Balaji Class 9 Maths Solutions Chapter 13 Quadrilateral Ex 13.3 चतुर्भज
प्रश्न 1.
सिद्ध कीजिए कि किसी त्रिभुज में उसके शीर्ष से आधार पर डाली गयी माध्यिका उसकी अन्य दो भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड समद्विभाजित करता है।
हलः
ज्ञात है: एक ∆ABC जिसमें E तथा F, AB तथा AC के मध्य बिन्दु हैं। शीर्ष A से BC पर एक रेखाखण्ड AD खींचा जो EF को R पर काटता है।
सिद्ध करना है: AR = RD
रचना: PAQ,BC के समान्तर रेखा खींची।
उपपत्तिः E तथा F, AB तथा AC के मध्य बिन्दु हैं। (दिया है)
∴ EF || BC
PAQ||BC
∴ PAQ|| EF || BC
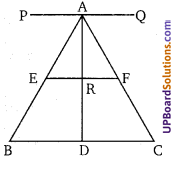
∴ PAQ, EF तथा BC तीन समान्तर रेखायें हैं जो तिर्यक रेखा AB के बीच बराबर अन्त:खण्ड काटती हैं। अतः इन्हीं समान्तर रेखाओं के बीच तिर्यक रेखा AD के बीच बने अन्तः खण्ड भी बराबर होंगे।
∴ AR = RD
![]()
प्रश्न 2.
सिद्ध कीजिए कि समलम्ब चतुर्भुज की असमान्तर भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड समान्तर भुजाओं के योग का आधा होता है।
हलः
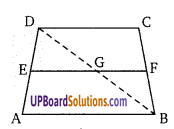
ज्ञात है: ABCD एक समलम्ब है जिसकी भुजाएँ AB व DC एक दूसरे के समान्तर है।
E तथा F क्रमशः AD तथा BC के मध्य बिन्दु हैं। EF को मिलाया।
सिद्ध करना है:
![]()
उपपत्तिः ∆ABD में, बिन्दु E, भुजा AD का मध्य बिन्दु है तथा EG, भुजा AB के समान्तर है।
∴ बिन्दु G, BD का मध्य बिन्दु है …(1)

प्रश्न 3.
सिद्ध कीजिए कि समलम्ब चतुर्भुज की असमान्तर भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड समान्तर भुजाओं के समान्तर होता हैं।
हलः
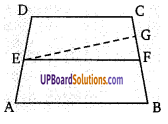
ज्ञात है: E तथा F, AD तथा BC के मध्य बिन्दु हैं।
सिद्ध करना है: EF||AB तथा EF||DC
रचनाः माना EF, AB के समान्तर नहीं है। इसलिए EG एक रेखा ऐसी खींची जिससे EG|| AB तथा EG||EG|| AB परन्तु EG तथा EF एक प्रतिच्छेद बिन्दु E पर काटती हैं।
परन्तु दो प्रतिच्छेदी रेखा एक रेखा के समान्तर नहीं हो सकती।
∴ EG तथा EF एक ही रेखा होगी।
∴ AB|| EF|| DC
![]()
प्रश्न 4.
ABCD एक समान्तर चतुर्भुज है। जिसमें E व F क्रमशः AB व CD के मध्य बिन्दु हैं। सिद्ध कीजिए कि-
(i) AF||EC
(ii) CE व AF विकर्ण BD को समत्रिभाजित करते हैं। [NCERT]
हलः
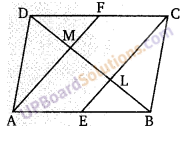
ज्ञात है: ABCD एक समान्तर चतुर्भुज में E तथा F क्रमश: AB तथा CD के मध्य बिन्दु हैं।
(i) सिद्ध करना हैः AF|| EC
उपपत्तिः (i) ∆ADF तथा ∆BCE में,
AD = BC (समान्तर चतुर्भुज की भुजाएँ)
DF = EB (समान्तर चतुर्भुज की भुजाएँ)
∠ADC = ∠ABC (समान्तर चतुर्भुज के सम्मुख कोण)
अतः ∆ADF ≅ ∆BCE
∴ AF = EC
∴ AFCE एक समान्तर चतुर्भुज होगा। (∴ AE||FC तथा AE = FC)
अतः समान्तर चतुर्भुज में AF||EC
(ii) ∵ समान्तर चतुर्भुज AECF में तिर्यक रेखा BD है। समान्तर चतुर्भुज ABCD में तिर्यक रेखा DB द्वारा काटे गये अन्त:खण्ड बराबर होंगे
∴ DM = ML = LB
अत: CE व AF विकर्ण BD को समत्रिभाजित करते हैं।
प्रश्न 5.
एक समलम्ब चतुर्भुज में उसके आधार के समान्तर एक रेखा उसकी असमान्तर भुजाओं में से एक को समद्विभाजित करती है। सिद्ध कीजिए कि यह इसके किसी विकर्ण को भी समद्विभाजित करेगी।
हलः
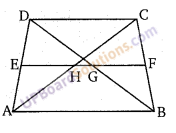
E, AD का मध्य बिन्दु है।
∴ DE = EA
AB||DC|| EF
तिर्यक रेखा DA पर बने अन्त:खण्ड DE = EA (जो दिया है)
∴ तिर्यक रेखा DB पर बने अन्त:खण्ड DG = GB होंगे।
AB के समान्तर रेखा E से होते हुए H,G पर प्रतिच्छेद करते हुए F तक खींची गयी है।
∴ बिन्दु F, CB का मध्य बिन्दु होगा।
DC|| AB
∴ तिर्यक रेखा CB पर बने अन्त:खण्ड CF = FB तथा तिर्यक रेखा CA पर बने अन्त:खण्ड CH = HA
![]()
प्रश्न 6.
ABCD एक समान्तर चतुर्भुज है तथा E व F क्रमश: AB व CD के मध्य D, बिन्दु हैं। एक अन्य रेखा GH, AD,EF व BC को क्रमशः G,P व H बिन्दुओं पर प्रतिच्छेद करती है। सिद्ध कीजिए कि GP = PH
हलः
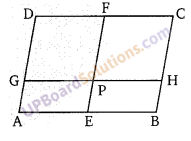
ABCD एक समान्तर चतुर्भुज है। E तथा F, AB तथा CD के मध्य बिन्दु हैं।
∴ AD||BC, AB तिर्यक रेखा काटती है।
∴ अन्त:खण्ड AE = EB
∴ DC तिर्यक रेखा काटती है।
∴ अन्त:खण्ड DF = FC
बिन्दु E को F से मिलाने पर वह बिन्दु P से होकर जाती है।
∴ तिर्यक रेखा GH के अन्त:खण्ड GP = PH होंगे।