Balaji Class 9 Maths Solutions Chapter 11 Triangles and Its Angles Ex 11.1 त्रिभुज एवं उसके गुण
Ex 11.1 Triangles and Its Angles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
यदि एक त्रिभुज के दो कोण बराबर है तब दोनों की विपरीत भुजा बराबर है या नहीं?
हलः
एक त्रिभुज के दो कोण बराबर है तब उस त्रिभुज की सम्मुख भुजाएं भी बराबर होगी।
![]()
प्रश्न 2.
एक त्रिभुज की बराबर भुजाओं के विपरीत कोण बराबर है या नहीं?
हलः
बराबर
प्रश्न 3.
यदि एक त्रिभुज की भुजाएँ 5 सेमी, 6 सेमी तथा 11 सेमी हैं तब त्रिभुज का नाम बताइए।
हलः
∵ किसी त्रिभुज की रचना के लिए दो भुजाओं का योग तीसरी भुजा से बड़ा होना चाहिए परन्तु 5 + 6 = 11, 11, के बराबर है।
∴ त्रिभुज की रचना सम्भव नहीं है।
प्रश्न 4.
यदि एक त्रिभुज की भुजाएँ 5 सेमी, 4 सेमी तथा 3 सेमी हैं तब त्रिभुज का नाम बताइए।
हलः :
∵ 3 + 4 = 7 > 5
अतः त्रिभुज की रचना सम्भव है।
(5)2 = (3)2 + (4)2 .
∴ यह एक समकोण त्रिभज है।
प्रश्न 5.
एक त्रिभुज की दो भुजाओं का योग, हमेशा तीसरी भुजा से अधिक होता है या नहीं?
हलः
एक त्रिभुज की दो भुजाओं का योग, हमेशा तीसरी भुजा से अधिक होता है। हाँ
प्रश्न 6.
यदि एक त्रिभुज के सभी कोण बराबर है, तब इनमें प्रत्येक कोण ज्ञात कीजिए।
हलः
एक त्रिभुज के तीनों कोणों का योग = 180°
∠A + ∠B + ∠C = 180° …………. (1)
माना ∠A = x, ∠B = x, ∠C = x
∴ x + x + x = 180°
3x = 180°
x = [latex]\frac{180^{\circ}}{3}[/latex] = 60°
∴ ∠A = ∠B = ∠C = 60°
![]()
प्रश्न 7.
यदि एक समकोण त्रिभुज के दो न्यूनकोण बराबर है, तब प्रत्येक न्यूनकोण ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
यदि ∠A = 90° तथा ∠B = ∠C
तब 90° + ∠B + ∠C = 180°
∠B + ∠C = 180° – 90° = 90°
प्रत्येक ∠B = ∠C = 45°
Ex 11.1 Triangles and Its Angles लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)
प्रश्न 8.
एक त्रिभुज के कोण 2 : 3 : 7 के अनुपात में है। त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हलः
माना
∆ABC का ∠A = 2x
∠B = 3x
∠C = 7x
∴ ∠A + ∠B + ∠C = 180°
2x + 3x + 7x = 180°
12x = 180°
x = [latex]\frac{180^{\circ}}{12}[/latex] = 15°
∴ ∠A = 2 × 15 = 30°
∠B = 3 × 15 = 45°
∠C = 7 × 15 = 105°
प्रश्न 9.
∆ABC में, ∠A + ∠B = 65° तथा / B+ ∠C =140°, त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
65° + ∠C = 180°
∠C = 180°- 65° = 115°
तथा ∠A + ∠B + ∠C = 180°
∠A + 140° = 180°
∠A = 180° – 140° = 40°
∵ ∠A + ∠B = 65°
40° + ∠B = 65°
∴∠B = 65° – 40° = 25°
प्रश्न 10.
∆ABC में, यदि ∠B = 76° तथा ∠C = 48° है, तो ∠A ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
∠A + 76° + 48° = 180°
∠A = 180° – 124° = 56°
![]()
प्रश्न 11.
∆ABC में, यदि ∠B = 105° तथा ∠C =50° है, तो ∠A ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
∠A + 105° + 50° = 180°
∠A = 180° – 155° = 25°
प्रश्न 12.
एक त्रिभुज के दो कोणों का योग, तीसरे कोण के बराबर है। तीसरे कोण की माप ज्ञात कीजिए।
हल:
∆ABC में, (∠A + ∠B) + ∠C = 180°
∠A + ∠B = ∠C ……………. (1)
∠C + ∠C = 180°
2∠C = 180°
∠C = [latex]\frac{180^{\circ}}{2}[/latex] = 90°
तीसरा कोण ∠C = 90°
प्रश्न 13.
यदि एक त्रिभुज के कोण 2 : 3 : 4 के अनुपात में है। कोण ज्ञात कीजिए। (NCERT Exemplar)
हल:
∆ABC के कोण ∠A : ∠B : ∠C = 2 : 3 : 4
माना ∠A = 2x, ∠B = 3x, ∠C = 4x
∠A + ∠B + ∠C = 180°
2x + 3x + 4x = 180° ⇒ 9x = 180°
x = [latex]\frac{180^{\circ}}{9}[/latex] = 20°
∴∠A = 2 × 20° = 40°, ∠B = 3 × 20° = 60°, ∠C = 4 × 20°= 80°
Ex 11.1 Triangles and Its Angles लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)
प्रश्न 14.
एक ∆ABC में, 15∠A = 10∠B = 6∠C हो, तो ∠A, ∠B तथा ∠C ज्ञात कीजिए।
हलः
15∠A = 10∠B = 6∠C
माना
∠B = x
15∠A = 10x

प्रश्न 15.
एक ∆ABC में, यदि ∠A = 55°, ∠B = 40° तब ∠C ज्ञात कीजिए।
हल:
∆ABC में,
∠A + ∠ B + ∠C = 180°
55° + 40° + ∠C = 180°
∠C = 180° – 95° = 85°
![]()
प्रश्न 16.
A, B, C एक त्रिभुज के तीन कोण हैं। यदि A – B = 15°, B – C = 30° हो, तो ∠A, ∠B और ∠C ज्ञात कीजिए।
हल:
A – B = 15° ⇒ A = B + 15° ………….(1)
B – C = 30° ⇒ C = B – 30° …………(2)
∵ ∠A + ∠B + ∠C = 180°
B + 15° + B + B – 30° = 180°
3B – 15° = 180°
3B = 180° + 15° = 195°
∴ B = [latex]\frac{195^{\circ}}{3}[/latex] = 65°
∴ समीकरण (1) से
∠A = 65° + 15° = 80°
∠C = 65° – 30° = 35°
प्रश्न 17.
एक त्रिभुज के दो कोणों का योग 106° है तथा उनका अन्तर 10° है। त्रिभुज के सभी कोण ज्ञात कीजिए।
हलः
माना A के दो कोण ∠A तथा ∠B है।
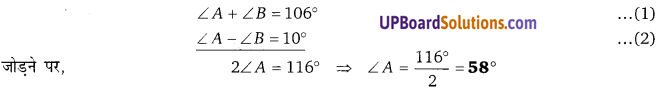
समीकरण (1) में ∠A का मान रखने पर
58° + ∠B = 106°
∠B = 106° – 58° = 48°
तथा ∠C = 180° – (∠A + ∠B) = 180° (58° + 48°) = 180° – 106° = 74°
![]()
प्रश्न 18.
दिये गये चित्र में, AB||DC यदि x = [latex]\frac{4 y}{3}[/latex], y = [latex]\frac{3 z}{8}[/latex] हो, तो ∠BCD ज्ञात कीजिए।
हल:
∵ AB|| DC तथा BD तिर्यक रेखा है।
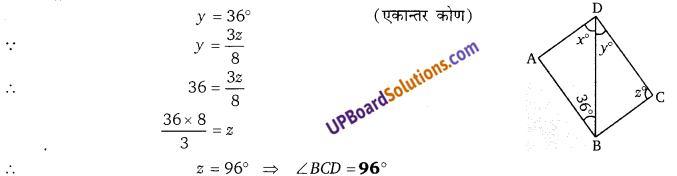
प्रश्न 19.
एक ∆ABC में, ∠A – ∠B = 33° तथा ∠B – ∠C = 18° हो, तो त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
∠A – ∠B = 33° ⇒ ∠A = 2B + 33° …………. (1)
∠B – ∠C = 18° ⇒ ∠B – 18° = ∠C ……………. (2)
∵ ∠A + ∠B + ∠C = 180°
∠B + 33°+ ∠B + ∠B – 18° = 180°
3∠B + 15° = 180°
3∠B = 180° – 15° = 165°
∠B = [latex]\frac{165^{\circ}}{3}[/latex] = 55°
∴ ∠A = ∠B + 33° = 55 + 33 = 88°
∴ ∠C = ∠B – 18 = 55 – 18 = 37°
![]()
प्रश्न 20.
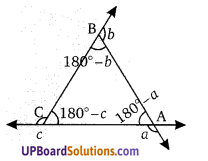
दिये गये चित्र में, सिद्ध कीजिए कि ∠a + ∠b + ∠c = 360°
हलः
∠BAC + ∠ABC + ∠ACB = 180°
180 – ∠a + 180 – ∠b + 180 – ∠c = 180°
360° = ∠a + ∠b + ∠c
Ex 11.1 Triangles and Its Angles दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 21.
एक त्रिभुज ABC है जिसमें ∠A = 72°, ∠B तथा ∠C के अन्तः समद्विभाजक बिन्दु O पर मिलते हैं तो∠BOC का परिमाण ज्ञात कीजिए।
हलः
माना ∠ABC = x तथा ∠ACB = y

प्रश्न 22.
दिये गये चित्र में, AE, ∠CAD का अर्द्धक है तथा ∠B = ∠C तो सिद्ध कीजिए कि AE||BC
हलः
माना
∠CAD = 2x
∴ ∠DAE = ∠CAE = x
∠B = ∠C
∠CAD, ∆ABC का बहिष्कोण है।
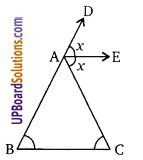
∴ ∠CAD = ∠ABC + ∠ACB
∴ ∠ABC + ∠ACB = 2x
परन्तु ∠ABC = ∠ACB
∴ प्रत्येक ∠ABC = ∠ACB = x°
∴ ∠EAC = ∠ACB = x° (परन्तु ये एकान्तर कोण हैं।)
AE ||BC
![]()
प्रश्न 23.
दिये गये चित्र में, AB||CD है। x और y के मान ज्ञात कीजिए।
हल:
∵ AB||CD
∠FED = ∠EMB
58 = y + 20
58 – 20 = y
∴ y = 38°
∴ ∠MEB = 180 – (58 + 22)
= 180° – 80° = 100°
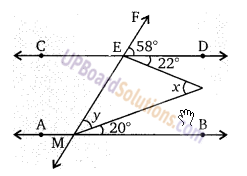
∆EBM में,
x + y + 100 = 180
x + 38 + 100 = 180
x = 180 – 138 = 42°
प्रश्न 24.
दिये गये चित्र में, x और y के मान ज्ञात कीजिए।
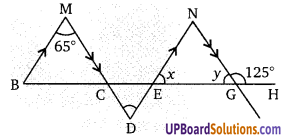
हल:
∵ y + 125 = 180 (रैखिक युग्म कोण)
y = 180 – 125 = 55°
∠CDE = ∠BMC = 65° (एकान्तर कोण)
तथा ∠CDN = ∠ENG = 65° (एकान्तर कोण)
∆NEG में, x + y + 65 = 180
∴ x + 55 + 65 = 180
x = 180 – 120 = 60°
![]()
प्रश्न 25.
निम्न प्रत्येक में x का मान ज्ञात कीजिए।
हलः
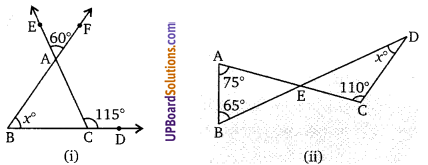
चित्र (i) में,
∠EAF = ∠BAC = 60° [शीर्षाभिमुख कोण]
∆ABC का बहिष्कोण ∠ACD है।
∠ACD = ∠BAC + ∠ABC .
115° = 60° + x
115° – 60° = x
x = 55°
चित्र (ii) में, ∆ABE में ∠AEB = 180 – (75 + 65)
= 180 – 140 = 40°
∠CED = ∠AEB = 40° [शीर्षाभिमुख कोण]
∆ECD में, 40 + 110 + x = 180°
150 + x = 180°
x = 180° – 150° = 30°
प्रश्न 26.
एक त्रिभुज के कोणों को परिमाण के बढ़ते हुए क्रम में रखा गया है यदि दो क्रमागत कोणों के बीच का अन्तर 10° है तो तीनों कोणों को ज्ञात कीजिए।
हलः
माना त्रिभुज के तीन कोण क्रमशः x, x + 10, x + 20 हैं।
∴ x + x + 10+ x + 20 = 180
3x + 30 = 180
3x = 180 – 30 = 150°
x = [latex]\frac{150}{3}[/latex] = 50°
∴ त्रिभुज के तीन कोण क्रमश: 50°, 60°, 70° है।
![]()
प्रश्न 27.
दिये गये चित्र में, ∆ABC के सभी कोणों की माप ज्ञात कीजिए।
हल:
∆ABC में,
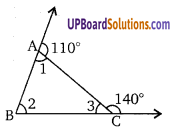
∠1 = 180 – 110 = 70°
∠3 = 180 – 140 = 40°
∠2 = 180 – (70 + 40) = 180 – 110 = 70°