Balaji Class 9 Maths Solutions Chapter 12 Congruence of Triangles Ex 12.1 त्रिभुजों की सर्वांगसमता
प्रश्न 1.
दिये गये चित्र में, AD = CB, AB = CD तथा EF, BD को G पर समद्विभाजित करता है तो सिद्ध कीजिए कि G, EF का मध्य बिन्दु है।
हल:
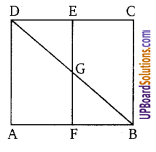
∵ AB = CB = CD … (1)
∆DEG तथा ∆GFB में
DG = GB (दिया है)
∠FGB = ∠DGE (शीर्षाभिमुख कोण)
DE = FB (दिया है)
अतः ∆DEG ≅ ∆GFB
∴ EG = GF
![]()
प्रश्न 2.
सिद्ध कीजिए कि एक समबाहु त्रिभुज की माध्यिकाएँ सर्वांगसम होती हैं।
हलः

प्रश्न 3.
एक चतुर्भुज ABCD है। जिसमें AB = CD तथा चतुर्भुज का एक अन्तः बिन्दु O इस प्रकार है कि OA = OD तथा OB = OC तो सिद्ध कीजिए कि BC || AD.
हलः
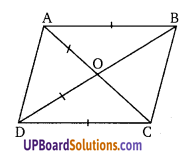
परन्तु ये एकान्तर कोण हैं
∴ AB || DC
अत: ABCD एक समान्तर चतुर्भुज होगा।
∴ BC|| AD
प्रश्न 4.
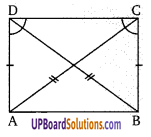
दिये गये चित्र में, AD = BC तथा AC = BD तो सिद्ध कीजिए कि ∠ADC = ∠BCD
हल:
प्रश्न 5.
दिये गये चित्र में, एक समांतर चतुर्भुज ABCD तथा ∆BXC और ∆AYD इस प्रकार है कि BX = DY तथा CX = AY तो सिद्ध कीजिए कि-
(i) BX || DY
(ii) XY और BD एक दूसरे को समद्विभाजित करते हैं।
हल:
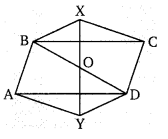
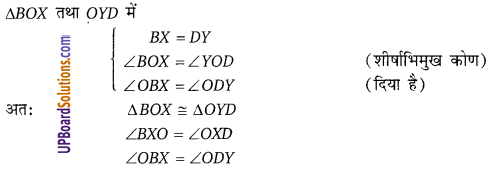
परन्तु ये एकान्तर कोण है।
(i) ∴ BX || YD
(ii) XO = OY तथा BO = OD
∴ XY, BD एक दूसरे को समद्विभाजित करते हैं।
![]()
प्रश्न 6.
एक चतुर्भुज की चारों भुजाएँ बराबर हैं तो सिद्ध कीजिए कि इसके कोण, विकर्ण द्वारा समद्विभाजित होते हैं। हलः
