Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.6

Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.6 बहुपद तथा उनके गुणनखण्ड

Ex 5.6 Polynomial and their Factors अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Question)

निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए।
प्रश्न 1.
x² + 7x + 12
हल:
x² + 7x + 12 = x² + (3 + 4)x + 12 12 = 3 × 4
= x² + 3x + 4x + 12 = x(x + 3) + 4(x + 3) = (x + 3)(x + 4)

प्रश्न 2.
x² – 14x + 48
हल:
x² – 14x + 48 = x² – (6 + 8)x + 48 (48 = 6 × 8)
= x² – 6x – 8x + 48 = x(x – 6) – 8(x – 6) = (x – 6)(x – 8)

प्रश्न 3.
x² – 7x – 18
हल:
x² – 7x – 18 = x² – (9 – 2)x – 18 = x² – 9x + 2x – 18 = x(x – 9) + 2(x – 9) = (x – 9)(x + 2)

प्रश्न 4.
x² – 25x + 84
हल:
x² – 25x + 84 = x² – (21 + 4)x + 84 (84 = 4 × 21)
= x² – 21x – 4x + 84= x(x -21)- 4(x – 21)= (x – 21)(x – 4)

प्रश्न 5.
2x² + 7x + 6
हल:
2x² + 7x + 6 = 2x² + (3 + 4)x + 6                         (2 × 6 = 12 ⇒ 12 = 3 × 4)
= 2x² + 3x + 4x + 6 = x(2x + 3) + 2(2x + 3) = (2x + 3)(x + 2)

प्रश्न 6.
2x² – 13x + 15
हलः
2x² – 13x + 15 = 2x² – (3 + 10)x + 15 (2 × 15 = 30 ⇒ 30 = 3 × 10)
= 2x² – 3x – 10x + 15 = x(2x – 3) – 5(2x – 3) = (2x – 3)(x – 5)

प्रश्न 7.
3x² – 14x + 8
हल:
3x² – 14x + 8 = 3x² – (2 + 12)x + 8 (3 × 8 = 24 ⇒ 24 = 12 × 2)
= 3x² – 2x – 12x + 8= x(3x – 2) – 4(3x – 2) = (3x – 2)(x – 4 )

प्रश्न 8.
3x² + 10x – 8
हलः
3x² + 10x – 8= 3x² + (12 – 2)x – 8 (3 × 8 = 24 ⇒ 24 = 2× 12)
= 3x² + 12x – 2x – 8 = 3x(x + 4) – 2(x + 4)= (x + 4)(3x – 2)

Ex 5.6 Polynomial and their Factors लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 9.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 8(x + 2)² + 2(x + 2) – 15
(ii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) – 15(2x – 1)²
(iii) (x² – 2x)² – 23(x² – 2x) + 120
(iv) (x + 2y)² + 5(x + 2y)(2x + y) + 6(2x + y)²
हलः
(i) 8(x + 2)² + 2(x + 2) – 15
माना x + 2 = y
= 8y² + 2y – 15
= 8y² +(12 – 10)y – 15 (8 × 15 = 120 ⇒ 120 = 12 × 10)
= 8y² + 12y – 10y – 15 = 4y(2y + 3) – 5(2y + 3)
= (2y + 3)(4y – 5)=[2(x + 2) + 3] [4(x + 2) – 5]
= [2x + 4 + 3][4x + 8 – 5) = (2x + 7) (4x + 3)

(ii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) – 15(2x – 1)²
हलः
x² + 7x = y तथा 2x – 1 = z
= 12y² – 8yz – 15z²
= 12y² – (18 – 10)yz – 15z² (12 × 15 = 180 ⇒ 180 = 2 × 2 × 3 × 3 × 5)
= 12y² – 18ýz + 10yz – 15z²
= 6y (2y – 3z) + 5z(2y – 3z) = (2y – 3z)(6y + 5z)
= [2(x² + 7x) – 3(2x – 1)][6(x² + 7x) + 5(2x – 1)]
= [2x² + 14x – 6x + 3] [6x² + 42x + 10x – 5]
= [2x² + 8x + 3][6x² + 52x – 5]

(iii) (x² – 2x)² – 23(x² – 2x) + 120
हलः
x² – 2x = y
=y² – 23y + 120
= y² – (8 + 15)y + 120 (120 = 8 × 15)
= y² – 8y – 15y + 120 = y(y – 8) – 15(y – 8)
= (y – 15)(y – 8)
= (x² – 2x – 15)(x² – 2x – 8) (15 = 3 × 5 व 8 = 4 × 2)
= [x² – (5 – 3)x – 15][x² – (4 – 2)x – 8]
= [x² – 5x + 3x – 15][x² – 4x + 2x – 8]
=[x(x – 5) + 3(x – 5)][x(x – 4) + 2(x – 4)]
= [(x + 3)(x – 5)][(x – 4)(x + 2)]

(iv) (x + 2y)² + 5(x + 2y)(2x + y) + 6(2x + y)²
हलः
माना x + 2y = m तथा 2x + y = n
= m² + 5mn + 6n² = m² +(2 + 3)mn +6n²
= m² + 2mn + 3mn + 6n² = m(m + 2n) + 3n(m + 2n)
= (m + 2n)(m + 3n)
यहाँ [x + 2y + 2(2x + y)][x + 2y + 3(2x + y)]
=[x + 2y + 4x + 2y][x + 2y + 6x + 3y] = [5x + 4y][7x + 5y]

प्रश्न 10.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) [latex]\frac{1}{3} x^{2}[/latex] – 2x – 9
(ii) [latex]\frac{1}{4} x^{2}[/latex] + x – 3
(iii) 8x³ – 2x²y – 15xy²
(iv) 9x³y +41x²y² + 20xy³
हलः


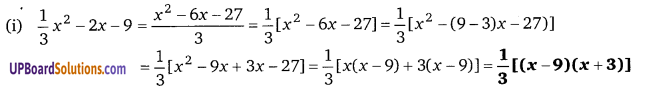
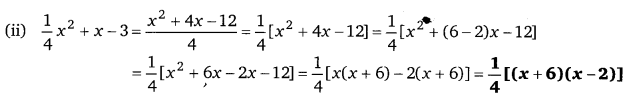
(iii) 8x³ – 2x²y – 15xy² = x[8x² – 2xy -15y²]
= x[8x² – (12 – 10)xy -15y²] (∵ 8 × 15 = 120 ⇒ 120 = 12× 10)
= x[8x² – 12xy + 10xy – 15y²]
= x[4x(2x – 3y) + 5y(2x – 3y)] = x(2x – 3y)(4x + 5y)

(iv) 9x³y + 41x²y² + 20xy³ = xy[9x² + 41xy + 20y²]
= xy[9x² + (36 + 5)xy + 20y²] (9 × 20 = 180 ⇒ 180 = 2 × 2 × 3 × 3 × 5)
= xy[9x² + 36xy + 5xy + 20y²]
= xy[9x(x + 4y) + 5y (x + 4y)] = xy(9x + 5y)(x + 4y)

प्रश्न 11.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x² +4x – 21
(ii) x² – 7x + 12
(iii) x² – 21x + 108
(iv) x² + 5x – 36
हल:
(i) x² + 4x – 21 = x² + (7 – 3)x – 21 (21 = 3 × 7)
= x² + 7x – 3x – 21 = x(x + 7) – 3(x + 7) = (x + 7)(x – 3)

(ii) x² – 7x + 12 = x² – (3 + 4)x + 12 (12 = 2 × 2 × 3)
= x² – 3x – 4x + 12 = x(x – 3) – 4(x – 3) = (x – 3)(x – 4)

(iii) x² – 21x + 108 = x² – (12 + 9)x + 108 (108 = 2 × 2 × 3 × 3 × 3 = 12 × 9)
= x² – 12x – 9x + 108 = x(x – 12)- 9(x – 12) = (x – 12)(x – 9)

(iv) x² + 5x – 36 = x² + (9 – 4)x – 36 (36 = 2 × 2 × 3 × 3)
= x² + 9x – 4x – 36 = x(x + 9)- 4(x + 9) = (x + 9)(x – 4)

प्रश्न 12.
निम्न व्यंजकों के गुणनखण्ड इनके मध्य पद को विभक्त करके कीजिए
(i) x⁴ + 3x² – 28
(ii) x⁴ – 5x² + 4
हल:
(i) x⁴ + 3x² – 28 = x⁴ + (7 – 4)x² – 28 (∵ 28 = 2 × 2 × 7)
= x⁴ + 7x² – 4x² – 28 = x²(x² + 7) – 4(x² + 7)
= (x² + 7)(x² – 4) = (x² + 7)[(x)⁴ – (2)⁴] = (x² + 7)(x + 2)(x – 2)

(ii) x⁴ – 5x² + 4 = x⁴ – (1 + 4)x² + 4 (∵ 4 = 1 × 4)
= x⁴ – x² – 4x² + 4 = x²(x² – 1) – 4(x² – 1) = (x² – 1)(x² – 4)
= [(x)² – (1)²][(x²) – (2)²] = (x + 1)(x – 1)(x + 2)(x – 2)

प्रश्न 13.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x² + [latex]4 \sqrt{2} x[/latex] + 6
(ii) x² + [latex]5 \sqrt{3} x[/latex] + 12
(iii) x² + [latex]5 \sqrt{5} x[/latex] + 30
(iv) x² + [latex]6 \sqrt{6} x[/latex] + 48
हलः

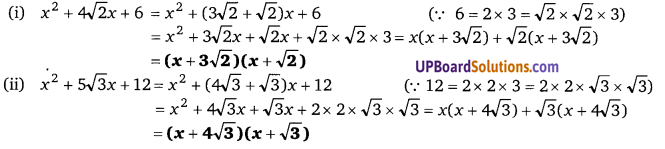
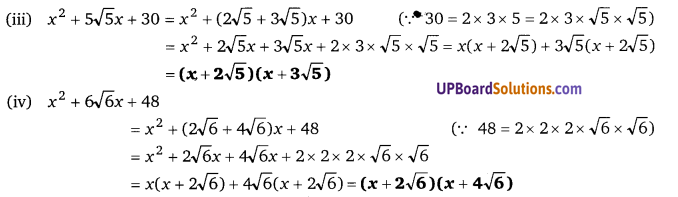
प्रश्न 14.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) [latex]\left(5 x-\frac{1}{x}\right)^{2}+5\left(5 x-\frac{1}{x}\right)+6[/latex]
(ii) (p + q)² – 20(p + q) – 125
(iii) (a² – a)² – 8(a² – a) + 12
(iv) (x² – 4x)(x² – 4x – 1) – 20
(v) (x² + x)² + 4(x² + x) – 12
(vi) (3x – 4)² – (3x – 4) – 42
हलः

(ii) (p + q)² – 20(p + q) – 125
माना P + q = x
= x² – 20x – 125 = x² – (25 – 5)x – 125
= x² – 25x + 5x – 125 = x(x – 25) + 5(x – 25)
= (x + 5)(x – 25)
∴ (p + q – 25)(p + q + 5)

(iii) (a² – a)² – 8(a² – a) + 12
माना a² – a = x
→ = x² – 8x + 12
= x² – (2 + 6)x + 12 = x² – 2x – 6x +12
= x(x – 2) – 6(x – 2) = (x – 2)(x – 6)
∴ (a² – a – 2)(a² – a – 6)
=[a² – (2 – 1)a – 2][a² – (3 – 2)a – 6]
=[a – 2a + a – 2][a² – 3a + 2a – 6]
= [a(a – 2) + 1(a – 2)][a(a – 3) + 2(a – 3)]
= (a – 2)(a + 1)(a – 3)(a + 2)

(iv) (x² – 4x)(x² – 4x -1) – 20
माना x² – 4x = y
⇒ = y (y – 1) – 20 = y² – y – 20
= y² – (5 – 4)y – 20
= y² – 5y + 4y – 20
= y(y – 5) + 4(y – 5) = (y – 5)(y + 4)
∴ (x² – 4x – 5)(x² – 4x + 4)
= [x² – (5 – 1)x – 5][x² – (2 + 2)x + 4]
= [x² – 5x + x – 5][x² – 2x – 2x + 4]
= [x(x – 5) + 16x – 5)][x(x – 2) – 2(x -2)]
= (x – 5) (x + 1) (x – 2) (x – 2) = (x – 5)(x + 1)(x – 2)²

(v) (x² + x)² + 46x² + x) – 12
माना x² + x = y
= y² + 4y – 12
= y² + (6 – 2)y – 12 = y² + 6y – 2y -12
= y(y + 6) – 2(y + 6) = (y + 6)(y – 2)
∴ (x² + x + 6) (x² + x – 2)
= (x² + x + 6)[x² + (2 – 1)x – 2] = (x² + x + 6)[x² + 2x – x – 2] = (x² + x + 6)[x(x + 2) – 1(x + 2)]
= (x² + x + 6)(x – 1)(x + 2)

(vi) (3x – 4)² – (3x – 4) – 42
माना 3x – 4 = y
→ = y² – y – 42 (∵ 42 = 2 × 3 × 7 = 6 × 7)
= y² – (7 – 6)y – 42 = y² – 7y + 6y – 42
= y(y – 7) + 6(y – 7) = (y – 7)(y + 6)
∴ (3x – 4 – 7)(3x – 4 + 6)
= (3x – 11)(3x + 2)

Ex 5.6 Polynomial and their Factors लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 15.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x⁴ – x² – 12
(ii) m⁸ – 11m⁴n⁴ – 80n⁸
हल:
(i) x⁴ – x² – 12
= x⁴ – (4 – 3)x² – 12
= x² – 4x² + 3x² – 12 = x²(x² – 4) + 3(x² – 4)
= (x² – 4)(x² + 3) = (x)² – (2)²(x² + 3)
= (x + 2)(x – 2)(x² + 3)

(ii) m⁸ – 11m⁴n⁴ – 80n⁸ (∵ 80 = 2 × 2 × 2 × 2 × 5)
= m⁸ – (16 – 5)m⁴n⁴ – 80n⁸
= m⁸ – 16m⁴n⁴ + 5m⁴n⁸ – 80n⁸ = m⁴ (m⁴ – 16n⁴) + 5n⁴(m⁴ – 16n⁴)
= (m⁴ + 5n⁴)(m⁴ – 16n⁴) = (m⁴ + 5n⁴)(m² + 4n²)(m² – 4n²)
= (m⁴ + 5n⁴)(m² + 4n)(m + 2n)(m – 2n)

प्रश्न 16.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 2x² + 13x + 20
(ii) 6x² + 11x + 3
(iii) 9x² + 27x + 20
(iv) 2x² – 11x – 63
(v) 10x² – 9x – 7
(vi) 21x² + 5x – 6
हल:
(i) 2x² + 13x + 20 (∵ 2 × 20 = 2 × 2 × 2 × 5)
= 2x² + (5 + 8)x + 20 = 2x² + 5x + 8x + 20
= x(2x + 5) + 4(2x + 5) = (2x + 5)(x + 4)

(ii) 6x² + 11x +3 (∵ 6x 3 = 18 = 2 × 3 × 3)
= 6x² + (2 + 9)x + 3 = 6x² + 2x + 9x + 3
= 2x(3x + 1) + 3(3x + 1) = (3x + 1)(2x +3)

(iii) 9x² + 27x + 20 = 9x² + (12 + 15)x + 20 (∵ 9 × 20 = 3 × 3 × 2 × 2 × 5)
= 9x² + 12x + 15x + 20 = 3x(3x + 4) + 5(3x + 4)= (3x + 4)(3x + 5)

(iv) 2x² – 11x – 63 = 2x² – (18 – 7)x – 63 (∵ 2 × 63 = 2 × 3 × 3 × 7)
= 2x² – 18x + 7x – 63 = 2x(x – 9) + 7(x – 9) = (x – 9)(2x + 7)

(v) 10x² – 9x – 7 = 10x² – (14 – 5)x – 7 (∵ 10 × 7 = 2 × 5 × 7)
= 10x² – 14x + 5x -7 = 2x(5x – 7) + 1(5x – 7) = (5x – 7)(2x + 1)

(vi) 21x² + 5x – 6 = 21x² + (14 – 9)x – 6 (∵ 21 × 6 = 3 × 7 × 2 × 3)
= 21x² + 14x – 9x – 6 = 7x (3x + 2) – 3(3x + 2) = (3x + 2)(7x – 3)

प्रश्न 17.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) [latex]\frac{1}{2} x^{2}[/latex] + 4x + 6
(ii) 2x² – x + [latex]\frac{1}{8}[/latex]
हलः

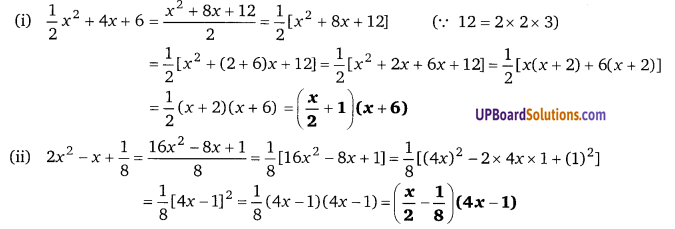
प्रश्न 18.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 7(x + 2y)² – 25(x + 2y) + 12
(ii) 8(a + 1)² +2(a + 1)(b + 2) – 15(b + 2)²
(iii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) + (2x – 1)²
(iv) 2(y² + 2y)² – 5(y² + 2y) + 3
(v) 6(x² + 4x)² – 11(x² + 4x)- 10
हलः
(i) 7(x + 2y)² – 25(x + 2y) + 12
माना x + 2y = z
= 7z²– 25z + 12
= 7z² – (21 + 4)z + 12 (∵ 7 × 12 = 7 × 2 × 2 × 3)
=7z² – 21z – 4z + 12 = 7z(z – 3) – 4(z – 3)
= (z – 3)(7z – 4) =(x + 2y – 3)[7(x + 2y) – 4]
(x + 2y – 3)(7x + 14y – 4)

(ii) 8(a + 1)² + 2(a + 1)(b + 2) – 15(b + 2)²
माना (a + 1) = x तथा (b + 2) = y
= 8x² + 20y – 15y²
= 8x² +(12 – 10)xy – 15y² (∵ 15 × 8 = 120 = 2 × 2 × 2 × 3 × 5)
= 8x² + 12xy – 10xy – 15y²
= 4x(2x + 3y) – 5y (2x + 3y) = (2x + 3y)(4x – 5y)
⇒ [2(a + 1) + 3(b + 2)][4(a + 1) – 5(b + 2)]
= [2a + 2+ 3b + 6][4a + 4 – 5b – 10]
= [2a + 3b + 8][4a – 5b – 6]

(iii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) + (2x – 1)²
माना x² + 7 x = m तथा 2x – 1 = n
12m² – 8mn +n²
= 12m² – (6 + 2)mn + n² (∵ 12 × 1 = 12 = 2 × 2 × 3)
= 12m² – 6mn – 2mn + n²
= 6m(2m – n) – n(2m – n)= (6m – n)(2m – n)
= [6(x² + 7x) – 2x + 1][2(x² + 7x) – 2x + 1]
= (6x² + 42x – 2x + 1)(2x² + 14x – 2x + 1)
= (6x² + 40x + 1)(2x² + 12x + 1)

(iv) 2(y² + 2y)² – 5(y² + 2y) + 3
माना y² + 2y = m
= 2m² – 5m + 3 = 2m² – (2 + 3)m + 3 (∵ 2 × 3 = 6)
= 2m² – 2m – 3m + 3 = 2m(m – 1) – 3(m – 1)
= [(2m – 3)(m – 1)] = [2(y² + 2y) – 3][y² + 2y – 1]
=[2y² + 4y – 3][y² + 2y – 1]

(v) 6(x² + 4x)² – 11(x² + 4x) – 10
माना x² + 4x = m
= 6m² – 11m – 10
= 6m² -(15 – 4)m – 10 (∵ 10 × 6 = 60 = 2 × 2 × 3 × 5)
= 6m² – 15m + 4m – 10 = 3m(2m – 5) + 2(2m – 5)
= (2m – 5)(3m + 2) = [2(x² + 4x) – 5][3(x² + 4x) + 2]
= [2x² + 8x – 5][3x² + 12x + 2]

प्रश्न 19.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए

हलः

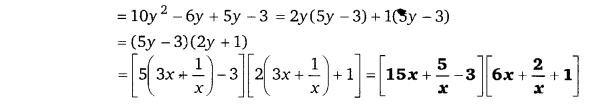
प्रश्न 20.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए

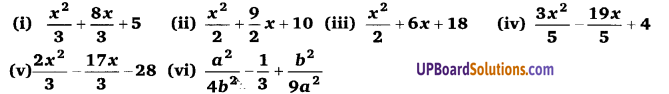
हलः

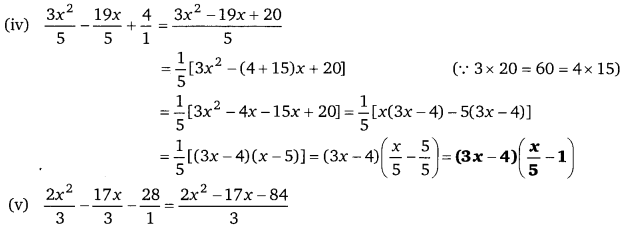
प्रश्न 21.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए

हलः

प्रश्न 22.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 9a³b + 41a²b² + 20ab³
(ii) ax² + (4a² – 3b)x – 12ab
(iii) 25x² + 10xy – 8y²
(iv) 4x² + 20xy + 25y²
हलः
(i) 9a²b + 41a²b² + 20ab³ = ab[9a² + 41ab + 20b²] (∵ 9 × 20 = 180 = 2 × 2 × 3 × 3 × 5)
= ab[9a² + (36 + 5)ab + 20b²] = ab[9a² + 36ab + 5ab + 20b²]
= ab[9a(a + 4b) + 5b(a + 4b)] = ab(9a + 5b)(a + 4b)]

(ii) ax² + (4a² – 3b)x – 12ab = ax² + 4a²x – 3bx – 12ab = ax(x + 4a) – 3b(x + 4a)
= (x + 4a)(ax – 3b)

(iii) 25x² + 10xy – 8y² = 25x² + (20 – 10)xy – 8y² (∵ 25 × 8 = 200 = 2 × 2 × 2 × 5 × 5)
= 25x² + 20xy – 10xy – 8y² = 5x(5x + 4y) – 2y(5x + 4y)
= (5x + 4y)(5x – 2y)

(iv) 4x² + 20xy + 25y² = 4x² + (10 + 10)xy + 25y² (∵ 4 × 25 = 100 = 10 × 10)
= 4x² + 10xy + 10xy + 25y² = 2x(2x + 5y) + 5y (2x + 5y)
= (2x + 5y)(2x + 5y)

Balaji Publications Mathematics Class 9 Solutions