Class 10

Balaji Class 10 Maths Solutions Chapter 14 Statistics Ex 14.3 सांख्यिकी

Ex 14.3 Statistics अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि प्रेक्षणों की संख्या (n) विषम है तब माध्यिका ज्ञात कीजिए।
हलः
यदि आँकड़ों की संख्या (n) विषम है (UPBoardSolutions.com) तब माध्यिका = [latex]\left(\frac{n+1}{2}\right)[/latex] वाँ पद

प्रश्न 2.
एक टैस्ट परीक्षा में 10 विद्यार्थियों द्वारा प्राप्तांक है :
35, 12, 18, 22, 32, 11, 14, 41, 26, 30 तब प्राप्त प्राप्तांक की माध्यिका ज्ञात कीजिए।
हलः
आँकड़ों को आरोही क्रम में रखने पर
11, 12, 14, 18, 22, 26, 30, 32, 35, 41
आँकड़ों की संख्या, n = 10 (सम संख्या)

प्रश्न 3.
आँकड़ों 3, 13, 9, 0, 5, 18, 7 की माध्यिका ज्ञात कीजिए।
हलः
आँकड़ों को आरोही क्रम में रखने पर- 0, 3, 5, 7, 9, 13, 18
आँकड़ों की संख्या n = 7 (विषम संख्या)
माध्यिका = [latex]\frac{n+1}{2}[/latex] वाँ पद
= [latex]\frac{7+1}{2}=\frac{8}{2}[/latex] = 4 वाँ पद = 7

प्रश्न 4.
आँकड़ों 0, 1, 0, 2, 3, 2, 3, 4 की माध्यिका ज्ञात कीजिए।
हलः
आँकड़ों को आरोही क्रम में (UPBoardSolutions.com) रखने पर – 0, 0, 1, 2, 2, 3, 3, 4
n = 8 (सम संख्या)

Ex 14.3 Statistics दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 5.
एक कक्षा में 41 विद्यार्थियों द्वारा प्राप्तांक का विवरण निम्नलिखित सारणी में दर्शाया गया है। तब माध्यिका ज्ञात कीजिए।

हलः
आँकड़ों को आरोही क्रम में रखने पर

n = 41 (विषम संख्या)
∴ माध्यिका = [latex]\frac{41+1}{2}=\frac{42}{2}[/latex] = 21 वाँ पद
∴ प्राप्तांकों की माध्यिका = 22

प्रश्न 6.
निम्नलिखित बंटन की माध्यिका ज्ञात कीजिए। (UP 2010, 13)

हलः
आँकड़ों को आरोही क्रम में (UPBoardSolutions.com) रखने पर

∴ n = 41 (विषम संख्या)
माध्यिका = [latex]\frac{61+1}{2}=\frac{62}{2}[/latex] = 31 वाँ पद
∴ व्यय की माध्यिका = 15

प्रश्न 7.
निम्नलिखित बंटन के लिए माध्यिका ज्ञात कीजिए। (UP 2009, 10)

हलः
आँकड़ों को आरोही क्रम में रखने पर

प्रश्न 8.
निम्नलिखित बंटन के लिए माध्यिका ज्ञात कीजिए। (UP 2009, 13, 14)

हलः
आँकड़ों को आरोही क्रम में (UPBoardSolutions.com) रखने पर

प्रश्न 9.
निम्नलिखित आँकडों की माध्यिका 525 है। x तथा y ज्ञात कीजिए यदि सभी बारम्बारताओं का योग 100 है।

हलः

बारम्बारताओं का योग = 100
16 + x + 17 + 20 + 15 + y = 100
x + y + 68 = 100
x + y = 100 – 68 (UPBoardSolutions.com)
x + y = 32 …(1)
∵ माध्यिका = 525 है, जोकि वर्ग 500-600 में है।

25 = 5 (17 – x)
25 = 85 – 5x
5x = 85 – 25
x = [latex]\frac{60}{5}[/latex]
x = 12
x का मान समी० (1) में रखने पर,
12 + y = 32
y= 32 (UPBoardSolutions.com) – 12
y = 20
अतः x = 12, y = 20

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 14 Statistics Ex 14.2 सांख्यिकी

प्रश्न 1.
निम्नलिखित सारणी के लिए, प्रत्येक घर के व्यय (₹ में) का माध्य, लघु विधि द्वारा ज्ञात कीजिए।

हलः

प्रश्न 2.
निम्नलिखित सारणी का समान्तर माध्य, पद विचलन विधि द्वारा ज्ञात कीजिए।

हलः

प्रश्न 3.
निम्नलिखित सारणी का समान्तर माध्य, पद विचलन विधि द्वारा ज्ञात कीजिए।

हलः

प्रश्न 4.
निम्नलिखित आँकडों का समान्तर माध्य ज्ञात कीजिए।

(NCERT Exemplar)
हलः

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 9 Constructions Ex 9.1 रचनाएँ

प्रश्न 1.
एक 10 सेमी लम्बी रेखा को 3 : 2 के अनुपात में अन्त:विभाजित करें।
हलः
रचना के चरणः
चरण 1: एक रेखाखण्ड (UPBoardSolutions.com) AB = 10 सेमी खींचिए।

चरण 2: एक किरण AX, एक न्यूनकोण ∠ BAX बनाते हुए खींची।
चरण 3: AX के सापेक्ष बिन्दुओं  5 (= 3 + 2) A₁, A₂, A₃, A₄ तथा A₅ को इस प्रकार चिन्हित कीजिए कि
AA₁ = A₁A₂ = … = A₄A₅
चरण 4: A₅B को मिलाया।
चरण 5: बिन्दु A₃ से, A₃P || A₅B खींचा जो रेखाखण्ड AB को बिन्दु P पर काटता है। स्पष्टतः P वह बिन्दु है जो रेखाखण्ड AB को 3 : 2 के अनुपात में विभाजित करता है।

प्रश्न 2.
एक ∆ ABC की रचना कीजिए जिसमें AB = 4 सेमी, BC = 5 सेमी, AC = 6 सेमी, ∆ ABC के समरूप एक त्रिभुज की रचना कीजिए जिसकी प्रत्येक भुजा, ∆ ABC की संगत भुजा की [latex]\frac{2}{3}[/latex] है। (NCERT)
हलः
रचना के चरणः

चरण 1: एक रेखा BC = 5 सेमी खींची।
चरण 2: B को केन्द्र मानकर’ 4 सेमी त्रिज्या का एक चाप खींचा।
चरण 3: पुन:C को केन्द्र मानकर 6 सेमी (UPBoardSolutions.com) त्रिज्या का एक दूसरा चाप खींचा जो पहले चाप को बिन्दु A पर काटता है।
चरण 4: ∆ABC बनाने के लिए रेखाखण्ड AB तथा AC को मिलाया।
चरण 5: रेखाखण्ड BC के नीचे एक न्यूनकोण ∠CBX खींचा।
चरण 6: रेखाखण्ड BX तीन बिन्दुओं B₁, B₂, B₃ को इस प्रकार चिन्हित किया कि
BB₁ = B₁B₂ = B₂B₃
चरण 7: B₃C को मिलाया।
चरण 8: बिन्दु B₂ से B₂D ||B₃C खींची जोकि रेखाखण्ड BC को बिन्दु D पर काटती है।
चरण 9: बिन्दु D से, DE ||CA खींची जोकि AB को बिन्दु E पर काटती है।
अत: ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 3.
एक ∆ ABC की रचना कीजिए जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हैं। एक ऐसे त्रिभुज की रचना कीजिए जो ∆ ABC के समरूप हो तथा जिसकी भुजाएँ, ∆ ABC की संगत भुजाओं की। [latex]\frac{4}{3}[/latex] है। (NCERT)
हलः
रचना के चरणः

चरण 1: एक सीधी रेखा BC = 7 सेमी खींची।
चरण 2: बिन्दु B से, एक न्यूनकोण ∠CBX = 45° खींचा और कोण BCY = 180° – (45° + 105°) = 30° खींचा।
चरण 3: ∆ABC प्राप्त करने के लिए (UPBoardSolutions.com) BX को मिलाया तथा CY, इसे बिन्दु A पर प्रतिच्छेद करता है।
चरण 4: ∆ABC के शीर्ष A के सम्मख एक न्यूनकोण CB खींचा।
चरण 5: रेखाखण्ड BZ पर चार बिन्दुओं B₁, B₂, B₃, B₄ को इस पर चिन्हित करते हैं कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄
चरण 6: बिन्दु B₃ से C को मिलाया।
चरण 7: B₃C के समान्तर एक रेखा B₄C’ खींची जोकि रेखाखण्ड BC को बिन्दु C’ पर प्रतिच्छेद करती है।
चरण 8: CA के समान्तर बिन्दु C’ से जाती हुई एक रेखा खींची जोकि बाहृय रेखाखण्ड BA को बिन्दु A’ पर प्रतिच्छेद करती है।
अत: ∆A BC’ ही अभीष्ट त्रिभुज है, जोकि ∆ABC के समरूप है।

प्रश्न 4.
एक समकोण त्रिभुज की रचना कीजिए जिसमें भुजाएँ (कर्ण को छोडकर ) 5 सेमी तथा 4 सेमी हैं। फिर एक, दूसरे त्रिभुज की रचना कीजिए जिसकी भुजाएँ, दिए गए त्रिभुज की [latex]\frac{5}{3}[/latex] गुनी है।
हलः
रचना के चरणः

चरण 1: BC = 5 सेमी की एक रेखा खींचिए।
चरण 2: B पर एक समकोण बनायें और AB = 4 सेमी काट लें।
चरण 3: AC को मिला दें तो ∆ ABC दिया गया समकोण त्रिभुज है।
चरण 4: B से एक न्यूनकोण ∠CBY ‘नीचे की ओर बनायें।
चरण 5: BY पर 5 बिंदुओं B₁, B₂, B₃, B₄ तथा B, इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
चरण 6: B₃C को मिला दे।
चरण 7: बिंदु B₅ से B₅D||B₃C (UPBoardSolutions.com) खींचे जो BC के बढ़े भाग को D पर काटे।
चरण 8: D से, DE || CA खींचे BA के बढ़े भाग को E पर काटे।
तब ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 5.
एक ∆ PQR की रचना कीजिए जिसकी भुजाएँ QR = 7 सेमी, PQ = 6 सेमी तथा ∠PQR = 60° फिर एक, दूसरे त्रिभुज की रचना कीजिए जिसकी भुजाएँ, ∆ PQR की संगत भुजाओं की [latex]\frac{3}{5}[/latex] है
हलः
रचना के चरणः

चरण 1: PQ = 6 सेमी की सरल रेखा खींचें।
चरण 2: बिन्दुQ, से ∠ PQY = 60° बनायें और QR = 7 सेमी काटे।
चरण 3: PR को मिला दे। ∆ PQR ही अभीष्ट त्रिभुज है।
चरण 4: P से एक किरण PX नीचे की ओर एक न्यूनकोण ∠QPX बनाते हुए खींचे।
चरण 5: PX पर पाँच बिंदुओं (UPBoardSolutions.com) P₁, P₂,P₃, P₄ और P₅ इस प्रकार अंकित करें । कि
PP₁ = P₁P₂ = P₂P₃ = P₃P₄ = P₄P₅
चरण 6: P₅ को Q से मिलायें।
चरण 7: P₃ से P₃Q’ ||P₅Q खींचे जो PQ को Q’ पर प्रतिच्छेद करें।
चरण 8: Q’ से Q R’ ||QR खींचे जो PR को R’ पर प्रतिच्छेद करती है
तब ∆ PQ’ R’ ही अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ PQR की भुजाओं की [latex]\frac{3}{5}[/latex] है।

प्रश्न 6.
एक समद्विबाहु त्रिभुज की रचना कीजिए जिसका आधार 8 सेमी तथा ऊँचाई 4 सेमी है तथा तब एक ऐसे त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए गए, समद्विबाहु त्रिभुज की संगत भुजाओं की [latex]\frac{3}{2}[/latex] गुनी है   (NCERT)
हलः
रचना के चरणः

चरण 1: BC = 8 सेमी की एक रेखा खींचिए।
चरण 2: B पर एक समकोण बनाइयें और AB = 4 सेमी काट लें।
चरण 3: AC को मिला दें तो ∆ ABC दिया गया समकोण त्रिभुज है।
चरण 4: B से एक न्यूनकोण ∠CBY नीचे की ओर बनाइयें।
चरण 5: BY पर तीन बिंदुओं (UPBoardSolutions.com) B₁, B₂, B₃ इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃
चरण 6: B₂C को मिला दें।
चरण 7: बिंदु B₃ से B₃D||B₂C खींचे जो BC के बढ़े भाग को D पर काटे।
चरण 8: D से, DE || CA खींचे BA के बढ़े भाग को E पर काटे।
तब ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 7.
एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ 5 सेमी, 5.5 सेमी तथा 6.5 सेमी हैं। तब एक, दूसरे त्रिभुज की रचना कीजिए जिसकी भुजाएँ, दिए गए त्रिभुज की भुजाओं की [latex]\frac{3}{5}[/latex] गुनी है।
हलः
रचना के चरणः

चरण 1: BC = 5.5 सेमी का एक रेखाखण्ड खींचिए।
चरण 2: B को केन्द्र मानकर 5 सेमी त्रिज्या का एक चाप खींचें।
चरण 3: C को केन्द्र मानकर 6.5 सेमी त्रिज्या का एक दूसरा चाप खींचें जो पहले चाप को A पर प्रतिच्छेद करे।
चरण 4: AB और AC को मिला दें। इस तरह ∆ ABC प्राप्त हुआ।
चरण 5: BC के नीचे एक न्यूनकोण (UPBoardSolutions.com) ∠CBX बनायें।
चरण 6: BX पर पाँच बिंदुओं B₁, B₂, B₃, B₄, B₅ इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
चरण 7: B₅C को मिला दें।
चरण 8: बिन्दु B₃ से B₃D||B₅C खींचें जो BC से D पर मिले।
चरण 9: D से, DE || CA खींचें BA को E पर मिले।
तब ∆EBD अभीष्ट त्रिभुज है जिसकी प्रत्येक भुजा ∆ABC की संगत भुजाओं की [latex]\frac{3}{5}[/latex] गुनी है।

प्रश्न 8.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 6 सेमी, AB = 5 सेमी तथा ∠ABC = 60° तब एक ऐसा त्रिभुज बनाइए जिसकी भुजाएँ, ∆ ABC की संगत भुजाओं का [latex]\frac{3}{4}[/latex] वाँ भाग हो। (NCERT)
हलः
रचना के चरणः

चरण 1: AB = 5 सेमी की सरल रेखा खींचें।
चरण 2: बिन्दु B, से ∠ ABY = 60° बनायें और BC = 6 सेमी काटे।
चरण 3: AC को मिला दें। ∆ ABC ही अभीष्ट त्रिभुज है।
चरण 4: A से एक किरण AX नीचे की ओर एक न्यूनकोण ∠ BAX = 60° बनाते हुए खींचे।
चरण 5: AX पर चार बिंदुओं (UPBoardSolutions.com) A₁, A₂, A₃ और A₄ इस प्रकार अंकित करें कि
AA₁ = A₁A₂ = A₂A₃ = A₃A₄
चरण 6: A₄B को मिलायें।
चरण 7: A₃ से A₃B’ ||A₄B खींचें जो AB को B’ पर प्रतिच्छेद करें।
चरण 8: B’ से B’C’ ||BC खींचें जो AC को C’ पर प्रतिच्छेद करती है तब ∆ AB’C’ ही अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ ABC की भुजाओं की [latex]\frac{3}{4}[/latex] है।

प्रश्न 9.
एक समकोण त्रिभुज की रचना कीजिए जिसमें भुजाओं (कर्ण को छोड़कर) की लम्बाई 8 सेमी तथा 6 सेमी हैं तब एक, दूसरा त्रिभुज बनाइए जिसकी भुजाएँ पहले त्रिभुज की संगत भुजाओं की [latex]\frac{3}{4}[/latex] गुनी है।
हलः
रचना के चरणः

चरण 1: BC = 8 सेमी की एक रेखा खींचिए।
चरण 2: B पर एक समकोण बनाइयें और AB = 6 सेमी काट लें।
चरण 3: AC को मिला दें तो ∆ ABC दिया गया समकोण त्रिभुज है।
चरण 4: B से एक न्यूनकोण ∠ CBY नीचे की ओर बनाइये।
चरण 5: BY पर चार बिंदुओं (UPBoardSolutions.com) B₁, B₂, B₃ तथा B₄ इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄
चरण 6: B₄C को मिला दे।
चरण 7: बिन्दु B₃ से B₃D||B₄C खींचें जो BC को D पर प्रतिच्छेद करे।
चरण 8: D से, DE || CA खींचे, जो BA को E पर प्रतिच्छेद करे। तब ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 10.
एक समकोण त्रिभुज ABC की रचना कीजिए जिसमें AB = 6 सेमी, BC = 8 सेमी तथा ∠B = 90° तथा बिन्दु B से रेखा AC पर एक लम्ब BD डाले तथा बिन्दुओं B,C तथा D से गुजरने वाला एक वृत्त खींचा गया। A से इस वृत्त पर स्पर्श रेखायें खींचें।
हलः

यहाँ एक समकोण ∆ABC है जिसमें AB = 6 सेमी, BC = 8 सेमी तथा ∠B = 90° BD, AC पर लम्ब है।
हमे बिन्दु A से वृत्त BDC पर दो स्पर्श रेखायें खींचनी हैं। यहाँ रचना के चरण निम्नलिखित हैं
चरण 1: BC = 8 सेमी और AB =.6 सेमी के रेखाखण्ड खींचे जोकि एक-दूसरे पर लम्ब हों।
चरण 2: AC को मिला दें, इस प्रकार ∆ ABC ही अभीष्ट समकोण त्रिभुज है।
चरण 3: BC के मध्य बिन्दु (UPBoardSolutions.com) F को केन्द्र लेकर FB = 4 सेमी त्रिज्या का एक वृत्त खींचें जो AC को D पर काटता है तथा B, C तथा D से होकर गुजरता है।
चरण 4: A को केन्द्र मानकर 6 सेमी त्रिज्या का चाप खींचें जो वृत्त को E पर काटता है।
चरण 5: AE को मिला दें।
तब AE एक अभीष्ट स्पर्श रेखा है तथा AB पहले ही B पर स्पर्श रेखा है।

प्रश्न 11.
8 सेमी लम्बाई का एक रेखाखण्ड AB खींचे। A को केन्द्र मानकर, 4 सेमी त्रिज्या का एक वत्त खींचे तथा B को केन्द्र मानकर एक 3 सेमी त्रिज्या का दूसरा वृत्त खींचें। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखायें खींचे। (NCERT)
हलः

दिया गया रेखाखण्ड AB = 8 सेमी। दो वृत्त जिनके केन्द्र A और B तथा त्रिज्यायें क्रमशः 4 सेमी और 3 सेमी हैं।
हमें प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से दो-दो स्पर्श रेखायें खींचनी हैं।
रचना के चरण निम्नलिखित हैं:
चरण 1. AB = 8 सेमी का एक रेखाखण्ड खींचें।
चरण 2. A केन्द्र से 4 सेमी त्रिज्या का एक वृत्त खींचें।
चरण 3. B केन्द्र से 3 सेमी त्रिज्या का दूसरा वृत्त खींचें।
चरण 4. रेखाखण्ड AB को (UPBoardSolutions.com) समद्विभाग करें। माना कि L, AB का मध्य बिंदु है।
चरण 5. L को केन्द्र मानकर, AL त्रिज्या का एक बिन्दुवत् वृत्त खींचें। यह दोनों वृत्तों (A केन्द्र वाले तथा B केन्द्र वाले वृत्तों को) को P, Q, R तथा S बिन्दुओं पर काटते हैं।
चरण 6. AP, AQ, BR तथा BS को मिला दें।
तब प्राप्त रेखायें ही अभीष्ट स्पर्श रेखायें हैं।

प्रश्न 12.
3.5 सेमी त्रिज्या के एक वृत्त के बिन्दु P से दो स्पर्श रेखायें खींचे जिसकी वृत्त के केन्द्र से दूरी 6.2 सेमी है।
हलः

यहाँ 3.5 सेमी त्रिज्या वाले एक वृत्त के केन्द्र से 6.2 सेमी दूरी पर एक बिन्दु P है। हमें दिये गये बिन्दु P से वृत्त की दो स्पर्श रेखायें खींचनी हैं।
रचना के चरण निम्नलिखित हैं:
चरण 1. O के केन्द्र से 3.5 सेमी त्रिज्या का वृत्त खींचें।
चरण 2. OP को मिला दें और इसे समद्विभाग करें। मान लें कि M, OP का मध्य बिन्दु है।
चरण 3. M को केन्द्र मानकर, (UPBoardSolutions.com) MP त्रिज्या का एक वृत्त खींचे, जो वृत्त को बिन्दुओं A तथा B पर काटता है।
चरण 4. PA तथा PB को मिलाएँ।
तब PA और PB ही वृत्त पर दो अभीष्ट स्पर्श रेखायें हैं।

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 14 Statistics Ex 14.1 सांख्यिकी

Ex 14.1 Statistics लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
एक कक्षा में प्रतिदिन अनुपस्थित विद्यार्थियों की संख्या के 120 दिनों के बारे में निम्नलिखित बारंबारता सारणी में दिया गया है।

प्रतिदिन अनुपस्थित विद्यार्थियों की संख्या का माध्य ज्ञात कीजिए।
हलः

समान्तर माध्य [latex]\overline{x}=\frac{\Sigma f x}{n}=\frac{423}{120}[/latex] = 3.53

प्रश्न 2.
निम्नलिखित सारणी का समान्तर माध्य ज्ञात कीजिए।

हलः

प्रश्न 3.
निम्नलिखित वितरण में, एक महीने में एक फैक्ट्री के 160 मजदूरों की दुर्घटनाओं की संख्या दी गई है। दुर्घटनाओं की औसत संख्या ज्ञात कीजिए।

हलः

प्रश्न 4.
यदि निम्नलिखित आँकडों का माध्य 6 है तो p का मान ज्ञात कीजिए।

हलः

Ex 14.1 Statistics दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 5.
निम्नलिखित सारणी में 108 छात्रों के अंक दर्शाये गये हैं। अंकों के समान्तर माध्य की गणना कीजिए।

हलः

प्रश्न 6.
एक फैक्ट्री के मजदूरों की आयु नीचे दी गई है। मजदूरों की औसत आयु ज्ञात कीजिए।

हलः

प्रश्न 7.
कक्षा 10 के 80 विद्यार्थियों के गणित में अंको को नीचे दर्शाया गया है। गणित में औसत अंको की गणना कीजिए।

हलः

Balaji Publications Mathematics Class 10 Solutions

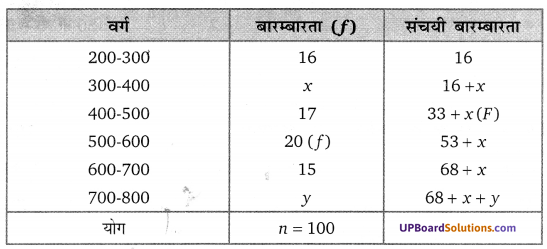
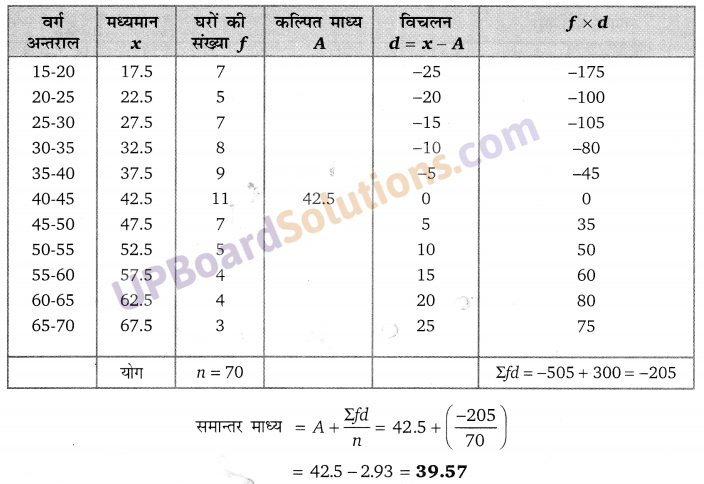
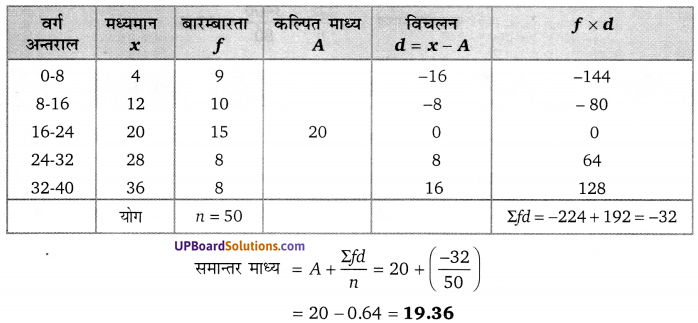
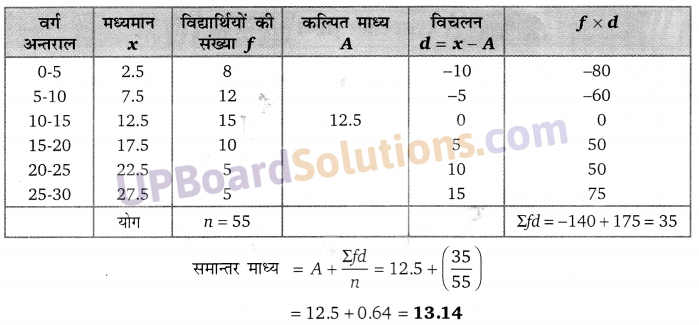
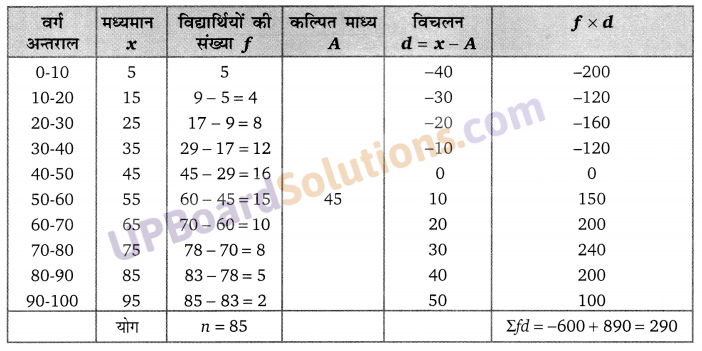
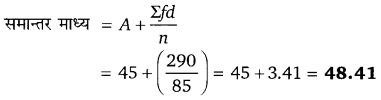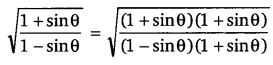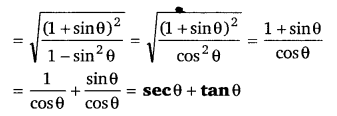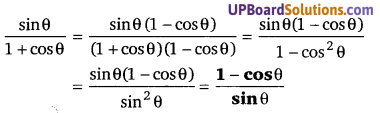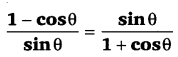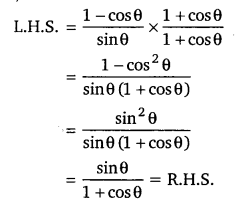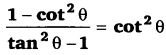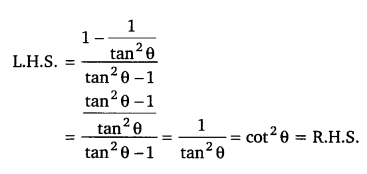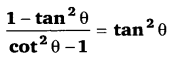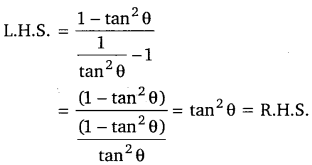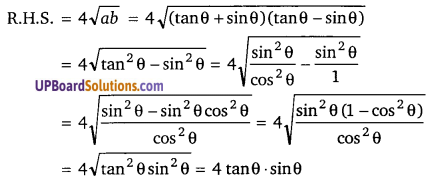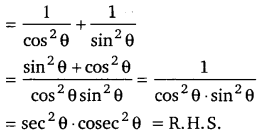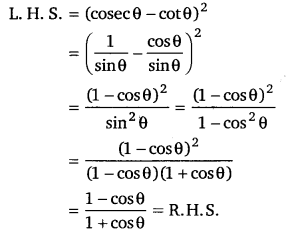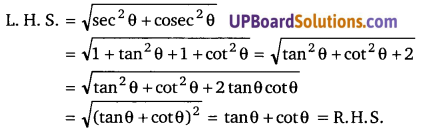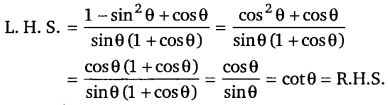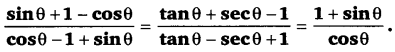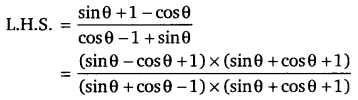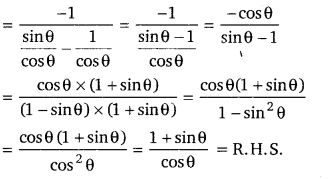Balaji Class 10 Maths Solutions Chapter 10 Trigonometrical Ratios and Identities Ex 10.4 त्रिकोणमितीय अनुपात एवं असमिकाएँ

Ex 10.4 Trigonometrical Ratios and Identities अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि sinθ = cost तब θ का मान ज्ञात कीजिए।
हल:
∵ sinθ = cosθ

प्रश्न 2.
sin²θ sec²θ का मान ज्ञात कीजिए।
हल:
sin² θ · sec²θ (UPBoardSolutions.com) = sin²θ · [latex]\frac{1}{\cos ^{2} \theta}[/latex]
= tan²θ

प्रश्न 3.
secθ sinθ का मान ज्ञात कीजिए।
हलः
secθ ·sinθ = [latex]\frac{1}{\cos \theta}[/latex]·sin²
= tanθ

प्रश्न 4.
(secθ – tanθ) (secθ + tanθ) का मान ज्ञात कीजिए।
हलः
(secθ – tanθ)(secθ + tanθ) = sec²θ – tan²θ
=1

प्रश्न 5.
यदि cosθ = [latex]\frac{a}{b}[/latex], तब sine का मान ज्ञात कीजिए।
हलः

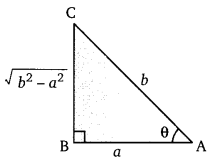
प्रश्न 6.
यदि tanθ = [latex]\frac{a}{b}[/latex], तब [latex]\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}[/latex] का मान ज्ञात कीजिए।
हलः

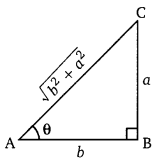
प्रश्न 7.
यदि x = a cosθ, y = b sinθ, a (b²x² + a²y²) का मान ज्ञात कीजिए।
हलः
x = acosθ तथा y = bsinθ

प्रश्न 8.
(sin⁴ θ – cos⁴ θ + 1) cosec²θ का मान ज्ञात कीजिए।
हलः
(sin⁴ θ – cos⁴ θ + 1)cosec²θ
= [(sin²θ)² – (cos² θ)² + 1]cosec²θ
= [(sin²θ + cos² θ) (UPBoardSolutions.com) (sin² θ – cos²θ) + 1]·cosec²θ
= [1(sin² θ – cos²θ) + sin²θ + cos² θ]cosec²θ
= (sin² θ – cos²θ + sin² θ + cos²θ).cosec²θ
= 2 sin²θ × [latex]\frac{1}{\sin ^{2} \theta}[/latex] = 2

प्रश्न 9.
[latex]\sqrt{\frac{1+\sin \theta}{1-\sin \theta}}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

प्रश्न 10.
[latex]\sqrt{\frac{1+\sin \theta}{1-\sin \theta}}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

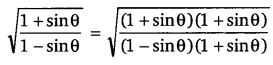
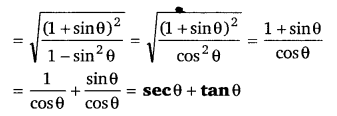
प्रश्न 11.
[latex]\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

प्रश्न 12.
[latex]\frac{\sin \theta}{1+\cos \theta}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

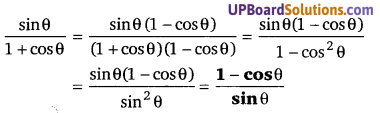
प्रश्न 13.
(1 + tanθ + secθ)(1 + cotθ – cosecθ) का मान ज्ञात कीजिए।
हलः
(1 + tanθ + secθ) (UPBoardSolutions.com) (1 + cotθ – cosecθ)

प्रश्न 14.
sin² θ + sin⁴ θ = (यदि cosθ + cos² θ = 1) का मान ज्ञात कीजिए।
हलः
यदि cosθ + cos²θ = 1
coso = 1 – cos² θ
cosθ = (UPBoardSolutions.com) sin²θ
या sin² θ = cos ²
तब sin²θ + sin⁴ θ = sin² θ(1 + sin²θ)
= cos θ(1 + cosθ)
= cosθ + cos² θ = 1

Ex 10.4 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-I)

निम्न को सिद्ध कीजिए-

प्रश्न 15.
(1 – sin²θ) sec²θ = 1
हलः
L.H.S. = (1 – sin² θ)sec²θ
= cos² θ – sec² θ (UPBoardSolutions.com) (सर्वसम्मिका sin²θ + cos²θ = 1 से)
= cos ²θ·[latex]\frac{1}{\cos ^{2} \theta}[/latex]
= 1 = R.H.S

प्रश्न 16.
(secθ + tanθ)² = [latex]\frac{1+\sin \theta}{1-\sin \theta}[/latex]
हलः
L.H.S. = (secθ + tanθ)²

प्रश्न 17.
(sin θ – cosθ)(cotθ + tanθ) = secθ – cosec θ
हलः

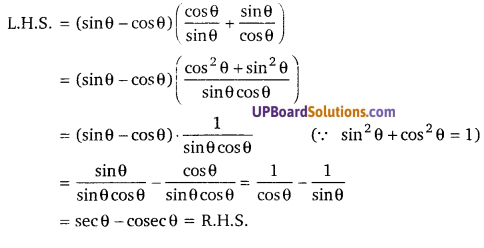
प्रश्न 18.
[latex]\frac{\sec \theta-\tan \theta}{\sec \theta+\tan \theta}[/latex] = 1 – 2 secθ tan θ + 2 tan²θ
हलः

प्रश्न 19.

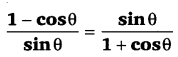
हलः
अंश का परिमेयकरण (UPBoardSolutions.com) करने पर,

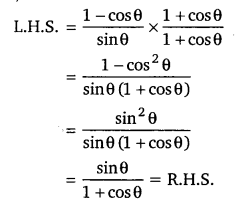
प्रश्न 20.
(1 – sinθ) (1 + sin θ) (1 + tan²θ) = 1
हलः
L.H.S. = (1 – sinθ)(1 + sinθ)(1 + tan²θ)
= (1 – sin²θ)sec²θ
= cos²θ · (UPBoardSolutions.com) sec²θ
= cos²θ [latex]\frac{1}{\cos ^{2} \theta}[/latex] = 1 = R.H.S.

प्रश्न 21.

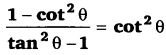
हलः

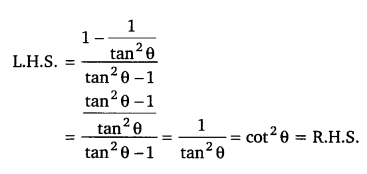
प्रश्न 22.

हलः

प्रश्न 23.

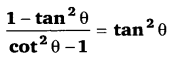
हलः

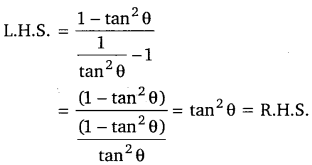
Ex 10.4 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 24.
यदि tan θ + sin θ = a, tanθ – sin θ = b, तब सिद्ध कीजिए a² – b² = 4[latex]\sqrt{a b}[/latex]
हलः
L.H.S. = a² – b²
= (tan θ + sinθ)² – (UPBoardSolutions.com) (tan θ – sinθ)²
= tan² θ + sin² θ + 2 tanθsinθ – tan² θ – sin²θ + 2 tanθ sin²
= 4 tanθ sinθ

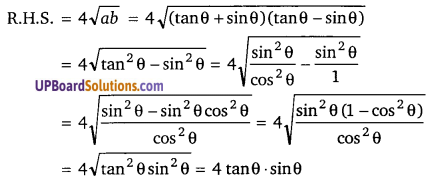
∴ L.H.S. = R.H.S.

प्रश्न 25.
यदि asin ³ θ + b cos³ θ = sin θ cosθ in a sinθ – b cos θ = 0, तब सिद्ध कीजिए कि a² + b² = 1
हलः
asin³ θ + bcos ³ θ = sinθ cosθ … (1)
asinθ – bcos θ = 0 … (2)
समीकरण (2) से,
asinθ = bcos θ …(3)
समीकरण (1) से, asinθ, का मान रखने पर
(asinθ).sin²θ + bcos³ θ = sinθ cosθ
bcosθsin²θ + bcos³θ = (UPBoardSolutions.com) sinθ cosθ
bcos θ(sin²θ + cos²θ) = sinθ cosθ
bcosθ (1) = sin θcosθ
∴ b = sin θ …(4)
समीकरण (3) से, b का मान रखने पर
asinθ = sin θcos θ
∴ a = cos θ
L.H.S. = a² + b² …(5)
= cos ²θ + sin²θ
= 1 = R.H.S.

सिद्ध कीजिए कि –

प्रश्न 26.
tanθ – cotθ = [latex]\frac{2 \sin ^{2} \theta-1}{\sin \theta \cos \theta}=\frac{1-2 \cos ^{2} \theta}{\sin \theta \cos \theta}[/latex]
हलः

प्रश्न 27.
sec² θ + cosec²θ = sec² θ cosec²θ (UP 2000, 02)
हलः
L. H. S. = sec²θ + (UPBoardSolutions.com) cosec²θ

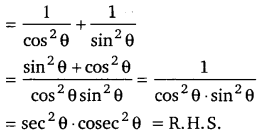
प्रश्न 28.
(cosecθ – cotθ)² = [latex]\frac{1-\cos \theta}{1+\cos \theta}[/latex] (NCERT)
हलः
L. H. S. = (cosecθ – cotθ)²

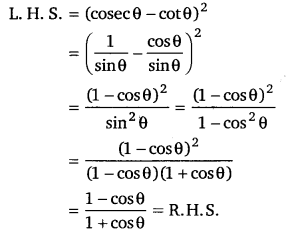
प्रश्न 29.
[latex]\sqrt{\sec ^{2} \theta+\csc ^{2} \theta}[/latex] = tanθ + cotθ
हलः

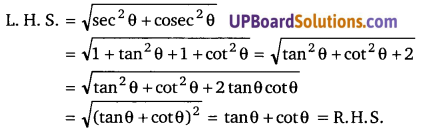
प्रश्न 30.
[latex]\frac{1+\cos \theta}{1-\cos \theta}[/latex] = (cosecθ + cotθ)²
हलः

Ex 10.4 Trigonometrical Ratios and Identities दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 31.
सिद्ध कीजिए कि tan² A – tan² B = [latex]\frac{\sin ^{2} A-\sin ^{2} B}{\cos ^{2} A \cos ^{2} B}=\frac{\cos ^{2} B-\cos ^{2} A}{\cos ^{2} B \cos ^{2} A}[/latex]
हलः

प्रश्न 32.
सिद्ध कीजिए [latex s = 2]\frac{\cot \theta+\csc \theta-1}{\cot \theta-\csc \theta+1}=\frac{1+\cos \theta}{\sin \theta}[/latex]
हलः

प्रश्न 33.
सिद्ध कीजिए [latex s=2]\frac{1+\cos \theta-\sin ^{2} \theta}{\sin \theta(1+\cos \theta)}=\cot \theta[/latex] (UP 2012)
हलः

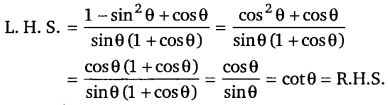
प्रश्न 34.
सिद्ध कीजिए [latex s=2]\frac{\csc \theta+\cot \theta}{\csc \theta-\cot \theta}[/latex] = (cosecθ + cotθ)² = 1 + 2 cot² θ + 2 cosecθ cotθ.
हलः

प्रश्न 35.
सिद्ध कीजिए

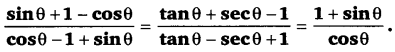
हलः

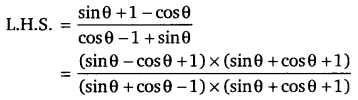
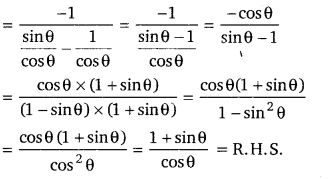
प्रश्न 36.
यदि sinθ + cosθ = p a secθ + cosecθ = q, तब सिद्ध कीजिए कि
q(p² – 1) = 2p
हलः
L. H. S. = 9(p² – 1)- 2p
= (sec θ + cosec θ) (UPBoardSolutions.com) [(sin θ + cos θ)² – 1]

∵ (sinθ + cosθ) = P
= P × 2 = 2P = R.H.S.

प्रश्न 37.
यदि cosθ + sinθ = [latex] \sqrt{{2}} [/latex] · cosθ, तब सिद्ध कीजिए कि (cosθ – sinθ) = [latex] \sqrt{{2}} [/latex] · sinθ
हलः
यदि cosθ + sinθ = [latex] \sqrt{{2}} [/latex]cosθ
दोनों पक्षों का वर्ग करने पर,
(cosθ + sinθ)² = ([latex] \sqrt{{2}} [/latex] cosθ)²
cos²θ + sin²θ + 2cosθ sinθ = 2cos²θ
sin²θ = 2cos²θ – cos²θ (UPBoardSolutions.com) = 2sinθ · cosθ
cos²θ – 2cosθ·sinθ = sin²θ
cos²θ + sin²θ – 2cosθ·sinθ = sin²θ + sin²θ
(cosθ – sinθ)² = 2sin²θ
cosθ – sinθ = [latex] \sqrt{{2}} [/latex] sinθ इति सिद्धम्।

प्रश्न 38.
यदि sinθ – cosθ = 0 तब सिद्ध कौजिए कि sin⁴θ + cos⁴θ = [latex]\frac{1}{2}[/latex]
हलः
दिया है, sinθ – cosθ = 0
दोनों और वर्ग करने पर,
(sinθ – cosθ)² = 0
sin²θ + cos²θ – 2sinθ cosθ = 0
1 – 2 sinθ cosθ = 0
1 = 2sinθ cosθ
sinθ·cosθ = [latex]\frac{1}{2}[/latex]
L. H. S. = sin⁴θ + cos⁴θ
= (sin²θ)² + (cos²θ)² + 2sin²θcos²θ – 2sin²θcos²θ
= (sin²θ + cos²θ)² – 2(sinθ·cosθ)²
= (1)² – 2[latex]\left(\frac{1}{2}\right)^{2}[/latex] (UPBoardSolutions.com)
= 1 – 2 × [latex]\frac{1}{4}[/latex] = 1 – [latex]\frac{1}{2}=\frac{1}{2}[/latex] = R.H.S

प्रश्न 39.
यदि [latex]\frac{x}{a}[/latex]cosθ + [latex]\frac{y}{b}[/latex] sinθ = 1 व [latex]\frac{x}{a}[/latex]sinθ – [latex]\frac{y}{b}[/latex] cosθ = 1, तब सिद्ध कीजिए कि [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}[/latex] = 2
हलः

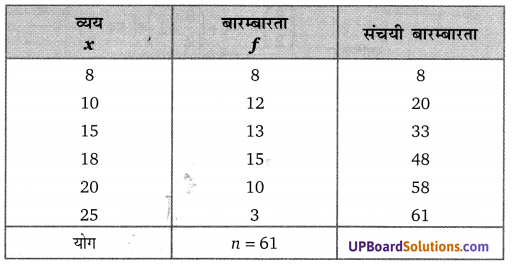
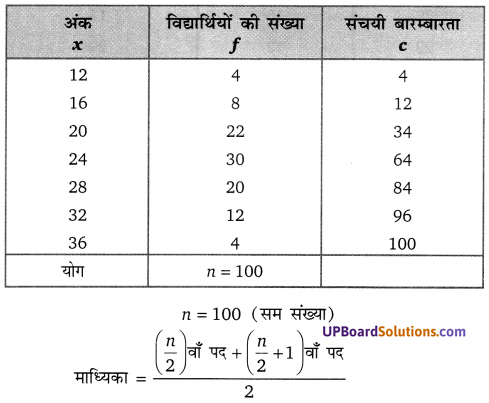
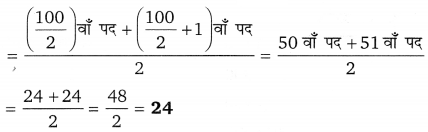
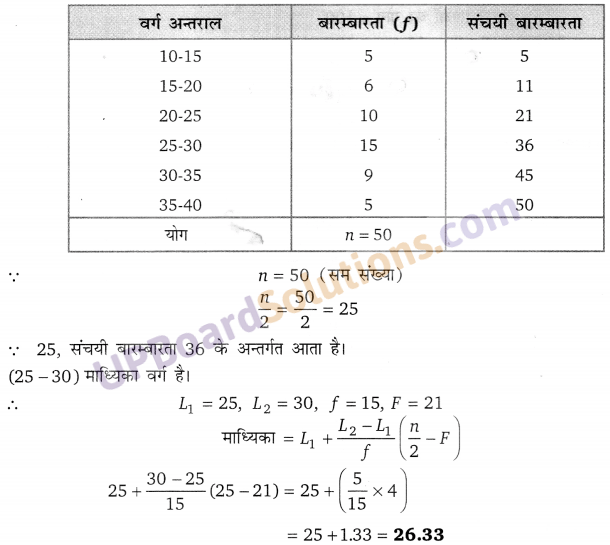
Balaji Publications Mathematics Class 10 Solutions