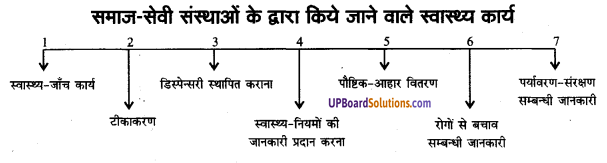
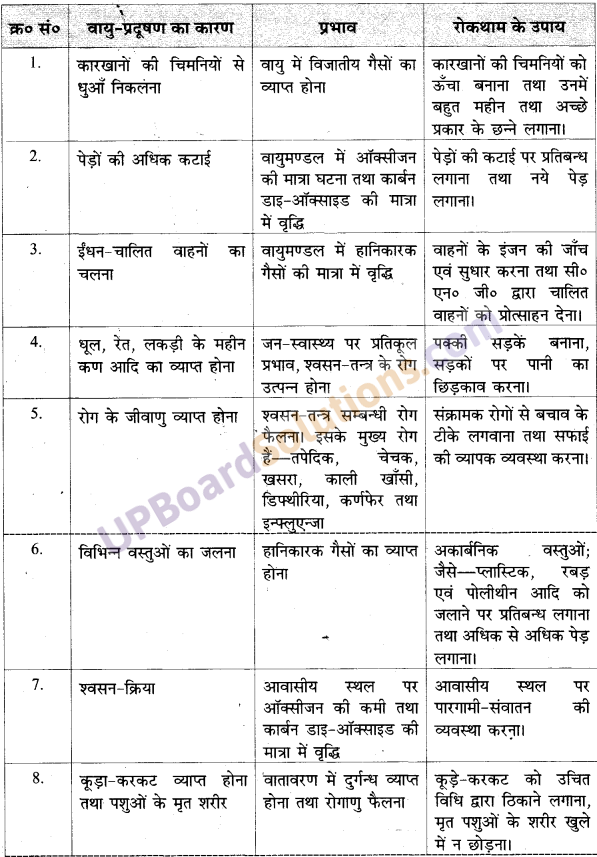
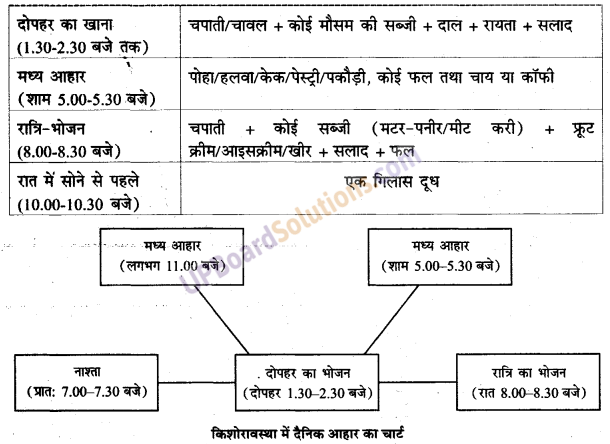
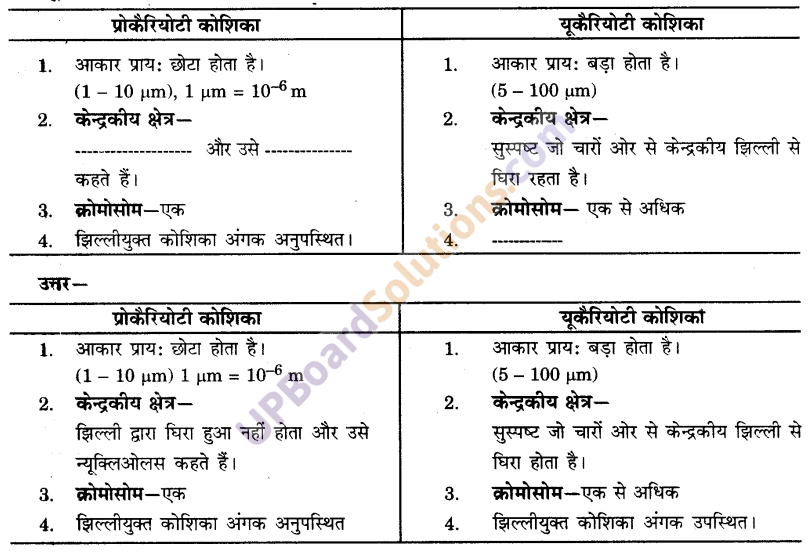
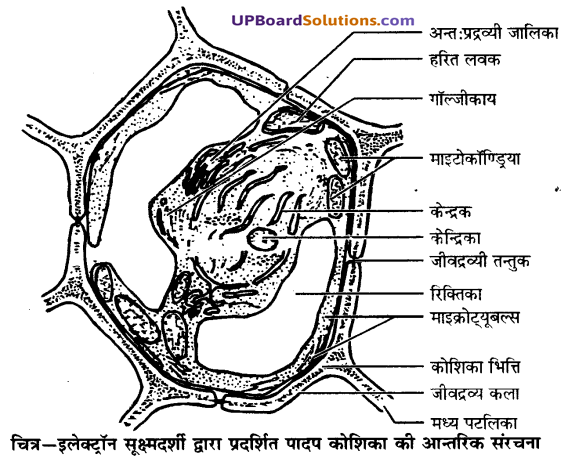
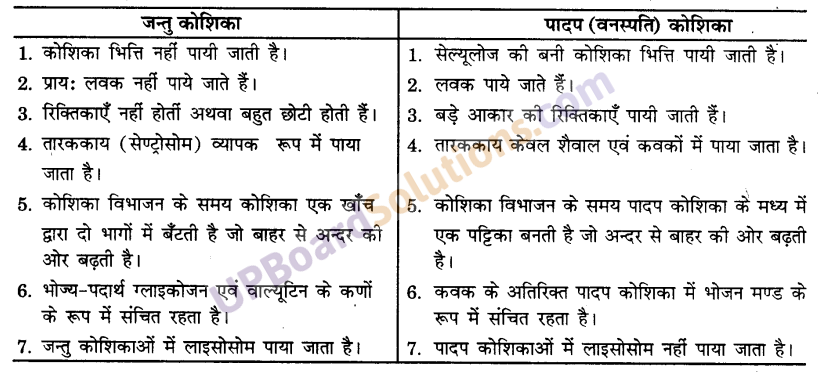
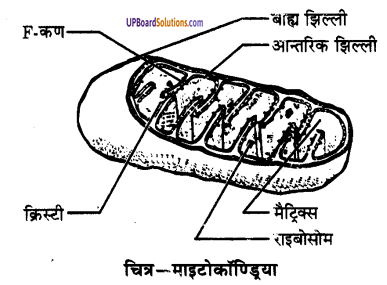
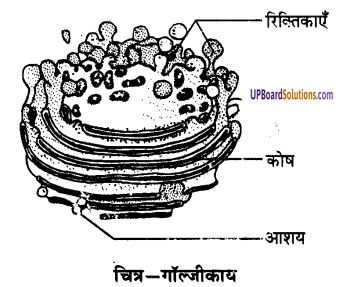
UP Board Solutions for Class 9 Social Science Economics Chapter 3 निर्धनता : एक चुनौती
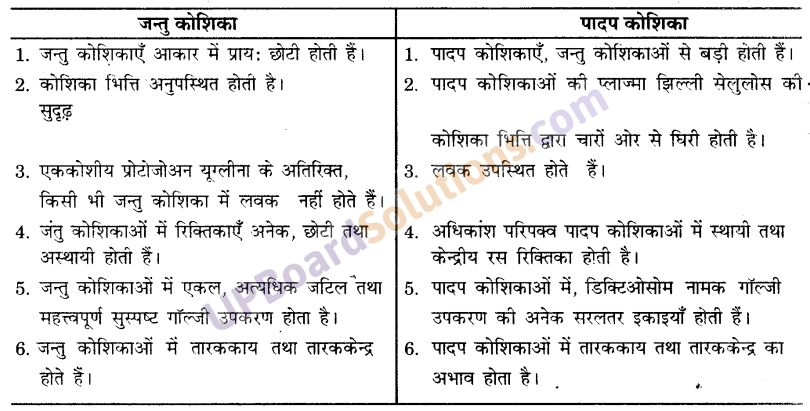
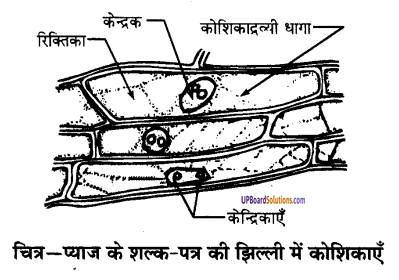
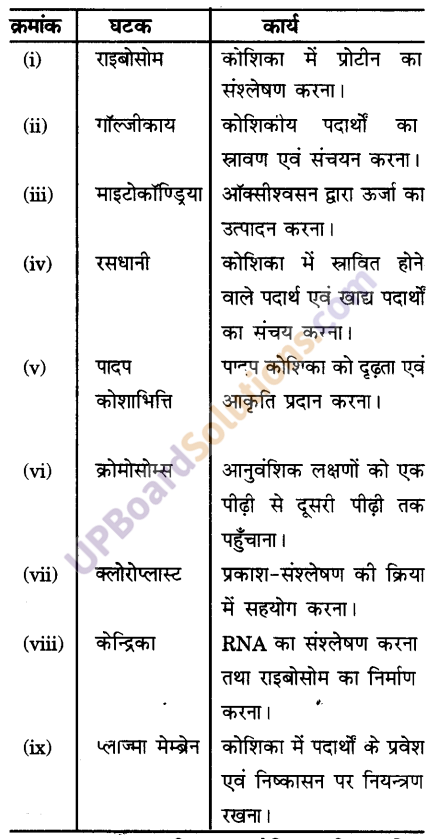
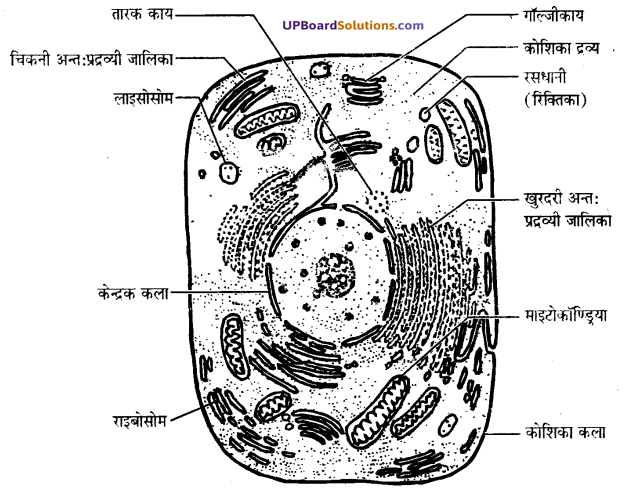
These Solutions are part of UP Board Solutions for Class 9 Social Science. Here we have given UP Board Solutions for Class 9 Social Science Economics Chapter 3 निर्धनता : एक चुनौती
पाठ्य-पुस्तक के प्रश्नोत्तर
प्रश्न 1.
भारत में निर्धनता रेखा का आकलन कैसे किया जाता है?
उत्तर:
भारत में निर्धनता रेखा का आकलन करने के लिए आय या उपभोग स्तरों पर आधारित एक सामान्य पद्धति का प्रयोग किया जाता है। भारत में गरीबी रेखा का निर्धारण करते समय जीवन निर्वाह हेतु खाद्य आवश्यकता, कपड़ों, जूतों, ईंधन और प्रकाश, शैक्षिक एवं चिकित्सा सम्बन्धी आवश्यकताओं को प्रमुख माना जाता है। निर्धनता रेखा का आकलन करते समय खाद्य आवश्यकता के लिए वर्तमान सूत्र वांछित कैलोरी आवश्यकताओं पर आधारित है। खाद्य वस्तुएँ जैसे अनाज, दालें, आदि मिलकर इस आवश्यक (UPBoardSolutions.com) कैलोरी की पूर्ति करती है। भारत में स्वीकृत कैलोरी आवश्यकता ग्रामीण क्षेत्रों में 2400 कैलोरी प्रति व्यक्ति प्रतिदिन एवं नगरीय क्षेत्रों में 2100 कैलोरी प्रति व्यक्ति प्रतिदिन है। चूंकि ग्रामीण क्षेत्रों में रहने वाले लोग अधिक शारीरिक कार्य करते हैं, अतः ग्रामीण क्षेत्रों में कैलोरी आवश्यकता शहरी क्षेत्रों की तुलना में अधिक मानी गई है।
अनाज आदि रूप में इन कैलोरी आवश्यकताओं को खरीदने के लिए प्रति व्यक्ति मौद्रिक व्यय को, कीमतों में वृद्धि को ध्यान में रखते हुए समयसमय पर संशोधित किया जाना है। इन परिकल्पनाओं के आधार पर वर्ष 2000 में किसी व्यक्ति के लिए निर्धनता रेखा का निर्धारण ग्रामीण क्षेत्रों में १ 328 प्रतिमाह और शहरी क्षेत्रों में २ 454 प्रतिमाह किया गया था।
![]()
प्रश्न 2.
क्या आप समझते हैं कि निर्धनता आकलन का वर्तमान तरीका सही है?
उत्तर:
वर्तमान निर्धनता अनुमान पद्धति पर्याप्त निर्वाह स्तर की बजाय न्यूनतम स्तर को महत्त्व देती है। सिंचाई और क्रान्ति के फैलाव ने कृषि के क्षेत्र में कई नौकरियों के अवसर दिए लेकिन भारत में इसका प्रभाव कुछ भागों तक ही सीमि रहा है। सार्वजनिक और निजी दोनों क्षेत्रों के उद्योगों ने नौकरियों के (UPBoardSolutions.com) अवसर दिए हैं। लेकिन ये नौकरी लेने वालों की अपेक्षा बहुत कम है। निर्धनता को विभिन्न संकेतकों के द्वारा जाना जा सकता है। जैसे अशिक्षा का स्तर, कुपोषण के कार मान्य प्रतिरोधक क्षमता में कमी, स्वास्थ्य सेवाओं तक कम पहुँच, नौकरी के कम अवसर, पीने के पानी में कमी, सफाई व्यवस्था आदि। सामाजिक अपवर्जन और असुरक्षा के आधार पर निर्धनता का विश्लेषण अब सामान्य है। गरीबी पर सामाजिक उपेक्षा एवं गरीबी का शिकार होने की प्रवृत्ति के आधार पर भी विचार किया जा सकता है।
प्रश्न 3.
भारत में 1973 से निर्धनता की प्रवृत्तियों की चर्चा करें।
उत्तर:
भारत में 1973 से निर्धनता की प्रवृत्ति को निम्न तालिका द्वारा प्रदर्शित किया गया है-
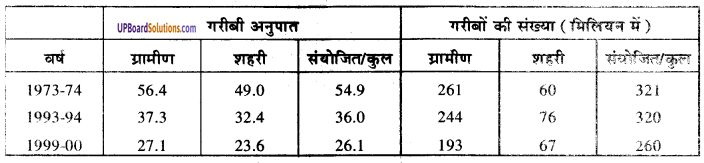
प्रश्न 4.
भारत में निर्धनता की अंतर-राज्य असमानताओं का एक विवरण प्रस्तुत करें।
उत्तर:
भारत में निर्धनता की अन्तर्राज्य असमानता का वितरण निम्नलिखित तालिका द्वारा स्पष्ट है
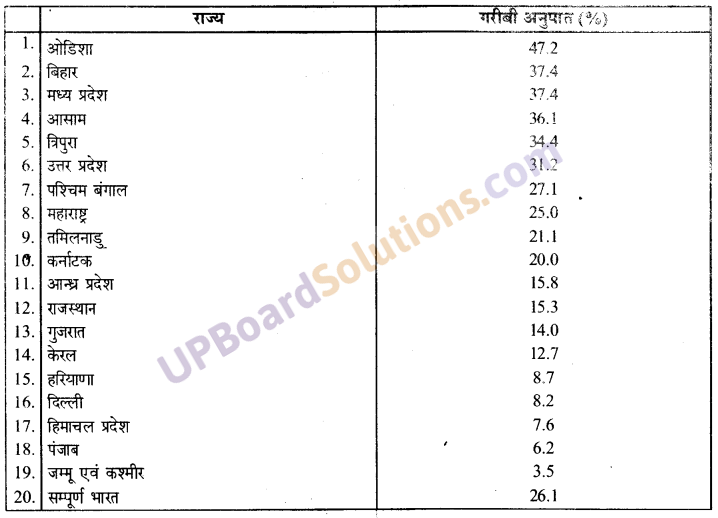
भारत के निश्चित क्षेत्रों के गरीबी अनुपात (1999-2000) से यह स्पष्ट होता है कि ओडिशा भारत का सबसे गरीब राज्य है जिसकी 47.2% जनसंख्या गरीबी रेखा से नीचे रहती है। जम्मू-कश्मीर में सबसे कम 3.5% लोग गरीबी रेखा के नीचे रहते हैं। भारत में कुल 26.1% लोग निर्धनता की रेखा के नीचे हैं।
प्रश्न 5.
उन सामाजिक और आर्थिक समूहों की पहचान करें जो भारत में निर्धनता के समक्ष निरुपाय हैं।
उत्तर:
अनुसूचित जाति, अनुसूचित जनजाति तथा अन्य पिछड़े वर्ग के परिवार उन सामाजिक समूहों में शामिल हैं, जो निर्धनता के प्रति सर्वाधिक असुरक्षित हैं। इसी प्रकार, आर्थिक समूहों में सर्वाधिक असुरक्षित समूह, ग्रामीण कृषि श्रमिक परिवार और नगरीय अनियमित मजदूर परिवार हैं। इसके अलावा महिलाओं, वृद्ध लोगों और बच्चियों को अति निर्धन माना जाता है क्योंकि उन्हें सुव्यवस्थित ढंग से परिवार के उपलब्ध संसाधनों तक पहुँच से वंचित रखा जाता है।
प्रश्न 6.
भारत में अन्तर्राज्यीय निर्धनता में विभिन्नता के कारण बताइए।
उत्तर:
भारत में अन्तर्राज्यीय निर्धनता में विभिन्नता के प्रमुख कारण इस प्रकार हैं
- केन्द्रीय प्रादेशिक सरकार समान रूप से सभी क्षेत्रों में समान निवेश नहीं करती।
- दूर स्थित ग्रामीण क्षेत्रों, पहाड़ी एवं रेगिस्तानी इलाकों की अवहेलना की जाती है।
- प्राकृतिक आपदा जैसे—बाढ़, तूफान, सूनामी का सभी राज्यों में न होना।
- प्रत्येक राज्य में निर्धन लोगों का अनुपात एकसमान नहीं है।
- प्रत्येक राज्य का प्राकृतिक वातावरण, जलवायु, मिट्टी, वर्षा आदि समान नहीं है।
- प्रत्येक राज्य समान रूप से मानव संसाधन अर्थात् शिक्षा और स्वास्थ्य का विकास नहीं कर पाए हैं।
- प्रत्येक राज्य में भूमि सुधार का कार्य समान नहीं हुआ है।
![]()
प्रश्न 7.
वैश्विक निर्धनता की प्रवृत्तियों की चर्चा करें।
उत्तर:
विश्व बैंक के अनुसार सार्वभौमिक निर्धनता जो 1990 में 28% थी, घटकर 2001 में 21% हो गयी। निर्धनता में स्थिरता से चीन एवं दक्षिणी एशिया के देशों में मानवीय संसाधनों में वृद्धि के कारण कम है। भारत, पाकिस्तान, श्रीलंका, नेपाल, भूटान एवं बांग्लादेश में तेजी से निर्धनता में कमी नहीं हुई है।

प्रश्न 8.
निर्धनता उन्मूलन की वर्तमान सरकारी रणनीति की चर्चा करें।
उत्तर:
भारत से निर्धनता उन्मूलन करने हेतु निम्नलिखित उपाय अपनाये गए हैं|
- आर्थिक विकास में वृद्धि–आर्थिक विकास की दर में वृद्धि करना निर्धनता उन्मूलन हेतु महत्त्वपूर्ण कदम है। राष्ट्रीय आय में जनसंख्या के अनुपात में वृद्धि तेजी से होनी चाहिए तभी आर्थिक विकास में वृद्धि हो सकती है।
- भूमि सुधार-निर्धनता दूर करने के लिए भूमि की हदबंदी कानून के अन्तर्गत प्राप्त भूमि को भूमिहीन एवं गरीब किसानों में बाँट देना चाहिए। भूमि के बिखराव को रोकना चाहिए और खेतों की चकबंदी की जानी चाहिए।
- जनसंख्या पर नियंत्रण-गरीबी को अधिक सीमा तक कम किया जा सकता है यदि हम परिवार नियोजन पर जोर दें। जनसंख्या नियंत्रण से प्रति व्यक्ति आय में वृद्धि होगी। यह जनसंख्या वृद्धि की दर में एवं आर्थिक संसाधनों के बीच अन्तर करने में सहायक होगा।
- अत्यधिक रोज़गार के अवसर-ग्रामीण एवं शहरी क्षेत्रों में रोज़गार के अवसरों को बढ़ाकर भारत में बेरोज़गारी को कम किया जा सकता है। इस प्रकार सार्वजनिक कार्य विस्तृत पैमाने (extensive scale) पर प्रारम्भ किया। जाना चाहिए। लघु एवं कुटीर उद्योग को प्रोत्साहित (UPBoardSolutions.com) करना चाहिए। मानवशक्ति का कुशल उपयोग निःसंदेह अर्थव्यवस्था में आय उत्पन्न करेगी और इससे गरीबी को कुछ सीमा तक कम किया जा सकता है।
प्रश्न 9.
निम्नलिखित प्रश्नों के संक्षेप में उत्तर दें
(क) मानव निर्धनता से आप क्या समझते हैं?
(ख) निर्धनों में भी सबसे निर्धन कौन हैं?
(ग) राष्ट्रीय ग्रामीण रोजगार गारंटी अधिनियम, 2005 की मुख्य विशेषताएँ क्या हैं?
उत्तर:
(क) “मानव निर्धनता’ की अवधारणा मात्र-आय की न्यूनता तक ही सीमित नहीं है। इसका अर्थ है किसी व्यक्ति को राजनीतिक, सामाजिक और आर्थिक अवसरों का उचित स्तर न मिलना। अशिक्षा, रोजगार के अवसरों की कमी, स्वास्थ्य सेवा की सुविधाओं और सफाई व्यवस्था में कमी, जाति, लिंग-भेद आदि मानव निर्धनता के कारक हैं।
(ख) महिलाओं, वृद्ध लोगों और बच्चों को अति निर्धन माना जाता है क्योंकि उन्हें सुव्यवस्थित ढंग से परिवार के उपलब्ध संसाधनों तक पहुँच से वंचित रखा जाता है।
(ग) राष्ट्रीय ग्रामीण रोजगार गारंटी अधिनियम, 2005 (एन.आर.ई.जी.ए.) की विशेषताएँ निम्नलिखित हैं
- 200 जिलों में प्रत्येक वर्ष गृहस्थ को 100 दिन के रोजगार का आश्वासन प्रदान करना। बाद में यह योजना 600 | जिलों में कर दी गई।
- 1/3 आरक्षित कार्य (jobs) महिलाओं के लिए होंगे।
- केन्द्रीय सरकार राष्ट्रीय रोज़गार आश्वासन कोष का निर्माण करेगी।
- यदि कार्य 50 दिन के भीतर प्रदान नहीं कराया गया तो प्रतिदिन रोज़गार भत्ता दिया जाएगा।
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
भारत और चीन की निर्धनता में कमी के आँकड़ों के बारे में बताइए।
उत्तर:
भारत में निर्धनता का अनुपात 1990 के 20 प्रतिशत से बढ़कर 2001 में 21 प्रतिशत हो गया है। चीन में निर्धनता की संख्या 1981 के 60.6 करोड़ से घटकर 2001 में 21.2 करोड़ हो गयी।
![]()
प्रश्न 2.
सरकार द्वारा चलाए गए निर्धनता निरोधी कार्यक्रम ज्यादा कारगर साबित क्यों नहीं हो रहा है?
उत्तर:
निर्धनता निरोधी कार्यक्रम के कम प्रभावी होने का एक मुख्य कारण उचित कार्यान्वयन और सही लक्ष्य निश्चित करने की।
प्रश्न 3.
उन पाँच राज्यों के नाम बताएँ जहाँ निर्धनता सबसे कम और सबसे अधिक है।
उत्तर:
भारत के पाँच सबसे कम निर्धन राज्य-जम्मू कश्मीर, पंजाब, हिमाचल प्रदेश, हरियाणा, केरल। भारत के पाँच सबसे अधिक निर्धन राज्य–ओडिशा, बिहार, झारखण्ड, मध्य प्रदेश, असम।
प्रश्न 4.
भारत में निर्धनता के किन्हीं दो कारणों का उल्लेख कीजिए।
उत्तर:
भारत की दीर्घकालिक बेरोजगारी में वृद्धि होना।
स्वतन्त्रता के पश्चात् भूमि और अन्य संसाधनों का असमान वितरण।
प्रश्न 5.
भारत में निर्धनता सम्बन्धी चुनौतियों का उल्लेख कीजिए।
उत्तर:
(क) लैंगिक समता तथा निर्धनों में सम्मान ।
(ख) शिक्षा व रोजगार सुरक्षा उपलब्ध कराना
(ग) न्यूनतम आवश्यक आय की उपलब्धता
(घ) सभी को स्वास्थ्य सेवाएँ उपलब्ध कराना।
प्रश्न 6.
उन पाँच देशों का उल्लेख कीजिए, जिनकी ज्यादातर जनसंख्या गरीबी रेखा से नीचे है।
उत्तर:
- नाइजीरिया,
- बांग्लादेश,
- भारत,
- पाकिस्तान,
- चीन।।
प्रश्न 7.
उन पाँच राज्यों का नामोल्लेख कीजिए जिनकी अल्पसंख्या गरीबी की रेखा के नीचे हैं
उत्तर:
- जम्मू-कश्मीर,
- गोवा,
- पंजाब,
- हरियाणा,
- हिमाचल प्रदेश।
![]()
प्रश्न 8.
उन पाँच राज्यों के नाम बताइए जिनमें लोगों का अधिकांश भाग गरीबी रेखा से नीचे है।
उत्तर:
- ओडिशा,
- बिहार,
- मध्य प्रदेश,
- उत्तर प्रदेश,
- पश्चिम बंगाल।
लघु उत्तरीय प्रश्न
प्रश्न 1.
देश में गरीबी दूर करने के लिए सरकार द्वारा शुरू की गयी योजनाओं का उल्लेख कीजिए।
उत्तर:
- राष्ट्रीय ग्रामीण रोजगार आश्वासन अधिनियम (NREGA), 2005
- राष्ट्रीय कार्य के बदले भोजन योजना (NFWP), 2004
- प्रधानमंत्री रोज़गार योजना (PMRY), 1993
- ग्रामीण रोज़गार विकास योजना (REGP), 1995
- स्वर्णजयंती ग्राम स्वरोज़गार योजना (SGSY), 1999
- प्रधानमंत्री ग्रामोद्योग योजना (PMGY), 2000
- अन्त्योदय अन्न योजना (AAY)
प्रश्न 2.
‘आर्थिक संवृद्धि एवं निर्धनता उन्मूलन के बीच घनिष्ठ सम्बन्ध है।’ स्पष्ट कीजिए।
उत्तर:
विकास की उच्च दर ने निर्धनता को कम करने में एक महत्त्वपूर्ण भूमिका निभाई है। 1980 के दशक से भारत | की आर्थिक संवृद्धि-दर विश्व में सबसे अधिक रही। संवृद्धि-दर 1970 के दशक के करीब 3.5 प्रतिशत के औसत से बढ़कर 1980 और 1990 के दशक में 6 प्रतिशत के करीब पहुँच गई। अधिक संवृद्धि-दर निर्धनता उन्मूलन को कम करने में सहायक (UPBoardSolutions.com) होती है। इसलिए यह स्पष्ट होता जा रहा है कि आर्थिक संवृद्धि और निर्धनता उन्मूलन के बीच एक घनिष्ठ सम्बन्ध है। आर्थिक संवृद्धि अवसरों को व्यापक बना देती है और मानव विकास में निवेश के लिए आवश्यक संसाधन उपलब्ध कराती है। यह शिक्षा में निवेश से अधिक आर्थिक प्रतिफल पाने की आशा में लोगों को अपने बच्चों को लड़कियों सहित स्कूल भेजने के लिए प्रोत्साहित करती है।
प्रश्न 3.
सरकार की वर्तमान निर्धनता-निरोधी रणनीतियाँ किन दो कारकों पर आधारित हैं? स्पष्ट कीजिए।
उत्तर:
निर्धनता-उन्मूलन भारत की विकास रणनीति का प्रमुख उद्देश्य रहा है। सरकार की वर्तमान निर्धनता-निरोधी रणनीति मुख्य रूप से निम्न दो कारकों पर आधारित है
लक्षित निर्धनता-निरोधी कार्यक्रम-सरकार ने निर्धनता को समाप्त करने के लिए कई निर्धनता-निरोधी कार्यक्रम चलाए। जैसे-राष्ट्रीय ग्रामीण रोजगार गारंटी अधिनियम, 2005, प्रधानमंत्री रोजगार योजना, ग्रामीण रोजगार सृजन, स्वर्ण जयंती ग्राम स्वरोज़गार योजना, प्रधानमंत्री ग्रामोदय योजना, अंत्योदय अन्न योजना, राष्ट्रीय काम के बदले अनाज।
आर्थिक संवृद्धि को प्रोत्साहन-विकास की उच्च दर ने निर्धनता को कम करने में एक महत्त्वपूर्ण भूमिका निभाई है। 1980 के दशक से भारत की आर्थिक संवृद्धि-दर विश्व में सबसे अधिक रही। संवृद्धि-दर 1970 के दशक के करीब 3.5 प्रतिशत के औसत से बढ़कर 1980 और 1990 के (UPBoardSolutions.com) दशक में 6 प्रतिशत के करीब पहुँच गई। इसलिए यह स्पष्ट होता जा रहा है कि आर्थिक संवृद्धि और निर्धनता उन्मूलन के बीच एक घनिष्ठ सम्बन्ध है। आर्थिक संवृद्धि अवसरों को व्यापक बना देती है और मानव विकास में निवेश के लिए आवश्यक संसाधन उपलब्ध कराती है।
प्रश्न 4.
गरीबी की विशेषताएँ बताइए।
उत्तर:
गरीब चाहे ग्रामीण हों या शहरी उनकी विशेषताएँ लगभग एक जैसी होती हैं। उनकी सामान्य विशेषताओं को नीचे समझाया गया है–
- भूख, भुखमरी एवं कुपोषण-अपर्याप्त भोजन गरीबी की महत्त्वपूर्ण विशेषता है। यह कुपोषण भूख और भुखमरी को पैदा करती है।
- बुरा स्वास्थ्य एवं शिक्षा-बुरा स्वास्थ्य एवं बुरी शिक्षा सदैव गरीबी का ही परिणाम होता है।
- कार्य का निरंतर न होना, सौदेबाजी की क्षमता में कमी-गरीब लोग बेरोज़गारी, अल्प रोज़गार एवं मौसमी बेरोज़गारी के शिकार होते हैं जो उनकी मज़दूरी को कम करता है और इससे दुबारा उनकी गरीबी बढ़ती है। 4. सीमित आर्थिक अवसर-गरीबी संसाधनों की कमी से (UPBoardSolutions.com) पीड़ित होती है। गरीबों को सीमित आर्थिक अवसरों की उपलब्धता के कारण फिर गरीबी का सामना करना पड़ता है। यह गरीब लोगों को निर्धनता के चक्र से निकलने नहीं देती।
![]()
प्रश्न 5.
गरीब कौन है और इसकी पहचान किस आधार पर की जा सकती है?
उत्तर:
सामान्य तौर पर एक व्यक्ति तब तक गरीब माना जाता है यदि वह भूमिहीन है, कृषि मजदूर, शहरी मजदूर, गंभीर ऋणग्रस्तता के शिकार, बुरा स्वास्थ्य, भूख एवं भुखमरी में है। गरीब लोग कुपोषण, बेरोज़गारी, परिवार के बड़े आकार, असहाय एवं दुर्भाग्य के शिकार (UPBoardSolutions.com) होते हैं। योजना आयोग के अनुसार वह व्यक्ति जो गरीबी रेखा से नीचे है, गरीब है। ग्रामीण क्षेत्रों में जिनके पास 2400 से कम एवं शहरी क्षेत्रों में 2100 से कम कैलोरी है।
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
आर्थिक विकास की दर में वृद्धि के उपाय बताइए।
उत्तर:
आर्थिक विकास की दर में वृद्धि गरीबी को दूर करने के लिए सबसे महत्त्वपूर्ण कार्य है। इसके लिए निम्नलिखित कार्य किए जा सकते हैं
- देश के पिछड़े हुए क्षेत्रों में कुटीर एवं लघु उद्योगों का निर्माण करना।
- देश के प्राकृतिक, मानवीय एवं पूँजी संसाधनों का कुशलतम उपयोग करना।
- सार्वजनिक अनुत्पादित व्यय के स्थान पर सार्वजनिक उत्पादित व्यय को प्राथमिकता देना।
- गरीब लोगों के लिए पूर्ण एवं अधिक उत्पादित रोज़गार।।
- गरीबों को न्यूनतम एवं उपयुक्त मजदूरी।
- समाज के गरीब वर्गों के लिए स्वयं रोज़गार के अवसरों में वृद्धि करना।
- गरीब श्रमिकों की श्रम उत्पादकता में वृद्धि के लिए शिक्षा, प्रशिक्षण एवं स्वास्थ्य की व्यवस्था करना।
प्रश्न 2.
ग्रामीण गरीब की विशेषताएँ बताइए तथा शहरी गरीबी के कारण बताइए।
उत्तर:
ग्रामीण गरीब की प्रमुख विशेषताएँ इस प्रकार हैं
गंभीर ऋणग्रस्तता–एक ग्रामीण गरीब के पास सीमित साधन होते हैं। उसकी आय उसके परिवार की आधारभूत आवश्यकताओं को सन्तुष्ट करने में अपर्याप्त होती है। इस प्रकार वह ऊँची ब्याज दर पर ऋण प्राप्त करने के लिए मजबूर होता है।
बाल श्रम–बच्चों को अपने माता-पिता की कम आय में सहायता करने की आवश्यकता होती है। इसलिए उन्हें ग्रामीण फैक्ट्रियों या ढाबों में श्रमिक के रूप में कार्य करना पड़ता है।
ईंधन के रूप में गोबर एवं लकड़ी का उपयोग करना-गंभीर गरीबी के कारण ग्रामीण लोग अपना खाना पकाने के लिए ईंधन के रूप में गोबर एवं लकड़ी का उपयोग करते हैं। वह ईंधन के रूप में कोयला, मिट्टी का तेल, बिजली एवं गैस के खर्चे को सहन नहीं कर सकते।
भूमिहीन–ग्रामीण गरीबों के पास अपनी भूमि नहीं होती। यदि कोई भूमि का टुकड़ा होता है तो यह बहुत छोटा टुकड़ा होता है जो उसके परिवार की आवश्यकताओं को सन्तुष्ट नहीं कर सकता।
कृषि श्रमिक–अपर्याप्त एवं भूमि के टुकड़े का नहीं होना ग्रामीण व्यक्ति को कार्य से वंचित रखता है। इस प्रकारउन्हें कृषि श्रमिक के रूप में साहूकारों के पास कार्य करना पड़ता है और वह स्वयं को शोषण के लिए उन्हें समर्पित कर देते हैं। अधिकांश कार्य मौसमी एवं अस्थायी होते हैं एवं परेशानियाँ जारी रहती हैं।
कच्ची घर-ग्रामीण मज़दूरों का घर कच्चा होता है, जहाँ दीवारें मिट्टी की एवं छत सामान्य तौर पर घास-फूस एवं लकड़ियों से बनी होती है। यह घर तेज हवा, वर्षा एवं ठंड का सामना करने में असमर्थ होते हैं। शहरी गरीबी के प्रमुख कारण इस प्रकार हैं
- बुरा स्वास्थ्य-गरीबी, भुखमरी, ऋणग्रस्तता एवं मानसिक परेशानी को पैदा करती है जो बुरे स्वास्थ्य को बढ़ावा | देती है और जो कार्य की हानि करके गरीबी में दोबारा योगदान देती है।
- अस्वच्छता एवं बिजली की अनुपलब्धता-सफाई सुविधाओं का झुग्गी-झोंपड़ी के क्षेत्रों में अभाव है। सामान्य तौर पर बिजली उपलब्ध नहीं है। अस्वच्छता गंभीर बीमारियों एवं बुरे स्वास्थ्य का कारण होती है।
- स्वच्छ पीने के पानी की अनुपलब्धता-यह बहुत दुख की बात है कि इन असहाय एवं दुर्भाग्य लोगों को पीने को स्वच्छ पानी भी उपलब्ध नहीं है।
- झुग्गी-झोंपड़ी के निवासी-शहरी गरीब आवासीय क्षेत्रों में घर का प्रबन्ध नहीं कर सकते। इसलिए वह अपने घर शहर के किनारे एवं झुग्गी-झोंपड़ी के क्षेत्रों में बनाते हैं जो गंदे, अस्वच्छ कीचड़ एवं कूड़ा करकट वाले होते | हैं और मानवीय निवास के लिए अनुपयुक्त हैं।
- निरक्षरता-गरीबी एवं निरक्षरता दोनों एक-दूसरे पर निर्भर हैं। गरीबी, निरक्षरता को बढ़ाती है और निरक्षरता गरीबी को सामान्य तौर पर गरीब बच्चों को अपने माता-पिता की कम आय में सहायता के लिए कार्य करना पड़ता है। स्कूल जाने के लिए उनके पास समय एवं पैसा नहीं होता।
- अनिरन्तर रोज़गार-शहरी गरीबों के पास सामान्य तौर पर निरन्तर कार्य नहीं होता। कुछ समय वह कार्यरत होते हैं और वर्ष के कई महीने तक वह बेरोज़गार होते हैं। वह मौसमी एवं वार्षिक बेरोज़गारी के शिकार होते हैं। जो उनके जीवन को कठिन बनाती है।
प्रश्न 3.
विश्व में प्रत्येक व्यक्ति के लिए भोजन है फिर भी लोग भूख की वजह से क्यों मरते हैं?
उत्तर:
निर्धनता का आशय है भोजन एवं आवास का अभाव। यह एक अवस्था है जहाँ व्यक्ति की मूलभूत सुविधाएँ जैसे–चिकित्सा सुविधा, शैक्षिक सुविधा, आधारभूत नागरिक सुविधायें प्रप्त नहीं कर पाता। यूनाइटेड नेशन के अनुसार लगभग 25000 लोग प्रतिदिन भूख या भूख-सम्बन्धी बीमारियों के कारण मर जाते हैं, जिनमें अधिकतर बच्चे होते हैं। हालांकि विश्व में प्रत्येक व्यक्ति के लिए भोजन है परन्तु उसे खरीदने के लिए पैसों की कमी के कारः लोग कुपोषित हैं, वे कमजोर और बीमार रहते हैं। इस कारण वे कम काम कर पाते हैं (UPBoardSolutions.com) जिससे वे और निर्धन तथा भूखे हाते जाते हैं।
यह चक्र उनके और उनके परिवार वालों के लिए मृत्यु तक चलता रहता है। इस समस्या को सुलझाने के लि। कई कार्यक्रम भी चलाए । ‘खाने के लिए काम कार्यक्रम-जिसमें व्यस्कों को स्कूल बनाने, कुएं खोदने, सड़कें बनाने आदि के काम के लिए रवाना दिया जाता है। इससे निर्धनों को पोषण मिलता है और निर्धनता को समाप्त करने के लिए संरचना तैयार होती है। ‘ग्वाने के लिए शिक्षा कार्यक्रम –जिसमें बच्चों को भोजन दिया जाता है जब वे स्कूल में उपस्थित हो। उनकी शिक्षा उन्हें भूख और वैश्विक निर्धनत बचा सकती है।
![]()
प्रश्न 4.
सरकार द्वारा संचालित निर्धनता निरोधी रणनीतियों का उल्लेख कीजिए।
उत्तर:
सरकार द्वारा संचालित निर्धनता निधी रणनीतियों का विवर!
ग्रामीण रोजगार सृजन कार्यक्रम
- के इस कार्यक्रम को 1995 में आरम्भ किया गया।
- इसका उद्देश्य ग्रामीण क्षेत्रों और छोटे शहरों में स्वराजः के अनः जिन ३रन है।\दसवीं पंचवर्षीय योजना में इस कार्यक्रम के अन्तर्गत 2 लाख नए जिगार के अवसर सृजित करने का नक्ष्य गल्ला गया है
स्वर्ण जयंती ग्राम स्वरोजगार योजना
- इस कार्यक्रम का आरम्भ 1999 में किया गया।इस कार्यक्रम का उद्देश्य सहायता प्राप्त निर्धन परिवारों के सहाय।
- सही में ३ बैंक ऋण और सरकारी सहायिकी के संयोजन द्वारा निर्धनता रेखा से ऊपर लाना ।
प्रधानमंत्री ग्रामोदय योजना
- यह योजना 2000 में आरम्भ की गई।
- इसके अन्तर्गत प्राथमिक स्वास्थ्य, प्राथमिक शिक्षा, ग्रामीण आश्रय, ग्रामीण पेयजल और ग्रामीण विद्युतीकरण जैसी मूल सुविधाओं के लिए राज्यों को अतिरिक्त केन्द्रीय महायता प्रदान की जाती है।
राष्ट्रीय काम के बदले अनाज कार्यक्रम
- यह कार्यक्रम 2004 में देश के सबसे पिछड़े 150 जिलों में लागू किया गया था। यह कार्यक्रम उन सभी ग्रामी निर्धनों के लिए है, जिन्हें मजदूरी पर रोजगार की आवश्यकता है और जो अकुशल शारीरिक काम करने के इच्छुक हैं।
- इसके लिए राज्यों को खाद्यान्न निःशुल्क उपलब्ध कराए जा रहे हैं।
प्रधानमंत्री रोजगार योजना
• इस योजना को 1993 में आरम्भ किया गया।
• इस कार्यक्रम का उद्देश्य ग्रामीण क्षेत्रों और छोटे शहरों में शिक्षित बेरोजगार युवाओं के लिए स्वरोजगार के अवसर सृजित करना है।
• इस कार्यक्रम में लघु व्यवसाय और उद्योग स्थापित करने में उनकी सहायता की जाती है।
राष्ट्रीय ग्रामीण रोजगार गारंटी अधिनियम, 2005
- राष्ट्रीय ग्रामीण रोजगार गारंटी अधिनियम, 2005 को सितम्बर, 2005 में पारित किया गया।
- प्रत्येक ग्रामीण परिवार को 100 दिन के सुनिश्चित रोजगार का प्रावधान करता है। | प्रारम्भ में यह विधेयक प्रत्येक वर्ष देश के 200 जिलों में और बाद में इस योजना का विस्तार 600 जिलों में किया गया। प्रस्तावित रोजगारों का एक तिहाई रोजगार महिलाओं के लिए (UPBoardSolutions.com) आरक्षित है। केन्द्र सरकार राष्ट्रीय रोजगार गारंटी कोष भी स्थापित करेगी।
- इसी तरह राज्य सरकारें भी योजना के कार्यान्वयन के लिए राज्य स्वरोजगार गारंटी कोष की स्थापना करेंगी। कार्यक्रम के अन्तर्गत अगर आवेदक को 15 दिन के अंदर रोजगार उपलब्ध नहीं कराया गया तो वह दैनिक बेरोजगारी भत्ते का हकदार होगा।
Hope given UP Board Solutions for Class 9 Social Science Economics Chapter 3 are helpful to complete your homework.
If you have any doubts, please comment below. UP Board Solutions try to provide online tutoring for you.