Class 9

UP Board Solutions for Class 9 Maths Chapter 8 Quadrilaterals (चतुर्भुज)

These Solutions are part of UP Board Solutions for Class 9 Maths. Here we have given UP Board Solutions for Class 9 Maths Chapter 8 Quadrilaterals (चतुर्भुज).

प्रश्नावली 8.1

प्रश्न 1.
एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं। इस चतुर्भुज के सभी कोण ज्ञात कीजिए।
हल :
चतुर्भुज के कोणों का अनुपात 3 : 5 : 9 : 13 है।
अतः माना कि चतुर्भुज के कोण क्रमशः 3x, 6x, 9x और 13x हैं।
चतुर्भुज के (अन्तः) कोणों का योग = 360°
3x + 5x + 9x + 13x = 360°
⇒ 30x = 360°
⇒ x = 12°
पहला कोण = 3x = 3 x 12 = 36°
दूसरा कोण = 5x = 5 x 12 = 60°
तीसरा कोण = 9x = 9 x 12 = 108°
तथा चौथा कोण = 13x = 13 x 12 = 156°
अतः चतुर्भुज के कोण क्रमशः 36°, 60°, 108° व 156° हैं।

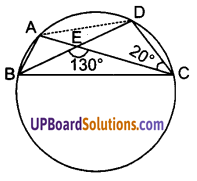
प्रश्न 2.
यदि एक समान्तर चतुर्भुज के विकर्ण बराबर हों तो दर्शाइए कि वह एक आयत है।

हल :
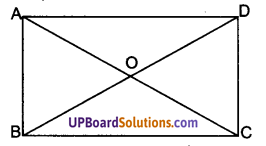
दिया है : चतुर्भुज ABCD एक समान्तर चतुर्भुज है। जिसमें विकर्ण AC = BD है। विकर्णो का प्रतिच्छेद बिन्दु O है।
सिद्ध करना है : चतुर्भुज ABCD एक आयत है।
उपपत्ति : समान्तर चतुर्भुज ABCD के बिकर्ण AC और BD हैं जो O पर प्रतिच्छेद करते हैं।
तथा AC = BD
AO + OC = BO + OD (चित्र से) …(1)
AC और BD समान्तर चतुर्भुज के विकर्ण हैं और बिन्दु O पर काटते हैं।
AO = OC और BO = OD ……(2)
तब समीकरण (1) व (2) से,
AO + AO = BO + BO
⇒ AO = BO
AO = BO = CO = OD
तब ∆OAD में,
AO = OD
⇒ ∠ADO = ∠DAO (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।)
∠AOB, ∆OAD का बहिष्कोण है।
∠AOB = ∠DAO + ∠ADO
⇒ ∠AOB = DAO + ∠DAO (∠ADO = ∠DAO)
⇒ ∠AOB = 2 ∠DAO …(3)
और ∆OAB में भी, AO = OB ⇒ ∠ABO = ∠BAO (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।)
∠AOD, ∆OAB का बहिष्कोण है,
∠AOD = ∠BAO + ∠ABO
∠AOD = ∠ BAO + ∠BAO (∠ABO = ∠BAO)
∠AOD = 2 ∠BAO …(4)
समीकरण (3) व (4) को जोड़ने पर,
∠AOB + ∠AOD = 2 ∠DAO + 2 ∠BAO
⇒ ∠BOD = 2 (∠DAO + ∠BAO) = 2 ∠BAD (चित्र से)
2 ∠BAD = 180° (क्योंकि BOD एक ऋजु रेखा है।)
∠BAD = 90°
चतुर्भुज ABCD में ∠A = 90°
चतुर्भुज ABCD एक समान्तर चतुर्भुज है
तथा ∠A + ∠D = 180° (अन्त:कोणों का योग)
∠D = ∠A = ∠D = 90° (∠A = 90°)
तब ∠B और ∠C में से भी प्रत्येक 90° होगा।
समान्तर चतुर्भुज ABCD में, AB = CD और BC = DA
और ∠A = ∠B = ∠C = ∠D = 90°
अतः समान्तर चतुर्भुज ABCD एक आयत है।
Proved.

प्रश्न 3.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।

हल :
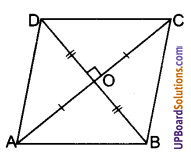
ज्ञात है : एक चतुर्भुज ABCD जिसके विकर्ण AC और BD एक-दूसरे को बिन्दु D 0 पर परस्पर समकोण पर समद्विभाजित करते हैं।
अर्थात् ∠AOD = ∠COD = 90°
तथा OA = OC तथा OB = OD
सिद्ध करना है : चतुर्भुज ABCD एक समचतुर्भुज है।
उपपत्ति: ∆AOD
तथा ∆COB में, OA = OC (दिया है।)
∠AOD = ∠ COB (शीर्षाभिमुख कोण हैं।)
OD = OB (दिया है।)
∆AOD = ∆COB (S.A.S. से)
∠OAD = ∠OCB (C.P.C.T.)
परन्तु ∠OAD = ∠CAD
तथा ∠OCB = ∠ACB
∠CAD = ∠ACB
इससे प्रदर्शित होता है कि AD और BC को तिर्यक रेखा AC द्वारा काटने पर बने एकान्तर अन्त: कोण CAD तथा ACB बराबर हैं जो केवल तभी सम्भव है जबकि AD एवं BC एक-दूसरे के समान्तर हों।
AD एवं BC एक-दूसरे के समान्तर हैं। …(1)
इसी प्रकार सिद्ध किया जा सकता है कि AB एवं DC एक-दूसरे के समान्तर हैं।
इस प्रकार सिद्ध हुआ कि ABCD एक समान्तर चतुर्भुज है।
अब हम दिखाएँगे कि AB = BC = CD = DA
∆AOD तथा ∆COD में,
OA = OC (दिया है।)
∠AOD = ∠COD = 90° (दिया है।)
OD = OD (उभयनिष्ठ है।)
∆AOD = ∆COD (S.A.S. से)
AD = CD (C.P.C.T.)
इससे प्रदर्शित होता है कि ABCD एक ऐसा समान्तर चतुर्भुज है जिसकी क्रमागत भुजाओं का एक युग्म AD, CD बराबर है।
अतः समान्तर चतुर्भुज ABCD एक समचतुर्भुज है।
Proved.

प्रश्न 4.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।

हल :
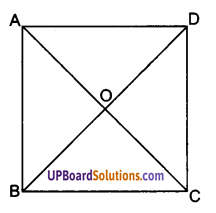
दिया है : चतुर्भुज ABCD एक वर्ग है जिसके विकर्ण AC और BD परस्पर बिन्दु O पर काटते हैं। सिद्ध करना है:
AC = BD और ∠AOB एक समकोण या 90° उपपत्ति: चतुर्भुज ABCD एक वर्ग है।
AB = BC = CD = DA
∠A = ∠B= ∠C = ∠D = 90°
तब ∆ABC और ∆BCD समकोण त्रिभुज हैं।
अब ∆ABC और ∆DCB में,
AB = DC (वर्ग की भुजाएँ हैं।)
∠B= ∠C (प्रत्येक 90°)
BC = BC (उभयनिष्ठ भुजा है।)
∆ABC = ∆DCB (S.A.S. से)
AC = BD (C.P.C.T.)
चतुर्भुज ABCD एक वर्ग है।
AB = BC = CD = DA
AB = CD और BC = DA
चतुर्भुज ABCD एक समान्तर चतुर्भुज भी है।
इसके विकर्ण AC तथा BD परस्पर (बिन्दु O पर) समद्विभाजित करेंगे।
AO = BO = CO = DO
अब ∆AOB और ∆COB में,
AO = CO (ऊपर सिद्ध किया है।)
AB = CB (वर्ग की भुजाएँ हैं।)
BO = BO (उभयनिष्ठ भुजा है।)
∆AOB = ∆COB (S.S.S. से)
∠AOB = ∠COB (C.P.C.T.) …(1)
परन्तु AOC (विकर्ण) एक ऋजु रेखा है,
∠AOB + ∠BOC = 180°
समीकरण (1) व (2) के हल से,
∠AOB = ∠COB = 90°
अतः वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं।
Proved.

प्रश्न 5.
दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हों और वे परस्पर समकोण पर समद्विभाजित करें तो वह एक वर्ग होता है।

हल :
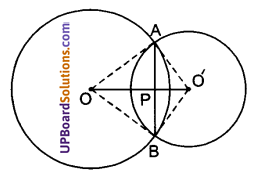
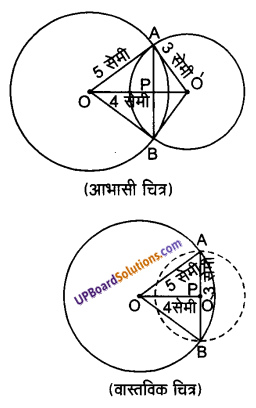
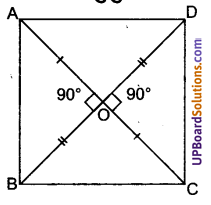
दिया है: ABCD एक चतुर्भुज है जिसमें विकर्ण AC और BD बराबर हैं तथा एक-दूसरे को बिन्दु O पर इस प्रकार काटते हैं कि AO = OC तथा BO = OD तथा AC ⊥ BD
सिद्ध करना है : चतुर्भुज ABCD एक वर्ग है।
उपपत्ति : चतुर्भुज ABCD के विकर्ण परस्पर बिन्दु O पर समद्विभाजित करते हैं।
चतुर्भुज ABCD एक समान्तर चतुर्भुज है।
AB = CD …(1)
तथा AB || CD …(2)
अब ∆ABC और ∆DCB में,
AB = DC (ऊपर सिद्ध किया है।)
AC = DB (दिया है।)
BC = BC (उभयनिष्ठ भुजा है।)
∆ABC = ∆DCB (S.S.S. से)
∠B = ∠C (C.P.C.T.) …(3)
AB || CD समीकरण (2) से, और BC एक तिर्यक प्रतिच्छेदी रेखा है।
∠B + ∠C = 180° (अन्त:कोणों का योग) …(4)
समीकरण (3) व (4) से,
∠B = 90° और ∠C = 90°
इस प्रकार चतुर्भुज ABCD एक ऐसा समान्तर चतुर्भुज है जिसका प्रत्येक कोण 90° है।
AC = BD और ये बिन्दु O पर परस्पर समद्विभाजित होते हैं।
AO = BO = CO = DO
AC ⊥ BD ⇒ ∠AOB = 90° तथा ∠ BOC = 90°
तब ∆AOB तथा ∆COB में,
AO = CO (विकर्ण परस्पर समद्विभाजित करते हैं।)
∠AOB= ∠COB (प्रत्येक समकोण है।)
BO = BO (दोनों त्रिभुजों की उभयनिष्ठ भुजा है।)
∆AOB = ∆COB (S.A.S. से)
AB = BC (C.P.C.T.)
तब चतुर्भुज ABCD में,
AB = BC, AB = CD और BC = DA
AB = BC = CD = DA और ∠B = 90°
अर्थात् चारों भुजाएँ बराबर हैं और अन्त:कोण समकोण हैं।
अतः चतुर्भुज ABCD एक वर्ग है।
Proved.

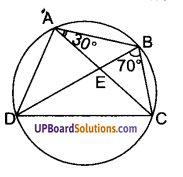
प्रश्न 6.
समान्तर चतुर्भुज ABCD का विकर्ण AC, ∠A को समद्विभाजित करता है। दर्शाइए कि
(i) यह ∠C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।

हल :
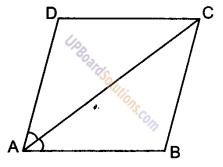
दिया है : चतुर्भुज ABCD एक समान्तर चतुर्भुज है जिसमें विकर्ण AC, ∠A को समद्विभाजित करता है
अर्थात् ∠ BAC = ∠DAC
सिद्ध करना है :
(i) विकर्ण AC, ∠C को भी समद्विभाजित करता है।
(ii) ABCD एक समचतुर्भुज है।
उपपत्ति : (i) चतुर्भुज ABCD एक समान्तर चतुर्भुज है।
AB || CD तथा BC || DA
AB || CD और AC एक तिर्यक रेखा है।
∠ BAC = ∠ACD (एकान्तर कोण) …(1)
इसी प्रकार, BC || DA और AC एक तिर्यक रेखा है।
∠DAC = ∠ACB (एकान्तर कोण) …(2)
AC, ∠A को समद्विभाजित करता है।
∠BAC = ∠DAC
समीकरण (1) व (2) से,
∠ACB = ∠ACD
अर्थात् AC, ∠C को भी समद्विभाजित करती है।
(ii) ∠BAC = ∠DAC और ∠DAC = ∠ACB
∠BAC = ∠ACB
तब ∆ABC में,
∠BAC = ∠ACB
BC = AB (त्रिभुज में समान कोणों की सम्मुख भुजाएँ समान होती हैं।)
परन्तु ABCD एक समान्तर चतुर्भुज है।
AB = CD तथा BC = DA
AB = BC = CD = DA
चतुर्भुज ABCD एक समचतुर्भुज होगा।
Proved.

प्रश्न 7.
ABCD एक समचतुर्भुज है। दर्शाइए विकर्ण AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD, कोणों B और D दोनों को समद्विभाजित करता है।

हल :
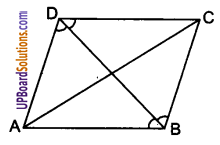
दिया है : ABCD एक समचतुर्भुज है।।
सिद्ध करना है : विकर्ण AC, ∠A और ∠C दोनों को समद्विभाजित करता है
तथा विकर्ण BD, ∠B तथा ∠D दोनों को समद्विभाजित करता है।
उपपत्ति : चतुर्भुज ABCD एक समचतुर्भुज है।
AB = BC = CD = DA
∆ABC में,
AB = BC के ∠ACB = ∠BAC …(1) (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।)
समचतुर्भुज एक समान्तर चतुर्भुज भी होता है।
AB || CD और AC तिर्यक रेखा है।
∠BAC = ∠ACD (एकान्तर कोण) …(2)
समीकरण (1) व (2) से,
∠ACB = ∠ACD (एकान्तर कोण) …(3)
अर्थात् AC, ∠C का समद्विभाजक है।
BC || DA तथा AC तिर्यक रेखा है के
∠ACB= ∠DAC (एकान्तर कोण) …(4)
तब समीकरण (1) व (4) से,
∠DAC = ∠BAC
अर्थात् AC, ∠A का समद्विभाजक है।
अतः AC, ∠A व ∠C दोनों का समद्विभाजक है।
BC || DA और BD तिर्यक रेखा है।
∠ADB = ∠CBD (एकान्तर कोण) …(5)
इसी प्रकार ∠ABD = ∠ BDC (एकान्तर कोण) …(6)
और : ∆BCD में,
BC = CD ⇒ ∠BDC = ∠CBD …(7)
(त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।)
तब समीकरण (5) व (7) से,
∠ADB = ∠BDC
अर्थात् BD, ∠D का समद्विभाजक है।
समीकरण (6) व (7) से,
∠ABD = ∠CBD
अर्थात् BD, ∠B का समद्विभाजक है।
BD, ∠B व ∠D दोनों का समद्विभाजक है।
अत: विकर्ण AC, ∠A व ∠C को समद्विभाजित करता है और BD, ∠B व ∠D को समद्विभाजित करता है।
Proved.

प्रश्न 8.
ABCD एक आयत है जिसमें विकर्ण AC दोनों कोणों A व C को समद्विभाजित करता है। दर्शाइए कि
(i) ABCD एक वर्ग है।
(ii) BD, दोनों कोणों B और D को समद्विभाजित करता है।

हल :
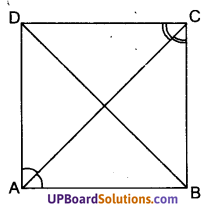
दिया है : चतुर्भुज ABCD एक आयत है जिसमें विकर्ण AC, ∠A व ∠C दोनों को समद्विभाजित करता है।
BD आयत का दूसरा विकर्ण है।
सिद्ध करना है :
(i) चतुर्भुज ABCD एक वर्ग है।
(ii) BD, ∠B और ∠D दोनों को समद्विभाजित करता है।
उपपत्ति : (i) चतुर्भुज ABCD एक आयत है।
AB = CD तथा ∠A = 90°
विकर्ण AC, ∠A तथा ∠C दोनों को समद्विभाजित करता है।
∠BAC = ∠DAC और ∠BCA = ∠DCA
∆ABC तथा ∆ADC में,
∠BAC =∠DAC (दिया है।)
AC = AC (उभयनिष्ठ भुजा है।)
∠BCA = ∠DCA (दिया है।)
∆ABC = ∆ADC (A.S.A. से)
AB = DA (C.P.C.T.) …(1)
चतुर्भुज ABCD में,
AB = CD; BC = DA;
AB = BC = CD = DA
तथा ∠A = 90° [समीकरण (1) से ]
अतः चतुर्भुज ABCD एक वर्ग है।
Proved.
(ii) ∆BCD में,
BC = CD ⇒ BDC = ∠CBD (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।)
अब वर्ग की सम्मुख भुजाएँ समान्तर होती हैं।
अर्थात AB || CD और BD तिर्यक रेखा है।
∠BDC = ∠ABD (एकान्तर कोण) …(2)
समीकरण (1) व (2) से,
∠ABD = ∠CBD
अर्थात् BD, ∠B का समद्विभाजक है।
इसी प्रकार, BC || DA और BD तिर्यक रेखा है।
∠CBD = ∠ADB (एकान्तर कोण) …(3)
समीकरण (1) व (3) से,
∠BDC = ∠ADB
अर्थात् BD, ∠D का समद्विभाजक है।
अत: BD, ∠B तथा ∠D दोनों को समद्विभाजित करता है।
Proved.

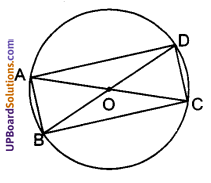
प्रश्न 9.
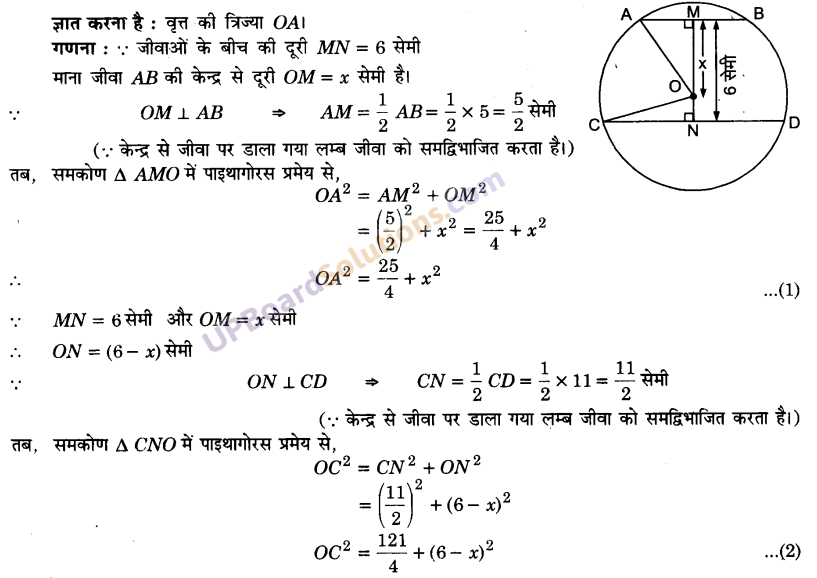
समान्तर चतुर्भुज ABCD के विकर्ण BD पर दो बिन्दु P और Q इस प्रकार स्थित हैं कि DP = BQ है। दर्शाइए कि
(i) ∆APD = ∆CQB
(ii) AP = CQ
(iii) ∆AQB = ∆CPD
(iv) AQ = CP
(v) APCQ एक समान्तर चतुर्भुज है।

हल :
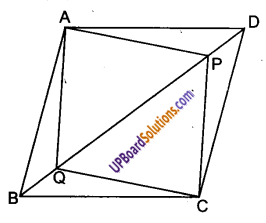
दिया है : चतुर्भुज ABCD एक समान्तर चतुर्भुज है और BD उसका एक विकर्ण है।
BD पर P और Q दो बिन्दु इस प्रकार स्थित हैं कि DP = BQ है।
AP, AQ, CP वे C रेखाखण्ड खींचे गए हैं जिनसे चतुर्भुज APCQ बनता है।
सिद्ध करना है :
(i) ∆APD = ∆CQB
(ii) AP = CQ
(iii) ∆AQB = ∆CPD
(iv) AQ = CP
(v) APCQ एक समान्तर चतुर्भुज है।
उपपत्ति : चतुर्भुज ABCD समान्तर चतुर्भुज है ।
AB = CD तथा और
AB || CD तथा BC|| DA
(i) BC || DA और BD एक तिर्यक रेखा है।
∠ADB = ∠CBD ⇒ ∠ADP = ∠CBQ (एकान्तर कोण)
अब, ∆APD और ∆CQB में,
DA = BC (दिया है।)
∠ADP = ∠CBQ (ऊपर सिद्ध किया है।)
DP = BQ (दिया है।)
∆APD = ∆CQB (S.A.S. से)
Proved.
(ii) ∆APD = ∆CQB
AP = CQ (C.P.C.T.)
Proved.
(iii) AB || CD और BD तिर्यक रेखा है।
∠ABD = ∠BDC के ∠ABQ = ∠PDC (एकान्तर कोण)
अब ∆AQB और ∆CPD में, AB = CD (दिया है।)
∠ABQ = ∠PDC (ऊपर सिद्ध किया है।)
BQ = DP (दिया है।)
∆AQB = ∆CPD (S.A.S. से)
Proved.
(iv) ∆AQB = ∆CPD
AQ = CP (C.P.C.T.)
Proved.
(v) चतुर्भुज APCR में सम्मुख भुजाएँ AP = CQ और AQ = CP [भाग (i) तथा (iv) से]
अत: चतुर्भुज APCQ एक समान्तर चतुर्भुज है।
Proved.

प्रश्न 10.
ABCD एक समान्तर चतुर्भुज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं। दर्शाइए कि
(i) ∆APB = ∆CQD
(ii) AP = CQ

हल :
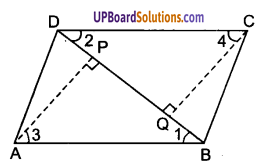
दिया है: चतुर्भुज ABCD एक समान्तर चतुर्भुज है जिसका एक विकर्ण BD है।
BD पर शीर्ष A से AP और शीर्ष C से CQ लम्ब खींचा गया है।
सिद्ध करना है :
(i) ∆APB = ∆CQD
(ii) AP = CQ
उपपत्ति:
(i) चतुर्भुज ABCD एक समान्तर चतुर्भुज है।
AB = CD तथा AB || CD
AB || CD और विकर्ण BD एक तिर्यक रेखा है।
∠ABD = ∠BDC (एकान्तर कोण)
∠1 = ∠2
AP ⊥ BD ⇒ ∠APB= 90°
∆APB में, ∠PAB = 180° – (∠APB + ∠ABP) (त्रिभुज के अन्त:कोणों का योग 180° होता है।)
∠PAB = 180° – (90° + ∠1) = 90° – ∠1
∠3 = 90° – ∠1
इसी प्रकार, CQ ⊥ BD ⇒ ∠CQD = 90°
∆CQD में,
∠QCD = 180° – (∠CQD + ∠CDQ)
= 180° – 90° – ∠2 = 90° – ∠2
∠4 = 90° – 21 (∠1 = ∠2)
∠3 = 90° – ∠1 और ∠4 = 90° – ∠1
∠3 = ∠4 …(2)
तब ∆APB और ∆CQD की तुलना करने पर,
∠1 = ∠2 [समीकरण (1) से]
AB = CD (दिया है।)
∠3 = ∠4 [समीकरण (2) से]
∆APB = ∆CQD (A.S.A. से)
Proved.
(ii) ∆APB = ∆CQD
AP = CQ (C.P.C.T.)
Proved.

प्रश्न 11.
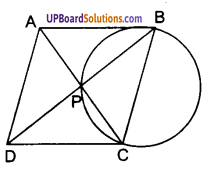
∆ABC और ∆DEF में, AB = DE, AB || DE, BC = EF और BC || EF है। शीर्षों A, B और C को क्रमशः शीर्षों D, E और F से जोड़ा जाता है। दर्शाइए कि
(i) चतुर्भुज ABED एक समान्तर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
(iii) AD || CF और AD = CF है।
(iv) चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
(v) AC = DF है।
(vi) ∆ABC = ∆DEF है।

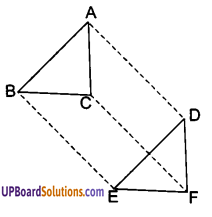
हल :
दिया है : ∆ABC और ∆DEF दो त्रिभुज हैं जिनमें AB = DE और AB || DE तथा BC = EF और BC || EF हैं। शीर्षों A, B व C को क्रमशः शीर्षों D, E व F से ऋजु रेखाखण्डों द्वारा जोड़ा गया है।
सिद्ध करना है :
(i) चतुर्भुज ABED एक समान्तर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
(iii) AD || CF और AD = CF है।
(iv) चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
(v) AC = DF है।
(vi) ∆ABC = ∆DEF है।
उपपत्ति :
(i) चतुर्भुज ABED में,
AB = DE और AB || DE
चतुर्भुज ABED की सम्मुख भुजाओं AB वे DE का एक युग्म बराबर और समान्तर है।
अत: चतुर्भुज ABED एक समान्तर चतुर्भुज है।
Proved.
(ii) चतुर्भुज BEFC में, BC = EF और BC || EF
चतुर्भुज BEFC की सम्मुख भुजाओं BC और EF का एक युग्म बराबर और समान्तर है।
अतः चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
Proved.
(iii) चतुर्भुज ABED समान्तर चतुर्भुज है।
AD = BE और AD || BE चतुर्भुज BEFC एक समान्तर चतुर्भुज है।
BE = CF
BE || CF दोनों को मिलाकर,
AD = BE = CF और AD || BE || CF
अतः AD = CF और AD || CF
Proved.
(iv) चतुर्भुज ACFD में,
AD = CF और AD || CF
अर्थात् सम्मुख भुजाओं का एक युग्म बराबर और समान्तर है।
अतः चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
Proved.
(v) चतुर्भुज ACFD एक समान्तर चतुर्भुज है।
सम्मुख भुजाओं के युग्म बराबर होंगे।
अत: AC = DF
Proved.
(vi) ∆ABC और ∆DEF की तुलना करने पर,
AB = DE (दिया है।)
AC = DF (अभी सिद्ध किया है।)
BC = EF (दिया है।)
∆ABC = ∆DEF (S.S.S. से)
Proved.

प्रश्न 12.
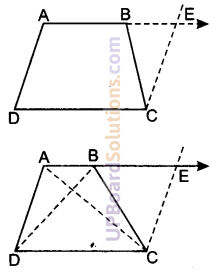
ABCD एक समलम्ब है, जिसमें AB || DC और AD = BC है। दर्शाइए कि
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC = ∆BAD
(iv) विकर्ण AC = विकर्ण BD

हल :
दिया है : चतुर्भुज ABCD एक समलम्ब है, जिसमें AB || DC और AD = BC है।
सिद्ध करना है :
(i) ∠A = ∠B
(ii) ∠C = ∠D
(iii) ∆ABC = ∆BAD
(iv) विकर्ण AC = विकर्ण BD
रचना : विकर्ण AC तथा BD खींचे।
AB को आगे बढ़ाया और बिन्दु C से DA के समान्तर रेखा खींची जो बढ़ी हुई ABP को बिन्दु E पर काटे।
उपपत्ति : (i) : समलम्ब चतुर्भुज ABCD में AB|| DC और AB को बढ़ाया गया है।
AE || DC और AD || CE (रचना से) …(2)
चतुर्भुज ADCE एक समान्तर चतुर्भुज है।
∠DAE = ∠DCE (सम्मुख कोण) …(3)
∠ADC = ∠AEC (सम्मुख कोण) …(4)
AB || DC और BC एक तिर्यक रेखा है
∠BCD = ∠CBE (एकान्तर कोण) …(5)
चतुर्भुज ADCEएक समान्तर चतुर्भुज है।
AD = CE परन्तु दिया है कि
AD = BC
BC = CE
∠BEC = ∠CBE (त्रिभुज में समान भुजाओं के सम्मुख कोण समान होते हैं।) …(6)
अब समान्तर चतुर्भुज ADCE में,
∠A = ∠DCE (समीकरण (3) से)
= ∠ BCD +∠BCE (चित्र से)
=∠CBE +∠BCE (समीकरण (5) से)
= ∠ BEC+∠BCE (समीकरण (6) से)
= ∠CBA (∠CBA, ∆BCE का बहिष्कोण है।)
∠A = ∠B (समलम्ब ABCD में)
Proved.
(ii) AB || CD और AD तिर्यक रेखा है।
∠A + ∠D = 180° (अन्त:कोणों का योग)
∠D = 180° – ∠A
∠D = 180° – ∠B [∠A= ∠B भाग (i) से)]
इसी प्रकार, AB || CD और BC तिर्यक रेखा है।
∠ABC + ∠BCD = 180° (अन्त:कोणों का योग)
∠ BCD = 180° – ∠ABC
∠C = 180° – ∠B
तब ∠C व ∠D की तुलना करने पर,
∠C = ∠D
Proved.
(iii) ∆ABC और ∆BAD में,
BC = AD (दिया है।)
∠A = ∠B [भाग (1) से)]
AB = AB (उभयनिष्ठ भुजा है।)
∆ABC = ∆BAD (S.A.S. से)
(iv) ∆ABC = ∆BAD
AC = BD (C.P.C.T.)
अतः समलम्ब का विकर्ण AC = विकर्ण BD
Proved.

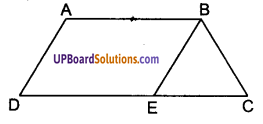
प्रश्नावली 8.2

प्रश्न 1.
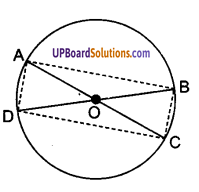
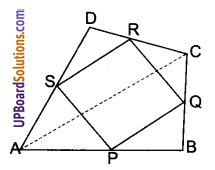
ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। AC उसका एक विकर्ण है। दर्शाइए कि
(i) SR || AC और SR = [latex]\frac { 1 }{ 2 }[/latex] AC है।
(ii) PQ = SR है।
(iii) PQRS एक समान्तर चतुर्भुज है।

हल :
दिया है : चतुर्भुज ABCD में P, Q, R व S क्रमश: भुजाओं AB, BC, CD व DA के मध्ये-बिन्दु हैं।
P, Q, R व S को ऋजु रेखाखण्ड PQ, QR, RS व SP द्वारा जोड़कर चतुर्भुज PQRS प्राप्त किया गया है।
सिद्ध करना है :
(i) SR || AC और SR = AC
(ii) PQ = SR
(iii) PQRS एक समान्तर चतुर्भुज है।
उपपत्ति : (i) ∆ACD में,
CD का मध्य-बिन्दु R तथा AD का मध्य-बिन्दु S है।
किसी त्रिभुज की दो भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर और तीसरी भुजा का आधा होता है।
अतः रेखाखण्ड SR || AC और SR = [latex]\frac { 1 }{ 2 }[/latex] AC होगा। …(1)
Proved.
(ii) ∆ABC में, AB का मध्य-बिन्दु P है और BC का मध्यबिन्दु Q है।
रेखाखण्ड PQ || AC और PQ = [latex]\frac { 1 }{ 2 }[/latex] AC
अब (1) और (2) से
PQ || SR और PQ = SR
अतः PQ = SR
Proved.
(iii) ऊपर सिद्ध हुआ है कि PQ || SR और PQ = SR
चतुर्भुजं PQRS में P और RS सम्मुख भुजाओं का युग्म है जो परस्पर बराबर भी है और समान्तर भी।
अत: चतुर्भुज PQRS एक समान्तर चतुर्भुज होगी।
Proved.

प्रश्न 2.
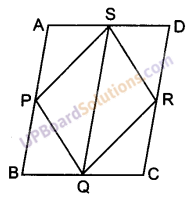
ABCD एक समचतुर्भुज है और P, Q, R, S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक आयत है।

हल :
दिया है: ABCD एक समचतुर्भुज है। जिसकी भुजाओं AB, BC, CD, DA के मध्य-बिन्दु क्रमशः P, Q, R, S हैं।
सिद्ध करना है : PQRS एक आयत है।
रचना : रेखाखण्ड QS को मिलाया।
उपपत्ति : ABCD एक समचतुर्भुज है,
AB = BC = CD = DA
तथा ∠A = ∠C और ∠B = ∠D
P, Q, R, S क्रमश: AB, BC, CD, DA के मध्य-बिन्दु हैं।
AP = BP = BQ = CQ = CR = RD = DS = AS
∆APS और ∆QCR में,
AP = CR (दिया है।)
∠A = ∠C (दिया है।)
AS = CQ (दिया है।)
∆APS = ∆CRQ (S.A.S. से)
PS = QR (C.P.C.T.) …(1)
∆PBQ तथा ∆RDS में,
BP = DR (दिया है।)
∠B = ∠D (दिया है।)
BQ = DS (दिया है।)
∆PBQ = ∆RDS (S.A.S. से)
PQ = RS (C.P.C.T.) …(2)
AB || CD और बिन्दु Q तथा S क्रमश: BC और DA के मध्य-बिन्दु हैं।
QS || AB तथा QS = CD
QS || AB और PS तिर्यक रेखा है।
∠PSQ= ∠ APS (एकान्तर कोण)
परन्तु ∠ APS = ∠ASP (AS = AP)
∠ PSQ = ∠ ASP …(3)
इसी प्रकार, ∠RSQ = ∠DSR …(4)
∠ ASP +∠PSQ + ∠RSQ +∠DSR = 180° (एक रेखा पर बने कोण)
∠PSQ + ∠ PSQ + ∠RSQ + ∠RSQ = 180° [समीकरण (3) व (4) से]
2 (∠PSQ + ∠RSQ) = 180°
2 ∠S = 180° या ∠S = 90°
(∠S = ∠PSQ + ∠RSQ)…(5)
समीकरण (1) और (2) से,
PQRS एक समान्तर चतुर्भुज है और समीकरण (5) से उसका एक अन्त:कोण समकोण है।
अतः PQRS एक आयत है।
Proved.

प्रश्न 3.
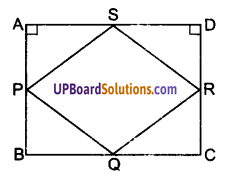
ABCD एक आयत है जिसमें P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं। दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है।

हल :
दिया है : चतुर्भुज ABCD एक आयत है जिसकी भुजाओं AB, BC, CD और DA के मध्य-बिन्दु क्रमशः P, Q, R और S हैं।
रेखाखण्ड PG, QR, RS और SP एक चतुर्भुज PQRS बनाते हैं।
सिद्ध करना है : चतुर्भुज PQRS एक समचतुर्भुज है।
उपपत्ति: ΔAPS और ΔDRS में,
AS = DS (S, AD का मध्य-बिन्दु है)।
∠A = ∠D (आयत के अन्त:कोण)
AP = DR (P, AB का तथा R, CD का मध्य बिन्दु है तथा AB = CD)
ΔAPS = ΔDRS (S.A.S. से)
SP = SR (C.P.C.T.) …(1)
ΔAPS और ΔBPQ में,
AP = BP (P, AB का मध्य-बिन्दु है)
∠A = ∠B (आयत के अन्त:कोण)
AS = BQ (AD = BC और S तथा Q इनके क्रमश: मध्य-बिन्दु हैं)
ΔAPS = ΔBPQ (S.A.S. से)
SP = QP (C.P.C.T.) …(2)
ΔAPS और ΔCRQ में,
AP = CR (AP = [latex]\frac { 1 }{ 2 }[/latex] AB = [latex]\frac { 1 }{ 2 }[/latex] CD = RC) (प्रत्येक समकोण)
∠A = ∠C
AS = CQ ( AS = [latex]\frac { 1 }{ 2 }[/latex] AD = [latex]\frac { 1 }{ 2 }[/latex] BC = QC)
ΔAPS = ΔCRQ (S.A.S. से)
SP = QR (C.P.C.T.) …(3)
समीकरण (1), (2) और (3) से,
SP = RS = PQ = QR
PQRS एक समचतुर्भुज है।
Proved.

प्रश्न 4.
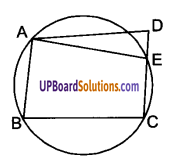
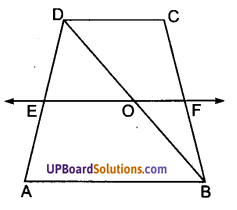
ABCD एक समलम्ब है, जिसमें AB || CD है। साथ ही BD एक विकर्ण है और E भुजा AD का मध्य-बिन्दु है। E से होकर एक रेखा AB के समान्तर खींची गई है जो BC को F पर प्रतिच्छेद करती है। दर्शाइए कि F भुजा BC का मध्य-बिन्दु है।

हल :
दिया है : चतुर्भुज ABCD एक समलम्ब है जिसमें AB || CD है। BD. समलम्ब ABCD का एक विकर्ण है।
भुजा AD का मध्य-बिन्दु E है।
E से AB के समान्तर एक रेखा EF खींची गई है जो BC को बिन्दु F पर तथा BD को बिन्दु O पर प्रतिच्छेद करती है।
सिद्ध करना है : F, BC का मध्य-बिन्दु है।
उपपत्ति : ΔABD में, बिन्दु E भुजा AD का मध्य-बिन्दु है और चूँकि EF, AB के समान्तर है।
बिन्दु O, BD को समद्विभाजित करेगा अर्थात् O, भुजा BD का मध्य-बिन्दु है।
AB || CD और EF || AB
EF || CD या OF || CD
अब ΔBCD में,
O, BD को मध्य-बिन्दु है
और OF || CD, जो BC को F पर प्रतिच्छेद करती है।
अत: F, BC का मध्य-बिन्दु है।
Proved.

प्रश्न 5.
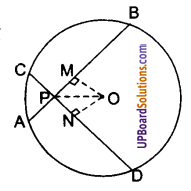
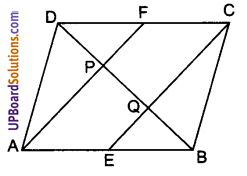
एक समान्तर चतुर्भुज ABCD में E और F क्रमशः भुजाओं AB और CD के मध्य-बिन्दु हैं। दर्शाइए कि रेखाखण्ड AF और CE विकर्ण BD को समत्रिभाजित करते हैं।

हल :
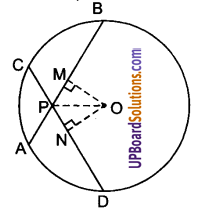
दिया है : ABCD एक समान्तर चतुर्भुज है। बिन्दु E और F क्रमश: उसकी भुजाओं AB तथा CD के मध्य-बिन्दु हैं।
उसका विकर्ण BD, रेखाखण्डों AF तथा CE से क्रमशः बिन्दुओं P और Q पर विभक्त होता है।
सिद्ध करना है : BD को AF और CE तीन बराबर भागों में बाँटते हैं
अर्थात् DP = PQ = QB
उपपत्ति : ABCD एक समान्तर चतुर्भुज है।
AB || CD तथा AB = CD
और E तथा F क्रमश: AB और CD के मध्य-बिन्दु हैं।
AE || CF और AE = CF
AECF एक समान्तर चतुर्भुज है।
AF || CE ……(1)
AP|| EQ …(2)
PF || CQ …(3)
ΔDQC में, बिन्दु F, भुजा CD का मध्य-बिन्दु है। (ज्ञात है।)
और PF || CQ (समीकरण (3) से)
P, DQ का मध्य-बिन्दु है।
DP = PQ …(4)
पुनः ΔABP में, बिन्दु E भुजा AB का मध्य-बिन्दु है
और EQ || AP (समीकरण (2) से)
Q, BP का मध्य-बिन्दु है। QB = PQ …(5)
समीकरण (4) और (5) से, DP = PQ = QB
अतः रेखाखण्ड AF और CE, विकर्ण BD को तीन बराबर भागों में विभक्त करते हैं।
Proved.

प्रश्न 6.
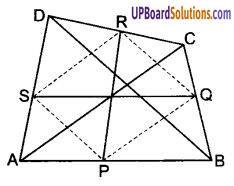
दर्शाइए कि चतुर्भुज की सम्मुख भुजाओं के मध्य बिन्दुओं को मिलाने वाले रेखाखण्ड परस्पर समद्विभाजित करते हैं।

हल :
दिया है : चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA के मध्य-बिन्दु क्रमशः P, Q, R, S हैं।
सम्मुख भुजाओं AB और CD के मध्य-बिन्दुओं P और R को मिलाकर रेखाखण्ड PR बनता है
तथा BC और DA के मध्य-बिन्दुओं Q और S को मिलाकर रेखाखण्ड QS बनता है।
सिद्ध करना है : PR और QS परस्पर समद्विभाजित करते हैं।
रचना : रेखाखण्ड PQ, QR, RS और SP को मिलाइए
तथा विकर्ण AC और BD खींचिए।
उपपत्ति: ΔABC में,
P, AB का तथा Q, BC का मध्य-बिन्दु है।
PQ = [latex]\frac { 1 }{ 2 }[/latex] AC और PQ || AC …(1)
पुनः ΔACD में, R, CD का ओर S, DA का मध्य-बिन्दु है।
RS = [latex]\frac { 1 }{ 2 }[/latex] AC और RS || AC
PQ = RS और PQ || RS [समीकरण (1) व (2) से]
PQRS एक समान्तर चतुर्भुज है।
समान्तर चतुर्भुज PQRS के विकर्ण PR तथा SQ हैं।
अत: PR तथा SQ परस्पर समद्विभाजित करते हैं।
Proved.

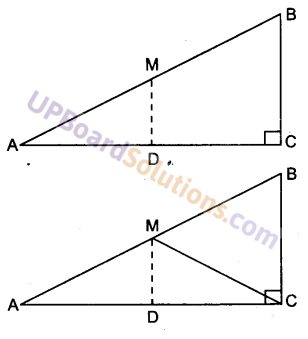
प्रश्न 7.
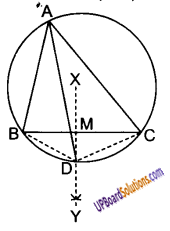
ABC एक त्रिभुज है जिसका कोण C समकोण है। कर्ण AB के मध्य-बिन्दु M से होकर BC के समान्तर खींची गई रेखा AC को D पर प्रतिच्छेद करती है। दर्शाइए कि :
(i) D भुजा AC का मध्य-बिन्दु है।
(ii) MD ⊥ AC है।
(iii) CM = MA = [latex]\frac { 1 }{ 2 }[/latex] AB है। .

हल:
दिया है: ΔABC में ∠C समकोण है और AB कर्ण है जिसका मध्य-बिन्दु M है।
बिन्दु M से एक रेखा BC के समान्तर खींची गई है जो AC को बिन्दु D पर प्रतिच्छेद करती है।
सिद्ध करना है :
(i) D भुजा AC का मध्य-बिन्दु है।
(ii) MD ⊥ AC
(iii) CM = MA = [latex]\frac { 1 }{ 2 }[/latex] AB
रचना : रेखाखण्ड CM खींचा।
उपपत्ति : (i) ΔABC में,
M कर्ण AB का मध्य-बिन्दु है और M से BC के समान्तर खींची गई Aरेखा AC को बिन्दु D पर प्रतिच्छेद करती है जिससे MD || BC है।
अतः बिन्दु D, AC का मध्य-बिन्दु होगा।
Proved.
(ii) MD || BC और तिर्यक रेखा AC इन्हें प्रतिच्छेद करती है।
∠MDA = ∠C
∠MDA = 90°
MD ⊥ AD या MD ⊥ AC
अतः (iii) ΔMDA तथा ΔMDC में,
AD = CD (D, AC का मध्य-बिन्दु है।)
∠MDA = ∠MDC (MD ⊥ AC)
MD = MD (उभयनिष्ठ भुजा है।)
ΔMDA = ΔMDC (S.A.S. से)
MA = CM (C.P.C.T.)
परन्तु M, AB का मध्य-बिन्दु है जिससे
MA = [latex]\frac { 1 }{ 2 }[/latex] AB
अतः CM = MA = [latex]\frac { 1 }{ 2 }[/latex] AB
Proved.

We hope the UP Board Solutions for Class 9 Maths Chapter 8 Quadrilaterals (चतुर्भुज) help you. If you have any query regarding UP Board Solutions for Class 9 Maths Chapter 8 Quadrilaterals (चतुर्भुज), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 9 Home Science Chapter 11 व्यक्तिगत सज्जा : उचित वेशभूषा

These Solutions are part of UP Board Solutions for Class 9 Home Science . Here we have given UP Board Solutions for Class 10 Home Science Chapter 11 व्यक्तिगत सज्जा : उचित वेशभूषा.

विस्तृत उत्तरीय प्रश्न

प्रश्न 1:
व्यक्तिगत सज्जा से क्या तात्पर्य है? व्यक्तिगत सज्जा हेतु वस्त्रों का चयन करते समय आप किन-किन मुख्य बातों का ध्यान रखेंगी?
या
व्यक्तिगत सज्जा और वेशभूषा में वस्त्रों का क्या स्थान है? किसी व्यक्ति के लिए वस्त्रों के चयन में कौन-सी सावधानियाँ अपेक्षित हैं?
उत्तर:
उपयुक्त वेशभूषा व्यक्तिगत सज्जा का मूल आधार है। सुन्दर एवं उपयुक्त वस्त्रों से मनुष्य का बाहरी व्यक्तित्व आकर्षक हो जाता है, आत्मविश्वास में वृद्धि होती है एवं इससे मनुष्य को मानसिक प्रसन्नता होती है। उपयुक्त वस्त्र आयु, लिंग, व्यवसाय, अवसर एवं ऋतुओं के अनुकूल होते हैं। ये मनुष्य को शारीरिक सुख एवं आराम प्रदान करने के साथ-साथ उसके रहन-सहन के स्तर के भी परिचायक होते हैं। अतः (UPBoardSolutions.com) संक्षेप में हम कह सकते हैं कि व्यक्तिगत सज्जा व्यक्ति-विशेष के मानसिक, आर्थिक, सामाजिक, अवसर के अनुकूल एवं रहन-सहन के अपेक्षित स्तर को बनाए रखने व प्रदर्शित करने की प्रभावशाली विधि है।

व्यक्तिगत सज्जा का अर्थ
उपर्युक्त सामान्य परिचय के आधार पर व्यक्तिगत सज्जा का अर्थ स्पष्ट किया जा सकता है। वास्तव में, व्यक्ति के बाहरी व्यक्तित्व को निखारने एवं आकर्षक बनाने के लिए व्यक्ति द्वारा अपनाए जाने वाले समस्त उपायों एवं साधनों को ही सम्मिलित रूप से व्यक्तिगत सज्जा कहा जाता है। व्यक्तिगत सज्जा के माध्यम से व्यक्ति अपने शरीर अर्थात् व्यक्तित्व के प्रकट रूप को अधिक-से-अधिक आकर्षक, निखरा हुआ तथा प्रभावशाली बनाने का प्रयास करते हैं। व्यक्तिगत सज्जा का मुख्यतम साधन वेशभूषा है। उत्तम वेशभूषा द्वारा (UPBoardSolutions.com) व्यक्तिगत सज्जा में विशेष योगदान प्राप्त होता है। वेशभूषा के अतिरिक्त व्यक्ति द्वारा किया जाने वाला श्रृंगार, बाल सँवारने का ढंग, बातचीत करने का ढंग, उठने-बैठने का ढंग तथा व्यक्ति के हाव-भाव व्यक्तिगत सज्जा के महत्त्वपूर्ण कारक हैं। इन सभी कारकों के प्रति जागरूक व्यक्ति निश्चित रूप से उत्तम व्यक्तिगत सज्जा को प्रदर्शित कर सकता है तथा समाज में आकर्षण का केन्द्र बन सकता है।

वस्त्रों का चयन करते समय ध्यान रखने योग्य बातें वस्त्र केवल तन ढकने का ही कार्य नहीं करते वरन् व्यक्ति-विशेष के बाहरी व्यक्तित्व को आकर्षक एवं प्रभावशाली बनाने में भी महत्त्वपूर्ण योगदान देते हैं। अत: उपयुक्त वस्त्रों का चयन करते समय उनकी निम्नवर्णित विशेषताओं को दृष्टिगत रखना चाहिए

(1) आकर्षक एवं आरामदायक वस्त्र-वस्त्रों का चयन करते समय देखें कि

• (क) वस्त्र सही फिटिंग अथवा शारीरिक माप वाले एवं सुन्दर होने चाहिए,
• (ख) वस्त्र न तो बहुत पुराने और न ही आधुनिकतम चलन के हों,
• (ग) रंगों का चयन अवसर, व्यवसाय एवं आयु के अनुरूप हो,
• (घ) चयन का आधार किसी की नकल के अनुसार न होकर अपने कद-काठी व रुचि के अनुसार होना चाहिए।

उपर्युक्त नियमों के अनुरूप चयनित वस्त्र देखने में अच्छे लगते हैं, आरामदायक होते हैं एवं व्यक्ति-विशेष की सामाजिक प्रतिष्ठा में वृद्धि करते हैं।

(2) ऋतुओं के अनुकूल वस्त्र:
विभिन्न ऋतुओं में प्रायः उनके अनुकूल ही वस्त्र पहनने चाहिए; जैसे कि ग्रीष्म ऋतु में सूती एवं शरद ऋतु में ऊनी वस्त्र ही आरामदायक रहते हैं। सूती वस्त्र शरीर से निकलने वाले पसीने को सोखकर ठण्डेपन का आभास कराते हैं, जबकि ऊनी वस्त्र शीत ऋतु में शारीरिक ऊष्मा को अन्दर ही रोककर शरीर को गर्म रखते हैं।

(3) अवसरानुकूल वस्त्र:
घर में सामान्यतः सूती वस्त्र पहनने में हर प्रकार की सुविधा रहती है, परन्तु विशिष्ट अवसरों (विवाह, जन्मदिन व अन्य महत्त्वपूर्ण उत्सव आदि) पर मूल्यवान् व सुन्दर वस्त्र पहनना सामाजिक प्रतिष्ठा बनाए रखने के लिए आवश्यक है; जैसे कि विवाह अथवा जन्मदिन के अवसर पर जरीदार (UPBoardSolutions.com) बनारसी साड़ियाँ, रेशमी व कृत्रिम तन्तुओं से निर्मित सुन्दर व आधुनिक फैशन के वस्त्र पहनने से एकत्रित जनसमूह के मध्य सम्मान एवं प्रशंसा प्राप्त होती है।

(4) मजबूत व टिकाऊ वस्त्र:
प्रायः पक्के रंगों के मजबूत व टिकाऊ वस्त्र खरीदने राहिए। उदाहरण के लिए टेरीकॉट, नायलॉन, टेरीलीन आदि वस्त्र सूती व रेशमी वस्त्रों से अधिक मजबूत व टिकाऊ होते हैं। अतः इनका यथासम्भव अधिक उपयोग आर्थिक दृष्टि से लाभदायक रहता है।

(5) सरलता से धुलने वाले वस्त्र:
सामान्यतः कृत्रिम तन्तुओं से निर्मित वस्त्रों को धोना सरल होता है, क्योंकि ये न तो सिकुड़ते हैं और न ही सूखने में अधिक समय लेते हैं। मोटे सूती वस्त्रों को धोने में अधिक श्रम की आवश्यकता होती है तथा इन पर लगे दाग व धब्बे भी सहज ही दूर नहीं होते। मूल्यवान ऊनी, रेशमी व जरीदार वस्त्रों की धुलाई कठिन व महँगी होने के कारण इन्हें सावधानीपूर्वक विशिष्ट अवसरों पर ही उपयोग में लाना चाहिए।

(6) सिकुड़न व सिलवट मुक्त वस्त्र:
वस्त्र खरीदते समय यह अवश्य ध्यान रखें कि धुलाई का उस पर क्या प्रभाव पड़ सकता है। एक उपयोगी वस्त्र न तो धोने पर सिकुड़ना चाहिए और न ही उसमें अनावश्यक सिलवटें पड़नी चाहिए। उदाहरणार्थ टेरीकॉट, टेरीलीन, रेयॉन इत्यादि वस्त्र। इन वस्त्रों पर इस्तरी (प्रेस) करने के श्रम की भी पर्याप्त बचत होती है।

(7) आर्थिक क्षमता के अनुरूप वस्त्र:
वस्त्र खरीदते समय पारिवारिक बजट का विशेष ध्यान रखना चाहिए, क्योंकि ऐसा न करने पर प्रायः मानसिक क्लेश उत्पन्न होता है तथा पारिवारिक अर्थव्यवस्था भी प्रभावित होती है। अतः सामान्यतः अपनी आर्थिक क्षमता के अनुरूप वस्त्रों को खरीदना ही विवेकपूर्ण रहता है।

प्रश्न 2:
वस्त्रों के चयन के मुख्य आधार कौन-कौन से हैं? समझाइए।
या
शारीरिक विशेषताओं, आयु एवं लिंग के अनुसार वस्त्रों का चयन आप किस प्रकार करेंगी?
उत्तर:
मनुष्य के दैनिक जीवन के लिए उपयुक्त वस्त्रों का अत्यधिक महत्त्व है। उपयुक्त वस्त्रों को चयन कोई सरल कार्य नहीं है। इसके लिए व्यक्ति विशेष की आर्थिक, सामाजिक, मानसिक, आयु वर्ग एवं व्यवसाय सम्बन्धी परिस्थितियों का विशेष ध्यान रखना पड़ता है।
उपर्युक्त सभी कारकों को ध्यान में रखते हुए उचित वस्त्रों के चयन के निम्नलिखित आधार माने जा सकते हैं

1.  शारीरिक विशेषताएँ,
2.  लिंग एवं आयु,
3. व्यवसाय एवं पद,
4. मौसम एवं भौगोलिक परिस्थिति।

(1) शारीरिक विशेषताएँ:
वस्त्रों का चयन करते समय शारीरिक विशेषताओं को ध्यान में रखना अत्यधिक आवश्यक है। उदाहरणस्वरूप–औसत कद वाले व्यक्तियों पर प्रायः सभी प्रकार के वस्त्र अच्छे लगते हैं। लम्बे कद की स्त्रियों को साड़ी और ब्लाउज के विभिन्न रंग, बड़े डिजाइन व हल्के रंगों का प्रयोग करना चाहिए। (UPBoardSolutions.com) नाड़े कद की स्त्रियों को लम्बी दिखाई पड़ने के लिए एक ही रंग की साड़ी व ब्लाउज, जो कि ऊपर से नीचे की ओर धारियों वाले, छोटे डिजाइन के व हल्के रंग के हों, पहनने चाहिए।
विभिन्न कद एवं आकार वाले व्यक्तियों को अपनी लम्बाई व चौड़ाई के अनुसार वस्त्रों का चयन करना चाहिए।

(2) लिंग एवं आयु:
विभिन्न व्यक्तियों के लिए वेशभूषा के चयन हेतु अलग-अलग नियम होते हैं, जिन्हें निम्नांकित विवरण से समझा जा सकता है

(i) पुरुषों के लिए:
सही शारीरिक माप वाले कपड़े पहनने से बाहरी व्यक्तित्व आकर्षक दिखाई पड़ता है। वस्त्र चाहे संख्या में कम हों परन्तु उनकी अच्छी सिलाई आवश्यक है। पुरुषों को अपनी आर्थिक क्षमता के अनुसार उपयुक्त वस्त्र खरीदने चाहिए। महँगे होने के कारण सूट का कपड़ा सदैव टिकाऊ, आकर्षक व गहरे रंग का लेना चाहिए जिससे इसे बार-बार ड्राइक्लीन न कराना पड़े। नवयुवक पर प्रायः चमकीले अथवा गहरे रंग के वस्त्र आकर्षक लगते हैं, जबकि अधेड़ावस्था में हल्के व सौम्य रंग के वस्त्र ही ठीक रहते हैं।

(ii) स्त्रियों के लिए:
महिलाओं के लिए प्रायः साड़ी व ब्लाउज ही अधिक महत्त्वपूर्ण वस्त्र होते हैं। दैनिक उपयोग के लिए सूती साड़ियाँ सर्वोत्तम रहती हैं। विशेष अवसरों के लिए जरीदार बनारसी साड़ियाँ, काँचीवरम की साड़ियाँ तथा गुजराती बंधेज की साड़ियाँ उपयोग में लाई जाती हैं। सामान्य अवसरों के लिए हैण्डलूम की साड़ियाँ, आरगेण्डी व चिकन की साड़ियाँ तथा कृत्रिम तन्तुओं से निर्मित साड़ियाँ अधिक उपयुक्त रहती हैं। (UPBoardSolutions.com) साड़ियों के साथ अधिकतर अनुरूप (मैचिंग) रंग के ब्लाउज उपयुक्त रहते हैं। इसके लिए 2×2 रूबिया, पॉपलीन व रेशमी वस्त्रों का चयन उचित रहता है। मूल्यवान साड़ियों के साथ प्रायः ब्लाउज के लिए अतिरिक्त कपड़ा साड़ी के साथ ही जुड़ा मिलता है। कम आयु की महिलाओं के लिए प्रायः चटकीले रंग उपयुक्त रहते हैं, जो कि सहज ही हैण्डलूम व कृत्रिम तन्तुओं से निर्मित साड़ियों में उपलब्ध हो जाते हैं।

(iii) बच्चों के लिए:
बच्चे अधिक खेलते-कूदते हैं; अतः उनके वस्त्र मजबूत कपड़े के होने चाहिए। बाल्यावस्था में शारीरिक वृद्धि होने के कारण बच्चों के कपड़े थोड़े ढीले व संख्या में कम होने चाहिए। वस्त्रों की सिलाई कराते समय सींवनों में अतिरिक्त कपड़ा छोड़ने से इन्हें आवश्यकतानुसार ढीला किया जा सकता है। बच्चों के वस्त्रों के बटन मजबूती से लगे होने चाहिए। विशेष अवसरों के लिए बच्चों को महँगे वस्त्र दिलाए जा सकते हैं।

(iv) शिशुओं के लिए:
शिशुओं की त्वचा कोमल होती है; अतः इनके वस्त्र मुलायम कपड़ों (रेशमी, सूती व ऊनी आदि) के बनवाने चाहिए। शिशुओं को प्रायः हल्के गुलाबी, नीले, नारंगी आदि रंगों के झबले, रोम्पर, फ्रॉक, टी-शर्ट व लैंगिंग्स पहनाए जाते हैं।

(3) व्यवसाय एवं पद:
व्यवसाय एवं पद का सीधा सम्बन्ध मनुष्य की आर्थिक क्षमता एवं सामाजिक स्थिति में होता है। छोटे व्यवसाई अथवा छोटी नौकरी करने वाले व्यक्ति आय कम होने के कारण वस्त्रों पर अधिक व्यय नहीं कर सकते। इनके लिए प्रायः सूती व टेरीकॉट के वस्त्र ही अधिक उपयुक्त रहते हैं। अधिक आय वर्ग के व्यक्ति अधिक मूल्य के रेडीमेड अथवा अन्य प्रकार के अनेक वस्त्र प्रयोग कर सकते हैं। (UPBoardSolutions.com) कुछ विशिष्ट व्यवसायों एवं सेवाओं में वस्त्रों की निर्धारित सीमाएँ होती हैं; जैसे कि सेवा के समय में चिकित्सक, सेना व पुलिस कर्मचारी व वकील इत्यादि एक निश्चित पोशाक पहनने के लिए बाध्य होते हैं। व्यापारियों एवं दुकानदारों को कुर्ता-धोती अथवा कुर्ता-पाजामा पहनने में सुविधा रहती है। उच्च अधिकारियों, अध्यापक एवं अध्यापिकाओं को सौम्य रंग एवं फैशन के वस्त्र पहनने उपयुक्त रहते

(4) मौसम एवं भौगोलिक परिस्थिति:
वस्त्रों के चयन के लिए मौसम व स्थान-विशेष की भौगोलिक परिस्थितियों का एक अलग ही महत्त्व है। ग्रीष्म ऋतु में हल्के रंग के सूती वस्त्र तथा शीत ऋतु में विभिन्न प्रकार के गहरे रंग के ऊनी वस्त्र अधिक उपयुक्त रहते हैं। इसी प्रकार ठण्डे प्रदेशों में शीत ऋतु के वस्त्र तथा गर्म प्रदेशों में ग्रीष्म ऋतु के वस्त्र उपयोग करना आवश्यक होता है।

लघु उत्तरीय प्रश्न

प्रश्न 1:
स्पष्ट कीजिए कि उचित वेशभूषा से व्यक्तित्व में निखार आता है।
उत्तर:
प्रत्येक व्यक्ति के व्यक्तित्व को निखारने में उसकी वेशभूषा का विशेष योगदान एवं महत्त्व होता है। यदि व्यक्ति अपनी आयु, व्यवसाय, अवसर, ऋतु एवं लिंग के अनुसार वेशभूषा धारण करता है। तो उस व्यक्ति का व्यक्तित्व सामान्य रूप से आकर्षक एवं प्रभावशाली प्रतीत होता है। जो व्यक्ति उचित वेशभूषा धारण करता है, उसके प्रति अन्य व्यक्तियों का व्यवहार भी सौम्य होता है। यह एक मनोवैज्ञानिक तथ्य (UPBoardSolutions.com) है कि उचित वेशभूषा धारण करने वाले व्यक्ति में एक प्रकार का अतिरिक्त आत्म-विश्वास भी जाग्रत होता है, इससे भी व्यक्ति के व्यक्तित्व में क्रमश: निखार आता है। इस प्रकार स्पष्ट है कि व्यक्ति-व्यक्तित्व को निखारने वाले कारकों में उचित वेशभूषा का महत्त्वपूर्ण स्थान है।

प्रश्न 2:
अवसर के अनुकूल व्यक्तिगत वेशभूषा कैसी होनी चाहिए? कम-से-कम पाँच |.. बिन्दुओं का उल्लेख कीजिए।
उत्तर:
प्रत्येक व्यक्ति को अपने दैनिक एवं सामाजिक जीवन में विभिन्न अंवसरों एवं परिस्थितियों से गुजरना पड़ता है। यदि उसको सामान्य जीवन घरेलू परिस्थितियों में व्यतीत होता है, तो उसे कभी-कभी यात्रा पर भी जाना होता है और अनेक बार विवाह, जन्म-दिन आदि अनेक महत्त्वपूर्ण (UPBoardSolutions.com) सामाजिक उत्सवों में भी भाग लेना पड़ता है। प्रत्येक अवसर के लिए अनुकूल व्यक्तिगत वेशभूषा को चयन व्यक्तिगत सज्जा के नियमानुसार करने से उसके आत्मविश्वास एवं सामाजिक प्रतिष्ठा में वृद्धि होती है। आइए इस सम्बन्ध में कुछ उपयोगी नियमों का अवलोकन करें

(1) मौसम सम्बन्धी नियम:
मौसम के अनुसार सूती व रेशमी (ग्रीष्म ऋतु) अथवा ऊनी (शीत ऋतु) वस्त्र उपयोग में लाने चाहिए।

(2) मजबूती व टिकाऊपन सम्बन्धी नियम:
सामान्य घरेलू जीवन में मजबूत व टिकाऊ वस्त्र पहनना लाभदायक रहता है। रसोई-गृह में सूती वस्त्रों व शेष समय में हैण्डलूम व कृत्रिम तन्तुओं से निर्मित वस्त्रों का उपयोग सर्वोत्तम रहता है।

(3) आरामदायक व उपयुक्त फिटिंग सम्बन्धी नियम:
सदैव ऐसे वस्त्रों का चयन करना चाहिए जो कि शारीरिक आराम में बाधा न डालें। सही शारीरिक माप अथवा फिटिंग वाले वस्त्र पहनने से बाहरी व्यक्तित्व के आकर्षण में वृद्धि होती है।

(4) रंगों के संयोग का नियम:
रंग प्रायः परस्पर या तो समन्वित होते हैं अथवा विरोधाभासी। लाल एवं गुलाबी, गहरा व हल्का नीला, सफेद व काला इत्यादि रंगों के अद्भुत संयोग के उदाहरण हैं। इनका विवेकपूर्ण उपयोग सदैव लाभदायक रहता है।

(5) विशिष्ट अवसर सम्बन्धी नियम:
विवाह, जन्मोत्सव आदि उत्सवों में व्यक्तिगत वेशभूषा का चुनाव इस प्रकार करना चाहिए कि शरीर के असुन्दर भाग ढके रहें तथा सुन्दर अंगों का आवश्यक प्रदर्शन हो सके। इन अवसरों पर मूल्यवान वस्त्रों, जैसे जरीदार व रेशमी साड़ियों का उपयोग प्रतिष्ठा एवं सौन्दर्य में वृद्धि करता है।

प्रश्न 3:
व्यक्तिगत सज्जा हेतु वस्त्रों के विवेकपूर्ण चयन से आप क्या समझती हैं?
उत्तर:
व्यक्तिगत सज्जा के सारे नियमों का पालन करने पर भी यदि कोई व्यक्ति वस्त्रों को क्रय करते समय अपने विवेक का प्रयोग नहीं करता है, तो सब कुछ व्यर्थ हो सकता है। वस्त्रों के सुन्दर एवं उपयुक्त चुनाव के साथ निम्नलिखित सिद्धान्तों का पालन अवश्य किया जाना चाहिए

(1) बजट के अनुसार खरीदारी:
आप अपने बजट के अनुसार ही वस्त्रों का चयन करें। फिजूलखर्ची आप व आपके परिवार में असन्तोष उत्पन्न कर सकती है।

(2) सोच-समझकर खरीदारी:
वस्त्रों की उद्देश्यहीन खरीदारी न करें। अवसरों एवं आवश्यकताओं को दृष्टिगत रखकर की गई खरीदारी सदैव सुख एवं सन्तोष प्रदान करती है।

(3) मूल्य देखकर खरीदारी:
अधिक मूल्य के वस्त्र केवल आवश्यकता पड़ने पर ही खरीदें। सदैव अच्छी जगह से वस्त्र खरीदें। यदि वस्त्र सिलवाने हों, तो सोच-समझकर आवश्यक कपड़ा ही खरीदें। इससे कपड़ा व्यर्थ नहीं होगा और धन की बचत होगी।

(4) वस्त्रों की उचित देखभाल:
आपके पास वस्त्रं कर्म हों अथवा अधिक, उनकी उचित देखभाल करना अति आवश्यक है। इससे वस्त्रों को लम्बे समय तक प्रयोग में लाया जा सकता है।

प्रश्न 4:
बाजार से वस्त्रों को खरीदते समय आप किन-किन बातों का विशेष ध्यान रखेंगी?
उत्तर:
उपयुक्त वस्त्रों के चयन के अनेक नियम हैं, जिनमें कुछ इतने आवश्यक हैं जिनकी अवहेलना नहीं की जानी चाहिए। वस्त्रों के लिए कपड़ा खरीदते समय निम्नलिखित बातों को ध्यान में रखना आवश्यक है

1. बाजार जाने से पूर्व ही यह निश्चित कर लेना आवश्यक है कि कपड़ा दैनिक उपयोग के लिए खरीदना है अथवा किसी विशिष्ट अवसर के लिए।
2. कपड़ा मजबूत व टिकाऊ होना चाहिए।
3. कपड़े का रंग पक्का होना चाहिए।
4.  कपड़ा सिकुड़न मुक्त है अथवा नहीं, इसकी जाँच कर लेनी चाहिए।
5.  सूती कपड़ों पर सनफोराइज्ड व कलैण्डर्ड की मोहर व ऊनी कपड़ों पर वूलमार्क व आई० एस० आई० मार्क अवश्य देख लेना चाहिए।
6. कई अच्छी दुकानों पर जाकर कपड़े के सही मूल्य का अनुमान लगाकर ही उसे खरीदना चाहिए।

प्रश्न 5:
स्कूल जाने वाले बालक-बालिकाओं की वेशभूषा का विवरण प्रस्तुत कीजिए।
उत्तर:
सामान्य रूप से सभी स्कूलों द्वारा छात्र-छात्राओं की वेशभूषा निर्धारित तथा निश्चित होती है इसलिए स्कूल जाने वाले बालक-बालिकाओं को स्कूल द्वारा निर्धारित यूनिफॉर्म ही धारण करनी चाहिए। यूनिफॉर्म धारण करने से स्कूल के सभी छात्र-छात्राओं में एकरूपता बनी रहती है तथा किसी प्रकार के भेदभाव या ऊँच-नीच के अन्तर के विकसित होने की आशंका नहीं रहती। स्कूल जाने वाले छात्र-छात्राओं की (UPBoardSolutions.com) वेशभूषा को तैयार करवाते समय ध्यान रखना चाहिए कि उनकी वेशभूषा चुस्त तथा अच्छी फिटिंग वाली ही होनी चाहिए। सामान्य रूप से ऐसा कपड़ा चुनना चाहिए जिसमें शीघ्र सिलवटें तथा शिकन न पड़े। स्कूल जाने वाले बच्चों की यूनिफॉर्म के लिए पक्के रंग वाला कपड़ा ही लेना चाहिए तथा उसकी धुलाई भी सरल होनी चाहिए। कपड़ों के अतिरिक्त बच्चों की वेशभूषा में जूतों, मोजों, बेल्ट तथा बैज आदि भी ठीक दशा में होने चाहिए।

प्रश्न 6:
तीज-त्योहार के अवसर पर पहनी जाने वाली वेशभूषा का वर्णन कीजिए।
उत्तर:
तीज-त्योहार के अवसर अपने आप में कुछ विशिष्ट अवसर होते हैं। इन विशिष्ट अवसरों पर वेशभूषा धारण करने में भी विशेष ध्यान रखना चाहिए। इन अवसरों की प्रकृति तथा उत्साह के वातावरण को ध्यान में रखते हुए रंग-बिरंगे आकर्षक तथा भड़कीले वस्त्र भी पहने जा सकते हैं। व्यक्ति अपनी रुचि के अनुसार आधुनिक अथवा पारम्परिक किसी भी प्रकार के वस्त्र पहन सकता है। अनेक महिलाएँ इन अवसरों पर लहँगा-चुनरी, गरारा अथवा भारी साड़ियाँ पहना करती हैं। कुछ किशोरावस्था की लड़कियाँ इन अवसरों पर जीन्स अथवा (UPBoardSolutions.com) स्कर्ट आदि पहनना अधिक पसन्द करती हैं। जहाँ तक बनाव श्रृंगार का प्रश्न है, इन अवसरों पर पर्याप्त छूट होती है। अपनी रुचि एवं आयु के अनुसार पर्याप्त श्रृंगार किया जा सकता है। सुविधा के अनुसार आभूषण भी पहने जा सकते हैं। यदि इस अवसर पर मेले में अथवा भीड़-भाड़ वाले स्थान पर जाना हो, तो सुरक्षा के पहलू को अवश्य ही ध्यान में रखना चाहिए।

प्रश्न 7:
खेल के समय धारण की जाने वाली वेशभूषा का विवरण दीजिए।
उत्तर:
खेल के समय व्यक्ति को विभिन्न प्रकार की शारीरिक क्रियाएँ करनी पड़ती हैं तथा सभी क्रियाएँ प्रायः तीव्र गति से करनी पड़ती हैं। इस स्थिति में शरीर से अधिक पसीना निकलता है। अतः इन तथ्यों को ध्यान में रखकर ही खेल के समय की वेशभूषा का निर्धारण करना चाहिए तथा उसका निर्माण ऐसे कपड़े से किया जाना चाहिए जिसमें अवशोषकता का गुण विद्यमान हो ताकि खेल के समय वो शरीर से निकलने (UPBoardSolutions.com) वाले पसीने को सोख सके। इसके अतिरिक्त खेल के समय धारण की जाने वाली वेशभूषा ऐसे कपड़े की होनी चाहिए जिससे धोना सरल हो। खेल के समय जूतों तथा मोजों का भी विशेष ध्यान रखना चाहिए। हल्के तथा आरामदायक जूते पहनना ही अच्छा रहती है।

प्रश्न 8:
रात्रि-भोज के अवसर पर पहनी जाने वाली वेशभूषा का वर्णन कीजिए।
उत्तर:
रात्रि-भोज के अवसर सामान्य रूप से हर्ष, उल्लास एवं प्रसन्नता के अवसर होते हैं। रात्रि-भोज के अवसर पर अधिक औपचारिकता नहीं होती तथा प्रत्येक व्यक्ति अपनी रुचि के अनुसार आकर्षक एवं सुन्दर वेशभूषा पहन सकता है। इस अवसर पर यदि चाहें तो सीमित रूप से भड़कीली तथा आत्म-प्रदर्शन में सहायक वेशभूषा भी पहनी जा सकती है। महिलाएँ यदि चाहें तो रात्रि-भोज के अवसर पर चमकीले, भड़कीले तथा जरी-गोटे वाले बहुमूल्य वस्त्र भी पहन सकती हैं। आधुनिक फैशन के अनुसार इन अवसरों पर साटन तथा वेलवेट के वस्त्र पहनने का भी प्रचलन है। रात्रि-भोज के अवसर पर वेशभूषा के साथ-साथ अपनी रुचि के अनुसार कम या (UPBoardSolutions.com) अधिक श्रृंगार भी किया जा सकता है। बालों को सजाने के लिए ताजे फूलों का गजरा भी लगाया जा सकता है। यदि चाहें तो परफ्यूम भी इस्तेमाल किया जा सकता है। इस अवसर पर एक निश्चित सीमा के अन्तर्गत रहते हुए शारीरिक सौष्ठव का प्रदर्शन भी किया जा सकता है। रात्रि-भोज के अवसर पर यदि चाहें तो गहने भी पहने जो सकते हैं, परन्तु सुरक्षा का समुचित ध्यान रखना चाहिए।

प्रश्न 9:
यात्रा के समय धारण की जाने वाली वेशभूषा का उल्लेख कीजिए।
उत्तर:
प्रत्येक व्यक्ति को अपने जीवन में कभी-न-कभी छोटी अथवा लम्बी यात्री पर जाना ही। पड़ता है। कुछ व्यक्तियों को तो नियमित रूप से ही यात्रा पर जाना पड़ता है। यात्रा के समय भी व्यक्ति को अपनी वेशभूषा का चुनाव सूझ-बूझपूर्वक करना चाहिए। यात्रा के समय धारण की जाने वाली वेशभूषा का अनिवार्य गुण उसका सुविधादायक होना है। यात्रा के समय वही वेशभूषा धारण की जानी चाहिए, जो लम्बे समय तक सीट पर बैठने अथवा लेटने में सुविधाजनक हो। इस अवसर पर ऐसे वस्त्र धारण करना उत्तम माना जाता है जो (UPBoardSolutions.com) शीघ्र ही क्रश न होते हों अर्थात् शीघ्र ही सिलवटें पड़ने वाले वस्त्र यात्रा के समय धारण नहीं करने चाहिए। सामान्य रूप से यात्रा के समय किसी प्रकार का विशेष बनाव-श्रृंगार नहीं किया जाना चाहिए। जहाँ तक कीमती आभूषणों का प्रश्न है, यात्रा के समय इन्हें बिल्कुल भी धारण नहीं किया जाना चाहिए अन्यथा किसी अनहोनी के घटित होने की निरन्तर आशंका बनी रहती है।

प्रश्न 10:
कामकाजी महिलाओं के लिए कार्य के समय पहनी जाने वाली वेशभूषा का वर्णन कीजिए।
उत्तर:
कामकाजी महिलाओं को अपने कार्य के समय वेशभूषा का विशेष ध्यान रखना चाहिए। इस अवसर पर प्रत्येक स्थिति में वेशभूषा की सौम्यता का विशेष रूप से ध्यान रखना चाहिए। कार्यस्थल की औपचारिकता को अवश्य ध्यान में रखना चाहिए तथा किसी भी स्थिति में महिलाओं को अधिक चटकदार तथा दिखावटी वेशभूषा नहीं पहननी चाहिए। इस समय अधिक श्रृंगार भी नहीं करना चाहिए, केवल हल्का-सा अति आवश्यक श्रृंगार ही करना चाहिए। बिन्दी, हल्की लिपस्टिक तथा माँग भरना (यदि विवाहित हों तो) ही पर्याप्त होता है। (UPBoardSolutions.com) कार्य-स्थल पर खनखनाहट वाले गहने भी नहीं पहनने चाहिए। इससे कार्य-स्थल के वातावरण में व्यवधान उत्पन्न होता है तथा अशोभनीय प्रतीत होता है। सामान्य रूप से कोई तेज सुगन्ध वाला परफ्यूम या तेल भी नहीं लगाना चाहिए। संक्षेप में कहा जा सकता है कि महिलाओं द्वारा कार्य-स्थल पर पहनी जाने वाली वेशभूषा में अनावश्यक आकर्षण तथा भड़कीलेपन का प्रदर्शन नहीं होना चाहिए, बल्कि उसके माध्यम से सौम्यता, गरिमा तथा सादगी का ही प्रदर्शन होना चाहिए।

प्रश्न 11:
शोक के अवसर पर धारण की जाने वाली वेशभूषा का विवरण दीजिए।
उत्तर:
शोक के अवसर पर उल्लास एवं उमंग का नितान्त अभाव होता है। इस अवसर पर परस्पर संवेदना तथा सहानुभूति प्रकट की जाती है। शोक के अवसर पर जहाँ तक हो सके बिल्कुल सादी वेशभूषा ही धारण की जानी चाहिए। हमारे समाज में पारम्परिक रूप से इस अवसर पर सफेद अथवा हल्के (UPBoardSolutions.com) रंगों की वेशभूषा ही धारण की जाती है। कुछ समाजों में शोक के अवसर पर काले रंग की वेशभूषा धारण की जाती है। शोक के अवसर पर सादी वेशभूषा धारण करने के साथ ही साथ किसी प्रकार का बनाव-श्रृंगार भी नहीं किया जाता। संक्षेप में कहा जा सकता है कि शोक के अवसर पर व्यक्ति की वेशभूषा से सादगी का प्रदर्शन होना चाहिए, न कि दिखावे तथा आकर्षण का।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:
व्यक्तिगत सज्जा क्या है?
उत्तर:
व्यक्तिगत सज्जा से तात्पर्य उस महत्त्वपूर्ण कारक से है जो व्यक्ति के बाहरी व्यक्तित्व को निखारने में उल्लेखनीय भूमिका निभाता है। इस कारक के अन्तर्गत सामान्य रूप से उचित वेशभूषा, श्रृंगार के ढंग, बालों को सँवारने के ढंग, बातचीत करने के ढंग, उठने-बैठने के ढंग तथा व्यक्ति के हाव-भावों को सम्मिलित किया जाता है।

प्रश्न 2:
व्यक्तिगत सज्जा क्यों आवश्यक है?
उत्तर:
व्यक्तिगत सज्जा मनुष्य की रुचि एवं रहन-सहन के स्तर की परिचायक होती है। उपयुक्त सज्जा मनुष्य को आत्मविश्वास, सामाजिक प्रतिष्ठा एवं मानसिक प्रसन्नता प्रदान करती है तथा उसके बाहरी व्यक्तित्व को आकर्षक एवं प्रभावशाली बनाती है।

प्रश्न 3:
व्यक्तिगत सज्जा का मूल आधार क्या है?
उत्तर:
उपयुक्त वेशभूषा व्यक्तिगत सज्जा का मूल आधार है।

प्रश्न 4:
वेशभूषा के लिए कपड़े का चुनाव करते समय ध्यान रखने योग्य मुख्य गुण क्या हैं?
उत्तर:
वेशभूषा के लिए कपड़ा

1.  आकर्षक एवं आरामदायक होना चाहिए,
2. मजबूत एवं टिकाऊ होना चाहिए,
3. सरलता से धुलने वाला होना चाहिए तथा
4.  आर्थिक बजट के अनुरूप होना चाहिए।

प्रश्न 5:
ग्रीष्म ऋतु में कौन-से वस्त्र उपयुक्त रहते हैं?
उत्तर:
ग्रीष्म ऋतु में सूती वस्त्र अधिक उपयुक्त रहते हैं।

प्रश्न 6:
ग्रीष्म ऋतु के वस्त्रों में कौन-कौन सी मुख्य विशेषताएँ होनी चाहिए?
उत्तर:
ग्रीष्म ऋतु के वस्त्र पसीना सोखने वाले, महीन, सफेद अथवा हल्के रंगों के होने चाहिए।

प्रश्न 7:
रसोई गृह में नायलॉन व टेरीलीन के वस्त्र पहनने से क्या हानि हो सकती है?
उत्तर:
ये वस्त्र आग शीघ्र पकड़ते हैं; अतः इन्हें भोजन बनाते समय नहीं पहनना चाहिए।

प्रश्न 8:
छोटे बच्चों के वस्त्र किस प्रकार के होने चाहिए?
उत्तर:
बच्चों के लिए सदैव चमकीले एवं भड़कीले वस्त्र लेने चाहिए। इसके साथ-साथ इस बात का भी ध्यान रखना चाहिए कि बच्चों के वस्त्रों का कपड़ा नर्म तथा मुलायम होना चाहिए।

प्रश्न 9:
वृद्ध व्यक्तियों को किस रंग के वस्त्र धारण करने चाहिए ?
उत्तर:
वृद्ध व्यक्तियों को सफेद या हल्के रंगों के वस्त्र ही धारण करने चाहिए।

प्रश्न 10:
अिंक पूफ का क्या अर्थ है?
उत्तर:
कुछ रासायनिक पदार्थों का प्रयोग कर कपड़ा सिकुड़ने से मुक्त बनाया जाता है, इसी को श्रिंक पूफ कहते हैं।

प्रश्न 11:
मौसम के अनुसार वस्त्र पहनना क्यों आवश्यक है?
उत्तर:
मौसम के अनुसार वस्त्र पहनना इसलिए आवश्यक है जिससे कि मौसम के प्रभाव से बचा जा सके।

प्रश्न 12:
वर्षा ऋतु में कौन-से वस्त्रों से अधिक आराम मिलता है?
उत्तर:
वर्षा ऋतु में सूती व महीन वस्त्रों से अधिक आराम मिलता है।

वस्तुनिष्ठ प्रश्न

प्रश्न:
प्रत्येक प्रश्न के चार वैकल्पिक उत्तर दिए गए हैं। इनमें से सही विकल्प चुनकर लिखिए

(1) व्यक्तिगत सज्जा के लिए आवश्यक है
(क) उचित वेशभूषा,
(ख) श्रृंगार एवं उचित केश विन्यास,
(ग) बात करने तथा उठने-बैठने का उचित ढंग,
(घ) उपर्युक्त सभी।

(2) वस्त्रों का चुनाव करते समय ध्यान में रखना चाहिए
(क) कपड़े का गुण,
(ख) कपड़े की सुन्दरता तथा आकर्षण,
(ग) कपड़े का मूल्य,
(घ) ये सभी।

(3) खेल के समय वस्त्र धारण करने चाहिए ।
(क) मोटे तथा मजबूत,
(ख) कृत्रिम तन्तुओं से बने,
(ग) पसीना सोखने की क्षमता वाले,
(घ) पुराने तथा घटिया।

(4) घरेलू जीवन में उपयोग के लिए सर्वोत्तम वस्त्र हैं
(क) सूती,
(ख) रेशमी,
(ग) जरीदार,
(घ) आधुनिक फैशन के।

(5) सफेद अथवा हल्के रंगों के वस्त्र पहनने चाहिए
(क) शीत ऋतु में,
(ख) ग्रीष्म ऋतु में,
(ग) वर्षा ऋतु में,
(घ) इन सभी में।।

(6) व्यक्तिगत सज्जा से वृद्धि होती है
(क) सामाजिक प्रतिष्ठा में,
(ख) व्यक्तित्व के आकर्षण में,
(ग) मानसिक सन्तोष में,
(घ) इन सभी में।

(7) काले रंग के व्यक्ति को वस्त्र पहनने चाहिए
(क) सफेद रंग के,
(ख) हल्के रंग के,
(ग) गहरे रंग के,
(घ) किसी भी रंग के।

(8) लम्बे कद की महिलाओं को साड़ी व ब्लाउज पहनने चाहिए
(क) समान रंग के,
(ख) भिन्न रंग के
(ग) सफेद रंग के,
(घ) काले रंग के।

(9) शिशु के वस्त्र बने होने चाहिए
(क) सूती तन्तु से,
(ख) टेरीलीन के तन्तु से,
(ग) नायलॉन के तन्तु से,
(घ) किसी भी तन्तु से।।

(10) स्कूल जाने वाले बालक-बालिकाओं को धारण करनी चाहिए
(क) रंग-बिरंगी वेशभूषा,
(ख) मजबूत वेशभूषा,
(ग) सस्ती वेशभूषा,
(घ) स्कूल द्वारा निर्धारित वेशभूषा।

(11) पसीना सोखने की क्षमता वाले वस्त्र हैं
(क) ऊनी वस्त्र,
(ख) टेरीलीन के वस्त्र,
(ग) रेशमी वस्त्र,
(घ) सूती वस्त्र।

उत्तर:
(1) (घ) उपर्युक्त सभी,
(2) (घ) इन सभी,
(3) (ग) पसीना सोखने की क्षमता वाले,
(4) (क) सूती,
(5) (ख) ग्रीष्म ऋतु में,
(6) (घ) ये सभी में,
(7) (ख) हल्के रंग के,
(8) (ख) भिन्न रंग के,
(9) (क) सूती तन्तु से,
(10) (घ) स्कूल द्वारा निर्धारित वेशभूषा,
(11) (घ) सूती वस्त्र।

We hope the UP Board Solutions for Class 9 Home Science Chapter 11 व्यक्तिगत सज्जा : उचित वेशभूषा help you. If you have any query regarding UP Board Solutions for Class 9 Home Science Chapter 11 व्यक्तिगत सज्जा : उचित वेशभूषा, drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 9 Hindi Chapter 6 निष्ठामूर्ति कस्तूरबा (गद्य खंड)

These Solutions are part of UP Board Solutions for Class 9 Hindi. Here we have given UP Board Solutions for Class 9 Hindi Chapter 6 निष्ठामूर्ति कस्तूरबा (गद्य खंड).

विस्तृत उत्तरीय प्रश्न 

प्रश्न 1. निम्नांकित गद्यांशों में रेखांकित अंशों की सन्दर्भ सहित व्याख्या और तथ्यात्मक प्रश्नों के उत्तर दीजिए-
(1) चाहे दक्षिण अफ्रीका में हों या हिन्दुस्तान में, सरकार के खिलाफ लड़ाई के समय जब-जब चारित्र्य का तेज प्रकट करने का मौका आया कस्तूरबा हमेशा इस दिव्य कसौटी से सफलतापूर्वक पार हुई हैं।
             इससे भी विशेष बात यह है कि बड़ी तेजी से बदलते हुए आज के युग में भी आर्य सती स्त्री का जो आदर्श हिन्दुस्तान ने अपने हृदय में कायम रखा है, उस आदर्श की जीवित प्रतिमा के रूप में राष्ट्र पूज्य कस्तूरबा को पहचानता। है। इस तरह की विविध लोकोत्तर योग्यता के कारण आज सारा राष्ट्र कस्तूरबा की पूजा करता है।
प्रश्न
(1) गद्यांश का संदर्भ लिखिए।
(2) रेखांकित अंश की व्याख्या कीजिए।
(3) किस योग्यता के कारण सारा राष्ट्र कस्तूरबा की पूजा करता है?

उत्तर-

1. सन्दर्भ- प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक ‘हिन्दी गद्य’ के ‘निष्ठामूर्ति कस्तूरबा’ नामक पाठ से अवतरित है। इसके लेखक उच्चकोटि के विचारक काका कालेलकर हैं। प्रस्तुत अवतरण में कस्तूरबा के गुणों का वर्णन किया गया है।
2. रेखांकित अंशों की व्याख्या- कस्तूरबा का वर्णन करते हुए लेखक कहता है कि चाहे भारत में हो या दक्षिण अफ्रीका में सरकार के खिलाफ संघर्ष के अवसर पर कस्तूरबा पीछे नहीं रहीं और उसका सफलतापूर्वक संचालन किया। इससे भी महत्त्वपूर्ण बात यह है कि कस्तूरबा ने आदर्श भारतीय नारी के स्वरूप का विधिवत् पालन किया है। भारत ने स्त्री का जो आदर्श अपने (UPBoardSolutions.com) हृदय में धारण किया है, कस्तूरबा उसकी प्रतिमूर्ति थीं। इन्हीं गुणों के कारण कस्तूरबा भारतीय समाज में समादृत हैं।
3. विविध लोकोत्तर योग्यता के कारण आज सारा राष्ट्र कस्तूरबा की पूजा करता है।

(2) दुनिया में दो अमोघ शक्तियाँ हैं-शब्द और कृति । इसमें कोई शक नहीं कि ‘शब्दों’ ने सारी पृथ्वी को हिला दिया है। किन्तु अन्तिम शक्ति तो ‘कृति’ की है। महात्मा जी ने इन दोनों शक्तियों की असाधारण उपासना की है। कस्तूरबा ने इन दोनों शक्तियों में से अधिक श्रेष्ठ शक्ति कृति की नम्रता के साथ उपासना करके सन्तोष माना और जीवनसिद्धि प्राप्त की।
प्रश्न
(1) उपर्युक्त गद्यांश का संदर्भ लिखिए।
(2) रेखांकित अंश की व्याख्या कीजिए।
(3) कस्तूरबा कैसी महिला थीं?
(4) शब्द और कृति क्या है?
(5) गाँधी जी ने किसकी उपासना की?
[शब्दार्थ-अमोघ = अचूक। कृति = रचना। सिद्धि = जीवन की श्रेष्ठता।]

उत्तर-

1. सन्दर्भ- प्रस्तुत पद्यावतरण हमारी पाठ्य-पुस्तक ‘हिन्दी गद्य’ में संकलित एवं काका कालेलकर द्वारा लिखित । ‘निष्ठामूर्ति कस्तूरबा’ नामक निबन्ध से लिया गया है जो गाँधी युग के जलते चिराग’ नामक पुस्तक से उद्धृत है। लेखक कस्तूरबा के जीवन की विशेषताओं का उल्लेख करते हुए विश्व की महानतम् शक्तियों (शब्द और कृति) में ‘बा’ को ‘कृति’ की उपासिका बतलाता है।
2. रेखांकित अंशों की व्याख्या- शब्द अर्थात् ‘कहना’ तथा कृति अर्थात् ‘करना’ वास्तव में इस संसार की ये ही दो अचूक शक्तियाँ हैं। इसमें कोई संदेह नहीं कि शब्दों की शक्ति ऐसी है जिसने सारे विश्व को प्रभावित कर रखा है, किन्तु शब्दों की अपेक्षा ‘कृति’ वाली शक्ति और भी महत्त्व रखती है। महात्मा गाँधी ने उक्त दोनों शक्तियों की असाधारण साधना की थी अर्थात् उन्होंने कथनी (UPBoardSolutions.com) और करनी में सामंजस्य स्थापित किया था, किन्तु कस्तूरबा ने सबसे पहले महत्त्वपूर्ण शक्ति ‘कृति’ की नम्रतापूर्वक साधना की और अपने जीवन को सफल सिद्ध किया। ‘बा’ ने केवल काम करने को ही महत्त्व दिया और इसी के बल पर वे सर्वपूज्य हो गयीं। दक्षिणी अफ्रीका की सरकार ने गाँधी जी को जब जेल भेज दिया तो कस्तूरबा ने अपना बचाव तक नहीं किया और न कहीं निवेदन किया। वे एक दृढ़ संकल्प वाली महिला थीं।
3. कस्तूरबा एक दृढ़ संकल्प वाली महिला थीं।
4. शब्द और कृति दो अमोघ शक्तियाँ हैं।
5. गाँधी जी ने शब्द और कृति दोनों शक्तियों की असाधारण उपासना की है।

(3) यह सब श्रेष्ठता या महत्ता कस्तूरबा में कहाँ से आयी? उनकी जीवन-साधना किस प्रकार की थी? शिक्षण के द्वारा उन्होंने बाहर से कुछ नहीं लिया था। सचमुच, (UPBoardSolutions.com) उनमें तो आर्य आदर्श को शोभा देनेवाले कौटुम्बिक सद्गुण ही थे। असाधारण मौका मिलते ही और उतनी ही असाधारण कसौटी आ पड़ते ही उन्होंने स्वभावसिद्ध कौटुम्बिक सद्गुण व्यापक किये और उनके जोरों पर हर समय जीवन-सिद्धि हासिल की। सूक्ष्म प्रमाण में या छोटे पैमाने पर जो शुद्ध साधना की जाती है उसका तेज इतना लोकोत्तरी होता है कि चाहे कितना ही बड़ा प्रसंग आ पड़े, व्यापक प्रमाण में कसौटी हो, चारित्र्यवान् मनुष्य को अपनी शक्ति का सिर्फ गुणाकार ही करने का होता है।
प्रश्न
(1) उपर्युक्त गद्यांश का संदर्भ लिखिए।
(2) रेखांकित अंश की व्याख्या कीजिए।
(3) चारित्र्यवान् मनुष्य को अपनी शक्ति का क्या करना होता है?
(4) चारित्र्यवान व्यक्ति की क्या विशेषता होती है? |
(5) किस साधना का तेज लोकोत्तरी होता है?

उत्तर-

1. सन्दर्भ- प्रस्तुत गद्यावतरण हमारी पाठ्य-पुस्तक ‘हिन्दी गद्य’ में संकलित एवं काका कालेलकर द्वारा लिखित ‘निष्ठामूर्ति कस्तूरबा’ पाठ से अवतरित है। प्रस्तुत अवतरण में कस्तूरबा के कौटुम्बिक सद्गुणों का वर्णन है।
2. रेखांकित अंशों की व्याख्या- कस्तूरबा ने शिक्षण द्वारा कुछ नहीं ग्रहण किया था, बल्कि उन्होंने जो कुछ सीखा-समझा वह व्यवहारतः था । वास्तव में उनमें आदर्श कौटुम्बिक सद्गुण थे, बल्कि अवसर मिलने पर उन्होंने स्वभाव सिद्ध पारिवारिक सद्गुणों का विस्तार किया और (UPBoardSolutions.com) उसी के बल पर जीवन में सफलता प्राप्त की। छोटे पैमाने पर जो साधना की जाती है उसमें असीम शक्ति होती है। चरित्रवान व्यक्ति सदैव कसौटी पर खरा उतरता है। कस्तूरबा एक चरित्रवान् महिला थीं। अपने चारित्रिक गुणों और कौटुम्बिक सदगुणों के कारण उन्होंने भारतीय समाज में ख्याति प्राप्त की।
3. चारित्र्यवान् मनुष्य को अपनी शक्ति का सिर्फ गुणाकर ही करना होता है।
4. चारित्र्यवान् व्यक्ति की विशेषता है कि उसमें कौटुम्बिक सद्गुण होते हैं।
5. शुद्ध साधना का तेज लोकोत्तरी होता है।

प्रश्न 2. काका कालेलकर का जीवन-परिचय देते हुए उनके कृतित्व पर प्रकाश डालिए।

प्रश्न 3. भाषा-शैली को स्पष्ट करते हुए कालेलकर जी की साहित्यिक विशेषताएँ लिखिए।

प्रश्न 4, काका कालेलकर का जीवन एवं साहित्यिक परिचय दीजिए।
अथवा काका कालेलकर का साहित्यिक परिचय देते हुए उनकी रचनाओं का उल्लेख कीजिए।

काका कालेलकर
( स्मरणीय तथ्य )

जन्म-सन् 1885 ई० । मृत्यु-सन् 1981 ई०। जन्म-स्थान- महाराष्ट्र में सतारा जिला।
अन्य बातें -हिन्दी, गुजराती, बंगला, अंग्रेजी, मराठी भाषाओं पर पूरा अधिकार, राष्ट्रभाषा का प्रचार ।
भाषा- सरल, ओजस्वी, प्रवाहपूर्ण ।
शैली- सजीव, प्रभावपूर्ण, कल्पना की उड़ान।
साहित्य- संस्मरण, यात्रा वर्णन, सर्वोदय, हिमालय प्रवास, लोकमाता, उस पार के पड़ोसी, जीवन लीला, बापू की झाँकियों, जीवन का काव्य आदि।

• जीवन-परिचय- काका कालेलकर का जन्म महाराष्ट्र के सतारा जिले में 1 दिसम्बर, सन् 1885 ई० को हुआ था। कालेलकर हिन्दी के उन उन्नायक साहित्यकारों में से हैं जिन्होंने अहिन्दी भाषा क्षेत्र का होकर भी हिन्दी सीखकर उसमें लिखना प्रारम्भ किया। उन्होंने राष्ट्रभाषा के प्रचार-कार्य को राष्ट्रीय कार्यक्रम के अन्तर्गत माना है। काका कालेलकर ने सबसे पहले हिन्दी लिखी और फिर (UPBoardSolutions.com) दक्षिण भारत में हिन्दी प्रचार को कार्य प्रारम्भ किया। अपनी सूझबूझ, विलक्षणता और व्यापक अध्ययन के कारण उनकी गणना देश के प्रमुख अध्यापकों एवं व्यवस्थापकों में होती है। काका साहब उच्चकोटि के विचारक एवं विद्वान् थे। भाषा प्रचार के साथ-साथ इन्होंने हिन्दी और गुजराती में मौलिक रचनाएँ भी की हैं। सन् 1981 ई० में आपकी मृत्यु हो गयी।
• कृतियाँ- काको साहब की कृतियाँ निम्नलिखित हैं –
  1. निबन्ध-संग्रह- जीवन-साहित्य, जीवन का काव्य-इन विचारात्मक निबन्धों में इनके संत व्यक्तित्व और प्राचीन भारतीय संस्कृति की सुन्दर झलक मिलती है।
  2. आत्म-चरित्र- ‘धर्मोदय’ तथा ‘जीवन लीला’–इनमें काका साहब के यथार्थ व्यक्तित्व की सजीव झाँकी है।
  3. यात्रा-वृत्त- ‘हिमालय-प्रवास’, ‘लोकमाता’, ‘यात्रा’, ‘उस पार के पड़ोसी’ आदि प्रसिद्ध यात्रावृत्त हैं।
  4. संस्मरण- ‘संस्मरण’ तथा ‘बापू की झाँकी’-इन रचनाओं में महात्मा गाँधी के जीवन का चित्रण है।
  5. सर्वोदय-साहित्य- आपकी ‘सर्वोदय’ रचना में सर्वोदय से सम्बन्धित विचार हैं।
  6. साहित्यिक परिचय- काका साहब एक सिद्धहस्त मॅझे हुए लेखक थे। किसी भी सुन्दर दृश्य का वर्णन अथवा पेचीदी समस्या का सुगम विश्लेषण उनके लिए आनन्द का विषय है। उनके यात्रा-वर्णन में पाठकों को देश-विदेश के भौगोलिक विवरणों के साथ-साथ वहाँ की विभिन्न समस्याओं तथा सामाजिक एवं सांस्कृतिक विशेषताओं की जानकारी भी (UPBoardSolutions.com) हो जाती है। काका साहब देश की विभिन्न भाषाओं के अच्छे जानकार हैं। उन्होंने प्रायः अपने ग्रन्थों का अनुवाद विभिन्न भारतीय भाषाओं में स्वयं प्रस्तुत किया है। इनके विचारों में संस्कृति और परम्पराओं में एक नवीन क्रान्तिकारी दृष्टिकोणों का समावेश रहता है।
  7. भाषा-शैली- काका साहब की भाषा अत्यन्त ही सरल और ओजस्वी है। उसमें एक आकर्षक धारा है जिसमें सूक्ष्म दृष्टि एवं विवेचनात्मक तर्कपूर्ण विचार की अभिव्यक्ति होती है। उनकी भाषा में एक नयी चित्रमयता के साथ-साथ विचारों की मौलिकता के स्पष्ट दर्शन होते हैं। भाषा के साथ-साथ उनकी शैली अत्यन्त ही ओजस्वी है। इन्होंने अपने निबन्धों में प्राय: व्याख्यात्मक शैली का प्रयोग किया है। कुछ रचनाओं में प्रबुद्ध विचारक के उपदेशात्मक शैली के दर्शन होते हैं ।

लघु उत्तरीय प्रश्न

प्रश्न 1. कस्तूरबा में एक आदर्श भारतीय नारी के कौन-कौन से गुण विद्यमान थे?
उत्तर- कस्तूरबा गाँधी एक पतिव्रता महिला थीं। वे अत्यन्त धार्मिक महिला थीं। गीता और तुलसी कृत रामायण में उनकी अगाध श्रद्धा थी। आलस्य नाम की चीज उनके अन्दर थी ही नहीं। आश्रम में कस्तूरबा लोगों के लिए माँ के समान थीं।

प्रश्न 2. स्वयं में शिक्षा के अभाव की पूर्ति ‘बा’ ने किस प्रकार की?
उत्तर- कस्तूरबा अनपढ़ थीं। उनका भाषा-ज्ञान सामान्य देहाती से अधिक नहीं था। बापू के साथ वे दक्षिण अफ्रीका में रहीं इसलिए वह कुछ अंग्रेजी समझने लगी थीं।

प्रश्न 3. ‘शब्द’ और ‘कृति’ से लेखक का क्या तात्पर्य है? कस्तूरबा के सम्बन्ध में सोदाहरण स्पष्ट कीजिए।
उत्तर- दुनिया में दो अमोघ शक्तियाँ हैं-शब्द और कृति। इसमें कोई शक नहीं है कि शब्दों ने सारी पृथ्वी को हिला दिया है, किन्तु अन्तिम शक्ति तो कृति ही है। महात्मा जी (UPBoardSolutions.com) ने इन दोनों शक्तियों की असाधारण उपासना की है। कस्तूरबा ने इन दोनों शक्तियों में से अधिक श्रेष्ठ शक्ति कृति की नम्रता के साथ उपासना करके सन्तोष माना और जीवनसिद्धि प्राप्त की।

प्रश्न 4. ‘निष्ठामूर्ति कस्तूरबा’ पाठ से दस महत्त्वपूर्ण वाक्य लिखिए।
उत्तर- कस्तूरबा अनपढ़ थीं। उनका भाषा-ज्ञान सामान्य देहाती से अधिक नहीं था। कस्तूरबा को गीता पर असाधारण श्रद्धा थी। उनकी निष्ठा का पात्र दूसरा ग्रन्थ था तुलसीकृत रामायण। कस्तूरबा रामायण भी ठीक ढंग से कभी पढ़ न सकीं। आश्रम में कस्तूरबा हम लोगों के लिए माँ के समान थीं। आज के जमाने में स्त्री-जीवन-सम्बन्ध के हमारे आदर्श हमने काफी बदल लिये हैं।

प्रश्न 5. कस्तूरबा से सम्बन्धित संक्षिप्त गद्यांश लिखिए।
उत्तर- वह भले ही अशिक्षित रही हों, संस्था चलाने की जिम्मेदारी लेने की महत्त्वाकांक्षा भले ही उनमें कभी जागी न हो, लेकिन देश में क्या चल रहा है उसकी सूक्ष्म जानकारी वह प्रश्न पूछकर या अखबारों के ऊपर नजर डालकर प्राप्त कर ही लेती थीं।

प्रश्न 6. कस्तूरबा के ‘मूक किन्तु तेजस्वी बलिदान’ की कहानी लिखिए।
उत्तर- सती कस्तूरबा सिर्फ अपने संस्कारों के कारण पातिव्रत्य धर्म को, कुटुम्ब वत्सलता को और तेजस्विता को चिपकाये रहीं और उसी के बल पर महात्मा जी के महात्म्य की (UPBoardSolutions.com) बराबरी में आ सकीं। आज हिन्दू, मुस्लिम, सिख, ईसाई, पारसी, बौद्ध आदि अनेक धर्मों के लोगों का यह विशाल देश अत्यन्त निष्ठा के साथ कस्तूरबा की पूजा करता है।

प्रश्न 7. कस्तूरबा की मितभाषिता एवं कर्तव्यनिष्ठा के गुणों को प्रकट करनेवाले प्रसंगों एवं घटनाओं का वर्णन अपने शब्दों में कीजिए।
उत्तर- आश्रम में चाहे बड़े-बड़े नेता आयें या मामूली कार्यकर्ता, उनके खाने-पीने का प्रबन्ध कस्तूरबा ही करती थीं। प्राणघातक बीमारी से मुक्त होने के बाद रसोई के कार्यों में हाथ बँटाती थीं । कस्तूरबा में आर्य आदर्श को शोभा देनेवाले कौटुम्बिक सद्गुण थे।

प्रश्न 8. ‘निष्ठामूर्ति कस्तूरबा’ पाठ की भाषा-शैली की दो विशेषताएँ लिखिए।
उत्तर- ‘निष्ठामूर्ति कस्तूरबा’ पाठ की भाषा-शैली विवेचनात्मक है। भाषा अपेक्षाकृत संस्कृतनिष्ठ एवं परिष्कृत है।

प्रश्न 9. कस्तूरबा के गुणों को अपने शब्दों में लिखिए।
उत्तर- कस्तूरबा आदर्श भारतीय महिला थीं। वे पतिव्रता स्त्री थीं। वे आश्रम में बच्चों की देखभाल करती थीं। आश्रम में कस्तूरबा लोगों के लिए माँ समान थीं। गीता और रामायण में उनकी अगाध श्रद्धा थी।

प्रश्न 10. काका कालेलकर की भाषा-शैली की दो विशेषताएँ लिखिए।
उत्तर- काका कालेलकर की भाषा परिष्कृत खड़ीबोली है। उसमें प्रवाह, ओज तथा अकृत्रिमता है। इन्होंने विवेचनात्मक, विवरणात्मक तथा व्यंग्यात्मक शैलियों का प्रयोग किया है।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1. काका कालेलकर की दो रचनाओं के नाम लिखिए।
उत्तर- काका कालेलकर की दो रचनाएँ जीवन काव्य तथा हिमालय प्रवास हैं।

प्रश्न 2. काका कालेलकर किस युग के लेखक माने जाते हैं?
उत्तर- काका कालेलकर शुक्ल एवं शुक्लोत्तर युग के लेखक माने जाते हैं।

प्रश्न 3. राष्ट्रभाषा प्रचार को राष्ट्रीय कार्यक्रम मानने वाले हिन्दी लेखक का नाम बताइए।
उत्तर- राष्ट्रभाषा प्रचार को राष्ट्रीय कार्यक्रम मानने वाले हिन्दी लेखक का नाम है काका कालेलकर ।

प्रश्न 4. कस्तूरबा कौन थीं?
उत्तर- कस्तूरबा महात्मा गाँधी की पत्नी थीं।

प्रश्न 5. निम्नलिखित में से सही वाक्य के सम्मुख सही (√) का चिह्न लगाइए-
(अ) कस्तूरबा अनपढ़ थीं।                                                                  (√)
(ब) ‘निष्ठामूर्ति कस्तूरबा’ पाठ विवेचनात्मक शैली में लिखा गया है।       (√)
(स) कालेलकर जी का सम्पर्क टैगोर से नहीं था।                                  (×)
(द) दुनिया में ‘शब्द’ और ‘कृति’ दो अमोघ शक्तियाँ हैं।                         (√)

व्याकरण-बोध

प्रश्न 1. निम्नलिखित शब्दों में सन्धि-विच्छेद करते हुए सन्धि का नाम भी लिखिए-
लोकोत्तर, सत्याग्रह, गुणाकर, महत्त्वाकांक्षा, एकाक्षरी, प्रत्युत्पन्न।
उत्तर-
लोकोत्तर        –    लोक + उतर           – गुण सन्धि
सत्याग्रह         –    सत्य + आग्रह          – दीर्घ सन्धि
गुणाकर          –     गुण + आकर         – दीर्घ सन्धि
महत्त्वाकांक्षा   –    महत्त्व + आकांक्षा   – दीर्घ सन्धि
एकाक्षरी         –    एक + अक्षरी          –  दीर्घ सन्धि
प्रत्युत्पन्न          –   प्रति + उत्पन्न           – यण सन्धि

प्रश्न 2.निम्नलिखित में समास-विग्रह करते हुए समास का नाम लिखिए-
माँ-बाप, देश-सेवा, राष्ट्रमाता, प्राणघातक, बन्धनमुक्ते, धर्मनिष्ठा।
उत्तर-
माँ-बाप      =  माँ और बाप           =    द्वन्द्व समास
देश-सेवा    =  देश के लिए सेवा    =    सम्प्रदान तत्पुरुष
राष्ट्रमाता     =  राष्ट्र की माता           =   सम्बन्ध तत्पुरुष
प्राणघातक =  प्राण के लिए घातक   =   सम्प्रदान तत्पुरुष
बन्धनमुक्त  =  बंधन से मुक्त           =   करण तत्पुरुष
धर्मनिष्ठा     =  धर्म में निष्ठा              =    अधिकरण तत्पुरुष

प्रश्न 3. निम्नलिखित विदेशज शब्दों के लिए हिन्दी शब्द लिखिए –
अमलदार, कायम, जिद्द, हासिल, कतई, खुद।
उत्तर-
अमलदार –   ग्राह्य
जिद्द         –    हठ
कतई       –   बिल्कुल
कायम      –   स्थिर
हासिल     –    प्राप्त
खुद          –   स्वयं

We hope the UP Board Solutions for Class 9 Hindi Chapter 6 निष्ठामूर्ति कस्तूरबा (गद्य खंड) help you. If you have any query regarding UP Board Solutions for Class 9 Hindi Chapter 6 निष्ठामूर्ति कस्तूरबा (गद्य खंड), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 9 Maths Chapter 10 Circle (वृत्त)

These Solutions are part of UP Board Solutions for Class 9 Maths. Here we have given UP Board Solutions for Class 9 Maths Chapter 10 Circle (वृत्त).

प्रश्नावली 10.1

प्रश्न 1.
खाली स्थान भरिए।
(i) वृत्त का केन्द्र वृत्त के ……………….. में स्थित है (बहिर्भाग/अभ्यन्तर)।
(ii) एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के ………… में स्थित होता है (बहिर्भाग/अभ्यन्तर)।
(iii) वृत्त की सबसे बड़ी जीवा वृत्त का ……………… होती है।
(iv) एक चाप ………………… होता है, जब इसके सिरे एक व्यास के सिरे हों।
(v) वृत्तखण्ड एक चाप तथा ……………….. के बीच का भाग होता है।
(vi) एक वृत्त, जिस तल पर स्थित है, उसे ………………….. भागों में विभाजित करता है।
हल :
(i) वृत्त का केन्द्र वृत्त के अभ्यन्तर में स्थित होता है।
(ii) एक बिन्दु, जिसकी वृत्त के केन्द्र से दूरी त्रिज्या से अधिक हो, वृत्त के बहिर्भाग में स्थित होता है।
(iii) वृत्त की सबसे बड़ी जीवा वृत्त का व्यास होती है।
(iv) एक चाप अर्धवृत्त होता है, जब इसके सिरे एक व्यास के सिरे हों।
(v) वृत्तखण्ड एक चाप तथा जीवा के बीच का भाग होता है।
(vi) एक वृत्त, जिस तल पर स्थित है, उसे तीन भागों में विभाजित करता है।

प्रश्न 2.
लिखिए, सत्य या असत्य। अपने उत्तर के कारण दीजिए।
(i) केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखण्ड वृत्त की त्रिज्या होती है।
(ii) एक वृत्त में समान लम्बाई की परिमित जीवाएँ होती हैं।
(iii) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भाग दीर्घ चाप होता है।
(iv) वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।
(v) त्रिज्यखण्ड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।
(vi) वृत्त एक समतल आकृति है।
हल :
(i) केन्द्र को वृत्त पर किसी बिन्दु से मिलाने वाला रेखाखण्ड वृत्त की त्रिज्या होती है’ कथन सत्य है।
(ii) एक वृत्त में समान लम्बाई की परिमित जीवाएँ होती हैं कथन असत्य है क्योंकि किसी वृत्त में समान लम्बाई की अपरिमित जीवाएँ होती हैं।
(iii) यदि एक वृत्त को तीन बराबर चापों में बाँट दिया जाए, तो प्रत्येक भागे दीर्घ चाप होता है’ कथन असत्य है। क्योंकि वृत्त के आधे से कम भाग को अन्तरित करने वाला चाप लघु चाप होता है।
(iv) ‘वृत्त की एक जीवा, जिसकी लम्बाई त्रिज्या से दो गुनी हो, वृत्त का व्यास है।’ कथन सत्य है।
(v) ‘त्रिज्यखण्ड, जीवा एवं संगत चाप के बीच का क्षेत्र होता है।’ कथन असत्य है।
(vi) ‘वृत्त एक समतल आकृति है’ कथन सत्य है।

प्रश्नावली 10.2

प्रश्न 1.
याद कीजिए कि दो वृत्त सर्वांगसम होते हैं, यदि उनकी त्रिज्याएँ बराबर हों। सिद्ध कीजिए कि सर्वांगसम वृत्तों की बराबर जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करती हैं।

हल :
दिया है : केन्द्र O वाला एक वृत्त है जिसकी एक जीवा AB है।
केन्द्र O वाला एक अन्य वृत्त है जिसकी एक जीवा CD है। दोनों वृत्त सर्वांगसम हैं और जीवा AB जीवा CD के बराबर है।
जीवा AB केन्द्र O पर ∠ AOB तथा जीवा CD केन्द्र O’ पर ∠ CO’D अन्तरित करती है।
सिद्ध करना है : ∠AOB = ∠COD
रचना : त्रिज्याएँ OA, OB, O’C व O’D खींचिए।
उपपत्ति: ∆AOB तथा ∆CO’D में,
AB = CD (दिया है।)
OA = O’C (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं।)
OB = O’D (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं)
∆AOB = ∆COD (S.S.S. से)
∠AOB = ∠COD (C.P.C.T.)
Proved.

प्रश्न 2.
सिद्ध कीजिए कि यदि सर्वांगसम वृत्तों की जीवाएँ उनके केन्द्रों पर बराबर कोण अन्तरित करें, तो जीवाएँ बराबर होती हैं।

हल :
दिया है : O तथा O’ केन्द्रों वाले दो सर्वांगसम वृत्त हैं। जिनकी जीवाएँ AB व CD उनके केन्द्रों O तथा O’ पर क्रमशः ∠AOB व ∠CO’D
इस प्रकार अन्तरित करती हैं कि ∠AOB = ∠ CO’D है।
सिद्ध करना है : जीवा AB = जीवा CD
उपपत्ति: ∆AOB और ∆CO’D में,
OA = O’C (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं।)
∠AOB = ∠ COD (दिया है।)
OB = O’D (सर्वांगसम वृत्तों की त्रिज्याएँ बराबर होती हैं।)
∆AOB = ∆COD (S.A.S. से)
AB = CD (C.P.C.T.)
अतः जीवा AB = जीवा CD
Proved.

प्रश्नावली 10.3

प्रश्न 1.
वृत्तों के कई युग्म (जोड़े) खींचिए। प्रत्येक जोड़े में कितने बिन्दु उभयनिष्ठ हैं? उभयनिष्ठ बिन्दुओं की अधिकतम संख्या क्या है?
हल :
प्रश्न के निर्देश के अनुसार नीचे विभिन्न वृत्तों के युग्म खींचे गए हैं। इन्हें ध्यान से देखिए :

दोनों युग्मों में कोई बिन्दु उभयनिष्ठ नहीं है।

दोनों युग्मों में केवल एक बिन्दु उभयनिष्ठ है।

प्रत्येक युग्म में दो बिन्दु उभयनिष्ठ हैं। अतः दो वृत्तों के उभयनिष्ठ बिन्दु की अधिकतम संख्या = 2

प्रश्न 2.
मान लीजिए आपको एक वृत्त दिया है। एक रचना इसके केन्द्र को ज्ञात करने के लिए दीजिए।

हल :
दिया है : अज्ञात केन्द्र वाला एक वृत्त।। ज्ञात करना है : वृत्त का केन्द्र।
रचना :
(1) वृत्त की परिधि पर तीन बिन्दु A, B व C लिए।
(2) जीवाएँ AB व BC खींचीं।
(3) जीवा AB व जीवा BC दोनों के लम्ब समद्विभाजक खींचे जो परस्पर बिन्दु O पर काटते हैं।
बिन्दु O वृत्त का अभीष्ट केन्द्र है।

प्रश्न 3.
यदि दो वृत्त परस्पर दो बिन्दुओं पर प्रतिच्छेद करें, तो सिद्ध कीजिए कि उनके केन्द्र उभयनिष्ठ जीवा के लम्ब-समद्विभाजक पर स्थित हैं।

हल :
दिया है : O तथा O’ केन्द्र वाले दो वृत्त हैं जो परस्पर दो बिन्दुओं A तथा B पर प्रतिच्छेद करते हैं। AB वृत्तों की उभयनिष्ठ जीवा है और OO’ उनके केन्द्रों को मिलाने वाली रेखा है। AB और OO’ एक-दूसरे को बिन्दु P पर काटते हैं।
सिद्ध करना है : OO’, AB का लम्ब समद्विभाजक है।
रचना : वृत्तों की त्रिज्याएँ OA, OB, O’A व O’B खींचीं।
उपपत्ति: ∆OAO’ तथा ∆OBO’ में,
OA = OB (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)
O’A= O’B (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)
OO’ = OO’ (उभयनिष्ठ भुजा है)
Δ ΟΑΟ’ = Δ ΟΒΟ’ (S.S.S. से)
∆AOO’ = ∆BOO’ या
∠AOP = ∠ BOP (C.P.C.T.)
तब ∆AOP और ∆BOP में,
OA = OB (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)
∠ AOP = ∠ BOP (ऊपर सिद्ध किया है।)
OP = OP (उभयनिष्ठ भुजा है)
∆AOP = ∆BOP
AP = BP और ∠OPA = ∠OPB
AP = BP;
अत: OO’ बिन्दु P पर AB को समद्विभाजित करता है। :
∠OPA = ∠OPB और APB एक रेखा (उभयनिष्ठ जीवा) है।
∠OPA + ∠OPB = 180°
हल करने पर, ∠OPA = 90° व ∠OPB = 90°
अतः OO” उभयनिष्ठ जीवा AB का लम्ब-समद्विभाजक है।

प्रश्नावली 10.4

प्रश्न 1.
5 सेमी और 3 सेमी त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों के बीच की दूरी 4 सेमी है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।

हुल :
दिया है: O तथा O’ केन्द्रों वाले वृत्तों की त्रिज्याएँ OA तथा O’A क्रमशः 5 सेमी व 3 सेमी हैं।
उनके केन्द्रों के बीच की दूरी OO’ = 4 सेमी है।
ज्ञात करनी है : उभयनिष्ठ जीवा AB की माप। गणना
∆OAO’ की भुजाएँ O’A = 3 सेमी,
OO’ = 4 सेमी व OA = 5 सेमी हैं।
तब, OA² = (25) और O’A² +(OO’)² = (3)² + (4)² = 25
OA² = O’A² + OO’² (पाइथागोरस प्रमेय से)
अतः ∆OAO’ समकोणीय है।
∠ AOO’ = 90°
परन्तु APB उभयनिष्ठ जीवा है जो OO” पर लम्ब होना चाहिए।
अतः P और O’ एक ही बिन्दु है अर्थात्
त्रिज्या AO’ = उभयनिष्ठ जीवा का भाग AP
उभयनिष्ठ जीवा का भाग AP = AO’ = 3 सेमी
केन्द्र रेखा OO’ उभयनिष्ठ जीवा AB की लम्ब-समद्विभाजक होगी।
AB = 2 x AP = 2 x 3 = 6 सेमी
अत: उभयनिष्ठ जीवा की लम्बाई = 6 सेमी।

प्रश्न 2.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खण्ड दूसरी जीवा के संगत खण्डों के बराबर हैं।

हल :
दिया है : O केन्द्र वाले एक वृत्त की AB व CD दो बराबर जीवाएँ हैं जो एक-दूसरे को वृत्त के अन्दर बिन्दु P पर काटती हैं।
सिद्ध करना है : AP = CP तथा BP = DP
रचना : वृत्त के केन्द्र O से जीवा AB पर OM तथा जीवा CD पर ON लम्बे खींचे।। रेखाखण्ड OP खींचा।
उपपत्ति : OM ⊥ AB ⇒ ∠OMP = 90°
और ON ⊥ CD ⇒ ∠ONP = 90°
∆OMP और ∆ONP समकोणीय हैं।
तब, समकोण ∆OMP तथा ∆ONP में,
OM = ON (जीवा AB = जीवा CD)
OP = OP (उभयनिष्ठ जीवा है।)
∠OMP = ∠ONP (प्रत्येक 90°)
∆OMP = ∆ONP (R.H.S. से)
MP = NP (C.P.C.T.) …(1)
OM ⊥ AB
AM = BM
AP + PM = BM
AP = BM – PM
AP = [latex]\frac { 1 }{ 2 }[/latex] AB – PM (∵ AM = BM = [latex]\frac { AB }{ 2 }[/latex]) …..(2)
और ON ⊥ CD
CN = DN
CP + PN = DN
CP = DN – PN
CP = [latex]\frac { 1 }{ 2 }[/latex] CD – PN (CN = DN = [latex]\frac { CD }{ 2 }[/latex])
CP = [latex]\frac { 1 }{ 2 }[/latex] AB – PM [CD = AB तथा समीकरण (1) से PN = PM] …(3)
अब समीकरण (2) व (3) से,
AP = CP
AB = CD (दिया है।)
AP + BP = CP + DP (चित्र से) परन्तु
AP = CP (ऊपर सिद्ध किया है।)
घटाने पर BP = DP
अत: AP = CP और BP = DP
अर्थात एक जीवा AB के खण्ड दूसरी जीवा CD के संगत खण्डों के बराबर हैं।
Proved.

प्रश्न 3.
यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केन्द्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।

हल :
दिया है : केन्द्र O के वृत्त की दो बराबर जीवाएँ AB और CD जो बिन्दु P पर प्रतिच्छेदन करती हैं।
सिद्ध करना है: रेखाखण्ड OP, से जीवाओं AB व CD द्वारा बने ∠BPO = ∠DPO
रचना : केन्द्र O से AB और CD पर क्रमशः OM और ON लम्ब डाले।
उपपत्ति : जीवा AB = जीवा CD
OM = ON
अब ΔOPM और ΔOPN में,
OM = ON (दिया है।)
∠OMP = ∠ONP (प्रत्येक समकोण है।)
OP = OP (उभयनिष्ठ भुजा है।)
ΔOPM = ΔOPN (R.H.S. से)
अतः ∠MPO = NPO यो ∠BPO = ∠DPO (C.P.C.T.)
Proved.

प्रश्न 4.
यदि एक रेखा दो संकेन्द्रीय वृत्तों (एक ही केन्द्र वाले वृत्त) को, जिनका केन्द्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है।

हल :
दिया है : दो संकेन्द्रीय वृत्तों का केन्द्र 0 है। एक ऋजु रेखा वृत्तों को बिन्दुओं A, B, C और D पर प्रतिच्छेदित करती है।
सिद्ध करना है : AB = CD
रचना : वृत्त के केन्द्र O से हैं पर OM लम्ब डाला।
उपपत्ति : रेखा l बड़े वृत्त को बिन्दुओं A तथा D पर काटती है।
AB वृत्त की जीवा है और OM उस पर केन्द्र से डाला गया लम्ब है।
AM = MD ……..(1)
रेखा l छोटे वृत्त को बिन्दुओं B तथा C पर काटती है।
BC वृत्त की जीवा है और OM उस पर केन्द्र से खींचा गया लम्ब है।
BM = MC ……..(2)
समीकरण (1) में से (2) को घटाने पर,
AM – BM = MD – MC
अतः AB = CD
Proved.

प्रश्न 5.
एक पार्क में बने 5 मीटर त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 मीटर हो तो रेशमा और मनदीप के बीच की दूरी क्या है?

हल :
दिया है। एक पार्क में 5 मीटर त्रिज्या का एक वृत्त बना है जिसका केन्द्र O है। तीन लड़कियाँ रेशमा, सलमी और मनदीप वृत्त पर क्रमशः A, B व C स्थानों पर खड़ी हैं। रेशमा और सलमा के बीच की दूरी AB = 6 मीटर तथा सलमा और मनदीप के बीच दूरी BC = 6 मीटर है।
ज्ञात करना है : रेशमा और मनदीप के बीच की दूरी = AC
गणना : त्रिज्याएँ OA और OB खींचीं और माना कि OB, AC को बिन्दु P पर काटती है।
ΔOAB में, OA = 5 मीटर (त्रिज्या), OB = 5मीटर (त्रिज्या) तथा AB = 6 मीटर।
माना OA = 5 मीटर = a, OB = 5 मीटर = b और AB = 6 मीटर = c अर्धपरिमाप

प्रश्न 6.
20 मीटर त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कॉलोनी में स्थित है। तीन लड़के अंकुर, सैय्यद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
हल :
दिया है : O केन्द्र वाला एक वृत्त के आकार का पार्क है जिसकी त्रिज्या OA या OB = 20 मीटर है। वृत्त की परिधि पर तीन लड़के एक-दूसरे से बराबर दूरी पर A, B व C स्थानों पर ऐसे बैठे हैं कि
AB = BC = AC

प्रश्नावली 10.5

प्रश्न 1.
केन्द्र O वाले एक वृत्त पर तीन बिन्दु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है। यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिन्दु है तो ∠ADC ज्ञात कीजिए।

हल :
दिया है : O केन्द्र वाला एक वृत्त है जिसकी परिधि पर A, B और C तीन बिन्दु इस प्रकार हैं कि ∠AOB = 60° और ∠ BOC = 30° हैं।
चाप ABC के अतिरिक्त वृत्त की परिधि पर एक बिन्दु D है जो चाप ABC के साथ ∠ ADC बनाता है।
ज्ञात करना है: ∠ADC गणना : ∠AOB = 60° और ∠BOC = 30°
जोड़ने पर, ∠AOB + ∠ BOC = 60° + 30°= 90°
∠ AOC = 90°
∠AOC, चाप ABC द्वारा केन्द्र पर बना कोण है।
वृत्त की शेष परिधि पर चाप ABC द्वारा बना कोण ∠ADC, ∠AOC का आधा होगा।
∠ADC = [latex]\frac { 1 }{ 2 }[/latex] ∠AOC = [latex]\frac { 1 }{ 2 }[/latex] x 90° = 45°
∠ADC = 45°

प्रश्न 2.
किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है। जीवा द्वारा लघु चाप के किसी बिन्दु पर अन्तरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिन्दु पर भी अन्तरित कोण ज्ञात कीजिए।

हल:
दिया है। एक वृत्त का केन्द्र 0 है। उसकी एक जीवा AB वृत्त की त्रिज्या OA के बराबर है। वृत्त के लघु चाप ACB पर एक बिन्दु C तथा दीर्घ चाप ADB पर एक बिन्दु D है। चाप ACB द्वारा बिन्दु D पर अन्तरित ∠ADB तथा चाप ADB द्वारा बिन्दु C पर अन्तरित ∠ACB है।
ज्ञात करना है : ∠ACB व ∠ADB
विश्लेषण व गणना :
जीवा AB = वृत्त की त्रिज्या OA या OB
AB = OA = OB
ΔABC समबाहु त्रिभुज है।
∠AOB = 60° जो चाप ACB द्वारा केन्द्र पर अन्तरित कोण है। :
चाप ACB द्वारा वृत्त की शेष परिधि के बिन्दु D पर अन्तरित ∠ADB = ∠AOB
∠ADB = [latex]\frac { 1 }{ 2 }[/latex] x ADB
= [latex]\frac { 1 }{ 2 }[/latex] x 60° = 30°
इसी प्रकार, चाप ADB द्वारा वृत्त के केन्द्र O पर अन्तरित वृहत्कोण AOB = 360° – 60° = 300°
तब चाप ADB द्वारा वृत्त की शेष परिधि के बिन्दु C पर अन्तरित कोण ।
∠ACB = [latex]\frac { 1 }{ 2 }[/latex] वृहत्कोण ∠AOB = [latex]\frac { 1 }{ 2 }[/latex] x 30° = 150°
अतः ∠ACB = 150° तथा ∠ADB = 30°

प्रश्न 3.
∠PQR = 100° है, जहाँ P, Q तथा R, केन्द्र O वाले एक वृत्त पर स्थित Q बिन्दु हैं। ∠OPR ज्ञात कीजिए।

हल :
दिया है : O केन्द्र का एक वृत्त है जिसकी परिधि पर P, Q व R तीन बिन्दु हैं।
ज्ञात करना है : ∠OPR
गणना : दीर्घ चाप PR द्वारा वृत्त के केन्द्र पर बना कोण वृहत्कोण ∠POR है और इस चाप द्वारा शेष परिधि PQR के बिन्दु Q पर बना ∠PQR है।
∠PQR = [latex]\frac { 1 }{ 2 }[/latex] x वृहत्कोण ∠POR
100° = [latex]\frac { 1 }{ 2 }[/latex] वृहत्कोण ∠POR
वृहत्कोण ∠ POR = 200°
तब, शेष कोण POR = 360° – 200° = 160°
अब, ΔPOR में,
OR = OP (वृत्त की त्रिज्याएँ)
∠OPR = ∠ORP (समान भुजाओं के सम्मुख कोण)
पुन: ΔPOR में,
∠OPR + ∠ POR + ∠ORP = 180° (त्रिभुज के अन्त:कोणों को योग 180° होता है।)
∠OPR + 160° + ∠OPR = 180° (∠ORP = ∠OPR)
2 ∠OPR = 180° – 160° = 20°
∠OPR = 10°
अतः ∠OPR = 10°

प्रश्न 4.
∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए।

हल :
दिया है : दी गई आकृति में ∠ABC = 69° और ∠ACB = 31° है।
ज्ञात करना है : ∠BDC का मान।
गणना : ΔABC में,
∠ BAC + ∠ABC + ∠ ACB = 180° (त्रिभुज के अन्त:कोणों का योग 180° होता है।)
∠ BAC + 69° + 31° = 180°
∠BAC = 180° – (69° + 31°) = 180° – 100°
∠BAC = 80°
∠BAC व ∠BDC एक ही वृत्तखण्ड के कोण हैं और ∠ BAC = 80° है।
∠BAC = ∠ BDC = 80°
अत: ∠BDC = 80°

प्रश्न 5.
एक वृत्त पर A, B, C और D चार बिन्दु हैं। AC और BD एक बिन्दु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠ BEC = 130° तथा ∠ECD = 20° है।
∠BAC ज्ञात कीजिए।

हल :
दिया है : दी गई आकृति में एक वृत्त की परिधि पर A, B, C और D चार बिन्दु BF हैं।
AC और BD बिन्दु E पर प्रतिच्छेद करते हैं।
∠BEC = 130° तथा ∠ECD = 20°
ज्ञात करना है: ∠BAC
रचना : AD को मिलाया।
गणना : ∠ ECD = 20° या ∠ACD = 20°
∠ABD वे ∠ACD एक ही वृत्तखण्ड के कोण हैं।
∠ABD = 20° (∠ACD = 20°)
∠ABE = 20°
ΔABE में ∠BEC बहिष्कोण है।
∠ BAE + ∠ ABE = ∠BEC
∠ BAE + 20° = 130° (दिया है ∠BEC = 130°)
∠BAE = 130° – 20° = 110°
∠ BAC = 110° (∠BAE = ∠BAC)
अत: ∠BAC = 110°

प्रश्न 6.
ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30°हो तो ∠BCDज्ञात कीजिए।
पुनः यदि AB = BC हो तो 2 ECD ज्ञात कीजिए।

हल :
दिया है: ABCD एक चक्रीय चतुर्भुज है जिसमें विकर्ण AC व BD एक-दूसरे को बिन्दु E पर प्रतिच्छेद करते हैं।
∠DBC = 70° व ∠BAC = 30° और AB = BC है।
ज्ञात करना है : ∠ BCD और ∠ECD
गणना : ∠DAC व ∠DBC एक ही वृत्तखण्ड के कोण हैं।
∠ DAC = ∠DBC के ∠DAC = 70° (∠DBC = 70°)
तब, चतुर्भुज ABCD में,
∠DAB = ∠DAC + ∠BAC = 70° + 30°
∠DAB = 100°
ABCD चक्रीय चतुर्भुज है।
∠DAB + ∠BCD = 180° (सम्मुख कोणों का योग 180° होता है।)
100° + ∠ BCD = 180°
∠ BCD = 180° – 100° = 80°
∠BCD = 80°
अब ΔABC में, AB = BC
∠ACB = ∠BAC (समान भुजाओं के सम्मुख कोण)
∠ACB = 30° (∠ BAC = 30°)
ऊपर हम सिद्ध कर चुके हैं कि
∠BCD = 80°
∠ACD + ∠ACB = 80° (चित्र से)
∠ACD + 30° = 80° (∠ACB = 30°)
∠ACD = 80° – 30° = 50°
∠ECD = 50° (∠ ECD = ∠ACD)
अतः ∠BCD = 80° और ∠ECD = 50°

प्रश्न 7.
यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।

हल :
दिया है: ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण AC और BD वृत्त के व्यास हैं जो परस्पर बिन्दु O पर काटते हैं।
सिद्ध करना है : ABCD एक आयत है।
उपपत्ति : विकर्ण AC और BD व्यास हैं।
AC = BD
O वृत्त का केन्द्र है।
OA = OC तथा OB = OD
चतुर्भुज ABCD के विकर्ण AC और BD एक-दूसरे को समद्विभाजित करते हैं।
ABCD समान्तर चतुर्भुज है।
∠B = ∠D
परन्तु ABCD चक्रीय चतुर्भुज भी है जिससे
∠B + ∠D = 180° (सम्मुख कोणों का योग = 180°)
उक्त दोनों तथ्यों से ∠B = 90° तथा ∠D = 90°
इसी प्रकार, ∠A = 90° तथा ∠D = 90°
इस प्रकार चतुर्भुज ABCD एक ऐसा समान्तर चतुर्भुज है जिसके अन्त:कोण समकोण हैं।
अत: ABCD एक आयत है।
Proved.

प्रश्न 8.
यदि एक समलम्ब की असमान्तर भुजाएँ बराबर हों तो सिद्ध कीजिए कि वह चक्रीय है।

हल :
दिया है : समलम्ब चतुर्भुज ABCD में भुजा AD = भुजा BC .
सिद्ध करना है : ABCD चक्रीय चतुर्भुज होगा।
रचना : AD के समान्तर रेखाखण्ड BE खींचा।
उपपत्ति : समान्तर चतुर्भुज ABED में,
∠BAD = ∠BED …..(1)
तथा AD = BE
परन्तु
AD = BC (दिया है।)
BC = BE
तब ΔBEC एक समद्विबाहु त्रिभुज हुआ।
∠BEC = ∠ BCE (समान भुजाओं के सम्मुख कोण) …(2)
∠ BEC + ∠ BED = 180° (ऋजु कोण)
∠ BCE + ∠ BAD = 180° [समीकरण (1) व (2) से ]
∠ BCD +∠ BAD = 180°
इससे स्पष्ट है कि चतुर्भुज ABCD के दो सम्मुख अन्त: कोणों का योग दो समकोण के बराबर है।
अत: चतुर्भुज ABCD चक्रीय चतुर्भुज है।
Proved.

प्रश्न 9.
दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखण्ड ABD और PBQवृत्तों को A, D और P, Q पर क्रमशः प्रतिच्छेद करते हुए खींचे गए हैं। सिद्ध कीजिए कि ∠ACP = ∠QCD है।

हल :
दिया है : दो वृत्त दी गई आकृति के अनुसार बिन्दुओं B और C पर प्रतिच्छेद करते हैं। दो रेखाखण्ड ABD और PBQ बिन्दु B से जाते हैं। पहला रेखाखण्ड ABD वृत्तों को A व D पर तथा दूसरी PBQ वृत्तों को Pव पर प्रतिच्छेद करता है। C से P और D को मिलाकर ∠ACP और ∠QCD बनाए गए हैं।
सिद्ध करना है :
∠ACP = ∠QCD
उपपत्ति : रेखाखण्ड ABD और PBQ परस्पर बिन्दु B पर काटते हैं।
∠ABP = ∠QBD (शीर्षाभिमुख कोण) …(1)
∠ABP और ∠ACP एक वृत्तखण्ड के कोण हैं।
∠ABP = ∠ACP …(2)
इसी प्रकार, ∠QCD और ∠QBD एक ही वृत्तखण्ड के कोण हैं।
∠QCD = ∠QBD ……(3)
तब समीकरण (1) व (2) से,
∠ACP = ∠QBD …(4)
अब समीकरण (3) व (4) से,
∠ACP = ∠QCD
अतः ∠ACP = ∠QCD
Proved.

प्रश्न 10.
यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।

हल :
दिया है : ABC एक त्रिभुज है जिसकी भुजाओं AB तथा AC को व्यास मानकर दो वृत्त खींचे गए हैं जो परस्पर बिन्दु X पर काटते हैं।
सिद्ध करना है : बिन्दु X, त्रिभुज की तीसरी भुजा BC पर स्थित है।
रचना : रेखाखण्ड AX खींचिए।
उपपत्ति : AB वृत्त का व्यास है तथा बिन्दु X वृत्त की परिधि पर स्थित है,
∠AXB = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)
पुनः AC वृत्त का व्यास है तथा बिन्दु X वृत्त की परिधि पर स्थित है,
∠AXC = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)
∠AXB + ∠AXC = 90° + 90° = 180°
अर्थात ∠ BXC = 180° = ऋजुकोण
अत: B, X और C एक ही रेखा में स्थित हैं।
वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
Proved.

प्रश्न 11.
उभयनिष्ठ कर्ण AC वाले दो समकोण त्रिभुज ABC और ADC हैं। सिद्ध कीजिए कि ∠ CAD = ∠CBD है।

हल :
दिया है : ΔABC और ΔADC दो समकोण त्रिभुज हैं जिनका कर्ण AC उभयनिष्ठ है। रेखाखण्ड BD खींचा गया है।
सिद्ध करना है : ∠CAD = ∠ CBD
रचना : AC को व्यास मानकर वृत्त खींचा। उपपत्ति
ΔABC समकोण त्रिभुज है जिसका कर्ण AC है।
∠B = 90°
पुनः ΔADC समकोण त्रिभुज है जिसका कर्ण AC है।
∠ D = 90°
तब चतुर्भुज ABCD में, ∠B + ∠D = 180°
ABCD चक्रीय चतुर्भुज है। (सम्मुख कोणों का योग 180° है।)
बिन्दु A, B, C और D एक वृत्त पर हैं।
∠CAD और ∠CBD एक ही वृत्तखण्ड के कोण हैं;
अतः बराबर होंगे।
अतः ∠ CAD = ∠CBD

प्रश्न 12.
सिद्ध कीजिए कि चक्रीय समान्तर चतुर्भुज एक आयत होता है।

हल :
दिया है । समान्तर चतुर्भुज ABCD एक चक्रीय चतुर्भुज है।
सिद्ध करना है : चतुर्भुज ABCD एक आयत है।
उपपत्ति : ABCD एक चक्रीय चतुर्भुज है, इसके सम्मुख कोणों का योग 180° के बराबर होगा।
∠ A + ∠C = 180°
परन्तु समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।
∠A = ∠C
अत: समीकरण (1) से,
∠A = ∠C = 90° इसी प्रकार,
∠B = ∠D = 90°
ABCD का प्रत्येक अन्त:कोण 90° के बराबर है।
अत: ABCD एक आयत है।
Proved.

प्रश्नावली 10.6 (ऐच्छिक)

प्रश्न 1.
सिद्ध कीजिए कि दो प्रतिच्छेद करते हुए वृत्तों के केन्द्रों की रेखा दोनों प्रतिच्छेद बिन्दुओं पर समान कोण अन्तरित करती है।

हल :
दिया है : O₁ तथा O₂ केन्द्रों वाले दो वृत्त एक-दूसरे को दो बिन्दुओं A तथा B पर प्रतिच्छेद करते हैं।
केन्द्र रेखा O₁O₂ प्रतिच्छेद बिन्दु A पर ∠O₁AO₂ तथा B पर ∠O₁BO₂ अन्तरित करती है।
सिद्ध करना है : ∠O₁AO₂ = ∠O₁BO₂
उपपत्ति: ΔO₁AO₂ तथा ΔO₁BO₂ में,
O₁A = O₁B (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)
O₂A = O₂B (एक ही वृत्त की त्रिज्याएँ बराबर होती हैं।)
O₁O₂ = O₁O₂ (दोनों त्रिभुजों की उभयनिष्ठ भुजा है)
ΔO₁AO₂ = ΔO₁BO₂ (S.S.S. से)
∠O₁AO₂ = ∠O₁BO₂ (C.P.C.T.)
Proved.

प्रश्न 2.
एक वृत्त की 5 सेमी तथा 11 सेमी लम्बी दो जीवाएँ AB और CD समान्तर हैं और केन्द्रकी विपरीत दिशा में स्थित हैं। यदि AB और CD के बीच की दूरी 6 सेमी हो, तो वृत्त की त्रिज्या ज्ञात कीजिए।
हल :
दिया है : O त्रिज्या का एक वृत्त है जिसमें AB तथा CD दो समान्तर जीवाएँ केन्द्र O के विपरीत ओर स्थित हैं जिनकी लम्बाइयाँ क्रमश: 5 सेमी व 11 सेमी हैं। जीवाओं के बीच की (लाम्बिक) दूरी 6 सेमी है अर्थात MON = 6 सेमी जबकि MON ⊥ AB व MON ⊥ CD

प्रश्न 3.
किसी वृत्त की दो समान्तर जीवाओं की लम्बाइयाँ 6 सेमी और 8 सेमी हैं। यदि छोटी जीवा केन्द्र से 4 सेमी की दूरी पर हो, तो दूसरी जीवा केन्द्र से कितनी दूर है?

प्रश्न 4.
मान लीजिए कि कोण ABC का शीर्ष एक वृत्त के बाहर स्थित है और कोण की भुजाएँ वृत्त से बराबर जीवाएँ AD और CE काटती हैं। सिद्ध कीजिए कि 2 ABC जीवाओं AC तथा DE द्वारा केन्द्र पर अन्तरित कोणों के अन्तर का आधा है।

प्रश्न 5.
सिद्ध कीजिए कि समचतुर्भुज की किसी भी भुजा को व्यास मानकर खींचा गया वृत्त, उसके विकर्णो के प्रतिच्छेद बिन्दु से होकर जाता है।

हल :
दिया है ABCD एक समचतुर्भुज है जिसमें AC और BD विकर्ण हैं जिनका । प्रतिच्छेद बिन्दु P है।
भुजी BC को व्यास मानकर एक वृत्त खींचा गया है।
सिद्ध करना है: BC को व्यास मानकर खींचा गया वृत्त विकर्मों के प्रतिच्छेद बिन्दु P से होकर जाएगा।
उपपत्ति : ABCD एक समचतुर्भुज है और उसके विकर्ण AC तथा BD परस्पर बिन्दु P पर प्रतिच्छेद करते हैं।
∠CPB = 90°
A CPB एक समकोण त्रिभुज है जिसका कर्ण BC है।
तब समकोण ∆CPB का ∆CPB अर्धवृत्त में स्थित होगा जिसका व्यास BC है।
अत: BC को व्यास मानकर खींचा गया वृत्त बिन्दु P (विकर्मों का प्रतिच्छेद बिन्दु) से होकर जाएगा।
Proved.

प्रश्न 6.
ABCD एक समान्तर चतुर्भुज है। A, B और C से जाने वाला वृत्त CD(यदि आवश्यक हो तो बढ़ाकर) को E पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AE = AD है।

हल :
दिया है : ABCD एक समान्तर चतुर्भुज है जिसके शीर्षों A, B और C से एक वृत्त खींचा गया है जो भुजा CD को E पर काटता है। सिद्ध करना है :
AE = AD
उपपत्ति : ABCD एक समान्तर चतुर्भुज है, ∠B = ∠D …(1) (समान्तर चतुर्भुज के सम्मुख कोण बराबर होते हैं।)
A, B, C से जाने वाला वृत्त CD को E पर काटता है,
ABCE एक चक्रीय चतुर्भुज है। AED = ∠B …(2)
समीकरण (1) व (2) से,
∠ AED = ∠D (= ∠ADE)
∆ADE में,
∠AED = ∠ADE
∆ADE समद्विबाहु त्रिभुज है जिसमें
AD = AE (समान कोणों की सम्मुख भुजाएँ समान होती हैं।)
अतः AD = AE
Proved.

प्रश्न 7.
AC और BD एक वृत्त की जीवाएँ हैं जो परस्पर समद्विभाजित करती हैं। सिद्ध कीजिए :
(i) AC और BD व्यास हैं।
(ii) ABCD एक आयत है।

हल :
दिया है: AC तथा BD एक वृत्त की जीवाएँ हैं जो एक-दूसरे को बिन्दु 0 पर समद्विभाजित करती हैं। सिद्ध करना है :
(i) AC तथा BD वृत्त के व्यास हैं।
(ii) ABCD एक आयत है।
रचना : चतुर्भुज ABCD को पूरा किया।
उपपत्ति : (i) जीवा AC और BD एक-दूसरे को बिन्दु O पर समद्विभाजित करती हैं।
OA = OB = OC = OD
तब, OA, OB, OC और OD एक ऐसे वृत्त की त्रिज्याएँ हैं जिसका केन्द्र O है।
तब, AC = OA + OC = त्रिज्या + त्रिज्या = 2 x त्रिज्या
AC वृत्त का व्यास है।
BD भी O से होकर जाती है, तब BD भी वृत्त का व्यास है।
Proved.
(ii) AC व्यास है, तब ∠B = 90° तथा ∠D = 90° और BD व्यास है,
तब ∠A = 90° तथा ∠C = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)
तब, ABCD एक ऐसा चतुर्भुज है जिसका प्रत्येक अन्त: कोण 90° है तथा विकर्ण एक-दूसरे को अर्धित करते हैं।
अत: ABCD एक आयत है।
Proved.

प्रश्न 8.
त्रिभुज ABC के कोणों A, B और C के समद्विभाजक उसके परिवृत्त को क्रमशः बिन्दुओं D, E और F पर प्रतिच्छेदित करते हैं। | सिद्ध कीजिए कि ∆DEF के कोण 90° – [latex]\frac { A }{ 2 }[/latex], 90° – [latex]\frac { B }{ 2 }[/latex] और 90° – [latex]\frac { C }{ 2 }[/latex] हैं।

प्रश्न 9.
दो सर्वांगसम वृत्त परस्पर बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से होकर कोई रेखाखण्ड PAQइस प्रकार खींचा गया है कि P और २ दोनों वृत्तों पर स्थित हैं। सिद्ध कीजिए कि BP = BQ है।

हल :
दिया है : दो वृत्तों के केन्द्र O₁ व O₂ हैं और वे बिन्दुओं A और B पर प्रतिच्छेद करते हैं। A से एक रेखा PAQ खींची गई है जो वृत्तों से बिन्दुओं P और Q पर मिलती है।
सिद्ध करना है : रेखाखण्ड BP = रेखाखण्ड BQ
रचना : जीवा AB तथा त्रिज्याएँ O₁A, O₁B, O₁A तथा O₂B खींचीं
उपपत्ति : जीवा AB दोनों वृत्तों में उभयनिष्ठ है और दोनों वृत्त सर्वांगसम हैं।
O1 केन्द्र वाले वृत्त का चाप AB = O₂ केन्द्र वाले वृत्त का चाप AB
∠AO₁B = ∠AOB (सर्वांगसम वृत्तों के समान चाप केन्द्र पर समान कोण अन्तरित करते हैं।)
∠APB = ∠AQB (परिधि पर अन्तरित कोण)
अब : ΔQBP में,
∠APB = ∠AQB (ऊपर सिद्ध हुआ है।)
∠BPQ = ∠BQP
अत: BQ = BP (सम्मुख कोण बराबर होने पर सम्मुख भुजाएँ भी बराबर होती हैं।)
Proved.

प्रश्न 10.
किसी त्रिभुज ABC में, यदि ∠A का समद्विभाजक तथा BC का लम्बे समद्विभाजक प्रतिच्छेद करें, तो सिद्धकीजिए कि वे ΔABC के परिवृत्त पर प्रतिच्छेद करेंगे।

हल :
दिया है : ΔABC के आधार BC का लम्ब समद्विभाजक XY है।
ABDC, ΔABC का परिवृत्त है। लम्ब समद्विभाजक XY परिवृत्त को D पर काटता है। XY, BC को M पर काटता है।।
सिद्ध करना है : ∠A का समद्विभाजक भी बिन्दु D से होकर जाएगा।
रचना : DB तथा DC को मिलाया।
उपपत्ति : XY, BC का लम्ब समद्विभाजक है और यह परिवृत्त को बिन्दु D पर काटता है।
बिन्दु D, परिवृत्त पर भी है और XY पर भी।
ΔBDM और ΔCDM में,
BM = CM (XY, BC का लम्ब समद्विभाजक है।)
∠BMD = ∠CMD (XY ⊥ BC अर्थात प्रत्येक 90°)
MD = MD (उभयनिष्ठ भुजा है।)
ΔBDM = ΔCDM (S.A.S. से)
BD = CD (C.P.C.T.)
बिन्दु D, परिवृत्त पर भी स्थित है।
परिवृत्त में, जीवा BD = जीवा CD
चाप BD= चाप CD (समान चाप किसी वृत्त की समान जीवाएँ काटती हैं।)
चाप BD द्वारा बिन्दु A पर अन्तरित कोण = चाप CD द्वारा बिन्दु A पर अन्तरित कोण
∠BAD = ∠CAD
अत: A का समद्विभाजक AD भी बिन्दु D से होकर जाता है।
Proved.

We hope the UP Board Solutions for Class 9 Maths Chapter 10 Circle (वृत्त) help you. If you have any query regarding Chapter 10 Circle (वृत्त), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 9 Hindi Chapter 4 गिल्लू (गद्य खंड)

These Solutions are part of UP Board Solutions for Class 9 Hindi. Here we have given UP Board Solutions for Class 9 Hindi Chapter 4 गिल्लू (गद्य खंड).

(विस्तृत उत्तरीय प्रश्न)

प्रश्न 1. निम्नांकित गद्यांशों में रेखांकित अंशों की सन्दर्भ सहित व्याख्या और तथ्यपरक प्रश्नों के उत्तर दीजिये –
(1) सोनजुही में आज एक पीली कली लगी है। उसे देखकर अनायास ही उस छोटे जीव का स्मरण हो आया, जो इस लता की सघन हरीतिमा में छिपकर बैठता था और फिर मेरे निकट पहुँचते ही कन्धे पर कूदकर मुझे चौंका देता था। तब मुझे कली की खोज रहती थी, पर आज उस लघुप्राणी की खोज है।
परन्तु वह तो अब तक इन सोनजुही की जड़ में मिट्टी होकर मिल गया होगा कौन जाने स्वर्णिम कली के बहाने वही मुझे चौंकाने ऊपर आ गया हो अचानक एक दिन सवेरे कमेर से बरामदे में आकर मैंने देखा, दो कौए एक गमले के चारों ओर चोंचों से छुवाछुवौवल-जैसा खेल खेल रहे हैं। यह कागभुशुण्डि भी विचित्र पक्षी है-एक साथ समादरित, अनादरित, अति सम्मानित, अति अवमानित।
प्रश्न
(1) उपर्युक्त गद्यांश का संदर्भ लिखिए।
(2) रेखांकित अंशों की व्याख्या कीजिए।
(3) गिल्लू को कहाँ समाधि दी गयी?
[शब्दार्थ-सोनजुही = पीले फूलोंवाली एक लता। अनायास = अचानक। सघन हरीतिमा = घनी हरियाली। लघुप्राणी = छोटे से जीव।]

उत्तर-

1. सन्दर्भ- प्रस्तुत अवतरण पाठ्य-पुस्तक ‘हिन्दी गद्य’ में संकलित एवं महादेवी वर्मा द्वारा लिखित ‘गिल्लू’ नामक पाठ से अवतरित है। महादेवी जी को सोनजुही की लता में एक पीली कली को देखकर गिलहरी के बच्चे ‘गिल्लू’ की याद आ जाती है। लेखिका ने एक कोमल लघुप्राणी (गिलहरी) की प्रकृति का मानवीय संवेदना तथा समता के आधार पर चित्रण किया है।
2. रेखांकित अंशों की व्याख्या- लेखिका कहती है कि सोनजुही की लता में मुझे जो एक पीली कली दिखायी दे रही है, उसको देखकर मुझे एक छोटे-से कोमल प्राणी गिलहरी के बच्चे ‘गिल्लू’ का संस्मरण हो रहा है। जिस प्रकार लताओं के बीच उसकी कली छिपी हुई है, ठीक उसी प्रकार गिल्लू भी उसी लता में छिपकर बैठता था। जब मैं लता के निकट कलियों एवं पुष्पों को लेने जाती थी, तो लता के बीच छिपा हुआ गिल्लू मेरे कंधे पर कूदकर मुझे अचानक चौंका देता था। वह इस जगत् से जीवन (UPBoardSolutions.com) समाप्त कर चुका है, किन्तु मेरी आँखें उसे आज भी खोज रही हैं। लेकिन अब वह इस सोनजुही की जड़ में मिट्टी होकर मिल गया होगा। शायद वह इसे स्वर्णिम कली के बहाने मुझे चौंकाने के लिए ऊपर आ गया हो। इसे कौन जान सकता है।
   एक दिन अचानक मैंने कमरे से बरामदे में आकर देखा कि दो कौए एक गमले में चोंचों से छुवा-छुवौवल का खेल खेल रहे हैं। धार्मिक ग्रन्थों में कौए का वर्णन ‘कागभुशुण्डि’ के नाम से किया गया है। बड़ा ही अद्भुत प्राणी है। लोक मानस में यह एक साथ विरोधी व्यवहार प्राप्त करता है। कभी यह अत्यधिक आदर प्राप्त करता है और कभी अनादर, कभी सम्मानित होता है और कभी अपमानित।
3. गिल्लू की सोनजुही की लता के नीचे समाधि दी गयी।

(2) मेरे पास बहुत-से पशु-पक्षी हैं और उनका मुझसे लगाव भी कम नहीं है, परन्तु उनमें से किसी को मेरे साथ मेरे थाली में खाने की हिम्मत हुई है, ऐसा मुझे स्मरण नहीं आता।
               गिल्लू इनमें अपवाद था। मैं जैसे ही खाने के कमरे में पहुँचती, वह खिड़की से निकलकर आँगन की दीवार, बरामदा पार करके मेज पर पहुँच जाता और मेरी थाली में बैठ जाना चाहता । बड़ी कठिनाई से मैंने उसे थाली के पास बैठना सिखाया, जहाँ बैठकर वह मेरी थाली में से एक-एक (UPBoardSolutions.com) चावल उठाकर बड़ी सफाई से खाता रहता । काजू उसका प्रिय खाद्य था और कई दिन काजू न मिलने पर वह अन्य खाने की चीजें या तो लेना बन्द कर देता था या झूले के नीचे फेंक देता था।
प्रश्न
(1) उपर्युक्त गद्यांश का संदर्भ लिखिए।
(2) रेखांकित अंश की व्याख्या कीजिए।
(3) गिल्लू को क्या बेहद पसंद था?

उत्तर- 

1. सन्दर्भ- प्रस्तुत गद्यांश पाठ्य-पुस्तक ‘हिन्दी गद्य’ में संकलित एवं महादेवी वर्मा द्वारा लिखित ‘गिल्लू’ पाठ से उद्धृत है। प्रस्तुत अवतरण में गिल्लू के खान-पान का वर्णन है।
2. रेखांकित अंशों की व्याख्या-लेखिका कहती है कि मेरे पास बहुत से पशु-पक्षी हैं। सभी के साथ मेरा असीम लगाव है, लेकिन किसी को मेरे साथ मेरी थाली में खाने की हिम्मत नहीं हुई। गिल्लू इसका अपवाद था। मैं खाना खाने के लिए जैसे ही मेज के पास जाती गिल्लू (UPBoardSolutions.com) कूद-फाँदकर खाने की मेज पर पहुँच जाता और मेरी थाली में बैठना चाहता। मैंने बड़ी मुश्किल से उसे थाली के पास बैठना सिखाया। उसके बाद गिल्लू मेरी थाली के पास बैठकर एक-एक चावल निकालकर खाता था। काजू उसे बेहद पसंद था। यदि कई दिन काजू न मिले तो अन्य चीजें भी खाना बन्द कर देता था। या झूले, के नीचे गिरा देता था।
3. गिल्लू को काजू बेहद पसंद था।

(3) मेरी अस्वस्थता में वह तकिये पर सिरहाने बैठकर अपने नन्हें-नन्हें पंजों से ये मेरे सिर और बालों को इतने हौले-हौले सहलाता रहता कि उसका हटना एक परिचारिका के हटने के समान लगता।
          गर्मियों में जब मैं दोपहर में काम करती रहती तो गिल्लू ने बाहर जाता, न अपने झूले में बैठता। उसने मेरे निकट रहने के साथ गर्मी से बचने का एक सर्वथा नया उपाय खोज निकाला था। वह मेरे पास रखी सुराही पर लेट जाता और इस प्रकार समीप भी रहता और ठण्डक में भी रहता।
          गिलहरियों के जीवन की अवधि दो वर्ष से अधिक नहीं होती, अत: गिल्लू की जीवन-यात्रा का अन्त आ ही गया। दिनभर उसने न कुछ खाया और न बाहर गया। रात में अन्त की यातना में भी वह अपने झूले से उतरकर मेरे बिस्तर पर आया और ठण्डे पंजों से मेरी वही उँगली पकड़कर हाथ से चिपक गया, जिसे उसने अपने बचपन की मरणासन्न स्थिति में पकड़ा था।
          पंजे इतने ठण्डे हो रहे थे कि मैंने जागकर हीटर जलाया और उसे उष्णता देने का प्रयत्न किया, परन्तु प्रभात की प्रथम किरण के स्पर्श के साथ ही वह किसी और जीवन में जागने के लिए सो गया ।
प्रश्न
(1) उपर्युक्त गद्यांश का संदर्भ लिखिए।
(2) रेखांकित अंश की व्याख्या कीजिए।
(3) गिल्लू गर्मी से बचने के लिए किस पर लेट जाता था?

उत्तर-

1. सन्दर्भ- प्रस्तुत गद्यांश हमारी पाठ्य-पुस्तक ‘हिन्दी गद्य’ में संकलित एवं महादेवी वर्मा द्वारा लिखित ‘गिल्लू’ नामक पाठ से अवतरित है। प्रस्तुत अवतरण में लेखिका ने बताया है कि यदि मैं घर पर रहती तो गिल्लू सदैव मेरे निकट ही रहना चाहता था।
2. रेखांकित अंशों की व्याख्या- लेखिका कहती है कि गर्मियों में जब मैं अपने लिखने-पढ़ने में व्यस्त रहती तो गिल्लू न बाहर जाता था और न ही अपने झूले पर जाता था। वह सदैव मेरे करीब ही रहता था। गिल्लू गर्मी से बचने के लिए मेरे पास रखी सुराही पर लेट जाता था। इस तरह वह एक पल भी मुझसे अलग नहीं होना चाहता था।
   गिलहरियों की जीवनावधि बहुत अल्प होती है, मुश्किल से दो वर्ष । इसलिए जब गिल्लू की जीवन-यात्रा का न्त करीब आया तो उसने दिनभर ने कुछ (UPBoardSolutions.com) खाया-पिया और न ही बाहर गया। रात में अपने झूले से उतरकर मेरे बिस्तर पर आ और मेरी उँगली पकड़कर मेरे हाथ से चिपक गया जिसे उसने अपने बचपन की मरणासन्न स्थिति में पकड़ा था। उसका शरीर अल ठण्डा पड़ गया था। मैंने हीटर जलाकर उसे गर्मी प्रदान करने का प्रयास किया लेकिन गिल्लू का अन्त तो करीब था। प्रात:कानते ही उसने इस संसार से विदा ले ली।
3. गिल्लू गर्मी से बचने के लिए सुराही पर लेट जाता था।

प्रश्न 2. महादेवी वर्मा का जीवन-परिचय एवं कृतियों का उल्लेख कीजिए।

प्रश्न 3. महादेवी वर्मा के जीवन एवं साहित्यिक परिचय को अपने शब्दों में लिखिए।

प्रश्न 4. महादेवी वर्मा के साहित्यिक परिचय एवं भाषा-शैली पर प्रकाश डालिए।

प्रश्न 5. महादेवी वर्मा के व्यक्तित्व एवं कृतित्व पर प्रकाश डालिए।
अथवा महादेवी वर्मा को साहित्यिक परिचय देते हुए उनकी रचनाओं का उल्लेख कीजिए।

महादेवी वर्मा
( स्मरणीय तथ्य )

 जन्म-सन् 1907 ई०। मृत्यु-सन् 1987 ई०। जन्म-स्थान-फर्रुखाबाद। पिता- गोविन्दप्रसाद वर्मा। माता- श्रीमती हेमरानी।। शिक्षा- एम० ए०। पति-रूपनारायण किन्तु परित्यक्ता।
अन्य बातें – ‘चाँद’ पत्र का सम्पादन, ‘साहित्य संसद्’ की स्थापना ।
काव्यगत विशेषताएँ- छायावादी, रहस्यवादी रचनाएँ, वेदना की प्रधानता। 

• जीवन-परिचय- श्रीमती महादेवी वर्मा का जन्म फर्रुखाबाद जिले के एक सम्पन्न कायस्थ परिवार में अन् 1907 ई० में हुआ था। इनकी प्रारम्भिक शिक्षा इन्दौर में हुई । प्रयोग विश्वविद्यालय से संस्कृत में एम० ए० करने ३, वात् ये प्रयाग महिला विद्यापीठ में प्रधानाचार्या हो गयीं। तब से अन्त तक इसी पद पर कार्य किया। बीच में कुछ वषों 1: आपने चाँद” नामक मासिक पत्रिका का भी सम्पादन किया था। इन्हें ‘सेकसरिया’ एवं ‘मंगलाप्रसाद पुरस्कार’ भी प्राप्त हो चुके हैं। इनकी विद्वता पर भारत (UPBoardSolutions.com) सरकार ने इन्हें ‘पद्मभूषण’ की उपाधि से अलंकृत किया है। ये उत्तर प्रदेश विज्ञान परिषद् की सम्मानित सदम्या भी रह चुकी हैं। सन् 1987 में इनका देहावसान हो गया था।
• कृतियाँ- महादेवी जी का कृतित्व गुणात्मक दृष्टि से तो अति समृद्ध है ही, परिमाण की दृष्टि से भी कम नहीं है। इनकी प्रम् । रचनाएँ निम्नलिखित हैं ‘क्षणदा’, ‘ श्रृंखला की कड़ियाँ’, ‘साहित्यकार की आस्था तथा निबन्ध’ उनके प्रसिद्ध निबन्ध-संग्रह हैं। ‘अतीत के चलचित्र’, ‘पथ के साथी’, ‘स्मृति की रेखाएँ’, ‘मेरा परिवार’ उनके संस्मरणों और रेखाचित्रों के संग्रह हैं। ‘हिन्दी का विवेचनात्मक गद्य’ और काव्य-ग्रन्थों की भूमिकाओं तथा फुटकर आलोचनात्मक निबन्धों में उनका सजग आलोचक-रूप व्यक्त हुआ है। | ‘नीहार’, ‘रश्मि’, ‘नीरजा’, ‘सांध्यगीत’, ‘यामा’, ‘दीपशिखा’ आदि उनके कविता-संग्रह हैं। ‘चाँद’ और ‘ आधुनिक कवि’ का उन्होंने सम्पादन किया। |
• साहित्यिक परिचय- महादेवी जी का मुख्य साहित्यिक क्षेत्र काव्य है तथापि ये उच्चकोटि की गद्य रचनाकार भी हैं। एक ओर जहाँ वे विशिष्ट गम्भीर शैली में आलोचनाएँ लिख सकती हैं, दूसरी ओर ‘ श्रृंखला की कड़ियाँ’ में विवेचनात्मक गद्य भी प्रस्तुत कर सकती हैं। इन्होंने नारी-जगत् की समस्याओं को प्राय: अपने निबन्धों का वर्ण्य-विषय बनाया है। पथ के साथी’ में कुछ प्रमुख (UPBoardSolutions.com) साहित्यकारों के ‘अतीत के चलचित्र’ एवं ‘स्मृति की रेखाओं में मार्मिक रेखाचित्र प्रस्तुत किया है। मेरा परिवार में कुछ पालतू पशु-पक्षियों के शब्द-चित्र बड़ी ही मार्मिक शैली में चित्रित किये गये हैं। महादेवी जी के काव्य में आध्यात्मिक वेदना का पुट है। इनका काव्य वर्णनात्मक और इतिवृत्तात्मक न होकर गीतिकाव्य है जिसमें लाक्षणिकता और व्यंजकता का बाहुल्य है।
• भाषा शैली– महादेवी की भाषा शुद्ध खड़ीबोली है, जिसमें संस्कृत के तत्सम शब्दों का प्रयोग हुआ है। भाषा में का मक चित्रमयता सर्वत्र देखने योग्य है। इनकी गद्य रचनाओं में भी काल की चित्रमयता, मधुरता एवं कल्पनाशीलता विद्यमान रहती है जिसमें पाठकों को एक अनोखी आत्मीयता के दर्शन होते हैं। शब्दों का चयन एवं वाक्य-विन्यास अत्यन्त ही कलात्मक है। गद्य में लाक्षणिकता के पुट से एक मधुर व्यंग्य की सृष्टि होती है। भाषा संस्कृतनिष्ठ होने पर भी उसमें शुष्कता और दुर्बोधता का अभाव है। भावों की अभिव्यक्ति में आपको अद्वितीय सफलता मिली है।

उदाहरण

1. विवरणात्मक शैली- “हिमालय के प्रति मेरी आसक्ति जन्मजात है। इसके पर्वतीय अंचलों में मौन हिमानी और मुखर निर्झरी, निर्जन वन और कलेवर भरे आकाश वाला रामगढ़ मुझे विशेष रूप से आकर्षित करता रहा है।” – प्रणाम
2. विवेचनात्मक शैली- ”महान् साहित्यकार अपनी कृति में इस प्रकार व्याप्त रहता है कि उसे कृति से पृथक् रखकर देखना उसके व्यक्तिगत जीवन की सब रेखाएँ जोड़ लेना ही कष्टसाध्य होता है। एक के तौलने में दूसरा तुल जाता और दूसरे को नापने में पहला नप जाता है।” – प्रणाम
3. आत्मव्यंजक शैली- “मेरे काक पुराण के विवेचन में अचानक बाधा आ पड़ी क्योंकि गमले और दीवार की सन्धि में छिपे एकें छोटे-से जीव पर मेरी दृष्टि गयी। निकट आकर देखा, गिलहरी का छोटा बच्चा है।”   -गिल्लू

( लघु उत्तरीय प्रश्न )

प्रश्न 1. इस पाठ से लेखिका के स्वभाव आदि के बारे में आपको क्या-क्या ज्ञात होता है?
उत्तर- इस पाठ से लेखिका के स्वभाव के बारे में जानकारी मिलती है कि लेखिका का स्वभाव दयालु है। वह जीवजन्तुओं पर दया करती है। गिल्लू का उन्होंने घायलावस्था में (UPBoardSolutions.com) उपचार किया। उसको वह अपने साथ भोजन कराती थी। गिल्लू परिवार का सदस्य जैसा था।

प्रश्न 2. लेखिका ने अपनी रचनाओं में किन-किन शैलियों का प्रयोग किया है?
उत्तर- लेखिका में अपनी रचनाओं में चित्रोपमे वर्णनात्मक शैली, विवेचनात्मक शैली, मात्रात्मक शैली, व्यंग्यात्मक शैली, आलेकारिक शैली; ‘सूक्ति शैली, ‘उद्धरण शैलियों का प्रयोग किया है।

प्रश्न 3. गिल्लू कौन था? उसकी विशेषताओं को अपने शब्दों में लिखिए।
उत्तर- गिल्लू एक जीव था। वह बहुत ही जानकार था। वह लेखिका की थाली में बैठकर खाना खाता था। जब गिल्लू को भूख लगती थी तो वह चिक-चिक की आवाज करता था। काजू उसे बेहद पसन्द था। यदि उसे काजू नहीं मिलता था तो पिंजड़े में रखी दूसरी चीजें वह गिरा देता था।

प्रश्न 4. महादेवी वर्मा को ‘विरह की गायिका’ के रूप में आधुनिक मीरा’ किस आधार पर कहा जाता है? स्पष्ट | कीजिए।
उत्तर- रहस्यवाद एवं प्रकृतिवाद पर आधारित इनको छायावादी साहित्य हिन्दी साहित्य की अमूल्य विरासत के रूप में स्वीकार किया जाता है। विरह की गायिका के रूप में महादेवी जी को आधुनिक मीरा कहा जाता है। महादेवी जी के कुशल सम्पादन के परिणामस्वरूप ही ‘चाँद’ पत्रिका नारी जगत् की सर्वश्रेष्ठ पत्रिका बन सकी।

प्रश्न 5. लेखिका ने कौए को समादरित, अनादरित, अतिसम्मानित तथा अतिअवमानित क्यों कहा है?
उत्तर- पितृपक्ष में कौए का महत्त्व बढ़ जाता है। इसके अतिरिक्त किसी प्रियजन के आने की सूचना अपने कर्कश स्वर में देता है। इसलिए यह समादरित और अति (UPBoardSolutions.com) सम्मानित है। हम कौए के काँव-काँव करने को अवमानना के अर्थ में ही प्रयुक्त करते हैं इसलिए अनादरित और अतिअवमानित है।

प्रश्न 6. गिल्लू को लेखिका ने किन परिस्थितियों में प्राप्त किया?
उत्तर- लेखिका की गमले और दीवार की सन्धि में छिपे एक छोटे-से जीव पर दृष्टि गयी। निकट जाकर देखा, उसमें गिलहरी का एक छोटा-सा बच्चा था, जो सम्भवतः घोंसले से गिर पड़ा था। कौए उस पर चोंच से प्रहार कर रहे थे। ऐसी स्थिति में लेखिका ने उसे आश्रय दिया।

प्रश्न 7. गिल्लू के किन-किन व्यवहारों से पता चलता है कि वह समझदार प्राणी था?
उत्तर- भूख लगने पर गिल्लू चिक-चिक करके सूचना देता था। काजू और बिस्कुट मिल जाने पर पंजे से पकड़कर कुतरकुतर कर खाता । लेखिका कहती है कि जब मैं खाने की मेज पर बैठती तो गिल्लू थाली के पास आकर बैठ जाता और एक-एक चावल मेरी थाली से निकालकर खाता। गर्मी के मौसम में गर्मी से बचने के लिए कमरे में रखी मेरी सुराही पर लेट जाता। इससे यह मालूम होता है कि गिल्लू एक समझदार प्राणी था।

प्रश्न 8. गिल्लू पाठ से दस सुन्दर वाक्य लिखिए।
उत्तर- सोनजुही में आज एक पीली कली लगी है। हमारे बेचारे पुरखे न गरुड़ के रूप में आ सकते हैं, न मयूर के, न हंस । के। मैं उसे गिल्लू कहकर बुलाने लगी। भूख लगने पर वह चिक-चिक की आवाज करती। काजू या बिस्कुट मिल जाने पर पंजे से पकड़कर उसे कुतरता रहता था। फिर (UPBoardSolutions.com) गिल्लू के जीवन का प्रथम बसन्त आया। नीम-चमेली की गन्ध मेरे कमरे में हौले-हौले आने लगी। मेरे पास बहुत से पशु-पक्षी थे। गिल्लू इनमें अपवाद था। जब मैं खाने की मेज पर बैठती तो गिल्लू मेरी थाली के पास बैठ जाता और थाली में से एक-एक चावल निकालकर कुतरता रहता। मेरे साथ खाने की हिम्मत अन्य पशु-पक्षियों की कभी नहीं हुई। काजू गिल्लू का प्रिय खाद्य था। कई दिन तक काजू न मिलने पर वह अन्य खाने की चीजें या तो लेना बन्द कर देता था या झूले के नीचे फेंक देता था।

प्रश्न 9. लेखिका के किन व्यवहारों से ज्ञात होता है कि गिल्लू को वह अपने परिवार के एक सदस्य की तरह मानती थी?
उत्तर- लेखिका गिल्लू को अपने परिवार के सदस्य की तरह थाली में खाना खिलाती थी। उसे बिस्कुट और काजू खिलाती थी।

प्रश्न 10. अपने किसी पालतू जन्तु के विषय में वर्णन कीजिए।
उत्तर- मेरे पास एक नेवला है। यह बहुत ही जानकार जन्तु है। यह पूरे घर में टहलता रहता है। जब मैं घर से बाहर निकलता हूँ तो यह भी मेरे साथ निकल पड़ता है। यह घर के आस-पास कीड़े-मकोड़ों को खाता रहता है। नेवले के कारण घर के आस-पास सर्प का भय नहीं होता है।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1. महादेवी वर्मा की दो रेखाचित्र कृतियों का नामोल्लेख कीजिए।
उत्तर- ‘स्मृति की रेखाएँ’ और ‘अतीत के चलचित्र’ महादेवी वर्मा के दो रेखाचित्र हैं।

प्रश्न 2. निम्नलिखित में से सही वाक्य के सम्मुख सही (√) का चिह्न लगाइए –
(अ) गिल्लू तीन वर्ष तक महादेवी जी के घर में रहा।                  (×)
(ब) गिल्लू महादेवी जी के साथ उनकी थाली में भी खाता था।     (√)
(स) गिल्लू को कौए ने मार डाला था।                                         (×)
(द) सोनजुही की लता के नीचे गिल्लू को समाधि दी गयी।           (√)

प्रश्न 3. महादेवी वर्मा किस युग की लेखिका थीं?
उत्तर- महादेवी वर्मा शुक्लोत्तर युग की लेखिका थीं। 

प्रश्न 4. गिलहरियों के जीवन की अवधि कितने वर्ष की होती है?
उत्तर- गिलहरियों के जीवन की अवधि दो वर्ष की होती है।

प्रश्न 5. ‘गिल्लू’ नामक पाठ महादेवी जी की किस कृति से लिया गया है?
उत्तर- ‘गिल्लू’ नामक पाठ महादेवी जी द्वारा लिखित ‘मेरा परिवार’ नामक पुस्तक से लिया गया है।

व्याकरण-बोध

प्रश्न 1.‘समादरित’ शब्द का सन्धि-विच्छेद करते हुए सन्धि का नाम बताइए –
उत्तर- समादरित – सम + आदरित – दीर्घ सन्धि

प्रश्न 2. वाक्य-विश्लेषण कीजिए –
यह कागभुशुण्डि भी विचित्र पक्षी है-एक साथ समादरित, अनादरित, अति सम्मानित, अति अवमानित।
उत्तर- कागभुशुण्डि एक ऐसा विचित्र पक्षी है जिसका आदर भी होता है, अनादर भी होता है, जो सम्मानित भी होता है और अपमानित भी।

प्रश्न 3. निम्नलिखित शब्दों का वाक्य-प्रयोग कीजिए –
गिल्लू, सोनजुही, बसंत, जाली, काजू, गिलहरी।
उत्तर-

• गिल्लू – महादेवी वर्मा ने जिस गिलहरी को पाला था उसका नाम गिल्लू रखा।
  
• सोनजुही- सोनजुही में एक पीली कली लगी है।
  
• बसंत- बसंत का मौसम अत्यन्त प्यारा होता है।
  
• जाली- गिल्लू काजू न पाने पर अन्य चीजें काट-काटकर जाली से गिरा देता था।
  
• काजू- गिल्लू को काजू बहुत पसन्द था।
  
• गिलहरी- गिलहरी की अवधि दो वर्ष होती है।

We hope the UP Board Solutions for Class 9 Hindi Chapter 4 गिल्लू (गद्य खंड) help you. If you have any query regarding UP Board Solutions for Class 9 Hindi Chapter 4 गिल्लू (गद्य खंड), drop a comment below and we will get back to you at the earliest.