Class 9

Balaji Class 9 Maths Solutions Chapter 10 Lines and Angle Ex 10.2 रेखाएँ एवं कोण

Ex 10.2 Lines and Angle अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
दी गयी आकृति में, AB || DE तो सिद्ध कीजिए कि ∠ABC + ∠BCD = 180°+ ∠CDE
हलः
बिन्दु C से होकर एक रेखा MCN खींची जबकि AB || MN
माना
∠MCD = x
∠MCB = y

∠CDE = ∠ MCD = x
LHS ∵ ∠ABC + ∠BCD = 180 – y + x + y [∵ ∠ABC = ∠BCN = 180°- y एकान्तर कोण]
= 180 + x = 180 + ∠CDE = RHS

प्रश्न 2.
दी गयी आकृति में, AB, CD के समान्तर है, x ज्ञात कीजिए।
हलः

∵ AB||CD
बिन्दु T से होती हुई AB तथा CD के समान्तर रेखा MN खींची।
∠ TAB + ∠ATN = 180° (अन्तः कोण युग्म)
140 + ∠ATN – 180°
∠ATN = 180 – 140 = 40°
∵ ∠DCT + ∠NTC = 180°
150 + ∠NTC = 180°
∠NTC = 180 – 150 = 30°
∴ x = ∠ATN + ∠NTC = 40 + 30 = 70°

प्रश्न 3.
निम्न प्रत्येक आकृति में x° का मान ज्ञात कीजिए।

हल:
(i) AB तथा CD के समान्तर एक रेखा FEM खींची।
∠ABE + ∠FEB = 180°
140 + ∠FEB = 180°
∠FEB = 180 – 140 = 40°
∠CDE + ∠FED = 180°
135 + ∠FED = 180° (अन्तः युग्म कोण)
∠FED = 180 – 135 = 45°
∴ ∠FEB + ∠FED = 40 + 45 = 85°
∴ x = 85°

(ii) बिन्दु E से होती हुई एक रेखा MN खींची
∠MEA = ∠BAE = 50° (एकान्तर कोण)
∠MEC = ∠ECD = 70° (एकान्तर कोण)
∴ ∠MEA + ∠MEC = 50 + 70 = 120°
∴ x = 120°

(iii) बिन्दु E से होती हुई MN रेखा खींची
माना ∠MEB = a
a = 180°- 60° = 120°
∴ b = 180°- 30° = 150°
∵ x = a + b
= 120° + 150° = 270°

प्रश्न 4.
दी गयी आकृति में, AB|| CD तथा कोई बिन्दु P दर्शाया गया है तो सिद्ध कीजिए कि ∠ABP + ∠BPD + ∠CDP = 360°
हल:

∵ AB||CD
तथा P बिन्दु से होती हुई एक सरल रेखा EF खींची
माना ∠BPE = x तथा ∠DPE = y
∠MBP = 180 – ∠ABP ……….. (1)
तथा ∠NDP = 180 – ∠PDC …………..(2)
∠MBP = x (एकान्तर कोण)
∠NDP = y (एकान्तर कोण)
समीकरण (1) से 180 – ∠ABP = x ……… (3)
समीकरण (2) से 180 – ∠PDC = y …………. (4)
समीकरण (3) व (4) को जोडने पर,
180 – ∠ABP + 180 – ∠PDC = x + y
360 – ∠ABP – ∠CDP = ∠BPD
∴ 360° = ∠ABP + ∠BPD + ∠CDP

प्रश्न 5.
दी गयी आकृति में, x ज्ञात कीजिए।
हल:
∆ABC का बहिष्कोण = x
∆ का बहिष्कोण अपने सम्मुख अन्तः कोणों के योग के बराबर होता है

∴ ∠CBD = ∠ACB + ∠CAB
∴ ∠CBD = 70 + 60 = 130°
∴ x = 130°

प्रश्न 6.
दी गयी आकृति में, l||m||n और ∠1 = 60°, ∠2 ज्ञात कीजिए।
हल:

∠1 = 60° ∵ l || m || n
∠1 = ∠3 (संगत कोण)
= 60°
∴ ∠4 = 180° – 60° = 120°
∠2 = ∠4 = 120° (एकान्तर कोण)

प्रश्न 7.
आकृति में, भुजाओं BA और DC द्वारा निर्मित एक चतुर्भुज दर्शाया गया है तो सिद्ध कीजिए कि a + b = x + y यदि AB||DC.
हलः

∵ ∠BCD = 180 – a
∠BAD = 180 – b
चतुर्भुज के चारो कोणों का योग = 360
180 – a + y + 180 – b + x = 360
x + y = a + b

प्रश्न 8.
दी गयी आकृति में, AB||CD और ∠F = 30°, तो ∠ECD ज्ञात कीजिए।
हलः

∵ ∠AFE = 30°
∠ECH = ∠AFE = 30° (एकान्तर कोण)
∠ECD = 30 + 90 = 120°

प्रश्न 9.
दी गयी आकृति में, यदि AC||DE, तब x का मान ज्ञात कीजिए।
हलः

∠MCD = 180° – ∠EDC
= 180° – 55° = 125
x = ∠MCD (शीर्षाभिमुख कोण)
= 125°

प्रश्न 10.
दी गयी आकृति में, ∠ABC की भुजाओं BA और BC, ∠DEF की क्रमशः भुजाओं ED और EF के समान्तर है तो सिद्ध कीजिए कि ∠ABC + ∠DEF = 180°
हल:
∵ ∠ABC + ∠EDC = 180° (अन्तः युग्म कोण) …………….(1)
परन्तु ∠EDC = ∠DEF ………….. (2)

समीकरण (2) का मान समीकरण (1) में रखने पर
∠ABC + ∠DEF = 180°

प्रश्न 11.
दी गयी आकृति में AB||CD और DE||CF, तो x और y ज्ञात कीजिए।
हलः

∵ AB || CD
∴ ∠BAC = ∠ACD
50 = y (एकान्तर कोण) …………(1)
∵ DE ||CF
x = 70 + y (एकान्तर कोण) …………(2)
समीकरण (2) में y का मान रखने पर
x = 70 + 50 = 120°

प्रश्न 12.
दी गयी आकृति में BD||CE, तो x, y और z ज्ञात कीजिए।
हलः

∠ FDE = 180 – 120 = 60°
∴ y = 60° (संगत कोण)
∠DBC = 180 – 70 = 110°
∆ABD में,
∠DBC = ∠BAD + ∠ADB
110 = x + 60
(∵ ∠ADB = 180 – 120 = 60°)
x = 110 – 60 = 50°
x = 50°
z = ∠BCE = 70° (संगत कोण)

प्रश्न 13.
दी गयी आकृति में समान्तर रेखायें l, m, n एक तिर्यक रेखा P द्वारा क्रमशः x, y और z पर प्रतिच्छेद होती है। तो ∠1, ∠2 तथा ∠3 ज्ञात कीजिए।
हलः

∠4 = 180° – 50° = 130°
∠4 = ∠1 = 130° (संगत कोण)
∠1 = ∠2 = 130° (संगत कोण)
∠3 = ∠1 = 130° (एकान्तर कोण)

प्रश्न 14.
दी गयी आकृति में l₁||l₂ और m₁|| m₂ क्यों हैं, कारण दीजिए?
हलः

∠NQR = QRS = 130°
परन्तु ये एकान्तर कोण हैं।
∴ m₁||m₂
∠PQR = 180° – 130° = 50°
∠MPS = ∠PQR = 50° (संगत कोण)
∴ l₁||l₂

Ex 10.2 Lines and Angle विविध प्रश्नावली

प्रश्न 1.
चित्र में x और y के मान ज्ञात कीजिए और सिद्ध कीजिए कि AB||CD.
हल:
AB||CD
x = 130° (संगत कोण)
y = 130° (शीर्षाभिमुख कोण)

प्रश्न 2.
चित्र में, यदि AB||CD, CD||EF और y : z = 3 : 7, तो x का मान ज्ञात कीजिए।
हलः
∠EPN = ∠CNM

180 – z = y
∴ y + z = 180° …………..(1)
माना ∠y = 3a
∠z = 7a
3a + 7a = 180
10a = 180 ⇒ a = [latex]\frac{180}{10}[/latex] = 18
∴ y = 3 × 18 = 54°
∵ z + y = 180
∴ z + 54 = 180°
∴ z = 180 – 54 = 126°
∴ ∠x = 2x = 126° (संगत कोण)

प्रश्न 3.
चित्र में, यदि AB||CD, EF⊥CD और ∠GED = 126°, ∠AGE, ∠GEF और ∠FGE ज्ञात कीजिए। (NCERT)
हल:

∵ AB||CD
∠AGE = ∠GED = 126° (एकान्तर कोण)
∠GEF = 126° – ∠FED
= 126° – 90° = 36°
∠FGE = 180° – ∠AGE = 180 – 126 = 54°

प्रश्न 4.
चित्र में यदि PQ||ST, ∠PQR = 110° और ∠RST = 130° तो ∠QRS ज्ञात कीजिए। (NCERT)
हलः

PQ को आगे M तक बढ़ाया
तथा
∠AMR = 130° (संगत कोण)
∠MQR = 180°- 110 = 70°
∠QMR = 180 – 130 = 50°
∆QRM में तथा ∠QRS = 180°- (∠MQR + ∠QMR)
= 180°- (70 + 50)
= 180 – 120 = 60°

प्रश्न 5.
चित्र में यदि AB||CD, ∠APQ = 50° और ∠PRD = 127° तो और y ज्ञात कीजिए।
हल:
∆PQR में, AB||CD
x = 50° (एकान्तर कोण)
∵ बहिष्कोण ∠PRD = ∠QPR + ∠PQR
∠PRD = y + x
127 = y + 50
127 – 50 = y
77° = y

प्रश्न 6.
चित्र में PQ और RS दो दर्पण है जो एक-दूसरे के समान्तर रखे गये है। एक आपतन किरण AB दर्पण PQ से B पर टकराती है और परावर्तित किरण पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुनः CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB||CD है।
हलः

∵ ∠3 = ∠4 ……………. (1)
P तथा ∠1 = ∠2 …………. (2)
परन्तु ∠3 = ∠2 …………… (3) (एकान्तर कोण) ,
समीकरण (1) व (3) से ∠2 = ∠4 …………….. (4)
समीकरण (2) व (3) से ∠1 = ∠3 ………………… (5)
समीकरण (4) व (5) को जोड़ने पर
∠2 + ∠1 = ∠4 + ∠3
∴ ∠BCD = ∠ABC
परन्तु ये एकान्तर कोण है।
∴ AB||CD

प्रश्न 7.
चित्र में ∆PQR की भुजाएँ QP और RQ को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है। यदि ∠SPR = 135° है और ∠PQT = 110° है तो ∠PRQ ज्ञात कीजिए। (NCERT)
हलः

∠QPR = 180 – 135 = 45°
∠PQT = ∠QPR + ∠PRQ
(∆ का बहिष्कोण अपने सम्मुख अन्तः कोणों के योग के बराबर होता है)
110 = 45 + ∠PRQ
110 – 45 = ∠PRQ
65° = ∠PRQ

प्रश्न 8.
चित्र में ∠X = 62°, ∠XYZ = 547, यदि ∆XYZ में YO और ZO क्रमशः ∠XYZ और ∠XZY के समद्विभाजक हैं तो ∠OZY और ∠YOZ ज्ञात कीजिए।
हल:
∆XYZ में ∠XZY = 180°– (62 + 54)
180 – 116 = 64°
∵ YO तथा ZO क्रमशः ∠XYZ तथा ∠XZY के समद्विभाजक है।

∴ ∠OYZ = [latex]\frac{54}{2}[/latex] = 27
तथा ∠OZY = [latex]\frac{64}{2}[/latex] = 32°
∠YOZ = 180 – (27 + 32)
= 180 – 59 = 121°

प्रश्न 9.
चित्र में यदि AB||DE, ∠BAC = 35°, ∠CDE = 53° तो ∠DCE ज्ञात कीजिए। (NCERT)
हलः

∵ AB||DE
∠BAC = ∠DEC = 35° (एकान्तर कोण)
∆CDE में,
∠DCE = 180° – (53 + 35)
= 180 – 88 = 92°

प्रश्न 10.
चित्र में यदि रेखाएं PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती है कि ∠PRT = 40°, ∠RPT = 95° और ∠TSQ = 75°, तो ∠SQT ज्ञात कीजिए। (NCERT)
हल:

∆PRT में, PTR = 180 – (95 + 40)
= 180 – 135 = 45°
∠PTR = ∠QTS = 45° (शीर्षाभिमुख कोण)
∠TQS = 180 – (45 + 75)
= 180 – 120 = 60°

प्रश्न 11.
चित्र में यदि PS ⊥ RS, PT||SR और ∠STR = 28° और ∠QRT = 65° तो x और y के मान ज्ञात कीजिए। (NCERT)
हलः

बहिष्कोण
∠QRT = ∠STR + ∠TSR
65 = 28 + ∠TSR
65 – 28 = ∠TSR
37 = ∠TSR
x = 37° [एकान्तर कोण]
∆TPS में,
90 + x + y = 180
90 + 37 + y = 180
127 + y = 180
y = 180 – 127 ⇒ y = 53°

प्रश्न 12.
चित्र में ∆PQR की भुजा QR को एक बिन्दु तक बढाया गया। यदि ∠PQR और ∠PRS के समअर्द्धक, बिन्दु T पर मिलते है तब सिद्ध कीजिए कि ∠QTR = [latex]\frac{1}{2}[/latex]∠QPR (NCERT)
हल:

∵ ∠QPR = 180 – ∠PQR – ∠PRQ
= 180 – 2∠TQR – (180 – ∠PRS)
= 180 – 2∠TQR – 180+∠PRS
= -2TQR + 2∠TRS
= 2(∠TRS – ∠TQR)
= 2∠QTR
या [latex]\frac{1}{2}[/latex] ∠QPR = ∠QTR

Ex 10.2 Lines and Angle बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
यहाँ x के किस मान के लिए l || m होगी?
(a) 20
(b) 30
(c) 50
(d) 45
हलः

l||m होगी, यदि संगत कोण बराबर होंगे। तब
2x – 30° = x + 20°
⇒ 2x – x = 30° + 20°
⇒ x = 50°
अतः विकल्प (c) सही है।

प्रश्न 2.
x के किस मान के लिए l||m होगी?
(a) 25
(b) 35
(c) 45
(d) इनमें से कोई नहीं
हल:

l||m होगी, यदि
4x + (3x + 5) – 180°
⇒ 7x + 5 = 180°
⇒ 7x = 180 – 5 = 175°
⇒ x =[latex]\frac{175^{\circ}}{7}[/latex] = 25°
अतः विकल्प (a) सही है।

प्रश्न 3.
यदि दो कोण परस्पर पूरक हैं तब प्रत्येक कोण है
(a) न्यूनकोण
(b) समकोण
(c) अधिक कोण
(d) इनमें से कोई नहीं
हलः
न्यूनकोण।
अतः विकल्प (a) सही है।

प्रश्न 4.
एक कोण की माप उसके पूरक की 5 गुनी है तब कोण की माप है।
(a) 25°
(b) 50°
(c) 75°
(d) इनमें से कोई नहीं
हलः
माना कोण = x°, पूरक कोण = (90 – x)°
तब x = 5(90°- x)
⇒ x = 450° – 5x
⇒ x + 5x = 450° ⇒ 6x = 450
⇒ x = [latex]\frac{450}{6}[/latex] = 75°
अतः विकल्प (c) सही है।

प्रश्न 5.
एक कोण जिसकी माप 180° से अधिक किन्तु 360° से कम हो, कहलाता है
(a) परावर्तित कोण
(b) न्यून कोण
(c) अधिक कोण
(d) ऋजु कोण
हलः
परावर्तित कोण
अत: विकल्प (a) सही है।

प्रश्न 6.
दो पूरक कोण इस प्रकार हैं कि एक की माप का दोगुना, अन्य की माप के तीन गुने के बराबर है। दो मापों का बड़ा है।
(a) 54°
(b) 64°
(c) 63°
(d) इनमें से कोई नहीं
हलः
माना बड़ा कोण = x°, पूरक कोण = (90 –x)°
2x = 3 × (90 – x)
2x = 270° – 3x ⇒ 5x = 270°
⇒ x = [latex]\frac{270}{5}[/latex] = 54°
अतः विकल्प (a) सही है।

प्रश्न 7.
दो सरल रेखाएँ AB और CD, एक-दूसरे को 0 पर काटती हैं। यदि ∠BOD = 63° तब ∠BOC =
(a) 63°
(b) 17°
(c) 153°
(d) 117°
हलः

∠BOD + ∠ BOC = 180°
⇒ 63° + ∠ BOC = 180°
⇒ ∠BOC = 180° – 63°
⇒ ∠BOC = 117°
अतः विकल्प (d) सही है।

प्रश्न 8.
यदि AB = x + 3, BC = 2x और AC = 4x – 5, तब x के किस मान के लिए B, AC पर स्थित है?
(a) 5
(b) 6
(c) 8
(d) इनमें से कोई नहीं
हलः
बिन्दु B, AC पर स्थित होगा, यदि
AC = AB + BC
⇒ 4x – 5 = x + 3 + 2x
⇒ 4x – 5 = 3x + 3 ⇒ x = 8
अतः विकल्प (c) सही है।

प्रश्न 9.
कोण की माप जो स्वयं का पूरक है
(a) 45°
(b) 55°
(c) 90°
(d) इनमें से कोई नहीं
हलः
45°
अतः विकल्प (a) सही है।

प्रश्न 10.
एक त्रिभुज का एक बाह्य कोण 110° और दो अन्तः विपरीत कोण बराबर हैं। ये बराबर कोण है
(a) 45°
(b) 55°
(c) 90°
(d) इनमें से कोई नहीं
हलः
माना अन्त:कोण = x°
तब बाह्य कोण = अन्त:कोणों का योग
110° = x° + x°
⇒ 2x = 110° ⇒ x = [latex]\frac{110^{\circ}}{2}[/latex] = 55°
अतः विकल्प (b) सही है।

प्रश्न 11.
यदि एक त्रिभुज का एक कोण, अन्य दो कोणों के योग के बराबर है तब त्रिभुज है (NCERT Exemplar)
(a) समकोण
(b) समद्विबाहु
(c) समबाहु
(d) इनमें से कोई नहीं
हलः
समकोण।
अतः विकल्प (a) सही है।

प्रश्न 12.
यदि दो सम्पूरक कोणों के बीच का अन्तर 40° है तब कोण है.
(a) 70°, 120°
(b) 70°, 110°
(c) 210°, 150°
(d) इनमें से कोई नहीं
हलः
माना कोण = x°; सम्पूरक कोण = (180° – x)
x – (180° – x) = 40°
⇒ 2x = 220° ⇒ x = [latex]\frac{220}{2}[/latex] = 110°
सम्पूरक कोण = 180° – 110° = 70°
अतः विकल्प (b) सही है।

प्रश्न 13.
यदि दो पूरक कोणों के बीच का अनुपात 2 : 3 है तब कोण है
(a) 36°, 54°
(b) 30°, 60°
(c) 20°, 70°
(d) इनमें से कोई नहीं
हलः
माना एक कोण = x°, पूरक कोण = (90° – x)

अतः विकल्प (a) सही है।

प्रश्न 14.
संलग्न चित्र में, यदि l||m, तब x =
(a) 30°
(b) 40°
(c) 70°
(d) इनमें से कोई नहीं

हलः

यदि l||m, तब
∠EDO = ∠COB = 70°
⇒ ∠BOA = 180° – 70° = 110°
∆ABO में, x°+ 110°+ 30° = 180°
x = 180° – 140°
⇒ x = 40°
अतः विकल्प (b) सही है।

प्रश्न 15.
संलग्न चित्र में, यदि AB||CD, तब x =
(a) 110°
(b) 115°
(c) 100
(d) इनमें से कोई नहीं

हलः
∠FAE = 180 – 132 = 48°
∵ PF ||CE
⇒ ∠FAE = ∠AEC = 48°
तथा AB||CD
⇒ ∠AEC = ∠ECD = 48°

∵ PA||CE
⇒ ∠APG = ∠ECP = 180 – 148 =32°
अतः बिन्दु C पर
x + ∠ECD + ∠ECP = 180°
x + 48 + 32 = 180°
⇒ x = 180° – 80 = 100°
अतः विकल्प (c) सही है।

प्रश्न 16.
यदि AB और CD दो समान्तर रेखाएँ हैं, PQ, AB और CD को क्रमशः E तथा F पर काटती है। EL, ∠FEB का समद्विभाजक है यदि ∠LEB = 35%, तब ∠CFQ =
(a) 90°
(b) 65°
(c) 110°
(d) 140°
हलः

दिया है,
∠LEB = 35°
∵ EL, ∠FEB का समद्विभाजक है, तब
∠FEL = 70°
⇒ ∠AEF = 180° – 70° = 110°
⇒ ∠CFQ = ∠AEF = 110° (एकान्तर कोण)
∴ ∠CFQ = 110°
अतः विकल्प (c) सही है।

प्रश्न 17.
तिर्यक रेखा के एक ही ओर यदि दो अन्तः कोणों का अनुपात 2 : 3 है तो बड़ा कोण = (NCERT)
(a) 56°
(b) 125°
(c) 108°
(d) इनमें से कोई नहीं
हलः
दो अन्त:कोणों का अनुपात = 2 : 3
अतः कोण = 2x तथा 3x
तब 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = [latex]\frac{180}{5}[/latex] = 36°
अतः बड़ा कोण = 3 × 36° = 108°
अतः विकल्प (c) सही है।

प्रश्न 18.
एक कोण इसके सम्पूरक के तीन गुने के बराबर है। कोण की माप है
(a) 125°
(b) 130°
(c) 135°
(d) 120°
हलः
माना कोण = x°; सम्पूरक कोण = (180° – x)
तब x = 3(180° – x)
⇒ x = 540 – 3x
⇒ 4x = 540 ⇒ x = [latex]\frac{540}{4}[/latex] = 135°
अतः विकल्प (c) सही है।

प्रश्न 19.
दिया गया है कि ∠POR = 3x और ∠QOR = 2x + 10°, यदि POQ एक सरल रेखा है तब x =
(a) 25°
(b) 30°
(c) 34°
(d) 44°
हल:
∵ POQ एक सरल रेखा है।
∴ ∠POR + ∠QOR = 180°
⇒ 3x + 2x + 10 = 180°
⇒ 5x + 10 = 180°
⇒ 5x = 180° – 10 = 170
⇒ x = [latex]\frac{170}{5}[/latex] = 34°
अतः विकल्प (c) सही है।

प्रश्न 20.
दो पूरक कोण इस प्रकार हैं कि एक की माप का दोगुना, अन्य की माप के तीन गुने के बराबर है। छोटे कोण की माप है।
(a) 36°
(b) 40°
(c) 56°
(d) इनमें से कोई नहीं
हलः
माना एक कोण = x°, पूरक कोण = (90° – x)
⇒ 3x = 2(90 – x)
⇒ 3x = 180 – 2x
⇒ 5x = 180° ⇒ x = [latex]\frac{180}{5}[/latex] = 36°
अतः विकल्प (a) सही है।

प्रश्न 21.
संलग्न चित्र में, यदि l||m तब x =
(a) 95°
(b) 45°
(c) 55°
(d) 65°
हल:

∵ l||m
तब ∠BAO = ∠OCD = 40
∆OAB में, ∠OAB + ∠ABO + ∠BOA = 180°
40° + 55° + ∠BOA = 180°
∠BOA = 180° – 95 = 85°
अब बिन्दु O पर,
x + ∠AOB = 180°
⇒ x + 85 = 180°
⇒ x = 180° – 85 = 95°
अतः विकल्प (a) सही है।

प्रश्न 22.
संलग्न चित्र में, l||m और m||n यदि x : y = 3 : 2 तब x =
(a) 108°
(b) 72°
(c) 1200
(d) इनमें से कोई नहीं
हलः

दिया है, x : y = 3 : 2
⇒ x = 3k, y = 2k
x + y = 3k +2k
5k = 180° ⇒ k = [latex]\frac{180^{\circ}}{5}[/latex] = 36°
⇒ x = 3 × 36 = 108°
अतः विकल्प (a) सही है।

प्रश्न 23.
एक त्रिभुज का एक बाह्य कोण 105° है तथा इसके अन्तः विपरीत कोण बराबर हैं तब प्रत्येक बराबर कोण की माप है (NCERT Exemplar)

हलः
माना अन्तः कोण = x°
तब त्रिभुज का बाह्य कोण = अन्तः कोणों का योग
105° = x + x
⇒ 2x = 105 ⇒ x = [latex]\frac{105}{2}=52 \frac{1}{2}^{\circ}[/latex]
अतः विकल्प (b) सही है।

प्रश्न 24.
यदि एक त्रिभुज का एक कोण 130, है तब अन्य दो कोणों के समद्विभाजकों के बीच कोण है (NCERT Exemplar)
(a) 145°
(b) 155°
(c) 65°
(d) इनमें से कोई नहीं
हल:
∆DAB में, ∠AOB = 130°
तथा PA तथा PB क्रमशः ∠OAB तथा ∠OBA के समद्विभाजक हैं।
माना ∠OAB = 2x, ∠OBA = 2y

तब ∠OAP = ∠PAB = x
तथा ∠OBP = ∠PBA = y
∆APB में, x + y + ∠APB = 180°
∠APB = 180° – (x + y) …………………. (1)
∆AOB में, 2x + 2y + 130° = 180°
2x + 2y = 50
x + y = 25 …………………….(2)
समी० (2) से x + y का मान समी० (1) में रखने पर,
∠APB = 180 – 25 = 155°
अतः विकल्प (b) सही है।

प्रश्न 25.
दिए गए चित्र में ज्ञात कीजिए कि a + b =
(a) 127°
(b) 107°
(c) 45°
(d) 54°
हलः


अतः विकल्प (a) सही है।

प्रश्न 26.
संलग्न चित्र में, AOB एक सरल रेखा है। ∠COD की माप =
(a) 80°
(b) 60°
(c) 120°
(d) 160°
हलः
बिन्दु O पर,

x + 20 + 2x – 20 + 60 = 180°
⇒ 3x + 60° = 180°
⇒ 3x = 120°
⇒ x = 40°
∠COD = 2 × 40 – 20 = 60°
अतः विकल्प (b) सही है।

प्रश्न 27.
यदि एक कोण की माप, उसके सम्पूरक कोण की माप की दोगुनी है। तब इसकी माप है
(a) 90°
(b) 110°
(c) 135°
(d) 120°
हलः
माना कोण = x, सम्पूरक कोण = 180° – x
x = 2(180° – x)
⇒ x = 360° – 2x
⇒ 3x = 360° ⇒ x = [latex]\frac{360^{\circ}}{3}[/latex] = 120°
अतः विकल्प (d) सही है।

प्रश्न 28.
एक कोण की माप जो स्वयं का सम्पूरक है
(a) 90°
(b) 110°
(c) 45°
(d) 135°
हलः
90°
अतः विकल्प (a) सही है।

प्रश्न 29.
(90°-x) का पूरक है
(a) x
(b) 90°+ x
(c) –x
(d) इनमें से कोई नहीं
हलः
(90° – x) का पूरक कोण = 90° – (90°– x)
= 90° – 90° + x = x
अतः विकल्प (a) सही है।

प्रश्न 30.
एक कोण की माप जो स्वयं का पूरक है
(a) 30°
(b) 90°
(c) 45°
(d) इनमें से कोई नहीं
हलः
माना कोण = x, पूरक कोण = 90° –x
x = 90° – x
⇒ x + x = 90°
⇒ 2x = 90° ⇒ x = [latex]\frac{90}{2}[/latex] = 45°
अतः विकल्प (c) सही है।

Ex 10.2 Lines and Angle स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
यह दिया गया है कि ∠XYZ = 64° और XY को एक बिन्दु P तक बढ़ाया गया है। दी गयी जानकारी से एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समअर्द्धक करती है तो ∠XYQ और परावर्तित ∠QYP ज्ञात कीजिए।
हलः
∵ YQ किरण, ∠ZYP को समअर्द्धक करती है
माना ∠ZYQ = ∠QYP = x
64 + x + x = 180
64 + 2x = 180
2x = 180 – 64 = 116
x = [latex]\frac{116}{2}[/latex] = 58

∴ ∠XYQ = 64 + x = 64 + 58 = 122°
∠QYP = 58°
परावर्तित कोण ∠QYP = 360 – 58 = 302°

प्रश्न 2.
सिद्ध कीजिए कि यदि दो रेखायें परस्पर प्रतिच्छेद करती है तब शीर्षाभिमुख कोण बराबर हैं।
हलः
रेखा AB व CD एक दूसरे को बिन्दु O पर प्रतिच्छेद करती है।
∠AOC + ∠AOD = 180° ………………….. (1)
∠AOD + ∠BOD = 180° ……………… (2)

समीकरण (1) व (2) की तुलना से
∠AOC + ∠AOD = ∠AOD + ∠BOD
∴ ∠AOC = ∠BOD
इसी प्रकार सिद्ध कर सकते हैं कि ∠AOD = ∠BOC
∴ शीर्षाभिमुख कोण बराबर होते हैं।

प्रश्न 3.
सलंग्न चित्र में, OD, ∠AOC का और OE, ∠BOC का समद्विभाजक है तथा OD⊥OE तो सिद्ध कीजिए कि बिन्दु A, O और B सरेख हैं।
हलः

∵ OD⊥OE ∴ ∠DOE = 90° ………………. (1)
माना ∠AOC = 2x तथा ∠BOC = 2y
∴ ∠AOD = ∠COD = x
तथा ∠BOE = ∠COE = y
∵ ∠AOD + ∠DOC + ∠COE + ∠BOE
= x + x + y + y = 2x + 2y
= 2(x + y)
= 2 × 90° = 180°
∵ समीकरण (1) से ∠DOE = ∠DOC + ∠COE = x + y = 90°
∴ AOB एक सरल रेखा है तथा A,O,B संरेख है।

प्रश्न 4.
यदि एक तिर्यक द्वारा दो समान्तर रेखायें प्रतिच्छेद होती हैं तब सिद्ध कीजिए कि किन्ही दो के संगत कोणों के समद्विभाजक समान्तर हैं।
हल:

माना AB||CD तथा MN एक तिर्यक रेखा काटती है।
∠MPB = ∠MQD (संगत कोण)
2 से भाग करने पर
[latex]\frac{\angle M P B}{2}=\frac{\angle M Q D}{2}[/latex]
∴ ∠MPT = ∠MQV
परन्तु ये संगत कोण है
PT||QN

प्रश्न 5.
संलग्न चित्र में ∆PQR की भुजा QR को एक बिन्दु S तक बढ़ाया गया है। यदि ∠PQR और ∠PRS के समद्विभाजक बिन्दु T पर मिलते हैं, तो सिद्ध कीजिए कि ∠QTR = [latex]\frac{1}{2}[/latex]∠QPR
हलः

∵ ∠QPR = 180 – ∠PQR – ∠PRQ
= 180 – 2∠TQR – (180 – ∠PRS)
= 180 – 2∠TQR – 180+∠PRS
= -2TQR + 2∠TRS
= 2(∠TRS – ∠TQR)
= 2∠QTR
या [latex]\frac{1}{2}[/latex] ∠QPR = ∠QTR

प्रश्न 6.
यदि एक तिर्यक रेखा द्वारा दो समान्तर रेखाएँ प्रतिच्छेद होती हैं तो सिद्ध कीजिए कि अन्तः कोणों के दो युग्मों के समद्विभाजक, एक आयत के रूप के हैं।
हलः

∠APQ, ∠BPQ तथा ∠PQC तथा ∠PQD के समद्विभाजक खीचें।
माना ∠BPQ = ∠QPB = x
∵ 2x + 2y = 180
x + y = 90 ………….. (1)
∵ x + y = 90
∴ चारों कोण 90° के होंगे।
∆PTQ तथा PSQ में सिद्ध कर सकते हैं कि PT = QS तथा TQ = PS
अत: PTQS एक आयत है।

प्रश्न 7.
सिद्ध कीजिए कि एक युग्म के समद्विभाजकों के शीर्षाभिमुख कोण, एक समान सरल रेखा पर है।
हलः

∠1 = ∠3 ………….. (1)
∠2 = ∠4 ………….. (2)
एक रेखा EF खींची।
∠2 = ∠x + ∠y, ∠2 + ∠1 + ∠4 + ∠3 = 360°,
∠4 = ∠m + ∠n रखने पर
∠x + ∠y + ∠1 + ∠m + ∠n + ∠3 = 360° (∠x +∠1 + ∠m) + (∠y + ∠3 + ∠n) = 360°
∴ प्रत्येक ∠x + ∠1 + ∠m = ∠y + ∠3 + ∠n
∴ शीर्षाभिमुख कोण ∠2 व ∠4 एक समान रेखा पर स्थित हैं = 180°

प्रश्न 8.
यदि दो सरल रेखायें परस्पर प्रतिच्छेद करती हैं। तो सिद्ध कीजिए कि एक कोण के समद्विभाजक के विपरीत किरण, शीर्षाभिमुख कोण को प्रतिच्छेद करती है।
हलः
माना ∠AOT = m तथा ∠TOD = n
m + z + y = 180 ……………… (1)
n + x + y = 180 …………….. (2)
समीकरण (1) व (2) की तुलना से
m + z + y = n + z + y

∴ m = n
∴ रेखा TM, शीर्षाभिमुख कोण को प्रतिच्छेद करती हैं।

प्रश्न 9.
यदि दो सरल रेखायें एक रेखा पर लम्ब है तो सिद्ध कीजिए कि वे परस्पर समान्तर हों?
हलः
यदि PQ व MN रेखा AB पर लम्ब हैं।
∵ ∠AQP = ∠ANM = 90°
परन्तु ये संगत कोण हैं।
∴ PQ||MN

प्रश्न 10.
सिद्ध कीजिए कि यदि एक कोण की दो भुजा, दूसरे कोण की भुजा के लम्बवत् है तो कोण या तो बराबर होंगे या सम्पूरक।
हलः
कोण बराबर होंगे यदि उनका योग 180° होगा अर्थात् सम्पूरक होंगे।

प्रश्न 11.
संलग्न चित्र में, यदि PQ⊥PS, PQ ||RS, ∠SQR = 28° तथा ∠QRT = 65° तो x, y और z के मान ज्ञात कीजिए।
हलः

∵ PQ⊥PS तथा ∠SPQ = 90°
∆SQR में,
z = 180 – 65 = 115°
∵ PQ||RS, ∠PQR = ∠QRT
x + 28 = 65
x = 65 – 28 = 37°
समकोण ∆PSQ में, y = 180 – (90 + 37)
= 180 – 127 = 53°

प्रश्न 12.
दिये गये चित्र में, यदि ∠COE = 2x° और / BOD = x°, तो x ज्ञात कीजिए। (जहाँ OD, ∠AOB का समद्विभाजक है और OE, ∠AOC का समद्विभाजक है)
हलः

∵ OD, ∠AOB का समद्विभाजक है
∴ ∠AOD =∠BOD = x
तथा OE, ∠AOC का समद्विभाजक है
∠COE =∠AOE = 2x
∴ ∠BOD + ∠AOD + ∠AOE +∠COE = 180
x + x + 2x + 2x = 180
6x = 180
x = [latex]\frac{180}{6}[/latex] = 30°

प्रश्न 13.
यदि दो सरल रेखाएँ परस्पर इस प्रकार प्रतिच्छेद करती है, कि एक के कोण की माप 90° है, तो सिद्ध कीजिए कि प्रत्येक के शेष कोण की माप 90° है।
हलः
l तथा m रेखाएँ एक-दूसरे को इस प्रकार प्रतिच्छेद करती हैं, कि
∠AOB = 90°
तब शेष ∠AOB = ∠AOC = 180°- 90° = 90°
इसी प्रकार ∠BOD =∠ COD = 90°

प्रश्न 14.
यदि एक कोण की भुजा क्रमशः अन्य दूसरे कोण की भुजा के समान्तर है, तो सिद्ध कीजिए कि दो कोण या तो बराबर हैं, या सम्पूरक।
हलः
कोण बराबर होंगे यदि उनका कोण 180° होगा अर्थात् सम्पूरक होंगे।

प्रश्न 15.
यदि दो सरल रेखाएँ समान रेखा के लम्बवत् हैं तो सिद्ध कीजिए कि वे परस्पर समान्तर हैं।
हलः
यदि PQ व MN रेखा AB पर लम्ब है।

∴ ∠AQP = ∠ANM = 90°
परन्तु ये संगत कोण हैं।
PQ||MN

Balaji Publications Mathematics Class 9 Solutions

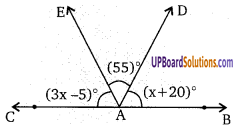
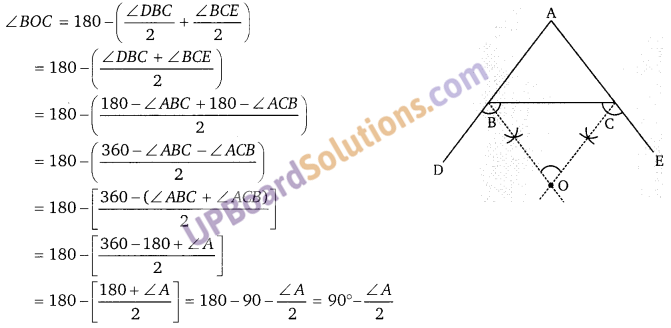
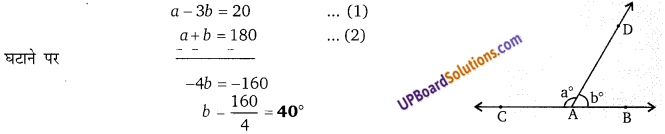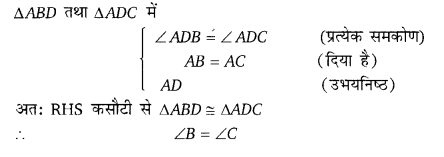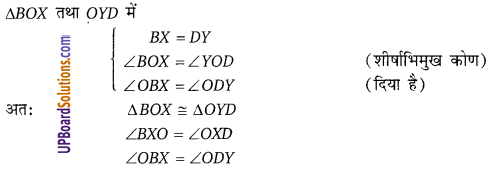Balaji Class 9 Maths Solutions Chapter 13 Quadrilateral Ex 13.4 चतुर्भज

Ex 13.4 Quadrilateral अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
किसी आयत के प्रत्येक कोण की माप ज्ञात कीजिए।
हलः
आयत का प्रत्येक कोण 90° होता है।

प्रश्न 2.
वर्ग की चारों भुजाओं में निम्न में से कौन-सा सम्बन्ध है?
(a) असमान
(b) समान
(c) दो समान हैं
(d) इनमें से कोई नहीं
हलः
वर्ग की चारों भुजाएँ समान होती हैं। अतः विकल्प (b) सही है।

प्रश्न 3.
समबाहु त्रिभुज की भुजाओं के मध्य बिन्दुओं को मिलाने से बना त्रिभुज कौन-सा त्रिभुज होता है?
हलः
समबाहु ∆ की तीनों भुजाओं के मध्य बिन्दुओं को मिलाने पर एक समबाहु त्रिभुज बनता है।

प्रश्न 4.
एक समान्तर चतुर्भुज में यदि विकर्ण बराबर तथा परस्पर लम्ब हों तो यह किस प्रकार का त्रिभुज होगा?
हलः
वह समान्तर चतुर्भुज में जिसमें विकर्ण समान लम्बाई के तथा एक दूसरे के लम्बवत् होते हैं, वह वर्ग होता है।

प्रश्न 5.
समान्तर चतुर्भुज की सम्मुख भुजाएँ होती हैं-
(a) समान्तर
(b) बराबर
(c) (a) व (b) दोनों
(d) इनमें से कोई नहीं
हलः
समान्तर चतुर्भुज की सम्मुख भुजाएं समान तथा समान्तर होते हैं। अतः विकल्प (c) सही है।

प्रश्न 6.
निम्न में से किसमें विकर्ण परस्पर लम्बवत् होते हैं?
(a) आयत
(b) समचतुर्भुज
(c) समान्तर चतुर्भुज
(d) इनमें से कोई नहीं
हल:
आयत में विकर्ण एक दूसरे के लम्बवत होते हैं। अतः विकल्प (a) सही है।

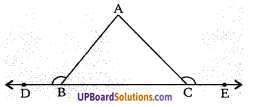
प्रश्न 7.
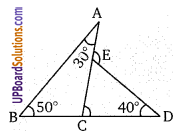
∆ABC में, यदि AD माध्यिका व E, AD का मध्य बिन्दु है। BE को मिलाया तथा ऐसे बढ़ाया कि यह AC
को F पर प्रतिच्छेद करती है तब AF का मान ज्ञात कीजिए।
हल:
[latex]A F=\frac{1}{6} A C[/latex]

प्रश्न 8.
समचतुर्भुज के मध्य बिन्दुओं को मिलाकर बनने वाली आकृति है (NCERT Exemplar)
(a) समचतुर्भुज
(b) आयत
(c) वर्ग
(d) इनमें से कोई नहीं
हलः
समचतुर्भुज के मध्य बिन्दुओं को मिलाने पर आयत बनता है। अतः विकल्प (b) सही है।

प्रश्न 9.
वर्ग की भुजाओं के मध्य बिन्दुओं को मिलाकर बनने वाला चतुर्भुज है-
(a) वर्ग
(b) आयत
(c) समान्तर चतुर्भुज
(d) इनमें से कोई नहीं
हलः
वर्ग के मध्य बिन्दुओं को मिलाने पर बना चतुर्भुज वर्ग होता है। अतः विकल्प (a) सही है।

प्रश्न 10.
समान्तर चतुर्भुज में यदि एक कोण 90° है तो यह है एक-
(a) समचतुर्भुज
(b) आयत
(c) वर्ग
(d) इनमें से कोई नहीं
हलः
यदि समान्तर चतुर्भुज का एक कोण 90° है तो समान्तर चतुर्भुज एक आयत होगा। अतः विकल्प (b) सही है।

प्रश्न 11.
एक समचतुर्भुज का एक कोण यदि 90° है तो यह है एक-
(a) समलम्ब चतुर्भुज
(b) वर्ग
(c) आयत
(d) इनमें से कोई नहीं
हलः
यदि किसी समचतुर्भुज का एक कोण 90° है तो वह वर्ग होगा। अत: विकल्प (b) सही है।

प्रश्न 12.
निम्न में से किसमें सभी चारों भुजाएँ बराबर होगी ?
(a) वर्ग
(b) समचतुर्भुज
(c) (a) व (b) दोनों
(d) इनमें से कोई नहीं
हलः
वर्ग तथा समचतुर्भुज की चारों भुजाएं समान होती हैं। अतः विकल्प (c) सही है।

Ex 13.4 Quadrilateral लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 13.
सिद्ध कीजिए कि यदि एक समान्तर चतुर्भुज के विकर्ण परस्पर लम्ब हैं, तब यह एक समचतुर्भुज होता [NCERT]
हलः
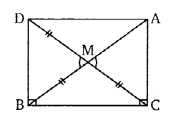
ज्ञात हैः एक समान्तर चतुर्भुज ABCD जिसके विकर्ण AC तथा BD बराबर हैं।

सिद्ध करना है: ABCD एक आयत है
उपपत्ति: ∆ABC तथा ∆DCB में;
AB = CD (समान्तर चतुर्भुज ABCD की सम्मुख भुजाएँ)
BC (उभयनिष्ठ भुजा)
AC = BD (ज्ञात है)
अतः ∆ABC = ∆DCB
∴ ∠ABC = ∠DCB
समान्तर चतुर्भुज ABCD में तिर्यक रेखा BC के एक की ओर स्थित ∠ABC तथा ∠DCB का योगफल 180° होगा।
∴ ∠ABC + ∠DCB = 180°
समान्तर चतुर्भुज का प्रत्येक कोण समकोण होता है।
∠ABC = 90° (∴ ∠ABC = ∠DCB)
∴ ABCD समचतुर्भुज है।

प्रश्न 14.
सिद्ध कीजिए कि यदि एक चतुर्भुज के विकर्ण परस्पर लम्ब समद्विभाजक हैं तो वह एक समचतुर्भुज होता [NCERT]
हलः
ज्ञात है: एक समान्तर चतुर्भुज ABCD जिसके विकर्ण AC तथा BD एक-दूसरे पर लम्ब हैं।

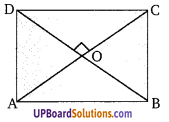
सिद्ध करना है: ABCD एक समचतुर्भुज है।
उपपत्तिः माना विकर्ण AC तथा BD एक दूसरे को बिन्दु O पर काटते हैं। समान्तर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
समान्तर चतुर्भुज ABCD में, OA = OC
∆AOD तथा ∆COD में, OA =OC (अभी सिद्ध किया है)
∠AOD = ∠COD (प्रत्येक समकोण)
OD उभयनिष्ठ
अतः ∆AOD ≅ ∆COD
AD = CD
अतः ABCD एक ऐसा समान्तर चतुर्भुज है जिसकी क्रमागत भुजाएँ AD,CD बराबर हैं।
अतः ABCD एक समचतुर्भुज है।

प्रश्न 15.
सिद्ध कीजिए कि यदि किसी चतुर्भुज के विकर्ण बराबर तथा समकोण पर समद्विभाजित हैं तो वह एक वर्ग होता है। [NCERT]
हलः
ज्ञात है: एक समान्तर चतुर्भुज ABCD जिसके विकर्ण AC एवं BD बराबर हैं तथा एक दूसरे पर लम्ब हैं।
सिद्ध करना है: ABCD एक वर्ग है।
उपपत्ति: माना विकर्ण AC व BD एक दूसरे को बिन्दु O पर काटते हैं।
∵ समान्तर चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं।
समान्तर चतुर्भुज ABCD में |
OB = OD … (1)

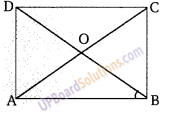
∆AOB तथा ∆AOD में,
A0 उभयनिष्ठ
∠AOB = ∠AOD (प्रत्येक समकोण)
OB =OD [समी० (1) से]
अतः
∆AOB ≅ ∆AOD
AB = AD …(2)
परन्तु समान्तर चतुर्भुज ABCD की सम्मुख भुजायें होने के कारण
AB = CD तथा AD = BC …. (3)
समीकरण (2) तथा (3) से, AB = BC = CD = AD … (4)
अब ∆ABD तथा ∆BAC में, AB उभयनिष्ठ
AD = BC [समी० (4) से]
BD = AC (ज्ञात है)
∴ ∆ABD ≅ ∆BAC
∴ ∠DAB = ∠CBA
∴ ABCD एक समान्तर चतुर्भुज है।
∴ सम्मुख भुजाएं AD एवं BC एक दूसरे के समान्तर हैं।
∴ AD तथा BC एक दूसरे के समान्तर हैं उन्हें तिर्यक रेखा AB क्रमशः A व B पर काटती हैं।
∴ तिर्यक रेखा AB के एक ही ओर स्थित अन्त:कोणों ∠DAB और ∠CBA का योग 180° होता है।
∠DAB + ∠CBA = 180° …(6)
समीकरण (5) व (6) से, ∠DAB + ∠CBA = 90° …(7)
∴ समीकरण (4) व (7) से प्रदर्शित होता है कि ABCD एक ऐसा समान्तर चतुर्भुज है। जिसकी सभी भुजाएं बराबर तथा प्रत्येक कोण समकोण है।
अत: ABCD एक वर्ग है।

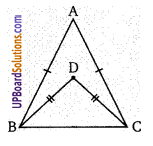
प्रश्न 16.
त्रिभुज ABC की माध्यिका AD को X की ओर बढ़ाते हैं तो AD = DX तो सिद्ध कीजिए ABXC एक समान्तर चतुर्भुज है।
हलः
ज्ञात है: ∆ABC में माध्यिका AD को बिन्दु X तक बढ़ाया गया है जिससे AD = DX
सिद्ध करना है: ABXC एक समान्तर चतुर्भुज है।
रचना: BX तथा XC को मिलाया।
उपपत्तिः
AD = DX
BD = DC
∆ABD तथा ∆ADC में,

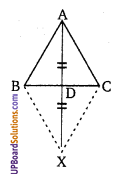
AD = DX (ज्ञात है)
BD = DC (ज्ञात है)
∠ADB = ∠ADC (प्रत्येक समकोण)
अतः
∆ABD ≅ ∆ADC
AB = CX
इसी प्रकार सिद्ध कर सकते हैं कि BX = AC
इसलिए ABXC एक समान्तर चतुर्भुज है।

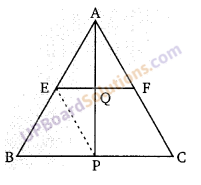
प्रश्न 17.
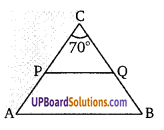
त्रिभुज ABC में E व F क्रमशः AB व AC के मध्य बिन्दु हैं। BC पर एक शीर्ष लम्ब AP है। जो EF को
बिन्दु Q पर प्रतिच्छेद करता है। सिद्ध कीजिए AQ = PQ
हल:

Ex 13.4 Quadrilateral दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 18.
ABCD एक समचतुर्भुज है। सिद्ध कीजिए कि विकर्ण AC, ∠A व ∠C को तथा विकर्ण BD, ∠B व ∠D को समद्विभाजित करते हैं। [NCERT]
हलः

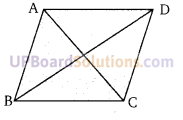
ज्ञात है: ABCD एक समचतुर्भुज है जिसके विकर्ण AC तथा BD हैं।
सिद्ध करना है: ∠BAC = ∠DAC तथा ∠ACB = ∠ACD
तथा ∠ABD = ∠DBC तथा ∠ADB = ∠BDC
उपपत्ति: ∆ABC तथा ∆ADC में,
AB = DC (समचतुर्भुज की भुजाएँ)
BC = AD (समचतुर्भुज की भुजाएँ)
AC उभयनिष्ठ
अतः ∆ABC ≅ ∆ADC
∴ ∠BAC = ∠CAD तथा ∠BCA = ∠ACD
इसी प्रकार सिद्ध कर सकते हैं कि ∠ABD = ∠DBC तथा ∠ADB = ∠BDC

प्रश्न 19.
सिद्ध कीजिए कि चतुर्भुज की सम्मुख भुजाओं के मध्य बिन्दुओं को मिलाने वाले रेखाखण्ड परस्पर समद्विभाजित करते हैं। (NCERT)
हलः

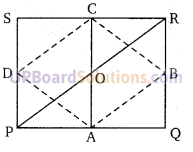
ज्ञात है: A,B,C,D क्रमश: PQ, QR, RS तथा SP के मध्य बिन्दु हैं। AC तथा BD बिन्दु O पर अन्त:खण्ड खींचे गये हैं।
सिद्ध करना है: AO = CO तथा DO = OB
रचनाः AB, BC,CD तथा DA को मिलाया।
उपपत्तिः ∆PQR में, A, B PQ तथा QR के मध्य बिन्दु हैं।
AB||PR
∆PSR में, DC||PR समी० (1) व (2) से AB||DC तथा AB = DC
समान्तर चतुर्भुज ABCD में, AO = CO तथा DO = BO

प्रश्न 20.
ABCD एक समचतुर्भुज है तथा P, Q,R व S क्रमश: AB, BC, CD व DA के मध्य बिन्दु हैं। सिद्ध कीजिए कि PQRS एक आयत है।
हल:
∆ABC में P तथा Q, AB व BC के मध्य बिन्दु हैं। AC को मिलाया।

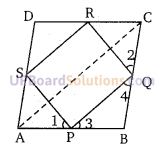
इसी प्रकार ∆ADC में R तथा S,CD तथा DA के मध्य बिन्दु हैं।

समी० (1) व (2) से PQ|| RS तथा PQ = SR
चतुर्भुज PQRS में, PQ तथा SR समान तथा समान्तर हैं।
∴ PQRS एक समान्तर चतुर्भुज है।
∴ AB, BC समचतुर्भुज की भुजाएं हैं।

प्रश्न 21.
सिद्ध कीजिए कि यदि चतुर्भुज के सम्मुख कोण समान हो तो वह समान्तर चतुर्भुज होता है। [NCERT]
हलः

Ex 13.4 Quadrilateral इतिसिद्धम् बहविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
एक समचतुर्भुज की आसन्न भुजाओं के मध्य बिन्दुओं को मिलाने पर प्राप्त आकृति है एक-
(a) आयत
(b) वर्ग
(c) समान्तर चतुर्भुज
(d) इनमें से कोई नहीं
हलः
एक आयत।
अतः विकल्प (a) सही है।

प्रश्न 2.
एक वर्ग की आसन्न भुजाओं के मध्य बिन्दुओं को मिलाने पर प्राप्त आकृति है, एक-
(a) आयत
(b) वर्ग
(c) समचतुर्भुज
(d) इनमें से कोई नहीं
हलः
वर्ग। अतः विकल्प (b) सही है।

प्रश्न 3.
यदि एक चतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं तब आकृति है एक-
(a) आयत
(b) समान्तर चतुर्भुज
(c) समचतुर्भुज
(d) इनमें से कोई नहीं
हलः
समचतुर्भुज। अतः विकल्प (c) सही है।

प्रश्न 4.
निम्न में से कौन-सी आकृति के विकर्ण बराबर हैं?
(a) आयत
(b) समान्तर चतुर्भुज
(c) समचतुर्भुज
(d) इनमें से कोई नहीं
हलः
आयत। अतः विकल्प (a) सही है।

प्रश्न 5.
यदि एक समान्तर चतुर्भुज ABCD के दो आसन्न कोण ∠A = ∠B है, तब समान्तर चतुर्भुज है-
(a) आयत
(b) समलम्ब चतुर्भुज
(c) समचतुर्भुज
(d) इनमें से कोई नहीं
हलः
आयत। अतः विकल्प (a) सही है।

प्रश्न 6.
एक समचतुर्भुज की आसन्न भुजाओं के मध्य बिन्दुओं को मिलाने पर प्राप्त आकति है, एक-
(a) वर्ग
(b) आयत
(c) समचतुर्भुज
(d) इनमें से कोई नहीं
हलः
समचतुर्भुज। अतः विकल्प (c) सही है।

प्रश्न 7.
यदि एक समलम्ब चतुर्भुज की समान्तर भुजाएँ क्रमशः a और b हैं, तो असमान्तर भुजाओं के मध्य बिन्दुओं को मिलाने वाली रेखा है-
(a) [latex]\frac{\boldsymbol{a}+\boldsymbol{b}}{2}[/latex]
(b) [latex]\frac{\boldsymbol{a}-\boldsymbol{b}}{2}[/latex]
(c) [latex]\frac{2 a b}{a+b}[/latex]
(d) इनमें से कोई नहीं
हलः
असमान्तर भुजाओं के मध्य बिन्दुओं को मिलाने वाली रेखा = [latex]\frac{\boldsymbol{a}+\boldsymbol{b}}{2}[/latex]
अतः विकल्प (a) सही है।

प्रश्न 8.
समान आधार व समान समान्तर भुजाओं पर दो समान्तर भुजाएं हैं। उनके क्षेत्रफलों का अनुपात-
(a) 1 : 2
(b) 2 : 1
(c) 1 : 1
(d) इनमें से कोई नहीं
हल:
1 : 1
अतः विकल्प (c) सही है।

प्रश्न 9.
निम्न में से कौन-सा समान्तर चतुर्भुज के लिए सत्य है?
(a) विपरीत भुजाएँ बराबर हैं।
(b) विपरीत कोण बराबर हैं।
(c) विकर्ण एक-दूसरे को समद्विभाजित करते हैं।
(d) सभी सत्य हैं।
हलः
सभी सत्य हैं। अतः विकल्प (d) सही है।

प्रश्न 10.
यदि एक चतुर्भुज के तीन कोणों की माप 56°,115° और 84° है तब चौथे कोण की माप है।
(a) 105°
(b) 100°
(c) 110°
(d) इनमें से कोई नहीं
हल:
∵ चतुर्भुज के चारों कोणों का योग 360° होता है। अतः
56+115+ 84+ X = 360°
x = 360° – 255
=105°
अतः विकल्प (a) सही है।

प्रश्न 11.
यदि एक चतुर्भुज के कोण A,B,C और D अनुपात 3:7:6:4 के क्रम में लिये गये हैं तब ABCD है एक- (NCERT Exemplar)
(a) समचतुर्भुज
(b) समलम्ब चतुर्भुज
(c) समान्तर चतुर्भुज
(d) इनमें से कोई नहीं
हल:
3x +7x+6x +4x = 360°
20x = 360°
x = 180
∠A = 3 × 18 = 54°,
∠B = 7 × 18 = 126°,
∠C = 6 × 18 = 108°,
∠D = 4 × 18 = 72°
∠A + ∠B = 180° तथा
∠C + ∠D = 180°
अतः विकल्प (b) सही है।

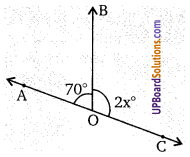
प्रश्न 12.
एक चतुर्भुज के तीन कोण 75°,90° और 75° है। चौथा कोण हैं (NCERT Exemplar)
(a) 60°
(b) 90°
(c) 120°
(d) इनमें से कोई नहीं
हलः
माना चौथा कोण x° है। तब ।
75+ 90 + 75+ x = 360°
240 + x = 360°
x = 360°- 240°
x = 120°
अतः विकल्प (c) सही है।

प्रश्न 13.
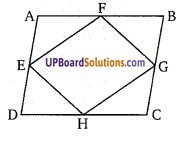
एक समान्तर चतुर्भुज का परिमाप 32 सेमी है। यदि छोटी भुजा 6.5 सेमी है तब बड़ी भुजा की माप है
(a) 9.5 सेमी
(b) 9 सेमी
(c) 8.5 सेमी
(d) इनमें से कोई नहीं
हलः
माना बड़ी भुजा x है, तब परिमाप
32 = 2x + 2 × 6.5
32 = 2x + 13
2x = 32 – 13 ⇒ 2x = 19

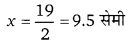
अतः विकल्प (a) सही है।

प्रश्न 14.
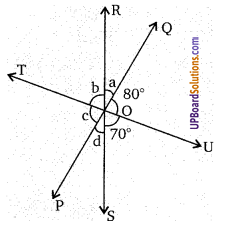
एक समान्तर चतुर्भुज ABCD में यदि ∠A = 80° और ∠B =
(a) 100°
(b) 120°
(c) 130°
(d) इनमें से कोई नहीं
हल:

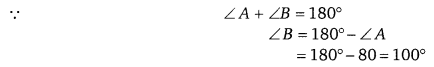
अतः विकल्प (a) सही है।

प्रश्न 15.
यदि एक समचतुर्भुज ABCD है तब ∠A – ∠C =
(a) 60°
(b) 90°
(c) 0
(d) इनमें से कोई नहीं
हलः
किसी समचतुर्भुज में यदि ∠A तथा ∠C, समकोण हों, तो
∠A – ∠C = 0
अतः विकल्प (c) सही है।

प्रश्न 16.
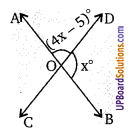
एक समान्तर चतुर्भुज ABCD के विकर्ण AC और BD बिन्दु O पर प्रतिच्छेद करते हैं यदि ∠DAC = 34° और ∠AOB = 75° तब ∠DBC =
(a) 34°
(b) 75°
(c) 41°
(d) इनमें से कोई नहीं
हल:
∴ ∠DAC = 34°

प्रश्न 17.
एक समचतुर्भुज ABCD इस प्रकार कि ∠ACB = 40° तब ∠ADB = (NCERT Exemplar)
(a) 50°
(b) 60°
(c) 90°
(d) इनमें से कोई नहीं
हल:

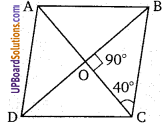
∴ ∠ACB = 40°
∴ ∠COB = 90°

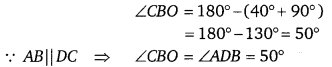
अतः विकल्पं (a) सही है।

प्रश्न 18.
एक समान्तर चतुर्भुज के कोणों के समद्विभाजकों द्वारा बनी आकृति है एक-
(a) वर्ग
(b) समचतुर्भुज
(c) समान्तर चतुर्भुज
(d) आयत हलः आयत।
अतः विकल्प (d) सही है।

प्रश्न 19.
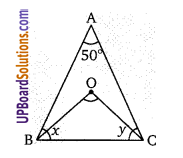
संलग्न चित्र में, एक समचतुर्भुज ABCD इस प्रकार है कि ∠ACB = 50° तब ∠ADB =
(a) 50°
(b) 60°
(c) 40°
(d) इनमें से कोई नहीं

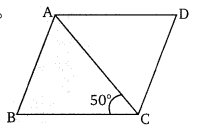
हलः

Ex 13.4 Quadrilateral स्वमल्यांकन परीक्षण (Self Assessment Test)

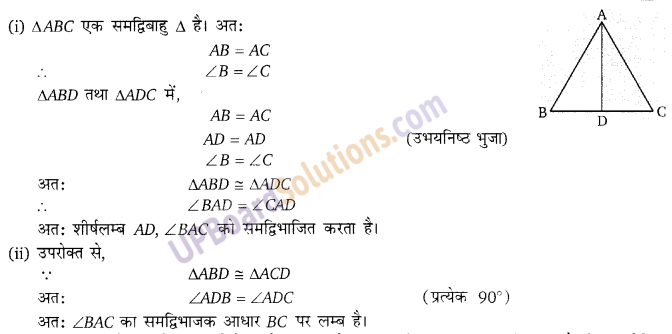
प्रश्न 1.
सिद्ध कीजिए कि एक समान्तर चतुर्भुज की विपरीत भुजाओं के मध्य बिन्दुओं को मिलाने वाली सरल रेखा, समान्तर भुजाओं के अन्य युग्म से समान्तर होती है।
हलः
∵ ABCD एक समान्तर चतुर्भुज है।
∴ AB||DC तथा AD|| BC
(i) ∵ AB||DC व DA व CB तिर्यक रेखा हैं।

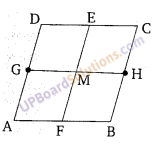
मध्य बिन्दुओं E, F को मिलाने वाली रेखा EF के अन्त:खण्ड EM = MF
तथा मध्य बिन्दुओं G,H को मिलाने वाली रेखा GH के अन्त:खण्ड GM = MH होंगे।
अत: AB||GH|| DC तथा AD|| FE||BC होंगे।

प्रश्न 2.
एक समचतुर्भुज PQRS है। विकर्ण PR और QS, O पर प्रतिच्छेद करते हैं। तो सिद्ध कीजिए कि इस प्रकार बने सभी चार कोण सर्वांगसम हैं।
हलः
∵ समचतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं तथा समचतुर्भुज की चारों भुजाएं समान होती हैं।
PQ = QR = RS = SP

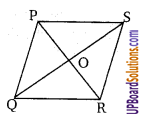
∆POQ, ∆POS, ∆QOR तथा ∆SOR भुजा-भुजा-भुजा प्रतिबन्ध से सर्वांगसम होंगे।

प्रश्न 3.
एक चतुर्भुज के कोण 3:5:9 : 13 के अनुपात में हैं। चतुर्भुज के सभी कोण ज्ञात कीजिए। [NCERT]
हलः
माना चतुर्भुज के कोण = 3x, 5x, 9x, 13x
∵ चतुर्भुज के चारों कोणों का योगफल = 360°
3x + 5x + 9x + 13x = 360°
30x = 360°

∴ चतुर्भुज के कोण = 36°, 60°, 108°, 156°

प्रश्न 4.
दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं तथा एक-दूसरे को समकोण पर समद्विभाजित करते हैं। [NCERT]
हलः

प्रश्न 5.
एक समान्तर चतुर्भुज ABCD का विकर्ण AC, ∠A को समद्विभाजित करता है तो सिद्ध कीजिए कि-
(i) यह ∠C को भी समद्विभाजित करता है। [NCERT]
(ii) ABCD एक समचतुर्भुज है।
हलः
AB||DC तथा AC तिर्यक रेखा काटती है।
∠1 = ∠3 (एकान्तर कोण )

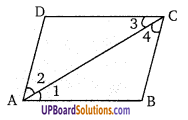
AD||BC तथा AC तिर्यक रेखा काटती है।
∠2 = ∠4 (एकान्तर कोण)
∵ AC, ∠A का अर्द्धक है।
∴ ∠1 = ∠2
∴ ∠3 = ∠4
∴ सम्मुख कोण समान हैं तथा ABCD एक समचतुर्भुज है।

प्रश्न 6.
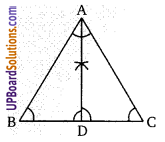
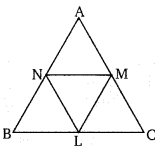
ABC एक समबाहु त्रिभुज है तथा L,M,N क्रमशः भुजाओं BC, CA और AB के मध्य बिन्दु हैं तो दर्शाइये कि ∆LMN एक समबाहु त्रिभुज है।
हलः
माना समबाहु ∆ की भुजा AB = BC = CA = x सेमी
∵ किसी त्रिभुज में दो भुजाओं के मध्य बिन्दुओं को मिलाने वाली रेखा तीसरी भुजा के समान्तर तथा उससे आधी होती है।

प्रश्न 7.
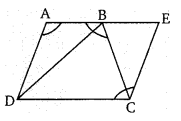
एक समलम्ब चतुर्भुज ABCD इस प्रकार है कि AB||CD तथा AD = BC तो दर्शाइए कि
(i) ∠A = ∠B
(ii) ∠C = ∠D (NCERT)
(iii) ∆ABC ≅ ∆BAD
(iv) विकर्ण AC = विकर्ण BD
हल:
AB को बढ़ाया और C से होकर DA के समान्तर एक रेखा खींची जो बढी हुई भुजा AB को E पर प्रतिच्छेद करे।
∵ AECD एक समान्तर चतुर्भुज है।

प्रश्न 8.
एक समचतुर्भुज की भुजाओं के मध्य बिन्दुओं को मिलाने पर एक चतुर्भुज बनता है। सिद्ध कीजिए कि वह एक आयत होगा।
हलः

प्रश्न 9.
एक चतुर्भुज ABCD की भुजाओं AB, BC, CD और DA के मध्य बिन्दु क्रमश: P, Q, R और है तथा जिसमें AC = BD है तो सिद्ध कीजिए कि PQRS एक समचतुर्भुज है। (NCERT)
हल:

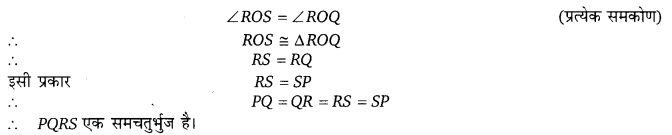
प्रश्न 10.
ABCD एक समचतुर्भुज है जिसमें भुजा AB की D से ऊँचाई, AB को समद्विभाजित करती है। तो समचतुर्भुज के कोण ज्ञात कीजिए।
हल:

प्रश्न 11.
एक समान्तर चतुर्भुज के एक अधिक कोण के शीर्ष से, समान्तर चतुर्भुज की दो ऊँचाइयों के बीच का कोण 60° है। एक समान्तर चतुर्भुज के कोण ज्ञात कीजिए।
हलः

प्रश्न 12.
एक चतुर्भुज ABCD है जिसमें P, Q,R और क्रमशः भुजाओं AB, BC, CD और DA के मध्य बिन्दु हैं AC एक विकर्ण है तो दर्शाइए कि-
(i) SR||AC और SR = [latex]\frac{1}{2}[/latex]AC
(ii) PQ = SR
(iii) PQRS एक समान्तर चतुर्भुज है।
हल:

प्रश्न 13.
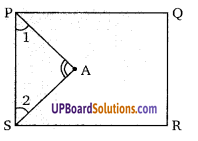
एक समद्विबाहु समकोण त्रिभुज में, एक वर्ग बनाया गया है। वर्ग और त्रिभुज का एक कोण उभयनिष्ठ है। दर्शाइए कि उभयनिष्ठ कोण के शीर्ष के विपरीत, वर्ग का शीर्ष कर्ण को समद्विभाजित करता है। (NCERT Exemplar)
हल:

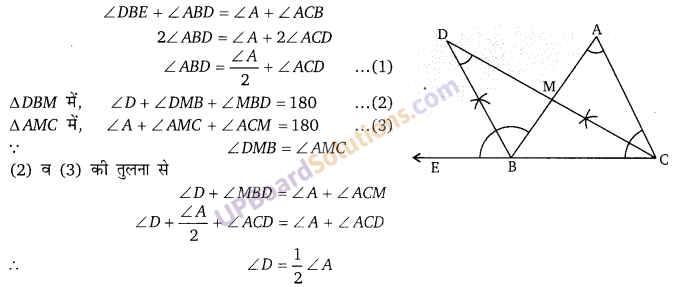
प्रश्न 14.
एक ∆ABC में, D,E और F क्रमशः भुजाओं BC, CA और AB के मध्य बिन्दु हैं। यदि भुजाओं AB, BC और CA की लम्बाइयाँ क्रमशः 7 सेमी, 8 सेमी, 9 सेमी हैं तो दर्शाइए कि ∆DEF का परिमाप 12 सेमी है।
हल:

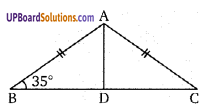
प्रश्न 15.
माना एक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AB = AC यदि D,E और F क्रमशः भुजाओं BC, CA और AB के मध्य बिन्दु हैं तो दर्शाइए कि रेखाखण्ड AD और EF एक-दूसरे को समकोण पर समद्विभाजित करती है।
हलः

प्रश्न 16.
ABCD एक पतंग है जिसमें AB = AD और BC = CD तो सिद्ध कीजिए कि भुजाओं के मध्य बिन्दुओं को मिलाने पर प्राप्त आकृति एक आयत है।
हल:

प्रश्न 17.
एक ∆ABC में, A, B और C से, भुजाओं BC, CA और AB के समान्तर रेखा R खींचे जाने पर प्राप्त आकृति ∆PQR है। तो दर्शाइए कि BC = [latex]\frac{1}{2}[/latex]QR.
हल:

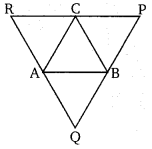
बिन्दु A से BC के समान्तर RQ, बिन्दु B से AC के समान्तर PQ तथा बिन्दु C से AB Aके समान्तर RP रेखायें खींची गयी है।
∴ ∆PQR बनता है।
अतः बिन्दु A, B, C क्रमश: APQR की भुजाओं RQ, QP तथा PR के मध्य बिन्दु होंगे।

प्रश्न 18.
एक समान्तर चतुर्भुज का परिमाप 22 सेमी है यदि बड़ी भुजा की माप 6.5 सेमी है दर्शाइए कि छोटी भुजा की माप 4.5 सेमी है।
हल:
समान्तर चतुर्भुज का परिमाप = 2(a + b)
जहाँ a व b क्रमशः समान्तर चतुर्भुज की भुजाएं है।

प्रश्न 19.
यदि एक समान्तर चतुर्भुज के कोण, इसके आसन्न कोण का [latex]\frac{4}{5}[/latex] तो समान्तर चतुर्भुज के कोण ज्ञात कीजिए।
हलः

प्रश्न 20.
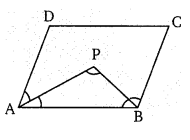
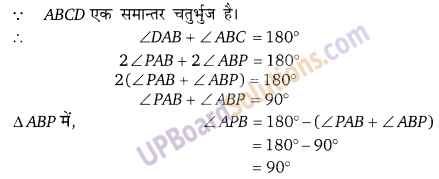
संलग्न चित्र में, एक समान्तर चतुर्भुज ABCD है जिसमें ∠A और ∠B के समद्विभाजक एक बिन्दु P पर प्रतिच्छेद करते हैं, दर्शाइए कि ∠APB = 90°
हलः

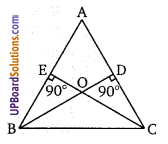
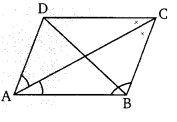
प्रश्न 21.
संलग्न चित्र में, ABCD एक समान्तर चतुर्भुज है, E, AB का मध्य बिन्दु है। और CE, ∠BCD को समद्विभाजित करता है। तो सिद्ध कीजिए कि
(i) AE = AD
(ii) DE, ∠ADC को समद्विभाजित करता है।
(iii) ∠DEC = 90°

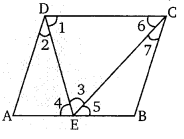
हलः

प्रश्न 22.
यदि एक समान्तर चतुर्भुज का एक विकर्ण, समान्तर चतुर्भुज के कोणों में से एक को समद्विभाजित करता है तो सिद्ध कीजिए कि यह, इसके विपरीत कोण को भी समद्विभाजित करता है तथा दोनों विकर्ण
हलः
समान्तर चतुर्भुज ABCD का विकर्ण AC, उसे दो समान त्रिभुजों में बाँटता है
∆ADC तथा ∆ABC में,
AB = DC (समान्तर चतुर्भुज की भुजाएँ)
AD = BC (समान्तर चतुर्भुज की भुजाएँ)
AC उभयनिष्ठ अतः
∆ADC ≅ ∆ABC
∠BCA = ∠DCA

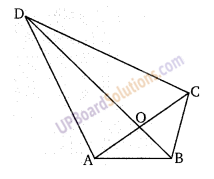
प्रश्न 23.
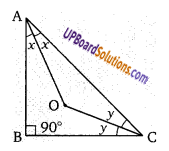
यदि ABCD एक चतुर्भुज है जिसके विकर्ण AC और BD,O पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए किः
(i) (AB + BC + CD + DA) > (AC + BD)
(ii) (AB + BC + CD + DA) < 2(AC + BD)
हलः

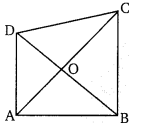
प्रश्न 24.
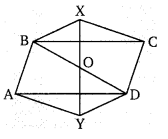
संलग्न चित्र में, एक बिन्दु 0, एक समचतुर्भुज ABCD के भीतर इस प्रकार लिया गया है कि OB = OD तो दर्शाइए कि A,0 और C समान रेखा में हैं।
हलः

प्रश्न 25.
एक चतुर्भुज के विकर्ण लम्बवत् हैं तो दिखाइये कि चतुर्भुजीव आकृति में, इसकी भुजाओं के मध्य बिन्दुओं को मिलाने पर प्राप्त आकृति एक आयत है। (NCERT)
हलः
स्वयं हल कीजिए।

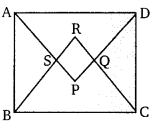
प्रश्न 26.
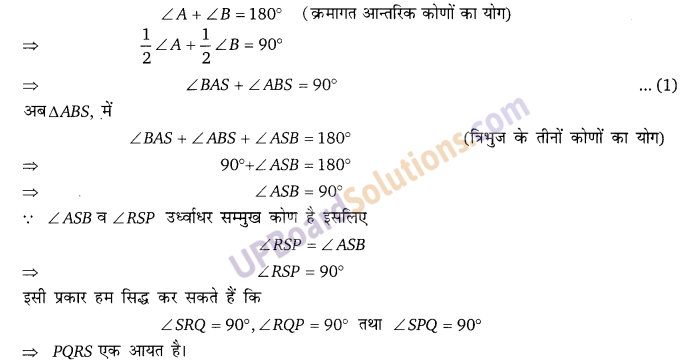
सिद्ध कीजिए कि एक समान्तर चतुर्भुज के कोणों के समद्विभाजकों द्वारा घिरा क्षेत्र एक आयत है।
हलः
दिया है: ABCD एक समान्तर चतुर्भुज है जिसमें कोणों A, B,C,D के समद्विभाजक क्रमशः बिन्दुओं P,Q, R व
S पर प्रतिच्छेद कर एक चतुर्भुज PQRS बनाते हैं।
सिद्ध करना है: PQRS एक आयत हैं।
उपपत्तिः ∵ ABCD एक समान्तर चतुर्भुज है
इसलिए, AD|| BC
∵ AD||BC तथा तिर्यक रेखा AB उसे क्रमशः बिन्दु A व B पर प्रतिच्छेद करती है।

प्रश्न 27.
एक वर्ग की भुजाओं के मध्य बिन्दुओं को मिलाने पर प्राप्त आकृति एक वर्ग होता है।
हलः

प्रश्न 28.
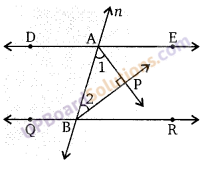
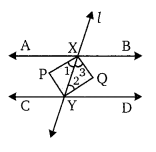
यदि एक तिर्यक, दो समान्तर रेखाओं को काटती है तो दर्शाइए कि अन्तः कोणों के समद्विभाजक एक आयत बनाते हैं।
हलः
दिया है। दो समान्तर भुजाएँ AB व CD तथा तिर्यक रेखा l जो AB को X तथा CD को Y पर काटती है। आन्तरिक कोणों के समद्विभाजक बिन्दु P व Q पर प्रतिच्छेद करते हैं।

प्रश्न 29.
समान्तर चतुर्भुज ABCD के विकर्ण BD को तीन बराबर भागों में बिन्दु P व Q से बाँटा जाता है, सिद्ध कीजिए कि CQ, AP के समान्तर है।
हलः
स्वयं हल कीजिए।

प्रश्न 30.
ABCD एक समान्तर चतुर्भुज है। AD को E तक इस प्रकार बढ़ाया गया है कि DE = DC तथा EC का बढ़ा भाग, AB के बढ़े भाग F में मिलता है तो सिद्ध कीजिए कि BF = BC
हलः
स्वयं हल कीजिए।

प्रश्न 31.
ABCD एक समान्तर चतुर्भुज है। AD पर एक बिन्दु P पर इस प्रकार है कि AP = [latex]\frac{1}{3}[/latex]AD तथा BC पर एक बिन्दु Q इस प्रकार है कि CQ = [latex]\frac{1}{3}[/latex]BC तो सिद्ध कीजिए कि AQCP एक समान्तर चतुर्भुज है।
हलः
स्वयं हल कीजिए।

प्रश्न 32.
एक समान्तर चतुर्भुज ABCD है। E तथा F क्रमश: AB तथा AD के मध्य बिन्दु हैं। कोई रेखा GH है जो AD, EF और BC को क्रमश: G,P और H पर प्रतिच्छेद करती है तो सिद्ध कीजिए कि GP = PH.
हलः
स्वयं हल कीजिए।

प्रश्न 33.
ABC एक त्रिभुज है तथा A, B और C से, BC, CA और AB के समान्तर रेखाएँ खींची गई हैं जो क्रमशः P,Q तथा R पर प्रतिच्छेद करती हैं तो सिद्ध कीजिए कि ∆PQR का परिमाप, ∆ABC के परिमाप का दोगुना है।
हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 10 Lines and Angle Ex 10.1 रेखाएँ एवं कोण

Ex 10.1 Lines and Angle अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि दो पूरक कोणों के बीच का अनुपात 2 : 3 है। तब कोण ज्ञात कीजिए।
हलः
माना दो पूरक (कोटिपूरक) कोण = 2x, 3x
∵ दो पूरक कोणों का योग 90° होता है।
∴ 2x + 3x = 90°
5x = 90
x = [latex]\frac{90}{5}[/latex] = 18
∴ दो पूरक कोण = 2 × 18 =36° तथा 3 × 18 = 54°

प्रश्न 2.
यदि दो सम्पूरक कोणों के बीच का अन्तर 40° है। तब कोण ज्ञात कीजिए।
हलः
माना दो सम्पूरक कोण = x,
180 – x दो सम्पूरक कोणों का अन्तर = 40
x – (180 – x) = 40
x – 180 + x = 40
2x = 220
x = [latex]\frac{220}{2}[/latex] = 110
सम्पूरक कोण = 110°, 70°

प्रश्न 3.
एक त्रिभुज का बाह्य कोण 110° है और इसके दो अन्तः विपरीत कोण बराबर हैं। तब ये कोण ज्ञात कीजिए।
हलः
माना ∠ABC = ∠BAC = x

∵ A का बहिष्कोण, अपने सम्मुख अन्तः कोणो के योग के बराबर होता है
∴ ∠ACD = ∠BAC + ∠ABC
110 = x + x
110 = 2x
[latex]\frac{110}{2}[/latex] = x
∴ x = 55°

प्रश्न 4.
यदि एक त्रिभुज का एक कोण, अन्य दो कोणों के योग के बराबर है तब त्रिभुज का नाम बताइये?
हलः
माना
∆ के कोण = x, y, z
∵ x + y = z (दिया है) ………………… (i)
∵ ∆ के तीनों कोणो का योग = 180°
x + y + z = 180°
समीकरण (1) से,
z + z = 180°
2z = 180°
z = [latex]\frac{180}{2}[/latex] = 90
∴ यह त्रिभुज एक समकोण त्रिभुज है।

प्रश्न 5.
एक त्रिभुज के कोणों का अनुपात 2 : 3 : 4 है। तब त्रिभुज का नाम बताइए।
हलः
माना ∆ के तीन कोण = 2x, 3x, 4x
∆ के तीनो कोणो का योगफल = 180°
2x + 3x +4x = 180°
9x = 180°
x = [latex]\frac{180}{9}[/latex] = 20
∴ ∆ के कोण = 40°, 60°, 80°
∴ यह एक न्यूनकोण ∆ है।

प्रश्न 6.
यदि एक त्रिभुज का एक कोण 110° है तब अन्य दो कोणों के समअर्द्धको के बीच का कोण ज्ञात कीजिए।
हल:
∆ABC में माना
∠A = x
∠C = y
∠B = 110°

∠A + ∠B + ∠C = 180°
⇒ x + 110 + y = 180
⇒ x + y = 180 – 110 = 70
∵ [latex]\frac{x}{2}+\frac{y}{2}=\frac{70}{2}[/latex] = 35
माना ∠A व ∠C के समअर्द्धको के बीच का कोण = z
तब [latex]\frac{x}{2}+\frac{y}{2}+z[/latex] = 180°
समीकरण (1) से,
35 + z = 180°
z = 180 – 35 = 145°

Ex 10.1 Lines and Angle लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 7.
निम्नलिखित को परिभाषित कीजिए
(i) कोण
(ii) एक कोण का अभ्यन्तर
(iii) न्यूनकोण
(iv) अधिक कोण
(v) सम्पूरक कोण
(vi) पूरक कोण
हलः
(i) कोण- दो रेखाओं के परस्पर झुकाव से बनने वाली आकृति को कोण कहते है। जैसे AB व AC दो किरणें हैं। AB तथा AC के झुकाव से ∠BAC बनता है।

(ii) एक कोण का अभ्यन्तर (Interior of an Angle)- समतल का वह भाग जो किरण AB व AC के बीच स्थित है। ∠BAC का अभ्यन्तर कहलाता है।
(iii) न्यूनकोण- 90° से छोटे या कम कोण को न्यूनकोण कहते हैं।
(iv) अधिक कोण- 90° से बड़े कोण को अधिक कोण कहते हैं।
(v) सम्पूरक कोण- जिन दो कोणों का योग 180° होता है, सम्पूरक कोण कहलाते हैं जैसे 40° का सम्पूरक कोण 140° है।
(vi) पूरक कोण- जिन दो कोणों का योग 90° होता है, पूरक कोण कहलाते हैं जैसे 40° का पूरक कोण 50° होता है।

प्रश्न 8.
कौन-सा कोण स्वयं का कोटिपूरक होता है?
हलः
माना कोण = x
पूरक कोण = x
∴ x + x = 90
2x = 90 ⇒ x = [latex]\frac{90}{2}[/latex] = 45
∴ कोण = 45° स्वयं का कोटिपूरक होता है।

प्रश्न 9.
कौन-सा कोण स्वयं का सम्पूरक होता है?
हलः
माना कोण = x
सम्पूरक कोण = x
∴ x + x = 180°
2x = 180 ⇒ x = [latex]\frac{180}{2}[/latex] = 90°
∴ कोण = 90° स्वयं का सम्पूरक कोण होता है।

प्रश्न 10.
निम्नलिखित प्रत्येक के सम्पूरक कोण का मापन ज्ञात कीजिए।
(i) 54°
(ii) 1300
(iii) 1720
हलः
(i) 54° का सम्पूरक कोण = 180 – 54 = 126°
(ii) 130° का सम्पूरक कोण = 180 – 130 = 50°
(iii) 172° का सम्पूरक कोण = 180 – 172 = 8°

प्रश्न 11.
निम्नलिखित प्रत्येक कोण का पूरक कोण लिखिए।
(i) 77°
(ii) 65°10’20”
(iii) 485942″
हलः
(i) 77° का पूरक कोण = 90 – 77 = 13°
(ii) 65°10′ 20″ का पूरक कोण = 90 – (65°10′ 20″) = 24°49’40”
(iii) 48°59’42” का पूरक कोण = 90 – (48°59’42”) =41°0’18”

प्रश्न 12.
यदि एक कोण, उसके पूरक में, 10° का अन्तर है। कोण ज्ञात कीजिए।
हलः
माना कोण = x
पूरक कोण = 90 – x
x – (90 – x) = 10
x – 90 + x = 10
2x = 100
x = 50°
∴ कोण = 50°

प्रश्न 13.
यदि कोण (2x – 10)° और (x – 5)° पूरक कोण है तब x ज्ञात कीजिए।
हल:
∵ कोण (2x – 10) तथा (x – 5) पूरक कोण है।
∴ 2x – 10 + x – 5 = 90
3x = 90 + 15
3x = 105
x = [latex]\frac{105}{3}[/latex] = 35°

प्रश्न 14.
यदि एक कोण का सम्पूरक, उसके पूरक के तीन गुने के बराबर है। तो कोण का मापन ज्ञात कीजिए।
हलः
माना कोण = x
पूरक कोण = 90 – x
सम्पूरक कोण = 180 – x
प्रश्नानुसार, 180 – x = 3(90 – x)
180 – x = 270 – 3x
2x = 90
x = [latex]\frac{90}{2}[/latex] = 45
कोण = 45°

प्रश्न 15.
दो सम्पूरक कोण 3 : 7 के अनुपात में हैं, कोण ज्ञात कीजिए।
हलः
माना
पहला कोण = 3x
दूसरा कोण = 7x
प्रश्नानुसार, 3x + 7x = 180°
10x = 180°
x = [latex]\frac{180}{10}[/latex] = 18
∴ पहला कोण = 3 × 18 = 54°
दूसरा कोण = 7 × 18 = 126°

Ex 10.1 Lines and Angle लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 16.
दी गयी आकृति में, OA और OB विपरीत किरणें हैं। x का मान ज्ञात कीजिए तथा ∠AOC तथा ∠BOD भी ज्ञात कीजिए।
हलः

∠AOB = 180°
∠AOC + ∠COD + ∠BOD = 180°
x + 20 + x + x + 10 = 180
3x + 30 = 180
3x = 180 – 30
3x = 150
x = [latex]\frac{150}{3}[/latex] = 50°
∴ ∠AOC = 50 + 20 = 70°
∠BOD = 50 + 10 = 60°

प्रश्न 17.
चित्र में, AB और AC विपरीत किरणें हैं। यदि (a – 3b) = 20° तो कोण a और b ज्ञात कीजिए।
हल:
∵ हम जानते हैं कि किरण CAB में a + b = 180° है।

समीकरण (1) में b का मान रखने पर a – 3 × 40 = 20
a = 20+ 120
a = 140°

प्रश्न 18.
दी गई आकृति में, दो सरल रेखाएं AB और CD एक बिन्दु O पर प्रतिच्छेद करती है। यदि ∠BOD = x° और ∠AOD = (4x – 5)° तो x का मान ज्ञात कीजिए तथा निम्न को ज्ञात कीजिए।

(i) ∠BOD
(ii) ∠AOD
(iii) ∠AOC
(iv) ∠BOG
हलः
∠ BOD + ∠AOD = 180
x + 4x – 5 = 180°
5x = 180+ 5
5x = 185
x = [latex]\frac{185}{5}[/latex] = 37°
(i) ∠BOD = 37°
(ii) ∠AOD = 4x – 5 = 4 × 37 – 5 = 148 – 5 = 143°
(iii) ∠AOC = ∠BOD = 37° (शीर्षाभिमुख कोण)
(iv) ∠BOC = ∠AOD = 143° (शीर्षाभिमुख कोण)

प्रश्न 19.
दी गयी आकृति में, AOC एक रेखा है। x का मान ज्ञात कीजिए।

हल:
AOC एक सरल रेखा है।
70 + 2x = 180°
2x = 180 – 70 = 110
x = [latex]\frac{110}{2}[/latex] = 55°

प्रश्न 20.
दी गयी आकृति में, BAC एक रेखा है। x का मान ज्ञात कीजिए तथा ∠CAE व ∠BAD ज्ञात कीजिए।

हलः
∴ बिन्दु A पर बने तीनों कोणों का योग = 180°
∴ 3x – 5 + 55 + x + 20 = 180°
4x + 70 = 180
4x = 180 – 70 = 110
x = [latex]\frac{110}{4}[/latex] = 27°30′
∴ ∠CAE = (3x 27°30′ – 5)
= 82°30′ – 5°= 77°30′
∴ ∠BAD = 27°30′ + 20 = 4730′

प्रश्न 21.
दी गयी आकृति में, POS एक रेखा है। x का मान ज्ञात कीजिए।

हल:
∵ POS एक सरल रेखा है।
∠POQ + ∠QOR + ∠ROS = 180°
60 + 4x + 40 = 180
4x = 180 – 100 = 80
x = [latex]\frac{80}{4}[/latex] = 20°

प्रश्न 22.
निम्न दी गयी आकृति में, तीन समरेखीय रेखायें एक बिन्दु O पर प्रतिच्छेद करती हैं। रुपीय कोण दर्शाये ( चित्र में) गये हैं। a, b, c और d के मान ज्ञात कीजिए।

हलः
∵ ∠b = 70° (शीर्षाभिमुख कोण)
∠c = 80° (शीर्षाभिमुख कोण)
∴ PQ एक सरल रेखा है।
∠a + ∠b + ∠c = 180°
∠a + 70 + 80 = 180°
∠a = 180° – 150° = 30°
∠d = ∠a = 30° (शीर्षाभिमुख कोण)

प्रश्न 23.
सभी में आसन्न कोणों के कितने युग्म है? दी गयी आकृति में इन्हें क्या नाम दे सकते हैं?

हलः
10 युग्म है, जो निम्न प्रकार है।
∠AOB तथा ∠BOC
∠AOB तथा ∠BOD
∠AOB तथा ∠BOE
∠AOC तथा ∠COD
∠AOC तथा ∠COE
∠AOD तथा ∠DOE
∠BOC तथा ∠COD
∠BOC तथा ∠COE
∠BOD तथा ∠DOE
∠COD तथा ∠DOE

प्रश्न 24.
चित्र में, यदि ∠AOC + ∠BOD = 284° तो सभी चार कोण ज्ञात कीजिए।

हलः
यदि ∠AOC + ∠BOD = 284°
माना ∠AOD = ∠BOC = x
∠AOC + ∠BOD + ∠AOD + ∠BOC = 360
284 + ∠AOD + ∠BOC = 360
∠AOD + ∠BOC = 360 – 284 = 76
∴ x + x = 76
2x = 76 ⇒ x = [latex]\frac{76}{2}[/latex] = 38°
∴ ∠AOC = 180° – 38 = 142°
∠BOD = 142° (शीर्षाभिमुख कोण)

प्रश्न 25.
चित्र में, ∠ACB एक रेखा इस प्रकार है कि ∠DCA = 5x और ∠DCB = 4x, x का मान ज्ञात कीजिए तथा ∠DCB और ∠DCA ज्ञात कीजिए।

हल:
∠ACB एक सरल कोण है।
∴ ∠ACD + ∠ BCD = 180
⇒ 5x + 4x = 180
⇒ 9x = 180
⇒ x = [latex]\frac{180}{9}[/latex] = 20
∴ ∠ BCD = 4x = 4 × 20 = 80°
तथा ∠ACD = 5x = 5 × 20 = 100°

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 13 Quadrilateral Ex 13.3 चतुर्भज

प्रश्न 1.
सिद्ध कीजिए कि किसी त्रिभुज में उसके शीर्ष से आधार पर डाली गयी माध्यिका उसकी अन्य दो भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड समद्विभाजित करता है।
हलः
ज्ञात है: एक ∆ABC जिसमें E तथा F, AB तथा AC के मध्य बिन्दु हैं। शीर्ष A से BC पर एक रेखाखण्ड AD खींचा जो EF को R पर काटता है।
सिद्ध करना है: AR = RD
रचना: PAQ,BC के समान्तर रेखा खींची।
उपपत्तिः E तथा F, AB तथा AC के मध्य बिन्दु हैं। (दिया है)
∴ EF || BC
PAQ||BC
∴ PAQ|| EF || BC

∴ PAQ, EF तथा BC तीन समान्तर रेखायें हैं जो तिर्यक रेखा AB के बीच बराबर अन्त:खण्ड काटती हैं। अतः इन्हीं समान्तर रेखाओं के बीच तिर्यक रेखा AD के बीच बने अन्तः खण्ड भी बराबर होंगे।
∴ AR = RD

प्रश्न 2.
सिद्ध कीजिए कि समलम्ब चतुर्भुज की असमान्तर भुजाओं के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड समान्तर भुजाओं के योग का आधा होता है।
हलः

ज्ञात है: ABCD एक समलम्ब है जिसकी भुजाएँ AB व DC एक दूसरे के समान्तर है।
E तथा F क्रमशः AD तथा BC के मध्य बिन्दु हैं। EF को मिलाया।
सिद्ध करना है:

उपपत्तिः ∆ABD में, बिन्दु E, भुजा AD का मध्य बिन्दु है तथा EG, भुजा AB के समान्तर है।
∴ बिन्दु G, BD का मध्य बिन्दु है …(1)

प्रश्न 3.
सिद्ध कीजिए कि समलम्ब चतुर्भुज की असमान्तर भुजाओं के मध्य-बिन्दुओं को मिलाने वाला रेखाखण्ड समान्तर भुजाओं के समान्तर होता हैं।
हलः

ज्ञात है: E तथा F, AD तथा BC के मध्य बिन्दु हैं।
सिद्ध करना है: EF||AB तथा EF||DC
रचनाः माना EF, AB के समान्तर नहीं है। इसलिए EG एक रेखा ऐसी खींची जिससे EG|| AB तथा EG||EG|| AB परन्तु EG तथा EF एक प्रतिच्छेद बिन्दु E पर काटती हैं।
परन्तु दो प्रतिच्छेदी रेखा एक रेखा के समान्तर नहीं हो सकती।
∴ EG तथा EF एक ही रेखा होगी।
∴ AB|| EF|| DC

प्रश्न 4.
ABCD एक समान्तर चतुर्भुज है। जिसमें E व F क्रमशः AB व CD के मध्य बिन्दु हैं। सिद्ध कीजिए कि-
(i) AF||EC
(ii) CE व AF विकर्ण BD को समत्रिभाजित करते हैं। [NCERT]
हलः

ज्ञात है: ABCD एक समान्तर चतुर्भुज में E तथा F क्रमश: AB तथा CD के मध्य बिन्दु हैं।
(i) सिद्ध करना हैः AF|| EC
उपपत्तिः (i) ∆ADF तथा ∆BCE में,
AD = BC (समान्तर चतुर्भुज की भुजाएँ)
DF = EB (समान्तर चतुर्भुज की भुजाएँ)
∠ADC = ∠ABC (समान्तर चतुर्भुज के सम्मुख कोण)
अतः ∆ADF ≅ ∆BCE
∴ AF = EC
∴ AFCE एक समान्तर चतुर्भुज होगा। (∴ AE||FC तथा AE = FC)
अतः समान्तर चतुर्भुज में AF||EC
(ii) ∵ समान्तर चतुर्भुज AECF में तिर्यक रेखा BD है। समान्तर चतुर्भुज ABCD में तिर्यक रेखा DB द्वारा काटे गये अन्त:खण्ड बराबर होंगे
∴ DM = ML = LB
अत: CE व AF विकर्ण BD को समत्रिभाजित करते हैं।

प्रश्न 5.
एक समलम्ब चतुर्भुज में उसके आधार के समान्तर एक रेखा उसकी असमान्तर भुजाओं में से एक को समद्विभाजित करती है। सिद्ध कीजिए कि यह इसके किसी विकर्ण को भी समद्विभाजित करेगी।
हलः

E, AD का मध्य बिन्दु है।
∴ DE = EA
AB||DC|| EF
तिर्यक रेखा DA पर बने अन्त:खण्ड DE = EA (जो दिया है)
∴ तिर्यक रेखा DB पर बने अन्त:खण्ड DG = GB होंगे।
AB के समान्तर रेखा E से होते हुए H,G पर प्रतिच्छेद करते हुए F तक खींची गयी है।
∴ बिन्दु F, CB का मध्य बिन्दु होगा।
DC|| AB
∴ तिर्यक रेखा CB पर बने अन्त:खण्ड CF = FB तथा तिर्यक रेखा CA पर बने अन्त:खण्ड CH = HA

प्रश्न 6.
ABCD एक समान्तर चतुर्भुज है तथा E व F क्रमश: AB व CD के मध्य D, बिन्दु हैं। एक अन्य रेखा GH, AD,EF व BC को क्रमशः G,P व H बिन्दुओं पर प्रतिच्छेद करती है। सिद्ध कीजिए कि GP = PH
हलः

ABCD एक समान्तर चतुर्भुज है। E तथा F, AB तथा CD के मध्य बिन्दु हैं।
∴ AD||BC, AB तिर्यक रेखा काटती है।
∴ अन्त:खण्ड AE = EB
∴ DC तिर्यक रेखा काटती है।
∴ अन्त:खण्ड DF = FC
बिन्दु E को F से मिलाने पर वह बिन्दु P से होकर जाती है।
∴ तिर्यक रेखा GH के अन्त:खण्ड GP = PH होंगे।

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 13 Quadrilateral Ex 13.2 चतुर्भज

प्रश्न 1.
ABCD एक समचतुर्भुज है। EABF एक सरल रेखा इस प्रकार है कि EA = AB = BF तो सिद्ध कीजिए कि ED व FC को बढ़ाने पर ये समकोण पर प्रतिच्छेद करती हैं।
हलः
समचतुर्भुज ABCD में,
∵ AB = BC = CD = DA
∴ EA = AB = BF (दिया है)
EA = AD = DC
ED = AC
∴ EP|| AC

∵ समचतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं
तथा लम्बवत् होते हैं।
∴ ∠DOC = 90°
∴ ∆DOC तथा ∆PDC में,
DC उभयनिष्ठ
∠PDC = ∠OCD (एकान्तर कोण)
∠ODC = ∠PCD (एकान्तर कोण)
अतः ∆DOC ≅ ∆PDC
∴ ∠DOC = ∠DPC = 90°

प्रश्न 2.
सिद्ध कीजिए कि समलम्ब चतर्भज के सम्मुख कोण सम्पुरक होते हैं।
हलः
ज्ञात हैः एक समलम्ब ABCD जिसमें AB||CD तथा AD = BC
सिद्ध करना हैः ∠B + ∠D = 180°

प्रश्न 3.
चित्र में, AD व BE त्रिभुज ABC की माध्यिकाएँ हैं तथा BE||DF तो सिद्ध कीजिए कि CF = [latex]\frac{1}{4}[/latex]AC
हलः
∵ BE||DF तथा BC का मध्य बिन्दु D है।
तिर्यक रेखा BC पर बने अन्त:खण्ड BD = DC
इसी प्रकार तिर्यक रेखा AC पर बने अन्त:खण्ड

EF = FC …(1)
AE = EC (∵ E, AC का मध्य बिन्दु है)
AE = EF + FC
AE = FC + FC [समी० (1) से ]
AE = 2FC

प्रश्न 4.
चित्र में, ABCD एक समान्तर चतुर्भुज है तथा P, भुजा DC का मध्य बिन्दु है। C से PA के समान्तर एक ऐसी रेखा खींचिए कि DA को बढ़ाने से यह बिन्दु Q पर तथा AB को बिन्दु R पर मिलती है। सिद्ध कीजिए कि DQ =2AD तथा CQ = 2CR
हल:
∵ AP||QC, तिर्यक रेखा DC द्वारा काटे गये अन्त:खण्ड DP = PC ….(1)
इसी प्रकार तिर्यक रेखा AB द्वारा काटे गये अन्त:खण्ड AR = RB ….(2)
∵ AB||CD
∴ तिर्यक रेखा द्वारा काटा गया अन्त:खण्ड

CR = RQ
या CQ = 2CR
इसी प्रकार DQ = 2AD

प्रश्न 5.
चित्र में, AB||CD||EF||GH व Ax = XY = YH । यदि AC = 1.5 सेमी तो AG का मान ज्ञात कीजिए।
हल:
AX|| XY|| YH यदि AC = 1.5 सेमी
तिर्यक रेखा AH द्वारा काटे गये अन्त:खण्ड
AX = XY = YH

∴ तिर्यक रेखा AG द्वारा काटे गये अन्त:खण्ड
AC = CE = EG = 1.5 सेमी
AG = AC + CE + EG = 1.5 + 1.5 + 1.5 = 4.5 सेमी

प्रश्न 6.
चित्र में, ∆ABC की भुजा AC को E तक ऐसे बढ़ाते हैं कि CE = [latex]\frac{1}{2}[/latex]AC यदि D,BC का मध्य बिन्दु है तथा ED को बढ़ाने पर वह AB से F बिन्दु पर मिलती है। तथा CP व DQ, BA के समान्तर है सिद्ध कीजिए कि FD = [latex]\frac{1}{3}[/latex]FE
हलः

CE = [latex]\frac{1}{2}[/latex]AC …(1)
D, BC का मध्य बिन्दु है
∴ BD = DC
∆BDF तथा ∆DCP में, BD = DC (दिया है)
∠BDF = ∠CDP (शीर्षाभिमुख कोण)
∠FBD = ∠BCP (एकान्तर कोण)
अतः ∆BDF = ∆DCP
FD = DP …(2)
∴ AB||CP तथा तिर्यक रेखा FE के द्वारा बने अन्त:खण्ड FD = DP [समी० (2) से अभी सिद्ध किया है]
∴ तिर्यक रेखा AE के द्वारा बने अन्त:खण्ड
AQ = QC …(3)
समी० (1) व (3) से, [latex]C E=\frac{1}{2} \times 2 Q C[/latex]
CE = QC …(4)
इसी प्रकार DQ||CP की तिर्यक रेखा FE पर बने अन्त:खण्ड
DP = PE
∴ समी० (2) से,
FD = [latex]\frac{1}{3}[/latex] FE

प्रश्न 7.
चित्र में, ABC एक समकोण त्रिभुज है तथा ∠B = 90° दिया है AB = 9 सेमी, AC = 15 सेमी। D व E क्रमशः AB व AC के मध्य बिन्दु हैं तब BC की लम्बाई ज्ञात कीजिए।
हलः

पाइथागोरस प्रमेय से,
AC² = AB² + BC²
(15)² = 9² + BC²
225 – 81 = BC²
144 = BC²
BC = [latex]\sqrt{144}[/latex] = 12 सेमी

प्रश्न 8.
ABCD एक समान्तर चतुर्भुज है। बिन्दु P, DC का मध्य बिन्दु है तथा Q, AC DF पर एक ऐसा बिन्दु है कि CQ = [latex]\frac{1}{4}[/latex]AC। यदि PQ को बढ़ाने पर वह BC से R बिन्दु पर मिलती है तो सिद्ध कीजिए कि R,BC का मध्य बिन्दु है।
हलः

प्रश्न 9.
सिद्ध कीजिए कि किसी समलम्ब चतुर्भुज के विकर्णों के मध्य बिन्दुओं को मिलाने वाले रेखाखण्ड उसकी समान्तर भुजाओं के समान्तर तथा उनके अन्तर से आधा होता है।
हलः
ज्ञात हैः एक समलम्ब ABCD जिसकी भुजाएं AB तथा DC एक दुसरे के समान्तर हैं
तथा P एवं Q विकर्ण AC व BD के मध्य बिन्दु हैं। PQ को मिलाया।
सिद्ध करना है: PQ, AB या DC के समान्तर है।


रचनाः DP को मिलाया तथा आगे बढ़ाया जिससे वह AB से बिन्दु R पर मिलती है।
उपपत्तिः ∵ AB व DC एक दूसरे के समान्तर हैं जिन्हें तिर्यक रेखा AC, बिन्दु A व C पर काटती है। अब ∆APR तथा ∆DPC में
∠1 = ∠2 (एकान्तर अन्त:कोण)
AP = CP (∵ P, AC का मध्य बिन्दु है)
∠3 = ∠4 (शीर्षाभिमुख कोण)
अतः ∆APR ≅ ∆DPC
AR = DC …(1)
PR = DP …(2)
समी० (2) से प्रदर्शित होता है कि P, DR का मध्य बिन्दु है। इस प्रकार ∆DRB में P तथा Q क्रमशः भुजा DR तथा DB के मध्य बिन्दु हैं।
∴ PQ, भुजा RB के समान्तर है।
या PQ.AB के समान्तर है।
∵ RB, AB का एक भाग है।
∴ PQ, AB तथा DC के समान्तर है।
∴ AB व DC एक दुसरे के समान्तर हैं।

प्रश्न 10.
BM व CN किसी त्रिभुज ABC के शीर्ष A से जाने वाली रेखा पर लम्ब है यदि L,BC का मध्य बिन्दु है सिद्ध कीजिए कि LM = LN
हलः

ज्ञात है: BM तथा CN रेखा AN पर लम्ब खींचे गये हैं तथा L, BC का मध्य बिन्दु हैं।
सिद्ध करना है: LM = LN
उपपत्तिः ∆BML तथा ∆LNC में,
BL = LC (ज्ञात है)
∠BML = ∠CNL (प्रत्येक समकोण)
∠MLB = ∠CLN (शीर्षाभिमुख कोण)
अतः ∆BML ≅ ∆LNC
∴ LM = LN

Balaji Publications Mathematics Class 9 Solutions