Class 9

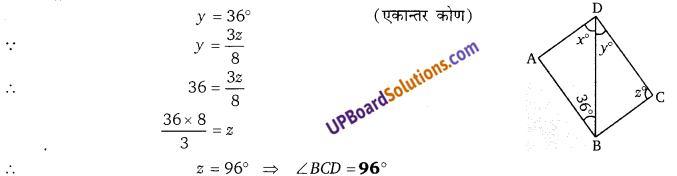
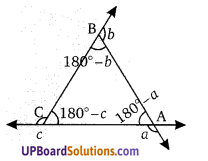
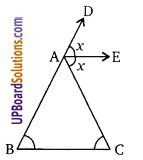
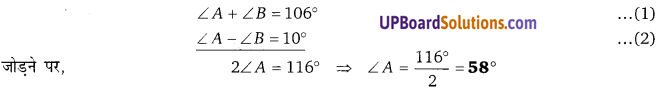Balaji Class 9 Maths Solutions Chapter 15 Circle Ex 15.1 वृत्त

Ex 15.1 Circle अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
चित्र में O, वृत्त का केन्द्र, जीवा AB = 10 सेमी तथा व्यास AC = 26 सेमी है। जीवा AB की वृत्त के केन्द्र से दूरी ज्ञात कीजिए। [UP 2001, 03]
हल:

प्रश्न 2.
एक वृत्त की जीवा की लम्बाई 16 सेमी तथा वृत्त के केन्द्र से इसकी दूरी 6 सेमी है। तब वृत्त की त्रिज्या ज्ञात कीजिए।
हलः

प्रश्न 3.
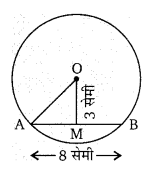
वृत्त की एक जीवा की लम्बाई 8 सेमी तथा वृत्त के केन्द्र से इसकी दूरी 3 सेमी है। तब वृत्त की त्रिज्या ज्ञात कीजिए। [UP 2003]
हलः

प्रश्न 4.
वृत्त के लघु वृत्तखण्ड का कोण ज्ञात कीजिए। [UP 2000]
हलः
अधिक कोण

प्रश्न 5.
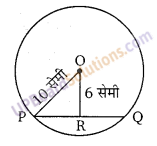
एक वृत्त का केन्द्र 0 तथा त्रिज्या OP = 10 सेमी है। जीवा PQ पर लम्ब OR की लम्बाई 6 सेमी है। तब PQ का मान ज्ञात कीजिए। [UP 2000]
हलः
समकोण ∆OPR में, (OP)² = (OR)² + (PR)²
(10)² = (6)² + (PR)²
100 = 36 + (PR)²
100 – 36 = (PR)²
∴ PR = [latex]\sqrt{64}[/latex] = 8 सेमी
∴ जीवा PQ = 2 × PR = 2 × 8 = 16 सेमी

प्रश्न 6.
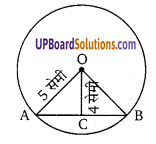
चित्र में, 0 वृत्त का केन्द्र है तथा OA = 5 सेमी।0 से AB पर लम्ब OC की लम्बाई 4 सेमी है तब जीवा AB का मान ज्ञात कीजिए। (UP 2009, 10, 11)
हलः
समकोण ∆OAC में,
(OA)² = (AC)² + (OC)²
(5)² = (AC)² + (4)²
25 = (AC)² +16
25 -16 = (AC)²
या (AC)² = 9
∴ AC = [latex]\sqrt{9}[/latex] = 3 सेमी
∴ जीवा AB = 2 × AC = 2 × 3 = 6 सेमी

प्रश्न 7.
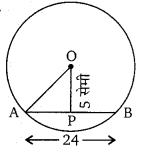
चित्र में, O वृत्त का केन्द्र है तथा एक जीवा AB = 24 सेमी है। जीवा की वृत्त के केन्द्र O से दूरी 5 सेमी है। तब वृत्त का व्यास ज्ञात कीजिए। (UP 2009)
हलः
समकोण ∆OAP में,
(OA)² = (OP)² + (AP)²
(OA)² = (5)² + (12)² (∵ AP = AB /2)
(OA)² = 25 +144 = 169
OA = [latex]\sqrt{169}[/latex] = 13 सेमी
∴ वृत्त का व्यास = 2 × त्रिज्या
= 2 – 13 = 26 सेमी

प्रश्न 8.
चित्र में, O वृत्त का केन्द्र है तथा एक जीवा AB = 30 सेमी है तथा इसका व्यास AD = 34 सेमी है। जीवा AB की केन्द्र O से दूरी ज्ञात कीजिए।
हलः

Ex 15.1 Circle लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-I)

प्रश्न 9.
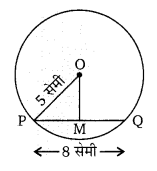
एक 5 सेमी त्रिज्या वाले वृत्त के केन्द्र से 8 सेमी की एक जीवा की दूरी ज्ञात कीजिए। [UP 2005]
हल:
वृत्त की त्रिज्या OP = 5 सेमी
∵ वृत्त के केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।

प्रश्न 10.
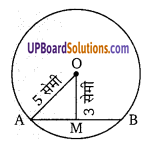
एक 5 सेमी त्रिज्या वाले वृत्त के केन्द्र से 3 सेमी की दूरी पर जीवा की लम्बाई ज्ञात कीजिए। (UP 2006)
हलः
समकोण ∆OAM में,
(OA)² = (OM)² + (AM )²
(5)² = (3)² + (AM)²
25 = 9 + (AM)²
25 – 9 = (AM)²
16 = (AM)²
∴ AM = [latex]\sqrt{16}[/latex] = 4 सेमी
∴ जीवा AB = 2 × AM = 2 × 4 = 8 सेमी

प्रश्न 11.
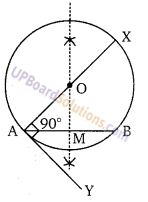
एक वृत्त की एक चाप दी गयी है। प्रदर्शित कीजिए कि वृत्त को पूरा कैसे किया जायेगा?
हलः
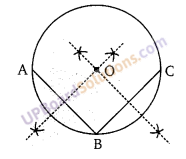
एक वृत्त का चाप AXB दिया है। वृत्त का केन्द्र ज्ञात करने के लिए AB को मिलाया। जीवा AB का लम्बार्द्धक खींचा, जो चाप को M बिन्दु पर काटता है। बिन्दु A अथवा B से कोई न्यूनकोण बनाती AY रेखा नीचे की ओर खींची। रेखा AY पर 90° का कोण बनाते हुए AX रेखा खींची जो AB के लम्बार्द्धक को बिन्दु O पर काटती है। अब बिन्दु 0 को केन्द्र मानकर OA त्रिज्या परकार में लेकर एक वृत्त खींचा जो दिये गये । चाप को ही पूर्ण करता है।

प्रश्न 12.
दिये गये वृत्त का केन्द्र ज्ञात करने की विधि बताइये।
हलः
(1) वृत्त पर तीन बिन्दु A, B,C लिए।
(2) AB तथा BC को मिलाया।
(3) AB तथा BC के लम्ब समद्विभाजक खींचे जो एक-दूसरे को बिन्दु O पर
काटते हैं।
(4) बिन्दु O वृत्त का अभीष्ट केन्द्र है।

Ex 15.1 Circle लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 13.
चित्र में, 0 वृत्त का केन्द्र, त्रिज्या 5 सेमी तथा OP ⊥ AB, OQ ⊥ CD व AB||CD, AB = 6 सेमी, CD = 8 सेमी है। PQ का मान ज्ञात कीजिए।
हलः

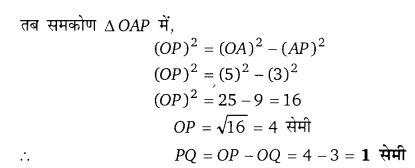
प्रश्न 14.
यदि वृत्त का व्यास उसकी प्रत्येक जीवा को समद्विभाजित करता है तब सिद्ध कीजिए कि उसकी जीवाऐं समान्तर हैं।
हलः
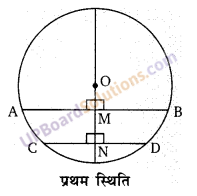
प्रथम स्थिति : यदि वृत्त की दो जीवाऐं वृत्त के एक ही ओर हैं।
∵ वृत्त के केन्द्र तथा जीवा के मध्य बिन्दु को मिलाने वाली रेखा जीवा पर लम्ब होती है।
∠OMA = ∠OMB = 90° (प्रत्येक 90°)
∠ONC = ∠OND = 90° (प्रत्येक 90°)
∠OMA = ∠ONC = 90° (संगत कोण)
तथा
∠OMB = ∠OND = 90° (संगत कोण)
परन्तु ये संगत कोण तभी बराबर होंगे जबकि AB ||CD
द्वितीय स्थिति : यदि वृत्त की दोनों जीवाऐं वृत्त के केन्द्र के विपरीत ओर हैं।
∵ वृत्त के केन्द्र तथा जीवा के मध्य बिन्दु को मिलाने वाली रेखा जीवा पर लम्ब होती है।
∠OMA = ∠OMB = 90° (प्रत्येक 90°)
∠ONC = ∠OND = 90° (प्रत्येक 90°)
∠OMA = ∠OND = 90° तथा
∠OMB = ∠ONC = 90°
परन्तु ये कोण एकान्तर कोण हैं। ये कोण एकान्तर तभी हो सकते हैं जबकि
AB||CD
∵ वृत्त की जीवायें AB तथा CD समान्तर होंगी।

प्रश्न 15.
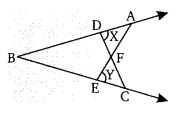
दो समान वृत्त परस्पर P व Q बिन्दुओं पर प्रतिच्छेद करते हैं। P से एक रेखा, वृत्तों पर बिन्दु A व B से मिलती है। सिद्ध कीजिए कि QA = QB
हलः

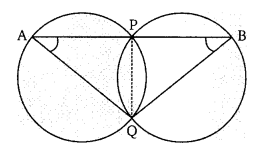
चाप PQ दोनों वृत्तों में उभयनिष्ठ हैं।
∴ ∠QAP = ∠QBP
PQ उभयनिष्ठ जीवा
तथा
∠APQ = ∠QPB
(वृत्तों के शेष कोणों द्वारा बने कोण)
अतः ∆APQ ≅ ∆BPQ
∴ QA = QB

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 11 Triangles and Its Angles Ex 11.1 त्रिभुज एवं उसके गुण

Ex 11.1 Triangles and Its Angles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि एक त्रिभुज के दो कोण बराबर है तब दोनों की विपरीत भुजा बराबर है या नहीं?
हलः
एक त्रिभुज के दो कोण बराबर है तब उस त्रिभुज की सम्मुख भुजाएं भी बराबर होगी।

प्रश्न 2.
एक त्रिभुज की बराबर भुजाओं के विपरीत कोण बराबर है या नहीं?
हलः
बराबर

प्रश्न 3.
यदि एक त्रिभुज की भुजाएँ 5 सेमी, 6 सेमी तथा 11 सेमी हैं तब त्रिभुज का नाम बताइए।
हलः
∵ किसी त्रिभुज की रचना के लिए दो भुजाओं का योग तीसरी भुजा से बड़ा होना चाहिए परन्तु 5 + 6 = 11, 11, के बराबर है।
∴ त्रिभुज की रचना सम्भव नहीं है।

प्रश्न 4.
यदि एक त्रिभुज की भुजाएँ 5 सेमी, 4 सेमी तथा 3 सेमी हैं तब त्रिभुज का नाम बताइए।
हलः :
∵ 3 + 4 = 7 > 5
अतः त्रिभुज की रचना सम्भव है।
(5)² = (3)² + (4)² .
∴ यह एक समकोण त्रिभज है।

प्रश्न 5.
एक त्रिभुज की दो भुजाओं का योग, हमेशा तीसरी भुजा से अधिक होता है या नहीं?
हलः
एक त्रिभुज की दो भुजाओं का योग, हमेशा तीसरी भुजा से अधिक होता है। हाँ

प्रश्न 6.
यदि एक त्रिभुज के सभी कोण बराबर है, तब इनमें प्रत्येक कोण ज्ञात कीजिए।
हलः
एक त्रिभुज के तीनों कोणों का योग = 180°
∠A + ∠B + ∠C = 180° …………. (1)
माना ∠A = x, ∠B = x, ∠C = x
∴ x + x + x = 180°
3x = 180°
x = [latex]\frac{180^{\circ}}{3}[/latex] = 60°
∴ ∠A = ∠B = ∠C = 60°

प्रश्न 7.
यदि एक समकोण त्रिभुज के दो न्यूनकोण बराबर है, तब प्रत्येक न्यूनकोण ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
यदि ∠A = 90° तथा ∠B = ∠C
तब 90° + ∠B + ∠C = 180°
∠B + ∠C = 180° – 90° = 90°
प्रत्येक ∠B = ∠C = 45°

Ex 11.1 Triangles and Its Angles लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 8.
एक त्रिभुज के कोण 2 : 3 : 7 के अनुपात में है। त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हलः
माना
∆ABC का ∠A = 2x
∠B = 3x
∠C = 7x
∴ ∠A + ∠B + ∠C = 180°
2x + 3x + 7x = 180°
12x = 180°
x = [latex]\frac{180^{\circ}}{12}[/latex] = 15°
∴ ∠A = 2 × 15 = 30°
∠B = 3 × 15 = 45°
∠C = 7 × 15 = 105°

प्रश्न 9.
∆ABC में, ∠A + ∠B = 65° तथा / B+ ∠C =140°, त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
65° + ∠C = 180°
∠C = 180°- 65° = 115°
तथा ∠A + ∠B + ∠C = 180°
∠A + 140° = 180°
∠A = 180° – 140° = 40°
∵ ∠A + ∠B = 65°
40° + ∠B = 65°
∴∠B = 65° – 40° = 25°

प्रश्न 10.
∆ABC में, यदि ∠B = 76° तथा ∠C = 48° है, तो ∠A ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
∠A + 76° + 48° = 180°
∠A = 180° – 124° = 56°

प्रश्न 11.
∆ABC में, यदि ∠B = 105° तथा ∠C =50° है, तो ∠A ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
∠A + 105° + 50° = 180°
∠A = 180° – 155° = 25°

प्रश्न 12.
एक त्रिभुज के दो कोणों का योग, तीसरे कोण के बराबर है। तीसरे कोण की माप ज्ञात कीजिए।
हल:
∆ABC में, (∠A + ∠B) + ∠C = 180°
∠A + ∠B = ∠C ……………. (1)
∠C + ∠C = 180°
2∠C = 180°
∠C = [latex]\frac{180^{\circ}}{2}[/latex] = 90°
तीसरा कोण ∠C = 90°

प्रश्न 13.
यदि एक त्रिभुज के कोण 2 : 3 : 4 के अनुपात में है। कोण ज्ञात कीजिए। (NCERT Exemplar)
हल:
∆ABC के कोण ∠A : ∠B : ∠C = 2 : 3 : 4
माना ∠A = 2x, ∠B = 3x, ∠C = 4x
∠A + ∠B + ∠C = 180°
2x + 3x + 4x = 180° ⇒ 9x = 180°
x = [latex]\frac{180^{\circ}}{9}[/latex] = 20°
∴∠A = 2 × 20° = 40°, ∠B = 3 × 20° = 60°, ∠C = 4 × 20°= 80°

Ex 11.1 Triangles and Its Angles लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 14.
एक ∆ABC में, 15∠A = 10∠B = 6∠C हो, तो ∠A, ∠B तथा ∠C ज्ञात कीजिए।
हलः
15∠A = 10∠B = 6∠C
माना
∠B = x
15∠A = 10x

प्रश्न 15.
एक ∆ABC में, यदि ∠A = 55°, ∠B = 40° तब ∠C ज्ञात कीजिए।
हल:
∆ABC में,
∠A + ∠ B + ∠C = 180°
55° + 40° + ∠C = 180°
∠C = 180° – 95° = 85°

प्रश्न 16.
A, B, C एक त्रिभुज के तीन कोण हैं। यदि A – B = 15°, B – C = 30° हो, तो ∠A, ∠B और ∠C ज्ञात कीजिए।
हल:
A – B = 15° ⇒ A = B + 15° ………….(1)
B – C = 30° ⇒ C = B – 30° …………(2)
∵ ∠A + ∠B + ∠C = 180°
B + 15° + B + B – 30° = 180°
3B – 15° = 180°
3B = 180° + 15° = 195°
∴ B = [latex]\frac{195^{\circ}}{3}[/latex] = 65°
∴ समीकरण (1) से
∠A = 65° + 15° = 80°
∠C = 65° – 30° = 35°

प्रश्न 17.
एक त्रिभुज के दो कोणों का योग 106° है तथा उनका अन्तर 10° है। त्रिभुज के सभी कोण ज्ञात कीजिए।
हलः
माना A के दो कोण ∠A तथा ∠B है।

समीकरण (1) में ∠A का मान रखने पर
58° + ∠B = 106°
∠B = 106° – 58° = 48°
तथा ∠C = 180° – (∠A + ∠B) = 180° (58° + 48°) = 180° – 106° = 74°

प्रश्न 18.
दिये गये चित्र में, AB||DC यदि x = [latex]\frac{4 y}{3}[/latex], y = [latex]\frac{3 z}{8}[/latex] हो, तो ∠BCD ज्ञात कीजिए।
हल:
∵ AB|| DC तथा BD तिर्यक रेखा है।

प्रश्न 19.
एक ∆ABC में, ∠A – ∠B = 33° तथा ∠B – ∠C = 18° हो, तो त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
∠A – ∠B = 33° ⇒ ∠A = 2B + 33° …………. (1)
∠B – ∠C = 18° ⇒ ∠B – 18° = ∠C ……………. (2)
∵ ∠A + ∠B + ∠C = 180°
∠B + 33°+ ∠B + ∠B – 18° = 180°
3∠B + 15° = 180°
3∠B = 180° – 15° = 165°
∠B = [latex]\frac{165^{\circ}}{3}[/latex] = 55°
∴ ∠A = ∠B + 33° = 55 + 33 = 88°
∴ ∠C = ∠B – 18 = 55 – 18 = 37°

प्रश्न 20.
दिये गये चित्र में, सिद्ध कीजिए कि ∠a + ∠b + ∠c = 360°
हलः
∠BAC + ∠ABC + ∠ACB = 180°
180 – ∠a + 180 – ∠b + 180 – ∠c = 180°
360° = ∠a + ∠b + ∠c

Ex 11.1 Triangles and Its Angles दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 21.
एक त्रिभुज ABC है जिसमें ∠A = 72°, ∠B तथा ∠C के अन्तः समद्विभाजक बिन्दु O पर मिलते हैं तो∠BOC का परिमाण ज्ञात कीजिए।
हलः
माना ∠ABC = x तथा ∠ACB = y

प्रश्न 22.
दिये गये चित्र में, AE, ∠CAD का अर्द्धक है तथा ∠B = ∠C तो सिद्ध कीजिए कि AE||BC
हलः
माना
∠CAD = 2x
∴ ∠DAE = ∠CAE = x
∠B = ∠C
∠CAD, ∆ABC का बहिष्कोण है।

∴ ∠CAD = ∠ABC + ∠ACB
∴ ∠ABC + ∠ACB = 2x
परन्तु ∠ABC = ∠ACB
∴ प्रत्येक ∠ABC = ∠ACB = x°
∴ ∠EAC = ∠ACB = x° (परन्तु ये एकान्तर कोण हैं।)
AE ||BC

प्रश्न 23.
दिये गये चित्र में, AB||CD है। x और y के मान ज्ञात कीजिए।
हल:
∵ AB||CD
∠FED = ∠EMB
58 = y + 20
58 – 20 = y
∴ y = 38°
∴ ∠MEB = 180 – (58 + 22)
= 180° – 80° = 100°

∆EBM में,
x + y + 100 = 180
x + 38 + 100 = 180
x = 180 – 138 = 42°

प्रश्न 24.
दिये गये चित्र में, x और y के मान ज्ञात कीजिए।

हल:
∵ y + 125 = 180 (रैखिक युग्म कोण)
y = 180 – 125 = 55°
∠CDE = ∠BMC = 65° (एकान्तर कोण)
तथा ∠CDN = ∠ENG = 65° (एकान्तर कोण)
∆NEG में, x + y + 65 = 180
∴ x + 55 + 65 = 180
x = 180 – 120 = 60°

प्रश्न 25.
निम्न प्रत्येक में x का मान ज्ञात कीजिए।
हलः

चित्र (i) में,
∠EAF = ∠BAC = 60° [शीर्षाभिमुख कोण]
∆ABC का बहिष्कोण ∠ACD है।
∠ACD = ∠BAC + ∠ABC .
115° = 60° + x
115° – 60° = x
x = 55°
चित्र (ii) में, ∆ABE में ∠AEB = 180 – (75 + 65)
= 180 – 140 = 40°
∠CED = ∠AEB = 40° [शीर्षाभिमुख कोण]
∆ECD में, 40 + 110 + x = 180°
150 + x = 180°
x = 180° – 150° = 30°

प्रश्न 26.
एक त्रिभुज के कोणों को परिमाण के बढ़ते हुए क्रम में रखा गया है यदि दो क्रमागत कोणों के बीच का अन्तर 10° है तो तीनों कोणों को ज्ञात कीजिए।
हलः
माना त्रिभुज के तीन कोण क्रमशः x, x + 10, x + 20 हैं।
∴ x + x + 10+ x + 20 = 180
3x + 30 = 180
3x = 180 – 30 = 150°
x = [latex]\frac{150}{3}[/latex] = 50°
∴ त्रिभुज के तीन कोण क्रमश: 50°, 60°, 70° है।

प्रश्न 27.
दिये गये चित्र में, ∆ABC के सभी कोणों की माप ज्ञात कीजिए।
हल:
∆ABC में,

∠1 = 180 – 110 = 70°
∠3 = 180 – 140 = 40°
∠2 = 180 – (70 + 40) = 180 – 110 = 70°

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 12 Congruence of Triangles Ex 12.2 त्रिभुजों की सर्वांगसमता

प्रश्न 1.
दिये गये चित्र में यदि ∠X = ∠Y तथा AB = CB तब सिद्ध कीजिए कि AE = CD
हल:

प्रश्न 2.
यदि एक चतुर्भुज के विकर्ण उन कोणों को समद्विभाजित करते हैं, जिनसे वे जुड़े हुए हैं तो सिद्ध कीजिए कि वे विकर्ण परस्पर लम्बवत् हैं।
हल:

प्रश्न 3.
ABC एक न्यूनकोण त्रिभुज है। B से AC पर लम्ब, Cसे AB पर लम्ब के बराबर है तो सिद्ध कीजिए कि AB = AC हल:
∆BCE तथा ∆BCF में

प्रश्न 4.
एक समकोण त्रिभुज में, एक न्यूनकोण अन्य कोण का दुगुना है, तो सिद्ध कीजिए कि कर्ण, छोटी भुजा का दुगुना है।
हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 6 Remainder Theorem and Factor Theorem Ex 6.3 शेषफल प्रमेय तथा गुणनखण्ड प्रमेय

गुणनखण्ड प्रमेय का प्रयोग करके निम्न बहुपदों के गुणनफल ज्ञात कीजिए।
प्रश्न 1.
x³ +13x² + 32x + 20; यदि (x + 2) इसका एक गुणनखण्ड है।
हलः
x³ + 13x² + 32x + 20 का (x + 2) एक गुणनखण्ड है।

गुणनखण्ड = (x + 2)[x² +11x + 10]
= (x + 2)[x² + (10 + 1)x + 10]
= (x + 2)[x² + 10x + x + 10]
= (x + 2)[x(x + 10) + 1(x + 10)]
= (x + 2)(x + 10)(x + 1)

प्रश्न 2.
x³ – 6x² + 3x + 10; यदि (x – 2) इसका एक गुणनखण्ड है।
हल:
x³ – 6x² + 3x + 10 का एक गुणनखण्ड (x – 2) है।

गुणनखण्ड = (x – 2)[x² – 4x – 5]
= (x – 2)[x² – (5 – 1)x – 5]
= (x – 2)[x² – 5x + x – 5]
= (x – 2)[x(x – 5) + 1(x – 5)]
= (x – 2)(x – 5)(x + 1)

प्रश्न 3.
x³ + 13x² + 31x – 45; यदि (x + 9) इसका एक गुणनखण्ड है।
हलः
x³ + 13x² + 31x – 45 का एक गुणनखण्ड (x + 9) है।

गुणनखण्ड = (x + 9)[x² + 4x – 5]
= (x + 9)[x² + (5 – 1)x -5]
= (x + 9)[x² + 5x – x -5]
= (x + 9)[x(x + 5) – 1(x + 5)]
= (x + 9)(x + 5)(x – 1)

प्रश्न 4.
9x³ – 27x² – 100x + 300; यदि (3x + 10) इसका एक गुणनखण्ड है।
हल:
9x³ – 27x² – 100x + 300 का एक गुणनखण्ड (3x + 10) है।

गुणनखण्ड = (3x + 10)[3x² – 19x + 30]
= (3x + 10)[3x² – (10 + 9)x + 30]
= (3x + 10)[3x² – 10x – 9x + 30]
= (3x + 10)[x(3x – 10) – 3(3x – 10)]
= (3x + 10)(3x – 10)(x – 3)

प्रश्न 5.
x⁴ – 7x³ + 9x² + 7x – 10; यदि (x – 1) इसका एक गुणनखण्ड है।
हल:
x⁴ – 7x³ + 9x² – 10 का एक गुणनखण्ड (x – 1) है।

x³ – 6x² + 3x + 10 में x = -1 रखने पर
शेषफल = (-1)³ – 6(-1)² + 3(-1) + 10
= -1 – 6 – 3 + 10 = 0
∴ (x + 1) भी इसका एक गुणनखण्ड होगा।

गुणनखण्ड = (x -1)(x + 1)[x² – 7x + 10]
= (x – 1)(x + 1)[x² – (5 + 2)x + 10]
= (x – 1)(x + 1)[x² – 5x – 2x + 10]
= (x – 1)(x + 1)[x(x – 5) – 2(x – 5)]
= (x – 1)(x + 1)(x – 5)(x – 2)

प्रश्न 6.
x³ + 6x² + 11x + 6
हल:
x³ + 6x² + 11x + 6
अतः इनमें से ऋणात्मक मान रखे जायेंगे।
x = -1 रखने पर = (-1)³ + 6(-1)² + 11(-1) + 6 = -1 + 6 – 11 + 6 = 0
अतः (x + 1) इसका एक गुणनखण्ड है।

गुणनखण्ड = (x + 1)[x² + 5x + 6]
= (x + 1)[x² + (2 + 3)x + 6]
= (x + 1)[x² + 2x + 3x + 6]
= (x + 1)[x(x + 2) + 3(x + 2)]
= (x + 1)(x + 2)(x + 3)

प्रश्न 7.
x³ + 7x² + 7x – 15
हल:
x³ + 7x² + 7x – 15                 (∵ 15 = 1 × 3 × 5)
x = 1 रखने पर = (1)³ + 7(1)² + 7(1) – 15 = 1 + 7 + 7 – 15 = 0
अतः (x – 1) इसका एक गुणनखण्ड है।

∴ गुणनखण्ड = (x – 1)[x² + 8x +15]
= (x – 1)[x² + (3 + 5)x + 15]
= (x – 1)[x² + 3x + 5x + 15]
= (x – 1)[x(x + 3) + 5(x + 3)]
= (x – 1)(x + 3)(x + 5)

प्रश्न 8.
a³ + b³ + c³ – 3abc
हल:
a³ + b³ + c³ – 3abc में a = -(b + c) रखने पर
=[-(b + c)]³ + b³ + c³ + 3(b + c)bc = -[b³ + c³ + 3bc(b + c)] + b³ + c³ + 3b²c + 3bc³ = 0
अतः (a + b + c) इसका एक गुणनखण्ड है।

∴ a³ + b³ + c³ – 3abc के गुणनखण्ड = (a + b + c)(a² + b² + c² – ab – bc – ca)

प्रश्न 9.
x⁴ + x³ – 7x² – x + 6
हलः
x⁴ + x³ – 7x² – x + 6 (∵ 6 = 1 × 2 × 3)
x = 1 रखने पर = (1)⁴ + (1)³ – 7(1)² – 1 + 6 = 1 + 1 – 7 – 1 + 6 = 0
अतः (x – 1) इसका एक गुणनखण्ड है। .
x = -1 रखने पर = (-1)⁴ + (-1)³ – 7(-1)² – (-1) + 6 = 1 – 1 – 7 + 1 + 6 = 8 – 8 = 0
अतः (x + 1) भी इसका एक गुणनखण्ड है।
∴ (x + 1)(x – 1) = (x² – 1) बहुपद का गुणनखण्ड होगा।

∴ गुणनखण्ड = (x + 1)(x – 1)[x² + x – 6]
= (x + 1)(x – 1)[x² + (3 – 2)x – 6] = (x + 1)(x – 1)[x² + 3x – 2x – 6]
= (x + 1)(x – 1)[x(x + 3) – 2(x + 3)]
= (x + 1)(x – 1)(x + 3)(x – 2)

प्रश्न 10.
2y³ – 5y² – 19y + 42
हलः
2y³ – 5y² – 19y + 42 (∵ 42 = 2 × 3 × 7)
y = 2 रखने पर = 2(2)³ – 5(2)² – 19(2) + 42 = 16 – 20 – 38 + 42 = 58 – 58 = 0
अतः (y – 2) इसका एक गुणनखण्ड है।

∴ गुणनखण्ड = (y – 2)[2y² – y – 21]
= (y – 2)[2y² – (7 – 6)y – 21] = (y – 2)[2y² – 7y + 6y – 21]
= (y – 2)[y (2y – 7) + 3(2y – 7)]
= (y – 2)(y + 3)(2y – 7)

प्रश्न 11.
x⁴ – 5x³ – 7x² + 41x – 30
हल:
x⁴ – 5x³ – 7x² + 41x – 30 (∵ 30 = 1 × 2 × 3 × 5)
x = 1 रखने पर = (1)⁴ – 5(1)³ – 7(1)² + 41(1) – 30 = 1 – 5 – 7 + 4 1 – 30 = 42 – 42 = 0
अतः (x -1) इसका एक गुणनखण्ड है।
x = 2 रखने पर = (2)⁴ – 5(2)³ – 7(2)² + 41(2) – 30 = 16 – 40 – 28 + 82 – 30 = 98 – 98 = 0
अतः (x – 2) भी इसका एक गुणनखण्ड है।।
(x – 1)(x – 2) = x² – 2x – x + 2 = x² – 3x + 2 इसके गुणनखण्ड है।

∴ गुणनखण्ड = (x – 1)(x – 2)[x² – 2x – 15]
= (x – 1)(x – 2)[x² – (5 – 3)x – 15] = (x -1)(x – 2)[x² – 5x + 3x – 15]
= (x – 1)(x – 2)[x(x – 5) + 3(x – 5)] = (x – 1)(x – 2)(x – 5)(x + 3)

प्रश्न 12.
a⁴ + 2a³ – 2a² + 2a – 3
हलः
a⁴ + 2a³ – 2a² + 2a – 3 (∵ 3 = 1 × 3)
a = 1 रखने पर = (1)⁴ + 2(1)³ – 2(1)² + 2(1) – 3 = 1 + 2 – 2 + 2 – 3 = 5 – 5 = 0
अतः (a – 1) इसका एक गुणनखण्ड है।
a = -3 रखने पर = (-3)⁴ + 2(-3)³ – 2(-3)² + 2(-3) – 3 = 81 – 54 – 18 – 6 – 3 = 81 – 81 = 0
अतः (a + 3) भी इसका एक गुणनखण्ड है।
इसलिए (a – 1)(a + 3) = a² + 3a – a – 3 = a² + 2a – 3 इसका गुणनखण्ड है।

∴ गुणनखण्ड = (a – 1)(a + 3)(a² + 1)

प्रश्न 13.
4x⁴ – 12x³ – x² + 27x – 18
हलः
4x⁴ – 12x³ – x² + 27x – 18 (∵ 18 = 1 × 2 × 3 × 3)
x = 1 रखने पर = 4(1)⁴ – 12(1)³ – (1)² + 27(1) – 18 = 4 – 12 – 1 + 27 – 18 = 31 – 31 = 0
अतः (x – 1) इसका एक गुणनखण्ड है।
इसी प्रकार x = 2 रखने पर = 4(2)⁴ – 12(2)³ – (2)² + 27(2) – 18
= 4 × 16 – 12 × 8 – 4 + 27 × 2 – 18
= 64 – 96 – 4 + 54 – 18 = 118 – 118 = 0
अतः (x – 2) इसका एक गुणनखण्ड है।
(x – 1)(x – 2) = x² – 2x – x + 2 = x² – 3x + 2 इसका गुणनखण्ड है।

∴ गुणनखण्ड = (x – 1)(x – 2)(4x² – 9) = (x – 1)(x – 2)(2x + 3)(2x – 3)

प्रश्न 14.
x⁴ + 10x³ + 35x² + 50x + 24
हल:
x⁴ + 10x³ + 35x² + 50x + 24 (∵ 24 = 1 × 2 × 2 × 2 × 3)
x = -1 रखने पर = (-1)⁴ + 10(-1)³ + 35(-1)² + 50(-1) + 24
= 1 – 10 + 35 – 50 + 24 = 60 – 60 = 0
अतः (x + 1) इसका एक गुणनखण्ड है।
x = -2 रखने पर = (-2)⁴ + 10(-2)³ + 35(-2)² + 50(-2) + 24
= 16 – 80 + 140 – 100 + 24 = 180 – 180 = 0
अतः (x + 2) भी इसका एक गुणनखण्ड है।
∴ (x + 1)(x + 2) = x² + 3x + 2 इसका गुणनखण्ड है।

गुणनखण्ड = (x + 1)(x + 2)[x² + 7x + 12]
= (x + 1)(x + 2)[x² + (3 + 4)x + 12] = (x + 1)(x + 2)[x² + 3x + 4x + 12]
= (x + 1)(x + 2)[x(x + 3)+ 4(x + 3)] = (x + 1)(x + 2)(x + 3)(x + 4)

प्रश्न 15.
3a⁴ + 28a³ + 87a² + 98a + 24
हलः
3a⁴ + 28a³ + 87a² + 98a + 24      (∵ 24 = 1 × 2 × 3 × 4)
a = -2 रखने पर = 3(-2)⁴ + 28(-2)³ + 87(-2)² + 98(-2) + 24
= 48 – 224 + 348 – 196 + 24 = 420 – 420 = 0
अतः (a + 2) इसका एक गुणनखण्ड है।
a = -3 रखने पर = 3(-3)⁴ + 28(-3)³ + 87(-3)² + 98(-3) + 24
= 243 – 756 + 783 – 294 + 24 = 1050 – 1050 = 0
अतः (a + 3) भी इसका एक गुणनखण्ड है।
(a + 2)(a + 3) = a² + 5a + 6 इसका गुणनखण्ड है।

∴ गुणनखण्ड = (a + 2)(a + 3)[3a² + 13a + 4] = (a + 2)(a + 3)[3a² + (12 + 1)a + 4]
= (a + 2)(a + 3)[3a² + 12a + a + 4] = (a + 2)(a + 3)[3a(a + 4) + 1(a + 4)]
= (a + 2)(a + 3)(3a + 1)(a + 4)

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 20 Statistics Ex 20.1 सांख्यिकी

प्रश्न 1.
शब्द “सांख्यिकी’ द्वारा
(i) एकवचन रूप में,
(ii) बहुवचन रूप में तुम क्या समझते हो?
हलः
सांख्यिकी वह विज्ञान है जिसमें किसी अनुसन्धान क्षेत्र से सम्बन्धित आँकडो का संकलन, वर्गीकरण, सारणीकरण, प्रस्तुतीकरण, विश्लेषण निर्वचन तथा पूर्वानुमान, किसी निश्चित उद्देश्य की पूर्ति हेतू किया जाता है।

प्रश्न 2.
30 विद्यार्थियों ने एक परीक्षा में निम्न अंक प्राप्त किए-
20, 23, 28, 30, 32, 34, 35, 36, 36, 40, 41, 42, 43, 44, 45, 45, 48, 44, 50, 50, 52, 53, 54, 56, 56, 58, 61, 62, 65, 65
वर्ग अन्तराल 20-29, 30-39, 40-49, 50-59 तथा 60-69 लेकर इन्हें बारंबारता बंटनीय रूप में दर्शाइये।
हलः

प्रश्न 3.
एक सोसाइटी में 30 घरों के पानी के बिल (र में ) नीचे दिये गये हैं।
वर्ग-माप 10 लेकर एक वर्गीकृत बारंबारता बंटन सारणी के रूप में निरूपित कीजिए:
30, 32, 45, 54, 74, 78, 108, 112, 66, 76, 88, 40, 14, 20, 15, 35, 44, 66 , 75, 84, 95, 96, 102, 110, 88, 74, 112, 14, 34, 44
हलः

प्रश्न 4.
निम्नलिखित आँकड़ों के प्रयोग से एक बारंबारता सारणी बनाइयेः
315, 320, 324, 317, 324, 319, 320, 317, 323, 325, 316, 318, 321, 322, 325, 319, 324, 321, 316, 319, 320, 320, 322, 323.
हल:

प्रश्न 5.
नीचे 16 विद्यार्थियों की लम्बाइयाँ इंचों में दी गई हैं। 5 के वर्ग-अन्तराल के प्रयोग से एक बारंबारता
बंटन सारणी बनाइये :
62, 70, 72, 64, 65, 71, 70, 60, 64, 72, 60, 61, 69, 70, 64, 71
हलः

प्रश्न 6.
एक बंटन के वर्ग-चिह्न 104, 114, 124, 134, 144, 154 तथा 164 हैं। वर्ग-माप तथा वर्ग-सीमा निकालिये।
हलः
वर्ग माप = 10
वर्ग सीमा = 100-110,110-120, 120-130,130-140,140-150, 150-160,160-170, 170-180 है।

प्रश्न 7.
एक सोसाइटी के 40 घरों के बिजली के बिल (र में) नीचे दिये गये हैं :
116, 127, 107, 100, 80, 82, 91, 101, 65, 95,87,81, 105, 129, 92, 75, 89, 78,87, 81, 59,52, 65, 101, 115, 108,95, 65, 98, 62,84, 76, 63, 128, 121, 61, 118, 108, 116, 130.
वर्गीकृत-बारंबारता सारणी बनाइये।
हलः

प्रश्न 8.
नीचे दिये गये आँकड़ों से एक बारंबारता सारणी तैयार कीजिए।
90, 97, 92, 95, 93, 95, 93, 85, 93, 85, 83, 77, 83, 77, 74, 60, 71, 65, 74, 80, 87, 82, 81, 76, 61, 63, 58, 58, 56, 57
हलः

प्रश्न 9.
30 विद्यार्थियों के गणित में अन्तिम अंक निम्न प्रकार दिये गये हैं:
53, 61, 48, 60, 78, 68, 55, 100, 67, 90, 75, 88, 77, 37, 84, 58, 60, 48, 62, 56, 44, 58, 52, 64, 98, 59, 70, 39, 56, 60.
(i) इन अंकों को आरोही क्रम में व्यवस्थित कीजिए। जैसे – 30-39 एक समूह, 40-49 दूसरा समूह आदि।
(ii) अधिकतम स्कोर क्या है?
(iii) निम्नतम स्कोर क्या है?
(iv) परास क्या है?
(v) यदि उत्तीर्ण अंक 40 है तो कितने अनुत्तीर्ण हैं?
(vi) 75 या अधिक अंक कितने विद्यार्थियों ने प्राप्त किए?
(vii) 50 से 60 के बीच कौन-सा प्रेक्षण वास्तव में नहीं होगा।
(viii) 50 से कम अंक कितनों ने प्राप्त किए?
हलः
(i) सारणी 30-49, 40-49, 50-59, 60-69, 70-79, 80-89, 90-99 तथा 100-109 तक बनाओ।
(ii) 100
(iii) 37
(iv) 63
(v) 2
(vi) 8
(vii) 51, 54,57
(viii) 5

प्रश्न 10.
दी गई समावेशी श्रृंखला को अपवर्जी श्रृंखला में बदलिए :

हलः
अपवर्जी सारणी

प्रश्न 11.
वर्ग अन्तराल 13.5 – 15.5 का मध्य-बिन्दु क्या है?
हल:
14.5

Balaji Publications Mathematics Class 9 Solutions