Balaji Class 9 Maths Solutions Chapter 1 Real Numbers Ex 1.2

Balaji Class 9 Maths Solutions Chapter 1 Real Numbers Ex 1.2 वास्तविक संख्याएँ

प्रश्न 1.
निम्न प्रत्येक सात दशमलव को पूर्णांकों के भागफल में व्यक्त कीजिए।
(i) 0.9
(ii) -0.67
(iii) -0.35
(iv) 1.075
हल:

प्रश्न 2.
निम्न प्रत्येक आवर्ती दशमलव को पूर्णांकों के भागफल के रूप में व्यक्त कीजिए।
(i) [latex]0 . \overline{7}[/latex]
(ii) [latex]0 . \overline{57}[/latex]
(iii) [latex]0 . \overline{134}[/latex]
(iv) [latex]0 . \overline{2341}[/latex]
(v) [latex]5 . \overline{317}[/latex]
हलः

प्रश्न 3.
5 और 6 के बीच तीन परिमेय संख्याएँ लिखिए।
हलः

प्रश्न 4.
0.5 और 0.6 के बीच तीन अपरिमेय संख्याएँ लिखिए।
हलः
0.5 व 0.6 के बीच तीन अपरिमेय संख्याएँ = 0.515115111……
= 0.535335333……
= 0.575775777……

प्रश्न 5.
[latex]\sqrt{2}[/latex] और [latex]\sqrt{7}[/latex] के बीच तीन अपरिमेय संख्याएँ लिखिए।
हल:
[latex]\sqrt{2}, \sqrt{7}[/latex] के बीच अपरिमेय संख्या = [latex]\sqrt{3}, \sqrt{5}, \sqrt{6}[/latex]

प्रश्न 6.
[latex]\sqrt{2}[/latex] का दशमलव के दो स्थानों तक परिमेय सन्निकटन ज्ञात कीजिए।
हलः
[latex]\sqrt{2}[/latex] = 1.4142135 से 1.4142136

प्रश्न 7.
जाँच कीजिए कि निम्नलिखित संख्याएँ परिमेय है या अपरिमैय

हल:

प्रश्न 8.
कारण सहित बताइये कि किसी संख्या p के लिए, 3 + [latex]\sqrt{p}[/latex] एक अपरिमेय संख्या है।
हलः
माना, x = 3 + [latex]\sqrt{p}[/latex] एक अपरिमेय संख्या है।
x − 3 = [latex]\sqrt{p}[/latex]
वर्ग करने पर, x² + 9 – 6x = p ……………..(1)
x² भी परिमेय संख्या होगी परन्तु x अपरिमेय संख्या है।
समीकरण (1) से,
p एक अपरिमेय संख्या है समीकरण (1) से सिद्ध होता है कि अपरिमेय संख्या p के लिए ही 3 + [latex]\sqrt{p}[/latex] अपरिमेय होगा।

प्रश्न 9.
सिद्ध कीजिए कि ([latex]\sqrt{3}-\sqrt{2}[/latex]) अपरिमेय है।
हलः
माना, ([latex]\sqrt{3}-\sqrt{2}[/latex]) एक परिमेय संख्या है।

अतः हमारी परिकल्पना कि [latex]\sqrt{3}-\sqrt{2}[/latex] एक परिमेय संख्या है, गलत है
इसलिए [latex]\sqrt{3}-\sqrt{2}[/latex] एक अपरिमेय संख्या है।

प्रश्न 10.
सिद्ध कीजिए कि 7, एक परिमेय संख्या का घन नही हैं।
हलः
माना 7, एक परिमेय संख्या x का घन है।
7 = x³
0 = x³ -7
∴ x. एक परिमेय संख्या नही है
∴ हमारी परिकल्पना x एक परिमेय संख्या है,
गलत है .:. x परिमेय संख्या नहीं है
∴ 7, एक परिमेय संख्या का घन नहीं है।
वास्तविक संख्याएँ

Ex 1.2 Real Numbers  अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

निम्न संख्याओं का दशमलव रूप में प्रसार कीजिए। (प्रश्न 1- 5) [NCERT]
प्रश्न 1.
[latex]\frac{7}{8}[/latex]
हलः

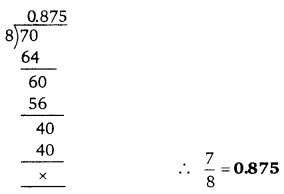
प्रश्न 2.
[latex]\frac{2157}{625}[/latex]
हलः

प्रश्न 3.
[latex]\frac{8}{3}[/latex]
हलः

प्रश्न 4.
[latex]\frac{15}{4}[/latex]
हलः

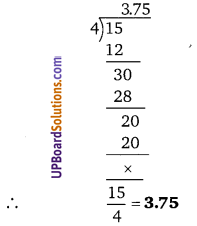
प्रश्न 5.
[latex]\frac{-22}{13}[/latex]
हलः

निम्न संख्याओं को [latex]\frac{m}{n}[/latex] के रूप में व्यक्त कीजिए। (प्रश्न 6-13)

प्रश्न 6.
[latex]0 . \overline{3}[/latex]
हलः

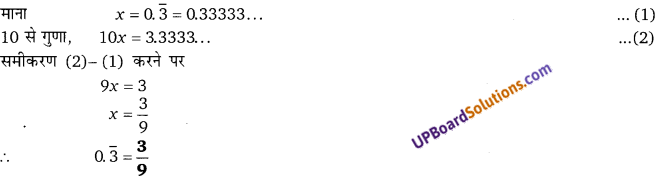
प्रश्न 7.
[latex]0 . \overline{1}[/latex]
हलः

प्रश्न 8.
[latex]0 . \overline{585}[/latex]
हलः

प्रश्न 9.
[latex]23 . \overline{43}[/latex]
हलः
माना x = 23.434343…. ………..(1)
100 से गुणा करने पर, 100x = 2343.434343… ………..(2)
समीकरण (2)- समीकरण (1) करने पर
99x = 2320
x = [latex]\frac{2320}{99}[/latex]

प्रश्न 10.
[latex]0 . \overline{23}[/latex]
हलः

प्रश्न 11.
[latex]4 . \overline{32}[/latex]
हलः

प्रश्न 12.
7.010
हलः

प्रश्न 13.
[latex]0 . \overline{621}[/latex]
हलः

प्रश्न 14.
0.1 और 0.12 के बीच दो अपरिमेय संख्याओं को ज्ञात करें।
हलः
0.1 और 0.12 के बीच दो अपरिमेय संख्याएँ =.1010010001…
तथा .1101001000100001…

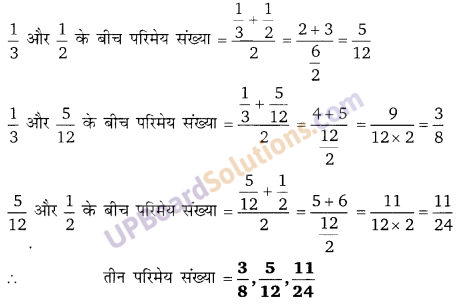
प्रश्न 15.
[latex]\frac{1}{3}[/latex] और [latex]\frac{1}{2}[/latex] के बीच तीन परिमेय संख्याओं को ज्ञात करें।
हलः

प्रश्न 16.
[latex]\frac{1}{5}[/latex] और [latex]\frac{1}{4}[/latex] के बीच तीन परिमेय संख्याओं को ज्ञात करें। (NCERT Exemplar)
हलः

प्रश्न 17.
[latex]3 \frac{1}{8}[/latex] का दशमलव रूप में प्रसार करें।
हलः
[latex]3 \frac{1}{8}=\frac{25}{8}[/latex] = 3.125

प्रश्न 18.
[latex]0.2 \overline{45}[/latex] को एक साधारण भिन्न के रूप में व्यक्त करें।
हलः
माना x = 0.2454545…

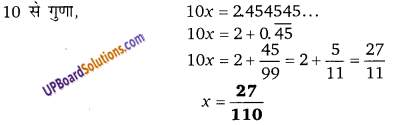
प्रश्न 19.
निम्नलिखित में से कौन-सी संख्या एक अपरिमेय संख्या है?
(a) [latex]\sqrt{\frac{25}{49}}[/latex]
(b) [latex]\sqrt{5}[/latex]
(c) [latex]\sqrt{36}[/latex]
(d) इनमें से कोई नहीं
हल:
विकल्प (b), [latex]\sqrt{5}[/latex]

प्रश्न 20.
निम्न में से कौन-सा कथन सत्य है?

हलः
विकल्प (c) π अपरिमेय है और [latex]\frac{22}{7}[/latex] परिमेय है।

प्रश्न 21.
निम्न में से कौन-सा एक कथन सत्य नहीं है?
(a) एक अपरिमेय संख्या का दशमलव प्रसार अनवसानी (असांत) और अनावर्ती है।
(b) दो अपरिमेय संख्याओं का योग, एक परिमेय या एक अपरिमेय संख्या होना चाहिए।
(c) एक परिमेय और एक अपरिमेय संख्या का योग हमेशा अपरिमेय होता है।
(d) सभी सत्य है।
हल:
विकल्प (d) सभी सत्य है।

प्रश्न 22.
निम्नलिखित में परिमेय संख्या ज्ञात कीजिए।
(a) π
(b) 0
(c) [latex]\sqrt{2}[/latex]
(d) इनमें से कोई नहीं
हल:
0, विकल्प (b)

Ex 1.2 Real Numbers  लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 23.
[latex]\sqrt{3}[/latex] और [latex]\sqrt{11}[/latex] के बीच एक परिमेय संख्या ज्ञात कीजिए।
हलः

प्रश्न 24.
संख्या [latex]\sqrt{5}[/latex] का दशमलव प्रसार ज्ञात कीजिए।
हलः
[latex]\sqrt{5}[/latex] = 2.23606797749…
अनवसानी (असांत) और अनावर्ती

प्रश्न 25.
दो वास्तविक संख्याओं के बीच कितनी परिमेय और अपरिमेय संख्याएँ होती हैं?
हलः
अनन्त

प्रश्न 26.
निम्नलिखित में से कौन-सा कथन सत्य है?
(a) प्रत्येक पूर्णांक एक परिमेय संख्या है।
(b) एक वास्तविक संख्या या तो परिमेय होती है या अपरिमेय।
हलः
(a) सत्य
(b) सत्य

प्रश्न 27.
दो अपरिमेय संख्याओं की गुणा की प्रकृति ज्ञात कीजिए।
हलः
दो अपरिमेय संख्याओं की गुणा परिमेय भी हो सकती है तथा अपरिमेय भी हो सकती है।

प्रश्न 28.
[latex]\sqrt{2}[/latex] और [latex]\sqrt{3}[/latex] के बीच एक परिमेय संख्या ज्ञात कीजिए।
हलः

प्रश्न 29.
संख्या (3 -[latex]\sqrt{7}[/latex] )(3 + [latex]\sqrt{7}[/latex] ) का प्रकार ज्ञात कीजिए।
हलः

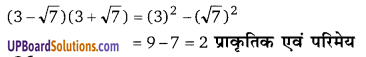
प्रश्न 30
[latex]\frac{36}{100}[/latex] का दशमलव रूप ज्ञात कीजिए। [NCERT]
हलः
[latex]\frac{36}{100}[/latex] = 0.36

प्रश्न 31.
सिद्ध कीजिए कि एक परिमेय संख्या का दशमलव निरूपण या तो सांत होता है या आवर्ती।
हलः
परिमेय संख्या का दशमलव निरूपण करने पर दशमलव के बाद अंकों की संख्या सीमित है
जैसे- [latex]\frac{3}{4}[/latex] = 0.75 या [latex]\frac{5}{8}[/latex] = 0.625
परन्तु यदि अंको की संख्या सीमित नहीं है और अंको के एक समूह की क्रमानुसार पुनरावृत्ति हो तो उसे आवर्ती दशमलव कहते हैं। जैसे-

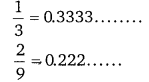
प्रश्न 32.
सिद्ध कीजिए कि एक अपरिमेय संख्या का दशमलव निरूपण न तो सांत होता है और न ही आवर्ती।
हलः
अपरिमेय संख्या, जिसे [latex]\frac{p}{q}[/latex] (जहाँ p व q पूर्णांक तथा q ≠ 0) है, के रूप में व्यक्त नही किया जा सकता है।
परिमेय संख्या का दशमलव निरूपण सांत तथा आवर्ती होता है। इसके विपरीत अपरिमेय संख्या का दशमलव निरूपण न तो सांत और ना ही आवर्ती होते हैं। जैसे- [latex]\sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{11}[/latex] आदि अपरिमेय संख्याएँ जो परिमेय नहीं है, दशमलव के रूप में प्रदर्शित करने पर वे न तो सांत होती हैं और न ही आवर्ती।

प्रश्न 33.
सिद्ध कीजिए कि एक संख्या रेखा पर प्रत्येक बिन्दु, एक एकल वास्तविक संख्या निरूपित करता है।
हलः
सभी परिमेय संख्याएँ तथा अपरिमेय संख्याएँ साथ ली गई हैं जो वास्तविक संख्याओं से ली गई है सभी परिमेय एवं अपरिमेय संख्या, वास्तविक संख्याओं का समुच्चय है। सभी परिमेय व अपरिमेय संख्या, संख्या रेखा पर वास्तविक संख्याएं निरूपित है इसलिए इसे संख्या रेखा के स्थान पर वास्तविक संख्या रेखा कहते हैं।

Ex 1.2 Real Numbers स्वमल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
क्या शून्य (0) एक परिमेय संख्या है? क्या इसे [latex]\frac{p}{q}[/latex], p, q ∈ Z, q ≠ 0 के रूप में व्यक्त किया जा सकता
हलः
हाँ 0 को [latex]\frac{p}{q}[/latex] के रूप में व्यक्त किया जा सकता है
0 = [latex]\frac{\mathbf{0}}{\mathbf{1}}=\frac{\mathbf{0}}{\mathbf{2}}=\frac{\mathbf{p}}{\mathbf{q}}[/latex]

प्रश्न 2.
निम्न में सही (T) व गलत (F) छाटियें।
(i) प्रत्येक प्राकृत संख्या, पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णांक एक पूर्ण संख्या होती है।।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है
हलः
(i) T
(ii) F
(iii) F

प्रश्न 3.
सिद्ध कीजिए कि प्रत्येक धनात्मक पूर्णांक संख्याओं का वर्गमूल अपरिमेय संख्या नही होती।
हलः
(i) यदि n कोई पूर्ण वर्ग संख्या नहीं है तो [latex]\sqrt{n}[/latex] परिमेय संख्या नहीं होती है।
∴ [latex]\sqrt{n} \neq \frac{p}{q}[/latex] जहाँ p व q पूर्णांक है तथा q ≠ 0
जैसे- [latex]\sqrt{2}, \sqrt{3}, \sqrt{5}[/latex] आदि

(ii) यदि n कोई पूर्ण वर्ग संख्या है तो [latex]\sqrt{n}[/latex] एक परिमेय संख्या होती है।
[latex]\sqrt{n}=\frac{p}{q}[/latex] जहाँ p व q पूर्णांक है तथा q ≠ 0
जैसे- [latex]\sqrt{4}, \sqrt{9}, \sqrt{16}, \sqrt{25}[/latex] आदि

प्रश्न 4.
सिद्ध कीजिए कि 3.142678 एक परिमेय संख्या है। .
हलः
∵ 3.142678 = [latex]\frac{3142678}{1000000}=\frac{1571339}{500000}[/latex]
जिसे [latex]\frac{p}{q}[/latex] लिखा जा सकता है यह एक परिमेय संख्या है।

प्रश्न 5.
हम जानते हैं कि प्रत्येक परिमेय संख्या [latex]\frac{p}{q}[/latex] (p, q ∈ Z, q ≠ 0) के रूप की होती है। जहाँ p व 4 में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड नहीं होता तथा इसका दशमलव प्रसार सांत होता है। किस गुण को संतुष्ट करेगा?
हलः
q एक अभाज्य गुणनखण्ड होगा।

प्रश्न 6.
यदि n एक अभाज्य संख्या है तो सिद्ध कीजिए कि [latex]\sqrt{n}[/latex], परिमेय संख्या नहीं है।
हलः
माना n एक अभाज्य संख्या है। माना [latex]\sqrt{n}[/latex] एक परिमेय संख्या है।

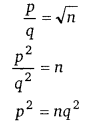
⇒ ∴ n, p² का एक गुणनखण्ड है।
⇒ n, p का एक गुणनखण्ड है।
माना p = nm (किसी भी प्राकृतिक संख्या m के लिए)
⇒ p² = n²m²
⇒ nq² = n²m²
⇒ q² = nm²
⇒ n, q² का एक गुणनखण्ड है
⇒ n,q का एक गुणनखण्ड है
परन्तु n, p का भी एक गुणनखण्ड है तथा q का गुणनखण्ड है
∴ n, p व q दोनों का गुणनखण्ड है यह परिकल्पना कि p व q का कोई उभयनिष्ठ गुणनखण्ड गलत है। अत: हमारी परिकल्पना कि [latex]\sqrt{n}[/latex] एक परिमेय संख्या है, गलत है।
अतः [latex]\sqrt{n}[/latex] एक परिमेय संख्या नहीं है।

प्रश्न 7.
यदि a > b > 0 तब सिद्ध कीजिए कि [latex]\sqrt{a b}[/latex] सदैव a व b के बीच स्थित है।
हल:
∵ यदि a और b दो भिन्न धनात्मक परिमेय संख्याएं इस प्रकार हैं कि ab किसी परिमेय संख्या का एक पूर्ण वर्ग नहीं है। तब [latex]\sqrt{a b}[/latex] एक a व b के बीच स्थित अपरिमेय संख्या है।
∴ a < [latex]\sqrt{a b}[/latex] < b

प्रश्न 8.
माना m a n दो धनात्मक पूर्णांक इस प्रकार हैं कि m ≥ 1, n ≥ 1 तथा m पूर्ण n वाँ घात नहीं है अर्थात् कोई ऐसा पूर्णांक p नहीं है जिसके लिए pⁿ = m, सिद्ध कीजिए कि ऐसी कोई परिमेय संख्या a नहीं हैं जिसके लिए aⁿ = m.
हलः
pⁿ = m ………………… (1)
aⁿ = m ………………… (2)
(1) व (2) की तुलना से,
pⁿ = aⁿ
दोनों पक्षों की तुलना से, p= परन्तु यह सम्भव नहीं है ।
∴ ऐसी कोई परिमेय संख्या a नहीं है
जिसके लिए aⁿ = m

प्रश्न 9.
(i) सम अभाज्य संख्या लिखिये।
(ii) 5 व 6 के बीच कितनी वास्तविक संख्याएँ हैं?
(iii) वास्तविक संख्याओं के लिए धनात्मक तत्समक ज्ञात कीजिए।
(iv) परिमेय संख्याओं के लिए गुणन तत्समक ज्ञात कीजिए।
हलः
(i) 2
(ii) अनन्त
(iii) 0
(iv) 1

प्रश्न 10.
[latex]\frac{1}{9}[/latex] का दशमलव प्रसार लिखकर [latex]\frac{2}{9}, \frac{4}{9}, \frac{5}{9}[/latex], के मान ज्ञात कीजिए।
हलः

प्रश्न 11.
सिद्ध कीजिए कि एक अशून्य परिमेय संख्या तथा अपरिमेय संख्या का योग अपरिमेय संख्या होती है।
हलः
माना x एक परिमेय संख्या है तथा y एक अपरिमेय संख्या है।
तब हमें दिखाना है कि (x + y) एक अपरिमेय संख्या है।
माना x + y परिमेय संख्या है।
∵ दो परिमेय संख्याओं का अन्तर भी परिमेय ही होता है।
∴ (x + y) – x भी एक परिमेय संख्या है।
∴ y एक परिमेय संख्या है परन्तु y एक अपरिमेय संख्या है।
∴ हमारी परिकल्पना हैं कि x + y एक परिमेय संख्या है, गलत है
अत: x + y एक अपरिमेय संख्या है।

प्रश्न 12.
सिद्ध कीजिए कि एक अशून्य परिमेय संख्या तथा अपरिमेय संख्या का गुणनफल एक अपरिमेय संख्या होती है।
हलः
माना x एक अशून्य परिमेय संख्या तथा y एक अपरिमेय संख्या है
तो हमें दर्शाना है कि xy एक अपरिमेय संख्या है।
माना y एक परिमेय संख्या है।
∵ दो अशून्य परिमेय संख्याओं का भागफल भी परिमेय ही होता है
∴ xy परिमेय तथा x परिमेय संख्या है।
∴ भागफल ⇒ [latex]\left(\frac{x y}{x}\right)[/latex] भी एक परिमेय संख्या है।
⇒ y एक परिमेय संख्या है।
परन्तु y एक अपरिमेय संख्या है।
इसलिए हमारी अभिधारणा (परिकल्पना) कि xy एक परिमेय संख्या है, गलत है
∴ xy एक अपरिमेय संख्या है।

प्रश्न 13.
0.232332333233332… व 0.2525525552555552… के बीच दो परिमेय संख्याऐं ज्ञात कीजिए।
हलः
माना a = 0.232332333233332……..
b = 0.2525525552555552…….
a तथा b दोनों अपरिमेय संख्या है।
a व b में दशमलव के बाद का पहला स्थान एक ही (2) है परन्तु दूसरा स्थान a में 3 व b में 5 है।
∴ c = 0.25 तथा d = 0.2525 ऐसी परिमेय संख्या होगी।
जिससे a < c < d < b

प्रश्न 14.
[latex]0 . \overline{1}[/latex] व 0.1101 के बीच एक अपरिमेय संख्या ज्ञात कीजिए।
हलः
[latex]0 . \overline{1}[/latex] = 0.111111…..
तथा 0.1101 के बीच एक अपरिमेय संख्या = 0.111101001000100001…

प्रश्न 15.
सिद्ध कीजिए कि [latex]\sqrt{3}+\sqrt{5}[/latex] एक अपरिमेय संख्या है।
हलः
माना [latex]\sqrt{3}+\sqrt{5}[/latex] एक परिमेय संख्या है।

∴ हमारी परिकल्पना कि [latex]\sqrt{3}+\sqrt{5}[/latex] एक परिमेय संख्या है, गलत है अतः [latex]\sqrt{3}+\sqrt{5}[/latex] एक अपरिमेय संख्या ही होगी।

Balaji Publications Mathematics Class 9 Solutions