Balaji Class 9 Maths Solutions Chapter 6 Remainder Theorem and Factor Theorem Ex 6.1 शेषफल प्रमेय तथा गुणनखण्ड प्रमेय
Ex 6.1 Remainder Theorem and Factor Theorem अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
बहुपद 5x3 – 2x2 – 7x + 1 को x से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब 5x3 – 2x2 – 7x + 1 को x से विभाजित किया जाता है तो x = 0 रखने पर
शेषफल = 0 – 0 – 0 + 1 = 1
![]()
प्रश्न 2.
बहुपद p(x) को (x – a) से भाग देने पर शेषफल ज्ञात कीजिए।
हल:
जब P(x) को (x – a) से विभाजित किया जाता है तो x – a = 0
∴ x = a रखने पर
शेषफल = P(a)
प्रश्न 3.
बहुपद p(x) को (ax – b) से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब P(x) को (ax – b) से विभाजित किया जाता है तो ax – b = 0 या x = [latex]\frac{b}{a}[/latex] रखने पर
शेषफल = [latex]\boldsymbol{P}\left(\frac{\boldsymbol{b}}{\boldsymbol{a}}\right)[/latex]
प्रश्न 4.
बहुपद x3 – 2x2 + x + 1 को (x – 1) से भाग देने पर शेषफल ज्ञात कीजिए।
हल:
x3 – 2x2 + x + 1 को (x – 1) से विभाजित किया जाता है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)3 – 2(1)2 + 1 + 1 = 1 – 2 + 1 + 1 = 1
प्रश्न 5.
बहुपद x31 + 31 को (x + 1) से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब x31 + 31 को (x + 1) से विभाजित किया जाता है तो x + 1 = 0 या x = 0 – 1 = -1
शेषफल = (-1)31 + 31 = -1 + 31 = 30
प्रश्न 6.
बहुपद 3x3 – 4x2 + 7x – 5 को (x – 3) से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब 3x3 – 4x3 + 7x – 5 को (x – 3) से विभाजित किया जाता है तो x – 3 = 0 या x = 3 रखने पर
शेषफल = 3(3)3 – 4(3)2 + 7(3) – 5 = 3. 27 – 36 + 21 – 5 = 81 – 36 + 21 – 5 = 102 – 41 = 61
![]()
प्रश्न 7.
बहुपद x3 + 5x2 – 2 को (x – 1) से भाग देने पर शेषफल ज्ञात कीजिए।
हल:
x3 + 5x2 – 2 को (x – 1) से विभाजित किया जाता है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)3 + 5(1)2 – 2 = 1 + 5 – 2 = 4
Ex 6.1 Remainder Theorem and Factor Theorem लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)
प्रश्न 8.
शेषफल ज्ञात कीजिए यदि 3x3 – 4x2 + 7x – 5 को (x + 3) से भाग दिया जाता है।
हलः
जब 3x3 – 4x2 + 7x – 5 को (x + 3) से विभाजित किया जाता है तो
x + 3 = 0 या X = 0 – 3 = -3 रखने पर
शेषफल = 3(-3)3 – 4(-3)2 + 7(-3) – 5 = 3(-27) – 4(9) – 21 – 5
= -81 – 36 – 21 – 5 = -143
प्रश्न 9.
x = 3 पर p(x) का मान ज्ञात कीजिए यदि p(x) = 3x2 – 4x + [latex]\sqrt{17}[/latex]
हल:
P(x) = 3x2 – 4x + [latex]\sqrt{17}[/latex], यदि x = 3
शेषफल = 3(3)2 – 4 × 3 + [latex]\sqrt{17}[/latex] = 27 – 12 + [latex]\sqrt{17}[/latex] = 15 + [latex]\sqrt{17}[/latex]
प्रश्न 10.
शेषफल ज्ञात कीजिए यदि f (x) = 3x4 + 29x3 – 5a2x2 + 5x को (x – a) से भाग दिया जाता है।
हल:
f(x) = 3x4 + 29x3 – 5a2x2 + 5x को (x – a) से विभाजित किया जाता है तो
x – a = 0 या x = 0 + a = a
शेषफल = 3a4 + 29a3 – 5a2. a2 + 5a = 3a4 + 29a3 – 5a4 + 5a = -2a4 + 29a3 + 5a
![]()
प्रश्न 11.
शेषफल ज्ञात कीजिए यदि P(x) = x3 – 3x2 + 4x + 50 को (x – 3) से भाग दिया जाता है।
हल:
P(x) = x3 – 3x2 + 4x + 50 को (x -3) से भाग किया जाता है तो x – 3 = 0 या x = 3 रखने पर
शेषफल = (3)3 – 3(3)2 + 4 × 3 + 50 = 27 – 27 + 12 + 50 = 62
Ex 6.1 Remainder Theorem and Factor Theorem लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)
प्रश्न 12.
शेषफल प्रमेय का प्रयोग करते हुए निम्न में शेषफल ज्ञात कीजिए जब f(x) को g(x) से भाग दिया जाता है।

हल:
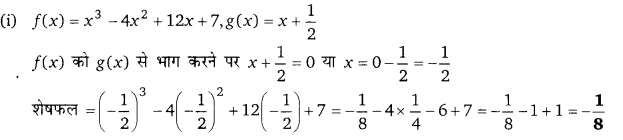

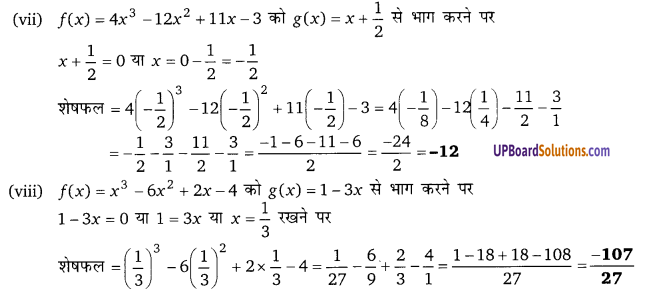
प्रश्न 13.
सिद्ध कीजिए कि 2x3 + 13x2 + x – 70, (x – 2) से विभाजित है।
हल:
2x3 + 13x3 + x – 70 को (x – 2) से भाग करने पर x – 2 = 0 या x = 2 रखने पर
शेषफल = 2(2)3 + 13(2)2 + 2 – 70 = 16 + 52 + 2 – 70 = 0
अत: 2x3 + 13x2 + x – 70, (x – 2) से पूर्णतया विभाजित होगा।
![]()
प्रश्न 14.
यदि बहुपदों px3 + 4x2 + 3x – 4 व x3 – 4x + p को (x – 3) से भाग करने पर समान शेषफल प्राप्त होते हैं तो सिद्ध कीजिए कि p = -1 (NCERT Exemplar)
हलः
जब Px3 + 4x2 + 3x – 4 को (x – 3) से भाग करने पर x – 3 = 0 या x = 3 रखने पर
शेषफल = P(3)3 + 4(3)2 + 3(3) – 4 = 27P + 36 + 9 – 4 = 27P + 41
जब x3 – 4x + P को (x – 3) से भाग करने पर x – 3 = 0 या x = 3 रखने पर
शेषफल = 33 – 4(3) + P = 27 – 12 + P = 15 + P
∴ 27P + 41 = 15 + P
27P – P = 15 – 41
26P = -26.
P = [latex]\frac{-26}{26}[/latex] = -1
प्रश्न 15.
यदि px3 + 9x2 + 4x – 10 को (x + 3) से भाग देने पर -22 शेषफल प्राप्त होता है तो p का मान ज्ञात कीजिए।
हलः
जब Px3 + 9x3 + 4x – 10 को (x + 3) से भाग किया जाता है तो x + 3 = 0 या x = -3 रखने पर
शेषफल = P(-3)3 + 9(-3)2 + 4(-3) – 10 = -22
-27P + 81 – 12 – 10 = -22
-27P = -22 – 81 + 22
– 27P = -81
P = [latex]\frac{-81}{-27}[/latex] = 3
प्रश्न 16.
यदि बहुपद f (x) = x4 – 2x3 + 3x2 – ax + b को (x – 1) और (x + 1) से भाग देने पर शेषफल क्रमशः 5 व 19 प्राप्त होते हैं, तो a व b के मान ज्ञात कीजिए।
हलः
यदि f(x) = x4 – 2x3 + 3x2 – ax + b को (x – 1) से भाग किया जाता है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)4 – 2(1)3 + 3(1)2 – a(1) + b = 1 – 2 + 3 – a + b = 2 – a + b
प्रश्नानुसार, 2 – a + b = 5
-a + b = 5 – 2 = 3 ⇒ – a + b = 3 ………………(1)
प्रश्नानुसार, यदि f(x) को (x + 1) से भाग किया जाता है तो
x + 1 = 0 या x = -1 रखने पर
शेषफल = (-1)4 – 2(-1)3 + 3(-1)2 – a(-1) + b
= 1 + 2 + 3 + a + b
= 6 + a + b
तथा 6 + a + b = 19
a + b = 19 – 6
a + b = 13 ………………(2)
(1) व (2) जोडने पर,
2b = 16
b = [latex]\frac{16}{2}[/latex] = 8
समी० (2) मे b का मान रखने पर, a + 8 = 13
a = 13 – 8 = 5
अतः a = 5 व b = 8
![]()
प्रश्न 17.
बहुपद x3 + px2 + qx + 6 को जब (x – 3) से भाग दिया जाता है तो शेषफल 3 तथा जब (x – 2) से भाग दिया जाता है तो शेषफल शून्य प्राप्त होता है। p व 4 के मान ज्ञात कीजिए।
हलः
यदि x3 + px2 + qx + 6 को (x – 3) से भाग किया जाता है तो x – 3 = 0 या x = 3 रखने पर
शेषफल = (3)3 + p(3)2 + q(3) + 6 = 3
27 + 9p + 3q + 6 = 3
9p + 3q + 33 = 3
9p + 3q = 3 – 33
9p + 3q = -30
3(3p + q) = -30
3p + q =[latex]\frac{-33}{3}[/latex] = -10 ……………(1)
यदि x3 + px2 + qx + 6 को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर
शेषफल = (2)3 + p(2)3 + q(2) + 6 = 0
8 + 4p + 2q + 6 = 0
4p + 2q = -14
2(2p + q) = -14
2p + q =[latex]\frac{-14}{2}[/latex] =-7 …………….(2)
समीकरण (1) व (2) को हल करने पर,

समीकरण (1) में p का मान रखने पर,
3 × -3 + q = -10
-9 + q = -10
q = -10 + 9 = -1
अतः p = -3, q = -1
प्रश्न 18.
बहुपद kr4 + 3x3 + 6 को (x – 2) से भाग देने पर प्राप्त शेषफल, दूसरे बहुपद 2x3 + 17x + k को (x – 2) से भाग देने पर प्राप्त शेषफल का दोगुना है। k का मान ज्ञात कीजिए।
हलः
बहुपद kr4 + 3x3 + 6 को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर शेषफल
= k(2)4 + 3(2)3 + 6
= 16k + 24 + 6 = 16k + 30
और जब 2x3 + 17x + k को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर
शेषफल = 2(2)3 + 17(2) + k = 2 × 8 + 34 + k = 50 + k
प्रश्नानुसार,
16k + 30 = 2(50 + k)
16k + 30 = 100 + 2k
16k – 2k = 100 – 30
14k = 70
k = [latex]\frac{70}{14}[/latex] = 5
![]()
प्रश्न 19.
यदि बहुपदों 9x3 + 3x2 – 13 तथा 2x3 – 5x + a को (x – 2) से भाग देने पर समान शेषफल प्राप्त होते हैं तो a का मान ज्ञात कीजिए।
हलः
बहुपद 9x3 + 3x2 – 13 को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर,
शेषफल = 9(2)3 + 3(2)2 – 13 = 72 + 12 – 13 = 71
बहुपद 2x3 – 5x + a को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर,
शेषफल = 2(2)3 – 5(2) + a = 16 – 10 + a या 6 + a
प्रश्नानुसार, 6 + a = 71
a = 71 – 6 = 65