Balaji Class 9 Maths Solutions Chapter 9 Introduction to Euclid’s Geometry Ex 9.1 यूक्लिड की ज्यामिति का परिचय
Ex 9.1 Introduction to Euclid’s Geometry अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
एक बिन्दु की विमायें ज्ञात कीजिए। (NCERT Exemplar)
हलः 0
![]()
प्रश्न 2.
एक ठोस की विमायें ज्ञात कीजिए। (NCERT Exemplar)
हलः
3
प्रश्न 3.
एक सतह की विमायें ज्ञात कीजिए। (NCERT Exemplar)
हल:
2
प्रश्न 4.
तीन असंरेख बिन्दुओं से गुजरने वाले समतलों की संख्या ज्ञात कीजिए।
हलः
1
प्रश्न 5.
सतह की सीमाओं के नाम लिखो। (NCERT Exemplar)
हलः
वक्र
प्रश्न 6.
ठोस की सीमाओं के नाम लिखो। (NCERT Exemplar)
हलः
पृष्ठ
![]()
प्रश्न 7.
यदि दो बराबर संख्याओं में एक बराबर संख्या जोड़ी जाती है तो परिणामी संख्याएँ बराबर होती हैं यह है
(a) अभिग्रहित
(b) परिभाषा
(c) उपपत्ति
(d) अभिधारणा
हलः
(a) अभिग्रहित
Ex 9.1 Introduction to Euclid’s Geometry लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 8.
(i) एक दिये गये बिन्दु से कितनी रेखाएं खींची जा सकती है?
(ii) एक रेखा के निरूपण हेतु कितने बिन्दुओं की आवश्यकता होगी?
(iii) क्या, रेखा की कोई लम्बाई होती है?
(iv) तीन संरेख बिन्दुओं से निर्धारित होने वाले रेखाखण्ड का नाम बताइये।
हलः
(i) अनन्त
(ii) दो
(iii) नहीं
(iv) यदि P, Q, R तीन सरैख बिन्दु है तो PQ, QR, PR रेखाखण्ड होंगे।
प्रश्न 9.
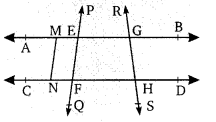
संलग्न चित्र में निम्न के नाम बताइये।
(i) 6 बिन्दु
(ii) 5 रेखाखण्ड
(iii) 4 किरणें
(iv) 4 रेखाएं
(v) 4 संरेख बिन्दु
हलः
(i) 6 बिन्दु = A, B,C, D, E, F
(ii) 5 रेखाखण्ड = [latex]\overline{\boldsymbol{E} \boldsymbol{F}}, \overline{\boldsymbol{G} \boldsymbol{H}}, \overline{\boldsymbol{E} \boldsymbol{G}}, \overline{\boldsymbol{F} \boldsymbol{H}}, \overline{\boldsymbol{M} \boldsymbol{N}}[/latex]
(iii) 4 किरणों = [latex]\overrightarrow{E P}, \overrightarrow{G R}, \overrightarrow{G B}, \overrightarrow{H D}[/latex]
(iv) 4 रेखाएं = [latex]\stackrel{\leftrightarrow}{\mathrm{AB}}, \stackrel{\leftrightarrow}{\mathrm{CD}}, \stackrel{\leftrightarrow}{\mathrm{PQ}} \stackrel{\leftrightarrow}{\mathrm{RS}}[/latex]
(v) 4 संरेख बिन्दु = M,E,G,B
![]()
प्रश्न 10.
निम्न में से कौन सा कथन सत्य है?
(i) एक रेखाखण्ड की कोई लम्बाई नहीं होती।
(ii) एक रेखाखण्ड का एक ही सिरा होता है।
(iii) प्रत्येक किरण की लम्बाई निश्चित होती है।
(iv) किरण AB = किरण BA
(v) दो विभिन्न बिन्दु सदैव एक रेखा को निर्धारित करते हैं।
(vi) एक बिन्दु से एक ही रेखा गुजरती है।
(vii) तीन रेखाएं समवर्ती होती हैं यदि उनका एक ही उभयनिष्ठ बिन्दु है।
हलः
(i) असत्य
(ii) असत्य
(iii) असत्य
(iv) असत्य
(v) सत्य
(vi) असत्य
(vii) सत्य
प्रश्न 11.
प्रमेय एवं अभिग्रहित में क्या अन्तर है?
हलः
पहले से प्राप्त परिणामों के आधार पर कुछ अभिग्रहित जो कथन बनाते हैं उस प्रमेय कहते हैं।
तथा वे कल्पनाऐं जिन्हें बिना (UPBoardSolutions.com) सिद्ध किये सत्य कथन मान लिया गया तथा जिन्हें निरन्तर प्रयोग किया गया, अभिग्रहित कहलाते हैं।
जैसे- (i) बराबर के आधे भी बराबर होते हैं।
(ii) यदि a = b तब [latex]\frac{1}{2}[/latex]a = [latex]\frac{1}{2}[/latex] b एक अभिग्रहित है।
प्रश्न 12.
कब किरण XY, रेखाखण्ड XZ के समान्तर होगी?
हलः
जब X, Y, Z संरेख हों।
प्रश्न 13.
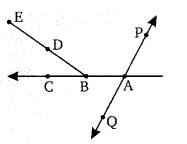
संलग्न चित्र से निम्न के उत्तर दीजिए।
(a) क्या A, B, C संरेख बिन्दु हैं?
(b) क्या A, B, D संरेख बिन्दु हैं?
(c) BD + DE = BE?
(d) AC ∩ BC = BC?
हलः
(a) हाँ
(b) नहीं
(c) हाँ
(d) हाँ
![]()
प्रश्न 14.
रिक्त स्थानों की पूर्ति करें।
(a) एक रेखाखण्ड के ……….. सिरे होते हैं।
(b) समवर्ती रेखायें ……….., बिन्दु (ओं) से गुजरती हैं।
हलः
(a) दो
(b) एक
Ex 9.1 Introduction to Euclid’s Geometry बहविकल्पीय प्रश्न (Multiple Choice Questions)
सही विकल्प का चयन कीजिए।
प्रश्न 1.
निम्न में किसकी उपपत्ति की आवश्यकता होती है। (NCERT Exemplar)
(a) प्रमेय
(b) अभिग्रहित
(c) अभिधारणा
(d) इनमें से कोई नहीं
हलः
प्रमेय
अतः विकल्प (a) सही है।
प्रश्न 2.
यूक्लिड ने अपनी पाठ्य पुस्तक ‘दी इलीमैन्ट’ को कितने भागों में बाँटा? (NCERT Exemplar)
(a) 12 अध्याय
(b) 13 अध्याय
(c) 11 अध्याय
(d) इनमें से कोई नहीं
हल:
13 अध्याय
अतः विकल्प (b) सही है।
प्रश्न 3.
यदि x = 23, y = 23 तब x = y, यह यूक्लिड का कौन-सा अभिग्रहित है?
(a) 6 वाँ
(b) 5 वाँ
(c) 4 वाँ
(d) इनमें से कोई नहीं
हलः
6वाँ
अतः विकल्प (a) सही है।
प्रश्न 4.
पिरामिड का आधार (NCERT Exemplar)
(a) केवल आयत
(b) केवल त्रिभुज
(c) कोई बहुभुज
(d) इनमें से कोई नहीं
हलः
कोई बहुभुज।
अतः विकल्प (c) सही है।
Ex 9.1 Introduction to Euclid’s Geometry स्वमूल्यांकन परीक्षण (Self Assessment Test)
प्रश्न 1.
निम्न में से सही कथन के लिए सत्य तथा गलत के लिए असत्य लिखें। (NCERT Exemplar)
(i) वह कथन जिसे सिद्ध किया गया है, अभिग्रहित कहलाता है।
(ii) एक सतह की भुजाएँ, वक्र होती हैं।
(iii) दो प्रतिच्छेदी रेखाएं कभी समान्तर नहीं होती।
(iv) दो बराबर वस्तुओं को दोगुना करने पर प्राप्त संख्याएँ भी बराबर होती हैं।
(v) ठोस की सीमाएँ, वक्र होती हैं।
हलः
(i) असत्य
(ii) सत्य
(iii) सत्य
(iv) सत्य
(v) असत्य
![]()
प्रश्न 2.
निम्न कथन को पढ़ें
एक वर्ग ऐसा बहुभुज है जो चार बराबर रेखाखण्डों से बना है तथा सभी कोण समकोण होते हैं। वह पद बताइये जो इस परिभाषा के लिए आवश्यक है।
हलः
यूक्लिड की अभिधारणा।
प्रश्न 3.
दो अभिधारणायें लें
(i) दो भिन्न-2 बिन्दुओं A व B के बीच, एक तीसरे बिन्दु C का अस्तित्व है। जो A व B के बीच है।
(ii) तीन विभिन्न बिन्दुओं का अस्तित्व है जो एक रेखा पर नहीं है।
क्या इन अभिकल्पनाओं में कोई अपरिभाषित पद है? क्या ये यूक्लिड अभिग्रहित का अनुसरण करते हैं?
हलः
ये यूक्लिड के अभिग्रहित का अनुसरण करते हैं।
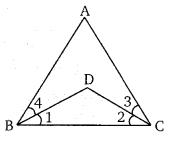
प्रश्न 4.
संलग्न चित्र में यदि ∠ABC = ∠ACB, ∠3 = ∠4, तब सिद्ध कीजिए कि ∠1 = ∠2. (NCERT Exemplar) .
हलः
∠ABC = ∠ACB
∠4 + ∠1 = ∠3 + ∠2
∵ ∠3 – ∠4 (दिया है)
∴ ∠1 = ∠2
प्रश्न 5.
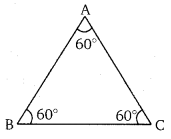
सिद्ध कीजिए कि किसी दिये रेखाखण्ड पर एक समबाहु त्रिभुज बनाया जा सकता है।
हलः
यदि BC एक रेखाखण्ड दिया है। बिन्दु B तथा C पर रेखाखण्ड BC के बराबर दो रेखाखण्ड AB तथा AC काटें, जिससे ∠ABC तथा ∠ACB 60° के कोण बनते हैं। इस प्रकार AB तथा AC को मिलाया। अत: ∆ABC एक समबाहु ∆ बनेगा।
प्रश्न 6.
सिद्ध कीजिए कि प्रत्येक रेखाखण्ड का एक और केवल एक मध्य बिन्दु होता है।
हलः
यूक्लिड के अभिग्रहित से एक ही वस्तु के आधे परस्पर बराबर होते हैं। अतः प्रत्येक रेखाखण्ड का एक और केवल एक मध्य बिन्दु होता है।
प्रश्न 7.
क्या यूक्लिड की पांचवी अभिधारणा समान्तर रेखाओं का अस्तित्व स्वीकार करती है।
हलः
इसके अनुसार यदि दो रेखायें एक ही रेखा के समान्तर हैं तो वे एक दूसरे के भी समान्तर होंगे।
![]()
प्रश्न 8.
किसी रेखा के समान्तर, दो समान्तर रेखाएं परस्पर समान्तर होती हैं।
हलः
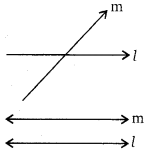
माना m तथा n के समान्तर नही हैं तब m और n एक बिन्दु P पर प्रतिच्छेद करती है –
इस प्रकार l के बाहर एक बिन्दु P से, दो रेखायें m और n, l के समान्तर है। यह (समान्तर जो समान्तर अभिग्रहित का विलोम है, हमारी कल्पना गलत है।
m ∥ n

प्रश्न 9.
दो विभिन्न रेखाओं का एक से अधिक उभयनिष्ठ बिन्दु नहीं हो सकता। सिद्ध कीजिए।
हलः
यदि l और m दो भिन्न रेखायें है माना l ∩ m में दो बिन्दु P व Q है तब ! के बिन्दु P और Q हैं।
तथा m के बिन्दु P और Q हैं। किन्तु यहाँ दो (UPBoardSolutions.com) भिन्न बिन्दुओं से केवल और केवल एक l रेखा गुजरती है इसलिए l = m अतः यह मानना कि और m दो भिन्न रेखायें है, गलत है अत: दो भिन्न रेखाओं में एक से अधिक बिन्दु उभयनिष्ठ नहीं हो सकता।
प्रश्न 10.
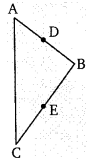
दिये गये चित्र में AD = [latex]\frac{1}{2}[/latex] AB तथा BE = [latex]\frac{1}{2}[/latex] BC, यदि AB = BC सिद्ध कीजिए कि AD = CE
हलः
∵ AB = BC .
∴ [latex]\frac{1}{2}[/latex] AB = [latex]\frac{1}{2}[/latex] BC
∴ AD = CE
प्रश्न 11.
माना किसी रेखा पर तीन बिन्दु P, Q व R हैं यदि P व R के बीच बिन्दु Q है तब सिद्ध C कीजिए कि PR – QR = PQ
हलः
यदि एक सरल रेखा पर तीन बिन्दु इस प्रकार स्थित हैं कि Q, P तथा R के बीच में स्थित है, तब
सिद्ध करना है : PR – QR = PQ
उपपत्ति : सदिश विश्लेषण से,

परिमाण लेने पर, PR – QR = PQ
प्रश्न 12.
संलग्न चित्र में AC = XD व C, AB का तथा D, XY के मध्य बिन्दु हैं। यूक्लिड अभिग्रहित का प्रयोग करके सिद्ध कीजिए कि AB = XY
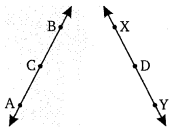
हलः
∵ C, AB का मध्य बिन्दु है, तब
AC = BC = [latex]\frac{A B}{2}[/latex] ………………(1)
यदि D, XY का मध्य बिन्दु है, तब
XD = DY = [latex]\frac{X Y}{2}[/latex]
दिया है : AC = XD
[latex]\frac{A B}{2}=\frac{X Y}{2}[/latex] [समी० (1) व (2) से]
⇒ AB = XY यही सिद्ध करना था।
![]()
प्रश्न 13.
नीचे दिये गये चित्र से सिद्ध कीजिए कि AB = CD, यदि AC = BD
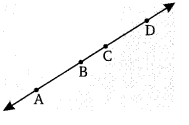
हलः
यदि
AC = BD
AD = AB + BD …………….. (1)
AD = AC + CD …………….(2)
समी० (1) व (2) से,
AB + BD = AC + CD [∵AC = BD]
AB = CD
प्रश्न 14.
यदि कोई बिन्दु 0, बिन्दुओं P व R के मध्य स्थित है तथा PO = OR तब सिद्ध कीजिए कि
PO = (1/2)PR
हलः
![]()
∵ बिन्दु 0, बिन्दुओं P व R के मध्य स्थित है, तब
PO = OR
= PR – PO
⇒ PO + PO = PR
⇒ 2PO = PR
⇒ PO = [latex]\frac{1}{2}[/latex] PR
प्रश्न 15.
यदि कोई बिन्दु E बिन्दुओं D व F के बीच इस प्रकार स्थित है कि DE = EF, सिद्ध कीजिए कि
DE = [latex]\frac{1}{2}[/latex] DF
हलः
![]()
दिया है,
DE = EF
= DF – DE
⇒ DE + DE = DF
⇒ 2DE = DF
⇒ DE = [latex]\frac{1}{2}[/latex] DF