Balaji Class 9 Maths Solutions Chapter 13 Quadrilateral Ex 13.2

Balaji Class 9 Maths Solutions Chapter 13 Quadrilateral Ex 13.2 चतुर्भज

प्रश्न 1.
ABCD एक समचतुर्भुज है। EABF एक सरल रेखा इस प्रकार है कि EA = AB = BF तो सिद्ध कीजिए कि ED व FC को बढ़ाने पर ये समकोण पर प्रतिच्छेद करती हैं।
हलः
समचतुर्भुज ABCD में,
∵ AB = BC = CD = DA
∴ EA = AB = BF (दिया है)
EA = AD = DC
ED = AC
∴ EP|| AC

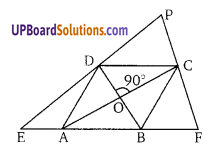
∵ समचतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं
तथा लम्बवत् होते हैं।
∴ ∠DOC = 90°
∴ ∆DOC तथा ∆PDC में,
DC उभयनिष्ठ
∠PDC = ∠OCD (एकान्तर कोण)
∠ODC = ∠PCD (एकान्तर कोण)
अतः ∆DOC ≅ ∆PDC
∴ ∠DOC = ∠DPC = 90°

प्रश्न 2.
सिद्ध कीजिए कि समलम्ब चतर्भज के सम्मुख कोण सम्पुरक होते हैं।
हलः
ज्ञात हैः एक समलम्ब ABCD जिसमें AB||CD तथा AD = BC
सिद्ध करना हैः ∠B + ∠D = 180°

प्रश्न 3.
चित्र में, AD व BE त्रिभुज ABC की माध्यिकाएँ हैं तथा BE||DF तो सिद्ध कीजिए कि CF = [latex]\frac{1}{4}[/latex]AC
हलः
∵ BE||DF तथा BC का मध्य बिन्दु D है।
तिर्यक रेखा BC पर बने अन्त:खण्ड BD = DC
इसी प्रकार तिर्यक रेखा AC पर बने अन्त:खण्ड

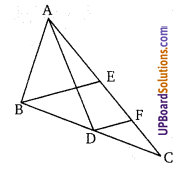
EF = FC …(1)
AE = EC (∵ E, AC का मध्य बिन्दु है)
AE = EF + FC
AE = FC + FC [समी० (1) से ]
AE = 2FC

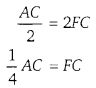
प्रश्न 4.
चित्र में, ABCD एक समान्तर चतुर्भुज है तथा P, भुजा DC का मध्य बिन्दु है। C से PA के समान्तर एक ऐसी रेखा खींचिए कि DA को बढ़ाने से यह बिन्दु Q पर तथा AB को बिन्दु R पर मिलती है। सिद्ध कीजिए कि DQ =2AD तथा CQ = 2CR
हल:
∵ AP||QC, तिर्यक रेखा DC द्वारा काटे गये अन्त:खण्ड DP = PC ….(1)
इसी प्रकार तिर्यक रेखा AB द्वारा काटे गये अन्त:खण्ड AR = RB ….(2)
∵ AB||CD
∴ तिर्यक रेखा द्वारा काटा गया अन्त:खण्ड

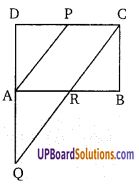
CR = RQ
या CQ = 2CR
इसी प्रकार DQ = 2AD

प्रश्न 5.
चित्र में, AB||CD||EF||GH व Ax = XY = YH । यदि AC = 1.5 सेमी तो AG का मान ज्ञात कीजिए।
हल:
AX|| XY|| YH यदि AC = 1.5 सेमी
तिर्यक रेखा AH द्वारा काटे गये अन्त:खण्ड
AX = XY = YH

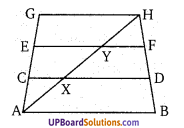
∴ तिर्यक रेखा AG द्वारा काटे गये अन्त:खण्ड
AC = CE = EG = 1.5 सेमी
AG = AC + CE + EG = 1.5 + 1.5 + 1.5 = 4.5 सेमी

प्रश्न 6.
चित्र में, ∆ABC की भुजा AC को E तक ऐसे बढ़ाते हैं कि CE = [latex]\frac{1}{2}[/latex]AC यदि D,BC का मध्य बिन्दु है तथा ED को बढ़ाने पर वह AB से F बिन्दु पर मिलती है। तथा CP व DQ, BA के समान्तर है सिद्ध कीजिए कि FD = [latex]\frac{1}{3}[/latex]FE
हलः

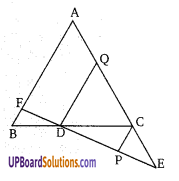
CE = [latex]\frac{1}{2}[/latex]AC …(1)
D, BC का मध्य बिन्दु है
∴ BD = DC
∆BDF तथा ∆DCP में, BD = DC (दिया है)
∠BDF = ∠CDP (शीर्षाभिमुख कोण)
∠FBD = ∠BCP (एकान्तर कोण)
अतः ∆BDF = ∆DCP
FD = DP …(2)
∴ AB||CP तथा तिर्यक रेखा FE के द्वारा बने अन्त:खण्ड FD = DP [समी० (2) से अभी सिद्ध किया है]
∴ तिर्यक रेखा AE के द्वारा बने अन्त:खण्ड
AQ = QC …(3)
समी० (1) व (3) से, [latex]C E=\frac{1}{2} \times 2 Q C[/latex]
CE = QC …(4)
इसी प्रकार DQ||CP की तिर्यक रेखा FE पर बने अन्त:खण्ड
DP = PE
∴ समी० (2) से,
FD = [latex]\frac{1}{3}[/latex] FE

प्रश्न 7.
चित्र में, ABC एक समकोण त्रिभुज है तथा ∠B = 90° दिया है AB = 9 सेमी, AC = 15 सेमी। D व E क्रमशः AB व AC के मध्य बिन्दु हैं तब BC की लम्बाई ज्ञात कीजिए।
हलः

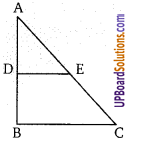
पाइथागोरस प्रमेय से,
AC² = AB² + BC²
(15)² = 9² + BC²
225 – 81 = BC²
144 = BC²
BC = [latex]\sqrt{144}[/latex] = 12 सेमी

प्रश्न 8.
ABCD एक समान्तर चतुर्भुज है। बिन्दु P, DC का मध्य बिन्दु है तथा Q, AC DF पर एक ऐसा बिन्दु है कि CQ = [latex]\frac{1}{4}[/latex]AC। यदि PQ को बढ़ाने पर वह BC से R बिन्दु पर मिलती है तो सिद्ध कीजिए कि R,BC का मध्य बिन्दु है।
हलः

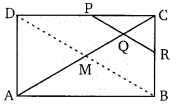
प्रश्न 9.
सिद्ध कीजिए कि किसी समलम्ब चतुर्भुज के विकर्णों के मध्य बिन्दुओं को मिलाने वाले रेखाखण्ड उसकी समान्तर भुजाओं के समान्तर तथा उनके अन्तर से आधा होता है।
हलः
ज्ञात हैः एक समलम्ब ABCD जिसकी भुजाएं AB तथा DC एक दुसरे के समान्तर हैं
तथा P एवं Q विकर्ण AC व BD के मध्य बिन्दु हैं। PQ को मिलाया।
सिद्ध करना है: PQ, AB या DC के समान्तर है।


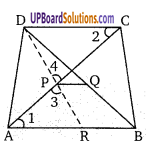
रचनाः DP को मिलाया तथा आगे बढ़ाया जिससे वह AB से बिन्दु R पर मिलती है।
उपपत्तिः ∵ AB व DC एक दूसरे के समान्तर हैं जिन्हें तिर्यक रेखा AC, बिन्दु A व C पर काटती है। अब ∆APR तथा ∆DPC में
∠1 = ∠2 (एकान्तर अन्त:कोण)
AP = CP (∵ P, AC का मध्य बिन्दु है)
∠3 = ∠4 (शीर्षाभिमुख कोण)
अतः ∆APR ≅ ∆DPC
AR = DC …(1)
PR = DP …(2)
समी० (2) से प्रदर्शित होता है कि P, DR का मध्य बिन्दु है। इस प्रकार ∆DRB में P तथा Q क्रमशः भुजा DR तथा DB के मध्य बिन्दु हैं।
∴ PQ, भुजा RB के समान्तर है।
या PQ.AB के समान्तर है।
∵ RB, AB का एक भाग है।
∴ PQ, AB तथा DC के समान्तर है।
∴ AB व DC एक दुसरे के समान्तर हैं।

प्रश्न 10.
BM व CN किसी त्रिभुज ABC के शीर्ष A से जाने वाली रेखा पर लम्ब है यदि L,BC का मध्य बिन्दु है सिद्ध कीजिए कि LM = LN
हलः

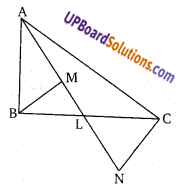
ज्ञात है: BM तथा CN रेखा AN पर लम्ब खींचे गये हैं तथा L, BC का मध्य बिन्दु हैं।
सिद्ध करना है: LM = LN
उपपत्तिः ∆BML तथा ∆LNC में,
BL = LC (ज्ञात है)
∠BML = ∠CNL (प्रत्येक समकोण)
∠MLB = ∠CLN (शीर्षाभिमुख कोण)
अतः ∆BML ≅ ∆LNC
∴ LM = LN

Balaji Publications Mathematics Class 9 Solutions