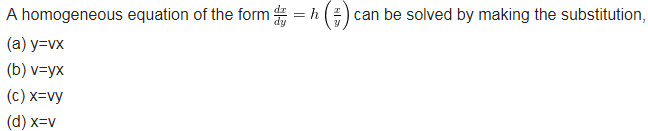Prasanna

UP Board Solutions for Class 11 Physics Chapter 8 Gravitation (गुरुत्वाकर्षण ) are part of UP Board Solutions for Class 11 Physics . Here we have given UP Board Solutions for Class 11 Physics Chapter 8 Gravitation (गुरुत्वाकर्षण )

Board	UP Board
Textbook	NCERT
Class	Class 11
Subject	Physics
Chapter	Chapter 8
Chapter Name	Gravitation
Number of Questions Solved	77

UP Board Solutions for Class 11 Physics Chapter 8 Gravitation (गुरुत्वाकर्षण )

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
निम्नलिखित के उत्तर दीजिए
(a) आप किसी आवेश का वैद्युत बलों से परिरक्षण उस आवेश को किसी खोखले चालक के भीतर रखकर कर सकते हैं। क्या आप किसी पिण्ड का परिरक्षण, निकट में रखे पदार्थ के गुरुत्वीय प्रभाव से, उसे खोखले गोले में रखकर अथवा किसी अन्य साधनों द्वारा कर सकते हैं?
(b) पृथ्वी के परितः परिक्रमण करने वाले छोटे अन्तरिक्षयान में बैठा कोई अन्तरिक्ष यात्री गुरुत्व बल का संसूचन नहीं कर सकता। यदि पृथ्वी के परितः परिक्रमण करने वाला अन्तरिक्ष स्टेशंन आकार में बड़ा है, तब क्या वह गुरुत्व बल के संसूचन की आशा कर सकता है?
(c) यदि आप पृथ्वी पर सूर्य के कारण गुरुत्वीय बल की तुलना पृथ्वी पर चन्द्रमा के कारण गुरुत्व बल से करें, तो आप यह पाएँगे कि सूर्य का खिंचाव चन्द्रमा के खिंचाव की तुलना में अधिक है (इसकी जाँच आप स्वयं आगामी अभ्यासों में दिए गए आँकड़ों की सहायता से कर सकते हैं) तथापि चन्द्रमा के खिंचाव का ज्वारीय प्रभाव सूर्य के ज्वारीय प्रभाव से अधिक है। क्यों?
उत्तर-
(a) गुरुत्वीय प्रभाव से किसी पिण्ड का परिरक्षण किसी भी प्रकार से अथवा साधन से नहीं किया जा सकता।
(b) हाँ, यदि अन्तरिक्ष स्टेशन पर्याप्त रूप में बड़ा है तो (UPBoardSolutions.com) यात्री उस स्टेशन के कारण गुरुत्व बल का संसूचन कर सकता है।
(c) किसी ग्रह के कारण ज्वारीय प्रभाव दूरी के घन के व्युत्क्रमानुपाती होता है; अत: यह गुरुत्वीय बल से मुक्त है। चूंकि सूर्य की पृथ्वी से दूरी, चन्द्रमा की पृथ्वी से दूरी की तुलना में बहुत अधिक है; अतः चन्द्रमा के कारण ज्वारीय प्रभाव अधिक होता है।

प्रश्न 2.
सही विकल्प का चयन कीजिए
(a) बढ़ती तुंगता के साथ गुरुत्वीय त्वरण बढ़ता/घटता है।
(b) बढ़ती गहराई के साथ (पृथ्वी को एकसमान घनत्व का गोला मानकर) गुरुत्वीय त्वरण बढता/घटता है।
(c) गुरुत्वीय त्वरण पृथ्वी के द्रव्यमान/पिण्ड के द्रव्यमान पर निर्भर नहीं करता।
(d) पृथ्वी के केन्द्र से r₂, तथा r₁ दूरियों के दो बिन्दुओं के बीच स्थितिज ऊर्जा- अन्तर के लिए सूत्र – G Mm (1/r₂ -1/r₁) सूत्र mg (r₂ – r₁) से अधिक/कम यथार्थ है।
उत्तर-
(a) घटता है।
(b) घटता है।
(c) पिण्ड के द्रव्यमान पर निर्भर नहीं करता।
(d) अधिक यथार्थ है।

प्रश्न 3.
मान लीजिए एक ऐसा ग्रह है जो सूर्य के परितः पृथ्वी की तुलना में दोगुनी चाल से गति करता है, तब पृथ्वी की कक्षा की तुलना में इसका कक्षीय आमाप क्या है?
हल-
माना पृथ्वी का परिक्रमण काल = T_E
तब ग्रह का परिक्रमण काल T_P = [latex s=2]\frac { { T }_{ E } }{ 2 } [/latex] (दिया है)
माना इनके कक्षीय आमाप क्रमशः R_E तथा R_P हैं,

अर्थात् ग्रह का आमाप पृथ्वी के आमाप से 0.631 गुना छोटा है।

प्रश्न 4.
बृहस्पति के एक उपग्रह, आयो (Io) की कक्षीय अवधि 1.769 दिन तथा कक्षा की त्रिज्या 4.22×10⁸ m है। यह दर्शाइए कि बृहस्पति का द्रव्यमान सूर्य के द्रव्यमान का लगभग 1/1000 गुना है।
हल-
बृहस्पति के उपग्रह का परिंक्रमण काल

प्रश्न 5.
मान लीजिए कि हमारी आकाशगंगा में एक सौर द्रव्यमान के 2.5×10¹¹ तारे हैं। मंदाकिनीय केन्द्र से 50,000ly दूरी पर स्थित कोई तारा अपनी एक परिक्रमा पूरी करने में कितना समय लेगा? आकाशगंगा का व्यास 10⁵ ly लीजिए।
हल-
प्रश्नानुसार, तारा आकाशगंगा के परितः R = 50,000 ly त्रिज्या के वृत्तीय (UPBoardSolutions.com) पथ पर घूमती है। आकाशगंगा का द्रव्यमान M = 2.5×10¹¹ × सौर द्रव्यमान

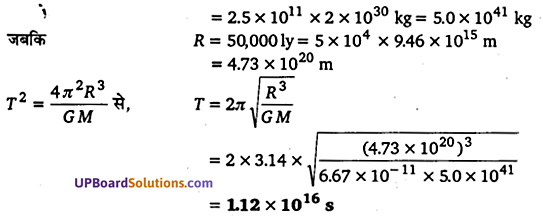
प्रश्न 6.
सही विकल्प का चयन कीजिए–
(a) यदि स्थितिज ऊर्जा का शून्य अनन्त पर है तो कक्षा में परिक्रमा करते किसी उपग्रह की कुल ऊर्जा इसकी गतिज/स्थितिज ऊर्जा का ऋणात्मक है।
(b) कक्षा में परिक्रमा करने वाले किसी उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने | के लिए आवश्यक ऊर्जा समान ऊँचाई (जितनी उपग्रह की है) के किसी स्थिर पिण्ड को | पृथ्वी के प्रभाव से बाहर प्रक्षेपित करने के लिए आवश्यक ऊर्जा से अधिक/कम होती है।
उत्तर-
(a) गतिज ऊर्जा का ऋणात्मक है।
(b) कम होती है।

प्रश्न 7.
क्या किसी पिण्ड की पृथ्वी से पलायन चाल
(a) पिण्ड के द्रव्यमान,
(b) प्रक्षेपण बिन्दु की अवस्थिति,
(c) प्रक्षेपण की दिशा,
(d) पिण्ड के प्रमोचन की अवस्थिति की ऊँचाई पर निर्भर करती है?
उत्तर-
(a) नहीं,
(b) नहीं,
(c) नहीं,
(d) हाँ, निर्भर करती है।

प्रश्न 8.
कोई धूमकेतु सूर्य की परिक्रमा अत्यधिक दीर्घवृत्तीय कक्षा में कर रहा है। क्या अपनी कक्षा में धूमकेतु की शुरू से अन्त तक
(a) रैखिक चाल,
(b) कोणीय चाल,
(c) कोणीय संवेग,
(d) गतिज ऊर्जा,
(e) स्थितिज ऊर्जा,
(f) कुल ऊर्जा नियत रहती है? सूर्य के अति निकट आने पर धूमकेतु के द्रव्यमान में ह्रास को नगण्य मानिए।
उत्तर-
(a) नहीं,
(b) नहीं,
(c) हाँ, कोणीय संवेग नियत रहता है,
(d) नहीं,
(e) नहीं,
(f) हाँ, कुल ऊर्जा नियत रहती है।

प्रश्न 9.
निम्नलिखित में से कौन-से लक्षण अन्तरिक्ष में अन्तरिक्ष यात्री के लिए दुःखदायी हो सकते हैं? \
(a) पैरों में सूजन,
(b) चेहरे पर सूजन,
(c) सिरदर्द,
(d) दिविन्यास समस्या।
उत्तर-
(b), (c) तथा (d)।

प्रश्न 10.
एकसमान द्रव्यमान घनत्व के अर्द्धगोलीय खोलों द्वारा परिभाषित ढोल के पृष्ठ के केन्द्र पर गुरुत्वीय तीव्रता की दिशा [देखिए चित्र-8.1] (i) a, (ii) b, (iii) c, (iv) 0 में किस तीर द्वारा दर्शाई जाएगी?

उत्तर-
यदि हमे गोले को पूरा कर दें तो केन्द्र पर नेट तीव्रता शून्य होगी। इसका यह अर्थ है कि केन्द्र पर दोनों अर्द्धगोलों के कारण तीव्रताएँ परस्पर विपरीत तथा बराबर होंगी। अतः दिशा (iii) c द्वारा प्रदर्शित होगी।

प्रश्न 11.
उपर्युक्त समस्या में किसी यादृच्छिक बिन्दु P पर गुरुत्वीय तीव्रता किस तीर
(i) d,
(ii) e,
(iii) f,
(iv) g द्वारा व्यक्त की जाएगी?
उत्तर-
(ii) e द्वारा प्रदर्शित होगी।

प्रश्न 12.
पृथ्वी से किसी रॉकेट को सूर्य की ओर दागा गया है। पृथ्वी के केन्द्र से किस दूरी पर रॉकेट | पर गुरुत्वाकर्षण बल शून्य है? सूर्य का द्रव्यमान = 2×10³⁰ kg, पृथ्वी का द्रव्यमान = 6×10²⁴ kg| अन्य ग्रहों आदि के प्रभावों की उपेक्षा कीजिए (कक्षीय त्रिज्या = 1.5×10¹¹ m)।
हल-
माना पृथ्वी के केन्द्र से x मीटर की दूरी पर रॉकेट पर गुरुत्वाकर्षण बल शून्य है। इस क्षण रॉकेट की सूर्य से दूरी = (r – x) मीटर

जहाँ r = सूर्य तथा पृथ्वी के बीच की दूरी अर्थात् पृथ्वी की कक्षीय त्रिज्या = 1.5×10¹¹ मीटर यह तब भी सम्भव है जबकि –
पृथ्वी द्वारा रॉकेट पर आरोपित गुरुत्वाकर्षण बल = सूर्य द्वारा रॉकेट पर आरोपित गुरुत्वाकर्षण बल

प्रश्न 13.
आप सूर्य को कैसे तोलेंगे, अर्थात् उसके द्रव्यमान का आकलन कैसे करेंगे? सूर्य के परितः पृथ्वी की कक्षा की औसत त्रिज्या 1.5×10⁸ km है।।
हल-
पृथ्वी के परित: उपग्रह के परिक्रमण काल के सूत्र [latex s=2]T=2\pi \sqrt { \frac { { r }^{ 3 } }{ { GM }_{ e } } } [/latex] , के अनुरूप सूर्य के परितः पृथ्वी का परिक्रमण काल
[latex s=2]T=2\pi \sqrt { \frac { { r }^{ 3 } }{ { GM }_{ e } } } [/latex] (जहाँ M, = सूर्य का द्रव्यमान) (UPBoardSolutions.com)

प्रश्न 14.
एक शनि-वर्ष एक पृथ्वी-वर्ष का 29.5 गुना है। यदि पृथ्वी सूर्य से 1.5×10⁸ km दूरी पर है, तो शनि सूर्य से कितनी दूरी पर है?
हल-
पृथ्वी की सूर्य से दूरी R_SE = 1.5×10⁸ km
माना पृथ्वी का परिक्रमण काल = T_E
तब शनि का परिक्रमण काल T_S = 29.5TE
शनि की सूर्य से दूरी R_SS = ?
परिक्रमण कालों के नियम से,

प्रश्न 15.
पृथ्वी के पृष्ठ पर किसी वस्तु का भार 63N है। पृथ्वी की त्रिज्या की आधी ऊँचाई पर पृथ्वी के कारण इस वस्तु पर गुरुत्वीय बल कितना है?
हल-
यदि पृथ्वी तल पर गुरुत्वीय त्वरण g हो, तो पृथ्वी तल से h ऊँचाई पर गुरुत्वीय त्वरण
[latex s=2]{ g }^{ I }=g{ \left( 1+\frac { h }{ { R }_{ e } } \right) }^{ 2 } [/latex]
यदि वस्तु का द्रव्यमान m हो तो दोनों पक्षों में m से गुणा करने पर,
[latex s=2]m{ g }^{ I }=\frac { mg }{ { \left( 1+\frac { h }{ { R }_{ e } } \right) }^{ 2 } } [/latex] (जहाँ Re = पृथ्वी की त्रिज्या)
यहाँ mg = पृथ्वी के पृष्ठ पर वस्तु का भार = 63 न्यूटन
mg’ = पृथ्वी तल से h ऊँचाई पर वस्तु का भार अर्थात् पृथ्वी के कारण वस्तु पर गुरुत्वीय बल F_g तथा h = R_e/2

प्रश्न 16.
यह मानते हुए कि पृथ्वी एकसमान घनत्व का एक गोला है तथा इसके पृष्ठ पर किसी वस्तु का भार 250 N है, यह ज्ञात कीजिए कि पृथ्वी के केन्द्र की ओर आधी दूरी पर इस वस्तु का भार क्या होगा?
हल-
पृथ्वी तल से h गहराई पर गुरुत्वीय त्वरण
[latex s=2]{ g }^{ I }=g\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex] (जहाँ R_e = पृथ्वी की त्रिज्या)
अथवा [latex s=2]m{ g }^{ I }=mg\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex]
यहाँ पृथ्वी के पृष्ठ पर वस्तु का भार mg = 250 N
h = R_e/2(जहाँ R_e = पृथ्वी की त्रिज्या)
mg’ = इस गहराई पर वस्तु का भार w’
[latex s=2]\therefore { W }^{ I }=250N\left( 1-\frac { \frac { { R }_{ e } }{ 2 } }{ { R }_{ e } } \right) =\left( 250\times \frac { 1 }{ 2 } \right) N[/latex]
= 125 N

प्रश्न 17.
पृथ्वी के पृष्ठ से ऊर्ध्वाधरतः ऊपर की ओर कोई रॉकेट 5 km s^-1 की चाल से दागा जाता है। पृथ्वी पर वापस लौटने से पूर्व यह रॉकेट पृथ्वी से कितनी दूरी तक जाएगा? पृथ्वी का द्रव्यमान = 6.0×10²⁴ kg; पृथ्वी की माध्य त्रिज्या = 6.4×10⁶ m तथा G = 6.67×10^-11N-m²/kg^-2.
हल-
माना रॉकेट का द्रव्यमान = m; पृथ्वी से ऊर्ध्वाधरत: ऊपर की ओर रॉकेट का प्रक्षेप्य वेग ν = 5 किमी-से^-1 = 5×10³ मी-से^-1
माना रॉकेट पृथ्वी पर वापस लौटने से पूर्व पृथ्वी से अधिकतम (UPBoardSolutions.com) दूरी H ऊँचाई तक जाता है। अत: इस ऊँचाई पर रॉकेट का वेग शून्य हो जाता है।
ऊर्जा संरक्षण सिद्धान्त से पृथ्वी तल से महत्तम ऊँचाई पर
पहुँचने पररॉकेट की गतिज ऊर्जा में कमी = उसकी गुरुत्वीय स्थितिज ऊर्जा में वृद्धि –

प्रश्न 18.
पृथ्वी के पृष्ठ पर किसी प्रक्षेप्य की पलायन चाल 11.2 kms^-1 है। किसी वस्तु को इस चाल की तीन गुनी चाल से प्रक्षेपित किया जाता है। पृथ्वी से अत्यधिक दूर जाने पर इस वस्तु की चाल क्या होगी? सूर्य तथा अन्य ग्रहों की उपस्थिति की उपेक्षा कीजिए।
हल-
पृथ्वी के पृष्ठ पर पलायन चाल [latex s=2]{ \nu }_{ e }=\sqrt { \left( \frac { 2G{ M }_{ e } }{ { R }_{ e } } \right) } …(1) [/latex]
यहाँ पृथ्वी के पृष्ठ पर वस्तु का प्रक्षेप्य वेग ) ν = 3ν_e;
माना पृथ्वी से अत्यधिक दूर (अनन्त पर) चाल = ν_f
ऊर्जा संरक्षण के सिद्धान्त से, पृथ्वी तल पर कुल ऊर्जा = अनन्त पर कुल ऊर्जा
अर्थात् पृथ्वी तल पर (गतिज ऊर्जा + स्थितिज ऊर्जा) = अनन्त पर (गतिज ऊर्जा + स्थितिज ऊर्जा)

प्रश्न 19.
कोई उपग्रह पृथ्वी के पृष्ठ से 400 km ऊँचाई पर पृथ्वी की परिक्रमा कर रहा है। इस उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने में कितनी ऊर्जा खर्च होगी? उपग्रह का द्रव्यमान = 200 kg; पृथ्वी का द्रव्यमान = 6.0×10²⁴ kg; पृथ्वी की त्रिज्या = 6.4×10⁶ m तथा G = 6.67×10^-11 N m² kg^-2.
हल-
पृथ्वी के परितः उपग्रह की कक्षा की त्रिज्या r = R_e + h
r = 6.4×10⁶ मीटर + 400×10³ मीटर
= 68×10⁵ मीटर = 6.8×10⁶
मीटर अतः इस कक्षा में घूमते हुए उपग्रह की कुल ऊर्जा
[latex s=2]E=-\left( \frac { { GM }_{ e }m }{ 2r } \right) [/latex]
(जहाँ m = उपग्रह का द्रव्यमान, M_e = पृथ्वी का द्रव्यमान)
पृथ्वी के.गुरुत्वीय प्रभाव से उपग्रह को बाहर (UPBoardSolutions.com) निकालने के लिए इसको दी जाने वाली आवश्यक ऊर्जा

प्रश्न 20.
दो तारे, जिनमें प्रत्येक का द्रव्यमान सूर्य के द्रव्यमान (2×10³⁰ kg) के बराबर है, एक-दूसरे की ओर सम्मुख टक्कर के लिए आ रहे हैं। जब वे 10⁹ km दूरी पर हैं तब इनकी चाल उपेक्षणीय है। ये तारे किस चाल से टकराएँगे? प्रत्येक तारे की त्रिज्या 10⁴ km है। यह मानिए कि टकराने के पूर्व तक तारों में कोई विरूपण नहीं होता (G के ज्ञात मान का उपयोग कीजिए)।
हल-
दिया है, प्रत्येक तारे को द्रव्यमान (माना) M = 2×10³⁰ किग्रा तथा तारों के बीच प्रारम्भिक दूरी (माना) r₁ = 10⁹ किमी = 10¹² मी।
तारों की प्रारम्भिक कुल ऊर्जा E_i = प्रारम्भिक गतिज ऊर्जा + प्रारम्भिक स्थितिज ऊर्जा
[latex s=2]=0+\left[ -\frac { GMM }{ { r }_{ 1 } } \right] =-\left[ \frac { { GM }^{ 2 } }{ { r }_{ 1 } } \right] [/latex]
जब दोनों तारे परस्पर टकराते हैं, तो उनके बीच की दूरी r₂ = 2×x तारे की त्रिज्या = 2R यदि तारों का ठीक टकराने से पूर्व वेग ν हो अर्थात् वे ν चाल से टकराते हैं, तो तारों की कुल अन्तिम ऊर्जा E_f = अन्तिम गतिज ऊर्जा + अन्तिम स्थितिज ऊर्जा

प्रश्न 21.
दो भारी गोले जिनमें प्रत्येक का द्रव्यमान 100 kg तथा त्रिज्या 0.10 m है किसी क्षैतिज मेज पर एक-दूसरे से 1.0 m दूरी पर स्थित हैं। दोनों गोलों के केन्द्रों को मिलाने वाली रेखा। के मध्य बिन्दु पर गुरुत्वीय बल तथा विभव क्या है? क्या इस बिन्दु पर रखा कोई पिण्ड सन्तुलन में होगा? यदि हाँ, तो यह सन्तुलन स्थायी होगा अथवा अस्थायी?
हल-
प्रत्येक गोले का द्रव्यमान इसके केन्द्र पर निहित माना जा सकता है।
अतः ! C_AC_B = r = 1.0 मीटर तथा m_A = m_B = 100 किग्रा
दोनों गोलों के केन्द्रों को मिलाने वाली रेखा के मध्य बिन्दु M की प्रत्येक गोले के केन्द्र से

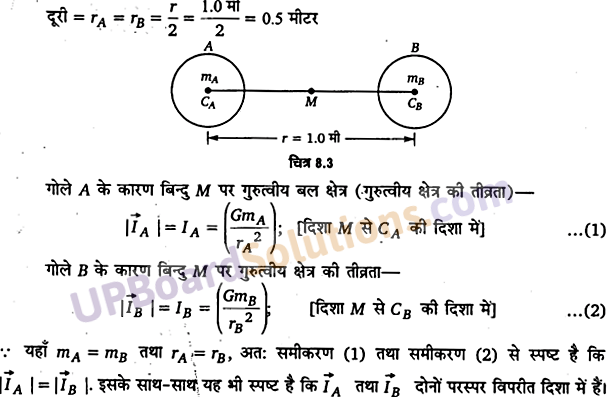
अतः ये एक-दूसरे को निरस्त कर देगी। इसलिए M पर परिणामी गुरुत्व क्षेत्र की तीव्रता = शून्य। परन्तु गुरुत्वीय क्षेत्र की तीव्रता की परिभाषा से यह M बिन्दु पर रखे एकांक द्रव्यमान पर लगने वाले गुरुत्वीय बल को व्यक्त करेगी। इसलिए गोले के मध्य बिन्दु M पर रखे किसी भी पिण्ड पर गुरुत्वीय बल शून्य होगा। गोले A के कारण बिन्दु M पर गुरुत्वीय बिभव

चूँकि ऊपर सिद्ध किया जा चुका है कि मध्य बिन्दु M पर रखे किसी भी पिण्ड पर परिणामी गुरुत्वीय
बल = शून्य
अतः मध्य बिन्दु M पर रखा पिण्ड सन्तुलन में होगा।।
अब यदि पिण्ड को थोड़ा-सा मध्य बिन्दु से किसी भी गोले की ओर विस्थापित कर दिया जाये तो वह एक नेट गुरुत्वीय बल के कारण इस बिन्दु से दूर विस्थापित होता चला जायेगा। अतः पिण्ड का सन्तुलन अस्थायी है।

अतिरिक्त अभ्यास

प्रश्न 22.
जैसा कि आपने इस अध्याय में सीखा है कि कोई तुल्यकाली उपग्रह पृथ्वी के पृष्ठ से लगभग 36,000 km ऊँचाई पर पृथ्वी की परिक्रमा करता है। इस उपग्रह के निर्धारित स्थल पर पृथ्वी के गुरुत्व बल के कारण विभव क्या है? (अनन्त पर स्थितिज ऊर्जा शून्य लीजिए) पृथ्वी का द्रव्यमान= 6.0×10²⁴ kg, पृथ्वी की त्रिज्या= 6400 km.
हल-
दिया है : पृथ्वी की त्रिज्या R_E = 6400 km = 6.4 x 10⁶ m,
पृथ्वी तल से ऊँचाई h = 360×10⁶ m,
पृथ्वी का द्रव्यमान M_E = 6.0×10²⁴ kg
उपग्रह के निर्धारित स्थल पर गुरुत्वीय विभव ।

प्रश्न 23.
सूर्य के द्रव्यमान से 2.5 गुने द्रव्यमान का कोई तारा 12 km आमाप से निपात होकर 1.2 परिक्रमण प्रति सेकण्ड से घूर्णन कर रहा है (इसी प्रकार के संहत तारे को न्यूट्रॉन तारा कहते हैं। कुछ प्रेक्षित तारकीय पिण्ड, जिन्हें पल्सार कहते हैं, इसी श्रेणी में आते हैं)। इसके विषुवत वृत्त पर रखा कोई पिण्ड, गुरुत्व बल के कारण, क्या इसके पृष्ठ से चिपका रहेगा? (सूर्य का द्रव्यमान= 2×10³⁰ kg)
हल-
घूर्णन करते तारे की विषुवतं तल पर रखे पिण्ड पर निम्न दो बल कार्य करते हैं
(i) गुरुत्वीय बल F_G = mg (अन्दर की ओर)
(ii) अपकेन्द्र बल F_e = mω²R

प्रश्न 24.
कोई अन्तरिक्षयान मंगल पर ठहरा हुआ है। इस अन्तरिक्षयान पर कितनी ऊर्जा खर्च की जाए कि इसे सौरमण्डल से बाहर धकेला जा सके। अन्तरिक्षयान का द्रव्यमान = 1000 kg; सूर्य का द्रव्यमान = 2×10³⁰ kg; मंगल का द्रव्यमान= 6.4×10²³ kg; मंगल की त्रिज्या = 3395 km; मंगल की कक्षा की त्रिज्यां = 228×10⁸ km तथा  G = 6.67×10^-11 N m² kg^-2.
हल-
दिया है : यान का द्रव्यमान m = 1000 kg = 10³ kg
सूर्य का द्रव्यमान M_S = 2×10³⁰ kg,
मंगल का द्रव्यमान M_M = 6.4×10²³ kg
मंगल की त्रिज्या R = 3395 km = 3395 x 10⁶ m,
मंगल की कक्षा की त्रिज्या r = 2.28×10¹¹ m
∵ यान मंगल की सतह पर है; अत: इसकी सूर्य से दूरी r_M के बराबर होगी।
∴ सूर्य के कारण यान की गुरुत्वीय स्थितिज ऊर्जा = [latex s=2]-\frac { { GM }_{ S }m }{ r } [/latex]
तथा मंगल के कारण यान की गुरुत्वीय स्थितिज ऊर्जा (UPBoardSolutions.com) = [latex s=2]-\frac { { GM }_{ M }m }{ R } [/latex]
यान की कुल ऊर्जा = [latex s=2]-Gm\left( \frac { { M }_{ S } }{ r } +\frac { { M }_{ M } }{ R } \right) [/latex] [∴ गतिज ऊर्जा = 0]
माना इस यान पर K ऊर्जा खर्च की जाती है, जिसे पाकर यह सौरमण्डल से बाहर चला जाता है। सौरमण्डल से बाहर, सूर्य तथा मंगल के सापेक्ष इसकी कुल ऊर्जा शून्य हो जाएगी। ऊर्जा संरक्षण के नियम से,

प्रश्न 25.
किसी रॉकेट को मंगल ग्रह के पृष्ठ से 2 kms^-1 की चाल से ऊध्र्वाधर ऊपर दागा जाता है। यदि मंगल के वातावरणीय प्रतिरोध के कारण इसकी 20% आरम्भिक ऊर्जा नष्ट हो जाती है, तब मंगल के पृष्ठ पर वापस लौटने से पूर्व यह रॉकेट मंगल से कितनी दूरी तक जाएगा? मंगल का द्रव्यमान = 6.4×10²³ kg; मंगल की त्रिज्या = 3395 km तथा G = 6.67×10^-11 N m² kg^-2.
हल-
रॉकेट का मंगल के पृष्ठ से प्रक्षेप्य वेग ) = 20 किमी-से^-1
= 2×10³ मी-से^-1
∴रॉकेट की आरम्भिक ऊर्जा E_i = गतिज ऊर्जा = [latex s=2]\frac { 1 }{ 2 } m{ \nu }^{ 2 } [/latex]
परन्तु 20% आरम्भिक ऊर्जा नष्ट हो जाती है।
अतः केवल वह अवशेष गतिज ऊर्जा जो स्थितिज (UPBoardSolutions.com) ऊर्जा में रूपान्तरित होती है = E_i का , 80%

परीक्षोपयोगी प्रश्नोत्तर

ब-विकल्पीय प्रश्न

प्रश्न 1.
कैपलर के द्वितीय नियम के अनुसार सूर्य को किसी ग्रह से मिलाने वाली रेखा समान समय , अन्तरालों में समान क्षेत्रफलं तय करती है। यह परिणाम किसके संरक्षण पर आधारित है?
(i) रेखीय संवेग
(ii) कोणीय संवेग
(iii) ऊर्जा
(iv) आवेश
उत्तर-
(ii) कोणीय संवेग ।

प्रश्न 2.
ग्रहों की गति से सम्बन्धित कैपलर का तृतीय नियम है .
(i) T∝r
(ii) T∝r²
(ii) T∝r³
(iv) T∝r^3/2
उत्तर-
(iii) T∝r³

प्रश्न 3.
ग्रहों की गति में निम्न में से कौन-सी भौतिक राशि संकलित रहती है?
(i) गतिज ऊर्जा
(ii) स्थितिज ऊर्जा
(iii) रेखीय ऊर्जा
(iv) कोणीय संवेग
उत्तर-
(iv) कोणीय संवेग

प्रश्न 4. एक ग्रह सूर्य के चारों तरफ चक्कर लगा रहा है जैसा कि चित्र 8.4 में दर्शाया गया है। ग्रह का अधिकतम वेग होगा ।

(i) A पर
(ii) B पर
(iii) C पर
(iv) D पर
उत्तर-
(ii) B पर।

प्रश्न 5. यदि पृथ्वी व सूर्य के बीच की दूरी वर्तमान दूरी की आधी होती है, तो एक वर्ष में दिनों की संख्या होगी
(i) 64.5
(ii) 129
(iii) 182.5
(iv) 730
उत्तर-
(ii) 129 दिन

प्रश्न 6.
यदि पृथ्वी का द्रव्यमान M_e, तथा त्रिज्या R_e है, तो गुरुत्वीय त्वरण g तथा गुरुत्वाकर्षण स्थिरांक G में अनुपात है।
(i) [latex s=2]\frac { { { R }^{ 2 } }_{ e } }{ { M }_{ e } } [/latex]
(ii) [latex s=2]\frac { { M }_{ e } }{ { { R }^{ 2 } }_{ e } } [/latex]
(iii)[latex s=2]{ M }_{ e }{ { R }^{ 2 } }_{ e } [/latex]
(iv)[latex s=2]\frac { { M }_{ e } }{ { R }_{ e } } [/latex]
उत्तर-
(ii) [latex s=2]\frac { { M }_{ e } }{ { { R }^{ 2 } }_{ e } } [/latex]

प्रश्न 7. पृथ्वी की त्रिज्या 6400 किमी तथा पृथ्वी पर गुरुत्वीय त्वरण 10 मी/से² है। यदि h ऊँचाई पर गुरुत्वीय त्वरण 2.5 मी/से² हो, तो h का मान होगा।
(i) 3200 किमी.
(ii) 6400 किमी
(iii) 9600 किमी
(iv) 12800 किमी
उत्तर-
(i) 6400 किमी

प्रश्न 8. g_e तथा g_p, क्रमशः पृथ्वी तल पर तथा अन्य ग्रह के तल पर गुरुत्वीय त्वरण हैं। ग्रह का द्रव्यमान व त्रिज्या दोनों पृथ्वी की तुलना में दोगुने हैं, तब
(i) g_e = g_p
(ii) g_p = 2g_p
(iii) g_p = 2g_e
(iv)[latex s=2]{ g }_{ p }=\frac { { g }_{ e } }{ \sqrt { 2 } } [/latex]
उत्तर-
(ii) g_e = 2g_p

प्रश्न 9.
किसी पिण्ड का पलायन वेग उसके
(i) द्रव्यमान के अनुक्रमानुपाती होता है ।
(ii) द्रव्यमान के वर्ग के अनुक्रमानुपाती होता है।
(iii) द्रव्यमान के व्युत्क्रमानुपाती होता है।
(iv) द्रव्यमान पर निर्भर नहीं करता है।
उत्तर-
(iv) द्रव्यमान पर निर्भर नहीं करता है।

प्रश्न 10.
संचार उपग्रह INISAT-II B का पृथ्वी के परितः परिक्रमण काल है।
(i) 12 घण्टे
(ii) 24 घण्टे
(iii) 48 घण्टे
(iv) 30 दिन
उत्तर-
(i) 24 घण्टे ।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
किसी उपग्रह को ग्रह के परितः घूमने के लिए आवश्यक अभिकेन्द्र बल कहाँ से प्राप्त होता है?
उत्तर-
उपग्रह तथा ग्रह के बीच लगने वाले गुरुत्वाकर्षण बल से।

प्रश्न 2.
g तथा G में क्या सम्बन्ध होता है?
उत्तर-
g = GM_e/R²_e
जहाँ M_e. व R_e क्रमशः पृथ्वी के द्रव्यमान तथा त्रिज्या एवं G = सार्वत्रिक गुरुत्वाकर्षण नियतांक।

प्रश्न 3.
पृथ्वी तल पर ‘g’ का मान कहाँ अधिकतम तथा कहाँ न्यूनतम होता है?
उत्तर-
g का मान ध्रुवों पर अधिकतम तथा भूमध्य (UPBoardSolutions.com) रेखा पर न्यूनतम होता है।

प्रश्न 4,
पृथ्वी के केन्द्र पर ‘g’ का मान कितना होता है?
उत्तर-
शून्य।

प्रश्न 5.
भूमध्य रेखा पर g’ का मान ध्रुवों की अपेक्षा कम होता है, क्यों?
उत्तर-
(i) ध्रुवों पर पृथ्वी चपटी है (अर्थात् पृथ्वी का भूमध्य रेखीय व्यासं, उसके ध्रुवीय व्यास की अपेक्षा अधिक होता है।)
(ii) पृथ्वी अपनी अक्ष के परितः घूर्णन करती है।

प्रश्न 6.
‘g’ के मान पर कौन-कौन से कारक प्रभाव डालते हैं?
उत्तर-
टू के मान पर निम्नलिखित तीन कारक प्रभाव डालते हैं
(i) पृथ्वी पर अक्षांशीय स्थिति,
(ii) पृथ्वी तल से ऊँचाई तथा
(iii) पृथ्वी तल से गहराई।

प्रश्न 7.
पृथ्वी सतह से h ऊँचाई पर गुरुत्वीय क्षेत्र की तीव्रता एवं गुरुत्वीय विभव से सम्बन्धित समीकरण लिखिए।
उत्तर-
गुरुत्वीय क्षेत्र की तीव्रता [latex s=2]{ I }_{ G }=\frac { { GM }_{ e } }{ { \left( { R }_{ e }+h \right) }^{ 2 } } [/latex] न्यूटन/किग्रा
गुरुत्वीय विभवे [latex s=2]V_{ G }=\frac { { GM }_{ e } }{ { \left( { R }_{ e }+h \right) } } [/latex]
जहाँ R_e = पृथ्वी की त्रिज्या अतः |
V_G = – I_G (R_e + h)

प्रश्न 8.
G का मात्रक लिखिए। इसे सार्वत्रिक नियतांक क्यों कहते हैं?
उत्तर-
G का मात्रक न्यूटन-मीटर²/किग्रा² है। चूंकि G का मान कणों की प्रकृति, माध्यम, समय, ताप । आदि पर निर्भर नहीं करता है, इसलिए इसे सार्वत्रिक नियतांक कहते हैं। प्रश्न 9. भूमध्य रेखा पर किसी वस्तु का भार ध्रुवों पर भार की तुलना में कम क्यों (UPBoardSolutions.com) होता है? उत्तर-चूंकि ध्रुवों की अपेक्षा भूमध्य रेखा पर g का मान कम होता है तथा भार W = mg, अतः ध्रुवों की ‘अपेक्षा भूमध्य रेखा पर वस्तु का भार कम होता है।

प्रश्न 10.
गुरुत्वीय क्षेत्र की तीव्रता की परिभाषा दीजिए।
उत्तर-
गुरुत्वीय क्षेत्र के अन्तर्गत किसी बिन्दु पर एकांक द्रव्यमान पर कार्य करने वाला गुरुत्वाकर्षण बेल उस बिन्दु पर ‘गुरुत्वीय क्षेत्र की तीक्रेता’ कहलाती है।

प्रश्न 11.
पृथ्वी की सतह के एक स्थान पर स्थित 25 किग्रा के एक पिण्ड पर 250 न्यूटन का बल लग रहा है। उस स्थान पर गुरुत्वीय क्षेत्र की तीव्रता का क्या मान है’ –
हल-
[latex s=2]{ I }_{ G }=\frac { F }{ m } =\frac { 250 }{ 25 } =10 [/latex] न्यूटन/किया।

प्रश्न 12.
पृथ्वी तल पर गुरुत्वीय त्वरण g = 10.0 मी/से² तथा पृथ्वी की त्रिज्या R = 6.4×10⁶ मी है। पृथ्वी के केन्द्र से 2R दूरी पर गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए।
हल-
पृथ्वी के केन्द्र से प्रक्षेपण बिन्दु की दूरी, r = 2R मी
गुरुत्वीय क्षेत्र की तीव्रता

प्रश्न 13.
गुरुत्वीय त्वरण से क्या तात्पर्य है?
उत्तर-
पृथ्वी के गुरुत्वाकर्षण बल के कारण स्वतन्त्रतापूर्वक पृथ्वी की ओर गिरती हुई वस्तु में उत्पन्न त्वरण गुरुत्वीय त्वरण कहलाता है।

प्रश्न 14. पृथ्वी तल से कितना नीचे जाने पर गुरुत्वीय त्वरण पृथ्वी तल पर गुरुत्वीय त्वरण का
(i) आधा रह जायेगा,
(ii) चौथाई रह जायेगा।
हल-
पृथ्वी तल से नीचे जाने पर गुरुत्वीय त्वरण [latex s=2]{ g }^{ I }=g\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex]

प्रश्न 15.
क्या पलायन वेग का मान पिण्ड के द्रव्यमान पर निर्भर करता है?
उत्तर-
नहीं।

प्रश्न 16.
पृथ्वी तल पर पलायन वेग का मान कितना होता है?
उत्तर-
11.2 किमी/सेकण्ड।

प्रश्न 17.
पृथ्वी के समीप परिक्रमा करने वाले कृत्रिम उपग्रह के कक्षीय वेग एवं पलायन वेग में सम्बन्ध लिखिए।
उत्तर-
[latex s=2]{ \nu }_{ e }={ { \nu } }_{ O }\sqrt { 2 } [/latex]

प्रश्न 18.
पृथ्वी के पृष्ठ से पलायन वेग 11 किमी/से है। किसी दूसरे ग्रह की त्रिज्या पृथ्वी की अपेक्षा दोगुनी है तथा उसका द्रव्यमान पृथ्वी की अपेक्षा 2.88 गुना अधिक है। इस ग्रह से पलायन वेग कितना होगा?
हल-

प्रश्न 19.
पृथ्वी तल से किसी पिण्ड का पलायन वेग 11.2 किमी/से है। यदि किसी अन्य ग्रह की त्रिज्या पृथ्वी की त्रिज्या की 1/3 तथा द्रव्यमान पृथ्वी के द्रव्यमान का 1/4 हो तो उस ग्रह से पलायन वेग कितना होगा?
हल-

प्रश्न 20.
पृथ्वी के परितः वृत्ताकार कक्षा में घूमते हुए कृत्रिम उपग्रह के परिक्रमण काल का सूत्र प्रयुक्त संकेतांकों का अर्थ बताते हुए लिखिए।
उत्तर-
T=2π[latex s=2]\sqrt { \frac { { r }^{ 3 } }{ { GM }_{ e } } } [/latex]
r = (R_e+h)
T = परिक्रमण काल, G = सार्वत्रिक गुरुत्वाकर्षण, r = त्रिज्या, R_e = पृथ्वी की त्रिज्या
तथा M_e = पृथ्वी का द्रव्यमान

प्रश्न 21.
एक उपग्रह पृथ्वी-तल के समीप एक कक्षा में परिक्रमण कर रहा है। पृथ्वी की त्रिज्या 6.4×10⁶ मीटर मानते हुए, उपग्रह की कक्षीय चाल तथा परिक्रमण काल ज्ञात कीजिए। (g=9.8 मी/से²)
हल-

प्रश्न 22.
समझाइए कि तुल्पकाली उपग्रह क्या होता है। इसकी उपयोगिता क्या है?
उत्तर-
जिस उपग्रह का पृथ्वी के परितः परिक्रमण काल 24 घण्टे होता है उसे तुल्यकाली उपग्रह कहते हैं। यह पृथ्वी के सापेक्ष सदैव स्थिर दिखायी देता है, अत: इसको भू-स्थिर उपग्रह भी कहते हैं। इसका उपयोग दूरसंचार में किया जाता है।

प्रश्न 23.
पृथ्वी की परिक्रमा कर रहे अन्तरिक्ष यान में बैठे मनुष्य का भार कितना होता है?
उत्तर-
शून्य।

लघु उत्तरीय प्रश्न

प्रश्न 1.
कैपलर के ग्रहों की गति सम्बन्धी नियम लिखिए।
या ग्रहों के गति सम्बन्धी कैपलर के नियमों का उल्लेख कीजिए।
उत्तर
कैपलर के ग्रहों की गति सम्बन्धी नियम
(i) सभी ग्रह सूर्य के चारों ओर दीर्घ-वृत्ताकार कक्षाओं (elliptical orbits) में चक्कर लगाते हैं तथा सूर्य, उन कक्षाओं के एक फोकस पर स्थित होता है।
(ii) सूर्य तथा किसी ग्रह को मिलाने वाली रेखा बराबर समय-अन्तराल में बराबर क्षेत्रफल पार (sweep) करती है, ° सूर्य अर्थात् प्रत्येक ग्रह की क्षेत्रीय चाल (areal speed) नियत S . रहती है। अत: जब ग्रह सूर्य के समीप होता है, तो उसकी चाल p (UPBoardSolutions.com) अधिकतम होती है तथा जब दूर होता है, तो उसकी चाल न्यूनतम होती है। चित्र 8.5 में एक ग्रह की कक्षा को दर्शाया गया है। यदि यह ग्रह किसी दिये समय-अन्तराल में A से B तक जाता है तथा उतने ही समय-अन्तराल में C से D तक जाता है, तब क्षेत्रफल SAB तथा SCD आपस में बराबर होंगे।

(iii) सूर्य के चारों ओर किसी भी ग्रह के परिक्रमण काल का वर्ग उसकी दीर्घवृत्तीय कक्षा के अर्द्ध-दीर्घ अक्ष (semi-major axis) के घन के अनुक्रमानुपाती होता है।
अत: ‘यदि किसी ग्रह का सूर्य के चारों ओर परिक्रमण काल T तथा उसकी दीर्घवृत्तीय कक्षा की अर्द्ध-दीर्घ अक्ष a हो तो तृतीय नियम के अनुसार T² ∝ a³ अथवा T²/a³ = नियतांक अर्थात् सभी ग्रहों के लिए T³/a³ का मान नियत रहता है।

प्रश्न 2.
ग्रहों की गति सम्बन्धी कैपलर के नियमों से सिद्ध कीजिए कि किसी ग्रह पर लगने वाला बल सूर्य से उसकी दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
उत्तर-
कैपलर के नियमों से न्यूटन के निष्कर्ष- न्यूटन ने पाया कि अधिकांश ग्रहों (बुध व प्लूटो को छोड़कर) की सूर्य के चारों ओर की कक्षाएँ लगभग वृत्ताकार हैं। कैपलर के द्वितीय नियम के अनुसार, किसी ग्रह की क्षेत्रीय चाल नियत रहती है। अत: वृत्ताकार कक्षा में ग्रह की रेखीय (UPBoardSolutions.com) चाल (ν) नियत होगी। चूंकि यह वृत्ताकार पथ पर चल रहा है; अत: ग्रह पर केन्द्र (सूर्य) की ओर अभिकेन्द्र बल F लगता है तथा
F = mv²/r,
जहाँ m ग्रह का द्रव्यमान, ν ग्रह की रेखीय चाल तथा r वृत्ताकार कक्षा की त्रिज्या है।
यदि ग्रह का परिक्रमण काल T है, तो

इस प्रकार कैपलर के नियमों के आधार पर न्यूटन ने निम्नलिखित निष्कर्ष निकाले
1. ग्रह पर एक अभिकेन्द्र बल (F) कार्य करता है जिसकी दिशा सूर्य की ओर होती है।
2. यह बल ग्रह की सूर्य से औसत दूरी के वर्ग के व्युत्क्रमानुपाती होता है (F ∝1/r²)।
3. यह बल ग्रह के द्रव्यमान के अनुक्रमानुपाती होता है (F ∝ m) ।
इन निष्कर्षों के साथ-साथ न्यूटन ने यह बताया कि कैपलर के नियम केवल सूर्य एवं ग्रह के बीच ही सत्य नहीं हैं, अपितु ब्रह्माण्ड में स्थित किन्हीं भी दो पिण्डों के लिए भी सत्य हैं।

प्रश्न 3.
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण नियम लिखिए तथा इसके आधार पर G की परिभाषा दीजिए।
उत्तर-
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण नियम-इस नियम के अनुसार किन्हीं दो द्रव्य-कणों के. बीच लगने वाला गुरुत्वाकर्षण बल कणों के द्रव्यमानों के गुणनफल के अनुक्रमानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। बल की दिशा दोनों कणों को मिलाने वाली रेखा के साथ होती है।

अतः “गुरुत्वाकर्षण नियतांक उस पारस्परिक आकर्षण बल के बराबर होता है जो एकांक दूरी पर रखे एकांक द्रव्यमान के दो द्रव्य-कणों के बीच कार्य करता है तथा जिसकी दिशा कणों को मिलाने वाली रेखा के अनुदिश होती है।”

प्रश्न 4.
गुरुत्वीय बन्धन ऊर्जा से क्या तात्पर्य है? एक मनुष्य जिसका भार पृथ्वी की सतह पर W है, यदि वह पृथ्वी की सतह से पृथ्वी की त्रिज्या की 3 गुना ऊँचाई पर जाता है, तो उस स्थान पर
| उसका भार ज्ञात कीजिए।
उत्तर-
गुरुत्वीय बन्धन ऊर्जा-“पृथ्वी के चारों ओर परिक्रमण करते हुए किसी पिण्ड अथवा उपग्रह को अपनी कक्षा छोड़कर अनन्त पर चले जाने के लिए आवश्यक ऊर्जा को बन्धन ऊर्जा कहते हैं।” पृथ्वी के समीप परिक्रमण करते हुए उपग्रह की (UPBoardSolutions.com) कुल ऊर्जा [latex s=2]-\frac { 1 }{ 2 } \left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex] होती है। अत: उपग्रह को अनन्त पर भेजने के लिए उपग्रह को [latex s=2]+\frac { 1 }{ 2 } \left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex] ऊर्जा देनी होगी जिससे उसकी कुल ऊर्जा E शून्य हो जाएगी।
अतः पृथ्वी के समीप परिक्रमण करते उपग्रह की बन्धन ऊर्जा = [latex s=2]+\frac { 1 }{ 2 } \left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex]

प्रश्न 5.
सूर्य से दो ग्रहों की दूरियाँ क्रमशः 10¹¹ मीटर तथा 10¹⁰ मीटर हैं। इनकी चालों का । अनुपात ज्ञात कीजिए।
हल-
कैपलर के तृतीय नियम के अनुसार, T² = Kr³
जहाँ, T ग्रह का आवर्तकाल तथा r ग्रह की सूर्य से दूरी है। यदि ग्रहों के आवर्तकाल T1 व T2 तथा सूर्य से दूरियाँ क्रमशः r1 व r2 हों, तो ।

प्रश्न 6.
यदि दो ग्रहों की त्रिज्याएँ r1 तथा r2 हों एवं उनके माध्य घनत्व d1 तथा d2, हों तो सिद्ध कीजिए कि दोनों ग्रहों पर गुरुत्वीय त्वरणों का अनुपात r1d1 :r2d2 होगा।
हल-
चूँकि द्रव्यमान M = आयतन x घनत्व = [latex s=2]\frac { 4 }{ 3 } \pi { r }^{ 3 }\times d [/latex]

प्रश्न 7.
पृथ्वी तल से किस ऊँचाई पर g का मान वही है जो एक 100 किमी गहरी खाई में है?
हल-
माना पृथ्वी तल से h ऊँचाई पर होगा। ,
100 किमी गहरी खाई में g का मान ।

प्रश्न 8.
पृथ्वी की त्रिज्या 6.4×10⁶ मी है। पृथ्वी तल से 800 किमी की ऊँचाई पर गुरुत्वीय विभव तथा गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए। (g = 10 मी/से²)
हल-
पृथ्वी के केन्द्र से प्रक्षेपण बिन्दु की दूरी

प्रश्न 9.
पृथ्वी के केन्द्र से उस बिन्दु की दूरी ज्ञात कीजिए जहाँ पृथ्वी के गुरुत्वीय क्षेत्र की तीव्रता 2.5 न्यूटन/किग्रा हो। उस बिन्दु पर गुरुत्वीय विभव की गणना कीजिए। (g= 10 मी/से², पृथ्वी की त्रिज्या R_e = 6.4×10⁶ मी)
हल-

प्रश्न 10.
सूर्य से एक ग्रह की दूरी, पृथ्वी की अपेक्षा 4 गुनी है। सूर्य के चारों ओर पृथ्वी का परिक्रमण काल एक वर्ष है। उस ग्रह का परिक्रमण काल ज्ञात कीजिए।
हल-
माना पृथ्वी से सूर्य की दूरी = r1 तथा पृथ्वी का सूर्य के परितः परिक्रमण काल T = 1 वर्ष
प्रश्नानुसार, ग्रह से सूर्य की दूरी r2 = 4r1 तथा ग्रह का (UPBoardSolutions.com) परिक्रमण काल = T2
कैपलर के तृतीय नियम से,

विस्तृत उत्तरीय प्रश्न

प्रश्न 1.
गुरुत्वीय त्वरण से क्या तात्पर्य है? पृथ्वी की सतह से h ऊँचाई पर गुरुत्वीय त्वरण के लिए | व्यंजक पृथ्वी की सतह पर गुरुत्वीय त्वरण तथा पृथ्वी की त्रिज्या के पदों में प्राप्त कीजिए। या पृथ्वी तल से ऊपर तथा नीचे जाने पर ‘g’ के मान में विचरण की विवेचना कीजिए। क्या दोनों परिस्थितियों में g के घटने की दर समान होगी?
उत्तर-
पृथ्वी तल से ऊँचाई के साथ ‘g’ के मान में विचरण
गुरुत्वीय त्वरण- “स्वतन्त्रतापूर्वक पृथ्वी की ओर गिरती हुई किसी वस्तु के वेग में 1 सेकण्ड में होने वाली वृद्धि अर्थात् त्वरण को गुरुत्वीय त्वरण कहते हैं। इसे ‘g’ से प्रदर्शित करते हैं।
पृथ्वी तल से ऊपर जाने पर ऊँचाई में वृद्धि के साथ-साथ गुरुत्वीय त्वरण का मान घटता जाता है। इस तथ्य को निम्न प्रकार से समझाया जा सकता है
माना पृथ्वी का द्रव्यमान M_e है, जिसको इसके केन्द्र O पर ही निहित माना जा सकता है तथा R_e इसकी त्रिज्या है। यदि m द्रव्यमान की वस्तु पृथ्वी तल पर बिन्दु A पर स्थित है (चित्र 8.6) तो न्यूटन के गुरुत्वाकर्षण नियमानुसार वस्तु पर पृथ्वी का (UPBoardSolutions.com) गुरुत्वाकर्षण बल [latex s=2]F=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex]
यह बल ही पृथ्वी तल पर इस वस्तु का भार mg होगा।
अतः [latex s=2]mg=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex] …(i)
(जहाँ g = पृथ्वी तल पर गुरुत्वीय त्वरण है।) जब इस वस्तु को पृथ्वी तल से h. ऊँचाई पर स्थित बिन्दु P पर रखा जायेगा, जहाँ गुरुत्वीय त्वरण g’ हो, तो उपर्युक्त समी० (1) के अनुरूप इस स्थान पर ।


उपर्युक्त समी० (3) से स्पष्ट है कि पृथ्वी तल से ऊपर जाने पर h के बढ़ने के साथ-साथ गुरुत्वीय त्वरण g'<g अर्थात् गुरुत्वीय त्वरण का मान घटता जाता है तथा अनन्त पर h = ∞ के लिए यह शून्य हो जाएगा।
पृथ्वी तल से गहराई के साथ ‘g’ के मान में  विचरण “पृथ्वी तल से नीचे जाने पर गहराई में वृद्धि के साथ-साथ गुरुत्वीय त्वरण का मान घटता जाता है।” इस तथ्य को निम्नवत् समझा जा सकता है
माना m द्रव्यमान की कोई वस्तु पृथ्वी के अन्दर इसकी सतह से h। गहराई पर स्थित बिन्दु P पर रखी है (चित्र 8.7) जिसकी पृथ्वी के केन्द्र O से दूरी (R_e-h) होगी। इस अवस्था में यदि O को केन्द्र मानकर एक गोला खींचा जाये जिसकी त्रिज्या (R, – h) हो तो (UPBoardSolutions.com) वस्तु अन्दर वाले ठोस गोले के तल पर स्थित होगी तथा बाहरी कवच के अन्दर होगी। परन्तु किसी भी खोखले गोल कवच के भीतर स्थित वस्तु पर आकर्षण बल शून्य होता है; अतः केवल अन्दर वाले ठोस गोले के कारण ही वस्तु पर आकर्षण बल कार्य करेगा। अन्दर वाले ठोस गोले का द्रव्यमान M_e‘ = (R_e – h) त्रिज्या के गोले का आयतन x पृथ्वी का माध्य घनत्व
= [latex s=2]=\frac { 4 }{ 3 } \pi { \left( { R }_{ e }-h \right) }^{ 3 }\times \rho [/latex]
अत: न्यूटन के गुरुत्वाकर्षण नियमानुसार, अन्दर वाले गोले के कारण वस्तु पर आकर्षण बल


अत: जैसे-जैसे हम पृथ्वी तल से नीचे की ओर जाते हैं, h में वृद्धि के साथ-साथ गुरुत्वीय त्वरण का मान घटता जाता है तथा पृथ्वी के केन्द्र O पर (जहाँ h = R_e) इसका मान शून्य हो जाता है। उपर्युक्त दोनों परिस्थितियों में ‘g’ के घटने की दर समान नहीं होगी, बल्कि पृथ्वी तल से गहराई में जाने की तुलना में तल से ऊँचाई पर जाने पर गुरुत्वीय त्वरण तेजी से घटता है।

प्रश्न 2.
पृथ्वी के केन्द्र से दूरी पर कोई पिण्ड जिसका द्रव्यमान m है, की गुरुत्वीय स्थितिज ऊर्जा के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
पृथ्वी की सतह पर गुरुत्वीय स्थितिज ऊर्जा-माना पृथ्वी तल के बिन्दु (UPBoardSolutions.com) A पर m द्रव्यमान का एक पिण्ड स्थित है। यदि पृथ्वी का द्रव्यमान M_e. तथा त्रिज्या R_e. हो, तो पृथ्वी द्वारा पिण्ड पर लगा गुरुत्वाकर्षण बल [latex s=2]{ F }_{ A }=G\left( \frac { { M }_{ e }m }{ { { R }^{ 2 } }_{ e } } \right) [/latex]
माना A से अनन्त तक की दूरी को छोटे-छोटे भागों AB, BC, CD, ….. में विभाजित किया गया है तथा बिन्दुओं B, C, D, ….. की पृथ्वी के केन्द्र से दूरियाँ क्रमशः R₁, R₂, R₃,…… हैं। यदि पिण्ड बिन्दु B पर हो तो उस पर लगा गुरुत्वाकर्षण बल
[latex s=2]{ F }_{ B }=G\left( \frac { { M }_{ e }m }{ { { R }^{ 2 } }_{ 1 } } \right) [/latex]
चूँकि बिन्दु A व B बहुत समीप हैं; अत: A व B के बीच लगे बल का मान, A व B पर लगे बलों के गुणोत्तर माध्य (geometric mean) के बराबर लिया जा सकता है। अतः A व B के बीच माध्य बल

प्रश्न 3.
गुरुत्वीय त्वरण तथा गुरुत्वाकर्षण नियतांक में सम्बन्ध लिखिए। पृथ्वी तल से कितना (i) नीचे जाने पर (ii) ऊपर जाने पर गुरुत्वीय त्वरण पृथ्वी पर गुरुत्वीय त्वरण का आधा रह जायेगा? (R_e = 6400 किमी)
उत्तर-
‘g’ तथा ‘G’ में सम्बन्धमाना पृथ्वी का द्रव्यमान M_e तथा त्रिज्या R_e है तथा पृथ्वी का कुल द्रव्यमान उसके केन्द्र पर संकेन्द्रित माना जा सकता है। माना m द्रव्यमान की एक वस्तु पृथ्वी के धरातल से नगण्य ऊँचाई पर स्थित है। अत: इस वस्तु की पृथ्वी के केन्द्र से दूरी R_e ही मानी जा सकती है। अब, न्यूटन के गुरुत्वाकर्षण नियम से पृथ्वी द्वारा वस्तु पर लगाया गया आकर्षण बल
[latex s=2]{ F }=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex] …(1)
इस बल F के कारण ही वस्तु में गुरुत्वीय त्वरण ! उत्पन्न होता है। न्यूटन के गति विषयक द्वितीय नियम के आधार पर
बल = द्रव्यमान x त्वरण
F = m x g …(2)
समी० (1) तथा समी० (2) की तुलना करने पर,
[latex s=2]mg=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex]
अथवा [latex s=2]g=\frac { { GM }_{ e } }{ { { R }^{ 2 } }_{ e } } [/latex] …(3)
समीकरण (3) ही g तथा G में सम्बन्ध व्यक्त करती है। चूंकि इस व्यंजक में वस्तु का समान द्रव्यमान m नहीं आता, अतः गुरुत्वीय त्वरण g का मान गिरने वाली वस्तु के द्रव्यमान पर निर्भर नहीं करता। इसलिए यदि वायु की अनुपस्थिति में भिन्न-भिन्न द्रव्यमान वाली वस्तुओं को समान ऊँचाई से गिराया। जाए तो उनमें उत्पन्न त्वरण (g) समान होने के कारण वे सभी वस्तुएँ पृथ्वी तल पर एक साथ पहुंचेगी। वायु की उपस्थिति में उत्प्लावन प्रभाव व श्यानकर्षण के कारण सभी वस्तुओं के त्वरण भिन्न-भिन्न पाये जाते हैं। इस दशा में भारी वस्तु पृथ्वी-तल पर पहले पहुँचेगी। | (i) पृथ्वी-तल से नीचे जाने पर गुरुत्वीय त्वरण ।
[latex s=2]{ g }^{ I }=g\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex]

प्रश्न 4.
गुरुत्वीय विभव की परिभाषा दीजिए। पृथ्वी के केन्द्र से r दूरी पर किसी m द्रव्यमान के पिण्ड के गुरुत्वीय विभव का सूत्र व्युत्पादित कीजिए।
उत्तर-
गुरुत्वीय विभव (Gravitational potential)-एकांक द्रव्यमान को अनन्त से गुरुत्वीय क्षेत्र के भीतर किसी बिन्दु तक लाने में जितना कार्य होता है, उसे उस बिन्दु पर ‘गुरुत्वीय विभव’ कहते हैं। चूंकि यह कार्य क्षेत्र द्वारा किया जाता है; अतः गुरुत्वीय विभव सदैव ऋणात्मक होता है। यदि m किग्रा द्रव्यमान को अनन्त से गुरुत्वीय क्षेत्र के किसी बिन्दु तक लाने में W जूल कार्य प्राप्त होता है तो उस बिन्दु पर गुरुत्वीय विभव (- W/m) जूल/किग्रा होगा।

यह एक अदिश राशि है। इसका मात्रक जूल/किग्रा तथा विमा [L²T^-2] है।
M द्रव्यमान के कारण r दूरी पर गुरुत्वीय विभव का व्यंजक- माना कि M द्रव्यमान का एक पिण्ड बिन्दु O पर स्थित है। माना पिण्ड के गुरुत्वीय क्षेत्र में बिन्दु O से r मीटर दूरी पर स्थित बिन्दु A पर गुरुत्वीय विभव ज्ञात करना है। इसके लिए हम पहले m किग्रा (UPBoardSolutions.com) द्रव्यमान के एक पिण्ड को A से अनन्त तक ले जाने में गुरुत्वाकर्षण बल के विरुद्ध किये गये कार्य की गणना निम्नवत् करेंगेA से अनन्त तक की दूरी को छोटे-छोटे भागों AB, BC, CD,… में विभाजित हुआ मान लेते हैं। बिन्दुओं B, C, D,… की बिन्दु 0 से दूरियाँ क्रमशः r1, r2, r3,…मीटर हैं। बिन्दु A पर स्थित m किग्रा द्रव्यमान के पिण्ड पर M के कारण गुरुत्वाकर्षण बल [latex s=2]{ F }_{ A }=G\left( \frac { Mm }{ { r }^{ 2 } } \right) [/latex]
यदि पिण्ड B पर हो, तब उस पर गुरुत्वाकर्षण बल [latex s=2]{ F }_{ B }=G\left( \frac { Mm }{ { r1 }^{ 2 } } \right) [/latex]
चूँकि A व B एक-दूसरे के बहुत निकट हैं; अतः A व B के बीच गुरुत्वाकर्षण बल का मान, A व B पर लगे बलों के गुणोत्तर माध्य (geometric mean) के बराबर ले सकते हैं।
अतः A व B के बीच माध्य बल ।

प्रश्न 5.
पृथ्वी तल से किसी ऊँचाई में स्थित बिन्दु पर गुरुत्वीय क्षेत्र की तीव्रता का मान 2.5 न्यूटन/किग्रा है। उस बिन्दु पर गुरुत्वीय विभव की गणना कीजिए। (g=100 मी/से² तथा पृथ्वी की त्रिज्या R = 6.4×10⁶ मी)
हल-
गुरुत्वीय क्षेत्र की तीव्रता [latex s=2]I=\left( \frac { GM }{ { r }^{ 2 } } \right) [/latex] ..(1)
तथा . गुरुत्वीय विभव [latex s=2]V=-\left( \frac { GM }{ { r } } \right) [/latex] …(2)
समी० (1) व समी० (2) से,
V= -I x r
∴ परन्तु समी० (1) से

प्रश्न 6.
पृथ्वी के पृष्ठ से किसी पिण्ड के पलायन वेग के व्यंजक का निगमन कीजिए। पृथ्वी के पृष्ठ के समीप किसी उपग्रह की कक्षीय चाल तथा पलायन वेग में सम्बन्ध भी बताइए।
उत्तर-
पलायन वेग- वह न्यूनतम वेग जिससे किसी वस्तु को पृथ्वी तल से फेंकने पर वह पृथ्वी के आकर्षण क्षेत्र से बाहर निकल जाये; अर्थात् वापस लौटकर पृथ्वी पर न आ सके, पलायन वेग कहलाता है। इसे ν_e, से व्यक्त करते हैं।
पलायन वेग के लिए व्यंजक-अनन्त पर गुरुत्वीय स्थितिज ऊर्जा शून्य मानने पर, (UPBoardSolutions.com) पृथ्वी तल पर स्थित m द्रव्यमान के पिण्ड की गुरुत्वीय स्थितिज ऊर्जा [latex s=2]U=-\left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex]
जहाँ M_e पृथ्वी का द्रव्यमान तथा R_e पृथ्वी की त्रिज्या है।
अतः m द्रव्यमान के पिण्ड को पृथ्वी तल से अनन्त तक ले जाने के लिए GM_e.m/R_e कार्य करना पड़ता है। अतः यदि पिण्ड m को इतने वेग से फेंके कि उसकी गतिज ऊर्जा, कार्य GM,m/R, के बराबर हो तो वह पृथ्वी के गुरुत्वीय क्षेत्र के बाहर चला जाएगा; अर्थात् अनन्त पर चला जाएगा अर्थात् पृथ्वी से सदैव के लिए पलायन कर जाएगा। यही पलायन ऊर्जा होगी।
अतः पलायन ऊर्जा [latex s=2]=+\left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex] …(1)
इस दशा में पिण्ड को दिया गया वेग ही पिण्ड को पलायन वेग ν_e, होगा। अत: पिण्ड की गतिज ऊर्जा mu. होगी।

अथवा पलायन वेग [latex s=2]{ \upsilon }_{ e }=\sqrt { 2g{ R }_{ e } } [/latex] …(3)
उपर्युक्त समी० (2) तथा (3) पृथ्वी तल से किसी पिण्ड के पलायन वेग के लिए अभीष्ट व्यंजक के दो विभिन्न रूप हैं। चूंकि इन सूत्रों में पिण्ड का द्रव्यमान m तथा प्रक्षेपण कोण θ नहीं आता है; अतः पलायन वेग ν_e , का मान फेंके गये पिण्ड के द्रव्यमान तथा प्रक्षेपण कोण पर निर्भर नहीं करता है। अतः
पृथ्वी पर प्रत्येक पिण्ड के लिए पलायन वेग का मान एक ही होता है; चाहे उसका द्रव्यमान कुछ भी हो और वह क्षैतिज के साथ किसी भी कोण पर प्रक्षेपित किया जाये।
यह ग्रह की त्रिज्या एवं ग्रह के गुरुत्वीय त्वरण पर निर्भर करता है।
यदि किसी कृत्रिम उपग्रह को पलायन वेग के बराबर वेग से क्षैतिज दिशा में प्रक्षेपित किया जाए तो उसका पथ परवलयाकार होगा।
पलायन वेग तथा कक्षीय वेग-पलायन वेग किसी पिण्ड को पृथ्वी तल से दिया गया (UPBoardSolutions.com) वह वेग है। जिससे फेंके जाने पर पिण्ड पृथ्वी तल से सदैव के लिए पलायन कर जाये; अर्थात् अनन्त पर चला जाये,जबकि कक्षीय वेग किसी पिण्ड को पृथ्वी तल से कुछ ऊँचाई पर ले जाकर दिया गया वह क्षैतिज वेग है। जिससे कि पिण्डे पृथ्वी के चारों ओर वृत्ताकार कक्षा में परिक्रमण करने लगे।
कक्षीय चाल तथा पलायन वेग में सम्बन्ध-पृथ्वी के पृष्ठ के निकट किसी उपग्रह की कक्षीय चाल

प्रश्न 7.
पृथ्वी की सतह से h ऊँचाई पर किसी कृत्रिम उपग्रह की कक्षीय चाल के लिए व्यंजक स्थापित कीजिए। दर्शाइए कि उपग्रह का वेग उसके द्रव्यमान पर निर्भर नहीं करता है। या , उपग्रहों की कक्षीय चाल के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
जिस तरह विभिन्न ग्रह सूर्य के चारों ओर परिक्रमा करते हैं, उसी तरह कुछ आकाशीय पिण्ड इन ग्रहों (planets) के चारों ओर भी चक्कर लगाते हैं। इन पिण्डों को उपग्रह (satellites) कहते हैं; जैसे चन्द्रमा पृथ्वी के चारों ओर वृत्तीय कक्षा में चक्कर लगाता है। अतः पृथ्वी एक ग्रह तथा चन्द्रमा पृथ्वी का एक उपग्रह है।
उपग्रह की कक्षीय चाल-पृथ्वी के चारों ओर वृत्तीय कक्षा जिसकी त्रिज्या r है, में कक्षीय चाल υ_o, से परिक्रमण कर रहे उपग्रह (द्रव्यमान m) पर एक अभिकेन्द्र बल (mυ_o²/r) लगता है जो पृथ्वी द्वारा उपग्रह पर लगाये गये गुरुत्वाकर्षण बल (GM_em/r²) से प्राप्त होता है, जहाँ M_e पृथ्वी का द्रव्यमान है |

यदि उपग्रह पृथ्वी तल से h ऊँचाई पर है तो पृथ्वी के केन्द्र से उपग्रह की दूरी r = R_e +h
जहाँ R_e पृथ्वी की त्रिज्या है। r का यह मान समी० (1) में रखने पर,

स्पष्ट है कि कक्षीय चाल उपग्रह के द्रव्यमान पर निर्भर नहीं करती है। यह केवल उसकी पृथ्वी तल से ऊँचाई पर निर्भर करती है।
यदि उपग्रह पृथ्वी तल के अति समीप है; अर्थात् h<<R_e, तब h को R_e की तुलना में नगण्य मान सकते हैं।
अत: समी० (3) से

उपग्रह की कक्षीय चाल (वेग) के उपर्युक्त सूत्रों में उपग्रह का द्रव्यमान नहीं आता है, अत: इससे सिद्ध होता है कि उपग्रह की कक्षीय चाल (वेग) उसके द्रव्यमान पर निर्भर नहीं करती है। अतः भिन्न-भिन्न द्रव्यमान के दो कृत्रिम उपग्रह एक ही कक्षा में साथ-साथ एक ही कक्षीय चाल से परिभ्रमण करेंगे।

प्रश्न 8.
पृथ्वी तल से h ऊँचाई पर पृथ्वी की परिक्रमा कर रहे कृत्रिम उपग्रह के परिक्रमण काल के | लिए सूत्र स्थापित कीजिए। या किसी उपग्रह के परिक्रमण काल का व्यंजक प्राप्त कीजिए।
उत्तर-
कृत्रिम उपग्रह का परिक्रमण काल-यदि कृत्रिम उपग्रह की वृत्तीय कक्षा की त्रिज्या । हो, (UPBoardSolutions.com) जहाँ r = R_e + h (जिसमें R_e = पृथ्वी की त्रिज्या तथा h = पृथ्वी तल से कृत्रिम उपग्रह की ऊँचाई) तो उपग्रह का परिक्रमण काले अर्थात् पृथ्वी के चारों ओर एक चक्कर पूरा करने में लगा समय

प्रश्न 9.
पृथ्वी के समीप परिक्रमा करने वाले उपग्रह की सम्पूर्ण ऊर्जा के लिए सूत्र स्थापित कीजिए। इसको मान ऋणात्मक क्यों होता है?
उत्तर-
पृथ्वी के चारों ओर परिक्रमा करता हुआ उपग्रह पृथ्वी के गुरुत्वीय क्षेत्र में रहता है, इसलिए उपग्रह में स्थितिज ऊर्जा होती है तथा उपग्रह की गति के कारण इसमें गतिज ऊर्जा होती है। इस प्रकार पृथ्वी के चारों ओर परिक्रमा करते हुए उपग्रह की स्थितिज एवं गतिज ऊर्जाओं का योग ही इसकी कुल ऊर्जा होती है। अनन्त पर किसी पिण्ड की गुरुत्वीय स्थितिज ऊर्जा शून्य मानते हुए पृथ्वी तल पर स्थित m द्रव्यमान के पिण्ड की गुरुत्वीय स्थितिज ऊर्जा निम्नलिखित सूत्र से व्यक्त की जाती है
[latex s=2]{ U }_{ e }=-\left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex]
(जहाँ M_e = पृथ्वी का द्रव्यमान तथा R_e = पृथ्वी की त्रिज्या)
यदि कोई कृत्रिम उपग्रह पृथ्वी तल के समीप ही पृथ्वी की परिक्रमा वृत्तीय कक्षा में कर रहा हो तो उसकी कक्षीय त्रिज्या r को R_e के बराबर मान सकते हैं। तब यदि उपग्रह का द्रव्यमान m हो तो उसकी गुरुत्वीय स्थितिज ऊर्जा U = U_e ही होगी

उपग्रह की कुल ऊर्जा के सूत्र में ऋणात्मक चिह्न इस तथ्य का प्रतीक है कि उपग्रह की कुल ऊर्जा ऋणात्मक है। इसका एक विशेष अर्थ है। अनन्त पर (r= ∞) उपग्रह की गतिज ऊर्जा व स्थितिज ऊर्जा दोनों ही शून्य हैं; अतः अनन्त पर उपग्रह की कुल ऊर्जा शून्य है। परन्तु (UPBoardSolutions.com) गतिज ऊर्जा ऋणात्मक नहीं हो सकती। तब कुल ऊर्जा ऋणात्मक होने का अर्थ है कि उपग्रह को अनन्त पर भेजने के लिए अर्थात् कुल ऊर्जा शून्य करने के लिए हमें उपग्रह को ऊर्जा देनी पड़ेगी। जब तक परिक्रमण करते उपग्रह को अतिरिक्त ऊर्जा प्राप्त नहीं होगी तब तक वह अपनी कक्षा नहीं छोड़ेगा अर्थात् बन्द कक्षा में ही परिक्रमण करता रहेगा, अर्थात् उपग्रह पृथ्वी से बद्ध (bound) रहेगा।

We hope the UP Board Solutions for Class 11 Physics Chapter 8 Gravitation help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 8 Gravitation, drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 12 Maths Chapter 10 Vector Algebra (सदिश बीजगणित) are part of UP Board Solutions for Class 12 Maths. Here we have given UP Board Solutions for Class 12 Maths Chapter 10 Vector Algebra (सदिश बीजगणित)

Board	UP Board
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 10
Chapter Name	Vector Algebra
Exercise	Ex 10.1, Ex 10.2, Ex 10.3, Ex 10.4
Number of Questions Solved	54
Category	UP Board Solutions

UP Board Solutions for Class 12 Maths Chapter 10 Vector Algebra

प्रश्नावली 10.1

प्रश्न 1.
उत्तर से 30° पूर्व में 40 किमी के विस्थापन को आलेखीय निरूपण कीजिए।
हल-
20 किमी को 1 सेमी मानते हुए 2 सेमी का एक रेखाखण्ड OP, OY की दायीं ओर OY के साथ 30° का कोण बनाते हुए खींचा गया। इस प्रकार सदिश [latex ]\overrightarrow { OP } [/latex] OY से 30° पूर्व में किमी 40 किमी के विस्थापन को निरूपित करता है।

प्रश्न 2.
निम्नलिखित मापों को अदिश एवं सदिश के रूप में श्रेणीबद्ध कीजिए।
(i) 10 किग्रा,
(ii) 2 मीटर उत्तर-पश्चिम,
(iii) 40°,
(iv) 40 वाट,
(v) 10^-19 कूलॉम,
(vi) 20 मी/से.
हल-
(i) अदिश-यहाँ इकाई किग्रा जो द्रव्यमान का मात्रक है तथा हम जानते हैं कि द्रव्यमान एक अदिश राशि है, अतः 10 किग्रा भी एक अदिश राशि है।
(ii) सदिश-2 मी उत्तर-पश्चिम एक सदिश राशि है क्योंकि इसमें परिमाण (2 मी) तथा दिशा । (उत्तर-पश्चिम) दोनों विद्यमान हैं।
(iii) अदिश-40° एक कोण को प्रदर्शित करता है हम जानते हैं कि कोण एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(iv) अदिश-यहा इकाई वाट है जोकि शक्ति का मात्रक है तथा कार्य करने की शक्ति एक अदिश राशि है, अत: 40 वाट भी एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(v) अदिश-10^-19 कुलाम एक अदिश राशि है क्योंकि इसमें केवल परिमाण विद्यमान है।
(vi) सदिश-यहाँ दिया गया मात्रक मी/से है जोकि त्वरण का मात्रक है तथा त्वरण एक सदिश राशि है। अत: 20 मी/से एक सदिश राशि है क्योंकि इसमें परिमाण के साथ दिशा भी विद्यमान है।

प्रश्न 3.
निम्नलिखित को अदिश एवं सदिश राशियों के रूप में श्रेणीबद्ध कीजिए
(i) समय कालांश
(ii) दूरी
(iii) बल
(iv) वेग
(v) कार्य
हल-
(i) अदिशे-समय कालांश एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(ii) अदिश-दूरी एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।
(iii) सदिश-बल एक सदिश राशि है क्योंकि इसमें परिमाण व दिशा दोनों विद्यमान है।
(iv) सदिश-वेग एक सदिश राशि है क्योंकि इसमें परिमाण व दिशा दोनों विद्यमान है।
(v) अदिश-कार्य एक अदिश राशि है क्योंकि इसमें केवल परिमाण होता है।

प्रश्न 4.
चित्र में निम्नलिखित सदिशों को पहचानिए
(i) सह आदिम
(ii) समान
(iii) संरेख परन्तु असमान

हल-
(i) सहआदिम [latex ]\overrightarrow { a } ,\overrightarrow { d } [/latex]
(ii) [latex ]\overrightarrow { b } ,\overrightarrow { d } [/latex]
(iii) [latex ]\overrightarrow { a } ,\overrightarrow { c } [/latex]

प्रश्न 5.
निम्नलिखित के उत्तर सत्य व असत्य के रूप में दीजिए–
(i) [latex ]\overrightarrow { a } ,\overrightarrow { a } [/latex] संरेखीय हैं।
(ii) दो संरेख सदिशों का परिमाण सदैव समान होता है।
(iii) दो समान परिमाण वाले सदिश संरेख होते हैं।
(iv) दो समान परिमाण वाले संरेखीय सदिश समान होते हैं।
हल-
(i) क्योंकि प्रत्येक सदिश स्वयं के संरेख होता है। अत: कथन सत्य है।
(ii) दो संरेख सदिशों के परिमाण भिन्न-भिन्न हो सकते हैं। अत: कथन असत्य है।
(iii) असत्य
(iv) सत्य।

प्रश्नावली 10.2

प्रश्न 1.
निम्नलिखित सदिशों के परिमाण का परिकलन कीजिए

हल-

प्रश्न 2.
समान परिमाण वाले दो विभिन्न सदिश लिखिए।
हल-

प्रश्न 3.
समान दिशा वाले दो विभिन्न सदिश लिखिए।
हल-

प्रश्न 4.
x और y के मान ज्ञात कीजिए ताकि सदिश

समान हों।
हल-

प्रश्न 5.
एक सदिश का प्रारम्भिक बिन्दु (2, 1) है और अन्तिम बिन्दु (-5, 7) है। इस सदिश के अदिश एवं सदिश घटक ज्ञात कीजिए।
हल-
माना सदिश के प्रारम्भिक वे अन्तिम बिन्दु क्रमशः A (2, 1), B (-5, 7) हैं।

प्रश्न 6.
सदिश

का योगफल ज्ञात कीजिए।
हल-

प्रश्न 7.
सदिश

के अनुदिश एक पात्रक सदिश ज्ञात कीजिए।
हल-

प्रश्न 8.
सदिश [latex ]\overrightarrow { PQ } [/latex] के अनुदिश मात्रक सदिश ज्ञात कीजिए जहाँ विन्दु P और Q क्रमशः (1, 2, 3) और (4, 5, 6) हैं।
हल-
बिन्दु P(1, 2, 3) तथा Q(4, 5, 6) को मिलाने वाला सदिश

प्रश्न 9.

हल-

प्रश्न 10.
सदिश [latex ]5\hat { i } -\hat { j } +2\hat { k } [/latex] के अनुदिश एक ऐसा सदिश ज्ञात कीजिए। जिसका परिमाण 8 इकाई है।
हल-

प्रश्न 11.
दर्शाइए कि सदिश

संरेख हैं।
हल-

प्रश्न 12.
सदिश [latex ]\hat { i } +2\hat { j } +3\hat { k } [/latex] की दिक्-कोज्या ज्ञात कीजिए।
हल-

प्रश्न 13.
बिन्दुओं A(1,2,-3) एवं B(-1,-2,1) को मिलाने वाले एवं A से B की तरफ दिष्ट सदिश की दिक् – कोज्या ज्ञात कीजिए।
हल-
A (x1, y1, z1) और B (x2, y2, z2) को मिलाने वाले एवं A से B की तरफ ओर सदिश

प्रश्न 14.
दर्शाइए कि सदिश [latex ]\hat { i } +\hat { j } +\hat { k } [/latex] अक्षों OX, OY, OZ के साथ बराबर झुका हुआ है।
हल-
सदिश [latex ]\hat { i } +\hat { j } +\hat { k } [/latex] की दिक्-कोज्याएँ क्रमशः

चूँकि सदिश की दिक्-कोज्याएँ समान हैं अत: सदिश अक्षों से समान कोण बनाता है।

प्रश्न 15.
बिन्दुओं

को मिलाने वाली रेखा को 2:1 के अनुपात में
(i) अन्तः,
(ii) बाह्य, विभाजित करने वाले विन्दु R का स्थिति सदिश ज्ञात कीजिए।
हल-
(i) अन्त: विभाजन

प्रश्न 16.
दो बिन्दुओं P (2, 3, 4) और Q(4, 1, -2) को मिलाने वाले सदिश का मध्यबिन्दुज्ञात कीजिए।
हल-

प्रश्न 17.
दर्शाइए कि बिन्दु A, B और C जिनके स्थिति सदिश क्रमशः

है, एक समकोण त्रिभुज के शीर्षों का निर्माण करते हैं।
हल-

प्रश्न 18.

हल-

प्रश्न 19.

हल-

प्रश्नावली 10.3

प्रश्न 1.

हल-

प्रश्न 2.

हल-

प्रश्न 3.
सदिश [latex]\hat { i } +\hat { j } [/latex] पर सदिश [latex]\hat { i } -\hat { j } [/latex] का प्रक्षेप ज्ञात कीजिए।
हल-

प्रश्न 4.

हल-

प्रश्न 5.

हल-

प्रश्न 6.

हल-

प्रश्न 7.

हल-

प्रश्न 8.

हल-

प्रश्न 9.

हल-

प्रश्न 10.

हल-

प्रश्न 11.

हल-

प्रश्न 12.

हल-

प्रश्न 13.

हल-

प्रश्न 14.

हल-

प्रश्न 15.

हल-

प्रश्न 16.
दर्शाइए कि बिन्दु A(1,2,2, B(2,6, 3) और C(3, 10,- 1) संरेख हैं।
हल-
दिया है, बिन्दु ABC के स्थिति सदिश क्रमशः (1, 2, 7), (2, 6, 3) और (3, 10,- 1) हैं।
माना O मूल बिन्दु है। तब ।

प्रश्न 17.

हल-

प्रश्न 18.

हल-

प्रश्नावली 10.4

प्रश्न 1.

हल-

प्रश्न 2.

हल-

प्रश्न 3.

हल-

प्रश्न 4.

हल-

प्रश्न 5.

हल-

प्रश्न 6.

हल-

प्रश्न 7.

हल-

प्रश्न 8.

हल-

प्रश्न 9.
एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष A(1,1, 2), B (2, 3, 5) और C(1, 5, 5) हैं।
हल-

प्रश्न 10.

हल-

प्रश्न 11.

हल-

We hope the UP Board Solutions for Class 12 Maths Chapter 10 Vector Algebra (सदिश बीजगणित) help you. If you have any query regarding UP Board Solutions for Class 12 Maths Chapter 10 Vector Algebra (सदिश बीजगणित), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry (त्रिविमीय ज्यामिति) are part of UP Board Solutions for Class 12 Maths. Here we have given UP Board Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry (त्रिविमीय ज्यामिति)

Board	UP Board
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 11
Chapter Name	Three Dimensional Geometry
Exercise	Ex 11.1, Ex 11.2, Ex 11.3
Number of Questions Solved	36
Category	UP Board Solutions

UP Board Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry

प्रश्नावली 11.1

प्रश्न 1.
यदि एक रेखा x,y और z-अक्ष के साथ क्रमश: 90°, 135°, 45° के कोण बनाती है तो इसकी दिक् कोसाइन ज्ञात कीजिए।
हल-
माना रेखा की दिक् कोसाइन क्रमशः l, m, n हैं, तब
l = cos 90°, m = cos 135°, n = cos 45°
l = 0, [latex ]m=-\frac { 1 }{ \sqrt { 2 } } [/latex], [latex]n=\frac { 1 }{ \sqrt { 2 } } [/latex]

प्रश्न 2.
एक रेखा की दिक् कोसाइन ज्ञात कीजिए जो निर्देशाक्षों के साथ समान कोण बनाती है।
हल-
माना रेखा निर्देशाक्षों के साथ समान कोण α बनाती है, क्ब रेखा की दिक् कोसाइन
l = cosα, m = cos α, n = cos α
परन्तु l² + m² + n² = 1
⇒ cos²α + cos²α + cos²α = 1

प्रश्न 3.
यदि एक रेखा के दिक्-अनुपात –  18, 12, – 4 हैं तो इसकी दिक्-कोज्याएँ क्या हैं?
हल-
दिया है, a = – 18, b = 12, c = – 4

प्रश्न 4.
दर्शाइए कि बिन्दु (2, 3, 4), (-1, -2, 1), (5, 8, 7) संरेख हैं।
हल-
बिन्दुओं P (2, 3, 4) और Q(-1, -2, 1) को मिलाने वाली रेखा के दिक् अनुपात
( – 1 – 2), ( – 2 – 3), (1 – 4) अर्थात् – 3, – 5, – 3 हैं।
बिन्दुओं Q(-1,-2, 1) और R(5, 8, 7) को मिलाने वाली रेखा के दिक् अनुपात 5-(-1), 8-(-2), 7-1 अर्थात् 6, 10, 6 हैं।
∴PQ और QR के दिक् अनुपात समानुपाती हैं।
∴PQ और QR समान्तर हैं।
पुन: चूँकि PQ और QR में बिन्दु Q उभयनिष्ठ है।
अतः P, Q और R संरेख बिन्दु हैं।

प्रश्न 5.
एक त्रिभुज की भुजाओं की दिक् कोसाइन ज्ञात कीजिए। यदि इसके शीर्ष बिन्दु (3, 5, -4), (-1,1, 2) और (-5, – 5, – 2) हैं।
हल-
माना त्रिभुज की भुजाओं के शीर्ष बिन्दु क्रमशः A(3, 5, -4), B(-1, 1, 2) और C(-5, -5, -2) हैं।

प्रश्नावली 11.2

प्रश्न 1.
दर्शाइए कि दिक्-कोज्याएँ

वाली तीन रेखाएँ परस्पर लम्बवत् हैं।
हल-
दो रेखाएँ जिनकी दिक्-कोज्याएँ क्रमशः l1, m1, n1 और l2, m2, n2 परस्पर लम्बवत् होंगी
यदि l1l2 + m1m2 + n1n2 = 0

प्रश्न 2.
दर्शाइए कि बिन्दुओं (1,-1, 2), (3,4,-2) से होकर जाने वाली रेखा बिन्दुओं (0,3,2) और (3, 5, 6) से जाने वाली रेखा पर लम्ब है।
हल-
दिए गए बिन्दु A (1, – 1, 2), B (3,4, -2) से होकर जाने वाली रेखा के दिक्-अनुपात 3 – 1, 4 + 1, -2 – 2 या 2, 5, -4 हैं।
बिन्दु C (0, 3,2) और D (3, 5, 6) से होकर जाने वाली रेखा के दिक्-अनुपात 3 – 0, 5 – 3, 6 – 2 या 3, 2, 4 है।।
हम जानते हैं कि रेखाएँ जिनके दिक् अनुपात (a1, b1, c1) तथा (a2, b2, c2) है परस्पर लम्बवत होंगी यदि और केवल
a1a2 + b1b2 + c1c2 = 0
यहाँ a1a2 + b1b2 + c1c2 = 2 x 3 + 5 x 2 + (- 4) x4
= 6 + 10 – 16
= 16 – 16 = 0
अतः रेखा AB तथा CD एक-दूसरे पर लंब हैं।। इति सिद्धम्

प्रश्न 3.
दर्शाइए कि बिन्दुओं (4,7, 8), (2, 3, 4) से होकर जाने वाली रेखा बिन्दुओं (-1, -2, 1) (1, 2, 5) से जाने वाली रेखा के समान्तर हैं।
हल-
बिन्दु A (4, 7, 8), B(2, 3, 4) से होकर जाने वाली रेखा AB के दिक्-अनुपात a1, b1, c1 क्रमशः 2 – 4, 3 – 7, 4 – 8 या -2, -4, -4 हैं।
बिन्दु C (-1, – 2, 1) और D (1, 2, 5) से होकर जाने वाली रेखा CD के दिक्-अनुपात a2, b2, c2, क्रमशः 1 – (-1), 2 – (-2), 5 – 1 या 2, 4, 4 हैं।

अतः AB || CD इति सिद्धम्

प्रश्न 4.
बिन्दु (1, 2, 3) से गुजरने वाली रेखा का समीकरण ज्ञात कीजिए जो सदिश [latex]3\hat { i } +2\hat { j } -2\hat { k } [/latex] के समान्तर है।
हल-

प्रश्न 5.
बिन्दु जिसका स्थिति सदिश [latex]2\hat { i } -\hat { j } +4\hat { k } [/latex] से होकर जाने वाली व सदिश [latex]\hat { i } +2\hat { j } -\hat { k } [/latex] के समान्तर रेखा को सदिश और कार्तीय समीकरण ज्ञात कीजिए।
हल-

प्रश्न 6.
उस रेखा का समीकरण ज्ञात कीजिए जो बिन्दु (-2, 4, -5) से जाती है और

के समान्तर है।
हल-

प्रश्न 7.
एक रेखा का कार्तीय समीकरण

है। इसका सदिश समीकरण ज्ञात कीजिए।
हल-

प्रश्न 8.
मूलबिन्दु और (5,-2, 3) से जाने वाली रेखा का समीकरण सदिश व कार्तीय रूपों में ज्ञात कीजिए।
हल-

प्रश्न 9.
बिन्दुओं (3, -2, -5) और (3, -2, 6) से होकर जाने वाली रेखा का समीकरण सदिश व कार्तीय रूप में ज्ञात कीजिए।
हल-
दिये गये बिन्दुओं A(3,-2, -5) व B(3, -2, 6) के स्थिति सदिश ।

प्रश्न 10.
निम्नलिखित रेखायुग्मों के बीच का कोण ज्ञात कीजिए।

हल-

प्रश्न 11.
निम्नलिखित रेखायुग्मों के बीच का कोण ज्ञात कीजिए

हल-
(i) दी गई रेखाओं के दिक् अनुपात क्रमश: 2, 5, -3 और -1, 8, 4 है।
यदि दी गई रेखाओं के मध्य कोण θ है, तब

प्रश्न 12.

हल-

प्रश्न 13.

हल-

प्रश्न 14.

हल-

प्रश्न 15.

हल-

प्रश्न 16.
रेखाएँ, जिनके सदिश समीकरण निम्नलिखित हैं, के बीच की न्यूनतम दूरी ज्ञात कीजिए।

हल-

प्रश्न 17.
रेखाएँ, जिनके सदिश समीकरण निम्नलिखित हैं, के बीच की न्यूनतम दूरी ज्ञात कीजिए।

हल-

प्रश्नावली 11.3

प्रश्न 1.
निम्नलिखित प्रश्नों में से प्रत्येक में समतल के अभिलम्ब की दिक् कोसाइन और मूलबिन्दु से दूरी ज्ञात कीजिए।
(a) z = 2
(b) x + y + z = 1
(c) 2x + 3y – z = 5
(d) 5y + 8 = 0
हल-
(a) दिये गये समतल का समीकरण z = 2
इसकी तुलना समतल के मानक समीकरण lx + my + nz = p से करने पर,
समतल की मूलबिन्दु से दूरी
p = 2 मात्रक तथा
समतल के अभिलम्ब की दिक् केसाइन l = 0, m = 0, n = 1
(b) दिये गये समतल का समीकरण x + y + z = 1

प्रश्न 2.
उस समतल का समीकरणे ज्ञात कीजिए जो मूलबिन्दु से 7 मात्रक दूरी पर है, और सदिश [latex ]3\hat { i } +5\hat { j } -6\hat { k } [/latex] पर अभिलम्ब है।
हल-
यहाँ p = 7 मात्रक

प्रश्न 3.
निम्नलिखित समतलों का कार्तीय समीकरण ज्ञात कीजिए

हल-

प्रश्न 4.
निम्नलिखित स्थितियों में मूलबिन्दु से खींचे गये लम्ब के पाद के निर्देशांक ज्ञात कीजिए।
(a) 2x + 3y + 4z – 12 = 0
(b) 3y + 4z – 6 = 0
(c) x + y + z = 1
(d) 5y + 8 = 0
हल-
(a) माना मूलबिन्दु से समतल पर डाले गये लम्ब के पाद P के निर्देशांक
(x1, y1, z1) हैं, तब रेखा OP के दिक् अनुपात x1, y1, z1 हैं।
समतल के समीकरण को अभिलम्ब रूप में लिखने पर,

प्रश्न 5.
निम्नलिखित प्रतिबन्यों के अन्तर्गत समतलों को सदिश एवं कार्तीय समीकरण ज्ञात कीजिए।
(a) बिन्दु (1, 0, -2) से जाता है और सदिश [latex ]\hat { i } +\hat { j } -\hat { k } [/latex] पर अभिलम्ब है।
(b) बिन्दु (1, 4, 6) से जाता है और [latex ]\hat { i } -2\hat { j } +\hat { k } [/latex] पर लम्ब है।
हल-

प्रश्न 6.
उन समतलों के समीकरण ज्ञात कीजिए जो निम्नलिखित बिन्दुओं से गुजरते हैं।
(a) (1, 1 ,-1), (6, 4, -5), (-4, -2, 3)
(b) (1, 1, 0), (1, 2, 1), (-2, 2, -1)
हल-

प्रश्न 7.
समतल 2x + y – z = 5 द्वारा काटे गए अन्तःखण्डों को ज्ञात कीजिए।
हल-

प्रश्न 8.
उस समतल का समीकरण ज्ञात कीजिए जिसका y-अक्ष पर अन्त:खण्ड 3 और जो तल ZOX के समान्तर है।
हल-
ZOX के समान्तर तल का समीकरण y = a
यह तल y-अक्ष पर अन्त:खण्ड 3 बनाता है।
⇒ a = 3
समतल अभीष्ट का समीकरण y = 3

प्रश्न 9.
उस समतल का समीकरण ज्ञात कीजिए जो समतलों 3x – y + 2z – 4 = 0 और x + y + z – 2 = 0 के प्रतिच्छेदन तथा बिन्दु (2, 2, 1) से होकर जाता है।
हल-
दिये गये समतलों के प्रतिच्छेदन से जाने वाले समतल का समीकरण
(3x – y + 2z – 4) + λ(x + y + z – 2) = 0 …(1)
यह बिन्दु (2, 2, 1) से होकर जाता है, तब

प्रश्न 10.

हल-
उपरोक्त प्रश्न की भाँति स्वयं हल कीजिए।

प्रश्न 11.
तलों x + y + z = 1 और 2x + 3y + 4z = 5 की प्रतिच्छेदन रेखा से होकर जाने वाले तथा तल x – y + z = 0 पर लम्बवत् तल का समीकरण ज्ञात कीजिए।
हल-
तलों x + y + z = 1 और 2x + 3y + 4z = 5 की प्रतिच्छेदन रेखा से जाने वाले समतल का समीकरण ।
(x + y + z – 1) + λ (2x + 3y + 4z – 5) = 0
(1 + 2λ)x + (1 + 3λ)y + (1 + 4λ)z – 5λ – 1 = 0 ….(1)
समतल (1) तल x – y + z = 0 पर लम्ब है।
(1 + 2λ).(1) + (1 + 3λ).(-1) + (1 + 4λ).(1) = 0
1 + 2λ – 1 – 3λ + 1 + 4λ = 0

प्रश्न 12.

हल-

प्रश्न 13.
निम्नलिखित प्रश्नों में ज्ञात कीजिए कि क्या दिए गए समतलों के युग्म समान्तर हैं अथवा लम्बवत् हैं और उस स्थिति में, जब ये न तो समान्तर हैं और न ही लम्बवत्, उनके बीच का कोण ज्ञात कीजिए।
(a) 7x + 5y + 6z + 30 = 0 और 3x – y – 10z + 4= 0
(b) 2x + y + 3z – 2 = 0 और x – 2y + 5 = 0
(c) 2x – 2y + 4z + 5 = 0 और 3x – 3y + 6z – 1 = 0
(d) 2x – y + 3z – 1 = 0 और 2x – y + 3z + 3 = 0
(c) 4x + 8y + z – 8 = 0 और y + z – 4 = 0
हल-
दिए गए समतल a1x + b1y + c1z + d1 = 0 और a2x + b2y + c2z + d2 = 0 हैं।

प्रश्न 14.
निम्नलिखित प्रश्नों में प्रत्येक दिए गए बिन्दु से दिए गए संगत समतलों की दूरी ज्ञात कीजिए।

हल-
हम जानते है। कि बिन्दु (x1, y1, z1) की समतल ax + by + cz + d = 0 से दूरी

We hope the UP Board Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry (त्रिविमीय ज्यामिति) help you. If you have any query regarding UP Board Solutions for Class 12 Maths Chapter 11 Three Dimensional Geometry (त्रिविमीय ज्यामिति), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 12 Maths Chapter 9 Differential Equations (अवकल समीकरण) are part of UP Board Solutions for Class 12 Maths. Here we have given UP Board Solutions for Class 12 Maths Chapter 9 Differential Equations (अवकल समीकरण)

Board	UP Board
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 9
Chapter Name	Differential Equations
Exercise	Ex 9.1, Ex 9.2, Ex 9.3, Ex 9.4, Ex 9.5, Ex 9.6
Number of Questions Solved	95
Category	UP Board Solutions

UP Board Solutions for Class 12 Maths Chapter 9 Differential Equations

प्रश्नावली 9.1.

1 से 10 तक के प्रश्नों में प्रत्येक अवकल समीकरण की कोटि एवं घात (यदि परिभाषित हो) ज्ञात कीजिए

प्रश्न 1.

हल-
दी गई अवकल समीकरण अवकलजों में बहुपद समीकरण नहीं है।
∴ इसकी घात परिभाषित नहीं है। जबकि कोटि = 4

प्रश्न 2.
y’ + 5y = 0
हल-
चूँकि अवकल समीकरण में उपस्थित उच्चतम कोटि की अवकलज y’ है जिसकी कोटि 1 तथा घात 1 है। अतः समीकरण की कोटि 1 तथा घात 1 है।

प्रश्न 3.

हल-
कोटि = 2, घात = 1

प्रश्न 4.

हल-
कोटि = 2
चूँकि समीकरण का बायाँ पक्ष अवकलजों में बहुपद नहीं है।
अतः इसकी घात परिभाषित नहीं है।

प्रश्न 5.

हल-
चूँकि दिए गए अवकल समीकरण में उच्चतम कोटि का अवकलज [latex ]\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } [/latex] है जिसकी कोटि 2 तथा घात 1 है। अतः अवकल समीकरण की कोटि 2 तथा घात 1 है।

प्रश्न 6.
(y”’)² + (y”)³ + (y’)⁴ + y⁵ = 0
हल-
चूँकि दिए गए अवकल समीकरण में उच्चतम कोटि का अवकलज (y”’)² है जिसकी कोटि 3 तथा घात 1 है। अत: अवकल समीकरण की कोटि 3 तथा घात 2 है।

प्रश्न 7.
y”‘ + 2y” + y’ = 0
हल-
चूँकि दिए गए अवकल समीकरण में उच्चतम कोटि का अवकलज y”’ है जिसकी कोटि 3 तथा घात 1 है। अतः अवकल समीकरण की कोटि 3 तथा घात 1 है।

प्रश्न 8.
y’ + y = e^x
हल-
चूँकि दिए गए अवकल समीकरण में उच्चतम कोटि का अवकलज y’ है जिसकी कोटि 1 तथा घात 1 है। अत: अवकल समीकरण की कोटि 1 तथा घात 1 है।

प्रश्न 9.
y” + (y’)² + 2y = 0
हल-
चूँकि दिए गए अवकल समीकरण में उच्चतम कोटि का अवकलज y” है जिसकी कोटि 2 तथा घात 1 है। अत: अवकल समीकरण की कोटि 2 तथा घात 1 है।

प्रश्न 10.
y” + 2y’ + siny = 0
हल-
चूँकि दिए गए अवकल समीकरण में उच्चतम कोटि का अवकलज y” है तथा यह y’, y” में बहुपदी है। अत: अवकल समीकरण की कोटि 2 तथा घात 1 है।

प्रश्न 11.
अवकल समीकरण

की घात है
(a) 3
(b) 2
(c) 1
(d) परिभाषित नहीं है।
हल-
दी गई समीकरण y’, y” में बहुपद समीकरण नहीं है। अत: इस अवकल समीकरण की घात परिभाषित नहीं है। अतः विकल्प (d) सही है।

प्रश्न 12.
अवकल समीकरण

की कोटि है
(a) 2
(b) 1
(c) 0
(d) परिभाषित नहीं है।
हल-
अवकल समीकरण में उच्चतम अवकलज

कोटि 2 है।
अतः विकल्प (a) सही है।

प्रश्नावली 9.2

1 से 10 तक प्रत्येक प्रश्न में सत्यापित कीजिए कि दिया हुआ फलन (स्पष्ट अथवा अस्पष्ट) संगत अवकल समीकरण का हल है

प्रश्न 1.
y = e^x + 1 : y” – y’ = 0
हल-
दिया है y = e^x + 1, अवकल समीकरण y” – y’ = 0
x के सापेक्ष अवकलन करने पर,

समीकरण (2) में से (1) को घटाने पर,
y”- y’ = e^x – e^x = 0
अतः y = e^x + 1 अवकल समीकरण y” – y’ = 0 का हल है।

प्रश्न 2.
y = x² + 2x + C : y’ – 2x – 2 = 0
हल-
दिया है, y = x² + 2x + C
x के सापेक्ष अवकलन करने पर, y’ = 2x + 2 + 0 ⇒ y’ – 2x – 2 = 0
∴y = x² + 2x + C, अवकल समीकरण y’ – 2x – 2 = 0 का हल है।

प्रश्न 3.
y = cos x + C : y’ + sin x = 0
हल-
दिया है, y = cos x + C
x के सापेक्ष अवकलन करने पर,
y’ = – sin x + 0 या y’ + sin x = 0
∴y = cos x + C, अवकल समीकरण y’ + sin x = 0 का हल है।

प्रश्न 4.
दिखाइए कि [latex ]y=\sqrt { 1+{ x }^{ 2 } } [/latex], अवकल समीकरण [latex ]{ y }^{ I }=\frac { xy }{ 1+{ x }^{ 2 } } [/latex], का एक हल है।
हल-
दिया गया फलन [latex ]y=\sqrt { 1+{ x }^{ 2 } } [/latex] …(1)
(1) का x में सापेक्ष अवकलन करने पर,

प्रश्न 5.
y = Ax : xy’ = y (x ≠ 0)
हल-
दिया है, y = Ax ..(1)
x के सापेक्ष अवकलन करने पर, y’ = A x 1 ..(2)

xy’ = y (x ≠ 0) का हल y = Ax है।

प्रश्न 6.
दिखाइए कि y = xsin x, अवकल समीकरण [latex ]x{ y }^{ I }=y+x\sqrt { { x }^{ 2 }-{ y }^{ 2 } } [/latex] (x≠0 और x > y अथवा x < – y) का एक हल है।
हल-
दिया गया फलन y = xsinx …(1)
x के सापेक्ष अवकलन करने पर, y’ = x cos x + sin x . 1 = x cos x + sinx

प्रश्न 7.
दिखाइए कि xy = logy + C अवकल समीकरण

का हल है।
हल-
दिया है। xy = log y + C …(1)
दोनों पक्षों का x के सापेक्ष अवकलन करने पर,

प्रश्न 8.
दिखाइए कि y – cosy = x अवकल समीकरण (y siny + cosy + x)[latex s=2]\frac { dy }{ dx }=y[/latex] का एक हल है।
हल-
दिया गया फलन
y – cos y = X …(1)
(1) का x के सापेक्ष अवकलन करने पर,

प्रश्न 9.
x + y = tan^-1 y : y²y’ + y² + 1 = 0
हल-
दिया है,

प्रश्न 10.
सत्यापित कीजिए कि [latex ]y=\sqrt { { a }^{ 2 }-{ x }^{ 2 } } [/latex], x∈ [-a, a] अवकल समीकरण [latex ]x+y\frac { dy }{ dx } =0[/latex] का एक हल है।
हल-
प्रश्नानुसार, [latex s=2]y=\sqrt { { a }^{ 2 }-{ x }^{ 2 } } [/latex] …(1)

प्रश्न 11.
चौथे क्रम के अंतर समीकरण के सामान्य समाधान में मनमानी स्थिरांक की संख्या निम्न है:
(a) 0
(b) 2
(c) 3
(d) 4
हल-
(b) चौथे क्रम के अंतर समीकरण के सामान्य समाधान में 4 मनमानी स्थिरांक हैं।
क्योंकि इसमें भिन्न समीकरण के क्रम के रूप में मनमानी स्थिरांक की एक ही संख्या होती है।

प्रश्न 12.
तीसरे क्रम के अंतर समीकरण के विशेष समाधान में मनमानी स्थिरांक की संख्या निम्न है:
(a) 3
(b) 2
(c) 1
(d) 0
हल-
(d)मनमानी स्थिरांक = 0 की संख्या
क्योंकि विशेष समाधान मनमानी स्थिरांक से मुक्त है।

प्रश्नावली 9.3

1 से 5 तक प्रत्येक प्रश्न में, स्वेच्छ अचरों a तथा b को विलुप्त करते हुए दिए हुए वक्रों के कुल को निरूपित करने वाला अवकल समीकरण ज्ञात कीजिए।

प्रश्न 1.
[latex ]\frac { x }{ a } +\frac { y }{ b } =1[/latex]
हल-
दिया है, [latex ]\frac { x }{ a } +\frac { y }{ b } =1[/latex]
x के सापेक्ष अवकलन करने पर,

अतः अभीष्ट अवकल समीकरण y” = 0 है।

प्रश्न 2.
y² = a(b² – x²)
हल-
दिया है,
y² = a(b² – x²) ..(1)

प्रश्न 3.
y = ae^3x + be^-2x
हल-
दिया है,
y = ae^3x + be^-2x ..(1)

प्रश्न 4.
y = e^2x (a + bx)
हल-
दिया है,
y = e^2x (a + bx) …(1)

प्रश्न 5.
y = e^x (a cosx + b sinx)
हल-
दिया है,
y = e^x (a cosx + b sinx) …(1)

प्रश्न 6.
y-अक्ष को मूलबिन्दु पर स्पर्श करने वाले वृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए।
हल-
वृत्त y को मल बिन्दु पर स्पर्श करने वाले वृत्त केन्द्र x अक्ष पर होगा। माना (a, 0) वृत्त का केन्द्र तथा a वृत्त की त्रिज्या है, तब वृत्त का समीकरण
(x-a)² + y² = a²
या x² + a² – 2ax + y² = a²
या x² + y² – 2ax = 0 …(1)
x के सापेक्ष अवकलन करने पर,


जोकि अभीष्ट अवकल समीकरण है।

प्रश्न 7.
ऐसे परवलयों के कुल का अवकल समीकरण निर्मित कीजिए जिनका शीर्ष मूलबिन्दु पर है और जिनको अक्ष धनात्मक y-अक्ष की दिशा में है।
हल-
ऐसे परवलय के कुल का समीकरण जिसका शीर्ष मूल बिन्दू तथा अक्ष OY है, निम्नवत् है, …(1)
x² = 4ay
x के सापेक्ष अवकलन करने पर,


प्रश्न 8.
ऐसे दीर्घवृत्तों के कुल का अवकल समीकरण ज्ञात कीजिए जिनकी नाभियाँ y-अक्ष पर हैं तथा जिनका केन्द्र मूलबिन्दु है।
हल-
ऐसे दीर्घवृत्त के कुल का समीकरण जिसकी नाभियाँ y-अक्ष पर हैं तथा जिसका केन्द्र मूल बिन्दु पर है।

प्रश्न 9.
ऐसे अतिपरवलयों के कुल का अवकल समीकरण ज्ञात कीजिए जिसकी नाभियाँ x-अक्ष पर हैं तथा जिनका केन्द्र मूल बिन्दु पर है।
हल-
दिये गये अतिपरवलय कुल का समीकरण

यही अभीष्ट अवकल समीकरण है।

प्रश्न 10.
ऐसे वृत्तों के कुल की अवकल समीकरण ज्ञात कीजिए जिनका केन्द्र y-अक्ष पर है और जिनकी त्रिज्या 3 इकाई है।
हल-
दिये गये वृत्त कुल का समीकरण x² + (y – b)² = 9 …(1)

यही अभीष्ट अवकल समीकरण है।

प्रश्न 11.
निम्नलिखित में से कौन सा अंतर समीकरण है

के रूप में सामान्य समाधान?

हल-

प्रश्न 12.
निम्न में से किन अंतर समीकरणों में वाई y = x एक्स का विशेष समाधान है?

हल-

प्रश्नावली 9.4

1 से 10 तक के प्रश्नों में प्रत्येक अवकल समीकरण को व्यापक हल ज्ञात कीजिए।

प्रश्न 1

हल-
दिया है,

चरों को अलग-अलग करके समाकलन करने पर,

प्रश्न 2

हल-
दिया है,

चरों का पृथक्करण करके समाकलन करने पर,

जोकि अभीष्ट हल है।

प्रश्न 3.

हल-
दिया है,

चरों का पृथक्करण करने पर,

जोकि अभीष्ट हल है।

प्रश्न 4.
sec² x tan y dx + sec² y tan x dy = 0
हल-
दिया है, sec² x tan y dx + sec² y tan x dy = 0

जोकि अभीष्ट हल है।

प्रश्न 5.
अवकल समीकरण (e^x + e^-x) dy – (e^x – e^-x)dx = 0 को हल कीजिए।
हल-
दिया गया अवकल समीकरण
(e^x + e^-x) dy – (e^x – e^-x) dx = 0 यी (e^x + e^-x) dy = (e^x – e^-x) dx

प्रश्न 6.

हल-
दिया है,

जोकि अभीष्ट हल है।

प्रश्न 7.
y log y dx – x dy = 0
हल-
दिया है,
y log y dx – x dy = 0

जोकि अभीष्ट हल है।

प्रश्न 8.

हल-

प्रश्न 9.

हल-

प्रश्न 10.

हल-

प्रश्न 11 से 14 तक के प्रश्नों में, प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबन्ध को सन्तुष्ट करने वाला विशिष्ट हल ज्ञात कीजिए।

प्रश्न 11.
(x³ + x² + x + 1)[latex ]\frac { dy }{ dx }[/latex] = 2x² + x; y = 1 यदि x = 0
हल-
दिया है, (x³ + x² + x + 1)[latex ]\frac { dy }{ dx }[/latex] = 2x² + x
या (x³ + x² + x + 1) dy = (2x² + x) dx

प्रश्न 12.

हल-

प्रश्न 13.

हल-

प्रश्न 14.

हल-


प्रश्न 15.
बिन्दु (0, 0) से गुजरने वाले ऐसे वक्र का समीकरण ज्ञात कीजिए जिसका अवकल समीकरण y’ = e^x sin x है।
हल-
दिया गया अवकल समीकरण y’ = e^x sin x

प्रश्न 16.
अवकल समीकरण xy[latex ]\frac { dy }{ dx }[/latex] = (x + 2) (y + 2) के लिए बिन्दु (1,-1) से गुजरने वाला वक्र ज्ञात कीजिए।
हल-
दिया गया अवकल समीकरण, xy[latex ]\frac { dy }{ dx }[/latex] = (x + 2) (y + 2)

प्रश्न 17.
बिन्दु (0,-2) से होकर जाने वाले ऐसे वक्र का समीकरण ज्ञात कीजिए जिसके किसी बिन्दु पर स्पर्श रेखा की प्रवणता और उस बिन्दु के y निर्देशांक का गुणनफल उस बिन्दु के x निर्देशांक के बराबर है।
हल-

प्रश्न 18.
एक वक्र के किसी बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता स्पर्श बिन्दु को बिन्दु (-4,-3) से मिलाने वाले रेखाखण्ड की प्रवणता की दुगुनी है। यदि यह वक्र बिन्दु (-2, 1) से गुजरता है तो इस वक़ की समीकरण ज्ञात कीजिए।
हल-

प्रश्न 19.
एक गोलाकार गुब्बारे का आयतन जिसे हवा भरकर फुलाया जा रहा है, स्थिर गति से बदल रहा है। यदि आरम्भ में इस गुब्बारे की त्रिज्या 3 इकाई है और 3 सेकण्ड बाद 6 इकाई है, तो t सेकण्ड बाद उस गुब्बारे की त्रिज्या ज्ञात कीजिए।
हल-
माना किसी समय ‘t’ पर गुब्बारे की त्रिज्या r तथा आयतन V है।

प्रश्न 20.
किसी बैंक में मूलधन में वृद्धि r% वार्षिक की दर से होती है। यदि Rs 100, 10 वर्षों में दुगुने हो जाते हैं, तो r को मान ज्ञात कीजिए। (log_e2= 0.6931)
हल-
माना मूलधन P है, तब प्रश्नानुसार

प्रश्न 21.
किसी बैंक में मूलधन की वृद्धि 5% वार्षिक की दर से होती है। इस बैंक में Rs 1000 जमा कराए जाते हैं। ज्ञात कीजिए कि 10 वर्ष बाद यह राशि कितनी हो जाएगी?(e^0.5 = 1.648)
हल-

प्रश्न 22.
किसी जीवाणु समूह में जीवाणुओं की संख्या 1,00,000 है। 2 घण्टों में इनकी संख्या में 10% की वृद्धि होती है। कितने घण्टों में जीवाणुओं की संख्या 2,00,000 हो जाएगी, यदि जीवाणुओं के वृद्धि की दर उनकी उपस्थित संख्या के समानुपाती हैं?
हल-
माना जीवाणु समूह की संख्या जब t = 0 है, 1,00,000 और किसी समय t पर N है।

प्रश्न 23.

हल-

प्रश्नावली 9.5

1 से 10 तक के प्रत्येक प्रश्न में दर्शाइए कि दिया हुआ अवकल सम्मकरण समघातीय है और इनमें से प्रत्येक को हल कीजिए

प्रश्न 1.
(x² + xy) dy = (x² + y²)dx
हल-
दिया गया समीकरण

प्रश्न 2.

हल-

प्रश्न 3.
(x – y)dy – (x + y)dx = 0
हल-

प्रश्न 4.
(x² – y²) dx + 2xy dy = 0
हल-
दिया है, (x² – y²) dx + 2xy dy = 0

प्रश्न 5.

हल-

प्रश्न 6.

हल-

प्रश्न 7.

हल-

प्रश्न 8.

हल-

प्रश्न 9.

हल-

प्रश्न 10.
(1 + e^x/y)dx + e^x/y(1 – x/y)dy = 0
हल-

11 से 15 तक के प्रश्नों में प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबन्धको सन्तुष्ट करने वाला विशिष्ट हल ज्ञात कीजिए।

प्रश्न 11.
अवकल समीकरण (x + y)dy + (x – y) dx = 0 का विशेष हल ज्ञात कीजिए जबकि y = 1 यदि x =1
हल-
दिया गया अवकल समीकरण

प्रश्न 12.
अवकल समीकरण x² dy + (xy + y²) dx = 0 का विशेष हल ज्ञात कीजिए जबकि y = 1 यदि x = 1
हल-
दिया गया अवकल समीकरण

प्रश्न 13.
अवकल समीकरण

का विशेष हल ज्ञात कीजिए जबकि [latex ]y=\frac { \pi }{ 4 } [/latex] यदि x = 1
हल-

प्रश्न 14.
अवकल समीकरण

का विशेष हल ज्ञात कीजिए जबकि y = 0 यदि x = 1
हल-
दिया हुआ अवकल समीकरण

प्रश्न 15.
अवकल समीकरण
हल-

का विशेष हल ज्ञात कीजिए जबकि y = 2 यदि x = 1

प्रश्न 16.

हल-
(c) x = vy

प्रश्न 17.

हल-
(d)

प्रश्नावली 9.6

1 से 12 तक के प्रश्नों में, प्रत्येक अवकल समीकरण का व्यापक हल ज्ञात कीजिए

प्रश्न 1.

हल-
दी गई अवकल समीकरण रैखिक अवकल समीकरण है।
P = 2 तथा Q = sin x

प्रश्न 2.

हल-

प्रश्न 3.

हल-

प्रश्न 4
अवकल समीकरण

का व्यापक हल ज्ञात कीजिए।
हल-
दी गई अवकल समीकरण रैखिक अवकल समीकरण है।
P = sec x ,Q = tan x

प्रश्न 5.
अवकल समीकरण

का व्यापक हल ज्ञात कीजिए।
हल-

प्रश्न 6.
अवकल समीकरण

का व्यापक हल ज्ञात कीजिए।
हल-

प्रश्न 7.
अवकल समीकरण

का व्यापक हल ज्ञात कीजिए।
हल-

प्रश्न 8.
अवकल समीकरण (1+x²)dy + 2xy dx = cotx dx ,(x≠0) का व्यापक हल ज्ञात कीजिए।
हल-

प्रश्न 9.
अवकल समीकरण

का व्यापक हल ज्ञात कीजिए।
हल-

प्रश्न 10.
अवकल समीकरण

का व्यापक हल ज्ञात कीजिए।
हल-

प्रश्न 11.
अवकल समीकरण y dx + (x – y²)dy = 0 का व्यापक हल ज्ञात कीजिए।
हल-


प्रश्न 12.
अवकल समीकरण

का व्यापक हल ज्ञात कीजिए।
हल-

13 से 15 तक के प्रश्नों में प्रत्येक अवकल समीकरण के लिए दिए हुए प्रतिबन्धको सन्तुष्ट करने वाला विशिष्ट हुल ज्ञात कीजिए।

प्रश्न 13.

हल-


प्रश्न 14.

हल-

प्रश्न 15.

हल-

प्रश्न 16.
मूल विन्दु से होकर जाने वाले एक वक्र का समीकरण ज्ञात कीजिए यदि इस वक्र के किसी बिन्दु (x, y) पर स्पर्श रेखा की प्रवणता उस बिन्दु के निर्देशांकों के योग के बराबर है।
हल-
माना दिया गया वक्र y = f(x) है,
तब प्रश्नानुसार [latex ]\frac { dy }{ dx }=x+y[/latex]

प्रश्न 17.
विन्दु 0, 2) से होकर जाने वाले वक्र का समीकरण ज्ञात कीजिए यदि इस वक्र के किसी विन्दुके निर्देशांकों का योग उस बिन्दु पर खींची गई स्पर्श रेखा की प्रवणता के परिमाण से 5 अधिक है।
हल-
माना दिया गया वक्र y = f(x) है।
तब प्रश्नानुसार [latex ]x+y=\frac { dy }{ dx }+5[/latex]

प्रश्न 18.

हल-

प्रश्न 19.

हल-

We hope the UP Board Solutions for Class 12 Maths Chapter 9 Differential Equations (अवकल समीकरण) help you. If you have any query regarding UP Board Solutions for Class 12 Maths Chapter 9 Differential Equations (अवकल समीकरण), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 12 Maths Chapter 8 Application of Integrals (समाकलनों के अनुप्रयोग) are part of UP Board Solutions for Class 12 Maths. Here we have given UP Board Solutions for Class 12 Maths Chapter 8 Application of Integrals (समाकलनों के अनुप्रयोग)

Board	UP Board
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 8
Chapter Name	Application of Integrals
Exercise	Ex 8.1, Ex 8.2
Number of Questions Solved	20
Category	UP Board Solutions

UP Board Solutions for Class 12 Maths Chapter 8 Application of Integrals

प्रश्नावली 8.1

प्रश्न 1.
वक्र y² = x, रेखाओं x = 1,y = 4 एवं x-अक्ष से धिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
अभीष्ट क्षेत्रफल

प्रश्न 2.
प्रथम चतुर्थांश में वक्र y² = 9x, x = 2 x = 4 एवं x-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
अभीष्ट क्षेत्रफल

प्रश्न 3.
प्रथम चतुर्थांश में x² = 4y, y = 2 y = 4 एवं y-अक्ष से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिया हुआ वक्र x² = 4y, y-अक्ष के प्रति सममित है। तथा हमें प्रथम चतुर्थांश में क्षेत्रफल ज्ञात करना
∴ अभीष्ट क्षेत्रफल = क्षेत्रफल ABCDA

प्रश्न 4
दीर्घवृत्त [latex ]\frac { { x }^{ 2 } }{ 16 } +\frac { { y }^{ 2 } }{ 9 } =1[/latex] से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-

प्रश्न 5.
दीर्घवृत्त [latex ]\frac { { x }^{ 2 } }{ 4 } +\frac { { y }^{ 2 } }{ 9 } =1[/latex] से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिया है, दीर्घवृत्त का समीकरण
[latex ]\frac { { x }^{ 2 } }{ 4 } +\frac { { y }^{ 2 } }{ 9 } =1[/latex]
∵9 > 4

प्रश्न 6.
प्रथम चतुर्थांश में वृत्त x² + y² = 4, रेखा x = √3 y एवं x-अक्ष द्वारा घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिए गए वृत्त का समीकरण x² + y² = 4 है जिसका केन्द्र (0, 0) और त्रिज्या 2 के समान

प्रश्न 7.
छेदक रेखा [latex ]x=\frac { a }{ \sqrt { 2 } } [/latex] द्वारा वृत्त x² + y² = a² के छोटे भाग का क्षेत्रफल ज्ञात कीजिए
हल-
अभीष्ट क्षेत्रफल = 2 (क्षेत्रफल MAPM)
(क्योंकि वृत्त x-अक्ष के प्रति सममित है)

प्रश्न 8.
यदि वक्र x = y² एवं रेखा x = 4 से घिरा हुआ क्षेत्रफल रेखा x = a द्वारा दो बराबर भागों में विभाजित होता है। तो a का मान ज्ञात कीजिए।
हल-
दिया गया वक्र
x = y² …(1)
एवं रेखा x = 4 ..(2)
(1) एक परवलय है जिसको शीर्ष (0, 0) है तथा (2) एक रेखा है जो कि y-अक्ष के समान्तर है तथा इससे 4 इकाई दूरी पर है। माना रेखा x = a, क्षेत्रफल को दो बराबर भागों में विभाजित करती है। इसलिए कुल क्षेत्रफल

प्रश्न 9.
परवलय y = x² एवं y = |x| से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिया हुआ परवलय
y = x² y-अक्ष के प्रति सममित है।
परवलय y = x² व y = x के प्रतिच्छेद बिन्दु के लिए।
y = x² में y = x रखने पर,
⇒x = x²
⇒x(x – 1) = 0
⇒x = 0, x = 1
पुन: चूँकि y = |x| ∴y = x, – x y = 1, -1
अत: अभीष्ट प्रतिच्छेद बिन्दु (-1, 1), (0, 0) व (1, 1)
इसलिए अभीष्ट क्षेत्रफल = 2 [क्षेत्रफल ∆APO – क्षेत्रफल ∆OAP]

प्रश्न 10.
वक्र x² = 4y एवं रेखा x = 4y – 2 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिया गया वक्र x² = 4y ….(1)
तथा दी गई रेखा x = 4y – 2 …(2)
(1) और (2) को हल करने पर,
(4y – 2)² = 4y
या 16y² – 16y + 4 – 4y = 0
या 16y² – 20y + 4 = 0
या 4y² – 5y + 1 = 0
या (y – 1)(4y – 1) = 0

प्रश्न 11.
वक्र y² = 4 एवं रेखा x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिया गया वक्र y² = 4x, एक परवलय का समीकरण है। जिसका शीर्ष (0, 0) है और OX इसका अक्ष है जिसके सापेक्ष परवलय सममित है तथा रेखा का समीकरण x = 3 है।
y² = 4x …(1)
में x = 3 रखने पर,
y² = 4 x 3 = 12
⇒ y = √12
∴अभीष्ट क्षेत्रफल = क्षेत्र OPQ का. क्षेत्रफल
= 2 x OLQ का क्षेत्रफल
(केवल प्रथम चतुर्थांश में छायांकित क्षेत्र)


अत: अभीष्ट क्षेत्रफल 8√3 वर्ग इकाई है।

प्रश्न 12.

हल-

प्रश्न 13.

हल-

प्रश्नावली 8.2

प्रश्न 1.
परवलय x² = 4y और वृत्त 4x² + 4y² = 9 के मध्यवर्ती क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिए गए वृत्त का समीकरण 4x² + 4y² = 9 तथा परवलय का समीकरण x² = 4y है।
परवलय x² = 4y का शीर्ष (0, 0) है और OY सममित रेखा है।

प्रश्न 2.
दो वृत्तों x² + y² = 1 एवं (x – 1)² + y =1 से आबद्ध क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिए हुए वृत्तों के समीकरण हैं– x² + y² = 1 …(1)
(x – 1)² + y = 1 …(2)
समीकरण (1) ऐसा वृत्त है जिसका केन्द्र मूल बिन्दु O पर है। और जिसकी त्रिज्या 1 इकाई है। समीकरण (2) एक ऐसा वृत्त है।
जिसका केन्द्र C(1, 0) है और जिसकी त्रिज्या 1 इकाई है।
समीकरण (1) और (2) को हल करने पर,
(x – 1)² + y² = x² + y²
या x² – 2x + 1 + y² = x² + y²

प्रश्न 3.
वक्रों y = x² + 2, y = x, x = 0 एवं x = 3 से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हल-
दिए गये वक्रों के समीकरण y = x² + 2 …(1)
y = x …(2)
x = 0 …(3)
x = 3 …(4)
अभीष्ट क्षेत्रफल = छायांकित क्षेत्रफल

प्रश्न 4.
समाकलन का उपयोग करते हुए एक ऐसे त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष (-1, 0), (1, 3) एवं (3, 2) हैं।
हल-
माना दिए हुए तीन बिन्दु A(-1, 0), B (1, 3) तथा C (3, 2) हैं।
हम जानते हैं कि, बिन्दु (x1, y1), (x2, y2) को मिलाने वाली रेखा की समीकरण


समीकरण (4) में ∆ ABL, समलम्ब BCML तथा ∆ ACM के क्षेत्रफलों के मान रखने पर, ∆ABC का क्षेत्रफल = 3 + 5 – 4 = 4 वर्ग इकाई

प्रश्न 5.
समाकलन का उपयोग करते हुए एक ऐसे त्रिकोणीय क्षेत्र का क्षेत्रफल ज्ञात कीजिए जिसकी भुजाओं के समीकरण y = 2x + 1,y = 3x + 1 एवं = 4 हैं।
हल-
भुजाओं के समीकरण

y = 2x + 1 ..(1)
y = 3x + 1 ..(2)
x = 4 ..(3)
(1) और (2) को हल करने पर,
2x + 1 = 3x + 1 ⇒ x = 0 ∴ y = 1
∴(1) और (2) का प्रतिच्छेद बिन्दु (0, 1) है।
(1) और (3) को हल करने पर,
y = 8 + 1 = 9
∴(1) और (3) का प्रतिच्छेद बिन्दु (4, 9) है।
(2) और (3) को हल करने पर, y = 12 + 1 = 13; x = 4
∴(2) और (3) का प्रतिच्छेद बिन्दु (4, 13) है।

प्रश्न 6.

हल-

प्रश्न 7.

हल-

We hope the UP Board Solutions for Class 12 Maths Chapter 8 Application of Integrals (समाकलनों के अनुप्रयोग) help you. If you have any query regarding UP Board Solutions for Class 12 Maths Chapter 8 Application of Integrals (समाकलनों के अनुप्रयोग), drop a comment below and we will get back to you at the earliest.