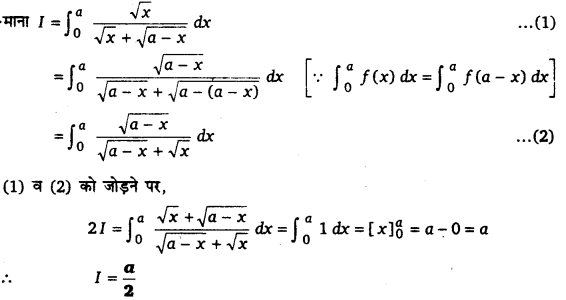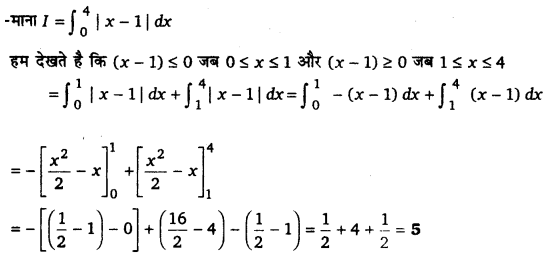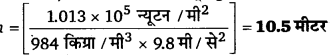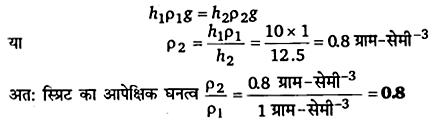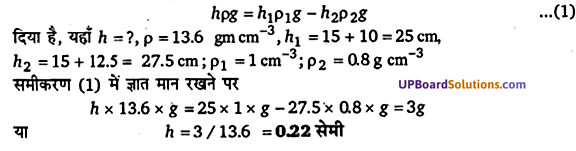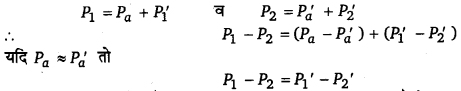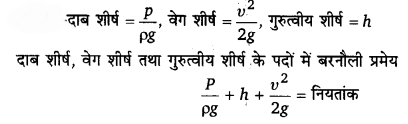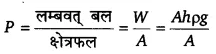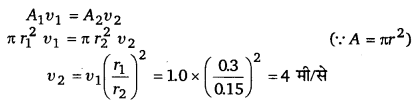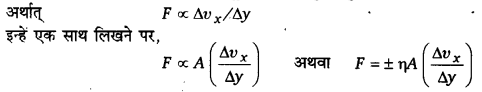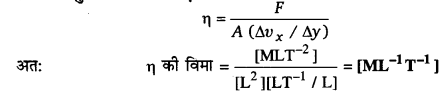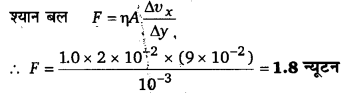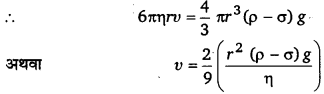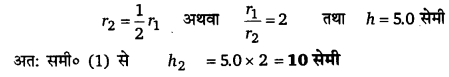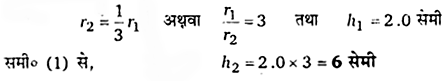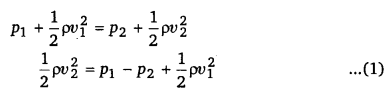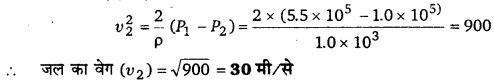UP Board Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids (तरलों के यान्त्रिक गुण) are part of UP Board Solutions for Class 11 Physics . Here we have given UP Board Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids (तरलों के यान्त्रिक गुण)
| Board |
UP Board |
| Textbook |
NCERT |
| Class |
Class 11 |
| Subject |
Physics |
| Chapter |
Chapter 10 |
| Chapter Name |
Mechanical Properties Of Fluids |
| Number of Questions Solved |
150 |
UP Board Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids (तरलों के यान्त्रिक गुण)
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर
प्रश्न 1.
स्पष्ट कीजिए क्यों
(a) मस्तिष्क की अपेक्षा मानव का पैरों पर रक्त चाप अधिक होता है।
(b) 6 km ऊँचाई पर वायुमण्डलीय दाब समुद्र-तल पर वायुमण्डलीय दाब का लगभग आधा हो जाता है, यद्यपि वायुमण्डल का विस्तार 100 km से भी अधिक ऊँचाई तक है। |
(c) यद्यपि दाब, प्रति एकांक क्षेत्रफल पर लगने वाला बल होता है तथापि द्रवस्थैतिक दाब एक अदिश राशि है।
उत्तर-
(a) पैरों के ऊपर रक्त स्तम्भ की ऊँचाई मस्तिष्क के ऊपर रक्त स्तम्भ की ऊँचाई से अधिक होती है। चूंकि द्रव स्तम्भ का दाब गहराई के अनुक्रमानुपाती होता है; अत: पैरों पर रक्त दाब मस्तिष्क पर रक्त दाब की तुलना में अधिक होता है।
(b) पृथ्वी के गुरुत्वीय प्रभाव के कारण वायु के अणु पृथ्वी के समीप बने रहते हैं अधिक ऊँचाई तक नहीं जा पाते। इसी कारण 6:km से अधिक ऊँचाई पर जाने पर वायु बहुत ही विरल हो जाती है और घनत्व बहुत कम हो जाता है। चूँकिं तरल-दाब, तरल के घनत्व के अनुक्रमानुपाती होता है; अतः 6 km से ऊपर की वायु का कुल दाब अत्यन्त कम होता है; अत: पृथ्वी-तल से 6 km की ऊँचाई पर वायुमण्डलीय दाबं समुद्र तल पर वायुमण्डलीय दाब का आधा रह जाता है।
(c) पास्कल के नियम के अनुसार किसी बिन्दु पर द्रव-दाब सभी दिशाओं में समान रूप से लगता है, अर्थात् दाब के साथ कोई दिशा नहीं जोड़ी जा सकती; अत: दाब एक अदिश राशि है।।
प्रश्न 2.
स्पष्ट कीजिए क्यों
(a) पारे का काँच के साथ स्पर्श कोण अधिककोण होता है जबकि जल का काँच के साथ स्पर्श कोण न्यूनकोण होता है।
(b) काँच के स्वच्छ समतल पृष्ठ पर जल फैलने का प्रयास करता है जबकि पारा उसी पृष्ठ पर बूंदें | बनाने का प्रयास करता है। (दूसरे शब्दों में जल काँच को गीला कर देता है जबकि पारा ऐसा नहीं करता है।)
(c) किसी द्रव का पृष्ठ-तनाव पृष्ठ के क्षेत्रफल पर निर्भर नहीं करता है।
(d) जल में घुले अपमार्जकों के स्पर्श कोणों का मान कम होना चाहिए।
(e) यदि किसी बाह्य बल का प्रभाव न हो तो द्रव बूंद की आकृति सदैव गोलाकार होती है।
उत्तर-
(a) पारे के अणुओं के बीच ससंजक बल, पारे व काँच के अणुओं के बीच आसंजक बल से अधिक होता है, इस कारण काँच व पारे का स्पर्श कोण अधिककोण होता है।
इसके विपरीत जल के अणुओं के बीच ससंजक बल, काँच व जल (UPBoardSolutions.com) के अणुओं के बीच आसंजक बल से कम होता है, इस कारण जल तथा काँच के बीच स्पर्श कोण न्यूनकोण होता है। |
(b) खण्ड (a) के उत्तर में वर्णित कारण यहाँ भी लागू होता है।
(c) रबड़ की झिल्ली को खींचने पर उसमें तनाव बढ़ जाता है परन्तु किसी द्रव के मुक्त पृष्ठ का क्षेत्रफल बढ़ा देने पर उसके तनाव में कोई परिवर्तन नहीं आता; अत: द्रव का पृष्ठ-तनाव उसके मुक्त क्षेत्रफल पर निर्भर नहीं करता।।
(d) अपसार्जक घुले होने पर जल का पृष्ठ-तनाव कम हो जाता है; अतः स्पर्श कोण भी कम हो जाता है।
(e) बाह्य बल की अनुपस्थिति में बूंद की आकृति केवल पृष्ठ-तनाव द्वारा निर्धारित होती है। पृष्ठ-तनाव के कारण बूंद न्यूनतम मुक्त क्षेत्रफल वाली आकृति ग्रहण करना चाहती है। चूंकि एक दिए गए आयतन के लिए गोले का मुक्त पृष्ठ न्यूनतम होता है; अतः बूंद की आकृति पूर्ण गोलाकार हो जाती

प्रश्न 3.
प्रत्येक प्रकथन के साथ संलग्न सूची में से उपयुक्त शब्द छाँटकर उस प्रकथन के रिक्त स्थान की पूर्ति कीजिए
(a) व्यापक रूप में व्रवों का पृष्ठ-तनाव ताप बढने पर…….है। (बढ़ता/घटता)
(b) गैसों की श्यानता ताप बढ़ने पर………है, जबकि द्रवों की श्यानता ताप बढने पर……..है। (बढ़ती/घटती)।
(c) दृढ़ता प्रत्यास्थता गुणांक वाले ठोसों के लिए अपरूपण प्रतिबल……….के अनुक्रमानुपाती होता है, जबकि द्रवों के लिए वह……….के अनुक्रमानुपाती होता है। (अपरूपण विकृति/अपरूपण विकृति की दर) ।
(d) किसी तरल के अपरिवर्ती प्रवाह में आए किसी संकीर्णन पर प्रवाह की चाल में वृद्धिमें…….. का अनुसरण होता है। (संहति का संरक्षण/बरनौली सिद्धान्त)
(e) किंसी वायु सुरंग में किसी वायुयान के मॉडल में प्रक्षोभ की चाल वास्तविक वायुयान के प्रक्षोभ के लिए क्रांतिक चाल की तुलना में………होती है। (अधिक/कम)
उत्तर-
(a) घटता
(b) बढ़ती, घटती,
(c) अपरूपण विकृति, अपरूपण विकृति की दर,
(d) संहति को संरक्षण,
(e) अधिक।
प्रश्न 4.
निम्नलिखित के कारण स्पष्ट कीजिए
(a) किसी कागज़ की पट्टी को क्षतिज रखने के लिए आपको उस कागज़ पर ऊपर की ओर हवा फेंकनी चाहिए, नीचे की ओर नहीं।
(b) जब हम किसी जल टोंटी को अपनी उँगलियों द्वारा बन्द करने का प्रयास करते हैं तो उँगलियों के बीच की खाली जगह से तीव्र जल धाराएँ फूट निकलती हैं।
(c) इंजेक्शन लगाते समय डॉक्टर के अंगूठे द्वारा आरोपित दाब की अपेक्षा सुई का आकार दवाई की बहिःप्रवाही धारा को अधिक अच्छा नियन्त्रित करता है।
(d) किसी पात्र के बारीक छिद्र से निकलने वाला तरल उस पर पीछे की ओर प्रणोद आरोपित करता है।
(e) कोई प्रचक्रमान क्रिकेट की गेंद वायु में परवलीय प्रपथ का अनुसरण नहीं करती।
उत्तर-
(a) कागज़ के ऊपर फेंक मारने से ऊपर वायु का वेग अधिक हो जाएगा। क्षैतिज प्रवाह के लिए बरनौली प्रमेय [latex s=2]\left( P+\frac { 1 }{ 2 } { \rho \nu }^{ 2 } \right) [/latex] = नियत के अनुसार कागज़ के ऊपर वायु दाब, नीचे की तुलना में कम हो जाएगा। इससे कागज़ पर उत्थापक बल लगेगा जो कागज़ को नीचे नहीं गिरने देगा। |
(b) टोंटी को उँगलियों द्वारा बन्द करने पर जल उँगलियों के बीच की खाली जगह से निकलने लगता है। यहाँ धारा का अनुप्रस्थ क्षेत्रफल टोंटी के अनुप्रस्थ क्षेत्रफल से कम होता है; अतः अविरतता के सिद्धान्त (A1ν1 = A2ν2) से जल का वेग अधिक हो जाता है। |
(c) अविरतता के सिद्धान्त से, समान दाब आरोपित किए जाने पर भी, सुई बारीक होने पर (अनुप्रस्थ क्षेत्रफल कम होने पर) बहि:प्रवाही धारा का प्रवाह वेग बढ़ जाता है; अत: बहि:प्रवाह वेग सुई के आकार से अधिक नियन्त्रित होता है।
(d) जब कोई तरल किसी पात्र में बने बारीक छिद्र से बाहर आता है तो अविरतता के सिद्धान्त से वह उच्च बहि:स्राव वेग प्राप्त कर लेता है। बाह्य बल की अनुपस्थिति में पात्र + तरल का संवेग संरक्षित रहता है; अतः पात्र विपरीत दिशा में संवेग प्राप्त करता है, अर्थात् बाहर निकलता हुआ द्रव पात्र पर : विपरीत दिशा में प्रणोद आरोपित करता है।
(e) घूमती हुई गेंद अपने साथ वायु को खींचती है; अतः गेंद के ऊपर तथा नीचे वायु के वेग में अन्तर आ जाता है; अतः दाबों में भी अन्तर आ जाता है। इसके कारण गेंद पर भार के अतिरिक्त एक अन्य बल भी लगने लगता है और गेंद को पथ परवलयाकार नहीं रह जाता।।
प्रश्न 5.
ऊँची एड़ी के जूते पहने 50 kg संहति की कोई बालिका अपने शरीर को 1.0 cm व्यास की एक ही वृत्ताकार एड़ी पर सन्तुलित किए हुए है। क्षैतिज फर्श पर एड़ी द्वारा आरोपित दाब ज्ञात कीजिए।
हल-
वृत्ताकार एड़ी की त्रिज्या R = व्यास /2 = 1.0 सेमी/2
= 0.5 सेमी = 5 x 10-3 मीटर
वृत्ताकार एड़ी का क्षेत्रफल A = πR2 =3.14 (5 x 10-3 मी)2
= 78.50 x 10-6 मी2
एड़ी पर पड़ने वाला बल F = बालिका का भार = mg
= 50 किग्रा x 9.8 मी/से2 =490 न्यूटन
क्षैतिज फर्श पर एड़ी द्वारा आरोपित दाब = एड़ी पर आरोपित दाब


प्रश्न 6.
टॉरिसेली के वायुदाबमापी में पारे का उपयोग किया गया था। पास्कल ने ऐसा ही वायुदाबमापी 984 kg m-3 घनत्व की फ्रेंच शराब का उपयोग करके बनाया। सामान्य वायुमण्डलीय दाब के लिए शराब-स्तम्भ की ऊँचाई ज्ञात कीजिए।
हल-
h ऊँचाई के शराब स्तम्भ का दाब P = h.ρ.g
शराब स्तम्भ की ऊँचाई h = [latex s=2]\frac { P }{ \rho .g } [/latex]
यहाँ P = 1 वायुमण्डलीय दाब
= 1.013 x 105Pa = 1.013 x 105 न्यूटन/मी2
शराब का घनत्व ρ = 984 किग्रा/मी3 तथा g = 9.8 मी/से2
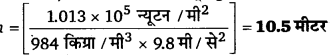
प्रश्न 7.
समुद्र तट से दूर कोई ऊध्र्वाधर संरचना 109 Pa के अधिकतम प्रतिबल को सहन करने के लिए बनाई गई है। क्या यह संरचना किसी महासागर के भीतर किसी तेल कूप के शिखर पर रखे जाने के लिए उपयुक्त है? महासागर की गहराई लगभग 3km है। समुद्री धाराओं की उपेक्षा कीजिए।
हल-
यदि समुद्र के जल द्वारा आरोपित दाब, संरचना द्वारा सहन किये जा सकने वाले अधिकतम प्रतिबल से कम होगा तो संरचना महासागर के भीतर तेल कूप के शिखर पर रखे जाने के लिए उपयुक्त होगी। समुद्र जल द्वारा आरोपित दाब
P = hρg
यहाँ h = 3 किमी = 3 x 103 मीटर,
जल का घनत्व = 103 किग्रा – मी-3 तथा g = 9.8 मी/ से2
P =3 x 103 मी x 103 किग्रा -मी3 x 9.8 मी-से-2
= 2.94 x 107 न्यूटन /मी2 = 2.94 x 107 Pa
चूँकि P < अधिकतम प्रतिबल 109 Pa; अत: संरचना आवश्यक कार्य के लिए उपयुक्त है।
प्रश्न 8.
किसी द्रवचालित आटोमोबाइल लिफ्ट की संरचना अधिकतम 3000 kg संहति की कारोंको उठाने के लिए की गई है। बोझ को उठाने वाले पिस्टन की अनुप्रस्थ काट का क्षेत्रफल 425 cm2 है। छोटे पिस्टन को कितना अधिकतम दाब सहन करना होगा?
हल-
पास्कल के नियम के अनुसार,
छोटे पिस्टन पर अधिकतम दाब = बोझ उठाने वाले बड़े पिस्टन पर दाब

प्रश्न 9.
किसी U-नली की दोनों भुजाओं में भरे जल तथा मेथेलेटिड स्पिरिट को पारा एक-दूसरे से पृथक् करता है। जब जल तथा पारे के स्तम्भ क्रमशः 10 cm तथा 12.5 cm ऊँचे हैं तो दोनों भुजाओं में पारे का स्तर समान है। स्पिरिट का आपेक्षिक घनत्व ज्ञात कीजिए।
हल-
U-नली की एक भुजा में जल स्तम्भ के लिए,
h1 = 10.0 सेमी; ρ1 (घनत्व) = 1 g-cm-3
U-नली की दूसरी भुजा में मेथेलेटिड स्प्रिट के लिए,
h2 =12.5 सेमी; ρ2 =?
चूंकि दोनों भुजाओं में पारे का तल समान है अत: इस तल पर दोनों भुजाओं के स्तम्भों के दाब भी समान होंगे। अर्थात् ।
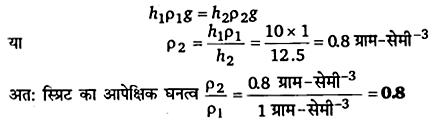
प्रश्न 10.
यदि प्रश्न 9 की समस्या में, U-नली की दोनों भुजाओं में इन्हीं दोनों द्रवों को और उड़ेल कर दोनों द्रवों के स्तम्भों की ऊँचाई 15 cm और बढ़ा दी जाए तो दोनों भुजाओं में पारे के स्तरों में क्या अन्तर होगा? (पारे का आपेक्षिक घनत्व = 13.6)
हल-
माना कि U-नली की दोनों भुजाओं में पारे के तलों का अन्तर h है तथा ρ पारे का घनत्व है, तो ,
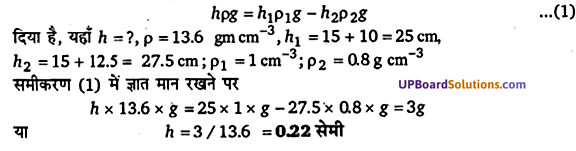

प्रश्न 11.
क्यो,बरनौली समीकरण का उपयोग किसी नदी की किसी क्षिपिका के जल-प्रवाह का विवरण देने के लिए किया जा सकता है? स्पष्ट कीजिए।
उत्तर-
बरनौली प्रमेय का समीकरण केवल धारारेखी प्रवाह पर लागू होता है। चूंकि नदी की क्षिफ्रिका (UPBoardSolutions.com) का जल-प्रवाह धारारेखी प्रवाह नहीं होता; अत: इसका विवरण देने के लिए बरनौली समीकरण का प्रयोग नहीं किया जा सकता।
प्रश्न 12.
बरनौली समीकरण के अनुप्रयोग में यदि निरपेक्ष दाब के स्थान पर प्रमापी दाब (गेज़ दाब) का प्रयोग करें तो क्या इससे कोई अन्तर पड़ेगा? स्पष्ट कीजिए।
उत्तर-
बरनौली समीकरण के अनुसार,

माना दो बिन्दुओं पर वायुमण्डलीय दाब Pq तथा Pq हैं व गेज दाब क्रमशः P’ व P; हैं तब
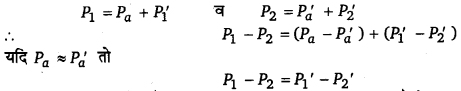
अर्थात् यदि दोनों बिन्दुओं के वायुमण्डलीय दाबों में बहुत कम अन्तर है तो परम दाब के स्थान पर गेज़ दाब का प्रयोग करने से कोई, अन्तर नहीं पड़ेगा।
प्रश्न 13.
किसी 1.5 m लम्बी 10 cm त्रिज्या की क्षैतिज नली से ग्लिसरीन का अपरिवर्ती प्रवाह हो रहा है। यदि नली के एक सिरे पर प्रति सेकण्ड एकत्र होने वाली ग्लिसरीन का परिमाण 4.0 x 10-3 kg s-1 है तो नली के दोनों सिरों के बीच दाबान्तर ज्ञात कीजिए। (ग्लिसरीन का घनत्व = 1.3 x 103 kg m-3 तथा ग्लिसरीन की श्यानता = 0.83 Pas) आप यह भी जाँच करना चाहेंगे कि क्या इस नली में स्तरीय प्रवाह की परिकल्पना सही है?
हल-
धारा-रेखीय प्रवाह मानते हुए नली में ग्लिसरीन के प्रवाह की दर के प्वॉइजली के सूत्र [latex s=2]Q=\frac { \pi \rho { r }^{ 4 } }{ 8\eta { l }^{ 4 } } [/latex]
से नली के सिरों के बीच दाबान्तर


यह धारा-रेखी प्रवाह के लिए मान्य अधिकतम मान 2000 से काफी कम है। अतः नली में ग्लिसरीन को प्रवाह धारा-रेखी है।।
प्रश्न 14.
किसी आदर्श वायुयान के परीक्षण प्रयोग में वायु-सुरंग के भीतर पंखों के ऊपर और नीचे के पृष्ठों पर वायु-प्रवाह की गतियाँ क्रमशः 70 ms-1 तथा 63 ms-1 हैं। यदि पंख का क्षेत्रफल 2.5 m2 है तो उस पर आरोपित उत्थापक बल परिकलित कीजिए। वायु का घनत्व 1.3 kg m-3 लीजिए।
हल-
बरनौली प्रमेय के अनुसार, वायु के. क्षैतिज प्रवाह के लिए

जहाँ P1 = वायुयान पंख के ऊपर दाब तथा P2 = पंख के नीचे दाब
υ1 = पंख की ऊपरी सतह पर वायु का वेग तथा υ2 = निचली सतह पर वायु का वेग
∴ पंख की ऊपरी सतह की तुलना में निचली सतह पर दाब आधिक्य अर्थात् पंखों की सतहों के बीच दाबान्तर

प्रश्न 15.
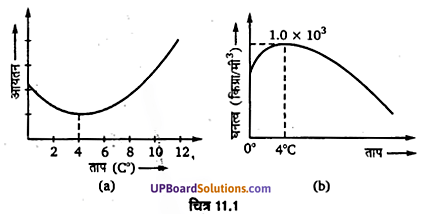
चित्र-10.1 (a) तथा (b) किसी द्रव (श्यानताहीन) का अपरिवर्ती प्रवाह दर्शाते हैं। इन दोनों चित्रों में से कौन-सही नहीं है? कारण स्पष्ट कीजिए।
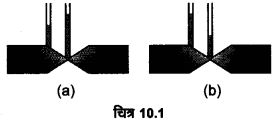
उत्तर-
चित्र-10.1 (a) सही नहीं है। नलिका की ग्रीवा में अनुप्रस्थ क्षेत्रफल कम है; अत: अविरतता के सिद्धान्त से यहाँ वेग अधिक होगा; अत: बरनौली प्रमेय से यहाँ जल का दाब कम होगा जबकि चित्र (a) में ग्रीवा पर जल दाब अधिक दिखाया गया है।

प्रश्न 16.
किसी स्प्रे पम्प की बेलनाकार नली की अनुप्रस्थ काट का क्षेत्रफल 8.0 cm2 है। इस नली के एक सिरे पर 1.0 mm व्यास के 40 सूक्ष्म छिद्र हैं। यदि इस नली के भीतर द्रव के प्रवाहित होने की दर 1.5 m min-1 है तो छिद्रों से होकर जाने वाले द्रव की निष्कासन-चाल ज्ञात कीजिए।
हल-
नली की अनुप्रस्थ-काट का क्षेत्रफल A1 = 8 x 10-4 मी2

प्रश्न 17.
U-आकार के किसी तार को साबुन के विलयन में डुबोकर बाहर निकाला गया जिससे उस पर एक पतली साबुन की फिल्म बन गई। इस तार के दूसरे सिरे पर फिल्म के सम्पर्क में एक फिसलने वाला हलका तार लगा है जो 1.5 x 10-2 N भार (जिसमें इसका अपना भार भी सम्मिलित है) को सँभालता है। फिसलने वाले तार की लम्बाई 30 cm है। साबुन की फिल्म का पृष्ठ-तनाव कितना है?
हल-
तार की लम्बाई l = 30 cm = 0.3 m
तार पर लटका भार W = 1.5 x 10-2 N
माना फिल्म का पृष्ठ-तनाव S है, तब फिल्म के एक ओर के पृष्ठ (UPBoardSolutions.com) के कारण तार पर F1 = S x l बल लगेगा।
∴ दोनों पृष्ठों के कारण तार पर बल
F = 2F1 = 2sl
यह बल भार को सन्तुलित करता है; अतः
2Sl = W

प्रश्न 18.
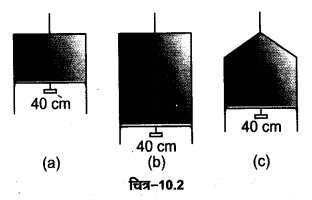
निम्नांकित चित्र-10.2 (a) में किसी पतली द्रव-फिल्म को 4.5 x 10-2 N का छोटा भार सँभाले दर्शाया गया है। चित्र (b) तथा (c) में बनी इसी द्रव की फिल्में इसी ताप पर कितना भार सँभाल सकती हैं? अपने उत्तर को प्राकृतिक नियमों के अनुसार स्पष्ट कीजिए।
उत्तर-
चित्र-10.2 (a), (b) व (c) प्रत्येक में फिल्म के नीचे वाले किनारे की लम्बाई 40 cm (समान) है।
इस किनारे पर फिल्म के पृष्ठ-तनाव S के कारण समान बल F = S x 2l लगेगा।
यही बल लटके हुए भार को साधता है। चूंकि साधने वाला बल प्रत्येक दशा में समान है; अतः चित्र-10.2 (b) व (C) में भी वही भार 4.5 x 10-2 N सँभाला जा सकता है।

प्रश्न 19.
3.00 mm त्रिज्या की किसी पारे की बूंद के भीतर कमरे के ताप पर दाब क्या है? 20°C ताप पर पारे का पृष्ठ तनाव 4.65 x 10-1 N m-1 है। यदि वायुमण्डलीय दाब 101 x 105 Pa है तो पारे की बूंद के भीतर दाब-आधिक्य भी ज्ञात कीजिए।
हल-
दिया है : त्रिज्या r =3.00 mm = 3.00 x 10-3m,
वायुमण्डलीय दाब Pa = 1.01 x 105 Pa
20°C पर पारे का पृष्ठ-तनाव S =4.65 x 10-1Nm-1

प्रश्न 20.
5.00 mm त्रिज्या के किसी साबुन के विलयन के बुलबुले के भीतर दाब-आधिक्य क्या है? 20°C ताप पर साबुन के विलयन का पृष्ठ-तनाव 2.50 x 10-2 Nm-1 है। यदि इसी विमा का कोई वायु का बुलबुला 1.20 आपेक्षिक घनत्व के साबुन के विलयन से भरे किसी पात्र में 40.0 cm गहराई पर बनता तो इस बुलबुले के भीतर क्या दाब होता, ज्ञात कीजिए। (1 वायुमण्डलीय दाब = 101 x 105 Pa)
हल-
(a) बुलबुले की त्रिज्या r = 5.00 mm = 5.0 x 10-3 m,
विलयन का पृष्ठ-तनाव S = 2.50 x 10-2 Nm-1
साबुन के घोल का बुलबुला वायु में बनता है; अतः इसके दो मुक्त पृष्ठ होंगे।


अतिरिक्त अभ्यास
प्रश्न 21.
1.0 m2 क्षेत्रफल के वर्गाकार आधार वाले किसी टैंक को बीच में ऊर्ध्वाधर विभाजक दीवार द्वारा दो भागों में बाँटा गया है। विभाजक दीवार के नीचे 20 cm2 क्षेत्रफल का कब्जेदार दरवाजा है। टैंक का एक भाग जल से भरा है तथा दूसरा भाग 1.7 आपेक्षिक घनत्व के अम्ल से भरा है। दोनों भाग 40 m ऊँचाई तक भरे गए हैं। दरवाजे को बन्द रखने के लिए आवश्यक बल परिकलित कीजिए।
हुल-
दरवाजे को बन्द रखने के लिए आवश्यक बल
F = विभाजक दीवार के दोनों ओर का दाबान्तर x दरवाजे का क्षेत्रफल
= (अम्ल स्तम्भ का दाब – जल स्तम्भ का दाब) x A

प्रश्न 22.
चित्र-10.3 (a) में दर्शाए अनुसार कोई मैनोमीटर किसी बर्तन में भरी गैस के दाब का पाठ्यॉक लेता है। पम्प द्वारा कुछ गैस बाहर निकालने के पश्चात मैनोमीटर चित्र 10.3 (b)] में दर्शाए अनुसार पाठ्यांक लेता है। मैनोमीटर में पारा भरा है तथा वायुमण्डलीय दाब का मान 76 cm मरकरी (Hg) है।
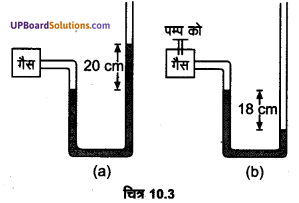
(i) प्रकरणों (a) तथा (b) में बर्तन में भरी गैस के निरपेक्ष दाब तथा प्रमापी दाब cm (Hg) के मात्रक में लिखिए।
(ii) यदि मैनोमीटर की दाहिनी भुजा में 13.6 cm ऊँचाई तक जल (पारे के साथ | अमिश्रणीय) उड़ेल दिया जाए तो प्रकरण (b) में स्तर में क्या परिवर्तन होगा? (गैस के आयतन में हुए थोड़े परिवर्तन की उपेक्षा कीजिए।)
हस-
वायुमण्डलीय दाब P0 = 76 सेमी पारा ।
(i) चित्र 10.3 (a) में
निरपेक्ष दाब P = P0 + 20 सेमी पारा ।
= 76 सेमी पारा + 20 सेमी पारा = 96 सेमी पारा
‘प्रमापी (गेज) दाब = (P – P0) = 20 सेमी पारा
चित्र 10.3 (b) में,
निरपेक्ष दाब P = P0 – 18 सेमी पारा
= 76 सेमी पारा – 18 सेमी पारा
= 58 सेमी पारा
प्रमापी (गेज) दाब = (P – P0) = -18 सेमी पारा
यह ऋणात्मक (-) चिह्न यह दर्शाता है कि बर्तन में भरी गैस का दाब वायुमण्डलीय दाब से कम है।
(ii) यदि मैनोमीटर की दाहिनी भुजा में 13.6 सेमी ऊँचाई तक जल उड़ेल दिया जाता है, तो चित्र 10.4 के अनुसार मैनोमीटर की दाहिनी भुजा में पारे। का तल नीचे गिरता है तथा बायीं भुजा में यह ऊपर उठता है ताकि तली पर दोनों ओर के दाब समान हो जायें। माना पारे का दाहिनी भुजा से बायीं भुजा में स्थानान्तरण x सेमी है। अत: दोनों भुजाओं में पारे। के स्तम्भ का अन्तर 2x सेमी होगा।
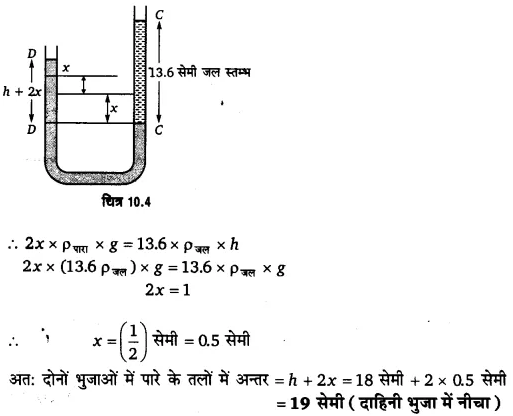

प्रश्न 23.
वो पात्रों के आधारों के क्षेत्रफल समान हैं परन्तु आकृतियाँ भिन्न-भिन्न हैं। पहले पात्र में दूसरे पात्र की अपेक्षा किसी ऊँचाई तक भरने पर दोगुना जल आता है। क्या दोनों प्रकरणों में पात्रों के आधारों पर आरोपित बल समान हैं? यदि ऐसा है तो भार मापने की मशीन पर रखे एक ही ऊँचाई तक जल से भरे दोनों पात्रों के पाठ्यांक भिन्न-भिन्न क्यों होते हैं?
हल-
माना प्रत्येक पात्र में जल-स्तम्भ की ऊँचाई h तथा आधार का क्षेत्रफल A है तो
आधार पर बल = जल-स्तम्भ का दाब x क्षेत्रफल
= h ρ g × A = A h ρ g
∵A व h दोनों के लिए समान है तथा ρ व g अचर राशियाँ हैं।
∴दोनों पात्रों के आधारों पर समान बल आरोपित होंगे। भार मापने वाली मशीन, पात्र के आधार पर आरोपित बल को मापने के स्थान पर पात्र + जल का भार मापती है।
∵ एक पात्र में दूसरे की अपेक्षा दोगुना जल है; अतः भार मापने की मशीन के पाठ्यांक अलग-अलग होंगे।
प्रश्न 24.
रुधिर-आधान के समय किसी शिरा में, जहाँ दाब 2000 Pa है, एक सुई धेसाई जाती है। रुधिर के पात्र को किस ऊँचाई पर रखा जाना चाहिए ताकि शिरा में रक्त ठीक-ठीक प्रवेश कर सके। (रुधिर का घनत्व = 1.06 x 103 kg m-3)
हुल-
शिरा में रक्त दाब P = 2000 Pa, रक्त का घनत्व ρ = 1.06 x 103 kg m-3
माना कि रक्त के पात्र की सुई से ऊँचाई = h
रक्त के शिरा में ठीक-ठीक प्रवेश करने हेतु, h ऊँचाई वाले रक्त स्तम्भ का दाब, (UPBoardSolutions.com) शिरा में रक्त स्तम्भ के दाब के ठीक बराबर होना चाहिए।

प्रश्न 25.
बरनौली समीकरण व्युत्पन्न करने में हमने नली में भरे तरल पर किए गए कार्य को तरल की गतिज तथा स्थितिज ऊर्जाओं में परिवर्तन के बराबर माना था।
(a) यदि क्षयकारी बल, उपस्थित हैं, तब नली के अनुदिश तरल में गति करने पर दाब में परिवर्तन किस प्रकार होता है?
(b) क्या तरल का वेग बढ़ने पर क्षयकारी बल अधिक महत्त्वपूर्ण हो जाते हैं? गुणात्मक रूप में चर्चा कीजिए।
उत्तर-
(a) क्षयकारी बल की अनुपस्थिति में बहते हुए द्रव के एकांक आयतन की कुल ऊर्जा स्थिर रहती है परन्तु क्षयकारी बल की उपस्थिति में नली में तरल के प्रवाह को बनाए रखने के लिए क्षयकारी बल के विरुद्ध कार्य करना पड़ता है। इस कारण नली के अनुदिश चलने पर तरल का दाब अधिक तेजी से घटता जाता है। यही कारण है कि शहरों में जल की टंकी से बहुत दूरी पर स्थित मकानों की ऊँचाई टंकी से कम होने पर भी जल उनकी ऊपर वाली मंजिल तक नहीं पहुँच पाता। तरलों के यान्त्रिक गुण, 267
(b) हाँ, तरलं का वेग बढ़ने पर तरल की अपरूपण दर बढ़ जाती है; अतः क्षयकारी बल (श्यान बल) और अधिक महत्त्वपूर्ण हो जाते हैं।
प्रश्न 26.
(a) यदि किसी धमनी में रुधिर का प्रवाह पटलीय प्रवाह ही बनाए रखना है तो | 2 x 10-3 m त्रिज्या की किसी धमनी में रुधिर-प्रवाह की अधिकतम चाल क्या होनी चाहिए?
(b) तद्नुरूपी प्रवाह-दर क्या है ? (रुधिर की श्यानता 2.084 x 10-3 Pas लीजिए।
हल-
(a) धमनी रुधिर प्रवाह की अधिकतम चाल = क्रान्तिक वेग [latex s=2]{ \nu }_{ c }=\frac { { R }_{ e }\eta }{ \rho d } [/latex]
परन्तु धारा-रेखी प्रवाह के लिए रेनॉल्ड संख्या का अधिकतम मान
Re =2000


प्रश्न 27.
कोई वायुयान किसी निश्चित ऊँचाई पर किसी नियत चाल से आकाश में उड़ रहा है तथा इसके दोनों पंखों में प्रत्येक का क्षेत्रफल 25 m2 है। यदि वायु की चाल पंख के निचले पृष्ठ पर 180 kmh-1 तथा ऊपरी पृष्ठ पर 234 km h-1 है तो वायुयान की संहति ज्ञात कीजिए। (वायु का घनत्व 1 kgm-3 लीजिए।) ।
हल-
वायुयान के एक पंख पर उत्थापक बल = (P2 – P1) x A
अतः दोनों पंखों पर उत्थापक बल F =2 (P2 – P1) x A


प्रश्न 28.
मिलिकन तेल की बूंद प्रयोग में, 2.0 x 10-5 m त्रिज्या तथा 1.2 x 103 kg m-3 घनत्व की किसी बूंद की सीमान्त चाल क्या है? प्रयोग के ताप पर वायु की श्यानता 1.8 x 10-5 Pas लीजिए। इस चाल पर बूंद पर श्यान बल कितना है? (वायु के कारण बूंद पर उत्प्लावन बल की उपेक्षा कीजिए।)
हल-
किसी तरल (वायु) में गिरती हुई तेल की बूंद का सीमान्त वेग
[latex s=2]{ \nu }_{ r }=\frac { 2(\rho -\sigma ){ r }^{ 2 }.g }{ 9\eta } [/latex]
यहाँ वायु के कारण उत्प्लावन बल की उपेक्षा की गयी है। अतः σ को नगण्य अर्थात् शून्य मानते हुए
[latex s=2]{ \nu }_{ r }=\frac { 2\rho { r }^{ 2 }.g }{ 9\eta } [/latex]
परन्तु यहाँ बूंद (तेल) का घनत्व ρ = 1.2 x 103 किग्रा-मी-3, बूंद की त्रिज्या
r = 2.0 x 10-5 मीटर, बूंद का श्यानता गुणांक η = 1.8 x 10-5 Pa.s
तथा g = 9.8 मी/से2.


प्रश्न 29.
सोडा काँच के साथ पारे का स्पर्श कोण 140° है। यदि पारे से भरी द्रोणिका में 1.00 mm त्रिज्या की काँच की किसी नली का एक सिरा डुबोया जाता है तो पारे के बाहरी पृष्ठ के स्तर की तुलना में नली के भीतर पारे का स्तर कितना नीचे चला जाता (पारे का घनत्व = 136 x 103kg m-3)
हल-
केशनली की त्रिज्या r = 1.00 mm = 10-3 m, स्पर्श कोण θ = 140°,
पारे का घनत्व ρ = 13.6 x 103 kg m-3, पृष्ठ-तनाव S = 0.4355 N m-1
माना पारे का स्तर केशनली में h ऊँचाई ऊपर उठता है तो

प्रश्न 30.
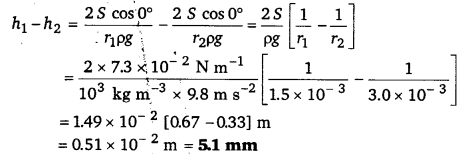
3.0 mm तथा 6.0 mm व्यास की दो संकीर्ण नलियों को एक साथ जोड़कर दोनों सिरों से खुली एक U-आकार की नली बनाई जाती है। यदि इस नली में जल भरा है तो इस नली की दोनों भुजाओं में भरे जल के स्तरों में क्या अन्तर है? प्रयोग के ताप पर जल का पृष्ठ-तनाव 7.3 x 10-2 N m-1 है। स्पर्श कोण शून्य लीजिए तथा जल का घनत्व 10 x 103 kg m-3 लीजिए। (g = 9.8 ms-2)
हल-
त्रिज्याएँ r1 = 1.5 x 10-3 m, r2 = 3.0 x 10-3 m,
जल का पृष्ठ-तनाव S = 7.3 x 10-2 N m-1,
जल का घनत्व ρ = 1.0 x 103 kg m-3, g = 9.8 ms-2
पृष्ठ-तनाव की अनुपस्थिति में दोनों नलिकाओं में जल का तल समान ऊँचाई पर (UPBoardSolutions.com) होता। माना। पृष्ठ-तनाव के कारण जल दोनों ओर क्रमशः h1 व h2 ऊँचाई तक चढ़ता है तो दोनों नलिकाओं में जल के तल का अन्तर
परिकलित्र/कम्प्यूटर पर आधारित प्रश्नोत्तर
प्रश्न 31.
(a) यह ज्ञात है कि वायु का घनत्व ρ, ऊँचाई y (मीटरों में) के साथ इस सम्बन्ध के अनुसार घटता है:
ρ = ρ0e-y/y0
यहाँ समुद्र तल पर वायु का घनत्व ρ0 = 1.25 kg m-3 तथा y0 एक नियतांक है। घनत्व में इस परिवर्तन को वायुमण्डल का नियम कहते हैं। यह संकल्पना करते हुए कि वायुमण्डल का ताप नियत रहता है (समतापी अवस्था) इस नियम को प्राप्त कीजिए। यह भी मानिए कि g का मान नियत रहता है।
(b) 1425 m³ आयतन का हीलियम से भरा कोई बड़ा गुब्बारा 400 kg के किसी पेलोड को उठाने के काम में लाया जाता है। यह मानते हुए कि ऊपर उठते समय गुब्बारे की त्रिज्या नियत रहती है, गुब्बारा कितनी अधिकतम ऊँचाई तक ऊपर उठेगा? . [y0 = 8000 m तथा ρHe = 0.18 kg m-3 लीजिए।]
हल-
(a) समुद्र तल से ऊँचाई पर वायु के एक काल्पनिक बेलन पर विचार कीजिए जिसका अनुप्रस्थ क्षेत्रफल A है। माना बेलन की ऊँचाई dy है। बेलन के निचले तथा ऊपर वाले सिरों पर वायु दाब क्रमशः P तथा P + dP हैं।




परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न
प्रश्न 1.
दाब का मात्रक है ।।
(i) न्यूटन
(ii) न्यूटन-मी
(iii) न्यूटन-मी2
(iv) न्यूटन/मी2
उत्तर-
(iv) न्यूटन/मी2
प्रश्न 2.
एक व्यक्ति द्वारा भूमि पर सर्वाधिक दाब तब लगेगा, जब वह
(i) लेटा हो ।
(ii) बैठा हो
(iii) एक पैर पर खड़ा हो।
(iv) दोनों पैरों पर खड़ा हो
उत्तर-
(iii) एक पैर पर खड़ा हो
प्रश्न 3.
यदि क्षेत्रफल एक-चौथाई हो जाए, तो दाब
(i) दोगुना हो जायेगा ।
(ii) चौथाई रह जायेगा।
(iii) चार गुना हो जायेगा
(iv) वही रहेगा
उत्तर-
(iii) चार गुना हो जायेगा।
प्रश्न 4.
द्रव दाब निर्भर करता है।
(i) केवल द्रव की गहराई पर
(ii) केवल द्रव के घनत्व पर
(iii) केवल गुरुत्वीय त्वरण पर ,
(iv) गहराई, घनत्व तथा गुरुत्वीय त्वरण तीनों पर
उत्तर-
(iv) गहराई, घनत्व तथा गुरुत्वीय त्वरण तीनों पर
प्रश्न 5.
वायुमण्डलीय दाब का अचानक गिर जाना प्रदर्शित करता है।
(i) तूफान
(ii) वर्षा
(iii) स्वच्छ मौसम
(iv) शीत लहर
उत्तर-
(i) तूफान
प्रश्न 6.
बल F, दाब P तथा क्षेत्रफल A में सम्बन्ध है।
(i) F = [latex s=2]\frac { P }{ A }[/latex]
(ii) A = F x P
(iii) F = A x P
(iv) F² = P x A
उत्तर-
(i) F = A x P

प्रश्न 7.
एक गोताखोर समुद्र में 30 मी की गहराई पर तैर रहा है उस पर लगने वाला कुल दाब का मान होगा (समुद्री जल का घनत्व) = 1000 किग्रा/मी3, 1 वायुमण्डलीय दाब = 10 x 105 न्यूटन/मी2
(i) 4 वायुमण्डलीय दाब
(ii) 10 वायुमण्डलीय दाब
(iii) 12 वायुमण्डलीय दाब
(iv) 5 वायुमण्डलीय दाब ।
उत्तर-
(i) 4 वायुमण्डलीय दाब
प्रश्न 8.
हाइड्रोलिक ब्रेक का कार्य सिद्धान्त आधारित है।
(i) चार्ल्स नियम पर ।
(ii) पास्कल नियम पर
(iii) बॉयल नियम पर
(iv) इनमें से किसी पर भी नहीं
उत्तर-
(i) पास्कल नियम पर
प्रश्न 9. एक जहाज समुद्र पर तैरता है क्योंकि
(i) जहाज द्वारा विस्थापित पानी का भार जहाज के भार के बराबर है।
(ii) जहाज द्वारा विस्थापित पानी का भार जहाज के भार से अधिक है।
(iii) जहाज द्वारा विस्थापित पानी का भार जहाज के भार से कम है।
(iv) प्रत्येक पिण्ड अवश्य ही तैरता है।
उत्तर-
(ii) जहाज द्वारा विस्थापित पानी का भार जहाज के भार से अधिक है।
प्रश्न 10.
लकड़ी का एक टुकड़ा जल में पूरा डुबोकर रखा गया है। टुकड़े पर जल का उत्क्षेप, टुकड़े के भार की अपेक्षा होगा ।
(i) अधिक
(ii) बराबर
(iii) कम
(iv) शून्य
उत्तर-
(i) अधिक
प्रश्न 11.
जल में किसी पत्थर के टुकड़े का भार उसके वायु में वास्तविक भार की तुलना में होगा
(i) बराबर :
(ii) भारी
(iii) हल्का
(iv) शून्य
उत्तर-
(iii) हल्का
प्रश्न 12. बरनौली प्रमेय पूर्णतया सत्य है।
(i) आदर्श द्रव के धारा-रेखी प्रवाह के लिए।
(ii) आदर्श द्रव के विक्षुब्ध’ प्रवाह के लिए।
(iii) वास्तविक द्रव के धारा-रेखी प्रवाह के लिए
(iv) किसी भी द्रव के किसी भी प्रकार के प्रवाह के लिए
उत्तर-
(i) आदर्श द्रव के धारा-रेखी प्रवाह के लिए
प्रश्न 13. बरनौली प्रमेय आधारित है।
(i) संवेग संरक्षण पर
(ii) ऊर्जा संरक्षण पर
(iii) द्रव्यमान संरक्षण पर
(iv) वेग संरक्षण पर,
उत्तर-
(ii) ऊर्जा संरक्षण पर

प्रश्न 14. एक वायुयान कार्य करता है।
(i) आर्किमिडीज के सिद्धान्त पर
(ii) पास्कल के नियम पर
(iii) बरनौली सिद्धान्त पर
(iv) स्टोक्स के नियम पर
उत्तर-
(iii) बरनौली सिद्धान्त पर
प्रश्न 15. जल से भरे बर्तन में मुक्त तल से 3.2 मीटर गहराई पर एक छिद्र है। यदि गुरुत्वीय त्वरण 10 मी/से2 हो तो जल का बहिसाव वेग होगा।
(i) 5.7 मी/से
(ii) 5.7 सेमी/से
(iii) 8.0 मी/से
(iv) 32 मी/से
उत्तर-
(iii) 8.0 मी/से ।
प्रश्न 16..किसी असमान त्रिज्या वाली नली में जल बह रहा है। नली में प्रविष्टि तथा निकासी सिरों की त्रिज्याओं का अनुपात 3:2 है। नली में प्रविष्ट करने वाले तथा निकलने वाले जल के वेगों का अनुपात होगा
(i) 8:27
(ii) 4:9
(iii) 1:1
(iv) 9:4
उत्तर-
(ii) 4:9
प्रश्न 17. ताप के बढ़ने पर श्यानता गुणांक ।
(i) गैसों तथा द्रवों दोनों का बढ़ता है।
(ii) गैसों तथा द्रवों दोनों का घटता है।
(iii) गैसों का बढ़ता है तथा द्रवों का घटता है।
(iv) गैसों का घटता है तथा द्रवों का बढ़ता है।
उत्तर-
(ii) गैसों का बढ़ता है तथा द्रवों का घटता है।
प्रश्न 18. दो छोटी गोलियाँ जिनकी त्रिज्याओं का अनुपात 1:2 है, किसी श्याने द्रव से होकर गिर रही हैं। उनकी सीमान्त चालों का अनुपात होगा।
(i) 1:2
(ii) 1:4
(iii) 2:1
(iv) 4:1
उत्तर-
(ii) 1:4 .
प्रश्न 19.
श्यान द्रव में सीमान्त वेग से गिरने वाले पिण्ड का त्वरण होता है
(i) शून्य
(ii) g
(iii) g से अधिक
(iv) g से कम
उत्तर-
(i) शून्य ।

प्रश्न 20. वर्षा की एक छोटी बूंद सीमान्त चाल से नीचे गिर रही है। इस बूंद से दोगुनी त्रिज्या वाली दूसरी बूंद का सीमान्तवेग होगा
(i) ν
(ii) 2ν
(iii) 8ν
(iv) 4ν
उत्तर-
(iv) 4ν
प्रश्न 21.
वर्षा की बूंद की वायु में सीमान्त चाल थे बराबर है।
(i) ν = krη
(ii) ν = kr²η
(iii) ν = krη²
(iv) ν = kr²/η
उत्तर-
(iv) ν = kr²/η
प्रश्न 22.
द्रव का पृष्ठ तनाव
(i) पृष्ठ क्षेत्रफल के साथ बढ़ता है।
(ii) पृष्ठ क्षेत्रफल के साथ घटता है।
(iii) ताप के साथ बढ़ता है।
(iv) ताप के साथ घटता है।
उत्तर-
(iv) ताप के साथ घटता है।
प्रश्न 23. पृष्ठ तनाव का विमीय सूत्र है।
(i) [MLT²]
(ii) [ML²T²]
(iii)[MT-2]
(iv) [MLT-1]
उत्तर-
(iii) [MT-2]
प्रश्न 24.
किसी केशनली में जल 4 सेमी की ऊँचाई तक चढ़ता है। यदि नली की अनुप्रस्थ-काट का क्षेत्रफल एक-चौथाई कर दिया जाये तो जल किस ऊँचाई तक चढेगा?
(i) 2 सेमी :
(ii) 4 सेमी
(iii) 8 सेमी
(iv) 12 सेमी
उत्तर-
(iii) 8 सेमी
प्रश्न 25.
साबुन के घोल के बुलबुले की त्रिज्या R तथा पृष्ठ तनाव T है, बुलबुले के भीतर आधिक्य दाब का सूत्र है।
(i) T/R
(ii) 2T/R
(iii)4T/R
(iv) T/2R
उत्तर-
(iii) 4T/R
प्रश्न 26. वर्षा की बूंद की वायु में सीमान्त चाल है।
(i) ν =krη
(ii) ν = kr²η
(iii) ν = krη²
(iv) ν = kr²η
जहाँ r, जल की बूंद की त्रिज्या, η वायु का श्यानता. गुणांक तथा k नियतांक है।.
उत्तर-
(iv) ν = kr²/η
प्रश्न 27.
2 x 10-6 मी2 पृष्ठ क्षेत्रफल की एक गोलाकार बूंद है, जिसके द्वेव का पृष्ठ-तनाव 7.5 x 10-2 न्यूटन/मी है। यह समान त्रिज्या की 8 गोलाकार बूंदों में विभक्त हो जाती है। इस प्रक्रिया में किया गया कार्य होगा ।
(i) 0.75 x 10-7 जूल
(ii) 1.5 x 10-7 जूल
(iii) 4.5 x 10-7 जूल।
(iv)3.0 x 10-7 जूल
उत्तर-
(ii) 1.5 x 10-7 जूल ।

प्रश्न 28. जल की एक बड़ी बूंद को 27 छोटी बूंदों में स्प्रे किया गया है। छोटी बूंद के भीतर दाब आधिक्य बड़ी बूंद की अपेक्षा कितना होगा?
(i) दोगुना ।
(ii) तीन गुना
(iii) आधा
(iv) एक-तिहाई
उत्तर-
(ii) तीन गुना ।
प्रश्न 29. एक ऊर्ध्वाधर केशनली में जल 10 सेमी लम्बाई तक चढ़ता है। यदि नली को 45° झुका दिया जाये तो नली के चढ़े हुए जल की लम्बाई होगी।
(i) 10 सेमी.
(ii) 10√2 सेमी
(iii) [latex s=2]\frac { 10 }{ \sqrt { 2 } } [/latex] सेमी
(iv) 5 सेमी
उत्तर-
(ii) 10√2 सेमी :
प्रश्न 30. साबुन के दो बुलंबुलों के अन्दर आधिक्य दाब क्रमशः 1.01 वायुमण्डल और 1.02 वायुमण्डल हैं। इन बुलबुलों के आयतनों का अनुपात है।
(i) 102 : 101
(ii) (102)2 : (101)3
(iii) 8:1
(iv) 2:1
उत्तर-
(ii) (102)2 : (101)3
प्रश्न 31.
साबुन के दो बुलबुलों की त्रिज्याएँ 2:1 के अनुपात में हैं। उनके भीतर आधिक्य दाब को अनुपात है।
(i) 1: 2
(ii) 2:1
(ii) 4:1
(iv) 1:4
उत्तर-
(i) 1: 2
प्रश्न 32.
लोहे की एक सूई पानी की सतह पर तैरती है। इस परिघटना का कास्ण है।
(i) द्रव का उत्प्लावन
(ii) श्यानता
(iii) पृष्ठ तनाव
(iv) गुरुत्वीय त्वरण
उत्तर-
(ii) पृष्ठ तनाव
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
दाब से क्या तात्पर्य है। इसका मात्रक लिखिए।
उत्तर-
द्रव द्वारा सम्पर्क सतह के प्रति एकांक क्षेत्रफल पर आरोपित (UPBoardSolutions.com) अभिलम्बवत् बल को दाब कहते हैं। दाब का मात्रक न्यूटन/मी अथवा पास्कल होता है।
प्रश्न 2.
बल तथा दाब में सम्बन्ध का सूत्र लिखिए।
उत्तर-

प्रश्न 3.
द्रव में किसी गहराई hपर द्रव-दाब क्या होगा?
उत्तर-
P= hdg
प्रश्न 4.
यदि बल को चार गुना तथा तल के क्षेत्रफल को आधा कर दें तो दोब, प्रारम्भिक दाब का कितने गुना हो जायेगा?
उत्तर-
आठ गुना।
प्रश्न 5.
द्रव का दाब किस पर निर्भर करता है?
उत्तर-
द्रव स्तम्भ की ऊँचाई पर।
प्रश्न 6.
तरल दाब से क्या तात्पर्य है। इसके लिए सूत्र बताइए।
उत्तर-
किसी पात्र या बर्तन में उपस्थित तरल द्वारा पात्र या बर्तन की दीवारों के प्रति एकांक क्षेत्रफल पर आरोपित बल को तरल दाब कहते हैं। द्रव के स्वतन्त्र तल से h गहराई पर द्रव के दाब, P = hρg यहाँ, ρ = द्रव का घनत्व, g = गुरुत्वीय त्वरण

प्रश्न 7.
कील एक सिरे से नुकीली क्यों बनाते हैं?
उत्तर-
जिससे कम बल लगाकर भी दाब अधिक लगे।
प्रश्न 8.
यदि बल को नियत रखा जाए तथा क्षेत्रफल आधा कर दिया जाए तो दाब पर क्या प्रभाव पड़ेगा?
उत्तर-
हम जानते हैं कि, दाब

दाब, क्षेत्रफल के व्युत्क्रमानुपाती होता है। अत: क्षेत्रफल आधा कर देने पर दाब दोगुना हो जाएगा।
प्रश्न 9.
हमें वायुमण्डलीय दाब का अनुभव क्यों नहीं होता?
उत्तर-
रक्त दाब के कारण हमें वायुमण्डलीय दाब का अनुभव नहीं होगा।
प्रश्न 10.
वायुमण्डल में बहुत अधिक ऊपर जाने पर रक्तनलिकाओं के फटने का डर क्यों रहता है?
उत्तर-
वायुदाब कम होने के कारण तथा रक्तदाब से सन्तुलन बिगड़ने के कारण।”
प्रश्न 11.
स्पिन करती टेनिस की गेंद एक सरल रेखा पर नचलकर वक्राकार पथ पर क्यों चलती है?
उत्तर-
गेंद के ऊपर वायु-दाब अधिक तथा गेंद के नीचे कम होता है। इस दाबान्तर के कारण गेंद सरल रेखा में न चलकर, नीचे की ओर झुकते हुए वक्राकार पथ पर चलती है।
प्रश्न 12.
पास्कल नियम के दो अनुप्रयोग बताइए।
उत्तर-
द्रवचालित ब्रेक, द्रवचालित लिफ्ट।
प्रश्न 13.
आर्किमिडीज के सिद्धान्त के आधार पर द्रव के आपेक्षिक घनत्व का सूत्र लिखिए।
उत्तर-
द्रव का आपेक्षिक घनत्व

प्रश्न 14.
किसी ठोस को किसी द्रव में डुबोने पर ठोस के भार में कितनी कमी होती है?
उत्तर-
उसके द्वारा हटाये गये द्रव के भार के बराबर
प्रश्न 15.
एक कॉर्क जल पर तैर रही है। इसका आभासी भार क्या है?
उत्तर-
शून्य, क्योंकि कॉर्क का भार कॉर्क पर जल के (UPBoardSolutions.com) प्रणोद (Upthrust) द्वारा सन्तुलित हो जाता है।
प्रश्न 16.
गेज दाब को समझाइए। उत्तर-द्रव के अन्दर किसी बिन्दु पर द्रव स्थैतिक दाब (p’) तथा वायुमण्डलीय दाब (PA) का अन्तर उस बिन्दु पर
गेज दाब कहलाता है।
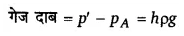
प्रश्न 17.
धारा रेखीय प्रवाह से आप क्या समझते हैं?
उत्तर-
यदि द्रव के प्रवाह में किसी एक बिन्दु से होकर गुजरने वाले द्रव के सभी कण एक ही वेग से, एक ही मार्ग से होकर गुजरें, तब यह प्रवाह धारा रेखीय प्रवाह कहलाता है।
प्रश्न 18.
आदर्श द्रव के धारा रेखीय प्रवाह के अविरतता के सिद्धान्त का उल्लेख कीजिए।
उत्तर-
इस सिद्धान्त के अनुसार, यदि कोई द्रव किसी असमान अनुप्रस्थ-परिच्छेद की नलिका में धारा रेखीय प्रवाह में बह रहा हो, तब प्रत्येक बिन्दु पर नली के अनुप्रस्थ-काट का क्षेत्रफल (A) तथा द्रव के वेग (ν) का गुणनफल नियत रहता है, अर्थात् A x ν = नियतांक
प्रश्न 19.
आदर्श द्रव के धारा रेखीय प्रवाह के लिए बरनौली का प्रमेय समीकरण प्रयुक्त चिह्नों का अर्थ । बताते हुए लिखिए।
उत्तर-
बरनौली का समीकरण p = [latex s=2]\frac { 1 }{ 2 }[/latex]ρν² + ρgh नियतांक
जहाँ p = दाब, ρ = द्रव का घनत्व, ν = द्रव प्रवाह का वेग, g = गुरुत्वीय त्वरण, h = पृथ्वी तल से स्थान की ऊँचाई ।
इसके अतिरिक्त p,[latex s=2]\frac { 1 }{ 2 }[/latex]ρν² (UPBoardSolutions.com) तथा ρgh क्रमशः दाब ऊर्जा, गतिज ऊर्जा तथा स्थितिज ऊर्जा को व्यक्त करते हैं।

प्रश्न 20.
बरनौली प्रमेय में दाब शीर्ष, वेग शीर्ष तथा गुरुत्वीय शीर्ष के लिए सूत्र लिखिए।
उत्तर-
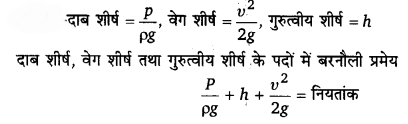
प्रश्न 21.
एक टंकी की ऊँचाई hहै। टंकी की दीवार में नीचे से hऊँचाई पर एक सूक्ष्म छिद्र है। जब टंकी को पानी से पूरा भर लिया जाता है, तो छिद्र से पानी कितने वेग से निकलेगा तथा कितनी क्षैतिज दूरी पर गिरेगा?
हल-
चित्र 10.6 में A तथा B बिन्दुओं पर बरनौली प्रमेय लगाने पर,

प्रश्न 22.
क्रिकेट तथा टेनिस के खेल में चक्रण (spin) करती हुई गेंद अपने मार्ग से घूम जाती है, इसकी व्याख्या किस सिद्धान्त या प्रमेय के आधार पर की जा सकती है?
उत्तर-
बरनौली प्रमेय के आधार पर।
प्रश्न 23.
ऊँचाई के साथ जाने पर वायु के घनत्व पर क्या प्रभाव पड़ता है?
उत्तर-
वायु का घनत्व कम होता जाता है।
प्रश्न 24.
लकड़ी के एक पिण्ड का भार w तथा आयतन v है। जल पर तैराने पर पिण्ड का भार कितना होगा?
उत्तर-
शून्य।
प्रश्न 25.
जब गुब्बारा उड़ता हुआ किसी निश्चित ऊँचाई पर पहुँच कर रुक जाता है तो उस स्थान की वायु तथा गुब्बारे में भरी गैस के घनत्व में क्या सम्बन्ध होगा?
उत्तर-
दोनों के घनत्व बराबर होंगे।
प्रश्न 26. सन्तुलित भौतिक तुला के एक पलड़े के नीचे तेजी से हवा चलाने पर तुला के सन्तुलन पर क्या प्रभाव पड़ेगा?
उतर-
पलड़े के नीचे वायु-वेग बढ़ने से दाब कम हो (UPBoardSolutions.com) जायेगा। अत: पलड़ा कुछ नीचे झुक जायेगा।

प्रश्न 27.
गहरा जल सदैव शान्त होता है, कारण बताइए।
उत्तर-
गहरे जल का द्रवस्थैतिक दाब अधिक होता है इसलिए वहाँ जल का वेग कम होगा अर्थात् जल शान्त होगा।
प्रश्न 28.
नदी के किनारे जल का वेग कम तथा बीच में अधिक होता है?
उत्तर-
नदी के किनारे जल का वेग कम तथा बीच में अधिक इसलिए होता है क्योंकि स्थिर पृष्ठ से दूर जाने पर जल की परतों का वेग बढ़ता है।
प्रश्न 29.
श्यानता गुणांक को परिभाषित कीजिए। इसकी विमा और मात्रक भी लिखिए।
उत्तर-
किसी द्रव का श्यानता गुणांक उस द्रव की एकांक सम्पर्क क्षेत्रफल वाली दो परतों के बीच कार्यरत् । श्यान बल के परिमाण के बराबर होता है, जबकि परतों के मध्य वेग-प्रवणता एकांक होती है। इसका SI मात्रक किग्रा/मी-से तथा विमा [ML-1T-1] होती है।
प्रश्न 30.
जल, वायु, रक्त तथा शहद में कौन सबसे अधिक श्यान होता है तथा कौन सबसे कम?
उत्तर-
शहद, वायु।
प्रश्न 31.
श्यान बल से सम्बन्धित स्टोक का सूत्र लिखिए।
उत्तर-
श्यान बल F = 6πηrν.
प्रश्न 32.
श्यान व्रव में गिरती हुई गोली की सीमान्त चाल के लिए सूत्र लिखिए।
उत्तर-
सीमान्त चाल [latex s=2](\nu )=\frac { 2 }{ 9 } \frac { { r }^{ 2 }(\rho -\sigma ) }{ \eta } g[/latex]
जहाँ, r = गोली की त्रिज्या, g = गुरुत्वीय त्वरण, (UPBoardSolutions.com) σ = श्यान द्रव का घनत्व, ρ = गोली के पदार्थ का घनत्व,η = द्रव का श्यानता गुणांक
प्रश्न 33.
किसी व्रव का क्रान्तिक वेग किन-किन बातों पर निर्भर करता है?
उत्तर-
द्रव की श्यानता पर, द्रव के घनत्व पर तथा नली की त्रिज्या पर
[latex s=2]\left( { \nu }_{ c }=\frac { k\eta }{ \rho a } \right) [/latex]
प्रश्न 34.
क्या वर्षा की गिरती बूंदों की चाल लगातार बढ़ती जाती है? क्या बड़ी व छोटी बूंदें पृथ्वी पर एक ही चाल से पहुँचती हैं?
उत्तर-
नहीं, वे एक सीमान्त चाल से नीचे गिरती हैं। नहीं, बड़ी बूंद की सीमान्त चाल अधिक होती है।

प्रश्न 35.
किसी श्यान द्रव में गिरती हुई गोली का त्वरण शून्य कब होता है?
उत्तर-
जब गोली पर लगने वाला नेट बल शून्य हो।
प्रश्न 36.
आकाश में बादल तैरते क्यों दिखाई देते हैं? ।
उत्तर-
जब जल की वाष्प धूल के कणों पर संघनित्र होती है, तो शुरू में बूंदें बहुत छोटी होती हैं तथा वायु की श्यानता के कारण यह सीमान्त चाल प्राप्त कर लेती हैं तथा नीचे की ओर बहुत धीमी चाल से चलती हैं, क्योंकि यह चाल बूंदों की त्रिज्या जो कि बहुत छोटी है, के वर्ग के अनुक्रमानुपाती होती है; इन्हें ही बादल कहते हैं तथा ये आकाश में तैरते प्रतीत होते हैं।
प्रश्न 37.
किसी द्रव के पृष्ठ-तनाव की परिभाषा दीजिए।
उत्तर-
किसी द्रव का पृष्ठ-तनाव वह बल है जो कि द्रव के पृष्ठ पर खींची गई किसी काल्पनिक रेखा की एकांक लम्बाई पर पृष्ठ के तेल में तथा रेखा के लम्बवत् कार्य करता है। इसका S.I. मात्रक न्यूटन/मीटर है।
प्रश्न 38.
किसी द्रव में बने हुए वायु के बुलबुले के भीतर दाब-आधिक्य का सूत्र लिखिए।
उत्तर-
p = [latex s=2]\frac { 2T }{ R }[/latex]
प्रश्न 39.
पृष्ठ-तनाव की परिभाषा पृष्ठीय ऊर्जा के पदों में दीजिए।
उत्तर-
T पृष्ठ-तनाव वाले द्रव के पृष्ठीय क्षेत्रफल में ΔA की वृद्धि करने में किया गया कार्य अर्थात् | पृष्ठीय ऊर्जा w = T x ΔA अथवा [latex s=2]T=\frac { W }{ \Delta A } [/latex] यदि ΔA = 1, तो W = T, अत: किसी द्रव का पृष्ठ-तनाव उस कार्य के बराबर होता है जो (UPBoardSolutions.com) नियत ताप पर उस द्रव के पृष्ठ के क्षेत्रफल में एकांक वृद्धि कर दे। अत: पृष्ठ-तनाव का मात्रक जूल/मी² भी लिखा जा सकता है।
प्रश्न 40.
गर्म सूप ठण्डे सूप की अपेक्षा अधिक स्वादिष्ट लगता है। क्यों?
उत्तर-
ठण्डे सूप की अपेक्षा गर्म सूप का पृष्ठ-तनाव कम होता है। अतः गर्म सूप ठण्डे सूप की अपेक्षा जीभ का अधिक क्षेत्रफल घेरता है जिससे कि वह ठण्डे सूप की तुलना में अधिक स्वादिष्ट लगता है।।
प्रश्न 41.
पृष्ठ ऊर्जा में क्या परिवर्तन होगा, यदि जल की एक बड़ी बूंद को अनेक छोटी-छोटी बूंदों में विभक्त किया जाये?
उत्तर-
पृष्ठ ऊर्जा बढ़ जाएगी।
प्रश्न 42.
किसी केशिका नली में जल के उन्नयन का सूत्र लिखिए।
उत्तर-
h =2T cos θ/rρg.
प्रश्न 43.
दो साबुन के बुलबुलों की त्रिज्याओं का अनुपात 1:4है। उनके आधिक्य दाबों का अनुपात क्या होगा?
उत्तर-
p ∝ 1/R ⇒ p1 : p2 = R2: R1 = 4 : 1
प्रश्न 44.
द्रव की छोटी बूंदें लगभग गोल आकार क्यों धारण कर लेती हैं? समझाइए।
उत्तर-
पृष्ठ-क्नाव के कारण द्रव का स्वतन्त्र तल सिकुड़कर न्यूनतम क्षेत्रफल ग्रहण करने की प्रवृत्ति रखता है। चूंकि किसी दिये हुए आयतन के लिए गोले के पृष्ठ का क्षेत्रफल (surface area) न्यूनतम (minimum) होता है। इसलिए द्रव की छोटी बूंदें लगभग गोल आकार धारण कर लेती हैं।

प्रश्न 44.
साबुन के घोल का पृष्ठ-तनाव 30 x 10-2 न्यूटन/मी है। इसका क्या अर्थ है?
उत्तर-
इसका अर्थ है कि साबुन के घोल के पृष्ठ पर खींची गयी काल्पनिक रेखा की एक मीटर लम्बाई पर इसके लम्बवत् 3.0 x 10-2 न्यूटन स्पर्शरेखीय बल कार्य करेगा।
प्रश्न 46.
स्पर्श कोण क्या है?
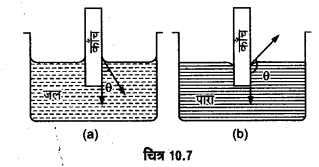
उत्तर-
“द्रव व ठोस के स्पर्श बिन्दु से द्रव के पृष्ठ पर खींची गयी स्पर्श रेखा तथा ठोस के (UPBoardSolutions.com) पृष्ठ पर द्रव के अन्दर की ओर खींची गयी स्पर्श रेखा के बीच बने कोण को उस ठोस व द्रव के लिए स्पर्श कोण कहते हैं।” चित्र 10.7 में स्पर्श कोण को θ से प्रदर्शित किया गया है।
प्रश्न 47.
खेत की जुताई करने से उसकी नमी रुकती है। भौतिक सिद्धान्त की सहायता से व्याख्या कीजिए।
उत्तर-
फसल में पानी देने के बाद गुड़ाई कर दी जाती है और वर्षा के बाद किसान खेत की जुताई कर देता है। पानी देने के बाद मिट्टी में केशिकाएँ बन जाती हैं जिनमें पानी का वाष्पीकरण होता रहता है परन्तु गुड़ाई या जुताई करने के बाद ये केशिका नलियाँ टूट जाती हैं जिससे पानी का वाष्पीकरण नहीं हो पाता है। अतः मिट्टी में नमी बनी रहती है।
प्रश्न 48.
लोहे का घनत्व जल की अपेक्षा अधिक होता है, फिर भी लोहे की । पतली सूई जल पर तैर सकती है। क्यों?
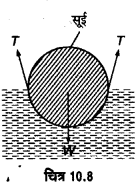
उत्तर-
एक स्वच्छ पतली सूई को स्याही सोखते पर रखकर धीरे से पानी की सतह पर रखते हैं। सोखता कुछ देर तक पानी को सोखकर गीला होता रहता है। और अन्त में डूब जाता है, परन्तु सुई पानी पर तैरती रहती है। इसका कारण जल का पृष्ठ-तनाव ही है। चित्र 10.8 में जल के (UPBoardSolutions.com) पृष्ठ पर तैरती हुई सूई का ॐ अनुप्रस्थ-काट दिखाया गया है। जल के पृष्ठ पर तैरती हुई सूई पर दो बल लगते (i) पृष्ठ-तनाव बल T, (ii) सूई का भार W। पृष्ठ-तनाव का परिणामी बल । ऊर्ध्वाधर दिशा में ऊपर की ओर लगता है जो सूई के भार W को सन्तुलित करता है। फलस्वरूप सूई तैरती है।
प्रश्न 49.
समुद्र की लहरों को शान्त करने के लिए लहरों पर तेल डाल देते हैं; क्यों?
उत्तर-
तेल डाल देने पर, तेज हवा तेल को जल के पृष्ठ पर हवा की दिशा में दूर तक फैला देती है। बिना तेल वाले जल का पृष्ठ तनाव तेल वाले जल से अधिक होता है। अत: बिना तेल वाला जल तेल वाले जल । को वायु की विपरीत दिशा में खींचता है जिससे की लहरें शान्त हो जाती हैं।
प्रश्न 50.
पृष्ठ-तनाव पर किन बातों का प्रभाव पड़ता है?
उत्तर-
पृष्ठ-तनाव पर निम्नलिखित बातों को प्रभाव पड़ता है
1. ताप का प्रभाव Effect of temperature ताप बढ़ने से संसंजक बल का मान घट जाता है। | जिसके फलस्वरूप पृष्ठ-तनाव घट जाता है। क्रान्तिक ताप पर पृष्ठ-तनाव शून्य होता है।
2. संदूषण का प्रभाव Effect of contamination यदि द्रव के तल पर धूल, कोई चिकनाई; जैसे- ग्रीस या तेल हो, तो इससे द्रव का पृष्ठ-तनाव घट जाता है।
3. विलेय का प्रभाव Effect of solute प्रयोगों से ज्ञात होता है कि जल का पृष्ठ तनाव उसमें घोले गये पदार्थ व उसकी घुलनशीलता पर निर्भर करता है। उदाहरण के लिए, जल में नमक घोलने पर जल का पृष्ठ-तनाव बढ़ जाता है। इसके विपरीत जल में साबुन घोलने पर जल को पृष्ठ-तनाव घट जाता

लघु उत्तरीय प्रश्न
प्रश्न 1. द्रव दाब के नियम लिखिए।
उत्तर-
द्रव दाब के नियम-ये नियम निम्नलिखित हैं
1. किसी द्रव के भीतर एक ही क्षैतिज तल में स्थित सभी बिन्दुओं पर दाब समान होता है।
2. द्रव से भरे बीकर में डूबे पिण्ड अथवा उसकी दीवारों पर द्रव द्वारा आरोपित दाब पिण्ड के पृष्ठ के प्रत्येक बिन्दु के लम्बवत् कार्य करता है।
3. स्थिर द्रव के भीतर किसी बिन्दु पर दाब द्रव के मुक्त पृष्ठ से उस बिन्दु की गहराई के अनुक्रमानुपाती है।
4. किसी द्रव का दाब उसके घनत्व के अनुक्रमानुपीती होता है।
5. द्रव दाब बीकर के क्षेत्रफल पर निर्भर नहीं करता। अतः दाब परिकलन के लिए द्रव के स्तम्भ की । ऊँचाई व घनत्व महत्त्वपूर्ण हैं। पात्र की आकृति व आधार का अनुप्रस्थ-काट द्रव दाब की गणना में महत्त्व नहीं रखता है।
प्रश्न 2.
एक द्रव स्तम्भ द्वारा उत्पन्न दाब का व्यंजक प्राप्त कीजिए। या तरल स्तम्भ के कारण दाबे का व्यंजक प्राप्त कीजिए।
उत्तर-
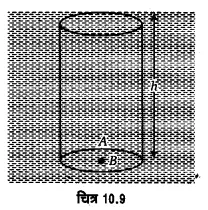
तरल स्तम्भ के कारण दाब Pressure due to fluid column- द्रव के भीतर स्थित किसी बिन्दु पर दाब माना कि किसी द्रव में उसके स्वतंत्र तल से h गहराई पर कोई बिन्दु B स्थित है, जहाँ पर हमें द्रव के दाब का मान ज्ञात करना है। बिन्दु B को केन्द्र मानकर कोई वृत्त खींचो। माना कि इस वृत्त का क्षेत्रफल A है। इस क्षेत्रफल पर द्रव द्वारा आरोपित बल, इस पर खड़े h ऊँचाई के बेलनाकार द्रव स्तम्भ के भार के बराबर होगा।
अब द्रव स्तम्भ का आयतन V= क्षेत्रफल x ऊँचाई = A x h
यदि द्रव का घनत्व ρ हो, तो द्रव स्तम्भ का द्रव्यमान |
m = V x ρ = A x H x ρ
तथा द्रव का स्तम्भ का भार W = mg = Ahρg
जहाँ g गुरुत्वीय त्वरण है।
यह लम्बवत् भार (बल) w बिन्दु B के चारों ओर A क्षेत्रफल पर आरोपित रहता है। अतः बिन्दु B पर द्रव का दाब
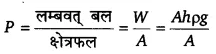
अत: द्रव के अन्दर किसी बिन्दु पर द्रव के कारण दाब द्रव की सतह से उस बिन्दु तक की गहराई, द्रव के घनत्व तथा गुरुत्वीय त्वरण के गुणनफल के बराबर होता है।
अतः उपर्युक्त सूत्र किसी तरल (द्रव अथवा गैस) के h ऊँचाई के स्तम्भ के कारण दाब का सूत्र है। इस सूत्र में एक ही द्रव के लिए ρ नियत तथा स्थान विशेष के लिए g नियत होता है अत: P ∝ h. अतः दिए गये द्रव के अन्दर किसी बिन्दु पर दांब, द्रव के स्वतन्त्र तल से उस बिन्दु की गहराई के अनुक्रमानुपाती होता है। यह उस बर्तन के आकार अथवा आकृति पर निर्भर नहीं करता जिसमें द्रव रखा जाता है।
प्रश्न 3.
आर्किमीडिज का सिद्धान्त लिखिए।
उत्तर-
आर्किमीडिज का सिद्धान्त–इसके अनुसार, “जब कोई वस्तु किसी द्रव में (UPBoardSolutions.com) पूरी अथवा आंशिक रूप से डुबोई जाती है तो उसके भार में कमी प्रतीत होती है। भार में यह आभासी कमी उस वस्तु द्वारा हटाये गये द्रव के भार के बराबर होती है।”
माना किसी वस्तु का वायु में भार W1, तथा द्रव में डुबोने पर वस्तु का भार W2 है;
अत: द्रव में डूबने से वस्तु के भार में आभासी कमी = W1 – W2,
यदि वस्तु के द्रव में डूबे भाग का आयतन V हो तो इसके द्वारा हटाये गये द्रव का आयतन भी v ही होगा। यदि द्रव का घनत्व d हो तो ।
वस्तु. द्वारा हटाये गये द्रव का द्रव्यमान = V x d
हटाये गये द्रव का भार = V x d x g
अत: आर्किमिडीज के सिद्धान्त से, वस्तु के भार में कमी
(W1-W2) = V x d x g
प्रश्न 4.
उत्प्लावन (उत्क्षेप) से क्या तात्पर्य है? उत्प्लावन का सूत्र प्राप्त कीजिए।
उत्तर-
उत्प्लावन बल अथवा उत्क्षेप तथा उत्प्लावन केन्द्र प्रत्येक द्रव अपने अन्दर पूर्ण अथवा आंशिक रूप से डूबी वस्तु पर ऊपर की ओर एक बल लगाता है। इस बल को उत्प्लावन बल अथवा. उत्क्षेप कहते हैं। किसी वस्तु पर द्रव का उत्क्षेप वस्तु द्वारा हटाए गए भार के बराबर होता है। यह बल वस्तु द्वारा हटाए गए द्रव के गुरुत्व केन्द्र पर कार्य करता है, इसे उत्प्लावन केन्द्र कहते हैं। उत्प्लावन बल के कारण ही द्रव में डूबी वस्तुएँ अपने वास्तविक भार से हल्की लगती हैं। यदि ρ घनत्व वाले किसी द्रव में किसी वस्तु का V आयतन डूबा है तो वस्तु पर द्रव का उत्क्षेप = हटाए गए द्रव का भार
= वस्तु का डूबा हुआ आयतन x द्रव का घनत्व x g = Vρg
प्रश्न 5.
प्लवन या तैरने का नियम लिखिए।
उत्तर-
तैरनेका नियम-जब कोई वस्तु किसी द्रव में आंशिक या पूर्ण रूप से डूबी या तैरती है तो वस्तु का कुल भार डूबे हुए भाग द्वारा हटाये गये द्रव के भार के बराबर होता है।

प्रश्न 6.
भारी वाहनों के पहियों के टायर काफी चौड़े क्यों बनाये जाते हैं?
उत्तर-
भारी वाहनों के पहियों के टायर चौड़े होने से (क्षेत्रफल A अधिक है) सड़क अथवा जमीन पर लगने वाला दाब (P = F / A) कम हो जाता है, क्योंकि वाहन का भार अधिक क्षेत्रफल पर लगता है, इसीलिए वाहन के पहिये सड़क में धंसने से बच जाते हैं।
प्रश्न 7
ऊँट रेगिस्तान में आसानी से क्यों चल लेता है?
उत्तर-
सूत्र दाब =बल/क्षेत्रफल से, ऊँट के पैर चौड़े होने के कारण इनका क्षेत्रफल अधिक होता है, अतः पृथ्वी पर दाब कम लगता है। इस कारण पैरों के नीचे की पृथ्वी धंसती नहीं है, अतः ऊँट रेगिस्तान में आसानी से चल लेता है।
प्रश्न 8.
रेलगाड़ी की पटरियों के नीचे लकड़ी या लोहे के चौड़े स्लीपर क्यों लगाये जाते हैं?
उत्तर-
यदि पटरियों के नीचे चौड़े स्लीपर न लगाये जायें तो पटरियाँ अधिक दबाव के कारण जमीन में धंस सकती हैं। पटरियों के नीचे स्लीपर लगाने से क्षेत्रफल अधिक हो जाता है जिसके कारण दाब कम पड़ता है और पटरी जमीन में नहीं धंसती।
प्रश्न 9.
लोहे से बना जहाज समुद्र में तैरता है, परन्तु लोहे का ठोस टुकड़ा (कील) डूब जाता है, क्यों? सम्बन्धित नियम देते हुए कथन की व्याख्या कीजिए।
उत्तर-
लोहे की कील की बनावट इस प्रकार की होती है कि उसका भार, उसके द्वारा हटाये गये जल के भार से बहुत अधिक होता है। इसी कारण वह जल में डूब जाती है। इसके विपरीत, लोहे का जहाज तैरता रहता है। इसका कारण यह है कि जहाज का ढाँचा अवतल होता है तथा अन्दर से खोखला बनाया जाता है। जैसे ही जहाज समुद्र में प्रवेश करता है तो उसके द्वारा (उसकी बनावट के कारण) इतना जल हटा दिया जाता है कि उसके द्वारा हटाये गये जल का भार, जहाज (जहाज व उसके समस्त समान सहित) के कुल भार के बराबर हो जाता है। इसी कारण पास्कल के सिद्धान्त के अनुसार, जहाज तैरता रहता है।
प्रश्न 10.
हिमखण्ड जल पर क्यों तैरता है?
उत्तर-
हिमखण्ड का घनत्व, जल के घनत्व से कम होता है, जिससे हिमखण्ड के आयतन के बराबर जल का उत्क्षेप-बल हिमखण्ड के भार से अधिक हो जाता है और हिमखण्ड जल पर तैरता रहता है। तैरते समय हिमखण्ड का केवल उतना आयतन ही जल में डूबता है, जितने आयतन के द्वारा हटाये गये जल का भार हिमखण्ड के भार के बराबर होता है।
प्रश्न 11.
0.02 मी2 तथा 0.04 मी2 परिच्छेद क्षेत्रफल के दो क्षैतिज पाइप एक-दूसरे से जुड़े हैं, जिसमें जल बह रहा है। पहले पाइप में जल की चाल 16 मी/से तथा दाब 2.0 x 104 न्यूटन/मी2 है। दूसरें पाइप में जल की चाल तथा दाब की गणना कीजिए।
हल-
दिया है, पहले पाइप के परिच्छेद का क्षेत्रफल (A1) = 0.02 मी2
दूसरे पाइप के परिच्छेद का क्षेत्रफल (A1) = 0.04 मी2
पहले पाइप में जल की चाल = (ν1) = 16 मी/से
पहले पाइप में जल का (UPBoardSolutions.com) दाब (ρ1) = 2 x 104 न्यूटन/मी2
अविरतता के सिद्धान्त से, A1ν1 = A2ν2

प्रश्न 12.
असमान परिच्छेद की एक बेलनाकार पाइप में जल प्रवाहित हो रहा है। एक स्थान पर नली की त्रिज्या 0.3 मी है तथा जल का वेग 1.0 मी/से है। दूसरे स्थान पर जहाँ नली की त्रिज्या 0.15 मी है, वहाँ पर जल के वेग की गणना कीजिए।
हल-
यहाँ, नली के पहले स्थान की त्रिज्या (r1) = 0.3 मी,
नली के दूसरे स्थान की त्रिज्या (r2) = 0.15 मी
नली के पहले स्थान पर जल का वेग (ν1) = 1.0 मी/से
नली के दूसरे स्थान पर जल का वेग (ν2)) = ?
अविरतता के सिद्धान्त से,
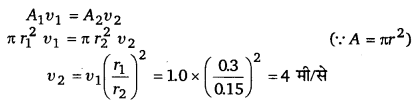
अतः जल का वेग = 4 मी/से है।

प्रश्न 13.
हवाई जहाज में पंखों के सामने के किनारे गोलाई में तथा पीछे के किनारे चपटे क्यों होते हैं?
उत्तर-
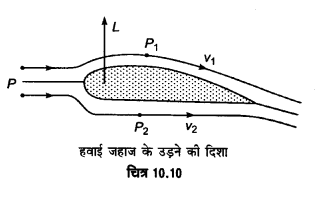
हवाई जहाज के पंख की आकृति इस प्रकार रखी जाती है कि उसकी ऊपरी सतह की वक्रता निचली सतह की वक्रता से अधिक होती है। तथा, सामने का किनारा गोल तथा पीछे का किनारा चपटा रखा जाता है (चित्र 10.10)। जब हवाई जहाज दौड़ लगाता है तब पंख के ऊपुर तथा नीचे से होकर वायु की धारा बहती है। (चित्र’10.10) से स्पष्ट है कि पंख के ऊपर का पृष्ठ कुछउभरा तथा ।
नीचे का पृष्ठ सीधा है। अत: वायु को पंख के ऊपर, नीचे की अपेक्षा अधिक दूरी तय करनी पड़ती है, फलतः वायु की धारा का वेग ऊपरी पृष्ठ पर अधिक तथा निचले पृष्ठ पर कम होता है। इस कारण ऊपरी पृष्ठ पर कम दाब तथा निचले पृष्ठ पर अधिक दाब कार्य करता है तथा वायुयान के पंख पर इन दोनों दाबों के अन्तर (P2 – P1) के बराबर एक प्रणोद (thrust) L कार्य करता है तथा पंख ऊपर को उठने लगता है।
प्रश्न 14.
श्यानता-गुणांक की परिभाषा दीजिए। इसका विमीय सूत्र तथा M.K.S. मात्रक लिखिए। या श्यानता-गुणांक की परिभाषा दीजिए।
उत्तर-
श्यानता-गुणांक-धारा-रेखीय प्रवाह के लिए द्रव की किन्हीं दो पर्तों के मध्य लगने वाला (UPBoardSolutions.com) श्यान-बल निम्नलिखित बातों पर निर्भर करता है–
1. यह पर्तों के सम्पर्क क्षेत्रफल (A) के अनुक्रमानुपाती होता है, अर्थात् ।
F∝A
2. यह पर्यों के बीच की वेग-प्रवणत Δνx/Δy के अनुक्रमानुपाती होता है, अर्थात्
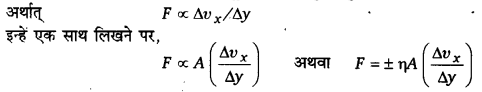
जहाँ η (ईटा) एक नियतांक है, जिसे द्रव का श्यानता-गुणांक (coefficient of viscosity) कहते हैं। यदि A = 1 तथा 20/Δνx/Δy = 1 हो, तो η = ± F, अर्थात् किसी द्रव का श्यानता-गुणांक उस श्यान बल के बराबर है जो एकांक क्षेत्रफल वाली पर्तों के बीच कार्य करता है, जबकि पर्तों के बीच एकांक वेग-प्रवणता हो।
उपर्युक्त सूत्र में ± चिह्न का अर्थ है कि बल F दो पर्यों के बीच अन्योन्य बल है। द्रव की किसी पर्त पर उससे ऊपर वाली पर्त आगे की ओर बल लगाती है, जबकि उससे नीचे वाली पर्त उस पर पीछे की ओर बल लगाती है।
श्यानता-गुणांक की विमा एवं मात्रक
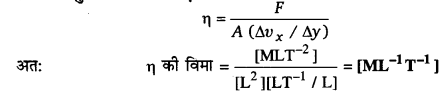
η का मात्रक (M.K.S. में) किग्रा/मीटर-सेकण्ड है। इसका एक अन्य मात्रक प्वॉइज है।
1 किग्रा/(मीटर-सेकण्ड) = 10 प्वॉइज

प्रश्न 15.
200 वर्ग सेमी क्षेत्रफल की एक समतल प्लेट तथा एक और बड़ी प्लेट के बीच ग्लिसरीन की 1 मिमी मोटी तह है। यदि ग्लिसरीन का श्यानता-गुणांक 1.0 किग्रा/मीटर-सेकण्ड हो, तो प्लेट को 9 सेमी/सेकण्ड के वेग से चलाने के लिए कितना बल चाहिए?
हल-
प्रश्नानुसार, η = 1.0 किग्रा/(मीटर-सेकण्ड),
A = 200 वर्ग सेमी = 2 x 10-2 वर्ग मीटर,
Δνx = 9 x 10-2 मीटर/सेकण्ड
तथा Δy = 1 मिमी = 10-3 मीटर
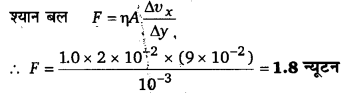
प्रश्न 16.
स्टोक्स के सूत्र का प्रयोग कर किसी श्यान द्रव में गिरते हुए एक गोलीय पिण्ड के सीमान्त वेग के लिए सूत्र प्राप्त कीजिए।
उत्तर-
स्टोक्स का नियम–स्टोक्स ने सिद्ध किया कि यदि r त्रिज्या की गोली किसी पूर्णत: समांग वे अनन्त विस्तार वाले तरल माध्यम में वेग ν से गति करे तो गोली पर कार्य करने वाला श्यान बल । F = 6πηrν होता है जो सदैव गोलीं की गति की विपरीत दिशा में लगता है, (UPBoardSolutions.com) जहाँ η उस द्रव का श्यानता-गुणांक है।।
सीमान्त वेग की गणना-माना कोई गोली जिसकी त्रिज्या r तथा घनत्व ρ है, σ घनत्व वाले द्रव में गिर रही है, जबकि द्रव का श्यानता-गुणांक η है। जब गोली सीमान्त वेग प्राप्त कर लेती है तो इस पर निम्नलिखित दो बल कार्य करते हैं—
1. नीचे की ओर कार्य करने वाला प्रभावी बल = [latex s=2]V(\rho -\sigma )g=\frac { 4 }{ 3 } \pi { r }^{ 3 }(\rho -\sigma )g[/latex]
2. ऊपर की ओर कार्य करने वाला श्यान बल = 6πηrν
चूँकि गोली नियत वेग से चल रही है अर्थात् त्वरण शून्य है। अतः इस पर लगने वाला नेट बल। शून्य होना चाहिए; अर्थात् उपर्युक्त दोनों बल बराबर होने चाहिए।
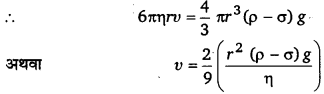
अतः गोली की सीमान्त चाल गोली की त्रिज्या के वर्ग के अनुक्रमानुपाती होती है।
प्रश्न 17.
किसी द्रव की पृष्ठ-ऊर्जा की व्याख्या कीजिए। द्रव के मुक्त पृष्ठ के क्षेत्रफल प्रसार में किए गए कार्य का व्यंजक प्राप्त कीजिए।
उत्तर-

द्रव की पृष्ठ-ऊर्जा जब द्रव के पृष्ठ का क्षेत्रफल बढ़ाया जाता है तो द्रव के कुछ अणु उसके अन्दर से मुक्त पृष्ठ पर आते हैं। इन अणुओं को मुक्त पृष्ठ के ठीक नीचे वाले अणुओं के आकर्षण-बल के विरुद्ध कुछ कार्य करना पड़ता है। यह कार्य, निर्मित हुए नवीन पृष्ठ में स्थितिज ऊर्जा के रूप में संचित हो जाता है। इस अतिरिक्त पृष्ठ-क्षेत्रफल के बढ़ने पर शीतलन (cooling) भी होता है। अत: बाहर से कुछ ऊष्मा पृष्ठ में आकर इसे पुन: प्रारम्भिक ताप पर ले आती है। इस प्रकार पृष्ठ को कुछ ऊर्जा बाहर से भी प्राप्त हो जाती है। इससे स्पष्ट है कि द्रव-पृष्ठ में स्थित अणु अपनी स्थिति के कारण कुछ अतिरिक्त (additional) ऊर्जा (UPBoardSolutions.com) रखते हैं। अत: द्रव के मुक्त पृष्ठ के प्रति एकांक क्षेत्रफल की इस अतिरिक्त ऊर्जा को ‘द्रव की पृष्ठ-ऊर्जा’ (surface energy of liquid) कहते हैं। द्रव के पृष्ठ का क्षेत्रफल बढ़ाने में किये गये कार्य व पृष्ठ-तनाव में सम्बन्ध माना एक मुड़े हुए तार ABC तथा उस पर बिना घर्षण खिसकने वाले सीधे तार PQ के बीच किसी द्रव की फिल्म । बनी है (चित्र 10.11)। हम जानते हैं कि पृष्ठ तनाव के कारण फिल्म का मुक्त पृष्ठ सिकुड़ने की चेष्टा करता है, अत: तार PQ ऊपर की ओर (फिल्म की ओर) चलेगा। तार PQ को साम्यावस्था में रखने के लिए इस पर एकसमान बल F नीचे की ओर लगाना होगा।
प्रयोगों से ज्ञात होता है कि बल F को मानतार PQ के सम्पर्क में A फिल्म की लम्बाई l के अनुक्रमानुपाती होता है। चूंकिं फिल्म में । दो मुक्त पृष्ठ होते हैं (एक बाहर वाला तथा दूसरा अन्दर वाला),
अतः F ∝ 2l
अथवा F = T x 2l = 2Tl
जहाँ T एक नियतांक है जो कि द्रव का पृष्ठ-तनाव कहलाता है।
माना तार PQ को ∆x दूरी से नीचे खिसकाया जाता है जिससे यह नवीन स्थिति P’ Q’ में आ जाता है। इस क्रिया में द्रव की फिल्म के क्षेत्रफल में वृद्धि होती है। फिल्म के क्षेत्रफल में वृद्धि के लिए किया गया यान्त्रिक कार्य W = बल x दूरी
= F x ∆x = (2Tl) ∆x =T x (2l∆x)
परन्तु 2l ∆x = फिल्म के दोनों पृष्ठों के क्षेत्रफल में होने वाली कुल वृद्धि = ∆A
अत: W = T x ∆A अथवा [latex s=2]T=\frac { W }{ \Delta A } [/latex]
यदि ∆A = 1; तब T = w, अतः द्रव के पृष्ठ के एकांक क्षेत्रफल को बढ़ाने में किया गया कार्य पृष्ठ-तनाव T के बराबर है। इस आधार पर हम पृष्ठ-तनाव की परिभाषा निम्न प्रकार कर सकते हैं
“नियत ताप पर द्रव के मुक्त पृष्ठ के क्षेत्रफल में एकांक वृद्धि करने के लिए किया गया कार्य द्रव को पृष्ठ-तनाव कहलाता है।”
इस परिभाषा के आधार पर पृष्ठ-तनाव के मात्रक को जूल/मी² से भी व्यक्त कर सकते हैं।
ताप बढ़ाने पर पृष्ठ-तनाव का मान घटता है।

प्रश्न 18.
पारे की एक बूंद की कमरे के ताप पर त्रिज्या 3 मिमी है। उसी ताप पर पारे का पृष्ठ तनाव 0.465 न्यूटन/मी है। बूंद के भीतर आधिक्य दाब तथा कुल दाब ज्ञात कीजिए। वायुमण्डलीय दाब 1.01 x 105 न्यूटन/मी2 है।
हल-
माना कि पारे का पृष्ठ-तनाव = T, बूंद की त्रिज्या = R

प्रश्न 19.
पानी की 1000 छोटी बूंदों को, जिनमें प्रत्येक की त्रिज्या 0.01 मिमी है, मिलाकर एक बड़ी बूंद बनाने में मुक्त ऊर्जा की गणना कीजिए। पानी का पृष्ठ-तनाव =7 x 10-2 न्यूटन/मी।
हल-
माना बड़ी बूंद की त्रिज्या R = 0.01 मिमी तथा छोटी बूंद की त्रिज्या r है,
अतः एक बड़ी बूंद का आयतन = 1000 (UPBoardSolutions.com) छोटी बूंदों का आयतन

प्रश्न 20.
एक केशनली में जल 5.0 सेमी ऊपर चढ़ता है। यदि एक अन्य केशनली की त्रिज्या इसकी आधी हो तो उसमें जल की ऊँचाई क्या होगी?
हल-
चूँकि किसी केशनली में चढ़े द्रव-स्तम्भ की ऊँचाई उसकी नली की त्रिज्या के व्युत्क्रमानुपाती होती है अर्थात् h∝1/r अर्थात् hr = नियतांक
∴ यदि r1 वा r2 त्रिज्या वाली केशनलियों में द्रव-स्तम्भ की ऊँचाइयाँ क्रमश: h1 व h2 हों, तो
h1r1 = h2r2
अथवा
h2 = h1(r1/r2) …(1)
परन्तु यहाँ दूसरी केशनली की त्रिज्या = [latex s=2]\frac { 1 }{ 2 }[/latex](पहली केशनली की त्रिज्या)
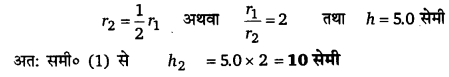
प्रश्न 21.
एक केशनलिका जिसकी त्रिज्या 0.4 मिमी है, जल में ऊध्र्वाधर डुबाई जाती है। ज्ञात कीजिए कि केशनलिका में जल कितनी ऊँचाई तक चढेगा? यदि इस केश नलिका को ऊध्र्वाधर रेखा से 60° झुका दें तो नली की कितनी लम्बाई तक जल चढेगा? जल का पृष्ठ-तनाव 7.0 x 10-2 न्यूटन/मी है।
हल-
दिया है, r = 0.4 मिमी = 0.4 x 10-3 मी,
T = 7.0 x 10-2 न्यूटन/मी,
θ = 0° अर्थात् cos θ = cos 0° = 1 एवं g = 9.8 मी/से2,
जल का घनत्व ρ = 103 किग्रा/मी3


प्रश्न 22.
साबुन के घोल से 2.0 सेमी त्रिज्या का बुलबुला फेंककर बनाने में कितना कार्य करना पड़ेगा? साबुन के घोल का पृष्ठ तनाव 0.03 न्यूटन/मी है।
हल-
साबुन के घोल का पृष्ठ तनाव T = 0.03 न्यूटन/मी
बुलबुले की त्रिज्या R =2 सेमी या 2 x 10-2 मीटर
साबुन के घोल के बुलबुले में 2 मुक्त पृष्ठ होते हैं।
अत: घोल से R मीटर त्रिज्या का बुलबुला फेंककर बनाने में इसके पृष्ठीय क्षेत्रफल में कुल वृद्धि

प्रश्न 23.
किसी द्रव के एक बूंद की त्रिज्या 5 x 10-3 मीटर है। द्रव बूंद के भीतर आधिक्य दाब की गणना कीजिए। द्रव का पृष्ठ तनाव 0.5 न्यूटन/मीटर है।
हल-
बूंद की त्रिज्या = R = 5 x 10-3 मीटर,
द्रव का पृष्ठ तनाव T = 0.5 न्यूटन/मीटर
द्रव की बूंद के भीतर आधिक्य दाब,

प्रश्न 24.
एक केशनली में पानी 2.0 सेमी ऊपर चढ़ता है। यदि एक अन्य केशनली की त्रिज्या उसकी एक-तिहाई हो, तो उसमें पानी कितना चढेगा?
हल-
किसी केशनली में चढ़े स्तम्भ की ऊँचाई उसकी नली की त्रिज्या (UPBoardSolutions.com) के व्युत्क्रमानुपाती होती है अर्थात् । h ∝ [latex s=2]\frac { 1 }{ r }[/latex] अर्थात् hr = नियतांक।
माना r1 वे r2 त्रिज्या वाली केशनलियों में द्रव-स्तम्भ की ऊँचाइयाँ क्रमश: h1 व h2 हों, तो
h1 r1 = h2 r2
या, h2 = h1 (r1/r2) …(1)
परन्तु दूसरी केशनली की त्रिज्या = [latex s=2]\frac { 1 }{ 3 }[/latex](पहली केशनली की त्रिज्या)
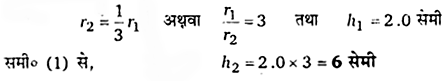
विस्तृत उत्तरीय प्रश्न
प्रश्न 1.
तरल दाब के पास्कल का नियम लिखिए। हाइड्रोलिक लिफ्ट के सिद्धान्त और कार्यविधि की व्याख्या कीजिए। या पास्कल का नियम लिखिए।
उत्तर-
पास्कल का नियम-द्रव में दाब के संचरण के सम्बन्ध में वैज्ञानिक पास्कल ने सन् 1653 में एक नियम प्रतिपादित किया था जो पास्कल का नियम कहलाता है। इसे द्रव के दाब संचरण का नियम भी कहा जाता है।
इस नियम के अनुसार, “किसी बर्तन में रखे द्रव की संतुलन अवस्था में द्रव के किसी भाग पर आरोपित दाब (बिना क्षय हुए) द्रव द्वारा सभी दिशाओं में समान रूप से ( परिमाण में) संचरित कर दिया जाता है।”
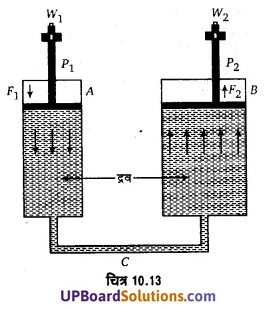
द्रव चालित लिफ्ट (Hydraulic lift)-यह भारी वस्तुओं; जैसे-कार, मोटरगाड़ी, ट्रक आदि को ऊपर उठाने के प्रयोग में लायी जाती है। इसका कार्य सिद्धान्त पास्कल के नियम पर आधारित है।
सिद्धान्त (Principle)– पास्कल के नियम के अनुसार, द्रव के किसी स्थान पर आरोपित दाब अन्य सभी स्थानों पर समान परिमाण में संचरित होता है। अतः कम परिमाण के दाब को अपेक्षाकृत बहुत बड़े क्षेत्रफल पर संचरित करके उस क्षेत्रफल पर (UPBoardSolutions.com) कार्यरत अधिक बल प्राप्त किया जा सकता है। यह तथ्य निम्न प्रकार समझा जा सकता हैं —
उपर्युक्त चित्र 10.13 में A तथा B दो बेलनाकार बर्तन हैं जिनकी अनुप्रस्थ-काट क्रमश: A1 तथा A2 है एवं A2 > A1। इनको परस्पर क्षैतिज नली C द्वारा जोड़ दिया गया है। माना बर्तन A में लगे पिस्टन P1 पर भार W1 रखने पर इस पर लगाया गया बल F1 है।
अत: इसके द्वारा A में भरे द्रव पर आरोपित दाब P = [latex s=2]P=\left( \frac { { F }_{ 1 } }{ { A }_{ 1 } } \right) [/latex]
पास्कल के नियम के अनुसार यही दाब नली C से संचरित होकर बर्तन B में भरे द्रव के प्रत्येक बिन्दु पर संचरित हो जाता है। इसलिए B में लगे पिस्टन P2 पर भी P दाब लगेगा।
अतः इसे पर ऊपर की ओर कार्यरत् बल ।
F2 = P x A2 = (F1/A1 ) x A2
अथवा [latex s=2]{ F }_{ 2 }={ F }_{ 1 }\left( \frac { A_{ 2 } }{ { A }_{ 1 } } \right) [/latex] …(1)
∵ A2 > A1 अत: F2 > F1 अतः A2, क्षेत्रफल A1 से जितना गुना बड़ा होगा पिस्टने P2, पर उतने गुना अधिक बल लगेगा जिससे कि P2 पर रखे भार W2(> W1) को P1 पर बहुत कम बल लगाकर उठाया जा सकता है।
F2/F1 को इस मशीन का यांत्रिक लाभ कहते हैं।

रचना तथा कार्यविधि—इसमें दो खोखले बेलनाकार बर्तन A तथा B होते हैं। A का परिच्छेद क्षेत्रफल A1,B के परिच्छेद क्षेत्रफल A2 से बहुत कम होता है। इन बर्तनों की तली में क्रमश: वाल्व V1 तथा V2, लगे होते हैं। बर्तन A को वाल्व V1 द्वारा तेल के एक टैंक से जोड़ दिया जाता है। इस बर्तन में लगे पिस्टन P1 को ऊपर-नीचे करने के लिए एक लीवर की व्यवस्था होती है। बर्तन B को वाल्व V2, के द्वारा नली T के माध्यम से बर्तन A से जोड़ दिया जाता है तथा इसको वाल्व V3 के द्वारा तेल टैंक से जोड़ दिया जाता है (चित्र 10.14)।
जब पिस्टन P1 को लीवर द्वारा ऊपर उठाया जाता है तो बर्तन A में पिस्टन P1 के नीचे दाब कम हो जाता है। अत: वाल्व V1 द्वारा टैक से तेल बर्तन A में चढ़ जाता है। अब लीवर के द्वारा पिस्टन P1 को नीचे गिरा देते हैं जिससे द्रव का दाब बढ़ जाता है। दाब में यह वृद्धि नली T द्वारा बर्तन B में संचरित हो जाती है जिससे इसमें लगे पिस्टन P2, पर (A2/A1) गुना बड़ा बल कार्य करता है। इसके कारण पिस्टन P2, ऊपर उठता है जिससे कि उस पर रखा हुआ भार (जैसे- मोटरगाड़ी) भी ऊपर उठ जाता है। जब काम पूरा हो जाता है तो वाल्व V3, द्वारा बर्तन B के अतिरिक्त तेल को तेल टैंक में वापस भेज दिया जाता है और पिस्टन P2 नीचे होकर अपनी पूर्वावस्था में आ जाता है।

प्रश्न 2.
किसी 3000 किग्रा द्रव्यमान के वाहन को उठाने के लिए एक हाइड्रॉलिक पम्प का निर्माण किया गया है, जिसके बड़े पिस्टन का क्षेत्रफल 900 सेमी2 है। यदि छोटे पिस्टन का क्षेत्रफल 10 सेमी2 हो तो बताइए इस कार्य के लिए उस पर कितना बल आरोपित करना पड़ेगा?
उत्तर
दिया है, वाहन का द्रव्यमान (m) = 3000 किग्रा
छोटे पिस्टन का क्षेत्रफल, (A1) = 10 सेमी2 = 10 x 10-4 मी2
बड़े पिस्टन का क्षेत्रफल (A2) = 900 सेमी2 = 900 x 10-4 मी2
बड़े पिस्टन के लिए, (F2) = mg = 3000 x 9.8 = 29400 न्यूटन
छोटे पिस्टन के लिए, F1 = ?
पास्कल के नियम से, [latex s=2]\frac { { F }_{ 1 } }{ { A }_{ 1 } } =\frac { { F }_{ 2 } }{ { A }_{ 2 } } [/latex]
छोटे पिस्टन के लिए आरोपित बल,
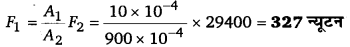
प्रश्न 3.
आदर्श द्रव किसे कहते हैं? सिद्ध कीजिए कि किसी नली में आदर्श द्रव का धारारेखीय प्रवाह होने पर नली के अनुप्रस्थ-परिच्छेद एवं द्रव के वेग का गुणनफल स्थिर रहता है। या आदर्श द्रव के धारा-रेखीय प्रवाह की अविरतता के सिद्धान्त का उल्लेख कीजिए। या आदर्श द्रवों के सांतत्य प्रवाह का समीकरण स्थापित कीजिए।
उत्तर-
आदर्श द्रव-वह द्रव जिसमें
(i) शून्य सम्पीड्यता तथा
(ii) शून्य श्यानता होती है; आदर्श द्रव कहलाता है।

उपपत्ति—मान लीजिए कि एक असम्पीड्य तथा अश्यान द्रव एक असमान अनुप्रस्थ-काट की नली XY में होकर बह रहा है। माना कि नली के X व Y सिरों पर अनुप्रस्थ-काट के क्षेत्रफल क्रमशः A1 व A2 हैं तथा द्रव का वेग ν1 व ν2 है। (UPBoardSolutions.com) माना कि द्रव का घनत्व ρ है। सिरे X से प्रवेश करने वाला द्रव एक सेकण्ड में ν1 दूरी तय करता है। अतः एक सेकण्ड में सिरे X पर क्षेत्रफल A1 से गुजरने वाले द्रव का आयतन = A1 x ν1
∴1 सेकण्ड में सिरे x से गुजरने वाले द्रव का द्रव्यमान = ρ x A1 x ν1
इसी प्रकार, 1 सेकण्ड में सिरे Y से गुजरने वाले द्रव का द्रव्यमान = ρ x A2 x ν2
अब, क्योंकि सिरे X में जो भी द्रव प्रवेश करता है वह दूसरे सिरे Y से बाहर निकल जाता है, उपर्युक्त दोनों द्रव्यमान बराबर हैं,
अर्थात् ρ x A1 x ν1 = ρ x A2 x ν2
अर्थात् A1 x ν1 = A2 x ν2
या। A x ν = नियतांक
स्पष्ट है कि नली में प्रत्येक स्थान पर नली के अनुप्रस्थ-काट के क्षेत्रफल तथा द्रव के वेग का गुणनफल एक नियतांक होता है। उपर्युक्त समीकरण को सांतत्य समीकरण (Equation of continuity) भी कहते हैं।
इस सिद्धान्त को द्रवों के बहने का अविरतता का सिद्धान्त’ भी कहते हैं।
प्रश्न 4.
बरनौली के प्रमेय का उल्लेख कर उसको सिद्ध कीजिए। या बरनौली के प्रमेय के कथन को लिखिए तथा सम्बन्धित समीकरण को स्थापित कीजिए।
उत्तर-
बरनौली की प्रमेय-जब कोई असम्पीड्य तथा अश्यान द्रव (अथवा गैस) एक स्थान से दूसरे स्थान तक धारा-रेखीय प्रवाह में बहता है तो इसके मार्ग के प्रत्येक बिन्दु पर इसके एकांक आयतन की कुल ऊर्जा अर्थात् दाब ऊर्जा, गतिज ऊर्जा तथा स्थितिज ऊर्जा का योग एक नियतांक होता है। अर्थात्

इस प्रकार बरनौली प्रमेय बहते हुए द्रव (अथवा गैस) के लिए ऊर्जा-संरक्षण का सिद्धान्त है।
उपपत्ति-चित्र 10.16 में एक असमान अनुप्रस्थ-काट की नली में एक असम्पीड्य तथा अश्यान द्रव प्रवाहित हो रहा है। द्रव का प्रवाह धारा-रेखीय है। माना पृथ्वी तल से h1, ऊँचाई पर नली की अनुप्रस्थ-काट का क्षेत्रफल A1, द्रव का वेग ν1, व दाब P1 है तथा पृथ्वी तल से h2; ऊँचाई पर नली की अनुप्रस्थ-काट का क्षेत्रफल A2, द्रव का वेग ν2, व दाब P2 है। यहाँ A2 < A1 है। इसलिए । ν1 < ν2 होगा।
अनुप्रस्थ परिच्छेद A1 पर प्रवेश करने वाले द्रव पर P1 x A1 बल कार्य करता है। इस बल के अन्तर्गत द्रवे 1 सेकण्ड में ν1 दूरी तय करता है; अत: 1 सेकण्ड में A1 सिरे पर प्रवेश करने वाले द्रव पर
किया गया कार्य = बेल x दूरी = P1 x A1 x ν1
इसी प्रकार अनुप्रस्थ-परिच्छेद A2, पर निकलने वाला द्रव, बल = P2 x A2, के विरुद्ध कार्य करता है।
तथा 1,सेकण्ड में ν2 दूरी तय करता है।
अतः 1 सेकण्ड में A2 सिरे से निकलने वाले द्रव द्वारा किया गया कार्य
= P2 x A2 x ν2
द्रव पर किया गया नेट कार्य = P1 x A1 x ν1 – P2 x A2 x ν2 …(1)
परन्तु A1 x ν1 तथा A2 x ν2 , क्रमशः एक (UPBoardSolutions.com) सिरे से प्रवेश करने वाले व दूसरे सिरे से निकलने वाले द्रव का आयतन है जो आपस में बराबर होंगे।
अतः A1 ν1 = A2 ν2 = m/ρ
जहाँ एक सेकण्ड में प्रवेश करने वाले द्रव का द्रव्यमान m तथा द्रव का घनत्व ρ है।
द्रव पर किया गया नेट कार्य = (P1 – P2)m/ρ


अत: किसी द्रव के क्षैतिज व धारा-रेखीय प्रवाह के लिए प्रत्येक बिन्दु पर दाब तथा द्रवे के एकांक आयतन की गतिज ऊर्जा का योग एक नियतांक होता है।
बरनौली प्रमेय समीकरण से यह स्पष्ट है कि किसी प्रवाहित द्रव (अथवा गैस) में जिस स्थान पर द्रव का वेग कम होता है, वहाँ दाब अधिक हो जाता है तथा जिस स्थान पर वेग अधिक होता है, वहाँ दाब कम हो जाता है। यदि हम द्रव को किसी ऐसी नली में प्रवाहित (UPBoardSolutions.com) करें जिसके बीच का भाग संकीर्ण हो, तो इस भाग में द्रव का वेग सबसे अधिक होगा तथा दाब सबसे कम होगा। प्रवाहित द्रव के दाब-शीर्ष, वेर्ग-शीर्ष तथा गुरुत्वीय-शीर्ष- बरनौली की समीकरण (6) को ρg से भाग देने पर,

इसमें P/ρg को ‘दाब-शीर्ष’ (pressure head), ν²/2g को ‘वेग-शीर्ष’ (velocity head) तथा h को ‘गुरुत्वीय-शीर्ष’ (gravitational head) कहते हैं। इन तीनों की विमाएँ ऊँचाई की विमा [L] के समतुल्य हैं। इनके योग को ‘सम्पूर्ण शीर्ष’ (total head) कहते हैं। अत: बरनौली प्रमेय को निम्न प्रकार भी कहा जा सकता है —
आदर्श द्रव के धारा-रेखा प्रवाह में द्रव के किसी बिन्दु पर दाब-शीर्ष, वेग-शीर्ष तथा गुरुत्वीय-शीर्ष का योग सदैव नियत रहता है। यह यांत्रिक ऊर्जा संरक्षण को व्यक्त करती है।

प्रश्न 5.
बरनौली के प्रमेय के आधार पर कणित्र की कार्यविधि समझाइए।
उत्तर-
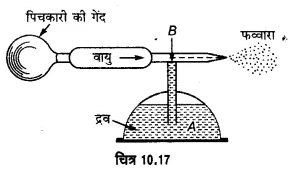
कणित्र (Atomizer)-यह रंग अथवा सुगन्धित द्रव को छिड़कने, कार, स्कूटर पर पेण्ट करने, नाइयों द्वारा सिर पर जल फुहारने, डॉक्टरों द्वारा नाक, कान को धोने व गले में दवाई को छिड़कने के काम आता है। इसमें एक साधारण पिचकारी होती है, जिसके मुख पर एक केशनली (capillary tube) लगा दी जाती है। केशनली का निचला सिरा बर्तन में भरे द्रव में डूबा रहता है। जब पिचकारी की गेंद को दबाते हैं, तो वायु अत्यधिक वेग से निकलती है, जिससे पिचकारी के मुँह पर दाब गतिज ऊर्जा बढ़ने से (बरनौली प्रमेय के आधार पर) घट जाता है। दाब के घटने से केशिका नली में द्रव चढ़कर पिचकारी के मुँह तक आ जाता है और दोबारा पिचकारी की गेंद को दबाने पर यह वायु के साथ मिलकर फव्वारे के रूप में बाहर निकलता है।।
प्रश्न. 6.
आदर्श द्रवों के प्रवाह से सम्बन्धित बरनौली की प्रमेय लिखिए। जल से भरे एक बर्तन की दीवार में बने एक छिद्र से जल का स्वतन्त्र तल h ऊँचाई पर है। छिद्र से निकलने वाले जल के बहिःस्राव वेग के लिए व्यंजक स्थापित कीजिए।
उत्तर-
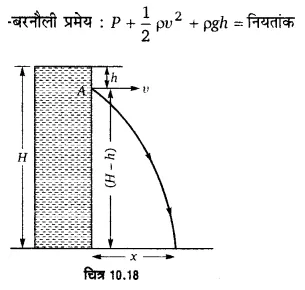
बहिःस्राव वेग के लिए व्यंजक–चित्र 10.18 में एक बर्तन दर्शाया गया है जिसमें H ऊँचाई तक द्रव भरा है। माना द्रव का घनत्व p है। बर्तन द्रव के स्वतन्त्र तल से h गहराई पर एक छिद्र A है। माना A से निकलने वाले द्रव का बहि:स्राव वेग » है। द्रव के स्वतन्त्र तल पर गतिज ऊर्जा शून्य है, केवल स्थितिज ऊर्जा है। परन्तु A से निकलने वाले द्रव में स्थितिज तथा गतिज दोनों ही प्रकार की ऊर्जाएँ हैं। बरनौली प्रमेय के अनुसार, द्रव के स्वतन्त्र तल पर तथा छिद्र A पर द्रव के एकांक आयतन की कुल ऊर्जा अर्थात् दाब ऊर्जा,
गतिज ऊर्जा तथा स्थितिज ऊर्जाओं का योग बराबर होना चाहिए। । यदि वायुमण्डलीय दाब P हो, तो


अत: यदि छिद्र बर्तन की दीवार के ठीक बीच में है तो द्रव की धार सबसे अधिक दूर (बर्तन में द्रव की ऊँचाई के बराबर दूरी पर) गिरती है।

प्रश्न 7.
चित्र 10.19 के अनुसार एक क्षैतिज नलिका में जल प्रवाहित होता है। बिन्दु A व B के मध्य 5 मिमी पारे का दाब परिवर्तन है जहाँ अनुप्रस्थ परिच्छेद 20 सेमी2 तथा 10 सेमी2 है। नलिका में जल प्रवाह की दर ज्ञात कीजिए। (पारे का घनत्व = 1.36 x 103 किग्रा/मी3, जल का घनत्व = 1.0 x 103 किग्रा/मी)

हल-
दिया है, A1 = 20 सेमी2 = 20 x 10-4 मी2
A2 = 10 सेमी2 = 10 x 10-4 मी2
प्रश्नानुसार, दाब में परिवर्तन P1 – P2 = 5 मिमी
पारा स्तम्भ पर दाब = hdg = 5 x 10-3 x 13.6 x 103 x 9.8
= 666.4 न्यूटन/मी2
अविरतता के सिद्धान्त से,

प्रश्न 8.
एक क्षैतिज पाइप में जल बहता है, जिसका एक सिरा वाल्व द्वारा बन्द है और पाइप में लगे दाबमापी का पाठ्यांक 5.5 x 105 न्यूटन/मी2 है। पाइप में लगे वाल्व को खोल देने पर दाबमापी का पाठ्यांक 10 x 105 न्यूटन/मी2 रह जाता है। पाइप में प्रवाहित जल के वेग की गणना कीजिए।
उत्तर-
दिया है, जल का घनत्व, (ρ) = 1.0 x 103 किग्रा/मी3
बन्द सिरे के कारण दाबमापी का पाठ्यांक (P1) = 5.5 x 105 न्यूटन/मी2
न्यूटन/मी खुले सिरे के कारण दाबमापी का पाठ्यांक (P) = 1.0 x 105 न्यूटन/मी2
बरनौली प्रमेय से,
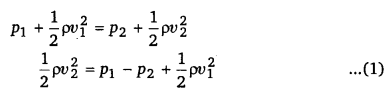
चूंकि प्रारम्भिक अवस्था में वाल्व बन्द होता है इसलिए ν1 = 0 होगा।
अत: समीकरण (1) से
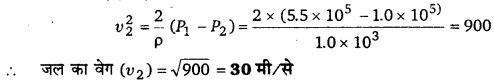

प्रश्न 9.
एक छोटा गोला जिसका द्रव्यमान M व घनत्व d1 है। एक ग्लिसरीन भरे पात्र में डाला जाता है। कुछ समय पश्चात् गोले का वेग स्थिर हो जाता है। यदि ग्लिसरीन का घनत्व d2 है, तो गोले पर लगने वाले श्यान बल की गणना कीजिए।
उत्तर-
यहाँ गोले का द्रव्यमान = M, गोले का घनत्व = d1
ग्लिसरीन का घनत्व = d2

प्रश्न 10.
पृष्ठ-तनाव तथा केशिकात्व की परिभाषा दीजिए। इसका एस० आई० मात्रक बताइए। काँच की केशनली में चढे द्रव-स्तम्भ की ऊँचाई, त्रिज्या तथा द्रव के पृष्ठ-तनाव में सम्बन्ध का सूत्र स्थापित कीजिए।
उत्तर-
पृष्ठ-तनाव (Surface tension)-प्रत्येक द्रव में मुक्त पृष्ठ पर एक तनाव बल कार्य करता है; जिसके कारण उसका स्वतन्त्र पृष्ठ एक तनी झिल्ली की भाँति व्यवहार करता है। यदि इस मुक्त पृष्ठ में चित्र 10.20 की भाँति किसी भी दिशा में एक सरल रेखा AB (UPBoardSolutions.com) की कल्पना की जाये तो रेखा के किसी भी ओर का पृष्ठ रेखा के अपने विपरीत ओर के पृष्ठ पर कर्षण (pulling) बल F लगाता है। यह बल पृष्ठ के तल में तथा इस रेखा के लम्बवत् कार्य करता है। इस रेखा AB की एकांक लम्बाई पर कार्य करने वाले बल का परिमाण ही द्रव के पृष्ठ-तनाव की माप है।
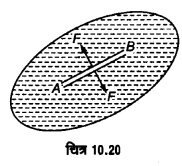
यदि रेखा AB की लम्बाई । हो और इसके किसी ओर भी कार्य करने वाला सम्पूर्ण बल F हो, तो पृष्ठ तनाव T = [latex s=2]\frac { F }{ l }[/latex].
यदि l = 1, तो T = F
अत: किस द्रव का पृष्ठ-तनाव वह बल है जो द्रव के पृष्ठ पर खींची गयी काल्पनिक रेखा की एकांक लम्बाई पर पृष्ठ के तल में तथा कल्पित रेखा के लम्बवत् कार्य करता है।
पृष्ठ-तनाव का एस० आई० मात्रक न्यूटन/मीटर है।
केशिकात्व Capillarity द्रव का वह गुण-धर्म जिसके कारण किसी केशनली को इसमें खड़ा करने पर यह नली के बाहर द्रव के तल की तुलना में नली में ऊपर चढ़ता है या नीचे उतरता है, केशिकात्व कहलाता है।
काँच की केशनली में चढ़े द्रव-स्तम्भ की ऊँचाई, त्रिज्या तथा द्रव के पृष्ठ-तनाव में सम्बन्ध चित्र 10.21 (a) में जल के एक बीकर में काँच की केशनली खड़ी की गई है जिसमें जल के तल से h ऊँचाई तक जल चढ़ता है। माना कि जल की पृष्ठ-तनाव T है। नली में जल का अवतल-पृष्ठ AEB है। इसकी परिधि 2πr नली की दीवारों के सम्पर्क में है, जहाँ r केशनली की त्रिज्या है। इसकी एकांक लम्बाई पर जल के पृष्ठ-तनाव के कारण बल T नली की दीवार से θ कोण पर जल के अन्दर की ओर लगता है, θ जल-काँच के लिए स्पर्श कोण है।
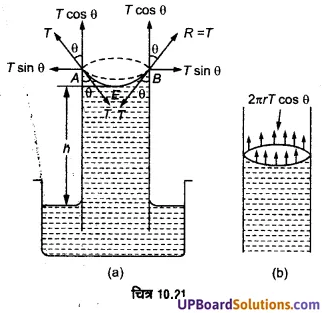
नली की दीवार भी प्रतिक्रिया के कारण उतना ही बल T जल के वक्र पृष्ठ की परिधि पर बाहर की ओर लगाती है। इस बल को ऊर्ध्व और क्षैतिज दो घटेकों, T cos θ और T sin θ में वियोजित करते हैं। T cos θ ऊर्ध्व दिशा में परिधि 2πr की प्रत्येक एकांक लम्बाई (UPBoardSolutions.com) पर ऊपर की ओर कार्य करता है; अत: प्रतिक्रिया बल का मान 2πr x T cos θ के बराबर होता है जो नली में चढ़े जल के स्तम्भ के भार को साधता है। चूंकि T sin θ परिधि पर बाहर की ओर लगता है, अतः पूरी परिधि के लिए उनका परिणामी बेल शून्य होगा। यदि जल का घनत्व ρ हो, तो जल के स्तम्भ का भार = πr²h x ρ x g
सन्तुलन की अवस्था में । 2πr x T cos θ =πr²h x ρ x g
[latex s=2]T=\frac { rhg\rho }{ 2cos\theta } [/latex]
उपर्युक्त सूत्र से स्पष्ट है कि यदि जल काँच का स्पर्श-कोण θ ज्ञात हो, तो h तथा r के मान ज्ञात करके जल के पृष्ठ-तनाव T की गणना की जा सकती है।
शुद्ध जल एवं साफ काँच के लिए स्पर्श कोण θ लगभग शून्य है; अत: cos θ = 1, इस प्रकार
[latex s=2]T=\frac { rhg\rho }{ 2 } [/latex]

प्रश्न 11.
काँच की नली में द्रव के मुक्त पृष्ठ की आकृति की व्याख्या कीजिए। द्रव के वक्र पृष्ठ के दो पाश्र्वो के बीच दाबान्तर क्यों होता है?
उत्तर-
काँच की नली में द्रव के मुक्त पृष्ठ की आकृति जब कोई द्रव किसी ठोस के स्पर्श में आता है तो स्पर्श-तल के समीप द्रव का पृष्ठ वक्रीय हो जाता है। वक्रता की प्रकृति द्रव के अणुओं के बीच संसंजक-बल तथा द्रव व ठोस के अणुओं के बीच आसंजक-बल के सापेक्ष परिणामों पर निर्भर करती है।

चित्र 10.22 (a) में जल एक काँच की नली की दीवार के सम्पर्क में दिखाया गया है। माना कि काँच के समीप द्रव के मुक्त पृष्ठ पर एक अणु A है तथा इस अणु पर दो आकर्षण-बल कार्य करते हैं।
(i) परिणामी आसंजक-बल P, जो A के समीप वाले ठोस के अणुओं के आकर्षण के कारण A पर कार्य करता है। इसकी दिशा ठोस के पृष्ठ के लम्बवत् है।।
(ii) परिणामी संसंजक-बल Q, जो A के समीप द्रव के अन्य अणुओं के आकर्षण के कारण A पर द्रव के अन्दर की ओर एक दिशा में कार्य करता है।
जल व काँच के अणुओं के बीच लगेने वाला आसंजक-बल, जल के ही अणुओं के बीच परस्पर लगने वाले संसंजक-बल से बड़ा होता है। अत: बेल P, बल Q से बड़ा होगा। चित्र 3.7(a) से स्पष्ट है कि इन दोनों बलों का परिणामी बल R, जल से बाहर की ओर को होगा।
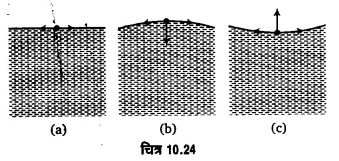
चित्र 10.22 (b) में पारे को काँच की नली की दीवार के सम्पर्क में दिखाया गया है। पारे के अणुओं के बीच संसंजक-बल, पारे व काँच के अणुओं के बीच लगने वाले आसंजक-बल से कहीं अधिक बड़ा होता है। अत: इस दशा में पारे के मुक्त पृष्ठ पर अणु A पर बल Q, बल P से बड़ा होगा तथा इनका परिणामी बल R पारे के भीतर की ओर को होगा। परिणामी बल R, जल अथवा पारे के मुक्त पृष्ठ के सभी अणुओं पर कार्य करता है। दीवार से दूर स्थित अणुओं के लिए आसंजक-बल P घटता जाता है तथा संसंजक-बल Q अधिकाधिक ऊध्वधर होता जाता है। अतः परिणामी बल R भी अधिकाधिक उध्वधर होता जाता है। मुक्त पृष्ठ के बीच वाले भाग में P लगभग शून्य हो जाता है तथा Q ऊर्ध्वाधर हो जाता है। अतः परिणामी बल बिल्कुल ऊर्ध्वाधर हो जाता है। [चित्र 10.23 (a), (b)]

यदि द्रव का मुक्त पृष्ठ साम्यावस्था में है तो पृष्ठ के किसी अणु पर कार्य करने वाला परिणामी बल पृष्ठ के लम्बवत् होना चाहिये। अत: द्रव का पृष्ठ प्रत्येक स्थान पर परिणामी बल के लम्बवत् हो जाता है। यही कारण है कि काँच की नली में जल का मुक्त पृष्ठ अवतल आकृति धारण कर लेता है तथा पारे का मुक्त पृष्ठ उत्तल आकृति। प्रत्येक दशा में बीच में परिणामी बल ऊर्ध्वाधर होता है, अतः बीच में मुक्त पृष्ठ क्षैतिज होता है [चित्र 10.23 (a), (b)]।
द्रव के वक्र पृष्ठ के पाश्व के बीच दाबान्तर
किसी द्रव के पृष्ठ में स्थित कोई अणु, पृष्ठ के दूसरे अणुओं द्वारा सभी दिशाओं में आकर्षित होता है। यदि द्रव का पृष्ठ समतल हो [चित्र 10.24 (a)] तो अणु सभी दिशाओं में समान रूप से आकर्षित होता है। अतः अणु पर पृष्ठ-तनाव के कारण परिणामी बल शून्य होता है। परन्तु यदि द्रव का पृष्ठ उत्तल हो तो प्रत्येक अणु पर लगने वाले आकर्षण-बलों को एक परिणामी घटक पृष्ठ के लम्बवत् अन्दर की ओर होता है [चित्र 10.24 (b)]। इसी प्रकार, यदि द्रव का पृष्ठ अवतल हो तो प्रत्येक अणु पर पृष्ठ-तनाव के कारण एक परिणामी बल पृष्ठ के लम्बवत् बाहर की ओर को लगता है [चित्र 10.24 (c)]। अत: वक्र पृष्ठ के सन्तुलन के लिये, पृष्ठ के दोनों पार्यों के बीच दाबान्तर होना चाहिये जिससे कि आधिक्य-दाब (excess of pressure) के कारण लगने वाला बल पृष्ठ-तनाव के कारण उत्पन्न परिणामी बल को सन्तुलित कर सके। स्पष्ट है कि पृष्ठ के अवतल पाश्र्व पर दाब उत्तल पाश्र्व की अपेक्षा अधिक होना चाहिये। दाबों पर यह अन्तर 2T/R के बराबर होता है, जहाँ T द्रव का पृष्ठ-तनाव है तथा R पृष्ठ की त्रिज्या है।

प्रश्न 12.
किसी साबुन के बुलबुले के भीतर आधिक्य-दाब के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
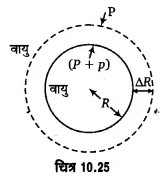
साबुन के घोल के बुलबुले के भीतर आधिक्य-दाब माना कि त्रिज्या R का एक बुलबुला, पृष्ठ-तनाव T के साबुन के घोल से बना है (चित्र 10.25)। माना बुलबुले के बाहर दाब P है तथा भीतर P + p है। इस प्रकार बुलबुले के भीतर आधिक्य-दाब p है। माना कि यह आधिक्य-दाब बुलबुले के पृष्ठ को अभिलम्बवत् बाहर की ओर दूरी ∆R धकेलता है, जहाँ ∆R इतना सूक्ष्म है कि बुलबुले के भीतर दाब अपरिवर्तित रहता है। अतः आधिक्य-दाब के कारण उत्पन्न बल द्वारा किया गया कार्य
w = बल x विस्थापन ।
= (आधिक्य-दाब x क्षेत्रफल) x विस्थापन
= (p x 4πR²) x ∆R …(1)
साबुन के घोल के बुलबुले के दो पृष्ठ वायु के सम्पर्क में हैं, एक बुलबुले के भीतर तथा एक बुलबुले के बाहर। अतः उपरोक्त विस्थापन के कारण बुलबुले के पृष्ठ-क्षेत्रफल में कुल वृद्धि
∆A = 2[4π(R + ∆R)²-4πR²]
= 8π[R + (∆R)²+ 2R∆R – R²]
= 16πR(∆R)
अल्प पद (∆R)² को छोड़ने पर
अतः ‘पृष्ठ ऊर्जा में वृद्धि = पृष्ठ-क्षेत्रफल में वृद्धि x पृष्ठ तनाव
= 16πR(∆R) x T …(2)
ऊर्जा में वृद्धि, आधिक्य-दाब के कारण किये गये कार्य से होती है।
अत: समीकरण (1) तथा (2) को बराबर रखने पर,
(p x 4πR²) x ∆R= 16 πR(∆R)xT
अथवा
[latex s=2]p=\frac { 4T }{ R } [/latex]
प्रश्न 13.
द्रव की बूंद के भीतर आधिक्य-दाब का व्यंजक निगमित कीजिए।
उत्तर-
द्रव की बूंद के भीतर आधिक्य-दाब माना कि द्रव की एक बूंद की त्रिज्या R है तथा द्रव का पृष्ठ-तनाव T है (चित्र 10.26)। बूंद के पृष्ठ पर स्थित द्रव के अणुओं पर, पृष्ठ-तनाव के कारण, एक परिणामी बल पृष्ठ के अभिलम्बवत् ‘भीतर की ओर को’ कार्यरत् है। अत: बूंद के (UPBoardSolutions.com) भीतर दाब, बाह्य दाब से अधिक होना चाहिए। बूंद के भीतर यह आधिक्य-दाब बाहर की
ओर को एक बल लगाता है जो पृष्ठ तनाव के बल को सन्तुलित करता है तथा बूंद साम्यावस्था में बनी रहती है।
माना कि बूंद के बाहर दाब P है तथा भीतर P+p है। इस प्रकार, बूंद के भीतर आधिक्य-दाब p है। माना कि यह आधिक्य-दाब बूंद के पृष्ठ को अभिलम्बवत् बाहर की ओर दूरी ∆R तक धकेलता है, जहाँ ∆R इतना सूक्ष्म है कि बूंद के भीतर दाब अपरिवर्तित रहता है। आधिक्य-दाब p के कारण उत्पन्न बल द्वारा किया गया यान्त्रिक कार्य
w = बल x विस्थापन
= (आधिक्य दाब x क्षेत्रफल) x विस्थापन

We hope the UP Board Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 10 Mechanical Properties Of Fluids, drop a comment below and we will get back to you at the earliest.
![]()







![]()
















![]()
![]()
















![]()
![]()
![]()



![]()
![]()

![]()












![]()

![]()


![]()
![]()
![]()

![]()
![]()

![]()
![]()
![]()
![]()




![]()







![]()









![]()





![]()






![]()
![]()








![]()

![]()



![]()
![]()



![]()










![]()



![]()



![]()