Prasanna

UP Board Solutions for Class 12 Maths Chapter 4 Determinants (सारणिक) are part of UP Board Solutions for Class 12 Maths. Here we have given UP Board Solutions for Class 12 Maths Chapter 4 Determinants (सारणिक)

Board	UP Board
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 4
Chapter Name	Determinants
Exercise	Ex 4.1, Ex 4.2, Ex 4.3, Ex 4.4, Ex 4.5, Ex 4.6
Number of Questions Solved	68
Category	UP Board Solutions

UP Board Solutions for Class 12 Maths Chapter 4 Determinants

प्रश्नावली 4.1

प्रश्न 1.
मान ज्ञात कीजिए ।

हल-

प्रश्न 2.
मान ज्ञात कीजिए

हल-
(i)

(ii)

= (x² – x + 1)(x + 1) – (x + 1) (x – 1)
= (x + 1)[x² – x + 1 – x + 1]
= (x + 1)(x² – 2x + 2)
= x³ – 2x² + 2x + x² – 2x + 2
= x³ – x² + 2

प्रश्न 3.
यदि [latex s=2]A=\begin{bmatrix} 1 & 2 \\ 4 & 2 \end{bmatrix}[/latex] तो दिखाइए कि |2A| = 4|A|
हल-
|A|= 1 x 2 – 4 x 2 = -6

प्रश्न 4.
यदि [latex s=2]A=\left[ \begin{matrix} 1 & 0 & 1 \\ 0 & 1 & 2 \\ 0 & 0 & 4 \end{matrix} \right] [/latex] हो तो दिखाइए कि |3A| = 27|A|
हल-
|A| = 1.(1 x 4 – 0 x 2) – 0 + 0 = 4

∴ बायाँ पक्ष = |3A| = 3 (3 x 12 – 0 x 6) – 0 + 0
= 108
= 27 x 4
= 27|A] = दायाँ पक्ष

प्रश्न 5.
निम्नलिखित सारणिकों के मान ज्ञात कीजिए

हल-
(i) द्वितीय पंक्ति के सापेक्ष प्रसार करने पर,

प्रश्न 6.
यदि [latex s=2]A=\left[ \begin{matrix} 1 & 1 & -2 \\ 2 & 1 & -3 \\ 5 & 4 & -9 \end{matrix} \right] [/latex], तो |A| ज्ञात कीजिए।
हल-
प्रथम पंक्ति के सापेक्ष प्रसार करने पर,

= [1 x (-9) – 4 x (-3)] – (1) [2x(-9) – 5x(-3)] + (-2)[2×4 – 5×1]
= 3 + 3 – 6
= 0

प्रश्न 7.
x के मान ज्ञात कीजिए।

हल-

प्रश्न 8.
यदि

हो तो x बराबर है
(A) 6
(B) ±6
(C) -6
(D) 0
हल-
दिया है,

दोनों ओर सारणिक का विस्तार करने पर,
x × x – 2 × 18 = 6 × 6 – 2 × 18
x² – 36 = 36 – 36
x² – 36 = 0
⇒ x² = 36
x = ±6
अतः विकल्प (B) सही है।

प्रश्नावली 4.2

बिना प्रसरण किए और सारणिकों के गुणधर्मों का प्रयोग करके निम्नलिखित प्रश्न 1 से 5 को सिद्ध कीजिए

प्रश्न 1.

हल-
बायाँ पक्ष = ∆

∵ यहाँ दो स्तम्भ (C1 = C3) बराबर है। इति सिद्धम्

प्रश्न 2.

हल-
माना बायाँ पक्ष = ∆

∵ यहाँ पहले स्तम्भ C1 के सभी अवयव शून्य हैं। इति सिद्धम्

प्रश्न 3.

हल-
माना बायाँ पक्ष =

∵ यहाँ तीसरे स्तम्भ C3 के सभी अवयव शून्य हैं। इति सिद्धम्

प्रश्न 4.

हल-

∵ यहाँ प्रथम स्तम्भ तथा तृतीय स्तम्भ (C1 = C3) बराबर हैं। इति सिद्धम्

प्रश्न 5.

हल-
माना


R2 और R3 में से -1 उभयनिष्ठ लेने पर इति सिद्धम्

सारणिकों के गुणधर्मों का प्रयोग करके प्रश्न 6 से 14 तक को सिद्ध कीजिए

प्रश्न 6.

हल-

प्रश्न 7.

हल-

प्रश्न 8.

हल-

प्रश्न 9.

हल-

प्रश्न 10.

हल-

प्रश्न 11.

हल-
(i)

प्रश्न 12.

हल-

प्रश्न 13.

हल-

प्रश्न 14.

हल-

प्रश्न 15.
यदि A एक 3×3 कोटि का वर्ग आव्यूह है तो |kA| का मान होगा
(A) k[A]
(B) k² |A|
(C) k³ |A|
(D) 3k|A |
हल –
| kA| को |A| के पद में व्यक्त करने पर

प्रश्न 16.
निम्नलिखित में से कौन-सा कथन सही है?
(A) सारणिक एक वर्ग आव्यूह है।
(B) सारणिक एक आव्यूह से सम्बद्ध एक संख्या है।
(C) सारणिक एक वर्ग आव्यूह से सम्बद्ध एक संख्या है।
(D) इनमें से कोई नहीं।
हल-
हम जानते हैं कि प्रत्येक n क्रम के वर्ग आव्यूह A = [a_ij] जहाँ a_ij = A का (ij) वा अवयव है, को किसी व्यंजक या संख्या के साथ संबद्ध किया जा सकता है जिसे सारणिक कहते हैं।
अतः विकल्प (C) सही है।

प्रश्नावली 4.3

प्रश्न 1.
दिए गए शीर्ष बिन्दुओं वाले त्रिभुजों का क्षेत्रफल ज्ञात कीजिए
(i) (1, 0), (6, 0), 4, 3)
(ii) (2, 7), (1, 1), (10, 8)
(iii) (-2, -3), (3, 2), (-1, – 8)
हल-
शीर्ष बिन्दुओं (x₁, y₁), (x₂, y₂), (x₃, y₃) से होकर जाने वाले त्रिभुज का क्षेत्रफल

प्रश्न 2.
दर्शाइए कि बिन्दु A(a, b + c), B (b, c + a) और c(c, a + b) संरेख हैं।
हल-
ज्ञात है, त्रिभुज के शीर्ष A (a, b + c), B(b, c + a) और C (c, a + b)

प्रश्न 3.
प्रत्येक में k का मान ज्ञात कीजिए यदि त्रिभुजों का क्षेत्रफल 4 वर्ग इकाई है। जहाँ शीर्ष बिन्दु निम्नलिखित हैं।
(i) (k, 0), 4, 0), (0, 2)
(ii) (-2, 0), (0, 4), (0, k)
हल-

प्रश्न 4.
(i) सारणिकों का प्रयोग करके (1, 2) और (3, 6) को मिलाने वाली रेखा का समीकरण ज्ञात कीजिए।
(ii) सारणिकों का प्रयोग करके (3, 1) और (9, 3) को मिलाने वाली रेखा को समीकरण ज्ञात कीजिए।
हल-
(i) माना कोई बिन्दु (x, y) है।
इसलिए त्रिभुज के शीर्ष (x, y), (1, 2), (3,6) होंगे।

(ii) माना बिन्दुओं A(3, 1) और B(9, 3) को मिलाने वाली रेखा पर बिन्दु P(x, y) है। तब बिन्दु A, P और B संरेख हैं।
∴ क्षेत्रफल (∆APB) = 0

प्रश्न 5.
यदि शीर्ष (2,-6), (5, 4) और (k, 4) वाले त्रिभुज का क्षेत्रफल 35 वर्ग इकाई हो तो k का मान है|
(a) 12
(b) -2
(c) -12,-2
(d) 12,-2
हल-
दिया है, त्रिभुज के शीर्ष (2, -6), (5, 4) तथा (k, 4)

धनात्मक चिह्न लेने पर, 7 = 5 – k ⇒ k = 5 – 7 = – 2
ऋणात्मक चिह्न लेने पर, -7 = 5 – k ⇒ – 12 = – k ⇒ k = 12
अतः k = 12, -2
अत: विकल्प (d) सही है।

प्रश्नावली 4.4

निम्नलिखित सारणिकों के अवयवों के उपसारणिक एवं सहखण्ड लिखिए।

प्रश्न 1.
निम्नलिखित सारणिकों के अवयवों के उपसारणिक एवं सहखण्ड ज्ञात कीजिए

हल-
(i) उपसारणिक M₁₁ = 3, M₁₂ = 0, M₂₁ = -4, M₂₂ = 2
तथा सहखण्ड A₁₁ = 3, A₁₂ = 0, A₂₁ = -(-4) = 4, A₂₂ = 2
(ii) उपसारणिक M₁₁ =d, M₁₂ = b, M₂₁ = c, M₂₂ = a
तथा सहखण्ड A₁₁ = d, A₁₂ = -b, A₂₁ = -c A₂₂ = a

प्रश्न 2.
निम्नलिखित सारणिकों के अवयवों के उपसारणिक एवं सहखण्ड ज्ञात कीजिए

हल-

प्रश्न 3.
दूसरी पंक्ति के अवयवों के सहखण्डों का प्रयोग करके

का मान ज्ञात कीजिए।
हल-
दूसरी पंक्ति के सहखण्ड इस प्रकार होंगे

प्रश्न 4
तीसरे स्तम्भ के अवयवों के सहखण्डों का प्रयोग करके

का मान ज्ञात कीजिए।
हल-
तीसरे स्तम्भ के सहखण्ड इस प्रकार होंगे

∆ = a₁₃ A₁₃ + a₂₃ A₂₃ + a₃₃ A₃₃
= yz(z – y) + zx(x – z) + xy (y – x)
= yz² – y²z + zx² – z²x + xy² – x²y
= zx² – x²y + xy² – z²x + yz² – y²z
= x²(z – y) + x(y – z)(y + z) + yz(z – y)
= (z – y)[x² – x(y + z) + yz]
= (z – y)[x² – xy – xz + yz]
= (z – y)[x(x – y) – z(x – y)]
= (z – y)(x – y)(x – z)
= (x – y)(y – z)(z – x)

प्रश्न 5
यदि

और a_ij का सहखण्ड A_ij हो तो Δ का मान निम्नलिखित रूप में व्यक्त किया जाता है–
(a) a₁₁ A₃₁ + a₁₂ A₃₂ + a₁₃ A₃₃
(b) a₁₁ A₁₁ + a₁₂ A₂₁ + a₁₃ A₃₁
(c) a₂₁ A₁₁ + a₂₂ A₁₂ + a₂₃ A₁₃
(d) a₁₁ A₁₁ + a₂₁ A₂₁ + a₃₁ A₃₁
हल-
∆ = किसी पंक्ति अथवा स्तम्भ के अवयवों तथा उनके संगत महखण्डों के गुणन का योग
C₁ स्तम्भ के अवयव (a₁₁, a₂₁, a₃₁)
इनके सहखण्ड A₁₁, A₂₁, A₃₁
⇒ ∆ = a₁₁ A₁₁ + a₂₁ A₂₁ + a₃₁ A₃₁
अत: विकल्प (d) सही है।

प्रश्नावली 4.5

प्रश्न 1 और 2 में प्रत्येक आव्यूह का सहखण्डज (adjoint) ज्ञात कीजिए।

प्रश्न 1.

हल-

प्रश्न 2.

हल-

प्रश्न 3 और 4 में सत्यापित कीजिए कि A (adj A) = (adj A). A = |A|.I है।

प्रश्न 3.

हल-

प्रश्न 4.

हल-

प्रश्न 5 से 11 में दिए गए प्रत्येक आव्यूहों के व्युत्क्रम (जिनका अस्तित्व हो ) ज्ञात कीजिए।

प्रश्न 5.

हल-

प्रश्न 6.

हल-

प्रश्न 7.

हल-

प्रश्न 8.

हल-

प्रश्न 9.

हल-

प्रश्न 10.

हल-

प्रश्न 11.

हल-

प्रश्न 12.

हल-

प्रश्न 13.
यदि [latex s=2]A=\begin{bmatrix} 3 & 1 \\ -1 & 2 \end{bmatrix}[/latex] है तो दर्शाइए कि A² – 5A + 7I = 0 है। इसकी सहायता से A^-1 ज्ञात कीजिए।
हल-

प्रश्न 14.
आव्यू [latex s=2]A=\begin{bmatrix} 3 & 2 \\ 1 & 1 \end{bmatrix}[/latex] के लिए a और b ऐसी संख्याएँ ज्ञात कीजिए ताकि A² + aA + bI = 0 है।
हल-
प्रश्नानुसार,
A² + aA + bI = 0

प्रश्न 15.

हल-

प्रश्न 16.

हल-

प्रश्न 17.
यदि A, 3×3 कोटि का आव्यूह है तो |adj A| का मान है|
(a) |A|
(b) |A|²
(c) |A|³
(d) 3|A|
हल-
चूँकि हम जानते हैं कि |adj A| = |A|^n-1 यहाँ n = 3
∴ |adj A| = |A|²
अत: विकल्प (b) सही है।

प्रश्न 18.
यदि A कोटि 2 को व्युत्क्रमणीय आव्यूह है तो det (A^-1) बराबर है
(a) det (A)
(b) [latex s=2]\frac { 1 }{ det(A) }[/latex]
(c) 1
(d) 0
हल-

प्रश्नावली 4.6

निम्नलिखित प्रश्नों 1 से 6 तक दी गई समीकरण निकायों का संगत अथवा असंगत के रूप में वर्गीकरण कीजिए।

प्रश्न 1
x + 2y = 2
2x + 3y = 3
हल-

प्रश्न 2
2x – y = 5
x + y = 4
हल-

प्रश्न 3
x + 3y = 5
2x + 6y = 8
हल-

प्रश्न 4.
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
हल-

प्रश्न 5
3x – y – 2z = 2
2y – z = – 1
3x – 5y = 3
हल-

प्रश्न 6
5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = – 1
हल-

निम्नलिखित प्रश्न 7 से 14 तक प्रत्येक समीकरण निकाय को आव्यूह विधि से हल कीजिए।

प्रश्न 7.
5x + 2y = 4
7x + 3y = 5
हल-
दिया हुआ समीकरण निकाय
5x + 2y = 4
7x + 3y = 5

प्रश्न 8.
2x – y = – 2
3x + 4y = 3
हल-
दिया हुआ समीकरण निकाय
2x – y = – 2
3x + 4y = 3
समीकरण निकाय AX = B के रूप में लिखा जा सकता है अत: x = A^-1B

प्रश्न 9.
4x – 3y = 3
3x – 5y = 7
हल-

प्रश्न 10.
5x + 2y = 3
3x + 2y = 5
हल-

प्रश्न 11.
2x + y + z = 1
x – 2y – z = [latex]\frac { 3 }{ 2 }[/latex]
3y – 5z = 9
हल-

प्रश्न 12.
x – y + 2 = 4
2x + y – 3z = 0
x + y + z = 2
हल-
दिया हुआ समीकरण निकाय
x – y + 2 = 4
2x + y – 3z = 0
x+ y + z = 2
समीकरण निकाय AX = B के रूप में लिखा जा सकता है अतः x = A^-1B

प्रश्न 13.
2x + 3y + 3z = 5
x – 2y + z = – 4
3x – y – 2z = 3
हल-

प्रश्न 14.
x – y + 2z = 7
3x + 4y – 5z = – 5
2x – y + 3z = 12
हल-

प्रश्न 15.
यदि [latex s=2]A=\left[ \begin{matrix} 2 & -3 & 5 \\ 3 & 2 & -4 \\ 1 & 1 & -2 \end{matrix} \right] [/latex] है तो A^-1 ज्ञात कीजिए।
A^-1 का प्रयोग करके निम्नलिखित समीकरण निकाय को हल कीजिए
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = -3
हल-

प्रश्न 16.
4 किग्रा प्याज, 3 किग्रा गेहूँ और 2 किग्रा चावल मूल्य Rs 60 है 2 किग्रा प्याज, 4 किग्रा गेहूँ और 6 किग्रा चावल का मूल्य Rs 90 है। 6 किग्रा प्याज, 2 किग्रा गेहूँ और 3 किग्रा चावल का मूल्य Rs 70 है। आव्यूह द्वारा प्रत्येक का मूल्य प्रति किग्रा ज्ञात कीजिए।
हल-
माना प्याज का मूल्य Rs प्रतिकिग्रा = x
गेहूं का मूल्य Rs प्रतिकिग्रा = y
चावल को मूल्य Rs प्रतिकिग्रा = z
तब दिये गये प्रतिबन्धों के अनुसार,
4x + 3y + 2z = 60;
2x + 4y + 6z = 90;
6x + 2y + 3z = 70
इस समीकरण निकाय को AX = B के रूप में इस प्रकार लिखा जा सकता है।

We hope the UP Board Solutions for Class 12 Maths Chapter 4 Determinants (सारणिक) help you. If you have any query regarding UP Board Solutions for Class 12 Maths Chapter 4 Determinants (सारणिक), drop a comment below and we will get back to you at the earliest.

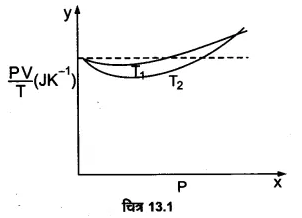
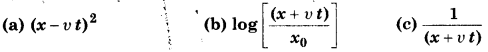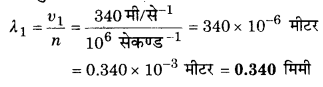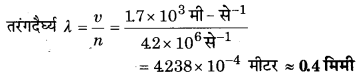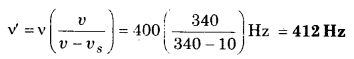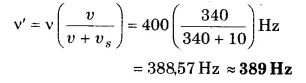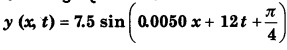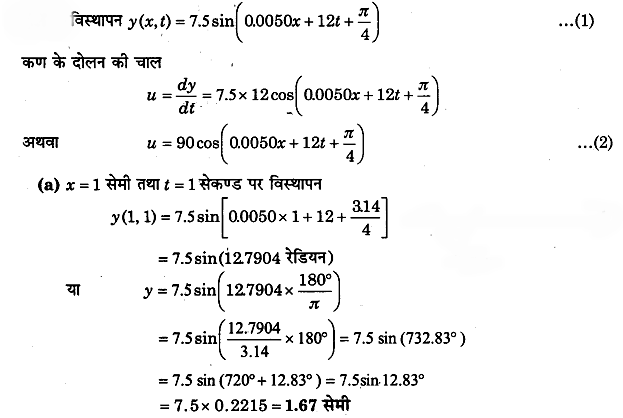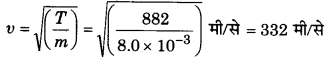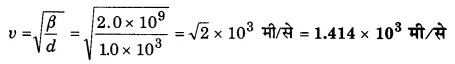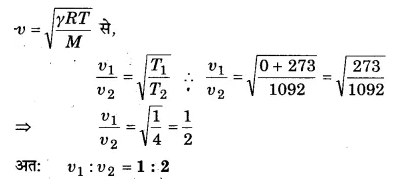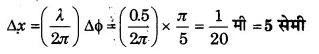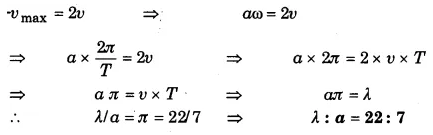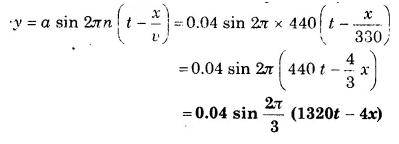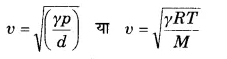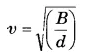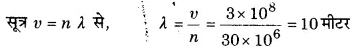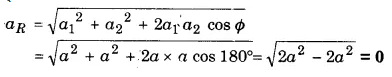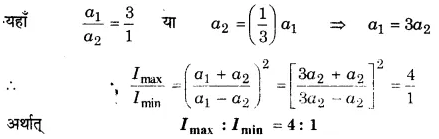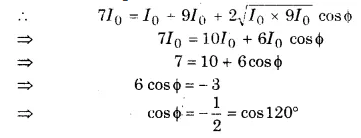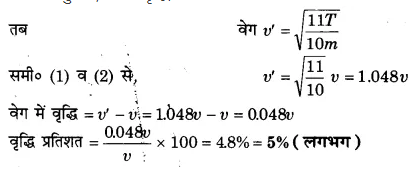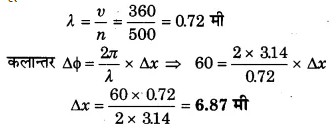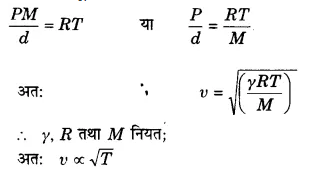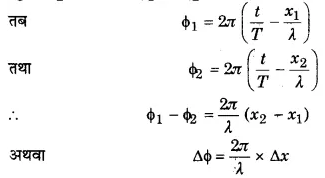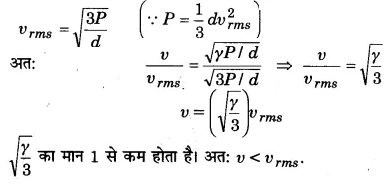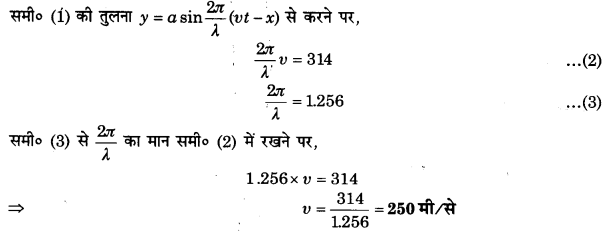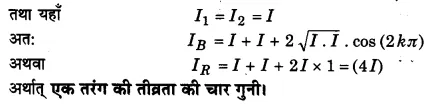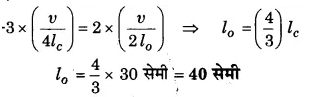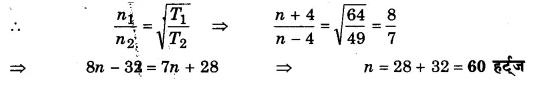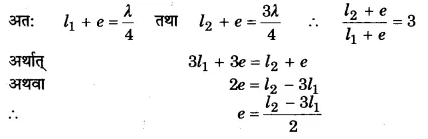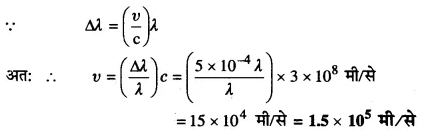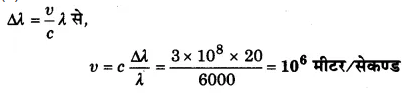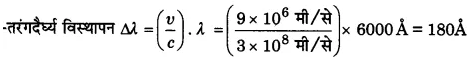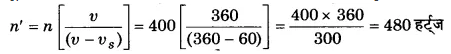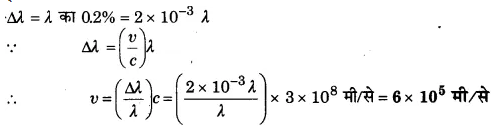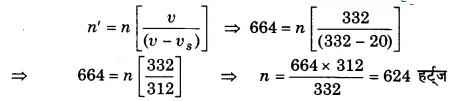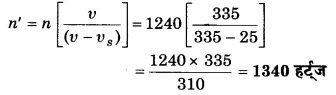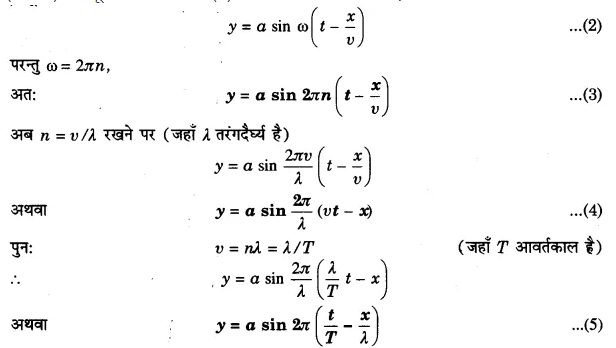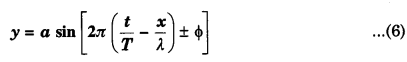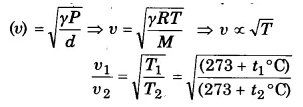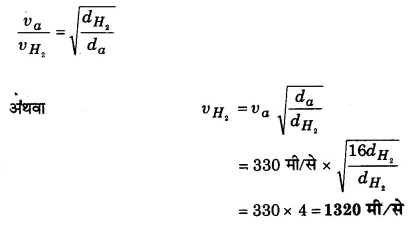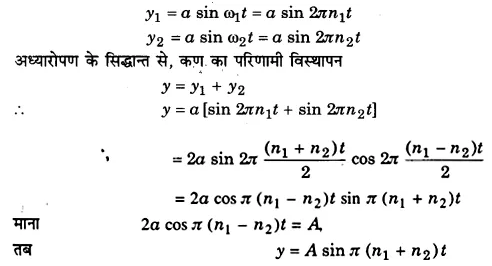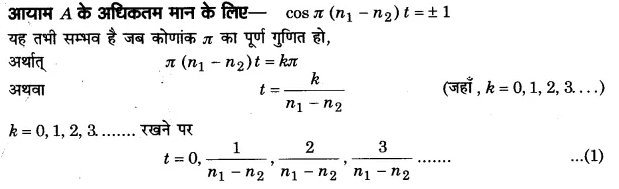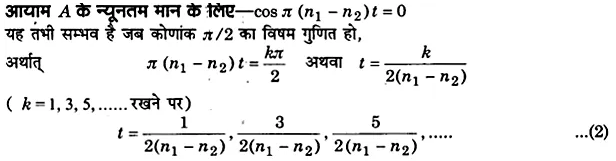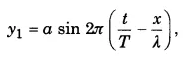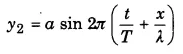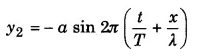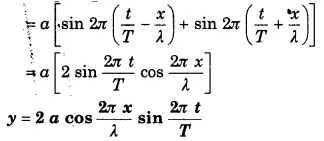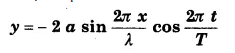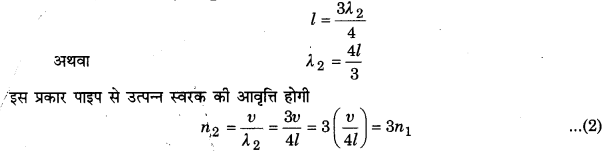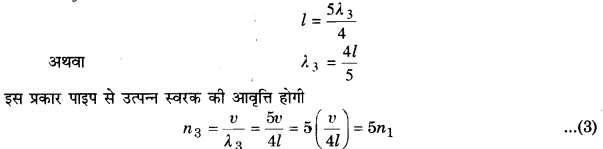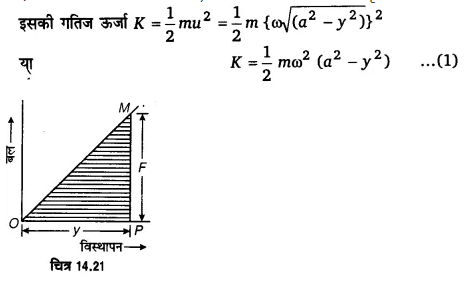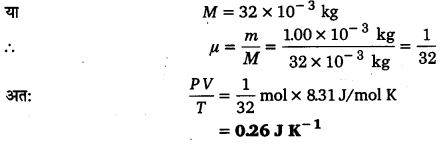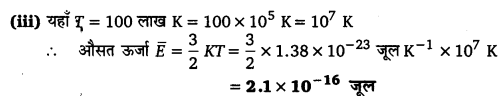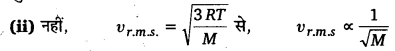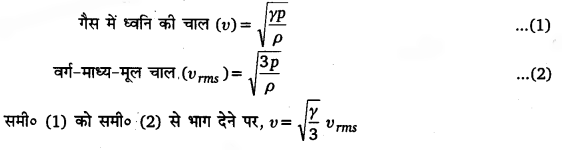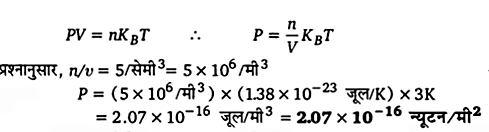UP Board Solutions for Class 11 Physics Chapter 15 Waves (तरंगें) are part of UP Board Solutions for Class 11 Physics . Here we have given UP Board Solutions for Class 11 Physics Chapter 15 Waves (तरंगें)

Board	UP Board
Textbook	NCERT
Class	Class 11
Subject	Physics
Chapter	Chapter 15
Chapter Name	Waves
Number of Questions Solved	177

UP Board Solutions for Class 11 Physics Chapter 15 Waves (तरंगें)

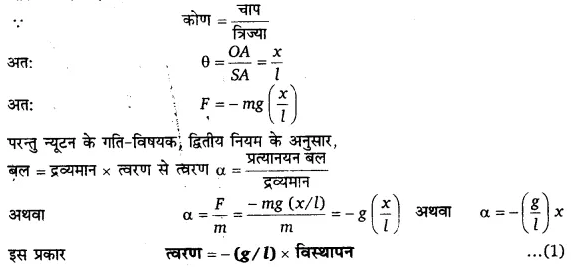
अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
2.50 kg द्रव्यमान की 20 cm लम्बी तानित डोरी पर 200 N बल का तनाव है। यदि इस डोरी के एक सिरे को अनुप्रस्थ झटका दिया जाए, तो उत्पन्न विक्षोभ कितने समय में दूसरे सिरे तक पहुँचेगा?
हल-
डोरी का द्रव्यमान m = 250 kg, लम्बाई l = 20 cm = 0.2 m
तथा डोरी का तनाव T = 200 N

प्रश्न 2.
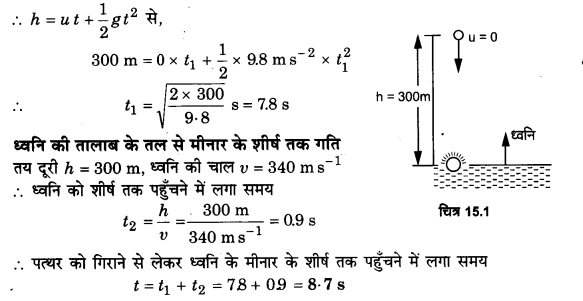
300 m ऊँची मीनार के शीर्ष से गिराया गया पत्थर मीनार के आधार पर बने तालाब के पानी से टकराता है। यदि वायु में ध्वनि की चाल 340 ms^-1 है तो पत्थर के टकराने की ध्वनि मीनार के शीर्ष पर पत्थर गिराने के कितनी देर बाद सुनाई देगी?(g = 9. 8 ms^-2)
हल-
माना पत्थर को तालाब तक पहुँचने में t1 तथा ध्वनि को तालाब से मीनार के शीर्ष तक पहुँचने में t2 समय लगता है।
पत्थर की मीनार के शीर्ष से तालाब तक गति ।
u = 0, h = 300 m, g = 9.8 ms^-2, समय = t1

प्रश्न 3.
12.0 m लम्बे स्टील के तार का द्रव्यमान 2.10 kg है। तीर में तनाव कितना होना चाहिए ताकि उस तार पर किसी अनुप्रस्थ तरंग की चाल 20°C पर शुष्क वायु में ध्वनि की चाल (343 ms^-1) के बराबर हो।
हल-
यहाँ L = 120 मीटर लम्बे तार का द्रव्यमान M = 2.10 किग्रा तथा तार में अनुप्रस्थ तरंग की चाल v = 343 मी-से^-1

प्रश्न 4.

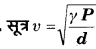
का उपयोग करके स्पष्ट कीजिए कि वायु में ध्वनि की चाल क्यों
(a) दाब पर निर्भर नहीं करती,
(b) ताप के साथ बढ़ जाती है, तथा
(c) आर्द्रता के साथ बढ़ जाती है?
उत्तर-
(a) वायु में ध्वनि की चाल पर दाब का प्रभाव-वायु में ध्वनि की चाल के सूत्र

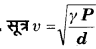
से। प्रतीत होता है कि दाब P के बदलेने पर ध्वनि की चाल v का मान भी बदल जाएगा परन्तु वास्तव में ऐसा नहीं होता।
माना’ परमताप T पर किसी गैस के 1 ग्राम-अणु द्रव्यमान का आयतन V तथा दाब P है।
यदि गैस का अणुभार M तथा घनत्व d हो तो


(c) वायु में ध्वनि की चाल पर आर्द्रता का प्रभावे-आर्द्र वायु (जलवाष्प मिली हुई) का घनत्व d, शुष्कं वायु के घनत्व की तुलना में कम होता है। इस कारण आर्द्र वायु में ध्वनि की चाल शुष्क वायु की तुलना में बढ़ जाती है।

प्रश्न 5.
आपने यह सीखा है कि एक विमा में कोई प्रगामी तरंग फलन y = f (x t) द्वारा निरूपित की जाती है, जिसमें x तथा t को x – vt अथवा x + vt है अर्थात y = f (x ± vt) संयोजन में प्रकट होना चाहिए। क्या इसका प्रतिलोम भी सत्य है? नीचे दिए गए y के प्रत्येक फलन का परीक्षण करके यह बताइए कि क्या वह किसी प्रगामी तरंग को निरूपित कर सकता है

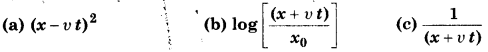
उत्तर-
इसका प्रतिलोम सत्य नहीं है। फलन f(x ± ut) को प्रगामी तरंग निरूपित करने के लिए इस फलन को प्रत्येक क्षण तथा प्रत्येक बिन्दु पर निश्चित तथा परिमित होना चाहिए।
(a) जब x →∞ अथवा t →∞ तो फलन (x – vt)² अपरिमित हो जाएगा; अत: यह फलन प्रगामी तरंग को निरूपित नहीं कर सकता।
(b) जब x →∞ अथवा t →∞ तो फलन log [latex s=2]log\left( \frac { x+\upsilon t }{ { x }_{ 0 } } \right) [/latex] अपरिमित हो जाएगा; अत: यह फलन प्रगामी तरंग को निरूपित नहीं कर सकता।
(c) जब x →∞ अथवा t →∞ तो यह फलन परिमित बना रहेगा; अत: यह फलन सम्भवतया प्रगामी तरंग को निरूपित कर सकता है।

प्रश्न 6.
कोई चमगादड़ वायु में 1000 kHz आवृत्ति की पराश्रव्य ध्वनि उत्सर्जित करता है। यदि यह ध्वनि जल के पृष्ठ से टकराती है तो
(a) परावर्तित ध्वनि, तथा (b) पारगमित ध्वनि की तरंगदैर्घ्य ज्ञात कीजिए। वायु तथा जल में ध्वनि की चाल क्रमशः 340 ms^-1 तथा 1486 ms^-1है।
हल-
यहाँ आपतित तरंग की आवृत्ति ,
n = 1000 kHz = 10⁶ Hz = 10⁶ सेकण्ड^-1
वायु में ध्वनि की चाल υ1 = 340 मी-से^-1
जल में ध्वनि की चाल υ2 = 1486 मी-से^-1
(a) परावर्तित ध्वनि वायु में ही गति करेगी। अतः उसकी तरंगदैर्घ्य ।

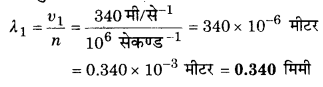
(b) पारगमित ध्वनि की आवृत्ति भी n ही होगी क्योंकि अपवर्तन से आवृत्ति नहीं बदलती है तथा यह जल में, गति करेगी। अतः इसकी तरंगदैर्घ्य

प्रश्न 7.
किसी अस्पताल में ऊतकों में ट्यूमरों का पता लगाने के लिए पराश्रव्य स्कैनर का प्रयोग किया जाता है। उस ऊतक में ध्वनि में तरंगदैर्ध्य कितनी है जिसमें ध्वनि की चाल 1.7 kms^-1 है? स्कैनर की प्रचालन आवृत्ति 4.2 MHz है।
हल-
ध्वनि की चाल v = 1.7 किमी-से^-1 = 1.7 x 10³ मी-से^-1
आवृत्ति n = 4.2 MHz = 4.2×10⁶ से^-1

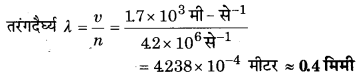
प्रश्न 8.
किसी डोरी पर कोई अनुप्रस्थ गुणावृत्ति तरंग का वर्णन

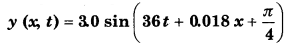
द्वारा किया जाता है। यहाँ x तथा y सेण्टीमीटर में तथा t सेकण्ड में है। x की धनात्मक दिशा बाएँ से दाएँ है।
(a) क्या यह प्रगामी तरंगे है अथवा अप्रगामी ? यदि यह प्रगामी तरंग है तो इसकी चाल तथा संचरण की दिशा क्या है?
(b) इसका आयाम तथा आवृत्ति क्या है?
(c) उद्गम के समय इसकी आरम्भिक कला क्या है?
(d) इस तरंग में दो क्रमागंत शिखरों के बीच की न्यूनतम दूरी क्या है?
हल-
(a) दिए गए समी० को पुनर्व्यवस्थित करके निम्नलिखित प्रकार से लिखा जा सकता है

प्रश्न 9.
प्रश्न 8 में वर्णित तरंग के लिए x = 0 cm, 2 cm तथा 4 cm के लिए विस्थापन (y) और समयं (t) के बीच ग्राफ आलेखित कीजिए। इन ग्राफों की आकृति क्या है? आयाम, आवृत्ति अथवा कला में से किन पहलुओं में प्रगामी तरंग में दोलनी गति एक बिन्दु से दूसरे बिन्दु पर भिन्न है?
हल-
दी गयी प्रगामी तरंग का समीकरण

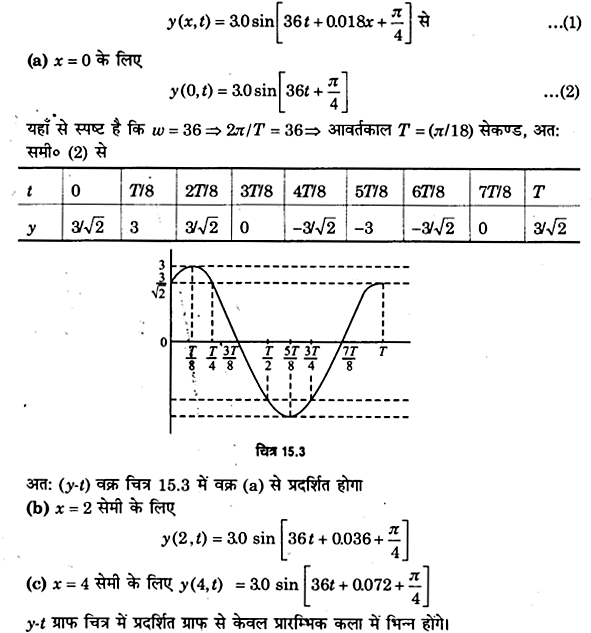
प्रश्न 10.
प्रगामी गुणावृत्ति तरंग y (x,t) = 20 cos 2π (10t – 0.0080x + 0.35) जिसमें x तथा y को m में तथा t को s में लिया गया है, के लिए उन दो दोलनी बिन्दुओं के बीच कलान्तर कितना है जिनके बीच की दूरी है
(a) 4m
(b) 0.5 m
(c) [latex s=2]\frac { \lambda }{ 2 } [/latex]
(d) [latex s=2]\frac { 3\lambda }{ 4 }  [/latex]
हल-
दिए गये समी० y (x,t) = 20 cos 2π (10t – 0.0080x + 0.35) की तुलना प्रामाणिक समीकरण

प्रश्न 11.
दोनों सिरों पर परिबद्ध किसी तानित डोरी पर अनुप्रस्थ विस्थापन को इस प्रकार व्यक्त किया गया है

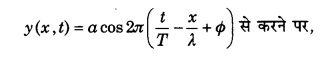
जिसमें x तथा y को मीटर में तथा १ को सेकण्ड में लिया गया है। इसमें डोरी की लम्बाई 1.5 m है जिसकी संहति 30 x 10^-2 kg है। निम्नलिखित का उत्तर दीजिए
(a) यह फलन प्रगामी रंग अथवा अप्रगामी तरंग में से किसे निरूपित करता है?
(b) इसकी व्याख्या विपरीत दिशाओं में गमन करती दो तरंगों के अध्यारोपण के रूप में करते | हुए प्रत्येक तरंग की तरंगदैर्घ्य, आवृत्ति तथा चाल ज्ञात कीजिए।
(c) डोरी में तनाव ज्ञात कीजिए।
हल-
(a) दिया गया फलन दो आवर्तफलनों के गुणनफल के रूप में हैं जिसमें एक x का ज्या फलन तथा दूसरा t का कोज्या फलन है। अत: यह अप्रगामी तरंग को व्यक्त करता है।
(b) ∵ 2 sin A• cos B = sin (A + B) + sin (A – B)

प्रश्न 12.
(i) प्रश्न 11 में वर्णित डोरी पर तरंग के लिए बताइए कि क्या डोरी के सभी बिन्दु समान  (a) आवृत्ति, (b) कला, (c) आयाम से कम्पन करते हैं? अपने उत्तरों को स्पष्ट कीजिए।
(ii) एक सिरे से 0.375 m दूर के बिन्दु का आयाम कितना है?
हले-
(i) (a) निस्पन्द के अतिरिक्त डोरी के सभी बिन्दुओं की आवृत्ति n = 60 सेकण्ड^-1 समान है।
(b) एक लूप में सभी बिन्दु समान कला में कम्पन करते हैं। (निस्पन्द के अतिरिक्त)
(c) दी गयी अप्रगामी तरंग फलन से x दूरी पर तुरंग का आयाम

प्रश्न 13.
नीचे किसी प्रत्यास्थ तरंग (अनुप्रस्थ अथवा अनुदैर्घ्य) के विस्थापन को निरूपित करने वाले x तथा t के फलन दिए गए हैं। यह बताइए कि इनमें से कौन (i) प्रगामी तरंग को, (ii) अप्रगामी तरंग को, (iii) इनमें से किसी भी तरंग को निरूपित नहीं करता है।
(a) y = 2 cos (3x) sin 10t
(b) y = 2√x-vt
(c) = 3 sin (5x – 0.5t) + 4 cos (5x – 0.5t)
(d) y = cos x sint + cos 2x sin 2t
उत्तर-
(a) यह फलन एक अप्रगामी तरंग निरूपित करता है।
(b) x→∞ अथवा t →∞ पर फलन अपरिमित हो जाता है; अत: यह किसी भी प्रकार की तरंग को निरूपित नहीं करता।
(c) दिया गया फलन -अक्ष की धन दिशा (एक ही दिशा) में चलने वाली दो तरंगों, जिनके बीच [latex s=2]\left( \frac { \pi }{ 2 } \right) [/latex] का कलान्तर है, के अध्यारोपण से बनी तरंग को प्रदर्शित करता है; अत: यह एक प्रगामी तरंग है।
(d) दिया गया फलन y = cosxsint + cos2xt sin 2t, दो अप्रगामी तरंगों के अध्यारोपण को प्रदर्शित करता है।

प्रश्न 14.
दो दृढ़ टेकों के बीच तानित तार अपनी मूल विधा में 45 Hz आवृत्ति से कम्पन करता है। इस तार का द्रव्यमान 3.5 x 10^-2 kg तथा रैखिक द्रव्यमान घनत्व 40 x 10-2 kg m^-1 है। (a) तार पर अनुप्रस्थ तरंग की चाल क्या है, तथा (b) तार में तनाव कितना है?
हल-
तार की मूल आवृत्ति n = 45 हज = 45 सेकण्ड^-1
तार का रैखिक घनत्व अर्थात् एकांक लम्बाई का द्रव्यमान

प्रश्न 15.
एक सिरे एर खुली तथा दूसरे सिरे पर चलायमान पिस्टन लगी 1 m लम्बी नलिका, किसी नियत आवृत्ति के स्रोत (340 Hz आवृत्ति का स्वरित्र द्विभुज) के साथ, जब नलिका में वायु कॉलम 25.5 cm अथवा 79.3 cm होता है तब अनुनाद दर्शाती है। प्रयोगशाला के ताप पर वायु में ध्वनि की चाल का आकलन कीजिए। कोर के प्रभाव को नगण्य मान सकते हैं।
हल-
यदि अनुनादित वायु-स्तम्भों की पहली दो क्रमिक लम्बाइयाँ l1 व l2 हैं तथा स्वरित्र द्विभुज की आवृत्ति n हो, तो वायु-स्तम्भ में ध्वनि की चाल ।
v = 2n(l2 – l1)
= 2x 340 सेकण्ड^-1 x (79.3-25.5) सेमी
= 36584 सेमी/सेकण्ड ।
= 365.84 मीटर/सेकण्डे

प्रश्न 16.
100 cm लम्बी स्टील-छड़ अपने मध्य बिन्दु पर परिबद्ध है। इसके अनुदैर्ध्य कम्पनों की मूल आवृत्ति2.53 kHz है। स्टील में ध्वनि की चाल क्या है?

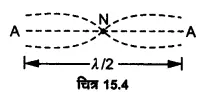
हल-
l = 100 सेमी = 1.00 मीटर की छड़ के मध्यबिन्दु पर परिबद्ध होने पर इसमें अनुदैर्ध्य कम्पन दिए चित्र 15.4 की भाँति होंगे। मध्य बिन्दु पर निस्पन्द तथा छड़ के स्वतन्त्र सिरों पर प्रस्पन्द बनेंगे। चित्र से स्पष्ट है कि

प्रश्न 17.
20 cm लम्बाई के पाइप का एक सिरा बन्द है। 430 Hz आवृत्ति के स्रोत द्वारा इस पाइप की कौन-सी गुणावृत्ति विधा अनुनाद द्वारा उत्तेजित की जाती है? यदि इस पाइप के दोनों | सिरे खुले हों तो भी क्या यह स्रोत इस पाइप के साथ अनुनाद करेगा? वायु में ध्वनि की चाल 340 ms^-1 है।
हल-
बन्द ऑर्गन पाइप की लम्बाई l = 20 सेमी = 0.20 मीटर
वायु में ध्वनि की चाल v = 340 मी/से
∴ बन्द ऑर्गन पाइप की मूल आवृत्ति

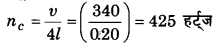
यह प्रथम संनादी होगा इसके तृतीय एवं पाँचवें संनादी की आवृत्ति क्रमशः 3n_c = 1275 Hz तथा 5n_c = 2125 Hz होंगी। अतः 430 Hz आवृत्ति के स्रोत द्वारा पाइप की पहली गुणावृत्ति (मूलस्वरक) अनुनाद द्वारा उत्तेजित की जा सकती है।
पाइप के दोनों सिरे खुले होने पर उसकी (खुले ऑर्गन पाइप) मूल आवृत्ति
[latex s=2]{ n }_{ 0 }=\frac { \upsilon }{ 2l } [/latex] = 2x 425 = 850 Hz
इनके द्वितीय, तृतीय…. संनादी की आवृत्तियाँ क्रमशः 2n₀ = 1700 Hz, 3n₀ = 2550 Hz होंगी। अतः 430 Hz आवृत्ति के स्रोत से इसका कोई भी संनादी उत्तेजित नहीं हो सकेगा। इसलिए पाइप के दोनों सिरे खुले होने पर दिया हुआ 430 Hz आवृत्ति वाला स्रोत इसके साथ अनुनाद नहीं करेगा।
वैकल्पिक विधि-माना 430 Hz आवृत्ति का स्वरित्र N वें संनादी के साथ अनुनाद करता है।

परन्तु N पूर्णांक होना चाहिए। अतः दोनों सिरों पर खुला पाइप 430 Hz आवृत्ति के स्रोत दाब किसी भी विधा में अनुनाद द्वारा उत्तेजित नहीं हो सकता है।

प्रश्न 18.
सितार की दो डोरियाँ A तथा B एक साथ ‘गा’ स्वर बजा रही हैं तथा थोड़ी-सी बेसुरी होने के कारण 6 Hz आवृत्ति के विस्पन्द उत्पन्न कर रही हैं। डोरी A का तनाव कुछ घटाने पर । विस्पन्द की आवृत्ति घटकर 3 Hz रह जाती है। यदि A की मूल आवृत्ति 324 Hz है तो B की आवृत्ति क्या है ?
हल-
दिया है डोरी A की आवृत्ति n_A = 324 Hz
प्रति सेकण्ड विस्पन्दों की संख्या x = 6
∴डोरी B की सम्भव आवृत्तियाँ n_B = n_A ± x = (324 ± 6) Hz
= 330 Hz अथवा 318 Hz
तनी हुई डोरी की आवृत्ति n ∝√T (तनाव के नियम से)
अत: डोरी A पर तनाव घटाने से इसकी आवृत्ति घटेगी। यदि B की सही आवृत्ति 330 Hz मान ली जाए। तो n_A = 324 Hz के घटने पर 330 Hz से उसका अन्तर 6 से अधिक आयेगा अर्थात् विस्पन्द बढ़ेंगे परन्तु विस्पन्द आवृत्ति घट रही है, अत: B की सही आवृत्ति 330 Hz न होकर 318 Hz ही होगी; चूँकि तनाव घटाने पर जब A की आवृत्ति 324 से घटकर 321 रह जायेगी तब 318 से इसका अन्तर 3 आयेगा, जो प्रश्न के अनुकूल है।

प्रश्न 19.
स्पष्ट कीजिए क्यों (अथवा कैसे)-
(a) किसी ध्वनि तरंग में विस्थापन निस्पन्द, दाब प्रस्पन्द होता है और विस्थापन प्रस्पन्द, दाब निस्पन्द होता है।
(b) आँख न होने पर भी चमगादड़ अवरोधकों की दूरी, दिशा, प्रकृति तथा आकार सुनिश्चित कर लेते हैं।
(c) वायलिन तथा सितार के स्वरों की आवृत्तियाँ समान होने पर भी हम दोनों से उत्पन्न स्वरों में भेद कर लेते हैं।
(d) ठोस अनुदैर्घ्य तथा अनुप्रस्थ दोनों प्रकार की तरंगों का पोषण कर सकते हैं जबकि गैसों में केवल अनुदैर्ध्य तरंगें ही संचरित हो सकती हैं, तथा ।
(e) परिक्षेपी माध्यम में संचरण के समय स्पन्द की आकृति विकृत हो जाती है।
उत्तर-
(a) ध्वनि तरंगों में जहाँ माध्यम के कणों का विस्थापन न्यूनतम (विस्थापन निस्पन्द) होता है वहाँ कण अत्यधिक पास-पास होते हैं अर्थात् वहाँ दाब अधिकतम (दाब प्रस्पन्द) होता है तथा जहाँ विस्थापन महत्तम (विस्थापन-प्रस्पन्द) होता है वहाँ कण दूर-दूर होते हैं अर्थात् वहाँ दाब न्यूनतम (दाब निस्पन्द) होता है।
(b) चमगादड़ उच्च आवृत्ति की पराश्रव्य तरंगें उत्सर्जित करते हैं। ये तरंगें अवरोधकों से टकराकर वापस लौटती हैं तो चमगादड़ इन्हें अवशोषित कर लेते हैं। परावर्तित तरंग की आवृत्ति तथा तीव्रता की प्रेषित तरंग से तुलना करके चमगादड़ अवरोधकों की दूरी, दिशा, प्रकृति तथा आकार सुनिश्चित कर लेते हैं।
(c) प्रत्येक स्वर में एक मूल स्वरक के साथ कुछ अधिस्वरक भी उत्पन्न होते हैं। यद्यपि वायलिन तथा सितार से उत्पन्न स्वरों में मूल स्वरकों की आवृत्तियाँ समान रहती हैं परन्तु उनके साथ उत्पन्न होने वाले अधिस्वरकों की संख्या, आवृत्तियाँ तथा आपेक्षिक तीव्रताओं में भिन्नता होती है। इसी भिन्नता के कारण इन्हें पहचान लिया जाता है।
(d) ठोसों में आयतन प्रत्यास्थता के साथ-साथ अपरूपण प्रत्यास्थती भी पाई जाती है; अत: ठोसों में दोनों प्रकार की तरंगें संचरित हो सकती हैं। इसके विपरीत गैसों में केवल आयतन प्रत्यास्थता ही पाई जाती है; अत: गैसों में केवल अनुदैर्ध्य तरंगें ही संचरित हो पाती हैं।
(e) प्रत्येक ध्वनि स्पन्द कई विभिन्न तरंगदैर्यों की तरंगों का मिश्रण होता है। जब यह स्पन्द परिक्षेपी माध्यम में प्रवेश करता है तो ये तरंगें अलग-अलग वेगों से गति करती हैं; अत: स्पन्द की आकृति विकृत हो जाती है।

प्रश्न 20.
रेलवे स्टेशन के बाह्य सिगनल पर खड़ी कोई रेलगाड़ी शान्त वायु में 400 Hz आवृत्ति की सीटी बजाती है।
(i) प्लेटफॉर्म पर खड़े प्रेक्षक के लिए सीटी की आवृत्ति क्या होगी जबकि रेलगाड़ी (a) 10 ms^-1 चाल से प्लेटफॉर्म की ओर गतिशील है, तथा (b) 10 ms^-1 चाल से प्लेटफॉर्म से दूर जा रही है?
(ii) दोनों ही प्रकरणों में ध्वनि की चाल क्या है? शान्त वायु में ध्वनि की चाल 340 ms^-1 लीजिए।
हल-
(i) सीटी की आवृत्ति ν = 400 Hz,
रेलगाड़ी की चाल υ_s = 10 m s^-1
शान्त वायु में ध्वनि की चाल υ = 340 ms^-1
(a) जब रेलगाड़ी (ध्वनि-स्रोत) स्थिर प्रेक्षक की ओर गतिशील है तो प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति ।

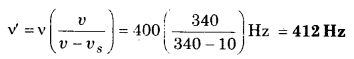
(b) जब रेलगाड़ी (स्रोत) स्थिर प्रेक्षक से दूर जा रही है तो प्रेक्षक द्वारा सुनी गई ध्वनि की आवृत्ति,

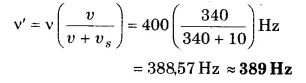
(ii) दोनों प्रकरणों में ध्वनि की चाल 340 m s^-1 (अपरिवर्तित) है।

प्रश्न 21.
स्टेशन यार्ड में खड़ी कोई रेलगाड़ी शान्त वायु में 400 Hz आवृत्ति की सीटी बजा रही है। तभी 10 ms^-1 चाल से यार्ड से स्टेशन की ओर वायु बहने लगती है। स्टेशन के प्लेटफॉर्म पर खड़े किसी प्रेक्षक के लिए ध्वनि की आवृत्ति, तरंगदैर्घ्य तथा चाल क्या हैं? क्या यह स्थिति तथ्यतः उस स्थिति के समरूप है जिसमें वायु शान्त हो तथा प्रेक्षक 10 ms^-1 चाल से यार्ड की ओर दौड़ रहा हो? शान्त वायु में ध्वनि की चाल 340 ms^-1 ले सकते हैं।
हल-
सीटी की आवृत्ति ν = 400 Hz, शान्त वायु में ध्वनि की चाल υ = 340 ms^-1
वायु की (प्रेक्षक की ओर) चाल W = 10 m s^-1
∵रेलगाड़ी (स्रोत) तथा प्रेक्षक दोनों स्थिर हैं; अतः υ_s = 0, υ₀ = 0

नहीं, यदि प्रेक्षक यार्ड की ओर दौड़ेगा, तो प्रभावी तरंगदैर्घ्य घट जाएगी तथा आवृत्ति बढ़ जाएगी जबकि ध्वनि की चाल अपरिवर्तित रहेगी।

अतिरिक्त अभ्यास

प्रश्न 22.
किसी डोरी पर कोई प्रगामी गुणावृत्ति तरंग इस प्रकार व्यक्त की गई है।

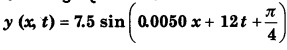
(a) x = 1cm तथा t = 1s पर किसी बिन्दु का विस्थापन तथा दोलन की चाल ज्ञात कीजिए। क्या यह चाल तरंग संचरण की चाल के बराबर है?
(b) डोरी के उन बिन्दुओं की अवस्थिति ज्ञात कीजिए जिनका अनुप्रस्थ विस्थापन तथा चाल उतनी ही है जितनी x = 1cm पर स्थित बिन्दु की समय t = 2s,5 s तथा 11s पर है।
हल-

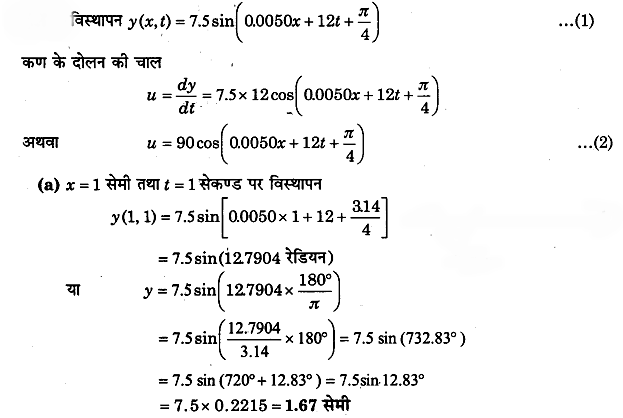
प्रश्न 23.
ध्वनि का कोई सीमित स्पन्द (उदाहरणार्थ सीटी की ‘पिप) माध्यम में भेजा जाता है। (a) क्या इस स्पन्द की कोई निश्चित (i) आवृत्ति, (ii) तरंगदैर्घ्य, (iii) संचरण की चाल है? (b) यदि स्पन्द दर 1स्पन्द प्रति 20 s है अर्थात सीटी प्रत्येक 20 s के पश्चात सेकण्ड , के कुछ अंश के लिए बजती है तो सीटी द्वारा उत्पन्न स्वर की आवृत्ति (1/20) Hz अथवा 0.05 Hz है?
उत्तर-
(a) नहीं, किसी स्पन्द की कोई निश्चित आवृत्ति अथवा तरंगदैर्घ्य नहीं होती। स्पन्द के संचरण की चाल निश्चित है जो माध्यम में ध्वनि की चाल के बराबर है।
(b) नहीं, स्पन्द की आवृत्ति [latex s=2]\frac { 1 }{ 20 }[/latex] Hz अथवा 0.05 Hz नहीं है।

प्रश्न 24.
80 x 10^-3 kg m^-1 रैखिक द्रव्यमान घनत्व की किसी लम्बी डोरी का एक सिरा 256 Hz आवृत्ति के विद्युत चालित स्वरित्र द्विभुज से जुड़ा है। डोरी का दूसरा सिरा किसी स्थिर घिरनी के ऊपर गुजरता हुआ किसी तुला के पलड़े से बँधा है जिस पर 90 kg के बाट लटके हैं। घिरनी वाला सिरा सारी आवक ऊर्जा को अवशोषित कर लेता है जिसके कारण इस सिरे से परावर्तित तरंगों का आयाम नगण्य होता है। t = 0 पर डोरी के बाएँ सिरे । (द्विभुज वाले सिरे) x = 0 पर अनुप्रस्थ विस्थापन शून्य है (y = 0) तथा वह y-अक्ष की धनात्मक दिशा के अनुदिश गतिशील है। तरंग का आयाम 5.0 cm है। डोरी पर इस तरंग का वर्णन करने वाले अनुप्रस्थ विस्थापन y को x तथा t के फलन के रूप में लिखिए।
हल-
डोरी का रैखिक घनत्व m = 8.0 x 10^-3 किग्रा/मीटर; ।
डोरी पर आरोपित तनाव T = Mg = 90 x 9.8 न्यूटन = 882 न्यूटन
∴तनी हुई डोरी में संचरित अनुप्रस्थ तरंग की चाल ।

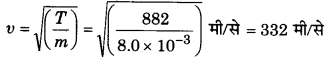
डोरी में संचरित तरंग की आवृत्ति = इसके एक सिरे से जुड़े स्वरित्र की आवृत्ति = 256 Hz

प्रश्न 25.
किसी पनडुब्बी से आबद्ध कोई ‘सोनार निकाय 40.0 kHz आवृत्ति पर प्रचालन करता है। कोई शत्रु-पनडुब्बी 360 kmh^-1 चाल से इस सोनार की ओर गति करती है। पनडुब्बी से परावर्तित ध्वनि की आवृत्ति क्या है? जल में ध्वनि की चाल 1450 ms^-1 लीजिए।
हल-
सोनार द्वारा प्रेषित तरंगे की आवृत्ति ν = 40.0 kHz
जल में ध्वनि की चाल υ = 1450 m s^-1

प्रश्न 26.
भूकम्प पृथ्वी के भीतर तरंगें उत्पन्न करते हैं। गैसों के विपरीत, पृथ्वी अनुप्रस्थ (S) तथा अनुदैर्घ्य (P) दोनों प्रकार की तरंगों की अनुभूति कर सकती है।S तरंगों की प्रतिरूपी चाल लगभग 40 km s^-1 तथा P तरंगों की प्रतिरूपी चाल लगभग 80 km s^-1 है। कोई भूकम्प-लेखी किसी भूकम्प की PतथाS तरंगों को रिकार्ड करता है। पहली P तरंग, पहली S तरंग की तुलना में 4 मिनट पहले पहुँचती है। यह मानते हुए कि तरंगें सरल रेखामें गमन करती हैं यह ज्ञात कीजिए कि भूकम्प घटित होने वाले स्थान की दूरी क्या है?
हल-
माना भूकम्प घटित होने वाले स्थान की भूकम्प-लेखी से दूरी x km है।
दिया है : S तरंगों की चाल υ1 = 4 km s^-1 = 4 x 60 km/min
तथा P तरंगों की चाल υ2 = 8 km s^-1 = 8 x 60 km/min

प्रश्न 27.
कोई चमगादड़ किसी गुफा में फड़फड़ाते हुए पराश्रव्य ध्वनि उत्पन्न करते हुए उड़ रहा है। मान लीजिए चमगादड़ द्वारा उत्सर्जित पराश्रव्य ध्वनि की आवृत्ति 40 kHz है। किसी दीवार की ओर सीधा तीव्र झपट्टा मारते समय चमगादड़ की चाल ध्वनि की चाल की 0.03 गुनी है। चमगादड़ द्वारा सुनी गई दीवार से परावर्तित ध्वनि की आवृत्ति क्या है?
हल-
माना ध्वनि की चाल = υ_r उत्सर्जित तरंग की आवृत्ति v = 40 kHz
तब चमगादड़ की चाल υ₁ = 0.03 υ
माना दीवार द्वारा ग्रहण की गई तरंग की आभासी आवृत्ति ν1 है।।
इस दशा में स्रोत, श्रोता की ओर गतिमान है जबकि श्रोता (दीवार) स्थिर है,

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न
प्रश्न 1.
वायु में ध्वनि की चाल N. T. P. पर 300 मी/से है। यदि वायुदाब बढकर चार गुना हो जाये तो ध्वनि की चाल होगी ।
(i) 150 मी/से
(ii) 300 मी/से
(iii) 600 मी/से
(iv) 120 मी/से
उत्तर-
(ii) 300 मी/से

प्रश्न 2.
ध्वनि की चाल अधिकतम है।
(i) वायु में
(ii) जल में ।
(iii) निर्वात् में
(iv) स्टील (इस्पात) में
उत्तर-
(iv) स्टील (इस्पात) में

प्रश्न 3.
वांगु में ध्वनि की चाल पर किस भौतिक राशि का प्रभाव नहीं पड़ता है? |
(i) ताप
(ii) दाब
(iii) आर्द्रता
(iv) वायु वेग
उत्तर-
(ii) दाब।

प्रश्न 4.
तनी हुई डोरी में तनाव T तथा डोरी की एकांक लम्बाई का द्रव्यमान m हो तो डोरी में तरंग संचरण का वेग होगा

उत्तर-
[latex s=2]\sqrt { \frac { T }{ m } } [/latex]

प्रश्न 5.
जब ध्वनि तरंगें किसी गैसीय माध्यम से चलती हैं तो माध्यम के किसी बिन्दु पर प्रक्रिया होती है ।
(i) समतापी
(ii) समदाबी
(iii) रुद्धोष्म
(iv) समआयतनिक
उत्तर-
(iii) रुद्धोष्म

प्रश्न 6.
0°C पर वायु में ध्वनि की चाल 332 मी/से है। 35°C पर वायु में ध्वनि की चाल होगी
(i) 325 मी/से
(ii) 332 मी/से
(iii) 353 मी/से
(iv) 367 मी/से
उत्तर-
(iii) 353 मी/से

प्रश्न 7.
वायु में ध्वनि तरंगों की चाल के लिए न्यूटन का सूत्र है।

जहाँ P वायुमण्डलीय दाब तथा d वायु का घनत्व है।
उत्तर-
(ii)[latex s=2]\sqrt { \frac { P }{ d } } [/latex]

प्रश्न 8.
किसी गैस A में 26°C ताप पर ध्वनि का वेग वही है जो एक दूसरी गैस B में 325°C पर है। A तथा B के अणभारों का अनुपात होगा।
(i) 26 : 235
(ii) 325 : 36
(iii) 1 : 2
(iv) 2 : 1
उत्तर-
(iii) 1 : 2

प्रश्न 9.
एक अनुप्रस्थ तरंग का समीकरण है
9 = 20 sin π (0.02 – 2t) जहाँ y और x सेमी में हैं तथा t सेकण्ड में है। इसकी तरंगदैर्ध्य सेमी में होगी
(i) 50
(ii) 100
(iii) 200
(iv) 10
उत्तर-
(ii) 100

प्रश्न 10.
दो ध्वनि तरंगों के समीकरण हैं- y = a sin (ωt – kr) तथा y =a cos (ωt – kx) जहाँ संकेतों के अर्थ सामान्य हैं। इनमें कलान्तर है।

उत्तर-
(iii) π/2

प्रश्न 11.
निम्नलिखित दो तरंगों- [latex s=2]{ y }_{ 1 }={ a }_{ 1 }sin\left( \omega t-\frac { 2\pi }{ \lambda } x \right) [/latex]
तथा [latex s=2]{ y }_{ 2 }={ a }_{ 2 }sin\left( \omega t-\frac { 2\pi }{ \lambda } x+\phi \right) [/latex] के बीच पधान्तर होगा

उत्तर-
(iii) [latex s=2]\left( \frac { \lambda }{ 2\pi } \right) \phi [/latex]

प्रश्न 12.
एक तरंग की चाल 360 मी/सेकण्ड तथा आवृत्ति 500 हर्ट्ज है। दो निकटवर्ती कणों के बीच कलान्तर 60° है। उनके बीच पथान्तर होगा।
(i) 0.72 मीटर
(ii) 12 सेमी
(iii) 120 सेमी
(iv) 0.72 सेमी
उत्तर-
(ii) 12 सेमी

प्रश्न 13.
यदि दो तरंगों की तीव्रता का अनुपात 1:16 है, तो उनके आयामों का अनुपात होगा
(i) 1:16
(ii) 1:4
(iii) 4:1
(iv) 8:1
उत्तर-
(ii) 1 : 4

प्रश्न 14.
निम्नलिखित में कौन-सा समीकरण तरंग का है?
(i) y = A(ωt – kx)
(ii) y = Asin(ωt)
(iii) y = Acos(ωt)
(iv) y = Asin(at – bx + c)
उत्तर-
(ii) y = Asin(ωt)

प्रश्न 15.
एक प्रगामी तरंग का समीकरण, [latex s=2]y=0.5sin\left( 100t-\frac { x }{ 50 } \right) [/latex] है, जहाँ x व y सेमी में तथा t सेकण्ड में है। तरंग का वेग है।
(i) 100 मी/से
(ii) 150 मी/से
(iii) 200 मी/से
(iv) 50 मी/से
उत्तर-
(iv) 50 मी/से

प्रश्न 16.
व्यतिकरण की घटना का कारण है।
(i) कलान्तर
(ii) आयाम परिवर्तन
(iii) वेग परिवर्तन
(iv) तीव्रता
उत्तर-
(i) कलान्तर

प्रश्न 17.
विनाशी व्यतिकरण के लिए दो तरंगों के बीच पथान्तर होना चाहिए
(i) शून्य
(ii) 2 के बराबर
(iii) 2/2 का विषम गुणक
(iv) 2/2 का सम गुणक
उत्तर-
(iii) 2/2 का विषम गुणक

प्रश्न 18. लगभग समान आवृत्तियों के दो ध्वनि तरंगों के अध्यारोपण से उत्पन्न विस्पन्द का वेग होता
(i) ध्वनि के वेग के बराबर
(ii) ध्वनि के वेग से अधिक
(iii) ध्वनि के वेग से कम ।
(iv) शून्य
उत्तर-
(iv) शून्य

प्रश्न 19.
दो तरंगें y = 0.1 sin 316 t तथा y = 0.1 sin 310 t एक ही दिशा में चल रही हैं तो विस्पन्द की आवृत्ति है।
(i) 37
(ii) 6
(iii) 3
(iv) 37
उत्तर-
(i) 3

प्रश्न 20.
यदि व्यतिकरण करने वाली दो तरंगों की तीव्रताओं का अनुपात 16 : 9 है, तो व्यतिकरण प्रारूप में महत्तम एवं न्यूनतम तीव्रताओं का अनुपात है [संकेत : [latex s=2]{ a }_{ 1 }{ a }_{ 2 }=\sqrt { { I }_{ 1 }/{ I }_{ 2 } } [/latex]]
(i) 4 : 3
(ii) 49 : 1
(iii) 25 : 7
(iv) 256 : 81
उत्तर-
(ii) 49 : 1

प्रश्न 21.
दो ध्वनि-स्रोत एक साथ बजने पर 0.25 सेकण्ड में 2 विस्पन्द उत्पन्न करते हैं। उनकी आवृत्तियों का अन्तर है।
(i) 2
(ii) 4
(iii) 8
(iv) 1
उत्तर-
(iii) 8

प्रश्न 22.
एक अज्ञात आवृत्ति का स्रोत S, 256 हर्ट्ज आवृत्ति के स्रोत के साथ 2 विस्पन्द/ सेकण्ड तथा 260 हर्ट्ज आवृत्ति के स्रोत के साथ 6 विस्पन्द/सेकण्ड उत्पन्न करता है। स्रोत S की आवृत्ति है।
(i) 258 हज
(ii) 254 हज़
(iii) 266 हज़
(iv) 262 हज़
उत्तर-
(ii) 254 हज

प्रश्न 23.
तनी हुई डोरी में उत्पन्न तरंगें होती हैं।
(i) अनुप्रस्थ प्रगामी ।
(ii) अनुदैर्ध्य प्रगामी
(iii) अनुप्रस्थ अप्रगामी
(iv) अनुदैर्ध्य अप्रगामी
उत्तर-
(iii) अनुप्रस्थ अप्रगामी

प्रश्न 24.
एक तने हुए तार के अनुप्रस्थ कम्पनों की आवृत्ति 50% बढ़ाने के लिए इसका तनाव बढ़ाना चाहिए।
(i) 150%
(ii) 125%
(iii) 100%
(iv) 50%
उत्तर-
(ii) 125%

प्रश्न 25.
तरंगदैर्घ्य λ की अप्रगामी तसंग के दो निकटवर्ती निस्पन्दों के बीच की दूरी है।
(i) 2λ
(ii) λ / 2
(iii) λ
(iv) λ/4
उत्तर-
(ii) λ/ 2

प्रश्न 26.
500 हर्ट्ज आवृत्ति की किसी अप्रगामी तरंग को एक निस्पन्द तथा निकटवर्ती प्रस्पन्द के बीच की दूरी 20 सेमी है। तरंग की चाल है।
(i) 200 मी/से।
(ii) 400 मी/से
(iii) 50 मी/से।
(iv) 100 मी/से
उत्तर-
(ii) 400 मी/से

प्रश्न 27.
एक स्वरमापी का तार द्वितीयक अधिस्वरक (overtone) में कम्पन कर रहा है। हम कह सकते हैं कि उसमें उपस्थित हैं।
(i) दो निस्पन्द, दो प्रस्पन्द
(ii) तीन निस्पन्द, दो पुस्पन्द
(iii) चार निस्पन्द, तीन प्रस्पन्द
(iv) तीन निस्पन्द, तीन प्रस्पन्द
उत्तर-
(iii) चार निस्पन्द, तीन प्रस्पन्द

प्रश्न 28.
एक सिरे पर बन्द ऑर्गन पाइप में अनुनाद तब उत्पन्न होता है, जब पाइप की लम्बाई होती
(i) λ/8
(ii) λ/2
(iii) λ
(iv) λ/4
उत्तर-
(iv) λ/4

प्रश्न 29.
एक श्रोता किसी मिल के साइरन की ध्वनि सुन रहा है, जबकि वह मिल की ओर जा रहा है। श्रोता को साइरन की ध्वनि सुनायी देगी
(i) बढ़ती हुई
(ii) घटती हुई
(iii) अपरिवर्तित
(iv) इनमें से कोई नहीं
उत्तर-
(i) बढ़ती हुई

प्रश्न 30.
जब श्रोता किसी स्थिर स्रोत से दूर जा रहा होता है तो सुने गए स्वर की आवृत्ति वास्तविक आवृत्ति से होती है।
(i) अधिक
(ii) कम
(iii) बराबर
(iv) इनमें से कोई नहीं
उत्तर-
(ii) कम

प्रश्न 31.
एक कार एक श्रोता की ओर आ रही है। उसके हॉर्न की ध्वनि की आवृत्ति श्रोता को 2.5% बढ़ी हुई प्रतीत होती है। यदि ध्वनि की चाल 338 मी/से हो, तो कार की चाल है।
(i) 8 मी/से ।
(ii) 6 मी/से
(iii) 800 मी/से
(iv) 7.5 मी/से
उत्तर-
(i) 8 मी/से

प्रश्न 32.
ध्वनि की प्रबलता L तथा तीव्रता I के बीच सम्बन्ध है।
(i) L = log I
(ii) L = k log I
(iii) I = k log L
(iv) I = log L
उत्तर-
(ii) L = k log I

प्रश्न 33.
किसी व्यक्ति की आवाज पहचानी जाती है उसकी
(i) प्रबलता से
(ii) तारत्व से
(iii) गुणता से।
(iv) स्वर-अन्तराल से
उत्तर-
(iii) गुणता से

प्रश्न 34.
सांगीतिक ध्वनि की गुणवत्ता निर्भर करती है।
(i) आवृत्ति पर
(ii) आयाम पर
(iii) तरंग वेग पर
(iv) संनादियों की संख्या पर
उत्तर-
(iv) संनादियों की संख्या पर

प्रश्न 35.
निम्नलिखित में से कौन-सी सांगीतिक विशेषता नहीं है?
(i) तारत्व
(ii) प्रबलता
(iii) गुणवत्ता
(iv) तीव्रता
उत्तर-
(iv) तीव्रता

प्रश्न 36.
ध्वनि का तारत्व निर्भर करता है।
(i) ध्वनि की तीव्रता पर
(ii) ध्वनि की आवृत्ति पर।
(iii) तरंग रूप पर
(iv) तीव्रता तथा तरंग रूप पर
उत्तर-
(ii) ध्वनि की आवृत्ति पर

प्रश्न 37.
एक ध्वनि-स्रोत, श्रोता से दूर जा रहा है। श्रोता को स्रोत की वास्तविक आवृत्ति की 25% से कम की ध्वनि आवृत्ति प्रतीत होती है। यदि ध्वनि की चाल υ है, तो स्रोत की चाल है।
(i) υ / 4
(ii) υ / 3
(iii) 3υ
(iv) 4υ
उत्तर-
(iii) 3υ

प्रश्न 38.
एक ध्वनि स्रोत तथा श्रोता दोनों एक-दूसरे की ओर एकसमान चाल u से गति कर रहे हैं। यदि श्रोता को सुनाई पड़ने वाली आवृत्ति, वास्तविक आवृत्ति की दोगुनी हो, तो ध्वनि की चाल है।
(i) 3v
(ii) 2u
(iii) u
(iv) u/ 2
उत्तर-
(ii) 2u

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
नियत ताप पर वायु में आर्द्रता बढ़ने पर वायु में ध्वनि के वेग पर क्या प्रभाव पड़ता है?
उत्तर-
शुष्क वायु का घनत्व आर्द्र वायु (जलवाष्प मिली हुई) से अधिक होता है। अतः यदि आर्द्र वायु के लिएy का मान वही लें जोकि शुष्क वायु के लिए होता है तब सूत्र [latex s=2]\upsilon =\sqrt { (\gamma P/d) } [/latex] से स्पष्ट है कि आर्द्र वायु में ध्वनि की चाल शुष्क वायु की अपेक्षा कुछ बढ़ जाती है। यही कारण है कि वर्षा ऋतु में रेल की सीटियाँ तथा अन्य ध्वनि ग्रीष्म ऋतु की अपेक्षा अधिक दूरी तक सुनाई देती है।

प्रश्न 2.
रेल की पटरी पर एक व्यक्ति चोट मारकर ध्वनि उत्पन्न करता है। इस स्थान से 1 किलोमीटर की दूरी पर कान लगाकर बैठे दूसरे व्यक्ति को दो ध्वनियाँ सुनायी देती हैं। कारण बताइए।
उत्तर-
एक ध्वनि रेल की पटरी में होकर तथा दूसरी ध्वनि वायु में होकर आती है।

प्रश्न 3.
ध्वनि के वेग ज्ञात करने के न्यूटन के सूत्र में लाप्लास ने संशोधन क्यों किया?
या , लाप्लास संशोधन क्या है?
उत्तर-
लाप्लास ने बताया कि ध्वनि संचरण के समय विरलन के स्थान पर ताप घट जाता है तथा सम्पीडन के स्थान पर ताप बढ़ जाता है। अत: ध्वनि संचरण के अन्तर्गत माध्यम का ताप स्थिर नहीं रहता है, जबकि न्यूटन के अनुसार, ताप स्थिर बताया गया था। इसीलिए न्यूटन के सूत्र में लाप्लास ने संशोधन किया।

प्रश्न 4.
गैसों में अनुप्रस्थ तरंगें उत्पन्न नहीं होती हैं। क्यों?
उत्तर-
क्योंकि गैसों में दृढ़ता नहीं होती है।

प्रश्न 5.
शुष्क वायु की अपेक्षा नम वायु में ध्वनि की चाल अधिक होती है। क्यों?
उत्तर-
शुष्क वायु की अपेक्षा नमवायु का घनत्व कम होता है। अत: [latex s=2]\upsilon =\sqrt { E/d } [/latex] से d के कम होने से इसमें ध्वनि की चाल अधिक होती है।।

प्रश्न 6.
“ध्वनि की चाल उसकी आवृत्ति पर निर्भर नहीं करती।” इस कथन के लिए अपने दैनिक जीवन का कोई उदाहरण दीज़िए।
उत्तर-
यदि किसी समय किसी स्थान पर विभिन्न वाद्य यन्त्रों से ध्वनियाँ उत्पन्न की जायें (जिनकी . आवृत्तियाँ भिन्न-भिन्न होती हैं) तो कान पर विभिन्न ध्वनियाँ एक ही साथ सुनायी देती हैं। अत: ध्वनि की चाल, आवृत्ति पर निर्भर नहीं करती।।

प्रश्न 7.
ध्वनि की चाल क्या आई हाइड्रोजन में शुष्क हाइड्रोजन की अपेक्षा अधिक होगी?
उत्तर-
हाइड्रोजन की अपेक्षा जल-वाष्प का घनत्व अधिक होता है, अत: आर्द्र हाइड्रोजन का घनत्व शुष्क हाइड्रोजन की अपेक्षा अधिक हो जाने के कारण उसमें ध्वनि की चाल कम हो जाती है।

प्रश्न 8.
आकाश में बिजली की गरज तथा दीप्ति एकसाथ उत्पन्न होती है, परन्तु बिजली की गरज उसकी दीप्ति के कुछ क्षणों के पश्चात् सुनायी पड़ती है, क्यों?
उत्तर-
क्योंकि ध्वनि की चाल की तुलना में प्रकाश की चाल बहुत अधिक होती है इसलिए बिजली की गरज (ध्वनि) उसकी चमक (दीप्ति अर्थात् प्रकाश) के कुछ देर बाद सुनायी पड़ती है।

प्रश्न 9.
लोहे की लम्बी नली के एक सिरे पर कान लगाया जाये और कोई दूसरे सिरे पर आघात करें, तो ठोंकने की आवाज दो बार सुनायी देती है, क्यों? कौन-सी ध्वनि पहले सुनायी देगी और क्यों?
उत्तर-
एक ध्वनि नली के पदार्थ अर्थात् लोहे में होकर जाती है तथा दूसरी वायु में होकर। लोहे एवं वायु में ध्वनि की चाल अलग-अलग होने से ध्वनि को समान दूरी तय करने में अलग-अलग समय लगता है जिससे दो ध्वनि सुनायी पड़ती हैं। ठोस में ध्वनि की चाल वायु की अपेक्षा 15 गुनी अधिक होती है। अत: जो ध्वनि लोहे में होकर जाती है वह पहले पहुँचती है।

प्रश्न 10.
वायु की अपेक्षा CO₂ गैस में ध्वनि अधिक तीव्र क्यों सुनायी देती है?
उत्तर-
वायु की अपेक्षा CO₂ गैस का घनत्व अधिक होने के कारण तीव्रता बढ़ जाती है।

प्रश्न 11.
यदि जल का आयतन प्रत्यास्थता गुणांक 2.0×10⁹ न्यूटन/मी ² तथा घनत्व 1.0×10³ किग्रा /मी³ हो तो जल में ध्वनि की चाल कितनी होगी?
हल-

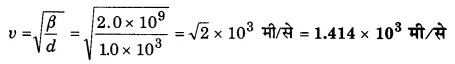
प्रश्न 12.
0°C तथा 1092 K तापों पर वायु में ध्वनि की चालों का अनुपात ज्ञात कीजिए।
हल-

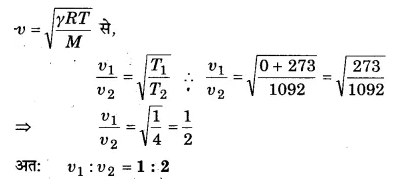
प्रश्न 13.
किसी माध्यम में एक तरंग की तरंगदैर्घ्य 0.5 भी है। इस माध्यम में इस तरंग के कारण दो बिन्दुओं के बीच कलान्तर π/5 है। इन दो बिन्दुओं के बीच न्यूनतम दूरी ज्ञात कीजिए।
हल-
कलान्तर ∆φ = (2π/λ) ∆x,
अतः , पथान्तर

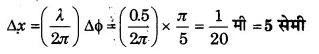
प्रश्न 14.
एक प्रगामी तरंग की चाल 400 मी/से तथा आवृत्ति 500 हर्ट्ज है। यदि दो निकटवर्ती कणों के बीच कलान्तर π/4 रेडियन है तो उनके बीच पथान्तर ज्ञात कीजिए।
हल-

प्रश्न 15.
किसी तरंग में दो बिन्दुओं के बीच पथान्तर [latex ]\frac { \lambda }{ 4 } [/latex] है, तो उनके बीच कलान्तर कितना होगा?
हल-

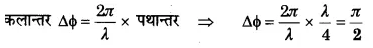
प्रश्न 16.
किसी समतल प्रगामी तरंग में कण के वेग का अधिकतम मान तरंग वेग का दोगुना है। तरंगदैर्घ्य तथा तरंग आयाम का अनुपात निकालिए।
हल-

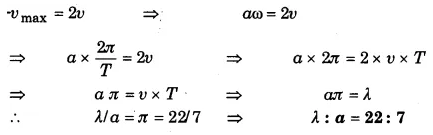
प्रश्न 17.
इस समतल प्रगामी तरंग का समीकरण लिखिए जो धनात्मक X-अक्ष के अनुदिश चल रही है। जिसका आयाम 0.04 मी, आवृत्ति 440 हर्ट्ज तथा चाल 330 मी/से है।
हल-

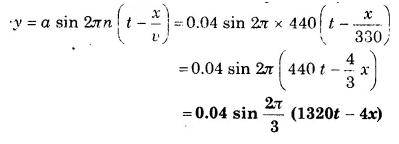
प्रश्न 18.
किसी गैस में ध्वनि तरंगों की चाल के लिए लाप्लास का सूत्र लिखिए।
उत्तर-

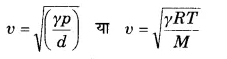
प्रश्न 19.
किसी गैस में अनुदैर्ध्य तरंगों की चाल के लिए न्यूटन का सूत्र लिखिए।
उत्तर-

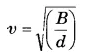
प्रश्न 20.
एक रेडियो प्रसारण केन्द्र की आवृत्ति 30 मेगाहर्ट्ज है। केन्द्र से प्रसारित तरंगों की तरंगदैर्घ्य ज्ञात कीजिए। (प्रकाश की चाल c = 3×10⁸ मी/से)
हल-
रेडियो प्रसारण केन्द्र की आवृत्ति (n) = 30 मेगाहर्ट्ज या 30×10⁶ हज
रेडियो तरंग की चाल, υ = c = 3×10⁸ मी/से ।

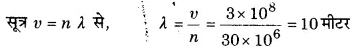
अतः केन्द्र से प्रसारित तरंगों की तरंगदैर्घ्य 10 मी होगी।

प्रश्न 21.
तरंगों का अध्यारोपण का सिद्धान्त लिखिए।
उत्तर-
तरंगों का अध्यारोपण का सिद्धान्त (Principle of superposition of waves)—किसी माध्यम में दो अथवा दो से अधिक प्रगामी तरंगें एक साथ परन्तु एक-दूसरे की गति को बिना प्रभावित किये चल सकती हैं। अत: माध्यम के प्रत्येक कण का किसी क्षण परिणामी विस्थापन दोनों तरंगों द्वारा अलग-अलग उत्पन्न विस्थापनों के सदिश (vector) योग के बराबर होता है। इस सिद्धान्त को ‘अध्यारोपण का सिद्धान्त’ कहते हैं।

प्रश्न 22.
तरंगों के अध्यारोपण से कितने प्रकार के प्रभाव प्राप्त होते हैं? कौन-कौन से?
उत्तर-
तरंगों के अध्यारोपण से तीन प्रकार के प्रभाव प्राप्त होते हैं
(i) व्यतिकरण,
(ii) विस्पन्द,
(iii) अप्रगामी तरंगें।

प्रश्न 23.
समान तरंगदैर्घ्य और समान आयाम की दो तरंगें किसी बिन्द पर 180° कलान्तर पर, मिलती हैं। वहाँ पर परिणामी आयाम क्या होगा?
हल-

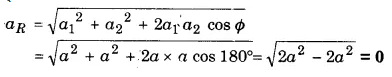
प्रश्न 24.
समान आवृत्ति वाली दो तरंगों के आयामों का अनुपात 3:1 है। इनके अध्यारोपण से उत्पन्न परिणामी तरंग की अधिकतम तथा न्यूनतम तीव्रताओं का अनुपात ज्ञात कीजिए।
हल-

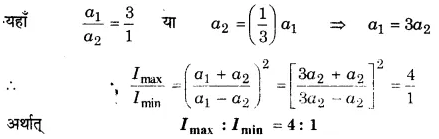
प्रश्न 25.
कला-सम्बद्ध स्रोतों से आप क्या समझते हैं?
उत्तर-
ऐसे दो स्रोतों को जिनके बीच कलान्तर सदेव नियत रहता है, कला-सम्बद्ध स्रोत (coherent sources) कहते हैं। दो कला-सम्बद्ध स्रोतों से हम स्थायी (sustained) व्यतिकरण प्रतिरूप प्राप्त कर सकते हैं। ऐसे स्रोत किसी युक्ति द्वारा एक ही स्रोत से प्राप्त किये जाते हैं।

प्रश्न 26.
ध्वनि के व्यतिकरण पर आधारित दो यन्त्रों के नाम लिखिए।
उत्तर-
क्विण्के की नली, स्वरित्र द्विभुज।।

प्रश्न 27.
प्रकाश के व्यतिकरण का एक प्राकृतिक तथा एक प्रायोगिक उदाहरण बताइए।
उत्तर-
तेल की परत का रंगीन दिखायी देना, यंग का प्रयोग।

प्रश्न 28.
विस्पन्द बनने की आवश्यक शर्त क्या है?
उत्तर-
अध्यारोपण करने वाली तरंगों की आवृत्तियों में बहुत थोड़ा अन्तर अवश्य होना चाहिए।

प्रश्न 29.
दो स्वरित्रों की आवृत्तियाँ 256 हर्ट्ज तथा 280 हर्टज हैं। एक ध्वनि स्रोत इन दोनों ही स्वरित्रों से 12 विस्पन्द प्रति सेकण्ड उत्पन्न करता है। इस स्रोत की आवृत्ति निकालिए।
हल-
पहले स्वरित्र के साथ विस्पन्दों के आधार पर
ध्वनि स्रोत की सम्भव आवृत्तियाँ = 256 ± 12 = 268 या 244 Hz
दूसरे स्वरित्र के साथ विस्पन्दों के आधार पर
ध्वनि स्रोत की सम्भव्र आवृत्तियाँ = 280 ± 12 = 268 या 292 Hz
उपर्युक्त दोनों दशाएँ 268 हज उभयनिष्ठ है।
अत: स्रोत की सही आवृत्ति = 268 Hz

प्रश्न 30.
256 हर्ट्ज तथा 260 हंट्ज आवृत्ति के दो स्वरित्रों को एक साथ कम्पित कराने पर 1.5 सेकण्ड में बनने वाले विस्पन्दों की संख्या ज्ञात कीजिए।
हल-
प्रति सेकण्ड विस्पन्दों की संख्या = ध्वनि स्रोतों की आवृत्तियों का अन्तर
= 260 – 256 = 4
1.5 सेकण्ड में विस्पन्दों की संख्या = 4 x 1.5 = 6

प्रश्न 31.
समान आवृत्ति की दो तरंगें जिनकी तीव्रताएँ I तथा 9I0 हैं, अध्यारोपित की जाती हैं। यदि किसी बिन्दु पर परिणामी तीव्रता 7I हो तो उस बिन्दु पर तरंगों के बीच न्यूनतम कलान्तर ज्ञात कीजिए।
हल-
परिणामी तीव्रता I = I₁ + I₂ + [latex s=2]2\sqrt { { I }_{ 1 }{ I }_{ 2 } } cos\phi [/latex]
जहाँ φ किसी बिन्दु पर मिलने वाली तरंगों के बीच कलान्तर है।

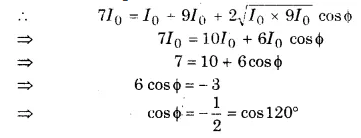
कलान्तर φ = 120°

प्रश्न 32.
दो ध्वनि स्रोत एक साथ बजाने पर 0.20 सेकण्ड में 2 विस्पन्द उत्पन्न होते हैं। विस्पन्द की आवृत्ति ज्ञात कीजिए।
हल-
0.20 सेकण्ड में उत्पन्न विस्पन्द = 2
1 सेकण्ड में उत्पन्न विस्पन्द = [latex s=2]\frac { 2 }{ 0.20 }[/latex] = 10 विस्पंद/सेकण्ड = 10 हर्ट्ज़

प्रश्न 33.
किसी तनी हुई डोरी में अनुप्रस्थ तरंगों की चाल का सूत्र लिखिए। प्रयुक्त संकेतों के अर्थ लिखिए।
उत्तर-
तनी हुई डोरी में अनुप्रस्थ तरंग की चाल [latex s=2]\upsilon =\sqrt { \frac { T }{ m } } [/latex]
जहाँ T डोरी में तनाव तथा m डोरी की एकांक लम्बाई का द्रव्यमान है।

प्रश्न 34.
किसी तनी हुई डोरी के तनाव बल में 10% की वृद्धि कर देने पर, उसमें बनने वाली अनुप्रस्थ तरंग की चाल में कितने प्रतिशत परिवर्तन हो जाएगा?
हल-
तनी हुई डोरी में अनुप्रस्थ तरंग की चाल [latex s=2]\upsilon =\sqrt { \frac { T }{ m } } [/latex] …(1)
जहाँ T डोरी में तनाव तथा m डोरी की एकांक लम्बाई का द्रव्यमान है।
अत: प्रश्नानुसार, 10% वृद्धि करने पर तनाव = [latex s=2]\frac { 11T }{ 10 }[/latex]

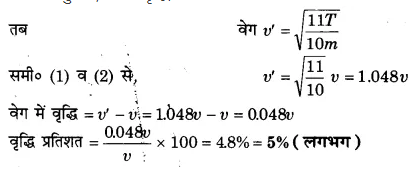
प्रश्न 35.
किसी अप्रगामी तरंग का समीकरण लिखिए। संकेतों के अर्थ स्पष्ट कीजिए।
उत्तर-

प्रश्न 36.
स्वरमापी के नाद पर दीवार में छिद्र क्यों बने होते हैं?
उत्तर-
ताकि नाद पट के भीतर की वायु का सम्बन्ध बाहरी वायु से बना रहे। ऐसा करने से स्वरित्र के तार के कम्पन सेतु से होकर नाद पट के भीतर की वायु में चले जाते हैं तथा छिद्रों से बाहर की वायु में आ जाते हैं। जिससे बाहर की वायु के कम्पित होने से ध्वनि की तीव्रता बढ़ जाती है।

प्रश्न 37.
एक प्रगामी तरंग जिसकी आवृत्ति 500 हर्ट्ज है, 360 मी/से के वेग से चल रही है। उन दो बिन्दुओं के बीच की दूरी क्या होगी जिनमें 60° का कलान्तर हो?
हल-
दिया है, तरंग की आवृत्ति (n) = 500 हर्ट्ज, वेग (υ) = 360 मी/से :
माना दो बिन्दुओं के बीच की दूरी = ∆x
सूत्र υ = nλ रे,

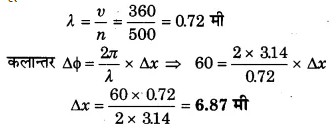
प्रश्न 38.
अप्रगामी तरंग बनने के लिए आवश्यक प्रतिबन्ध क्या है ?
या अप्रगार्मी’तरंगें बनने की प्रमुख शर्त बताइए।
उत्तर-
बद्ध माध्यम का होना अप्रगामी तरंग बनने के लिए आवश्यक प्रतिबन्ध है।

प्रश्न 39.
क्या कारण है कि खुले पाइप का स्वर बन्द पाइप के स्वर की अपेक्षा अधिक मधुर होता है?
उत्तर-
किसी स्वर के संनादियों की संख्या जितनी अधिक होती है वह उतना ही मधुर होता है। बन्द पाइप में केवल विषम संनादी जबकि खुले पाइप में सम तथा विषम दोनों प्रकार के संनादी उत्पन्न होते हैं। अत: खुले पाइप में संनादियों की संख्या बन्द पाइप में संनादी की अपेक्षा अधिक होने से इसका स्वर मधुर होता है।

प्रश्न 40.
(i) एक तारा पृथ्वी की ओर 6 x 10⁶ मी/से की चाल से गति कर रहा है। यदि उससे प्राप्त किसी स्पेक्ट्रमी रेखा की तरंगदैर्घ्य 5800 Å है, तो उसकी पृथ्वी पर आभासी तरंगदैर्घ्य  ज्ञात कीजिए। [प्रकाश की चाल 3×10⁸ मी/से]
(ii) पृथ्वी की ओर 100 किमी/सेकण्ड की चाल से आते हुए दूरस्थ सितारे से निकली 5000 Å की स्पेक्ट्रमी रेखा की तरंगदैर्ध्य में विस्थापन की गणना कीजिए।
(iii) एक तारा 10 किमी/से के वेग से हमसे दूर जा रहा है। इस तारे से उत्सर्जित 6000 Å की स्पेक्ट्रमी रेखा की तरंगदैर्ध्य में विस्थापन की गणना कीजिए।
हल-

प्रश्न 41.
पृथ्वी एक स्थिर तारे की ओर 2×10³ किमी/सेकण्ड के वेग से गति कर रही है। यदि तारे के प्रकाश की वास्तविक तरंगदैर्घ्य 6000 Å हो, तो पृथ्वी पर उसकी आभासी तरंगदैर्घ्य ज्ञात कीजिए। प्रकाश की चाल c = 3×10⁸ मी/से है।
हल-

प्रश्न 42.
खाली कमरे में ध्वनि तेज तथा भरे कमरे में मन्द सुनायी पड़ती है, क्यों?
उत्तर-
भरे कमरे में ध्वनि का कुछ भाग अवशोषित हो जाने के कारण ध्वनि की तीव्रता कम हो जाती है। जिससे ध्वनि मन्द सुनायी पड़ती है।

प्रश्न 43.
बाँसुरी और वायलिन में मुख्य अन्तर क्या है?
उत्तर-
बाँसुरी एक ऑर्गन पाइप है, जबकि वायलिन तनी डोरी का वाद्य-यन्त्र है।

प्रश्न 44.
सितार में भिन्न-भिन्न आवृत्ति के स्वर उत्पन्न होते हैं, क्यों?
उत्तर-
तार का तनाव बदलकर स्वरमेल किया जाता है तथा तारों को हाथ से विभिन्न स्थानों पर दबाकर तार की कम्पित लम्बाई परिवर्तित करके भिन्न-भिन्न आवृत्तियों के स्वर उत्पन्न किये जाते हैं।

प्रश्न 45.
वेबर-फैशनर नियम क्या है?
उत्तर-
L = k log I जहाँ, L= प्रबलता, I = तीव्रता, k = नियतांक है।
इसे वेबर-फैशनर नियम कहते हैं।

प्रश्न 46.
स्वर-अन्तराल से आप क्या समझते हैं?
उत्तर-
दो शुद्ध स्वरों की आवृत्तियों की निष्पत्ति को उन दो स्वरों के बीच का स्वर-अन्तराल कहते हैं। यदि n1 व n2 आवृत्तियों के दो स्वर हैं, तो उनका स्वर-अन्तराल = n2/ n1.

प्रश्न 47.
सांगीतिक ध्वनि एवं शोर में अन्तर स्पष्ट कीजिए।
उत्तर-
1. जो ध्वनि हमारे कानों को सुखद अर्थात् प्रिय लगती है, सांगीतिक ध्वनि कहलाती है तथा जो ध्वनि हमारे कानों को अप्रिय लगती है, शोर ध्वनि कहलाती है।
2. सांगीतिक ध्वनि किसी वस्तु के एक निश्चित आवृत्ति के नियमित कम्पनों द्वारा उत्पन्न होती है, जबकि शोर ध्वनि वस्तुओं के अनियमित कम्पनों से उत्पन्न होती है।

प्रश्न 48.
ध्वनि की आवृत्ति तथा तारत्व में क्या अन्तर है?
उत्तर-
आवृत्ति का भौतिक मापन सम्भव है, तारत्व का नहीं।

प्रश्न 49.
माध्यम का घनत्व बढ़ा दिए जाने पर ध्वनि की प्रबलता पर क्या प्रभाव पड़ेगा?
उत्तर-
माध्यम का घनत्व बढ़ाने से ध्वनि की तीव्रता (I = 2π² n² α² ρυ) बढ़ जाती है; अतः प्रबलता (L = k log I), I के बढ़ने पर बढ़ जाएगी; अर्थात् माध्यम का घनत्व बढ़ने से प्रबलता बढ़ती है।

प्रश्न 50.
एक तारे के H₂ रेखाओं के स्पेक्ट्रम (6563Å) में डॉप्लर विस्थापन 6.563Å है। पृथ्वी से दूर जाते हुए तारे के वेग की गणना कीजिए।
हल-
∆λ = 6.563Å

लघु उत्तरीय प्रश्न

प्रश्न 1.
वायु में ध्वनि की चाल पर ताप का क्या प्रभाव पड़ता है ? आवश्यक सूत्र का निगमन कीजिए।
या किसी गैस में ध्वनि की चाल पर ताप के प्रभाव की विवेचना कीजिए। 1°C ताप बढाने पर वायु में ध्वनि की चाल पर कितना परिवर्तन होगा?
उत्तर-
वायु में ध्वनि की चाल [latex s=2]\upsilon =\sqrt { \left( \frac { \gamma P }{ d } \right) } [/latex] …(1)
जहाँ P = दाब, d = घनत्व तथा γ = C_p/C_υ = 1.41
वायु के लिए (P/d) का मान वायु के ताप पर निर्भर करता है। वायु का ताप बढ़ाने पर दो सम्भावनाएँ। होती हैं। यदि वायु प्रसारित होने के लिए स्वतन्त्र है तो वह गर्म करने पर फैल जायेगी और उसका घनत्व (d) कम हो जायेगा, जबकि दाब (P) नहीं बदलेगा। इस प्रकार (P/d) का मान बढ़ जायेगा। यदि वायु एक बर्तन में बन्द है तो गर्म करने पर उसका दाब बढ़ जायेगा, जबकि घनत्व वही रहेगा। पुनः (P/d) का मान बढ़ेगा। अत: उपर्युक्त दोनों स्थितियों में वायु को गर्म करने पर (P/d) के बढ़ने से सूत्र (1) में ध्वनि की चाल बढ़ जायेगी।
सूत्र का निगमन–एक ग्राम-अणु गैस (वायु) का आयतन V = M/d,
जहाँ M गैस का अणुभार तथा d घनत्व है।
PV = RT सूत्र में V का मान रखने पर,

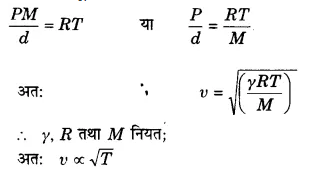
अत: किसी गैस (वायु) में ध्वनि की चाल गैस के परमताप के वर्गमूल के अनुक्रमानुपाती होती है। 1°C ताप बढ़ाने पर वायु में ध्वनि की चाल 0.61 मी/से बढ़ जाती है।

प्रश्न 2.
एक सरल आवर्त प्रगामी तरंग के लिए समीकरण लिखिए। प्रयुक्त संकेतों का अर्थ लिखिए। आयाम तथा तरंगदैर्घ्य का अर्थ तरंग के सम्बन्ध में समझाइए।
उत्तर-
सरल आवर्त प्रगामी तरंग का समीकरण
[latex s=2]y=asin\quad 2\pi \left( \frac { t }{ T } -\frac { x }{ \lambda } \right) [/latex]
जहाँ a कम्पन का आयाम, t समय, T आवर्तकाल, λ तरंगदैर्घ्य तथा x दूरी है।
तरंग के सम्बन्ध में आयाम एवं तरंगदैर्ध्य की परिभाषा ।
(i) तरंग का आयाम- माध्यम का कोई भी कण अपनी साम्यावस्था के दोनों ओर जितना अधिक-से-अधिक विस्थापित होता है, उस दूरी को तरंग का आयाम कहते हैं। इसे a से निरूपित करते हैं।
(ii) तरंगदैर्घ्य- माध्यम के किसी भी कण के एक पूरे कम्पन के समय में तरंग जितनी दूरी तय करती है, उसे तरंगदैर्ध्य कहते हैं, अथवा किसी तरंग में समान कला वाले दो निकटतम कणों के बीच की दूरी को तरंगदैर्ध्य कहते हैं। इसे λ से निरूपित करते हैं।

प्रश्न 3.
किसी प्रगामी तरंग में विस्थापन के लिए व्यंजक लिखिए। उसमें स्थित किन्हीं दो बिन्दुओं के बीच कलान्तर (∆φ) तथा अथान्तर (∆x) के बीच सम्बन्ध स्थापित कीजिए।
उत्तर-
माना कि किसी माध्यम में सरल आवर्त प्रगामी तरंग +X दिशा में चल रही है। मूल बिन्दु से x दूरी पर स्थित माध्यम के कण का किसी समय t पर विस्थापन निम्नलिखित समीकरण द्वारा व्यक्त होता है
[latex s=2]y=asin\quad 2\pi \left( \frac { t }{ T } -\frac { x }{ \lambda } \right) [/latex] …(1)
इस समीकरण में sin का कोणांक (argument) [latex s=2]2\pi \left( \frac { t }{ T } -\frac { x }{ \lambda } \right) [/latex] है। यह इसे कण की, जिसकी स्थिति x है, समय t पर कला (φ) है। माना कि समय t पर दो कणों की कलाएँ, जिनकी मूल बिन्दु से दूरियाँ x1 व x2 हैं, क्रमशः φ1 व φ2 हैं। तब

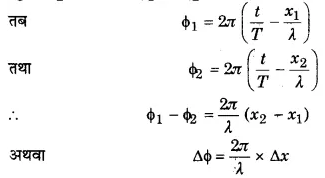
यही अभीष्ट सम्बन्ध है। आवर्तकाल T के पदों में प्रगामी तरंग का समीकरण उपर्युक्त समी० (1) है।

प्रश्न 4.
किसी प्रगामी तरंग में स्थान x तथा समय t पर विस्थापन y है।
y (x, t) = 1.5 sin(1000t – 3.3x)
जहाँ y तथा x मीटर में तथा t सेकण्ड में है। तरंग की चाल तथा उसकी गति की दिशा ज्ञात कीजिए।
हल-
दी, गई समीकरण y(x, t) = 1.5sin (1000t – 3.3x) की समीकरण

प्रश्न 5.
ऑक्सीजन में ध्वनि की चाल 640 मी/से है। हीलियम तथा ऑक्सीजन के उस मिश्रण में ध्वनि की चाल ज्ञात कीजिए जिसमें हीलियम तथा ऑक्सीजन के आयतनों का अनुपात 5:1 है। (M_He = 4, M_O2, = 32)
हल-
माना कि हीलियम तथा ऑक्सीजन के मिश्रण में हीलियम तथा ऑक्सीजन के आयतन क्रमशः V_He व V_O हैं तथा घनत्व क्रमश: d_He एवं d_O हैं। तब, मिश्रण में हीलियम तथा ऑक्सीजन के द्रव्यमान क्रमश: V_He, d_He व V_O d_O होंगे। यदि मिश्रण का घनत्व d_mix हो, तब

प्रश्न 6.
X-अक्ष दिशा में आने वाली एक प्रगामी तरंग का समीकरण y = 0.06 sin 2π (200t – x) है। यह तरंग एक दृढ तल से परावर्तित होती है तो उसका आयाम पहले का 1/3 रह जाता है। परावर्तित तरंग का समीकरण ज्ञात कीजिए।
हल-
दिया है, X-अक्ष दिशा में जाने वाली प्रगामी तरंग का समीकरण,
y = 0.06 sin 2π(200 t – 3) …(1)
समीकरण (1) से आयाम a = 0.06
प्रश्नानुसार, परावर्तित तरंग का आयाम = 0.06 x [latex s=2]\frac { 1 }{ 3 }[/latex] = 0.02
अतः परावर्तित तरंग का समीकरण, y = -0.02 sin 2π (200 t + x)

प्रश्न 7.
किसी गैस में ध्वनि की चाल तथा उसी गैस के अणुओं की वर्ग-माध्य-मूल चाल υ_rms में सम्बन्ध का सूत्र लिखिए।
उत्तर-
किसी गैस में ध्वनि की चाल [latex s=2]\upsilon =\sqrt { \frac { \gamma P }{ d } } [/latex]
जहाँ P = गैस का दाब; d = गैस का घनत्व
इसी गैस के अणुओं की वर्ग-माध्य-मूल चाल

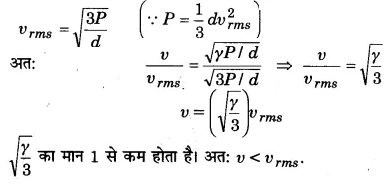
अर्थात् किसी गैस में ध्वनि की चाल, उस गैस के अणुओं की वर्ग-माध्य-मूल चाल से कम होती है।

प्रश्न 8.
एक प्रगामी तरंग y = 2sin(314t – 1.256x) की चाल ज्ञात कीजिए, जहाँ t सेकण्ड में तथा x मीटर में है।
हल-
दिया है, प्रगामी तरंग का समीकरण,
y = 2 sin (314t – 1.256x) …(1)

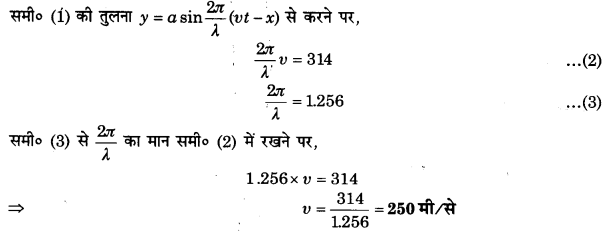
प्रश्न 9.
समान तीव्रता की दो तरंगें व्यतिकरण कर रही हैं। संपोषी व्यतिकरण के स्थान पर परिणामी तीव्रता एक तरंग की तीव्रता की कितनी गुनी होगी?
हल-
[latex s=2]{ I }_{ R }={ I }_{ 1 }+{ I }_{ 2 }+2\sqrt { { I }_{ 1 }{ I }_{ 2 } } cos\phi [/latex]
(संपोषी व्यतिकरण के लिए φ = 2kπ, जहाँ k = 0,1, 2, …..)

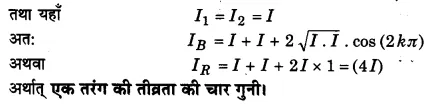
प्रश्न 10.
कभी-कभी दूर के रेडियो स्टेशन तो सुने जाते हैं किन्तु पास वाले स्टेशन सुनायी नहीं देते क्यों?
उत्तर-
पास वाले रेडियो स्टेशन से आने वाली रेडियो तरंगों तथा पृथ्वी से अत्यधिक ऊँचाई पर स्थित आयनमण्डल से परावर्तित होकर आने वाली रेडियो तरंगों के बीच पथान्तर (λ/2) का विषम गुणक रह जाने के कारण पास वाले रेडियो स्टेशन सुनायी नहीं दे पाते, जबकि दूर वाले स्टेशन से आने वाली रेडियो तरंगों तथा आयनमण्डल से परावर्तित तरंगों के बीच पथान्तर (λ/2) का पूर्ण-गुणक होने के कारण ये स्टेशन सुनायी देते है।

प्रश्न 11.
दो तरंगों की तरंगदैर्ध्य क्रमशः 49 सेमी तथा 50 सेमी हैं। यदि कमरे का ताप 30°C हो, तो दोनों तरंगों में प्रति सेकण्ड कितने विस्पन्द उत्पन्न होंगे ? 0°C पर ध्वनि का वेग 332 मी/से है।
हल-

प्रश्न 12.
16 स्वरित्र श्रेणी क्रम में इस प्रकार रखे हैं कि प्रत्येक स्वरिंत्र के साथ 2 विस्पन्द/सेकण्ड उत्पन्न करता है। यदि अन्तिम स्वरित्र की आवृत्ति पहले स्वरित्र की आवृत्ति की दोगुनी हो तो पहले स्वरित्र की आवृत्ति ज्ञात कीजिए।
हल-
माना पहले स्वरित्र की आवृत्ति n है तो दूसरे की (n + 2). तीसरे की (n + 4) तथा 16 वें की n + (16 – 1) x 2 = n + 30 होगी।
परन्तु n + 30 = 2n
⇒n = 30
अत: पहले स्वरित्र की आवृत्ति 30 हर्ट्ज़ होगी।

प्रश्न 13.
एक ध्वनि स्रोत 262 Hz तथा 278 Hz आवृत्तियों के दो स्वरित्रों (द्विभुजों में से प्रत्येक के साथ 8 विस्पन्द प्रति सेकण्ड उत्पन्न करता है। स्रोत की आवृत्ति ज्ञात कीजिए।
हल-
पहली शर्त के अनुसार सम्भव आवृत्तियाँ = 262 ± 8 = 270 या 254 हज
इसी प्रकार दूसरी शर्त के अनुसार, सम्भव आवृत्तियाँ = (278 ± 8) = 286 या 270 हर्ट्ज
∵ दोनों में 270 हर्ट्ज उभयनिष्ठ है।
अतः स्रोत की आवृत्ति 270 हर्ट्ज है।

प्रश्न 14.
मूल आवृत्ति, संनादी तथा अधिस्वरक में अन्तर लिखिए।
उत्तर-
मूल आवृत्ति, संनादी तथा अधिस्वरक में अन्तर- किसी भी वाद्ययन्त्र से उत्पन्न विभिन्न आवृत्तियों के स्वरों में न्यूनतम आवृत्ति मूल आवृति कहलाती है। इसके अतिरिक्त अन्य आवृत्तियों वाले स्वर अधिस्वरक कहलाते हैं तथा जो आवृत्तियाँ मूल आवृत्ति की पूर्ण गुणक होती हैं; वे संनादी कहलाते हैं।

प्रश्न 15.
संनादी से क्या तात्पर्य है ? उदाहरण देकर समझाइए।
उत्तर-
जिन अधिस्वरकों की आवृत्तियाँ मूल-स्वरक की आवृत्ति की पूर्ण गुणज होती हैं, उन स्वरकों को संनादी कहते हैं। मूल स्वर प्रथम संनादी कहलाता है। जिस अधिस्वरक की आवृत्ति, मूल-स्वरक की आवृत्ति से दोगुनी होती है, उसे द्वितीय संनादी कहते हैं। दूसरे, चौथे, छठे इत्यादि संनादी को सम संनादी (even harmonic) तथा तीसरे, पाँचवें, सातवें इत्यादि संनादी को विषम संनादी (odd harmonic) कहते हैं। उदाहरणार्थ-तनी हुई डोरी अथवा वायु स्तम्भों में उत्पन्न संनादी। किसी ध्वनि में संनादियों की संख्या जितनी अधिक होती है वह उतनी ही मधुर प्रतीत होती है।

प्रश्न 16.
दो बन्दनलिकाओं को एक साथ कम्पन कराने से 5 विस्पन्द प्रति सेकण्ड उत्पन्न होते हैं। यदि उनकी लम्बाइयों का अनुपात 21:20 हो, तो उनकी आवृत्तियाँ क्या होंगी ?
हल-

प्रश्न 17.
एक बन्द ऑर्गन पाइप के प्रथम अधिस्वरक की आवृत्ति वही है जो खुले ऑर्गन पाइप के । प्रथम अधिस्वरक की है। यदि बन्द ऑर्गन पाइप की लम्बाई 30 सेमी हो तो खुले ऑर्गन | पाइप की लम्बाई ज्ञात कीजिए।
हल-

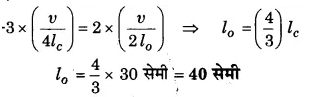
प्रश्न 18.
एक अप्रगामी तरंगे का समीकरण है- y = 4.0 sin 6.28 x cos 314 t, जहाँ y तथा x सेमी में एवं t सेकण्ड में हैं। दो अध्यारोपित तरंगों की चाल एवं दो क्रमागत निस्पन्दों के बीच की दूरी ज्ञात कीजिए।
हल-
यदि प्रगामी तरंग का आयाम a, कम्पन-काल T तथा तरंगदैर्घ्य λ हो तो इनसे उत्पन्न अप्रगामी तरंग की समीकरण इस प्रकार होगी [latex s=2]y=2a\quad sin\frac { 2\pi x }{ \lambda } cos\frac { 2\pi t }{ T } [/latex]
इसकी दी हुई समीकरण y = 4.0 sin 6.28x cos 314t से तुलना करने पर

प्रश्न 19.
एक स्वरित्र द्विभुज को एक सोनोमीटर तार के साथ कम्पन कराते हैं। जब तार की लम्बाई 105 सेमी तथा 95 सेमी होती है तो दोनों अवस्थाओं में 5 विस्पन्द प्रति सेकण्ड सुनाई देते हैं। ज्ञात कीजिए (i) स्वरित्र द्विभुज की आवृत्ति, (ii) दोनों दशाओं में तार के कम्पन की आवृत्ति।
हल-
(i), माना स्वरित्र की आवृत्ति = n चूँकि n ∝ 1/l,
अतः l1 = 105 सेमी पर तार की आवृत्ति n1 = n – 5
तथा l2 = 95 सेमी पर तार की आवृत्ति n2 = n + 5
∴n1l1 = n2l2
अतः (n – 5) x 105 = (n + 5) x 95
105 n – 525 = 95n + 475
या (105n – 95n) = 475 + 525
10n = 1000 या n = 100 हर्ट्ज़
(ii) ∴ पहली दशा में तार की आवृत्ति = n – 5 = 100 – 5 = 95 हज
तथा दूसरी दशा में तार की आवृत्ति = n + 5 = 100 + 5 = 105 हज

प्रश्न 20.
एक स्वरित्र द्विभुज सोनोमीटर के 40 सेमी लम्बे तार के साथ कम्पन करता है, तो 4 विस्पन्द प्रति सेकण्ड सुनायी पड़ते हैं, जबकि तार पर तनाव 64 न्यूटन है। तार के तनाव को घटाकर 49 न्यूटन कर देने पर फिर उतने ही विस्पन्द सुनाई पड़ते हैं। द्विभुज की आवृत्ति ज्ञात कीजिए।
हल-
माना स्वरित्र की आवृत्ति n है। यह दोनों तनावों पर तार के साथ 4 विस्पन्द प्रति सेकण्ड उत्पन्न करता है तथा तनाव के नियम से, तने तार की आवृत्ति n ∝√T; अत: T1 = 64 न्यूटन
तनाव पर आवृत्ति n1 = (n + 4) तथा T2 = 49 न्यूटन
तनावे पर आवृत्ति n2 = (n – 4), अतः तनाव के उपर्युक्त नियमानुसार,

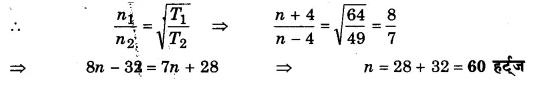
प्रश्न 21.
अनुनाद नली के अंत्य संशोधन का सूत्र स्थापित कीजिए।
उत्तर-
अनुनाद नली द्वाराअंत्यसंशोधन ज्ञात करना- अनुनाद नली में प्रस्पन्द ठीक खुले सिरे पर न बनकर थोड़ा बाहर की ओर e दूरी पर बनता है। अतः अनुनाद की पहली व दूसरी स्थिति में वायु स्तम्भ की लम्बाई l1 + e तथा l2 + e होगी।

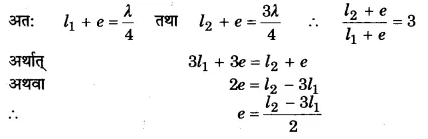
इस सूत्र से अनुनाद नली का अंत्य संशोधन ज्ञात किया जा सकता है।

प्रश्न 22.
एक खुली ऑर्गन नलिका की मूल आवृत्ति 512 हर्ट्ज है। यदि इसका एक सिरा बन्द कर दिया जाए तो इसकी आवृत्ति क्या होगी?
हल-

प्रश्न 23.
प्रकाश में डॉप्लर प्रभाव क्या है?
उत्तर-
प्रकाश में डॉप्लर का प्रभाव- यदि कोई प्रकाश-स्रोत किसी प्रेक्षक की ओर आ रहा है तो प्रकाश की आभासी आवृत्ति बढ़ जाती है (अर्थात् तरंगदैर्घ्य घट जाती है)। अत: इसकी स्पेक्ट्रमी रेखाएँ स्पेक्ट्रम के बैंगनी भाग की ओर को विस्थापित हो जाती हैं। इसके विपरीत, यदि प्रकाश-स्रोत प्रेक्षक से दूर जा रहा है तो स्पेक्ट्रमी रेखाएँ स्पेक्ट्रम के लाल भाग की ओर को विस्थापित हो जाती हैं। प्रकाश-स्रोत तथा प्रेक्षक की सापेक्ष गति के कारण, प्रकाश की आवृत्ति (अथवा तरंगदैर्ध्य) में प्रेक्षित आभासी परिवर्तन को ‘प्रकाश में डॉप्लर प्रभाव’ कहते हैं।

प्रश्न 24.
स्पेक्ट्रमी रेखाओं के डॉप्लर विस्थापन के लिए एक व्यंजक का निगमन कीजिए। तारों की ।। गति के अध्ययन में इसके अनुप्रयोग की विवेचना कीजिए।
उत्तर-
डॉप्लर विस्थापन- प्रकाश-स्रोत तथा प्रेक्षक के बीच दूरी परिवर्तन के कारण प्रकाश-स्रोत से उत्सर्जित प्रकाश की वास्तविक तरंगदैर्घ्य तथा प्रेक्षित तरंगदैर्घ्य (आभासी तरंगदैर्ध्य) का अन्तर डॉप्लर विस्थापन कहलाता है। इसको निम्नांकित सूत्र से व्यक्त किया जाता है
डॉप्लर विस्थापन ∆λ = [latex ]\frac { \upsilon }{ c } [/latex] λ
जहाँ, v = प्रकाश-स्रोत या प्रेक्षक का वेग, c = प्रकाश का वेग तथा λ = वास्तविक तरंगदैर्घ्य
जब प्रेक्षक तथा प्रकाश-स्रोत के बीच की दूरी घट रही हो, तो– सापेक्षिकता के सिद्धान्त (theory of relativity) से यह सिद्ध किया जा सकता है कि स्रोत की आभासी आवृत्ति

जहाँ v प्रकाश की वास्तविक आवृत्ति,υ प्रकाश स्रोत अथवा प्रेक्षक की चाल तथा c प्रकाश की चाल है। स्पष्ट है कि इस दशा में प्रेक्षक को प्रकाश की आवृत्ति बढ़ी हुई प्रतीत होगी, अर्थात् स्पेक्ट्रमी रेखा स्पेक्ट्रम के बैंगनी सिरे की ओर विस्थापित होंगी।
डॉप्लर विस्थापन ज्ञात करने के लिए, माना स्रोत से उत्सर्जित प्रकाश की वास्तविक तिरंगदैर्घ्य λ तथा आभासी तरंगदैर्घ्य λ है।।

जब स्रोत व प्रेक्षक के बीच की दूरी बढ़ रही हो ।
तब स्रोत की आभासी आवृत्ति

स्पष्ट है कि इस दशा में प्रेक्षक को प्रकाश की आवृत्ति घटी हुई अर्थात् तरंगदैर्घ्य बढ़ी हुई प्रतीत होगी। इसलिए स्पेक्ट्रमी रेखाएँ स्पेक्ट्रम के लाल भाग की ओर विस्थापित हो जाएँगी। परन्तु उपर्युक्त की भाँति गणना करने पर तरंगदैर्घ्य विस्थापन का निम्नलिखित समी० प्राप्त होगा

अत: उपर्युक्त समी० (2) व (4) से स्पष्ट है कि दोनों दशाओं में डॉप्लर विस्थापन का सूत्र समान है। डॉप्लर विस्थापन से तारों की गति का अनुमान- तारे तथा गैलेक्सी प्रकाशमान होने से प्रकाश उत्सर्जित करते हैं। इनके वेग का अनुमान लगाने के लिए उनसे प्राप्त प्रकाश के स्पेक्ट्रम का चित्र खींचा जाता है। स्पेक्ट्रम में कुछ तत्त्वों; जैसे—हाइड्रोजन, हीलियम, पारा इत्यादि की रंगीन रेखाएँ दिखाई पड़ती हैं जिनकी तरंगदैर्घ्य ज्ञात की जाती है। ये रेखाएँ प्रयोगशाला में भी इस तत्त्व का स्पेक्ट्रम लेकर देखी जा सकती हैं तथा इनकी तरंगदैर्घ्य निश्चित होती है। यदि इन स्पेक्ट्रमों की तुलना करने पर यह ज्ञात होता है। कि तारे के स्पेक्ट्रम में किसी रेखा की तरंगदैर्घ्य, प्रयोगशाला में लिये गये स्पेक्ट्रम में उसी रेखा की तरंगदैर्ध्य से अधिक है, तो तारा पृथ्वी से दूर जा रहा है और यदि कम है, तो तारा पृथ्वी की ओर आ ; रहा है। यदि किसी रेखा के लिए तरंगदैर्ध्य में यह अन्तर ∆λ हो, तब,

प्रश्न 25.
दूर स्थित तारे से आते हुए प्रकाश का स्पेक्ट्रोमीटर से फोटोग्राफ लिया जाता है और यह देखा जाता है कि तरंगदैर्ध्य में बड़ी तरंगदैर्घ्य की ओर 0.50% का विचलन मिलता है। तारे का वेग ज्ञात कीजिए। (प्रकाश का वेग = 3 x 10⁸ मी/से)
हल-
∆λ = λ का 0.05% = 5 x 10^-4 λ

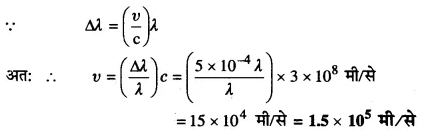
प्रश्न 26.
किसी तारे से आने वाली 6000 Å की स्पेक्ट्रमी रेखा की तरंगदैर्घ्य 5980 Å में मिलती है। बताइए कि
(i) तारा पृथ्वी की ओर आ रहा है अथवा इससे दूर जा रहा है।
(ii) नक्षत्र (तारे) का वेग क्या है?
हल-
(i) ∆λ = 20 Å तरंगदैर्घ्य घट रही है, अत: तारा पृथ्वी की ओर आ रहा है।
(ii)

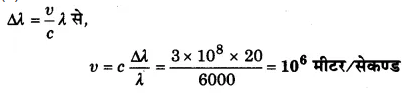
प्रश्न 27.
एक तारा पृथ्वी की ओर 9 x 10⁶ मी/से की चाल से गति कर रहा है। यदि उससे प्राप्त किसी स्पेक्ट्रमी रेखा की तरंगदैर्घ्य 6000 Å हो, तो उसकी पृथ्वी पर आभासी तरंगदैर्घ्य ज्ञात कीजिए।
(प्रकाश की चाल = 3 x 10⁸ मी/से)
हल-

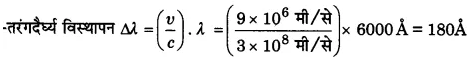
चूँकि तारा पृथ्वी की ओर आ रहा है अर्थात् प्रकाश-स्रोत के बीच की दूरी घट रही है, अत: तरंगदैर्घ्य भी घटेगी, अतः पृथ्वी पर आभासी तरंगदैर्घ्य λ’ = λ – ∆λ = 6000 Å -180 Å = 5820 Å

प्रश्न 28.
एक तारा पृथ्वी से 10⁵ मी/से वेग से दूर जा रहा है। यदि उससे प्राप्त स्पेक्ट्रमी रेखा की तरंगदैर्ध्य 6000 Å है तो प्रयोगशाला में इस स्पेक्ट्रमी रेखा की तरंगदैर्ध्य क्या होगी? ।(प्रकाश का वेग c = 3 x 10⁸ मी/से)
हल-

प्रश्न 29.
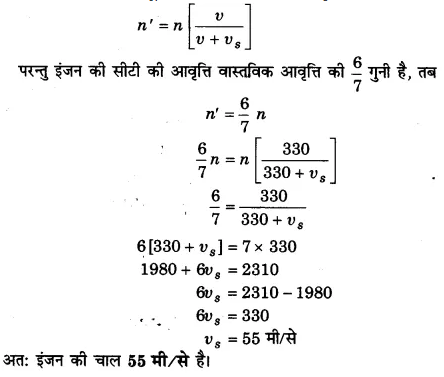
जब कोई इंजन किसी स्थिर ध्वनि से दूर जाता है तो इंजन की सीटी की आवृत्ति वास्तविक आवृत्ति की 6/7 गुनी प्रतीत होती है। इंजन की चाल की गणना कीजिए। (वायु में ध्वनि की चाल 330मी/से) है।
हल-
इंजन किसी स्थिर ध्वनि से दूर जाता है, तो आभासी आवृत्ति

प्रश्न 30.
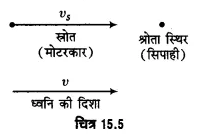
एक ध्वनि स्रोत एवं श्रोता एक-दूसरे के विपरीत दिशा में, एकसमान चाल 36 किमी/घण्टा से गति करते हैं। यदि स्रोत से आने वाली ध्वनि की आवृत्ति श्रोता को 1980 हर्ट्ज की प्राप्त हो तो स्रोत की वास्तविक आवृत्ति क्या है? (वायु में ध्वनि की चाल = 340 मी/से है)।

हल-
यदि ध्वनि-स्रोत तथा श्रोता क्रमशः υ_s व υ_o वेगों से ध्वनि की दिशा में चल रहे हों तो श्रोता को सुनाई देने वाली आभासी आवृत्ति ।

जहाँ n स्रोत की वास्तविक आवृत्ति है तथा υ ध्वनि की चाल है।
प्रश्नानुसार, स्रोत (मोटरकार) ध्वनि की दिशा में चल रहा है तथा श्रोता (सिपाही) स्थिर है (चित्र 15.5)। इस प्रकार

प्रश्न 31.
एक इंजन 60 मीटर/सेकण्ड की चाल से एक स्थिर श्रोता की ओर आ रहा है। उसकी वास्तविक आवृत्ति 400 हर्ट्ज है। श्रोता द्वारा सुनी गयी आभासी आवृत्ति की गणना कीजिए। ध्वनि की चाल 360 मीटर/सेकण्ड है।
हल-
इंजन की चाल (υ_s) = 60 मीटर/सेकण्ड
वास्तविक आवृत्ति (n) = 400 हर्ट्ज ।
चूँकि इंजन स्थिर श्रोता की ओर आ रहा है, तब आभासी आवृत्ति

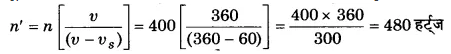
अतः श्रोता द्वारा सुनी गयी आभासी आवृत्ति 480 हर्ट्ज है।

प्रश्न 32.
पृथ्वी से दूर जाते हुए तारे के प्रकाश की प्रेक्षित तरंगदैर्घ्य वास्तविक तरंगदैर्ध्य से 0.2 प्रतिशत अधिक प्रतीत होती है। तारे की चाल ज्ञात कीजिए।
हल-

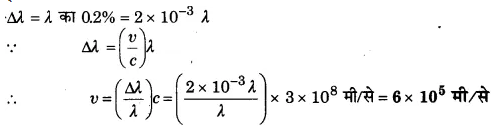
प्रश्न 33.
एक ध्वनि-स्रोत स्थिर श्रोता की ओर 20 मी/से की चाल से आ रहा है। यदि श्रोता को सुनाई देने वाली आभासी आवृत्ति 664 कम्पन/सेकण्ड है तो ध्वनि सोत की वास्तविक आवृत्ति ज्ञात कीजिए। ध्वनि की चाल 332 मीटर/सेकण्ड है।
हल-
ध्वनि-स्रोत की चाल υ_s = 20 मी/से
आभासी आवृत्ति (n’) = 664 कम्पन/सेकण्ड
∵ ध्वनि-स्रोत स्थिर श्रोता की ओर आ रहा है, तब वास्तविक आवृत्ति

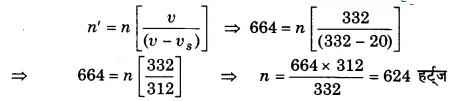
अतः ध्वनि-स्रोत की वास्तविक आवृत्ति 624 हर्ट्ज है।

प्रश्न 34.
यदि एक गतिमान मनुष्य को स्थिर स्रोत की ध्वनि का तारत्व 10 प्रतिशत गिरा हुआ लगता है तो उसकी चाल एवं दिशा ज्ञात कीजिए।
हल-
श्रोतों को सुनाई पड़ने वाली आवृत्ति

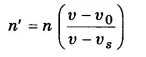
जहाँ n वास्तविक आवृत्ति है तथा υ_o व υ_s क्रमशः श्रोता के स्रोत के ध्वनि की दिशा में वेग हैं।

प्रश्न 35.
एक इंजन 1240 हर्ट्ज आवृत्ति की सीटी बजाता हुआ 90 किमी/घण्टा के वेग से एक पहाड़ी की ओर जा रहा है। एक स्पष्ट प्रति ध्वनि ड्राइवर को सुनाई देती है। प्रति ध्वनि की आभासी आवृत्ति इस ड्राइवर को कितनी प्रतीत होगी? ध्वनि की चाल 335 मी/से है।।
हल-
इंजन की चाल (υ_s) = 90 किमी/घण्टा = [latex s=2]\frac { 90X5 }{ 18 }[/latex] मी/से = 25 मी/से
वास्तविक आवृत्ति (n) = 1240 हज़।
चूँकि इंजन स्थिर श्रोता की ओर आ रहा है, तब प्रतिध्वनि की आभासी आवृत्ति

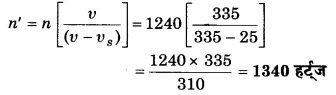
विस्तृत उत्तरीय प्रश्न

प्रश्न 1.
एक समतल प्रगामी तरंग के विस्थापन समीकरण की स्थापना कीजिए।
उत्तर-
यदि किसी माध्यम में तरंग के संचरित होने पर माध्यम के कण अपनी साम्य स्थिति के दोनों ओर सरल आवर्त गति करते हैं, तो इस तरंग को सरल आवर्त अथवा समतल प्रगामी तरंग (progressive wave) कहते हैं।
माना किसी माध्यम में ध्वनि तरंग धनात्मक X-अक्ष की दिशा में संचरित हो रही है तथा इसकी चाल है। माना कि हम समय का मापन उस क्षण से प्रारम्भ करते हैं जब मूल बिन्दु O पर स्थित कण अपना कम्पन प्रारम्भ करता है। यदि t सेकण्ड पश्चात् इस कण का विस्थापन y हो, तो ।
y = a sin ωt …(1)

जहाँ a कम्पन का आयाम, ω = 2πn तथा n तरंग की आवृत्ति है। समीकरण (1) बिन्दु O पर स्थित कण के लिए सरल आवर्त गति का समीकरण है। ज्यों-ज्यों तरंग O से आगे अन्य कणों तक पहुँचती है, त्यों-त्यों ये कम्पन करने लगते हैं।
यदि तरंग की चाल υ हो तो वह कण 1 से x दूरी पर स्थित कण 6 तक x/υ सेकण्ड में पहुँचेगी। अतः कण 6, कण 1 से x/υ सेकण्ड के बाद अपना कम्पन प्रारम्भ करेगा। इस प्रकार किसी समय कण 6 का विस्थापन वही है जो उस समय से x/υ सेकण्ड पहले कण 1 का था, अर्थात् t पर कण 6 का विस्थापन वही होगा जो (t – x/υ) पर कण 1 का था। समीकरण (1) में t के स्थान पर (t – x/υ) रखकर हम कण 1 का समय है t – (x/υ) पर विस्थापन प्राप्त कर सकते हैं। अतः मूल बिन्दु (कण 1) से x दूरी पर स्थित कण (6) की समय t पर विस्थापन होगा।

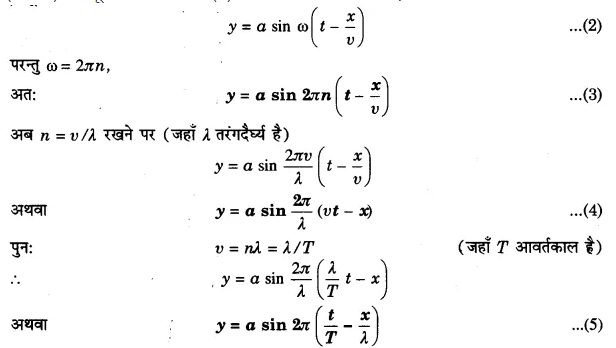
समीकरण (3), (4) वे (5) + X दिशा में चलने वाली सरल आवर्त प्रगामी तरंग की समीकरण है। यदि तरंग -X दिशा में चल रही है तो उपर्युक्त समीकरणों में sin के कोणांक में (-) के स्थान पर (+) लिखना होगा।
यदि +X दिशा में चलने वाली तरंग तथा किसी अन्य तरंग में कलान्तर φ हो तो उस तरंग का समीकरण होगा।

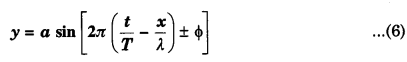
प्रश्न 2.
एक समतल प्रगामी तरंग का विस्थापन समीकरण निम्नवत् है
y = 0.5 sin(314t – 1.57x) मीटर
इस तरंग का आयाम, आवृत्ति एवं चाल ज्ञात कीजिए। इसके चलने की दिशा भी बताइए।
हल-
दिया है, y = 0.5sin(314t – 1.57x) दी गयी समीकरण की तुलना

प्रश्न 3.
किसी माध्यम (गैस) में अनुदैर्घ्य (ध्वनि) तरंगों की चाल के लिए न्यूटन का सूत्र लिखिए। इस सूत्र में लाप्लास के संशोधन की व्याख्या कीजिए।
उत्तर-
सर्वप्रथम न्यूटन ने गणना द्वारा यह सिद्ध किया कि यदि किसी माध्यम को प्रत्यास्थता गुणांक E तथा घनत्व d हो, तो उसे माध्यमं में ध्वनि की चाल υ निम्नलिखित सूत्र द्वारा प्राप्त की जाती है
[latex s=2]\upsilon =\sqrt { \left( \frac { E }{ d } \right) } [/latex]
यह किसी भी माध्यम में अनुदैर्ध्य तरंगों की चाल का व्यापक सूत्र है।
न्यूटन के अनुसार, जब अनुदैर्ध्य तरंग किसी गैस माध्यम में चलती है तो गैस का ताप अपरिवर्तित रहता है। अत: उपर्युक्त सूत्र में E को गैस का समतापी आयतन प्रत्यास्थता गुणांक ले सकते हैं जिसका मान गैस के प्रारम्भिक दाब P के बराबर होता है। अत: न्यूटन के अनुसार किसी गैस में ध्वनि की चाल होती है।
[latex s=2]\upsilon =\sqrt { \left( \frac { P }{ d } \right) } [/latex] …(1)
इस सूत्र द्वारा जब 0°C पर, P (= 1.01 x 10⁵ न्यूटन/मीटर²) तथा d ( = 1.29 किग्रा/मीटर³) के मान रखकर υ के मान की गणना करते हैं तो इसका मान 279.8 मीटर/सेकण्ड प्राप्त होता है। परन्तु प्रयोगों द्वारा 0°C पर वायु में ध्वनि की चाल 331 मीटर/सेकण्ड प्राप्त होती है। अत: न्यूटन के सूत्र में कुछ त्रुटि सम्मिलित है। इस त्रुटि का संशोधन लाप्लास ने किया। लाप्लास का संशोधन-लाप्लास के अनुसार, जब गैस में अनुदैर्ध्य तरंगें चलती हैं तो सम्पीडन एवं विरलन एकान्तर क्रम में बहुत ही शीघ्रता से होते हैं। इस कारण सम्पीडन के समय उत्पन्न ऊष्मा माध्यम से बाहर नहीं जा पाती और न ही विरलन के समय ऊष्मा की कमी को माध्यम के बाहर से ऊष्मा प्राप्त कर पूरा किया जा सकता है। इसके अतिरिक्त ऊष्मा का यह आदान-प्रदान गैस का ऊष्मा का कुचालक होने के कारण भी सम्भव नहीं है। इस प्रकार गैस में ध्वनि संचरण के समय ऊष्मा की मात्रा स्थिर रहती है, परन्तु ताप बदल जाता है। इस प्रकार न्यूटन के सूत्र में E गैस का रुद्धोष्म आयतन-प्रत्यास्थता गुणांक होना चाहिए जिसका मान γP होता है।

यह मान प्रयोगों द्वारा प्राप्त मान के बराबर है।
अत: लाप्लासे का संशोधन ध्वनि की वायु में चाल के प्रेक्षित मान की पुष्टि करता है।
समी० (2) वायु अर्थात् गैसीय माध्यम में ध्वनि की चाल के लिए लाप्लास का सूत्र भी कहलाता है जो लाप्लास द्वारा किया गया न्यूटन के सूत्र का संशोधित रूप है।

प्रश्न 4.
गैस में ध्वनि की चाल को प्रभावित करने वाले विभिन्न कारक क्या हैं? गैस में ध्वनि की चाल पर ताप वृद्धि का क्या प्रभाव पड़ता है? आवश्यक सूत्र का निगमन कीजिए।
हल-
गैस में ध्वनि की चाल को प्रभावित करने वाले कारक निम्नलिखित होते हैं
(i) दाब का प्रभाव-ध्वनि की चाल (υ) = [latex s=2]\sqrt { \frac { \gamma P }{ d } } =\sqrt { \frac { \gamma RT }{ M } } [/latex]
स्थिर ताप पर, [latex s=2]\frac { P }{ d } =\frac { RT }{ M } [/latex] = नियतांक
अत: स्थिर ताप पर ध्वनि की चाल पर गैस के दाब का कोई प्रभाव नहीं पड़ता।
(ii) ताप का प्रभाव-ताप बढ़ने पर ध्वनि की चाल बढ़ती है।
ध्वनि की चाल

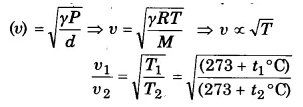
अर्थात् किसी गैस में ध्वनि की चाल गैस के परमताप के वर्गमूल के अनुक्रमानुपाती होती है।
(iii) आर्द्रता का प्रभाव-आर्द्रता बढ़ने पर वायु का घनत्व घट जाता है, अत: सूत्र [latex s=2]\upsilon =\sqrt { \frac { \gamma P }{ d } } [/latex] के परिणामस्वरूप वायु में ध्वनि की चाल बढ़ जाती है। समान तापक्रम पर नम वायु (बारिश) में , ध्वनि की चाल शुष्क वायु (गर्मियों में) की तुलना में अधिक होती है।
d नम वायु υ शुष्क वायु
(iv) माध्यम की गति का प्रभाव–यदि माध्यम (गैस वायु) ω वेग से ध्वनि संचरण की दिशा में गतिशील हो, तब
ध्वनि का परिणामी वेग = υ + ω cos θ
(v) आवृत्ति अथवा तरंगदैर्घ्य का प्रभाव-ध्वनि तरंगों की आवृत्ति अथवा तरंगदैर्ध्य का ध्वनि की चाल पर कोई प्रभाव नहीं पड़ता है।

प्रश्न 5.
सामान्य ताप व दाब पर 4 ग्राम हीलियम 22.4 लीटर आयतन घेरती है। इस अवस्था में हीलियम में ध्वनि की चाल ज्ञात कीजिए। दिया गया है—γ = 1.67 तथा 1 वायुमण्डल दाब = 10⁵ न्यूटन/मी²।
हल-
यहाँ सामान्य दाब P =1 वायुमण्डल दाब = 10⁵ न्यूटन/मीटर²
सामान्य ताप व दाब पर हीलियम का घनत्व

प्रश्न 6.
किस ताप पर ऑक्सीजन में ध्वनि की चाल वही होगी जो कि 14°C पर नाइट्रोजन में है? ऑक्सीजन व नाइट्रोजन के अणुभार क्रमशः 32 व 28 हैं।
हल-
यदि किसी गैस का अणुभार : M तथा परमताप T हो तो उस गैस में ध्वनि की चाल
[latex s=2]\upsilon =\sqrt { \gamma RT/M } [/latex]
जहाँ R सार्वत्रिक गैस-नियतांकं है।
माना कि ताप t पर ऑक्सीजन में ध्वनि की चाल वही है जो 14°C पर नाइट्रोजन में है। अब

प्रश्न 7.
सामान्य ताप तथा दाब पर वायु में ध्वनि की चाल 330 मी/से है। हाइड्रोजन गैस में ध्वनि की चाल की गणना कीजिए। हाइड्रोजन गैस वायु की तुलना में 16 गुनी हल्की है।
हल-
किसी गैस में ध्वनि की चाल [latex s=2]\upsilon =\sqrt { (\gamma P/d) } [/latex], जहाँ P गैस का दाब है,d घनत्व है तथा γ गैस की दो विशिष्ट ऊष्माओं का अनुपात है। यहाँ स्पष्ट है कि समान दाब पर विभिन्न गैसों में ध्वनि की चाल υ∝l/√d अर्थात् घनत्व के वर्गमूल के व्युत्क्रम में होगी। इसलिए यदि सामान्य ताप व दाब पर वायु तथा हाइड्रोजन में ध्वनि की चाल क्रमश: υ_a तथा υ_H2 एवं इनके घनत्व क्रमशः d_a तथा d_H2 हों, तो

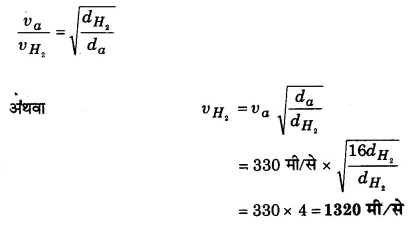
प्रश्न 8.
एक तरंग समीकरण [latex s=2]y=3sin\pi \left[ \frac { x }{ 4.0 } -\frac { t }{ 0.025 } \right] [/latex]
से प्रदर्शित है, जहाँ y तथा x सेमी में एवं t सेकण्ड में है। ज्ञात कीजिए
(i) तरंग की चाल
(ii) 2.0 सेमी दूर स्थित कणों के मध्य कलान्तर।
हल-
दी गई तरंग की समीकरण है।
[latex s=2]y=3sin\pi \left[ \frac { x }{ 4.0 } -\frac { t }{ 0.025 } \right] [/latex]
इसकी मानक समीकरण y = a sin(kx – ωt) से तुलना करने पर,
a = 3 सेमी

प्रश्न 9.
एक तनी हुई डोरी में अनुप्रस्थ तरंग चाल का व्यंजक लिखिए तथा उसमें प्रयुक्त प्रतीकों का अर्थ बताइए। एक तने हुए तार की लम्बाई 1.0 मीटर तथा द्रव्यमान 0.2 ग्राम है। यदि तार से 2.5 किग्रा को भार लटक रहा हो और तार दो खण्डों में कम्पन कर रहा हो, तो तार से उत्पन्न स्वर की आवृत्ति ज्ञात कीजिए। (g = 10 मी/से²)
हल-
तनी हुई डोरी में अनुप्रस्थ तरंग की चाल υ = (T/m)
(जहाँ T डोरी में तनाव तथा m डोरी की एकांक लम्बाई का द्रव्यमान है। यदि डोरी के एक सिरे से M द्रव्यमान लटकाकर उसमें T तनाव आरोपित किया जाए तो T = Mg तथा डोरी की त्रिज्या r, घनत्व d

प्रश्न 10.
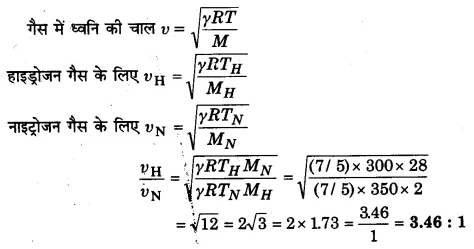
27°C पर हाइड्रोजन एवं 77°C पर नाइट्रोजन गैसों में ध्वनि की चालों का अनुपात ज्ञात कीजिए।
हल-
दिया है, हाइड्रोजन का ताप (T_H) = 27°C या 27 + 273 = 300 K
नाईट्रोजन का ताप (T_N) = 77°C
यो 77 + 273 = 350 K

प्रश्न 11.
एक तने हुए पतले तार में संचरित अनुप्रस्थ तरंग का विस्थापन समीकरण निम्नलिखित है-y = 0.021 sin (30t + 2) मी, जहाँ t सेकण्ड एवं x मीटर में है। यदि तार के पदार्थ का रेखीय घनत्व 1.6 x 10^-4 किग्रा/मी हो तो तरंग-वेग तथा तार में तनाव ज्ञात कीजिए।
हल-
दिया है, अनुप्रस्थ तरंग का विस्थापन समीकरण,
y = 0.021 sin (30t + 2x)
इसकी मानक समीकरण, y = sin (ωt – kx) से तुलना करने पर,
a = 0.021 सेमी, ω = 30, k = 2

प्रश्न 12.
व्यतिकरण से क्या तात्पर्य है? तरंगों के संपोषी तथा विनाशी व्यतिकरण के लिए आवश्यक शर्ते व्युत्पादित कीजिए।
उत्तर-
व्यतिकरण-दो तरंगों के अध्यारोपण के कारण तीव्रता के पुनर्वितरण से तीव्रता के महत्तम व न्यूनतम होने की घटना को तरंगों का व्यतिकरण कहते हैं।
संपोषी व्यतिकरण के लिए आवश्यक शर्ते
परिणामी तीव्रता के सूत्र [latex s=2]I={ I }_{ 1 }+{ I }_{ 2 }+2\sqrt { ({ I }_{ 1 }{ I }_{ 2 }) } cos\phi [/latex] से स्पष्ट है कि किसी बिन्दु पर संपोषी व्यतिकरण अर्थात् अधिकतम तीव्रता के लिए

अतः संपोषी व्यतिकरण के लिए आवश्यक शर्त निम्न हैं
(i) दोनों तरंगों के बीच कलान्तर शून्य अथवा π का सम गुणक होना चाहिए, अर्थात् तरंगें एक ही कला में मिलनी चाहिए।
(ii) दोनों तरंगों के बीच पथान्तर शून्य अथवा तरंगदैर्घ्य λ का पूर्ण गुणक होना चाहिए।
अतः संपोषी व्यतिकरण की दशा में परिणामी तीव्रता के सूत्र में cos φ = 1 रखने पर,
परिणामी तीव्रता का अधिकतंम मान ।

प्रश्न 13.
विस्पन्द से आप क्या समझते हैं? सिद्ध कीजिए कि प्रति सेकण्ड उत्पन्न विस्पन्दों की संख्या दो ध्वनि स्रोतों की आवृत्तियों के अन्तर के बराबर होती है।
उत्तर-
विस्पन्द (Beats)-जब ‘लगभग बराबर आवृत्ति वाली दो ध्वनि तरंगें एक साथ उत्पन्न की जाती हैं, तो माध्यम में उनके अध्यारोपण से प्राप्त ध्वनि की तीव्रता बारी-बारी से घटती और बढ़ती रहती है। ध्वनि की तीव्रता में होने वाले इस चढ़ाव व उतराव को ‘विस्पन्द’ (beat) कहते हैं। एक चढ़ाव तथा एक उतराव को मिलाकर एक विस्पन्द’ (one beat) कहते हैं। प्रति सेकण्ड ध्वनि की तीव्रता में होने वाले चढ़ाव व उतराव की संख्या को ‘विस्पन्द आवृत्ति’ (beat frequency) कहते हैं।
विस्पन्द उत्पन्न होने के लिए आवश्यक दशा (condition) यह है कि दोनों स्रोतों की आवृत्तियों में थोड़ा अन्तर अवश्य होना चाहिए।
माना दो ध्वनि-स्रोतों की आवृत्तियाँ n1 व n2 हैं (n1 आवृत्ति n2 आवृत्ति से कुछ अधिक है)। माना प्रत्येक ध्वनि का आयाम a है तथा दोनों तरंगें एक ही दिशा में जा रही हैं। माना इन तरंगों द्वारा माध्यम के किसी कण का विस्थापन क्रमशः y1 व y2 है, तब सरल आवर्त गति के समीकरण के अनुसार,

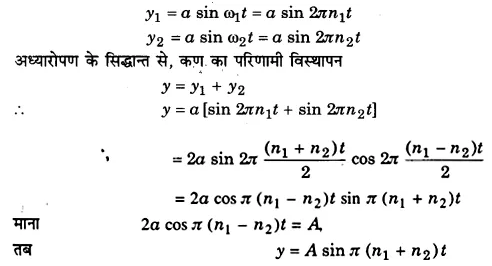
इस समीकरण से स्पष्ट है कि दोनों तरंगों के अध्यारोपण से कण एक सरल आवर्त गति करता है जिसका आयाम a है तथा जो समय t पर निर्भर करता है। चूंकि cos π(n1 – n2) t का अधिकतम मान ±1 तथा न्यूनतम मान 0 हो सकता है; अत: A का अधिकतम मान ± 2a तथा न्यूनतम मान 0 होगा।

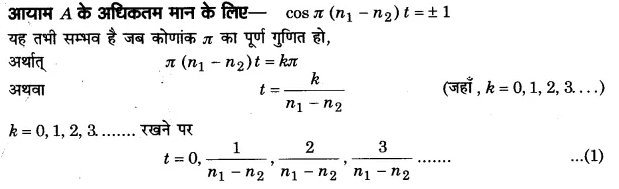
अत: इन क्षणों पर आयाम का मान अधिकतम होगा जिसके फलस्वरूप ध्वनि की तीव्रता (I = kA²) भी अधिकतम होगी।
दो लगातार अधिकतम तीव्रताओं के बीच समयान्तराल = 1/(n1 – n2) सेकण्ड है। अत: एक सेकण्ड में (n1 – n2) बार तीव्रता अधिकतम होगी।

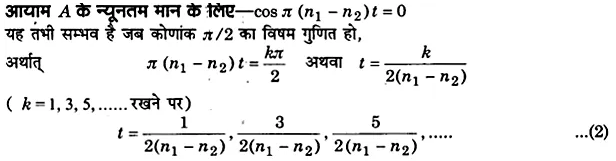
अतः इन क्षणों पर आयाम न्यूनतम होगा जिसके फलस्वरूप ध्वनि की तीव्रता भी न्यूनतम होगी। उपर्युक्त समीकरणों (1) तथा (2) से स्पष्ट है कि अधिकतम तीव्रताओं के ठीक बीच-बीच में न्यूनतम तीव्रताएँ आती
दो लगातार न्यूनतम तीव्रताओं के बीच समयान्तराल = [latex s=2]\frac { 1 }{ n1 – n2 }[/latex] सेकण्ड अर्थात् प्रति सेकण्ड (n1 – n2) बार तीव्रता न्यूनतम होती है।
इससे स्पष्ट है कि ध्वनि की तीव्रता में एक सेकण्ड में (n1 – n2) चढ़ाव तथा (n1 – n2) उतराव आते हैं, जबकि एक चढ़ाव तथा एक उतराव को मिलाकर एक विस्पन्द कहते हैं, अर्थात् एक सेकण्ड में n1 – n2 विस्पन्द सुनाई देंगे।
अत: विस्पन्दों की प्रति सेकण्ड संख्या (अर्थात् विस्पन्द-आवृत्ति)
= n1 – n2 = ध्वनि-स्रोतों की आवृत्तियों का अन्तर

प्रश्न 14.
अप्रगामी तरंग समीकरण व्युत्पन्न कीजिए। प्रस्पन्द तथा निस्पन्द बनने की शर्ते बताइए। दर्शाइए कि दो क्रमागत प्रस्पन्दों के बीच की दूरी तरंगदैर्घ्य की आधी होती है।
उत्तर-
अप्रगामी तरंग की समीकरण (Equation of stationary wave)-माना कि आयाम a की एक समतल प्रगामी तरंग चाल υ में X-अक्ष की धन दिशा में चल रही है। इस तरंग की समीकरण निम्न

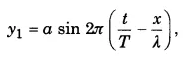
जहाँ λ प्रगामी तरंग की तरंगदैर्घ्य है तथा T कम्पन-काल है। माना कि यह तरंग किसी मुक्त (free) सिरे से टकराती है और परावर्तित तरंग X-अक्ष की ऋण दिशा में अग्रसर होती है। तब परावर्तित तरंग की समीकरण निम्न होगी

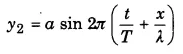
परन्तु यदि यही तरंग किसी दृढ़ (rigid) सिरे से परावर्तित हो तब परावर्तित तरंग की समीकरण निम्न होगी

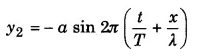
दोनों परावर्तित तरंगों में से किसी को भी लेकर अप्रगामी तरंग की समीकरण प्राप्त की जा सकती है।
नीचे मुक्त सिरे से परावर्तित तरंग लेकर अप्रगामी तरंग का समीकरण प्राप्त किया गया है।
माना कि आपतित तरंग के कारण किसी बिन्दु x का किसी क्षण t पर विस्थापन y1 है तथा परावर्तित
तरंग के कारण विस्थापन y2 है। तब, अध्यारोपण के सिद्धान्त से,
उस बिन्दु का परिणामी विस्थापन y = y1 + y2

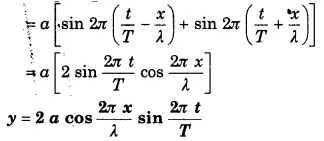
यही अप्रगामी तरंग की समीकरण है। इस समी० में x = 0, λ/2, 2λ/2, 3λ/2,…….. रखने पर cos (2π x/λ) को मान एकान्तर क्रम से +1 तथा -1 हो जाता है। इससे स्पष्ट है कि इन बिन्दुओं पर अन्य बिन्दुओं की तुलना में विस्थापन y सदैव अधिकतम होता है। ये बिन्दु ही ‘प्रस्पन्द’ (antinodes) हैं तथा एक-दूसरे से λ/2 की दूरी पर स्थित हैं। इसी प्रकार, x = λ/4,3λ/4,5λ/4,…… रखने पर cos (2π x/λ) का मान शून्य हो जाता है। इससे स्पष्ट है कि इन बिन्दुओं पर विस्थापन y शून्य हो जाता है। ये बिन्दु ही ‘निस्पन्द’ (nodes) हैं तथा ये भी एक दूसरे से λ/2 की दूरी पर हैं।
यदि हम दृढ़ सिरे से परावर्तित तरंग लें तब अप्रगामी तरंग की निम्न समीकरण प्राप्त होगी—

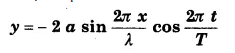
इस दशा में x = 0,λ/2, 2λ/2, 3λ/2,…… पर निस्पन्द तथा x = λ/4,3λ/4,5λ/4,…… पर प्रस्पन्द होंगे। यहाँ से स्पष्ट है कि दो क्रमागत निस्पन्दों तथा दो क्रमागत प्रस्पन्दों के बीच की दूरी तरंगदैर्ध्य की आधी (λ/2) होती है।

प्रश्न 15.
अप्रगामी तरंगों से आप क्या समझते हैं? इनकी मुख्य विशेषताएँ लिखिए।
उत्तर-
अप्रगामी तरंगें (Stationary waves)–जब किसी बद्ध माध्यम में सभी प्रकार से समान दो अनुदैर्घ्य अथवा दो अनुप्रस्थ प्रगामी तरंगें एक ही चाल से परन्तु विपरीत दिशाओं में चलती हैं, तो उनके अध्यारोपण के फलस्वरूप उत्पन्न नयी तरंग माध्यम में स्थिर प्रतीत होती है। इस प्रकार प्राप्त नयी तरंग अप्रगामी तरंग कहलाती है।
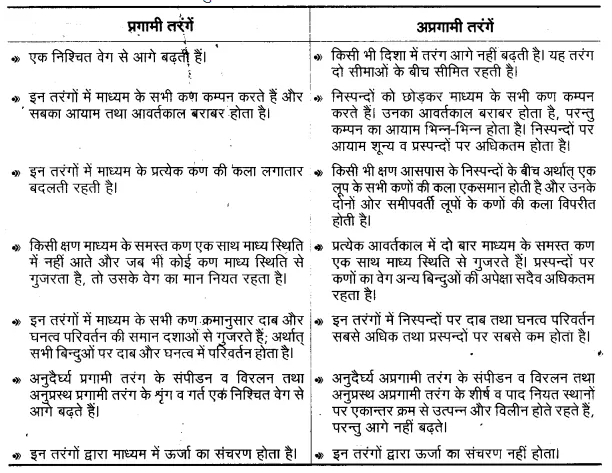
अप्रगामी तरंगों की मुख्य विशेषताएँ-अप्रगामी तरंगों की मुख्य विशेषताएँ निम्नलिखित हैं|
1. बद्ध माध्यम के कुछ कण सदैव अपने ही स्थान पर स्थिर रहते हैं; अर्थात् उनका विस्थापन शून्य होता है। ये निस्पन्द कहलाते हैं। ये समान दूरियों पर स्थित होते हैं। अप्रगामी तरंगों के अनुदैर्घ्य होने की दशा में निस्पन्दों पर दाब तथा घनत्व में परिवर्तन महत्तम होता है।
2. अप्रगामी तरंग में निस्पन्दों के बीच में कुछ बिन्दु ऐसे होते हैं जिनका विस्थापन महत्तम होता है। ये प्रस्पन्द कहलाते हैं। अप्रगामी तरंगों के अनुदैर्ध्य होने की दशा में प्रस्पन्दों पर दाब तथा घनत्व में कोई परिवर्तन नहीं होता।
3. दो क्रमागत निस्पन्दों अथवा दो क्रमागत प्रस्पन्दों के बीच की दूरी λ/2 होती है। एक निस्पन्द तथा उसके पास वाले प्रस्पन्द की दूरी λ/4 होती है।
4. किसी भी क्षण दो पास-पास स्थित निस्पन्दों के बीच सभी कणों की कला समान होती है। वे साथ-साथ गति करते हुए अपनी-अपनी अधिकतम विस्थापने की स्थिति में पहुँचते हैं तथा साथ-ही-साथ अपनी साम्यावस्था से गुजरते हैं।
5. किसी भी क्षण किसी निस्पन्द के दोनों ओर के कणों का कलान्तर 180° होता है, अर्थात् दोनों ओर के कण विपरीत कला में कम्पन करते हैं।
6. माध्यम के सभी बिन्दु एक आवर्तकाल में दो बार एक साथ अपनी-अपनी साम्यावस्था में से गुजरते हैं। दूसरे शब्दों में, दो बार अप्रगामी तरंग एक सीधी रेखा का रूप ग्रहण करती है।।

प्रगामी तथा अप्रगामी तरंगों की तुलना

प्रश्न 16.
एक अप्रगामी तरंग का समीकरण y = 10 cos[latex s=2]\frac { \pi x }{ 15 } [/latex] cos 100 πt है, जहाँ y तथा x सेमी में तथा t सेकण्ड में है। ज्ञात कीजिए–
(i) मूल प्रगामी तरंगों की आवृत्ति तथा तरंगदैर्घ्य
(ii) मूल प्रगामी तरंगों के समीकरण।
हल-
(i) जब X-अक्ष की धन दिशा में जाती प्रगामी तरंग को लिया जाए तो,
y = a cos (ωt – kx) लिया जाए तो मुक्त तल से परावर्तित तरंग।
y = a cos (ωt + kx) होगी।
इन दोनों के अध्यारोपण से उत्पन्न अप्रगामी तरंग का समीकरण होगा
y = 2a cos ωt · cos kx ….(1)

प्रश्न 17.
एक सिरे पर बन्द वायु स्तम्भ की मूल-आवृत्ति का सूत्र निगमित कीजिए तथा समझाइए कि उसमें केवल विषम प्रकार के संनादी उत्पन्न होते हैं।
उत्तर-
बन्द ऑर्गन पाइप में वायु स्तम्भ के कम्पन-

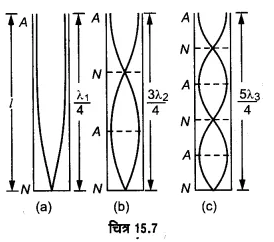
किसी बन्द पाइप के खुले सिरे पर फेंक मारने पर पाइप की वायु में अनुदैर्ध्य तरंगें खुले सिरे से बन्द सिरे की ओर चलती हैं। बन्द सिरा एक दृढ़ परिसीमा की भाँति इस तरंग को परावर्तित (विरलन की दशा को विरलन के रूप में और संपीडन की दशा को संपीडन के रूप में) करता है और परावर्तित तरंग खुले सिरे की ओर चलती हैं। खुला सिरा एक मुक्त परिसीमा की भाँति इसे परावर्तित (विरलन की दशा को संपीडन के रूप में और संपीडन की दिशा को विरलन के रूप में) करके पुनः बन्द सिरे की ओर भेजता है। इस प्रकार पाइप के वायु स्तम्भ में दो ।
अनुदैर्ध्य तरंगें विपरीत दिशाओं में चलने लगती हैं। इनके अध्यारोपण से अप्रगामी अनुदैर्ध्य तरंगें उत्पन्न होती हैं। पाइप के बन्द सिरे पर वायु के कणों को कम्पन करने की बिल्कुल स्वतन्त्रता नहीं होती। अत: वहाँ सदैव निस्पन्द (node) बनता है। इसके विपरीत पाइप के खुले सिरे पर वायु के कणों को कम्पन करने की सबसे अधिक स्वतन्त्रता होती है; अतः वहाँ सदैव प्रस्पन्द (antinode) होता है। बन्द पाइप के खुले सिरे पर ‘धीरे-से’ फेंक मारने पर वायु स्तम्भ में कम्पन चित्रे 15.7 (a) की भाँति होंगे अर्थात् खुले सिरे पर प्रस्पन्द (A) तथा बन्द सिरे पर निस्पन्द (N) होगा। एक निस्पन्द और पास वाले प्रस्पन्द के बीच की दूरी (λ1/4) होती है। अत: यदि पाइप की लम्बाई l तथा तरंगदैर्घ्य λ1 हो, तो ।

इस प्रकार पाइप से उत्पन्न स्वरक की आवृत्ति होगी

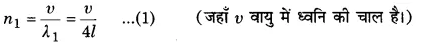
इस स्वरक को पाइप का ‘मूल-स्वरक’ (fundamental node) अथवा ‘पहला संनादी’ (first harmonic) कहते हैं। स्पष्ट है कि मूल-स्वरक की आवृत्ति पाइप की लम्बाई के व्युत्क्रमानुपाती होती है।
बन्द पाइप के खुले सिरे पर जोर से फेंक मारने पर वायु स्तम्भ में मूल-स्वरक से ऊँची आवृत्ति के स्वरक उत्पन्न किये जा सकते हैं, जिन्हें ‘अधिस्वरक’ (overtones) कहते हैं। तब वायु स्तम्भ में कम्पन चित्र 15.7 (b) तथा 15.7 (c) के अनुसार होते हैं जिनमें पाइप के खुले तथा बन्द सिरों के बीच में भी निस्पन्द व प्रस्पन्द होते हैं।
चित्र 15.7 (b) में एक पाइप के बन्द व खुले सिरों के बीच में एक प्रस्पन्द (A) व एक निस्पन्द (N) है। यदि इस स्थिति में तरंगदैर्घ्य λ2, हो, तो

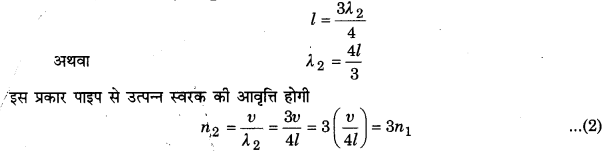
अर्थात् इस दशा में पाइप से उत्पन्न स्वरक की आवृत्ति मूल-स्वरक की आवृत्ति की तीन गुनी है। अत: यह बन्द पाइप का पहला अधिस्वरक’ है। इसे ‘तीसरा संनादी’ भी कह सकते हैं।
चित्र 15.7 (c) में पाइप के बन्द व खुले सिरों के बीच में दो निस्पन्द व दो प्रस्पन्द हैं। यदि इस स्थिति में तरंगदैर्घ्य λ3 हो, तो

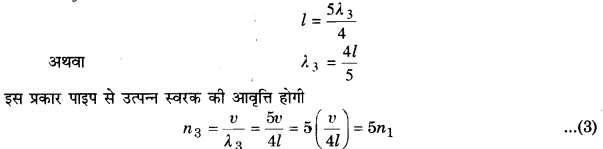
अर्थात् इस दशा में पाइप से उत्पन्न स्वरक की आवृत्ति मूल-स्वरक की आवृत्ति की पाँच गुनी है। अतः यह ‘पाँचवाँ संनादी’ अथवा ‘दूसरा अधिस्वरक’ है। इसी प्रकार आगे के अधिस्वरकों की आवृत्तियाँ भी ज्ञात की जा सकती हैं। समीकरण (1), (2) व (3) से स्पष्ट है कि |
n1 : n2 : m3 ………….= 1: 3: 5:…………..
अर्थात् बन्द पाइप से केवल ‘विषम संनादी’ ही उत्पन्न हो सकते हैं।

प्रश्न 18.
सिद्ध कीजिए कि दोनों ओर खुले ऑर्गन पाइप में सम और विषम दोनों प्रकार के संनादी उत्पन्न होते हैं।
उत्तर-
अप्रगामी तरंग का समीकरण

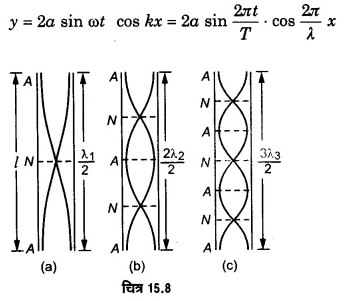
खुले ऑर्गन पाइप में वायु स्तम्भ के कम्पन–किसी खुले पाइप के एक सिरे पर फेंक मारने पर पाइप की वायु में अनुदैर्ध्य तरंगें एक सिरे से दूसरे सिरे की ओर चलती हैं। दूसरा सिरा एक मुक्त परिसीमा की भाँति इसे परावर्तित (विरलन की दशा को संपीडन के रूप में और संपीडन की दशा को विरलन के रूप में) करता है और परावर्तित तरंग पहले सिरे की ओर चलती है। पहला सिरा भी एक मुक्त परिसीमा की भाँति इसे परावर्तित करके पुन: दूसरे सिरे की ओर भेजता है। इस प्रकार पाइप के वायु स्तम्भ में दो अनुदैर्ध्य तरंगें विपरीत दिशाओं में चलने लगती हैं। उनके अध्यारोपण से अप्रगामी अनुदैर्ध्य तरंगें उत्पन्न होती हैं। चूँकि पाइप दोनों सिरों पर खुला है; अत: दोनों सिरों पर सदैव प्रस्पन्द होते हैं। पाइप के सिरे पर धीरे-से फेंक मारने पर वायु स्तम्भ में कम्पन चित्र 15.8 (a) की भाँति होंगे अर्थात् दोनों सिरे प्रस्पन्द (A) तथा उनके बीच एक निस्पन्द (N) होगा। दो प्रस्पन्दों के बीच की दूरी (λ/2) होती है। अतः यदि पाइप की लम्बाई । से तथा तरंगदैर्घ्य λ1 हो, तो

जहाँ υ वायु में ध्वनि की चाल है। पाइप से उत्पन्न कम-से-कम आवृत्ति के इस स्वरक को ‘मूलस्वरक’ अथवा ‘पहला संनादी’ कहते हैं।
पाइप के सिरे पर जोर से फेंक मारने पर वायु स्तम्भ में मूल-स्वरके से ऊँची आवृत्ति के स्वरक उत्पन्न किये जा सकते हैं, जिन्हें ‘अधिस्वरक’ कहते हैं। तब वायु स्तम्भ में कम्पन चित्र 15.8 (b) तथा 15.8 (c) के अनुसार होते हैं।
चित्र 15.8 (b) में पाइप के सिरों के बीच दो निस्पन्द हैं। यदि इस स्थिति में तरंगदैर्घ्य λ2, हो, तो

अर्थात् इस दशा में पाइप से उत्पन्न स्वरक की आवृत्ति मूल-स्वरक की आवृत्ति से दो गुनी है। अत: यह ‘द्वितीय संनादी’ अथवा ‘पहला अधिस्वरक’ है।।
चित्र 15.8 (c) में पाइप के सिरों के बीच तीन निस्पन्द हैं। यदि इस स्थिति में तरंगदैर्घ्य λ3 हो, तो

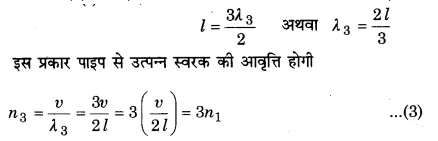
अर्थात् इस दशा में पाइप से उत्पन्न स्वरक की आवृत्ति मूल-स्वरक की आवृत्ति से तीन गुनी है। अत: यह तीसरा संनादी अथवा ‘दूसरा अधिस्वरक’ है। इस प्रकार आगे के अधिस्वरकों की आवृत्तियाँ भी ज्ञात की जा सकती हैं। समीकरण (1), (2) व (3) से स्पष्ट है कि खुले पाइप के मूल स्वरक तथा अधिस्वरकों में निम्नलिखित सम्बन्ध है
n1 : n2 : n3 ….= 1: 2: 3….
अर्थात् खुले ऑर्गन पाइप से सम तथा विषम दोनों प्रकार के संनादी उत्पन्न हो सकते हैं।

प्रश्न 19.
संनादी से आप क्या समझते हैं? सिद्ध कीजिए कि तनी हुई डोरी में सम तथा विषम दोनों प्रकार के संनादी उत्पन्न होते हैं।
उत्तर-
संनादी (Harmonics)– यदि किसी ध्वनि-स्रोत से उत्पन्न मूल-स्वरक तथा अधिस्वरकों की आवृत्तियाँ हारमोनिक श्रेणी में हों तो इन स्वरकों को संनादी कहते हैं। डोरी के मूल-स्वरक तथा अधिस्वरक

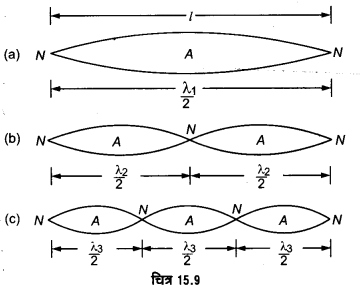
-जब किसी तनी हुई डोरी (अथवा तार) के मध्य-बिन्दु को धीरे से खींचकर छोड़ते हैं तो डोरी एक खण्ड में कम्पन करती है, तब इसके सिरों पर निस्पन्द (N) तथा बीच में प्रस्पन्द (A) बनते हैं,
चित्र 15.9 (a)। इस दशा में डोरी में उत्पन्न स्वरक को ‘मूल-स्वरक’ कहते, हैं। दो पास-पास वाले निस्पन्दों के बीच की दूरी λ/2 होती है, (λ तरंगदैर्घ्य)। यदि मूल-स्वरक की स्थिति में तरंगदैर्घ्य λ1 हो तथा डोरी की लम्बाई l हो, तो

यह डोरी (अथवा तार) की मूल आवृत्ति है।
यदि डोरी के मध्य-बिन्दु को किसी हल्के पंख से छूते हुए उसे किसी सिरे से चौथाई लम्बाई पर लम्बवत् खींचकर छोड़ दें तो डोरी दो खण्डों में कम्पन करने लगती है, चित्र 15.9 (b)। यदि इस दशा में तरंगदैर्घ्य λ2 हो, तो।

प्रश्न 20.
एक बन्द ऑर्गन पाइप के दूसरे अधिस्वरक तथा उसी लम्बाई के खुले ऑर्गन पाइप के ‘ पहले अधिस्वरक की आवृत्तियों में 150 हर्ट्ज का अन्तर है। बन्द व खुले पाइपों की मूल आवृत्तियाँ क्या हैं?
हल-
माना कि बन्द व खुले पाइपों की मूल आवृत्तियाँ क्रमशः n1 व n2 हैं, प्रत्येक पाइप की लम्बाई l है तथा वायु में ध्वनि की चाल υ है। तब

प्रश्न 21.
एक अप्रगामी तरंग को उत्पन्न करने वाली अवयवी तरंगों के आयाम, आवृत्ति एवं वेग। क्रमशः 8 सेमी, 30 हर्ट्ज एवं 180 सेमी/सेकण्ड हैं। अप्रगामी तरंग का समीकरण प्राप्त कीजिए।
हल-
अप्रगामी तरंग उत्पन्न करने वाली अवयवी तरंगों का आयाम a = 8 सेमी
आवृत्ति n = 30 हर्ट्ज = 30 सेकण्ड^-1 तथा वेग υ = 180 सेमी/सेकण्ड

प्रश्न 22.
डॉप्लर प्रभाव क्या है? एक स्थिर ध्वनि-स्रोत की ओर एक श्रोता एकसमान वेग से गति कर रहा है। श्रोता द्वारा सुनी गयी आभासी आवृत्ति के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
डॉप्लर प्रभाव-जब श्रोता और ध्वनि के स्रोत के बीच आपेक्षिक गति (relative motion) होती है, तो श्रोता को ध्वनि की आवृत्ति बदलती हुई प्रतीत होती है। आपेक्षिक गति से जब श्रोता तथा ध्वनि-स्रोत के मध्य दूरी बढ़ रही होती है तो आवृत्ति घटती हुई और जब दूरी घट रही होती है तो आवृत्ति बढ़ती हुई प्रतीत होती है। ध्वनि स्रोत तथा श्रोता के मध्य आपेक्षिक गति के कारण ध्वनि-स्रोत की आवृत्ति में उत्पन्न आभासी परिवर्तन (apparent change) का अध्ययन सर्वप्रथम डॉप्लर ने सन् 1842 में किया था, इसी कारण इसे डॉप्लर प्रभाव कहते हैं।

जब ध्वनि स्रोत स्थिर तथा श्रोता इसकी ओर गतिमान है तो आभासी आवृत्ति का व्यंजक- माना कि ध्वनि-स्रोत S स्थिर  (υ_s – 0) है तथा श्रोता O चाल υ₀ से ध्वनि के चलने की दिशा के विपरीत चलकर स्रोत की ओर तरंगें जा रहा है।
यदि ध्वनि-स्रोत की मूल आवृत्ति n हो तथा ध्वनि की चाल υ हो, तो तरंगदैर्घ्य [latex s=2]\lambda =\frac { \upsilon }{ n } [/latex]
यदि श्रोता भी स्थिर होता तो वह 1 सेकण्ड में ध्वनि-स्रोत से आने वाली n तरंगें सुनता है [चित्र तरंगें 15.10 (a)] परन्तु चूँकि वह स्वयं 1 सेकण्ड में υ₀ दूरी स्रोत की ओर तय कर लेता है [चित्रे 15.10 (b)]। अत: वह इन तरंगों के अतिरिक्त दूरी υ₀ में फैली υ₀/λ तरंगों को भी सुन सकेगा।

अतः 1 सेकण्ड में श्रोता द्वारा सुनी गयी कुल तरंगों की संख्या अर्थात् आभासी आवृत्ति ।

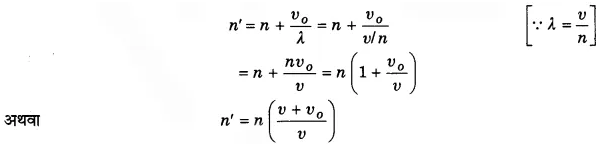
जो कि वास्तविक आवृत्ति n से अधिक है।

प्रश्न 23.
यदि कोई ध्वनि स्रोत तथा श्रोता दोनों ही एक-दूसरे की तरफ गति कर रहे हों तो ध्वनि की आभासी आवृत्ति के लिए सूत्र निगमन कीजिए।
उत्तर-
माना कि ध्वनि स्रोत तथा श्रोता दोनों ही ध्वनि की गति की दिशा में ध्वनि का वेग क्रमशः υ तथा υ वेग से चल रहे हैं (चित्र 15.11)। (ध्वनि की दिशा s सदैव ध्वनि स्रोत से श्रोता की ओर होती है।) आरम्भ में यदि यह माना जाये कि श्रोता स्थिर है, तो ध्वनि स्रोत की गति के कारण आभासी आवृत्ति

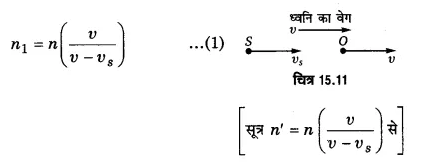
अब यदि श्रोता भी गतिमान हो जाए, तो n1, उसके लिए वास्तविक आवृत्ति होगी तथा माना श्रोता द्वारा सुनी गयी आवृत्ति n1 से बदलकर n’ हो जाती है तो

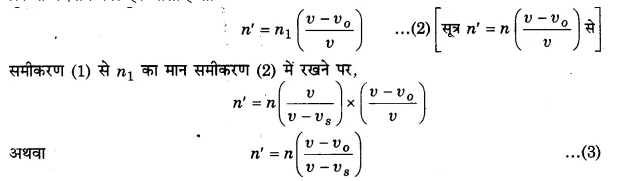
यदि स्रोत अथवा श्रोता में से किसी के चलने की दिशा ध्वनि की दिशा के विपरीत हो तो समीकरण (3) में उसके वेग υ अथवा υ का चिह्न बदल जायेगा।

प्रश्न 24.
किसी रेलवे प्लेटफॉर्म पर खड़ा एक व्यक्ति एक इंजन की सीटी को सुनता है जो एक स्थिर चाल से आकर बिना रुके हुए उसी चाल से आगे निकल जाता है। जैसे ही इंजन उससे आगे निकलता है, उस व्यक्ति को सीटी की आवृत्ति में 11 kHz से 9 kHz के अन्तर होने का आभास होता है। इंजन की चाल तथा सीटी की वास्तविक आवृत्ति की गणना कीजिए। (वायु में ध्वनि की चाल = 300 मी/से)।
हल-
दिया है,υ0 = 0,υ = 300 मी/से, n’ = 11kHz = 11000 Hz, n” = 9 kHz = 9000 Hz, υ६ =?
जब इंजन व्यक्ति की ओर आ रहा है तब आवृत्ति

प्रश्न 25.
एक स्थिर श्रोता की ओर जाते हुए ध्वनि स्रोत की आभासी आवृत्ति के सूत्र का निगमन कीजिए।
या n आवृत्ति का एक गतिमान स्रोत υ चाल से एक स्थिर श्रोता की ओर आ रहा है। ध्वनि का वेग υ कीजिए। है। श्रोता द्वारी सुनी गई आभासी आवृत्ति के लिए सूत्र का निगमन कीजिए।
या स्थिर श्रोता की ओर एक गतिमान स्रोत एकसमान वेग से जा रहा है तो आभासी आवृत्ति का सूत्र निगमित कीजिए।
उत्तर-
स्थिर श्रोता की ओर जाते हुए ध्वनि स्रोत की आभासी आवृत्ति का सूत्र- चित्र 15.12 में S व O क्रमशः ध्वनि-स्रोत तथा श्रोता की स्थितियों को व्यक्त करते हैं।

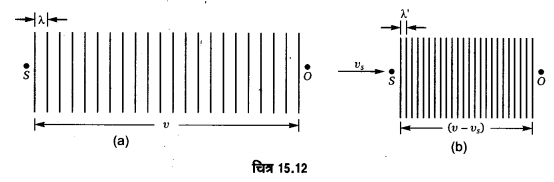
माना कि ध्वनि-स्रोत की मूल (वास्तविक) आवृत्ति n है तथा ध्वनि की चाल υ है। स्पष्ट है कि स्रोत से 1 सेकण्ड में n तरंगें निकलेंगी जो चाल υ से चलेंगी। यदि स्रोत अपने स्थान पर स्थिर है, तो यह n तरंगें SO = υ दूरी में फैल जायेंगी [चित्र 15.12 (a)]। इस प्रकार एक तरंग की लम्बाई अथवा तरंगदैर्घ्य [latex s=2]\lambda =\frac { \upsilon }{ n } [/latex]
अब माना कि ध्वनि-स्रोत चाल υ से श्रोता की ओर गति करता है, अर्थात् स्रोत ध्वनि तरंगों के पीछे-पीछे चल रहा है। तब 1 सेकण्ड में निकलने वाली n तरंगें υ दूरी में न फैलकर υ – υ, दूरी में फैलेगी, क्योंकि 1 सेकण्ड में ध्वनि-स्रोत O की ओर υ दूरी चल लेता है [चित्र 15.12 (b)]। फलतः तरंगदैर्ध्य छोटी हो जायेगी। मान लीजिए यह λ है।
इस प्रकार श्रोता को λ’ तरंगदैर्घ्य की तरंगें प्राप्त होंगी। अत: उसको ध्वनि की आवृत्ति बदली हुई प्रतीत होगी। मान लीजिए यह आभासी आवृत्ति n’ है। तब ।

जो कि वास्तविक आवृत्ति n से अधिक है।

प्रश्न 26.
एक रेडार स्टेशन से एक वायुयान की ओर 6 x 10 हर्ट्ज आवृत्ति के संकेत भेजे जाते हैं। यदि वायुयान से परावर्तित संकेत की आवृत्ति भेजे गये संकेत की आवृत्ति से 1x 10 हर्ट्ज अंधिक मालूम पड़े तो बताइए कि वायुयान किस दिशा में किस वेग से जा रहा है? (c = 30 x 10 मीटर/सेकण्ड).
हल-
संकेतों की आभासी आवृत्ति बढ़ी हुई प्रतीत होती है; इसका अर्थ है कि रेडार स्टेशन तथा वायुयान के बीच दूरी घट रही है अर्थात् वायुयान रेडार स्टेशन की ओर आ रहा है।
माना कि भेजे गये रेडार संकेत की वास्तविक आवृत्ति ν है। यदि वायुयान का रेडार स्टेशन की ओर उपगमन वेग υ है, तब सापेक्षिकता के सिद्धान्त से,

= 250 मीटर/सेकण्ड
यह वायुयान का उपगमन वेग है।

प्रश्न 27.
एक श्रोता किसी वेग से एक स्थिर ध्वनि स्रोत की ओर आकर उसी वेग से दूसरी ओर चला जाता है। श्रोता के निकट आते समय तथा दूर जाते समय की आभासी आवृत्तियों का अनुपात [latex s=2]\frac { 6 }{ 5 }[/latex] है। श्रोता के वेग की गणना कीजिए। वायु में ध्वनि की चाल 330 मी/से है।
हल-
ना श्रोता का वेग υ है।
जब श्रोता स्रोत के निकट आता है तब आभासी आवृत्ति

अतः श्रोता का वेग 30 मी/से है।

We hope the UP Board Solutions for Class 11 Physics Chapter 15 Waves help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 15 Waves, drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Physics Chapter 14 Oscillations (दोलन) are part of UP Board Solutions for Class 11 Physics . Here we have given UP Board Solutions for Class 11 Physics Chapter 14 Oscillations (दोलन)

Board	UP Board
Textbook	NCERT
Class	Class 11
Subject	Physics
Chapter	Chapter 14
Chapter Name	Oscillations
Number of Questions Solved	76

UP Board Solutions for Class 11 Physics Chapter 14 Oscillations (दोलन)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
नीचे दिए गए उदाहरणों में कौन आवर्ती गति को निरूपित करता है?
(i) किसी तैराक द्वारा नदी के एक तट से दूसरे तट तक जाना और अपनी एक वापसी यात्रा पूरी करना।
(ii) किसी स्वतन्त्रतापूर्वक लटकाए गए दण्ड चुम्बक को उसकी N-S दिशा से विस्थापित कर छोड़ देना।
(iii) अपने द्रव्यमान केन्द्र के परितः घूर्णी गति करता कोई हाइड्रोजन अणु।
(iv) किसी कमान से छोड़ा गया तीर।
उत्तर-
(i) यह आवश्यक नहीं है कि तैराक को प्रत्येक बार वापस लौटने में समान समय ही लगे; अत: यह गति आवर्ती गति नहीं है।
(ii) दण्ड चुम्बक को विस्थापित करके छोड़ने पर उसकी गति आवर्ती गति होगी।
(iii) यह एक आवर्ती गति है।
(iv) तीर छूटने के बाद कभी-भी वांपस प्रारम्भिक स्थिति में नहीं लौटता; अत: यह आवर्ती गति नहीं है।

प्रश्न 2.
नीचे दिए गए उदाहरणों में कौन (लगभग) सरल आवर्त गति को तथा कौन आवर्ती परन्तु सरल आवर्त गति निरूपित नहीं करते हैं?
(i) पृथ्वी की अपने अक्ष के परितः घूर्णन गति।।
(ii) किसी U-नली में दोलायमान पारे के स्तम्भ की गति।
(iii) किसी चिकने वक्रीय कटोरे के भीतर एक बॉल बेयरिंग की गति जब उसे निम्नतम बिन्द से कुछ ऊपर के बिन्दु से मुक्त रूप से छोड़ा जाए।
(iv) किसी बहुपरमाणुक अणु की अपनी साम्यावस्था की स्थिति के परितः व्यापक कम्पन।
उत्तर-
(i) आवर्ती गति परन्तु सरल आवर्त गति नहीं।
(ii) सरल आवर्त गति।
(iii) सरल आवर्त गति।
(iv) आवर्ती गति परन्तु सरल आवर्तः गति नहीं।

प्रश्न 3. चित्र-14.1 में किसी कण की रैखिक गति के लिए चार x-t आरेख दिए गए हैं। इनमें से कौन-सा आरेख आवर्ती गति का निरूपण करता है? उस गति का आवर्तकाल क्या है? (आवर्ती गति वाली गति का)।

उत्तर-
(a) ग्राफ से स्पष्ट है कि कण कभी भी अपनी गति की पुनरावृत्ति नहीं करता है; अत: यह गति, आवर्ती गति नहीं है।
(b) ग्राफ से ज्ञात है कि कण प्रत्येक 2 s के बाद अपनी गति की पुनरावृत्ति करता है; अतः यह गति एक आवर्ती गति है जिसका आवर्तकाल 2 s है।
(c) यद्यपि कण प्रत्येक 3 s के बाद अपनी प्रारम्भिक स्थिति में लौट रहा है परन्तु दो क्रमागत प्रारम्भिक स्थितियों के बीच कण अपनी गति की पुनरावृत्ति नहीं करता; अत: यह गति आवर्त गति नहीं है।
(d) कण प्रत्येक 2 s के बाद अपनी गति को दोहराता है; अत: यह गति एक आवर्ती गति है जिसका आवर्तकाले 2 s है।

प्रश्न 4. नीचे दिए गए समय के फलनों में कौन (a) सरल आवर्त गति (b) आवर्ती परन्तु सरल आवर्त गति नहीं, तथा (e) अनावर्ती गति का निरूपण करते हैं। प्रत्येक आवर्ती गति का आवर्तकाल ज्ञात कीजिए: (ω कोई धनात्मक अचर है)

उत्तर-
(a) दिया गया फलन x = sin ωt – cos ωt


(e) तथा (f) में दिए गए दोनों फलन न तो आवर्त गति निरूपित करते हैं और न ही सरल आवर्त गति निरूपित करते हैं।

प्रश्न 5.
कोई कण एक-दूसरे से 10 cm दूरी पर स्थित दो बिन्दुओं A तथा B के बीच रैखिक सरल आवर्त गति कर रहा है। A से B की ओर की दिशा को धनात्मक दिशा मानकर वेग, त्वरण
तथा कण पर लगे बल के चिह्न ज्ञात कीजिए जबकि यह कण
(a) A सिरे पर है,
(b) B सिरे पर है।
(c) A की ओर जाते हुए AB के मध्य बिन्दु पर है,
(d) A की ओर जाते हुए 8 से 2 cm दूर है,
(e) B की ओर जाते हुए से 3 cm दूर है, तथा
(f) A की ओर जाते हुए 8 से 4 cm दूर है।
उत्तर-
स्पष्ट है कि बिन्दु A तथा बिन्दु B अधिकतम विस्थापन की स्थितियाँ हैं तथा इनका मध्य बिन्दु O (मोना), सरल आवर्त गति का केन्द्र है।

(a) ∴ बिन्दु A पर कण का वेग शून्य होगा।
कण के त्वरण की दिशा बिन्दु A से साम्यावस्था O की ओर होगी; अतः त्वरण धनात्मक होगा।
कण पर बल, त्वरण की ही दिशा में होगा; अत: बल धनात्मक होगा।
(b) बिन्दु B पर भी कण का वेग शून्य होगा।
कण का त्वरण B से साम्यावस्था O की ओर दिष्ट होगा; अतः त्वरण ऋणात्मक होगा।
बल भी ऋणात्मक होगा।
(c) AB का मध्य बिन्दु 0 सरल आवर्त गति का केन्द्र है।
∴ कण B से A की ओर चलते हुए 0 से गुजरता है; अत: वेग BA के अनुदिश है, अर्थात् वेग ऋणात्मक है।
बिन्दु ०पर त्वरण तथा बल दोनों शून्य हैं।
(d) B से 2 cm दूरी पर कण B तथा 0 के बीच होगा।
∴ कण B से A की ओर जा रहा है; अतः वेग ऋणात्मक होगा।
यहाँ त्वरण भी B से O की ओर दिष्ट है; अतः त्वरण भी ऋणात्मक है।
‘बले भी ऋणात्मक है।
(e) ∴ कण-B की ओर जा रहा है; अतः वेग धनात्मक है।
∴ कण A व O के बीच है; अत: त्वरण A से O की ओर दिष्ट है; अत: त्वरण भी धनात्मक है।
बल भी धनात्मक है।
(f) ∴ कण A की ओर जा रहा है; अत: वेग ऋणात्मक है।
कण B तथा O के बीच है तथा त्वरण B से O की ओर (अर्थात् B से A की ओर दिष्ट है; अतः त्वरण ऋणात्मक है।
बल भी ऋणात्मक है।

प्रश्न 6.
नीचे दिए गए किसी कण के त्वरण तथा विस्थापन के बीच सम्बन्धों में से किससे सरल आवर्त गति सम्बद्ध है:
(a) a = 0.7 x
(b) a = -200x²
(c) a = -10
(d) a = 100x³
उत्तर-
उपर्युक्त में से केवल सम्बन्ध (c) में a =-10x अर्थात् त्वरण विस्थापन के अनुक्रमानुपाती है तथा विस्थापन के विपरीत दिशा में है; अत: केवल यही सम्बन्ध सरल आवर्त गति को निरूपित करता है।

प्रश्न 7.
सरल आवर्त गति करते किसी कण की गति का वर्णन नीचे दिए गए विस्थापन फलन द्वारा किया जाता है। x(t) = A cos (ωt + φ) यदि कण की आरम्भिक (t = 0) स्थिति 1 cm तथा उसका आरम्भिक वेग πcms^-1 है। तो कण का आयाम तथा आरम्भिक कला कोण क्या है? कण की कोणीय आवृत्ति π^-1 है। यदि सरल आवर्त गति का वर्णन करने के लिए कोज्या (cos) फलन के स्थान पर हम ज्या (sin) फूलन चुनें; x = B sin (ωt + α), तो उपर्युक्त आरम्भिक प्रतिबन्धों में कण का आयाम तथा आरम्भिक कला कोण क्या होगा?
हल-
दिया है : कोणीय आवृत्ति ω = r rad s^-1, t = 0 पर x = 1 cm
तथा प्रारम्भिक वेग u = πcm s^-1
सरल आवर्त गति की समीकरण x = A cos (ωt + φ)
x = A cos (πt + φ)
t = 0 तथा x = 1 रखने पर, 1 = A cos φ ..(1)

प्रश्न 8.
किसी कमानीदार तुलां का पैमानी 0 से 50 kg तक अंकित है और पैमाने की लम्बाई 20 cm है। इस तुला से लटकाया गया कोई पिण्ड, जब विस्थापित करके मुक्त किया जाता है, 0.6 s के आवर्तकाल से दोलन करता है। पिण्ड का भार कितना है?
हल-

प्रश्न 9.
1200 Nm^-1 कमानी-स्थिरांक की कोई कमानी चित्र-14.3 में दर्शाए अनुसार किसी क्षैतिज मेज से जड़ी है। कमानी के मुक्त। सिरे से 3kg द्रव्यमान का कोई पिण्ड जुड़ा है। इस पिण्ड को एक ओर 2.0 cm दूरी तक खींचकर मुक्त किया जाता है,
(i) पिण्ड के दोलन की आवृत्ति,
(ii) पिण्ड का अधिकतम त्वरण, तथा ।
(iii) पिण्ड की अधिकतम चाल ज्ञात कीजिए।

हल-
यहाँ बृल नियतांक k = 1200 न्यूटन-मीटर^-1, m = 3 किग्रा; कमानी का अधिकतम विस्तार अर्थात् आयाम a = 2.0 सेमी = 2 x 10^-2 मीटर

प्रश्न 10.
अभ्यास प्रश्न 9 में, मान लीजिए जब कमानी अतानित अवस्था में है तब पिण्ड की स्थिति x = 0 है तथा बाएँ से दाएँ की दिशा x-अक्ष की धनात्मक दिशा है। दोलन करते पिण्ड के विस्थापन x को समय के फलन के रूप में दर्शाइए, जबकि विराम घड़ी को आरम्भ (t = 0) करते समय पिण्ड,
(a) अपनी माध्य स्थिति,
(b) अधिकतम तानित स्थिति, तथा
(c) अधिकतम सम्पीडन की स्थिति पर है।
सरल आवर्त गति के लिए ये फलन एक-दूसरे से आवृत्ति में, आयाम में अथवा आरम्भिक कला में किस रूप में भिन्न है ।
हल-
उपर्युक्त प्रश्न में आयाम a = 0.20 मीटर =2 सेमी।

प्रश्न 11.
चित्र-14.4 में दिए गए दो आरेख दो वर्तुल गतियों के तद्नुरूपी हैं। प्रत्येक आरेख पर वृत्त की त्रिज्या परिक्रमण-काल, आरम्भिक स्थिति और परिक्रमण की दिशा दर्शाई गई है। प्रत्येक प्रकरण में, परिक्रमण करते कण के त्रिज्य-सदिश के x-अक्ष पर प्रक्षेप की तदनुरूपी सरल आवर्त गति ज्ञात कीजिए।

हल-
(a) माना वृत्त पर गति करता हुआ कण किसी समय । पर P से स्थिति A में पहुँच जाता है।
माना ∠POA = θ
AB, बिन्दु A से x-अक्ष पर लम्ब है।
तब ∠ BAO = θ
आवर्तकाल T = 2s

प्रश्न 12.
नीचे दी गई प्रत्येक सरल आवर्त गति के लिए तदनुरूपी निर्देश वृत्त का आरेख खींचिएं। घूर्णी कण की आरम्भिक (t = 0) स्थिति, वृत्त की त्रिज्या तथा कोणीय चाल दर्शाइए। सुगमता के लिए प्रत्येक प्रकरण में परिक्रमण की दिशा वामावर्त लीजिए। (x को cm में तथा t को s में लीजिए।)।

हल-
(a) दिया है : सरल आवर्त गति का समीकरण [latex s=2]x=-2sin\left( 3t+\frac { \pi }{ 3 } \right) [/latex]
यह गति समय का ज्या (sine) फलन है;
अतः कोणीय विस्थापन, y-अक्ष से नापा जाएगा।
दिए गए समीकरण में t = 0 रखने पर,

प्रश्न 13.
चित्र-14.7(a) में k बल-स्थिरांक की किसी कमानी के । एक सिरे को किसी दृढे आधार से जकड़ा तथा दूसरे मुक्त। सिरे से एक द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के मुक्त सिरे पर बल F आरोपित करने से कमानी तन जाती है चित्र-14.7 (b) में उसी कमानी के दोनों मुक्त सिरों से द्रव्यमान जुड़ा दर्शाया गया है। कमानी के दोनों सिरों को चित्र-14.7 में समान बल F द्वारा तानित किया गया है।

(i) दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या है?
(ii) यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन का आवर्तकाल ज्ञात कीजिए।
हल-
(i) माना कमानी का अधिकतम विस्तार x_max है, तब
चित्र (a)

(b) में-चूँकि इस बार कमानी किसी स्थिर वस्तु से सम्बद्ध नहीं है; अतः दूसरे पिण्ड पर लगे बल का कार्य केवल कमानी को स्थिर रखना है।
अतः विस्तार अभी भी केवल एक ही बल के कारण होगा।

(ii) चित्र (a) में माना कि पिण्ड को खींचकर छोड़ने पर, वापसी की गति करता पिण्ड किसी क्षण साम्यावस्था से x दूरी पर है तब कमानी में प्रत्यानयन बल F = -kx होगा।
यदि पिण्ड का त्वरण ‘a है तो F = ma

चित्र (b) में-इस दशा में, निकाय का द्रव्यमान केन्द्र अर्थात् कमानी का मध्य बिन्दु स्थिर रहेगा और दोनों पिण्ड दोलन करेंगे।
इस अवस्था में हम मान सकते हैं कि प्रत्येक पिण्ड मूल कमानी की आधी लम्बाई से जुड़ा है तथा ऐसे प्रत्येक भाग का कमानी स्थिरांक 2k होगा। यदि किसी क्षण, कोई पिण्ड साम्यावस्था से x दूरी पर है तो कमानी के संगत भाग में प्रत्यानयन बल F = -2kx होगा। यदि पिण्ड का त्वरण a है तो
ma = F => ma = -2kx या ।

प्रश्न 14.
किसी रेलगाड़ी के इंजन के सिलिण्डर हैड में पिस्टन का स्ट्रोक (आयाम को दोगुना) 1.0 m का है। यदि पिस्टन 200 rad/min की कोणीय आवृत्ति से सरल आवर्त गति करता है तो उसकी अधिकतम चाल कितनी है?
हल-
पिस्टन का आयाम a = स्ट्रोक/2 = 1.0 मी/2 = 0.5 मीटर तथा
इसकी कोणीय आवृत्ति ω = 200 रेडियन/मिनट = (200/60) रे/से = 10/3 रे/से
पिस्टन की अधिकतम चाल u_max = aω = 20 = 0.5 मीटर x (10/3) रे/से
=1.67 मी-से^-1

प्रश्न 15.
चन्द्रमा के पृष्ठ पर गुरुत्वीय त्वरण 1.7 ms^-2 है। यदि किसी सरल लोलक का पृथ्वी के पृष्ठ पर आवर्तकाल 3.5 s है तो उसका चन्द्रमा के पृष्ठ पर आवर्तकाल कितना होगा? (पृथ्वी के पृष्ठ पर g = 9.8 ms^-2)
हल-
सरल लोलक का आवर्तकाल [latex s=2]T=2\pi \sqrt { \frac { l }{ g } } [/latex] लोलक विशेष के लिए नियत; अत: T ∝1/√g इसलिए यदि पृथ्वी एवं चन्द्रमा पर गुरुत्वीय त्वरण क्रमशः g_e व g_m एवं आवर्तकाल क्रमश: T_e व T_m हो

प्रश्न 16.
नीचे दिए गए प्रश्नों के उत्तर दीजिए
(a) किसी कण की सरल आवर्त गति के आवर्तकाल का मान उस कण के द्रव्यमान तथा बल-स्थिरांक पर निर्भर करता है: [latex s=2]T=2\pi \sqrt { \frac { m }{ k } } [/latex]। कोई सरल लोलक सन्निकट सरल आवर्त गति करता है। तब फिर किसी लोलक का आवर्तकाल लोलक के द्रव्यमान पर निर्भर क्यों नहीं करता?
(b) किसी सरल लोलक की गति छोटे कोण के सभी दोलनों के लिए सन्निकट सरल आवर्त गति होती है। बड़े कोणों के दोलनों के लिए एक अधिक गूढ विश्लेषण यह दर्शाता है कि का मान [latex s=2]2\pi \sqrt { \frac { l }{ g } } [/latex] से अधिक होता है। इस परिणाम को समझने के लिए किसी गुणात्मक कारण का चिन्तन कीजिए।
(c) कोई व्यक्ति कलाई घड़ी बाँधे किसी मीनार की चोटी से गिरता है। क्या मुक्त रूप से गिरते समय उसकी घड़ी यथार्थ समय बताती है?
(d) गुरुत्व बल के अन्तर्गत मुक्त रूप से गिरते किसी केबिन में लगे सरल लोलक के दोलन की आवृत्ति क्या होती है?
उत्तर-
(a) जब दोलन स्प्रिंग के द्वारा होते हैं तो बल नियंताक k का मान केवल स्प्रिंग पर निर्भर करता है। न कि गतिमान कण के द्रव्यमान पर। इसके विपरीत सरल लोलक के लिए बल नियतांक

कण के द्रव्यमान के अनुक्रमानुपाती होता है; अत: [latex s=2]\frac { m }{ k }[/latex] का मान नियत बना रहता है।
इसलिए आवर्तकाल m पर निर्भर नहीं करता।
(b) सरल लोलक के लिए प्रत्यानयन बल F =- mg sin θ
यदि θ छोटा है तो sin θ ≈ θ = [latex s=2]\frac { x }{ l }[/latex]

अर्थात् यह गति सरल आवर्त होगी तथा आवर्तकाल [latex s=2]2\pi \sqrt { \frac { l }{ g } } [/latex]
यदि θ छोटा नहीं है तो हम sin θ ≈ θ नहीं ले सकेंगे तब गति सरल आवर्त नहीं रहेगी; अत: आवर्तकाल [latex s=2]2\pi \sqrt { \frac { l }{ g } } [/latex] से बड़ा होगा।
(c) हाँ, क्योकि कलाई घड़ी का आवर्तकाल गुरुत्वीय त्वरण के मान में परिवर्तन से प्रभावित नहीं होता।
(d) मुक्त रूप से गिरते केबिन में गुरुत्वीय त्वरण का प्रभावी मान g’.= 0 होगा।
∴ लोलक का आवर्तकाल [latex s=2]2\pi \sqrt { \frac { l }{ g } } [/latex] अनन्त हो जाएगा तथा आवृत्ति शून्य हो जाएगी।

प्रश्न 17.
किसी कार की छत से l लम्बाई का कोई सरल लोलक, जिसके लोलक का द्रव्यमान M है, लटकाया गया है। कार R त्रिज्या की वृत्तीय पथ पर एकसमान चाल u से गतिमान है। यदि लोलक त्रिज्य दिशा में अपनी साम्यावस्था की स्थिति के इधर-उधर छोटे दोलन करता है तो इसका आवर्तकाल क्या होगा?
उत्तर-

कार जब मोड़ पर मुड़ती है तो उसकी गति में त्वरण, [latex s=2]\frac { { \upsilon }^{ 2 } }{ R } [/latex] (अभिकेन्द्र त्वरण) होता है। इस प्रकार कार एक अजड़त्वीय निर्देश तन्त्र है। इसलिए गोलक पर एक छद्म बल [latex s=2]\frac { m{ \upsilon }^{ 2 } }{ R } [/latex] वृत्तीय पथ के बाहर की ओर लगेगा जिसके कारण लोलक ऊर्ध्वाधर रहने के स्थान पर थोड़ा तिरछा हो जाएगा।
इस समय गोलक पर दो बले क्रमशः भार mg तथा अपकेन्द्र बल [latex s=2]\frac { m{ \upsilon }^{ 2 } }{ R } [/latex] लगेंगे।
यदि गोलक के लिए g का प्रभावी मान g’ है तो गोलक पर प्रभावी बल mg’ होगा जो कि उक्त दो बलों का परिणामी है।।

प्रश्न 18.
आधार क्षेत्रफल A तथा ऊँचाई h के एक कॉर्क का बेलनाकार टुकड़ा ρ1 घनत्व के किसी द्रव में तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतन्त्र छोड़ देते हैं, यह दर्शाइए कि कॉर्क
ऊपर-नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल [latex s=2]T=2\pi \sqrt { \frac { h\rho }{ { \rho }_{ 1 }g } } [/latex] है।
यहाँ ρ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमन्दन को नगण्य मानिए।)
उत्तर-
द्रव में तैरते बेलनाकार बर्तन के दोलन—माना कॉर्क के टुकड़े का द्रव्यमान m है। माना साम्यावस्था में इसकी l लम्बाई द्रव में डूबी है। (चित्र-14.9)।
तैरने के सिद्धान्त से, कॉर्क के डूबे भाग द्वारा हटाए गए द्रव का भार कॉर्क के भार के बराबर होगा,

जब कॉर्क को द्रव में नीचे की ओर दबाकर छोड़ा जाता है तो यह ऊपर-नीचे दोलन करने लगता है। माना किसी क्षण इसका साम्यावस्था से नीचे की ओर विस्थापन y है। इस स्थिति में, इसकी y लम्बाई द्वारा विस्थापित द्रव का उत्क्षेप बेलनाकार बर्तन को प्रत्यानयन बल (F) प्रदान करेगा।
अतः F = – A y ρ1 g
यहाँ पर ऋण चिह्न यह प्रदर्शित करता है कि प्रत्यानयन बल F, कॉर्क के टुकड़े के विस्थापन के विपरीत दिशा में लग रहा है; अतः टुकड़े का त्वरण

प्रश्न 19.
पारे से भरी किसी U नली का एक सिरा किसी चूषण पम्प से जुड़ा है तथा दूसरा सिरा वायुमण्डल में खुला छोड़ दिया गया है। दोनों स्तम्भों में कुछ दाबान्तर बनाए रखा जाता है। यह दर्शाइए कि जब चूषण पम्प को हटा देते हैं, तब U नली में पारे का स्तम्भ सरल आवर्त गति करता है।
उत्तर-

सामान्यत: U नली में द्रव (पारा) भरने पर उसके दोनों स्तम्भों व में पारे का तल समान होगा। परन्तु चूषण पम्प द्वारा दाबान्तर बनाये रखने की स्थिति में यदि स्तम्भ में पारे का तल सामान्य स्थिति से y दूरी नीचे है । तो दूसरे स्तम्भ में यह सामान्य स्थिति से y दूरी ऊपर होगा। अत: दोनों । । स्तम्भ में पारे के तलों का अन्तर = 2y, चूषण पम्प हटा लेने पर U नली के दायें स्तम्भ में पारे पर नीचे की ओर कार्य करने वाला बल = 2y ऊँचाई के पारा स्तम्भ का भार = 2y ρga.
जहाँ a = U नली स्तम्भों की अनुप्रस्थ काट का क्षेत्रफल
ρ = पारे का घनत्व; g = गुरुत्वीय त्वरण
अत: बायीं भुजा में पारा ऊपर की ओर चढ़ेगा तथा इस पर कार्य करने वाला प्रत्यानयन बल (जिसके अन्तर्गत यह गति करेगा)
F = -2yρga, दोनों स्तम्भों में पारे के स्तम्भ की ऊँचाई समान होने की स्थिति में यदि ऊँचाई h हो तो U नली में भरे पारे के स्तम्भ की कुल लम्बाई = 2h अतः पारे का कुल द्रव्यमान m = 2h x ρ x a

अतिरिक्त अभ्यास

प्रश्न 20.
चित्र-14.11 में दर्शाए अनुसार V आयतन के किसी वायु कक्ष की ग्रीवा (गर्दन) की अनुप्रस्थ कोर्ट का क्षेत्रफल a है। इस ग्रीवा में m द्रव्यमान की कोई गोली बिना किसी घर्षण के ऊपर-नीचे गति कर सकती है। यह दर्शाइए कि जब गोली को थोड़ा नीचे दबाकर मुक्त छोड़ देते हैं तो वह सरल आवर्त गति करती है। दाब-आयतन विचरण को समतापी मानकर दोलनों के आवर्तकाल का व्यंजक ज्ञात कीजिए (चित्र-14.11 देखिए)। वायु ।
उत्तर-

माना साम्यावस्था में जब गैस का आयतन V है तो इसका दाब P है। साम्यावस्था से गेंद को अल्पविस्थापन x देने पर माना गैस का दाब बढ़कर (P + ∆P) तथा आयतन घटकर V – ∆V रह जाता है। समतापीय परिवर्तन के लिए बॉयल के नियम से ।
P x V = (P + ∆P)(V – ∆V)
अथवा PV = PV – P.∆V + ∆P.V – ∆P.∆V
चूँकि ∆P व ∆V अल्प राशियाँ हैं, अतः ∆P, ∆V को नगण्य मानते हुए 0 = -P ∆V + ∆P.V

प्रश्न 21.
आप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं। यह मानिए कि आप इस । वाहन की निलम्बन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं। जब समस्त | वाहन इस पर रखा जाता है, तब निलम्बन 15 cm आनमित होता है। साथ ही, एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोतरी हो जाती है, निम्नलिखित के मानों को आकलन कीजिए
(a) कमानी स्थिरांक तथा
(b) कमानी तथा एक पहिए के प्रघात अवशोषक तन्त्र के लिए अवमन्दन स्थिरांक b. यह मानिए कि प्रत्येक पहिया 750 kg द्रव्यमान वहन करता है।
हल-
(a) दिया है : वाहन का द्रव्यमान, M = 3000 kg, निलम्बन का झुकाव x = 15 cm
वाहन में चार कमानियाँ होती हैं; अत: प्रत्येक कमानी पर कुल भार को एक-चौथाई भार पड़ेगा।
अतः . एक कमानी हेतु [latex s=2]F=\frac { 1 }{ 4 }[/latex]
F = kx से,

प्रश्न 22.
यह दर्शाइए कि रैखिक सरल आवर्त गति करते किसी कण के लिए दोलन की किसी अवधि की औसत गतिज ऊर्जा उसी अवधि की औसत स्थितिज ऊर्जा के समान होती है।
उत्तर-
माना m द्रव्यमान का कोई कण ω कोणीय आवृत्ति से सरल आवर्त गति कर रहा है जिसका आयाम a है।
माना गति अधिकतम विस्थापन की स्थिति से प्रारम्भ होती है तब t समय में कण का विस्थापन
x = a cos ωt …(1)
इस क्षण कण की गतिज ऊर्जा ।

प्रश्न 23.
10 kg द्रव्यमान की कोई वृत्तीय चक्रिका अपने केन्द्र से जुड़े किसी तार से लटकी है। चक्रिका को घूर्णन देकर तार में ऐंठन उत्पन्न करके मुक्त कर दिया जाता है। मरोड़ी दोलन का आवर्तकाल 1.5 s है। चक्रिका की त्रिज्या 15 cm है। तार का मरोड़ी कमानी नियतांक ज्ञात कीजिए। [मरोड़ी कमानी नियतांक α सम्बन्ध J = -αθ द्वारा परिभाषित किया जाता है, यहाँ J प्रत्यानयन बल युग्म है तथा θ ऐंठन कोण है।
हल-
दिया है : चक्रिका का द्रव्यमान m = 10 kg, मरोड़ी दोलन का आवर्तकाल T = 1.5 s,
चक्रिका की त्रिज्या = 0.15 m
केन्द्र से जाने वाली तथा तेल के लम्बवत् अक्ष के परितः चक्रिका का

प्रश्न 24.
कोई वस्तु 5 cm के आयाम तथा 0.2 सेकण्ड के आवर्तकाल से सरल आवर्त गति करती है। वस्तु का त्वरण तथा वेग ज्ञात कीजिए जब वस्तु का विस्थापन
(a) 5 cm,
(b) 3 cm,
(c) 0 cm हो।
हल-
यहाँ वस्तु का आयाम a = 5 सेमी = 0.05 मीटर, आवर्तकाल T = 0.2 सेकण्ड
∴कोणीय आवृत्ति ω = 2π/T = 2π/0.2 सेकण्ड
= 10π रे/से = 10π से^-1
(a) यहाँ विस्थापन y = 5 सेमी = 5 x 10^-2 मीटर = 0.05 मीटर

प्रश्न 25.
किसी कमानी से लटका एक पिण्ड एक क्षैतिज तल में कोणीय वेग ω से घर्षण या अवमन्दन रहित दोलन कर सकता है। इसे जब x₀ दूरी तक खींचते हैं और खींचकर छोड़ देते हैं तो यह सन्तुलन केन्द्र से समय t = 0 पर v₀ वेग से गुजरता है। प्राचल ω,x₀, तथा v₀ के पदों में परिणामी दोलन का आयाम ज्ञात कीजिए।(संकेतः समीकरण x = acos (ωt + θ) से प्रारंभ कीजिए। ध्यान रहे कि प्रारम्भिक वेग ऋणात्मक है।)
हल-
माना सरल आवर्त गति का समीकरण ।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1.
सरल आवर्त गति करते हुए कण का आवर्तकाल होता है।

उत्तर-

प्रश्न 2.
सरल लोलक का आवर्तकाल दोगुना हो जायेगा जब उसकी प्रभावी लम्बाई कर दी जाती है
(i) दोगुनी।
(ii) आधी
(iii) चार गुनी
(iv) चौथाई
उत्तर-
(iii) चार गुनी ।

प्रश्न 3.
सरल लोलक के आवर्तकाल का सूत्र है [latex s=2]T=2\pi \sqrt { \left( l/g \right) } [/latex] जहाँ संकेतों के अर्थ सामान्य हैं। l तथा T के बीच खींचा गया ग्राफ होगा
(i) सरल रेखा
(ii) परवलय
(iii) वृत्त
(iv) दीर्घवृत्त
उत्तर-
(ii) परवलय

प्रश्न 4.
अनुनाद के लिए बाह्य आवर्ती बल की आवृत्ति तथा कम्पन करने वाली वस्तु की स्वाभाविक आवृत्ति का अनुपात होगा।
(i) 1
(ii) शून्य
(iii)1 से अधिक
(iv) 1 से कम
उत्तर-
(i) 1

प्रश्न 5.
अनुनाद की दशा में दोलनों का आयाम
(i) न्यूनतम होता है।
(ii) अधिकतम होता है।
(ii) शून्य होता है।
(iv) इनमें से कोई नहीं
उत्तर-
(i) अधिकतम होता है ।

प्रश्न 6.
एक कण सरल आवर्त गति कर रहा है जिसका आयाम A है। एक पूर्ण दोलन में कण द्वारा चली गयी दूरी है।
(i) 2A
(ii) 0
(iii) A
(iv) 4A
उत्तर-
(iii) A

प्रश्न 7.
किसी सरल आवर्त गति का आयाम a है तथा आवर्तकाल T है। अधिकतम तात्कालिक वेग होगा

उत्तर-
(iii) [latex s=2]\frac { 2\pi a }{ T } [/latex]

प्रश्न 8.
सरल आवर्त गति करते कण का अधिकतम विस्थापन की स्थिति में त्वरण होता है।
(i) अधिकतम
(ii) न्यूनतम
(iii) शून्य
(iv) न अधिकतम और न न्यूनतम
उत्तर-
(i) अधिकतम

प्रश्न 9.
सरल आवर्त गति करते हुए कण की साम्य स्थिति से दूरी पर स्थितिज ऊर्जा होती है।

उत्तर-
(ii) [latex s=2]\frac { 1 }{ 2 } m{ \omega }^{ 2 }{ a }^{ 2 }[/latex]

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
आवर्ती गति से क्या तात्पर्य है?
उत्तर-
जब कोई वस्तु एक निश्चित समयान्तराल में एक निश्चित पथ पर बार-बार अपनी गति को दोहराती है, तो उसकी गति आवर्ती गति कहलाती है।

प्रश्न 2.
सरल आवर्त गति की विशेषताएँ लिखिए।
उत्तर-
(i) यह गति एक निश्चित बिन्दु (कण की माध्य स्थिति) के इधर-उधर होती है।
(ii) कण पर कार्यरत् प्रत्यानयन बल अर्थात् कण का त्वरण सदैव माध्य स्थिति से कण के विस्थापन के अनुक्रमानुपाती होता है।
(iii) प्रत्यानयन बल (अर्थात् त्वरण) की दिशा सदैव माध्य स्थिति की ओर दिष्ट रहती है।

प्रश्न 3.
संरल लोलक के अलावा सरल आवर्त गति के दो उदाहरण दीजिए।
उत्तर-
(1) स्प्रिंग से लटके द्रव्यमान की गति तथा
(2) जल पर तैरते लकड़ी के बेलन को थोड़ा जल में दबाकर छोड़ देने पर उसकी गति।

प्रश्न 4.
सेकण्ड पेण्डुलम क्या होता है?
उत्तर-
वह सरल लोलक जिसका आवर्तकाल 2 सेकण्ड होता है, सेकण्ड लोलक (पेण्डुलम) कहलाता है।

प्रश्न 5.
आवर्तकाल किसे कहते हैं?
उत्तर-
एक दोलन पूरा करने में कोई वस्तु जितना समय लेती है उसे उसका आवर्तकाल कहते हैं। इसे T से प्रदर्शित करते हैं।

प्रश्न 6.
आवृत्ति तथा आवर्तकाल में सम्बन्ध लिखिए।
उत्तर-
आवृत्ति = 1/ आवर्तकाल

प्रश्न 7.
सरल आवर्त गति करते हुए कण का साम्य स्थिति से 5 सेमी की दूरी पर त्वरण 20 सेमी/से² है। इसका आवर्तकाल ज्ञात कीजिए।
हल-

प्रश्न 8.
एक कण सरल आवर्त गति कर रहा है तथा उसका त्वरण [latex s=2]\overrightarrow { a } =-{ 4\pi }^{ 2 }\overrightarrow { X } [/latex], जहाँ [latex s=2]\overrightarrow { X } [/latex] कण की साम्य स्थिति से उसका विस्थापन है। कण का आवर्तकाल निकालिए।
हल-

प्रश्न 9.
सरल आवर्त गति करते हुए किसी कण का आयाम 5 सेमी तथा आवर्तकाल 2 सेकण्ड है। कण के त्वरण का अधिकतम मान निकालिए।
हल-

प्रश्न 10.
सरल आवर्त गति का समीकरण y = 2sin 200πt है। दोलन की आवृत्ति का मान ज्ञात कीजिए।
हल-
दिया है, y = 2sin 200πt
सरल आवर्त गति के समीकरण [latex s=2]y=asin\left( \frac { 2\pi }{ T } \right) t[/latex] से उपर्युक्त समीकरण की तुलना करने पर
[latex s=2]\frac { 2 }{ T }=200[/latex] ⇒ 2n = 200 [latex s=2]\left( \because \frac { 1 }{ T } =n \right) [/latex]
n = 100

प्रश्न 11.
सरल आवर्त गति करने वाले कण का विस्थापन समीकरण लिखिए तथा इसके दो चक्करों के लिए समय-विस्थापन वक्र खींचिए।
उत्तर-
सरल आवर्त गति करने वाले कण का विस्थापन समीकरण
y = asin ωt …(1)
समी० (1) में, ω = 2π/T रखने पर
[latex s=2]y=asin\left( \frac { 2\pi t }{ T } \right) [/latex]
इस समीकरण की सहायता से हमेसरले आवर्त गति करते किसी कण के विस्थापन y तथा समय t है के बीच ग्राफ खींच सकते हैं। इसके लिए हम समीकरण (1) के द्वारा विभिन्न समयों पर विस्थापन ज्ञात करते हैं।

प्रश्न 12.
सरल आवर्त गति करने वाले कण के वेग का सूत्र लिखिए तथा इसका समय-वेग वक्र खींचिए।
या सरल आवर्त गति के लिए समय और वेग में ग्राफ प्रदर्शित कीजिए।
उत्तर-
सरल आवर्त गति करने वाले कण के वेग का सूत्र

प्रश्न 13.
एक कण ‘r” त्रिज्या के वृत्त की परिधि पर ‘V’ चाल से गति करता है। आधे तथा पूरे आवर्तकाल के बाद इसका विस्थापन ज्ञात कीजिए।
उत्तर-
आधे आवर्तकाल के कण का विस्थापन r+r = 2r होगा तथा पूरे आवर्तकाल के बाद इसका विस्थापन शून्य होगा।

प्रश्न 14.
सरल आवर्त गति के लिए समय और विस्थापन में ग्राफ प्रदर्शित कीजिए।
उत्तर

प्रश्न 15.
सरल आवर्त गति करने वाले कण के वेग का सूत्र लिखिए तथा इसका समय-त्वरण ग्राफ खीचिए।
उत्तर-
सरल आवर्त गति करने वाले कण के वेग का सूत्र,

प्रश्न 16.
पृथ्वी पर सेकण्ड लोलक की लम्बाई की गणना कीजिए। पृथ्वी पर g का मान 9.8 मी/से² है। (π = 3.14)
हल-

अत: पृथ्वी तल पर सेकण्ड लोलक की लम्बाई लगभग 1 मीटर होती है।

प्रश्न 17.
500 ग्राम का एक गोला, 1.0 मीटर लम्बी डोरी से लटका है। क्षैतिज स्थिति से मुक्त करने पर यह ऊर्ध्वतल में दोलन करने लगता है। दोलनों के दौरान जब डोरी ऊर्ध्व से 60° कोण पर है। तब डोरी में तनाव ज्ञात कीजिए।
हल-

दिया है,
गोले का द्रव्यमान (m) = 500 ग्राम
= 0.5 किग्रा
∵ डोरी क्षैतिज स्थिति में है, अत: डोरी में तनाव
T = mg cos θ
T = 0.5 x 10 x cos60 = 0.5 x 10 x [latex s=2]\frac { 1 }{ 2 }[/latex] = 2.5 न्यूटन

प्रश्न 18.
एक कण सरल आवर्त गति कर रहा है। किसी क्षण इसका विस्थापन y = a/2 है। कण मध्यमान स्थिति से गति प्रारम्भ करता है। इस स्थिति के लिए कला की गणना कीजिए।
हल-
कला-विस्थापन का समीकरण ।

प्रश्न 19.
किसी लिफ्ट में लटकाये गए एक सरल लोलक के दोलन के आवर्तकाल पर क्या प्रभाव पड़ता है जब लिफ्ट एक त्वरण α से ऊपर चढ़ रही है?
उत्तर-
जब लिफ्ट α त्वरण से ऊपर की ओर त्वरित होती है तो प्रभावी α का मान बढ़कर (α + α) हो जाता है। अतः आवर्तकाल T घट जाता है।

प्रश्न 20.
किसी स्प्रिंग के बल नियतांक की परिभाषा दीजिए।
हल-
यदि किसी स्प्रिंग पर F बल लगाने से उसकी लम्बाई में x वृद्धि हो जाए तो
F ∝ x या F = kx
जहाँ k = स्प्रिंग का बल नियतांक। यदि x = 1 तो k = F,
अत: किसी स्प्रिंग का बल नियतांक उस बल के बैराबर है जो उसकी लम्बाई में एकांक वृद्धि कर दे। इसका मात्रक न्यूटन/मीटर है।

प्रश्न 21.
प्रणोदित दोलन क्या होते हैं? उदाहरण देकर स्पष्ट कीजिए। या प्रणोदित कम्पन क्या है? इनके दो उदाहरण दीजिए।
उत्तर-
प्रणोदित दोलन (Forced oscillations)-जब किसी दोलन करने वाली वस्तु पर कोई ऐसा बाह्य आवर्त बल लगाते हैं जिसकी आवृत्ति, वस्तु की स्वाभाविक आवृत्ति से भिन्न हो, तो वस्तु आवर्त बल की आवृत्ति से दोलन करने लगती है। ऐसे दोलनों को प्रणोदित दोलन (forced oscillations) कहते हैं।
उदाहरणार्थ-(i) जब तने हुए पतले तार में प्रत्यावर्ती धारा प्रवाहित की जाती है और तार को चुम्बक के ध्रुवों के बीच रखते हैं तो तार प्रत्यावर्ती धारा की आवृत्ति से कम्पन करने लगता है।
(ii) सितार, वायलिन व स्वरमापी के तार पर जब किसी आवृत्ति का स्वर उत्पन्न किया जाता है तो इसके कम्पन, सेतु द्वारा खोखले ध्वनि बोर्ड में पहुँच जाते हैं। इससे बोर्ड के अन्दर की वायु में प्रणोदित दोलन उत्पन्न हो जाते हैं।

प्रश्न 22.
प्रणोदित तथा अनुनादी कम्पनों में क्या अन्तर है?
उत्तर-
अनुनादी कम्पन प्रणोदित कम्पनों की ही एक विशेष अवस्था है। प्रणोदित कम्पन में वस्तु पर आरोपित आवर्त बल की आवृत्ति कम्पन करने वाली वस्तु की स्वाभाविक आवृत्ति से भिन्न होती है तथा कम्पन का आयाम छोटा होता है, जबकि अनुनादी कम्पन से आरोपित आवर्त बल की आवृत्ति वस्तु की स्वाभाविक आवृत्ति के बराबर होती है तथा कम्पनों का आयाम महत्तम होता है।

प्रश्न 23.
मुक्त तथा प्रणोदित दोलनों में प्रत्येक का एक-एक उदाहरण देकर अन्तर समझाइए।
उत्तर
मुक्त तथा प्रणोदित दोलन में अन्तर । मुक्त दोलन

प्रश्न 24.
तार वाले वाद्य-यन्त्रों में प्रधान तार के साथ अन्य तार क्यों लगाये जाते हैं?
उत्तर-
प्रधान तार से उत्पन्न आवृत्ति के साथ अनुनादित होकर स्वर की तीव्रता बढ़ाने के लिए प्रधान तार के साथ अन्य तार लगाये जाते हैं जो विभिन्न आवृत्तियों के लिए समस्वरित (tuned) रहते हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
एक सरल लोलक का गोलक एक जल से भरी गेंद है। गेंद की तली में एक बारीक छेद कर देने पर गोलक के आवर्तकाल पर क्या प्रभाव पड़ेगा?
उत्तर-
जैसे-जैसे जल बाहर निकलेगा, लोलक का गुरुत्व केन्द्र नीचे आता जाएगा और लोलक की प्रभावी लम्बाई बढ़ती जाएगी, जिससे आवर्तकाल बढ़ता जाएगा। जब गेंद आधे से अधिक खाली हो जाएगी तब लोलक का गुरुत्व केन्द्र पुनः ऊपर उठने लगेगा और लोलक की प्रभावी लम्बाई पुनः घटने लगेगी तथा आवर्तकाल भी घटने लगेगा। जब गेंद पूरी खाली हो जाएगी, तब लोलक का गुरुत्व केन्द्र पुनः गेंद के केन्द्र पर आ जाएगा तथा आवर्तकाल को मान प्रारम्भिक मान के बराबर हो जाएगा।

प्रश्न 2.
एक कण 6.0 सेमी आयाम तथा 6.0सेकण्ड के आवर्तकाल से सरल आवर्त गति कर रहा है। अधिकतम विस्थापन की स्थिति से आयाम के आधे तक आने में यह कितना समय लेगा?
हल-
अधिकतम विस्थापन की स्थिति में कण का विस्थापन समीकरण :

प्रश्न 3.
सरल आवर्त गति करते हुए एक कण का साम्य स्थिति में 4 सेमी दूरी पर त्वरण 16 सेमी सेकण्ड² है। इसका आवर्तकाल ज्ञात कीजिए।
हल-
∵सरल आवर्त गति करते हुए कण का आवर्तकाल

प्रश्न 4.
सरल आवर्त गति करते हुए किसी कण का अधिकतम वेग 100 सेमी/से तथा अधिकतम त्वरण 157 सेमी/से² है। कण का आवर्तकाल ज्ञात कीजिए।
हल-
अधिकतम वेग a_ω = 100 सेमी/से ।

प्रश्न 5.
एक सेकण्ड लोलक को ऐसे स्थान पर ले जाया जाता है जहाँg का मान 981 सेमी/से² के स्थान पर 436 सेमी/से² है। लोलक का उस स्थान पर आवर्तकाल ज्ञात कीजिए।
हल-
सेकण्ड लोलक का आवर्तकाल [latex s=2]T=2\pi \sqrt { \frac { l }{ g } } [/latex] …(1)
स्थान बदलने पर आवर्तकाल [latex s=2]{ T }^{ ‘ }=2\pi \sqrt { \frac { l }{ { g }^{ ‘ } } } [/latex] ….(2)

प्रश्न 6.
2 किग्रा द्रव्यमान का एक पिण्ड भारहीन स्प्रिंग जिसका बल नियतांक 200 न्यूटन/मी है, से लटका है। पिण्ड को नीचे की ओर 20 सेमी विस्थापित करके छोड़ दिया जाता है। ज्ञात कीजिए
(i) पिण्ड की अधिकतम चाल,
(ii) पिण्ड-स्प्रिंग निकाय की कुल ऊर्जा।
हल-
(i) स्प्रिंग में अधिकतम खिंचाव x_max = 20 सेमी = 0.20 मी पिण्ड को नीचे की उपर्युक्त दूरी से विस्थापित करके छोड़ देने पर यदि इसकी अधिकतम चाल υ_max हो तो।
पिण्ड की अधिकतम गतिज ऊर्जा = स्प्रिंग के अधिकतम खिंचाव पर प्रत्यास्थ स्थितिज ऊर्जा

(ii) स्प्रिंग से लटके पिण्ड को खींचकर छोड़ देने पर स्प्रिंग की प्रत्यास्थ स्थितिज ऊर्जा पिण्ड की गतिज ऊर्जा तथा स्थितिज ऊर्जा परस्पर परिवर्तित होती रहती है।
पिण्ड-स्प्रिंग निकाय की कुल ऊर्जा = अधिकतम खिंचाव पर स्प्रिंग की स्थितिज ऊर्जा

प्रश्न 7.
जब एक भारहीन स्प्रिंग से 0.5 किग्रा का बाट लटकाया जाता है, तो उसकी लम्बाई में 0.02 मीटर की वृद्धि हो जाती है। स्प्रिंग का बल नियतांक एवं उसमें संचित ऊर्जा की गणना कीजिए। G = 9.8 मी/से²)
हल-

प्रश्न 8.
एक स्प्रिंग पर 0.60 किग्रा का पिण्ड लटकाने पर उसकी लम्बाई 0.25 मी बढ़ जाती है। यदि स्प्रिंग से 0.24 किग्रा का एक पिण्ड लटकाकर नीचे खींचकर छोड़ दिया जाए तो स्प्रिंग का आवर्तकाल कितना होगा? (g = 10 मी/से²)
हल-
M=0.60 किग्रा, g = 10 मी/से² ।
स्प्रिंग की लम्बाई में वृद्धि ∆x = 0.25 मी

प्रश्न 9.
0.25 किग्रा द्रव्यमान की एक वस्तु जब किसी स्प्रिंग से लटकायी जाती है तो स्प्रिंग की। लम्बाई 5 सेमी बढ़ जाती है। जब 0.4 किग्रा की वस्तु इससे लटकांयी जाती है तब स्प्रिंग के दोलन का आवर्तकाल ज्ञात कीजिए। (g = 10 मी/से²)
हल-
वस्तु को द्रव्यमान (M) = 0.25 किग्रा, g = 10 मी/से²
स्प्रिंग की लम्बाई में वृद्धि ∆x = 5 सेमी = 5 x 10^-2 मीटर

प्रश्न 10.
0.40 किग्रा द्रव्यमान के एक पिण्ड को एक आदर्श स्प्रिंग से लटकाने पर स्प्रिंग की लम्बाई 2.0 सेमी बढ़ जाती है। यदि इस स्प्रिंग से 2.0 किग्रा द्रव्यमान के पिण्ड को लटकाया जाए तो दोलन का आवर्तकाल क्या होगा? (g = 10 मी/से²)
हल-
पिण्ड का द्रव्यमान (M) = 0.40 किग्रा, g = 10 मी/से²
स्प्रिंग की लम्बाई में वृद्धि Δx = 2 सेमी = 2 x 10^-2 मीटर

विस्तृत उत्तरीय प्रश्न

प्रश्न 1.
सरल आवर्त गति से आप क्या समझते हैं। सरल लोलक के आवर्तकाल के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
सरल आवर्त गति-जब किसी कण की अपनी साम्य स्थिति के इधर-उधर एक सरल रेखा में गति इस प्रकार की होती है कि इस पर लग रहा त्वरण (अथवा बल) प्रत्येक स्थिति में कण के विस्थापन के अनुक्रमानुपाती रहती है तथा सदैव साम्य स्थिति की ओर दिष्ट होता है तो कण की गति को सरल आवर्त गति कहते हैं।
सरल लोलक के आवर्तकाल का व्यंजक-चित्र 14.18 में एक सरल लोलक दर्शाया गया है जिसकी प्रभावी लम्बाई 1 है तथा उसके गोलक का द्रव्यमान m है। गोलक को बिन्दु S से लटकाया गया है तथा गोलक की साम्य स्थिति O है। मान लीजिए दोलन करते समय गोलक किसी क्षण स्थिति A में है, जबकि

इसका विस्थापन OA = x है। इस स्थिति में धागा ऊर्ध्वाधर से θ कोण बनाता है तथा गोलक पर । निम्नलिखित दो बल लगते है– .
1. गोलक का भार mg जो उसके गुरुत्व केन्द्र पर ठीक नीचे की ओर ऊध्र्वाधर दिशा में लगता है।
2. धागे में तनाव का बल T’ जो धागे के अनुदिश निलम्बन बिन्दु S की ओर लगता है।
भार mg को दो भागों में वियोजित किया जा सकता है : घटक mg Cos θ जो कि धागे के अनुदिश T’ की विपरीत दिशा में लगता है तथा घटक mg sin θ जो कि धागे की लम्बवत् दिशा में लगता है। धागे में तनाव T’ तथा घटक mg cos θ का परिणामी (T’ – mg cos θ), गोलक को l त्रिज्या के वृत्तीय पथ पर चलने के लिए आवश्यक अभिकेन्द्र बल (mv²/l) प्रदान करता है; जबकि घटक mg sin θ गोलक को साम्य स्थिति O में लौटाने का प्रयत्न करता है। यही गोलक पर कार्य करने वाला प्रत्यानयन बल (restoring force) है।
अतः गोलक पर प्रत्यनियन बल F = – mg sin θ
(जबकि θ, कोणीय विस्थापन से छोटा है एवं इसे रेडियन में नापा जाता है।)
ऋण चिह्न यह व्यक्त करता है कि बल F, विस्थापन θ के घटने की दिशा में है अर्थात् साम्य स्थिति की ओर को दिष्ट है।

समीकरण (1) में (g/l) किसी निश्चित स्थान पर किसी दी हुई प्रभावी लम्बाई के सरल लोलक के लिए नियतांक है; अत: त्वरण ∝ – (विस्थापन) स्पष्ट है कि गोलक का त्वरण विस्थापन के अनुक्रमानुपाती है तथा उसकी दिशा विस्थापन x के विपरीत है। क्योंकि θ का मान कम रखा जाता है, अत: चाप OA लगभग ऋजु-रेखीय होगा। इस प्रकार लोलक सरल रेखा में गति करेगा। अतः गोलक की गति सरल आवर्त गति है।

प्रश्न 2.
सरल आवर्त गति करते हुए किसी कण के वेग का सूत्र प्राप्त कीजिए।
उत्तर-

सरल आवर्त गति में कण का वेग (Velocity of a particle in S.H.M.)—निर्देश वृत्त की परिधि पर चलते कण P के वेग v को परस्पर दो लम्बवत् घटकों में वियोजित करने पर (चित्र 14.19);
v का PN के समान्तर घटक = v sin θ
v का PN के लम्बवत् घटक = v cos θ
घटक v cos θ, कण P से वृत्त के व्यास पर खींचे गये लम्ब के पाद N की गति की दिशा OA के समान्तर है। अत: यह पाद N के वेग के बराबर है। इस प्रकार, पाद N का वेग u = v cos θ

इस समीकरण से यह पता चलता है कि सरल आवर्त गति करते हुए किसी कण का वेग (u) उसके विस्थापन (y) के साथ-साथ बदलता है। जब विस्थापन शून्य होता है (y = 0) अर्थात् जब । कण अपनी साम्य स्थिति से गुजरता है तब वेग अधिकतम होता है (u_max = aω) तथा जब विस्थापन अधिकतम होता है (y = a) तब वेग शून्य होता है (u = 0).

प्रश्न 3.
यदि पृथ्वी के केन्द्र से होकर पृथ्वी के आर-पार एक सुरंग बनाई जाए तथा उस सुरंग में एक पिण्ड छोड़ा जाए तो दिखाइए कि पिण्ड का त्वरण सदैव सुरंग के मध्य बिन्दु (अर्थात पृथ्वी के केन्द्र) से विस्थापन के अनुक्रमानुपाती होता है। यह भी सिद्ध कीजिए कि इसका आवर्तकाल पृथ्वी के समीप परिक्रमा करते हुए उपग्रह के आवर्तकाल के बराबर होगा।
उत्तर-

चित्र 14.20 में पृथ्वी के केन्द्र से गुजरने वाली एक सुरंग AB को प्रदर्शित किया गया है तथा O पृथ्वी का केन्द्र है। m द्रव्यमान के एक पिण्ड को इस सुरंग के भीतर गति करने के लिए छोड़ा गया है। माना किसी क्षण पिण्ड बिन्दु P पर है, जहाँ इसका पृथ्वी के केन्द्र O से विस्थापन x है। इस समय पिण्डे x त्रिज्या के ठोस गोले के बाह्य पृष्ठ पर स्थित है। अत: पिण्ड पर पृथ्वी का गुरुत्वीय बल x त्रिज्या के गोले के गुरुत्वीय बल के बराबर होगा, जो P से O की दिशा में कार्य करेगा।

इस प्रकार, पिण्ड का त्वरण α, विस्थापन x के अनुक्रमानुपाती है तथा इसकी दिशा विस्थापन x के विपरीत है। अतः पिण्ड की गति सरल आवर्त गति है।

प्रश्न 4.
एक कण सरल आवर्त गति कर रहा है। यदि माध्य स्थिति से x1 तथा x2 दूरियों पर कण का वेग क्रमशः u1 तथा u2 हैं, तो सिद्ध कीजिए कि इसका आवर्तकाल [latex s=2]T=2x\sqrt { \left[ \frac { { { x }^{ 2 } }_{ 2 }-{ { x }^{ 2 } }_{ 1 } }{ { { u }^{ 2 } }_{ 1 }-{ { u }^{ 2 } }_{ 2 } } \right] } [/latex] होगा।
हल-

प्रश्न 5.
सरल आवर्त गति करते हुए पिण्ड की दोलन गतिज ऊर्जा, स्थितिज ऊर्जा तथा सम्पूर्ण ऊर्जा के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
गतिज ऊर्जा (Kinetic energy)-सरल आवर्त गति करते हुए कण को जब किसी क्षण उसकी साम्य स्थिति से विस्थापन y हो तो उस क्षण उसका वेग latex s=2]u=\omega \sqrt { \left( { a }^{ 2 }-{ y }^{ 2 } \right) } [/latex]
जहाँ a = कण का आयाम तथा ) ω = कण की कोणीय आवृत्ति। यदि पिण्ड (कण) का द्रव्यमान m हो

स्थितिज ऊर्जा (Potential energy)-सरल आवर्त गति करते हुए कण । का जब किसी क्षण उसकी साम्य स्थिति से विस्थापन y है तो उस क्षण ||
उसका त्वरण α =- ω²y (जहाँ ω = कोणीय आवृत्ति)।
यदि कण का द्रव्यमान m हो तो इस क्षण कण पर लगने वाला प्रत्यानयन बल F = द्रव्यमान x त्वरण
F = m x α = m x (-ω²y) =-mω²y
ऋण चिह्न केवल बल की दिशा (विस्थापन y के विपरीत) का प्रतीक है।’
अतः बल का परिमाण F = mω²y
यदि हम कण पर लगे बल F तथा कण के विस्थापन y के बीच एक ग्राफ खींचे तो चित्र 14.21 की भाँति एक सरल रेखा प्राप्त होती है। यह एक बल विस्थापन ग्राफ है। अत: इस ग्राफ (सरल रेखा) तथा विस्थापन अक्ष के बीच घिरा क्षेत्रफल कण पर किये गये कार्य अर्थात् कण की स्थितिज ऊर्जा को व्यक्त करेगा।

इस प्रकार समी० (4) से स्पष्ट है कि सरल आवर्त गति करते कण (पिण्ड) की कुल ऊर्जा आयाम के वर्ग (a²) के तथा आवृत्ति के वर्ग (n²) के अनुक्रमानुपाती होती है।

प्रश्न 6.
बल नियतांक k की भारहीन स्प्रिंग से लटके हुए एक द्रव्यमान m के पिण्ड के ऊध्र्वाधर दोलनों के आवर्तकाल के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
स्प्रिंग से लटके पिण्ड की गति (Motion of a body suspended by a spring)—चित्रं 14.22 (a) में एक हल्की (भारहीन) स्प्रिंग दर्शायी गई है, जिसकी सामान्य लम्बाई L है तथा यह एक दृढ़ आधार से लटकी है। जब इसके निचले सिरे पर m द्रव्यमान का एक पिण्ड लटकाया जाता है तो पिण्ड के भार से इसमें खिंचाव उत्पन्न होता है। माना यह खिंचाव अथवा स्प्रिंग की लम्बाई में वृद्धि l है। चित्र 14.22 (b) में स्प्रिंग अपनी प्रत्यास्थता के कारण द्रव्यमान m पर एक प्रत्यानयन बल F ऊपर ऊर्ध्व दिशा में लगाती है। हम जानते हैं कि स्प्रिंग के लिए हुक का नियम सत्य होता है। अतः हुक के नियम से F = – kl.
जहाँ k स्प्रिंग का बल नियतांक है। इसे स्प्रिंग नियतांक (spring constant) भी कहते हैं। इसका मात्रक ‘न्यूटन/मीटर’ होता है। उपर्युक्त समीकरण में ऋण चिह्न इस बात का संकेत करता है कि प्रत्यानयन बल F विस्थापन के विपरीत दिशा में है। इस स्थिति में पिण्ड पर लगने वाला एक दूसरा बल पिण्ड का भार mg है। चूंकि इस स्थिति में पिण्ड स्थायी सन्तुलन अवस्था में है, अतः इस पर परिणामी बल शून्य होना चाहिए।

अत: F + mg = 0
-kl + mg = 0
mg = kl …(1)
अब, यदि पिण्डे को थोड़ा नीचे खींचकर छोड़ दिया जाये तो यह अपनी साम्य स्थिति के ऊपर-नीचे दोलन करने लगता है। माना दोलन करते समय किसी क्षण पिण्ड का
साम्य स्थिति से विस्थापन y दूरी नीचे की ओर है [चित्र 14.22 (c)]। इस क्षण स्प्रिंग की लम्बाई (L + l) से करता हुआ बढ़कर (L + l + y) हो जाती है; अर्थात् स्प्रिंग की लम्बाई में कुल वृद्धि (l + y) ह्येगी। अतः इस देशा में स्प्रिंग द्वारा पिण्ड पर लगाया गया प्रत्यानयन बल
F’ = – k(l + y) = – kl – ky
पिण्ड पर दूसरा बल अब भी उसका भार mg ही है। चूंकि इस दशा में पिण्ड गतिशील है। अत: इस पर लगने वाला परिणामी बल
F” = F’ + mg = (- kl – ky) + mg
परन्तु समी० (1) से, mg = kl
∴ F” = -kl – ky + kt या F” = – ky
अत: पिण्ड में उत्पन्न त्वरण α = बल/द्रव्यमान = F”/m
α = -(ky/m) ,[latex s=2]\alpha =-\left( \frac { k }{ m } \right) y[/latex] …(2)
चूँकि पिण्ड विशेष के लिए m नियत तथा स्प्रिंग के लिए k नियत है, अत: समी० (2) में राशि (k/m) नियतांक है।
अतः α ∝ -y
इस प्रकार स्प्रिंग से लटके पिण्ड के दोलन करते समय इसमें त्वरण α पिण्ड की साम्य स्थिति से उसके विस्थापन y के अनुक्रमानुपाती है, तथा ऋण चिह्न (-) इस तथ्य का प्रतीक है कि त्वरण की दिशा विस्थापन की दिशा के विपरीत है। अंतः पिण्ड की गति सरल आवर्त है।

प्रश्न 7.
आरेख की सहायता से अवमन्दित कम्पन को समझाइए। अवमन्दित कम्पन के दो उदाहरण दीजिए। अवमन्दित कम्पन को प्रणोदित कम्पन में बदलने के लिए क्या करना पड़ता है?
उत्तर-

अवमन्दित कम्पन (Damped Vibrations)-किसी वस्तु के कम्पन करते समय कोई-न-कोई बाह्य अवमन्दक बल (damping force) अवश्य विद्यमान रहता है जिसके कारण कम्पन करती वस्तु की ऊर्जा लगातार घटती रहती है, इसके परिणामस्वरूप वस्तु के कम्पन का आयाम भी निरन्तर घटता जाता है या कुछ समय पश्चात् वस्तु कम्पन करना बन्द कर देती है। यह वह स्थिति है जब वस्तु को दी गयी कुल ऊर्जा समाप्त हो चुकी होती है।
इस प्रकार बाह्य अवमन्दक बलों के विरुद्ध दोलन करने, वाली वस्तु की ऊर्जा का निरन्तर कम होते रहना ऊर्जा क्षय कहलाता है। इस ऊर्जा क्षय के कारण ही कम्पित वस्तु के कम्पनों का आयाम धीरे-धीरे घटता जाता है। ऐसे कम्पन को जिनका ओयार्म समय के साथ घटता जाता है, अवमन्दित कम्पन (damped vibrations) कहते है।
उदाहरणार्थ- (i) सरल लोलक के गोलक के दोलन करते समय लोलक को लटकाने वाले दृढ़ आधार का घर्षण तथा वायु की श्यानता बाह्य अवमन्दक का कार्य करते हैं जिससे इसके दोलनों का आयाम धीरे-धीरे घटता जाता है तथा अन्त में गोलक दोलन करना बन्द कर देता है।
(ii) ऊध्र्वाधर स्प्रिंग से लटके पिण्ड को थोड़ा नीचे खींचकर छोड़ देने पर पिण्ड के दोलन अवमन्दित दोलन हैं। यहाँ पिण्ड का वायु के साथ घर्षण (श्यानता) अवमन्दक-बल का कार्य करता है। अवमन्दित कम्पन को प्रणोदित कम्पन में बदलने के लिए कम्पित ‘वस्तु पर बाह्य आवर्त बल आरोपित करना होता है।

प्रश्न 8.
अनुनाद से क्या तात्पर्य है? व्याख्या कीजिए। ध्वनि अनुनाद, यान्त्रिक अनुनाद तथा विद्युत चुम्बकीय अनुनाद के एक-एक उदाहरण दीजिए।
उत्तर-
जब किसी दोलन करने वाली वस्तु पर कोई बाह्य आवर्त बल लगाया जाता है तो वस्तु बल की आवृत्ति से प्रणोदित दोलन करने लगती है। यदि बाह्य बल की आवृत्तिवस्तु की स्वाभाविक आवृत्ति के बराबर (अथवा इसकी पूर्ण गुणज) हो तो वस्तु के प्रणोदित दोलनों का आयाम बहुत बढ़ जाता है। इस घटना को अनुनाद (resonance) कहते हैं। बाह्य बल और वस्तु की आवृत्ति में थोड़ा-सा ही अन्तर होने पर आयाम बहुत कम हो जाता है। स्पष्ट है कि अनुनाद, प्रणोदित दोलनों की ही एक विशेष अवस्था है।
अनुनाद की व्याख्या-जब बाह्य बल की आवृत्ति वस्तु की स्वाभाविक आवृत्ति के बराबर होती है तो दोनों समान कला में कम्पन करते हैं। अतः आवर्त बल द्वारा लगाये गये उत्तरोत्तर आवेग वस्तु की ऊर्जा लगातार बढ़ाते जाते हैं और वस्तु का आयाम लगातार बढ़ता जाता है। सिद्धान्त रूप से वस्तु का आयाम अनन्त तक बढ़ता रहना चाहिए, परन्तु व्यवहार में दोलन करती हुई वस्तु में वायु के घर्षण तथा ध्वनि विकिरण के कारण ऊर्जा-क्षय होता रहता है। दोलन आयाम बढ़ने के साथ-साथ ऊर्जा-क्षय भी बढ़ता जाता है और एक ऐसी स्थिति आ जाती है कि बाह्य बल द्वारा प्रति दोलन दी गई ऊर्जा, वस्तु द्वारा प्रति । दोलन में ऊर्जा-क्षय के बराबर हो जाती है। इस स्थिति में आयाम का बढ़ना रुक जाता है।
उदाहरणार्थ
1. ध्वनि अनुनाद
(i) डोरियों में कम्पन-यदि समान आवृत्ति की दो डोरियाँ एक ही बोर्ड पर तनी हों तथा उनमें से एक को कम्पित किया जाये तो दूसरी स्वयं कम्पन करने लगती है।
(ii) बर्तन में जल भरना-काँच के एक लम्बे जार के मुँह पर किसी स्वरित्र को बजाकर रखने पर एक धीमी ध्वनि सुनाई देती है। जार में पानी भरना शुरू कर देने पर जार के वायु-स्तम्भ की लम्बाई कम होने लगती है एवं एक निश्चित लम्बाई पर तेज ध्वनि सुनाई पड़ती है। इसका कारण यह है कि एक निश्चित लम्बाई पर वायु स्तम्भ की स्वाभाविक आवृत्ति, स्वरित्र की आवृत्ति के बराबर हो जाती है और अनुनाद के कारण वायु स्तम्भ में बड़े आयाम के कम्पन होते हैं जिससे ध्वनि तेज सुनाई देती है।
(iii) वातावरण के कम्पन-कान के ऊपर खाली गिलास रखने पर गुनगुन की ध्वनि सुनाई पड़ती है। इसका कारण यह है कि वातावरण में अनेक प्रकार के कम्पन उपस्थित रहते हैं। इन कम्पनों में से जिसकी आवृत्ति गिलास के भीतर वायु की स्वाभाविक आवृत्ति के बराबर होती है, वे वायु को अनुनादित करते हैं।

2. यान्त्रिक अनुनाद
सेना का पुल पार करना-जब सेना किसी पुल को पार करती है तब सैनिक कदम मिलाकर नहीं चलते। इसका कारण यह है कि यदि सैनिकों के कदमों की आवृत्ति, पुल की स्वाभाविक आवृत्ति के बराबर हो जायेगी तो पुल में बड़े आयाम के कम्पन होने लगेंगे और पुल के टूटने का खतरा हो जाएगा।

3. विद्युत-चुम्बकीय अनुनाद
रेडियो-यह विद्युत अनुनाद का उदाहरण है। विभिन्न प्रसारण केन्द्रों से अलग-अलग आवृत्तियों पर तरंगें प्रसारित की जाती हैं। रेडियो पर एक L-C परिपथ लगा होता है। इसमें लगे संधारित्र की धारिता (C) बदलने पर L-C परिपथ की आवृत्ति [latex s=2]\left( t=\frac { 1 }{ 2\pi \sqrt { LC } } \right) [/latex] बदल जाती है। जब इस विद्युत परिपथ की का आवृत्ति किसी प्रसारण केन्द्र (स्टेशन) की आवृत्ति के बराबर हो जाती है तो विद्युत परिपथ उन तरंगों को ग्रहण कर लेता है और स्टेशन से प्रोग्राम सुनाई देने लगती है।

We hope the UP Board Solutions for Class 11 Physics Chapter 14 Oscillations help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 14 Oscillations, drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Physics Chapter 13 Kinetic Theory (अणुगति सिद्धान्त) are part of UP Board Solutions for Class 11 Physics . Here we have given UP Board Solutions for Class 11 Physics Chapter 13 Kinetic Theory (अणुगति सिद्धान्त)

Board	UP Board
Textbook	NCERT
Class	Class 11
Subject	Physics
Chapter	Chapter 13
Chapter Name	Kinetic Theory
Number of Questions Solved	58

UP Board Solutions for Class 11 Physics Chapter 13 Kinetic Theory (अणुगति सिद्धान्त)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
ऑक्सीजन के अणुओं के आयतन और STP पर इनके द्वारा घेरे गए कुल आयतन का अनुपात ज्ञात कीजिए। ऑक्सीजन के एक अणु का व्यास 3Å लीजिए।
हल-
आवोगाद्रो की परिकल्पना के अनुसार S T P पर गैस के 1 मोल द्वारा घेरा गया आयतन
V = 22.4 लीटर = 22.4 x 10^-3 मी³
तथा 1 ग्राम मोल में अणुओं की संख्या = आवोगाद्रो संख्या
N = 6.02 x 10²³
ऑक्सीजन के एक अणु की त्रिज्या
r = व्यास/2 = 3 Å/2= 1.5 x 10^-10 मी
∴ ऑक्सीजन के एक अणु का आयतन

प्रश्न 2.
मोलर आयतन, STP पर किसी गैस (आदर्श) के 1 मोल द्वारा घेरा गया आयतन है। (STP:1 atm दाब, 0°C ताप)। दर्शाइए कि यह 22.4 लीटर है।
हल-
S.T.P. का अर्थ P = 1 वायुमण्डलीय दाब = 1.013 x 105 न्यूटन-मीटर^-2
तथा T = 0+273 = 273 K है तथा R = 8.31 जूल/मोल-K
∴ (1 मोल के लिए) आदर्श गैस समीकरण PV = RT से ।

= 22.395 x 10^-3 मी^-3 ≈ 22.4 लीटर

प्रश्न 3.
चित्र-13.1 में ऑक्सीजन के 100 x 10^-3kg द्रव्यमान के लिए PV/T एवं P में, दो अलग-अलग तापों पर ग्राफ दर्शाए गए हैं।
(a) बिन्दुकित रेखा क्या दर्शाती है?
(b) क्या संत्य है : T1 > T2 अथवा T1 < T2?
(c) y-अक्ष पर जहाँ वक्र मिलते हैं वहाँ [latex s=2]\frac { PV }{ T }[/latex] का मान क्या है?

(d) यदि हम ऐसे ही ग्राफ 100 x 10^-3 kg हाइड्रोजन के लिए बनाएँ तो भी क्या उस बिन्दु पर जहाँ वक़ y-अक्ष से मिलते हैं [latex s=2]\frac { PV }{ T }[/latex] का मान यही होगा? यदि नहीं, तो हाइड्रोजन के कितने द्रव्यमान के लिए [latex s=2]\frac { PV }{ T }[/latex] का मान (कम दाब और उच्च ताप के क्षेत्र के लिए वही होगा? H₂ का अणु द्रव्यमान = 2.02 u, O₂ का अणु द्रव्यमान = 32.0 u, R = 8.31 J mol^-1K^-1)
उत्तर-
(a) बिन्दुकित रेखा यह दर्शाती है, कि राशि [latex s=2]\frac { PV }{ T }[/latex] नियत है। यह तथ्य केवल आदर्श गैस के लिए सत्य है; अतः बिन्दुकित रेखा आदर्श गैस का ग्राफ है।
(b) हम देख सकते हैं कि ताप T2 पर ग्राफ की तुलना में ताप T1 पर गैस का ग्राफ आदर्श गैस के ग्राफ के अधिक समीप है अर्थात् ताप T2 पर ऑक्सीजन गैस का आदर्श गैस के व्यवहार से विचलन अधिक है।
हम जानते हैं कि वास्तविक गैसें निम्न ताप पर आदर्श गैस के व्यवहार से अधिक विचलित होती है।
अतः T1 > T2
(c) जिस बिन्दु पर ग्राफ y-अक्ष पर मिलते हैं ठीक उसी बिन्दु से आदर्श गैस का ग्राफ भी गुजरता है;
अतः इस बिन्दु पर ऑक्सीजन गैस, आदर्श गैस समीकरण का पालन करेगी।
अत: PV = µRT से, [latex s=2]\frac { PV }{ T }[/latex] = µR
∵ गैस का द्रव्यमान m= 1.00 x 10^-3 kg जबकि गैस का ग्राम अणुभार M = 32g

(d) इस बिन्दु पर गैस, आदर्श गैस समीकरण का पालन करेगी; अतः [latex s=2]\frac { PV }{ T }[/latex] = µR होगा। परन्तु समान द्रव्यमान हाइड्रोजन गैस में ग्राम-अणुओं की संख्या भिन्न होगी; अत: हाइड्रोजन गैस के लिए [latex s=2]\frac { PV }{ T }[/latex] का मान भिन्न होगा।
H₂ गैस के लिए [latex s=2]\frac { PV }{ T }[/latex] = µR का वही मान प्राप्त करने के लिए हमें ग्राम-अणुओं की संख्या वही [latex s=2]\left( \mu =\frac { 1 }{ 32 } \right) [/latex] लेनी होगी।

प्रश्न 4.
एक ऑक्सीजन सिलिण्डर जिसका आयतन 30 L है, में ऑक्सीजन का आरम्भिक दाब 15 atm एवं ताप 27°c है। इसमें से कुछ गैस निकाल लेने के बाद प्रमापी (गेज) दाब गिरकर 11 atm एवं ताप गिरकर 17°C हो जाता है। ज्ञात कीजिए कि सिलिण्डर से ऑक्सीजन की कितनी मात्रा निकाली गई है? (R = 8.31 J mol^-1K^-1, ऑक्सीजन का अणु द्रव्यमान O₂ = 32u )
हल-
μ ग्राम मोल के लिए आदर्श गैस समीकरण
PV = μ RT (जहाँ μ = m/M)
अतः PV= (m/M) RT
(जहाँ m= ग्राम में द्रव्यमान, M = ग्राम में अणुभार)

प्रश्न 5.
वायु का एक बुलबुला, जिसका आयतन 1.0 cm³ है, 40 m गहरी झील की तली से जहाँ ताप 12°c है, उठकर ऊपर पृष्ठ पर आता है जहाँ ताप 35°c है। अब इसका आयतन क्या होगा?
हल-
दिया है : बुलबुले का आयतन V1 = 1.0 cm³ = 1.0 x 10^-6m³
अन्तिम आयतन V2 = ?

प्रश्न 6.
एक कमरे में, जिसकी धारिता 25.0 m³ है, 27°C ताप और 1 atm दाब पर, वायु के कुल अणुओं (जिनमें नाइट्रोजन, ऑक्सीजन, जलवाष्प और अन्य सभी अवयवों के कण सम्मिलित हैं) की संख्या ज्ञात कीजिए।
हल-
दिया है : कमरे की धारिता V = 25.0 m³, ताप T = 27 + 273 = 300K,
दाब P = 1 atm = 1.01 x 10⁵ N m^-2
कुल अणुओं की संख्या = ?

प्रश्न 7.
हीलियम परमाणु की औसत तापीय ऊर्जा का आकलन कीजिए-
(i) कमरे के ताप (27°C) पर।
(ii) सूर्य के पृष्ठीय ताप (6000 K) पर।
(iii) 100 लाख केल्विन ताप (तारे के क्रोड का प्रारूपिक ताप) पर।
हल-
हीलियम एक परमाणु गैस है। अत: परमाणु की औसत तापीय ऊर्जा अणु की औसत तापीय ऊर्जा ही होगी। किसी गैस के एक अणु की औसत तापीय ऊर्जा (गतिज ऊर्जा) [latex s=2]\overline { E } =\frac { 3 }{ 2 } K.T[/latex] (जहाँ T = परमताप,

प्रश्न 8.
समान धारिता के तीन बर्तनों में एक ही ताप और दाब पर गैसे भरी हैं। पहले बर्तन में निऑन (एकपरमाणुक) गैस है, दूसरे में क्लोरीन (द्विपरमाणुक) गैस है और तीसरे में यूरेनियम हेक्साफ्लोराइड (बहुपरमाणुक) गैस है। क्या तीनों बर्तनों में गैसों के संगत अणुओं की संख्या समान है? क्या तीनों प्रकरणों में अणुओं की υ_r.m.s (वर्ग-माध्य-मूल चाल) समान है?
उत्तर-
(i) हाँ, चूँकि आवोगाद्रो परिकल्पना के अनुसार समान परिस्थितियों में गैसों के समान आयतन में अणुओं की संख्या समान होती है। (ii) नहीं,

तीनों गैसों के ग्राम-अणु भार अलग-अलग हैं; अतः अणुओं की वर्ग-माध्य-मूल चाल भी अलग-अलग होगी।

प्रश्न 9.
किस ताप पर ऑर्गन गैस सिलिण्डर में अणुओं की υ_r.m.s,-20°C पर हीलियम गैस परमाणुओं की υ_r.m.s के बराबर होगी? (Ar का परमाणु द्रव्यमान = 39.9u एवं हीलियम का परमाणु द्रव्यमान = 4.0u)
हल-

प्रश्न 10.
नाइट्रोजन गैस के एक सिलिण्डर में, 2.0 atm दाब एवं 17°C ताप पर, नाइट्रोजन अणुओं के माध्य मुक्त पथ एवं संघट्ट आवृत्ति का आकलन कीजिए। नाइट्रोजन अणु की त्रिज्या लगभग 1.0 Å लीजिए। संघट्ट-काल की तुलना अणुओं द्वारा दो संघट्टों के बीच स्वतन्त्रतापूर्वक चलने में लगे समय से कीजिए। (नाइट्रोजन का आणविक द्रव्यमान = 28.0u)
हल-
P = 2.0, वायुमण्डलीय = 2 x 1.013 x 10⁵ = 2.026 x 10⁵ न्यूटन मीटर^-2,
T = 17°C = 17 + 273 = 290 K
1 मोल गैस के लिए, PV = RT

अतिरिक्त अभ्यास

प्रश्न 11.
1 मीटर लम्बी संकरी (और एक सिरे पर बन्द) नली क्षैतिज रखी गई है। इसमें 76 cm लम्बाई भरा पारद सूत्र, वायु के 15 cm स्तम्भ को नली में रोककर रखता है। क्या होगा यदि खुला सिरा नीचे की ओर रखते हुए नली को ऊर्ध्वाधर कर दिया जाए?
हल-
प्रारम्भ में जब नली क्षैतिज है, तब बन्द सिरे पर रोकी गई वायु का दाब वायुमण्डलीय दाब के बराबर होगा क्योंकि यह वायु, वायुमण्डलीय दाब के विरुद्ध पारे के स्तम्भ को पीछे हटने से रोकती है।
∴ P1 = वायुमण्डलीय दाब
= 76 सेमी पारद स्तम्भ का दाब
यदि नली का अनुप्रस्थ क्षेत्रफल A सेमी² है तो वायु का आयतन V1 = 15 सेमी X A सेमी² = 15A सेमी³ । जब नली का खुला सिरा नीचे की ओर रखते हुए ऊध्र्वाधर करते हैं तो खुले सिरे पर बाहर की ओर से वायुमण्डलीय दाब (76 सेमी पारद स्तम्भ का दाब) काम करता है जब कि ऊपर की ओर से 76 सेमी पारद सूत्र का दाब तथा बन्द सिरे पर एकत्र वायु की दाब काम करते हैं। चूँकि खुले सिरे पर पारद स्तम्भ + वायु का दाब अधिक है अतः पारद स्तम्भ सन्तुलन में नहीं रह पाता और नीचे गिरते हुए, वायु को बाहर निकाल देता है।
माना पारद स्तम्भ की h लम्बाई नली से बाहर निकल जाती है।
तब, पारद स्तम्भ की शेष ऊँचाई = (76 – h)
सेमी जबकि बन्द सिरे पर वायु स्तम्भ की लम्बाई = (15 + 9 + h) सेमी
= (24 + h) सेमी
वायु का आयतन V2 = (24 + h) A सेमी³

अतः h = 23.8 सेमी अथवा – 47.8 सेमी (जो अनुमान्य है।)
इसलिए h = 23.8 सेमी ≈ 24 सेमी ।
अतः लगभग 24 सेमी पारा बाहर निकल जायेगा। शेष पारे का 52 सेमी ऊँचा स्तम्भ तथा 4.8 सेमी वायु स्तम्भ इसमें जुड़कर बाह्य वायुमण्डल के साथ संतुलन में रहते हैं। (यहाँ पूरे प्रयोग की अवधि में ताप को नियत माना गया है तब ही बॉयल के नियम का प्रयोग किया है।)

प्रश्न 12.
किसी उपकरण से हाइड्रोजन गैस 28:7 सेमी³/से की दर से विसरित हो रही है। उन्हींस्थितियों में कोई दूसरी गैस 7.2 सेमी³/से की दर से विसरित होती है। इस दूसरी गैस
को पहचानिए।
[संकेत-ग्राहम के विसरण नियम R1/R2 = (M2 /M1)^1/2 का उपयोग कीजिए, यहाँ R1, R2 क्रमशः गैसों की विसरण दर तथा M1 एवं M2 उनके आणविक द्रव्यमान हैं। यह नियम अणुगति सिद्धान्त का एक सरल परिणाम है।]
हल-
किसी गैस के विसरण की दर । गैस अणुओं के वर्ग माध्य मूल वेग के अनुक्रमानुपाती होती है अर्थात्

अतः दूसरी गैस ऑक्सीजन है। (चूंकि ऑक्सीजन का अणुभार 32 होता है।)

प्रश्न 13.
साम्यावस्था में किसी गैस का घनत्व और दाब अपने सम्पूर्ण आयतन में एकसमान हैं। यह पूर्णतया सत्य केवल तभी है जब कोई भी बाह्य प्रभाव न हो। उदाहरण के लिए गुरुत्व से प्रभावित किसी गैस स्तम्भ का घनत्व (और दाब) एकसमान नहीं होता है। जैसा कि आप आशा करेंगे इसका घनत्व ऊँचाई के साथ घटता है। परिशुद्ध निर्भरता ‘वातावरण के नियम

से दी जाती है, यहाँ n2, n1 क्रमशः h2 व h1 ऊँचाइयों पर संख्यात्मक घनत्व को प्रदर्शित करते हैं। इस सम्बन्ध का उपयोग द्रव-स्तम्भ में निलम्बित किसी कण के अवसादने साम्य के लिए समीकरण

को व्युत्पन्न करने के लिए कीजिए, यहाँ ρ निलम्बित कण का घनत्व तथा ρ’ चारों तरफ के माध्यम का घनत्व है। N_A आवोगाव्रो संख्या तथा R सार्वत्रिक गैस नियतांक है। (संकेतः निलम्बित कण के आभासी भार को जानने के लिए आर्किमिडीज के सिद्धान्त का उपयोग कीजिए)
उत्तर-
वातावरण के नियम के अनुसार,

जबकि m द्रव्यमान का कण वायु में साम्यावस्था में तैर रहा है। यदि कण ρ’ वाले किसी द्रव में छोड़ा गया है तो इस कण पर द्रव के कारण उत्क्षेप भी कार्य करेगा। ऐसी स्थिति में हमें उक्त सूत्र में mg के स्थान पर कण का आभासी भार रखना होगा।
माना कण का आयतन V तथा घनत्व ρ है तब ।
कण का आभासी भार = mg – उत्क्षेप

प्रश्न 14.
नीचे कुछ ठोसों व द्रवों के घनत्व दिए गए हैं। उनके परमाणुओं की आमापों का आकलन (लगभग) कीजिए।

[ संकेतः मान लीजिए कि परमाणु ठोस अथवा द्रव प्रावस्था में दृढ़ता से बँधे हैं, तथा आवोगाव्रो संख्या के ज्ञात मान का उपयोग कीजिए। फिर भी आपको विभिन्न परमाणवीय आकारों के लिए अपने द्वारा प्राप्त वास्तविक संख्याओं का बिल्कुल अक्षरशः प्रयोग नहीं करना चाहिए क्योंकि दृढ़ संवेष्टन सन्निकटन की रूक्षता के परमाणवीय आकार कुछ Å के पास में हैं ]
हल-

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न
प्रश्न 1.
27°C ताप पर एक बर्तन में भरी हुई एक मोल हाइड्रोजन गैस का दाब P है। उसी आयतन के दूसरे बर्तन में 127°C ताप पर एक मोल हीलियम गैस भरी है। इसका दाब होगा

उत्तर-
(iii) [latex s=2]\frac { 4 }{ 3 }p[/latex]

प्रश्न 2.
किसी बर्तन में P₀ दाब पर गैस है। यदि सभी अणुओं के द्रव्यमान आधे और उनकी चाल दोगुनी कर दी जाये तो परिणामी दाब होगा
(i) 4P₀
(ii) 2P₀
(iii) P₀
(iv) P₀/2
उत्तर-
(ii) 2P₀

प्रश्न 3.
सामान्य ताप एवं दाब पर 1 सेमी³ हाइड्रोजन एवं 1 सेमी³ ऑक्सीजन गैसें ली गयी हैं। हाइड्रोजन के अणुओं की संख्या n1 तथा ऑक्सीजन के अणुओं की संख्या n2 है। सही विकल्प होगा

उत्तर-
(i) [latex s=2]\frac { { n }_{ 1 } }{ { n }_{ 2 } } =\frac { 1 }{ 16 } [/latex]

प्रश्न 4.
एक आदर्श गैस का दाब P और इसके एकांक आयतन की गतिज ऊर्जा E में परस्पर सम्बन्ध है।

उत्तर-
(iii)[latex s=2]P=\frac { 2 }{ 3 }E[/latex]

प्रश्न 5.
एक ग्राम-अणु गैस की गतिज ऊर्जा सामान्य ताप तथा दाब पर E है। 273°C पर इसकी गतिज ऊर्जा होगी।
(i) [latex s=2]\frac { E }{ 4 }[/latex]
(ii) [latex s=2]\frac { E }{ 2 }[/latex]
(iii) 2E
(iv) 4E
उत्तर-
(iii) 2E

प्रश्न 6.
किसी वास्तविक गैस के लिए P तथा v में परिवर्तन चार विभिन्न तपों T1, T2, T3 व T4 पर प्रदर्शित है। गैस का क्रान्तिक ताप है। विभिन्न तापों T1, T2, T3 तथा T4 पर किसी वास्तविक गैस का दाब P बढ़ाने पर आयतन v में परिवर्तन चित्र 13.3 में प्रदर्शित है। गैस का क्रान्तिक ताप है।

(i) T1
(ii) T2
(iii) T3
(iv) T4
उत्तर-
(ii) T2

प्रश्न 7.
40°C पर किसी गैस के अणुओं की औसत गतिज ऊर्जा है। वह ताप, जिस पर यह ऊर्जा 2E हो जाएगी, है।
(i) 80°C
(ii) 160° C
(ii) 273°C
(iv) 353°C
उत्तर-
(i) 80°C

प्रश्न 8.
1 मोल नाइट्रोजन गैस के दाब व ताप बदल जाते हैं । जब प्रयोग को उच्च दाब तथा उच्च ताप पर किया 2.0 जाता है। प्राप्त परिणाम चित्र 13.4 में प्रदर्शित है। [latex s=2]\frac { PV }{ RT }[/latex] का P के साथ सही परिवर्तन प्रदर्शित होगा

(i) वक्र 1 से
(ii) वक्र 4 से।
(iii) वक्र 3 से
(iv) वक्र 2 से
उत्तर-
(ii) वक्र 4 से

प्रश्न 9.
कमरे के ताप पर हाइड्रोजन तथा ऑक्सीजन के अणुओं की वर्ग-माझ्य-मूल चालों का अनुपात है
(i) 4:1
(ii) 8:1
(iii) 12:1
(iv) 16:1
उत्तर-
(i) 4:1

प्रश्न 10.
किसी गैस का परमताप चार गुना बढ़ा दिया जाता है। गैस के अणुओं की वर्ग-माध्य-मूल चाल हो जायेगी।
(i) 4 गुना
(ii) 16 गुना
(iii) 1/4 गुना
(iv) 2 गुना
उत्तर-
(iv) 2 गुना

प्रश्न 11.
दो आदर्श गैसों के अणुओं के वर्ग-माध्य-मूल वेग समान हैं। गैसों के अणुभार क्रमशः M1 और M2 एवं परमताप क्रमशःT1 और T2 हैं तो,

उत्तर-
(ii) [latex s=2]\frac { T_{ 1 } }{ T_{ 2 } } =\frac { M_{ 1 } }{ M_{ 2 } } [/latex]

प्रश्न 12.
समान ताप पर दो गैसों के वाष्प घनत्वों का अनुपात 4 : 5 है। इनके अणुओं के वर्ग-माध्य-मूल वेगों का अनुपात होगा।
(i) 1 : 2.25
(ii) 2:3
(iii)3:2
(iv) 4:9
उत्तर-
(iii) 3 : 2

प्रश्न 13.
एक पक्षी आकाश में उड़ रहा है। इसके गति की स्वातन्त्र्य कोटि की संख्या है।
(i) 3
(ii) 2
(iii) 1
(iv) 0
उत्तर-
(i) 3

प्रश्न 14.
किसी द्विपरमाणविक अणु की स्थानान्तरीय तथा घूर्णीय स्वातन्त्र्य कोटियों की कुल संख्या होगी
(i) 2
(ii) 3
(iii) 4
(iv) 5
उत्तर-
(iv) 5

प्रश्न 15.
किसी एकपरमाणविक गैस के एक अणु की स्वातन्त्र्य कोटियों की संख्या होगी।
(i) 1
(ii) 2
(iii) 3
(iv) 4
उत्तर-
(iii) 3

प्रश्न 16.
एक चींटी मेज के पृष्ठ पर चल रही है। इसके चलने की स्वातन्त्रय कोटि है।
(i) शून्य
(ii) 1
(iii) 2
(iv) 3
उत्तर-
(iii) 2

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
आदर्श गैस का अवस्था समीकरण किसे कहते हैं?
उत्तर-
किसी आदर्श गैस के निश्चित द्रव्यमान के आयतन, ताप व दाब में सम्बन्ध बताने वाले समीकरण को आदर्श गैस समीकरण या आदर्श गैस को अवस्था समीकरण कहते हैं।

प्रश्न 2.
वास्तविक गैसों के लिए वाण्डरवाल्स समीकरण लिखिए तथा प्रमुख प्रतीकों के अर्थ बताइए।
उत्तर-
वास्तविक गैसों के लिए वाण्डरवाल्स समीकरण निम्न है।

जहाँ P = दाब, V = आयतन, R = सार्वत्रिक गैस नियतांक
a तथा b = त्रुटि सुधार नियतांक

प्रश्न 3.
अणुगति सिद्धान्त के आधार पर गैस के दाब का सूत्र लिखिए। प्रयुक्त संकेतांकों का अर्थ लिखिए।
उत्तर-

जहाँ m = एक अणु का द्रव्यमान,n = V आयतन में अणुओं की संख्या तथा [latex s=2]{ \overline { \nu } }^{ 2 }[/latex] = अणुओं का वर्ग-माध्य-मूल वेग।

प्रश्न 4.
दो गैसें समान ताप, दाब तथा आयतन पर मिश्रित की गयी हैं। यदि तप्प और आयतन में । परिवर्तन न हो तो मिश्रण का परिणामी दाब क्या होगा?
उत्तर-
डाल्टने के आंशिक दाब के अनुसार परिणामी दाब = P1 + P2
परन्तु यहाँ P1 = P2 = P (माना) अतः परिणामी दाब = P+ P = 2P
अतः मिश्रण का दाब एक गैस के दाब का दोगुना होगा।

प्रश्न 5.
1 सेमी³ ऑक्सीजन और 1 सेमी³ नाइट्रोजन सामान्य ताप एवं दाब पर हैं। इन गैसों में अणुओं की संख्याओं का अनुपात क्या है?
हल-
अणुगति सिद्धान्त से,

चूँकि दोनों एक ही ताप पर हैं, अत: अणुओं की माध्य गतिज ऊर्जाएँ बराबर होंगी। तब

प्रश्न 6.
किसी ठोस को दबाने पर उनके परमाणुओं की स्थितिज ऊर्जा घटती है अथवा बढ़ती है।
उत्तर-
बढ़ती है।

प्रश्न 7.
किसी गैस के दाब तथा प्रति एकांक आयतन की गतिज ऊर्जा में सम्बन्ध स्थापित कीजिए।
उत्तर-
गैसों के अणुगति सिद्धान्त के अनुसार

प्रश्न 8.
किस ताप पर किसी गैस के अणुओं की माध्य गतिज ऊर्जा 27°C ताप पर गतिज ऊर्जा की 1/3 होगी?
हल-
चूँकि

प्रश्न 9.
किसी गैस के परमताप को चार गुना बढ़ा दिया गया। इसके अणुओं के वर्ग-माध्य-मूल वेग में क्या परिवर्तन होगा?
उत्तर-
∴ ν_rms ∝ √t; यदि परमताप को 4 गुना बढ़ा देने से वर्ग-माध्य-मूल वेग √4 गुना अर्थात् 2 गुना बढ़ जायेगा।

प्रश्न 10.
किसी गैस में ध्वनि की चाल तथा उसकी गैस के अणुओं की वर्ग-माध्य-मूल चाल (ν_rms) में सम्बन्ध का सूत्र लिखिए।
उत्तर-

लनु उत्तरीय प्रश्न

प्रश्न 1.
अणुगति सिद्धान्त के आधार पर बॉयल तथा चाल्र्स के नियमों की व्याख्या कीजिए।
उत्तर-
बॉयल के नियम की व्याख्या-अणुगति सिद्धान्त से एक निश्चित द्रव्यमान की गैस द्वारा आरोपित दाब

प्रश्न 2.
किसी गैस को सम्पीडित करने में किये गये कार्य को समझाइए।
उत्तर-
गैस को सम्पीडित करने में किया गया कार्य-माना एक आदर्श गैस एक पिस्टन लगे सिलिण्डर में भरी है, गैस का दाब P, आयतन V तथा ताप T है, जब गैस को सम्पीडित किया जाता है, तो उसके लिए μ मोलों के लिए आदर्श गैस समीकरण । PV = μT से,[latex s=2]\frac { PV }{ T }[/latex] = μR का मान नियत रहता है। गैस को सम्पीडित करने में गैस पर कुछ कार्य करना पड़ता है। यदि P दाब पर गैस का आयतन dV कम हो जाये, तो गैस पर कृत कार्य,

dw = PdV
गैस का आयतन V1 से V2 तक सम्पीडित करने में गैस पर किया गया कार्य

कृत कार्य का मान गैस को सम्पीडित करने के प्रक्रम पर भी निर्भर करता है। उदाहरण के लिए, समदाबी, समतापी व रुद्धोष्म प्रक्रमों में कृत कार्य भिन्न-भिन्न होते हैं। यदि गैस वास्तविक है, तो गैस को सम्पीडित करने में अन्तरआण्विक बलों के विरुद्ध भी कार्य करना पड़ता है।

प्रश्न 3.
अन्तरिक्ष के किसी क्षेत्र में प्रति घन सेमी में औसतन केवल 5 अणु हैं तथा वहाँ ताप 3 है। उस क्षेत्र में गैस का दाब क्या है? बोल्ट्ज मैन नियतांक R= 1.38 x 10^-23 जूल/K
हल-
यदि गैस के किसी द्रव्यमान में n अणु हों तब गैस के इस द्रव्यमान के लिए निम्नलिखित समीकरण होगी

प्रश्न 4.
एक बर्तन में भरी गैस का ताप 400 Kहै और दाब 2.78 x 10^-3 न्यूटन/भी² है। बर्तन के 1 सेमी³ आयतन में अणुओं की संख्या ज्ञात कीजिए। बोल्ट्जमैन नियतांक K = 1.38 x 10^-23 जूल/केल्विन।
हल-
आदर्श गैस समीकरण PV = nK_BT से,

प्रश्न 5.
वायु से भरे हुए एक कमरे का आयतन 41.4 मी³ है। वायु का ताप 27°C तथा दाब 1.0 x 10⁵ न्यूटन/मी² है। वायु के कुल अणुओं की संख्या ज्ञात कीजिए।
हल-
आदर्श गैस समीकरण PV = nK_BT से,

प्रश्न 6.
क्रान्तिक ताप के आधार पर वाष्प तथा गैस में अन्तर स्पष्ट कीजिए।
उत्तर-
वाष्प तथा गैस दोनों ही किसी पदार्थ की गैसीय अवस्था के दो नाम हैं। इनमें अन्तर यह है कि जो पदार्थ साधारण ताप व दाब पर द्रव या ठोस अवस्था में होते हैं उनके गैसीय अवस्था में आ जाने पर उनको वाष्प कहते हैं; जैसे—कपूर की वाष्प, जलवाष्प आदि। परन्तु जो पदार्थ साधारण ताप व दाब पर ही गैसीयं अवस्था में होते हैं, वे गैस कहलाते हैं। उदाहरणार्थ-वायु, ऑक्सीजन आदि। गैस को दाब डालकर द्रवित करने के लिए पहले उसे क्रान्तिक ताप तक ठण्डा करना पड़ता है, परन्तु वाष्प को केवल दाब डालकर ही द्रवित किया जा सकता है। अतः क्रान्तिक ताप से ऊपर पदार्थ गैस तथा नीचे वाष्प की भाँति व्यवहार करता है।

प्रश्न 7.
दिखाइए कि गैस के अणुओं का वर्ग-माध्य-मूल वेग गैस के परमताप के वर्गमूल के अनुक्रमानुपाती होता है।
हल-
गैस के अणुओं के वेगों के वर्गों का माध्य का वर्गमूल, गैस के अणुओं का वर्ग-माध्य-मूल वेग कहलाता है। उसे ν_rms से प्रदर्शित करते हैं।

अत: किसी गैस के अणुओं का वर्ग-माध्य-मूल वेग गैस के परमताप के वर्गमूल के अनुक्रमानुपाती होता है।

प्रश्न 8.
27°C पर ऑक्सीजन (आणविक भार = 32) के लिए अणुओं का वर्ग-माध्य-मूल वेग तथा 4 ग्राम गैस की गतिज ऊर्जा भी ज्ञात कीजिए। (गैस नियतांक R = 8.31 जूल/मोल-K)
हल-
T = 27°C = 27 + 273 = 300 K, M = 32

प्रश्न 9.
किसी गैस का प्रारम्भिक ताप – 73°c है। इसे किस ताप तक गर्म करना चाहिए जिससे
(i) गैस के अणुओं का वर्ग-माध्य-मूल वेग दोगुना हो जाये?
(ii) अणुओं की औसत गतिज ऊर्जा दोगुनी हो जाए?
हल-
प्रारम्भिक परमताप T1 = (-73 + 273) K = 200 K; माना इसको t2°C तक गर्म किया जाना चाहिए जिसका संगत परमताप T2K.

प्रश्न 10.
यदि किसी गैस का ताप 127°C से बढ़ाकर 527°C कर दिया जाये तो उसके अणुओं का वर्ग-माध्य-मूल वेग कितना हो जायेगा?
हल-

प्रश्न 11.
किस ताप पर ऑक्सीजन के अणुओं का औसत वेग पृथ्वी से पलायन कर जाने के लिए पर्याप्त होगा? पृथ्वी का पलायन वेग = 11.2 किमी/से, ऑक्सीजन के एक अणु का द्रव्यमान = 5.34 x 10^-26 किग्रा, बोल्ट्जमैन नियतांक K = 1.38 x 10^-23 जूल/K
हल-
माना ऑक्सीजन के एक अणु का द्रव्यमान m है। अणु की पलायन ऊर्जा [latex s=2]\frac { 1 }{ 2 } m{ { v }_{ e } }^{ 2 }[/latex] होगी, जहाँ v_e पृथ्वी से पलायन करने का वेग है।
अणुगति सिद्धान्त के अनुसार, TK ताप पर एक अणु की माध्य गतिज ऊर्जा [latex s=2]E=\frac { 3 }{ 2 } K{ _{ B } }T[/latex] होती है, जहाँ K_B बोल्ट्जमैन नियतांक है।

प्रश्न 12.
4.0 ग्राम ऑक्सीजन गैस की 27°C ताप पर कुल आन्तरिक ऊर्जा की गणना कीजिए। (ऑक्सीजन गैस की स्वातन्त्रय कोटियों की संख्या 5 तथा गैस नियतांक R = 2.0 कैलोरी/मोल-केल्विन है)
हल-

विस्तृत उत्तरीय प्रश्न

प्रश्न 1.
आदर्श गैस समीकरण PV = RT स्थापित कीजिए तथा R का विमीय सूत्र एवं मात्रक ज्ञात कीजिए।
आदर्श गैस के अवस्था समीकरण की सहायता से गैस नियतांक (R) का विमीय-सूत्र ज्ञात कीजिए।
उत्तर-
आदर्श गैस समीकरण—किसी आदर्श गैस के निश्चित द्रव्यमान के आयतने, ताप व दाब में सम्बन्ध बतलाने वाले समीकरण को आदर्श गैस समीकरण अथवा आदर्श गैस का अवस्था समीकरण (equation of state) कहते हैं।
माना आदर्श गैस की प्रारम्भिक अवस्था में इसके निश्चित द्रव्यमान के दाब, आयतन व ताप क्रमशः P1 V1 तथा T1 हैं। किसी अन्य अवस्था में इनके मान बदलकर माना P2, V2 तथा T2 हो जाते हैं। गैस की अवस्था में होने वाले इस परिवर्तन को निम्न दो पदों में पूर्ण हुआ माना जा सकता है|
(i) ताप नियत रखते हुए यदि ताप T1 स्थिर रखते हुए दाब P1 से बदलकर P2 कर दिया जाए। तथा आयतन V1 से बदलकर V’ हो जाए तो बॉयल के नियम से
P1V1 = P2V’
अथवा V’= P1V1/P2 …(1)
(ii) दाब नियत रखते हुए-यदि दाब P2 नियत रखते हुए परमताप T1 से बदलकर T2 कर दिया जाये तो आयतन V’ से बदलकर V2 हो जायेगा। अत: चार्ल्स के नियम के अनुसार,

यही गैस समीकरण है। नियतांक । को विशिष्ट गैस नियतांक (specific gas constant) कहते हैं। इसका मान गैस की प्रकृति तथा द्रव्यमान पर निर्भर करता है, अर्थात् भिन्न-भिन्न गैसों के एक ही द्रव्यमान के लिए अथवा एक ही गैस के भिन्न-भिन्न द्रव्यमानों के लिए इसका मान भिन्न-भिन्न होता है। यदि हम एक ग्राम-अणु अर्थात् 1मोल गैस लें तो गैस-नियतांकr का मान सभी गैसों के लिए बराबर होगा। तब इसको सार्वत्रिक-गैस-नियतांक (universal gas constant) कहते हैं तथा । इसे R से व्यक्त करते हैं।
अतः 1 मोल अर्थात् 1 ग्राम-अणु गैस के लिए समीकरण (3) को नया रूप निम्नलिखित होगा
PV = RT …(4)
समीकरण (4) गैस-नियमों के आधार पर प्राप्त की गयी है। चूंकि गैस के नियम एक आदर्श गैस के लिए पूर्णत: सत्य हैं; अतः समीकरण PV = RT भी एक आदर्श गैस के 1 ग्राम मोल के लिए पूर्णतः सत्य होगी। अतः इसको आदर्श गैस समीकरण कहते हैं। R का विमीय सूत्र तथा मात्रक,

प्रश्न 2.
गैस के अणुगति सिद्धान्त की परिकल्पनाओं का उल्लेख कीजिए।
उत्तर-
गैस के अणुगति सिद्धान्त की परिकल्पनाएँ-गैसों का अणुगति सिद्धान्त निम्नलिखित परिकल्पनाओं पर आधारित है–
1. प्रत्येक गैस छोटे-छोटे कणों से मिलकर बनी होती है जिन्हें अणु कहते हैं।
2. किसी गैस के अणु दृढ़, पूर्णतः प्रत्यास्थ (perfectly elastic), गोलाकार व सभी प्रकार से एकसमान होते हैं।
3. अणुओं का आकार अत्तराणुक अन्तराल की तुलना में नगण्य होता है। अतः अणुओं का अपना आयतन गैस के आयतचे की तुलना में नगण्य होता है।
4. साधारणत: अणुओं के बीच किसी प्रकार का बल नहीं लगता; अत: ये नियत चाल से ऋजु-रेखीय पथों पर गति करते हैं। परन्तु जब दो अणु एक-दूसरे के अत्यन्त निकट आ जाते हैं तो उनके बीच प्रतिकर्षण बल कार्य करने लगता है जिससे उनकी चाल तथा गति की दिशा बदल जाती है। फलस्वरूप, अणु नये सरल रेखीय पथ पर गति प्रारम्भ करते हैं। इस घटना को दो अणुओं के बीच ‘टक्कर’ (collision) कहते हैं। अत: दो क्रमागत टक्करों के बीच गैस के अणु सरल रेखा में गति करते हैं। दो क्रमागत टक्करों के बीच गैस के अणु द्वारा तय की गयी औसत दूरी को ‘औसत मुक्त पथ’ (mean free path) कहते हैं। इस प्रकार अणु सभी सम्भव वेग से सभी सम्भव दिशाओं में अनियमित गति करते हैं।
5. ये अणु बर्तन की दीवारों से टकराते हैं किन्तु इन टक्करों से गैस का आयतन नहीं बदलता अर्थात् गैस के प्रति एकांक आयतन में अणुओं की संख्या स्थिर रहती है।
6. दो अणुओं की टक्कर पूर्णतः प्रत्यास्थ होती है। टक्कर के समय उनके मध्य आकर्षण या प्रतिकर्षण बल नहीं लगता जिससे टक्कर में गतिज ऊर्जा संरक्षित रहती है।
7. दो अणुओं की टक्कर क्षणिक होती है अर्थात् टक्कर का समय उनके द्वारा स्वतन्त्रतापूर्वक चलने | में लिए गये समय की तुलना में नगण्य होता है।
8. अणुओं की गति पर गुरुत्वाकर्षण के प्रभाव को नगण्य माना जा सकता है। अतः गुरुत्वाकर्षण बल के कारण भी अणुओं के वितरण पर कोई प्रभाव नहीं पड़ता।

प्रश्न 3.
आदर्श गैस समीकरण लिखिए। वास्तविक गैसों के लिए वाण्डर वाल्स के संशोधनों को समझाइए तथा इससे संशोधित गैस समीकरण प्राप्त कीजिए।
उत्तर-
आदर्श गैस समीकरण-1 मोल गैस के लिए आदर्श गैस समीकरण है PV = RT, जहाँ P = दाब,V = आयतन, R = गैस नियतांक तथा T = परमताप है।
वाण्डर वाल्स गैस समीकरण-बॉयल के नियमानुसार, स्थिर ताप पर गैस के एक निश्चित द्रव्यमान के लिए दाब (P) व्र आयतन (V) का गुणनफल PV एक नियतांक होता है। प्रयोगों द्वारा देखा गया है। कि कोई भी वास्तविक गैस इस नियम का पूर्णतः पालन नहीं करती। उच्च दाबों तथा निम्न तापों पर गैस बॉयल के नियम से बहुत अधिक विचलित हो जाती है। अतः वाण्डर वाल्स ने वास्तविक गैसों के इस व्यवहार की व्याख्या करने के लिए आदर्श मॉडल में निम्न लिखित दो संशोधन किये
1. अणुओं का अशून्य आकार (Finite size of molecules)–आदर्श गैस समीकरण PV = RT को प्राप्त करने में यह माना गया था कि गैस के अणुओं का आयतन, गैस के आयतन V की तुलना में नगण्य है तथा गैस का सम्पूर्ण आयतन अणुओं की गति के लिए उपलब्ध है। परन्तु सभी अणुओं का आयतन कुछ स्थान घेरता है जिससे आदर्श गैस के आयतन का प्रभावी आयतन (V – b) होगा, जहाँ । एक नियतांक है। अत: हम आदर्श गैस समीकरण PV = RT में v के स्थान पर (V – b) रखेंगे।
2. अन्तरा-अणुक बल (Inter-molecular force)–आदर्श गैस मॉडल में यह भी माना गया था कि गैस के अणुओं के मध्ये कोई बल आरोपित नहीं होता। यह मान्यता वास्तविक गैसों पर लागू नहीं होती है। गैस का प्रत्येक अणु दूसरे अणु पर बल लगाता है जिसे अन्तर आणविक बल कहते हैं। साधारण दाबों पर गैस के अणु बहुत दूर-दूर होते हैं; अत: उनके बीच अन्तर आणविक बल लगभग शून्य होता है। दाब बढ़ने के साथ-साथ अणु भी पास-पास आ जाते हैं और वे एक-दूसरे को आकर्षित करने लगते हैं। बर्तन के मध्य स्थित अणु (जैसे P) पर चारों ओर से आकर्षण बल कार्य करते हैं; अत: उस पर कोई प्रभावी बल नहीं लगता। जो अणु दीवार के पास होता है उस पर एक बल अन्दर की ओर लगता है, जिससे दीवार के टकराते समय उसके संवेग में कुछ कमी आ जाती है। अतः अणु द्वारा दीवार पर आरोपित बल आदर्श गैस मॉडल में प्राप्त बल से कम होता है। इसके फलस्वरूप दीवार पर वास्तविक गैस का दाब, आदर्श गैस के दाब से कम होता है। यदि यह कमी β है तो आदर्श गैस समीकरण में P के स्थान पर (P + β) रखेंगे। β का मान दीवार के समीप अंणु को आकर्षित करने वाले अणुओं की प्रति एकांक आयतन में संख्या पर तथा दीवार के प्रति एकांक क्षेत्रफल पर प्रति सेकण्ड टकराने वाले अणुओं की संख्या पर निर्भर करता है। ये दोनों ही गैस के घनत्व के अनुक्रमानुपाती होते हैं।

प्रश्न 4.
गैसों के अणु गतिज सिद्धान्त के आधार पर किसी आदर्श गैस के दाब का सूत्र लिखिए और इसके आधार पर बॉयल के नियम की व्याख्या कीजिए।
उत्तर-
गैसों के गतिज सिद्धान्त के आधार पर किसी आदर्श गैस का दाब सूत्र निम्नवत् है
[latex s=2]P=\frac { 1 }{ 3 } e{ v }^{ 2 }[/latex]
बॉयल का नियम इस नियम के अनुसार, नियत ताप पर किसी गैस के एक निश्चित द्रव्यमान का आयतन V उसके दाब P के व्युत्क्रमानुपाती होता है।
[latex s=2]V=\propto \frac { 1 }{ P } [/latex]
PV = नियतांक …(1)
इस प्रकार, यदि हम किसी गैस के ताप को नियत रखते हुए उसके दाब को दोगुना कर दें तो उसका आयतन आधा रह जायेगा अथवा दाब को आधा कर देने पर आयतन दोगुना हो जायेगा।

व्यापक रूप में, नियत ताप पर किसी दिये गये द्रव्यमान की गैस के प्रारम्भिक दाब व आयतन P1 व V1 हों तथा अन्तिम दाब व आयतन P2 व V2 हों, तो बॉयल के नियम से, P1V1 = P2V2, चित्र 13.7 में किसी गैस के लिए विभिन्न नियत तापों T1, T2, व T3 (T1 > T2 > T3) पर P तथा v के बीच प्रायोगिक वक्र तथा सैद्धान्तिक वक्र तुलना के लिए साथ-साथ दर्शाये गये हैं। बिन्दुकित वक्र समीकरण (1) के आधार पर खींचे गये हैं जो सैद्धान्तिक वक्र दर्शाते हैं, जबकि चिकने (smooth line) वक्र प्रायोगिक रूप से P तथा V के प्राप्त मानों के आधार पर खींचे गये हैं। इनसे यह स्पष्ट है कि निम्न दाब तथा उच्च ताप पर सैद्धान्तिक तथा प्रायोगिक वक्रों में संगति स्पष्ट दृष्टिगोचर होती है, परन्तु उच्च दाबों तथा निम्न तापों पर उनमें बहुत अधिक विचलन पाया जाता है। इसका कारण यह है कि निम्न दाबों तथा उच्च तापों पर गैस के अणु दूर-दूर होते हैं और उनके बीच अन्तरआणविक बल उपेक्षणीय होते हैं। अन्तरआणविक बलों की अनुपस्थिति में गैस आदर्श गैस की तरह व्यवहार करती है। इस प्रकार, दाब व ताप की सभी अवस्थाओं में गैसें बॉयल के नियम का पूर्ण रूप से पालन नहीं करती , हैं, केवल निम्न दाब तथा उच्च ताप पर ही वे ऐसा करती हैं।

प्रश्न 5.
गैसों के अणुगति सिद्धान्त के आधार पर किसी आदर्श गैस के दाब का व्यंजक लिखिए तथा इसकी सहायता से अणुओं की गतिज ऊर्जा तथा गैस के ताप में सम्बन्ध स्थापित कीजिए।
उत्तर-
दाब

आणविक गतिज ऊर्जा एवं ताप में सम्बन्ध–माना किसी गैस के 1 ग्राम-अणु (1 मोल) का द्रव्यमान अर्थात् अणुभार M तथा इसके अणुओं का वेग-वर्ग-माध्य [latex s=2]{ \overline { v } }^{ 2 }[/latex] है तो 1 ग्राम-अणु गैस की गतिज ऊर्जा

अर्थात् औसत गतिज ऊर्जा प्रारम्भिक औसत गतिज ऊर्जा की दोगुनी हो जायेगी।

प्रश्न 6.
माध्य-मुक्त पथ के लिए व्यंजक का निगमन कीजिए।
उत्तर-
माध्य-मुक्त पथ के लिए व्यंजक-माना कि किसी बर्तन में एक अणु के अतिरिक्त अन्य सभी अणु स्थिर हैं। माना कि प्रत्येक अणु d व्यास का गोला है। गतिशील अणु उन सभी अणुओं से टकरायेगा जिनके केन्द्र इसके केन्द्र से d दूरी पर स्थित होंगे [चित्र-13.8 (a)]।

माना कि एक बर्तन में गैस भरी है तथा उसके प्रति एकांक आयतन में n अणु हैं। प्रत्येक अणु का व्यास d है। माना इस गैस का केवल एक अणु ७ वेग से गतिमान है तथा शेष सभी अणु स्थिर हैं। गतिमान अणु उन सभी अणुओं से टकरायेगा जिनके केन्द्र इसके केन्द्र से d दूरी पर हैं [चित्र 13.8 (b)]। ∆t समय में इस अणु द्वारा चली दूरी = v ∆t. अतः ∆t समय में यह अणु उन सभी अणुओं से टकराएगा जो d त्रिज्या तथा ) v ∆t लम्बाई के सिलिण्डर में हैं।
सिलिण्डर का आयतन = πd²v∆t
सिलिण्डर में अणुओं की संख्या = (πd²v∆t) x n
यह गतिशील अणु द्वारा ∆t समय में अन्य अणुओं से टक्करों की संख्या है। गतिशील अणु ∆t समय में v∆t दूरी तय करता है। अतः अणु का ।

We hope the UP Board Solutions for Class 11 Physics Chapter 13 Kinetic Theory help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 13 Kinetic Theory, drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions (प्रतिलोम त्रिकोणमितीय फलन) are part of UP Board Solutions for Class 12 Maths. Here we have given UP Board Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions (प्रतिलोम त्रिकोणमितीय फलन)

Board	UP Board
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 2
Chapter Name	Inverse Trigonometric Functions
Exercise	Ex 1.1, Ex 1.2
Number of Questions Solved	35
Category	UP Board Solutions

UP Board Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions

प्रश्नावली 2.1

प्रश्न 1.
[latex s=2]{ sin }^{ -1 }\left( -\frac { 1 }{ 2 } \right) [/latex] का मुख्य मान ज्ञात कीजिए।
हल-

प्रश्न 2.
[latex s=2]{ cos }^{ -1 }\left( \frac { \sqrt { 3 } }{ 2 } \right) [/latex] का मुख्य मान ज्ञात कीजिए।
हल-
cos^-1 की मुख्य मान शाखा परिसर [0, π] है।

प्रश्न 3.
cosec^-1 (2) का मुख्य मान ज्ञात कीजिए।
हल-

प्रश्न 4.
tan^-1 (-√3) का मुख्य मान ज्ञात कीजिए।
हल-

प्रश्न 5.
[latex s=2]{ cos }^{ -1 }\left( -\frac { 1 }{ 2 } \right) [/latex] का मुख्य मान ज्ञात कीजिए।
हल-
cos^-1 की मुख्य मान शाखा परिसर [0, π] है।

प्रश्न 6.
tan^-1(-1) का मुख्य मान ज्ञात कीजिए।
हल-

प्रश्न 7.
[latex s=2]{ sec }^{ -1 }\left( \frac { 2 }{ \sqrt { 3 } } \right) [/latex] का मुख्य मान ज्ञात कीजिए।
हल-

प्रश्न 8.
cot^-1(√3) का मुख्य मान ज्ञात कीजिए।
हल-
cot^-1 का मुख्य मान शाखा परिसर (0, π) है।

प्रश्न 9.
[latex s=2]cos^{ -1 }\left( \frac { -1 }{ \sqrt { 2 } } \right) [/latex] का मान ज्ञात कीजिए।
हल-
cos^-1 का मुख्य मान शाखा परिसर [0, π] है।

प्रश्न 10.
cosec^-1 (-√2) का मुख्य मान ज्ञात कीजिए।
हल-

प्रश्न 11.

का मान ज्ञात कीजिए।
हल-

प्रश्न 12.

का मान ज्ञात कीजिए।
हल-

प्रश्न 13.
यदि sin^-1 x = y, तो

हल-

प्रश्न 14.
tan^-1√3 – sec^-1(-2) का मान बराबर है

हल-

प्रश्नावली 2.2

निम्नलिखित को सिद्ध कीजिए–

प्रश्न 1.

हल-
माना sin^-1x = θ ∴ sin θ = x
पुनः sin 3θ = 3 sin³ θ – 4 sin० θ
⇒ sin 3θ = 3x – 4x³
⇒ 3θ = sin^-1(3x – 4x³)
∴ 3sin^-1x = sin^-1(3x – 4x³) इति सिद्धम्

प्रश्न 2.

हल-
माना cos^-1 x = θ ∴ cosθ = x
∴ cos 3θ = 4cos³θ – 3 cos θ
⇒ cos 3θ = 4x³ – 3x
⇒ 3θ = cos^-1(4x³ – 3x)
∴ 3cos^-1x = cos^-1(4x³ – 3x) इति सिद्धम्

प्रश्न 3.

हल-

प्रश्न 4.

हल-

निम्नलिखित फलनों को सरलतम रूप में लिखिए

प्रश्न 5.

हल-

प्रश्न 6.

हल-

प्रश्न 7.

हल-

प्रश्न 8.

हल-

प्रश्न 9.

हल-

प्रश्न 10.

हल-

प्रश्न 11.

हल-

प्रश्न 12.
cot (tan^-1 a + cot^-1 a)
हल-
माना y = cot (tan^-1 a + cot^-1 a)

प्रश्न 13.

हल-

प्रश्न 14.

हल-

प्रश्न 15.

हल-


प्रश्न 16.

हल-

प्रश्न 17.

हल-

प्रश्न 18.

हल-

प्रश्न 19.

हल-

प्रश्न 20.

हल-

प्रश्न 21.
tan^-1√3 – cot^-1(-√3) का मान है
(A) π
(B) [latex]-\frac { \pi }{ 2 } [/latex]
(C) 0
(D) 2√3
हल-

We hope the UP Board Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions (प्रतिलोम त्रिकोणमितीय फलन) help you. If you have any query regarding UP Board Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions (प्रतिलोम त्रिकोणमितीय फलन), drop a comment below and we will get back to you at the earliest.
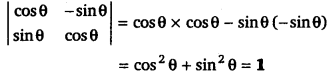
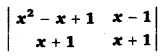
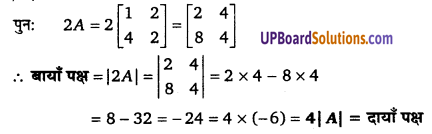
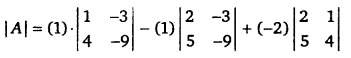
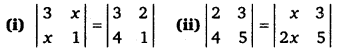
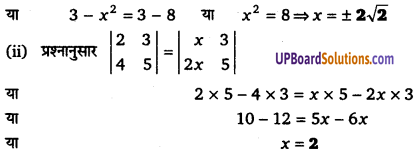
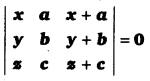
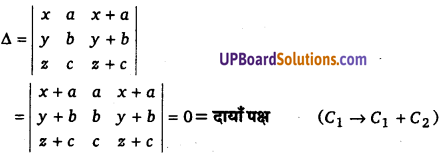
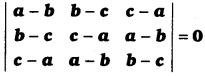
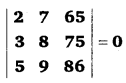
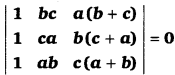
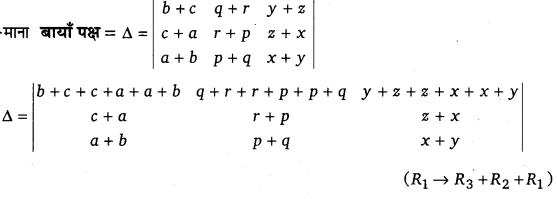
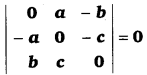
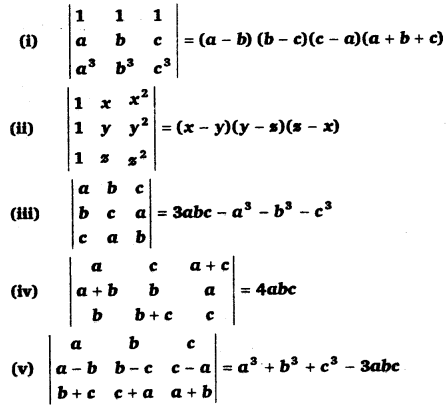
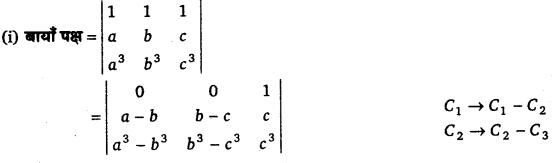
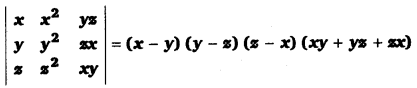
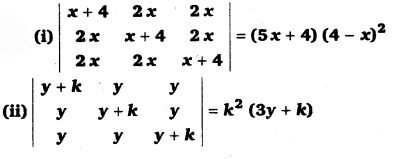
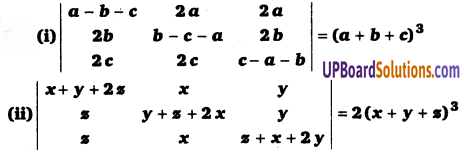
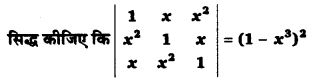
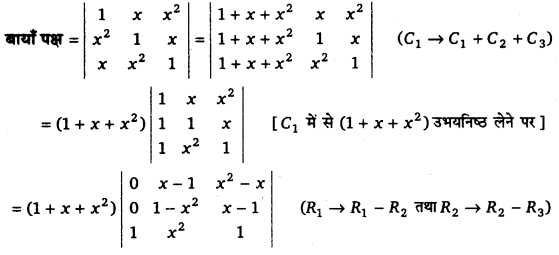
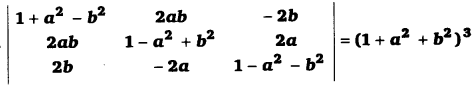
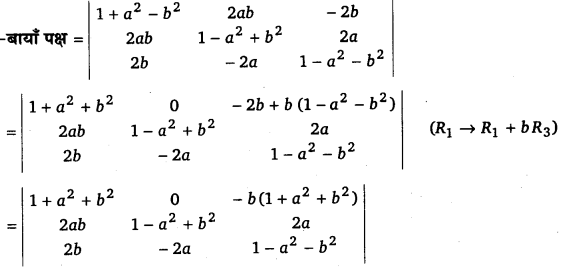
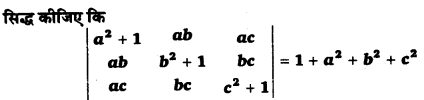
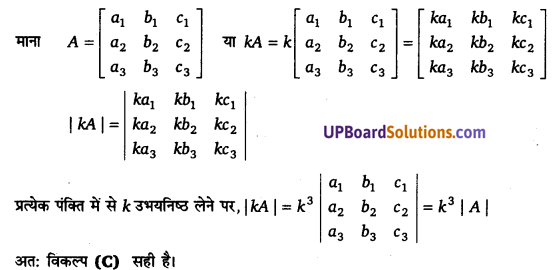
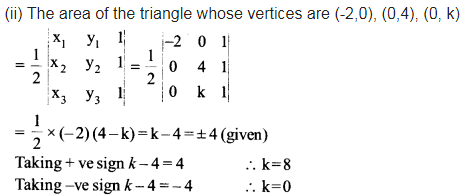
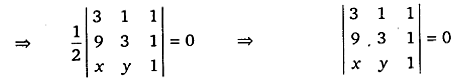
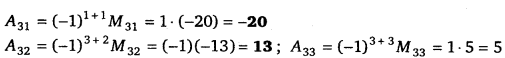
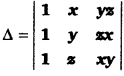
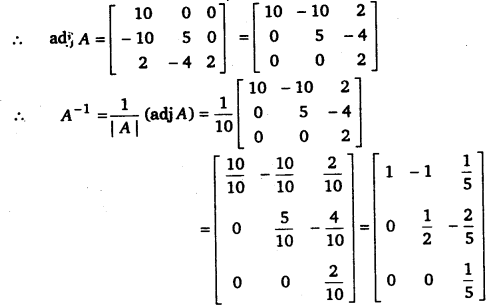
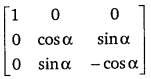
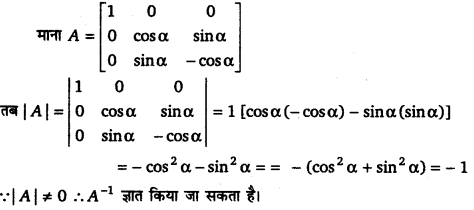
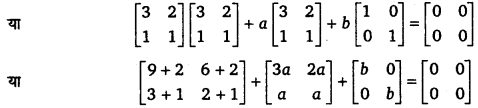