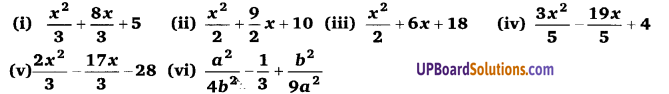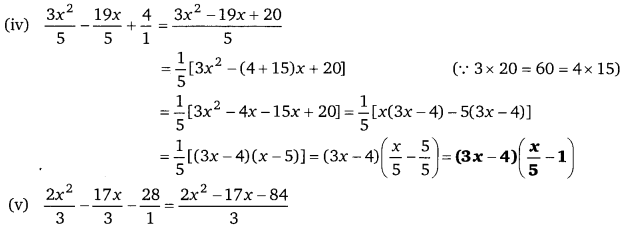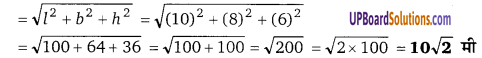Safia

Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.3 बहुपद तथा उनके गुणनखण्ड

Ex 5.3 Polynomial and their Factors अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Question

प्रश्न 1.
जब एक बहुपद x² + 4x + 5 कों (x + 3) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
बहुपद x² + 4x + 5 को (x + 3) से भाग करने पर शेषफल प्राप्त करने के लिए x + 3 = 0 या
x = 0 – 3 = -3 बहुपद में रखते है।
∴ शेषफल = (-3)² + 4(-3) + 5 = 9 – 12 + 5 = 2

प्रश्न 2.
जब एक बहुपद x² + 6x + 9 को (x + 3) से भाग दिया जाता है. तब शेषफल ज्ञात कीजिए।
हलः
बहुपद x² + 6x + 9 को (x + 3) से भाग करने पर
x + 3 = 0 या x = -3 रखने पर
∴ शेषफल = (-3)² + 6(-3) + 9 = 9 – 18 + 9 = 0

प्रश्न 3.
जब एक बहुपद x³ – 7x + 6 को (x – 1) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
बहुपद x³ – 7x + 6 को (x – 1) से भाग करने पर
x – 1 = 0 या x = 1
शेषफल = (1)³ – 7(1) + 6 = 1 – 7 + 6 = 0

प्रश्न 4.
जब बहुपद (x³ + 1) को (x + 1) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
(x³ + 1) को (x + 1) से भाग करने पर
x + 1 = 0 या x = 0 – 1 = -1 बहुपद में रखने पर शेषफल = (-1)³ + 1 = -1 + 1 = 0

प्रश्न 5.
जब बहुपद x³ + 3x + 3 को (x + 2) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
यदि बहुपद x² + 3x + 3 को (x + 2) से भाग किया जाए तो x + 2 = 0 या x = 0 – 2 = -2 रखने पर
शेषफल = (-2)² + 3(-2) + 3 = 4 – 6 + 3 = 1

प्रश्न 6.
जब बहुपद x⁶ + x⁴ – x² +1 को x – 2 से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
यदि बहुपद x⁶ + x⁴ – x² + 1 को (x – 2) से भाग किया जाए तो x – 2 = 0 या x = 2 रखने पर
शेषफल = (2)⁶ + (2)⁴ – (2)² + 1 = 64 + 16 – 4 + 1 = 77

प्रश्न 7.
यदि x¹⁵ – 199 को (x – 1) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
यदि x¹⁵ – 199, (x – 1) से विभाजित है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)¹⁵ – 199 = 1 – 199 = -198

प्रश्न 8.
बहुपद x³ – 3x² + 4x – 12 का एक गुणनखण्ड ज्ञात कीजिए।
हल:
x³ – 3x² + 4x – 2 में x = 1 रखने पर शेषफल 0 नहीं है।
x = 2 रखने पर शेषफल 0 नहीं है।
x = 3 रखने पर शेषफल = (3)³ – 3(3)² + 4(3) – 12 = 27 – 27 + 12 – 12 = 0
इसलिए (x -3) इसका एक गुणनखण्ड है।

प्रश्न 9.
यदि p(-3) = 0 तब बहुपद p(x) का गुणनखण्ड ज्ञात कीजिए।
हलः
यदि p(-3) = 0 तब p(x) का एक गुणनखण्ड (x + 3) होगा।

प्रश्न 10.
बहुपद 2x³ + 4x + 6 का एक गुणनखण्ड ज्ञात कीजिए।
हल:
2x³ + 4x + 6 का एक गुणनखण्ड (x + 1) होगा।
यदि x + 1 = 0 या x = 0 – 1 = -1 रखने पर
शेषफल = 2(-1)² + 4(-1) + 6 = -2 – 4 + 6 = 0

प्रश्न 11.
(x – 3) निम्न में से किस बहुपद का गुणनखण्ड होगा?
(a) 2x² – x – 15
(b) x² + 9
(c) 3x² + 5x + 7
(d) इनमें से कोई नहीं
हलः
(a) (x – 3), 2x² – x – 15 का एक गुणनखण्ड है। क्योंकि x – 3 = 0 या x = 3 रखने पर
शेषफल = 2(3)² – 3 – 15 = 18 – 3 – 15 = 0

प्रश्न 12.
(x + 1) निम्न में से किसका गुणनखण्ड नहीं है।
(a) x² – 4x – 3
(b) x² + 4x + 3
(c) x² – 1
(d) इनमें से कोई नहीं
हलः
(a) (x + 1), x² – 4x – 3 का एक गुणनखण्ड नहीं है।
∵ x+1 = 0 या X = 0-1 = -1 रखने पर
शेषफल = (-1)² – 4(-1) – 3 = 1 + 4 – 3 = 2 ≠ 0

प्रश्न 13.
यदि (2x + 1) बहुपद 4x² – kx + k का एक गुणनखण्ड है, तो k का मान ज्ञात कीजिए।
हलः
∵ (2x + 1), 4x² – kx + k का गुणनखण्ड है।
∴ 2x + 1 = 0 या 2x = -1 या x = [latex]-\frac{1}{2}[/latex] रखने पर
शेषफल = 0

प्रश्न 14.
यदि (x – 1) बहुपद x³ + kx² + 142x – 120 का एक गुणनखण्ड है, तो k का मान ज्ञात कीजिए।
हल:
∵ (x – 1) बहुपद x³ + kx² + 142x – 120 का एक गुणनखण्ड है।
∴ x – 1 = 0 या x = 1 रखने पर,
शेषफल = 0
(1)³ + k(1)² + 142 × 1 – 120 = 0
1 + k + 142 – 120 = 0
k + 23 = 0 ⇒ k = -23

प्रश्न 15.
यदि [latex]x+\frac{1}{2}[/latex] बहुपद px² – 4px +3 का एक गुणनखण्ड है, तो p का मान ज्ञात कीजिए।
हल:
यदि [latex]x+\frac{1}{2}[/latex], px² – 4px + 3 का एक गणुखण्ड है।
∴ [latex]x+\frac{1}{2}[/latex] = 0 या x = [latex]-\frac{1}{2}[/latex] -रखने पर शेषफल

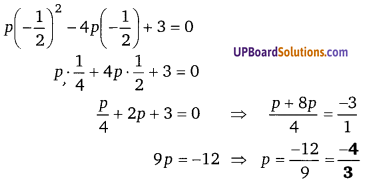
Ex 5.3 Polynomial and their Factors  लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 16.
निम्न प्रत्येक में, बहुपद f(x) को g(x) से भाग दीजिए तथा भागफल व शेषफल के मान ज्ञात कीजिए।
(i) f(x) = 5x² + 3x + 1; , g(x) = 2x
(ii) f(x) = x³ – 14x² + 37x – 60; g(x) = x – 2
(iii) f(x) = x³ – 3x² + 4x + 2; g(x) = x – 1
(iv) f(x) = x³ + 3x² – 12x + 4; g(x) = x – 2
(v) f(x) = 2x² – 3x + 5; g(x) = x – a
हलः
(i) f(x) = 5x² + 3x + 1 तथा g(x) = 2x

(ii) f(x) = x³ – 14x² + 37x – 60 तथा g(x) = x – 2

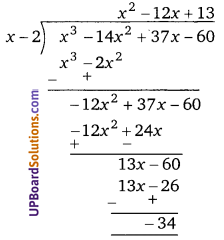
भागफल = x² – 12x + 13 तथा शेषफल = -34

(iii) f(x) = x³ – 3x² + 4x + 2 तथा g(x) = x – 1

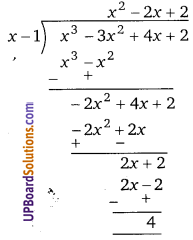
भागफल = x² – 2x + 2
शेषफल = 4

(iv) f(x) = x³ + 3x² – 12x + 4 तथा g(x) = x – 2

भागफल = x² + 5x – 2
शेषफल = 0

(v) f(x) = 2x² – 3x + 5 तथा g(x) = x – a

भागफल = 2x + 2a – 3 तथा शेषफल = 2a² – 3a + 5

Ex 5.3 Polynomial and their Factors  दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 17.
सिद्ध कीजिए कि x² – 4x + 3 बहुपद x³ – 3x² – x + 3 का एक गुणनखण्ड है।
हलः

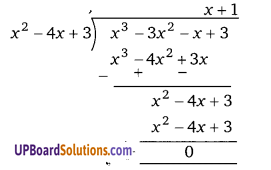
∵ x³ – 3x² – x + 3, x² – 4x + 3 से पूर्णतया विभाजित है।
∴ x² – 4x + 3 इसका एक गुणनखण्ड है।।

प्रश्न 18.
सिद्ध कीजिए कि x² – x + 2 बहुपद x³ – 3x² + 4x – 4 का एक गुणनखण्ड है।
हलः

∵ x³ – 3x² + 4x – 4, x² – x + 2 से पूर्णतया विभाजित है।
∴ x² – x + 2 इसका एक गुणनखण्ड है।

प्रश्न 19.
सिद्ध कीजिए कि x – 3 बहुपद x³ – 2x² + 3x – 18 का एक गुणनखण्ड है।
हलः

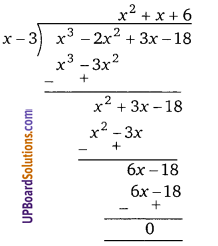
∵ x³ – 2x² + 3x – 18, x – 3 से पूर्णतया विभाजित है।
∴ x – 3 इसका एक गुणनखण्ड है।

प्रश्न 20.
निम्न प्रत्येक में f(x) को g(x) से भाग कीजिए तथा भागफल व शेषफल के मान ज्ञात कीजिए।
(i) f(x) = x + 5x³ + 3x² + 5x + 3; g(x) = x² + 4x + 2
(ii) f(x) = 6x⁵ + 4x⁴ – 3x³ + x + 1; g(x) = 3x² – x + 1
(iii) f(x) = x⁵ + x⁴ + x³ + x² + 2x + 2; g(x) = x + 1
हल:
(i) f(x) = x⁵ + 5x³ + 3x² + 5x + 3 तथा g(x) = x² + 4x + 2

भागफल = x³ – 4x² + 19x – 65
शेषफल = 227x + 133

(ii) f(x) = 6x⁵ + 4x⁴ – 3x³ + x + 1 तथा g(x) = 3x² – x + 1

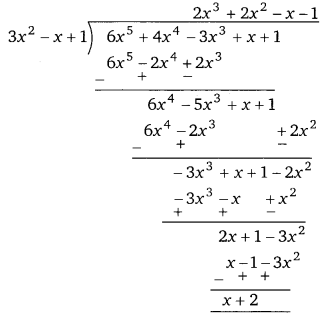
भागफल = 2x³ + 2x² – x – 1
शेषफल = x + 2

(iii) f(x) = x⁵ + x⁴ + x³ + x² + 2x + 2 तथा g(x) = x³ + 1

भागफल = x² + x + 1 तथा शेषफल = x + 1

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 18 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder Ex 18.2 घन, घनाभ तथा लम्बवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन

Ex 18.2 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
एक घन का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 96 सेमी है। (NCERT Exemplar)
हलः
घन का पृष्ठीय क्षेत्रफल = 96
6 × a² = 96
a² = [latex]\frac{96}{6}[/latex] = 16 (∴ a = 4 सेमी)
घन का आयतन = a³ = (4)³ = 64 सेमी³

प्रश्न 2.
एक कमरे के फर्श का क्षेत्रफल 15 मी² है। यदि ऊँचाई 4 मी है तब कमरे में जा सकने वाली हवा का आयतन ज्ञात कीजिए।
हलः
कमरे में जा सकने वाली हवा का आयतन = l × b × h
= 15 × 4 = 60 मी³
= 60,000 डेसी मी³

प्रश्न 3.
एक घनाभ का आयतन 12 सेमी है। एक घनाभ का आयतन (सेमी³ में) ज्ञात कीजिए जिसकी भुजा, इस घनाभ की दोगुनी है।
हलः
घनाभ का आयतन V₁ = 12 सेमी³
घनाभ की प्रत्येक विमा 2 गुनी होने पर बने घनाभ का आयतन V₂ = 2 × 2 × 2 × V₁
= 8V₁ = 8 × 12 = 96 सेमी³

प्रश्न 4.
यदि दो घनों के आयतन 8 : 1 के अनुपात में है तब इनके कोरों का अनुपात ज्ञात कीजिए।
हलः

प्रश्न 5.
एक घन का पार्श्व पृष्ठीय क्षेत्रफल 256 मी² है घन का आयतन ज्ञात कीजिए। (NCERT Exemplar)
हलः

प्रश्न 6.
एक घन का आयतन 512 सेमी है, कुल पृष्ठीय क्षेत्रफल (सेमी’ में) ज्ञात कीजिए।
हलः
घन का आयतन = 512
a = 512
a³ = (8)³
∴ a = 8 सेमी
कुल पृष्ठीय क्षेत्रफल = 6a² = 6 × (8) = 6 × 64 = 384 सेमी ²

प्रश्न 7.
10 सेमी भुजा वाले एक घनाकार बर्तन में पूर्णतया आने वाली छड़ी की लम्बाई ज्ञात कीजिए।
हलः
घनाकार बर्तन में पूर्णतया आने वाली छडी की लम्बाई
= घन का विकर्ण = 10[latex]\sqrt{3}[/latex] सेमी

प्रश्न 8.
दो घनों के आयतन 1 : 27 के अनुपात में है इनके पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हलः

प्रश्न 9.
1.5 मीटर गहरी तथा 30 मीटर चौड़ी एक नहर में 3 किमी/घण्टा की दर से पानी बह रहा है। समुद्र में प्रति मिनट आने वाले पानी का आयतन (मी में) ज्ञात कीजिए।
हलः
पानी का आयतन = l × b × h

प्रश्न 10.
एक झरने में 5 सेमी वर्षा होती है। 2 हेक्टेयर क्षेत्र में पड़ने वाले मानी का कुल आयतन (मी में ) ज्ञात कीजिए।
हलः

Ex 18.2 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 11.
6 सेमी भुजा के दो घनों को फलक-दर-फलक मिलाया जाता है। इस प्रकार बने घनाभ का आयतन ज्ञात कीजिए।
हलः
दो घनों को मिलाने पर बने घनाभ की लम्बाई l = 12 सेमी
b = 6 सेमी
h = 6 सेमी
घनाभ का आयतन = l × b × h = 12 × 6 × 6 = 432 सेमी

प्रश्न 12.
एक घन का कुल पृष्ठीय क्षेत्रफल 294 सेमी है। इसका आयतन ज्ञात कीजिए।
हलः
घन का कुल पृष्ठीय क्षेत्रफल = 294

प्रश्न 13.
एक सिनेमा हॉल की विमाएं 100 मी × 50 मी × 18 मी है। यदि एक व्यक्ति को 150 मी हवा की आवश्यकता है तो सिनेमा हॉल में कुल कितने व्यक्ति बैठ सकते हैं।
हल:

प्रश्न 14.
एक गोदाम की विमाएँ 30 मी × 25 मी × 8 मी है। 2 मी × 1.25 मी × 0.4 मी विमा वाली कितनी लकड़ी की पेटी इसमें रखी जा सकती है ?
हल:

प्रश्न 15.
एक आयताकार ठोस घनाभ जिसका आयतन v है के तीन लगातार फलकों के क्षेत्रफल A,B व C हैं। सिद्ध कीजिए कि V² = ABC
हल:

प्रश्न 16.
25 मी × 9.8 मी के आकार के एक कमरे में 100 व्यक्ति सो सकते हैं। यदि एक व्यक्ति को 12.25 मी³ हवा की आवश्यकता होती है तो कमरे की लम्बाई ज्ञात कीजिए।
हलः
100 व्यक्तियों को सोने के लिए आवश्यक हवा = 100 × 12.25 = 1225 मी³

प्रश्न 17.
एक घन का आयतन 1000 सेमी है। इसका कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः
घन का आयतन = 1000 सेमी³
a³ = 1000 = (10)³
a = 10 सेमी कुल पृष्ठीय क्षेत्रफल = 6 × a² = 6 × (10)²
= 6 × 100 = 600 सेमी²

प्रश्न 18.
18 मी × 12 मी × 9 मी के आकार के घनाभ से 3 मी भुजा वाले कितने घन काटे जा सकते हैं?
हलः

Ex 18.2 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 19.
आयताकार रूप के खेती के एक प्लाट की विमाएँ 240 मी × 180 मी है। इसके चारों ओर 10 मीटर चौड़ा एक गड्ढा खोदा गया है। तथा इसमें से निकली मिट्टी को समान रूप से प्लाट में फैलाया जाता है। जिससे उसकी सतह का स्तर 25 सेमी बढ़ जाता है। गड्ढ़े की गहराई ज्ञात कीजिए।
हल:
मिट्टी के पड़ने से प्लाट की मिट्टी का आयतन = 240 × 180 × 0.25 मी³

प्रश्न 20.
एक आयताकार टैंक की आधार पर विमायें 225 मी × 162 मी है। 60 सेमी × 45 सेमी की विमा के एक पाईप से टैंक के अन्दर किस दर से पानी डाला जाये जिससे 5 घण्टे में इसमें पानी का स्तर 20 सेमी बढ़ जाये।
हलः
माना आयताकार टैंक में पानी की ऊँचाई = 20 सेमी = 0.2 मीटर
माना आयताकार टैंक में पानी का आयतन = 225 × 162 × 0.2 मी³

प्रश्न 21.
8 मीटर लम्बा, 6 मीटर चौड़ा तथा 3 मीटर गहरा, एक घनाभकार गड्ढ़ा खुदवाने में ₹30 प्रति मी की दर से होने वाला व्यय ज्ञात कीजिए।
(NCERT)
हलः
घनाभकार गड्ढे का आयतन = l × b × h
= 8 × 6 × 3 = 144 मी
घनाभकार गड्ढा खुदवाने में कुल खर्च =144 × 30 = ₹ 4320

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.6 बहुपद तथा उनके गुणनखण्ड

Ex 5.6 Polynomial and their Factors अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Question)

निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए।
प्रश्न 1.
x² + 7x + 12
हल:
x² + 7x + 12 = x² + (3 + 4)x + 12 12 = 3 × 4
= x² + 3x + 4x + 12 = x(x + 3) + 4(x + 3) = (x + 3)(x + 4)

प्रश्न 2.
x² – 14x + 48
हल:
x² – 14x + 48 = x² – (6 + 8)x + 48 (48 = 6 × 8)
= x² – 6x – 8x + 48 = x(x – 6) – 8(x – 6) = (x – 6)(x – 8)

प्रश्न 3.
x² – 7x – 18
हल:
x² – 7x – 18 = x² – (9 – 2)x – 18 = x² – 9x + 2x – 18 = x(x – 9) + 2(x – 9) = (x – 9)(x + 2)

प्रश्न 4.
x² – 25x + 84
हल:
x² – 25x + 84 = x² – (21 + 4)x + 84 (84 = 4 × 21)
= x² – 21x – 4x + 84= x(x -21)- 4(x – 21)= (x – 21)(x – 4)

प्रश्न 5.
2x² + 7x + 6
हल:
2x² + 7x + 6 = 2x² + (3 + 4)x + 6                         (2 × 6 = 12 ⇒ 12 = 3 × 4)
= 2x² + 3x + 4x + 6 = x(2x + 3) + 2(2x + 3) = (2x + 3)(x + 2)

प्रश्न 6.
2x² – 13x + 15
हलः
2x² – 13x + 15 = 2x² – (3 + 10)x + 15 (2 × 15 = 30 ⇒ 30 = 3 × 10)
= 2x² – 3x – 10x + 15 = x(2x – 3) – 5(2x – 3) = (2x – 3)(x – 5)

प्रश्न 7.
3x² – 14x + 8
हल:
3x² – 14x + 8 = 3x² – (2 + 12)x + 8 (3 × 8 = 24 ⇒ 24 = 12 × 2)
= 3x² – 2x – 12x + 8= x(3x – 2) – 4(3x – 2) = (3x – 2)(x – 4 )

प्रश्न 8.
3x² + 10x – 8
हलः
3x² + 10x – 8= 3x² + (12 – 2)x – 8 (3 × 8 = 24 ⇒ 24 = 2× 12)
= 3x² + 12x – 2x – 8 = 3x(x + 4) – 2(x + 4)= (x + 4)(3x – 2)

Ex 5.6 Polynomial and their Factors लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 9.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 8(x + 2)² + 2(x + 2) – 15
(ii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) – 15(2x – 1)²
(iii) (x² – 2x)² – 23(x² – 2x) + 120
(iv) (x + 2y)² + 5(x + 2y)(2x + y) + 6(2x + y)²
हलः
(i) 8(x + 2)² + 2(x + 2) – 15
माना x + 2 = y
= 8y² + 2y – 15
= 8y² +(12 – 10)y – 15 (8 × 15 = 120 ⇒ 120 = 12 × 10)
= 8y² + 12y – 10y – 15 = 4y(2y + 3) – 5(2y + 3)
= (2y + 3)(4y – 5)=[2(x + 2) + 3] [4(x + 2) – 5]
= [2x + 4 + 3][4x + 8 – 5) = (2x + 7) (4x + 3)

(ii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) – 15(2x – 1)²
हलः
x² + 7x = y तथा 2x – 1 = z
= 12y² – 8yz – 15z²
= 12y² – (18 – 10)yz – 15z² (12 × 15 = 180 ⇒ 180 = 2 × 2 × 3 × 3 × 5)
= 12y² – 18ýz + 10yz – 15z²
= 6y (2y – 3z) + 5z(2y – 3z) = (2y – 3z)(6y + 5z)
= [2(x² + 7x) – 3(2x – 1)][6(x² + 7x) + 5(2x – 1)]
= [2x² + 14x – 6x + 3] [6x² + 42x + 10x – 5]
= [2x² + 8x + 3][6x² + 52x – 5]

(iii) (x² – 2x)² – 23(x² – 2x) + 120
हलः
x² – 2x = y
=y² – 23y + 120
= y² – (8 + 15)y + 120 (120 = 8 × 15)
= y² – 8y – 15y + 120 = y(y – 8) – 15(y – 8)
= (y – 15)(y – 8)
= (x² – 2x – 15)(x² – 2x – 8) (15 = 3 × 5 व 8 = 4 × 2)
= [x² – (5 – 3)x – 15][x² – (4 – 2)x – 8]
= [x² – 5x + 3x – 15][x² – 4x + 2x – 8]
=[x(x – 5) + 3(x – 5)][x(x – 4) + 2(x – 4)]
= [(x + 3)(x – 5)][(x – 4)(x + 2)]

(iv) (x + 2y)² + 5(x + 2y)(2x + y) + 6(2x + y)²
हलः
माना x + 2y = m तथा 2x + y = n
= m² + 5mn + 6n² = m² +(2 + 3)mn +6n²
= m² + 2mn + 3mn + 6n² = m(m + 2n) + 3n(m + 2n)
= (m + 2n)(m + 3n)
यहाँ [x + 2y + 2(2x + y)][x + 2y + 3(2x + y)]
=[x + 2y + 4x + 2y][x + 2y + 6x + 3y] = [5x + 4y][7x + 5y]

प्रश्न 10.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) [latex]\frac{1}{3} x^{2}[/latex] – 2x – 9
(ii) [latex]\frac{1}{4} x^{2}[/latex] + x – 3
(iii) 8x³ – 2x²y – 15xy²
(iv) 9x³y +41x²y² + 20xy³
हलः


(iii) 8x³ – 2x²y – 15xy² = x[8x² – 2xy -15y²]
= x[8x² – (12 – 10)xy -15y²] (∵ 8 × 15 = 120 ⇒ 120 = 12× 10)
= x[8x² – 12xy + 10xy – 15y²]
= x[4x(2x – 3y) + 5y(2x – 3y)] = x(2x – 3y)(4x + 5y)

(iv) 9x³y + 41x²y² + 20xy³ = xy[9x² + 41xy + 20y²]
= xy[9x² + (36 + 5)xy + 20y²] (9 × 20 = 180 ⇒ 180 = 2 × 2 × 3 × 3 × 5)
= xy[9x² + 36xy + 5xy + 20y²]
= xy[9x(x + 4y) + 5y (x + 4y)] = xy(9x + 5y)(x + 4y)

प्रश्न 11.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x² +4x – 21
(ii) x² – 7x + 12
(iii) x² – 21x + 108
(iv) x² + 5x – 36
हल:
(i) x² + 4x – 21 = x² + (7 – 3)x – 21 (21 = 3 × 7)
= x² + 7x – 3x – 21 = x(x + 7) – 3(x + 7) = (x + 7)(x – 3)

(ii) x² – 7x + 12 = x² – (3 + 4)x + 12 (12 = 2 × 2 × 3)
= x² – 3x – 4x + 12 = x(x – 3) – 4(x – 3) = (x – 3)(x – 4)

(iii) x² – 21x + 108 = x² – (12 + 9)x + 108 (108 = 2 × 2 × 3 × 3 × 3 = 12 × 9)
= x² – 12x – 9x + 108 = x(x – 12)- 9(x – 12) = (x – 12)(x – 9)

(iv) x² + 5x – 36 = x² + (9 – 4)x – 36 (36 = 2 × 2 × 3 × 3)
= x² + 9x – 4x – 36 = x(x + 9)- 4(x + 9) = (x + 9)(x – 4)

प्रश्न 12.
निम्न व्यंजकों के गुणनखण्ड इनके मध्य पद को विभक्त करके कीजिए
(i) x⁴ + 3x² – 28
(ii) x⁴ – 5x² + 4
हल:
(i) x⁴ + 3x² – 28 = x⁴ + (7 – 4)x² – 28 (∵ 28 = 2 × 2 × 7)
= x⁴ + 7x² – 4x² – 28 = x²(x² + 7) – 4(x² + 7)
= (x² + 7)(x² – 4) = (x² + 7)[(x)⁴ – (2)⁴] = (x² + 7)(x + 2)(x – 2)

(ii) x⁴ – 5x² + 4 = x⁴ – (1 + 4)x² + 4 (∵ 4 = 1 × 4)
= x⁴ – x² – 4x² + 4 = x²(x² – 1) – 4(x² – 1) = (x² – 1)(x² – 4)
= [(x)² – (1)²][(x²) – (2)²] = (x + 1)(x – 1)(x + 2)(x – 2)

प्रश्न 13.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x² + [latex]4 \sqrt{2} x[/latex] + 6
(ii) x² + [latex]5 \sqrt{3} x[/latex] + 12
(iii) x² + [latex]5 \sqrt{5} x[/latex] + 30
(iv) x² + [latex]6 \sqrt{6} x[/latex] + 48
हलः

प्रश्न 14.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) [latex]\left(5 x-\frac{1}{x}\right)^{2}+5\left(5 x-\frac{1}{x}\right)+6[/latex]
(ii) (p + q)² – 20(p + q) – 125
(iii) (a² – a)² – 8(a² – a) + 12
(iv) (x² – 4x)(x² – 4x – 1) – 20
(v) (x² + x)² + 4(x² + x) – 12
(vi) (3x – 4)² – (3x – 4) – 42
हलः

(ii) (p + q)² – 20(p + q) – 125
माना P + q = x
= x² – 20x – 125 = x² – (25 – 5)x – 125
= x² – 25x + 5x – 125 = x(x – 25) + 5(x – 25)
= (x + 5)(x – 25)
∴ (p + q – 25)(p + q + 5)

(iii) (a² – a)² – 8(a² – a) + 12
माना a² – a = x
→ = x² – 8x + 12
= x² – (2 + 6)x + 12 = x² – 2x – 6x +12
= x(x – 2) – 6(x – 2) = (x – 2)(x – 6)
∴ (a² – a – 2)(a² – a – 6)
=[a² – (2 – 1)a – 2][a² – (3 – 2)a – 6]
=[a – 2a + a – 2][a² – 3a + 2a – 6]
= [a(a – 2) + 1(a – 2)][a(a – 3) + 2(a – 3)]
= (a – 2)(a + 1)(a – 3)(a + 2)

(iv) (x² – 4x)(x² – 4x -1) – 20
माना x² – 4x = y
⇒ = y (y – 1) – 20 = y² – y – 20
= y² – (5 – 4)y – 20
= y² – 5y + 4y – 20
= y(y – 5) + 4(y – 5) = (y – 5)(y + 4)
∴ (x² – 4x – 5)(x² – 4x + 4)
= [x² – (5 – 1)x – 5][x² – (2 + 2)x + 4]
= [x² – 5x + x – 5][x² – 2x – 2x + 4]
= [x(x – 5) + 16x – 5)][x(x – 2) – 2(x -2)]
= (x – 5) (x + 1) (x – 2) (x – 2) = (x – 5)(x + 1)(x – 2)²

(v) (x² + x)² + 46x² + x) – 12
माना x² + x = y
= y² + 4y – 12
= y² + (6 – 2)y – 12 = y² + 6y – 2y -12
= y(y + 6) – 2(y + 6) = (y + 6)(y – 2)
∴ (x² + x + 6) (x² + x – 2)
= (x² + x + 6)[x² + (2 – 1)x – 2] = (x² + x + 6)[x² + 2x – x – 2] = (x² + x + 6)[x(x + 2) – 1(x + 2)]
= (x² + x + 6)(x – 1)(x + 2)

(vi) (3x – 4)² – (3x – 4) – 42
माना 3x – 4 = y
→ = y² – y – 42 (∵ 42 = 2 × 3 × 7 = 6 × 7)
= y² – (7 – 6)y – 42 = y² – 7y + 6y – 42
= y(y – 7) + 6(y – 7) = (y – 7)(y + 6)
∴ (3x – 4 – 7)(3x – 4 + 6)
= (3x – 11)(3x + 2)

Ex 5.6 Polynomial and their Factors लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 15.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x⁴ – x² – 12
(ii) m⁸ – 11m⁴n⁴ – 80n⁸
हल:
(i) x⁴ – x² – 12
= x⁴ – (4 – 3)x² – 12
= x² – 4x² + 3x² – 12 = x²(x² – 4) + 3(x² – 4)
= (x² – 4)(x² + 3) = (x)² – (2)²(x² + 3)
= (x + 2)(x – 2)(x² + 3)

(ii) m⁸ – 11m⁴n⁴ – 80n⁸ (∵ 80 = 2 × 2 × 2 × 2 × 5)
= m⁸ – (16 – 5)m⁴n⁴ – 80n⁸
= m⁸ – 16m⁴n⁴ + 5m⁴n⁸ – 80n⁸ = m⁴ (m⁴ – 16n⁴) + 5n⁴(m⁴ – 16n⁴)
= (m⁴ + 5n⁴)(m⁴ – 16n⁴) = (m⁴ + 5n⁴)(m² + 4n²)(m² – 4n²)
= (m⁴ + 5n⁴)(m² + 4n)(m + 2n)(m – 2n)

प्रश्न 16.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 2x² + 13x + 20
(ii) 6x² + 11x + 3
(iii) 9x² + 27x + 20
(iv) 2x² – 11x – 63
(v) 10x² – 9x – 7
(vi) 21x² + 5x – 6
हल:
(i) 2x² + 13x + 20 (∵ 2 × 20 = 2 × 2 × 2 × 5)
= 2x² + (5 + 8)x + 20 = 2x² + 5x + 8x + 20
= x(2x + 5) + 4(2x + 5) = (2x + 5)(x + 4)

(ii) 6x² + 11x +3 (∵ 6x 3 = 18 = 2 × 3 × 3)
= 6x² + (2 + 9)x + 3 = 6x² + 2x + 9x + 3
= 2x(3x + 1) + 3(3x + 1) = (3x + 1)(2x +3)

(iii) 9x² + 27x + 20 = 9x² + (12 + 15)x + 20 (∵ 9 × 20 = 3 × 3 × 2 × 2 × 5)
= 9x² + 12x + 15x + 20 = 3x(3x + 4) + 5(3x + 4)= (3x + 4)(3x + 5)

(iv) 2x² – 11x – 63 = 2x² – (18 – 7)x – 63 (∵ 2 × 63 = 2 × 3 × 3 × 7)
= 2x² – 18x + 7x – 63 = 2x(x – 9) + 7(x – 9) = (x – 9)(2x + 7)

(v) 10x² – 9x – 7 = 10x² – (14 – 5)x – 7 (∵ 10 × 7 = 2 × 5 × 7)
= 10x² – 14x + 5x -7 = 2x(5x – 7) + 1(5x – 7) = (5x – 7)(2x + 1)

(vi) 21x² + 5x – 6 = 21x² + (14 – 9)x – 6 (∵ 21 × 6 = 3 × 7 × 2 × 3)
= 21x² + 14x – 9x – 6 = 7x (3x + 2) – 3(3x + 2) = (3x + 2)(7x – 3)

प्रश्न 17.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) [latex]\frac{1}{2} x^{2}[/latex] + 4x + 6
(ii) 2x² – x + [latex]\frac{1}{8}[/latex]
हलः

प्रश्न 18.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 7(x + 2y)² – 25(x + 2y) + 12
(ii) 8(a + 1)² +2(a + 1)(b + 2) – 15(b + 2)²
(iii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) + (2x – 1)²
(iv) 2(y² + 2y)² – 5(y² + 2y) + 3
(v) 6(x² + 4x)² – 11(x² + 4x)- 10
हलः
(i) 7(x + 2y)² – 25(x + 2y) + 12
माना x + 2y = z
= 7z²– 25z + 12
= 7z² – (21 + 4)z + 12 (∵ 7 × 12 = 7 × 2 × 2 × 3)
=7z² – 21z – 4z + 12 = 7z(z – 3) – 4(z – 3)
= (z – 3)(7z – 4) =(x + 2y – 3)[7(x + 2y) – 4]
(x + 2y – 3)(7x + 14y – 4)

(ii) 8(a + 1)² + 2(a + 1)(b + 2) – 15(b + 2)²
माना (a + 1) = x तथा (b + 2) = y
= 8x² + 20y – 15y²
= 8x² +(12 – 10)xy – 15y² (∵ 15 × 8 = 120 = 2 × 2 × 2 × 3 × 5)
= 8x² + 12xy – 10xy – 15y²
= 4x(2x + 3y) – 5y (2x + 3y) = (2x + 3y)(4x – 5y)
⇒ [2(a + 1) + 3(b + 2)][4(a + 1) – 5(b + 2)]
= [2a + 2+ 3b + 6][4a + 4 – 5b – 10]
= [2a + 3b + 8][4a – 5b – 6]

(iii) 12(x² + 7x)² – 8(x² + 7x)(2x – 1) + (2x – 1)²
माना x² + 7 x = m तथा 2x – 1 = n
12m² – 8mn +n²
= 12m² – (6 + 2)mn + n² (∵ 12 × 1 = 12 = 2 × 2 × 3)
= 12m² – 6mn – 2mn + n²
= 6m(2m – n) – n(2m – n)= (6m – n)(2m – n)
= [6(x² + 7x) – 2x + 1][2(x² + 7x) – 2x + 1]
= (6x² + 42x – 2x + 1)(2x² + 14x – 2x + 1)
= (6x² + 40x + 1)(2x² + 12x + 1)

(iv) 2(y² + 2y)² – 5(y² + 2y) + 3
माना y² + 2y = m
= 2m² – 5m + 3 = 2m² – (2 + 3)m + 3 (∵ 2 × 3 = 6)
= 2m² – 2m – 3m + 3 = 2m(m – 1) – 3(m – 1)
= [(2m – 3)(m – 1)] = [2(y² + 2y) – 3][y² + 2y – 1]
=[2y² + 4y – 3][y² + 2y – 1]

(v) 6(x² + 4x)² – 11(x² + 4x) – 10
माना x² + 4x = m
= 6m² – 11m – 10
= 6m² -(15 – 4)m – 10 (∵ 10 × 6 = 60 = 2 × 2 × 3 × 5)
= 6m² – 15m + 4m – 10 = 3m(2m – 5) + 2(2m – 5)
= (2m – 5)(3m + 2) = [2(x² + 4x) – 5][3(x² + 4x) + 2]
= [2x² + 8x – 5][3x² + 12x + 2]

प्रश्न 19.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए

हलः

प्रश्न 20.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए

हलः

प्रश्न 21.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए

हलः

प्रश्न 22.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 9a³b + 41a²b² + 20ab³
(ii) ax² + (4a² – 3b)x – 12ab
(iii) 25x² + 10xy – 8y²
(iv) 4x² + 20xy + 25y²
हलः
(i) 9a²b + 41a²b² + 20ab³ = ab[9a² + 41ab + 20b²] (∵ 9 × 20 = 180 = 2 × 2 × 3 × 3 × 5)
= ab[9a² + (36 + 5)ab + 20b²] = ab[9a² + 36ab + 5ab + 20b²]
= ab[9a(a + 4b) + 5b(a + 4b)] = ab(9a + 5b)(a + 4b)]

(ii) ax² + (4a² – 3b)x – 12ab = ax² + 4a²x – 3bx – 12ab = ax(x + 4a) – 3b(x + 4a)
= (x + 4a)(ax – 3b)

(iii) 25x² + 10xy – 8y² = 25x² + (20 – 10)xy – 8y² (∵ 25 × 8 = 200 = 2 × 2 × 2 × 5 × 5)
= 25x² + 20xy – 10xy – 8y² = 5x(5x + 4y) – 2y(5x + 4y)
= (5x + 4y)(5x – 2y)

(iv) 4x² + 20xy + 25y² = 4x² + (10 + 10)xy + 25y² (∵ 4 × 25 = 100 = 10 × 10)
= 4x² + 10xy + 10xy + 25y² = 2x(2x + 5y) + 5y (2x + 5y)
= (2x + 5y)(2x + 5y)

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.2 बहुपद तथा उनके गुणनखण्ड

Ex 5.2 Polynomial and their Factors अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
बहुपद x⁶ + 5x² + 7 की घात ज्ञात कीजिए।
हलः
बहुपद x⁶ + 5x² + 7 की घात 6 है क्योंकि बहुपद की सबसे बड़ी घात 6 है।

प्रश्न 2.
बहुपद 3x + 7 की घात क्या है?
हलः
बहुपद 3x + 7 की घात 1 है क्योंकि बहुपद की सबसे बड़ी घात 1 है।

प्रश्न 3.
2 घात का बहुपद बताइए?
हल:
x² + 2x + 1 की घात 2 है।

प्रश्न 4.
बहुपद x²(3x⁴ + 7x – 5) की घात ज्ञात कीजिए।
हल:
x²(3x⁴ + 7x – 5) = 3x⁶ + 7x³ – 5x² की घात 6 है।

प्रश्न 5.
यदि f(x) की घात = 36 तथा g(x) की घात = 20 तब f(x)+g(x) की घात ज्ञात कीजिए।
हलः
बहुपद f(x) की घात = 36
बहुपद g(x) की घात = 20
f(x) + g(x) की घात 36 होगी क्योंकि यह घात दोनों में बड़ी घात है।

प्रश्न 6.
यदि f(x) की घात = m तथा g(x) की घात = n, m < n, तब f (x) + g(x) की घात ज्ञात कीजिए।
हल:
यदि बहुपद f(x) की घात m तथा बहुपद g(x) की घात n है। यदि m < n तब f(x) + g(x) की घात n होगी क्योंकि n, m से बड़ी घात है।

प्रश्न 7.
यदि f (x) की घात = m तथा g(x) की घात = n, m > n, तब f(x) + g(x) की घात ज्ञात कीजिए।
हलः
यदि बहुपद f(x) की घात m तथा बहुपद g(x) की घात n है तथा m > n, तब f(x) + g(x) की घात m होगी क्योंकि m, n से बड़ी घात है।

प्रश्न 8.
यदि f(x) = x⁷ – x + 2x² + 1 व g(x) = -x⁷ + x – 2 तब f(x) + g(x) की घात ज्ञात कीजिए।
हल:
f(x) = x⁷ – x⁵ + 2x² + 1, g(x) = -x⁷ + x – 2
∴ f(x) + g(x) = –x⁵ + 2x² + x – 1
इसमें सबसे बड़ी घात 5 है।
∴ f(x) + g(x) की घात 5 होगी।

प्रश्न 9.
दिये गये प्रश्न 8 में f(x) – g(x) की घात क्या है? हलः प्रश्न 8 से F(x) – g(x) = 2x⁷ – x⁵ + 2x² – x + 3
इसमें सबसे बड़ी घात 7 है।
∴ f(x) – g(x) की घात 7 होगी।

Ex 5.2 Polynomial and their Factors  लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 10.
निम्न में से प्रत्येक बहुपद की घात ज्ञात कीजिए
(i) 0 (NCERT Exemplar)
(ii) 7
(iii) x
(iv) x + 7
(v) x² + 2x +7
(vi) 4x³ + [latex]\sqrt{5} x^{2}[/latex] – 2x + [latex]\frac{5}{7}[/latex]
(vii) (x + 5)(4x + 7)
(viii) 6x(x² + 7)
हलः
(i) 0 एक शून्य बहुपद है, इसकी कोई घात नहीं होती।
(ii) 7 एक अचर बहुपद है, इसकी घात शून्य है।
(iii) x में सबसे बड़ी घात 1 है। इसलिए इसकी घात एक है।
(iv) x + 7 में सबसे बड़ी घात 1 है। इसलिए इसकी घात एक है।
(v) x² + 2x + 7 में x की सबसे बड़ी घात 2 है। इसलिए इसकी घात दो है।
(vi) 4x³ + [latex]\sqrt{5} x^{2}[/latex] – 2x + [latex]\frac{5}{7}[/latex] में x की सबसे बड़ी घात 3 है। इसलिए इसकी घात तीन है।
(vii) (x + 5)(4x + 7) = 4x² + 27x + 35 में x की सबसे बड़ी घात 2 है। इसलिए इसकी घात दो है।
(viii) 6x(x² +7) = 6x² + 42x में x की सबसे बड़ी घात 3 है। इसलिए इसकी घात तीन है।

प्रश्न 11.
यदि f (x) = 2x² +3x +1 व g(x) = 0 तब f(x).g(x) ज्ञात कीजिए।
हलः
f(x) = 2x² + 3x +1, g(x) = 0
f(x) . g(x) = (2x² + 3x + 1) . 0 = 0

प्रश्न 12.
x² – 4 को x³ – 4 बनाने के लिए क्या जोडें?
हलः
माना x² – 4 में A जोड़ा जाए जिससे योगफल x³ – 4 हो जाए।
∴ x² – 4 + A = x³ – 4
∴ A = x³ – 4 – x² + 4
A = x² – 2

प्रश्न 13.
बहुपद x⁴ + 3x³ + 4x² – 3x – 6 से 3x³ + 4x² – x + 3 प्राप्त करने के लिए क्या घटायें।
हलः
माना x⁴ + 3x³ + 4x² – 3x – 6 में से A घटाया जाए, जिससे शेषफल 3x³ + 4x² – x + 3 प्राप्त हो जाए।
x⁴ + 3x³ + 4x² – 3x – 6 – A = 3x³ + 4x² – x +3
-A = 3x³ + 4x² – x + 3 – x⁴ – 3x³ – 4x² + 3x + 6
-A = -x⁴ + 2x + 9
∴ A = x⁴ – 2x – 9
∴ x⁴ – 2x – 9 घटाया जाएगा।

Ex 5.2 Polynomial and their Factors  लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 14.
बहुपद x⁴ – x² + x + 2 से x² + x + 4 प्राप्त करने के लिये क्या जोडें?
हलः
माना x⁴ – x² + x + 2 में A जोड़ा जाए जिससे x² + x + 4 प्राप्त हो जाए।
x⁴ – x² + x + 2 + A = x² + x +4
∴ A = x² + x + 4 – x⁴ + x² – x – 2 = -x⁴ + 2x² + 2

प्रश्न 15.
7x³ + x² – 3x + 4 प्राप्त करने के लिये बहुपद 8x³ – 3x² + 5x – 9 में क्या जोडें?
हलः
माना 8x³ – 3x² + 5x – 9 में A जोड़ा जाए जिससे 7x³ + x² – 3x + 4 प्राप्त हो जाए।
8x³ – 3x² + 5x – 9 + A.= 7x³ + x² – 3x +4
∴ A = 7x³ + x² – 3x + 4 – 8x³ + 3x² – 5x + 9
= -x³ + 4x² – 8x + 13

प्रश्न 16.
x³ – 7x² + 5 प्राप्त करने के लिये बहुपद x⁴ – x² + 2x + 3 में क्या जोडें?
हलः
माना x⁴ – x² + 2x + 3 में A जोड़ा जाए जिससे x³ – 7x² + 5 प्राप्त हो जाए।
x⁴ – x² + 2x + 3 + A = x – 7x² + 5
∴ A = x³ – 7x² + 5 – x⁴ + x² – 2x – 3
= -x⁴ + x³ – 6x² – 2x + 2

प्रश्न 17.
-x² + 3x³ – 2x + 4 प्राप्त करने के लिये बहुपद x² – 3x³ + 2x – 4 में से क्या घटायें?
हलः
माना x² – 3x³ + 2x – 4 में से A घटाया जाए जिससे –x² + 3x³ – 2x + 4 प्राप्त हो।
x² – 3x³ + 2x – 4 – A = -x² + 3x³ – 2x + 4
∴ x² – 3x³ + 2x – 4 + x² – 3x³ + 2x – 4 = A
-6x³ + 2x² + 4x – 8 = A

प्रश्न 18.
संख्या 2 प्राप्त करने के लिये बहपदं x³ – 3x² + 2x – 1 से क्या घटायें?
हलः
माना x³ – 3x² + 2x – 1 में से A घटाया जाए जिससे शेषफल 2 प्राप्त हो।
x³ – 3x² + 2x – 1 – A = 2
x³ – 3x² + 2x – 1 – 2 = A
x³ – 3x² + 2x – 3 = A

प्रश्न 19.
संख्या 1 प्राप्त करने के लिये बहुपद x³ – 2x² + 4x + 1 से क्या घटायें?
हलः
माना x³ – 2x² + 4x + 1 में से A घटाया जाए जिससे शेषफल 1 प्राप्त हो।
x³ – 2x² + 4x + 1 – A = 1
x³ – 2x² + 4x + 1 – 1 = A
x³ – 2x² + 4x = A

प्रश्न 20.
बहुपद x⁴ – 3x³ + 2x + 6 व x⁴ – 3x² + 6x + 2 के योग मे से x³ – 3x + 4 घटाइये।
हलः
योगफल = x⁴ – 3x³ + 2x + 6 + x⁴ – 3x² + 6x + 2 = 2x⁴ – 3x³ – 3x² + 8x + 8
अन्तर = 2x⁴ – 3x³ – 3x² + 8x + 8 – (x³ – 3x + 4)
= 2x⁴ – 3x³ – 3x² + 8x + 8 – x³ + 3x – 4 = 2x⁴ – 4x³ – 3x² + 11x + 4

प्रश्न 21.
बहुपद x² – 3x³ + 2x + 5 व 2x⁴ – 3x³ + 9x +12 के योग में से 5x³ – 3x² + 8 घटाइये।
हलः
योगफल = x⁴ – 3x³ + 2x + 5 + 2x⁴ – 3x³ + 9x + 12 = 3x⁴ – 6x³ + 11x + 17
अन्तर = 3x⁴ – 6x + 11x + 17 – (5x³ – 3x² + 8) = 3x⁴ – 6x³ + 11x + 17 – 5x³ + 3x² – 8
= 3x⁴ – 11x³ + 3x² + 11x + 9

प्रश्न 22.
यदि p(x) = x³ – x² + 2 तथा g(x) = x +1 तब p(x) + g(x) तथा p(x) – g(x) की घात ज्ञात कीजिए।
हलः
(i) p(x) = x³ – x² + 2 तथा g(x) = x +1
p(x) + g(x) = x³ – x² + 2 + x + 1 = x³ – x² + x + 3
p(x) + g(x) की घात 3 है।।

(ii) p(x) – g(x) = x³ – x² + 2 – x – 1 = x³ – x² – x +1
p(x) – g(x) की घात 3 है।

प्रश्न 23.
निम्न बहुपद युग्मों का योग ज्ञात कीजिए।
(i) 3x² + 5x – 2 ; -3x² – 5x + 6
(ii) 3x² -7x + 5; 6x³; + 5x – 7
(iii) x² + x – 7; x³ + x² + 3x + 4
(iv) x³ – 5x² + x + 2; x³ – 3x² + 2x + 1
(v) x⁶ – 3x⁴; x⁴ + x³ + 2x² – 6
हलः
(i) योगफल = (3x² + 5x – 2) + (-3x² – 5x + 6) = 4
(ii) योगफल = (3x² – 7x + 5) + (6x³ + 5x – 7) = 6x³ + 3x² – 2x – 2
(iii) योगफल = (x² + x -7) + (x³ + x² + 3x + 4) = x³ + 2x² + 4x – 3
(iv) योगफल = (x³ – 5x² + x + 2) + (x³ – 3x² + 2x + 1) = 2x³ – 8x² + 3x + 3
(v) योगफल = (x⁶ – 3x⁴) + (x⁴ + x³ + 2x² – 6) = x⁶ – 2x⁴ + x³ + 2x² – 6

प्रश्न 24.
निम्न में पहले बहुपद में से दूसरा बहुपद घटाइये।
(i) x³ + x + 1; 1 – x – x²
(ii) 6x³ +5x² + 4x – 3; 4x³ – 2x² + 7x – 1
(iii) x³ + x² + x + 1; x³ – x² + x – 1
(iv) x⁴ – 3x³ + 2x + 6; x⁴ – 3x³ – 6x + 2
(v) 3x⁷ – 2x² + 3; x⁶ – 3x⁴ + x² + x
हल:
(i) अन्तर = (x³ + x + 1) – (1 – x – x²) = x³ + x + 1 – 1 + x + x² = x³ + x² + 2x
= x(x² + x + 2)

(ii) अन्तर = 6x³ + 5x² + 4x – 3 – (4x³ – 2x² + 7x – 1)
= 6x³ + 5x² + 4x – 3 – 4x³ + 2x² – 7x + 1 = 2x³ + 7x² – 3x – 2

(iii) अन्तर = (x³ + x² + x + 1) – (x³ – x² + x – 1) = x³ + x² + x + 1 – x³ + x² – x + 1
= 2x² +2

(iv) अन्तर = (x⁴ – 3x³ + 2x + 6) – (x⁴ – 3x³ – 6x + 2)
= x⁴ – 3x³ + 2x + 6 – x⁴ + 3x³ + 6x – 2 = 8x + 4

(v) अन्तर = (3x⁷ – 2x² + 3) – (x⁶ – 3x⁴ + x² + x)
= 3x⁷ – 2x² + 3 – x + 3x⁴ – x² – x = 3x⁷ – x⁶ + 3x⁴ – 3x² – x + 3

प्रश्न 25.
निम्न बहुपदों का गुणनफल ज्ञात कीजिए।
(i) x² – 4x + 4; x – 2
(ii) x² + 3x + 2; x² + 3x +1
(iii) 3x³ + x² + x; x + 2
(iv) 3x + 2; x² + x + 1
हल:
(i) गुणनफल = (x² – 4x + 4)(x – 2) = x³ – 2x² – 4x² + 8x + 4x – 8 = x³ – 6x² + 12x – 8

(ii) गुणनफल = (x² + 3x + 2)(x² + 3x + 1)
= x⁴ + 3x³ + x² + 3x³ + 9x² + 3x + 2x² + 6x + 2
= x⁴ + 6x³ + 12x² + 9x + 2

(iii) गुणनफल = (3x³ + x² + x)(x + 2) = 3x⁴ + 6x³ + x³ + 2x² + x² + 2x
=3x⁴ + 7x³ + 3x² + 2x

(iv) गुणनफल = (3x + 2)(x² + x + 1) = 3x³ + 3x² + 3x + 2x² + 2x + 2
= 3x³ +5x² + 5x + 2

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 18 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder Ex 18.1 घन, घनाभ तथा लम्बवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन

Ex 18.1 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
एक छड़ की अधिकतम लम्बाई ज्ञात कीजिए जिसे 10 मीx 8 मीx 6 मी विमा वाले एक कमरे में रखा जा सकता है।
हलः
छड़ की अधिकतम लम्बाई = घनाभ का विकर्ण

प्रश्न 2.
यदि एक घनाभ की लम्बाई, चौड़ाई तथा गहराई का योग 19 सेमी है तथा इसका विकर्ण 515 है तब इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 3.
यदि ऊँचाई h तथा त्रिज्या r वाले एक ठोस लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल, इसके कुल पृष्ठीय क्षेत्रफल का [latex]\frac{1}{3}[/latex] है तब h ज्ञात कीजिए।
हलः
लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
कुल पृष्ठीय क्षेत्रफल = 2πr(h +r)

प्रश्न 4.
एक बेलन में, त्रिज्या दोगुनी है तथा ऊँचाई आधी है तो वक्र पृष्ठीय क्षेत्रफल होगाः
(a) समान
(b) आधा
(c) दोगुना
(d) इनमें से कोई नहीं
हलः
(a) बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
त्रिज्या दो गुनी तथा ऊँचाई आधी करने पर

वक्र पृष्ठीय क्षेत्रफल समान रहेगा।

प्रश्न 5.
एक घनाभ 12 सेमी लम्बा, 9 सेमी चौड़ा तथा 8 सेमी ऊँचा है इसका कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः
घनाभ की 1 = 12 सेमी,
b = 9 सेमी,
h = 8 सेमी
कुल पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2(12 × 9 + 9 × 8 + 8 × 12)
= 2(108 + 72 + 96) = 2(276) = 552 सेमी²

प्रश्न 6.
यदि एक घन के एक विकर्ण की लम्बाई 813 सेमी है तब इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 7.
तीन बराबर घन, एक आसन्नीय क्रम में रखे गये हैं तब घनाभ के कुल पृष्ठीय क्षेत्रफल से तीनों घनों के पृष्ठीय क्षेत्रफलों के योग का अनुपात ज्ञात कीजिए।
हलः
तीन घनों का वक्र पृष्ठीय क्षेत्रफल = 3 × 6a² = 18a²
बने घनाभ का वक्र पृष्ठीय क्षेत्रफल = 2(b + bh + hl)
(l = 3a, b = a, h = a)
= 2[3a² + a² + 3a²] = 14a²
अनुपात = 14a² : 18a² = 7 : 9

Ex 18.1 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 8.
एक घनाभ का पृष्ठीय क्षेत्रफल 1300 सेमी है। यदि इसकी चौड़ाई 10 सेमी है तथा ऊँचाई 20 सेमी है तो इसकी लम्बाई ज्ञात कीजिए।
हल:

प्रश्न 9.
तीन घनों जिनमें प्रत्येक की भुजा 4 सेमी है की बाह्य सतहों को आपस में जोड़ दिया गया है तो प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। हलः
तीन घनों को आपस में जोड़ने पर प्राप्त घनाभ की लम्बाई
l = 4 + 4 + 4 = 12 सेमी
b = 4 सेमी
h = 4 सेमी
अतः घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2(12 × 4 + 4 × 4 + 4 × 12)
= 2(48 + 16 + 48) = 2 × 112 = 224 सेमी²

प्रश्न 10.
एक घनाभ का कुल पृष्ठीय क्षेत्रफल 372 सेमी है तथा इसका पार्श्व पृष्ठीय क्षेत्रफल 180 सेमी है। इसके आधार का क्षेत्रफल ज्ञात कीजिए।
हलः
घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 (आधार का क्षेत्रफल)
372 = 180 + 2 (आधार का क्षेत्रफल)
372 – 180 = 2 (आधार का क्षेत्रफल)
192 = 2 × आधार का क्षेत्रफल

प्रश्न 11.
8 सेमी भुजा वाले एक घन का पार्श्व पृष्ठीय क्षेत्रफल तथा कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः
घन की भुजा = 8 सेमी
पार्श्व पृष्ठीय क्षेत्रफल = 4 × (भुजा)² = 4 × (8)²
= 4 × 64 = 256 सेमी²
कुल पृष्ठीय क्षेत्रफल = 6 × (भुजा)² = 6 × (8)²
= 6 × 64 = 384 सेमी²

प्रश्न 12.
यदि एक घनाभ की लम्बाई, चौड़ाई और ऊँचाई क्रमश: 15 सेमी, 10 सेमी तथा 20 सेमी है तो इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [NCERT]
हलः
घनाभ की 1 = 15 सेमी,
b = 10 सेमी
h = 20 सेमी
कुल पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2(15 × 10 + 10 × 20 – 20 × 15)
= 2(150 – 200 – 300)
= 2(650) = 1300 सेमी²

प्रश्न 13.
एक आयताकार हॉल के फर्श का परिमाप 250 मी है तथा ऊँचाई 6 मी है। चारों दीवारों का क्षेत्रफल ज्ञात कीजिए।
हलः
हाँल की चारों दीवारों का क्षेत्रफल = 2(l + b) × h
= परिमाप × ऊँचाई = 250 × 6 = 1500 मी²

प्रश्न 14.
24 सेमी × 12 सेमी × 5 सेमी आकार के एक डिब्बे को बनाने के लिए आवश्यक गत्ते का क्षेत्रफल ज्ञात कीजिए।
हलः
डिब्बे का क्षेत्रफल = 2(lb + bh + hl)
= 2(24 × 12 + 12 × 5 + 5 × 24) = 2(288+ 60 + 120)
= 2(468) = 936 सेमी²

प्रश्न 15.
एक घनाभ की लम्बाई, चौड़ाई और गहराई का योग 19 सेमी है तथा इसके विकर्ण की लम्बाई 11 सेमी है। घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 16.
एक घनाभ की विमाएँ 1 : 2 :3 के अनुपात में हैं तथा इसका कुल पृष्ठीय क्षेत्रफल 88 मी2 है। विमाएँ ज्ञात कीजिए।
हलः

प्रश्न 17.
तीन घनों जिनमें प्रत्येक की भुजा 5 सेमी है की बाह्य सतहों को आपस में जोड़ दिया गया है। परिणामी घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः
घनों को जोडने पर प्राप्त घनाभ की लम्बाई l = 5 + 5 + 5
= 15 सेमी, b = 5 सेमी, h = 5 सेमी
परिणामी घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2(15 × 5+ 5 × 5 – 5 × 15)
= 2(75 + 25 + 75) = 2 × 175 = 350 सेमी²

प्रश्न 18.
एक आयताकार हॉल के फर्श का परिमाप 250 मी है। इसकी ऊँचाई 6 मी है। ₹ 6 प्रति मीटर की दर से इसकी चारों दीवारों पर पुताई कराने का खर्च ज्ञात कीजिए।
हॉल की चारो दीवारो का क्षेत्रफल = 2(l + b) × h
= परिमाप × ऊँचाई
= 250 × 6 = 1500 मी²
कुल खर्च = 1500 × 6 =₹9000

प्रश्न 19.
एक घनाभ का कुल पृष्ठीय क्षेत्रफल 40 मी2 है तथा इसका पार्श्व पृष्ठीय क्षेत्रफल 26 मी2 है। इसके आधार का क्षेत्रफल ज्ञात कीजिए।
हलः
घनाभ का कुल पृष्ठीय क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल + 2 × आधार का क्षेत्रफल
40 = 26 + 2 × आधार का क्षेत्रफल
40 – 26 = 2 × आधार का क्षेत्रफल
14 = 2 × आधार का क्षेत्रफल

∴ आधार का क्षेत्रफल = 7 मी²

प्रश्न 20.
एक शीतगृह की लम्बाई, इसकी चौड़ाई की दोगुनी है। इसकी ऊँचाई 3 मी है। इसकी चारों दीवारों (दरवाजों सहित) का क्षेत्रफल 108 मी2 है। इसका आयतन ज्ञात कीजिए।
हलः
l = 2b … (1)
h = 3 …(2)
चारो दीवारो का क्षेत्रफल = 2(l + b) × h

Balaji Publications Mathematics Class 9 Solutions