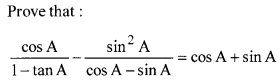These Sample papers are part of CBSE Sample Papers for Class 10 Maths. Here we have given CBSE Sample Papers for Class 10 Maths Paper 9.
CBSE Sample Papers for Class 10 Maths Paper 9
| Board | CBSE |
| Class | X |
| Subject | Maths |
| Sample Paper Set | Paper 9 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 9 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.
Time allowed: 3 Hours
Maximum Marks: 80
General Instructions
- All questions are compulsory.
- The question paper consists of 30 questions divided into four sections A, B, C and D.
- Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each.
- There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
- Use of calculators is not permitted.
Section – A
Question 1.
What is the condition for the decimal expansion of a rational number to terminate? Explain with the help of an example.
Question 2.
In the given figure ∆ACB ~ ∆APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP = 2.8 cm, then find AC.
Question 3.
An equation has been given as [latex]\frac { c }{ { x }^{ 2 } } +\frac { k }{ x }[/latex] = 1. Find the relation between c and k if x has real values.
Question 4.
If sec 2 A = cosec (A – 42°) where 2 A is acute angle, then find the value of A [NTSE 2015]
Question 5.
Find the next term of A.P. √2,√8,√18……..
Question 6.
Find the ratio in which the point P ([latex]\frac { 3 }{ 4 } [/latex],[latex]\frac { 5 }{ 12 } [/latex]) divides the line segment joining the points A ([latex]\frac { 1 }{ 2 } [/latex],[latex]\frac { 3 }{ 2 } [/latex]) and B (2, -5).
Section – B
Question 7.
How many three digit natural numbers are divisible by 7 ?
Question 8.
A certain class has ‘s’ students. If a student is picked at random, the probability of picking a boy is [latex]\frac { 8 }{ 13 } [/latex] If the class has 24 boys, what is the value of ‘s’?
Question 9.
A bag contains 40 coins, consisting of ₹ 2, ₹ 5 and ₹ 10 denominations. If a coin is drawn at random, the probability of drawing a ₹ 2 coin is [latex]\frac { 5 }{ 8 } [/latex] If x ₹ 2 coins are removed from the bag and then a coin is drawn at random, the probability of drawing a ₹ 2 coin is [latex]\frac { 1 }{ 2 } [/latex] . Find the value of x.
Question 10.
Solve the following system of equations :
[latex]\frac { 4 }{ X } [/latex] + 5y = 7 ; [latex]\frac { 3 }{ x } [/latex] + 4y = 5
Question 11.
If the pth term of an A.P. is [latex]\frac { 1 }{ Q } [/latex] and qth term is [latex]\frac { 1 }{ P } [/latex]. Prove that the sum of the first pq terms is [latex]\frac { 1 }{ 2 } [/latex] (pq +1)
Question 12.
If (3,0), (2, a) and (b, 6) are the vertices of a ∆ ABC, whose centroid is (2, 5). Find the values of a and b.
Section – C
Question 13.
Prove that √2 + √5 is irrational.
Question 14.
Quadratic polynomial 2x2 – 3x + 1 has zeroes as a and β Now form a quadratic polynomial whose zeroes are 3α and 3β.
Question 15.
Prove that the points (a, a), (-a,-a) and (-√3 a,√3 a) are the vertices of an equilateral triangle.|
Question 16.
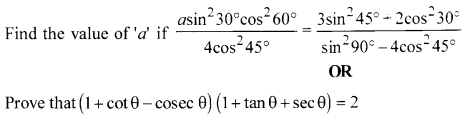
Question 17.
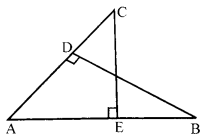
In a triangle ABC, AD ⊥ BC, If AD2 = BD.DC, prove that ∆ABC is right angle triangle.
OR
AD is the median of ∆ABC. The bisector of ∠ADB and ∠ADC meet AB and AC at points E and F. Prove that EF || BC.
Question 18.
In figure, PQRS is a square lawn with side PQ = 42 metres. Two circular flower beds are there on the sides PS and QR with centre at O, the intersection of its diagonals. F ind the total area of the two flower beds (shaded parts).
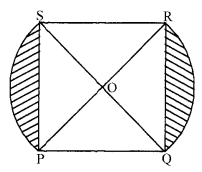
Question 19.
The mean of x1, x2, x3, …., xn is [latex]\overline { x } [/latex] If (a – 2b) is added to each ofthe observations, show that the mean of the new observations is [latex]\overline { x } [/latex] + (a – 2b)
Question 20.
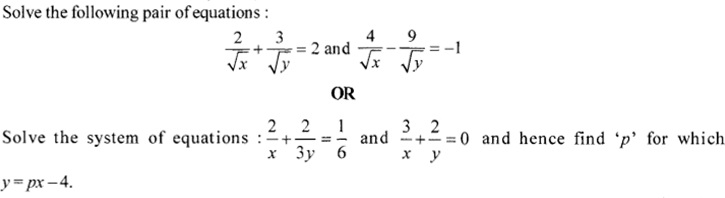
Question 21.
If a circle touches the side BC of a triangle ABC at P and extended sides AB and AC at Q and R, respectively, prove that AQ = [latex]\frac { 1 }{ 2 } [/latex] (BC + CA + AB)
Question 22.
A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 31 cm. Find the total surface area ofthe toy. (use π = [latex]\frac { 22 }{ 7 } [/latex])
OR
The rain water from a roof 22 m × 20 m drains into a cylindrical vessel having diameter of base 2 m and height 3.5 m. Ifthe vessel is just lull, find the rainfall in cm.
Section – D
Question 23.
If the sum of p terms of an A.P. is q and the sum of q terms is p then, show that sum of (p – q) terms = (p – q) (1 + [latex]\frac { 2q }{ P } [/latex])
Question 24.
From a window (h meters high above the ground) of a house in a street, the angles of elevation and depression of the top and the foot of another house on the opposite side of the street are θ and Φ respectively, Show that the height of the opposite house is h (1 + tan θ cot Φ)) meters.
OR
A pole 5 m high is fixed on the top of the tower. The angles of elevation of the top of the pole observed from a point A on the ground is 60° and the angle of depression ofthe point ‘A’ from the top of the tower is 45°. Find the height of the tower.
Question 25.
Out of a certain number of Saras birds one-fourth the number arc moving in lotus plants, [latex]\frac { 1 }{ 9 } [/latex] th coupled with [latex]\frac { 1 }{ 4 } [/latex] th as well as 7 times the square root of the number move on a hill, 56 birds remain in Vacula tree. What is the total number of birds?
Question 26.
A bucket open at the top, and made up of a metal sheet is in the form of a frustum of a cone. The depth of the bucket is 24 cm and the diameters of its upper and lower circular ends are 30 cm and 10 cm respectively. Find the cost of metal sheet used in it at the rate of ₹ 10 per 100 cm2. [Use π = 3.14],
Question 27.
Find the value of
(1 + tan θ + sec θ) (1 + cot θ – cosec θ).
Question 28.
Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter and on opposite sides of its centre, each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.
Question 29.
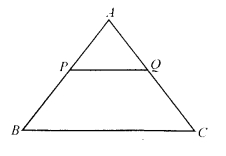
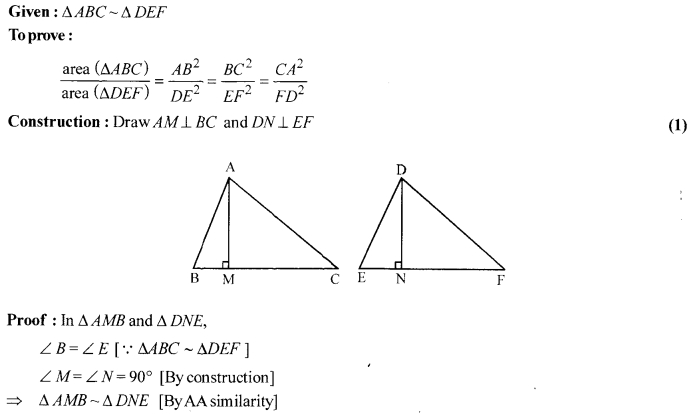
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides.
OR
In a right triangle, prove that the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Question 30.
On the sports day of a school, 300 students participated. Their ages are given in the following distribution :
| Age (in years) | 5 – 7 | 7 – 9 | 9 – 11 | 11 – 13 | 13 – 15 | 15 – 17 | 17 – 19 |
| Number of students | 67 | 33 | 41 | 95 | 36 | 13 | 15 |
Find the mode of the data.
OR
Monthly expenditures of milk in 100 families of a housing society are given in the following frequency distribution :
|
Monthly expenditure (in ₹) |
0 – 175 | 175 – 350 | 350 – 525 | 525 – 700 | 700 – 875 | 875 – 1050 | 1050 – 1225 |
| Number of families | 10 | 14 | 15 | 21 | 28 | 7 | 5 |
Find the mode for this distribution.
SOLUTIONS
Section – A
Solution: 1
The decimal expansion of a rational number terminates, if the denominator of rational number. [latex]\frac { p }{ q } [/latex], where p and q are co-prime can be expressed as 2m 5n, while m and n are non-negative integers.
e.g., [latex]\frac { 3 }{ 10 } [/latex] = [latex]\frac { 3 }{ { 2 }^{ 1 }\times { 5 }^{ 1 } } [/latex] = 0.3 (1)
Solution: 2

Solution: 3
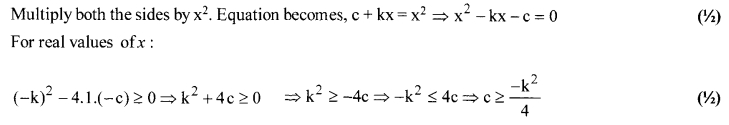
Solution: 4
sec 2A = cosec (A – 42°)
cosec (90° – 2A) = cosec (A – 42°)
90° – 2A = A – 42°
3A = 132°
A = 44° (1)
Solution: 5
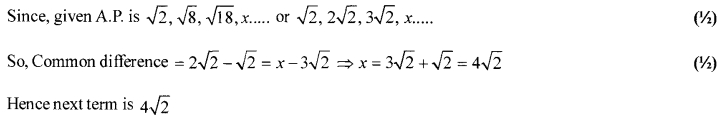
Solution: 6

Section – B
Solution: 7
Since, the numbers which are less than 1000 and divisible by 7 is [ [latex]\frac { 1000 }{ 7 } [/latex] ] i.e., 142. (1/2)
Now, the numbers which are less than 100 and divisible by 7 is [ [latex]\frac { 100 }{ 7 } [/latex] ] i.e., 14. (1/2)
So, the numbers which have three digits and divisible by 7 is 142 – 14 i.e., 128. (1)
Hence, there are total 128 three-digit natural numbers which are divisible by 7.
Solution: 8
Probability of picking a boy = [latex]\frac { Number of boys }{ Total students } [/latex] (1)
⇒ [latex]\frac { 8 }{ 13 } [/latex] = [latex]\frac { 24 }{ s } [/latex] ⇒ s = 24 × [latex]\frac { 13 }{ 8 } [/latex] ⇒ s = 3 × 13 ⇒ s = 39 (1)
Solution: 9
Total number of coins = 40
let number of ₹ 2 coins is C.
∵ P (drawing a ₹2 coins is c) = [latex]\frac { 5 }{ 8 } [/latex] ⇒ [latex]\frac { c }{ 40 } [/latex] = [latex]\frac { 5 }{ 8 } [/latex] ⇒ c = 25 (1)
Now, [latex]\frac { 25-x }{ 40-x } [/latex] = [latex]\frac { 1 }{ 2 } [/latex] ⇒ x = 10 (1)
Solution: 10

Solution: 11

Solution: 12
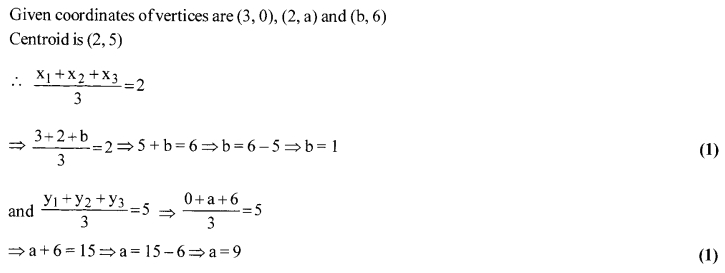
Section – C
Solution: 13
Let us assume on the contrary that √2 + √5 is rational number. Then, there exist co-prime positive integers a and b such that

Solution: 14

Solution: 15

Solution: 16

Solution: 17
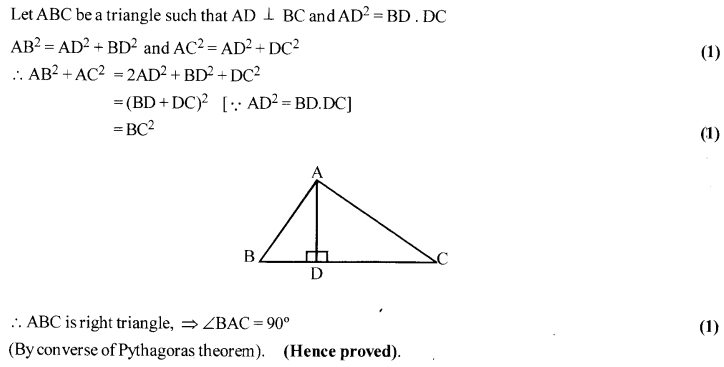
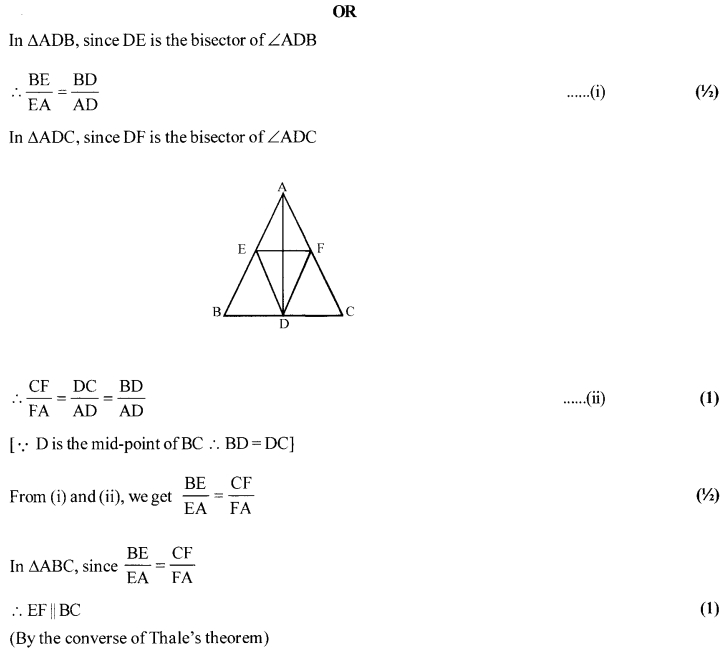
Solution: 18

Solution: 19

Solution: 20


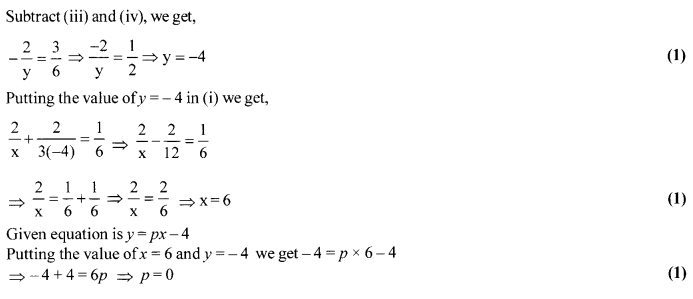
Solution: 21
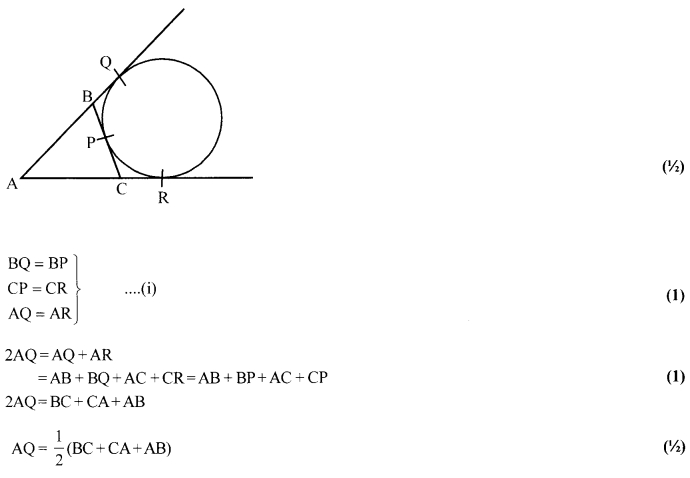
Solution: 22


Section – D
Solution: 23

Solution: 24
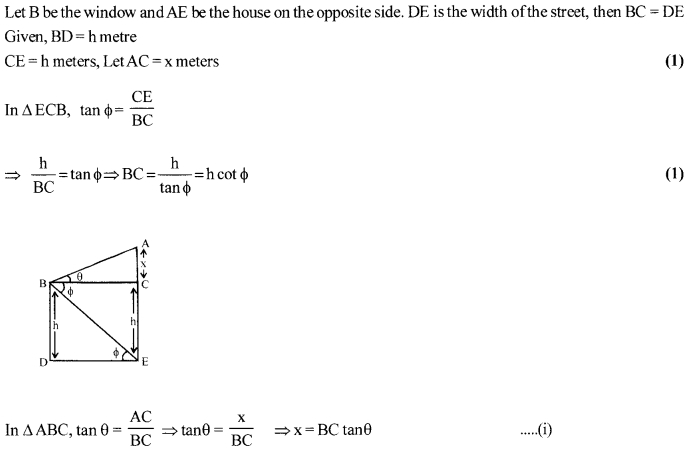

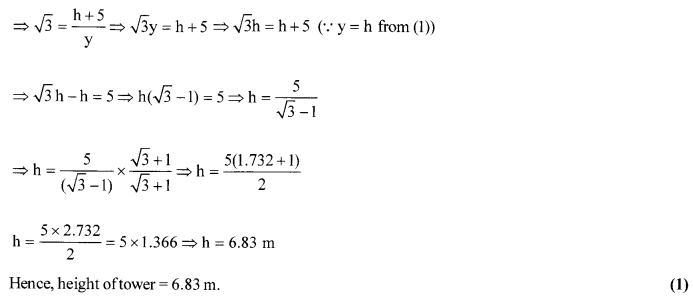
Solution: 25
Let the total number of birds be x.
∴ Numbe of birds moving in lotus plants = [latex]\frac { x }{ 4 } [/latex]
Number of birds moving on a hill = [latex]\frac { x }{ 9 } [/latex] + [latex]\frac { x }{ 4 } [/latex] + 7 √x (1)
Number of birds in Vacula tree = 56.
Using the given informations, we have
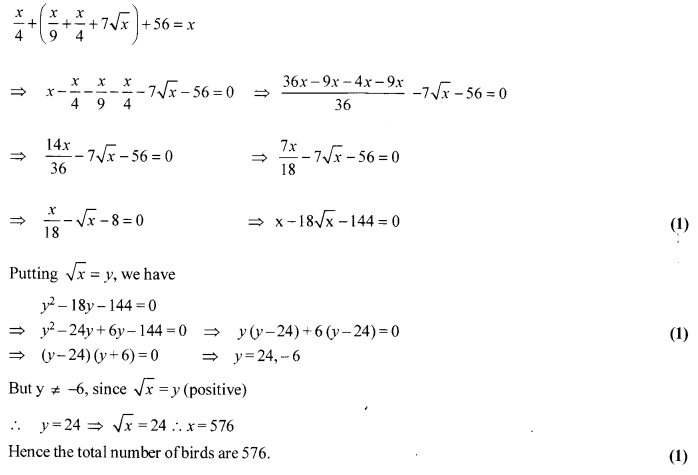
Solution: 26
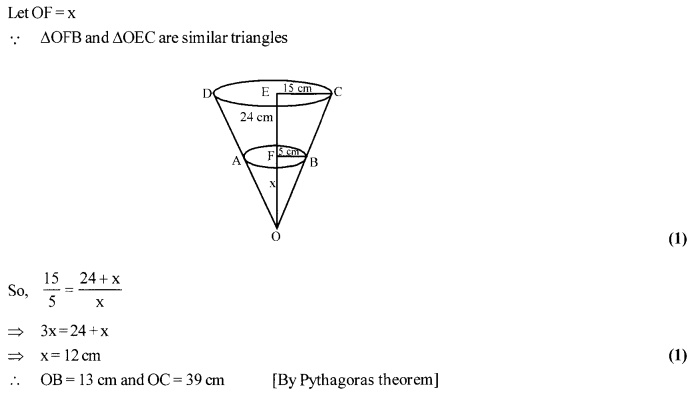
Total surface area of bucket
= Curved surface area of frustum + base area of lower circular end ABA
= (π × 15 × 39 – π × 5 × 13) + π (5)2
= 520 π + 25 π = 54 π cm2 (1)
So, total cost of metal sheet = ₹ 545 π × 0.1
= ₹ 54.5 × 3.14 = ₹ 171.13
Hence, cost of required metal sheet is ₹ 171.13. (1)
Solution: 27
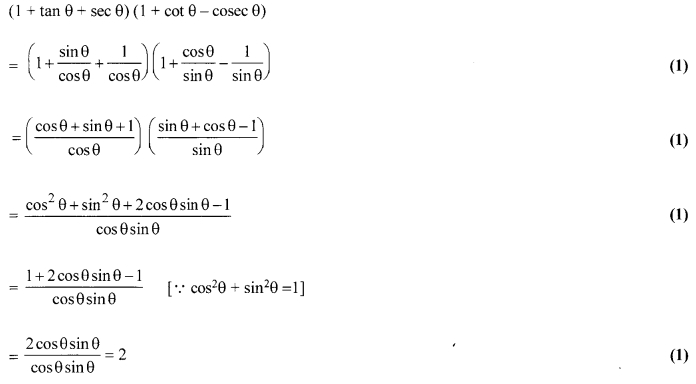
Solution: 28
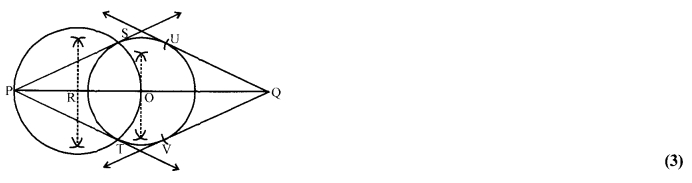
Steps of construction :
- Draw a line segment PQ of length (2 × 7 = 14) cm. (1)
- Draw perpendicular bisector of PQ, which intersects PQ at O.
- With centre O and radius 3 cm, draw a circle,
- Draw perpendicular bisector ofPO, which intersects PO at R.
- With centre R and radius RP or RO, draw a circle, which intersects the circle drawn in step (iii), at S and T.
- Draw rays PS and PT
- With centre Q and radius equal to PS (or PT), draw arcs intersecting the circle drawn in step (iii) at U andV.
- Draw rays QU and QV.
Thus, PS, PT, QU and QV are required tangents.
Solution: 29


Solution: 30

We hope the CBSE Sample Papers for Class 10 Maths paper 9 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths paper 9, drop a comment below and we will get back to you at the earliest.