Class 11

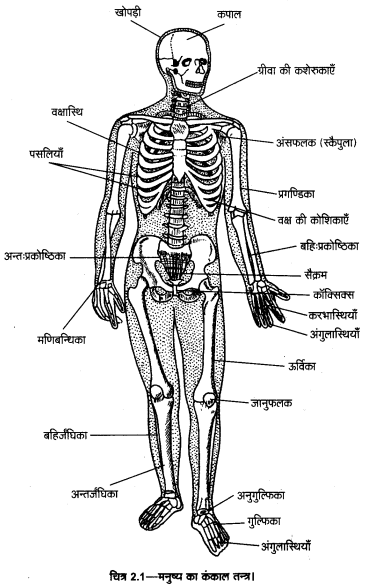
UP Board Solutions for Class 11 Physics Chapter 1 Physical World (भौतिक जगत)

These Solutions are part of UP Board Solutions for Class 11 Physics. Here we have given UP Board Solutions for Class 11 Physics Chapter 1 Physical World (भौतिक जगत).

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1:
विज्ञान की प्रकृति से सम्बन्धित कुछ अत्यन्त पारंगत प्रकथन आज तक के महानतम वैज्ञानिकों में से एक अल्बर्ट आइन्स्टाइन द्वारा प्रदान किए गए हैं। आपके विचार से आइन्स्टाइन को उस समय क्या तात्पर्य था, जब उन्होंने कहा था-“संसार के बारे में सबसे अधिक अबोधगम्य विषय यह है कि यह बोधगम्य है?”
उत्तर:
हमारे चारों ओर, उपस्थित ब्रह्माण्ड अत्यन्त जटिल है तथा इसमें होने वाली परिघटनाएँ भी अत्यन्त जटिल हैं, परन्तु विज्ञान के अनेक नियम ऐसे हैं जो इन सभी परिघटनाओं की व्याख्या करने में पूर्णतः समर्थ हैं। अतः जब कोई घटना हम पहली बार देखते या सुनते हैं, वह अबोधगम्य होती है, परन्तु जब हम उस घटना से सम्बन्धित सिद्धान्त, नियम, तथ्य आदि का गहन विश्लेषण करते हैं तो वह घटना हमारे लिए बोधगम्य हो जाती है। अत: (UPBoardSolutions.com) भौतिक जगत से सम्बद्ध प्रत्येक तथ्य की सुस्पष्ट व्याख्या विज्ञान विषय में उपलब्ध है। जब हमारी जिज्ञासु प्रवृत्ति किसी तथ्य से सम्बद्ध वैज्ञानिक दृष्टिकोण जानना चाहती है तो हम उसे जान लेते हैं जिससे जटिल से जटिल परिघटना भी हमारे लिए आश्चर्य का कारण नहीं बनती; अतः आइन्स्टाइन का यह कथन तर्कसंगत है।

प्रश्न 2:
“प्रत्येक महान भौतिक सिद्धान्त अपसिद्धान्त से आरम्भ होकर धर्मसिद्धान्त के रूप में  समाप्त होता है।” इस तीक्ष्ण टिप्पणी की वैधता के लिए विज्ञान के इतिहास से कुछ उदाहरण लिखिए।
उत्तर:
पारम्परिक रूढ़िवादी विचारधारा के विरोध में प्रगट किया गया मत मात्र किवदन्ती माना जाता है। और सर्वमान्य र्निविरोध माना जाने वाला तथ्य नियम होता है। कोपरनिकसे का जिओसैन्ट्रिक सिद्धान्त प्रारम्भ में एक किवदन्ती के रूप में चर्चा का विषय बना, किन्तु टाइकोब्राहं तथा जॉन्स कैपलर द्वारा प्रतिपादित और समर्पित पाये जाने के उपरान्त उसको सर्वमान्य रूप से मान लिया गया। अत: यह नियम बन गया।

प्रश्न 3:
“सम्भव की कला ही राजनीति है।” इसी प्रकार “समाधान की कला ही विज्ञान है।” विज्ञान की प्रकृति तथा व्यवहार पर इस सुन्दर सूक्ति की व्याख्या कीजिए।
उत्तर:
राजनीति में सब कुछ सम्भव होता है। राजनीतिज्ञ अवसरवादी होते हैं। उनकी न कोई आचार संहिता होती है, न कोई नियम और न कोई उसूल। उनका एकमात्र लक्ष्य सत्ता में बना रहना होता है, साधन चाहे उचित हो अथवा अनुचित। किन्तु वैज्ञानिक घटनाओं का सावधानीपूर्वक निरीक्षण करता है। समंक व । संकलित करता है तथा उनका विश्लेषण करता है और प्राप्त निष्कर्षों के आधार पर नियमों का प्रतिपादन करता है। इस प्रकार यह प्रकृति के रहस्यों का उद्घाटन करता है। उसका एकमात्र ध्येय नियमों का पालन तथा प्रतिपादन करना होता है।

प्रश्न 4:
यद्यपि अब भारत में विज्ञान तथा प्रौद्योगिकी का विस्तृत आधार है तथा यह तीव्रता से फैल भी रहा है, परन्तु फिर भी इसे विज्ञान के क्षेत्र में विश्व नेता बनने की अपनी क्षमता को कार्यान्वित करने में काफी दूरी तय करनी है। ऐसे कुछ महत्त्वपूर्ण कारक लिखिए जो आपके विचार से भारत में विज्ञान के विकास में बाधक रहे हैं?
उत्तर:
आज भारत विज्ञान और प्रौद्योगिकी में विश्व में अपना स्थान बना चुका है और उसके पास अपना एक विस्तृत आधार है। चाहे वह मानव संसाधन, सूचना प्रौद्योगिकी, रॉके , आयुर्विज्ञान, परिवहन, रक्षायन्त्र, नाभिकीय विज्ञान, अनुसन्धान और बायोटेक्नोलॉजी तथा (UPBoardSolutions.com) इंजीनियरिंग कोई भी क्षेत्र क्यों न हो लेकिन फिर भी कुछ कारण ऐसे हैं जिनसे यह विश्व में आज भी एकमान्य वैज्ञानिक शक्ति नहीं है, जिसके निम्नलिखित कारण हैं

1.  विज्ञान प्रबन्धन पर नौकरशाही का कब्जा है।
2.  अनुसन्धान तथा प्रौद्योगिकी में सामंजस्य का अभाव होता है।
3.  भारत में कुछ मूलभूत सुविधाओं की कमी।
4. वैज्ञानिकों के लिए रोजगार के सीमित अवसरों की उपलब्धि।
5. इस देश में प्रारम्भिक अनुसन्धान के लिए प्रचुर धन की आवश्यकता।

प्रश्न 5:
किसी भी भौतिक विज्ञानी ने इलेक्ट्रॉन के कभी भी दर्शन नहीं किए हैं, परन्तु फिर भी सभी भौतिक विज्ञानियों का इलेक्ट्रॉन के अस्तित्व में विश्वास है। कोई बुद्धिमान, परन्तु अन्धविश्वासी व्यक्ति इसी तुल्यरूपता को इस तर्क के साथ आगे बढ़ाता है कि यद्यपि किसी ने देखा नहीं है, परन्तु भूतों का अस्तित्व है। आप इस तर्क का खण्डन किस प्रकार करेंगे?
उत्तर:
इलेक्ट्रॉन की उपस्थिति की मान्यता के आधार पर अनेक घटनाएँ घटित होती देखी गयी हैं और घटित भी की जा रही हैं। इसके सम्बन्ध में कुछ सिद्धान्त प्रतिपादित किये गये तथा उनको प्रायोगिक रूप में सिद्ध पाया गया किन्तु भूत की उपस्थिति सिद्ध करने के लिए न तो कोई प्रायोगिक प्रमाण मिला है और न ही तत्सम्बन्धी कोई घटना भी अवलोकित हुई है जिससे इसकी उपस्थिति सिद्ध हो सके। यह एक केवल कल्पना : मात्र तथा अंधविश्वास है।

प्रश्न 6:
जापान के एक विशेष समुद्र तटीय क्षेत्र में पाए जाने वाले केकड़े के कवचों (खोल) में से अधिकांश समुरई के अनुश्रुत चेहरे से मिलते-जुलते प्रतीत होते हैं। नीचे इस प्रेक्षित तथ्य की दो व्याख्याएँ दी गई हैं। इनमें से आपको कौन-सा वैज्ञानिक स्पष्टीकरण लगता है?
(i) कई शताब्दियों पूर्व किसी भयानक समुद्री दुर्घटना में एक युवा समुरई डूब गया। उसकी बहादुरी के लिए श्रद्धांजलि के रूप में प्रकृति ने अबोधगम्य ढंगों द्वारा उसके चेहरे को केकड़े के कवचों पर अंकित करके उसे उस क्षेत्र में अमर बना दिया।
(ii) समुद्री दुर्घटना के पश्चात उस क्षेत्र के मछुआरे अपने मृत नेता के सम्मान में सद्भावना प्रदर्शन के लिए, उस हर केकड़े के कवच को जिसकी आकृति संयोगवश समुरई से मिलती-जुलती प्रतीत होती थी, उसे वापस समुद्र में फेंक देते थे। परिणामस्वरूप केकड़े के कवचों की इस प्रकार की विशेष आकृतियाँ अधिक समय तक विद्यमान रहीं और इसीलिए कालान्तर में इसी आकृति का आनुवंशतः जनन हुआ। यह कृत्रिम वरण द्वारा विकास का एक उदाहरण है।
(नोट : यह रोचक उदाहरण कार्ल सागन की पुस्तक “दि कॉस्मॉस’ से लिया गया है। यह इस (UPBoardSolutions.com) तथ्य पर प्रकाश डालता है कि प्रायः विलक्षण तथा अबोधगम्य तथ्य जो प्रथम दृष्टि में अलौकिक प्रतीत होते हैं वास्तव में साधारण वैज्ञानिक व्याख्याओं द्वारा स्पष्ट होने योग्य बन जाते हैं। इसी प्रकार के अन्य उदाहरणों पर विचार कीजिए।)
उत्तर:
प्रश्न में दिए गए दोनों कथनों

1.  तथा
2.  में से कथन
3. प्रेक्षित तथ्य का वैज्ञानिक स्पष्टीकरण देने में पर्याप्त रूप से समर्थ है।

प्रश्न 7:
दो शताब्दियों से भी अधिक समय पूर्व इंग्लैण्ड तथा पश्चिमी यूरोप में जो औद्योगिक क्रान्ति हुई थी उसकी चिंगारी का कारण कुछ प्रमुख वैज्ञानिक तथा प्रौद्योगिक उपलब्धियाँ थीं। ये उपलब्धियाँ क्या थीं?
उत्तर:
जिन मुख्य उपलब्धियों के कारण औद्योगिक क्रान्ति का जन्म हुआ है वह निम्न प्रकार से हैं

1.  विद्युत की खोज से ऊर्जा प्राप्ति डाइनमो तथा मोटर की रूपरेखा।
2.  ऊष्मा और ऊष्मागतिकी पर आधारित इंजन का आविष्कार।
3.  हाथ की अपेक्षा कपास से 300 गुना गति से बिनौले अलग करने वाली सूती मशीन।
4.  विस्फोटकों की खोज से न केवल सैन्य बलों, अपितु खनिज दोहन में भी आशातीत सफलता प्राप्त हुई है।
5.  लोहे को उच्च श्रेणी के स्टील में बदलने (UPBoardSolutions.com) वाली ब्लास्ट भट्टी।
6.  गुरुत्व के अध्ययन से गोलों/तोपों/बन्दूकों से गोली की गति के अध्ययन की खोज।

प्रमुख वैज्ञानिकों के नाम की सूची निम्नवत् है

1.  क्रिश्चन हाइगेन,
2. गैलिलियो गैलिली,
3.  माइकल फैराडे तथा
4.  आइजक न्यूटन।

प्रश्न 8:
प्रायः यह कहा जाता है कि संसार अब दूसरी औद्योगिक क्रान्ति के दौर से गुजर रहा है, जो समाज में पहली क्रान्ति की भाँति आमूलचूल परिवर्तन ला देगी। विज्ञान तथा प्रौद्योगिकी के उन प्रमुख समकालीन क्षेत्रों की सूची बनाइए जो इस क्रान्ति के लिए उत्तरदायी हैं।
उत्तर:
विज्ञान और तकनीक की उपलब्धियाँ जो औद्योगिक क्रान्ति लाने में सक्षम हैं, उनमें से प्रमुख निम्नलिखित हैं

1. लेजर तकनीक जिसके द्वारा रक्तस्राव के बिना शल्य क्रिया सम्भव हो सकी है तथा जिसके द्वारा रॉकेट तथा उपग्रहों को नियन्त्रित किया जा सकता है।
2.  सुपरकण्डक्टरों का निर्माण जिसके द्वारा कमरे के ताप पर विद्युत शक्ति बिना हानि के प्रेषित की जा सकती है।
3.  कम्प्यूटर का बढ़ता हुआ प्रभाव और प्रयोग जिसने मानव की कार्यकुशलता कई गुनी बढ़ा दी है।
4.  बायोटेक्नोलॉजी का अद्भुत विकास।

प्रश्न 9:
बाईसवीं शताब्दी के विज्ञान तथा प्रौद्योगिकी पर अपनी निराधार कल्पनाओं को आधार मानकर लगभग 1000 शब्दों में कोई कथा लिखिए।
उत्तर:
आज हम सदर देशों की यात्रा वाययान, रेलमार्ग अथवा मोटरकार द्वारा करते हैं जो पेटोल अथवा डीजल से चलते हैं। बाईसवीं शताब्दी तक पहुँचते-पहुँचते हम दूर आकाश में स्थित ग्रहों तथा उपग्रहों की यात्रा कर सकेंगे जिनकी अनुमानित दूरी हजारों प्रकाश वर्ष से भी अधिक है। अनुमान है कि वे यान ईंधन रहित होंगे।
आज उपग्रह को स्थापित करने के लिए रॉकेट का प्रयोग आवश्यक है (UPBoardSolutions.com) और उसके लिए उपयुक्त प्लेटफॉर्म का होना भी आवश्यक है, किन्तु बाईसवीं शताब्दी के आते-आते विज्ञान की प्रगति उस अवस्था तक पहुँच जाएगी कि पृथ्वी से प्रेषित यानों को रिमोट कंट्रोल द्वारा संचालित किया जा सकेगा। यही नहीं आकाश में भ्रमण करती हुई कार्यशाला भी होगी जो किसी यान में त्रुटि आने पर उसकी आवश्यक देखभाल और मरम्मत भी कर सकेगी।

प्रश्न 10:
विज्ञान के व्यवहार पर अपने ‘नैतिक दृष्टिकोणों को रचने का प्रयास कीजिए। कल्पना कीजिए कि आप स्वयं किसी संयोगवश ऐसी खोज में लगे हैं जो शैक्षिक दृष्टि से रोचक है। परन्तु उसके परिणाम निश्चित रूप से मानव समाज के लिए भयंकर होने के अतिरिक्त कुछ नहीं होंगे। फिर भी यदि ऐसा है तो आप इस दविधा के हल के लिए क्या करेंगे?
उत्तर:
वैज्ञानिक का कार्य प्रकृति के सत्य की खोज करना और उसे फिर प्रकाशन माध्यम से संसार के सामने प्रस्तुत करना है। इसमें कोई भी सन्देह नहीं है कि एक ही खोज का प्रभाव मानव पर उत्थान और विनाश दोनों के लिये उपयोगी किया जा सकता है। यह बात वैज्ञानिक खोज के व्यावहारिक उपयोग करने वाले पर निर्भर है। यहाँ पर यह बात भी सम्भव हो सकती है कि जो खोज आज विनाशकारी है, वह आगे चलकर लाभकारी भी सिद्ध हो सकती है। यदि मैं एक वैज्ञानिक अन्वेषक हूँ और माना कि मैं स्टेम सेल पर कार्य कर रहा हूँ तो वैज्ञानिक आविष्कारक के रूप में मेरा दायित्व है कि उसके परिणाम समाज के सामने प्रस्तुत करू। राजनेता इसका उपयोग एक विशेष मानव जाति के विकास के लिए करते हैं या फिर डॉक्टर इसका उपयोग विभिन्न रोगों के उपचार के लिए करते हैं, इस बात का ध्यान रखना मेरा कार्य नहीं है। आइस्टाइन ने E = mc² का सूत्र संसार को दिया लेकिन इसका उपयोग हिरोशिमा व नागासाकी पर परमाणु बम गिराने में होगा ऐसा उसने कभी भी नहीं सोचा था। आज यह समीकरण संसार में ऊर्जा उत्पादन के कार्य में लाई जा रही है, जो कि मानव कल्याण का कार्य ही है।

प्रश्न 11:
किसी भी ज्ञान की भाँति विज्ञान का उपयोग भी, उपयोग करने वाले पर निर्भर करते हुए, अच्छा अथवा बुरा हो सकता है। नीचे विज्ञान के कुछ अनुप्रयोग दिए गए हैं। विशेषकर कौन-सा अनुप्रयोग अच्छा है, बुरा है अथवा ऐसा है कि जिसे स्पष्ट रूप से वर्गबद्ध नहीं किया जा सकता? इसके बारे में अपने दृष्टिकोणों को सूचीबद्ध कीजिए

1.  आम जनता को चेचक के टीके लगाकर इस रोग को दबाना और अन्ततः इस रोग से जनता को मुक्ति दिलाना। (भारत में इसे पहले ही प्रतिपादित किया जा चुका है।)
2.  निरक्षरता का विनाश करने तथा समाचारों एवं धारणाओं के जनसंचार के लिए टेलीविजन।
3.  जन्म से पूर्व लिंग-निर्धारण।
4. कार्यदक्षता में वृद्धि के लिए कम्प्यूटर।
5. पृथ्वी के परितः कक्षाओं में मानव-निर्मित उपग्रहों की स्थापना।
6. नाभिकीय शस्त्रों का विकास।
7.  रासायनिक तथा जैव-युद्ध की नवीन तथा शक्तिशाली तकनीकों का विकास।
8.  पीने के लिए जल का शोधन।
9. प्लास्टिक शल्य क्रिया।
10. क्लोनिंग।

उत्तर:

1.  उत्तम-भारत देश इस संक्रामक रोग से पूर्णतया मुक्त हो चुका है।
2. उत्तम-इसके द्वारा शिक्षा का प्रसार होता है एवं साथ ही मनोरंजन और ज्ञान में वृद्धि होती है।
3.  इस ज्ञान का दुरुपयोग सम्भव है। बहुधा भ्रूण के कन्या होने पर (UPBoardSolutions.com) गर्भपात करा दिया जाता है जो भ्रूण हत्या है और सर्वथा अनुचित भी।।
4. उत्तम-कार्यकुशलता बढ़ती है।
5.  उत्तम-उपग्रह की स्थापना ने संचार व्यवस्था में क्रान्ति ला दी है।
6.  अवांछित-ये सामूहिक विनाश का कारण होते हैं तथा इनके प्रयोग से जो विनाश का तांडव होता है उसका न तो अनुमान लगाया जा सकता है न
7. इस पर कोई प्रतिबन्ध लगाया जा सकता है।
8.  इनका प्रयोग मानवता के विपरीत है या कहिए अमानवीय है।
9. श्रेष्ठ – शुद्ध पेयजल मिलने से अनेक रोगों की सम्भावना समाप्त हो जाती है।
10.  उत्तम-विकृति दूर की जा सकती है।
11. उत्तम-निस्संतान दंपत्ति लाभान्वित हो सकते हैं।

प्रश्न 12:
भारत में गणित, खगोलिकी, भाषा विज्ञान, तर्क तथा नैतिकता में महान विद्वत्ता की एक लम्बी एवं अटूट परम्परा रही है। फिर भी इसके साथ एवं समान्तर, हमारे समाज में बहुत से अन्धविश्वासी तथा रूढ़िवादी दृष्टिकोण व परम्पराएँ फली-फूली हैं और दुर्भाग्यवश ऐसा अभी भी हो रहा है और बहुत-से शिक्षित लोगों में व्याप्त है। इन दृष्टिकोणों का विरोध करने के लिए अपनी रणनीति बनाने में आप अपने विज्ञान के ज्ञान का उपयोग किस प्रकार करेंगे?
उत्तर:
भारत में रूढ़िवादिताएँ और अतार्किक कर्मकाण्ड काफी प्रचलित हैं। इनको समाज से हटाना कोई छोटा-सा सुगम मार्ग नहीं है। इन व्यवहारों को जन्म देने वाले कुछ कारण निम्नलिखित हैं

1. समाज के बड़े भाग को शिक्षा से वंचित रखना।
2.  लोगों में विज्ञान के प्रति ज्ञान का अभाव रहना।
3. शासक तथा भूमि मालिकों का स्वार्थ।
4.  जाति प्रथाः ।
5.  दूसरों को अज्ञानी रखकर उन पर शासन करने की लालसा रखना।

ज्यादा-से-ज्यादा इलेक्ट्रॉनिक संचार माध्यम, जैसे- रेडियो, टी०वी०, समाचार-पत्र, विज्ञान प्रदर्शनियाँ आदि के द्वारा विज्ञान एवं तकनीकी के विकास में लोगों की रुचि को जाग्रत करके व्यवहार को बदलने से अपने ध्येय की प्राप्ति हो सकती है। इससे लोग शिक्षित हो सकते हैं। (UPBoardSolutions.com) अभिभावकों को अपने बच्चों को शिक्षित करने के लिये उन्हें स्कूल भेजने के लिये प्रेरित किया जाना चाहिए। भारत की बढ़ती हुई जनसंख्या पर नियन्त्रण पाने के लिये हमें वैज्ञानिक पद्धतियों को अपनाना अतिआवश्यक है। यह एक विस्फोटक स्थिति है। इससे लोगों में विज्ञान के प्रति विश्वास उत्पन्न होगा और विज्ञान के ज्ञान का सदुपयोग होगा।

प्रश्न 13:
यद्यपि भारत में स्त्री तथा पुरुषों को समान अधिकार प्राप्त हैं, फिर भी बहुत से लोग महिलाओं की स्वाभाविक प्रकृति, क्षमता, बुद्धिमत्ता के बारे में अवैज्ञानिक विचार रखते हैं। तथा व्यवहार में उन्हें गौण महत्त्व तथा भूमिका देते हैं। वैज्ञानिक तक तथा विज्ञान एवं अन्य क्षेत्रों में महान महिलाओं का उदाहरण देकर इन विचारों को धाराशायी कीजिए तथा अपने को स्वयं तथा दूसरों को भी समझाइए कि समान अवसर दिए जाने पर महिलाएँ पुरुषों के समकक्ष होती हैं।
उत्तर:
जन्म से पूर्व तथा जन्म के पश्चात् आहार के पोषक तत्वों का एक बड़ा भाग मानव-मस्तिष्क के विकास में योगदान करता है। यह मानव-मस्तिष्क स्त्री अथवा पुरुष किसी का भी हो सकता है। यदि हम स्त्रियों के प्राचीन इतिहास तथा वर्तमान स्थिति पर ध्यान केन्द्रित करें तो हम देखते हैं कि स्त्रियों की स्थिति सदैव सम्मानजनक रही है तथा उन्होंने अनेक उत्कृष्ट कार्य किए हैं। वे प्रत्येक कार्य में सक्षम हैं तथा किसी भी दशा में पुरुषों से कम नहीं हैं। जब्र कभी भी स्त्रियों को अवसर प्राप्त हुआ है, आश्चर्यजनक परिणाम सामने आए हैं। झाँसी की रानी लक्ष्मीबाई, सती अनुसूया (महर्षि अत्रि की पत्नी), रानी कर्मावती, नूरजहाँ, श्रीमती सरोजिनी नायडू, मैडम क्युरी, कल्पना चावला, मार्गेट थेचर, श्रीमती भण्डारनाइके, इन्दिरा गांधी, बछेन्द्री पॉल, श्रीमती संतोष यादव आदि अनेक नाम स्त्रियों के स्वर्णिम इतिहास का वर्णन करते हैं। (UPBoardSolutions.com) आज के समय में सानिया मिर्जा का नाम भी स्त्री-जगत में शीर्षस्थ स्थान पर है। इन स्त्रियों को अवसर प्राप्त हुआ तथा इन्होंने अपनी अपूर्व-क्षमता का परिचय दिया। आज भारत सरकार ने रक्षा-सेवाओं के द्वार भी स्त्रियों के लिए खोल दिए हैं तथा वहाँ भी स्त्रियों ने अपनी कार्यदक्षता सिद्ध कर दी है।
अतः यह सत्य है कि समान अवसर दिए जाने पर महिलाएँ पुरुषों के समकक्ष होती हैं।

प्रश्न 14:
“भौतिकी के समीकरणों में सुन्दरता होना उनका प्रयोगों के साथ सहमत होने की अपेक्षा अधिक महत्त्वपूर्ण है।” यह मत महान ब्रिटिश वैज्ञानिक पी०ए०एम० डिरैक का था। इस दृष्टिकोण की समीक्षा कीजिए। इस पुस्तक में ऐसे सम्बन्धों तथा समीकरणों को खोजिए जो आपको सुन्दर लगते हैं।
उत्तर:
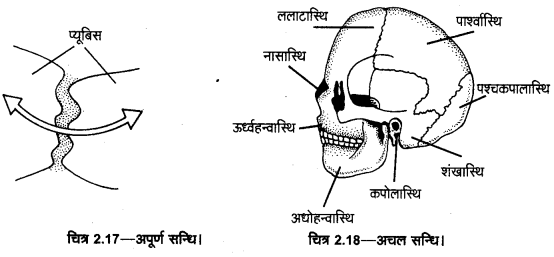
यह कथन असत्य नहीं है। भौतिकी के समीकरण प्रयोगों से मिलने चाहिए और साथ ही सरल और सुन्दर भी होने चाहिए। आइन्स्टाइन का समीकरण (E = mc²) एक ऐसा ही समीकरण है जो बहुत सुन्दर और याद करने में सरल है। लेकिन इस समीकरण ने बीसवीं शताब्दी में विज्ञान एवं समाज का चेहरा ही बदल दिया है। दूसरा समीकरण F = G है जो कि सामान्य एवं सुन्दर है। एक दी गई स्थिति में इस समीकरण ने खगोल विज्ञान की समझ में ही आमूलचूल परिवर्तन कर दिया है। भौतिकी में कुछ अन्य ऐसे ही समीकरण निम्नवत् हैं
F = mg, E= [latex]\frac { 1 }{ 2 }[/latex] mν², P = mν, E= hν तथा स्थितिज ऊर्जा U = mgh

प्रश्न 15:
यद्यपि उपर्युक्त प्रक्कथन विवादास्पद हो सकता है परन्तु अधिकांश भौतिक विज्ञानियों का यह मत है कि भौतिकी के महान नियम एक ही साथ सरल एवं सुन्दर होते हैं। डिरैक के अतिरिक्त जिन सुप्रसिद्ध भौतिक विज्ञानियों ने ऐसा अनुभव किया उनमें से कुछ के नाम इस प्रकार हैं-आइन्स्टाइन, बोर, हाइजेनबर्ग, चन्द्रशेखर तथा फाइनमैन। आपसे अनुरोध है कि आप भौतिकी के इन विद्वानों तथा अन्य महानायकों द्वारा रचित सामान्य पुस्तकों एवं लेखों तक पहुँचने के लिए विशेष प्रयास अवश्य करें। (इस पुस्तक के अन्त में दी गई ग्रन्थ-सूची देखिए)। इनके लेख सचमुच प्रेरक हैं।
उत्तर:

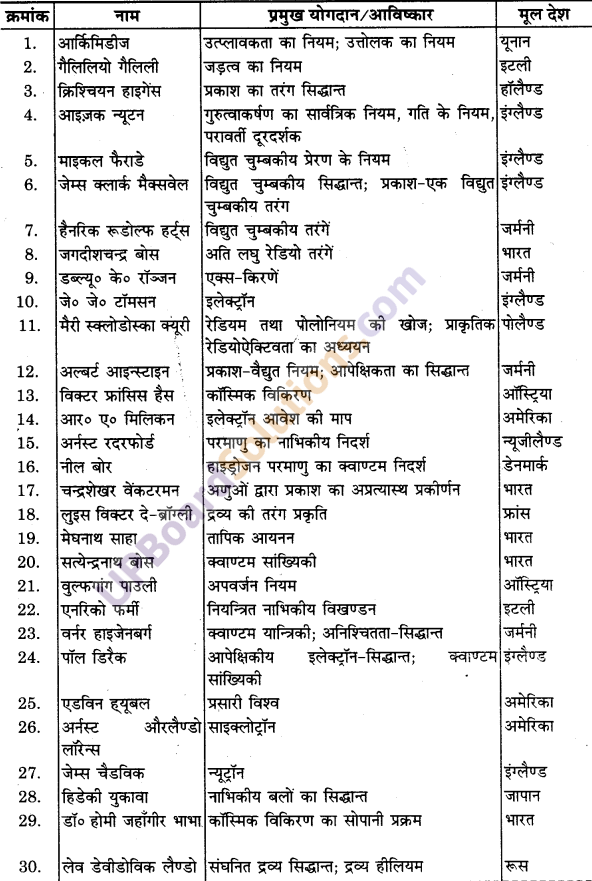
प्रश्न 16:
विज्ञान की पाठ्य-पुस्तकें आपके मन में यह गलत धारणा उत्पन्न कर सकती हैं कि विज्ञान पढ़ना शुष्क तथा पूर्णतः अत्यन्त गम्भीर है एवं वैज्ञानिक भुलक्कड़, अन्तर्मुखी, कभी न हँसने वाले अथवा खीसे निकालने वाले व्यक्ति होते हैं। विज्ञान तथा वैज्ञानिकों का यह चित्रण पूर्णतः आधारहीन है। अन्य समुदाय के मनुष्यों की भाँति वैज्ञानिक भी विनोदी होते हैं। तथा बहुत से वैज्ञानिकों ने तो अपने वैज्ञानिक कार्यों को गम्भीरता से पूरा करते हुए अत्यन्त विनोदी प्रकृति के साथ साहसिक कार्य करके अपना जीवन व्यतीत किया है। गैमो तथा फाइनमैन इसी शैली के दो भौतिक विज्ञानी हैं। ग्रन्थ सूची में उनके द्वारा रचित पुस्तकों को पढ़ने में आपको आनन्द प्राप्त होगा।
उत्तर:
फाइनमैन तथा गैमो द्वारा रचित इन पुस्तकों के नाम निम्नलिखित हैं

1. आर० पी० फाइनमैन द्वारा रचित ‘Surely you are joking, Mr. Feynman’, बेन्टन बुक्स (1986)।
2.  जी गैमो द्वारा रचित ‘Mr. Tompkins in paperback’, कैम्ब्रिज यूनिवर्सिटी (UPBoardSolutions.com) प्रेस (1987)। उपर्युक्त पुस्तकों को पढ़ने पर ज्ञात होता है कि वैज्ञानिक भी अन्य समुदाय के मनुष्यों की भाँति ही विनोदी होते हैं। विज्ञान विषय पढ़ना शुष्क तथा पूर्णतः गम्भीर नहीं हैं यदि इसका अध्ययन हम रुचिपूर्वक, तथ्यों को भली-भाँति समझकर करें।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1:
भौतिक शास्त्र है।
(i) भौतिक विषयों का अध्ययन
(ii) भौतिक वस्तुओं का अध्ययन
(iii) प्रकृति के विभिन्न घटनाक्रमों का अध्ययन
(iv) विकल्प (ii) एवं (iii) दोनों
उत्तर:
(iv) विकल्प (ii) एवं (iii) दोनों

प्रश्न 2:
नोबेल पुरस्कार प्राप्त करने वाले प्रथम भारतीय वैज्ञानिक थे
(i) श्री जे०सी० बोस
(ii) एचजे० भाभा
(iii) एम० एन० शाह
(iv) सर सी०वी० रमन
उत्तर:
(iv) सर सी०वी० रमन

प्रश्न 3:
गुरुत्वाकर्षण की खोज की
(i) बेथे ने
(ii) आइन्सटाइन ने
(iii) न्यूटन ने
(iv) रदरफोर्ड ने
उत्तर:
(iii) न्यूटन ने

प्रश्न 4:
रेडियोधर्मिता की खोज किसके द्वारा की गयी?
(i) चैडविक
(ii) रदरफोर्ड
(iii) बेकुरल
(iv) रॉञ्जन
उत्तर:
(iii) बेकुरल

प्रश्न 5:
प्रथम इलेक्ट्रॉनिक कम्प्यूटर का आविष्कार हुआ
(i) 1942 में
(ii) 1946 में
(iii) 1947 में
(iv) 1948 में
उत्तर:
(ii) 1946 में

प्रश्न 6:
अब्दुस सलाम को निम्न में से किस क्षेत्र में नोबेल पुरस्कार प्राप्त हुआ?
(i) अणुओं द्वारा प्रकाश का अप्रत्यास्थ प्रकीर्णन
(ii) दुर्बल तथा विद्युत चुम्बकीय बलों का एकीकरण
(iii) अति चालकता
(iv) लेसर तकनीक
उत्तर:
(ii) दुर्बल तथा विद्युत चुम्बकीय बलों का एकीकरण

प्रश्न 7:
टेलीविजन का आविष्कार किया
(i) राइट ब्रदर्स ने
(ii) मूलर ने
(iii) बेयर्ड ने
(iv) गोडार्ड ने
उत्तर:
(iii) बेयर्ड ने

प्रश्न 8:
डी-ब्रॉगली सम्बन्धित है।
(i) जर्मनी से
(ii) इंग्लैण्ड से
(iii) फ्रांस से
(iv) अमेरिका से
उत्तर:
(iii) फ्रांस से

प्रश्न 9:
परमाणु के नाभिक की खोज की थी
(i) न्यूटन
(ii) थॉमसन
(ii) रदरफोर्ड
(iv) मैक्सवेल
उत्तर:
(iii) रदरफोर्ड

प्रश्न 10:
द्रव्यमान-ऊर्जा की तुल्यता किस वैज्ञानिक ने स्थापित की?
(i) जूल
(i) न्यूटन
(iii) आइन्सटाइन
(iv) फैराडे
उत्तर:
(iii) आइन्सटाइन

प्रश्न 11:
प्रकृति में पाया जाने वाला सबसे अधिक निर्बल बल है।
(i) गुरुत्वाकर्षण बल ,
(ii) वैद्युत चुम्बकीय बल ,
(iii) दुर्बल नाभिकीय बल
(iv) प्रबल नाभिकीय बल
उत्तर:
(i) गुरुत्वाकर्षण बल

प्रश्न 12:
प्रबल नाभिकीय बल विद्युत चुम्बकीय बलों की अपेक्षा होता है।
(i) 100 गुना क्षीण
(ii) 100 गुना प्रबल
(iii) 10⁶ गुना क्षीण
(iv) 10⁶ गुना प्रबल
उत्तर:
(ii) 100 गुना प्रबल

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:
भौतिकी क्या है?
उत्तर:
भौतिकी विज्ञान की वह शाखा है जिसके अन्तर्गत प्रकृति एवं प्राकृतिक घटनाओं का अध्ययन किया जाता है।

प्रश्न 2:
उस वैज्ञानिक का नाम लिखिए जिसने x-किरणों की खोज की।
उत्तर:
डब्ल्यू० के० रॉञ्जन।

प्रश्न 3:
उस वैज्ञानिक का नाम बताइये जिसे विज्ञान की दो पृथक-पृथक शाखाओं में नोबेल पुरस्कार मिला।
उत्तर:
मैडम मेरी स्कलेडोवेक क्यूरी (Skladowak Curie) को भौतिकी में वर्ष 1903 में तथा रसायन विज्ञान में वर्ष 1911 में नोबेल पुरस्कार मिला।

प्रश्न 4:
बेतार सन्देश के आविष्कारक का नाम क्या है?
उत्तर:
बेतार सन्देश के आविष्कारक जी० मार्कोनी थे।

प्रश्न 5:
मैक्सवेल का नाम किस वैज्ञानिक सिद्धान्त से सम्बद्ध है?
उत्तर:
वैद्युत चुम्बकीय सिद्धान्त

प्रश्न 6:
भौतिकी में तीन संरक्षण नियमों के नाम बताइए।
उत्तर:
ऊर्जा संरक्षण का नियम, रेखीय संवेग संरक्षण का नियम तथा वैद्युत आवेश संरक्षण का नियम।

प्रश्न 7:
रेखीय संवेग संरक्षण का नियम लिखिए।
उत्तर:
रेखीय संवेग संरक्षण का नियम–यदि कणों के किसी निकाय पर कार्य करने वाला बाह्य बल शून्य है, तो उस निकाय का संवेग संरक्षित रहता है।

प्रश्न 8:
द्रव्यमान तथा ऊर्जा का तुल्यता का नियम बताइए तथा इसका एक उदाहरण दीजिए।
उत्तर:
आइन्सटाइन के अनुसार, द्रव्यमान तथा ऊर्जा पृथक्-पृथक् अस्तित्व वाली भौतिक राशियाँ नहीं हैं, बल्कि एक ही राशि के दो रूप हैं। द्रव्यमान को ऊर्जा में तथा ऊर्जा को द्रव्यमान में बदला जा सकता है। द्रव्यमान तथा ऊर्जा के बीच तुल्य सम्बन्ध, E = mc², जहाँ E ऊर्जा तथा (UPBoardSolutions.com) m द्रव्यमान हैं। इसके अनुसार यदि ऊर्जा E विलुप्त हो जाए, तो द्रव्यमान m बढ़ जाता है और यदि द्रव्यमान m नष्ट हो जाए तो इसके समतुल्य ऊर्जा E उत्पन्न होती है।
उदाहरण–सूर्य पर चल रही नाभिकीय संलयन की क्रियाओं में सूर्य का द्रव्यमान निरन्तर ऊर्जा में परिवर्तित हो रहा है।

लघु उत्तरीय प्रश्न

प्रश्न 1:
वैज्ञानिक विधि क्या है? वैज्ञानिक विधि के विभिन्न चरणों की व्याख्या कीजिए।
उत्तर:
भौतिक जगत की प्राकृतिक घटनाओं का क्रमबद्ध एवं सुव्यवस्थित ज्ञान प्राप्त करने के लिए जो । विधि अपनायी जाती है, उसे वैज्ञानिक विधि कहते हैं। वैज्ञानिक विधि निम्नलिखित चार चरणों में पूर्ण की जाती है।

1. क्रमबद्ध प्रेक्षण Systematic observations:
प्राकृतिक घटना अथवा अध्ययन के लिए चुनी गई समस्या से सम्बन्धित भौतिक राशियों के पर्याप्त संख्या में प्रेक्षण लिए जाते हैं और उन्हें सुव्यवस्थित करके उनका विश्लेषण किया जाता है।

2. परिकल्पना की रचना Construction of hypothesis:
प्राप्त प्रेक्षणों का विश्लेषण करने के लिए एक कार्यकारी मॉडल (working model) तैयार किया जाता है, जिसे परिकल्पना कहते हैं। इसमें समस्या को गणितीय रूप में अभिव्यक्त किया जाता हैं।

3. परिकल्पना का परीक्षण Testing of the hypothesis:
बनाई गई परिकल्पना का परीक्षण करने के लिए, उस परिकल्पना के आधार पर कुछ निष्कर्ष निकाले जाते हैं एवं उनका सत्यापन करने के लिए नए प्रयोग भी किए जाते हैं।

4. सिद्धान्त की स्थापना Establishment of theory:
यदि परिकल्पना सत्यापित हो जाती है, तो उसे अन्तिम सिद्धान्त मान लिया जाता है। यदि परिकल्पना सत्यापित नहीं हो पाती है तो उसमें संशोधन किए जाते हैं अथवा नई परिकल्पना तैयार की जाती है और उसके परीक्षण के लिए पुनः नये प्रयोग किए जाते हैं। इसी क्रम को तब तक जारी रखते हैं जब तक प्रयोगों द्वारा पूर्णत: सत्यापित अन्तिम सिद्धान्त प्राप्त न हो जाये।

प्रश्न 2:
आवेश-संरक्षण का नियम लिखिए। उदाहरण दीजिए।
उत्तर:
जब दो वस्तुओं को परस्पर रगड़ा जाता है, तो दोनों वस्तुओं पर एक साथ विपरीत प्रकृति परन्तु समान परिमाण के आवेश उत्पन्न हो जाते हैं। अर्थात् दोनों वस्तुओं पर उत्पन्न आवेश की कुल मात्रा शून्य ही रहती है। इस बात को हम इस प्रकार भी कह सकते (UPBoardSolutions.com) हैं कि “न तो आवेश उत्पन्न किया जा सकता है और न ही नष्ट किया जा सकता है।” यह कथन ही “आवेश-संरक्षण का नियम”(Law of conservation of charge) कहलाता है। प्रत्येक प्राकृतिक घटना में, जहाँ वैद्युत आवेश का आदान-प्रदान होता है, इस नियम को सत्य पाया गया है।

उदाहरणार्थ:
इलेक्ट्रॉन तथा पॉजिट्रॉन का संयोग आवेश-संरक्षण को प्रदर्शित करता है। इलेक्ट्रॉन पर ऋणावेश होता है तथा पॉजिट्रॉन पर ठीक इलेक्ट्रॉन के आवेश के बराबर परिमाण का धनावेश होता है।
अतः दोनों के आवेश का कुल योग शून्य होता है। ये दोनों परस्पर संयोग करके दो γ-प्रोटॉन उत्पन्न करते हैं जिसमें प्रत्येक पर आवेश शून्य ही होता है।
अतः संयोग से पूर्व कुल आवेश = संयोग के पश्चात् कुल आवेश।

विस्तृत उत्तरीय प्रश्न

प्रश्न 1:
भौतिकी का प्रौद्योगिकी से सम्बन्ध उदाहरणों सहित स्पष्ट कीजिए।
उत्तर:
भौतिकी तथा प्रौद्योगिकी के बीच सम्बन्ध–भौतिकी तथा प्रौद्योगिकी के बीच घनिष्ठ सम्बन्ध है। भौतिकी के सिद्धान्तों पर प्रौद्योगिकी को प्रयुक्त कर अनेक मशीनें तथा उपकरण बनाए गए हैं जो समाज के लिए अत्यधिक लाभकारी सिद्ध हुए हैं। इसके उदाहरण निम्नलिखित हैं

1.  टेलीफोन, टेलीग्राफ और टेलेक्स के विकास से हम दूर तक बात कर सकते हैं । समाचार भेज सकते हैं।
2.  रेडियो, टेलीविजन और सैटेलाइट (satellite) के विकास से संचार साधन (communication) में क्रान्ति (revolution) ओ गयी।
3. इलेक्ट्रॉनिक (electronic), कम्प्यूटर, लेसर (laser) के विकास से समाज (society) को अत्यधिक लाभ हुआ है।
4.  विद्युत-चुम्बकीय प्रेरण (electro-magnetic induction) (UPBoardSolutions.com) के सिद्धान्त पर विद्युत का उत्पादन आधारित है।
5. ऊष्मागतिकी (thermodynamics) के नियम पर आधारित ऊष्मा इंजन, पेट्रोल इंजन, डीजल इंजन आदि से सामान को एक स्थान से दूसरे स्थान पर ले जाना।
6.  न्यूक्लीयर चेन प्रतिक्रिया (nuclear chain reaction) को नियन्त्रित करके न्यूक्लीयर रिएक्टर से शक्ति (power) का उत्पादन करना।
7.  रॉकेट की उड़ान न्यूटन के गति के तीसरे नियम पर आधारित है।
8.  बर्नोली के सिद्धान्त पर हवाई जहाज का उड़ना।
9. भौतिकी के अध्ययन से ही लेसर (laser) का आविष्कार हुआ है जिससे समाज को अधिक लाभ पहुँचा है।
10. X-किरणों का व्यवहार औषधि विज्ञान (medical science) में किया जाता है। कुछ प्रौद्योगिक उपलब्धियाँ एवं उनसे सम्बन्धित भौतिकी के सिद्धान्तों को नीचे सारणी में दिया गया है

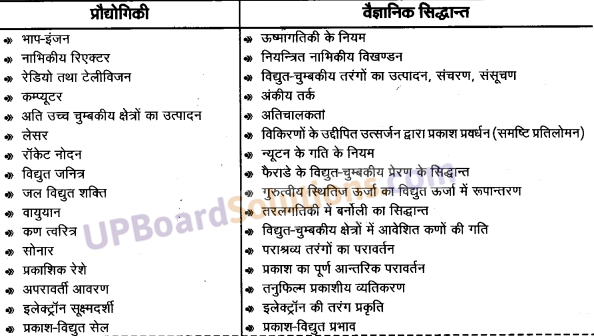
प्रश्न 2:
प्रकृति के मूल बल कौन-कौन से हैं? प्रत्येक के प्रमुख गुण लिखिए। उदाहरण सहित बलों के एकीकरण को समझाइए।
या
प्रकृति के चार मूल बल कौन-कौन से हैं। उनका वर्णन कीजिए।
उत्तर:
प्रकृति केमल बल: प्रकृति में चार प्रकार के मूल बल हैं जो निम्नलिखित हैं-

1.  गुरुत्वाकर्षण बल,
2. विद्युत चुम्बकीय बल,
3.  प्रबल नाभिकीय बल तथा
4. दुर्बल नाभिकीय बल।

1. गुरुत्वाकर्षण बल:
न्यूटन के अनुसार, ब्रह्माण्ड में प्रत्येक द्रव्य-कण दूसरे द्रव्य-कण को अपनी ओर आकर्षित करता है तो इन कणों के बीच एक आकर्षण बल लगता है। यही आकर्षण बल गुरुत्वाकर्षण बल कहलाता है।

न्यूटन के गुरुत्वाकर्षण बल के नियमानुसार, किन्हीं दो पिण्डों के बीच कार्यरत् गुरुत्वाकर्षण बल उनके द्रव्यमानों के गुणनफल के अनुक्रमानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह एक सार्वत्रिक बल है।

जहाँ m₁ व m₂ = पिण्डों के द्रव्यमान तथा r = द्रव्यमानों के बीच की दूरी गुरुत्वाकर्षण बलों के गुण निम्नलिखित हैं

1. ये बल सदैव आकर्षणात्मक होते हैं तथा कभी भी प्रतिकर्षणात्मक नहीं होते हैं।
2. ये प्रकृति में सबसे दुर्बल बंल होते हैं।
3. ये विस्तृत दूरियों पर भी कार्यरत् रहते हैं।
4.  ये दूरी सम्बन्धी व्युत्क्रम वर्ग के नियम का पालन करते हैं।
5.  ये केन्द्रीय बल होते हैं अर्थात् दोनों वस्तुओं के केन्द्रों को जोड़ने वाली रेखा के अनुदिश कार्य करते हैं।
6. ये बल संरक्षी बल होते हैं।

2. विद्युत चुम्बकीय बल:
आवेशित कणों के बीच कार्यरत् बल को विद्युत चुम्बकीय बल कहते हैं। स्थिर आवेशित कणों के बीच कार्यरत् बल को कूलॉम के नियम द्वारा व्यक्त किया जाता है, इसीलिए इसे कूलॉम का नियम भी कहते हैं।

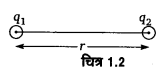
कूलॉम के अनुसार, किन्हीं दो स्थिर बिन्दु आवेशों के बीच कार्यरत् स्थिर वैद्युत बल, आवेशों के परिमाणों के गुणनफल के अनुक्रमानुपाती तथा उनकी बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है।

जहाँ, q₁ q₂= कार्यरत् आवेश तथा r = कार्यरत् आवेशों के बीच की दूरी है। समान आवेशों के बीच कार्यरत् बल प्रतिकर्षण तथा असमान आवेशों के बीच कार्यरत् वैद्युत बल आकर्षण प्रकृति का होता है।

विद्युत चुम्बकीय बलों के गुण निम्नलिखित हैं

1. ये बल आकर्षणात्मक अथवा प्रतिकर्षणात्मक हो सकते हैं।
2.  ये बल कूलॉम के नियम का पालन करते हैं।
3. ये दूरी सम्बन्धी व्युत्क्रम वर्ग के नियम का पालन करते हैं।
4.  दो प्रोटॉनों के बीच स्थिर वैद्युत बल किसी भी स्थिर दूरी के लिए गुरुत्वाकर्षण बल की तुलना में 10³⁶ गुना प्रबल होते हैं।
5. ये अधिक दूरी तक प्रभावी नहीं होते हैं।
6. ये केन्द्रीयै बल होते हैं।
7.  ये संरक्षी बल होते हैं।

3. प्रबल नाभिकीय बल:
वे बल जो एक नाभिक में न्यूट्रॉनों तथा प्रोटॉनों को परस्पर साथ-साथ बाँधे रखते हैं, प्रबल नाभिकीय बल कहलाते हैं। अतः ये बल दो प्रोटॉनों अथवा दो न्यूट्रॉनों अथवा एक
टॉन व एक न्यूट्रॉन के बीच कार्यरत रहते हैं, जबकि ये कण परस्पर एक-दूसरे के काफी निकट होते हैं। जब दो न्यूक्लिऑन परस्पर 10-15 मीटर दूरी पर होते हैं तो उनके बीच प्रबल नाभिकीय आकर्षण बल इतनी ही दूरी पर स्थित दो प्रोटॉनों के बीच लगने वाले प्रतिकर्षणात्मक वैद्युत बल की तुलना में 10 गुना प्रबल होता है।

प्रबल नाभिकीय बलों के गुण निम्नलिखित हैं

1. नाभिकीय बल आकर्षण बल हैं।
2. ये बल अत्यन्त प्रबल हैं। मानव जानकारी में अब तक जितने भी बल ज्ञात हैं उनमें सबसे अधिक तीव्र नाभिकीय बल ही हैं।
3.  ये वैद्युत बल नहीं हैं। यदि ये वैद्युत बल होते तो इनके कारण प्रोटॉनों के बीच प्रतिकर्षण होता और नाभिक की संरचना सम्भव न हो पाती।
4.  ये गुरुत्वीय बल भी नहीं हैं। दो न्यूक्लिऑनों के बीच गुरुत्वीय (UPBoardSolutions.com) बल बहुत क्षीण होते हैं, जबकि नाभिकीय बल अत्यन्त तीव्र हैं। अत: नाभिकीय बल मूलत: गुरुत्वीय बल नहीं हो सकते।
5. ये बल आवेश पर किसी प्रकार भी निर्भर नहीं करते अर्थात् विभिन्न न्यूक्लिऑनों के बीच
   (जैसे-प्रोटॉन-प्रोटॉन के बीच, न्यूट्रॉन-न्यूट्रॉन के बीच, प्रोटॉन-न्यूट्रॉन के बीच) बल एकसमान (uniform) होते हैं।
6.  ये बल अत्यन्त लघु परिसर (short range) के हैं। अत: ये बहुत कम दूरी (केवल नाभिकीय व्यास, 10^-15 मीटर के अन्दर) तक ही प्रभावी होते हैं।

4. दुर्बल नाभिकीय बल:
इन बलों की उत्पत्ति की खोज रेडियोधर्मिता में β-रूप की घटना के दौरान हुई। ये बल अल्प जीवन काल वाले कणों के बीच अन्योन्य प्रक्रियाओं के फलस्वरूप उत्पन्न बल हैं। दुर्बल नाभिकीय बलों के गुण निम्नलिखित हैं|

1.  ये बल आकर्षणात्मक अथवा प्रतिकर्षणात्मक हो सकते हैं।
2.  ये बल कूलॉम के नियम का पालन करते हैं।
3. ये दूरी सम्बन्धी व्युत्क्रम वर्ग के नियम का पालन करते हैं।
4.  दो प्रोटॉनों के बीच स्थिर वैद्युत बल किसी भी स्थिर दूरी के लिए गुरुत्वाकर्षण बल की तुलना में 10³⁶ गुना प्रबल होते हैं।
5.  ये अधिक दरी तक प्रभावी नहीं होते हैं।
6. ये केन्द्रीय बल होते हैं।
7.  ये संरक्षी बल होते हैं।
8. विद्युत चुम्बकीय बलों का क्षेत्र कण फोटॉन होता है जिस पर कोई आवेश नहीं होता है तथा जिसका विराम द्रव्यमान शून्य होता है।

बलों का एकीकरण:
एकीकरण भौतिकी की मूलभूत खोज है। भौतिकी की महत्त्वपूर्ण उन्नति प्राय: विभिन्न सिद्धान्तों तथा प्रभाव क्षेत्रों के एकीकरण की ओर ले जाती है। न्यूटन ने पार्थिव तथा खगोलीय प्रभाव क्षेत्रों को अपने गुरुत्वाकर्षण के सर्वमान्य नियम के अधीन एकीकृत किया। ऑस्टेंड तथा फैराडे ने प्रायोगिक खोजों द्वारा दर्शाया कि व्यापक रूप में वैद्युत तथा चुम्बकीय परिघटनाएँ अविच्छेद्य हैं। मैक्सवेल की इस खोज ने, कि प्रकाश विद्युत चुम्बकीय तरंगें हैं, (UPBoardSolutions.com) विद्युत चुम्बकत्व तथा प्रकाशिकी को एकीकृत किया। आइंस्टाइन ने गुरुत्व तथा विद्युत चुम्बकत्व को एकीकृत करने का प्रयास किया परन्तु अपने इस साहसिक कार्य में सफल न हो सके। परन्तु इससे भौतिक विज्ञानियों की, बलों के एकीकरण के उद्देश्य के लिए, उत्साहपूर्वक आगे बढ़ने की प्रक्रिया रुकी नहीं।

We hope the UP Board Solutions for Class 11 Physics Chapter 1 Physical World (भौतिक जगत) help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 1 Physical World (भौतिक जगत) drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations (सम्मिश्र संख्याएँ और द्विघातीय समीकरण)

These Solutions are part of UP Board Solutions for Class 11 Maths. Here we have given UP Board Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations (सम्मिश्र संख्याएँ और द्विघातीय समीकरण).

प्रश्नावली 5.1

प्रश्न 1 से 10 तक की सम्मिश्र संख्याओं में प्रत्येक को a + ib के रूप में व्यक्त कीजिए।

प्रश्न 1.
(5i) ([latex]\frac { -3 }{ 5 }[/latex] i)
हल:

प्रश्न 2.
i⁹ + i¹⁹
हल:

प्रश्न 3.
i^-39
हल:

प्रश्न 4.
3(7 + i7) + i (7 + i7)
हल:
3(7 + i7) + i (7 + i7)
= 21 + 21i + 7i + 7i²
= 21 + 28i + 7(-1) [∵ i² = -1]
= 21 – 7 + 28i
= 14 + 28j

प्रश्न 5.
(1 – i) – (-1 + i6)
हल:
(1 – i) – (-1 + i6)
= (1 – i) + (1 – 6i) (UPBoardSolutions.com)
= 1 – i + 1 – 6i
= 2 – 7i

प्रश्न 8.
(1 – i)⁴
हल:

प्रश्न 9.
([latex]\frac { 1 }{ 3 }[/latex] + 3i)³
हल:

प्रश्न 10.
(-2 – [latex]\frac { 1 }{ 3 }[/latex] i)³

प्रश्न 11 से 13 तक की सम्मिश्र संख्याओं में प्रत्येक का गुणात्मक प्रतिलोम ज्ञात कीजिए।
प्रश्न 11.
4 – 3i.

प्रश्न 12.
√5 + 3i.

प्रश्न 13.
-i.
हल:
-1 का गुणात्मक प्रतिलोम
(UPBoardSolutions.com)

प्रश्न 14.
निम्नलिखित व्यंजक को a + ib के रूप में व्यक्त कीजिए:

प्रश्नावली 5.2

प्रश्न 1 से 2 तक सम्मिश्र संख्याओं में प्रत्येक का मापांक और कोणांक ज्ञात कीजिए:
प्रश्न 1.
z = -1 – i√3

प्रश्न 2.
-√3 + i.

प्रश्न 3 से 8 तक सम्मिश्र संख्याओं में प्रत्येक को ध्रुवीय रूप में रूपांतरित कीजिए:
प्रश्न 3.
1 – i

प्रश्न 4.
-1 + i.

प्रश्न 5.
-1 – i.

प्रश्न 6.
-3.

प्रश्न 7.
√3 + i

प्रश्न 8.
i.

प्रश्नावली 5.3

निम्नलिखित समीकरणों में से प्रत्येक को हल कीजिए:
प्रश्न 1.
x² + 3 = 0.
हल:
x² + 3 = 0 या x² = -3 या x = ± √-3 = ± √3 i.

प्रश्न 2.
2x² + x + 1 = 0.

प्रश्न 3.
x² + 3x + 9 = 0.

प्रश्न 4.
-x² + x – 2 = 0.

प्रश्न 5.
x² + 3x + 5 = 0.

प्रश्न 6.
x² – x + 2 = 0.

प्रश्न 7.
√2 x² + x + √2 = 0.

प्रश्न 8.
√3 x² – √2 x + 3√3 = 0.

प्रश्न 9.
x² + x + [latex]\frac { 1 }{ \surd 2 }[/latex] = 0

प्रश्न 10.
x² + [latex]\frac { x }{ \surd 2 }[/latex] + 1 = 0

अध्याय 5 पर विविध प्रश्नावली

प्रश्न 6 से 9 में दिए गए प्रत्येक समीकरण को हल कीजिए:

प्रश्न 6.
3x² – 4x + [latex]\frac { 20 }{ 3 }[/latex] = 0.

प्रत 7.
x² – 2x + [latex]\frac { 3 }{ 2 }[/latex] = 0.

प्रश्न 8.
21x² – 28x + 10 = 0.

We hope the UP Board Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations (सम्मिश्र संख्याएँ और द्विघातीय समीकरण) help you. If you have any query regarding UP Board Solutions for Class 11 Maths Chapter 5 Complex Numbers and Quadratic Equations (सम्मिश्र संख्याएँ और द्विघातीय समीकरण), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Home Science Chapter 2 कंकाल तन्त्र (Skeletal System)

UP Board Solutions for Class 11 Home Science Chapter 2 कंकाल तन्त्र

UP Board Class 11 Home Science Chapter 2 विस्तृत उत्तरीय प्रश्नोत्तर

प्रश्न 1.
कंकाल तन्त्र से आप क्या समझती हैं? अस्थियों की सामान्य संरचना भी स्पष्ट कीजिए।
उत्तर:
कंकाल तन्त्र (The Skeletal System):
कशेरुकी प्राणियों अर्थात् रीढ़ की हड्डी वाले प्राणियों के शरीर का अवलोकन करने पर स्पष्ट होता है कि उनके शरीर का आकार सुनिश्चित होता है। उनके शरीर में एक विशिष्ट प्रकार की दृढ़ता एवं गतिशीलता देखी जा सकती है। इन प्राणियों के शरीर के इन विशिष्ट गुणों एवं गतिविधियों को बनाए रखने के लिए अलग से एक तन्त्र या संस्थान होता है, जिसे अंस्थि संस्थान अथवा कंकाल तन्त्र (skeletal system) कहा जाता है। अस्थि संस्थान में अनेक छोटी-बड़ी अस्थियाँ होती हैं, जो परस्पर व्यवस्थित ढंग से सम्बद्ध होती हैं। ये अस्थियाँ ही सम्मिलित रूप से शरीर को निश्चित आकार तथा व्यवस्थित गति प्रदान करती हैं। अस्थियाँ ही शरीर को साधने का कार्य करती हैं। इन समस्त तथ्यों को ध्यान में रखते हुए हम कह सकते हैं कि अस्थि संस्थान या कंकाल तन्त्र शरीर का वह महत्त्वपूर्ण तन्त्र है, जो विभिन्न अस्थियों की पारस्परिक सम्बद्ध व्यवस्था द्वारा शरीर को आकार, दृढ़ता तथा गति प्रदान करता है। कंकाल तन्त्र के दो भाग माने जाते हैं

(क) बाह्य कंकाल (exoskeleton): ऐसी संरचनाएँ जो शरीर के बाहरी स्तर अर्थात् त्वचा (skin) पर स्थित होती हैं; जैसे—बाल, नाखून आदि।

(ख) अन्तःकंकाल (endoskeleton): यह अनेक पृथक्-पृथक् टुकड़ों से बना एक पिंजर या ढाँचा (framework) है। यह अधिकांशत: अस्थियों (bones) का बना होता है, जिनके सहयोग के लिए अनेक उपास्थियाँ (cartilages) भी होती हैं। एक सामान्य वयस्क व्यक्ति के शरीर में कुल 206 .. अस्थियाँ होती हैं।

अस्थियों की संरचना (Structure of Bones):
अस्थियाँ तथा उपास्थियाँ सजीव होती हैं। अस्थियों का निर्माण भ्रूणावस्था में उपास्थियों के रूप में होता है। इनमें से अधिकांश उपास्थियाँ; विभिन्न खनिजों, जैसे कैल्सियम, मैग्नीशियम आदि के कार्बोनेट्स, फॉस्फेट्स आदि के जमा हो जाने के कारण; अस्थियों के रूप में परिवर्तित हो जाती हैं तथा कुछ उपास्थियों के ही रूप में रह जाती हैं। उपास्थियों से ‘अस्थियों में परिवर्तन की इस क्रिया को अस्थिभवन (ossification) कहते हैं। अस्थियों को ढकने वाला आवरण अत्यन्त कड़ा होता है। इसे अस्थिच्छद (periosteum) कहते हैं। लम्बी अस्थियाँ खोखली होती हैं। इनकी गुहा को अस्थिगुहा । कहते हैं तथा इसमें एक विशेष गूदे जैसा पदार्थ भरा रहता है, जिसे अस्थि मज्जा (bone marrow) कहते हैं। इसी में अनेक रुधिर केशिकाएँ, तन्त्रिकाएँ आदि भी होती हैं। अस्थि मज्जा में रुधिर कणों का निर्माण होता है।
अन्त:कंकाल को स्थिति के अनुसार निम्नलिखित दो भागों में बाँटा जा सकता है

• अक्षीय कंकाल (axial skeleton) तथा
• अनुबन्धी कंकाल (appendicular skeleton)

अन्त:कंकाल को अग्रांकित तालिका द्वारा भली प्रकार समझा जा सकता है-

प्रश्न 2.
शरीर के कंकाल तन्त्र एवं अस्थियों की क्या उपयोगिता है?
अथवा “अस्थियाँ शरीर को आकृति, गति, दृढ़ता एवं सुरक्षा प्रदान करती हैं।” इस कथन को ध्यान में रखते हुए, शरीर में अस्थियों की उपयोगिता को स्पष्ट कीजिए।
अथवा टिप्पणी लिखिए-अस्थि तन्त्र के कार्य।
अथवा शरीर में अस्थि तन्त्र की क्या भूमिका है?
अथवा मानव शरीर में अस्थियों के क्या कार्य एवं महत्त्व हैं?
उत्तर:
शरीर में कंकाल तन्त्र और अस्थियों की उपयोगिता एवं कार्य (Utility and Functions of Skeletal System and Bones in Body):
कंकाल तन्त्र अर्थात अस्थियों की व्यवस्था शरीर के लिए अत्यन्त उपयोगी है। इनके निम्नलिखित महत्त्वपूर्ण कार्य हैं

शरीर को आकृति प्रदान करना: कंकाल तन्त्र शरीर को आकार प्रदान करता है। अस्थियाँ बाहर से त्वचा द्वारा ढकी रहती हैं। त्वचा तथा अस्थियों के मध्य मांसपेशियाँ होती हैं। यदि शरीर में अस्थियाँ न होती तो शरीर मांस का एक बड़ा-सा लोथड़ा होता तथा उसका सधा रह पाना सम्भव न होता।

शरीर को गति प्रदान करना: प्राणि-शरीर में अस्थि संस्थान का एक महत्त्वपूर्ण कार्य शरीर को गति प्रदान करना भी है। शरीर के विभिन्न अंगों की गति अस्थियों तथा मांसपेशियों के सहयोग से ही सम्भव हो पाती है। शरीर की कुछ अस्थियाँ तो आपस में जुड़कर उत्तोलक के रूप में कार्य करती हैं। शरीर को सुचारु रूप से गतिशील बनाने में अस्थि-संस्थान में अस्थि-सन्धियों की व्यवस्था है।

शरीर के भीतरी कोमल अंगों को सुरक्षा प्रदान करना: हमारे शरीर में कई स्थानों पर अस्थियाँ मिलकर एक खोखला सन्दूक-सा बनाती हैं, जिसमें हमारे शरीर के कोमल अंग सुरक्षित रहते हैं। उदाहरण के लिए खोपड़ी के अन्दर मस्तिष्क, पसलियों आदि से बने पिंजर में हृदय व फेफड़े तथा रीढ़ की अस्थि या कशेरुक दण्ड के तन्त्रिकीय नाल में रीढ़ रज्जु या सुषुम्ना सुरक्षित रहती है।

शरीर को दृढ़ता प्रदान करना: अस्थियों की उपस्थिति के कारण शरीर में दृढ़ता आती है। यदि शरीर में अस्थियाँ न होती तो शरीर में आघात सहने की शक्ति भी नहीं होती। अस्थियों की सहायता से ही हम भारी-से-भारी बोझ उठा सकते हैं।

रक्त कणों का निर्माण: कंकाल की अस्थियों की अस्थि-गुहा में विद्यमान अस्थि-मज्जा में लाल रक्त कणिकाओं का निर्माण होता है। यदि अस्थियों के मज्जा वाले भाग में किसी प्रकार का विकार या अनियमितता आ जाती है तो रक्त कणिकाओं का निर्माण भी अनियमित हो जाता है। अस्थियों द्वारा निरन्तर रक्त कणिकाओं के निर्माण को ध्यान में रखते हुए ही अस्थियों को लाल रक्त कणिकाओं के निर्माण की फैक्ट्रियाँ भी कहा जाता है।

पेशियों को जुड़ने का स्थान देना: विभिन्न मांसपेशियाँ अस्थियों के साथ जुड़ी होती हैं। इसी से अनेक प्रकार की गतियाँ होती हैं तथा शरीर चलने-फिरने एवं अन्य कार्य करने का आधार प्राप्त करता है। वास्तव में अस्थि-सन्धियाँ तथा मांसपेशियाँ मिलकर ही शरीर के अंगों को गतिशीलता प्रदान करती हैं।

बाहरी कंकाल के रूप में उपयोगिता: बाल तथा नाखून भी कंकाल तन्त्र के ही एक रूप हैं। कंकाल तन्त्र का यह बाहरी भाग भी हमारे लिए विशेष उपयोगी है। बाल तथा नाखून भी शरीर को अनेक प्रकार से सुरक्षा प्रदान करते हैं।

श्रवण तथा श्वसन में सहायता प्रदान करना: हमारे कंकाल तन्त्र में विद्यमान विभिन्न उपास्थियाँ श्रवण तथा श्वसन में सहायक होती हैं। वास्तव में कान के अन्दर के भाग, वायु नलिकाओं के छल्ले तथा पसलियों का कुछ भाग उपास्थि से निर्मित होता है। ये उपास्थियाँ श्रवण तथा श्वसन क्रियाओं में सहायक होती हैं।

कैल्सियम को संचित करना: हमारे शरीर के लिए कैल्सियम की विशेष उपयोगिता एवं महत्त्व है। शरीर के लिए आवश्यक कैल्सियम की अधिकांश मात्रा अस्थियों में ही संचित रहती है। इस दृष्टिकोण से भी हम अस्थियों को शरीर के लिए उपयोगी मानते हैं।

प्रश्न 3.
मानव कपाल या खोपड़ी का संक्षिप्त परिचय दीजिए। शरीर के इस भाग में पायी जाने वाली अस्थियों के नाम एवं रचना आदि बताइए।
उत्तर:
मनुष्य की खोपड़ी (skull) में कुल 22 अस्थियाँ पायी जाती हैं। इनमें से 8 अस्थियाँ मस्तिष्क कोष में तथा 14 चेहरे में पायी जाती हैं। ये अस्थियाँ ऊपर से चपटी, दोनों ओर से गोल व पीछे से अण्डाकार होती हैं। खोपड़ी हमारी गर्दन के ऊपरी भाग पर टिकी रहती है। गर्दन के सहारे खोपड़ी को विभिन्न दिशाओं में घुमाया जा सकता है। हम केवल पीछे की दिशा में खोपड़ी को नहीं घुमा सकते।

खोपड़ी की विभिन्न अस्थियाँ (Various Bones of Skull):
मानव कपाल या खोपड़ी को हम दो भागों में बाँट सकते हैं-
(1) मस्तिष्क कोष (cranium),
(2) चेहरा (face)

1. मस्तिष्क कोष (Cranium)
यह आठ अस्थियों से मिलकर बना होता है। यह एक डिब्बे (box) के समान है, जिसके अन्दर मस्तिष्क सुरक्षित रहता है। इन आठों अस्थियों का संक्षिप्त परिचय निम्नलिखित है

ललाटास्थि (frontal bone): यह कपाल या खोपड़ी के सामने की अस्थि है। इससे ललाट या मस्तक (forehead) बनता है। इसी में हमारी आँखों के दो गड्ढे भी होते हैं। यह संख्या में एक होती है।

पाश्र्वास्थियाँ (parietal bones): ये अस्थियाँ कपाल की सतह तथा अगल-बगल के भाग बनाती हैं। ये सिर की गोलाई के साथ दोनों ओर मुड़ी रहती हैं। ये सामने की ओर ललाटास्थि से पीछे की ओर पश्चादास्थि से जाकर जुड़ती हैं। ये संख्या में दो होती हैं।

पश्चादास्थि (occipital bone): यह खोपड़ी या कपाल के पीछे का भाग तथा कुछ नीचे का भाग बनाती है। इसके निचले भाग में लगभग 4 सेमी का एक गोल छिद्र बना होता है। इसको महाछिद्र (foramen magnum) कहते हैं। इसमें होकर मस्तिष्क तथा सुषुम्ना का आपस में सम्बन्ध रहता है। इस छिद्र के सामने की ओर दो उभार दिखाई देते हैं। इनकी सहायता से एक जोड़ बनता है, जिससे मनुष्य सिर को आगे व पीछे की ओर कर सकता है। यह संख्या में एक होती है।

शंखास्थि (temporal bones): इनके द्वारा कनपटी की अस्थि बनती है। इनके दोनों ओर एक-एक छिद्र होता है, जो कान के अन्दर के भाग से सम्बन्ध रखते हैं। कानों के पीछे का भाग इन्हीं अस्थियों से मिलकर बना है। ये संख्या में दो होती हैं।

जतूकास्थि (sphenoid bone): यह अस्थि देखने में पंख फैलाए चमगादड़ के समान लगती है। यह कपाल के धरातल के नीचे सामने की ओर ललाटास्थि से मिलकर चक्षुगुहा बनाती है। यह खोपड़ी या कपाल की अन्य अस्थियों के बीच जुड़ी रहती है। यह संख्या में एक होती है।

झर्झरास्थि या बहुछिद्रास्थि (ethmoid bone): कपाल में यह एक विचित्र प्रकार की अस्थि होती है जो मस्तिष्क की गुहा को नाक से पृथक् करती है। यह नाक के ऊपरी भाग में दो छिद्र बनाती है। इसमें अनेक छोटे-छोटे छिद्र होते हैं, जिनमें होकर तन्त्रिकाएँ मस्तिष्क में जाती व आती हैं। ललाटास्थि ये आठों अस्थियाँ आपस में विशेष प्रकार की अचल सन्धियों द्वारा जुड़ी रहती हैं।

2. चेहरा (Face)
इसमें 14 अस्थियाँ पायी जाती हैं, जिनके नाम एवं सामान्य परिचय इस प्रकार है-

ऊपरी जबड़े की अस्थियाँ (upper jaw bones): ये अस्थियाँ मुँह के ऊपरी भाग में होती हैं। प्रत्येक अस्थि में 8 गड्डे होते हैं, जिनके अन्दर ऊपर के 16 दाँत लगे रहते हैं। ऊपर के तालू का भाग भी इन्हीं अस्थियों से मिलकर बनता है। ये संख्या में दो होती हैं।

निचले जबड़े की अस्थि (lower jaw bone): इस अस्थि द्वारा ठोड़ी बनती है। यह चेहरे की सबसे मजबूत अस्थि है। इसमें भी 16 गड्डे पाए जाते हैं, जिनमें नीचे के 16 दाँत लगे रहते हैं। यह एक ही अस्थि होती है।

गाल या कपोलास्थियाँ (cheek bones): ये अस्थियाँ दोनों ओर के गालों का निर्माण करती हैं जिससे गाल उभरे हुए दिखाई देते हैं। ये अस्थियाँ संख्या में दो होती हैं।

तालू की अस्थियाँ (palate bones): इनके द्वारा तालू का पिछला भाग बनता है। ये संख्या में दो होती हैं।

नाक की अस्थियाँ (nasal bones): इनके द्वारा नाक के दोनों नथुनों की बाहरी दीवार बनती है। ये संख्या में दो होती हैं।

स्पंजी अस्थियाँ (spongy bones): इनके द्वारा नाक के अन्दर के भाग बनते हैं। इनका आकार सीप के समान होता है। ये स्पंज के समान मुलायम होती हैं। ये संख्या में दो होती हैं।

अश्रु अस्थियाँ (lachrymal bones): इनका सम्बन्ध अश्रुओं से होता है। इनसे होकर आँसू आँखों से नाक में आ जाते हैं। इनकी संख्या दो होती है।

नाक का पर्दा (vomer bone): इस अस्थि के द्वारा नाक दो भागों में विभाजित हो जाती है। इसकी संख्या एक होती है। इस प्रकार मस्तिष्क कोष की 8 तथा चेहरे की 14 अस्थियाँ मिलकर कपाल या खोपड़ी की कुल 22 अस्थियाँ होती हैं।

प्रश्न 4.
मेरुदण्ड में कितनी कशेरुकाएँ पायी जाती हैं? किसी एक कशेरुका का चित्र सहित वर्णन कीजिए। अथवा रीढ़ की अस्थि में झुकाव क्यों होते हैं? ये कितने होते हैं और शरीर में इनकी क्या उपयोगिता है?
उत्तर:
रीढ़ की अस्थियाँ या कशेरुक दण्ड (Vertebral Column or Back Bone):
मेरुदण्ड या कशेरुक दण्ड शरीर के लिए आधार का कार्य करता है। यह अनेक छल्ले के आकार की टेढ़ी-मेढ़ी अस्थियों की एक श्रृंखला है, जो पीठ के बीचोबीच गर्दन में प्रारम्भ होकर नीचे मलद्वार के 6-7 सेमी ऊपर तक एक स्तम्भ की भाँति फैली होती है। इसमें कुल मिलाकर 26 अस्थियाँ होती हैं। छोटे बच्चे के कशेरुक दण्ड में 33 अस्थियाँ होती हैं, बड़े होने पर नीचे की 9 अस्थियों में से पिछली 5 मिलकर एक और अन्तिम 4 मिलकर एक अस्थि बन जाती है। इस प्रकार कुल 26 अस्थियाँ रह जाती हैं। इन छोटी-छोटी अस्थियों को कशेरुकाएँ कहा जाता है। इनका वर्गीकरण इस प्रकार है-

कशेरुकाओं का वर्गीकरण (Classification of Vertebral):
एक वयस्क व्यक्ति की कशेरुक दण्ड की कुल 26 कशेरुकाओं को उनके स्थान एवं स्थिति के अनुसार पाँच वर्गों में बाँटा जाता है, जिन्हें क्रमश:
(i) ग्रीवा प्रदेश की कशेरुकाएँ,
(ii) वक्षीय कशेरुकाएँ,
(iii) कटिप्रदेशीय कशेरुकाएँ,
(iv) त्रिक कशेरुकाएँ तथा
(v) अनुत्रिक कशेरुकाएँ कहा जाता है। इन पाँचों वर्गों की कशेरुकाओं का सामान्य विवरण निम्नवर्णित है

ग्रीवा प्रदेश की कशेरुकाएँ (Cervical vertebrae): ये संख्या में 7 होती हैं और गर्दन का भाग बनाती हैं। इनकी पहली और दूसरी कशेरुका पर ही मनुष्य की खोपड़ी टिकी रहती है। कशेरुक दण्ड के इस भाग की प्रथम दो कशेरुकाओं की बनावट अन्य कशेरुकाओं की बनावट से कुछ भिन्न होती है। इनमें से पहली कशेरुका को शीर्षधरा (altas) कहते हैं तथा इसी कशेरुका पर हमारी खोपड़ी टिकी रहती है। दूसरी कशेरुका को अक्षक (axis) कहते हैं।

वक्षीय कशेरुकाएँ (Thoracic vertebrae): ये संख्या में 12 होती हैं, इनके बाहरी किनारों से पसली की अस्थियाँ जुड़ी रहती हैं। ये आगे की ओर छाती की अस्थि से जुड़कर छाती का पिंजर बनाती हैं।

कटिप्रदेशीय कशेरुकाएँ (Lumbar vertebrae): ये आकार में सबसे बड़ी तथा मजबूत होती हैं। ये सारे शरीर का भार सहन करने में सक्षम होती हैं। ये संख्या में 5 होती हैं।

त्रिक कशेरुकाएँ (Sacral vertebrae): आरम्भ में ये 5 होती हैं, किन्तु युवावस्था में आपस में मिलकर एक हो जाती हैं, जिसे त्रिकास्थि कहते हैं।

अनुत्रिक कशेरुकाएँ (Caudal vertebrae): ये अन्तिम 4 कशेरुकाएँ भी बड़े होने पर मिलकर एक हो जाती हैं, जिसे अनुत्रिकास्थि कहते हैं। इनको पूँछ की कशेरुकाएँ भी कह सकते हैं।

कशेरुकाओं की संरचना (Structure of Vertebra):

प्रथम 2 और अन्तिम 9 को छोड़कर सभी कशेरुकाओं की आकृति लगभग समान तथा नगदार अंगूठी के समान होती है। सामान्य रूप से प्रत्येक कशेरुका को तीन भागों में बाँटा जा सकता है

कशेरुककाय (Body): यह अंगूठी के नग की भाँति ठोस एवं मोटा होता है। यह कशेरुका के अगले भाग का निर्माण करता है।।

तन्त्रिका चाप (Neural arch): कशेरुककाय के पिछले भागों से मिलकर जो हिस्सा घेरा बनाता है, उसे तन्त्रिका चाप कहा जाता है। इससे बनी नली में ही सुषुम्ना रहती है।

प्रवर्ध (Projections): कशेरुका के तन्त्रिका चाप से तीन उभार निकलते हैं। घेरे के दोनों ओर के उभारों को अनुप्रस्थ प्रवर्ध तथा बीच के नुकीले उभार को तन्त्रिका कण्टक कहा जाता है।कशेरुकाएँ आपस में इस प्रकार जुड़ी रहती हैं कि मुड़ने या झुकने के बाद भी ये टूटती नहीं हैं। प्रत्येक दो कशेरुकाओं के बीच में एक उपास्थि की तह होती है, जिसके कारण कशेरुकाएँ आपस में रगड़ नहीं खाती हैं। सभी कशेरुकाएँ एक-दूसरे के ऊपर इस प्रकार रखी रहती हैं कि बीच में एक नली-सी बन जाती है, जिसे तन्त्रिका नाल (neural canal) कहते हैं।

कशेरुक दण्ड की सबसे पहली कशेरुका, जिसे एटलस या शीर्षधरा (atlas) कहते हैं, खोपड़ी के लिए आधार का कार्य करती है। इसके अगले सिरे पर 2 गोल गड्ढे होते हैं, जिनमें खोपड़ी के दोनों पश्च उभार स्थित रहते हैं। इसी प्रकार पहली ग्रीवा कशेरुका, जिसे अक्षीय कशेरुका (axis) कहते हैं, में खोपड़ी कुछ इस प्रकार स्थित रहती है कि खोपड़ी को सरलता से घुमाया जा सकता है। इस जोड़ को खूटीदार जोड़ कहते हैं।

कशेरुक दण्ड के झुकाव (Curvatures of Vertebral Column):
मनुष्यों की रीढ़ की हड्डी या कशेरुक दण्ड बिल्कुल सीधी नहीं होती बल्कि इसमें चार झुकाव होते हैं जिनका विवरण निम्नवर्णित है-
1. गर्दन का झुकाव (पीछे की ओर);
2. वक्ष का झुकाव (आगे की ओर);
3. कमर का झुकाव (पीछे की ओर);
4. श्रोणि का झुकाव (आगे की ओर)।

इन झुकावों के कारण ही मनुष्य सिर या कन्धों पर भारी बोझ आसानी से ढो सकता है क्योंकि झुकाव होने के कारण ही इनमें अधिक विस्तारण एवं संकुचन की क्षमता होती है। इसके अतिरिक्त कशेरुक दण्ड के इन झुकावों के कारण ही वक्ष तथा उदर के अंगों को आवश्यक सुरक्षा प्राप्त होती है। इन झुकावों के ही परिणामस्वरूप हमारा शरीर सधा रहता है।

इस प्रकार कशेरुक दण्ड मानव शरीर का आधार है, जिस पर सिर टिका रहता है तथा हाथ-पैर जुड़े रहते हैं। वक्ष प्रदेश की कशेरुकाओं में पसलियाँ जुड़ी रहती हैं, जो उनसे मिलकर छाती का पिंजर बनाने में सहायक होती हैं।

प्रश्न 5.
मनुष्य के वक्ष की रचना तथा कार्यों का वर्णन कीजिए।
उत्तर:
मनुष्य के वक्ष की रचना (Structure of Human Thorax):
वक्ष (thorax) की संरचना दूर से देखने पर सन्दूक (box) के समान दिखाई देती है। इसके अन्दर हृदय, फेफड़े आदि कोमल अंग सुरक्षित रहते हैं। इसका निर्माण आगे की ओर वक्षास्थि या उरोस्थि (sternum) तथा पसलियों (ribs) से तथा पीछे की ओर मेरुदण्ड (vertebral column) से होता है।

(क) उरोस्थि (Sternum):
यह छाती के सामने का भाग होता है, जो चपटा, पतला, चौड़ा तथा मजबूत होता है। इसकी लम्बाई 15 से 18 सेमी होती है। इसका ऊपरी भाग लगभग 12 से 15 सेमी चौड़ा होता है, जो नीचे तक धीरे-धीरे सँकरा होता जाता है। इस पर पसलियाँ (ribs) जुड़ी रहती हैं। उरोस्थि या वक्षास्थि को तीन प्रमुख भागों में बाँटा गया है-

1. मैनुब्रियम (manubrium): स्टर्नम के ऊपरी चौड़े भाग को मैनुब्रियम कहते हैं। इसका ऊपरी भाग अवतल होता है, जिसमें हँसली की अस्थि के भाग जुड़े रहते हैं।

2. ग्लैडियोलस (gladiolus): यह बीच का लम्बा व पतला भाग है। यह कई भागों में बँटा रहता है।

3. जिफाइड (xiphoid): यह स्टर्नम का सबसे निचला भाग है, जो छोटा तथा कार्टिलेज का बना होता है। पूरी उरोस्थि में बराबर दूरी पर 7 गड्ढे होते हैं, जिनमें पसलियों के सिरे उपास्थियों (cartilages) के द्वारा जुड़े रहते हैं।

(ख) पसलियाँ (Ribs):
वक्षास्थि या उरोस्थि (sternum) के साथ मिलकर पसलियाँ वक्ष के पिंजर का निर्माण करती हैं। इसके अन्दर अनेक कोमल अंग; जैसे हृदय, फेफड़े आदि सुरक्षित रहते हैं। पसलियाँ संख्या में 24 होती हैं। ये वक्ष में दोनों ओर 12-12 स्थित होती हैं। एक ओर की पहली 7 पसलियाँ सामने की ओर वक्षास्थि (sternum) से सीधी ही सम्बन्धित हैं। पसलियों के इन 7 जोड़ों को वास्तविक या सच्ची पसलियाँ कहते हैं। इसके बाद की पसलियाँ अर्थात् आठवीं, नवीं और दसवीं पसलियाँ वक्षास्थि से सीधी सम्बन्धित नहीं होतीं वरन् कार्टिलेज की सहायता से अपने ऊपर की पसली से जुड़ी रहती हैं। इसी कारण इन पसलियों को असत्य पसलियाँ कहते हैं।

अन्तिम दो पसलियाँ (ग्यारहवीं और बारहवीं) किसी भी रूप में वक्षास्थि से नहीं जुड़ी होती वरन् ये सामने की ओर स्वतन्त्र होकर निकली रहती हैं। ये काफी छोटी होती हैं। इन्हें प्लावी या तैरने वाली पसलियाँ (floating ribs) कहते हैं। इन दोनों पसलियों के बीच मांसपेशियाँ जुड़ी रहती हैं। ये मांसपेशियाँ साँस लेने में बहुत सहायता करती हैं। साँस लेते समय ये मांसपेशियाँ पसलियों को उठा तथा दबाकर हवा फेफड़ों में भरने तथा फेफड़ों से बाहर निकालने में बहुत सहायता करती हैं। इसी कारण इन मांसपेशियों को अन्तःपर्शका मांसपेशी भी कहते हैं।

प्रश्न 6.
शरीर की अधोशाखाओं अथवा टाँगों की अस्थियों का चित्र सहित विवरण प्रस्तुत कीजिए।
उत्तर:
अधोशाखाएँ अथवा टाँगों की अस्थियाँ (Bones of Lower Extremities or Hind limbs):
शरीर की अधोशाखा अथवा टाँग की अस्थियों की रचना को स्पष्ट करते हुए कहा जा सकता है कि इसके चार भाग होते हैं, जिनका संक्षिप्त परिचय निम्नवर्णित है

1. जंघा या ऊरु (thigh) की अस्थियाँ-इसके अन्तर्गत श्रोणि मेखला तथा घुटनों के बीच का भाग आता है। जंघा अथवा ऊरु में एक ही लम्बी अस्थि होती है, जिसे ऊर्वास्थि या ऊर्विका कहते हैं। यह शरीर की एक बहुत मजबूत और सबसे लम्बी अस्थि है। इसका ऊपरी सिरा गोल होता है और सिर कहलाता है। यह श्रोणि उलूखल में स्थित रहता है। यहाँ कन्दुक खल्लिका सन्धि पायी जाती है। इसके नीचे का कुछ भाग तिरछा होता है और ग्रीवा कहलाता है। शेष भाग गात्र है। निचला सिरा चौड़ा होता है, इसके दोनों ओर दो उभार तथा बीच में एक खाँच होती है। उसी में घुटने की अस्थि स्थित होती है।

2. पिंडली (shank) की अस्थियाँ–यह भाग घुटने से टखने के बीच पाया जाता है। घुटने के स्थान पर कब्जा सन्धि पायी जाती है। इस भाग में 2 अस्थियाँ होती हैं-
(i) अन्तःजंधिका या टिबिया (tibia) तथा
(ii) बहिःजंघिका या फिबुला (fibula)
अन्त:जंघिका पैर के अंगूठे की ओर होती है और बहि:जंघिका पैर की कनिष्ठा उँगली की ओर की अस्थि है। बहि:जंघिका का ऊपरी सिरा मोटा और चौड़ा होता है। इसका गात्र ऊपर से नीचे की ओर कुछ कम चौड़ा और चपटा होता है। इसके सिरे पर टखने की अस्थियाँ जुड़ती हैं। अन्तःजंघिका अपेक्षाकृत पतली और कमजोर होती है। इसका गात्र भी गोल पतली नली के समान होता है। ऊपरी सिरा चौकोर-सा होता है और ऊर्वास्थि से जुड़ा होता है। नीचे का सिरा एक ओर कुछ उभरा होता है और टखने की अस्थि से जुड़ा होता है।

3. घुटने की अस्थि (knee cap): इसमें एक तिकोनी अस्थि होती है, जिसे जान्त्रिका या पटेला (patella) कहते हैं। यह ऊर्विका के नीचे के सिरे पर एक छोटी अस्थि है और दोनों ओर इन अस्थियों से बँधी रहती है। टाँग की गति होने पर इसका ऊपरी भाग फिसलता हुआ प्रतीत होता है।

4. पैर (foot) की अस्थियाँ: ये तीन भागों में स्थित होती हैं-

• टखना (ankle): पैर का पिछला भाग टखना (tarsals) कहलाता है। टखने (tarsals) में 7 अस्थियाँ होती हैं। सातों अस्थियाँ एक-दूसरे से आकार में भिन्न होती हैं। इनमें 1 अस्थि, जो सबसे बड़ी होती है, एड़ी बनाती है। सातों अस्थियाँ दो पंक्तियों में बँटकर बराबर से आपस में जुड़ी रहती हैं और नीचे की ओर तलुवे की टिबिया अस्थि से जुड़ती हैं।
• तलुआ (sole): पैर के तलुवे में 5 अस्थियाँ होती हैं। इन्हें मेटाटार्सल्स (metatarsals) कहते हैं। ये पतली और लम्बी होती हैं, जो ऊपर की ओर टखने की अस्थियों से और नीचे की ओर उँगलियों की अस्थियों से होती हैं।
• उँगलियाँ या पोर (phalanges): पैर में अँगूठा और 4 उँगलियाँ होती हैं। अँगूठे में 2 और उँगलियों में 3-3 अस्थियाँ पायी जाती हैं। कुल 14 अस्थियाँ होती हैं। एक सिरे पर ये तलवे की अस्थियों से जुड़ी होती हैं तथा इनके दूसरे सिरे पर नाखून होते हैं।

प्रश्न 7.
शरीर की ऊर्ध्व शाखाओं अथवा बाहु की अस्थियों का चित्र सहित विवरण प्रस्तुत कीजिए। अथवा बाँह की हड्डियों का नामांकित सचित्र वर्णन कीजिए।
उत्तर:
ऊर्ध्व शाखाएँ अथवा बाहु की अस्थियाँ (Bones of Upper Extremities or Fore limbs):
सम्पूर्ण बाहु को हम तीन भागों में विभाजित कर सकते हैं

1. ऊपरी बाहु (Upper arm)-कन्धे से कोहनी तक का भाग ऊपरी बाहु कहलाता है। इसमें कन्धे से कोहनी तक केवल एक ही लम्बी अस्थि होती है। इस अस्थि को प्रगण्डिका या रामरस (humerus) कहा जाता है। इस अस्थि के बीच का लम्बा गोल भाग गात्र कहलाता है। ऊपर का उभरा हुआ गोल भाग अस्थि का सिर (head) कहलाता है। इस अस्थि का सिर अंस उलूखल में स्थित होकर स्कन्ध सन्धि बनाता है, जिस पर बाहु घूमती है। यह सन्धि कन्दुक खल्लिका सन्धि होती है। प्रगण्डिका के नीचे के सिरे पर एक उभार होता है, जो कोहनी पर अग्रबाहु की दोनों अस्थियों से जुड़ा रहता है।

2. अग्रबाहु (Forearm)-बाहु के नीचे कोहनी से कलाई तक का भाग अग्रबाहु कहलाता है। कोहनी पर कब्जा सन्धि होती है। इसमें दो अस्थियाँ होती हैं, जिनके नाम रेडियस या बहिःप्रकोष्ठास्थि तथा अल्ना या अन्तःप्रकोष्ठास्थि हैं। हथेली को सामने की ओर फैलाने पर बहि:प्रकोष्ठास्थि बाहर की ओर तथा अन्त:प्रकोष्ठास्थि भीतर की ओर रहती है। ये दोनों अस्थियाँ प्रगण्डिका की अपेक्षा छोटी और पतली होती हैं (अँगूठे की ओर वाली अस्थि बहिःप्रकोष्ठास्थि और कनिष्ठा या छोटी उँगली की ओर वाली अस्थि अन्तःप्रकोष्ठास्थि कहलाती है)। ऊपर की ओर केवल अन्तःप्रकोष्ठास्थि; प्रगण्डास्थि के निचले जान्विका भाग से मिलकर कोहनी की सन्धि बनाती है। नीचे की ओर ये दोनों अस्थियाँ कलाई की 8 अस्थियों में से प्रथम पंक्ति की 4 अस्थियों से मिलकर कलाई या बहिःप्रकोष्ठास्थि मणिबन्ध की सन्धि बनाती हैं।

हाथ की अस्थियों को हम तीन भागों में बाँट सकते हैं-
(i) कलाई,
(ii) हथेली तथा
(iii) उँगलियाँ।
कलाई में विभिन्न आकार की 8 छोटी-छोटी अस्थियाँ होती हैं, जो एक-दूसरे से पृथक् होती हैं, किन्तु दृढ़ स्नायुओं के द्वारा एक-दूसरे से जुड़ी रहती हैं।

3. हाथ (Hand): इसके नीचे हथेली की 5 अंगुलास्थियाँ अस्थियाँ होती हैं, जिन्हें करभास्थि (metacarpals) कहते हैं। इनके ऊपरी सिरे कलाई की ओर कुछ चौकोर से रहते हैं और कलाई की अस्थियों को नीचे की पंक्ति से बाँधे रहते हैं। पाँचों करभास्थियों के आकार में थोड़ा-थोड़ा अन्तर होता है। अंगूठे से जुड़ने वाली अस्थि सबसे छोटी और मोटी होती है। कनिष्ठा उँगली से जुड़ने वाली अस्थि सबसे पतली और बीच की उँगलियों से जुड़ने वाली अस्थि सबसे लम्बी होती है। अँगूठे में 2, शेष चारों उँगलियों में 3-3 अस्थियाँ पायी जाती हैं। इस प्रकार हाथ में कुल 14 अस्थियाँ होती हैं।


प्रश्न 8.
मानव शरीर की अंस मेखला और श्रोणि मेखला की अस्थि-संरचना का चित्र सहित वर्णन चित्र 2.8-हाथ की अस्थियाँ। कीजिए।
उत्तर:
(क) मनुष्य की अंस मेखला (Pectoral girdle of Man):
मनुष्य की अंस मेखला के दोनों अर्द्ध-भाग अलग-अलग होते हैं। प्रत्येक अर्द्ध-भाग एक तिकोनी और चपटी अस्थि से बना होता है, जिसे स्कैपुला (scapula) कहते हैं। यह भाग पीठ व गर्दन के दोनों ओर तथा पसलियों के पीछे स्थित होता है। अस्थि का चौड़ा भाग ऊपर की ओर तथा नुकीला भाग नीचे की ओर होता है। स्कैपुला के पीछे के भाग में एक उभार होता है, जो एक उठी हुई छोटी-सी दीवार की तरह लगता है। यह कण्टक (spine) कहलाता है। इसी के कारण अंस मेखला दो भागों में विभाजित हो जाती है।

अंस मेखला का ऊपरी भाग चपटा हो जाता है। इसे ऐक्रोमियन प्रवर्ध (acromian process) कहते हैं। इसी भाग से हँसली की अस्थि जुड़ी रहती है, जिससे मनुष्य में उठे हुए कन्धे (shoulders) बन जाते हैं। इसी सिरे के पास स्कैपुला में एक गड्ढा होता है, जिसे अंस उलूखल (glenoid cavity) कहते हैं। इस गड्ढे में अग्रबाहु की प्रगण्डिका (humerus) का गोल सिर स्थित रहता है। यह जोड़ (सन्धि) कन्दुक-खल्लिका सन्धि कहलाता है। इसीलिए हम हाथ को चारों ओर सुविधापूर्वक घुमा सकते हैं। अंस मेखला भी पसलियों के साथ केवल मांसपेशियों से जुड़ी रहती है।

अंस मेखला के कार्य (Functions of Pectoral girdle):
अंस मेखला विशेष कार्यों के कारण एक महत्त्वपूर्ण अस्थि है। इसके कार्य इस प्रकार हैं

• कन्धे का निर्माण इस अस्थि के द्वारा ही होता है।
• हँसली की अस्थि का एक सिरा इसी से जुड़ा रहता है जिसका दूसरा सिरा स्टर्नम से जुड़ा रहता है।
• इसी अस्थि के अंस उलूखल में अग्रबाहु (प्रगण्डिका) का ऊपरी भाग (सिर) स्थित होता है। एक विशेष प्रकार की सन्धि होने के कारण ही भुजा चारों ओर आसानी से घुमाई जा सकती है।

(ख) श्रोणि मेखला (Pelvic girdle):
मनुष्य के उदर के नीचे कूल्हे के भाग में कई अस्थियों का सम्मिलित रूप होता है, जिसे श्रोणि मेखला (pelvic girdle) कहते हैं।
श्रोणि मेखला दो अर्धांशों से मिलकर बनी होती है। इसके दोनों अर्द्ध-भाग पीछे और सामने आपस में जुड़कर एक घेरा बनाते हैं, जो पुरुषों की अपेक्षा स्त्रियों में अधिक चौड़ा होता है। दोनों ओर की श्रोणि मेखलाएँ रचना में समान होती हैं। बालकों में प्रत्येक श्रोणि मेखला अलग-अलग रहती है। बड़े होने पर ये एक-दूसरे से जुड़ हैं और उदर गुहा (abdominal cavity) का निचला भाग बनाती हैं। इसी भाग में अनेक अनुत्रिकास्थि । आन्तरांग सुरक्षित रहते हैं। प्रत्येक कूल्हे की अस्थि के ऊपरी भाग में प्याले के आकार का गड्डा-सा होता है, जिसे श्रोणि उलूखल या ऐसीटाबुलम (acetabulum) कहते हैं। इसी गड्ढे में टाँग की अस्थि ऊर्वास्थि (femur) का सिरा फँसा रहता है। प्रत्येक श्रोणि मेखला के तीन भाग होते हैं-

• इलियम (ileum) या नितम्बास्थि: यह श्रोणि मेखला का ऊपरी चौड़ा तथा चपटा भाग होता है, जो पीछे की तरफ त्रिकास्थि (sacrum) से जुड़ा रहता है।
• इश्चियम (ischium) या आसनास्थि: यह नीचे वाला सबसे छोटा तथा गाँठदार भाग है। हमारा शरीर इन्हीं गाँठों पर सधा रहता है तथा इन्हीं से हमें बैठने में सहायता मिलती है।
• प्यूबिस या जंघास्थि (pubis): श्रोणि मेखला का यह भाग इलियम तथा इश्चियम के मध्य होता है। यह अस्थि छोटे आकार की होती है।

श्रोणि मेखला के कार्य (Functions of Pelvic girdle):
श्रोणि मेखला के कार्य निम्नलिखित हैं-

• इससे बैठने तथा शरीर को साधने में सहायता मिलती है।
• इसके श्रोणि उलूखल में टाँगों की अस्थि का ऊपरी भाग सन्धि बनाता है।
• इसके द्वारा कूल्हे का निर्माण होता है।
• इससे हम अपने पैरों को घुमा सकते हैं।

प्रश्न 9.
अस्थि सन्धि से क्या आशय है? शरीर में पायी जाने वाली विभिन्न अस्थि सन्धियों का सामान्य परिचय दीजिए।
अथवा अस्थि सन्धि कितने प्रकार की होती हैं? मानव शरीर में इनका क्या कार्य है?
अथवा चल सन्धि के प्रकार लिखिए। ऐसी किसी एक प्रकार की सन्धि का वर्णन कीजिए।
अथवा चल सन्धियों के प्रकार उदाहरणसहित समझाइए।
अथवा गेंद-गड्डा सन्धि का चित्र बनाइए।
उत्तर:
अस्थि सन्धि (Bone Joints):
कशेरुकीय जन्तुओं के शरीर में अनेक छोटी-बड़ी अस्थियाँ होती हैं, जो किसी-न-किसी रूप में एक-दूसरे से जुड़ी रहती हैं और शरीर का ढाँचा बनाकर इसे विशिष्ट आकार प्रदान करती हैं। शरीर में दो या अधिक अस्थियों के मिलने के स्थान एवं व्यवस्था को अस्थि-सन्धि या अस्थि-जोड़ (joint) कहते हैं। सन्धि स्थल पर कुछ मजबूत सूत्र या तन्तु जुड़े रहते हैं, जो इनको बाँधने में सहायता करते हैं।

इसके अतिरिक्त सन्धि स्थल पर मिलने वाले स्थान उपास्थि आदि से ढके रहते हैं। अस्थि सन्धियों की शरीर में महत्त्वपूर्ण भूमिका एवं कार्य हैं। सन्धियाँ शरीर के विभिन्न अंगों की गति पर नियन्त्रण करती हैं। प्राणियों की शारीरिक गतिविधियों को सम्भव बनाने के लिए ही अस्थि-सन्धियों की व्यवस्था है। अस्थि-सन्धियों के ही कारण व्यक्ति विभिन्न प्रकार की सुव्यवस्थित गतियाँ करता है तथा विशिष्ट कार्य करता है। अस्थि-सन्धियों का प्रमुख कार्य शरीर को गतिशीलता एवं क्रियाशीलता प्रदान करना है।

अस्थि सन्धियो के प्रकार (Kinds of Bone Joints):
अस्थि सन्धियाँ तीन प्रकार की होती हैं-
(1) पूर्ण सन्धि या चल सन्धि,
(2) अपूर्ण सन्धि, तथा
(3) अचल सन्धि।

1. पूर्ण सन्धि (Perfect joint): इन्हें चल सन्धि भी कहते हैं। इस सन्धि में भाग लेने वाली अस्थियों के सिरों पर उपास्थि की टोपी मढ़ी रहती है। दोनों जुड़ने वाली अस्थियों के बीच थोड़ी-सी जगह रहती है, जो साइनोवियल गुहा (synovial cavity) कहलाती है। यह साइनोवियल कला (synovial membrane) से ढकी रहती है। साइनोवियल गुहा में साइनोवियल द्रव (synovial fluid) भरा रहता है। इस प्रकार द्रव भरी एक थैली बन जाती है, जिसे साइनोवियल कैप्सूल कहते हैं। बाहर की ओर दोनों अस्थियों के सिरे स्नायु (ligaments) चित्र द्वारा परस्पर जुड़े रहते हैं। पूर्ण सन्धि या चल सन्धि निम्नलिखित प्रकार की होती हैं-

कन्दुक-खल्लिका सन्धि (ball and socket अंस मेखला joint): इसे गेंद-गड्डा सन्धि भी कहते हैं। इस सन्धि में एक अस्थि का गोल उभरा सिरा दूसरी अस्थि के सिरे पर पाए जाने वाले गड्डे में स्थित रहता है। इससे उभरे सिरे वाली अस्थि चारों ओर घुमाई जा सकती है। कूल्हे का जोड़ तथा कन्धे का जोड़ इसके उदाहरण हैं।

कब्जा सन्धि (hinge joint): इस सन्धि के अन्तर्गत एक अस्थि के सिरे का उभार दूसरी अस्थि के गड्डे में इस प्रकार फिट होता है कि उभरे सिरे वाली अस्थि दरवाजे की तरह केवल एक ही दिशा में पूरी मुड़ती है। विपरीत दिशा में गति नहीं हो सकती। घुटने, कुहनी तथा उँगलियों के पोरों के जोड़ इसके उदाहरण हैं। रेडियस

विवर्त या खुंटी सन्धि (pivot joint): इसमें एक अस्थि खूटी की तरह स्थिर रहती है तथा दूसरी अस्थि इसके गड्डे द्वारा इसके ऊपर फिट होकर चारों ओर घूमती है। स्तनधारियों में दूसरे कशेरुक, प्रथम ग्रीवा कशेरुक के ओडोण्टॉइड प्रवर्ध (odontoid process), शीर्षधरा (atlas) तथा खोपड़ी की सन्धि इसी प्रकार की सन्धि है। इस प्रकार की अस्थि-सन्धि को अंगठे का धुराग्र सन्धि भी कहा जाता है।

पर्याण या सैडिल सन्धि (saddle joint): यह कार्पल सन्धि कन्दुक-खल्लिका सन्धि से मिलती-जुलती है, परन्तु इसमें बॉल तथा सॉकेट दोनों ही कम विकसित होते हैं। हाथ के अंगठे की चित्र 2.15–सैडिल सन्धिा मेटाकार्पल्स तथा कार्पल्स के बीच ऐसी ही सन्धि होती है। इसी सन्धि के कारण अंगठा अन्य उँगलियों की अपेक्षा रेडियस 7 अल्ना इधर-उधर अधिक घुमाया जा सकता है।

var en farauf het (gliding joint): इसमें दोनों अस्थियाँ एक-दूसरी पर फिसल सकती हैं। कार्पल्स – कशेरुकों के योजी प्रवर्धा (zygapo-physes) के बीच तथा प्रबाहु की रेडियोअल्ना और कलाई के बीच इसी प्रकार की सन्धि पायी जाती है।

2. अपूर्ण सन्धि (Imperfect joint): इस प्रकार की सन्धि में दोनों अस्थियाँ केवल उपास्थियों द्वारा एक-दूसरी से जुड़ी होती हैं। इनमें गति बहुत ही सीमित होती है। दोनों प्यूबिस अस्थियों के बीच ऐसी ही सन्धि होती है।

3. अचल सन्धि (immovable joint): इसमें अस्थियाँ सीवन (sutures) द्वारा परस्पर जुड़ी रहती हैं और हिलने-डुलने में असमर्थ होती हैं। इसीलिए इसे अचल सन्धि कहते हैं। खोपड़ी की अस्थियों में इसी प्रकार की सन्धियाँ होती हैं।

UP Board Class 11 Home Science Chapter 2 लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
मानव शरीर में पायी जाने वाली अस्थियों के विभिन्न प्रकारों का उल्लेख कीजिए।
उत्तर:
अस्थियों के प्रकार
प्रायः सभी अस्थियों की आन्तरिक रचना एकसमान होती है, परन्तु उनके बाहरी आकार में पर्याप्त भिन्नता पायी जाती है। आकार की भिन्नता के आधार पर मानव शरीर की अस्थियों के निम्नलिखित प्रकार हैं

• लम्बी अस्थियाँ (Long bones): इनका आकार लम्बा होता है। इन अस्थियों के दो सिरे होते हैं, दोनों सिरों पर ये मुठिया के समान गोल होती हैं। बाँहों तथा टाँगों की अस्थियाँ इसी प्रकार की होती हैं। ये अस्थियाँ ऊपर से कड़ी तथा अन्दर से खोखली होती हैं। इस खोखली जगह को मज्जा गहा कहते हैं जिसमें अस्थि-मज्जा भरा रहता है। मांसपेशियों की सहायता से इन अस्थियों में गति उत्पन्न होती है।
• चपटी अस्थियाँ (Flat bones): ये अस्थियाँ आकार में चपटी होती हैं और ऐसे स्थानों पर पायी जाती हैं, जहाँ सुरक्षा की आवश्यकता अधिक होती है। इस प्रकार की अस्थियाँ सामान्य रूप से आपस में मिलकर ऐसी रचना का निर्माण करती हैं, जिसमें शरीर के कोमल अंग सुरक्षित रहते हैं। खोपड़ी, चेहरे, पीठ एवं छाती इत्यादि की अस्थियाँ इसी प्रकार की होती हैं।
• घनाकार अस्थियाँ (Cubical bones): ये अस्थियाँ शरीर में ऐसे स्थानों पर पायी जाती हैं, जहाँ पर शक्ति की आवश्यकता होती है। ये अस्थियाँ ऊपर से कठोर तथा अन्दर से खोखली होती हैं; जैसे—कलाई तथा टखने की अस्थियाँ।
• छोटी अस्थियाँ (Small bones): ये अस्थियाँ पतली तथा कुछ छोटी होती हैं; जैसे-हथेली तथा उँगलियों की अस्थियाँ।
• वक्राकार अस्थियाँ (Curved bones): इन अस्थियों का आकार समान नहीं होता है। ये कहीं गोल, कहीं लम्बी, चौड़ी या कहीं नुकीली होती हैं। उदाहरण के लिए रीढ़ की अस्थि, कनपटी तथा जबड़े की अस्थियाँ इत्यादि।
• विषम अस्थियाँ (Irregular bones): इनका आकार विषम होता है। इस प्रकार का उदाहरण मेरुदण्ड की अस्थियाँ हैं।

प्रश्न 2.
मानव कंकाल के मुख्य भागों तथा अस्थियों की संख्या का उल्लेख कीजिए।
उत्तर:
मानव कंकाल के मुख्य भाग तथा अस्थियों की संख्या
मनुष्य के अस्थिपंजर अर्थात् कंकाल तन्त्र का अध्ययन प्रमुख रूप से तीन भागों में बाँटकर करते हैं

1. खोपड़ी (Skull): खोपड़ी अन्दर से खोखली होती है, जिसमें मस्तिष्क स्थित होता है। इसके आगे की ओर कुछ विषम अस्थियाँ होती हैं, जिनके द्वारा मनुष्य के चेहरे तथा निचले जबड़े को आकार मिलता है। खोपड़ी कुल 22 अस्थियों के मिलने से बनती है। ऊपरी भाग 8 अस्थियों से मिलकर बना होता है जिसमें मस्तिष्क सुरक्षित रहता है। ये सभी अस्थियाँ चपटी, पतली तथा दृढ़ होती हैं। चेहरे में कुल 14 अस्थियाँ होती हैं, जिनमें कुछ बड़ी तथा कुछ छोटी होती हैं।

2. धड़ (Trunk): कंकाल तन्त्र का यह दूसरा भाग है जो कि कुल 64 अस्थियों से मिलकर बनता है। इसमें 33 अस्थियाँ रीढ़ में होती हैं तथा 24 पसलियाँ होती हैं। इनके अतिरिक्त 1 छाती की, 2 कन्धे की, 2 हँसली की तथा 2 मेखला की अस्थियाँ होती हैं।

3. ऊर्ध्व तथा अधर शाखाएँ (Upper and lower extremities): कंकाल तन्त्र के इस भाग के अन्तर्गत ऊपरी बाहु, अग्रबाहु, हाथ तथा जंघा, घुटना, पैर इत्यादि की अस्थियाँ आती हैं। इन भागों में 60 अस्थियाँ हाथों या बाँहों में तथा 60 ही टाँगों या पैरों में होती हैं।
इस प्रकार मानव कंकाल में कुल मिलाकर 206 अस्थियाँ होती हैं।

प्रश्न 3.
अस्थियाँ लाल रक्त कणों के निर्माण की फैक्टरियाँ क्यों कही जाती हैं? समझाइए।
उत्तर:
मनुष्य सहित सभी स्तनधारियों की लम्बी अस्थियों में खोखले स्थान अर्थात् मज्जा गुहा (marrow cavity) होती है। इस गुहा में एक गूदे के समान पदार्थ भरा रहता है। इस पदार्थ को अस्थि मज्जा (bone marrow) कहते हैं। अस्थि मज्जा में रुधिर केशिकाएँ, तन्त्रिकाएँ आदि होती हैं। इसी मज्जा में लाल रक्त कणिकाओं (red blood corpuscles) का निर्माण होता है। इसीलिए अस्थियों को ‘लाल रक्त कणों के निर्माण की फैक्टरी’ कहा जाता है। मनुष्य में लाल रक्त कण थोड़े ही समय तक जीवित रहते हैं; अत: मृत हुए कणों के स्थान पर नए लाल रक्त कण सदैव ही आवश्यक होते हैं। इसीलिए इनका निर्माण भी सदैव होते रहना चाहिए और यह कार्य अस्थियाँ सदैव करती रहती हैं; अर्थात् इनमें उत्पादन भी सदैव ही होता रहता है।

प्रश्न 4.
हमारे शरीर के कोमल अंगों की सुरक्षा अस्थियाँ किस प्रकार करती हैं? स्पष्ट कीजिए। .
उत्तर:
अस्थियों द्वारा कोमल अंगों की सुरक्षा
अस्थियाँ शरीर के लगभग सभी अंगों को सुरक्षा प्रदान करती हैं, परन्तु शरीर में जो अति कोमल किन्तु विशिष्ट अंग हैं, उनको ये विशेष प्रकार की संरचनाएँ स्थान, कोष्ठ या सन्दूक के समान आकार बनाकर विशेष सुरक्षा प्रदान करती हैं। उदाहरण के लिए आँख, कान, नाक जैसी अति महत्त्वपूर्ण, संवेदनशील तथा कोमल ज्ञानेन्द्रियों को विशेष सुरक्षा; अस्थियाँ अक्षिकोष्ठ (orbit), श्रवण कोष्ठ (auditory capsule) तथा घ्राण कोष्ठ (olfactory chamber) बनाकर देती हैं।

हमें ज्ञात है कि मस्तिष्क एक अति कोमल अंग है और सम्पूर्ण शरीर की समस्त क्रियाओं पर यह किसी-न-किसी प्रकार तन्त्रिकीय नियन्त्रण रखता है। मस्तिष्क करोटि (cranium) में स्थित होता है, जो एक बन्द सन्दूक के समान संरचना है। सुषुम्ना कशेरुक दण्ड की तन्त्रिकीय नाल में सुरक्षित रहती है। फेफड़े, हृदय आदि संरचनाओं को तो अपनी क्रियाशीलता के लिए विशेष स्थान भी चाहिए और असीम सुरक्षा भी। यह सुरक्षा वक्षीय पिंजर (thoracic cage) बनाकर कशेरुक दण्ड, उरोस्थि तथा पसलियाँ देती हैं। अंस मेखला, श्रोणि मेखलाओं आदि की संरचना भी इसी प्रकार मेहराबदार होती है, जो विभिन्न आन्तरांगों को पूर्ण तथा महत्त्वपूर्ण सुरक्षा देने में सक्षम है।

प्रश्न 5.
शरीर के लिए अस्थि सन्धियों के महत्त्व का उल्लेख कीजिए। अथवा मानव शरीर में अस्थि सन्धियों का क्या कार्य है?
उत्तर:
शरीर के लिए अस्थि सन्धियों का महत्त्व अथवा कार्य
अस्थि-संस्थान की सुचारु क्रियाशीलता तथा शरीर की समस्त गतिविधियों के लिए अस्थि सन्धियाँ विशेष रूप से आवश्यक तथा महत्त्वपूर्ण हैं। वास्तव में, शरीर में अस्थि सन्धियों की उपस्थिति के कारण ही विभिन्न गतियाँ होती हैं। गमन भी इसका ही उदाहरण है। यदि शरीर में अस्थि सन्धियाँ न होतीं तो समस्त शरीर एक गतिहीन मूर्ति की भाँति होता तथा चल-फिर भी नहीं पाता। शरीर द्वारा श्वास लेना, शरीर का झुकाव आदि भी अस्थियों के मध्य पायी जाने वाली सन्धियों पर ही निर्भर होता है। विभिन्न प्रकार की इन गतियों के लिए सन्धियों का प्रकार भी निश्चित होता है।

किसी अंग के किसी विशेष दिशा में गति करने के लिए एक विशेष प्रकार की सन्धि की ही व्यवस्था होती है; उदाहरण के लिए कुहनी की सन्धि एक कब्जेदार सन्धि है जो हाथ को पीछे मुड़ने से रोकती है, जबकि कन्धे की सन्धि जो एक कन्दुक-खल्लिका सन्धि है, सम्पूर्ण बाहु को किसी भी दिशा में घूमने देती है। इसी प्रकार कशेरुकदण्ड के साथ खोपड़ी की सन्धि अत्यन्त महत्त्वपूर्ण है जो बिना शरीर घुमाए खोपड़ी को इधर-उधर घुमाने में सहायता प्रदान करती है। यह एक खूटीदार सन्धि है। इसमें गति न होने से इन सन्धियों के मध्य मस्तिष्क सुरक्षित एक स्थान पर स्थिर रहता है। इनकी उपस्थिति के कारण बाल्यावस्था में मस्तिष्क इत्यादि के विकसित होने में कोई बाधा नहीं पड़ती। बाद में ये सन्धियाँ अचल हो जाती हैं और मजबूत कपाल का निर्माण करती हैं। इस प्रकार स्पष्ट है कि अस्थि सन्धियाँ हमारे शरीर के लिए अनेक प्रकार से उपयोगी हैं।

प्रश्न 6.
अस्थि सन्धियों में होने वाली विभिन्न गतियों का उल्लेख कीजिए।
उत्तर:
अस्थि सन्धियों में होने वाली गतियाँ
हमारे शरीर में विद्यमान अस्थि सन्धियों के परिणामस्वरूप निम्नलिखित गतियाँ होती हैं

1. संकुचन (Contraction): जब एक अंग दूसरे अंग की तरफ खिंचता है तो उसे संकुचन कहते हैं। उदाहरण के लिए कुहनी मोड़कर अग्रबाहु को पश्चबाहु के पास लाया जा सकता है। इसे कुहनी का संकुचन कहेंगे।

2. फैलना (Extension): यह उपर्युक्त क्रिया के विपरीत क्रिया होती है; जैसे-अग्रबाहु का सामने की तरफ फैलने के बाद बाहु से दूर चला जाना।

3. पर्यावर्तन (Circumduction): जब कोई अंग अपने अक्ष पर इस प्रकार घूमे कि चारों ओर घूमकर एक शंकु बन जाए तो इस प्रकार की गति को पर्यावर्तन कहते हैं। अस्थि सन्धियों की उपर्युक्त मुख्य गतियों के अतिरिक्त दो अन्य प्रकार की गतियाँ भी देखी जा सकती हैं, जिन्हें क्रमश: अभिवर्तन तथा अपवर्तन कहा जाता है। अभिवर्तन (Adduction) के अन्तर्गत शरीर के किसी अंग को शरीर की मध्य रेखा की ओर खींचने की क्रिया होती है। इससे भिन्न अपवर्तन (Abduction) के अन्तर्गत शरीर के किसी अंग को शरीर की मध्य रेखा से बाहर की ओर ले जाया जाता है।

प्रश्न 7.
मनुष्यों द्वारा बाहुओं एवं सिर को घुमाने की क्रिया को स्पष्ट कीजिए।
उत्तर:
मनुष्य अपनी बाहुओं को कन्धे के स्थल से विभिन्न दिशाओं में सरलता से घुमा लेता है तथा सिर को भी विभिन्न दिशाओं में सरलता से घुमा सकता है। बाहुओं एवं सिर की इन गतियों के लिए अस्थि सन्धियाँ ही जिम्मेदार हैं। इन स्थलों पर होने वाली गतियों का स्पष्टीकरण निम्नवर्णित है-

(क) बाहुओं को चारों तरफ घुमाने की क्रिया का स्पष्टीकरण:
मनुष्य की बाहु में एक अस्थि का सिरा गेंद के समान गोल होता है और दूसरी अस्थि का सिरा प्याले की तरह होता है। गेंद वाला सिरा, प्यालेनुमा आकार वाले सिरे में स्थित रहता है और इसे सरलता से चारों ओर घुमाया जा सकता है। कन्धे में प्रगण्डिका (humerus) अस्थि का गोल सिरा अंस फलक के प्यालेनुमा गड्ढे, अंस उलूखल (acetabulum) में स्थित होकर घूमता है; अतः मनुष्य अपनी बाहुओं को चारों तरफ घुमा सकता है।

(ख) सिर को घुमाना:
मनुष्य का सिर (खोपड़ी) रीढ़ की अस्थि (कशेरुक दण्ड) के साथ एक विशेष प्रकार की सन्धि बनाता है। इसको बनाने में प्रथम और द्वितीय कशेरुकाओं की अत्यधिक स्पष्ट भूमिका होती है। वास्तव में प्रथम ग्रीवा कशेरुक, जिसे अक्षीय कशेरुक कहते हैं, से एक खूटी की तरह का प्रवर्ध निकला रहता है, जिस पर खोपड़ी में उपस्थित गड्डा टिका रहता है। इस प्रकार की सन्धि को विवर्त अथवा खूटी सन्धि (pivot joint) कहते हैं। इस प्रकार की सन्धि के कारण ही हम अपने सिर को इधर-उधर, केवल पीछे की दिशा को छोड़कर सरलता से घुमा सकते हैं।

प्रश्न 8.
कोहनी की सन्धि का संक्षिप्त वर्णन कीजिए।
उत्तर:
कोहनी की सन्धि
यह एक कब्जेदार सन्धि (hinge joint) है। यह ऊपर की ओर प्रगण्डास्थि (humerus) तथा नीचे की ओर बहिःप्रकोष्ठास्थि (radius) व अन्तःप्रकोष्ठास्थि (ulna) के साथ मिलकर बनी सन्धि है। इन अस्थियों में से प्रगण्डास्थि का सिरा तो गोल तथा घिरौं (pulley) की तरह होता है, जिसे ट्रॉक्लिया (trochlea) कहते हैं तथा अन्तःप्रकोष्ठिका अपेक्षाकृत बड़ी होती है और एक प्रवर्ध के रूप में ऊपर की ओर निकली रहती है। इसको ऑलीक्रेनन प्रवर्ध (olecraneon process) कहते हैं। इसी प्रवर्ध के पीछे भीतर की ओर इस अस्थि पर एक गहरा गड्ढा होता है, जिसे सिगमॉइड कूप (sigmoid notch) कहते हैं। इसी खात (गड्डे) में प्रगण्डास्थि की ट्रॉक्लिया फँसी रहती है और चल जोड़ बनाती है। प्रवर्ध के कारण इस जोड़ की विशेषता है कि यह अग्रबाहु को केवल आगे की ओर मुड़ने देता है, बाहर या पीछे की ओर नहीं और एक कब्जे की तरह कार्य करता है।

प्रश्न 9.
यदि अस्थि टूट जाती है तो उसका प्राथमिक उपचार किस प्रकार से होता है? अथवा हड्डी टूट का उपचार लिखिए।
उत्तर:
अस्थि की टूट का उपचार
किसी भी प्रकार से अस्थि के टूट जाने पर तुरन्त किए जाने वाले मुख्य प्राथमिक उपचार निम्नलिखित हैं-

• तुरन्त किसी अस्थि विशेषज्ञ से सम्पर्क करना चाहिए।
• जिस अंग की अस्थि टूट गई हो, उस अंग को खपच्चियों का सहारा देकर सही स्थिति में रखकर तिकोनी पट्टी बाँध देनी चाहिए। .
• यदि कोहनी तथा कलाई के आस-पास की अस्थि टूटी हो तो झोली द्वारा सहारा देना चाहिए। (4) यदि अस्थि के टूटने के साथ-साथ रक्त भी बह रहा हो तो सर्वप्रथम रक्तस्राव रोकना चाहिए।
• यदि व्यक्ति आघात से अथवा भय से मूछित हो गया हो तो उसे होश में लाने का प्रयत्न करना चाहिए।
• जिस व्यक्ति की अस्थि टूटी हो उसे इस प्रकार लिटाया जाना चाहिए कि उसे पूरा आराम मिल सके। उसे अधिक हिलाना-डुलाना नहीं चाहिए।
• घायल व्यक्ति का साहस बढ़ाना चाहिए। उससे सहानुभूति रखनी चाहिए।
• शरीर को गर्म रखने के लिए कोई गर्म पेय पदार्थ देना चाहिए।

UP Board Solutions for Class 11 Home Science Chapter 2 अति लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
‘अस्थि संस्थान’ अथवा ‘कंकाल तन्त्र’ का अर्थ एक वाक्य में लिखिए।
उत्तर:
शरीर में विद्यमान समस्त अस्थियों की व्यवस्था को ही अस्थि संस्थान या कंकाल तन्त्र कहते हैं।

प्रश्न 2.
अस्थि संस्थान की उपयोगिता संक्षेप में लिखिए। अथवा शरीर में अस्थियों की क्या उपयोगिता है?
उत्तर:
अस्थि संस्थान शरीर को आकृति, गति, दृढ़ता तथा सुरक्षा प्रदान करता है। यह लाल रक्त कणों के निर्माण का कार्य तथा मांसपेशियों के जुड़ने का स्थान प्रदान करता है।

प्रश्न 3.
शरीर की अस्थियाँ छूने में कैसी प्रतीत होती हैं?
उत्तर:
शरीर की अस्थियाँ छूने में कठोर प्रतीत होती हैं।

प्रश्न 4.
अस्थियों की बनावट कैसी होती है?
उत्तर:
अस्थियाँ बाहर से कठोर तथा अन्दर से खोखली होती हैं।

प्रश्न 5.
अस्थियों के खोखले भाग को क्या कहते हैं?
उत्तर:
अस्थियों के खोखले भाग को ‘अस्थि-गुहा’ कहते हैं।

प्रश्न 6.
उपास्थियों से अस्थियों में परिवर्तन की क्रिया को क्या कहते हैं?
उत्तर:
उपास्थियों से अस्थियों में परिवर्तन की क्रिया को अस्थिभवन (ossification) कहते हैं।

प्रश्न 7.
अस्थियों को मजबूत करने के लिए कौन-सा तत्त्व महत्त्वपूर्ण है?
उत्तर:
अस्थियों को मजबूत करने के लिए ‘कैल्सियम’ नामक तत्त्व महत्त्वपूर्ण है।

प्रश्न 8.
अस्थि-गहा में क्या भरा रहता है?
उत्तर:
अस्थि-गुहा में ‘अस्थि-मज्जा’ नामक गूदेदार पदार्थ भरा रहता है।

प्रश्न 9.
मानव शरीर में कुल कितनी अस्थियाँ पायी जाती हैं?
उत्तर:
मानव शरीर में कुल 206 अस्थियाँ पायी जाती हैं।

प्रश्न 10.
मानव शरीर में कितने प्रकार की अस्थियाँ पायी जाती हैं?
उत्तर:
मानव शरीर में छह प्रकार की अस्थियाँ पायी जाती हैं, जिन्हें लम्बी, चपटी, घनाकार, छोटी, वक्राकार तथा विषम अस्थियाँ कहा जाता है।

प्रश्न 11.
मानव शरीर में लम्बी अस्थियाँ कहाँ-कहाँ पायी जाती हैं?
उत्तर:
मानव शरीर में लम्बी अस्थियाँ बाँहों तथा टाँगों में पायी जाती हैं।

प्रश्न 12.
मानव कपाल में किस प्रकार की अस्थियाँ पायी जाती हैं?
उत्तर:
मानव कपाल में चपटी अस्थियाँ पायी जाती हैं।

प्रश्न 13.
मानव शरीर में छोटी अस्थियाँ मुख्य रूप से कहाँ-कहाँ पायी जाती हैं?
उत्तर:
मानव शरीर में हाथों तथा पैरों की उँगलियों में छोटी अस्थियाँ पायी जाती हैं।

प्रश्न 14.
खोपड़ी में कुल कितनी अस्थियाँ पायी जाती हैं?
उत्तर:
खोपड़ी में कुल 22 अस्थियाँ होती हैं, जिनमें से 8 कपाल में तथा 14 चेहरे में पायी जाती हैं।

प्रश्न 15.
वयस्क व्यक्ति के मेरुदण्ड में कुल कितनी अस्थियाँ (कशेरुकाएँ) पायी जाती हैं तथा उन्हें क्या कहते हैं?
उत्तर:
वयस्क व्यक्ति के मेरुदण्ड में कुल 26 अस्थियाँ (कशेरुकाएँ) पायी जाती हैं तथा उन्हें .. कशेरुकाएँ कहते हैं।

प्रश्न 16.
शैशवावस्था में मेरुदण्ड में कुल कितनी अस्थियाँ (कशेरुकाएँ) पायी जाती हैं?
उत्तर:
शैशवावस्था में मेरुदण्ड में कुल 33 अस्थियाँ (कशेरुकाएँ) पायी जाती हैं।

प्रश्न 17.
वक्ष में कुल कितनी पसलियाँ पायी जाती हैं?
उत्तर:
वक्ष में कुल 24 पसलियाँ पायी जाती हैं।

प्रश्न 18.
अस्थि सन्धि से क्या आशय है?
उत्तर:
अस्थि संस्थान में जहाँ दो या दो से अधिक अस्थियाँ परस्पर सम्बद्ध होती हैं, उस स्थान एवं व्यवस्था को अस्थि सन्धि कहते हैं।

प्रश्न 19.
शरीर के लिए अस्थि सन्धियों की क्या उपयोगिता है? अथवा शरीर में कंकाल सन्धियों की दो उपयोगिताएँ लिखिए।
उत्तर:
(i) अस्थि सन्धियाँ शरीर को गति प्रदान करती हैं,
(ii) कंकाल तन्त्र को व्यवस्था प्रदान करती हैं।

प्रश्न 20.
अस्थि सन्धि के प्रकार लिखिए।
उत्तर:
अस्थि सन्धियाँ मुख्य रूप से दो प्रकार की होती हैं-चल सन्धियाँ तथा अचल सन्धियाँ। चल सन्धियाँ पाँच प्रकार की होती हैं-कन्दुक-खल्लिका सन्धि, कब्जा सन्धि, विवर्त या खुंटी सन्धि, पर्याण या सैडिल सन्धि तथा प्रसर या विसी सन्धि।

प्रश्न 21.
चल सन्धियाँ किसे कहते हैं?
उत्तर:
जिन अस्थि सन्धियों में एक अथवा अधिक दिशा में गति होती है, उन्हें चल सन्धि कहते हैं।

प्रश्न 22.
चल सन्धि के प्रकार लिखिए।
उत्तर:
चल सन्धियाँ दो प्रकार की होती हैं—अपूर्ण चल सन्धि तथा पूर्ण चल सन्धि।

प्रश्न 23.
किन्हीं दो सन्धियों के नाम बताइए।
उत्तर:
कन्दुक-खल्लिका सन्धि, कब्जा सन्धि, खूटीदार सन्धि, प्रसर सन्धि तथा पर्याण सन्धि।

प्रश्न 24.
घुटनों तथा कोहनी के स्थान पर किस प्रकार की सन्धि पायी जाती है?
उत्तर:
घुटनों तथा कोहनी के स्थान पर कब्जा सन्धि पायी जाती है।

प्रश्न 25.
पर्याण सन्धि शरीर के किस अंग में पायी जाती है?
उत्तर:
पर्याण सन्धि अँगूठे में पायी जाती है।

प्रश्न 26.
अचल सन्धि से क्या आशय है?
उत्तर:
जब दो या दो से अधिक अस्थियाँ परस्पर इस प्रकार से सम्बद्ध होती हैं कि उनमें किसी भी प्रकार की गति नहीं होती तो उस सन्धि-व्यवस्था को अचल सन्धि कहते हैं।

प्रश्न 27.
हमारे शरीर में अचल सन्धियाँ कहाँ पायी जाती हैं?
उत्तर:
हमारे शरीर में खोपड़ी में अचल सन्धियाँ पायी जाती हैं।

UP Board Solutions for Class 11 Home Science Chapter 2 बहुविकल्पीय प्रश्नोत्तर

निर्देश : निम्नलिखित प्रश्नों के उत्तर में दिए गए विकल्पों में से सही विकल्प का चयन कीजिए

प्रश्न 1.
शरीर को निश्चित आकार तथा व्यवस्थित गति प्रदान करने में महत्त्वपूर्ण भूमिका है(क) पेशीतन्त्र की
(ख) कंकाल तन्त्र की
(ग) पाचन तन्त्र की
(घ) उपर्युक्त सभी की।
उत्तर:
(ख) कंकाल तन्त्र की।

प्रश्न 2.
शरीर की विभिन्न अस्थियाँ व्यवस्थित होकर बनाती हैं(क) सम्पूर्ण शरीर को
(ख) अस्थि संस्थान को
(ग) शरीर के आधार को
(घ) शरीर की सुन्दरता को।
उत्तर:
(ख) अस्थि संस्थान को।

प्रश्न 3.
अस्थियों का निर्माण होता है
(क) कैल्सियम से
(ख) रक्त मज्जा से
(ग) अस्थि-कोशिकाओं से
(घ) खनिज लवणों से।
उत्तर:
(ग) अस्थि-कोशिकाओं से।

प्रश्न 4.
निम्नलिखित में से कौन-सा तत्त्व अथवा अवयव हड्डी-निर्माण के लिए आवश्यक नहीं
(क) कैल्सियम
(ख) फॉस्फोरस
(ग) सोडियम
(घ) विटामिन ‘D’.
उत्तर:
(ग) सोडियम।

प्रश्न 5.
अस्थि कोशिकाओं का आकार होता है(क) गोल
(ख) पतला एवं लम्बा
(ग) चपटा
(घ) अनियमित।
उत्तर:
(घ) अनियमित।

प्रश्न 6.
अस्थि-संस्थान का कार्य है
(क) शरीर को निश्चित आकृति एवं दृढ़ता प्रदान करना
(ख) लाल रक्त कणों का निर्माण करना
(ग) शरीर को गति प्रदान करना
(घ) उपर्युक्त सभी कार्य।
उत्तर:
(घ) उपर्युक्त सभी कार्य।

प्रश्न 7.
एक वयस्क मनुष्य के शरीर में कुल कितनी अस्थियाँ पायी जाती हैं
(क) 106
(ख) 206
(ग) 212
(घ) 200.
उत्तर:
(ख) 206.

प्रश्न 8.
अस्थि का कड़ापन किस तत्त्व के कारण होता है
(क) लौह तत्त्व
(ख) सोडियम
(ग) मैग्नीशियम
(घ) कैल्सियम।
उत्तर:
(घ) कैल्सियम।

प्रश्न 9.
मानव के मस्तिष्क कोष में कितनी अस्थियाँ पायी जाती हैं.
(क) 10
(ख) 8
(ग) 22
(घ) 14.
उत्तर:
(ख) 8.

प्रश्न 10.
खोपड़ी में कुल कितनी अस्थियाँ पायी जाती हैं
(क) 22
(ख) 24
(ग) 206
(घ) 306.
उत्तर:
(क) 22.

प्रश्न 11.
चेहरे में कुल कितनी अस्थियाँ होती हैं
(क) 24
(ख) 12
(ग) 14
(घ) 28.
उत्तर:
(ग) 14.

प्रश्न 12.
छोटे बच्चों के शरीर में रीढ़ की अस्थि में कुल कशेरुकाएँ (अस्थियाँ ) होती हैं
(क) 26 .
(ख) 33
(ग) 30
(घ) 31.
उत्तर:
(ख) 33.

प्रश्न 13.
एक वयस्क व्यक्ति की रीढ़ की अस्थि में कुल कशेरुकाएँ होती हैं
(क) 33
(ख) 26
(ग) 30
(घ) 28.
उत्तर:
(ख) 26.

प्रश्न 14.
व्यक्ति के शरीर में कुल पसलियाँ होती हैं
(क) 22
(ख) 26
(ग) 24
(घ) 28.
उत्तर:
(ग) 24.

प्रश्न 15.
मानव शरीर में मुक्त पशुकाएँ ( पसलियाँ) (फ्लोटिंग रिब्स ) कौन-सी होती हैं
(क) नवीं तथा दसवीं
(ख) पहली तथा दूसरी
(ग) पाँचवीं तथा छठी
(घ) ग्यारहवीं तथा बारहवीं।
उत्तर:
(घ) ग्यारहवीं तथा बारहवीं।

प्रश्न 16.
कोहनी का जोड़ कौन-सा जोड़ कहलाता है–
(क) विवर्त
(ख) कब्जेदार
(ग) फिसलने वाला
(घ) खूटीदार।
उत्तर:
(ख) कब्जेदार।

प्रश्न 17.
कूल्हे तथा कन्धे के स्थान पर किस प्रकार की अस्थि सन्धि पायी जाती है
(क) अपूर्ण चल सन्धि
(ख) कब्जेदार सन्धि
(ग) कन्दुक-खल्लिका सन्धि
(घ) फिसलने वाली सन्धि।
उत्तर:
(ग) कन्दुक-खल्लिका सन्धि।

प्रश्न 18.
शंख अस्थियाँ पायी जाती हैं…
(क) कान में
(ख) हाथ में
(ग) कपाल में
(घ) घुटनों में।
उत्तर:
(ग) कपाल में।

प्रश्न 19.
मानव के मस्तिष्क कोष (कपाल) की अस्थियाँ किस प्रकार की सन्धि से जुड़ी रहती हैं
(क) चल सन्धि
(ख) अपूर्ण सन्धि
(ग) अचल सन्धि
(घ) कब्जा सन्धि।
उत्तर:
(ग) अचल सन्धि।

प्रश्न 20.
अचल सन्धि शरीर में कहाँ पायी जाती है
(क) चेहरे में
(ख) कलाई में
(ग) कपाल में
(घ) कोहनी में।
उत्तर:
(ग) कपाल में।

UP Board Solutions for Class 11 Home Science

UP Board Solutions for Class 11 Maths Chapter 7 Permutations and Combinations (क्रमचय और संचयं)

These Solutions are part of UP Board Solutions for Class 11 Maths. Here we have given UP Board Solutions for Class 11 Maths Chapter 7 Permutation and Combinations (क्रमचय और संचयं).

प्रश्नावली 7.1

प्रश्न 1.
अंक 1, 2, 3, 4 और 5 से कितनी 3 अंकीय संख्याएँ बनाई जा सकती हैं, यदि
(i) अंकों की पुनरावृत्ति की अनुमति हो।
(ii) अंकों की पुनरावृत्ति की अनुमति नहीं हो।
हल:
3 अंकीय संख्या में 3 स्थान होते हैं : इकाई, दहाई और सैकड़ा।
(i) इकाई का स्थान 5 तरीकों से भरा जा सकता है क्योंकि 1, 2, 3, 4, 5 में से कोई भी एक अंक लिया जा सकता है।
दहाई का स्थान भी 5 तरीकों से भरा जा (UPBoardSolutions.com) सकता है क्योंकि पुनरावृत्ति की अनुमति है।
1, 2, 3, 4, 5 में से कोई भी अंक लिया जा सकता है।
इसी प्रकार सैकड़े का स्थान भी 5 तरीकों से भरा जा सकता है।
3 अंकीय संख्याओं की संख्या = 5 x 5 x 5 = 125.

(ii) इकाई का स्थान 1, 2, 3, 4, 5 में से कोई-से एक अंक को लेकर 5 तरीकों से भरा जा सकता है।
दहाई का स्थान 4 तरीकों से भरा जा सकता है क्योंकि एक अंक पहले ही चयनित कर लिया गया। पुनरावृत्ति की अनुमति नहीं है।
सैकड़े का स्थान 3 तरीकों से भरा जा सकता है क्योंकि 2 अंक पहले ही चयनित कर लिए गए हैं।
3 अंकीय संख्याओं की संख्या = 5 x 4 x 3 = 60.

प्रश्न 2.
अंकः1, 2, 3, 4, 5, 6 से कितनी 3 अंकीय सम संख्याएँ बनाई जा सकती हैं, यदि अंकों की पुनरावृत्ति की जा सकेती है?
हल:
इकाई का स्थान 2, 4, 6 में से एक को लेकर 3 तरीकों से भरा जा सकता है।
क्योंकि पुनरावृत्ति की जा सकती है, दहाई का स्थान 6 तरीकों से भरा जा सकता है।
इसी प्रकार सैकड़े का स्थान भी 6 तरीकों से ही भरा जा सकता है।
3 अंकीय संख्याओं की संख्या = 6 x 6 x 3 = 108.

प्रश्न 3.
अंग्रेजी वर्णमाला के प्रथम 10 अक्षरों से कितने 4 अक्षरों के कोड बनाए जा सकते हैं, यदि किसी भी अक्षर की पुनरावृत्ति नहीं की जा सकती?
हल:
4 अक्षरों वाले कोड में 4 स्थान हैं। प्रत्येक अक्षर के लिए एक स्थान चाहिए।
पहले स्थान को 10 तरीकों से, दूसरे स्थान को 9 तरीकों से, तीसरे स्थान को 8 तरीकों से और चौथे स्थान को 7 तरीकों से भर सकते हैं क्योंकि पुनरावृत्ति की अनुमति नहीं है।
एक अक्षर दुबारा नहीं लिखा जा सकता।
चार अक्षर वाले कोडों की संख्या = 10 x 9 x 8 x 7 = 5040.

प्रश्न 4.
0 से 9 तक के अंकों का प्रयोग करके कितने 5 अंकीय टेलीफोन नम्बर बनाए जा सकते हैं, यदि प्रत्येक नम्बर 67 से आरम्भ होता है और कोई अंक एक बार से अधिक नहीं आता है?
हल:
पांच अंकीय नम्बर में 5 स्थान हैं जिसमें पहले और दूसरे को I और II से निरूपित किया गया है। I और II स्थान पर 6 और 7 को रखा गया है।
शेष 8 अंकों में से एक-एक अंक लेकर I, IV और V स्थान को भरना है। स्थान III को (UPBoardSolutions.com) 8 तरीकों से, स्थान IV को 7 तरीकों से तथा स्थान V को 6 तरीकों से भर सकते है।
5 अंकीय टेलीफोन नम्बरों की संख्या = 8 x 7 x 6 = 336 .

प्रश्न 5.
एक सिक्का तीन बार उछाला जाता है और परिणाम अंकित कर लिए जाते हैं। परिणामों की संभव संख्या क्या है?
हल:
एक बार सिक्का उछालने से दो में से एक भाग ऊपर आता है अर्थात T या H जबकि H चित्त और T पट को निरूपित करते हैं।
एक बार सिक्का उछालने से दो परिणाम होते हैं।
तीन बार सिक्का उछालने से 2 x 2 x 2 = 8 परिणाम होंगे।
ये परिणाम इस प्रकार है :
TTT, TTH, THT, HTT, HHT, HTH, THH, HHH

प्रश्न 6.
भिन्न-भिन्न रंगों के 5 झंडे दिए हुए हैं। इससे कितने विभिन्न संकेत बनाए जा सकते हैं, यदि प्रत्येक संकेत में 2 झंडों, एक के नीचे दूसरे के प्रयोग की आवश्यक पड़ती है?
हल:
झंडे के ऊपर का स्थान भरने के 5 तरीके हैं। एक झंडा प्रयोग होने के बाद 4 झंडे (UPBoardSolutions.com) रह जाते हैं। नीचे का दूसरा स्थान 4 तरीकों से भरा जा सकता है।
कुल संकेतों की संख्या = 5 x 4 = 20.

प्रश्नावली 7.2

प्रश्न 1.
मान निकालिए:
(i) 8!
(ii) 4! – 3!
हल:
(i) 8! = 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40320.
(ii) 4! – 3! = 4 x 3 x 2 x 1 – 3 x 2 x 1 = 24 – 6 = 18.

प्रश्न 2.
क्या 3! + 4! = 7!
हल:
बायाँ पक्ष = 3! + 4! = 3! + 4! = 3 x 2 x 1 + 4 x 3 x 2 x 1 = 6 + 24 = 30
दायाँ पक्ष = 7! = 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040
अत: 3! + 4! ≠ 7!

प्रश्नावली 7.3

प्रश्न 1.
1 से 9 तक के अंकों को प्रयोग करके कितनी 3 अंकीय संख्याएं बनाई जा सकती हैं, यदि किसी भी अंक को दोहराया नहीं गया है?
हल:
3 अंकीय संख्या में तीन स्थान होते हैं: इकाई, दहाई और सैकड़ा।
इकाई के स्थान को 9 तरीकों से, दहाई के स्थान को 8 तरीकों से और सैकड़े के स्थान को 7 तरीकों से भरा जा सकता है।
3 अंकीय संख्याओं की संख्या = 9 x 8 x 7 = 504.

प्रश्न 2.
किसी भी अंक को दोहराए बिना कितनी 4 अंकीय संख्याएँ होती हैं?
हल:
0 से 9 तक कुल 10 अंक हैं। 10 में से 4 अंक लेकर संख्याओं की संख्या = 10[latex]{ P }_{ 4 }[/latex] = 10 x 9 x 8 x 7 = 5640
इनमें वे संख्याएं सम्मिलित हैं जिनमें हजार के स्थान पर 0 है।
0 को हजार के स्थान पर रखने पर और शेष स्थानों पर कोई तीन अंक रखने पर कुल संख्याओं की संख्या
= 9[latex]{ P }_{ 3 }[/latex] = 9 x 8 x 7 = 504
चार अंकीय संख्याओं की संख्या = 5040 – 504 = 4536.

प्रश्न 3.
अंक 1, 2, 3, 4, 6, 7 को प्रयुक्त करने से कितनी 3 अंकीय सम संख्याएँ बनाई जा सकती हैं, यदि कोई भी अंक दोहराया नहीं गया है?
हल:
2, 4, 6 में से किसी एक को इकाई के स्थान पर रखने से सम संख्या बनती है।
इकाई का स्थान 3 तरीकों से भरा जा सकता है।
दहाई के स्थान को 5 तरीकों से और सैकड़े के स्थान को 4 (UPBoardSolutions.com) तरीकों से भरा जा सकता है।
3 अंकीय सम संख्याओं की संख्या = 3 x 5 x 4 = 60.

प्रश्न 4.
अंक 1, 2, 3, 4, 5 के उपयोग द्वारा कितनी 4 अंकीय संख्याएँ बनाई जा सकती हैं। यदि कोई भी अंक दोहराया नहीं गया है? इनमें से कितनी सम संख्याएँ होंगी?
हल:
(i) 5 में से 4 अंक लेकर संख्याओं की संख्या = 5[latex]{ P }_{ 4 }[/latex] = 5 x 4 x 3 x 2 = 120
(ii) इकाई के स्थान पर 2 या 4 रखने से संख्या सम बनती है।
इस प्रकार इकाई का स्थान 2 तरीकों से, दहाई का स्थान 4 तरीकों से, सैकड़े का स्थान 3 तरीकों से और हजार का स्थान 2 तरीकों से भरा जा सकता है।
4 अंकीय सम संख्याओं की संख्या = 2 x 4 x 3 x 2 = 48.

प्रश्न 5.
8 व्यक्तियों की समिति में, हम कितने प्रकार से एक अध्यक्ष और एक उपाध्यक्ष चुन सकते हैं, यह मानते हुए कि एक व्यक्ति एक से अधिक पद पर नहीं रह सकता है?
हल:
8 व्यक्तियों में से एक को अध्यक्ष चुनने के तरीके = 8
अध्यक्ष चुनने के बाद 7 व्यक्तियों में से एक उपाध्यक्ष चुना जाना है।
उपाध्यक्ष चुनने के तरीके = 7
एक अध्यक्ष और एक उपाध्यक्ष को 8 x 7 = 56 तरीकों से चुना जा सकता है।

प्रश्न 8.
EQUATION शब्द के अक्षरों में से प्रत्येक को तथ्यतः केवल एक बार उपयोग करके कितने अर्थपूर्ण या अर्थहीन शब्द बन सकते हैं?
हल:
शब्द EQUATION में कुल 8 अक्षर हैं।
इन अक्षरों से बनने वाले शब्दों ( जो अर्थपूर्ण या अर्थहीन हैं) (UPBoardSolutions.com) की संख्या = [latex]\frac { 8! }{ \left( 8-8 \right) ! }[/latex] = 8!
= 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 40320.

प्रश्न 9.
MONDAY शब्द के अक्षरों से कितने अर्थपूर्ण या अर्थहीन शब्द बन सकते हैं, यह मानते हुए कि किसी भी अक्षर की पुनरावृत्ति नहीं की जाती है,
(i) एक समय में 4 अक्षर लिए जाते हैं?
(ii) एक समय में सभी अक्षर लिए जाते हैं?
(iii) सभी अक्षरों का प्रयोग किया जाता है, किन्तु प्रथम अक्षर एक स्वर है?
हल:
(i) MONDAY शब्द में कुल 6 अक्षर हैं।
6 अक्षरों में से 4 अक्षर एक समय पर लेकर कुल शब्दों की संख्या = 6[latex]{ P }_{ 4 }[/latex] = 6 x 5 x 4 x 3 = 360
जबकि शब्द अर्थपूर्ण या अर्थहीन हो सकते हैं।
(ii) सभी अक्षरों को एक साथ लेकर शब्दों की संख्या = 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720.
(iii) पहले स्थान पर A या O रखना है। यह दो तरीकों से हो सकता है।
शेष 5 स्थान 5! = 120 तरीकों से भरे जा सकते हैं।
उन शब्दों की संख्या जो स्वर से प्रारम्भ होते हैं = 2 x 120 = 240.

प्रश्न 10.
MISSISSIPPIशब्द के अक्षरों से बने भिन्न-भिन्न क्रमचयों में से कितनों में चारों I एक साथ नहीं आते हैं?
हुल:
शब्द MISSISSIPPI में कुल 11 अक्षर हैं जिसमें M, एक बार; I चार बार; S (UPBoardSolutions.com) चार बार, तथा P दो बार प्रयुक्त हो रहे हैं।

प्रश्न 11.
PERMUTATIONS शब्द के अक्षरों को कितने तरीकों से व्यवस्थित किया जा सकता है, यदि
(i) चयनित शब्द का प्रारंभ P से तथा अंत S से होता है।
(ii) चयनित शब्द में सभी स्वर एक साथ हैं।
(iii) चयनित शब्द में P तथा S के मध्य सदैव 4 अक्षर हों?
हल:
PERMUTATIONS शब्द में कुल 12 अक्षर हैं जिनमें T – 2 है, शेष सब भिन्न हैं।
(i) P और 9 के स्थान स्थिर कर दिए (UPBoardSolutions.com) गए हैं।
शेष अ६ से बने शब्दों की संख्या = [latex]\frac { 10! }{ 2! }[/latex] = 1814400.

(ii) सभी स्वरों को एक साथ कर दिया गया है।
(EUAIO)PRMTTNS जिनमें 2T हैं।
उन शब्दों की संख्या जब स्वर एक साथ है।
= [latex]\frac { 8! }{ 2! }[/latex] x 5!
= [latex]\frac { 40320 x 120 }{ 2 }[/latex]
= 2419200.

(iii) P तथा 5 के बीच चार अक्षर होने चाहिए।
मान लीजिए 12 अक्षरों के स्थानों का नाम 1, 2, 3, …… 12 रख दिया है।
1 2 3 4 5 6 7 8 9 10 11 12
इस प्रकार P को स्थान 1, 2, 3, 4, 5, 6, 7 पर रखा जा सकता है तो S को स्थान 6, 7, 8, 9, 10, 11, 12 पर रखा जा सकता है।
P और S को 7 स्थानों पर रखा जा सकता है।
इसी प्रकार S और P को 7 स्थानों पर रखा जा सकता है।
P और S या S और P को 7 + 7 = 14 तरीकों से रखा जा सकता
शेष [latex]\frac { 10! }{ 2! }[/latex] अक्षरों को 10 तरीकों से व्यवस्थित किया जा सकता है।
उन शब्दों की संख्या जब P और S के बीच में 4 अक्षर हों
= [latex]\frac { 10! }{ 2! }[/latex] x 14 = 10! x 7 = 25401600.

प्रश्नावली 7.4

प्रश्न 3.
किसी वृत्त पर स्थित 21 बिन्दुओं से होकर जाने वाली कितनी जीवाएँ खींची जा सकती हैं?
हल:
21 बिन्दुओं में कोई 2 बिन्दु मिलाने से एक जीवा प्राप्त होती है।

प्रश्न 4.
5 लड़के और 4 लड़कियों में से 3 लड़के और 3 लड़कियों की टीमें बनाने के कितने तरीके हैं?

प्रश्न 5.
6 लाल रंग की, 5 सफेद रंग की और 5 नीले रंग की गेंदों में से 9 गेंदों के चुनने के तरीकों की संख्या ज्ञात कीजिए, यदि प्रत्येक संग्रह में प्रत्येक रंग की 3 गेंदें हैं।

प्रश्न 6.
52 पत्तों की एक गड्डी में से 5 पत्तों को लेकर बनने वाले संचयों की संख्या निर्धारित कीजिए, यदि प्रत्येक संचय में तथ्यतः एक इक्का हो।

प्रश्न 7.
17 खिलाड़ियों में से, जिनमें केवल 5 गेंदबाजी कर सकते हैं, एक क्रिकेट टीम के 11 खिलाड़ियों का चयन कितने प्रकार से किया जा सकता है, यदि प्रत्येक टीम में तथ्यतः 4 गेंदबाज हैं?

प्रश्न 8.
एक थैली में 5 काली तथा 6 लाल गेंदें हैं। 2 काली तथा 3 लाल गेंदों के चयन के तरीकों की संख्या निर्धारित कीजिए।

प्रश्न 9.
9 उपलब्ध पाठ्यक्रमों में से, एक विद्यार्थी 5 पाठ्यक्रमों का चयन कितने प्रकार से कर सकता है, यदि प्रत्येक विद्यार्थी के लिए 2 विशिष्ट पाठ्यक्रम अनिवार्य हैं?

अध्याय 7 पर विविध प्रश्नावली

प्रश्न 1.
DAUGHTER शब्द के अक्षरों से, कितने अर्थपूर्ण या अर्थहीन शब्दों की रचना की जा सकती है, जबकि प्रत्येक शब्द में 2 स्वर तथा 3 व्यंजन हों?

प्रश्न 2.
EQUATION शब्द के अक्षरों से कितने, अर्थपूर्ण या अर्थहीन, शब्दों की रचना की जा सकती है, जबकि स्वर तथा व्यंजन एक साथ रहते हैं?
हल:
EQUATION शब्द में कुल 8 अक्षर हैं जिनमें 5 स्वर और 3 व्यंजन हैं।
स्वर अक्षरों का क्रमसंचय = 5! = 5 x 4 x 3 x 2 x 1 = 120
व्यंजन अक्षरों का क्रमसंचय = 3! = 3 x 2 x 1 = 6
स्वरों और अक्षरों को 2 तरीकों से लिखा (UPBoardSolutions.com) जा सकता है, पहले स्वर ले या व्यंजन लें।
EQUATION शब्द के अक्षरों से बनने वाले शब्द जब स्वर तथा व्यंजन एक साथ आएँ = 120 x 6 x 2 = 1440.

प्रश्न 3.
9 लड़के और 4 लड़कियों से 7 सदस्यों की एक समिति बनानी है, यह कितने प्रकार से किया सकता है, जबकि समिति में
(i) तथ्यत: 3 लड़कियाँ हैं?
(ii) न्यूनतम 3 लड़कियाँ हैं?
(iii) अधिकतम 3 लड़कियाँ हैं?

प्रश्न 4.
यदि शब्द EXAMINATION के सभी अक्षरों से बने विभिन्न क्रमचयों को शब्द कोष की तरह सूचीबद्ध किया जाता है, तो E से प्रारम्भ होने वाले प्रथम शब्द से पूर्व कितने शब्द हैं?

प्रश्न 5.
0, 1, 3, 5, 7 तथा 9 अंकों से, 10 से विभाजित होने वाली और बिना पुनरावृत्ति किए कितनी 6 अंकीय संख्याएँ बनाई जा सकती हैं?

प्रश्न 6.
अंग्रेजी वर्णमाला में 5 स्वर तथा 21 व्यंजन हैं। इस वर्णमाला में 2 भिन्न स्वरों और 2 भिन्न व्यंजनों वाले कितने शब्दों की रचना की जा सकती है?

प्रश्न 7.
किसी परीक्षा के एक प्रश्न पत्र में 12 प्रश्न हैं जो क्रमशः 5 तथा 7 प्रश्नों वाले दो खण्डों में विभक्त हैं अर्थात खंड 1 और खण्ड II, एक विद्यार्थी का प्रत्येक खंड से न्यूनतम 3 प्रश्नों का चयन करते हुए कुल 8 प्रश्नों को हल करना है। एक विद्यार्थी कितने प्रकार से प्रश्नों का चयन कर सकता है ?

प्रश्न 8.
52 पत्तों की एक गड्डी में से 5 पत्तों के संचय की संख्या निर्धारित कीजिए, यदि 5 पत्तों के प्रत्येक चयन (संचय) में तथ्यतः एक बादशाह है।

प्रश्न 9.
5 पुरुषों और 4 महिलाओं को एक पंक्ति में इस प्रकार बैठाया जाता है कि महिलाएँ सम स्थानों पर बैठती हैं। इस प्रकार कितने विन्यास संभव हैं ?
हल:
4 महिलाओं का 4 सम स्थानों पर बैठाने के विन्यास = 4! = 24
5 पुरुषों को 5 विषम स्थानों पर बैठाना (UPBoardSolutions.com) के तरीके = 5! = 120
4 महिलाओं को सम स्थानों पर और 5 पुरुषों को विषम स्थानों पर बैठाने के विन्यास = 4! x 5! = 24 x 120 = 2880.

प्रश्न 10.
25 विद्यार्थियों की एक कक्षा से 10 का चयन एक भ्रमण दल के लिए किया जाता है। तीन विद्यार्थी ऐसे हैं, जिन्होंने यह निर्णय लिया है कि या तो वे तीनों दल में शामिल होंगे या उनमें से कोई भी दल में शामिल नहीं होगा। भ्रमण दल का चयन कितने प्रकार से किया जा सकता है?
हल:
25 विद्यार्थियों में से 10 विद्यार्थियों को भ्रमण दल में शामिल करना है। परन्तु 10 विद्यार्थियों में से 3 ऎसे हैं
(i) जब तीनों भ्रमण दल में शामिल होते हैं या (ii) तीनों नहीं होते है।
(i) जब तीनों विद्यार्थी टीम में शामिल होते हैं तो भ्रमण दल का चयन करने के तरीके = 22[latex]{ C }_{ 7 }[/latex]
(ii) जब तीनों विद्यार्थी भ्रमण दल में शामिल नहीं होते हैं तो चयन करने के तरीके = 22[latex]{ C }_{ 10 }[/latex]
दोनो दशाओं में भ्रमण दल का चयन करने के तरीके = 22[latex]{ C }_{ 7 }[/latex] + 22[latex]{ C }_{ 10 }[/latex]

प्रश्न 11.
ASSASSINATION शब्द के अक्षरों के कितने विन्यास बनाए जा सकते हैं जबकि सभी sएक साथ रहें ?
हुल:
ASSASSINATION में कुल 13 अक्षर हैं जिसमें A तीन बार, S चार बार, I दो बार तथा N दो बार प्रयुक्त हो रहे हैं।
4 – S को एक साथ रहना है। अतः उसे एक अक्षर मान लिया। इस प्रकार इसमें 10 अक्षर रह गए जिसमें 3 – A, 2 – 1 और 2 – N समान हैं।
इस शब्द के अक्षरों का विन्यास जब S एक साथ (UPBoardSolutions.com) रहते हो

We hope the UP Board Solutions for Class 11 Maths Chapter 7 Permutation and Combinations (क्रमचय और संचयं) help you. If you have any query regarding UP Board Solutions for Class 11 Maths Chapter 7 Permutation and Combinations (क्रमचय और संचयं), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Physics Chapter 8 Gravitation (गुरुत्वाकर्षण ) are part of UP Board Solutions for Class 11 Physics . Here we have given UP Board Solutions for Class 11 Physics Chapter 8 Gravitation (गुरुत्वाकर्षण )

Board	UP Board
Textbook	NCERT
Class	Class 11
Subject	Physics
Chapter	Chapter 8
Chapter Name	Gravitation
Number of Questions Solved	77

UP Board Solutions for Class 11 Physics Chapter 8 Gravitation (गुरुत्वाकर्षण )

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
निम्नलिखित के उत्तर दीजिए
(a) आप किसी आवेश का वैद्युत बलों से परिरक्षण उस आवेश को किसी खोखले चालक के भीतर रखकर कर सकते हैं। क्या आप किसी पिण्ड का परिरक्षण, निकट में रखे पदार्थ के गुरुत्वीय प्रभाव से, उसे खोखले गोले में रखकर अथवा किसी अन्य साधनों द्वारा कर सकते हैं?
(b) पृथ्वी के परितः परिक्रमण करने वाले छोटे अन्तरिक्षयान में बैठा कोई अन्तरिक्ष यात्री गुरुत्व बल का संसूचन नहीं कर सकता। यदि पृथ्वी के परितः परिक्रमण करने वाला अन्तरिक्ष स्टेशंन आकार में बड़ा है, तब क्या वह गुरुत्व बल के संसूचन की आशा कर सकता है?
(c) यदि आप पृथ्वी पर सूर्य के कारण गुरुत्वीय बल की तुलना पृथ्वी पर चन्द्रमा के कारण गुरुत्व बल से करें, तो आप यह पाएँगे कि सूर्य का खिंचाव चन्द्रमा के खिंचाव की तुलना में अधिक है (इसकी जाँच आप स्वयं आगामी अभ्यासों में दिए गए आँकड़ों की सहायता से कर सकते हैं) तथापि चन्द्रमा के खिंचाव का ज्वारीय प्रभाव सूर्य के ज्वारीय प्रभाव से अधिक है। क्यों?
उत्तर-
(a) गुरुत्वीय प्रभाव से किसी पिण्ड का परिरक्षण किसी भी प्रकार से अथवा साधन से नहीं किया जा सकता।
(b) हाँ, यदि अन्तरिक्ष स्टेशन पर्याप्त रूप में बड़ा है तो (UPBoardSolutions.com) यात्री उस स्टेशन के कारण गुरुत्व बल का संसूचन कर सकता है।
(c) किसी ग्रह के कारण ज्वारीय प्रभाव दूरी के घन के व्युत्क्रमानुपाती होता है; अत: यह गुरुत्वीय बल से मुक्त है। चूंकि सूर्य की पृथ्वी से दूरी, चन्द्रमा की पृथ्वी से दूरी की तुलना में बहुत अधिक है; अतः चन्द्रमा के कारण ज्वारीय प्रभाव अधिक होता है।

प्रश्न 2.
सही विकल्प का चयन कीजिए
(a) बढ़ती तुंगता के साथ गुरुत्वीय त्वरण बढ़ता/घटता है।
(b) बढ़ती गहराई के साथ (पृथ्वी को एकसमान घनत्व का गोला मानकर) गुरुत्वीय त्वरण बढता/घटता है।
(c) गुरुत्वीय त्वरण पृथ्वी के द्रव्यमान/पिण्ड के द्रव्यमान पर निर्भर नहीं करता।
(d) पृथ्वी के केन्द्र से r₂, तथा r₁ दूरियों के दो बिन्दुओं के बीच स्थितिज ऊर्जा- अन्तर के लिए सूत्र – G Mm (1/r₂ -1/r₁) सूत्र mg (r₂ – r₁) से अधिक/कम यथार्थ है।
उत्तर-
(a) घटता है।
(b) घटता है।
(c) पिण्ड के द्रव्यमान पर निर्भर नहीं करता।
(d) अधिक यथार्थ है।

प्रश्न 3.
मान लीजिए एक ऐसा ग्रह है जो सूर्य के परितः पृथ्वी की तुलना में दोगुनी चाल से गति करता है, तब पृथ्वी की कक्षा की तुलना में इसका कक्षीय आमाप क्या है?
हल-
माना पृथ्वी का परिक्रमण काल = T_E
तब ग्रह का परिक्रमण काल T_P = [latex s=2]\frac { { T }_{ E } }{ 2 } [/latex] (दिया है)
माना इनके कक्षीय आमाप क्रमशः R_E तथा R_P हैं,

अर्थात् ग्रह का आमाप पृथ्वी के आमाप से 0.631 गुना छोटा है।

प्रश्न 4.
बृहस्पति के एक उपग्रह, आयो (Io) की कक्षीय अवधि 1.769 दिन तथा कक्षा की त्रिज्या 4.22×10⁸ m है। यह दर्शाइए कि बृहस्पति का द्रव्यमान सूर्य के द्रव्यमान का लगभग 1/1000 गुना है।
हल-
बृहस्पति के उपग्रह का परिंक्रमण काल

प्रश्न 5.
मान लीजिए कि हमारी आकाशगंगा में एक सौर द्रव्यमान के 2.5×10¹¹ तारे हैं। मंदाकिनीय केन्द्र से 50,000ly दूरी पर स्थित कोई तारा अपनी एक परिक्रमा पूरी करने में कितना समय लेगा? आकाशगंगा का व्यास 10⁵ ly लीजिए।
हल-
प्रश्नानुसार, तारा आकाशगंगा के परितः R = 50,000 ly त्रिज्या के वृत्तीय (UPBoardSolutions.com) पथ पर घूमती है। आकाशगंगा का द्रव्यमान M = 2.5×10¹¹ × सौर द्रव्यमान

प्रश्न 6.
सही विकल्प का चयन कीजिए–
(a) यदि स्थितिज ऊर्जा का शून्य अनन्त पर है तो कक्षा में परिक्रमा करते किसी उपग्रह की कुल ऊर्जा इसकी गतिज/स्थितिज ऊर्जा का ऋणात्मक है।
(b) कक्षा में परिक्रमा करने वाले किसी उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने | के लिए आवश्यक ऊर्जा समान ऊँचाई (जितनी उपग्रह की है) के किसी स्थिर पिण्ड को | पृथ्वी के प्रभाव से बाहर प्रक्षेपित करने के लिए आवश्यक ऊर्जा से अधिक/कम होती है।
उत्तर-
(a) गतिज ऊर्जा का ऋणात्मक है।
(b) कम होती है।

प्रश्न 7.
क्या किसी पिण्ड की पृथ्वी से पलायन चाल
(a) पिण्ड के द्रव्यमान,
(b) प्रक्षेपण बिन्दु की अवस्थिति,
(c) प्रक्षेपण की दिशा,
(d) पिण्ड के प्रमोचन की अवस्थिति की ऊँचाई पर निर्भर करती है?
उत्तर-
(a) नहीं,
(b) नहीं,
(c) नहीं,
(d) हाँ, निर्भर करती है।

प्रश्न 8.
कोई धूमकेतु सूर्य की परिक्रमा अत्यधिक दीर्घवृत्तीय कक्षा में कर रहा है। क्या अपनी कक्षा में धूमकेतु की शुरू से अन्त तक
(a) रैखिक चाल,
(b) कोणीय चाल,
(c) कोणीय संवेग,
(d) गतिज ऊर्जा,
(e) स्थितिज ऊर्जा,
(f) कुल ऊर्जा नियत रहती है? सूर्य के अति निकट आने पर धूमकेतु के द्रव्यमान में ह्रास को नगण्य मानिए।
उत्तर-
(a) नहीं,
(b) नहीं,
(c) हाँ, कोणीय संवेग नियत रहता है,
(d) नहीं,
(e) नहीं,
(f) हाँ, कुल ऊर्जा नियत रहती है।

प्रश्न 9.
निम्नलिखित में से कौन-से लक्षण अन्तरिक्ष में अन्तरिक्ष यात्री के लिए दुःखदायी हो सकते हैं? \
(a) पैरों में सूजन,
(b) चेहरे पर सूजन,
(c) सिरदर्द,
(d) दिविन्यास समस्या।
उत्तर-
(b), (c) तथा (d)।

प्रश्न 10.
एकसमान द्रव्यमान घनत्व के अर्द्धगोलीय खोलों द्वारा परिभाषित ढोल के पृष्ठ के केन्द्र पर गुरुत्वीय तीव्रता की दिशा [देखिए चित्र-8.1] (i) a, (ii) b, (iii) c, (iv) 0 में किस तीर द्वारा दर्शाई जाएगी?

उत्तर-
यदि हमे गोले को पूरा कर दें तो केन्द्र पर नेट तीव्रता शून्य होगी। इसका यह अर्थ है कि केन्द्र पर दोनों अर्द्धगोलों के कारण तीव्रताएँ परस्पर विपरीत तथा बराबर होंगी। अतः दिशा (iii) c द्वारा प्रदर्शित होगी।

प्रश्न 11.
उपर्युक्त समस्या में किसी यादृच्छिक बिन्दु P पर गुरुत्वीय तीव्रता किस तीर
(i) d,
(ii) e,
(iii) f,
(iv) g द्वारा व्यक्त की जाएगी?
उत्तर-
(ii) e द्वारा प्रदर्शित होगी।

प्रश्न 12.
पृथ्वी से किसी रॉकेट को सूर्य की ओर दागा गया है। पृथ्वी के केन्द्र से किस दूरी पर रॉकेट | पर गुरुत्वाकर्षण बल शून्य है? सूर्य का द्रव्यमान = 2×10³⁰ kg, पृथ्वी का द्रव्यमान = 6×10²⁴ kg| अन्य ग्रहों आदि के प्रभावों की उपेक्षा कीजिए (कक्षीय त्रिज्या = 1.5×10¹¹ m)।
हल-
माना पृथ्वी के केन्द्र से x मीटर की दूरी पर रॉकेट पर गुरुत्वाकर्षण बल शून्य है। इस क्षण रॉकेट की सूर्य से दूरी = (r – x) मीटर

जहाँ r = सूर्य तथा पृथ्वी के बीच की दूरी अर्थात् पृथ्वी की कक्षीय त्रिज्या = 1.5×10¹¹ मीटर यह तब भी सम्भव है जबकि –
पृथ्वी द्वारा रॉकेट पर आरोपित गुरुत्वाकर्षण बल = सूर्य द्वारा रॉकेट पर आरोपित गुरुत्वाकर्षण बल

प्रश्न 13.
आप सूर्य को कैसे तोलेंगे, अर्थात् उसके द्रव्यमान का आकलन कैसे करेंगे? सूर्य के परितः पृथ्वी की कक्षा की औसत त्रिज्या 1.5×10⁸ km है।।
हल-
पृथ्वी के परित: उपग्रह के परिक्रमण काल के सूत्र [latex s=2]T=2\pi \sqrt { \frac { { r }^{ 3 } }{ { GM }_{ e } } } [/latex] , के अनुरूप सूर्य के परितः पृथ्वी का परिक्रमण काल
[latex s=2]T=2\pi \sqrt { \frac { { r }^{ 3 } }{ { GM }_{ e } } } [/latex] (जहाँ M, = सूर्य का द्रव्यमान) (UPBoardSolutions.com)

प्रश्न 14.
एक शनि-वर्ष एक पृथ्वी-वर्ष का 29.5 गुना है। यदि पृथ्वी सूर्य से 1.5×10⁸ km दूरी पर है, तो शनि सूर्य से कितनी दूरी पर है?
हल-
पृथ्वी की सूर्य से दूरी R_SE = 1.5×10⁸ km
माना पृथ्वी का परिक्रमण काल = T_E
तब शनि का परिक्रमण काल T_S = 29.5TE
शनि की सूर्य से दूरी R_SS = ?
परिक्रमण कालों के नियम से,

प्रश्न 15.
पृथ्वी के पृष्ठ पर किसी वस्तु का भार 63N है। पृथ्वी की त्रिज्या की आधी ऊँचाई पर पृथ्वी के कारण इस वस्तु पर गुरुत्वीय बल कितना है?
हल-
यदि पृथ्वी तल पर गुरुत्वीय त्वरण g हो, तो पृथ्वी तल से h ऊँचाई पर गुरुत्वीय त्वरण
[latex s=2]{ g }^{ I }=g{ \left( 1+\frac { h }{ { R }_{ e } } \right) }^{ 2 } [/latex]
यदि वस्तु का द्रव्यमान m हो तो दोनों पक्षों में m से गुणा करने पर,
[latex s=2]m{ g }^{ I }=\frac { mg }{ { \left( 1+\frac { h }{ { R }_{ e } } \right) }^{ 2 } } [/latex] (जहाँ Re = पृथ्वी की त्रिज्या)
यहाँ mg = पृथ्वी के पृष्ठ पर वस्तु का भार = 63 न्यूटन
mg’ = पृथ्वी तल से h ऊँचाई पर वस्तु का भार अर्थात् पृथ्वी के कारण वस्तु पर गुरुत्वीय बल F_g तथा h = R_e/2

प्रश्न 16.
यह मानते हुए कि पृथ्वी एकसमान घनत्व का एक गोला है तथा इसके पृष्ठ पर किसी वस्तु का भार 250 N है, यह ज्ञात कीजिए कि पृथ्वी के केन्द्र की ओर आधी दूरी पर इस वस्तु का भार क्या होगा?
हल-
पृथ्वी तल से h गहराई पर गुरुत्वीय त्वरण
[latex s=2]{ g }^{ I }=g\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex] (जहाँ R_e = पृथ्वी की त्रिज्या)
अथवा [latex s=2]m{ g }^{ I }=mg\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex]
यहाँ पृथ्वी के पृष्ठ पर वस्तु का भार mg = 250 N
h = R_e/2(जहाँ R_e = पृथ्वी की त्रिज्या)
mg’ = इस गहराई पर वस्तु का भार w’
[latex s=2]\therefore { W }^{ I }=250N\left( 1-\frac { \frac { { R }_{ e } }{ 2 } }{ { R }_{ e } } \right) =\left( 250\times \frac { 1 }{ 2 } \right) N[/latex]
= 125 N

प्रश्न 17.
पृथ्वी के पृष्ठ से ऊर्ध्वाधरतः ऊपर की ओर कोई रॉकेट 5 km s^-1 की चाल से दागा जाता है। पृथ्वी पर वापस लौटने से पूर्व यह रॉकेट पृथ्वी से कितनी दूरी तक जाएगा? पृथ्वी का द्रव्यमान = 6.0×10²⁴ kg; पृथ्वी की माध्य त्रिज्या = 6.4×10⁶ m तथा G = 6.67×10^-11N-m²/kg^-2.
हल-
माना रॉकेट का द्रव्यमान = m; पृथ्वी से ऊर्ध्वाधरत: ऊपर की ओर रॉकेट का प्रक्षेप्य वेग ν = 5 किमी-से^-1 = 5×10³ मी-से^-1
माना रॉकेट पृथ्वी पर वापस लौटने से पूर्व पृथ्वी से अधिकतम (UPBoardSolutions.com) दूरी H ऊँचाई तक जाता है। अत: इस ऊँचाई पर रॉकेट का वेग शून्य हो जाता है।
ऊर्जा संरक्षण सिद्धान्त से पृथ्वी तल से महत्तम ऊँचाई पर
पहुँचने पररॉकेट की गतिज ऊर्जा में कमी = उसकी गुरुत्वीय स्थितिज ऊर्जा में वृद्धि –

प्रश्न 18.
पृथ्वी के पृष्ठ पर किसी प्रक्षेप्य की पलायन चाल 11.2 kms^-1 है। किसी वस्तु को इस चाल की तीन गुनी चाल से प्रक्षेपित किया जाता है। पृथ्वी से अत्यधिक दूर जाने पर इस वस्तु की चाल क्या होगी? सूर्य तथा अन्य ग्रहों की उपस्थिति की उपेक्षा कीजिए।
हल-
पृथ्वी के पृष्ठ पर पलायन चाल [latex s=2]{ \nu }_{ e }=\sqrt { \left( \frac { 2G{ M }_{ e } }{ { R }_{ e } } \right) } …(1) [/latex]
यहाँ पृथ्वी के पृष्ठ पर वस्तु का प्रक्षेप्य वेग ) ν = 3ν_e;
माना पृथ्वी से अत्यधिक दूर (अनन्त पर) चाल = ν_f
ऊर्जा संरक्षण के सिद्धान्त से, पृथ्वी तल पर कुल ऊर्जा = अनन्त पर कुल ऊर्जा
अर्थात् पृथ्वी तल पर (गतिज ऊर्जा + स्थितिज ऊर्जा) = अनन्त पर (गतिज ऊर्जा + स्थितिज ऊर्जा)

प्रश्न 19.
कोई उपग्रह पृथ्वी के पृष्ठ से 400 km ऊँचाई पर पृथ्वी की परिक्रमा कर रहा है। इस उपग्रह को पृथ्वी के गुरुत्वीय प्रभाव से बाहर निकालने में कितनी ऊर्जा खर्च होगी? उपग्रह का द्रव्यमान = 200 kg; पृथ्वी का द्रव्यमान = 6.0×10²⁴ kg; पृथ्वी की त्रिज्या = 6.4×10⁶ m तथा G = 6.67×10^-11 N m² kg^-2.
हल-
पृथ्वी के परितः उपग्रह की कक्षा की त्रिज्या r = R_e + h
r = 6.4×10⁶ मीटर + 400×10³ मीटर
= 68×10⁵ मीटर = 6.8×10⁶
मीटर अतः इस कक्षा में घूमते हुए उपग्रह की कुल ऊर्जा
[latex s=2]E=-\left( \frac { { GM }_{ e }m }{ 2r } \right) [/latex]
(जहाँ m = उपग्रह का द्रव्यमान, M_e = पृथ्वी का द्रव्यमान)
पृथ्वी के.गुरुत्वीय प्रभाव से उपग्रह को बाहर (UPBoardSolutions.com) निकालने के लिए इसको दी जाने वाली आवश्यक ऊर्जा

प्रश्न 20.
दो तारे, जिनमें प्रत्येक का द्रव्यमान सूर्य के द्रव्यमान (2×10³⁰ kg) के बराबर है, एक-दूसरे की ओर सम्मुख टक्कर के लिए आ रहे हैं। जब वे 10⁹ km दूरी पर हैं तब इनकी चाल उपेक्षणीय है। ये तारे किस चाल से टकराएँगे? प्रत्येक तारे की त्रिज्या 10⁴ km है। यह मानिए कि टकराने के पूर्व तक तारों में कोई विरूपण नहीं होता (G के ज्ञात मान का उपयोग कीजिए)।
हल-
दिया है, प्रत्येक तारे को द्रव्यमान (माना) M = 2×10³⁰ किग्रा तथा तारों के बीच प्रारम्भिक दूरी (माना) r₁ = 10⁹ किमी = 10¹² मी।
तारों की प्रारम्भिक कुल ऊर्जा E_i = प्रारम्भिक गतिज ऊर्जा + प्रारम्भिक स्थितिज ऊर्जा
[latex s=2]=0+\left[ -\frac { GMM }{ { r }_{ 1 } } \right] =-\left[ \frac { { GM }^{ 2 } }{ { r }_{ 1 } } \right] [/latex]
जब दोनों तारे परस्पर टकराते हैं, तो उनके बीच की दूरी r₂ = 2×x तारे की त्रिज्या = 2R यदि तारों का ठीक टकराने से पूर्व वेग ν हो अर्थात् वे ν चाल से टकराते हैं, तो तारों की कुल अन्तिम ऊर्जा E_f = अन्तिम गतिज ऊर्जा + अन्तिम स्थितिज ऊर्जा

प्रश्न 21.
दो भारी गोले जिनमें प्रत्येक का द्रव्यमान 100 kg तथा त्रिज्या 0.10 m है किसी क्षैतिज मेज पर एक-दूसरे से 1.0 m दूरी पर स्थित हैं। दोनों गोलों के केन्द्रों को मिलाने वाली रेखा। के मध्य बिन्दु पर गुरुत्वीय बल तथा विभव क्या है? क्या इस बिन्दु पर रखा कोई पिण्ड सन्तुलन में होगा? यदि हाँ, तो यह सन्तुलन स्थायी होगा अथवा अस्थायी?
हल-
प्रत्येक गोले का द्रव्यमान इसके केन्द्र पर निहित माना जा सकता है।
अतः ! C_AC_B = r = 1.0 मीटर तथा m_A = m_B = 100 किग्रा
दोनों गोलों के केन्द्रों को मिलाने वाली रेखा के मध्य बिन्दु M की प्रत्येक गोले के केन्द्र से

अतः ये एक-दूसरे को निरस्त कर देगी। इसलिए M पर परिणामी गुरुत्व क्षेत्र की तीव्रता = शून्य। परन्तु गुरुत्वीय क्षेत्र की तीव्रता की परिभाषा से यह M बिन्दु पर रखे एकांक द्रव्यमान पर लगने वाले गुरुत्वीय बल को व्यक्त करेगी। इसलिए गोले के मध्य बिन्दु M पर रखे किसी भी पिण्ड पर गुरुत्वीय बल शून्य होगा। गोले A के कारण बिन्दु M पर गुरुत्वीय बिभव

चूँकि ऊपर सिद्ध किया जा चुका है कि मध्य बिन्दु M पर रखे किसी भी पिण्ड पर परिणामी गुरुत्वीय
बल = शून्य
अतः मध्य बिन्दु M पर रखा पिण्ड सन्तुलन में होगा।।
अब यदि पिण्ड को थोड़ा-सा मध्य बिन्दु से किसी भी गोले की ओर विस्थापित कर दिया जाये तो वह एक नेट गुरुत्वीय बल के कारण इस बिन्दु से दूर विस्थापित होता चला जायेगा। अतः पिण्ड का सन्तुलन अस्थायी है।

अतिरिक्त अभ्यास

प्रश्न 22.
जैसा कि आपने इस अध्याय में सीखा है कि कोई तुल्यकाली उपग्रह पृथ्वी के पृष्ठ से लगभग 36,000 km ऊँचाई पर पृथ्वी की परिक्रमा करता है। इस उपग्रह के निर्धारित स्थल पर पृथ्वी के गुरुत्व बल के कारण विभव क्या है? (अनन्त पर स्थितिज ऊर्जा शून्य लीजिए) पृथ्वी का द्रव्यमान= 6.0×10²⁴ kg, पृथ्वी की त्रिज्या= 6400 km.
हल-
दिया है : पृथ्वी की त्रिज्या R_E = 6400 km = 6.4 x 10⁶ m,
पृथ्वी तल से ऊँचाई h = 360×10⁶ m,
पृथ्वी का द्रव्यमान M_E = 6.0×10²⁴ kg
उपग्रह के निर्धारित स्थल पर गुरुत्वीय विभव ।

प्रश्न 23.
सूर्य के द्रव्यमान से 2.5 गुने द्रव्यमान का कोई तारा 12 km आमाप से निपात होकर 1.2 परिक्रमण प्रति सेकण्ड से घूर्णन कर रहा है (इसी प्रकार के संहत तारे को न्यूट्रॉन तारा कहते हैं। कुछ प्रेक्षित तारकीय पिण्ड, जिन्हें पल्सार कहते हैं, इसी श्रेणी में आते हैं)। इसके विषुवत वृत्त पर रखा कोई पिण्ड, गुरुत्व बल के कारण, क्या इसके पृष्ठ से चिपका रहेगा? (सूर्य का द्रव्यमान= 2×10³⁰ kg)
हल-
घूर्णन करते तारे की विषुवतं तल पर रखे पिण्ड पर निम्न दो बल कार्य करते हैं
(i) गुरुत्वीय बल F_G = mg (अन्दर की ओर)
(ii) अपकेन्द्र बल F_e = mω²R

प्रश्न 24.
कोई अन्तरिक्षयान मंगल पर ठहरा हुआ है। इस अन्तरिक्षयान पर कितनी ऊर्जा खर्च की जाए कि इसे सौरमण्डल से बाहर धकेला जा सके। अन्तरिक्षयान का द्रव्यमान = 1000 kg; सूर्य का द्रव्यमान = 2×10³⁰ kg; मंगल का द्रव्यमान= 6.4×10²³ kg; मंगल की त्रिज्या = 3395 km; मंगल की कक्षा की त्रिज्यां = 228×10⁸ km तथा  G = 6.67×10^-11 N m² kg^-2.
हल-
दिया है : यान का द्रव्यमान m = 1000 kg = 10³ kg
सूर्य का द्रव्यमान M_S = 2×10³⁰ kg,
मंगल का द्रव्यमान M_M = 6.4×10²³ kg
मंगल की त्रिज्या R = 3395 km = 3395 x 10⁶ m,
मंगल की कक्षा की त्रिज्या r = 2.28×10¹¹ m
∵ यान मंगल की सतह पर है; अत: इसकी सूर्य से दूरी r_M के बराबर होगी।
∴ सूर्य के कारण यान की गुरुत्वीय स्थितिज ऊर्जा = [latex s=2]-\frac { { GM }_{ S }m }{ r } [/latex]
तथा मंगल के कारण यान की गुरुत्वीय स्थितिज ऊर्जा (UPBoardSolutions.com) = [latex s=2]-\frac { { GM }_{ M }m }{ R } [/latex]
यान की कुल ऊर्जा = [latex s=2]-Gm\left( \frac { { M }_{ S } }{ r } +\frac { { M }_{ M } }{ R } \right) [/latex] [∴ गतिज ऊर्जा = 0]
माना इस यान पर K ऊर्जा खर्च की जाती है, जिसे पाकर यह सौरमण्डल से बाहर चला जाता है। सौरमण्डल से बाहर, सूर्य तथा मंगल के सापेक्ष इसकी कुल ऊर्जा शून्य हो जाएगी। ऊर्जा संरक्षण के नियम से,

प्रश्न 25.
किसी रॉकेट को मंगल ग्रह के पृष्ठ से 2 kms^-1 की चाल से ऊध्र्वाधर ऊपर दागा जाता है। यदि मंगल के वातावरणीय प्रतिरोध के कारण इसकी 20% आरम्भिक ऊर्जा नष्ट हो जाती है, तब मंगल के पृष्ठ पर वापस लौटने से पूर्व यह रॉकेट मंगल से कितनी दूरी तक जाएगा? मंगल का द्रव्यमान = 6.4×10²³ kg; मंगल की त्रिज्या = 3395 km तथा G = 6.67×10^-11 N m² kg^-2.
हल-
रॉकेट का मंगल के पृष्ठ से प्रक्षेप्य वेग ) = 20 किमी-से^-1
= 2×10³ मी-से^-1
∴रॉकेट की आरम्भिक ऊर्जा E_i = गतिज ऊर्जा = [latex s=2]\frac { 1 }{ 2 } m{ \nu }^{ 2 } [/latex]
परन्तु 20% आरम्भिक ऊर्जा नष्ट हो जाती है।
अतः केवल वह अवशेष गतिज ऊर्जा जो स्थितिज (UPBoardSolutions.com) ऊर्जा में रूपान्तरित होती है = E_i का , 80%

परीक्षोपयोगी प्रश्नोत्तर

ब-विकल्पीय प्रश्न

प्रश्न 1.
कैपलर के द्वितीय नियम के अनुसार सूर्य को किसी ग्रह से मिलाने वाली रेखा समान समय , अन्तरालों में समान क्षेत्रफलं तय करती है। यह परिणाम किसके संरक्षण पर आधारित है?
(i) रेखीय संवेग
(ii) कोणीय संवेग
(iii) ऊर्जा
(iv) आवेश
उत्तर-
(ii) कोणीय संवेग ।

प्रश्न 2.
ग्रहों की गति से सम्बन्धित कैपलर का तृतीय नियम है .
(i) T∝r
(ii) T∝r²
(ii) T∝r³
(iv) T∝r^3/2
उत्तर-
(iii) T∝r³

प्रश्न 3.
ग्रहों की गति में निम्न में से कौन-सी भौतिक राशि संकलित रहती है?
(i) गतिज ऊर्जा
(ii) स्थितिज ऊर्जा
(iii) रेखीय ऊर्जा
(iv) कोणीय संवेग
उत्तर-
(iv) कोणीय संवेग

प्रश्न 4. एक ग्रह सूर्य के चारों तरफ चक्कर लगा रहा है जैसा कि चित्र 8.4 में दर्शाया गया है। ग्रह का अधिकतम वेग होगा ।

(i) A पर
(ii) B पर
(iii) C पर
(iv) D पर
उत्तर-
(ii) B पर।

प्रश्न 5. यदि पृथ्वी व सूर्य के बीच की दूरी वर्तमान दूरी की आधी होती है, तो एक वर्ष में दिनों की संख्या होगी
(i) 64.5
(ii) 129
(iii) 182.5
(iv) 730
उत्तर-
(ii) 129 दिन

प्रश्न 6.
यदि पृथ्वी का द्रव्यमान M_e, तथा त्रिज्या R_e है, तो गुरुत्वीय त्वरण g तथा गुरुत्वाकर्षण स्थिरांक G में अनुपात है।
(i) [latex s=2]\frac { { { R }^{ 2 } }_{ e } }{ { M }_{ e } } [/latex]
(ii) [latex s=2]\frac { { M }_{ e } }{ { { R }^{ 2 } }_{ e } } [/latex]
(iii)[latex s=2]{ M }_{ e }{ { R }^{ 2 } }_{ e } [/latex]
(iv)[latex s=2]\frac { { M }_{ e } }{ { R }_{ e } } [/latex]
उत्तर-
(ii) [latex s=2]\frac { { M }_{ e } }{ { { R }^{ 2 } }_{ e } } [/latex]

प्रश्न 7. पृथ्वी की त्रिज्या 6400 किमी तथा पृथ्वी पर गुरुत्वीय त्वरण 10 मी/से² है। यदि h ऊँचाई पर गुरुत्वीय त्वरण 2.5 मी/से² हो, तो h का मान होगा।
(i) 3200 किमी.
(ii) 6400 किमी
(iii) 9600 किमी
(iv) 12800 किमी
उत्तर-
(i) 6400 किमी

प्रश्न 8. g_e तथा g_p, क्रमशः पृथ्वी तल पर तथा अन्य ग्रह के तल पर गुरुत्वीय त्वरण हैं। ग्रह का द्रव्यमान व त्रिज्या दोनों पृथ्वी की तुलना में दोगुने हैं, तब
(i) g_e = g_p
(ii) g_p = 2g_p
(iii) g_p = 2g_e
(iv)[latex s=2]{ g }_{ p }=\frac { { g }_{ e } }{ \sqrt { 2 } } [/latex]
उत्तर-
(ii) g_e = 2g_p

प्रश्न 9.
किसी पिण्ड का पलायन वेग उसके
(i) द्रव्यमान के अनुक्रमानुपाती होता है ।
(ii) द्रव्यमान के वर्ग के अनुक्रमानुपाती होता है।
(iii) द्रव्यमान के व्युत्क्रमानुपाती होता है।
(iv) द्रव्यमान पर निर्भर नहीं करता है।
उत्तर-
(iv) द्रव्यमान पर निर्भर नहीं करता है।

प्रश्न 10.
संचार उपग्रह INISAT-II B का पृथ्वी के परितः परिक्रमण काल है।
(i) 12 घण्टे
(ii) 24 घण्टे
(iii) 48 घण्टे
(iv) 30 दिन
उत्तर-
(i) 24 घण्टे ।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
किसी उपग्रह को ग्रह के परितः घूमने के लिए आवश्यक अभिकेन्द्र बल कहाँ से प्राप्त होता है?
उत्तर-
उपग्रह तथा ग्रह के बीच लगने वाले गुरुत्वाकर्षण बल से।

प्रश्न 2.
g तथा G में क्या सम्बन्ध होता है?
उत्तर-
g = GM_e/R²_e
जहाँ M_e. व R_e क्रमशः पृथ्वी के द्रव्यमान तथा त्रिज्या एवं G = सार्वत्रिक गुरुत्वाकर्षण नियतांक।

प्रश्न 3.
पृथ्वी तल पर ‘g’ का मान कहाँ अधिकतम तथा कहाँ न्यूनतम होता है?
उत्तर-
g का मान ध्रुवों पर अधिकतम तथा भूमध्य (UPBoardSolutions.com) रेखा पर न्यूनतम होता है।

प्रश्न 4,
पृथ्वी के केन्द्र पर ‘g’ का मान कितना होता है?
उत्तर-
शून्य।

प्रश्न 5.
भूमध्य रेखा पर g’ का मान ध्रुवों की अपेक्षा कम होता है, क्यों?
उत्तर-
(i) ध्रुवों पर पृथ्वी चपटी है (अर्थात् पृथ्वी का भूमध्य रेखीय व्यासं, उसके ध्रुवीय व्यास की अपेक्षा अधिक होता है।)
(ii) पृथ्वी अपनी अक्ष के परितः घूर्णन करती है।

प्रश्न 6.
‘g’ के मान पर कौन-कौन से कारक प्रभाव डालते हैं?
उत्तर-
टू के मान पर निम्नलिखित तीन कारक प्रभाव डालते हैं
(i) पृथ्वी पर अक्षांशीय स्थिति,
(ii) पृथ्वी तल से ऊँचाई तथा
(iii) पृथ्वी तल से गहराई।

प्रश्न 7.
पृथ्वी सतह से h ऊँचाई पर गुरुत्वीय क्षेत्र की तीव्रता एवं गुरुत्वीय विभव से सम्बन्धित समीकरण लिखिए।
उत्तर-
गुरुत्वीय क्षेत्र की तीव्रता [latex s=2]{ I }_{ G }=\frac { { GM }_{ e } }{ { \left( { R }_{ e }+h \right) }^{ 2 } } [/latex] न्यूटन/किग्रा
गुरुत्वीय विभवे [latex s=2]V_{ G }=\frac { { GM }_{ e } }{ { \left( { R }_{ e }+h \right) } } [/latex]
जहाँ R_e = पृथ्वी की त्रिज्या अतः |
V_G = – I_G (R_e + h)

प्रश्न 8.
G का मात्रक लिखिए। इसे सार्वत्रिक नियतांक क्यों कहते हैं?
उत्तर-
G का मात्रक न्यूटन-मीटर²/किग्रा² है। चूंकि G का मान कणों की प्रकृति, माध्यम, समय, ताप । आदि पर निर्भर नहीं करता है, इसलिए इसे सार्वत्रिक नियतांक कहते हैं। प्रश्न 9. भूमध्य रेखा पर किसी वस्तु का भार ध्रुवों पर भार की तुलना में कम क्यों (UPBoardSolutions.com) होता है? उत्तर-चूंकि ध्रुवों की अपेक्षा भूमध्य रेखा पर g का मान कम होता है तथा भार W = mg, अतः ध्रुवों की ‘अपेक्षा भूमध्य रेखा पर वस्तु का भार कम होता है।

प्रश्न 10.
गुरुत्वीय क्षेत्र की तीव्रता की परिभाषा दीजिए।
उत्तर-
गुरुत्वीय क्षेत्र के अन्तर्गत किसी बिन्दु पर एकांक द्रव्यमान पर कार्य करने वाला गुरुत्वाकर्षण बेल उस बिन्दु पर ‘गुरुत्वीय क्षेत्र की तीक्रेता’ कहलाती है।

प्रश्न 11.
पृथ्वी की सतह के एक स्थान पर स्थित 25 किग्रा के एक पिण्ड पर 250 न्यूटन का बल लग रहा है। उस स्थान पर गुरुत्वीय क्षेत्र की तीव्रता का क्या मान है’ –
हल-
[latex s=2]{ I }_{ G }=\frac { F }{ m } =\frac { 250 }{ 25 } =10 [/latex] न्यूटन/किया।

प्रश्न 12.
पृथ्वी तल पर गुरुत्वीय त्वरण g = 10.0 मी/से² तथा पृथ्वी की त्रिज्या R = 6.4×10⁶ मी है। पृथ्वी के केन्द्र से 2R दूरी पर गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए।
हल-
पृथ्वी के केन्द्र से प्रक्षेपण बिन्दु की दूरी, r = 2R मी
गुरुत्वीय क्षेत्र की तीव्रता

प्रश्न 13.
गुरुत्वीय त्वरण से क्या तात्पर्य है?
उत्तर-
पृथ्वी के गुरुत्वाकर्षण बल के कारण स्वतन्त्रतापूर्वक पृथ्वी की ओर गिरती हुई वस्तु में उत्पन्न त्वरण गुरुत्वीय त्वरण कहलाता है।

प्रश्न 14. पृथ्वी तल से कितना नीचे जाने पर गुरुत्वीय त्वरण पृथ्वी तल पर गुरुत्वीय त्वरण का
(i) आधा रह जायेगा,
(ii) चौथाई रह जायेगा।
हल-
पृथ्वी तल से नीचे जाने पर गुरुत्वीय त्वरण [latex s=2]{ g }^{ I }=g\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex]

प्रश्न 15.
क्या पलायन वेग का मान पिण्ड के द्रव्यमान पर निर्भर करता है?
उत्तर-
नहीं।

प्रश्न 16.
पृथ्वी तल पर पलायन वेग का मान कितना होता है?
उत्तर-
11.2 किमी/सेकण्ड।

प्रश्न 17.
पृथ्वी के समीप परिक्रमा करने वाले कृत्रिम उपग्रह के कक्षीय वेग एवं पलायन वेग में सम्बन्ध लिखिए।
उत्तर-
[latex s=2]{ \nu }_{ e }={ { \nu } }_{ O }\sqrt { 2 } [/latex]

प्रश्न 18.
पृथ्वी के पृष्ठ से पलायन वेग 11 किमी/से है। किसी दूसरे ग्रह की त्रिज्या पृथ्वी की अपेक्षा दोगुनी है तथा उसका द्रव्यमान पृथ्वी की अपेक्षा 2.88 गुना अधिक है। इस ग्रह से पलायन वेग कितना होगा?
हल-

प्रश्न 19.
पृथ्वी तल से किसी पिण्ड का पलायन वेग 11.2 किमी/से है। यदि किसी अन्य ग्रह की त्रिज्या पृथ्वी की त्रिज्या की 1/3 तथा द्रव्यमान पृथ्वी के द्रव्यमान का 1/4 हो तो उस ग्रह से पलायन वेग कितना होगा?
हल-

प्रश्न 20.
पृथ्वी के परितः वृत्ताकार कक्षा में घूमते हुए कृत्रिम उपग्रह के परिक्रमण काल का सूत्र प्रयुक्त संकेतांकों का अर्थ बताते हुए लिखिए।
उत्तर-
T=2π[latex s=2]\sqrt { \frac { { r }^{ 3 } }{ { GM }_{ e } } } [/latex]
r = (R_e+h)
T = परिक्रमण काल, G = सार्वत्रिक गुरुत्वाकर्षण, r = त्रिज्या, R_e = पृथ्वी की त्रिज्या
तथा M_e = पृथ्वी का द्रव्यमान

प्रश्न 21.
एक उपग्रह पृथ्वी-तल के समीप एक कक्षा में परिक्रमण कर रहा है। पृथ्वी की त्रिज्या 6.4×10⁶ मीटर मानते हुए, उपग्रह की कक्षीय चाल तथा परिक्रमण काल ज्ञात कीजिए। (g=9.8 मी/से²)
हल-

प्रश्न 22.
समझाइए कि तुल्पकाली उपग्रह क्या होता है। इसकी उपयोगिता क्या है?
उत्तर-
जिस उपग्रह का पृथ्वी के परितः परिक्रमण काल 24 घण्टे होता है उसे तुल्यकाली उपग्रह कहते हैं। यह पृथ्वी के सापेक्ष सदैव स्थिर दिखायी देता है, अत: इसको भू-स्थिर उपग्रह भी कहते हैं। इसका उपयोग दूरसंचार में किया जाता है।

प्रश्न 23.
पृथ्वी की परिक्रमा कर रहे अन्तरिक्ष यान में बैठे मनुष्य का भार कितना होता है?
उत्तर-
शून्य।

लघु उत्तरीय प्रश्न

प्रश्न 1.
कैपलर के ग्रहों की गति सम्बन्धी नियम लिखिए।
या ग्रहों के गति सम्बन्धी कैपलर के नियमों का उल्लेख कीजिए।
उत्तर
कैपलर के ग्रहों की गति सम्बन्धी नियम
(i) सभी ग्रह सूर्य के चारों ओर दीर्घ-वृत्ताकार कक्षाओं (elliptical orbits) में चक्कर लगाते हैं तथा सूर्य, उन कक्षाओं के एक फोकस पर स्थित होता है।
(ii) सूर्य तथा किसी ग्रह को मिलाने वाली रेखा बराबर समय-अन्तराल में बराबर क्षेत्रफल पार (sweep) करती है, ° सूर्य अर्थात् प्रत्येक ग्रह की क्षेत्रीय चाल (areal speed) नियत S . रहती है। अत: जब ग्रह सूर्य के समीप होता है, तो उसकी चाल p (UPBoardSolutions.com) अधिकतम होती है तथा जब दूर होता है, तो उसकी चाल न्यूनतम होती है। चित्र 8.5 में एक ग्रह की कक्षा को दर्शाया गया है। यदि यह ग्रह किसी दिये समय-अन्तराल में A से B तक जाता है तथा उतने ही समय-अन्तराल में C से D तक जाता है, तब क्षेत्रफल SAB तथा SCD आपस में बराबर होंगे।

(iii) सूर्य के चारों ओर किसी भी ग्रह के परिक्रमण काल का वर्ग उसकी दीर्घवृत्तीय कक्षा के अर्द्ध-दीर्घ अक्ष (semi-major axis) के घन के अनुक्रमानुपाती होता है।
अत: ‘यदि किसी ग्रह का सूर्य के चारों ओर परिक्रमण काल T तथा उसकी दीर्घवृत्तीय कक्षा की अर्द्ध-दीर्घ अक्ष a हो तो तृतीय नियम के अनुसार T² ∝ a³ अथवा T²/a³ = नियतांक अर्थात् सभी ग्रहों के लिए T³/a³ का मान नियत रहता है।

प्रश्न 2.
ग्रहों की गति सम्बन्धी कैपलर के नियमों से सिद्ध कीजिए कि किसी ग्रह पर लगने वाला बल सूर्य से उसकी दूरी के वर्ग के व्युत्क्रमानुपाती होता है।
उत्तर-
कैपलर के नियमों से न्यूटन के निष्कर्ष- न्यूटन ने पाया कि अधिकांश ग्रहों (बुध व प्लूटो को छोड़कर) की सूर्य के चारों ओर की कक्षाएँ लगभग वृत्ताकार हैं। कैपलर के द्वितीय नियम के अनुसार, किसी ग्रह की क्षेत्रीय चाल नियत रहती है। अत: वृत्ताकार कक्षा में ग्रह की रेखीय (UPBoardSolutions.com) चाल (ν) नियत होगी। चूंकि यह वृत्ताकार पथ पर चल रहा है; अत: ग्रह पर केन्द्र (सूर्य) की ओर अभिकेन्द्र बल F लगता है तथा
F = mv²/r,
जहाँ m ग्रह का द्रव्यमान, ν ग्रह की रेखीय चाल तथा r वृत्ताकार कक्षा की त्रिज्या है।
यदि ग्रह का परिक्रमण काल T है, तो

इस प्रकार कैपलर के नियमों के आधार पर न्यूटन ने निम्नलिखित निष्कर्ष निकाले
1. ग्रह पर एक अभिकेन्द्र बल (F) कार्य करता है जिसकी दिशा सूर्य की ओर होती है।
2. यह बल ग्रह की सूर्य से औसत दूरी के वर्ग के व्युत्क्रमानुपाती होता है (F ∝1/r²)।
3. यह बल ग्रह के द्रव्यमान के अनुक्रमानुपाती होता है (F ∝ m) ।
इन निष्कर्षों के साथ-साथ न्यूटन ने यह बताया कि कैपलर के नियम केवल सूर्य एवं ग्रह के बीच ही सत्य नहीं हैं, अपितु ब्रह्माण्ड में स्थित किन्हीं भी दो पिण्डों के लिए भी सत्य हैं।

प्रश्न 3.
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण नियम लिखिए तथा इसके आधार पर G की परिभाषा दीजिए।
उत्तर-
न्यूटन का सार्वत्रिक गुरुत्वाकर्षण नियम-इस नियम के अनुसार किन्हीं दो द्रव्य-कणों के. बीच लगने वाला गुरुत्वाकर्षण बल कणों के द्रव्यमानों के गुणनफल के अनुक्रमानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। बल की दिशा दोनों कणों को मिलाने वाली रेखा के साथ होती है।

अतः “गुरुत्वाकर्षण नियतांक उस पारस्परिक आकर्षण बल के बराबर होता है जो एकांक दूरी पर रखे एकांक द्रव्यमान के दो द्रव्य-कणों के बीच कार्य करता है तथा जिसकी दिशा कणों को मिलाने वाली रेखा के अनुदिश होती है।”

प्रश्न 4.
गुरुत्वीय बन्धन ऊर्जा से क्या तात्पर्य है? एक मनुष्य जिसका भार पृथ्वी की सतह पर W है, यदि वह पृथ्वी की सतह से पृथ्वी की त्रिज्या की 3 गुना ऊँचाई पर जाता है, तो उस स्थान पर
| उसका भार ज्ञात कीजिए।
उत्तर-
गुरुत्वीय बन्धन ऊर्जा-“पृथ्वी के चारों ओर परिक्रमण करते हुए किसी पिण्ड अथवा उपग्रह को अपनी कक्षा छोड़कर अनन्त पर चले जाने के लिए आवश्यक ऊर्जा को बन्धन ऊर्जा कहते हैं।” पृथ्वी के समीप परिक्रमण करते हुए उपग्रह की (UPBoardSolutions.com) कुल ऊर्जा [latex s=2]-\frac { 1 }{ 2 } \left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex] होती है। अत: उपग्रह को अनन्त पर भेजने के लिए उपग्रह को [latex s=2]+\frac { 1 }{ 2 } \left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex] ऊर्जा देनी होगी जिससे उसकी कुल ऊर्जा E शून्य हो जाएगी।
अतः पृथ्वी के समीप परिक्रमण करते उपग्रह की बन्धन ऊर्जा = [latex s=2]+\frac { 1 }{ 2 } \left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex]

प्रश्न 5.
सूर्य से दो ग्रहों की दूरियाँ क्रमशः 10¹¹ मीटर तथा 10¹⁰ मीटर हैं। इनकी चालों का । अनुपात ज्ञात कीजिए।
हल-
कैपलर के तृतीय नियम के अनुसार, T² = Kr³
जहाँ, T ग्रह का आवर्तकाल तथा r ग्रह की सूर्य से दूरी है। यदि ग्रहों के आवर्तकाल T1 व T2 तथा सूर्य से दूरियाँ क्रमशः r1 व r2 हों, तो ।

प्रश्न 6.
यदि दो ग्रहों की त्रिज्याएँ r1 तथा r2 हों एवं उनके माध्य घनत्व d1 तथा d2, हों तो सिद्ध कीजिए कि दोनों ग्रहों पर गुरुत्वीय त्वरणों का अनुपात r1d1 :r2d2 होगा।
हल-
चूँकि द्रव्यमान M = आयतन x घनत्व = [latex s=2]\frac { 4 }{ 3 } \pi { r }^{ 3 }\times d [/latex]

प्रश्न 7.
पृथ्वी तल से किस ऊँचाई पर g का मान वही है जो एक 100 किमी गहरी खाई में है?
हल-
माना पृथ्वी तल से h ऊँचाई पर होगा। ,
100 किमी गहरी खाई में g का मान ।

प्रश्न 8.
पृथ्वी की त्रिज्या 6.4×10⁶ मी है। पृथ्वी तल से 800 किमी की ऊँचाई पर गुरुत्वीय विभव तथा गुरुत्वीय क्षेत्र की तीव्रता ज्ञात कीजिए। (g = 10 मी/से²)
हल-
पृथ्वी के केन्द्र से प्रक्षेपण बिन्दु की दूरी

प्रश्न 9.
पृथ्वी के केन्द्र से उस बिन्दु की दूरी ज्ञात कीजिए जहाँ पृथ्वी के गुरुत्वीय क्षेत्र की तीव्रता 2.5 न्यूटन/किग्रा हो। उस बिन्दु पर गुरुत्वीय विभव की गणना कीजिए। (g= 10 मी/से², पृथ्वी की त्रिज्या R_e = 6.4×10⁶ मी)
हल-

प्रश्न 10.
सूर्य से एक ग्रह की दूरी, पृथ्वी की अपेक्षा 4 गुनी है। सूर्य के चारों ओर पृथ्वी का परिक्रमण काल एक वर्ष है। उस ग्रह का परिक्रमण काल ज्ञात कीजिए।
हल-
माना पृथ्वी से सूर्य की दूरी = r1 तथा पृथ्वी का सूर्य के परितः परिक्रमण काल T = 1 वर्ष
प्रश्नानुसार, ग्रह से सूर्य की दूरी r2 = 4r1 तथा ग्रह का (UPBoardSolutions.com) परिक्रमण काल = T2
कैपलर के तृतीय नियम से,

विस्तृत उत्तरीय प्रश्न

प्रश्न 1.
गुरुत्वीय त्वरण से क्या तात्पर्य है? पृथ्वी की सतह से h ऊँचाई पर गुरुत्वीय त्वरण के लिए | व्यंजक पृथ्वी की सतह पर गुरुत्वीय त्वरण तथा पृथ्वी की त्रिज्या के पदों में प्राप्त कीजिए। या पृथ्वी तल से ऊपर तथा नीचे जाने पर ‘g’ के मान में विचरण की विवेचना कीजिए। क्या दोनों परिस्थितियों में g के घटने की दर समान होगी?
उत्तर-
पृथ्वी तल से ऊँचाई के साथ ‘g’ के मान में विचरण
गुरुत्वीय त्वरण- “स्वतन्त्रतापूर्वक पृथ्वी की ओर गिरती हुई किसी वस्तु के वेग में 1 सेकण्ड में होने वाली वृद्धि अर्थात् त्वरण को गुरुत्वीय त्वरण कहते हैं। इसे ‘g’ से प्रदर्शित करते हैं।
पृथ्वी तल से ऊपर जाने पर ऊँचाई में वृद्धि के साथ-साथ गुरुत्वीय त्वरण का मान घटता जाता है। इस तथ्य को निम्न प्रकार से समझाया जा सकता है
माना पृथ्वी का द्रव्यमान M_e है, जिसको इसके केन्द्र O पर ही निहित माना जा सकता है तथा R_e इसकी त्रिज्या है। यदि m द्रव्यमान की वस्तु पृथ्वी तल पर बिन्दु A पर स्थित है (चित्र 8.6) तो न्यूटन के गुरुत्वाकर्षण नियमानुसार वस्तु पर पृथ्वी का (UPBoardSolutions.com) गुरुत्वाकर्षण बल [latex s=2]F=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex]
यह बल ही पृथ्वी तल पर इस वस्तु का भार mg होगा।
अतः [latex s=2]mg=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex] …(i)
(जहाँ g = पृथ्वी तल पर गुरुत्वीय त्वरण है।) जब इस वस्तु को पृथ्वी तल से h. ऊँचाई पर स्थित बिन्दु P पर रखा जायेगा, जहाँ गुरुत्वीय त्वरण g’ हो, तो उपर्युक्त समी० (1) के अनुरूप इस स्थान पर ।


उपर्युक्त समी० (3) से स्पष्ट है कि पृथ्वी तल से ऊपर जाने पर h के बढ़ने के साथ-साथ गुरुत्वीय त्वरण g'<g अर्थात् गुरुत्वीय त्वरण का मान घटता जाता है तथा अनन्त पर h = ∞ के लिए यह शून्य हो जाएगा।
पृथ्वी तल से गहराई के साथ ‘g’ के मान में  विचरण “पृथ्वी तल से नीचे जाने पर गहराई में वृद्धि के साथ-साथ गुरुत्वीय त्वरण का मान घटता जाता है।” इस तथ्य को निम्नवत् समझा जा सकता है
माना m द्रव्यमान की कोई वस्तु पृथ्वी के अन्दर इसकी सतह से h। गहराई पर स्थित बिन्दु P पर रखी है (चित्र 8.7) जिसकी पृथ्वी के केन्द्र O से दूरी (R_e-h) होगी। इस अवस्था में यदि O को केन्द्र मानकर एक गोला खींचा जाये जिसकी त्रिज्या (R, – h) हो तो (UPBoardSolutions.com) वस्तु अन्दर वाले ठोस गोले के तल पर स्थित होगी तथा बाहरी कवच के अन्दर होगी। परन्तु किसी भी खोखले गोल कवच के भीतर स्थित वस्तु पर आकर्षण बल शून्य होता है; अतः केवल अन्दर वाले ठोस गोले के कारण ही वस्तु पर आकर्षण बल कार्य करेगा। अन्दर वाले ठोस गोले का द्रव्यमान M_e‘ = (R_e – h) त्रिज्या के गोले का आयतन x पृथ्वी का माध्य घनत्व
= [latex s=2]=\frac { 4 }{ 3 } \pi { \left( { R }_{ e }-h \right) }^{ 3 }\times \rho [/latex]
अत: न्यूटन के गुरुत्वाकर्षण नियमानुसार, अन्दर वाले गोले के कारण वस्तु पर आकर्षण बल


अत: जैसे-जैसे हम पृथ्वी तल से नीचे की ओर जाते हैं, h में वृद्धि के साथ-साथ गुरुत्वीय त्वरण का मान घटता जाता है तथा पृथ्वी के केन्द्र O पर (जहाँ h = R_e) इसका मान शून्य हो जाता है। उपर्युक्त दोनों परिस्थितियों में ‘g’ के घटने की दर समान नहीं होगी, बल्कि पृथ्वी तल से गहराई में जाने की तुलना में तल से ऊँचाई पर जाने पर गुरुत्वीय त्वरण तेजी से घटता है।

प्रश्न 2.
पृथ्वी के केन्द्र से दूरी पर कोई पिण्ड जिसका द्रव्यमान m है, की गुरुत्वीय स्थितिज ऊर्जा के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
पृथ्वी की सतह पर गुरुत्वीय स्थितिज ऊर्जा-माना पृथ्वी तल के बिन्दु (UPBoardSolutions.com) A पर m द्रव्यमान का एक पिण्ड स्थित है। यदि पृथ्वी का द्रव्यमान M_e. तथा त्रिज्या R_e. हो, तो पृथ्वी द्वारा पिण्ड पर लगा गुरुत्वाकर्षण बल [latex s=2]{ F }_{ A }=G\left( \frac { { M }_{ e }m }{ { { R }^{ 2 } }_{ e } } \right) [/latex]
माना A से अनन्त तक की दूरी को छोटे-छोटे भागों AB, BC, CD, ….. में विभाजित किया गया है तथा बिन्दुओं B, C, D, ….. की पृथ्वी के केन्द्र से दूरियाँ क्रमशः R₁, R₂, R₃,…… हैं। यदि पिण्ड बिन्दु B पर हो तो उस पर लगा गुरुत्वाकर्षण बल
[latex s=2]{ F }_{ B }=G\left( \frac { { M }_{ e }m }{ { { R }^{ 2 } }_{ 1 } } \right) [/latex]
चूँकि बिन्दु A व B बहुत समीप हैं; अत: A व B के बीच लगे बल का मान, A व B पर लगे बलों के गुणोत्तर माध्य (geometric mean) के बराबर लिया जा सकता है। अतः A व B के बीच माध्य बल

प्रश्न 3.
गुरुत्वीय त्वरण तथा गुरुत्वाकर्षण नियतांक में सम्बन्ध लिखिए। पृथ्वी तल से कितना (i) नीचे जाने पर (ii) ऊपर जाने पर गुरुत्वीय त्वरण पृथ्वी पर गुरुत्वीय त्वरण का आधा रह जायेगा? (R_e = 6400 किमी)
उत्तर-
‘g’ तथा ‘G’ में सम्बन्धमाना पृथ्वी का द्रव्यमान M_e तथा त्रिज्या R_e है तथा पृथ्वी का कुल द्रव्यमान उसके केन्द्र पर संकेन्द्रित माना जा सकता है। माना m द्रव्यमान की एक वस्तु पृथ्वी के धरातल से नगण्य ऊँचाई पर स्थित है। अत: इस वस्तु की पृथ्वी के केन्द्र से दूरी R_e ही मानी जा सकती है। अब, न्यूटन के गुरुत्वाकर्षण नियम से पृथ्वी द्वारा वस्तु पर लगाया गया आकर्षण बल
[latex s=2]{ F }=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex] …(1)
इस बल F के कारण ही वस्तु में गुरुत्वीय त्वरण ! उत्पन्न होता है। न्यूटन के गति विषयक द्वितीय नियम के आधार पर
बल = द्रव्यमान x त्वरण
F = m x g …(2)
समी० (1) तथा समी० (2) की तुलना करने पर,
[latex s=2]mg=\frac { { GM }_{ e }m }{ { { R }^{ 2 } }_{ e } } [/latex]
अथवा [latex s=2]g=\frac { { GM }_{ e } }{ { { R }^{ 2 } }_{ e } } [/latex] …(3)
समीकरण (3) ही g तथा G में सम्बन्ध व्यक्त करती है। चूंकि इस व्यंजक में वस्तु का समान द्रव्यमान m नहीं आता, अतः गुरुत्वीय त्वरण g का मान गिरने वाली वस्तु के द्रव्यमान पर निर्भर नहीं करता। इसलिए यदि वायु की अनुपस्थिति में भिन्न-भिन्न द्रव्यमान वाली वस्तुओं को समान ऊँचाई से गिराया। जाए तो उनमें उत्पन्न त्वरण (g) समान होने के कारण वे सभी वस्तुएँ पृथ्वी तल पर एक साथ पहुंचेगी। वायु की उपस्थिति में उत्प्लावन प्रभाव व श्यानकर्षण के कारण सभी वस्तुओं के त्वरण भिन्न-भिन्न पाये जाते हैं। इस दशा में भारी वस्तु पृथ्वी-तल पर पहले पहुँचेगी। | (i) पृथ्वी-तल से नीचे जाने पर गुरुत्वीय त्वरण ।
[latex s=2]{ g }^{ I }=g\left( 1-\frac { h }{ { R }_{ e } } \right) [/latex]

प्रश्न 4.
गुरुत्वीय विभव की परिभाषा दीजिए। पृथ्वी के केन्द्र से r दूरी पर किसी m द्रव्यमान के पिण्ड के गुरुत्वीय विभव का सूत्र व्युत्पादित कीजिए।
उत्तर-
गुरुत्वीय विभव (Gravitational potential)-एकांक द्रव्यमान को अनन्त से गुरुत्वीय क्षेत्र के भीतर किसी बिन्दु तक लाने में जितना कार्य होता है, उसे उस बिन्दु पर ‘गुरुत्वीय विभव’ कहते हैं। चूंकि यह कार्य क्षेत्र द्वारा किया जाता है; अतः गुरुत्वीय विभव सदैव ऋणात्मक होता है। यदि m किग्रा द्रव्यमान को अनन्त से गुरुत्वीय क्षेत्र के किसी बिन्दु तक लाने में W जूल कार्य प्राप्त होता है तो उस बिन्दु पर गुरुत्वीय विभव (- W/m) जूल/किग्रा होगा।

यह एक अदिश राशि है। इसका मात्रक जूल/किग्रा तथा विमा [L²T^-2] है।
M द्रव्यमान के कारण r दूरी पर गुरुत्वीय विभव का व्यंजक- माना कि M द्रव्यमान का एक पिण्ड बिन्दु O पर स्थित है। माना पिण्ड के गुरुत्वीय क्षेत्र में बिन्दु O से r मीटर दूरी पर स्थित बिन्दु A पर गुरुत्वीय विभव ज्ञात करना है। इसके लिए हम पहले m किग्रा (UPBoardSolutions.com) द्रव्यमान के एक पिण्ड को A से अनन्त तक ले जाने में गुरुत्वाकर्षण बल के विरुद्ध किये गये कार्य की गणना निम्नवत् करेंगेA से अनन्त तक की दूरी को छोटे-छोटे भागों AB, BC, CD,… में विभाजित हुआ मान लेते हैं। बिन्दुओं B, C, D,… की बिन्दु 0 से दूरियाँ क्रमशः r1, r2, r3,…मीटर हैं। बिन्दु A पर स्थित m किग्रा द्रव्यमान के पिण्ड पर M के कारण गुरुत्वाकर्षण बल [latex s=2]{ F }_{ A }=G\left( \frac { Mm }{ { r }^{ 2 } } \right) [/latex]
यदि पिण्ड B पर हो, तब उस पर गुरुत्वाकर्षण बल [latex s=2]{ F }_{ B }=G\left( \frac { Mm }{ { r1 }^{ 2 } } \right) [/latex]
चूँकि A व B एक-दूसरे के बहुत निकट हैं; अतः A व B के बीच गुरुत्वाकर्षण बल का मान, A व B पर लगे बलों के गुणोत्तर माध्य (geometric mean) के बराबर ले सकते हैं।
अतः A व B के बीच माध्य बल ।

प्रश्न 5.
पृथ्वी तल से किसी ऊँचाई में स्थित बिन्दु पर गुरुत्वीय क्षेत्र की तीव्रता का मान 2.5 न्यूटन/किग्रा है। उस बिन्दु पर गुरुत्वीय विभव की गणना कीजिए। (g=100 मी/से² तथा पृथ्वी की त्रिज्या R = 6.4×10⁶ मी)
हल-
गुरुत्वीय क्षेत्र की तीव्रता [latex s=2]I=\left( \frac { GM }{ { r }^{ 2 } } \right) [/latex] ..(1)
तथा . गुरुत्वीय विभव [latex s=2]V=-\left( \frac { GM }{ { r } } \right) [/latex] …(2)
समी० (1) व समी० (2) से,
V= -I x r
∴ परन्तु समी० (1) से

प्रश्न 6.
पृथ्वी के पृष्ठ से किसी पिण्ड के पलायन वेग के व्यंजक का निगमन कीजिए। पृथ्वी के पृष्ठ के समीप किसी उपग्रह की कक्षीय चाल तथा पलायन वेग में सम्बन्ध भी बताइए।
उत्तर-
पलायन वेग- वह न्यूनतम वेग जिससे किसी वस्तु को पृथ्वी तल से फेंकने पर वह पृथ्वी के आकर्षण क्षेत्र से बाहर निकल जाये; अर्थात् वापस लौटकर पृथ्वी पर न आ सके, पलायन वेग कहलाता है। इसे ν_e, से व्यक्त करते हैं।
पलायन वेग के लिए व्यंजक-अनन्त पर गुरुत्वीय स्थितिज ऊर्जा शून्य मानने पर, (UPBoardSolutions.com) पृथ्वी तल पर स्थित m द्रव्यमान के पिण्ड की गुरुत्वीय स्थितिज ऊर्जा [latex s=2]U=-\left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex]
जहाँ M_e पृथ्वी का द्रव्यमान तथा R_e पृथ्वी की त्रिज्या है।
अतः m द्रव्यमान के पिण्ड को पृथ्वी तल से अनन्त तक ले जाने के लिए GM_e.m/R_e कार्य करना पड़ता है। अतः यदि पिण्ड m को इतने वेग से फेंके कि उसकी गतिज ऊर्जा, कार्य GM,m/R, के बराबर हो तो वह पृथ्वी के गुरुत्वीय क्षेत्र के बाहर चला जाएगा; अर्थात् अनन्त पर चला जाएगा अर्थात् पृथ्वी से सदैव के लिए पलायन कर जाएगा। यही पलायन ऊर्जा होगी।
अतः पलायन ऊर्जा [latex s=2]=+\left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex] …(1)
इस दशा में पिण्ड को दिया गया वेग ही पिण्ड को पलायन वेग ν_e, होगा। अत: पिण्ड की गतिज ऊर्जा mu. होगी।

अथवा पलायन वेग [latex s=2]{ \upsilon }_{ e }=\sqrt { 2g{ R }_{ e } } [/latex] …(3)
उपर्युक्त समी० (2) तथा (3) पृथ्वी तल से किसी पिण्ड के पलायन वेग के लिए अभीष्ट व्यंजक के दो विभिन्न रूप हैं। चूंकि इन सूत्रों में पिण्ड का द्रव्यमान m तथा प्रक्षेपण कोण θ नहीं आता है; अतः पलायन वेग ν_e , का मान फेंके गये पिण्ड के द्रव्यमान तथा प्रक्षेपण कोण पर निर्भर नहीं करता है। अतः
पृथ्वी पर प्रत्येक पिण्ड के लिए पलायन वेग का मान एक ही होता है; चाहे उसका द्रव्यमान कुछ भी हो और वह क्षैतिज के साथ किसी भी कोण पर प्रक्षेपित किया जाये।
यह ग्रह की त्रिज्या एवं ग्रह के गुरुत्वीय त्वरण पर निर्भर करता है।
यदि किसी कृत्रिम उपग्रह को पलायन वेग के बराबर वेग से क्षैतिज दिशा में प्रक्षेपित किया जाए तो उसका पथ परवलयाकार होगा।
पलायन वेग तथा कक्षीय वेग-पलायन वेग किसी पिण्ड को पृथ्वी तल से दिया गया (UPBoardSolutions.com) वह वेग है। जिससे फेंके जाने पर पिण्ड पृथ्वी तल से सदैव के लिए पलायन कर जाये; अर्थात् अनन्त पर चला जाये,जबकि कक्षीय वेग किसी पिण्ड को पृथ्वी तल से कुछ ऊँचाई पर ले जाकर दिया गया वह क्षैतिज वेग है। जिससे कि पिण्डे पृथ्वी के चारों ओर वृत्ताकार कक्षा में परिक्रमण करने लगे।
कक्षीय चाल तथा पलायन वेग में सम्बन्ध-पृथ्वी के पृष्ठ के निकट किसी उपग्रह की कक्षीय चाल

प्रश्न 7.
पृथ्वी की सतह से h ऊँचाई पर किसी कृत्रिम उपग्रह की कक्षीय चाल के लिए व्यंजक स्थापित कीजिए। दर्शाइए कि उपग्रह का वेग उसके द्रव्यमान पर निर्भर नहीं करता है। या , उपग्रहों की कक्षीय चाल के लिए व्यंजक प्राप्त कीजिए।
उत्तर-
जिस तरह विभिन्न ग्रह सूर्य के चारों ओर परिक्रमा करते हैं, उसी तरह कुछ आकाशीय पिण्ड इन ग्रहों (planets) के चारों ओर भी चक्कर लगाते हैं। इन पिण्डों को उपग्रह (satellites) कहते हैं; जैसे चन्द्रमा पृथ्वी के चारों ओर वृत्तीय कक्षा में चक्कर लगाता है। अतः पृथ्वी एक ग्रह तथा चन्द्रमा पृथ्वी का एक उपग्रह है।
उपग्रह की कक्षीय चाल-पृथ्वी के चारों ओर वृत्तीय कक्षा जिसकी त्रिज्या r है, में कक्षीय चाल υ_o, से परिक्रमण कर रहे उपग्रह (द्रव्यमान m) पर एक अभिकेन्द्र बल (mυ_o²/r) लगता है जो पृथ्वी द्वारा उपग्रह पर लगाये गये गुरुत्वाकर्षण बल (GM_em/r²) से प्राप्त होता है, जहाँ M_e पृथ्वी का द्रव्यमान है |

यदि उपग्रह पृथ्वी तल से h ऊँचाई पर है तो पृथ्वी के केन्द्र से उपग्रह की दूरी r = R_e +h
जहाँ R_e पृथ्वी की त्रिज्या है। r का यह मान समी० (1) में रखने पर,

स्पष्ट है कि कक्षीय चाल उपग्रह के द्रव्यमान पर निर्भर नहीं करती है। यह केवल उसकी पृथ्वी तल से ऊँचाई पर निर्भर करती है।
यदि उपग्रह पृथ्वी तल के अति समीप है; अर्थात् h<<R_e, तब h को R_e की तुलना में नगण्य मान सकते हैं।
अत: समी० (3) से

उपग्रह की कक्षीय चाल (वेग) के उपर्युक्त सूत्रों में उपग्रह का द्रव्यमान नहीं आता है, अत: इससे सिद्ध होता है कि उपग्रह की कक्षीय चाल (वेग) उसके द्रव्यमान पर निर्भर नहीं करती है। अतः भिन्न-भिन्न द्रव्यमान के दो कृत्रिम उपग्रह एक ही कक्षा में साथ-साथ एक ही कक्षीय चाल से परिभ्रमण करेंगे।

प्रश्न 8.
पृथ्वी तल से h ऊँचाई पर पृथ्वी की परिक्रमा कर रहे कृत्रिम उपग्रह के परिक्रमण काल के | लिए सूत्र स्थापित कीजिए। या किसी उपग्रह के परिक्रमण काल का व्यंजक प्राप्त कीजिए।
उत्तर-
कृत्रिम उपग्रह का परिक्रमण काल-यदि कृत्रिम उपग्रह की वृत्तीय कक्षा की त्रिज्या । हो, (UPBoardSolutions.com) जहाँ r = R_e + h (जिसमें R_e = पृथ्वी की त्रिज्या तथा h = पृथ्वी तल से कृत्रिम उपग्रह की ऊँचाई) तो उपग्रह का परिक्रमण काले अर्थात् पृथ्वी के चारों ओर एक चक्कर पूरा करने में लगा समय

प्रश्न 9.
पृथ्वी के समीप परिक्रमा करने वाले उपग्रह की सम्पूर्ण ऊर्जा के लिए सूत्र स्थापित कीजिए। इसको मान ऋणात्मक क्यों होता है?
उत्तर-
पृथ्वी के चारों ओर परिक्रमा करता हुआ उपग्रह पृथ्वी के गुरुत्वीय क्षेत्र में रहता है, इसलिए उपग्रह में स्थितिज ऊर्जा होती है तथा उपग्रह की गति के कारण इसमें गतिज ऊर्जा होती है। इस प्रकार पृथ्वी के चारों ओर परिक्रमा करते हुए उपग्रह की स्थितिज एवं गतिज ऊर्जाओं का योग ही इसकी कुल ऊर्जा होती है। अनन्त पर किसी पिण्ड की गुरुत्वीय स्थितिज ऊर्जा शून्य मानते हुए पृथ्वी तल पर स्थित m द्रव्यमान के पिण्ड की गुरुत्वीय स्थितिज ऊर्जा निम्नलिखित सूत्र से व्यक्त की जाती है
[latex s=2]{ U }_{ e }=-\left( \frac { { GM }_{ e }m }{ { R }_{ e } } \right) [/latex]
(जहाँ M_e = पृथ्वी का द्रव्यमान तथा R_e = पृथ्वी की त्रिज्या)
यदि कोई कृत्रिम उपग्रह पृथ्वी तल के समीप ही पृथ्वी की परिक्रमा वृत्तीय कक्षा में कर रहा हो तो उसकी कक्षीय त्रिज्या r को R_e के बराबर मान सकते हैं। तब यदि उपग्रह का द्रव्यमान m हो तो उसकी गुरुत्वीय स्थितिज ऊर्जा U = U_e ही होगी

उपग्रह की कुल ऊर्जा के सूत्र में ऋणात्मक चिह्न इस तथ्य का प्रतीक है कि उपग्रह की कुल ऊर्जा ऋणात्मक है। इसका एक विशेष अर्थ है। अनन्त पर (r= ∞) उपग्रह की गतिज ऊर्जा व स्थितिज ऊर्जा दोनों ही शून्य हैं; अतः अनन्त पर उपग्रह की कुल ऊर्जा शून्य है। परन्तु (UPBoardSolutions.com) गतिज ऊर्जा ऋणात्मक नहीं हो सकती। तब कुल ऊर्जा ऋणात्मक होने का अर्थ है कि उपग्रह को अनन्त पर भेजने के लिए अर्थात् कुल ऊर्जा शून्य करने के लिए हमें उपग्रह को ऊर्जा देनी पड़ेगी। जब तक परिक्रमण करते उपग्रह को अतिरिक्त ऊर्जा प्राप्त नहीं होगी तब तक वह अपनी कक्षा नहीं छोड़ेगा अर्थात् बन्द कक्षा में ही परिक्रमण करता रहेगा, अर्थात् उपग्रह पृथ्वी से बद्ध (bound) रहेगा।

We hope the UP Board Solutions for Class 11 Physics Chapter 8 Gravitation help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 8 Gravitation, drop a comment below and we will get back to you at the earliest.