Class 9

UP Board Solutions for Class 9 Science Chapter 4 Structure of the Atom (परमाणु की संरचना)

These Solutions are part of UP Board Solutions for Class 9 Science. Here we have given UP Board Solutions for Class 9 Science Chapter 4 Structure of the Atom (परमाणु की संरचना).

पाठ्य – पुस्तक के प्रश्नोत्तर

पाठगत प्रश्न (पृष्ठ संख्या – 53)

प्रश्न 1.
केनाल किरणें क्या हैं ?
उत्तर-
केनाल किरणें- जब विसर्जन नलिका में बहुत कम दाब पर छिद्र युक्त कैथोड लेकर विद्युत विसर्जन किया जाता है तो छिद्र युक्त कैथोड से एक प्रकार की किरणें निकलती हैं जिनकी (UPBoardSolutions.com) दिशा कैथोड किरणों के विपरीत होती है। ये किरणें धनावेशित कणों से मिलकर बनी होती हैं। जिन्हें प्रोटॉन कहा गया। इनका द्रव्यमान हाइड्रोजन के एक परमाणु के द्रव्यमान के बराबर पाया गया।

प्रश्न 2.
यदि किसी परमाणु में एक इलेक्ट्रॉन तथा एक प्रोटॉन है तो उसमें कोई आवेश होगा या नहीं ?
उत्तर-
यदि किसी परमाणु में एक इलेक्ट्रॉन तथा एक प्रोटॉन होगा, तो उस पर कोई आवेश नहीं होगा क्योंकि इलेक्ट्रॉन पर उपस्थित ऋण आवेश प्रोटॉन पर उपस्थित धन आवेश को उदासीन कर देगा।

पाठगत प्रश्न (पृष्ठ संख्या – 56)

प्रश्न 1.
परमाणु उदासीन है, इस तथ्य को टामसन के मॉडल के आधार पर स्पष्ट कीजिए।
उत्तर-
टॉमसन के परमाणे मॉडल के अनुसार परमाणु धन आवेशित गोले का बना होता है और इलेक्ट्रॉन उसमें फँसे होते हैं। क्योंकि धनात्मक आवेश तथा इलेक्ट्रॉन पर उपस्थित ऋणात्मक आवेश परिमाण में समान होते हैं।
अतः परमाणु उदासीन होता है।

प्रश्न 2.
रदरफोर्ड के परमाणु मॉडल के अनुसार, परमाणु के नाभिक में कौन-सा अवपरमाणुक कण विद्यमान है?
उत्तर-
रदरफोर्ड के परमाणु मॉडल के अनुसार, परमाणु के नाभिक में धनावेशित कण प्रोटॉन विद्यमान है।

प्रश्न 3.
तीन कक्षाओं वाले बोर के परमाण मॉडल का चित्र बनाइये।।
उत्तर-
तीन कक्षाओं वाले बोर के परमाणु का मॉडल चित्र निम्न प्रकार से है। तीन कक्षाएँ क्रमशः K, L तथा M द्वारा दिखाई गई हैं

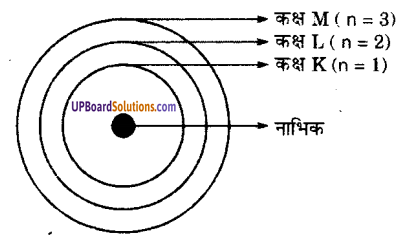
प्रश्न 4.
क्या अल्फा किरणों का प्रकीर्णन प्रयोग सोने के अतिरिक्त दूसरी धातु की पन्नी से संभव होगा?
उत्तर-
अल्फा किरणों के प्रकीर्णन प्रयोग में सोने की पन्नी को इसलिए चुना गया क्योंकि सोने की परत बहुत पतली अवस्था में प्राप्त हो सकती है अर्थात् 1000 परमाणुओं की मोटाई (UPBoardSolutions.com) के बराबर। यदि दूसरी भारी धातु लें तो हम इतनी पतली परत वाली पन्नी प्राप्त नहीं कर सकते अतः अल्फा किरणों का प्रकीर्णन तो इससे भी संभव होगा परन्तु परिणाम इतने स्पष्ट नहीं होंगे जितने सोने की पन्नी से प्राप्त होंगे।

पाठगत प्रश्न (पृष्ठ संख्या – 56)

प्रश्न 1.
परमाणु के तीन अवपरमाणुक कणों के नाम लिखिए।
उत्तर-
परमाणु के तीन प्रमुख कण हैं-इलेक्ट्रॉन, प्रोटॉन, और न्यूट्रॉन।

प्रश्न 2.
होलियम परमाणु का परमाणु द्रव्यमान 4u है तथा उसके नाभिक में दो प्रोटॉन होते हैं। इसमें कितने न्यूट्रान होंगे?
उत्तर-
न्यूट्रॉनों की संख्या = परमाणु द्रव्यमान – प्रोटॉन की संख्या = 4 – 2 = 2

पाठगत प्रश्न (पृष्ठ संख्या – 57)

प्रश्न 1.
कार्बन और सोडियम के परमाणुओं के लिए इलेक्ट्रॉन-वितरण लिखिए।
उत्तर-

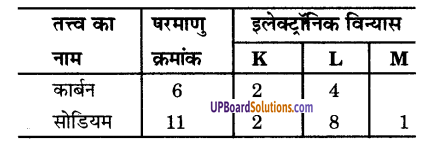
प्रश्न 2.
अगर किसी परमाणु का K और L कोश भरा है, तो उस परमाणु में इलेक्ट्रॉनों की संख्या क्या होगी ?
उत्तर-
K (पहला कक्ष)
इसमें इलेक्ट्रॉनों की संख्या = 2
L (दूसरा कक्ष)
इसमें इलेक्ट्रॉनों की संख्या = 8
अतः परमाणु में कुल इलेक्ट्रॉन = 2 + 8 = 10.

पाठगत प्रश्न (पृष्ठ संख्या – 58)

प्रश्न 1.
क्लोरीन, सल्फर और मैग्नीशियम की परमाणु संख्या से आप इनकी संयोजकता कैसे प्राप्त करेंगे?
उत्तर-
(i) क्लोरीन परमाणु संख्या = 17
इलेक्ट्रॉनिक विन्यास = 2, 8, 7
क्लोरीन के बाह्यतम कोश को पूर्ण करने के लिए केवल 1 इलेक्ट्रॉन की आवश्यकता होती है। इसलिए इसकी संयोजकता 1 है।
(ii) सल्फर परमाणु क्रमांक = 16
इलेक्ट्रॉनिक विन्यास = 2, 8, 6
क्योंकि इसके बाह्यतम कोश में 6 इलेक्ट्रॉन उपस्थित होते हैं।
अत: इसे पूर्ण रूप से भरने के लिए 2 इलेक्ट्रॉन की आवश्यकता होती है। अतः इसकी संयोजकता 2 है।
(iii) मैग्नीशियम परमाणु क्रमांक = 12
इलेक्ट्रॉनिक विन्यास = 2, 8, 2
क्योंकि इसके बाह्यतम कोश में 2 इलेक्ट्रॉन हैं
अतः इसकी संयोजकता 2 होगी।

पाठगत प्रश्न (पृष्ठ संख्या – 59)

प्रश्न 1.
यदि किसी परमाणु में इलेक्ट्रॉनों की संख्या 8 है और प्रोटॉनों की संख्या भी 8 है तब,
(a) परमाणु की परमाणुक संख्या क्या है ?
(b) परमाणु का क्या आवेश है ?
उत्तर-
(a) परमाणु संख्या = प्रोटॉनों की संख्या = 8
(b) प्रोटॉनों की संख्या = 8
धनात्मक आवेश = 8
इलेक्ट्रॉनों की संख्या = 8
ऋणात्मक आवेश = 8
कुल आवेश = + 8 (- 8) = 0

प्रश्न 2.
पाठ्य-पुस्तक की सारणी 4.1 की सहायता से ऑक्सीजन और सल्फर परमाणुओं की द्रव्यमान संख्या ज्ञात कीजिए।
उत्तर-
(i) ऑक्सीजन की द्रव्यमान संख्या = प्रोटॉनों की संख्या + न्यूट्रॉनों की संख्या = 8 + 8 = 16 u
(ii) सल्फर की परमाणु द्रव्यमान संख्या = प्रोटॉनों की संख्या + न्यूट्रॉनों की संख्या = 16 + 16 = 32 u

पाठगत प्रश्न (पृष्ठ संख्या – 60)

प्रश्न 1.
चिन्ह H, D और T के लिए प्रत्येक में पाए जाने वाले तीन अवपरमाणुक कणों को सारणीबद्ध कीजिए।

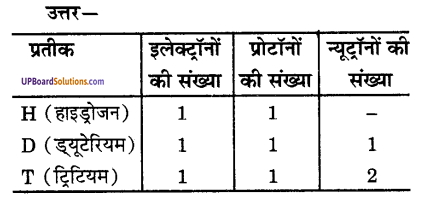
प्रश्न 2.
समस्थानिक और समभारिक के किसी एक युग्म का इलेक्ट्रॉनिक विन्यास लिखिए।
उत्तर-
कार्बन के समस्थानिक हैं
[latex]_{ 6 }^{ 12 }{ C }[/latex] और [latex]_{ 6 }^{ 14 }{ C }[/latex]
[latex]_{ 6 }^{ 12 }{ C }[/latex] (कार्बन-12)
प्रोटॉनों की संख्या = 8
इलेक्ट्रॉनों की संख्या = 6
न्यूट्रॉन की संख्या = 12 – 6 = 6
इलेक्ट्रॉनिक विन्यास = 2, 4
[latex]_{ 6 }^{ 14 }{ C }[/latex] (कार्बन-14)
इलेक्ट्रॉन की संख्या = 6
न्यूट्रॉन की संख्या = 14 – 6 = 8
प्रोटॉन की संख्या = 6
इलेक्ट्रॉनिक विन्यास = 2, 4
समभारिक
[latex]_{ 18 }^{ 40 }{ Ar }[/latex] आर [latex]_{ 20 }^{ 40 }{ Ca }[/latex]
[latex]_{ 18 }^{ 40 }{ Ar }[/latex] (ऑर्गन)
इलेक्ट्रॉन की संख्या = 18
प्रोटॉन की संख्या = 18
न्यूट्रॉन की संख्या = 40 – 18 = 22
इलेक्ट्रॉनिक विन्यास = 2, 8, 8, 4
[latex]_{ 20 }^{ 40 }{ Ca }[/latex] (कैल्सियम)
इलेक्ट्रॉन की संख्या = 20
प्रोटॉन की संख्या = 20
न्यूट्रॉन की संख्या = 40 – 20 = 20
इलेक्ट्रॉनिक विन्यास = 2, 8, 8, 2

अभ्यास के प्रश्न (पृष्ठ संख्या 61 – 63)

प्रश्न 1.
इलेक्ट्रॉन, प्रोटॉन और न्यूट्रॉन के गुणों की तुलना कीजिए।
उत्तर-
इलेक्ट्रॉन, प्रोटॉन व न्यूटॉन के गुणों की तुलना-

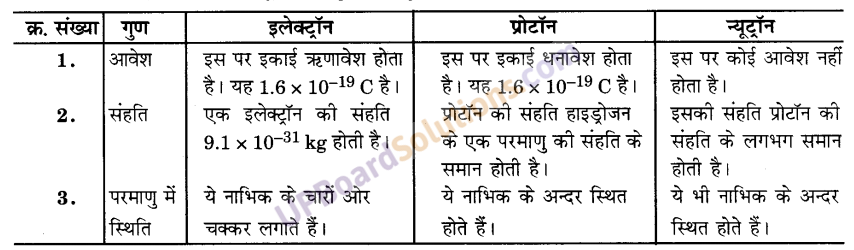
प्रश्न 2.
जे. जे. टामसन के परमाणु मॉडल की क्या सीमाएँ हैं ?
उत्तर-
जे.जे. टामसन ने परमाणु को एक गोले के रूप में प्रतिपादित किया, जिसमें प्रोटॉनों की उपस्थिति के कारण धनात्मक आवेश होता है और इलेक्ट्रॉन इसके अन्दर धंसे होते हैं। टॉमसन के पास इसे प्रायोगिक रूप में सिद्ध करने का कोई प्रमाण नहीं था और इस मॉडल द्वारा दूसरे वैज्ञानिकों द्वारा किये गये प्रयोगों के परिणामों को भी नहीं समझाया जा सकता है।

प्रश्न 3.
रदरफोर्ड के परमाणु मॉडल की क्या सीमाएँ हैं ?
उत्तर –
रदरफोर्ड के परमाणु मॉडल की कमियाँ-रदरफोर्ड (UPBoardSolutions.com) ने प्रस्तावित किया कि इलेक्ट्रॉन धनावेशित नाभिक के चारों ओर घूमते हैं (या चक्कर लगाते हैं)।

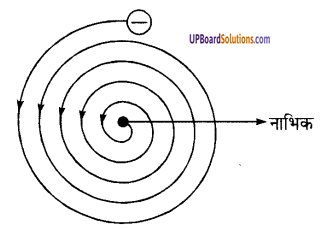
चित्र- चक्कर लगाता इलेक्ट्रॉन नाभिक में प्रवेश करता हुआ
अतः नाभिक व घूमने वाले इलेक्ट्रॉनों के मध्य आकर्षण बल इलेक्ट्रॉनों के अपकेन्द्रिय बल से संतुलित हो जाता है। परन्तु जब आवेशित वस्तु वृत्ताकार पथ पर घूमती है तो वह विकिरण उत्सर्जित करती है, जिससे ऊर्जा में हानि होती है। इसके फलस्वरूप इलेक्ट्रॉनों को नाभिक में गिर जाना चाहिए। (UPBoardSolutions.com) अगर ऐसा होता तो परमाणु अस्थिर हो जायेगा। परन्तु परमाणु स्थायी है। इन सब तथ्यों की रदरफोर्ड व्याख्या न कर सका और परमाणु की स्थिरता के कारण की व्याख्या भी नहीं कर सका।

प्रश्न 4.
बोर के परमाणु मॉडल की व्याख्या कीजिए।
उत्तर-
बोर का परमाणु मॉडल- रदरफोर्ड के परमाणु मॉडल की त्रुटियों का निवारण करके बोर ने परमाणु का नया मॉडल प्रस्तावित किया। उसकी मुख्य धाराएँ निम्नलिखित हैं|

1. इलेक्ट्रॉन परमाणु के नाभिक के चारों ओर निश्चित कक्षाओं में चक्कर लगाते हैं जिन्हें कक्ष कहते हैं।
2. एक इलेक्ट्रॉन जब किसी कक्ष में चक्कर लगाता है तो उसमें निश्चित ऊर्जा होती है और ऊर्जा का विकिरण नहीं होता।
3. प्रत्येक कक्ष की अपनी निश्चित ऊर्जा होती है। इसीलिए उन्हें ऊर्जा स्तर कहा जाता है।
   
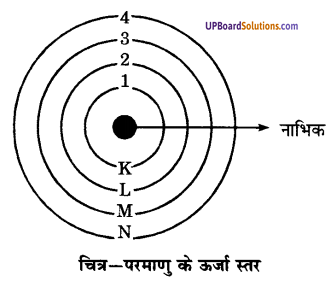
4. इन ऊर्जा स्तरों को K, L, M, N… द्वारा या 1, 2, 3, 4 … द्वारा प्रदर्शित करते हैं।

प्रश्न 5.
इस अध्याय में दिए सभी परमाणु मॉडलों की तुलना कीजिए।
उत्तर-
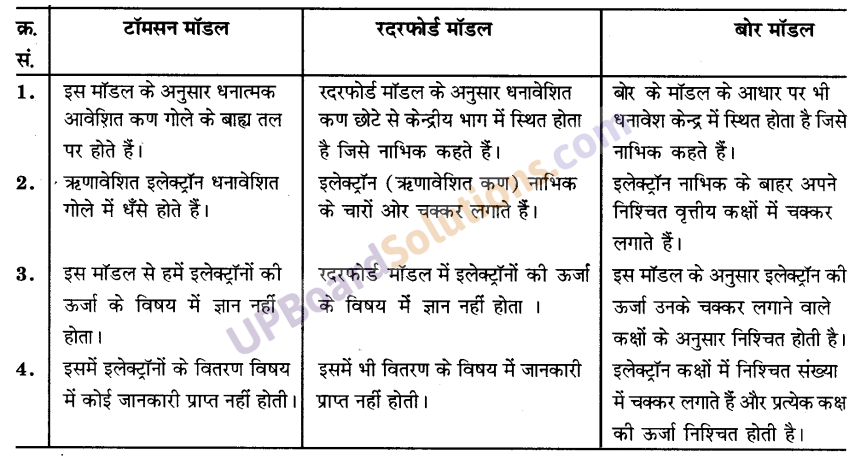
इस अध्याय में टॉमसन, रदरफोर्ड व बोर के परमाणु मॉडल दिये गये हैं। इनकी तुलना निम्न प्रकार से कर सकते हैं-

प्रश्न 6.
पहले अठारह तत्त्वों के विभिन्न कक्षों में इलेक्ट्रॉन वितरण के नियमों को लिखिए।
उत्तर-
प्रथम 18 तत्त्वों के इलेक्ट्रॉनिक विन्यास लिखने के लिए प्रयोग किए गए नियम निम्न प्रकार से हैं

1. किसी भी कक्ष में उपस्थित इलेक्ट्रॉन की संख्या एक सूत्र 2n² द्वारा ज्ञात की जाती है, जहाँ n = कक्ष की संख्या या ऊर्जा स्तर की संख्या। अतः अधिकतम इलेक्ट्रॉनों की संख्या
   पहले कक्ष (K) में होगी = 2 x 1² = 2
   दूसरे कक्ष (L) में होगी = 2 x 2² = 8
   तीसरे कक्ष (M) में होगी = 2 x 3² = 18
   चौथे कक्ष (N) में होगी = 2 x 4² = 32
2. बाह्यतम कोष में अधिकतम आठ इलेक्ट्रॉन रखे जा सकते हैं।
3. पहले कक्ष में इलेक्ट्रॉनों की संख्या पूर्ण होने पर शेष इलेक्ट्रॉन दूसरे कक्ष में जा सकते हैं अर्थात् कक्ष क्रमानुसार ही भरे जाते हैं।

प्रश्न 7.
सिलिकॉन व ऑक्सीजन का उदाहरण लेते हुए संयोजकता की परिभाषा दीजिए।
उत्तर-
किसी तत्त्व की संयोग करने की क्षमता को उसकी संयोजकता कहते हैं। यह उस परमाणु के बाह्यतम कोश (कक्ष) में उपस्थित इलेक्ट्रॉनों की संख्या से ज्ञात (UPBoardSolutions.com) की जाती है।
यदि बाह्यतम कोश में इलेक्ट्रॉनों की संख्या चार या उससे कम हो तो संयोजकता = बाह्यतम कोश में उपस्थित इलेक्ट्रॉनों की संख्या।
उदाहरण- सिलिकॉन (Si) की परमाणु संख्या 14 है।
अतः इसका इलेक्ट्रॉनिक विन्यास = 2, 8, 4
सिलिकॉन की संयोजकता = 4
यदि बाह्यतम कोश में उपस्थित इलेक्ट्रॉनों की संख्या चार से अधिक हो तो
संयोजकता = 8 – (बाह्यतम कोश में इलेक्ट्रॉनों की संख्या)
उदाहरण- ऑक्सीजन (O) की परमाणु संख्या 8 है।
इसका इलेक्ट्रॉनिक वितरण = 2, 6
अतः इसकी संयोजकता = 8 – 6 = 2

प्रश्न 8.
उदाहरण सहित व्याख्या कीजिए-परमाणु संख्या, द्रव्यमान संख्या, समस्थानिक और समभारिक। समस्थानिकों के कोई दो उपयोग लिखिए।
उत्तर-

1. परमाणु संख्या – परमाणु के नाभिक में पाए जाने वाले (धनावेशित कण) प्रोटॉनों की संख्या को परमाणु संख्या कहते हैं।
   इसे Z द्वारा दर्शाया जाता है।
   उदाहरण-
   • कार्बन की परमाणु संख्या 6 है क्योंकि इसके नाभिक में 6 प्रोटॉन पाए जाते हैं।
   • ऑक्सीजन की परमाणु संख्या 8 है क्योंकि ऑक्सीजन के परमाणु के नाभिक में 8 प्रोटॉन पाए जाते हैं।
2. द्रव्यमान संख्या – परमाणु के नाभिक में पाए जाने वाले प्रोटॉन व न्यूट्रॉन की कुल संख्या को द्रव्यमान संख्या कहते हैं।
   द्रव्यमान संख्या = प्रोटॉन की संख्या + न्यूट्रॉन की संख्या
   उदाहरण-
   • ऑक्सीजन की द्रव्यमान संख्या (परमाणु द्रव्यमान) 16 है क्योंकि ऑक्सीजन के परमाणु के नाभिक में 8 प्रोटॉन व 8 न्यूट्रॉन है।
     अतः द्रव्यमान संख्या = 8 + 8 = 16
   • सोडियम की द्रव्यमान संख्या 23 है क्योंकि सोडियम के नाभिक में 11 प्रोटॉन व 12 न्यूट्रॉन हैं।
     अतः द्रव्यमान संख्या = 11 + 12 = 23

समस्थानिक – एक ही तत्त्व के वे परमाणु जिनके परमाणु संख्या समान परन्तु द्रव्यमान संख्या भिन्न-भिन्न हों, समस्थानिक कहलाते हैं।

समस्थानिकों के दो उपयोग-

1. यूरेनियम के एक समस्थानिक का उपयोग परमाणु भट्टी में ईंधन के रूप में किया जाता है।
2. कैंसर के उपचार में कोबाल्ट के एक समस्थानिक का उपयोग होता है।
3. पेंघा रोग के उपचार में आयोडीन के समस्थानिक का उपयोग होता है।

प्रश्न 9.
Na⁺ के पूरी तरह से भरे हुए K वे L कोश होते हैं- व्याख्या कीजिए।
उत्तर-
Na की परमाणु संख्या = 11
Na⁺ में उपस्थित इलेक्ट्रॉन की संख्या = 11 – 1 = 10
Na⁺ का इलेक्ट्रॉनिक विन्यास = K, L = 2, 8
अत: Na⁺ में K तथा L कोश पूरी तरह भरे होते हैं।

प्रश्न 10.
अगर ब्रोमीन परमाणु दो समस्थानिकों [[latex]_{ 35 }^{ 79 }{ Br }[/latex] (49.7%) तथा [latex]_{ 35 }^{ 81 }{ Br }[/latex] (50.3%)] के रूप में हैं, तो ब्रोमीन परमाणु के औसत परमाणु द्रव्यमान की गणना कीजिए।

प्रश्न 11.
एक तत्त्व X का परमाणु द्रव्यमान 16.2 u है तो इसके किसी एक नमूने में समस्थानिक [latex]_{ 8 }^{ 16 }{ X }[/latex] और [latex]_{ 8 }^{ 18 }{ X }[/latex] का प्रतिशत क्या होगा?

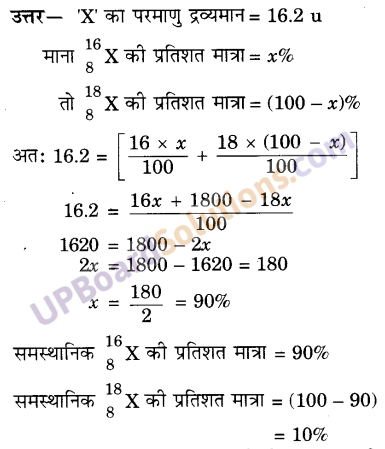
प्रश्न 12.
यदि तत्त्व का Z = 3 हो तो उस तत्त्व की संयोजकता क्या होगी? उस तत्त्व का नाम भी लिखिए।
उत्तर-
दिया है- Z = 3
इलेक्ट्रॉनिक विन्यास = 2, 1
तत्त्व की संयोजकता = 1
तत्त्व का नाम = लीथियम (Li)

प्रश्न 13.
दो परमाणु स्पीशीज के केन्द्रकों का संघटन नीचे दिया गया है
प्रोटॉन = 6(X) 6(Y)
न्यूट्रॉन = 6(X) 8(Y)
X और Y की द्रव्यमान संख्या ज्ञात कीजिए। इन दोनों स्पीशीज में क्या सम्बन्ध है?
हल-
X की द्रव्यमान संख्या = प्रोटॉन + न्यूट्रॉन = 6 + 6 = 12u
Y की द्रव्यमान संख्या = प्रोटॉन + न्यूट्रॉन = 6 + 8 = 14u
X और Y दोनों में प्रोटॉनों की संख्या समांन है अर्थात् दोनों की परमाणु संख्या समान है। परन्तु उनकी द्रव्यमान संख्या भिन्न है।
अतः दोनों एक ही तत्त्व के समस्थानिक हैं।

प्रश्न 14.
निम्नलिखित कथनों में से सही पर “T” और गलत पर “F” लिखिए
(a) जे. जे. टॉमसन ने यह प्रस्तावित किया था कि परमाणु के केन्द्रक में केवल न्यूक्लीयॉन्स होते हैं।
(b) एक इलेक्ट्रॉन और प्रोटॉन मिलकर न्यूट्रॉन का निर्माण करते हैं इसलिए यह अनावेशित होता है।
(c) इलेक्ट्रॉन का द्रव्यमान प्रोटॉन से लगभग [latex]\frac { 1 }{ 2000 }[/latex] गुना होता है।
(d) आयोडीन के समस्थानिक का इस्तेमाल टिंक्चर आयोडीन बनाने में होता है। इसका उपयोग दवा के रूप में होता है।
उत्तर-
(a) F, (b) F, (c) T, (d) T.

प्रश्न संख्या 15, 16, 17 और 18 में सही के सामने (✓) का चिह्न और गलत के सामने (✗) का चिह्न लगाइए।

प्रश्न 15. रदरफोर्ड का अल्फा कण प्रकीर्णन प्रयोग किसकी खोज के लिए उत्तरदायी था
(a) परमाणु केन्द्रक
(b) इलेक्ट्रॉन
(c) प्रोटॉन
(d) न्यूट्रॉन
उत्तर-
(a) ✓
(b) ✗
(c) ✗
(d) ✗

प्रश्न 16.
एक तत्त्वे के समस्थानिक में होते हैं
(a) समान भौतिक गुण
(b) भिन्न रासायनिक गुण
(c) न्यूट्रॉनों की अलग-अलग संख्या
(d) भिन्न परमाणु संख्या
उत्तर-
(a) ✗
(b) ✗
(c) ✓
(d) ✗

प्रश्न 17.
Cl^– आयन में संयोजकत्ना-इलेक्ट्रॉनों की संख्या है
(a) 16
(b) 8
(c) 17
(d) 18
उत्तर-
(a) ✗
(b) ✓
(c) ✗
(d) ✗

प्रश्न 18.
सोडियम का सही इलेक्ट्रॉनिक विन्यास निम्न में कौन-सा है ?
(a) 2, 8
(b) 8, 2, 1
(c) 2, 1, 8
(d) 2, 8, 1
उत्तर-
(a) ✗
(b) ✗
(c) ✗
(d) ✓

प्रश्न 19.
निम्नलिखित सारणी को पूरा कीजिए-

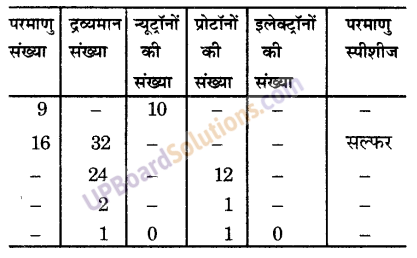
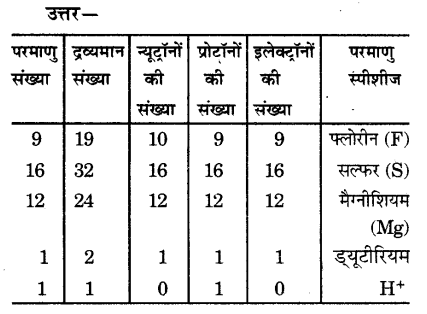
अन्य महत्वपूर्ण प्रश्नोत्तर

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
कैथोड किरणों से उत्पन्न होने वाली दूसरी किरण का नाम बताइये जिसका उपयोग चिकित्सा क्षेत्र में किया जाता है।
उत्तर-
कैथोड किरणों से उत्पन्न होने वाली दूसरी किरण का नाम एक्स-किरणें (X-Rays) है जिसका उपयोग चिकित्सा क्षेत्र में किया जाता है।

प्रश्न 2.
X-किरणें किन्हें कहते हैं अथवा X-किरणों को परिभाषित कीजिए।
उत्तर-
X-किरणें (X-Rays)- जब कैथोड किरणें उच्च गलनांक (UPBoardSolutions.com) की किसी धातु जैसे टंगस्टन (W) के लक्ष्य से टकराती हैं तो अत्यधिक ऊर्जा वाली आवेशरहित किरणे प्राप्त होती हैं, जिन्हें x-किरणें कहते हैं।

प्रश्न 3.
कैथोड किरणों के दो गुण लिखिए।
उत्तर-
कैथोड किरणों के दो गुण-
(1) ये किरणें ऋणावेशित होती हैं।
(2) इनमें गतिज ऊर्जा होती है।

प्रश्न 4.
X-किरणों की खोज किसने की थी ?
उत्तर-
X-किरणों की खोज डब्ल्यू. के. रान्टजन (W. K. Rontgen) ने की थी।

प्रश्न 5.
X-किरणें किस प्रकार उत्पन्न होती हैं ?
उत्तर-
कैथोड किरणों के उच्च गलनांक की भारी धातु से टकराने से X-किरणें उत्पन्न होती हैं।

प्रश्न 6.
रान्टजन किरणें किन्हें कहते हैं और क्यों?
उत्तर-
X-किरणों को उसके खोजकर्ता के नाम पर रान्टजन किरणें भी कहते हैं।

प्रश्न 7.
धन किरणें’ किन्हें कहते हैं ? अथवा धन किरणों को परिभाषित कीजिए।
उत्तर-
धन किरणें या ऐनोड किरणें (Positive Rays or Anode Rays)- जब विसर्जन नलिका प्रयोग को छिद्रयुक्त कैथोड से दुहराते हैं तो छिद्रयुक्त कैथोड के पीछे परदे पर एक मन्द दीप्ति दिखाई देती है। यह दीप्ति किन्हीं धनावेशित कणों से बनी किरणों की उपस्थिति के कारण होती है। इन किरणों को धन किरणें या ऐनोड किरणें कहते हैं।

प्रश्न 8.
धन किरणों या ऐनोड किरणों की खोज किसने की थी ?
उत्तर-
धन किरणों या ऐनोड किरणों की खोज ई. गोल्डस्टीन (E. Goldstein) ने की थी।

प्रश्न 9.
ऐनोड किरणों को केनाल किरणें क्यों कहा जाता है ?
उत्तर-
ऐनोड किरणों को केनाल किरणें (Canal Rays) भी कहा जाता है, क्योंकि ये कैथोड के छिद्रों या केनाल में से होकर निकलती हैं।

प्रश्न 10.
धन किरणों को ऐनोड किरणें क्यों कहते हैं?
उत्तर-
धन किरणे ऐनोड से कैथोडं की ओर चलती हैं, इसलिए इन्हें ऐनोंड किरणें कहते हैं।

प्रश्न 11.
कैथोड एवं ऐनोड किरणों का कोई एक गुण लिखिए जिसमें दोनों समानता दशति हैं।
उत्तर-
दोनों में गतिज ऊर्जा होती है जिससे दोनों ही (UPBoardSolutions.com) अपने मार्ग में रखे हल्के पहिये को घुमा देती हैं।

प्रश्न 12.
कैथोड किरणों का अध्ययन किसने किया ?
उत्तर-
कैथोड किरणों का अध्ययन सर जे.जे.टॉमसने ने 1897 में किया था।

प्रश्न 13.
कैथोड किरणें कैसे प्राप्त करते हैं ?
उत्तर-
कैथोड किरणों को प्राप्त करना-विसर्जन नलिका में निम्न दाब (लगभग 0.001 मिमी पारे के तल) पर उच्च विभव पर विद्युत प्रवाहित करके कैथोड किरणें प्राप्त करते हैं।

प्रश्न 14.
कैसे सिद्ध होता है कि कैथोड किरणें सीधी रेखा में चलती हैं ?
उत्तर-
यदि कैथोड किरणों के मार्ग में कोई ठोस वस्तु रख दी जाये तो उसकी छाया दिखाई देती है। इससे सिद्ध होता है कि कैथोड किरणें सीधी रेखा में चलती हैं।

प्रश्न 15.
कैसे सिद्ध होता है कि कैथोड किरणें गतिज ऊर्जा युक्त कणों से बनी हैं ?
उत्तर-
यदि कैथोड किरणों के मार्ग में किसी धातु की हल्की चकरी रख दी जाये तो चकरी घूमने लगती है। इससे सिद्ध होता है कि कैथोड किरणें ऐसे कणों से बनी हैं जिनमें गतिज ऊजी होती है।

प्रश्न 16.
कैसे सिद्ध होता है कि कैथोड किरणें ऋणावेशित कण हैं ?
उत्तर-
कैथोड किरणें जब विद्युत क्षेत्र से होकर गुजरती हैं तो धन प्लेट की ओर आकर्षित होती हैं। इससे सिद्ध होता है कि कैथोड किरणें ऋणावेशित कणों से बनी होती हैं।

प्रश्न 17.
प्रोटॉन के आवेश तथा द्रव्यमान का अनुपात (e/m) कितना होता है ?
उत्तर-प्रोटॉन के आवेश तथा द्रव्यमान का अनुपात (e/m) का मान 9.58 x 104 कूलॉम प्रति ग्राम होता है।

प्रश्न 18.
परमाणु का पहला मॉडल किस वैज्ञानिक ने दिया ?
उत्तर-
परमाणु को पहला मॉडल जे. जे. टॉमसन (J. J. Thomson) ने दिया।

प्रश्न 19.
रदरफोर्ड के परमाणु मॉडल के दो दोष कौन-कौन से थे ?
अथवा
रदरफोर्ड के परमाणु मॉडल के महत्त्वपूर्ण दोष क्या
उत्तर-
रदरफोर्ड के परमाणु मॉडल के दोष- रदरफोर्ड के परमाणु मॉडल के दो दोष निम्नलिखित हैं
(1) परमाणु के स्थायित्व की व्याख्या न कर पाना ।
(2) परमाणु के विभिन्न स्पेक्ट्रम की व्याख्या न करे पाना।

प्रश्न 20.
नील बोर के परमाणु मॉडल के अनुसार जब इलेक्ट्रॉन एक ही ऊर्जा स्तर में घूमता है तब वह ऊर्जा का उत्सर्जन करता है या अवशोषण या इलेक्ट्रॉन की ऊर्जा में कोई परिवर्तन नहीं होता, उत्तर दीजिए।
उत्तर-
इलेक्ट्रॉन की ऊर्जा में कोई परिवर्तन नहीं होता।

प्रश्न 21.
कक्षा या ऊर्जा स्तर किसे कहते हैं ?
उत्तर-
कक्षा या ऊर्जा स्तर (Shells or Energy Levels)- “नाभिक के चारों ओर निश्चित ऊर्जा वाले वे पथ जिनमें इलेक्ट्रॉन घूमते रहते हैं: कक्षा, कोश या ऊर्जा-स्तर कहलाते हैं।”

प्रश्न 22.
बोर के परमाणु मॉडल में (K, L, M, N) कक्षाओं में से नाभिक की निकटतम कक्षा कौन-सी है ?
उत्तर-
बोर के परमाणु मॉडल में K कक्षा नाभिक (UPBoardSolutions.com) की निकटतम कक्षा है।

प्रश्न 23.
किसी कक्षा में इलेक्ट्रॉन की अधिकतम संख्या कितनी हो सकती है?
उत्तर-
किसी कक्षा में इलेक्ट्रॉन की अधिकतम संख्या 2n² हो सकती है जहाँ कक्षा का क्रमांक है।

प्रश्न 24.
सबसे बाहरी कक्षा (कोश) में और उसके अन्दर वाली कक्षा में अधिकतम कितने इलेक्ट्रॉन हो सकते हैं ?
उत्तर-
सबसे बाहरी कक्षा (कोश) में अधिकतम 8 इलेक्ट्रॉन तथा उसके अन्दर वाली कक्षा (कोश) में अधिकतम 18 इलेक्ट्रॉन हो सकते हैं।

प्रश्न 25.
संयोजी कोश को परिभाषित कीजिए।
उत्तर-
संयोजी कोश-किसी परमाणु के बाह्यतम कोश को संयोजी कोश कहते हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
टॉमसन के परमाणु मॉडल के दो मुख्य अभिगृहीतियाँ बताइये।
उत्तर-
(i) परमाणु धन आवेशित गीले को बना होता है और इलेक्ट्रॉन उसमें फँसे होते हैं।
(ii) ऋणात्मक और धनात्मक आवेश परिमाण में समान होते हैं। इसलिए परमाणु वैद्युतीय रूप से उदासीन होते हैं।

प्रश्न 2.
समस्थानिक तथा समभारिक में दो अन्तर लिखिए।
उत्तर-
समस्थानिक (Isotopes)-
(1) परमाणु संख्या समान लेकिन द्रव्यमान संख्या भिन्न होती है।
(2) प्रोटॉनों की संख्या समान होती है।
समभारिक (Isobars)-
(1) परमाणु संख्या अलग-अलग होती है लेकिन द्रव्यमान संख्या समान होती है।
(2) प्रोटॉनों की संख्या भिन्न होती है।

प्रश्न 3.
निम्नलिखित सारणी में कुछ तत्त्वों की द्रव्यमान संख्या तथा परमाणु संख्या दी गई है :

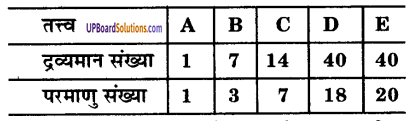
(a) उपर्युक्त सारणी से एक जोड़ा समभारिक चुनिए।
(b) उपर्युक्त सारणी में दिये गए तत्त्व ‘B’ की संयोजकता क्या होगी ?
उत्तर-
(a) D तथा E समभारिक हैं क्योंकि इनकी परमाणु संख्याएँ (40) परन्तु भिन्न-भिन्न द्रव्यमान संख्याएँ क्रमशः 18 तथा 20 हैं।
(b) B का इलेक्ट्रॉनिक विन्यास = 2, 5
अत: B की संयोजकता = 3, 5

प्रश्न 4.
एक तत्त्व ‘X’ का इलेक्ट्रॉनिक विन्यास 2, 8, 2 है।
(a) इलेक्ट्रॉन की संख्या ज्ञात कीजिए जो तत्व x में उपस्थित है।
(b) इसकी परमाणु संख्या लिखिए।
(c) यह तत्त्व ‘X’ एक धातु है या अधातु?
(d) तत्त्व X की संयोजकता ज्ञात कीजिए।
हल-
(a) X में उपस्थित इलेक्ट्रॉनों की संख्या = 2 + 8 + 2 = 12
(b) X की परमाणु संख्या = 12
(c) तत्त्व X एक धातु है।
(d) X की संयोजकता = 2

प्रश्न 5.
इलेक्ट्रॉन, प्रोटॉन एवं न्यूट्रॉन के गुणों की तुलना कीजिए तथा इनकी परमाणु में स्थिति एवं इनके खोजकर्ता का नाम लिखिए।
अथवा
इलेक्ट्रॉन, प्रोटॉन एवं न्यूट्रॉन की आवेश एवं (UPBoardSolutions.com) द्रव्यमान के तुलना कीजिए। इन कणों के खोजकर्ता का नाम एवं परमाणु क्रमांक में इनका स्थान लिखिए।
उत्तर-
इलेक्ट्रॉन, प्रोटॉन एवं न्यूट्रॉन के गुणों की तुलना-

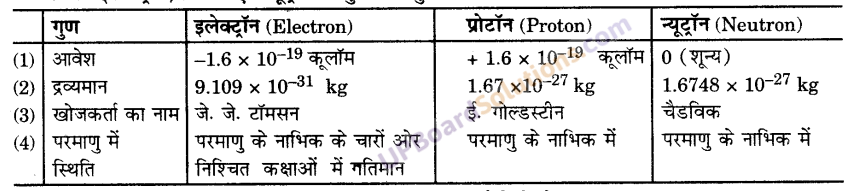
प्रश्न 6.
रदरफोर्ड के प्रयोग का चित्र बनाइये तथा इसके निष्कर्ष लिखिये।
उत्तर-
रदरफोर्ड के प्रयोग का चित्र-

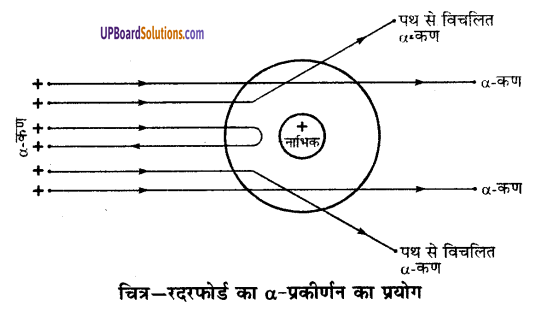
रदरफोर्ड के प्रयोग के निष्कर्ष
(1) प्रयोग में परमाणु के केन्द्रीय भाग से टकराकर कुछ α-कण वापस लौट आते हैं इससे निष्कर्ष निकलता है कि परमाणु का केन्द्रक ठोस, अभेद्य तथा प्रतिकर्षी है।
(2) अधिकांश α-कण स्वर्ण पत्र में बिना छेद किये सरल रेखा से बाहर निकल जाते हैं इससे निष्कर्ष निकलता है कि परमाणु खोखला है।
(3) कुछ α-कण विचलित हो जाते हैं इससे निष्कर्ष निकलता है कि परमाणु में ऋणावेशित कण हैं।

प्रश्न 7.
(a) नीचे दी गई स्पीशीज में किसमें 18 इलेक्ट्रॉन हैं ?
Ca²⁺, K⁺, Na, Cl, Ar
(b) किसी तत्त्व के सभी समस्थानिकों के रासायनिक गुण एकसमान होते हैं। कारण लिखिए।
उत्तर-
(a) Ca²⁺, K⁺, Cl, Ar
(b) समस्थानिकों में इलेक्ट्रॉनों की संख्या समान है, तब उनका इलेक्ट्रॉन विन्यास तथा संयोजकता इलेक्ट्रॉन की संख्या भी समान होगी।
अतः समस्थानिकों के रासायनिक गुण एकसमान होते हैं।

प्रश्न 8.
नील बोर द्वारा अपने परमाणु मॉडल में शामिल नई संकल्पनाएँ बताइए। इस मॉडल को दिखाने के लिए एक रेखाचित्र खींचिए।
उत्तर-
बोर के मॉडल में शामिल नई संकल्पनाएँ हैं
(i) निश्चित ऊर्जायुक्त कुछ खास कक्षाएँ ही स्वीकार्य हैं।
(ii) जब तक कोई इलेक्ट्रॉन कण ऊर्जा स्तर में गतिशील है, इसमें ऊर्जा की हानि या लाभ नहीं होता।
(iii) जब इलेक्ट्रॉन ऊर्जा ग्रहण करते हैं तो उच्च ऊर्जा स्तर में पहुँच जाते हैं। जब ऊर्जा की हानि होती है तो निम्न ऊर्जा स्तर पर आ जाते हैं। इसे चित्र द्वारा दिखाया गया है।

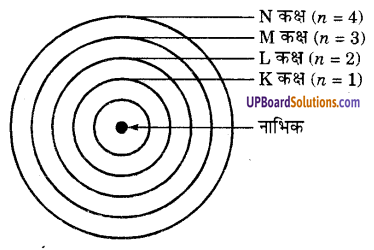
प्रश्न 9.
एक तत्त्व [latex]_{ 8 }^{ 16 }{ X }[/latex] के रूप में निरूपित होता है। ज्ञात कीजिए-
(a) तत्त्व x में इलेक्ट्रॉनों की संख्या,
(b) तत्त्व x की द्रव्यमान संख्या,
(c) तत्त्व x में न्यूट्रॉनों की संख्या।।
हल-
(a) तत्त्व x में इलेक्ट्रॉनों की संख्या = 8
(b) तत्त्व x की द्रव्यमान संख्या = 16
(c) तत्त्व x में न्यूट्रॉनों की संख्या = 16 – 8 = 8

प्रश्न 10.
(a) किसी परमाणु के तीन अवपरमाणुक कणों के नाम लिखिए।
(b) किसी तत्त्व में परमाणु की L कक्षा में पाँच इलेक्ट्रॉन हैं-
(i) तत्त्व की परमाणु संख्या क्या है ?
(ii) इसकी संयोजकता व्यक्त कीजिए।
(iii) तत्त्व को पहचानिए तथा इसका नाम लिखिए।
हल-
(a) किसी परमाणु के तीन अवपरमाणुक कणों के नाम हैं : इलेक्ट्रॉन, प्रोटॉन तथा न्यूट्रॉन।
(b) K कोश में इलेक्ट्रॉनों की संख्या = 2
L कोश में इलेक्ट्रॉनों की संख्या = 5
(i) तत्त्व की परमाणु संख्या 2 + 5 = 7
(ii) तत्त्व की संयोजकता।
(iii) तत्त्व नाइट्रोजन (N) है।

प्रश्न 11.
(a) हीलियम तथा बेरीलियमें दोनों में ही संयोजकता कक्षा में 2 इलेक्ट्रॉन होते हैं। हीलियम एक अक्रिय गैस है जबकि बेरीलियम एक धातु है। पुष्टि कीजिए।
(b) हाइड्रोजन का अस्तित्व तीन समस्थानिक रूपों में होता है। हाइड्रोजन के समस्थानिक रासायनिक रूप से समान क्यों होते हैं ?
उत्तर-
(a) हीलियम के बाह्यतम कक्ष में इलेक्ट्रॉनों की संख्या उसकी अधिकतम संख्या के बराबर है अतः हीलियम एक अक्रिय गैस है। बेरीलियम तत्त्व धातु है क्योंकि यह इलेक्ट्रॉन त्याग करके धनात्मक आयन बनाता है।
(b) समस्थानिकों में इलेक्ट्रॉनों की संख्या समान है। अतः उनका इलेक्ट्रॉन विन्यास और संयोजकता इलेक्ट्रॉन की संख्या भी समान होती है। अत: हाइड्रोजन के समस्थानिक रासायनिक रूप से समान होते हैं।

प्रश्न 12.
समस्थानिक और समभारिक क्या होते हैं ? क्लोरीन के दो समस्थानिक कौन-कौन से हैं ? क्लोरीन के प्राकृतिक नमूने में इनका क्या अनुपात होता है ? क्लोरीन परमाणु का औसत परमाणु द्रव्यमान परिकलित कीजिए।
उत्तर-
समस्थानिक- एक ही तत्त्व के परमाणु जिनकी परमाणु संख्या समान तथा द्रव्यमान भिन्न होता है, समस्थानिक कहलाते हैं।
समभारिक- वे परमाणु जिनकी द्रव्यमान संख्या समान होती है परन्तु परमाणु क्रमांक भिन्न होते हैं, समभारिक कहलाते हैं।

प्रश्न 13.
परमाणु नाभिक के आवश्यक गुणधर्मों की व्याख्या कीजिए।
उत्तर-
परमाणु नाभिक के गुणधर्म :
(i) परमाणु नाभिक धनावेश युक्त होता है।
(ii) परमाणु का सम्पूर्ण द्रव्यमान उसके नाभिक में ही स्थित होता है।
(iii) परमाणु नाभिक की त्रिज्या 10^-13 से 10^-12 cm होती है, जबकि सम्पूर्ण परमाणु की त्रिज्या लगभग 10^-8 cm होती है।
अत: परमाणु का अधिकांश भाग रिक्त होता है।

प्रश्न 14.
टॉमसन परमाणु मॉडल, रदरफोर्ड परमाणु मॉडल तथा बोर परमाणु मॉडलों की तुलना कीजिए।
उत्तर-
टॉमसन परमाणु मॉडल – टॉमसन ने तरबूज के समान परमाणु मॉडल प्रस्तावित किया जिसमें परमाणु का धनावेश तरबूज के खाने वाले भाग की भाँति फैला हुआ है, जबकि इलेक्ट्रॉन (ऋणावेश) धनावेशित गोले में तरबूज के बीज की भाँति फँसे हैं। ऋणावेश तथा धनावेश परिमाण में समान होते हैं। इसलिए परमाणु विद्युतीय उदासीन होता है।

रदरफोर्ड परमाणु मॉडल – इसके अनुसार, परमाणु में धनावेशित केन्द्र, जिसे नाभिक कहते हैं, होता है और इलेक्ट्रॉन स्थिर कक्षा में चक्कर लगाते हैं। नाभिक का आकार, परमाणु के आकार की तुलना में अत्यन्त कम या उपेक्षणीय होता है।

बोर परमाणु मॉडल – बोर परमाणु मॉडल के अनुसार इलेक्ट्रॉन केवल कुछ निश्चित कक्षाओं में ही चक्कर लगा सकते हैं, जिन्हें इलेक्ट्रॉनों की विविक्त कक्षा कहते हैं। जब इलेक्ट्रॉन इन विविक्त कक्षाओं में चक्कर लगाते हैं तो उनकी ऊर्जा का विकिरण नहीं होता।

प्रश्न 15.
सिलिकॉन और ऑक्सीजन का उदाहरण लेते हुए संयोजकता की परिभाषा दीजिए।
उत्तर-
परमाणु के अन्तिम कोश (बाह्यतम कोश) में विद्यमान इलेक्ट्रॉन, संयोजी इलेक्ट्रॉन कहलाते हैं। किसी परमाणु द्वारा स्थायित्व (अष्टक) प्राप्त करने के लिए, त्यागे गए या प्राप्त या साझा किए गए इलेक्ट्रॉनों की संख्या, उसकी संयोजकता कहलाती है। परमाणु द्वारा अष्टक पूरा करने की क्रिया में संयोजी इलेक्ट्रॉनों का ही स्थानान्तरण या साझा होता है अर्थात संयोजी इलेक्ट्रॉन ही परमाणु की संयोजकता निर्धारित करते हैं। उदाहरणार्थ-सिलिकॉन का परमाणु क्रमांक 14 है। इसका इलेक्ट्रॉनिक विन्यास 2, 8, 4 होगा। इसमें 4 संयोजी इलेक्ट्रॉन उपस्थित हैं अर्थात् इसकी संयोजकता 4 है।
ऑक्सीजन का परमाणु क्रमांक 8 है। इसका इलेक्ट्रॉनिक विन्यास 2, 6 होगा। इसमें 6 संयोजी इलेक्ट्रॉन उपस्थित हैं। ऑक्सीजन परमाणु की प्रवृत्ति दो इलेक्ट्रॉन ग्रहण करके अष्टक प्रदान करने की होती है। अतः इसकी संयोजकता 2 है।

प्रश्न 16.
Na⁺, K⁺, Al^3-, O^2- और F^– में कौन-से समइलेक्ट्रॉनी हैं ?
उत्तर-
समइलेक्ट्रॉनी स्पीशीज में इलेक्ट्रॉन की संख्या समान होती है।

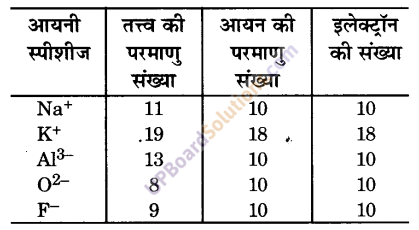
उपर्युक्त सारणी से स्पष्ट है कि Na⁺, K⁺, Al^3-, O^2- और F^– में 10^-10 इलेक्ट्रॉन हैं। अतः ये समइलेक्ट्रॉनी हैं।

प्रश्न 17.
रदरफोर्ड का परमाणु मॉडल क्या है?
उत्तर-
रदरफोर्ड का परमाणु मॉडल (Atomic Model of Rutherford) – रदरफोर्ड ने अपने α-कणों के प्रकीर्णन के प्रयोग द्वारा प्राप्त निष्कर्षों के आधार पर परमाणु का एक मॉडल प्रस्तुत किया जो निम्न प्रकार है

1. परमाणु का अधिकांश द्रव्यमान इसके केन्द्र में निहित है अतः परमाणु के केन्द्रीय भाग में प्रोटॉन एवं न्यूट्रॉन विद्यमान हैं। ये कण न्यूक्लिऑन कहलाते हैं। परमाणु के इस सूक्ष्म केन्द्र को नाभिक या केन्द्रक कहते हैं।
2. केन्द्रक के चारों ओर का अधिकांश भाग रिक्त होता है।
   
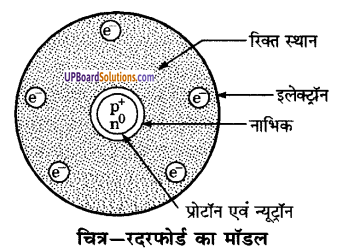
3. परमाणु के केन्द्रक के चारों ओर इलेक्ट्रॉन गतिशील होते हैं।
4. नाभिक का आकार परमाणु के आकार की तुलना में बहुत छोटा होता है।
5. चूँकि परमाणु उदासीन होता है अतः परमाणु में उपस्थित प्रोटॉन एवं इलेक्ट्रॉन की संख्या बराबर होती है।

प्रश्न 18.
रदरफोर्ड के परमाणु मॉडल के महत्त्वपूर्ण दोषों की व्याख्या कीजिए।
उत्तर-
रदरफोर्ड के परमाणु मॉडल के महत्त्वपूर्ण दोषों की व्याख्या (Explanation of Defects of Rutherford’s Atomic Model)-

1. परमाणु के स्थायित्व की व्याख्या न कर पाना – रदरफोर्ड के परमाणु मॉडल का पहला दोष यह है कि यह परमाणु के स्थायित्व की व्याख्या नहीं करता है। मैक्सवैल के अनुसार, कोई भी आवेशित कण गतिमान होने पर निरन्तर विद्युत चुम्बकीय तरंगों को विकरित करेगा, जिसमें उसकी ऊर्जा में लगातार कमी होते रहने से उसे अपनी राह (कक्षा) घटानी पड़ेगी और ऐसा करते हुए अन्त में इलेक्ट्रॉन नाभिक में गिरकर नष्ट हो जायेगा परन्तु वास्तव में ऐसा घटित नहीं होता।
2. परमाणु में विविक्त स्पेक्ट्रम की व्याख्या न कर पाना – रदरफोर्ड के परमाणु मॉडल का दूसरा प्रमुख दोष यह है कि यह परमाणु के विविक्त स्पेक्ट्रम की व्याख्या भी नहीं कर पाता। रदरफोर्ड के अनुसार इलेक्ट्रॉन की कक्षा की त्रिज्या निरन्तर बदलती रहने के कारण सतत् स्पेक्ट्रम बनना चाहिए परन्तु रैखिक स्पेक्ट्रम प्राप्त होता है।

दीर्घ उत्तरीय प्रश्नप्रश्न

प्रश्न 1.
बोर का परमाणु मॉडल समझाइये।
उत्तर-
बोर का परमाणु मॉडल-नील्स बोर ने क्वाण्टम सिद्धान्त के आधार पर परमाणु संरचना का सरल मॉडल प्रस्तुत किया। इस मॉडल की प्रमुख अभिधारणाएँ निम्नलिखित हैं

1. परमाणु के केन्द्र में नाभिक होता है, जिसमें धनावेशित कण (प्रोटॉन) उपस्थित होता है।
2. इलेक्ट्रॉन नाभिक के चारों ओर निश्चित ऊर्जा वाले पथ में घूमते हैं। ये निश्चित ऊर्जा वाले पथ कक्षा, कोश या ऊर्जा-स्तर कहलाते हैं।
3. कक्षाओं के क्रम को (n) द्वारा व्यक्त किया जाता है जहाँ n = 1, 2, 3, 4….. हैं जो क्रमशः K, L, M, N…. आदि से व्यक्त किये जा सकते हैं।
4. n के बढ़ते मान के साथ ये कक्षाएँ नाभिक से दूर होती जाती हैं और उनकी ऊर्जा क्रमशः बढ़ती जाती है। कक्षा k की ऊर्जा सबसे कम होती है। तथा यह नाभिक के निकटतम होती है।
5. बोर के अनुसार यदि कोई इलेक्ट्रॉन एक ही ऊर्जा स्तर या कक्षा में घूमता रहे तो इस इलेक्ट्रॉन की ऊर्जा में कोई परिवर्तन नहीं होता है।
6. इलेक्ट्रॉन जब बाहर से ऊर्जा ग्रहण करता है तो उत्तेजित होकर निकटतम उच्च ऊर्जा स्तर में चला जाता है और जब ये ऊर्जा का उत्सर्जन करता है तब निकटतम निम्न ऊर्जा के स्तर में चला जाता है।

प्रश्न 2.
इलेक्ट्रॉन वितरण की बोर-बरी योजना क्या है ? इसके अनुसार इलेक्ट्रॉनों की व्यवस्था लिखिए।
उत्तर-
इलेक्ट्रॉनवितरणकबर-बरीयोजना – इलेक्ट्रॉन वितरण के लिए बोर-बरी ने निम्न योजना प्रस्तुत की जिसे बोर-बरी की योजना कहते हैं। इसके प्रमुख बिन्दु निम्नलिखित हैं
(i) परमाणु की किसी भी कक्षा में इलेक्ट्रॉनों की | अधिकतम संख्या 2n² होती है, जहाँ n कक्षा की क्रम संख्या है जो नाभिक से बाहर की ओर गिनी जाती है। इस तरह इलेक्ट्रॉनों की अधिकतम संख्या पहली कक्षा में 2, दूसरी में 8, तीसरी में 18, चौथी में 32 एवं पाँचवीं में 50 होती है।
(ii) सबसे बाहर वाली कक्षा में 8 एवं उसके अन्दर वाली कक्षा में 18 से अधिक इलेक्ट्रॉन कभी नहीं हो सकते।
(iii) किसी कक्षा में 8 इलेक्ट्रॉन होने पर नई कक्षा प्रारम्भ हो जाती है चाहे उसकी अधिकतम सीमा कुछ भी हो।
(iv) सबसे बाहर की कक्षा में 2 से अधिक और उसके अन्दर वाली में 8 से अधिक इलेक्ट्रॉन तब तक नहीं होते जब तक अन्य अन्दर की कक्षाएँ 2n² से पूर्ण न हो जायें।

प्रश्न 3.
रिक्त स्थान भरिए-(इलेक्ट्रॉन विन्यास पूर्ण कीजिए)

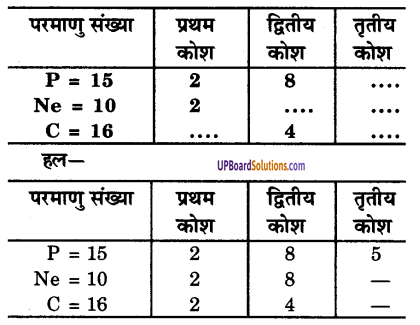
प्रश्न 4.
क्लोरीन तत्त्व ([latex]_{ 17 }^{ 35 }{ Cl }[/latex]) के उदाहरण से उसकी परमाणु संरचना का मॉडल बनाइये।
हल-
क्लोरीन परमाणु संरचना का मॉडल-

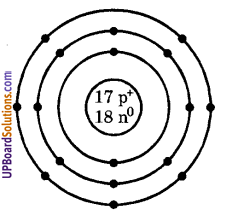
चित्र- क्लोरीन की परमाणु संरचना
क्लोरीन का परमाणु क्रमांक Z = 17
क्लोरीन की द्रव्यमान संख्या A = 35
प्रोटॉन की संख्या p = Z = 17
न्यूट्रॉन की संख्या n = A – Z = 35 – 17 = 18
इलेक्ट्रॉन की संख्या e = p = 17
इलेक्ट्रॉन का वितरण e = 17 = 2, 8, 7

प्रश्न 5.
[latex]_{ 18 }^{ 40 }{ Ar }[/latex] (आर्गन तत्व) की परमाणु संरचना बनाइये।
उत्तर –
[latex]_{ 18 }^{ 40 }{ Ar }[/latex] (आर्गन तत्व) की परमाणु संरचना

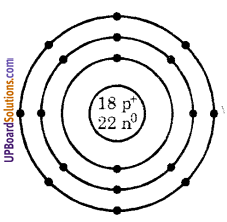
चित्र- आर्गन की परमाणु संरचना
आर्गन को परमाणु क्रमांक Z = 18
आर्गन की द्रव्यमान संख्या A = 40
प्रोटॉन की संख्या p = 18
न्यूट्रॉन की संख्या n = A – Z = 40 – 18 = 22
इलेक्ट्रॉन की संख्या e = p = 18
इलेक्ट्रॉन का वितरण e = 18 = 2, 8, 8

प्रश्न 6.
दो तत्त्वों A और B के परमाणुओं के अवपरमाणुक कण नीचे दिए गए हैं। उसका अध्ययन कीजिए तथा निम्न प्रश्नों के उत्तर दीजिए। अपने उत्तर की सत्यता सिद्ध कीजिए।

(i) दोनों में से किसके परमाणु का आकार बड़ा है?
(ii) दोनों में से किसका नाभिक प्रबल है?
(iii) तत्त्व A तथा B की प्रकृति की व्याख्या कीजिए।
उत्तर-
(i) B के परमाणु का आकार बड़ा है क्योंकि B में तीन कोश होते हैं जबकि A में एक कोश होता है।
(ii) B का नाभिक प्रबल है क्योंकि A की द्रव्यमान संख्या 2 + 2 = 4 है जबकि B की द्रव्यमान संख्या 11 + 12 = 23 है।
(iii) A अधातु है जबकि B धातु है। A गैस है तथा B के बाह्यतम कोश में एक इलेक्ट्रॉन है जिसका यह आसानी से त्याग कर सकता है।

प्रश्न 7.
(a) रदरफोर्ड के अल्फा कण प्रकीर्णन प्रयोग में निम्न निष्कर्ष व्युत्पन्न करने के लिए प्रायोगिक प्रमाण दीजिए।
(i) परमाणु के भीतर का अधिकतर भाग खाली होता है।
(ii) परमाणु का केन्द्र धनावेशित होता है।
(b) एक तत्त्व की द्रव्यमान संख्या 32 तथा परमाणु संख्या 16 है, ज्ञात कीजिए :
(i) तत्त्व के परमाणु में न्यूट्रॉनों की संख्या।
(ii) परमाणु के बाह्यतम कोश में इलेक्ट्रॉनों की संख्या ।
(c) रदरफोर्ड के परमाण्वीय मॉडल के आधार पर नाभिक में कौन-सा अवपरमाणुक कण विद्यमान होता है ?
उत्तर-
(a) (i) परमाणु के भीतर का अधिकतर भाग खाली होता है क्योंकि अधिकतर अल्फा कण बिना विक्षेपित हुए सोने की पन्नी को पार कर सीधे निकल गये।
(ii) कुछ α-कण अपने मूल पथ से थोड़ा विक्षेपित हो जाते हैं इससे सिद्ध होता है कि परमाणु का केन्द्र धनावेशित भाग है।
(b) तत्त्व की द्रव्यमान संख्या = 32
तत्त्व की परमाणु संख्या = 16
प्रोटॉनों की संख्या = परमाणु संख्या = 16
न्यूट्रॉनों की संख्या = द्रव्यमान संख्या – प्रोटॉनों की संख्या = 32 – 16 = 16
(ii) तत्त्व का इलेक्ट्रॉन विन्यास = 2, 8, 6
परमाणु के बाह्यतम कोश में इलेक्ट्रॉनों की संख्या = 6
(c) प्रोटॉन।

प्रश्न 8.
(a) उस अवपरमाणुक कण का नाम लिखिए जिसकी खोज जे. चैडविक ने की थी। इस कण पर कौन-सा आवेश होता है ? यह कण परमाणु के कौन-से भाग में स्थित होता है ?
(b) रदरफोर्ड के परमाणु मॉडल के प्रयोग के तीन चरणों की सूची बनाइए।
(c) एक उदाहरण देते हुए समभारिक परमाणु की परिभाषा लिखिए।
(d) यह निष्कर्ष किस वैज्ञानिक ने निकाला था कि परमाणु की अपेक्षा नाभिक का साइज बहुत छोटा होता है।
उत्तर-
(a) जे. चैडविक ने न्यूट्रॉन की खोज की थी। न्यूट्रॉन अनावेशित होता है। यह कण परमाणु के नाभिक में होता है।
(b) (i) रदरफोर्ड ने रेडियोऐक्टिव तत्त्व रेडियम को लैड के बॉक्स के भीतर रखकर प्राप्त अल्फा कणों को एक बारीक स्लिट से गुजारकर इन्हें पुंज के रूप में प्राप्त किया।
(ii) इस पुंज को उन्होंने एक भारी धातु, जैसे-गोल्ड के अत्यन्त पतली पन्नी पर डाला।
(iii) इससे ये अल्फा कण प्रकीर्णित हो गए तथा बहुत-से अल्फा कण पन्नी से पार होकर पीछे लगे जिंक सल्फाइड के मध्य जाकर टकरा गए।
(c) समभारिक – समभारिक, विभिन्न परमाणु संख्याओं परन्तु समान द्रव्यमान संख्या वाले विभिन्न तत्त्वों के परमाणु हैं। समभारिकों में, उनके नाभिकों में प्रोटॉनों की भिन्न संख्या होती है परन्तु उनमें न्यूक्लिआनो (प्रोटानों + न्यूट्रॉनों) की संख्या समान होती है। समभारिकों के उदाहरण आर्गन [latex]_{ 18 }^{ 40 }{ Ar }[/latex] और कैल्सियम [latex]_{ 20 }^{ 40 }{ Ca }[/latex] है।
(d) रदरफोर्ड ने निष्कर्ष निकाला था कि परमाणु की अपेक्षा नाभिक का साइज बहुत छोटा होता है।

प्रश्न 9.
परमाणु क्रमांक 1 से 18 तक के तत्त्वों के परमाणुओं का इलेक्ट्रॉन-विन्यास दीजिए।
उत्तर-
परमाणु क्रमांक 1 से 18 तक के तत्त्वों का इलेक्ट्रॉन विन्यास

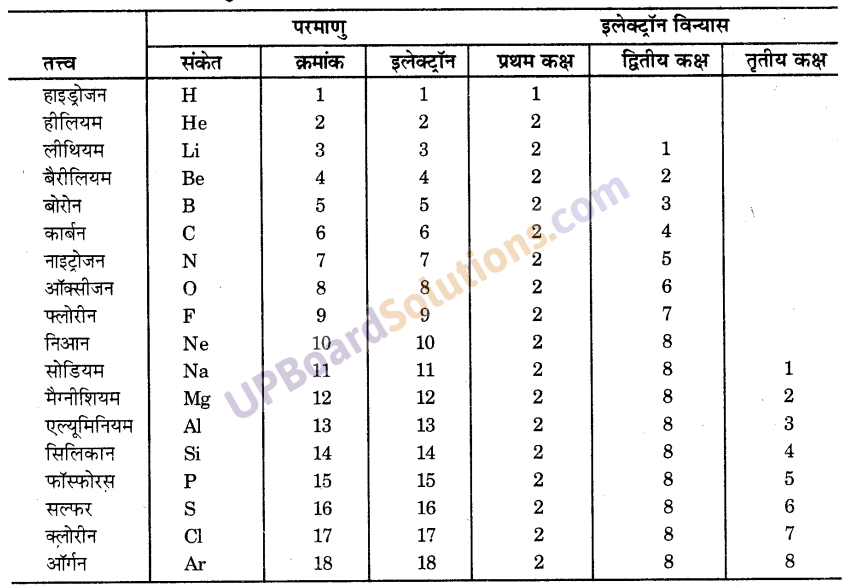
प्रश्न 10.
संयोजकता इलेक्ट्रॉन का महत्व लिखिए व तत्त्व की संयोजकता निर्धारण में इसकी भूमिका बताइए।
उत्तर-
संयोजकता – किसी तत्त्व के परमाणु द्वारा दिए जाने, लिए जाने या साझेदारी किए जाने वाले इलेक्ट्रॉन की संख्या, उस तत्त्व को संयोजकता कहलाती है।
हम जानते हैं कि किसी रासायनिक अभिक्रिया में केवल बाह्यतम कक्ष में उपस्थित इलेक्ट्रॉन या संयोजकता इलेक्ट्रॉन ही भाग लेते हैं।
अत: संयोजकता निर्धारण में संयोजकता इलेक्ट्रॉन ही महत्वपूर्ण होते हैं। यदि किसी तत्त्व के परमाणु के संयोजकता इलेक्ट्रॉन 1, 2 या 3 हैं तो उसकी संयोजकता क्रमशः 1, 2 या 3 होगी। यदि तत्त्व के बाह्यतम कक्ष में 4 से 8 इलेक्ट्रॉन हैं तो उसकी संयोजकता (संयोजकता इलेक्ट्रॉन–8) होगी।
उदाहरणार्थ – क्लोरीन या फ्लोरीन के बाह्यतम कक्ष में 7 इलेक्ट्रॉन हैं, तब उनकी संयोजकता 7 – 8 = -1 होगी।
अतः क्लोरीन या फ्लोरीन के आयन को Cl^– या F^– से प्रदर्शित करेंगे।

अभ्यास प्रश्न

बहुविकल्पीय प्रश्न

1. चैडविक ने खोज की थी
(a) इलेक्ट्रॉन की
(b) प्रोटॉन की
(c) न्यूट्रॉन की
(d) रेडियम की।

2. परमाणु के केन्द्रक में होते हैं
(a) इलेक्ट्रॉन
(b) प्रोटॉन
(c) न्यूट्रॉन
(d) प्रोटॉन तथा न्यूट्रॉन !

3. प्रोटॉन की खोज का श्रेय था
(a) चैडविक को
(b) गोल्डस्टीन को
(c) जे. जे. टॉमसन को
(d) रदरफोर्ड को।

4. X-किरणों की खोज की थी
(a) राण्टजन ने
(b) चैडविक ने
(c) मैडम क्यूरी ने
(d) गोल्डस्टीन ने।

5. समान परमाणु क्रमांक एवं भिन्न परमाणु भार वाले परमाणु कहलाते हैं
(a) समस्थानिक
(b) समभारिक
(c) समन्यूट्रानिक
(d) उपर्युक्त में से कोई नहीं।

6. निम्न किरणों में से सबसे अधिक बेधन क्षमता किसमें होती है?
(a) α-किरणे
(b) X-किरणें
(c) γ-किरणे
(d) कैथोड किरणें

7. सोने की पन्नी द्वारा अल्फा कण प्रकीर्णन का प्रयोग किया
(a) टॉमसन ने
(b) रदरफोर्ड ने
(c) बोर ने
(d) उपरोक्त सभी ने।

8. परमाणु धन आवेश का गोला है, बताया
(a) टॉमसन ने
(b) रदरफोर्ड ने
(c) बोर ने
(d) उपरोक्त सभी ने।

9. इलेक्ट्रॉन कुछ निश्चित कक्षाओं में चक्कर लगाते हैं, प्रतिपादित किया
(a) टॉमसन ने
(b) रदरफोर्ड ने
(c) बोर ने
(d) उपरोक्त सभी ने।

10. अवपरमाणुक कण है
(a) इलेक्ट्रॉन
(b) प्रोटॉन
(c) न्यूट्रॉन
(d) ये सभी।

11. दूसरे कक्ष में इलेक्ट्रॉन की अधिकतम संख्या है
(a) 2
(b) 4
(c) 18
(d) 8

12. डाल्टन के परमाणु सिद्धान्त की कमी थी
(a) उसने परमाणु को अविभाज्य बताया
(b) वह एक ही प्रकार के परमाणुओं से बने विभिन्न पदार्थों के अलग-अलग गुणों की व्याख्या न कर सका।
(c) क्यों कुछ कार्बनिक यौगिकों को संश्लेषण सम्भव नहीं है, स्पष्ट नहीं हो सका।
(d) उपर्युक्त सभी।

13. प्रोटियम में नहीं होता
(a) प्रोटॉन
(b) इलेक्ट्रॉन
(c) न्यूटॉन
(d) ये सभी।

14. दो न्यूट्रॉन होते हैं
(a) ड्यूटीरियम में
(b) ट्राइटियम में
(c) प्रोटियम में
(d) उपर्युक्त सभी में।

15. Ca व Ar के परमाणु हैं
(a) समस्थानिक
(b) समभारिक
(c) समावयव
(d) ये सभी।

16. फ्लोरीन की परमाणु संख्या 9 है, F^– में इलेक्ट्रॉन की कुल संख्या होगी
(a) 9
(b) 8
(c) 10
(d) 19

17. किसी तत्त्व के समस्थानिकों में
(a) प्रोटॉन की संख्या भिन्न होती है।
(b) इलेक्ट्रॉन की संख्या भिन्न होती है।
(c) न्यूट्रॉन की संख्या भिन्न होती है।
(d) न्यूट्रॉन की संख्या समान होती है।

18. जब एक न्यूट्रॉन विघटित होता है तो ……… उत्पन्न होता है।
(a) एक प्रोटॉन
(b) एक इलेक्ट्रॉन
(c) एक न्यूट्रॉन व एक इलेक्ट्रॉन
(d) एक प्रोटॉन व एक इलेक्ट्रॉन

19. रेडियो आइसोटोप डेटिंग में ……. करते हैं।
(a) 12C परमाणु की
(b) 10C परमाणु की
(c) 14C परमाणु की
(d) 3C परमाणु की।

20. परमाणु संख्या 16 वाले तत्त्वे की संयोजकता है
(a) 6
(b) 4
(c) 1
(d) 2

21. एक तत्त्व A की परमाणु संख्या 40 व तत्त्व B की परमाणु संख्या 11 है। A व B के विषय में कौन-सा कथन सत्य है-
(a) A, B से अधिक सक्रिय है।
(b) B, A से अधिक सक्रिय है।
(c) B रासायनिक रूप से अक्रिय
(d) A व B समान रूप से सक्रिय हैं।

22. निम्न में कौन-सा कथन असत्य है
(a) भारी तत्त्व रेडियोधर्मी होते हैं।
(b) α-कण धन आवेशिते हैं।
(c) β-कण आवेश रहित हैं।
(d) समस्थानिकों की परमाणु संख्या समान होती है।

23. कैल्सियम परमाणु संख्या 20 की संयोजकता है
(a) 1
(b) 2
(c) 3
(d) 6.

24. P-32 प्रयोग किया जाता है
(a) कैंसर
(b) थायरॉइड
(c) ल्यूकेमिया
(d) धमनी की रुकावट।

25. I-131 ……………के उपचार में प्रयोग किया जाता है।
(a) कैंसर के उपचार में
(b) थायरॉइड विकार में
(c) ल्यूकेमिया में
(d) धमनी की रुकावट में।

26. इलेक्ट्रॉन पर आवेश है
(a) 1.6 x 10^-19 C
(b) 9.1 x 10^-16 C
(c) 1.9 x 10^-16 C
(d) 6.1 x 10^-19 C

27. ……………… आवेश रहित हैं।
(a) न्यूट्रॉन
(b) प्रोटॉन
(c) इलेक्ट्रॉन
(d) इलेक्ट्रॉन व न्यूट्रॉन।

28. भारी तत्त्वों के नाभिक में ………. नहीं पाया जाता
(a) प्रोटॉन
(b) न्यूट्रॉन
(c) इलेक्ट्रॉन
(d) इलेक्ट्रॉन वे प्रोटॉन

29. हाइड्रोजन परमाणु में ………….. नहीं पाया जाता
(a) प्रोटॉन
(b) न्यूट्रॉन
(c) इलेक्ट्रॉन
(d) इलेक्ट्रॉन व प्रोटॉन।

30. कैथोड किरणों का प्रयोग सर्वप्रथम ……… किया।
(a) चैडविक ने
(b) जे. जे. टॉमसन ने
(c) नील बोर ने
(d) रदरफोर्ड ने।

31. सोने की पतली पन्नी पर α-कण की बौछार
वाला प्रयोग सर्वप्रथम किसने किया
(a) चैडविक ने
(b) जे. जे. टॉमसन ने
(c) नील बोर ने
(d) रदरफोर्ड ने।

32. न्यूट्रॉन की खोज की
(a) चैडविक ने
(b) जे. जे. टॉमसन ने
(c) नील बोर ने
(d) रदरफोर्ड ने।

33. इलेक्ट्रॉन होता है
(a) द्रव्यमान में प्रोटॉन का [latex]\frac { 1 }{ 1838 }[/latex] वां भाग व धन आवेशित
(b) द्रव्यमान में प्रोटॉन के बराबर व ऋण आवेशित
(c) द्रव्यमान में प्रोटॉन का 1/1838 व ऋण आवेशित
(d) द्रव्यमान में प्रोटॉन के बराबर व धन आवेशित

34. किसी परमाणु में प्रोटॉन की संख्या होती है
(a) न्यूट्रॉन के बराबर
(b) इलेक्ट्रॉन के बराबर
(c) परमाणु द्रव्यमान के बराबर
(d) कोई निश्चित नहीं।

35. यदि किसी तत्त्व के परमाणु में 9 प्रोटॉन व 10 न्यूट्रॉन हों तो उसका परमाणु द्रव्यमान है
(a) 19
(b) 9
(c) 10
(d) 1.

36. Na का परमाणु द्रव्यमान 23 व परमाणु क्रमांक 11 है तो उसके परमाणु में न्यूट्रॉन होंगे
(a) 11
(b) 12
(c) 23
(d) कोई निश्चित नहीं

37. संयोजकता इलेक्ट्रॉन परमाणु के ……. कक्ष में उपस्थित होते हैं।
(a) प्रथम कक्ष
(b) द्वितीय कक्ष
(c) बाह्यतम
(d) किसी भी।

38. यदि किसी तत्त्व का बाह्यतम कक्ष प्रथम कक्षे से तो वह बाह्यतम कक्ष में ……… इलेक्ट्रॉन होने पर ही अक्रिय गैस का विन्यास प्राप्त कर लेगा
(a) 2
(b) 4
(c) 6
(d) 8.

39. प्रत्येक तत्त्वं अपने बाह्यतम कक्ष में ……… इलेक्ट्रॉन पूरे करने का प्रयत्न करता है।
(a) 2
(b) 4
(c) 6
(d) 8.

उत्तरमाला

1. (c)
2. (d)
3. (b)
4. (a)
5. (a)
6. (c)
7. (b)
8. (a)
9. (c)
10. (d)
11. (d)
12. (d)
13. (c)
14. (b)
15. (b)
16. (c)
17. (c)
18. (d)
19. (c)
20. (d)
21. (b)
22. (c)
23. (b)
24. (c)
25. (b)
26. (a)
27. (a)
28. (c)
29. (b)
30. (b)
31. (d)
32. (a)
33. (c)
34. (b)
35. (a)
36. (b)
37. (c)
38. (a)
39. (d)

We hope the UP Board Solutions for Class 9 Science Chapter 4 Structure of the Atom (परमाणु की संरचना) help you. If you have any query regarding UP Board Solutions for Class 9 Science Chapter 4 Structure of the Atom (परमाणु की संरचना), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes (पृष्ठीय क्षेत्रफल एवं आयतन)

These Solutions are part of UP Board Solutions for Class 9 Maths. Here we have given UP Board Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes (पृष्ठीय क्षेत्रफल एवं आयतन).

प्रश्नावली 13.1

प्रश्न 1. 1.5 मीटर लम्बा 1.25 मीटर चौड़ा और 65 सेमी गहरा प्लास्टिक का एक डिब्बा बनाया जाना है। इसे ऊपर से खुला रखना है। प्लास्टिक शीट की मोटाई को नगण्य मानते हुए निर्धारित कीजिए।
(i) डिब्बा बनाने के लिए आवश्यक प्लास्टिक शीट का क्षेत्रफल।
(ii) इस शीट का मूल्य, यदि 1 मीटर शीट का मूल्य 20 है।
हल :
(i) प्लास्टिक के डिब्बे की लम्बाई (l) = 1.5 मीटर,
चौड़ाई (b) = 1.25 मीटर तथा
ऊँचाई h = 65 सेमी या 0.65 मीटर [: 1 मीटर = 100 सेमी]
डिब्बा ऊपर से खुला है; अतः इसमें 1 फलक कम होगा।
अतः डिब्बे को पृष्ठ = सम्पूर्ण पृष्ठीय क्षेत्रफल – ऊपरी फलक का क्षेत्रफल
= 2 (lb + bh + hl) – (l x b)
= 2 [(1.5 x 1.25) + (1.25 x 0.65) +(0.65 x 1.5)] – (1.5 x 1.25)
= 2 [1.875 + 0.8125 + 0.975] – 1.875
= 2 [3.6625] – 1.875
= 7.325 – 1.875
= 5.45 वर्ग मीटर
अतः डिब्बा बनाने के लिए आवश्यक प्लास्टिक शीट का क्षेत्रफल = 5.45 वर्ग मीटर।
(ii) 1 वर्ग मीटर शीट का मूल्य = 20
5.45 वर्ग मीटर शीट का मूल्य = (5.45 x 20) = 109.00
अतः आवश्यक प्लास्टिक शीट का मूल्य = 109

प्रश्न 2. एक कमरे की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 5 मीटर, 4 मीटर और 3 मीटर हैं। 7.50 प्रति मीटर की दर से इस कमरे की दीवारों और छत पर सफेदी कराने का व्यय ज्ञात कीजिए।
हल :
कमरे की लम्बाई (l) = 5 मीटर, चौड़ाई (b) = 4 मीटर व ऊँचाई (h) = 3 मीटर
कमरे की चारों दीवारों का क्षेत्रफल = परिमाप x ऊँचाई
= 2 (l + b) x h = 2 (5 + 4) x 3 वर्ग मीटर
= 18 x 3 वर्ग मीटर
= 64 वर्ग मीटर
छत का क्षेत्रफल = लम्बाई x चौड़ाई = l x b = (5 x 4) = 20 वर्ग मीटर
जिस भाग में सफेदी करानी है, उसका क्षेत्रफल = (54 + 20) वर्ग मीटर = 74 वर्ग मीटर
1 वर्ग मीटर पर सफेदी कराने का व्यय = 7.50
74 वर्ग मीटर पर सफेदी कराने का व्यय = (74 x 7.50) = 555
अतः कमरे की दीवारों और छत पर सफेदी कराने का व्यय = 555

प्रश्न 3. किसी आयताकार हॉल के फर्श की परिमाप 250 मीटर है। यदि के 10 प्रति मीटर² की दर से चारों दीवारों पर पेंट कराने की लागत के 15,000 है तो इस हॉल की ऊँचाई ज्ञात कीजिए।
हल :
माना हॉल की ऊँचाई h मीटर है।
हॉल की परिमाप = 250 मीटर
हाल की चारों दीवारों का क्षेत्रफल = हॉल की परिमाप x ऊँचाई। = 250 x h = 250h वर्ग मीटर
तब हॉल की दीवारों को पेंट कराने का व्यय = हॉल की चारों दीवारों का क्षेत्रफल x पेंट कराने की मूल्य-दर = 250h x 0 = 2,500 h
परन्तु दिया है 10 प्रति मीटर² की दर से हॉल की दीवारों को पेंट कराने का व्यय 15,000 है।
2500 h = 15000 ⇒ h = [latex]\frac { 15000 }{ 2500 }[/latex] = 6 मीटर
अत: हॉल की ऊँचाई = 6 मीटर।

प्रश्न 4. किसी डिब्बे में भरा हुआ पेंट 9.375 मीटर² के क्षेत्रफल पर पेंट करने के लिए पर्याप्त है। इस डिब्बे के पेंट से 22.5 सेमी x 10 सेमी x 7.5 सेमी विमाओं वाली कितनी ईंट पेंट की जा सकती हैं?
हल :
ईंट की विमाएँ 22.5 सेमी x 10 सेमी x 7.5 सेमी हैं।
माना l = 22.5 सेमी, b = 10 सेमी और h = 7.5 सेमी
प्रत्येक ईंट (घनाभ) का पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 [(22.5 x 10) + (10 x 7.5) + (7.5 x 22.5)]
= 2225.0 + 75.0 + 168.75
= 2 x 468.75
= 937.5 वर्ग सेमी
अब माना कि ईंटों की अभीष्ट संख्या n है।
कुल ईंटों का क्षेत्रफल = 937.5 n वर्ग सेमी
परन्तु प्रश्न में दिया है कि पेंट 9.375 वर्ग मीटर क्षेत्रफल पर पेंट करने के लिए पर्याप्त है।
937.5n वर्ग सेमी = 9.375 वर्ग मीटर।
⇒ 937.5 n वर्ग सेमी = 9.375 x 10,000 वर्ग सेमी (1 वर्ग मीटर = 10,000 वर्ग सेमी)
⇒ 937.5 n वर्ग सेमी = 93,750
⇒ n = 100
अत: ईंटों की अभीष्ट संख्या = 100

प्रश्न 5. एक घनाकार डिब्बे का एक किनास 10 सेमी लम्बाई का है तथा एक अन्य घनाभाकार डिब्बे की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 12.5 सेमी, 10 सेमी और 8 सेमी हैं।
(i) किस डिब्बे का पाश्र्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना कम है?
हल :
(i) घनाकार डिब्बे का पार्श्व-पृष्ठीय क्षेत्रफल = 4 x भुजा² [भुजा = 10 सेमी]
= 4 x (10)² = 400 वर्ग सेमी
घनाभाकार डिब्बे का पार्श्व-पृष्ठीय क्षेत्रफल = परिमाप x ऊँचाई = 2 (l + b) x h = 2 (12.5 + 10) x 8
[l = 12.5 सेमी, b = 10 सेमी तथा h = 8 सेमी]
= 16 x 22.5
= 360.0 वर्ग सेमी
अतः स्पष्ट है कि घनाकार डिब्बे का पाश्र्व पृष्ठ क्षेत्रफल (400 – 360) = 40 वर्ग सेमी अधिक है।
(ii) घनाकार डिब्बे का सम्पूर्ण पृष्ठीय क्षेत्रफल = 6 x भुजा² = 6 x (10)² = 600 वर्ग सेमी
तथा
पृष्ठीय क्षेत्रफल और आयतन 343 तथा घनाभाकार डिब्बे का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2 (lb + bh+ hl)
= 2 [(12.5 x 10) + (10 x 8) + (8 x 12.5)]
= 2[125 + 80 + 100]
= 2 x 305
= 610 वर्ग सेमी
अतः स्पष्ट है कि घनाकार डिब्बे का कुल पृष्ठीय क्षेत्रफल (610 – 600) = 10 वर्ग सेमी कम है।

प्रश्न 6. एक छोटा पौधा-घर (greenhouse) सम्पूर्ण रूप से शीशे की पट्टियों से (आधार भी सम्मिलित है) घर के अन्दर ही बनाया गया है और शीशे की पट्टियों को टेप द्वारा चिपका कर रोका गया है। यह पौधा-घर 30 सेमी लम्बा, 25 सेमी चौड़ा और 25 सेमी ऊँचा है।
(i) इसमें प्रयुक्त शीशे की पट्टियों का क्षेत्रफल क्या है?
(ii) सभी 12 किनारों के लिए कितने टेप की आवश्यकता है?
हल :
(i) पौधा-घर की लम्बाई (l) = 30 सेमी,
चौड़ाई (b) = 25 सेमी व ऊँचाई (h) = 25 सेमी।
पौधा-घर (घनाभ) का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2 [(30 x 25) + (25 x 25) + (25 x 30)]
= 2 [750 + 625 + 750]
= 2 x 2125
= 4250 वर्ग सेमी।
अतः पौधा-घर बनाने में प्रयुक्त काँच का क्षेत्रफल = 4250 वर्ग सेमी।
(ii) 12 किनारों में 4 लम्बाइयाँ, 4 चौड़ाइयाँ व 4 ऊँचाइयाँ होती हैं।
सभी किनारों की माप = 4 (लम्बाई + चौड़ाई + ऊँचाई) = 4 (l + b + h)
= 4 (30 + 25 + 25) सेमी
= 4 x 80 सेमी
= 320 सेमी
अतः आवश्यक टेप की लम्बाई = 320 सेमी।

प्रश्न 7. शान्ति स्वीट स्टाल अपनी मिठाइयों को पैक करने के लिए गत्ते के डिब्बे बनाने का ऑर्डर दे रहा था। दो मापों के डिब्बों की आवश्यकता थी। बड़े डिब्बों की माप 25 सेमी x 20 सेमी x 5 सेमी और छोटे डिब्बों की माप 15 सेमी x 12 सेमी x 5 सेमी थीं। सभी प्रकार की अतिव्याप्तता (overlaps) के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर अतिरिक्त गत्ता लगेगा। यदि गत्ते की लागत 4 रुपये प्रति 1000 सेमी 2 है तो प्रत्येक प्रकार के 250 डिब्बे बनवाने की कितनी लागत आएगी?
हल :
बड़े डिब्बे की विमाएँ 25 सेमी x 20 सेमी x 5 सेमी हैं।
l = 25 सेमी, b = 20 सेमी और h = 5 सेमी
बड़े डिब्बे का पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2 [(25 x 20) + (20 x 5) + (5 x 25)]
= 2(500 + 100 + 125)
= 2 x 725
= 1450 वर्ग सेमी।
250 डिब्बों का पृष्ठीय क्षेत्रफल = 250 x 1450 = 3,62,500 वर्ग सेमी.
छोटे डिब्बे की विमाएँ 15 सेमी x 12 सेमी x 5 सेमी हैं।
L = 15 सेमी, B = 12 सेमी व H = 5 सेमी
छोटे डिब्बे का पृष्ठीय क्षेत्रफल = 2 (LB + BH + HL)
= 2 [(15 x 12) + (12 x 5) + (5 x 15)]
= 2[180+ 60+75]
= 2 x 315
= 630 वर्ग सेमी
250 डिब्बों का पृष्ठीय क्षेत्रफल = 630 x 250 = 1,57,500 वर्ग सेमी
प्रत्येक प्रकार के 250 डिब्बों का कुल पृष्ठीय क्षेत्रफल = (3,62,500 + 1,57,500) वर्ग सेमी = 5,20,000 वर्ग सेमी।
अतिव्याप्तता (overlaps) के लिए आरक्षित क्षेत्रफल = 5,20,000 का 5% (दिया है।)
= 5,20,000 x [latex]\frac { 5 }{ 100 }[/latex] = 26,000 वर्ग सेमी
डिब्बों के निर्माण में लगे गत्ते का कुल क्षेत्रफल = प्रत्येक प्रकार के 250 डिब्बों का कुल पृष्ठीय क्षेत्रफल + अतिव्याप्तता के लिए आरक्षित क्षेत्रफल
= (5,20,000+ 26,000) वर्ग सेमी
= 5,46,000 वर्ग सेमी|
1000 वर्ग सेमी के लिए गत्ते की लागत = 4
1 वर्ग सेमी के लिए गत्ते की लागत = [latex]\frac { 4 }{ 1000 }[/latex]
5,46,000 वर्ग सेमी के लिए गत्ते की लागत = [latex]\frac { 4 }{ 1000 }[/latex] x 546000 = 2184
अतः प्रत्येक प्रकार के 250 डिब्बे बनवाने की लागत = 2184

प्रश्न 8. परवीन अपनी कार खड़ी करने के लिए, एक सन्दूक के प्रकार के ढाँचे जैसा एक अस्थायी स्थान तिरपाल की सहायता से बनाना चाहती है, जो कार को चारों ओर से और ऊपर से ढक ले (सामने वाला फलक लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है)। यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा। नगण्य होगा, आधार विमाओं 4 मीटर x 3 मीटर और ऊँचाई 2.5 मीटर वाले इस ढाँचे को बनाने के लिए कितने तिरपाल की आवश्यकता होगी?
हल :
ढाँचे की विमाएँ 4 मीटर x 3 मीटर x 2.5 मीटर हैं।
माना l = 4 मीटर, b = 3 मीटर व h = 2.5 मीटर
ढाँचे को पाश्र्व पृष्ठीय क्षेत्रफल = परिमाप x ऊँचाई = 2 (l + b) x h = 2 (4 + 3) x 2.5 = 14 x 2.5 = 35 वर्ग मीटर
तथा छत या ऊपर के पृष्ठ का क्षेत्रफल = l x b = 4 x 3 = 12 वर्ग मीटर
कुल क्षेत्रफल = 35 + 12 = 47 वर्ग मीटर
अतः ढाँचे के निर्माण में 47 वर्ग मीटर तिरपाल की आवश्यकता होगी।

प्रटनावली 13.2

जब तक अन्यथा न कहा जाए, π = [latex]\frac { 22 }{ 7 }[/latex] लीजिए।
प्रश्न 1. ऊँचाई 14 सेमी वाले एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 88 सेमी है। बेलन के आधार का व्यास ज्ञात कीजिए।
हल :
माना बेलन के आधार का व्यास = 2R सेमी है। [जहाँ R बेलन की त्रिज्या है।]
तथा
बेलन की ऊँचाई (h) = 14 सेमी
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πRh = 2 x [latex]\frac { 22 }{ 7 }[/latex] x R x 14 = 88 R वर्ग सेमी
परन्तु दिया है, बेलन का वक्र पृष्ठीय क्षेत्रफल = 88 वर्ग सेमी
88R = 88 ⇒ R = 1 सेमी
अतः बेलन का व्यास = 2R = 2 x 1 = 2 सेमी।

प्रश्न 2. धातु की एक चादर से 1 मीटर ऊँची और 140 सेमी व्यास के आधार वाली एक बन्द बेलनाकार टंकी बनाई जानी है। इस कार्य के लिए कितने वर्ग मीटर चादर की आवश्यकता होगी?
हल : धातु की टंकी का व्यास = 140 सेमी
धातु की टंकी की त्रिज्या r = [latex]\frac { 140 }{ 2 }[/latex] = 70 सेमी = [latex]\frac { 70 }{ 100 }[/latex] [1 मीटर = 100 सेमी] = 0.7 मीटर
तथा टंकी की ऊँचाई h = 1 मीटर
टंकी का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2πr (h + r)
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 0.7 x (1 + 0.7)
= 4.4 x 1.7 = 7.48 वर्ग मीटर
अतः टंकी को बनाने में प्रयुक्त चादर का क्षेत्रफल = 7.48 वर्ग मीटर।

प्रश्न 3. धातु का एक पाइप 77 सेमी लम्बा है। इसके एक अनुप्रस्थ काट का आन्तरिक व्यास 4 सेमी और बाहरी व्यास 4.4 सेमी है, ज्ञात कीजिए।
(i) आन्तरिक वक्र पृष्ठीय क्षेत्रफल
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल
(iii) कुल पृष्ठीय क्षेत्रफल

हल :
धातु के पाइप की लम्बाई या ऊँचाई (h) = 77 सेमी
पाइप के अनुप्रस्थ काट का आन्तरिक व्यास = 4 सेमी
पाइप के अनुप्रस्थ काट की आन्तरिक त्रिज्या = [latex]\frac { 4 }{ 2 }[/latex] = 2 सेमी
पाइप के अनुप्रस्थ काट का बाहरी व्यास = 4.4 सेमी
पाइप के अनुप्रस्थ काट की बाहरी त्रिज्या R = [latex]\frac { 4.4 }{ 2 }[/latex] = 2.2 सेमी
(i) तब पाइप का आन्तरिक वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 2 x 77 वर्ग सेमी
= 968 वर्ग सेमी।
(ii) बाहरी वक्र पृष्ठीय क्षेत्रफल = 2πrh
2 x [latex]\frac { 22 }{ 7 }[/latex] x 2.2 x 77 वर्ग सेमी
= 2 x 22 x 2.2 x 11 वर्ग सेमी = 1064.8 वर्ग सेमी।
(iii) पाइप का कुल पृष्ठीय क्षेत्रफल = आन्तरिक पृष्ठ + बाहरी पृष्ठ + दोनों वलयाकार सिरों का क्षेत्रफल
= 968 + 1064.8 + 2π(R² – r²)
= 2032.8 + 2 x [latex]\frac { 22 }{ 7 }[/latex] (2.2² – 2²)
= 2032.8+ 2 x [latex]\frac { 22 }{ 7 }[/latex] (4.84 – 4)
= 2032.8+ (2 x [latex]\frac { 22 }{ 7 }[/latex] x 0.84)
= (2032.8 + 5.28) वर्ग सेमी
= 2038.08 वर्ग सेमी।

प्रश्न 4. एक रोलर (roller) का व्यास 84 सेमी है और लम्बाई 120 सेमी है। एक खेल के मैदान को एक बार समतल करने के लिए 500 चक्कर लगाने पड़ते हैं। खेल के मैदान का वर्ग मीटर में क्षेत्रफल ज्ञात कीजिए।
हल :
रोलर को व्यास = 84 सेमी = 0.84 मीटर [1 मीटर = 100 सेमी]
रोलर की त्रिज्या (r) = [latex]\frac { 0.84 }{ 2 }[/latex] = 0.42 मीटर
और रोलर की लम्बाई (h) = 120 सेमी = 1.20 मीटर
रोलर का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 0.42 x 1.20 वर्ग मीटर
= 3.168 वर्ग मीटर
रोलर द्वारा 1 चक्कर लगाकर समतल किया गया मैदान का क्षेत्रफल = 3.168 वर्ग मीटर
रोलर द्वारा 500 चक्कर लगाकर समतल किया गया मैदान का क्षेत्रफल = 500 x 3.168 वर्ग मीटर = 1584 वर्ग मीटर
अतः खेल के मैदान का क्षेत्रफल = 1584 वर्ग मीटर।

प्रश्न 5. किसी बेलनाकार स्तम्भ का व्यास 50 सेमी है और ऊँचाई 3.5 मीटर है। 12.50 प्रति वर्ग मीटर की दर से इस स्तम्भ के वक्र पृष्ठ पर पेंट कराने का व्यय ज्ञात कीजिए।
हल : बेलनाकार स्तम्भ का व्यास = 50 सेमी = 0.5 मीटर [1 मीटर = 100 सेमी]
बेलनाकार स्तम्भ की त्रिज्या (r) = [latex]\frac { 0.5 }{ 2 }[/latex] मीटर = 0.25 मीटर
स्तम्भ की ऊँचाई (h) = 3.5 मीटर
बेलनाकार स्तम्भ का वक्र पृष्ठ = 2πrh
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 0.25 x 3.5 वर्ग मीटर
= 5.5 वर्ग मीटर
1 वर्ग मीटर पर पेंट कराने का व्यय = 12.50
5.5 वर्ग मीटर पर पेंट कराने का व्यय = (5.5 x 12.50) = 68.75
अतः स्तम्भ पर पेंट कराने का व्यय = 68.75

प्रश्न 6. एक लम्ब वृत्तीय बेलन का वक्र पृष्ठीय क्षेत्रफल 4.4मीटर है। यदि बेलन के आधार की त्रिज्या 0.7 मीटर है तो उसकी ऊँचाई ज्ञात कीजिए।
हल :
माना लम्ब वृत्तीय बेलन की ऊँचाई h मीटर है।
तथा बेलन की त्रिज्या (r) = 0.7 मीटर
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 0.7 x h = 4.4h वर्ग मीटर
परन्तु दिया है, बेलन का वक्र पृष्ठीय क्षेत्रफल = 4.4 वर्ग मीटर
4.4 h = 4.4 ⇒ h = 1 मीटर
अतः बेलन की ऊँचाई = 1 मीटर।

प्रश्न 7. किसी वृत्ताकार कुएँ को आन्तरिक व्यास 3.5 मीटर है और यह 10 मीटर गहरा है। ज्ञात कीजिए :
(i) आन्तरिक वक्र पृष्ठीय क्षेत्रफल।
(ii) 40 रुपये प्रति मीटर की दर से इसके वक्र पृष्ठ पर प्लास्टर कराने का व्यय।
हल :
वृत्ताकार कुएँ का आन्तरिक व्यास = 3.5 मीटर
वृत्ताकार कुएँ की आन्तरिक त्रिज्या r = [latex]\frac { 3.5 }{ 2 }[/latex] मीटर
तथा कुएँ की गहराई (h) = 10 मीटर
(i) कुएँ का आन्तरिक वक्र पृष्ठीय क्षेत्रफल = 2πrh
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x [latex]\frac { 3.5 }{ 2 }[/latex] x 10 वर्ग मीटर = 110 वर्ग मीटर।
(ii) 1 वर्ग मीटर पर प्लास्टर कराने का व्यय = 40
110 वर्ग मीटर पर प्लास्टर कराने का व्यय = (110 x 40) = 4400
अत: कुएँ के वक्र पृष्ठ पर प्लास्टर कराने की व्यय = 4400

प्रश्न 8. गरम पानी द्वारा गरम रखने वाले एक संयन्त्र में 28 मीटर लम्बाई और 5 सेमी व्यास वाला एक बेलनाकार पाइप है। इस संयन्त्र में गर्मी देने वाला कुल कितना पृष्ठ है?
हल :
बेलनाकार पाइप का व्यास = 5 सेमी = 0.05 मीटर
बेलनाकार पाइप की त्रिज्या (r) = [latex]\frac { 0.05 }{ 2 }[/latex] = 0.025 मीटर
पाइप की लम्बाई (h) = 28 मीटर
पाइप का वक्र पृष्ठ = 2πrh
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 0.025 x 28 वर्ग मीटर = 4.4 वर्ग मीटर
अतः संयन्त्र में गर्मी देने वाला कुल पृष्ठ = 4.4 वर्ग मीटर।

प्रश्न 9. ज्ञात कीजिए।
(i) एक बेलनाकार पेट्रोल की बन्द टंकी का पाश्र्व या वक्र पृष्ठीय क्षेत्रफल, जिसका व्यास 4.2 मीटर है और ऊँचाई 4.5 मीटर है।
(ii) इस टंकी को बनाने में कुल कितना इस्पात (steel) लगा होगा, यदि कुल इस्पात का भाग बनाने में नष्ट हो गया है?

प्रश्न 10. संलग्न आकृति में, आप एक लैम्प शेड का फ्रेम देख रहे हैं। इसे एक सजावटी कपड़े से ढका जाना है। इस फ्रेम के आधार का व्यास 20 सेमी है और ऊँचाई 30 सेमी है। फ्रेम के ऊपर और नीचे मोड़ने के लिए दोनों ओर 2.5 सेमी अतिरिक्त कपड़ा भी छोड़ा जाना है। ज्ञात कीजिए कि लैम्प शेड को ढकने के लिए कुल कितने कपड़े की आवश्यकता होगी।

हल : लैम्प शेड वृत्ताकार है।
लैम्प शेड के आधार का व्यास = 20 सेमी
लैम्प शेड के आधार की त्रिज्या (r) = [latex]\frac { 20 }{ 2 }[/latex] = 10 सेमी
और लैम्प शेड की ऊँचाई (h) = 30 सेमी
लैम्प शेड को सजाने में दोनों ओर 2.5 सेमी कपड़ा अतिरिक्त छोड़ा जाता है।
कपड़े की लम्बाई (h1) = (30 + 2.5 + 2.5) सेमी = 35 सेमी।
कपड़े का क्षेत्रफल = 2πrh1
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 10 x 35 वर्ग सेमी = 2200 वर्ग सेमी
अत: लैम्प शेड को ढकने के लिए आवश्यक कपड़े का क्षेत्रफल 2200 वर्ग सेमी होगा।

प्रश्न 11. किसी विद्यालय के विद्यार्थियों से एक आधार वाले बेलनाकार कलमदानों को गत्ते से बनाने और सजाने की प्रतियोगिता में भाग लेने के लिए कहा गया। प्रत्येक कलमदान को 3 सेमी त्रिज्या और 10.5 सेमी ऊँचाई का होना था। विद्यालय को इसके लिए प्रतिभागियों को गत्ता देना था। यदि इसमें 35 प्रतिभागी थे, तो विद्यालय को कितना गत्ता खरीदना पड़ा होगा?
हल :
कलमदान की त्रिज्या (r) = 3 सेमी
और कलमदान की ऊँचाई (h) = 10.5 सेमी।
बेलनाकार कलमदान का वक्र पृष्ठीय क्षेत्रफल = 2πrh

प्रश्नावली 13.3

जब तक अन्यथा न कहा जाए π = [latex]\frac { 22 }{ 7 }[/latex] लीजिए।
प्रश्न 1. एक शंकु के आधार का व्यास 10.5 सेमी है और इसकी तिर्यक ऊँचाई 10 सेमी है। इसका वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

प्रश्न 2. एक शंकु का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए, जिसकी तिर्यक ऊँचाई 21 मीटर है और आधार का व्यास 24 मीटर है।
हल :
शंकु के आधार का व्यास = 24 मीटर

प्रश्न 3. एक शंकु का वक्र पृष्ठीय क्षेत्रफल 308 सेमी है और इसकी तिर्यक ऊँचाई 14 सेमी है। ज्ञात कीजिए :
(i) आधार की त्रिज्या,
(ii) शंकु का कुल पृष्ठीय क्षेत्रफल।
हल :
(i) माना शंकु के आधार की त्रिज्या सेमी है।
शंकु की तिर्यक ऊँचाई (l) = 14 सेमी
शंकु का वक्र पृष्ठीय क्षेत्रफल = πrl

प्रश्न 4. शंकु के आकार का एक तम्बू 10 मीटर ऊँचा है और उसके आधार की त्रिज्या 24 मीटर है। ज्ञात कीजिए:
(i) तम्बू की तिर्यक ऊँचाई।
(ii) तम्बू में लगे कैनवास (canvas) की लागत, यदि 1 मीटर कैनवास की लागत 70 है।

प्रश्न 5. 8 मीटर ऊँचाई और आधार की त्रिज्या 6 मीटर वाले एक शंकु के आकार का तम्बू बनाने में 3 मीटर चौड़े तिरपाल की कितनी लम्बाई लगेगी? यह मान कर चलिए कि इसकी सिलाई और कटाई में 20 सेमी तिरपाल अतिरिक्त लगेगा। (π = 3.14 का प्रयोग कीजिए।)

प्रश्न 6. शंकु के आधार की एक गुम्बज की तिर्यक ऊँचाई और आधार का व्यास क्रमशः 25 मीटर और 14 मीटर हैं। इसकी वक्र पृष्ठ पर 210 प्रति 100 मीटर की दर से सफेदी कराने का व्यय ज्ञात कीजिए।

प्रश्न 7. एक जोकर की टोपी एक शंकु के आकार की है, जिसके आधार की त्रिज्या 7 सेमी और ऊँचाई 24 सेमी है। इसी प्रकार की 10 टोपियाँ बनाने के लिए आवश्यक गत्ते का क्षेत्रफल ज्ञात कीजिए।

प्रश्न 8. किसी बस स्टॉप को पुराने गत्ते से बने 50 खोखले शंकुओं द्वारा सड़क से अलग किया हुआ है। प्रत्येक शंकु के आधार का व्यास 40 सेमी है और ऊँचाई 1 मीटर है। यदि इन शंकुओं की बाहरी पृष्ठों को पेंट करवाना है और पेंट की दर 12 प्रति मीटर है, तो इनको पेंट कराने में कितनी लांगत आएगी? (π = 3.14 और √1.04 = 1.02 को प्रयोग कीजिए।)

प्रश्नावली 13.4

जब तक अन्यथा न कहा जाए, π = [latex]\frac { 22 }{ 7 }[/latex] लीजिए।
प्रश्न 1. निम्नलिखित त्रिज्या वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 10.5 सेमी
(ii) 5.6 सेमी
(iii) 14 सेमी।

प्रश्न 2. निम्नलिखित व्यास वाले गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए :
(i) 14 सेमी,
(ii) 21 सेमी,
(iii) 3.5 मीटर।

प्रश्न 3. 10 सेमी त्रिज्या वाले एक अर्धगोले का कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (π = 3.14 लीजिए।)

प्रश्न 4. एक गोलाकार गुब्बारे में हवा भरने पर, उसकी त्रिज्या 7 सेमी से 14 सेमी हो जाती है। इन दोनों अस्थितियों में, गुब्बारे के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
पहले गुब्बारे की त्रिज्या (r) = 7 सेमी
गुब्बारे का पृष्ठीय क्षेत्रफल = 4πr² = 4π x 7 x 7 वर्ग सेमी = 196 वर्ग सेमी।
हवा भरने के बाद गुब्बारे की त्रिज्या (R) = 14 सेमी
हवा भरने के बाद गुब्बारे का पृष्ठीय क्षेत्रफल = 4πR² = 4π x 14 x 14 वर्ग सेमी = 784π वर्ग सेमी।
अतः गुब्बारे के पृष्ठीय क्षेत्रफलों में अनुपात = 196π : 784π = 1 : 4

प्रश्न 5. पीतल से बने एक अर्द्धगोलाकार कटोरे का आन्तरिक व्यास 10.5 सेमी है। 16 प्रति 100 सेमी की दर से इसके आन्तरिक पृष्ठ पर कलई कराने का व्यय ज्ञात कीजिए।

प्रश्न 6. उस गोले की त्रिज्या ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 वर्ग सेमी है।

प्रश्न 7. चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। इन दोनों के पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हल :
चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है।
चन्द्रमा की त्रिज्या भी पृथ्वी की त्रिज्या की लगभग एक-चौथाई होगी।
माना चन्द्रमा की त्रिज्या। है तब पृथ्वी की त्रिज्या 4r होगी।
तब चन्द्रमा का पृष्ठीय क्षेत्रफल = 4πr² वर्ग सेमी।
और पृथ्वी का पृष्ठीय क्षेत्रफल = 4π (4r)² = 64πr² वर्ग सेमी।
अत: चन्द्रमा और पृथ्वी के पृष्ठीय क्षेत्रफलों में अनुपात = 4πr² : 64πr² = 1 : 16

प्रश्न 8. एक अर्द्धगोलाकार कटोरा 0. 25 सेमी मोटी स्टील से बना है। इस कटोरे की आन्तरिक त्रिज्या 5 सेमी है। कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।

हल : कटोरे की आन्तरिक त्रिज्या (r) = 5 सेमी
कटोरे की चादर की मोटाई (d) = 0.25 सेमी|
कटोरे की बाहरी त्रिज्या (R) = आन्तरिक त्रिज्या + मोटाई = 5 + 0.25 = 5.25 सेमी।
अर्द्धगोलाकार कटोरे का बाहरी पृष्ठ = 2πR²
= 2 x [latex]\frac { 22 }{ 7 }[/latex] x 5.25 x 5.25 वर्ग सेमी। = 173.
अतः कटोरे का बाहरी वक्र पृष्ठीय क्षेत्रफल= 173. 25 वर्ग सेमी।

प्रश्न 9. एक लम्बवृत्तीय बेलन त्रिज्या वाले एक गोले को पूर्णतया घेरे हुए है ज्ञात कीजिए:
(i) गोले का पृष्ठीय क्षेत्रफल ।
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल
(iii) ऊपर (i) और (ii) में प्राप्त क्षेत्रफलों का अनुपात

हल :
चित्र में लम्ब वृत्तीय बेलन गोले को पूर्णतया घेरे हुए है।
बेलन की त्रिज्या (R) = गोले की त्रिज्या (r)
(i) गोले का पृष्ठीय क्षेत्रफल = 4πr²
(ii) बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πRH
चित्र से स्पष्ट है कि बेलन की ऊँचाई H = गोले का व्यास = 2r
बेलन का वक्र पृष्ठीय क्षेत्रफल = 2πR (2r) = 2πr (2r) (R = r) = 4πr²
अतः बेलन का वक्र पृष्ठीय क्षेत्रफल = 4πr²
(iii) उक्त दोनों के पृष्ठीय क्षेत्रफलों में अनुपात = 4πr² : 4πr² = 1 : 1

प्रश्नावली 13.5

प्रश्न 1. माचिस की डिब्बी के माप 4 सेमी x 2.5 सेमी x 1.5 सेमी हैं। ऐसी 12 डिब्बियों के एक पैकेट का आयतन क्या होगा?
हल :
माचिस की डिब्बी की माप 4 सेमी x 2.5 सेमी x 1.5 सेमी है।
माना l = 4 सेमी, b = 2.5 सेमी तथा h = 1.5 सेमी
माचिस की डिब्बी (घनाभ) का आयतन = lbh = 4 x 2.5 x 1.5 घन सेमी = 15 घन सेमी
1 माचिस की डिब्बी का आयतन = 15 घन सेमी
12 माचिस की डिब्बियों का आयतन = 12 x 15 = 180 घन सेमी
अतः 12 माचिसों के पैकेट का आयतन = 180 घन सेमी।

प्रश्न 2. एक घनाभाकार पानी की टंकी 6 मीटर लम्बी, 5 मीटर चौड़ी और 4.5 मीटर गहरी है। इसमें कितने लीटर पानी आ सकता है?(1 घन मीटर = 1000 लीटर)
हल :
घनाभाकार टंकी की लम्बाई (l) = 6 मीटर, चौड़ाई (b) = 5 मीटर
और गहराई (h) = 4.5 मीटर।
टंकी का आयतन = lbh = 6 x 5 x 4.5 घन मीटर = 135 घन मीटर
टंकी में समाहित हो सकने वाले पानी का आयतन = 135 घन मीटर
= 135 x 1000 लीटर [1 घन मीटर = 1000 लीटर)
= 1,35,000 लीटर
अतः टंकी में 1,35,000 लीटर पानी आ सकता है।

प्रश्न 3. एक घनाभाकार बर्तन 10 मीटर लम्बा और 8 मीटर चौड़ा है। इसको कितना ऊँचा बनाया जाए कि इसमें 380 घन मीटर द्रव आ सके?
हुल :
माना h मीटर ऊँचा बर्तन होना चाहिए।
घनाभाकार बर्तन की लम्बाई (l) = 10 मीटर और
चौड़ाई (b) = 8 मीटर
घनाभाकार बर्तन का आयतन = lbh = 10 x 8 x h = 80h घन मीटर
बर्तन में समा सकने वाले द्रव का आयतन 380 घन मीटर है।
80 h = 380 ⇒ h = 4.75 मीटर
अतः बर्तन की ऊँचाई = 4.75 मीटर।

प्रश्न 4. 8 मीटर लम्बा, 6 मीटर चौड़ा और 3 मीटर गहरा एक घनाभाकार गड्ढा खुदवाने में 80 प्रति घन मीटर की दर से होने वाला व्यय ज्ञात कीजिए।
हल :
घनाभाकार गड्ढे की लम्बाई (l) = 8 मीटर,
चौड़ाई. (b) = 6 मीटर
तथा गहराई (h) = 3 मीटर
गड्ढे का ओयतन = lbh = (8 x 6 x 3) घन मीटर = 144 घन मीटर
1 घन मीटर गड्ढा खुदवाने का व्यय = 30
144 घन मीटर गड्ढा खुदवाने का व्यय = 30 x 144 = 4320
अतः गड्ढा खुदवाने में होने वाला व्यय = 4320

प्रश्न 5. एक घनाभाकार टंकी की धारिता 50,000 लीटर पानी की है। यदि इस टंकी की लम्बाई और गहराई क्रमशः 2.5 मीटर और 10 मीटर है, तो इसकी चौड़ाई ज्ञात कीजिए।
हल :
माना टंकी की चौड़ाई b मीटर है।
टंकी की लम्बाई (l) = 2.5 मीटर
और टंकी की गहराई (h) = 10 मीटर।
घनाभाकार टंकी का आयतन = lbh = 2.5 x b x 10 घन मीटर = 25b घन मीटर
टंकी की धारिता = 25b घन मीटर = 25b x 1000 लीटर (1 घन मीटर = 1000 लीटर) = 25,000 लीटर
परन्तु प्रश्न में दिया है कि टंकी की धारिता 50,000 लीटर है।
25000 b = 50,000 ⇒ b = 25,000
अतः टंकी की चौड़ाई = 2 मीटर।

प्रश्न 6. एक गाँव जिसकी जनसंख्या 4000 है, को प्रतिदिन प्रति व्यक्ति 150 लीटर पानी की आवश्यकता है। इस गाँव में 20 मीटर x 15 मीटर x 6 मीटर मापों वाली एक टंकी बनी हुई है। इस टंकी का पानी वहाँ कितने दिन के लिए पर्याप्त होगा?
हुल : गाँव की जनसंख्या = 4000
प्रति व्यक्ति प्रतिदिन पानी की आवश्यकता = 150 लीटर
प्रतिदिन गाँव के लिए आवश्यक पानी की मात्रा = 4000 x 150 लीटर = 6,00,000 लीटर
= 600 घन मीटर (1000 लीटर = 1 घन मीटर)
टंकी की लम्बाई (l) = 20 मीटर,
टंकी की चौड़ाई (b) = 15 मीटर
तथा टंकी की ऊँचाई (h) = 6 मीटर
टंकी का आयतन = lbh = 20 x 15 x 6 घन मीटर = 1800 घन मीटर।

अतः पानी से भरी टंकी गाँव के लिए 3 दिन के लिए पर्याप्त होगी।

प्रश्न 7. किसी गोदाम की मापें 40 मीटर x 25 मीटर x 15 मीटर हैं। इस गोदाम में 1.5 मीटर x 1.25 मीटर x 0.5 मीटर की माप वाले लकड़ी के कितने अधिकतम क्रेट (crate) रखे जा सकते हैं?
हल :
माना लकड़ी के n क्रेट रखे जा सकते हैं।
प्रत्येक क्रेट की माप 1.5 मीटर x 1.25 मीटर x 0.5 मीटर है।
अर्थात क्रेट की लम्बाई (l) = 1.5 मीटर,
क्रेट की चौड़ाई (b) = 1.25 मीटर
क्रेट की ऊँचाई (h) = 0.5 मीटर
प्रत्येक क्रेट का आयतन = lbh = 1.5 x 1.25 x 0.5 घन मीटर = 0.9375 घन मीटर
सभी n क्रेट्स का आयतन = 0.9375n घन मीटर
गोदाम की माप 40 मीटर x 25 मीटर x 15 मीटर है।
‘अर्थात गोदाम की लम्बाई (l1) = 40 मीटर,
गोदाम की चौड़ाई (b1) = 25 मीटर
तथा गोदाम की ऊँचाई (h1) = 15 मीटर
गोदाम का आयतन = l1b1h1 = 40 x 25 x 15 घन मीटर = 15,000 घन मीटर
गोदाम का आयतन लकड़ी के n क्रेट्स के आयतन के बराबर होना चाहिए।
0.9375 n = 15,000 ⇒ n = 16,000
अतः गोदाम में 16,000 क्रेट्स रखे जा सकते हैं।

प्रश्न 8. 12 सेमी भुजा वाले एक ठोस घन को बराबर आयतन वाले 8 घनों में काटा जाता है। नए घन की भुजा क्या होगी? साथ ही, इन दोनों घनों के पृष्ठीय क्षेत्रफलों का अनुपात भी ज्ञात कीजिए।

प्रश्न 9. 3 मीटर गहरी और 40 मीटर चौड़ी एक नदी 2 किमी प्रति घण्टा की चाल से बहकर समुद्र में गिरती है। एक मिनट में समुद्र में कितना पानी गिरेगा?
हल :
नदी की गहराई (h) = 3 मीटर
और चौड़ाई (b) = 40 मीटर
नदी का परिच्छेद क्षेत्रफल (Sectional Area) = h x b = 3 x 40 = 120 वर्ग मीटर
नदी के पानी की चाल 2 किमी प्रति घण्टा है।
1 मिनट में नदी के विस्थापित पानी की लम्बाई = [latex]\frac { 2 x 1000 }{ 60 }[/latex] = [latex]\frac { 100 }{ 3 }[/latex]
1 मिनट में बहने वाले पानी का आयतन = [latex]\frac { 100 }{ 3 }[/latex] x 120 घन मीटर = 4000 घन मीटर
अतः 1 मिनट में समुद्र में 4000 घन मीटर पानी गिरेगा।

प्रश्नावली 13.6

जब तक अन्यथा न कहा जाए, 1 = लीजिए।
प्रश्न 1. एक बेलनाकार बर्तन के आधार की परिधि 132 सेमी और उसकी ऊँचाई 25 सेमी है। इस बर्तन में कितने लीटर पानी आ सकता है? (1000 सेमी3 = 1 लीटर)

प्रश्न 2. लकड़ी के एक बेलनाकार पाइप को आन्तरिक व्यास 24 सेमी है और बाहरी व्यास 28 सेमी है। इस पाइप की लम्बाई 35 सेमी है। इस पाइप का द्रव्यमान ज्ञात कीजिए, यदि 1 सेमी लकड़ी का द्रव्यमान 0.6 ग्राम है।
हल : लकड़ी के बेलनाकार पाइप का आन्तरिक व्यास = 24 सेमी।
आन्तरिक त्रिज्या (r) = [latex]\frac { 24 }{ 2 }[/latex] = 12 सेमी

प्रश्न 3. एक सोफ्ट ड्रिंक (soft drink) दो प्रकार के पैकों में उपलब्ध है:
(i) लम्बाई 5 सेमी और चौड़ाई 4 सेमी वाले एक आयताकार आधार का टिन का डिब्बा जिसकी ऊँचाई 15 सेमी है और
(ii) व्यास 7 सेमी वाले वृत्तीय आधार और 10 सेमी ऊँचाई वाला एक प्लास्टिक का बेलनाकार डिब्बा। किस डिब्बे की धारिता अधिक है और कितनी अधिक है?
हल :
टिन (आयताकार आधार वाले) के डिब्बे की लम्बाई (l) = 5 सेमी,
चौड़ाई (b) = 4 सेमी और ऊँचाई (h) = 15 सेमी
टिन के डिब्बे का आयतन = lbh = 5 x 4 x 5 घन सेमी। = 300 घन सेमी
टिन के डिब्बे की धारिता = 300 घन सेमी
प्लास्टिक के (वृत्तीय आधार वाले) डिब्बे का व्यास = 7 सेमी
वृत्तीय आधार वाले डिब्बे की त्रिज्या (r’) = [latex]\frac { 7 }{ 2 }[/latex] सेमी
डिब्बे की ऊँचाई (h’) = 10 सेमी
बेलनाकार डिब्बे का आयतन = π (r’)² h’
= [latex]\frac { 22 }{ 7 }[/latex] x [latex]\frac { 7 }{ 2 }[/latex] x [latex]\frac { 7 }{ 2 }[/latex] x 10 घन सेमी
= 385 घन सेमी
बेलनाकार डिब्बे की धारिता = 385 घन सेमी|
अतः स्पष्ट है कि बेलनाकार डिब्बे की धारिता अधिक है तथा यह आयताकार आधार वाले डिब्बे की धारिता से (385 – 300) = 85 घन सेमी अधिक है।

प्रश्न 4. यदि एक बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 सेमी है और उसकी ऊँचाई 5 सेमी है, तो ज्ञात कीजिए :
(i) आधार की त्रिज्या,
(ii) बेलन का आयतन (π = 3.14 लीजिए)
हल :
(i) माना बेलन के आधार की त्रिज्या सेमी है।
दिया है, बेलन की ऊँचाई (h) = 5 सेमी
बेलन का पाश्र्व पृष्ठीय क्षेत्रफल = 2πrh वर्ग सेमी = 2 x 3.14 x r x 5 वर्ग सेमी = 31.4r वर्ग सेमी
परन्तु प्रश्न में दिया है कि बेलन का पार्श्व पृष्ठीय क्षेत्रफल 94.2 सेमी है।
31.4r = 94.2 ⇒ r = 3
अतः बेलन के आधार की त्रिज्या = 3 सेमी।
(ii) बेलन की त्रिज्या (r) = 3 सेमी तथा
बेलन की ऊँचाई (h) = 5 सेमी बेलन का आयतन = πr²h = 3.14 x 3 x 3 x 5 घन सेमी = 3.14 x 45 घन सेमी = 141.3 घन सेमी।
अतः बेलन का आयतन = 141.3 घन सेमी।

प्रश्न 5. 10 मीटर गहरे एक बेलनाकार बर्तन की आन्तरिक वक्र पृष्ठ को पेंट कराने का व्यय 2200 है। यदि पेंट कराने की दर 20 प्रति मीटर है तो ज्ञात कीजिए :
(i) बर्तन का आन्तरिक वक्र पृष्ठीय क्षेत्रफल
(ii) आधार की त्रिज्या
(iii) बर्तन की धारिता

प्रश्न 6. ऊँचाई 1 मीटर वाले एक बेलनाकार बर्तन की धारिता 15.4 लीटर है। इसको बनाने के लिए कितने वर्ग मीटर धातु की शीट की आवश्यकता होगी?

प्रश्न 7. सीसे की एक पेंसिल (lead pencil) लकड़ी के एक बेलन के अभ्यन्तर में ग्रेफाइट (graphite) से बने ठोस बेलन को डाल कर बनाई गई है। पेंसिल का व्यास 7 मिमी है और ग्रेफाइट का व्यास 1 मिमी है। यदि पेंसिल की लम्बाई 14 सेमी है, तो लकड़ी का आयतन और ग्रेफाइट का आयतन ज्ञात कीजिए।
हल : पेंसिल का व्यास = 7 मिमी = 0.7 सेमी [1 मिमी = [latex]\frac { 1 }{ 10 }[/latex] सेमी
पेसिल की त्रिज्या (r) = [latex]\frac { 0.7 }{ 2 }[/latex] सेमी = 0.35 सेमी
पेंसिल की लम्बाई (h) = 14 सेमी
पेंसिल का आयतन = πr²h = [latex]\frac { 22 }{ 7 }[/latex] x 0.35 x 0.35 x 14 घन सेमी = 5.39 घन सेमी।
ग्रेफाइट रॉड का व्यास = 1 मिमी = 0.1 सेमी
ग्रेफाइट रॉड की त्रिज्या (r’) = [latex]\frac { 0.1 }{ 2 }[/latex] = 0.05 सेमी
ग्रेफाइट रॉड की लम्बाई (h) = 14 सेमी
ग्रेफाइट रॉड का आयतन = π(r’)²h
= [latex]\frac { 22 }{ 7 }[/latex] x 0.05 x 0.05 x 14 घन सेमी = 0.11 घन सेमी
पेंसिल में लगी लकड़ी का आयतन = पेंसिल का आयतन – ग्रेफाइट रॉड का आयतन = (5.39 – 0.11) घन सेमी = 5.28 घन सेमी
अतः लकड़ी का आयतन 5.28 घन सेमी और ग्रेफाइट का आयतन 0.11 घन सेमी है।

प्रश्न 8. एक अस्पताल (hospital) के एक रोगी को प्रतिदिन 7 सेमी व्यास वाले एक बेलनाकार कटोरे में सूप (soup) दिया जाता है। यदि यह कटोरा सूप से 4 सेमी ऊँचाई तक भरा जाता है, तो इस अस्पताल में 250 रोगियों के लिए प्रतिदिन कितना सूप तैयार किया जाता है?
हल : बेलनाकार कटोरे का व्यास = 7 सेमी
कटोरे की त्रिज्या (r) = [latex]\frac { 7 }{ 2 }[/latex] सेमी
कटोरे की ऊँचाई (h) = 4 सेमी
बेलनाकार कटोरे में डाले गए सूप का आयतन = πr²h
= [latex]\frac { 22 }{ 7 }[/latex] x [latex]\frac { 7 }{ 2 }[/latex] x [latex]\frac { 7 }{ 2 }[/latex] x 4 घन सेमी
= 154 घन सेमी।
1 रोगी के लिए आवश्यक सूप की मात्रा = 154 घन सेमी
250 रोगियों के लिए आवश्यक सूप की मात्रा = 250 x 154 घन सेमी = 38,500 घन सेमी
= [latex]\frac { 38500 }{ 1000 }[/latex]
= 38.5 लीटर
अत: प्रतिदिन 38,500 घन सेमी या 38.5 लीटर सूप तैयार किया जाता है।

प्रश्नावली 13.7

जब तक अन्यथा न कहा जाए, π = [latex]\frac { 22 }{ 7 }[/latex] लीजिए।
प्रश्न 1. उस लम्ब वृत्तीय शंकु का आयतन ज्ञात कीजिए, जिसकी|
(i) त्रिज्या 6 सेमी और ऊँचाई 7 सेमी है।
(ii) त्रिज्या 3.5 सेमी और ऊँचाई 12 सेमी है।

प्रश्न 2. शंकु के आकार के उस बर्तन की लीटरों में धारिता ज्ञात कीजिए जिसकी
(i) त्रिज्या 7 सेमी और तिर्यक ऊँचाई 25 सेमी है।
(ii) ऊँचाई 12 सेमी और तिर्यक ऊँचाई 13 सेमी है।

प्रश्न 3. एक शंकु की ऊँचाई 15 सेमी है। यदि उसका आयतन 1570 सेमी है, तो इसके आधार की त्रिज्या ज्ञात कीजिए। (π = 3.14 प्रयोग कीजिए।)

प्रश्न 4. यदि 9 सेमी ऊँचाई वाले एक लम्बे वृत्तीय शंकु का आयतन 48 7 सेमी है तो इसके आधार का व्यास ज्ञात कीजिए।

प्रश्न 5. ऊपरी व्यास 3.5 मीटर वाले शंकु के आकार का एक गड्ढा 12 मीटर गहरा है। इसकी धारिता किलोलीटरों में कितनी है?

प्रश्न 6. एक लम्ब वृत्तीय शंकु का आयतन 9856 सेमी है। यदि इसके आधार का व्यास 28 सेमी है तो ज्ञात कीजिए।
(i) शंकु की ऊँचाई
(ii) शंकु की तिर्यक ऊँचाई
(iii) शंकु का वक्र पृष्ठीय क्षेत्रफल

प्रश्न 7. भुजाओं 5 सेमी, 12 सेमी और 13 सेमी वाले एक समकोण त्रिभुज ABC को भुजा 12 सेमी के परितः घुमाया जाता है। इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए।

प्रश्न 8. यदि प्रश्न 7 के त्रिभुज ABC को यदि भुजा 5 सेमी के परितः घुमाया जाए, तो इस प्रकार प्राप्त ठोस का आयतन ज्ञात कीजिए। प्रश्न 7 और 8 में प्राप्त किए गए दोनों ठोसों के आयतनों का अनुपात भी ज्ञात कीजिए।

प्रश्न 9. गेहूँ की एक ढेरी 10.5 मीटर व्यास और 3 मीटर ऊँचाई वाले एक शंकु के आकार की है। इसका आयतन ज्ञात कीजिए। इस ढेरी को वर्षा से बचाने के लिए कैनवास से ढका जाता है। वाँछित कैनवास का क्षेत्रफल ज्ञात कीजिए।

प्रश्नावली 13.8

जब तक अन्यथा न कहा जाए, π = [latex]\frac { 22 }{ 7 }[/latex] लीजिए।
प्रश्न 1. उस गोले का आयतन ज्ञात कीजिए जिसकी त्रिज्या निम्नलिखित हैं
(i) 7 सेमी
(ii) 0.63 मीटर

प्रश्न 2. उस ठोस गोलाकार गेंद द्वारा हटाए गए (विस्थापित) पानी का आयतन ज्ञात कीजिए, जिसका व्यास निम्नलिखित है :
(i) 28 सेमी
(ii) 0.21 मीटर।

प्रश्न 3. धातु की एक गेंद को व्यास 4.2 सेमी है। यदि इस धातु का घनत्व 8.9 ग्राम प्रति घन सेमी है तो इस गेंद का द्रव्यमान ज्ञात कीजिए।

प्रश्न 4. चन्द्रमा का व्यास पृथ्वी के व्यास का लगभग एक-चौथाई है। चन्द्रमा का आयतन पृथ्वी के आयतन की कौन-सी भिन्न है?

प्रश्न 5. व्यास 10.5 सेमी वाले एक अर्द्ध-गोलाव कार कटोरे में कितने लीटर दूध आ सकता है?

प्रश्न 6. एक अर्द्ध-गोलाकार टंकी 1 सेमी मोटी एक लोहे की चादर (sheet) से बनी है। यदि इसकी आन्तरिक त्रिज्या 1 मीटर है, तो इस टंकी के बनाने में लगे लोहे का आयतन ज्ञात कीजिए।

प्रश्न 7. उस गोले का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 154 वर्ग सेमी है।

प्रश्न 8. किसी भवन का गुम्बद एक अर्द्ध-गोले के आकार का है। अन्दर से, इसमें सफेदी कराने में 498.96 व्यय हुए। यदि सफेदी कराने की दर 2 प्रति वर्ग मीटर है, तो ज्ञात कीजिए।
(i) गुम्बद का आन्तरिक वक्र पृष्ठीय क्षेत्रफल
(ii) गुम्बद के अन्दर की हवा का आयतन।
हल :
(i) माना अर्द्ध-गोलाकार गुम्बद की त्रिज्या मीटर है।
अर्द्ध-गोलाकार गुम्बद खोखला होता है।
अर्द्ध-गोलाकार गुम्बद को आन्तरिक पृष्ठ = 2πr² वर्ग मीटर

प्रश्न 9. लोहे के संत्ताइस ठोस गोलों को पिघलाकर, जिनमें से प्रत्येक की त्रिज्या है और पृष्ठीय क्षेत्रफल S है, एक बड़ा गोला बनाया जाता है, जिसका पृष्ठीय क्षेत्रफल S’ है। ज्ञात कीजिए :
(i) नए गोले की त्रिज्या r’
(ii) S और S’ का अनुपात।

प्रश्न 10. दवाई का एक कैपसूल (capsule) 3.5 मिमी व्यास का एक गोला (गोली) है। इस कैपसूल को भरने के लिए कितनी दवाई (घन मिमी में) की आवश्यकता होगी?

प्रश्नावली 13.9 (ऐच्कि)

प्रश्न 1. एक लकड़ी के बुक-शैल्फ (book-shelf) की बाहरी विमाएँ 85 सेमी निम्नलिखित हैं :
ऊँचाई = 110 सेमी, गहराई = 25 सेमी, चौड़ाई = 85 सेमी। प्रत्येक स्थान पर तख्तों की मोटाई 5 सेमी है। इसके बाहरी फलकों पर पॉलिश कराई जाती है। और आन्तरिक फलकों पर पेंट किया जाना है। यदि पॉलिश कराने की दर 20 पैसे प्रति सेमी है और पेंट कराने की दर 10 पैसे प्रति सेमी है तो इस बुक-शैल्फ पर पॉलिश और पेंट कराने का कुल व्यय ज्ञात कीजिए।

हल :
दिया है, ऊँचाई = 110 सेमी, गहराई = 25 सेमी तथा चौड़ाई = 85 सेमी तख्तों की मोटाई = 5 सेमी।
पॉलिश वाले भाग का क्षेत्रफल = चार दीवारों का क्षेत्रफल + बुक-शैल्फ के पीछे का क्षेत्रफल + सामने की पट्टिकाओं का क्षेत्रफल
= [(2 x गहराई x ऊँचाई) + (2 x चौड़ाई x गहराई) + (चौड़ाई x ऊँचाई) + {2 x ऊँचाई x मोटाई) + 4 x (चौड़ाई – 5 – 5) मोटाई }]
= [(2 x 25 x 110 + 2 x 85 x 25) + 85 x 10 + {2 x 110 x 5 + 4 x (85 – 10) x 5}]
= [2 (110 + 85) x 25 + 110 x 85 + 110 x 5 x 2 + (75 x 5) x 4]
= 9750 + 9350 + 1100 + 1500
= 21700 वर्ग सेमी
अब प्रति वर्ग सेमी पर पॉलिश कराने का व्यय = 20 पैसे = [latex]\frac { 20 }{ 100 }[/latex] [1 पैसा = [latex]\frac { 1 }{ 100 }[/latex] ]
21700 वर्ग सेमी पर पॉलिश कराने का व्यय = (21700 x [latex]\frac { 20 }{ 100 }[/latex]) = 4340
आन्तरिक वक्र पृष्ठ = विमाओं 75 सेमी x 30 सेमी x 20 सेमी के प्रत्येक 3 घनाभों का कुल वक्र पृष्ठ – विमाओं 75 सेमी x 30 सेमी x 20 सेमी के प्रत्येक 3 घनाभों के सामने के फलक का क्षेत्रफल

प्रश्न 2. किसी घर के कम्पाउण्ड की सामने की दीवार को 21 सेमी व्यास वाले लकड़ी के गोलों को छोटे आधारों पर टिकाकर सजाया जाता है, जैसा कि संलग्न आकृति में दिखाया गया है। इस प्रकार के आठ गोलों का प्रयोग इस कार्य के लिए किया जाना है और इन गोलों को चाँदी वाले रंग में पेंट करवाना है। प्रत्येक आधार 1.5 सेमी त्रिज्या और ऊँचाई 7 सेमी का एक बेलन है तथा इन्हें काले रंग से पेंट करवाना है। यदि चाँदी के रंग का पेंट करवाने की दर 25 पैसे प्रति सेमी है तथा काले रंग के पेंट करवाने की दर 5 पैसे प्रति सेमी हो, तो पेंट करवाने का कुल व्यय ज्ञात कीजिए।

प्रश्न 3. एक गोले के व्यास में 25% की कमी हो जाती है। उसका वक्र पृष्ठीय क्षेत्रफल कितने प्रतिशत कम हो गया है?

We hope the UP Board Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes (पृष्ठीय क्षेत्रफल एवं आयतन) help you. If you have any query regarding UP Board Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes (पृष्ठीय क्षेत्रफल एवं आयतन), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति)

These Solutions are part of UP Board Solutions for Class 9 Maths. Here we have given UP Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति).

प्रश्नावली 1.1

प्रश्न 1.
क्या शून्य एक परिमेय संख्या है? क्या आप इसे [latex]\frac { p }{ q }[/latex] के रूप में लिख सकते हैं जहाँ p और q पूर्णाक हैं और q ≠ 0 है?
हल :
हाँ, शून्य एक परिमेय संख्या है।
इसे [latex]\frac { p }{ q }[/latex] के रूप में लिखा जा सकता है।
0 = [latex]\frac { 0 }{ 4 }[/latex] , [latex]\frac { 0 }{ 5 }[/latex] , [latex]\frac { 0 }{ 8 }[/latex] ,……….

प्रश्न 2.
3 और 4 के मध्य 6 परिमेय संख्याएँ ज्ञात कीजिए।
हल :
6 परिमेय संख्याएँ ज्ञात करने के लिए, 3 और 4 को (6 + 1) = 7 से गुणा और भाग करते हैं।

प्रश्न 3.
[latex]\frac { 3 }{ 5 }[/latex] और [latex]\frac { 4 }{ 5 }[/latex] के बीच पाँच परिमेय संख्याएँ ज्ञात कीजिए।
हल :
चूँकि दी गई परिमेय संख्याओ का हर समान है।
पाँच परिमेय संख्याएँ ज्ञात करने के लिए, [latex]\frac { 3 }{ 5 }[/latex] और [latex]\frac { 4 }{ 5 }[/latex] को (5 + 1) = 6 से गुणा और भाग करते हैं।

प्रश्न 4.
नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए :
(i) प्रत्येक प्राकृत संख्या एक पूर्ण संख्या होती है।
(ii) प्रत्येक पूर्णाक एक पूर्ण संख्या होती है।
(iii) प्रत्येक परिमेय संख्या एक पूर्ण संख्या होती है।
हल :
(i) क्योंकि सभी प्राकृत संख्याएँ {1, 2, 3, 4, ….}, पूर्ण संख्याओं {0, 1, 2, 3, 4, ….} में समाहित हैं। अतः कथन सत्य है।
(ii) क्योंकि ऋणात्मक पूर्णाक, पूर्ण संख्याओं में समाहित नहीं है। अतः कथन असत्य है।
(iii) क्योंकि परिमेय संख्याओं के संग्रह में भिन्ने एवं दशमलव संख्याएँ होती हैं जो पूर्ण संख्याओं के संग्रह में समाहित नहीं हैं। अतः कथन असत्य है।

प्रश्नावली 1.2

प्रश्न 1.
नीचे दिए गए कथन सत्य हैं या असत्य? कारण के साथ अपने उत्तर दीजिए :
(i) प्रत्येक अपरिमेय संख्या एक वास्तविक संख्या होती है।
(ii) संख्या रेखा का प्रत्येक बिन्दु √m के रूप का होता है जहाँ m एक प्राकृत संख्या है।
(iii) प्रत्येक वास्तविक संख्या एक अपरिमेय होती है।
हल :
(i) क्योंकि वास्तविक संख्याओं का संग्रह परिमेय और अपरिमेय संख्याओं से मिलकर बना है अतः प्रत्येक अपरिमेय संख्या वास्तविक होती है। अत: कथन सत्य है।
(ii) यदि m एक प्राकृतिक संख्या है तो संख्या रेखा पर केवल 1, 2, 3, 4,……. बिन्दु ही स्थित होने चाहिए।
जबकि संख्या रेखा पर दो क्रमिक संख्याओं के मध्य अनन्त “संख्याएँ होती हैं। अत: कथन असत्य है।
(iii) क्योंकि वास्तविक संख्याओं के संग्रह में परिमेय और अपरिमेय दोनों प्रकार की संख्याएँ होती हैं। अत: प्रत्येक वास्तविक संख्या का अपरिमेय होना आवश्यक नहीं है। अतः कथन असत्य है।

प्रश्न 2.
क्या सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय होते हैं? यदि नहीं, तो एक ऐसी संख्या के वर्गमूल का उदाहरण दीजिए जो एक परिमेय संख्या है।
हल :
नहीं, सभी धनात्मक पूर्णांकों के वर्गमूल अपरिमेय नहीं होते हैं।
उदाहरणार्थ : √9 = 3 एक परिमेय संख्या है।

प्रश्न 3.
दिखाइए कि संख्या रेखा पर √5 को किस प्रकार निरूपित किया जा सकता है?

प्रश्नावली 1.3

प्रश्न 1.
निम्नलिखित भिन्नों को दशमलव रूप में लिखिए और बताइए कि प्रत्येक को दशमलव प्रसार किस प्रकार का है :

प्रश्न 3.
निम्नलिखित को [latex]\frac { p }{ q }[/latex] के रूप में व्यक्त कीजिए, जहाँ p और q पूर्णाक है तथा q ≠ 0 है :

प्रश्न 4.
0.99999…. को [latex]\frac { p }{ q }[/latex] के रूप में व्यक्त कीजिए। क्या आप अपने उत्तर से आश्चर्यचकित हैं? अपने अध्यापक और कक्षा के सहयोगियों के साथ उत्तर की सार्थकता पर चर्चा कीजिए।

प्रश्न 5.
[latex]\frac { 1 }{ 17 }[/latex] के दशमलव प्रसार में अंकों के पुनरावृत्ति खण्ड में अंकों की अधिकतम संख्या क्या हो सकती है? अपने उत्तर की जाँच करने के लिए विभाजन-क्रिया कीजिए।
हल:
[latex]\frac { 1 }{ 17 }[/latex] में हर 17 है। अत: भाग करने पर 1 से 16 तक की कोई भी संख्याएँ शेषफल के रूप में प्राप्त हो सकती है। उसके उपरान्त अंकों की पुनरावृत्ति अवश्य होगी।
अतः [latex]\frac { 1 }{ 17 }[/latex] के दशमलव प्रसार के पुनरावृत्ति खण्ड में अधिकतम अंक = 16

प्रश्न 6.
[latex]\frac { p }{ q }[/latex] , q ≠ 0 के रूप में परिमेय संख्याओं के अनेक उदाहरण लीजिए, जहाँ p और q पूर्णांक हैं, जिनका 1 के अतिरिक्त अन्य कोई उभयनिष्ठ गुणनखण्ड नहीं है और जिसका सांत दशमलव निरूपण (प्रसार) है। क्या आप यह अनुमान लगा सकते हैं कि q को कौन-सा गुण अवश्य सन्तुष्ट करना चाहिए?
हल :
[latex]\frac { p }{ q }[/latex] के रूप में परिमेय संख्याओं का दशमलव प्रसार सांत तभी होगा जब p को qसे भाग देने पर शेषफल शून्य हो। जबकि p और g में 1 के अतिरिक्त कोई उभयनिष्ठ गुणनखण्ड न हो जहाँ p और q पूर्णांक हैं तथा q ≠ 0 है।
किसी संख्या को भाग करने पर शेषफल शून्य तभी होगा जबकि
(1) भाजक 2 या 2 की कोई घात हो।
(2) भाजक 5 या 6 की कोई घात हो।
(3) भाजक 2 की किसी घात और 5 की किसी घात का गुणनफल हो।
अतः q को 2 अथवा 5 अथवा इनकी किसी घात के बराबर होना चाहिए अथवा 2 की किसी घात और 5 की किसी घात के गुणन के बराबर होना चाहिए।
अर्थात q = 2^m x 5ⁿ जहाँ m और n पूर्ण संख्याएँ हैं।

प्रश्न 7.
ऐसी तीन संख्याएँ लिखिए जिनके दशमलव प्रसार अनवसानी अनावर्ती हो।
हल :
सभी अपरिमेय संख्याओं के दशमलव प्रसार अनवसानी अनावर्ती होते हैं।
ऐसी तीन संख्याएँ √2, √3, √5 हैं।

प्रश्न 8.
परिमेय संख्याओं [latex]\frac { 5 }{ 7 }[/latex] और [latex]\frac { 9 }{ 11 }[/latex] के बीच की तीन अलग-अलग अपरिमेय संख्याएँ ज्ञात कीजिए।

प्रश्न 9.
बताइए कि निम्नलिखित संख्याओं में कौन-कौन सी संख्याएँ परिमेय और कौन-कौन भी संख्याएँ अपरिमेय हैं :

प्रश्नावली 1.4

प्रश्न 1.
उत्तरोत्तर आवर्धन करके संख्या-रेखा पर 3.765 को देखिए।
हल :
चरण 1 : दी गई संख्या 3 तथा 4 के मध्य स्थित है।
चरण 2 : 3 और 4 के मध्य अन्तराल का आवर्धन करते हैं तथा इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 3 : दी गई संख्या 3.7 और 3.8 के मध्य स्थित हैं।
चरण 4 : 3.7 और 3.8 के मध्य अन्तराल को 10 बराबर भागों में विभाजित करते हैं तथा इसका आवर्धन करते हैं।
चरण 5 : दी गई संख्या 3.76 तथा 3.77 के मध्य स्थित हैं।
चरण 6 : 3.76 और 3.77 के मध्य अन्तराल का आवर्धन करते हैं तथा इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 7 : चरण-6 के आवर्धन में 3.765 पाँचवाँ भाग हैं।

प्रश्न 2.
4 दशमलव स्थानों तक संख्या-रेखा पर 4.26 को देखिए।
हल :
चरण 1 : संख्या रेखा पर दी गई संख्या 4.26, 4 तथा 5 के मध्य स्थित हैं। (4 दशमलव स्थानों तक संख्या 4.2626 हैं।)
चरण 2 : 4 तथा 5 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 3 : दी गई संख्या 4.2626, 4.2 तथा 4.3 के मध्य स्थित हैं।
चरण 4 : 4.2 तथा 4.3 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 5 : दी गई संख्या 4.26 और 4.27 के मध्य स्थित हैं।
चरण 6 : 4.26 तथा 4.27 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 7 : दी गई संख्या 4.262 तथा 4.263 के मध्य स्थित हैं।
चरण 8 : 4.262 तथा 4.263 के मध्य अन्तराल का आवर्धन करते हैं और इसे 10 बराबर भागों में विभाजित करते हैं।
चरण 9 : चरण-8 के आवर्धन में 4.2626 छठवाँ भाग हैं।

प्रश्नावली 1.5

प्रश्न 1.
बताइए नीचे दी गयी संख्याओं में कौन-कौन परिमेय हैं और कौन-कौन अपरिमेय हैं :

प्रश्न 2.
निम्नलिखित व्यंजकों में से प्रत्येक व्यंजक को सरल कीजिए।

प्रश्न 3.
आपको याद होगा कि π को एक वृत्त की परिधि (c) और उसके व्यास (d) के अनुपात से परिभाषित किया जाता है अर्थात् π = [latex]\frac { c }{ d }[/latex] है। यह इस तथ्य का अन्तर्विरोध करता हुआ प्रतीत होता है कि π अपरिमेय है। इस अन्तर्विरोध का निराकरण आप किस प्रकार करेंगे?

c और d को किसी पैमाने से मापने पर हमें केवल सन्निकट माप प्राप्त होती है जिससे यह पता नहीं चल पाती कि c या d परिमेय संख्याएँ हैं या अपरिमेय संख्याएँ हैं। इसी कारण हमें c और d को परिमेय संख्याएँ समझने का भ्रम उत्पन्न होता है। और हम c और d के अनुपात 7 को परिमेय संख्या समझने की ओर अग्रसर होते है जिससे अन्तर्विरोध उत्पन्न होता है। वास्तव में 7 के अपरिमेय होने में कोई अन्तर्विरोध नहीं है।

प्रश्न 4.
संख्या रेखा पर √9.3 को निरूपित कीजिए।
हल :

रेखाखण्ड AB = 9.3 मात्रक और BC = 1 मात्रक इस प्रकार खींचते हैं कि ABC एक सरल रेखा है।
AC का मध्य-बिन्दु M ज्ञात करते हैं तथा AC को व्यास लेकर अर्द्धवृत्त खींचते हैं।
∠ABD = 90° बनाते हैं जो अर्द्धवृत्त को D पर काटता है।
अब संख्या रेखा पर B को केन्द्र लेकर BD त्रिज्या से चाप लगाते हैं जो संख्या रेखा को P पर काटता है।
अब √9.3 = BP अर्थात् बिन्दु P संख्या रेखा पर √9.3 को निरूपित करती है।

प्रश्न 5.
निम्नलिखित के हरों का परिमेयकरण कीजिए ।

प्रश्नावली 1.6

प्रश्न 1.
ज्ञात कीजिए :

प्रश्न 2.
ज्ञात कीजिए।

प्रश्न 3.
सरल कीजिए :

We hope the UP Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति) help you. If you have any query regarding UP Board Solutions for Class 9 Maths Chapter 1 Number systems (संख्या पद्धति), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 9 Social Science Geography Chapter 4 जलवायु

These Solutions are part of UP Board Solutions for Class 9 Social Science. Here we have given UP Board Solutions for Class 9 Social Science Geography Chapter 4 जलवायु.

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1.
नीचे दिए गए चार विकल्पों में से सही उत्तर का चयन करें :
(i) नीचे दिए गए स्थानों में किस स्थान पर विश्व में सबसे अधिक वर्षा होती है?
(क) सिलचर
(ख) चेरापूँजी
(ग) मॉसिनराम
(घ) गुवाहाटी

(ii) ग्रीष्म ऋतु में उत्तरी मैदानों में बहने वाली पवन को निम्नलिखित में से क्या कहा जाता है?
(क) काल वैशाखी
(ख) व्यापारिक पवनें
(ग) लू
(घ) इनमें से कोई नहीं

(iii) निम्नलिखित में से कौन-सी कारण भारत के उत्तर-पश्चिम भाग में शीत ऋतु में होने वाली वर्षा के लिए उत्तरदायी है?
(क) चक्रवातीय अवदाब
(ख) पश्चिमी विक्षोभ
(ग) मानसून की वापसी
(घ) दक्षिण-पश्चिम मानसून

(iv) भारत में मानसून का आगमन निम्नलिखित में से कब होता है?
(क) मई के प्रारंभ में
(ख) जून के प्रारंभ में
(ग) जुलाई के प्रारंभ में
(घ) अगस्त के प्रारंभ में

(v) निम्नलिखित में से कौन-सी भारत में शीत ऋतु की विशेषता है?
(क) गर्म दिन एवं गर्म रातें
(ख) गर्म दिन एवं ठंडी रातें
(ग) ठंडा दिन एवं ठंडी रातें
(घ) ठंडा दिन एवं गर्म रातें
उत्तर:
(i) (ग) मॉसिनराम
(ii) (ग) लू
(iii) (ख) पश्चिमी विक्षोभ
(iv) (ख) जून के प्रारंभ में
(v) (ग) ठंडा दिन एवं ठंडी रातें।

प्रश्न 2.
निम्न प्रश्नों के संक्षेप में उत्तर दीजिए-

1. भारत की जलवायु को प्रभावित करने वाले कौन-कौन से कारक हैं?
2. भारत में मानसूनी प्रकार की जलवायु क्यों है?
3. भारत के किस भाग में दैनिक तापमान अधिक होता है एवं क्यों?
4. किन पवनों के कारण मालाबार तट पर वर्षा होती है?
5. जेट धाराएँ क्या हैं तथा वे किस प्रकार भारत की जलवायु को प्रभावित करती हैं?
6. मानसून को परिभाषित करें। मानसून में विराम से आप क्या समझते हैं?
7. मानसून को एक सूत्र में बाँधने वाला क्यों समझा जाता है?

उत्तर:

1. भारत की जलवायु को मुख्य रूप से तीन कारक प्रभावित करते हैं। ये हैं-
   1. अक्षांश,
   2. ऊँचाई,
   3. वायुदाब एवं पवनें।
2. भारत में मानसूनी जलवायु होने के प्रमुख कारण इस प्रकार हैं
   1. मानसूनी जलवायु में मौसम के अनुसार पवनों की दिशा में परिवर्तन होता है।
   2. भारत की जलवायु में भी पवनें गर्मी में समुद्र से स्थल की ओर तथा शीत ऋतु में स्थल से समुद्र की ओर चलती हैं।
3. भारत में सबसे अधिक दैनिक तापमान भारत के मरुस्थल में होता है क्योंकि रेत शीघ्र गर्म होने से दिन में तापमान अधिक होता है।
4. मालाबार तट पर दक्षिण-पश्चिमी पवनों के कारण वर्षा होती है।
5. क्षोभमंडल की ऊपरी परत में पश्चिम से पूर्व की ओर तथा पूर्व से पश्चिम की ओर चलने वाली तीव्रगामी वायु धाराओं को जेट प्रवाह कहते हैं। पश्चिमी जेट प्रवाह के मार्ग में हिमालय तथा तिब्बत के पठार अवरोधक का काम करते हैं।
   इस प्रकार यह प्रवाह दो भागों में बँट जाता है-
   1. उत्तरी जेट प्रवाह
   2. दक्षिणी जेट प्रवाह।
      उत्तरी जेट प्रवाह हिमालय के उत्तर में तथा दक्षिणी जेट प्रवाह हिमालय के दक्षिण में बहता है। जेट की दक्षिणी शाखा हमारे देश की जलवायु को प्रभावित करती है। जेट प्रवाह शीतकालीन चक्रवातों को भारत तक पहुँचाने में सहायक होते हैं। भारत की मानसून पवनों की दिशा को निर्धारित करने में जेट प्रवाह प्रभावशाली भूमिका निभाते हैं।
6. मानसून अरबी भाषा का शब्द है जिसका शाब्दिक अर्थ ‘मौसम’ है। मानसूनी जलवायु में मौसम के अनुसार पवनों की दिशा में परिवर्तन आ जाता है-गर्मी में समुद्र से स्थल की ओर सर्दी में स्थल से समुद्र की ओर। मानसून में विराम का अर्थ है वह शुष्क समय जिसमें वर्षा नहीं होती।
7. विभिन्न अक्षाशों में स्थित होने एवं उच्चावच लक्षणों के कारण भारत की मौसम संबंधी परिस्थितियों में बहुत अधिक भिन्नताएँ पाई जाती हैं। किन्तु ये भिन्नताएँ मानसून के कारण कम हो जाती हैं क्योंकि मानसून पूरे भारत में बहती हैं। सम्पूर्ण भारतीय भूदृश्य, इसके जीव तथा (UPBoardSolutions.com) वनस्पति, इसका कृषि-चक्र, मानव-जीवन तथा उनके त्योहार-उत्सव, सभी इस मानसूनी लय के चारों ओर घूम रहे हैं।

मानसून के आगमन का पूरे देश में भरपूर स्वागत होता है। भारत में मानसून के आगमन का स्वागत करने के लिए विभिन्न त्योहार मनाए जाते हैं। मानसून झुलसाती गर्मी से राहत प्रदान करती है। मानसून वर्षा कृषि क्रियाकलापों के लिए पानी उपलब्ध कराती है। वायु प्रवाह में ऋतुओं के अनुसार परिवर्तन एवं इससे जुड़ी मौसम संबंधी परिस्थितियाँ ऋतुओं का एक लयबद्ध चक्र उपलब्ध कराती हैं जो पूरे देश को एकता के सूत्र में बाँधती है। ये मानसूनी पवनें हमें जल प्रदान कर कृषि की प्रक्रिया में तेजी लाती हैं एवं सम्पूर्ण देश को एकसूत्र (UPBoardSolutions.com) में बाँधती हैं। नदी घाटियाँ जो इन जलों को संवहन करती हैं, उन्हें भी एक नदी घाटी इकाई का नाम दिया जाता है। भारत के लोगों का सम्पूर्ण जीवन मानसून के इर्द-गिर्द घूमता है। इसलिए मानसून को एक सूत्र में बाँधने वाला समझा जाता है।

प्रश्न 3.
उत्तर-भारत में पूर्व से पश्चिम की ओर वर्षा की मात्रा क्यों घटती जाती है?
उत्तर:
हवाओं में निरंतर कम होती आर्द्रता के कारण उत्तर भारत में पूर्व से पश्चिम की ओर वर्षा की मात्रा कम होती जाती है। बंगाल की खाड़ी से उठने वाली आर्द्र पवनें जैसे-जैसे आगे और आगे बढ़ती हुई देश के आंतरिक भागों में जाती हैं, वे अपने साथ लायी गयी अधिकतर आर्द्रता खोने लगती हैं। इसी के परिणामस्वरूप पूर्व से पश्चिम की ओर वर्षा धीरे-धीरे घटने लगती है। राजस्थान एवं गुजरात के कुछ भागों में बहुत कम वर्षा होती है। कोलकाता से दिल्ली की ओर बढ़ने पर वर्षा धीरे-धीरे घटती जाती है। उदाहरण के लिए, (UPBoardSolutions.com) कोलकाता में जहाँ 162 सेमी वर्षा होती है वहीं वाराणसी में 107 सेमी तथा दिल्ली में 56 सेमी वर्षा होती है। मानसून शाखा का दबाव और उसकी आर्द्रता पश्चिम की ओर क्रमशः घटती जाती है। यही कारण है कि मानसून की इस शाखा के दिल्ली तक पहुँचते-पहुँचाते वर्षा करने की क्षमता घटती जाती है।

प्रश्न 4.
कारण बताएँ-

1. भारतीय उपमहाद्वीप में वायु की दिशा में मौसमी परिवर्तन क्यों होता है?
2. भारत में अधिकतर वर्षा कुछ ही महीनों में होती है।
3. तमिलनाडु तट पर शीत ऋतु में वर्षा होती है।
4. पूर्वी तट के डेल्टा वाले क्षेत्र में प्रायः चक्रवात आते हैं।
5. राजस्थान, गुजरात के कुछ भाग तथा पश्चिमी घाट का वृष्टि छाया क्षेत्र सूखा प्रभावित क्षेत्र है।

उत्तर:
(1) भारतीय उपमहाद्वीप में वायु की दिशा में मौसमी परिवर्तन-भारतीय उपमहाद्वीप में मानसून पवनों की दिशा में मौसमी परिवर्तन का मूल कारण स्थल एवं जल पर विपरीत वायुदाब क्षेत्रों को विकसित होना है। यह वायु के तापमान के कारण होता है। स्पष्ट है कि स्थल एवं जल असमान रूप से गर्म होते हैं। ग्रीष्म ऋतु में समुद्र की अपेक्षा स्थल भाग अधिक गर्म हो जाता है। परिणामस्वरूप स्थल भाग के आंतरिक क्षेत्रों में निम्न वायुदाब क्षेत्र विकसित हो जाता है। जबकि समुद्री क्षेत्रों में उच्च वायुदाब का क्षेत्र होता है। अतः समुद्री पवनें समुद्र से स्थल की ओर गतिशील होती हैं। शीत ऋतु में स्थिति इसके विपरीत होती है अर्थात् पवन स्थल से समुद्र की ओर गतिशील होती है।

(2) भारत में अधिकतर वर्षा कुछ ही महीनों में होती है भारत के अधिकांश भागों में जून से सितम्बर के मध्य वर्षा होती है। भारत में मई माह में भारत के उत्तरी भाग में गर्मी बहुत पड़ती है। फलस्वरूप यहाँ की वायु हल्की होकर ऊपर उठ जाती है जिससे यहाँ वायुदाब कम हो जाता है। जबकि हिंद महासागर पर वायुदाब अधिक होता है। पवन प्रवाह का यह सर्वमान्य नियम है कि वह उच्च वायुदाब से निम्न (UPBoardSolutions.com) वायुदाब की ओर संचरित होती है। ऐसे में पवनें हिंद महासागर से भारत के उत्तरी भाग की ओर चलने लगती हैं। जलवाष्प से परिपूर्ण ये पवनें अपनी सम्पूर्ण आर्द्रता भारत में ही समाप्त कर देती हैं। ये पवनें जून से सितंबर तक भारत में सक्रिय रहती हैं। यही कारण है कि भारत में अधिकांश वर्षा जून से सितंबर माह की अवधि में होती है। भारत में मानसून की अवधि 100 से 120 दिन तक होती है।

(3) तमिलनाडु तट पर शीत ऋतु में वर्षा-पीछे हटते मानसून की ऋतु सितंबर से आरंभ हो जाती है। अब पवनें धरातल से समुद्र की ओर बहने लगती हैं। इसलिए ये शुष्क होती हैं और स्थल भाग पर वर्षा नहीं करतीं। जिस समय ये पवनें बंगाल की खाड़ी पर पहुँचती हैं तो वहाँ से ये आर्द्रता ग्रहण कर लेती हैं। अब ये उत्तरी-पूर्वी पवनों के प्रभाव में आकर इनकी दिशा भी उत्तर-पूर्व से दक्षिण-पश्चिम की ओर हो जाती है। और ये पवनें उत्तरी-पूर्वी मानसून के रूप में तमिलनाडु तट पर पहुँचती हैं। आर्द्रता ग्रहण की हुई ये पवनें तमिलनाडु तट पर शीत ऋतु में वर्षा करती हैं। अक्टूबर-नवंबर में पीछे हटते मानसून और बंगाल की खाड़ी पर उत्पन्न होने वाले उष्ण कटिबंधीय चक्रवातों के मिले-जुले प्रभाव से पूर्वी तट पर भारी वर्षा होती है। तमिलनाडु तट पर अक्टूबर-नवंबर में भारी वर्षा होती है।

(4) पूर्वी तट के डेल्टा में चक्रवात-बंगाल की खाड़ी में प्रायः निम्न वायुदाब का क्षेत्र बनता रहता है जबकि इस समय पूर्वी तट पर स्थित कृष्णा, कावेरी तथा गोदावरी के डेल्टा प्रदेश में अपेक्षाकृत वायुदाब का उच्च क्षेत्र होता है। पूर्वी तट के डेल्टा वाले क्षेत्र में प्रायः चक्रवात आते हैं। ऐसा इस कारण होता है क्योंकि अंडमान सागर पर पैदा होने वाला चक्रवातीय दबाव मानसून एवं अक्टूबर-नवंबर के दौरान उपोष्ण कटिबंधीय जेट धाराओं द्वारा देश के आंतरिक भागों की ओर स्थानांतरित कर दिया जाता है। ये चक्रवात विस्तृत क्षेत्र में भारी वर्षा (UPBoardSolutions.com) करते हैं। ये उष्ण कटिबंधीय चक्रवात प्रायः विनाशकारी होते हैं। गोदावरी, कृष्णा एवं कावेरी नदियों के डेल्टा प्रदेशों में अक्सर चक्रवात आते हैं, जिसके कारण बड़े पैमाने पर जान एवं माल की क्षति होती है। कभी-कभी ये चक्रवात ओडिशा, पश्चिम बंगाल एवं बांग्लादेश के तटीय क्षेत्रों में भी पहुँच जाते हैं। कोरोमंडल तट पर अधिकतर वर्षा इन्हीं चक्रवातों तथा अवदाबों से होती है।

(5) राजस्थान, गुजरात के कुछ भाग तथा पश्चिमी घाट की वृष्टि छाया क्षेत्र सूखा प्रभावित क्षेत्र है—राजस्थान तथा गुजरात के कुछ क्षेत्र अरबसागरीय मानसून शाखा द्वारा प्रभावित होते हैं–इस शाखा के बीच कोई प्राकृतिक अवरोधक नहीं है जो मानसून पवनों को रोककर राजस्थान तथा गुजरात के कुछ क्षेत्र में वर्षा करा सके। अरावली पर्वतमाला इस मानसून शाखा के समानांतर स्थित होने के कारण यह वर्षा कराने में असमर्थ रहती है। मरुभूमि होने के कारण यहाँ वाष्पीकरण अधिक होता है, संघनन नहीं होता। वनस्पतिविहीन होने के कारण वायुमंडलीय आर्द्रता यहाँ आकर्षित नहीं होती।
पश्चिमी घाट के वृष्टि छाया क्षेत्र सूखा से प्रवाहित होने के कारण-

1. यह क्षेत्र पश्चिमी घाट के पूर्व में स्थित है।
2. पश्चिमी घाट के वृष्टि छाया क्षेत्र में स्थित होने के कारण यहाँ वर्षा नहीं होती।
3. इससे यहाँ प्रायः सूखा पड़ने की संभावना रहती है।

प्रश्न 5.
भारत की जलवायु अवस्थाओं की क्षेत्रीय विभिन्नताओं को उदाहरण सहित समझाइए।
उत्तर:
भारत की उत्तर दिशा में हिमालय पर्वत के निर्णायक प्रभाव तथा दक्षिण में महासागर होने के बावजूद भी तापमान आर्द्रता एवं वर्षा में विविधता विद्यमान है।
जलवायु में इस विभिन्नता के निम्नलिखित कारण हैं-

1. उदाहरण के लिए, गर्मियों में राजस्थान के कुछ क्षेत्रों में, उत्तर-पश्चिमी भारत में तापमान 60 डिग्री सेल्सियस होता है जबकि उसी समय देश के उत्तर में जम्मू-कश्मीर के पहलगाम में तापमान 20 डिग्री सेल्सियस हो सकता है।
   सर्दियों की किसी रात में जम्मू-कश्मीर के द्रास में तापमान -45 डिग्री सेल्सियस तक हो सकता है, जबकि तिरुवनंतपुरम् में यह 22 डिग्री सेल्सियस हो सकता है।
2. अण्डमान व निकोबार एवं केरल में दिन व रात के तापमान में बहुत कम भिन्नता होती है।
3. एक अन्य विभिन्नता वर्षण में है। जबकि हिमालय के ऊपरी भागों में वर्षण अधिकतर हिम के रूप में होता है, देश के शेष भागों में वर्षा होती है। (UPBoardSolutions.com) मेघालय में 400 सेमी से लेकर लद्दाख एवं पश्चिमी राजस्थान में वार्षिक वर्षण 10 सेमी से भी कम होती है।
4. देश के अधिकतर भागों में जून से सितंबर तक वर्षा होती है, लेकिन कुछ क्षेत्रों जैसे तमिलनाडु तट पर अधिकतर वर्षा अक्टूबर एवं नवम्बर में होती है।
5. उत्तरी मैदान में वर्षा की मात्रा सामान्यतः पूर्व से पश्चिम की ओर घटती जाती है।

प्रश्न 6.
मानसूनी अभिक्रिया की व्याख्या करें।
उत्तर:
किसी भी क्षेत्र का वायुदाब एवं उसकी पवनें उस क्षेत्र की अक्षांशीय स्थिति एवं ऊँचाई पर निर्भर करती हैं। भारत की जलवायु में ऋतुओं के अनुसार पवनों की दिशा उलट जाती है। मानसून के रचनातंत्र में भारतीय उपमहाद्वीप के उत्तरी पर्वत सर्वाधिक महत्त्वपूर्ण भूमिका निभाते हैं। वे मानसून पवनों के प्रवाह को नियंत्रित करते हैं। इसी प्रकार की भूमिका पश्चिमी घाट भी निभाते हैं।

भारत में जलवायु तथा संबंधित मौसमी अवस्थाएँ निम्नलिखित वायुमंडलीय अवस्थाओं से संचालित होती हैं-
(1) पश्चिमी चक्रवाती विक्षोभ – हिमालय पर्वत के दक्षिण में प्रवाहित होने वाली उपोष्ण कटिबन्धीय पश्चिमी जेट धाराएँ जाड़े के महीने में देश के उत्तर एवं उत्तर पश्चिमी भागों में उत्पन्न होने वाले पश्चिमी चक्रवाती विक्षोभों के लिए उत्तरदायी हैं।

(2) वायुदाब एवं धरातलीय पवनें – वायु का संचार उच्च वायुदाब से निम्न वायुदाब की ओर होता है। शीत ऋतु में हिमालय के उत्तर में उच्च वायुदाब क्षेत्र होता है। ठण्डी शुष्क हवाएँ इस क्षेत्र से दक्षिण में सागर के ऊपर कम वायुदाब क्षेत्र की ओर बहती हैं। ग्रीष्म ऋतु के दौरान मध्य एशिया के साथ उत्तर-पश्चिमी भारत के ऊपर कम वायुदाब क्षेत्र विकसित हो जाता है। परिणामस्वरूप, कम वायुदाब प्रणाली दक्षिण गोलार्द्ध की दक्षिणपूर्वी व्यापारिक पवनों को आकर्षित करती है। ये व्यापारिक पवने विषुवत रेखा को पार करने के उपरांत कोरिआलिस बल के कारण दाहिनी ओर मुड़ते हुए भारतीय उपमहाद्वीप पर स्थित निम्न दाब की ओर बहने लगती हैं।

विषुवत् रेखा को पार करने के बाद ये पवनें दक्षिण-पश्चिमी दिशा में बहने लगती हैं और भारतीय प्रायद्वीप में दक्षिण-पश्चिमी मानसून के रूप में प्रवेश करती हैं। इन्हें दक्षिण पश्चिमी मानसून के नाम से जाना जाता है। ये पवनें गर्म महासागरों के ऊपर से बहते हुए आर्द्रता ग्रहण करती हैं और भारत (UPBoardSolutions.com) की मुख्यभूमि पर विस्तृत वर्षण लाती हैं। इस प्रदेश में, ऊपरी वायु परिसंचरण पश्चिमी प्रवाह के प्रभाव में रहता है। भारत में होने वाली वर्षा मुख्यतः दक्षिण-पश्चिमी मानसून पवनों के कारण होती है। मानसून की अवधि 100 से 120 दिनों के बीच होती है। इसलिए देश में होने वाली अधिकतर वर्षा कुछ ही महीनों में केंद्रित है।

(3) जेट वायु धाराएँ – जेट वायु धाराएँ क्षोभमण्डल में अत्यधिक ऊँचाई पर एक संकरी पट्टी में स्थित होती हैं। इन हवाओं की गति ग्रीष्म ऋतु में 110 किमी प्रति घण्टा एवं सर्दी में 184 किमी प्रति घण्टा के बीच विचलन करती रहती है। हिमालय पर्वत के उत्तर की ओर पश्चिमी जेट धाराएँ एवं ग्रीष्म ऋतु की अवधि में भारतीय प्रायद्वीप में बहने वाली पश्चिम जेट धाराओं की उपस्थिति मानसून को प्रभावित करती हैं। जब उष्णकटिबंधीय पूर्वी दक्षिण प्रशांत महासागर में उच्च वायुदाब होता है तो उष्णकटिबंधीय पूर्वी हिन्द महासागर में निम्न वायुदाब होता है।

किन्तु कुछ निश्चित वर्षों में वायुदाब परिस्थितियाँ विपरीत हो जाती हैं और पूर्वी प्रशांत महासागर में पूर्वी हिन्द महासागर की अपेक्षाकृत निम्न वायुदाब होता है। दाब की अवस्था में इस नियतकालिक परिवर्तन को दक्षिणी दोलन के नाम से जाना जाता है। एलनीनो, दक्षिणी दोलन से जुड़ा हुआ एक लक्षण है। यह एक गर्म समुद्री जलधारा है, जो पेरू की ठंडी धारा के स्थान पर प्रत्येक 2 या 5 वर्ष के अंतराल में पेरू तट से होकर बहती है। दाब की अवस्था में परिवर्तन का संबंध एलनीनो से है। हवाओं में निरंतर कम होती आर्द्रता के कारण उत्तर भारत में पूर्व से पश्चिम की ओर वर्षा की मात्रा कम होती जाती है।
बंगाल की खाड़ी शाखा से उठने वाली आर्द्र पवनें (UPBoardSolutions.com) जैसे-जैसे आगे, और आगे बढ़ती हुई देश के आंतरिक भागों में जाती हैं, वे अपने साथ लाई गई अधिकतर आर्द्रता खोने लगती हैं। परिणामस्वरूप पूर्व से पश्चिम की ओर वर्षा धीरे-धीरे घटने लगती है। राजस्थान एवं गुजरात के कुछ भागों में बहुत कम वर्षा होती है।

प्रश्न 7.
शीत ऋतु की अवस्था एवं उसकी विशेषताएँ बताएँ।।
उत्तर:
उत्तरी भारत में शीत ऋतु मध्य नवम्बर से शुरू होकर फरवरी तक विद्यमान रहती है। इस मौसम में आकाश मेघरहित एवं स्वच्छ रहता है। तापमान कम रहता है और मन्द गति से हवाएँ चलती हैं। तापमान दक्षिण से उत्तर की ओर बढ़ने पर घटता जाता है। दिसम्बर एवं जनवरी सबसे ठंडे महीने होते हैं। उत्तर में तुषारापात सामान्य है तथा हिमालय के उपरी ढालों पर हिमपात होता है। इस ऋतु में देश में उत्तर-पूर्वी व्यापारिक पवनें प्रवाहित होती हैं। ये स्थल से समुद्र की ओर बहती हैं तथा इसलिए देश के अधिकतर भाग में शुष्क मौसम होता है। इन पवनों के कारण कुछ मात्रा में वर्षा तमिलनाडु के तट पर होती है, क्योंकि वहाँ ये पवनें समुद्र से स्थल की ओर बहती हैं जिससे ये अपने साथ आर्द्रता लाती हैं।

देश के उत्तरी भाग में, एक कमजोर उच्च दाब का क्षेत्र बन जाता है, जिसमें हलकी पवनें इस क्षेत्र से बाहर की ओर प्रवाहित होती हैं। उच्चावच से प्रभावित होकर ये पवन पश्चिम एवं उत्तर-पश्चिम से गंगा घाटी में बहती है। शीत ऋतु में उत्तरी मैदानों में पश्चिम एवं उत्तर-पश्चिम से चक्रवाती विक्षोभ का अंतर्वाह विशेष लक्षण है। यह कम दाब वाली प्रणाली भूमध्यसागर एवं पश्चिमी एशिया के ऊपर उत्पन्न होती है (UPBoardSolutions.com) तथा पश्चिमी पवनों के साथ भारत में प्रवेश करती है। इसके कारण शीतकाल में मैदानों में वर्षा होती है तथा पर्वतों पर हिमपात, जिसकी उस समय बहुत अधिक आवश्यकता होती है। यद्यपि शीतकाल में वर्षा की कुल मात्रा कम होती है, लेकिन ये रबी फसलों के लिए बहुत ही महत्त्वपूर्ण होती है।

प्रश्न 8.
भारत में होने वाली मानसूनी वर्षा एवं उसकी विशेषताएँ बताएँ।
उत्तर:
भारत में वार्षिक वर्षा की औसत मात्रा 118 सेंटीमीटर के लगभग है। यह समस्त वर्षा मानसूनी पवनों द्वारा प्राप्त होती है।
इस मानसूनी वर्षा की विशेषताएँ इस प्रकार हैं-

1. भारत में मानसून की अवधि जून से शुरू होकर सितम्बर के मध्य तक होती है। इसकी औसत अवधि 100 से 120 दिन तक होती है। मानसून के आगमन के साथ ही सामान्य वर्षा में अचानक वृद्धि हो जाती है। यह वर्षा लगातार कई दिनों तक होती रहती है। आर्द्रतायुक्त पवनों के जोरदार गरज व चमक के साथ अचानक आगमन को ‘मानसून प्रस्फोट’ के नाम से जाना जाता है।
2. मानसून में आई एवं शुष्क अवधियाँ होती हैं जिन्हें वर्षण में विराम कहा जाता है।
3. वार्षिक वर्षा में प्रतिवर्ष अत्यधिक भिन्नता होती है।
4. यह कुछ पवनविमुखी ढलानों एवं मरुस्थल को छोड़कर भारत के शेष क्षेत्रों को पानी उपलब्ध कराती है।
5. वर्षा का वितरण भारतीय भूदृश्य में अत्यधिक असमान है। मौसम के प्रारंभ में पश्चिमी घाटों की पवनमुखी ढालों पर भारी वर्षा होती है अर्थात् 250 सेमी से अधिक। दक्कन के पठार के वृष्टि छाया क्षेत्रों एवं मध्य प्रदेश, राजस्थान, गुजरात, तथा लेह में बहुत कम वर्षा होती हैं। सर्वाधिक वर्षा देश के उत्तरपूर्वी क्षेत्रों में होती है।
6. उष्णकटिबंधीय दबाव की आवृत्ति एवं प्रबलता मानसून वर्षण की मात्रा एवं अवधि को निर्धारित करते हैं।
7. भारत के उत्तर पश्चिमी राज्यों से मानसून सितम्बर के प्रारंभ में वापसी शुरू कर देती है। अक्टूबर के मध्य तक यह देश के उत्तरी हिस्से से पूरी तरह लौट जाती है और दिसम्बर तक शेष भारत से भी मानसून लौट जाता है।
8. मानसून को इसकी अनिश्चितता के कारण भी जाना जाता है। जहाँ एक ओर यह देश के कुछ हिस्सों में बाढ़ ला देता है, वहीं दूसरी ओर यह देश के कुछ हिस्सों में सूखे का कारण बन जाता है।

भारत में मानसूनी वर्षा के प्रभाव को निम्न रूप में देखा जा सकता है-

1. मानसून भारत को एक विशिष्ट जलवायु पैटर्न उपलब्ध कराती है। इसलिए विशाल क्षेत्रीय भिन्नताओं की उपस्थिति के बावजूद मानसून देश और इसके लोगों को एकता के सूत्र में पिरोने वाला प्रभाव डालती है।
2. भारतीय कृषि मुख्य रूप से मानसून से प्राप्त पानी पर निर्भर है। देरी से, कम या अधिक मात्रा में वर्षा का फसलों पर नकारात्मक प्रभाव डालती है।
3. वर्षा के असमान वितरण के कारण देश में कुछ सूखा संभावित क्षेत्र हैं जबकि कुछ बाढ़ से ग्रस्त रहते हैं।

मानचित्र कौशल

प्रश्न 1.
भारत के रेखा मानचित्र पर निम्नलिखित को दर्शाएँ-

1. 400 सेमी से अधिक वर्षा वाले क्षेत्र
2. 20 सेमी से कम वर्षा वाले क्षेत्र।।
3. भारत में दक्षिण-पश्चिम मानसून की दिशा

उत्तर:

अन्य महत्त्वपूर्ण प्रश्नोत्तर

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
पीछे हटते हुए मानसून की ऋतु की दो प्रमुख विशेषताएँ बताइए।
उत्तर:

1. पीछे मानसून का निम्न वायुदाब का गर्त कमजोर पड़ जाता है तथा इसका स्थान उच्च वायुदाब ले लेता है।
2. इस ऋतु में पृष्ठीय पवनों की दिशा उलटनी शुरू हो जाती है। अक्टूबर तक मानसूनी पवनें पीछे हटने लगती

प्रश्न 2.
‘आगे बढ़ते हुए मानसून की ऋतु’ की दो विशेषताएँ बताइए।
उत्तर:

1. आगे बढ़ते हुए मानसून की ऋतु में भारत भर में वर्षा होती है।
2. मानसून की प्रभावी ऋतु में दक्षिण से उत्तर की ओर तथा पूर्व से पश्चिम की ओर वर्षा की मात्रा घटती जाती

प्रश्न 3.
भारत में सर्वाधिक वर्षा कब और कहाँ होती है?
उत्तर:
भारत में सर्वाधिक वर्षा मेघालय के मॉसिनराम में होती है। यह भारत ही नहीं बल्कि विश्व का सर्वाधिक वर्षा वाला स्थान है। यह स्थान गारो, खासीं और जैयन्तिया नामक तीन पहाड़ियों से घिरा हुआ है जिसके कारण बंगाल की खाड़ी से चलने वाली मानसूनी पवनें तीनों पहाड़ियों से टकराकर भारी वर्षा करती हैं।

प्रश्न 4.
‘काल वैशाखी’ किसे कहते हैं?
उत्तर:
मई माह में कभी-कभी तेज हवाओं के साथ गरज व चमक के साथ भारी वर्षा होती है। इसके साथ ही प्रायः हिम वृष्टि भी होती है। वैशाख का महीना होने के कारण पश्चिम बंगाल में इसे ‘काल वैशाखी’ कहते हैं।

प्रश्न 5.
‘क्वार की उमस’ से आप क्या समझते हैं?
उत्तर:
मानसून की वापसी होने से आसमान निर्मल होता है और तापमान में वृद्धि होती है। दिन का तापमान उच्च होता. है जबकि रातें ठण्डी एवं सुहानी होती हैं। स्थल अभी भी (UPBoardSolutions.com) आई होता है। दिन में उच्च तापमान व आर्द्रता वाली अवस्था के कारण दिन का मौसम कष्टकारी होता है। इसे सामान्यतः ‘क्वार की उमस के नाम से जाना जाता है।

प्रश्न 6.
महावट किसे कहते हैं?
उत्तर:
शीत ऋतु में उत्तरी मैदानों में पश्चिम एवं उत्तर-पश्चिम से चक्रवाती विक्षोभ का अंतर्वाह विशेष लक्षण है। यह कम दाब वाली प्रणाली भूमध्य सागर एवं पश्चिमी एशिया के ऊपर उत्पन्न होती है तथा पश्चिमी पवनों के साथ भारत में प्रवेश करती है। इसके कारण शीतकाल में मैदानों में वर्षा होती है तथा पर्वतों पर हिमपात जिसकी उस समय बहुत अधिक आवश्यकता होती है। यद्यपि शीतकाल में वर्षा को स्थानीय तौर पर महावट कहा जाता है।

प्रश्न 7.
दक्षिणी पश्चिम मानसून पवनें किसे कहा जाता है?
उत्तर:
गर्मी के दिनों में वायु की दिशा पूरी तरह से परिवर्तित हो जाती है। वायु दक्षिण में स्थित हिंद महासागर के उच्च दाब वाले क्षेत्र से दक्षिण पूर्वी दिशा में बहते हुए विषुवत् वृत्त को पार कर दाहिनी ओर मुड़ते हुए भारतीय उपमहाद्वीप पर स्थित निम्न दाब की ओर बहने लगती है। इन्हें दक्षिण-पश्चिम मानसून पवनों के नाम से जाना जाता है।

प्रश्न 8.
एलनीनो किसे कहते हैं?
उत्तर:
ठंडी पेरू जलधारा के स्थान पर अस्थायी तौर पर गर्म जलधारा के विकास को एलनीनो का नाम दिया गया है। एलनीनो स्पैनिश शब्द है, जिसका अर्थ होता है बच्चा तथा जो (UPBoardSolutions.com) कि बेबी क्राइस्ट को व्यक्त करता है क्योंकि यह धारा क्रिसमस के समय बहना शुरू करती है। एलनीनो की उपस्थिति समुद्र की सतह के तापमाम को बढ़ा देती है तथा उस क्षेत्र में व्यापारिक पवनों को शिथिल कर देती है।

प्रश्न 9.
कोरिआलिस बल किसे कहते हैं?
उत्तर:
पृथ्वी के अपनी धुरी पर घूमने के कारण उत्पन्न आभासी बल को कोरिआलिस बल कहते हैं। कोरिआलिस बल के कारण पवन उत्तरी गोलार्द्ध में दाहिनी ओर और दक्षिणी गोलार्द्ध में बायीं ओर मुड़ जाती है। हवाओं के इस प्रकार मुड़ने को ‘फेरेल का नियम’ कहते हैं।

प्रश्न 10.
पश्चिमी विक्षोभ से आप क्या समझते हैं?
उत्तर:
भारत, पाकिस्तान, अफगानिस्तान एवं नेपाल में भूमध्य सागर से उत्पन्न होने वाले अतिरिक्त उष्णकटिबंधीय तूफानों को पश्चिमी विक्षोभ कहा जाता है जो सर्दियों के दौरान भारतीय उपमहाद्वीप के उत्तर-पश्चिमी भागों में अचानक वर्षा एवं हिमपात का कारण बनते हैं।

प्रश्न 11.
अन्तः उष्णकटिबंधीय अभिसरण क्षेत्र किसे कहते हैं?
उत्तर:
ये विषुवतीय अक्षांशों में विस्तृत गर्त एवं निम्न दाब का क्षेत्र होता है। यहीं पर उत्तर-पूर्वी एवं दक्षिण-पूर्वी व्यापारिक पवनें आपस में मिलती हैं। यह अभिसरण क्षेत्र विषुवत् वृत्त के लगभग समानांतर होता है, लेकिन सूर्य की आभासी गति के साथसाथ यह उत्तर या दक्षिण की ओर खिसकता है।

प्रश्न 12.
भारत में शीत ऋतु की दो प्रमुख विशेषताएँ बताइए।
उत्तर:

1. भारत में शीत ऋतु-नवम्बर, दिसम्बर, जनवरी तथा फरवरी महीने में होती है।
2. यह ऋतु अत्यन्त सुहानी एवं आनन्दप्रद होती है। दिन के समय शीतल मंद समीर चलती है, लेकिन जाड़े की रातें शीतलहर के दौरान कष्टदायक होती हैं।
3. पर्वतीय क्षेत्रों में बर्फवारी होने से वहाँ पर पेयजल तक की समस्या हो जाती है। पीने के लिए भी पानी गर्म करना पड़ता है।

प्रश्न 13.
दक्षिण-पश्चिम मानसून की उत्पत्ति के कारण बताइए।
उत्तर:
इस मानसून की उत्पत्ति देश के उत्तर-पश्चिमी मैदानी भाग में कम वायुदाब उत्पन्न हो जाने के कारण होती है। जून के प्रारंभ तक निम्न वायुदाब का यह क्षेत्र इतना प्रबल हो जाता है कि दक्षिणी गोलार्द्ध की व्यापारिक पवनें भी इस ओर खिंच आती हैं। इन दक्षिण-पूर्वी व्यापारिक वनों की उत्पत्ति समुद्र से होती है। हिन्द महासागर में विषुवत रेखा को पार करके ये पवनें बंगाल की खाड़ी तथा अरब सागर में आ जाती हैं। (UPBoardSolutions.com) इनकी दिशा दक्षिण-पश्चिम हो जाती है तथा विषुवतीय गर्म धाराओं के ऊपर से गुजरने के कारण ये भारी मात्रा में आर्द्रता ग्रहण कर लेती हैं। इसके बाद ये भारत के वायुसंचरण का अंग बन जाती हैं। दक्षिण-पश्चिम दिशा के कारण इन्हें दक्षिण-पश्चिम मानसून कहा जाता है।

प्रश्न 14.
शीत ऋतु में उत्तरी भारत में होने वाली वर्षा का क्या कारण है? इस वर्षा का महत्त्व भी बताइए।
उत्तर:
शीत ऋतु में उत्तरी भारत में पश्चिमी विक्षोभों द्वारा वर्षा होती है। इनकी उत्पत्ति भूमध्य सागर से होती है। ये विक्षोभ मार्ग में फारस की खाड़ी तथा केस्पियन सागर से कुछ आर्द्रता ग्रहण कर लेते हैं और उत्तरी भारत में पहुँचकर हल्की वर्षा करते हैं।
उत्तरी भारत में होने वाली शीतकालीन वर्षा रबी की फसल, विशेष रूप से गेहूँ के लिए अत्यन्त लाभप्रद होती है।

प्रश्न 15.
यदि अरब सागर, बंगाल की खाड़ी तथा हिमालय पर्वत न होते तो भारत की जलवायु पर क्या प्रभाव पडता?
उत्तर:

1. यदि हिमालय पर्वत न होता तो भारत मानसूनी वर्षा से वंचित रह जाता क्योंकि मानसूनी हवाएँ हिमालय से टकरा कर वर्षा करने के बजाय उससे आगे निकल जातीं तथा वर्षा कहीं और होती। हिमालय न होता तो उत्तर में चीन से आने वाली भयानक बर्फीली हवाएँ उत्तर-भारत को जमा देतीं।
2. यदि अरब सागर न होता तो पश्चिमी घाट के पश्चिमी भाग पर अधिक वर्षा न होती। इसके अतिरिक्त पश्चिमी तटीय भागों के तापमान में विषमता आ जाती।
3. यदि बंगाल की खाड़ी न होती तो देश के पूर्वी तट (तमिलनाडु) पर शीत ऋतु में वर्षा न होती। इसके अलावा यहाँ के तापमान में भी विषमता आ जाती।

लघु उत्तरीय प्रश्न

प्रश्न 1.
मानसून के आगमन की विशेषताएँ बताइए।
उत्तर:
मानसून के आगमन की प्रमुख विशेषताएँ इस प्रकार हैं-

1. मानसून की शुरुआत जून माह में होती है। जून के प्रारंभ में उत्तरी मैदानों में निम्न दाब की अवस्था तीव्र हो जाती है। यह दक्षिणी गोलार्द्ध की व्यापारिक हवाओं को आकर्षित करता है। ये अपने साथ इस महाद्वीप में बहुत अधिक मात्रा में नमी लाती है।
2. मानसून से संबंधित एक अन्य परिघटना है, ‘वर्षा में विराम’। वर्षा में विराम का अर्थ है कि मानसूनी वर्षा एक समय में कुछ दिनों तक ही होती हैं। मानसून में आने वाले ये विराम मानसूनी गर्त की गति से संबंधित होते हैं।
3. मानसून को इसकी अनिश्चितता के कारण जाना जाता है। जब यह एक हिस्से में बाढ़ का कारण बनता है, उसी समय यह किसी दूसरे भाग में अकाल का कारण बन सकता है।
4. मौसम के प्रारंभ में पश्चिम घाट के पवनमुखी भागों में भारी वर्षा लगभग 250 सेमी से अधिक होती है। दक्कन का पठार एवं मध्य प्रदेश के कुछ भागों में भी वर्षा होती है, यद्यपि ये क्षेत्र वृष्टि छाया क्षेत्र में आते हैं।
5. इस मौसम की अधिकतर वर्षा खासी पहाड़ी के दक्षिणी श्रृंखलाओं में स्थित मॉसिनराम विश्व में सबसे अधिक औसत वर्षा प्राप्त करता है।

प्रश्न 2.
ग्रीष्म ऋतु की प्रमुख विशेषताएँ बताइए।
उत्तर:
ग्रीष्म ऋतु मार्च से जून तक रहती है। इसकी प्रमुख विशेषताएँ इस प्रकार हैं-

1. ग्रीष्म ऋतु में धूलभरी गर्म और शुष्क हवाएँ चलती हैं जिन्हें ‘लू’ कहते हैं। ये हवायें दिन के समय उत्तर एवं उत्तर पश्चिम भारत में गतिशील रहती हैं। ये देर शाम तक गतिशील रहती हैं। इस हवा का मानव स्वास्थ्य पर घातक प्रभाव होता है।
2. उत्तर भारत में मई के महीने में धूलभरी आँधियाँ चलती हैं। ये धूलभरी आंधियाँ तापमान घटाकर लोगों को राहत पहुँचाती हैं। आँधियों के बाद ठण्डी हवा चलती है और कभी-कभी हल्की वर्षा भी होती है।
3. ग्रीष्म ऋतु के दौरान कभी-कभी तेज हवाओं के साथ गरजवाली मूसलधारे वर्षा भी होती है। कभी-कभी वर्षा के साथ ओला वृष्टि भी होती है।

प्रश्न 3.
वृष्टि छाया क्षेत्र से आप क्या समझते हैं?
उत्तर:
वह क्षेत्र जो किसी पर्वत की पवनविमुख ढाल पर पड़ता है वृष्टि छाया क्षेत्र कहलाता है। ऊँचे पर्वत ठण्डी व गर्म पवनों के लिए रुकावट का काम करते हैं किन्तु यदि ये वर्षा करने वाली पवनों को रोकने के लिए पर्याप्त ऊँचे होते तो ये वर्षा भी करा सकते थे। पर्वत की पवनविमुख ढाल शुष्क रह जाती है। उदाहरण के लिए, पश्चिमी घाट तथा पूर्वी घाट भारत के प्रमुख वृष्टि छाया क्षेत्र हैं।

प्रश्न 4.
लौटती हुई मानसून के समय मौसमी विशेषताओं को प्रस्तुत कीजिए।
उत्तर:
लौटती हुई मानसून के समय मौसम की दशाएँ इस प्रकार होती हैं-

1. अक्टूबर-नवम्बर को मध्यकाल लौटती हुई मानसून का समय होता है। यह वर्षा ऋतु के गर्म मौसम से सर्दी के शुष्क मौसम में परिवर्तित होने का समय है।
2. भारत के पूर्वी तट के डेल्टाई क्षेत्र में चक्रवात सामान्यतः आते रहते हैं। गोदावरी, कृष्णा एवं कावेरी नदियों में सघन आबादी वाले डेल्टा प्रदेशों में अक्सर चक्रवात आते हैं, जिसके कारण बड़े पैमाने पर जान एवं माल की क्षति होती है।
3. कभी-कभी ये चक्रवात ओडिशा, पश्चिम बंगाल एवं बांग्लादेश के तटीय क्षेत्रों में भी पहुँच जाते हैं। कोरोमंडल तट पर अधिकतर वर्षा इन्हीं चक्रवातों तथा अवदाबों से होती हैं।
4. दिन में आर्द्रता अधिक व तापमान उच्च होता है जबकि रातें ठण्डी, और सुहानी होती हैं। इसे सामान्यतः ‘क्वार की उमस’ के नाम से जाना जाता है।
5. अक्टूबर के उत्तरार्द्ध में, विशेषकर उत्तरी भारत में तापमान तेजी से गिरने लगता है। नवम्बर के प्रारंभ में, उत्तर पश्चिम भारत के ऊपर निम्न दाब वाली अवस्था बंगाल की खाड़ी पर स्थानांतरित हो जाती है। यह स्थानांतरण चक्रवाती निम्न दाब से संबंधित होता है, जो कि अंडमान सागर के ऊपर उत्पन्न होता है।

प्रश्न 5.
दक्षिणी दोलन को स्पष्ट कीजिए तथा इसकी विशेषताएँ भी बताइए।
उत्तर:
जब उष्णकटिबंधीय पूर्वी-दक्षिणी प्रशान्त महासागर में उच्च वायुदाब होता है तो उष्णकटिबंधीय पूर्वी हिन्द महासागर में निम्न वायुदाब होता है। लेकिन कुछ निश्चित वर्षों में वायुदाब परिस्थितियाँ विपरीत हो जाती हैं तथा पूर्वी प्रशान्त महासागर में हिन्द महासागर की अपेक्षा निम्न वायुदाब होता है। वायुदाब की इस अवस्था में इस नियतकालिक परिवर्तन को दक्षिणी दोलन कहते हैं।

एलनीनो दक्षिणी दोलन से जुड़ी हुई एक महत्त्वपूर्ण विशेषता है। यह एक गर्म समुद्री जलधारा है जो पेरू की ठण्डी धारा के स्थान पर प्रत्येक 2 से 5 वर्ष के अंतराल में पेरू तट (UPBoardSolutions.com) से होकर प्रवाहित होती है। वायुदाब की इस अवस्था में परिवर्तन का सम्बन्ध ‘एलनीनो’ से है। एलनीनो का विपरीत प्रभाव भारत के मानसून पर पड़ता है। एलनीनो के प्रभाव से भारत में वर्षा देर से या फिर कम होती है।

प्रश्न 6.
‘मानसून’ शब्द का अर्थ तथा मानसूनी वर्षा की विशेषताएँ बताइए।
उत्तर:
‘मानसून’ शब्द की उत्पत्ति अरबी भाषा के शब्द ‘मौसम’ से हुई है। मौसम का शाब्दिक अर्थ ऋतु है। इस प्रकार मानसून का अर्थ ऐसी ऋतु से है, जिसमें पवनों की दिशा पूरी तरह से उलट जाती है। मौसम वैज्ञानिकों के द्वारा मानसून की परिभाषा इस प्रकार की गई है-“शुष्क गर्म वायु को पूरी तरह हटाकर विषुवतीय समुद्री वायु का स्थल भागों तथा सागरीय क्षेत्र में तीन से लेकर पाँच किमी की ऊँचाई तक फैल जाना है।”
मानसूनी वर्षा की प्रमुख विशेषताएँ निम्नलिखित हैं-

1. देश के अधिकांश भागों में अधिक वर्षा दक्षिण-पश्चिमी मानसून में होती है। इस अवधि (जून से सितम्बर तक चार महीनों की अवधि) में 90% वर्षा होती है, शेष 10% वर्षा वर्ष के 8 महीनों में होती है।
2. शीत ऋतु में अधिकतर वर्षा तमिलनाडु तथा आंध्र प्रदेश के तटीय प्रदेशों में होती है। इस अवधि में उत्तर-पश्चिमी भारत में वर्षा पश्चिमी विक्षोभों से होती है।
3. समस्त देश में वर्षा की अवधि, मात्रा एवं प्रकृति अनिश्चित, अनियमित और असमान है।
4. सामान्यतः वर्षा पूर्व से पश्चिम तथा दक्षिण से उत्तर की ओर कम होती जाती है।

प्रश्न 7.
शीत ऋतु में पश्चिमी विक्षोभ भारत की जलवायु को किस प्रकार प्रभावित करते हैं? इस सम्बन्ध में तीन तथ्य स्पष्ट करो।
उत्तर:
देश के उत्तरी भागों में तापमान तथा वायु में आर्द्रता शीत ऋतु में कम होती है। शीत ऋतु में आकाश स्वच्छ होता है तथा शीतल-मंद समीर संचरित होती है एवं दिन वर्षारहित होते हैं। इस सुहावने मौसम में कभी-कभी क्षीण चक्रवातीय अवदाबों के आ जाने के कारण मौसम में एकदम परिवर्तन हो जाते हैं। इससे उत्तरी-पश्चिमी भागों में शीत ऋतु में पश्चिमी विक्षोभों से वर्षा होती है।
इसके निम्नलिखित कारण हैं-

1. इन पश्चिमी विक्षोभों से उत्तरी भारत में हल्की वर्षा होती है क्योंकि इनको भारत में प्रवेश करते ही हिमालय के ढालों पर चढ़कर घनीभूत होना होता है।
2. इनसे पश्चिमी हिमालय के क्षेत्रों में भारी हिमपात होता है। वर्षा के साथ कभी ओला-वृष्टि भी होती है।
3. इन चक्रवातीय अवदाबों को पश्चिमी विक्षोभ कहते हैं। इनकी उत्पत्ति पूर्वी भूमध्य सागर में होती है। यहाँ से ये पूर्व की ओर पछुआ हवाओं के प्रभाव में बढ़ते हैं। एशिया, ईरान, अफगानिस्तान और पाकिस्तान को पार करते हुए, देश के उत्तर-पश्चिमी भागों में प्रवेश कर जाते हैं। मार्ग में कैस्पियन सागर तथा फारस की खाड़ी से भी आर्द्रता ग्रहण कर लेते हैं।
4. पश्चिमी जेट स्ट्रीम इन पवनों को सोखकर (UPBoardSolutions.com) इनकी गति तेज कर देता है।

प्रश्न 8.
भारत की चारों ऋतुओं के नाम उनके महीनों के साथ लिखिए।
उत्तर:

1. शीत ऋतु-दिसम्बर, जनवरी, फरवरी।
2. ग्रीष्म ऋतु-मार्च, अप्रैल, मई।
3. आगे बढ़ते मानसून की ऋतु-जून, जुलाई, अगस्त, सितम्बर।
4. पीछे हटते मानसून की ऋतु -अक्टूबर, नवम्बर, दिसम्बर।

प्रश्न 9.
त्रिवेंद्रम की जलवायु सम क्यों है? दो कारण बताइए।
उत्तर:
समुद्र तटवर्ती स्थानों और क्षेत्रों की जलवायु सम होती है। जल अपना समकारी प्रभाव स्थल पर छोड़ता है। अतः तटवर्ती क्षेत्र गर्मियों में न अधिक गर्म और न ठंड में अधिक ठंडे होते हैं। त्रिवेन्द्रम के तटवर्ती क्षेत्रों का दैनिक तथा वार्षिक तापपरिसर दोनों ही कम होते हैं। त्रिवेन्द्रम का वार्षिक तापक्रम अधिकतम 28° सेन्टीग्रेड व न्यूनतम तापमान 26° सेन्टीग्रेड रहता है। इस तरह त्रिवेन्द्रम का वार्षिक ताप परिसर 28° – 26° = 2° सेन्टीग्रेड है।

प्रश्न 10.
दैनिक ताप परिसर का क्या अर्थ है? उदाहरण देकर स्पष्ट कीजिए।
उत्तर:
किसी स्थान के अधिकतम व न्यूनतम दैनिक तापमान में अंतर को दैनिक ताप परिसर कहते हैं अर्थात् किसी स्थान के पिछले 24 घण्टों के अधिकतम और न्यूनतम तापमान के अंतर को दैनिक ताप परिसर कहते हैं। उदाहरण के लिए 8 अक्टूबर, 2017 ई. को दिल्ली अधिकतम तापमान 33.7° तथा न्यूनतम तापमान 19.1° था। इस प्रकार दिल्ली का दैनिक ताप परिसर 33.7° – 19.1° = 14.6° से हुआ।

प्रश्न 11.
वार्षिक ताप परिसर किसे कहते हैं? इसे एक उदाहरण देकर स्पष्ट कीजिए।
उत्तर:
किसी स्थान पर वर्ष में पाए जाने वाले अधिकतम तापमान और न्यूनतम तापमान के अंतर को वार्षिक ताप परिसर कहते हैं अर्थात् वर्ष के औसत अधिकतम और औसत न्यूनतम वाले महीनों के तापमान के अंतर को वार्षिक तापपरिसर कहते हैं। उदाहरण के लिए दिल्ली के सबसे गर्म महीने का औसत तापमान 33.3° से. तथा सबसे ठंडे महीने का औसत तापमान 14.4° से. है। अतः यहाँ वार्षिक ताप परिसर 33.3° – 14.4° = 18.9° से. है।

प्रश्न 12.
सम जलवायु किसे कहते हैं? भारत में सम जलवायु वाले दो स्थानों के नाम बताइए।
उत्तर:
जब किसी क्षेत्र या देश के सबसे अधिक गर्म तथा सबसे अधिक ठंडे महीने के तापमान में बहुत कम अंतर होता है, तो उस क्षेत्र, स्थान या देश की जलवायु को सम जलवायु कहते हैं अर्थात् जब किसी क्षेत्र या देश में तापमान की परिस्थितियाँ वर्षभर प्रायः समान रहती हैं, तो उसकी जलवायु सम कहलाती है। उदाहरण के लिए त्रिवेंद्रम और मुंबई की जलवायु सम है।

प्रश्न 13.
विषम जलवायु से क्या अभिप्राय है? भारत में विषम जलवायु वाले दो स्थानों के नाम लिखिए।
उत्तर:
किसी देश अथवा क्षेत्र के वार्षिक तापमानों और वर्षा की मात्रा में बहुत अंतर पाया जाता है, वहाँ की जलवायु का स्वरूप विषम होता है। तापमान की विषमता चाहे दैनिक हो अथवा वार्षिक वह विषम जलवायु के निर्धारण में महत्त्वपूर्ण भूमिका अदा करती है। उदाहरण के लिए, थार मरुस्थल में दिन का तापमान ग्रीष्म ऋतु में 50° से. को भी पार कर जाता है और रात के समय तापमान हिमांक बिंदु तक गिर जाता है। दिल्ली, जोधपुर, लेह आदि का वार्षिक ताप परिसर अधिक है। अतः इनकी जलवायु विषम है।

प्रश्न 14.
“हिमालय के समकारी प्रभाव के बावजूद तापमान, आर्द्रता एवं वर्षण में भिन्नता बनी रहती है।”
उदाहरण सहित व्याख्या करें।
उत्तर:
भारत में उत्तर में हिमालय तथा दक्षिण में सागर के समकारी प्रभाव के बावजूद तापमान, आर्द्रता एवं वर्षण में क्षेत्रीय भिन्नता बनी रहती है। ऐसा किसी स्थान की जलवायु को प्रभावित करने वाले छह कारकों के कारण है जो इस प्रकार हैं- अक्षांश, तुंगता, ऊँचाई, वायुदाब एवं पवनतंत्र, समुद्र (UPBoardSolutions.com) से दूरी, महासागरीय धाराएँ तथा उच्चावच लक्षण। उदाहरण के लिए गर्मियों में राजस्थान के कुछ क्षेत्रों में, उत्तर-पश्चिमी भारत में तापमान 50°C होता है जबकि उसी समय देश में उत्तर में जम्मू-कश्मीर के पहलगाम में तापमान 20°C हो सकता है। सर्दियों की किसी रात में जम्मू-कश्मीर के द्रास में तापमान -45 डिग्री सेल्सियस तक हो सकता है, जबकि तिरुवनंतपुरम् में यह 22 डिग्री सेल्सियस हो सकता है।

प्रश्न 15.
भारत के पूर्वी तटीय क्षेत्र के संभावित खतरों को स्पष्ट कीजिए।
उत्तर:
भारत के पूर्वी तट के डेल्टाई क्षेत्र में अक्सर चक्रवात आते हैं। ऐसा इस कारण होता है क्योंकि अण्डमान सागर में उत्पन्न होने वाला चक्रवातीय दबाव मानसून एवं अक्टूबर-नवम्बर के दौरान उपोष्ण कटिबंधीय जेट धाराओं द्वारा देश के आंतरिक भागों की ओर स्थानान्तरित कर दिया जाता है। ये चक्रवात बड़े क्षेत्र में भारी वर्षा करते हैं। ये उष्णकटिबंधीय चक्रवात प्रायः विनाशकारी होते हैं। कृष्णा, गोदावरी, कावेरी नदियों के डेल्टा प्रदेशों में प्रायः चक्रवात आते रहते हैं, जिसके कारण बड़े पैमाने पर धन-जन की हानि होती है। ये चक्रवात कभी-कभी ओडिशा एवं पश्चिम बंगाल के तटीय क्षेत्रों में भी पहुँच जाते हैं। इन्हीं चक्रवातों के अवदाबों के चलते कोरोमण्डल तट पर अधिकांश वर्षा होती है।

प्रश्न 16.
दक्षिण-पश्चिम मानसून की अरब सागर शाखा से भारत के किन भागों में वर्षा होती है?
उत्तर:
दक्षिण-पश्चिम मानसून की अरब सागर शाखा को तीन उपशाखाओं में बाँटा जा सकता है-

1. पश्चिमी घाट को प्रभावित करने वाली शाखा
2. विंध्या-सर्तपुड़ा मध्य शाखा
3. सौराष्ट्र-कच्छ शाखा।

1. पश्चिमी घाट शाखा – अरब सागर शाखा जब दक्षिण-पश्चिम से उत्तर-पूर्व की ओर गतिशील होती है, तो पश्चिमी घाट उसके मार्ग में अवरोधक बन जाते हैं। यहाँ इन पवनों को बाध्य होकर ऊपर चढ़ना पड़ता है। इस प्रक्रिया में संघनन बहुत तेजी से होता है। फलतः पश्चिमी घाट के पवनाभिमुख ढालों पर भारी वर्षा होती है। यह देश के अधिक वर्षा प्राप्त करने वाले क्षेत्रों में गिना जाता है। पश्चिमी घाट के पूर्वी भागों में ये (UPBoardSolutions.com) पवनें बहुत कम वर्षा कर पाती हैं। पश्चिम तटीय भागों में दक्षिण से उत्तर की ओर कम वर्षा होती है। मालाबार तट अधिक वर्षा प्राप्त करता है, जबकि कोंकण तट पर कम वर्षा होती है।

2. विंध्या-सतपुड़ा मध्य शाखा – यह शाखा विंध्या और सतपुड़ा पर्वतों के मध्य में होकर अपना मार्ग बनाती है। नर्मदा घाटी को पार कर छोटानागपुर तथा राजमहल की पहाड़ियों तक पहुँचाती है। इस क्षेत्र में पहुँचकर यहाँ अपेक्षाकृत अधिक वर्षा करने में समर्थ होती है। इस शाखा से पश्चिम से पूर्व की ओर वर्षा कम होती जाती है।

3. सौराष्ट्र-कच्छ शाखा – यह शाखा गुजरात तथा राजस्थान से होकर पंजाब के मैदान तक पहुँचती है। इसके मार्ग में अरावली का विस्तार पवनों के समानांतर है। अतः यह शाखा बेरोक-टोक हिमालय प्रदेश के पर्वतीय भागों तक पहुँचती । है। यहाँ हिमालय से अवरोध पाकर कश्मीर, पंजाब तथा हरियाणा में सामान्य वर्षा करने में समर्थ होती है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
दक्षिणी-पश्चिमी मानसून उत्तरी-पूर्वी मानसून से किस प्रकार भिन्न है? कोई चार अंतर लिखिए।
उत्तर:
उत्तरी-पूर्वी मानसून एवं दक्षिणी-पश्चिमी मानसून में अंतर-

उत्तरी-पूर्वी मानसून	दक्षिणी-पश्चिमी मानसून
1. भारत में दिसंबर से फरवरी तक की अवधि में उत्तर पूर्व से दक्षिण-पश्चिम की ओर चलने वाली पवनों को उत्तर-पूर्वी मानसून पवनें कहते हैं।	1. भारत में जून से सितंबर तक की अवधि में दक्षिण-पश्चिम से उत्तर-पूर्व की ओर चलने वाली आर्द्र पवनों को दक्षिण पश्चिम मानसून कहते हैं।
2. ये पवनें शीतकाल में देश के उत्तरी भागों में उच्च दाब की स्थिति पैदा होने के कारण देश के इस भाग से बाहर की ओर बहने लगती हैं।	2. इस अवधि में भारत के उत्तर-पश्चिमी भागों में निम्न दाब क्षेत्र पाया जाता है।
3. ये पवनें शीतकाल में स्थल से चलती हैं। अतः शुष्क एवं ठंडी होती हैं।	3. ये पवनें उष्णकटिबंधीय समुद्री भागों से चलकर आती हैं। अतः ये पवनें गर्म और आई होती हैं।
4. ये पवनें बंगाल की खाड़ी से आर्द्रता ग्रहण कर तमिलनाडु के तट पर वर्षा करती हैं।	4. इन पवनों से देश के अधिकांश भागों में लगभग 90 प्रतिशत वर्षा होती है।
5. देश के शेष भागों में स्वच्छ आकाश, निम्न तापमान व आर्द्रता, मंद समीर और वर्षारहित मौसम सुहावना होता है।	5. दक्षिण-पश्चिमी मानसून दो शाखाओं-बंगाल की खाड़ी और  अरब सागर में बँट जाता है।

प्रश्न 2.
सम और विषम जलवायु में अंतर स्पष्ट कीजिए।
उत्तर:
सम और विषम जलवायु में अंतर –

सम जलवायु	विषम जलवायु
1. इस प्रकार की जलवायु समुद्र तटवर्ती क्षेत्रों में पाई जाती है। केरल के तटीय भागों में सम जलवायु पाई जाती है।	1. विषम जलवायु महाद्वीपों के आंतरिक भागों में पाई जाती है। भारत के भीतरी भागों की जलवायु विषम है। दिल्ली और  कानपुर क्षेत्रों की जलवायु विषम है।
2. सम जलवायु समुद्र तटवर्ती क्षेत्रों में मिलने के कारण इसे अनुसमुद्री या समुद्री जलवायु कहते हैं।	2. महाद्वीपों के आंतरिक भागों में इस प्रकार की जलवायु मिलने के कारण, इसे महाद्वीपीय जलवायु भी कहते हैं।
3. ग्रीष्म ऋतु में न अधिक गर्मी तथा शीत ऋतु में न अधिक ठंड का पड़ना ही सम जलवायु की विशेषता है।	3. महाद्वीपीय जलवायु को अर्थ ऐसी जलवायु से है, जिसमें ग्रीष्म ऋतु में अधिक गर्मी तथा शीत ऋतु में अधिक ठंड पड़ती है।
4. सम जलवायु वाले क्षेत्रों में वार्षिक ताप परिसर कम होता है। इन भागों में दैनिक ताप परिसर वार्षिक ताप परिसर से अधिक होता है।	4. विषम जलवायु वाले क्षेत्रों में वार्षिक ताप परिसर अधिक पाया जाता है। उच्च वार्षिक ताप परिसर के साथ दैनिक  ताप परिसर भी अधिक होता है।
5. सम जलवायु प्रदेशों में वर्षा की अवधि और वर्षा की मात्रा प्रायः दोनों ही अधिक होते हैं।	5. विषम जलवायु वाले क्षेत्रों में वर्षा की अवधि और वर्षा की मात्रा दोनों ही कम पाई जाती है।

प्रश्न 3.
किसी क्षेत्र की जलवायु को प्रभावित करने वाले प्रमुख कारकों को वर्णन कीजिए।
उत्तर:
किसी क्षेत्र की जलवायु को छह प्राकृतिक कारक प्रभावित करते हैं, जिनका विवरण इस प्रकार है-
(1) उच्चावचे – ऊँचे पर्वत शीतल व गर्म वायु को रोकने का कार्य करते हैं। यदि इन पर्वतों की ऊँचाई इतनी हो कि वे वर्षा लाने वाली वायु के मार्ग को रोकने में सक्षम होते हैं तो वे उस क्षेत्र में वर्षा लाने में समर्थ होते हैं। पर्वतों के पवनविमुख ढाल अपेक्षाकृत सूखे रहते हैं।

(2) वायुदाब एवं पवनें – किसी क्षेत्र-विशेष को वायुदाब एवं उसकी पवनें उस क्षेत्र की अक्षांशीय स्थिति एवं ऊँचाई पर निर्भर करती हैं। इस प्रकार यह तापमान एवं वर्षण की प्रवृत्ति को भी प्रभावित करता है।

(3) महासागरीय धाराएँ – समुद्र की ओर से स्थल की ओर आने वाली पवनों के साथ-साथ महासागरीय धाराएँ भी तटीय क्षेत्रों की जलवायु को प्रभावित करती हैं। उदाहरण के लिए, कोई भी तटीय क्षेत्र जहाँ गर्म या ठण्डी जलधाराएँ प्रवाहित होती हैं और वायु की दिशा समुद्र से तट की ओर होती है, तब वह तट गर्म या ठण्डा हो जाएगा।

(4) सागर तट से दूरी – जैसे-जैसे स्थलीय क्षेत्र की सागर से दूरी बढ़ती जाती है, तो इसका समकारी प्रभाव घटने लगता है। इस तरह यह तापमान तथा वर्षा की प्रवृत्ति को प्रभावित करता है। इसे महाद्वीपीय अवस्था कहते हैं। महाद्वीपीय व्यवस्था का आशय है कि गर्मी में बहुत अधिक गर्मी और सर्दी में बहुत अधिक ठण्ड पड़ती है।

(5) स्थलीय क्षेत्र की ऊँचाई – भारत के उत्तर में पर्वत हैं जिनकी औसत ऊँचाई लगभग 6,000 मीटर है। भारत का तटीय क्षेत्र भी विशाल है, जहाँ अधिकतम ऊँचाई लगभग 30 मीटर है। हिमालय पर्वत मध्य एशिया से आने वाली सर्द हवाओं को इस उपमहाद्वीप में आने से रोकता है यही कारण है कि मध्य एशिया की अपेक्षा भारत में ठंड अपेक्षाकृत कम होती है। जैसे-जैसे हम पृथ्वी की सतह से ऊँचे स्थानों (UPBoardSolutions.com) की ओर जाते हैं, वायुमंडल विरल होता जाता है तथा तापमान गिरने लगता है। इसलिए पहाड़ियाँ गर्मियों में अपेक्षाकृत ठण्डी होती हैं।

(6) अक्षांशीय स्थिति – पृथ्वी की गोलाई के कारण, इसे प्राप्त सौर ऊर्जा की मात्रा अक्षांशों के अनुसार अलग-अलग होती है। तापमान विषुवत् वृत्त से ध्रुवों की ओर घटता जाता है। कर्क वृत्त देश के मध्य भाग, पश्चिम में कच्छ के रन से लेकर पूर्व में मिजोरम से होकर गुजरती है। देश का लगभग आधा भाग कर्क रेखा के दक्षिण में स्थित है, जो उष्णकटिबंधीय क्षेत्र में आता है। कर्क रेखा के उत्तर में स्थित शेष भाग उपोष्ण कटिबंध में आता है। इसलिए भारत की जलवायु में उष्णकटिबंधीय जलवायु एवं उपोष्ण कटिबंधीय जलवायु दोनों की विशेषताएँ पाई जाती हैं।

प्रश्न 4.
ग्रीष्म ऋतु में भारत की जलवायु-दशा का विवेचन कीजिए।
उत्तर:
भारत में मार्च, अप्रैल, मई और जून माह को ग्रीष्म काल में शामिल किया जाता है। ग्रीष्मकाल में सम्पूर्ण भारत में उच्च तापमान और निम्न वायुदाब का क्षेत्र बन जाता है। ग्रीष्म ऋतु में देश के उत्तर-पश्चिमी भागों में शुष्क और गर्म हवाएँ चलती हैं। इन शुष्क एवं गर्म पवनों का स्थानीय (UPBoardSolutions.com) नाम ‘लू’ है। मई माह में पंजाब, हरियाणा, राजस्थान और उत्तर प्रदेश में शाम के समय धूलभरी आँधियाँ चलती हैं। कभी-कभी इन आँधियों के पश्चात् हल्की वर्षा होती है, जिससे कष्टदायक गर्मी से कुछ राहत मिलती है।

ग्रीष्म ऋतु के अंत में केरल तथा कर्नाटक के तटीय भागों में मानसून से पूर्व की वर्षा होती है, जिसका स्थानीय नाम आम्रवृष्टि है। इस समय दक्कन के पठार पर अपेक्षाकृत उच्चदाब होने के कारण, मानसून से पूर्व की वर्षा का क्षेत्र आगे । नहीं बढ़ पाता है। इस ऋतु में बंगाल और असोम में भी उत्तर-पश्चिमी तथा उत्तरी पवनों द्वारा वर्षा की तेज बौछारें पड़ती हैं।

प्रश्न 5.
वायुदाब व पवन-तंत्र किसी स्थान की जलवायु को किस प्रकार प्रभावित करते हैं? स्पष्ट कीजिए।
उत्तर:
भूगोल वेत्ताओं के अनुसार पवनें उच्च वायुदाब से निम्न वायुदाब की ओर प्रवाहित होती हैं। सर्दियों में हिमालय के उत्तर में उच्च वायुदाब क्षेत्र बना होता है। इसीलिए ठण्डी शुष्क पवनें इस क्षेत्र से महासागरों की ओर निम्न दाब क्षेत्रों की ओर दक्षिण दिशा में बहती हैं। गर्मियों में भीतरी एशिया तथा उत्तर-पश्चिमी भारत में निम्न वायुदाब क्षेत्र उत्पन्न हो जाता है। इसके परिणामस्वरूप, वायु दक्षिण में स्थित हिंद महासागर के उच्च दाब वाले क्षेत्र से दक्षिण-पूर्वी दिशा में बहते हुए विषुवत् वृत्त को पार कर दाहिनी ओर मुड़ते हुए भारतीय उपमहाद्वीप पर स्थित निम्न दाब की ओर बहने लगती है।

इन्हें दक्षिण-पश्चिम मानसून पवनों के नाम से जाना जाता है। ये पवनें कोष्ण महासागरों के ऊपर से बहती हैं, नमी ग्रहण करती हैं तथा भारत की मुख्य भूमि पर वर्षा करती हैं। इस प्रदेश में, ऊपरी वायु परिसंचरण पश्चिमी प्रवाह के प्रभाव में रहता है। भारत में होने वाली वर्षा मुख्यतः दक्षिण-पश्चिमी मानसून पवनों के कारण होती है। मानसून की अवधि 100 से 120 दिन के बीच होती है। इसलिए देश में होने वाली अधिकतर वर्षा कुछ ही महीनों में केंद्रित है।

(1) पश्चिमी चक्रवाती विक्षोभ एवं उष्णकटिबंधीय चक्रवात – हिमालय के दक्षिण से बहने वाली उपोष्ण कटिबंधीय पश्चिमी जेट धाराएँ शीत ऋतु के महीनों में देश के उत्तर एवं उत्तर-पश्चिमी भागों में उत्पन्न होने वाले पश्चिमी चक्रवातीय विक्षोभों के लिए जिम्मेदार हैं। भारत, पाकिस्तान, अफगानिस्तान एवं नेपाल में भूमध्यसागर से उत्पन्न होने वाले अतिरिक्त उष्णकटिबंधीय तूफानों का पश्चिमी विक्षोभ कहा जाता है जो (UPBoardSolutions.com) सर्दियों के दौरान भारतीय उपमहाद्वीप के उत्तर-पश्चिमी भागों में अचानक वर्षा एवं हिमपात का कारण बनते हैं। यह पश्चिमी विक्षोभों के कारण होने वाला गैर-मानसूनी वर्षण है। इन तूफानों को मिलने वाली आर्द्रता का स्रोत भूमध्य सागर एवं अटलांटिक महासागर है।

(2) कोरिआलिस बल – भारतीय उपमहाद्वीप में पवनों की दिशा में मौसम के अनुरूप परिवर्तन कोरिआलिस बल के कारण होता है। भारत उत्तर पूर्वी पवनों के क्षेत्र में स्थित है। ये पवनें उत्तरी गोलार्द्ध के उपोष्ण कटिबंधीय उच्च दाब पट्टियों से उत्पन्न होती हैं। ये दक्षिण की ओर बहती, कोरिआलिस बल के कारण दाहिनी ओर विक्षेपित होकर विषुवतीय निम्न दाब वाले क्षेत्रों की ओर बढ़ती हैं।

(3) जेट धाराएँ – क्षोभमंडल में अत्यधिक ऊँचाई पर एक सँकरी पट्टी में स्थित हवाएँ होती हैं। इनकी गति गर्मी में 110 किमी प्रति घंटा एवं सर्दी में 184 किमी प्रति घंटा के बीच विचलन करती है। हिमालय के उत्तर की ओर पश्चिमी जेट धाराओं की गतिविधियों एवं गर्मियों के दौरान भारतीय प्रायद्वीप पर बहने वाली पश्चिमी जेट धाराओं की उपस्थिति मानसून को प्रभावित करती है। प्रायः जब उष्णकटिबंधीय पूर्वी दक्षिण प्रशांत महासागर में उच्च वायुदाब होता है। तो-उष्णकटिबंधीय पूर्वी हिन्द महासागर में निम्न वायुदाब होता है।

किन्तु कुछ निश्चित वर्षों में वायुदाब परिस्थितियाँ विपरीत हो जाती हैं और पूर्वी प्रशांत महासागर में पूर्वी हिन्द महासागर की अपेक्षाकृत निम्न वायुदाब होता है। दाब की अवस्था में इस नियतकालिक परिवर्तन को दक्षिणी दोलन के नाम से जाना जाता है। एलनीनो, दक्षिणी दोलन । से जुड़ा हुआ एक लक्षण है। यह एक गर्म समुद्री जलधारा है, जो पेरू की ठंडी धारा के स्थान पर प्रत्येक 2 या 5 वर्ष के अंतराल में पेरू तट से होकर बहती है। दाब की अवस्था में परिवर्तन का संबंध एलनीनो से है।

इसलिए इस परिघटना को एंसो-(ENSO) (एलनीनो दक्षिणी दोलन) कहा जाता है। हवाओं में निरंतर कम होती आर्द्रता के कारण उत्तर भारत में पूर्व से पश्चिम की ओर वर्षा की मात्रा कम होती जाती है। बंगाल की खाड़ी शाखा से उठने वाली आर्ट पवनें जैसे-जैसे आगे, और आगे बढ़ती हुई देश के आंतरिक (UPBoardSolutions.com) भागों में जाती हैं, वे अपने साथ लाई गई अधिकतर आर्द्रता खोने लगती हैं। परिणामस्वरूप पूर्व से पश्चिम की ओर वर्षा धीरे-धीरे घटने लगती है। राजस्थान एवं गुजरात के कुछ भागों में बहुत कम वर्षा होती है।

प्रश्न 6.
मानसून की एकता स्थापित करने वाले विभिन्न कारकों को उदाहरण सहित प्रस्तुत कीजिए।
उत्तर:
भारत में तापमान और वर्षा के वितरण को देखने एवं स्वरूप को समझने से इस बात का आभास होता है कि भारत की जलवायु में पर्याप्त विषमता है। लेकिन भारत अपनी जलवायु सम्बन्धी एकता के लिए जाना जाता है। इस मानसूनी एकता को प्रदान करने में जिन कारकों का विशेष योगदान है उसमें उत्तर दिशा में स्थित हिमालय पर्वत और वर्षा की प्रवृत्ति का विशेष योगदान है।

(1) हिमालय की विशिष्ट स्थिति – भारत की उत्तरी सीमा पर हिमालय पर्वतमालाओं का विस्तार उत्तर-पश्चिम से उत्तर पूर्व की ओर लगभग 3,000 किमी में है। ये पर्वतमालाएँ भारत के लिए अनेक प्रकार से वरदान सिद्ध हुई हैं। वास्तव में ये जलवायु विभाजक हैं तथा भारत के लिए बंद बक्से का काम करती हैं। शीतकाल में मध्य एशिया से चलने वाली ठंडी और शुष्क पवनों को ये पर्वत, भारत में आने से रोककर उसे ठंडा होने से बचाते हैं। दूसरी ओर दक्षिण-पश्चिमी मानसून पवनें जो उष्णआई होती हैं, उन्हें रोककर ये पर्वतमालाएँ वर्षा करने के लिए बाध्य करती हैं।

इस प्रकार भारत में वर्षा के वितरण को प्रभावित करने में इनका महत्त्वपूर्ण योगदान है। इन पर्वतों के कारण देश में उष्णकटिबंधीय जलवायु दशाएँ पैदा होती हैं। ग्रीष्म ऋतु में प्रायः सारे देश में जलवायु की समान दशाएँ पाई जाती हैं। जलवायु की विषमताओं तथा एक प्रदेश से दूसरे प्रदेश में परिवर्तनशीलता के होते हुए भी मानसून के कारण प्रतिवर्ष ऋतुओं के चक्र की एक लय बनी रहती है। इस ऋतु लय का प्रभाव भूमि, वनस्पति, प्राणी वर्ग, कृषि कार्य एवं संपूर्ण भारतीय जीवन पर पड़ता है।

(2) भारत में वर्षा की प्रवृत्ति – भारत के विभिन्न भागों में वर्षा की मात्रा उच्चावच पर निर्भर रहती है। फिर भी एक लंबे शुष्क और गर्म मौसम के बाद सारे देश में मानसून की पहली बरसात की तीव्रता से प्रतीक्षा की जाती है। रबी की फसल घर में ले आने के बाद कश्मीर से कन्याकुमारी तथा गुजरात से गुवाहाटी तक का किसान बड़ी बेसब्री के साथ आकाश में बादलों को वर्षा के लिए निहारता रहता है ताकि वर्षा से (UPBoardSolutions.com) उसकी जमीन की प्यास बुझ सके तथा वह अपने कृषि कार्य में लग सके। लेकिन वर्षा की प्रवृत्ति मानसून की सनक पर निर्भर करती है। समय, मात्रा एवं स्थान के अनुसार वर्षा की अनिश्चितता एवं अनियमितता पाई जाती है। इसका प्रभाव सारे देश पर पड़ता है।

मानचित्र कौशल

प्रश्न 1.
भारत के राजनैतिक रेखा मानचित्र पर निम्नलिखित को नामांकित करते हुए स्थिति दर्शाएँ-

• तिरुवनंतपुरम्
• चेन्नई
• जयपुर
• बंगलुरु
• मुंबई
• कोलकाता
• शिलांग उत्तर
• नागपुर

उत्तर:

प्रश्न 2.
नीचे दिए गए मानचित्र का ध्यानपूर्वक अध्ययन कीजिए और उसके नीचे के प्रश्नों के उत्तर लिखिए-

1. 1 सितम्बर और 15 सितम्बर के मध्य मानसून वापसी का समय किन दो अक्षरों द्वारा दिखाया गया है?
2. 1 अक्टूबर और 15 अक्टूबर के मध्य मानसून वापसी का समय किन दो अक्षरों से दिखाया गया है?

उत्तर:

1. अ तथा ब
2. स तथा द.
   

Hope given UP Board Solutions for Class 9 Social Science Geography Chapter 4 are helpful to complete your homework.

If you have any doubts, please comment below. UP Board Solutions try to provide online tutoring for you.

UP Board Solutions for Class 9 Social Science History Chapter 1 फ्रांसीसी क्रान्ति

These Solutions are part of UP Board Solutions for Class 9 Social Science. Here we have given UP Board Solutions for Class 9 Social Science History Chapter 1 फ्रांसीसी क्रान्ति.

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1.
फ्रांस में क्रान्ति की शुरुआत किन परिस्थितियों में हुई?
उत्तर:
फ्रांस में क्रान्ति की शुरुआत निम्न परिस्थितियों में हुई-
1. राजनैतिक कारण-तृतीय स्टेट के प्रतिनिधियों ने मिराब्यो एवं आबेसिए के नेतृत्व में स्वयं को राष्ट्रीय सभा घोषित कर इस बात की शपथ ली कि जब तक वे लोग सम्राट की शक्तियों को सीमित करने तथा अन्यायपूर्ण विशेषाधिकारों वाली सामंतवादी प्रथा को समाप्त करने वाला संविधान नहीं बना लेंगे तब तक राष्ट्रीय सभा को भंग नहीं करेंगे। राष्ट्रीय सभा जिस समय संविधान बनाने में व्यस्त थी, उस समय (UPBoardSolutions.com) सामंतों को विस्थापित करने के लिए अनेक स्थानीय विद्रोह हुए। अपने पिता की मृत्यु के बाद सन् 1774 ई. में ‘लुईस सोलहवाँ ‘ फ्रांस का राजा बना था। वह एक सज्जन परन्तु अयोग्य शासक था। राजा पर उसकी पत्नी ‘मैरी एंटोइनेट’ को भारी प्रभाव था।

प्रांतीय प्रशासन दो भागों में बँटा हुआ था जिन्हें क्रमशः ‘गवर्नमेंट’ तथा ‘जनरेलिटी’ के नामों से जाना जाता था। फ्रांसीसी शासन में एकरूपता का अभाव था। देश के भिन्न-भिन्न भागों में भिन्न-भिन्न प्रकार के कानून लागू थे। इसी बीच खाद्य संकट गहरा गया तथा जनसाधारण का गुस्सा गलियों में फूट पड़ा। 14 जुलाई को सम्राट ने सैन्य टुकड़ियों को पेरिस में प्रवेश करने के आदेश दिये। इसके प्रत्युत्तर में सैकड़ों क्रुद्ध पुरुषों एवं महिलाओं ने स्वयं की सशस्त्र टुकड़ियाँ बना लीं। ऐसे ही लोगों की एक सेना बास्तील किले की जेल (सम्राट की निरंकुश शक्ति का प्रतीक) में जा घुसी और उसको नष्ट कर दिया। इस प्रकार फ्रांसीसी क्रांति का प्रारंभ हुआ और व्यवस्था बदलने को आतुर लोग क्रांति में शामिल हो गए।

2. फ्रांस की आर्थिक परिस्थितियाँ-बूळू वंश का लुई सोलहवाँ 1774 में फ्रांस का राजा बना। उसने ऑस्ट्रिया की राजकुमारी मैरी एंटोइनेट से विवाह किया। उसके सत्तासीन होने के समय फ्रांस का कोष रिक्त था। राज्य पर कर्ज का बोझ निरंतर बढ़ रहा था। राज्य की कर (UPBoardSolutions.com) व्यवस्था असमानता और पक्षपात के सिद्धांत पर निर्मित होने के कारण अत्यंत दूषित थी। कर दो प्रकार के थे- प्रत्यक्ष कर (टाइल) और धार्मिक कर (टाइद)। पादरी वर्ग और कुलीन वर्ग जिनका फ्रांस की लगभग 40% भूमि पर स्वामित्व था, प्रत्यक्ष करों से पूर्ण मुक्त थे तथा अप्रत्यक्ष करों से भी प्रायः मुक्त थे। ऐसे समय में अमेरिका के ब्रिटिश उपनिवेशों के स्वतंत्रता संग्राम में भाग लेने के सरकारी निर्णय ने स्थिति को और अधिक गंभीर बना दिया।

सेना का रखरखाव, दरबार का खर्च, सरकारी कार्यालयों या विश्वविद्यालयों को चलाने जैसे अपने नियमित खर्च निपटाने के लिए सरकार कर बढ़ाने पर बाध्य हो गई। कर बढ़ाने के प्रस्ताव को पारित करने के लिए फ्रांस के सम्राट लुई सोलहवें ने 5 मई, 1789 ई. को एस्टेट के जनरल की सभा बुलाई। प्रत्येक एस्टेट को सभा में एक वोट डालने की अनुमति दी गई। तृतीय एस्टेट ने इस अन्यायपूर्ण प्रस्ताव का विरोध किया। उन्होंने सुझाव रखा कि प्रत्येक सदस्य का एक वोट होना चाहिए। सम्राट ने इंस अपील को ठुकरा दिया तथा तृतीय एस्टेट (UPBoardSolutions.com) के प्रतिनिधि सदस्य विरोधस्वरूप सभा से वाक आउट कर गए। फ्रांसीसी जनसंख्या में भारी बढ़ोत्तरी के कारण इस समय खाद्यान्न की माँग बहुत बढ़ गई थी। परिणामस्वरूप, पावरोटी (अधिकतर लोगों के भोजन का मुख्य भाग) के भाव बढ़ गए। बढ़ती कीमतों व अपर्याप्त मजदूरी के कारण अधिकतर जनसंख्या जीविका के आधारभूत साधन भी वहन नहीं कर सकती थी। इससे जीविका संकट उत्पन्न हो गया तथा अमीर और गरीब के मध्य दूरी बढ़ गई।

3. दार्शनिकों का योगदान- इस काल में फ्रांसीसी समाज में मांटेस्क्यू, वोल्टेयर तथा रूसो आदि विचारकों के विचारों के कारण तर्कवाद का प्रसार आरम्भ हुआ। इन विचारकों ने अपने साहित्य द्वारा पादरियों, चर्च की सत्ता तथा सामंती व्यवस्था की जड़ों को हिला दिया। अठारहवीं सदी के दौरान मध्यम वर्ग शिक्षित एवं धनी बन कर उभरा। सामंतवादी समाज द्वारा प्रचारित विशेषाधिकार प्रणाली उनके हितों के विरुद्ध थी। शिक्षित होने के कारण इस वर्ग के सदस्यों की पहुँच फ्रांसीसी एवं अंग्रेज राजनैतिक एवं सामाजिक दार्शनिकों (UPBoardSolutions.com) द्वारा सुझाए गए समानता एवं आजादी के विभिन्न-विचारों तक थी। ये विचार सैलून एवं कॉफीघरों में जनसाधारण के बीच चर्चा तथा वाद-विवाद के फलस्वरूप पुस्तकों एवं अखबारों के द्वारा लोकप्रिय हो गए। दार्शनिकों के विचारों ने महत्त्वपूर्ण भूमिका निभाई। जॉन लॉक, जीन जैक्स रूसो एवं मांटेस्क्यू ने राजा के दैवीय सिद्धान्त को नकार दिया।

4. सामाजिक परिस्थितियाँ- फ्रांस में सामंतवादी प्रथा प्रचलित थी, जो तीन वर्गों में प्रचलित थी। इन वर्गों को एस्टेट कहते थे। प्रथम एस्टेट में पादरी वर्ग आता था। इनका देश की 10% भूमि पर अधिकार था। द्वितीय एस्टेट में फ्रांस का कुलीन वर्ग सम्मिलित था। इनका देश की 30% भूमि पर अधिकार था। तृतीय एस्टेट में फ्रांस की लगभग 94% जनसंख्या आती थी। इस वर्ग में मध्यम वर्ग (लेखक, डॉक्टर, जज, वकील, अध्यापक, असैनिक अधिकारी आदि), किसानों, मजदूरों और दस्तकारों को सम्मिलित किया जाता था। यह (UPBoardSolutions.com) केवल तृतीय एस्टेट ही थी जो सभी कर देने को बाध्य थी। पादरी एवं कुलीन वर्ग के लोगों को सरकार को कर देने से छूट प्राप्त थी परन्तु सरकार को कर देने के साथ-साथ किसानों को चर्च को भी कर देना पड़ता था। यह एक अन्यायपूर्ण स्थिति थी जिसने तृतीय एस्टेट के सदस्यों में असंतोष की भावना को बढ़ावा दिया।

5. तात्कालिक कारण- लुई सोलहवें ने 5 मई, 1789 ई. को नए करों के प्रस्ताव हेतु 1614 ई. में निर्धारित संगठन के आधार पर तीनों एस्टेट की एक बैठक बुलाई। तृतीय एस्टेट की माँग थी कि सभी एस्टेट की एक संयुक्त बैठक बुलाई जाए तथा ‘एक व्यक्ति एक मत’ के आधार पर मतदान कराया जाए। लुई सोलहवें ने ऐसा करने से मना कर दिया। अतः 20 जून को तृतीय एस्टेट के प्रतिनिधि टेनिस कोर्ट में एकत्रित हुए तथा नवीन संविधान बनाने की घोषणा की।

प्रश्न 2.
फ्रांसीसी समाज के किन तबकों को क्रान्ति का फायदा मिला? कौन-से समूह सत्ता छोड़ने के लिए मजबूर हो गए? क्रांति के नतीजों से समाज के किन समूहों को निराशा हुई होगी?
उत्तर:
फ्रांसीसी क्रान्ति से सर्वाधिक लाभ तृतीय एस्टेट के धनी सदस्यों को हुआ। तृतीय एस्टेट में किसान, मजदूर, वकील, छोटे अधिकारीगण, अध्यापक, डॉक्टर एवं व्यवसायी शामिल थे। क्रांति से पहले इन्हें सभी कर अदा करने पड़ते थे। साथ ही इन लोगों को पादरियों और कुलीनों के द्वारा अपमानित भी किया जाता था। लेकिन क्रांति के बाद उनके साथ समाज के उच्च वर्ग के समान व्यवहार किया जाने लगा। (UPBoardSolutions.com) पादरियों एवं कुलीन वर्ग के लोगों को अपने विशेषाधिकारों को त्यागने पर विवश होना पड़ा। क्रान्ति के परिणामों से महिलाओं को निराशा हुई क्योंकि वे लैंगिक आधार पर पुरुषों की समानता का अधिकार हासिल नहीं कर सकीं।

प्रश्न 3.
उन्नीसवीं और बीसवीं सदी की दुनिया के लिए फ्रांसीसी क्रान्ति कौन-सी विरासत छोड़ गई?
उत्तर:
इस क्रान्ति से विश्व के लोगों को निम्न विरासत प्राप्त हुई-

1. फ्रांसीसी क्रान्ति वैश्विक स्तर पर मानव इतिहास की महत्त्वपूर्ण घटनाओं में से एक है।
2. यह विश्व का पहला ऐसा राष्ट्रीय आंदोलन था जिसने स्वतंत्रता, समानता और भाई-चारे जैसे विचारों को अपनाया।
   19वीं व 20वीं सदी के प्रत्येक देश के लोगों के लिए ये विचार आधारभूत सिद्धान्त बन गए।
3. राजा राममोहन राय जैसे नेता फ्रांसीसियों द्वारा राजशाही एवं उसके निरंकुशवाद के विरुद्ध प्रचारित विचारों से अत्यधिक प्रभावित थे।
4. इस क्रान्ति ने जनता की आवाज को प्रश्रय दिया। जनता उस समय दैवी अधिकार की धारणा, सामंती विशेषाधिकार, दास प्रथा एवं नियंत्रण को समाप्त करके योग्यता को सामाजिक उत्थान का आधार बनाना चाहती थी।
5. इसने यूरोप के लगभग सभी देशों सहित दक्षिण अमेरिका में प्रत्येक क्रान्तिकारी आंदोलन को प्रेरित किया।
6. इसने ‘राष्ट्रवादी आंदोलन को बढ़ावा दिया। इस क्रांति ने पोलैण्ड, जर्मनी, नीदरलैण्ड तथा इटली के लोगों को अपने देशों में राष्ट्रीय राज्यों की स्थापना हेतु प्रेरित किया।
7. इसने राजतंत्रात्मक स्वेच्छाचारी शासन का अन्त कर यूरोप तथा विश्व के अन्य भागों में गणतंत्र की स्थापना को बढ़ावा दिया।
8. इसने देश के सभी नागरिकों के लिए समान अधिकार की अवधारणा का प्रचार किया जो बाद में कानून के सम्मुख लोगों की समानता की धारणा का आधार बना।

प्रश्न 4.
उन जनवादी अधिकारों की सूची बनाएँ जो आज हमें मिले हुए हैं और जिनका उद्गम फ्रांसीसी क्रान्ति में है।
उत्तर:
ऐसे लोकतांत्रिक अधिकार जिनका हम आज सरलता से प्रयोग करते हैं तथा जिनका उद्भव फ्रांस की क्रान्ति के फलस्वरूप हुआ था, उनका विवरण इस प्रकार है-

1. धार्मिक स्वतंत्रता का अधिकार
2. शोषण के विरुद्ध अधिकार
3. संवैधानिक उपचारों का अधिकार
4. विचार अभिव्यक्ति का अधिकार
5. समानता का अधिकार
6. स्वतंत्रता का अधिकार
7. एकत्र होने तथा संगठन बनाने का अधिकार
8. सांस्कृतिक एवं शैक्षणिक अधिकार
9. संपत्ति का अधिकार।

प्रश्न 5.
क्या आप इस तर्क से सहमत हैं कि सार्वभौमिक अधिकारों के सन्देश में नाना अंतर्विरोध थे?
उत्तर:
विश्व में नागरिक अधिकारों की प्रथम घोषणा का प्रयास संभवतः फ्रांस में ही किया गया। फ्रांस के सार्वभौमिक अधिकारों के संदेश में स्वतंत्रता, समानता एवं बंधुत्व के तीन मौलिक सिद्धान्तों पर बल दिया गया। वर्तमान में सभी लोकतांत्रिक देशों द्वारा इन सिद्धान्तों को अंगीकार (UPBoardSolutions.com) किया गया है।
लेकिन यह सत्य है कि फ्रांस का सार्वभौमिक अधिकारों का संदेश अनेक विरोधाभासों से घिरा हुआ है जिनका विवरण इस प्रकार है-

1. व्यापार और कार्य की स्वतंत्रता का कोई उल्लेख नहीं था।
2. स्वतंत्रता को अधिक प्रोत्साहन दिया गया था।
3. व्यक्ति के चहुँमुखी विकास को लक्ष्य नहीं बनाया गया।
4. शिक्षा के अधिकार को कोई महत्त्व नहीं दिया गया।
5. घोषणा में कहा गया था कि “कानून सामान्य इच्छा की अभिव्यक्ति है। सभी नागरिकों को व्यक्तिगत रूप से या अपने प्रतिनिधियों के माध्यम से इसके निर्माण में भाग लेने का अधिकार है। कानून की नजर में सभी नागरिक समान हैं।” किन्तु जब फ्रांस एक संवैधानिक राजशाही बना तो लगभग 30 लाख नागरिक जिनमें 25 वर्ष से कम आयु के पुरुष एवं महिलाएँ शामिल थीं, उन्हें बिल्कुल वोट ही नहीं डालने दिया गया।
6. फ्रांस ने उपनिवेशों पर कब्जा करना व उनकी संख्या बढ़ाना जारी रखा।
7. फ्रांस में उन्नीसवीं सदी के पूर्वार्द्ध तक दासप्रथा जारी रही।

प्रश्न 6.
नेपोलियन के उदय को कैसे समझा जा सकता है?
उत्तर:
नेपोलियन का उदय 1796 में निर्देशिका के पतन के बाद हुआ। निदेशकों का प्रायः विधान सभाओं से झगड़ा होता था जो कि बाद में उन्हें बर्खास्त करने का प्रयास करती। निर्देशिका राजनैतिक रूप से अत्यधिक अस्थिर थी; अतः नेपोलियन सैन्य तानाशाह के रूप में सत्तारूढ़ हुआ। सन् 1804 में नेपोलियन बोनापार्ट ने स्वयं को फ्रांस का सम्राट बना लिया। 1799 ई. में डायरेक्टरी के शासन का अंत करके वह फ्रांस का प्रथम काउंसल बन गया। शीघ्र ही शासन की समस्त शक्तियाँ उसके हाथों में केंद्रित हो गईं।

सन् 1793-96 के मध्य फ्रांसीसी सेनाओं ने लगभग सम्पूर्ण पश्चिमी यूरोप पर विजय हासिल कर ली। जब नेपोलियन माल्टा, मिस्र और सीरिया की ओर बढ़ा (1797-99) तथा इटली से फ्रांसीसियों को बाहर ढकेल दिया गया तब सत्ता पर नेपोलियन का कब्जा हुआ, फ्रांस ने अपने खोए हुए भूखण्ड पुनः वापस ले लिए। उसने आस्ट्रिया को 1805 में, प्रशा को 1806 में और रूस को 1807 में परास्त किया। समुद्र के ऊपर ब्रिटिश नौ सेना पर फ्रांसीसी अपना प्रभुत्व कायम नहीं कर सके। अंततः लगभग सारे यूरोपीय देशों ने मिलकर 1813 ई. में लिव्जिंग (UPBoardSolutions.com) में फ्रांस को परास्त किया। बाद में इन मित्र राष्ट्रों की सेनाओं ने पेरिस (फ्रांस की राजधानी) पर अधिकार कर लिया। जून, 1815 ई. में नेपोलियन ने वाटरलू में पुनः विजय प्राप्त करने का असफल प्रयास किया। नेपोलियन ने अपने शासन काल में निजी संपत्ति की सुरक्षा और नाप-तोल की एक समान दशमलव प्रणाली सम्बन्धी कानून बनाए।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
गिलोटिन किसे कहते हैं?
उत्तर:
यह दो स्तम्भों और एक फरसे से मिलकर बना एक ऐसा यंत्र है जिसमें फरसा ऊपर से नीचे की ओर आता है ओर नीचे लिटाये गए मृत्युदण्ड प्राप्त व्यक्ति का एक ही बार में सिर धड़ से अलग कर देता है। फ्रांसीसी क्रांति के बाद इस यंत्र का बड़े पैमाने पर उपयोग किया गया।

प्रश्न 2.
आतंक के राज्य से क्या आशय है?
उत्तर:
फ्रांस में क्रान्ति के बाद अस्तित्व में आयी रोब्सपियर सरकार में कुलीन एवं पादरी, दूसरे राजनीतिक दल के सदस्यों, रोब्सपियर की कार्य-पद्धति से असहमत पार्टी के सदस्यों को बंदी बनाकर जेल में डाल दिया जाता था। इन बंदियों पर क्रान्तिकारी अदालत में मुकदमा चलाया जाता था। दोष सिद्ध होने पर इन लोगों को गिलोटिन पर चढ़ा दिया जाता था।

प्रश्न 3.
रोब्सपियर सरकार के दो प्रमुख कार्य बताइए।
उत्तर:
रोब्सपियर सरकार के दो प्रमुख कार्य इस प्रकार हैं-

1. खाद्यान्न संकट को देखते हुए मांस और पावरोटी की बिक्री हेतु राशनिंग व्यवस्था लागू कर दी गयी।
2. मजदूरी और कीमतों की अधिकतम सीमा निर्धारित करने वाला कानून बनाया गया।

प्रश्न 4.
रोब्सपियर को गिलोटिन पर चढ़ाने का कारण बताइए।
उत्तर:
रोब्सपियर की कठोर नीतियों को फ्रांस में निर्ममता से लागू किया गया, जिसमें हजारों निर्दोष लोग भी सन्देह में मारे गए। सन् 1794 में न्यायालय द्वारा रोब्सपियर को उत्पीड़ने का दोषी ठहराया गया और बंदी बना लिया गया तथा अगले ही दिन उसे गिलोटिन पर चढ़ा दिया गया।

प्रश्न 5.
‘सोसाइटी ऑफ रेवोल्यूशनरी एण्ड रिपब्लिकन विमेन’ की प्रमुख माँग बताइए।
उत्तर:
इस क्लब की प्रमुख माँग थी कि फ्रांस के समाज में महिला-पुरुष के बीच लैंगिक आधार पर विभेद न करके उन्हें एक समान माना जाए और समान राजनीतिक अधिकार प्रदान किए जाएँ।

प्रश्न 6.
नेपोलियन बोनापार्ट का उदय किस प्रकार हुआ?
उत्तर:
डायरेक्टरी शासन के दौरान फ्रांस में डायरेक्टरी के सदस्यों के मध्य परस्पर झगड़ा विधान परिषदों से होता था और विधान परिषद् डायरेक्टरी को बर्खास्त करने का प्रयास करती थी। डायरेक्टरी की राजनीतिक अस्थिरता ने
सेनिक तानाशाह नेपोलियन बोनापार्ट के उद्भव का मार्ग प्रशस्त किया।

प्रश्न 7.
फ्रांस के राष्ट्रीय गान को किस नाम से जाना जाता है?
उत्तर:
फ्रांस के राष्ट्रीय गान को ‘मार्सिले’ नाम से जाना जाता है।

प्रश्न 8.
जैकोबिन क्लब के नेता का नाम लिखिए। उत्तर मेक्समिलियन रोबेस्प्येर।। प्रश्न 9. फ्रांसीसी क्रांति के समय फ्रांस पर किस शासक का शासन था?
उत्तर:
लुईस XVI (सोलहवाँ) का।

प्रश्न 10.
लुईस सोलहवाँ फ्रांस की राजगद्दी पर कब आसीन हुआ था?
उत्तर:
1774 ई. में।

प्रश्न 11.
लुईस XVI किस राजवंश से संबंधित था?
उत्तर:
बूबों राजवंश।

प्रश्न 12.
फ्रांसीसी समाज किन तीन प्रमुख वर्गों में बँटा हुआ था?
उत्तर:

1. प्रथम एस्टेट,
2. द्वितीय एस्टेट,
3. तृतीय एस्टेट।

प्रश्न 13.
धार्मिक करों को किस नाम से जाना जाता था?
उत्तर:
टाइद।

प्रश्न 14.
एस्टेट जनरल की बैठक में तीनों वर्गों के कितने-कितने प्रतिनिधि आमंत्रित किए गए थे?
उत्तर:
प्रथम एस्टेट (300 प्रतिनिधि), द्वितीय एस्टेट (300 प्रतिनिधि)।

प्रश्न 15.
एस्टेट जनरल की बैठक में किन वर्गों का प्रवेश वर्जित था?
उत्तर:

1. किसानों,
2. औरतों,
3. कारीगरों।

प्रश्न 16.
बास्तील का पतन कब हुआ?
उत्तर:
14 जुलाई, 1789 ई.।

प्रश्न 17.
नेशनल असेम्बली ने सामंती व्यवस्था के उन्मूलन का आदेश कब पारित किया?
उत्तर:
4 अगस्त, 1789 ई.।

प्रश्न 18.
त्रिभुज के अन्दर रोशनी बिखेरती आँख किसका प्रतीक है?
उत्तर:
त्रिभुज के अन्दर रोशनी बिखेरती सर्वदर्शी आँख ज्ञान का प्रतीक है।

प्रश्न 19.
फ्रांस के राष्ट्रीय रंग कौन-से हैं?
उत्तर:

1. लाल,
2. सफेद,
3. नीला।

प्रश्न 20.
प्रारम्भिक वर्षों में क्रांतिकारी सरकार ने महिलाओं के जीवन में सुधार के लिए किस तरह के कानून पास किए?
उत्तर:
सरकारी विद्यालयों की स्थापना के साथ ही सभी (UPBoardSolutions.com) लड़कियों के लिए स्कूली शिक्षा को अनिवार्य बना दिया गया। अब पिता उन्हें उनकी मर्जी के खिलाफ शादी के लिए बाध्य नहीं कर सकते थे।

प्रश्न 21.
18वीं सदी में फ्रांसीसी समाज कितने एस्टेट्स में बँटा हुआ था?
उत्तर:
18वीं सदी में फ्रांसीसी समाज तीन एस्टेट्स में बँटा हुआ था-

1. प्रथम एस्टेट-पादरी वर्ग,
2. द्वितीय एस्टेट–कुलीन वर्ग,
   तृतीय एस्टेट-बड़े व्यवसायी, व्यापारी, अदालती कर्मचारी, वकील, किसान, कारीगर, छोटे किसान, भूमिहीन, मजदूर, नौकर।

प्रश्न 22.
18वीं सदी में फ्रांस में किस नए सामाजिक वर्ग का उदय हुआ?
उत्तर:
मध्यम वर्ग का।

प्रश्न 23.
एस्टेट जनरल (प्रतिनिधि सभा) की अन्तिम बैठक कब हुई थी?
उत्तर:
1614 ई.।

प्रश्न 24.
‘द सोशल कॉन्ट्रैक्ट’ नामक पुस्तक किसने लिखी थी?
उत्तर:
रूसो।

प्रश्न 25.
जैकोबिन सरकार के पतन के बाद फ्रांस में किस तरह की सरकार स्थापित हुई?
उत्तर:
जैकोबिन सरकार के पतन के उपरान्त एक नया संविधान लागू किया गया जिसने समाज के संपत्तिहीन नागरिकों को मताधिकार से वंचित रखा। संविधान में दो चुनी गई विधान परिषदों का प्रावधान था। इन परिषदों ने पाँच सदस्यों वाली एक कार्यपालिका डाइरेक्ट्री को नियुक्त किया जिसे डाइरेक्ट्री शासन कहा गया।

प्रश्न 26.
तीसरे एस्टेट की अधिकांश महिलाएँ किस तरह के कार्य करती थीं?
उत्तर:
तीसरे एस्टेट की अधिकांश महिलाएँ जीविका निर्वाह के लिए काम करती थीं। वे सिलाई, बुनाई, कपड़ों की धुलाई करती थीं, बाजारों में फल-फूल और सब्जियाँ बेचती थीं अथवा संपन्न घरों में घरेलू काम करती थीं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
फ्रांस की क्रान्तिकारी महिला ओलिम्प डि गाजेस (1748-1793) के बारे में आप क्या जानते हैं?
उत्तर:
फ्रांस की क्रान्तिकालीन राजनीति में सक्रिय ओलिम्प सबसे महत्त्वपूर्ण महिला थी। उन्होंने फ्रांस के संविधान नथा ‘पुरुष एवं नागरिक अधिकार घोषणापत्र’ का विरोध किया क्योंकि उनमें महिलाओं को मानव मात्र के मूलभूत अधिकारों से वंचित किया गया था। इसलिए उन्होंने 1791 ई. में ‘महिला एवं नागरिक अधिकार घोषणापत्र तैयार किया जिसे महारानी एवं नेशनल असेंबली के सदस्यों पर यह माँग करते हुए (UPBoardSolutions.com) भेजा गया था कि वे इस पर कार्यवाही करें। सन् 1793 में ओलिम्प ने महिला क्लवों को जबरन बंद करने के लिए जैकोबिन सरकार की आलोचना की। उन पर नेशनल कन्वेंशन द्वारा मुकदमा चलाया गया तथा फाँसी पर लटका दिया गया।

प्रश्न 2.
फ्रांस की क्रान्ति के बाद समता स्थापित करने के लिए रोबेस्प्येर सरकार ने कौन-से नियम बनाए?
उत्तर:

1. बोलचाल और संबोधन में भी बराबरी का आचार-व्यवहार लागू करने की कोशिश की गई। परंपरागत मॉन्स्यूर (महाशय) एवं मदाम (महोदया) के स्थान पर अब सभी फ्रांसीसी पुरुषों एवं महिलाओं को सितोयेन (नागरिक) एवं सितोयीन (नागरिका) नाम से संबोधित किया जाने लगा।
2. चर्को को बन्द कर दिया गया और उनके भवनों को बैरक या दफ्तर बना दिया गया।
3. रोबेस्प्येर सरकार ने कानून बना कर मजदूरी एवं कीमतों की अधिकतम सीमा तय कर दी।
4. गोश्त एवं पावरोटी की राशनिंग कर दी गई।
5. किसानों को अपना अनाज शहरों में ले जाकर सरकार द्वारा तय कीमत पर बेचने के लिए बाध्य किया गया।
6. महँगे सफेद आटे के इस्तेमाल पर रोक लगा दी गई। सभी नागरिकों के लिए साबुत गेहूं से बनी और बराबरी का प्रतीक मानी जाने वाली ‘समता रोटी खाना अनिवार्य कर दिया गया।

प्रश्न 3.
फ्रांस में जून, 1793 ई. से जुलाई, 1794 ई. के बीच के कालखण्ड को ‘आतंक का राज्य’ क्यों कहते हैं?
उत्तर:
फ्रांस में जून, 1793 से जुलाई, 1794 ई. तक के फ्रांसीसी शासन को ‘आतंक का राज्य के नाम से संबोधित किया जाता है। इसके पीछे निम्न तथ्य उत्तरदायी हैं-

1. चर्चे को बन्द कर दिया गया और उनके भवनों को बैरक या दफ्तर बना दिया गया।
2. रोब्सपियर ने अपनी नीतियों को सख्ती से लागू किया। उसके लिए दया का अर्थ था देशद्रोह। उसके एक साल के शासन काल में हजारों व्यक्तियों को मृत्यु-दण्ड दिया गया जिसके कारण उसके सहयोगी भी उसके दुश्मन बन गए और 27 जुलाई, 1794 ई. को उसे कैद कर लिया गया।
3. क्योंकि इस काल में शासन के समस्त सूत्र जैकोबिन क्लब के नेता रोब्सपियर के हाथों में केन्द्रित हो गए थे। उसके अनुसार फ्रांस का कल्याण क्रांति की सफलता में ही निहित है और क्रांति की सफलता आतंक का राज्य स्थापित करके ही प्राप्त की जा सकती है। इस उद्देश्य की पूर्ति के लिए उसने सभी असहमत वर्गों के नेताओं तथा व्यक्तियों को गिरफ्तार कर लिया तथा दोषी व्यक्तियों को गिलोटिन पर चढ़ाकर मृत्युदण्ड दे दिया गया।
4. उसने देश की रक्षा के लिए सेना की भर्ती आरंभ की और शीघ्र ही 7,50,000 फ्रेंच सेना तैयार हो गई।
5. उसने मजदूरी तथा कीमतों की (UPBoardSolutions.com) अधिकतम सीमा निर्धारित की। गोश्त तथा पावरोटी की राशनिंग आरम्भ कर दी गई।
   इस प्रकार उसने महँगाई रोकने के लिए अनेक प्रयास किए।

प्रश्न 4.
जैकोबिन क्लब से आप क्या समझते हैं?
उत्तर:
जैकोबिन क्लब की शुरुआत क्रान्ति के आरम्भिक समय में ही हो चुकी थी। शुरुआत में जैकोबिन के अनुयायी उदार तथा सुधारवादी ही थे। लेकिन धीरे-धीरे उसकी नीति उग्र होती गयी, फलस्वरूप मिराबो लाफाएत जैसे नरम विचार वाले सदस्य उससे पृथक् ही हो गए। परिणाम यह हुआ कि क्लब पर रोब्सपियर जैसे उग्र विचारक का नियंत्रण हो गया। इस क्लब का नाम पेरिस के भूतपूर्व कान्वेंट ऑफ सेंट जैकब के नाम पर पड़ा। इस क्लब का प्रधान स्थान पेरिस था। इस क्लब के सदस्य लम्बी धारीदार पतलून पहनते थे इसलिए इन्हें ‘सौं कुलॉत’ भी कहा जाता था। इसकी 400 के लगभग शाखाएँ थीं जो सारे देश में फैली हुई थीं। धीरे-धीरे यह क्लब अधिक शक्तिशाली हो गया और उसका प्रभाव इतना बढ़ गया कि फ्रांसीसी क्रांति के पश्चात् फ्रांस की सत्ता पर जैकोबिनों को नियन्त्रण स्थापित हो गया।

प्रश्न 5.
कुलीन वर्ग के फ्रांस से पलायन के क्या कारण थे?
उत्तर:
14 जुलाई, 1789 ई. को फ्रांस की क्रुद्ध भीड़ बास्तील के किले पर धावा बोलकर उसे नष्ट कर दिया तथा वहाँ के जेल में बन्द कैदियों को मुक्त कर दिया। ग्रामीण क्षेत्रों में यह अफवाह फैल गयी कि जागीरों के मालिक भाड़े पर लठैतोंलुटेरों के गिरोह बुला लिए हैं जो पकी फसलों को नष्ट करने के लिए निकल पड़े हैं। अनेक जिलों में भय से आक्रान्त किसानों ने कुदालों और बेलचों से ग्रामीण किलों पर आक्रमण कर दिए। किसानों ने अन्न भण्डारों को लूट लिया तथा लगान सम्बन्धी दस्तावेजों को आग के हवाले कर दिया। ऐसी अराजक स्थिति में बड़ी संख्या में कुलीन अपनी जागीरें छोड़कर पलायन कर गए।
और उन्होंने पड़ोसी देशों में शरण लेकर अपना जीवन सुरक्षित किया।

प्रश्न 6:
क्रान्तिकालीन फ्रांस में महिलाओं की भूमिका का वर्णन कीजिए।
उत्तर:
फ्रांस में सामाजिक परिवर्तन लाने में महिलाओं की उल्लेखनीय भूमिका है। महिलाओं ने अपने जीवन में सुधार लाने के लिए क्रान्तिकारी सरकार पर आवश्यक कदम उठाने के लिए दबाव डाला। तत्कालीन फ्रांसीसी महिलाएँ अपने पतियों एवं परिवार की आर्थिक रूप से सहायता करने के (UPBoardSolutions.com) लिए सिलाई-बुनाई, कपड़े धोने, बाजार में फूल, फल तथा सब्जियाँ बेचने का कार्य करती थीं। अपनी स्थिति में सुधार तथा इस पर चर्चा झुरने के लिए उन्होंने अनेक राजनैतिक क्लब एवं अखबार शुरू किए तथा कई महत्त्वपूर्ण मुद्दे उठाए, जो इस प्रकार हैं-

1. उनकी माँगों में यह भी शामिल था कि उन्हें भी पुरुषों के समान राजनैतिक अधिकार दिए जाएँ।
2. उन्होंने मताधिकार, सभा में चुने जाने एवं राजनैतिक पद ग्रहण कर सकने की भी माँग की।
3. फ्रांस के विभिन्न शहरों में लगभग साठ क्लब अस्तित्व में आए।
4. सभी वर्गों की महिलाओं को शिक्षा एवं व्यावसायिक प्रशिक्षण दिया जाए।
5. उन्होंने माँग की कि उन्हें भी उन दिनों पुरुषों को दी जा रही उच्च मजदूरी के समान ही मजदूरी मिले।

प्रश्न 7.
फ्रांस की क्रान्ति का फ्रांस पर प्रभाव बताइए।
उत्तर:
फ्रांस की क्रान्ति के फ्रांस पर निम्न महत्त्वपूर्ण प्रभाव पड़े-

1. फ्रांसीसी क्रांति ने जनता की माँगों का समर्थन किया, दैवीय अधिकार के विचार, सामन्ती विशेषाधिकारों, दासत्व तथा नियंत्रण की समाप्ति तथा सामाजिक उत्थान के लिए योग्यता को आधार बनाया।
2. फ्रांस में राजशाही का अन्त हो गया। फ्रांस गणतंत्र बन गया।
3. पुरुष एवं नागरिक अधिकारों की घोषणा भी फ्रांसीसी क्रांति की देन थी जिसने समानता एवं अभिव्यक्ति की स्वतंत्रता जैसे अधिकार दिए।

प्रश्न 8.
फ्रांस के 1791 ई. के संविधान की विशेषता बताइए।
उत्तर:

1. निर्वाचक की योग्यता पाने के लिए और पुनः सभा का सदस्य बनने के लिए लोगों को उच्च श्रेणी का करदाता होना आवश्यक था।
2. सभी नागरिकों को वोट देने का अधिकार नहीं था। केवल 25 वर्ष से अधिक आयु के पुरुष जो कि कम से कम एक मजदूर की 3 दिन की मजदूरी के समान कर अदा करते थे उन्हें ही सक्रिय नागरिक का दर्जा प्रदान किया गया अर्थात् उन्हें ही वोट देने का अधिकार था। बचे हुए सभी पुरुषों तथा सभी महिलाओं को निष्क्रिय नागरिक का दर्जा दिया गया था।
3. सन् 1791 के संविधान ने कानून बनाने की (UPBoardSolutions.com) शक्ति राष्ट्रीय सभा को दे दी जो कि अप्रत्यक्ष रूप से चुनी जाती थी अर्थात् नागरिक किसी चुनने वाले समूह को वोट देते तथा वह समूह फिर सभा को चुनता।।

प्रश्न 9.
फ्रांस में सेंसरशिप की समाप्ति का प्रभाव बताइए।
उत्तर:
1789 ई. में बास्तील के पतन के बाद जो सबसे महत्त्वपूर्ण कानून अस्तित्व में आया, वह ‘सेंसरशिप की समाप्ति’ से सम्बन्धित था। इसके प्रभाव का विवरण इस प्रकार है-

1. नाटक, संगीत और उसकी जुलूसों में असंख्य लोग जाने लगे।
2. स्वतंत्रता और न्याय के बारे में राजनीतिज्ञों व दार्शनिकों के पांडित्यपूर्ण लेखन को समझने और उससे जुड़ने का यह लोकप्रिय तरीका था क्योंकि किताबों को पढ़ना तो मुट्ठी भर शिक्षितों के लिए ही संभव था।
3. अब अधिकारों के घोषणापत्र ने भाषण एवं अभिव्यक्ति की स्वतंत्रता को नैसर्गिक अधिकार घोषित कर दिया। परिणामस्वरूप फ्रांस के शहरों में अखबारों, पर्चा, पुस्तकों एवं छपी हुई तस्वीरों की बाढ़ आ गई जहाँ से वह तेजी से गाँव-देहात तक जा पहुँची। उनमें फ्रांस में घट (UPBoardSolutions.com) रही घटनाओं एवं परिवर्तनों का ब्यौरा और उन पर टिप्पणी होती थी।
4. प्रेस की स्वतंत्रता का मतलब यह था कि किसी भी घटना पर परस्पर विरोधी विचार भी व्यक्त किए जा सकते थे।
   प्रिंट माध्यम का उपयोग करके एक पक्ष ने दूसरे पक्ष को अपने दृष्टिकोण से सहमत कराने की कोशिश की।

प्रश्न 10.
18वीं सदी से पहले फ्रांसीसी उपनिवेशों में दास-प्रथा का उल्लेख कीजिए।
उत्तर:
18वीं सदी से पहले फ्रांसीसी उपनिवेशों में दास प्रथा इस प्रकार थी-
(1) दास-व्यापार सत्रहवीं शताब्दी में शुरू हुआ। फ्रांसीसी सौदागर बोर्दै और नान्ते बंदरगाह से अफ्रीका तट पर जहाज ले जाते थे, जहाँ वे स्थानीय सरदारों से दास खरीदते थे। दासों को दाग कर एवं हथकड़ियाँ डालकर अटलांटिक महासागर के पार कैरिबिआई देशों तक तीन माह की लम्बी समुद्री-यात्रा के लिए जहाजों में ढूंस दिया जाता था। वहाँ उन्हें बागान-मालिकों को बेच दिया जाता था। दास-श्रुम के बल पर यूरोपीय बाजारों में चीनी, कॉफी एवं नील की बढ़ती माँग को पूरा करना संभव हुआ। बोर्दे और नान्ते जैसे बंदरगाह फलते-फूलते दास-व्यापार के कारण। ही समृद्ध नगर बन गए।

(2) फ्रांसीसी उपनिवेशों में से कैरिबिआई उपनिवेश-मार्टिनिक, गॉडेलोप और सैन डोमिंगों-तंबाकू, नील, चीनी एवं कॉफ़ी जैसी वस्तुओं के महत्त्वपूर्ण आपूर्तिकर्ता थे। अपरिचित एवं दूर देश जाने और काम करने के प्रति यूरोपियों की अनिच्छा का मतलब था–बागानों में श्रम की कमी। इस कमी को यूरोप, अफ्रीका एवं अमेरिका के बीच त्रिकोणीय दास-व्यापार द्वारा पूरा किया गया।

प्रश्न 11. 
फ्रांस में दास प्रथा का उन्मूलन किस प्रकार हुआ?
उत्तर:
फ्रांस में दास प्रथा का उन्मूलन निम्न प्रकार हुआ-

1. फ्रांस में दास प्रथा की अधिक निन्दा 18वीं सदी में नहीं हुई। नेशनल असेंबली में लम्बी बहस के बाद भी यह निर्धारित नहीं किया जा सका कि समस्त फ्रांसीसी प्रजा को समान अधिकार प्रदान किया जाए या नहीं। किन्तु दास-व्यापार पर निर्भर व्यापारियों के विरोध के भय के फलस्वरूप नेशनल असेंबली कोई कानून पारित नहीं कर सकी।
2. 1794 ई. के कन्वेंशन ने फ्रांसीसी उपनिवेशों में स्थित दासों को मुक्त करने सम्बन्धी कानून पारित कर दिया। यह कानून मात्र 10 वर्ष तक लागू रहा। दस वर्ष बाद (UPBoardSolutions.com) नेपोलियन ने दास-प्रथा पुनः शुरू कर दी। अब फ्रांस में सक्रिय बागान मालिकों को अपने आर्थिक हित साधने के लिए अफ्रीकी नीग्रो लोगों को गुलाम बनाने की स्वतंत्रता मिल गयी।
3. सन् 1848 में फ्रांसीसी उपनिवेशों में दास-प्रथा का पूरी तरह उन्मूलन कर दिया गया।

प्रश्न 12.
18वीं सदी के फ्रांस में महिलाओं की स्थिति स्पष्ट कीजिए।
उत्तर:
18वीं सदी के फ्रांस में महिलाओं की स्थिति निम्न प्रकार थी-

1. अधिकांश महिलाओं के पास पढ़ाई-लिखाई तथा व्यावसायिक प्रशिक्षण के मौके नहीं थे। केवल कुलीनों की लड़कियाँ अथवा तीसरे एस्टेट के धनी परिवारों की लड़कियाँ ही कॉन्वेंट में पढ़ पाती थीं, इसके बाद उनकी शादी कर दी जाती थी।
2. कामकाजी महिलाओं को अपने परिवार का पालन-पोषण भी करना पड़ता था-जैसे खाना पकाना, पानी लाना, लाइन लगाकर पावरोटी लाना और बच्चों की देख-रेख करना आदि। उनकी मजदूरी पुरुषों की तुलना में कम थी।
3. महिलाएँ शुरू से ही फ्रांसीसी समाज में इतने अहम् परिवर्तन लाने वाली गतिविधियों में सक्रिय रूप से शामिल थीं। उन्हें उम्मीद थी कि उनकी भागीदारी क्रांतिकारी सरकार को उनका जीवन सुधारने हेतु ठोस कदम उठाने के लिए प्रेरित करेगी।
4. तीसरे एस्टेट की अधिकांश महिलाएँ जीविका निर्वाह के लिए काम करती थीं। वे सिलाई-बुनाई, कपड़ों की धुलाई करती थीं, बाजारों में फल-फूल-सब्जियाँ, बेचती थीं अथवा संपन्न घरों में घरेलू काम करती थीं। बहुत सारी महिलाएँ , वेश्यावृत्ति करती थीं।

प्रश्न 13.
फ्रांस में व्याप्त आर्थिक तनाव क्रान्ति में किस प्रकार सहायक बना?
उत्तर:
लुई सोलहवाँ 1774 ई. में फ्रांस का राजा बना। उस समय फ्रांस का राजकोष रिक्त था। सेना का रखरखाव, दरबार का खर्च, सरकारी कार्यालयों या विश्वविद्यालयों को चलाने जैसे अपने नियमित खर्च निपटाने के लिए सरकार कर बढ़ाने पर बाध्य हो गई। कर बढ़ाने के प्रस्ताव को पारित करने के लिए फ्रांस के सम्राट लुई सोलहवें ने 5 मई, 1789 ई. को एस्टेट्स के जनरल की सभा बुलाई। प्रत्येक एस्टेटस को सभा में एक वोट डालने की अनुमति दी गई। तृतीय एस्टेट्स ने इस अन्यायपूर्ण प्रस्ताव का विरोध किया।

उन्होंने सुझाव रखा कि प्रत्येक सदस्य का एक वोट होना चाहिए। सम्राट ने इस अपील को ठुकरा दिया तथा तृतीय एस्टेट्स के प्रतिनिधि सदस्य विरोधस्वरूप सभा से वाक आउट कर गए। फ्रांसीसी जनसंख्या में भारी बढ़ोत्तरी के कारण इस समय खाद्यान्न की माँग बहुत बढ़ गई थी। परिणामस्वरूप, (UPBoardSolutions.com) पावरोटी’ (अधिकतर लोगों के भोजन को मुख्य भाग) के भाव बढ़ गए। बढ़ती कीमतों व अपर्याप्त मजदूरी के कारण अधिकतर जनसंख्या जीविका के आधारभूत साधन भी वहन नहीं कर सकती थी। इससे जीविका संकट उत्पन्न हो गया तथा अमीर और गरीब के मध्य दूरी बढ़ गई।

प्रश्न 14.
फ्रांस में जीविका संकट किन परिस्थितियों में उत्पन्न हुआ?
उत्तर:
फ्रांस की जनसंख्या में तेजी से वृद्धि हो रही थी। फ्रांस की जनसंख्या 1715 ई. में 2 करोड़ 30 लाख से बढ़कर 1789 ई. में 2 करोड़ 80 लाख हो गयी। फलस्वरूप इससे खाद्यान्न की माँग बहुत तेजी से बढ़ी। इसलिए पावरोटी की कीमत भी तेजी से बढ़ी क्योंकि यह आम आदमी का भोजन थी। बहुत से कामगार कारखानों में मजदूर का काम करते थे जिनके मालिक उनकी मजदूरी निर्धारित करते थे। किन्तु उनकी (UPBoardSolutions.com) मजदूरी बढ़ती कीमतों के हिसाब से नहीं बढ़ रही थी। इसलिए अमीर और गरीब के बीच की दूरी बढ़ गई। जब कभी अकाल पड़ता या ओलावृष्टि होती तो फसल कम होने से स्थिति और बिगड़ जाती। इससे जीविका संकट पैदा हुआ।

प्रश्न 15.
फ्रांसीसी क्रान्ति में दार्शनिकों का योगदान बताइए।
उत्तर:
फ्रांसीसी क्रान्ति में दार्शनिकों की भूमिका को हम निम्न प्रकार से स्पष्ट कर सकते हैं-

1. फ्रांसीसी दार्शनिकों ने क्रांतिकारी विचार प्रदान किए एवं फ्रांस के लोगों को अपने अधिकारों के लिए लड़ने हेतु प्रेरित किया। उन्होंने सम्राट की अक्षमता की सफलतापूर्वक कलई खोली और लोगों को उसे चुनौती देने के लिए उकसाया।
2. इन दार्शनिकों के इन विचारों पर सैलून एवं कॉफी-घरों में गहन चर्चा हुई और ये विचार पुस्तकों एवं अखबारों के द्वारा जनसाधारण के बीच फैल गए। इसने 1789 ई. में होने वाली क्रांति का मार्ग प्रशस्त किया।
3. जॉन लॉक ने राजा के दैवीय एवं स्वेच्छाचारी सिद्धान्त को नकार दिया।
4. रूसो ने लोगों एवं उनके प्रतिनिधियों के बीच एक सामाजिक करार पर आधारित सरकार का विचार सामने रखा।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
फ्रांसीसी क्रान्ति की शुरुआती घटनाओं का विश्लेषण कीजिए।
उत्तर:
(i) एस्टेट्स जनरल की बैठक- 5 मई, 1789 ई. को फ्रांस के शासक लुई सोलहवें ने नए करों के प्रस्ताव को 1614 ई. में निर्धारित संगठन के आधार पर वर्साय के महल में एस्टेट्स जनरल की बैठक बुलाई। इस सभा में प्रथम और द्वितीय एस्टेट के 300-300 प्रतिनिधि और तृतीय एस्टेट के 600 प्रतिनिधियों को बुलाया गया। मतदान की प्राचीन पद्धति के अनुसार एस्टेट के प्रत्येक वर्ग को एक मत देने का अधिकार दिया गया था लेकिन लुई सोलहवाँ लोकतांत्रिक सिद्धान्त के आधार पर एक व्यक्ति एक मत’ को अपनाने के स्थान पर (UPBoardSolutions.com) कुलीन-वर्ग और साधारण वर्ग की माँगों के बीच समझौता कराना चाहता था। लुई चाहता था कि वित्तीय प्रश्न पर एक व्यक्ति एक मत’ का सिद्धान्त अपनाया जाए तथा अन्य माँगों पर वर्ग के आधार पर मतदान का सिद्धान्त अपनाया जाए।

(ii) राष्ट्रीय सभा की स्थापना- 6 मई, 1789 ई. को राष्ट्रीय सभा की बैठक के दूसरे दिन यह प्रश्न उपस्थित हुआ कि तीन एस्टेट के सदस्य अलग-अलग भवनों में मतदान करेंगे या एक साथ एक भवन में मतदान करेंगे। सर्वसाधारण वर्ग ने अलग बैठने से मना कर दिया। सरकार ने इस गतिरोध को समाप्त करने का कोई प्रयास नहीं किया। अंततः सर्वसाधारण वर्ग के प्रतिनिधियों ने स्वयं को राष्ट्रीय सभा घोषित करके एक क्रान्तिकारी कदम उठाया। क्रमशः कुलीन व पादरी वर्ग के लोग राष्ट्रीय सभा में सम्मिलित हो गए। अंततः 26 जून को लुई सोलहवें ने विवश होकर कुलीन वर्ग का सर्वसाधारण वर्ग के साथ बैठक का आदेश जारी कर दिया।

(iii) संविधान का प्रारूप- राष्ट्रीय सभा ने संविधान का प्रारूप तैयार कर दिया जिसका प्रमुख उद्देश्य सम्राट की शक्तियों को सीमित करना तथा एक संवैधानिक राजतंत्र की स्थापना करना था जिसमें शक्तियों को विधायिका, कार्यपालिका व न्यायपालिका में बाँटा जा सके।

(iv) बास्तील का पतन- किसी अप्रिय स्थिति से निपटने के लिए सम्राट ने पेरिस में सेना को एकत्रित करना आरम्भ कर दिया। सेना को एकत्रित होता देख जन आक्रोश भड़क उठा। पेरिस में आर्थिक असन्तोष को लेकर जगहजगह दंगे भड़क उठे। ये दंगे उस भुखमरी, महँगाई और बेरोजगारी के फलस्वरूप शुरू हुए थे, जो तत्कालीन पेरिस में व्याप्त थी। आक्रोशित जनता ने 14 जुलाई को बास्तील के किले पर धावा बोल दिया। बास्तील का पतन निरंकुश शासन के पतन का प्रतीक था। फ्रांस में प्रत्येक वर्ष 14 जुलाई का दिन राष्ट्रीय (UPBoardSolutions.com) त्योहार के रूप में मनाया जाता है। धीरे-धीरे यह आंदोलन गाँवों में फैल गया। किसानों ने ग्रामीण किलों को नष्ट करके अन्न भंडारों को लूट लिया और लगान संबंधी दस्तावेजों को नष्ट कर दिया गया। कुलीन-वर्ग के लोग बड़ी संख्या में दूसरे क्षेत्रों अथवा देशों में पलायन कर गए।

(v) संवैधानिक राजतंत्र की स्थापना- जनता की शक्ति को भाँपते हुए फ्रांस के राजा लुई सोलहवें ने संवैधानिक राजतंत्र को मान्यता प्रदान कर दी। इस प्रकार फ्रांस में संवैधानिक राजतंत्र की स्थापना हो गई। राष्ट्रीय सभा ने एक आदेश पारित किया जिसके द्वारा धार्मिक करों को समाप्त कर दिया गया, चर्च के स्वामित्व वाली जमीन जब्त कर ली गई, पादरी-वर्ग को उसके विशेषाधिकारों को छोड़ने के लिए विवश किया गया तथा सामंती व्यवस्था के उन्मूलन का आदेश पारित किया गया।

प्रश्न 2.
फ्रांस की क्रान्ति के समय फ्रांस की राजनीतिक स्थिति का विवेचन कीजिए।
उत्तर:
(i) फ्रांस की क्रान्ति के समय फ्रांस पर लुई सोलहवें को शासन था। 1774 ई. में अपने पितामह की मृत्यु के बाद वह कठिन परिस्थिति में सिंहासनारूढ़ हुआ, उस समय राजकोष रिक्त था। राजा के ऊपर अत्यधिक ऋण भार था। इस परिस्थिति से बाहर निकलने के लिए जिस योग्यता की आवश्यकता थी, वह लुई में नहीं थी।

(ii) दूसरे फ्रांसीसी राजाओं की भाँति उसकी पत्नी मैरी इंटोइनेट का शासन पर अत्यधिक प्रभाव था। उसकी इच्छा शक्ति बड़ी दृढ़ थी, उसमें साहस था और तुरंत निर्णय भी कर सकती थी। इस प्रकार जो गुण राजा में नहीं थे वे उसमें विद्यमान थे परन्तु उसमें भी शासन की समस्याओं को समझने तथा (UPBoardSolutions.com) उनका समाधान करने की योग्यता नहीं थी। उसे अपने आमोद-प्रमोद से मतलब था। वह सदा लोभी, चाटुकारों से घिरी रहती थी जो उस समय की व्यवस्था से लाभ उठाते थे और इसी कारण सुधार के शत्रु थे।

वह शासन-कार्य में हस्तक्षेप करती रहती थी, मंत्रियों की नियुक्ति में दखल देती थी और सदा षड्यंत्रों में लगी रहती थी जिसके परिणाम सदा फ्रांस के हित के विपरीत होते थे। इन कारणों से तथा उसके विलासमय जीवन एवं अत्यधिक खर्चीले रहन-सहन से राज्य की कठिनाइयाँ बढ़ती रहीं। इस काल में फ्रांस का शासन भी बड़ा अक्षम, अव्यवस्थित और खर्चीला था। शासन का प्रमुख राजा था। उसकी सहायता के लिए पाँच समितियाँ होती थीं जो कानून बनाती थीं, राज्यादेश निकालती थीं और राज्य का समस्त
आंतरिक एवं बाह्य कार्य-संचालन करती थीं। यह व्यवस्था राजधानी में थी।

(iii) तत्कालीन फ्रांस के प्रांतीय शासन को दो प्रकार के प्रांतों में बाँटा गया था। एक प्रकार के प्रांत गवर्नमेंट कहलाते थे, जिनकी संख्या 40 थी। इनमें से अधिकांश फ्रांस के प्राचीन प्रांत थे। इनका शासन में कोई सहभागिता नहीं था। इन प्रांतों के गवर्नर उच्च वर्ग के कुलीन लोग होते थे। ये लोग अधिक वेतन पाते थे और राजा के सानिध्य में ऐशो-आराम की जिन्दगी व्यतीत करते थे।

(iv) शासन का वास्तविक कार्य फ्रांस के 36 अन्य प्रान्त करते थे, जिन्हें जेनरेलिटी कहते थे। प्रत्येक जेनरेलिटी में राजा द्वारा नियुक्त एक कर्मचारी होता था जिसे इंटेंडेट कहते थे। ये कर्मचारी मध्यम वर्ग के लोग होते थे तथा राजा के आदेशों का पालन करते थे। इन्हें जन आकांक्षाओं की ओर ध्यान (UPBoardSolutions.com) देने की स्वतंत्रता नहीं थी। इसलिए ये अपने अधीन काम करने वालों में बहुत अलोकप्रिय होते थे।

(v) सरकारी पदों पर नियुक्ति योग्यता के आधार पर नहीं बल्कि पहुँच के आधार पर होती थी। स्थानीय स्वशासन की कोई व्यवस्था नहीं थी।

(vi) स्थानीय कर्मचारियों को भी छोटी-छोटी बातों के लिए केन्द्र से आदेश प्राप्त करना पड़ता था। इस तरह शासन में जनता की भूमिका नगण्य थी। इसी के परिणामस्वरूप क्रांति के समय जब जनता ने शासन-सूत्र अपने हाथ में लिया तो अनेक गल्तियाँ भी कीं।

प्रश्न 3.
फ्रांस के नए संविधान में शक्तियों का विभाजन किस प्रकार किया गया था? स्पष्ट कीजिए।
उत्तर:
फ्रांस में नया संविधान बनाने के लिए राष्ट्रीय सभा ने 6 जुलाई, 1789 को एक समिति गठित की थी। इस नवनियुक्त समिति ने दो आधार पर संविधान तैयार किया-
(i) जनता की प्रभुता और
(ii) शक्ति विभाजन।

इस तरह संविधान पर मांटेस्क्यू का प्रभाव स्पष्ट था। संविधान में शक्तियों का विभाजन-

1. विधायिका,
2. कार्यपालिका और
3. न्यायपालिका के मध्य किया गया जिनका विवरण इस प्रकार है–

(1) विधायिका- नए संविधान के अन्तर्गत एक सदनीय विधान सभा की स्थापना की गयी। इसमें प्रत्यक्ष रूप से निर्वाचित 745 सदस्य रखे गए, जिनका कार्यकाल दो वर्ष निर्धारित किया गया। निर्वाचन के लिए नागरिक दो भागों में विभक्त किए गए। जिन नागरिकों की अवस्था कम से कम 25 वर्ष की थी, जो कम से कम 3 दिन की आय कर के रूप में देते थे और जिनके नाम नगरपालिका के रजिस्टरों में तथा राष्ट्रीय रक्षक-दल में दर्ज थे वे सक्रिय नागरिकों की श्रेणी में रखे गए, शेष निष्क्रिय नागरिक रहे। सक्रिय नागरिक प्रति सौ (UPBoardSolutions.com) नागरिकों के लिए एक फ्रांसीसी क्रान्ति निर्वाचक चुनते थे और इन निर्वाचकों का ‘निर्वाचक-मंडल’ प्रतिनिधि चुनता था। निर्वाचक के लिए यह आवश्यक था कि वह संपत्ति का स्वामी हो और वर्ष में 10 दिन की आय कर के रूप में देता हो।

प्रतिनिधि कोई भी सक्रिय नागरिक चुना जा सकता था, उसके लिए भूमि का स्वामी होना और 54 फ्रैंक कर के रूप में देना आवश्यक था। परन्तु न्यायिक अथवा प्रशासनिक पद पर नियुक्त कोई भी व्यक्ति विधान-सभा का सदस्य नियुक्त नहीं हो सकता था। इस विधान सभा को कानून-निर्माण के पूर्ण अधिकार थे। उस पर एकमात्र नियंत्रण राजा के ‘स्थगनकारी निषेध’ (सस्पेंशन वीटो) का था। राजा किसी भी कानून को दो सत्रों के लिए स्वीकार करने से इनकार कर सकता था, परन्तु उसका यह अधिकार आर्थिक बातों में लागू नहीं होता था।

(2) कार्यपालिका- कार्यपालिका प्रमुख के रूप में राजा का अस्तित्व बना रहा। उसे मंत्रियों की नियुक्ति, सेना का नेतृत्व एवं विदेश नीति को निर्धारित करने का अधिकार प्राप्त था, लेकिन विधान सभा उसके प्रभाव से पूरी तरह मुक्त थी। वह विधानसभा के अधिवेशन आमंत्रित नहीं कर सकता था, न उसे भंग कर सकता था और न ही उसके सामने कानून के प्रस्ताव ही प्रस्तुत कर सकता था। उसे केवल स्थगनकारी निषेध का अधिकार मिला। न्यायालयों तथा न्यायाधीशों पर भी उसका कोई अधिकार नहीं रहा। उसके मंत्री विधानसभा (UPBoardSolutions.com) के सदस्य नहीं हो सकते थे और इस तरह उन पर सभा का कोई नियंत्रण नहीं था। इस प्रकार राष्ट्रीय सभा ने इंग्लैण्ड का अनुकरण करके सांविधानिक एकतंत्र स्थापित किया, परन्तु इसके साथ मांटेस्क्यू के सिद्धान्त तथा अमेरिका के उदाहरण के अनुसार कार्यपालिका और विधायिका का परस्पर कोई संबंध नहीं रखा।

(3) न्यायपालिका- फ्रांस की राष्ट्रीय सभा ने देश में प्रचलित प्राचीन न्याय-व्यवस्था के स्थान पर नए केन्द्रीय एवं स्थानीय न्यायालयों का निर्माण किया। इन न्यायालयों के न्यायाधीशों के लिए सक्रिय न्यायाधीशों द्वारा निर्वाचन की व्यवस्था की गयी। मुद्रायुक्त पत्रों का चलन अवरुद्ध कर दिया गया (UPBoardSolutions.com) और जूरी द्वारा मुकदमे पर विचार करने की व्यवस्था की गयी।

प्रश्न 4.
पुरुष एवं नागरिक घोषणा-पत्र के प्रमुख बिन्दुओं को स्पष्ट कीजिए।
उत्तर:

1. मनुष्य स्वतंत्र पैदा होते हैं, स्वतंत्र रहते हैं जो और उनके अधिकार समान होते हैं।
2. कानून सम्मत प्रक्रिया के बाहर किसी व्यक्ति को न तो दोषी ठहराया जा सकता है और न ही गिरफ्तार या नजरबंद किया जा सकता है।
3. स्वतंत्रता का आशय ऐसे काम करने की शक्ति से है जो औरों के लिए नुकसानदेह न हो।
4. समाज के लिए किसी भी हानिकारक कृत्य पर पाबंदी लगाने का अधिकार कानून के पास है।
5. कानून सामान्य इच्छा की अभिव्यक्ति है। सभी नागरिकों को व्यक्तिगत रूप से या अपने प्रतिनिधियों के माध्यम से इसके निर्माण में भाग लेने का अधिकार है। कानून की नजर में सभी नागरिक समान हैं।
6. प्रत्येक नागरिक बोलने, लिखने और छापने के लिए आजाद है। लेकिन कानून द्वारा निर्धारित प्रक्रिया के तहत ऐसी स्वतंत्रता के दुरुपयोग की जिम्मेदारी भी उसी की होगी।
7. सार्वजनिक सेना तथा प्रशासन के खर्चे चलाने के लिए एक सामान्य कर लगाना अपरिहार्य था। सभी नागरिकों पर उनकी आय के अनुसार समान रूप से कर लगाया जाना चाहिए।
8. चूँकि सम्पत्ति का अधिकार एक पावन एवं अनुलंघनीय अधिकार है, अतः किसी भी व्यक्ति को इससे वंचित नहीं किया जा सकता है, जब तक कि विधि द्वारा स्थापित प्रक्रिया के तहत सार्वजनिक आवश्यकता के लिए संपत्ति का अधिग्रहण करना आवश्यक न हो। ऐसे मामले में अग्रिम मुआवजा जरूर दिया जाना चाहिए।
9. प्रत्येक राजनीतिक संगठन का लक्ष्य आदमी के नैसर्गिक एवं अहरणीय अधिकारों को संरक्षित रखना है। ये अधिकार हैं—स्वतंत्रता, संपत्ति, सुरक्षा एवं शोषण के प्रतिरोध का अधिकार।
10. समग्र सम्प्रभुता का स्रोत राज्य में निहित है; कोई भी समूह या व्यक्ति ऐसा अनधिकार प्रयोग नहीं करेगा जिसे जनता की सत्ता की स्वीकृति न मिली हो।

प्रश्न 5.
फ्रांस में राजतंत्र का अन्त एवं गणतन्त्र की स्थापना किस प्रकार हुई?
उत्तर:
1791 ई. में फ्रांस की राष्ट्रीय सभा ने संविधान का पूर्ण प्रपत्र तैयार किया। संविधान द्वारा राजा के अधिकार सीमित करते हुए शासन की शक्तियाँ विधायिका, कार्यपालिका एवं न्यायपालिका में वितरित की गयीं। इस प्रकार फ्रांस को संवैधानिक राजतंत्र में रूपांतरित किया गया। संविधान का प्रारम्भ (UPBoardSolutions.com) पुरुष एवं नागरिक अधिकारों की घोषणा के साथ हुआ जिन्हें नैसर्गिक एवं अहरणीय रूप में स्थापित किया गया जिन्हें कोई नहीं छीन सकता था। यह सरकार का कर्तव्य था कि वह प्रत्येक नागरिक के प्राकृतिक अधिकारों की रक्षा करे।

यद्यपि लुई सोलहवें ने संविधान पर हस्ताक्षर कर दिए थे बथापि उसने प्रशा के राजा से गुप्त समझौता कर लिया। इससे पहले कि लुई सोलहवाँ सन् 1789 की गर्मियों से चली आ रही घटनाओं को दबाने की अपनी योजनाओं पर अमल कर पाता, राष्ट्रीय सभा ने प्रशा एवं ऑस्ट्रिया के विरुद्ध युद्ध की घोषणा का प्रस्ताव पारित कर दिया। जनसंख्या के बड़े वर्गों का यह विश्वास था कि क्रांति को आगे बढ़ाने की आवश्यकता थी क्योंकि 1791 ई. के संविधान ने धनी वर्ग को ही राजनैतिक अधिकार प्रदान किए थे।

राजनैतिक क्लब उन लोगों के लिए एक महत्त्वपूर्ण बैठक स्थल बन गए जो सरकार की नीतियों पर चर्चा करना चाहते थे और अपनी रणनीति की योजना बनाई जाती थी। इनमें से एक जैकोबिन क्लब था। जैकोबिन क्लब के सदस्य मुख्यतः समाज के कम समृद्ध वर्ग से सम्बन्ध रखते थे जैसे कि छोटे दुकानदार, कारीगर, जूते बनाने वाले, पेस्ट्री बनाने वाले, घड़ीसाज, छपाई करने वाले, नौकर तथा दैनिक (UPBoardSolutions.com) मजदूर आदि। उनके नेता का नाम मैक्समिलियन रोब्सपियर था। इन जैकोबिन लोगों को सौं कुलॉत के नाम से जाना जाने लगा। सौं कुलॉत लोग इसके अतिरिक्त एक लाल टोपी भी पहनते थे जो आजादी का प्रतीक थी।

1792 ई. की गर्मियों में जैकोबिन लोगों ने प्रशा के विरुद्ध विद्रोह की योजना बनाई जो कि कम आपूर्ति एवं खाने-पीने की चीजों की बढ़ती कीमतों से गुस्साए हुए थे। 10 अगस्त की सुबह उन्होंने ट्यूलेरिए के महल पर आक्रमण कर दिया, राजा के रक्षकों को मार डाला और स्वयं राजा को घण्टों तक बंधक बनाए रखा। बाद में सभा ने शाही परिवार को जेल में डाल देने का प्रस्ताव पारित किया। चुनाव कराए गए तथा तब से 21 वर्ष या उससे अधिक आयु के सभी पुरुष, चाहे उनके पास संपत्ति हो या नहीं, सभी को वोट डालने का अधिकार मिल गया।

फ्रांस में नवनिर्वाचित सभा को कन्वेंशन नाम दिया गया। 21 सितम्बर, 1792 ई. को फ्रांस गणतन्त्र घोषित कर दिया गया। इसी के साथ फ्रांस में वंशानुगत राजतंत्र का अन्त हो गया। (UPBoardSolutions.com) न्यायालय ने राजद्रोह के आरोप में लुई सोलहवें कों मृत्युदण्ड की सजा सुनाई। प्लेस डी ला कन्कोर्ड में 21 जनवरी, 1793 ई. को लुई सोलहवें को फाँसी दे दी गयी और इसके बाद रानी मैरी इंटोइनेट को भी फाँसी दे दी गयी।

प्रश्न 6.
ओलिम्प डि गॉजेस के घोषणा-पत्र में उल्लिखित मूल अधिकारों का वर्णन कीजिए।
उत्तर:
ओलिम्प डि गाँजेस के घोषणा-पत्र में उल्लिखित मूल अधिकारों का वर्णन इस प्रकार है-

1. कानून सामान्य इच्छा की अभिव्यक्ति होनी चाहिए। सभी महिला एवं पुरुष नागरिकों का या तो व्यक्तिगत रूप से
   या अपने प्रतिनिधियों के माध्यम से विधि-निर्माण में दखल होना चाहिए। यह सभी के लिए समान होना चाहिए। सभी महिला एवं पुरुष नागरिक अपनी योग्यता एवं प्रतिभा के बल पर समान रूप से एवं बिना किसी भेदभाव के हर तरह के सम्मान वे सार्वजनिक पद के हकदार हैं।
2. कोई भी महिला अपवाद नहीं है। वह विधिसम्मत प्रक्रिया द्वारा अपराधी ठहराई जा सकती है, गिरफ्तार और नजरबंद की जा सकती है। पुरुषों की तरह महिलाएँ भी इस कठोर कानून का पालन करें।
3. औरत जन्मना स्वतंत्र है और अधिकारों में पुरुष के समान है।
4. सभी राजनीतिक संगठनों का लक्ष्य पुरुष एवं महिला के नैसर्गिक अधिकारों को संरक्षित करना है। ये अधिकार हैं स्वतंत्रता, संपत्ति, सुरक्षा और सबसे बढ़कर शोषण के प्रतिरोध का अधिकार।
5. समग्र संप्रभुता का स्रोत राष्ट्र में निहित है जो पुरुषों एवं महिलाओं के संघ के सिवाय कुछ नहीं है।

प्रश्न 7.
फ्रांस की क्रान्ति के बाद महिलाओं की स्थिति में आए परिवर्तनों का विवेचन कीजिए।
उत्तर:
फ्रांस की क्रान्ति के बाद महिलाओं की स्थिति में निम्न परिवर्तन घटित हुए-
(i) फ्रांस में आतंक के राज के दौरान देश में सक्रिय महिला अधिकारों के प्रति चेतना का प्रसार करने वाले क्लबों को | बन्द कर दिया गया। साथ ही महिलाओं की राजनीतिक गतिविधियों पर अंकुश लगा दिया गया। अनेक राजनीतिक रूप से सक्रिय महिलाओं को बन्दी बनाया गया तथा उनमें से कुछ को मृत्युदण्ड दे दिया गया।

(ii) मताधिकार और समान वेतन के लिए महिलाओं का आंदोलन अगली सदी में भी अनेक देशों में चलता रहा।
मताधिकार का संघर्ष उन्नीसवीं सदी के अंत एवं बीसवीं सदी के प्रारंभ तक अंतर्राष्ट्रीय मताधिकार आंदोलन के जरिए जारी रहा। क्रांतिकारी आंदोलन के दौरान फ्रांसीसी महिलाओं की (UPBoardSolutions.com) राजनीतिक सरगर्मियों को प्रेरक स्मृति के रूप में जिंदा रखा गया। अंततः सन् 1946 में फ्रांस की महिलाओं ने मताधिकार हासिल कर लिया।

(iii) फ्रांस की क्रांति के काल में ही महिलाओं ने अपने अधिकारों की माँग को लेकर अनेक महिला राजनीतिक क्लबों की स्थापना आरम्भ कर दी थी। ‘द सोसाइटी ऑफ रेवलूशनरी एण्ड रिपब्लिकन विमेन’ सबसे मशहूर क्लब था। उनकी एक प्रमुख माँग यह थी कि महिलाओं को पुरुषों के समान राजनीतिक अधिकार प्राप्त होने चाहिए। महिलाएँ इस बात से निराश हुईं कि 17 ई. के संविधान में उन्हें निष्क्रिय नागरिक का दर्जा दिया गया था। महिलाओं ने मताधिकार, असेंबली के लिए चुने जाने तथा राजनीतिक पदों की माँग रखी। उनका
मानना था कि तभी नई सरकार में उनके हितों का प्रतिनिधित्व हो पाएगा।

(iv) प्रारम्भिक वर्षों में क्रांतिकारी सरकार ने महिलाओं के जीवन में सुधार लाने वाले कुछ कानून लागू किए। सरकारी विद्यालयों की स्थापना के साथ ही सभी लड़कियों के लिए स्कूली शिक्षा को अनिवार्य बना दिया गया। अब पिता उन्हें उनकी मर्जी के खिलाफ शादी के लिए बाध्य नहीं कर सकते थे। शादी को स्वैच्छिक अनुबन्ध माना गया और नागरिक कानूनों के तहत उनका पंजीकरण किया जाने लगा। (UPBoardSolutions.com) तलाक को कानूनी रूप दे दिया गया और मर्द-औरत दोनों को ही इसकी अर्जी देने का अधिकार दिया गया। अब महिलाएँ व्यावसायिक प्रशिक्षण ले सकती थीं, कलाकार
बन सकती थीं और छोटे-छोटे व्यवसाय चला सकती थीं।

प्रश्न 8.
फ्रांसीसी क्रान्ति के लिए प्रथम एस्टेट का उत्तरदायित्व सिद्ध कीजिए।
उत्तर:
फ्रांस में प्रथम एस्टेट में पादरी वर्ग को शामिल किया जाता था। इस वर्ग में एक लाख तीस हजार के लगभग पादरी थे और इनका देश की 10 प्रतिशत भूमि पर नियंत्रण था। चर्च भी किसानों से टाइद (धार्मिक कर) नामक कर वसूलता था। इन्हें सरकारी करों से मुक्ति प्राप्त थी। साथ ही चर्च राज्य को दिए जाने वाले पंचवर्षीय अनुदान के द्वारा सरकार पर वित्तीय दबाव डालने की स्थिति में थे। फ्रांस की शिक्षा पद्धति, प्रचार के साधन तथा नैतिक व अनैतिक में अन्तर करने का अधिकार भी उन्हीं के हाथ में था।

फ्रांस का चर्च 18वीं सदी में बहुत अधिक बदनाम तथा अलोकप्रिय हो गया था। इस अलोकप्रियता के कारण पादरियों के व्यक्तिगत चरित्र, एवं जीवन से कम तथा तत्कालीन ऐतिहासिक परिस्थितियों से अधिक संबद्ध थे। व्यक्तिगत तौर पर आम पादरी का आचरण अपने युग के अनुकूल ही था, उससे बुरा नहीं। लोगों की नजरों में खटकने वाली बात तो यह थी कि चर्च की बढ़ती हुई सम्पदा के साथ पादरी अपने धार्मिक (UPBoardSolutions.com) कर्तव्यों की उपेक्षा करते जा रहे थे। चर्च की अलोकप्रियता का एक मुख्य कारण फ्रांस, विशेषकर उसके नगरों तथा मध्यम-वर्ग के व्यक्तियों में लोकप्रिय होती हुई संशयवाद की प्रवृत्ति थी जिसके प्रभाव में ईश्वर का अस्तित्व तथा चर्च की उपयोगिता दोनों ही विवाद का विषय बन गए थे।

एक दूसरा कारण चर्च के सामंतीय अधिकार तथा उनका कठोरता के साथ लागू किया जाना था, जिसके कारण किसानों में उसके विरुद्ध असंतोष उत्पन्न होता रहा। अन्त में पादरीवर्ग के अन्दर ही एकता को अभाव था। चर्च के उच्च पदों पर कुलीन-वर्ग के वंशजों का एकाधिकार था और इससे छोटे पादरियों में असंतोष बढ़ा तथा वे चर्च के प्रजातंत्रीय स्वरूप की स्थापना हेतु उत्सुक हो रहे थे।

प्रश्न 9.
फ्रांस का मध्यम वर्ग तत्कालीन व्यवस्था से क्यों असन्तुष्ट था? स्पष्ट कीजिए।
उत्तर:
तत्कालीन फ्रांस के मध्यम वर्ग में लेखक, डॉक्टर, वकील, जज, अध्यापक और असैनिक अधिकारी जैसे शिक्षित व्यक्ति तथा व्यापारी, बैंकर और कारखाने वाले धनी व्यक्ति सम्मिलित थे। समाज में इस वर्ग का आर्थिक दृष्टि से अत्यन्त महत्त्व था। मध्यम वर्ग उन लोगों का अग्रगामी था, जिन्होंने 19वीं सदी में आर्थिक व सामाजिक परिवर्तन लाने में महत्त्वपूर्ण भूमिका निभायी।
मध्यम वर्ग तत्कालीन व्यवस्था से निम्न कारणों से असन्तुष्ट था-

(i) कुलीन-वर्ग के साथ ही तत्कालीन शासन-पद्धति से भी मध्यम-वर्ग के औद्योगिक एवं व्यावसायिक अंग को शिकायत थी। समाज का यह वर्ग मात्र एक उद्देश्य लेकर चल रहा था–भौतिक सम्पत्ति की वृद्धि; किन्तु तत्कालीन शासन उसके इस उद्देश्य की पूर्ति में अपनी गलत नीतियों के कारण बाधक सिद्ध हो रहा था।

(ii) मध्यम-वर्ग का बुद्धिजीवी भाग आदर्श भावना से भी प्रेरित था। यह आदर्श था विवेक एवं बुद्धि पर आधारित समाज की संरचना जिसमें सभी कुछ तर्कसंगत हो।

(iii) इतिहास में व्यापारियों-उद्योगपतियों के ये समूह बिलकुल नए थे, किन्तु अमेरिका के फ्रांसीसी उपनिवेशों से व्यापार करने के कारण ये बहुत धनी हो गए थे और इनका महत्त्व बहुत बढ़ गया था। इनमें से कुछ ने जमीन खरीद ली थी और उनके पास बड़ी-बड़ी जमींदारियाँ हो गई थीं। इन व्यक्तियों के पास पर्याप्त धन था, इसलिए राज्य, पादरी और अभिजात-वर्ग सभी इनके ऋणी थे।

सामाजिक दृष्टि से वह स्तर पर आधारित श्रेणीबद्ध समाज के विरोधी न होकर समर्थक ही थे और उनकी महत्त्वाकांक्षा थी कि सामाजिक सीढ़ी की ऊँची पदान पर उन्हें स्थान मिले किन्तु रक्त के आधार पर श्रेणीबद्ध फ्रेंच समाज में कुलीन-वर्ग ने उस स्थान से उन्हें वंचित कर रखा था। इस प्रकार 18वीं शताब्दी का फ्रेंच बुर्जुआ (मध्यम-वर्ग) अपने को एक अजीब स्थिति में पाता था। उसके पास धन था, उसके पास (UPBoardSolutions.com) योग्यता थी किन्तु इस धन और योग्यता के अनुरूप समाज में प्रतिष्ठा नहीं थी, सरकारी पद नहीं थे। इस विषमता को तभी दूर किया जा सकता था जब सामंतीय समाज के ढाँचे को नष्ट कर दिया जाए।

प्रश्न 10.
क्रांति से पहले की फ्रांस की आर्थिक स्थिति का विश्लेषण कीजिए।
उत्तर:
क्रान्ति ( 1789 ) से पहले फ्रांस की आर्थिक स्थिति- फ्रांस की आर्थिक स्थिति अत्यन्त कठिन दौर से गुजर रही थी, ऐसे में सरकार की फिजूलखर्ची ने दशा को और भी शोचनीय बना दिया। उस समय फ्रांस में कर दो प्रकार के थेप्रत्यक्ष और परोक्ष। प्रत्यक्ष कर (टाइल) जायदाद, व्यक्तिगत संपत्ति तथा आय पर लिए जाते थे। कुलीन वर्ग और पादरी इनमें से कुछ करों से तो बिल्कुल मुक्त थे और शेष करों से प्रायः मुक्त थे, क्योंकि कर निर्धारण करने वाले राज्य-कर्मचारी डरकर उन पर नाममात्र का कर लगाया करते थे। उसकी सारी कमी शेष जनता पर कर लगाकर पूरी की जाती थी और इस प्रकार उस पर करों का अत्यधिक भार था। कुलीन-वर्ग और पादरी भी सम्पन्न थे, रुपये में तीन आने भी कर नहीं देते थे जबकि मध्यमवर्ग के व्यक्ति से प्रायः दस गुना कर वसूल लिया जाता था। परोक्ष करों में मुख्य रूप से नमक, शराब, तंबाकू आदि पर लिए जाने वाले कर थे।

दूषित कर-व्यवस्था के फलस्वरूप राज्य जनता की सम्पत्ति का राष्ट्रीय कामों के लिए उपयोग नहीं कर सकता था। उसकी वाणिज्य-नीति भी ऐसी थी जिसमें राज्य में सम्पत्ति की उत्पत्ति भी पूरी तरह न हो पाती थी। फ्रेंच व्यापार अभी पूरी तरह से उन्नति नहीं कर पाया था। इस दोषपूर्ण अर्थ-व्यवस्था का परिणाम यह निकला कि राज्य का व्यय सदैव ही उसकी आय से अधिक रहा था तथा इस घाटे की पूर्ति हेतु सरकार को ऋण का आश्रय लेना पड़ा। अमेरिका के ब्रिटिश उपनिवेशों के स्वतंत्रता-संग्राम में भाग लेने के सरकारी निर्णय ने स्थिति को (UPBoardSolutions.com) और अधिक गंभीर बना दिया। अगर इस संघर्ष में सम्मिलित होने के समय को फ्रांस सरकार के संकट का प्रारम्भ-बिन्दु माना जाए तो अत्युक्ति न होगी। इस संघर्ष की सफल समाप्ति ने फ्रांस में स्वतंत्रता की भावना को बल ही प्रदान नहीं किया अपितु उसका आर्थिक भार सरकार के लिए एक असह्य बोझ सिद्ध हुआ जिसे सम्हाल न सकने के कारण वह टूटकर बिखर गई।

Hope given UP Board Solutions for Class 9 Social Science History Chapter 1 are helpful to complete your homework.

If you have any doubts, please comment below. UP Board Solutions try to provide online tutoring for you.