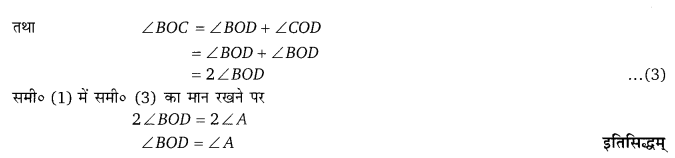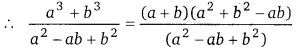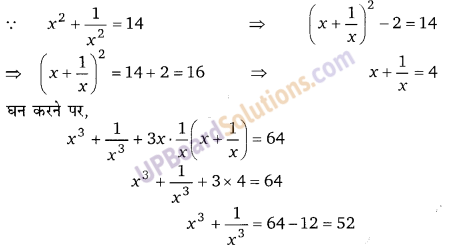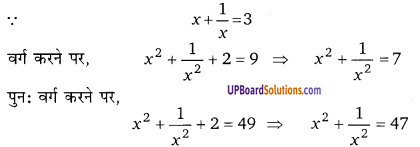Class 9

UP Board Solutions for Class 9 Home Science Chapter 12 भोजन का पाचन एवं सम्बन्धित शरीर-क्रिया विज्ञान

These Solutions are part of UP Board Solutions for Class 9 Home Science . Here we have given UP Board Solutions for Class 10 Home Science Chapter 12 भोजन का पाचन एवं सम्बन्धित शरीर-क्रिया विज्ञान.

विस्तृत उत्तरीय प्रश्न

प्रश्न 1:
पाचन तन्त्र के अंगों का चित्र सहित वर्णन कीजिए। छोटी आँत में भोजन किस प्रकार पचता है?
या
आहारनाल का चित्र बनाइए और उसके मुख्य भागों के नाम लिखिए। या पाचन नलिका का चित्र बनाइए तथा पाचन में सक्रिय रूप से भाग लेने वाले अंगों का वर्णन कीजिए।
उत्तर:
आहारनाल एवं पाचन तन्त्र

भोजन एवं पेय पदार्थों का हमारे शरीर में प्रवेश मुख द्वारा होता है तथा पाचन क्रिया के पश्चात् इनके अवशिष्ट पदार्थों का निकास मल द्वार द्वारा होता है। मुख एवं मल द्वार को परस्पर सम्बन्धित करने वाली नली को पाचन नली अथवा आहारनाल कहते हैं। आहारनाल के विभिन्न भाग हैं, जिनका आकार तथा कार्य भिन्न-भिन्न होता है। आहारनाल के सभी भाग मुख्य रूप से ग्रहण किए गए आहार के पाचन का कार्य करते हैं। (UPBoardSolutions.com) आहारनाल के अतिरिक्त अर्थात् इसके बाहर भी कुछ ऐसे अंग हैं जो आहार के पाचन में विशेष सहायता एवं योगदान प्रदान करते हैं। इन अंगों को आहार के पाचन में सहायक अंग माना जाता है। यकृत, अग्न्याशय तथा पित्ताशय इसी वर्ग के अंग हैं। आहारनाल तथा इससे सम्बन्धित पाचन क्रिया में सहायक अंग सम्मिलित रूप से पाचन तन्त्र अथवा पाचन संस्थान का निर्माण करते हैं अर्थात् आहार के पाचन एवं शोषण में प्रत्यक्ष रूप से भाग लेने वाले तथा अप्रत्यक्ष रूप से सहायता प्रदान करने वाले सभी अंगों को सम्मिलित रूप से पाचन तन्त्र कहा जा सकता है। इस प्रकार हमारे पाचन तन्त्र के दो भाग होते हैं

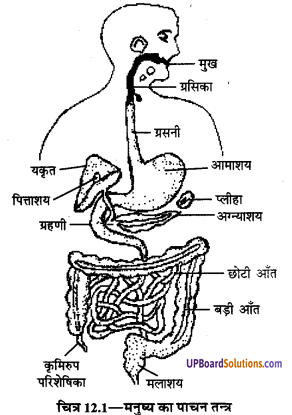
(1) आहारनाल तथा
(2) पाचन क्रिया में सहायक अंग।

(i) आहारनाल
यह पाचन तन्त्र को मुख्य भाग है। यह लगभग 9 मीटर लम्बी होती है। समान व्यास की न होकर यह ‘भिन्न-भिन्न स्थानों पर भिन्न-भिन्न आकार के अंगों का निर्माण करती है। आहारनाल के मुख्य अंग निम्नलिखित हैं

1. मुख तथा मुखगुहा,
2.  ग्रसनी,
3. ग्रासनली,
4.  आमाशय,
5.  पक्वाशय,
6.  छोटी आँत,
7. बड़ी आँत।

(i) मुख तथा मुखगुहा:
दो ओष्ठों से घिरा आहारनाल का प्रवेश द्वार मुख कहलाता है, जो कि अन्दर की ओर मुखगुहा में खुलता है। मुखगुहा आगे की ओर ऊपर-नीचे जबड़ों तथा पीछे की ओर गालों से घिरी होती है। मुखगुहा की छत तालू कहलाती है। दाँत मुखगुहा के महत्त्वपूर्ण अंग हैं। ये ऊपर व नीचे के जबड़ों में कुल (UPBoardSolutions.com) मिलाकर संख्या में 32 होते हैं। ये भोजन को चबाने का कार्य करते हैं। मुखगुहा में तीन जोड़ी लार ग्रन्थियाँ होती हैं, जिनसे निकलने वाली लार चबाते समय भोजन में मिलकर उसे लसलसा बनाती है। लार में टायलिन नामक किण्व (एन्जाइम) होती है जो कि श्वेतसारी पदार्थ (स्टार्च) को शर्करा में परिवर्तित कर देती है।

(ii) ग्रसनी( फैरिंक्स):
यह कीप के आकार की रचना होती है जो कि मुखगुहा के पीछे की ओर स्थित होती है।

(iii) ग्रासनली (इसोफेगस):
यह लगभग 25 सेमी लम्बी नली होती है जो कि गर्दन से उदरगुहा तक स्थित होती है। इसे अन्ननलिका (oesophagus) भी कहते हैं। इसकी भीतरी सतह श्लेष्मिक कला की बनी होती है, जिससे श्लेष्म निकला करता है।

(iv) आमाशय-आमाशय (stomach):
मशक के आकार का होता है तथा उदरगुहा में अनुप्रस्थ रूप में स्थित होता है। इसका एक सिरा बड़ा, परन्तु दुसरा सिरा सँकरा होता है। भोजन नलिका (इसोफेगस) का अन्तिम सिरा आमाशय से जुड़ा रहता है। इसकी लम्बाई 25 सेमी तथा चौड़ाई 10 सेमी होती है। इसमें ग्रास नली से भोजन आता है। आमाशय की दीवार में श्लेष्म ग्रन्थियों के अतिरिक्त जठर ग्रन्थियाँ भी होती हैं।

(v) पक्वाशय-आमाशय से आगे चलने पर पाचन:
तन्त्र का जो अंग प्रारम्भ होता है, उसे पक्वाशय या ग्रहणी (duodenum) कहते हैं। इसका आरम्भ आमाशय के निचले द्वारे से होता है। इसकी आकृति अंग्रेजी वर्णमाला के अक्षर ‘C’ के समान होती है। इसकी लम्बाई लगभग 25 सेमी होती है। यकृत से पित्त-नली तथा अग्न्याशय से क्लोम नली इसके निचले हिस्से में आकर मिलती है।

(vi) क्षुद्रांत्र अथवा छोटी आँत:
रचना-यह लगभग 5 मीटर लम्बी अत्यधिक कुण्डलित नली होती है, इसको दो भागों में विभाजित किया जा सकता है

(क) मध्यान्त्र:
यह लगभग 2.5 मीटर लम्बी व 4 सेमी चौड़ी नली होती है। इसकी दीवारों में रुधिरवाहिनियों का जाल बिछा होता है।
(ख) क्षेषान्त्र:
यह लगभग 2.25 मीटर लम्बी व 4 सेमी चौड़ी अत्यधिक कुण्डलित नली होती है। ग्रहणी को छोड़कर शेष छोटी आँत में अँगुली के आकार की रचनाएँ होती हैं, जो कि रसांकुर कहलाती हैं। सलवटों एवं रसांकुरों जैसे उभारों के फलस्वरूप आंत्रीय दीवार की अवशोषण सतह कई सौ गुना बढ़ (UPBoardSolutions.com) जाती है। आन्त्रीय दीवार में रसांकुरों के बीच-बीच में श्लेष्मिक कला आन्त्रीय ग्रन्थियों का निर्माण करती हैं, जिनमें भोजन के पाचन में सहायक आन्त्रीय रस बना करते हैं।

(vii) बड़ी आँत अथवा वृहदान्त्र:
बड़ी आँत लगभग 1.5 से 2.0 मीटर लम्बी व 6 सेमी चौड़ी होती है। इनके तीन प्रमुख भाग होते हैं

(क) अन्धात्र:
यह लगभग 6 सेमी लम्बी व 7.5 सेमी चौड़ी थैली के आकार की रचना होती है। इसके एक ओर लगभग 9 सेमी लम्बी उँगली के आकार की अवशेष रचना निकलती है। इसे कृमिरूप परिशेषिका (वर्मीफोर्म एपेन्डिक्स) कहते हैं। इसका हमारे शरीर में कोई उपयोग या कार्य नहीं है।

(ख) कोलोन:
यह लगभग 1.25 मीटर लम्बी व 6 सेमी चौड़ी नलिका होती है। यह उल्टे ‘C’ के आकार में रहकर सम्पूर्ण छोटी आँत को घेरे रहती है। यह अन्त में मलाशय में खुलती है।

(ग) मलाशय:
यह लगभग 12 सेमी लम्बी व 4 सेमी चौड़ी नली होती है, जिसका अन्तिम सिरा शरीर से बाहर खुलता है। इसे गुदाद्वार (एनस) कहते हैं। इसमें पाई जाने वाली मांसपेशियाँ
आवश्यकतानुसार संकुचित होकर व फैलकर गुदाद्वार को बन्द करती व खोलती हैं।

(2) पाचन क्रिया में सहायक अंग:

(1) यकृत (लिवर):
पाचन क्रिया के लिए यह एक महत्त्वपूर्ण सहायक अंग है। यह शरीर के दाहिने ओर नीचे की पसलियों के पीछे तथा मध्य पट के ठीक नीचे पाई जाने वाली भूरे रंग की शरीर की सबसे बड़ी ग्रन्थि होती है। इसका भार लगभग 1.5 किलोग्राम होता है। यकृत लगभग हरे-पीले रंग का पित्त नामक पाचक रस बनाता है जो कि यकृत वाहिनी द्वारा पित्ताशय तक पहुँचता रहता है।

(2) पित्ताशय(गॉल ब्लेडर ):
यह नाशपाती के आकार की एक थैली होती है जो कि यकृत के पीछे की ओर स्थित होती है। इसमें पित्त रस संचित रहता है, जो कि समय-समय पर आवश्यकतानुसार पित्तवाहिनी के द्वारा ग्रहणी में पहुँचता है।

(3) क्लोम अथवा अग्न्याशय (पैंक्रियास):
यह आमाशय के ठीक पीछे उदर की पिछली दीवार से सटी हुई होती है। यह ग्रहणी से प्लीहा तक फैली हुई होती है। यह लगभग 16 सेमी लम्बी व 4 सेमी चौड़ी होती है। यह अग्न्याशय रस बनाती है जो कि ग्रहणी में अग्न्याशय वाहिनी द्वारा पहुँचकर पाचन क्रिया में सहायता करता है।

प्रश्न 2:
दाँत कितने प्रकार के होते हैं? विभिन्न प्रकार के दाँतों के क्या कार्य हैं?
उत्तर:
दाँतों के प्रकार एवं कार्य दाँतों का मुख्य कार्य भोजन चबाना है। मनुष्य के दाँत जीवन में दो बार निकलते हैं; अतः मनुष्य द्विबार-दन्ती होता है। इस आधार पर मनुष्य के दाँत निम्नलिखित प्रकार के होते हैं
(1) अस्थायी या दूध के दाँत,
(2) स्थायी दाँत।

(1) अस्थायी या दूध के दाँत:
जन्म के समय ये दाँत बच्चे के मसूड़ों के अन्दर छिपे होते हैं। जन्म के 6 से 7 माह बाद बढ़ते हुए 2-3 वर्ष की आयु होने तक ये पूर्णरूप से निकल आते हैं। ये संख्या में 20 होते हैं।

(2) स्थायी दाँत:
लगभग 6 वर्ष की आयु अथवा इसके बाद दूध के दाँत गिरने लगते हैं। प्रायः 18 वर्ष तक की आयु में 28 दाँत निकलते हैं। पिछले 4 दाँत (अकल दाढ़) सामान्यत: 20-25 वर्ष की आयु में निकलते हैं। इस प्रकार कुल 32 दाँत होते हैं। इनमें से प्रत्येक जबड़े में 16 दाँत होते हैं।

स्थायी दाँतों के प्रकार

आकार एवं कार्य के आधार पर समस्त दाँतों को निम्नलिखित चार प्रकारों में वर्गीकृत किया जाता है

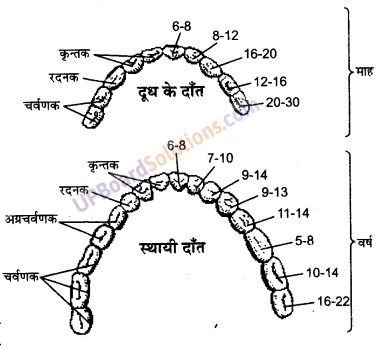
(i) कृन्तक अथवा छेदक (इनसीजर्स ):
ये सबसे आगे कीओर के संख्या में चार होते हैं। इनमें से प्रत्येक छैनी के समान धारदार होता है। ये भोजन को कुतरने के काम आते हैं।

(ii) रदनक (केनाइन):
यह कृन्तक के दोनों ओर स्थित होते हैं तथा संख्या में दो होते हैं। ये लम्बे एवं नुकीले होते हैं तथा भोजन को । चीरने-फाड़ने का कार्य करते हैं। चर्वणकर

(iii) अग्रचर्वणक( प्रिमोलर्स):
ये संख्या में चार तथा रदनक दाँतों के दोनों ओर दो-दो की संख्या में स्थित होते हैं। इनके सिरे चपटे व चौकोर होते हैं। ये भोजन को कुचलने व पीसने का कार्य करते हैं।

(iv) चर्वणक( मोलर्स):
ये संख्या में 6 तथा अग्रचर्वणक के पीछे तीन-तीन दोनों ओर स्थित होते हैं। इनके सिरे भी चपटे व चौकोर होते हैं तथा भोजन को कुचलने व पीसने का कार्य करते हैं। (UPBoardSolutions.com) दाँत ऊपर तथा नीचे के जबड़ों में बने गड्डों में दृढ़ता से स्थित होते हैं। मसूड़े इनको और दृढ़ता प्रदान करते हैं। एक वयस्क मनुष्य के 32 दाँतों को निम्नलिखित दन्त सूत्र के द्वारा प्रदर्शित किया जा सकता है

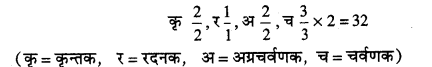
सभी प्रकार के दाँतों की संरचना लगभग समान होती है। ये जबड़े की अस्थि के गड्ढों में अपने मूल वाले भाग में जमे रहते हैं। एक सीमेन्ट जैसे पदार्थ से दाँत की अस्थि के साथ पकड़ अत्यधिक मजबूत होती है। इसके अतिरिक्त इसके निचले भाग पर मसूढ़े चढ़े रहते हैं। सभी दाँत डेन्टाइन (dentine) नामक पदार्थ से बने होते हैं। यह पदार्थ हड्डी से भी मजबूत होता है। प्रत्येक दाँत तीन भागों में विभक्त होता हैं। (UPBoardSolutions.com) दाँत अन्दर से खोखला होता है। इस खोखले भाग को दन्त गुहा (pulp cavity) कहते हैं, जो दन्त मज्जा से भरी होती है। इसमें अनेक सूक्ष्म रक्त नलिकाएँ, स्नायु जाल तथा तन्तु पाए जाते हैं। प्रत्येक दाँत के मूल में एक छोटा छेद होता है। इसी छेद से ये कोशिकाएँ तथा नलिकाएँ इत्यादि दन्त मज्जा में आती

प्रश्न 3:
आमाशय की रचना का वर्णन कीजिए। आमाशय में भोजन का पाचन किस प्रकार होता है? समझाइए।
या
आमाशय का सचित्र वर्णन कीजिए। यह भोजन की पाचन-क्रिया में किस प्रकार सहायता देता है?
या
‘आमाशय में उपस्थित जठर रस भोजन को पचाने में सहायक होता है।’ सिद्ध कीजिए।
या
आमाशय की रचना एवं उसके कार्य का विस्तृत वर्णन कीजिए।
उत्तर:
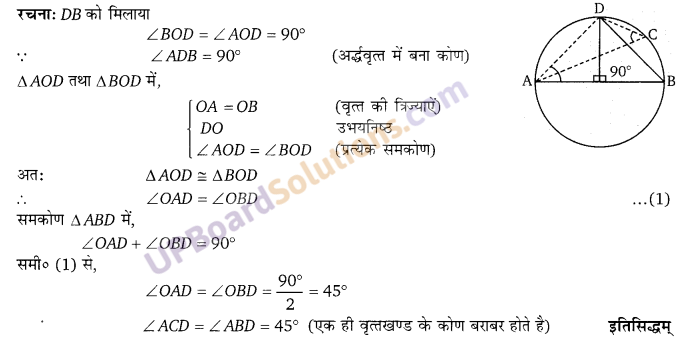
आमाशय की रचना:

आमाशय आहार-नाल को एक प्रमुख भाग है। आमाशय एक थैले के आकार की रचना होती है। इसकी लम्बाई लगभग 25 सेमी व चौड़ाई। 10 सेमी होती है। यह ऊपर की ओर ग्रासनली से तथा नीचे की ओर ग्रहणी से जुड़ा रहता है। उदरगुहा में इसका चौड़ा सिरी बाई ओर तथा सँकरा सिरा दाहिनी ओर होता है। यह मध्य पट के ठीक नीचे की ओर स्थित होता है। यह ऊपर की ओर हृदय प्लीहा द्वार तथा नीचे की ओर जठर-निर्गम द्वार द्वारा खुलता है। इसकी दीवार की संरचना ग्रासनली की दीवार की भाँति होती है, परन्तु यह ग्रासनली (UPBoardSolutions.com) से अपेक्षाकृत मोटी व दृढ़ होती है। इसमें पेशियों के अधिक स्तर होते हैं। आमाशय की दीवार में प्रायः वर्तुल व अनुलम्ब पेशियों के अतिरिक्त तिर्यक पेशियों का एक स्तर और होता है। आमाशय की दीवार में श्लेष्म अग्न्याशय ग्रन्थियों के अतिरिक्त जठर ग्रन्थियाँ भी पाई जाती हैं। इन ग्रन्थियों में जठर रस बनता है। आमाशय की दीवार में अनेक ग्रहणी जठर निर्गम द्वार उभरी हुई सलवटें होती हैं जो कि इसके क्षेत्रफल को कई गुना बढ़ा देती हैं।

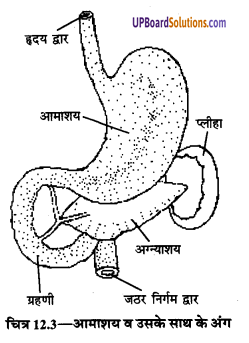
भोजन का पाचन:
आमाशय में आने वाला भोजन पिसी हुई अवस्था में होता है तथा इसमें लार तथा श्लेष्मक मिली हुई होती है। आमाशय की भीतरी दीवार में श्लेष्मिक झिल्ली होती है, जिसमें नली के आकार की अनेक जठर ग्रन्थियाँ होती हैं। इनसे जठर रस नामक पाचक रस का स्राव होता है। (UPBoardSolutions.com) आमाशय धीमी व तरंग गति से संकुचन व प्रसरण की क्रिया करता है, जिसके फलस्वरूप भोजन और महीन पिसता है तथा इसमें जठर रस भली प्रकार मिल जाता है। जठर रस में नमक का अम्ल (हाइड्रोक्लोरिक एसिड) व कुछ महत्त्वपूर्ण किण्व होती हैं। आमाशय में आते समय भोजन क्षारीय होता है, परन्तु जठर रस के मिलने पर यह अम्लीय हो जाता है। जठर रस के दो महत्त्वपूर्ण कार्य हैं

1. भोजन में उपस्थित कीटाणुओं को मार देता है,
2. पेप्सिन नामक किण्व को प्रोटीन्स पर क्रिया करने के लिए प्रोत्साहित करता है। जठर रस में निम्नलिखित किण्व पाई जाती है

(क) रेनिन:
यह किण्व नमक के अम्ल की उपस्थिति में क्रियाशील होती है। यह दूध को फाड़कर उसकी प्रोटीन को अलग कर देती है तथा दूध के ठोस भाग केसीन को जमाकर पाचन क्रिया में मदद करती है। यह किण्व केवल बच्चों में ही पाई जाती है तथा वयस्क पुरुष एवं महिलाओं में इसका पूर्णरूप से अभाव होता है।

(ख) पेप्सिन:
यह किण्व प्रारम्भ में पेप्सिनोजन नामक निष्क्रिय अवस्था में स्रावित होती है। बाद में यह जठर रस में उपस्थित नमक के अम्ल के सम्पर्क में आकर पेप्सिन में परिवर्तित हो जाती है। पेप्सिन प्रोटीन्स से क्रिया कर उन्हें प्रोटिओजिज व पेप्टोन्स में बदल देती है। आमाशय में भोजन प्रायः तीन-चार घण्टों तक (UPBoardSolutions.com) रहता है। इस अवधि में भोजन अम्लीय हो जाता है। तथा भूरे रंग की लेई (पल्प) के समान हो जाता है। भोजन की इस अवस्था को ‘काइम’ कहते हैं।

प्रश्न 4:
पक्वाशय तथा छोटी आँत में होने वाले आहार के पाचन एवं शोषण का विवरण प्रस्तुत कीजिए।
उत्तर:
आहार के पाचन में पक्वाशय तथा छोटी आँत का महत्त्वपूर्ण योगदान होता है। आहार नाल के इन भागों में होने वाले पाचन एवं शोषण का विवरण निम्नलिखित है

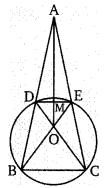
पक्वाशय की रचना:
आमाशय से आगे चलने पर पाचन-तन्त्र का जो अंग प्रारम्भ होता है, उसे पक्वाशय या ग्रहणी (duodenum) कहते हैं। इसका आरम्भ आमाशय के निचले द्वार से होता है। इसकी आकृति अंग्रेजी वर्णमाला के अक्षर ‘C’ के समान होती है। इसकी लम्बाई लगभग 25 सेमी होती है। यकृत (UPBoardSolutions.com) से पित्त-नली तथा अग्नाशय से क्लोम-नली इसके निचले हिस्से में आकर मिलती हैं। जैसे ही भोजन आमाशय से आहारनाल के इस भाग (पक्वाशय) में आता है, वैसे ही विभिन्न रस यहाँ पहुँचने लगते हैं, जो भोजन के पाचन में सहायक होते हैं।

छोटी आँत की रचना:
आहार नाल के पक्वाशय से आगे वाले भाग को छोटी आँत कहते हैं। छोटी आँत की लम्बाई लगभग 5 मीटर होती है तथा आकार में यह कुण्डलित-नली जैसी होती है। इसका प्रथम आधा भाग
लगभग 2.5 मीटर लम्बी तथा 4 सेमी चौड़ी नली के रूप में होता है। इस नली की दीवारों में रुधिर-वाहिनियों का जाल वाहिनी बिछा होता है। छोटी आँत का शेष आधा भागे लगभग 2.5 मीटर लम्बी तथा 4 सेमी चौड़ी अत्यधिक कुण्डलित नली के रूप में होता है। छोटी आँत में भीतरी सतह पर छोटे-छोटे उँगली के आकार के उभार आँत की गुहा में लटके ते हैं, जिन्हें रसांकुर (villus) कहते हैं। सिलवटों तथा (UPBoardSolutions.com) रसांकुर जैसे उभारों के कारण आंत्रीय दीवार के इस भीतरी तल का क्षेत्रफल कई सौ गुना बढ़ जाता है। प्रत्येक रसांकुर (villus) में एक मोटी लसिका। वाहिनी (lymph vessel) तथा कई रुधिर वाहिनियाँ (blood vessels) होती हैं, जो जाल बनाती हैं। शेष दीवा में रसांकुरों के बीच-बीच में श्लेष्मिक कला सँसकर नालाकार, आंत्रीय ग्रन्थियाँ (intestinal glands) बनाती है। ये ग्रन्थिया पाचक आत्रीय रस (intestinal juice) बनाती है।

पक्वाशय तथा छोटी आँत में भोजन का पाचन

पाचन-क्रिया में ग्रहणी का बहुत महत्त्व है। इसमें पित्ताशय व यकृत से ‘पित्त नली’ तथा अग्न्याशय अथवा पेंक्रियास से ‘अग्न्याशय नली आकर खुलती है। पित्ताशय से पित्त-रस व अग्न्याशय से अग्न्याशय रस, वाहिनियों अथवा नलियों द्वारा ग्रहणी में प्रवेश कर भोजन के पाचन में सहायता करते हैं।

पित्त-रस:
इसमें कोई किण्व अथवा एन्जाइम नहीं होता है। पित्त-रस में सोडियम बाइकार्बोनेट अधिक मात्रा में होता है। इसके प्रमुख कार्य निम्नलिखित हैं

1. यह भोजन की अम्लीय प्रकृति को उदासीन कर इसे क्षारीय बना देती हैं, जिसके फलस्वरूप
   विभिन्न किण्व भोजन पर क्रिया कर पाते हैं।
2. यह वसा का विखण्डन करके उसे छोटी-छोटी बूंदों में परिवर्तित कर देता है। इस स्थिति में वसा का पाचन सरल हो जाता है।

अग्न्याशय-रस:
यह आमाशय के पीछे स्थित अग्न्याशय ग्रन्थि में बनता है। यह एक महत्त्वपूर्ण पाचक-रस है, जिनमें तीन प्रकार के किण्व पाए जाते हैं। इनके नाम व प्रमुख कार्य निम्नलिखित हैं

(i) एमिलॉप्सिन:
यह किण्व भोजन के अवशेष स्टार्च को माल्टोज शर्करा में बदल देता है।

(ii) ट्रिप्सिन:
यह एक महत्त्वपूर्ण किण्व है, जो कि भोजन की शेष प्रोटिओजिन एवं पेप्टोन्स से क्रिया कर उन्हें पेप्टाइड्स व अमीनो अम्ल में परिवर्तित कर देता है।

(iii) स्टीएप्सिन:
यह तृतीय प्रकार का किण्व है, जो कि इमल्सिफाइड वसा को वसीय अम्लों व ग्लिसरॉल में परिवर्तित कर देता है।

शेष क्षुद्रान्त्र अथवा छोटी आँत में भोजन का पाचन एवं अवशोषण होता है। छोटी आँत में एक प्रकार का आन्त्र-रसे बनती है, जो कि पाचन-क्रिया में सहायता करता है। इसमें निम्न प्रकार के किण्व पाए जाते हैं।

(i) इप्सिन( पेप्टिडेज):
यह भोजन में शेष बची प्रोटीन व पेप्टाइड्स को अमीनो अम्ल में बदल देता है।
(ii) माल्टेस:
यह माल्टेस शर्करा को ग्लूकोस शर्करा में परिवर्तित कर देता है।
(iii) लैक्टेस:
यह किण्व लैक्टोस को ग्लूकोस एवं गैलेक्टोस शर्करा में बदल देता है।
(iv) सुक्रेस (इंवरटेस):
यह किण्व सुक्रोस शर्करा को ग्लूकोस व फ्रक्टोस शर्करा में परिवर्तित कर देता है।
(v) लाइपेस:
यह अत्यन्त सूक्ष्म मात्रा में पाया जाने वाला किण्व है, जो कि वसा को वसीय अम्लों एवं ग्लिसरॉल में परिवर्तित करता है।

भोजन का अवशोषण:
छोटी आँत में भोजन पूर्णरूप से पचकर रक्त में मिल जाने योग्य हो जाता है। अमीनो अम्ल वे सामान्य शर्करा (ग्लूकोस, फ्रक्टोस व गैलेक्टोस) रसांकुरों द्वारा अवशोषित होकर रक्त में पहुँच जाते हैं। शर्करा का शरीर की आवश्यकता से अधिक भाग ग्लाइकोजन के रूप में यकृत में (UPBoardSolutions.com) संचित होता रहता है तथा आवश्यकता पड़ने पर ही उपयोग में आता है। पचे हुए वसा पदार्थों (वसीय अम्ल एवं ग्लिसरॉल) का अवशोषण लिम्फ वैसल्स अथवा लसीकाओं द्वारा होकर लसीका तन्त्र में पहुँचता है। छोटी आँत में भोजन बहुत धीरे-धीरे चलकर लगभग चार घण्टों में बड़ी आँत तक पहुँचता है।

प्रश्न 5:
पाचन तन्त्र में यकृत के कार्यों का वर्णन कीजिए।
या
यकृत की रचना चित्र बनाकर समझाइए। इसके कार्यों का वर्णन कीजिए।
या
यकृत का शरीर में क्या महत्त्व है? पाचन क्रिया में इसके प्रमुख कार्यों का वर्णन कीजिए।
उत्तर:
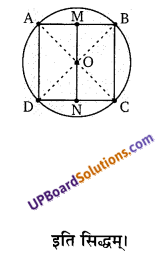
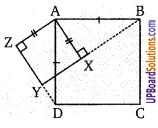
यकृत (लिवर) की रचना

यह शरीर की सबसे बड़ी ग्रन्थि होती है। इसका आकार थैले के समान तथा भार लगभग डेढ़ किलोग्राम तक होता है। इससे लगी हुई एक छोटी थैली जैसी रचना होती है, जिसे पित्ताशय कहते हैं। यह पित्तवाहिनी द्वारा ग्रहणी में खुलती है। एक गहरी दबी रेखा यकृत को दो भागों में विभाजित करती है। दाहिना भाग बीच से बड़ा होता है। यह अष्ट्रकोणीय कोशाओं से बना होता है। यकृत में दो (UPBoardSolutions.com) रक्तवाहिकाएँ रक्त लेकर आती हैं। यकृत-धमनी यकृत में शुद्ध तथा पोर्टल शिरा यकृत से अशुद्ध रक्त ले जाती है। यकृत में प्रतिदिन 500 से 700 ग्राम पित्त रस का निर्माण होता है। पित्त रस असंख्य छोटी-छोटी यकृत नलिकाओं द्वारा एक बड़ी यकृतवाहिनी तक पहुँचता है जो कि इस पित्ताशय तक ले जाती है।

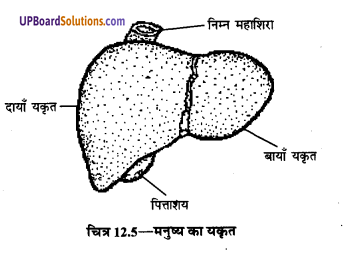
यकृत के कार्य

यकृत मानव शरीर की एक महत्त्वपूर्ण ग्रन्थि है। मानव-शरीर में यकृत की अत्यधिक महत्त्वपूर्ण भूमिका है। यकृत के कुछ महत्त्वपूर्ण कार्य निम्नलिखित हैं।

(1) पित्त रस का निर्माण:
यकृत प्रतिदिन लगभग 500 से 700 ग्राम पित्त रस बनाता है जो कि पित्ताशय में संचित रहता है।

(2) शर्करा को संचित करना:
यकृत रक्त शर्करा का सन्तुलन बनाए रखने में सहायता करता है। यह पाचन क्रिया के फलस्वरूप बनी शर्करा की आवश्यकता से अधिक मात्रा को ग्लाइकोजने में परिवर्तित कर अपने भीतर संचित कर लेता है तथा आवश्यकता पड़ने पर पुनः शर्करा में परिवर्तित कर रक्त में प्रवाहित कर देता है।

(3) पौष्टिक तत्वों को संचित करना:
यकृत लोहा, ताँबा व अनेक विटामिन्स को संचित रखता है।

(4) हानिकारक जीवाणुओं को नष्ट करना:
यकृत की कोशिकाएँ अनेक जीवाणुओं को नष्ट कर देती हैं।

(5) मृत लाल रक्त कोशिकाओं को नष्ट करना:
यकृत रक्त में उपस्थित मृत लाल कोशिकाओं को नष्ट करता रहता है।

(6) फाइब्रिनोजन का निर्माण:
यह फाइब्रिनोजन नामक प्रोटीन का निर्माण करता है जो कि रक्त को जमाने में सहायता करती है।

(7) हिपेरिन का निर्माण:
यकृत हिपेरिन बनाता है जो कि ऍक्त को जमने से रोकती है।

(8) नाइट्रोजनयुक्त हानिकारक पदार्थों को दूर करनी:
आवश्यकता से अधिक अमीनो अम्लों के विखण्डन के फलस्वरूप यूरिया तथा शर्करा बनते हैं। यूरिया गुर्दो के द्वारा शरीर से बाहर निकल जाता है।

(9) रक्त के आयतन में वृद्धि करना:
यकृत अस्थायी रूप से जल को संचित कर रक्त को तनु अथवा जलयुक्त करता रहता है।

(10) पाचन क्रिया में सक्रिय सहयोग:
यकृत पित्त रस का निर्माण करता है जो कि वसा के पाचन में सहायता करता है तथा भोजन की अम्लीयता को प्रभावहीन कर उसे क्षारीय बनाता है।

(ii) विषैले पदार्थों का निष्कासन:
यकृत विषैले पदार्थों तथा धात्वीय विषौं को निष्कासित करता है। अतः भोजन के माध्यम से विष के फलस्वरूप हुई मृत्यु में मृतक के यकृत का पोस्टमार्टम परीक्षण में अत्यधिक महत्त्व रखता है।

(12) लाल रक्त कोशिकाओं का निर्माण:
भ्रूण अवस्था में इन कोशिकाओं का निर्माण यकृत द्वारा होता है, जबकि वयस्कों में ये अस्थि-मज्जा में बनती हैं।

यकृत का शरीर में महत्त्व

यकृत शरीर में सबसे बड़ी ग्रन्थि है। इसका शरीर के सम्पूर्ण चयापचय में अत्यधिक महत्त्व है। शरीर की लगभग सभी क्रियाओं में इसका कोई-न-कोई हिस्सा होता है अथवा इस क्रिया को करने में यह नियन्त्रक का कार्य करता है। इसके महत्त्व को कुछ बिन्दुओं द्वारा इस प्रकार स्पष्ट कर सकते हैं

1.  यह शरीर की अनेकानेक उपापचई क्रियाओं को चलाता है; जैसे— भोजन में आए विभिन्न पोषक पदार्थों को तोड़ना-जोड़ना अथवा उनका आवश्यकतानुसार स्वरूप परिवर्तित करना।
2. शरीर के लिए संग्राहक (store house) का कार्य करना; जैसे-ग्लाइकोजन के रूप में श्वेतासार (कार्बोज) एकत्र करना।।
3.  पित्त रस का निर्माण करना जो शरीर की मुख्य पाचक क्रिया में सहायता करता है।
4.  शरीर में आए हुए अथवा उप-उत्पादों के रूप में शरीर में बन गए विषों को नष्ट करना।
5.  विभिन्न बेकार मृत तथा टूटी-फूटी कोशिकाओं को नष्ट करना तथा उन्हें पित्त रस के द्वारा शरीर से बाहर निकालने का प्रब्रन्ध करना; जैसे- शरीर के साथ आई तथा रुधिर की बेकार कोशिकाओं को नष्ट करता है।

प्रश्न 6:
पाचन प्रणाली में पाए जाने वाले विभिन्न पाचक रसों के नाम व उनके कार्यों का वर्णन कीजिए।
यो
पाचन क्रिया में भाग लेने वाले किन्हीं दो सहायक रसों के विषय में बताइए तथा उनके कार्यों का वर्णन कीजिए।
उत्तर:
भोजन में प्राय: कार्बोहाइड्रेट्स, प्रोटीन्स एवं वसा होते हैं। पाचन प्रणाली में इनका पचन सामान्यत: मुखगुहा, आमाशय तथा छोटी आँत में होता है। पाचन तन्त्र के इन तीन अंगों में विभिन्न प्रकार के पाचक रस पाचन क्रिया में अपना-अपना योगदान देते हैं। मानव पाचन प्रणाली में प्रायः चार निम्नलिखित प्रकार के पाचक रस पाए जाते हैं

1.  लार एवं लार ग्रन्थियाँ,
2.  आमाशयिक रस (गैस्ट्रिक जूस),
3. पित्त रस,
4.  क्लोम अथवा अग्न्याशय रस।

(1) लार एवं लार ग्रन्थियाँ:
मुखगुहा के अन्दर सामान्यतः तीन जोड़े अथवा कुल छह लार ग्रन्थियाँ पाई जाती हैं। इनका विवरण निम्नलिखित है–

(क) कर्ण पूर्व अथवा पेरोटिड ग्रन्थियाँ:
ये संख्या में दो तथा कान के नीचे स्थित होती हैं।

( ख) जिह्वाधर अथवा सबलिंगुअल ग्रन्थियाँ:
ये भी संख्या में दो होती हैं तथा जिह्वा के नीचे स्थित होती हैं।

(ग) अधोहनु अथवा सबमैक्सिलरी ग्रन्थियाँ:
ये निचले जबड़े के नीचे स्थित होती हैं। इनकी संख्या भी दो होती है।

लार के कार्य:

1.  भोजन को गीला व चिकनी करके निगलने में सहायता करती है।
2. चबाते समय भोजन में मिलकर उसे लेई के समान बनने में सहायता करती है, जिससे यह सहज ही ग्रसनी में चला जाता है।
3. लार के अन्दर टायलिन नामक किण्व होती है जो कि श्वेतसार पर क्रिया कर उसे शर्करा में परिवर्तित करती है।
4. लार विभिन्न पदार्थों को अपने में घोलकर उनका स्वाद बोध कराती है।
   6 मास तक शिशुओं में लार-ग्रन्थियों के स्राव का अभाव होता है; अतः उन्हें श्वेतसारयुक्त भोजन न देना हितकर रहता है।

(2) आमाशयिक रस:
आमाशय की श्लेष्मिक झिल्ली से बनी दीवार में अनेक आमाशयिक अथवा जठर ग्रन्थियाँ पाई जाती हैं। इनसे जठर रस स्राव होता है, जिसमें कि हाइड्रोक्लोरिक अथवा नमक का अम्ल एवं दो प्रकार की किण्व पाई जाती हैं। ये किण्व होते हैं-रेनिन तथा पेप्सिन। रेनिन के प्रभाव से दूध दही के रूप में परिवर्तित हो जाता है तथा पेप्सिन के प्रभाव से प्रोटीन, पेप्टोन में परिवर्तित हो जाती
है।

(3) पित्त रस:
यकृत प्रतिदिन 500 से 700 ग्राम पित्त रस का निर्माण करता है। पित्त रस पित्ताशय में संचित होता है, जहाँ से यह पित्त वाहिनी द्वारा समय-समय पर ग्रहणी में पहुँचकर पाचन क्रिया (UPBoardSolutions.com) में सहायता करता है। पित्त रस में कोई एन्जाइम या किण्व नहीं होते परन्तु यह अग्न्याशयिक रस की सहायता करता है तथा इसकी सहायता से वसा का पाचन सरल हो जाता है।

(4) क्लोम अथवा अग्न्याशय रस:
यह आमाशय के पीछे स्थित अग्न्याशय ग्रन्थि अथवा पैंक्रियास में बनता है। इसमें तीन प्रकार की किण्व पाई जाती हैं जो कि पाचन क्रिया में महत्त्वपूर्ण योगदान देती हैं। ये किण्व होते हैं

1.  एमिलॉप्सिन,
2.  ट्रिप्सिन तथा
3. लाइपेस। ऐमिलॉप्सिन भोजन में बिना पचे हुए स्टार्च को शक्कर में बदल देता है। ट्रिप्सिन नामक खमीर भोजन के प्रोटीन को पेप्टोन में परिवर्तित कर देता है तथा लाइपेस नामक किण्व के प्रभाव से आहार की वसा क्रमश: ग्लिसरॉल तथा वसी-अम्ल में परिवर्तित हो जाती है।

प्रश्न 7:
शरीर में अग्न्याशय के कार्यों का वर्णन कीजिए।
उत्तर:
अग्न्याशय के कार्य

अग्न्याशय एक बाह्य ग्रन्थि है जो आहारनाल के आमाशय तथा पक्वाशय के मध्य स्थित होती है। यह एक संयुक्त ग्रन्थि है तथा दो प्रकार के प्रमुख कार्य करती है

1. पाचक ग्रन्थि के रूप में इसकी अनेक कोशिकाएँ, जो विभिन्न पिण्डकों को बनाती हैं, अग्न्याशिक रस (pancreatic juice) बनाती हैं। यह इससे पक्वाशय में एक अग्न्याशिक नलिका के द्वारा पहुँचाता है तथा भोजन में आए हुए विभिन्न अवयवों को पचाने का कार्य करता है। इस (UPBoardSolutions.com) रस में कई पाचक एन्जाइम होते हैं; जैसे-ट्रिप्सिन, एमाइलॉप्सिन, लाइपेस आदि जो भोजन के विभिन्न अवयवों; जैसे प्रोटीन्स, पेप्टोन्स, मण्ड, वसा आदि पर क्रिया करके इनको सरल तथा रुधिर में अवशोषण के योग्य स्वरूप प्रदान करते हैं।
2. अग्न्याशय की संयोजी ऊतक में विशेष प्रकार की कोशिकाओं के समूह होते हैं, जिन्हें लैंगरहेन्स की द्विपिकाएँ कहा जाता है। ये अन्तःस्रावी (endocrine) ग्रन्थियाँ हैं तथा इन्सुलिन, ग्लूकैगॉन आदि हार्मोन्स स्रावित करती हैं। ये हार्मोन्स रुधिर द्वारा यकृत (liver) में पहुँचते हैं। ये हॉर्मोन्स ग्लाइकोजेनेसिस, ग्लाइकोजेनोलिसस आदि क्रियाओं में भाग लेते हैं। इन्हीं क्रियाओं के फलस्वरूप रुधिर में ग्लूकोस की मात्रा का नियमन होता है।

लघु उत्तरीय प्रश्न

प्रश्न 1:
मनुष्य के मुख में कौन-सा रस बनता है? उसका भोजन पर क्या प्रभाव पड़ता है?
उत्तर:
मनुष्य के मुख में तीन जोड़ी लार ग्रन्थियाँ पाई जाती हैं। ये लार स्रावित करती हैं। लार प्रारम्भिक पाचक रस है जो कि मुखगुहा में भोजन के पाचन में सहायता करता है।
लार भोजन को गीला एवं चिकना कर निगलने में सहायता करती है। लार द्वारा लेई के समान बना चिकना भोजन सहज ही ग्रसनी में प्रवेश कर जाता है। लार भोजन को घोलकर उसके विभिन्न तत्त्वों का स्वाद बोध कराती है। इसमें टायलिन नामक किण्व होती है। टायलिन भोजन के श्वेतसार को अंगूरी शर्करा में परिवर्तित करती है। यही कारण है कि श्वेतसारयुक्त भोजन मुंह में चबाने के पश्चात् मीठा लगने लगता है। ।

प्रश्न 2:
जीभ में पाई जाने वाली स्वादग्रन्थियाँ कितने प्रकार की होती हैं और उनके क्या कार्य हैं।
उत्तर:
मुखगुहा के तल पर एक मांसल जीभ होती है जो कि पीछे की ओर मुखगुहा से जुड़ी होती है तथा आगे की ओर स्वतन्त्र रहती है। यह भोजन को ग्रहण करने में सहायता देती है। जीभ के ऊपर छोटे-छोटे दाने होते हैं, जिन्हें संवेदी अंकुर अथवा स्वादांकुर कहते हैं। इन्हीं स्वादांकुरों के द्वारा हम भोजन के (UPBoardSolutions.com) विभिन्न स्वादों का ज्ञान प्राप्त कर पाते हैं। जीभ पर इनका क्रम होता है-खट्टा, मीठा, नमकीन एवं कड़वा। बच्चों के स्वादांकुर वयस्कों की अपेक्षा अधिक संवेदनशील होते हैं। स्वादांकुर हमारे लिए दो प्रकार से महत्त्वपूर्ण हैं

• ये भोजन के विभिन्न स्वादों (खट्टा, मीठा, कड़वी आदि) का ज्ञान कराते हैं।

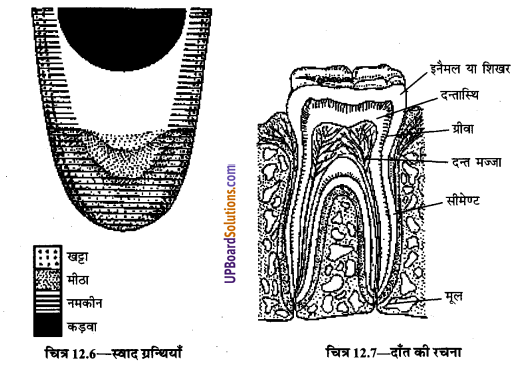
• हानिकारक एवं अप्राकृतिक स्वाद वाली खाद्य सामग्रियों से परिचित कराते हैं। इस प्रकार हम इनके उपभोग से बच पाते हैं।

प्रश्न 3:
दाँत की सामान्य रचना स्पष्ट करते हुए उसके मुख्य भागों का उल्लेख कीजिए।
उत्तर:
दाँत की रचना

बाहरी रूप से दाँत भिन्न-भिन्न आकार के तथा भिन्न-भिन्न कार्य करने वाले होते हैं, परन्तु जहाँ तक दाँत की संरचना का प्रश्न है, सभी दाँतों की संरचना एक समान ही होती है। सभी दाँत एक बहुत अधिक मजबूत पदार्थ के बने होते हैं जिसे डेण्टाइन कहते हैं। यह पदार्थ हड्डी से भी अधिक मजबूत होता है। (UPBoardSolutions.com) सभी दाँत अपने मूल वाले भाग से जबड़े की हड्डी में बने गड्डे जैसे स्थान पर जमे रहते हैं। दाँत को हड्डी के साथ मजबूती से जोड़ने के लिए एक सीमेण्ट जैसा पदार्थ सहायक होता है। दाँत को स्थिर रखने में मसूड़े भी महत्त्वपूर्ण योगदान प्रदान करते हैं। दाँत के तीन मुख्य भाग होते हैं ।

(i) शिखर (Crown):
मसूड़े के बाहर दिखाई देने वाले भाग को शिखर कहते हैं। इस भाग पर एक सफेद चमकीली परत चढ़ी रहती है, जिसे इनेमल (enamel) कहते हैं। यह इनेमल ही दाँत की बाहरी प्रहारों से रक्षा करता है।

(ii) ग्रीवा (Neck):
यह मसूड़े के अन्दर दबा हुआ भाग है। इस भाग में इनेमल नहीं होता परन्तु यह भाग कठोर डेण्टाइन से बना होता है। डेण्टाइन के आन्तरिक भाग में दन्त कोष्ठ होता है। इस कोष्ठ या गुहा में पल्प या दन्त मज्जा भरा रहता है। यह लसलसा पदार्थ होता है, जिसमें रक्त वाहिनियाँ तथा स्नायु तन्तु फेले रहते हैं। यदि पल्प नष्ट हो जाए, तो सारा दाँत ही नष्ट हो जाता है।

(iii) मूल (Root):
यह दाँत का अन्तिम भाग है। यह ग्रीवा के नीचे तथा मसूड़ों के अन्दर स्थित होता है। यह पीले रंग की एक विशेष पर्त से ढका रहता है, जिसे सीमेण्ट कहते हैं। यह मसूड़ों के भीतर दाँतों की जड़ों को भली-भाँति जमाने का कार्य करता है। भिन्न-भिन्न प्रकार के दाँतों के मूल भाग की संख्या भिन्न-भिन्न होती है। चर्वणक दाँतों में तीन, प्रचर्वणक में दो तथा अन्य दाँतों में केवल एक-एक मूल ही होती है।

प्रश्न 4:
किण्व अथवा एन्जाइम क्या हैं? पाचन प्रणाली में पाई जाने वाली विभिन्न एन्जाइम के नाम व उत्पत्ति स्थान बताइए।
उत्तर:
किण्व सिद्धान्त रूप से प्रोटीन्स के बने होते हैं, तु सभी प्रोटीन्स किण्व के समान कार्य नहीं करती हैं। अतः किण्व वे जटिल प्रोटीन्स हैं जो कि उत्प्रेरक के समान कार्य करती हैं। ये श्वेतसार, प्रोटीन्स तथा वसा आदि से क्रिया कर उन्हें शरीर द्वारा स्वीकार योग्य छोटे-छोटे घुलनशील अणुओं में परिवर्तित कर देती हैं तथा स्वयं इन पर किसी प्रकार का प्रभाव नहीं पड़ता है। पाचन प्रणाली में पाई जाने वाली कुछ प्रमुख किण्व निम्नलिखित हैं

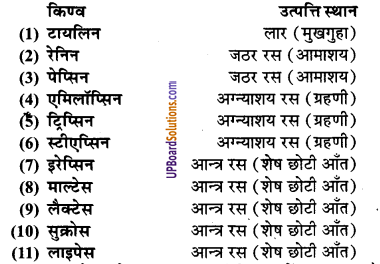
प्रश्न 5:
भोजन के पाचन तथा स्वांगीकरण में क्या अन्तर है?
उत्तर:
भोजन को जिस रूप में ग्रहण करते हैं उसे हमारा शरीर तब तक नहीं स्वीकारता जब तक कि वह घुलनशील रूप में परिवर्तित न हो जाए। भोजन का उसके घुलनशील रूप में रक्त द्वारा अवशोषण होता है तथा इसके बाद रक्त परिभ्रमण के द्वारा वह शरीर के विभिन्न अंगों में वितरित होता है। पाचन प्रणाली के विभिन्न भागों में स्रावित पाचक रसों की प्रतिक्रिया के फलस्वरूप भोजन का घुलनशील तथा रक्त में अवशोषित होने योग्य हो जाना ही भोजन का पाचन कहलाता है।
क्षुद्रान्त्र अथवा छोटी आँत में भोजन का अवशोषण होता है। क्षुद्रान्त्र की विलाई में पाई जाने वाली कोशिकाएँ जल, लवण, शर्करा व अमीनो अम्ल का अवशोषण करती हैं। यह (UPBoardSolutions.com) अवशोषित भोजन छोटी आँत की श्लेष्मिक झिल्ली की कोशिकाओं द्वारा रक्त में पहुँचा दिया जाता है तथा वसा एवं ग्लिसरॉल आदि अवशोषित होकरे लसीका-वाहिनियों में पहुंचते हैं। इस प्रकार पचे हुए भोजन के आवश्यक तत्त्वों का रुधिर तथा लसीका तन्त्र में पहुँचने को स्वांगीकरण कहते हैं। स्वांगीकरण के परिणामस्वरूप ही शरीर ग्रहण किए गए आहार से लाभान्वित होता है। यदि किसी कारणवश आहार के स्वांगीकरण की प्रक्रिया बिगड़ जाए, तो उस स्थिति में पौष्टिक एवं सन्तुलित
आहार ग्रहण करना भी व्यर्थ ही होता है।

प्रश्न 6:
अग्न्याशय ग्रन्थि पर संक्षिप्त टिप्पणी लिखिए।
उत्तर:
अग्न्याशय अथवा क्लोम ग्रन्थि (पेंक्रियास)

आमाशय के ठीक पीछे उदर की पिछली दीवार से सटी हुई अग्न्याशय अथवा क्लोम नामक ग्रन्थि होती है। यह ग्रहणी से प्लीहा तक फैली हुई होती है। इसका दाहिना सिरा ग्रहणी की ओर तथा बायाँ भाग प्लीहा की ओर होता है। यह 16 सेमी लम्बी व 4 सेमी चौड़ी होती है। अग्न्याशय वाहिनी द्वारा अग्न्याशय रस ग्रहणी तक पहुँचता है। अग्न्याशय वाहिनी के साथ-साथ पित्ताशय वाहिनी भी ग्रहणी में खुलती है। अग्न्याशय ग्रन्थि से अग्न्याशय रस स्रावित होता है। इसमें तीन महत्त्वपूर्ण किण्वे

1.  एमिलप्सिन,
2. स्ट्रीएप्सिन तथा
3.  ट्रिप्सिन होती हैं। ये तीनों ही किण्व या एन्जाइम पाचन क्रिया में महत्त्वपूर्ण योगदान प्रदान करते हैं।

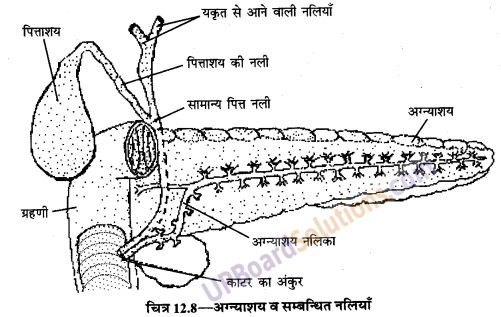
प्रश्न 7:
टिप्पणी लिखिए-प्लीहा या तिल्ली।
उत्तर:
प्लीहा या तिल्ली हमारे शरीर में पाई जाने वाली एक ग्रन्थि है। इसका रंग बैंगनी तथा आकार सेम के बीज के समान होता है। यह ग्रन्थि हमारे शरीर में आमाशय के बाईं ओर पसलियों के बीच में तथा क्लोम ग्रन्थि के दाहिनी ओर स्थित होती है। इसकी लम्बाई 12 सेमी तथा वजन 375 ग्राम होता है। यह आँत तथा वृक्क से भी मिली हुई रहती है। यह ग्रन्थि मुलायम और पिलपिली-सी होती है। इसके भीतर की ओर एक दबा हुआ (UPBoardSolutions.com) गड़ा-सा होता है, जो इसका द्वार है। इस द्वार से ही रक्त-नलिकाएं इसेमें प्रवेश करती हैं और बाहर निकलती हैं। यद्यपि प्लीहा का पाचन-संस्थान से कोई सीधा सम्बन्ध नहीं होता, तथापि यह मानव शरीर का एक आवश्यक अंग है और पाचन क्रिया में भी कुछ सहायता करता है। इसके बढ़ जाने पर भोजन ठीक प्रकार से नहीं पचता और प्रायः पेट में पीड़ा होती है। यह अपने अन्दर रक्त को शोषित करके संचित कर लेती है। इस प्रकार तिल्ली रक्त-कोषागार का कार्य करती है तिल्ली के मुख्य कार्य हैं-रक्त जमा करना, रक्त बनाना, पुराने एवं घिसे हुए रक्त कणों को नष्ट करना, यूरिया बनाने में सहायता करना तथा शरीर को सुरक्षित रखना।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:
पाचन-तन्त्र से क्या आशय है?
उत्तर:
आहार के पाचन एवं शोषण में प्रत्यक्ष रूप से भाग लेने वाले तथा इस कार्य में अप्रत्यक्ष रूप से सहायता प्रदान करने वाले सभी अंगों को सम्मिलित रूप से पाचन-तन्त्र कहा जा सकता है।

प्रश्न 2:
आहारनाल या आहार मार्ग से क्या आशय है?
उत्तर:
शरीर के अन्दर मुख से लेकर मल-द्वार तक के मार्ग को आहारनाल या आहार मार्ग कहा जाता है।

प्रश्न 3:
आहारनाल के मुख्य अंगों या भागों का उल्लेख कीजिए।
उत्तर:
आहारनाल के मुख्य अंग या भाग हैं

1.  मुख तथा मुख-गुहा,
2.  ग्रसनी,
3. ग्रासनली,
4.  आमाशय,
5. पक्वाशय,
6. छोटी आँत तथा
7. बड़ी आँत।

प्रश्न 4:
आहारनाल के अतिरिक्त पाचन-तन्त्र के अन्य सहायक अंगों का उल्लेख कीजिए।
उत्तर:
आहारनाल के अतिरिक्त पाचन-तन्त्र के अन्य सहायक अंग हैं—यकृत, पित्ताशय तथा क्लोम या अग्न्याशय।

प्रश्न 5:
दाँतों को सुरक्षित रखने के दो उपाय बताइए।
उत्तर:

1.  सुबह उठकर तथा रात्रि को सोने से पूर्व प्रतिदिन दाँतों को मंजन अथवा पेस्ट से साफ करना चाहिए।
2.  दाँतों में दर्द अथवा अन्य कोई परेशानी होने पर तुरन्त दन्त चिकित्सक को दिखाना चाहिए।

प्रश्न 6:
दाँतों के कौन-कौन से तीन भाग होते हैं?
उत्तर:
प्रत्येक दाँत के तीन भाग होते हैं

1. मूल अथवी जड़े,
2. ग्रीवा तथा
3.  शिखर।

प्रश्न 7:
मनुष्यों में कितने प्रकार के दाँत पाए जाते हैं?
उत्तर:
मनुष्यों में चार प्रकार के दाँत पाए जाते हैं।

प्रश्न 8:
पचे भोजन का अवशोषण आहारनाल के किस भाग में होता है?
उत्तर:
पचे भोजन का अवशोषण आहारनाल के छोटी आँत नामक भाग में होता है।

प्रश्न 9:
मनुष्यों में कितनी लार ग्रन्थियाँ पाई जाती हैं?
उत्तर:
मनुष्य में तीन जोड़ी (कुल छह) लार ग्रन्थियाँ पाई जाती हैं।

प्रश्न 10:
हमें लार से क्या लाभ हैं?
उत्तर:
लार भोजन को चिकना व लेई के समान बनाती है। इसमें पाई जाने वाली टायलिन नामक किण्व श्वेतसीर को अंगूरी शर्करा में बदल देती है।

प्रश्न 11:
पित्त रस किस ग्रन्थि में बनता है तथा कहाँ संचित रहता है?
उत्तर:
पित्तं रस यकृत में बनता है तथा पित्ताशय में संगृहीत होता है।

प्रश्न 12:
रेनिन आहारनाल के किस भाग में मिलता है तथा इसका क्या कार्य है?
उत्तर:
यह आमाशय के जठर रस में पाया जाता है तथा दूध को फाड़कर इसके केसीन (ठोस भाग) को पृथक् कर देता है।

प्रश्न 13:
भोजन के पाचन से क्या तात्पर्य है?
उत्तर:
भोजन के पाचन से तात्पर्य है किण्व की उपस्थिति में भोजन के अघुलनशील (अविलेय) अवयवों का घुलनशील (विलेय) अवस्था में परिवर्तित होना, जिससे कि वे रक्त में अवशोषित हो सकें।

प्रश्न 14:
भोजन का पाचन आहारनाल में कहाँ-कहाँ होता है?
उत्तर:
भोजन का पाचन आहारनाल में मुखगुहा, आमाशय तथा छोटी आँत में होता है।

प्रश्न 15:
यकृत के कोई दो महत्त्वपूर्ण कार्य बताइए।
उत्तर:
(1) यकृत पित्त रस का निर्माण करता है।
(2) अतिरिक्त श्वेतसार; ग्लाइकोजन के रूप में यकृत में संचित रहती है।

प्रश्न 16:
जठर रस में कौन-सा अम्ल पाया जाता है?
उत्तर:
जठर रस में नमक का अम्ल पाया जाता है।

प्रश्न 17:
एन्जाइम क्या हैं? पाचन में इनका क्या कार्य है?
उत्तर:
एन्जाइम या किण्व वे जटिल प्रोटीन्स हैं जो कि उत्प्रेरक के समान कार्य करती हैं। ये श्वेतसार, प्रोटीन्स तथा वसा आदि से क्रिया कर इन्हें शरीर द्वारा स्वीकार योग्य, छोटे-छोटे घुलनशील अणुओं में परिवर्तित कर पाचन क्रिया में महत्त्वपूर्ण योगदान देती हैं।

प्रश्न 18:
वमन या उल्टी क्यों होती है?
उत्तर:
जब मस्तिष्क में वमन केन्द्र उत्तेजित हो जाता है तथा जी मिचलाने लगता है तो ऐसी दशा में ग्रासनली का द्वार खुल जाता है और पेशियों के संकुचन में उल्टियाँ हो जाती हैं।

प्रश्न 19:
स्वांगीकरण का क्या अर्थ है?
उत्तर:
भोजन का कोशिकाओं में पहुँचकर जीवद्रव्य का अंश बन जाना स्वांगीकरण कहलाता है।

प्रश्न 20:
वसा के पाचन में सहायक पाचक रसों के नाम लिखिए।
उत्तर:
वसा के लिए पाचक रस मुख्यतः पित्त रस की उपस्थिति में अग्न्याशिक रस है, जिसमें लाइपेस नामक किण्व होता है। इसके अतिरिक्त यह किण्व आन्त्र रस में भी होता है।

वस्तुनिष्ठ प्रश्न

प्रश्न:
प्रत्येक प्रश्न के चार वैकल्पिक उत्तर दिए गए हैं। इनमें से सही विकल्प चुनकर लिखिए

(1) पाचन तन्त्र का प्रमुख कार्य है ।
(क) प्राणी की भूख को शान्त करना,
(ख) ग्रहण किए गए आहार के स्वाद का आनन्द लेना,
(ग) आहार को ग्रहण करना, उसका पाचन तथा पोषक तत्वों का अवशोषण करना
(घ) उपर्युक्त में से कोई नहीं।

(2) ग्रसनी के बाद भोजन कहाँ जाता है?
(क) आमाशय में,
(ख) क्षुद्रान्त्र में,
(ग) ग्रहणी में,
(घ) बड़ी आँत में।

(3) एक वयस्क मनुष्य के कितने दाँत होते हैं?
(क) 28,
(ख) 30,
(ग) 32,
(घ) 34

(4) रदनक दाँतों की संख्या कितनी होती है?
(क) दो जोड़े,
(ख) चार जोड़े,
(ग) छह जोड़े,
(घ) एक जोड़ा।

(5) पाचन तन्त्र में सर्वाधिक अवशोषण कहाँ होता है?
(क) यकृत में,
(ख) पित्ताशय में,
(ग) प्लीहा में,
(घ) छोटी आँत में।

(6) भोजन पीसने का कार्य करते हैं
(क) रदनक दाँत,
(ख) अग्र चर्वणक दाँत,
(ग) कृन्तक दाँत,
(घ) चवर्णक दाँत।

(7) मुँह में कितनी लार ग्रन्थियाँ होती हैं?
(क) छः,
(ख) आठ,
(ग) दस,
घ) दो।

(8) लार में टायलिन नामक किण्व नहीं पाई जाती है
(क) महिलाओं में,
(ख) पुरुषों में,
(ग) छः मासे तक के शिशुओं में,
(घ) छः वर्ष के बच्चों में।

(9) यकृत को भार होता है
(क) 1.5 किलोग्राम,
(ख) 2.5 किलोग्राम,
(ग) 0.5 किलोग्राम,
(घ) 5.0 किलोग्राम।

(10) रेनिन नामक किण्व पाया जाता है
(क) केवल महिलाओं में,
(ख) केवल बच्चों में,
(ग) केवल पुरुषों में,
(घ) इन सभी में।

(11) वसा को वसीय अम्लों एवं ग्लिसरॉल में परिवर्तित करने वाला किण्व है
(क) लैक्टेस,
(ख) लाइपेस,
(ग) सुक्रोस,
(घ) माल्टेस।

(12) स्टार्च को माल्टोज शर्करा में परिवर्तित करने वाला किण्व है
(क) ट्रिप्सिन,
(ख) स्टीएप्सिन,
(ग) इरेप्सिन,
(घ) एमिलप्सिन।

(13) सिद्धान्त रूप से सभी किण्व होते हैं
(क) श्वेतसार,
(ख) शर्करा,
(ग) प्रोटीन्स,
(घ) वसा।

(14) छोटी आँत की सामान्यतः लम्बाई होती है
(क) 5 मीटर,
(ख) 10 मीटर,
(ग) 15 मीटर,
(घ) 20 मीटर।

(15) यकृत अतिरिक्त शर्करा को किस वस्तु में परिवर्तित कर देता है?
(क) ग्लाइकोजन में,
(ख) सेलुलोस में,
(ग) एन्जाइम में,
(घ) ग्लिसरॉल में।

(16) लार में उपस्थित किण्व का क्या नाम है?
(क) लाइपेस,
(ख) रेनिन,
(ग) टायलिन,
(घ) पेप्सिन।

उत्तर:
(1) (ग) आहार को ग्रहण करना, उसका पाचन तथा पोषक-तत्त्वों का अवशोषण करना,
(2) (क) आमाशय में,
(3) (ग) 32,
(4) (क) दो जोड़े,
(5) (घ) छोटी आँत में,
(6) (घ) चर्वणक दाँत,
(7) (क) छः,
(8) (ग) छ: मास तक के शिशुओं में,
(9) (क) 1.5 किलोग्राम,
(10) (ख) केवल बच्चों में,
(11) (ख) लाइपेस,
(12) (घ) एमिलॉप्सिन,
(13) (ग) प्रोटीन्स,
(14) (क) 5 मीटर,
(15) (क) ग्लाइकोजन में,
(16) (ग) टायलिन।

We hope the UP Board Solutions for Class 9 Home Science Chapter 12 भोजन का पाचन एवं सम्बन्धित शरीर-क्रिया विज्ञान help you. If you have any query regarding UP Board Solutions for Class 9 Home Science Chapter 12 भोजन का पाचन एवं सम्बन्धित शरीर-क्रिया विज्ञान, drop a comment below and we will get back to you at the earliest.

Balaji Class 9 Maths Solutions Chapter 15 Circle Ex 15.2 वृत्त

Ex 15.2 Circle अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
एक वृत्त की जीवा उसकी त्रिज्या के बराबर है। जीवा द्वारा लघु चाप पर अन्तरित कोण ज्ञात कीजिए।
हल:

प्रश्न 2.
दीर्घ वृत्त का कोण निम्न में से कौन-सा होता है?
(a) न्यूनकोण
(b) अधिककोण
(c) समकोण
(d) इनमें से कोई नहीं
हलः
(a) दीर्घवृत्त खण्ड का कोण न्यूनकोण होता है।

प्रश्न 3.
दिये गये चित्र में, 0 केन्द्र वाले वृत्त के अन्दर एक समबाहु ∆ ABC है तब ∠BOC का मान ज्ञात कीजिए।
हलः

समबाहु ∆ABC में, ∠BAC = 60°
(∵ समबाहु ∆ का प्रत्येक कोण 60° होता है।)
वृत्त के केन्द्र पर बना कोण ∠BOC = 2 × वृत्त की परिधि पर बना कोण
∠BOC = 2 × ∠BAC = 2 × 60° = 120°

प्रश्न 4.
चित्र में, O वृत्त का केन्द्र है तथा रेखा OB, ∠AOC की अर्द्धक है। तब ∠ABC का मान ज्ञात कीजिए। (UP 2004)
हलः

प्रश्न 5.
चित्र में, O वृत्त का केन्द्र है तथा ∠ACB व ∠ADB समान वृत्तखण्ड के कोण हैं तब ∠ADB व ∠ACB में सम्बन्ध ज्ञात कीजिए।
हल:
∠ADB तथा ∠ACB एक ही वृत्तखण्ड AB द्वारा बने कोण हैं।
∴ ∠ADB = ∠ACB

प्रश्न 6.
ABCD एक चक्रीय चतुर्भुज है। यदि ∠DAB = 70° तब ∠DCB का मान ज्ञात कीजिए।
हलः
∵ चक्रीय चतुर्भुज के सम्मुख कोणों का योगफल 180° होता है।
∴ ∠BAD + ∠BCD = 180°
70°+ ∠BCD = 180°
∠BCD = 180°- 70°= 110°

प्रश्न 7.
चित्र में, O वृत्त का केन्द्र है x का मान ज्ञात कीजिए।
हलः
वृत्त के चाप BC द्वारा केन्द्र पर बना कोण
∠BOC = 2 × उसी चाप द्वारा वृत्त के बिन्दु A पर बना ∠BAC
∴ x = 2 × 62.5
=125°

Ex 15.2 Circle लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-I)

प्रश्न 8.
निम्न चित्रों में, x के मान ज्ञात कीजिए।

हलः
(i) एक ही वृत्तखण्ड में बने कोण समान होते हैं।
∴ ∠QPR = ∠QSR = 30°
∆ PQR में, x = 180° – (30° + 110°) (∴ ∆ के तीनों कोणों का योग = 180°)
= 180°-140° = 40°
(ii) एक ही वृत्तखण्ड में बने कोण समान होते हैं।
∴ ∠PRO = ∠PSQ = 40°
∆ OSQ में, x = 180° – (120°+ 40°)
=180° – 160°
= 20°
(iii) ∆ PQO में, PO = OQ (वृत्त की त्रिज्याएँ)
∴ ∠QPO = ∠PQO = 30°
∆OQR में, RO = OQ (वृत्त की त्रिज्याएँ)
∴ ∠QRO = ∠OQR = 45°
∴ ∠PQR = ∠PQO + ∠RQO
= 30°+ 45° = 75°
केन्द्र O पर बना ∠POR = x
= 2 × ∠PQR
= 2 × 75° =150
(iv) ∵ PQRS एक चक्रीय चतुर्भुज है।
∴ ∠PQR = 180°-140°= 40°
(∵ चक्रीय चतुर्भुज के सम्मुख कोणों का योग = 180°)
:: ∆PQR एक समकोण त्रिभुज है।
∴ ∠PRQ = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)
∆PQR में,
x = 180°– (90°+ 40°)
= 180°-130° = 50°

Ex 15.2 Circle लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 9.
चित्र में, 0 वृत्त का केन्द्र है तब सिद्ध कीजिए कि ∠POR = 2(∠PRQ + ∠QPR)
हलः

वृहत् कोण
∠POR = 2 × ∠PQR (वृहत् चाप PR द्वारा बने कोण)
∴ 360° – लघु ∠POR = 2(180°- ∠PRQ – ∠QPR)
360°- ∠POR = 360°-2(∠PRQ + ∠QPR)
∴ ∠POR = 2(∠PRQ + ∠QPR)

प्रश्न 10.
चित्र में, PQRS एक चक्रीय चतुर्भुज है तथा O वृत्त का केन्द्र है। यदि ∠QOs = 160° है। तो ∠QRS व ∠QMS के मान ज्ञात कीजिए।
हलः
चाप SQ द्वारा केन्द्र 0 पर बना कोण = 2 × चाप SQ द्वारा शेष परिधि पर बना कोण
160°= 2 × ∠SPQ

Ex 15.2 Circle दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 11.
चित्र में, O वृत्त का केन्द्र है, PQT एक सरल रेखा है तथा ∠RQT = 65° तब x व y के मान ज्ञात कीजिए।
हलः
∵ PQRS एक चक्रीय चतुर्भुज है।
∴ ∠PQR = 180°- y
∴ ∠PQT = 180°
∠PQR + ∠RQT – 180°
180° – y +65°= 180°
∴ y = 65°
∵ ∠PQR = 180°- 65° = 115°
∴ वृहत् ∠POR = 2 × ∠PQR
x = 2 × 115° = 230°

प्रश्न 12.
निम्न चित्र में, ABC एक समबाहु त्रिभुज है तब ∠BDC व ∠BEC के मान ज्ञात कीजिए।
हल:

प्रश्न 13.
निम्न चित्र में, P, Q, R व L, M, N संरेखीय बिन्दुओं के दो समुच्चय हैं। सिद्ध कीजिए कि PL||RN
हलः
चक्रीय चतुर्भुज के सम्मुख कोणों का योग 180° होता है।
∠LPQ + ∠LMQ = 180° …(1)
∠QMN + ∠NRQ = 180° …(2)
समीकरण (1) व (2) को जोड़ने पर
∠LPQ + ∠LMQ + ∠QMN + ∠NRQ = 180°+180°
∠LPQ + ∠LMQ + 180°- ∠LMQ + ∠NRQ = 360°
∠LPQ + ∠NRQ = 360°- 180°= 180°
इसी प्रकार सिद्ध कर सकते हैं कि
∠PLN + ∠MNR = 180°
∵ क्रमागत अन्तः कोणों का योगफल 180° है।
∴ PL || RN

Ex 15.2 Circle बहविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
तीन असंरेख बिन्दुओं से खींचे जा सकने वाले वृत्तों की संख्या है।
(a) 1
(b) 2
(c) 3
(d) इनमें से कोई नहीं
हल:
1
अतः विकल्प (a) सही है।

प्रश्न 2.
दो सर्वांगसम वृत्तों के केन्द्र O व O’ हैं। प्रथम वृत्त के चाप AB का अंश माप 50° तथा दूसरे वृत्त के चाप AB’ का अंशमाप 75° है तो AB : A’B’ =
(a) 1 : 2
(b) 2 : 4
(c) 2 : 3
(d) इनमें से कोई नहीं
हल:

अतः विकल्प (c) सही है।

प्रश्न 3.
किसी वृत्त की दो जीवाएं AB तथा CD केन्द्र से 3.5 सेमी दूरी पर हैं, तब-
(a) AB = CD
(b) AB > CD
(c) AB < CD (d) इनमें से कोई नहीं हलः ∵ केन्द्र से समान दूरी पर स्थित जीवाएँ लम्बाई में समान होती हैं। अतः AB = CD अतः विकल्प (a) सही है। प्रश्न 4. एक ही वृत्त में बराबर चापों द्वारा केन्द्र पर बने कोण α व β हैं, तब- (a) a = B (b) 4 > B
(c) a <B
(d) इनमें से कोई नहीं
हलः
∵ एक ही वृत्त में बराबर चापों द्वारा केन्द्र पर बने कोण समान होते हैं।
अत: α = β
अत: विकल्प (a) सही है।

प्रश्न 5.
यदि किसी चक्रीय चतुर्भुज का एक कोण 80° है तो सम्मुख कोण का मान है-
(a) 90°
(b) 100°
(c) 110°
(d) इनमें से कोई नहीं
हलः
∵ चक्रीय चतुर्भुज में आमने-सामने के कोणों का योग 180° होता है।
अतः सम्मुख कोण = 180 – 80
= 100° होगा।
अतः विकल्प (b) सही है।

प्रश्न 6.
यदि किसी चतुर्भुज में दो सम्मुख कोणों की माप 70° व 110° हैं तो वह चतुर्भुज निम्न में से किस प्रकार का है?
(a) समान्तर चतुर्भुज
(b) समचतुर्भुज
(c) चक्रीय चतुर्भुज
(d) इनमें से कोई नहीं
हलः
चक्रीय चतुर्भुज। अतः विकल्प (c) सही है।

प्रश्न 7.
बराबर वृत्तों में बराबर चापों के संगत जीवाओं की लम्बाई का अनुपात होगा।
(a) 1 : 2
(b) 1 : 1
(c) 2 : 1
(d) इनमें से कोई नहीं
हल:
1 : 1
अतः विकल्प (b) सही है।

प्रश्न 8.
किसी वृत्त का व्यास AB है। AB के बाहर वृत्त पर बिन्दु C है तो ∠ACB =
(a) 100°
(b) 0°
(c) 60°
(d) 90°
हल:
∵ अर्द्धवृत्त में स्थित कोण समकोण होता है।
अत: ∠ACB = 90°
अतः विकल्प (d) सही है।

Ex 15.2 Circle स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
एक वृत्त की, 5 सेमी तथा 11 सेमी लम्बाई की क्रमशः दो जीवाएँ परस्पर समान्तर हैं तथा इसके केन्द्र के विपरीत है यदि AB और CD के बीच की दूरी 6 सेमी है, तो वृत्त की त्रिज्या ज्ञात कीजिए। (NCERT)
हलः

प्रश्न 2.
एक वृत्त की दो समांतर जीवाओं की लम्बाईयाँ 6 सेमी तथा 8 सेमी हैं यदि छोटी जीवा केन्द्र से एक 4 सेमी की दूरी पर है, केन्द्र से अन्य जीवा की दूरी ज्ञात कीजिए।
हलः
∆APM में, AM² = AP² + PM²
= (3)² + (4)²
= 9 + 16 = 25
AM = [latex]\sqrt{25}[/latex] = 5
वृत्त की त्रिज्या AM = CM = 5 सेमी
अब ∆MCQ में, MC² = MQ² + CQ²
(5)² = MQ² + (4)²
25 – 16 = MQ
∴ MQ = 19 = 3 सेमी
∴ केन्द्र से दूसरी जीवा की दूरी = 3 सेमी

प्रश्न 3.
एक पार्क में बने 20 मीटर त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ A,B और C खेल रही हैं। A एक गेंद को B के पास, B, C के पास C,A के पास फेंकती है। यदि A और B के बीच और B और C के बीच की प्रत्येक दूरी 24 मीटर है, तो A और C के बीच की दूरी ज्ञात कीजिए।
हलः

प्रश्न 4.
40 मीटर त्रिज्या का एक वृत्तीय पार्क, एक कॉलोनी में स्थित है। तीन लड़के A, B और C इसकी परिसीमा पर बराबर दूरी पर बैठे है और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए हैं। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
हल:

प्रश्न 5.
एक वृत्त की जीवाएँ AC और BD एक-दूसरे को समद्विभाजित करती है सिद्ध कीजिए कि-
(i) AC और BD व्यास है। (NCERT)
(ii) ABCD एक आयत है।
हल:
∵ AC व BD एक दूसरे को समद्विभाजित करती है।
∴ AO × OC = BO × OD [परन्तु AO = OC तथा BO = OD]
OA² = BO²
या OA = BO
इसी प्रकार OA = OD
तथा OC = OD तथा OC = OD
अत: AC और BD वृत्त के व्यास होंगे।

प्रश्न 6.
संलग्न चित्र में, AB वृत्त का व्यास है तथा CD एक जीवा वृत्त की त्रिज्या के बराबर है। AC व BD को जब बढ़ाया जाता है, तो वे बिन्दु E पर मिलती है। सिद्ध कीजिए for ∠AEB = 60° (NCERT)
हलः

प्रश्न 7.
एक चक्रीय चतुर्भुज के विकर्ण समकोण पर है। सिद्ध कीजिए कि किसी एक भुजा जिसे पीछे की ओर बढ़ाया गया है पर इसके प्रतिच्छेद बिन्दु से 6 लम्ब विपरीत भुजा को समद्विभाजित करता है। (NCERT)
हलः

प्रश्न 8.
यदि एक वृत्त की दो बराबर जीवाएँ, वृत्त के अन्दर प्रतिच्छेद करती है तो सिद्ध कीजिए कि इन जीवाओं
का प्रतिच्छेद बिन्दु, वृत्त के केन्द्र से समान कोण बनाता है।
हलः
माना वृत्त का केन्द्र O है। बिन्दु O से जीवा AB तथा CD पर क्रमशः लम्ब OM तथा ON
खींचे।
अब ∆OMP तथा ∆OPN में,

प्रश्न 9.
यदि एक त्रिभुज की दो भुजाओं को व्यास मानकर, वृत्त खींचे गए हैं, तो सिद्ध कीजिए इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है। (NCERT)
हलः

प्रश्न 10.
केन्द्र O के एक वृत्त में, जीवाएँ AB और CD परिधि के अन्दर E पर प्रतिच्छेद करती है तो सिद्ध कीजिए कि ∠AOC + ∠BOD = 2 ∠AEC
हलः

प्रश्न 11.
यदि O, एक AABC का परिकेन्द्र है तथा OD ⊥ BC तो सिद्ध कीजिए कि ∠BOD = ∠A
हलः

प्रश्न 12.
एक वृत्त के दो व्यास परस्पर समकोण पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि उनके अंत बिन्दुओं को जोड़ने से बना चतुर्भुज, एक वर्ग होता है।
हल:

प्रश्न 13.
केन्द्र O के एक वृत्त का व्यास AB है तथा त्रिज्या OD, AB के लम्बवत् है यदि चाप DB पर कोई बिन्दु C है तो दर्शाइये कि ∠BAD = ∠ACD = 45°
हलः

प्रश्न 14.
एक समद्विबाहु त्रिभुज की बराबर भुजाओं AB और AC पर क्रमशः बिन्दु D तथा E इस प्रकार है कि B,C,E और D एकवृत्तीय चतुर्भुज है। यदि 0,CD और BE का प्रतिच्छेद बिन्दु है तो सिद्ध कीजिए कि AO, रेखाखण्ड DE का समद्विभाजक है।
हलः

प्रश्न 15.
सिद्ध कीजिए कि चक्रीय समलम्ब की असमान्तर भुजाएँ बराबर होती हैं। (UP 2006)
हल:

प्रश्न 16.
सिद्ध कीजिए कि किसी वृत्त में जो जीवा केन्द्र के निकट होती है। दूर वाली से अधिक बड़ी होती है। (UP 2005)
हलः
यदि वृत्त जिसका केन्द्र O है। O से जीवा AB तथा CD पर डाले गए लम्ब क्रमश: OM तथा ON हैं।

प्रश्न 17.
सिद्ध कीजिए कि किसी समकोण त्रिभुज में कर्ण के मध्य बिन्दु के सामने वाले शीर्ष से खींचा गया रेखाखण्ड कर्ण का आधा होता है। (UP 2006, 08, 09)
हल:

प्रश्न 18.
यदि किसी चक्रीय चतुर्भुज की सम्मुख भुजाओं का एक-युग्म बराबर हो, तो सिद्ध कीजिए कि उनके विकर्ण भी बराबर होंगे। (UP 2012)
हल:
∵ AB = CD
अतः वृत्त की दो जीवाएँ बराबर होंगी यदि केन्द्र से उनकी दूरी बराबर हों, तब
OM = ON
∆AMO तथा ∆DNO में, AM = DN
OM = ON
∠AMO = ∠DNO
∆AMO ≅ ∆DNO
अतः OA = OD
इसी प्रकार OB = OC
अतः विकर्ण AC = BD

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.7 बहुपद तथा उनके गुणनखण्ड

प्रश्न 1.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x³ – 8y³
(ii) a³ – 0.216
(iii) 16a⁴ + 54a
(iv) a⁶ – 7a³ – 8
हलः
(i) x³ – 8y³ = (x)³ – (2y)³ = (x – 2y)(x² + 4y² + 2xy)

(ii) a³ – 0.216 = (a)³ – (0.6)³ = (a – 0.6)(a² – 0.36 + 0.6 a)

(iii) 16a⁴ + 54a = 2a(8a³ + 27) = 2a[(2a)³ + (3)³] = 2a[(2a + 3)(4a² + 9 – 6a)]

(iv) a⁶ – 7a³ – 8 = a – (8 – 1)a³ – 8 = a⁶ – 8a³ + a³ – 8 = a (a³ – 8) – 1(a³ – 8)
= (a³ – 8)(a³ + 1) = [(a)³ – (2)³][(a)³ + (1)³]
= (a – 2)(a² + 4 + 2a)(a + 1)(a + 1 – a)

प्रश्न 2.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) x³ + 64
(ii) 1 – 125y³
(iii) [latex]\frac{p^{3}}{343}[/latex] + 8q³
(iv) 7m⁴n – 7mn⁴
(v) x⁷y⁷ – xy
हलः
(i) x³ + 64 = (x)³ + (4)³ = (x + 4)(x² + 16 – 4x)

(ii) 1-125y 3 = (1)³ – (5y)³ = (1 – 5y)(1 + 25y² + 5y)

(iii) [latex]\frac{p^{3}}{343}+8 q^{3}=\left(\frac{p}{7}\right)^{3}+(2 q)^{3}=\left(\frac{p}{7}+2 q\right)\left(\frac{p^{2}}{49}+4 q^{2}-\frac{2}{7} p q\right)[/latex]

(iv) 7m⁴n – 7mn⁴ = 7mn(m³ – n³) = 7mn[(m)³– (n)³] = 7mn[(m – n)(m² + n² + mn)]

(v) x⁷y⁷ – xy = xy(x⁶y⁶ – 1) = xy[(x²y²)³ – (1)³].
= y[(x²y² – 1)(x⁴y⁴ + 1 + x²y²]
= xy [(xy)² – (1)²) (x⁴y⁴ – 1 + 2x²y² xy²)]
= xy (xy + 1)(xy – 1)[(x²y² + 1)² – (xy)²]
= xy(xy + 1)(xy – 1)(x²y² + 1 + xy)(x²y² + 1 – xy)

प्रश्न 3.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) (a + 2b)³ – (a – 2b)³
(ii) a³ + b³ + c(a² – ab + b²)
(iii) x⁶ – 7x³ – 8
(iv) x³ – 3x² + 3x + 7
हल:
(i) (a + 2b)³ – (a – 2b)³ = (a + 2b – a + 2b) [(a + 2b)² + (a – 2b)² + (a + 2b) (a – 2b)]
= (4b)[a² + 4b² + 4ab + a² + 4b² – 4ab + a² – 4b²]
= (4b)[3a² + 4b²]

(ii) a³ + b³ + c(a² – ab + b²) = (a + b)(a + b² – ab) + c(a² – ab + b)
= (a² + b² – ab)[a + b + c]

(iii) x⁶ – 7x³ – 8 = x⁶ – (8 – 1)x³ – 8 (∵ 8 = 1 × 8)
= x⁶ – 8x³ + x³ – 8 = x³ (x³ – 8) +1(x³ – 8) = (x³ – 8)(x³ + 1)
=[(x)³ – (2)³][(x)³ + (1)³] = (x – 2)(x² + 4 + 2x)(x + 1)(x² + 1 – x)

(iv) x³ – 3x² + 3x + 7
माना f(x) = x³ – 3x² + 3x + 7
x + 1 = 0
x = -1 रखने पर,
= (-1)³ – 3(-1)² + 3 × (-1) +7
= -1 – 3 – 3 + 7 = -7 + 7 = 0
∵ (x + 1), f(x) का एक गुणनखण्ड है।
अतः

अत: x³ – 3x² + 3x + 7 के गुणनखण्ड (x + 1)(x² – 4x + 7) है।

प्रश्न 4.
निम्न व्यंजकों को सरल करके उनके मान ज्ञात कीजिए

हलः

Ex 5.7 Polynomial and their Factors स्वमूल्यांकन परीक्षण (Self Assessment Test)

निम्न के गुणनखण्ड कीजिए।
प्रश्न 1.
[latex]27 p^{3}-\frac{1}{216}-\frac{9}{2} p^{2}+\frac{1}{4} p[/latex] (NCERT)
हलः
[latex](3 p)^{3}+\left(-\frac{1}{6}\right)^{3}+3(3 p)\left(-\frac{1}{6}\right)\left(3 p-\frac{1}{6}\right)=\left(3 p-\frac{1}{6}\right)^{3}[/latex]

प्रश्न 2.
49a² + 70ab + 25b²
हलः
(7a)² + 2 × 7a × 5b + (5b)²
सूत्र [x² + 2xy + y² = (x + y)] से
= (7a + 5b)²

प्रश्न 3.
4x² + y² + z² – 4xy -2yz + 4xz
हलः
(2x)² + (-y)² + (z)² + 2. (2x)(-y) + 2(-y) (z) + 2. (2x)(z)
= (2x – y + z)² = (2x – y + z)(2x – y + z)

प्रश्न 4.
64m³ – 343n³
हलः
64m³ – 343n³ = (4m)³ – (7n)³ = (4m – 7n)(16m² + 49n² + 28mn)

प्रश्न 5.
27 – 125a³ – 135a + 225a²    (NCERT)
हलः
27 – 125a³ – 135a + 225a²
= (3)³ – (5a) – 45a(3 – 5a) = (3 – 5a)(9 + 25a² + 15a) – 45a(3 – 5a)
= (3 – 5a)(9 + 25a² + 15a – 45a) = (3 – 5a)(9 + 25a² – 30a)
= (3 – 5a)[(3)² + (5a)² – 2 × 3 × 5a]
= (3 – 5a) (3 – 5a)² = (3 – 5a)³

प्रश्न 6.
8a³ – b³ – 12a²b + 6ab²      (NCERT)
हल:
8a³3 – b³ – 12a²b + 6ab²
= (2a)³ – (b)³ – 6ab (2a – b) = (2a – b)(4a² + b² + 2ab) – 6ab(2a – b)
= (2a – b) [4a² + b² + 2ab – 6ab] = (2a – b)[4a² + b² – 4ab]
= (2a – b)[(2a)² + (b²) – 2 × 2a × b]
= (2a – b)(2a – b)² = (2a – b)³

प्रश्न 7.
64a³ – 27b³ – 144a²b + 108ab²
हलः
(4a)³ – (3b)³ – 36ab(4a – 3b)
= (4a – 3b)(16a² + 9b² + 12ab) – 36ab(4a – 3b)
= (4a – 3b)(16a² + 9b² + 12ab – 36ab) = (4a – 3b)(16a² + 9b² – 24ab)
= (4a – 3b)[(4a)² + (3b)² – 2 × 4a × 3b]
= (4a – 3b)[4a – 3b]² = (4a – 3b)³

प्रश्न 8.
8a³ + b³ + 12a²b + 6ab² (NCERT)
हलः
(2a) + (b)³ + 6ab(2a + b)
= (2a + b)(4a² + b² – 2ab) + 6ab(2a + b)
= (2a + b)[4a² + b² – 2ab + 6ab]
= (2a + b)[4a² + b² + 4ab]
= (2a + b)[(2a)² + (b)² + 2 × 2a × b]
= (2a + b)(2a + b)² = (2a + b)³

प्रश्न 9.
[latex]27 p^{3}-\frac{1}{216}-\frac{9}{2} p^{2}+\frac{1}{4} p[/latex]
हलः
[latex](3 p)^{3}+\left(-\frac{1}{6}\right)^{3}+3(3 p)\left(-\frac{1}{6}\right)\left(3 p-\frac{1}{6}\right)=\left(3 p-\frac{1}{6}\right)^{3}[/latex]

प्रश्न 10.
27x³ + y³ + z³ – 9xyz
हलः
(3x)³ + (y)³ + (z)³ – 3(3x)(y)(z)
= (3x + y + z)[(3x)2 + y² + z² – 3xy – yz – 3xz]
= (3x + y + z)[9x² + y² + z² – 3xy – yz – 3xz]

प्रश्न 11.
सिद्ध कीजिए कि a² + b² + 2(ab + bc + ca) = (a + b)(a + b + 2c)
हलः
L.H.S. = a² + b² + 2(ab + bc + ca) = a² + b² + 2ab + 2bc + 2ca
= (a + b)² + 2c(a + b) = (a + b)[a + b + 2c] = R.H.S.

प्रश्न 12.
सिद्ध कीजिए कि 8a³ – b³ – 4ax + 2bx = (2a – b)(4a² + 2ab + b² – 2x)
हलः
L.H.S. = 8a³ – b³ – 4ax + 2bx
= (2a)³ – (b)³ – 2x(2a – b) = (2a – b)(4a² + b² + 2ab) – 2x(2a – b)
= (2a – b)(4a² + b² + 2ab – 2x) = R.H.S.

प्रश्न 13.
सिद्ध कीजिए कि [latex]\frac{64}{125} x^{3}-8-\frac{96}{25} x^{2}+\frac{48}{5} x=\left(\frac{4 x}{5}-2\right)^{3}[/latex]
हलः

प्रश्न 14.
सिद्ध कीजिए कि a³x³ – 3a²bx² + 3ab²x – b³ = (ax – b)³ हलः
L.H.S. = ax³ – b³ – 3a²bx² + 3ab²x
= (ax)³ – (b)³ – 3abx(ax – b) = (ax – b)(a²x² + b² + abx) – 3abx(ax – b)
= (ax – b)(a²x² + b² + abx – 3abx) = (ax – b)(a²x² + b² – 2abx)
= (ax – b)(ax – b)² = (ax – 1)³ = R. H.S.

प्रश्न 15.
सिद्ध कीजिए कि a³ + b³ + 1 + 3ab = (a – b + 1)(a³ + b³ + ab – a + b + 1)
हलः
L.H.S. = (a)³ + (-b)³ + (1)³ – 3(a)(-b)(1)
= (a – b + 1)(a² + b² +1+ ab + b-a)
[∵ x³ + y² + z³ – 3xy² = (x + y + z)(x² + y² + z² – xy – yz – zx)]
∴ a³ – b³ + 1 + 3ab = (a – b + 1)(a² + b² + ab + a + b + 1) = R.H.S.

प्रश्न 16.
यदि p = 2 – a, तब सिद्ध कीजिए कि a³ + 6ap + p³ – 8 = 0
हलः
L.H.S. =a³ + 6ap + p – 8
= a³ – 8 + 6ap + p³ = (a – 2)(a² + 4 + 2a) + p(6a + p²)
p = 2 – a रखने पर
= (a − 2)(a² + 4 + 2a) +(2 – a)(6a + 4 + a² – 4a)
= (a − 2)(a² + 4 + 2a) – (a − 2)(a² + 2a + 4)
= (a – 2)[a² + 4 + 2a – a² – 2a – 4] = 0 = R. H.S.

प्रश्न 17.
यदि x = 2y+6, तब सिद्ध कीजिए कि x³ – 8y³ – 36xy – 216 =0 (NCERT Exemplar) .
हल:
L.H.S. = x³ – 8y³ – 36xy – 216
= (x)³ – (2y)³ – 36xy – 216 = (x – 2y)(x² +4y² + 2xy) – 36xy – 216
x = 2y + 6 रखने पर
= [2y + 6 – 2y][(2y + 6)² + 4y² + 2(2y + 6)y] – 36(2y + 6)y – 216
= 6[4y² + 36 + 24y + 4y² + 4y² + 12y] – 72y² – 216y – 216 = 0 = R.H.S.

प्रश्न 18.
यदि x + y = -4, तब सिद्ध कीजिए कि x + y³ – 12xy + 64 = 0 (NCERT Exemplar)
हल:
x³ + y³ – 12xy + 64
= (x + y) (x² + y² – xy) – 12xy + 64= (-4)(x² + y² – xy) – 12xy + 64
= -4x² – 4y² + 4xy – 12xy + 64 = -4x² – 4y² – 8xy + 64
= -4x² – 4(-4 – x)² – 8x(-4 – x) + 64 [y = -4 – x रखने पर]
= -4x² – 4(16 + x² + 8x) + 32x + 8x² + 64 = 0 = R.H.S.

प्रश्न 19.
यदि a² + b² + c² = 250 और ab+ bc + ca = 3, तब सिद्ध कीजिए कि a + b+ c = ±16
हलः
सूत्र (a + b + c) = a² + b² + c² + 2(ab + bc + ca) .
(a + b + c)2 = 250 + 2 × 3 = 250 + 6 = 256
(a + b + c) = [latex]\sqrt{256}[/latex] = ± 16

प्रश्न 20.
सिद्ध कीजिए कि

हलः
माना a = 0.013 तथा b = 0.007

= a + b = 0.013 + 0.007 = 0.020

प्रश्न 21.
यदि a + b ≠ 0 तब सिद्ध कीजिए कि समीकरण a(x – a) = 2ab – b(x – b) का हल x = a + b होता है|
हलः
∵ a(x – a) = 2ab – b(x – b)
⇒ ax – a² – 2ab + bx – b² = 0
x(a + b) = a² + b² + 2ab
x(a + b) – (a + b)² = 0
(a + b){x – (a + b)} = 0
a + b ≠ 0 अत: x – (a + b) = 0
x = (a + b)

प्रश्न 22.
सिद्ध कीजिए कि 2(a² + b²) = (a + b)² तब a = b
हलः
∵ 2(a + b²) = (a + b)²
⇒ 2(a² + b²) = a² + b² + 2ab
⇒ 2a² + 2b² = a² + b² + 2ab
⇒ a² + b² – 2ab = 0
⇒ (a – b)² = 0 ⇒ a = b

प्रश्न 23.
सिद्ध कीजिए कि 1 – x² + 2xy – y² = (1 + x – y)(1 – x + y)
हलः
L.H.S. = 1 – x² + 2xy – y²
= 1 – (x² – 2xy + y²) = 1² – (x – y)²
= (1 + x – y)(1 – x + y) = R.H.S.

प्रश्न 24.

हलः

प्रश्न 25.

हलः

प्रश्न 26.

हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 12 Congruence of Triangles Ex 12.1 त्रिभुजों की सर्वांगसमता

प्रश्न 1.
चित्र में वर्ग ABCD में एक बिन्दु x है। AX पर एक वर्ग AXYZ बनाया जाता है। सिद्ध कीजिए कि BX = DZ
हलः
समकोण ∆AXB तथा समकोण ∆AZD में
AB = AD (वर्ग की भुजाएँ)
AZ = AX (वर्ग की भुजाएँ)

R.H.S समरूपता से
∆AXB ≅ ∆AZD
∴ BX = DZ

प्रश्न 2.
दिये गये चित्र में AD और BC परस्पर O पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए:
(i) AB = CD तथा AC = BD
(ii) ∠BCD = ∠CBA तथा ∠DAC = ∠ADB
हलः

(i) ∆AOB तथा ∆COD में,

प्रश्न 3.
एक त्रिभुज ABC की माध्यिकाएँ BE और CF बराबर हैं। तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु है। (संकेतः माध्यिकाओं का प्रतिच्छेद बिन्दु इन्हें 2:1 के अनुपात में विभाजित करता है।)
हल:

प्रश्न 4.
दिये गये चित्र में, एक वर्ग PQRS तथा SRT एक समबाहु त्रिभुज है तो सिद्ध कीजिए (NCERT)
(i) PT = QT
(ii) ∠QRT = 150°
हलः

प्रश्न 5.
ABC एक समबाहु त्रिभुज है, D कोई इसका अन्तः केन्द्र है। DC पर एक समद्विबाहु त्रिभुज DEC खींचा गया है। [चित्र में दिखाये (DE = DC) अनुसार] तो सिद्ध कीजिए कि ∆BDC तथा ∆CDE सर्वांगसम हैं।
हल:

प्रश्न 6.
भुजा AB = AC का एक समद्विबाहु त्रिभुज ABC है तथा ∠B तथा ∠C के समद्विभाजक परस्पर O पर
प्रतिच्छेद करते हैं। तो सिद्ध कीजिए कि BO = CO तथा AO, ∠BAC का समद्विभाजक है।
हल:

प्रश्न 7.
दिये गये चित्र में, BA ⊥ AC तथा DE ⊥ EF इस प्रकार है कि BA = DE तथा DF = BC तो सिद्ध कीजिए कि AC = EF
हलः

प्रश्न 8.
दिये गये चित्र में, QX तथा RX, ∆PQR के क्रमशः ∠Q तथा ∠R के समद्विभाजक हैं यदि XS ⊥ QR तथा XT ⊥ PQ तो सिद्ध कीजिए-
(i) ∆XTQ = ∆XSQ
(ii) PX, ∠P का समद्विभाजक है।
हलः

प्रश्न 9.
चित्र में, ∠1 = ∠2, AC ⊥ CD तथा AB ⊥ BD तो सिद्ध कीजिए कि BD = CD
हलः

प्रश्न 10.
एक ∆PQR की भुजाएँ PQ व PR समान हैं तथा PR और PQ पर बिंदु S और T इस प्रकार हैं कि ∠PSQ और ∠PTR समकोण हैं तो सिद्ध कीजिए कि त्रिभुज PTR और PSQ सर्वांगसम हैं। यदि QS तथा RT, X पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए कि PTX तथा PSX सर्वांगसम हैं।
हलः

प्रश्न 11.
दिये गये चित्र में, AB = EF, BC = DE, AB ⊥ BD तथा FE ⊥ CE तो सिद्ध कीजिए कि ∆ABD = ∆FEC
हलः

प्रश्न 12.
चित्र में, AB = AC तथा ∠ACD = 115°, तब ∠BAC = ?
हल:

प्रश्न 13.
चित्र में, ABCD एक वर्ग है तथा EF, BD के समांतर है। R, EF का मध्य बिन्दु है A तो सिद्ध कीजिए कि-
(i) BE = DF
(ii) AR, ∠BAD का समद्विभाजक है।
(iii) यदि AR को बढ़ाते हैं तो यह C से होकर गुजरेगा।
हल:

प्रश्न 14.
चित्र में, यदि AB = 3 सेमी, AC = 3 सेमी तथा ∠A = 50° तब ∠B = ?
हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 10 Lines and Angle Ex 10.2 रेखाएँ एवं कोण

Ex 10.2 Lines and Angle अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
दी गयी आकृति में, AB || DE तो सिद्ध कीजिए कि ∠ABC + ∠BCD = 180°+ ∠CDE
हलः
बिन्दु C से होकर एक रेखा MCN खींची जबकि AB || MN
माना
∠MCD = x
∠MCB = y

∠CDE = ∠ MCD = x
LHS ∵ ∠ABC + ∠BCD = 180 – y + x + y [∵ ∠ABC = ∠BCN = 180°- y एकान्तर कोण]
= 180 + x = 180 + ∠CDE = RHS

प्रश्न 2.
दी गयी आकृति में, AB, CD के समान्तर है, x ज्ञात कीजिए।
हलः

∵ AB||CD
बिन्दु T से होती हुई AB तथा CD के समान्तर रेखा MN खींची।
∠ TAB + ∠ATN = 180° (अन्तः कोण युग्म)
140 + ∠ATN – 180°
∠ATN = 180 – 140 = 40°
∵ ∠DCT + ∠NTC = 180°
150 + ∠NTC = 180°
∠NTC = 180 – 150 = 30°
∴ x = ∠ATN + ∠NTC = 40 + 30 = 70°

प्रश्न 3.
निम्न प्रत्येक आकृति में x° का मान ज्ञात कीजिए।

हल:
(i) AB तथा CD के समान्तर एक रेखा FEM खींची।
∠ABE + ∠FEB = 180°
140 + ∠FEB = 180°
∠FEB = 180 – 140 = 40°
∠CDE + ∠FED = 180°
135 + ∠FED = 180° (अन्तः युग्म कोण)
∠FED = 180 – 135 = 45°
∴ ∠FEB + ∠FED = 40 + 45 = 85°
∴ x = 85°

(ii) बिन्दु E से होती हुई एक रेखा MN खींची
∠MEA = ∠BAE = 50° (एकान्तर कोण)
∠MEC = ∠ECD = 70° (एकान्तर कोण)
∴ ∠MEA + ∠MEC = 50 + 70 = 120°
∴ x = 120°

(iii) बिन्दु E से होती हुई MN रेखा खींची
माना ∠MEB = a
a = 180°- 60° = 120°
∴ b = 180°- 30° = 150°
∵ x = a + b
= 120° + 150° = 270°

प्रश्न 4.
दी गयी आकृति में, AB|| CD तथा कोई बिन्दु P दर्शाया गया है तो सिद्ध कीजिए कि ∠ABP + ∠BPD + ∠CDP = 360°
हल:

∵ AB||CD
तथा P बिन्दु से होती हुई एक सरल रेखा EF खींची
माना ∠BPE = x तथा ∠DPE = y
∠MBP = 180 – ∠ABP ……….. (1)
तथा ∠NDP = 180 – ∠PDC …………..(2)
∠MBP = x (एकान्तर कोण)
∠NDP = y (एकान्तर कोण)
समीकरण (1) से 180 – ∠ABP = x ……… (3)
समीकरण (2) से 180 – ∠PDC = y …………. (4)
समीकरण (3) व (4) को जोडने पर,
180 – ∠ABP + 180 – ∠PDC = x + y
360 – ∠ABP – ∠CDP = ∠BPD
∴ 360° = ∠ABP + ∠BPD + ∠CDP

प्रश्न 5.
दी गयी आकृति में, x ज्ञात कीजिए।
हल:
∆ABC का बहिष्कोण = x
∆ का बहिष्कोण अपने सम्मुख अन्तः कोणों के योग के बराबर होता है

∴ ∠CBD = ∠ACB + ∠CAB
∴ ∠CBD = 70 + 60 = 130°
∴ x = 130°

प्रश्न 6.
दी गयी आकृति में, l||m||n और ∠1 = 60°, ∠2 ज्ञात कीजिए।
हल:

∠1 = 60° ∵ l || m || n
∠1 = ∠3 (संगत कोण)
= 60°
∴ ∠4 = 180° – 60° = 120°
∠2 = ∠4 = 120° (एकान्तर कोण)

प्रश्न 7.
आकृति में, भुजाओं BA और DC द्वारा निर्मित एक चतुर्भुज दर्शाया गया है तो सिद्ध कीजिए कि a + b = x + y यदि AB||DC.
हलः

∵ ∠BCD = 180 – a
∠BAD = 180 – b
चतुर्भुज के चारो कोणों का योग = 360
180 – a + y + 180 – b + x = 360
x + y = a + b

प्रश्न 8.
दी गयी आकृति में, AB||CD और ∠F = 30°, तो ∠ECD ज्ञात कीजिए।
हलः

∵ ∠AFE = 30°
∠ECH = ∠AFE = 30° (एकान्तर कोण)
∠ECD = 30 + 90 = 120°

प्रश्न 9.
दी गयी आकृति में, यदि AC||DE, तब x का मान ज्ञात कीजिए।
हलः

∠MCD = 180° – ∠EDC
= 180° – 55° = 125
x = ∠MCD (शीर्षाभिमुख कोण)
= 125°

प्रश्न 10.
दी गयी आकृति में, ∠ABC की भुजाओं BA और BC, ∠DEF की क्रमशः भुजाओं ED और EF के समान्तर है तो सिद्ध कीजिए कि ∠ABC + ∠DEF = 180°
हल:
∵ ∠ABC + ∠EDC = 180° (अन्तः युग्म कोण) …………….(1)
परन्तु ∠EDC = ∠DEF ………….. (2)

समीकरण (2) का मान समीकरण (1) में रखने पर
∠ABC + ∠DEF = 180°

प्रश्न 11.
दी गयी आकृति में AB||CD और DE||CF, तो x और y ज्ञात कीजिए।
हलः

∵ AB || CD
∴ ∠BAC = ∠ACD
50 = y (एकान्तर कोण) …………(1)
∵ DE ||CF
x = 70 + y (एकान्तर कोण) …………(2)
समीकरण (2) में y का मान रखने पर
x = 70 + 50 = 120°

प्रश्न 12.
दी गयी आकृति में BD||CE, तो x, y और z ज्ञात कीजिए।
हलः

∠ FDE = 180 – 120 = 60°
∴ y = 60° (संगत कोण)
∠DBC = 180 – 70 = 110°
∆ABD में,
∠DBC = ∠BAD + ∠ADB
110 = x + 60
(∵ ∠ADB = 180 – 120 = 60°)
x = 110 – 60 = 50°
x = 50°
z = ∠BCE = 70° (संगत कोण)

प्रश्न 13.
दी गयी आकृति में समान्तर रेखायें l, m, n एक तिर्यक रेखा P द्वारा क्रमशः x, y और z पर प्रतिच्छेद होती है। तो ∠1, ∠2 तथा ∠3 ज्ञात कीजिए।
हलः

∠4 = 180° – 50° = 130°
∠4 = ∠1 = 130° (संगत कोण)
∠1 = ∠2 = 130° (संगत कोण)
∠3 = ∠1 = 130° (एकान्तर कोण)

प्रश्न 14.
दी गयी आकृति में l₁||l₂ और m₁|| m₂ क्यों हैं, कारण दीजिए?
हलः

∠NQR = QRS = 130°
परन्तु ये एकान्तर कोण हैं।
∴ m₁||m₂
∠PQR = 180° – 130° = 50°
∠MPS = ∠PQR = 50° (संगत कोण)
∴ l₁||l₂

Ex 10.2 Lines and Angle विविध प्रश्नावली

प्रश्न 1.
चित्र में x और y के मान ज्ञात कीजिए और सिद्ध कीजिए कि AB||CD.
हल:
AB||CD
x = 130° (संगत कोण)
y = 130° (शीर्षाभिमुख कोण)

प्रश्न 2.
चित्र में, यदि AB||CD, CD||EF और y : z = 3 : 7, तो x का मान ज्ञात कीजिए।
हलः
∠EPN = ∠CNM

180 – z = y
∴ y + z = 180° …………..(1)
माना ∠y = 3a
∠z = 7a
3a + 7a = 180
10a = 180 ⇒ a = [latex]\frac{180}{10}[/latex] = 18
∴ y = 3 × 18 = 54°
∵ z + y = 180
∴ z + 54 = 180°
∴ z = 180 – 54 = 126°
∴ ∠x = 2x = 126° (संगत कोण)

प्रश्न 3.
चित्र में, यदि AB||CD, EF⊥CD और ∠GED = 126°, ∠AGE, ∠GEF और ∠FGE ज्ञात कीजिए। (NCERT)
हल:

∵ AB||CD
∠AGE = ∠GED = 126° (एकान्तर कोण)
∠GEF = 126° – ∠FED
= 126° – 90° = 36°
∠FGE = 180° – ∠AGE = 180 – 126 = 54°

प्रश्न 4.
चित्र में यदि PQ||ST, ∠PQR = 110° और ∠RST = 130° तो ∠QRS ज्ञात कीजिए। (NCERT)
हलः

PQ को आगे M तक बढ़ाया
तथा
∠AMR = 130° (संगत कोण)
∠MQR = 180°- 110 = 70°
∠QMR = 180 – 130 = 50°
∆QRM में तथा ∠QRS = 180°- (∠MQR + ∠QMR)
= 180°- (70 + 50)
= 180 – 120 = 60°

प्रश्न 5.
चित्र में यदि AB||CD, ∠APQ = 50° और ∠PRD = 127° तो और y ज्ञात कीजिए।
हल:
∆PQR में, AB||CD
x = 50° (एकान्तर कोण)
∵ बहिष्कोण ∠PRD = ∠QPR + ∠PQR
∠PRD = y + x
127 = y + 50
127 – 50 = y
77° = y

प्रश्न 6.
चित्र में PQ और RS दो दर्पण है जो एक-दूसरे के समान्तर रखे गये है। एक आपतन किरण AB दर्पण PQ से B पर टकराती है और परावर्तित किरण पथ BC पर चलकर दर्पण RS से C पर टकराती है तथा पुनः CD के अनुदिश परावर्तित हो जाती है। सिद्ध कीजिए कि AB||CD है।
हलः

∵ ∠3 = ∠4 ……………. (1)
P तथा ∠1 = ∠2 …………. (2)
परन्तु ∠3 = ∠2 …………… (3) (एकान्तर कोण) ,
समीकरण (1) व (3) से ∠2 = ∠4 …………….. (4)
समीकरण (2) व (3) से ∠1 = ∠3 ………………… (5)
समीकरण (4) व (5) को जोड़ने पर
∠2 + ∠1 = ∠4 + ∠3
∴ ∠BCD = ∠ABC
परन्तु ये एकान्तर कोण है।
∴ AB||CD

प्रश्न 7.
चित्र में ∆PQR की भुजाएँ QP और RQ को क्रमशः बिन्दुओं S और T तक बढ़ाया गया है। यदि ∠SPR = 135° है और ∠PQT = 110° है तो ∠PRQ ज्ञात कीजिए। (NCERT)
हलः

∠QPR = 180 – 135 = 45°
∠PQT = ∠QPR + ∠PRQ
(∆ का बहिष्कोण अपने सम्मुख अन्तः कोणों के योग के बराबर होता है)
110 = 45 + ∠PRQ
110 – 45 = ∠PRQ
65° = ∠PRQ

प्रश्न 8.
चित्र में ∠X = 62°, ∠XYZ = 547, यदि ∆XYZ में YO और ZO क्रमशः ∠XYZ और ∠XZY के समद्विभाजक हैं तो ∠OZY और ∠YOZ ज्ञात कीजिए।
हल:
∆XYZ में ∠XZY = 180°– (62 + 54)
180 – 116 = 64°
∵ YO तथा ZO क्रमशः ∠XYZ तथा ∠XZY के समद्विभाजक है।

∴ ∠OYZ = [latex]\frac{54}{2}[/latex] = 27
तथा ∠OZY = [latex]\frac{64}{2}[/latex] = 32°
∠YOZ = 180 – (27 + 32)
= 180 – 59 = 121°

प्रश्न 9.
चित्र में यदि AB||DE, ∠BAC = 35°, ∠CDE = 53° तो ∠DCE ज्ञात कीजिए। (NCERT)
हलः

∵ AB||DE
∠BAC = ∠DEC = 35° (एकान्तर कोण)
∆CDE में,
∠DCE = 180° – (53 + 35)
= 180 – 88 = 92°

प्रश्न 10.
चित्र में यदि रेखाएं PQ और RS बिन्दु T पर इस प्रकार प्रतिच्छेद करती है कि ∠PRT = 40°, ∠RPT = 95° और ∠TSQ = 75°, तो ∠SQT ज्ञात कीजिए। (NCERT)
हल:

∆PRT में, PTR = 180 – (95 + 40)
= 180 – 135 = 45°
∠PTR = ∠QTS = 45° (शीर्षाभिमुख कोण)
∠TQS = 180 – (45 + 75)
= 180 – 120 = 60°

प्रश्न 11.
चित्र में यदि PS ⊥ RS, PT||SR और ∠STR = 28° और ∠QRT = 65° तो x और y के मान ज्ञात कीजिए। (NCERT)
हलः

बहिष्कोण
∠QRT = ∠STR + ∠TSR
65 = 28 + ∠TSR
65 – 28 = ∠TSR
37 = ∠TSR
x = 37° [एकान्तर कोण]
∆TPS में,
90 + x + y = 180
90 + 37 + y = 180
127 + y = 180
y = 180 – 127 ⇒ y = 53°

प्रश्न 12.
चित्र में ∆PQR की भुजा QR को एक बिन्दु तक बढाया गया। यदि ∠PQR और ∠PRS के समअर्द्धक, बिन्दु T पर मिलते है तब सिद्ध कीजिए कि ∠QTR = [latex]\frac{1}{2}[/latex]∠QPR (NCERT)
हल:

∵ ∠QPR = 180 – ∠PQR – ∠PRQ
= 180 – 2∠TQR – (180 – ∠PRS)
= 180 – 2∠TQR – 180+∠PRS
= -2TQR + 2∠TRS
= 2(∠TRS – ∠TQR)
= 2∠QTR
या [latex]\frac{1}{2}[/latex] ∠QPR = ∠QTR

Ex 10.2 Lines and Angle बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
यहाँ x के किस मान के लिए l || m होगी?
(a) 20
(b) 30
(c) 50
(d) 45
हलः

l||m होगी, यदि संगत कोण बराबर होंगे। तब
2x – 30° = x + 20°
⇒ 2x – x = 30° + 20°
⇒ x = 50°
अतः विकल्प (c) सही है।

प्रश्न 2.
x के किस मान के लिए l||m होगी?
(a) 25
(b) 35
(c) 45
(d) इनमें से कोई नहीं
हल:

l||m होगी, यदि
4x + (3x + 5) – 180°
⇒ 7x + 5 = 180°
⇒ 7x = 180 – 5 = 175°
⇒ x =[latex]\frac{175^{\circ}}{7}[/latex] = 25°
अतः विकल्प (a) सही है।

प्रश्न 3.
यदि दो कोण परस्पर पूरक हैं तब प्रत्येक कोण है
(a) न्यूनकोण
(b) समकोण
(c) अधिक कोण
(d) इनमें से कोई नहीं
हलः
न्यूनकोण।
अतः विकल्प (a) सही है।

प्रश्न 4.
एक कोण की माप उसके पूरक की 5 गुनी है तब कोण की माप है।
(a) 25°
(b) 50°
(c) 75°
(d) इनमें से कोई नहीं
हलः
माना कोण = x°, पूरक कोण = (90 – x)°
तब x = 5(90°- x)
⇒ x = 450° – 5x
⇒ x + 5x = 450° ⇒ 6x = 450
⇒ x = [latex]\frac{450}{6}[/latex] = 75°
अतः विकल्प (c) सही है।

प्रश्न 5.
एक कोण जिसकी माप 180° से अधिक किन्तु 360° से कम हो, कहलाता है
(a) परावर्तित कोण
(b) न्यून कोण
(c) अधिक कोण
(d) ऋजु कोण
हलः
परावर्तित कोण
अत: विकल्प (a) सही है।

प्रश्न 6.
दो पूरक कोण इस प्रकार हैं कि एक की माप का दोगुना, अन्य की माप के तीन गुने के बराबर है। दो मापों का बड़ा है।
(a) 54°
(b) 64°
(c) 63°
(d) इनमें से कोई नहीं
हलः
माना बड़ा कोण = x°, पूरक कोण = (90 –x)°
2x = 3 × (90 – x)
2x = 270° – 3x ⇒ 5x = 270°
⇒ x = [latex]\frac{270}{5}[/latex] = 54°
अतः विकल्प (a) सही है।

प्रश्न 7.
दो सरल रेखाएँ AB और CD, एक-दूसरे को 0 पर काटती हैं। यदि ∠BOD = 63° तब ∠BOC =
(a) 63°
(b) 17°
(c) 153°
(d) 117°
हलः

∠BOD + ∠ BOC = 180°
⇒ 63° + ∠ BOC = 180°
⇒ ∠BOC = 180° – 63°
⇒ ∠BOC = 117°
अतः विकल्प (d) सही है।

प्रश्न 8.
यदि AB = x + 3, BC = 2x और AC = 4x – 5, तब x के किस मान के लिए B, AC पर स्थित है?
(a) 5
(b) 6
(c) 8
(d) इनमें से कोई नहीं
हलः
बिन्दु B, AC पर स्थित होगा, यदि
AC = AB + BC
⇒ 4x – 5 = x + 3 + 2x
⇒ 4x – 5 = 3x + 3 ⇒ x = 8
अतः विकल्प (c) सही है।

प्रश्न 9.
कोण की माप जो स्वयं का पूरक है
(a) 45°
(b) 55°
(c) 90°
(d) इनमें से कोई नहीं
हलः
45°
अतः विकल्प (a) सही है।

प्रश्न 10.
एक त्रिभुज का एक बाह्य कोण 110° और दो अन्तः विपरीत कोण बराबर हैं। ये बराबर कोण है
(a) 45°
(b) 55°
(c) 90°
(d) इनमें से कोई नहीं
हलः
माना अन्त:कोण = x°
तब बाह्य कोण = अन्त:कोणों का योग
110° = x° + x°
⇒ 2x = 110° ⇒ x = [latex]\frac{110^{\circ}}{2}[/latex] = 55°
अतः विकल्प (b) सही है।

प्रश्न 11.
यदि एक त्रिभुज का एक कोण, अन्य दो कोणों के योग के बराबर है तब त्रिभुज है (NCERT Exemplar)
(a) समकोण
(b) समद्विबाहु
(c) समबाहु
(d) इनमें से कोई नहीं
हलः
समकोण।
अतः विकल्प (a) सही है।

प्रश्न 12.
यदि दो सम्पूरक कोणों के बीच का अन्तर 40° है तब कोण है.
(a) 70°, 120°
(b) 70°, 110°
(c) 210°, 150°
(d) इनमें से कोई नहीं
हलः
माना कोण = x°; सम्पूरक कोण = (180° – x)
x – (180° – x) = 40°
⇒ 2x = 220° ⇒ x = [latex]\frac{220}{2}[/latex] = 110°
सम्पूरक कोण = 180° – 110° = 70°
अतः विकल्प (b) सही है।

प्रश्न 13.
यदि दो पूरक कोणों के बीच का अनुपात 2 : 3 है तब कोण है
(a) 36°, 54°
(b) 30°, 60°
(c) 20°, 70°
(d) इनमें से कोई नहीं
हलः
माना एक कोण = x°, पूरक कोण = (90° – x)

अतः विकल्प (a) सही है।

प्रश्न 14.
संलग्न चित्र में, यदि l||m, तब x =
(a) 30°
(b) 40°
(c) 70°
(d) इनमें से कोई नहीं

हलः

यदि l||m, तब
∠EDO = ∠COB = 70°
⇒ ∠BOA = 180° – 70° = 110°
∆ABO में, x°+ 110°+ 30° = 180°
x = 180° – 140°
⇒ x = 40°
अतः विकल्प (b) सही है।

प्रश्न 15.
संलग्न चित्र में, यदि AB||CD, तब x =
(a) 110°
(b) 115°
(c) 100
(d) इनमें से कोई नहीं

हलः
∠FAE = 180 – 132 = 48°
∵ PF ||CE
⇒ ∠FAE = ∠AEC = 48°
तथा AB||CD
⇒ ∠AEC = ∠ECD = 48°

∵ PA||CE
⇒ ∠APG = ∠ECP = 180 – 148 =32°
अतः बिन्दु C पर
x + ∠ECD + ∠ECP = 180°
x + 48 + 32 = 180°
⇒ x = 180° – 80 = 100°
अतः विकल्प (c) सही है।

प्रश्न 16.
यदि AB और CD दो समान्तर रेखाएँ हैं, PQ, AB और CD को क्रमशः E तथा F पर काटती है। EL, ∠FEB का समद्विभाजक है यदि ∠LEB = 35%, तब ∠CFQ =
(a) 90°
(b) 65°
(c) 110°
(d) 140°
हलः

दिया है,
∠LEB = 35°
∵ EL, ∠FEB का समद्विभाजक है, तब
∠FEL = 70°
⇒ ∠AEF = 180° – 70° = 110°
⇒ ∠CFQ = ∠AEF = 110° (एकान्तर कोण)
∴ ∠CFQ = 110°
अतः विकल्प (c) सही है।

प्रश्न 17.
तिर्यक रेखा के एक ही ओर यदि दो अन्तः कोणों का अनुपात 2 : 3 है तो बड़ा कोण = (NCERT)
(a) 56°
(b) 125°
(c) 108°
(d) इनमें से कोई नहीं
हलः
दो अन्त:कोणों का अनुपात = 2 : 3
अतः कोण = 2x तथा 3x
तब 2x + 3x = 180°
⇒ 5x = 180°
⇒ x = [latex]\frac{180}{5}[/latex] = 36°
अतः बड़ा कोण = 3 × 36° = 108°
अतः विकल्प (c) सही है।

प्रश्न 18.
एक कोण इसके सम्पूरक के तीन गुने के बराबर है। कोण की माप है
(a) 125°
(b) 130°
(c) 135°
(d) 120°
हलः
माना कोण = x°; सम्पूरक कोण = (180° – x)
तब x = 3(180° – x)
⇒ x = 540 – 3x
⇒ 4x = 540 ⇒ x = [latex]\frac{540}{4}[/latex] = 135°
अतः विकल्प (c) सही है।

प्रश्न 19.
दिया गया है कि ∠POR = 3x और ∠QOR = 2x + 10°, यदि POQ एक सरल रेखा है तब x =
(a) 25°
(b) 30°
(c) 34°
(d) 44°
हल:
∵ POQ एक सरल रेखा है।
∴ ∠POR + ∠QOR = 180°
⇒ 3x + 2x + 10 = 180°
⇒ 5x + 10 = 180°
⇒ 5x = 180° – 10 = 170
⇒ x = [latex]\frac{170}{5}[/latex] = 34°
अतः विकल्प (c) सही है।

प्रश्न 20.
दो पूरक कोण इस प्रकार हैं कि एक की माप का दोगुना, अन्य की माप के तीन गुने के बराबर है। छोटे कोण की माप है।
(a) 36°
(b) 40°
(c) 56°
(d) इनमें से कोई नहीं
हलः
माना एक कोण = x°, पूरक कोण = (90° – x)
⇒ 3x = 2(90 – x)
⇒ 3x = 180 – 2x
⇒ 5x = 180° ⇒ x = [latex]\frac{180}{5}[/latex] = 36°
अतः विकल्प (a) सही है।

प्रश्न 21.
संलग्न चित्र में, यदि l||m तब x =
(a) 95°
(b) 45°
(c) 55°
(d) 65°
हल:

∵ l||m
तब ∠BAO = ∠OCD = 40
∆OAB में, ∠OAB + ∠ABO + ∠BOA = 180°
40° + 55° + ∠BOA = 180°
∠BOA = 180° – 95 = 85°
अब बिन्दु O पर,
x + ∠AOB = 180°
⇒ x + 85 = 180°
⇒ x = 180° – 85 = 95°
अतः विकल्प (a) सही है।

प्रश्न 22.
संलग्न चित्र में, l||m और m||n यदि x : y = 3 : 2 तब x =
(a) 108°
(b) 72°
(c) 1200
(d) इनमें से कोई नहीं
हलः

दिया है, x : y = 3 : 2
⇒ x = 3k, y = 2k
x + y = 3k +2k
5k = 180° ⇒ k = [latex]\frac{180^{\circ}}{5}[/latex] = 36°
⇒ x = 3 × 36 = 108°
अतः विकल्प (a) सही है।

प्रश्न 23.
एक त्रिभुज का एक बाह्य कोण 105° है तथा इसके अन्तः विपरीत कोण बराबर हैं तब प्रत्येक बराबर कोण की माप है (NCERT Exemplar)

हलः
माना अन्तः कोण = x°
तब त्रिभुज का बाह्य कोण = अन्तः कोणों का योग
105° = x + x
⇒ 2x = 105 ⇒ x = [latex]\frac{105}{2}=52 \frac{1}{2}^{\circ}[/latex]
अतः विकल्प (b) सही है।

प्रश्न 24.
यदि एक त्रिभुज का एक कोण 130, है तब अन्य दो कोणों के समद्विभाजकों के बीच कोण है (NCERT Exemplar)
(a) 145°
(b) 155°
(c) 65°
(d) इनमें से कोई नहीं
हल:
∆DAB में, ∠AOB = 130°
तथा PA तथा PB क्रमशः ∠OAB तथा ∠OBA के समद्विभाजक हैं।
माना ∠OAB = 2x, ∠OBA = 2y

तब ∠OAP = ∠PAB = x
तथा ∠OBP = ∠PBA = y
∆APB में, x + y + ∠APB = 180°
∠APB = 180° – (x + y) …………………. (1)
∆AOB में, 2x + 2y + 130° = 180°
2x + 2y = 50
x + y = 25 …………………….(2)
समी० (2) से x + y का मान समी० (1) में रखने पर,
∠APB = 180 – 25 = 155°
अतः विकल्प (b) सही है।

प्रश्न 25.
दिए गए चित्र में ज्ञात कीजिए कि a + b =
(a) 127°
(b) 107°
(c) 45°
(d) 54°
हलः


अतः विकल्प (a) सही है।

प्रश्न 26.
संलग्न चित्र में, AOB एक सरल रेखा है। ∠COD की माप =
(a) 80°
(b) 60°
(c) 120°
(d) 160°
हलः
बिन्दु O पर,

x + 20 + 2x – 20 + 60 = 180°
⇒ 3x + 60° = 180°
⇒ 3x = 120°
⇒ x = 40°
∠COD = 2 × 40 – 20 = 60°
अतः विकल्प (b) सही है।

प्रश्न 27.
यदि एक कोण की माप, उसके सम्पूरक कोण की माप की दोगुनी है। तब इसकी माप है
(a) 90°
(b) 110°
(c) 135°
(d) 120°
हलः
माना कोण = x, सम्पूरक कोण = 180° – x
x = 2(180° – x)
⇒ x = 360° – 2x
⇒ 3x = 360° ⇒ x = [latex]\frac{360^{\circ}}{3}[/latex] = 120°
अतः विकल्प (d) सही है।

प्रश्न 28.
एक कोण की माप जो स्वयं का सम्पूरक है
(a) 90°
(b) 110°
(c) 45°
(d) 135°
हलः
90°
अतः विकल्प (a) सही है।

प्रश्न 29.
(90°-x) का पूरक है
(a) x
(b) 90°+ x
(c) –x
(d) इनमें से कोई नहीं
हलः
(90° – x) का पूरक कोण = 90° – (90°– x)
= 90° – 90° + x = x
अतः विकल्प (a) सही है।

प्रश्न 30.
एक कोण की माप जो स्वयं का पूरक है
(a) 30°
(b) 90°
(c) 45°
(d) इनमें से कोई नहीं
हलः
माना कोण = x, पूरक कोण = 90° –x
x = 90° – x
⇒ x + x = 90°
⇒ 2x = 90° ⇒ x = [latex]\frac{90}{2}[/latex] = 45°
अतः विकल्प (c) सही है।

Ex 10.2 Lines and Angle स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
यह दिया गया है कि ∠XYZ = 64° और XY को एक बिन्दु P तक बढ़ाया गया है। दी गयी जानकारी से एक आकृति खींचिए। यदि किरण YQ, ∠ZYP को समअर्द्धक करती है तो ∠XYQ और परावर्तित ∠QYP ज्ञात कीजिए।
हलः
∵ YQ किरण, ∠ZYP को समअर्द्धक करती है
माना ∠ZYQ = ∠QYP = x
64 + x + x = 180
64 + 2x = 180
2x = 180 – 64 = 116
x = [latex]\frac{116}{2}[/latex] = 58

∴ ∠XYQ = 64 + x = 64 + 58 = 122°
∠QYP = 58°
परावर्तित कोण ∠QYP = 360 – 58 = 302°

प्रश्न 2.
सिद्ध कीजिए कि यदि दो रेखायें परस्पर प्रतिच्छेद करती है तब शीर्षाभिमुख कोण बराबर हैं।
हलः
रेखा AB व CD एक दूसरे को बिन्दु O पर प्रतिच्छेद करती है।
∠AOC + ∠AOD = 180° ………………….. (1)
∠AOD + ∠BOD = 180° ……………… (2)

समीकरण (1) व (2) की तुलना से
∠AOC + ∠AOD = ∠AOD + ∠BOD
∴ ∠AOC = ∠BOD
इसी प्रकार सिद्ध कर सकते हैं कि ∠AOD = ∠BOC
∴ शीर्षाभिमुख कोण बराबर होते हैं।

प्रश्न 3.
सलंग्न चित्र में, OD, ∠AOC का और OE, ∠BOC का समद्विभाजक है तथा OD⊥OE तो सिद्ध कीजिए कि बिन्दु A, O और B सरेख हैं।
हलः

∵ OD⊥OE ∴ ∠DOE = 90° ………………. (1)
माना ∠AOC = 2x तथा ∠BOC = 2y
∴ ∠AOD = ∠COD = x
तथा ∠BOE = ∠COE = y
∵ ∠AOD + ∠DOC + ∠COE + ∠BOE
= x + x + y + y = 2x + 2y
= 2(x + y)
= 2 × 90° = 180°
∵ समीकरण (1) से ∠DOE = ∠DOC + ∠COE = x + y = 90°
∴ AOB एक सरल रेखा है तथा A,O,B संरेख है।

प्रश्न 4.
यदि एक तिर्यक द्वारा दो समान्तर रेखायें प्रतिच्छेद होती हैं तब सिद्ध कीजिए कि किन्ही दो के संगत कोणों के समद्विभाजक समान्तर हैं।
हल:

माना AB||CD तथा MN एक तिर्यक रेखा काटती है।
∠MPB = ∠MQD (संगत कोण)
2 से भाग करने पर
[latex]\frac{\angle M P B}{2}=\frac{\angle M Q D}{2}[/latex]
∴ ∠MPT = ∠MQV
परन्तु ये संगत कोण है
PT||QN

प्रश्न 5.
संलग्न चित्र में ∆PQR की भुजा QR को एक बिन्दु S तक बढ़ाया गया है। यदि ∠PQR और ∠PRS के समद्विभाजक बिन्दु T पर मिलते हैं, तो सिद्ध कीजिए कि ∠QTR = [latex]\frac{1}{2}[/latex]∠QPR
हलः

∵ ∠QPR = 180 – ∠PQR – ∠PRQ
= 180 – 2∠TQR – (180 – ∠PRS)
= 180 – 2∠TQR – 180+∠PRS
= -2TQR + 2∠TRS
= 2(∠TRS – ∠TQR)
= 2∠QTR
या [latex]\frac{1}{2}[/latex] ∠QPR = ∠QTR

प्रश्न 6.
यदि एक तिर्यक रेखा द्वारा दो समान्तर रेखाएँ प्रतिच्छेद होती हैं तो सिद्ध कीजिए कि अन्तः कोणों के दो युग्मों के समद्विभाजक, एक आयत के रूप के हैं।
हलः

∠APQ, ∠BPQ तथा ∠PQC तथा ∠PQD के समद्विभाजक खीचें।
माना ∠BPQ = ∠QPB = x
∵ 2x + 2y = 180
x + y = 90 ………….. (1)
∵ x + y = 90
∴ चारों कोण 90° के होंगे।
∆PTQ तथा PSQ में सिद्ध कर सकते हैं कि PT = QS तथा TQ = PS
अत: PTQS एक आयत है।

प्रश्न 7.
सिद्ध कीजिए कि एक युग्म के समद्विभाजकों के शीर्षाभिमुख कोण, एक समान सरल रेखा पर है।
हलः

∠1 = ∠3 ………….. (1)
∠2 = ∠4 ………….. (2)
एक रेखा EF खींची।
∠2 = ∠x + ∠y, ∠2 + ∠1 + ∠4 + ∠3 = 360°,
∠4 = ∠m + ∠n रखने पर
∠x + ∠y + ∠1 + ∠m + ∠n + ∠3 = 360° (∠x +∠1 + ∠m) + (∠y + ∠3 + ∠n) = 360°
∴ प्रत्येक ∠x + ∠1 + ∠m = ∠y + ∠3 + ∠n
∴ शीर्षाभिमुख कोण ∠2 व ∠4 एक समान रेखा पर स्थित हैं = 180°

प्रश्न 8.
यदि दो सरल रेखायें परस्पर प्रतिच्छेद करती हैं। तो सिद्ध कीजिए कि एक कोण के समद्विभाजक के विपरीत किरण, शीर्षाभिमुख कोण को प्रतिच्छेद करती है।
हलः
माना ∠AOT = m तथा ∠TOD = n
m + z + y = 180 ……………… (1)
n + x + y = 180 …………….. (2)
समीकरण (1) व (2) की तुलना से
m + z + y = n + z + y

∴ m = n
∴ रेखा TM, शीर्षाभिमुख कोण को प्रतिच्छेद करती हैं।

प्रश्न 9.
यदि दो सरल रेखायें एक रेखा पर लम्ब है तो सिद्ध कीजिए कि वे परस्पर समान्तर हों?
हलः
यदि PQ व MN रेखा AB पर लम्ब हैं।
∵ ∠AQP = ∠ANM = 90°
परन्तु ये संगत कोण हैं।
∴ PQ||MN

प्रश्न 10.
सिद्ध कीजिए कि यदि एक कोण की दो भुजा, दूसरे कोण की भुजा के लम्बवत् है तो कोण या तो बराबर होंगे या सम्पूरक।
हलः
कोण बराबर होंगे यदि उनका योग 180° होगा अर्थात् सम्पूरक होंगे।

प्रश्न 11.
संलग्न चित्र में, यदि PQ⊥PS, PQ ||RS, ∠SQR = 28° तथा ∠QRT = 65° तो x, y और z के मान ज्ञात कीजिए।
हलः

∵ PQ⊥PS तथा ∠SPQ = 90°
∆SQR में,
z = 180 – 65 = 115°
∵ PQ||RS, ∠PQR = ∠QRT
x + 28 = 65
x = 65 – 28 = 37°
समकोण ∆PSQ में, y = 180 – (90 + 37)
= 180 – 127 = 53°

प्रश्न 12.
दिये गये चित्र में, यदि ∠COE = 2x° और / BOD = x°, तो x ज्ञात कीजिए। (जहाँ OD, ∠AOB का समद्विभाजक है और OE, ∠AOC का समद्विभाजक है)
हलः

∵ OD, ∠AOB का समद्विभाजक है
∴ ∠AOD =∠BOD = x
तथा OE, ∠AOC का समद्विभाजक है
∠COE =∠AOE = 2x
∴ ∠BOD + ∠AOD + ∠AOE +∠COE = 180
x + x + 2x + 2x = 180
6x = 180
x = [latex]\frac{180}{6}[/latex] = 30°

प्रश्न 13.
यदि दो सरल रेखाएँ परस्पर इस प्रकार प्रतिच्छेद करती है, कि एक के कोण की माप 90° है, तो सिद्ध कीजिए कि प्रत्येक के शेष कोण की माप 90° है।
हलः
l तथा m रेखाएँ एक-दूसरे को इस प्रकार प्रतिच्छेद करती हैं, कि
∠AOB = 90°
तब शेष ∠AOB = ∠AOC = 180°- 90° = 90°
इसी प्रकार ∠BOD =∠ COD = 90°

प्रश्न 14.
यदि एक कोण की भुजा क्रमशः अन्य दूसरे कोण की भुजा के समान्तर है, तो सिद्ध कीजिए कि दो कोण या तो बराबर हैं, या सम्पूरक।
हलः
कोण बराबर होंगे यदि उनका कोण 180° होगा अर्थात् सम्पूरक होंगे।

प्रश्न 15.
यदि दो सरल रेखाएँ समान रेखा के लम्बवत् हैं तो सिद्ध कीजिए कि वे परस्पर समान्तर हैं।
हलः
यदि PQ व MN रेखा AB पर लम्ब है।

∴ ∠AQP = ∠ANM = 90°
परन्तु ये संगत कोण हैं।
PQ||MN

Balaji Publications Mathematics Class 9 Solutions