Class 9

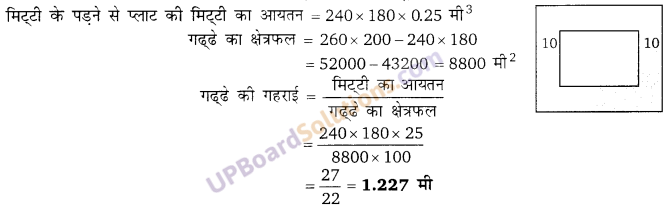
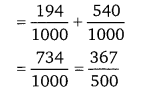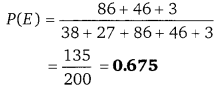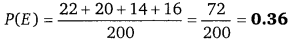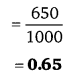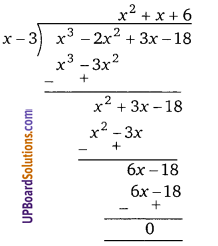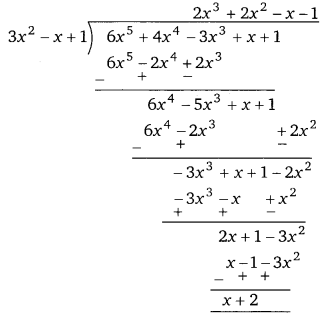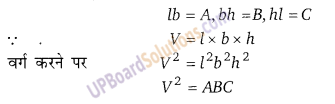Balaji Class 9 Maths Solutions Chapter 18 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder Ex 18.3 घन, घनाभ तथा लम्बवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन

Ex 18.3 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
r त्रिज्या तथा h ऊँचाई वाले लम्बवृत्तीय बेलन का आयतन है- [UP 2005,06, 07]
(a) [latex]\frac{1}{3} \pi r^{2} h[/latex] घन इकाई
(b) [latex]\pi \boldsymbol{r}^{2} \boldsymbol{h}[/latex] घन इकाई
(c) [latex]\frac{4}{3} \pi r^{2} h[/latex] घन इकाई
(d) 2 πr घन इकाई
हलः
लम्बवृत्तीय बेलन का आयतन = πr²h
⇒ विकल्प (b) सही है।

प्रश्न 2.
h सेमी ऊँचाई तथा r सेमी आधार त्रिज्या वाले लम्बवृत्तीय बेलन का वक्रपृष्ठ होगा- [UP 2005]
(a) 4πrh सेमी²
(b) 3πrh सेमी²
(c) 2πrh सेमी²
(d) πrh सेमी²
हलः
वक्रपृष्ठ = 2πrh सेमी²
⇒ विकल्प (c) सही है।

प्रश्न 3.
समान आधार त्रिज्या वाले दो बेलनों की ऊँचाईयों में अनुपात 2:5 है। उनके वक्रपृष्ठों का अनुपात होगा- [UP 2006]
(a) 2 : 5
(b) 5 : 2
(c) 3 : 2
(d) 2 : 3
हलः

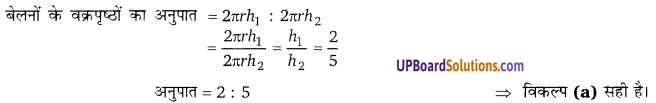
प्रश्न 4.
एक बेलन का आयतन 924 घन सेमी तथा वक्रपृष्ठ 264 वर्ग सेमी हो तो उसकी ऊँचाई होगी-
(a) 4 मीटर
(b) 5 मीटर
(c) 6 सेमी
(d) 7 मीटर
हलः
बेलन का आयतन = 924 समी³
πr²h = 924 ….(1)
बेलन का वक्रपृष्ठ = 264 सेमी²
2πrh = 264 ….(2)

प्रश्न 5.
दो बेलनों की त्रिज्याओं का अनुपात 2 :3 है तथा उनकी ऊँचाईयों का अनुपात 5 : 3 है तब उनके आयतनों का अनुपात होगा (UP 2006,09, 14) (a) 27 : 20
(b) 20 : 27
(c) 9 : 4
(d) 4 : 9
हलः

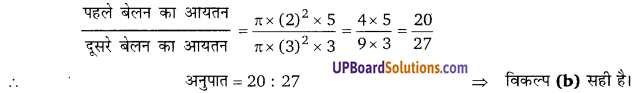
प्रश्न 6.
एक बेलन का व्यास 14 सेमी तथा ऊँचाई 20 सेमी है तब बेलन का वक्रपृष्ठ होगा- [UP 2004, 09]
(a) 440 सेमी²
(b) 220 सेमी²
(c) 880 सेमी²
(d) 1760 सेमी²
हलः

Ex 18.3 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 7.
उस लम्बवृत्तीय बेलन का आयतन तथा वक्रपृष्ठ ज्ञात कीजिए जिसकी ऊँचाई 21 सेमी तथा आधार की त्रिज्या 5 सेमी है।
हलः
बेलन की त्रिज्या r = 5 सेमी, बेलन की ऊँचाई, h = 21 सेमी
बेलन का आयतन = πr²h

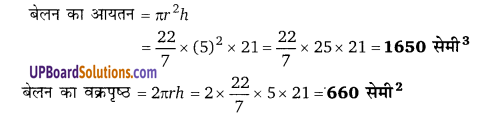
प्रश्न 8.
एक बेलन का आयतन 5544 सेमी है तथा इसकी ऊँचाई 16 सेमी है। इसकी त्रिज्या तथा वक्रपृष्ठ ज्ञात कीजिए।
हलः

प्रश्न 9.
एक बेलन का वक्रपृष्ठ 1210 सेमी है तथा इसका व्यास 20 सेमी है। इसकी ऊँचाई तथा आयतन ज्ञात कीजिए। [UP 2009]
हल:
बेलन के वक्रपृष्ठ का क्षेत्रफल = 1210 सेमी²
आधार का व्यास = 20 सेमी

प्रश्न 10.
एक लम्बवृत्तीय बेलन के आधार की परिधि 22 सेमी है। यदि बेलन की ऊँचाई 10 सेमी हो, तो बेलन का आयतन ज्ञात कीजिए। (π = 22/7) [UP 2001]
हलः
लम्बवृत्तीय बेलन की परिधि = 22 सेमी
2πr = 22

प्रश्न 11.
एक लम्बवृत्तीय बेलन का सम्पूर्ण पृष्ठ 1540 वर्ग सेमी है। यदि बेलन की ऊँचाई इसके आधार की त्रिज्या की चार गुनी हो तब बेलन के आधार की त्रिज्या ज्ञात कीजिए। [UP 2001, 04]
हलः

Ex 18.3 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 12.
44 सेमी लम्बे तथा 20 सेमी चौड़े आयताकार कागज को इसकी लम्बाई के सापेक्ष मोड़कर एक बेलन बनाया गया है। इस प्रकार निर्मित बेलन का आयतन ज्ञात कीजिए। [UP 2008]
हलः
कागज को 44 सेमी लम्बाई के अनुदिश मोड़ने पर बने बेलन की परिधि = 20 सेमी

प्रश्न 13.
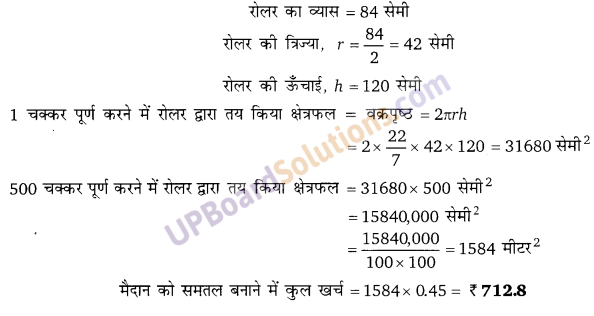
120 सेमी लम्बे रोलर का व्यास 84 सेमी है। एक मैदान को समतल करने के लिए यह पूरे 500 चक्कर काटता है। 45 पैसे प्रति वर्ग मीटर की दर से पूरे मैदान को समतल करने में लगी राशि ज्ञात कीजिए।
हलः

प्रश्न 14.
1.5 सेमी व्यास तथा 0.2 सेमी मोटाई के कितने सिक्के गलाये जायें ताकि 10 सेमी ऊँचाई तथा 4.5 सेमी व्यास का एक लम्बवृत्तीय बेलन बनाया जा सके?
हलः

प्रश्न 15.
20 सेमी लम्बे लोहे के एक पाईप का बाह्य व्यास 25 सेमी है। यदि पाईप की मोटाई 1 सेमी हो तो पाईप – का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हलः

Ex 18.3 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 16.
यदि एक बेलनाकार बर्तन के व्यास में 5% की कमी हो तो इसकी लम्बाई में कितने प्रतिशत की वृद्धि होगी। यदि इसके आयतन में कोई परिवर्तन नहीं होता? [UP 2009]
हलः
माना बेलन की प्रारम्भिक लम्बाई = h सेमी
बेलन का प्रारम्भिक व्यास = A सेमी
बेलन की प्रारम्भिक त्रिज्या = 4 सेमी

प्रश्न 17.
लोहे के एक ठोस आयताकार बक्से की विमाएं 4.4 सेमी, 2.6 मीटर, 1 मीटर हैं, को पिघलाकर एक खोखले बेलनाकार पाईप जिसकी आन्तरिक त्रिज्या 30 सेमी तथा मोटाई 5 सेमी है, के अन्दर रखा जाता है। पाईप की लम्बाई ज्ञात कीजिए।
हलः

Ex 18.3 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
यदि V आयतन वाले घन के विकर्ण की लम्बाई l है तो-
(a) 27V² = l⁶
(b) [latex]\sqrt{3}[/latex] V = l³
(c) 3V = l³
(d) इनमें से कोई नहीं
हलः

प्रश्न 2.
एक आयताकार ठोस की लम्बाई, चौड़ाई एवं ऊँचाई में अनुपात 3 : 2 : 1 है। यदि ठोस का आयतन 48 सेमी³ है तो इसका पृष्ठीय क्षेत्रफल =
(a) 32 सेमी²
(b) 88 सेमी²
(c) 128 सेमी²
(d) इनमें से कोई नहीं
हलः
l = 3k,
b = 2k,
h = k
ठोस आयतन = lbh

अतः विकल्प (b) सही है।

प्रश्न 3.
V आयतन वाले घन की प्रत्येक भुजा को यदि दोगुना कर दिया जाये तो नये घन का आयतन =
(a) 2V
(b) 4 v
(c) 8V
(d) इनमें से कोई नहीं
हलः
माना घन की भुजा = a
घन का आयतन V = a³
यदि घन की भुजा को दोगुना कर दिया जाए तो घन की भुजा = 2a
अब घन का आयतन = (2a)³ = 8a³ = 8V
अतः विकल्प (c) सही है।

प्रश्न 4.
यदि एक घन की सभी भुजाओं का योग 36 सेमी है, तब इसका आयतन (सेमी³ में) =
(a) 27
(b) 217
(c) 72
(d) इनमें से कोई नहीं
हल:

प्रश्न 5.
10 सेमी × 9 सेमी × 6 सेमी विमा वाले घनाभ के अन्दर रखे जा सकने वाले 3 सेमी भुजा वाले घनों की संख्या =
(a) 12
(b) 18
(c) 28
(d) इनमें से कोई नहीं
हलः
एक घनाभ का आयतन = 10 × 9 × 6 = 540 घन सेमी
एक घन का आयतन = (3)³ = 3 × 3 × 3 = 27 घन सेमी

प्रश्न 6.
लम्ब वृत्तीय बेलन का ऊर्ध्वाधर शंकु परिच्छेद होता है। एक-
(a) समचतुर्भुज
(b) वर्ग
(c) आयत
(d) इनमें से कोई नहीं
हलः
आयत।
अतः विकल्प (c) सही है।

प्रश्न 7.
लोहे की एक सीट से 2 मीटर व्यास तथा 40 मीटर लम्बाई का एक लम्ब वृत्तीय बेलन बनाना है। इसके लिए आवश्यक लोहे की सीट का आयतन = (मी² में)
(a) 40π
(b) 60π
(c) 80π
(d) इनमें से कोई नहीं
हलः

प्रश्न 8.
एक लम्ब वृत्तीय बेलन की ऊँचाई 6 गुनी बढ़ायी गयी है तथा इसका आधार का क्षेत्रफल 1/9 घटाया गया है तब पार्श्व पृष्ठीय क्षेत्रफल कितने गुना बढ़ेगा?
(a) 2
(b) 1/2
(c) 1/3
(d) इनमें से कोई नहीं
हलः

प्रश्न 9.
r त्रिज्या तथा h ऊँचाई का एक बेलन ऊपर व नीचे से बन्द है तब बेलन का कुल पृष्ठीय क्षेत्रफल =
(a) πr(r + h)
(b) 2πr (r + h)
(c) 2πr (2r +h)
(d) इनमें से कोई नहीं
हलः
कुल पृष्ठीय क्षेत्रफल = बेलन का पार्श्व पृष्ठ +2 × आधार का क्षेत्रफल

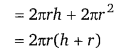
अतः विकल्प (b) सही है।

प्रश्न 10.
एक तार की त्रिज्या घटकर 1 हो गयी है। यदि उसका आयतन समान रहता है तो उसकी लम्बाई होगी-
(a) 3 गुना
(b) 9 गुना
(c) 2 गुना
(d) इनमें से कोई नहीं
हलः

Ex 18.3 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder स्वमूल्यांकन परीक्षण(Self Assessment Test)

प्रश्न 1.
मंजू अपने क्रिसमस वृक्ष को सजाना चाहती है। वह इस वृक्ष को लकड़ी के एक आयताकार बॉक्स पर रखना चाहती है। जिसे सान्ताक्लोज के चित्र के साथ एक रंगीन कागज से ढका जाना है। उसका यह जानना आवश्यक है कि उसे कितना कागज खरीदना चाहिए यदि उपरोक्त बॉक्स की लम्बाई, चौड़ाई एवं ऊँचाई 80 सेमी, 40 सेमी, 20 सेमी है तो उसे 40 सेमी भुजा वाली कागज की कितनी वर्गाकार
शीटों की आवश्यकता है।
हलः
1 = 80 सेमी, b = 40 सेमी, h = 20 सेमी
घनाभ का पृष्ठ = 2(lb + bh + hl)
= 2(80 × 40 + 40 × 20 + 20 × 80)
= 2(3200 + 800 + 1600) = 2(5600) = 11200 सेमी²

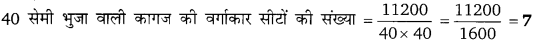
प्रश्न 2.
हरी ने अपने घर के लिए, ढक्कन वाली एक घनाकार पानी की टंकी बनवानी है। जिसका प्रत्येक बाहरी किनारा 1.5 मीटर लम्बा है। वह इस टंकी के बाहरी पृष्ठ पर तलों को जोड़ते हुए 25 सेमी भुजा वाली वर्गाकार टाइल्स लगवाता है। यदि टाइलों की लागत ₹ 360 प्रति दर्जन है। तो उसे टाईल लगवाने में कितना खर्च करना पड़ेगा?
हलः
घनाकार टंकी का बाहरी पृष्ठ (चारो दीवारो + ढक्कन) = 5 × (150)² = 5 × 150 × 150 सेमी²
= 112500 सेमी²

प्रश्न 3.
प्रवीण अपनी कार खड़ी करने के लिए, एक सन्दक के प्रकार के ढाँचे जैसा एक अस्थायी स्थान तिरपाल की सहायता से बनाना चाहता है। जो कार को चारों ओर से और ऊपर से ढक लें। (सामने वाला फल लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है।) यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा नगण्य होगा, आधार विमाओं 4 मीटर × 3 मीटर × 2.5 मीटर वाले इस ढाँचें को बनाने के लिए कितने तिरपाल की आवश्यकता होगी। (NCERT)
हलः
यहाँ, 1 = 4 मी०, b = 3 मी०, h = 2.5 मी०
अभीष्ट तिरपाल = [2(1 + b) × h + lb]
=[2(4+ 3) × 2.5 + 4 × 3] = (2 × 7 × 2.5 + 12)
= 35 + 12 = 47 मी²

प्रश्न 4.
एक लकड़ी के बुक शेल्फ की बाहरी विमाएं निम्न हैं : ऊँचाई 110 सेमी, गहराई = 25 सेमी, चौडाई = 85 सेमी। प्रत्येक स्थान पर तख्तों की मोटाई 5 सेमी है। इसके बाहरी फलकों पर पॉलिश करायी जाती है और आन्तरिक फलकों पर पेंट किया जाना है। यदि पॉलिश कराने की दर 20 पैसे प्रति सेमी2 है। और पेंट कराने की दर 10 पैसे प्रति सेमी है, तो बुक शेल्फ पर पेंट व पॉलिश कराने का कुल व्यय ज्ञात कीजिए।
हलः

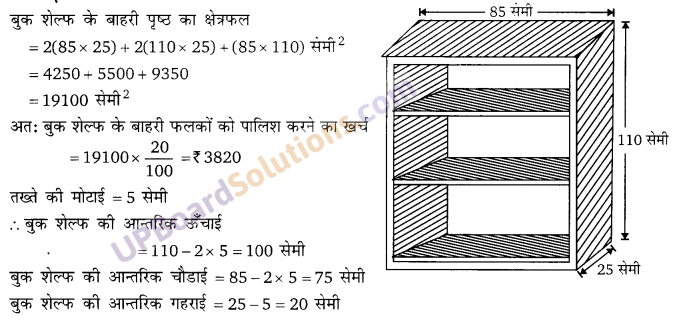
प्रश्न 5.
एक खुले मैदान में 10 मीटर लम्बी एक दीवार का निर्माण किया जाना था। दीवार की ऊचाई 4 मीटर है और उसकी मोटाई 24 सेमी है। यदि इस दीवार को 24 सेमी × 12 सेमी × 8 सेमी विमाओं वाली ईंटों से बनाया जाता है तो इसके लिए कितनी ईंटों की आवश्यकता होगी।
हलः

प्रश्न 6.
एक बच्चा भव ब्लॉकों से खेल रहा है। जो एक घन के आकार के हैं। उसने इनसे आकृति में दर्शाये अनुसार 3 सेमी एक ढाँचा बना लिया है। प्रत्येक घन का किनारा 3 सेमी है। बच्चे द्वारा बनाये गये ढाँचे का आयतन ज्ञात कीजिए।
हलः

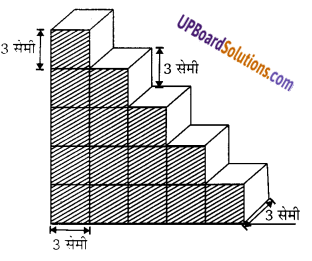
प्रश्न 7.
संसद भवन के 20 बेलनाकार खम्बों की सफाई करनी है। यदि प्रत्येक खम्बे का व्यास 0.50 मी तथा ऊँचाई 4 मी है तो ₹ 2.50 प्रति वर्ग मीटर की दर से उन्हें साफ करने में कुल व्यय ज्ञात कीजिए।
हलः

प्रश्न 8.
एक मन्दिर के दो खम्बे बेलनाकार रूप के है। यदि प्रत्येक खम्बे के आधार की त्रिज्या 20 सेमी तथा ऊँचाई 10 मीटर है तो इस तरह के 14 खम्बे बनाने में कुल कितने कंक्रीट मिश्रण की आवश्यकता होगी।
हल:

प्रश्न 9.
एक मेले में, एक स्टाल कीपर के पास 15 सेमी आधार त्रिज्या वाले बेलनाकार बर्तनों में 32 सेमी ऊँचाई तक सन्तरे का जूस भरा है। उन्हें 3 सेमी त्रिज्या वाले बेलनाकार बर्तन में 8 सेमी ऊँचाई तक भरकर प्रत्येक को ₹ 3 में बेचा जाता है। पूरे जूस को बेचकर वह कितने रुपये प्राप्त करेगा।
हलः

प्रश्न 10.
एक कमरे की विमाएं 12.5 मी × 9 मी × 7 मी है। उसमें दो दरवाजें तथा 4 खिड़की है। प्रत्येक दरवाजे की माप 2.5 मी × 1.2 मी तथा खिड़की की माप 1.5 मी × 1 मी है। सिद्ध कीजिए कि ₹ 3.50 प्रति वर्ग मीटर की दर से दीवारों को रंगने में कुल ₹ 1011.50 खर्च होगें।
हलः
कमरे की चारो दीवारो का क्षेत्रफल = 2(l + b) × h = 2(12.5 + 9) × 7
= 2 × 21.5 × 7 = 301 मी²
दो दरवाजों का क्षेत्रफल = 2 × 2.5 × 1.2 = 6 मी²
4 खिडकी का क्षेत्रफल = 4 × 1.5 × 1 = 6 मी²
दरवाजों तथा खिडकी को छोडकर दीवारों का शेष क्षेत्रफल = 301 – 6 – 6 = 289 मी²
दीवारों को रंगने में कुल खर्च = 289 × 3.50 = ₹ 1011.50

प्रश्न 11.
एक हॉल की लम्बाई एवं चौड़ाई का अनुपात 4 : 3 है तथा इसकी ऊँचाई 5.5 मीटर है। इसकी दीवारों को ₹ 6.60 प्रति वर्ग मीटर की दर से सजाने में कुल ₹ 5082 का खर्च आता है। सिद्ध कीजिए कि हॉल की लम्बाई व चौड़ाई क्रमशः 40 मीटर व 30 मीटर होगी।
हलः
माना
हॉल की लम्बाई = 4x मी
हॉल की चौडाई = 3x मी
हॉल की ऊचाई = 5.5 मी

प्रश्न 12.
9 सेमी भुजा वाला एक घन पानी से भरे एक आयताकार बर्तन में पूर्णतया डूब जाता है। यदि आधार की विमाएं 15 सेमी व 12 सेमी है। तो सिद्ध कीजिए कि पानी के स्तर में हुई बढ़ोत्तरी 4.05 सेमी होगी।
हलः
पानी में डुबाये गये घन का आयतन = ऊपर उठे पानी का आयतन
(9)³ = 15 × 12 × h
729 = 15 × 12 × h

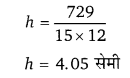
∴ पानी के स्तर में हुई बढोतरी = 4.05 सेमी

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 21 Probability Ex 21.1 प्रायिकता

Ex 21.1 Probability अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि एक घटना E के होने की प्रायिकता P है तब निम्नलिखित में से कौन-सा सत्य है?
(a) 0 ≤ p ≤ 1
(b) 0 < p < 1
(c) p > 1
(d) इनमें से कोई नहीं
हलः
विकल्प (a)

प्रश्न 2.
निम्न में से कौन-सी एक घटना की प्रायिकता नहीं हो सकती है?
(a) 0
(b) 1
(c) 2
(d) इनमें से कोई नहीं
हलः
विकल्प (c)

प्रश्न 3.
निम्न में से कौन-सी एक घटना की प्रायिकता नहीं हो सकती है?
(a) [latex]\frac{1}{3}[/latex]
(b) [latex]\frac{3}{4}[/latex]
(c) [latex]\frac{5}{4}[/latex]
(d) इनमें से कोई नहीं
हल:
विकल्प (c)

प्रश्न 4.
निम्न में सही सम्बन्ध ज्ञात कीजिए।
(a) P(E) = 1+ P([latex]\overline{\boldsymbol{E}}[/latex])
(b) P(E) + P([latex]\overline{\boldsymbol{E}}[/latex]) = 1
(c) P(E)- P([latex]\overline{\boldsymbol{E}}[/latex]) = 0
(d) इनमें से कोई नहीं
हलः
विकल्प (a)

प्रश्न 5.
एक घटना E के लिए, यदि P(E) = [latex]\frac{3}{7}[/latex] तब P([latex]\overline{\boldsymbol{E}}[/latex]) ज्ञात कीजिए।
हल:

प्रश्न 6.
ताश के पत्तों के एक पैकेट में, लाल रंग की संख्या ज्ञात कीजिए।
हलः
लाल रंग के पत्तों की संख्या = 26

प्रश्न 7.
एक सिक्के को 100 बार निम्न बारम्बारताओं के साथ उछाला गया है, चित् = 45, पट = 55 तब एक
चित् प्राप्त होने की प्रायिकता ज्ञात कीजिए।
हलः

प्रश्न 8.
एक सिक्के को 200 बार उछाला गया है तब 79 बार चित् आता है। एक चित् की प्रायिकता ज्ञात
कीजिए।
हल:

प्रश्न 9.
E₁ और E₂ एक घटना के केवल दो परिणाम है तथा P(E₁) = 0.32 तब P(E₂) का मान ज्ञात कीजिए।
हल:
P(E₁) + P(E₂)
0.32 + P(E₂) = 1
P(E₂) = 1 – 0.32 = 0.68

प्रश्न 10.
एक परीक्षण में, एक सिक्के को 500 बार उछाला गया है यदि चित् 280 बार ऊपर आता है तब एक पट प्राप्त करने की प्रायिकता ज्ञात कीजिए।
हल:
चित् आने के प्रकार = 280
∴ पट आने के प्रकार = 500 – 280 = 220

प्रश्न 11.
400 विद्यार्थियों के एक सर्वेक्षण में, 160 गणित को पसन्द करते हैं तथा अन्य इसे पसन्द नहीं करते हैं।
एक विद्यार्थी के यादृच्छया चुने जाने पर गणित को पसन्द करने की प्रायिकता ज्ञात कीजिए।
हलः

प्रश्न 12.
लूडो के एक खेल में एक पासे को फेंकने पर एक सम संख्या प्राप्त होने की प्रायिकता ज्ञात कीजिए।
हलः
सम संख्या = 2,4,6 (कुल 3 संख्याएँ)
कुल संख्या = 1,2,3,4,5,6 (कुल 6 संख्याएँ)
प्रायिकता [latex]=\frac{3}{6}=\frac{1}{2}[/latex]

प्रश्न 13.
एक क्रिकेट मैच में, एक बल्लेबाज खेली गई 400 गेंदों में 8 बार चौका मारता है तब प्रायिकता ज्ञात कीजिए कि वह चौका नहीं मारता है।
हलः
कुल गेंदे = 400

प्रश्न 14.
एक पासे को 1000 बार फेंका गया है तथा प्राप्त आंकड़ों को निम्न प्रकार लिख लिया गया है

यदि पासे को एक बार फिर से फेंका गया है तब प्रायिकता ज्ञात कीजिए कि यह 5 को दिखाता है।
हलः
5 आने के अनुकूल प्रकार = 150 + 1 = 151
पासे को फेंकने पर कुल प्रकार = 1000 + 1 = 1001

Ex 21.1. Probability लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 15.
एक सिक्के को 150 बार उछाला जाता है तथा परिणाम लिख लिये जाते हैं। परिणामों का बारम्बारता बंटन नीचे दिया गया है-

एक अकेले परीक्षण में एक चित प्राप्त होने की प्रायिकता ज्ञात कीजिए।
हलः
एक अकेले परीक्षण में एक चित प्राप्त होने की प्रायिकता
P(E) = [latex]\frac{85}{150}[/latex] = 0.56

प्रश्न 16.
दो सिक्के एक साथ 500 बार उछाले गये हैं तथा निम्न परिणाम प्राप्त किए गए हैं।

इन घटनाओं की प्रत्येक के होने की प्रायिकता ज्ञात कीजिए।
हलः
2 चित् आने की प्रायिकता = [latex]\frac{105}{500}[/latex] = 0.21

प्रश्न 17.
एक समूह में से 80 बल्बों को यादृच्छया चुना गया है तथा उनका जीवन समय (घंटों में ) नीचे दी गई बारम्बारता सारणी के रूप में लिख लिया गया है|

समूह में से एक बल्ब को यादृच्छया चुना गया है तब प्रायिकता ज्ञात कीजिए कि इसका जीवन 1150
घंटे है।
हलः
1150 घण्टे जीवन वाले बल्बों की संख्या = 0
प्रायिकता = 0

प्रश्न 18.
एक मौसम केन्द्र के रिकॉर्ड को देखने से पता चलता है कि पिछले 250 क्रमागत दिनों में दिए गए मौसम
पूर्वानुमानों में से 175 बार उसके पूर्वानुमान सही रहे हैं। प्रायिकता ज्ञात कीजिए कि एक दिए गए दिन पर पूर्वानुमान
(i) सही था
(ii) सही नहीं था। (NCERT)
हलः
एक दिए गए दिन पर पूर्वानुमान की प्रायिकता,

प्रश्न 19.
एक पासे को 100 बार फेंका गया है यदि एक सम संख्या प्राप्त होने की प्रायिकता [latex]\frac{2}{5}[/latex] है। एक विषम संख्या कितनी बार प्राप्त होगी?
हलः
सम संख्या प्राप्त होने की प्रायिकता = [latex]\frac{2}{5}[/latex]
∴ विषम संख्या प्राप्त होने की प्रायिकता = [latex]1-\frac{2}{5}=\frac{3}{5}[/latex]
∴ विषम संख्या प्राप्त होने के प्रकार= [latex]\frac{3}{5} \times 100[/latex] = 60

प्रश्न 20.
एक थैले में 4 सफेद गेंद तथा अन्य लाल गेंदे हैं यदि थैले से एक सफेद गेंद निकालने की प्रायिकता [latex]\frac{2}{5}[/latex] है। थैले में लाल गेंदों की संख्या ज्ञात कीजिए।
हलः
सफेद गेंद = 4

कुल गेंदे = 10
लाल गेंदों की संख्या = 10 – 4 = 6 गेंदे

Ex 21.1. Probability दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 21.
मासिक इकाई परीक्षा में, एक विद्यार्थी द्वारा प्राप्त अंकों का प्रतिशत नीचे दिया गया है-

प्रायिकता ज्ञात कीजिए कि विद्यार्थी प्राप्त करता है-
(i) 70% से अधिक अंक
(ii) 70% से कम अंक
(iii) 75% से अधिक
हल:
(i) 70% से अधिक अंक = 3 बार
∴ 70% से अधिक अंक आने की प्रायिकता P(E) = [latex]\frac{3}{5}[/latex] = 0.6
(ii) 70% से कम अंक = 2 बार
70% से कम अंक आने की प्रायिकता P(E) = [latex]\frac{2}{5}[/latex] = 0.4
(iii) 75% से अधिक अंक आने की प्रायिकता P(E) = [latex]\frac{1}{5}[/latex] = 0.2

प्रश्न 22.
निम्नलिखित सारणी 400 नियॉन लैम्पों के जीवन समय को दर्शाती है-

एक बल्ब यादृच्छया चुना गया है। प्रायिकता ज्ञात कीजिए कि चुने गये बल्ब का जीवन समय है
(i) 400 से कम
(ii) 300 से 800 घंटों के बीच
(iii) कम-से-कम 700 घंटे
हल:
(i) 400 से कम जीवन काल दर्शाने वाले बल्बों की प्रायिकता = [latex]\frac{14}{400}=\frac{7}{200}[/latex]

प्रश्न 23.
बीजों के 5 थैलों में से प्रत्येक थैले से पचास बीज यादृच्छया चुनकर उन्हें ऐसी मानकीकृत अवस्थाओं में
रखा गया जो अंकुरण के अनुकूल है। 20 दिन बाद प्रत्येक संग्रह में अंकुरित हुए बीजों की संख्या गिन कर नीचे दर्शाये अनुसार एक सारणी में लिखी गई है-

निम्नलिखित बीजों के अंकुरण की प्रायिकता क्या है? [NCERT]
(i) एक थैले में 40 से अधिक बीज?
(ii) एक थैले में 49 बीज?
(iii) एक थैले में, 35 से अधिक बीज?
हल:

(ii) एक थैले में 49 बीज होने की प्रायिकता = 0
(iii) एक थैले में, 35 से अधिक बीज होने की प्रायिकता = [latex]\frac{210}{210}[/latex] = 1

प्रश्न 24.
एक फैक्ट्री के 30 मजदूरों की आय (र में) का बारम्बारता बंटन नीचे दिया गया है-

एक मजदूर को यादृच्छया चुने जाने पर, प्रायिकता ज्ञात कीजिए कि उसकी आय है-
(i) ₹ 150 से कम
(ii) ₹ 210 कम से कम
(iii) ₹ 150 के बराबर या अधिक किन्तु ₹ 210 से कम
हलः
(i) ₹ 150 से कम आय वाले वाले मजदूर के चुने जाने की प्रायिकता = [latex]\frac{7}{30}[/latex]
(ii) ₹ 210 से कम आय वाले वाले मजदूर के चुने जाने की प्रायिकता = [latex]\frac{23}{30}[/latex]
(iii) ₹ 150 के बराबर या अधिक किन्तु ₹ 210 से कम आय वाले मजदूर के चुने जाने की प्रायिकता = [latex]\frac{16}{30}[/latex] = [latex]\frac{8}{15}[/latex]

Ex 21.1. Probability बहविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
एक सिक्के को 200 बार उछालने पर, 112 बार चित् तथा 88 बार पट प्राप्त हुए एक सिक्के की एक
उछाल में एक पट प्राप्त होने की प्रायिकता है-
(a) 10/25
(b) 11/25
(c) 14/25
(d) इनमें से कोई नहीं
हलः
200 उछाल में 88 बार पट प्राप्त होता है।
अतः एक सिक्के की एक उछाल में एक पट प्राप्त होने की प्रायिकता
[latex]=\frac{88}{200}=\frac{11}{25}[/latex]
अतः विकल्प (b) सही है।

प्रश्न 2.
एक सिक्के की 50 उछालों में, 32 बार पट आता है यदि एक सिक्का यादृच्छया उछाला जाता है तो एक चित् प्राप्त होने की प्रायिकता है-
(a) [latex]\frac{9}{25}[/latex]
(b) [latex]\frac{10}{25}[/latex]
(c) [latex]\frac{11}{25}[/latex]
(d) इनमें से कोई नहीं
हलः
एक चित् प्राप्त होने की प्रायिकता = [latex]\frac{18}{50}=\frac{9}{25}[/latex]
अतः विकल्प (a) सही है।

प्रश्न 3.
एक सिक्का 100 बार उछाला जाता है तब एक चित् के प्राप्त होने की प्रायिकता है-
(a) [latex]\frac{41}{100}[/latex]
(b) [latex]\frac{57}{100}[/latex]
(c) [latex]\frac{43}{100}[/latex]
(d) इनमें से कोई नहीं
हलः
चित् आने के प्रकार = 100 – 57 = 43
एक चित् आने की प्रायिकता = [latex]\frac{43}{100}[/latex]
अतः विकल्प (c) सही है।

प्रश्न 4.
दो सिक्के 1000 बार उछाले गये हैं तथा परिणाम निम्न प्रकार लिखे गये हैं-

एक सिक्के को यादृच्छया उछाला गया तब अधिक से अधिक एक चित् प्राप्त होने की प्रायिकता है-
(a) [latex]\frac{367}{500}[/latex]
(b) [latex]\frac{97}{500}[/latex]
(c) [latex]\frac{403}{500}[/latex]
(d) इनमें से कोई नहीं
हलः
अधिक से अधिक चित् प्राप्त होने की प्रायिकता = P(0) + P(1)

अतः विकल्प (a) सही है।

प्रश्न 5.
60 व्यक्तियों के एक समूह में, 35 कॉफी पसन्द करते हैं। इस समूह से यदि एक व्यक्ति यादृच्छया चुना गया तब उसके कॉफी न पसन्द करने की प्रायिकता है-
(a) [latex]\frac{3}{12}[/latex]
(b) [latex]\frac{5}{12}[/latex]
(c) [latex]\frac{7}{12}[/latex]
(d) इनमें से कोई नहीं
हलः
कॉफी पसन्द न करने वाले व्यक्तियों की संख्या = 60 – 35 = 25
कॉफी पसन्द न करने वाले एक व्यक्ति की प्रायिकता = [latex]\frac{25}{60}=\frac{5}{12}[/latex]
अतः विकल्प (b) सही है।

प्रश्न 6.
यदि एक खेल को जीतने की प्रायिकता 0.8 है, तब खेल को हारने की प्रायिकता है-
(a) 1
(b) 0
(c) 0.2
(d) इनमें से कोई नहीं
हलः
खेल को हारने की प्रायिकता = 1 – 0.8 = 0.2
अतः विकल्प (c) सही है।

प्रश्न 7.
एक पासे की 65 उछालों में, निम्न परिणाम लिखे गये हैं-

एक पासा यादृच्छया फेंका गया, तब एक अभाज्य संख्या प्राप्त होने की प्रायिकता है-
(a) [latex]\frac{31}{65}[/latex]
(b) [latex]\frac{33}{65}[/latex]
(c) [latex]\frac{3}{65}[/latex]
(d) इनमें से कोई नहीं
हलः
अभाज्य संख्याएँ = 10 + 12 + 9 = 31
एक अभाज्य संख्या प्राप्त होने की प्रायिकता = [latex]\frac{31}{65}[/latex]
अतः विकल्प (a) सही है।

प्रश्न 8.
एक सिक्के को 60 बार उछालने पर, 35 बार पट् आया है। एक चित् प्राप्त होने की प्रायिकता है-
(a) [latex]\frac{5}{12}[/latex]
(b) [latex]\frac{7}{12}[/latex]
(c) [latex]\frac{5}{12}[/latex]
(d) इनमें से कोई नहीं
हलः
चित् आने की संख्या = 60 – 35 = 25
एक चित् प्राप्त होने की प्रायिकता = [latex]\frac{25}{60}=\frac{5}{12}[/latex]
अतः विकल्प (a) सही है।

Ex 21.1. Probability स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
जैसे सिक्के को उछालने की संख्या बढ़ती है, तब चित् एवं पट् का अनुपात [latex]\frac{1}{2}[/latex]- है। क्या ये सत्य है? यदि
नहीं, तो सत्य मान लिखिये।
हलः

प्रश्न 2.
सांख्यिकी विषय के बारे में विद्यार्थियों के विचार जानने के लिए 200 विद्यार्थियों का एक सर्वेक्षण किया गया तथा प्राप्त आंकड़े निम्न सारणी में लिखे गये हैं-

प्रायिकता ज्ञात कीजिए कि यादृच्छया चुना गया विद्यार्थी-
(i) सांख्यिकी को पसन्द करता है।
(ii) सांख्यिकी को पसन्द नहीं करता है।
हल:

प्रश्न 3.
निम्न सारणी से

(i) प्रायिकता ज्ञात कीजिए कि एक विद्यार्थी गणित परीक्षा में 20% से कम अंक प्राप्त करता है।
(ii) प्रायिकता ज्ञात कीजिए कि एक विद्यार्थी 60 या से अधिक अंक प्राप्त करता है।
हलः
(i) 20% से कम अंक प्राप्त करने वाले विद्यार्थी की प्रायिकता = [latex]\frac{7}{90}[/latex]
(ii) 60 या 60 से अधिक अंक प्राप्त करने वाले विद्यार्थी की प्रायिकता = [latex]\frac{15+8}{90}=\frac{23}{90}[/latex]

प्रश्न 4.
एक वयस्त सड़क पर एक निश्चित समय अन्तराल में गुजरने वाली 60 कारों में बैठे व्यक्तियों की संख्या निम्न तालिका में दी गयी है-

माना एक कार इस समय के बाद गुजरती है तब प्रायिकता ज्ञात कीजिए कि
(i) उसमें केवल दो व्यक्ति बैठे हों।
(ii) उसमें तीन से कम व्यक्ति बैठे हों।
(iii) उसमें दो से अधिक व्यक्ति बैठे हों।
हल:
(i) कार में केवल 2 व्यक्ति ही बैठे हो, इसकी प्रायिकता = [latex]\frac{16}{60}[/latex] = 0.267
(ii) कार में 3 से कम व्यक्ति बैठे हो, इसकी प्रायिकता = [latex]\frac{22+16}{60}[/latex] = [latex]\frac{38}{60}[/latex] = 0.63
(iii) दो से अधिक व्यक्ति बैठे हो. इसकी प्रायिकता = [latex]\frac{12+6+4}{60}[/latex] = [latex]\frac{22}{60}[/latex] = 0.367

प्रश्न 5.
60 विद्यार्थियों के घर से स्कूल की दूरी निम्न तालिका में दी गयी है।

तब प्रायिकता ज्ञात कीजिए कि विद्यार्थी स्कूल से
(i) 7 किमी से कम दूरी पर रहता है।
(ii) 7 किमी से अधिक परन्तु 10 किमी से कम दूरी पर रहता है।
(iii) 10 किमी से अधिक दूरी पर रहता है।
हलः
(i) 7 किमी से कम दूरी पर रहने की प्रायिकता = [latex]\frac{35}{35+20+5}=\frac{35}{60}[/latex] = 0.583
(ii) 7 किमी से अधिक परन्तु 10 किमी से कम दूरी पर रहता है, इसकी प्रायिकता = [latex]\frac{20}{60}[/latex] = 0.333
(iii) 10 किमी से अधिक दूरी पर रहता है, इसकी प्रायिकता = [latex]\frac{5}{60}[/latex] = 0.083

प्रश्न 6.
दो पासों को 500 बार उछाला जाता है प्रत्येक बार उसके ऊपर वाले सिरों पर आने वाली संख्याओं का योग निम्न प्रकार है।

प्रायिकता
यदि पासे को एक ओर बार उछाला जाता है तब प्रायिकता ज्ञात कीजिए कि प्राप्त
(i) 3 हैं
(ii) 10 से अधिक है
(iii) ≤ 5
(iv) 8 व 12 के बीच
हलः

प्रश्न 7.
पिछले 200 कार्य दिवसों पर एक मशीन द्वारा प्रदत्त त्रुटि वाले उपकरणों की संख्या निम्न है।

तब प्रायिकता ज्ञात कीजिए कि आने वाले में
(i) कोई त्रुटिपूर्ण उपकरण न हो।
(ii) कम से कम एक त्रुटिपूर्ण उपकरण हो।
(iii) 5 से अधिक त्रुटिपूर्ण उपकरण न हो।
हल:
(i) कोई त्रुटिपूर्ण उपकरण न हो, इसकी प्रायिकता = [latex]\frac{50}{200}[/latex] = 0.25
(ii) कम से कम एक त्रुटिपूर्ण उपकरण हो, इसकी प्रायिकता

प्रश्न 8.
एक सर्वे में एक फैक्टरी में मजदूरों की आयु निम्न प्रकार प्राप्त हुई है।

एक मजदूर यादृच्छया चुना जाता है तब प्रायिकता ज्ञात कीजिए कि चुने हुए व्यक्ति की आयु
(i) 40 वर्ष या उससे अधिक हो
(ii) 40 से कम हो
(iii) 30 से 39 के बीच हो
(iv) 39 से अधिक परन्तु 60 से कम हो।
हलः
(i) 40 वर्ष या उससे अधिक आयु वाले मजदूर को चुनने की प्रायिकता

(ii) 40 वर्ष से कम आयु वाले मजदूर को चुनने की प्रायिकता = [latex]\frac{38+27}{200}[/latex]
= [latex]\frac{65}{200}[/latex] = 0.325
(iii) 30 वर्ष से 39 के बीच आयु के मजदूर को चुनने की प्रायिकता
= [latex]\frac{27}{200}[/latex] = 0.135
(iv) 39 वर्ष से अधिक परन्तु 60 से कम आयु के मजदूर चुनने की प्रायिकता
= [latex]\frac{86+46}{200}=\frac{132}{200}[/latex] = 0.66

प्रश्न 9.
दो सिक्कों को 500 बार उछाला जाता है तथा निम्न परिणाम प्राप्त किये जाते हैं।
दो चित् : 95 बार
एक पट : 290 बार
कोई चित् नही : 115 बार
इनमें प्रत्येक घटना के घटित होने की प्रायिकता ज्ञात कीजिए।
हलः

प्रश्न 10.
गेहूं के 11 बैग, जिनमें प्रत्येक पर 5 किग्रा गेहूँ होने के बारे में लिखा है, में वास्तव में निम्न भार पाये गये-
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00
प्रायिकता ज्ञात कीजिए कि इनमें से यादृच्छया तीन बैग निकालने पर उनमें 5 किग्रा से ज्यादा गेहूँ हो।
हलः
5 किग्रा से ज्यादा गेंहूँ वाले बैग की संख्या = 7
प्रायिकता P(E) = [latex]\frac{n(E)}{n(S)}=\frac{7}{11}[/latex]

प्रश्न 11.
टेलीफोन डायरेक्ट्री के एक पन्ने पर 200 टेलीफोन नम्बर लिखे हैं उनमें से इकाई स्थान के अंक की बारम्बारता निम्न तालिका में दी गयी है।

एक संख्या यादृच्छया चुनी जाती है। प्रायिकता ज्ञात कीजिए। इकाई स्थान पर संख्या-
(i) 6
(ii) 3 का गुणक (अशून्य) है
(iii) एक अशून्य सम संख्या है
(iv) एक विषम संख्या है
हलः
(i) इकाई स्थान पर संख्या 6 आये, इसकी प्रायिकता

(ii) 3 का गुणक (अशून्य) है, इसकी प्रायिकता

(iii) एक अशून्य सम संख्या है, इसकी प्रायिकता

(iv) एक विषम संख्या है, इसकी प्रायिकता

प्रश्न 12.
दो सिक्को को 1000 बार उछालने पर परिणामों की बारंबारता निम्न प्राप्त होगी।

यदि दो सिक्को को पुनः उछाला जाता है तब प्रायिकता ज्ञात कीजिए कि उस पर
(i) कम से कम एक चित् आये।
(ii) अधिक से अधिक एक चित् आये।
हलः
(i) कम से कम एक चित् आये, इसकी प्रायिकता

(ii) अधिक से अधिक एक चित् आये, इसकी प्रायिकता = [latex]\frac{340+310}{1000}[/latex]

प्रश्न 13.
निम्न तालिका में कक्षा IX के 39 विद्यार्थियों के जन्म माह को दर्शाती है।

प्रायिकता ज्ञात कीजिए कि विद्यार्थी अगस्त में पैदा हुआ हो।
हलः
अगस्त माह में पैदा होने वाले विद्यार्थी की प्रायिकता P(E) = [latex]\frac{5}{39}[/latex]

प्रश्न 14.
मासिक यूनिट टैस्ट में एक विद्यार्थी द्वारा प्राप्त अंकों का विवरण निम्न है।

प्रायिकता ज्ञात कीजिए कि विद्यार्थी ने
(i) कम से कम 60% अंक प्राप्त किये हों।
(ii) 70% व 80% के बीच अंक प्राप्त किये हों।
(iii) 75% व उससे अधिक अंक प्राप्त किये हों।
(iv) 65% से कम अंक प्राप्त किये हों।
हल:
(i) कम से कम 60% अंक प्राप्त किये हों, इसकी प्रायिकता = [latex]\frac{4}{5}[/latex] = 0.8
(ii) 70% व 80% के बीच अंक प्राप्त किये हों, इसकी प्रायिकता = [latex]\frac{1}{5}[/latex] =0.2
(iii) 75% व उससे अधिक अंक प्राप्त किये हों, इसकी प्रापि = [latex]\frac{2}{5}[/latex] = 0.4
(iv) 65% से कम अंक प्राप्त किये हों, इसकी प्रायिकता = [latex]\frac{3}{5}[/latex] = 0.6

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.4 बहुपद तथा उनके गुणनखण्ड

Ex 5.4 Polynomial and their Factors अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Question)

प्रश्न 1.
8x + 12y के गुणनखण्ड ज्ञात कीजिए।
हलः
8x + 12y = 2 × 2 × 2 × x + 2 × 2 × 3 × y = 4(2x + 3y)

प्रश्न 2.
x³ + x² के गुणनखण्ड ज्ञात कीजिए।
हलः
x³ + x² = x × x × x + x × x = x × x(x + 1) = x²(x + 1)

प्रश्न 3.
x² + x + y + xy के गुणनखण्ड ज्ञात कीजिए।
हल:
x² + x + y + xy = [x² + x] + [y + xy] = x(x + 1) + y(x + 1) = (x + 1)(x + y)

प्रश्न 4.
x² – x + y – xy के गुणनखण्ड ज्ञात कीजिए।
हल:
x² – x + y – xy = x(x – 1) – y(x – 1) = (x – 1)(x – y)

Ex 5.4 Polynomial and their Factors  लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

निम्न बहुपदों के गुणनखण्ड ज्ञात कीजिए

प्रश्न 5.
ax + cx – ay – cy
हलः
ax + cx – ay – cy = x(a + c) – y(a + c) = (a + c)(x – y)

प्रश्न 6.
mx – 2my – nx + 2ny
हल:
mx – 2my – nx + 2ny = mx – nx – 2my + 2ny = x(m – n) – 2y(m – n) = (m – n)(x – 2y)

प्रश्न 7.
ab + cd + ad + bc
हलः
ab + cd + ad + bc = ab + ad + cd + bc = a(b + d) + c(b + d)= (b + d)(a + c)

प्रश्न 8.
ax – bx + by + cy – cx – ay
हलः
ax – bx + by + cy – cx – ay = ax – bx – cx – ay + by + cy
= x(a – b – c) – y(a – b – c) = (a – b – c)(x – y)

प्रश्न 9.
mx + ny – nx – my
हलः
mx – ny – nx + my = mx – nx – my + ny = x(m – n) – y(m – n) = (m – n)(x – y)

प्रश्न 10.
ax + cy – ac – xy
हलः
ax + cy – ac – xy = ax – ac – xy + y = a(x – c) – y(x – c) = (x – c)(a – y)

प्रश्न 11.
9a³b²c – 27a²b³c² – 36a²b²c³
हलः
9a³b²c – 27a²b³c² – 36a²b²c³ = 9a²b²c(a – 3bc – 4c²)

प्रश्न 12.
8a²b(a – b)² – 4a²(a – b)³
हलः
8a²b(a – b)² – 4a² (a – b)³ = 4a²(a – b)²[2b – (a – b)]
= 4a² (a – b)²[2b – a + b] = 4a²(a – b)²[3b – a]

प्रश्न 13.
(p + q + r)² + x[p + q + r) – y(p + q + r)
हलः :
(p + q + r)² + x(p + q + r) – y(p + q + r) = (p + q + r)[p + q + r + x – y]

प्रश्न 14.
(p + q)³ + (p + q)² + (p + q)
हलः
(p + q)³ + (p + q)² + (p + q) = (p + q)[(p + q)² + (p + q) + 1]

Ex 5.4 Polynomial and their Factors  लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

निम्न बहुपदों के गुणनखण्ड कीजिए।
प्रश्न 15.
7(x + y)³ +14(x + y)² +28(x + y)
हलः
7(x + y)³ + 14(x + y)² + 28(x + y) = 7(x + y)[(x + y)² + 2(x + y) + 4]
= 7(x + y)[x² + y² + 2xy + 2x + 2y + 4]

प्रश्न 16.
a³bc + ab³c – abc³
हलः
a³bc + ab³c – abc³ = abc(a² + b² – c²)

प्रश्न 17.
(x² + 3x)² – 5(x² + 3x) – y(x² + 3x) + 5y
हलः
(x² + 3x)² – 5(x² + 3x) – y(x² + 3x) + 5y = (x² + 3x)[x² + 3x – 5] – y[x² + 3x – 5]
= [x² + 3x – 5][x² + 3x – y]

प्रश्न 18.
ab(x² + y²)+ xy(a² + b²)
हलः
ab(x² + y²) + xy(a² + b²)= abx² + aby² + xya² + xyb² = abx² + xya² + aby² + xyb²
= ax(bx + ay ) + by (ay + bx) = (ax + by)(bx + ay)

प्रश्न 19.
x⁵ + x⁴ – 2x² – 2x
हलः
x⁵ + x⁴ – 2x² – 2x = x{x⁴ + x³ – 2x – 2] = x[x³(x + 1) – 2(x + 1)]= x[(x³ – 2)(x + 1)]

प्रश्न 20.
ab(c² + 1) + c(a² + b²)
हलः
ab(c² + 1) + c(a² + b²) = abc² + ab + ca² + cb² = abc² + ca² + ab + cb²
= ac(bc + a) + b(a + bc) = (bc + a)(ac + b)

प्रश्न 21.
x² + [latex]\frac{1}{x^{2}}[/latex] + 2 – 3x – [latex]\frac{3}{x}[/latex]
हलः
[latex]x^{2}+\frac{1}{x^{2}}+2-3 x-\frac{3}{x}=\left(x+\frac{1}{x}\right)^{2}-3\left(x+\frac{1}{x}\right)=\left(x+\frac{1}{x}\right)\left[x+\frac{1}{x}-3\right][/latex]

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.3 बहुपद तथा उनके गुणनखण्ड

Ex 5.3 Polynomial and their Factors अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Question

प्रश्न 1.
जब एक बहुपद x² + 4x + 5 कों (x + 3) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
बहुपद x² + 4x + 5 को (x + 3) से भाग करने पर शेषफल प्राप्त करने के लिए x + 3 = 0 या
x = 0 – 3 = -3 बहुपद में रखते है।
∴ शेषफल = (-3)² + 4(-3) + 5 = 9 – 12 + 5 = 2

प्रश्न 2.
जब एक बहुपद x² + 6x + 9 को (x + 3) से भाग दिया जाता है. तब शेषफल ज्ञात कीजिए।
हलः
बहुपद x² + 6x + 9 को (x + 3) से भाग करने पर
x + 3 = 0 या x = -3 रखने पर
∴ शेषफल = (-3)² + 6(-3) + 9 = 9 – 18 + 9 = 0

प्रश्न 3.
जब एक बहुपद x³ – 7x + 6 को (x – 1) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
बहुपद x³ – 7x + 6 को (x – 1) से भाग करने पर
x – 1 = 0 या x = 1
शेषफल = (1)³ – 7(1) + 6 = 1 – 7 + 6 = 0

प्रश्न 4.
जब बहुपद (x³ + 1) को (x + 1) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
(x³ + 1) को (x + 1) से भाग करने पर
x + 1 = 0 या x = 0 – 1 = -1 बहुपद में रखने पर शेषफल = (-1)³ + 1 = -1 + 1 = 0

प्रश्न 5.
जब बहुपद x³ + 3x + 3 को (x + 2) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
यदि बहुपद x² + 3x + 3 को (x + 2) से भाग किया जाए तो x + 2 = 0 या x = 0 – 2 = -2 रखने पर
शेषफल = (-2)² + 3(-2) + 3 = 4 – 6 + 3 = 1

प्रश्न 6.
जब बहुपद x⁶ + x⁴ – x² +1 को x – 2 से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
यदि बहुपद x⁶ + x⁴ – x² + 1 को (x – 2) से भाग किया जाए तो x – 2 = 0 या x = 2 रखने पर
शेषफल = (2)⁶ + (2)⁴ – (2)² + 1 = 64 + 16 – 4 + 1 = 77

प्रश्न 7.
यदि x¹⁵ – 199 को (x – 1) से भाग दिया जाता है तब शेषफल ज्ञात कीजिए।
हलः
यदि x¹⁵ – 199, (x – 1) से विभाजित है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)¹⁵ – 199 = 1 – 199 = -198

प्रश्न 8.
बहुपद x³ – 3x² + 4x – 12 का एक गुणनखण्ड ज्ञात कीजिए।
हल:
x³ – 3x² + 4x – 2 में x = 1 रखने पर शेषफल 0 नहीं है।
x = 2 रखने पर शेषफल 0 नहीं है।
x = 3 रखने पर शेषफल = (3)³ – 3(3)² + 4(3) – 12 = 27 – 27 + 12 – 12 = 0
इसलिए (x -3) इसका एक गुणनखण्ड है।

प्रश्न 9.
यदि p(-3) = 0 तब बहुपद p(x) का गुणनखण्ड ज्ञात कीजिए।
हलः
यदि p(-3) = 0 तब p(x) का एक गुणनखण्ड (x + 3) होगा।

प्रश्न 10.
बहुपद 2x³ + 4x + 6 का एक गुणनखण्ड ज्ञात कीजिए।
हल:
2x³ + 4x + 6 का एक गुणनखण्ड (x + 1) होगा।
यदि x + 1 = 0 या x = 0 – 1 = -1 रखने पर
शेषफल = 2(-1)² + 4(-1) + 6 = -2 – 4 + 6 = 0

प्रश्न 11.
(x – 3) निम्न में से किस बहुपद का गुणनखण्ड होगा?
(a) 2x² – x – 15
(b) x² + 9
(c) 3x² + 5x + 7
(d) इनमें से कोई नहीं
हलः
(a) (x – 3), 2x² – x – 15 का एक गुणनखण्ड है। क्योंकि x – 3 = 0 या x = 3 रखने पर
शेषफल = 2(3)² – 3 – 15 = 18 – 3 – 15 = 0

प्रश्न 12.
(x + 1) निम्न में से किसका गुणनखण्ड नहीं है।
(a) x² – 4x – 3
(b) x² + 4x + 3
(c) x² – 1
(d) इनमें से कोई नहीं
हलः
(a) (x + 1), x² – 4x – 3 का एक गुणनखण्ड नहीं है।
∵ x+1 = 0 या X = 0-1 = -1 रखने पर
शेषफल = (-1)² – 4(-1) – 3 = 1 + 4 – 3 = 2 ≠ 0

प्रश्न 13.
यदि (2x + 1) बहुपद 4x² – kx + k का एक गुणनखण्ड है, तो k का मान ज्ञात कीजिए।
हलः
∵ (2x + 1), 4x² – kx + k का गुणनखण्ड है।
∴ 2x + 1 = 0 या 2x = -1 या x = [latex]-\frac{1}{2}[/latex] रखने पर
शेषफल = 0

प्रश्न 14.
यदि (x – 1) बहुपद x³ + kx² + 142x – 120 का एक गुणनखण्ड है, तो k का मान ज्ञात कीजिए।
हल:
∵ (x – 1) बहुपद x³ + kx² + 142x – 120 का एक गुणनखण्ड है।
∴ x – 1 = 0 या x = 1 रखने पर,
शेषफल = 0
(1)³ + k(1)² + 142 × 1 – 120 = 0
1 + k + 142 – 120 = 0
k + 23 = 0 ⇒ k = -23

प्रश्न 15.
यदि [latex]x+\frac{1}{2}[/latex] बहुपद px² – 4px +3 का एक गुणनखण्ड है, तो p का मान ज्ञात कीजिए।
हल:
यदि [latex]x+\frac{1}{2}[/latex], px² – 4px + 3 का एक गणुखण्ड है।
∴ [latex]x+\frac{1}{2}[/latex] = 0 या x = [latex]-\frac{1}{2}[/latex] -रखने पर शेषफल

Ex 5.3 Polynomial and their Factors  लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 16.
निम्न प्रत्येक में, बहुपद f(x) को g(x) से भाग दीजिए तथा भागफल व शेषफल के मान ज्ञात कीजिए।
(i) f(x) = 5x² + 3x + 1; , g(x) = 2x
(ii) f(x) = x³ – 14x² + 37x – 60; g(x) = x – 2
(iii) f(x) = x³ – 3x² + 4x + 2; g(x) = x – 1
(iv) f(x) = x³ + 3x² – 12x + 4; g(x) = x – 2
(v) f(x) = 2x² – 3x + 5; g(x) = x – a
हलः
(i) f(x) = 5x² + 3x + 1 तथा g(x) = 2x

(ii) f(x) = x³ – 14x² + 37x – 60 तथा g(x) = x – 2

भागफल = x² – 12x + 13 तथा शेषफल = -34

(iii) f(x) = x³ – 3x² + 4x + 2 तथा g(x) = x – 1

भागफल = x² – 2x + 2
शेषफल = 4

(iv) f(x) = x³ + 3x² – 12x + 4 तथा g(x) = x – 2

भागफल = x² + 5x – 2
शेषफल = 0

(v) f(x) = 2x² – 3x + 5 तथा g(x) = x – a

भागफल = 2x + 2a – 3 तथा शेषफल = 2a² – 3a + 5

Ex 5.3 Polynomial and their Factors  दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 17.
सिद्ध कीजिए कि x² – 4x + 3 बहुपद x³ – 3x² – x + 3 का एक गुणनखण्ड है।
हलः

∵ x³ – 3x² – x + 3, x² – 4x + 3 से पूर्णतया विभाजित है।
∴ x² – 4x + 3 इसका एक गुणनखण्ड है।।

प्रश्न 18.
सिद्ध कीजिए कि x² – x + 2 बहुपद x³ – 3x² + 4x – 4 का एक गुणनखण्ड है।
हलः

∵ x³ – 3x² + 4x – 4, x² – x + 2 से पूर्णतया विभाजित है।
∴ x² – x + 2 इसका एक गुणनखण्ड है।

प्रश्न 19.
सिद्ध कीजिए कि x – 3 बहुपद x³ – 2x² + 3x – 18 का एक गुणनखण्ड है।
हलः

∵ x³ – 2x² + 3x – 18, x – 3 से पूर्णतया विभाजित है।
∴ x – 3 इसका एक गुणनखण्ड है।

प्रश्न 20.
निम्न प्रत्येक में f(x) को g(x) से भाग कीजिए तथा भागफल व शेषफल के मान ज्ञात कीजिए।
(i) f(x) = x + 5x³ + 3x² + 5x + 3; g(x) = x² + 4x + 2
(ii) f(x) = 6x⁵ + 4x⁴ – 3x³ + x + 1; g(x) = 3x² – x + 1
(iii) f(x) = x⁵ + x⁴ + x³ + x² + 2x + 2; g(x) = x + 1
हल:
(i) f(x) = x⁵ + 5x³ + 3x² + 5x + 3 तथा g(x) = x² + 4x + 2

भागफल = x³ – 4x² + 19x – 65
शेषफल = 227x + 133

(ii) f(x) = 6x⁵ + 4x⁴ – 3x³ + x + 1 तथा g(x) = 3x² – x + 1

भागफल = 2x³ + 2x² – x – 1
शेषफल = x + 2

(iii) f(x) = x⁵ + x⁴ + x³ + x² + 2x + 2 तथा g(x) = x³ + 1

भागफल = x² + x + 1 तथा शेषफल = x + 1

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 18 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder Ex 18.2 घन, घनाभ तथा लम्बवृत्तीय बेलन का पृष्ठीय क्षेत्रफल एवं आयतन

Ex 18.2 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
एक घन का आयतन ज्ञात कीजिए जिसका पृष्ठीय क्षेत्रफल 96 सेमी है। (NCERT Exemplar)
हलः
घन का पृष्ठीय क्षेत्रफल = 96
6 × a² = 96
a² = [latex]\frac{96}{6}[/latex] = 16 (∴ a = 4 सेमी)
घन का आयतन = a³ = (4)³ = 64 सेमी³

प्रश्न 2.
एक कमरे के फर्श का क्षेत्रफल 15 मी² है। यदि ऊँचाई 4 मी है तब कमरे में जा सकने वाली हवा का आयतन ज्ञात कीजिए।
हलः
कमरे में जा सकने वाली हवा का आयतन = l × b × h
= 15 × 4 = 60 मी³
= 60,000 डेसी मी³

प्रश्न 3.
एक घनाभ का आयतन 12 सेमी है। एक घनाभ का आयतन (सेमी³ में) ज्ञात कीजिए जिसकी भुजा, इस घनाभ की दोगुनी है।
हलः
घनाभ का आयतन V₁ = 12 सेमी³
घनाभ की प्रत्येक विमा 2 गुनी होने पर बने घनाभ का आयतन V₂ = 2 × 2 × 2 × V₁
= 8V₁ = 8 × 12 = 96 सेमी³

प्रश्न 4.
यदि दो घनों के आयतन 8 : 1 के अनुपात में है तब इनके कोरों का अनुपात ज्ञात कीजिए।
हलः

प्रश्न 5.
एक घन का पार्श्व पृष्ठीय क्षेत्रफल 256 मी² है घन का आयतन ज्ञात कीजिए। (NCERT Exemplar)
हलः

प्रश्न 6.
एक घन का आयतन 512 सेमी है, कुल पृष्ठीय क्षेत्रफल (सेमी’ में) ज्ञात कीजिए।
हलः
घन का आयतन = 512
a = 512
a³ = (8)³
∴ a = 8 सेमी
कुल पृष्ठीय क्षेत्रफल = 6a² = 6 × (8) = 6 × 64 = 384 सेमी ²

प्रश्न 7.
10 सेमी भुजा वाले एक घनाकार बर्तन में पूर्णतया आने वाली छड़ी की लम्बाई ज्ञात कीजिए।
हलः
घनाकार बर्तन में पूर्णतया आने वाली छडी की लम्बाई
= घन का विकर्ण = 10[latex]\sqrt{3}[/latex] सेमी

प्रश्न 8.
दो घनों के आयतन 1 : 27 के अनुपात में है इनके पृष्ठीय क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हलः

प्रश्न 9.
1.5 मीटर गहरी तथा 30 मीटर चौड़ी एक नहर में 3 किमी/घण्टा की दर से पानी बह रहा है। समुद्र में प्रति मिनट आने वाले पानी का आयतन (मी में) ज्ञात कीजिए।
हलः
पानी का आयतन = l × b × h

प्रश्न 10.
एक झरने में 5 सेमी वर्षा होती है। 2 हेक्टेयर क्षेत्र में पड़ने वाले मानी का कुल आयतन (मी में ) ज्ञात कीजिए।
हलः

Ex 18.2 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 11.
6 सेमी भुजा के दो घनों को फलक-दर-फलक मिलाया जाता है। इस प्रकार बने घनाभ का आयतन ज्ञात कीजिए।
हलः
दो घनों को मिलाने पर बने घनाभ की लम्बाई l = 12 सेमी
b = 6 सेमी
h = 6 सेमी
घनाभ का आयतन = l × b × h = 12 × 6 × 6 = 432 सेमी

प्रश्न 12.
एक घन का कुल पृष्ठीय क्षेत्रफल 294 सेमी है। इसका आयतन ज्ञात कीजिए।
हलः
घन का कुल पृष्ठीय क्षेत्रफल = 294

प्रश्न 13.
एक सिनेमा हॉल की विमाएं 100 मी × 50 मी × 18 मी है। यदि एक व्यक्ति को 150 मी हवा की आवश्यकता है तो सिनेमा हॉल में कुल कितने व्यक्ति बैठ सकते हैं।
हल:

प्रश्न 14.
एक गोदाम की विमाएँ 30 मी × 25 मी × 8 मी है। 2 मी × 1.25 मी × 0.4 मी विमा वाली कितनी लकड़ी की पेटी इसमें रखी जा सकती है ?
हल:

प्रश्न 15.
एक आयताकार ठोस घनाभ जिसका आयतन v है के तीन लगातार फलकों के क्षेत्रफल A,B व C हैं। सिद्ध कीजिए कि V² = ABC
हल:

प्रश्न 16.
25 मी × 9.8 मी के आकार के एक कमरे में 100 व्यक्ति सो सकते हैं। यदि एक व्यक्ति को 12.25 मी³ हवा की आवश्यकता होती है तो कमरे की लम्बाई ज्ञात कीजिए।
हलः
100 व्यक्तियों को सोने के लिए आवश्यक हवा = 100 × 12.25 = 1225 मी³

प्रश्न 17.
एक घन का आयतन 1000 सेमी है। इसका कुल पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः
घन का आयतन = 1000 सेमी³
a³ = 1000 = (10)³
a = 10 सेमी कुल पृष्ठीय क्षेत्रफल = 6 × a² = 6 × (10)²
= 6 × 100 = 600 सेमी²

प्रश्न 18.
18 मी × 12 मी × 9 मी के आकार के घनाभ से 3 मी भुजा वाले कितने घन काटे जा सकते हैं?
हलः

Ex 18.2 Surface Area and Volume of a Cube, Cuboid and Right Circular Cylinder दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 19.
आयताकार रूप के खेती के एक प्लाट की विमाएँ 240 मी × 180 मी है। इसके चारों ओर 10 मीटर चौड़ा एक गड्ढा खोदा गया है। तथा इसमें से निकली मिट्टी को समान रूप से प्लाट में फैलाया जाता है। जिससे उसकी सतह का स्तर 25 सेमी बढ़ जाता है। गड्ढ़े की गहराई ज्ञात कीजिए।
हल:
मिट्टी के पड़ने से प्लाट की मिट्टी का आयतन = 240 × 180 × 0.25 मी³

प्रश्न 20.
एक आयताकार टैंक की आधार पर विमायें 225 मी × 162 मी है। 60 सेमी × 45 सेमी की विमा के एक पाईप से टैंक के अन्दर किस दर से पानी डाला जाये जिससे 5 घण्टे में इसमें पानी का स्तर 20 सेमी बढ़ जाये।
हलः
माना आयताकार टैंक में पानी की ऊँचाई = 20 सेमी = 0.2 मीटर
माना आयताकार टैंक में पानी का आयतन = 225 × 162 × 0.2 मी³

प्रश्न 21.
8 मीटर लम्बा, 6 मीटर चौड़ा तथा 3 मीटर गहरा, एक घनाभकार गड्ढ़ा खुदवाने में ₹30 प्रति मी की दर से होने वाला व्यय ज्ञात कीजिए।
(NCERT)
हलः
घनाभकार गड्ढे का आयतन = l × b × h
= 8 × 6 × 3 = 144 मी
घनाभकार गड्ढा खुदवाने में कुल खर्च =144 × 30 = ₹ 4320

Balaji Publications Mathematics Class 9 Solutions