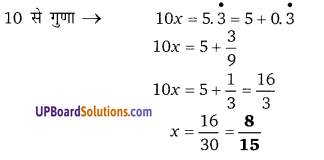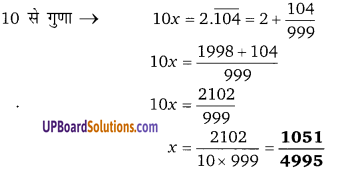UP Board Solutions for Class 9 Sanskrit Chapter 9 पत्र-लेखनम् (रचना) are the part of UP Board Solutions for Class 9 Sanskrit. Here we have given UP Board Solutions for Class 9 Sanskrit Chapter 9 पत्र-लेखनम् (रचना).
| Board |
UP Board |
| Textbook |
NCERT |
| Class |
Class 9 |
| Subject |
Sanskrit |
| Chapter |
Chapter 9 |
| Chapter Name |
पत्र-लेखनम् (रचना) |
| Category |
UP Board Solutions |
UP Board Solutions for Class 9 Sanskrit Chapter 9 पत्र-लेखनम् (रचना)
नवीं कक्षा में प्रार्थना-पत्र या निमन्त्रण-पत्र लिखने के लिए आते हैं। नवीं कक्षा के छात्रों से यह अपेक्षा की जाती है कि वे सरल संस्कृत में अपने विचार व्यक्त कर सकें।
प्रधानाचार्य या अन्य अधिकारियों को लिखे गये पत्र प्रार्थना-पत्र कहलाते हैं। प्रार्थना-पत्र लिखते समय प्रथम पंक्ति में बायीं ओर सेवायाम्’ या ‘प्रतिष्ठायाम्’ लिखकर दूसरी पंक्ति में (UPBoardSolutions.com) अधिकारी के पद के सामने ‘महोदय’ लिखा जाता है। इसके बाद अगली पंक्ति में कार्यालय का नाम लिखकर उसके आगे नगर या ग्राम को नाम लिखते हुए ‘स्थ’ जोड़ देते हैं।
इसके बाद ‘श्रीमान् या ‘महोदय’ लिखकर पत्र प्रारम्भ कर दिया जाता है। पत्र के अन्त में भवदीय:/भवदीया लिखकर नाम, पता तथा दिनांक लिखा जाता है।

1. विवाहोत्सव में सम्मिलित होने के लिए अवकाश हेतु प्रधानाचार्य को प्रार्थना-पत्र।
सेवायाम्,
श्रीमन्तः प्रधानाचार्य महोदयः
दिगम्बर जैन इण्टर कॉलेज,
बडौतस्थः
श्रीमन्तः
सविनयमिदं निवेद्यते यत् मम ज्येष्ठः भ्रातुः राकेशकुमारस्य विवाहः आगामिनि नवम्बरमासस्य पञ्चदशे दिनाङ्के निश्चितोऽस्ति। वरयात्रा दिल्ली नगर प्रस्थास्यति। मयापि तत्रावश्यमेव गन्तव्यम्। अतोऽहं पञ्चानां दिवसानां नवम्बरमासस्य चतुर्दश दिनाङ्कतः तस्यैव मासस्य अष्टादश दिनाङ्के यावत् (14-11-2014 से 18-11-2014 पर्यन्तम्) अवकाशं प्रार्थयामि। आशासे भवन्तः पञ्चानां दिवसानाम् अवकाशं स्वीकृत्य माम् अनुगृह्णीयुः।
बड़ौतनगरात्। आज्ञाकारी शिष्यः
दिनाङ्कः 30-10-2014 विपिन कुमार जैन:
नवम कक्षास्थः
2. आकस्मिक अवकाश (रुग्णावकाश) के लिए प्रधानाचार्या को प्रार्थना-पत्र
सेवायम्,
श्रीमती प्रधानाचार्या महोदया।
जैन स्थानकवासी कन्या इण्टर कॉलेज,
बडौतस्थः
महोदया!
सविनयं निवेदयामि यत् अहं गत दिवसात् ज्वरपीडिता (UPBoardSolutions.com) शय्याग्रस्ता अस्मि। बलवती शिरोवेदना च मां व्यथयति। अतोऽद्याहं विद्यालयमुपस्थातुं सर्वथाऽक्षमाऽस्मि। अतोऽद्यत: अगस्तमासस्य द्वादश दिनाङ्के यावत् त्रिदिवसानां रुग्णावकाशं स्वीकृत्य अनुगृह्णातु मां भवती।
बडौतनगरात्। भवदीया शिष्या
दिनाङ्क: 10-8-2014 रश्मि रानी जैन
नवम कक्षेया
3. धन भेजने के लिए पिता को पत्र
मुजफ्फरनगरात्
दिनाङ्क 19-9-2014
परमपूज्यो: पितृचरणयोः
सादरं प्रणतयः सन्तुतराम्।
अत्र कुशलं तत्रास्तु। बहुदिनादारभ्य नाद्यावधि भवत्पत्रं प्राप्तं मया। अत: मे चेत: चिन्तातुरः विद्यते। अस्माकम् अर्द्धवार्षिकी परीक्षा नातिदूरं वर्तते, अतोऽहमध्ययने नितरां संलग्नोऽस्मि। अहं सर्वेषु विषयेषु नितरां परिश्रमं करोमि। आशासेऽहम् अर्द्धवार्षिकपरीक्षायां सर्वाधिकान् अङ्कान् प्राप्य सफलतां प्राप्स्यामि। संस्कृत पाठ्यपुस्तकं क्रेतुम् धनस्य आवश्यकता अस्ति। कृपया धनं प्रेषयतु। मातृश्चरणयोः मे प्रणाम: कथनीयः। झटिति गृहस्य वृत्तं लेखनीयम्।।
भवताम् आज्ञाकारी पुत्रः
हरीशः कुमारः

4. मित्र को भ्रमण हेतु जाने के लिए पत्र प्रियवर तरुणः!
मयराष्ट्रतः सप्रेम नमोऽस्तु ते।
दिनाङ्कः 20-10-2014
अत्र कुशलं तत्र कुशली भवान्। अहं शरदवकोशेषु कश्मीरप्रदेशम् अटितुमिच्छामि। भवान् अपि मया सह गच्छेत्। तत्रगिरिभ्यः जलप्रवाहाः निर्झराश्चं पतन्ति। सेब-नङ्ग-अक्षोट फलानां च तत्र बाहुल्यमस्ति। तस्योत्तरस्यां दिशि हिमाच्छादितः हिमालयः तिष्ठति। तत्र औषधयः, उत्तम काष्ठादीनि (UPBoardSolutions.com) बहूनि उपयोगीनि वस्तूनि समुपलभ्यन्ते। तत्रोषित्वा स्वास्थ्यं शोभनम् आनन्दलाभश्च भविष्यति। त्वया भ्रमणविषये त्वरितम् उत्तरं देयम्।
भवदीयः अभिन्नहृदयः
हिमांशुः
नयम कक्षेयः
5. परिवार की कुशलता को जानने के लिए छोटे भाई को पत्र
प्रिय अनुज राजेशः
शुभाशिषः
अद्य प्रातः अहं सकुशलं प्रयागं समागतः। अत्र सर्व पूर्ववत् विद्यते। परिवारस्य मधुरस्मृतयः मां भृशं पीडयन्ति। मम प्रस्थानकाले मात्रा किञ्चिद् अवस्था आसीत्। तस्याः स्वास्थस्य आत्मनः अध्ययनस्य चिन्ता त्वया सावधानतया कर्त्तव्या। परिवारस्य कुशलवार्ता: पत्रेण सूचनीयाः।।
शुभेच्छुः दिनाङ्कः 29-10-2014
विकास कुमारः
प्रयाग विश्वविद्यालयस्य
गङ्गानाथ झा छात्रावासः
6. प्रधानाचार्य को शुल्क-मुक्ति के लिए प्रार्थना-पत्र
प्रतिष्ठाया।
श्रीमन्तः प्रधानाचार्य महोदयः
दिगम्बर जैन इण्टर कालेज,
बडौतस्थः
पूज्य गुरुदेव,
सेवायां नम्र निवेदनम् अस्ति यत् अहम् एकः निर्धन: ग्रामीण छात्रः अस्मि। मम पितुः एकः सामान्य कृषकः सन्ति। अहं विद्यालयस्य मासिक शुल्कं दातुं अक्षमः अतः शुल्क-मुक्ति स्वीकृति प्रदानाय प्रार्थये। आशास्ति यद् भवन्त: मां शुल्क-मुक्ति प्रदानेन अनुगृहीष्यन्ति नूनम्।
दिनाङ्कः 7-8-2014
भवतां आज्ञाकारी शिष्यः
विकास कुमार जैन
कक्षा 9 (अ)
7. जन्म-दिन के प्रीतिभोज में सम्मिलित होने के लिए एक निमन्त्रण पत्र।
श्रीमन्तः
मया आत्मनः तनुजस्य आयुष्मतः विपिनकुमारस्य जन्मदिनं सम्पादयितुं जूनमासस्य षष्ठ्यां तारिकायां एकस्मिन् समारोहे सायं सप्तवादनकाले एकः प्रीतिभोज: समायोजितः। भवन्तं प्रार्थयामि यत् तस्यां शुभवेलायाम् आत्मनः समुपस्थित्या माम् अनुगृह्णतु।
सहारनपुरतः
दिनाङ्कः 1-6-2014
भवदीयः दर्शनोत्सुकः
श्रीचन्द्रः
8. पुत्र के विवाह में आमन्त्रित करने के लिए निमन्त्रण पत्र
श्रीमन्तः
भवन्तः एतद् विदित्वा नूनं हर्षमनुभविष्यन्ति यत् परमात्मनः महत्यनुकम्पया मम ज्येष्ठपुत्रस्य राकेशकुमारस्य शुभ परिणयं संस्कारः गाजियाबाद वास्तव्यस्य श्री अरुणकुमारस्य ज्येष्ठपुत्र्या सङ्गीता नामिकया सह नवम्बरमासस्य षोडशतारिकायां रविवासरे सायं चतुर्वादनसमये सम्पत्यस्यते। अतः भवन्तः सादरं (UPBoardSolutions.com) प्रार्थ्यन्ते यत् सपरिवारम् अस्यां मङ्गलवेलायां निर्दिष्टसमये समागत्य वरवधूयुगलं शुभाशीर्वाद प्रदानेन अवश्यम् अनुग्रहीष्यन्ति। भवतां वरयात्रा-सम्मेलनमपि अपेक्ष्यते।
2582, धर्मपुरतः
दिल्लीनगरात्
दिनाङ्कः 6-11-2013
भवतां दर्शनाभिलाषी
सतीशचन्द्रः

9. गाँव की स्वच्छता और साक्षरता के लिए ग्राम-प्रधान को प्रार्थना पत्र
सेवायाम्,
ग्रामप्रधान महोदयः!
पसौण्डा (गाजियाबाद)।
महोदय!
सविनयं निवेद्यते यत् अस्माकं ग्रामे दूषित जलप्रवाहस्य समुचिता व्यवस्था नास्ति। तत्र जलप्रवाहिणी नैकापि नालिका नास्ति। अत: मार्गेषु दूषितं जलं भरितम् अस्ति। मार्गेषु सर्वत्र पङ्काधिक्यम् । अभवत्। जनानां यातायातम् अपि दुर्भरम् अभवत्। मशकानां बाहुल्यम् अपि तत्र अभवत्। अस्माकं ग्रामे बहुसङ्ख्यजनाः निरक्षराः सन्ति। अयम् अस्मभ्यं लज्जाजनकः अस्ति। अहं भवन्तं निवेदयामि (UPBoardSolutions.com) यत् दूषितजलस्य निस्सारणाय प्रणालिकाः कारयतु स्वच्छतायाश्च साक्षरताप्रसारस्य च समुचितं प्रबन्धनम् अपि आशु कारयतु भवान्।
दिनाङ्कः 22-11-2014
भवदीयः
प्रकाशचन्द्रः
पसौण्डा (गाजियाबाद)
10. पुस्तक-विक्रेता से पुस्तकें मैंगवाने के लिए पत्र
सेवाणम्,
व्यवस्थापक महोदयः!
विद्या प्रकाशन मन्दिरम्
टी० पी० नगरम्, मयराष्ट्रम्।
महोदय!
भवता प्रकाशितानि अधोलिखितानि पुस्तकानि वी० पी० पी० द्वारा आशु प्रेषणीयानि :
(1) हाईस्कूल हिन्दी गौरवम् •••••••••••••••••• एक प्रति
(2) हाईस्कूल संस्कृत गौरवम् : ••••••••••••••• एक प्रति
दिनाङ्कः 2-11-2014
भवदीय
रामप्रतापः शर्मणः
शर्मा-निकेतनम्, अलोपीबागः, प्रयागः
11. मामा अथवा पिता की कुशल-क्षेम जानने के लिए उनको पत्र।
मयराष्ट्रीत्
दिनाङ्कः 20-2-2014
पूज्यपाद मातुल महोदय:/परमपूज्ययोः पितृचरणयोः
सादरं वन्दे/सादरं प्रणतयः सन्तुतराम्। अत्र कुशलं तत्रास्तु। बहुकालादारभ्य भवतः कुशलपत्रं नायातम्। अतः मे हृदयः व्याकुलितः अस्ति। मम वार्षिकीपरीक्षा नातिदूरेऽस्ति। अतोऽहं अध्ययने नितरां संलग्नोऽस्मि। आशासेऽहं . वार्षिकपरीक्षायां सर्वाधिकान् अङ्कान् प्राप्य सफलता प्राप्स्यामि। मातृचरणयोः मे प्रणामः कथनीयः। अविलम्ब गृहस्य वृत्तं लेखनीयम्।
भवतः आज्ञाकारी
भागिनेयः/पुत्रः
देवदत्तः
12. विद्यालय के वार्षिकोत्सव में सम्मिलित होने एवं मुख्य अतिथि पद की स्वीकृति देने के लिए जिलाधिकारी को पत्र
प्रतिष्ठायाम्
माननीय जिलाधिकारी महोदय:
मयराष्ट्रतः
मान्य महोदयः
अस्माकं विद्यालयस्य वार्षिकोत्सवः फरवरी मासस्य सप्तमे दिनाङ्के आयोज्यते। तत्र विविधाः प्रतियोगिता आयोजिताः भविष्यन्ति। सायङ्काले षष्ठवादने कालिदासस्य (UPBoardSolutions.com) अभिज्ञानशाकुन्तलम्’ नाटकं छात्रैः अभिनीयते। तदनन्तरं पुरस्कारवितरणं विधास्यते। तस्य उत्सवस्य मुख्य-अतिथिपदम् अलङ्कर्तुं भवान् विद्यालयपरिवारेण अभ्यर्थितः
भवन्तः कृपया अस्य उत्सवस्य प्रमुख-अतिथित्वं वोढुं स्वकरकमलैः पुरस्कारान् च वितरितुम् आत्मनः स्वीकृत्या अस्मन् अनुगृह्णन्तु।
भवदीयः
विकास शर्मणः
छात्रसङ्गप्रधानः
देवनागरी इण्टर कॉलेजः,
मयराष्ट्रः

13. पुत्र के जन्मोत्सव पर सम्मिलित होने के लिए मित्रों को निमन्त्रण-पत्र
सुहवरेः
परमपितुः परमेश्वरस्य कृपा मम गृहे विगत रविवासरे मध्याह्नकाले पुत्रो जातः। तस्य नामकरण संस्कारः मम सदने अस्यैव मासस्य एकोनविंशतितारिकायां सम्पन्नः भविष्यति। तस्मिन् भवन्तः मम आवासं समागत्य नवजातं शुभाशिषा अभिषिच्य मया सह च सूक्ष्मं जलपानं स्वीकृत्य माम् अनुगृह्णन्तु।
भवदीयः
राहुल चौहानः
64, शिवालयः, बुढानाद्वारः
मयराष्ट्रः।
We hope the UP Board Solutions for Class 9 Sanskrit Chapter 9 पत्र-लेखनम् (रचना) help you. If you have any query regarding UP Board Solutions for Class 9 Sanskrit Chapter 9 पत्र-लेखनम् (रचना), drop a comment below and we will get back to you at the earliest.


![]()




![]()