UP Board Solutions for Class 12 Maths Chapter 1 Relations and Functions (सम्बन्ध एवं फलन) are part of UP Board Solutions for Class 12 Maths. Here we have given UP Board Solutions for Class 12 Maths Chapter 1 Relations and Functions (सम्बन्ध एवं फलन)
| Board | UP Board |
| Textbook | NCERT |
| Class | Class 12 |
| Subject | Maths |
| Chapter | Chapter 1 |
| Chapter Name | Relations and Functions |
| Exercise | Ex 1.1, Ex 1.2, Ex 1.3, Ex 1.4, |
| Number of Questions Solved | 55 |
| Category | UP Board Solutions |
UP Board Solutions for Class 12 Maths Chapter 1 Relations and Functions
Chapter 1 Relations and Functions Ex 1.1
We have to find the L.C.M of 12,18 and 24. Now,. Write the given number in their form of multiple.
प्रश्न 1.
निर्धारित कीजिए कि क्या निम्नलिखित सम्बन्धों में से प्रत्येक स्वतुल्य, सममित तथा संक्रामक हैं
(i) से (iv) व उनके हल के लिए प्रश्नावली 1 (A) का प्रश्न 1 देखें।
(v) किसी विशेष समय पर किसी नगर के निवासियों के समुच्चय में निम्नलिखित सम्बन्ध R
(a) R = { (x, y) : x तथा y एक ही स्थान पर कार्य करते हैं }
(b) R = { (x, y) : x तथा y एक ही मोहल्ले में रहते हैं }
(c) R = { (x, y) : x, y से ठीक-ठीक 7 सेमी लम्बा है }
(d) R = { (x, y) : x, y की पत्नी है}
(e) R = { (x, y) : x, y के पिता हैं }
हल :
(v) माना A = किसी विशेष समय पर किसी नगर के निवासियों का समुच्चय
(a)
R = { (x, y) : x तथा y एक ही स्थान पर कार्य करते हैं }
R स्वतुल्य है, क्योंकि प्रत्येक व्यक्ति उस नगर में उस विशेष समय पर कार्यरत है। R सममित है, क्योंकि x , y एक ही स्थान पर एक समय पर कार्यरत हैं तो y, x भी उसी स्थान पर उस समय कार्यरत हैं। R संक्रामक है, क्योंकि x, y तथा y, z एक नगर में एक ही समय पर कार्यरत हैं तो उस नगर में उसी समय x, z भी कार्यरत हैं।
अतः
स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक है।
(b)
R = { (x , y) : x तथा y एक ही मोहल्ले में रहते हैं }
R स्वतुल्य है, क्योंकि उस स्थान का प्रत्येक व्यक्ति वहीं पर रहता है। R सममित है, क्योकि x और y एक स्थान पर रहते हैं तथा उसी स्थान पर y और x भी रहते हैं। R संक्रामक है, क्योंकि x , y तथा y, z एक स्थान पर रहते हैं तब x , z भी उसी स्थान पर रहते हैं।
अतः
स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक है।
(c)
R = { (x, y) : x, y से ठीक-ठीक 7 सेमी लम्बा है।
R स्वतुल्य नहीं है, क्योंकि कोई भी व्यक्ति अपने आप से 7 सेमी अधिक लम्बा नहीं हो सकता। R सममित नहीं है, क्योंकि y, x से ठीक 7 सेमी अधिक लम्बा है तब x, y से 7 सेमी लम्बा नहीं हो सकता। R संक्रामक नहीं है, क्योंकि x, y से तथा y, z से ठीक 7 सेमी लम्बे तो x, y से ठीक 7 सेमी अधिक लम्बा नहीं हो सकता।
अतः
स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक में से कोई भी नहीं है।
(d)
R = { (x, y) : x, y की पत्नी है}
R स्वतुल्य नहीं है, क्योंकि x स्वयं अपनी ही पत्नी नहीं हो सकती है। R सममित नहीं है, क्योंकि यदि x, y की पत्नी है तो y, x की पत्नी नहीं हो सकती। R संक्रामक नहीं है, क्योंकि यदि x, y की पत्नी है तो y किसी की भी पत्नी नहीं हो सकती।
अतः
स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक नहीं है।
(e)
R = { (x, y) : x, y के पिता हैं}
R स्वतुल्य नहीं है, क्योंकि x अपना ही पिता नहीं हो सकता। R सममित नहीं है, क्योंकि यदि x, y का पिता है तो y, x का पिता नहीं हो सकता। R संक्रामक नहीं है, क्योंकि x, y का y, z का पिता है तो x, z का पिता नहीं हो सकता।
अतः
स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक नहीं है।
![]()
The LCM of 12 and 16 is 48.
प्रश्न 2.
सिद्ध कीजिए कि वास्तविक संख्याओं के समुच्चय R में R = { (a, b) : a ≤ b2}, द्वारा परिभाषित सम्बन्ध R, न तो स्वतुल्य है, न सममित है और न ही संक्रामक है।
हल :
माना A = वास्तविक संख्याओं का समुच्चय है और R = { (a, b) : a ≤ b2}
- R स्वतुल्य नहीं है, क्योंकि ,[latex s=2]\frac { 1 }{ 2 } [/latex], [latex s=2]\frac { 1 }{ 4 } [/latex] से कम नहीं है।
- R सममित नहीं है, क्योंकि a ≤ b2 तो b, a2 से कम या बराबर नहीं है, जैसे -2 < 52 परन्तु 5, 22 से कम नहीं है।
- R संक्रामक नहीं है, माना a = 2, b = -2 और c = -1 तब 2 < (-2)2, -2 < (-1)2 परन्तु 2, (-1)2 से कम नहीं है।
अत:
1,2 तथा 3 से स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक नहीं है।
प्रश्न 3.
जाँच कीजिए कि क्या समुच्चय{ 1, 2, 3, 4, 5, 6 } में R = { (a, b) : b = a + 1} द्वारा परिभाषित सम्बन्ध R स्वतुल्य, सममित या संक्रामक है।
हल :
दिया है, A = {1, 2, 3, 4, 5, 6} तथा R = { a, b ) : b = a + 1}
- R स्वतुल्य नहीं है, क्योंकि a, a + 1 के बराबर नहीं हो सकता।
माना 4 = 1, 1, (1 + 1) = 2 के बराबर नहीं हो सकता। - R सममित नहीं है, क्योंकि b = a + 1
तब a ≠ b + 1 यदि b = 1 + 1 = 2, 1 ≠ 2 + 1 - R संक्रामक नहीं है, क्योंकि b = a + 1, c = b + 1
तो c ≠ a + 1 यदि b = 1 + 1 = 2 तथा c = 2 + 1 = 3 तो 3 ≠ 1 + 1
अत:
1, 2 तथा 3 से स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक नहीं है।
प्रश्न 4.
सिद्ध कीजिए कि R में R = { (a, b) : a ≤ b}, द्वारा परिभाषित सम्बन्ध R स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है।
हल :
माना R कोई वास्तविक संख्याओं का समुच्चय है तथा R = { (a, b):a≤b}
- R स्वतुल्य है, क्योंकि a ≤ a ⇒ a = a
- R सममित नहीं है, क्योंकि a, b से कम है तब b, a से कम नहीं है।
यदि 1, 2 से कम है तब 2, 1 से कम नहीं हो सकती। - R संक्रामक है, क्योंकि a ≤ b और b ≤ c तब a ≤ b
अत:
1, 2 व 3 से स्पष्ट है कि R स्वतुल्य और संक्रामक है परन्तु सममित नहीं है।
![]()
प्रश्न 5.
वास्तविक संख्याओं के समुच्चय 5 में सम्बन्ध R, R = {(a, b): <b} द्वारा परिभाषित है, तो इसकी स्वतुल्यता, सममितता और संक्रमकता की जाँच कीजिए।
हल :
स्वतुल्यता :

प्रश्न 6.
सिद्ध कीजिए कि समुच्चय {1,2,3} में R = { (1,2), (2,1) } द्वारा प्रदत्त सम्बन्ध R सममित है किन्तु न तो स्वतुल्य है और न संक्रामक है।
हल :
दिया है, A = {1, 2, 3} तथा R = { (1, 2), (2, 1) }
- R स्वतुल्य नहीं है, क्योंकि (1, 1), (2, 2), (3, 3) ∉ R
- R सममित है, क्योंकि (1, 2) ∈ R और (2, 1) ∈ R
- R संक्रामक नहीं है, क्योंकि R में केवल 2 ही अवयव हैं, जबकि संक्रामक होने के लिए तीन अवयव का होना आवश्यक हैं।
अत:
1, 2 व 3 से स्पष्ट है कि R न तो स्वतुल्य है और न ही संक्रामक है परन्तु R सममित है। इति सिद्धम्
प्रश्न 7.
सिद्ध कीजिए कि किसी कॉलेज के पुस्तकालय की समस्त पुस्तकों के समुच्चय A में R = { (x, y) : x तथा y में पेजों की संख्या समान है } द्वारा प्रदत्त सम्बन्ध R एक तुल्यता सम्बन्ध
हल :
दिया है, A किसी कॉलेज के पुस्तकालय की समस्त पुस्तकों का समुच्चय है। तथा R = { (x, y) : x तथा y में पेजों की संख्या समान है }
- R स्वतुल्य है, क्योंकि बराबर पृष्ठों वाली प्रत्येक पुस्तक में पृष्ठों की संख्या बराबर होगी।
- R सममित है, क्योंकि x, y पुस्तकों में पृष्ठ बराबर है तो y, x पुस्तकों में भी पृष्ठ बराबर होगे।
- R संक्रामक है, क्योंकि x, y तथा y, z पुस्तकों में पृष्ठ बराबर हैं तो x, z पुस्तकों में भी पृष्ठ बराबर होंगे।
अत:
1, 2 व 3 से स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक है। इसलिए R तुल्यता सम्बन्ध है।
![]()
प्रश्न 8.
सिद्ध कीजिए कि A = {1, 2, 3, 4, 5} में, R = { (a, b) :|a – b| सम है } द्वारा प्रदत्त सम्बन्ध R एक तुल्यता सम्बन्ध है। प्रमाणित कीजिए कि {1, 3, 5} के सभी अवयव एक-दूसरे से सम्बन्धित हैं और समुच्चय {2, 4} के सभी अवयव एक-दूसरे से सम्बन्धित हैं परन्तु {1, 3 ,5} का कोई भी अवयव {2, 4} के किसी अवयव से सम्बन्धित नहीं है।
हल :
दिया है, A = {1, 2, 3, 4, 5} तथा R = { (a, b) : |a – b| एक सम संख्या } = { (1, 3), (1, 5), (2, 4), (3, 5)}
(a) तुल्यता सम्बन्ध सिद्ध करने के लिए प्रश्नावली 1 (A) के प्रश्न 10 का हल देखें।
(b) समुच्चय {1, 3, 5} में |1 -3|,|1 -5|,|3 -5| सभी सम संख्याएँ हैं। सभी अवयव एक-दूसरे से सम्बन्धित हैं। समुच्चय {2, 4} में |2 -4| एक सम संख्या है।
अतः
इसमें अवयव एक-दूसरे से सम्बन्धित हैं। परन्तु {1, 3, 5}, {2, 4} के अवयव आपस में सम्बन्धित नहीं हैं|1 -2|, |3 -4|,|3 -5|| सम संख्याएँ नहीं हैं। (इति सिद्धम्)
प्रश्न 9.
सिद्ध कीजिए कि समुच्चय A = { x ∈ z : 0 ≤ x ≤ 12 }, में दिए गए निम्नलिखित सम्बन्धों R में से प्रत्येक एक तुल्यता सम्बन्ध है :
(i) R = { (a, b) : |a – b|, 4 का एक गुणज है},
(ii) R = { (a, b) : a = b}, प्रत्येक दशा में 1 से सम्बन्धित अवयवों को ज्ञात कीजिए।
हल :
दिया है, A = {x ∈ z : 0≤ x ≤ 12} = {0, 1, 2, 3, 4, ….., 12}
(i)
R = { (a, b) :|a – b|, 4 का एक गुणज है } ,
= { (1, 5), (1, 9), (2, 6), (2, 10), (3, 7), 3, 11),(4, 8) (4, 12), (5, 9), (6, 10), (7, 11), (8, 12),(0, 4), (0, 8), (0, 12), (0, 0), (1, 1), (2, 2), (3, 3), …, (12, 12)}
- R स्वतुल्य है, यदि a – b= 4k ⇒ k = 0
- R सममित है, यदि | a – b| =| b – a| = 4k
- R संक्रामक है, यदि a – b, 4 का गुणज है तथा b – c, 4 का गुणज है। तो a – b + b – c = |a – c| भी 4 का एक गुणज होगा।
अत:
1, 2 व 3 से स्पष्ट है कि R, स्वतुल्य, सममित तथा स्वतुल्य है।
अत:
R एक तुल्यता सम्बन्ध है।
1 से सम्बन्धित अवयव = {1, 5, 9}
(ii)
R = { (a, b) : a = b} ∴ R = { (0, 0), (1, 1), (2, 2), (3, 3),…. (12, 12) }
- 4 = 1 = (a, a) = R
∴R स्वतुल्य है। - R सममित है, यदि 4 = b = b = d
- R संक्रामक है, यदि 1 = b,
b = c ⇒ a = c अर्थात a, b, c तीनों बराबर हैं।
अत:
1, 2 तथा 3 से स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक है।
अंतः
R एक तुल्यता सम्बन्ध है।
1 से सम्बन्धित अवयव = { 1 }
![]()
प्रश्न 10.
ऐसे सम्बन्ध का उदाहरण दीजिए, जो
(i) सममित हो परन्तु न तो स्वतुल्य हो और न संक्रामक हो।
(ii) संक्रामक हो परन्तु न तो स्वतुल्य हो और न सममित हो।
(iii) स्वतुल्य तथा सममित हो किन्तु संक्रामक न हो।
(iv) स्वतुल्य तथा संक्रामक हो किन्तु सममित न हो।
(v) सममित तथा संक्रामक हो किन्तु स्वतुल्य न हो।
हल :
(i)
माना A एक समतल में सरल रेखाओं का समुच्चय है तथा R = { (a, b) : a, b पर लम्ब है }
- रेखा a, b पर लम्ब है तो b रेखा a पर लम्ब है।
∴ R सममित सम्बन्ध है। - R स्वतुल्य नहीं है, क्योंकि रेखा a अपने आप पर ही लम्ब नहीं हो सकती है।
- R संक्रामक नहीं है, यदि a रेखा b पर लम्ब है, b रेखा c पर लम्ब है तो a रेखा c पर लम्ब नहीं
(ii)
माना A एक वास्तविक संख्याओं का समुच्चय है। तथा R = { (a, b) : a > b}
- R संक्रामक है, यदि a > b और b > c = a > c
- R स्वतुल्य नहीं है, a अपने आप से बड़ी संख्या नहीं है।
- R सममित नहीं है, यदि a > b तो b, a से बड़ा नहीं है।
(iii)
माना A = {1, 2, 3} तथा R = { (1, 1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2) }
समतुल्य व सममित है। परन्तु संक्रामक नहीं है क्योंकि (1, 2) ∈ R, (2, 3) ∈ R, परन्तु (1, 3) ∉ R
(iv)
माना A = {1, 2, 3} तथा
R = { (a, b) : a ≤ b} = {(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3) }
- R स्वतुल्य है, क्योंकि (1, 1), (2, 2), (3, 3) ∈ R
- R संक्रामक है, क्योंकि (1, 2), (2, 3) ∈ R = (1, 3) ∈ R
- R सममित नहीं है, यदि a < b परन्तु b, a से कम नहीं है।
![]()
(v)
माना A = {1, 2, 3} तब R = { (1, 1), (2, 2), (1, 2), (2, 1)} सममित व संक्रामक है, ।
परन्तु स्वतुल्य नहीं हैं क्योकि (3, 3) ∉R
प्रश्न 11.
सिद्ध कीजिए कि किसी समतल में स्थित बिन्दुओं के समुच्चय में R : { ( P, Q : बिन्दु P की मूलबिन्दु से दूरी, बिन्दु Qकी मूलबिन्दु से दूरी के समान है} द्वारा प्रदत्त सम्बन्ध R एक तुल्यता सम्बन्ध है। पुनः सिद्ध कीजिए कि बिन्दु P ≠ (0,0) से सम्बन्धित सभी बिन्दुओं का समुच्चय P से होकर जाने वाले एक ऐसे वृत्त को निरूपित करता है, जिसका केन्द्र मूलबिन्दु पर है।
हल :
दिया है, A समतल में बिन्दुओं को समुच्चय है। तथा R = { ( P, Q) : मूलबिन्दु से P तथा Q की दूरी समान है }
= { (P, Q) : OP = OQ}
- R स्वतुल्य है, क्योंकि OP अपने ही बराबर है।
- R सममित है, यक्योंकि OP = OQ ⇒ OQ = OP
- R संक्रामक है, क्योंकि OP = OQ,
OQ = QR ⇒ OP =QR
1, 2 तथा 3 से स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक है।
अत:
R तुल्यता सम्बन्ध है। चूँकि o मूलबिन्दु है तथा P वृत्त की परिधि पर रहता है अर्थात् यदि OP = K ⇒ बिन्दु P एक वृत्त पर रहता है जो 0 से K दूरी पर है। अतः बिन्दु P ≠ (0, 0) से सम्बन्धित सभी बिन्दुओं का समुच्चय P से होकर जाने वाले एक ऐसे वृत्त को निरूपित करता है, जिसका केन्द्र मूलबिन्दु पर है। (इति सिद्धम्)
![]()
प्रश्न 12.
सिद्ध कीजिए कि समस्त त्रिभुजों के समुच्चय A में, R = { (T1 T2) : T1 T2, के समरूप है} द्वारा परिभाषित सम्बन्ध R एक तुल्यता सम्बन्ध है। भुजाओं 3, 4, 5 वाले समकोण त्रिभुज T1 भुजाओं 5, 12, 13 वाले समकोण त्रिभुज T2, तथा भुजाओं 6, 8, 10 वाले समकोण त्रिभुज T3 पर विचार कीजिए। T1 T2 और T3 में से कौन-से त्रिभुज परस्पर सम्बन्धित हैं?
हल :
तुल्यता संबंध सिद्ध करने के लिए प्रश्नावली 1 (A) के प्रश्न 16 का हल देखें।
(i)
त्रिभुज , की भुजाएँ 3, 4, 5 हैं त्रिभुज T, की भुजाएँ 5, 12, 13 हैं तथा त्रिभुज T3 की भुजाएँ 6, 8, 10 हैं। चूँकि त्रिभुज T1, की भुजाएँ 3, 4, 5, त्रिभुज T2, की भुजाओं 5, 12, 13 के समानुपाती नहीं है। इसी प्रकार त्रिभुज T2 , की भुजाएँ 5, 12, 13 त्रिभुज T3 की भुजाओं 6, 8, 10 के समानुपाती नहीं है, इसलिए ये त्रिभुज समरूप त्रिभुज नहीं होंगे।
पुनः
त्रिभुज T3 तथा T3 की भुजाएँ समानुपाती हैं, इसलिए यह समरूप त्रिभुज है।
अत:
त्रिभुज T1 तथा T3 आपस में सम्बन्धित है।
प्रश्न 13.
सिद्ध कीजिए कि समस्त बहुभुजों के समुच्चय A में, R = { (p1, p2) : p1, तथा p2 }, की भुजाओं की संख्या समान है। प्रकार से परिभाषित सम्बन्ध R एक तुल्यता सम्बन्ध है। 3,4 और 5 लम्बाई की भुजाओं वाले समकोण त्रिभुज से सम्बन्धित समुच्चय A के सभी अवयवों का समुच्चय ज्ञात कीजिए।
हल :
दिया है, A समस्त बहुभुजों का समुच्चय है। तथा R = { (p1, p2) : p1, p2, की भुजाओं की संख्या बराबर है।
(i)
- R स्वतुल्य है, क्योंकि प्रत्येक बहुभुज की भुजाओं की संख्या स्वयं के समान होती है।
- R सममित है, यदि बहुभुज p1, p2, की भुजाएँ n है तो बहुभुज p2 और p1,की भुजाएँ भी n ही होंगी।
- R संक्रामक है, यदि बहुभुज p1, p2 औरp2, p3 प्रत्येक की n भुजाएँ है तो p1 और p3 की भुजाएँ भी n ही होंगी।
अतः
1, 2 तथा 3 से स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक हैं।
अतः
R एक तुल्यता सम्बन्ध है।
(ii)
सभी त्रिभुजों का समुच्चय त्रिभुज T से सम्बन्धित है।
प्रश्न 14.
मान लीजिए कि X Y – तल में स्थित समस्त रेखाओं का समुच्चय L है और L में R = { (L1,L2) : L1 समान्तर है L2 के } द्वारा परिभाषित सम्बन्ध R है। सिद्ध कीजिए कि R एक तुल्यता सम्बन्ध है। रेखा y = 2 x + 4 से सम्बन्धित समस्त रेखाओं का समुच्चय ज्ञात कीजिए।
हल :
दिया है, L किसी X Y- तल में स्थित समस्त रेखाओं का समुच्चय है।
तथा R = { (L1, L2) : L1 समान्तर है L2 के }
(i)
- R स्वतुल्य है, क्योंकि प्रत्येक रेखा अपने आप के समान्तर है।
- R सममित है, यदि L1 रेखा, L2 के समान्तर है तो L2 रेखा, L1 के भी समान्तर होगी।
- R संक्रामक है, यदि L1, L2 और L2, L3 समान्तर रेखाएँ हैं तो L1और L3 भी समान्तरे रेखाएँ होंगी।
अतः
1, 2 तथा 3 से स्पष्ट है कि R स्वतुल्य, सममित तथा संक्रामक है।
अतः
R एक तुल्यता सम्बन्ध है।
इति सिद्धम्
(ii)
माना y = 2 x + c, जबकि c का मान कुछ भी हो सकता है।
अतः
y = 2 x +4 से सम्बन्धित रेखाओं का समुच्चय y = 2 x + c है।
![]()
प्रश्न 15.
मान लीजिए कि समुच्चय {(1, 2, 3, 4)} में, R = { (1, 2), (2, 2), (1, 1), (4, 4), (1, 0, (3, 3), (3, 2)} द्वारा परिभाषित सम्बन्ध में है। निम्नलिखित में से सही उत्तर चुनिए।
(A) R स्वतुल्य तथा सममित है किन्तु संक्रामक नहीं है।
(B) R स्वतुल्य तथा संक्रामक है किन्तु सममित नहीं है।
(C) R सममित तथा संक्रामक है किन्तु स्वतुल्य नहीं है।
(D) R एक तुल्यता सम्बन्ध है।
हल :
दिया है, A = {1, 2, 3, 4}
तथा R = { (1, 2), (2, 2), (1, 1), 4, 4), (1, 3), (3, 3), (3, 2) }
- R स्वतुल्य है, क्योकि (1, 1), (2, 2), (3, 3), (4, 4) ∈ R
- R सममित नहीं है, क्योंकि (1,2) ∈ R परन्तु (2,1) ∉ R
- R संक्रामक है, क्योंकि (1, 3) ∈ R,(3, 2) ∈ R = (1, 2) ∈ R
अत:
1, 2 तथा 3 से स्पष्ट है कि R स्वतुल्य तथा संक्रामक है परन्तु सममित नहीं है।
अत:
विकल्प (B) सही है।
प्रश्न 16.
यदि प्राकृतिक संख्याओं के समुच्चय N में सम्क्न्ध में इस प्रकार है कि R = {(a, b) : a = b -2, b> 6} तो सही उत्तर चुनिए ।
(a) (2,4) ∈ R,
(b) (3, 8) ∈ R,
(c) (6, 8) ∈ R
(d) (8, 7) ∈ R
हल :
6 = 8 – 2, तथा 8 > 6
∴ (6, 8) ∈ R
अत: विकल्प (c) सही है।
Chapter 1 Relations and Functions Ex 1.2
प्रश्न 1.
सिद्ध कीजिए कि f(x) = [latex s=2]\frac { 1 }{ x }[/latex] द्वारा परिभाषित फलन f : R* → R* एकैकी तथा आच्छादक है, जहाँ R* सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है। यदि प्रान्त R* को N से बदल दिया जाए, जबकि सहप्रांत पूर्ववत R* ही रहे, तो भी क्या यह परिणाम सत्य होगा?
हल :
(a)
(i) दिया है, f (x) = [latex s=2]\frac { 1 }{ x }[/latex] यदि f (x1) = f (x2) ⇒ [latex s=2]\frac { 1 }{ { x }_{ 1 } }[/latex] = [latex s=2]\frac { 1 }{ { x }_{ 2 } } [/latex]
x1 = x2
अत:
प्रान्त के प्रत्येक अवयव का एक ही प्रतिबिम्ब है।
अतः
f एकैकी फलन है।
(ii)
दिया है, ye
y = [latex s=2]\frac { 1 }{ x }[/latex]
x = [latex s=2]\frac { 1 }{ y }[/latex]
y ≠ 0
सहप्रान्त का प्रत्येक अवयव प्रान्त में क्रमश: एक ही अवयव का प्रतिबिम्ब है।
∴ f आच्छादक फलन है।
∴ f एकैकी व आच्छादक फलन है।
(b)
यदि प्रान्त R को N से बदल दिया जाता है तब सहप्रान्त R वही रहे तो f : N → R
जब f (x1) = f (x2)
⇒ [latex s=2]\frac { 1 }{ { x }_{ 1 } }[/latex] = [latex s=2]\frac { 1 }{ { x }_{ 2 } } [/latex]
x1 = x2 ∈ N
⇒ f एकैकी है।
परन्तु सहप्रान्त का प्रत्येक अवयव प्रान्त के अवयव का प्रतिबिम्ब न हो।

इस प्रकार f एकैकी है परन्तु आच्छादक नहीं है। (इति सिद्धम्)
![]()
प्रश्न 2.
निम्नलिखित फलनों की एकैक (Injective) तथा आच्छादी (Surjective) गुणों की जाँच कीजिए :
(i) f (x) = x2 द्वारा प्रदत्त f : N → N फलन है।
(ii) f (x) = x2 द्वारा प्रदत्त f : Z → Z फलन है।
(iii) f (x) = x2 द्वारा प्रदत्त f : R → R फलन है।
(iv) f (x) = x3 द्वारा प्रदत्त f : N → N फलन है।
(v) f (x) = x3 द्वारा प्रदत्त f : Z → Z फलन है।
हल :
(i)
दिया है, f ( x ) = x2 और f : N → N
(a)
f ( x1 ) = f ( x2 ) ⇒ [latex]{ x }_{ 2 }^{ 1 }[/latex]
⇒ x1 = x2 ,
⇒ x1 = x2 ∈ N
f एकैकी है।
(b)
परन्तु सहप्रान्त में ऐसे कुछ अवयव हैं जो प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं हैं।
उदाहरणार्थ :
माना 3 सहप्रान्त में है तो 3 प्रान्त के किसी भी अवयव को प्रतिबिम्ब नहीं होगा।
∴ f आच्छादक नहीं है।
अत:
f एकैकी है परन्तु आच्छादक नहीं है।
(ii)
f (x) = x2 f : Z → Z , जबकि f (x) = x2
(a)
f (-1) = f (1) = 1 ⇒ -1 और 1 का प्रतिबिम्ब 1 है।
∵ प्रान्त के दो भिन्न-भिन्न अवयवों -1 और 1 का परिसर R में एक ही f-प्रतिबिम्ब 1 पर है।
∵ प्रतिबिम्ब समान है।
∴ f एकैकी नहीं है।
(b)
सहप्रान्त में ऐसे अवयव हैं जो प्रान्त के किसी अवयव में प्रतिबिम्ब नहीं हैं।
उदाहरणार्थ-3
सहप्रान्त में है, परन्तु 3 प्रान्त के किसी अवयव का प्रतिबिम्ब नहीं है।
∴ f आच्छादक नहीं है।
अत:
f न तो एकैकी है और न ही आच्छादक है।
(iii)
f : R → R, यदि f (x) = x2
(a)
( -1 )2 = (1)2 = f (-1) = f (1)
अतः
-1 और 1 का प्रतिबिम्ब 1 है। अर्थात् प्रान्त के दो भिन्न-भिन्न अवयवों -1 और 1 का परिसर R में एक ही f- प्रतिबिम्ब 1 है। अर्थात् प्रतिबिम्ब समान है,
∴ f एकैकी नहीं है।
(b)
-2 सहप्रान्त में है परन्तु यह प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं है।
अत:
f आच्छादक नहीं है।
∴ f न तो एकैकी है और न ही आच्छादक है।

प्रश्न 3.
सिद्ध कीजिए कि f(x) = [x] द्वारा प्रदत्त महत्तम पूर्णाक फलन f : R – R, न तो एकैकी है और न आच्छादक है, जहाँ [x], x से कम या उसके बराबर महत्तम पूर्णांक को निरूपित करता है।
हल :
स्पष्ट है कि f(x) का प्रान्त = R
तथा f(x) = 0 Y x e[0, 1)
∴ f : R → R एकैकी नहीं है।
पुनः f(x) केवल पूर्णांक मान ग्रहण करता है।
∴ सह प्रान्त के अपूर्णांक अवयव प्रान्त के किसी भी अवयव के प्रतिबिम्ब नहीं हैं।
∴ f : R → R आच्छादक नहीं है।
अत: f : R → R न तो एकैकी है और न ही आच्छादक।
![]()
प्रश्न 4.
सिद्ध कीजिए कि f ( x ) =| x | द्वारा प्रदत्त मापांक फलन f : R→ R, न तो एकैकी है। और न आच्छादक है, जहाँ | x | बराबर x , यदि x धन या शून्य है तथा| x | बराबर – x, यदि x ऋण है।
हल :
यहाँ f : R → R, जबकि f ( 3 ) = [x]
(a)
f (-1) = |- 1 | = 1, f(1) = |1| = 1
-1 और 1 का एक ही प्रतिबिम्ब है।
अत:
प्रान्त के दो भिन्न-भिन्न अवयवों -1 और 1 का परिसर R में एक ही f – प्रतिबिम्ब 1 है।
∵ प्रतिबिम्ब समान है।
इसलिए f एकैकी नहीं है।
(b)
सहप्रान्त की कोई भी ऋणात्मक संख्या प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं है।
∴ f आच्छादक नहीं है।
अत:
f न तो एकैकी है और न ही आच्छादक है। इति सिद्धम्
प्रश्न 5.
सिद्ध कीजिए कि f :R → R

हल :
स्पष्टतया f(2) = 1 तथा f (3) = 1
∴ f(2) = f(3) जबकि 2 ≠ 3
∴ f एकैकी नहीं है। f का परिसर = {1, 0, -1} c R
∴ f अन्तः क्षेपी है।
अतः फलन न तो एकैकी है और न आच्छादक।
प्रश्न 6.
मान लीजिए कि A = {1, 2, 3}, B = {4, 5, 6, 7} तथाf = { (1, 4), (2, 5), (3, 6) } A से B तक एक फलन है। सिद्ध कीजिए कि f एकैकी है।

हल :
दिया है, A ={1, 2, 3}, B = {4, 5, 6, 7}
f : A → B इस प्रकार है कि f = { (1, 4 ), ( 2, 5 ), ( 3, 6 ) } A के प्रत्येक अवयव का अलग-अलग प्रतिबिम्ब है। इसलिए f एकैकी है।
( इति सिद्धम् )
प्रश्न 7.
निम्नलिखित में से प्रत्येक स्थिति में बताइये कि क्या दिए हुए फलन एकैकी, आच्छादक अथवा एकैकी आच्छादी (bijective) हैं। अपने उत्तर का औचित्य भी बताइये।
(i) f (x) = 3 – 4 द्वारा परिभाषित फलन f : R → R है।
(ii) f (x) = 1 + x2 द्वारा परिभाषित फलन f : R → R है।
हल :
(i)
यहाँ f : R – R, यदि f(x) = 3 – 4 x

अत:
f, बहु-एक फलन है।
∴ f एकैकी नहीं है।
(b)
पुनः x के प्रत्येक वास्तविक मान के लिए (1 + x) का मान सदैव 1 या 1 से बड़ा होगा।
∴ परिसर R में 1 से छोटे अवयव (0 तथा ऋणात्मक संख्याएँ ), डोमेन R के किसी भी अवयव के f-प्रतिबिम्ब नहीं होंगे।
∴ f – अन्त:क्षेपी फलन है अर्थात् आच्छादक नहीं है।
इसलिए दिया हुआ फलन न तो एकैकी है और न ही आच्छादक है।
![]()
प्रश्न 8.
मान लीजिए A तथा B दो समुच्चय हैं। सिद्ध कीजिए किf : A × B → B × A, इस प्रकार हैं कि f (a, b) = f (b, a) एक एकैकी आच्छादक फलन है।
हल :

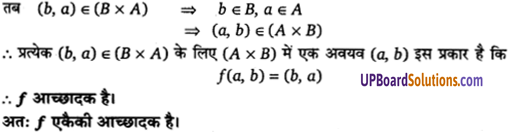
प्रश्न 9.
दिखाइए कि फलन f : N → N जोकि

हल :

प्रश्न 10.
मान लीजिए कि A= R → { 3 } तथा B = R – { 1 } हैं। (x) = [latex s=2]\frac { x-2 }{ x-3 } [/latex] द्वारा परिभाषित फलन f : A → B पर विचार कीजिए। क्या । एकैकी तथा आच्छादक है? अपने का औचित्य भी बतलाइए।
हल :
दिया है , f : A → B , तथा
A= R → { 3 } तथा B = R – { 1 } हैं। (x) = [latex s=2]\frac { x-2 }{ x-3 } [/latex] द्वारा परिभाषित फलन f : A → B पर विचार कीजिए। क्या । एकैकी तथा आच्छादक है? अपने का औचित्य भी बतलाइए।

इससे सिद्ध होता है कि सहडोमेन R का स्वेच्छ अवयव y ≠ 1, डोमेन R के अवयव x का f-प्रतिबिम्ब है अर्थात् सहडोमेन R का प्रत्येक अवयव, डोमेन R के किसी-न-किसी अवयव का f-प्रतिबिम्ब अवयव है।
फलन f का परिसर = सहडोमेन R फलन f आच्छादक है।
इसलिए दिया हुआ फलन । एकैकी तथा आच्छादक है।
प्रश्न 11.
मान लीजिए : R – R; f (3) = * द्वारा परिभाषित है। सही उत्तर का चयन कीजिए।
(a) एकैकी आच्छादक है।
(b) f बहुएक आच्छादक है।
(c) f एकैकी है किन्तु आच्छादक नहीं है,
(d) f न तो एकैकी है और न आच्छादक है।
हल :
दिया है, f : R → R, यदि f (x) = x4
(i) f(-1) = (-1)4 = 1, f(1) = 14 = 1
f(-1) = f(1)
∴ -1 और 1 का प्रतिबिम्ब 1 है। इसलिए f एकैकी नहीं है।
(ii) सहप्रान्त का अवयव -1 प्रान्त के किसी भी अवयव का प्रतिबिम्ब नहीं है। इसलिए f आच्छादक नहीं है। अत: f न तो एकैकी है और न ही आच्छादक है।
अत: विकल्प (d) सही है।
![]()
प्रश्न 12.
मान लीजिए कि f(a) = 3x द्वारा परिभाषित फलन f : R → R है। सही उत्तर चुनिए :
(a) f एकैकी आच्छादक है
(b) f बहुएक आच्छादक है।
(c) f एकैकी है परन्तु आच्छादक नहीं है
(d) f न तो एकैकी है और न आच्छादक है।
हल :

इससे सिद्ध होता है कि सहडोमेन R का स्वेच्छ अवयव y, डोमेन R के किसी-न-किसी अवयव का f-प्रतिबिम्ब अवश्य है। फलन f का परिसर = सहडोमेन R, फलन / आच्छादक है। इसलिए f एकैकी तथा आच्छादक है। अतः विकल्प (a) सही है।
Chapter 1 Relations and Functions Ex 1.3
प्रश्न 1.
मान लीजिए कि f : {1, 3, 4} {1,2, 5} तथा f : {1,2, 5} {1, 3}, f = { (1, 2), (3, 5), (4, 10} तथा g = { (1, 3), (2, 3), (5, 10} द्वारा प्रदत्त हैं। gof ज्ञात कीजिए।
हल :
दिया है, f : { 1, 3, 4 } → { 1, 2, 5 } तथा g : { 1, 2, 5 } → { 1 , 3 } .

प्रश्न 2.
मान लीजिए कि f, g तथा h, R से R तक दिए फलन हैं। सिद्ध कीजिए कि
(f + g) oh = foh + goh
(f.g) oh = (foh). (goh)

प्रश्न 3.
gof तथा fog ज्ञात कीजिए, यदि
(i) f (x) = | x | तथा g (x) =| 5 x – 2|
(ii) f (x) = g x3 तथा g (x) = x1/3
हल :

प्रश्न 4.
यदि y(x) = [latex]\frac { 4x+3 }{ 6x-4 } ,x\neq \frac { 2 }{ 3 }[/latex] तो सिद्ध कीजिए कि सभी [latex]x\neq \frac { 2 }{ 3 }[/latex] के लिए fof (x) = x है। f का प्रतिलोम भी ज्ञात कीजिए।
हल :
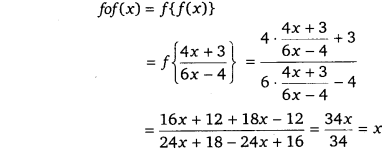
f का प्रतिलोम तभी ज्ञात किया जा सकता है जब f एकैकी आच्छादक हो। f एकैकी है माना कि x1 x2 ∈ प्रान्त तब f (x1) = f(x2)

प्रश्न 5.
कारण सहित बताइए कि क्या निम्नलिखित फलनों के प्रतिलोम हैं ?
(i) f : {1, 2, 3, 4} → {10} जहाँ f = {(1, 10), (2, 10), (3, 10), 4, 10)}
(ii) g: {5, 6, 7, 8} → {1, 2, 3, 4} जहाँ g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h : {2, 3, 4, 5} → {7, 9, 11, 13} जहाँ h = {(2, 7), (3, 9), (4, 11), (5, 13)}
हल :
(i) नहीं, क्योंकि एक बहुएक फलन है।
(ii) नहीं, इयोंकि g एक बहुएक फलन है।
(iii) हाँ, क्योंकि h एक एकैकी आच्छादक फलन है।
![]()
प्रश्न 6.
यदि f :[-1, 1] → Y: f(x) = [latex]\frac { x }{ x+2 } ,x\neq -2[/latex] तथा Y = परिसर (f) तो दिखाइए कि f-1 व्युत्क्रमणीय है तथा ज्ञात कीजिए।
हल :

प्रश्न 7.
f (x) = 4 x + 3 द्वारा प्रदत्त फलन f : R → R पर विचार कीजिए। सिद्ध कीजिए कि f व्युत्क्रमणीय है। f का प्रतिलोम फलन ज्ञात कीजिए।
हल :

प्रश्न 8.
f(x) = x + 4 द्वारा प्रदत्त फलन f : R → [4,∞) पर विचार कीजिए। सिद्ध कीजिए किf व्युत्क्रमणीय है तथा का प्रतिलोम -1,f (y) = [latex]\sqrt { y-4 } [/latex] द्वारा प्राप्त होता है, जहाँ R सभी ऋणेतर वास्तविक संख्याओं का समुच्चय है।
हल :

प्रश्न 9.
यदि f : R+ → [-5, ∞]: f (3) = 9x2 + 6x – 5 तो सिद्ध कीजिए कि f व्युत्क्रमणीय है तथा f-1(y) = [latex]\left( \frac { \sqrt { Y+6-1 } }{ 3 } \right)[/latex]
हल :
उपरोक्त प्रश्न की भाँति स्वयं हल करें।
प्रश्न 10.
मान लीजिए कि f : X→ Y एक व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f को प्रतिलोम फलन अद्वितीय (unique) है।
हल :

प्रश्न 11.
f : { 1, 2, 3} {a, b, c}, f (1) = a, f (2) = b तथा f (3) = c द्वारा प्रदत्त फलन f पर विचार कीजिए। f -1 ज्ञात कीजिए और सिद्ध कीजिए कि (f -1 )-1 = f है।
हल :

प्रश्न 12.
मान लीजिए कि f : A → B एक व्युत्क्रमणीय फलन है। सिद्ध कीजिए कि f-1 का प्रतिलोम f है अर्थात् (f-1)-1 = f है।
हल :


प्रश्न 13.
प्रश्नावली 1(C) का प्रश्न 5 व हल देखें।
प्रश्न 14.
प्रश्नावली 1(C) का प्रश्न 20 व हल देखें।
Chapter 1 Relations and Functions Ex 1.4
प्रश्न 1.
प्रश्नावली 1(D) का प्रश्न 1 व हल देखें।
प्रश्न 2.
प्रश्नावली 1(D) का प्रश्न 2 व हल देखें।
![]()
प्रश्न 3.
प्रश्नावली 1(D) का प्रश्न 16 व हल देखें।
प्रश्न 4.
प्रश्नावली 1(D) का प्रश्न 17 व हल देखें।
प्रश्न 5.
मान लीजिए कि समुच्चय { 1,2,3,4,5 } में एक द्विआधारी संक्रिया *’, a *’ b = a तथा b का HCF द्वारा परिभाषित है। क्या संक्रिया *’ उपर्युक्त प्रश्न 4 में परिभाषित संक्रिया * के समान है? अपने उत्तर का औचित्य भी बतलाइए।
हल :
प्रश्नानुसार, समुच्चय {1, 2, 3, 4, 5} संक्रिया a *’ b H.C.F. a तथा b द्वारा परिभाषित है। द्विआधारी संक्रिया * के लिए सारणी निम्नलिखित होगी ।
| *’ | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 1 | 1 | 1 | 1 |
| 2 | 1 | 2 | 1 | 2 | 1 |
| 3 | 1 | 1 | 3 | 1 | 1 |
| 4 | 1 | 2 | 1 | 4 | 1 |
| 5 | 1 | 1 | 1 | 1 | 5 |
यह संक्रिया सारणी प्रश्न 4 में दी गई संक्रिया सारणी के समान है।
अतः
द्विआधारी संक्रिया *’ तथा * समान होगी।
प्रश्न 6.
मान लीजिए कि N में एक द्विआधारी संक्रिया *, a* b = a तथा b का L.C.M. द्वारा परिभाषित है। निम्नलिखित ज्ञात कीजिए।
(i) 5 * 7, 20 * 16
(ii) क्या संक्रिया * क्रमविनिमेय है?
(iii) क्या * साहचर्य है?
(iv) N में * का तत्समक अवयव ज्ञात कीजिए।
(v) N के कौन-से अवयव * संक्रिया के लिए व्युत्क्रमणीय हैं?
हल:
प्रश्न में समुच्चय N = प्राकृत संख्याओं का समुच्चय में * संक्रिया, a * b = a, b का L.C.M. द्वारा परिभाषित है।
(i)
5 * 7 = 5 व 7 का L.C.M. = 35
20 * 16 = 20 वे 16 का L.C.M. = 80
∴ 5 * 7 = 35 , 20 *16 = 80
(ii)
a*b = a, b का L.C.M.
b* a = b, a का L.C.M.
∵ a * b तथा b* a का L.C.M. बराबर है।
इसलिए
⇒ a * b = b * a
∵ स्पष्ट है कि संक्रिया * क्रमविनिमेय द्विआधारी संक्रिया है।
(iii)
a * (b * c) = a * (b, c का L.C.M.)
= a, b, c का L.C.M.
(a*b)* c = (a, b का L.C.M.) *C
= a, b, c का L.C.M.
∵ a* (b * c) तथा (a * b)* c के L.C.M. बराबर हैं।
⇒ (a * b)* c = a * (b* c)
∴ स्पष्ट है कि संक्रिया * साहचर्य द्विआधारी संक्रिया है।
(iv)
* संक्रिया का तत्समक अवयव 1 है।
1 * a = a * 1 = a
(v)
N * N → N, * संक्रिया का a * b = a, b का L.C.M. द्वारा परिभाषित किया गया है। यदि a = 1, b = 1, a * b = 1 अन्यथा नहीं
⇒ 1 * 1 =1
⇒ 1 के लिए व्युत्क्रमणीय है।
प्रश्न 7.
प्रश्नावली 1(D) का प्रश्न 12 व हल देखें।
प्रश्न 8.
प्रश्नावली 1(D) का प्रश्न 13 व हल देखें।
![]()
प्रश्न 9.
प्रश्नावली 1(D) का प्रश्न 9 व हल देखें।
प्रश्न 10.
प्रश्न 9 में दी गई संक्रियाओं में किसी का तत्समक है, वह बतलाइए।
हल :
(i)
दिया है, a * b = a – b यदि e तत्समक अवयव हो तब ।
a * e = a – e तथा e * a = e – a
a – e ≠ e – a ⇒ a * e ≠ e * a
अत :
स्पष्ट है कि e का अस्तित्व नहीं है।
(ii)
दिया है, a * b = a2 + b2
∴ a * e = a2 + e2 तथा e * a = e2+a2
∵ हम देखते हैं कि
a *e = e * a ≠ 1
अत :
स्पष्ट है कि e का अस्तित्व नहीं है।
(iii)
दिया है, a * b = a+ ab
a* e = a + ae तथा
∵ हम देखते हैं कि a * e ≠ e * a ≠ a
अत :
स्पष्ट है कि e का अस्तित्व नहीं है।
(iv)
दिया है, a* b = (a – b)2
a * e = (a – e)2 ≠ a तथा e * a = (e – a)2 ≠ a
a * e =e * a ≠ a
अत :
स्पष्ट है कि e का अस्तित्व नहीं है।

अतः
स्पष्ट है कि e का अस्तित्व नहीं है।
प्रश्न 11.
प्रश्नावली 1(D) का प्रश्न 14 व हल देखें।
प्रश्न 12.
बताइए कि क्या निम्नलिखित कथन सत्य हैं या असत्य हैं। औचित्य भी बतलाइए।
(i) समुच्चय N में किसी भी स्वेच्छ द्विआधारी संक्रिया * के लिए a * a = a, ∀ a ∈ N
(ii) यदि N में * किसी क्रमविनिमेय द्विआधारी संक्रिया है तो a* (b * c) = (c * b) * a
हल :
प्रश्नानुसार, द्विआधारी संक्रिया समुच्चय N पर इस प्रकार परिभाषित की गयी है कि a * a = a, ∀ a ∈ N
(i)
यहाँ पर * संक्रिया में केवल एक ही अवयव का प्रयोग किया गया है।
अत :
स्पष्ट है कि यह कथन असत्य है।
(ii)
वास्तविक संख्याओं में समुच्चय पर संक्रिया * क्रमविनिमेय है।
b * c = c * b
∴ तथा (c * b) * a = (b * c) * a = a * (b * c)
∴ a* (b * c) = (c * b) * a
∴ यह कथन सत्य है।
![]()
प्रश्न 13.
a * b= a3 + b3 प्रकार से परिभाषित N में एक द्विआधारी संक्रिया * पर विचार कीजिए। अब निम्नलिखित में से सही उत्तर का चयन कीजिए
(A) * साहचर्य तथा क्रमविनिमेय दोनों है।
(B) * क्रमविनिमेय है किन्तु साहचर्य नहीं है।
(C) * साहचर्य है किन्तु क्रमविनिमेय नहीं है।
(D) * न तो क्रमविनिमेय है और न साहचर्य है।
हल :
प्रश्नानुसार, द्विआधारी संक्रिया * को समुच्चय N पर इस प्रकार परिभाषित किया गया है कि
a * b= a3 + b3


We hope the UP Board Solutions for Class 12 Maths Chapter 1 Relations and Functions (सम्बन्ध एवं फलन) help you. If you have any query regarding UP Board Solutions for Class 12 Maths Chapter 1 Relations and Functions (सम्बन्ध एवं फलन), drop a comment below and we will get back to you at the earliest.
thankyou sir