UP Board Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms (जीवों में विविधता)
These Solutions are part of UP Board Solutions for Class 9 Science. Here we have given UP Board Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms (जीवों में विविधता).
पाठ्य – पुस्तक के प्रश्नोत्तर
पाठगत प्रश्न (पृष्ठ संख्या – 91)
प्रश्न 1.
हम जीवधारियों का वर्गीकरण क्यों करते
उत्तर-
जीवों को वर्गीकरण इनकी विविधता के अध्ययन को सरल बनाता है इससे हमारी एक झलक से सभी जीवों की एक तस्वीर हमारे सामने आ जाती है तथा भिन्न-भिन्न जीवों (UPBoardSolutions.com) के मध्य आपसी सम्बन्धों के अध्ययन में भी सहायता करता है अतः इसी कारण हम जीवों का वर्गीकरण करते हैं।

प्रश्न 2.
अपने चारों ओर फैले जीव रूपों की विभिन्नता के तीन उदाहरण दें।
उत्तर-
- हम अपने आस-पास सूक्ष्म जीवाणुओं को देखते हैं जिनके आकार कुछ माइक्रोमीटर तक ही होता है। और बहुत कम समय तक ही जीवित रहते हैं, जैसे प्लाज्मोडियम, अमीबा, नीली-हरी शैवाल इत्यादि।
- हम 30 मीटर या इससे बड़े जीव भी देखते हैं जो काफी लम्बे समय तक जीवित रहते हैं, जैसे नीली व्हेल आदि।
- हमें इसे भी अधिक बड़े व हजारों वर्षों तक जीवित रहने वाले जीव भी मिलते हैं, जैसे रैड वुड आदि।
पाठगत प्रश्न (यून संख्या – 92)
प्रश्न 1.
जीवों के वर्गीकरण के लिए सर्वाधिक मूलभूत लक्षण क्या ले सकता है?
(a) उनका निवास स्थान
(b) उनकी कोशिका संरचना।।
उत्तर-
हमारे विचार के अनुसार जीवों के वर्गीकरण का आधारे उन कोशिकाओं का प्रकार है जिनके द्वारा उनका शरीर बना है क्योंकि जीव की सभी क्रियाएँ कोशिका (UPBoardSolutions.com) की रचना पर ही आधारित होती हैं। जीव एककोशी है या बहुकोशी, उसमें केन्द्रक झिल्ली सहित है या झिल्ली रहित यही कोशिका के गुण जीव को प्रभावित करते हैं।
प्रश्न 2.
जीवों के प्रारम्भिक विभाजन के लिए किस मृल लक्षण को आधार बनाया गया?
उनर-
वह मूल लक्षण जिस पर जीवों का प्रारंभिक विभाजन आधारित है वह कोशिका का स्वभाव है अर्थात् वह कोशिका ससीम केद्रक है। ससीम केन्द्रक कोशिका में एक केन्द्रक होता है जो कोशिका के सभी कोशिकीय कार्य जैसे विभाजन की क्षमता और बहुकोशिकीय जीव बनाने की क्षमता इत्यादि गुण पाए जाते हैं जिससे फिर ये विशेष कार्य योग्य बन जाते हैं। इसलिए इस गुण को प्राथमिक गुण माना जाता है।
प्रश्न 3.
किस आधार पर जन्तुओं और वनस्पति को एक दूसरे से भिन्न वर्ग में रखा जाता है?
उत्तर-
पौधों और जन्तुओं को विभिन्न वर्गों में रखने का आधार कोशिकाओं की संरचना व भोजन संश्लेषण करने की क्षमता है। यदि कोशिका की संरचना में कौर कोशिका भीति का होना, पर्णहरित पाया जाना, सूर्य के प्रकाश में भोजन का संश्लेषण करने की क्षमता से तो पौधों के वर्ग में होते हैं। (UPBoardSolutions.com) दूसरी ओर जिन कोशिकाओं में कोशिका भीति के स्थान पर कोशिका झिल्ली पाई जाती है और पर्णहरित नहीं होता तथा वे अपने भोजन का संश्लेषण नहीं करते बल्कि दूसरों के स्वरा,(पौ) बनाए गए भोजन ग्रहण करते हैं जन्तु वर्ग में वर्गीकृत किए जाते हैं। इसी आधार पर पौधे व जन्तु अलग-अलग वर्ग में रखे रोए हैं।’

पाठगत प्रश्न (पृष्ठ संख्या – 93)
प्रश्न 1.
आदिम जीव किन्हें कहते हैं ? ये तथाकथित उन्नत जीवों से किस प्रकार भिन्न हैं?
उत्तर-
पुरातन जीवों को साधारण व आदिम जीव कहा जाता है क्योंकि उनमें कोई विशेष परिवर्तन नहीं हुआ। नए जीवों को जटिल या विकसित जीव कहते हैं क्योंकि उनमें अधिक परिवर्तन हुआ है और उन्होंने अभी ही विशेष डिजाइन के शरीर को ग्रहण किया है।
प्रश्न 2.
क्या उन्नत जीव और जटिल जीव एक होते हैं?
उत्तर-
हाँ, विकसित जीव व जटिल जीव एक समान (जैसे) ही है क्योंकि विकास के समय में ही उनकी जटिलता में वृद्धि हुई है। अतः यह कहना गलत नहीं होगा। कि नए बने या विकसित जीव ही अधिक जटिल जीव हैं।
पाठ्गत प्रश्न (पृष्ठ संख्या – 96)
प्रश्न 1.
मोनेरा या प्रोटिस्टा जैसे जीवों के वर्गीकरण के मापदंड क्या हैं ?
उत्तर-
जीवों को मोनेरा या प्रोटिस्टा किंगडम में वर्गीकृत करने का आधार उनकी कोशिका संरचना, पोषण विधि, पोषण का स्रोत और शारीरिक रचना है। मोनेरा को आर्किबैक्टीरीय और यूबैक्टीरिया (जीवाणु) में विभाजित किया जाता है।
प्रश्न 2.
प्रकाश संश्लेषण करने वाले एककोशिक, यूकैरियोदी जीवों को आप किस जगत में संगै ?
उत्तर-
पादप जगत में रखते हैं।
प्रश्न 3.
वर्गीकरण के विभिन्न पदानुक्रमों में किस समूहमें सर्वाधिक समान लक्षण वाले सबसे कम जीवों को और किस समूह में सबसे ज्यादा संख्या में जीवों को रखा जायेगा ?
उत्तर-
स्पीसीज में सबसे कम जीव लेकिन अधिकतम समानताएँ वाले जीव रखे गये हैं। जरात में सबसे अधिक जीव रखे जाते हैं।
पाठ्गत प्रश्न (पृष्ठ संख्या – 99)
प्रश्न 1.
सरलतम पौधों को किस वर्ग में रखा गया है ?
उत्तर-
सरलतम पौधे थैलोफाइटा वर्ग में रखे गये हैं।

प्रश्न 2.
टेरिडोफाइटा और फैनरोगैमस में क्या अन्तर है ?
उत्तर-
टेरिडोफाइटा – इसमें भ्रूण (एम्ब्रीओ) नग्न होता है जिसे बी एणु कहते हैं। इस डिवीजन में देह तना, पत्तियों व जड़ों से बनी है। संवहन तंत्र विद्यमान होता है। बीज नहीं बनते। इसीलिए इन्हें क्रिप्टोगेमस (बिना बीज) पौधे कहते हैं। सभी फर्न इसी से सम्बन्धित हैं।
फैनरोगेम्स – इनमें देह असली तना, पत्तियाँ व जड़ में विभाजित होती है। इसमें जनन ऊतक बीज बनाते है। निषेवन के पश्चात् भ्रूण बनता है जिसमें संगृहीत भोजन होता है जो अकुरण में सहायक होता है। अतः यह टेरिडोफाइटा से अधिक विकसित होता है। इसमें संवहन तंत्र भी अच्छी प्रकार विकसित होता है। बीज फलों में बन्द होते या नहीं इसी आधार पर इन्हें वर्गीकृत करते हैं।
प्रश्न 3.
जिम्नोस्पर्म और एन्जियोस्पर्म एक-दूसरे से किस प्रकार भिन्न हैं ?
उत्तर-
जैसे तो दोनों वर्ग (डिवीजन) फैनरोगेम्स में पौधे जड़, तने, पत्तियाँ व बीज में विभाजित होते हैं, फिर भी बीजों के अन्तर के आधार पर इन्हें दो वर्गों में विभाजित किया जाता है
- जिम्नोस्पर्म – इनमें बीज फलों में बन्द नहीं होते। अतः इन्हें नग्नबीजी भी कहते हैं। ये पौधे काष्ठीय व सदाबहार होते हैं।
उदाहरण-पाइनस, साइकस, सिड्स।
- एन्जियोस्पर्म – इनमें बीज फलों में बन्द होते हैं, अतः ये आवृतबीजी कहलाते हैं। बीजों में बीजपत्रों की संख्या के आधार पर इन्हें दो वर्गों में बाँटा गया है-
- एकबीजपत्र वाले एक बीजपत्री और
- दो बीजपत्र वाले पौधे द्विबीजपत्री कहलाते हैं।
अत: दोनों में से कुछ सीमा तक जिम्नोस्पर्म अधिक विकसित समझे जाते हैं।
उदाहरण- पैफियोपडिलम (एकबीजपत्री), आइपोमिया (द्विबीजपत्री)।
पाठगत प्रश्न (पृष्ठ संख्या – 105)
प्रश्न 1.
पोरीफेरा और सिलेन्ट्रेटा वर्ग के जन्तुओं में क्या अन्तर है ?
उत्तर-
दोनों वर्ग के जन्तुओं में निम्नलिखित अन्तर है-
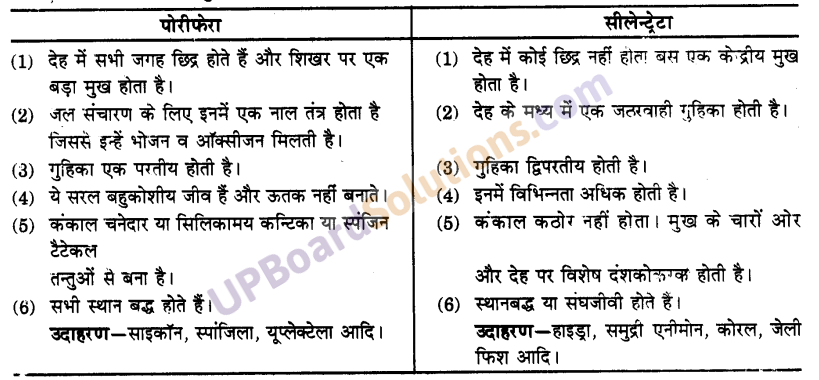
प्रश्न 2.
एनीलिडा के जन्तु आर्थोपोडा के जन्तुओं से किस प्रकार भिन्न हैं?
उत्तर-
एनीलिडा के जीव आर्थोपोडा के जीवों से निम्न गुणों में भिन्न है-

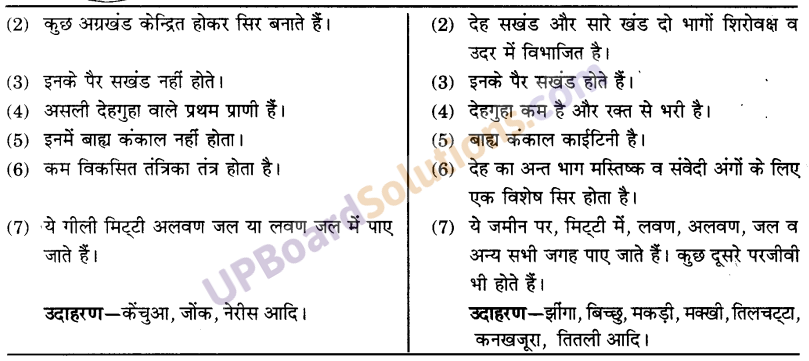
प्रश्न 3.
जल-स्थलचर और सरीसृप में क्या अंतर हैं ?
उत्तर-
जल-स्थलचर और सरीसृप में निम्नलिखित अंतर हैं-
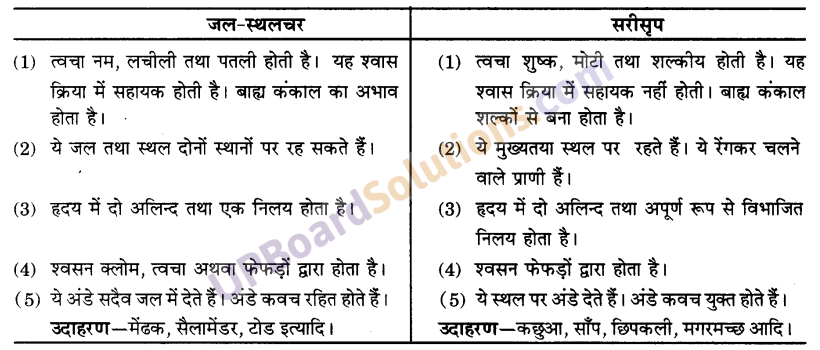
प्रश्न 4.
पक्षी वर्ग और स्तनपायी वर्ग के जंतुओं में क्या अंतर है?
उत्तर-
पक्षी तथा स्तनपायी वर्ग के जंतुओं में निम्नलिखित अंतर हैं-
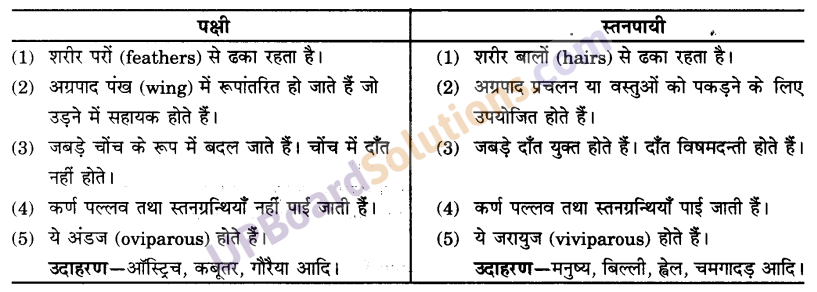
अभ्यास प्रश्न (पृष्ठ संख्या – 107)
प्रश्न 1.
जीवों के वर्गीकरण से क्या लाभ है ?
उत्तर-
जीवों के वर्गीकरण के निम्नलिखित लाभ हैं
- वर्गीकरण करने से जीवों का अध्ययन करना सरल हो जाता है।
- वर्गीकरण सभी जीवों की एकदम स्पष्ट तस्वीर प्रस्तुत करता है।
- इससे विभिन्न जीवों के समूहों के बीच आपसी सम्बन्धों के बारे में जानकारी मिलती है।
- यह अन्य जैविक विज्ञान के विकास को आधार प्रदान करता है।

प्रश्न 2.
वर्गीकरण में पदानुक्रम निर्धारण के लिए दो लक्षणों में से आप किस लक्षण का चयन करेंगे ?
उत्तर-
वर्गीकरण के पदानुक्रम के लक्षणों का चयन हम निम्नरूप से कर सकते हैं
- हम जीव के निर्माण की इकाई अर्थात् कोशिका को ध्यान में रखेंगे, इसके बाहर कोशिका झिल्ली है या कोशिका भित्ति, इसमें केन्द्रक है कोशिकांगों में झिल्ली है, (UPBoardSolutions.com) उनके कार्य और उनकी उत्पत्ति जैसे सभी गुणों का अध्ययन करेंगे। इस प्रकार इन गुणों के विकास के आधार पर ही उनका वर्गीकरण करेंगे।
- हमें यह भी देखना है अर्थात् अध्ययन करना होगा कि जीव स्वपोषी (स्वयं भोजन बनाना) है या परपोषी (दूसरों को बनाया भोजन ग्रहण करना)। यह विशेष गुण भी वर्गीकरण में सहायता करता है।
प्रश्न 3.
जीवों के पाँच जगत में वर्गीकरण के आधार की व्याख्या कीजिए।
उत्तर-
जीवों को पाँच मुख्य किंगडम में वर्गीकृत करने के लिए प्रयोग किए गए कुछ आधार निम्नलिखित है-
- वे जीव असीमकेन्द्री कोशिका से बने हैं या ससीमकेन्द्री कोशिका से। यदि उनकी संरचना असीमकेन्द्री कोशिका से बनी है तो वे प्राथमिक श्रेणी में आते हैं परन्तु यदि वे ससीमकेन्द्री कोशिका से बने हैं तो वे अपेक्षाकृत विकसित जीव होंगे।
- जीवों की रचना एक कोशिका से है या वे बहुकोशी हैं। एककोशीय जीव निम्न फाइलमों में होंगे और बहुकोशीय जटिल होंगे।
- कोशिकाओं के बाहर कोशिका भित्ति या कोशिका झिल्ली, यदि बाहर कोशिका भित्ति होगी तो उनका आधार कठोर व अधिक सुरक्षात्मक होगा, साथ-ही-साथ अधिक जटिल व विकसित होंगे।
- जीव स्वपोषी है या परपोषी। स्वपोषी पौधों की श्रेणी व परपोषी जन्तुओं की किंगडम में होंगे।
प्रश्न 4.
पादप जगत के प्रमुख वर्ग कौन हैं? इस वर्गीकरण का क्या आधार है?
उत्तर-
पादप प्रमुख पाँच वर्ग में बाँटे जाते हैं। ये पाँच वर्ग निम्नलिखित हैं
- थैलोफाइटा – इस प्रकार के पौधों के शरीर में विभाजन नहीं होता ये थैलस के रूप में होते हैं जैसे शैवाल, काई।
- ब्रायोफाइटा – इसमें पौधे का शरीर तने व पत्तियों के रूप में विभाजित होता है। कोई जल संवहन के लिए ऊतक विशेष नहीं होते, जैसे-मार्केशिया, मॉस इत्यादि।
- टैरीडोफाइटा – पादप जड़, तना व पत्तियों के रूप में बँटा होता है। जल संवहन के लिए विशेष ऊतक पाए जाते हैं। जैसे-मारसीलिया आदि।
ऊपरलिखित तीन विभाजन के पौधों के बीज नहीं होते। इनमें केवल नग्न भुण होता है जिन्हें बीजाणु (spores) कहते हैं। इनको सम्मिलित रूप से क्रिप्टोगेम्स कहते हैं। जिन पौधों में बीज पाए जाते हैं उन्हें फैनरोगेम्स कहते हैं। इनको दो भागों में बाँटते हैं-
(i) जिम्नोस्पर्म
(ii) एन्जियोस्पर्म
(i) जिम्नोस्पर्म – इन पौधों के बीज नग्न होते हैं। ये पौधे सदाबहार व काष्ठीय होते हैं जैसे-पाइनस व साइकस आदि।
(ii) एन्जियोस्पर्म – इन पौधों के बीज आवृतबीजी होते हैं। पौधों में फल व फूल भी लगते हैं। बीजों में एक या दो बीजपत्र पाए जाते हैं जो अंकुरण में सहायता करते हैं। एक बीजपत्र वाले बीजों को एकबीजपत्री (गेहूँ, चावल आदि) और दो बीजपत्र वालों को द्विबीजपत्री (चना, मटर, मॅग आदि) कहते हैं।
वर्गीकरण का आधार – विभाजनों का पहला आधार है कि पौधे का शरीर जड़, तने, और पत्ती में विभाजित है। या नहीं। दूसरे स्तर पर देखते हैं कि जल व अन्य पदार्थों के संवहन के लिए विशेष प्रकार के ऊतक उपस्थित हैं। तीसरे स्तर पर हमारा आधार होगा कि क्या पौधा बीज उत्पन्न करने में सक्षम है यदि है तो वे बीज आवृतबीजी हैं या नग्नबीजी । आवृतबीजी है तो उनमें कितने बीजपत्र (एक या दो) हैं। यह सभी पौधों के विभाजन के मुख्य आधार हैं।
प्रश्न 5.
जन्तुओं और पौधों के वर्गीकरण के आधारों में मूल अन्तर क्या है?
उत्तर-
पौधों के विभाजन का आधार जन्तुओं के विभाजन (वकर) आधार से भिन्। है। इस विभाजन का मुख्य आः उनकी रचना की उगलता है। पौधों की कोशिका में कोशिका भित्ति होती है और ये अपना भोजन पर्णहरिम (हरावर्णक) की सहायता से सूर्य के प्रकाश में भोजन को संश्लेषण करते हैं। ऐौधे स्थिर होते हैं। जन्तु की को में रोई कोशिका भित्ति ही होती, ये पौधों द्वारा, भोजन ग्रहण करते हैं (परपोषी)। ये गति कर (UPBoardSolutions.com) सकते हैं। इन सभी गुणों के अन्तर को ही वर्गीकरण का आधार माना जाता है जिससे वर्ग, उराव इयादि में जन्तुओं को वर्गीकृत किया जाता है।

प्रश्न 6.
वटा (कशेरुक प्राणी) को विभिन्न वर्गों में बाँटने के आधार की व्याख्या कीजिए।
उत्तर-
सभी वर्टीब्रेटा (कशेरुक प्राणियों) में मेरुदंड पाई जाती है। यह पृष्ठीय खोखली मेरुजु को घेरे रहती है। ग्रसनी विदर या क्लोम विदर प्रायः भ्रूण अवस्था में ही पाए जाते हैं। जलीय जंतुओं; जैसे मछली की वयस्क अवस्था में क्लोम (gills) पाए जाते हैं। मेरुरज्जु का अग्रभाग मस्तिष्क बनाता है। सिर पर नेत्र, कर्ण तथा घ्राणग्राही आदि संवेदी अंग होते हैं। अंतः कंकाल सुविकसित होता है। पेशियाँ अंतः कंकाल से लगी होती हैं। पेशियाँ तथा अस्थियाँ प्रचलन में सहायक होती हैं। वर्टीबेटा के वर्गीकरण के मुख्य आधार – वर्टीब्रेटा के वर्गीकरण के मुख्य आधार निम्नलिखित हैं-
- वयस्क अवस्था में या भ्रूण अवस्था में क्लोम विदर का पाया जाना।
- त्वचा पर श्लेष्म ग्रन्थियाँ, स्वेद ग्रन्थियाँ, तैल ग्रन्थियाँ, दुग्ध ग्रन्थियाँ आदि का पाया जाना । ।
- बाह्य काल शल्क, हॉर्नीप्लेट्स, पर (feathers), बाल से बना हुआ।
- अंतः कंकाल उपास्थि या अस्थि से बना हुआ।
- श्वसन क्लोम, त्वचा या फेफड़ों द्वारा।
- हृदय में वेश्मों की संख्या
- अग्रपादों का पंखों में रूपांतरण।
- असमतापी या समतापी।
- अंडज या जरायुज।
- अंडे जल में देना या जल से बाहर देना। अंडे कवचरहित या कवचयुक्त।
अन्य महत्वपूर्ण प्रश्नोत्तर
लघु उत्तरीय प्रश्न
प्रश्न 1.
जीतन की विविधता किसे कहते हैं ?
अथवा
नैव विविधग’ से क्या समझते हो ?
उत्तर-
नै विविधता या जीवन की विविधता (Diversits of Life) – जीवों में पाई जाने वाली विभिन्नता या अग्नता को सीवन की विविधता या जैव विविधता रूदने हैं।
प्रश्न 2.
जीवो के वर्गीकरण से क्या तात्पर्य है ?
उत्तर-
लीटों का वर्गीकरण (Classification of living organisms) – नीवों को खोजकर पहचानने, नाम देने तथा इनके गुणों एवं आदतों का पता लगाकर समूहबद्ध करने की क्रिया के जीवों का वर्गीकरण कहते हैं।
प्रश्न 3.
र्गिकी से आप क्या सम्झते हैं ?
उत्तर-
वर्गकी (Taxonomy) – विज्ञान की वह शाखा (UPBoardSolutions.com) जिसके अन्तर्गत जीवों के वर्गीकरण का अध्ययन किया जाता है, वर्गिकी कहलाती है।
प्रश्न 4.
विकासात्मक वर्गीकरण किसे कहते हैं ?
उत्तर-
विकासात्मक वर्गीकरण (Evolutionary Classification) – जो वर्गीकरण विकास के आधार पर किया जाता है उसे विकासात्मक वर्गीकरण कहते हैं।
प्रश्न 5.
वर्गीकरण का पिता किसे कहा जाता है?
उत्तर-
कैरोलस लीनियस को वर्गीकरण का पिता कहा जाता है।

प्रश्न 6.
जगत-मोनेरा के उदाहरण दीजिए।
उत्तर-
जगत-मोनेरा के उदाहरण-जीवाणु, नीली- हरी शैवाल।
प्रश्न 7.
जगत-प्रोटिस्टा के उदाहरण दीजिए।
उत्तर-
जगत-प्रोटिस्टा के उदाहरण-अमीबा, पैरामीशियम।
प्रश्न 8.
जगत-प्लाण्टी के उदाहरण दीजिए।
उत्तर-
जगत- प्लाण्टी के उदाहरण-शैवाल, आवृतबीजी पौधे।
प्रश्न 9.
जगत-फंजाई के उदाहरण दीजिए।
उत्तर-
जगत-फजाई के उदाहरण-सभी कवक।
प्रश्न 10.
जगत-ऐनीमेलिया के उदाहरण दीजिए।
उत्तर-
जगत-ऐनीमेलिया के उदाहरण-सभी बहुकोशिकीय जन्तु जैसे-फीताकृमि, केंचुआ इत्यादि।
प्रश्न 11.
सर्वप्रथम नामकरण पद्धति किसने प्रारम्भ की ?
उत्तर-
सर्वप्रथम नामकरण की पद्धति कैरोलस लीनियस ने प्रारम्भ की।

प्रश्न 12.
ब्रायोफाइटा के उदाहरण दीजिए।
उत्तर-
ब्रायोफाइटा के उदाहरण-मॉस।
प्रश्न 13.
टेरिडोफाइटा के उदाहरण दीजिए।
उत्तर-
टेरिडोफाइटा के उदाहरण-फर्न
प्रश्न 14.
अनावृतबीजी के उदाहरण दीजिए।
उत्तर-
अनावृतबीजी के उदाहरण- पाइनस, साइकस, विलियम सोनिया।
प्रश्न 15.
आवृतबीजी के उदाहरण दीजिए।
उत्तर-
आवृतबीजी के उदाहरण-आम, सरसों, गेहूँ।
प्रश्न 16.
एकबीजपत्री के उदाहरण दीजिए।
उत्तर-
एकबीजपत्री के उदाहरण-मक्का, गेहूँ, जौ, प्याज
प्रश्न 17.
द्विबीजपत्री के उदाहरण दीजिए।
उत्तर-
द्विबीजपत्री के उदाहरण-चना, सरसों, मटर, आम।

प्रश्न 18.
अमीबा किस संघ का प्राणी है ?
उत्तर-
अमीबा प्रोटोजोआ संघ का प्राणी है।
प्रश्न 19.
अमीबा के चलन अंग का नाम बताइये।
उत्तर-
अमीबा के चलन अंग का नाम कूटपाद है।
प्रश्न 20.
अमीबा में चलन (गति) किस अंग द्वारा होता है ?
अथवा
कूटपाद द्वारा किस जन्तु में चलन होता है ?
उत्तर-
अमीबा में चलन कूटपाद द्वारा होता है।
प्रश्न 21.
यूग्लीना किस संघ का प्राणी है ?
उत्तर-
युग्लीना प्रोटोजोआ संघ का प्राणी है।
प्रश्न 22.
यूग्लीना के चलन अंग का नाम बताइये।
उत्तर-
युग्लीना के चलन अंग का नाम फ्लैजिला है।
प्रश्न 23.
यूग्लीना में चलन (गति) किस अंग द्वारा होता है ?
अथवा
फ्लैजिला द्वारा किस जन्तु में चलन होता है ?
उत्तर-
युग्लीना में चलन फ्लैजिला द्वारा होता है।

प्रश्न 24.
सीलिया द्वारा गति किस जन्तु में होती
अथवा
पैरामीशियम में किस अंग के द्वारा गति होती है ?
उत्तर-
पैरामीशियम में गति सीलिया द्वारा होती है।
प्रश्न 25.
संघ-मोलस्का के जन्तुओं के उदाहरण दीजिए।
अथवा
संघ-मोलस्का के दो जन्तुओं के नाम लिखिए।
उत्तर-
संघ-मोलस्का के जन्तुओं का नाम-पाइला, यूनियो (सीप), ऑक्टोपस।
प्रश्न 26.
संघ-इकाइनोडर्मेटा के प्रमुख जन्तुओं के नाम लिखिए।
उत्तर-
संघ-इकाइनोडर्मेटा के जन्तुओं के नाम-स्टारफिश, सी-आरचिन, सी-कुकुम्बर।
प्रश्न 27.
स्टारफिश में चलन किस अंग द्वारा होता है ? नाम बताइये।
उत्तर-
स्टारफिश में चलन नाल पादों (Tube feet) द्वारा होता है।
प्रश्न 28.
मत्स्य वर्ग के जन्तुओं के नाम लिखिए।
उत्तर-
मत्स्य वर्ग के जन्तुओं के नाम-शार्क, रोहू (लेबियो), समुद्री घोड़ा (हिप्पोकैम्पस)
प्रश्न 29.
एम्फीबिया वर्ग के जन्तुओं के नाम लिखिए।
उत्तर-
एम्फीबिया वर्ग के जन्तुओं के नाम-मेंढक, टोड।

प्रश्न 30.
पक्षी वर्ग के उदाहरण दीजिए।
उत्तर-
पक्षी वर्ग के जन्तुओं के उदाहरण-मोर, कबूतर, मुर्गा
लघु उत्तरीय प्रश्न
प्रश्न 1.
सम्पूर्ण जीव जगत को कितने जगतों में विभाजित किया गया है ? उनके नाम लिखिए।
उत्तर-
जीव जगत का विभाजन-सम्पूर्ण जीव जगत को निम्न दो जगतों में विभाजित किया गया है
- पादप जगत (Plant Kingdom)
- जन्तु जगत (Animal Kingdom)
प्रश्न 2.
द्विजगत वर्गीकरण किसे कहते हैं ?
उत्तर-
द्विजगत वर्गीकरण-जिस वर्गीकरण में सम्पूर्ण जीवों को दो जगतों में विभाजित किया गया है, उसे द्विजगत वर्गीकरण कहते हैं।
प्रश्न 3.
द्विजगत वर्गीकरण किस वैज्ञानिक ने किया था ?
उत्तर-
द्विजगत वर्गीकरण स्वीडिस के वैज्ञानिक कैरोलस लीनियस ने किया था।
प्रश्न 4.
कैरोलस लीनियस की वर्गीकरण से सम्बन्धित पुस्तक का नाम क्या है ?
उत्तर-
कैरोलस लीनियस की वर्गीकरण से सम्बन्धित पुस्तक का नाम सिस्टेमा नेचुरी (Systema Naturae) है।
प्रश्न 5.
जीवों का आधुनिक वर्गीकरण किस वैज्ञानिक ने किया ?
उत्तर-
जीवों का आधुनिक वर्गीकरण आर. एच. ह्विटेकर ने किया।
प्रश्न 6.
पाँच जगत वर्गीकरण या आधुनिक वर्गीकरण किसे कहते हैं ?
उत्तर-
आधुनिक वर्गीकरण या पाँच जगत वर्गीकरण-जिस वर्गीकरण में सम्पूर्ण जीवों को पाँच जगतों में विभाजित किया गया है
उस वर्गीकरण को आधुनिक वर्गीकरण या पाँच जगत वर्गीकरण कहते हैं।

प्रश्न 7.
जीवों के नामकरण की पद्धति की क्या आवश्यकता है?
अथवा
जीवों के वैज्ञानिक नामों की क्या आवश्यकता है?
उत्तर-
जीवों को विभिन्न स्थानों पर विभिन्न नामों से पुकारा जाता था।
अतः सम्पूर्ण विश्व में अध्ययन के लिए जीवों के ऐसे नामों की आवश्यकता हुई जो विश्वभर में एकसमान हों। ऐसे नामों को वैज्ञानिक नाम कहा गया।
प्रश्न 8.
द्विनाम पद्धति क्या है ?
उत्तर-
द्विनाम पद्धति (Binomial system) – जिस पद्धति में जीवों का नाम दो शब्दों में रखा जाता है, जिसमें पहला शब्द वंश (Genus) और दूसरा शब्द उसकी जाति (Species) को बतलाता है, उस पद्धति को द्विनाम पद्धति कहते हैं।
प्रश्न 9.
त्रिनाम पद्धति क्या है ?
उत्तर-
त्रिनाम पद्धति-जिस पद्धति में जीवों का नाम तीन शब्दों का रखा जाता है, जिसमें पहला शब्द वंश, दूसरा शब्द उसकी जाति तथा तीसरा शब्द उसकी उपजाति को बतलाता है, उस पद्धति को त्रिनाम पद्धति कहते हैं।
प्रश्न 10.
त्रिनाम पद्धति की क्या आवश्यकता पड़ी?
उत्तर-
त्रिनाम पद्धति की आवश्यकताकभी-कभी अलग-अलग वातावरण में रहने वाले एक ही जाति में कुछ भिन्नताएँ आ जाती हैं। इस समस्या को दूर करने के लिए त्रिनाम पद्धति की आवश्यकता पड़ी।
प्रश्न 11.
पादप जगत को कितने प्रभागों में बाँटा गया है? उनके नाम लिखिए।
उत्तर-
पादप जगत का वर्गीकरण- पादप जगत को निम्न तीन भागों में विभाजित किया गया है
- शैवाल (Algae),
- ब्रायोफाइटा (Bryophyta) तथा
- ट्रेकियोफाइटा (Tracheophyta)

प्रश्न 12.
ट्रेकियोफाइटा को कितने उप-प्रभाग में बाँटा गया है? नाम लिखिए।
उत्तर-
ट्रेकियोफाइटा का वर्गीकरण-ट्रेकियोफाइटा को निम्न तीन उप-प्रभागों में बाँटा गया है
- टेरिडोफाइटा (Pteridophyta)
- अनावृतबीजी (Gymnosperms)
- आवृतबीजी (Angiosperm)
प्रश्न 13.
आवृत्तबीजी पौधों को कितने वर्गों में बाँटा गया है? उनके नाम लिखिए।
उत्तर-
आवृत्तबीजी पौधों का वर्गीकरण आवृतबीजी पौधों को निम्न दो वर्गों में बाँटा गया है
- एकबीजपत्री (Monocotyledons)
- द्विबीजपत्री (Dicotyledons)
प्रश्न 14.
जन्तु जगत को कितने उप-जगतों में विभाजित किया गया है? उनके नाम लिखिये।
उत्तर-
जन्तु जगत का वर्गीकरण- जन्तु जगत को निम्नांकित उप-जगत में विभाजित किया गया है
- अपृष्ठवंशी या अकशेरुकी या नॉन-कॉडेटा (Non-chordata)
- पृष्ठवंशी या कशेरुकी या कॉउँटा (Chordata)
प्रश्न 15.
मेंढक को एम्फीबिया वर्ग में क्यों रखा गया है?
उत्तर-
मेंढक एक असमतापी उभयचर है जिसमें एम्फीबिया वर्ग के लगभग सभी लक्षण मौजूद हैं इसलिए इसे एम्फीबिया वर्ग में रखा गया है।
प्रश्न 16.
वर्गीकरण के लाभ लिखिए।
उत्तर-
वर्गीकरण के लाभ-वर्गीकरण के निम्नलिखित प्रमुख लाभ हैं
- जीवों की पहचान होना।
- जीवों की विविधता का ज्ञान होना।
- जीवों के आपसी सम्बन्धों का ज्ञान होना।
- जीवों के उत्पत्ति की जानकारी होना।
- जीवों के विकास के क्रम का ज्ञान होना।

प्रश्न 17.
द्विजगत वर्गीकरण की कमियाँ बताइये।
उत्तर-
द्विजगत वर्गीकरण की कमियाँ-द्विजगत वर्गीकरण की निम्नलिखित कमियाँ हैं
- एककोशिकीय एवं बहुकोशिकीय जीवों को साथ-साथ रखना।
- प्रोकैरियोटिक एवं यूकैरियोटिक को साथ-साथ रखना।
- स्वपोषी एवं विषमपोषी जीवों को साथ-साथ रखना।
- जन्तु समूहों में कुछ पादपों एवं पादप समूहों में कुछ जन्तुओं को रखना।
प्रश्न 18.
वे पाँच लक्षण कौन-कौन से हैं जिनके आधार पर आधुनिक वर्गीकरण किया गया?
उत्तर-
निम्नलिखित पाँच लक्षणों के आधार पर आधुनिक वर्गीकरण किया गया|
- कोशिका की जटिलता प्रोकैरियोटिक या यूकैरियोटिक।
- पोषण विधियाँ।
- जीवन शैली।
- जीव जगत की संगठनात्मक जटिलता-एक कोशिकीयता एवं बहुकोशिकीयता।
- जीवों का विकासात्मक या जातिवृत्तीय सम्बन्ध।
प्रश्न 19.
पाँच जगत वर्गीकरण (आधुनिक वर्गीकरण) की कमियाँ बताइये।
उत्तर-
पाँच जगत वर्गीकरण (आधुनिक वर्गीकरण) की कमियाँ-इस वर्गीकरण की निम्नलिखित कमियाँ हैं
- एककोशिकीय शैवालों को अलग रखना।
- प्रोटिस्टा जगत का विविधतापूर्ण होना।
- जीवों की उत्पत्ति को बहुस्रोत वाली दर्शाना।
- विषाणु का स्थान निश्चित न होना।
- मिलते-जुलते गुणों वाले जीवों को दूर रखना।
प्रश्न 20.
शैवालों के लक्षण लिखिए।
उत्तर-
शैवाल के लक्षण
- इनका शरीर शूकायवत (Thalloid) होता है। अर्थात् यह जड़, तना एवं पत्ती में विभेदित नहीं होता है।
- ये स्वपोषी जीव होते हैं।
- इनके शरीर में संवहनी ऊतक नहीं पाया जाता है।
- ये जलीय वातावरण या नम स्थानों में पाये जाते हैं।
प्रश्न 21.
ब्रायोफाइटा के लक्षण लिखिए।
उत्तर-
ब्रायोफाइटा के लक्षण
- ये असंवहनी (Non-vascular), हरित लवक युक्त पौधे हैं।
- इनमें निषेचन के बाद भ्रूण (Embryo) बनता है तथा इनके निषेचन के लिए जल आवश्यक है।
- इनमें प्रतिपृष्ठ सतह पर मूलरोमों के समान रचनाएँ पाई जाती हैं जिन्हें मूलाभास (Rhizoids) कहते हैं।
- कुछ विकसित ब्रायोफाइट्स में तने सदृश रचनाएँ पाई जाती हैं।
- ये नम भूमि या पेड़ की छालों आदि पर पाये जाते हैं।
प्रश्न 22.
ट्रेकियोफाइटा के लक्षण लिखिए।
उत्तर-
ट्रेकियोफाइटा के लक्षण
- इनमें संवहनी ऊतक जाइलम (Xylem) एवं फ्लोएम (Phloem) पाये जाते हैं।
- इनका शरीर विभिन्न परिस्थितियों में रहने के लिए अनुकूलित होता है।
- ये पौधे जड़, तना तथा पत्ती में विभेदित होते हैं।
- इनमें श्रम विभाजन पाया जाता है।

प्रश्न 23.
टेरिडोफाइटा के लक्षण लिखिए।
उत्तर-
टेरिडोफाइटा के लक्षण
- इनका शरीर जड़, तना तथा पत्ती में विभेदित होता है।
- इनमें संवहनी ऊतक पाया जाता है जो जाइलम एवं फ्लोएम का बना होता है।
- ये पुष्पहीन होते हैं अतः इनमें बीज का निर्माण ही नहीं होता।
- इनका मुख्य पौधा बीजाणुभिद् होता है जिस पर बीजाणु पैदा होते हैं, जो अंकुरित होकर युग्मोद्भिद पौधे का निर्माण करते हैं।
प्रश्न 24.
जिम्नोस्पर्म (अनावृत्तबीजी) के लक्षण लिखिए।
उत्तर-
जिम्नोस्पर्म (अनावृत्तबीजी) के लक्षण
- इन पौधों के बीजों के चारों तरफ कोई आवरण नहीं पाया जाता है अतः इनके बीज नग्नं बीज होते हैं।
- इनमें वायु द्वारा परागण होता है।
- ये पौधे बहुवर्षी, काष्ठीय तथा मरुद्भिद स्वभाव के होते हैं।
- इनका संवहनी ऊतक जाइलम एवं फ्लोएम में विभेदित रहता है।
प्रश्न 25.
एन्जियोस्पर्म (आवृत्तबीजी) के लक्षण लिखिए।
उत्तर-
एन्जियोस्पर्म (आवृत्तबीजी) के लक्षण
- इन पौधों के बीजों के चारों ओर आवरण पाया जाता है।
- इनमें दोहरे निषेचन की क्रिया पाई जाती है।
- इनमें वातावरण के प्रति बहुत अधिक अनुकूलन पाया जाता है।
- ये परजीवी (अमरबेल), मृतजीवी (ऑर्किड), सहजीवी (दाल वाले पादप) तथा स्वपोषी रूप में पाये जाते हैं।
प्रश्न 26.
एकबीजपत्री के लक्षण लिखिए।
उत्तर-
एकबीजपत्री के लक्षण
- इनके बीजों में केवल एक बीजपत्र पाया जाता है।
- इनकी पत्तियों में समानान्तर शिराविन्यास पाया जाता है।
- इनकी पत्तियाँ अवृन्त रहती हैं।
- इनमें प्रायः रेशेदार (झकड़ा) जड़े होती हैं।
- इनके पुष्पों के तीन भाग या इसके गुणांक में होते हैं।
प्रश्न 27.
द्विबीजपत्री के लक्षण लिखिए।
उत्तर-
द्विबीजपत्री के लक्षण
- इनके बीजों में दो बीजपत्र पाये जाते हैं।
- इनकी पत्तियों में जालिकावत् शिराविन्यास होता है।
- इनकी पत्तियाँ प्रायः सवृन्त होती हैं।
- इनमें मूसला जड़ पाई जाती है।
- इनके पुष्प के भाग चार या पाँच या इनके गुणांक में होते हैं।

प्रश्न 28.
एम्फीबिया वर्ग (उभयचरों) के लक्षण लिखिए।
उत्तर-
वर्ग-उभयचर या एम्फीबिया (ClassAmphibia) के लक्षण
- ये जन्तु उभयचर होते हैं अर्थात् ये अपना जीवनयापन जल एवं थल दोनों में करते हैं।
- इनकी त्वचा, नम, चिकनी एवं ग्रन्थिमय होती है।
- ये असमतापी या शीत रुधिर प्राणी होते हैं।
- इनमें बाह्य निषेचन होता है।
प्रश्न 29.
सरीसृप या रेप्टीलिया वर्ग के लक्षण लिखिए।
उत्तर-
वर्ग-सरीसृप या रेष्टीलिया (Class-Reptilia) के लक्षण
- ये जन्तु असमतापी तथा रेंगकर चलने वाले जलचर एवं स्थलचर होते हैं।
- इनके हृदय में दो अलिंद एवं एक निलय अर्थात् तीन कोष्ठ पाये जाते हैं।
- इनकी त्वचा रूखी एवं ग्रन्थिविहीन होती है। लेकिन इनकी त्वचा पर शल्क पाये जाते हैं।
प्रश्न 30.
पक्षी वर्ग के लक्षण लिखिए।
उत्तर-
पक्षी वर्ग (Class-Aves) के लक्षण
- ये समतापी या गर्म रक्त प्राणी हैं।
- इनका शरीर सिर, धड़ एवं पूँछ में बँटा होता है।
- इनके हृदय में चार कोष्ठ अर्थात् दो अलिंद एवं दो निलय पाये जाते हैं।
- इनके कंकाल में छोटे-छोटे कोष्ठ पाये जाते हैं। जिनमें हवा भरी होती है अर्थात् इनकी हड्डियाँ खोखली एवं हल्की होती हैं। इनसे इन जन्तुओं को उड़ने में सहायता मिलती है।
दीर्घ उत्तरीय प्रश्न
प्रश्न 1.
ऐसे लक्षणों के तीन वास्तविक उदाहरण उद्धत कीजिए जो पदानुक्रम वर्गीकरण के लिए प्रयोग किए जाते हैं।
उत्तर-
(i) एक यूकैरियोटी कोशिका में केन्द्रक समेत कुछ झिल्ली से घिरे कोशिकांग होते हैं, जिसके कारण कोशिकीय क्रिया अलग-अलग कोशिकाओं में दक्षतापूर्वक होती रहती है। यही कारण है कि जिन कोशिकाओं में झिल्लीयुक्त कोशिकांग और केन्द्रक नहीं होते हैं, उनकी जैव रासायनिक (UPBoardSolutions.com) प्रक्रियाएँ भिन्न होती हैं। इसका असर कोशिकीय संरचना के सभी पहलुओं पर पड़ता है। इसके अतिरिक्त केन्द्रकयुक्त कोशिकाओं में बहुकोशिक जीव के निर्माण की क्षमता होती है क्योंकि वे किसी विशेष कार्यों के लिए विशिष्टीकृत हो सकते हैं। इसलिए कोशिकीय संरचना और कार्य वर्गीकरण का आधारभूत लक्षण है।
(ii) कोशिकाएँ जो एक साथ समूह बनाकर किसी जीव का निर्माण करती हैं, उनमें श्रम-विभाजन पाया जाता है। शारीरिक संरचना में सभी कोशिकाएँ एक समान नहीं होती हैं, बल्कि कोशिकाओं के समूह कुछ विशेष कार्यों के लिए विशिष्टीकृत हो जाते हैं। यही कारण है कि जीवों की शारीरिक संरचना में इतनी विभिन्नता होती है।
(iii) स्वयं भोजन बनाने की क्षमता रखने वाले और बाहर से भोजन प्राप्त करने वाले जीवों की शारीरिक संरचना में आवश्यक भिन्नता पाई जाती है।

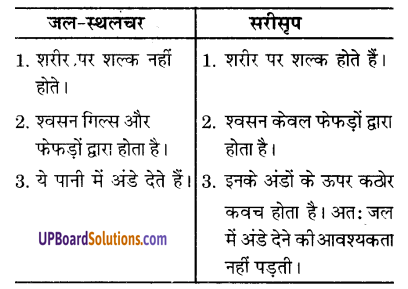
प्रश्न 2.
जल-स्थलचर और सरीसृप में तीन अन्तर लिखिए।
उत्तर-
जल-स्थलचर और सरीसृप में तीन अन्तर निम्नलिखित हैं-
प्रश्न 3.
फाइलम कॉडेटा के तीन विशेष लक्षण बताइए।
उत्तर-
फाइलम (संघ) कॉडेटा (chordata) के विशेष लक्षण निम्नलिखित हैं
- जीवन की किसी न किसी अवस्था में नोटोकॉर्ड (notochord) अवश्य पाई जाती है।
- तंत्रिका रज्जु (nerve chord) खोखला तथा पृष्ठतलीय होता है।
- हृदय अधर तल पर स्थित होता है। चल रुधिराणु हीमोग्लोबिन के कारण श्वसन में सहायक होते हैं।
प्रश्न 4.
उन तीन मुख्य लक्षणों का उल्लेख कीजिए जिन्हें जीवों को वर्गीकृत करने के लिए ध्यान में रखा गया है।
उत्तर-
जीवों को वर्गीकृत करने के लिए निम्नलिखित लक्षणों को ध्यान में रखा गया है|
- जीव प्रोकेरियोटी या यूकेरियोटी (UPBoardSolutions.com) कोशिका का बना है।
- कोशिकाएँ स्वतंत्र हैं या बहुकोशिकीय संगठन और जटिल जीव के रूप में हैं।
- कोशिकाओं में कोशिका भित्ति है। वे अपना भोजन संश्लेषित करते हैं।
प्रश्न 5.
वर्ग जल-स्थलचर की छह विशेषतायें लिखिए।
उत्तर-
जल-स्थलचर वर्ग की छह विशेषतायें
- जीव जल तथा नम स्थानों में स्थल पर रहते हैं। शीत रुधिर एवं अंडज वर्टीब्रेट।
- त्वचा मुलायम, आर्द्र तथा बिना स्केल की होती
- अधिकतर पाँच अँगुलियों वाले दो जोड़ी हाथ होते हैं।
- नेत्र गोलक इधर-उधर घुमाये जा सकते हैं।
- नासा छिद्र होते हैं।
- जीभ चिपचिपी एवं श्लेष्मिक झिल्ली से जुड़ी होती है।

प्रश्न 6.
वर्ग सरीसृप की छः विशेषतायें लिखिए।
उत्तर-
सरीसृप वर्ग की छह विशेषतायें
- ये अधिकांश थलचर हैं।
- त्वचा सूखी एवं शल्कों से ढकी होती है।
- शीत रुधिर चाले जंतु हैं।
- श्वसन मुख्य रूप से फेफड़ों से होता है।
- शरीर सिर, ग्रीवा, धड़ तथा पूँछ में बँटा होता है।
- अंत: कंकाल अस्थियों (bones) का बना होता है।
प्रश्न 7.
(a) अमीबा किस संघ का प्राणी है ? इसका प्राप्ति स्थान क्या है ? यह एक स्थान से दूसरे स्थान पर कैसे जाता है ?
(b) कवक अपना भोजन क्यों नहीं बना पाते हैं?
(c) सीलेण्टरॉन क्या है ? किन्हीं दो जंतुओं के नाम लिखिए जिनमें सीलेण्टरॉन पाई जाती है।
उत्तर-
(a) अमीबा प्रोटियस (Amoeba proteus) – संघ प्रोटोजोआ का एक कोशिकीय प्राणी है। यह साधारणतः पोखरों, तालाबों की कीचड़ में पाया जाने वाला सूक्ष्म जीव है। इसमें चलन पादाभ या कूटपाद द्वारा होता है।
(b) कवकों में पर्णहरित (chlorophyll) – नहीं होता, अतः वे अपना भोजन नहीं बना पाते। ये विषमपोषी (heterotrophic) या परपोषी होते हैं। ये मृतपोषी, परजीवी या सहजीवी होते हैं।
(c) सीलेण्टरॉन देहगुहा तथा आहारनाल दोनों का कार्य करने वाली गुहा (cavity) होती है। उदाहरण-हाइड्रा या ओबीलिया।
प्रश्न 8.
“जीवों के वर्गीकरण का जैव विकास से निकट का सम्बन्ध है।” क्या आप इसे कथन से सहमत हैं ? एक उदाहरण के साथ टिप्पणी कीजिए।
उत्तर-
जैव विकास की अवधारणा को वर्गीकरण से संबंधित करके देखें तो दो तरह के जीव पाये जाते हैं
(i) आदिम अथवा निम्न जीव।
(ii) उन्नंत अथवा उच्च जीव।
(i) आदिम अथवा निम्न जीव – वे जीव जिनकी शारीरिक संरचना में प्राचीन काल से लेकर आज तक कोई विशेष परिवर्तन नहीं हुआ है, आदिम अथवा निम्न जीव कहलाते हैं।
(ii) उन्नत अथवा उच्च जीव – वे जीव जिनकी शारीरिक संरचना में प्राचीन काल से आज तक पर्याप्त परिवर्तन हुआ है, उन्नत अथवा उच्च जीव कहलाते हैं। वर्गीकरण में हम जीवों को सरल से जटिल की तरफ व्यवस्थित करने का प्रयास करते हैं, जैसा कि निर्विवाद प्रमाणित हो चुका (UPBoardSolutions.com) है कि जीवों का विकास सरल से जटिल की ओर या आदिम से उन्नत की ओर हुआ। शारीरिक संरचना में समय के साथ या विकास के साथ परिवर्तन आते गये। अत: वर्गीकरण जैव विकास से निकट संबंधित है।
प्रश्न 9.
निम्न में से प्रत्येक का एक उदाहरण दीजिए
(i) अंडे देने वाला एक स्तनपायी।
(ii) एक मछली जिसका कंकाल केवल उपास्थि का बना होता है।
(iii) कवकों की कुछ प्रजातियाँ जो नील हरित शैवाल (साइनोबैक्टीरिया) के साथ स्थायी अंतर्सम्बन्ध बनाती हैं।
(iv) पादप वर्ग का उभयचर।
उत्तर-
(i) प्लेटिपस,
(ii) शार्क,
(iii) लाइकेन,
(iv) ब्रायोफाइट।

प्रश्न 10.
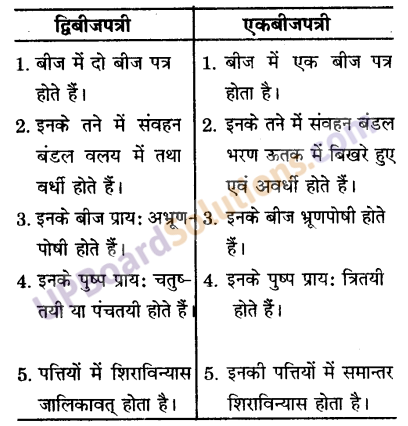
द्विबीजपत्री एवं एकबीजपत्री में पाँच अन्तर लिखिए।
उत्तर-
द्विबीजपत्री एवं एकबीजपत्री में पाँच प्रमुख अन्तर निम्नलिखित हैं-
प्रश्न 11.
वंश कोशिका किस संघ के जन्तुओं में पाई जाती है? इस संघ के दो उदाहरण दीजिए।
उत्तर-
दंश कोशिका संघ सीलेण्टरेटा के जन्तुओं में पाई जाती है। इस संघ के दो जन्तु हाइड्रा तथा ओबीलिया हैं।
प्रश्न 12.
बरसात में रास्ता फिसलने वाला क्यों हो जाता है ? ऐसी दशा उत्पन्न करने वाले इन जीवों को किस संघ में रखते हैं ?
उत्तर-
बरसात में रास्ते में नमी के कारण नीले-हरे शैवाल (UPBoardSolutions.com) उग आते हैं। इन शैवालों की कोशिका भित्ति से काफी मात्रा में श्लेष्मक होता है। अतः रास्ता फिसलने वाला हो जाता है। इन जीवों को संघ साइनोफाइटा में रखते हैं।
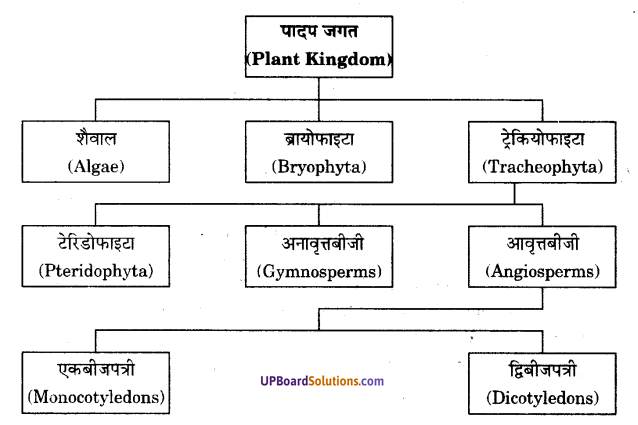
प्रश्न 13.
पादप जगत के वर्गीकरण का रेखाचित्र बनाइये।
उत्तर-
पादप जगत के वर्गीकरण रेखाचित्र-
प्रश्न 14.
अपृष्ठवंशी या अकशेरुकी या नॉनकॉर्डेटा के विशिष्ट लक्षण लिखिए।
अथवा
उप-जगत नॉन-कॉडेटा के मुख्य लक्षण लिखिए।
उत्तर-
अपृष्ठवंशी (अकशेरुकी) या नॉन-कॉउँटा (Non-chordata) के विशिष्ट लक्षण
- शरीर में मेरुदण्ड का अभाव रहता है।
- रक्त में लाल रक्त कणिकाओं का अभाव रहता है।
- मस्तिष्क ठोस होता है।
- हृदय स्पष्ट नहीं होता। यदि उपस्थित रहता है। तो शरीर के पृष्ठ तल पर उपस्थित रहता है।
- शरीर पर बाह्य कंकाल (Exoskeleton) पाया जाता है।

प्रश्न 15.
अकशेरुकी (अपृष्ठवंशी या नॉनकॉडेटा) को कितने संघों में विभाजित किया गया है? उनके नाम लिखिए।
अथवा
नॉन-कॉडेटा के वर्गों के नाम लिखिए।
उत्तर-
अकशेरुकी, अपृष्ठवंशी या नॉन-कार्डेटा (Non-chordata) का वर्गीकरण – इस उप-जगत को निम्नलिखित 9 संघों में विभाजित किया गया है
- प्रोटोजोआ (Protozoa),
- पोरीफेरा (Porifera),
- सीलेन्टरेटा (Coelenterata)
- प्लैटीहेल्मेन्थीस (Platyhelminthes),
- निमैटहेल्मिन्थीस (Nemathelminthes)
- ऐनेलिडा (Annelida)
- आर्थोपोडा (Arthropoda)
- मोलस्का (Mollusca)
- इकाइनोडर्मेटा (Echinodermata)
प्रश्न 16.
संघ-पोरीफेरा के लक्षण लिखिए।
उत्तर-
संघ-पोरीफेरा (Phylum-Porifera) के लक्षण-
- ये जन्तु बहुकोशिकीय होते हैं।
- ये जन्तु द्विस्तरीय (Diploblastic) होते हैं।
- इस संघ के जन्तुओं में मुख नहीं होता, परन्तु छोटे-छोटे रन्ध्र (Ostia) ही मुख का कार्य करते हैं।
प्रश्न 17.
संघ-सीलेन्टरेटा के लक्षण लिखिए।
उत्तर-
संघ-सीलेन्टरेटा (Phylum-Coelenterata)-
- ये जन्तु द्विस्तरीय (Diploblastic) होते हैं।
- इनके शरीर में लम्बी केन्द्रीय गुहा होती है।
- इन जन्तुओं की पीढ़ियों में एकान्तरण होता है।
- ये जन्तु द्विलिंगी (Bisexual) होते हैं।
- इनमें श्रम विभाजन पाया जाता है।
अभ्यास प्रश्न
बहुविकल्पीय प्रश्न
1. कूटपाद से गति करता है
(a) अमीबा
(b) कॉकरोच
(c) केचुआ
(d) पैरामीशियम।
2. श्रम विभाजन पाया जाता है
(a) मनुष्य में
(b) हाइड्रा में
(c) मेंढक में
(d) पक्षियों में
3. अमीबा निम्न वर्ग का प्राणी है
(a) पोरीफेरा
(b) सीलेन्टरेटा
(c) प्रोटोजोआ
(d) प्लेटीहेल्मिन्थीस।

4. ऑर्थोपोडा संघ का जन्तु है
(a) बिच्छू
(b) हाईड्रा
(c) ऑक्टोपस
(d) केंचुआ।
5. स्टारफिश में चलन होता है
(a) कूटपाद से
(b) सीलिया से
(c) टाँगों से
(d) नाल पादों से।
6. सीलेण्टेरेटा फाइलम का जन्तु है
(a) सी एनीमोन
(b) स्पांज
(c) यूग्लीना
(d) टेपवर्म
7. अमीबा और पैरामीशियम हैं
(a) एनीलिड
(b) आर्थोपोड
(c) सीलेन्टरेट
(d) प्रोटिस्टा।
8. फाइलम प्लेटीहेलमिन्थीज का जन्तु है
(a) सी एनीमोन
(b) स्पॉन्ज
(c) यूग्लीना
(d) टेपवर्म

9. पोरीफेरा फाइलम का जन्तु है
(a) सी एनीमोन
(b) स्पॉन्ज
(c) यूग्लीना
(d) टेपवर्म
(d) टपवमा
10. एस्केहेलमिन्थीज फाइलम का जन्तु है
(a) पिन वर्म
(b) टेपवर्म
(c) फ्लेट वर्म
(d) फ्लूक।
11. आर्थोपोडा का उदाहरण है
(a) केचुआ।
(b) जोंक
(c) मकड़ी।
(d) एस्केरिस
12. कौन मोलस्क फाइलम का जन्तु है
(a) केंचुआ।
(b) ऑक्टोपस
(c) कॉकरोच
(d) घरेलू मक्खी
13. उपफाइलम वर्टीब्रेटा का उदाहरण है
(a) डोलियोलम
(b) मेंढक
(c) ब्रान्कियोस्टोमा
(d) पायरोसोमा।

14. गिल्स के द्वारा श्वसन किसमें नहीं होता
(a) टोरपीडो में
(b) डॉगफिश में
(c) छिपकली में
(d) सी हॉर्स में।
15. गर्म रुधिर वाला जन्तु है
(a) गौरेया
(b) साँप
(c) मेंढक
(d) डॉग फिश
16. शीत रुधिर वाला जन्तु है
(a) कबूतर
(b) मेंढक
(c) कौआ
(d) बकरी।
17. तीन प्रकोष्ठों वाला हृदय पाया जाता है|
(a) फ्लाइंग लिजार्ड में
(b) एनावास में
(c) डॉग फिश में
(d) उपर्युक्त सभी में।
18. चार प्रकोष्ठों वाला हृदयं पाया जाता है
(a) उल्लू में
(b) चिम्पैंजी में
(c) कुत्ते में
(d) उपरोक्त सभी में।
19. स्तनधारी वर्ग का जन्तु है
(a) उल्लू
(b) चिम्पैंजी
(c) कौआ
(d) इनमें में से कोई भी नहीं।
20. मनुष्य का वैज्ञानिक नाम है
(a) एबेना
(b) होमोसेपियन्स
(c) पेन्थरालियो
(d) इनमें से कोई नहीं।
21. द्विपदीय नाम पद्धति को शुरू किया
(a) ई. एच. हीकल ने
(b) रॉबर्ट व्हिटेकर ने
(c) केरोलस लीनियस ने
(d) डार्विन ने।

22. जुड़े हुए पैर पाए जाते हैं
(a) एनीलिडा में
(b) आर्थोपोडा में
(c) सीलेण्टरेटा.में
(d) इनमें से कोई नहीं।
23. अप्रत्यक्ष जननांगे पाये जाते हैं
(a) जिम्नोस्पर्म में
(b) एंजियोस्पर्म में
(c) टेरिडोफाइट में
(d) इनमें से कोई नहीं।
24. किसमें थैलस नहीं पाया जाता
(a) शैवाल
(b) मॉस
(c) कवक
(d) लाइकेन।
25. शैवाल है
(a) एस्परजीलस
(b) पेनीसिलियम
(c) एगारीकस
(d) यूलोथ्रिक्स।
26. यूलोथिक्स है
(a) एल्गी
(b) कवक
(c) टेरिडोफाइट
(d) ब्रायोफाइटा
27. ब्रायोफाइटा का उदाहरण है
(a) नील हरित शैवाल
(b) जीवाणु
(c) लिवर वर्ट
(d) फर्न
28. टेरिडोफाइटा का उदाहरण है
(a) यूलोथिरेक्स
(b) जीवाणु
(c) लिवर वर्ट।
(d) फर्न

29. जिम्नोस्पर्म है
(a) हॉर्नवर्ट
(b) फर्न
(c) लिवरवर्ट
(d) साइकस।
30. एन्जियोस्पर्म है
(a) मटर
(b) हॉर्नवर्ट
(c) फर्न
(d) मॉस।
31. पेनिसीलियम सदस्य है
(a) शैवाल का
(b) कवक का
(c) टेरियोफाइट का
(d) फेनरोगेम का।
32. प्रोटोजोआ है-
(a) सी एनीमोन।
(b) स्पांज
(c) यूग्लीना
(d) टेपवर्म
33. नग्न बीज पाये जाते हैं
(a) जिम्नोस्पर्म में
(b) एंजियोस्पर्म में
(c) टेरिडोफाइट में
(d) इन सभी में।
34. बीज फल के अन्दर पाये जाते हैं
(a) जिम्नोस्पर्म में
(b) एंजियोस्पर्म में
(c) टेरिडोफाइट में
(d) इन सभी में।

35. द्विकोष्ठकीय हृदय पाया जाता है
(a) मछली में
(b) साँप में
(c) मेंढक में
(d) छिपकली में।
36. त्रिकोष्ठीय हृदय पाया जाता है
(a) साँप में
(b) मेंढक में
(c) छिपकली में
(d) इन सभी में
37, चार कोष्ठकीय हृदय पाया जाता है
(a) मेंढक में
(b) छिपकली में
(c) मगरमच्छ में
(d) उपर्युक्त में से किसी में नहीं।
38. चार कोष्ठकीय हृदय पाया जाता है
(a) मगरमच्छ में
(b) मनुष्य में
(c) कुत्ते में
(d) उपर्युक्त सभी में।
39. पक्षी वर्ग को जन्तु नहीं है|
(a) मोर
(b) चमगादड़
(c) कबूतर
(d) गौरैया।
40. अंडज है
(a) मछली
(b) मेंढक
(c) साँप
(d) ये सभी।

41. शिशु को जन्म देते हैं
(a) स्तनपायी
(b) सरीसृप
(c) पक्षी
(d) ये सभी।
उत्तरमाला
- (a)
- (b)
- (c)
- (a)
- (d)
- (a)
- (d)
- (d)
- (b)
- (a)
- (c)
- (b)
- (b)
- (c)
- (a)
- (b)
- (a)
- (d)
- (b)
- (b)
- (c)
- (b)
- (c)
- (b)
- (d)
- (a)
- (c)
- (d)
- (d)
- (a)
- (b)
- (c)
- (a)
- (b)
- (a)
- (d)
- (c)
- (d)
- (b)
- (d)
- (a)
We hope the UP Board Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms (जीवों में विविधता) help you. If you have any query regarding UP Board Solutions for Class 9 Science Chapter 7 Diversity in Living Organisms (जीवों में विविधता), drop a comment below and we will get back to you at the earliest.
![]()
![]()
![]()
![]()







