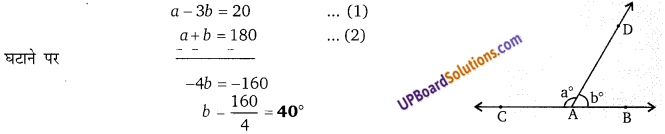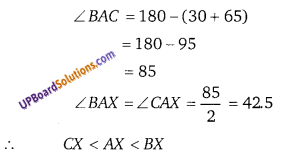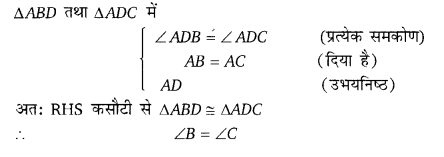Safia

Balaji Class 10 Maths Solutions Chapter 14 Statistics Ex 14.2 सांख्यिकी

प्रश्न 1.
निम्नलिखित सारणी के लिए, प्रत्येक घर के व्यय (₹ में) का माध्य, लघु विधि द्वारा ज्ञात कीजिए।

हलः

प्रश्न 2.
निम्नलिखित सारणी का समान्तर माध्य, पद विचलन विधि द्वारा ज्ञात कीजिए।

हलः

प्रश्न 3.
निम्नलिखित सारणी का समान्तर माध्य, पद विचलन विधि द्वारा ज्ञात कीजिए।

हलः

प्रश्न 4.
निम्नलिखित आँकडों का समान्तर माध्य ज्ञात कीजिए।

(NCERT Exemplar)
हलः

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 9 Constructions Ex 9.1 रचनाएँ

प्रश्न 1.
एक 10 सेमी लम्बी रेखा को 3 : 2 के अनुपात में अन्त:विभाजित करें।
हलः
रचना के चरणः
चरण 1: एक रेखाखण्ड (UPBoardSolutions.com) AB = 10 सेमी खींचिए।

चरण 2: एक किरण AX, एक न्यूनकोण ∠ BAX बनाते हुए खींची।
चरण 3: AX के सापेक्ष बिन्दुओं  5 (= 3 + 2) A₁, A₂, A₃, A₄ तथा A₅ को इस प्रकार चिन्हित कीजिए कि
AA₁ = A₁A₂ = … = A₄A₅
चरण 4: A₅B को मिलाया।
चरण 5: बिन्दु A₃ से, A₃P || A₅B खींचा जो रेखाखण्ड AB को बिन्दु P पर काटता है। स्पष्टतः P वह बिन्दु है जो रेखाखण्ड AB को 3 : 2 के अनुपात में विभाजित करता है।

प्रश्न 2.
एक ∆ ABC की रचना कीजिए जिसमें AB = 4 सेमी, BC = 5 सेमी, AC = 6 सेमी, ∆ ABC के समरूप एक त्रिभुज की रचना कीजिए जिसकी प्रत्येक भुजा, ∆ ABC की संगत भुजा की [latex]\frac{2}{3}[/latex] है। (NCERT)
हलः
रचना के चरणः

चरण 1: एक रेखा BC = 5 सेमी खींची।
चरण 2: B को केन्द्र मानकर’ 4 सेमी त्रिज्या का एक चाप खींचा।
चरण 3: पुन:C को केन्द्र मानकर 6 सेमी (UPBoardSolutions.com) त्रिज्या का एक दूसरा चाप खींचा जो पहले चाप को बिन्दु A पर काटता है।
चरण 4: ∆ABC बनाने के लिए रेखाखण्ड AB तथा AC को मिलाया।
चरण 5: रेखाखण्ड BC के नीचे एक न्यूनकोण ∠CBX खींचा।
चरण 6: रेखाखण्ड BX तीन बिन्दुओं B₁, B₂, B₃ को इस प्रकार चिन्हित किया कि
BB₁ = B₁B₂ = B₂B₃
चरण 7: B₃C को मिलाया।
चरण 8: बिन्दु B₂ से B₂D ||B₃C खींची जोकि रेखाखण्ड BC को बिन्दु D पर काटती है।
चरण 9: बिन्दु D से, DE ||CA खींची जोकि AB को बिन्दु E पर काटती है।
अत: ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 3.
एक ∆ ABC की रचना कीजिए जिसमें BC = 7 सेमी, ∠B = 45°, ∠A = 105° हैं। एक ऐसे त्रिभुज की रचना कीजिए जो ∆ ABC के समरूप हो तथा जिसकी भुजाएँ, ∆ ABC की संगत भुजाओं की। [latex]\frac{4}{3}[/latex] है। (NCERT)
हलः
रचना के चरणः

चरण 1: एक सीधी रेखा BC = 7 सेमी खींची।
चरण 2: बिन्दु B से, एक न्यूनकोण ∠CBX = 45° खींचा और कोण BCY = 180° – (45° + 105°) = 30° खींचा।
चरण 3: ∆ABC प्राप्त करने के लिए (UPBoardSolutions.com) BX को मिलाया तथा CY, इसे बिन्दु A पर प्रतिच्छेद करता है।
चरण 4: ∆ABC के शीर्ष A के सम्मख एक न्यूनकोण CB खींचा।
चरण 5: रेखाखण्ड BZ पर चार बिन्दुओं B₁, B₂, B₃, B₄ को इस पर चिन्हित करते हैं कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄
चरण 6: बिन्दु B₃ से C को मिलाया।
चरण 7: B₃C के समान्तर एक रेखा B₄C’ खींची जोकि रेखाखण्ड BC को बिन्दु C’ पर प्रतिच्छेद करती है।
चरण 8: CA के समान्तर बिन्दु C’ से जाती हुई एक रेखा खींची जोकि बाहृय रेखाखण्ड BA को बिन्दु A’ पर प्रतिच्छेद करती है।
अत: ∆A BC’ ही अभीष्ट त्रिभुज है, जोकि ∆ABC के समरूप है।

प्रश्न 4.
एक समकोण त्रिभुज की रचना कीजिए जिसमें भुजाएँ (कर्ण को छोडकर ) 5 सेमी तथा 4 सेमी हैं। फिर एक, दूसरे त्रिभुज की रचना कीजिए जिसकी भुजाएँ, दिए गए त्रिभुज की [latex]\frac{5}{3}[/latex] गुनी है।
हलः
रचना के चरणः

चरण 1: BC = 5 सेमी की एक रेखा खींचिए।
चरण 2: B पर एक समकोण बनायें और AB = 4 सेमी काट लें।
चरण 3: AC को मिला दें तो ∆ ABC दिया गया समकोण त्रिभुज है।
चरण 4: B से एक न्यूनकोण ∠CBY ‘नीचे की ओर बनायें।
चरण 5: BY पर 5 बिंदुओं B₁, B₂, B₃, B₄ तथा B, इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
चरण 6: B₃C को मिला दे।
चरण 7: बिंदु B₅ से B₅D||B₃C (UPBoardSolutions.com) खींचे जो BC के बढ़े भाग को D पर काटे।
चरण 8: D से, DE || CA खींचे BA के बढ़े भाग को E पर काटे।
तब ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 5.
एक ∆ PQR की रचना कीजिए जिसकी भुजाएँ QR = 7 सेमी, PQ = 6 सेमी तथा ∠PQR = 60° फिर एक, दूसरे त्रिभुज की रचना कीजिए जिसकी भुजाएँ, ∆ PQR की संगत भुजाओं की [latex]\frac{3}{5}[/latex] है
हलः
रचना के चरणः

चरण 1: PQ = 6 सेमी की सरल रेखा खींचें।
चरण 2: बिन्दुQ, से ∠ PQY = 60° बनायें और QR = 7 सेमी काटे।
चरण 3: PR को मिला दे। ∆ PQR ही अभीष्ट त्रिभुज है।
चरण 4: P से एक किरण PX नीचे की ओर एक न्यूनकोण ∠QPX बनाते हुए खींचे।
चरण 5: PX पर पाँच बिंदुओं (UPBoardSolutions.com) P₁, P₂,P₃, P₄ और P₅ इस प्रकार अंकित करें । कि
PP₁ = P₁P₂ = P₂P₃ = P₃P₄ = P₄P₅
चरण 6: P₅ को Q से मिलायें।
चरण 7: P₃ से P₃Q’ ||P₅Q खींचे जो PQ को Q’ पर प्रतिच्छेद करें।
चरण 8: Q’ से Q R’ ||QR खींचे जो PR को R’ पर प्रतिच्छेद करती है
तब ∆ PQ’ R’ ही अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ PQR की भुजाओं की [latex]\frac{3}{5}[/latex] है।

प्रश्न 6.
एक समद्विबाहु त्रिभुज की रचना कीजिए जिसका आधार 8 सेमी तथा ऊँचाई 4 सेमी है तथा तब एक ऐसे त्रिभुज की रचना कीजिए, जिसकी भुजाएँ दिए गए, समद्विबाहु त्रिभुज की संगत भुजाओं की [latex]\frac{3}{2}[/latex] गुनी है   (NCERT)
हलः
रचना के चरणः

चरण 1: BC = 8 सेमी की एक रेखा खींचिए।
चरण 2: B पर एक समकोण बनाइयें और AB = 4 सेमी काट लें।
चरण 3: AC को मिला दें तो ∆ ABC दिया गया समकोण त्रिभुज है।
चरण 4: B से एक न्यूनकोण ∠CBY नीचे की ओर बनाइयें।
चरण 5: BY पर तीन बिंदुओं (UPBoardSolutions.com) B₁, B₂, B₃ इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃
चरण 6: B₂C को मिला दें।
चरण 7: बिंदु B₃ से B₃D||B₂C खींचे जो BC के बढ़े भाग को D पर काटे।
चरण 8: D से, DE || CA खींचे BA के बढ़े भाग को E पर काटे।
तब ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 7.
एक त्रिभुज की रचना कीजिए जिसकी भुजाएँ 5 सेमी, 5.5 सेमी तथा 6.5 सेमी हैं। तब एक, दूसरे त्रिभुज की रचना कीजिए जिसकी भुजाएँ, दिए गए त्रिभुज की भुजाओं की [latex]\frac{3}{5}[/latex] गुनी है।
हलः
रचना के चरणः

चरण 1: BC = 5.5 सेमी का एक रेखाखण्ड खींचिए।
चरण 2: B को केन्द्र मानकर 5 सेमी त्रिज्या का एक चाप खींचें।
चरण 3: C को केन्द्र मानकर 6.5 सेमी त्रिज्या का एक दूसरा चाप खींचें जो पहले चाप को A पर प्रतिच्छेद करे।
चरण 4: AB और AC को मिला दें। इस तरह ∆ ABC प्राप्त हुआ।
चरण 5: BC के नीचे एक न्यूनकोण (UPBoardSolutions.com) ∠CBX बनायें।
चरण 6: BX पर पाँच बिंदुओं B₁, B₂, B₃, B₄, B₅ इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅
चरण 7: B₅C को मिला दें।
चरण 8: बिन्दु B₃ से B₃D||B₅C खींचें जो BC से D पर मिले।
चरण 9: D से, DE || CA खींचें BA को E पर मिले।
तब ∆EBD अभीष्ट त्रिभुज है जिसकी प्रत्येक भुजा ∆ABC की संगत भुजाओं की [latex]\frac{3}{5}[/latex] गुनी है।

प्रश्न 8.
एक त्रिभुज ABC की रचना कीजिए जिसमें BC = 6 सेमी, AB = 5 सेमी तथा ∠ABC = 60° तब एक ऐसा त्रिभुज बनाइए जिसकी भुजाएँ, ∆ ABC की संगत भुजाओं का [latex]\frac{3}{4}[/latex] वाँ भाग हो। (NCERT)
हलः
रचना के चरणः

चरण 1: AB = 5 सेमी की सरल रेखा खींचें।
चरण 2: बिन्दु B, से ∠ ABY = 60° बनायें और BC = 6 सेमी काटे।
चरण 3: AC को मिला दें। ∆ ABC ही अभीष्ट त्रिभुज है।
चरण 4: A से एक किरण AX नीचे की ओर एक न्यूनकोण ∠ BAX = 60° बनाते हुए खींचे।
चरण 5: AX पर चार बिंदुओं (UPBoardSolutions.com) A₁, A₂, A₃ और A₄ इस प्रकार अंकित करें कि
AA₁ = A₁A₂ = A₂A₃ = A₃A₄
चरण 6: A₄B को मिलायें।
चरण 7: A₃ से A₃B’ ||A₄B खींचें जो AB को B’ पर प्रतिच्छेद करें।
चरण 8: B’ से B’C’ ||BC खींचें जो AC को C’ पर प्रतिच्छेद करती है तब ∆ AB’C’ ही अभीष्ट त्रिभुज है जिसकी भुजाएँ ∆ ABC की भुजाओं की [latex]\frac{3}{4}[/latex] है।

प्रश्न 9.
एक समकोण त्रिभुज की रचना कीजिए जिसमें भुजाओं (कर्ण को छोड़कर) की लम्बाई 8 सेमी तथा 6 सेमी हैं तब एक, दूसरा त्रिभुज बनाइए जिसकी भुजाएँ पहले त्रिभुज की संगत भुजाओं की [latex]\frac{3}{4}[/latex] गुनी है।
हलः
रचना के चरणः

चरण 1: BC = 8 सेमी की एक रेखा खींचिए।
चरण 2: B पर एक समकोण बनाइयें और AB = 6 सेमी काट लें।
चरण 3: AC को मिला दें तो ∆ ABC दिया गया समकोण त्रिभुज है।
चरण 4: B से एक न्यूनकोण ∠ CBY नीचे की ओर बनाइये।
चरण 5: BY पर चार बिंदुओं (UPBoardSolutions.com) B₁, B₂, B₃ तथा B₄ इस प्रकार अंकित करें कि
BB₁ = B₁B₂ = B₂B₃ = B₃B₄
चरण 6: B₄C को मिला दे।
चरण 7: बिन्दु B₃ से B₃D||B₄C खींचें जो BC को D पर प्रतिच्छेद करे।
चरण 8: D से, DE || CA खींचे, जो BA को E पर प्रतिच्छेद करे। तब ∆EBD अभीष्ट त्रिभुज है।

प्रश्न 10.
एक समकोण त्रिभुज ABC की रचना कीजिए जिसमें AB = 6 सेमी, BC = 8 सेमी तथा ∠B = 90° तथा बिन्दु B से रेखा AC पर एक लम्ब BD डाले तथा बिन्दुओं B,C तथा D से गुजरने वाला एक वृत्त खींचा गया। A से इस वृत्त पर स्पर्श रेखायें खींचें।
हलः

यहाँ एक समकोण ∆ABC है जिसमें AB = 6 सेमी, BC = 8 सेमी तथा ∠B = 90° BD, AC पर लम्ब है।
हमे बिन्दु A से वृत्त BDC पर दो स्पर्श रेखायें खींचनी हैं। यहाँ रचना के चरण निम्नलिखित हैं
चरण 1: BC = 8 सेमी और AB =.6 सेमी के रेखाखण्ड खींचे जोकि एक-दूसरे पर लम्ब हों।
चरण 2: AC को मिला दें, इस प्रकार ∆ ABC ही अभीष्ट समकोण त्रिभुज है।
चरण 3: BC के मध्य बिन्दु (UPBoardSolutions.com) F को केन्द्र लेकर FB = 4 सेमी त्रिज्या का एक वृत्त खींचें जो AC को D पर काटता है तथा B, C तथा D से होकर गुजरता है।
चरण 4: A को केन्द्र मानकर 6 सेमी त्रिज्या का चाप खींचें जो वृत्त को E पर काटता है।
चरण 5: AE को मिला दें।
तब AE एक अभीष्ट स्पर्श रेखा है तथा AB पहले ही B पर स्पर्श रेखा है।

प्रश्न 11.
8 सेमी लम्बाई का एक रेखाखण्ड AB खींचे। A को केन्द्र मानकर, 4 सेमी त्रिज्या का एक वत्त खींचे तथा B को केन्द्र मानकर एक 3 सेमी त्रिज्या का दूसरा वृत्त खींचें। प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से स्पर्श रेखायें खींचे। (NCERT)
हलः

दिया गया रेखाखण्ड AB = 8 सेमी। दो वृत्त जिनके केन्द्र A और B तथा त्रिज्यायें क्रमशः 4 सेमी और 3 सेमी हैं।
हमें प्रत्येक वृत्त पर दूसरे वृत्त के केन्द्र से दो-दो स्पर्श रेखायें खींचनी हैं।
रचना के चरण निम्नलिखित हैं:
चरण 1. AB = 8 सेमी का एक रेखाखण्ड खींचें।
चरण 2. A केन्द्र से 4 सेमी त्रिज्या का एक वृत्त खींचें।
चरण 3. B केन्द्र से 3 सेमी त्रिज्या का दूसरा वृत्त खींचें।
चरण 4. रेखाखण्ड AB को (UPBoardSolutions.com) समद्विभाग करें। माना कि L, AB का मध्य बिंदु है।
चरण 5. L को केन्द्र मानकर, AL त्रिज्या का एक बिन्दुवत् वृत्त खींचें। यह दोनों वृत्तों (A केन्द्र वाले तथा B केन्द्र वाले वृत्तों को) को P, Q, R तथा S बिन्दुओं पर काटते हैं।
चरण 6. AP, AQ, BR तथा BS को मिला दें।
तब प्राप्त रेखायें ही अभीष्ट स्पर्श रेखायें हैं।

प्रश्न 12.
3.5 सेमी त्रिज्या के एक वृत्त के बिन्दु P से दो स्पर्श रेखायें खींचे जिसकी वृत्त के केन्द्र से दूरी 6.2 सेमी है।
हलः

यहाँ 3.5 सेमी त्रिज्या वाले एक वृत्त के केन्द्र से 6.2 सेमी दूरी पर एक बिन्दु P है। हमें दिये गये बिन्दु P से वृत्त की दो स्पर्श रेखायें खींचनी हैं।
रचना के चरण निम्नलिखित हैं:
चरण 1. O के केन्द्र से 3.5 सेमी त्रिज्या का वृत्त खींचें।
चरण 2. OP को मिला दें और इसे समद्विभाग करें। मान लें कि M, OP का मध्य बिन्दु है।
चरण 3. M को केन्द्र मानकर, (UPBoardSolutions.com) MP त्रिज्या का एक वृत्त खींचे, जो वृत्त को बिन्दुओं A तथा B पर काटता है।
चरण 4. PA तथा PB को मिलाएँ।
तब PA और PB ही वृत्त पर दो अभीष्ट स्पर्श रेखायें हैं।

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 14 Statistics Ex 14.1 सांख्यिकी

Ex 14.1 Statistics लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 1.
एक कक्षा में प्रतिदिन अनुपस्थित विद्यार्थियों की संख्या के 120 दिनों के बारे में निम्नलिखित बारंबारता सारणी में दिया गया है।

प्रतिदिन अनुपस्थित विद्यार्थियों की संख्या का माध्य ज्ञात कीजिए।
हलः

समान्तर माध्य [latex]\overline{x}=\frac{\Sigma f x}{n}=\frac{423}{120}[/latex] = 3.53

प्रश्न 2.
निम्नलिखित सारणी का समान्तर माध्य ज्ञात कीजिए।

हलः

प्रश्न 3.
निम्नलिखित वितरण में, एक महीने में एक फैक्ट्री के 160 मजदूरों की दुर्घटनाओं की संख्या दी गई है। दुर्घटनाओं की औसत संख्या ज्ञात कीजिए।

हलः

प्रश्न 4.
यदि निम्नलिखित आँकडों का माध्य 6 है तो p का मान ज्ञात कीजिए।

हलः

Ex 14.1 Statistics दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 5.
निम्नलिखित सारणी में 108 छात्रों के अंक दर्शाये गये हैं। अंकों के समान्तर माध्य की गणना कीजिए।

हलः

प्रश्न 6.
एक फैक्ट्री के मजदूरों की आयु नीचे दी गई है। मजदूरों की औसत आयु ज्ञात कीजिए।

हलः

प्रश्न 7.
कक्षा 10 के 80 विद्यार्थियों के गणित में अंको को नीचे दर्शाया गया है। गणित में औसत अंको की गणना कीजिए।

हलः

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 10 Lines and Angle Ex 10.1 रेखाएँ एवं कोण

Ex 10.1 Lines and Angle अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि दो पूरक कोणों के बीच का अनुपात 2 : 3 है। तब कोण ज्ञात कीजिए।
हलः
माना दो पूरक (कोटिपूरक) कोण = 2x, 3x
∵ दो पूरक कोणों का योग 90° होता है।
∴ 2x + 3x = 90°
5x = 90
x = [latex]\frac{90}{5}[/latex] = 18
∴ दो पूरक कोण = 2 × 18 =36° तथा 3 × 18 = 54°

प्रश्न 2.
यदि दो सम्पूरक कोणों के बीच का अन्तर 40° है। तब कोण ज्ञात कीजिए।
हलः
माना दो सम्पूरक कोण = x,
180 – x दो सम्पूरक कोणों का अन्तर = 40
x – (180 – x) = 40
x – 180 + x = 40
2x = 220
x = [latex]\frac{220}{2}[/latex] = 110
सम्पूरक कोण = 110°, 70°

प्रश्न 3.
एक त्रिभुज का बाह्य कोण 110° है और इसके दो अन्तः विपरीत कोण बराबर हैं। तब ये कोण ज्ञात कीजिए।
हलः
माना ∠ABC = ∠BAC = x

∵ A का बहिष्कोण, अपने सम्मुख अन्तः कोणो के योग के बराबर होता है
∴ ∠ACD = ∠BAC + ∠ABC
110 = x + x
110 = 2x
[latex]\frac{110}{2}[/latex] = x
∴ x = 55°

प्रश्न 4.
यदि एक त्रिभुज का एक कोण, अन्य दो कोणों के योग के बराबर है तब त्रिभुज का नाम बताइये?
हलः
माना
∆ के कोण = x, y, z
∵ x + y = z (दिया है) ………………… (i)
∵ ∆ के तीनों कोणो का योग = 180°
x + y + z = 180°
समीकरण (1) से,
z + z = 180°
2z = 180°
z = [latex]\frac{180}{2}[/latex] = 90
∴ यह त्रिभुज एक समकोण त्रिभुज है।

प्रश्न 5.
एक त्रिभुज के कोणों का अनुपात 2 : 3 : 4 है। तब त्रिभुज का नाम बताइए।
हलः
माना ∆ के तीन कोण = 2x, 3x, 4x
∆ के तीनो कोणो का योगफल = 180°
2x + 3x +4x = 180°
9x = 180°
x = [latex]\frac{180}{9}[/latex] = 20
∴ ∆ के कोण = 40°, 60°, 80°
∴ यह एक न्यूनकोण ∆ है।

प्रश्न 6.
यदि एक त्रिभुज का एक कोण 110° है तब अन्य दो कोणों के समअर्द्धको के बीच का कोण ज्ञात कीजिए।
हल:
∆ABC में माना
∠A = x
∠C = y
∠B = 110°

∠A + ∠B + ∠C = 180°
⇒ x + 110 + y = 180
⇒ x + y = 180 – 110 = 70
∵ [latex]\frac{x}{2}+\frac{y}{2}=\frac{70}{2}[/latex] = 35
माना ∠A व ∠C के समअर्द्धको के बीच का कोण = z
तब [latex]\frac{x}{2}+\frac{y}{2}+z[/latex] = 180°
समीकरण (1) से,
35 + z = 180°
z = 180 – 35 = 145°

Ex 10.1 Lines and Angle लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 7.
निम्नलिखित को परिभाषित कीजिए
(i) कोण
(ii) एक कोण का अभ्यन्तर
(iii) न्यूनकोण
(iv) अधिक कोण
(v) सम्पूरक कोण
(vi) पूरक कोण
हलः
(i) कोण- दो रेखाओं के परस्पर झुकाव से बनने वाली आकृति को कोण कहते है। जैसे AB व AC दो किरणें हैं। AB तथा AC के झुकाव से ∠BAC बनता है।

(ii) एक कोण का अभ्यन्तर (Interior of an Angle)- समतल का वह भाग जो किरण AB व AC के बीच स्थित है। ∠BAC का अभ्यन्तर कहलाता है।
(iii) न्यूनकोण- 90° से छोटे या कम कोण को न्यूनकोण कहते हैं।
(iv) अधिक कोण- 90° से बड़े कोण को अधिक कोण कहते हैं।
(v) सम्पूरक कोण- जिन दो कोणों का योग 180° होता है, सम्पूरक कोण कहलाते हैं जैसे 40° का सम्पूरक कोण 140° है।
(vi) पूरक कोण- जिन दो कोणों का योग 90° होता है, पूरक कोण कहलाते हैं जैसे 40° का पूरक कोण 50° होता है।

प्रश्न 8.
कौन-सा कोण स्वयं का कोटिपूरक होता है?
हलः
माना कोण = x
पूरक कोण = x
∴ x + x = 90
2x = 90 ⇒ x = [latex]\frac{90}{2}[/latex] = 45
∴ कोण = 45° स्वयं का कोटिपूरक होता है।

प्रश्न 9.
कौन-सा कोण स्वयं का सम्पूरक होता है?
हलः
माना कोण = x
सम्पूरक कोण = x
∴ x + x = 180°
2x = 180 ⇒ x = [latex]\frac{180}{2}[/latex] = 90°
∴ कोण = 90° स्वयं का सम्पूरक कोण होता है।

प्रश्न 10.
निम्नलिखित प्रत्येक के सम्पूरक कोण का मापन ज्ञात कीजिए।
(i) 54°
(ii) 1300
(iii) 1720
हलः
(i) 54° का सम्पूरक कोण = 180 – 54 = 126°
(ii) 130° का सम्पूरक कोण = 180 – 130 = 50°
(iii) 172° का सम्पूरक कोण = 180 – 172 = 8°

प्रश्न 11.
निम्नलिखित प्रत्येक कोण का पूरक कोण लिखिए।
(i) 77°
(ii) 65°10’20”
(iii) 485942″
हलः
(i) 77° का पूरक कोण = 90 – 77 = 13°
(ii) 65°10′ 20″ का पूरक कोण = 90 – (65°10′ 20″) = 24°49’40”
(iii) 48°59’42” का पूरक कोण = 90 – (48°59’42”) =41°0’18”

प्रश्न 12.
यदि एक कोण, उसके पूरक में, 10° का अन्तर है। कोण ज्ञात कीजिए।
हलः
माना कोण = x
पूरक कोण = 90 – x
x – (90 – x) = 10
x – 90 + x = 10
2x = 100
x = 50°
∴ कोण = 50°

प्रश्न 13.
यदि कोण (2x – 10)° और (x – 5)° पूरक कोण है तब x ज्ञात कीजिए।
हल:
∵ कोण (2x – 10) तथा (x – 5) पूरक कोण है।
∴ 2x – 10 + x – 5 = 90
3x = 90 + 15
3x = 105
x = [latex]\frac{105}{3}[/latex] = 35°

प्रश्न 14.
यदि एक कोण का सम्पूरक, उसके पूरक के तीन गुने के बराबर है। तो कोण का मापन ज्ञात कीजिए।
हलः
माना कोण = x
पूरक कोण = 90 – x
सम्पूरक कोण = 180 – x
प्रश्नानुसार, 180 – x = 3(90 – x)
180 – x = 270 – 3x
2x = 90
x = [latex]\frac{90}{2}[/latex] = 45
कोण = 45°

प्रश्न 15.
दो सम्पूरक कोण 3 : 7 के अनुपात में हैं, कोण ज्ञात कीजिए।
हलः
माना
पहला कोण = 3x
दूसरा कोण = 7x
प्रश्नानुसार, 3x + 7x = 180°
10x = 180°
x = [latex]\frac{180}{10}[/latex] = 18
∴ पहला कोण = 3 × 18 = 54°
दूसरा कोण = 7 × 18 = 126°

Ex 10.1 Lines and Angle लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 16.
दी गयी आकृति में, OA और OB विपरीत किरणें हैं। x का मान ज्ञात कीजिए तथा ∠AOC तथा ∠BOD भी ज्ञात कीजिए।
हलः

∠AOB = 180°
∠AOC + ∠COD + ∠BOD = 180°
x + 20 + x + x + 10 = 180
3x + 30 = 180
3x = 180 – 30
3x = 150
x = [latex]\frac{150}{3}[/latex] = 50°
∴ ∠AOC = 50 + 20 = 70°
∠BOD = 50 + 10 = 60°

प्रश्न 17.
चित्र में, AB और AC विपरीत किरणें हैं। यदि (a – 3b) = 20° तो कोण a और b ज्ञात कीजिए।
हल:
∵ हम जानते हैं कि किरण CAB में a + b = 180° है।

समीकरण (1) में b का मान रखने पर a – 3 × 40 = 20
a = 20+ 120
a = 140°

प्रश्न 18.
दी गई आकृति में, दो सरल रेखाएं AB और CD एक बिन्दु O पर प्रतिच्छेद करती है। यदि ∠BOD = x° और ∠AOD = (4x – 5)° तो x का मान ज्ञात कीजिए तथा निम्न को ज्ञात कीजिए।

(i) ∠BOD
(ii) ∠AOD
(iii) ∠AOC
(iv) ∠BOG
हलः
∠ BOD + ∠AOD = 180
x + 4x – 5 = 180°
5x = 180+ 5
5x = 185
x = [latex]\frac{185}{5}[/latex] = 37°
(i) ∠BOD = 37°
(ii) ∠AOD = 4x – 5 = 4 × 37 – 5 = 148 – 5 = 143°
(iii) ∠AOC = ∠BOD = 37° (शीर्षाभिमुख कोण)
(iv) ∠BOC = ∠AOD = 143° (शीर्षाभिमुख कोण)

प्रश्न 19.
दी गयी आकृति में, AOC एक रेखा है। x का मान ज्ञात कीजिए।

हल:
AOC एक सरल रेखा है।
70 + 2x = 180°
2x = 180 – 70 = 110
x = [latex]\frac{110}{2}[/latex] = 55°

प्रश्न 20.
दी गयी आकृति में, BAC एक रेखा है। x का मान ज्ञात कीजिए तथा ∠CAE व ∠BAD ज्ञात कीजिए।

हलः
∴ बिन्दु A पर बने तीनों कोणों का योग = 180°
∴ 3x – 5 + 55 + x + 20 = 180°
4x + 70 = 180
4x = 180 – 70 = 110
x = [latex]\frac{110}{4}[/latex] = 27°30′
∴ ∠CAE = (3x 27°30′ – 5)
= 82°30′ – 5°= 77°30′
∴ ∠BAD = 27°30′ + 20 = 4730′

प्रश्न 21.
दी गयी आकृति में, POS एक रेखा है। x का मान ज्ञात कीजिए।

हल:
∵ POS एक सरल रेखा है।
∠POQ + ∠QOR + ∠ROS = 180°
60 + 4x + 40 = 180
4x = 180 – 100 = 80
x = [latex]\frac{80}{4}[/latex] = 20°

प्रश्न 22.
निम्न दी गयी आकृति में, तीन समरेखीय रेखायें एक बिन्दु O पर प्रतिच्छेद करती हैं। रुपीय कोण दर्शाये ( चित्र में) गये हैं। a, b, c और d के मान ज्ञात कीजिए।

हलः
∵ ∠b = 70° (शीर्षाभिमुख कोण)
∠c = 80° (शीर्षाभिमुख कोण)
∴ PQ एक सरल रेखा है।
∠a + ∠b + ∠c = 180°
∠a + 70 + 80 = 180°
∠a = 180° – 150° = 30°
∠d = ∠a = 30° (शीर्षाभिमुख कोण)

प्रश्न 23.
सभी में आसन्न कोणों के कितने युग्म है? दी गयी आकृति में इन्हें क्या नाम दे सकते हैं?

हलः
10 युग्म है, जो निम्न प्रकार है।
∠AOB तथा ∠BOC
∠AOB तथा ∠BOD
∠AOB तथा ∠BOE
∠AOC तथा ∠COD
∠AOC तथा ∠COE
∠AOD तथा ∠DOE
∠BOC तथा ∠COD
∠BOC तथा ∠COE
∠BOD तथा ∠DOE
∠COD तथा ∠DOE

प्रश्न 24.
चित्र में, यदि ∠AOC + ∠BOD = 284° तो सभी चार कोण ज्ञात कीजिए।

हलः
यदि ∠AOC + ∠BOD = 284°
माना ∠AOD = ∠BOC = x
∠AOC + ∠BOD + ∠AOD + ∠BOC = 360
284 + ∠AOD + ∠BOC = 360
∠AOD + ∠BOC = 360 – 284 = 76
∴ x + x = 76
2x = 76 ⇒ x = [latex]\frac{76}{2}[/latex] = 38°
∴ ∠AOC = 180° – 38 = 142°
∠BOD = 142° (शीर्षाभिमुख कोण)

प्रश्न 25.
चित्र में, ∠ACB एक रेखा इस प्रकार है कि ∠DCA = 5x और ∠DCB = 4x, x का मान ज्ञात कीजिए तथा ∠DCB और ∠DCA ज्ञात कीजिए।

हल:
∠ACB एक सरल कोण है।
∴ ∠ACD + ∠ BCD = 180
⇒ 5x + 4x = 180
⇒ 9x = 180
⇒ x = [latex]\frac{180}{9}[/latex] = 20
∴ ∠ BCD = 4x = 4 × 20 = 80°
तथा ∠ACD = 5x = 5 × 20 = 100°

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 12 Congruence of Triangles Ex 12.4 त्रिभुजों की सर्वांगसमता

प्रश्न 1.
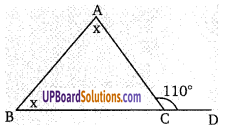
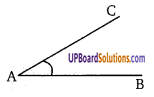
चित्र में, AB = AC तथा BC को बढ़ाने पर कोई बिन्दु D है तो सिद्ध कीजिए कि (NCERT Exemplar)
हलः
∵ AB = AC …(1)
∆ACD में ∠ACD अधिक कोण है
तथा ∠ADC न्यूनकोण है।

∴ अधिक कोण की सम्मुख भुजा बड़ी तथा न्यूनकोण की सम्मुख भुजा छोटी होती है।
∴ AD > AC
AD > AB (समीकरण (1) से)

प्रश्न 2.
एक त्रिभुज ABC में यदि ∠A = 45° और ∠B = 70° तब त्रिभुज की छोटी और बड़ी भुजा ज्ञात कीजिए।
हलः
∠C = 180 – (∠A + ∠B)
= 180 – (45 + 70)

= 180 – 115 = 65°
सबसे बड़ा कोण = 70°
सबसे छोटा कोण = 45°
∴ सबसे बडा कोण की सम्मुख भुजा AC सबसे बड़ी तथा सबसे छोटे कोण की सम्मुख भुजा BC सबसे छोटी है।

प्रश्न 3.
क्या हम 3 सेमी, 4 सेमी और 5 सेमी लम्बाई की भुजा वाला त्रिभुज खींच सकते हैं?
हल:
∵ 3+ 4 = 7 > 5, 4 + 5 > 3 तथा 3 + 5 > 4
∵ त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा है।
∴ ∆ की रचना सम्भव है।

प्रश्न 4.
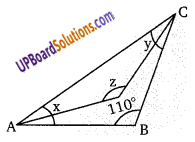
दिये गये चित्र में, AB = AC तो सिद्ध कीजिए कि AF > AE
हलः ::
AB = AC
∠B = ∠C … (1)

∠AFE = ∠CFD (शीर्षाभिमुख कोण) … (2)
∆ABD में, ∠AEF = ∠B + ∠EDB … (3)
बहिष्कोण समीकरण (2) व (3) से सिद्ध होता है।
∠AEF > ∠AFE
∴ AF > AE

प्रश्न 5.
एक त्रिभुज ABC में AB > AC, ∠B तथा ∠C के समद्विभाजक P पर मिलते हैं तो सिद्ध कीजिए कि BP > CP
हल:

प्रश्न 6.
सिद्ध कीजिए कि एक त्रिभुज का परिमाप, उसकी ऊँचाइयों के योग से बड़ा होता है।
हलः
एक ∆ABC में AM, BN तथा PC ∆ की ऊचाईयाँ है।
∆ABM में, ∠AMB समकोण है
∴ AB > AM … (1)

∆BNC में, ∠BNC समकोण है
BC > BN … (2)
∆APC में, ∠APC समकोण है
AC > PC … (3)
समीकरण (1) + (2) + (3) करने पर
AB + BC + AC > AM + BN + PC
∴ ∆ का परिमाप > ∆ की ऊँचाईयाँ

प्रश्न 7.
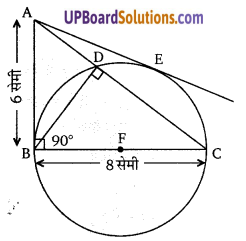
दिये गये चित्र में, O वृत्त का केन्द्र है तथा XY व्यास है। तो सिद्ध कीजिए कि XY > XZ
हल:
∵ XY व्यास है तथा XZ वृत्त की एक जीवा है
∵ वृत्त का व्यास, वृत्त की सबसे बड़ी जीवा होती है।
∵ XY > XZ

प्रश्न 8.
सिद्ध कीजिए कि त्रिभुज की सबसे बड़ी भुजा के सम्मुख कोण 60° से बड़ा होता है।
हल:
∆ABC में, AB = BC = AC
∴ ∠A = ∠B = ∠C = 60°
परन्तु यदि इनमें से एक भुजा बड़ी है तो दोनों भुजायें छोटी होगी तो सबसे बड़ी भुजा का सम्मुख कोण 60° से बड़ा होता है।

Ex 12.4 Congruence of Triangles विविध प्रश्नावली

Ex 12.4 Congruence of Triangles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
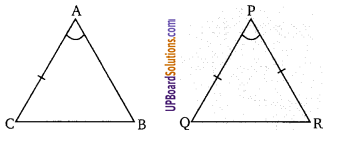
∆ABC तथा ∆PQR में, AB = PR तथा ∠A = ∠P तब SAS कथन द्वारा प्रतिबंध ज्ञात कीजिए कि दोनों त्रिभुज सर्वांगसम होंगे। (NCERT Exemplar)
हल:
∆ABC ≅ ∆PQR होगे यदि AC = PQ

प्रश्न 2.
संलग्न चित्र में, यह दिया है कि ∆ABD = ∆BAC अभिगृहित ज्ञात कीजिए जिसके द्वारा त्रिभुज सर्वांगसम हैं।
हलः
सर्वांगसमता की RHS कसौटी द्वारा।

प्रश्न 3.
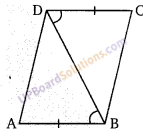
संलग्न चित्र में, यदि AB = DC, ∆ABD ≅ ∆CDB तब ∠ABD = ∠CDB को सिद्ध करने के लिए प्रयोग किए जाने वाले सर्वांगसमता नियम को ज्ञात कीजिए।
हल:
∆ABD ≅ ∆CDB होंगे सर्वांगसमता SAS कसौटी से।

प्रश्न 4.
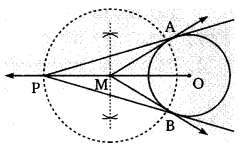
संलग्न चित्र में, यह दिया है कि ∆OAP ≅ ∆OBP अभिगृहित ज्ञात कीजिए जिसके द्वारा त्रिभुज सर्वांगसम है।
हल:

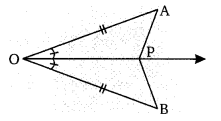
∆OAP तथा ∆OBP में,
OA = OB (दिया है)
∠AOP = ∠BOP (दिया है)
OP (उभयनिष्ठ)
सर्वांगसमता की SAS कसौटी से ∆OAP ≅ ∆OBP

प्रश्न 5.
∆PQR में, यदि ∠R > ∠Q तब निम्नलिखित में से कौन-सा एक सत्य है? (NCERT Exemplar)
(a) PR > PQ
(b) QR > PR
(c) PQ > PR
(d) इनमें से कोई नहीं
हलः

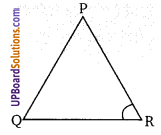
∆PQR में, ∠R > ∠Q तो PQ > PR
विकल्प (c) सही है।

प्रश्न 6.
यदि एक त्रिभुज की दो भुजाओं की लम्बाईयाँ 5 सेमी तथा 1.5 सेमी हैं। तब त्रिभुज की तीसरी भुजा की लम्बाई निम्न में से कौन-सी नहीं हो सकती है? (NCERT Exemplar)
(a) 3.4 सेमी
(b) 3.6 सेमी
(c) 3.8 सेमी
(d) 4.1 सेमी
हलः
∵ ∆ की रचना करने के लिए दो भुजाओं का योग हमेशा तीसरी भुजा से अधिक होना चाहिए।
∴ विकल्प (a) में 3.4 सेमी लेने पर त्रिभुज की रचना सम्भव नहीं है इसलिए ∆ की तीसरी भुजा 3.4 सेमी नहीं हो सकती।

प्रश्न 7.
∆AOC में तथा ∆XYZ में ∠A = ∠X, AO = XZ, AC = XY, तब सर्वांगसमता नियम ज्ञात कीजिए जिसके द्वारा ∆AOC ≅ ∆XZY
हल:
SAS कसौटी द्वारा।

प्रश्न 8.
संलग्न चित्र में, AD = BC तथा ∠BAD = ∠ABC तब ∠ACB ज्ञात D कीजिए।
हलः


SAS कसौटी से ∆ACB ≅ ∆ADB
∴ ∠ACB = ∠ADB

प्रश्न 9.
यदि दो समकोण त्रिभुज ABC और DEF क्रमश: B और E पर समकोण है जो RHS द्वारा सर्वांगसम है तब निम्न में से कौन-सा एक सत्य है?
(a) AC = DF
(b) AB = DE
(c) (a) और (b) दोनों सत्य हैं
(d) इनमें से कोई नहीं
हलः
विकल्प (c) सत्य है।

प्रश्न 10.
एक समकोण त्रिभुज में, एक न्यूनकोण अन्य का दोगुना है तब निम्न में से कौन-सा सत्य है?
(a) कर्ण = छोटी भुजा का दोगुना
(b) कर्ण = [latex]\frac{3}{4}[/latex] × छोटी भुजा
(c) एक न्यूनकोण 40° है
(d) इनमें से कोई नहीं
हलः
कर्ण = छोटी भुजा का दो गुना। अत: विकल्प (a) सही है।

प्रश्न 11.
∆ABC में, यदि AD माध्यिका है तब निम्न में से कौन-सा एक सत्य है?
(a) AB + AC > 2AD
(b) AB + AC < 2 AD
(c) AB + AC = 2 AD
(d) इनमें से कोई नहीं
हलः
विकल्प (a) सही है।

प्रश्न 12.
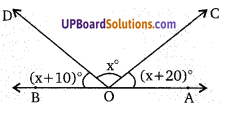
संलग्न चित्र में, ∠ABD : ∠ACD का अनुपात ज्ञात कीजिए।
हल:

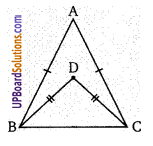
∆ABC में, AB = AC
∴ ∠B = ∠C … (1)
∆BCD में, DB = DC
∠DBC = ∠DCB … (2)
समीकरण (1) – (2) करने पर,
∠B – ∠DBC = ∠C – ∠DCB
∠ABD = ∠DCA
∴ ABD : ACD = 1 : 1

प्रश्न 13.
निम्न में से कौन-सी त्रिभुजों की सर्वांगसमता के लिए एक कसौटी नहीं है? (NCERT Exemplar)
(a) SAS
(b) SSS
(c) ASA
(d) SSA
हल:
विकल्प (d) SSA

प्रश्न 14.
∆ABC में ∠B = 35°, ∠C = 65° तथा AD, ∠BAC का समद्विभाजक BC से D पर मिलता है। तब निम्न में से कौन-सा सत्य है?
(a) BD > AD > CD
(b) AD > BD > CD
(c) AD > CD > BD
(d) इनमें से कोई नहीं

हलः
विकल्प (a) सही है।

प्रश्न 15.
यदि एक त्रिभुज के दो शीर्षलम्बों की ऊँचाईयाँ, विपरीत भुजाओं के बराबर है तब त्रिभुज का नाम बताइये।
हलः
समद्विबाहु त्रिभुज।

प्रश्न 16.
यदि ∆PQR ≅ ∆EFD तब ∠E ज्ञात कीजिए।
हलः
∠E = ∠P

प्रश्न 17.
यदि ∆PQR ≅ ∆EFD तब ED ज्ञात कीजिए।
हलः
ED = PR

प्रश्न 18.
एक समद्विबाहु त्रिभुज में, यदि शीर्ष कोण, आधार कोणों के योग से दोगुना है तब त्रिभुज के शीर्ष कोण की माप ज्ञात कीजिए।
हल:

प्रश्न 19.
∆ABC में यदि AB = AC तथा BC को D तक इस प्रकार बढ़ाया गया है कि ∠ACD = 100° तब ∠A ज्ञात कीजिए।
हलः

प्रश्न 20.
यदि ∆ABC ≅ ∆ACB तब कौन-सी भुजाओं के लिए ∆ABC समद्विबाहु है।
हलः
AB = BC

Ex 12.4 Congruence of Triangles लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-1)

प्रश्न 21.
एक समद्विबाहु त्रिभुज ABC है जिसमें AB = AC,BE और CF इसकी दो माध्यिकाएँ हैं तो सिद्ध कीजिए कि BE = CF
हलः

प्रश्न 22.
एक वर्ग ABCD की एक भुजा CD पर, एक समद्विबाहु त्रिभुज CDE है तो दिखाइये कि ∆ADE ≅ ∆BCE
हल:

प्रश्न 23.
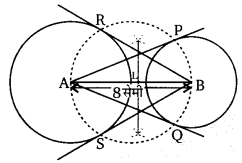
एक रेखाखंड AB है तथा रेखा । इसकी लाम्बिक समद्विभाजक है यदि एक बिंदु P, l पर स्थित है तो दिखाइये कि P, A तथा B से समदूरस्थ है। (NCERT)
हल:

प्रश्न 24.
एक चतुर्भुज ABCD में, AC = AD तथा AB, ∠A को समद्विभाजित करता है तो दिखाइये कि ∆ABC ≅ ∆ABD
हल:

प्रश्न 25.
एक समद्विबाहु त्रिभुज का ऊर्ध्वाधर कोण 100° है तो दिखाइये कि इसका आधार कोण 40° है।
हलः

∵ ∆ABC में
AB = BC
∠BAC = ∠ACB = 40°

प्रश्न 26.
संलग्न चित्र में, एक वर्ग ABCD है तथा P, AD का मध्य बिंदु है, BP और CP मिलाये गये हैं। तो सिद्ध कीजिए कि ∠PCB = ∠PBC
हल:

प्रश्न 27.
संलग्न चित्र में, बिंदु P और Q, BC पर इस प्रकार है कि BQ = CP तथा AP = AQ तो दिखाइये कि AB = AC
हलः

प्रश्न 28.
सिद्ध कीजिए कि एक त्रिभुज की बराबर भुजाओं के विपरीत कोण भी बराबर होते हैं।
हलः

Ex 12.4 Congruence of Triangles लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 29.
एक चतुर्भुज ABCD में, यदि विकर्ण AC, ∠A को समद्विभाजित करता है तथा AB = AD तब दिखाइये कि ∠CBA = ∠CDA
हल:

प्रश्न 30.
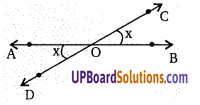
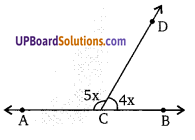
संलग्न चित्र में, ∆ABC में, ∠B = 30°, ∠C=65° तथा ∠A का समद्विभाजक BC पर X में मिलता है। दिखाइये कि CX < AX < BX
हलः

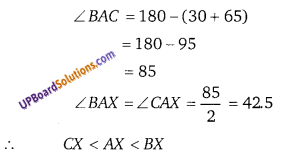
प्रश्न 31.
संलग्न चित्र में, O, AB तथा CD का मध्य बिंदु है। तो सिद्ध कीजिए कि AC = BD
हल:

प्रश्न 32.
सिद्ध कीजिए कि एक त्रिभुज की बराबर कोणों की विपरीत भुजाएँ भी बराबर होती हैं।
हल:
रचना- बिन्दु A से आधार BC पर लम्ब AM डाला। समकोण ∆AMB तथा समकोण ∆AMC में

प्रश्न 33.
एक न्यूनकोण त्रिभुज ABC है। B से AC पर लम्ब, C से AB पर लम्ब के बराबर है तो सिद्ध कीजिए कि AB = AC
हलः

प्रश्न 34.
सिद्ध कीजिए कि किसी त्रिभुज (समबाहु त्रिभुज से अलग) सबसे बड़ी भुजा के विपरीत कोण 60° से बड़ा होता है। (NCERT Exemplar)
हलः
समबाहु ∆ से अलग दो स्थिति होगी
(i) अधिक कोण त्रिभुज में सबसे बड़ी भुजा के विपरीत कोण 60° से बड़ा होता है।

(ii) न्यूनकोण त्रिभुज में सबसे बड़ी भुजा के विपरीत कोण 60° से अधिक ही होगा।

Ex 12.4 Congruence of Triangles दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 35.
सिद्ध कीजिए कि एक समबाहु त्रिभुज की माध्यिकाएँ बराबर होती हैं।
हल:

प्रश्न 36.
संलग्न चित्र में, AB = AC, CH = CB तथा HK || BC यदि ∠CAX = 137°तब ∠CHR ज्ञात कीजिए।
हल:

प्रश्न 37.
दिखाइये कि एक चतुर्भुज ABCD में AB + BC + CD + DA > AC + BD
हल:

प्रश्न 38.
संलग्न चित्र में, एक समबाहु त्रिभुज ABC है। PQ||AC तथा AC को R तक इस प्रकार बढ़ाया है कि CR = BP तो दिखाइये कि QR, PC को समद्विभाजित करता है।
हल:

प्रश्न 39.
सिद्ध कीजिए कि एक समद्विबाहु त्रिभुज के शीर्ष से माध्यिका, उर्ध्वाधर कोण को समद्विभाजित करती है।
हल:

प्रश्न 40.
संलग्न चित्र में, यदि x = y तथा AB = CB तब सिद्ध कीजिए कि AE = CD
हल:

Ex 12.4 Congruence of Triangles बहु विकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
एक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AB = AC तथा AD आधार BC की माध्यिका है तब ∠BAD =
(a) 50°
(b) 55°
(c) 65°
(d) 75°
हलः

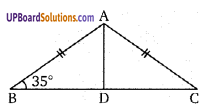
अतः विकल्प (b) सही है।

प्रश्न 2.
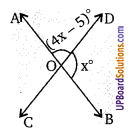
संलग्न चित्र में, AB > AC निम्न में से कौन-सा एक सत्य है?
(a) AB > AD
(b) AB < AD
(c) AB = AD
(d) इनमें से कोई नहीं हलः
∵ AB > AC … (1)

⇒ ∠3 > ∠2 [∵ बड़ी भुजा के सामने का कोण बड़ा होता है]
परन्तु ∠4 > ∠2
क्योंकि ∠4, ∆ABD का बहिष्कोण है तथा यह किसी भी अन्तकोण से बड़ा होता है।
तब ∠5 > ∠2 से
⇒ AB > AD
अतः विकल्प (a) सही है।

प्रश्न 3.
संलग्न चित्र में, BE L CA तथा CF | BA इस प्रकार हैं कि BE = CF तो निम्न में से कौन-सा सत्य है?
(a) ∆ABE ≅ ∆AFC
(b) ∆ABE ≅ ∆ACF
(c) (a) व (b) दोनों सत्य हैं
(d) इनमें से कोई नहीं
हल:

∆ABE तथा ∆ACF में, BE = CF (दिया है)
∠AEB = ∠AFC (प्रत्येक 90°)
∠BAE = ∠CAF (उभयनिष्ठ)
अतः ∆ABE ≅ ∆ACF
अतः विकल्प (b) सही है।

प्रश्न 4.
संलग्न चित्र में, AE = DB, CB = EF तथा ∠ABC = ∠FED तब निम्न में से कौन-सा सत्य है?

(a) ∆ABC ≅ ∆DEF
(b) ∆ABC ≅ ∆EFD
(c) (a) व (b) दोनों सत्य हैं
(d) इनमें से कोई नहीं
हलः :

Ex 12.4 Congruence of Triangles स्विमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
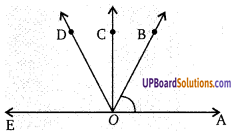
रेखा l कोण A की समद्विभाजक है तथा । पर कोई बिंदु B है। BP और BQ बिन्दु B से ∠A की भुजाओं पर लम्ब हैं तो दिखाइये कि-
(i) ∆APB ≅ ∆AQB
(ii) BP = BQ
हल:

प्रश्न 2.
C पर समकोण, एक समकोण ∆ABC में M, कर्ण AB का मध्य बिंदु है। C को M से मिलाया गया है तथा एक बिन्दु D तक इस प्रकार बढ़ाया गया है कि DM = CM बिंदु D को बिंदु B से मिलाया गया है तो दिखाइये कि
(i) ∆AMC = ∆BMD
(ii) ∠DBC एक समकोण है।
(iii) ∆DBC ≅ ∆ACB
(iv) CM = [latex]\frac{1}{2}[/latex]FAB

हलः

प्रश्न 3.
एक समद्विबाहु ∆ABC में AB = AC, ∠B तथा ∠C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं A को O से मिलाया तो दिखाइये कि-
(i) OB = OC
(ii) AO, ∠A को समद्विभाजित करता है।
हल:

प्रश्न 4.
एक त्रिभुज ABC है जिसमें ऊँचाईयाँ BE और CF भुजाओं AC और AB के बराबर हैं तो दिखाइये कि-
(i) ∆ABE ≅ ∆ACF
(ii) AB = AC, अर्थात् ABC एक समद्विबाहु त्रिभुज है।
हल:

प्रश्न 5.
समान आधार BC पर दो समद्विबाहु त्रिभुज ABC तथा DBC हैं तथा BC की समान भुजा पर शीर्ष A और D हैं यदि AD को बढ़ाने पर, BC को P पर प्रतिच्छेद करती है।
(i) ∆ABD ≅ ∆ACD
(ii) ∆ABP ≅ ∆ACP
(iii) AP, ∠A व ∠D को समद्विभाजित करते हैं।
(iv) AP, BC का लम्बअर्द्धक है।

हलः

प्रश्न 6.
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC, AD ⊥ BC खींच तो दिखाइये कि ∠B = ∠C
हल:

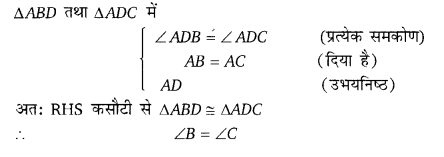
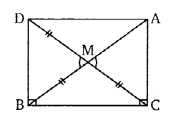
प्रश्न 7.
संलग्न चित्र में, ∠B < ∠A, ∠C <∠D तो दिखाइये कि AD > BC
हल:

प्रश्न 8.
यदि एक उभयनिष्ठ आधार के दो समद्विबाहु त्रिभुज हैं। तो सिद्ध कीजिए कि इनके शीर्षों को मिलाने वाली रेखा इन दोनों को समकोण पर समद्विभाजित करती है।
हलः

प्रश्न 9.
संलग्न चित्र में, AD, ∆ABC की माध्यिका है यदि AD पर दो लम्ब BL और CM खींचे गये हैं तथा AD को बढ़ाया गया है तो सिद्ध कीजिए कि BL = CM
हलः

∆BLD तथा ∆DMC में
∠BLP = ∠DMC (प्रत्येक 90°)
∠BDL = ∠MDC (शीर्षाभिमुख कोण)
BD = DC [ ∵ D, BC का मध्य बिन्दु है]
अतः ∆BLD ≅ ∆DMC
BL = CM

प्रश्न 10.
संलग्न चित्र में, एक त्रिभुज ABC है, जो B पर समकोण है। यदि भुजा BC पर एक वर्ग BCDE है तथा AC पर एक वर्ग ACFG है तो दिखाइये कि AD = BF
हलः

प्रश्न 11.
संलग्न चित्र में, OA = OB तथा OP = OQ तो सिद्ध कीजिए किः
(i) PX = Qx
(ii) AX = BX
हल:

प्रश्न 12.
यदि एक समद्विबाहु त्रिभुज के आधार को दोनों ओर को बढ़ाया गया है तो सिद्ध कीजिए की इस प्रकार बने बहिष्कोण परस्पर बराबर हैं।
हल:

प्रश्न 13.
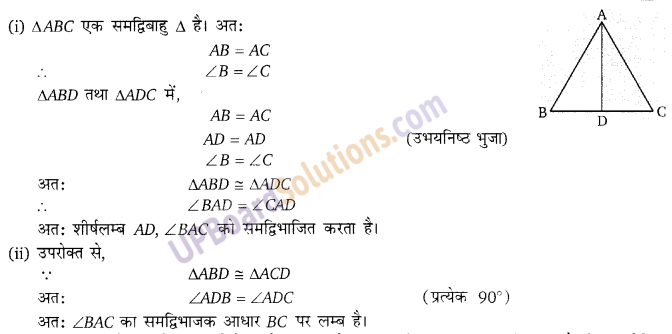
सिद्ध कीजिए किं ∆ABC एक समद्विबाहु त्रिभुज होगा यदि निम्न में से कोई एक शर्त पूरी होती है।
(i) शीर्षलम्ब AD, ∠BAC को समद्विभाजित करता है।
(ii) ∠BAC का समद्विभाजक आधार BC पर लम्ब है।
हल:

प्रश्न 14.
बिन्दु A पर प्रतिच्छेद करने वाली दो रेखाओं l व m से समान दूरी पर स्थित एक बिन्दु P है। सिद्ध कीजिए कि AP उनके बीच के कोण को समद्विभाजित करते हैं।
हलः

प्रश्न 15.
दो रेखायें AB व CD बिन्दु पर इस प्रकार प्रतिच्छेद करती हैं कि BC, AD के बराबर तथा समान्तर हैं। सिद्ध कीजिए कि AB व CD रेखाएँ, बिन्दु O पर प्रतिच्छेद करती हैं।
हलः
दिया है- BC = AD तथा BC || AD
सिद्ध करना है- AB तथा CD रेखाएँ, बिन्दु O पर प्रतिच्छेद करती हैं।
उपपत्ति- ∆AOD तथा ∆BOC में,
AD = BC
∠OAD = ∠OBD (एकान्तर कोण)
∠ADO = ∠OCB (एकान्तर कोण)
∆AOD ≅ ∆BOC
अत: ∠AOD = ∠BOC
अत: AB तथा CD रेखाएँ, बिन्दु O पर प्रतिच्छेद करती हैं।

Balaji Publications Mathematics Class 9 Solutions