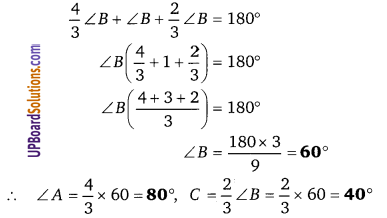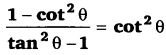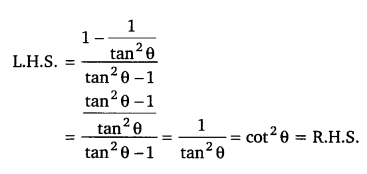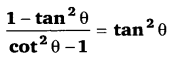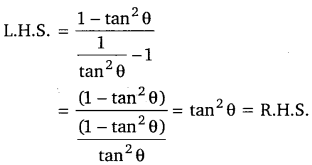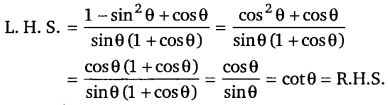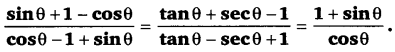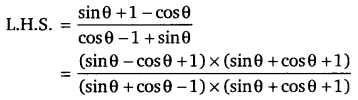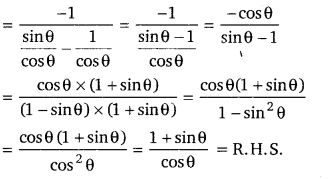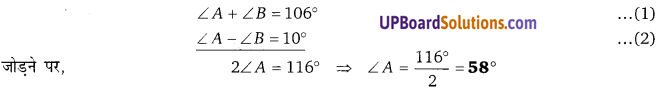Safia

Balaji Class 9 Maths Solutions Chapter 12 Congruence of Triangles Ex 12.1 त्रिभुजों की सर्वांगसमता

प्रश्न 1.
दिये गये चित्र में, AD = CB, AB = CD तथा EF, BD को G पर समद्विभाजित करता है तो सिद्ध कीजिए कि G, EF का मध्य बिन्दु है।
हल:

∵ AB = CB = CD … (1)
∆DEG तथा ∆GFB में
DG = GB (दिया है)
∠FGB = ∠DGE (शीर्षाभिमुख कोण)
DE = FB (दिया है)
अतः ∆DEG ≅ ∆GFB
∴ EG = GF

प्रश्न 2.
सिद्ध कीजिए कि एक समबाहु त्रिभुज की माध्यिकाएँ सर्वांगसम होती हैं।
हलः

प्रश्न 3.
एक चतुर्भुज ABCD है। जिसमें AB = CD तथा चतुर्भुज का एक अन्तः बिन्दु O इस प्रकार है कि OA = OD तथा OB = OC तो सिद्ध कीजिए कि BC || AD.
हलः

परन्तु ये एकान्तर कोण हैं
∴ AB || DC
अत: ABCD एक समान्तर चतुर्भुज होगा।
∴ BC|| AD

प्रश्न 4.
दिये गये चित्र में, AD = BC तथा AC = BD तो सिद्ध कीजिए कि ∠ADC = ∠BCD
हल:

प्रश्न 5.
दिये गये चित्र में, एक समांतर चतुर्भुज ABCD तथा ∆BXC और ∆AYD इस प्रकार है कि BX = DY तथा CX = AY तो सिद्ध कीजिए कि-
(i) BX || DY
(ii) XY और BD एक दूसरे को समद्विभाजित करते हैं।
हल:


परन्तु ये एकान्तर कोण है।
(i) ∴ BX || YD
(ii) XO = OY तथा BO = OD
∴ XY, BD एक दूसरे को समद्विभाजित करते हैं।

प्रश्न 6.
एक चतुर्भुज की चारों भुजाएँ बराबर हैं तो सिद्ध कीजिए कि इसके कोण, विकर्ण द्वारा समद्विभाजित होते हैं। हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 11 Triangles and Its Angles Ex 11.2 त्रिभुज एवं उसके गुण

Ex 11.2 Triangles and Its Angles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
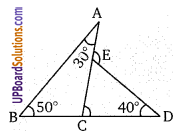
संलग्न चित्र में, ∠BAC = 30°, ∠ABC = 50° तथा ∠CDE = 40°, तो ∠AED ज्ञात कीजिए।
हलः
बहिष्कोण
∠ACD = ∠ABC + ∠CAB
= 50 + 30 = 80°
बहिष्कोण ∠AED = ∠ACD + ∠ EDC
= 80 + 40 = 120°

(∵ A का बहिष्कोण, अपने सम्मुख अन्तः कोणों के योग के बराबर होता है।)

प्रश्न 2.
∆ABC में, भुजा BC को D तक बढ़ाया गया है। यदि ∠ABC = 40° और ∠ACD = 120° तो ∠A ज्ञात कीजिए।
हल:
∆ABC का बहिष्कोण ∠ACD है।

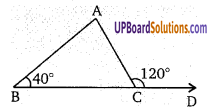
∠ACD = ∠ABC + ∠ BAC
120 = 40 + ∠ BAC
120 – 40 = ∠ BAC
80° = ∠BAC

प्रश्न 3.
संलग्न चित्र में, BO तथा CO क्रमशः ∠B और ∠C के समद्विभाजक है यदि ∠A = 50° तब ∠BOC ज्ञात कीजिए।
हलः

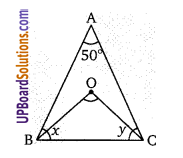
माना ∠ABC = x ∴ ∠OBC =[latex]\frac{x}{2}[/latex]
तथा ∠ACB = y तथा ∠OCB = [latex]\frac{y}{2}[/latex]
∆ABC में, 50 + x + y = 180
x + y = 180 – 50 = 130°
∆OBC में, BOC = [latex]180-\left(\frac{x}{2}+\frac{y}{2}\right)=180-\left(\frac{130}{2}\right)[/latex]
= 180 – 65 = 115°

प्रश्न 4.
एक त्रिभुज ABC की भुजा BC को बायीं ओर को D तक बढ़ाया गया है तथा दाँयी ओर को E तक बढ़या गया है तथा यहाँ ∠ABD = 125° और ∠ACE = 130° तब ∠A ज्ञात कीजिए।
हल:

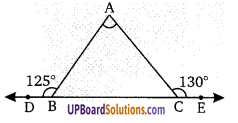
∆ABC में,
∠ABC = 180 – 125 = 55°
∠ACB = 180 – 130 = 50°
∆ABC में, ∠ABC + ∠ACB + ∠ BAC = 180°
55 + 50 + ∠BAC = 180°
105 + ∠ BAC = 180°
∠BAC = 180 – 105 = 75°

प्रश्न 5.
∆ABC में, BD⊥AC, ∠CAE = 30° और ∠CBD = 40° तब ∠AEB ज्ञात कीजिए।
हलः

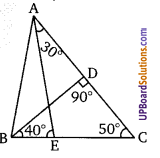
∠BCD = 180° – (40+ 90)
= 180 – 130
= 50°
तथा ∠AEB = ∠EAC + ∠ACE
∠AEB = 30 + 50
= 80°

Ex 11.2 Triangles and Its Angles लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 6.
∆ABC में, यदि 3∠A = 4∠B = 6∠C तो ∠A, ∠B और ∠C ज्ञात कीजिए।
हल:
∆ABC में,
∠A = [latex]\frac{4}{3} \angle B[/latex]
∠C = [latex]\frac{4}{6} \angle B=\frac{2}{3} \angle B[/latex]
∵ ∠A + ∠B + ∠C = 180°

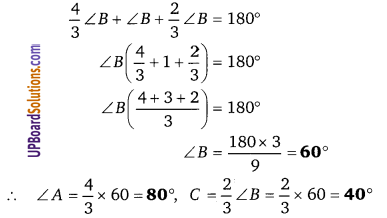
प्रश्न 7.
∆PQR में, यदि ∠P – ∠Q = 42° और ∠Q – ∠R = 21° तब ∠P, ∠Q और ∠R ज्ञात कीजिए।
हलः
∠P = 42° + ∠Q तथा ∠R = ∠Q – 21°
∆PQR में, ∵ ∠P + ∠Q + ∠R = 180°
42°+ ∠Q + ∠Q + ∠Q – 21° = 180°
3∠Q + 21° = 180°
3∠Q = 180° – 21° = 159°
∠Q = [latex]\frac{159}{3}[/latex] = 53°
∠P = 42 + 53 = 95°
∴ ∠R = 53 – 21 = 32°

प्रश्न 8.
∆ABC में, ∠A + ∠B = 125° और ∠A + ∠C = 113° तब ∠A, ∠B और ∠C ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B = 125° ………..(1)
∠A + ∠C = 113° ………… (2)
समीकरण (1) से, ∠A = 125° – ∠B ……………… (3)
समीकरण (2) से, ∠C = 113° – ∠A ………………….. (4)
∵ ∠A + ∠B + ∠C = 180
125 – ∠B + ∠B + 113 – ∠A = 180
238 – ∠A = 180
238 – 180 = ∠A ⇒ ∠A = 58°
समीकरण (3) में ∠A का मान रखने पर
58 = 125 – ∠B
∠B = 125 – 58 = 67°
समीकरण (2) में ∠A का मान रखने पर
58 + ∠C = 113
∠C = 113 – 58 = 55°

प्रश्न 9.
∆ABC में, यदि ∠A + ∠B = 108° और ∠B + ∠C = 130° तो ∠A, ∠B और ∠C ज्ञात कीजिए।
हलः
∵ ∠A + ∠B = 108°
∴ ∠A = 108° -∠B …………..(1)
तथा
∠B + ∠C = 130°
∠C = 130° – ∠B
∵ ∠A + ∠B + ∠C = 180
108 – ∠B + ∠B + 130 – ∠B = 180
238 – ∠B = 180
238 – 180 = ∠B ⇒ ∠B = 58°
∠C = 130 – 58 = 72°
∠A = 108 – 58 = 50°

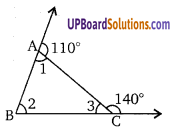
प्रश्न 10.
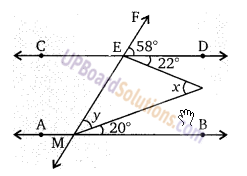
निम्न चित्र में x का मान ज्ञात कीजिए।
हलः

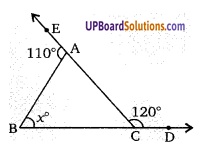
∠ACD = 120°
∠ACB = 180 – 120 = 60°
बहिष्कोण ∠BAE = ∠ABC + ∠ACB
110 = x + 60
110 – 60 = x
50° = x

Ex 11.2 Triangles and Its Angles लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 11.
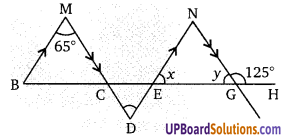
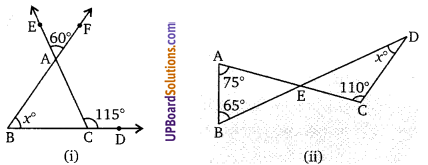
निम्न प्रत्येक में x का मान ज्ञात कीजिए।

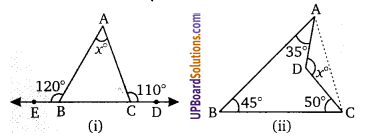
हलः
चित्र (i) में,
∠ACB = 180 – 110 = 70°
∆ABC में, ∠EBA बहिष्कोण है।
∠EBA = ∠BAC + ∠ACB
120 = x + 70
120 – 70 = x
∴ x = 50°
चित्र (ii) में, AD = DC (दिया है)
∴ ∠DAC = ∠DCA = a (माना)
∆ADC में, x + ∠DAC + ∠DCA = 180
x + a + a = 180
x + 2a = 180 ……………. (1)
∆ABC में, 45 + 35 + 50 + a + a = 180
130 + 2a = 180
2a = 180 – 130 = 50°
a = [latex]\frac{50}{2}[/latex] = 25°
समीकरण (1) में a का मान रखने पर
x + 2 × 25 = 180
x + 50 = 180 ⇒ x = 180 – 50 = 130°

प्रश्न 12.
चित्र में, एक समबाहु ∆EAB, एक वर्ग ABCD के ऊपर अध्यारोपित है। x और y के मान ज्ञात कीजिए।
हलः
समबाहु ∆EAB में, ∠ABE = 60° तथा ∠ABC = 90° [वर्ग ABCD के कोण]
∠EBC = 60 + 90 = 150°

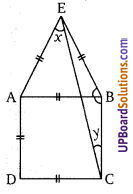
∆EBC में, EB = BA = BC
∠CEB + y = 180 – 150 = 30°
प्रत्येक ∠CEB = y = [latex]\frac{30}{2}[/latex] = 15°
∵ ∆EAB एक समबाहु A है।
∴ ∠AEB = 60°
∴ x + ∠CEB = 60°
x + 15 = 60° ⇒ x = 60 – 15 = 45°

प्रश्न 13.
चित्र में, AB, ∠DAC को 1 : 3 के अनुपात में विभाजित करता है और AB = DB, x का मान ज्ञात कीजिए।
हलः
∵ AB, ∠ DAC को 1 : 3 के अनुपात में विभाजित करती है।

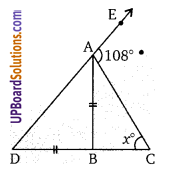
माना ∠ DAB = a
∠BAC = 3a
∴ a + 3a + 108 = 180 ⇒ 4a = 180 – 108 = 72°
a = [latex]\frac{72}{4}[/latex] = 18°
∴ ∠DAB = 18°
∴ ∠ADB = 18°
∠BAC = 3 × 18 = 54°
∴ ∠DAC = 18 + 54 = 72°
∆ADC में, ∠DAC + ∠ADC + x = 180°
72 + 18 + x = 180°
90 + x = 180° ⇒ x = 180 – 90 = 90°

प्रश्न 14.
चित्र में, CD⊥AB, ∠ABE = 130° तथा ∠BAC = 70°, तो x और y ज्ञात कीजिए।
हलः
∠BDC, ∆ADC का बहिष्कोण है।

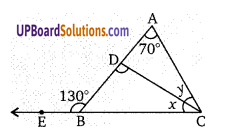
∠BDC = ∠DAC + ∠ACD
90 = 70 + y
90 – 70 = y
∴ y = 20°
∴ ∠ABE, ∆ABC का बहिष्कोण है।
∠ABE = ∠BAC + ∠BCA
130 = 70 + x + y
130 = 70 + x + 20
130 – 70 – 20 = x
40° = x

प्रश्न 15.
यदि ∠ABD = 125° तथा ∠ACE = 130° तब ∠ BAC ज्ञात कीजिए।
हलः

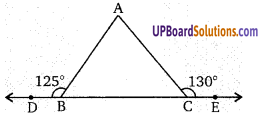
∠ABC = 180 – 125 = 55° [रैखिक युग्म कोण]
∠ACE, ∆ABC का बहिष्कोण है।
∴ ∠ACE = ∠ABC + ∠BAC
130 = 55 + ∠BAC
130 – 55 = ∠BAC
75° = ∠BAC

Ex 11.2 Triangles and Its Angles दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 16.
∆ABC में, भुजाओं AB और AC को क्रमश: D तथा E तक बढ़ाया गया है। ∠DBC और ∠ECB के समद्विभाजक एक बिन्दु 0 पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए कि ∠BOC = 90° – [latex]\frac{1}{2}[/latex]∠A
हल:

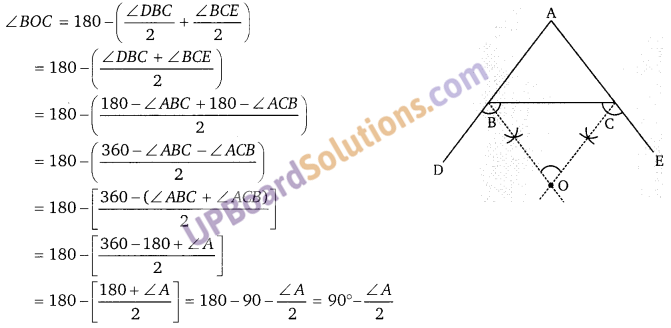
प्रश्न 17.
एक ∆ABC की भुजा BC को दोनों ओर को बढ़ाया गया है तो सिद्ध कीजिए कि दोनों बाह्य कोणों का योग ∠A से 180° बड़ा होगा।
हलः
सिद्ध करना है: ∠ABD + ∠ACE = ∠A + 180°
∆ का बहिष्कोण अपने सम्मुख अन्तः कोणों के योग के बराबर होता है।

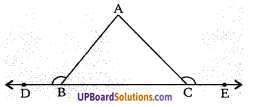
उपपत्तिः
∠ABD = ∠A + ∠ACB
∠ABD = ∠A + 180 – ∠ACE
∠ABD + ∠ACE = ∠A + 180°

प्रश्न 18.
यदि एक त्रिभुज के आधार कोण के समद्विभाजक द्वारा 135° का एक कोण बना है। तो सिद्ध कीजिए कि त्रिभुज समकोण है।
हलः

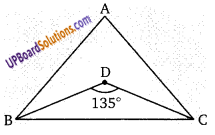
माना ∆ABC में,
∠B = 2x तथा ∠C = 2y
∴ ∠DBC = [latex]\frac{2 x}{2}[/latex] = x
∠DCB = [latex]\frac{2 y}{2}[/latex] = y
∆BDC में,
x + y + 135 = 180
x + y = 180 – 135 = 45°
∆ABC में, ∠ABC + ∠ BCA + ∠BAC = 180
2x + 2y + ∠BAC = 180
2(x + y) + ∠BAC = 180
समीकरण (1) से
2 × 45 + ∠BAC = 180
∠BAC = 180 – 90 = 90°
∴ ∆ABC एक समकोण त्रिभुज है।

प्रश्न 19.
एक त्रिभुज ABC है। B पर बाह्य कोण का समद्विभाजक तथा ∠C का समद्विभाजक परस्पर D पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए कि ∠D = [latex]\frac{1}{2}[/latex]∠A
हलः

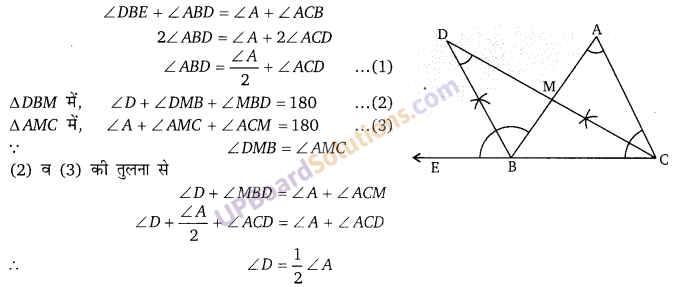
प्रश्न 20.
एक ∆ABC में, AD, ∠A का समद्विभाजक है तथा ∠C > ∠B तो सिद्ध कीजिए कि ∠ADB > ∠ADC
हलः

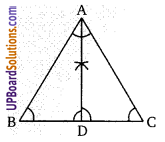
∵ ∠C > ∠B
AB > AC [बड़े कोण की सम्मुख भुजा बड़ी होती है।]
∆ABD तथा ∆ADC में,
∠ADB > ∠ADC

Ex 11.2 Triangles and Its Angles बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
एक ∆ABC में, ∠B = ∠C तथा किरण AX, बहिष्कोण DAC को समद्विभाजित करती है। यदि ∠DAX = 70° तब ∠ACB =
(a) 60°
(b) 70°
(c) 45°
(d) इनमें से कोई नहीं
हलः

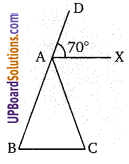
∠B = ∠C
तथा AX, बहिष्कोण DAC को समद्विभाजित करती है, तब
∠DAX = 70°
∠XAC = 70°
∵ AX||BC तथा AC तिर्यक रेखा इन्हें काटती हैं।
तब ∠XAC = ∠ACB = 70°
अतः विकल्प (b) सही है।

प्रश्न 2.
यदि एक समकोण त्रिभुज के न्यूनकोण के समद्विभाजक O पर मिलते हैं तब दोनों समद्विभाजकों के बीच कोण O है
(a) 90°
(b) 45°
(c) 145°
(d) 135°
हलः

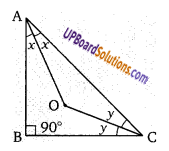
∠ABC = 90°
माना∠BAC = 2x, ∠BCA = 2y
OA, OC क्रमशः ∠BAC तथा ∠BCA के समद्विभाजक हैं।
तब ∠BAO = ∠OAC = x
∠BCO = ∠OCA = y
∆AOC में, x + y + ∠AOC = 180°
∠AOC = 180° – (x + y) …………… (1)
∆ABC में, 2x + 2y + 90° = 180°
x + y = 45
समी० (1) व समी० (2) से,
∠AOC = 180° – 45° = 135°
अतः विकल्प (d) सही है।

प्रश्न 3.
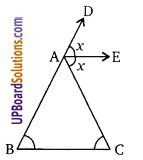
∆ABC में, यदि ∠A = 100°, AD, ∠A को समद्विभाजित करता है तथा AD⊥BC तब ∠B =
(a) 40°
(b) 50°
(c) 60°
(d) 90°
हलः

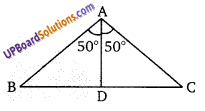
∵ AD, ∠A को समद्विभाजित करता है, अतः ।
∠BAD = ∠CAD = 50°
∆ABD में,
∠ABD + 50 + 90 = 180
∠ABD = 180 – 140 = 40°
अतः विकल्प (a) सही है।

प्रश्न 4.
एक समद्विबाहु त्रिभुज में शीर्ष पर एक बहिष्कोण 95° है तथा इसका एक बना हुआ अभिमुख कोण है
(a) 180°
(b) [latex]47 \frac{1}{2}^{\circ}[/latex]
(c) 90°
(d) 270°
हल:

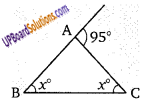
2x = 95°
x = [latex]\frac{95}{2}=47 \frac{1}{2}^{\circ}[/latex]
अतः विकल्प (b) सही है।

प्रश्न 5.
एक ∆ABC में, ∠A = 50° तथा BC को एक बिंदु D तक बढ़ाया गया है। यदि ∠ABC और ∠ACD के समद्विभाजक E पर मिलते हैं तब ∠E =
(a) 35°
(b) 45°
(c) 25°
(d) इनमें से कोई नहीं
हलः

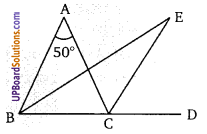
माना ∠ABC = 2x तथा ∠ACD = 2y
तब BE, ∠ABC का समद्विभाजक है, अतः
∠ABE = ∠EBC = x
तथा CE, ∠ACD का समद्विभाजक है, अतः
∠ACE = ∠ECD = y
∠ACD, ∆ABC का बहिष्कोण है। अत:
∠ACD = ∠CAB + ∠ABC
2y = 50° + 2x ⇒ y – x = 25° …………..(1)
∆BCE में, ∠EBC + ∠ECB + ∠BEC = 180°
x + (180° – y) + ∠BEC = 180°
∠BEC = 180° – 180° + y – x = (y – x) = 25°
अतः ∠E = 25°
अतः विकल्प (c) सही है।

प्रश्न 6.
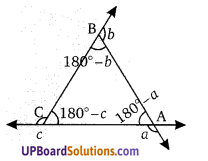
∆ABC के B तथा C पर बहिष्कोणों के समद्विभाजक O पर मिलते हैं यदि ∠A = x° तब ∠BOC =

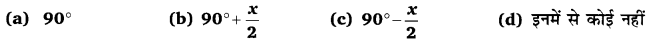
हलः

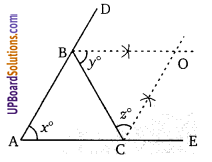
माना ∠CBD = 2y तथा ∠BCE = 2x
∵ BO तथा CO क्रमश: कोण ∠CBD तथा ∠BCE के समद्विभाजक हैं, तब
∠DBO = ∠OBC = y°
∠BCO = ∠COE = x°
∆ABC के ∠B तथा ∠C बहिष्कोण हैं, तब
∠DBC = x + ∠BCA ⇒ 2y = x + 180° – 2z
⇒ 2y + 2z = x + 180°
y + z = [latex]\frac{x}{2}[/latex] + 90°
∆BOC में, ∠BOC = 180° – (y + z)
= [latex]180^{\circ}-\left(\frac{x}{2}+90^{\circ}\right)=\left(90^{\circ}-\frac{x}{2}\right) [/latex]
अतः विकल्प (c) सही है।

प्रश्न 7.
यदि एक त्रिभुज के कोण 3 : 4 : 5 के अनुपात में है तब छोटा कोण है
(a) 45°
(b) 30°
(c) 60°
(d) 35°
हलः
कोणों में अनुपात = 3 : 4 : 5 तब कोण = 3x, 4x, 5x
3x + 4x + 5x = 180° ⇒ 12x = 180°
x = [latex]\frac{180^{\circ}}{12}[/latex] = 15
सबसे छोटा कोण = 3x = 3 × 15 = 45°
अतः विकल्प (a) सही है।

प्रश्न 8.
यदि एक त्रिभुज का एक कोण 110° का है, तब अन्य दो कोणों के समद्विभाजकों के बीच कोण हो सकता है
(a) 135°
(b) 160°
(c) 145°
(d) 90°
हलः

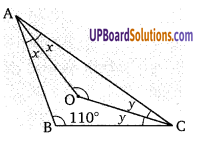
माना ∠BAC = 2.x, ∠BCA = 2y
∵ OA तथा OC, ∠BAC तथा /BCA के समद्विभाजक हैं, तब
∆ABC में, 2x + 2y + 110° = 180°
2x + 2y = 180° – 110°
2x + 2y = 70
⇒ x + y = 35
∆AOC में, ∠AOC + x + y = 180°
∠AOC = 180° – (x + y) = 180° – 35 = 145°
अतः विकल्प (c) सही है।

प्रश्न 9.
संलग्न चित्र में, OA तथा OB, ∠A और ∠B के समद्विभाजक है यदि ∠C = 30° तब ∠AOB =
(a) 45°
(b) 90°
(c) 180°
(d) 105°
हलः

माना ∠CAB = 2x, ∠CBA = 2y
∆ABC में, 2x + 2y + 30° = 180°
2x + 2y = 150° = x + y = 75° …………. (1)
∆OAB में, x + y + ∠AOB = 180°
∠AOB = 180° – (x + y)= 180° – 75° = 105°
अतः विकल्प (d) सही है।

प्रश्न 10.
चित्र में एक समद्विबाहु त्रिभुज ABC है जिसमें ∠A = ∠B तथा PQ||AB यदि ∠C = 70° तब ∠APQ =
(a) 45°
(b) 900
(c) 125°
(d) इनमें से कोई नहीं
हलः

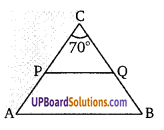
∠A = ∠B
∆ABC में, ∠A + ∠B + 70° = 180°
∠A + ∠A = 180° – 70°
2∠A = 110° ⇒ ∠A = 55°
∵ PQ|| AB ∴ ∠CPQ = ∠PAB = 55° (संगत कोण)
∠APQ = 180° – 55° = 125° अतः विकल्प (c) सही है।

Ex 11.2 Triangles and Its Angles  स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
यदि एक त्रिभुज का एक कोण, अन्य दो के योग के बराबर है तब सिद्ध कीजिए कि त्रिभुज एक समकोण त्रिभुज है।
हलः
माना ∆ के तीन कोण = ∠A, ∠B, ∠C
∠A = ∠B+ ∠C …………….(1)
∵ ∠A + ∠B + ∠C = 180
∠A + ∠A = 180
2∠A = 180
∠A = [latex]\frac{180}{2}[/latex] = 90°
∴ ∆ABC एक समकोण त्रिभुज है।

प्रश्न 2.
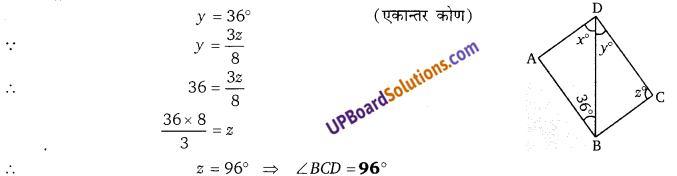
संलग्न चित्र में यदि AB||DE, ∠ BAC = 35° तथा ∠CDE = 53° तब दिखाइये कि ∠DCE = 92°
हलः

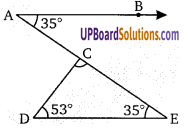
AB||DE
∠BAE = ∠AED = 35° (एकान्तर कोण)
∆CDE में, ∠DCE = 180 – (53 + 35)
= 180 – 88 = 92°

प्रश्न 3.
एक त्रिभुज ABC की भुजा BC दोनों ओर को बढ़ायी गयी है तो दिखाइये कि बने हुए बहिष्कोणों का योग, दो समकोण द्वारा ∠A से बड़ा है।
हलः

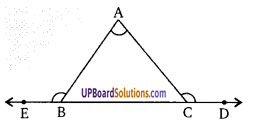
बहिष्कोण ∠ACD = ∠BAC + ∠ABC ……………(1)
बहिष्कोण ∠ABE = ∠BAC + ∠ACB …………. (2)
समीकरण (1) व (2) को जोड़ने पर
∠ACD + ∠ABE = ∠BAC + ∠ABC + ∠BAC + ∠ACB
= ∠BAC + (∠ABC + ∠BAC + ∠ACB)
= ∠BAC + 180°

प्रश्न 4.
∆ABC में, BD⊥AC तथा CE⊥AB, यदि BD तथा CE, O पर प्रतिच्छेद करते हैं तो सिद्ध कीजिए कि ∠BOC = 180° – ∠A
हलः

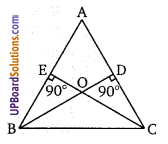
∠BOC = 180° – (∠OBC + ∠OCB) ……………. (1)
∆BDC में, ∠DBC + ∠BCD = 90 …………… (2)
∆BEC में, ∠EBC + ∠ECB = 90 ……………… (3)
∆ABC में, ∠A + ∠B + ∠C = 180 ………………. (4)
समीकरण (2) व (3) को जोड़ने पर
∠DBC + ∠ECB = 180 – ∠BCD – ∠EBC
= 180 – (180 -∠A) = ∠A ……………. (5)
समी० (1) में समी० (5) का मान रखने पर
∠BOC = 180° – ∠A

प्रश्न 5.
यदि एक त्रिभुज के दो कोणों का योग, तीसरे कोण के बराबर है तब तीसरा कोण ज्ञात कीजिए।
हलः
माना ∆ के तीन कोण = x, y, z
∵ x + y = z ………….(1)
x + y + z = 180
z + z = 180
2z = 180
∴ z = [latex]\frac{180}{2}[/latex] = 90°
तीसरा कोण = 90°

प्रश्न 6.
यदि एक त्रिभुज का प्रत्येक कोण, अन्य दो कोणों के योग से छोटा है तो दिखाइए कि यह न्यूनकोण त्रिभुज है।
हल:

∵ ∠A < ∠B + ∠C ………….(1)
∠B < ∠A + ∠C ………… (2)
∠C < ∠A + ∠B …………(3)
समीकरण (1) में दोनों और ∠A जोड़ने पर
2∠A < ∠A + ∠B + ∠C
2∠A < 180
∠A < [latex]\frac{180}{2}[/latex] < 90°
इसी प्रकार सिद्ध कर सकते हैं ∠B < 90°
∠C < 90° ∴ यह एक न्यूनकोण ∆ होगा।

प्रश्न 7.
एक ∆ABC की भुजा BC को नीचे दिये गये चित्र में दिखाये अनुसार एक बिन्दु D तक बढ़ाया गया है। ∠A का समद्विभाजक BC से L पर मिलता है। तो सिद्ध कीजिए कि ∠ABC + ∠ACD = 2∠ ALC ∠ACD = ∠CA∠ + ∠A∠C …(1) ∠ACD = ∠CAB + ∠A∠C
हल:

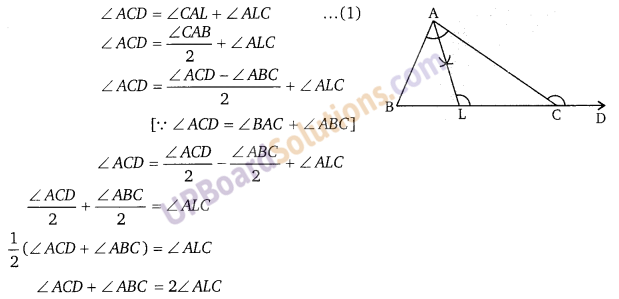
प्रश्न 8.
संलग्न चित्र में, चतुर्भुज PQRS के दो आसन्न कोण P और s के समद्विभाजक PA और SA हैं। तो सिद्ध कीजिए कि 2∠PAS = ∠Q +∠R
हल:

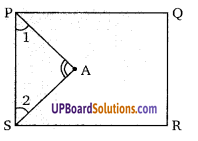
सिद्ध करना है। 2∠PAS = ∠Q + ∠R
∆PAS में, ∠ PAS = 180 – (∠1 + ∠2)
2 से गुणा करने पर,
2∠PAS = 360 – 2(∠1 + ∠2)
= 360 – (2∠1 + 2∠2)
= 360 – (∠P + ∠S)
= ∠Q + ∠R

प्रश्न 9.
संलग्न चित्र में, DE||QR और AP और BP क्रमश: ∠EAB तथा ∠RBA के समद्विभाजक है। तो दिखाइए कि ∠APB = 90°
हलः

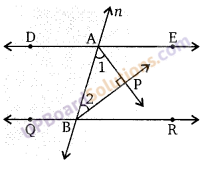
∵ DE ||QR
तथा AB एक तिर्यक रेखा है। समान्तर रेखाओं के एक ही ओर के अन्तः कोणों के युग्मों का योग 180°  होता है।
∴ ∠EAB + ∠ABR = 180
2∠1 + 2∠2 = 180
2(∠1 + ∠2) = 180
∠1 + ∠2 = 90
अब ∆PAB में, ∠APB + ∠1 + ∠2 = 180
∠APB + 90 = 180
∠APB = 180 – 90 = 90°

प्रश्न 10.
यदि एक त्रिभुज का एक कोण अन्य दो कोणों के योग से बड़ा है तो सिद्ध कीजिए कि त्रिभुज अधिक कोण वाला है।
हलः

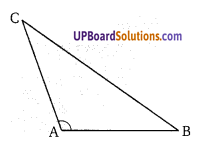
∠A > ∠B + ∠C
दोनों पक्षों में ∠A जोड़ने पर,
∠A + ∠A > ∠A + ∠B +∠C
⇒ 2∠A > 180°
⇒ ∠A > [latex]\frac{180^{\circ}}{2}[/latex] ⇒ ∠A > 90°
अतः ∠A , एक अधिककोण है।

प्रश्न 11.
यदि एक त्रिभुज का प्रत्येक कोण, अन्य दो कोणों के योग से कम है तो सिद्ध कीजिए कि त्रिभुज न्यूनकोण वाला है।
हलः

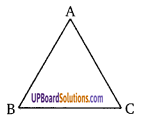
∵ ∠A < ∠B + ∠C …………(1)
∠B < ∠A + ∠C …………… (2)
∠C < ∠A + ∠B …………….(3)
समी० (1) में दोनों पक्षों में ∠A जोड़ने पर,
∠A + ∠A < ∠A + ∠B + ∠C
2∠A < 180°
∠A < [latex]\frac{180^{\circ}}{2}[/latex] ⇒ ∠A < 90°
अतः ∠A , एक न्यूनकोण है।

प्रश्न 12.
यदि एक त्रिभुज की भुजाएँ क्रम में बढ़ायी गयी है तो सिद्ध कीजिए कि बने हुए बहिष्कोणों का योग, चार सम कोणों के बराबर है।
हलः

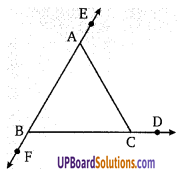
वृहत ∠A = ∠B + ∠C ………… (1)
वृहत ∠B = ∠A + ∠C …………… (2)
वृहत ∠C = ∠A + ∠B …………..(3)
समी० (1), (2) व (3) को जोड़ने पर,
वृहत [∠A + ∠B + ∠C ] = ∠B + ∠C + ∠A + ∠C + ∠A + ∠B
= 2[∠A + ∠B + ∠C] = 2 × 180° = 360°
= 4 × 90° = 4 समकोण

प्रश्न 13.
यदि एक त्रिभुज का एक कोण, अन्य दो कोणों के योग के बराबर है तो सिद्ध कीजिए कि त्रिभुज समकोण है।
हलः
∴ ∠A = ∠B + ∠C
दोनों पक्षों में ∠A जोड़ने पर,
∠A + ∠A = ∠A+ ∠B + ∠C
2∠A = 180°
∠A = [latex]\frac{180^{\circ}}{2}[/latex] = 90°
अत: ∆ABC एक समकोण त्रिभुज है।

प्रश्न 14.
∆ABC में, ∠B = 90° तथा BD⊥AC तो सिद्ध कीजिए कि ∠ABD = ∠ACB
हल:

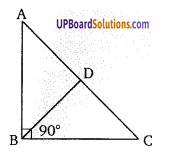
∵ BD⊥AC
∴ ∠BDA = ∠BDC = 90°
∆ABD में,
∠ABD + ∠A + ∠ADB = 180°
∠ABD + ∠A + 90°= 180°
∠ABD = 90°- ∠A ………….(1)
परन्तु
∠A + ∠B + ∠C = 180°
∠B + ∠C = 180° – ∠A
∠C = 180° – ∠A – ∠B
= 180° – ∠A – 90°
= 90° – ∠A ………….(2)
समी० (1) व (2) से,
∠ABD = ∠C = ∠ACB

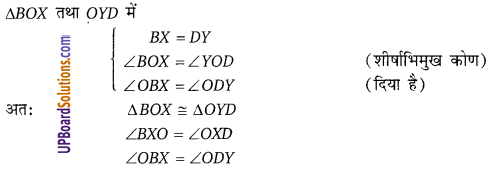
Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 15 Circle Ex 15.1 वृत्त

Ex 15.1 Circle अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
चित्र में O, वृत्त का केन्द्र, जीवा AB = 10 सेमी तथा व्यास AC = 26 सेमी है। जीवा AB की वृत्त के केन्द्र से दूरी ज्ञात कीजिए। [UP 2001, 03]
हल:

प्रश्न 2.
एक वृत्त की जीवा की लम्बाई 16 सेमी तथा वृत्त के केन्द्र से इसकी दूरी 6 सेमी है। तब वृत्त की त्रिज्या ज्ञात कीजिए।
हलः

प्रश्न 3.
वृत्त की एक जीवा की लम्बाई 8 सेमी तथा वृत्त के केन्द्र से इसकी दूरी 3 सेमी है। तब वृत्त की त्रिज्या ज्ञात कीजिए। [UP 2003]
हलः

प्रश्न 4.
वृत्त के लघु वृत्तखण्ड का कोण ज्ञात कीजिए। [UP 2000]
हलः
अधिक कोण

प्रश्न 5.
एक वृत्त का केन्द्र 0 तथा त्रिज्या OP = 10 सेमी है। जीवा PQ पर लम्ब OR की लम्बाई 6 सेमी है। तब PQ का मान ज्ञात कीजिए। [UP 2000]
हलः
समकोण ∆OPR में, (OP)² = (OR)² + (PR)²
(10)² = (6)² + (PR)²
100 = 36 + (PR)²
100 – 36 = (PR)²
∴ PR = [latex]\sqrt{64}[/latex] = 8 सेमी
∴ जीवा PQ = 2 × PR = 2 × 8 = 16 सेमी

प्रश्न 6.
चित्र में, 0 वृत्त का केन्द्र है तथा OA = 5 सेमी।0 से AB पर लम्ब OC की लम्बाई 4 सेमी है तब जीवा AB का मान ज्ञात कीजिए। (UP 2009, 10, 11)
हलः
समकोण ∆OAC में,
(OA)² = (AC)² + (OC)²
(5)² = (AC)² + (4)²
25 = (AC)² +16
25 -16 = (AC)²
या (AC)² = 9
∴ AC = [latex]\sqrt{9}[/latex] = 3 सेमी
∴ जीवा AB = 2 × AC = 2 × 3 = 6 सेमी

प्रश्न 7.
चित्र में, O वृत्त का केन्द्र है तथा एक जीवा AB = 24 सेमी है। जीवा की वृत्त के केन्द्र O से दूरी 5 सेमी है। तब वृत्त का व्यास ज्ञात कीजिए। (UP 2009)
हलः
समकोण ∆OAP में,
(OA)² = (OP)² + (AP)²
(OA)² = (5)² + (12)² (∵ AP = AB /2)
(OA)² = 25 +144 = 169
OA = [latex]\sqrt{169}[/latex] = 13 सेमी
∴ वृत्त का व्यास = 2 × त्रिज्या
= 2 – 13 = 26 सेमी

प्रश्न 8.
चित्र में, O वृत्त का केन्द्र है तथा एक जीवा AB = 30 सेमी है तथा इसका व्यास AD = 34 सेमी है। जीवा AB की केन्द्र O से दूरी ज्ञात कीजिए।
हलः

Ex 15.1 Circle लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-I)

प्रश्न 9.
एक 5 सेमी त्रिज्या वाले वृत्त के केन्द्र से 8 सेमी की एक जीवा की दूरी ज्ञात कीजिए। [UP 2005]
हल:
वृत्त की त्रिज्या OP = 5 सेमी
∵ वृत्त के केन्द्र से जीवा पर डाला गया लम्ब जीवा को समद्विभाजित करता है।

प्रश्न 10.
एक 5 सेमी त्रिज्या वाले वृत्त के केन्द्र से 3 सेमी की दूरी पर जीवा की लम्बाई ज्ञात कीजिए। (UP 2006)
हलः
समकोण ∆OAM में,
(OA)² = (OM)² + (AM )²
(5)² = (3)² + (AM)²
25 = 9 + (AM)²
25 – 9 = (AM)²
16 = (AM)²
∴ AM = [latex]\sqrt{16}[/latex] = 4 सेमी
∴ जीवा AB = 2 × AM = 2 × 4 = 8 सेमी

प्रश्न 11.
एक वृत्त की एक चाप दी गयी है। प्रदर्शित कीजिए कि वृत्त को पूरा कैसे किया जायेगा?
हलः
एक वृत्त का चाप AXB दिया है। वृत्त का केन्द्र ज्ञात करने के लिए AB को मिलाया। जीवा AB का लम्बार्द्धक खींचा, जो चाप को M बिन्दु पर काटता है। बिन्दु A अथवा B से कोई न्यूनकोण बनाती AY रेखा नीचे की ओर खींची। रेखा AY पर 90° का कोण बनाते हुए AX रेखा खींची जो AB के लम्बार्द्धक को बिन्दु O पर काटती है। अब बिन्दु 0 को केन्द्र मानकर OA त्रिज्या परकार में लेकर एक वृत्त खींचा जो दिये गये । चाप को ही पूर्ण करता है।

प्रश्न 12.
दिये गये वृत्त का केन्द्र ज्ञात करने की विधि बताइये।
हलः
(1) वृत्त पर तीन बिन्दु A, B,C लिए।
(2) AB तथा BC को मिलाया।
(3) AB तथा BC के लम्ब समद्विभाजक खींचे जो एक-दूसरे को बिन्दु O पर
काटते हैं।
(4) बिन्दु O वृत्त का अभीष्ट केन्द्र है।

Ex 15.1 Circle लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 13.
चित्र में, 0 वृत्त का केन्द्र, त्रिज्या 5 सेमी तथा OP ⊥ AB, OQ ⊥ CD व AB||CD, AB = 6 सेमी, CD = 8 सेमी है। PQ का मान ज्ञात कीजिए।
हलः

प्रश्न 14.
यदि वृत्त का व्यास उसकी प्रत्येक जीवा को समद्विभाजित करता है तब सिद्ध कीजिए कि उसकी जीवाऐं समान्तर हैं।
हलः
प्रथम स्थिति : यदि वृत्त की दो जीवाऐं वृत्त के एक ही ओर हैं।
∵ वृत्त के केन्द्र तथा जीवा के मध्य बिन्दु को मिलाने वाली रेखा जीवा पर लम्ब होती है।
∠OMA = ∠OMB = 90° (प्रत्येक 90°)
∠ONC = ∠OND = 90° (प्रत्येक 90°)
∠OMA = ∠ONC = 90° (संगत कोण)
तथा
∠OMB = ∠OND = 90° (संगत कोण)
परन्तु ये संगत कोण तभी बराबर होंगे जबकि AB ||CD
द्वितीय स्थिति : यदि वृत्त की दोनों जीवाऐं वृत्त के केन्द्र के विपरीत ओर हैं।
∵ वृत्त के केन्द्र तथा जीवा के मध्य बिन्दु को मिलाने वाली रेखा जीवा पर लम्ब होती है।
∠OMA = ∠OMB = 90° (प्रत्येक 90°)
∠ONC = ∠OND = 90° (प्रत्येक 90°)
∠OMA = ∠OND = 90° तथा
∠OMB = ∠ONC = 90°
परन्तु ये कोण एकान्तर कोण हैं। ये कोण एकान्तर तभी हो सकते हैं जबकि
AB||CD
∵ वृत्त की जीवायें AB तथा CD समान्तर होंगी।

प्रश्न 15.
दो समान वृत्त परस्पर P व Q बिन्दुओं पर प्रतिच्छेद करते हैं। P से एक रेखा, वृत्तों पर बिन्दु A व B से मिलती है। सिद्ध कीजिए कि QA = QB
हलः

चाप PQ दोनों वृत्तों में उभयनिष्ठ हैं।
∴ ∠QAP = ∠QBP
PQ उभयनिष्ठ जीवा
तथा
∠APQ = ∠QPB
(वृत्तों के शेष कोणों द्वारा बने कोण)
अतः ∆APQ ≅ ∆BPQ
∴ QA = QB

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 10 Maths Solutions Chapter 10 Trigonometrical Ratios and Identities Ex 10.4 त्रिकोणमितीय अनुपात एवं असमिकाएँ

Ex 10.4 Trigonometrical Ratios and Identities अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि sinθ = cost तब θ का मान ज्ञात कीजिए।
हल:
∵ sinθ = cosθ

प्रश्न 2.
sin²θ sec²θ का मान ज्ञात कीजिए।
हल:
sin² θ · sec²θ (UPBoardSolutions.com) = sin²θ · [latex]\frac{1}{\cos ^{2} \theta}[/latex]
= tan²θ

प्रश्न 3.
secθ sinθ का मान ज्ञात कीजिए।
हलः
secθ ·sinθ = [latex]\frac{1}{\cos \theta}[/latex]·sin²
= tanθ

प्रश्न 4.
(secθ – tanθ) (secθ + tanθ) का मान ज्ञात कीजिए।
हलः
(secθ – tanθ)(secθ + tanθ) = sec²θ – tan²θ
=1

प्रश्न 5.
यदि cosθ = [latex]\frac{a}{b}[/latex], तब sine का मान ज्ञात कीजिए।
हलः

प्रश्न 6.
यदि tanθ = [latex]\frac{a}{b}[/latex], तब [latex]\frac{\cos \theta+\sin \theta}{\cos \theta-\sin \theta}[/latex] का मान ज्ञात कीजिए।
हलः

प्रश्न 7.
यदि x = a cosθ, y = b sinθ, a (b²x² + a²y²) का मान ज्ञात कीजिए।
हलः
x = acosθ तथा y = bsinθ

प्रश्न 8.
(sin⁴ θ – cos⁴ θ + 1) cosec²θ का मान ज्ञात कीजिए।
हलः
(sin⁴ θ – cos⁴ θ + 1)cosec²θ
= [(sin²θ)² – (cos² θ)² + 1]cosec²θ
= [(sin²θ + cos² θ) (UPBoardSolutions.com) (sin² θ – cos²θ) + 1]·cosec²θ
= [1(sin² θ – cos²θ) + sin²θ + cos² θ]cosec²θ
= (sin² θ – cos²θ + sin² θ + cos²θ).cosec²θ
= 2 sin²θ × [latex]\frac{1}{\sin ^{2} \theta}[/latex] = 2

प्रश्न 9.
[latex]\sqrt{\frac{1+\sin \theta}{1-\sin \theta}}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

प्रश्न 10.
[latex]\sqrt{\frac{1+\sin \theta}{1-\sin \theta}}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

प्रश्न 11.
[latex]\frac{1-\tan ^{2} \theta}{1+\tan ^{2} \theta}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

प्रश्न 12.
[latex]\frac{\sin \theta}{1+\cos \theta}[/latex] का मान ज्ञात कीजिए। (NCERT)
हलः

प्रश्न 13.
(1 + tanθ + secθ)(1 + cotθ – cosecθ) का मान ज्ञात कीजिए।
हलः
(1 + tanθ + secθ) (UPBoardSolutions.com) (1 + cotθ – cosecθ)

प्रश्न 14.
sin² θ + sin⁴ θ = (यदि cosθ + cos² θ = 1) का मान ज्ञात कीजिए।
हलः
यदि cosθ + cos²θ = 1
coso = 1 – cos² θ
cosθ = (UPBoardSolutions.com) sin²θ
या sin² θ = cos ²
तब sin²θ + sin⁴ θ = sin² θ(1 + sin²θ)
= cos θ(1 + cosθ)
= cosθ + cos² θ = 1

Ex 10.4 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-I)

निम्न को सिद्ध कीजिए-

प्रश्न 15.
(1 – sin²θ) sec²θ = 1
हलः
L.H.S. = (1 – sin² θ)sec²θ
= cos² θ – sec² θ (UPBoardSolutions.com) (सर्वसम्मिका sin²θ + cos²θ = 1 से)
= cos ²θ·[latex]\frac{1}{\cos ^{2} \theta}[/latex]
= 1 = R.H.S

प्रश्न 16.
(secθ + tanθ)² = [latex]\frac{1+\sin \theta}{1-\sin \theta}[/latex]
हलः
L.H.S. = (secθ + tanθ)²

प्रश्न 17.
(sin θ – cosθ)(cotθ + tanθ) = secθ – cosec θ
हलः

प्रश्न 18.
[latex]\frac{\sec \theta-\tan \theta}{\sec \theta+\tan \theta}[/latex] = 1 – 2 secθ tan θ + 2 tan²θ
हलः

प्रश्न 19.

हलः
अंश का परिमेयकरण (UPBoardSolutions.com) करने पर,

प्रश्न 20.
(1 – sinθ) (1 + sin θ) (1 + tan²θ) = 1
हलः
L.H.S. = (1 – sinθ)(1 + sinθ)(1 + tan²θ)
= (1 – sin²θ)sec²θ
= cos²θ · (UPBoardSolutions.com) sec²θ
= cos²θ [latex]\frac{1}{\cos ^{2} \theta}[/latex] = 1 = R.H.S.

प्रश्न 21.

हलः

प्रश्न 22.

हलः

प्रश्न 23.

हलः

Ex 10.4 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 24.
यदि tan θ + sin θ = a, tanθ – sin θ = b, तब सिद्ध कीजिए a² – b² = 4[latex]\sqrt{a b}[/latex]
हलः
L.H.S. = a² – b²
= (tan θ + sinθ)² – (UPBoardSolutions.com) (tan θ – sinθ)²
= tan² θ + sin² θ + 2 tanθsinθ – tan² θ – sin²θ + 2 tanθ sin²
= 4 tanθ sinθ

∴ L.H.S. = R.H.S.

प्रश्न 25.
यदि asin ³ θ + b cos³ θ = sin θ cosθ in a sinθ – b cos θ = 0, तब सिद्ध कीजिए कि a² + b² = 1
हलः
asin³ θ + bcos ³ θ = sinθ cosθ … (1)
asinθ – bcos θ = 0 … (2)
समीकरण (2) से,
asinθ = bcos θ …(3)
समीकरण (1) से, asinθ, का मान रखने पर
(asinθ).sin²θ + bcos³ θ = sinθ cosθ
bcosθsin²θ + bcos³θ = (UPBoardSolutions.com) sinθ cosθ
bcos θ(sin²θ + cos²θ) = sinθ cosθ
bcosθ (1) = sin θcosθ
∴ b = sin θ …(4)
समीकरण (3) से, b का मान रखने पर
asinθ = sin θcos θ
∴ a = cos θ
L.H.S. = a² + b² …(5)
= cos ²θ + sin²θ
= 1 = R.H.S.

सिद्ध कीजिए कि –

प्रश्न 26.
tanθ – cotθ = [latex]\frac{2 \sin ^{2} \theta-1}{\sin \theta \cos \theta}=\frac{1-2 \cos ^{2} \theta}{\sin \theta \cos \theta}[/latex]
हलः

प्रश्न 27.
sec² θ + cosec²θ = sec² θ cosec²θ (UP 2000, 02)
हलः
L. H. S. = sec²θ + (UPBoardSolutions.com) cosec²θ

प्रश्न 28.
(cosecθ – cotθ)² = [latex]\frac{1-\cos \theta}{1+\cos \theta}[/latex] (NCERT)
हलः
L. H. S. = (cosecθ – cotθ)²

प्रश्न 29.
[latex]\sqrt{\sec ^{2} \theta+\csc ^{2} \theta}[/latex] = tanθ + cotθ
हलः

प्रश्न 30.
[latex]\frac{1+\cos \theta}{1-\cos \theta}[/latex] = (cosecθ + cotθ)²
हलः

Ex 10.4 Trigonometrical Ratios and Identities दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 31.
सिद्ध कीजिए कि tan² A – tan² B = [latex]\frac{\sin ^{2} A-\sin ^{2} B}{\cos ^{2} A \cos ^{2} B}=\frac{\cos ^{2} B-\cos ^{2} A}{\cos ^{2} B \cos ^{2} A}[/latex]
हलः

प्रश्न 32.
सिद्ध कीजिए [latex s = 2]\frac{\cot \theta+\csc \theta-1}{\cot \theta-\csc \theta+1}=\frac{1+\cos \theta}{\sin \theta}[/latex]
हलः

प्रश्न 33.
सिद्ध कीजिए [latex s=2]\frac{1+\cos \theta-\sin ^{2} \theta}{\sin \theta(1+\cos \theta)}=\cot \theta[/latex] (UP 2012)
हलः

प्रश्न 34.
सिद्ध कीजिए [latex s=2]\frac{\csc \theta+\cot \theta}{\csc \theta-\cot \theta}[/latex] = (cosecθ + cotθ)² = 1 + 2 cot² θ + 2 cosecθ cotθ.
हलः

प्रश्न 35.
सिद्ध कीजिए

हलः

प्रश्न 36.
यदि sinθ + cosθ = p a secθ + cosecθ = q, तब सिद्ध कीजिए कि
q(p² – 1) = 2p
हलः
L. H. S. = 9(p² – 1)- 2p
= (sec θ + cosec θ) (UPBoardSolutions.com) [(sin θ + cos θ)² – 1]

∵ (sinθ + cosθ) = P
= P × 2 = 2P = R.H.S.

प्रश्न 37.
यदि cosθ + sinθ = [latex] \sqrt{{2}} [/latex] · cosθ, तब सिद्ध कीजिए कि (cosθ – sinθ) = [latex] \sqrt{{2}} [/latex] · sinθ
हलः
यदि cosθ + sinθ = [latex] \sqrt{{2}} [/latex]cosθ
दोनों पक्षों का वर्ग करने पर,
(cosθ + sinθ)² = ([latex] \sqrt{{2}} [/latex] cosθ)²
cos²θ + sin²θ + 2cosθ sinθ = 2cos²θ
sin²θ = 2cos²θ – cos²θ (UPBoardSolutions.com) = 2sinθ · cosθ
cos²θ – 2cosθ·sinθ = sin²θ
cos²θ + sin²θ – 2cosθ·sinθ = sin²θ + sin²θ
(cosθ – sinθ)² = 2sin²θ
cosθ – sinθ = [latex] \sqrt{{2}} [/latex] sinθ इति सिद्धम्।

प्रश्न 38.
यदि sinθ – cosθ = 0 तब सिद्ध कौजिए कि sin⁴θ + cos⁴θ = [latex]\frac{1}{2}[/latex]
हलः
दिया है, sinθ – cosθ = 0
दोनों और वर्ग करने पर,
(sinθ – cosθ)² = 0
sin²θ + cos²θ – 2sinθ cosθ = 0
1 – 2 sinθ cosθ = 0
1 = 2sinθ cosθ
sinθ·cosθ = [latex]\frac{1}{2}[/latex]
L. H. S. = sin⁴θ + cos⁴θ
= (sin²θ)² + (cos²θ)² + 2sin²θcos²θ – 2sin²θcos²θ
= (sin²θ + cos²θ)² – 2(sinθ·cosθ)²
= (1)² – 2[latex]\left(\frac{1}{2}\right)^{2}[/latex] (UPBoardSolutions.com)
= 1 – 2 × [latex]\frac{1}{4}[/latex] = 1 – [latex]\frac{1}{2}=\frac{1}{2}[/latex] = R.H.S

प्रश्न 39.
यदि [latex]\frac{x}{a}[/latex]cosθ + [latex]\frac{y}{b}[/latex] sinθ = 1 व [latex]\frac{x}{a}[/latex]sinθ – [latex]\frac{y}{b}[/latex] cosθ = 1, तब सिद्ध कीजिए कि [latex]\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}[/latex] = 2
हलः

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 11 Triangles and Its Angles Ex 11.1 त्रिभुज एवं उसके गुण

Ex 11.1 Triangles and Its Angles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि एक त्रिभुज के दो कोण बराबर है तब दोनों की विपरीत भुजा बराबर है या नहीं?
हलः
एक त्रिभुज के दो कोण बराबर है तब उस त्रिभुज की सम्मुख भुजाएं भी बराबर होगी।

प्रश्न 2.
एक त्रिभुज की बराबर भुजाओं के विपरीत कोण बराबर है या नहीं?
हलः
बराबर

प्रश्न 3.
यदि एक त्रिभुज की भुजाएँ 5 सेमी, 6 सेमी तथा 11 सेमी हैं तब त्रिभुज का नाम बताइए।
हलः
∵ किसी त्रिभुज की रचना के लिए दो भुजाओं का योग तीसरी भुजा से बड़ा होना चाहिए परन्तु 5 + 6 = 11, 11, के बराबर है।
∴ त्रिभुज की रचना सम्भव नहीं है।

प्रश्न 4.
यदि एक त्रिभुज की भुजाएँ 5 सेमी, 4 सेमी तथा 3 सेमी हैं तब त्रिभुज का नाम बताइए।
हलः :
∵ 3 + 4 = 7 > 5
अतः त्रिभुज की रचना सम्भव है।
(5)² = (3)² + (4)² .
∴ यह एक समकोण त्रिभज है।

प्रश्न 5.
एक त्रिभुज की दो भुजाओं का योग, हमेशा तीसरी भुजा से अधिक होता है या नहीं?
हलः
एक त्रिभुज की दो भुजाओं का योग, हमेशा तीसरी भुजा से अधिक होता है। हाँ

प्रश्न 6.
यदि एक त्रिभुज के सभी कोण बराबर है, तब इनमें प्रत्येक कोण ज्ञात कीजिए।
हलः
एक त्रिभुज के तीनों कोणों का योग = 180°
∠A + ∠B + ∠C = 180° …………. (1)
माना ∠A = x, ∠B = x, ∠C = x
∴ x + x + x = 180°
3x = 180°
x = [latex]\frac{180^{\circ}}{3}[/latex] = 60°
∴ ∠A = ∠B = ∠C = 60°

प्रश्न 7.
यदि एक समकोण त्रिभुज के दो न्यूनकोण बराबर है, तब प्रत्येक न्यूनकोण ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
यदि ∠A = 90° तथा ∠B = ∠C
तब 90° + ∠B + ∠C = 180°
∠B + ∠C = 180° – 90° = 90°
प्रत्येक ∠B = ∠C = 45°

Ex 11.1 Triangles and Its Angles लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 8.
एक त्रिभुज के कोण 2 : 3 : 7 के अनुपात में है। त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हलः
माना
∆ABC का ∠A = 2x
∠B = 3x
∠C = 7x
∴ ∠A + ∠B + ∠C = 180°
2x + 3x + 7x = 180°
12x = 180°
x = [latex]\frac{180^{\circ}}{12}[/latex] = 15°
∴ ∠A = 2 × 15 = 30°
∠B = 3 × 15 = 45°
∠C = 7 × 15 = 105°

प्रश्न 9.
∆ABC में, ∠A + ∠B = 65° तथा / B+ ∠C =140°, त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
65° + ∠C = 180°
∠C = 180°- 65° = 115°
तथा ∠A + ∠B + ∠C = 180°
∠A + 140° = 180°
∠A = 180° – 140° = 40°
∵ ∠A + ∠B = 65°
40° + ∠B = 65°
∴∠B = 65° – 40° = 25°

प्रश्न 10.
∆ABC में, यदि ∠B = 76° तथा ∠C = 48° है, तो ∠A ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
∠A + 76° + 48° = 180°
∠A = 180° – 124° = 56°

प्रश्न 11.
∆ABC में, यदि ∠B = 105° तथा ∠C =50° है, तो ∠A ज्ञात कीजिए।
हल:
∆ABC में, ∠A + ∠B + ∠C = 180°
∠A + 105° + 50° = 180°
∠A = 180° – 155° = 25°

प्रश्न 12.
एक त्रिभुज के दो कोणों का योग, तीसरे कोण के बराबर है। तीसरे कोण की माप ज्ञात कीजिए।
हल:
∆ABC में, (∠A + ∠B) + ∠C = 180°
∠A + ∠B = ∠C ……………. (1)
∠C + ∠C = 180°
2∠C = 180°
∠C = [latex]\frac{180^{\circ}}{2}[/latex] = 90°
तीसरा कोण ∠C = 90°

प्रश्न 13.
यदि एक त्रिभुज के कोण 2 : 3 : 4 के अनुपात में है। कोण ज्ञात कीजिए। (NCERT Exemplar)
हल:
∆ABC के कोण ∠A : ∠B : ∠C = 2 : 3 : 4
माना ∠A = 2x, ∠B = 3x, ∠C = 4x
∠A + ∠B + ∠C = 180°
2x + 3x + 4x = 180° ⇒ 9x = 180°
x = [latex]\frac{180^{\circ}}{9}[/latex] = 20°
∴∠A = 2 × 20° = 40°, ∠B = 3 × 20° = 60°, ∠C = 4 × 20°= 80°

Ex 11.1 Triangles and Its Angles लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 14.
एक ∆ABC में, 15∠A = 10∠B = 6∠C हो, तो ∠A, ∠B तथा ∠C ज्ञात कीजिए।
हलः
15∠A = 10∠B = 6∠C
माना
∠B = x
15∠A = 10x

प्रश्न 15.
एक ∆ABC में, यदि ∠A = 55°, ∠B = 40° तब ∠C ज्ञात कीजिए।
हल:
∆ABC में,
∠A + ∠ B + ∠C = 180°
55° + 40° + ∠C = 180°
∠C = 180° – 95° = 85°

प्रश्न 16.
A, B, C एक त्रिभुज के तीन कोण हैं। यदि A – B = 15°, B – C = 30° हो, तो ∠A, ∠B और ∠C ज्ञात कीजिए।
हल:
A – B = 15° ⇒ A = B + 15° ………….(1)
B – C = 30° ⇒ C = B – 30° …………(2)
∵ ∠A + ∠B + ∠C = 180°
B + 15° + B + B – 30° = 180°
3B – 15° = 180°
3B = 180° + 15° = 195°
∴ B = [latex]\frac{195^{\circ}}{3}[/latex] = 65°
∴ समीकरण (1) से
∠A = 65° + 15° = 80°
∠C = 65° – 30° = 35°

प्रश्न 17.
एक त्रिभुज के दो कोणों का योग 106° है तथा उनका अन्तर 10° है। त्रिभुज के सभी कोण ज्ञात कीजिए।
हलः
माना A के दो कोण ∠A तथा ∠B है।

समीकरण (1) में ∠A का मान रखने पर
58° + ∠B = 106°
∠B = 106° – 58° = 48°
तथा ∠C = 180° – (∠A + ∠B) = 180° (58° + 48°) = 180° – 106° = 74°

प्रश्न 18.
दिये गये चित्र में, AB||DC यदि x = [latex]\frac{4 y}{3}[/latex], y = [latex]\frac{3 z}{8}[/latex] हो, तो ∠BCD ज्ञात कीजिए।
हल:
∵ AB|| DC तथा BD तिर्यक रेखा है।

प्रश्न 19.
एक ∆ABC में, ∠A – ∠B = 33° तथा ∠B – ∠C = 18° हो, तो त्रिभुज के प्रत्येक कोण की माप ज्ञात कीजिए।
हल:
∠A – ∠B = 33° ⇒ ∠A = 2B + 33° …………. (1)
∠B – ∠C = 18° ⇒ ∠B – 18° = ∠C ……………. (2)
∵ ∠A + ∠B + ∠C = 180°
∠B + 33°+ ∠B + ∠B – 18° = 180°
3∠B + 15° = 180°
3∠B = 180° – 15° = 165°
∠B = [latex]\frac{165^{\circ}}{3}[/latex] = 55°
∴ ∠A = ∠B + 33° = 55 + 33 = 88°
∴ ∠C = ∠B – 18 = 55 – 18 = 37°

प्रश्न 20.
दिये गये चित्र में, सिद्ध कीजिए कि ∠a + ∠b + ∠c = 360°
हलः
∠BAC + ∠ABC + ∠ACB = 180°
180 – ∠a + 180 – ∠b + 180 – ∠c = 180°
360° = ∠a + ∠b + ∠c

Ex 11.1 Triangles and Its Angles दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 21.
एक त्रिभुज ABC है जिसमें ∠A = 72°, ∠B तथा ∠C के अन्तः समद्विभाजक बिन्दु O पर मिलते हैं तो∠BOC का परिमाण ज्ञात कीजिए।
हलः
माना ∠ABC = x तथा ∠ACB = y

प्रश्न 22.
दिये गये चित्र में, AE, ∠CAD का अर्द्धक है तथा ∠B = ∠C तो सिद्ध कीजिए कि AE||BC
हलः
माना
∠CAD = 2x
∴ ∠DAE = ∠CAE = x
∠B = ∠C
∠CAD, ∆ABC का बहिष्कोण है।

∴ ∠CAD = ∠ABC + ∠ACB
∴ ∠ABC + ∠ACB = 2x
परन्तु ∠ABC = ∠ACB
∴ प्रत्येक ∠ABC = ∠ACB = x°
∴ ∠EAC = ∠ACB = x° (परन्तु ये एकान्तर कोण हैं।)
AE ||BC

प्रश्न 23.
दिये गये चित्र में, AB||CD है। x और y के मान ज्ञात कीजिए।
हल:
∵ AB||CD
∠FED = ∠EMB
58 = y + 20
58 – 20 = y
∴ y = 38°
∴ ∠MEB = 180 – (58 + 22)
= 180° – 80° = 100°

∆EBM में,
x + y + 100 = 180
x + 38 + 100 = 180
x = 180 – 138 = 42°

प्रश्न 24.
दिये गये चित्र में, x और y के मान ज्ञात कीजिए।

हल:
∵ y + 125 = 180 (रैखिक युग्म कोण)
y = 180 – 125 = 55°
∠CDE = ∠BMC = 65° (एकान्तर कोण)
तथा ∠CDN = ∠ENG = 65° (एकान्तर कोण)
∆NEG में, x + y + 65 = 180
∴ x + 55 + 65 = 180
x = 180 – 120 = 60°

प्रश्न 25.
निम्न प्रत्येक में x का मान ज्ञात कीजिए।
हलः

चित्र (i) में,
∠EAF = ∠BAC = 60° [शीर्षाभिमुख कोण]
∆ABC का बहिष्कोण ∠ACD है।
∠ACD = ∠BAC + ∠ABC .
115° = 60° + x
115° – 60° = x
x = 55°
चित्र (ii) में, ∆ABE में ∠AEB = 180 – (75 + 65)
= 180 – 140 = 40°
∠CED = ∠AEB = 40° [शीर्षाभिमुख कोण]
∆ECD में, 40 + 110 + x = 180°
150 + x = 180°
x = 180° – 150° = 30°

प्रश्न 26.
एक त्रिभुज के कोणों को परिमाण के बढ़ते हुए क्रम में रखा गया है यदि दो क्रमागत कोणों के बीच का अन्तर 10° है तो तीनों कोणों को ज्ञात कीजिए।
हलः
माना त्रिभुज के तीन कोण क्रमशः x, x + 10, x + 20 हैं।
∴ x + x + 10+ x + 20 = 180
3x + 30 = 180
3x = 180 – 30 = 150°
x = [latex]\frac{150}{3}[/latex] = 50°
∴ त्रिभुज के तीन कोण क्रमश: 50°, 60°, 70° है।

प्रश्न 27.
दिये गये चित्र में, ∆ABC के सभी कोणों की माप ज्ञात कीजिए।
हल:
∆ABC में,

∠1 = 180 – 110 = 70°
∠3 = 180 – 140 = 40°
∠2 = 180 – (70 + 40) = 180 – 110 = 70°

Balaji Publications Mathematics Class 9 Solutions