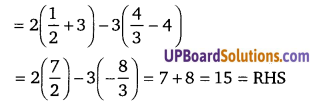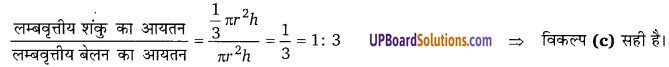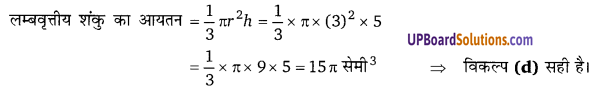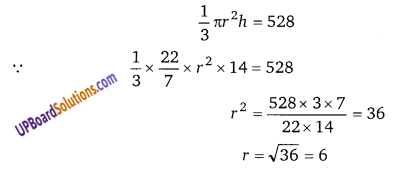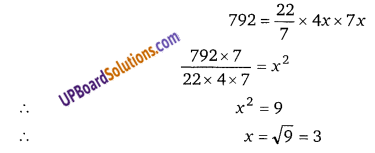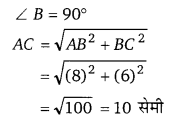Safia

Balaji Class 9 Maths Solutions Chapter 19 Surface Area and Volume of a Right Circular Cone and Sphere Ex 19.2 लम्बवृत्तीय शंकु एवं गोले का पृष्ठीय क्षेत्रफल एवं आयतन

Ex 19.2 Surface Area and Volume of a Right Circular Cone and Sphere बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
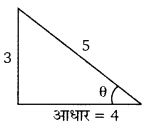
एक अर्द्धगोले की त्रिज्या 4 सेमी है, उसका वक्रपृष्ठ होगा- [UP 2006, 07]
(a) 647 वर्ग सेमी
(b) 487 वर्ग सेमी
(c) 327 वर्ग सेमी
हलः
अर्द्धगोला या गोलार्द्ध का वक्रपृष्ठ = 2πr² = 2 × T × (4)²
= 32π वर्ग सेमी

प्रश्न 2.
एक गोले का आयतन 38808 घन सेमी हो तो उसका वक्रपृष्ठ होगा-
(a) 1386 वर्ग सेमी
(b) 4158 वर्ग सेमी
(c) 5544 वर्ग सेमी
हलः

प्रश्न 3.
14 सेमी व्यास वाले अर्द्धगोले का सम्पूर्ण पृष्ठ है-
(a) 588 π वर्ग सेमी
(b) 392 π वर्ग सेमी
(c) 147 π वर्ग सेमी
(d) 98 π वर्ग सेमी
हलः
अर्द्धगोले का व्यास = 14 सेमी
अर्द्धगोले की त्रिज्या = [latex]\frac{14}{2}[/latex] = 7 सेमी
अर्द्धगोले का सम्पूर्ण पृष्ठ = 3πr²
= 3π(7)²
= 3π × 49 = 147π वर्ग सेमी
⇒ विकल्प (c) सही है।

प्रश्न 4.
10 सेमी त्रिज्या के गोले को पिघलाकर समान त्रिज्या की 8 ठोस गेंद बनायी गयी हैं। प्रत्येक गेंद का वक्रपृष्ठ है-
(a) 600 वर्ग सेमी
(b) 657 वर्ग सेमी
(c) 75 7 वर्ग सेमी
(d) 1007 वर्ग सेमी
हलः

प्रश्न 5.
दो गोलों की त्रिज्याओं का अनुपात 5 : 4 है, उनके सम्पूर्ण पृष्ठों का अनुपात है-
(a) 4 : 5
(b) 16 : 25
(c) 25 : 16
(d) 5 : 4
हलः

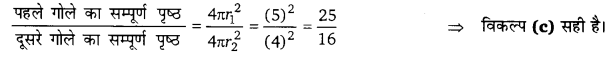
प्रश्न 6.
दो गोलों के आयतनों का अनुपात 1:27 है, उनकी त्रिज्याओं का अनुपात होगा-
(a) 1 : 3
(b) 1 : 9
(c) 3 : 1
(d) 9 : 1
हलः

Ex 19.2 Surface Area and Volume of a Right Circular Cone and Sphere अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 7.
4.2 सेमी त्रिज्या वाले गोले का आयतन व वक्रपृष्ठ ज्ञात कीजिए। [UP 2004,07]
हल:

प्रश्न 8.
उस गोले का वक्रपृष्ठ ज्ञात कीजिए जिसका आयतन 4851 घन मीटर है।
हलः

प्रश्न 9.
एक गोले का वक्रपृष्ठ 346.5 वर्ग मीटर है। इसकी त्रिज्या तथा आयतन ज्ञात कीजिए।
हलः
वक्रपृष्ठ = 346.5
4πr² = 346.5

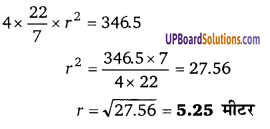
प्रश्न 10.
उस गोले की त्रिज्या ज्ञात कीजिए जिसका वक्रपृष्ठ 647 वर्ग सेमी है। [UP 2003]
हलः
गोले का वक्रपृष्ठ = 64π सेमी²
4πr² = 64 π

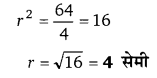
प्रश्न 11.
π के पदों में उस गोले का वक्रपृष्ठ व आयतन ज्ञात कीजिए। जिसका व्यास 3 सेमी है।
हलः
गोले का व्यास = 3 सेमी
गोले की त्रिज्या = [latex]\frac{3}{2}[/latex]

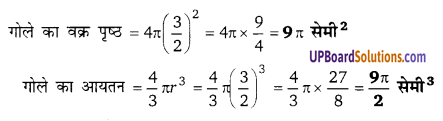
Ex 19.2 Surface Area and Volume of a Right Circular Cone and Sphere लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 12.
3.5 सेमी त्रिज्या के अर्द्धगोले का आयतन तथा सम्पूर्ण पृष्ठ ज्ञात कीजिए। [UP 2002]
हलः
अर्द्धगोले की त्रिज्या r = 3.5 सेमी

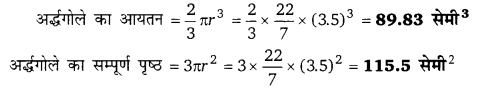
प्रश्न 13.
एक गोले के आयतन व वक्रपृष्ठ के आंकिक मान बराबर हैं। इनकी त्रिज्याएँ ज्ञात कीजिए। [UP 2003]
हल:
गोले का आयतन = गोले का सम्पूर्ण पृष्ठ

r = 3 सेमी

प्रश्न 14.
7 सेमी भुजा वाले घन से एक महत्तम गोला काटा गया है। गोले का आयतन ज्ञात कीजिए। (दिया है: π = 3.14)
हल:

प्रश्न 15.
10.5 सेमी त्रिज्या के धातु के एक गोले को पिघलाकर छोटे शंकु बनाये गये हैं। जिनमें प्रत्येक की त्रिज्या 3.5 सेमी तथा ऊँचाई 3 सेमी है। शंकुओं की कुल संख्या ज्ञात कीजिए।
हलः

Ex 19.2 Surface Area and Volume of a Right Circular Cone and Sphere दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 16.
एक गोलीय कोश का बाह्य व्यास 10 सेमी तथा अन्तः व्यास 9 सेमी है। इसके अन्दर भरी धातु का आयतन ज्ञात कीजिए।
हलः

प्रश्न 17.
समान वृत्तीय आधार तथा समान ऊँचाई का एक शंकु, एक अर्द्धगोला तथा एक बेलन बनाया गया है। इनके आयतनों का अनुपात ज्ञात कीजिए। [UP 2001]
हल:
h =r …… (1)
शंकु का आयतन : अर्द्धगोले का आयतन : बेलन का आयतन

प्रश्न 18.
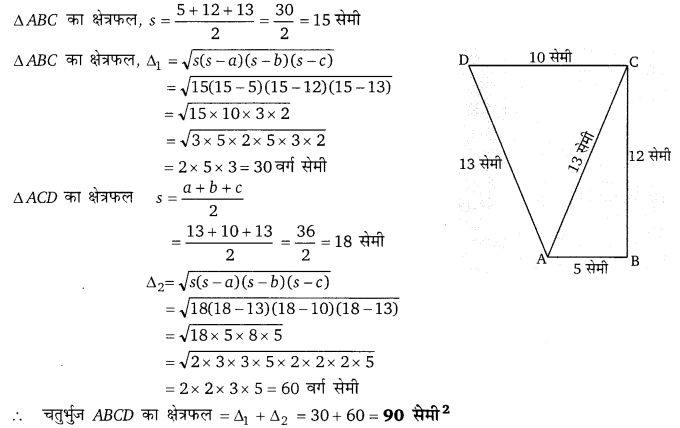
एक पात्र अर्द्धगोल कटोरे के रूप का है। जिसके ऊपर एक खोखला बेलन बना हुआ है। गोले का व्यास 14 सेमी तथा पात्र की कुल ऊँचाई 13 सेमी है। पात्र की धारिता ज्ञात कीजिए।
हलः

प्रश्न 19.
लोहे की एक ठोस गेंद की त्रिज्या 9 सेमी है। इसे पिघलाकर तीन छोटी ठोस गेंदे बनायी गयी है। यदि उनमें से दो की त्रिज्याएँ क्रमशः 8 सेमी और 6 सेमी है, तो तीसरी गेंद की त्रिज्या ज्ञात कीजिए। [UP 2016]
हलः
लोहे की ठोस गेंद का आयतन = पहली + दूसरी + तीसरी गेंद का आयतन माना तीसरी गेंद की त्रिज्या = r सेमी

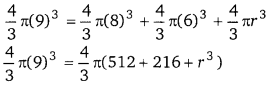
प्रश्न 20.
24 सेमी व्यास और 6 सेमी ऊँचे एक लम्बवृत्तीय शंकु को पिघलाकर बनाए गए ठोस गोले का पृष्ठीय क्षेत्रफल ज्ञात कीजिए। [UP 2016]
हलः

प्रश्न 21.
12 सेमी त्रिज्या के एक बेलनाकार टब में 20 सेमी ऊँचाई तक पानी भरा है। लोहे की एक गोलीय गेंद टब में डाली जाती है। और इस प्रकार पानी का स्तर 6.75 सेमी ऊपर उठ जाता है। गेंद की त्रिज्या ज्ञात कीजिए। [UP 2015,16]
हलः
गोलीय गेंद का आयतन = बेलनाकार टब में ऊपर उठे पानी का आयतन

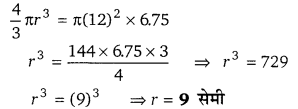
प्रश्न 22.
एक ठोस धातु के बेलन के दोनों सिरे अर्द्धगोलाकार है। इसकी सम्पूर्ण ऊँचाई 19 सेमी हैं तथा बेलन का व्यास 7 सेमी है। इस ठोस का भार ज्ञात कीजिए यदि 1 सेमी³ धातु का भार 4.5 ग्राम है।[latex]\left(\pi=\frac{22}{7}\right)[/latex]
हलः

Ex 19.2 Surface Area and Volume of a Right Circular Cone and Sphere बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
किसी लम्बवृत्तीय शंकु की त्रिज्या और ऊँचाई में 5 : 12 का अनुपात है। यदि शंकु का आयतन 314 घन मीटर हो तो आधार की त्रिज्या होगी-
(a) 1 मीटर
(b) 2 मीटर
(c) 4 मीटर
(d) 5 मीटर
हलः

प्रश्न 2.
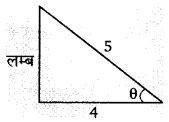
एक शंकु के आकार का तम्बू बनाने में 352 वर्ग मीटर कपड़ा लगा है, यदि तम्बू के आधार की त्रिज्या 3.5 मीटर हो तो उसकी तिर्यक ऊँचाई होगी-
(a) 32 मीटर
(b) 22 मीटर
(c) 35 मीटर
(d) 52 मीटर
हलः

प्रश्न 3.
यदि एक शंकु का वक्रपृष्ठ 1884 वर्ग मीटर तथा उसके आधार का व्यास 12 मीटर है तो शंकु की ऊँचाई होगी-
(a) 8 मीटर
(b) 18 मीटर
(c) 128 मीटर
(d) 110 मीटर
हलः

प्रश्न 4.
एक लम्बवृत्तीय शंकु की आधार त्रिज्या 14 सेमी तथा उसकी ऊँचाई 10.5 सेमी है तो शंकु का वक्रपृष्ठ होगा-
(a) 77 सेमी²
(b) 770 सेमी²
(c) 70 सेमी²
(d) इनमें से कोई नहीं
हलः
r = 14 सेमी, h = 10.5 सेमी

प्रश्न 5.
एक लम्बवृत्तीय शंकु के आधार का परिमाप 66 सेमी है। यदि शंकु की ऊँचाई 8 सेमी हो तो शंकु का आयतन होगा-
(a) 124 सेमी³
(b) 924 सेमी³
(c) 92.4 सेमी²
(d) इनमें से कोई नहीं
हलः

प्रश्न 6.
एक शंकु की ऊँचाई और आधार का व्यास क्रमशः 12 सेमी व 18 सेमी हैं तो इसकी तिर्यक ऊँचाई होगी-
(a) 15 सेमी
(b) 12 सेमी
(c) 8 सेमी
(d) इनमें से कोई नहीं
हलः

प्रश्न 7.
एक शंकु का आयतन 100 1 सेमी है। यदि उसके आधार की त्रिज्या 5 सेमी हो तो इसका वक्रपृष्ठ होगा-
(a) 65 7 सेमी²
(b) 6.5 0 सेमी²
(c) 65 सेमी²
(d) इनमें से कोई नहीं
हलः

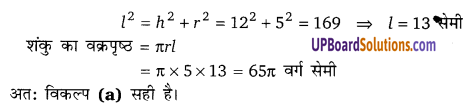
प्रश्न 8.
यदि किसी गोले का वक्रपृष्ठ 3247 सेमी है तो इसकी त्रिज्या होगी-
(a) 8 सेमी
(b) 9 सेमी
(c) 10 सेमी
(d) इनमें से कोई नहीं
हलः
गोले का वक्रपृष्ठ = 4πr² = 324π

अतः विकल्प (b) सही है।

प्रश्न 9.
एक तार का व्यास 5% कम कर दिया जाये तो उसकी लम्बाई कितने प्रतिशत बढ़ा दी जाये कि आयतन न बदले?
(a) 12%
(b) 10.8%
(c) 11%
(d) इनमें से कोई नहीं
हलः

प्रश्न 10.
एक बेलन की ऊँचाई तथा आधार की त्रिज्या दोनों 10% बढ़ा दी जाये तो बेलन के आयतन में वृद्धि होगी-
(a) 33%
(b) 30%
(c) 33.1%
(d) 100%
हलः
माना बेलन की ऊँचाई तथा आधार की त्रिज्या h व r हैं। तब बेलन का आयतन V₁ = πr²h…(1)
बेलन की ऊँचाई तथा त्रिज्या को 10% बढ़ाने पर, माना ऊँचाई h₁ तथा त्रिज्या r₁ है।

Ex 19.2 Surface Area and Volume of a Right Circular Cone and Sphere स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
5.25 सेमी त्रिज्या तथा तिर्यक ऊँचाई 10 सेमी वाले शंकु का वक्रपृष्ठ ज्ञात कीजिए।
हलः
r = 5.25 सेमी
1 = 10 सेमी

प्रश्न 2.
एक शंकु के आकार की क्रानकाब के चौड़े भाग की त्रिज्या 2.1 सेमी तथा लम्बाई 20 सेमी है। यदि 1 सेमी² क्षेत्रफल में औसतन 4 दाने आते हैं तो पूरी कॉब में कुल कितने दानें आयेगे?
हलः

प्रश्न 3.
माना के पास 551 वर्ग मीटर कपड़ा है। इससे इसे 7 मीटर आधार त्रिज्या का एक टैन्ट बनाना है। सिलने व कटिंग में कुल 1 वर्ग मीटर कपड़ा यदि खराब होता है तो इससे बने टैन्ट का आयतन ज्ञात कीजिए।
हलः

प्रश्न 4.
एक गोलीय बर्तन, 0.25 सेमी मोटाई वाले स्टील से बना है। बर्तन की आन्तरिक त्रिज्या 5 सेमी है। तो बर्तन का बाहरी पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः
बाहरी त्रिज्या R = 5 + 0.25 = 5.25 सेमी
आन्तरिक त्रिज्या r = 5 सेमी
बर्तन का बाहरी पृष्ठीय क्षेत्रफल = 4πR²

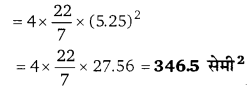
प्रश्न 5.
एक भवन का डोम अर्द्धगोलाकार है। इसकी त्रिज्या 63 डेकामी है। ₹ 2 प्रति वर्ग मीटर की दर से इसे रंगने में कुल लागत ज्ञात कीजिए।
हलः

प्रश्न 6.
r त्रिज्या व पृष्ठीय क्षेत्रफल S वाले घातु के 27 ठोस गोलों को पिघलाकर एक दूसरा गोला बनाया जाता है। जिसका पृष्ठीय क्षेत्रफल S’ है। निम्न के मान ज्ञात कीजिए-
(i) नये गोले की त्रिज्या r’
(ii) s व S’ का अनुपात।
हल:
27 गोलो का आयतन = 1 नये गोले का आयतन

प्रश्न 7.
दवाई का एक कैप्सूल 3.5 मिमी व्यास के गोले के आकार का है। इसको भरने के लिए कितनी दवाई की आवश्यकता होगी?
हल:

प्रश्न 8.
चन्द्रमा का व्यास लगभग पृथ्वी के व्यास का 1 है। चन्द्रमा का आयतन पृथ्वी के आयतन का कितना गुना है?
हलः

प्रश्न 9.
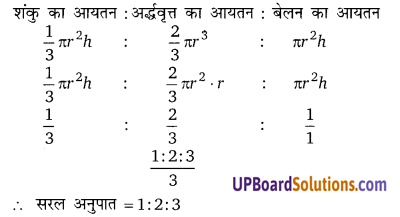
एक शंकु, अर्द्धवृत्त तथा बेलन समान आधार व समान ऊँचाई के हैं। सिद्ध कीजिए कि उनके आयतनों में 1 : 2 : 3 का अनुपात है।
हल:
शंकु का आयतन : अर्द्धवृत्त का आयतन : बेलन का आयतन

प्रश्न 10.
एक बेलन व एक शंकु के आधार की त्रिज्याएँ तथा ऊँचाई समान हैं। यदि उनके वक्रपृष्ठों का अनुपात 8 : 5 है तो सिद्ध कीजिए कि प्रत्येक की त्रिज्या एवं ऊँचाई में 3 : 4 का अनुपात है।
हलः

प्रश्न 11.
10 सेमी ऊँचे तथा 6 सेमी आधार त्रिज्या के एक लम्बवृत्तीय बेलन से समान आधार एवं ऊँचाई का एक शंकु काटा जाता है। शेष बचे ठोस का आयतन ज्ञात कीजिए।
हलः

प्रश्न 12.
28 सेमी व्यास की धातु की अर्द्धवृत्ताकार सीट को मोड़कर एक खुला शंक्वाकार कप बनाया गया है। कप की धारिता व गहराई ज्ञात कीजिए।
हलः
जब अर्द्धवृत्ताकार शीट को माड़कर एक खुला शंक्वाकार कप बनाया जाता है।

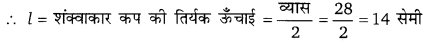
प्रश्न 13.
14 सेमी भुजा वाले घन में समायोजित होने वाले महत्तम लम्बवृत्तीय शंकु का आयतन ज्ञात कीजिए।
हलः

प्रश्न 14.
एक खिलौना लम्बवृत्तीय बेलन के आकार का है जिसके एक ओर एक अर्द्धवृत्त तथा दूसरी ओर एक शंकु है। बेलनाकार भाग की ऊँचाई एवं त्रिज्या क्रमश: 13 व 5 सेमी है। अर्द्धवृत्ताकार व शंक्वाकार भाग की त्रिज्या, बेलनाकार भाग की त्रिज्या के बराबर है। यदि शंक्वाकार भाग की ऊँचाई 12 सेमी है तो खिलौने का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हल:

प्रश्न 15.
एक अंर्द्धवृत्त पर एक शंकु अध्यारोपित है। इस रूप का लकड़ी का एक खिलौना है। शंकु के आधार का व्यास 6 सेमी तथा ऊँचाई 4 सेमी है। ₹ 5 प्रति 1000 वर्ग सेमी की दर से रंग करने की कुल लागत ज्ञात कीजिए।
हलः

प्रश्न 16.
एक अर्द्धवृत्त के ऊपर समान त्रिज्या व ऊँचाई का एक बेलन रखा है। यदि इसकी कुल लम्बाई 7 सेमी हो तो उसका वक्रपृष्ठ ज्ञात कीजिए।
हलः

प्रश्न 17.
एक बेलनाकार बर्तन जिसकी त्रिज्या 6 सेमी तथा ऊँचाई 15 सेमी है, आइसक्रीम से भरा है। परी आइसक्रीम को बराबर अर्द्धवृत्ताकार शीर्ष वाले शंकुओं में भरकर 10 बच्चों में बाँटना है। यदि शंक्वाकार भाग की ऊँचाई आधार की त्रिज्या से 4 गुनी है तो आइसक्रीम शंकु की त्रिज्या ज्ञात कीजिए।
हलः

प्रश्न 18.
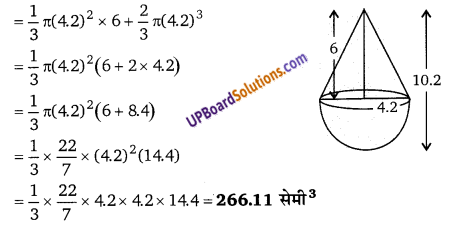
एक ठोस लकड़ी का खिलौना ‘अर्द्धवृत्त पर लम्बवृत्तीय शंकु के आकार का है। यदि अर्द्धवृत्त की त्रिज्या 4.2 सेमी तथा खिलौने की कुल ऊँचाई 10.2 सेमी है तो लकड़ी के खिलौने का आयतन ज्ञात कीजिए।
हलः
अर्द्धवृत्त की त्रिज्या = 4.2 सेमी लकडी के खिलौने का कुल आयतन = शंक्वाकार भाग का आयतन + अर्द्धवृत्ताकार भाग का आयतन

प्रश्न 19.
2 सेमी आन्तरिक तथा 4 सेमी बाहय त्रिज्या वाले खाली गोले को पिघलाकर 4 सेमी आधार त्रिज्या का एक शंकु बनाया गया है। शंकु की ऊँचाई एवं तिर्यक ऊँचाई ज्ञात कीजिए।
हलः

प्रश्न 20.
10.5 सेमी त्रिज्या की धातु का एक गोला पिघलाकर 3.5 सेमी त्रिज्या तथा 3 सेमी ऊँचाई के छोटे शंकु बनाये गये हैं। इस प्रकार बने शंकुओं की संख्या ज्ञात कीजिए।
हलः

प्रश्न 21.
एक गोले व शंकु की त्रिज्याएँ आधार एवं ऊँचाई के बराबर है। यदि उनके वक्रपृष्ठ 3 : 5 के अनुपात में है तब सिद्ध कीजिए कि प्रत्येक की त्रिज्या व ऊँचाई में अनुपात 3 : 4 होगा।
हलः
स्वयं हल कीजिए।

प्रश्न 22.
दो शंकुओं के आधार का व्यास बराबर है तथा उनकी तिर्यक ऊँचाईयों में 4 : 3 का अनुपात है। सिद्ध कीजिए कि उनके पृष्ठीय क्षेत्रफलों का अनुपात 4 : 3 है।
हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 10 Maths Solutions Chapter 10 Trigonometrical Ratios and Identities Ex 10.2 त्रिकोणमितीय अनुपात एवं असमिकाएँ

Ex 10.2 Trigonometrical Ratios and Identities अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
sec 45° का मान ज्ञात कीजिए।
हल:
sec 45° का मान (UPBoardSolutions.com) [latex] \sqrt{{2}} [/latex] होता है।

प्रश्न 2.
tan 60° का मान ज्ञात कीजिए।
हल:
tan60° का मांन [latex] \sqrt{{3}} [/latex] होता है।

प्रश्न 3.
यदि tanθ = [latex]\frac{1}{\sqrt{3}}[/latex], तब θ का मान ज्ञात कीजिए।
हलः
यदि tanθ = [latex]\frac{1}{\sqrt{3}}[/latex] तो tanθ = tan30° अत: θ = 30°

प्रश्न 4.
cos 60° × sin 60° का मान ज्ञात कीजिए।
हलः
cos60° × sin60° (UPBoardSolutions.com) = [latex]\frac{1}{2} \times \frac{\sqrt{3}}{2}=\frac{\sqrt{3}}{4}[/latex]

Ex 10.2 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-I)

प्रश्न 5.
यदि θ = 30°, तब सिद्ध कीजिए कि sin2θ = [latex]\frac{\sqrt{3}}{2}[/latex]
हलः
यदि θ = 30° ∴ sin20 = sin2 × 30° = sin60° = [latex]\frac{\sqrt{3}}{2}[/latex]

प्रश्न 6.
यदि θ = 45°, तब सिद्ध कीजिए कि sin2θ = 1
हलः
यदि θ = 45° ∴ sin20 (UPBoardSolutions.com) = sin2 × 45° = sin90° = 1

प्रश्न 7.
सिद्ध कीजिए कि sin30°.cosec30°.tan30° = [latex]\frac{1}{\sqrt{3}}[/latex]
हल:
sin30° × cosec30° × tan30° = [latex]\frac{1}{2} \times \frac{2}{1} \times \frac{1}{\sqrt{3}}=\frac{1}{\sqrt{3}}[/latex]

Ex 10.2 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

निम्न की सत्यता की जाँच कीजिए –
प्रश्न 8.
cos60° cos45° – sin60°sin 45° = [latex]\frac{\sqrt{2}-\sqrt{6}}{4}[/latex]
हल:
LHS = cos 60°.cos 45° – sin60°sin 45°

प्रश्न 9.
cos30°cos45° – sin30° sin 45° = [latex]\frac{\sqrt{3}-1}{2 \sqrt{2}}[/latex]
हलः
LHS = cos 30°cos 45° – sin30°sin 45°

प्रश्न 10.
cosec²30°sin² 45° – sec²60° = -2
हलः
LHS = (UPBoardSolutions.com) cosec ²30°sin²45° – sec²60°
= (2)² · [latex]\left(\frac{1}{\sqrt{2}}\right)^{2}[/latex] – (2)²
= 4·[latex]\frac{1}{2}[/latex] – 4 = – 2 = RHS

प्रश्न 11.
4cos²60° + 4sin² 45° – sin² 30° = [latex]\frac{1}{4}[/latex]
हल:
LHS = 4 cos²60° + 4sin² 45° – sin²30°

प्रश्न 12.
cos 90° = 1 – 2 sin² 45° = 2 cos² 45° – 1
हल:
cos 90° = 1 – 2 sin²45° = 2 cos² 45° – 1
LHS → cos 90 = 0
RHS = 1 – 2 sin² 45°

प्रश्न 13.
cos60° = 1 – 2 sin² 30° = 2 cos²30° – 1
हल:
cos 60° = 1 – 2 sin² 30° = 2 cos² 30° – 1

प्रश्न 14.
cos² 30° + cos² 45° + cos²60° = sin² 30° + sin² 45° + sin² 60°
हल:
LHS = cos²30° + (UPBoardSolutions.com) cos² 45° + cos²60°

Ex 10.2 Trigonometrical Ratios and Identities दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 15.
सिद्ध कीजिए कि cot² 30° + cot² 45° + cot² 60° = [latex]\frac{13}{3}[/latex]
हल:
LHS = cot² 30° + cot² 45° + cot²60°

प्रश्न 16.
सिद्ध कीजिए कि 2(sin² 45° + cot²30°) – 3(cosec²60° – sec²60°) = 15
हल:
LHS = 2(sin² 45° + cot²30°) – 3(cosec²60° – sec²60°)

प्रश्न 17.
सिद्ध कीजिए कि 4 cot² 45° – sec²60° + sin²30° = [latex]\frac{1}{4}[/latex]
हलः
LHS = 4cot² 45° – sec²60° + sin²30° (UPBoardSolutions.com)
= 4 x (1)² – (2)² + [latex]\left(\frac{1}{2}\right)^{2}[/latex]
= 4 – 4 + [latex]\frac{1}{4}[/latex] = [latex]\frac{1}{4}[/latex] = RHS

प्रश्न 18.
यदि tan(A – B) = [latex]\frac{1}{\sqrt{3}}[/latex], व tan(A + B) = [latex] \sqrt{{3}} [/latex], तब A व B के मान ज्ञात कीजिए।
हलः

A का मान समीकरण (2) में रखने पर 45° + B = 60°
B = 60° – 45° = 150

प्रश्न 19.
यदि sin(A – B) = cos(A + B) = [latex]\frac{1}{2}[/latex], तब A व B के मान ज्ञात कीजिए।
हलः

समी० (1) में A (UPBoardSolutions.com) का मान रखने पर
45° – B = 30°
– B = 30° – 450
– B = -15° ⇒ B = 150

प्रश्न 20.
यदि A = 30%, तो सिद्ध कीजिए कि –
(i) sin 3A = 3 sin A – 4 sin³ A

हलः
यदि A = 30°
sin³A = 3sinA – 4sin³ A
LHS → sin3 × 30° = sin90° = 1

प्रश्न 21.
यदि A = 45° तथा B = 30°, तो सिद्ध कीजिए कि –
(i) tan(A + B) = [latex]\frac{\tan A+\tan B}{1-\tan A \tan B}[/latex]
(ii) sin(A + B) = sin (UPBoardSolutions.com) A cos B + cos A sin B
(iii) cos(A – B) = cos A cos B + sin A sin B
हलः
यदि A = 45° और B = 30°

प्रश्न 22.
यदि θ = 30°, तब सिद्ध कीजिए कि cosθ = [latex]\sqrt{\frac{1+\cos 2 \theta}{2}}[/latex]
हलः

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 17 Heron’s Formula Ex 17.2 हीरोन का सूत्र

Ex 17.2 Heron’s Formula अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
दिये गये संलग्न चित्र में, समान्तर चतुर्भुज ABCD का क्षेत्रफल ज्ञात D कीजिए।
हलः

प्रश्न 2.
एक वर्ग और एक समबाहु त्रिभुज के परिमाप बराबर है। यदि वर्ग का विकर्ण [latex]12 \sqrt{2}[/latex] सेमी है, तब त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हलः
वर्ग का परिमाप = समबाहु ∆ का परिमाप
4a = समबाहु ∆ का परिमाप… (1)
वर्ग का विकर्ण = [latex]12 \sqrt{2}[/latex]

प्रश्न 3.
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए। जहाँ, AB = 7 सेमी, DA = 15 सेमी, AC = 9 सेमी, BC = 6 सेमी तथा CD = 12 सेमी हैं।
हल:

Ex 17.2 Heron’s Formula लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 4.
एक चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए, जिसमें AB = 5 सेमी, BC = 12 सेमी, CD = 10 सेमी, DA = 13 सेमी और AC = 13 सेमी हैं।
हल:

प्रश्न 5.
एक समचतुर्भुज का परिमाप 52 सेमी है। एक विकर्ण 24 सेमी है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हलः

Ex 17.2 Heron’s Formula दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 6.
किसी स्कूल के विद्यार्थियों ने सफाई अभियान के लिए एक रैली निकाली उन्होंने दो समूहों में, विभिन्न गलियों में चलकर मार्च किया। एक समूह ने गलियों AB, BC और CA में मार्च किया तथा अन्य समूह ने AC,CD और DA में मार्च किया। फिर उन्होंने इन गलियों द्वारा घेरे गए भागों को साफ किया यदि AB = 9 मी, BC = 40 मी, CD = 15 मी, DA = 28 मी तथा LB = 90° है, तो किस समूह ने अधिक सफाई की और कितनी अधिक विद्यार्थियों द्वारा सफाई किया गया कुल क्षेत्रफल भी ज्ञात कीजिए। [NCERT]
हलः

स्पष्ट है कि पहले समूह ने अधिक सफाई की ओर दूसरे समूह से 180 – 126² मी अधिक सफाई की । अब ,सफाई किया गया कुल क्षेत्रफल = 180 + 126 = 306 मी²

प्रश्न 7.
एक चतुर्भुज की भुजाएँ क्रमशः 5, 12, 14 और 15 मी के क्रम में ली गयी हैं तथा पहली दो भुजाओं के बीच का कोण समकोण है। इसका क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 8.
एक पार्क, एक चतुर्भुज ABCD के आकार में है जिसमें ∠C =90°, AB = 9 मी, BC = 12 मी, CD = 5 मी और AD = 8 मी है। इसका क्षेत्रफल कितना है? (NCERT)
हलः

प्रश्न 9.
एक आयताकार मैदान की लम्बाई को 50% बढ़ाया गया है और इसकी चौड़ाई को 50% घटाया गया है तब हमें एक नया आयताकार मैदान प्राप्त होता है। नये मैदान का क्षेत्रफल क्या होगा?
हलः
माना आयताकार मैदान की लम्बाई = x मी
आयताकार मैदान की चौड़ाई = y मी
आयताकार मैदान का क्षेत्रफल = xy मी

प्रश्न 10.
एक समचतुर्भुज के आकार की शीट जिसका परिमाप 32 मी है तथा जिसका एक विकर्ण 10 मी लम्बा है, की दोनों भुजाओं को ₹ 5 प्रति मी2 की दर से पेन्ट किया गया है। पेन्ट का व्यय ज्ञात कीजिए।
हलः

प्रश्न 11.
समचतुर्भुज का क्षेत्रफल 2016 सेमी है तथा इसकी भुजा 65 सेमी है। इसके विकर्ण ज्ञात कीजिए।
हलः

Ex 17.2 Heron’s Formula बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
एक ∆ ABC में, यदि AB = 7 सेमी, BC = 8 सेमी तथा CA = 5 सेमी है तो ∆ ABC का क्षेत्रफल है-
(a) 103[latex]\sqrt{3}[/latex] सेमी²
(b) 10 (3)² सेमी²
(c) 513 सेमी²
(d) इनमें से कोई नहीं
हलः
a = 7,
b = 8,
c = 5

अतः विकल्प (a) सही है।

प्रश्न 2.
एक समबाहु त्रिभुज का क्षेत्रफल 4-3 सेमी2 है, इसका अर्द्ध-परिमाप है
(a) 8 सेमी
(b) 10 सेमी
(c) 6 सेमी
(d) 4 सेमी
हलः

प्रश्न 3.
एक त्रिभुज की दो भुजाएँ 13 सेमी और 14 सेमी हैं तथा अर्द्ध-परिमाप 18 सेमी है तब त्रिभुज की तीसरी भुजा है-
(a) 8 सेमी
(b) 9 सेमी
(c) 10 सेमी
d) 11 सेमी
हलः

प्रश्न 4.
एक समबाहु त्रिभुज का क्षेत्रफल 2/3 सेमी 2 है, इसका अर्द्ध-परिमाप है-
(a) 3[latex]\sqrt{2}[/latex] सेमी
(b) 13 सेमी
(c) 4[latex]\sqrt{3}[/latex] सेमी
हलः

प्रश्न 5.
एक समद्विबाहु समकोण त्रिभुज की भुजा, जिसका कर्ण 5[latex]\sqrt{2}[/latex] सेमी है, होगी-
(a) 4 सेमी
(b) 5 सेमी
(c) 6 सेमी
(d) इनमें से कोई नहीं
हलः

प्रश्न 6.
एक त्रिभुज की भुजाएँ 13, 14 और 15 सेमी हैं तब इसका क्षेत्रफल है-
(a) 48 सेमी²
(b) 82 सेमी²
(c) 84 सेमी²
(d) इनमें से कोई नहीं
हलः

अतः विकल्प (c) सही है।

प्रश्न 7.
एक समकोण त्रिभुज का आधार 15 सेमी है तथा इसका कर्ण 25 सेमी है, तब इसका क्षेत्रफल है-
(a) 150 सेमी²
(b) 160 सेमी²
(c) 250 सेमी²
(d) इनमें से कोई नहीं
हलः

प्रश्न 8.
एक त्रिभुज की भुजाएँ 5:12:13 के अनुपात में है तथा इसका परिमाप 120 सेमी है इसका क्षेत्रफल है-
(a) 180 सेमी²
(b) 480 सेमी²
(c) 380 सेमी²
(d) इनमें से कोई नहीं
हल:

प्रश्न 9.
एक समकोण त्रिभुज का आधार 10 सेमी तथा कर्ण 26 सेबी हैं, त्रिभुज का क्षेत्रफल है-
(a) 20 सेमी²
(b) 120 सेमी²
(c) 260 सेमी²
(d) इनमें से कोई नहीं
हल:

प्रश्न 10.
आधार 6 सेमी तथा ऊँचाई 8 सेमी वाले एक त्रिभुज का क्षेत्रफल है-
(a) 24 सेमी²
(b) 34 सेमी²
(c) 48 सेमी
(d) इनमें से कोई नहीं
हलः

Ex 17.2 Heron’s Formula स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
एक त्रिभुज का क्षेत्रफल ज्ञात कीजिए, जिसकी दो भुजाएँ 8 सेमी और 11 सेमी है तथा परिमाप 32 सेमी
हलः

प्रश्न 2.
एक समकोण त्रिभुज का परिमाप 300 मी है। यदि इसकी भुजाएँ 3:5:7 के अनुपात में है तो त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 3.
एक समबाहु त्रिभुज का क्षेत्रफल [latex]16 \sqrt{3}[/latex] सेमी² है, इसका परिमाप ज्ञात कीजिए।
हलः

प्रश्न 4.
एक त्रिभुजाकार भूखण्ड की भुजाएँ 6:7:8 के अनुपात में है तथा परिमाप 420 मी है। त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 5.
भूमि का एक टुकड़ा, एक समचतुर्भुज ABCD के आधार का है जिसमें प्रत्येक भुजा की माप 100 मी है तथा विकर्ण AC, 160 मी लम्बा है। समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 6.
सफेद और काले रंग की त्रिभुजाकार चादरों को एक खिलौना बनाने में प्रयुक्त किया गया है (चित्र में दिखाये अनुसार ) खिलौना बनाने में प्रयुक्त काले और सफेद रंग की चादरों का कुल क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 7.
एक त्रिभुजाकार पार्क की भुजाएँ क्रमशः 8 मी, 10 मी और 6 मी हैं। 2 मी व्यास का एक छोटा वृत्ताकार क्षेत्र छोड़ा गया है तथा शेष बचे क्षेत्र को गुलाब उगाने के लिए प्रयुक्त किया गया है। गुलाबों को उगाने के लिए कितना क्षेत्रफल प्रयुक्त हुआ? (π = 3.14)
हलः
एक त्रिभुजाकार पार्क की भुजाएँ a = 8 मी,
b = 10 मी,
c = 6 मी

प्रश्न 8.
एक समद्विबाहु त्रिभुज की भुजा जो बराबर नहीं है कि माप 24 सेमी है तथा इसका क्षेत्रफल 60 सेमी 2 है दिये गये समद्विबाहु त्रिभुज का परिमाप ज्ञात कीजिए।
हलः

प्रश्न 9.
एक समांतर चतुर्भुज की आसन्न भुजाएँ 26 सेमी और 28 सेमी हैं तथा इसका एक विकर्ण 30 सेमी है। समांतर चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हल:

प्रश्न 10.
एक पार्क, एक चतुर्भुज ABCD के आकार का है जिसमें AB = 9 मी, BC = 12 मी, CD = 5 मी, AD = 8 मी और ∠C = 90° है। पार्क का क्षेत्रफल ज्ञात कीजिए।
हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 10 Maths Solutions Chapter 10 Trigonometrical Ratios and Identities Ex 10.1 त्रिकोणमितीय अनुपात एवं असमिकाएँ

Ex 10.1 Trigonometrical Ratios and Identities अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
यदि sinθ = [latex]\frac{3}{5}[/latex], तब tanθ का मान ज्ञात कीजिए।
हलः


पाइथागोरस प्रमेय से, (कर्ण)² = (लम्ब)² + (आधार)²
(5)² = (3)² + (UPBoardSolutions.com) (आधार)²
25 = 9 + (आधार)²
25 – 9 = (आधार)²
16 = (आधार)²
[latex] \sqrt{{16}} [/latex] = आधार
4 = आधार

प्रश्न 2.
यदि cosθ = [latex]\frac{1}{3}[/latex], तब sinθ का मान ज्ञात कीजिए।
हलः

पाइथागोरस प्रमेय से, (कर्ण)² = (लम्ब)² + (आधार)²
(3)² = (लम्ब)² + (1)²
9 = (लम्ब)² + 1
9 – 1 = (लम्ब)²
8 = (लम्ब)²

प्रश्न 3.
यदि costθ = [latex]\frac{4}{5}[/latex], तब tanθ का मान ज्ञात कीजिए।
हलः


पाइथागोरस प्रमेय से, (कर्ण)² = (लम्ब)² + (आधार)²
(5)² = (लम्ब)² + (4)
25 = (लम्ब)² + 16
25 – 16 = (UPBoardSolutions.com) (लम्ब)²
9 = (लम्ब)²
∴ लम्ब = [latex] \sqrt{{9}} [/latex] = 3

प्रश्न 4.
यदि secθ = 2, तब cot@ का मान ज्ञात कीजिए।
हलः


पाइथागोरस प्रमेय से, (कर्ण)² = (लम्ब)² + (आधार)²
(2)² = (लम्ब)² + (1)²
4 = (लम्ब)² + 1
4 – 1 = (लम्ब)²
3 = (लम्ब)²
∴ लम्ब = [latex] \sqrt{{3}} [/latex]

प्रश्न 5.
यदि tanθ = [latex]\frac{1}{\sqrt{3}}[/latex], तब [latex]\frac{2 \tan \theta}{1-\tan ^{2} \theta}[/latex] का मान ज्ञात कीजिए।
हलः
∵ tanθ = [latex]\frac{1}{\sqrt{3}}[/latex]

प्रश्न 6.
यदि sinθ = [latex]\frac{4}{5}[/latex], तब 3 secθ – 5 cosθ का मान ज्ञात कीजिए।
हलः

Ex 10.1 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 7.
यदि 4tan@ = 3, तब सिद्ध कीजिए कि : [latex]\frac{4 \sin \theta+3 \cos \theta}{8 \sin \theta+5 \cos \theta}=\frac{6}{11}[/latex]
हलः

प्रश्न 8.
यदि cosθ = [latex]\frac{\sqrt{3}}{2}[/latex], तब सिद्ध कीजिए कि 4 cos³θ – 3 cosθ = 0
हलः

प्रश्न 9.
यदि tanθ = [latex] \sqrt{{2}} [/latex] -1, तब सिद्ध कीजिए कि cotθ = [latex] \sqrt{{2}} [/latex] + 1
हलः

प्रश्न 10.
यदि cosθ = [latex]\frac{4}{5}[/latex], तब सिद्ध कीजिए कि [latex]\frac{\tan \theta}{1+\tan ^{2} \theta}=\frac{\sin \theta}{\sec \theta}[/latex]
हलः

प्रश्न 11.
यदि sinθ = [latex]\frac{\sqrt{3}}{2}[/latex], तब सिद्ध कीजिए कि 4 cos³θ – 3 cosθ = -1
हल:

प्रश्न 12.
यदि tanθ = 2, तब सिद्ध कीजिए कि secθ sinθ + tan²θ – cosec²θ = [latex]\frac{19}{4}[/latex]
हल:

Ex 10.1 Trigonometrical Ratios and Identities दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 13.
यदि sinθ = [latex]\frac{a}{b}[/latex], तब सिद्ध कीजिए कि (tanθ – cotθ) = [latex]\frac{2 a^{2}-b^{2}}{a \sqrt{b^{2}-a^{2}}}[/latex].
हलः

प्रश्न 14.
यदि cotθ = [latex]\frac{3}{4}[/latex], तब सिद्ध कीजिए कि [latex]\frac{\sin \theta+\cos \theta}{\sin \theta-\cos \theta}[/latex] = 7
हल:

प्रश्न 15.
यदि tanθ = [latex]\frac{a}{b}[/latex], तब सिद्ध कीजिए कि [latex]\frac{a \sin \theta-b \cos \theta}{a \sin \theta+b \cos \theta}=\frac{a^{2}-b^{2}}{a^{2}+b^{2}}[/latex]
हल:

प्रश्न 16.
यदि tanθ = [latex]\frac{4}{3}[/latex], तब सिद्ध कीजिए कि [latex]\sqrt{\frac{1+\sin \theta}{1-\sin \theta}}[/latex] = 3
हलः

प्रश्न 17.
यदि costθ = [latex]\frac{5}{13}[/latex], तब सिद्ध कीजिए कि [latex]\frac{2 \sin \theta-3 \cos \theta}{4 \sin \theta-9 \cos \theta}[/latex] = 3
हलः

प्रश्न 18.
यदि sinθ = [latex]\frac{4}{5}[/latex], तब सिद्ध कीजिए कि [latex]\frac{4 \tan \theta-5 \cos \theta}{\sec \theta+\cot \theta}=\frac{28}{29}[/latex]
हलः

प्रश्न 19.
यदि tanθ = [latex] \sqrt{{2}} [/latex] – 1, तब सिद्ध कीजिए कि sinθ cosθ = [latex]\frac{\sqrt{2}}{4}[/latex]
हलः

प्रश्न 20.
यदि cosecθ = [latex]\frac{5}{3}[/latex], तब सिद्ध कीजिए कि [latex]\frac{\cos \theta-\frac{1}{\tan \theta}}{2 \cot \theta}=-\frac{1}{5}[/latex]
हलः

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 19 Surface Area and Volume of a Right Circular Cone and Sphere Ex 19.1 लम्बवृत्तीय शंकु एवं गोले का पृष्ठीय क्षेत्रफल एवं आयतन

Ex 19.1 Surface Area and Volume of a Right Circular Cone and Sphere बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
समान व्यास व समान ऊँचाई वाले शंकु व बेलन के आयतनों का अनुपात हैं- [U.P. 2004, 06]
(a) 1 : 1
(b) 1 : 2
(c) 1 : 3
(d) 1 : 4
हलः

प्रश्न 2
एक लम्बवृत्तीय शंकु की लम्ब ऊँचाई 8 सेमी तथा इसके आधार का व्यास 12 सेमी है। इसकी तिर्यक ऊँचाई होगी
[U.P. 2005]
(a) 8 सेमी
(b) 10 सेमी
(c) 12 सेमी
(d) 20 सेमी
हलः
लम्बवृत्तीय शंकु की ऊर्ध्वाधर ऊँचाई, h = 8 सेमी
लम्बवृत्तीय शंकु के आधार का व्यास = 12 सेमी
लम्बवृत्तीय शंकु की त्रिज्या, r = [latex]\frac{12}{2}[/latex] = 6 सेमी
लम्बवृत्तीय शंकु में, (तिर्यक ऊँचाई)² = (त्रिज्या)² + (ऊर्ध्वाधर ऊँचाई)²
l² = r² + h²
l² = (6)² + (8)² = 36 + 64 = 100
l = [latex]\sqrt{100}[/latex] = 10 सेमी ⇒ विकल्प (b) सही है।

प्रश्न 3.
5 सेमी ऊँचाई तथा 3 सेमी आधार त्रिज्या वाले लम्बवृत्तीय शंकु का आयतन है- [U.P. 2002]
(a) 360 सेमी
(b) 480 सेमी
(c) 127 सेमी
(d) 151 सेमी
हलः
लम्बवृत्तीय शंकु की ऊँचाई, h = 5 सेमी
लम्बवृत्तीय शंकु की आधार की त्रिज्या, r = 3 सेमी

प्रश्न 4.
24 सेमी ऊँचाई के लम्बवृत्तीय शंकु का आयतन 1232 सेमी है। इसका वक्रपृष्ठ है- [U.P. 2009]
(a) 1254 सेमी²
(b) 704 सेमी²
(c) 550 सेमी²
(d) 154 सेमी²
हलः

प्रश्न 5.
एक शंकु की तिर्यक ऊँचाई 17 सेमी तथा त्रिज्या 8 सेमी हैं। तब इसकी लम्ब ऊँचाई है- [U.P. 2009]
(a) 9 सेमी
(b) 15 सेमी
(c) 20 सेमी
(d) 25 सेमी
हलः
लम्बवृत्तीय शंकु में, l² = r² + h²
(17)² = (8)² + h²
289 = 64 + h²
∴ h² = 289 – 64
h = [latex]\sqrt{225}[/latex] = 15 सेमी
⇒ विकल्प (b) सही है।

प्रश्न 6.
दो समान त्रिज्याओं वाले लम्बवृत्तीय शंकुओं के आयतन क्रमशः 47 व 9 घन मीटर हैं, उनकी ऊँचाइयों
का अनुपात है-
(a) [latex]\sqrt{2}[/latex] : [latex]\sqrt{3}[/latex]
(b) 2:3
(c) 4:9
(d) 16:8
हलः

Ex 19.1 Surface Area and Volume of a Right Circular Cone and Sphere अतिलघु उत्तरीय प्रश्न (Very Short Answer-Type Questions)

प्रश्न 7.
एक लम्बवृत्तीय शंकु के आधार की त्रिज्या 21 सेमी तथा ऊँचाई 20 सेमी है। शंकु का आयतन ज्ञात कीजिए।
[U.P. 2000]
हलः
लम्बवृत्तीय शंकु के आधार की त्रिज्या, r = 21 सेमी
लम्बवृत्तीय शंकु के आधार की ऊँचाई, h = 20 सेमी

प्रश्न 8.
उस लम्बवृत्तीय शंकु का वक्रपृष्ठ ज्ञात कीजिए जिसके आधार का व्यास 10 सेमी तथा ऊँचाई 12 सेमी
[U.P. 2001]
हलः
लम्बवृत्तीय शंकु के आधार का व्यास = 10
सेमी लम्बवृत्तीय शंकु के आधार की त्रिज्या, r = [latex]\frac{10}{2}[/latex] = 5 सेमी
लम्बवृत्तीय शंकु की ऊँचाई, h = 12 सेमी

प्रश्न 9.
एक लम्बवृत्तीय शंकु का व्यास 12 सेमी तथा तिर्यक ऊँचाई 10 सेमी है। इसका आयतन तथा सम्पूर्ण
पृष्ठ ज्ञात कीजिए।
हलः

प्रश्न 10.
24 सेमी ऊँचाई वाले लम्बवृत्तीय शंकु का वक्रपृष्ठ 550 वर्ग सेमी है। इसका आयतन ज्ञात कीजिए।
हलः
लम्बवृत्तीय शंकु की ऊँचाई, h = 24 सेमी

Ex 19.1 Surface Area and Volume of a Right Circular Cone and Sphere लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 11.
एक शंक्वाकार तम्बू में 528 मीटर हवा भरी है। यदि तम्बू की लम्ब ऊँचाई 14 मीटर है तो तम्बू का
व्यास ज्ञात कीजिए। (π = 22/7)
हलः
शंक्वाकार तम्बू का आयतन = 528 मीटर³
ऊर्ध्वाधर ऊँचाई, h = 14 मीटर

तम्बू का व्यास = 2 × r = 2 × 6 = 12 मीटर

प्रश्न 12.
एक शंकु की त्रिज्या तथा तिर्यक ऊँचाई में 4 : 7 का अनुपात है तथा इसका वक्रपृष्ठ 792 वर्ग सेमी है।
इसकी त्रिज्या ज्ञात कीजिए।
हलः
माना लम्बवृत्तीय शंकु की त्रिज्या, r = 4x
लम्बवृत्तीय शंकु की लम्बाई, l = 7x
वक्रपृष्ठ = πrl

∴ शंकु की त्रिज्या, r = 4 × 3 = 12 सेमी

प्रश्न 13.
24 सेमी लम्ब ऊँचाई वाले एक लम्बवृत्तीय शंकु का आयतन 616 सेमी है। इसका वक्रपृष्ठ ज्ञात कीजिए।
हलः
लम्बवृत्तीय शंकु की ऊर्ध्वाधर ऊँचाई, h = 24 सेमी
शंकु का आयतन = 616 सेमी³

प्रश्न 14.
8 मीटर ऊँचे तथा 4 मीटर व्यास वाले तांबे के एक ठोस बेलन को पिघलाकर 3 मीटर व्यास का एक
शंकु बनाया जाता है। शंकु की ऊँचाई ज्ञात कीजिए।
हलः

Ex 19.1 Surface Area and Volume of a Right Circular Cone and Sphere दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 15.
9 सेमी भुजा वाले घन से अधिकतम कितने आयतन का लम्बवृत्तीय शंकु बनाया जा सकता है?
हलः

प्रश्न 16.
एक समकोण त्रिभुज में समकोण बनाने वाली भुजाओं की लम्बाई 8 सेमी व 6 सेमी हैं। उसे कर्ण के परितः घुमाया जाता है। इस प्रकार उत्पादित द्विशंकु का सम्पूर्ण पृष्ठ ज्ञात कीजिए।
हलः

Balaji Publications Mathematics Class 9 Solutions