Balaji Class 10 Maths Solutions Chapter 3 Pair of Linear Equation in Two Variables Ex 3.5

Balaji Class 10 Maths Solutions Chapter 3 Pair of Linear Equation in Two Variables Ex 3.5 दो चर वाले रैखिक समीकरण युग्म

Ex 3.5 Pair of Linear Equation in Two Variables अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
k का वह मान ज्ञात कीजिए जिसके लिए रैखिक (UPBoardSolutions.com) समीकरण निकाय x + 2y = 3; 5x + ky = 15 के अनंततः अनेक हल हैं।
हलः
समीकरण निकाय x + 2y = 3 ……(1)
तथा 5x + ky = 15 …(2)
∵ समीकरण निकाय के अनंततः अनेक हल हैं।

प्रश्न 2.
a का मान ज्ञात कीजिए जिसके लिए समीकरण निकाय 9x – y = 25; 6x – ay = 3 का एक अद्वितीय हल है।
हलः
समीकरण निकाय 9x – y = 2 ….(1)
तथा 6x – 2y = 3 …(2)
∵ समीकरण निकाय एक अद्वितीय हल है

प्रश्न 3.
a का मान ज्ञात कीजिए जिसके लिए (UPBoardSolutions.com) समीकरण युग्म 10x + 5y = a – 5; 20x + 10y – a = 0 के अनंततः अनेक हल हैं।
हलः
समीकरण युग्म 10x + 5y = a – 5 …(1)
तथा 20x + 10y – a = 0
या 20x + 10 y = a …(2)
∵ समीकरण के अनंततः अनेक हल हैं।

प्रश्न 4.
यदि एक समीकरण युग्म संगत है तब रेखाएँ भी संगत होंगी या नहीं?
हलः
यदि एक समीकरण युग्म संगत है तब रेखाएँ भी संगत होंगी।

प्रश्न 5.
किस प्रकार के रैखिक समीकरण युग्म का आलेखीय हल नहीं होता।
हलः
यदि दोनों रेखायें समान्तर होंगी।

प्रश्न 6.
दो रैखिक समीकरणों का ग्राफ समानांतर (UPBoardSolutions.com) रेखाएँ हैं, तब रैखिक समीकरण युग्म के कितने हल होंगे?
हलः
कोई हल नहीं।

प्रश्न 7.
एक रैखिक समीकरण युग्म का अद्वितीय हल है। इसका आलेखीय रूप कितने बिन्दुओं पर प्रतिच्छेद करता है?
हलः
एक बिन्दु पर।

प्रश्न 8.
यदि दो रैखिक समीकरणों के आलेखीय रूप में प्रतिच्छेदक रेखाएँ हैं, तब रैखिक समीकरण युग्म के कितने हल हैं?
हलः
रैखिक समीकरण युग्म का 1 हल है।

प्रश्न 9.
यदि [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex] तब समीकरण निकाय a₁x + b₁y + c₁ = 0 और a₂x + b₂y + c₂ = 0 के कितने हल हैं?
हलः
यदि [latex]\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}} \neq \frac{c_{1}}{c_{2}}[/latex]
तब समीकरण निकाय का कोई हल नहीं है।

प्रश्न 10.
यदि [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex] तब समीकरण निकाय a₁x + b₁y + q = 0 और a₂x + b₂y + c₂ = 0 के कितने हल हैं?
हलः
यदि [latex]\frac{a_{1}}{a_{2}} \neq \frac{b_{1}}{b_{2}}[/latex]
तब समीकरण निकाय का एक अद्वितीय हल है।

Ex 3.5 Pair of Linear Equation in Two Variables लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 11.
k का मान ज्ञात कीजिए जिसके लिए निम्नलिखित (UPBoardSolutions.com) समीकरण निकाय का कोई हल नहीं है।
3x – y – 5 = 0; 6x – 2y – k = 0
हलः
समीकरण 3x – y – 5 = 0 …….(1)
तथा 6x – 2y – k = 0 ……….(2)
∵ समीकरण का कोई हल नहीं है

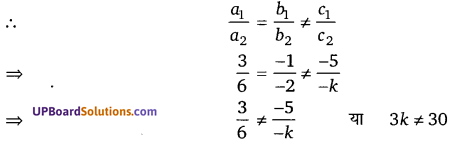
प्रश्न 12.
निम्नलिखित रैखिक समीकरण निकाय को आलेखीय विधि से हल कीजिए-
(i) 2x – y = 4
3y – x = 3
(ii) x – 2y = – 3
2x + y = 4
(iii) x – y + 1 = 0
4x + 3y = 24
(iv) 3x – 2y – 1 = 0
2x – 3y + 6 = 0
(v) 3x – 5y = 19
3y – 7x + 1 = 0
(vi) 2x – 3y =1
3x – 4y = 1
हलः
(i) समीकरण 2x – y = 4 ………………(1)
तथा 3y – x = 3 …………(2)
समी० (1) से, 2x – 4 = y या y = 2x – 4

उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखायें (UPBoardSolutions.com) बिन्दु (3, 2) पर प्रतिच्छेद करती हैं।
अतः x = 3, y = 2

(ii) समीकरण x – 2y = -3 ……..(1)
तथा 2x + y = 4 ……..(2)
समी० (1) से,
x – 2y = – 3
⇒ x + 3 = 2y
⇒ 2y = x + 3
⇒ y = [latex]\frac{x+3}{2}[/latex]

उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखायें बिन्दु (1, 2) पर काटती हैं।
अतः x = 1, y = 2

(iii) समीकरण (UPBoardSolutions.com) x – y + 1 = 0 …….(1)
तथा 4x + 3y = 24 …………..(2)
समी० (1) से, x – y + 1 = 0
या y = x + 1

उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखायें बिन्दु (3, 4) पर काटती हैं।
अत: x = 3, y = 4

(iv) समीकरण (UPBoardSolutions.com) 3x – 2y – 1 = 0 ………(1)
तथा 2x – 3y + 6 = 0 ………(2)
समी० (1) से, 3x – 2y – 1 = 0
⇒ 2y = 3x – 1


∵ दोनों रेखायें परस्पर बिन्दु B(3, 4) पर काटती हैं।
अतः x = 3 तथा y = 4

(v) समीकरण 3x – 5y = 19 ……..(1)
तथा 3y – 7x + 1 = 0 ……..(2)
संमी० (1) से, 3x – 19 = 5y
या y = [latex]\frac{3 x-19}{5}[/latex]

उपरोक्त ग्राफ से स्पष्ट है कि (UPBoardSolutions.com) दोनों रेखायें बिन्दु (- 2, – 5) पर काटती हैं।
अत: x = – 2, y = – 5

(vi) समीकरण निकाय 2x – 3y = 1 …………..(1)
तथा 3x – 4y = 1 …………(2)
समी० (1) से, 2x – 1 = 3y या [latex]\frac{2 x-1}{3}[/latex] = y
या y = [latex]\frac{2 x-1}{3}[/latex]


∵ दोनों रेखायें एक – दूसरे को बिन्दु ( – 1 – 1) पर काटती हैं।
अतः x = – 1 तथा y = – 1

प्रश्न 13.
समीकरण 3x – y + 9 = 0 और 3x + y = 0 तथा 3x + 4y – 6 = 0 (UPBoardSolutions.com) का आलेख दर्शाइये तथा रेखाओं और x – अक्ष से निर्मित त्रिभुज के शीर्ष भी ज्ञात कीजिए।
हलः
समीकरण 3x – y + 9 = 0 ……….(1)
तथा 3x + y = 0 ……(2)
तथा 3x + 4y – 6 = 0 ……(3)
समी० (1) से, 3x + 9 = y
या y = 3x + 9

प्रश्न 14.
निम्नलिखित रैखिक समीकरण युग्म (UPBoardSolutions.com) को प्रतिस्थापन विधि से हल करें-
(i) 7x – 15y = 2
x + 2y = 3 (NCERT)
(ii) 3x – y = 3
9x – 3y = 9 (NCERT)
(iii) s – t = 3
[latex]\frac{s}{3}+\frac{t}{2}[/latex] = 6 (NCERT)
(iv) [latex]\frac{\boldsymbol{x}}{\boldsymbol{a}}+\frac{\boldsymbol{y}}{\boldsymbol{b}}[/latex] = 2, a ≠ 0, b ≠ 0
ax – by = a² – b²
हल:
(i) समीकरण 7x – 15y = 2 ……..(1)
तथा x + 2y = 3 …..(2)
समी० (2) से, x = 3 – 2y ……………(3)
समी० (3) से x का मान समी० (1) में प्रतिस्थापित करने पर,
7(3 – 2y) – 15y = 2
21 – 14y – 15y = 2
21 – 29y = 2
या – 29y = 2 – 21
या – 29y = – 19
या y = [latex]\frac{19}{29}[/latex]
y का मान समी० (3) में रखने पर,

प्रश्न 15.
निम्नलिखित रैखिक समीकरण निकाय (UPBoardSolutions.com) को विलोपन विधि से हल करें-
(i) x + y = 5
2x – 3y = 4 (NCERT)
(ii) 3x – 5y = 4
9x – 2y = 7 (NCERT)
(iii) [latex]\frac{x}{2}+\frac{2 y}{3}[/latex] = -1
x = [latex]\frac{y}{3}[/latex] = 3 (NCERT)
(iv) [latex]\frac{3 a}{x}-\frac{2 b}{y}[/latex] + 5 = 0
[latex]\frac{a}{x}+\frac{3 b}{y}[/latex] – 2 = 0, x ≠ 0, y ≠ 0
हलः
विलोपन विधि से-
(i) समीकरण x + y = 5 ….(1)
तथा 2x – 3y = 4 ……(2)
समी० (1) को 3 से गुणा करने पर,

(ii) समीकरण 3x – 5y = 4 …..(1)
तथा 9x – 2y = 7 ….(2)
समी० (1) को 3 से गुणा करने पर,

प्रश्न 16.
निम्नलिखित रैखिक समीकरणों (UPBoardSolutions.com) को ब्रज-गुणन विधि से हल करें –
(i) 8x + 5y = 9
3x + 2y = 4 (NCERT)
(ii) 2x + 3y – 7 = 0
6x + 5y – 11 = 0 (NCERT)
हलः
ब्रज – गुणन विधि से-
(i) समीकरण 8x + 5y = 9
या 8x + 5y – 9 = 0 …(1)
तथा 3x + 2y = 4
या 3x + 2y – 4 = 0 ………(2)

(ii) समीकरण (UPBoardSolutions.com) 2x + 3y – 7 = 0 …(1)
तथा 6x + 5y – 11 = 0 …(2)

Ex 3.5 Pair of Linear Equation in Two Variables दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 17.
एक कक्षा के विद्यार्थियों को पंक्तियों में खड़ा होना है। यदि प्रत्येक पंक्ति में 4 विद्यार्थी अतिरिक्त हो तो पंक्तियों की संख्या 2 कम हो जाती है तथा यदि प्रत्येक पंक्ति में 4 विद्यार्थी कम हो तो 4 पंक्तियाँ और बनानी पड़ेंगी। कक्षा में विद्यार्थियों (UPBoardSolutions.com) की संख्या ज्ञात कीजिए।
हलः
माना प्रत्येक पंक्ति में विद्यार्थियों की संख्या = x
तथा पंक्तियों की संख्या = y
तब कक्षा में कुल विद्यार्थियों की संख्या = xy
प्रश्नानुसार, पहली शर्त,
प्रत्येक पंक्ति में विद्यार्थी = (x + 4)
तथा पंक्तियों की संख्या = (y – 2)
कुल विद्यार्थियों की संख्या = xy
(x + 4) × (y – 2) = xy
xy – 2x + 4y – 8 = xy
– 2x + 4y = xy – xy + 8
– 2x + 4y = 8 …(1)
तथा दूसरी शर्त,
प्रत्येक पंक्ति में विद्यार्थी = (x – 4)
पंक्तियों की संख्या = (y + 4)
कुल विद्यार्थियों की संख्या = xy
(x – 4)x (y + 4) = xy
xy + 4x – 4y – 16 = xy
4x – 4y = xy – xy + 16

x का मान समी० (1) में रखने पर,
– 2 × 12 + 4y = 8
या 4y = 8 + 24
4y = 32
या y = [latex]\frac{32}{4}[/latex] = 8
अतः कक्षा में कुल विद्यार्थियों की संख्या = xy = 12 × 8 = 96

प्रश्न 18.
2 वर्ष पहले, एक व्यक्ति की आयु अपने पुत्र की आयु से 5 (UPBoardSolutions.com) गुनी थी। दो वर्ष बाद, उसकी आयु उसके पुत्र की आयु के तीन गुने से 8 अधिक थी। पिता एवं पुत्र की वर्तमान आयु ज्ञात कीजिए।
हलः
माना पिता की वर्तमान आयु = x वर्ष तथा पुत्र की वर्तमान आयु = y वर्ष
प्रश्नानुसार,
पहली शर्त, (x – 2) = 5 × (y – 2)
x – 2 = 5y – 10
x – 5y = – 10 + 2 या x – 5y= – 8 ….(1)
तथा दूसरी शर्त, (x + 2) = 3x (y + 2) + 8
x + 2 = 3y + 6 + 8
या x – 3y = 14 – 2

y का मान समी० (1) में रखने पर,
x – 5 × 10 = – 8
x – 50 = – 8 या x = – 8 + 50
x = 42
अतः पिता की आयु = 42 वर्ष तथा पुत्र की आयु = 10 वर्ष

प्रश्न 19.
एक भिन्न का अंश, उसके हर से एक कम है। यदि अंश व हर दोनों में 3 (UPBoardSolutions.com) जोड़ा जाये तो वह भिन्न मूल भिन्न से [latex]\frac{3}{28}[/latex] अधिक हो जाती है। भिन्न ज्ञात कीजिए।
हलः
भिन्न का हर = x तथा अंश = x – 1

प्रश्न 20.
एक रेलगाड़ी एक नियत चाल से 300 किमी० चलती है। यदि रेलगाड़ी की (UPBoardSolutions.com) चाल 5 किमी०/घण्टा बढ़ा दी जाये, तो यात्रा पूरी करने में दो घण्टे कम लगते हैं। रेलगाड़ी की मूल चाल ज्ञात कीजिए।
हलः
माना रेलगाड़ी की मूल चाल = x km/hr
तब, 300 किमी की दूरी तय करने में रेलगाड़ी को लगा समय =  घण्टे
यदि रेलगाड़ी की चाल 5 km/h बढ़ा दी जाये तो
अब, रेलगाड़ी की चाल = (x + 5) km/h

प्रश्न 21.
m व n के वे मान ज्ञात कीजिए, जिनके लिए निम्न (UPBoardSolutions.com) समीकरण निकाय, अनंततः हल रखता है।
3x + 4y = 12;
(m + n)x + 2(m – n)y = 5m – 1
हलः
समीकरण 3x + 4y = 12 …(1)
तथा (m + n)x + 2(m – n)y = 5m – 1
∵ समीकरण निकाय के अनंततः हल है।

प्रश्न 22.
k के किस मान के लिए निम्न समीकरण निकाय अनंततः हल रखता है
2x – 3y = 7;
(k + 1)x + (1 – 2k)y = 5k – 4
हलः
समीकरण 2x – 3y – 7 = 0 ….(1)
तथा (k + 1)x + (1 – 2k)y = 5k – 4 …(2)
∵ समीकरण निकाय के अनंततः हल है।

अतः k = 5

प्रश्न 23.
दो अंकों की एक संख्या के दोनों अंकों का गुणनफल 14 है। (UPBoardSolutions.com) यदि संख्या में 45 जोड़ा जाये तो अंकों के स्थान बदल जाते हैं। संख्या ज्ञात कीजिए।
हलः
माना, इहाई का अंक = x तथा इकाई का अंक = y है।
तब अभीष्ट संख्या = (10x + y)
प्रश्नानुसार, पहली शर्त xy = 14
या y = [latex]\frac{14}{x}[/latex] …(1)
तथा दूसरी शर्त, 10x + y + 45 = 10 y + x
10x + y – 10y – x = – 45
या 9x – 9y = – 45
9(x – y) = – 45
या x – y = [latex]-\frac{45}{9}[/latex]
या x – y = – 5 …(2)
समी० (1) से y का मान समी० (2) में रखने पर,
x – [latex]\frac{14}{x}[/latex] = -5
या [latex]\frac{x^{2}-14}{x}[/latex] = -5
x² – 14 = – 5x
x² + 5x – 14 = 0
या x² + 7x – 2x – 14 = 0
x(x + 7) – 2(x + 7) = 0
(x + 7)(x – 2) – 0
x + 7 = 0 तथा x – 2 = 0
x = – 7 (अमान्य) x = 2
x का मान समी० (1) में रखने पर,
y = [latex]\frac{14}{2}[/latex] = 7
अतः अभीष्ट संख्या = 10x + y = 10 × 2 + 7 = 20 + 7 = 27

प्रश्न 24.
उस चक्रीय चतुर्भुज ABCD के कोण ज्ञात कीजिए, जिसमें
∠A = (4x + 20)°, ∠B = (3x – 5)°, ∠C = (4y)° तथा ∠D = (7y + 5)°
हल:
चक्रीय चतुर्भुज ABCD में,
∠A = (4x + 20), ∠B = (3x – – 5)°
∠C = (4y)° तथा ∠D = (7y + 5)°
∵ चक्रीय चतुर्भुज के सम्मुख कोणों का योगफल = 180°
∴ ∠A + ∠C = 180°
4x + 20 + 4y = 180 या 4x + 4y = 180 – 20
4x + 4y = 160 या 4(x + y) = 160

y का मान समी० (1) में रखने पर,
x + 15 = 40 या
x = 40 – 15 = 25
अतः ∠A = (4x + 20) = 4 × 25 + 20 = 100 + 20 = 120°
∠B = (3x – 5)° = 3 × 25 – 5 = 75 – 5 = 70°
∠C = 4y = 4 × 15 = 60°
∠D = (7y + 5)° = 7 × 15 + 5 = 105 + 5 = 110°

प्रश्न 25.
निम्न समीकरण निकाय को (UPBoardSolutions.com) हल कीजिए-

हलः


x का मान समी० (5) में रखने पर,
4 – y = 1
या 4 – 1 = y या y = 3
अतः x = 4 तथा y = 3

प्रश्न 26.
k के किस मान के लिए निम्न समीकरण (UPBoardSolutions.com) निकाय का कोई हल नहीं है।
(3k + 1)x + 3y – 2 = 0;
(k² + 1)x + (k – 2)y – 5 = 0
हलः
समीकरण निकाय
(3k + 1)x + 3y – 2 = 0 …(1)
(k² + 1)x + (k – 2)y – 5 = 0 …(2)
∵ समीकरण निकाय का कोई हल नहीं है,

(3k + 1) (k – 2) = 3 (k2 + 1)
3k² – 6k + k – 2 = 3k² + 3
3k² – 5k, – 3k² = 3 + 2
-5k = 5
-k = [latex]\frac{5}{5}[/latex] ⇒ -k = 1
अतः k = – 1

Balaji Publications Mathematics Class 10 Solutions