Class 10

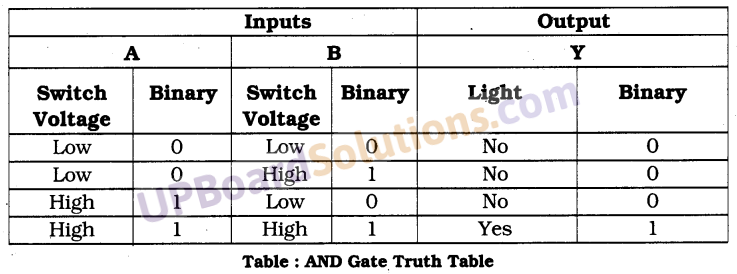
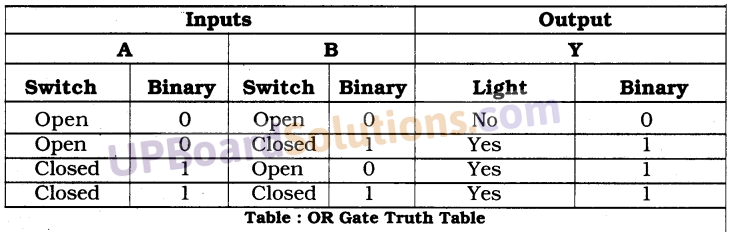
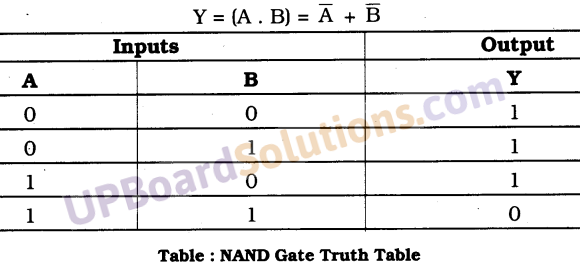
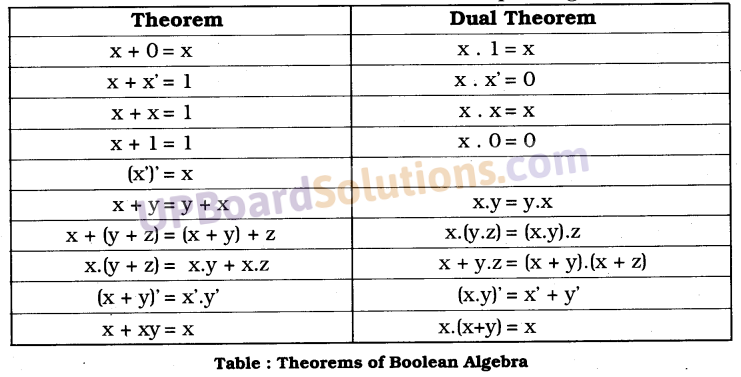
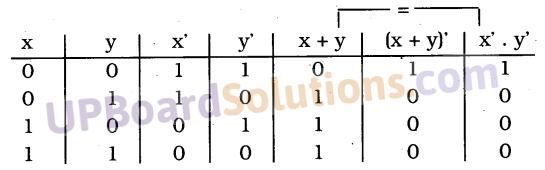
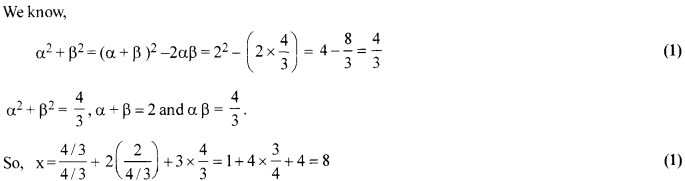UP Board Solutions for Class 10 Science Chapter 6 Life Processes (जैव-प्रक्रम)

These Solutions are part of UP Board Solutions for Class 10 Science. Here we have given UP Board Solutions for Class 10 Science Chapter 6 Life Processes.

पाठगत हल प्रश्न

[NCERT IN-TEXT QUESTIONS SOLVED]

खंड 6.1 ( पृष्ठ संख्या 105)

प्रश्न 1.
हमारे जैसे बहुकोशिकीय जीवों में ऑक्सीजन की आवश्यकता पूरी करने में विसरण क्यों अपर्याप्त है?
उत्तर
हम जानते हैं कि बहुकोशिकीय जीवों में सभी कोशिकाएँ अपने आसपास के पर्यावरण के सीधे संपर्क में नहीं रह सकती हैं। अतः साधारण विसरण द्वारा सभी कोशिकाओं और ऊतकों तक ऑक्सीजन की पूर्ति नहीं हो पाती है, क्योंकि यह अत्यंत (UPBoardSolutions.com) धीमी प्रक्रिया है। इसलिए वहन तंत्र द्वारा शरीर के विभिन्न अंगों तक ऑक्सीजन पहुँचाई जाती है।

प्रश्न 2.
कोई वस्तु सजीव है, इसका निर्धारण करने के लिए हम किस मापदंड का उपयोग करेंगे?
उत्तर
कोई वस्तु सजीव है इसका निर्धारण हम निम्न मापदंडों द्वारा कर सकते हैं|

1. गति
2. वृद्धि
3. श्वसन
4. उत्तेजनशीलता
5. पोषण इत्यादि।

प्रश्न 3.
किसी जीव द्वारा किन कच्ची सामग्रियों का उपयोग किया जाता है?
उत्तर
किसी जीव द्वारा निम्न कच्ची सामग्रियों के उपयोग किए जाते हैं

1. खाद्य पदार्थ (कार्बन आधारित)-यह जीवों के लिए ऊर्जा प्राप्त करने के लिए।
2. ऑक्सीजन श्वसन तथा ATP के रूप में ऊर्जा प्राप्त करने के लिए।
3. जल-भोजन के पाचन तथा शरीर के (UPBoardSolutions.com) अंदर अन्य कार्यों के लिए।
4. कार्बन डाइऑक्साइड [CO,]-पौधों में प्रकाश संश्लेषण का एक आवश्यक घटक।।

प्रश्न 4.
जीवन के अनुरक्षण के लिए आप किन-किन प्रक्रमों को आवश्यक मानेंगे?
उत्तर
जीवन के अनुरक्षण के लिए सभी जैव क्रियाएँ आवश्यक होती हैं; जैसे-पोषण, श्वसन, परिवहन, उत्सर्जन, वृद्धि आदि।

खंड 6.2 ( पृष्ठ संख्या 111)

प्रश्न 1.
स्वयंपोषी पोषण तथा विषमपोषी पोषण में क्या अंतर है?
उत्तर

प्रश्न 2.
प्रकाश संश्लेषण के लिए आवश्यक कच्ची सामग्री पौधे कहाँ से प्राप्त करते हैं?
उत्तर
प्रकाश संश्लेषण के लिए आवश्यक कच्ची सामग्री तथा उनके स्रोत निम्न हैं:

1. जल-पौधों की जड़े भूमि से जल प्राप्त करती हैं।
2. कार्बन-डाइऑक्साइड (CO)-पौधे इसे वायुमंडल से रंध्रों (Stomata) द्वारा प्राप्त करते हैं।
3. क्लोरोफिले-हरे पत्तों में क्लोरोप्लास्ट (UPBoardSolutions.com) होता है, जिसमें क्लोरोफिल मौजूद होते हैं।
4. सूर्य का प्रकाश-सूर्य से प्राप्त करते हैं।

प्रश्न 3.
हमारे आमाशय में अम्ल की भूमिका क्या है?
उत्तर
हमारे आमाशय में अम्ल की निम्नलिखित भूमिका है

1. आमाशय में HCl अम्ल की भूमिका आमाशय रस को अम्लीय बनाना है, क्योंकि एन्जाइम पेप्सिन केवल अम्लीय माध्यम में ही प्रभावशाली ढंग से प्रोटीनों का पाचन कर सकता है।
2. अम्ल का एक अन्य कार्य यह भी है कि ये भोजन में मौजूद हानिकारक जीवाणुओं को मार देते हैं।
3. यह अधपचे भोजन का किण्वन नहीं होने देता है।

प्रश्न 4.
पाचक एंजाइमों का क्या कार्य है?
उत्तर
पाचक एंजाइम अघुलनशील जटिल कार्बनिक अणुओं को सरल घुलनशील अणुओं में परिवर्तित कर देते हैं, ताकि क्षुद्रांत की भित्ति द्वारा सरलतापूर्वक अवशोषित कर लिए जाएँ।

प्रश्न 5.
पचे हुए भोजन को अवशोषित करने के लिए क्षुद्रांत्र को कैसे अभिकल्पित किया गया है?
उत्तर
क्षुद्रांत्र के आंतरिक आस्तर पर अनेक अँगुली जैसे प्रवर्ध होते हैं, जिन्हें दीर्घरोम कहते हैं, ये अवशोषण का सतही क्षेत्रफल बढ़ा देते हैं। दीर्घरोम में रुधिर वाहिकाओं की बहुतायत होती है, जो भोजन को अवशोषित करके शरीर की प्रत्येक (UPBoardSolutions.com) कोशिका तक पहुँचाती हैं।

खंड 6.3 (पृष्ठ संख्या 116)

प्रश्न 1.
श्वसन के लिए ऑक्सीजन प्राप्त करने की दिशा में एक जलीय जीव की अपेक्षा स्थलीय जीव किस प्रकार लाभप्रद है?
उत्तर

1. जलीय जीव जल में विलेय ऑक्सीजन का उपयोग करते हैं। क्योंकि जल में विलेय ऑक्सीजन की मात्रा वायु में ऑक्सजीन की मात्रा की तुलना में बहुत कम है, इसलिए जलीय जीवों की श्वास दर स्थलीय जीवों की अपेक्षा द्रुत गति से होती है।
2. स्थलीय जीवों में ऑक्सीजन भिन्न-भिन्न अंगों द्वारा अवशोषित की जाती है। इन सभी अंगों में एक रचना होती है, जो उस सतही क्षेत्रफल को बढ़ाती है जो ऑक्सीजन बाहुल्य वायुमंडल के संपर्क में रहता है।

प्रश्न 2.
ग्लूकोज़ के ऑक्सीकरण से भिन्न जीवों में ऊर्जा प्राप्त करने के विभिन्न पर्थ क्या हैं?
उत्तर
ग्लूकोज के ऑक्सीकरण से भिन्न जीवों में ऊर्जा प्राप्त करने के विभिन्न पथ इस प्रकार हैं:

प्रश्न 3.
मनुष्यों में ऑक्सीजन तथा कार्बन-डाइऑक्साइड का परिवहन कैसे होता है?
उत्तर
ऑक्सीजन का परिवहन-मानव शरीर के फुफ्फुस कूपिकाओं की रुधिर वाहिकाओं में RBC होते हैं, जिसमें मौजूद हीमोग्लोबिन ऑक्सीजन से संयुक्त होकर ऑक्सीहीमोग्लोबिन बनाता है तथा सभी ऊतकों एवं अंगों तक पहुँच जाता है। कार्बन-डाइऑक्साइड (co₂) का परिवहन-ऑक्सीजन की अपेक्षा CO₂ जल में अधिक विलेय है, इसलिए ऊतकों से फुफ्फुस तक परिवहन हमारे रुधिर (प्लाज्मा) में विलेय अवस्था में होता है।

प्रश्न 4.
गैसों के विनिमय के लिए मानव-फुफ्फुस में अधिकतम क्षेत्रफल को कैसे अभिकल्पित किया है?
उत्तर
फुफ्फुस के अंदर मार्ग छोटी और छोटी नलिकाओं में विभाजित हो जाता है, जो अंत में गुब्बारे जैसी रचना में अंतकृत हो जाता है, जिसे कूपिका कहते हैं। कूपिका एक सतह उपलब्ध कराती है। जिसमें गैसों का विनिमय हो सकता है। यदि (UPBoardSolutions.com) कूपिकाओं की सतह को फैला दिया जाए तो यह लगभग 80 से 100 वर्ग मीटर क्षेत्र ढक लेगी। इस तरह हमारे फुफ्फुस गैसों के विनिमय के लिए अधिकतम क्षेत्रफल बनाती है।

खंड 6.4 ( पृष्ठ संख्या 122)

प्रश्न 1.
मानव में वहन तंत्र के घटक कौन से हैं? इन घटकों के क्या कार्य हैं?
उत्तर
मानव में वहन तंत्र के घटक हैं-हृदय, रुधिर वाहिकाएँ और रुधिर। उनके कार्य इस प्रकार हैं :
1. हृदय (Heart)–यह एक पंप की तरह कार्य करता है।

2. रुधिर वाहिकाएँ (Blood Vessels):

1. धमनियाँ (Arteries)-हृदय से शरीर के सभी अंगों तक ऑक्सीजन युक्त रक्त (Oxygenated blood) | ले जाती हैं।
2. शिराएँ (Veins)-विभिन्न अंगों से हृदय तक वापस डीऑक्सीजनेटेड (De-Oxygenated) रक्त शुद्धिकरण के लिए लाती हैं।
3. कोशिकाएँ (capillaries)-धमनी छोटी-छोटी वाहिकाओं में विभाजित हो जाती है, जिसे कोशिकाएँ कहते हैं। रुधिर एवं आसपास की कोशिकाओं के मध्य पदार्थों का विनिमय होता है।

3. रुधिर या रक्त (Blood)-यह परिवहन का माध्यम है जो निम्नलिखित से बने हैं:

1. प्लाज्मा (Plasma)-भोजन के अणुओं, CO₂नाइट्रोजनी वर्त्य (nitrogenous wastes), लवण, हार्मोन, प्रोटीन आदि का विलीन रूप में वहन करता है।
2. RBC-इसमें हीमोग्लोबीन होता है, जो ऑक्सीजन को ले जाती है।
3. WBC-संक्रमण से लड़ने में सहायता करता है। यह शरीर में आए रोगाणुओं को मारकर शरीर को स्वस्थ बनाए रखता है।
4. प्लेटलेट्स (Plateletes)-रक्तस्राव के स्थान पर रुधिर का थक्का बनाकर मार्ग अवरुद्ध कर देती है।

प्रश्न 2.
स्तनधारी तथा पक्षियों में ऑक्सीजनित तथा विऑक्सीजनित रुधिर को अलग करना क्यों आवश्यक है?
उत्तर
हृदय का दायाँ व बायाँ बँटवारा ऑक्सीजनित तथा विऑक्सीजनित रुधिर को मिलने से रोकता है तथा शरीर को उच्च दक्षतापूर्ण ऑक्सीजन की पूर्ति करता है, क्योंकि पक्षी और स्तनधारी जंतुओं को अपने शरीर का तापक्रम बनाए रखने के (UPBoardSolutions.com) लिए निरंतर उच्च ऊर्जा की आवश्यकता होती है, जिसके लिए यह बहुत लाभदायक होता है।

प्रश्न 3.
उच्च संगठित पादप में वहन तंत्र के घटक क्या हैं?
उत्तर
उच्च संगठित पादप में निम्नलिखित वहन तंत्र होते हैं :

1. जाइलम ऊतक (Xylem tissue)-जाइलम ऊतक पादप के जड़ से खनिज लवण तथा जल इसके सभी अंगों तक पहुँचाता है। जाइलम ऊतक में जड़ों, तनों और पत्तियों की वाहिनिकाएँ तथा वाहिकाएँ आपस में जुड़कर जल संवहन वाहिकाओं का एक जाल बनाती हैं, जो पादप के सभी भागों से संबद्ध होता है।
2. फ्लोएम ऊतक (Phloem tissue)-भोजन तथा अन्य पदार्थों का संवहन (Translocation) पत्तियों से अन्य सभी अंगों तक फ्लोएम ऊतक द्वारा होता है।

प्रश्न 4.
पादप में जल और खनिज लवण का वहन कैसे होता है?
उत्तर
पापों में जल और खनिज लवण का वहन जाइलम ऊतक द्वारा होता है।

जड़ों की कोशिकाएँ मृदा के संपर्क में हैं तथा वे सक्रिय रूप से आयन प्राप्त करती हैं। यह जड़ और मृदा के मध्य आयन सांद्रण में एक अंतर उत्पन्न करता है। इस अंतर को समाप्त करने के लिए जल अनवरत गति से जड़ के जाइलम में जाता है और जल के स्तंभ का निर्माण करता है, जो लगातार ऊपर की ओर धकेला जाता है। यह दाब जल को ऊँचाई तक पहुँचाने में पर्याप्त नहीं होता है। पत्तियों के द्वारा वाष्पोत्सर्जन क्रिया द्वारा (UPBoardSolutions.com) रंध्र से जल की हानि होती है, जो एक चूषण उत्पन्न करता है, जो जल को जड़ों में उपस्थित जाइलम कोशिकाओं द्वारा खींचता है। अतः वाष्पोत्सर्जन कर्षण जल की गति के लिए एक मुख्य प्रेरक बल होता है।

प्रश्न 5.
पादप में भोजन का स्थानांतरण कैसे होता है?
उत्तर
पादप में भोजन का स्थानांतरण फ्लोएम ऊतक द्वारा होता है। प्रकाश संश्लेषण के उत्पादों के अलावा फ्लोएम अमीनो अम्ल तथा अन्य पदार्थों का परिवहन भी करता है। ये पदार्थ विशेष रूप से जड़ के भंडारण अंगों, फलों, बीजों तथा वृद्धि वाले अंगों में ले जाए जाते हैं। भोजन तथा अन्य पदार्थों का स्थानांतरण संलग्न साथी कोशिका की सहायता से चालनी नलिका में उपरिमुखी तथा अधोमुखी दोनों दिशाओं में होता है। सुक्रोज सरीखे पदार्थ फ्लोएम ऊतक में ए०टी०पी० से प्राप्त ऊर्जा से ही स्थानांतरित होते हैं।

खंड 6.5 ( पृष्ठ संख्या 124)

प्रश्न 1.
वृक्काणु (नेफ्रॉन) की रचना तथा क्रियाविधि का वर्णन कीजिए।
उत्तर
संरचना (Structure)-मानव शरीर में दो वृक्क होते हैं। प्रत्येक वृक्क नेफ्रॉन की अनेक इकाइयों से बना होता है। वृक्काणु (नेफॉन) वृक्क की क्रियात्मक इकाई होती है। नेफॉन में कप के आकार का बोमन संपुट (Bowman’s Capsule) होता है, जिसमें कोशिका गुच्छ (Glomerulus) होते हैं। यह रुधिर कोशिकाओं का एक गुच्छ होता है जो एफेरेन्ट कोशिकाओं द्वारा बने होते हैं। एफेरेन्ट धमनियाँ अशुद्ध रक्त नेफ्रॉन तक लाते हैं। कप के आकार का बोमन संपुट वृक्काणु के निलिकाकार भाग (Tubular part of rephron) का निर्माण करती है। जो संग्राहक वाहिनी (collecting duct) से जुड़ा होता है।

क्रियाविधि (Working)–वृक्क धमनी (Renal artery) ऑक्सीजनित रुधिर लाती है, जिसमें नाइट्रोजनी वर्त्य होते हैं। मूत्र बोमन संपुट में स्थित कोशिका गुच्छ (ग्लामेरूलस) में फिल्टर होकर कुंडली के आकार में नेफ्रॉन के नलिकाकार भाग में पहुँचता है। मूत्र में कुछ उपयोगी पदार्थ; जैसे-ग्लूकोज, अमीनों अम्ल, लवण तथा जले रह जाते हैं जो पुनः इस नलिकाकार भाग में अवशोषित कर लिए जाते हैं। इसके बाद मूत्र (UPBoardSolutions.com) संग्राहक वाहिनी में एकत्र हो जाती है तथा मूत्रवाहिनी; में प्रवेश करता है जहाँ से मूत्राशय में चली जाती है। अतः प्रत्येक वृक्क में बनने वाला मूत्र एक लंबी नलिका, मूत्रवाहिनी में प्रवेश करता है, जो वृक्क को मूत्राशय से जोड़ती है।

प्रश्न 2.
उत्सर्जी उत्पाद से छुटकारा पाने के लिए पादप किन विधियों का उपयोग करते हैं?
उत्तर
उत्सर्जी उत्पाद से छुटकारा पाने के लिए पादप निम्न विधियों को उपयोग करते हैं

1. प्रकाश संश्लेषण में O₂ उत्पाद के रूप में तथा CO₂ श्वसन क्रिया में रंध्रों द्वारा निष्कासित किए जाते हैं।
2. पौधे अतिरिक्त जल से वाष्पोत्सर्जन क्रिया द्वारा छुटकारा पा सकते हैं।
3. पौधों में निष्क्रिय पत्तियाँ समय-समय पर अलग होती रहती हैं, जिनमें अपशिष्ट उत्पाद संचित रहते हैं।
4. पादपों में अन्य अपशिष्ट उत्पाद रेजिन तथा गोंद के रूप में विशेष रूप से पुराने जाइलम में संचित रहते हैं।
5. पादप कुछ अपशिष्ट पदार्थों को अपने आसपास की मृदा में उत्सर्जित करते हैं।
6. बहुत से पादप अपशिष्ट उत्पाद कोशकीय रिक्तिका में संचित रहते हैं।

प्रश्न 3.
मूत्र’ बनने की मात्रा का नियमन किस प्रकार होता है?
उत्तर

1. जल की मात्रा पुनरवशोषण (Reabsorption) शरीर में उपलब्ध अतिरिक्त जल की मात्रा पर तथा कितना जल की मात्रा पर तथा कितना विलेय वयं उत्सर्जित करना है, पर निर्भर करती है।
2. जैसे गर्मी के दिनों में शरीर से अत्यधिक पसीने के द्वारा जल एवं लवण निष्कासित होते हैं। इसलिए वृक्क के द्वारा छने (filterate) हुए मूत्र में विद्यमान जल एवं लवण की अधिकांश मात्रा पुनः अवशोषित कर ली जाती है। अतः मूत्र (UPBoardSolutions.com) कम मात्रा में उत्सर्जित होते हैं इसके विपरीत सर्दियों में कम पसीना आता है, इसलिए मूत्र अधिक बनता है। जल एवं लवण पुनरवशोषण हार्मोन के द्वारा नियंत्रित होते हैं।
3. अत: मूत्र निर्माण पर नियंत्रण रक्त के ऑसमोटिक (osmotic) संतुलन को भी बनाए रखता है।

पाठ्यपुस्तक से हल प्रश्न

[NCERT TEXTBOOK QUESTIONS SOLVED]

प्रश्न 1.
मनुष्य में वृक्क एक तंत्र का भाग है, जो संबंधित है
(a) पोषण
(b) श्वसन
(C) उत्सर्जन
(d) परिवहन
उत्तर
(c) उत्सर्जन।।

प्रश्न 2.
पादप में जाइलम उत्तरदायी है
(a) जल का वहन
(b) भोजन का वहन
(C) अमीनो अम्ल का वहन
(d) ऑक्सीजन का वहन
उत्तर
(a) जल का वहन।।

प्रश्न 3.
स्वपोषी पोषण के लिए आवश्यक है
(a) कार्बन डाइऑक्साइड तथा जल
(b) क्लोरोफिल
(C) सूर्य का प्रकाश
(d) उपरोक्त सभी
उत्तर
(d) उपरोक्त सभी

प्रश्न 4.
पायरुवेट के विखण्डन से यह कार्बन-डाइऑक्साइड, जल तथा ऊर्जा देता है और यह क्रिया होती है
(a) कोशिका द्रव्य
(b) माइटोकॉन्ड्रिया
(C) हरित लवक
(d) केन्द्रक
उत्तर
(b) माइटोकॉन्ड्रिया।

प्रश्न 5.
हमारे शरीर में वसा का पाचन कैसे होता है? यह प्रक्रम कहाँ होता है?
उत्तर

• वसा का पाचन छोटी आँत में होता है।
• क्षुद्रांत में वसा बड़ी गोलिकाओं के रूप में होता है, जिससे उस पर एंजाइम का कार्य करना मुश्किल हो जाता है।
• लीवर द्वारा स्रावित पित्त लवण उन्हें छोटी (UPBoardSolutions.com) गोलिकाओं में खंडित कर देता है, जिससे एंजाइम की क्रियाशीलता बढ़ जाती है। यह इमल्सीकृत क्रिया कहलाती है।
• पित्त रस अम्लीय माध्यम को क्षारीय बनाता है, ताकि अग्न्याशय से स्रावित लाइपेज एंजाइम क्रियाशील हो सके।
• लाइपेज एंजाइम वसा को वसा अम्ल तथा ग्लिसरॉल में परिवर्तित कर देता है।
• पाचित वसा अंत में आंत्र की भित्रि अवशोषित कर लेती है।

प्रश्न 6.
भोजन के पाचन में लार की क्या भूमिका है?
उत्तर
भोजन के पाचन में लार की भूमिका निम्नलिखित है

1. लार भोजन को गीला करता है जिससे निगलने में आसानी होती है।
2. लार में एमिलेस (amylase) एंजाइम होता है, जो मंड (स्टार्च) के जटिल अणु को शर्करा में खंडित करता | है। (जटिल कार्बोहाइड्रेट को सरल कार्बोहाइड्रेड में बदलना)
3. इसमें मौजूद लाइसोजाइम हानिकारक जीवाणुओं को नष्ट कर देता है।

प्रश्न 7.
स्वपोषी पोषण के लिए आवश्यक परिस्थितियाँ कौन-सी हैं और उसके उपोत्पाद क्या हैं?
उत्तर
हरे पौधे स्वपोषी कहलाते हैं, क्योंकि प्रकाश संश्लेषण क्रिया द्वारा वे अपना भोजन स्वयं बनाते हैं। प्रकाश संश्लेषण के लिए आवश्यक परिस्थितियाँ निम्नलिखित हैं

1. 1. क्लोरोफिल-पौधों के हरे भाग में क्लोरोफिल होते हैं, जो प्रकाश ऊर्जा को अवशोषित करता है।
   2. सूर्य का प्रकाश-सूर्य के (UPBoardSolutions.com) प्रकाश से
   3. कार्बन डाइऑक्साइड-वायुमंडल से
   4. जल-पौधे जड़ों द्वारा भूमि से प्रकाश संश्लेषण की क्रिया को निम्न रासायनिक समीकरण द्वारा बनाया जाता है।
      
      अत: कार्बोहाइड्रेट (ग्लूकोज़), ऑक्सीजन तथा जल उपोत्पाद के रूप में प्राप्त होते हैं।

प्रश्न 8.
वायवीय श्वसन तथा अवायवीय श्वसन में क्या अंतर है? कुछ जीवों के नाम लिखिए जिनमें अवायवीय श्वसन होता है।
उत्तर

प्रश्न 9.
गैसों के अधिकतम विनिमय के लिए कूपिकाएँ किस प्रकार अभिकल्पित हैं?
उत्तर
कूपिका एक सतह उपलब्ध कराती है, जिससे गैसों का विनिमय हो सके। कूपिकाओं की भित्ति में रुधिर वाहिकाओं का विस्तीर्ण जाल होता है, जो वायु से ऑक्सीजन लेकर हमारे शरीर की सभी कोशिकाओं तक पहुँचाता है तथा रुधिर में विलेय Co₂ को कूपिकाओं में छोड़ने के लिए लाता है ताकि CO₂ हमारे शरीर से बाहर निकल जाए।

प्रश्न 10.
हमारे शरीर में हीमोग्लोबिन की कमी के क्या परिणाम हो सकते हैं?
उत्तर
हम जानते हैं कि मानव में श्वसन वर्णक हीमोग्लोबिन है, जो ऑक्सीजन के लिए उच्च बंधुता रखता है। इसकी कमी के कारण हमारे शरीर के विभिन्न अंगों में ऑक्सीजन की कमी हो जाएगी, जिससे ऊर्जा कम मात्रा में निर्मित होगी (UPBoardSolutions.com) और हम थकान का अनुभव करेंगे। हमारी श्वास गति भी बढ़ जाएगी। अतः हीमोग्लोबिन की कमी से एनीमिया
(anaeamia) होता है।

प्रश्न 11.
मनुष्य में दोहरा परिसंचरण की व्याख्या कीजिए। यह क्यों आवश्यक है?
उत्तर
मनुष्य के परिसंचरण तंत्र को दोहरा परिसंचरण इसलिए कहते हैं, क्योंकि प्रत्येक चक्र में रुधिर दो बार हृदय में जाती है। हृदय का दायाँ और बायाँ बँटवारा ऑक्सीजनित तथा विऑक्सीजनित रुधिर को मिलने से रोकता है। चूंकि हमारे । शरीर में उच्च ऊर्जा की आवश्यकता होती है, जिसके लिए उच्च दक्षतापूर्ण ऑक्सीजन जरूरी होता है। अतः शरीर का तापक्रम बनाए रखने तथा निरंतर ऊर्जा की पूर्ति के लिए यह (UPBoardSolutions.com) परिसंचरण लाभदायक होता है।

प्रश्न 12.
जाइलम तथा फ्लोएम में पदार्थों के वहन में क्या अंतर है?
उत्तर

प्रश्न 13.
फुफ्फुस में कूपिकाओं तथा वृक्क में वृक्काणु (नेफ्रॉन) की रचना तथा क्रियाविधि की तुलना कीजिए।
उत्तर

Hope given UP Board Solutions for Class 10 Science Chapter 6 are helpful to complete your homework.

If you have any doubts, please comment below. UP Board Solutions try to provide online tutoring for you.

UP Board Solutions for Class 10 Hindi Chapter 3 रसखान (काव्य-खण्ड)

These Solutions are part of UP Board Solutions for Class 10 Hindi. Here we have given UP Board Solutions for Class 10 Hindi Chapter 3 रसखान (काव्य-खण्ड).

कवि-परिचय

प्रश्न 1.
रसखान का संक्षिप्त जीवन-परिचय देते हुए उनकी रचनाओं को स्पष्ट कीजिए। [2010]
या
कवि रसखान का जीवन-परिचय दीजिए तथा उनकी एक रचना का नाम लिखिए। [2011, 12, 13, 14, 15, 17]
उत्तर
हिन्दी काव्य की श्रीवृद्धि न जाने कितने ही मुसलमान कवियों के द्वारा की गयी, किन्तु इन सभी कवियों में रसखान जैसा सुकोमल, सरस और ललित काव्य किसी का भी नहीं है। इन्हें अत्यधिक भावुक कवि-हृदय मिला था, जिसके कारण ये श्रीकृष्ण के दीवाने हो गये थे। इनके हृदय से निकला हुआ समस्त काव्य रस और भाव से आकुल कर देने वाला है। कृष्ण-भक्ति शाखा के ये अद्वितीय कवि माने जाते हैं।

जीवन-परिचय—-रसखान दिल्ली के पठान सरदार थे। इनका पूरा नाम सैयद इब्राहीम रसखान था। इनके द्वारा रचित ‘प्रेम वाटिका’ ग्रन्थ से यह संकेत प्राप्त होता है कि ये दिल्ली के राजवंश में उत्पन्न हुए थे और इनका रचना-काल जहाँगीर का राज्य-काल था। इनका जन्म सन् 1558 ई० (सं० 1615 वि०) के लगभग दिल्ली में हुआ था। ‘हिन्दी-साहित्य का प्रथम इतिहास के अनुसार इनका जन्म सन् 1533 ई० में पिहानी, जिला हरदोई (उ०प्र०) में हुआ था। हरदोई में सैयदों की बस्ती भी है। डॉ० नगेन्द्र ने भी अपने ‘हिन्दी-साहित्य के इतिहास में इनका जन्म सन् 1533 ई० के आस-पास ही स्वीकार किया है। (UPBoardSolutions.com) ऐसा माना जाता है कि इन्होंने दिल्ली में कोई विप्लव होता देखा, जिससे व्यथित होकर ये गोवर्धन चले आये और यहाँ आकर श्रीनाथ की शरणागत हुए। इनकी रचनाओं से यह प्रमाणित होता है कि ये पहले रसिक-प्रेमी थे, बाद में अलौकिक प्रेम की ओर आकृष्ट हुए और कृष्णभक्त बन गये। गोस्वामी बिट्ठलनाथ ने पुष्टिमार्ग में इन्हें दीक्षा प्रदान की थी। इनका अधिकांश जीवन ब्रजभूमि में व्यतीत हुआ। यही कारण है कि ये कंचन धाम को भी वृन्दावन के करील-कुंजों पर न्योछावर करने और अपने अगले जन्मों में ब्रज में शरीर धारण करने की कामना करते थे। कृष्णभक्त कवि रसखान की मृत्यु सन् 1618 ई० (सं० 1675 वि०) के लगभग हुई।

कृतियाँ (रचनाएँ)–रसखान की निम्नलिखित दो रचनाएँ प्रसिद्ध हैं—

(1) सुजान रसखान-इसकी रचना कवित्त और सवैया छन्दों में की गयी है। यह भक्ति और प्रेम-विषयक मुक्तक काव्य है। इसमें 139 भावपूर्ण छन्द हैं।
(2) प्रेमवाटिका—इसमें 25 दोहों में प्रेम के त्यागमय और निष्काम स्वरूप का काव्यात्मक वर्णन है। तथा प्रेम का पूर्ण परिपाक हुआ है।

साहित्य में स्थान-रसखान का स्थान भक्त-कवियों में विशेष महत्त्वपूर्ण है। इनके बारे में डॉ० विजयेन्द्र स्नातक ने लिखा है कि “इनकी भक्ति हृदय की मुक्त साधना है और इनका श्रृंगार वर्णन भावुक हृदय की उन्मुक्त अभिव्यक्ति है। इनके काव्य इनके स्वच्छन्द मन के (UPBoardSolutions.com) सहज उद्गार हैं। यही कारण है कि इन्हें स्वच्छन्द काव्य-धारा का प्रवर्तक भी कहा जाता है। इनके काव्य में भावनाओं की तीव्रता, गहनता और तन्मयता को देखकर भारतेन्दु जी ने कहा था-‘इन मुसलमान हरिजनन पैकोटिन हिन्दू वारिये।।

पद्यांशों की ससन्दर्भ व्याख्या सवैये

प्रश्न 1.
मानुष हौं तो वही रसखानि, बसौं बज गोकुल गाँव के ग्वारन ।
जौ पसु हौं तो कहा बस मेरो, चरौं नित नंद की धेनु मँझारन ॥
पाहन हौं तो वही गिरि को, जो धर्यौ कर छत्र पुरंदर-धारन ।
जो खग हौं तो बसेरो करौं मिलि कालिंदी-कूल कदंब की डारन ॥ [2009, 11, 18]
उत्तर
[ मानुष = मनुष्य। ग्वारन = ग्वाले। धेनु = गाय। मॅझारन = मध्य में। पाहन = पाषाण, पत्थर। पुरंदर = इन्द्रा खग = पक्षी। बसेरो करौं = निवास करू। कालिंदी-कूल = यमुना का किनारा। डारन = डाल पर, शाखा पर।]
सन्दर्भ-प्रस्तुत पद्य रसखान कवि द्वारा रचित ‘सुजान-रसखान’ से हमारी पाठ्य-पुस्तक ‘हिन्दी के ‘काव्य-खण्ड में संकलित ‘सवैये’ शीर्षक से अवतरित है।

[ विशेष—इस शीर्षक के शेष सभी पद्यों के लिए यही सन्दर्भ प्रयुक्त होगा। ]

प्रसंग-इस पद्य में रसखान ने पुनर्जन्म में विश्वास व्यक्त किया है और अगले जन्म में श्रीकृष्ण की जन्म-भूमि (ब्रज) में जन्म लेने एवं उनके समीप ही रहने की कामना की है।

व्याख्या-रसखान कवि कहते हैं कि हे भगवान्! मैं मृत्यु के बाद अगले जन्म में यदि मनुष्य के रूप में जन्म प्राप्त करू तो मेरी इच्छा है कि मैं ब्रजभूमि में गोकुल के ग्वालों के मध्य निवास करूं। यदि मैं पशु योनि में जन्म ग्रहण करू, जिसमें मेरा कोई वश (UPBoardSolutions.com) नहीं है, फिर भी मेरी इच्छा है कि मैं नन्द जी की गायों के बीच विचरण करता रहूँ। यदि मैं अगले जन्म में पत्थर ही बना तो भी मेरी इच्छा है कि मैं उसी गोवर्धन पर्वत का पत्थर बनें, जिसे आपने इन्द्र का घमण्ड चूर करने के लिए और जलमग्न होने से गोकुल ग्राम की रक्षा करने के लिए अपनी अँगुली पर छाते के समान उठा लिया था। यदि मुझे पक्षी योनि में भी जन्म लेना पड़ा तो भी मेरी इच्छा है कि मैं यमुना नदी के किनारे स्थित कदम्ब वृक्ष की शाखाओं पर ही निवास करू।

काव्यगत सौन्दर्य-

1. रसखान कवि की कृष्ण के प्रति असीम भक्ति को प्रदर्शित किया गया है। उनकी भक्ति इतनी उत्कट है कि वह अगले जन्म में भी श्रीकृष्ण के समीप ही रहना चाहते हैं।
2. भाषा– ब्रज।
3. शैली-मुक्तक
4. रस-शान्त एवं भक्ति।
5. छन्द-सवैया।
6. अलंकार-‘कालिंदी-कुल कदंब की डारन’ में अनुप्रास।
7. गुण–प्रसाद।

प्रश्न 2.
आजु गयी हुती भोर ही हौं, रसखानि रई बहि नंद के भौनहिं ।।
वाको जियौ जुग लाख करोर, जसोमति को सूख जात कह्यौ नहिं॥
तेल लगाइ लगाई कै अँजन, भौंहैं बनाई बनाई डिठौनहिं ।
डारि हमेलनि हार निहारत बारत ज्यौं पुचकारत छौनहिं ॥
उत्तर
[ हुती = थी। भोर = प्रात:काल। हौं = मैं। रई बहि = प्रेम में डूब गयी। भौनहिं = भवन में। वाको = उसका, यशोदा का। जुग = युग। डिठौनहिं == काला टीका। हमेलनि = हमेल (सोने का एक आभूषण) को। निहारत = देख रही थी। बारत = न्योछावर करते हुए। पुचकारत = पुचकार रही थी। छौनहिं = पुत्र को।]

प्रसंग-इसे पद्य में कवि ने श्रीकृष्ण के प्रति यशोदा के वात्सल्य भाव का चित्रण किया है।

व्याख्या-एक गोपी दूसरी गोपी से कहती है कि हे सखी ! आज प्रात:काल के समय श्रीकृष्ण के प्रेम में मग्न हुई मैं नन्द जी के घर गयी थी। मेरी कामना है कि उनका पुत्र श्रीकृष्ण लाखों-करोड़ों युगों तक जीवित रहे। यशोदा के सुख के बारे में (UPBoardSolutions.com) कुछ कहते नहीं बनता है; अर्थात् उनको अवर्णनीय सुख की प्राप्ति हो रही है। वे अपने पुत्र का श्रृंगार कर रही थीं। वे श्रीकृष्ण के शरीर में तेल लगाकर आँखों में काजल लगा रही थीं। उन्होंने उनकी सुन्दर-सी भौंहें सँवारकर बुरी नजर से बचाने के लिए माथे पर टीका (डिठौना) लगा दिया था। वे उनके गले में सोने का हार डालकर और एकाग्रता से उनके रूप को निहारकर अपने जीवन को न्योछावर कर रही थीं और प्रेमावेश में बार-बार अपने पुत्र को पुचकार रही थीं।

काव्यगत सौन्दर्य-

1. प्रस्तुत छन्द में माता यशोदा के वात्सल्य-भाव और श्रीकृष्ण के प्रात:कालीन श्रृंगार का अनुपम वर्णन किया गया है।
2. भाषा-ब्रज।
3.  शैली-चित्रात्मक और मुक्तक।
4. रसवात्सल्य
5. छन्द-सवैया।
6. अलंकार-यमक, अनुप्रास और पुनरुक्तिप्रकाश।
7. गुण–प्रसाद।

प्रश्न 3.
धूरि भरे अति सोभित स्यामजू, तैसी बनी सिर सुंदर चोटी ।
खेलत खात फिरै अँगनी, पग पैंजनी बाजति पीरी कछोटी ॥
वा छबि को रसखानि बिलोकत, वारत काम कला निज कोटी ।
काग के भाग बड़े सजनी हरि-हाथ सों लै गयौ माखन-रोटी ॥ [2012, 15]
उत्तर
[ बनी = सुशोभित। पैंजनी = पायजेब। पीरी = पीला। कछोटी = कच्छा। सजनी = सखी।] |

प्रसंग–इसे पद्य में कवि ने बालक कृष्ण के मोहक रूप का चित्रण किया है। श्रीकृष्ण के सौन्दर्य को देखकर एक गोपी अपनी सखी से उनके सौन्दर्य का वर्णन करती है।

व्याख्या–हे सखी! श्यामवर्ण के कृष्ण धूल से धूसरित हैं और अत्यधिक शोभायमान हो रहे हैं। वैसे ही उनके सिर पर सुन्दर चोटी सुशोभित हो रही है। वे खेलते और खाते हुए अपने घर के आँगन में विचरण कर रहे हैं। उनके पैरों में पायल बज रही है और (UPBoardSolutions.com) वे पीले रंग की छोटी-सी धोती पहने हुए हैं। रसखान कवि कहते हैं कि उनके उस सौन्दर्य को देखकर कामदेव भी उन पर अपनी कोटि-कोटि कलाओं को न्योछावर करता है। हे सखी! उस कौवे के भाग्य का क्या कहना, जो कृष्ण के हाथ से मक्खन और रोटी छीनकर ले गया। भाव यह है कि कृष्ण की जूठी मक्खन-रोटी खाने का अवसर जिसको प्राप्त हो गया, वह धन्य है।

काव्यगत सौन्दर्य-

1. प्रस्तुत छन्द में श्रीकृष्ण के बाल-सौन्दर्य का बड़ा ही मोहक वर्णन ” किया गया है।
2. भाषा-ब्रज
3. शैली—चित्रात्मक और मुक्तक
4. रसवात्सल्य और भक्ति।
5. छन्द-सवैया।
6. अलंकार-पद्य में सर्वत्र अनुप्रास, ‘वारत काम कला निज कोटी’ में प्रतीप।
7. गुण-माधुर्य।
8. भावसाम्य-गोस्वामी जी ने भी श्रीराम की धूल से भरी बाल छवि का ऐसा ही चित्र खींचा है-अति सुन्दर सोहत धूरि भरे, छवि भूरि अनंग की दूरि धरें।

प्रश्न 4.
जा दिन तें वह नंद को छोहरा, या बन धेनु चराई गयी है।
मोहिनी ताननि गोधन गावत, बेनु बजाइ रिझाइ गयौ है ॥
वा दिन सो कछु टोना सो कै, रसखानि हियै मैं समाई गयी है।
कोऊ न काहू की कानि करै, सिगरो ब्रज बीर बिकाइ गयौ है ।
उत्तर
[ छोहरा = पुत्र। धेनु = गाय। बेनु = वंशी। टोना = जादू। सिगरो = सम्पूर्ण।] |

प्रसंग-इस पद्य में ब्रज की गोपियों पर श्रीकृष्ण के मनमोहक प्रभाव का सुन्दर चित्रण हुआ है।

व्याख्या–एक गोपी दूसरी गोपी से कहती है कि हे सखी! जिस दिन से वह नन्द का लाड़ला बालक इस वन में आकर गायों को चरा गया है तथा अपनी मोहनी तान सुनाकर और वंशी बजाकर हम सबको रिझा गया है, उसी दिन से ऐसा जान पड़ता है (UPBoardSolutions.com) कि वह कोई जादू-सा करके हमारे मन में बस गया है। इसलिए अब कोई भी गोपी किसी की मर्यादा का पालन नहीं करती है, उन्होंने तो अपनी लज्जा एवं संकोच सब कुछ त्याग दिया है। ऐसा मालूम पड़ता है कि सम्पूर्ण ब्रज ही उस कृष्ण के हाथों बिक गया है, अर्थात् उसके वशीभूत हो गया है। ||

काव्यगत सौन्दर्य-

1. यहाँ गोपियों पर कृष्ण-प्रेम के जादू का सजीव वर्णन किया गया है।
2. भाषा-ब्रज।
3. शैली-मुक्तक।
4. छन्द-सवैया।
5. रस-शृंगार।
6. अलंकार-‘कोऊ न काहु की कानि करै’, ‘ब्रज बीर बिकाइ गयौ’, ‘बेनु बजाइ’, ‘गोधन गावत’ में अनुप्रास।
7. गुण-माधुर्य।
8. भावसाम्य-रसखान ने अन्यत्र भी इसी प्रकार का वर्णन किया है कोऊ न काहु की कानि करै, कछु चेटक सो जु कियौ जदुरैया।

प्रश्न 5.
कान्ह भये बस बाँसुरी के, अब कौन सखी, हमकौं चहिहै ।
निसद्यौस रहै सँग-साथ लगी, यह सौतिन तापन क्यौं सहिहै ॥
जिन मोहि लियौ मनमोहन कौं, रसखानि सदा हमकौं दहिहै ।
मिलि आओ सबै सखि, भागि चलें अब तो ब्रज मैं बँसुरी रहिहै ॥
उत्तर
[चहिहै = चाहेगा। निसद्यौस = रात-दिन। तापन = सन्तापों को। सहिहै = सहन करेगी। मोहि लियौ = मोहित कर लिया है। दहिहै = जलाती है।

प्रसंग-इन पंक्तियों में श्रीकृष्ण के वंशी-प्रेम एवं गोपियों के उसके प्रति सौतिया डाह का सजीव वर्णन किया गया है।

व्याख्या–एक गोपी अपनी सखी से कहती है कि हे सखी! श्रीकृष्ण अब बाँसुरी के वश में हो गये हैं, अब हमसे कौन प्रेम करेगा? श्रीकृष्ण हमसे बहुत प्रेम करते थे, किन्तु अब वे इस दुष्ट बाँसुरी से प्रेम करने लगे हैं। यह बाँसुरी रात-दिन उनके साथ लगी रहती है। यह अब गोपीरूपी सौत की ईष्र्या के सन्ताप को क्यों सहन करेगी? जिस बाँसुरी ने हमारे मन को मोहने वाले कृष्ण को अपने प्रेम से मोहित कर लिया है, वह हमें सदी ईर्ष्या से जलाती (UPBoardSolutions.com) रहेगी। हे सखी! आओ हम सब मिलकर ब्रज छोड़कर अन्यत्र चलें; क्योंकि यहाँ अब केवल बाँसुरी ही रह सकेगी अर्थात् कृष्ण के प्रेम से वंचित होकर हमारा अब ब्रज में निर्वाह नहीं हो सकता।

काव्यगत सौन्दर्य-

1. प्रस्तुत छन्द में गोपियों की मुरली के प्रति स्वाभाविक ईष्र्या का सजीव वर्णन किया गया है।
2. भाषा-सुललित ब्रज।
3. शैली—चित्रोपम मुक्तक
4. रस- श्रृंगार।
5. छन्द-सवैया
6. अलंकार-अनुप्रास।
7. भावसाम्य–महाकवि सूरदास ने भी मुरली के प्रति गोपियों की ऐसी ही ईष्र्या को व्यक्त किया है। उनकी गोपियाँ तो ईवश मुरली को ही चुरा लेना चाहती हैं

 सखी री, मुरली लीजै चोरि ।
जिनि गुपाल कीन्हें अपनें बस, प्रीति सबनि की तोरि॥

प्रश्न 6.
मोर-पखा सिर ऊपर राखिहौं, गुंज की माल गरें पहिरौंगी।
ओढिपितम्बर लै लकुटी, बन गोधन ग्वारन संग फिरौंगी॥
भावतो वोहि मेरो रसखानि, सो तेरे कहै सब स्वाँग करौंगी।
या मुरली मुरलीधर की, अधरान धरी अधरा न धरींगी ॥
उत्तर
[ मोर-पखा = मोर के पंखों से बना हुआ मुकुट गरें = गले में। पितम्बर = पीताम्बर, पीला वस्त्र। लकुटी = छोटी लाठी। स्वाँग = श्रृंगार अभिनय। अधरान = होंठों पर। अधरा न= होंठों पर नहीं

प्रसंग-प्रस्तुत सवैये में कृष्ण के वियोग में व्याकुल गोपियों की मनोदशा का मोहक वर्णन किया गया है। कृष्ण-प्रेम में मग्न गोपियाँ कृष्ण का वेश धारणकर अपने हृदय को सान्त्वना देती हैं।

व्याख्या-एक गोपी अपनी दूसरी सखी से कहती है कि हे सखी! मैं तुम्हारे कहने से अपने सिर पर मोर के पंखों से बना मुकुट धारण करूंगी, अपने गले में गुंजा की माला पहन लूंगी, कृष्ण की तरह पीले वस्त्र पहनकर और हाथ में लाठी लिये हुए (UPBoardSolutions.com) ग्वालों के साथ गायों को चराती हुई वन-वने घूमती रहूंगी। ये सभी कार्य मुझे अच्छे लगते हैं और तेरे कहने से मैं कृष्ण के सभी वेश भी धारण कर लूंगी, परन्तु उनके होठों पर रखी हुई बाँसुरी का अपने होठों से स्पर्श नहीं करूंगी। तात्पर्य यह है कि कृष्ण गोपियों के प्रेम की परवाह न करके दिनभर बाँसुरी को साथ रखते हैं और उसे अपने होंठों से लगाये रहते हैं; अत: गोपियाँ उसे सौत मानकर उसका स्पर्श भी नहीं करना चाहती हैं; क्योंकि वह श्रीकृष्ण के ज्यादा ही मुँह लगी हुई है।

काव्यगत सौन्दर्य-

1. प्रस्तुत छन्द में कृष्ण के प्रति गोपियों के अनन्य प्रेम और बाँसुरी के प्रति स्त्रियोचित ईष्र्या का स्वाभाविक चित्रण किया गया है।
2. भाषा-ब्रज।
3. शैली-मुक्तक।
4. गुणमाधुर्य।
5. रस-शृंगार।
6. छन्द-सवैया।
7. अलंकार-‘या मुरली मुरलीधर की, अधरान धरी अधरा न धरौंगी’ में अनुप्रास तथा यमक।

कवित्त

प्रश्न 1.
गोरज बिराजै भाल लहलही बनमाल,
आगे गैयाँ पाछे ग्वाल गावै मृदु बानि री।
तैसी धुनि बाँसुरी की मधुर-मधुर जैसी,
बंक चितवन मंद मंद मुसंकानि री ॥
कदम बिटप के निकट तटिनी के तट,
अटा चढ़ि चाहि पीत पट फहरानि री ।
रस बरसावै तन-तपनि बुझावै नैन,
प्राननि रिझावै वह आवै रसखानि री ॥
उत्तर
[ गोरज = गायों के पैरों से उड़ी हुई धूल। लहलही = शोभायमान हो रही है। बानि = वाणी। बंक = टेढ़ी। तटिनी = (यमुना) नदी। तन-तपनि = शरीर की गर्मी।]

सन्दर्भ-प्रस्तुत पंक्तियाँ रसखान कवि द्वारा रचित ‘सुजान-रसखान’ (UPBoardSolutions.com) से हमारी पाठ्य-पुस्तक ‘हिन्दी’ के ‘काव्य-खण्ड में संकलित ‘कवित्त’ शीर्षक से अवतरित हैं।

प्रसंग-इन पंक्तियों में सायं के समय वन से गायों के साथ लौटते हुए कृष्ण की अनुपम शोभा का वर्णन एक गोपी अपनी सखी से कर रही है।

व्याख्या-गोपी कहती है कि हे सखी! वन से गायों के साथ लौटते हुए कृष्ण के मस्तक पर गायों के चलने से उड़ी धूल सुशोभित हो रही है। उनके गले में वन के पुष्पों की माला पड़ी हुई है। कृष्ण के आगे-आगे गायें चल रही हैं और पीछे मधुर स्वर में गाते हुए ग्वाल-बाल चल रहे हैं। जितनी मधुर और बाँकी श्रीकृष्ण की चितवन है, उतनी ही बाँकी उनकी धीमी-धीमी मुस्कान हैं। उनकी इस मधुर छवि के अनुरूप ही उनकी वंशी की मधुर-मधुर तान है। हे सखी! कदम्ब वृक्ष के पास यमुना नदी के किनारे खड़े कृष्ण के पीले वस्त्रों का फहराना, जरा अटारी पर चढ़कर तो देख लो। रस की खान वह श्रीकृष्ण चारों ओर सौन्दर्य (UPBoardSolutions.com) और प्रेम-रस की वर्षा करते हुए शरीर और मन की जलन को शान्त कर रहे हैं। उनका सौन्दर्य नेत्रों की प्यास को बुझा रहा है और प्राणों को अपनी ओर खींचकर रिझा रहा है।

काव्यगत सौन्दर्य-

1. प्रस्तुत छन्द में गोचारण से लौटते हुए श्रीकृष्ण के अनुपम सौन्दर्य का मोहक चित्रण हुआ है।
2. भाषा-सरल, सरस ब्रज।
3.  शैली—मुक्तक।
4.  रस-शृंगार।
5.  छन्द-मनहरण कवित्त।
6. अलंकार-‘भाल लहलही बनमाल’ में अनुप्रास, ‘मधुर-मधुर, मन्द-मन्द में पुनरुक्तिप्रकाश तथा ‘रसखानि री’ में श्लेष का मंजुल प्रयोग द्रष्टव्य है।
7. गुण-माधुर्य।

काव्य-सौन्दर्य एवं व्याकरण-बोध

प्रश्न 1
निम्नलिखित पंक्तियों में कौन-सा रस है, उसके स्थायी भाव का नाम लिखिए
(क) तेल लगाइ लगाह के अंजन, भाँहँ बनाइ बनाइ डिठौनहिं ।
(ख) जिन मोहि लियौ मनमोहन , रसखानि सदा हम दहिहै ।
मिलि आओ सबै सखि भागि चलें अब तो ब्रज में बँसुरी रहिहै ।।
उत्तर
(क) रसवात्सल्य, स्थायी भाव-स्नेह (रति)।
(ख) रस-श्रृंगार, स्थायी भाव–रति।

प्रश्न 2
निम्नलिखित पंक्तियों में प्रयुक्त अलंकार का नाम बताते हुए उसका स्पष्टीकरण दीजिए
(क) वा छबि को रसखानि बिलोकत, वारत काम कला निज कोटी।
(ख) या मुरली मुरलीधर की, अधरान धरी अधरा न धराँगी ।
(ग) रस बरसावे तन-तपनि बुझावै नैन,
प्राननि रिझावै वह आवै रसखानि री ॥
उत्तर
(क) अनुप्रास-‘क’ वर्ण की आवृत्ति के कारण अनुप्रास अलंकार है।

प्रतीप-“वारत काम कला निज कोटी’ यहाँ कृष्ण (UPBoardSolutions.com) के सौन्दर्य को देखकर कामदेव स्वयं अपनी करोड़ों कलाएँ निछावर कर रहा है। उपमान को उपमेय बना देने के कारण यहाँ प्रतीप अलंकार है।

(ख) अनुप्रास, यमक-‘म’, ‘ध’, ‘र’ वर्गों की आवृत्ति के कारण अनुप्रास तथा एक ‘अधरान का अर्थ ‘होठों पर’ एवं दूसरे ‘अधरा न’ का अर्थ होठों पर नहीं होने के कारण यमक है।

(ग) श्लेष—यहाँ ‘रसखानि री’ के दो अर्थ–रस की खान श्रीकृष्ण तथा कवि रसखान हैं; अतः इसमें श्लेष है।

प्रश्न 3
सवैये और कवित्त का लक्षण लिखते हुए पाठ से एक-एक उदाहरण दीजिए।
उत्तर
सवैया–बाइस से छब्बीस तक के वर्णवृत्त सवैया कहलाते हैं। उदाहरण पाठ से देखें। |

कवित्त—यह दण्डक वृत्त है। इसके प्रत्येक चरण में 31 वर्ण होते हैं। (UPBoardSolutions.com) 16-15 वर्षों पर यति होती है। अन्त में एक गुरु वर्ण होता है। इसे मनहरण कवित्त भी कहते हैं। उदाहरण पाठ से देखें।

प्रश्न 4
निम्नलिखित शब्दों के खड़ी बोली रूप लिखिए-
करोर, सिगरी, दुति, लकुटी, काग, अँगुरी, भाजति, संजम।
उत्तर

We hope the UP Board Solutions for Class 10 Hindi Chapter 3 रसखान (काव्य-खण्ड) help you. If you have any query regarding UP Board Solutions for Class 10 Hindi Chapter 3 रसखान (काव्य-खण्ड), drop a comment below and we will get back to you at the earliest.

 

These Sample papers are part of CBSE Sample Papers for Class 10 Maths. Here we have given CBSE Sample Papers for Class 10 Maths Paper 11.

CBSE Sample Papers for Class 10 Maths Paper 11

Board	CBSE
Class	X
Subject	Maths
Sample Paper Set	Paper 10
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 11 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.

Time allowed: 3 Hours
Maximum Marks: 80 

 General Instructions

• All questions are compulsory.
• The question paper consists of 30 questions divided into four sections A, B, C and D.
• Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each.
• There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
• Use of calculators is not permitted.

Section – A

Question 1.
Write whether the rational number [latex]\frac { 7 }{ 75 } [/latex] will have a terminating decimal expansion or a non-terminating repeating decimal expansion.

Question 2.
Find the value (s) of k, if the quadratic equation 3x² – k √3x + 4 = 0 has equal roots.

Question 3.
Find the eleventh term from the last term of the AP: 27, 23, 19,… ,- 65.

How do you round 214.0822 to the nearest tenth? … Hint: We are given a decimal number.

Question 4.
Find the coordinates of the point on y- axis which is nearest to the point (-2, 5).

Question 5.
In given figure, ST || RQ, PS = 3 cm and SR = 4 cm. Find the ratio of the area of ∆ PST to the area of ∆ PRQ.

Question 6.
If cos A = [latex]\frac { 2 }{ 5 } [/latex] , find the value of 4 + 4 tan² A.

Section – B

Question 7.
If two positive integers p and q are written as p = a² b³ and q = a³ b; a, b are prime numbers, then verily: LCM (p, q) × HCF (p, q) = pq

Question 8.
The sum of first n terms of an AP is given by S_n = 2n² + 3n. Find the sixteenth term of the A.P.

Question 9.
Find the value (s) of k for which the pair of linear equations kx + y = k² and x + ky = 1 have infinitely many solutions.

Question 10.
If ( 1, [latex]\frac { p }{ 3 } [/latex] ) is the mid- point of the line segment joining the points (2,0) and ( 0, [latex]\frac { 2 }{ 9 } [/latex] ) then show that the line 5x + 3y + 2 = 0 passes through the point (-1 , 3p)

Question 11.
A box contains cards numbered 11 to 123. A card is drawn at random from the box. Find the probability that the number on the drawn card is

1. a square number
2. a multiple of 7.

To convert 10 11/16 to decimal you can use the long division method explained in our article fraction to decimal, which you can find in the header menu.

Question 12.
A box contains 12 balls of which some are red in colour. If 6 more red balls are put in the box and a ball is drawn at random, the probability of drawing a red ball doubles than what it was before. Find the number of red balls in the bag.

Section – C

Question 13.
Show that exactly one of the numbers n, n + 2 or n + 4 is divisible by 3.

Question 14.
Find all the zeroes of the polynomial 3x⁴ + 6x³ – 2x² – 10x – 5 if two of its zeroes are √ [latex]\frac { 5 }{ 3 } [/latex] and – √ [latex]\frac { 5 }{ 3 } [/latex]

Question 15.
Seven times a two digit number is equal to four times the number obtained by reversing the order of its digits. Ifthe difference ofthe digits is 3, determine the number.

Question 16.
In what ratio does the x-axis divide the line segment joining the points (-4,-6) and (-1, 7)? Find the co-ordinates of the point of division.
OR
The points A (4, -2), B (7,2), C (0,9) and D (-3,5) form a parallelogram. Find the length of the altitude of the parallelogram on the base AB.

Question 17.
In given figure ∠1 = ∠2 and ∆NSQ = ∆MTR, then prove that ∆ PTS ~ PRQ

OR
In an equilateral triangle ABC, D is a point on the side BC such that BD = [latex]\frac { 1 }{ 3 } [/latex] BC. Prove that 9 AD² = 7 AB²

Question 18.
In given figure XY and X’ Y’ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X’ Y’ at B. Prove that ∠ AOB = 90°.

Question 19.

Question 20.
In given figure ABPC is a quadrant of a circle ofradius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region

Question 21.
Water in a canal, 6 m wide and 1.5m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
OR
A cone of maximum size is carved out from a cube of edge 14 cm. Find the surface area of the remaining solid after the cone is carved out.

Question 22.
Find the mode of the following distribution of marks obtained by the students in an examination :

Marks obtained	0-20	20-40	40-60	60-80	80-100
Number of students	15	18	21	29	17

Given the mean of the above distribution is 53, using empirical relationship estimate the value of its median.

Question 23.
A train travelling at a uniform speed for 360 km would have taken 48 minutes less to travel the same distance if its speed were 5 km/hour more. Find the original speed of the train.
OR
Check whether the equation 5x² – 6x – 2 = 0 has real roots and if it has, find them by the method of completing the square. Also verify that roots obtained satisfy the given equation.

Question 24.
An AP consists of 3 7 terms. The sum of the three middle most terms is 225 and the sum of the last three terms is 429. Find the AP.

Question 25.
Show that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
OR
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Question 26.
Draw a triangle ABC with side BC = 7 cm, ∠B=45°, ∠A= 105°. 1 Then, construct a triangle whose sides are [latex]\frac { 4 }{ 3 } [/latex] times the corresponding sides of ∆ABC.

Question 27.

Question 28.
The angles of depression of the top and bottom of a building 50 metres high as observed from the top of a tower are 30° and 60°, respectively. Find the height of the tower and also the horizontal distance between the building and the tower.

Question 29.
Two dairy owners A and B sell flavoured milk filled to capacity in mugs of negligible thickness, which are cylindrical in shape with a raised hemispherical bottom. The mugs are 14 cm high and have diameter of 7 cm as shown in given figure. Both A and B sell flavoured milk at the rate of ₹ 80 per litre. The dairy owner A uses the formula nrh to find the volume of milk in the mug and charges ₹ 43.12 for it. The dairy owner B is of the view that the price of actual quantity of milk should be charged. What according to him should be the price of one mug of milk? Which value is exhibited by the dairy owner B ? [ use π = [latex]\frac { 22 }{ 7 } [/latex] )

Question 30.
The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency k.

Daily pocket allowance (in ₹)	11-13	13-15	15-17	17-19	19-21	21-23	23-25
Number of children	3	6	9	13	k	5	4

The following frequency distribution shows the distance (in metres) thrown by 68 students in a Javelin throw competition.

Distance (in m)	0-10	10-20	20-30	30-40	40-50	50-60	60-70
Number of students	4	5	13	20	14	8	4

Draw a less than type O give for the given data and find the median distance thrown using this curve.

Solutions

Solution 1.
Non terminating repeating decimal expansion.

Solution 2.
k = ± 4

Solution 3.
a₁₁ = -25

Solution 4.
(0,5)

Solution 5.
9 : 49

Solution 6.
4 + tan² A = 4 sec² A = 4 ( [latex]\frac { 5 }{ 2 } [/latex] ) ² = 25

Solution 7.
LCM (p, q) = a³ b³
HC,F (p, q) = a² b
LCM (p, q) × HCF (p, q) = a⁵ b⁴ = (a² b³)
(a³ b) = pq

Solution 8.
S_n = 2n² + 3n
S₁ = 5 = a₁
S₂ = a₁ + a₂ = 14 ⇒ a₂ = 9
d= a₂ – a₁ = 4
a₁₆ = a₁ + 15d = 5+ 15(4) = 65

Solution 9.

Solution 10.

Solution 11.

1. P (square number) = [latex]\frac { 8 }{ 113 } [/latex]
2. P (multiple of 7) = [latex]\frac { 16 }{ 113 } [/latex]

Solution 12.
Let number of red balls be = x
∴ P (red ball) = [latex]\frac { x }{ 12 } [/latex]
If 6 more red balls are added: The number of red balls = x + 6 P (red ball) = [latex]\frac { x+6 }{ 18 } [/latex]
Since, [latex]\frac { x+6 }{ 18 } [/latex] = 2 ( [latex]\frac { x }{ 12 } [/latex] ) ⇒ x = 3
There are 3 red balls in the bag.

Solution 13.
Let n = 3k, 3k + 1 or 3k+ 2.
(i) When n = 3k: n is divisible by 3.
n + 2 = 3k + 2 ⇒ n + 2 is not divisible by 3.
n + 4 = 3k + 4 = 3 (k + 1)+ 1 ⇒ n + 4 is not divisible by 3.

(ii) When n = 3k + 1: n is not divisible by 3.
n + 2 = (3k + 1) + 2 = 3k+ 3 = 3 (k+ 1) ⇒ n + 2 is divisible by 3.
n + 4 = (3k+ l) + 4 = 3k + 5 = 3(k+ 1) + 2 ⇒ n + 4isnotdivisibleby3.

(iii) When n = 3k + 2: n is not divisible by 3.
n + 2 = (3k+2) + 2 = 3k + 4 = 3(k+ 1)+ 1 ⇒ n + 2 is not divisible by 3.
n + 4 = (3k + 2)+ 4 = 3k+ 6 = 3(k + 2) ⇒ n + 4 is divisible by 3.
Hence exactly one of the numbers n, n + 2 or n + 4 is divisible by 3.

Solution 14.

Solution 15.
Let the ten’s and the units digit be y and x respectively.
So,the number is 10 y + x.
The number when digits are reversed is 10 x + y.
Now, 7(10y+ x) = 4(10x + y) ⇒ 2y = x …( 1)
Also x – y3 …(ii)
Solving (1) and (2),we get y = 3 and x = 6.
Hence the number is 36.

Solution 16.

Solution 17.
∠SQN = ∠TRM (CPCT as NSQ ≅ MTR)

Since, ∠P + ∠1 + ∠2 = ∠P + ∠PQR + ∠PRQ (Angle sum property)
⇒ ∠1 + ∠2 = ∠PQR + ∠PRQ
⇒ 2 ∠1 = 2 ∠PQR (as ∠1 = ∠2 and ∠PQR= ∠PRQ) ⇒ ∠1 = ∠PQR
Also ∠2 = ∠PRQ and ∠SPT = ∠QPR (common) ∆PTS ~ ∆PRQ (By AAA similarity criterion)

Solution 18.

Solution 19.

Solution 20.

Solution 21.

Solution 22.

Solution 23.

Solution 24.
Let the three middle most terms of the AP be a – d, a, a + d
We have, (a – d) +a + (a + d) = 225
⇒ 3 a = 225 ⇒ a = 75
Now, the AP is a – 18d,…,a – 2d, a – d, a, a + d,a + 2d,…,a + 18d
Sum of last three terms :
(a + 18d) + (a + 17d) + (a + 16d) = 429
⇒ 3a + 51 d = 429 ⇒ (a + 17d) = 143
⇒ 75 + 17d = 143 ⇒ d = 4
Now, first term = a – 18d = 75 – 18(4) = 3
∴ The AP is 3,7,11,…, 147.

Solution 25.
Given : A right triangle ABC right angled at B.
To prove : AC² = AB² + BC²
Construction : Draw BD ⊥ AC
Proof : In ∆ ADB and ∆ ABC
∠ADB = ∠ABC (each 90°)
∠BAD = ∠CAB (common)

Solution 26.
Draw ∆ABC in which BC = 7 cm, ∠B = 45°, ∠A = 105° and hence ∠C = 30°.
Construction of similar triangle A’ BC’ as shown below.

Solution 27.

Solution 28.

Solution 29.

Solution 30.

We hope the CBSE Sample Papers for Class 10 Maths paper 11 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths paper 11, drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 10 Computer Science Chapter 4 Discrete Mathematics

Discrete Mathematics Long Answer Type Questions (8 Marks)

Question 1.
How are characters created by Binary Numbers? What are its different codes? Explain with examples. (UP 2011)
Answer:
Computer Code: Computer codes are used to convert data into binary form to make the computer understand it. Apart from this, they are responsible for error-free signal flow in the computer. Three popular computer codes are:
BCD (Binary Coded Decimal): It is one of the earliest developed (UPBoardSolutions.com) memory codes. In this, every digit is converted into binary form separately:
e.g.,

But four-bit code can handle only 2⁴ = 16 dIfferent characters that are why it is extended to 6-bit code and It can handle 2⁶ = 64 different characters. It is 6-bit code and divided into two parts i.e., zone bit and character code.
Zone bit consists of Z bits and character zone consists of 4 bits.
To understand more look at the table given below:

EBCDIC (Extended Binary Coded Decimal Interchange Code): BCD can convert only 64 characters but we use more than 64 characters in computer to represent data. To overcome this problem, 2 more bits have been added to the zone bit to develop new 8-bit code and, that is why it is known as extended binary coded decimal interchange code. EBCDIC is 8- bit code which can encode 2⁸ = 256 different characters. It is similar to BCD in working but it has 4 bits in bit zone. To understand more table is given below:

ASCII (American Standard Code for Information Interchange): This code is the most popular and widely accepted computer code. It is the standard code for computers, developed by the American National Standards Institute in the year 1963 for (UPBoardSolutions.com) encoding different characters in the computer. It is used by almost every manufacturing company. ASCII codes are of two types:
(a) 7-bit Code: To encode 2⁷ = 128 characters with 3 bits in zone bit and four in character zone.


(b) 8-bit code: To encode 2⁸ = 256 characters with 4 bits in bit zone and 4 bits in character zone.

What is 5/8 as a decimal you ask? Converting the fraction 5/8 into a decimal is very easy.

Question 2.
Define character representation in computers. (UP 2008)
Or
What is meant by “character representation”? Explain one such code in detail. (UP 2009)
Or
What is meant by character coding? Explain one coding methods in detail. (UP 2016)
Or
What is Character Representation? (UP 2018)
Answer:
Character Representation: Physical devices used to store and process data in computers are two-state devices. A switch, for example, is a two-state device. It can be either ON or OFF. Electronic devices such as transistors used in computers must function reliably when operated as switches. Thus, all data to be stored and processed in computers are transformed or coded as strings of two symbols, one symbol to represent each state.

Coding of characters has been standardized to facilitate the exchange of recorded data between computers. The most popular standard is known as ASCII. Each letter is a unique combination of Binary Digits (BITS). That is, each letter (UPBoardSolutions.com) is a group of charged and uncharged transistors and it is grouped in such a way that a particular combination represents a specific character. A group of 8 BITS which is used to represent a character is called a byte. The length of 1 word is called word length which ranges from 1 byte to 64 bytes.
The internal code representation of string HARSH is:

Question 3.
Explain the Number System.
Answer:
Number System: Number systems are very important to understand because the design and organization of a computer system depend on it.
Number systems are basically of two types:
1. Non-positional Number System: In this number system, each symbol represents the same value regardless of its position in the number and the symbols are simply added to find out the value of a particular number. Since it is very difficult to perform arithmetical operations with such a number system, positional number systems have been developed.

2. Positional Number System: In a positional number system, there are only a few symbols (UPBoardSolutions.com) called digits, and these symbols represent different values depending on the position they occupy in the number.

The value of each digit in such a number is determined by three considerations :

1. The digit itself
   Face Value: The face value of a digit always remains the same regardless of its position in the number, e.g., the face value of 4 in 554, 40567 etc. is 4.
2. The position of the digit in the number.
   Place Value: Place value of a digit changes due to change in its position, e.g., place value of 2 in 4210 is 2 hundred, in 32,450 it is 2 thousand, etc.
3. The base of the number system (where the base is defined as the total number of digits available in the number system), e.g., Decimal number system has base 10 since it includes only 10 digits 0, 1, 2, ….., 9, to represent any number.

The various positional systems in use are:

1. Binary number system
2. Octal number system
3. Decimal number system
4. Hexadecimal number system.

Convert fraction 6 and 1/2 to decimal. What is 6 1/2 as a decimal? Answer: 6.5.

Question 4.
What are the logical operators? What are their different types? Explain operators making their Truth Table. (UP 2007, 08, 10)
Answer:
Logical Operators: AND, OR, and NOT are logical operators. Since these operators are operated on logical values 0 and 1, that is why these operators are called logical operators.

AND Operator: An AND operator is represented by the symbol ‘.’. Basically AND operator is used to performing logical multiplication. A, B, and C are three logical variables, where A, B, are input variables and C is the output variable. We can define the AND operator by listing all possible combinations of A and B and the resulting value of C in the operation A.B = C.

It may be noted that since the variables A and B can have only two possible values (0 or 1) so only four (22) combinations of inputs are possible as shown in the following table. The resulting output values for each of the four input combinations (UPBoardSolutions.com) are given in the table. Such a table is known as the truth table. Thus, the table is the truth table for the logical AND operator.

As we can observe from the truth table that in AND operation, the output will be 1 when all inputs are 1 else output will be 0.
OR Operator: An OR operator is represented by the symbol V. Basically an OR operator is used to perform logical addition. As in the previous example, A and B are input variables and C its output variable. We can define the OR operator by listing all possible combinations of A and B and the resulting value of C in the equation A + B = C. The truth table for Logical OR operator is shown in the following Table:

As we can observe from the truth table that in logical addition, the output will be 1 when any one input is 1. It means if all inputs are 0 then the output will be 0.

NOT Operator: The two operators (AND and OR) are binary operators because they operate on two variables. NOT operator denoted by is a Unary operator because it operates on a single variable. NOT operator is also known as complementation operator or inverse operator.
Thus, complement of A is [latex]\bar { A } [/latex]. Complement of (A + B) is [latex]\bar { (A+B } )[/latex]. If value
of [latex]\bar { A } [/latex] is 0 then value of A is 1 and if value of A is 1 then value of [latex]\bar { A } [/latex] is 0. (UPBoardSolutions.com) The truth table for logical NOT operator is shown in table.

Question 5.
Write about the postulates of Boolean Algebra.
Answer:
Postulates of Boolean Algebra: Boolean Algebra is an algebraic structure defined on a set of elements B together with two binary operators + and . provided the following postulates are satisfied:
(1) (a) Closure with respect to the operator +
(b) Closure with respect to the operator.

(2) (a) An identity element with respect to +, designated by
0 : X + 0 = 0 + X = X.
(b) An identify element with respect to designated by
1 : X . 1 = 1 . X = X.

(3) (a) Commutative with respect to + : X + Y = Y + X
(b) Commutative with respect to . : X . Y = Y . X

(4) (a) . is distributive over : : X . (Y + Z) = (X . Y) + (X . Z)
(b) + is distributive over . : X + (Y . Z) = (X + Y) . (X + Z)

(5) For every element X ∈ B, there exists an element [latex]\bar { X } [/latex] ∈ B such that:
(a) X × [latex]\bar { X } [/latex] = 1
(b) X . [latex]\bar { X } [/latex] = 0
The postulates listed above are called Huntington (1904) Postulates and need (UPBoardSolutions.com) no proof. They are used to prove the theorems of Boolean Algebra.

Question 6.
What are the different Gates in Boolean Algebra? (UP 2004, 05, 07)
Or
What is ‘Truth Table’? How is it helpful in understanding GATES? (UP 2006)
Or
Explain the working of a NAND Gate. Give its two application. (UP 2009, 10)
Or
How can you show that NAND is a Universal Gate? Explain with diagrams and truth tables. (UP 2011, 19)
Answer:
Truth Table: A table that shows all the input-output possibilities of a logic circuit is called a truth table.
There are several types of the truth table. AND, OR, NOT, NAND, NOR, XOR, XNOR Gates are described below:
(a) AND Gate: In English language, Input A is ANDed with Input B to get output Y.

The truth table illustrates four ways to express the logical ANDing of A and B.
The AND Gate works on the principle that output will be high when all the inputs (UPBoardSolutions.com) are high otherwise output will be low.

(b) OR Gate: In OR Gate, input A is ORed with input B to get output Y.


The OR Gate works on the principle that, if anyone input is high, the output will be high. Thus, the only case when output will be low is when all inputs are low i.e., 0.

(c) NOT Gate: The NOT Gate is an electronic circuit that generates an output signal which is the reverse of the input signal. A NOT gate is also known as an inverter because it inverts the input.

(d) NAND Gate: A NAND Gate is a complemented AND gate. That is, the output of NAND Gate will be 1 if anyone of the inputs is 0 and will be 0 when all the inputs are 1.

(e) NOR Gate: A NOR Gate is a complemented OR Gate. That is, the output of a NOR Gate will be 1 only when all inputs are 0 and will be 0 if any input represents a 1.

(f) XOR Gate (Exclusive-OR Gate): XOR Gate is a combination of AND, OR, and NOT (UPBoardSolutions.com) Gates. symbol denotes XOR operation. This Gate works on the principle that if an odd number of inputs are 1, the output will be 1 otherwise output will be 0.

As observed from the truth table, the output is 1 when odd numbers of inputs are 1.

(g) XNOR Gate (Exclusive-NOR Gate): Similarly, XNOR gate is also formed with a combination of AND, OR, and NOT gates. symbol denotes XNOR operation. Since this gate is the inverse of XOR gate, the output will be 0 when odd numbers of inputs are 1 otherwise output will be 1.

Question 7.
Explain the basic features of ASCII Code. (UP 2005, 08, 09, 10)
Or
Explain in detail the features of the ASCII character code. (UP 2007)
Answer:
ASCII: Binary numbers are coded to represent characters in the computer memory. Several codes are used for this purpose. One most commonly used code is the American Standard Code for Information Interchange (ASCII). ASCII has been adopted by several American computer manufacturers as their computer’s internal code. This code is popular in data communications, is used (UPBoardSolutions.com) almost exclusively to represent data internally in microcomputers, and is frequently found in the larger computers produced by some vendors.

ASCII is of two types: ASCII-7 and ASCII-8. ASCII-7 is a 7-bit code that represents 128 (27) different characters.
ASCII-8 is an extended version of ASCII-7. It is an 8-bit code that represents 256 (28) different characters rather than 128.
e.g. (i) A is given ASCII code 65.

Now if we convert 65 into Binary form we get 01000001 → 1 byte
In the same way, every character has its own ASCII value after converting into binary code stored on the computer.

Question 8.
Describe various Binary Arithmetic Operations. (UP 2008, 09, 11)
Or
What is binary arithmetic? Explain with suitable example. (UP 2017)
Answer:
Four basic arithmetic operations are performed inside a computer using binary numbers. These are addition, subtraction, multiplication, and division. Since binary numbers are made up of 0’s and 1’s, results of arithmetic operations are also in 0’s and 1’s only.

Binary Addition: Binary addition is performed in the same manner as decimal addition. However the binary system has only two digits, the addition table for binary arithmetic is very simple, consisting of only four entries. The complete table for binary addition is as follows:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0

Plus a carry of 1 to next higher column. Carryovers are performed in the same manner as in decimal arithmetic. Since 1 is the largest digit in the binary system, any sum greater than 1 requires that a digit be carried over.
Example:


Binary Subtraction: From the following table, it is clear that the lower digit is subtracted (UPBoardSolutions.com) from the upper digit. If the lower digit is larger than the upper digit, it is necessary to borrow from the column to the left which equals to 2 (10).
0 – 0 = 0
1 – 0 = 1
1 – 1 = 0
0 – 1 = 1
with borrow from the next column. Thus, the only case in which it is necessary to borrow is when 1 is subtracted from 0.
Example

Binary Multiplication: Multiplication in the binary system also follows the same general rules as decimal multiplication. The table for binary multiplication is as follows:
0 × 0 = 0
0 × 1 = 0
1 × 0 = 0
1 × 1 = 1
Example:

Binary Division: Binary division is, again, very simple. As in the decimal system (or in any other system), division by zero is meaningless, here too. Hence, the complete table for the binary division is as follows:
0/1 = 0
1/1 = 1
The division process is performed in a manner similar to the decimal division.
Example:

Discrete Mathematics Short Answer Type Questions (4 Marks)

Question 1.
What is the order of precedence in Boolean Algebra? (UP 2007, 09, 19)
Answer:
In a Boolean expression, many operators are used. The order in which they are operated is known as precedence. The precedence of Boolean operators is as follows:

1. The expression is scanned from left to right.
2. Expressions enclosed within parentheses are evaluated first.
3. All complement (NOT) operations are performed next.
4. All ‘.’ (AND) operations are performed after that.
5. Finally, all ‘+’ (OR) operations are performed in the end.

Question 2.
Define the Principal of Quality. (UP 2016)
Answer:
The Huntington Postulates have been listed in two parts: (a) and (b). One part may be obtained from the other if ‘+’ is interchanged ‘+’ with ‘.’ and ‘0’ in interchanged with ‘1’ and vice-versa. This important property of Boolean Algebra (UPBoardSolutions.com) is called Principle of Quality. This principle ensures that, if a theorem is proved using the postulates, then a dual theorem obtained interchanging ‘+’ with ‘.’ and ‘0’ with ‘1’ automatically holds and need not be proved separately.
The table below lists theorems and their corresponding dual theorems.

Question 3.
Write a note on De Morgan’s Theorems to prove it.
Answer:
Theorem (a): De Morgan’s Theorems: (x + y)’ = x’. y’
Proof: The truth table for proving this theorem is given below:

From the truth table, it is clear that both sides of the theorem are equal. Hence, the theorem is proved.
Theorem (b): (x + y)’ = x’ + y’
Proof: The truth table for proving this theorem is given below:

From the truth table, It is clear that both sides of the theorem are equal. Hence, the theorem is proved.
Theorems 6(a) and 6(b) are very important and useful. They are known as De Morgan’s theorems. They can be extended to n variables as given below:
(X₁ + X₂ + X₃ + ………. + X_n)’ = X₁‘ . X₂‘ . X₃‘ …….. X_n‘
(X₁ . X₂ . X₃. …… X_n)’ = X₁‘ + X’₂ + X₃‘ + ……….. + X_n‘

Question 4.
Write AND and OR LAWS of Discrete mathematics.
Answer:
AND LAWS: AND LAWS are the laws which work on logical multiplication. They are:
1. x . 1 = x
2. x . x’ = 0
3. x . x = x
4. x . 0 = 0
“The tabular representations of truth values of a compound statement based on the truth values of the prime connective ness of statements is called TRUTH TABLE.”
Truth table consists of horizontal lines (rows) and vertical lines (columns). If a compound statement consists of N statements, the number of rows will be 2^N. The number of columns in a truth table depends upon the number of relationships between these statements.

Discrete Mathematics Very Short Answer Type Questions (2 Marks)

Question 1.
Discuss De-Morgan’s Theorem. (UP 2014)
Answer:
First Theorem: This theorem states that the complement of a sum of the binary variable is equal to the product of the complement of the binary variables.
Second Theorem: The theorem states that the complement of a product of binary (UPBoardSolutions.com) variable is equal to the sum of the complement of the binary variable

Question 2.
What is the full form of ASCII? (UP 2014)
Answer:
The full form of ASGII is American Standard Code for Information Interchange.

Question 3.
If A = 0 and B = 1, then find the value of y from the following expression:
Y = (A . B)
Answer:
Y = [latex]\bar { (0.1 } )[/latex] = [latex]\bar { (0 } )[/latex] = 1

Question 4.
Give the name of the Boolean operators. (UP 2014)
Answer:
AND Operator, Or operator and NOT operator.

Question 5.
Write a full form of EBCDIC. (UP 2017)
Answer:
Extended Binay Coded Decimal Interchange Code.

Discrete Mathematics Objective Type Questions (1 Marks)

There are four alternative answers for each part of the questions. Select the (UPBoardSolutions.com) correct one and write in your answer book:

Question 1.
Each letter is a unique combination of:
(a) Bits
(b) Bytes
(c) Word length
(d) Binary.
Answer:
(a) Bits

Question 2.
A group of 8 bits which is used to represent a character is called :
(a) Bits
(b) Bytes
(c) Integer
(d) None of these.
Answer:
(b) Bytes

Question 3.
The most popular standard is known as:
(a) BCD
(b) ABC
(c) ASC
(d) ASCII
Answer:
(d) ASCII

Question 4.
In the hexadecimal number system, the base :
(a) 8
(b) 10
(c) 16
(d) None of these.
Answer:
(c) 16

Question 5.
The binay equivalent of the number (15)₁₀. (UP 2014)
(a) (1101)
(b) (1110)₂
(c) (1111)₂
(d) (1000)₂.
Answer:
(a) (1101)

Question 6.
Which logic gate has only one input and one output? (UP 2015)
(a) NOT
(b) NOR
(c) OR
(d) AND.
Answer:
(a) NOT

Question 7.
The value of the binary number (1010)₂ would be?
(a) (14)₁₀
(b) (12)₁₀
(c) (10)₁₀
(d) (11)₁₀
Answer:
(c) (10)₁₀

Question 8.
What is binary equivalent of [31]₁₀. (UP 2017)
(a) 10000
(b) 11111
(c) 100000
(d) 11110.
Answer:
(b) 11111

Question 9.
Which of the following is a single input logic gate? (UP 2018)
(a) NAND
(b) AND
(c) NOT
(d) NOR.
Answer:
(c) NOT

UP Board Solutions for Class 10 Computer Science