Class 11

UP Board Solutions for Class 11 Samanya Hindi काव्यांजलि Chapter 1 सन्त कबीरदास are part of UP Board Solutions for Class 11 Samanya Hindi. Here we have given UP Board Solutions for Class 11 Samanya Hindi काव्यांजलि Chapter 1 सन्त कबीरदास.

Board	UP Board
Textbook	NCERT
Class	Class 11
Subject	Samanya Hindi
Chapter	Chapter 1
Chapter Name	सन्त कबीरदास
Number of Questions	6
Category	UP Board Solutions

UP Board Solutions for Class 11 Samanya Hindi काव्यांजलि Chapter 1 सन्त कबीरदास

कवि का साहित्यिक परिवय और कृतियाँ

प्रश्न 1.
कबीर का जीवन-परिचय देते हुए उनकी काव्य-कृतियों (साहित्यिक योगदान) का उल्लेख कीजिए।
या
सन्त कबीर का साहित्यिक परिचय देते हुए उनकी कृतियों को उल्लेख कीजिए।

एक जनश्रुति के अनुसार इनका जन्म हिन्दू-परिवार में हुआ था। कहते हैं कि ये एक विधवा ब्राह्मणी के पुत्र थे, जिसने इन्हें लोक-लाज के भय से काशी के लहरतारा नामक स्थान पर तालाब के किनारे छोड़ दिया था, जहाँ से नीरू नामक एक जुलाहा एवं उसकी पत्नी नीमा नि:सन्तान होने के कारण इन्हें उठा लाये।

कबीर के जन्म-स्थान के सम्बन्ध में भी विद्वानों में मतभेद हैं, परन्तु अधिकतर विद्वान् इनका जन्म काशी में ही मानते हैं, जिसकी पुष्टि स्वयं कबीर का यह कथन भी करता है—काशी में परगट भये, हैं रामानन्द चेताये। इससे इनके गुरु का नाम भी पता चलता है कि प्रसिद्ध वैष्णव सन्त आचार्य रामानन्द से इन्होंने दीक्षा ग्रहण की। गुरुमन्त्र के रूप में इन्हें ‘राम’ नाम मिला, जो इनकी समग्र भावी साधना का आधार बना।

कबीर की पत्नी का नाम लोई था, जिससे इनके कमाल नामक पुत्र और कमाली नामक पुत्री उत्पन्न हुई। कबीर बड़े निर्भीक और मस्तमौला स्वभाव के थे। व्यापक देशाटन एवं अनेक साधु-सन्तों के सम्पर्क में आते रहने के कारण इन्हें विभिन्न धर्मों एवं सम्प्रदायों का ज्ञान प्राप्त हो गया था। ये बड़े सारग्राही एवं प्रतिभाशाली थे। कबीर की दृढ़ मान्यता थी कि मनुष्य को अपने कर्मों के अनुसार ही गति मिलती है, स्थान-विशेष के प्रभाव से नहीं। अपनी इसी मान्यता को सिद्ध करने के लिए अन्त समय में ये मगहर चले गये; क्योंकि लोगों की मान्यता थी कि काशी में मरने वाले को मुक्ति मिलती है, किन्तु मगहर में मरने वाले को नरक। अधिकतर विद्वानों ने माना है कि कबीर की मृत्यु संवत् 1575 ( सन् 1519) में हुई। इसके समर्थन में निम्नलिखित उक्ति प्रसिद्ध है-

साहित्यिक सेवाएँ—कबीर पढ़े-लिखे नहीं थे, किन्तु ये बहुश्रुत होने के साथ-साथ उच्च कोटि की प्रतिभा से सम्पन्न थे। आचार्य हजारीप्रसाद द्विवेदी ने भी स्पष्ट कहा है कि, ”कविता करना कबीर का लक्ष्य नहीं था, कविता तो उन्हें सेंत-मेंत में मिली वस्तु थी, उनका लक्ष्य लोकहित था।” इस दृष्टि से उनके काव्य में उनके दो रूप दिखाई पड़ते हैं—(1) सुधारक रूप तथा (2) साधक (या भक्त) रूप। उनके बाद वाले रूप में ही उनके सच्चे कवित्व के दर्शन होते हैं।

1. कबीर का सुधारक रूप—कबीरदास के समय में हिन्दुओं और मुसलमानों में कटुता चरम सीमा पर थी। कबीर ने इन दोनों को पास लाना चाहा। इसके लिए उन्होंने सामाजिक और धार्मिक दोनों स्तरों पर प्रयास किया।
   
2. कबीर का साधक ( या भक्त) रूप-सुधारक रूप में यदि कबीर में तर्कशक्ति और बुद्धि की प्रखरता देखने को मिलती है तो साधक रूप में उनके भावुक हृदय से मार्मिक साक्षात्कार होता है। कबीर के अनुसार मानव-जीवन की सार्थकता ईश्वर-दर्शन में है। उस ईश्वर को विभिन्न धर्मों के

अनुयायी अलग-अलग नामों से पुकारते हैं। कृतियाँ-कबीर लिखना-पढ़ना नहीं जानते थे। यह बात उन्होंने स्वयं कही है– मसि कागद छूयो नहीं, कलम गयो नहिं हाथ। उनके शिष्यों ने उनकी वाणियों का संग्रह ‘बीजक’ नाम से किया, जिसके तीन मुख्य भाग हैं-साखी, सबद (पद), रमैनी। हजारीप्रसाद द्विवेदी के अनुसार ‘बीजक’ का सर्वाधिक प्रामाणिक अंश ‘साखी’ है। इसके बाद सबद’ और अन्त में ‘रमैनी’ का स्थान है।

साहित्य में स्थान—कबीर के जीवन और सन्देश के सदृश ही उनकी कविता भी आडम्बरशून्य है। कविता की यह सादगी ही उसकी बड़ी शक्ति है। न जाने कितने सहृदय तो उनके साधक रूप की अपेक्षा उनके कवि रूप पर मुग्ध हैं और उन्हें हिन्दी के सिद्धहस्त महाकवियों की पंक्ति में अग्र स्थान का अधिकारी मानते हैं।

पद्यांशों पर आधारित प्रश्नोत्तर

We hope the UP Board Solutions for Class 11 Samanya Hindi काव्यांजलि Chapter 1 सन्त कबीरदास help you. If you have any query regarding UP Board Solutions for Class 11 Samanya Hindi काव्यांजलि Chapter 1 सन्त कबीरदास, drop a comment below and we will get back to you at the earliest.

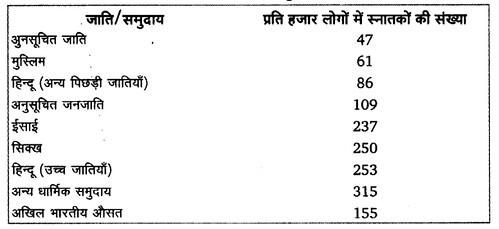
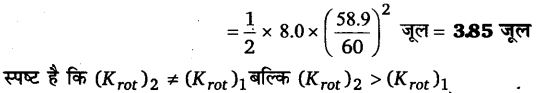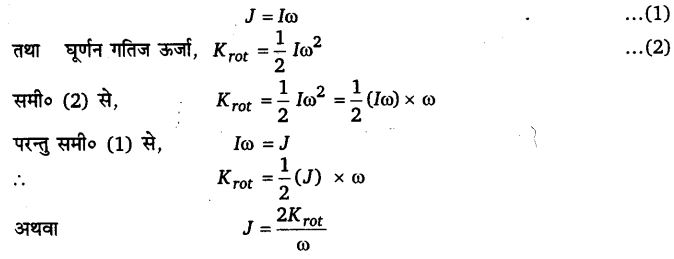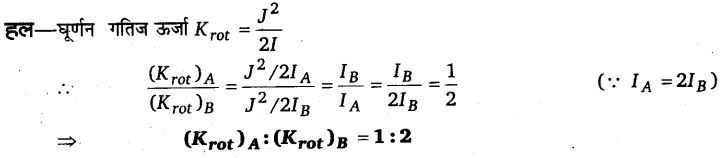UP Board Solutions for Class 11 Physics Chapter 7 System of particles and Rotational Motion (कणों के निकाय तथा घूर्णी गति)

These Solutions are part of UP Board Solutions for Class 11 Physics. Here we have given UP Board Solutions for Class 11 Physics Chapter 7 System of particles and Rotational Motion (कणों के निकाय तथा घूर्णी गति)

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
एकसमान द्रव्यमान घनत्व के निम्नलिखित पिण्डों में प्रत्येक के द्रव्यमान केन्द्र की अवस्थिति लिखिए –

(a) गोला
(b) सिलिण्डर
(c) छल्ला तथा
(d) घन।

क्या किसी पिण्ड का द्रव्यमान केन्द्र आवश्यक रूप से उस पिण्ड के भीतर स्थित होता है?

उत्तर :
गोला, सिलिण्डर, वलय तथा घन का द्रव्यमान केन्द्र उनको ज्यामितीय केन्द्र होता है। नहीं, द्रव्यमान केन्द्र आवश्यक रूप से पिण्ड के भीतर स्थित नहीं होता है, अनेक पिण्डों; जैसे-वलय में, खोखले गोले में, खोखले सिलिण्डर में द्रव्यमान केन्द्र पिण्ड के बाहर होता है, जहाँ कोई पदार्थ नहीं होता है।

प्रश्न 2.
HCl अणु में दो परमाणुओं के नाभिकों के बीच पृथकन लगभग 1.27 A (1Å = 10^-10 m) है। इस अणु के द्रव्यमान केन्द्र की लगभग अवस्थिति ज्ञात कीजिए। यह ज्ञात है कि क्लोरीन का परमाणु हाइड्रोजन के परमाणु की तुलना में 35.5 गुना भारी होता है तथा किसी परमाणु का समस्त द्रव्यमान उसके नाभिक पर केन्द्रित होता है।

प्रश्न 3.
कोई बच्चा किसी चिकने क्षैतिज फर्श पर एकसमान चाल υ से गतिमान किसी लम्बी ट्रॉली के एक सिरे पर बैठा है। यदि बच्चा खड़ा होकर ट्रॉली पर किसी भी प्रकार से दौड़ने लगता है, तब निकाय (ट्रॉली + बच्चा) के द्रव्यमान केन्द्र की चाल क्या है?
उत्तर :
चूंकि ट्रॉली एक चिकने क्षैतिज फर्श पर गति कर रही है; अतः फर्श के चिकना होने के कारण निकाय पर क्षैतिज दिशा में कोई बाह्य बल कार्य नहीं करता है। जब बच्चा ट्रॉली पर दौड़ता है तो बच्चे द्वारा ट्रॉली पर

प्रश्न 4.
दर्शाइए कि [latex]\xrightarrow { a } [/latex] एवं [latex]\xrightarrow { b } [/latex] के बीच बने त्रिभुज का क्षेत्रफल [latex]\xrightarrow { a } [/latex] x [latex]\xrightarrow { b } [/latex] के परिमाण का आधा है।

प्रश्न 5.
दर्शाइए कि [latex]\xrightarrow { a } [/latex].([latex]\xrightarrow { b } [/latex] x [latex]\xrightarrow { c } [/latex]) का परिमाण तीन सदिशों [latex]\xrightarrow { a } [/latex], [latex]\xrightarrow { b } [/latex] तथा [latex]\xrightarrow { c } [/latex] से बने समान्तर षट्फलक के आयतन के बराबर है।

अत: ज्यामितीय दृष्टिकोण से [latex]\xrightarrow { a } [/latex] •([latex]\xrightarrow { b } [/latex] x [latex]\xrightarrow { c } [/latex]) उस समान्तर षट्फलक का आयतन है, जिसकी तीन संलग्न भुजाएँ सदिशों [latex]\xrightarrow { a } [/latex], [latex]\xrightarrow { b } [/latex] व [latex]\xrightarrow { c } [/latex] से निरूपित होती हैं।

प्रश्न 6.
एक कण, जिसके स्थिति सदिश [latex]\xrightarrow { r } [/latex] के x, y, z – अक्षों के अनुदिश अवयव क्रमशः x,y,s हैं और रेखीय संवेग सदिश [latex]\xrightarrow { p } [/latex] के अवयव px, py, ps हैं, कोणीय संवेग [latex]\xrightarrow { 1 } [/latex] के अक्षों के अनुदिश अवयव ज्ञात कीजिए। दर्शाइए कि यदि कण केवल x-y तल में ही गतिमान हो तो। कोणीय संवेग का केवल z – अवयव ही होता है।

प्रश्न 7.
दो कण जिनमें से प्रत्येक का द्रव्यमान m एवं चाल υ है, d दूरी पर समान्तर रेखाओं के अनुदिश, विपरीत दिशाओं में चल रहे हैं। दर्शाइए कि इस द्विकण निकाय का सदिश कोणीय संवेग समान रहता है, चाहे हम जिस बिन्दु के परितः कोणीय संवेग लें।
उत्तर :
माना दो कण समान्तर रेखाओं AB तथा CD के अनुदिश परस्पर विपरीत दिशाओं में चाल से गति कर रहे हैं।

माना किसी क्षण इनकी स्थितियाँ क्रमश: बिन्दु P तथा Q हैं। हम एक बिन्दु O (UPBoardSolutions.com) के परितः इस निकाय का कोणीय संवेग ज्ञात करना चाहते हैं।

इस प्रकारं द्विकर्ण निकाय का बिन्दु O के परितः कोणीय संवेग केवल m, υ तथा रेखाओं के बीच की दूरी d पर निर्भर करता है अर्थात् यह कोणीय संवेग बिन्दु O की स्थिति पर निर्भर नहीं करता है।

अतः इस द्विकण निकाय का सभी बिन्दुओं के परितः कोणीय संवेग नियत है।

प्रश्न 8.
w भार की एक असंमांग छड़ को, उपेक्षणीय 3 भार वाली दो डोरियों से चित्र 7.4 में दर्शाए अनुसार लटकांकर विरामावस्था में रखा गया है। डोरियों द्वारा ऊध्र्वाधर से बने कोण क्रमशः 36.9° एवं 53.1° हैं। छड़ 2 m लम्बाई की है। छड़ के बाएँ सिरे से इसके गुरुत्व केन्द्र की दूरी d ज्ञात कीजिए।

हल : माना छड़ AB का गुरुत्व केन्द्र G, उसके एक सिरे A से ‘d दूरी पर स्थित है। (UPBoardSolutions.com) छड़ तीन बलों के अधीन सन्तुलन में है।

डोरियों में तनाव T₁ तथा T₂ डोरियों के अनुदिश ऊपर 3 की ओर कार्य करते हैं।

छड़ का भार W उसके गुरुत्व केन्द्र G पर ऊर्ध्वाधरत: नीचे की ओर कार्य करता है।

सन्तुलन की स्थिति में तीनों बलों की क्रिया-रेखाएँ एक ही बिन्दु O पर काटती हैं।

प्रश्न 9.
एक कार का भार 1800 kg है। इसकी अगली और पिछली धुरियों के बीच की दूरी 1.8 m है। इसका गुरुत्व केन्द्र, अगली धुरी से 1.05 m पीछे है। समतल धरती द्वारा। इसके प्रत्येक अगले और पिछले पहियों पर लगने वाले बल की गणना कीजिए।
हल : माना भूमि द्वारा प्रत्येक अगले पहिए पर आरोपित प्रतिक्रिया बल R₁ व प्रत्येक पिछले पहिए पर आरोपित प्रतिक्रिया बले R₂ है तब निकाय के ऊर्ध्वाधर सन्तुलन के लिए,
2R₁ + 2R₂ = W ……(1)
जहाँ W कार का भार है जो उसके (UPBoardSolutions.com) गुरुत्व केन्द्र G पर कार्यरत है।
G के सापेक्ष आघूर्ण लेने पर
2R₁ × 1.05 = 2R₂ × (1.8 – 1.05)
या
R₁ × 1.05 = R₂ × 0.75

प्रश्न 10.
(a) किसी गोले को, इसके किसी व्यास के परितः जड़त्व – आघूर्ण 2MR²/5 है, जहाँ M गोले का द्रव्यमान एवं R इसकी त्रिज्या है। गोले पर खींची गई स्पर्श रेखा के परितः इसका जड़त्व-आघूर्ण ज्ञात कीजिए।
(b) M द्रव्यमान एवं R त्रिज्या वाली किसी डिस्क का इसके किसी व्यास के परित; “जड़त्व-आघूर्ण MR² /4 है। डिस्क के लम्बवत् इसकी कोर से गुजरने वाली अक्ष के परितः
इस डिस्क (चकती) का जड़त्व-आघूर्ण ज्ञात कीजिए।
उत्तर :
(a) दिया है : गोले का द्रव्यमान = M, त्रिज्या = R
रेखा AB गोले की एक स्पर्श रेखा है जिसके परितः गोले का जड़त्व-आघूर्ण ज्ञात करना है। स्पर्श रेखा AB के समान्तर, गोले का एक व्यास PQ खींचा।
प्रश्नानुसार, व्यास PQ (जो कि गोले के केन्द्र से जाता है) के परितः गोले का जड़त्व-आघूर्ण।

प्रश्न 11.
समान द्रव्यमान और त्रिज्या के एक खोखले बेलन और एक ठोस गोले पर समान परिमाण के बल-आघूर्ण लगाए गए हैं। बेलन अपनी सामान्य सममित अक्ष के परितः घूम सकता है और गोला अपने केन्द्र से गुजरने वाली किसी अक्ष के परितः। एक दिए गए समय के बाद दोनों में कौन अधिक कोणीय चाल प्राप्त कर लेगा?
उत्तर :
खोखले बेलन का अपनी सामान्य सममित अक्ष के परितः जड़त्व आघूर्ण
I_c = MR² …..(1)
ठोस गोले का अपने केन्द्र से गुजरने वाली अक्ष के परित: जड़त्व आघूर्ण
I_s = [latex]\frac { 2 }{ 5 } [/latex] MR² …..(2)

प्रश्न 12.
20 kg द्रव्यमान का कोई ठोस सिलिण्डर अपने अक्ष के परितः 100 rad s^-1 की कोणीय चाल से घूर्णन कर रहा है। सिलिण्डर की त्रिज्या 0.25 m है। सिलिण्डर के घूर्णन से सम्बद्ध गतिज ऊर्जा क्या है? सिलिण्डर का अपने अक्ष के परितः कोणीय संवेग का परिमाण क्या है?
हल : ठोस सिलिण्डर का द्रव्यमान M = 20 किग्रा, सिलिण्डर की त्रिज्या R = 0.25 मी
∴ ठोस सिलिण्डर का अपनी अक्ष के परितः जड़त्व आघूर्ण,

प्रश्न 13.
(a) कोई बच्चा किसी घूर्णिका (घूर्णीमंच) पर अपनी दोनों भुजाओं को बाहर की ओर फैलाकर खड़ा है। घूर्णिका को 40 rev/min की कोणीय चाल से घूर्णन कराया जाता है। यदि बच्चा अपने हाथों को वापस सिकोड़कर अपना जड़त्व-आघूर्ण अपने आरम्भिक जड़त्व-आघूर्ण [latex]\frac { 2 }{ 5 } [/latex] गुना कर लेता है तो इस स्थिति में उसकी कोणीय चाल क्या होगी? यह मानिए कि घूर्णिका की घूर्णन गति घर्षणरहित है।

(b) यह दर्शाइए कि बच्चे की घूर्णन की नयी गतिज ऊर्जा उसकी आरम्भिक घूर्णन की गतिज ऊर्जा से अधिक है। आप गतिज ऊर्जा में हुई इस वृद्धि की व्याख्या किस प्रकार करेंगे?

अब चूँकि अन्तिम जड़त्व आघूर्ण प्रारम्भिक जड़त्व आघूर्ण का 2/5 है, अत: अन्तिम घूर्णन गतिज ऊर्जा प्रारम्भिक मान की 5/2 गुनी हो जायेगी अर्थात् घूर्णन की नयी गतिज ऊर्जा प्रारम्भिक गतिज ऊर्जा से अधिक है।

इसका कारण यह है कि बच्चे द्वारा हाथों को वापस सिकोड़ने में व्यय रासायनिक ऊर्जा घूर्णन गतिज ऊर्जा में बदल जाती है।

प्रश्न 14.
3 kg द्रव्यमान तथा 40 cm त्रिज्या के किसी खोखले सिलिण्डर पर कोई नगण्य द्रव्यमान की रस्सी लपेटी गई है। यदि रस्सी को 30 N बल से खींचा जाए तो सिलिण्डर का कोणीय त्वरण क्या होगा। रस्सी का रैखिक त्वरण क्या है? यह मानिए कि इस प्रकरण में कोई फिसलन नहीं है?
हल : यदि बेलन का द्रव्यमान M तथा त्रिज्या R हो तो यहाँ M = 3.0 किग्रा तथा R = 40 सेमी = 0.40 मीटर
अत: खोखले बेलन का अपनी अक्ष के परितः जड़त्व आघूर्ण –

प्रश्न 15.
किसी घूर्णक (रोटर) की 200 rads^-1 की एकसमान कोणीय चालक्नाए रखने के लिए एक इंजन द्वारा 180 N- m का बल-आघूर्ण प्रेषित करना आवश्यक होता है। इंजन के लिए आवश्यक शक्ति ज्ञात कीजिए। (नोट : घर्षण की अनुपस्थिति में एकसमान कोणीय वेग होने में यह समाविष्ट है कि बल-आघूर्ण शून्य है। व्यवहार में लगाए गए बल-आघूर्ण की। आवश्यकता घर्षणी बल-आघूर्ण को निरस्त करने के लिए होती है।) यह मानिए कि इंजन की दक्षता 100% है।
हल : दिया है ω = 200 rad s^-1 (नियत है), बल-आघूर्ण τ = 180 Nm
इंजन के लिए आवश्यक शक्ति
P = इंजन द्वारा घूर्णक को दी गई शक्ति [∵ η = 100%]
= τ ω = 180 N m × 200rad s^-1
= 36 × 10 w = 36 kW

प्रश्न 16.
R त्रिज्या वाली समांग डिस्क से [latex]\frac { R }{ 2 }[/latex] त्रिज्या का एक वृत्ताकार भाग काट कर निकाल दिया गया है। इस प्रकार बने वृत्ताकार सुराख का केन्द्र मूल डिस्क के केन्द्र से [latex]\frac { R }{ 2 }[/latex] दूरी पर है। अवशिष्ट डिस्क के गुरुत्व केन्द्र की स्थिति ज्ञात कीजिए।
उत्तर :
माना दिए हुए वृत्ताकार पटल का केन्द्र O और व्यास AB है।
OA = OB = R = त्रिज्या
इस पटल से, व्यास OB को एक वृत्त काट कर निकाल दिया जाता है।
स्पष्टत: दिए हुए पटल का गुरुत्व केन्द्र O पर तथा काटे गए वृत्त का गुरुत्व केन्द्र उसके केन्द्र G₁ पर होगा, जबकि
OG₁ = [latex]\frac { 1 }{ 2 }[/latex]. OB = [latex]\frac { 1 }{ 2 }[/latex] R

∵ वृत्तों के क्षेत्रफल उनकी त्रिज्याओं के वर्गों के अनुपात में होते हैं।

प्रश्न 17.
एक मीटर छड़ के केन्द्र के नीचे क्षुर-धार रखने पर वह इस पर सन्तुलित हो जाती है जब दो सिक्के, जिनमें प्रत्येक का द्रव्यमान 5 g है, 12.0 cm के चिह्न पर एक के ऊपर एक रखे जाते हैं तो छड़ 45.0 cm चिह्न पर सन्तुलित हो जाती है। मीटर छड़ का द्रव्यमान क्या है?

हल : माना मीटर छड़ का द्रव्यमान m g है।
प्रश्नानुसार, प्रथम स्थिति में छड़ अपने मध्य बिन्दु पर सन्तुलित होती है। इसका अर्थ यह है कि छड़ का गुरुत्व केन्द्र उसके मध्य बिन्दु पर है। दूसरी दशा में, छड़ पर दो बल लगे हैं,
(1) सिक्कों का भार W₁ = 10g, बिन्दु C पर जहाँ AC = 12 cm
(2) छड़ का भार W₂ = mg, मध्य बिन्दु G पर
छड़ D बिन्दु पर सन्तुलित होती है, जहाँ AD = 45 cm
यहाँ D आलम्ब है।
अतः आघूर्गों के सिद्धान्त से,

प्रश्न 18.
एक ठोस गोला, भिन्न नति के दो आनत तलों पर एक ही ऊँचाई से लुढ़कने दिया जाता है।

(a) क्या वह दोनों बार समान चाल से तली में पहुँचेगा?
(b) क्या उसको एक तल पर लुढ़कने में दूसरे से अधिक समय लगेगा?
(c) यदि हाँ, तो किस पर और क्यों?

उत्तर :
(a) θ झुकाव कोण तथा h ऊँचाई के आनत तल पर लुढ़कने वाले सममित पिण्ड का पृथ्वी तल पर पहुँचने पर वेग υ हो तो –

यहाँ पर स्पष्ट है कि गोले को तली पर पहुँचने का वेग आनत तल के झुकाव कोण 8 पर निर्भर नहीं करता, अतः गोला दोनों आनत तलों की तली पर समान चाल से पहुँचेगा।

(b) यदि आनत तल की लम्बाई s हो तथा गोले द्वारा तली तक पहुँचने में लिया गया समय t हो तो –

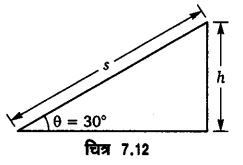
चूँकि लिया गया समय आनत तल के झुकाव कोण पर निर्भर करता है, अतः दोनों तलों पर लुढ़कने का समय भिन्न-भिन्न होगा।

(c) चूंकि t α 1/sin θ तथा 8 का मान बढ़ने से sin θ का मान बढ़ता है।
अतः θ के कम मान के लिए sin θ का मान कम होने के कारण t का मान अधिक होगा अर्थात् कम ढाल वाले तल पर लुढ़कने में लिया गया समय अधिक होगा।

प्रश्न 19.
2 m त्रिज्या के एक वलय (छल्ले) का भार 100 kg है। यह एक क्षैतिज फर्श पर इस प्रकार लोटनिक गति करता है कि इसके द्रव्यमान केन्द्र की चाल 20 cm/s हो। इसको रोकने के लिए कितना कार्य करना होगा ?
हल : छल्ले की त्रिज्या R =2 मी, इसका द्रव्यमान M = 100 किग्रा, द्रव्यमान केन्द्र की चाल υ = 2 सेमी/से = 0.20 मी/से।
चूँकि छल्ला लोटनिक गति करता आगे बढ़ रही है,
अतः इसकी कुल गतिज ऊर्जा K = स्थानान्तरीय गतिज ऊर्जा + घूर्णी गतिज ऊर्जा

प्रश्न 20.
ऑक्सीजन अणु का द्रव्यमान 5.30 × 10^-26 kg है तथा इसके केन्द्र से होकर गुजरने वाली और इसके दोनों परमाणुओं को मिलाने वाली रेखा के लम्बवत् अक्ष के परितः जड़त्व-आघूर्ण 1.94 × 10^-46 kg-m² है। मान लीजिए कि गैस के ऐसे अणु की औसत चाल 500 m/s है और इसके घूर्णन की गतिज ऊर्जा, स्थानान्तरण की गतिज ऊर्जा की दो-तिहाई है। अणु का औसत कोणीय वेग ज्ञात कीजिए।
हल : ऑक्सीजन अणु का द्रव्यमान M = 5.30 × 10^-26 किग्रा
इसका जड़त्व आघूर्ण I = 1.94 × 10^-46 किग्रा-मी²
अणु की औसत चाल υ = 500 मी/से

प्रश्न 21.
एक बेलन 30° कोण बनाते आनत तल पर लुढ़कता हुआ ऊपर चढ़ता है। आनत तल की तली में बेलन के द्रव्यमान केन्द्र की चाल 5 m/s है।
(a) आनत तल पर बेलन कितना ऊपर जाएगा?
(b) वापस तली तक लौट आने में इसे कितना समय लगेगा?

अतिरिक्त अभ्यास

प्रश्न 22.
जैसा चित्र-7.14 में दिखाया गया है, एक खड़ी होने वाली सीढी के दो पक्षों BA और CA की लम्बाई 1.6m है और इनको A पर कब्जा लगाकर जोड़ा गया है। इन्हें ठीक बीच में 0.5m लम्बी रस्सी DE द्वारा बाँधा गया है। सीढ़ी BA के अनुदिश B से 1.2 m की दूरी पर स्थित बिन्दु F से 40 kg का एक भार लटकाया गया है। यह मानते हुए कि फर्श घर्षणरहित है और सीढी का भार उपेक्षणीय है, रस्सी में तनाव और सीदी पर फर्श द्वारा लगाया गया बल ज्ञात कीजिए।(g =9.8 m/s² लीजिए)
[संकेत : सीढ़ी के दोनों ओर के सन्तुलन पर अलग-अलग विचार कीजिए]

हल : माना सीढ़ी के निचले सिरों पर फर्श की प्रतिक्रिया R1 तथा R2 है तथा डोरी का तनाव T है। माना सीढ़ी की दोनों भुजाएँ ऊध्र्वाधर से कोण से बनाती हैं [चित्र 7.15]।

प्रश्न 23.
कोई व्यक्ति एक घूमते हुए प्लेटफॉर्म पर खड़ा है। उसने अपनी दोनों बाहें फैला रखी हैं और उनमें से प्रत्येक में 5 kg भार पकड़ रखा है। प्लेटफॉर्म की कोणीय चाल 30 rev/min है। फिर वह व्यक्ति बाहों को अपने शरीर के पास ले आता है जिससे घूर्णन अक्ष से प्रत्येक भार की दूरी 90 cm से बदलकर 20 cm हो जाती है। प्लेटफॉर्म सहित व्यक्ति के जड़त्व आघूर्ण का मान 7.6 kg-m² ले सकते हैं।
(a) उसका नया कोणीय वेग क्या है? (घर्षण की उपेक्षा कीजिए)
(b) क्या इस प्रक्रिया में गतिज ऊर्जा संरक्षित होती है? यदि नहीं, तो इसमें परिवर्तन का स्रोत क्या है?

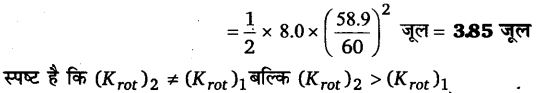
अत: इस प्रक्रिया में गतिज ऊर्जा संरक्षित नहीं रहती बल्कि बढ़ती है तथा इस परिवर्तन (वृद्धि) का स्रोत व्यक्ति की मांसपेशीय रासायनिक ऊर्जा का गतिज ऊर्जा में परिवर्तित होना है।

प्रश्न 24.
10 g द्रव्यमान और 500 m/s चाल वाली बन्दूक की गोली एक दरवाजे के ठीक केन्द्र में टकराकर उसमें अंतः स्थापित हो जाती है। दरवाजा 1.0m चौड़ा है और इसका द्रव्यमान 12 kg है। इसके एक सिरे पर कब्जे लगे हैं और यह इनसे गुजरती एक ऊर्ध्वाधर अक्ष के परितः लगभग बिना घर्षण के घूम सकता है; गोली के दरवाजे में अन्तःस्थापना के ठीक बाद इसका कोणीय वेग ज्ञात कीजिए।
[संकेत : एक सिरे से गुजरती ऊध्र्वाधर अक्ष के परितः दरवाजे का जड़त्व-आघूर्ण ML²/3 है]

प्रश्न 25.
दो चक्रिकाएँ जिनके अपने-अपने अक्षों (चक्रिका के अभिलम्बवत् तथा चक्रिका के केन्द्र से गुजरने वाले) के परितः जड़त्व-आघूर्ण I₁ तथा I₂ हैं और जो ω₁ तथा ω₂ कोणीय चालों से घूर्णन कर रही हैं, को उनके घूर्णन अक्ष सम्पाती करके आमने-सामने (सम्पर्क में) लाया जाता है।
(a) इस दो चक्रिका निकाय की कोणीय चाल क्या है?
(b) यह दर्शाइए कि इस संयोजित निकाय की गतिज ऊर्जा दोनों चक्रिकाओं की आरम्भिक गतिज ऊर्जाओं के योग से कम है। ऊर्जा में हुई इस हानि की आप कैसे व्याख्या करेंगे? ω₁ ≠ ω₂ लीजिए।
उत्तर :
(a) माना सम्पर्क में आने के पश्चात् दोनों चक्रिकाएँ उभयनिष्ठ कोणीय वेग ω से घूर्णन करती हैं।
∵ निकाय पर बाह्य बल आघूर्ण शून्य है, अतः निकाय का कोणीय संवेग संरक्षित रहेगा।

अर्थात् संयोजित निकाय की गतिज ऊर्जा चक्रिकाओं की आरम्भिक गतिज ऊर्जाओं के योग से कम है।

गतिज ऊर्जा में हानि, चक्रिकाओं की सम्पर्कित सतहों के बीच घर्षण बल के कारण हुई है।

प्रश्न 26.
(a) लम्बवत् अक्षों के प्रमेय की उपपत्ति करें। [संकेत:(x, y) तल के लम्बवत् मूलबिन्दु से गुजरती अक्ष से किसी बिन्दु x – y की दूरी का वर्ग (x² + y²) है।
(b) समान्तर अक्षों के प्रमेय की उपपत्ति करें। [संकेत : यदि द्रव्यमान केन्द्र को मूलबिन्दु ले लिया जाए ∑ [latex]\overrightarrow { m }[/latex] i [latex]\overrightarrow { r }[/latex] i = [latex]\overrightarrow { 0 }[/latex]

उत्तर :
(a) लम्बवत् अक्षों की प्रमेय (Theorem of Perpendicular Axes) – इस प्रमेय के अनुसार, “किसी समपटल का उसके तल के लम्बवत् तथा द्रव्यमान केन्द्र से जाने वाली अक्ष के परितः जड़त्व-आघूर्ण (I_s), समपटल के तल में स्थित तथा द्रव्यमान केन्द्र से जाने वाली दो परस्पर लम्बवत् अक्षों के परितः समपटल के जड़त्व-आघूर्णी (I_x तथा I_y) के योग के बराबर होता है।”

(b) समान्तर अक्षों की प्रमेय (Theorem of Parallel Axes) – इस प्रमेय के अनुसार, “किसी पिण्ड का किसी अक्ष के परितः जड़त्व-आघूर्ण I, उस पिण्ड के द्रव्यमान केन्द्र से होकर जाने वाली समान्तर अक्ष के परितः जड़त्व-आघूर्ण I_cm तथा पिण्ड के द्रव्यमान M व दोनों समान्तर अक्षों के बीच की लम्बे दूरी d के वर्ग के गुणनफल के योग के बराबर होता है।”
अर्थात् I = I_cm + Md²

उपपत्ति – माना पिण्ड के भीतर स्थित m द्रव्यमान के किसी कण की दी गई अक्ष AB से दूरी r है तथा द्रव्यमान केन्द्र C से गुजरने वाली AB के समान्तर अक्ष EF से कण की दूरी a है। माना दोनों अक्षों AB व EF के बीच की लम्बवत् दूरी 4 है। तब चित्र-7.17 से, r = a + d

 

प्रश्न 27.
सूत्र υ² = 2gh / (1 + k²/R²) को गतिकीय दृष्टि (अर्थात् बलों तथा बल-आघूर्गों विचार) से व्युत्पन्न कीजिए। जहाँ लोटनिक गति करते पिण्ड (वलय, डिस्क, बेलन या गोला) का आनत तल की तली में वेग है। आनत तल पर hवह ऊँचाई है जहाँ से पिण्ड गति प्रारम्भ करता है। K सममित अक्ष के परितः पिण्ड की घूर्णन त्रिज्या है और R पिण्ड की त्रिज्या है।
उत्तर :

माना M द्रव्यमान तथा R त्रिज्या का कोई गोलीय पिण्ड, जिसका द्रव्यमान केन्द्र C है, ऐसे आनत तल पर लुढ़कता है, जो क्षैतिज से θ कोण पर झुका है। इस स्थिति में पिण्ड पर निम्नलिखित बल कार्य करते हैं –

1. पिण्ड का भार Mg, ऊर्ध्वाधर नीचे की ओर
2. आनत तल की प्रतिक्रिया N, तल के लम्बवत् ऊपर की ओर
3. आनत तल द्वारा पिण्ड पर आरोपित स्पर्शरेखीय चित्र-7.18 स्थैतिक घर्षण-बल f_s आनत तल के समान्तर ऊपर की ओर।

घर्षण-बल f_s ही पिण्ड को फिसलने से रोकता है। माना पिण्ड के द्रव्यमान केन्द्र का आनत तल के अनुदिश नीचे की ओर रेखीय त्वरण a है। इन बलों को आनत तल के समान्तर तथा लम्बवत् घटकों में वियोजित करने पर,

प्रश्न 28.
अपने अक्ष पर ω₀ कोणीय चाल से घूर्णन करने वाली किसी चक्रिका को धीरे से (स्थानान्तरीय धक्का दिए बिना किसी पूर्णतः घर्षणरहित मेज पर रखा जाता है। चक्रिका की त्रिज्या R , है। चित्र-7.19 में दर्शाई चक्रिका के बिन्दुओं A, B तथा पर रैखिक वेग क्या हैं? क्या यहं चक्रिका चित्र में दर्शाई दिशा में लोटनिक गति करेगी?

उत्तर :
चूँकि चक्रिका तथा मेज के बीच कोई घर्षण बल नहीं है; अत: चक्रिका लोटनिक गति नहीं कर पाएगी तथा मेज के एक ही बिन्दु B के संम्पर्क में रहते हुए अपनी अक्ष के परितः शुद्ध घूर्णी गति करती रहेगी।
बिन्दु A की अक्ष से दूरी = R
∴बिन्दु A पर रैखिक वेग υ_A = R ω₀ तीर की दिशा में होगा।
इसी प्रकार बिन्दु B पर रैखिक वेग υ_B = R ω₀
बिन्दु B पर दिखाए गए तीर के विपरीत दिशा में होगा।
∵ बिन्दु C की अक्ष से दूरी = [latex]\frac { R }{ 2 } [/latex]
∴ बिन्दु C पर रैखिक वेग υ_c = [latex]\frac { R }{ 2 } [/latex] ω₀ क्षैतिजत: बाएँ से दाएँ को होगा।
यह पहले ही स्पष्ट है कि चक्रिका लोटनिक गति नहीं करेगी।

प्रश्न 29.
स्पष्ट कीजिए कि चित्र-7.19 में अंकित दिशा में चक्रिका की लोटनिक गति के लिए घर्षण होना आवश्यक क्यों है?
(a) B पर घर्षण बल की दिशा तथा परिशुद्ध लुढ़कन आरम्भ होने से पूर्व घर्षणी बल-आघूर्ण की दिशा क्या है?
(b) परिशुद्ध लोटनिक गति आरम्भ होने के पश्चात् घर्षण बल क्या है?
उत्तर :
चक्रिका मूलतः शुद्ध घूर्णी गति कर रही है जबकि लोटनिक गति प्रारम्भ होने का अर्थ घूर्णी गति के साथ-साथ स्थानान्तरीय गति का भी होना है, परन्तु स्थानान्तरीय गति प्रारम्भ होने के लिए बाह्य बल आवश्यक है। अत: चक्रिका की लोटनिक गति होने के लिए घर्षण बल (वर्णित परिस्थिति में एकमात्र बाह्य बले घर्षण बल ही हो सकता है) आवश्यक है।

(a) बिन्दु B पर घर्षण बल की दिशा तीर द्वारा प्रदर्शित दिशा में (बिन्दु B की अपनी गति की दिशा के विपरीत) है जबकि घर्षण बल के कारण उत्पन्न बल-आघूर्ण की दिशा कागज के तल के लम्बवत् बाहर की ओर है।

(b) घर्षण बल बिन्दु B को मेज के सम्पर्क बिन्दु के सापेक्ष विराम में लाना चाहता है, जब ऐसा हो जाता है तो परिशुद्ध लोटनिक गति प्रारम्भ हो जाती है।

अब चूँकि सम्पर्क बिन्दु पर कोई सरकन नहीं है; अतः घर्षण बल शून्य हो जाता है।

प्रश्न 30.
10 cm त्रिज्या की कोई ठोस चक्रिका तथा इतनी ही त्रिज्या का कोई छल्ला किसी क्षतिज मेज पर एक ही क्षण 10 π rad s^-1 की कोणीय चाल से रखे जाते हैं। इनमें से कौन पहले लोटनिक गति आरम्भ कर देगा। गतिज घर्षण गुणांक µ_k =0.2।
हल : माना मेज पर रखे जाने के t s पश्चात् कोई पिण्ड लोटनिक गति प्रारम्भ करता है। द्रव्यमान केन्द्र की स्थानान्तरीय गति प्रारम्भ कराने के लिए आवश्यक बल घर्षण बल से मिलता है। यदि इस दौरान द्रव्यमान केन्द्र का त्वरण a है तो
F = ma से, µ_k mg = ma


चक्रिका तथा छल्ले को लोटनिक गति’ प्रारम्भ करने में क्रमश: 0.17s तथा 0.25s लगेंगे। स्पष्ट है कि चक्रिको पहले लोटनिक गति प्रारम्भ करेगी।

प्रश्न 31.
10 kg द्रव्यमान तथा 15 cm त्रिज्या का कोई सिलिण्डर किसी 30° झुकाव के समतल पर परिशुद्धतः लोटनिक गति कर रहा है। स्थैतिक घर्षण गुणांक µ_s = 0.25 है।

(a) सिलिण्डर पर कितना घर्षण बल कार्यरत है?
(b) लोटन की अवधि में घर्षण के विरुद्ध कितना कार्य किया जाता है?
(c) यदि समतल के झुकाव θ में वृद्धि कर दी जाए तो के किस मान पर सिलिण्डर परिशुद्धतः लोटनिक गति करने की बजाय फिसलना आरम्भ कर देगा?

अतः जब नत समतल को झुकाव कोण 37° हो जायेगा तो सिलिण्डर फिसलने लगेगा।

प्रश्न 32.
नीचे दिए गए प्रत्येक प्रकथन को ध्यानपूर्वक पढिए तथा कारण सहित उत्तर दीजिए कि इनमें से कौन-सा सत्य है और कौन-सा असत्य?

(a) लोटनिक गति करते समय घर्षण बल उसी दिशा में कार्यरत होता है जिस दिशा में पिण्ड का द्रव्यमान केन्द्र गति करता है।
(b) लोटनिक गति करते समय सम्पर्क बिन्दु की तात्क्षणिक चाल शून्य होती है।
(c) लोटनिक गति करते समय सम्पर्क बिन्दु का तात्क्षणिक त्वरण शून्य होता है।
(d) परिशुद्ध लोटनिक गति के लिए घर्षण के विरुद्ध किया गया कार्य शून्य होता है।
(e) किसी पूर्णतः घर्षणरहित आनत समतल पर नीचे की ओर गति करते पहिये की गति फिसलन गति (लोटनिक गति नहीं) होगी।

उत्तर :

(a) सत्य, क्योंकि घर्षण बल ही पिण्ड में स्थानान्तरीय गति उत्पन्न करता है और इसी बल के कारण पिण्ड का द्रव्यमान केन्द्र आगे की ओर बढ़ता है।
(b) सत्य, जब सम्पर्क बिन्दु की सप गति समाप्त हो जाती है तभी लोटनिक गति प्रारम्भ होती है; अतः परिशुद्ध लोटनिक गति में सम्पर्क बिन्दु की तात्क्षणिक चाल शून्य होती है।
(e) असत्य, चूँकि वस्तु घूर्णन गति कर रही है; अतः सम्पर्क बिन्दु की गति में अभिकेन्द्र त्वरण अवश्य ही विद्यमान रहता है।
(d) सत्य, परिशुद्ध लोटनिक गति में सम्पर्क बिन्दु पर कोई सरकन नहीं होता; अतः घर्षण बल के विरुद्ध किया गया कार्य शून्य होता है।
(e) सत्य, घर्षण के अभाव में, आनत तल पर छोड़े गए पहिये का आनत तल के साथ सम्पर्क बिन्दु विराम में नहीं रहेगा अपितु पहिया भार के अधीन आनत तल के अनुदिश फिसलता जाएगा। अतः यह गति विशुद्ध सरकन गति होगी, लोटनिक नहीं।

प्रश्न 33.
कणों के किसी निकाय की गति को इसके द्रव्यमान केन्द्र की गति और द्रव्यमान केन्द्र के परितः गति में अलग-अलग करके विचार करना। दर्शाइए कि –
(a) [latex]\overrightarrow { P } [/latex] = [latex]\overrightarrow { P } [/latex] I = mi [latex]\overrightarrow { V } [/latex]
जहाँ है [latex]\overrightarrow { P } [/latex] i (mi द्रव्यमान वाले) i-वे कण का संवेग है और [latex]\overrightarrow { P } [/latex] i = mi [latex]\overrightarrow { v’ } [/latex] i ध्यान दें कि [latex]\overrightarrow { v’ } [/latex] i, द्रव्यमान केन्द्र के सापेक्ष i – वे कण का वेग है।
द्रव्यमान केन्द्र की परिभाषा का उपयोग करके यह भी सिद्ध कीजिए कि ∑ [latex]\overrightarrow { P’ } [/latex] i = 0

(b) K = K’ +[latex]\frac { 1 }{ 2 } [/latex] MV²
K कणों के निकाय की कुल गतिज ऊर्जा, K’ = निकाय की कुल गतिज ऊर्जा जबकि कणों की गतिज ऊर्जा द्रव्यमान केन्द्र के सापेक्ष ली जाए। MV²/2 सम्पूर्ण निकाय के (अर्थात् निकाय के द्रव्यमान केन्द्र के) स्थानान्तरण की गतिज ऊर्जा है।

(c) [latex]\overrightarrow { L } [/latex] = [latex]\overrightarrow { L’ } [/latex] + [latex]\overrightarrow { R } [/latex] X M [latex]\overrightarrow { V } [/latex]
जहाँ L’ = ∑ [latex]\overrightarrow { L } [/latex] i x [latex]\overrightarrow { P’ } [/latex] i , द्रव्यमान के परितः निकाय का कोणीय संवेग है जिसकी गणना में वेग द्रव्यमान केन्द्र के सापेक्ष मापे गए हैं। याद कीजिए [latex]\overrightarrow { r } [/latex] i = [latex]\overrightarrow { r } [/latex] i – [latex]\overrightarrow { R } [/latex] शेष सभी चिह्न अध्याय में प्रयुक्त विभिन्न राशियों के मानक चिह्न हैं। ध्यान दें कि [latex]\overrightarrow { L’ } [/latex] द्रव्यमान केन्द्र के परितः निकाय का कोणीय संवेग एवं M [latex]\overrightarrow { R } [/latex] x [latex]\overrightarrow { V } [/latex] इसके द्रव्यमान केन्द्र का कोणीय संवेग है।

(जहाँ [latex]\xrightarrow { \tau \prime } [/latex] ext द्रव्यमान केन्द्र के परितः निकाय पर लगने वाले सभी बाह्य बल आघूर्ण हैं।)
[संकेत – दव्यमान केन्द की परिभाषा एवं न्यूटन के गति के तृतीय नियम का उपयोग कीजिए। यह मान लीजिए कि किन्ही दो कणों के बीच के आन्तरिक बल उनको मिलाने वाली रेखा के अनुदिश कार्य करते हैं।]

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
वह बिन्दु जहाँ पर किसी निकाय या पिण्ड का सम्पूर्ण द्रव्यमान केन्द्रित माना जा सकता है, कहलाता है।
(i) ज्यामितीय केन्द्र
(ii) मध्य बिन्दु
(iii) द्रव्यमान केन्द्र
(iv) गुरुत्व केन्द्र
उत्तर :
(iii) द्रव्यमान केन्द्र

प्रश्न 2.
द्रव्यमान m तथा त्रिज्या वाली किसी वृत्ताकार डिस्क का इसके व्यास के परितः जड़त्व आघूर्ण होता है।
(i) mr²
(ii) mr² / 2
(iii) mr² / 4
(iv) 3/4 mr²
उत्तर :
(iii) mr² / 4

प्रश्न 3.
गोलीय कोश का जड़त्व आघूर्ण होगा
(i) MR²
(ii) MR² / 2
(iii) 2/5 MR²
(iv) 2/3 MR²
उत्तर :
(iv) 2/3 MR²

प्रश्न 4.
किसी अक्ष के परितः कोणीय वेग से घूमते हुए किसी पिण्ड के जड़त्व आघूर्ण I तथा कोणीय संवेग J में सम्बन्ध है।
(i) J= Iω²
(ii) J= Iω
(iii) I = Jω
(iv) I = Jω²
उत्तर :
(ii) J= Iω

प्रश्न 5.
किसी पिण्ड के जड़त्व आघूर्ण तथा कोणीय त्वरण के गुणनफल को कहते हैं।
(i) कोणीय संवेग
(ii) बल-आघूर्ण
(iii) बल
(iv) कार्य
उत्तर :
(ii) बल-आघूर्ण

प्रश्न 6.
यदि एक वस्तु के कोणीय संवेग में 50% की कमी हो जाए तो उसकी घूर्णन गतिज ऊर्जा में परिवर्तन होगा
(i) 125% की वृद्धि
(ii) 100% की कमी
(iii) 75% की वृद्धि
(iv) 75% की कमी
उत्तर :
(iv) 75% की कमी।

प्रश्न 7.
किसी अक्ष के परितः कोणीय वेग से घूमते किसी पिण्ड के जड़त्व आघूर्ण कोणीय त्वरण तथा बल आघूर्ण क्रमशःI, α तथा τ हैं, तब
(i) τ = Iα
(ii) τ = Iω
(iii) I = τω
(iv) α = τ I
उत्तर :
(i) τ = Iα

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
दृढ पिण्ड से क्या तात्पर्य है।
उत्तर :
यदि किसी पिण्ड पर बाह्य बल लगाने पर उसके कणों में एक-दूसरे के सापेक्ष कोई विस्थापन न हो तो ऐसे पिण्ड को दृढ़ पिण्ड कहते हैं।

प्रश्न 2.
किसी निकाय के द्रव्यमान केन्द्र से आप क्या समझते हैं?
उत्तर :
किसी निकाय का द्रव्यमान केन्द्र वह बिन्दु है जो पिण्ड के साथ इस प्रकार गति करता है, जैसे पिण्ड का समस्त द्रव्यमान उसी बिन्दु पर केन्द्रित हो तथा पिण्ड पर कार्यरत् सभी बल भी उसी पर कार्य कर रहे हों।

प्रश्न 3.
समान द्रव्यमान के वो कणों के द्रव्यमान केन्द्र की स्थिति क्या होती है?
उत्तर :
समान द्रव्यमान के दो कणों का द्रव्यमान केन्द्र (CM) उनको मिलाने वाली रेखा के मध्य बिन्दु पर होता है। होता है।

प्रश्न 4.
यदि दो कणों के निकाय में एक कण दूसरे की अपेक्षा भारी है तो इसका द्रव्यमान केन्द्र किस कण के निकट होगा?
उत्तर :
भारी कण के निकट।

प्रश्न 5.
समान द्रव्यमान के दो कणों के निकाय के द्रव्यमान केन्द्र को स्थिति सदिश क्या होगा?
उत्तर :
दोनों कणों के स्थिति सदिशों का औसत
अर्थात् [latex]\xrightarrow { r } [/latex] = ([latex]\xrightarrow { r1 } [/latex] + [latex]\xrightarrow { r2 } [/latex]) / 2

प्रश्न 6.
2.0 किग्रा तथा 1.0 किग्रा के दो पिण्ड क्रमशः (0, 0) मी तथा (3,0) मी पर स्थित हैं। इस निकाय के द्रव्यमान केन्द्र की स्थिति ज्ञात कीजिए।

प्रश्न 7.
यदि m द्रव्यमान वाले कण का स्थिति सदिश [latex]\xrightarrow { r1 } [/latex] तथा 2m द्रव्यमान वाले कण का स्थिति सदिश [latex]\xrightarrow { r2 } [/latex] हो, तो उस निकाय के द्रव्यमान केन्द्र का स्थिति सदिश क्या होगा?

प्रश्न 8.
रेखीय त्वरण तथा कोणीय त्वरण में सम्बन्ध का सूत्र लिखिए।
उत्तर :
a = rα

प्रश्न 9.
बल-आघूर्ण की परिभाषा दीजिए तथा इसका मात्रक लिखिए।
उत्तर :
जब किसी पिण्ड पर लगा हुआ कोई बाह्य बल, उस पिण्ड को किसी अक्ष के (UPBoardSolutions.com) परितः घुमाने की प्रवृत्ति रखता है, तो इस प्रवृत्ति को बल-आघूर्ण कहते हैं। इसका S.I. मात्रक न्यूटन-मीटर होता है।

प्रश्न 10.
किसी कण को बल में एक बिन्दु की ओर आरोपित किया जाता है। उस बिन्दु के परितः बल का आधूर्ण क्या होगा तथा क्यों?
उत्तर :
शून्य (क्योंकि बिन्दु से बेल की क्रिया की लम्बवत् दूरी शून्य होगी)।

प्रश्न 11.
किसी वस्तु का जड़त्व आघूर्ण किस बिन्द कण के लिए शून्य होता है?
उत्तर :
घूर्णन अक्ष पर स्थित बिन्दु कण के लिए।

प्रश्न 12.
किसी पिण्ड को जड़त्वं आघूर्ण किस अक्ष के परितः न्यूनतम होता है?
उत्तर :
उसके द्रव्यमान केन्द्र से गुजरने वाली अक्ष के परितः न्यूनतम होता है।

प्रश्न 13.
बल आघूर्ण, जड़त्व आघूर्ण तथा कोणीय त्वरण के बीच सम्बन्ध का सूत्र लिखिए।
या
घूर्णन गति हेतु बल आघूर्ण तथा जड़त्व आघूर्ण में सम्बन्ध लिखिए।
उत्तर :
τ = Ia

प्रश्न 14.
विभिन्न धातुओं से बने समान द्रव्यमान तथा समान त्रिज्या के दो गोलों में से एक ठोस तथा दूसरा खोखला है। यदि इन्हें एक साथ नत तल पर लुढ़काया जाता है तो कौन-सा गोला पहले नीचे पहुँचेगा? कारण सहित उत्तर दीजिए।
उत्तर :
ठोस गोला पहले नीचे पहुँचेगा, क्योकि खोखले गोले की अपेक्षा ठोस गोले का जड़त्व आघूर्ण कम होगा। अत: ठोस गोले की घूर्णन गति में खोखले गोले की अपेक्षा कम विरोध उत्पन्न होगा।

प्रश्न 15.
किसी छड़ का उसके एक सिरे से गुजरने वाली लम्बवत् अक्ष के परितः जड़त्व आघूर्ण ज्ञात करने के लिए जड़त्व आघूर्ण का कौन-सा प्रमेय प्रयोग में लाया जाता है, जबकि इसका जड़त्व आघूर्ण इसके द्रव्यमान केन्द्र से गुजरने वाली ऊर्ध्वाधर अक्ष के परितः दिया हो?
उत्तर :
समान्तर अक्षों की प्रमेय।

प्रश्न 16.
एक ठोस बेलन की त्रिज्या R, द्रव्यमान M तथा लम्बाई है। इसका अपनी अक्ष के परितः जड़त्व आघूर्ण का सूत्र क्या होगा? यदि बेलन खोखला हो तब सूत्र क्या होगा?
उत्तर :
I = [latex]\frac { 1 }{ 2 }[/latex] MR2 ; I = MR2

प्रश्न 17.
एक ठोस गोले का द्रव्यमान M तथा त्रिज्या R है। इसके व्यास के परितः जड़त्व आघूर्ण का सूत्र लिखिए। यदि इसी द्रव्यमान तथा त्रिज्या का खोखला गोला हो तब सूत्र क्या होगा?
उत्तर :
I = [latex]\frac { 2 }{ 5 }[/latex] MR2.

प्रश्न 18.
एक पतली छड़ का द्रव्यमान M तथा इसकी लम्बाई L है। इसके एक सिरे से गुजरने वाली लम्बवत् अक्ष के परितः छड़ को जड़त्व आघूर्ण क्या होगा?
उत्तर :
जड़त्व आघूर्ण I = ML² /12

प्रश्न 19.
धूर्णन गति में किए गए कार्य के लिए सूत्र लिखिए।
उत्तर :
घूर्णन गति में किया गया कार्य घूर्णन गतिज ऊर्जा के बराबर होता है।
अतः कार्य w = [latex]\frac { 1 }{ 2 } [/latex] Iω² जहाँ I = जड़त्व आघूर्ण तथा ω = कोणीय वेग

प्रश्न 20.
घूर्णन गति के तीनों समीकरणों को लिखिए तथा प्रयुक्त संकेतों के अर्थ बताइए।
उत्तर :
घूर्णन गति के समीकरण हैं –

प्रश्न 21.
किसी पिण्ड की घूर्णन गतिज ऊर्जा के लिए व्यंजक लिखिए। क्या यह घूर्णन अक्ष पर निर्भर करता है?
उत्तर :
Krot = [latex]\frac { 1 }{ 2 } [/latex] Iω2 हाँ।

प्रश्न 22.
22.2[latex]\sqrt { 2 } [/latex] मीटर त्रिज्या की एक चकती अपनी अक्ष के परितः घूर्णन कर रही है। उसकी घूर्णन (परिभ्रमण) त्रिज्या की गणना कीजिए।

लघु उत्तरीय प्रश्न

प्रश्न 1.
विलगित निकाय से क्या तात्पर्य है?
उत्तर :
विलगित निकाय (Isolated system) – विलगित निकाय वह होता है जिस पर कार्यरत् समस्त बाह्य बलों का सदिश योग शून्य हो।

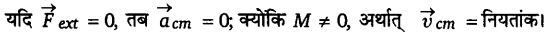
इस प्रकार, जब किसी निकाय पर लगने वाले सभी बाह्य बलों का सदिश योग शून्य होता है, तो द्रव्यमान केन्द्र का वेग नियत रहता है। रेडियोऐक्टिव क्षय में विभिन्न कण भिन्न-भिन्न वेगों से भिन्न-भिन्न दिशाओं में पलायन करते हैं, परन्तु उनके द्रव्यमान-केन्द्र का वेग नियत रहता है।

प्रश्न 2.
1 ग्राम, 2 ग्राम तथा 3 ग्राम के तीन बिन्दु द्रव्यमान XY- तल में क्रमशः (1,2), (0, -1) तथा (2,-3) बिन्दुओं पर स्थित हैं। निकाय के द्रव्यमान केन्द्र की स्थिति ज्ञात कीजिए।

प्रश्न 3.
कोणीय संवेग की परिभाषा दीजिए तथा दिखाइए कि किसी पिण्ड के कोणीय संवेग के परिवर्तन की दर उस पिण्ड पर लगाए गए बल-आघूर्ण के बराबर होती है।
उत्तर :
कोणीय संवेग की परिभाषा – घूर्णन गति में पिण्ड के विभिन्न अवयवी कणों के रेखीय (UPBoardSolutions.com) संवेगों के घूर्णन-अक्ष के परितः आघूर्गों का योग उस अक्ष के परितः पिण्ड का कोणीय संवेग कहलाता है। यह निम्नलिखित सूत्र से व्यक्त किया जाता है –

प्रश्न 4.
कोणीय संवेग संरक्षण का नियम लिखिए।
हल : इस नियम के अनुसार, यदि किसी घूर्णन के परित: घूमते हुए पिण्ड पर बाह्य बल आघूर्ण न लगाया जाए, तो उस पिण्ड का कोणीय संवेग नियत रहता है।
अर्थात् J = Iω = नियतांक

प्रश्न 5.
बल-युग्म से क्या तात्पर्य है? बल-युग्म के आघूर्ण का सूत्र लिखिए।
उत्तर :

बल-युग्म – जब किसी दृढ़ पिण्ड पर कोई ऐसे दो बल जो परिमाण में समान, दिशा में विपरीत व जिनकी क्रिया रेखाएँ भिन्न-भिन्न हों, साथ-साथ लगाये जाते हैं तो यह पिण्ड में बिना स्थानान्तरण के 40 घूर्णन उत्पन्न कर देते हैं (चित्र 7.22)। ऐसे बलों के युग्म को बल-युग्म कहते हैं।

बल-युग्म का आघूर्ण – बल-युग्म के बल के परिमाण वे उसकी भुजा की लम्बाई के गुणनफल को बल-युग्म को आघूर्ण कहते हैं। माना F परिमाण के दो बल एक दृढ़ छड़ AB जो बिन्दु O के परितः घूमने को स्वतन्त्र है, पर लगे हैं (चित्र 7.22)। तब छड़ AB पर कार्यरत् बल-युग्म का आघूर्ण,
τ = बिन्दु A पर कार्यरत् बल F का आधूर्ण + बिन्दु B पर कार्यरत् बल F का आघूर्ण
= F × AO + F × OB
= F × (AO + OB) = F × AB
परन्तु  AB = l,
∴ τ = F × l

प्रश्न 6.
एक पिण्ड जिसका जड़त्व आघूर्ण 3 किग्रा-मी2 है, विरामावस्था में है। इसे 6 न्यूटन-मीटर के बल आघूर्ण द्वारा 20 सेकण्ड तक घुमाया जाता है। पिण्ड का कोणीय विस्थापन ज्ञात कीजिए। पिण्ड पर किये गये कार्य की गणना भी कीजिए।

प्रश्न 7.
किसी छड़ की लम्बाई के लम्बवत् द्रव्यमान केन्द्र से गुजरने वाली अक्ष के परितः जड़त्व आघूर्ण 2.0 ग्राम-सेमी² है। इस छड़ की लम्बाई के लम्बवत छड़ के सिरे से गुजरने वाली अक्ष के परितः जड़त्व आघूर्ण कितना होगा?

प्रश्न 8.
वृत्ताकार छल्ले का व्यास के परितः जड़त्व आघूर्ण 4.0 ग्राम-सेमी है। छल्ले के केन्द्र से गुजरने वाली तथा तल के लम्बवत अक्ष के परितः जड़त्व आघूर्ण ज्ञात कीजिए।

प्रश्न 9.
m₁ तथा m₂ द्रव्यमान के दो कण l लम्बाई की भारहीन छड़ के सिरों पर रखे हैं। सिद्ध कीजिए कि छड़ के लम्बवत द्रव्यमान केन्द्र से गुजरने वाली अक्ष के परितः निकाय का जड़त्व आघूर्ण I = m¹ m²/(m¹ + m²) है।

प्रश्न 10.
कोणीय संवेग और घूर्णन गतिज ऊर्जा में सम्बन्ध स्थापित कीजिए।
उत्तर :
कोणीय संवेग और घूर्णन गतिज ऊर्जा में सम्बन्ध – यदि किसी घूर्णन अक्ष के परित: किसी पिण्ड का जड़त्व आघूर्ण I तथा कोणीय वेग ω हो तो उस पिण्ड को उसी घूर्णन अक्ष के परित: कोणीय संवेग


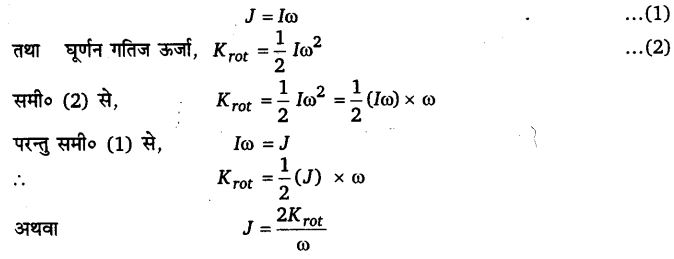
यही कोणीय संवेग और घूर्णन गतिज ऊर्जा में अभीष्ट सम्बन्ध है।

प्रश्न 11.
घूर्णन करते हुए दो पिण्डों A तथा B के कोणीय संवेग के मान बराबर हैं। A का जड़त्व आघूर्ण B के जड़त्व आघूर्ण का दोगुना है। Aतथा B की घूर्णन गतिज ऊर्जाओं का अनुपात निकालिए।

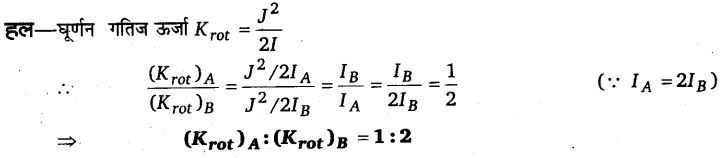
प्रश्न 12.
क्षैतिज समतल पर लुढ़कती हुई गेंद की घूर्णन गतिज ऊर्जा उसकी सम्पूर्ण गतिज ऊर्जा का कौन-सा भाग होगी?

प्रश्न 13.
10 किग्रा द्रव्यमान एवं 0.2 मीटर त्रिज्या की एक रिंग अपनी ज्यामितीय अक्ष के परितः 35 चक्कर/सेकण्ड की दर से घूम रही है। उसके जड़त्व आघूर्ण एवं घूर्णन गतिज ऊर्जा की गणना कीजिए।

प्रश्न 14.
5 किग्रा द्रव्यमान एवं 0.4 मी व्यास की एक रिंग अपनी ज्यामितीय अक्ष के परितः 840 चक्कर/मिनट की दर से घूम रही है। इसके कोणीय संवेग एवं घूर्णन गतिज ऊर्जा का परिकलन कीजिए।

प्रश्न 15.
15 किग्रा द्रव्यमान एवं 0.5 मीटर त्रिज्या की रिंग अपनी ज्यामितीय अक्ष के परितः 35 चक्कर/सेकण्ड की दर से घूम रही है। इसकी घूर्णन गतिज ऊर्जा की गणना कीजिए।

विस्तृत उत्तरीय प्रश्न

प्रश्न 1.
एकसमान छड़ के द्रव्यमान केन्द्र के लिए व्यंजक प्राप्त कीजिए।
उत्तर :
एकसमान छड़ का द्रव्यमान (अथवा संहति) केन्द्र – माना l लम्बाई की कोई समांग छड़ AB (चित्र 7.24) जिसका कुल द्रव्यमान m इसकी पूरी लम्बाई । पर एकसमान रूप से वितरित है। यह छड़ इस प्रकार से रखी है कि इसकी लम्बाई AB X-अक्ष के अनुदिश तथा उसका सिरा A समकोणिक निर्देशाक्षों XY के मूल-बिन्दु 0 पर स्थित है। अब चूंकि एक सर्वत्रसम छड़ ऐसे बिन्दु द्रव्यमानों (point masses) के समुच्चय का (UPBoardSolutions.com) निकाय होती है जो सतत् रूप से किसी रेखा के अनुदिश वितरित होते हैं। अतः ऐसे निकाय के द्रव्यमान-केन्द्र की स्थिति का निर्धारण समाकलन विधि द्वारा सर्वाधिक सुगमता से किया जा सकता है।

यहाँ यह मान लिया गया है कि छड़ की अनुप्रस्थ विमाएँ यथा चौड़ाई (आयताकारछड़ की दशा में) या व्यास (बेलनाकार छड़ की दशा में) अनुदैर्ध्य विमाओं (यथा लम्बाई या ऊँचाई) की तुलना में नगण्य है।

छड़ के एक छोटे से खण्ड CD जिसकी लम्बाई dx (जहाँ dx → 0) है तथा जो मूल-बिन्दु O से X दूरी पर स्थित है (चित्र 7.24) पर विचार कीजिए।

अर्थात् सर्वत्रसम छड़ का द्रव्यमाने-केन्द्र उसके मध्य-बिन्दु अर्थात् ज्यामितीय-केन्द्र पर स्थित होगा। सममिति का यही तर्क, समांग वलयों, चकतियो, गोलों और यहाँ तक कि वृत्ताकार या आयताकार अनुप्रस्थ काटे वाली मोटी छड़ों के लिए भी लागू होता है अर्थात् इनके ज्यामितीय-केन्द्र ही इनके द्रव्यमान-केन्द्र भी होते हैं।

प्रश्न 2.
किसी पिण्ड के कोणीय संवेग तथा जड़त्व आघूर्ण के बीच सम्बन्ध स्थापित कीजिए। इसके आधार पर जड़त्व आघूर्ण की परिभाषा दीजिए।
उतर :
कोणीय संवेग तथा जड़त्व आघूर्ण में सम्बन्ध – रेखीय गति में पिण्ड के द्रव्यमान m तथा उसके रेखीय वेग υ का गुणनफल पिण्ड का रेखीय संवेग कहलाता है। इसको p से प्रदर्शित करते हैं। अतः p = m × υ घूर्णन गति में पिण्ड के विभिन्न अवयवी कणों के रेखीय संवेगों के घूर्णन-अक्ष के परितः आघूर्णो का योग उस अक्ष के परितः पिण्ड का कोणीय संवेग कहलाता है। इसको Jसे प्रदर्शित करते हैं।

अत: “किसी पिण्ड के जड़त्व-आघूर्ण का मान घूर्णन-अक्ष के परितः पिण्ड के कोणीय संवेग के परिमाण के बराबर होता है, जबकि पिण्ड एक रेडियन/सेकण्ड के कोणीय वेग से घूर्णन गति कर रहा है।”

प्रश्न 3.
जड़त्व-आघूर्ण सम्बन्धी समकोणिक अक्षों के प्रमेय का उल्लेख कीजिए तथा उसको सिद्ध कीजिए।
उत्तर :
जड़त्व-आघूर्ण सम्बन्धी समकोणिक अक्षों की प्रमेय कथन-किसी समतल पंटल का उसके तल में ली गई दो परस्पर लम्बवत् अक्षों ox OY के परितः जड़त्व-आघूर्णो का योग, इन अक्षों के कटान-बिन्दु O में को जाने वाली तथा पटल के तल के लम्बवत् अक्ष Oz के परितः जड़त्व-अधूर्ण के बराबर होता है। अतः पटल का’ अक्ष Oz के परितः जड़त्व-आघूर्ण

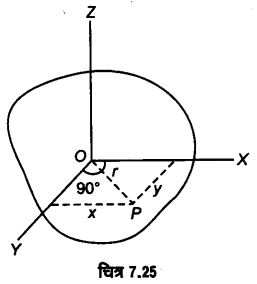
प्रश्न 4.
घूर्णन गति में बल-आधूर्ण एवं जड़त्व-आघूर्ण में सम्बन्ध स्थापित कीजिए तथा इस आधार पर जड़त्व-आघूर्ण की परिभाषा दीजिए।
उत्तर :
माना कोई पिण्ड किसी घूर्णन-अक्ष के परितः अचर कोणीय त्वरण α  (UPBoardSolutions.com)से घूर्णन गति कर रहा है। पिण्ड के सभी कणों का कोणीय त्वरण α ही होगा परन्तु रेखीय त्वरण अलग-अलग होंगे। माना कि पिण्ड के एक कण का द्रव्यमान m₁ है तथा इसकी घूर्णन-अक्ष से दूरी r₁ है। तब

अत: किसी वस्तु का किसी दी हुई अक्ष के सापेक्ष जड़त्व-आघूर्ण उस बल-आघूर्ण के बराबर होता है। जो वस्तु में एकांक कोणीय त्वरण उत्पन्न कर दे।

प्रश्न 5.
घूर्णन गतिज ऊर्जा के लिए व्यंजक का निगमन कीजिए।
उत्तर :
घूर्णन गतिज ऊर्जा – माना कोई पिण्ड किसी अक्ष के परित: एकसमान कोणीय वेग ω से घूर्णन गति कर रहा है। इस पिण्ड के सभी अवयवी कणों का कोणीय वेग ω ही होगा जबकि उनके रेखीय वेग भिन्न-भिन्न होंगे। माना घूर्णन अक्ष से r₁, r₂, r₃…. दूरियों (UPBoardSolutions.com) पर स्थित पिण्ड के अवयवी कणों के द्रव्यमान क्रमशः m₁, m₂, m₃…. तथा इनके रेखीय वेग क्रमश: v₁, v₂, v₃…. हैं।

We hope the UP Board Solutions for Class 11 Physics Chapter 7 System of particles and Rotational Motion (कणों के निकाय तथा घूर्णी गति) help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 7 System of particles and Rotational Motion (कणों के निकाय तथा घूर्णी गति) drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Physics Chapter 2 Units and Measurements (मात्रक एवं मापन)

These Solutions are part of UP Board Solutions for Class 11 Physics. Here we have given UP Board Solutions for Class 11 Physics Chapter 2 Units and Measurements (मात्रक एवं मापन).

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1:
रिक्त स्थान भरिए

(a) किसी 1 cm भुजा वाले घन का आयतन…..m³ के बराबर है।
(b) किसी 2 cm त्रिज्या व 10 cm ऊँचाई वाले सिलिण्डर का पृष्ठ क्षेत्रफल…..(mm)² बराबर है।
(c) कोई गाड़ी 18 kmem/h की चाल से चल रही है तो यह 1s में….m चलती है।
(d) सीसे का आपेक्षिक घनत्व 11.3 है। इसका घनत्व…….g cm^-3 या …. kg m^-3 है।
हल:
(a) ∵ घन का आयतन = ( भुजा)³ =(1 cm)³
= ([latex]\frac { 1 }{ 100 }[/latex] m)³  = (UPBoardSolutions.com) (10-2 m)³ [ 1cm=[latex]\frac { 1 }{ 100 }[/latex] = 10^-2 m)
=10^-6 m³

(b) सिलिण्डर का पृष्ठ क्षेत्रफल = वक्र पृष्ठ का क्षेत्रफल + दोनों वृत्तीय सिरों का क्षेत्रफल
=2πrh + 2πr²
= 2π (h +r)= 2x 3.14 x 2 cm (10 cm + 2 cm)
= 4 x 3:4 x 12cm² = 150.72 cm²
= 150.72 x (10mm)² (∵1 cm = 10 mm)
= 150.72 x 100(mm)² =1.5x 104 (mm)²

(c) गाड़ी की चाल = 18km/h
= 18x [latex]\frac { 5 }{ 18 }[/latex]m/s = 5 m s^-1
∴ 1s में तय दूरी = चाल x समय = 5ms^-1 x1 s=5 m

(d) सीसे का घनत्व = सीसे का आपेक्षिक-घनत्व x जल का घनत्व
= 11.3 x 1 g cm^-3 = 11.3 g cm^-3
[∵जल का घनत्व = 1 g cm^-3 या 10 kg m^-3]
या   सीसे का घनत्व = 11.3 x 10³ kg m^-3
= 1.13 x 104 kg m^-3

प्रश्न 2:
रिक्त स्थानों को मात्रकों के उचित परिवर्तन द्वारा भरिए
(a) 1 kg m² s^-2= ……g cm² s^-2
(b) 1 m = …. 1y
(c) 3.0 m s^-2 = …. km h^-2
(d) G= 6.67x 10^-11 Nm (kg)^-2 =……… (cm)3 s^-2 g^-1
हल:
(a) 1 kg m²s^-2 = 1 kg x 1m²s^-2
= (1000 g)x (100 cm)2x 1s^-2
= 1000 x 10000 g (cm)2 s^-2
= 10⁷g (cm)2 s^-2

प्रश्न 3:
ऊष्मा या ऊर्जा का मात्रक कैलोरी है और यह लगभग 4.2J के बराबर है, जहाँ 1J =1 kg m² s^-2 मान लीजिए कि हम मात्रकों की कोई ऐसी प्रणाली प्रयोग करते हैं जिसमें द्रव्यमान का मात्रक α kg के बराबर है, लम्बाई का मात्रक β m के बराबर है, समय का मात्रक γs के बराबर है तो यह प्रदर्शित कीजिए कि नए मात्रकों के पदों में कैलोरी का परिमाण 4.2 α^-1 β^-2 γ² है।
हल:
1 कैलोरी = 4.2.J = 4.2 kg-m²S^-2
ऊर्जा का विमीय सूत्र = [ML²F^-2]
माना दी गई दो मापन पद्धतियों में द्रव्यमान, लम्बाई (UPBoardSolutions.com) तथा समय के मात्रक क्रमशः M₁,L₁, T₁, तथा M₂,L₂, T₂, हैं।

प्रश्न 4:
इस कथन की स्पष्ट व्याख्या कीजिए : तुलना के मानक का विशेष उल्लेख किए बिना “किसी विमीय राशि को ‘बड़ा या छोटा कहना अर्थहीन है।” इसे ध्यान में रखते हुए नीचे दिए गए कथनों को जहाँ कहीं भी आवश्यक हो, दूसरे शब्दों में व्यक्त कीजिए
(a) परमाणु बहुत छोटे पिण्ड होते हैं।
(b) जेट वायुयान अत्यधिक गति से चलता है।
(c) बृहस्पति का द्रव्यमान बहुत ही अधिक है।
(d) इस कमरे के अन्दर वायु में अणुओं की संख्या बहुत अधिक है।
(e) इलेक्ट्रॉन, प्रोटॉन से बहुत भारी होता है।
(f) ध्वनि की गति प्रकाश की गति से बहुत ही कम होती है।
उत्तर:
सामान्यतया कहा जाता है कि परमाणु बहुत छोटा गोलीय पिण्ड है, परन्तु हम जानते हैं कि इलेक्ट्रॉन परमाणु से भी छोटा कण है, तब यह कहा जा सकता है कि इलेक्ट्रॉन की तुलना में परमाणु एक बड़ा पिण्ड है। इसके विपरीत क्रिकेट की गेंद की तुलना में परमाणु एक बहुत छोटा पिण्ड है। इस प्रकार हम देखते हैं कि परमाणु को किसी एक वस्तु की तुलना में बहुत छोटा कहा जा सकता है जबकि किसी अन्य वस्तु की तुलना में उसे बड़ा (UPBoardSolutions.com) कहा जा सकता है। यही बात किसी विमीय राशि के विषय में भी लागू होती है। कोई विमीय राशि, किसी दूसरी समान विमीय राशि की तुलना में बड़ी हो सकती है जबकि किसी अन्य, समान विमीय राशि से छोटी हो सकती है। अत: किसी विमीय राशि को छोटा या बंड़ा कहना तब तक अर्थहीन है जब तक कि तुलना के मानक को स्पष्ट उल्लेख ने किया गया हो।
(a) चीनी के एक दाने की तुलना में परमाणु बहुत छोटे पिण्ड होते हैं।
(b) जेट वायुयान, रेलगाड़ी की तुलना में अत्यधिक गति से चलता है।
(c) बृहस्पति का द्रव्यमान, पृथ्वी के द्रव्यमान की तुलना में बहुत ही अधिक है।
(d) इस कमरे के अन्दर वायु में अणुओं की संख्या, एक ग्राम-अणु गैस में उपस्थित अणुओं की संख्या ‘ से बहुत अधिक है। कथनों
(e) तथा
(f) को बदलने की आवश्यकता नहीं है।

प्रश्न 5:
लम्बाई का कोई ऐसा नया मात्रक चुना गया है जिसके अनुसार निर्वात में प्रकाश की चाल 1 है। लम्बाई के नए मात्रक के पदों में सूर्य तथा पृथ्वी के बीच की दूरी कितनी है, प्रकाश इस दूरी को तय करने में 8 min और 20 s लगाता है।
हल:
प्रकाश की चाल = 1 मात्रक S^-1
जबकि प्रकाश द्वारा लिया गया समय है t = 8 min 20 s
= (8x 60 + 20) s = 500s
∴ सूर्य तथा पृथ्वी के बीच की दूरी = प्रकाश की चाल x लगा समय
=1 मात्रक s^-1 x 500 s
= 500 मात्रक

प्रश्न 6:
लम्बाई मापने के लिए निम्नलिखित में से कौन-सा सबसे परिशुद्ध यन्त्र है
(a) एक वर्नियर कैलीपर्स जिसके वर्नियर पैमाने पर 20 विभाजन हैं।
(b) एक स्क्रूगेज जिसका चूड़ी अन्तराल 1 mm और वृत्तीय पैमाने पर 100 विभाजन हैं।
(c) कोई प्रकाशिक यन्त्र जो प्रकाश की तरंगदैर्घ्य की सीमा के अन्दर लम्बाई माप सकता है।
हल:

प्रश्न 7:
कोई छात्र 100 आवर्धन के एक सूक्ष्मदर्शी के द्वारा देखकर मनुष्य के बाल की मोटाई मापता है। वह 20 बार प्रेक्षण करता है और उसे ज्ञात होता है कि सूक्ष्मदर्शी के दृश्य क्षेत्र में बाल की औसत मोटाई 3.5 mm है। बाल की मोटाई का अनुमान क्या है?
हल:

प्रश्न 8.
निम्नलिखित के उत्तर दीजिए
(a) आपको एक धागा और मीटर पैमाना दिया जाता है। आप धागे के व्यास का अनुमान किस प्रकार लगाएँगे?
(b) एक स्क्रूगेज का चूड़ी अन्तराल 1.0 mm है और उसके वृत्तीय पैमाने पर 200 विभाजन हैं। क्या आप यह सोचते हैं कि वृत्तीय पैमाने पर विभाजनों की संख्या स्वेच्छा से बढ़ा देने पर स्क्रूगेज की यथार्थता में वृद्धि करना संभव है?
(c) वर्नियर कैलीपर्स द्वारा पीतल की किसी पतली छड़ का माध्य व्यास मापा जाना है। केवल 5 मापनों के समुच्चय की तुलना में व्यास के 100 मापनों के समुच्चय के द्वारा अधिक विश्वसनीय अनुमान प्राप्त होने की सम्भावना क्यों है?
उत्तर:
(a) इसके लिए हम एक बेलनाकार छड के ऊपर धागे को इस (UPBoardSolutions.com) प्रकार लपेटेंगे कि धागे के फेरे एक-दूसरे से सटे रहें। धागे के फेरों द्वारा घेरी गई छड़ की लम्बाई l को मीटर पैमाने की सहायता से नाप लेंगे। अब लपेटे गए फेरों की संख्या n को गिन लिया जाएगा।

प्रश्न 9:
किसी मकान का फोटोग्राफ 35 mm स्लाइड पर 1.75 cm ² क्षेत्र घेरता है। स्लाइड को | किसी स्क्रीन पर प्रक्षेपित किया जाता है और स्क्रीन पर मकान का क्षेत्रफल 1.55 m² है। प्रक्षेपित्र-परदा व्यवस्था का रेखीय आवर्धन क्या है?
हल:
स्लाइड पर मकान का क्षेत्रफल = 1.75 cm²
स्क्रीन पर मकान का क्षेत्रफल = 1.55 m2 = 1.55 (100 cm)
= 1.55x 10000 cm²

प्रश्न 10:
निम्नलिखित में सार्थक अंकों की संख्या लिखिए
(a) 0.007 m²
(b) 2.64 x 10²⁴ kg
(c) 0.2370 cm^-3
(d) 6.320 J
(e) 6.032 Nm^-2
(f) 0.000603² m²
उत्तर:
(a) 1, (b) 3, (e) 4, (d) 4, (e) 4, (f) 4.

प्रश्न 11:
धातु की किसी आयताकार शीट की लम्बाई, चौड़ाई व मोटाई क्रमशः 4,234 m, 1.005 m व 2.01 cm है। उचित सार्थक अंकों तक इस शीट का पृष्ठीय क्षेत्रफल व आयतन ज्ञात कीजिए।
हल:
यहाँ लम्बाई 4 = 4.234 m, चौड़ाई b =1.005 m
तथा मोटाई c = 2.01 cm = 0.0201 m
स्पष्ट है कि लम्बाई व चौड़ाई में 4-4 सार्थक अंक हैं जबकि मोटाई में 3 सार्थक अंक हैं।
∴ पृष्ठीय क्षेत्रफल तथा आयतन दोनों का (UPBoardSolutions.com) अधिकतम 3 सार्थक अंकों में पूर्णांकन करना होगा।
अब शीट का पृष्ठीय क्षेत्रफल
= 2x (ab + bc + ca)
= 2x [4.234 x 1.005 + 1.005 x 0.0201 + 0.0201 x 4234] m²
= 2x [4.25517 + 0.0202005 + 0.0851034] m²
= 2 x 4.3604739 m = 8.7209478 m = 8.72 m²
जबकि शीट का आयतन = ल० x चौ० x ऊँ०
= 4.234 m x 1.005 m x 0.0201 m
= 0.085528917 m³
= 0.0855 m³

प्रश्न 12:
पंसारी की तुला द्वारा मापे गए डिब्बे का द्रव्यमान 2.300 kg है। सोने के दो टुकड़े जिनका द्रव्यमान क्रमशः 20.15 g व 20.17 g है, डिब्बे में रखे जाते हैं
(a) डिब्बे का कुल द्रव्यमान कितना है,
(b) उचित सार्थक अंकों तक टुकड़ों के द्रव्यमानों में कितना अन्तर है?
हल:
(a) दिया है : डिब्बे का द्रव्यमान = 2300 kg
पहले टुकड़े का द्रव्यमान = 20.15 g = 0.02015 kg
दूसरे टुकड़े का द्रव्यमान = 2017 g= 0.02017 kg
∴ टुकड़े रखने के बाद डिब्बे का कुल द्रव्यमान
= 2.300 kg + 0.02015 kg + 0.02017kg
= 2.34032 kg
∵ तीनों मांपों में डिब्बे के द्रव्यमान में सबसे कम सार्थक अंक (4 अंक) हैं; अतः डिब्बे के कुल द्रव्यमान का अधिकतम चार सार्थक अंकों में पूर्णांकन करना होगा।
∴ डिब्बे का कुल द्रव्यमान = 2.340 kg

(b)∵ सोने के टुकड़ों के द्रव्यमानों में प्रत्येक में 4 सार्थक अंक हैं; अतः इनके अन्तर का अधिकतम
दशमलव के दूसरे स्थान तक पूर्णांकन करना होगा।
टुकड़ों के द्रव्यमानों का अन्तर = 20.17 g – 20.16 g= 0.02 g

प्रश्न 13:
कोई भौतिक राशि P, चार प्रेक्षण-योग्य राशियों a, b,c तथा d से इस प्रकार

a, b, c तथा d के मापने में प्रतिशत त्रुटियाँ क्रमशः 1%, 3%, 4% तथा 2% हैं। राशि P में प्रतिशत त्रुटि कितनी है? यदि उपर्युक्त सम्बन्ध का उपयोग करके P का परिकलित मान 3. 763 आता है तो आप परिणाम का किस मान तक निकटन करेंगे?
हल:

P के मान में त्रुटि 0.489 से स्पष्ट है कि P के मान में दशमलव (UPBoardSolutions.com) के पहले स्थान पर स्थित अंक ही संदिग्ध है; अत: P के मान को दशमलव के दूसरे स्थान तक लिखना व्यर्थ है। अतः P के मान का. दशमलव के पहले स्थान तक पूर्णांकन करना होगा।
अतः P का निकटतम मान = 3.763 = 3.8

प्रश्न 14:
किसी पुस्तक में, जिसमें छपाई की अनेक त्रुटियाँ हैं, आवर्त गति कर रहे किसी कण के विस्थापन के चार भिन्न सूत्र दिए गए हैं

(a = कण का अधिकतम विस्थापन, ν = कण की चाल, T = गति का आवर्तकाल)।
विमीय आधारों पर गलत सूत्रों को निकाल दीजिए।
उत्तर:
किसी त्रिकोणमितीय फलन का कोण एक विमाहीन राशि होती है।
सूत्र (b) तथा (c) में कोण vt तथा ! विमाहीन नहीं हैं; अत: उपर्युक्त दोनों सूत्र सही नहीं हैं। शेष दोनों सूत्र (a) तथा (d) सही हैं।

प्रश्न 15:
भौतिकी का एक प्रसिद्ध सम्बन्ध किसी कण के चल द्रव्यमान (moving mass) m, [latex]\frac { t }{ a }[/latex] विराम द्रव्यमान (rest mass) m₀, इसकी चाल ν और प्रकाश c की चाल  के बीच है। (यह सम्बन्ध सबसे पहले अल्बर्ट आइन्स्टाइन के विशेष आपेक्षिकता के सिद्धान्त के परिणामस्वरूप उत्पन्न हुआ था।) कोई छात्र इस सम्बन्ध को लगभग सही याद करता है। लेकिन स्थिरांक c को लगाना भूल जाता है। वह लिखता है

अनुमान लगाइए कि c कहाँ लगेगा?
उत्तर:
दिया गया सम्बन्ध है।

प्रश्न 16:
परमाण्विक पैमाने पर लम्बाई का सुविधाजनक मात्रक ऍग्स्ट्रॉम है और इसे [latex]\mathring { A }[/latex](1 [latex]\mathring { A }[/latex] = 10^-10m) द्वारा निर्दिष्ट किया जाता है। हाइड्रोजन के परमाणु का आमाप लगभग 0.5 A है। हाइड्रोजन परमाणुओं के एक मोल का m’ में कुल आण्विक आयतन कितना होगा?
हल:

प्रश्न 17:
किसी आदर्श गैस का एक मोल (ग्राम अणुक) मानक ताप व दाब पर 22.4L आयतन (ग्राम अणुक आयतन) घेरता है। हाइड्रोजन के ग्राम अणुक आयतन तथा उसके एक मोल के परमाण्विक आयतन का अनुपात क्या है? (हाइड्रोजन के (की आमाप लगभग 1[latex]\mathring { A }[/latex] मानिए)। यह अनुपात इतनी अधिक क्यों है?
हल:
एक मोल हाइड्रोजन गैस का (UPBoardSolutions.com) आयतन = 22.4
L =22.4 x 10^-3 m³
जबकि 1 मोल हाइड्रोजन गैस का परमाण्विक आयतन =3.15 x 10^-7 m³ (प्रश्न 16 के परिणाम से)

इसे अनुपात का मान इतना अधिक होने का अर्थ है कि गैस का आयतन उसमें उपस्थित अणुओं के वास्तविक आयतन की तुलना में बहुत अधिक होता है। इसका अन्य अर्थ यह है कि गैस के अणुओं के बीच बहुत अधिक खाली स्थान होता है।

प्रश्न 18:
इस सामान्य प्रेक्षण की स्पष्ट व्याख्या कीजिए : यदि आप तीव्र गति से गतिमान किसी रेलगाड़ी की खिड़की से बाहर देखें तो समीप के पेड़, मकान आदि रेलगाड़ी की गति की विपरीत दिशा में तेजी से गति करते प्रतीत होते हैं, परन्तु दूरस्थ पिण्ड (पहाड़ियाँ, चन्द्रमा, तारे आदि) स्थिर प्रतीत होते हैं। (वास्तव में क्योंकि आपको ज्ञात है कि आप चल रहे हैं, इसलिए ये दूरस्थ वस्तुएँ आपको अपने साथ चलती हुई प्रतीत होती हैं।)
उत्तर:
किसी वस्तु का हमारे सापेक्ष गति करते हुए प्रतीत होना, हमारे सापेक्ष वस्तु के कोणीय वेग पर निर्भर करता है न कि उसके रेखीय वेग पर। यद्यपि गाड़ी से यात्रा करते समय सभी वस्तुएँ समान वेग से हमारे पीछे की ओर गति करती हैं, परन्तु समीप स्थित वस्तुओं का हमारे सापेक्ष कोणीय वेग अधिक होता है; अतः वे तेजी से पीछे जाती प्रतीत होती हैं जबकि दूर स्थित वस्तुओं का हमारे सापेक्ष कोणीय वेग बहुत ही कम होता है; अतः वे हमें लगभग स्थिर प्रतीत होती हैं।

प्रश्न 19:
समीपी तारों की दूरियाँ ज्ञात करने के लिए लम्बन के सिद्धान्त का प्रयोग किया जाता है। सूर्य के परितः अपनी कक्षा में छः महीनों के अन्तराल पर पृथ्वी की अपनी, दो स्थानों को मिलाने वाली, आधार रेखा AB है। अर्थात आधार रेखा पृथ्वी की कक्षा के व्यास≈ 3x 10¹¹ m के लगभग बराबर है। लेकिन चूंकि निकटतम तारे भी इतने अधिक दूर हैं। कि इतनी लम्बी आधार रेखा होने पर भी वे चाप के केवल 1″ (सेकण्ड, चाप का) की कोटि का लम्बन प्रदर्शित करते हैं। खगोलीय पैमाने पर लम्बाई का सुविधाजनक मात्रक पारसेक है। यह किसी पिण्ड की वह दूरी है जो पृथ्वी से सूर्य तक की दूरी के बराबर आधार रेखा के दो विपरीत किनारों से चाप के 1′ का लम्बन प्रदर्शित करती है। मीटरों में एक पारसेक
कितना होता है?
हल:

प्रश्न 20:
हमारे सौर परिवार से निकटतम तारा 4.29 प्रकाश वर्ष दूर है। पारसेक में यह दूरी कितनी है? यह तारा (ऐल्फा सेटौरी नामक) तब कितना लम्बन प्रदर्शित करेगा जब इसे सूर्य के परितः अपनी कक्षा में पृथ्वी के दो स्थानों से जो छः महीने के अन्तराल पर हैं, देखा, जाएगा?
हल:

प्रश्न 21:
भौतिक राशियों का परिशुद्ध मापन विज्ञान की आवश्यकताएँ हैं। उदाहरण के लिए, किसी शत्रु के लड़ाकू जहाज की चाल सुनिश्चित करने के लिए बहुत ही छोटे समयान्तरालों पर इसकी स्थिति का पता लगाने की कोई यथार्थ विधि होनी चाहिए। द्वितीय विश्वयुद्ध में रेडार की खोज के पीछे वास्तविक प्रयोजन यही था। आधुनिक विज्ञानं के उन भिन्न उदाहरणों को सोचिए जिनमें लम्बाई, समय, द्रव्यमान आदि के परिशुद्ध मापन की आवश्यकता होती है। अन्य जिस किसी विषय में भी आप बता सकते हैं, परिशुद्धता की मात्रात्मक धारणा दीजिए।
उत्तर:
लम्बाई का मापन: विभिन्न यौगिकों के क्रिस्टलों में परमाणुओं के बीच की दूरी का मापन करते समय लम्बाई के परिशुद्ध मापन की आवश्यकता होती है।।

समय का मापन: फोको की विधि द्वारा किसी (UPBoardSolutions.com) माध्यम में प्रकाश की चाल ज्ञात करने के प्रयोग में समय के परिशुद्ध मापन की आवश्यकता होती है।

द्रव्यमान का मापन: द्रव्यमान स्पेक्ट्रमलेखी में परमाणुओं के द्रव्यमान का परिशुद्ध मापन किया जाता है।

प्रश्न 22:
जिस प्रकार विज्ञान में परिशुद्ध मापन आवश्यक है, उसी प्रकार अल्पविकसित विचारों तथा सामान्य प्रेक्षणों को उपयोग करने वाली राशियों के स्थूल आकलन कर सकना भी उतना ही महत्त्वपूर्ण है। उन उपायों को सोचिए जिनके द्वारा आप निम्नलिखित का अनुमान लगा सकते हैं-(जहाँ अनुमान लगाना कठिन है वहाँ राशि की उपरिसीमा पता लगाने का प्रयास कीजिए)
(a) मानसून की अवधि में भारत के ऊपर वर्षाधारी मेघों का कुल द्रव्यमान।
(b) किसी हाथी का द्रव्यमान।।
(c) किसी तूफान की अवधि में वायु की चाल।
(d) आपके सिर के बालों की संख्या।
(e) आपकी कक्षा के कमरे में वायु के अणुओं की संख्या।
उत्तर:
(a) सर्वप्रथम मौसम विभाग से पूरे भारत में हुई कुल वर्षा की माप की जानकारी लेंगे और वर्षा जल के आयतन को जल के घनत्व से गुणा करके वर्षा जल के द्रव्यमान की गणना कर लेंगे। इससे मेघों का द्रव्यमान ज्ञात हो जाएगा।
(b) ट्रक आदि का द्रव्यमान मापने वाले काँटे पर खड़ा करके हाथी को द्रव्यमान ज्ञात किया जा सकता है।
(c) किसी तूफान की अवधि में वायु द्वारा उत्पन्न दाब को मापकर, वायु की चाल का आकलन किया जा सकता है।
(d) सिर के 1cm² क्षेत्रफल में स्थित बालों को गिन लिया जाएगा। तत्पश्चात् सिर के क्षेत्रफल का आकलन करके इस क्षेत्रफल से 1cm² क्षेत्रफल में स्थित बालों की संख्या को गुणा करके सिर के बालों की संख्या का आकलन किया जा सकता है।
(e) कक्षा के कमरे में उपस्थित वायु का घनत्व नापकर 1cm³ आयतन में उपस्थित अणुओं की संख्या की गणना की जा सकती है। तत्पश्चात् कमरे के आयतन से गुणा करके कक्षा के कमरे में उपस्थित वायु के अणुओं की गणना की जा सकती है।

प्रश्न 23:
सूर्य एक ऊष्म प्लैज्मा (आयनीकृत पदार्थ) है जिसके आन्तरिक क्रोड का ताप 10⁷K से अधिक और बाह्य पृष्ठ का ताप लगभग 6000 K है। इतने अधिक ताप पर कोई भी पदार्थ ठोस या तरल प्रावस्था में नहीं रह सकता। आपको सूर्य का द्रव्यमान घनत्व किस परिसर में होने की आशा है? क्या यह ठोसों, तरलों या गैसों के घनत्वों के परिसर में है? क्या आपका अनुमान सही है, इसकी जाँच आप निम्नलिखित आँकड़ों के आधार पर कर सकते हैं- सूर्य का द्रव्यमान = 2.0×10³⁰ kg सूर्य की त्रिज्या = 7.0 x 10⁸ m.
हल:

प्रश्न 24:
जब बृहस्पति ग्रह पृथ्वी से 8247 लाख किलोमीटर दूर होता है तो इसके व्यास की कोणीय माप 35.72′ का चाप है। बृहस्पति का व्यास परिकलित कीजिए।
हल:
दिया है, बृहस्पति ग्रह की पृथ्वी से दूरी
s= 8247 लाख किलोमीटर = 8247 x 10⁵ किमी

अतिरिक्त अभ्यास

प्रश्न 25:
वर्षा के समय में कोई व्यक्ति चाल) के साथ तेजी से चला जा रहा है। उसे अपने छाते को टेढ़ा करके ऊर्ध्व के साथ 8 कोण बनाना पड़ता है। कोई विद्यार्थी कोण 8 व 9 के बीच निम्नलिखित सम्बन्ध व्युत्पन्न करता है-tan θ = ν
और वह इस सम्बन्ध के औचित्य की सीमा पता लगाता है: जैसी कि आशा की जाती है। यदि v→0 तो θ →0(हम यह मान रहे हैं कि तेज हवा नहीं चल रही है और किसी खड़े व्यक्ति के लिए वर्षा ऊध्वधरतः पड़ रही है)। क्या आप सोचते हैं कि यह सम्बन्ध सही हो सकता है? यदि ऐसा नहीं है तो सही सम्बन्ध का अनुमान लगाइए।
उत्तर:
दिए गए सम्बन्ध में,

∵ दोनों पक्षों की विमाएँ परस्पर समान नहीं हैं; अत: यह सम्बन्ध सही नहीं हो सकता। स्पष्ट है कि सही सम्बन्ध में दाएँ पक्ष की विमाएँ भी [L⁰] होनी चाहिए। माना वर्षा की बूंदें u वेग से ऊर्ध्वाधरत: नीचे गिर रही हैं, तब दाएँ पक्ष को विमाहीन करने के लिए ν को (UPBoardSolutions.com) u से भाग देना चाहिए।

प्रश्न 26:
यह दावा किया जाता है कि यदि बिना किसी बाधा के 100 वर्षों तक दो सीजियम घड़ियों को चलने दिया जाए तो उनके समयों में केवल 0.02 s का अन्तर हो सकता है। मानक सीजियम घड़ी द्वारा 1s के समय अन्तराल को मापने में यथार्थता के लिए इसका क्या अभिप्राय है?
हल:
कुल समय = 100 वर्ष, T = 100 x 365 x 24 x 60 x 60 s
100 वर्ष के अन्तराल में त्रुटि ∆T = 0.02s

प्रश्न 27:
एक सोडियम परमाणु का आमाप लगभग 2.5 [latex]\mathring { A }[/latex] मानते हुए उसके माध्य द्रव्यमान घनत्व का अनुमान लगाइए। (सोडियम के परमाणवीय द्रव्यमान तथा आवोगाद्रो संख्या के ज्ञात मान का प्रयोग कीजिए)। इस घनत्व की क्रिस्टलीय प्रावस्था में सोडियम के घनत्व 970 kg m^-3 के साथ तुलना कीजिए। क्या इन दोनों घनत्वों के परिमाण की कोटि समान है? यदि हाँ, तो क्यों?
हल:
सोडियम परमाणु का आमाप (त्रिज्या) = 2.5 [latex]\mathring { A }[/latex]= 2.5 x 10^-10 m
सोडियम का ग्राम परमाणु भार = 23 g= 23 x 10^-3 kg
एक ग्राम परमाणु में परमाणुओं की संख्या 6.023 x 10²³ होती है।

स्पष्ट है कि परमाणु का द्रव्यमान घनत्व तथा ठोस प्रावस्था में सोडियम का (UPBoardSolutions.com) घनत्व दोनों 103 की कोटि के हैं। इसका अर्थ यह है कि ठोस प्रावस्था में परमाणुओं के बीच खाली स्थान नगण्य होता है, अर्थात् ठोस प्रावस्था में परमाणु दृढ़तापूर्वक संकुलित होते हैं।

प्रश्न 28:
नाभिकीय पैमाने पर लम्बाई का सुविधाजनक मात्रक फर्मी है-(1f=10^-15 m)। नाभिकीय आमाप लगभग निम्नलिखित आनुभविक सम्बन्ध का पालन करते हैं r =r₀ A^1/3 जहाँ नाभिक की त्रिज्या,A इसकी द्रव्यमान संख्या और r₀, कोई स्थिरांक है जो लगभग 1.2 f के बराबर है। यह प्रदर्शित कीजिए कि इस नियम का अर्थ है कि विभिन्न नाभिकों के लिए नाभिकीय द्रव्यमान घनत्व लगभग स्थिर है। सोडियम नाभिक के द्रव्यमान घनत्व का आकलन कीजिए। प्रश्न 27 में ज्ञात किए गए सोडियम परमाणु के माध्य द्रव्यमान घनत्व के साथ इसकी तुलना कीजिए।
हल:
माना किसी नाभिक की द्रव्यमान संख्या A है तथा प्रत्येक न्यूक्लिऑन (न्यूट्रॉन तथा प्रोटॉन) का द्रव्यमान m₀ (नियतांक) है।

अर्थात् सोडियम नाभिक का घनत्व उसके परमाणु के घनत्व से लगभग 1015 गुना अधिक है। इसका अर्थ यह है कि परमाणु का अधिकांश भाग खोखला है तथा उसका अधिकांश द्रव्यमान उसके नाभिक में निहित है।

प्रश्न 29:
लेसर (LASER), प्रकाश के अत्यधिक तीव्र, एकवर्णी तथा एकदिश किरण-पुंज का स्रोत है। लेसर के इन गुणों का लम्बी दूरियाँ मापने में उपयोग किया जाता है। लेसर को प्रकाश के स्रोत के रूप में उपयोग करते हुए पहले ही चन्द्रमा की पृथ्वी से दूरी परिशुद्धता के साथ ज्ञात की जा चुकी है। कोई लेसर प्रकाश किरण-पुंज चन्द्रमा के पृष्ठ से परावर्तित होकर 2.56 s में वापस आ जाता है। पृथ्वी के परितः चन्द्रमा की कक्षा की त्रिज्या कितनी है?
हल:

प्रश्न 30:
जल के नीचे वस्तुओं को ढूंढने व उनके स्थान का पता लगाने के लिए सोनार (SONAR) में पराश्रव्य तरंगों का प्रयोग होता है। कोई पनडुब्बी सोनार से सुसज्जित है। इसके द्वारा जनित अन्वेषी तरंग और शत्रु की पनडुब्बी से परावर्तित इसकी प्रतिध्वनि की प्राप्ति के बीच काल विलम्ब 77.0 s है। शत्रु की पनडुब्बी कितनी दूर है? (जल में ध्वनि की चाल = 1450 m s^-1)
हल:

प्रश्न 31:
हमारे विश्व में आधुनिक खगोलविदों द्वारा खोजे गए सर्वाधिक दूरस्थ पिण्ड इतनी दूर हैं। कि उनके द्वारा उत्सर्जित प्रकाश को पृथ्वी तक पहुँचने में अरबों वर्ष लगते हैं। इन पिण्डों (जिन्हें क्वासर Quasar’ कहा जाता है) के कई रहस्यमय लक्षण हैं जिनकी अभी तक सन्तोषजनक व्याख्या नहीं की जा सकी है। किसी ऐसे क्वासर की km में दूरी ज्ञात कीजिए जिससे उत्सर्जित प्रकाश को हम तक पहुँचने में 300 करोड़ वर्ष लगते हों।
हल:

प्रश्न 32:
यह एक विख्यात तथ्य है कि पूर्ण सूर्यग्रहण की अवधि में चन्द्रमा की चक्रिका सूर्य की चक्रिका को पूरी तरह ढक लेती है। चन्द्रमा का लगभग व्यास ज्ञात कीजिए।
(पृथ्वी से चन्द्रमा की दूरी = 3.84 x 10⁸ m सूर्य का कोणीय व्यास = 1920′ )
हल:
माना कि चन्द्रमा का कोणीय व्यास = d
जबकि चन्द्रमा की पृथ्वी से दूरी = 3.84 x 10⁸ m

प्रश्न 33:
इस शताब्दी के एक महान भौतिकविद् (पी०ए०एम० डिरैक) प्रकृति के मूल स्थिरांकों (नियतांकों) के आंकिक मानों के साथ क्रीड़ा में आनन्द लेते थे। इससे उन्होंने एक बहुत ही रोचक प्रेक्षण किया। परमाणवीय भौतिकी के मूल नियतांकों (जैसे इलेक्ट्रॉन का द्रव्यमान, प्रोटॉन का द्रव्यमान तथा गुरुत्वीय नियतांक G) से उन्हें पता लगा कि वे एक ऐसी संख्या पर पहुँच गए हैं जिसकी विमा समय की विमा है। साथ ही, यह एक बहुत ही बड़ी संख्या थी और इसका परिमाण विश्व की वर्तमान आकलित आयु (~1500 करोड़ वर्ष) के करीब है। इस पुस्तक में दी गई मूल नियतांकों की सारणी के आधार पर यह देखने का प्रयास कीजिए कि क्या आप भी यह संख्या (या और कोई अन्य रोचक संख्या जिसे आप सोच सकते हैं) बना, सकते हैं? यदि विश्व की आयु तथा इस संख्या में समानता महत्त्वपूर्ण है तो मूल नियतांकों की स्थिरता किस प्रकार प्रभावित होगी?
हल:

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1:
निम्नलिखित में से कौन-सा S.I. मात्रक नहीं है?
(i) ऐम्पियर
(ii) केण्डिला
(iii) न्यूटन
(iv) केल्विन
उत्तर:
(iii) न्यूटन

प्रश्न 2:
निम्नलिखित में से कौन दूरी का मात्रक नहीं है?
(i) ऐंग्स्ट्रॉम
(ii) फर्मी
(iii) बार्न
(iv) पारसेक
उत्तर:
(iii) बार्न

प्रश्न 3.
पारसेक मात्रक है।
(i) समय का
(ii) दूरी को
(iii) आवृत्ति का
(iv) कोणीय संवेग का
उत्तर:
(ii) दूरी का

प्रश्न 4.
प्रकाश वर्ष मात्रक है।
(i) समय का
(ii) दूरी का
(iii) वेग का
(iv) प्रकाश की तीव्रता का
उत्तर:
(ii) दूरी का

प्रश्न 5:
नाभिकीय त्रिज्या 10^-15 मीटर कोटि की है। इसे व्यक्त करने के लिए उपयुक्त मात्रक है
(i) माइक्रोन
(ii) मिमी
(iii) ऐंग्स्ट्राम
(iv) फर्मी
उत्तर:
(iv) फर्मी

प्रश्न 6:
निम्नलिखित में से व्युत्पन्न मात्रक है।
(i) केण्डिला
(ii) किग्रा
(iii) न्यूटन
(iv) मीटर
उत्तर:
(iii) न्यूटन

प्रश्न 7:
1 मीटर तुल्य है।
(i) 10¹⁰ [latex]\mathring { A }[/latex]
(ii) 10⁸ [latex]\mathring { A }[/latex]
(iii) 10⁶ [latex]\mathring { A }[/latex]
(iv) 10⁵ [latex]\mathring { A }[/latex]
उत्तर:
(i) 10¹⁰ [latex]\mathring { A }[/latex]

प्रश्न 8.
एक माइक्रोन (μ) होता है।
(i) 10^-9 मी
(ii) 10^-12 मी
(iii) 10^-6 मी
(iv) 10^-15 मी
उत्तर:
(iv) 10^-15 मी

प्रश्न 9:
एक नैनोमीटर तुल्य है ।
(i) 10^-9 मिमी
(ii) 10^-6 सेमी
(iii) 10^-7 सेमी
(iv) 10^-9 सेमी
उत्तर:
(iii) 10^-7 सेमी

प्रश्न 10:
1 सेकण्ड तुल्य है।
(i) क्रिप्टॉन घड़ी के 1650763.73 आवर्गों के
(ii) क्रिप्टॉन घड़ी के 652189.63 आवर्ती के
(iii) सीजियम घड़ी के 1650763.73 आवर्ती के
(iv) सीजियम घड़ी के 91926317770 आवर्ती के
उत्तर:
(iv) सीजियम घड़ी के 91926317770 आवर्ती के

प्रश्न 11:
1 मीटर में Kr86 की कितनी तरंगदैर्ध्य होती है?
(i) 1553164.13
(ii) 1650763.73
(iii) 2348123.73
(iv) 652189.63
उत्तर:
(ii) 1650763.73

प्रश्न 12:
एक प्रकाश वर्ष दूरी बराबर है।
(i) 9.46 x 10¹⁰ किमी
(ii) 9.46 x 10¹² किमी
(iii) 9.46 x 10¹² मीटर
(iv) 9.46 x 10¹⁵ सेमी
उत्तर:
(ii) 9.46 x 10¹² किमी

प्रश्न 13:
10⁶ डाइन/सेमी² का दाब किसके बराबर है?
(i) 10⁷ न्यूटन/मीटर²
(ii) 10⁶ न्यूटन/मीटर²
(iii) 10⁵ न्यूटन/मीटर²
(iv) 10⁴ न्यूटन/मीटर²
उत्तर:
(iii) 10°न्यूटन/मीटर2,

अतिलघु उत्तरीय प्रश्न

प्रश्न 1:
किसी भौतिक राशि के मापन से क्या तात्पर्य है?
उत्तर:
किसी भौतिक राशि की इसके मात्रक से तुलना करना ही मापन कहलाता है।

प्रश्न 2:
किसी राशि की माप को पूर्णतया व्यक्त करने के लिए किन-किन बातों का ज्ञान होना आवश्यक है?
उत्तर:
किसी राशि की माप को पूर्णतया व्यक्त करने के लिए निम्नलिखित बातों का ज्ञान होना आवश्यक है

1.  मात्रक: जिसमें वह भौतिक राशि मापी जाती है।
2.  आंकिक मान: यह उस राशि के परिमाण को प्रदर्शित करता है अर्थात् यह बताता है कि उस राशि की माप में उसका मात्रक कितनी बार सम्मिलित है।

प्रश्न 3:
मात्रक कितने प्रकार के होते हैं?
उत्तर:
मात्रक दो प्रकार के होते हैं-
(i) मूल मात्रक,
(ii) व्युत्पन्न मात्रक।

प्रश्न 4:
S.I. प्रणाली क्या है?
उत्तर:
सात मूल मात्रकों तथा दो पूरक मूल मात्रकों पर आधारित माप की प्रणाली S.I. प्रणाली कहलाती है।।

प्रश्न 5:
MKS प्रणाली के मूल मात्रकों के नाम लिखिए।
उत्तर:
MKS प्रणाली के मूल मात्रक मीटर, किग्रा, सेकण्डे, ऐम्पियर, केण्डिला तथा केल्विन होते हैं।

प्रश्न 6:
शेक किस भौतिक राशि का मात्रक है?
उत्तर:
यह समय का मात्रक है तथा 1 शेक = 10^-8 सेकण्ड।

प्रश्न 7:
नाभिक के आकार को व्यक्त करने के लिए कौन-सा मात्रक प्रयुक्त किया जाता है? इसका मीटर से क्या सम्बन्ध है?
उत्तर:
फर्मी, जहाँ 1 फर्मी (F) = 10^-15 मीटर।

प्रश्न 8:
चन्द्रशेखर सीमा किस यौगिक राशि का मात्रक है?
उत्तर:
यह द्रव्यमान का मात्रक है तथा 1 CS.L.= 1.4 x सूर्य का द्रव्यमान।।

प्रश्न 9:
AU तथा [latex]\mathring { A }[/latex] क्या हैं? इनमें पारस्परिक सम्बन्ध क्या हैं?
उत्तर:
AU तथा [latex]\mathring { A }[/latex] लम्बाई के ही भिन्न-भिन्न मात्रक हैं। AU लम्बाई का खगोलीय मात्रक है तथा A लम्बाई की छोटा मात्रक है।।
1 AU =1.496 x 10²¹ [latex]\mathring { A }[/latex]

प्रश्न 10:
स्लग (Slug) क्या है? 1 स्लग में मीट्रिक टनों की संख्या कितनी होगी?
हल:
स्लग (Slug) बड़े द्रव्यमान मापने का एक मात्रक है।
तथा 1 स्लग = 14.59 किग्रा
∵ 1 मीट्रिक टन = 1000 किग्रा
∴ 1 स्लग =[latex]\frac { 14.59 }{ 1000 }[/latex]14.32 मीट्रिक टन
= 1459 x 10^-3  मीट्रिक टन

प्रश्न 11:
क्या प्रकाश वर्ष समय का मात्रक है?
उत्तर:
नहीं, प्रकाश वर्ष दूरी का मात्रक है।

प्रश्न 12:
माइक्रोसेकण्ड तथा शेक में क्या सम्बन्ध है?
हल:

प्रश्न 13:
प्रकाश वर्ष को परिभाषित कीजिए।
उत्तर:
1 प्रकाश वर्ष वह दूरी है जो प्रकाश निर्वात् में 1 वर्ष में तय करता है।
∴ 1 प्रकाश वर्ष = 9.46 x 10¹⁵ मीटर
या निर्वात् में 1 प्रकाश वर्ष = 9.46 x 10¹³ मीटर

प्रश्न 14:
1 सेकण्ड माध्य-सौर-दिवस का कौन-सा भाग होता है?
उत्तर:
1 सेकण्ड माध्य-सौर-दिवस का 86,400वाँ भाग होता है।

प्रश्न 15:
एक मीटर में कितने प्रकाश-वर्ष होते हैं?
उत्तर:
हम जानते हैं कि,

प्रश्न 16:
पृथ्वी से प्रेषित एक लेसर पुंज चन्द्रमा से परावर्तन के पश्चात पृथ्वी पर 2.6 सेकण्ड बाद वापस लौटता है। पृथ्वी से चन्द्रमा की दूरी ज्ञात कीजिए।
हल:
यहाँ, समय t = 2.6 सेकण्ड,
लेसर पुंज का वेग c = 3x 10⁸ मी/से

लघु उत्तरीय प्रश्न

प्रश्न 1:
मूल मात्रक क्या हैं? इनके चार गुण लिखिए।
उत्तर:
मूल राशियों के वे मात्रक जो एक-दूसरे से पूर्णतया स्वतन्त्र होते हैं तथा इनमें से किसी एक मात्रक को किसी अन्य मात्रक से बदला अथवा उससे सम्बन्धित नहीं किया जा सकता है, मूल मात्रक कहलाते हैं। लम्बाई, द्रव्यमान, समय, वैद्युतधारा, ऊष्मागतिक ताप, ज्योति तीव्रता तथा पदार्थ की मात्रा मूल मात्रक हैं। मूल. मात्रकों के गुण निम्नलिखित हैं

1.  यह बाह्य कारकों से अप्रभावित रहना चाहिए।
2.  यह सुपरिभाषित होना चाहिए।
3.  इसे सरलतापूर्वक निर्मित किया जाना चाहिए।
4.  इसका उपयोग सरल होना चाहिए।

प्रश्न 2:
व्युत्पन्न मात्रक किसे कहते हैं? किसी एक भौतिक राशि का व्युत्पन्नमात्रक प्राप्त कीजिए।
उत्तर:
मूल राशियों के अतिरिक्त अन्य सभी भौतिक राशियों के मात्रक एक अथवा अधिक मूल मात्रकों पर उपयुक्त घातें लगाकर प्राप्त किये जा सकते हैं। ऐसे मात्रकों को व्युत्पन्न मात्रक (derived units) कहते हैं। बल का व्युत्पन्न मात्रक (UPBoardSolutions.com) निम्न प्रकार से प्राप्त कर सकते हैं
बलु = द्रव्यमान x त्वरण
बल का मात्रक = किग्रा x मीटर/सेकण्ड^-2
= किग्रा-मीटर सेकण्ड^-2
परन्तु S.I. प्रणाली में बल का व्यावहारिक मात्रक न्यूटन होता है।
∴ 1 न्यूटन = 1 किग्रा-मीटर सेकण्ड^-2

प्रश्न 3:
गुरुत्वीय द्रव्यमान और जड़त्वीय द्रव्यमान में अन्तर स्पष्ट कीजिए।
उत्तर:
किसी वस्तु पर कार्यरतु पृथ्वी के गुरुत्वाकर्षण बल तथा पृथ्वी की ओर मुक्त रूप से गिरती वस्तु के गुरुत्वीय जनित त्वरण का अनुपात, वस्तु का गुरुत्वीय द्रव्यमान कहलाता हैं, जबकि किसी वस्तु पर लगाए गए कुल बाह्य बल तथा उसके कारण वस्तु में उत्फन त्वरण का अनुपात वस्तु का जड़त्वीय द्रव्यमान कहलाता है।

प्रश्न 4:
मापन की यथार्थता तथा परिशुद्धता में अन्तर स्पष्ट कीजिए।
उत्तर:

1.  किसी मापन की यथार्थता वह मान है जो हमें यह बताती है कि किसी राशि का मापित मान उसके वास्तविक मान के कितना निकट है, जबकि किसी मापन की परिशुद्धता यह बताती है कि वह राशि किस सीमा या विभेदन तक मापी गई है।
2. किसी भी मापक यन्त्र की यथार्थती उस यन्त्र में विद्यमान उसकी क्रमबद्ध त्रुटि पर निर्भर करती है, जबकि किसी भी मापक यन्त्र की परिशुद्धता यादृच्छिक त्रुटियों पर निर्भर करती है।

प्रश्न 5:
किसी राशि के परिमाण की कोटि से क्या तात्पर्य है? उदाहरण सहित समझाइये।
उत्तर:
यदि किसी राशि के परिमाण को उसके निकटतम 10 की पूर्णाक घात के रूप में लिखा जाए, तो प्राप्त परिमाण को इस राशि को कोटिमान (कोटि) कहते हैं।
उदाहरण:
किसी राशि 0.0025 = 2.5 x 10^-3 में 2.5, 3.16 से छोटा है, तो इस राशि का कोटिमान 10^-3 होगा, जबकि एक अन्य राशि 0.0035 = 3.5 x 10^-3 में 3.5, 3.16 से बड़ा है, तो इस राशि का कोटिमान 10^-3+1 = 10^-2 होगा।

प्रश्न 6:
पृथ्वी के व्यास के दो विपरीत छोरों से किसी आकाशीय पिण्ड का विस्थापनाभास (parallax) 60 सेकण्ड है। यदि पृथ्वी की त्रिज्या 64 x 10⁶ मीटर हो, तो पृथ्वी के केन्द्र से आकाशीय पिण्ड की दूरी ज्ञात कीजिए। इस दूरी को खगोलीय मात्रक में परिवर्तित कीजिए। (1 A.U.= 1.5 x 10¹¹ मीटर)
हल:

विस्तृत उत्तरीय प्रश्न

प्रश्न 1:
लम्बन तथा लम्बनकोण से क्या तात्पर्य है? पृथ्वी के निकट स्थित तारे की दूरी ज्ञात करने के लिए लम्बन विधि का वर्णन कीजिए।
उत्तर:
लम्बन तथा लम्बनकोण-जब हम किसी दीवार पर अंकित किसी चिह्न P को पहले अपनी बायीं आँख A(दायीं आँख B बन्द रखते हुए) देखते हैं और फिर उसी बिन्दु को अपनी दायीं आँख B से (बायीं आँख A बन्द रखते हुए) देखते हैं तो दीवार के सापेक्ष (UPBoardSolutions.com) चिह्न की स्थिति में आभासी विस्थापन दिखायी देता है। इस आभासी विस्थापन को ही लम्बन कहते हैं दूरी AB को आधार दूरी कहते हैं।

AP तथा BP के बीच का कोण θ लम्बनकोण कहलाता है।

पृथ्वी के निकट स्थित तारे की दूरी ज्ञात करना—दिए गए चित्र 2.3 में सूर्य S के परितः पृथ्वी की परिक्रमण कक्षा का व्यास AB है। N एक तारा है जो पृथ्वी के निकट स्थित है तथा इस तारे N की ही पृथ्वी से दूरी ज्ञात करनी है। चित्र 2.3 में F एक अन्य तारा है जो पृथ्वी से काफी दूरी पर स्थित है। माना किसी क्षण पृथ्वी की अपनी कक्षा में स्थिति A है। खगोलीय दूरदर्शी द्वारा ∠FAN = θ, ज्ञात कर । लिया जाता है। में ∠ANS =∠ FAN = θ.6 माह के समयान्तराल पर पृथ्वी अपनी कक्षा में स्थिति A के ठीक सामने स्थिति B में होगी। अब खगोलीय दूरदर्शी द्वारा ∠NBF = 8ज्ञात कर लिया जाता है।

∠BNS =∠ NBF = θ,
तथा ∠ANB=∠ANS + ∠BNS
= θ1 + θ2.
यह कोण तारे N द्वारा पृथ्वी के व्यास AB पर शीर्षाभिमुख बनने वाला कोण है।

प्रश्न 2:
आवोगाने विधि द्वारा परमाणु के आकार का आकलन किस प्रकार किया जा सकता है? समझाइए।
उत्तर:
आवोगाद्रो के अनुसार, पदार्थ के एक ग्राम-परमाणु में 6023 x 10²³ परमाणु होते हैं, जो पदार्थ का लगभग दो-तिहाई आयतेन घेरते हैं। माना पदार्थ का द्रव्यमान m, पदार्थ का परमाणु भार M, पदार्थ द्वारा घेरा गया आयतन V, परमाणु की त्रिज्या तथा आवोगाद्रो संख्या N है। तब,

चूंकि आयतन V, परमाणु भार M, आवोगाद्रो संख्या N तथा पदार्थ का द्रव्यमान m ज्ञात हैं, अतः परमाणु की त्रिज्या । नापी जा सकती है, जिसका मान लगभग 10-10 मीटर की कोटि का होता है।

We hope the UP Board Solutions for Class 11 Physics Chapter 2 Units and Measurements (मात्रक एवं मापन) help you. If you have any query regarding UP Board Solutions for Class 11 Physics Chapter 2 Units and Measurements (मात्रक एवं मापन) drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Political Science Political theory Chapter 4 Social Justice (सामाजिक न्याय)

These Solutions are part of UP Board Solutions for Class 11 Political Science. Here we have given UP Board Solutions for Class 11 Political Science Political theory Chapter 4 Social Justice (सामाजिक न्याय).

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1.
हर व्यक्ति को उसका प्राप्य देने का क्या मतलब है? हर किसी को उसका प्राप्य देने का मतलब समय के साथ-साथ कैसे बदला है?
उत्तर-
हर व्यक्ति को उसका प्राप्य देने का मतलब है न्याय में प्रत्येक व्यक्ति को उसका उचित भाग प्रदान करना। यह बात आज भी न्याय का महत्त्वपूर्ण अंग बनी हुई है। आज इस बात पर निर्णय के लिए विचार किया जाता है कि किसी व्यक्ति का प्राप्य क्या है? जर्मन दार्शनिक काण्ट के अनुसार, प्रत्येक मनुष्य की गरिमा होती है। अगर सभी व्यक्तियों की गरिमा स्वीकृत है, तो उनमें से हर एक को प्राप्य यह होगा कि उन्हें अपनी प्रतिभा के विकास और लक्ष्य की पूर्ति के लिए अवसर प्राप्त हों। न्याय के लिए आवश्यक है कि हम सभी व्यक्तियों को समुचित और समान महत्त्व दें।

समान लोगों के प्रति समान व्यवहार – आधुनिक समाज में बहुत-से लोगों को समान महत्त्व देने के बारे में आम सहमति है, लेकिन यह निर्णय करना सरल नहीं है कि प्रत्येक व्यक्ति को उसका प्राप्य कैसे दिया जाए। इस विषय में अनेक सिद्धान्त प्रस्तुत किए गए हैं। उनमें से एक है समकक्षों के साथ समान बरताव का सिद्धान्त। यह माना जाता है कि मनुष्य होने के कारण सभी व्यक्तियों में कुछ समान चारित्रिक विशेषताएँ होती हैं। इसीलिए वे समान अधिकार और समान बरताव के अधिकारी हैं। आज अधिकांश उदारवादी जनतन्त्रों में कुछ महत्त्वपूर्ण अधिकार प्रदान किए गए हैं। इनमें जीवन, स्वतन्त्रता और सम्पत्ति के अधिकार जैसे नागरिक अधिकार शामिल हैं। इसमें समाज के अन्य सदस्यों के साथ समान अवसरों के उपभोग करने का सामाजिक अधिकार और मताधिकार जैसे राजनीतिक अधिकार भी शामिल हैं। ये अधिकार व्यक्तियों को राज-प्रक्रियाओं में भागीदार बनाते हैं।

समान अधिकारों के अतिरिक्त समकक्षों के साथ समान बरताव के सिद्धान्त के लिए आवश्यक है कि लोगों के साथ वर्ग, जाति, नस्ल या लिंग के आधार पर भेदभव न किए जाए। उन्हें उनके काम और कार्य-कलापों के आधार पर जाँचा जाना चाहिए। इस आधार पर नहीं कि वे किस समुदाय के सदस्य हैं। इसीलिए अगर भिन्न जातियों के दो व्यक्ति एक ही काम करते हैं, चाहे वह पत्थर तोड़ने का काम हो या होटल में कॉफी सर्व करने का; उन्हें समान पारिश्रमिक मिलना चाहिए।

प्रश्न 2.
अध्याय में दिए गए न्याय के तीन सिद्धान्तों की संक्षेप में चर्चा करो। प्रत्येक को उदाहरण के साथ समझाइए।
उत्तर-
अध्याय में दिए गए न्याय के तीन सिद्धान्त निम्नलिखित हैं-
1. समान लोगों के लिए समान व्यवहार – इसका विवेचन हम प्रश्न 1 में कर चुके हैं।

2. समानुपातिक न्याय – समान व्यवहार न्याय का एकमात्र सिद्धान्त नहीं है। ऐसी परिस्थितियाँ हो सकती हैं जिनमें हम यह अनुभव करें कि प्रत्येक के साथ समान व्यवहार करना अन्याय होगा। उदाहरण के लिए; किसी विद्यालय में अगर यह निर्णय लिया जाए, कि परीक्षा में सम्मिलित होने वाले सभी लोगों को समान अंक दिए जाएँगे क्योंकि सभी एक ही स्कूल के विद्यार्थी हैं और सभी ने एक ही परीक्षा दी है, यह स्थिति कष्टपूर्ण हो सकती है, तब अधिक उचित यह रहेगा। कि छात्रों को उंनकी उत्तर-पुस्तिकाओं की गुणवत्ता और सम्भव हो तो इसके लिए उनके द्वारा किए गए प्रयास के अनुसार अंक प्रदान किए जाएँ। यह न्याय का समानुपातिक सिद्धान्त है।

3. मुख्य आवश्यकताओं का विशेष ध्यान – न्याय का तीसरा सिद्धान्त है-पारिश्रमिक या कर्तव्यों का वितरण करते समय लोगों की मुख्य आवश्यकताओं का ध्यान रखने का सिद्धान्त। इसे सामाजिक न्याय को बढ़ावा देने का एक तरीका माना जा सकता है। समाज के सदस्यों के रूप में लोगों की बुनियादी अवस्था और अधिकारों की दृष्टि से न्याय के लिए यह आवश्यक हो सकता है कि लोगों के साथ समान बरताव किया जाए, लेकिन लोगों के बीच भेदभाव न करना और उनके परिश्रम के अनुपात में उन्हें पारिश्रमिक देना भी यह सुनिश्चित करने के लिए शायद पर्याप्त न हो कि समाज में अपने जीवन के अन्य सन्दर्भो में भी लोग समानता का उपभोग करें या कि समाज समग्ररूप से न्यायपूर्ण हो जाए। लोगों की विशेष आवश्यकताओं को दृष्टिगत रखने का सिद्धान्त समान व्यवहार के सिद्धान्त को अनिवार्यतया खण्डित नहीं, बल्कि उसका विस्तार ही करता है।

प्रश्न 3.
क्या विशेष जरूरतों का सिद्धान्त सभी के साथ समान बरताव के सिद्धान्त के विरुद्ध है?
उत्तर-
विशेष जरूरतों या विकलांग व्यक्तियों को कुछ विशेष मामलों में असमान और विशेष सहायता के योग्य समझा जा सकता है। लेकिन इस पर सहमत होना सरल नहीं होता कि लोगों को विशेष सहायता देने के लिए उनकी किन असमानताओं को मान्यता दी जाए। शारीरिक विकलांगता, उम्र या अच्छी शिक्षा और स्वास्थ्य सुविधाओं तक पहुँच न होना कुछ ऐसे कारक हैं, जिन्हें विभिन्न देशों में बरताव का आधार समझा जाता है। यह माना जाता है कि जीवनयापन और अवसरों के बहुत उच्च स्तर के उपभोक्ता और उत्पादक जीवन जीने के लिए आवश्यक न्यूनतम बुनियादी सुविधाओं से भी वंचित लोगों से हर मामले में एक समान बरताव करेंगे उनके ऐसा करने पर यह आवश्यक नहीं है कि परिणाम समतावादी और न्यायपूर्ण समाज होगा बल्कि एक असमान समाज भी हो सकता है।

प्रश्न 4.
निष्पक्ष और न्यायपूर्ण वितरण को युक्तिसंगत आधार पर सही ठहराया जा सकता है। रॉल्स ने इस तर्क को आगे बढ़ाने में अज्ञानता के आवरण के विचार का उपयोग किस प्रकार किया?
उत्तर-
जीवन में विभिन्न प्रकरणों में हमारे समक्ष यह प्रश्न उत्पन्न हो जाता है कि हम ऐसे निर्णय पर कैसे पहुँचे जो निष्पक्ष हो और न्यायसंगत भी।
जॉन रॉल्स ने इस प्रश्न का उत्तर देने का प्रयास किया है। रॉल्स तर्क प्रस्तुत करते हैं कि निष्पक्ष और न्यायसंगत नियम तक पहुँचने का एकमात्र रास्ता यही है कि हम स्वयं को ऐसी परिस्थितियों में होने की कल्पना करें जहाँ हमें यह निर्णय लेना है कि समाज को कैसे संगठित किया जाए। जबकि हमें यह ज्ञात नहीं है कि उस समाज में हमरा क्या स्थान होगा। अर्थात् हम नहीं जानते कि किस प्रकार के परिवार में हम जन्म लेंगे, हम उच्च जाति के परिवार में जन्म लेंगे या निम्न जाति के, धनी होंगे या गरीब, सुविधासम्पन्न होंगे अथवा सुविधाहीन। रॉल्स तर्क प्रस्तुत करते हैं कि अगर हमें यह नहीं मालूम हो, इस मायने में, कि हम कौन होंगे और भविष्य के समाज में हमारे लिए कौन-से विकल्प खुले होंगे, तब हम भविष्य के उस समाज के नियमों और संगठन के बारे में जिस निर्णय का समर्थन करेंगे, वह समाज के अनेक सदस्यों के लिए अच्छा होगा।

रॉल्स ने इसे ‘अज्ञानता के आवरण’ में सोचना कहा है। रॉल्स आशा करते हैं कि समाज में अपने सम्भावित स्थान और सामर्थ्य के बारे में पूर्ण अज्ञानता की दशा में प्रत्येक व्यक्ति, आमतौर पर जैसे सब करते हैं, अपने स्वयं के हितों को दृष्टिगत रखकर निर्णय करेगा। चूँकि कोई नहीं जानता कि वह कौन होगा और उसके लिए क्या लाभप्रद होगा, इसलिए प्रत्येक व्यक्ति सबसे बुरी स्थिति को दृष्टिगत रखकर समाज की कल्पना करेगा। स्वयं के लिए सोच-विचार कर सकने वाले व्यक्ति के सामने यह स्पष्ट रहेगा कि जो जन्म से सुविधासम्पन्न हैं, वे कुछ विशेष अवसरों का उपभोग करेंगे। लेकिन दुर्भाग्य से यदि उनका जन्म समाज के वंचित वर्ग में हो जहाँ वैसा कोई अवसर न मिले, तब क्या होगा? इसलिए, अपने स्वार्थ में काम करने वाले प्रत्येक व्यक्ति के लिए यही उचित होगा कि वह संगठन के ऐसे नियमों के विषय में सोचे जो कमजोर वर्ग के लिए यथोचित अवसर सुनिश्चित कर सके। इस प्रयास से यह होगा कि शिक्षा, स्वास्थ्य, आवास जैसे महत्त्वपूर्ण संसाधन सभी लोगों को प्राप्त हों-चाहे वे उच्च वर्ग के हों या निम्न वर्ग के।

निश्चित रूप से अपनी पहचान को विस्मृत करना और अज्ञानता के आवरण’ में खड़ा होने की कल्पना करना किसी के लिए सहज नहीं है। लेकिन तब, अधिकांश लोगों के लिए यह भी उतना ही कठिन है। कि वे आत्मत्यागी बनें और अजनबी लोगों के साथ अपने सौभाग्य को बाँटें। यही कारण है कि हम आदतस्वरूप आत्मत्याग को वीरता से जोड़ते हैं। इन मानवीय दुर्बलताओं और सीमाओं को दृष्टिगत रखते हुए हमारे लिए ऐसे ढाँचे के बारे में सोचना अच्छा रहेगा जिसमें असाधारण कार्यवाहियों की आवश्यकता न रहे। ‘अज्ञानता के आवरण’ वाली स्थिति की विशेषता यह है कि उसमें लोगों से सामान्य रूप से विवेकशील मनुष्य बने रहने की उम्मीद बँधती है। उनसे अपने लिए सोचने और अपने हित में जो अच्छा हो, उसे चुनने की अपेक्षा रहती है।

अज्ञानता का कल्पित आवरण ओढ़न उचित कानूनों और नीतियों की प्रणाली तक पहुँचने का पहला कदम है। इससे यह प्रकट होगा कि विवेकशील मनुष्य न केवल सबसे बुरे सन्दर्भ को दृष्टिगत रखकर चीजों को देखेंगे, बल्कि वे यह भी सुनिश्चित करने का प्रयास करेंगे कि उनके द्वारा निर्मित नीतियाँ समग्र समाज के लिए लाभप्रद हों। दोनों चीजों को साथ-साथ चलना है। चूंकि कोई नहीं जानता कि वे वे आगामी समाज में कौन-सी जगह लेंगे, इसलिए हर कोई ऐसे नियम चाहेगी जो, अगर वे सबसे बुरी स्थिति में जीने वालों के बीच पैदा हों, तब भी उनकी रक्षा कर सके। लेकिन उचित तो यही होगा कि वे यह भी सुनिश्चित करने का प्रयास करें, कि उनके द्वारा चुनी गई नीतियाँ बेहतर स्थिति वालों को कमजोर न बना दे, क्योंकि यह सम्भावना भी हो सकती है कि वे स्वयं भविष्य के उस समाज में सुविधासम्पन्न स्थिति में जन्म लें। इसलिए यह सभी के हित में होगा कि निर्धारित नियमों और नीतियों से सम्पूर्ण समाज को लाभ होना चाहिए, किसी एक विशिष्ट वर्ग का नहीं। यहाँ निष्पक्षता विवेकसम्मत कार्यवाही का परिणाम है, न कि परोपकार अथवा उदारता का।

इसलिए रॉल्स तर्क प्रस्तुत करते हैं कि नैतिकता नहीं बल्कि विवेकशील चिन्तन हमें समाज में लाभ और भार के वितरण के मामले में निष्पक्ष होकर विचार करने की ओर प्रेरित करती है। इस उदारहण में हमारे पास पहले से बना-बनाया कोई लक्ष्य या नैतिकता के प्रतिमान नहीं होते हैं। हमारे लिए सबसे अच्छा क्या है, यह निर्धारित करने के लिए हम स्वतन्त्र होते हैं। यही विश्वास रॉल्स के सिद्धान्त को निष्पक्ष और न्याय के प्रश्न को हल करने को महत्त्वपूर्ण और सबल रास्ता तैयार कर देता है।

प्रश्न 5.
आमतौर पर एक स्वस्थ और उत्पादक जीवन जीने के लिए व्यक्ति की न्यूनतम बुनियादी जरूरतें क्या मानी गई हैं। इस न्यूनतम को सुनिश्चित करने में सरकार की क्या जिम्मेदारी है?
उत्तर-
आमतौर पर एक स्वस्थ और उत्पादक जीवन जीने के लिए व्यक्ति की बुनियादी न्यूनतम जरूरतें शरीर के लिए आवश्यक पोषक तत्त्वों की मात्रा, आवास, शुद्ध पेयजल की आपूर्ति, शिक्षा और न्यूनतम मजदूरी मानी गई हैं।
गरीबों को न्यूनतम बुनियादी सुविधाएँ उपलब्ध कराने की जिम्मेदारी सरकार को लेनी चाहिए। इसके लिए वह विभिन्न कार्यक्रम चला सकती है, निजी एजेंसियों की सेवाएँ भी ले सकती है। राज्य के लिए यह आवश्यक हो सकता है कि वह उन वृद्धों और रोगियों को विशेष सहायता प्रदान करे जो प्रतिस्पर्धा नहीं कर सकते। लेकिन इसके आगे राज्य की भूमिका नियम-कानून का ढाँचा बरकरार रखने तक ही। सीमित होनी चाहिए।

प्रश्न 6.
सभी नागरिकों को जीवन की न्यूनतम बुनियादी स्थितियाँ उपलब्ध कराने के लिए राज्य की कार्यवाही को निम्न में से कौन-से तर्क से वाजिब ठहराया जा सकता है?
(क) गरीब और जरूरतमन्दों को निःशुल्क सेवाएँ देना एक धर्मकार्य के रूप में न्यायोचित है।
(ख) सभी नागरिकों को जीवन का न्यूनतम बुनियादी स्तर उपलब्ध करवाना अवसरों की समानता सुनिश्चित करने का एक तरीका है।
(ग) कुछ लोग प्राकृतिक रूप से आलसी होते हैं और हमें उनके प्रति दयालु होना चाहिए।
(घ) सभी के लिए बुनियादी सुविधाएँ और न्यूनतम जीवन स्तर सुनिश्चित करना साझी मानवता और मानव अधिकारों की स्वीकृति है।
उत्तर-
(घ) सभी के लिए बुनियादी सुविधाएँ और न्यूनतम जीवन स्तर सुनिश्चित करना साझी मानवता और मानव अधिकारों की स्वीकृति है।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न

प्रश्न 1.
प्राचीन भारत में न्याय का सम्बन्ध था?
(क) धर्म से
(ख) ध्यान से
(ग) राज्य से
(घ) राजा से
उत्तर :
(क) धर्म से

प्रश्न 2.
‘दि रिपब्लिक’ किसकी रचना है?
(क) अरस्तू की
(ख) प्लेटो की
(ग) मैकियावली की
(घ) बोदां की
उत्तर :
(ख) प्लेटो की।

प्रश्न 3.
सुकरात कौन था?
(क) एक दार्शनिक
(ख) एक राजनीतिज्ञ
(ग) एक राजा
(घ) एक विद्यार्थी
उत्तर :
(क) एक दार्शनिक।

प्रश्न 4.
“हर मनुष्य की गरिमा होती है।” यह किसका कथन है?
(क) प्लेटो का
(ख) अरस्तू का
(ग) इमैनुएल काण्ट का।
(घ) रॉल्स का
उत्तर :
(ग) इमैनुएल काण्ट का।

प्रश्न 5.
न्याय की देवी आँखों पर पट्टी इसलिए अँधे रहती है क्योंकि –
(क) उसे निष्पक्ष रहना है।
(ख) वह देख नहीं सकती
(ग) यह एक परम्परा है।
(घ) वह स्त्री है।
उत्तर :
(क) उसे निष्पक्ष रहना है।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
सामाजिक न्याय का लक्ष्य क्या है?
उत्तर :
सामाजिक न्याय का लक्ष्य सामाजिक-आर्थिक न्याय की प्राप्ति है ताकि समाज निरन्तर अपने निर्धारित लक्ष्यों की ओर बढ़ सके।

प्रश्न 2.
न्याय के तीन सिद्धान्त कौन-से हैं?
उत्तर :

1. समान लोगों के प्रति समान बरताव।
2. समानुपातिक न्याय।
3. विशेष जरूरतों का विशेष ध्यान।

प्रश्न 3.
जॉन रॉल्स ने कौन-सा सिद्धान्त प्रस्तुत किया था?
उत्तर :
सुप्रसिद्ध राजनीतिक दार्शनिक जॉन रॉल्स ने न्यायोचित वितरण का सिद्धान्त प्रस्तुत किया है।

प्रश्न 4.
बुनियादी आवश्यकताएँ कौन-सी हैं?
उत्तर :
स्वस्थ रहने के लिए आवश्यक पोषक तत्त्वों की बुनियादी मात्रा, आवास, शुद्ध पेयजल की आपूर्ति, शिक्षा और न्यूनतम मजदूरी बुनियादी आवश्यकताएँ हैं।

प्रश्न 5.
मुक्त बाजार की एक विशेषता लिखिए।
उत्तर :
मुक्त बाजार साधारणतया पूर्व से ही सुविधासम्पन्न लोगों के लिए काम करते हैं।

लघु उत्तरीय प्रश्न

प्रश्न 1.
न्यायपूर्ण विभाजन के लिए क्या आवश्यक है?
उत्तर :
सामाजिक न्याय प्राप्त करने के लिए सरकारों को यह सुनिश्चित करना होता है कि कानून और नीतियाँ सभी व्यक्तियों पर निष्पक्ष रूप से लागू हों। लेकिन इतना ही काफी नहीं है इसमें कुछ और अधिक करने की आवश्यकता है। सामाजिक न्याय का सम्बन्ध वस्तुओं और सेवाओं के न्यायोचित वितरण से भी है, चाहे यह राष्ट्रों के बीच वितरण का मामला हो या किसी समाज के अन्दर विभिन्न समूहों और व्यक्तियों के बीच का। यदि समाज में गम्भीर सामाजिक या आर्थिक असमानताएँ हैं तो यह आवश्यक होगा कि समाज के कुछ प्रमुख संसाधनों की पुनर्वितरण हो, जिससे नागरिकों को जीने के लिए समतल धरातल मिल सके। इसलिए किसी देश के अन्दर सामाजिक न्याय के लिए यह आवश्यक है कि न केवल लोगों के साथ समाज के कानूनों और नीतियों के सन्दर्भ में समान बरताव किया जाए। बल्कि जीवन की स्थितियों और अवसरों के मामले में भी वे बहुत कुछ बुनियादी समानता का उपभोग करें।

प्रश्न 2.
नीचे दी गई स्थितियों की जाँच करें और बताएँ कि क्या वे न्यायसंगत हैं। अपने तर्क के साथ यह भी बताएँ कि प्रत्येक स्थिति में न्याय का कौन-सा सिद्धान्त काम कर रहा है –

1. एक दृष्टिहीन छात्र सुरेश को गणित का प्रश्नपत्र हल करने के लिए साढ़े तीन घण्टे मिलते हैं, जबकि अन्य सभी छात्रों को केवल तीन घण्टे।
2. गीता बैसाखी की सहायता से चलती है। अध्यापिका ने गणित का प्रश्नपत्र हल करने के लिए उसे भी साढ़े तीन घण्टे का समय देने का निश्चय किया।
3. एक अध्यापक कक्षा के कमजोर छात्रों के मनोबल को उठाने के लिए कुछ अतिरिक्त अंक देता है।
4. एक प्रोफेसर अलग-अलग छात्राओं को उनकी क्षमताओं के मूल्यांकन के आधार पर अलग-अलग प्रश्नपत्र बाँटता है।
5. संसद में एक प्रस्ताव विचाराधीन है कि संसद की कुल सीटों में से एक-तिहाई सीटें महिलाओं के लिए आरक्षित कर दी जाएँ।

उत्तर :

1. न्यायसंगत है। विशेष जरूरतों का ख्याल रखने का सिद्धान्त।
2. न्यायसंगत नहीं। यहाँ उपर्युक्त सिद्धान्त लागू नहीं होता।
3. न्यायसंगत नहीं। यहाँ समानुपातिक सिद्धान्त लागू नहीं होता।
4. न्यायसंगत नहीं। यहाँ न्यायपूर्ण बँटवारा नहीं है।
5. न्यायसंगत है। यहाँ ‘विशेष जरूरतों का विशेष ख्याल’ सिद्धान्त लागू होता है।

दीर्घ लघु उत्तरीय प्रश्न

प्रश्न 1.
सामाजिक न्याय दिलाने की दिशा में सरकार ने विकलांगों के लिए क्या कार्य किया है।
उत्तर :
विकलांगता के कारण विकलांगों को सामाजिक घृणा का सामना करना पड़ता है तथा उन्हें जीवन में आगे बढ़ने के अवसरों से मात्र उनकी विकलांगता के कारण वंचित कर दिया जाता है। इससे न केवल विकलांग व्यक्ति को वरन् उसके पूरे परिवार को अनेक अवांछित कठिनाइयों का सामना करना पड़ता है।

भारतीय संविधान विकलांगों को उनके काम, शिक्षा तथा सार्वजनिक सहायता के अधिकार दिलावने हेतु राज्यों को निर्देश देता है जिससे कि वे प्रभावी व्यवस्था लागू करें। भारत के विकलांगों के हितों से सम्बन्धित मुख्यतया निम्नलिखित तीन कानून पारित किए गए हैं –

1. भारतीय पुनर्वास परिषद् अधिनियम, 1992;
2. विकलांग-व्यक्ति को समान अवसर, अधिकारों की रक्षा और पूर्ण सहभागिता अधिनियम, 1995; तथा
3. आत्मविमोह, मस्तिष्क पक्षाघात, अल्पबुद्धिता तथा बहुविकलांगता प्रभावित व्यक्तियों के कल्याणार्थ राष्ट्रीय न्याय अधिनियम, 1999.

भारतीय पुनर्वास परिषद् अधिनियम, 1992 के द्वारा पुनर्वास परिषद् को वैधानिक दर्जा प्रदान किया गया है। यह विकलांगता के क्षेत्र में काम करने वाले विभिन्न श्रेणियों के कर्मचारियों के लिए चल रहे कार्यक्रमों तथा संस्थाओं को नियन्त्रित करता है।

प्रश्न 2.
विकलांग व्यक्ति अधिनियम, 1995 के क्या प्रावधान हैं?
उत्तर :
‘विकलांग व्यक्ति अधिनियम, 1995′ सर्वाधिक व्यापक है जो विकलांगों के लिए समग्र दृष्टिकोण रखता है। इसके अनसुार –

1. विकलांगों को सरकारी नौकरियों में 3 प्रतिशत आरक्षण दिया जाएगा तथा उन सार्वजनिक एवं निजी संस्थानों को प्रोत्साहन दिया जाएगा जो पाँच या पाँच से अधिक विकलांगों को अपने यहाँ नौकरी पर रखेंगे;
2. सरकार का उत्तरदायित्व है कि प्रत्येक विकलांग को 18 वर्ष की आयु तक नि:शुल्क शिक्षा प्रदान करे;
3. विकलांगों को घर बनाने के लिए व्यापार या फैक्टरी स्थापित करने के लिए अथवा विशेष मनोरंजन केन्द्र, विद्यालय या अनुसन्धान संस्थान खोलने के लिए भूमि का आवंटन रियायती दरों पर और प्राथमिकता के आधार पर दिया जाएगा;
4. इनके लिए रोजगार कार्यालय, विशेष बीमा पॉलिसियाँ तथा बेकारी भत्ते की व्यवस्था की जाएगी; तथा
5. विकलांगों के कल्याण के लिए एक मुख्य आयुक्त की नियुक्ति की जाएगी जो राज्यों के आयुक्तों द्वारा इन लोगों के कार्यों के लिए सामंजस्य स्थापित करे, इनके हितों की सुरक्षा हेतु । कार्य करे और उनकी शिकायतों की सुनवाई करे।

प्रश्न 3.
भारत में सामाजिक न्याय के सन्दर्भ में क्या कदम उठाए गए हैं?
उत्तर :
भारत में सामाजिक न्याय के सन्दर्भ में राज्य के नीति-निदेशक सिद्धान्तों में निम्नलिखित प्रावधान किए गए हैं

अनुच्छेद 38 – राज्य एक ऐसी सामाजिक व्यवस्था की प्राप्ति और संरक्षण द्वारा, जिसमें सामाजिक, आर्थिक और राजनीतिक न्याय राष्ट्रीय जीवन की सभी संस्थाओं का मार्गदर्शन करता है, जनसामान्य की भलाई को बढ़ावा देने का प्रयास करेगा।

अनुच्छेद 39 – विशेषतौर पर राज्य अपनी नीति को इन चीजों की उपलब्धि के लिए निर्देशित करेगा

(क) कि नागरिक, पुरुष और स्त्रियाँ, जीवन यापन के उचित साधनों पर समान अधिकार रखते हों।
(ख) कि आर्थिक ढाँचे का क्रियान्वयन ऐसा न हो कि साधारण मनुष्यों का अहित हो और सम्पत्ति तथा उत्पादन के साधन केन्द्रित हो जाएँ।
(ग) कि कामगारों के स्वास्थ्य, शक्ति और बच्चों की सुकुमार उम्र का दुरुपयोग न हो।

अनुच्छेद 43 – श्रमिकों के लिए जीवनोपयोगी वेतन प्राप्त कराने का राज्य प्रयत्न करे।

अनुच्छेद 46 – राज्य समाज के कमजोर वर्गों के शैक्षणिक और आर्थिक हितों की विशेष रूप से वृद्धि करे और उनका सामाजिक अन्याय तथा सभी प्रकार के शोषण से संरक्षण करे।

अनुच्छेद 47 – राज्य अपने नागरिकों के पौष्टिक स्तर और जीवन स्तर को ऊपर उठाने और सामाजिक स्वास्थ्य को उन्नत करने को अपने प्राथमिक कर्तव्यों में समझे।।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
सामाजिक न्याय से आप क्या समझते हैं? सामाजिक न्याय के लक्षणों का वर्णन कीजिए।
उत्तर :
एक अवधारणा के रूप में सामाजिक न्याय अपेक्षाकृत नया है। सर सी०के० एलन अपनी पुस्तक ‘आस्पैक्ट्स ऑफ जस्टिस’ में लिखते हैं –

आज हम ‘सामाजिक न्याय के बारे में बहुत कुछ सुनते हैं। मैं नहीं समझता कि वे जो इस कथन को बड़ी वाचालता से प्रयोग करते हैं, इसके क्या अर्थ लेते हैं, कुछ इसकी व्याख्या ‘अवसर की समानता के रूप में करते हैं। जो एक भ्रमिक कथन है, क्योंकि अवसर सभी लोगों के बीच समान नहीं हो सकता क्योंकि इसे ग्रहण करने की क्षमताएँ असमान हैं, मुझे भय है, कुछ इसका अर्थ यह लेते हैं कि यह उचित है मैं कहूँगा–विशाल हृदय कि प्राकृतिक मानवी असमानता की सूक्ष्मता को कम किए जाने के लिए हर प्रयास किया जाए और आत्मोन्नति के व्यावहारिक अवसरों में कोई बाधा नहीं डालनी चाहिए, वरन् उन्हें मदद पहुँचानी चाहिए।

सर एलन का यह कथन इस बात को प्रकट करता है कि सामाजिक न्याय की धारणा अस्पष्ट सी है। फिर भी इसमें कुछ तथ्य हैं। सामाजिक न्याय की अवधारणा में एक उचित और सुन्दर सामाजिक व्यवस्था जो सबके लिए उचित और सुन्दर है, सम्मिलित है।

सामाजिक न्याय का तात्पर्य उन लोगों को ऊपर उठाना है जो किन्हीं कारणों से कमजोर और कम अधिकारसम्पन्न हैं और जो जीवन की दौड़ में पीछे छूट गए हैं। अतः सामाजिक न्याय समाज के अधिक कमजोर और पिछड़े वर्गों को विशेष सुरक्षा प्रदान करता है।

भारत के पूर्व मुख्य न्यायाधीश के० सुब्बाराव के अनुसार-‘सामाजिक न्याय’ शब्द के सीमित और व्यापक दोनों अर्थ हैं। अपने सीमित अर्थ में इसका अभिप्राय है मनुष्य के व्यक्तिगत सम्बन्धों में व्याप्त अन्याय को सुधार। अपने विस्तृत अर्थ में यह मनुष्यों के राजनीतिक, सामाजिक और आर्थिक जीवन के असन्तुलन को दूर करता है। सामाजिक न्याय को दूसरे या बाद वाले अर्थ में समझा जाना चाहिए, क्योंकि तीनों ही क्रियाएँ आपस में सम्बद्ध हैं। सामाजिक न्याय अच्छे समाज के निर्माण में सहायक होता है।

प्रश्न 2.
सामाजिक न्याय स्वतन्त्रता और सामाजिक नियन्त्रण में सन्तुलन बनाए रखने का प्रयास करता है।’ विवेचना कीजिए।
उत्तर :
सामाजिक न्याय आधुनिक कल्याणकारी राज्य का निदेशक सिद्धान्त बन गया है। सामाजिक सुरक्षा के कदम, जैसे कि बेरोजगारी के मामले में सहायता, प्रसवकालीन लाभ और बीमारी, वृद्धावस्था तथा अपंगता के विरुद्ध बीमा, समाज के उन सदस्यों को सामाजिक न्याय दिलाने को उठाए गए हैं। जिनके पास अपने भरण-पोषण के साधन नहीं हैं और जो अपने परिवारों की देख-रेख नहीं कर पाते। सामाजिक न्याय को मात्र सामाजिक सुरक्षा के बराबर समझना गलत होगा। यह सामाजिक सुरक्षा से अधिक बड़े अर्थ का सूचक है और यह कमजोर तथा पिछड़े हुओं पर विशेष ध्यान दिए जाने पर जोर देता है। सामाजिक न्याय तथा समाजवाद के अर्थों में प्रायः भ्रान्ति पैदा हो जाती है क्योंकि दोनों ही असमानताओं को हटाने का प्रयास करते हैं। इन दोनों शब्दों को एक-दूसरे के लिए प्रयोग करना गलत है। समाजवाद अन्तिम विश्लेषण में उत्पादन के साधनों पर व्यक्तिगत अधिकार को समाप्त करने का उद्देश्य रखता है। समाजवादी व्यवस्था के अन्तर्गत उत्पादन के सभी साधन; जैसे-भूमि, पूँजी, कारखाने आदि सार्वजनिक अधिकार में ले लिए जाते हैं। एक ऐसी राजनीतिक व्यवस्था में जो सामाजिक न्याय के लिए वचनबद्ध है इस सीमा तक जाना आवश्यक नहीं है। सामाजिक न्याय की माँगों को उस देश में भी पूरा किया जा सकता है जिसने पूँजीवाद को अपनी आर्थिक व्यवस्था का आधार बनाए रखा है। आवश्यक यह है कि कानून, कर और अन्य युक्तियों से यह सुनिश्चित कर दिया जाए कि अच्छे जीवन के लिए आवश्यक न्यूनतम हालात प्रत्येक सदस्य को अधिकाधिक रूप में उपलब्ध कराए जाएँ। अनिवार्यतः इसका तात्पर्य समृद्ध लोगों के हाथ से समाज के गरीब वर्ग के हाथ में साधनों का हस्तान्तरण होना है, परन्तु इससे पूँजीवाद का अन्त नहीं होता। सामाजिक न्याय सदैव आर्थिक और सामाजिक असन्तुलनों को दूर करने का प्रयास करता है जैसा कि भारतीय उच्च न्यायालय ने एक महत्त्वपूर्ण फैसले में कहा था-“यह स्वतन्त्रता और सामाजिक नियन्त्रण में सन्तुलन बनाए रखने का प्रयास करता है।”

प्रश्न 3.
‘मुक्त बाजार बनाम राज्य का हस्तक्षेप’ विषय पर लघु निबन्ध लिखिए।
उत्तर :

मुक्त बाजार बनाम राज्य का हस्तक्षेप

मुक्त बाजार के समर्थकों का मानना है कि जहाँ तक सम्भव हो, लोगों को सम्पत्ति अर्जित करने के लिए तथा मूल्य, मजदूरी और लाभ के मामले में दूसरों के साथ अनुबन्ध और समझौतों में शामिल होने के लिए स्वतन्त्रत रहना चाहिए। उन्हें लाभ की अधिकतम मात्रा प्राप्त करने के लिए एक-दूसरे के साथ प्रतिद्वन्द्विता करने की छूट होनी चाहिए। यह मुक्त बाजार का सरल चित्रण है। मुक्त बाजार के समर्थक मानते हैं कि अगर बाजारों को राज्य के हस्तक्षेप से मुक्त कर दिया जाए, तो बाजारी कारोबार का योग कुल मिलाकर समाज में लाभ और कर्तव्यों का न्यायपूर्ण वितरण सुनिश्चित कर देगा। इससे योग्य और प्रतिभासम्पन्न लोगों को अधिक प्रतिफल प्राप्त होगा जबकि अक्षम लोगों को कम प्राप्त होगा। उनकी मान्यता है कि बाजारी वितरण का जो भी परिणाम हो, वह न्यायसंगत होगा।

हालाँकि, मुक्त बाजार के सभी समर्थक आज पूर्णतया अप्रतिबन्धित बाजार का समर्थन नहीं करेंगे। कई लोग अब कुछ प्रतिबन्ध स्वीकार करने के लिए तैयार होंगे। उदाहरण के रूप में, सभी लोगों के लिए न्यूनतम बुनियादी जीवन-मानक सुनिश्चित करने के लिए राज्य हस्तक्षेप करे, ताकि वे समान शर्तों पर प्रतिस्पर्धा करने में समर्थ हो सकें। लेकिन वे तर्क कर सकते हैं कि यहाँ भी स्वास्थ्य सेवा, शिक्षा तथा ” ऐसी अन्य सेवाओं के विकास के लिए बाजार को अनुमति देना ही लोगों के लिए इन बुनियादी सेवाओं की आपूर्ति का सबसे उत्तम उपाय हो सकता है। दूसरों शब्दों में, ऐसी सेवाएँ उपलब्ध कराने के लिए निजी एजेंसियों को प्रोत्साहित किया जाना चाहिए, जबकि राज्य की नीतियाँ इन सेवाओं को खरीदने के लिए लोगों को सशक्त बनाने का प्रयास करें। राज्य के लिए यह भी आवश्यक हो सकता है कि वह उन वृद्धों और रोगियों को विशेष सहायता प्रदान करे, जो प्रतिस्पर्धा नहीं कर सकते। लेकिन इसके आगे राज्य की भूमिका नियम-कानून का ढाँचा बनाए रखने तक ही सीमित रहनी चाहिए, जिससे व्यक्तियों के बीच जबरदस्ती और अन्य बाधाओं से मुक्त प्रतिद्वन्द्विता सुनिश्चित हो। उनका मानना है कि मुक्त बाजार उचित और न्यायपूर्ण समाज का आधार होता है। कहा जाता है कि बाजार किसी व्यक्ति की जाति या धर्म की परवाह नहीं करता। वह यह भी नहीं देखता कि आप पुरुष हैं या स्त्री। वह इन सबसे निरपेक्ष रहता है और उसका सम्बन्ध आपकी प्रतिभा और कौशल से है। अगर आपके पास योग्यता है। तो शेष सब बातें बेमानी हैं।

बाजारी वितरण के पक्ष में एक तर्क यह रखा जाता है कि यह हमें अधिक विकल्प प्रदान करता है। इसमें शक नहीं कि बाजार प्रणाली उपभोक्ता के तौर पर हमें अधिक विकल्प देती है। हम जैसा चाहें वैसा चावल पसन्द कर सकते हैं और रुचि के अनुसार विद्यालय जा सकते हैं, बशर्ते उनकी कीमत चुकाने के लिए हमारे पास साधन हों। लेकिन, बुनियादी वस्तुओं और सेवाओं के मामले में महत्त्वपूर्ण बात यह है कि अच्छी गुणवत्ता की वस्तुएँ और सेवाएँ लोगों के खरीदने लायक कीमत पर उपलब्ध हों। यदि निजी एजेंसियाँ इसे अपने लिए लाभदायक नहीं पाती हैं, तो वे उसे विशिष्ट बाजार में प्रवेश नहीं करेंगी अथवा सस्ती और घटिया सेवाएँ उपलब्ध कराएँगी। यही वजह है कि सुदूर ग्रामीण इलाकों में बहुत कम निजी विद्यालय हैं और कुछ खुले भी हैं; तो वे निम्नस्तरीय हैं। स्वास्थ्य सेवा और आवास के मामले में भी सच यही है। इन परिस्थितियों में सरकार को हस्तक्षेप करना पड़ता है।

मुक्त बाजार और निजी उद्यम के पक्ष में अक्सर सुनने में आने वाला दूसरा तर्क यह है कि वे जो सेवाएँ उपलब्ध कराते हैं, उनकी गुणवत्ता सरकारी संस्थानों द्वारा प्रदत्त सेवाओं से प्रायः अच्छी होती हैं। लेकिन इन सेवाओं की कीमत उन्हें गरीब लोगों की पहुँच से बाहर कर सकती है। निजी व्यवसाय वहीं जाना चाहता है, जहाँ उसे सर्वाधिक लाभ मिले और इसीलिए मुक्त बाजार ताकतवर, धनी और प्रभावशाली लोगों के हित में काम करने के लिए प्रवृत्त होता है। इसका परिणाम अपेक्षाकृत कमजोर और सुविधाहीन लोगों के लिए अवसरों का विस्तार करने की अपेक्षा अवसरों से वंचित करना हो सकता है।

तर्क तो वाद-विवाद दोनों पक्षों के लिए प्रस्तुत किए जा सकते हैं, लेकिन मुक्त बाजार साधारणतया पूर्व से ही सुविधासम्पन्न लोगों के हक में काम करने का रुझान दिखाते हैं। इसी कारण अनेक लोग तर्क करते हैं कि सामाजिक न्याय सुनिश्चित करने के लिए राज्य को यह सुनिश्चित करने की पहल करनी चाहिए कि समाज के सदस्यों को बुनियादी सुविधाएँ उपलब्ध हों।

We hope the UP Board Solutions for Class 11 Political Science Political theory Chapter 4 Social Justice (सामाजिक न्याय) help you. If you have any query regarding UP Board Solutions for Class 11 Political Science Political theory Chapter 4 Social Justice (सामाजिक न्याय), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Political Science Political theory Chapter 3 Equality (समानता)

These Solutions are part of UP Board Solutions for Class 11 Political Science. Here we have given UP Board Solutions for Class 11 Political Science Political theory Chapter 3 Equality (समानता).

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1.
कुछ लोगों का तर्क है कि असमानता प्राकृतिक है जबकि कुछ अन्य का कहना है कि वास्तव में समानता प्राकृतिक है और जो असमानता हम चारों ओर देखते हैं उसे समाज ने पैदा किया है। आप किस मत का समर्थन करते हैं? कारण दीजिए।
उत्तर-
प्राकृतिक असमानताएँ लोगों की जन्मजात विशिष्टताओं और योग्यताओं का परिणाम मानी जाती हैं। यह कथन सत्य है। इसे हम बदल नहीं सकते। दूसरी ओर वे सामाजिक असमानताएँ हैं जिन्हें समाज ने बदल दिया है। उदाहरण के लिए, कुछ समाज बौद्धिक कार्य करने वालों को शारीरिक कार्य करने वालों से अधिक महत्त्व देते हैं और उन्हें अलग तरीके से लाभ देते हैं। वे विभिन्न वंश, रंग या जाति के लोगों के साथ भिन्न-भिन्न व्यवहार करते हैं। हम इसी मत का समर्थन करते हैं क्योंकि बौद्धिक कार्य करने वाले पहले कार्य की संरचना करते हैं तभी शारीरिक कार्य करना सम्भव होता है।

प्रश्न 2.
एक मत है कि पूर्ण आर्थिक समानता न तो सम्भव है और न ही वांछनीय। एक समाज ज्यादा-से-ज्यादा बहुत अमीर और बहुत गरीब लोगों के बीच की खाई को कम करने का प्रयास कर सकता है। क्या आप इस तर्क से सहमत हैं? अपना तर्क दीजिए।
उत्तर-
हम इस तर्क से सहमत हैं। अगर किसी समाज में कुछ विशिष्ट वर्ग के लोग पीढ़ियों से बेशुमार धन-दौलत और इसके साथ प्राप्त होने वाली सत्ता का उपयोग करते हैं, तो समाज वर्गों में बँट जाता है। एक ओर वे, जो पीढ़ियों से धन, विशेषाधिकार और सता का उपयोग करते आए हैं और दूसरी ओर अन्य जो पीढ़ियों से गरीब बने हुए हैं। कालक्रम में यह वर्ग भेद, आक्रोश और हिंसा को बढ़ावा दे सकता है। इसलिए अमीरी-गरीबी के बीच की खाई को कम करने के प्रयास किए जा सकते हैं, इसे पाटा नहीं जा सकता।

प्रश्न 3.
नीचे दी गई अवधारणा और उसके उचित उदाहरणों में मेल बैठाएँ
(क) सकारात्मक कार्यवाही – (1) प्रत्येक वयस्क नागरिक को मत देने का अधिकार है।
(ख) अवसर की समानता – (2) बैंक वरिष्ठ नागरिकों को ब्याज की ऊँची दर देते हैं।
(ग) समान अधिकार – (3) प्रत्येक बच्चे को निःशुल्क शिक्षा मिलनी चाहिए।
उत्तर-
(ख) 1, (ग) 2, (क) 3.

प्रश्न 4.
किसानों की समस्या से सम्बन्धित एक सरकारी रिपोर्ट के अनुसार छोटे और सीमान्त किसानों को बाजार से अपनी उपज का उचित मूल्य नहीं मिलता। रिपोर्ट में सलाह दी गई कि सरकार को बेहतर मूल्य सुनिश्चित करने के लिए हस्तक्षेप करना चाहिए। लेकिन यह प्रयास केवल लघु और सीमान्त किसानों तक ही सीमित रहना चाहिए। क्या यह सलाह समानता के सिद्धान्त से सम्भव है?
उत्तर-
समानता के विषय पर सोचते समय हमें प्रत्येक व्यक्ति को बिल्कुल एक जैसा मानने और प्रत्येक व्यक्ति को मूलतः समान मानने में अन्तर करना चाहिए। मूलतः समान व्यक्तियों को विशेष स्थितियों में अलग-अलग व्यवहार की आवश्यकता हो सकती है। लेकिन ऐसे सभी मामलों में सर्वोपरि उद्देश्य समानता को बढ़ावा देना हो होगा। समानता के लक्ष्य को पाने के लिए अलग या विशे बर्ताव के बारे में सोंचा जा सकता है। इसके लिए औचित्य सिद्ध करना और सावधानीपूर्वक पुनर्विचार आवश्यक होता है।

प्रश्न 5.
निम्नलिखित में से किस में समानता के किस सिद्धान्त का उल्लंघन होता है और क्यों?
(क) कक्षा का हर बच्चा नाटक का पाठ अपना क्रम आने पर पढ़ेगा।
(ख) कनाडा सरकार ने दूसरे विश्वयुद्ध की समाप्ति से 1960 तक यूरोप के श्वेत नागरिकों को कनाड़ा में आने और बसने के लिए प्रोत्साहित किया।
(ग) वरिष्ठ नागरिकों के लिए अलग से रेलवे आरक्षण की एक खिड़की खेली गई।
(घ) कुछ वन क्षेत्रों को निश्चित आदिवासी समुदायों के लिए आरक्षित कर दिया गया है।
उत्तर-
(घ) में प्राकृतिक समानता के सिद्धान्त का उल्लंघन हुआ। वन क्षेत्र प्राकृतिक है, इस पर सभी का समान अधिकार है पर इसे आदिवासियों के लिए आरक्षित कर दिया गया है।

प्रश्न 6.
यहाँ महिलाओं को मताधिकार देने के पक्ष में कुछ तर्क दिए गए हैं। इनमें से कौन-से तर्क समानता के विचार से संगत हैं। कारण भी दीजिए।
(क) स्त्रियाँ हमारी माताएँ हैं। हम अपनी माताओं को मताधिकार से वंचित करके अपमानित नहीं करेंगे।
(ख) सरकार के निर्णय पुरुषों के साथ-साथ महिलाओं को भी प्रभावित करते हैं इसलिए शासकों के चुनाव में उनका भी मत होना चाहिए।
(ग) महिलाओं को मताधिकार न देने से परिवारों में मदभेद पैदा हो जाएँगे।
(घ) महिलाओं से मिलकर आधी दुनिया बनती है। मताधिकार से वंचित करके लम्बे समय तक उन्हें दबाकर नहीं रखा जा सकता है।
उत्तर-
(ख) तर्क समानता के विचार से संगत है। वास्तव में शासकीय निर्णय सम्पूर्ण समाज को प्रभावित करते हैं, इनमें महिलाएँ भी होती हैं इसलिए उन्हें मताधिकार से वंचित नहीं किया जाना चाहिए।
(घ) संसार में महिलाओं की भी पर्याप्त संख्या है ऐसे में उन्हें मताधिकार से दीर्घकाल के लिए वंचित नहीं किया जा सकता।

परीक्षोपयोगी प्रश्नोत्तर

बहुविकल्पीय प्रश्न
प्रश्न 1.
समानता का सही अर्थ क्या है?
(क) प्रत्येक व्यक्ति को अपने सही विकास के लिए समान सुविधाएँ प्राप्त हों और देश के
कानून के समक्ष सभी समान हों।
(ख) सभी को समान मजदूरी व सम्पत्ति प्राप्त हो
(ग) सभी को निवास की सुविधा
(घ) सभी को समान शिक्षा व रोजगार
उत्तर-
(क) प्रत्येक व्यक्ति को अपने सही विकास के लिए समान सुविधाएँ प्राप्त हों और देश के कानून के समक्ष सभी समान हों।

प्रश्न 2.
नागरिक या कानूनी समानता निम्नलिखित में किसकी विशेषता है?
(क) सभी प्रजातान्त्रिक सरकारों की
(ख) सभी प्रकार की सरकारों की
(ग) केवल तानाशाही सरकारों की
(घ) जिन देशों में लिखित संविधान है।
उत्तर-
(क) सभी प्रजातान्त्रिक सरकारों की।

प्रश्न 3.
कानून के समक्ष समानता निम्नलिखित श्रेणियों में किसके अन्तर्गत हैं?
(क) राजनीतिक समानता के अन्तर्गत
(ख) सामाजिक समानता के अन्तर्गत ।
(ग) नागरिक समानता के अन्तर्गत
(घ) आर्थिक समानता के अन्तर्गत
उत्तर-
(ग) नागरिक समानता के अन्तर्गत।

प्रश्न 4.
नकारात्मक दृष्टि से समानता का क्या अर्थ है?
(क) विशेष अधिकारों का अभाव
(ख) कमजोर वर्ग के लिए विशेष अधिकारों का प्रावधान
(ग) शासक वर्ग के लिए विशेष सुविधाओं की व्यवस्था
(घ) इनमें से कोई नहीं
उत्तर-
(क) विशेष अधिकारों का अभाव।

प्रश्न 5.
समानता को सकारात्मक अर्थ क्या है?
(क) समाज के सभी सदस्यों की प्राथमिक आवश्यकताओं की पूर्ति
(ख) सभी के लिए पर्याप्त अवसरों की व्यवस्था
(ग) समानता जो कानून की शक्ति द्वारा समर्थित होती है।
(घ) प्रकृति प्रदत्त समानता
उत्तर-
ख) सभी के लिए पर्याप्त अवसरों की व्यवस्था।

प्रश्न 6.
सामाजिक समानता का क्या अर्थ है?
(क) प्रत्येक व्यक्ति अपनी क्षमता के अनुसार कार्य करे
(ख) वर्तमान सामाजिक व्यवस्था को बदलने का कोई प्रयत्न न हो
(ग) जाति व धर्म के अन्तर के कारण किसी भी व्यक्ति को हीनता के भाव से पीड़ित न होना पड़े
(घ) कमजोर वर्ग की आर्थिक उन्नति के लिए विशेष प्रयत्न हों।
उत्तर-
(ग) जाति व धर्म के अन्तर के कारण किसी भी व्यक्ति को हीनता के भाव से पीड़ित न होना पड़े।

प्रश्न 7.
“आर्थिक समानता के अभाव में राजनीतिक स्वतन्त्रता केवल एक भ्रम है।” यह मत किसका है?
(क) प्लेटो
(ख) मार्क्स
(ग) कोल
(घ) लॉस्की
उत्तर-
(ग) कोल।

प्रश्न 8.
“स्वतन्त्रता तथा समानता एक-दूसरे की विरोधी हैं।” यह कथन किसका है?
(क) लॉर्ड एक्टन
ख) लॉस्की
(ग) कार्ल मार्क्स
(घ) प्लेटो
उत्तर-
(क) लॉर्ड एक्टन।

प्रश्न 9.
‘एक व्यक्ति एक वोट का सिद्धान्त किससे सम्बन्धित है? |
(क) आर्थिक समानता ।
(ख) राजनीतिक समानता
(ग) सामाजिक समानता
(घ) नागरिक समानता
उत्तर-
(ख) राजनीतिक समानता।

प्रश्न 10.
“समानता की उत्कट अभिलाषा के कारण स्वतन्त्रता की आशा ही व्यर्थ हो गई है। यह कथन किस विद्वान का है?
(क) लॉर्ड एक्टन
(ख) लासवैल
(ग) डेविड ईस्टन
(घ) फाइनर
उत्तर-
(क) लॉर्ड एक्टन।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
सामाजिक समानता का अर्थ लिखिए।
उत्तर–
प्रत्येक व्यक्ति को समाज में रहकर अपने सर्वांगीण विकास का अवसर प्राप्त होना ही सामाजिक समानता के अर्थ का परिचायक है।

प्रश्न 2.
समानता के दो प्रकार लिखिए।
उत्तर–
समानता के दो प्रकार हैं
(i) राजनीतिक समानता, तथा
(ii) आर्थिक समानता।

प्रश्न 3.
“स्वतन्त्रता और समानता एक-दूसरे की पूरक हैं।” एक तर्क दीजिए।
उत्तर-
लोकतन्त्र की सफलता के लिए स्वतन्त्रता और समानता दोनों ही आवश्यक हैं, इसलिए ये दोनों एक-दूसरे की पूरक हैं।

प्रश्न 4.
समानता के अधिकार को भारत के संविधान में किस अनुच्छेद से किस अनुच्छेद तक वर्णित किया गया है?
उत्तर-
समानता के अधिकार को भारतीय संविधान में अनुच्छेद 14 से 18 तक वर्णित किया गया है।

प्रश्न 5.
“आर्थिक स्वतन्त्रता के बिना राजनीतिक स्वतन्त्रता एक भ्रम है।” यह कथन किसका है?
उत्तर-
यह कथन प्रो० सी०ई०एम० जोड का है।

प्रश्न 6.
समानता के किसी एक प्रकार का वर्णन कीजिए।
उत्तर-
समानता का एक प्रकार है—प्राकृतिक समानता।

प्रश्न 7.
नागरिक समानता का क्या अर्थ है?
उत्तर-
नागरिक समानता का अर्थ है कि राज्य प्रत्येक नागरिक को वंश, जाति, धर्म, लिंग इत्यादि के आधार पर बिना भेदभाव किए समान रूप से नागरिक अधिकार प्रदान करे।

प्रश्न 8.
राजनीतिक समानता से क्या तात्पर्य है?
उत्तर–
राजनीतिक समानता से तात्पर्य है–समान राजनीतिक अधिकार।

प्रश्न 9.
प्राकृतिक समानता से क्या तात्पर्य है?
उत्तर–
प्राकृतिक समानता का अभिप्राय है कि प्रकृति ने सभी मनुष्यों को समान बनाया है।

प्रश्न 10.
सकारात्मक समानता से क्या अभिप्राय है?
उत्तर-
सकारात्मक समानता से अभिप्राय है कि प्रत्येक व्यक्ति को बिना किसी भेदभाव के विकास के समान अवसर प्रदान किए जाएँ।

लघु उत्तरीय प्रश्न

प्रश्न 1.
समानता के मार्क्सवादी दृष्टिकोण को संक्षेप में समझाइए।
उत्तर-
समानता के सन्दर्भ में मार्क्सवादी दृष्टिकोण इस बात का प्रतिपादन करता है कि जब तक समाज में विरोधी वर्गों का अस्तित्व रहेगा तब तक किसी भी रूप में समानता की स्थापना नहीं की जा सकती है। आर्थिक समानता को तब तक लागू नहीं किया जा सकता जब तक कि पूँजीवादी व्यवस्था पर आधारित व्यक्तिगत पूँजी को समाप्त करके उत्पादन, वितरण विनिमय के साधनों को समाज के सभी वर्गों में विभक्त न कर दिया जाए। अत: मार्क्सवादी आर्थिक असमानता को भी समाज में एक वर्ग के द्वारा दूसरे वर्ग के शोषण एवं उत्पीड़न के लिए उत्तरदायी मानता है। माक्र्स को यह भी मत है कि पूँजीवादी राज्यों में राजनीतिक एवं सामाजिक समानता का जो आडम्बर रचा जा रहा है उसने पूर्णतया भ्रमपूर्ण स्थिति उत्पन्न कर दी है। क्योंकि आर्थिक समानता के अभाव में किसी प्रकार की भी समानता स्थापित नहीं की जा सकती है।

प्रश्न 2.
नकारात्मक समानता का संक्षेप में वर्णन कीजिए।
उत्तर–
सामान्य रूप में नकारात्मक स्वतन्त्रता का अर्थ है, ‘विशेषाधिकारों का अन्त’। समाज के किसी वर्ग-विशेष को जन्म, धर्म, जाति या रंग के आधार पर किसी प्रकार के विशेष अधिकार प्रदान न किए जाएँ, तो यह नकारात्मक समानता का द्योतक है। राज्य को चाहिए कि वह बिना भेदभाव के नागरिकों को व्यक्ति के विकास के समान अवसर प्रदान करे। लोगों में प्राकृतिक कारणों से अर्थात् जन्मजात असमानता हो सकती है, परन्तु अप्राकृतिक कारणों से अर्थात् पैतृक परिस्थितियों अथवा राज्य द्वारा किए गए भेदभाव के परिणामस्वरूप किसी प्रकार की असमानता नहीं होनी चाहिए। छुआछूत का अन्त व सबको शैक्षणिक संस्थाओं में प्रवेश का अधिकार नकारात्मक समानता के उदाहरण हैं।

प्रश्न 3.
सकारात्मक समानता का संक्षेप में वर्णन कीजिए।
उत्तर–
सामान्यतया इसका अर्थ है कि प्रत्येक व्यक्ति को उसके व्यक्तित्व के विकास हेतु पर्याप्त अवसर मिलें तथा राज्य के द्वारा उनमें कोई बाधा उत्पन्न न की जाए। यदि सभी को समान अवसर न मिलें तो मनुष्य का सर्वांगीण विकास नहीं हो सकता है। प्रत्येक व्यक्ति को अपनी योग्यता व प्रतिभा विकसित करने का समान अवसर प्राप्त होना चाहिए। लॉस्की के अनुसार, “समानता का तात्पर्य एक-सा व्यवहार करना नहीं, इसका तो आग्रह इस बात के लिए है कि मनुष्यों को सुख का समान अधिकार प्राप्त होना चाहिए। उनके अधिकारों में किसी प्रकार का आधारभूत अन्तर स्वीकार नहीं किया जा सकता है। समानता मूलतः समाजीकरण की एक प्रक्रिया है—प्रथमतः इसका अभिप्राय विशेषाधिकारों की समाप्ति है -” और दूसरे, व्यक्तियों को विकास के पर्याप्त एवं समान अवसर उपलब्ध कराने से है।”
इस प्रकार राजनीति विज्ञान के समानता का तात्पर्य ऐसी परिस्थितियों के अस्तित्व से होता है जिससे व्यक्तियों को अपने व्यक्तित्व के विकास के समान अवसर मिलें, जिससे असमानता का अन्त हो जाए जिसका मूल सामाजिक असमानता है।

प्रश्न 4.
कानून के समक्ष समानता के सिद्धान्त को स्पष्ट कीजिए।
उत्तर-
कानून के समक्ष समानता का अर्थ होता है कि कानून के समक्ष सभी व्यक्ति समान है तथा इसके अन्तर्गत सभी व्यक्तियों के लिए राज्य समान कानून बनाता है तथा उन्हें समान रूप से लागू करता है। कानून के सम्बन्ध में राज्य धनी-निर्धन, ऊँच-नीच, गोरे-काले, साक्षर-निरक्षर आदि का कोई भेद नहीं करता है। जन्म, वंश, लिंग तथा जन्म-स्थान के आधार पर कानून किसी भी व्यक्ति को प्राथमिकता प्रदान नहीं करता है। पश्चिम बंगाल बनाम अनवर अली के मुकदमे में भारतीय उच्चतम न्यायालय ने कहा था कि समान परिस्थितियों में सभी लोगों के साथ कानून का व्यवहार एक-सा होना चाहिए। कानूनी समानता के सम्बन्ध में इसी प्रकार की बात डायसी ने भी कही थी। डायसी के शब्दों में, “हमारे देश में प्रत्येक अधिकारी चाहे वह प्रधानमंत्री हो या पुलिस का सिपाही अथवा का वसूल करने वाला, अवैधानिक कार्यों के लिए उतना ही दोषी माना जाएगा, जितना कि कोई अन्य नागरिका”

प्रश्न 5.
आर्थिक समानता के किन्हीं पाँच तत्त्वों का उल्लेख कीजिए।
उत्तर–
आर्थिक समानता के पाँच तत्त्व निम्नलिखित हैं

1.  प्रत्येक व्यक्ति की न्यूनतम भौतिक आवश्यकताओं की पूर्ति होनी चाहिए; जैसे-वस्त्र, भोजन तथा आवास आदि की सुविधाएँ।
2.  प्रत्येक व्यक्ति को रोजगार, पर्याप्त मजदूरी तथा विश्राम के लिए पर्याप्त अवकाश प्राप्त होना चाहिए।
3.  समान कार्य के लिए समान वेतन मिलना चाहिए।
4.  बेकारी, वृद्धावस्था, बीमारी व अन्य ऐसी स्थितियों में लोगों को राज्य की ओर से आर्थिक सहायता मिलनी चाहिए।
5.  विभिन्न लोगों में आर्थिक विषमता की दूरी कम-से-कम होनी चाहिए।

प्रश्न 6.
नीचे दी गई तालिका में विभिन्न समुदायों की शैक्षिक स्थिति से जुड़े कुछ आँकड़े दिए गए हैं। इन समुदायों की शैक्षिक स्थिति में जो अन्तर हैं, क्या वे महत्त्वपूर्ण हैं? क्या इन अन्तरों का होना केवल एक संयोग है या ये अन्तर जाति-व्यवस्था केअसर की ओर संकेत करते हैं? आप यहाँ जाति-व्यवस्था के अलावा और किन कारणों का प्रभाव देखते हैं।
शहरी भारत में उच्च शिक्षा में जातिगत समुदायों में असमानता

स्रोत- नेशनल सेम्पल सर्वे आर्गेनाइजेशन, 55 वाँ राउण्ड सर्वे,1999-2000.
उत्तर–
शैक्षिक स्थिति में अन्तर महत्त्वपूर्ण हैं, क्योंकि सभी को शिक्षा का समान अधिकार प्राप्त है। फिर भी यह अन्तर बना हुआ है जो हमारी शिक्षा व्यवस्था की कमियों पर हमारा ध्यान आकृष्ट करता है। इन अन्तरों का होना संयोग नहीं है। यह असफल शिक्षा प्रणाली का परिणाम है। इसका अन्य कारण
आर्थिक असमानता, जागरूकता की कमी भी है।

प्रश्न 7.
इन चित्रों पर एक नजर डालें।

ये चित्र क्या संकेत करते हैं?
उत्तर-
ये चित्र मनुष्यों के बीच नस्ल और रंग के आधार पर भेदभाव की ओर संकेत करते हैं। यह हममें से अधिकांश को अस्वीकार्य हैं। वास्तव में इस प्रकार का भेदभाव समानता के हमारे आत्म-बोध का उल्लंघन करता है। समानता का हमारा आत्म-बोध कहता है कि साझी मानवता के कारण सभी मनुष्य बराबर, सम्मान और परवाह के हकदार हैं।

प्रश्न 9.
अवसरों की समानता से क्या आशय है?
उत्तर-
अवसरों की समानता-
समानता की अवधारणा में यह निश्चित है कि सभी मनुष्य अपनी दक्षता और प्रतिभा को विकसित करने के लिए तथा अपने लक्ष्यों और आकांक्षाओं को पूरा करने के लिए समान अधिकार और अवसरों के हकदार हैं। इसका आशय यह है कि समाज में लोग अपनी पसन्द और प्राथमिकताओं के मामलों में अलग हो सकते हैं। उनकी प्रतिभा और योग्यताओं में भी अन्तर हो सकता है और हो सकता है इस कारण कुछ लोग अपने चुने हुए क्षेत्रों में शेष लोगों से अधिक सफल हो जाएँ। लेकिन केवल इसलिए कि कोई क्रिकेट में पहले पायदान पर पहुँच गया है या कोई बहुत सफल वकील बन गया है, समाज को असमान नहीं माना जा सकता। दूसरे शब्दों, में सामाजिक दर्जा, सम्पत्ति या विशेषाधिकारों में समानता का अभाव होना महत्त्वपूर्ण नहीं है लेकिन शिक्षा, स्वास्थ्य और सुरक्षित आवास जैसी बुनियादी चीजों की उपलब्धता में असमानताओं से कोई समाज असमान और अन्यायपूर्ण बनता है।

प्रश्न 10.
नीचे दी गई स्थितियों पर विचार करें। कया इनमें से किसी भी स्थिति में विशेष और विभेदकारी बरताव करना न्यायोचित होगा? ।

कामकाजी महिलाओं को मातृत्व अवकाश मिलना चाहिए।

•  एक विद्यालय में दो छात्र दृष्टिहीन हैं। विद्यालय को उनके लिए कुछ विशेष उपकरण खरीदने के लिए धनराशि खर्च करनी चाहिए।
• गीता बास्केटबॉल बहुत अच्छा खेलती है। विद्यालय को उसके लिए बॉस्केटबॉल कोर्ट | बनाना चाहिए जिससे वह अपनी योग्यता को और भी विकास कर सके।
• जीत के माता-पिता चाहते हैं कि वह पगड़ी पहने। इरफान चाहता है कि वह जुम्मे (शुक्रवार) को नमाज पढे, ऐसी बातों को ध्यान में रखते हुए स्कूल को जीत से यह आग्रह नहीं करना चाहिए कि वह क्रिकेट खेलते समय हेलमेट पहने और इरफान के अध्यापक को शुक्रवार को उससे दोपहर बाद की कक्षाओं के लिए रुकने को नहीं कहना चाहिए।

उत्तर-
कामकाजी महिलाओं को मातृत्व अवकाश मिलना चाहिए; इस स्थिति में विभेदकारी बरताव करना न्यायोचित होगा शेष प्रकरणों में विभेदकारी बरताव आवश्यक नहीं

दीर्घ लघु उत्तरीय प्रश्न

प्रश्न 1.
समानता से क्या आशय है? समानता के अन्तर्गत कौन-सी बातें आती हैं।
उत्तर–
समानती का वास्तविक अर्थ है कि सभी व्यक्तियों को अपने विकास के लिए समान सुअवसर प्राप्त हों। जन्म, सम्पत्ति, जाति, धर्म, रंग आदि के आधार पर जो सामाजिक जीवन के कृत्रिम आधार हैं। व्यक्ति में विभेद न किया जाए अर्थात् राज्य सभी नागरिकों को किसी प्रकार के भेदभाव के बिना उसकी बुद्धि और व्यक्तित्व के पूर्ण विकास के लिए समुचित अवसर प्रदान करे। आकांक्षा और योग्यता के रहते किसी व्यक्ति के विकास में बाधा नहीं आनी चाहिए। समानता के अन्तर्गत तीन मौलिक बातें आती हैं
प्रथम, किसी नागरिक, समुदाय, वर्ग या जाति के विरुद्ध किसी प्रकार की वैधिक अनर्हता (disqualification) नहीं रखनी चाहिए। द्वितीय, सभी को उन्नति और विकास के अवसर दिए जाएँ।
तृतीय, सभी को शिक्षा, आवास, भोजन और प्राथमिक सुविधाओं की प्राप्ति का पूरा-पूरा हक हो।” समानता की व्याख्या करते हुए लॉस्की ने कहा है-“समानता का पहला अर्थ है कि समाज में कोई विशेष हित वाला न हो, दूसरा प्रत्येक व्यक्ति को उन्नति के समान अवसर प्राप्त हों।

प्रश्न 2.
“आर्थिक समानता के अभाव में राजनीतिक स्वतन्त्रता निरर्थक है।” स्पष्ट कीजिए।
या आर्थिक समानता के बिना राजनीतिक स्वतन्त्रता एक भ्रम है।” इस कथन की विवेचना कीजिए।
उत्तर-
प्रो० लॉस्की ने लिखा है, “राजनीतिक समानता आर्थिक समानता के बिना निरर्थक है; क्योंकि राजनीतिक शक्ति आवश्यक रूप से आर्थिक शक्ति के हाथों में खिलवाड़ ही सिद्ध होगी। यदि व्यक्ति को समस्त राजनीतिक अधिकार; जैसे-मतदान का, चुनाव में प्रत्याशी होने का, सार्वजनिक पद धारण करने का आदि दे दिए जाएँ परन्तु उसे पेट भर खाना न मिले तो उसके लिए सम्पूर्ण प्रदत्त राजनीतिक अधिकार व्यर्थ हैं। एक गरीब व्यक्ति का धर्म, ईमान व राजनीति आदि सब-कुछ रोटी तक ही सीमित हैं। भारत में नागरिकों को मत अधिकार है पर रोजी छोड़कर मतदान केन्द्र पर जाने का परिणाम क्या होगा। लोगों को चुनाव में खड़े होने का अधिकार है, किन्तु चुनाव कितने महँगे होते हैं। क्या एक सामान्य व्यक्ति चुनाव लड़ सकता है। सामान्य व्यक्ति के पास जीवन-यापन करने के सीमित साधन होते हैं, फिर वह राजनीतिक अधिकारों का कैसे उपभोग करेगा? समाजवादी विचारक इस बात पर बल देते हैं कि आर्थिक स्वतन्त्रता के बिना राजनीतिक स्वन्तत्रता व्यर्थ है। राजनीतिक स्वतन्त्रता की उपलब्धि के लिए आर्थिक सुरक्षा की व्यवस्था की जानी चाहिए। आर्थिक विषमता को समाप्त करना। चाहिए जिससे मनुष्य का शोषण न हो।

प्रश्न 3.
समाजवाद क्या है? लोहिया की सप्तक्रान्तियाँ क्या थीं?
उत्तर–
समाजवाद असमानताओं के जवाब में उत्पन्न हुए कुछ राजनीतिक विचारों का समूह है। ये विशेषकर वे असमानताएँ थीं, जो औद्योगिक पूँजीवादी अर्थव्यवस्था से उत्पन्न हुईं और उसमें बाद तक बनी रहीं। समाजवाद का मुख्य उद्देश्य वर्तमान असमानताओं को न्यूनतम करना और संसाधनों का न्यायपूर्ण विभाजन है। हालाँकि समाजवाद के पक्षधर पूरी तरह से बाजार के विरुद्ध तो नहीं होते, लेकिन वे शिक्षा और स्वास्थ्य सेवा जैसे आधारभूत क्षेत्रों में सरकारी नियमन, नियोजन और नियन्त्रण का समर्थन अवश्य करते हैं।
भारत में प्रमुख समाजवादी चिन्तक राममनोहर लोहिया ने पाँच प्रकार की असमानताओं की पहचान की, जिनके विरुद्ध एक साथ लड़ना होगा-स्त्री-पुरुष असमानता, त्वचा के रंग पर आधारित असमानता, जातिगत असमानता, कुछ देशों का अन्य पर औपनिवेशिक शासन और नि:सन्देह आर्थिक असमानता है। यह आज स्वप्रमाणितं धारण लग सकती है, लेकिन लोहिया के समय में, समाजवादियों के बीच आमतौर पर यही तर्क चलता था कि असमानता का एकमात्र रूप वर्गीय असमानता है जिसके विरुद्ध संघर्ष अपरिहार्य है। दूसरी असमानताएँ गौण हैं या आर्थिक असमानता के समाप्त होते ही वे स्वतः समाप्त हो जाएगी। लोहिया का कहना था कि इन असमानताओं में से प्रत्येक की अलग-अलग जड़े हैं और इन सबके विरुद्ध अलग-अलग लेकिन एक साथ संघर्ष छेड़ने होंगे। उन्होंने एकांगी क्रान्ति की बात नहीं कही। उनके लिए उपर्युक्त पाँच असमानताओं के विरुद्ध संघर्ष का अर्थ था—पाँच क्रान्तियाँ। उन्होंने इस सूची में दो और क्रान्तियों को शामिल किया–व्यक्तित्व जीवन पर अन्यायपूर्ण अतिक्रमण के विरुद्ध नागरिक स्वतन्त्रता के लिए क्रान्ति तथा अंहिसा के लिए सत्याग्रह के पक्ष में शस्त्र त्याग के लिए क्रान्ति। ये ही सप्तक्रान्तियाँ थीं। यही लोहिया के अनुसार समाजवाद का आदर्श है।

दीर्घ उतरीय प्रश्न

प्रश्न 1.
समानता के कितने प्रकार होते हैं?
या समानता के विविध रूपों का विवेचन कीजिए। \
उत्तर-
समानता के भेद अथवा प्रकार
समानता के विभिन्न भेदों का संक्षिप्त विवरण निम्नलिखित है

1. प्राकृतिक समानता– प्लेटो के अनुसार, “प्राकृतिक समानता से अभिप्राय यह है कि सब मनुष्य जन्म से समान होते हैं। स्वाभाविक रूप से सभी व्यक्ति समान हैं, हम सबका निर्माण एक ही विश्वकर्मा ने एक ही मिट्टी से किया है। हम चाहे अपने को कितना ही धोखा दें, ईश्वर को निर्धन, किसान और शक्तिशाली राजकुमार सभी समान रूप से प्रिय हैं।”
आधुनिक युग में प्राकृतिक समानता को कोरी कल्पना माना जाता है। कोल के अनुसार, “मनुष्य शारीरिक बल, पराक्रम, मानसिक योग्यता, सृजनात्मक शक्ति, समाज-सेवा की भावना और सम्भवतः सबसे अधिक कल्पना-शक्ति में एक-दूसरे से मूलतः भिन्न हैं।” संक्षेप में, वर्तमान युग में प्राकृतिक समानता का आशय यह है कि प्राकृतिक रूप से नैतिक आधार पर ही सभी व्यक्ति समान हैं तथा समाज में व्याप्त विभिन्न प्रकार की असमानताएँ कृत्रिम हैं।

2. सामाजिक समानता- सामाजिक समानता का अर्थ यह है कि प्रत्येक व्यक्ति को समाज में
समान अधिकार प्राप्त हों और सबको समान सुविधाएँ मिलें। जिस समाज में जन्म, जाति, धर्म, लिंग इत्यादि के आधार पर भेदभाव नहीं किया जाता, वहाँ सामाजिक समानता होती है। संयुक्त राष्ट्र संघ के द्वारा जो मानव-अधिकारों की घोषणा की गयी है, उसमें सामाजिक समानता पर
विशेष बल दिया गया है।

3. नागरिक या कानूनी समानता– नागरिक समानता का अर्थ नागरिकता के समान अधिकारों से होता है। नागरिक समानता के लिए यह आवश्यक है कि सब नागरिकों के मूलाधिकार सुरक्षित हों तथा सभी नागरिकों को समान रूप से कानून का संरक्षण प्राप्त हो। नागरिक समानता की पहली अनिवार्यता यह है कि समस्त नागरिक कानून के समक्ष समान हों। यदि कानून धन, पद, जाति अथवा अन्य किसी आधार पर भेद करता है तो उससे नागरिक समानता समाप्त हो जाती है और नागरिकों में असमानता का उदय होता है।

4. राजनीतिक समानता- जब राज्य के सभी नागरिकों को शासन में भाग लेने का समान अधिकार प्राप्त हो तो वहाँ के लोगों को राजनीतिक समानता प्राप्त रहती है। राजनीतिक समानता के अनुसार प्रत्येक व्यक्ति को मत देने, निर्वाचन में खड़े होने तथा सरकारी नौकरी प्राप्त करने का समान अधिकार होता है। उनके साथ जाति, धर्म या अन्य किसी आधार पर कोई भेदभाव नहीं किया जाता। राजनीतिक समानता लोकतन्त्र की आधारशिला होती है।

5. धार्मिक समानता- धार्मिक समानता का अर्थ यह है कि धार्मिक मामलों में राज्य तटस्थ हो और सब नागरिकों को अपनी इच्छा से धर्म मानने की स्वतन्त्रता हो। राज्य धर्म के आधार पर | किसी प्रकार का भेदभाव न करे। प्राचीन और मध्यकाल में इस प्रकार की धार्मिक समानता का
अभाव था, परन्तु आज धर्म और राजनीति एक-दूसरे से अलग हो गये हैं और सामान्यत: राज्य नागरिकों के धार्मिक जीवन में हस्तक्षेप नहीं करता।

6. आर्थिक समानता- आर्थिक समानता का अभिप्राय यह है कि समाज में धन के वितरण की उचित व्यवस्था हो तथा मनुष्यों की आय में बहुत अधिक असमानता नहीं होनी चाहिए। लॉस्की के अनुसार, “आर्थिक समानता का अभिप्राय यह है कि राज्य में सभी को समान सुविधाएँ तथा अवसर प्राप्त हों।” इस सन्दर्भ में लॉर्ड ब्राइस का मत है कि “समाज से सम्पत्ति के सभी भेदभाव समाप्त कर दिये जाएँ तथा प्रत्येक स्त्री-पुरुष को भौतिक साधनों एवं सुविधाओं का समान भाग दिया जाए।”
संक्षेप में, आर्थिक समानता से सम्बन्धित प्रमुख बातें इस प्रकार हैं—
(i) समाज में सभी को समान रूप से व्यवसाय चुनने की स्वतन्त्रता हो।
(ii) प्रत्येक मनुष्य को इतना वेतन या पारिश्रमिक अवश्य प्राप्त हो कि वह अपनी न्यूनतम आर्थिक आवश्यकताओं की पूर्ति कर सके।
(iii) राज्य में उत्पादन और उपभोग के साधनों का वितरण और विभाजन इस प्रकार से हो कि
आर्थिक शक्ति कुछ ही व्यक्तियों या वर्गों के हाथों में केन्द्रित न हो सके। सी० ई० एम० जोड के अनुसार, “स्वतन्त्रता का विचार, जो राजनीतिक विचारधारा में बहुत महत्त्वपूर्ण है, जब आर्थिक क्षेत्र में लागू किया गया तो उससे विनाशकारी परिणाम निकले, जिसके फलस्वरूप समाजवादी और साम्यवादी विचारधाराओं का उदय हुआ, जो आर्थिक समानता पर विशेष बल देती हैं और जिनकी यह निश्चित धारणा है कि आर्थिक समानता के अभाव में वास्तविक राजनीतिक स्वतन्त्रता कदापि प्राप्त नहीं हो सकती।” वास्तविकता यह है कि आर्थिक समानता सभी प्रकार की स्वतन्त्रताओं का आधार है और आर्थिक समानता के बिना राजनीत्रिक स्वतन्त्रता केवल एक भ्रम है। प्रो० जोड के अनुसार, “आर्थिक समानता के
बिना राजनीतिक स्वतन्त्रता एक भ्रम है।’ |
(iv) सुदृढ़ राजनीतिक एवं नागरिक समानता की कल्पना अपेक्षित आर्थिक समानता की पृष्ठभूमि
| पर ही की जा सकती है।

7. शैक्षिक एवं सांस्कृतिक समानता- शैक्षिक समानता का अभिप्राय यह है कि प्रत्येक व्यक्ति को शिक्षा प्राप्त करने तथा अन्य योग्यताएँ विकसित करने का समान अवसर मिलना चाहिए और शिक्षा के क्षेत्र में जाति, धर्म, वर्ण और लिंग के आधार पर कोई भेदभाव नहीं किया जाना चाहिए। समानता का तात्पर्य यह है कि सांस्कृतिक दृष्टि से बहुसंख्यक और अल्पसंख्यक सभी वर्गों को अपनी भाषा, लिपि और संस्कृति बनाये रखने का अधिकार होना चाहिए। इसका महत्त्व इसी बात से सिद्ध हो जाता है कि इसे भारतीय संविधान में मूल अधिकारों के अन्तर्गत रखा जाता है। ‘

8. नैतिक समानता- इस समानता के अनुसार प्रत्येक व्यक्ति को अपने चरित्र का विकास करने के लिए अन्य व्यक्तियों के समान अधिकार प्राप्त होने चाहिए।

9. राष्ट्रीय समानता- प्रत्येक राष्ट्र समान है, चाहे कोई राष्ट्र छोटा हो या बड़ा। इसलिए प्रत्येक राष्ट
को विकास करने के समान अधिकार प्राप्त होने चाहिए।

प्रश्न 2.
समानता से आप क्या समझते हैं? क्या समानता और स्वतन्त्रता एक-दूसरे के पूरक हैं?
या स्वतन्त्रता एवं समानता का सम्बन्ध स्पष्ट कीजिए।
या “स्वतन्त्रता की समस्या का केवल एक ही हल है और वह हल समानता में निहित है।” इस
कथन की विवेचना कीजिए।
या समानता को परिभाषित कीजिए तथा स्वतन्त्रता के साथ इसके सम्बन्ध की व्याख्या कीजिए।
उत्तर-
समानता का अर्थ
साधारण रूप से समानता का अर्थ यह लगाया जाता है कि सभी व्यक्तियों को ईश्वर ने बनाया है; अतः सभी समान हैं और इसी कारण सभी को समान सुविधाएँ व आय का समान अधिकार होना चाहिए। इस प्रकार का मत व्यक्त करने वाले व्यक्ति प्राकृतिक समानती में विश्वास व्यक्त करते हैं, किन्तु यह विचार भ्रमपूर्ण है, क्योंकि प्रकृति ने ही मनुष्यों को बुद्धि, बल तथा प्रतिभा के आधार पर समान नहीं बनाया है। अप्पादोराय के शब्दों में, “यह स्वीकार करना कि सभी मनुष्य समान हैं, उतना ही भ्रमपूर्ण है जितना कि यह कहना कि भूमण्डल समतल है।”

मनुष्यों में असमानता के दो कारण हैं—प्रथम, प्राकृतिक और द्वितीय, सामाजिक या समाज द्वारा उत्पन्न। अनेक बार यह देखने में आता है कि प्राकृतिक रूप से समान होते हुए भी व्यक्ति असमान हो जाते हैं, क्योंकि आर्थिक समानता के अभाव में सभी को अपने व्यक्तित्व का विकास करने के समान अवसर उपलब्ध नहीं हो पाते। इस प्रकार समाज द्वारा उत्पन्न परिस्थितियाँ मनुष्य के बीच असमानता उत्पन्न कर देती हैं।

नागरिकशास्त्र की अवधारणा के रूप में समानता से हमारा तात्पर्य समाज द्वारा उत्पन्न इस असमानता का अन्त करने से होता है। दूसरे शब्दों में, समानता का तात्पर्य अवसर की समानता से है। सभी व्यक्तियों को अपने विकास के लिए समान सुविधाएँ व समान अवसर प्राप्त हों, ताकि किसी भी व्यक्ति को यह कहने का अवसर न मिले कि यदि उसे यथेष्ट सुविधाएँ प्राप्त होतीं तो वह अपने जीवन का विकास कर सकता था। इस प्रकार समाज में जाति, धर्म व भाषा के आधार पर व्यक्तियों में किसी प्रकार का भेद न किया जाना अथवा इन आधारों पर उत्पन्न विषमता का अन्त करना ही ‘समानता है। समानता की परिभाषा व्यक्त करते हुए लास्की ने लिखा है कि “समानता मूल रूप से समतल करने की प्रक्रिया है। इसीलिए समानता का प्रथम अर्थ विशेषाधिकारों का अभाव और द्वितीय अर्थ अवसरों की समानता से है।”

समानता के दो पक्ष : नकारात्मक और सकारात्मक– समानता की परिभाषा का विश्लेषण करने से यह स्पष्ट हो जाता है कि समानता के दो पक्ष हैं
(1) नकारात्मक तथा
(2) सकारात्मक। नकारात्मक पक्ष से तात्पर्य है कि सामाजिक क्षेत्र में किसी के साथ किसी प्रकार का भेदभाव न हो तथा सकारात्मक पक्ष का अर्थ है कि प्रत्येक व्यक्ति को अपने अधिकाधिक विकास के लिए समान अवसर प्राप्त हों। उदाहरणार्थ-शिक्षा की आवश्यकता सबके लिए होती है; अतः राज्य का यह कर्तव्य है कि वह अपने सब नागरिकों को शिक्षा प्राप्त करने का समान अवसर प्रदान करे।

समानता के विविध रूप

समानता के विविध रूपों में नागरिक समानता, सामाजिक समानता, राजनीतिक समानता, आर्थिक समानता, प्राकृतिक समानता, धार्मिक समानता एवं सांस्कृतिक और शिक्षा सम्बन्धी समानता प्रमुख हैं।

स्वतन्त्रता और समानता का सम्बन्ध

स्वतन्त्रता और समानता के पारस्परिक सम्बन्ध के विषय पर राजनीतिशास्त्रियों में पर्याप्त मतभेद हैं। और इस सम्बन्ध में प्रमुख रूप से दो विचारधाराओं का प्रतिपादन किया गया है, जो इस प्रकार हैं
1. स्वतन्त्रता और समानता परस्पर विरोधी हैं— कुछ व्यक्तियों द्वारा स्वतन्त्रता और समानता के जन-प्रचलित अर्थों के आधार पर इन्हें परस्पर विरोधी बताया गया है। उनके अनुसार स्वतन्त्रता अपनी इच्छानुसार कार्य करने की शक्ति का नाम है, जब कि समानता का तात्पर्य प्रत्येक प्रकार से सभी व्यक्तियों को समान समझने से है। इस आधार पर सामान्य व्यक्ति ही नहीं, वरन् डी० टॉकविले और एक्टन जैसे विद्वानों द्वारा भी इन्हें परस्पर विरोधी माना गया है। लॉर्ड एक्टन ‘एक स्थान पर लिखते हैं कि “समानता की उत्कृष्ट अभिलाषा के कारण स्वतन्त्रता की आशा ही
व्यर्थ हो गयी है।”

2. स्वतन्त्रता और समानता परस्पर पूरक हैं— उपर्युक्त प्रकार की विचारधारा के नितान्त विपरीत दूसरी ओर विद्वानों का बड़ा समूह है, जो स्वतन्त्रता और समानता को परस्पर विरोधी नहीं, वरन्। पूरक मानते हैं। रूसो, टॉनी, लॉस्की और मैकाइवर इस मत के प्रमुख समर्थक हैं और अपने मत की पुष्टि में इन विद्वानों ने निम्नलिखित तर्क दिये हैंस्वतन्त्रता और समानता को परस्पर विरोधी बताने वाले विद्वानों द्वारा स्वतन्त्रता और समानता की गलत धारणा को अपनाया गया है।

स्वतन्त्रता का तात्पर्य प्रतिबन्धों के अभाव’ या स्वच्छन्दता से नहीं है, वरन् इसका तात्पर्य केवल यह है कि अनुचित प्रतिबन्धों के स्थान पर उचित प्रतिबन्धों की व्यवस्था की जानी चाहिए और उन्हें अधिकतम सुविधाएँ प्रदान की जानी चाहिए, जिससे उनके द्वारा अपने व्यक्तित्व का विकास किया जा सके। इसी प्रकार पूर्ण समानता एक काल्पनिक वस्तु है और समानता का तात्पर्य पूर्ण समानता जैसी किसी काल्पनिक वस्तु से नहीं, वरन् व्यक्तित्व के विकास हेतु आवश्यक और पर्याप्त सुविधाओं से है, जिससे सभी व्यक्ति अपने व्यक्तित्व का विकास कर सकें और इस प्रकार उसे असमानता का अन्त हो सके, जिसका मूल कारण सामाजिक परिस्थितियों का भेद है। इस प्रकार स्वतन्त्रता और समानता दोनों ही व्यक्तित्व के विकास हेतु नितान्त आवश्यक हैं।

प्रश्न 3.
नारीवाद’ पर लघु निबन्ध लिखिए।
उत्तर-
नारीवाद स्त्री-पुरुष के समान अधिकारों का पक्ष लेने वाला राजनीतिक सिद्धान्त है। वे स्त्री व पुरुष नारीवादी कहलाते हैं, जो मानते हैं कि स्त्री-पुरुष के बीच की अनेक असमानताएँ न तो नैसर्गिक हैं और न ही आवश्यक। नारीवादियों का मानना है कि इन असमानताओं को बदला जा सकता है और स्त्री-पुरुष एक सम्पूर्ण जीवन व्यतीत कर सकते हैं।

नारीवाद के अनुसार, स्त्री-पुरुष असमानता ‘पितृसत्ता’ से आशय एक ऐसी सामाजिक, आर्थिक और सांस्कृतिक व्यवस्था से है जिसमें पुरुष को स्त्री से अधिक महत्त्व और शक्ति दी जाती है। पितृसत्ता इस मान्यता पर आधारित है कि पुरुष और स्त्री प्रकृति से भिन्न हैं और यही भिन्नता समाज में उनकी असमान स्थिति को न्यायोचित ठहराती है। नारीवादी इस दृष्टिकोण को सन्देह की दृष्टि से देखते हैं। इसके लिए वे स्त्री-पुरुष के जैविक विभेद और स्त्री-पुरुष के बीच सामाजिक भूमिकाओं के विभेद के बीच अन्तर करने का आग्रह करते हैं। जैविक या लिंग भेद प्राकृतिक और जन्मजात होता है, जबकि लैंगिकता समाजजनित है। इसे दूसरे शब्दों में इस प्रकार भी समझा जा सकता है कि मनुष्य का नर या मादा के रूप में जन्म होता है, लेकिन स्त्री या पुरुष को जिन सामाजिक भूमिकाओं में हम देखते हैं उन्हें समाज गढ़ता है। उदाहरण के लिए, यह जीव-विज्ञान का एक तथ्य है कि केवल स्त्री ही गर्भधारण करके बालक को जन्म दे सकती है, लेकिन जीव-विज्ञान के तथ्य में निहित नहीं है कि जन्म देने के बाद केवल स्त्री ही बालक का लालन-पालन करे। नारीवादियों ने यह स्पष्ट किया है कि स्त्री-पुरुष असमानता का अधिकांश भाग प्रकृति ने नहीं समाज ने पैदा किया है।

‘पितृसत्ता’ ने श्रम का कुछ ऐसा विभाजन किया है जिसमें स्त्री ‘निजी’ और ‘घरेलू’ किस्म के कार्यों के लिए जिम्मेदार है जबकि पुरुष की जिम्मेदारी सार्वजनिक’ और ‘बाहरी दुनिया में है। नारीवादी इस विभेद पर भी सवाल खड़े करते हैं। उनका कहना है कि अधिकतर महिलाएँ घर से बाहर अनेक क्षेत्रों में कार्यरत हैं। लेकिन घरेलू कामकाज की पूरी जिम्मेदारी केवल स्त्रियों के कन्धों पर है। नारीवादी इसे स्त्रियों के कन्धे पर दोहरा बोझ’ बताते हैं। हालाँकि इस दोहरे बोझ के बावजूद स्त्रियों को सार्वजनिक क्षेत्र के निर्णयों में ना के बराबर महत्त्व दिया जाता है।
नारीवादियों का मानना है कि निजी/सार्वजनिक के बीच यह विभेद और समाज या व्यक्ति द्वारा गढ़ी हुई लैगिक असमानता के सभी रूपों को मिटाया जा सकता है और मिटाया भी जाना चाहिए।

We hope the UP Board Solutions for Class 11 Political Science Political theory Chapter 3 Equality (समानता) help you. If you have any query regarding UP Board Solutions for Class 11 Political Science Political theory Chapter 3 Equality (समानता), drop a comment below and we will get back to you at the earliest.