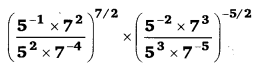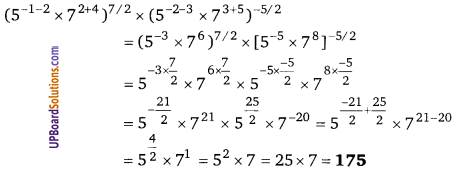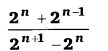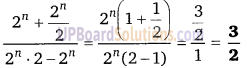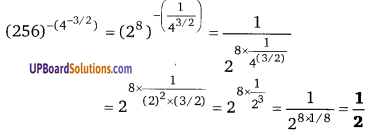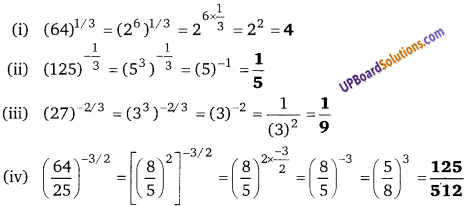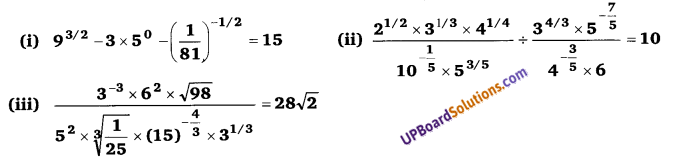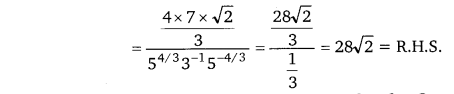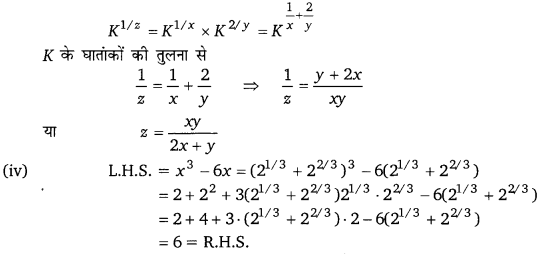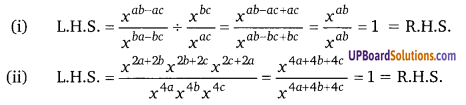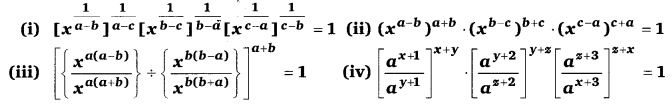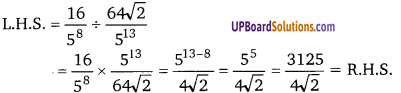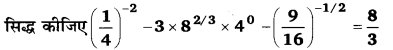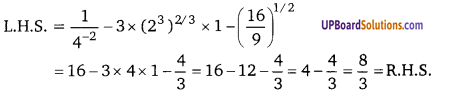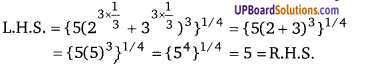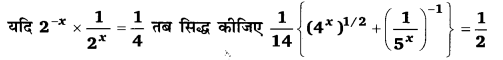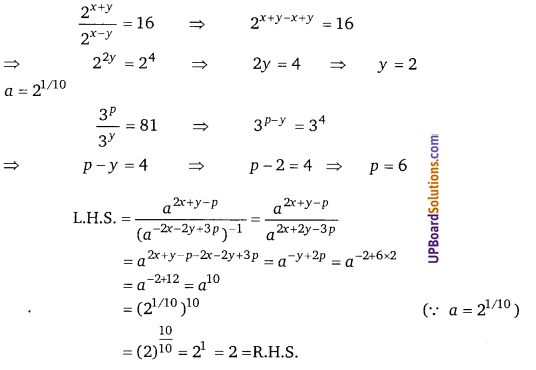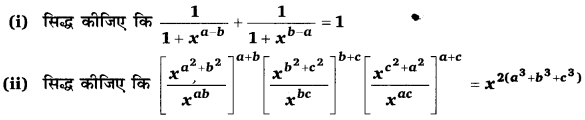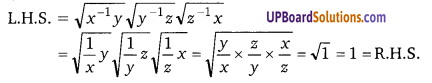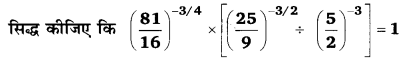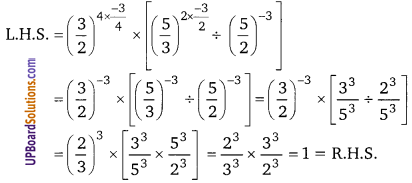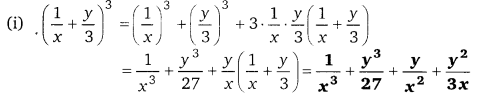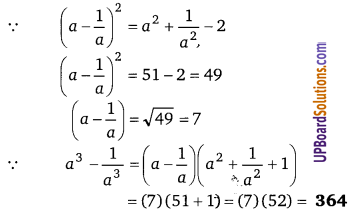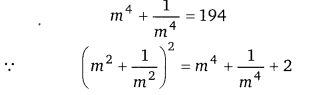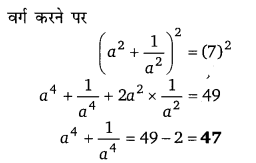Balaji Class 9 Maths Solutions Chapter 5 Polynomial and their Factors Ex 5.5 बहुपद तथा उनके गुणनखण्ड
Ex 5.5 Polynomial and their Factors अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Question)
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए। (प्रश्न 1 – 8)
प्रश्न 1.
x2 + 6x + 9
हल:
x2 + 6x + 9 = (x)2 + 2 × 3 × x + (3)2 = (x + 3)2
![]()
प्रश्न 2.
x2 – 14x + 49
हल:
x2 – 14x + 49 = (x)2 – 2 × 7 × x + (7)2 = (x – 7)2
प्रश्न 3.
9x2 – 12x + 4
हल:
9x2 – 12x + 4 = (3x)2 – 2 × 3x × 2 + (2)2 = (3x – 2)2
प्रश्न 4.
x2 – 18x + 81
हल:
x2 – 18x + 81 = (x)2 – 2 × 9 × x + (9)2 = (x – 9)2
प्रश्न 5.
x2 – 4x + 4
हल:
x2 – 4x + 4 = (x)2 – 2 × 2 × x + (2)2 = (x – 2)2
प्रश्न 6.
49 – 64x2
हल:
49 – 64x2 = (7)2 – (8x)2 = (7 + 8x)(7 – 8x)
![]()
प्रश्न 7.
16x2 – 9y2
हलः
16x2 – 9y2 = (4x)2 – (3y)2 = (4x + 3y)(4x – 3y)
प्रश्न 8.
5x2 – 80y2
हलः
5x2 – 80y2 = 5[x2 – 16y2] = 5[(x)2 – (4y)2] = 5[(x + 4y)(x – 4y)]
Ex 5.5 Polynomial and their Factors लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)
प्रश्न 9.
(x + y)(x – y) का मान ज्ञात कीजिए।
हलः
(x + y)(x – y)
वर्गान्तर सूत्र से = x2 – y2
प्रश्न 10.
(x + y)3 – x – y के गुणनखण्ड ज्ञात कीजिए।
हलः
(x + y)3 – x – y = (x + y)3 – (x + y)
= (x + y)[(x + y)2 – 1]
= (x + y)[(x + y)2 – (1)2]
= (x + y)[(x + y + 1)(x + y – 1)]
प्रश्न 11.
निम्न व्यंजकों के गुणनखण्ड ज्ञात कीजिए
(i) 9x2 – 25y2
(ii) 16 – 81x2
(iii) 100x2 – 81y2
(iv) (a + b)2 – 9c2
हल:
(i) 9x2 – 25y2 = (3x)2 – (5y)2 = (3x + 5y)(3x – 5y)
(ii) 16 – 81x2 = (4)2 – (9x)2 = (4 + 9x)(4 – 9x)
(iii) 100x2 – 81y2 = (10x)2 – (9y)2 = (10x + 9y) (10x – 9y)
(iv) (a + b)2 – 9c2 = (a + b)2 – (3c)2 = (a + b + 3c)(a + b – 3c)
Ex 5.5 Polynomial and their Factors लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)
निम्न बहुपदों के गुणनखण्ड ज्ञात कीजिए।
प्रश्न 12.
9x4 – 6x3b + x2b2
हल:
9x4 – 6x3b + x2b2 = x2[9x2 – 6xb + b2] = x2[(3x)2 – 2 × 3x × b + (b)2] = x2[(3x – b)]
![]()
प्रश्न 13.
x2 – x + [latex]\frac{1}{4}[/latex]
हलः
[latex]x^{2}-x+\frac{1}{4}=x^{2}-2 \times \frac{1}{2} \times x+\left(\frac{1}{2}\right)^{2}=\left(x-\frac{1}{2}\right)^{2}[/latex]
प्रश्न 14.
(a + b + c)2 + 2(a + b + c)(a – b – c)+ (a – b – c)2
हलः
(a + b + c)2 + 2(a + b + c) (a – b – c) + (a – b – c)2 = [(a + b + c) + (a – b – c)]2
= [a + b + c + a – b – c]2
= [2a]2 = 4a2
प्रश्न 15.
6x4 – 24x3y3 + 24y6x2
हल:
6x4 – 24x3y3 + 24y6x2 = 6x2[x2 – 4xy3 + 4y6]
= 6x2[(x)2 – 2 × x × 2y3 + (2y3)2] = 6x2(x – 2y3)2
प्रश्न 16.
121x2y2 + 110xyab + 25a2b2
हलः
121x2y2 + 110xyab + 25a2b2 = (11xy)2 + 2 × 11xy × 5ab + (5ab)2 = (11xy + 5ab)2
प्रश्न 17.
[latex]x^{2} z^{2}+\frac{1}{25} y^{2}-\frac{2}{5} x y z[/latex]
हल:
[latex]x^{2} z^{2}+\frac{1}{25} y^{2}-\frac{2}{5} x y z=(x z)^{2}+\left(\frac{1}{5} y\right)^{2}-2 \times x z \times \frac{1}{5} y=\left(x z-\frac{1}{5} y\right)^{2}[/latex]
प्रश्न 18.
3x3y – 243xy3
हलः
3x3y – 243xy3 = 3xy[x2 – 81y2] = 3xy[(x)2 – (9y)2] = 3xy[(x + 9y)(x – 9y)]
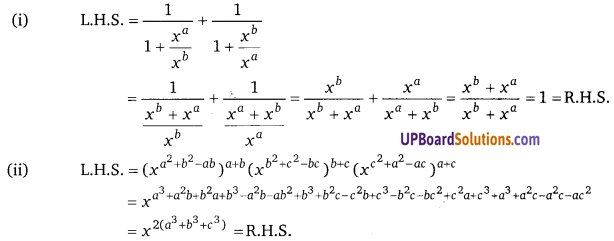
प्रश्न 19.
1 – 2xy – (x2 + y2)
हलः
1 – 2xy – (x2 + y2) = 1 – [2xy + x2 + y2] = (1)2 – [(x + y)2]
वर्गान्तर सूत्र से = (1 + x + y)(1 – x – y)
![]()
प्रश्न 20.
x2 + 6x + 9 – 25y2
हल:
x2 + 6x + 9 – 25y2 = x2 + 2 × 3 × x + (3)2 – (5y)2
= (x + 3)2 – (5y)2 = (x + 3 + 5y)(x + 3 – 5y)
प्रश्न 21.
2xy – (x2 + y2 – z2)
हल:
2xy – (x2 + y2 – z2) = 2xy – x2 – y2 + z2 = z2 – (x2 + y2 – 2xy) = z2 – (x – y)2
= (z + x – y)(z – x + y)
प्रश्न 22.
x2 – y2 – 2x + 1
हलः
x2 – y2 – 2x + 1 = x2 – 2x + 1 – y2
= (x)2 – 2 × x × 1 + (1)2 – y2
= (x – 1)2 – (y)2 = (x – 1 + y)(x – 1 – y)