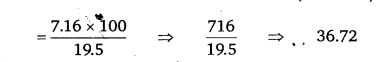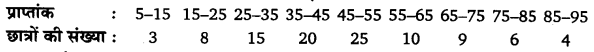Safia

CBSE Sample Papers for Class 10 Maths Paper 3

by

These Sample papers are part of CBSE Sample Papers for Class 10 Maths. Here we have given CBSE Sample Papers for Class 10 Maths Paper 3.

CBSE Sample Papers for Class 10 Maths Paper 1

Board CBSE
Class X
Subject Maths
Sample Paper Set Paper 3
Category CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 3 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.

Time allowed: 3 Hours
Maximum Marks: 80

General Instructions

  •  All questions are compulsory.
  • The question paper consists of 30 questions divided into four sections A, B, C andD.
  • Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
  • There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
  • Use of calculators is not permitted.

Section-A

Question 1.
Find an irrational between 3 and 5.

Question 2.
Find the distance between the points A(4, 5) and B(0, -3)

Question 3.
CBSE Sample Papers for Class 10 Maths Paper 3 img 1

Question 4.
Find the common difference ofthe AP [latex s=2]\frac { 1 }{ p } ,\frac { 1-p }{ p } ,\frac { 1-2p }{ p } ,[/latex] …….

Question 5.
Let ∆ABC ~ ∆DEF. Ifar (∆ABC) = 100 cm2, ar(∆DEF) = 196 cm2 andDE= 7, then find AB.

Question 6.
Solve the equation [latex s=2]\frac { 4 }{ x } [/latex] – 3 = [latex s=2]\frac { 5 }{ 2x+3 } [/latex] ; x ≠ 0, -[latex s=2]\frac { 3 }{ 2 } [/latex], for x.

Section-B

Question 7.
Find how many integers between 200 and 500 are divisible by 8.

Question 8.
Find the ratio in which the line segment joining the points A (3, -3) and B (-2, 7) is divided by x-axis. Also find the coordinates of the point of division.

Question 9.
Which type of equations x + 2y = 4 and 2x + y = 5 will be?

Question 10.
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.

Question 11.
A bag contains 15 white and some black balls. If the probability of drawing a black ball from the bag is thrice that of drawing a white ball, find the number of black balls in the bag.

Question 12.
Find the probability that in a family of 3 children, there will be at least one boy.

Section-C

Question 13.
If the H.C.F of 210 and 55 is expressible in the form 210 × 5 + 55y, find y.

Question 14.
If the polynomial f{x) = 3x4 + 3x3 – 11x2 – 5x + 10 is completely divisible by 3x2 – 5, find all its zeroes.

Question 15.
If sin 0 + cos 0 = p and sec 0 + cosec 0 = q, show that q (p2 -1) = 2p

Question 16.
Following frequency distribution shows the daily expenditure on milk of 30 households in a locality:
CBSE Sample Papers for Class 10 Maths Paper 3 img 2
Find the mode for the above data.

Question 17.
Solve the system of equations:
a(x + y) + b{x-y) = a2 – ab + b2
a(x + y)-b(x-y) = a2 + ab + b2

Question 18.
∆ ABC is right-angled at A. DEFG is a square as shown in the figure. Prove that DE2 = BD × EC
CBSE Sample Papers for Class 10 Maths Paper 3 img 3
OR
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.

Question 19.
Ifthe distances of P(x, y) from A(5, 1) and B (-1,5) are equal, then prove that 3x = 2y.
OR
Prove that the points (3,0), (6,4) and (-1, 3) are the vertices of a right angled isosceles triangle.

Question 20.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig.). Find the length of TP.
CBSE Sample Papers for Class 10 Maths Paper 3 img 4

Question 21.
In fig., a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use n = 3.14 and [latex]\sqrt { 3 } [/latex] = 1.73]
CBSE Sample Papers for Class 10 Maths Paper 3 img 5

Question 22.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel ofbase radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. 22
[Use π = [latex s=2]\frac { 22 }{ 7 } [/latex] ]
OR
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3[latex s=2]\frac { 5 }{ 9 } [/latex] cm. Find the diameter of the cylindrical vessel.

Section-D

Question 23.
The pth term of an A.P. is a and qth term is A Prove that the sum of its (p + q) terms is [latex s=2]\frac { p+q }{ 2 } \left\{ a+d+\frac { a-b }{ p-q } \right\} [/latex]

Question 24.
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base ofhillas30°. Find the distance of the hill from the ship and the height of the hill
OR
The angle of elevation of a bird from a point 50 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the bird above the lake.

Question 25.
For the following frequency distribution, find the value of f1 and f2, ifmean is given to be 50,
CBSE Sample Papers for Class 10 Maths Paper 3 img 6
OR
The following distribution gives the daily income of 50 workers of a factory.
CBSE Sample Papers for Class 10 Maths Paper 3 img 7
Convert the distribution above to a less than type cummulative frequency distribution and draw its ogive.

Question 26.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. Ifthe total surface area
of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. [Use π = [latex s=2]\frac { 22 }{ 7 } [/latex] ]

Question 27.
Sove for x : [latex]\frac { 1 }{ x+1 } +\frac { 3 }{ 5x+1 } =\frac { 5 }{ x+4 } [/latex] x ≠-1, -[latex s=2]\frac { 1 }{ 5 } [/latex],-4
OR
Two taps running together can fill a tank in 3[latex s=2]\frac { 1 }{ 13 } [/latex] hours. If one tap takes 3 hours more than the other to fill

Question 28.
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then prove that the angle opposite to the first side is a right angle.

Question 29.
Solve [latex]\frac { \cos ^{ 2 }{ \theta } -3\cos { \theta } +2 }{ \sin ^{ 2 }{ \theta } } [/latex] =1; (θ < 90°)

Question 30.
Draw a circle ofradius 2.5 cm. From a point P, 6 cm apart from the centre of the circle, draw two tangents to the circle.

Solutions
Section-A

Solution 1.
[latex]\sqrt { 3\times 5 } =\sqrt { 15 } [/latex] is an irrational between 3 and 5  (1)

Solution 2.
Here x1 = 4, y1 = 5, x2 = 0, y2 = -3
Using distance formula
CBSE Sample Papers for Class 10 Maths Paper 3 img 8

Solution 3.
CBSE Sample Papers for Class 10 Maths Paper 3 img 9

Solution 4.
CBSE Sample Papers for Class 10 Maths Paper 3 img 10

Solution 5.
CBSE Sample Papers for Class 10 Maths Paper 3 img 11

Solution 6.
CBSE Sample Papers for Class 10 Maths Paper 3 img 12

Section-B

Solution 7.
First number divisible by 8 between 200 and 500 is 208.
If form an A.P. = 208,216,224,……..,496.
Here, an = 496, a = 208, d = 8
an = a + (n – l)d  (1)
496 = 208 + (n-l)8
(n-1)8 = 496-208
(n-1) = [latex s=2]\frac { 288 }{ 8 } [/latex] ⇒ n-1=36 ⇒n=37   (1)

Solution 8.
CBSE Sample Papers for Class 10 Maths Paper 3 img 13

Solution 9.
CBSE Sample Papers for Class 10 Maths Paper 3 img 14

Solution 10.
Natural numbers between 101 and 999 divisible by 5 and 2 both, must be divisible by 10.
∴ {110,120,………, 990} are numbers divisible by both 2 and 5.   (1/2)
If forms anA.P., in which a = 110, d = 10 and an = 990.   (1/2)
an = a + (n-1)d ⇒ 990 = 110 + (n- 1) 10
⇒ 99 =11+ (n-1)=>88 + 1= n ⇒n = 89   (1)

Solution 11.
Since, number of white balls in the bag = 15
Let the number of black balls in the bag = x
As, P (drawing a black ball) = 3 x P (drawing a white ball)   (1)
[latex s=2]\frac { x }{ 15+x } =3\times \frac { 15 }{ 15+x } [/latex] ⇒ x=45 [∵x+15 ≠ 0]   (1)
Hence, the number ofblack balls in the bag is 45.

Solution 12.
S = {BBB, BBQ BGB, BGQ GBB, GBQ GGB, GGG} ; n(S) = 8
E = {BBB, BBQ BGB, BGQ GBB, GBQ GGB}; n(E) = 7  (1)
∴ P(E) = [latex]\frac { n(E) }{ n(S) } =\frac { 7 }{ 8 } [/latex] (1)

Section-C

Solution 13.
Let us first find the H.C.F. of 210and 55.
Applying Euclid’s division lemma on 210 and 55, we get
210=55 x3 + 45 ….(i) (1)
Since, the remainder 45 ^ 0. So, we now apply division lemma on the divisor 55 and the remainder 45 to get
55 = 45 × 1 + 10 ….(ii)     (1/2)
We consider the divisor 45 and the remainder 10 and apply division lemma to get
45 = 4 × 10 + 5 …(iii)   (1/2)
We consider the divisor 10 and the remainder 5 and apply division lemma to get
10=5 × 2 + 0….(iv)
We observe that the remainder at this stage is zero. So, the last divisor i.e., 5 is the H.C.F of210 and 55.
∴ 5 = 210 × 5 + 55y ⇒ y = [latex]\frac { -1045 }{ 55 } [/latex] = (-19)   (1)

Solution 14.
As 3x2 – 5 divides f(x) completely
∴ (3x2 – 5) is a factor of f(x)
⇒ 3[latex]\left( { x }^{ 2 }-\frac { 5 }{ 3 } \right) [/latex] is a factor of f(x)
CBSE Sample Papers for Class 10 Maths Paper 3 img 15

Solution 15.
CBSE Sample Papers for Class 10 Maths Paper 3 img 16

Solution 16.
CBSE Sample Papers for Class 10 Maths Paper 3 img 17
CBSE Sample Papers for Class 10 Maths Paper 3 img 18

Solution 17.
CBSE Sample Papers for Class 10 Maths Paper 3 img 19

Solution 18.
CBSE Sample Papers for Class 10 Maths Paper 3 img 20
CBSE Sample Papers for Class 10 Maths Paper 3 img 21
OR
CBSE Sample Papers for Class 10 Maths Paper 3 img 22

Solution 19.
Since, distance between (x, y) and (5,1) = Distance between (x, y) and (-1,5)
So, [latex]\sqrt { { (x-5) }^{ 2 }+{ (y-1) }^{ 2 } } =\sqrt { { (x-(-1)) }^{ 2 }+{ (y-5) }^{ 2 } } [/latex]  (1)
Squaring on both sides, we get
(x-5)2 + (y- 1)2 = (x+ 1)2+(y-5)2
(x2– lOx + 25) + (y2 -2y + 1) = (x2 + 2x + 1)+ (y2-10y + 25)  (1)
So, -12x = -8y ⇒ 12x = 8y ⇒ 3x = 2y (Hence proved).  (1)
OR
Let A (3,0), B(6,4) andC (-1,3) be the vertices of the triangle.
Using distance formula,
AB = [latex]\sqrt { { (4-0) }^{ 2 }+{ (6-3) }^{ 2 } } =\sqrt { 25 } [/latex] = 5 units   (1/2)
BC = [latex]\sqrt { { (3-4) }^{ 2 }+{ (-1-6) }^{ 2 } } =\sqrt { 50 } =5\sqrt { 2 } [/latex]  (1/2)
CA = [latex]\sqrt { { (0-3) }^{ 2 }+{ (3+1) }^{ 2 } } =\sqrt { 25 } [/latex] = 5 units   (1/2)
Now, (5)2 + (5)2 = [latex]{ \left( 2\sqrt { 5 } \right) }^{ 2 }[/latex]
=> AB2 + CA2 = BC2 [Follow Pythagoras theorem]   (1)
Also, AB = CA = 5 units
So, ∆ABC is a right-angled isosceles triangle.   (1/2)
Hence, the given points are the vertices of a right-angled isosceles triangle.

Solution 20.
CBSE Sample Papers for Class 10 Maths Paper 3 img 23
Solution 21.
Median and altitude of an equilateral triangle are same and passing through the centre of incircle and centre divides the median in ratio 2:1.
∴ In ∆ABD, ∠D = 90°
CBSE Sample Papers for Class 10 Maths Paper 3 img 24

By Pythagoras theorem
AD2 = AB2-BD2 ⇒ AD2 = 122 – 62
⇒ AD2 = 144-36
⇒ AD = [latex]\sqrt { 108 } [/latex] = 6[latex]\sqrt { 3 } [/latex] cm
AO:OD = 2: 1   (1)
∴OD = [latex s=2]\frac { 1 }{ 3 } [/latex] AD = [latex s=2]\frac { 1 }{ 3 } [/latex] × 6[latex]\sqrt { 3 } [/latex] = 2[latex]\sqrt { 3 } [/latex]   (1/2)
Now, radius of circle = 2[latex]\sqrt { 3 } [/latex] = 2 × 1.73 = 3.46 cm   (1/2)
Area of shaded region = Area of equilateral ∆ABC – Area of circle   (1)
= [latex]\frac { \sqrt { 3 } }{ 4 } [/latex](12)2 -(2[latex]\sqrt { 3 } [/latex])2 × π
= 1.73 × 36 – 12 × 3.14 = 62.28 – 37.68 = 24.6 cm2.

Solution 22.
Suppose,
r = Radius of the conical vessel = 5 cm
h = Height of the conical vessel = 24 cm
r2 = Radius of the cylindrical vessel = 10 cm
Suppose water rises up to a height h2 cm in the cylindrical vessel.
A.T.Q,
Volume of the water in cylindrical vessel = Volume of water in conical vessel
⇒[latex ]\pi { r }_{ 2 }^{ 2 }{ h }_{ 2 }=\frac { 1 }{ 3 } \pi { r }_{ 1 }^{ 2 }{ h }_{ 1 }[/latex] (1)
⇒[latex ]3{ r }_{ 2 }^{ 2 }{ h }_{ 2 }={ r }_{ 1 }^{ 2 }{ h }_{ 1 }[/latex] ⇒ 3 × 10 × 10 × h2 = 5 × 5 × 24 (1)
h2 = [latex s=2]\frac { 5\times 5\times 24 }{ 3\times 10\times 10 } [/latex] ⇒ h2 = 2 cm  (1)
Hence, the rise in the water level in the cylindrical vessel = 2 cm.
OR
Increase in the height of water level in the cylindrical vessel due to sphere (h) = [latex s=2]\frac { 32 }{ 9 } [/latex] cm
Radius of the sphere (R) = 6 cm  (1/2)
Suppose radius of the cylindrical vessel be r.
Volume ofwater in cylinder = Volume of sphere  (1)
πr2h = [latex s=2]\frac { 4 }{ 3 } [/latex]πR3
⇒ r2 = [latex s=2]\frac { 4\times { 6 }^{ 3 }\times 9 }{ 3\times 32 } [/latex] ⇒ r = [latex]\sqrt { 27\times 3 } [/latex] = 9cm (1)
Hence, diameter of the cylindrical vessel = 18 cm. (1/2)

Section-D

Solution 23.
CBSE Sample Papers for Class 10 Maths Paper 3 img 25

Solution 24.
CBSE Sample Papers for Class 10 Maths Paper 3 img 26
Suppose the man is standing on the deck of the ship at point A.
Suppose CE be the hill with base at C.  (1)
Given that the angle of elevation of point E from A is 60° and the angle of depression of point C from A is 30°.
∠DAE = 60°, ∠CAD = 30°  (1/2)
Now, ∠CAD = ∠ACB = 30° [Alternate angles]
AB = 10 m   (1/2)
Let ED = h m and BC = x m.
In ∆EAD, tan 60° = [latex s=2]\frac { ED }{ AD } [/latex] ⇒ [latex]\sqrt { 3 } [/latex] = [latex s=2]\frac { h }{ x } [/latex] ⇒ h = x[latex]\sqrt { 3 } [/latex] …..(i)   (1/2)

In ∆ABC, tan30° = [latex s=2]\frac { AB }{ BC } [/latex] ⇒ [latex]\frac { 1 }{ \sqrt { 3 } } [/latex] = [latex s=2]\frac { 10 }{ x } [/latex] ⇒ x = 10[latex]\sqrt { 3 } [/latex] …(ii)  (1/2)
So, distance of the hill from the ship = 10[latex]\sqrt { 3 } [/latex]m
From (i) and (ii), h = 10[latex]\sqrt { 3 } [/latex]×[latex]\sqrt { 3 } [/latex] = 30m
Hence, height of the hill = h+ 10 = 30+ 10 = 40 m. (1)
OR
Let A be the reflection ofthe bird B in the lake, then CB = CA = h metres (say).
CBSE Sample Papers for Class 10 Maths Paper 3 img 27
∴NB-{h — 50) m and    (1)
AN =(h + 50) m
Let ON be dmetres.
tan 60° = [latex s=2]\frac { h+50 }{ d } [/latex] ⇒ [latex]\sqrt { 3 } [/latex] =[latex s=2]\frac { h+50 }{ d } [/latex] and

tan 30° = [latex s=2]\frac { h-50 }{ d } [/latex] ⇒d = (h-50)[latex]\sqrt { 3 } [/latex]

Thus, 3 = [latex s=2]\frac { h+50 }{ h-50 } [/latex] ⇒ h = 100      (1)

Solution 25.
Let a = 50 and h = 20
CBSE Sample Papers for Class 10 Maths Paper 3 img 28
OR
Less than type frequency distribution
CBSE Sample Papers for Class 10 Maths Paper 3 img 29
We first draw the coordinate x-axis with lower limits of the daily income (in ?) along the horizontal axis and the cummulative frequency along the vertical axis. Then, we plot the points (120, 12), (140, 26), (160,34), (180,40), (200,50) and join these points by a free hand smooth curve.
CBSE Sample Papers for Class 10 Maths Paper 3 img 30

Solution 26.
Let the radius of base and height of the solid right circular cylinder be r cm and h cm, respectively,
Here, r + h = 37 ….(i)  (1/2)
Total surface area = 1628 sq cm
∴ 2πr(r + h)= 1628 …(ii)  (1/2)
From (i) and (ii), we get
2πr(37) =1628 => 2×[latex s=2]\frac { 22 }{ 7 } [/latex]×r = 44
∴ r =7cm  (1)
After substituting the value of r in (i), we get
7 + h = 37
∴ h = 30cm  (1)
Then, volume of the cylinder = πr2h
= [latex s=2]\frac { 22 }{ 7 } [/latex] ×7×7×30 = 4630 cm2    (1)
Therefore, the volume of the cylinder is 4,620 cm3.

Solution 27.
CBSE Sample Papers for Class 10 Maths Paper 3 img 31
OR
CBSE Sample Papers for Class 10 Maths Paper 3 img 32

Solution 28.
CBSE Sample Papers for Class 10 Maths Paper 3 img 33

Solution 29.
CBSE Sample Papers for Class 10 Maths Paper 3 img 34

Solution 30.
Given : Apoint P is at a distance of 6 cm. from the centre of a circle ofradius 2.5 cm.
Required : To draw two tangents to the circle from the given point P. (1)
CBSE Sample Papers for Class 10 Maths Paper 3 img 35
Step of construction:
1. DrawalinesegmentOPoflength6cm.
2. With centre O and radius equal to 2.5 cm, draw a circle.
3. Draw the right bisector of OP, intersecting OP at M. Let M be mid-point of OP.
4. Taking M as centre and MO as radius draw a circle which intersect the given circle in two points, say AandB.
5. Join PA and PB. These are the required tangents from P to the given circle. (1)

We hope the CBSE Sample Papers for Class 10 Maths paper 3 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths paper 3, drop a comment below and we will get back to you at the earliest.

CBSE Sample Papers for Class 10 Maths Paper 2

by

These Sample papers are part of CBSE Sample Papers for Class 10 Maths. Here we have given CBSE Sample Papers for Class 10 Maths Paper 2.

CBSE Sample Papers for Class 10 Maths Paper 2

Board CBSE
Class X
Subject Maths
Sample Paper Set Paper 2
Category CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 2 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.

Time allowed: 3 Hours
Maximum Marks: 80

General Instructions

  • All questions are compulsory.
  •  The question paper consists of 30 questions divided into four sections A, B, C andD.
  • Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
  •  There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
  • Use of calculators is not permitted.

Section-A

Question 1.
Identify: [latex s=2]\sqrt { \frac { 9 }{ \pi } } [/latex] as rational or irrational.

Question 2.
Find an arithmetic mean between 10[latex s=2]\frac { 1 }{ 2} [/latex] and 25[latex s=2]\frac { 1 }{ 2 } [/latex].

Question 3.
ABCD is a rectangle whose three vertices are B (4, 0), C (4, 3) and D (0, 3). What is the length of one of its diagonals ?

Question 4.
If cos 2A = sin(A – 15°), find A.

Question 5.
If x = – [latex s=2]\frac { 1 }{ 2} [/latex], is a solution of the quadratic equation 3x2 + 2kx – 3 = 0, find the value of k.

Question 6.
In the figure of ∆ABC, the points D and E are on the sides CA, CB respectively such that DE || AB, AD = 2x, DC=x + 3,BE = 2x-1 and CE=x. Then, find x.
CBSE Sample Papers for Class 10 Maths Paper 2 img 1

Section-B

Question 7.
Find the HCF of 1,656 and 4,025 by Euclid’s division algorithm.

Question 8.
If the point P (k – 1,2) is equidistant from the points A (3 ,k) and B (k, 5), find the values of k.

Question 9.
The probability of selecting a rotten apple randomly from a heap of900 apples is 0.18. What is the number of rotten apples in the heap?

Question 10.
The probability of selecting a red ball at random from ajar that contains only red, blue and orange balls
is [latex s=2]\frac { 1 }{ 4} [/latex]. The probability of selecting a blue ball at random from the same jar is [latex s=2]\frac { 1 }{ 3} [/latex]. If thejar contains 10 orange balls, find the total number of balls in the jar.

Question 11.
Sum of the ages of a father and the son is 40 years. If father’s age is three times that of his son, then find their respective ages.

Question 12.
If the ratio of the sum of first n terms of two A.P’s is (7n + 1): (4n + 27), find the ratio of their wth terms.

Section-C

Question 13.
Show that [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] is irrational

Question 14.
Obtain all other zeroes of the polynomial 4x4 + x3 – 72x2 – 18x, if two of its zeroes are 3[latex]\sqrt { 2 } [/latex] and -3[latex]\sqrt { 2 } [/latex] .

Question 15.
x-coordinate of a point P is twice its y-coordinate. If P is equidistant from Q (2, -5) and R (-3, 6), find the coordinates of P.
OR
The area of a triangle is 5 sq units. Two of its vertices are (2,1) and (3, -2). Ifthe third vertex is [latex s=2]\left( \frac { 7 }{ 2 } ,y \right) [/latex], find the value of y.

Question 16.
If [latex s=2]\frac { \cos { \alpha } }{ \cos { \beta } } [/latex] = m and [latex s=2]\frac { \cos { \alpha } }{ \sin { \beta } } [/latex] = n show that (m2 + n2)cos2 β n2
OR
Find the value of ‘x’ such that
2cos ec230° + x sin2 60°- [latex s=2]\frac { 3 }{ 4} [/latex]tan2 30° = 10

Question 17.
In figure, a quadrilateral ABCD is drawn to circumscribe a circle, with centre O, in such a way that the sides AB, BC, CD and DA touch the circle at the points P, Q, R and S respectively. Prove that AB + CD = BC + DA.
CBSE Sample Papers for Class 10 Maths Paper 2 img 2

Question 18.
In the given figure, ABCD is a rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure.
CBSE Sample Papers for Class 10 Maths Paper 2 img 3

Question 19.
A cubical block of side 10 cm is surmounted by a hemisphere. What is the largest diameter that the hemisphere can have? Find the cost of painting the total surface area of the solid so formed, at the rate of ? 5 per 100 sq. cm [Use π=3.14].
OR
504 cones, each of diameter 3.5 cm and height 3 cm, are melted and recast into a metallic sphere. Find the diameter of the sphere and hence find its surface area. [Use π = [latex s=2]\frac { 22 }{ 7 } [/latex]]

Question 20.
Find the sum of values of a and b for which the following system of linear equations has infinite number of solutions:
2x + 3y = 7
(a+b+ 1)x + (a+2b + 2)y = 4(a+ b)+ 1

Question 21.
In the given figure, S and T trisect the side QR of a right triangle PQR. Prove that HPT2 = 3 PR2 + 5 PS2
CBSE Sample Papers for Class 10 Maths Paper 2 img 4
OR
In the given figure PA, QB and RC, each are perpendicular to AC. Prove that [latex s=2]\frac { 1 }{ x } +\frac { 1 }{ z } =\frac { 1 }{ y } [/latex]
CBSE Sample Papers for Class 10 Maths Paper 2 img 5

Question 22.
The mean and median of 100 observations are 50 and 52 respectively. The value of the largest observation is 100. It was later found that it is 110 not 100. Find the true mean and median.

Section-D

Question 23.
If cos θ + [latex]\sqrt { 3 } [/latex] sin θ = 2sin θ
Show that sin θ – [latex]\sqrt { 3 } [/latex] cos θ = 2cos θ.

Question 24.
A well of diameter 4 m is dug 21 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 3 m to form an embankment. Find the height of the embankment.

Question 25.
Solve the following for x :[latex s=2]\frac { 1 }{ 2a+b+2x } =\frac { 1 }{ 2a } +\frac { 1 }{ b } +\frac { 1 }{ 2x } [/latex]
OR
Solve for x: [latex s=2]\frac { 1 }{ x+1 } +\frac { 1 }{ x+2 } =\frac { 4 }{ x+4 } [/latex], x ≠ -1,-2,-4

Question 26.
Prove that the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides
OR
In a right triangle, prove that the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Question 27.
The angles of depression of the top and bottom of a 50 m high building from the top of a tower are 45° and 60° respectively. Find the height of the tower and the horizontal distance between the tower and the
building, (use [latex]\sqrt { 3 } [/latex] = 1.73)
OR
vertical tower stands on a horizontal plane and is surmounted by a vertical flag staff of height h. At a point on the plane, the angles of elevation of the bottom and the top of the flag staff are α and β respectively. Prove that the height of the tower is ([latex s=2]\frac { h\tan { \alpha } }{ \tan { \beta } -\tan { \alpha } } \quad [/latex])

Question 28.
If [latex s=2]\frac { b+c-a }{ a } ,\frac { c+a-b }{ b } ,\frac { a+b-c }{ c } \quad [/latex] are in A.P. then prove [latex s=2]\frac { 1 }{ a } ,\frac { 1 }{ b } ,\frac { 1 }{ c } \quad [/latex] in A.P.

Question 29.
Draw a triangle ABC with sideBC = 7 cm. ∠B = 45°, ∠A = 105°. Construct a triangle whose sides are (4/3) times the corresponding side of ∆ ABC.

Question 30.
On the annual day of school, age-wise participation of students is given in the following frequency distribution table:
CBSE Sample Papers for Class 10 Maths Paper 2 img 6

Solutions:
Section-A

Solution 1.
[latexs=2]\sqrt { \frac { 9 }{ \pi } } =(3)\left( \frac { 1 }{ \sqrt { \pi } } \right) [/latex] = (rational) (irrational) = irrational (1)

Solution 2.
CBSE Sample Papers for Class 10 Maths Paper 2 img 7

Solution 3.
CBSE Sample Papers for Class 10 Maths Paper 2 img 8

According to the figure BD is the diagonal of ABCD. By distance formula BD
BD = [latex]\sqrt { { ({ x }_{ 2 }-{ x }_{ 1 }) }^{ 2 }+{ ({ y }_{ 2 }-{ y }_{ 1 }) }^{ 2 } } =\sqrt { { (4-0) }^{ 2 }+(0-3)^{ 2 } } [/latex]
= [latex]\sqrt { 25 } [/latex] = 5 units (1)

Solution 4.
sin(90° – 2A) = sin(A-15°)
⇒ 90°-2A = +4-15° ⇒ 3A = 105°  (1/2)
∴ A = 35°  (1/2)

Solution 5.
x = -[latex s=2]\frac { 1 }{ 2 } [/latex] is a solution of 3x2 + 2kx -3=0
Now, [latexs=2]{ 3\left( \frac { -1 }{ 2 } \right) }^{ 2 }+2k\left( \frac { -1 }{ 2 } \right) -3[/latex] = 0   (1/2)
[latex s=2]\frac { 3 }{ 4 } [/latex] -k -3 =0 ⇒ k = [latex s=2]\frac { -9 }{ 4 } [/latex]   (1/2)

Solution 6.
[latex s=2]\frac { CD }{ AD } =\frac { CE }{ BE } [/latex] ⇒ [latexs=2]\frac { x+3 }{ 2x } =\frac { x }{ 2x-1 } [/latex]  (1/2)
⇒ 5x = 3 ⇒ x = [latex s=2]\frac { 3 }{ 5 } [/latex]   (1/2)

Section-B

Solution 7.
Since 4025 > 1656,
∴4025 =1656 × 2 + 713
1656 = 713 × 2 + 230
713 = 230 × 3+23  (1)
230 = 23 × 10+0
So, HCF (1,656,4,025) = 23  (1)

Solution 8.
CBSE Sample Papers for Class 10 Maths Paper 2 img 9

Solution 9.
Since, the number of apples in the given heap = 900
And the probability of selecting a rotten apple randomly = 0.18
CBSE Sample Papers for Class 10 Maths Paper 2 img 10
Hence, the number of rotten apples in the heap will be 900 × 0.18 i.e.,162   (1)

Solution 10.
∵P (Red) = [latex s=2]\frac { 1 }{ 4 } [/latex], and, P (Blue) = [latex s=2]\frac { 1 }{ 3 } [/latex]
So, P (Orange) = 1-[latex]\frac { 1 }{ 4 } -\frac { 1 }{ 3 } =\frac { 5 }{ 12 } [/latex]   (1)
Therefore, [latex s=2]\frac { 5 }{ 12 } [/latex] ×(Total no. of balls) = 10
Hence, total no. of balls = [latex s=2]\frac { 10\times 12 }{ 5 } [/latex] = 24   (1)

Solution 11.
Let ages of father and son be x and y respectively.
x+y = 40 …(i)
x = 3y ….(ii)    (1)
By solving eqs. (i) and (ii)
x =30 andy = 10
Ages are 30 years and 10 years.   (1)

Solution 12.
CBSE Sample Papers for Class 10 Maths Paper 2 img 11
CBSE Sample Papers for Class 10 Maths Paper 2 img 12

Section-C

Solution 13.
Let us assume [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex], to the contrary, that [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] is rational.
∴ [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] = [latex s=2]\frac { p }{ q } [/latex] where p, q (q ≠ 0) are integers and p, q are co-prime.  (1)
⇒ [latex s=2]\frac { 2q }{ 5p } [/latex] = [latex]\sqrt { 3 } [/latex]  (1/2)
Since, 2, 5, p, q are integers
∴ [latex s=2]\frac { 2q }{ 5p } [/latex] is rational, and so [latex]\sqrt { 3 } [/latex] is rational.  (1)
But this contradicts the fact that [latex]\sqrt { 3 } [/latex] is irrational
Hence, [latex s=2]\frac { 2 }{ 5\sqrt { 3 } } [/latex] is irrational.  (1/2)

Solution 14.
CBSE Sample Papers for Class 10 Maths Paper 2 img 13
CBSE Sample Papers for Class 10 Maths Paper 2 img 14

Solution 15.
Let the y-coordinate of the point P be a.
And, its x-coordinate will be 2a.
So, the coordinates of the point P are (2a, a).
Since, the point P (2a, a) is equidistant from Q (2, -5) and R(-3,6).
∴ [latex]\sqrt { { (2a-2) }^{ 2 }+{ (a-(-5)) }^{ 2 } } =\sqrt { { (2a-(-3)) }^{ 2 }+{ (a-6) }^{ 2 } } [/latex]  (1)
[latex]\sqrt { { (2a-2) }^{ 2 }+{ (a+5) }^{ 2 } } =\sqrt { { (2a+3) }^{ 2 }+{ (a-6) }^{ 2 } } [/latex]
So, [latex]\sqrt { { 5a }^{ 2 }+2a+29 } =\sqrt { { 5a }^{ 2 }+45 } [/latex]   (1)
After squaring both sides, we get
5a2 + 2a + 29 = 5a2 + 45
5a2 + 2a – 5a2 = 45 – 29
Thus, a = 8
Hence, the coordinates of the point P are (16, 8).
OR
CBSE Sample Papers for Class 10 Maths Paper 2 img 15

Solution 16.
CBSE Sample Papers for Class 10 Maths Paper 2 img 16
CBSE Sample Papers for Class 10 Maths Paper 2 img 17
OR
CBSE Sample Papers for Class 10 Maths Paper 2 img 18

Solution 17.
As, the tangents drawn from the exterior point to a circle are equal in length.  (1/2)
So, DR=DS ….(i)
AP= AS …(ii)
BP = BQ …(iii)
CR=CQ ….(iv)    (1)
CBSE Sample Papers for Class 10 Maths Paper 2 img 19
Adding(i), (ii), (iii) and (iv), we get
DR + AP + BP + CR = DS + AS + BQ + CQ (1/2)
⇒ (DR + CR) + (AP + BP) = (DS + AS) + (BQ + CQ)
⇒ CD + AB = DA + BC
⇒ AB+CD = BC + DA (Hence Proved).    (1)

Solution 18.
Area of shaded region
= Area of rectangle – Area of semi-circle (1/2)
(14×21) – [latex s=2]\frac { 1 }{ 2 } \times \frac { 22 }{ 7 } \times { 7 }^{ 2 }[/latex] (1/2)
= 294 – 77 = 217 cm2 (1/2)
Perimeter of shaded region = (2 × 21) +14 + [latex s=2]\left( \frac { 22 }{ 7 } \times { 7 } \right) [/latex] (1)
= 42+14 + 22 = 78 cm (1/2)

Solution 19.
∵ Largest possible diameter ofhemisphere = 10 cm
So, radius ofhemisphere = 5 cm  (1/2)
Now, total surface area = 5(10)2 + 3.14 × (5)2 × 2   (1)
= 657 cm2  (1/2)
Hence, cost of painting = [latex s=2]\frac { 657\times 5 }{ 100 } [/latex] = ₹ 32.85
OR
CBSE Sample Papers for Class 10 Maths Paper 2 img 20

Solution 20.
CBSE Sample Papers for Class 10 Maths Paper 2 img 21
CBSE Sample Papers for Class 10 Maths Paper 2 img 22

Solution 21.
S and T trisect the side QR.
Let QS = ST = TR = x units
Let PQ = y units   (1/2)
In right ∆PQS, PS2 = PQ2 + QS2 (By Pythagoras Theorem)
= y2 + x2 …(i)  (1/2)
In right ∆PQR, PT2 = (By Pythagoras Theorem)
= y2 + (2x)2 = y2 + 4x2 ….(ii)  (1/2)
In right ∆PQR, PR22 = PQ2 + QR2(By Pythagoras Theorem)
=y2 + (3x)2 = y2 + 9x2 …(iii)  (1/2)
R.H.S. = 3 PR2 + 5 PS2
= 3(y2 + 9x2)+ 5(y2+x2) [From (i) and (iii)]
= 3y2 + 27x2 + 5y2 + 5x2 = 8y2 + 32x2
= 8(y2 + 4x2) = 8PT2 = L.H.S. [From(ii)]   (1)
Thus 8PT2 = 3PR2 + 5PS22
OR
In APAC and AQBC, We have
∠PAC = ∠QBC [Each = 90°]
∠PCA = ∠QCB [Common]   (1)
∴∆PAC ~ ∆QBC
∴ [latex s=2]\frac { x }{ y } =\frac { AC }{ BC } [/latex] i.e. [latexs=2]\frac { y }{ x } =\frac { BC }{ AC } [/latex] ..(i) (1/2)
CBSE Sample Papers for Class 10 Maths Paper 2 img 23

Solution 22.
CBSE Sample Papers for Class 10 Maths Paper 2 img 24

Section-D

Solution 23.
(cos θ + [latex]\sqrt { 3 } [/latex] sin θ)2 + (sin θ – [latex]\sqrt { 3 } [/latex] cos θ)2
= cos2 θ + 3sin2 θ + 2 [latex]\sqrt { 3 } [/latex] cos θ sin θ + sin2 θ + 3cos2 θ – 2 [latex]\sqrt { 3 } [/latex] cos θ sin θ  (1)
⇒ (2sin θ)2 + (sin θ – [latex]\sqrt { 3 } [/latex] cos θ)2 = (cos2 θ + sin2 θ) + 3 (sin2 θ + cos2 θ)  (1)
⇒ (sin θ – [latex]\sqrt { 3 } [/latex] cos θ)2 = 4 – 4 sin2 θ  (1/2)
⇒ (sin θ- [latex]\sqrt { 3 } [/latex] cos θ)2 = 4 cos2 θ  (1)
⇒ sin θ – [latex]\sqrt { 3 } [/latex] cos θ = 2 cos θ (Hence proved)  (1/2)

Solution 24.
Let r and h be the radius and depth of the well, respectively.
Here, r = [latex s=2]\frac { 4 }{ 2 } [/latex] = 2 m and h = 21 m  (1/2)
Let R and H be the outer radius and height of the embankment, respectively.
So, R = r + 3= 2 + 3 = 5m   (1)
As, volume of the earth to form the embankment = Volume of the earth dug out
π(R2-r2)H = πr2h   (1)
∴ H = [latex s=2]\frac { { r }^{ 2 }h }{ { R }^{ 2 }-{ r }^{ 2 } } [/latex]  (1/2)

∴ H = [latex s=2]\frac { { 2 }^{ 2 }\times 21 }{ { 5 }^{ 2 }-{ 2 }^{ 2 } } [/latex] = 4 m  (1)

Solution 25.
Since, [latex s=2]\frac { 1 }{ 2a+b+2x } =\frac { 1 }{ 2a } +\frac { 1 }{ b } +\frac { 1 }{ 2x } [/latex]
[latex s=2]\frac { 1 }{ 2a+b+2x } =\frac { 2xb+4ax+2ab }{ (2a)(b)(2x) } [/latex]   (1)
4abx = (2xb + 4ax + 2ab) (2a + b + 2x)
4abx = 12axb + 8a2x + 4a2b + 2xb2 + 2ab2 + 4x2b + 8ax2
x2 (4b + 8a) + x(8ab + 8a2 + 2b2) + (2ab2 + 4a2b) = 0 (1)
4x2 (2a + b) + x [4a (2a + b) + 2b (2a+ b)] + 2ab (b + 2a) = 0
4(2a + b) x[x + a] + 2b (2a + b) [x + a] = 0   (1)
(x + a) (2x + b) = 0 [ ∵ 2a + b ≠ 0]
x = -a, [latex s=2]\frac { -b }{ 2 } [/latex]
Hence, the value of x is -a and [latex s=2]\frac { -b }{ 2 } [/latex].   (1)
OR
CBSE Sample Papers for Class 10 Maths Paper 2 img 25

Solution 26.
CBSE Sample Papers for Class 10 Maths Paper 2 img 26
CBSE Sample Papers for Class 10 Maths Paper 2 img 27
OR
CBSE Sample Papers for Class 10 Maths Paper 2 img 28
CBSE Sample Papers for Class 10 Maths Paper 2 img 29

Solution 27.

CBSE Sample Papers for Class 10 Maths Paper 2 img 30
OR
CBSE Sample Papers for Class 10 Maths Paper 2 img 31
CBSE Sample Papers for Class 10 Maths Paper 2 img 32

Solution 28.
CBSE Sample Papers for Class 10 Maths Paper 2 img 33

Solution 29.
Steps of construction:
1.DrawBC = 7cm.
2. Draw a ray BX and CY such that ∠CBX = 45° and ∠BCY =180°- (45° + 105°) = 30°
Suppose BX and CY intersect each other at A. ∆ ABC so obtained is the given triangle.
3.  Draw a ray BZ making a suitable acute angle with BC on opposite side of vertex A with respect to B BC.
4.  Draw four (greater of 4 and 3 in 4/3) arcs intersecting the ray BZ at B1, B2, B3, B4 such that BB1 = B1B2 = B2B3 = B3B4.
5.  Join B3 to C and draw a line through B4 parallel to B3C, intersecting the extended line segment BC atC’.
6. Draw a line through C’ parallel to CA intersecting the extended line segment BA at A’. Triangle A’BC’ so obtained is the required triangle.    (1)
CBSE Sample Papers for Class 10 Maths Paper 2 img 34

Solution 30.
CBSE Sample Papers for Class 10 Maths Paper 2 img 35

We hope the CBSE Sample Papers for Class 10 Maths paper 2 help you. If you have any query regarding CBSE Sample Papers for Class 10 Maths paper 2, drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration

by

UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration (रासायनिक समन्वय तथा एकीकरण)

These Solutions are part of UP Board Solutions for Class 11 Biology. Here we have given UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration (रासायनिक समन्वय तथा एकीकरण).

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
निम्नलिखित की परिभाषा लिखिए-
(अ) बहिःस्रावी ग्रन्थियाँ
(ब) अन्तःस्रावी ग्रन्थियाँ
(स) हॉर्मोन।
उत्तर-
(अ) बहिःस्रावी ग्रन्थियाँ (Exocrine Glands) – ये सँकरी नलिकाओं के द्वारा सम्बन्धित भागों से जुड़ी रहती हैं। इन ग्रन्थियों से स्रावित तरल नलिकाओं द्वारा सम्बन्धित सतह पर मुक्त होता है। इन्हें वाहिनीयुक्त (ducted glands) भी कहते हैं; जैसे-लार ग्रन्थियाँ, आहारनाल की विभिन्न पाचक ग्रन्थियाँ, त्वचा की तैल ग्रन्थियाँ, पसीने की ग्रन्थि (sweat gland), यकृत आदि।

(ब) अन्तःस्रावी ग्रन्थियाँ (Endocrine Glands) – ये सम्बन्धित एपिथीलियम से (UPBoardSolutions.com) पृथक् हो जाने के कारण नलिकाविहीन (ductless) कहलाती हैं। इनसे स्रावित रसायनों को हॉर्मोन्स कहते हैं। इनका वितरण रक्त या ऊतक तरल द्वारा होता है। इन ग्रन्थियों में रक्त-केशिकाओं का घना जाल फैला रहता है; जैसे-थाइरॉइड, पैराथाइरॉइड, अधिवृक्क, पीयूष, पीनियल तथा थाइमस ग्रन्थियाँ आदि।

(स) हॉर्मोन (Hormone) – बैलिस एवं स्टारलिंग (Bayliss & Starling, 1903-1905) के अनुसार ये ऐसे सक्रिय सन्देशवाहक रसायन होते हैं जो बाह्य या अन्त:उद्दीपन के कारण शरीर के किसी भाग की अन्त:स्रावी कोशिकाओं द्वारा स्रावित होकर रक्त में पहुँचकर शरीर में संचारित होते हैं।
और इसकी सूक्ष्म मात्रा शरीर की लक्ष्य कोशिकाओं की कार्यिकी को प्रभावित करती है।

UP Board Solutions

प्रश्न 2.
हमारे शरीर में पाई जाने वाली अन्तःस्रावी ग्रन्थियों की स्थिति चित्र बनाकर प्रदर्शित कीजिए।
उत्तर-
अन्तःस्रावी ग्रन्थियों की स्थिति
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 1

प्रश्न 3.
निम्नलिखित द्वारा स्रावित हॉर्मोन का नाम लिखिए-
(अ) हाइपोथैलेमस
(ब) पीयूष ग्रन्थि
(स) थाइरॉइड
(द) पैराथाइरॉइड
(य) अधिवृक्क ग्रन्थि
(र) अग्न्याशय
(ल) वृषण।
(व) अण्डाशय
(श) थाइमस
(स) एट्रियम
(ह) जठर-आंत्रीय पथ
उत्तर-
(अ) गोनेडोट्रोपिन (GnRH),
(ब) वृद्धि हार्मोन (GH), प्रोलेक्टिनं (PRL), थाइरॉइड स्टिम्युलेटिंग हार्मोन (TSH), एडीनोकॉर्टिकोट्रोफिक हार्मोन (ACTH), ल्यूटिनाइजिंग हार्मोन (LH), फॉलिकल स्टीम्युलेटिंग हार्मोन (FSH), मिलेनोसाइट स्टिम्युलेटिंग हार्मोन (MSH), ऑक्सीटोसिन, वेसोप्रोसिन, (UPBoardSolutions.com) ग्लूकोकॉर्टिकॉइड, एन्ड्रोजन, एन्टीडाययूरेटिक हार्मोन (ADH)।
(स) थाइरॉक्सिन (T4) तथा ट्राइडोथाइरोनिन (T3), थाइरोकेल्सिटोनिन (TCT).
(द) पैराथाइरॉइड हार्मोन (PTH)।
(य) एड्रीनलिन अथवा एपिनेफ्रिन, नॉरएड्रीनलिन अथवा नॉरएपिनेफ्रिन।
(र) ग्लूकागॉन, इंसुलिन।
(ल) एंड्रोजन (टेस्टोस्टीरॉन)।
(व) एस्ट्रोजन तथा प्रोजेस्ट्रॉन।
(श) थॉयमोसिन।
(स) एट्रियल नेट्रीयूरेटिक फेक्टर (ANF)।
(ष) इरिथ्रोपोइटिन।
(ह) गैस्ट्रिन।

UP Board Solutions

प्रश्न 4.
रिक्त स्थानों की पूर्ति कीजिए-
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 2
उत्तर-
(अ) हाइपोथैलेमस,
(ब) थाइरॉइड ग्रन्थि,
(स) अधिवृक्क वल्कुट,
(द) वृषण अथवा अडाशय,
(य) त्वचा की रंग कोशिकाएँ (मिलैनोफोर्स)।

प्रश्न 5.
निम्नलिखित हॉर्मोन के कार्यों के बारे में टिप्पणी लिखिए-
(अ) पैराथाइरॉइड हॉर्मोन (पी०टी०एच)
(ब) थाइरॉइड हॉर्मोन,
(स) थाइमोसिन,
(द) एन्ड्रोजेन,
(य) एस्ट्रोजेन,
(र) इन्सुलिन एवं ग्लूकैगॉन।
उत्तर-
(अ) पैराथायरॉइड हॉर्मोन (Parathyroid Hormone) – ह कैल्सियम के अवशोषण तथा फॉस्फेट के उत्सर्जन को बढ़ाता है। अस्थि एवं दाँतों के विकास में सहायता करता है और पेशियों को क्रियाशील रखता है।
(ब) थाइरॉइड हॉर्मोन (Thyroid Hormone) –

  • ये ऑक्सीकारक उपापचय (Oxidative metabolism) को प्रेरित करके कोशिकाओं में ऊर्जा उत्पादन और उपापचय दर को बढ़ाते हैं और जीवन की रफ्तार को बनाए रखते हैं। ये हृदय स्पन्दन दर, प्रोटीन संश्लेषण, O2 एवं ग्लूकोस की खपत आदि (UPBoardSolutions.com) को बढ़ाते हैं।
  • थायरॉक्सिन कायान्तरण (metamorphosis) – के लिए आवश्यक होता है।
  • ये शीत रुधिर वाले जन्तुओं में त्वक्पतन (moulting) – को नियन्त्रित करते हैं।

UP Board Solutions

(स) थाइमोसिन (Thymosin) – यह T-लिम्फोसाइट्स के प्रचुरोद्भवन (proliferation) एवं विभेदीकरण द्वारा शरीर की सुरक्षा करता है। ये जीवाणुओं के प्रतिजन (antigens) को नष्ट करने के लिए प्रतिरक्षी का निर्माण करती है।
(द) एन्ड्रोजेन (Androgens) – इन्हें पौरुष-विकास हॉर्मोन (masculinization hormones) कहते हैं। ये सहायक जनन ग्रन्थियों के विकास को प्रेरित करते हैं। इनके प्रभाव से नर लैंगिक लक्षणों; जैसे-दाढ़ी-मूंछ का उगना, आवाज का भारी होना, अस्थियों का मजबूत होना, पेशियों और शरीर की सुडौलता, कन्धों को फैलाव आदि लक्षणों का विकास होता है।
(य) एस्ट्रोजेन (Estrogens) – इनके कारण स्त्रियों में यौवनारम्भ (puberty) होता है। मासिक धर्म प्रारम्भ (UPBoardSolutions.com) हो जाता है। स्तनों, दुग्ध ग्रन्थियों, गर्भाशय, योनि, लैबिया (labia) भगशिश्न (clitoris) आदि का विकास होता है। इस हॉर्मोन को नारी विकास (feminizing) हॉर्मोन कहते हैं।
(र) इन्सुलिन एवं ग्लूकैगॉन (Insulin and Glucagon) – ये कार्बोहाइड्रेट उपापचय का नियमन करते हैं। इन्सुलिन आवश्यकता से अधिक शर्करा को ग्लाइकोजन में बदलता है। इस क्रिया को ग्लाइकोजेनेसिस (glycogenesis) कहते हैं। ग्लाइकोजन शर्करा में संचित हो जाती है। रक्त में ग्लूकोस की मात्रा के कम होने पर ग्लूकैगॉन हॉर्मोन संचित ग्लाइकोजन को ग्लूकोस में बदल देता है। इसे ग्लाइकोजेनोलिसिस (glycogenolysis) कहते हैं।

प्रश्न 6.
निम्नलिखित के उदाहरण दीजिए-
(अ) हाइपरग्लाइसीमिक हॉर्मोन एवं हाइपोग्लाइसीमिक हॉर्मोन
(ब) हाइपरकैल्सीमिक हॉर्मोन
(स) गोनेडोट्रॉफिक हॉर्मोन
(द) प्रोजेस्टेशनल हॉर्मोन
(य) रक्तदाब निम्नकारी हॉर्मोन
(र) एन्ड्रोजेन एवं एस्ट्रोजेन।
उत्तर-
(अ) हाइपरग्लाइसीमिक हॉर्मोन; जैसे – ग्लूकैगॉन (glucagon) एवं ग्लूकोकॉर्टिकोएड्स (glucocorticoids)।
हाइपोग्लाइसीमिक हॉर्मोन; जैसे – इन्सुलिन (insulin) एवं ग्लूकोकॉर्टिकॉएड्स।
(ब) हाइपरकैल्सीमिक हॉर्मोन; जैसे पैराथॉर्मोन (Parathormone)।
(स)गोनेडोट्रॉफिक हॉर्मोन; जैसे – ल्यूटीनाइजिंग हॉर्मोन (LH), पुटिका प्रेरक हॉर्मोन (FSH)।
(द) प्रोजेस्टेशनल हॉर्मोन; जैसे – प्रोजेस्टेरॉन (progesterone) हॉर्मोन।
(य) रक्तदाब निम्नकारी हॉर्मोन; जैसे – पेप्टाइड हॉर्मोन या (atrial natriuretic factor, ANF)।
(र) एन्ड्रोजेन (androgens); जैसे – टेस्टोस्टेरॉन (testosterone)।
एस्ट्रोजेन (Estrogens); जैसे-एस्ट्रोन (estrone), एस्ट्रिओल (estriole)।

प्रश्न 7.
निम्नलिखित विकार किस हार्मोन की कमी के कारण होते हैं?
(अ) डायबिटीज
(ब) गॉइटर
(स) क्रिटिनिज्म
उत्तर-
(अ) इन्सुलिन स्रावण में कमी के कारण
(ब) आयोडीन व थाइरॉक्सिन हार्मोन की कमी के कारण
(स) वृद्धि हार्मोन (GH) की कमी के कारण।

प्रश्न 8.
एफ०एस०एच० की कार्य-विधिका संक्षेप में वर्णन कीजिए।
उत्तर-
एफ०एस०एच० की कार्य-विधि
यह पुरुषों में वृषणों की शुक्रजनन नलिकाओं (seminiferous tubules) की वृद्धि तथा शुक्राणुजनन (spermatogenesis) को प्रेरित करता है। स्त्रियों में यह अण्डाशय की प्रैफियन पुटिकाओं (Graafian follicles) की वृद्धि और विकास तथा अण्डजनन (oogenesis) को प्रेरित करता है। यह मादा हॉर्मोन एस्ट्रोजेन (estrogen) के स्रावण को प्रेरित करता है।
ऋणात्मक पुनर्निवेशन नियन्त्रण में स्त्रियों में यह प्रमुख हॉर्मोन एस्ट्रोजन (estrogen) तथा पुरुषों (UPBoardSolutions.com) में प्रमुख नर हॉर्मोन टेस्टोस्टेरॉन (testosterone) FSH के स्रावण का अवरोध करते हैं। स्त्रियों में 40 वर्ष की आयु के बाद अण्डाशयों पर FSH का प्रभाव बहुत कम हो जाता है; अत: मासिक धर्म, अण्डजनन तथा मादा हॉर्मोन स्रावण आदि समाप्त होने लगते हैं। इस स्थिति को रजोनिवृत्ति कहते हैं।

UP Board Solutions

प्रश्न 9.
निम्नलिखित के जोड़े बनाइए-
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 3

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
रुधिर दाब तथा हृदय स्पंदन किस हॉर्मोन से बढ़ जाते हैं?
(क) एड्रीनेलिन
(ख) थायरॉक्सिन
(ग) सीक्रिटिन
(घ) गैस्ट्रीन
उत्तर-
(क) एड्रीनेलिन

प्रश्न 2.
लैंगरहैन्स की द्वीपिकाएँ पायी जाती हैं।
(क) मस्तिष्क में
(ख) प्लीहा में
(ग) अग्न्याशय में
(घ) अण्डाशय में
उत्तर-
(ग) अग्न्याशय में

UP Board Solutions

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
किन्हीं दो न्यूरोहॉर्मोन्स के नाम लिखिए।
उत्तर-
ऐसीटिलकोलीन, डोपामीन, नॉर-एपीनेफ्रिन आदि।

प्रश्न 2.
ऐसीटिलकोलीन क्या है? इसके अभाव में शरीर पर क्या प्रभाव पड़ेगा?
उत्तर-
ऐसीटिलकोलीन एक तन्त्रिसंचारी पदार्थ है जो क्रोमेफिन कोशिकाओं को अपने (UPBoardSolutions.com) हॉर्मोन-नॉरएपिनेफ्रीन तथा एपिनेफ्रीन-मुक्त करने के लिए प्रेरित करता है। इसके अभाव में नॉरंएपिनेफ्रीन तथा एपिनेफ्रीन हॉर्मोनों का स्रावण प्रभावित होगा।

प्रश्न 3.
कौन-सा हॉर्मोन पानी तथा खनिज उपापचय का नियन्त्रण करता है?
उत्तर-
मिनरैलोकॉर्टिकॉएड्स (Mineralocorticoides)

प्रश्न 4.
एस्ट्रोजन का प्रमुख कार्य लिखिए।
उत्तर-
एस्ट्रोजन का कार्य स्त्रियों में गौण स्त्री लैंगिक लक्षणों के विकास को प्रेरित करना तथा अण्डाशय व गर्भाशय में होने वाले चक्रीय परिवर्तन को नियन्त्रित करना होता है।

प्रश्न 5.
डायबिटीज मैलीटस रोग क्या है? इस रोग के लक्षण एवं बचाव के दो उपाय लिखिए।
या
डायबिटीज मैलीटस रोग क्या है? इस रोग के दो लक्षण लिखिए।
उत्तर-
डायबिटीज मैलीटस-जब मनुष्य के मूत्र के साथ ग्लूकोज का ह्रास होने लगता है तो इस रोग को डायबिटीज मैलीटस कहते हैं।
लक्षण-
1. मूत्र बार-बार आता है।
2. भूख अधिक लगती है।
बचाव-
1. मनुष्य को संतुलित भोजन खाना चाहिए और नियमित व्यायाम करना चाहिए।
2. रोग हो जाने पर निश्चित समयान्तराल पर इंसुलिन के इंजेक्शन लगवाने चाहिए।

लघु उत्तरीय प्रश्न

प्रश्न 1.
हॉर्मोन्स क्या हैं? हॉर्मोन्स की क्रियाविधि का वर्णन कीजिए।
उत्तर-

हॉर्मोन्स

अन्त:स्रावी ग्रन्थियों द्वारा उत्पन्न रस जो सीधे रुधिर में संवहित किये जाते हैं, हॉर्मोन्स (hormones) कहलाते हैं। इन्हें रासायनिक सन्देशवाहक (chemical messenger) भी कहते हैं। इनकी रासायनिक प्रकृति अमीनो ऐसिड, प्रोटीन या स्टेरॉइड्स होती है। शरीर (UPBoardSolutions.com) में इनका प्रभाव किसी विशेष अंग में विशेष प्रकार की क्रिया आदि को प्रभावित व प्रेरित करना होता है। ये कार्य के बाद प्रायः विघटित हो जाते हैं। परिभाषा के रूप में बैलिस तथा स्टार्लिंग (Bayliss and Starling, 1902-1905) के अनुसार, हॉर्मोन एक ऐसा सक्रिय सन्देशवाहक पदार्थ होता है जो किसी बाह्य या अन्त:उद्दीपन के कारण शरीर के किसी भाग की अन्त:स्रावी कोशिकाओं से स्रावित होकर रुधिर में पहुँचता है और पूरे शरीर में संचरित होता है तथा इसकी सूक्ष्म मात्रा ही शरीर की अन्य कोशिकाओं, प्रायः किसी विशिष्ट भाग की लक्ष्य कोशिकाओं की कार्यिकी को प्रभावित करती है।

UP Board Solutions

हॉर्मोन्स की क्रिया-विधि

हॉर्मोन्सनिम्न प्रकार से अपनी क्रिया करते हैं-

  1. ये कोशिका को अधिक सक्रिय बनाने के लिए कोशिका कला (plasma membrane) की पारगम्यता बढ़ाकर उसे अधिक वरणात्मक पारगम्य (selectively permeable) बना देते हैं।
    इससे कोशिका के कार्य के लिए आवश्यक पदार्थ उसके भीतर आ-जा सकते हैं।
  2. हॉर्मोन्स कोशिकाओं में एन्जाइम्स (enzymes) को प्रेरित कर देते हैं जिससे वे अधिक सक्रिय हो जाते हैं।
  3. स्टेरॉइड प्रकार के हॉर्मोन्स कोशिका के केन्द्रक में पहुँचकर उसके जीन्स को प्रभावित करते हैं। इस प्रक्रिया में सक्रिय जीन को निष्क्रिय तथा सुप्त जीन को सक्रिय किया जाता है। इससे प्रोटीन संश्लेषण प्रभावित हो जाता है।

हॉर्मोन्स की क्रिया-विधि की सदरलैंड़ (Sutherland, 1971) ने इस प्रकार व्याख्या की है, हॉर्मोन प्रथम दूत (primary messenger) के रूप में कोशिका कला (plasma – membrane) में पाये जाने वाले ऐडीनिल साइलेज (adenyl cyclase) नामक एन्जाइम को प्रेरित करते हैं। एक एन्जाइम कोशिकाद्रव्य के ATP अणु का चक्रिक ऐडीनोसीन मोनोफॉस्फेट (cyclic AMP) में विघटन करता है। चक्रिक AMP द्वितीय दूत (second messenger) के रूप में कोशिकाओं को कई प्रकार से प्रभावित कर सकता है; जैसे-जीन को प्रभावित कर सकता है।” हॉर्मोन क्रिया में चक्रिक AMP की द्वितीय दूत के रूप में कार्य करने की व्याख्या पर सदरलैंड को नोबेल पुरस्कार (Nobel prize) से सम्मानित किया गया।

प्रश्न 2.
विटामिन तथा हॉर्मोन्स का तुलनात्मक वर्णन कीजिए।
उत्तर-
विटामिन – ये हमारे भोजन का महत्त्वपूर्ण अवयव होते हैं जो हमारे शरीर के लिए सूक्ष्म मात्रा में आवश्यक होते हैं। ये कार्बनिक पदार्थ होते हैं। हमारा शरीर इनका निर्माण नहीं कर सकता, परन्तु इनकी सूक्ष्म मात्रा हमारे जीवन के लिए आवश्यक है। यह हमें भोजन से प्राप्त होता है।
हॉर्मोन – हॉर्मोन्स अन्त:स्रावी ग्रन्थियों द्वारा उत्पन्न एक रस हैं जो सीधे ही हमारे रुधिर में संवहित (UPBoardSolutions.com) किये जाते हैं। इनकी रासायनिक प्रकृति अमीनो अम्ल, प्रोटीन या स्टेरॉइड्स होती है। शरीर में इनका प्रभाव किसी विशेष अंग में विशेष प्रकार की क्रिया आदि को प्रभावित व प्रेरित करना होता है। ये कार्ये के बाद प्रायः विघटित हो जाते हैं।

प्रश्न 3.
हरस्यूटिज्म रोग के कारण व लक्षण लिखिए।
या
कभी-कभी स्त्रियों में पुरुषों के द्वितीयक गौण लक्षण उत्पन्न हो जाते हैं। ऐसा क्यों होता है? कारण सहित समझाइए।
उत्तर-
हरस्यूटिज्म (Hirsutism) – अधिवृक्क ग्रन्थि तथा जनन अंगों से नर तथा मादा हॉर्मोन्स एन्ड्रोजेन्स तथा एस्ट्रोजेन्स स्रावित होते हैं। ये नर तथा मादा में द्वितीयक लक्षणों का विकास करते हैं। सामान्यतया अधिवृक्क ग्रन्थि से स्रावित लिंग हॉर्मोन्स का प्रभाव दिखाई नहीं देता, लेकिन अतिस्रावण के कारण स्त्री में पुरुषोचित लक्षण; जैसे-दाढ़ी-मूंछ निकल आना, आवाज का भारी होना, शरीर पर अधिक बालों का पाया जाना आदि प्रदर्शित होने लगते हैं। इन लक्षणों को हरस्यूटिज्म कहते हैं।”

प्रश्न 4.
“अग्न्याशय एक अन्तःस्रावी के साथ-साथ बहिःस्रावी ग्रन्थि भी है।” इस कथन की पुष्टि कीजिए।
या
सिद्ध कीजिए कि अग्न्याशय (पैन्क्रियाज) एक बहिःस्रावी एवं अन्तःस्रावी ग्रन्थि है।
या
अग्न्याशय एक मिश्रित ग्रन्थि है। समझाइए।
उत्तर-
अन्याशय ग्रहणी आमाशय के साथ ‘C’ आकार की रचना बनाती है। इसी के मध्य में यकृत तथा आमाशय के पीछे स्थित, मछली के आकार की कोमल एवं गुलाबी रंग की एक चपटी ग्रन्थि होती है जिसे अग्न्याशय कहते हैं। यह यकृत के बाद शरीर की सबसे बड़ी ग्रन्थि होती है। इसमें दो विभिन्न प्रकार के ग्रन्थिल ऊतक भाग होते हैं-
(i) बहिःस्रावी भाग (exocrine part)
(ii) अन्तःस्रावी भाग (endocrine pary)

UP Board Solutions

(i) बहिःस्रावी भाग – बहि:स्रावी ग्रन्थि के रूप में इस ग्रन्थि में पाचन के लिये अत्यन्त महत्त्वपूर्ण, अनेक एन्जाइम्स (enzymes) वाला अग्न्याशयिक रस (pancreatic juice) बनता है। अग्न्याशय की विभिन्न पालियों से छोटी-छोटी वाहिनियाँ उत्पन्न होती हैं जो मिलकर अग्न्याशयी वाहिनियों (pancreatic ducts) का निर्माण करती हैं। ये वाहिनियाँ पित्त वाहिनी (bile duct) में खुलती हैं, जो स्वयं ग्रहणी के समीपस्थ भाग से सम्बन्धित होती हैं।
(ii) अन्तःस्रावी भाग – अन्त:स्रावी ग्रन्थि के रूप में लैंगरहैन्स की द्वीपिकाओं से कार्बोहाइड्रेट उपापचय में महत्त्वपूर्ण हॉर्मोन्स बनते हैं।
उपर्युक्त विवरण के आधार पर हम कह सकते हैं कि अग्न्याशय एक अन्त:स्रावी ग्रन्थि के साथ-साथ बहि:स्रावी ग्रन्थि भी है। इसे मिश्रित ग्रन्थि भी कहा जाता है।

प्रश्न 5.
(क) इन्सुलिन कहाँ बनता है? इसका क्या कार्य है?
(ख) एपिनेफ्रिन तथा नॉर-एपिनेफ्रिन में एक अन्तर बताइए।
उत्तर-
(क) इन्सुलिन – लैंगरहैन्स की द्वीपिकाओं की कोशिकाओं से इन्सुलिन स्रावित होता है। यह आवश्यकता से अधिक ग्लूकोज को ग्लाइकोजन में बदल कर संचित कर देता है।
(ख) एपिनेफ्रिन तथा नॉर-एपिनेफ्रिन में अन्तर – ‘एपिनेफ्रिन हृदय स्पन्दन, श्वास दर, आधारीय (UPBoardSolutions.com) उपापचय दर (BMR) तथा रक्त में पोषक पदार्थों की मात्रा को बढ़ाता है। नॉर-एपिनेफ्रिन शरीर की रक्तवाहिनियों को संकुचित करके रक्तदाब को बढ़ाता है।

प्रश्न 6.
मानव शरीर में किसकी कमी से निम्नलिखित रोग उत्पन्न होते हैं? इन रोगों को होने से कैसे रोका जा सकता है?
(i) मधुमेह,
(ii) घेघा,
(iii) ऐडिसन रोग,
(iv) बौनापन,
(v) मिक्सीडेमा।
उत्तर-
(i) मधुमेह (Diabetes) – यह रोग इन्सुलिन हॉर्मोन की कमी से होता है। शर्करा युक्त पदार्थों के कम उपयोग एवं नियमित व्यायाम से मधुमेह को रोका जा सकता है।
(ii) घेघा (Goitre) – यह थाइरॉक्सिन हॉर्मोन की कमी से होता है। आयोडीन युक्त नमक का प्रयोग करने से घेघा रोग को होने से रोका जा सकता है।
(iii) ऐडिसन रोग (Addison’s disease) – ह रोग एड्रीनल हॉर्मोन की कमी के कारण होता है। शरीर से जल तथा सोडियम अधिक मात्रा में उत्सर्जित हो जाने से शरीर का निर्जलीकरण हो जाता है। पेशियाँ शिथिल हो जाती हैं और रक्तदाब कम हो जाता है।
(iv) बौनापन – यह रोग बचपन में वृद्धि हॉर्मोन की कमी के कारण होता है। वृद्धि हॉर्मोन पीयूष ग्रन्थि से स्रावित होता है। बचपन में थाइरॉक्सिन हॉर्मोन की कमी के कारण व्यक्ति बौना रहे जाता है। आयोडीन प्रचुर मात्रा में उपलब्ध होने पर थाइरॉक्सिन हॉर्मोन की कमी नहीं हो पाती है।
(v) मिक्सीडेमा – वयस्क अवस्था में हॉर्मोन की कमी से उपापचय दर कम हो जाने से समय से पहले बुढ़ापा आ जाता है। और रक्तदाब कम हो जाता है तथा जननक्षमता कम हो जाती है।

UP Board Solutions

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
अन्तःस्रावी एवं बहिःस्रावी ग्रन्थियों में अन्तर स्पष्ट कीजिए। किन्हीं दो अन्तःस्रावी ग्रन्थियों के नाम, उनसे निकलने वाले हॉर्मोन्स एवं कार्य लिखिए।
या
अन्तःस्रावी ग्रन्थियाँ क्या हैं ? मानव शरीर में पायी जाने वाली चार प्रमुख अन्तःस्रावी ग्रन्थियों (UPBoardSolutions.com) के नाम तथा उनके द्वारा स्रावित एक-एक हॉर्मोन का नाम और कार्य लिखिए।
या
बहिःस्रावी तथा अन्तःस्रावी ग्रन्थियों में अन्तर लिखिए।
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 4
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 5

अन्तःस्रावी ग्रन्थियाँ

तन्त्रिकीय नियन्त्रण के अतिरिक्त सभी जन्तुओं में किसी-न-किसी प्रकार का रासायनिक नियन्त्रण भी रहता है। कशेरुकियों में विशेषकरें, स्तनियों में रासायनिक नियन्त्रण को एक विशिष्ट तन्त्र होता है जिसे अन्त:स्रावी तन्त्र (endocrine system) कहते हैं। मनुष्य में तो यह (UPBoardSolutions.com) तन्त्र अतिविकसित होता है। अन्त:स्रावी अथवा एण्डोक्राइन (endocrine) ग्रन्थियों से अभिप्राय ऐसी ग्रन्थियों से है, जो आन्तरिक रूप से स्रावण करती हों। इनमें नलिकाएँ न पायी जाने के कारण इन्हें नलिकाविहीन ग्रन्थियाँ (ductless glands) भी कहते हैं। इन ग्रन्थियों से स्रावित होने वाले विशिष्ट पदार्थों को हॉर्मोन्स (hormones) कहते हैं। हॉर्मोन्स का शरीर के विभिन्न अंगों तक संचरण रुधिर प्रवाह के माध्यम से होता है।

UP Board Solutions
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 6
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 7

प्रश्न 2.
मनुष्य की पीयूष ग्रन्थि की संरचना तथा इसके द्वारा स्रावित विभिन्न हॉर्मोन्स के नाम व कार्यों का वर्णन कीजिए।
या
पीयूष ग्रन्थि द्वारा स्रावित दो हॉर्मोन्स के नाम तथा कार्यों का उल्लेख कीजिए।
उत्तर-
पीयूष ग्रन्थि पीयूष ग्रन्थि एक सेला टर्सिका नामक अस्थिल गुहा में स्थित होती है और एक वृंत द्वारा हाइपोथैलेमस से जुड़ी होती है। आन्तरिक रूप से पीयूष ग्रन्थि एडिनोहाइपोफाइसिस और न्यूरोहाइपोफाइसिस नामक दो भागों में विभाजित होती है। एडिनोहाइपोफाइसिस दो भागों का बना होता है-पार्स डिस्टेलिस और पार्स इंटरमीडिया। पार्स डिस्टेलिस को साधारणतया अग्र पीयूष ग्रन्थि कहते हैं, जिससे वृद्धि हॉर्मोन या सोमेटोट्रोपिन (GH), प्रोलैक्टिन (PRIL) या मेमोट्रोपिन, थाइरॉइड प्रेरक हॉर्मोन (TSH) एड्रिनोकॉर्टिकोट्रॉफिक हॉर्मोन (ACTH) या कॉर्टिकोट्रोफिन, ल्यूटीनाइजिंग हार्मोन (LH) और पुटिका प्रेरक हॉर्मोन का स्राव होता है। पार्स इंटरमीडिया एकमात्रे हॉर्मोन मैलेनोसाइट प्रेरक हॉर्मोन (MSH) या मेलेनोट्रोफिन का स्राव करता है। यद्यपि मानव में पार्स इंटरमीडिया (मध्यपिंड) पार्स डिस्टेलिस (दूरस्थ पिंड) से लगभग जुड़ा होता है। न्यूरोहाइपोफाइसिस (पार्स नर्वोसा) या पश्चपीयूष ग्रन्थि, हाइपोथैलेमस द्वारा उत्पादित किए जाने वाले हॉमन्स ऑक्सीटॉसिन और वेसोप्रेसिन का संग्रह और स्राव करती है। ये हॉर्मोन वास्तव में हाइपोथैलेमस द्वारा संश्लेषित होते हैं और तन्त्रिकाक्ष (axon) होते हुए पश्च पीयूष ग्रन्थि में पहुँचा दिए जाते हैं।

UP Board Solutions

वृद्धिकारी हॉर्मोन (GH) के अति स्राव से शरीर की असामान्य वृद्धि होती है जिसे जाइगेटिज्मया अतिकायकता (gigantism) कहते हैं और इसके अल्प स्राव से वृद्धि अवरुद्ध हो जाती है जिसे पिट्यूटरी ड्वार्फिज्म (बौनापन या वामनता) कहते हैं। प्रोलैक्टिन हॉर्मोन स्तन ग्रन्थियों की वृद्धि और उनमें दुग्ध निर्माण का नियंत्रण करता है। थाइरॉइड प्रेरक हॉर्मोन (TSH) थाइरॉइड ग्रन्थियों पर कार्य कर उनसे थाइरॉइड हॉर्मोन के संश्लेषण और स्रावण को प्रेरित करता है। एड्रिनोकॉर्टिकोट्रॉफिक हॉर्मोन (ACTH) एड्रीनल वल्कुट पर कार्य करता है और इसे ग्लूकोकॉर्टिकॉइड्स नामक स्टीरॉइड हॉर्मोन के संश्लेषण और स्रावण के लिए प्रेरित करता है। (UPBoardSolutions.com) ल्यूटिनाइजिंग (LH) और पुटिका प्रेरक हॉर्मोन (FSH) जननांगों की क्रिया को प्रेरित करते हैं और लिंगी हॉर्मोन का उत्पादन करते हैं अतः गोनेडोट्रोपिन कहलाते हैं। नरों में ल्यूटिनाइजिंग हॉर्मोन (LH), एंड्रोजेन नामक हॉर्मोन के संश्लेषण और स्राव के लिए प्रेरित करता है। इसी तरह नरों में पुटिका प्रेरक हॉर्मोन (FSH) और एंड्रोजेन शुक्रजनन (Spermatogenesis) को नियंत्रित करता है। मादाओं में ल्यूटिनाइजिंग हॉर्मोन (LH) पूर्ण विकसित पुटिकाओं (ग्राफियन पुटिका) से अण्डोत्सर्ग को प्रेरित करता है और ग्राफियन पुटिका के बचे भाग से कॉर्पस ल्यूटियम बनाता है। पुटिका प्रेरक हार्मोन (FSH) मादाओं में अण्डाशयी पुटिकाओं की वृद्धि और परिवर्धन को प्रेरित करता है।

मेलानोसाइट प्रेरक हॉर्मोन (MSH), मेलानोसाइट्स (मेलेनिन युक्त कोशिकाओं) पर क्रियाशील होता है तथा त्वचा की वर्णकता का नियमन करता है। ऑक्सीटॉसिन हमारे शरीर की चिकनी पेशियों पर कार्य करता है और उनके संकुचन को प्रेरित करता है। मादाओं में यह प्रसव के समय गर्भाशयी पेशियों के संकुचन और दुग्ध झुन्थियों से दूध के स्राव को प्रेरित करता है। वेसोप्रेसिन मुख्यतः वृक्क की दूरस्थ संवलित नलिका से जल एवं आयनों के पुनरावशोषण को प्रेरित करता है, जिससे मूत्र के साथ जल का ह्रास (डाइयूरेसिस) कम हो। अत: इसे प्रतिमूत्रल हॉर्मोन या एंटी-डाइयूरेटिक हार्मोन (ADH) भी कहते हैं।
UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration image 8

प्रश्न 3.
थाइरॉइड ग्रन्थि से उत्पन्न हॉर्मोन्स का वर्णन कीजिए। थाइरॉइड की अनियमितताओं के दुष्प्रभाव का उल्लेख कीजिए।
उत्तर-
थाइरॉइड ग्रन्थि थाइरॉइड ग्रन्थि श्वास नली के दोनों ओर स्थित दो पालियों से बनी होती है। दोनों पालियाँ संयोजी ऊतक की पतली पल्लीनुमा इस्थमस से जुड़ी होती हैं। प्रत्येक थाइरॉइड ग्रन्थि पुटकों (follicles) र भरण ऊतकों (stromal tissues) की बनी होती हैं। प्रत्येक थाइरॉइड पुटक एक गुहा को घेरे पुटक कोशिकाओं से निर्मित होता है। ये पुटक कोशिकाएँ दो हॉर्मोन, टेट्राआइडोथाइरोनीन (TA) अथवा थाइरॉक्सिन तथा ट्राइआइडोथायरोनीन (T) का संश्लेषण करती हैं। थाइरॉइड हॉर्मोन के सामान्य दर से संश्लेषण के लिए आयोडीन आवश्यक है। हमारे भोजन में आयोडीन की कमी से अवथाइरॉइडता (hypothyroidism) एवं थाइरॉइड ग्रन्थि (UPBoardSolutions.com) की वृद्धि हो जाती है। इस बीमारी को साधारणतया घेघा (goitre) कहते हैं। गर्भावस्था के समय अवथाइरॉइडता के कारण गर्भ में विकसित हो रहे बालक की वृद्धि विकृत हो जाती है। इससे बच्चे की अवरोधित वृद्धि (cretinism) या वामनता तथा मंदबुद्धि, त्वचा असामान्यता, मूकबधिरता आदि हो जाती है। वयस्क स्त्रियों में अवथाइरॉइडता मासिक चक्र को अनियमित कर देता है। थाइरॉइड ग्रन्थि के कैंसर अथवा इसमें गाँठों की वृद्धि से थाइरॉइड हॉर्मोन के संश्लेषण की दर असामान्य रूप से अधिक हो जाती है। इस स्थिति को थाइरॉइड अतिक्रियता (hyperthyroidism) कहते हैं, जो शरीर की कार्यिकी पर प्रतिकूल प्रभाव डालती है।

UP Board Solutions

थाइरॉइड हॉर्मोन आधारीय उपापचयी दर (basal metabolic rate) के नियमन में मुख्य भूमिका निभाते हैं। ये हॉर्मोन, लाल रक्त कणिकाओं के निर्माण की प्रक्रिया में भी सहायता करते हैं। थाइरॉइड हॉर्मोन कार्बोहाइड्रेट, प्रोटीन और वसा के उपापचय (संश्लेषण और विखंडन) को भी नियन्त्रित करते हैं। जल और विद्युत अपघट्यों का नियमन भी थाइरॉइड हॉर्मोन को प्रभावित करते हैं। थाइरॉइड ग्रन्थि से एक प्रोटीन हॉर्मोन, थाइरोकैल्सिटोनिन (TCT) का भी स्राव होता है (UPBoardSolutions.com) जो रक्त में कैल्सियम स्तर को नियन्त्रित करता है।

We hope the UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration (रासायनिक समन्वय तथा एकीकरण) help you. If you have any query regarding UP Board Solutions for Class 11 Biology Chapter 22 Chemical Coordination and Integration (रासायनिक समन्वय तथा एकीकरण), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination

by

UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination (तन्त्रिकीय नियन्त्रण एवं समन्वय)

These Solutions are part of UP Board Solutions for Class 11 Biology. Here we have given UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination (तन्त्रिकीय नियन्त्रण एवं समन्वय).

अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर

प्रश्न 1.
निम्नलिखित संरचनाओं का संक्षेप में वर्णन कीजिए–
(अ) मस्तिष्क
(ब) नेत्र
(स) कर्ण।
उत्तर-

(अ) मस्तिष्क की संरचना

मनुष्य में मस्तिष्क कपाल या क्रेनियम (cranium) के भीतर सुरक्षित रहता है। (UPBoardSolutions.com) मस्तिष्क तीन आवरणों से ढका रहती है जिन्हें मस्तिष्कावरण (meninges) कहते हैं। ये मस्तिष्कावरण हैं-
1. दृढतानिका (Duramater) – श्वेत तन्तुमय ऊतक की बनी होती है।
2. जालतानिका (Arachnoid mater) – यह मध्य की पर्त है।
3. मृदुतानिका (Piamater) – यह सबसे भीतरी आवरण है, जो मस्तिष्क के सम्पर्क में रहती है।
इस पर्त में रुधिर वाहिनियों का जाल बिछा रहता है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 1
इन झिल्लियों के बीच एक तरल भरा रहता है जिसे सेरेब्रोस्पाइनल तरल (cerebrospinal fluid) कहते हैं। यह द्रव पोषण, श्वसन तथा उत्सर्जन में सहायक है। यह बाहरी आघातों से कोमल मस्तिष्क की सुरक्षा भी करता है। मस्तिष्क को तीन भागों में बाँटा जा सकता है-

  1. अग्रमस्तिष्क (Fore brain)
  2. मध्य-मस्तिष्क (Mid brain)
  3. पश्चमस्तिष्क (Hind brain)

UP Board Solutions

1. अग्रमस्तिष्क या प्रोसेनसिफैलॉन
अग्र मस्तिष्क के तीन भाग होते हैं|
(i) घ्राण भाग,
(ii) सेरेब्रम तथा
(iii) डाइएनसिफैलॉन।

(i) मनुष्य में घ्राण भाग अवशेषी होता है तथा अग्रमस्तिष्क का मुख्य भाग सेरेब्रम होता है।
(ii) प्रमस्तिष्क या सेरेब्रम (Cerebrum) – मस्तिष्क का लगभग 2/3 भाग प्रमस्तिष्क होता है। प्रमस्तिष्क दो पालियों में बँटा होता है जिन्हें प्रमस्तिष्क गोलार्द्ध (cerebral hemispheres) कहते हैं। दोनों प्रमस्तिष्क गोलार्द्ध तन्त्रिका तन्तुओं की एक पट्टी द्वारा जुड़े रहते हैं जिसे कॉर्पस कैलोसम (corpus callosum) कहते हैं।

प्रमस्तिष्क में तन्त्रिका कोशिकाएँ इस प्रकार स्थित होती हैं कि इनके कोशिकाकाय बाहर की ओर स्थित होते हैं। इस भाग को प्रमस्तिष्क वल्कुट (cerebral cortex) कहते हैं। भीतर की ओर तन्त्रिका कोशिकाओं पर अक्षतन्तु (axon) स्थित होते हैं। यह भाग प्रमस्तिष्क मध्यांश (cerebral medulla) कहलाता है। बाहरी भाग धूसर (ग्रे) रंग का होता है। इसे धूसर द्रव्य (grey matter) कहते हैं। भीतरी भाग श्वेत (सफेद) रंग का होता है। इसे श्वेत द्रव्य (white matter) कहते हैं।

प्रमस्तिष्क की पृष्ठ सतह में तन्त्रिका तन्तुओं की अत्यधिक संख्या होने के कारण यह सतह अत्यधिक मोटी व वलनों वाली (folded) हो जाती है। इस सतह को नियोपैलियम (neopallium) कहते हैं। नियोपैलियम में उभरे हुए भागों को उभार या गायराई (gyri) तथा बीच के दबे भाग को खाँच या सल्काई (sulci) कहते हैं।

तीन गहरी दरारें प्रत्येक प्रमस्तिष्क गोलार्द्ध को चार मुख्य पालियों में बाँट देती हैं। इन्हें-
फ्रन्टल पालि (frontal lobe), पैराइटल पालि (parietal lobe), टैम्पोरल पालि (temporal lobe) तथा ऑक्सीपीटल पालि (Occipital lobe) कहते हैं।
प्रमस्तिष्क की गुहाओं को पाश्र्व मस्तिष्क गुहा या पैरासील (paracoel or lateral ventricles) कहते हैं।

(iii) अग्रमस्तिष्क पश्च या डाइएनसिफैलॉन (Diencephalon) – यह अग्रमस्तिष्क का पिछला भाग है। इसका पृष्ठ भाग पतला होता है तथा अधर भाग मोटा होता है जिसे हाइपोथैलेमस (hypothalamus) कहते हैं। हाइपोथैलेमस की अधर सतह पर इन्फन्डीबुलम (infundibulum) से जुड़ी पीयूष ग्रन्थि होती है। डाइएनसिफैलॉन की पृष्ठ सतह पर पीनियल काय (pineal body) तथा अग्र रक्त जालक (anterior choroid plexus) पाया जाता है।
डाइएनसिफैलॉन की गुहा तृतीय निलय (third ventricle) या डायोसील (diocoel) होती है, यह पार्श्व गुहाओं से मोनरो के छिद्र (foramen of Monaro) द्वारा जुड़ी रहती है।

2. मध्यमस्तिष्क या मीसेनसिफैलॉन
यह भाग स्तनियों में बहुत अधिक विकसित नहीं होता है। इसका पृष्ठ भाग चार दृक् पालियों के रूप में होता है, जिन्हें कॉर्पोरा क्वाड़िजेमिना (corpora quadrigemina) कहते हैं। मध्यमस्तिष्क के पाश्र्व व अधर भाग में तन्त्रिका ऊतक की पट्टियाँ होती हैं जिन्हें क्रूरा सेरेब्राई (crura cerebri) कहते हैं। ये पश्चमस्तिष्क को अग्रमस्तिष्क से जोड़ने का कार्य करती हैं। यहाँ दृक् तन्त्रिकाएँ एक-दूसरे को क्रॉस करके, ऑप्टिक कियाज्मा (optic chiasma) बनाती हैं। मध्यमस्तिष्क की संकरी गुहा को आइटर (iter) कहते हैं, जो तृतीय निलय को चतुर्थ निलय (fourth ventricle) से जोड़ती है।

3. पश्चमस्तिष्क या रॉम्बेनसिफैलॉन
यह मस्तिष्क का पश्च भाग है। इसे मस्तिष्क वृन्त (brain stalk) भी कहते हैं। पश्च मस्तिष्क के दो भाग होते हैं-
(i) अनुमस्तिष्क (cerebellum),
(ii) मस्तिष्क पुच्छ या मेडुला ऑब्लांगेटा (medulla oblongata)

UP Board Solutions

(i) अनुमस्तिष्क (Cerebellum) – यह प्रमस्तिष्क के पिछले भाग से सटा रहता है। अनुमस्तिष्क दो पाश्र्व गोलाद्घ (lateral hemispheres) का बना होता है। अनुमस्तिष्क में बाहरी धूसर द्रव्य तथा आन्तरिक श्वेत द्रव्य होता है। श्वेत द्रव्य में स्थान-स्थान पर धूसर द्रव्य प्रवेश करके वृक्ष की शाखाओं जैसी रचना बनाता है। इसे प्राणवृक्ष या आरबर विटी (arbor vitae) कहते हैं। अनुमस्तिष्क में गुहा अनुपस्थित होती है। अनुमस्तिष्क के अधर भाग में श्वेत (UPBoardSolutions.com) द्रव्य की एक पट्टी होती है जिसे पोंस वेरोली (pons varolli) कहते हैं।
(ii) मस्तिष्क पुच्छ या मेडुला ऑब्लांगेटा (Medulla Oblongata) – यह मस्तिष्क का सबसे पिछला भाग है जो आगे मेरुरज्जु के रूप में कपाल गुहा से बाहर निकलता है। मेडुला की पृष्ठ भित्ति पर पश्च रक्त जालक (posterior choroid plexus) स्थित होता है। मेडुला की गुहा को चतुर्थ निलय या मेटासील (fourth ventricle or metacoel) कहते हैं।

(ब) नेत्र की संरचना

मनुष्य में एक जोड़ी नेत्र चेहरे पर सामने की ओर नेत्र कपाल के नेत्र कोटर (eye orbit) में स्थित होते हैं। प्रत्येक नेत्र एक तरल से भरे गोलक के रूप में होता है। नेत्र गोलक का 4/5 भाग नेत्र कोटर में और लगभग 1/5 भाग नेत्र कोटर के बाहर स्थित होता है।
नेत्र गोलक की भित्ति तीन स्तरों से बनी होती है। सबसे बाहरी दृढ़पटल (sclera), मध्य रक्तकपटल (choroid) तथा भीतरी दृष्टिपटल (retina) है।
1. दृढ़पटल या स्क्ले रोटिक (Sclera or Sclerotic) – यह तन्तुमय संयोजी ऊतक का बना सबसे बाहरी स्तर है। इसका वह भाग जो नेत्र कोटर से बाहर होता है, पारदर्शी होता है तथा इसे कॉर्निया (cornea) कहते हैं।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 2
2. रक्तकपटल या कोरॉइड (Choroid) – ह नेत्र गोलक की भित्ति का मध्य स्तर है। रक्तकपटल संयोजी ऊतक का बना स्तर है जिसमें रुधिर केशिकाओं का घना जाल होता है। रक्तकपटल में रंगायुक्त कोशिकाएँ होती हैं, जिस कारण नेत्र का रंग काला, भूरा, सुनहरा या नीला दिखाई देता है।

रक्तकपटल का वह भाग जो कॉर्निया के नीचे होता है, थोड़ा पीछे हटकर एक पेशीय पर्दे जैसी रचना (diaphragm like) बनाता है जिसे आइरिस या उपतारा (iris) कहते हैं। आइरिस अरीय (radial) तथा वर्तुल पेशियों (circular muscles) का बना होता है। आइरिस के मध्य में एक गोल छिद्र होता है जिसे तारा या पुतली (pupil) कहते हैं। अरीय पेशियाँ तारे के छिद्र को बड़ा करती हैं; अतः इन्हें प्रसारी पेशियाँ (dilatory muscles) कहते हैं। वर्तुल पेशियाँ तारे के छिद्र को छोटा या संकुचित करती हैं; अतः इन्हें स्फिक्टर (अवरोधिनी) पेशियाँ (sphincter muscles) कहते हैं। तारा नेत्र में प्रवेश करने वाले प्रकाश की मात्रा को नियन्त्रित करता है।

UP Board Solutions
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 3
आइरिस के आधार पर रक्तकपटल अत्यधिक मोटा व पेशीयुक्त होकर सीलियरी काय (ciliary body) बनाता है।

3. दृष्टिपटल या रेटिना (Retina) – यह नेत्र भित्ति का सबसे भीतरी प्रकाश संवेदी (light sensitive) स्तर है।
रेटिना में रक्तकपटल की ओर एक पतला वर्णक स्तर (pigmented layer) तथा भीतर की ओर तन्त्रिका संवेदी स्तर होता है। तन्त्रिको संवेदी स्तर (neurosensory layer) प्रकाश के लिए संवेदनशील होता है। यह निम्नलिखित प्रकार की पर्यों से बना होता है-

(i) दृष्टि शलाकाओं एवं शंकुओं का स्तर (Layer of Rods and Cones) – शलाकाओं में दृष्टि पर्पल (visual purple) वर्णक रोडोप्सिन (rhodopsin) तथा शंकुओं में दृष्टि वॉयलेट (visual violet) वर्णक आयोडोप्सिन (iodopsin) पाए जाते हैं। शलाकाएँ प्रकाश व अन्धकार में भेद करती हैं, जबकि शंकु रंगों का ज्ञान कराते हैं।
(ii) द्विध्रुवीय न्यूरॉन का स्तर (Layer of Bipolar Neurons) – इसकी तन्त्रिका कोशिकाएँ दृष्टि शलाकाओं एवं शंकुओं के स्तर को गुच्छकीय कोशिकाओं के स्तर से जोड़ती हैं।
(iii) गुच्छकीय कोशिकाओं का स्तर (Layer of Ganglionic Cells) – इसकी कोशिकाओं के एक्सॉन तन्तु मिलकर दृक् तन्त्रिका (optic nerve) बनाते हैं। दृक् तन्त्रिका जिस स्थान से रेटिना से निकलती है, उसे अन्ध बिन्दु (blind spot) कहते हैं, इस स्थान पर प्रतिबिम्ब का निर्माण नहीं होता है।

नेत्र की मध्य अनुलम्ब अक्ष (optical axis) पर स्थित रेटिना के मध्य भाग को मध्य क्षेत्र (area centralis) कहते हैं। इस भाग को पीत बिन्दु (yellow spot) या मैकुला ल्यूटिया (macula lutea) भी कहते हैं। यहाँ उपस्थित एक छोटे से गड्ढे को फोविया सेन्ट्रैलिस (UPBoardSolutions.com) (fovea centralis) कहते हैं। इस स्थान पर सबसे स्पष्ट प्रतिबिम्ब बनता है।
लेन्स (Lens) – यह उभयोत्तल (biconvex), पारदर्शी, रंगहीन व लचीला होता है। यह आइरिस के ठीक पीछे स्थित होता है। लेन्स साधक स्नायु (suspensory ligament) द्वारा सीलियरी कार्य (ciliary body) से जुड़ा होता है।
तेजो वेश्म या ऐक्वस वेश्म (aqueous chamber) – कॉर्निया तथा लेन्स के बीच का स्थान होता है। इसमें जलीय तरल तेजोजल या ऐक्वस ह्यूमर (aqueous humor) भरा रहता है।
काचाभ वेश्म या विट्रियस वेश्म (vitreous chamber) – रेटिना व लेन्स के बीच को स्थान है। इसमें जैली सदृश काचाभ जल या विट्रियस ह्यूमर (vitreous humor) भरा रहता है। जलीय तेजोजल तथा जैली सदृश काचाभ जल सीलियरी कार्य द्वारा स्रावित होते हैं। ये नेत्र की गुहा में निश्चित दबाव बनाए रखते हैं जिससे दृष्टिपटल व अन्य नेत्रपटल यथास्थान बने रहें।
पलक (Eye Lids) – नेत्र कोटर के ऊपरी व निचले भागों में त्वचा के पेशीयुक्त भंज (folds) पलकों का निर्माण करते हैं। दोनों पलकें सचल होती हैं तथा नेत्र गोलक के खुले भाग को ढक सकती हैं। पलकों की भीतरी उपचर्म (epidermis) पारदर्शी होकर कॉर्निया के साथ समेकित हो जाती है। इसे
नेत्र श्लेष्मा या कन्जंक्टिवा (conjunctiva) – कहते हैं। पलकों पर बरौनियाँ (eye lashes) पाई जाती हैं।
खरगोश तथा अन्य स्तनियों में एक तीसरी पलक होती है, जिसे निमेषक पटल (nictitating membrane) कहते हैं। यह पलक नेत्रों की सुरक्षा का कार्य करती है। मनुष्य में यह अवशेषी होती है।
अश्रु ग्रन्थियाँ (Lachrymal Glands or Tear Glands) – प्रत्येक नेत्र के बाहरी ऊपरी कोने पर तीन अश्रु ग्रन्थियाँ स्थित होती हैं। इनका स्राव कॉर्निया व कन्जंक्टिवा को नम तथा स्वच्छ बनाए रखता है। नेत्र के भीतरी कोण पर एक अश्रु नलिका (lachrymal duct) होती है (UPBoardSolutions.com) जो फालतू स्राव को नासा वेश्म में पहुँचा देती है। जन्म के चार माह पश्चात् मानव शिशु में अश्रु ग्रन्थियाँ सक्रिय होती हैं।
मीबोमियन ग्रन्थियाँ (Meibomian glands) – ये पलकों में स्थित होती हैं तथा एक तैलीय पदार्थ का स्रावण करती हैं। यह तैलीय पदार्थ कॉर्निया पर फैलकर अश्रु ग्रन्थियों के स्रावण को पूरी कॉर्निया पर फैलाता है।

UP Board Solutions

(स) कर्ण की संरचना

कर्ण श्रवण तथा स्थैतिक सन्तुलन (hearing and equilibrium) का अंग है।
प्रत्येक कर्ण के तीन भाग होते हैं-
(i) बाह्य कर्ण,
(ii) मध्य कर्ण तथा
(iii) अन्त:कर्ण।

(i) बाह्य कर्ण
मनुष्य में बाह्य कर्ण के दो भाग होते हैं – कर्ण पल्लवे (pinna) तथा बाह्य कर्ण कुहर (external auditory canal)
कर्ण पल्लव केवल स्तनियों में ही पाए जाते हैं। ये लचीली उपास्थि से बनी पंखेनुमा रचना है। कर्ण पल्लव ध्वनि तरंगों को कर्ण कुहर में भेजता है। बाह्य कर्ण कुहर एक अस्थिल नलिका है, जो मध्य कर्ण से जुड़ी रहती है। बाह्य कर्ण कुहरे के अन्तिम सिरे पर एक पर्दे जैसी रचना कर्णपटह (tympanic membrane) होती है।

(ii) मध्य कर्ण
यह करोटि की टिप्पैनिक बुल्ला (tympanic bulla) नामक अस्थि की गुहा में स्थित होता है। मध्य कर्ण कण्ठ कर्ण नलिका या यूस्टेकियन नलिका (eustachian tube) द्वारा ग्रसनी (pharynx) से जुड़ा रहता है। मध्य कर्ण में तीन कर्ण अस्थिकाएँ (ear ossicles) होती हैं। इन्हें मैलियस, (UPBoardSolutions.com) इन्कस तथा स्टैपीज (malleus, incus and stapes) कहते हैं। मैलियस कान के पर्दे से सटी रहती है तथा स्टैपीज अन्त:कर्ण की ओर अण्डाकार गवाक्ष या फेनेस्ट्रा ओवेलिस (fenestra ovalis) पर स्थित होती है।
ये तीनों कर्ण अस्थिकाएँ ध्वनि तरंगों को बाह्य कर्ण से अन्त:कर्ण तक पहुँचाने का कार्य करती हैं। मध्य कर्ण दो छिद्रों द्वारा अन्त:कर्ण की गुहा से जुड़ा होता है, इन्हें अण्डाकार गवाक्ष या फेस्ट्रा ओवेलिस (fenestra ovalis) तथा वृत्ताकार गवाक्ष या फेनेस्ट्रा रोटन्डस (fenestra rotundus) कहते हैं। इन छिद्रों के ऊपर एक झिल्ली उपस्थित होती है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 4

UP Board Solutions

(iii) अन्तःकर्ण
अन्त:कर्ण करोटि की टैम्पोरल अस्थि के भीतर स्थित होता है। अन्त:कर्ण एक अर्द्धपारदर्शक झिल्ली से बनी जटिल रचना होती है, जिसे कलागहन (membranous labyrinth) कहते हैं। कलागहन अस्थि के बने कोष में स्थित रहता है जिसे अस्थीय लेबिरिन्थ (bony labyrinth) कहते हैं। अस्थीय लेबिरिन्थ में परिलसीका (perilymph) भरा रहता है, जिसमें कलागहन तैरता रहता है। कलागहन के भीतर अन्तःलसीका (endolymph) भरा रहता है। कलागहन के दो मुख्य भाग यूट्रिकुलस (utriculus) तथा सैक्यूलस (sacculus) होते हैं। दोनों भाग एक सँकरी सैक्यूलो-यूट्रिकुलर नलिका (sacculo-utricular duct) द्वारा जुड़े रहते हैं। यूट्रिकुलस से तीन अर्द्धवृत्ताकार नलिकाएँ (semicircular canals) निकलकर यूट्रिकुलस में ही खुल जाती हैं। अग्र तथा पश्च अर्द्धवृत्ताकार नलिकाएँ एकसाथ सहनलिका (crus commune) के रूप में निकलती हैं। अर्द्धवृत्ताकार नलिकाओं का अन्तिम भाग तुम्बिका (ampulla) के रूप में फूला होता है। सैक्यूलस से स्प्रिंग की तरह कुण्डलित कॉक्लियर (UPBoardSolutions.com) नलिका (cochlear duct) निकलती है। इसमें 2 कुण्डलन होते हैं।

प्रश्न 2.
निम्नलिखित की तुलना कीजिए-
(अ) केन्द्रीय तन्त्रिका तन्त्र और परिधीय तन्त्रिका तन्त्र
(ब) स्थिर विभव और सक्रिय विभव
(स) कोरॉइड और रेटिना।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 5
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 6

UP Board Solutions
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 7
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 8

प्रश्न 3.
निम्नलिखित प्रक्रियाओं का वर्णन कीजिए-
(अ) तन्त्रिका तन्तु की झिल्ली का ध्रुवीकरण
(ब) तन्त्रिका तन्तु की झिल्ली का विध्रुवीकरण
(स) तन्त्रिका तन्तु के समान्तर आवेगों का संचरण
(द) रासायनिक सिनेप्स द्वारा तन्त्रिका आवेगों का संवहन।
उत्तर-

(अ) तन्त्रिका तन्तु की झिल्ली का ध्रुवीकरण

UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 9
तन्त्रिका तन्तु के ऐक्सोप्लाज्म में Na+ की संख्या बहुत कम, परन्तु ऊतक तरल में लगभग 12 गुना अधिक होती है। ऐक्सोप्लाज्म में K+ की संख्या ऊतक तरल की अपेक्षा लगभग 30-35 गुना अधिक होती है। विसरण अनुपात के अनुसार Na+ की ऊतक तरल से ऐक्सोप्लाज्म में और K+ के ऐक्सोप्लाज्म से ऊतक तरल में विसरित होने की प्रवृत्ति होती है।
लेकिन तन्त्रिकाच्छद या न्यूरीलेमा (neurilemma) Na+ के लिए कम और K+ के लिए अधिक पारगम्य होती है। विश्राम अवस्था में ऐक्सोप्लाज्म में ऋणात्मक आयनों और ऊतक तरल में धनात्मक आयनों की अधिकता रहती है। तन्त्रिकाच्छद या न्यूरीलेमा की बाह्य सतह पर धनात्मक आयनों और (UPBoardSolutions.com) भीतरी सतह पर ऋणात्मक आयनों का जमाव रहता है। तन्त्रिकाच्छद की बाह्य सतह पर धनात्मक और भीतरी सतह पर 70 mV का ऋणात्मक आकेश रहता है। इस स्थिति में तन्त्रिकाच्छद या न्यूरीलेमा विद्युतावेशी या धुवण अवस्था (polarised state) में बनी रहती है। तन्त्रिकाच्छद (neurilemma) के इधर-उधर विद्युतावेशी अन्तर (electric charge difference) के कारण न्यूरीलेमा में बहुत-सी विभव ऊर्जा संचित रहती है। इसी ऊर्जा को विश्राम कला विभव कहते हैं। प्रेरणा संचरण में इसी ऊर्जा का उपयोग होता है।

UP Board Solutions

(ब) तन्त्रिका तन्तु की झिल्ली का विध्रुवीकरण

जब एक तन्त्रिका तन्तु को श्रेशहोल्ड उद्दीपन (threshold stimulus) दिया जाता है तो न्यूरीलेमा (neurilemma) की पारगम्यता बदल जाती है। यह Na+ के लिए अधिक पारगम्य हो जाती है और K+ के लिए अपारगम्य हो जाती है। इसके फलस्वरूप तन्त्रिका तन्तु विश्राम कला विभव की ऊर्जा का प्रेरणा संचरण के लिए उपयोग करने में सक्षम होते हैं। तन्त्रिका तन्तु को उद्दीपित करने पर इसके विश्राम कला विभव की ऊर्जा एक विद्युत प्रेरणा के रूप में, तन्तु के क्रियात्मक कला विभव में बदल जाती है। यह विद्युत प्रेरणा तन्त्रिकीय प्रेरणा होती है। Na+ ऐक्सोप्लाज्म में तेजी से प्रवेश करने लगते हैं, इसके फलस्वरूप तन्त्रिका तन्तु का विध्रुवीकरण होने लगता है। विध्रुवीकरण के फलस्वरूप न्यूरीलेमा की भीतरी सतह पर धनात्मक और बाह्य सतह पर ऋणात्मक विद्युत आवेश स्थापित हो जाता है। यह स्थिति विश्राम अवस्था के विपरीत होती है।

(स) तन्त्रिका तन्तु के समान्तर आवेगों का संचरण

जब तन्त्रिकाच्छद (न्यूरीलेमा) के किसी स्थान पर तन्त्रिका आवेग की उत्पत्ति होती है तो उत्पत्ति स्थल A पर तन्त्रिकाच्छद Na+ के लिए अधिक पारगम्य हो जाती है, जिसके फलस्वरूप Na+ तीव्र गति से अन्दर आने लगते हैं तथा न्यूरीलेमा की भीतरी सतह पर धनात्मक और बाह्य सतह पर ऋणात्मक आवेश स्थापित हो जाता है। आवेग स्थल पर विध्रुवीकरण हो जाने को क्रियात्मक विभव कहते हैं। क्रियात्मक विभव तन्त्रिकीय प्रेरणा के रूप में स्थापित हो जाता है।
तन्त्रिकाच्छद से कुछ आगे ‘B’ स्थल पर झिल्ली की बाहरी सतह पर धनात्मक और भीतरी सतह पर ऋणात्मक आवेश होता है। परिणामस्वरूप, तन्त्रिका आवेग A स्थल से ‘B’ स्थल की ओर आवेग का संचरण होता है। यह प्रक्रम सम्पूर्ण एक्सॉन में दोहराया जाता है। इसके प्रत्येक बिन्दु पर उद्दीपन को सम्पोषित किया जाता रहता है। उद्दीपन किसी भी स्थान पर अत्यन्त कम समय तक (0.001 से 0.005 सेकण्ड) तक ही रहता है। जैसे ही भीतरी सतह पर धनात्मक विद्युत आवेश +35mV होता है, तन्त्रिकाच्छद की पारगम्यता प्रभावित होती है। यह पुन: Na’ के लिए अपारगम्य और K’ के लिए अत्यधिक पारगम्य हो जाती है। K+ तेजी से ऐक्सोप्लाज्म में ऊतक तरल में जाने लगते हैं। सोडियम-पोटैशियम पम्प पुनः सक्रिय हो जाता है जिससे तन्त्रिको तन्तु विश्राम विभवे में आ जाता है। अब यह अन्य उद्दीपन के संचरण हेतु फिर तैयार हो जाता है।

(द) रासायनिक सिनैप्स द्वारा तन्त्रिका आवेगों को संवहन

अक्षतन्तु (axon) के अन्तिम छोर पर स्थित अन्त्य बटन (terminal button) तथा अन्य तन्त्रिका कोशिका के डेन्ड्राइट के मध्य एक युग्मानुबन्ध (synapse) होता है। अत: इस स्थान पर आवेग का संचरण विशेष रासायनिक पदार्थ ऐसीटिलकोलीन (acetylcholine) नामक न्यूरोहॉर्मोन (neurohormone) के द्वारा होता है। आवेग के प्राप्त होने पर अन्त्य बटन में उपस्थित स्रावी पुटिकाएँ (secretory vesicles) ऐसीटिलकोलीन स्रावित करती हैं। यही पदार्थ दूसरी तन्त्रिका कोशिका के डेण्ड्राईट (dendrites) में कार्यात्मक विभव (action potential) को स्थापित कर देता है। अब यही विभव, आवेग के रूप में अगले तन्त्रिका तन्तु की सम्पूर्ण लम्बाई में आगे बढ़ता जाता है। इस प्रकार, ऐसीटिलकोलीन एक रासायनिक दूत (chemical transmitter) की तरह कार्य करता है। बाद में, ऐसीटिलकोलीन (UPBoardSolutions.com) कोएन्जाइम-ऐसीटिलकोलीनेस्टेरेज (acetylcholinesterase) द्वारा विघटित कर दिया जाता है।

UP Board Solutions
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 10

प्रश्न 4.
निम्नलिखित का नामांकित चित्र बनाइए-
(अ) न्यूरॉन
(ब) मस्तिष्क
(स) नेत्र
(द) कर्ण।
उत्तर-
(अ) न्यूरॉने की संरचना (Structure of Neuron) – अभ्यास के अन्तर्गत दिए गए। प्रश्नोत्तर में लघु उत्तरीय प्रश्न 1 का उत्तर देखें।
(ब) मस्तिष्क की संरचना (Structure of Brain) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 1 का उत्तर देखें।
(स) नेत्र की संरचना (Structure of Eye) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 1 का उत्तर देखें।
(द) कर्ण की संरचना (Structure of Ear) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 1 का उत्तर देखें।

प्रश्न 5.
निम्नलिखित पर संक्षिप्त टिप्पणी लिखिए
(अ) तन्त्रीय समन्वयन
(ब) अग्रमस्तिष्क
(स) मध्यमस्तिष्क
(द) पश्चमस्तिष्क
(ध) रेटिना
(य) कर्ण अस्थिकाएँ
(र) कॉक्लिया
(ल) ऑर्गन ऑफ कॉरटाई
(व) सिनेप्स।
उत्तर-
(अ) तन्त्रीय समन्वयन (Nervous Coordination) – शरीर की विभिन्न क्रियाओं का नियन्त्रण तथा नियमन सूचना प्रसारण तन्त्र (communication system) द्वारा होता है। इसके अन्तर्गत तत्रिका तन्त्र (nervous system) तथा अन्तःस्रावी तन्त्र (Endocrine System) आते हैं। तन्त्रिका निर्माण तन्त्रिका कोशिकाओं (nerve cells) से होता है। ये कोशिकाएँ उत्तेजनशीलता एवं संवाहकता के लिए विशिष्टीकृत होती हैं। ये आवेगों को संवेदांगों से (UPBoardSolutions.com) ग्रहण करके केन्द्रीय तन्त्रिका तन्त्र तक और केन्द्रीय तन्त्रिका तन्त्र द्वारा होने वाली प्रतिक्रियाओं को अपवाहक (effectors) अंगों तक पहुँचाने का कार्य करती हैं। अपवाहक अंगों के अन्तर्गत मुख्यतया पेशियाँ तथा ग्रन्थियाँ आती हैं। केन्द्रीय तन्त्रिका तन्त्र उद्दीपनों की व्याख्या, विश्लेषण करके प्रतिक्रियाओं का निर्धारण करता है।

UP Board Solutions

(ब) अग्रमस्तिष्क (Fore brain) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 1 (अ) मस्तिष्क की संरचना के अन्तर्गत ‘अग्रमस्तिष्क’ (fore brain) देखिए।

(स) मध्यमस्तिष्क (Mid brain) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 1 (अ) मस्तिष्क की संरचना के अन्तर्गत ‘मध्य मस्तिष्क’ (mid brain) देखिए।

(द) पश्चमस्तिष्क (Hind brain) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 1 (अ) मस्तिष्क की संरचना के अन्तर्गत ‘पश्च मस्तिष्क’ (hind brain) देखिए।

(ध) रेटिना (Retina) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में नेत्र की संरचना के अन्तर्गत ‘रेटिना’ देखिए।

(य) कर्ण अस्थिकाएँ (Ear Ossicles) – मध्यकर्ण में तीन कर्ण अस्थिकाएँ चल सन्धियों द्वारा परस्पर जुड़ी रहती हैं। इन्हें क्रमशः मैलियस (malleus), इन्कस (incus) और स्टैपीज (stapes) कहते हैं।

  • मैलियस (Malleus) – यह हथौड़ीनुमा होती है। इसका बाह्य सँकरा भाग कर्णपटह से तथा भीतरी चौड़ा सिरा इन्कस से जुड़ा होता है।
  • इन्कस (Incus) – यह निहाई (anvil) के आकार की होती है। इसका बाहरी चौड़ा सिरा मैलियस से तथा भीतरी सँकरा भाग स्टैपीज से जुड़ा होता है।
  • स्टैपीज (Stapes) – यह रकाब (stirrup) के आकार की होती है। इसका सँकरा सिरा इन्कस से और चौड़ा सिरा फेनेस्ट्रा ओवैलिस (fenestra ovalis) से लगा होता है। कर्ण अस्थिकाएँ कर्णपटह पर होने वाले ध्वनि कम्पनों को अधिक प्रबल करके फेनेस्ट्रा ओवैलिस द्वारा अन्त:कर्ण में पहुँचाती हैं।

(र) कॉक्लिया (Cochlea) – मनुष्य का अन्तःकर्ण यो कलागहन (membranous labyrinth) दो मुख्य भागों से बना होता है। यूट्रिकुलस (utriculus) तथा सैक्यूलस (sacculus)। सैक्यूलस से स्प्रिंग की तरह कुण्डलित कॉक्लिया निकलता है। यह नलिकारूपी होता है। इसमें 2[latex s=2]\frac { 3 }{ 4 }[/latex] कुण्डलन होते हैं। इसके चारों ओर अस्थिल कॉक्लिया का आवरण होता है। कॉक्लिया की नलिका अस्थिल लेबिरिन्थ की भित्ति से जुड़ी रहती है जिससे अस्थिल लेबिरिन्थ की गुहा दो वेश्मों में बँट जाती है। पृष्ठ वेश्म को स्कैला वेस्टीबुली (scala vestibuli) कहते हैं तथा अधर वेश्म को स्कैला टिम्पैनी (scala tympani) कहते हैं। इन दोनों वेश्म के मध्य कॉक्लिया का वेश्म स्कैला मीडिया (scala media) होता है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 11

(ल) ऑर्गन ऑफ कॉरटाई (Organ of Corti) – कॉक्लिया नलिका की गुहा स्कैला मीडिया की पतली पृष्ठ भित्ति रीसनर्स कला (Reissner’s membrane) कहलाती है। अधर भित्ति मोटी होती है। इसे बेसीलर कला (basilar membrane) कहते हैं। बेसीलर कला के मध्य में कॉरटाई का अंग (organ of Corti) होता है। इसमें अवलम्ब कोशिकाओं के बीच-बीच में संवेदी कोशिकाएँ होती हैं। प्रत्येक संवेदी कोशिका के स्वतन्त्र तल पर स्टीरियोसीलिया (stereocilia) होते हैं। कॉरटाई के अंग के ऊपर टेक्टोरियल कला (tectorial membrane) स्थित होती है। संवेदी कोशिकाओं से निकले तन्त्रिका तन्तु मिलकर श्रवण तन्त्रिका (auditory nerve) का निर्माण करते हैं। कॉरटाई के अंग ध्वनि के उद्दीपनों को ग्रहण करते हैं।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 12

UP Board Solutions

(व) सिनैप्स (Synapse) – प्रत्येक तन्त्रिको कोशिका का अक्षतन्तु (axon) अपने स्वतन्त्र छोर पर टीलोडेन्ड्रिया (telodendria) या एक्सॉन अन्तस्थ (axon terminals) नामक शाखाओं में बँट जाता है। प्रत्येक शाखा का अन्तिम छोर घुण्डीनुमा होता है। इसे सिनैप्टिक बटन (synaptic button) कहते हैं। ये घुण्डियाँ समीपवर्ती तन्त्रिका कोशिका के डेण्ड्राइट्स के साथ सन्धि बनाती हैं। इन संधियों को सिनेप्स या युग्मानुबन्ध कहते हैं। युग्मानुबन्ध पर सूचना लाने वाली (UPBoardSolutions.com) तन्त्रिका कोशिका को पूर्व सिनैप्टिक (presynaptic) तथा सूचना ले जाने वाली तन्त्रिका कोशिका को पश्च सिनेप्टिक (post synaptic) कहते हैं। इनके मध्य भौतिक सम्पर्क नहीं होता। दोनों के मध्य लगभग 20 से 40 mµ का दरारनुमा सिनैप्टिक विदर होता है। इसमें ऊतक तरल भरा होता है। सिनैप्टिक विदर से उद्दीपन या प्रेरणाओं का संवहन तत्रिका संचारी पदार्थों; जैसे-ऐसीटिलकोलीन (acetylcholine) के द्वारा होता है।

प्रश्न 6.
निम्नलिखित पर संक्षिप्त टिप्पणी दीजिए-
(अ) सिनैप्टिक संचरण की क्रियाविधि
(ब) देखने की प्रक्रिया
(स) श्रवण की प्रक्रिया।
उत्तर-

(अ) सिनैप्टिक संचरण की क्रियाविधि

शेरिंगटन (Sherrington) ने दो तन्त्रिका कोशिकाओं के सन्धि स्थलों को युग्मानुबन्ध (synapsis) कहा। इसका निर्माण पूर्व सिनेप्टिक तथा पश्च सिनैप्टिक तृन्त्रिका तन्तुओं से होता है। युग्मानुबन्ध में पूर्व सिनैप्टिक तन्त्रिका के एक्सॉन या अक्षतन्तु के अन्तिम छोर पर स्थित सिनेप्टिक बटन (synaptic button) तथा पश्च सिनैप्टिक तन्त्रिका कोशिका के डेन्ड्राइट्स के मध्य सन्धि होती है। दोनों के मध्य सिनैप्टिक विदर (synaptic cleft) होता है, इससे उद्दीपन विद्युत तरंग के रूप में प्रसारित नहीं हो पाता। सिनैप्टिक बटन या घुण्डियों में सिनैप्टिक पुटिकाएँ (synaptic vesicles) होती हैं। ये तन्त्रिका संचारी पदार्थ (neurotransmitters) से भरी होती हैं। उद्दीपन या प्रेरणा के क्रियात्मक विभव के कारण Ca2+ ऊतक द्रव्य से सिनैप्टिक घुण्डियों में प्रवेश करते हैं तो सिनैप्टिक घुण्डियों से तन्त्रिका संचारी पदार्थ मुक्त होता है। यह तन्त्रिका संचारी पदार्थ पश्च सिनैप्टिक, तन्त्रिका के डेन्ड्राइट पर क्रियात्मक विभव को स्थापित कर देता है, इसमें लगभग 0.5 मिली सेकण्ड का समय लगता है।

प्रेरणा प्रसारण या क्रियात्मक विभव के स्थापित हो जाने के पश्चात् एन्जाइम्स द्वारा तन्त्रिका संचारी पदार्थ का विघटन कर दिया जाता है, जिससे अन्य प्रेरणा को प्रसारित किया जा सके। सामान्यतया सिनैप्टिक पुटिकाओं से ऐसीटिलकोलीन (acetylcholine) नामक तन्त्रिका संचारी पदार्थ मुक्त होता है। इसका विघटन ऐसीटिलकोलीनेस्टीरेज (acetylcholinesterase) एन्जाइम द्वारा होता है। एपिनेफ्रीन (epinephrine), डोपामीन (dopamine), हिस्टैमीन (histamine), सोमैटोस्टैटिन (somatostatine) आदि पदार्थ अन्य तन्त्रिका संचारी पदार्थ हैं। ग्लाइसीन (glycine) गामा-ऐमीनोब्यूटाइरिक (gamma aminobutyric acid-GABA) आदि तन्त्रिका संचारी पदार्थ प्रेरणाओं के प्रसारण को रोक देते हैं।

UP Board Solutions

(ब) देखने की प्रक्रिया

नेत्र कैमरे की भाँति कार्य करते हैं। ये प्रकाश की 380 से 760 नैनोमीटर तरंगदैर्घ्य (wave-length) की किरणों की ऊर्जा को ग्रहण करके इसे तन्त्रिका तन्तु के क्रिया विभव (action potential) में बदल देते हैं।

नेत्र की क्रिया-विधि
जब उचित आवृत्ति की प्रकाश तरंगें कॉर्निया पर पड़ती हैं, तब कॉर्निया तथा तेजोजल प्रकाश किरणों का अपवर्तन (refraction) कर देते हैं। ये किरणें तारे से होकर लेन्स पर पड़ती हैं। लेन्स इनका पूर्ण अपवर्तन कर देता है और उल्टा प्रतिबिम्ब रेटिना पर बना देता है। आइरिस तारे को छोटा या (UPBoardSolutions.com) बड़ा करके प्रकाश की मात्रा का नियन्त्रण करता है। तीव्र प्रकाश में तारा सिकुड़ जाता है तथा कम प्रकाश नेत्र के भीतर प्रवेश करता है। कम प्रकाश में तारा फैल जाता है तथा अधिक प्रकाश नेत्र के भीतर प्रवेश करता है।

नेत्र द्वारा समायोजन
सीलियरी काय तथा निलम्बन स्नाय (suspensory ligaments) लेन्स के फोकस में अन्तर लाकर वस्तु के प्रतिबिम्ब को रेटिना पर केन्द्रित करते हैं।
सामान्य अवस्था में नेत्र दूर की वस्तु देखने के लिए समायोजित रहता है। इस समय सीलियरी काय शिथिल (relaxed) रहता है तथा निलम्बन स्नायु तना रहता है। इससे लेन्स की फोकस दूरी अधिक हो जाती है और
दूर की वस्तु का स्पष्ट प्रतिबिम्ब बनता हैं।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 13
पास की वस्तु देखने के लिए सीलियरी काय में संकुचन तथा निलम्बन स्नायु में शिथिलन होता हैं।
इससे लेन्स छोटा व मोटा हो जाता है तथा इसकी फोकस दूरी कम हो जाती है। इससे पास की वस्तु का स्पष्ट प्रतिबिम्ब बनता है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 14

प्रकाश-रासायनिक परिवर्तन
जब विशिष्ट तरंगदैर्घ्य वाली प्रकाश की किरणें रेटिना पर पड़ती हैं, तब ये शलाकाओं तथा शंकुओं में उपस्थित रसायनों में परिवर्तन करती हैं।
जब प्रकाश की किरणें शलाकाओं के रोडोप्सिन पर पड़ती हैं, तब यह रेटिनीन (retinene) तथा ऑप्सिन (opsin) में टूट जाता है। अन्धकार में शलाकाओं में एन्जाइम्स की सहायता से रेटिनीन तथा ऑप्सिन रोडोप्सिन को, संश्लेषण करते हैं। यही कारण है कि जब हम तीव्र प्रकाश से अन्धकार में जाते। हैं, तब एकदम कुछ दिखाई नहीं देता किन्तु धीरे-धीरे स्पष्ट दिखाई देने लगता है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 15

UP Board Solutions
शंकुओं में आयोडोप्सिन उपस्थित होता है। इसको वर्णक घटक रेटिनीन तथा प्रोटीन घटक फोटोप्सिन होता है। शंकु तीन प्रारम्भिक रंगों को ग्रहण करते हैं, जो लाल, नीला व हरा होते हैं। इन्हीं तीन प्रकार के शंकुओं द्वारा विभिन्न मात्रा में उद्दीपन ग्रहण से अन्य रंगों का ज्ञान होता है। मनुष्य व दूसरे प्राइमेट्स में दोनों नेत्रों द्वारा एक ही प्रतिबिम्ब बनता है। ऐसी दृष्टि को द्विनेत्री दृष्टि (binocular vision) कहते हैं।

(स) श्रावण की प्रक्रिया

कर्ण के निम्नलिखित प्रमुख दो कार्य होते हैं-
(i) कर्ण का प्राथमिक कार्य शरीर का स्थैतिक तथा गतिक सन्तुलन बनाए रखना तथा
(ii) ध्वनि ग्रहण करना अर्थात् श्रवण क्रिया।
अन्त:कर्ण के कलागहन के कॉक्लिया में स्थित कॉरटाई का अंग ध्वनि के उद्दीपनों को ग्रहण करने के लिए उत्तरदायी है।

श्रवण क्रिया में कर्ण द्वारा एक विशेष आवृत्ति की ध्वनि कम्पनों को ग्रहण करके कॉरटाई के अंग में स्थित संवेदी कोशिकाओं तक भेजा जाता है। संवेदी कोशिकाएँ इन तरंगों को तन्त्रिका के क्रिया विभव में परिवर्तित कर देती हैं। मस्तिष्क के ध्वनि वल्कुट (auditory cortex) सुनने (UPBoardSolutions.com) का कार्य करता है। मनुष्य का कर्ण 16 से 20,000 साइकिल प्रति सेकण्ड की ध्वनि तरंगों को ग्रहण कर सकता है।
बाह्य कर्ण पल्लव ध्वनि तरंगों को कर्ण कुहर में भेज देता है। ध्वनि तरंगें कर्णपटह में कम्पन उत्पन्न करती हैं।

मध्य कर्ण की कर्ण अस्थिकाओं द्वारा कर्णपटह से कम्पन अण्डाकार गवाक्ष के ऊपर मढ़ी झिल्ली पर पहुँचते हैं। इसके फलस्वरूप अन्त:कर्ण के स्कैला वैस्टीबुली (scala vestibuli) के परिलसीका में कम्पन होने लगता है। यहाँ से कम्पन स्कैला टिम्पैनी (scala tympani) के परिलसीका में पहुँचते हैं।
रीसनर्स कला तथा बेसीलर कला में कम्पन होने से स्कैला मीडिया (scala media) के अन्त:लसीका में कम्पन होने लगता है जिससे कॉरटाई के अंग के संवेदी रोमों में कम्पन होने लगता है। संवेदी रोमों के कम्पन टेक्टोरियल कला में कम्पन उत्पन्न करके ध्वनि संवेदना की प्रेरणा उत्पन्न कर देते हैं। श्रवण तन्त्रिका द्वारा ध्वनि संवेदना मस्तिष्क के ध्वनि वल्कुट (auditory cortex) तक पहुँच जाती है। ध्वनि की तीव्रता संवेदी रोमों के कम्पन की तीव्रता से ज्ञात होती है। ध्वनि तरंगों के कम्पन वृत्ताकार गवाक्ष की झिल्ली से टकराकर समाप्त हो जाते हैं।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 16

प्रश्न 7.
(अ) आप किस प्रकार किसी वस्तु के रंग का पता लगाते हैं?
(ब) हमारे शरीर का कौन-सा भाग शरीर का सन्तुलन बनाए रखने में मदद करता है?
(स) नेत्र किस प्रकार रेटिना पर पड़ने वाले प्रकाश का नियमन करते हैं?
उत्तर-
(अ) नेत्र गोलक की रेटिना तन्त्रिको संवेदी (neurosensory) होती है। इसमें दृष्टि शलाकाएँ (rods) तथा दृष्टि शंकु (cones) पाए जाते हैं। शंकुओं में आयोडोप्सिन (iodopsin) दृष्टि वर्णक पाया जाता है। तीव्र प्रकाश में शंकु विभिन्न रंगों को ग्रहण करते हैं। शंकु तीन प्राथमिक रंगों लाल, हरे व नीले से सम्बन्धित भिन्न-भिन्न प्रकार के होते हैं। ये इन प्राथमिक रंगों को ग्रहण करते हैं। इन प्राथमिक रंगों के मिश्रण से विभिन्न रंगों का ज्ञान होता है।

UP Board Solutions

(ब) अन्त:कर्ण की अर्द्धचन्द्राकार नलिकाओं के तुम्बिका (ampulla), सैक्यूलस तथा यूट्रिकुलस शरीर का सन्तुलन बनाने का कार्य करती हैं।
यूट्रिकुलस तथा सैक्यूलस के मैकुला तथा अर्द्धचन्द्राकार नलिकाओं के तुम्बिका में स्थित संवेदी कूटों द्वारा गतिक (UPBoardSolutions.com) सन्तुलन (dynamic equilibrium) नियन्त्रित होता है। जब शरीर एक ओर को झुक जाती है, तब ऑटोकोनिया उसी ओर चले जाते हैं, जहाँ वे संवेदी कूटों को उद्दीपन प्रदान करते हैं। ‘इससे तन्त्रिका आवेग उत्पन्न होता है और मस्तिष्क में शरीर के झुकने की सूचना पहुँच जाती है। मस्तिष्क प्रेरक तन्त्रिकाओं द्वारा सम्बन्धित पेशियों को सूचना भेजकर शरीर का सन्तुलन बनाता है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 16

(स) रेटिना (retina) पर पड़ने वाले प्रकाश की मात्रा का नियमन उपतारा (iris) द्वारा किया जाता है। यह एक मुद्राकार, चपटा, मिलेनिन वर्णकयुक्त तन्तुपट (diaphragm) के रूप में होता है। इसके गोल छिद्र को तारा या पुतली (pupil) कहते हैं। उपतारा (iris) में अरेखित अरीय प्रसारी पेशियाँ (radial dilatory muscles) तथा अरेखित वर्तुल अवरोधिनी पेशियाँ (circular sphincter muscles) होती हैं। अरीय पेशियों के संकुचन से पुतली का व्यास बढ़ जाता है और वर्तुल पेशियों के संकुचन से पुतली का व्यास घट जाता है। इस प्रकार ये पेशियाँ क्रमशः मन्द प्रकाश और तीव्र प्रकाश में संकुचित होकर रेटिना पर पड़ने वाले प्रकाश की मात्रा का नियमन करती हैं।

प्रश्न 8.
(अ) सक्रिय विभवे उत्पन्न करने में Na+ की भूमिका का वर्णन कीजिए।
(ब) सिनैप्स पर न्यूरोट्रान्समीटर मुक्त करने में Ca++ की भूमिका का वर्णन कीजिए।
(स) रेटिना पर प्रकाश द्वारा आवेग उत्पन्न होने की क्रियाविधि का वर्णन कीजिए।
(द) अन्तःकर्ण में ध्वनि द्वारा तन्त्रिका आवेग उत्पन्न होने की क्रियाविधि का वर्णन कीजिए।
उत्तर-
(अ) सक्रिय विभव उत्पन्न करने में Na+ की भूमिका (Role of Na+ in the generation of Action Potential) – उद्दीपन के फलस्वरूप तन्त्रिकाच्छद या न्यूरीलेमा की Na+ के लिए पारगम्यता बढ़ जाने से, Na+ ऊतक तरल से ऐक्सोप्लाज्म में तेजी से पहुँचने लगते हैं। इसके फलस्वरूप तन्त्रिका तन्तु का विध्रुवीकरण हो जाता है और तन्त्रिका तन्तु का विश्राम कला विभव क्रियात्मक कला विभव में बदलकर प्रेरणा प्रसारण में सहायता करता है। (विस्तृत विवरण के लिए अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 3 (ब) का उत्तर देखिए।)

(ब) सिनैप्स पर न्यूरोट्रान्समीटर मुक्त करने में Ca++ की भूमिका (Role of Ca++ to release Neurotransmitters of Synapsis) – जब कोई तन्त्रिकीय प्रेरणा क्रियात्मक विभव के रूप में सिनैप्टिक घुण्डी पर पहुँचती है तो Ca++ ऊतक तरल से सिनेप्टिक घुण्डी में प्रवेश कर जाते हैं। इनके प्रभाव से सिनैप्टिक घुण्डी की सिनैप्टिक पूटिकाएँ इसकी कला से जुड़ जाती हैं। इससे सिनैप्टिक पुटिकाओं से तन्त्रिका संचारी पदार्थ (न्यूरोट्रान्समीटर) मुक्त होकर (UPBoardSolutions.com) सिनैप्टिक विदर के ऊतक तरल में पहुँच जाता है और पश्चसिनैप्टिक तन्त्रिका कोशिका के ड्रेन्ड्राइट्स पर रासायनिक उद्दीपन द्वारा क्रियात्मक विभव को स्थापित कर देता है।

(स) रेटिना पर प्रकाश द्वारा आवेग उत्पन्न होने की क्रियाविधि (Mechanism of generation of Light Impulse in the Retina) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 6 ‘ब’ के अन्तर्गत प्रकाश-रासायनिक परिवर्तन (photo-chemical changes) का विवरण देखिए।

(द) अन्तःकर्ण में ध्वनि द्वारा तन्त्रिका आवेग उत्पन्न होने की क्रियाविधि (Mechanism through which a Sound produces a Nerve Impulse in the Internal Ear) – अभ्यास के अन्तर्गत दिए गए प्रश्नोत्तर में प्रश्न 6 ‘स’ के अन्तर्गत देखिए।

UP Board Solutions

प्रश्न 9.
निम्नलिखित के बीच में अन्तर बताइए-
(अ) आच्छादित और अनाच्छादित तन्त्रिकाक्ष
(ब) दुम्राक्ष्य और तन्त्रिकाक्ष
(स) शलाका और शंकु
(द) थैलेमस तथा हाइपोथैलेमस
(य) प्रमस्तिष्क और अनुमस्तिष्क।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 17
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 18

UP Board Solutions
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 19
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 20
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 21

प्रश्न 10.
(अ) कर्ण का कौन-सा भाग ध्वनि की पिच का निर्धारण करता है?
(ब) मानव मस्तिष्क का सर्वाधिक विकसित भाग कौन-सा है?
(स) केन्द्रीय तन्त्रिका तन्त्र का कौन-सा भाग मास्टर क्लॉक की तरह कार्य करता है?
उत्तर-
(अ) कॉरटाई के अंग (organ of Corti) की संवेदनाग्राही कोशिकाएँ ध्वनि की पिच को निर्धारण करती हैं तथा उद्दीपनों को ग्रहण करके श्रवण तन्त्रिका (auditory nerve) में प्रेषित करती हैं।
(ब) प्रमस्तिष्क (cerebrum) मस्तिष्क का सर्वाधिक विकसित भाग है। यह मस्तिष्क का लगभग 80% भाग बनाता है।
(स) मस्तिष्क मास्टर क्लॉक की तरह कार्य करता है।

प्रश्न 11.
कशेरुकी के नेत्र का वह भाग जहाँ से दृक तन्त्रिका रेटिना से बाहर निकलती है, क्या कहलाता है-
(अ) फोविया
(ब) आइरिस
(स) अन्ध बिन्द
(द) ऑप्टिक किएज्मा (चाक्षुष किएज्मा)।
उत्तर-
(स) अन्ध बिन्दु (Blind spot)।

प्रश्न 12.
निम्नलिखित में भेद स्पष्ट कीजिए-
(अ) संवेदी तन्त्रिका एवं प्रेरक तन्त्रिका।
(ब) आच्छादित एवं अनाच्छादित तन्त्रिका तन्तु में आवेग संचरण।
(स) ऐक्विअस ह्युमर, (नेत्रोद) एवं विट्रियस ह्युमर (काचाभ द्रव)।
(द) अन्ध बिन्दु एवं पीत बिन्दु।
(य) कपालीय तन्त्रिकाएँ एवं मेरु तन्त्रिकाएँ।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 22
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 23

UP Board Solutions
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 24

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
रोडोप्सिन
(क) एक रंजक है जो नेत्र की रॉड कोशिकाओं में पाया जाता है।
(ख) एक प्रकार का प्रोटीन है जो तन्त्रिका के युग्मानुबंधन में पाया जाता है।
(ग) एक छोटी-सी हड्डी है जो मध्य कान में पायी जाती है ।
(घ) एक प्रकार का रासायनिक पदार्थ है जो अस्थि मज्जा में पाया जाता है।
उत्तर-
(क) एक रंजक है जो नेत्र की रॉड कोशिकाओं में पाया जाता है।

प्रश्न 2.
निम्नलिखित में से कौन आँखकी वास्तविक तन्त्रिका-संवेदी पटल है?
(क) कॉर्निया
(ख) स्कलीरा या दृढ़ पटल
(ग) दृष्टिपटल
(घ) रक्तके पटल
उत्तर-
(ग) दृष्टिपटल

UP Board Solutions

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
संवेदी एवं प्रेरक तन्त्रिका तन्तुओं के कार्य स्पष्ट कीजिए।
उत्तर-
संवेदी तन्त्रिका तन्तु ग्राही अंगों अर्थात् संवेदांगों से संवेदनाओं की प्रेरणाओं को केन्द्रीय तन्त्रिका तन्त्र में लाते हैं जबकि प्रेरक तन्त्रिका तन्तु प्रतिक्रियाओं की प्रेरणाओं अर्थात् चालक प्रेरणाओं को केन्द्रीय तन्त्रिका तन्त्र से अपवाही अंगों या ऊतकों में लाते हैं।

प्रश्न 2.
अपवाही (संर्वेदी) और अभिवाही (मोटर) तन्त्रिका कोशिका में क्या भेद है?
उत्तर-
संवेदी अंगों से उद्दीपनों को अभिवाही (afferent) तन्त्रिकाएँ मेरुरज्जु या मस्तिष्क में पहुँचाती हैं। (UPBoardSolutions.com) मेरुरज्जु या मस्तिष्क से प्रेरणाओं को अपवाही (efferent) तन्त्रिकाएँ पेशी, ऊतक या ग्रन्थि तक पहुँचाती हैं।

प्रश्न 3.
मानव मस्तिष्क के सेरीब्रम के दो कार्य लिखिए।
उत्तर-

  1. जटिल विचारों व क्रियाओं का अन्दर से नियन्त्रण।
  2. निर्णय करने की क्षमता।

लघु उत्तरीय प्रश्न

प्रश्न 1.
तन्त्रिका कोशिका या न्यूरॉन की संरचना का वर्णन कीजिए।
या
एक तन्त्रिका कोशिका का स्वच्छ नामांकित चित्र बनाइए तथा डेण्ड्राइट एवं एक्सॉन में अन्तर बताइए।
या
बहुध्रुवीय तन्त्रिका कोशिका का एक स्वच्छ नामांकित चित्र बनाइए (वर्णन की आवश्यकता नहीं है)।
उत्तर-

तन्त्रिका कोशिकाएँ या न्यूरॉन्स

तन्त्रिका कोशिकाएँ तन्त्रिका तन्त्र (nervous system) की संरचनात्मक तथा कार्यात्मक इकाइयाँ हैं। मस्तिष्क, सुषुम्ना एवं विभिन्न तन्त्रिकाओं में उपस्थित तन्त्रिका ऊतक (nervous tissue) में ये कोशिकाएँ अति महत्त्वपूर्ण हैं और भ्रूण की न्यूरोब्लास्ट (neuroblast) कोशिकाओं से बनती हैं। भ्रूणीय परिवर्द्धन में एक बार बन जाने के बाद तन्त्रिका कोशिकाएँ शरीर के साथ बड़ी तो होती रहती हैं, किन्तु विभाजित नहीं होती हैं तथा सदैव विभाजनान्तराल अवस्था (interphase) में ही रहती हैं।

संरचना तथा कार्यिकी में तन्त्रिका कोशिकाएँ शरीर की सर्वाधिक जटिल और लम्बी कोशिकाएँ होती हैं। प्रत्येक तन्त्रिका कोशिका की विशेषता उससे निकलने वाले प्रवर्ध (processes) होते हैं तथा इन प्रवर्षों में क्रियात्मक विभेदीकरण (physiological differentiation) होता है। कोशिका से निकलने वाले इन प्रवर्थों की संख्या के आधार पर इन्हें एक ध्रुवीय (unipolar), द्विध्रुवीय (bipolar) अथवा बहुध्रुवीय (multipolar) कहते हैं। अध्रुवीय (nonpolar) तन्त्रिका (UPBoardSolutions.com) कोशिकाएँ केवल निम्न श्रेणी के जन्तुओं में पायी जाती हैं। जिनमें प्रवर्ध तो होते हैं, किन्तु प्रवर्षों में क्रियात्मक विभेदीकरण नहीं होता है। इस प्रकार तन्त्रिका कोशिका के अग्र दो प्रमुख भाग होते हैं

1. कोशिकाकाय
यह तन्त्रिका कोशिका का प्रमुख भाग है जो गोल, अण्डाकार या अन्य आकार का हो सकता है। अनुमस्तिष्क (cerebellum) में कोशिकाकाय फ्लास्क (flask) की आकृति के होते हैं और पुरकिन्जे की कोशिकाएँ (Purkinje’s cell) कहलाते हैं। इसमें केन्द्रक (nucleus) प्रायः केन्द्र में, परिमाप में । बड़ा व गोलाकार होता है।

कोशिकाद्रव्य में महीन तन्त्रिको तन्तुक (neurofibrils), माइटोकॉण्ड्रिया (mitochondria), सूक्ष्म नलिकाएँ (microtubules), गॉल्जीकार्य (golgi complex), अन्त:प्रद्रव्यी जालिका (endoplasmic reticulum), वसा बिन्दुक (fat globules) आदि सामान्य संरचनाओं के अतिरिक्त अनियमित
आकार के बड़े-बड़े निसल के कण (Nissl’s granules) पाये जाते हैं।

UP Board Solutions

2. तन्त्रिका कोशिका प्रवर्ध
तन्त्रिको कोशिकाओं में प्रवर्ध निम्नलिखित दो प्रकार के होते हैं-
(i) वृक्षाभ (Dendrites) – कोशिकाकाय से निकलने वाले ये प्रवर्ध अपेक्षाकृत छोटे, सिरों की ओर क्रमशः सँकरे तथा शाखित होते हैं। कभी-कभी ये निकलने के स्थान से ही अत्यधिक शाखित होकर झाड़ी के समान (bushy) हो जाते हैं। इनमें निसल के कण, तन्त्रिका तन्तुक पाये जाते हैं।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 25

(ii) अक्ष तन्तु (Axon) – यह प्रवर्ध लगभग एक बराबर मोटाई का लम्बा तथा संख्या में एक ही
होता है। यह प्रायः स्वतन्त्र सिरे पर ही शाखित होता है और ये शाखाएँ अन्तिम शाखाएँ (telodendria) कहलाती हैं। अन्तिम शाखाओं पर गोल, घुण्डी की तरह के आकार के बटन (buttons) होते हैं। अक्ष तन्तु में निसल के कण राइबोसोम्स, गॉल्जी काय आदि नहीं होते हैं, किन्तु तन्त्रिका तन्तुक एवं अन्य कई प्रकार के कोशिकांग होते हैं। इसके बाहर आवरण के रूप में एक्सिओप्लाज्म (axioplasm) होता है। अक्ष तन्तु अनेक बार एक या अधिक आच्छदों से घिरा रहता है, तब इसे मज्जावृत (medullated) कहते हैं अन्यथा मज्जारहित (nonmedullated)। अक्ष तन्तु से बाहर उपस्थित कोमल आच्छद को न्यूरीलेमा (netirilemia) या श्वान का (UPBoardSolutions.com) आच्छद (sheath of Schwann) कहते हैं, जो श्वन कोशिकाओं (Schwann cells) से बना होता है। इस आच्छद के बाहर एक महीन आधारीय कला (basement membrane) होती है। इसके भी बाहर संयोजी ऊतक से बना हेनले का आच्छद (Henle’s sheath) पाया जाता है। श्वान कोशिकाओं से बना न्यूरीलेमा तथा अक्ष तन्तु के मध्य का आच्छद मायलिन आच्छद (myalin sheath) कहलाता है। मायलिन आच्छद निश्चित दूरियों पर विच्छिन्न (discontinuous) होती है। अतः इन स्थानों पर न्यूरीलेमा अक्ष तन्तु से चिपकी रहती है। इन स्थानों को रैन्वियर के नोड (nodes of Ranvier) कहते हैं।
कार्य
अक्ष तन्तु चेतनाओं को कोशिका से दूर ले जाते हैं। चेतना प्रेरणाओं को दूर-दूर तक ले जाने के लिए तन्तु एवं गुच्छकों (ganglia) में तन्त्रिका कोशिकाएँ अपने-अपने अक्ष तन्तुओं एवं वृक्षाभ की शाखाओं द्वारा एक-दूसरे से सम्बन्धित रहते हैं। इन स्थानों को युग्मानुबन्ध (synapse) कहते हैं। कोशिकाकाय तथा इसके वृक्षाभ (dendrites) संवेदनाओं को तन्त्रिका आवेग के रूप में प्राप्त करते अथवा उत्पन्न करते हैं, जबकि अक्ष तन्तु (axon) चेतनाओं के प्रसारण का कार्य करते हैं। इसलिए वृक्षाभों को अभिवाही (afferent) तथा अक्ष तन्तु को अपवाही (efferent) प्रवर्ध कहते हैं।

UP Board Solutions

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
तन्त्रिका तन्तु में तन्त्रिका आवेग की उत्पत्ति तथा इसके संचारण का सचित्र वर्णन कीजिए। या एक्सॉन में तन्त्रिका आवेग के समारम्भन (initiation) एवं चालन (conduction) का सचित्र वर्णन कीजिए। समझाइए कि तन्त्रिका आवेग स्वतः प्रचारी (self propagatory) होता है। यो युग्मानुबन्धन की संरचना तथा इसके पार प्रेरणा प्रसारण की क्रियाविधि का सचित्र वर्णन कीजिए। इस क्रिया में ऐसीटिलकोलीन की भूमिका की विवेचना कीजिए।
उत्तर-

एक्सॉन में तन्त्रिका आवेग का समारम्भन

किसी जन्तु में उपस्थित संवेदी कोशिकाएँ (sensory cells) प्रायः किसी भी प्रकार के उद्दीपन (stimulus) द्वारा उत्तेजित होने पर उद्दीपन को सम्बन्धित तन्त्रिका तन्तुओं (nerve fibres) में प्रेषित कर देती हैं, जिससे इसका आगे संवहन हो सके। तन्त्रिका तन्तुओं का यह उद्दीपन तन्त्रिका संवेग, आवेग या चेता प्रेरणा (nerve impulse) कहलाता है। तन्त्रिका आवेगों का संवहन एक विद्युत-रासायनिक प्रेरणा (electro-chemical impulse) के रूप में होता है। यह आवेग स्वप्रचारी (self propagatory) होता है तथा प्रारम्भ होने पर इसका अन्तिम सिरे तक होना आवश्यक होता है। तन्त्रिका आवेगों में निम्नलिखित लक्षण पाये जाते हैं।

  1. बाह्य उद्दीपन से उत्तेजित होने पर तन्त्रिका में आवेगों की लहर उठने लगती है।
  2. आवेगों का तन्त्रिका में संवहन केवल एक ही दिशा में होता है।
  3. सामान्यतः एक आवेग एक ही तन्त्रिका तन्तु तक सीमित रहता है।
  4. शरीर में तन्त्रिका तन्तु कई आवेगों को वहन कर पाते हैं।
  5. तन्त्रिका तन्तु आवेगों के संवहन की अवधि में अधिक ऊर्जा का उपभोग करते हैं।
  6. एक बार प्रारम्भ होने के पश्चात् आवेग के एक छोर से दूसरे अन्तिम छोर तक संवहन निश्चित होता है।

तन्त्रिका आवेगों का संवहन या चालन
तन्त्रिका तन्तु द्वारा आवेग का निर्माण तथा संवहन दोनों अत्यन्त जटिल एवं विद्युत-रासायनिक प्रक्रियाएँ। हैं तथा एक्सॉन की निम्नलिखित अवस्थाओं पर निर्भर करते हैं।
(i) एक्सिओप्लाज्म (axioplasm) का रासायनिक संघटन।
(ii) एक्सॉन के बाहर स्थित तरल वातावरण की रासायनिक दशा।
(iii) एक्सॉन की कोशिकाकला, एक्सोलेमा (axolemma) की पारगम्यता (permeability)।

UP Board Solutions

तन्त्रिका आवेगों का विद्युत-रासायनिक संवहन या चालन

तन्त्रिका आवेग के संवहन अथवा प्रसारण विधि की सम्पूर्ण प्रक्रिया को निम्नलिखित दो प्रावस्थाओं में विभक्त किया जा सकता है।
1. सुप्त कला विभव या विश्राम क्षमता
कोशिकाओं के बाह्य कोशिकीय माध्यम में ऊतक द्रव्य होता है। इसी माध्यम से कोशिकाएँ अपना सम्पूर्ण रासायनिक लेन-देन करती हैं। इस माध्यम में प्राय: सोडियम (Na+), क्लोराइड (Cl–) तथा बाइकार्बोनेट (HCO3–) आयन अधिक मात्रा में होते हैं। इसमें पोषक पदार्थ, (UPBoardSolutions.com) ऑक्सीजन कोशिकाओं के उपजात पदार्थ तथा कार्बन डाइऑक्साइड भी सामान्य रूप से उपस्थित होते हैं। तन्त्रिका कोशिका के एक्सिओप्लाज्म में प्रोटीन व अन्य कार्बनिक पदार्थों के साथ-साथ पोटैशियम (K+), मैग्नीशियम (Mg++) तथा फॉस्फेट (PO43- ) आयन प्रचुर मात्रा में पाये जाते हैं।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 26
विद्युत विभव (electric potential) में अन्तर होने पर भी धनात्मक एवं ऋणात्मक विद्युतावेशी आयन्स तन्त्रिका कोशिका की कला अर्थात् तन्त्रिका कला (neurilemma) के इधर-उधर गति करते हैं। जल, अकार्बनिक एवं सरल कार्बनिक अणुओं के लिए तन्त्रिका कला वरणात्मक रूप से पारगम्य (permeable) होती है। विश्रामावस्था में यह पोटैशियम (K+) तथा क्लोराइड (Cl–) आयन्स के लिए पारगम्य, परन्तु सोडियम (Na+) आयन्स के लिए लगभग अपारगम्य होती है। एक्सिओप्लाज्म (axioplasm) में पोटैशियम (K+) आयन्स ऊतक द्रव्य की अपेक्षा लगभग 30 गुना अधिक, परन्तु (Na+) वे क्लोराइड (CI) आयन्स लगभग 15 गुना कम होते हैं। इस प्रकार बनी विसरण प्रवणता के अनुसार K+ आयन्स एक्सिओप्लाज्म में गति करते हैं। चेष्ट आवागमन में आयन्स विसरण प्रवणता के विपरीत गति करते हैं अर्थात् K+ (UPBoardSolutions.com) आयन्स ऊतक द्रव्य से एक्सिओप्लाज्म में तथा Na+ आयन्स एक्सिओप्लाज्म से ऊतक द्रव में गति करते हैं। Na+ व K+ आयन्स की इस गति को ही सोडियम-पोटैशियम पम्प (sodium-potassium pump) कहते हैं। इस क्रिया में ऊतक द्रव व एक्सिओप्लाज्म के मध्य परासरणी सन्तुलन (osmotic equilibrium) बना रहता है। ऐक्सोलेमा की यह ध्रुवण अवस्था (polarized state) विश्राम अथवा सुप्त कला विभव कहलाती है।

UP Board Solutions

2. क्रियात्मक विभव अथवा प्रेरणा क्षमता
तन्त्रिका कला की एक विशेषता यह है कि उद्दीपन (stimulation) प्राप्त होने पर इसकी सोडियम (Na+) आयन्स की पारगम्यता में वृद्धि हो जाती है, जो इन कोशिकाओं को आवेशों के प्रसारण के योग्य बनाती है। यह प्रक्रिया निम्नांकित चरणों में पूर्ण होती है-
तन्त्रिका तन्तु में किसी बिन्दु पर उद्दीपन प्राप्त होने से इस स्थान पर तन्त्रिका कला की पारगम्यता बढ़ जाने के कारण Na+ आयन्स बड़ी संख्या में एक्सिओप्लाज्म में प्रवेश करने लगते हैं। इस प्रकार, उद्दीपन के स्थान पर तन्त्रिको कला में भीतर की ओर विपरीत विभव (reverse potential) बन जाता है। विश्रामावस्था से ठीक विपरीत परिवर्तन की इस क्रिया को नि: ध्रुवण (depolarization) कहते हैं। सोडियम-पोटैशियम पम्प लगभग 2-4 मिली सेकण्ड में Na+ व K+ की स्थिति सामान्य कर देता है, जिससे विश्राम क्षमता पुनः स्थापित हो जाती है। 2-4 मिली सेकण्ड का यह समय अनुत्तेजन अवधि (refractory period) कहलाता है। इस समय तन्त्रिका कला के इस बिन्दु पर नयी प्रेरण क्षमता नहीं बन पाती है और आवेग केवल साइटॉन से एक्सॉन की ओर ही चलता है। इसे पुनर्भुवण (repolarization) कहते हैं।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 27
मेड्यूलैटेड (medullated) तन्तुओं में आवेग केवल नोड्स (nodes) पर ही सम्पोषित होता है और यह कई गुनी तीव्र गति से प्रेषित होता है। प्रेषण की यह विधि उच्छ्ल न प्रसारण (saltatory transmission) कहलाती है।
युग्मानुबन्ध पर आवेग का हस्तान्तरण
तन्त्रिका कोशिका की स्वतन्त्र शाखाओं के स्वतन्त्र सिरों पर सिनैप्टिक घुण्डियाँ (synaptic knobs or buttons) होती हैं। इनके और इनसे सम्बन्धित अगली तन्त्रिका की डेण्ड्राइट्स के मध्य तरल पदार्थ से. भरा एक विशेष स्थान होता है जिसे सूत्रयुग्मन या युग्मानुबन्ध (synapse) कहते हैं। सिनैप्टि घुण्डियों में स्रावी पुटिकाएँ (secretory vesicles) होती हैं, जिन्हें सिनैप्टिक पुटिकाएँ (synaptic vesicles) भी कहते हैं। इनसे विशेष रासायनिक पदार्थ ऐसीटिलकोलीन (acetylcholine) स्रावित (UPBoardSolutions.com) होता है जो आवेग को सिनैप्टिक घुण्डी से अगले न्यूरॉन की शाखा में संचरित करता है तथा उसमें कार्यात्मक विभव (action potential) का निर्माण करता है। ऐसीटिलकोलीन के निर्माण व स्रावण के लिए कैल्सियम आयन्स (Ca+) की आवश्यकता होती है। क्रिया के पश्चात् इस पदार्थ का निष्क्रियण कोलीनेस्टेरेज (cholinesterase) नामक एन्जाइम के द्वारा होता है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 28
इस प्रकार आवेग युग्मानुबन्ध पर एक तन्त्रिका कोशिका से दूसरी तन्त्रिका कोशिका में एक ही दिशा में अर्थात् एकदिशात्मक (unidirectional) रूप में स्वसंचारित होता रहता है।

प्रश्न 2.
प्रतिवर्ती क्रिया को परिभाषित कीजिए। इस क्रिया को चित्र की सहायता से समझाइए।
या
प्रतिवर्ती क्रिया क्या है? इसके प्रकार एवं दो उदाहरण लिखिए।
या
प्रतिवर्ती चाप का नामांकित चित्र बनाइए।
या
प्रतिवर्ती क्रिया का सचित्र वर्णन कीजिए।
उत्तर-

प्रतिवर्ती क्रियाएँ तथा उनकी कार्य-विधि

प्रतिवर्ती क्रियाएँ अनैच्छिक क्रियाएँ हैं जिन पर मस्तिष्क का किसी भी प्रकार नियन्त्रण नहीं होता है। इन क्रियाओं में संवेदी प्रेरणा सुषुम्ना अथवा मस्तिष्क में पहुँचने पर तुरन्त ही चालक प्रेरणा के रूप में अपवाहक अंगों में स्थानान्तरित हो जाती है।
इस प्रकार प्रतिवर्ती क्रियाएँ अनायास, अविलम्ब, यन्त्रवत् एवं सहज ही घट्रित होती हैं। इस प्रकार की क्रियाओं का सर्वप्रथम पता हाल (Hall, 1833) ने लगाया था।

सुषुम्ना से प्रत्येक स्पाइनल तन्त्रिका (spinal nerve) दो मूलों के रूप में निकलती है। पहला संवेदी तन्तुओं (sensory fibres) से बना पृष्ठ मूल (dorsal root) तथा चालक तन्तुओं (motor fibres) से बना दूसरा अधर मूल (ventral root) कहलाता है। संवेदना प्राप्त होने पर आवेग (impulse) की लहर पृष्ठ मूल से होकर पृष्ठ मूल गुच्छक (dorsal root ganglion) में स्थित न्यूरॉन तथा उसके एक्सॉन (axon) में होती हुई सुषुम्ना के धूसर द्रव्य (grey matter) में पहुँचती हैं। यहाँ से सिनैप्टिक घुण्डियों (synaptic knobs) से होता हुआ आवेग चालक तन्त्रिका कोशिकाओं (motor nerve cells) के डेण्ड्राइट्स में जाता है। अब यह आवेग ज्यों-का-त्यों (UPBoardSolutions.com) चालक प्रेरणा बनकर प्रभावी अंग (effected organ) में पहुँचता है। प्रभावी अंगों की पेशियाँ तुरन्त क्रियाशील होकर इन्हें गति प्रदान करती हैं। संवेदांग से लेकर अपवाहक अंग (effector organ) तक के इस प्रकार के आवेग पथ को प्रतिवर्ती चाप (reflex arc) कहा जाता है।
UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination image 29
प्रतिवर्ती क्रियाएँ निम्नांकित दो प्रकार की होती हैं।

1. अबन्धित प्रतिवर्ती क्रियाएँ (Unconditional Reflex Actions) – इस प्रकार की प्रतिवर्ती क्रियाएँ प्राणियों में जन्म से मूल प्रवृत्ति (instinct) के रूप में होती हैं। ये क्रियाएँ स्पाइनल कॉर्ड (spinal cord) द्वारा नियन्त्रित होती हैं; जैसे-घोंसला बनाना, पक्षियों का देशान्तरण (migration) आदि।
2. प्रतिबन्धित प्रतिवर्ती क्रियाएँ (Conditioned Reflex Actions) – ये क्रियाएँ प्राणियों में अनुभव द्वारा विकसित होती हैं। इन क्रियाओं पर प्रारम्भ में तो प्रमस्तिष्क का नियन्त्रण रहता है, परन्तु बाद में ये स्वत: ही होने लगती हैं। नृत्य, तैरना, वाद्य, संगीत आदि इन क्रियाओं के सामान्य उदाहरण हैं।

UP Board Solutions

प्रतिवर्ती क्रियाओं के कुछ सामान्य उदाहरण
1. खाँसना एवं छींकना (Coughing and Sneezing) – श्वसन मार्ग में किसी ठोस कण के पहुँचने पर फेफड़ों से मुख के द्वारा तीव्र गति से वायु बाहर निकलती है, जिससे कि अवांछित कण वायु के दबाव से बाहर निकल जायें। तीव्र उच्छ्वास के कारण स्वर पट्टियों में कम्पन उत्पन्न होने से खाँसी (UPBoardSolutions.com) की ध्वनि उत्पन्न होती है। छींकने में भी ऐसा ही होता है, अन्तर केवल इतना है कि इसमें वायु मुख के स्थान पर नाक से बाहर निकलती है।
2. नेत्र प्रतिक्षेप क्रिया (Blinking Reflex of Eye) – किसी वस्तु के अचानक सामने आने पर पलकों का अविलम्ब झपकना नेत्र प्रतिक्षेप क्रिया कहलाता है।

We hope the UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination (तन्त्रिकीय नियन्त्रण एवं समन्वय) help you. If you have any query regarding UP Board Solutions for Class 11 Biology Chapter 21 Neural Control and Coordination (तन्त्रिकीय नियन्त्रण एवं समन्वय), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion

by

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion (परिक्षेपण के माप)

पाठ्य-पुस्तक के प्रश्नोत्तर

प्रश्न 1.
किसी बारम्बारता वितरण के समझने में परिक्षेपण का माप केन्द्रीय मान का एक अच्छा सम्पूरक है।’ टिप्पणी करें।
उत्तर :
परिक्षेपण यह दर्शाता है कि वितरण का मान उसके औसत मान से कितना भिन्न है। केन्द्रीय माप अथवा औसत प्रतिनिधि माप तो होता है किन्तु यह मान आँकड़ों में विद्यमान परिवर्तनशीलता को नहीं दर्शाता है। दूसरे शब्दों में, औसत वितरण के केवल एक पहलू के बारे में बताता है अर्थात् यह मूल्यों का एक प्रतिनिधि आकार है। इसे बेहतर ढंग से समझने के लिए मूल्यों अथवा मानों के प्रसरण को जानना अत्यन्त
आवश्यक है। इसके विपरीत, परिक्षेपण के माप आँकड़ों में बिखराव अथवा फैलाव के बारे में बताते हैं और वितरण के मामले में बेहतर जानकारी प्रदान करते हैं। अतः परिक्षेपण की माप आँकड़ों के वितरण को समझने में केन्द्रीय प्रवृत्ति की माप का एक अच्छा सम्पूरक है।

प्रश्न 2.
परिक्षेपण का कौन-सा माप सर्वोत्तम है और कैसे?
उत्तर :
परिक्षेपण के चार प्रमुख माप हैं
(क) परास (विस्तर),
(ख) चतुर्थक विचलन,
(ग) माध्य विचलन तथा
(घ) प्रमाप मानक विचलन।
उपर्युक्त में से कोई भी परिक्षेपण की माप-सीमाओं से परे नहीं है। प्रत्येक परिक्षेपण माप’ की अपनी विशेषताएँ एवं कमियाँ हैं। फिर भी मानक विचलन परिक्षेपण की मापों में सर्वाधिक उपयुक्त माप है, क्योंकि

  • यह सभी मानों पर आधारित होता है। इसलिए किसी भी माने में परिवर्तन, मानक विचलन के मान को प्रभावित करता है।
  • यह उद्गम से स्वतन्त्र है परन्तु पैमाने से नहीं।
  • यह कुछ उच्च सांख्यिकीय विधियों में भी प्रयुक्त होता है।
  • इसका बीजगणितीय विवेचन सम्भव है।

प्रश्न 3.
‘परिक्षेपण के कुछ माप मानों के प्रसरण पर निर्भर करते हैं, लेकिन कुछ, केन्द्रीय मान से | मानों के विचरण को परिकलित करते हैं। क्या आप सहमत हैं?
उत्तर :
परिक्षेपण के माप दो प्रकार के होते हैं-

1. परिक्षेपण के निरपेक्ष माप तथा
2. परिक्षेपण के सापेक्ष माप।

1. परिक्षेपण के निरपेक्ष माप – ये हैं–विस्तार, चतुर्थक विचलन, माध्य विचलन और प्रमाप विचलन। ये माप उसी इकाई में होते हैं जिसमें मौलिक मूल्य होते हैं। इसलिए जब मूल्यों में ज्यादा बिखराब पाया जाता है तो ये माप आँकड़ों के वितरण के बारे में भ्रम पैदा कर सकते हैं।
2. परिक्षेपण के सापेक्ष माप – ये हैं–विस्तार गुणांक, चतुर्थक विचलन गुणांक, माध्य विचलन गुणांक, मानक विचलन गुणांक एवं विचरण गुणांक। इन मूल्यों की इकाई नहीं होती। परिक्षेपण के निरपेक्ष माप आँकड़ों के बिखराव से प्रभावित होते हैं जबकि परिक्षेपण के सापेक्ष माप केन्द्रीय प्रवृत्ति से विचरण को मापते हैं।

प्रश्न 4.
एक कस्बे में 25% लोग हैं 45,000 से अधिक आय अर्जित करते हैं जबकि 75% लोग 18,000 से अधिक आय अर्जित करते हैं। परिक्षेपण के निरपेक्ष एवं सापेक्ष मानों का परिकलन कीजिए।
उत्तर :
अर्जित आय का अधिकतम मूल्य = ₹ 45,000
अर्जित आय का न्यूनतम मूल्य = 18,000
विस्तार = L – S
= 45,000 -18,000 = ₹ 27,000
विस्तार गुणंख = [latex s=2]\frac { l-S }{ l-S } =\frac { 45,000-18,000 }{ 45,000+18,000 }[/latex]
= [latex s=2]\frac { 27,000 }{ 63,000 } or\frac { 27 }{ 63 } or\frac { 3 }{ 7 }[/latex]
=0.43
परिक्षेपण का निरपेक्ष मान = ₹ 27,000
परिक्षेपण का सापेक्ष मान = ₹ 0.43.

प्रश्न 5.
एक राज्य के 10 जिलों की प्रति एकड़ गेहूँ व चावल फसल की उपज निम्नवत है|
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 1

प्रत्येक फसल के लिए परिकलन करें
(क) परास
(ख) चतुर्थक विचलन
(ग) माध्य से माध्य विचलन
(घ) मध्यिका से माध्य विचलन
(ङ) मानक विचलन
(च) किस फसल में अधिक विचरण है?
(छ) प्रत्येक फसल के लिए विभिन्न मापों के मानों की तुलना कीजिए।
उत्तर :
(क) परास
(i) गेहूँ
वितरण का अधिकतम मूल्य (L) = 25
वितरण का न्यूनतम मूल्य (S) = 9
परास = L-S
= 25 – 9 = 16
∴ गेहूं की फसल का परास = 16,

(ii) चावल
वितरण का अधिकतम मूल्य (L) = 34
वितरण का न्यूनतम मूल्य (S) = 12
परास = L – S
= 25 – 12 = 22
∴ चावल की फसल को परास = 22

(ख) चतुर्थक विचलन
(i) गेहूँ
गेहूं के उत्पादन का बढ़ता क्रम
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 2

(ii) चावल
चावल के उत्पादन का बढ़ता क्रम
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 3

(ग) माध्य से माध्य विचलन
(i) गेहूं
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 4
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 5
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 6

माध्य से माध्य विचलन
(i) गेहूँ के लिए 4.3
(ii) चाल के लिए =6
(घ) मध्यिका से माध्य विचलन
(i) गेहूँ
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 7 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 8 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 9

मध्यिका से माध्य विचलन
(i) गेहूँ के लिए = 4.3
(ii) चावल के लिए = 5.7

(ङ) मानक विचलन
(i) गेहूँ
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 10 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 11

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 12

मानक विचलन –

  • गेहूँ के लिए = 4,94
  • चावल के लिए = 7.16

(च) किस फसल में अधिक विचरण है?
(i) गेहूँ
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 13
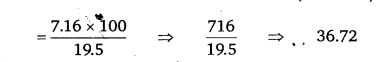
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 14

अतः चावल की उपज में विचरण अधिक है।
(छ) प्रत्येक फसल के लिए विभिन्न मापों के मानों की तुलना
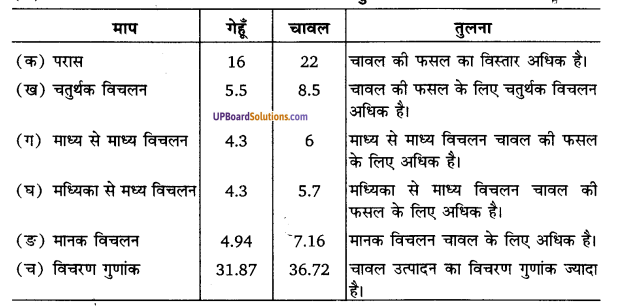
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 15

प्रश्न 6.
पूर्ववर्ती प्रश्न में, विचरण के सापेक्ष मापों को परिकलित कीजिए और वह मान बताइए जो आपके विचार से सर्वाधिक विश्वसनीय हो।
उत्तर :
(A) पिछले प्रश्न में, गेहूं की फसल के लिए विभिन्न परिक्षेपण के सापेक्ष माप एवं विचरण निम्न प्रकार हैं|
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 16 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 17

∴ मानक विचलन से विचरण गुणांक ज्यादा विश्वसनीय है।

प्रश्न 7.
किसी क्रिकेट टीम के लिए एक बल्लेबाज का चयन करना है। यह चयन x और y के बीच पाँच पूर्ववर्ती स्कोर के आधार पर करना है जो निम्नवत् है
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 18
किस बल्लेबाज को टीम में चुना जाना चाहिए
(क) अधिक रन स्कोर करने वाले को, या
(ख) अधक भरोसेमन्द बल्लेबाज को।
उत्तर :
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 19
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 20
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 21

उत्तर :
(क) ‘x’ का औसत स्कोर बल्लेबाज y की तुलना में ज्यादा है। अत: अधिक रन बनाने वाले बल्लेबाज के रूप में ‘x का चयन होना चाहिए।
(ख) विचरण गुणांक बल्लेबाज ‘x की तुलना में y का अधिक है। अत: विश्वसनीयता के आधार पर y का चयन किया जाना चाहिए।

प्रश्न 8.
दो ब्राण्डों के बल्बों की गुणवत्ता जाँचने के लिए, ज्वलन अवधि घण्टों में उनके जीवन-काल को, प्रत्येक ब्राण्ड के 100 बल्बों के आधार पर निम्नानुसार अनुमानित किया गया है–

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 22
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 23

(क) किस ब्राण्ड का जीवनकाल अधिक है?
(ख) कौन-सा ब्राण्ड अधिक भरोसेमन्द है?
उत्तर :

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 24
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 25 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 26

उत्तर :

  • औसत जीवनकाल बल्ब ‘क’ का ज्यादा है।
  • विचरण गुणांक का मान बल्ब ‘ख’ के लिए कम है; अत: बल्ब ‘क’ की तुलना में बल्ब ‘ख’ ज्यादा विश्वसनीय है।

प्रश्न 9.
एक कारखाने के 50 मजदूरों की औसत दैनिक मजदूरी ₹ 200 तथा मानक विचलन ₹ 40 था। प्रत्येक मजदूर की मजदूरी में है 20 की वृद्धि की गई। अब मजदूरों की औसत दैनिक मजदूरी एवं मानक विचलन क्या है? क्या मजदूरी में समानता आई है?
उत्तर :
‘सजदूरों की संख्या = ₹ 50
औसत दैनिक मजदूरी = ₹ 200
कुल मजदूरी = मजदूरों की संख्या × औसत मजदूरी
= 50 × 200 = ₹ 10,000
प्रत्येक मजदूर की मजदूरी में वृद्धि = ₹ 20, कुल वृद्धि = ₹ 50 × 20 = ₹ 1000
नई कुल मजदूरी = ₹ 10,000 + ₹ 1000= ₹ 11,000
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 27

प्रश्न 10.
पूर्ववर्ती प्रश्न में, यदि प्रत्येक मजदूर की मजदूरी में 10% की वृद्धि की जाए, तो माध्य एवं मानक विचलन पर क्या प्रभाव पड़ेगा?
उत्तर :
पूर्ववर्ती प्रश्न में,
औसत मजदूरी = ₹ 200
मानक मजदूरी = ₹ 40
मजदूरी में वृद्धि = ₹ 200 का 10%
= 200 x [latex s=2]\frac { 10 }{ 100 }[/latex] = ₹ 20
माध्य तथा मानक विचलन पर वही प्रभाव पड़ेगा जो पिछले प्रश्न में पड़ा था।

प्रश्न 11.
निम्नलिखित वितरण के लिए, माध्य से माध्य विचलन और मानक विचलन का परिकलन कीजिए
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 28
हल :
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 29

माध्य = 948
मानक विचलन = 26.17

प्रश्न 12.
10 मानों का योग 100 है और उनके वर्गों का योग 1090 है। विचरण गुणांक ज्ञात कीजिए।
उत्तर :
मानों की संख्या (N) = 10
10 मानों का योग = 100
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 30

परीक्षोपयोगी प्रश्नोत्तर
बहुविकल्पीय प्रश्न

प्रश्न 1.
“अपकिरण पदों के विचरण या अंतर को माप है।” यह परिभाषा किसने दी है?
(क) मार्शल
(ख) प्रो० एली
(ग) डॉ० बाउले
(घ) कॉनर
उत्तर :
(ग) डॉ०. बाउले।

प्रश्न 2.
किसी समंकमाला में सबसे बड़े पद’ तथा ‘सबसे छोटे पद’ के मूल्य के अंतर को क्या कहते हैं?
(क) विस्तार
(ख) प्रमाप
(ग) विचरण
(घ) बहुलक
उत्तर :
(क) विस्तार।

प्रश्न 3.
‘प्रथम अपकिरण घात’ कहते हैं
(क) बहुलक को
(ख) माध्य विचलन को
(ग) समान्तर माध्य को
(घ) अपकिरण को
उत्तर :
(ख) माध्य विचलन को।

प्रश्न 4.
प्रमाप विचलन का प्रयोग सर्वप्रथम किसने किया?
(क) कार्ल पियर्सन ने
(ख) प्रो० माल्थस ने
(ग) मिल ने
(घ) प्रो० मार्शल ने
उत्तर :
(क) कार्ल पियर्सन ने।

प्रश्न 5.
‘लॉरेंज वक्र का प्रयोग सर्वप्रथम किस अर्थशास्त्री ने किया था?
(क) प्रो० मार्शल ने
(ख) कार्ल पियर्सन ने
(ग) आरूकेण्ड्यू पिट ने
(घ) डॉ० मैक्स लॉरेंज ने
उत्तर :
(घ) डॉ० मैक्स लॉरेंज ने।

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
अपकिरण की परिभाषा दीजिए।
उत्तर :
“अपकिरण मदों के विचरण का माप है।”

प्रश्न 2.
औसत व अपकिरण में क्या अंतर है?
उत्तर :
औसत किसी श्रेणी की केन्द्रीय प्रवृत्ति है जबकि अपकिरण विभिन्न मदों तथा केन्द्रीय प्रवृत्ति के बिखराव के विस्तार को मापता है।।

प्रश्न 3.
अपकिरण के निरपेक्ष माप से क्या आशय है?
उत्तर :
अपकिर का निरपेक्ष माप वह होता है जो श्रृंखला की मौलिक इकाई में ही व्यक्त किया जाता है।

प्रश्न 4.
अपकिर के सापेक्ष माप से क्या आशय है?
उत्तर :
अपकिर क; सापेक्ष माप वह होता है जिसमें आँकड़ों के अंतर को अनुपात या प्रतिशत के रूप में व्यक्त किया जाता है।

प्रश्न 5.
विस्तार (Range) किसे कहते हैं?
उत्तर :
किसी श्रेणी के सबसे बड़े मूल्य (L) और सबसे छोटे मूल्य (S) के अंतर को विस्तार कहते हैं। (L – S)

प्रश्न 6.
विस्तार गुणांक (Coefficient of Range) क्या है?
उत्तर :
विस्तार गुणांक श्रेणी के सबसे बड़े मूल्य तथा सबसे छोटे मूल्य के अंतर तथा इनके योग का अनुपात है। [latex s=2](\frac { L-S }{ L+S } )[/latex]

प्रश्न 7
अंतर चतुर्थक विस्तार (InterQuartile Range) किसे कहते हैं?
उत्तर :
किसी श्रेणी के तृतीय (Q3) तथा प्रथम चतुर्थक Q5) के अंतर को अंतर चतुर्थक विस्तार कहते हैं। (Q3 – Q1)

प्रश्न 8.
चतुर्थक विचलन (Quartile Deviation) क्या है?
उत्तर :
चतुर्थक विचलन अंतर चतुर्थक विस्तार का आधा होता है। [latex s=2](\frac { { Q }_{ 3 }-{ Q }_{ 1 } }{ 2 } )[/latex]

प्रश्न 9.
चतुर्थक विचलने गुणांक (CoefficientofQuartile Deviation) किसे कहते हैं?
उत्तर :
यह अपकिरण की सापेक्ष माप है। इसका उपयोग दो या दो से अधिक श्रेणी पदों की तुलना के लिए किया जाता है। [latex s=2](\frac { { Q }_{ 3 }-{ Q }_{ 1 } }{ { Q }_{ 3 }+{ Q }_{ 1 } } )[/latex]

प्रश्न 10.
माध्य विचलने (Mean Deviation) की परिभाषा दीजिए।
उत्तर :
“श्रृंखला के किसी सांख्यिकीय माध्य (समान्तर माध्य, मध्यिका या भूयिष्ठक) से निकाले गए विभिन्न मूल्यों के विचलनों के समान्तर माध्य को उसका माध्य विचलन कहा जाता है।”

प्रश्न 11.
माध्य विचलन का गुणांक कैसे निकाला जाता है?
उत्तर :
माध्य विचलन का गुणांक निकालने के लिए माध्य विचलन को उसके औसत से भाग कर दिया जाता है।

पश्न 12.
माध्य विचलन को प्रमुख दोष बताइए।
उत्तर :
इसमें श्रेणी के औसत मूल्य से प्राप्त सभी विचलनों को धनात्मक मान लिया जाता है जबकि कुछ विचलन ऋणात्मक भी होते हैं।

प्रश्न 13.
प्रमाप विचलन को परिभाषित कीजिए।
उत्तर :
“प्रमाप विचलन समान्तर माध्य से श्रृंखला के विभिन्न मूल्यों के विचलनों के वर्गों के माध्य को वर्गमूल है।”

प्रश्न 14.
प्रमाप विचलन का गुणांक (Coefficient of Standard Deviation) क्या है?
उत्तर :
प्रमाप विचलन का गुणांक प्रमाप विचलन तथा समान्तर माध्य का अनुपात है। [latex s=2](\frac { \sigma }{ \overline { X } } )[/latex]

प्रश्न 15.
विचरण गुणांक (Coefficient of variation) क्या है?
उत्तर :
विचरण गुणांक प्रमाप विचलन का प्रतिशत रूप है। [latex s=2](\frac { \sigma }{ \overline { X } } \times 100)[/latex]

प्रश्न 16.
विचरण गुणांक और प्रमाप विचलन में क्या अंतर है?
उत्तर :
विचरण गुणंक माध्य में होने वाला प्रतिशत विचरण है जबकि प्रमाप विचलन माध्य में होने वाला कुल विचरण है।

प्रश्न 17.
लॉरेंज वक्र (Lorenz Curve) क्या है?
उत्तर :
लॉरेंज वक्र समान वितरण रेखा से वास्तविक वितरण के विचलन का बिन्दुरेखीय माप है।

प्रश्न 18.
समान वितरण रेखा किसे कहते हैं?
उत्तर :
OX अक्ष के O मापदण्ड को OY अक्ष के मापदण्ड से मिलाने से जो रेखा खींची जाती है, उसे समान वितरण रेखा कहते हैं।

प्रश्न 19.
लॉरेंज वक्र का दूसरा क्या नाम है?
उत्तर :
लॉरेंज वक्र का दूसरा नाम ‘संचयी प्रतिशत वक्र’ है।

लघु उत्तरीय प्रश्न

प्रश्न 1.
अपकिरण किसे कहते हैं? अपकिरण की माप के उद्देश्य बताइए।
उत्तर :

अपकिरण

अपकिरण शब्द का प्रयोग दो अर्थों में किया जाता है। प्रथम अर्थ में, अपकिरण से तात्पर्य समंक श्रेणी के सीमांत मूल्यों के अंतर या सीमा विस्तार से है। दूसरे अर्थ में-“अपकिरण श्रेणी के माध्य से निकाले गए विभिन्न पदों के विचलनों का माध्य है।”
डॉ. बाउले के अनुसार – “अपकिरण पदों के विचरण या अंतर का माप है।”

अपकिरण की माप के उद्देश्य

अपकिरण की माप के निम्नलिखित उद्देश्य हैं

  • श्रेणी के माध्य से विभिन्न पद मूल्यों की औसत दूरी ज्ञात करना;
  • श्रेणी की बनावट के बारे में सूचना प्राप्त करना;
  • पद मूल्यों का सीमा विस्तार ज्ञात करना;
  • तुलनात्मक अध्ययन द्वारा यह जानना कि किसमें विचरण की मात्रा अधिक है;
  • यह देखना कि माध्य द्वारा श्रेणी का किस सीमा तक प्रतिनिधित्व होता है।

प्रश्न 2.
परास या विस्तार (Range) क्या है? इसके गुण व दोष बताइए।
उत्तर :
किसी समंकमाला के सबसे बड़े और सबसे छोटे मूल्य के अंतर को विस्तार या परास (Range) कहते हैं। इसमें श्रेणी के अधिकतम मूल्य और न्यूनतम मूल्य ज्ञात किए जाते हैं। सूत्र रूप में
R = L -S
यहाँ, R = परास या विस्तार
L = श्रेणी का अधिकतम मूल्य
S = श्रेणी का निम्नतम मूल्य

विस्तार के गुण

  • यह अपकिरण की सबसे सरल माप है।
  • यह उन सीमाओं को स्पष्ट कर देता है जिसके मध्य ही समंकमाला के समस्त मूल्य फैले रहते हैं।
  • गुण नियंत्रण, मूल्यों के उच्चावचन तथा भौगोलिक अध्ययनों में यह बहुत उपयोगी है।

विस्तार के दोष

  • इससे समंकमाला के केवल उच्चतम और न्यूनतम मूल्य पर ही ध्यान दिया जाता है तथा अन्य मूल्यों की उपेक्षा की जाती है।
  • यह अपकिरण की एक संतोषजनक माप नहीं है।
  • इसके द्वारा श्रेणी की बनावट के बारे में जानकारी नहीं होती है।
  • यह अपकिरण की एक अस्थिर माप है।

प्रश्न 3.
निम्नलिखित का अर्थ एवं गुणन क्रिया समझाइए

(i) अंतर चतुर्थक विस्तार,
(ii) चतुर्थक विचलन,
(iii) चतुर्थक विचलन गुणांक।

उत्तर :

(i) अंतर चतुर्थक विस्तार

समंक श्रेणी के तृतीय चतुर्थक और प्रथम चतुर्थक के अंतर को ‘अंतर चतुर्थक विस्तार’ कहते हैं। गणन क्रिया निम्नलिखित प्रकार से है

  • पहले दोनों चतुर्थक ज्ञात किए जाते हैं।
  • निम्नांकित सूत्र का प्रयोग किया जाता है
    I.R. =Q3 – Q1

(ii) चतुर्थक विचलन

तृतीय चतुर्थक वः प्रथम चतुर्थक के अंतर के आधे को चतुर्थक विचलन’ (Quartile deviation) या ‘अर्द्ध-अंतर चतुर्थक विस्तार’ (Semi-inter quartile range) कहते हैं। सूत्र रूप में
QD =Q3 – Q1

(iii) चतुर्थक विचलन गुणांक

विभिन्न श्रेणियों के चतुर्थक विचलन की तुलना करने के लिए इसका सापेक्ष माप निकाला जाता है। यह सापेक्ष माप चतुर्थक विचलन गुणांक’ कहलाता है। सूत्र निम्न प्रकार है
Coeffi. of QD = [latex s=2]\frac { { Q }_{ 3 }-{ Q_{ 1 } } }{ { Q }_{ 3 }+{ Q_{ 1 } } }[/latex]

प्रश्न 4.
माध्य विचलन (Mean Deviation) किसे कहते हैं? माध्य विचलन के गुण व दोष बताइए।
उत्तर :
किसी श्रेणी का माध्य विचलन श्रेणी के सभी पद मूल्यों के वास्तविक माध्य से लिए गए विचलनों कैं। समान्तर माध्य होता है। मूल्यों के विचलन निकालते समय + चिह्नों को छोड़ दिया जाता है।
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 31a
माध्य विचलन के गुण-

  • माध्य विचलन एक उत्तम विधि है क्योंकि यह किसी भी माध्य द्वारा निकाला जा सकता है।
  • यह विचलन ज्ञात करने की एक सरल विधि है।
  • माध्य विचलन श्रेणी के सभी पदों पर आधारित होने के कारण अन्य मापों से श्रेष्ठ होता है।
  • इस माध्य द्वारा श्रेणी की बनावट के बारे में भी मालूम किया जा सकता है।
  • यह प्रमाप विचलने की तुलना में चरम मूल्यों से कम प्रभावित होता है।
  • यह वितरण के महत्त्व को स्पष्ट करने वाली माप है।
  • इसका प्रयोग आर्थिक, व्यापारिक एवं सामाजिक क्षेत्रों में पर्याप्त होता है।

माध्य विचलन के दोष-

  • चूँकि यह विभिन्न माध्यों से ज्ञात किया जाता है; अत: यह एक अनिश्चित माप है।
  • इसमें (+) और (-) चिह्नों को छोड़ दिया जाता है, इसलिए यह माप गणितीय दृष्टि से अशुद्ध है।
  • इसका बीजीय विवेचन संभव नहीं है।
  • विभिन्न माध्यों से ज्ञात माध्य विचलनों में समानता नहीं होती।

प्रश्न 5.
प्रमाप विचलन किसे कहते हैं? प्रमाप विचलन की विशेषताएँ बताइए।
उत्तर :
प्रमाप विचलन अपकिरण की एक आदर्श माप है। इसका आशय उसा माप से होता है जो कि पदों के समान्तर माध्य से लिए गए विचलनों के वर्गों के समान्तर माध्य का वर्गमूल है। विशेषताएँ-

  • इसके अंतर्गत विचलन सदैव समान्तर माध्य से ही लिए जाते हैं क्योंकि यह माध्य से केन्द्रीय प्रवृत्ति का सर्वश्रेष्ठ माप समझा जाता है।
  • इस माप के अंतर्गत बीजगणितीय चिह्न (+) तथा (-) को छोड़ा नहीं जाता बल्कि मूल्यों का वर्ग करने पर वे स्वयं ही धनात्मक हो जाते हैं।
  • विचलनों के वर्गों के योग में पदों की संख्या का भाग दिया जाता है तथा प्राप्त मूल्य का वर्गमूल निकाला जाता है। यही प्रमाप विचलन होता है।

प्रश्न 6.
प्रमाप विचलन के गुण व दोष बताइए।
उत्तर :
प्रेमाप विचलन के गुण-

  1. यह श्रेणी के सभी मूल्यां पर आधारित होता है।
  2. यह विशुद्ध गणितीय विधि पर आधारित है; अत: उच्चतर गणितीय रीतियों में इसका काफी प्रयोग होता है।
  3. अपकिरण की अन्य मापों की अपेक्षा प्रमाप विचलन पर निदर्शन परिवर्तनों का सबसे कम प्रभाव होता है।
  4. यह अपकिरण का एक स्पष्ट और निश्चित माप है जो प्रत्येक स्थिति में ज्ञात किया जा सकता है।
  5. इसके द्वारा सामान्य वक्र के क्षेत्र का निर्धारण स्पष्ट रूप से हो जाता है।
  6. इसका बीजीय विवेचन संभव है।
  7. अपकिरण का निम्नलिखित क्षेत्रों में अत्यधिक उपयोग किया जाता है
  • विभिन्न समूहों के विचरण की तुलना करने में।
  • दैव न्यादर्शों में विभिन्न मापों की अर्थपूर्णता की जाँच करने में।
  • प्रसामान्य वक्र के अधीनस्थ क्षेत्रफल की जाँच करने में।
  • सहसंबंध विश्लेषण में।
  • श्रेणी में मूल्य वितरण की सीमाएँ निर्धारित करने में।

प्रमाप विचलन के दोष-

  • अन्य मापों की अपेक्षा समझने में यह कठिन है।
  • यह चरम मूल्यों को अत्यधिक महत्त्व देता है।

प्रश्न 7.
लॉरेज वक्र क्या है? इसके गुण व दोष बताइए।
उत्तर :
लॉरेंज वक्र अपकिरण ज्ञात करने की एक बिंदुरेखीय रीति है। इसे संचयीप्रतिशत वक्र भी कहते हैं।
गुण –

  • यह आकर्षक व प्रभावशाली होता है।
  • यह समझने में सरल है।
  • इसकी सहायता से दो या दो से अधिक श्रेणियों की अपकिरण की मात्रा की तुलना की जा सकती है।
  • इससे मस्तिष्क पर बोझिल अंकों का भार नहीं पड़ता।

दोष –

  • इससे अपकिरण का अंकात्मक माप ज्ञात नहीं होता।
  • इसे बनाने की क्रिया कठिन है और इसे बनाने से पहले श्रेणी में काफी संशोधन करना पड़ता है।

प्रश्न 8.
विचरण गुणांक क्या है? इसका सूत्र लिखिए।
उत्तर :
विचरण गुणांक,Coefficient of Variation)-दो या दो से अधिक श्रेणियों में विचलन की तुलना करने के लिए विचरण गुणांक का प्रयोग किया जाता है। यह माप विचलन गुणांक का प्रतिशत रूप है। दूसरे शब्दों में, प्रमाप विचलन को समान्तर माध्य से भाग देकर भजनफल में 100 की गुणा करने से प्राप्त प्रतिशत ही ‘विचरण गुणांक’ होता है। सूत्र रूप में

Coeffi. of V. = [latex s=2]\frac { \sigma }{ \overline { X } } \times 100[/latex]

निर्वचन – जिस समंक श्रेणी का विचरण गुणांक अधिक होता है उसमें विचरण अधिक होता है और वह श्रेणी अधिक अस्थिर व असंगत मानी जाती है। इसके विपरीत, जिस श्रेणी में विचरण गुणांक कम होता है, वह अधिक स्थिर व संगत मानी जाती है।

दीर्घ उत्तरीय प्रश्न

प्रश्न 1.
अपकिरण अथवा परिक्षेपण का क्या अर्थ है? अपकिरण को माप करने की कौन-कौन सी
विधियाँ हैं?
या
अपकिरण का अर्थ एवं उददेश्य बताइए। सापेक्ष व निरपेक्ष अपकिरण से क्या आशय है?
अपकिरण के माप द्वितीय श्रेणी के माध्य क्यों कहलाते हैं?
उत्तर :

अपकिरण का अर्थ एवं परिभाषा

अपकिरण शब्द का दो अर्थों में प्रयोग किया जाता है। प्रथम अर्थ में, अपकिरण से तात्पर्य समंक श्रेणी के सीमान्त मूल्यों के अन्तर या सीमा विस्तार से है। दूसरे अर्थ में, अपकिरण श्रेणी के मध्य से निकाले गए विभिन्न पदों के विचलनों का माध्य’ है। अपकिरण की प्रमुख परिभाषाएँ निम्नलिखित हैं

1. डॉ० बाउले के अनुसार-“अपकिरण पदों के विचरण या अन्तर का माप है।”
2. कॉनर के अनुसार-“जिस सीमा तक व्यक्तिगत पद मूल्यों में भिन्नता होती है, उसके माप को अपकिरण कहते हैं।’

द्वितीय श्रेणी के माध्य – अपकिरण के माप ज्ञात करते समय पहले श्रेणी का सांख्यिकीय माध्य निकाला जाता है, फिर उस माध्य से विभिन्न मूल्यों के विचलनों का माध्य ज्ञात किया जाता है। माध्य से निकाले गए विचलनों का माध्य होने के कारण अपकिरण माप ‘द्वितीय श्रेणी के माध्य’ कहलाते हैं।

निरपेक्ष व सापेक्ष अपकिरण

जब किसी श्रेणी के विचरण का माप निरपेक्ष रूप में उस श्रेणी की इकाई में ही ज्ञात किया जाता है तो वह अपकिरण का निरपेक्ष माप कहलाता है। इस निरपेक्ष माप को सम्बन्धित माध्य से भाग देने पर जो अनुपात या प्रतिशत आता है, वह ‘अपकिरण का सापेक्ष माप’ कहलाता है।

अपकिरण के उद्देश्य

अपकिरण के माप के निम्नलिखित उद्देश्य हैं

  • श्रेणी के माध्य से विभिन्न पद मूल्यों की औसत दूरी ज्ञात करना।
  • श्रेणी की बनावट के बारे में सूचना प्राप्त करना।
  • पद मूल्यों का सीमा विस्तार ज्ञात करना।
  • तुलनात्मक अध्ययन द्वारा यह जानना कि किसमें विचरण की मात्रा अधिक हैं।
  • यह देखना कि माध्य द्वारा श्रेणी का किस सीमा तक प्रतिनिधित्व होता है।

अपकिरण ज्ञात करने की रीतियाँ

अपकिरण ज्ञात करने की निम्नलिखित रीतियाँ हैं
(अ) सीमा रीति (Methods of limits)–

1. विस्तार या परास (Range),
2. अन्तर चतुर्थक विस्तार (Inter quartile range),
3. शतमक विस्तार (Percentile range)।

(ब) विचलन माध्य रीति (Method of averaging deviations)

1. चतुर्थक विचलन (Quartile deviation),
2. माध्य विचलन (Mean deviation),
3. प्रमाप विचलन (Standard deviation),
4. विचरण गुणांक (Coefficient of variation)।

(स) बिन्दुरेखीय रीति (Graphic method),
लॉरेंज वक्र (Lorenz curve)।

प्रश्न 2.
विस्तार (परास) एवं विस्तार गुणांक क्या है? उदाहरणों की सहायता से इसकी गणन प्रक्रिया को समझाइए।
उत्तर :

विस्तार अथवा परास (Range)

किसी समंकमाला में सबसे बड़े पद’ तथा ‘सबसे छोटे पद’ के मूल्य के अन्तर को ‘विस्तार’ कहते हैं। यह अपकिरण की प्रारम्भिक माप है।
इसे दो प्रकार से व्यक्त किया जा सकता है-

  • समंकमाला के सबसे अधिक मूल्य तथा सबसे कम मूल्य के अन्तर के रूप में अथवी
  • समंकमाला के सबसे अधिक तथा सबसे कम मूल्य के रूप में।

उदाहरण के लिए, एक फार्म में 50 कर्मचारी कार्य करते हैं जिनके मासिक वेतन 1200 से लेकर ₹400 तक हैं, तो कहा जा सकता है कि वेतनों का विस्तार 1200 – 400 = ₹ 800 है। सूत्र रूप में
विस्तार = अधिकतम मूल्य – न्यूनतम मूल्य
(Range = Largest Value – Smallest Value)
अर्थात् R = L – S = 1200 – 400 = 800

विस्तार गुणांक (Coefficient of Range) – विस्तार अपकिरण की निरपेक्ष माप है जबकि विस्तार गुणांक अपकिरण की सापेक्ष माप है। विस्तार गुणांक श्रृंखलाओं को तुलनीय बनाता है। यह श्रृंखला के सबसे बड़े मूल्य (L) तथा सबसे छोटे मूल्य (S) के अन्तर (L – S) तथा इनके योग (L+ S) का अनुपात है। इसका सूत्र निम्न प्रकार है
विस्तार गुणांक (CR) – [latex s=2]\frac { L-S }{ L+S } [/latex]
यहाँ, L = श्रृंखला का अधिकतम मूल्य
S = श्रृंखला का न्यूनतम मूल्य
उपर्युक्त उदाहरण के अनुसार,
CR = [latex s=2]\frac { 1200-400 }{ 1200+400 } =\frac { 800 }{ 1600 } =0.5[/latex]
CR=0.5

विभिन्न सांख्यिकीय श्रृंखलाओं के विस्तार तथा विस्तार गुणांक की गणना
1. व्यक्तिगत श्रृंखला और विस्तार – सबसे बड़ी संख्या तथा सबसे छोटी संख्या का अंतर ही विस्तार (Range) कहलाता है।
उदाहरण 1. निम्नलिखित समंकों में विस्तार व विस्तार गुणांक ज्ञात कीजिए
10    72    36    85    35    52    76
हल :
विस्तार (R) = L – S
यहाँ, L = 85, S = 35
अतः विस्तार = 85 -35 = 50
R=50
विस्तार गणंख (CR) = [latex s=2]\frac { L-S }{ L+S } =\frac { 85-35 }{ 85+35 }[/latex]
= [latex s=2]\frac { 50 }{ 120 } =0.417[/latex]
CR = 0.417

2. खण्डित आवृत्ति श्रृंखला और विस्तार  इसमें सबसे बड़ी मद (Items) एवं सबसे छोटी मद का अंतर निकाला जाता है। इसमें आवृत्तियों पर ध्यान नहीं दिया जाता है।

उदाहरण 2. निम्नलिखित श्रेणी से विस्तार और विस्तार गुणांक ज्ञात कीजिए
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 32

3. अखण्डित श्रृंखला में विस्तार – इस श्रृंखला में विस्तार ज्ञात करने के लिए दो विधियों का प्रयोग किया जाता है
(अ) प्रथम विधि – इस विधि में सर्वप्रथम मदों के वर्गांतर के मध्य मूल्य को ज्ञात किया जाता है। मध्य मूल्यों की अधिकतम तथा न्यूनतम संख्याओं का अंतर ही विस्तार कहलाता है।
उदाहरण 3. निम्नलिखित श्रेणी में विस्तार व विस्तार गुणक ज्ञात कीजिए
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 33

(ब) द्वितीय विधि – इसमें आवृत्ति वितरण की प्रथम वर्गांतर की निचली सीमा तथा अन्तिम वर्गातर की. उच्चतम सीमा का अंतर निकाल लिया जाता है। इन दोनों सीमाओं के अंतर को विस्तार कहते हैं।
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 34

नोट – खण्डित तथा अखण्डित श्रेणी में विस्तार व विस्तार गुणांक ज्ञात करने के लिए आवृत्तियों का उपयोग नहीं होता। यदि अखण्डित श्रेणी समावेशी आधार पर दी हुई है तो उसे पहले समावेशी बना लेनी चाहिए।

प्रश्न 3.
अंतर चतुर्थक विस्तार (QR), चतुर्थक विचलन (QD) तथा चतुर्थक विचलन गुणांक (CQD) क्या हैं? उदाहरणों की सहायता से इनकी गणन प्रक्रिया समझाइए।
उतर :
अंतर चतुर्थक विस्तार (Inter Quartile Range)
सूत्र – IQR = Q3 – Q1
यहाँ, IQR = अंतर चतुर्थक विस्तार
Q3 = तृतीय चतुर्थक
Q1 = प्रथम चतुर्थक

गणन विधि – 

  • सर्वप्रथम तृतीय व प्रथम चतुर्थक ज्ञात किए जाते हैं।
  • उपर्युक्त सूत्र का प्रयोग करके अंतर चतुर्थक विस्तार ज्ञात किया जाता है।

चतुर्थक विचलन

चतुर्थक विचलन श्रेणी के चतुर्थ मूल्यों (तृतीय, चतुर्थक एवं प्रथम चतुर्थक) पर आधारित एक माप है। यह श्रेणी के तृतीय व प्रथम चतुर्थक के अंतर का आधा होता है। [latex s=2]QD=\frac { Q_{ 3 }-Q_{ 1 } }{ 2 }[/latex]

चतुर्थक विचलन गुणांक

चतुर्थक विचलन गुणांक अपकिरण की सापेक्ष माप है। इसे ज्ञात करने के लिए तीसरे तथा पहले चतुर्थकों के अंतर के आधे को इनके योग के आधे से भाग कर देते हैं। [latex s=2]CQD=\frac { Q_{ 3 }-Q_{ 1 } }{ Q_{ 3 }+Q_{ 1 } }[/latex]

चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक की विभिन्न
सांख्यिकीय श्रृंखलाओं में गणना

1. व्यक्तिगत श्रृंखला – व्यक्तिगत श्रृंखला में चतुर्थक विचलन निकालने के लिए पहले प्रथम चतुर्थक तथा तृतीय चतुर्थक को निम्नलिखित सूत्रों की सहायता से ज्ञात किया जाता है
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 35

इसके पश्चात् निम्नलिखित सूत्रों की सहायता से चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक ज्ञात किया जाता है
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 36

उदाहरण 1. निम्नलिखित आँकड़ों का अंतर चतुर्थक विस्तार, चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक ज्ञात कीजिए
आकार: 15    12    9    8    6    14    10
हल :
सर्वप्रथम श्रेणी को आरोही या अवरोही क्रम में रखेंगे और उसके उपरांत गणन क्रिया आरंभ करेंगे। अतः
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 37

2. खण्डित आवृत्ति श्रृंखला – खण्डित श्रृंखला में Q तथा Q5 संचयी आवृत्तियों की सहायता से ज्ञात की जाती हैं। सूत्र व्यक्तिगत श्रृंखला की भाँति ही है।
उदाहरण 2. निम्नलिखित समंकों से अंतर चतुर्थक विस्तार, चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक ज्ञात कीजिए
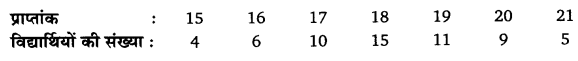
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 38

हल :
सर्वप्रथम संचयी आवृत्ति ज्ञात की जाएगी।

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 39 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 40

3. अखण्डित श्रृंखला – इसकी प्रक्रिया को निम्नांकित उदाहरण द्वारा स्पष्ट किया गया है
उदाहरण 3. निम्नलिखित समंकों में अंतर चतुर्थक विस्तार, चतुर्थक विचलन तथा चतुर्थक विचलन गुणांक ज्ञात कीजिए
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 41
हल :
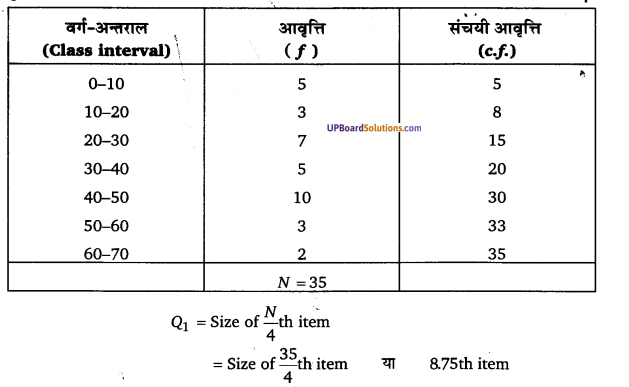
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 42
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 43 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 44

प्रश्न 4.
माध्य विचलन (Mean Deviation) व माध्य विचलन गुणांक (Coeff. of Mean Deviation) किसे कहते हैं? उदाहरणों की सहायता से माध्य विचलन की प्रक्रिया को समझाइए।
उत्तर :

माध्य विचलन (Mean Deviation)

माध्य विचलने का अभिप्राय विचलनों के समान्तर माध्य से होता है। जब किसी श्रेणी या समूह के किसी औसत (माध्य, मध्यिका या भूयिष्ठक) से उस श्रेणी के व्यक्तिगत पदों के विचलन लिए जाते हैं और विचलनों का समान्तर माध्य ज्ञात किया जाता है तो उसे ‘माध्य विचलन’ कहते हैं। माध्य विचलन को ‘प्रथम अपकिरण घात’ (First movement of dispersion) भी कहते हैं। क्लार्क तथा शैकाडे के अनुसार-“श्रृंखला के किसी सांख्यिकीय माध्य (समान्तर माध्य,मध्यिका या भूयिष्ठक) से निकाले गए विभिन्न मूल्यों के विचलनों के समान्तर माध्य को उसका माध्य विचलन कहा जाता है।”
नोट – माध्य विचलनकीगणनकेलिए सभी विचलनों को धनात्मक माना जाता है।
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 45

माथ्य विचलन गुणांक

माध्य विचलन गुणांक अपकिरण की सापेक्ष माप है। इसकी गणना के लिए माध्य विचलने को उसके माध्य या मध्यिका या भूयिष्ठक से भाग कर दिया जाता है। जिसके द्वारा माध्य विचलन की गणना की जाती है।
सूत्रे – माध्य से माध्य विचलन गुणांक
(i) C. of [latex]MD_{ \overline { X }  }=\frac { M{ D }_{ X } }{ \overline { X }  } [/latex]
(ii) C. of MDM = [latex s=2]\frac { MD_{ M } }{ M }[/latex]
(ii) C. of MDZ = [latex s=2]\frac { MD_{ Z } }{ Z }[/latex]

विभिन्न श्रृंखलाओं में माध्य विंचलन व माध्य विचलन गुणांक की गणना
1. व्यक्तिगत श्रेणी
व्यक्तिगत श्रेणी में माध्य विचलन ज्ञात करने की प्रक्रिया निम्नवत् है

  • सर्वप्रथम उस श्रेणी का समान्तर माध्य, मध्यिका या भूयिष्ठक निकाला जाता है।
  • प्राप्त माध्यों में से किसी भी माध्य द्वारा श्रेणी के व्यक्तिगत पदों से विचलन लिए जाते हैं।
  • विचलन लेते समय + और – चिह्नों को छोड़ दिया जाता है अर्थात् निरेपक्ष विचलन ज्ञात किए जाते हैं।
  • सभी विचलनों के योग को श्रेणी के पदों की संख्या से विभाजित कर दिया जाता है। यही माध्य विचलन कहलाता है।
  • सूत्रानुसार
    UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 46

नोट – सुविधा की दृष्टि से माध्य विचलन ज्ञात करने के लिए मध्यिका (Median) का ही प्रयोग करना चाहिए।

माध्य विचलन गुणांक
माध्य विचलन के निरपेक्ष माप को उसी माध्य से भाग देने पर जिससे कि विचलन लिए गए हैं, माध्य विचलन गुणांक प्राप्त हो जाता है।
सूत्रानुसार

(i) समान्तर माध्य से माध्य विचलन गुणांक = [latex s=2]\frac { MX_{ \overline { X } } }{ \overline { X } }[/latex]
(ii) मध्यिका से माध्य विचलन गुणांक =[latex s=2]\frac { MD_{ M } }{ M }[/latex]
(iii) बहुलक से माध्य विचलन गुणांक = [latex s=2]\frac { MD_{ z } }{ Z }[/latex]

उदाहरण 1. निम्नलिखित वेतनों में मध्य विचलन और इसके गुणांक की गणना कीजिए–
103, 50, 68, 110, 108, 105, 174, 103, 150, 200, 200, 225 103
हल :
सर्वप्रथम इन मूल्यों को आरोही क्रम में लिखा जाएगा
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 47 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 48

लघु रीति – व्यक्तिगत श्रेणी में माध्य विचलन लघु रीति द्वारा भी ज्ञात किया जा सकता है। इसके लिए निम्नलिखित प्रक्रिया अपनाई जाती है
मध्यिका से माध्य विचलन निकालना

  • सर्वप्रथम मध्यिका की गणना की जाती है जिससे विचलन लेने हैं।
  • मध्यिका मूल्य से अधिक मूल्यों का योग (∑XA) ज्ञात कर लिया जाता है। इसी प्रकार मध्यिका पद से कम मूल्यों का योग (∑Xg) ज्ञात कर लिया जाता है।
  • निम्नलिखित सूत्र का प्रयोग किया जाता है
    [latex s=2]MD_{ M }=\frac { \Sigma X_{ A }-\Sigma X_{ B } }{ N }[/latex]

मध्यिका के बाद के मूल्यों का योग
मध्यिका से पहले के मूल्यों का योग

समान्तर माध्य विचलन निकालना

  • सर्वप्रथम समान्तर माध्य (X) ज्ञात किया जाता है।
  • समान्तर माध्य से अधिक आकार वाले मूल्यों का जोड़ (EXA) तथा उससे कम आकार वाले मूल्यों का जोड़ (EXp) ज्ञात किया जाता है।
  • समान्तर माध्य से अधिक आकार वाले पदों की संख्या (NA) तथा उससे कम आकार वाले पदों की संख्या (Ng) ज्ञात की जाती है।
    सूत्रानुसार – [latex s=2]MD_{ \overline { X } }=\frac { \Sigma X_{ A }-\Sigma X_{ B }-(N_{ A }-N_{ B })X }{ N }[/latex]

उदाहरण 2. निम्नलिखित कीमतों के लिए माध्य और मध्यिका से माध्य विचलन तथा इसका गुणांक ज्ञात कीजिए
210    220    225    225    225    235    240    250    270    280
हल :
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 49 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 50

 

उदाहरण 3. लघु रीति द्वारा माध्य विचलन ज्ञात कीजिए
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 51
हल :
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 52 UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 53

2. खण्डित अथवा विच्छिन्न श्रेणी में माध्य विचलन ज्ञात करना
प्रत्यक्ष रीति – गणन क्रिया निम्नलिखित प्रकार से है

  • सर्वप्रथम वह माध्य ज्ञात किया जाता है जिससे विचलन निकालना है।
  • उस माध्य से प्रत्येक आकार को चिह्न रहित विचलन निकाल लिया जाता है। (| dM |) या (| dx |)
  • विचलनों में आवृत्तियों की गुणा करके योग [Σƒ | dM| या Σƒ | dx|] लगा लिया जाता है।
  • अंत में निम्नलिखित सूत्र को प्रयोग किया जाता है
    UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 54

माध्य विचलन गुणांक – माध्य विचलन गुणांक निकालने के लिए निरपेक्ष माप को उस माध्य से भाग दे दिया जाता है जिससे विचलन ज्ञात किए गए हैं; यथा
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 55

उदाहरण 4. निम्नलिखित समंकों से-

  • अपकिरण का मध्यिका गुणांक (Median coefficient of dispersion) तथा
  • अपकिरण का माध्य गुणांक (Mean coefficient of dispersion) निकालिए

UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 56
हल :
प्रत्यक्ष रीति – सर्वप्रथम मध्यिका तथा समान्तर माध्य का परिगणन किया जाएगा
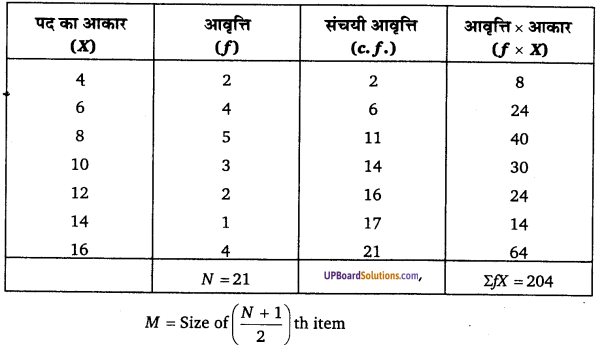
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 57
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 58
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 59
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 60

3. अविच्छिन्न श्रेणी
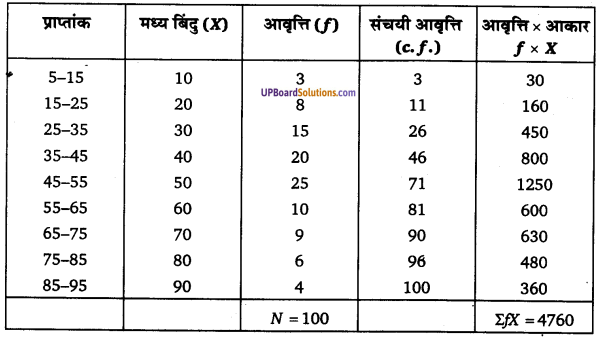
उदाहरण 5. 500 पात्रों के निम्न प्राप्तांक बंटन की सहायता से-

  • माध्यिका से और
  • समान्तर माध्य से माध्य विचलन ज्ञात कीजिए

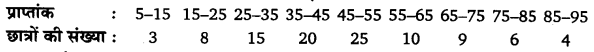
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 61
हल :
सर्वप्रियम समांतर व माधियक की गणना की जाएगी
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 62
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 63
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 64
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 65
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 66

प्रश्न 5.
विचरण गुणांक (Coefficient of variation) किसे कहते हैं? उदाहरण की सहायता से इसकी गणना विधि को समझाइए।
उत्तर :

विचरण गुणांक

विचरण गुणांक प्रमाप विचलन का प्रतिशत रूप है। यह किसी श्रृंखला पर आधारित अपकिरण गुणांक का 100 गुना होता है। दो या दो से अधिक श्रेणियों में अपकिरण की तुलना करने के लिए विचरण गुणांक का सहारा लिया जाता है। प्रमाप विचलन को समान्तर माध्य से भाग देकर भजनफल में 100 की गुणा करने से प्राप्त प्रतिशत विचरण गुणांक होता है।

कार्ल पियरसन के शब्दों में – “विचरण गुणांक माध्य में होने वाला प्रतिशत विचरण है। इसके लिए निम्नांकित सूत्र का प्रयोग किया जाता है
C.V. = [latex s=2]\frac { \sigma }{ \overline { X } } \times 100[/latex]
C.V. = Coeffi. of ox 100

नोट – जिस समंक श्रेणी का विचरण गुणांक अधिक होता है, उसमें विचरण अधिक होता है और वह श्रेणी अधिक अस्थिर अथवा असंगत मानी जाती है। इसके विपरीत, जिस श्रेणी में विचरण गुणांक कम होता है, वह अधिक स्थिर, एकरूप, सजातीय अथवा संगत मानी जाती है। प्रमाप विचलन के विभिन्न उदाहरणों में दी गई तालिका के आधार पर हम विचरण गुणांक की गणना इस प्रकार कर सकते हैं
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 67

उदाहरण 6. A तथा B टीम ने फुटबॉल मैच में निम्न प्रकार गोल किए
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 68

अपने खेल में कौन-सी टीम अधिक स्थिर है?
हल :
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 69
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 70
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 71

अत: टीम B अपने खेल में अधिक स्थिर है।

प्रश्न 6.
लॉरेंज वक्र किसे कहते हैं? इसके गुण व दोष बताइए। एक उदाहरण की सहायता से उसकी गणन क्रिया व निर्माण विधि को समझाइए।
उत्तर :

लॉरेंज वक्र (Lorenz Curve)

लॉरेंज वक्र अपकिरण ज्ञात करने की एक बिंदुरेखीय रीति है। इसे संचयी प्रतिशत वक्र (Cumulative Percentage Curve) भी कहते हैं। इसका प्रयोग सर्वप्रथम डॉ० मैक्स लॉरेंज ने आय और धन के वितरण का अध्ययन करने के लिए किया था।

गणन क्रिया व निर्माण विधि

  • मूल्यों या मध्ये मूल्यों के संचयी योग ज्ञात करते हैं। फिर अन्तिम संचयी योग को 100 मानकर प्रत्येक संचयी मूल्य को प्रतिशत में बदल देते हैं।
  • आवृत्तियों के संचयी योग ज्ञात करते हैं। फिर अन्तिम संचयी योग को 100 मानकर सभी आवृत्तियों को प्रतिशत में बदल देते हैं।
  • संचयी मूल्यों के प्रतिशत y-axis पर तथा संचयी आवृत्तियों के प्रतिशत x-axis पर रखे जाते हैं।
  • y-axis का माप 0-100 तक तथा x-axis का माप 100-0 तक लिखा जाता है।
  • x.axis के 0 तथा y-axis के 100 को एक सीधी रेखा द्वारा मिला दिया जाता है। इसे समान वितरण की रेखा (Line of Equal Distribution) कहते हैं।
  • संचयी आवृत्तियों के प्रतिशत और संचयी मूल्यों के प्रतिशत बिन्दुओं को मिला दिया जाता है। इस प्रकार जो वक्र तैयार होता है, उसे लॉरेंज वक्र कहते हैं।

निर्वचन (Interpretation) – लॉरेंज वक्र समान वितरण की रेखा से जितना अधिक दूर होगा, अपकिरण या वितरण में असमानता उतनी ही अधिक होगी। इसके विपरीत, यह वक्र समान वितरण की रेखा से जितना अधिक निकट होगा, अपकिरण की मात्रा उतनी ही कम होगी।

गुण –

  • यह आकर्षक व प्रभावशाली होता है।
  • यह समझने में सरल है।
  • इसकी सहायता से दो या दो से अधिक श्रेणियों की अपकिरण की मात्रा की तुलना की जा सकती है।
  • इससे मस्तिष्क पर बोझिल अंकों का भार नहीं पड़ता।

दोष –

  • इससे अपकिरण का अंकात्मक माप ज्ञात नहीं होता।
  • इसे बनाने की क्रिया कठिन है और इसे बनाने से पहले श्रेणी में काफी संशोधन करना पड़ता है।

उदाहरण 1. दो कारखानों में मजदूरी वितरण की असमानताओं की तुलना करने के लिए लॉरेंज वक्र की रचना कीजिए
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 72
UP Board Solutions for Class 11 Economics Statistics for Economics Chapter 6 Measures of Dispersion 73