UP Board Solutions for Class 10 Social Science Chapter 1 भारत : भौतिक स्वरूप (अनुभाग – तीन)
These Solutions are part of UP Board Solutions for Class 10 Social Science. Here we have given UP Board Solutions for Class 10 Social Science Chapter 1 भारत : भौतिक स्वरूप (अनुभाग – तीन).
विरत उत्तरीय प्रश्न
प्रश्न 1.
भारत का भौगोलिक वर्णन निम्नलिखित शीर्षकों के अन्तर्गत कीजिए [2016]
(क) स्थिति एवं विस्तार,
(ख) भू-आकृति (उच्चावच),
(ग) जल-निकास (प्रवाह)।
उत्तर :
(क) भारत की स्थिति एवं विस्तार
हिन्द महासागर के शीर्ष पर स्थित भारत एक विशाल देश है। इसका क्षेत्रफल 32,87,263 वर्ग किमी (2.43%) है। भारत 8°4′ से 37°6′ उत्तरी अक्षांशों और 687′ से 97°25′ पूर्वी देशान्तर के मध्य स्थित है। निकोबार द्वीप समूह में स्थित ‘इन्दिरा प्वॉइण्ट’ भारत का दक्षिणतम बिन्दु है। मुख्य स्थल पर कन्याकुमारी भारत का सबसे दक्षिण में स्थित बिन्दु है जब कि जम्मू-कश्मीर राज्य में स्थित इन्दिरा कोल’ सबसे उत्तरी बिन्दु। 26 दिसम्बर, 2009 में सूनामी के कारण भारत के सबसे दक्षिणी बिन्दु ‘इन्दिरा प्वॉइण्ट’ ने जल समाधि ले ली। 82°30′ पूर्वी देशान्तर रेखा भारत की प्रामाणिक देशान्तर रेखा है, (UPBoardSolutions.com) जो इलाहाबाद तथा चेन्नई से होकर गुजरती है। कर्क वृत्त (23°30′ उत्तरी अक्षांश) देश के लगभग मध्य से होकर गुजरती है; अत: देश का उत्तरी भाग उपोष्ण (सम-शीतोष्ण) कटिबन्ध में तथा दक्षिणी भाग उष्ण कटिबन्ध में पड़ता है। भारतीय मानक समय रेखा भारत के पाँच राज्यों-उत्तर प्रदेश, मध्य प्रदेश, छत्तीसगढ़, ओडिशा एवं आन्ध्र प्रदेश से गुजरती है। भारत का दक्षिणी भाग, जिसमें प्रायद्वीपी-भारत सम्मिलित है, उष्ण कटिबन्ध में आता है। उत्तरी भाग जिसमें मुख्यत: उत्तर का पर्वतीय मैदानी भाग है, उपोष्ण कटिबन्ध में आता है। तीन ओर से सागरों से घिरा होने के कारण यहाँ विशिष्ट मानसूनी जलवायु पायी जाती है, जो देश के समूचे अर्थतन्त्र को प्रभावित करती है। भारत यूरोप से ऑस्ट्रेलिया तथा दक्षिणी और पूर्वी एशियाई देशों के व्यापारिक मार्गों पर स्थित है। . इसलिए प्राचीन काल से ही यहाँ विदेशी व्यापार उन्नत रहा है।
भारतीय उपमहाद्वीप एक सुस्पष्ट भौगोलिक इकाई है, जिसमें एक विशिष्ट संस्कृति का विकास हुआ है। इस महाद्वीप के उत्तर-पश्चिम में पाकिस्तान, केन्द्र में भारत, उत्तर में नेपाल, उत्तर-पूर्व में भूटान तथा पूर्व में बाँग्लादेश सम्मिलित हैं। हिन्द महासागर में स्थित द्वीपीय देश श्रीलंका और मालदीव हमारे दक्षिणी पड़ोसी देश हैं। इन प्रदेशों की भौगोलिक स्थिति, जलवायु, प्राकृतिक मिट्टी तथा जनसंख्या की विशेषताओं में विभिन्नताएँ तथा विविधताएँ होते हुए भी उनमें एकात्मकता दिखायी पड़ती है। इसीलिए इसे उपमहाद्वीप कहा जाता है।
भारत विषुवत् रेखा के उत्तर में स्थित है। इस कारण यह उत्तरी गोलार्द्ध में आता है। प्रधान मध्याह्न रेखा (ग्रीनविच रेखा) के पूर्व में स्थित होने के कारण भारत पूर्वी गोलार्द्ध में आता है। हम जानते हैं कि मध्याह्न रेखा की मध्य स्थिति 90° पूर्वी देशान्तर है, जो भारत से ही होकर गुजरती है। 82°30′ पूर्वी मध्याह्न रेखा भारत की मानक मध्याह्न रेखा है। इससे पूर्वी गोलार्द्ध में भारत की केन्द्रीय स्थिति स्पष्ट हो जाती है। भारत एशिया महाद्वीप के दक्षिण (UPBoardSolutions.com) मध्य प्रायद्वीप में स्थित है। एशियो संसार में सबसे बड़ा तथा सबसे अधिक जनसंख्या वाला महाद्वीप है। अपनी भौगोलिक स्थिति के कारण ही भारत को प्राचीन काल से ही आर्थिक लाभ प्राप्त हुए हैं।

(ख) भारत का उच्चावच अथवा प्राकृतिक स्वरूप (बनावट)
उच्चावच से तात्पर्य किसी भू-भाग के ऊँचे व नीचे धरातल से है। सभी प्रकार के पहाड़ी, पठारी व मैदानी तथा मरुस्थलीय क्षेत्र मिलकर किसी क्षेत्र के उच्चावच का निर्माण करते हैं। उच्चावच की दृष्टि से भारत में अनेक विभिन्नताएँ मिलती हैं। इनका मूल कारण अनेक शक्तियों और संचालनों का परिणाम है, जो लाखों वर्ष पूर्व घटित हुई थीं। इसकी उत्पत्ति भूवैज्ञानिक अतीत के अध्ययन से स्पष्ट की जा सकती है। आज से 25 करोड़ वर्ष पूर्व भारतीय उपमहाद्वीप विषुवत् रेखा के दक्षिण में स्थित प्राचीन गोण्डवानालैण्ड का एक भाग था। अंगारालैण्ड नामक एक अन्य प्राचीन भूखण्ड विषुवत् रेखा के उत्तर में स्थित था। दोनों प्राचीन भूखण्डों के मध्य टेथिस नामक एक सँकरा, लम्बा, उथला सागर था। इन भूखण्डों की नदियाँ टेथिस में अवसाद जमा करती रहीं, जिससे कालान्तर में टेथिस सागर पट गया। पृथ्वी की आन्तरिक हलचलों के कारण दोनों भूखण्ड टूटे। गोण्डवानालैण्ड से भारत का प्रायद्वीप अलग हो गया तथा भूखण्डों के टूटे हुए भाग विस्थापित होने लगें। आन्तरिक हलचलों से टेथिस सागर के अवसादों की परतों में भिंचाव हुआ और उसमें विशाल मोड़ पड़े गये। इस प्रकार हिमालय पर्वत-श्रृंखला की रचना हुई। इसी कारण हिमालय को वलित पर्वत कहा जाता है।
हिमालय की उत्पत्ति के बाद भारतीय प्रायद्वीप और हिमालय के मध्य एक खाई या गर्त शेष रह गया। हिमालय से निकलने वाली नदियों ने स्थल का अपरदन करके अवसादों के उस गर्त को क्रमशः भरना शुरू किया जिससे विशाल उत्तरी मैदान की रचना (UPBoardSolutions.com) हुई। इस प्रकार भारतीय उपमहाद्वीप की भू-आकृतिक इकाइयाँ अस्तित्व में आयीं।
भारत एक विशाल देश है। भू-आकृतिक संरचना की दृष्टि से भारत में अनेक विषमताएँ एवं विभिन्नताएँ दृष्टिगोचर होती हैं। भारत का 29.3% भाग पर्वतीय, पहाड़ी एवं ऊबड़-खाबड़, 27.7% भाग पठारी तथा 43% भाग मैदांनी है। भारत में अन्य देशों की अपेक्षा मैदानी क्षेत्रों का विस्तार अधिक है (विश्व की औसत 41%)। देश में एक ओर नवीन मोड़दार पर्वत-श्रृंखलाएँ हैं तो दूसरी ओर विस्तृत तटीय मैदान, कहीं नदियों द्वारा समतल उपजाऊ मैदान हैं तो कहीं प्राचीनतम कठोर चट्टानों द्वारा निर्मित कटा-फटा पठारी भाग है।
(ग) जल-निकास : प्रवाह विस्तृत स्तरीय प्रश्न संख्या 6 देखें।
प्रश्न 2.
भारत को प्रमुख भू-आकृतिक विभागों में बाँटिए और भारतीय प्रायद्वीपीय पठार का वर्णन कीजिए।
या
भारत को भौतिक विभागों में विभाजित कीजिए तथा उनमें से किन्हीं एक का वर्णन निम्नलिखित शीर्षकों में कीजिए [2014]
(क) स्थिति का विस्तार, (ख) प्राकृतिक स्वरूप।
या
भारत को उच्चावच के आधार पर भौतिक विभागों में विभाजित कीजिए तथा उनमें से किसी। एक की स्थिति, विस्तार एवं भौतिक स्वरूप का वर्णन कीजिए। [2012]
या
भारत को विभिन्न भौतिक विभागों में बाँटिए और पूर्वी तथा पश्चिमी (UPBoardSolutions.com) मैदानों की विशेषताओं का वर्णन कीजिए। भारत को प्राकृतिक भागों में विभक्त कीजिए तथा उनमें से किसी एक की स्थिति, धरातल तथा मानव-जीवन का वर्णन कीजिए। [2016]
या
पूर्वी समुद्र तटीय मैदान की स्थिति एवं विस्तार का वर्णन कीजिए। [2017]
उत्तर :
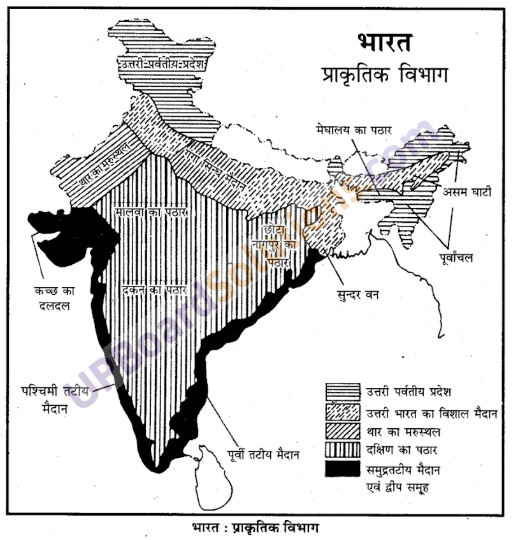
भारत का प्राकृतिक स्वरूप (बनावट)
भारत एक विशाल देश है। भू-आकृतिक संरचना की दृष्टि से भारत में अनेक विषमताएँ एवं विभिन्नताएँ दृष्टिगोचर होती हैं। भारत का 29.3% भाग पर्वतीय, पहाड़ी एवं ऊबड़-खाबड़; 27.7% भाग पठारी तथा 43% भाग मैदानी है। भारत में अन्य देशों की अपेक्षा मैदानी क्षेत्रों का विस्तार अधिक है (विश्व का औसत 41%)। देश में एक ओर नवीन मोड़दार पर्वत-श्रृंखलाएँ हैं, तो दूसरी ओर विस्तृत तटीय मैदान, कहीं नदियों द्वारा समतल उपजाऊ मैदान हैं तो कहीं प्राचीनतम कठोर चट्टानों द्वारा निर्मित कटा-फटा पठारी भाग है। इस प्रकार जम्मू से कन्याकुमारी तक भारत को उच्चावच अथवा भू-आकृतिक संरचना के अनुसार अग्रलिखित पाँच भागों में विभाजित किया जा सकता है
- उत्तरीय पर्वतीय प्रदेश,
- उत्तरी भारत का विशाल मैदान,
- दक्षिण का पठार,
- समुद्रतटीय मैदान एवं द्वीप समूह,
- थार का मरुस्थल।

इनका संक्षिप्त विवरण निम्नलिखित है-
(1) उत्तरी पर्वतीय प्रदेश– भारत के उत्तर में लगभग 2,500 किमी की लम्बाई तथा पूर्व में 150 किमी तथा पश्चिम में 400 किमी की चौड़ाई में उत्तरी अथवा हिमालय पर्वतीय प्रदेश का विस्तार है। यह पर्वत-श्रृंखला पूर्व से पश्चिम तक चाप के आकार में फैली हुई है। इस पर्वतीय प्रदेश का विस्तार लगभग 5 लाख वर्ग किमी है। यह मोड़दार पर्वतमाला तीन समानान्तर श्रेणियों-
- महान् हिमालय (हिमाद्रि हिमालय),
- लघु हिमालय,
- बाह्य हिमालय (शिवालिक हिमालय) में विस्तृत है। महान् हिमालय की औसत ऊँचाई 6,000 मीटर से अधिक होने के कारण ये श्रेणियाँ सदैव बर्फ से ढकी रहती हैं। विश्व की सर्वोच्च पर्वत-श्रेणी माउण्ट एवरेस्ट इसी हिमालय पर्वतमाला में स्थित है। समुद्र तल से इसकी ऊँचाई 8,848 मीटर है। हिमालय पर्वत उत्तरी भारत की अधिकांश नदियों का उद्गम स्थल तथा हरे-भरे वनों का भण्डार है। यहाँ बहने वाली नदियाँ (UPBoardSolutions.com) तीव्रगामी तथा अपनी युवावस्था में हैं। ये उत्तरी मैदानों में बहती हुई अरब सागर या बंगाल की खाड़ी में गिर जाती हैं। इनसे भारतीय उपमहाद्वीप की तीन प्रमुख नदियाँ सिन्धु, सतलुज तथा ब्रह्मपुत्र हिमालय के उस पार से निकलती हैं। हिमालय अपनी सुन्दर और रमणीक घाटियों के लिए विश्वविख्यात हैं, जिनमें कश्मीर घाटी, दून घाटी, कुल्लू और काँगड़ा घाटी पर्यटकों को अपनी ओर खींचती हैं।

(2) उत्तरी भारत का विशाल मैदान- उत्तरी भारत अथवा गंगा-ब्रह्मपुत्र का मैदान हिमालय पर्वत के दक्षिण में और दक्षिणी पठार के उत्तर में भारत का ही नहीं वरन् विश्व का सबसे अधिक उपजाऊ और घनी जनसंख्या वाला मैदान है। इसका क्षेत्रफल लगभग 7 लाख वर्ग किमी से अधिक है। इस मैदान की पश्चिम से पूरब की लम्बाई 2,414 किलोमीटर तथा उत्तर-दक्षिण की चौड़ाई 150 से 500 किलोमीटर है। इस मैदान का ढाल लगभग 25 सेण्टीमीटर प्रति किलोमीटर है। अरावली पर्वत-श्रेणी को छोड़कर इसका कोई भी भाग समुद्र तल से 150 मीटर से ऊँचा नहीं है।
यह मैदान सिन्धु, सतलुज, गंगा, यमुना, ब्रह्मपुत्र और उनकी अनेक सहायक नदियों द्वारा लाई गयी मिट्टी से बना है; अत: यह बहुत ही उपजाऊ है। इस मैदान के बीच में अरावली पर्वत आ जाने के कारण सिन्धु और उसकी नदियाँ पश्चिम में तथा गंगा और उसकी सहायक नदियाँ तथा ब्रह्मपुत्र पूर्व में बहती हैं। पश्चिमी मैदान का ढाल उत्तर से दक्षिण की ओर है और पूर्वी मैदान का ढाल उत्तर-पश्चिम से दक्षिण-पूर्व की ओर है। इस मैदान में गहराई (UPBoardSolutions.com) नहीं पायी जाती। सम्पूर्ण गंगा का मैदान बाँगर तथा खादर से निर्मित है। यहाँ देश की 45% जनसंख्या निवास करती है। प्रति वर्ष नदियाँ इस मैदान में उपजाऊ काँप मिट्टी अपने साथ लाकर बिछाती रहती हैं।
(3) दक्षिण का पठार(प्रायद्वीपीय पठार)– भारत के दक्षिण में प्राचीन ग्रेनाइट तथा बेसाल्ट की कठोर शैलों से बना दकन का पठार है, जिसे दक्षिण का पठार भी कहते हैं। यह राजस्थान से लेकर कुमारी अन्तरीप तक और पश्चिम में गुजरात से लेकर पूर्व की ओर पश्चिम बंगाल तक विस्तृत है। इसका आकार त्रिभुजाकार है एवं आधार उत्तर की ओर तथा शीर्ष दक्षिण की ओर है। पठार के उत्तर में। अरावली, विन्ध्याचल और सतपुड़ा की पहाड़ियाँ हैं, पश्चिम में ऊँचे पश्चिमी घाट और पूरब में निम्न पूर्वी घाट और दक्षिण में नीलगिरि पर्वत हैं।
इसके पश्चिमी भाग पर ज्वालामुखी द्वारा निर्मित लावा के निक्षेप हैं, जो काली मिट्टी के उपजाऊ क्षेत्र हैं। इस पठारी क्षेत्र पर अधिकांश नदियों ने गहरी घाटियाँ बना ली हैं। इस पठार की औसत ऊँचाई 500. से 750 मीटर है। इसको धरातल बहुत ही विषम है। इस पठारी भाग का क्षेत्रफल लगभग 16 लाख वर्ग किमी है। दकन का पठारी क्षेत्र खनिज पदार्थों का विशाल भण्डार है। इस पठार पर बहुमूल्य मानसूनी वन सम्पदा पायी जाती है। सागौन एवं चन्दन की बहुमूल्य लकड़ी इसी पठारी भाग में मिलती है। यह कृषि-उपजों का भण्डार तथा उद्योग-धन्धों का महत्त्वपूर्ण केन्द्र भी है।
इस पठार पर बहने वाली अधिकांश नदियाँ दक्षिण-पूर्व की ओर बहकर बंगाल की खाड़ी में गिरती हैं। महानदी, गोदावरी, कृष्णा तथा कावेरी ऐसी ही नदियाँ हैं। नर्मदा और ताप्ती नदियाँ भ्रंश घाटी में होकर बहती हैं तथा अरब सागर में गिरती हैं। अरब (UPBoardSolutions.com) सागर में गिरने वाली अन्य नदियाँ बहुत छोटी तथा तीव्रगामी हैं।

(4) समुद्रतटीय मैदान एवं द्वीप समूह– दकन के पठार के दोनों ओर पूर्वी तथा पश्चिमी तटीय क्षेत्रों पर पतली पट्टी के रूप में जो मैदान फैले हैं, उन्हें समुद्रतटीय मैदान कहते हैं। इन मैदानों का निर्माण सागर की लहरों तथा नदियों ने अपनी निक्षेप क्रियाओं द्वारा लाये गये अवसाद से किया है। इस मैदानी क्षेत्र को निम्नलिखित दो भागों में बाँटा जा सकता है
- पश्चिमी तटीय मैदान- यह मैदान पश्चिम में खम्भात की खाड़ी से लेकर कुमारी अन्तरीप तक फैला हुआ है। इसकी औसत चौड़ाई 64 किलोमीटर है। इसमें बहने वाली नदियाँ अत्यन्त तीव्रगामी हैं। इसके दक्षिणी मार्ग में नावों के लिए अनेक अनूप (Lagoons) पाये जाते हैं। नया । मंगलोर, कोचीन इन्हीं अनूपों पर स्थित हैं। यहाँ चावल, केला, गन्ना व रबड़ खूब पैदा होता है। ” कॉदला, मुम्बई व कोचीन इस तट पर स्थित अन्य प्रमुख बन्दरगाह हैं।
- पूर्वी तटीय मैदान– पश्चिमी तटीय मैदान की अपेक्षा यह मैदान अधिक (UPBoardSolutions.com) चौड़ा है। इसकी औसत | चौड़ाई 161 से 483 किलोमीटर है। यह उत्तर में गंगा के मुहाने से दक्षिण में कुमारी अंन्तरीप तक फैला हुआ है। कोलकाता, मद्रास (चेन्नई) व विशाखापत्तनम् इस तट के प्रमुख बन्दरगाह हैं।
द्वीप समूह–भारत के मुख्य स्थल भाग के पश्चात् सागरों के बीच में जो आकृतियाँ स्थित हैं वे द्वीपसमूह के रूप में जानी जाती हैं। ये भारत का अभिन्न अंग हैं। छोटे-बड़े मिलाकर कुल 247 द्वीप हैं, जो स्थिति-अनुसार निम्नलिखित दो भागों में बँटे हुए हैं—
- अरब सागरीय द्वीप-ये द्वीप अरब सागर के मुख्य स्थल (केरल तट) के पश्चिम में स्थित हैं। | इन द्वीपों की आकृति घोड़े की नाल या अँगूठी के समान है। इनका निर्माण अल्पजीवी सूक्ष्म प्रवाल जीवों के अवशेषों के जमाव से हुआ है। इसलिए इन्हें प्रवालद्वीप वलय (एटॉल) कहते हैं। इनमें लक्षद्वीप, मिनीकोय एवं अमीनीदीवी प्रमुख हैं। इन द्वीपों पर नारियल के वृक्ष बहुत अधिक उगाये जाते हैं। इन द्वीपों की संख्या 43 है तथा लक्षद्वीप का क्षेत्रफल मात्र 32 वर्ग किलोमीटर है। कवरत्ति यहाँ की राजधानी है।
- बंगाल की खाड़ी के द्वीप- बंगाल की खाड़ी में भी भारत के अनेक द्वीप हैं। इन्हें अण्डमान तथा निकोबार द्वीप समूह के नाम से पुकारते हैं। ये द्वीप बड़े भी हैं और संख्या में भी अधिक हैं। ये जल में डूबी हुई पहाड़ियों की श्रृंखला पर स्थित हैं। (UPBoardSolutions.com) इन द्वीपों में से कुछ की उत्पत्ति ज्वालामुखी के उद्गार से हुई है। भारत को एकमात्र सक्रिय ज्वालामुखी इन्हीं द्वीपों में एक बैरन द्वीप पर स्थित है। इनका विस्तार 590 किमी की लम्बाई तथा अधिकतम 50 किमी की चौड़ाई में अर्द्ध-चन्द्राकार रूप में बना हुआ है। ये द्वीप यहाँ एक समूह के रूप में पाये जाते हैं, जो एक-दूसरे से संकीर्ण खाड़ी द्वारा पृथक् होते हैं। इनकी कुल संख्या 204 है तथा पोर्ट ब्लेयर यहाँ की राजधानी है।
(5) थार का मरुस्थल- राजस्थान का उत्तर-पश्चिमी भाग रेगिस्तानी है जिसे ‘थार का मरुस्थल’ कहा जाता है। इस मरुस्थल का कुछ भाग पाकिस्तान में भी है। इस भाग में प्रतिदिन धूल व रेतभरी तेज हवाएँ चलती हैं, जो जगह-जगह रेत के टीले बना देती हैं। यहाँ 10 सेमी से भी कम वर्षा होती है, इसलिए यह भाग वर्ष भर शुष्क बना रहता है और पूरे भाग में पानी की कमी रहती है। अतः यहाँ ज्वार-बाजरा जैसी कम पानी वाली फसलें अधिक उगाई जाती हैं। यह मरुस्थलीय भाग 644 किमी लम्बा व लगभग 161 किमी चौड़ा है। इसका कुल क्षेत्रफल लगभग 1,04,000 वर्ग किमी है तथा इसका विस्तार हरियाणा, पंजाब, राजस्थान तथा उत्तरी गुजरात राज्यों में है। इस प्रदेश में अत्यन्त विरल । जनसंख्या निवास करती है। लूनी इस मरुस्थलीय प्रदेश की मुख्य मौसमी नदी है। यहाँ पर साँभर, डिंडवाना, लूनकरनसर, कुचामन तथा डेगाना खारे पानी की प्रमुख झीलें हैं, जिनसे नमक बनाया जाता है। कुछ भागों में ग्रेनाइट, नीस तथा शिस्ट चट्टानों की नंगी सतह दिखलायी पड़ती हैं। खनिज पदार्थों में ताँबा, जिप्सम पत्थर तथा मुल्तानी मिट्टी यहाँ मुख्यतः मिलती हैं। राजस्थान में झुंझुनू जिले के खेतड़ी नगर के पास ताँबे की अनेक खाने हैं। यहाँ ऊँट यातायात का प्रमुख साधन है, (UPBoardSolutions.com) जिसे रेगिस्तान का जहाज कहा जाता है। मरुस्थलीय संरचना एवं जलवायु की विषमताओं के कारण यह क्षेत्र आर्थिक दृष्टि से पिछड़ा हुआ है। पूर्व की ओर इन्दिरा गांधी नहर के बन जाने से धीरे-धीरे सम्बद्ध क्षेत्रों में विकास हो रहा है।

प्रश्न 3.
भारत के उत्तर में स्थित हिमालय पर्वत की बनावट कैसी है? इस प्रदेश का भौगोलिक वर्णन कीजिए।
या
हिमालय के कोई दो महत्त्व लिखिए। हिमालय पर्वत से होने वाले कोई पाँच लाभ लिखिए। [2011]
या
हिमालय पर्वतों की तीन समान्तर शृंखलाओं के नाम लिखिए और प्रत्येक की एक-एक विशेषता लिखिए। भारत के हिमालय पर्वतीय प्रदेश का वर्णन निम्नलिखित शीर्षकों में कीजिए- [2015]
(क) स्थिति एवं विस्तार, (ख) धरातलीय संरचना, (ग) जल-प्रवाह।
उत्तर :
हिमालय पर्वत की संरचना
भारत के उत्तर में हिमालय पर्वत चाप के आकार में तथा पश्चिम में सिन्धु नदी के मोड़.से पूर्व में ब्रह्मपुत्र नदी • के मोड़ तक 2,500 किमी की लम्बाई में चन्द्राकार रूप में फैले हैं। इसकी औसत चौड़ाई 150 से 400 किमी के बीच है। हिमालय; भारत और तिब्बत (चीन) के मध्य एक अवरोध के रूप में स्थित है। मुख्य हिमालय में विश्व की सर्वोच्च पर्वत-चोटियाँ पायी जाती हैं, जिनकी औसत ऊँचाई 6,000 मीटर से भी अधिक है। एशिया महाद्वीप में 97 (UPBoardSolutions.com) ऐसी ज्ञात चोटियाँ हैं, जिनकी ऊँचाई 7,500 मीटर से अधिक है। इनमें से 95 चोटियाँ भारत के इसी पर्वतीय प्रदेश में स्थित हैं। हिमालय की ये पर्वत-श्रेणियाँ सदैव बर्फ से ढकी रहती हैं, इसलिए इस पर्वतमाला का नाम हिमालय रखा गया है। इसका क्षेत्रफल लगभग 5 लाख वर्ग किमी है। भौगोलिक दृष्टि से हिमालय पर्वतीय प्रदेश को निम्नलिखित उपविभागों में बाँटा जा सकता है–
1. महान् या वृहद् हिमालय– हिमालय की यह पर्वत-श्रेणी सबसे ऊँची है, जिन्हें हिमाद्रि या वृहत्तर हिमालय भी कहा जाता है। इस पर्वत-श्रेणी की औसत ऊँचाई 6,000 मीटर से अधिक होने के कारण यह वर्षभर बर्फ से आच्छादित रहती है। इस पर्वत-श्रेणी की लम्बाई सिन्धु नदी के मोड़ से अरुणाचल प्रदेश में ब्रह्मपुत्र नदी के मोड़ तक 2,500 किमी तथा औसत चौड़ाई 25 किमी है। इस क्षेत्र में गंगोत्री, जेमू तथा मिलाम जैसे विशाल हिमनद (Glaciers) पाये जाते हैं, जिनकी लम्बाई 20 किमी से भी अधिक है। माउण्ट एवरेस्ट, कंचनजंगा, मकालू, धौलागिरि, नंगा पर्वत, गॉडविन-ऑस्टिन, त्रिशूल, बदरीनाथ, नीलकण्ठ, केदारनाथ आदि इस क्षेत्र के प्रमुख पर्वत-शिखर हैं। इन। पर्वत-श्रेणियों का निर्माण ग्रेनाइट, नीस, शिस्ट आदि कठोर और प्राचीन शैलों से हुआ है। माउण्ट एवरेस्ट (नेपाल देश में स्थित) विश्व की सर्वोच्च पर्वत-श्रेणी है, जिसकी ऊँचाई 8,848 मीटर है। महान् हिमालय में अनेक दरें पाये जाते हैं जिनमें शिपकीला, थांगला, नीति, लिपुलेख, बुर्जिल, माना, नाथुला तथा (UPBoardSolutions.com) जैलेपला आदि मुख्य हैं। इन्हीं दरों के मार्ग द्वारा भारत की सीमा के पार जाया जा सकता है। महान् हिमालय की पूर्वी सीमा पर ब्रह्मपुत्र तथा पश्चिमी सीमा पर सिन्धु नदियाँ गहरी एवं सँकरी घाटियों से होकर प्रवाहित होती हैं। वृहद् हिमालय और श्रेणियों के मध्य दो प्रमुख घाटियाँ हैंकाठमाण्डू की घाटी (नेपाल) और कश्मीर की घाटी (भारत)।

2. लघु या मध्य हिमालय- यह पर्वत-श्रेणी महान् हिमालय के दक्षिण में उसके समानान्तर फैली हुई है, जो 80 से 100 किमी तक चौड़ी है। इस श्रेणी की औसत ऊँचाई 2,000 से 3,500 मीटर तक है। तथा अधिकतम ऊँचाई 4,500 मीटर तक पायी जाती है। इस भाग में नदियाँ ‘वी’ (V) अकार की घाटियाँ तथा गहरी कन्दराएँ बनाकर बहती हैं, जिनकी गहराई 1,000 मीटर तक है। महान् और लघु हिमालय के मध्य कश्मीर, काठमाण्डू, काँगड़ा एवं कुल्लू की घाटियाँ महत्त्वपूर्ण स्थान रखती हैं। शीत-ऋतु में तीन-चार महीने यहाँ हिमपात होता है। ग्रीष्म ऋतु में ये पर्वतीय क्षेत्र उत्तम एवं स्वास्थ्यवर्द्धक जलवायु तथा मनमोहक प्राकृतिक सुषमा के कारण पर्यटन के केन्द्र बन जाते हैं। कश्मीर की जास्कर और पीर पंजाल इसकी महत्त्वपूर्ण श्रेणियाँ हैं, जो अनेक भुजाओं वाली हैं। इस श्रेणी की ऊँचाई 4,000 मीटर है। चकरौता, शिमला, मसूरी, नैनीताल, रानीखेत, दार्जिलिंग आदि स्वास्थ्यवर्द्धक पर्वतीय नगर लघु हिमालय में ही स्थित हैं, जहाँ प्रति वर्ष लाखों पर्यटक सैर के लिए जाते हैं। इस श्रेणी के उत्तरी ढाल मन्द, हैं, जब कि दक्षिणी ढाल तीव्र। इस पर्वतीय क्षेत्र में उपयोगी कोणधारी वृक्ष तथा ढालों पर घास उगती है। घास के इन मैदानों को कश्मीर में मर्ग (गुलमर्ग, खिलनमर्ग, सोनमर्ग) तथा उत्तराखण्ड में बुग्याल और पयार (गढ़वाल एवं कुमाऊँ हिमालय) के नाम से पुकारते हैं। इस भाग की संरचना में अवसादी शैलों की प्रधानता है, जिनमें अधिकांश चूने की चट्टानें विस्तृत क्षेत्र में फैली हैं।
3. उप-हिमालय या शिवालिक श्रेणियाँ अथवा बाह्य हिमालय- हिमालय की सबसे निचली तथा दक्षिणी पर्वत-श्रेणियाँ इसके अन्तर्गत आती हैं, जिन्हें बाह्य हिमालय या शिवालिक श्रेणियों के नाम से भी पुकारते हैं। यह हिमालय का नवनिर्मित भाग है, जो पंजाब में पोतवार बेसिन के दक्षिण से आरम्भ होकर पूर्व में कोसी नदी अर्थात् 87° देशान्तर तक विस्तृत है। इन पर्वत-श्रेणियों का निर्माण-काल बीस लाख वर्ष से दो करोड़ वर्ष के मध्य माना जाता है। शिवालिक श्रेणियों का निर्माण नदियों द्वारा लायी गयी अवसाद में मोड़ पड़ने से हुआ है, इसलिए इन पर अपरदन की क्रियाओं का विशेष प्रभाव पड़ा है। तिस्ता और (UPBoardSolutions.com) रायडॉक के निकट 50 किमी की चौड़ाई में इन पहाड़ियों का लोप हो जाता है। इनकी औसत चौड़ाई पश्चिम में 50 किमी और पूरब में 15 किमी है। ये पर्वत औसत रूप से 600 से 1,500 मीटर तक ऊँचे हैं। इस क्षेत्र में अनेक उपजाऊ तथा समतल विस्तृत घाटियाँ हैं, जिन्हें दून और द्वार कहते हैं; जैसे-देहरादून, पूर्वादून, कोठड़ीदून, पाटलीदून, हरिद्वार, कोटद्वार आदि।
भौगोलिक महत्त्व/लाभ
हिमालय पर्वत ने हमारे देश के भौतिक, आर्थिक, सांस्कृतिक तथा राजनीतिक स्वरूप का निर्माण किया है। इनके भौगोलिक महत्त्व/लाभ का वर्णन निम्नलिखित है
- ये पर्वत साइबेरिया और मध्यवर्ती एशिया की ओर से आने वाली बर्फीली, तूफानी और शुष्क हवाओं से भारत की रक्षा करते हैं।
- हिमालय की ऊँची-ऊँची हिमाच्छादित चोटियाँ उत्तरी भारत के तापमान एवं आर्द्रता (वर्षा) को | प्रभावित करती हैं। इसी के फलस्वरूप हिमालय में हिम नदियाँ, सदावाहिनी नदियाँ प्रारम्भ होती हैं, जो उत्तरी मैदान को उपजाऊ बनाती हैं।
- हिमालय के हिमाच्छादित शिखरों और नैसर्गिक दृश्यों के कारण इन पर्वतों का पर्यटकों के लिए महत्त्व बढ़ गया है।
- हिमालय की घाटी में जैसे ही वृक्षों की सीमा समाप्त होती है, वहाँ छोटे-छोटे चरागाह पाये जाते हैं, जिन्हें मर्ग कहते हैं; जैसे—गुलमर्ग, सोनमर्ग आदि। यहाँ कश्मीरी गड़रिये भेड़-बकरियाँ चराते हैं।
- हिमालय पर्वत से निकलने वाली सदावाहिनी नदियाँ अपने प्रवाह-मार्ग में प्राकृतिक जल-प्रपातों की . रचना करती हैं। ये जल-प्रपात जल-विद्युत शक्ति के उत्पादन में सहायक सिद्ध हुए हैं।
- शीत ऋतु में उत्तरी ध्रुवीय प्रदेश से ठण्डी एवं बर्फीली पवनें दक्षिण की ओर चला करती हैं। हिमालय | पर्वतमाला इन पर्वतों के मार्ग में बाधा बनकर भारत को ठण्ड से बचाती है। 7. हिमालय पर्वत पर पर्याप्त मात्रा में कोयला, पेट्रोल तथा अन्य खनिज पदार्थ प्राप्त होने की सम्भावना | व्यक्त की गयी है, जिससे इसका आर्थिक महत्त्व और अधिक बढ़ गया है।
- हिमालय पर्वतमाला भारत के उत्तर में पहरेदार की भाँति एक अभेद्य दीवार के रूप में खड़ी है, जो । आक्रमणकारियों से भारत की रक्षा करती है।
- हिमालय की कश्मीर घाटी को फलों का स्वर्ग कहा जाता है। यहाँ सेब, अखरोट, आड़, खुबानी, अंगूर व नाशपाती आदि फल उगाये जाते हैं। पर्वतीय ढालों पर चाय, सीढ़ीदार खेतों में चावेल व आलू की खेती भी की जाती है।
- हिमालय पर्वत के दोनों ढालों पर उपयोगी वनों का बाहुल्य है। इन वनों से विभिन्न उद्योगों के लिए कच्चे माल, उपयोगी इमारती लकड़ियाँ आदि प्राप्त होती हैं।
- हिमालय पर्वतमाला से अनेक जड़ी-बूटियाँ प्राप्त होती हैं, जो अनेक (UPBoardSolutions.com) रोगों की चिकित्सा में काम आती हैं। इसके अतिरिक्त हिमालय के वनों से शहद, आँवला, बेंत, गोंद, लाख, कत्था, बिरोजा आदि प्राप्त होते हैं, जो मानव की विविध आवश्यकताओं की पूर्ति करते हैं। हिमालय के अनेक पर्वतीय नगर ग्रीष्म-ऋतु में पर्यटकों के भ्रमण के लिए आकर्षण के केन्द्र बन जाते हैं।

प्रश्न 4.
भारत के उत्तरी विशाल मैदान का भौगोलिक वर्णन कीजिए तथा इसके आर्थिक महत्त्व का उल्लेख कीजिए। [2014]
या
भारत के उत्तरी मैदान की स्थिति व विस्तार को स्पष्ट कीजिए। इसकी कृषि के लिए क्या उपयोगिता है? [2010]
या
गंगा के मैदानी भाग का वर्णन निम्नलिखित शीर्षकों के अन्तर्गत कीजिए- [2011, 18]
(क) स्थिति, (ख) विस्तार, (ग) महत्त्व।
या
भारत के उत्तरी मैदानी भाग का वर्णन निम्नलिखित शीर्षकों में कीजिए- [2012]
(क) स्थिति, (ख) विस्तार, (ग) वनस्पति, (घ) व्यवसाय
या
भारत के उत्तरी विशाल मैदान का वर्णन निम्नलिखित शीर्षकों में कीजिए- [2016, 18]
(क) स्थिति एवं विस्तार, (ख) मिट्टियाँ, (ग) कृषि।
या
भारत का उत्तरी मैदानी क्षेत्र घना क्यों बसा है? कोई तीन कारण बताइए। [2018]
उत्तर :
उत्तर का विशाल मैदान नवीनतम भूखण्ड है। इस विशाल मैदान का निर्माण हिमालय पर्वतमाला की उत्पत्ति के बाद उत्तर में हिमालयं तथा दक्षिण में प्रायद्वीपीय पठार से निकलने वाली नदियों द्वारा बहाकर लायी गयी अवसाद से हुआ है। सिन्धु की सहायक सतलुज, रावी, झेलम, चिनाब, व्यास, गंगा तथा उसकी सहायक और ब्रह्मपुत्र व उसकी सहायक नदियों द्वारा बहाकर लायी गयी अवसाद के जमने से इस मैदान के निर्माण में विशेष (UPBoardSolutions.com) योगदान मिला है। इसे जलोढ़ मैदान के नाम से भी पुकारते हैं। यह जलोढ़ दो प्रकार की होती है—प्राचीन एवं नवीन। नवीन जलोढ़ अत्यधिक उपजाऊ होती है। अत: यह मैदान अत्यधिक उर्वर तथा घना आबाद है।

हिमालय पर्वत के दक्षिण तथा प्रायद्वीपीय पठार के उत्तर में यह मैदान भारत का ही नहीं, अपितु विश्व का सर्वाधिक उपजाऊ एवं सघन जनसंख्या वाला मैदान है। यहाँ देश की 45% जनसंख्या निवास करती है। इस मैदान का क्षेत्रफल 7 लाख वर्ग किमी है। पूर्व से पश्चिम इस मैदान की लम्बाई 2.414 किमी तथा चौडाई पश्चिम में 480 किमी है, जब कि पूर्व में यह केवल 145 किमी रह जाती है। यह एक समतल मैदान है, जिसका अधिकांश भाग समुद्र तल से 150 मीटर से अधिक ऊँचा नहीं है। इस मैदान का निर्माण काँप मिट्टी से हुआ है, जिसकी गहराई 400 मीटर तक मिलती है। इस मैदान का विस्तार उत्तरी राजस्थान, पंजाब, हरियाणा, दिल्ली, उत्तर प्रदेश, उत्तरी बिहार, पश्चिम बंगाल तथा असोम राज्यों में है।
विभिन्न प्राकृतिक कारकों तथा बहने वाली नदियों की प्राथमिकता के आधार पर इस वृहद् मैदान को तीन उप-विभागों में बाँटा गया है—
(1) पश्चिमी मैदान, (2) मध्यवर्ती मैदान एवं (3) पूर्वी मैदान।
1. पश्चिमी मैदान- इस भाग में पंजाब, राजस्थान और हरियाणा का पश्चिमी भाग सम्मिलित किया जाता है। सम्पूर्ण पश्चिमी मैदान की औसत ऊँचाई 150 से 300 मीटर तक है। इसको सामान्य ढाल उत्तर-पूर्व से दक्षिण-पश्चिम की ओर है। पश्चिमी मैदान के अन्तर्गत थार के मरुस्थल को भी सम्मिलित किया जाता है। इसे पश्चिमी शुष्क मैदान भी कहते हैं, जो 640 किलोमीटर लम्बा तथा 160 किलोमीटर चौड़ा है। यह नीची भूमि का (UPBoardSolutions.com) प्रदेश है।
यमुना नदी के पश्चिम में पंजाब और हरियाणा राज्यों में विस्तृत भाग पंजाब का मैदान कहलाता है। यह मैदान चौरस है तथा समुद्र तल से इसका धरातल 200 से 250 मीटर ऊँचा है। सिन्धु के मैदान का अधिकांश भाग अब पाकिस्तान में चला गया है।

2. मध्यवर्ती मैदान अथवा गंगा का मैदान– पश्चिम में यमुना नदी से लेकर पूर्व में बांग्लादेश की पश्चिमी सीमा तक लगभग 1,400 किलोमीटर लम्बा तथा उत्तर में शिवालिक पर्वत श्रेणी से दक्षिण में पठारी प्रदेश तक औसतन 300 किलोमीटर चौड़ा क्षेत्र मध्यवर्ती मैदान कहलाता है। इसे गंगा का मैदान भी कहते हैं। देश के सबसे महत्त्वपूर्ण तथा समतल इस मैदान का क्षेत्रफल 3,57,000 वर्ग किलोमीटर है। इस मैदान का ढाल सामान्यतः उत्तर-पश्चिम से दक्षिण-पूर्व की ओर 15 सेण्टीमीटर प्रति किलोमीटर है। .
ओ०एच०के० स्पेट ने इस विस्तृत मैदान को निम्नलिखित तीन उपविभागों में बाँटा है–
- ऊपरी गंगा का मैदान अथवा गंगा-यमुना दोआब-यह भाग पश्चिम में दिल्ली से पूर्व में इलाहाबाद तक विस्तृत है। इसका प्रमुख भाग गंगा-यमुना का दोआब है। यह मैदान यमुना, गंगा, शारदा, चम्बल नदियों द्वारा जमा किये गये अवसादों से बना है।
- मध्य गंगा का मैदान—यह इलाहाबाद से भागलपुर (बिहार) तक लगभग 1,62,200 वर्ग किलोमीटर क्षेत्र में फैला है। इसमें गंगा की सहायक नदियाँ–गोमती, घाघरा, गण्डक, कोसी, टोंस तथा सोन–बहती हैं। पूर्वी उत्तर प्रदेश तथा बिहार के मैदान इस भाग में स्थित हैं। यह मैदान दोमट तथा जलोढ़ मिट्टियों से बना है।
- निचला गंगा का मैदान अथवा गंगा का डेल्टा-इसके अन्तर्गत गंगा का डेल्टा प्रदेश आता है, जो पश्चिम बंगाल राज्य में फैला है। इसका क्षेत्रफल 79,100 वर्ग किलोमीटर है। इसका अधिकांश भाग बांग्लादेश में है। इस मैदान की औसत ऊँचाई समुद्र की सतह से 50 मीटर से भी कम है। कोलकाता के पास इसकी ऊँचाई केवल 6 मीटर है। यह संसार का सबसे बड़ा डेल्टा क्षेत्र है।
3. पूर्वी मैदान अथवा ब्रह्मपुत्र का मैदान– असोम राज्य में सदिया के उत्तर-पूर्व से लेकर धुवरी स्थान तक लगभग 650 किलोमीटर लम्बा एवं 100 किलोमीटर चौड़ा पूर्वी मैदान है। इसे ब्रह्मपुत्र का मैदान भी कहते हैं। इस मैदान के पश्चिमी भागों को (UPBoardSolutions.com) छोड़कर सभी ओर ऊँचे पहाड़ी भाग हैं। इस समतल भाग का ढाल क्रमशः उत्तर-पूर्व से दक्षिण-पूर्व की ओर कम होता जा रहा है।

उपर्युक्त मैदानों के अतिरिक्त हिमालय पर्वत के बाहरी ढाल पर कंकरीली बलुई मिट्टी के निक्षेप से बने भाग को भाबर का मैदान कहते हैं। भावर के आगे बारीक कंकड़, पत्थर, रेत और चिकनी मिट्टी से तराई का , मैदान बना है।।
भौगोलिक महत्त्व अथवा संसाधनों का आकलन
यह मैदान भारत के लगभग एक-तिहाई क्षेत्रफल को घेरे हुए है। अनुकूल जलवायु, उपजाऊ मिट्टी, सिंचाई की सुविधा तथा यातायात के मार्गों का विस्तृत जाल और जीवन की अन्य सुविधाएँ सुलभ हो जाने से सम्पूर्ण देश की लगभग 45% जनसंख्या इसी क्षेत्र में निवास करती है। यद्यपि भौगोलिक तथा आर्थिक दृष्टि से यह मैदान भारत का सर्वोत्तम भाग है, किन्तु भू-वैज्ञानिक दृष्टि से इसका महत्त्व अधिक नहीं है, क्योंकि यह भारत का नवीनतम भाग है और इसकी संरचना सरल है। इस मैदान का महत्त्व अग्रलिखित तथ्यों से स्पष्ट होता है
- इस मैदान की रचना उर्वर-काँप मिट्टी से होने के कारण यह कृषि सम्पन्न प्रदेश है तथा भारत का ‘अन्न भण्डार’ कहलाता है। तापमान व आर्द्रता की भिन्नता के आधार पर यहाँ फसलों की विविधता पायी जाती है।
- इस मैदान में असंख्य नदियाँ प्रवाहित होती हैं, जिनमें से अधिकांश हिमालय से निकलने वाली सदावाहिनी नदियाँ हैं। उत्तर प्रदेश व पंजाब के शुष्क भागों में सिंचाई के लिए ये विशेष उपयोगी हैं।
- उत्तरी मैदान की नदियों के मार्ग में ढाल प्रवणता बहुत कम है; अतएव ये नौकारोहण योग्य हैं।
- जहाँ कहीं भी नदियों के मार्ग में प्रपात स्थित हैं, वहाँ (UPBoardSolutions.com) जल-विद्युत शक्ति विकसित की गयी है।
- समतल एवं कोमल शैलों से निर्मित होने के कारण यहाँ सड़क व रेलमार्गों का उत्तम विकास सम्भव हुआ है।
- नवीन शैलों से निर्मित होने के कारण इस मैदान में खनिजों की कमी है। मैदान के पूर्वी एवं पश्चिमी छोरों पर कहीं-कहीं कोयला एवं पेट्रोलियम प्राप्त होने की सम्भावनाएँ अवश्य हैं।
- शताब्दियों से यह मैदान सघन जनसंख्या के पोषण में समर्थ रहा है। भारतीय सभ्यता एवं संस्कृति यहीं फली-फूली है।
- यह मैदान भारतीय इतिहास, राजनीति एवं धर्म का केन्द्र तथा भारत की समृद्धि एवं गौरव का प्रतीक रहा है।
यह क्षेत्र आर्थिक दृष्टि से भारत का सर्वोत्तम भाग है। भूमि समतल होने के कारण यहाँ रेलमार्गों व सड़कों का जाल बिछा हुआ है। इसके परिणामस्वरूप देश के बड़े-बड़े व्यापारिक और औद्योगिक केन्द्र यहाँ स्थित हैं। दिल्ली, कानपुर, पटना तथा कोलकाता जैसे प्रमुख नगर इसी क्षेत्र में बसे हैं।

मिट्टियाँ
उत्तरी विशाल मैदान में सर्वत्र काँप (जलोढ़) मिट्टी का विस्तार है। यह मिट्टी कृषि-उत्पादन में महत्त्वपूर्ण भूमिका निभाती है जिसका विस्तार 7.68 लाख वर्ग किमी क्षेत्र पर है। इसी कारण इस क्षेत्र में सघन जनसंख्या निवास करती है। काँप मिट्टियाँ हिमालय पर्वत से निकलने वाली सिन्धु, गंगा, ब्रह्मपुत्र एवं उनकी सहायक नदियों द्वारा लाई गयी अवसाद से निर्मित हुई हैं। यह मिट्टी हल्के भूरे रंग की होती है। इस मिट्टी में नाइट्रोजन, फॉस्फोरस और वनसपति के अंशों की कमी होती है तथा सिलिका एवं चूने के अंशों की प्रधानता होती है। यह मिट्टी पीली दोमट है। कुछ स्थानों पर यह चिकनी एवं बलुई होती है। उत्तरी विशाल मैदान की मिट्टियों को वर्षा की भिन्नता, क्षारीय गुणों, बालू एवं चीका की भिन्नता के आधार पर निम्नलिखित भागों में बाँटा जा सकता है
- पुरातन काँप- इसे बाँगर मिट्टी के नाम से भी पुकारा जाता है। इस मिट्टी का विस्तार उन क्षेत्रों में है। जहाँ नदियों की बाढ़ का पानी नहीं पहुँच पाता है। इसमें कहीं-कहीं कंकड़ भी पाये जाते हैं। खुरदरे एवं बड़े कणों वाली मिट्टी को भूड़ कहते हैं। इस मिट्टी में गन्ना एवं गेहूं अधिक उगाया जाता है।
- नवीन काँप- इसे खादर मिट्टी भी कहा जाता है। यह मिट्टी रेतीली एवं कम कंकरीली होती है। इस मिट्टी के क्षेत्रों में प्रतिवर्ष बाढ़े आती हैं तथा उनके द्वारा नवीन काँप मिट्टी बिछती रहती है। इस मिट्टी में नमी धारण करने की शक्ति अधिक होती है। कहीं-कहीं पर दलदल भी होती है। इसमें पोटाश, फॉस्फोरस, चूना एवं जीवांशों की मात्रा अधिक होती है।
- डेल्टाई काँप- यह मिट्टी नदियों के डेल्टा में पायी जाती है। यहाँ नदियाँ नवीन क़ाँप मिट्टी का जमाव करती रहती हैं, अत: यह मिट्टी अत्यधिक उपजाऊ होती है। इस मिट्टी के कण बहुत ही बारीक होते हैं। जिन फसलों को अधिक जल की (UPBoardSolutions.com) आवश्यकता होती है, उनमें सिंचाई की आवश्यकता पड़ती है। चावल, जूट, तम्बाकू, गेहूँ, तिलहन आदि इस मिट्टी की प्रमुख फसलें हैं। उत्तरी विशाल मैदान के दक्षिण-पश्चिम में मरुस्थलीय अथवा रेतीली मिट्टी पायी जाती है। वर्षा की कमी के कारण इसमें नमी की मात्रा कम होती है। जल की कमी के कारण यह मिट्टी अनुपजाऊ होती है।

कृषि
उत्तरी विशाल मैदान में कृषि के तौर पर मुख्यतः गन्ना, गेहूँ, कपास, ज्वार व बाजरा आदि फसलो पर जोर. दिया जाता है। ‘नकदी फसल के रूप में गन्ना प्रमुख है। इस क्षेत्र की कृषि की प्रमुख विशेषताएँ अग्र प्रकार हैं
1. खाद्य आवश्यकताओं की पूर्ति में सहायक-देश के साथ- साथ इस क्षेत्र की कृषि को मुख्य उद्देश्य क्षेत्र की विशाल जनसंख्या की खाद्य आवश्यकताओं की पूर्ति करना है। किन्तु अभी हाल के वर्षों में इसमें व्यापारिक और बाजारोन्मुख होने के प्रवृत्ति देखी जा रही है।
2. विशाल जनसंख्या का भारी दबाव- देश की कृषि की तरह इस क्षेत्र की कृषि पर जनसंख्या का भारी दबाव है। देश की जनसंख्या का बड़ा हिस्सा यहाँ निवास करता है जिसमें अधिकांश पूरी तरह कृषि पर निर्भर है। जनसंख्या के तेजी से बढ़ने के कारण प्रति व्यक्ति कृषि भूमि का औसत निरन्तर कम होता जा रहा है।
3. खाद्यान्नों की कृषि को प्रमुखता- इस क्षेत्र की कृषि में खाद्यान्नों की कृषि में प्रमुखता है। यह कृषिगत क्षेत्र का 76 प्रतिशत भाग और सम्पूर्ण कृषि उत्पादन का 80 प्रतिशत भाग प्रदान करते हैं। इसमें गन्ना, गेहूं, ज्वार, बाजरा, चना, मक्का एवं कुछ मात्रा में चावल आदि शामिल हैं।
4. कृषि फसलों में विविधता- यहाँ की कृषि में फसलों की विविधता देखने (UPBoardSolutions.com) को मिलती है। ऐसा इस क्षेत्र की जलवायु एवं भौतिक विशेषताओं में भिन्नता के कारण है। कभी-कभी तो एक ही खेत में एक साथ अनेक फसलें बोई जाती हैं।
5. खेत छोटे-छोटे टुकड़ों में- भौतिक, आर्थिक एवं सामाजिक कारणों से देश की तरह इस क्षेत्र में भी कृषि भूमि का आकार बहुत छोटे-छोटे खेतों के रूप में है। यह छोटे-छोटे खेत आधुनिक कृषि के दृष्टिकोण से उचित नहीं हैं।
6. वर्षा पर आधारित कृषि- इस क्षेत्र में कृषि अधिकांशत: वर्षा पर निर्भर है।
नदियों द्वारा लायी गयी बारीक मिट्टी से निर्मित तथा सिंचित होने के कारण यह मैदान बहुत उपजाऊ है। यहाँ गेहूँ, गन्ना, दाल-दलहन, कपास आदि की फसलें बड़े पैमाने पर पैदा की जाती हैं। इस क्षेत्र में अनेक तीर्थस्थल; जैसे-हरिद्वार, मथुरा, प्रयाग, काशी आदि स्थित हैं। यहाँ सारे देश से यात्रीगण आते हैं, जिस कारण इन स्थानों पर आर्थिक गतिविधियाँ प्रायः पूरे वर्ष चरम पर रहती हैं।

प्रश्न 5.
दक्षिण के प्रायद्वीपीय पठार की भौगोलिक रचना तथा आर्थिक महत्त्व का उल्लेख कीजिए।
या
भारत के दक्षिणी पठारी भाग का वर्णन निम्नलिखित शीर्षकों के अन्तर्गत कीजिए
(क) स्थिति, (ख) विस्तार, (ग) खनिज सम्पदा। [2014]
या
भारत के दक्षिणी पठारी भाग के किन्हीं तीन खनिज संसाधनों का वर्णन कीजिए। [2014]
या
भारत के दक्षिणी पठारी भाग की छः विशेषताएँ बताइए। [2014]
या
भारत के दक्षिणी पठारी भाग का वर्णन निम्नलिखित शीर्षकों में कीजिए- [2010]
(अ) धरातल, (ब) जल-प्रवाह प्रणाली, (स) भौगोलिक महत्त्व।
भारत के दक्षिणी प्रायद्वीपीय भाग में जल-प्रवाह (UPBoardSolutions.com) प्रणाली का संक्षिप्त वर्णन कीजिए। [2010]
या
दक्षिण के पठारी भाग की स्थिति, विस्तार तथा खनिज सम्पदा का वर्णन कीजिए। [2012]
या
दकन के पठार का संक्षिप्त वर्णन कीजिए। भारत के दक्षिणी पठारी भाग का वर्णन निम्नलिखित शीषकों में कीजिए- [2015]
(क) स्थिति एवं विस्तार, (ख) जल-प्रवाह प्रणाली, (ग) खनिज़।
या
भारत में दक्षिणी पठार का वर्णन निम्नलिखित शीर्षकों के अन्तर्गत कीजिए- [2016, 17]
(क) स्थिति एवं विस्तार, (ख) प्राकृतिक बनावट (भौतिक लक्षण) (ग) खनिज।
या
भारत के दक्षिणी पठार के किन्हीं तीन आर्थिक महत्त्व पर प्रकाश डालिए। [2018]
उत्तर :
दक्षिणी प्रायद्वीपीय पठार की भौगोलिक रचना (धरातल)
भारत के दक्षिण में प्राचीन ग्रेनाइट तथा बेसाल्ट की कठोर शैलों से निर्मित दकन (दक्षिण) को पठार है। यह विशाल प्रायद्वीपीय पठार प्राचीन गोण्डवानालैण्ड का ही एक अंग है, जो भारतीय उपमहाद्वीप का सबसे प्राचीन भूभाग है। यह पठारी प्रदेश 16 लाख वर्ग किमी क्षेत्रफल में विस्तृत है। इसकी आकृति त्रिभुजाकार है। इसके उत्तर में गंगा-सतलुज-ब्रह्मपुत्र का मैदान, पूर्व में पूर्वी तटीय मैदान एवं बंगाल की खाड़ी, दक्षिण में हिन्द महासागर तथा पश्चिम में पश्चिमी तटीय मैदान एवं अरब सागर स्थित है। इस पठार पर अनेक पर्वत विस्तृत हैं, जो मौसमी क्रियाओं; अर्थात् अपक्षय; द्वारा प्रभावित हैं। इस (UPBoardSolutions.com) भौतिक प्रदेश में सबसे अधिक धरातलीय विषमताएँ मिलती हैं। समुद्र-तल से इस पठार की औसत ऊँचाई 500 से 700 मीटर है। इस पठारी प्रदेश का विस्तार उत्तर में राजस्थान से लेकर दक्षिण में कुमारी अन्तरीप तक 1,700 किमी की लम्बाई तथा पश्चिम में गुजरात से लेकर पूर्व में पश्चिम बंगाल तक 1,400 किमी की चौड़ाई में है। प्राकृतिक दृष्टिकोण से इसकी उत्तरी सीमा अरावली, कैमूर तथा राजमहल की पहाड़ियों द्वारा निर्धारित होती है। यहाँ मौसमी क्रियाओं द्वारा चट्टानों का अपक्षरण होता रहता है। नर्मदा नदी की घाटी सम्पूर्ण प्रायद्वीपीय पठारी क्षेत्र को दो असमान भागों में विभाजित कर देती हैं। उत्तर की ओर के भाग को मालवा का पठार तथा दक्षिणी भाग को दकन ट्रैप या प्रायद्वीपीय पठार के नाम से पुकारते हैं। इस प्रदेश में निम्नलिखित स्थलाकृतिक विशिष्टताएँ पायी जाती हैं’

1. मालवा का पठार- मालवा का पठार ज्वालामुखी से प्राप्त लावे द्वारा निर्मित हुआ है, जिससे यह समतल हो गया है। इस पठार पर बेतवा, माही, पार्वती, काली-सिन्धु एवं चम्बल नदियाँ प्रवाहित होती हैं। चम्बल एवं उसकी सहायक नदियों ने इस पठार के उत्तरी भाग को बीहड़ तथा ऊबड़-खाबड़ गहरे खड्डों में परिवर्तित कर दिया है, जिससे अधिकांश भूमि खेती के अयोग्य हो गयी है। शेष भूमि समतल और उपजाऊ है। इस पठार का ढाल पूर्व तथा उत्तर-पूर्व की ओर है। विन्ध्याचल की पर्वत-श्रृंखलाएँ यहीं पर स्थित हैं।
2. विन्ध्याचल श्रेणी– प्रायद्वीपीय पठार के उत्तर-पश्चिमी भाग पर विन्ध्याचल श्रेणी का विस्तार है। इस श्रेणी के उत्तर-पश्चिम (राजस्थान) में अरावली श्रेणी स्थित है। यह श्रेणी अत्यधिक अपरदन के कारण निचली पहाड़ियों के रूप में दृष्टिगोचर होती है। विन्ध्याचल. श्रेणी के दक्षिण में नर्मदा की घाटी स्थित है। नर्मदा घाटी के दक्षिण में सतपुड़ा श्रेणी का विस्तार है, जो महानदी और गोदावरी के बीच स्थित है।
3. बुन्देलखण्ड एवं बघेलखण्ड का पठार- यह पठार मालवा पठार के उत्तर-पूर्व में स्थित है। यमुना एवं चम्बल नदियों ने इस पठार को काट-छाँटकर बीहड़ खड्डों का निर्माण किया है, जिससे यह असमतल तथा अनुपजाऊ हो गया है। इस पठार पर नीस, ग्रेनाइट, बालुका-पत्थर की चट्टानें तथा पहाड़ियाँ मिलती हैं।
4. छोटा नागपुर का पठार- यह पठार एक सुस्पष्ट पठारी इकाई है। इसके उत्तर व पूर्व में गंगा का मैदान है। इसका पश्चिमी मध्यवर्ती भाग 100 मीटर ऊँचा है, जिसे ‘पाट क्षेत्र’ कहते हैं। झारखण्ड राज्य के गया, हजारीबाग तथा राँची जिलों में यह पठार विस्तृत है। (UPBoardSolutions.com) महानदी, सोन, स्वर्ण-रेखा एवं दामोदर इस पठार की प्रमुख नदियाँ हैं। यहाँ ग्रेनाइट एवं नीस की शैलें पायी जाती हैं। यह पठार खनिज पदार्थों में बहुत धनी है। इसकी औसत ऊँचाई 400 मीटर है।
5. मेघालय का पठार- उत्तर-पूर्व में इस पठार को मिकिर की पहाड़ियों के नाम से पुकारते हैं। इसका | उत्तरी ढाल खड़ा है, जिसमें ब्रह्मपुत्र तथा उसकी सहायक नदियाँ प्रवाहित होती हैं। इसी पठार में गारो, खासी तथा जयन्तिया की पहाड़ियाँ विस्तृत हैं।
6. दकन का पठार- यह महाराष्ट्र पठार के नाम से भी जाना जाता है। इसका क्षेत्रफल 5 लाख वर्ग किमी है। इसका विस्तार मध्य प्रदेश, महाराष्ट्र, गुजरात, कर्नाटक, पश्चिमी तमिलनाडु एवं आन्ध्र प्रदेश राज्यों पर है। यह पठार बेसाल्ट शैलों से निर्मित है तथा खनिज पदार्थों में धनी है। यह पठार दो भागों में विभाजित है-तेलंगाना एवं दकन का पठार।

7. प्रायद्वीपीय पठार की प्रमुख पर्वत-श्रेणियाँ–यह पठारी प्रदेश अनाच्छादन की क्रियाओं से प्रभावित है। यहाँ विन्ध्याचल, सतपुड़ा एवं अरावली की पहाड़ियाँ प्रमुख हैं। इनकी औसत ऊँचाई 300 से 900 मीटर तक है।
8. पश्चिमी घाट– इन्हें सह्याद्रि की पहाड़ियों के नाम से भी पुकारा जाता है। ये पश्चिमी तट के समीप उसके समानान्तर विस्तृत हैं। इनकी औसत चौड़ाई 50 किमी है। इनका विस्तार मुम्बई के उत्तर से दक्षिण में कुमारी अन्तरीप तक लगभग 1,600 किमी है। थाकेघाट, भोरघाट व पालघाट यहाँ के प्रमुख दरें हैं। इस श्रेणी के उत्तर-पूर्व में पालनी तथा दक्षिण में इलायची की पहाड़ियाँ हैं। अनाईमुडी इसका सर्वोच्च शिखर (2,695 मीटर) है।
9. पूर्वीघाट– इस श्रेणी का विस्तार महानदी के दक्षिण में उत्तर-पूर्व दिशा से दक्षिण-पश्चिम दिशा की ओर नीलगिरि की पहाड़ियों तक 1,300 किमी की लम्बाई में है। इनकी औसत ऊँचाई 615 मीटर तथा औसत चौड़ाई उत्तर में 190 किमी तथा दक्षिण में 75 किमी है। इन घाटों को काटकर महानदी, गोदावरी, कृष्णा, कावेरी आदि नदियाँ पश्चिमी भागों से पूर्व की ओर बहती हुई उपजाऊ मैदान में डेल्टा बनाती हैं।
जल-प्रवाह प्रणाली
दक्षिण पठारी भाग की जल-प्रवाह प्रणाली में नर्मदा, ताप्ती, महानदी, कृष्णा, कावेरी, पेन्नार आदि नदियों का योगदान है। इनमें नर्मदा व ताप्ती पश्चिम की ओर बहकर अरब सागर में गिरती हैं। नर्मदा अमरकण्टक की पहाड़ियों से निकलती है तथा ताप्ती (UPBoardSolutions.com) मध्य प्रदेश के बैतूल जिले से निकलती है। यह दोनों नदियाँ सतपुड़ा के दक्षिण में सँकरी तथा गहरी भ्रंश घाटियों से होकर बहती हैं। महानदी, गोदावरी, कृष्णा, कावेरी तथा पेन्नार नदियाँ बंगाल की खाड़ी में गिरती हैं। साबरमती व माही नदियाँ कच्छ की खाड़ी में गिरती हैं।
भौगोलिक महत्त्व
प्रायद्वीपीय पठार के भौगोलिक-आर्थिक महत्त्व का वर्णन निम्नलिखित है—
- प्राचीन आग्नेय कायान्तरित शैलों से निर्मित होने के कारण यह भू-भाग खनिज सम्पन्न है। मध्य प्रदेश में मैंगनीज, संगमरमर, चूना-पत्थर, बिहार व उड़ीसा (ओडिशा) में लोहा व कोयला, कर्नाटक में सोना, आन्ध्र प्रदेश में कोयला, हीरा आदि आर्थिक महत्त्व के खनिज उपलब्ध होते हैं।
- लावा की मिट्टी कपास व गन्ने की खेती के लिए अत्युत्तम है। पहाड़ी क्षेत्रों में लैटेराइट मिट्टियाँ चाय, कहवा तथा रबड़ के लिए उपयुक्त हैं। गर्म मसाले, काजू, केला अन्य महत्त्वपूर्ण उपजें हैं।
- वनों में चन्दन, साल, सागौन, शीशम आदि बहुमूल्य लकड़ी तथा लाख, बीड़ी बनाने के लिए तेन्दू व टिमरु वृक्ष के पत्ते, हरड़, बहेड़ा, आँवला, चिरौंजी, अग्नि व रोशा घास आदि आर्थिक महत्त्व की गौण वन-उपजें प्राप्त होती हैं।
- पठारी धरातल पर प्रवाहित होने वाली नदियों के प्रपाती मार्ग में अनेक स्थानों पर जल-विद्युत शक्ति के विकास की सम्भावनाएँ उपलब्ध हैं। कठोर चट्टानी धरातल होने के कारण वर्षा के जल को एकत्रित करने के लिए जलाशय में बाँध की सुविधाएँ प्राप्त हैं।
- सामान्यतः प्रायद्वीपीय पठार की जलवायु उष्ण है, किन्तु उटकमण्ड, पंचमढ़ी, महाबलेश्वर आदि सुरम्य एवं स्वास्थ्यवर्द्धक स्थल पर्यटकों के लिए विशेष आकर्षण का केन्द्र हैं।
- विषम धरातल होने के कारण यहाँ आवागमन के साधनों का (UPBoardSolutions.com) समुचित विकास नहीं हो सका है। उत्तरी मैदान की तुलना में यहाँ कृषि भी अधिक विकसित नहीं है। चम्बल व अन्य नदियों के बीहड़ लम्बी अवधि तक डाकुओं व असामाजिक तत्वों के शरणस्थल रहे हैं। विन्ध्याचल एवं सतपुड़ा पर्वत प्राचीन काल से ही उत्तर एवं दक्षिण भारत के मध्य प्राकृतिक व सांस्कृतिक अवरोध रहे हैं; अतएव दक्षिणी भारत में उत्तर भारत से सर्वथा भिन्न संस्कृति विकसित हुई है।

प्रश्न 6.
भारत में जल-प्रवाह प्रणाली का वर्णन निम्नलिखित शीर्षकों में कीजिए
(क) पूर्वी तट का जल-प्रवाह, (ख) उत्तरी मैदानी भाग का जल-प्रवाह।
उत्तर भूतल की बनावट तथा नदियों के उद्गम के दृष्टिकोण से भारत के जल-प्रवाह तन्त्र को दो भागों में बाँटा जा सकता है- (क) उत्तरी मैदानी-भाग को जल-प्रवाह तथा (ख) प्रायद्वीपीय या दक्षिण भारत का जल-प्रवाह। दक्षिण भारत के जल-प्रवाह में कुछ जल अरब सागर में प्रवाहित होता है तथा कुछ। बंगाल की खाड़ी में। उत्तरी मैदानी भाग तथा पूर्वी तट जल-प्रवाह दोनों का वर्णन निम्नलिखित है–
(क) पूर्वी तट का जल-प्रवाह– इसे जल-प्रवाह में महानदी, गोदावरी, कृष्णा, कावेरी, पेन्नार आदि नदियाँ बंगाल की खाड़ी में गिरती हैं। इनका संक्षिप्त विवरण निम्नवत् है
- महानदी- इस नदी का उद्गम-स्रोत छत्तीसगढ़ के रायपुर जिले में फरसिया ग्राम के निकट स्थित एक तालाब से है। यह मध्य प्रदेश, महाराष्ट्र, ओडिशा, बिहार से होकर बंगाल की खाड़ी में गिरती है।
- गोदावरी- यह प्रायद्वीपीय भारत की सबसे बड़ी नदी है। यह महाराष्ट्र राज्य में नासिक से दक्षिण-पश्चिम में त्र्यम्बक गाँव से निकलती है। यह 1,465 किमी लम्बी है। यह मध्य प्रदेश, कर्नाटक, ओडिशा तथा आन्ध्र प्रदेश से होती हुई बंगाल की खाड़ी में गिरती है।
- कृष्णा- यह नदी महाबलेश्वर की पहाड़ियों से निकलती है। इसकी लम्बाई 1,400 किमी है। यह महाराष्ट्र, कर्नाटक तथा आन्ध्र प्रदेश से होकर बंगाल की खाड़ी में मिल जाती है।
- कावेरी- यह नदी कर्नाटक राज्य की नीलगिरि पर्वत-श्रेणियों से निकलती है। यह कर्नाटक तथा तमिलनाडु राज्यों से होकर बहती है। यह लगभग 815 किमी लम्बी है।
(ख) उत्तरी मैदानी भाग का जल-प्रवाह- उत्तरी मैदानी भाग के जल-प्रवाह तन्त्र (UPBoardSolutions.com) को तीन नदी तन्त्रों–सिन्धु नदी, गंगा नदी तथा ब्रह्मपुत्र नदी में विभाजित किया जा सकता है। इनका संक्षिप्त विवरण निम्नवत् है
- सिन्धु नदी तन्त्र– सिन्धु नदी तन्त्र- में पश्चिम हिमालय से निकलने वाली नदियाँ–सिन्धु, झेलम, चिनाब, रावी, व्यास और सतलुज आती हैं। ये सभी अरब सागर में गिरती हैं। इनका प्रवाह उत्तर से दक्षिण- पश्चिम की ओर है।
- गंगा नदी तन्त्र- गंगा नदी तन्त्र बंगाल की खाड़ी में मिलता है। इस तन्त्र की मुख्य नदी गंगा है। गंगा नदी, भागीरथी व अलकनन्दा नदियों का सम्मिलित रूप है। इसका उद्गम उत्तरकाशी जिले के ग्लेशियर से है। उद्गम स्थल से मुहाने तक गंगा नदी की लम्बाई 2,525 किमी है। इसकी मुख्य सहायक नदियाँ हैं-राम गंगा, गोमती, घाघरा, गण्डक, कोसी, यमुना तथा चम्बल। गंगा नदी तन्त्र का प्रवाह उत्तर से दक्षिण-पूर्व की ओर है।
- ब्रह्मपुत्र नदी तन्त्र– उत्तरी भारत के अपवाह का पूर्वी भाग ब्रह्मपुत्र व उसकी सहायक नदियों द्वारा बनाया गया है। ब्रह्मपुत्र भारत की सबसे बड़ी नदी है। यह तिब्बत में कैलाश पर्वत पर मानसरोवर झील से 80 किमी की दूरी पर 5,150 मीटर की ऊँचाई से निकलती है। लगभग 1,100 किमी तक महान् हिमालय के समानान्तर बहने के बाद यह नामचा-बरुआ के निकट दक्षिण की ओर मुड़कर असोम में दिहांग के नाम से प्रकट होती है। यहाँ से यह दक्षिण-पश्चिम की ओर बहती है।।

लघु उत्तरीय प्रश्न
प्रश्न 1.
ब्रह्मपुत्र की घाटी का संक्षिप्त विवरण दीजिए।
उत्तर :
ब्रह्मपुत्र का उद्गम स्थान तिब्बत में सिन्धु और सतलुज के उद्गम के निकट ही है। ब्रह्मपुत्र की लम्बाई सिन्धु नदी के बराबर है, परन्तु इसका अधिकांश विस्तार तिब्बत में है। तिब्बत में इसका नाम सांग है। नामचा-बरुआ नामक पर्वत के पास यह तीखा मोड़ लेकर भारत में प्रवेश करती है। अरुणाचल प्रदेश में इसे दिहांग के नाम से पुकारते हैं। लोहित, दिहांग तथा दीबांग के संगम के पश्चात् इसका नाम ब्रह्मपुत्र पड़ता है। बांग्लादेश के उत्तरी (UPBoardSolutions.com) भाग में इसका नाम जमुना है तथा मध्य भाग में इसे पद्मा कहते हैं। दक्षिण में पहुंचकर ब्रह्मपुत्र और गंगा आपस में मिल जाती हैं, तब इस संयुक्त धारा को मेघना कहते हैं।
प्रश्न 2.
भारत के उत्तरी विशाल मैदान का निर्माण किस प्रकार हुआ ?
उत्तर :
भारत का उत्तरी मैदान हिमालय तथा दक्षिणी प्रायद्वीपीय पठार के मध्य स्थित है। यह मैदान हिमालय तथा प्रायद्वीपीय पठार से निकलकर उत्तर की ओर बहने वाली नदियों द्वारा लायी गयी मिट्टियों से बना है। इन महीन मिट्टियों को जलोढ़क’ कहते हैं। उत्तरी मैदान जलोढ़कों द्वारा निर्मित एक समतल उपजाऊ भू-भाग है।
प्राचीनकाल में इसे मैदान के स्थान पर एक विशाल गर्त था। हिमालय पर्वतों के निर्माण के बाद हिमालय से निकलकर बहने वाली नदियों ने उस गर्त में गाद भरने शुरू किये। अनाच्छादन के कारकों ने हिमालय का अपरदन किया तथा भारी मात्रा में अवसाद (UPBoardSolutions.com) उस गर्त में एकत्रित होते गये। क्रमश: वह गर्त अवसादों से पट गया तथा उत्तरी मैदान की रचना हुई।

प्रश्न 3.
पश्चिमी तटीय मैदान की भौगोलिक स्थिति एवं विस्तार तथा उसकी तीन विशेषताओं का उल्लेख कीजिए। [2010]
या
भारत के पश्चिमी तटीय भाग के दोनों नामों को स्थिति सहित लिखिए।
उत्तर :
पश्चिमी तटीय मैदान एक सँकरी पट्टी के रूप में विस्तृत हैं। प्रायद्वीप के पश्चिम में खम्भात की खाड़ी से लेकर कुमारी अन्तरीप तक इस मैदान का विस्तार है। इसकी औसत चौड़ाई 64 किमी है, जब कि नर्मदा एवं ताप्ती नदियों के मुहाने के निकट ये 80 किमी तक चौड़े हैं। इस मैदान के उत्तरी भाग को कोंकण तथा दक्षिणी भाग को मालाबार कहते हैं। यहाँ सघन जनसंख्या पायी जाती है। इनकी स्थिति का विवरण अग्रलिखित है 10.
- कोंकण का मैदान– इस मैदान का विस्तार दमन से लेकर गोआ तक 500 किमी की लम्बाई में है। इस मैदान की चौड़ाई 50 से 60 किमी के बीच है तथा मुम्बई के निकट सबसे अधिक है।
- मालाबार का तटीय मैदान– इस मैदान का विस्तार मंगलोर से लेकर कन्याकुमारी तक 500 किमी की लम्बाई में है। इस पर लैगून नामक छोटी-छोटी तटीय झीलें पायी जाती हैं।
पश्चिमी तटीय मैदानों की प्रमुख तीन विशेषताएँ निम्नलिखित हैं
- ये मैदान एक सँकरी पट्टी के रूप में विस्तृत हैं। गुजरात में ये अधिकतम चौड़े हैं तथा दक्षिण की ओर सँकरे हैं।
- इस तट पर अनेक ज्वारनदमुख स्थित हैं जिनमें नर्मदा और ताप्ती के ज्वारनदमुख (एस्चुरी) मुख्य हैं।
- दक्षिण में केरल में अनेक लैगून या पश्चजल स्थित हैं। उनके मुख पर बालूमिति या रोधिकाएँ स्थित हैं।
प्रश्न 4.
पूर्वी तटीय मैदान की स्थिति, विस्तार तथा उसकी तीन विशेषताओं का उल्लेख कीजिए।
उत्तर :
प्रायद्वीपीय पठार के पूर्वी किनारे पर बंगाल की खाड़ी के तट तक तथा पूर्वी घाट के मध्य प० बंगाल से लेकर दक्षिण में कन्याकुमारी तक पूर्वी तटीय मैदानों का विस्तार है। तमिलनाडु में यह मैदान 100 से 120 किमी चौड़ा है। गोदावरी के डेल्टा के उत्तर में यह सँकरा है। कहीं-कहीं इसकी चौड़ाई 32 किमी तक है। इसकी तीन विशेषताएँ निम्नलिखित हैं—
- यह मैदान पश्चिमी तटीय मैदान से अधिक चौड़ा है। नदियों के डेल्टाओं के निकट विशेष रूप से यह अधिक चौड़ा है।
- नदी डेल्टाओं के मैदान अत्यधिक उर्वर तथा सघन आबाद हैं। महानदी, (UPBoardSolutions.com) गोदावरी, कृष्णा तथा कावेरी यहाँ बहने वाली नदियाँ हैं।
- डेल्टाओं में नदियों से अनेक नहरें निकाली गयी हैं, जो सिंचाई के महत्त्वपूर्ण साधन हैं। यहाँ अनेक लैंगून झीलें भी मिलती हैं, जिनमें ओडिशा की चिल्का, आन्ध्र प्रदेश की कोलेरू तथा तमिलनाडु की पुलीकट झीलें उल्लेखनीय हैं।

प्रश्न 5.
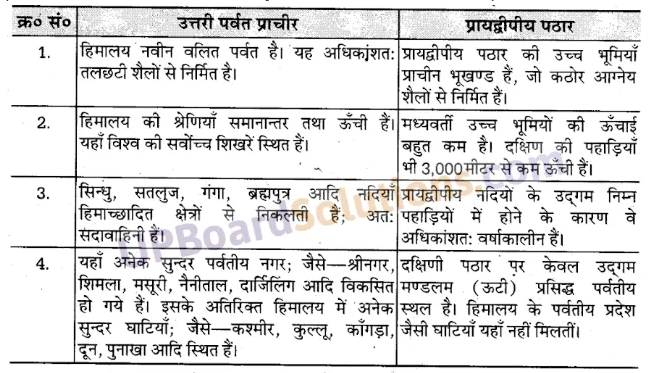
उत्तरी पर्वत प्राचीर तथा प्रायद्वीपीय पठार में क्या अन्तर है ?
उत्तर :
उत्तरी पर्वत प्राचीर तथा प्रायद्वीपीय पठार में निम्नलिखित अन्तर हैं


प्रश्न 6.
हिमालय की उत्पत्ति की विवेचना कीजिए। या हिमालय का निर्माण किस प्रकार हुआ ?
उत्तर :
हिमालय की उत्पत्ति या निर्माण-उच्चावच से तात्पर्य किसी भू-भाग के ऊँचे व नीचे धरातल से है। सभी प्रकार के पहाड़ी, पठारी व मैदानी तथा मरुस्थलीय क्षेत्र मिलकर किसी क्षेत्र के उच्चावच का निर्माण करते हैं। उच्चावच की दृष्टि से भारत में अनेक विभिन्नताएँ मिलती हैं। इनका मूल कारण अनेक शक्तियों और संचलनों का परिणाम है, जो लाखों वर्ष पूर्व घटित हुई थीं। इसकी उत्पत्ति भूवैज्ञानिक अतीत के अध्ययन से स्पष्ट की जा सकती है। आज से 25 करोड़ वर्ष पूर्व भारतीय उपमहाद्वीप विषुवत रेखा के दक्षिण में स्थित प्राचीन गोण्डवानालैण्ड का एक भाग था। अंगारालैण्ड नामक एक अन्य प्राचीन भूखण्ड विषुवत् रेखा के उत्तर (UPBoardSolutions.com) में स्थित था। दोनों प्राचीन भूखण्डों के मध्य टेथिस नामक एक सँकरा, लम्बा, उथला सागर था। इन भूखण्डों की नदियाँ टेथिस में अवसाद जमा करती रहीं, जिससे कालान्तर में टेथिस सागर पट गया। पृथ्वी की आन्तरिक हलचलों के कारण दोनों भूखण्ड टूटे। गोण्डवानालैण्ड से भारत का प्रायद्वीप अलग हो गया तथा भूखण्डों के टूटे हुए भाग विस्थापित होने लगे। आन्तरिक हलचलों से टेथिस सागर के अवसादों की परतों में भिंचाव हुआ और उसमें विशाल मोड़ पड़ गये। इस प्रकार हिमालय पर्वत-श्रृंखला की रचना हुई। इसी कारण हिमालय को वलित पर्वत कहा जाता है।
हिमालय की उत्पत्ति के बाद भारतीय प्रायद्वीप और हिमालय के मध्य एक खाई या गर्त शेष रह गया। हिमालय से उतरने वाली नदियों ने स्थल का अपरदन करके अवसादों के उस गर्त को क्रमशः भरना शुरू किया जिससे विशाल उत्तरी मैदान की रचना हुई। इस प्रकार भारतीय उपमहाद्वीप की भू-आकृतिक इकाइयाँ अस्तित्व में आयीं।
प्रश्न 7.
हिमालय से निकलने वाली नदियों तथा प्रायद्वीपीय भारत की नदियों में अन्तर स्पष्ट कीजिए।
उत्तर:
हिमालय से निकलने वाली नदियों तथा प्रायद्वीपीय नदियों में निम्नलिखित अन्तर हैं

प्रश्न 8.
दक्षिण के पठार में नहर बनाना क्यों कठिन है ? इसके दो कारण लिखिए।
उत्तर:
दक्षिण के पठार में भौगोलिक स्थितियाँ नहर बनाने के अनुकूल नहीं हैं। इसके दो कारण निम्नलिखित हैं
- चम्बल व उसकी सहायक नदियों ने इस पठार के उत्तरी भाग को बीहड़ तथा ऊबड़-खाबड़ गहरे खड्डों में परिवर्तित कर दिया है। यही स्थिति बुन्देलखण्ड एवं बघेलखण्ड के पठार की भी है, जहाँ पर चम्बल व यमुना नदी ने बीहड़ निर्मित किये हैं। यह क्षेत्र नहर बनाने के लिए उपयुक्त नहीं है।
- यह पठारी क्षेत्र अत्यन्त कठोर चट्टानों द्वारा निर्मित है। इन चट्टानों को तोड़कर (UPBoardSolutions.com) नहरें निकालना अत्यन्त महँगा व श्रम-साध्य कार्य है। इन्हीं कारणों से दक्षिण के पठार में नहरें बनाना कठिन है।
प्रश्न 9.
भारत के समुद्रतटीय मैदानों के आर्थिक महत्त्व का वर्णन कीजिए।
उत्तर :
प्रायद्वीपीय पठार के दोनों ओर पूर्वी तथा पश्चिमी तटीय क्षेत्रों पर पतली सँकरी पट्टी के रूप में जो मैदान फैले हैं, उन्हें समुद्रतटीय मैदान कहते हैं। ये क्रमश: पश्चिमी तथा पूर्वी समुद्रतटीय मैदान कहलाते हैं। इनका आर्थिक महत्त्व निम्नवत् है
1. पश्चिमी तटीय मैदान– प्रायद्वीप के पश्चिम में खम्भात की खाड़ी से लेकर कुमारी अन्तरीप तक इस मैदान का विस्तार है। नर्मदा तथा ताप्ती यहाँ की प्रमुख नदियाँ हैं। नदियों के मुहानों पर बालू जम जाने से यहाँ लैगून निर्मित होते हैं। इनमें मछलियाँ पकड़ी जाती हैं। उपयुक्त जलवायु तथा उत्तम मिट्टी के कारण यहाँ चावल, आम, केला, सुपारी, काजू, इलायची, गरम मसाले, नारियल आदि की फसलें उगायी जाती हैं। सागर तट पर नमक बनाने तथा मछलियाँ पकड़ने का व्यवसाय भी पर्याप्त रूप में विकसित हुआ है। भारत के प्रमुख पत्तन इन्हीं मैदानों में स्थित हैं। काँदला, मुम्बई ( न्हावाशेवा) व कोचीन इस तट के प्रमुख बन्दरगाह हैं।
2. पूर्वी तटीय मैदान– प्रायद्वीपीय पठारों के पूर्वी किनारों पर बंगाल की खाड़ी के तट तक तथा पूर्वी घाट के मध्य प० बंगाल से लेकर दक्षिण में कन्याकुमारी तक पूर्वी तटीय मैदानों का विस्तार है। इस मैदान में महानदी, गोदावरी, कृष्णा एवं कावेरी नदियों के डेल्टा विकसित हुए हैं। डेल्टाओं में नदियों से अनेक नहरें निकाली गयी हैं, जो सिंचाई का महत्त्वपूर्ण साधन हैं। यह तटीय मैदान उपजाऊ है तथा कहीं- कहीं पर कॉप मिट्टी से ढका है। यह मैदान कृषि की दृष्टि से बड़ा अनुकूल है। चावल, गन्ना, तम्बाकू व जूट इस मैदान की मुख्य उपज हैं।

प्रश्न 10.
भारत के पश्चिमी तथा पूर्वी तटीय मैदानों में दो मुख्य अन्तर लिखिए।
या
भारत के पूर्वी व पश्चिमी तटीय मैदानों की तुलना कीजिए। [2014]
उत्तर :
प्रायद्वीपीय पठार के दोनों ओर पूर्वी तथा पश्चिमी तटीय क्षेत्रों पर पतली पट्टी के रूप में जो मैदान फैले हैं, उन्हें समुद्रतटीय मैदान कहते हैं। इन मैदानों को दो क्षेत्रों में बाँटा जा सकता है-पूर्वी तटीय मैदान एवं पश्चिमी तटीय मैदान। इन दोनों मैदानों में दो मुख्य अन्तर निम्नलिखित हैं
- आकार–पश्चिमी तटीय मैदान एक सँकरी पट्टी के रूप में विस्तृत हैं। इनकी औसत चौड़ाई 64 किमी है तथा नर्मदा एवं ताप्ती के मुहाने के निकट ये 80 किमी चौड़े हैं, जबकि पूर्वी तटीय मैदान अपेक्षाकृत अधिक चौड़े हैं। इनकी औसत चौड़ाई (UPBoardSolutions.com) 161 से 483 किमी है।
- विस्तार–पश्चिमी तटीय मैदान प्रायद्वीप के पश्चिम में खम्भात की खाड़ी से लेकर कुमारी अन्तरीप तक फैले हैं, जबकि पूर्वी तटीय मैदान प्रायद्वीपीय पठारों के पूर्वी किनारों पर बंगाल की खाड़ी के तट तक तथा पूर्वी घाट के मध्य पश्चिमी बंगाल से लेकर दक्षिण में कन्याकुमारी तक विस्तृत हैं।
अतिलघु उत्तरीय प्रज,
प्रश्न 1.
भारत के अक्षांशीय एवं देशान्तरीय विस्तार को लिखिए। [2012]
उत्तर :
भारत हिन्द महासागर के शीर्ष पर स्थित एक विशाल देश है। इसका क्षेत्रफल 32,87,263 वर्ग किमी है। भारत 8°4′ उत्तर से 37°6′ उत्तरी अक्षांश और 68°7′ से 97°25′ पूर्वी देशान्तर के मध्य स्थित है।
प्रश्न 2.
क्षेत्रफल की दृष्टि से भारत का विश्व में कौन-सा स्थान है ?
उत्तर:
क्षेत्रफल की दृष्टि से भारत विश्व का सातवाँ विशाल देश है। इससे अधिक बड़े आकार वाले देश क्रमशः रूस, कनाडा, चीन, संयुक्त राज्य अमेरिका, ब्राजील तथा ऑस्ट्रेलिया हैं।

प्रश्न 3.
भारत की सीमाओं पर स्थित पड़ोसी देशों के नाम लिखिए।
उत्तर:
भारत की पूर्वी सीमा बांग्लादेश तथा म्यांमार से, पश्चिमी सीमा पाकिस्तान (UPBoardSolutions.com) व अफगानिस्तान से, उत्तरी सीमा चीन, नेपाल और भूटान से तथा दक्षिण में श्रीलंका से मिलती है।
प्रश्न 4.
भारतीय उपमहाद्वीप में कौन-कौन-से देश हैं ?
उत्तर:
भारतीय उपमहाद्वीप में पाकिस्तान,भारत, नेपाल, भूटान, बांग्लादेश, श्रीलंका तथा मालदीव देश सम्मिलित हैं।
प्रश्न 5.
हिमालय को नवीन वलित पर्वत क्यों कहते हैं ?
उत्तर:
हिमालय की उत्पत्ति टेथिस सागर में लगातार तलछटों के निक्षेप से बनी परतों में मोड़ पड़ जाने से हुई। भिंचाव की शक्तियों के कारण ये मोड़ ऊँचे उठते चले गये जो बाद में पर्वत बन गये। इसीलिए हिमालय को नवीन वलित पर्वत कहते हैं।
प्रश्न 6.
भारतीय उपमहाद्वीप का सबसे प्राचीन भू-भाग कौन-सा है ?
उत्तर:
भारतीय उपमहाद्वीप का सबसे प्राचीन भू-भाग विशाल प्रायद्वीपीय पठार है, जो उत्तरी मैदान के दक्षिण में स्थित है।
प्रश्न 7.
लक्षद्वीप किस सागर में स्थित है ?
उत्तर:
लक्षद्वीप अरब सागर में स्थित है।

प्रश्न 8.
उत्तर भारत के विशाल मैदानों की दो विशेषताओं का उल्लेख कीजिए। [2011]
उत्तर:
- उत्तर का विशाल मैदान सतलज, गंगा तथा ब्रह्मपुत्र नदियों के अपरदन से बना है।
- यह क्षेत्र अत्यधिक उपजाऊ है।
प्रश्न 9.
शिवालिक श्रेणी किन दो राज्यों में स्थित है ?
उत्तर:
शिवालिक श्रेणी
- पंजाब तथा
- उत्तराखण्ड राज्यों में स्थित है।
प्रश्न 10.
भारत के पश्चिमी तट के दक्षिणी भाग को किस नाम से जाना जाता है ?
उत्तर:
भारत के पश्चिमी तट के दक्षिणी भाग को ‘मालाबार’ (UPBoardSolutions.com) नाम से जाना जाता है।
प्रश्न 11.
हिमालय के दो सर्वोच्च शिखरों के नाम लिखिए।
उत्तर:
हिमालय के दो सर्वोच्च शिखर माउण्ट एवरेस्ट (नेपाल) तथा के-2 (भारत) हैं।
प्रश्न 12.
हिमालय की प्रमुख घाटियों के नाम बताइए। इनका क्या महत्त्व है ?
उत्तर:
हिमालय की प्रमुख घाटियों, जिन्हें ‘दून’ कहते हैं; के नाम हैं-देहरादून, पूर्वादून, कोठड़ीदून, पाटलीदून आदि। ये घाटियाँ अपनी प्राकृतिक सुन्दरता के लिए विश्वविख्यात हैं।

प्रश्न 13.
पूर्वांचल में पर्वत-श्रृंखलाओं के नाम लिखिए।
उत्तर:
पटकाई कूम, गारो-खासी जयन्तिया तथा चुसाई पहाड़ियाँ।
प्रश्न 14.
गंगा-ब्रह्मपुत्र नदियों के डेल्टा को हम किस नाम से जानते हैं?
उत्तर:
सुन्दरवन डेल्टा।
प्रश्न 15.
विशाल प्रायद्वीपीय पठार की दो प्रमुख विशेषताएँ लिखिए।
उत्तर:
विशाल प्रायद्वीपीय पठार की दो प्रमुख विशेषताएँ निम्नलिखित हैं
- यह विशाल प्रायद्वीपीय पठार भारतीय उपमहाद्वीप का सबसे प्राचीन भू-भाग है, जो गोण्डवाना–लैण्ड का ही एक अंग है।
- इस पठार का निर्माण त्रिभुजाकार आकृति में प्राचीन (UPBoardSolutions.com) ग्रेनाइट तथा बेसाल्ट की कठोर शैलों से हुआ है।
प्रश्न 16.
ब्रह्मपुत्र नदी भारत के किस राज्य में बहती है ?
उत्तर:
ब्रह्मपुत्र नदी भारत के असोम राज्य में बहती है।
प्रश्न 17.
सतपुड़ा पर्वत किन दो नदियों के बीच स्थित है ?
उत्तर:
सतपुड़ा पर्वत नर्मदा और ताप्ती नदियों के बीच स्थित है।

प्रश्न 18.
अरावली पहाड़ियाँ किस राज्य में स्थित हैं ?
उत्तर:
अरावली पहाड़ियाँ राजस्थान राज्य में स्थित हैं।
प्रश्न 19.
बंगाल की खाड़ी में गिरने वाली दो नदियों के नाम लिखिए। [2018]
उत्तर:
- महानदी तथा
- स्वर्ण रेखा नदी।
प्रश्न 20.
थार मरुस्थल कहाँ है ?
उत्तर:
थार मरुस्थल उत्तर-पश्चिमी भारत (राजस्थान) में है।
प्रश्न 21.
भारत और विश्व का सबसे बड़ा डेल्टा कौन-सा है ?
उत्तर:
भारत और विश्व का सबसे बड़ा डेल्टा गंगा-ब्रह्मपुत्र डेल्टा या सुन्दरवन है।
प्रश्न 22.
डेल्टा को परिभाषित कीजिए और किसी एक डेल्टा का नाम लिखिए। [2011, 12]
या
डेल्टा किसे कहते हैं? यह कैसे बनता है?
उत्तर:
जब नदियों में अवसाद की मात्रा ज्यादा हो जाती है तो (UPBoardSolutions.com) नदियों का पानी कई शाखाओं में होकर बहने लगता है, जिससे निक्षेपण क्षेत्र A के आकार का हो जाता है, जिसे ‘डेल्टा’ कहते हैं। सुन्दरवन डेल्टा विश्व का सबसे बड़ा डेल्टा है।

प्रश्न 23.
मालय के दो प्रमुख दरों के नाम लिखिए। [2011, 13, 16]
उत्तर:
हिमालय के दो प्रमुख दरों के नाम हैं–
प्रश्न 24.
अरब सागर में गिरने वाली दो नदियों के नाम लिखिए। [2011, 13]
उत्तर:
अरब सागर में गिरने वाली दो नदियाँ हैं–सिन्धु नदी तथा नर्मदा नदी।
प्रश्न 25.
भारत और चीन के बीच सीमा-रेखा का क्या नाम है ?
उत्तर:
भारत और चीन के बीच सीमा-रेखा का नाम मैकमोहन रेखा है।
प्रश्न 26.
कौन-सा दर्रा भारत के सिक्किम राज्य को तिब्बत से जोइता है ?
उत्तर:
नाथुला दर्रा भारत के सिक्किम राज्य को तिब्बत से जोड़ता है।
प्रश्न 27.
भारत के पश्चिम और दक्षिण में कौन-से सागर हैं? [2014]
उत्तर:
पश्चिम-(1) अरब सागर।
दक्षिण-(2) हिन्द महासागर।

प्रश्न 28.
डेल्टा तथा ज्वारनदमुख में अन्तर स्पष्ट कीजिए।
उत्तर :
जब नदियों में अवसाद की मात्रा ज्यादा हो जाती है तो नदियों का पानी कई शाखाओं में होकर बहने लगता है, जिससे निक्षेपण क्षेत्र A के आकार का हो जाता है, जिसे डेल्टा’ (Delta) कहते हैं तथा जब नदियाँ बिना डेल्टा का निर्माण किए सीधे समुद्र (UPBoardSolutions.com) में गिरती हैं तो उसे ‘ज्वारनदमुख’ कहते हैं।
बहुविकल्पीय
प्रश्न 1. भारत किस महाद्वीप में स्थित है?
(क) यूरोप में
(ख) अफ्रीका में
(ग) एशिया में
(घ) ऑस्ट्रेलिया में
2. भारत किस कटिबन्ध में स्थित है?
(क) उपोष्ण
(ख) उष्ण
(ग) शीतोष्ण
(घ) शीत
3. भारत की वह नदी जो ज्वारनदमुख बनाती है
(क) ताप्ती
(ख) महानदी
(ग) गोदावरी
(घ) लूनी
4. भारत के कुल क्षेत्रफल में मैदानी भाग हैं [2011]
(क) लगभग 43%
(ख) लगभग 40%
(ग) लगभग 33%
(घ) लगभग 30%

5. ‘शिपकी-ला’ दर्रा भारत को जोड़ता है [2011]
(क) पाकिस्तान से
(ख) चीन से
(ग) भूटान से
(घ) नेपाल से
6. भारत के दक्षिण में स्थित देश का नाम है [2012]
(क) श्रीलंका
(ख) नेपाल
(ग) चीन
(घ) म्यांमार
7. हिमालय पर्वत की सर्वोच्च चोटी है
(क) एवरेस्ट
(ख) कंचनजंगा
(ग) K-2
(घ) नन्दा
8. अरुणाचल प्रदेश में मुख्य दर्रा है[2011]
(क) नाथुला दर्रा
(ख) बोमडिला दर्रा
(ग) कराकोरम दर्रा
(घ) बोलन दर्रा

9. गंगा की सबसे बड़ी सहायक नदी है
(क) चम्बल
(ख) यमुना
(ग) बेतवा
(घ) नर्मदा
10. नन्दा देवी शिखर किस पर्वत से सम्बन्धित है?
(क) नीलगिरि पर्वत से
(ख) सतपुड़ा पर्वत से
(ग) हिमालय पर्वत से
(घ) मैकाले पर्वत से
11. भारत का सर्वोच्च शिखर कौन-सा है? [2011, 13, 14]
(क) गॉडविन ऑस्टिन
(ख) कंचनजंगा
(ग) नन्दा देवी ,
(घ) इनमें से कोई नहीं
12. भारत की स्थल सीमा की कुल लम्बाई कितनी है?
(क) 15,200 किमी.
(ख) 15,300 किमी
(ग) 15,400 किमी
(घ) 15,500 किमी

13. नीलगिरि पर्वत स्थित है [2011, 12, 13, 16]
(क) उत्तरी भारत में
(ख) दक्षिणी भारत में
(ग) पूर्वी भारत में
(घ) पश्चिमी भारत में
14. नाथूला दर्रा किस राज्य में स्थित है?
(क) अरुणाचल प्रदेश में
(ख) असोम में
(ग) सिक्किम में ।
(घ) मणिपुर में
15. बोमडिला दर्रा किस राज्य में स्थित है? [2010]
(क) सिक्किम में
(ख) हिमाचल प्रदेश में
(ग) जम्मू-कश्मीर में
(घ) अरुणाचल प्रदेश में
16. निम्नलिखित में से कौन-सी नदी अरब सागर में गिरती है? [2012, 13, 18]
(क) सतलुज
(ख) महानदी
(ग) ताप्ती
(घ) कावेरी

17. ऊटकमण्ड किस राज्य में स्थित है? [2012]
(क) केरल
(ख) कर्नाटक
(ग) तमिलनाडु
(घ) उत्तराखण्ड
18. शिवालिक पर्वत स्थित है [2012]
(क) उत्तरी भारत में
(ख) दक्षिणी भारत में
(ग) पूर्वी भारत में
(घ) पश्चिमी भारत में
19. जोजिला दर्रा जोड़ता है [2012]
(क) जम्मू और कठुआ को
(ख) जम्मू और ऊधमपुर को
(ग) श्रीनगर और लेह को
(घ) श्रीनगर और कुपवाड़ा को

20. निम्नलिखित में से कौन-सी सबसे बड़ी नदी है? [2011]
(क) गोदावरी
(ख) गंगा
(ग) कृष्णा
(घ) साबरमती
21. निम्नलिखित में से कौन-सी नदी बंगाल की खाड़ी में गिरती है? [2011]
(क) नर्मदा
(ख) गोदावरी
(ग) ताप्ती
(घ) साबरमती
22. शिपकी-ला दर्रा किस राज्य में है?
(क) उत्तराखण्ड
(ख) हिमाचल प्रदेश
(ग) सिक्किम
23. भारतीय गणराज्य में कितने राज्य हैं?
(क) 29
(ख) 28
(ग) 30
(घ) 35

24. कौन-सा समुद्र तट कोरोमण्डल तट कहा जाता है? [2013, 15]
(क) गुजरात का समुद्र तट
(ख) केरल का समुद्र तट
(ग) तमिलनाडु की समुद्र तट
(घ) ओडिशा का समुद्र तट
25. किस राज्य की तट रेखा सबसे लम्बी है? [2014]
(क) गुजरात
(ख) आन्ध्र प्रदेश
(ग) पश्चिम बंगाल
(घ) गोवा
26. भारतवर्ष का क्षेत्रफल है [2014]
(के) 32,87,263 वर्ग किमी
(ख) 33,87,364 वर्ग किमी
(ग) 30,80,362 वर्ग किमी
(घ) 31,80,664 वर्ग किमी
27. क्षेत्रफल की दृष्टि से सबसे बड़ा राज्य है [2014]
(क) मध्य प्रदेश
(ख) उत्तर प्रदेश
(ग) बिहार
(घ) राजस्थान

28. कंचनजंगा की ऊँचाई है [2015]
(क) 8598 मीटर
(ख) 7598 मीटर
(ग) 6598 मीटर
(घ) 5598 मीटर
29. संसार का सबसे बड़ा डेल्टा है [2015]
(क) अमेजन का डेल्टा ।
(ख) गंगा का डेल्टा
(ग) मिसीसिपी का डेल्टा
(घ) नील नदी का डेल्टा
30. माउण्ट एवरेस्ट की ऊँचाई है [2015, 16]
(क) 8848 मीटर
(ख) 7747 मीटर
(ग) 6646 मीटर
(घ) 5545 मीटर
31. भारत की सर्वोच्च श्रेणी की ऊँचाई है [2015]
(क) 8211 मीटर
(ख) 8611 मीटर
(ग) 8000 मीटर
(घ) 8302 मीटर
32. कंचनजंगा चोटी अवस्थित है [2015]
(क) जम्मू और कश्मीर में
(ख) उत्तराखण्ड में
(ग) सिक्किम में
(घ) हिमाचल प्रदेश में

33. मालाबार तट कहा जाता है [2015]
(क) पश्चिमी समुद्र तटीय मैदान का उत्तरी भाग
(ख) पश्चिमी समुद्र तटीय मैदान का दक्षिणी भाग
(ग) पूर्वी समुद्र तटीय मैदान का उत्तरी भाग
(घ) पूर्वी समुद्र तटीय मैदान का दक्षिणी भाग
34. मैकमोहन रेखा स्थित है [2015, 16]
(क) भारत तथा बांग्लादेश के मध्य
(ख) भारत तथा नेपाल के मध्य ।
(ग) भारत तथा पाकिस्तान के मध्य
(घ) भारत तथा चीन के मध्य
35. निम्नलिखित में से कौन पर्वतीय चोटी भारत में स्थित है? [2016]
(क) माउण्ट एवरेस्ट
(ख) धौला गिरि
(ग) अन्नपूर्णा
(घ) नन्दा देवी
36. निम्नलिखित में से किस राज्य में समुद्र तट नहीं है? [2017]
(क) महाराष्ट्र
(ख) गुजरात
(ग) केरल
(घ) मध्य
प्रदेश 37. गंगा नदी का उद्गम स्थल है [2017]
(क) तिब्बत का पठार
(ख) मानसरोवर झील
(ग) गोमुख हिमनद
(घ) नंगा पर्वत
38. नीलगिरि पर्वत स्थित है [2017]
(क) तमिलनाडु
(ख) कर्नाटक
(ग) केरल
(घ) आन्ध्र

प्रदेश 39. कन्याकुमारी स्थित है [2017]
(क) कर्नाटक
(ख) आन्ध्र प्रदेश
(ग) केरल
(घ) तमिलनाडु
40. नवीनतम पर्वतश्रेणी है
(क) नीलगिरि
(ख) सतपुड़ा
(ग) शिवालिक
(घ) विन्ध्य की पहाड़ियाँ
उत्तरमाला
1. (ग), 2. (क), 3. (क), 4. (क), 5. (ख), 6. (क), 7. (क), 8. (ख), 9. (ख), 10. (ग), 11. (ख), 12. (क), 13. (ख), 14. (ग), 15. (घ), 16. (ग), 17. (ग), 18. (क), 19. (ग), 20. (ख), 21. (ख), 22. (ख), 23. (क), 24. (ग), 25. (क), 26. (क), 27. (घ), 28. (क), 29. (ख), 30. (क), 31. (ख), 32. (ग), 33. (ख), 34. (घ) 35. (घ), 36. (घ), 37. (ग), 38. (क), 39. (घ), 40. (ग) |
We hope the UP Board Solutions for Class 10 Social Science Chapter 1 भारत : भौतिक स्वरूप (अनुभाग – तीन) help you. If you have any query regarding UP Board Solutions for Class 10 Social Science Chapter 1 भारत : भौतिक स्वरूप (अनुभाग – तीन), drop a comment below and we will get back to you at the earliest
![]()
![]()
![]()


