Balaji Class 10 Maths Solutions Chapter 12 Area Related to Circles Ex 12.4

Balaji Class 10 Maths Solutions Chapter 12 Area Related to Circles Ex 12.4 वृत्तों से सम्बन्धित क्षेत्रफल

प्रश्न 1.
वर्गाकार टैंक की भुजा 40 मीटर है। उसके चारों ओर अर्द्धवृत्ताकार चार प्लॉट हैं। ₹ 1.25 प्रति वर्ग मीटर की दर से उन्हें सींचने का कुल मूल्य ज्ञात कीजिए। (π = 3.14)
हलः
वर्गाकार टैंक की भुजा = 40 मीटर।

₹ 1.25 प्रति वर्ग मीटर की दर (UPBoardSolutions.com) से प्लॉटो को सींचने का कुल मूल्य
= 2512 × 1.25 = ₹3140

प्रश्न 2.
सिद्ध कीजिए कि r त्रिज्या के वृत्ताकार क्षेत्र के चारों ओर h मीटर चौड़ाई के एक वृत्ताकार रास्ते का क्षेत्रफल πh(2r + h) वर्ग मीटर है।
हलः
वृत्ताकार क्षेत्र की आन्तरिक त्रिज्या = r मीटर तथा वृत्ताकार रास्ते की चौड़ाई = h मीटर
तब, वृत्ताकार क्षेत्र की बाा त्रिज्या R = (r + h) मीटर

वृत्ताकार रास्ते का क्षेत्रफल = π(R² – r²)
= π[(r + h)² – r²]
= π[r² + h² +2rh – r²]
= π[h² +2rh]
= πh(h + 2r) वर्ग मीटर

प्रश्न 3.
एक 40 सेमी भुजा के वर्ग के रूप में डेन कवर है जिसके अन्दर 441 छेद हैं। जिनमें प्रत्येक का व्यास 1 सेमी है। छेद से अलग वर्गाकार प्लेट का क्षेत्रफल ज्ञात कीजिए।
हलः
वर्ग की भुजा a = 40 सेमी तब
वर्ग का क्षेत्रफल = a² = (40)² = 1600 सेमी²
छेद का व्यास (UPBoardSolutions.com) r = [latex]\frac{1}{2}[/latex] सेमी


अतः छेद से अलग वर्गाकार प्लेट का क्षेत्रफल
= 1600 – 346.5 = 1253.5 सेमी²

प्रश्न 4.
O केन्द्र तथा 21 सेमी व 7 सेमी त्रिज्या के दो संकेन्द्रीय वृत्तों की चाप क्रमशः AB व CD हैं। यदि ∠AOB = 30° तब छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (NCERT)

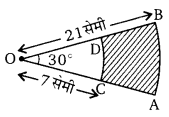
हलः
केन्द्र O वाले संकेन्द्रीय वृत्तों की त्रिज्यायें क्रमशः 21 सेमी व 7 सेमी हैं।
तथा ∠AOB = 30°
तब छायांकित क्षेत्र का क्षेत्रफल (UPBoardSolutions.com) = त्रिज्यखण्ड AOB का क्षेत्रफल – त्रिज्यखण्ड COD का क्षेत्रफल

प्रश्न 5.
40 मीटर व्यास का एक वृत्ताकार प्लॉट है। जिसके चारों ओर 3.5 मीटर चौड़ा एक रास्ता है। उस रास्ते पर ₹ 4 प्रति वर्ग मीटर के हिसाब से घास लगाने में कितना खर्च आयेगा?
हलः
वृत्ताकार प्लॉट का व्यास = 40 मीटर
वृत्ताकार प्लॉट की त्रिज्या r = [latex]\frac{40}{2}[/latex] = 20 मीटर
रास्ते की चौड़ाई = 3.5 मीटर
रास्ते सहित वृत्ताकार प्लॉट की त्रिज्या R = 20 + 3.5 = 23.5 मीटर
तब रास्ते का क्षेत्रफल = π [R² – r²]
= [latex]\frac{22}{7}[/latex](23.5)² – (20)²]
= [latex]\frac{22}{7}[/latex][552.25 – 400]
= [latex]\frac{22}{7}[/latex] × 152.25 = 22 × 21.75
= 478.5 सेमी²
रास्ते पर ₹ 4 प्रति वर्ग मीटर की दर से घास लगाने का खर्च = 478.5 × 4 = ₹1914

प्रश्न 6.
एक वृत्ताकार तालाब जिसका व्यास 17.5 मीटर है, के चारों ओर 2 मीटर चौड़ा एक रास्ता है। ₹ 25 प्रति वर्ग मीटर की दर से रास्ते बनाने में कुल लागत ज्ञात कीजिए। (π = 3.14)
हलः
वृत्ताकार तालाब का व्यास = 17.5 मीटर
वृत्ताकार तालाब की त्रिज्या r = [latex]\frac{17.5}{2}[/latex] = 8.75 मीटर
रास्ते की चौड़ाई = 2 मीटर
तब, रास्ते सहित वृत्ताकार तालाब की त्रिज्या R = 8.75 + 2
R = 10.75 मीटर
वृत्ताकार रास्ते का क्षेत्रफल = π(R² – r²)
= 3.14[(10.75)² – (8.75)²]
= 3.14[115.5625 – 76.5625]
= 3.14 × 39 = 122.46 मीटर²
₹ 25 प्रति वर्ग मीटर की दर से (UPBoardSolutions.com) रास्ता बनाने में कुल लागत = 122.46 × 25 = ₹ 3061.50

प्रश्न 7.
72 मीटर परिमाप वाले अर्द्धवृत्ताकार क्षेत्र के चारों ओर 3.5 मीटर चौड़ा एक रास्ता है। रास्ते का क्षेत्रफल ज्ञात कीजिए।
हलः
माना, अर्द्धवृत्ताकार क्षेत्र की त्रिज्या r मीटर है।
तब प्रश्नानुसार, अर्द्धवृत्ताकार क्षेत्र का परिमाप = 72 मीटर
2r + πr = 72 या r(2 + π) = 72

अर्द्धवृत्ताकार क्षेत्र के चारों ओर रास्ते की चौड़ाई = 3.5 मीटर
तब, रास्ते सहित अर्द्धवृत्ताकार क्षेत्र की (UPBoardSolutions.com) त्रिज्या R = 14 + 3.5 = 17.5 मीटर

प्रश्न 8.
24 सेमी भुजा वाले एक समबाहु त्रिभुज में उसकी भुजाओं को स्पर्श करते हुए एक वृत्त खींचा गया है। त्रिभुज के शेष भाग का क्षेत्रफल ज्ञात कीजिए। ([latex] \sqrt{{3}} [/latex] = 1.732)
हलः
माना, वृत्त की त्रिज्या ON = r सेमी
तथा समबाहु ∆ ABC की प्रत्येक भुजा a = 24 सेमी
∵ समबाहु A का प्रत्येक कोण 60° का होता है।
∴ ∠OBN = 30°

प्रश्न 9.
संलग्न चित्र में, AB व CD, O केन्द्र वाले एक वृत्त के व्यास हैं जो परस्पर लम्बवत् हैं। OD उसके समरूप वृत्त का व्यास है। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (NCERT)

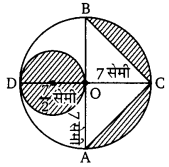
हलः
O केन्द्र वाले वृत्त के व्यास AB = CD = 14 सेमी
तथा समरूप वृत्त का व्यास OD = 7
सेमी माना, O केन्द्र वाले (UPBoardSolutions.com) वृत्त की त्रिज्य R = [latex]\frac{14}{2}[/latex] = 7 सेमी
तथा समरूप वृत्त की त्रिज्या r = [latex]\frac{7}{2}[/latex] सेमी
तब, छायांकित क्षेत्र का क्षेत्रफल = OD व्यास वाले वृत्त का क्षेत्रफल + अर्द्धवृत्त OACB का क्षेत्रफल – ∆ ABC का क्षेत्रफल

प्रश्न 10.
संलग्न चित्र में एक समबाहु त्रिभुज ABC जोकि O केन्द्र तथा 4 सेमी त्रिज्या वाले वृत्त के अन्दर स्थित है। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 4 सेमी

∵ समबाहु A ABC का प्रत्येक कोण 60° है। अर्थात् ∠ABC = 60°
∴ केन्द्र O पर बना कोण (UPBoardSolutions.com) AOC = 120°

प्रश्न 11.
50 मीटर भुजा वाले वर्गाकार क्षेत्र के चारों कोनों पर चार गाय इस प्रकार बांधी गयी हैं कि वे कभी भी एक-दूसरे से नहीं मिल सकती। कितना क्षेत्र बिना चरे रह जायेगा?

हलः
वर्गाकार क्षेत्र की भुजा a = 50 मीटर
∵ वर्गाकार क्षेत्र के चारों कोनों पर चार गाय बाँधी गयी हैं।
∴ गाय की रस्सी की लम्बाई (UPBoardSolutions.com) r = [latex]\frac{50}{2}[/latex] = 25 मीटर
तब बिना चरे क्षेत्र का क्षेत्रफल = वर्गाकार क्षेत्र का क्षेत्रफल – गाय द्वारा चरे भाग का क्षेत्रफल
= a² – 4 × त्रिज्यखण्ड का क्षेत्रफल

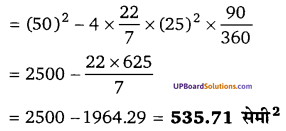
प्रश्न 12.
आयताकार मैदान की छोटी भुजाओं को व्यास मानकर दो अर्द्धवृत्त उसकी छोटी भुजाओं में जोड़े गये हैं। यदि आयत की भुजाएँ 36 मीटर व 24.5 मीटर हों तो मैदान का क्षेत्रफल ज्ञात कीजिए। (π = [latex]\frac{22}{7}[/latex])
हलः
आयताकार मैदान की लम्बाई = 36 मीटर
तथा आयताकार मैदान की चौड़ाई = 24.5 मीटर
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= 36 × 24.5 = 882 मीटर² 
∵ दो अर्द्धवृत्त आयत की छोटी भुजाओं (UPBoardSolutions.com) में जोड़े गये हैं।

अतः पूरे मैदान का क्षेत्रफल = 882 + 471.625
= 1353.625 मीटर²

प्रश्न 13.
एक आयताकार टुकडे की लम्बाई 20 मीटर व चौडाई 15 मीटर है। इसके चारों कोनों से 3.5 मीटर त्रिज्या के चार चतुर्थांश काटे गये हैं। शेष भाग का क्षेत्रफल ज्ञात कीजिए।
हलः
आयताकार टुकडे की लम्बाई l = 20 मीटर
आयताकार टुकडे की चौड़ाई b = 15 मीटर
चतुर्थांश की त्रिज्या r = 3.5 मीटर
तब शेष भाग का क्षेत्रफल = आयताकार (UPBoardSolutions.com) टुकडे का क्षेत्रफल – चारों चतुर्थांशों का क्षेत्रफल

प्रश्न 14.
एक समषटभुज, एक वृत्त के अन्दर स्थित है। यदि समषटभुज का क्षेत्रफल 24[latex] \sqrt{{3}} [/latex] वर्ग सेमी है तो वृत्त का क्षेत्रफल ज्ञात कीजिए। (π = 3.14)
हलः
समषटभुज ABCDEF का क्षेत्रफल = (UPBoardSolutions.com) 24[latex] \sqrt{{3}} [/latex] सेमी²

Balaji Publications Mathematics Class 10 Solutions