Class 11

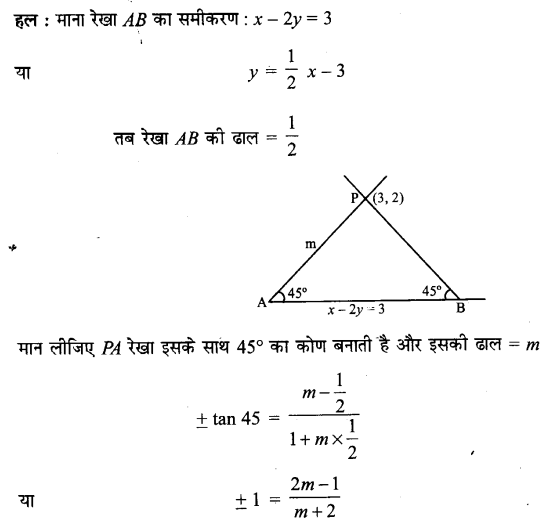
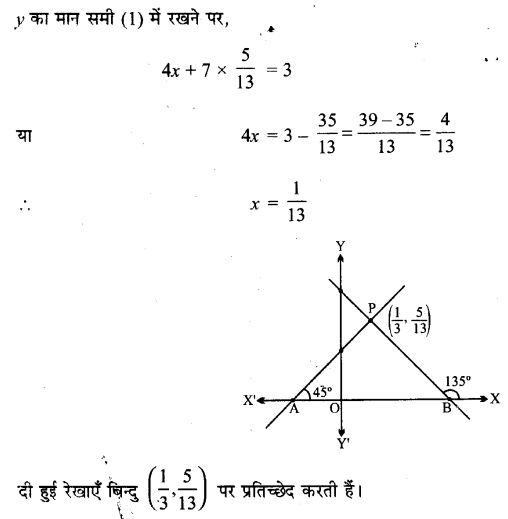
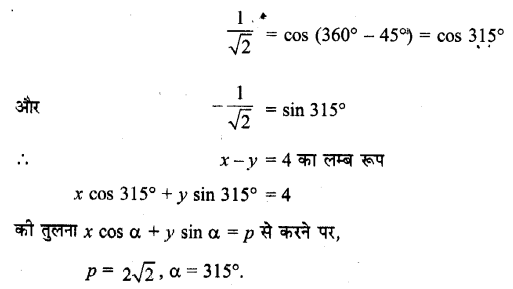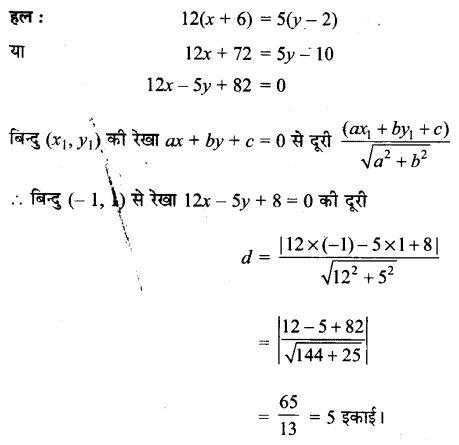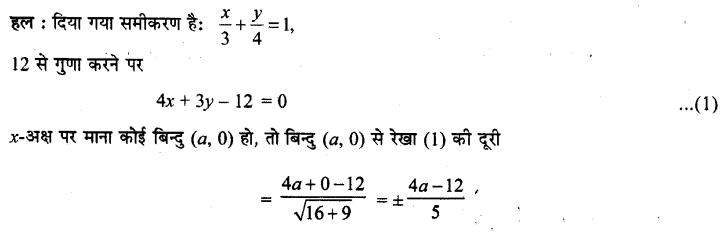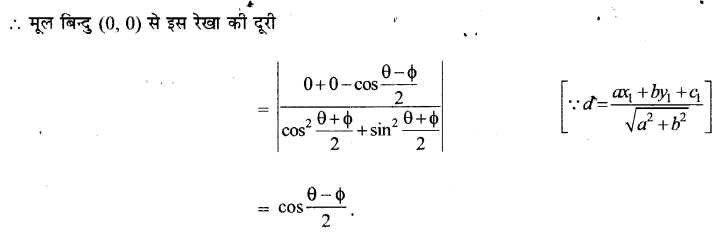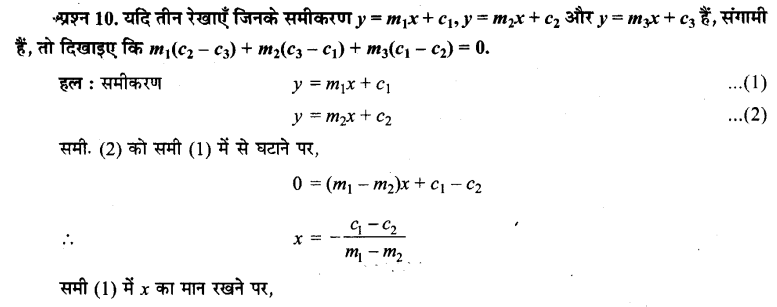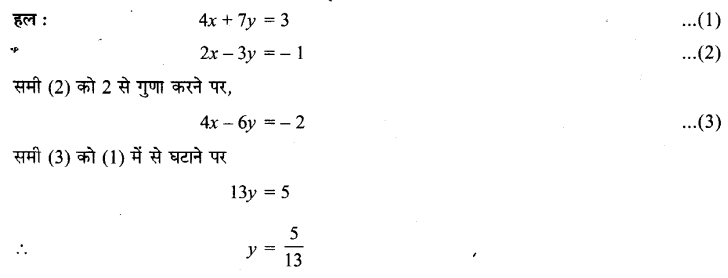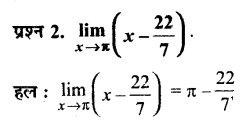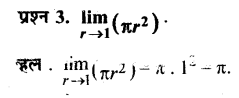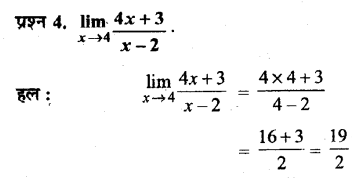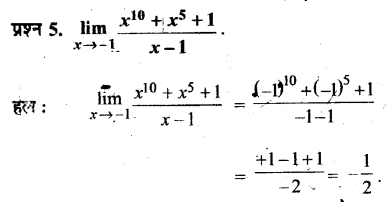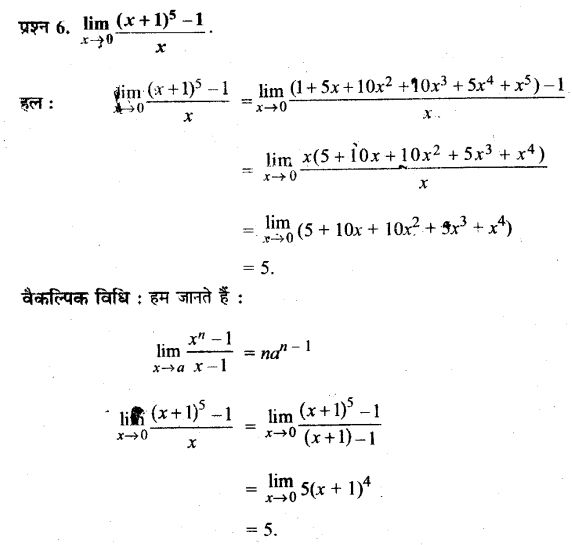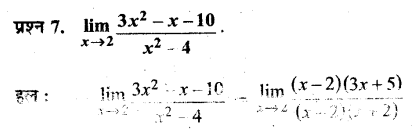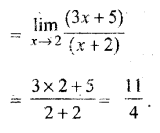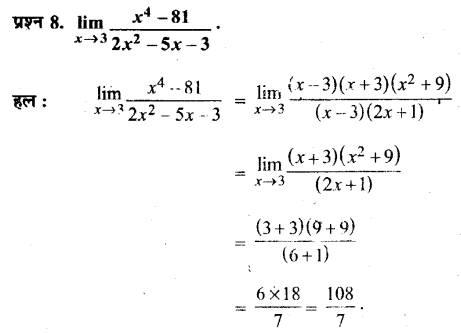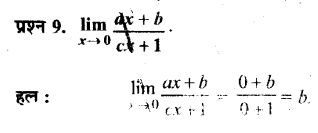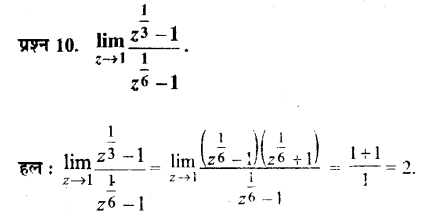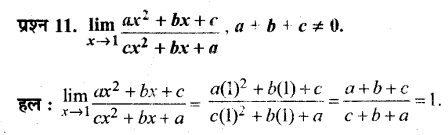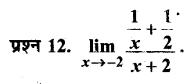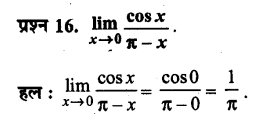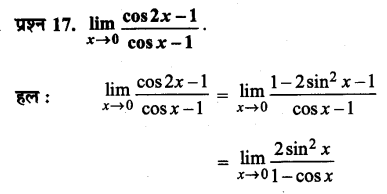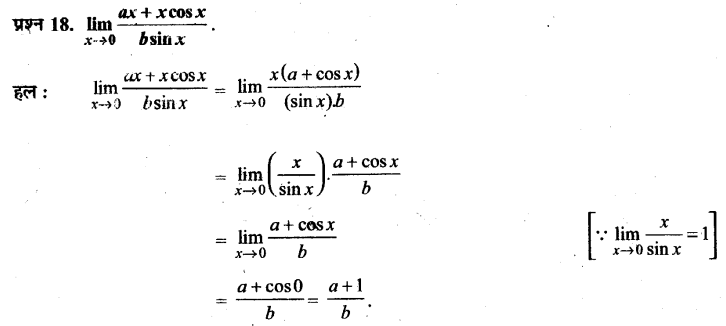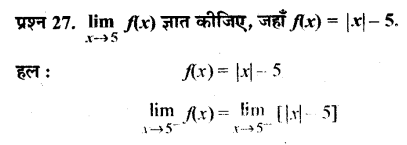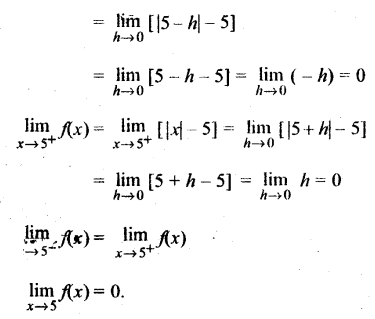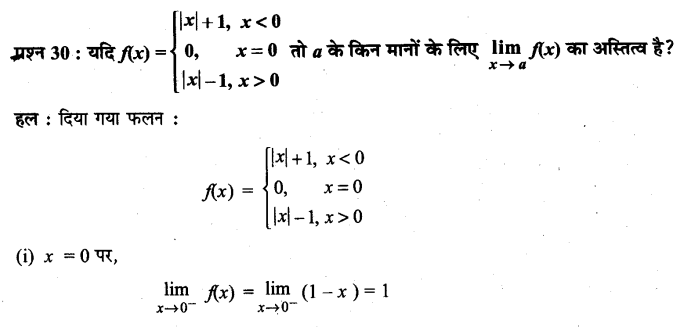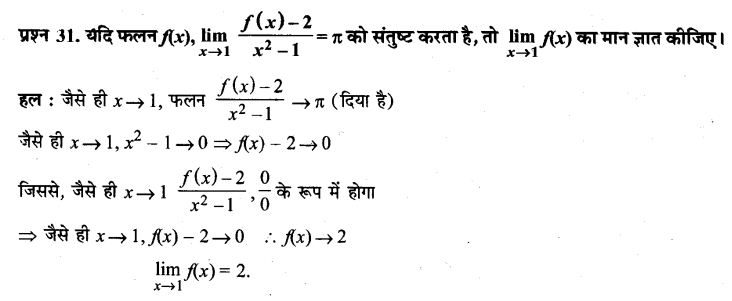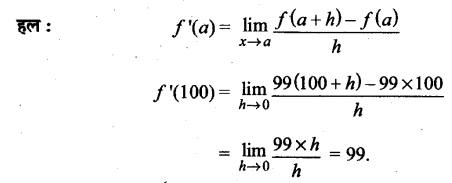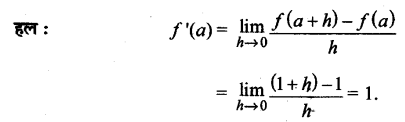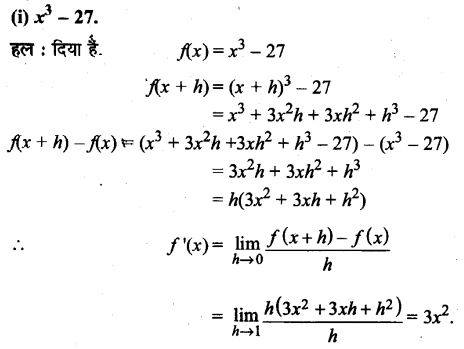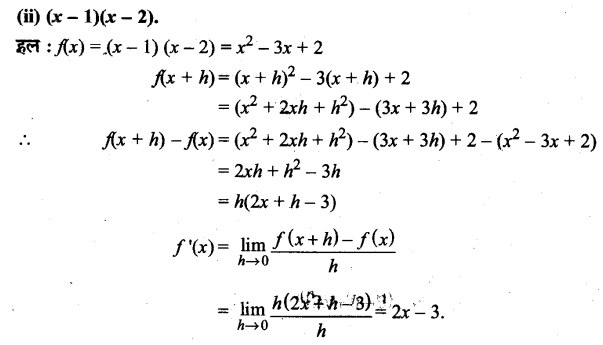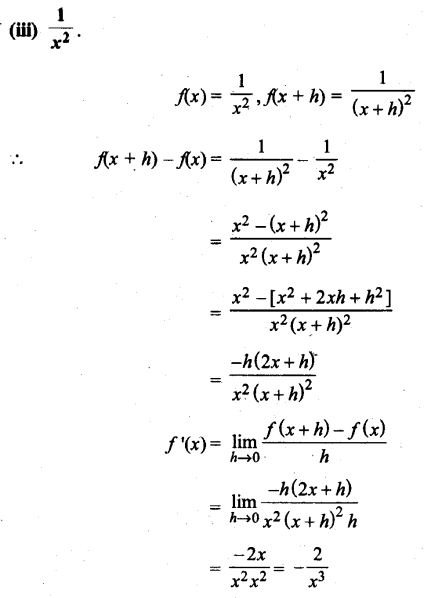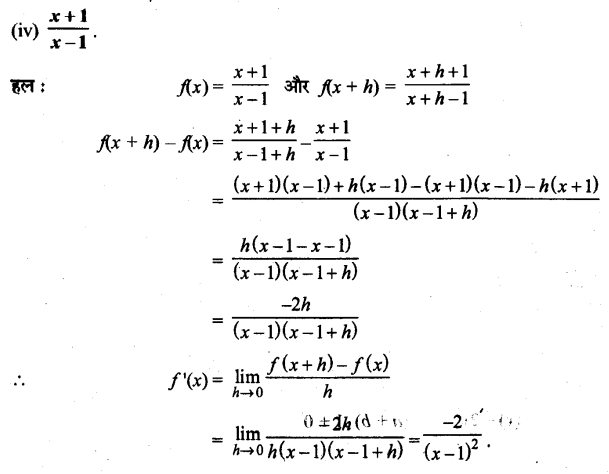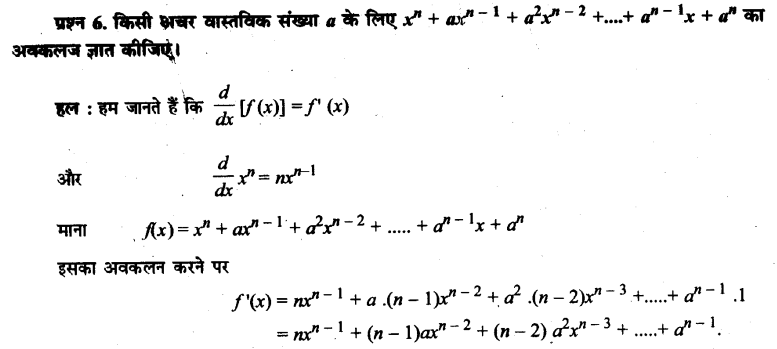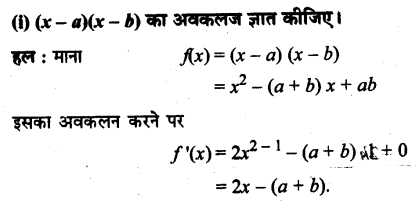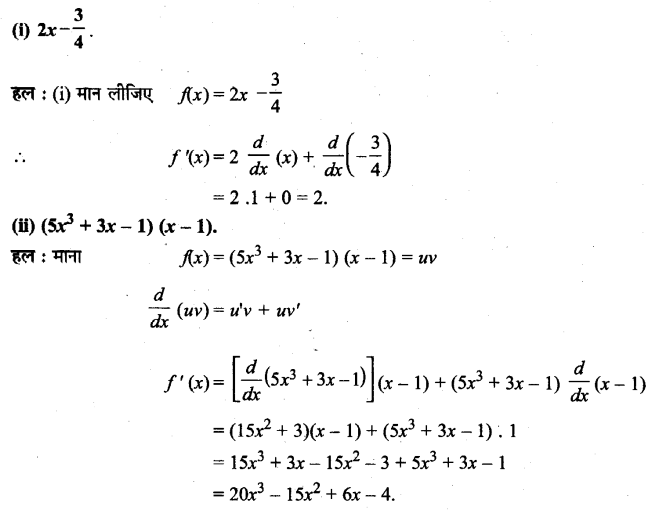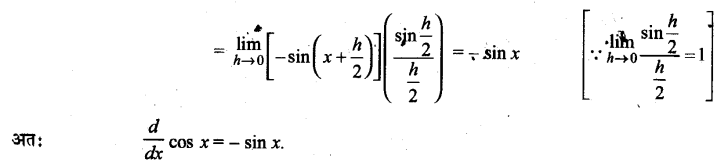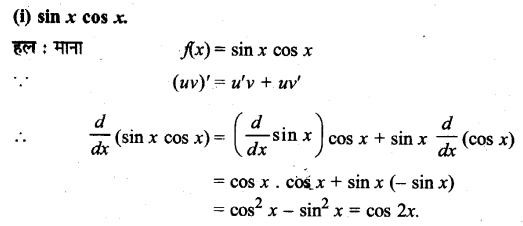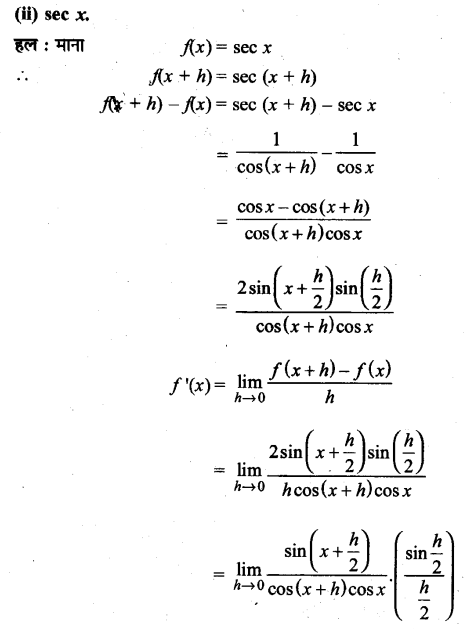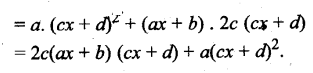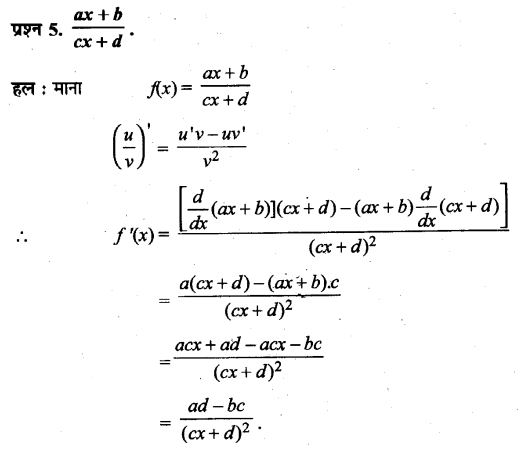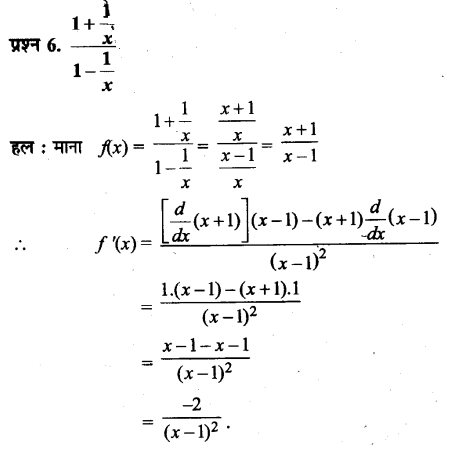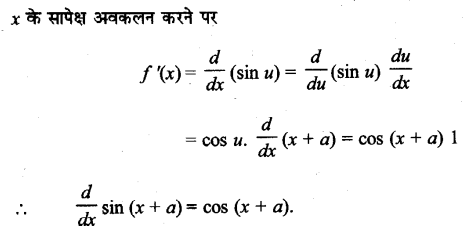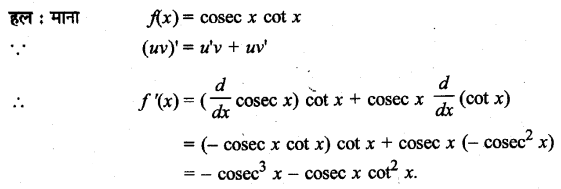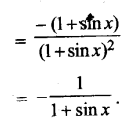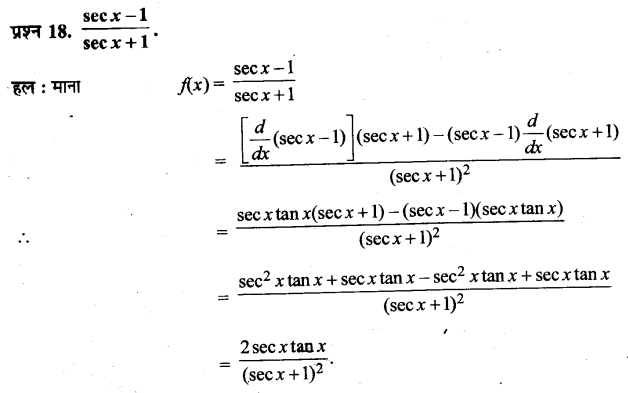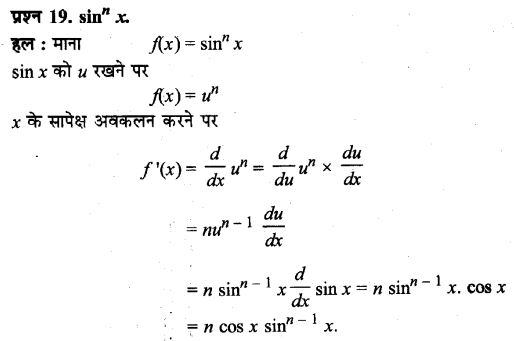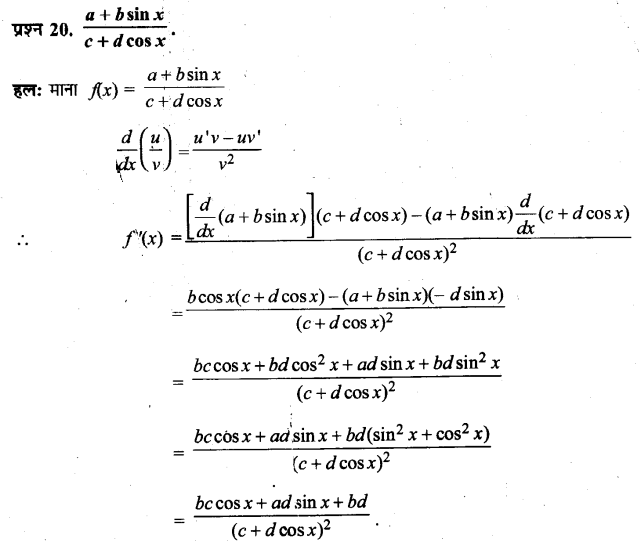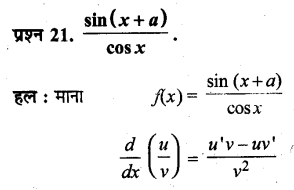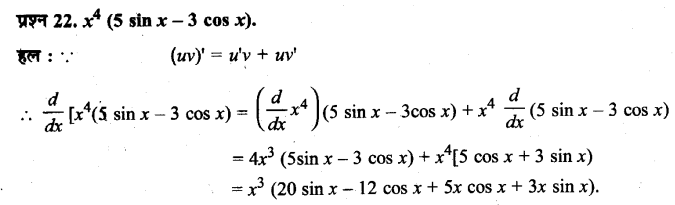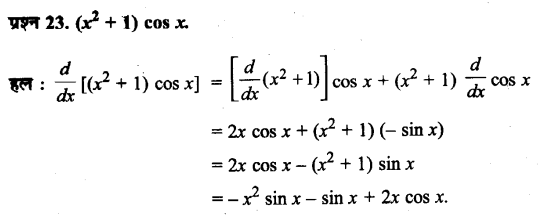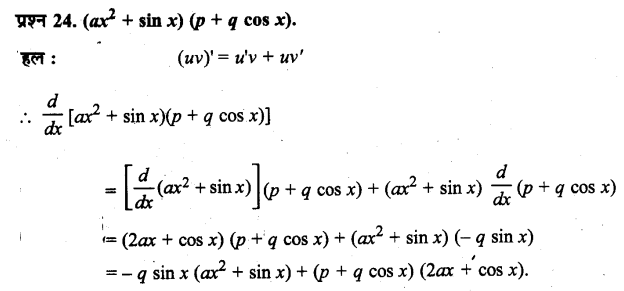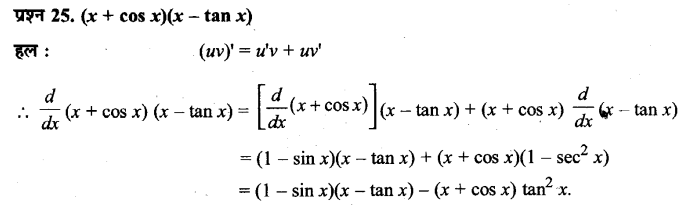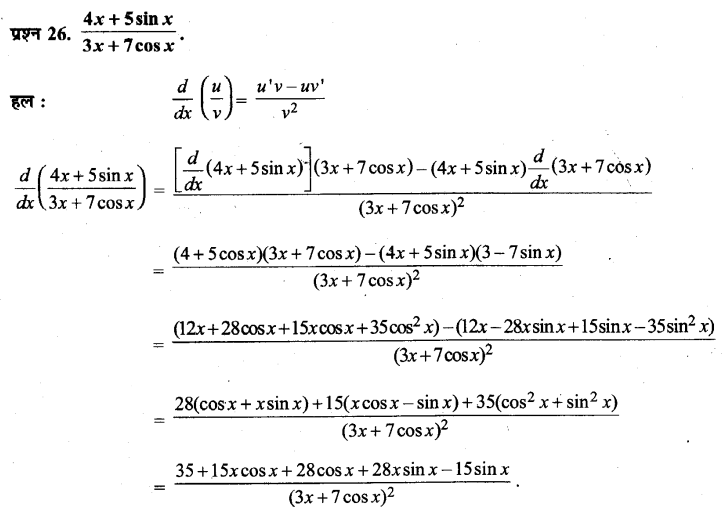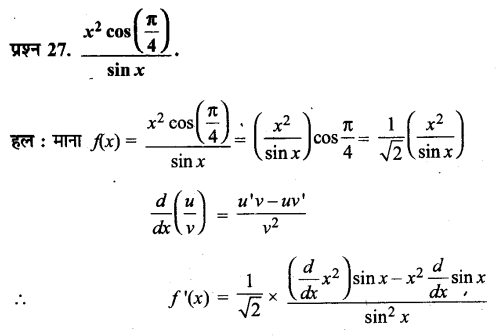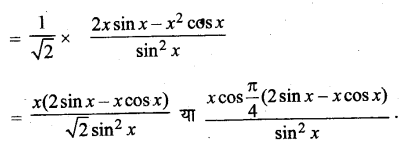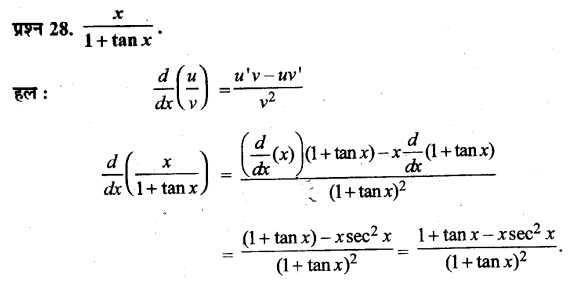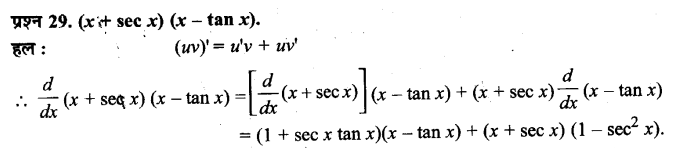UP Board Solutions for Class 11 History Chapter 1 From the Beginning of Time (समय की शुरुआत से)

These Solutions are part of UP Board Solutions for Class 11 History . Here we  given UP Board Solutions for Class 11 History Chapter 1 From the Beginning of Timehave

पाठ्य पुस्तक के प्रश्नोत्तर

संक्षेप में उत्तर दीजिए
प्रश्न 1.
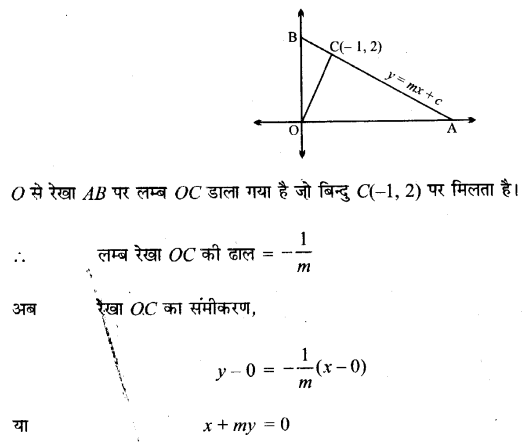
पृष्ठ 27 पर दिए गए सकारात्मक प्रतिपुष्टि व्यवस्था (Positive Feedback Mechanism) को दर्शाने वाले आरेख को देखिए। क्या आप उन निवेशों (Inputs) की सूची दे सकते हैं जो औजारों के निर्माण में सहायक हुए? औजारों के निर्माण से किन-किन प्रक्रियाओं को बल मिला?

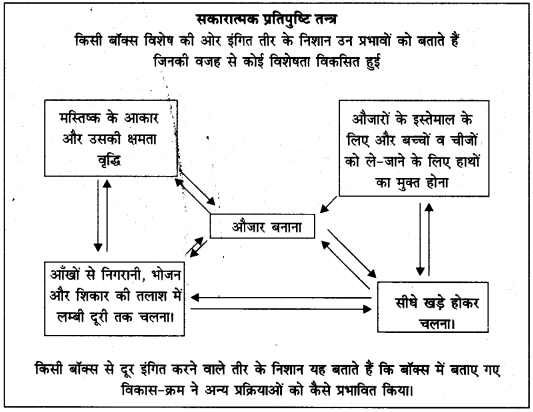
उत्तर :
(I)  निम्नलिखित निवेश (Inputs) औजार निर्माण में सहायक हुए

1. मस्तिष्क के आकार में वृद्धि हुई तथा उसकी क्षमता बढ़ी।
2.  वस्तुओं को उठाने, औजारों को बनाने तथा उपयोग के लिए हाथ स्वतन्त्र थे।
3. मानव अपने पैरों पर सीधा चलने लगा था।
4. आखेट और भोजन के लिए।

(II)  औजारों के निर्माण में निम्नलिखित प्रक्रियाएँ आगे बढ़ीं

1.  मानव की कार्यक्षमता में वृद्धि हो गई।
2.  मानव सरलता से आखेट करने लगा।
3.  वह मांस के बड़े टुकड़ों को छोटे-छोटे आकार में कर सकता था, जिससे उसे खाने में सरलता होने लगी।
4. औजारों के उपयोग से उसने घर बनाना भी सीखा।

प्रश्न 2.
मानव और लंगूर तथा वानरों जैसे स्तनपायियों के व्यवहार तथा शरीर रचना में कुछ समानताएँ पाई जाती हैं। इससे यह संकेत मिलता है कि सम्भवतः मानव का क्रमिक विकास वानरों से हुआ (क) व्यवहार और (ख) शरीर रचना शीर्षकों के अन्तर्गत दो अलग-अलग स्तम्भ बनाइए और उन समानताओं की सूची दीजिए। दोनों के बीच पाए जाने वाले उन अन्तरों का भी उल्लेख कीजिए जिन्हें आप महत्त्वपूर्ण समझते हैं?
उत्तर :
समानताएँ (व्यवहार) :

1. मानव, लंगूर और वानर ये तीनों ‘प्राइमेट’ स्तनपायी प्राणियों के एक अधिक बड़े समूह के अन्तर्गत एक समूह है।
2.  ये तीनों अपनी सन्तानों से प्यार करते हैं।
3.  तीनों चलते समय पैरों और हाथों का उपयोग करते हैं।
4. तीनों ही प्रजनन द्वारा सन्तान को जन्म देते हैं।
5. अपना और अपने बच्चों की सुरक्षा का ध्यान रखते हैं।

शारीरिक समानताएँ :

1.  तीनों के शरीर पर बाल पाए जाते हैं।
2.  सन्तान जन्म लेने से पूर्व अपेक्षाकृत दीर्घकाल तक माता के गर्भ में पलती है।
3. तीनों में स्तनपायी ग्रन्थियाँ पाई जाती हैं।

मानव, लंगूर तथा वानर में अन्तर

1. तीनों की खोपड़ियों की रचना में बड़ा अन्तर है।
2.  तीनों के दाँत भी भिन्न प्रकार के होते हैं।

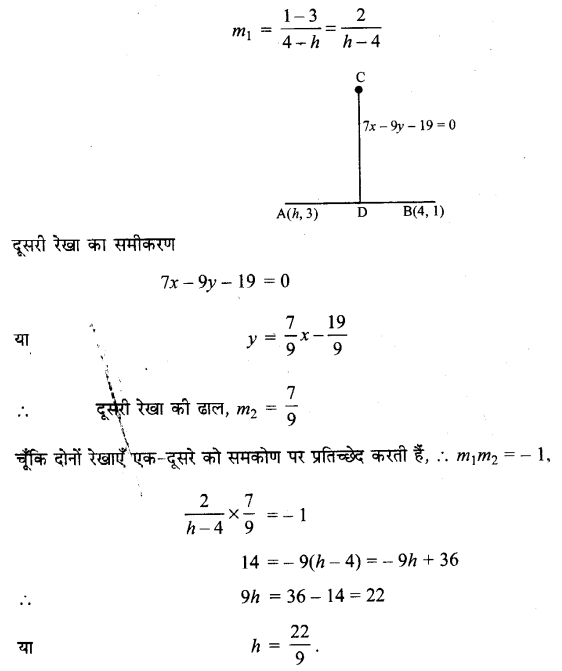
प्रश्न 3.
मानव उद्भव के क्षेत्रीय निरमंतरता मॉडल के पक्ष में दिए गए तर्कों पर चर्चा कीजिए। क्या आपके विचार से यह मॉडल पुरातात्त्विक साक्ष्य को युक्तियुक्त स्पष्टीकरण देता है?
उत्तर :
मानव उद्भव के क्षेत्रीय निरन्तरता मॉडल के पक्ष में निम्नलिखित तर्क दिए गए हैं

1. आधुनिक सभ्य मानवों में सर्वत्र शारीरिक और आनुवंशिक समरूपता पाई जाती है। इस समरूपता का कारण क्षेत्रीय निरन्तरता है।
2. सभी आधुनिक सभ्य मानवों के पूर्वज एक ही क्षेत्र अर्थात् अफ्रीका में उत्पन्न हुए थे और वहीं से अन्य स्थानों पर गए।
3. आधुनिक मानव के जो जीवाश्म इथोपिया में मिले हैं उनसे इनकी पुष्टि होती है।
4. आधुनिक सभ्य समाज में जो शारीरिक भिन्नताएँ दिखाई देती हैं उसका कारण उन लोगों का , परिस्थितियों के अनुसार स्वयं को तैयार करना है। इस प्रकार क्षेत्रीय निरन्तरता मॉडल पुरातात्त्विक साक्ष्य का सही-सही स्पष्टीकरण देता है। जिसकी पुष्टि पुरातात्त्विक साक्ष्य भी करते हैं।

प्रश्न 4.
इनमें से कौन-सी क्रिया के साक्ष्य व प्रमाण पुरातात्विक अभिलेख में सर्वाधिक मिलते हैं
(क) संग्रहण
(ख) औजार बनाना
(ग) आग का प्रयोग
उत्तर :
(ख) औजार बनाना

संक्षेप में निबन्ध लिखिए।

प्रश्न 5.
भाषा के प्रयोग से (क) शिकार करने और (ख) आश्रय बनाने के काम में कितनी मदद . मिली होगी? इस पर चर्चा कीजिए। इन क्रिया-कलापों के लिए विचार सम्प्रेषण के अन्य किन तरीकों का इस्तेमाल किया जा सकता था?
उत्तर :
शिकार करने और आश्रय या घर बनाने के कार्य में भाषा के प्रयोग से मानव को बहुत सुविधा प्राप्त हुई होगी। भाषा-विचार सम्प्रेषण का सर्वाधिक सशक्त माध्यम है। पहले भाषा का रूप हाव-भाव थे। होमोनिड भाषा में हाव-भाव या हाथों का संचालन सम्मिलित था। उच्चारित भाषा से पूर्व मौखिक या अशाब्दिक संचार का प्रयोग किया जाता था। मानव की वाणी का प्रारम्भ सम्भवतया प्राइमेट्स में पाए जाने वाले बुलावों की क्रिया से हुआ। प्रारम्भिक मानव एक-दूसरे को भाषा के माध्यम से शिकार का स्थान और उसका प्रकार बताता होगा। यही नहीं, शिकार किस प्रकार किया जाए, इसकी भी जानकारी प्राप्त करता होगा। कुछ पुरातत्त्वशास्त्रियों का विचार है कि भाषा, कला के साथ-साथ 40000-35000 वर्ष पूर्व विकसित हुई उच्चारित भाषा का विकास कला के साथ निकटतापूर्वक जुड़ा है। इसी कला के माध्यम से मानव को आश्रय या घर की सुविधा के विषय में ज्ञान प्राप्त हुआ होगा। घर बनाने की तकनीक, इसमें प्रयुक्त होने वाली सामग्री की जानकारी भी एक-दूसरे से भाषा के माध्यम से ही प्राप्त हुई होगी। विचार सम्प्रेषण केअन्य तरीकों के रूप में नृत्य, हाव-भाव का प्रदर्शन, चित्रकारी करना, रेखाएँ खींचना, लक्ष्य दिखाना आदि का प्रयोग किया जाता रहा होगा।

प्रश्न 6.
अध्याय के अन्त में दिए गए प्रत्येक कालानुक्रम में से किन्हीं दो घटनाओं को चुनिए और यह बताइए कि इनका क्या महत्त्व है?
उत्तर :
अध्याय के अन्त में दिए युए कालानुक्रम प्रथम की दो सम्मुख घटनाओं का वर्णन इस प्रकार है

1. आस्ट्रेलोपिथेकस : 56 लाख वर्ष पूर्व आस्ट्रेलोपिथिकस का उद्भव हुआ था। इसके मस्तिष्क का आकार होमो की अपेक्षा बड़ा था। जबंड़े अधिक भारी थे। दाँत भी बड़े थे। आस्ट्रेलोपिथिकस नाम लातिनी भाषा के शब्द ‘आस्ट्रेल’ अर्थात् दक्षिणी और यूनानी भाषा के शब्द ‘पिथिक्स’ यानी ‘वानर’ से मिलकर बना है। यह नाम इसलिए ‘दिया गया, क्योंकि मानव के आदिकालीन रूप में उसकी वानर अवस्था के अनेक लक्षण विमान रहे।
2. होमोसेपियन्स : होमोसैपियन्स अथवा आधुनिक मानव जो बुद्धिमान तथा चिन्तनशील कहलाता है। ये 1.9-1.6 लाख वर्ष पूर्व के हैं।

कालानुक्रम द्वितीय की दो घटनाएँ निम्नलिखित हैं

1.  स्वरतन्त्र का विकास : स्वरतन्त्र का सम्बन्ध बोली जाने वाली भाषा से है। पुरातत्त्वविदों
   का विचार है कि होमोबिलस के मस्तिष्क में कुछ ऐसी विशेषताएँ रही होंगी, जिनके कारण वे बोल सके होंगे। स्वरतन्त्र का विकास भी भाषा की उत्पत्ति में महत्त्वपूर्ण स्थान रखता है। स्वरतन्त्र का विकास लगभग 2 लाख वर्ष पूर्व हुआ। वास्तव में इसका सम्बन्ध आधुनिक मानवों से रहा है।
2.  चूल्हों के इस्तेमाल के बारे में पहला साक्ष्य (1,25,000 लाख वर्ष पूर्व) :
   1,25,000 वर्ष । पूर्व गुफाओं तथा खुले निवास क्षेत्र का प्रचलन प्रारम्भ हो गया था। इसके प्रमाण यूरोप के पुरास्थलों से मिलते हैं। दक्षिण फ्रांस में स्थित लेजरेट गुफा की दीवार को 12×4 मीटर आकार के एक निवास स्थान से सटाकर बनाया गया है। इसके अन्दर दो चूल्हे मिले हैं। चूल्हे आग के नियन्त्रित प्रयोग के परिचायक हैं। इसके कई लाभ थे। नियन्त्रित आग का प्रयोग गुफाओं के अन्दर प्रकाश और उष्णता मिलने में सहायक होता था। इससे भोजन भी पकाया जाता था। आग का प्रयोग खतरनाक जानवरों को भगाने में भी किया जाता रहा होगा।

परीक्षोपयोगी अन्य महत्त्वपूर्ण प्रश्नोत्तर

बहुविकल्पीय प्रश्न :
प्रश्न 1.
जीवाश्मों का अध्ययने क्यों आवश्यक है।
(क) जीवित मानव के लिए।
(ख) मानव की लुप्त प्रजातियों के लिए।
(ग) मृत जीवों के लिए ।
(घ) विशिष्ट अध्ययन हेतु
उत्तर :
(ख) मानव की लुप्त प्रजातियों के लिए।

प्रश्न 2.
पशुओं और कुत्तों को कब पालतू बनाया गया?
(क) 7000-6000 ई० पू०
(ख) 5000-4000 ई० पू०
(ग) 2000-3000 ई० पू०
(घ) 1000-1500 ई० पू०
उत्तर :
(क) 7000-6000 ई० पू०

प्रश्न 3.
प्रथम ओलम्पिक खेलों का आयोजन किस देश में हुआ?
(क) यूनान
(ख) एशिया
(ग) यूरोप
(घ) भारत
उत्तर :
(क) यूनान 

प्रश्न 4.
गेहूँ और जौ की खेती कहाँ प्रारम्भ हुई थी?
(क) भारत
(ख) यूनान
(ग) यूरोप
(घ) अफ्रीका
उत्तर :
(ग) यूरोप।

प्रश्न 5.
भीमबेटका के गुफाचित्र भारत के किस प्रदेश में हैं।
(क) गुजरात
(ख) महाराष्ट्र
(ग) मध्य प्रदेश
(घ) राजस्थान
उत्तर :
(ग) मध्य प्रदेश

प्रश्न 6.
प्राज्ञ मानव कहलाता है
(क) आस्ट्रेलोपिथिकस
(ख) होमोहैबिलस
(ग) होमोसैपियन्स
(घ) निअण्डरथल
उत्तर :
(ग) होमोसैपियन्स

प्रश्न 7.
सीधे खड़े होकर पैरों के बल चलने वाले मानव थे
(क) होमोहैबिलस
(ख) होमोइरेक्टस
(ग) होमोसैपियन्स
(घ) निअण्डरथल
उत्तर :
(ख) होमोइरेक्टस

अतिलघु उत्तरीय प्रश्न

प्रश्न 1.
जीवाश्म से क्या आशय है?
उत्तर :
जीवाश्म अत्यन्त प्राचीन वृक्ष, मानव तथा जानवरों के अवशेष हैं। ये पत्थर में परिवर्तित हो । जाते हैं तथा प्रायः चट्टानों में संचित रहते हैं। इस प्रकार जीवाश्म लाखों वर्षों तक सुरक्षित बने रहते हैं।

प्रश्न 2.
‘प्राइमेट्स से आप क्या समझते हैं?
उत्तर :
प्राइमेट्स स्तनधारियों के बड़े समूह के उपसमूह हैं। इसमें लंगूर, वानर तथा मानव को सम्मिलित किया जाता है। प्राइमेट्स का गर्भधारणकाल
अपेक्षाकृत लंबा होता है। इनमें स्तनग्रन्थियाँ पायी जाती हैं।

प्रश्न 3.
प्रारम्भ में मानव ने अपना भोजन किस प्रकार प्राप्त किया?
उत्तर :
प्रारम्भ में मानव ने अपना भोजन जानवरों का शिकार करके, भोजन की तलाश करके अंथवा वृक्षों से प्राप्त कंद-मूल से प्राप्त किया।

प्रश्न 4.
वे कौन-से कारक हैं जो प्रारम्भिक मानव इतिहास को समझने में हमारी सहायता करते हैं?
उत्तर :
निम्नलिखित कारक प्रारम्भिक मानव इतिहास को समझने में हमारी सहायता करते हैं

1.  जीवाश्म,
2.  पत्थर के औजार,
3. गुफाओं की चित्रकारी।

प्रश्न 5.
मानव विज्ञान के अध्ययन के विषय क्या हैं?
उत्तर :
मानव विज्ञान एक ऐसा विषय है जिसमें मानव संस्कृति और मानव जीवविज्ञान के उविकासीय पक्षों का अध्ययन किया जाता है।

प्रश्न 6.
नृवंशशास्त्र (Ethnography) शास्त्र के अध्ययन का विषय क्या है?
उत्तर :
नृवंशशास्त्र के अध्ययन का विषय समकालीन नृजातीय समूहों का विश्लेषणात्मक अध्ययन होता है। इसमें उनके रहन-सहन, खान-पान, आजीविका के साधन, प्रौद्योगिकी आदि की जाँच की जाती है।

प्रश्न 7.
भाषा की उत्पत्ति कब हुई?
उत्तर :
उच्चरित यानी बोली जाने वाली भाषा की उत्पत्ति के विषय में नृतत्त्वशास्त्रियों का मत है कि ‘होमोहैबिलस’ के मस्तिष्क में कुछ ऐसी विशेषताएँ थीं जिनके कारण उसके लिए बोलना सम्भव हुआ। इस प्रकार सम्भवतः भाषा का विकास 20 लाख वर्ष पूर्व हुआ होगा।

प्रश्न 8.
आस्ट्रेलोपिथिकस की खोज किसने की?
उत्तर :
आस्ट्रेलोपिथिकस की खोज सर्वप्रथम मैरी लिके (Mary Leakey) ने 17 जुलाई, 1959 को की थी।

प्रश्न 9.
प्रजातियों का वर्गीकरण कैसे किया गया है?
उत्तर :
आदिकालीन मानवों के अवशेषों को भिन्न-भिन्न प्रजातियों में वर्गीकृत किया गया है। इन प्रजातियों को अक्सर उनकी हड्डियों की रचना में पाए जाने वाले अन्तरों के आधार पर एक-दूसरे से । अलग किया जाता है।

प्रश्न 10.
होमिनिड्स के उपविभाग लिखिए।
उत्तर :
होमिनिड्स के उपविभाग हैं

1. आस्ट्रेलोपिथिकस
2.  होमो

प्रश्न 11.
आस्ट्रेलोपिथिकस तथा होमो के बीच क्या अन्तर है?
उत्तर :
आस्ट्रेलोपिथिकस तथा होमो के बीच मुख्य अन्तर मस्तिष्क के आकार, जबड़ों तथा दाँतों में आस्ट्रेलोपिथिकस मस्तिष्क का आकार होमो की अपेक्षा छोटा होता है। इसके अलावा आस्ट्रेलोपिथिकस के जबड़े होमो के मुकाबले भारी तथा दाँत लम्बे होते हैं।

प्रश्न 12.
पत्थर के औजार बनाने तथा प्रयोग करने के प्रारम्भिक साक्ष्य हमें कहाँ मिले?
उत्तर :
पत्थर के औजार बनाने तथा प्रयोग करने के प्रारम्भिक साक्ष्य हमें अफ्रीका महाद्वीप के इथियोपिया तथा कार्निया में मिले हैं।

प्रश्न 13.
पत्थर के औजारों का प्रयोग सर्वप्रथम किसके द्वारा किया गया?
उत्तर :
आस्ट्रेलोपिथिकस सम्भवतः पत्थर के औजार बनाने वाले सर्वप्रथम थे।

प्रश्न 14.
हादजा कौन है?
उत्तर :
हादजा शिकारियों तथा संग्राहकों का एक छोटा समूह है, जो दक्षिण अफ्रीका में ‘लेक इयासी एक खारे पानी की विभ्रंश घाटी में बनी झील के आस-पास रहते हैं।

प्रश्न 15.
लेजरेट गुफा के पास मिले निवास स्थल में चूल्हे (Hearths) किस बात के प्रतीक हैं।
उत्तर :
चूल्हे इस बात का प्रतीक हैं कि मानव आग का नियन्त्रित प्रयोग जानता था। आग से गुफाओं को गर्म रखने तथा उजाला करने में सहायता मिलती थीं।

प्रश्न 16.
प्रारम्भिक होमिनिड्स के खाद्य स्रोत कौन से थे?
उत्तर :
ऐसा माना जाता है कि प्रारम्भिक होमिनिड्स मृत जानवरों के शरीर में मांस तथा मज्जा प्राप्त करते होंगे। ये जानवर या तो प्राकृतिक रूप से मर जाते होंगे या अन्य जानवरों द्वारा मार दिए जाते होंगे। प्रश्न 17. मानव के सीधे खड़े होने की स्थिति का उसे क्या लाभ मिला? उत्तर-सीधा खड़ा होने तथा पिछले पैरों से चलना सीखना मानव के विकास की सबसे महत्त्वपूर्ण घटना थी। मानव अब स्वयं को दूसरे जानवरों से अलग कर सकता था। खड़ा होने पर मानव के आगे के अंग वस्तुओं को पकड़ने तथा औजारों का हथियारों के रूप में प्रयोग करने के लिए स्वतन्त्र थे।

प्रश्न 18.
मानव इतिहास में प्रमुख निर्णायक अवस्था कब आई?
उत्तर :
मानव इतिहास में प्रमुख निर्णायक अवस्था उस समय आई जब मानव ने भोजन की तलाश से कृषि करना सीखा।

प्रश्न 19.
होमो’ शब्द का अर्थ बताइए।
उत्तर :
‘होमो’ लैटिन भाषा का शब्द है जिसका अर्थ है ‘मानव’।

प्रश्न 20.
नृतत्त्वशास्त्रियों द्वारा सभी प्रजातियों के नाम किन भाषाओं से लिए गए हैं। एक उदाहरण दीजिए।
उत्तर :
नृतत्त्वशास्त्रियों द्वारा सभी प्रजातियों के नाम लैटिन तथा ग्रीक भाषाओं से लिए गए हैं, जैसेआस्ट्रेलोपिथिकस शब्द की उत्पत्ति लैटिन भाषा के ‘आस्ट्रल’ शब्द से हुई है, जिसका अर्थ है दक्षिणी तथा ग्रीक भाषा के शब्द ‘पिथिकोस’ से हुई, जिसका अर्थ है ‘वानर’।

प्रश्न 21.
ओल्डवर्ड गोर्ज क्यों प्रसिद्ध है?
उत्तर :
ओल्डवर्ड गोर्ज से आदिकालीन मानव के अनेक अवशेष मिले हैं, इसलिए यह प्रसिद्ध है।

प्रश्न 22.
आस्ट्रेलोपिथिकस कैसे लुप्त हो गया?
उत्तर :
हिमयुग के प्रारम्भ में तापमान और वर्षा की कमी के कारण जंगल कम हो गए और घास के मैदानों का क्षेत्रफल बढ़ता गया। फलस्वरूप आस्ट्रेलोपिथिकस के प्रारम्भिक रूप लुप्त हो गए।

प्रश्न 23.
गुफाओं में चित्रकारी क्यों की जाती थी?
उत्तर :

1.  शिकार करने में सफलता प्राप्त करने पर।
2.  गुफाएँ संगमस्थल थीं जहाँ लोगों के छोटे-छोटे समूह मिलते थे।

प्रश्न 24.
हादजा जनसमूह का भोजन क्या है?
उत्तर :
हादजा जनसमूह का भोजन 80% वनस्पतिजन्य और शेष 20% मांस और शहद से पूर्ण किया जाता है।

प्रश्न 25.
होमिनिड कहाँ निवास करते थे?
उत्तर :
होमिनिड पेड़ों की शाखाओं पर निवास करते थे।

प्रश्न 26.
आदिकालीन मानव के दो औजारों के नाम लिखिए।
उत्तर :

1. मँड़ासा,
2. हस्तकुठार,
3.  छेनी

लघु उत्तरीय प्रश्न :

प्रश्न 1.
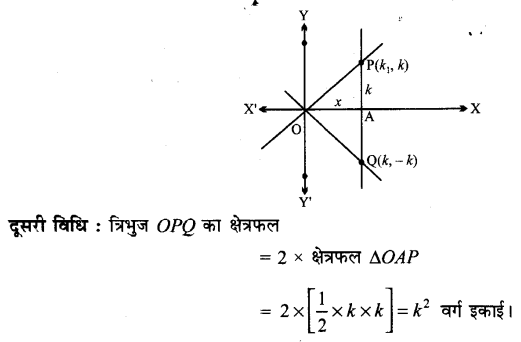
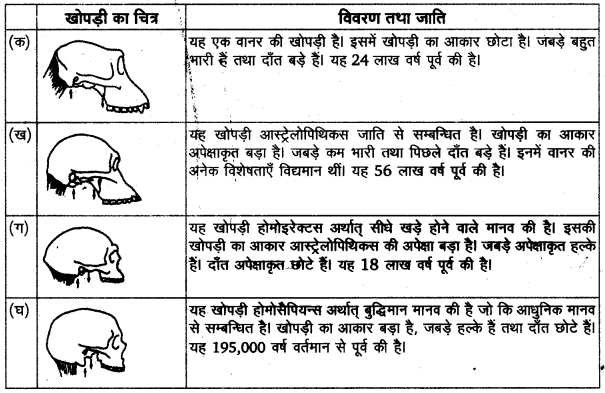
इन चार खोपड़ियों को देखिए

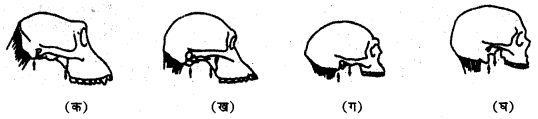
खोपड़ी—क, एक वानर की है।
खोपड़ी—ख, आस्ट्रेलोपिथिकस नामक प्रजाति की है (नीचे देखिए)
खोपड़ी–ग, होमोइरेक्टस (सीखे खड़े होकर चलने वाले आदमी) की है।
खोपड़ी-घ, होमोसेपियन्स (चिन्तनशील/प्राज्ञ मानव) नामक प्रजाति की है। आज के मानव इसी प्रजाति के हैं। इन खोपड़ियों में आप अधिक-से-अधिक जितनी समानताएँ और अन्तर देखते हैं उनकी सूची बनाइए; इस हेतु आप सबसे पहले इन खोपड़ियों का मस्तिष्क खोलो, जबड़ों और दाँतों को भली-भाँति देखिए।
उत्तर :
उपर्युक्त प्रस्तुत चार खोपड़ियाँ क, ख, ग, घ के विषय में हमारे अध्ययन का निष्कर्ष निम्न है

प्रश्न 2.
प्रजाति की प्रमुख विशेषताएँ लिखिए।
उत्तर :
प्रजाति की प्रमुख विशेषताएँ निम्नलिखित हैं
(i) प्रजाति जीवों का एक ऐसा समूह है जिसके नर और मादा सहवास के माध्यम से बच्चे पैदा कर सकते हैं।
(ii) ये बच्चे भी कालान्तर में सहवास करके सन्तान उत्पन्न करते हैं।
(iii) एक प्रजाति विशेष के सदस्य दूसरी प्रजाति के सदस्यों से सहवास करके सन्तान उत्पन्न नहीं कर सकते।
(iv) विभिन्न प्राणियों की आनुवंशिकी भी भिन्न-भिन्न होती है।

प्रश्न 3.
“जीवित प्राणियों में केवल मानवों में ही भाषा पाई जाती है।” स्पष्ट कीजिए।
उत्तर :
विश्व के समस्त जीवित प्राणियों में केवल मानव द्वारा ही भाषा का प्रयोग किया जाता है। भाषा के विकास से जुड़े निम्नलिखित मत हैंहोमोनिड मानव भाषा के रूप में हाव-भाव तथा हाथों की चेष्टा का उपयोग करता था। ध्वनि तथा हाव-भाव और चेहरे के भाव द्वारा अपनी बात समझाना बोल-चाल की भाषा से पूर्व का रूप था। मानव भाषा का प्रारम्भ प्राइमेट्स में पाई गई आवाजों से हुआ। प्रारम्भिक अवस्था में मानव के पास भाषा के रूप में कम ध्वनियाँ रही होंगी, धीरे-धीरे इनका विकास भाषा में हुआ होगा।

प्रश्न 4.
आदिमानव के दो पैरों पर चलने से क्या लाभ हुए?
उत्तर :
आदिमानव जब दो पैरों पर चला तो उसे निम्नलिखित लाभ हुए

1. दो पैरों पर खड़े होकर चलने की क्षमता के कारण उसके हाथ वस्तुओं को उठाकर ले जाने के लिए मुक्त हो गए।
2.  हाथों के प्रयोग से सन्तुलन बना और दो पैरों पर खड़े होकर चलने की कुशलता भी बढ़ गई।
3.  हाथों का इस्तेमाल औजार बनाने में काम आया।
4. चलने से उसकी शारीरिक ऊर्जा की खपत अन्य कार्यों में होने लगी।

प्रश्न 5.
आकृति (क) चिम्पैंजी की ठीक व सूक्ष्म पकड़ दर्शाती है।

आकृति (ख) होमिनिड़ की दुरुस्त व सूक्ष्म पकड़ दर्शाती है। आकृति (ग) मनुष्य के हाथ की सशक्त (Power) पकड़ दर्शाती है। हाथ की सशक्त पकड़ का विकास सम्भवतः ठीक व सूक्ष्म पकड़ से पहले ही हुआ होगा। चिम्पैंजी की ठीक पकड की तुलना मनुष्य के हाथ की ठीक व सूक्ष्म पकड़ से कीजिए। उन कामों की सूची बनाइए जिन्हें करते समय आप ठीक व पकड़ सूक्ष्म का इस्तेमाल करते हैं। आप किन-किन कामों को करने के लिए सशक्त पकड़ का प्रयोग करते हैं?
उत्तर :

हम यथार्थ मात्रता पकड़ के आधार पर औजार बनाने, छोटी-छोटी वस्तुओं को उठाने तथा उन्हें पकड़ने आदि का काम करते हैं। सशक्त पकड़ के आधार पर हम किसी वस्तु; जैसे-क्रिकेट का बैट, हॉकी, भाला, साइकिल, स्कूटर का हैंडिल आदि को पकड़ने का कार्य करते हैं।

प्रश्न 6.
कुछ स्थानों पर मानव-निर्मित औजार एक ही स्थान पर भारी मात्रा में मिले हैं। इसका क्यो कारण है?
उत्तर :
कुछ स्थानों, जैसे कीनिया में किलोंबे और ओलोर्जेसाइली में हजारों की संख्या में शल्य उपकरण और हस्तकुठार प्राप्त हुए हैं। ये 7 लाख से 5 लाख वर्ष प्राचीन हैं। एक ही स्थान पर हजारों की संख्या में औजार मिलने का कारण यह हो सकता है कि जिन स्थानों पर खाद्य प्राप्ति के संसाधन अधिक मात्रा में उपलब्ध थे वहाँ बार-बार आते-जाते रहे होंगे। वे लोग जाते समय वहाँ अपने क्रिया-कलापों और उपस्थिति के चिह्न; जैसे-शिल्प वस्तुएँ, औजार आदि छोड़ गए होंगे। धीरे-धीरे इन स्थानों पर औजारों का ढेर लग गया। जहाँ लोग कम आते थे वहाँ ये वस्तुएँ कम पाई गईं।

प्रश्न 7.
मानव द्वारा आखेट या शिकार कब प्रारम्भ किया गया?
उत्तर :
मानव द्वारा आखेट लगभग 5,00,000 वर्ष पूर्व प्रारम्भ किया गया। योजनाबद्ध तरीके से सोच-समझकर बड़े स्तनपायी जानवरों का शिकार और उनका वध करने का सबसे प्राचीन स्पष्ट साक्ष्य दो स्थानों से मिला है—दक्षिण इंग्लैण्ड में बॉक्स ग्रोव से 5 लाख वर्ष पूर्व का और जर्मनी में । शोनिजन से 4 लाख वर्ष पूर्व का। लगभग 35 हजार वर्ष पूर्व मानव के योजनाबद्ध तरीके से शिकार करने का साक्ष्य कुछ यूरोपीय खोज स्थलों से मिलता है। ऐसा लगता है कि पूर्व मानव
ने कुछ ऐसे स्थल जैसे कि नदी के पास दोलनी वेस्तोनाइस (चेक गणराज्य) को सोच-समझकर शिकार के लिए चुना था। रेन्डियर और घोड़ा जैसे स्थान बदलने वाले जानवरों के झुण्ड के झुण्ड पतझड़ और वसन्त के मौसम में सम्भवतः उस नदी के पार जाते थे आर तब उनका बड़े पैमाने पर शिकार किया जाता था।

चित्र-यूरोप

प्रश्न 8.
आदिमानव की औजार बनाने की पंच ब्लेड विधि को सचित्र समझाइए।
उत्तर-लगभग 11000 वर्ष पूर्व सिले हुए कपड़ों के प्राथमिक प्रमाण मिलते हैं। पंच ब्लेड विधि के द्वारा छोटे रूखानी जैसे औजार बनाए जाने लगे। इनकी सहायता से हड्डियों, बारहसिंगों के सींग, हाथीदाँत या लकड़ी पर नक्काशी की जाने लगी।

पंच ब्लेड विधि (The Punch Blade Technique)

(क) एक बड़े पत्थर का ऊपरी भाग पत्थर के हथौड़े से हटाया जाता है।
(ख) इससे एक सपाट तल (Flat Surface) बनता है जिसे चोट मारने वाला प्लेटफार्म (Striking platform) कहा जाता है।
(ग) इसे हथौड़े तथा पंच के द्वारा पीटा जाता है, जो कि हड्डी या बारहसिंगे के सींग के बने होते हैं।
(घ) इससे ब्लेड बनते हैं जिन्हें चाकुओं या रूखानियों (Chisels) के रूप में हड्डी बारहसिंगे की सींग, हाथीदाँत या लकड़ी पर नक्काशी अथवा खुदाई (Engraving) के लिए प्रयोग किया जा सकता है।
(ङ) हड्डी पर नक्काशी (Engraving) का एक उदाहरण। इस पर जानवरों के चित्रों को देखें।

एक फेंकने वाली बरछी (A Spear Hrowner)

प्रश्न 9.
होमोनिड्स के क्रियाकलाप के विषय में आप क्या जानते हैं?
उत्तर :
प्रस्तुत चित्र से स्पष्ट होता है कि एक ही स्थल पर होमोनिड्स, अन्य प्राइमेट्स तथा मांसाहारी पाए गए हैं। नृतत्त्वशास्त्रियों का विचार है कि प्रारम्भिक होमोनिड्स जैसे होमोहैबिलस जहाँ कहीं भी भोजन मिलता था उसका अधिकांश उपयोग करते थे। विभिन्न स्थानों पर सोते थे और अपना अधिकांश समय पेड़ों पर बिताते थे।

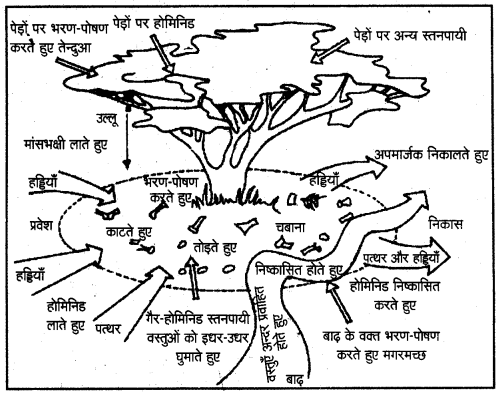
दीर्घ उत्तरीय प्रश्न :

प्रश्न 1.
आधुनिक मानव की उत्पत्ति के स्थान के विषय में प्रतिस्थापन मॉडल और क्षेत्रीय निरन्तरता मॉडल के बिन्दुओं की विवेचना कीजिए।
उत्तर :
आधुनिक मानव की उत्पत्ति के विषय में हुई खोजों के पश्चात् वैज्ञानिकों ने दो मॉडल विकसित किए|

1. क्षेत्रीय निरन्तरता मॉडल,
2. प्रतिस्थापन मॉडल।

 

1.  क्षेत्रीय निरन्तरता मॉडल : इस प्रतिरूप के अनुसार भिन्न-भिन्न प्रदेशों में रहने वाले होमोसैपियन्स का आधुनिक मानव के रूप में विकास धीरे-धीरे अलग गति से हुआ। इसीलिए आधुनिक मानव विश्व के विभिन्न भागों में पहली बार अलग अलग स्वरूप में दिखाई दिया।यह तर्क वर्तमान मानव के लक्षणों की विभिन्नताओं पर आधारित है।
   
2.  प्रतिस्थापन मॉडल : प्रतिस्थापन मॉडल में यह कल्पना की गई है कि मानव के सभी प्राचीन रूप, चाहे वे कहीं भी थे, बदल गए। उनका स्थान पूरी तरह आधुनिक मानव ने ले लिया। इस विचारधारा का समर्थन इस प्रमाण से होता है कि आधुनिक मानव में सभी जगह शारीरिक और जाननिक समरूपता दिखाई देती है।
   

प्रश्न 2.
प्रारम्भिक मानव के भोजन प्राप्त करने के तरीकों की विवेचना कीजिए।
उत्तर :
पुरातात्त्विक प्रमाणों से पता चलता है कि प्रारम्भिक मानव दो तरीकों से भोजन प्राप्त करते थे|

1.  संग्रहण द्वारा।
2. आखेट (शिकार) द्वारा।

 

1.  संग्रहण द्वारा : यत्र-तत्र बिखरे हुए खाद्य पदार्थों को खोजकर एकत्र करना, बिखरे हुए दाने, बीजों आदि को बटोरना और जल से मछली पकड़ना आदि संग्रहण है। प्रारम्भिक मानव अपने भोजन के लिए सम्भवतया इसी संग्रहण प्रक्रिया का सहारा लेता होगा। इस प्रक्रिया के कोई साक्ष्य प्राप्त नहीं हुए हैं।
   आखेट (शिकार) द्वारा : प्रारम्भिक मानव का भोजन प्राप्त करने का दूसरा प्रमुख तरीका आखेट था। प्राप्त साक्ष्यों से ज्ञात होता है कि आदिकालीन होमिनिड मृत जानवरों की मांस-मज्जा खुरचकर निकाल लेते थे और उसका भोजन के रूप में प्रयोग करते थे। इसके लिए वे पत्थर के औजारों का इस्तेमाल करते थे। ये औजार दक्षिण अफ्रीका में इथोपिया और केन्या में मिले हैं। सम्भवतया ये लोग स्तनपायी जानवरों, पक्षियों, चूहे, साँप और कीड़े-मकौड़ों को  अपना आहार बनाते होगे। आखेट या शिकार द्वारा भोजन प्राप्त करने का तरीका मानव ने 5 लाख वर्ष पूर्व ही अपना लिया था। आस्ट्रेलोपिथिकस सम्भवतः पत्थर के औजार बनाने वाले सबसे पहले थे। इनसे मांस-मज्जा खुरचकर वे उसका प्रयोग भोजन में करते थे।
   

योजनाबद्ध आखेट करने के सर्वाधिक प्राचीन प्रमाण दो स्थलों से प्राप्त हुए हैं ।

1. दक्षिणी इंग्लैण्ड में बॉक्स ग्रोव से—यह 5 लाख वर्ष पूर्व का है।
2. जर्मनी में स्कोनिंजन से—यह 4 लाख वर्ष पूर्व का है।
   वर्तमान समाज में भी अनेक जनजातियाँ संग्रहण और आखेट द्वारा अपना भरण-पोषण करती हैं, किन्तु इनकी तुलना प्राचीन समाज से नहीं की जा सकती है।

प्रश्न 3.
होमों का क्या अर्थ है? होमो जीवाश्मों का वर्गीकरण किस प्रकार किया गया है?
उत्तर :
‘होमो’ लैटिन भाषा का शब्द है जिसका अर्थ है ‘मानव’। नृतत्त्वशास्त्रियों द्वारा होमो को अनेक प्रजातियों में बाँटा गया है तथा प्रजातियों को उनकी विशिष्टताओं के आधार पर अलग-अलग नाम दिए गए हैं। होमो जीवाश्मों को निम्नलिखित वर्गों में बाँटा गया है

1. होमोबिलस : औजार बनाने वाले।
2.  होमोइरेक्टस : सीधे खड़े होकर पैरों के बल चलने वाले।
3.  होमोसेपियन्स : चिन्तनशील या प्राज्ञ मानव।
   
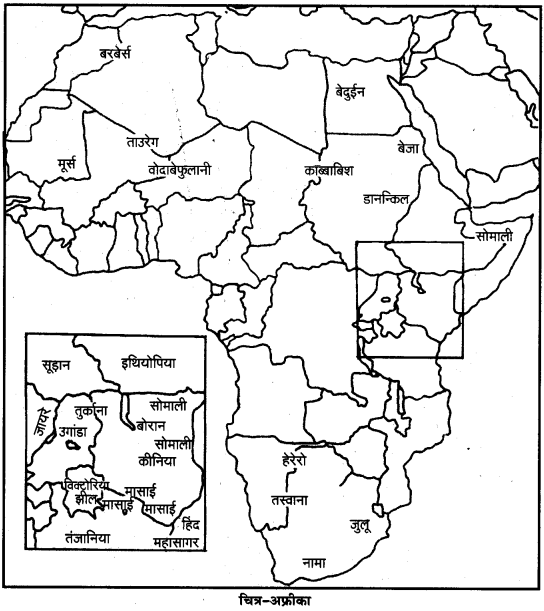
   होमोहबिलस के जीवाश्म इथियोपिया में ओमो तथा तंजानिया के ओल्ड्वर्ड गोर्ज में मिले हैं। होमोइरेक्टस के प्राचीनतम जीवाश्म अफ्रीका के कूबीफोरा तथा पश्चिमी तुर्काना, केन्या और जावा  के मोड़जोकर्ता तथा संकरित में मिले थे। होमोसैपियन्स आधुनिक मानव है। यह बुद्धिमान तथा चिन्तनशील माना जाता है।

विश्व में मानव प्रजातियों का विकास’

We hope the UP Board Solutions for Class 11 History Chapter 1 From the Beginning of Time help you. If you have any query regarding UP Board Solutions for Class 11 History Chapter 1 From the Beginning of Time , drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Maths Chapter 10 Straight Lines (सरल रेखाएँ)

These Solutions are part of UP Board Solutions for Class 11 Maths. Here we have given UP Board Solutions for Class 11 Maths Chapter 10 Straight Lines (सरल रेखाएँ).

प्रश्नावली 10.1

प्रश्न 1.
कार्तीय तल में एक चतुर्भुज खींचिए जिसके शीर्ष (-4, 5), (0, 7), (5, -5) और (-4, -2) हैं। इसका क्षेत्रफल भी ज्ञात कीजिए।
हल:
दिए गए बिन्दुओं (-4, 5), (0, 7), (5, -5) और (-4, -2) क्रमशः A, B, C, D द्वारा दर्शाया गया है। चतुर्भुज ABCD को दो भागों में बाँटा गया है।
जो ΔABD तथा ΔBDC के रूप में हैं।

प्रश्न 2.
2 भुजा के समबाहु त्रिभुज का आधार y-अक्ष के अनुदिश इस प्रकार है कि आधार का मध्य बिन्दु मूल बिन्दु पर है। त्रिभुज के शीर्ष ज्ञात कीजिए।
हल:
माना ΔABC की भुजा BC, y-अक्ष के अनुदिश है जिसका मध्य बिन्दु मूल बिन्दु O है।
⇒ B और C के शीर्ष बिन्दु (0, a) और (0, -a) हैं।
बिन्दु A, x-अक्ष पर है, AB = 2a, OB = a

प्रश्न 3.
P(x₁, y₁) और Q(x₂, y₂) के बीच की दूरी ज्ञात कीजिए जब :
(i) PQ, y-अक्ष के समांतर है,
(ii) PQ, x-अक्ष के समांतर है।
हल:
(i) जब कोई रेखा y-अक्ष के समांतर होती है तो उसे पर जितने भी बिन्दु होंगे उनके x-निर्देशांक बराबर होते हैं अर्थात् x₁ = x₂.

(ii) जब कोई रेखा x-अक्ष के समांतर लेती है तो उसके प्रत्येक बिन्दु का y-निर्देशांक बराबर होता है।
अर्थात्

प्रश्न 4.
x-अक्ष पर एक बिन्दु ज्ञात कीजिए जो (7, 6) और (3, 4) बिन्दुओं से समान दूरी पर है।
हल:
मान लीजिए x-अक्ष पर बिन्दु A(a, 0), बिन्दु B(7, 6) और C(3, 4) से समान दूरी पर है।

प्रश्न 5.
रेखा की ढाल ज्ञात कीजिए जो मूल बिन्दु और P(0, -4) तथा B(8, 0) बिन्दुओं को मिलाने वाले रेखाखंड के मध्य बिन्दु से जाती है।
हल:
बिन्दु P(0, -4) और B(8, 0) को मिलाने वाले रेखाखंड का मध्य बिन्दु

प्रश्न 6.
पाइथागोरस प्रमेय के प्रयोग बिना दिखलाइए कि बिन्दु (4, 4), (3, 5) और (-1, -1) एक समकोण त्रिभुज के शीर्ष हैं।
हल:
माना दिए गए बिन्दु A(4, 4), B(3, 5) और C(-1, -1) हैं, तब

प्रश्न 7.
उस रेखा का समीकरण ज्ञात कीजिए जो y-अक्ष की धन दिशा से वामावर्त मापा गया 30° का कोण बनाती है।
हल:
माना रेखों OP, y-अक्ष से वामावर्त 30° का कोण बनाती है।
x- अक्षे, की धन दिशा से 90° + 30° = 120° को कोण बनाती है।
रेखा OP की ढाल = tan 120 = -√3

यह रेखा मूलबिन्दु (0, 0) से होकर जाती है। रेखा का बिन्दु ढाल रूप है।
y – y₁ = m(x – x₁)
OP का समीकरण y – 0 = -√3 (x – 0)
y = -√3 x.

प्रश्न 8.
x का वह मान ज्ञात कीजिए जिसके लिए बिन्दु (x, -1), (2, 1) और (4, 5) संरेख हैं।
हल:
मान लीजिए बिन्दु A (x, -1), B (2, 1), C (4, 5) सरेख हैं यदि,
AB की ढाल = BC की ढाल

प्रश्न 9.
दूरी सूत्र का प्रयोग किए बिना दिखलाइए कि बिन्दु (-2, -1), (4, 0), (3, 3) और (-3, 2) एक समांतर चतुर्भुज के शीर्ष हैं।
हल:
मान लीजिए एक चतुर्भुज के शीर्ष A(-2, -1), B(4, 0), C(3, 3), तथा D(-3, 2) हैं।

प्रश्न 10.
x-अक्ष और (3, -1) और (4, -2) बिन्दुओं को मिलाने वाली रेखा के बीच का कोण ज्ञात कीजिए।
हल:
माना A(3, -1), B(4, -2) को मिलाने वाली रेखा AB की ढाल = [latex]\frac { -2+1 }{ 4-3 }[/latex] = [latex]\frac { -1 }{ 1 }[/latex] = -1
यदि x-अक्ष और AB के बीच से कोण हो, तो
tan θ = -1 = tan 135°
θ = 135°.

प्रश्न 11.
एक रेखा की ढाल दूसरी रेखा की ढाल का दुगुना है। यदि दोनों के बीच के कोण की स्पर्शज्या (tangent) [latex]\frac { 1 }{ 3 }[/latex] है तो रेखाओं की ढाल ज्ञात कीजिए।

प्रश्न 12.
एक रेखा (x1, y1) और (h, k) से जाती है। यदि रेखा की ढाल m है तो दिखाइए k – y₁ = m (h – x₁).
हल:
माना रेखा AB बिन्दु A(x₁, y₁) और B(h, k) से गुजरती हो, तब

प्रश्न 13.
यदि तीन बिन्दु (h, 0), (a, b) और (0, k) एक रेखा पर हैं तो दिखाइए कि [latex]\frac { a }{ h } +\frac { b }{ k } = 1[/latex]
हल:
मान लीजिए बिन्दु A (h, 0), B(a, b), तथा C(0, k) एक रेखा पर हों, तब

प्रश्न 14.
जनसंख्या और वर्ष के निम्नलिखित लेखाचित्र पर विचार कीजिए। (देखिए आकृति में) रेखा AB की ढाल ज्ञात कीजिए और इसके प्रयोग से बताइए कि वर्ष 2010 में जनसंख्या कितनी होगी ?
हल:
दी गयी आकृति में रेखा AB बिन्दु A(1985, 92) और B(1995, 97) से होकर जाती है।

प्रश्नावली 10.2

प्रश्न 1 से 8 तक रेखा का समीकरण ज्ञात कीजिए जो दिए गए प्रतिबंधों को संतुष्ट करता है।

प्रश्न 1.
x-अक्ष और y-अक्ष के समीकरण लिखिए।
हल:
x-अक्ष का समीकरण y = 0.
तथा y-अक्ष का समीकरण x = 0.

प्रश्न 2.
ढाल [latex]\frac { 1 }{ 2 }[/latex] और बिन्दु (-4, 3) से जाने वाली।
हल:
ढाल m = [latex]\frac { 1 }{ 2 }[/latex], बिन्दु (-4, 3)
अभीष्ट रेखा का समीकरण
y – y₁ = m(x – x₁)
y – 3 = [latex]\frac { 1 }{ 2 }[/latex] (x + 4)
2y – 6 = x + 4
x – 2y + 10 = 0.

प्रश्न 3.
बिन्दु (0, 0) से जाने वाली और ढाल m वाली।
हल:
दिया है : बिन्दु (0, 0), ढाल = m
ढाल m, तथा (x₁, y₁) से जाने वाली रेखा का समीकरण
y – y₁ = m(x – x₁)
y – 0 = m(x – 0)
अतः अभीष्ट समीकरण y = mx.

प्रश्न 4.
बिन्दुः(2, 2√3) से जाने वाली और x-अक्ष से 75° के कोण पर झुकी हुई।
हल:
चूँकि रेखा x-अक्ष के साथ 75° पर झुकी हुई है, तब रेखा की ढाल
m = tan 75° = tan (45° + 30°)

प्रश्न 5.
मूल बिन्दु के बाईं ओर ४-अक्ष को 3 इकाई की दूरी पर प्रतिच्छेद करने तथा ढाल -2 वाली।
हल:
मूल बिन्दु से बाईं ओर 3 इकाई की दूरी पर स्थित बिन्दु (-3, 0) होगा तथा ढाल m = – 2 m तथा (x₁, y₁) के द्वारा, रेखा का समीकरण,
y – y₁ = (x – x₁)
यहाँ x₁ = -3 तथा y₁ = 0 रखने पर,
y – 0 = -2 (x + 3) यो
y = -2x – 6
2x + y + 6 = 0.

प्रश्न 6.
मूल बिन्दु से ऊपर y-अक्ष को 2 इकाई की दूरी पर प्रतिच्छेद करने वाली और x-अक्ष की धन दिशा के साथ 30° का कोण बनाने वाली।
हल:
मूल बिन्दु से y-अक्ष पर 2 इकाई की दूरी पर स्थित बिन्दु (0, 2) होगा। x-अक्ष की धन दिशा के साथ रेखा 30° का कोण बनाती है।

प्रश्न 7.
बिन्दुओं (-1, 1) और (2, -4) से जाते हुए।

प्रश्न 8.
उस रेखा का समीकरण ज्ञात कीजिए जिसकी मूल बिन्दु से लांबिक दूरी 5 इकाई और लंब धन x-अक्ष से 30° को कोण बनाती है।
हल:
हम जानते हैं कि लंबे रूप में रेखा AB का समीकरण,

प्रश्न 9.
ΔPQR के शीर्ष P(2, 1), Q(-2, 3) और R(4, 5) हैं। शीर्ष R से जाने वाली माध्यिका का समीकरण ज्ञात कीजिए।

प्रश्न 10.
(-3, 5) से होकर जाने वाली और बिन्दु (2, 5) और (-3, 6) से जाने वाली रेखा पर लंब रेखा का समीकरण ज्ञात कीजिए।
हल:
बिन्दु A(2, 5) और B(-3, 6) से होकर जाने वाली रेखा का ढाल

प्रश्न 11.
एक रेखा (1, 0) तथा (2, 3) बिन्दुओं को मिलाने वाली रेखाखंड पर लम्ब है तथा उसको 1 : n के अनुपात में विभाजित करती है। रेखा का समीकरण ज्ञात कीजिए।
हल:
रेखा AB बिन्दु A(1, 0) तथा B(2, 3) से होकर जाती है।

प्रश्न 12.
एक रेखा का समीकरण ज्ञात कीजिए जो निर्देशांक अक्षों से समान अंत:खण्ड काटती है और बिन्दु (2, 3) से जाती है।
हल:
(i) रेखा AB बिन्दु P(2, 3) से होकर जाती है और निर्देशांक अक्षों पर समान अंत:खंड बनाती है।
OA = OB
∠BAO = 45°
∠BAX = 135°

AB की ढाल, m = tan 135° = -1
रेखा का समीकरण, y – y₁ = m(x – x₁)
जहाँ x₁ = 2, y₁ = 3 तथा m = -1
y – 3 = -1 (x – 2)
x + y – 5 = 0
x + y = 5.

प्रश्न 13.
बिन्दु (2, 2) से जाने वाली रेखा का समीकरण ज्ञात कीजिए जिसके द्वारा अक्षों से कटे अंत:खंडों का योम 9 है।
हल:
मान लीजिए P(2, 2) से होकर जाने वाली रेखा से अक्षों पर बने अंतः खंड a तथा b हैं।

प्रश्न 14.
बिन्दु (0, 2) से जाने वाली और धन x-अक्ष से [latex]\frac { 2\pi }{ 3 }[/latex] के कोण बनाने वाली रेखा का समीकरण ज्ञात कीजिए। इसके समांतर और y-अक्ष को मूल बिन्दु से 2 इकाई नीचे की दूरी पर प्रतिच्छेद करती हुई रेखा का समीकरण भी ज्ञात करो।
हल:
माना एक रेखा PQ बिन्दु P(0, 2) से होकर जाती है और धन x-अक्ष के साथ [latex]\frac { 2\pi }{ 3 }[/latex] का कोण बनाती है।

प्रश्न 15.
मूल बिन्दु से किसी रेखा पर डाला गया लम्ब रेखा से बिन्दु (-2, 9) पर मिलता है। रेखा का समीकरण ज्ञात कीजिए।
हल:
मान लीजिए रेखा AB पर मूल बिन्दु से डाला गया लम्ब AB पर मिलता है।

प्रश्न 16.
तांबे की छड़ की लम्बाई L (सेमी में) सेल्सियस ताप C का रैखिक फलन है। एक प्रयोग में यदि L = 124.942, जब C = 20 और L = 125.134 जब C = 110 हो, तो L को C के पदों में व्यक्त कीजिए।
हल:
L ताप C का रैखिक फलन है।
(20, 124.942), (110, 125.134) इसका रैखिक फलन है। इन दो बिन्दुओं से संतुष्ट फलन

प्रश्न 17.
किसी दूध भण्डार का स्वामी प्रति सप्ताह 980 लीटर दूध, 14 रू प्रति लीटर के भव से और 1220 लीटर दूध 16 रू प्रति लीटर के भाव से बेच सकता है। विक्रय मूल्य तथा मांग के मध्य के संबंध को रैखिक मानते हुए ज्ञात कीजिए कि प्रति सप्ताह वह कितना दूध 17 रू प्रति लीटर के भाव से बेच सकता है?
हल:
दूध के भाव और मात्रा में रैखिक सम्बन्ध है। यह रेखा दो बिन्दुओं (14, 980), (16, 1220) से होकर जाती है।
इससे प्राप्त रेखा का समीकरण,

प्रश्न 18.
अक्षों के बीच रेखाखंड का मध्य बिंदु P(a, b) है। दिखाइए कि रेखा का समीकरण [latex]\frac { x }{ a } +\frac { y }{ b } =\quad 2[/latex]
हल:
माना रेखा AB अक्षों पर p और q अंत:खंड बनते हैं।
बिन्दु A और B के क्रमशः निर्देशांक (p, 0) और (0, q) हैं।

प्रश्न 19.
अक्षों के बीच रेखाखण्ड को बिन्दु R(h, k), 1 : 2 के अनुपात में विभक्त करता है। रेखा का समीकरण ज्ञात कीजिए।
हल:
अक्षों के बीच रेखाखंड AB को R(h, k) AR : RB = 1 : 2 के अनुपात में विभक्त करता है।
मान लीजिए अक्षों पर अंत:खण्ड OA = a और OB = b है।

प्रश्न 20.
रेखा के समीकरण की संकल्पना का प्रयोग करते हुए सिद्ध कीजिए कि तीन बिन्दु (3, 0), (-2, -2) और (8, 2) संरेख हैं।
हल:
बिन्दु A(3, 0), B(2, -2) से होकर जाने वाली रेखा का समीकरण

प्रश्नावली 10.3

प्रश्न 1.
निम्नलिखित समीकरणों को ढाल अंत:खण्ड रूप में रूपान्तरित कीजिए और उनके ढाल तथा y-अंत:खण्ड ज्ञात कीजिए:
(i) x + 7y = 0
(ii) 6x + 3y – 5 = 0
(iii) y = 0.
हल:
(i) x + 7y = 0

प्रश्न 2.
निम्नलिखित समीकरणों को अंतःखण्ड रूप में रूपान्तरित कीजिए और अक्षों पर इनके द्वारा काटे गए अंत:खण्ड ज्ञात कीजिए:
(i) 3x + 2y – 12 = 0
(ii) 4x – 3y = 6
(iii) 3y + 2 = 0.

प्रश्न 3.
निम्नलिखित समीकरणों को लम्ब रूप में रूपान्तरित कीजिए। उनकी मूल बिन्दु से लॉबिक दूरियाँ और लम्ब तथा धन-अक्ष के बीच का कोण ज्ञात कीजिए
(i) x – √3 y + 8 = 0
(ii) y – 2 = 0
(iii) x – y = 4.

प्रश्न 4.
बिन्दु (-1, 1) की रेखा 12(x + 6) = 5(y – 2) से दूरी ज्ञात कीजिए।

प्रश्न 5.
x-अक्ष पर बिन्दुओं को ज्ञात कीजिए जिनकी रेखा [latex]\frac { x }{ 3 } +\frac { y }{ 4 } =\quad 1[/latex] से दूरियाँ 4 इकाई हैं।

प्रश्न 6.
समान्तर रेखाओं के बीच की दूरी ज्ञात कीजिए-
(i) 15x + 8y – 34 = 0 और 15x + 8y + 31 = 0
(ii) l(x + y) + p = 0 और l(x + y) – r = 0

प्रश्न 7.
रेखा 3x – 4y + 2 = 0 के समान्तर और बिन्दु (-2, 3) से जाने वाली रेखा का समीकरण ज्ञात कीजिए।

प्रश्न 8.
रेखा 4x – 7y + 5 = 0 पर लम्ब और x-अन्त:खण्ड 3 वाली रेखा का समीकरण ज्ञात कीजिए।

प्रश्न 9.
रेखाओं √3 x + y = 1 और x + √3 y = 1 के बीच का कोण ज्ञात कीजिए।

प्रश्न 10.
बिन्दुओं (h, 3) और (4, f) से जाने वाली रेखा, रेखा 7x – 9y – 19 = 0 को समकोण पर प्रतिच्छेद करती है। h का मान ज्ञात कीजिए।
हल:
माना रेखा AB बिन्दु A(h, 3), B(4, 1) से जाने वाली रेखा की ढाल,

प्रश्न 11.
सिद्ध कीजिए कि बिन्दु (x₁, y₁) से जाने वाली और रेखा Ax + By + C = 0 के समान्तर रेखा को समीकरण A(x – x₁) + B(y – y₁) = 0 है।

प्रश्न 12.
बिन्दु (2, 3) से जाने वाली दो रेखाएँ परस्पर 60° के कोण पर प्रतिच्छेद करती हैं। यदि एक रेखा की ढाल 2 है तो दूसरी रेखा का समीकरण ज्ञात कीजिए।
हल:
माना दूसरी रेखा की ढाल m है।
दोनों रेखाओं के बीच कोण

प्रश्न 13.
बिन्दुओं (3, 4) और (-1, 2) को मिलाने वाली रेखाखण्ड के लम्बे समद्विभाजक रेखा का समीकरण ज्ञात कीजिए।
हल:
माना बिन्दुओं A(3, 4) और B(-1, 2) को मिलाने वाले रेखाखण्ड का मध्य बिन्दु

प्रश्न 14.
बिन्दु (-1, 3) से रेखा 3x – 4y – 16 = 0 पर डाले गए लम्बपाद के निर्देशांक ज्ञात कीजिए।
हल:
मान लीजिए रेखा AB को समीकरप, 3x – 4y – 16 = 0 …… (i)

प्रश्न 15.
मूल बिन्दु से रेखा y = mx + c पर डाला गया लम्ब रेखा से बिन्दु (-1, 2) पर मिलता है। m और c के मान ज्ञात कीजिए।
हल:
माना रेखा AB का समीकरण, y = mx + c
रेखा AB की ढाल = m

प्रश्न 16.
यदि p और q क्रमशः मूल बिन्दु से रेखाओं x cosθ – y sinθ = k cos 2θ और x secθ + y cosecθ = k पर लम्ब की लंबाइयाँ हैं तो सिद्ध कीजिए कि p² + 4q² = k².
हल:
मूल बिन्दु (0, 0) से x cosθ – y sinθ = k cos 2θ की दूरी,

प्रश्न 17.
शीर्षों A (2, 3), B (4, -1) और C (1, 2) वाले त्रिभुज ABC के शीर्ष A से उसकी सम्मुख भुजा पर लम्बे डाला गया है। लम्बे की लम्बाई तथा समीकरण ज्ञात कीजिए।
हल:
मान लीजिए AM रेखा BC पर लंब डाला गया है।

अध्याय 10 पर विविध प्रश्नावली

प्रश्न 1.
k के मान ज्ञात कीजिए जब कि रेखा (k – 3) x – (4 – k²) y + k² – 7k + 6 = 0
(a) x-अक्ष के समान्तर है।
(b) y-अक्ष के समान्तर है।
(c) मूल बिन्दु से जाती है।
हल:
(i) x-अक्ष के समान्तर y = a
प्रश्न में दिए गए समीकरण में x का गुणांक = 0 या k – 3 = 0 अर्थात् k = 3.
(ii) y-अक्ष के समान्तर रेखा x = q
दिए गए समीकरण में y का गुणांक = 0 या 4 – k² = 0 अर्थात् k = ± 2.
(iii) यदि रेखा मूल बिन्दु से जाती है तो (0, 0) इसके समीकरण को संतुष्ट करेगा।
0 – 0 + k² – 7k + 6 = 0 या (k – 6) (k- 1) = 0 या k = 1, 6.

प्रश्न 2.
θ और p के मान ज्ञात कीजिए यदि समीकरण x cosθ + y sinθ = p रेखा √3 x + y + 2 = 0 को लम्ब रूप है।

प्रश्न 3.
उन रेखाओं के समीकरण ज्ञात कीजिए जिनके अक्षों से कटे अंत:खण्डों का योग और गुणनफल क्रमशः 1 और -6 हैं।

प्रश्न 4.
y-अक्ष पर कौन से बिन्दु ऐसे हैं, जिनकी [latex]\frac { x }{ 3 } +\frac { y }{ 4 } =\quad 1[/latex] से, दूरी 4 इकाई है।

प्रश्न 5.
मूल बिन्दु से बिन्दुओं (cosθ, sinθ) और (cosφ , sinφ) को मिलाने वाली रेखा की लांबिक दूरी ज्ञात कीजिए।
हल:
(cosθ, sinθ) और (cosφ , sinφ) को मिलाने वाली रेखा का समीकरण,

प्रश्न 6.
रेखाओं x – 7y + 5 = 0 और 3x + y = 0 के प्रतिच्छेद बिन्दु से खीचीं गई और y-अक्ष के समान्तर रेखा का समीकरण ज्ञात कीजिए।

प्रश्न 7.
रेखा [latex]\frac { x }{ 4 } +\frac { y }{ 6 } =\quad 1[/latex] पर लंब उस बिन्दु से खींची गई रेखा का समीकरण ज्ञात कीजिए जहाँ यह रेखा y-अक्ष से मिलती है।

प्रश्न 8.
रेखाओं y – x = 0, x + y = 0, और x – k = 0 से बने त्रिभुज का क्षेत्रफल ज्ञात कीजिए।

प्रश्न 9.
p का मान ज्ञात कीजिए जिससे तीन रेखाएँ 3x + y – 2 = 0, px + 2y – 3 = 0 और 2x – y – 3 = 0 एक बिन्दु पर प्रतिच्छेद करें।

प्रश्न 11.
बिन्दु (3, 2) से जाने वाली उस रेखा का समीकरण ज्ञात कीजिए जो रेखा x – 2y = 3 से 45° का कोण बनाती है।

प्रश्न 12.
रेखाओं 4x + 7y – 3 = 0 और 2x – 3y + 1 = 0 के प्रतिच्छेद बिन्दु से जाने वाली रेखा का समीकरण ज्ञात कीजिए जो अक्षों से समान अंतः खण्ड बनाती हैं।

प्रश्न 14.
(-1, 1) और (5, 7) को मिलाने वाली रेखाखण्ड को रेखा x + y = 4 किस अनुपात में विभाजित करती है ?
हल:
मान लीजिए बिन्दु P रेखाखण्ड AB को k : 1 के अनुपात में विभाजित करता है। जबकि A और B के क्रमशः (-1, 1) और (5, 7) निर्देशांक हैं।

प्रश्न 15.
बिन्दु (1, 2) से रेखा 4x + 7y + 5 = 0 की 2x – y = 0 के अनुदिश दूरी ज्ञात करो।
हल:
माना रेखा PC का समीकरण, 2x – y = 0 जिस पर बिन्दु P(1, 2) स्थित है।

प्रश्न 16.
बिन्दु (-1, 2) से खींची जा सकने वाली उस रेखा की दिशा ज्ञात कीजिए जिसका रेखा x + y = 4 से प्रतिच्छेदन बिन्दु दिए बिन्दु से 3 इकाई की दूरी पर है।
हल:
मान लीजिए अभीष्ट रेखा PQ की ढाल m है। रेखा PQ जो बिन्दु P(-1, 2) से होकर जाती है और ढाल m है, का समीकरण

प्रश्न 17.
समकोण त्रिभुज के कर्ण के अंत्य बिन्दु (1, 3) और (-4, 1) हैं। त्रिभुज के पाद (leg) (समकोणीय नाओं) का एक समीकरण ज्ञात कीजिए।
हल:
माना त्रिभुज ABC एक समकोणीय त्रिभुज है जिसका कर्ण AB है। A और B के निर्देशांक क्रमशः (1, 3) और (-4, 1) हैं।
मान लीजिए BC की ढाल m है।

प्रश्न 18.
किसी बिन्दु के लिए रेखा को दर्पण मानते हुए बिन्दु (3, 8) का रेखा x + 3y = 7 में प्रतिबिंब ज्ञात कीजिए।
हल:
माना देखा AB का समीकरण x + 3y = 7 है और बिन्दु P के निर्देशांक (3, 8) हैं।

प्रश्न 19.
यदि रेखाएँ y = 3x +1 और 2y = x + 3, रेखा y = mx + 4 पर समान रूप से आनत हो तो m का मान ज्ञात कीजिए।
हल:
रेखा AB का समीकरण, y = 3x + 1 की ढाल = 3
रेखा BC का समीकरण, y = mx + 4 की ढाल = m

प्रश्न 20.
यदि एक चर बिन्दु P(x, y) की रेखाओं x + y – 5 = 0 और 3x – 2y + 7 = 0 से लांबिक दूरियों का योग सदैव 10 रहे तो दर्शाइए कि P अनिवार्य रूप से एक रेखा पर गमन करता है।

प्रश्न 21.
समांतर रखाओं 9x + 6y – 7 = 0 और 3x + 2y + 6 = 0 से समदूरस्थ रेखा का समीकरण ज्ञात कीजिए।

प्रश्न 22.
बिन्दु (1, 2) से होकर जाने वाली एक प्रकाश किरण x-अक्ष के बिन्दु A से परावर्तित होती है और परावर्तित किरण बिन्दु (5, 3) से होकर जाती है। A के निर्देशांक ज्ञात कीजिए।
हल:
मान लीजिए BC, x-अक्ष के अनुदिश उस बिन्दु के निर्देशांक A (a, 0) है। AN इस पर लंब है। PA एक आपतित किरण है और AQ परावर्तित किरण है।

प्रश्न 24.
एक व्यक्ति समीकरणों 2x – 3y + 4 = 0 और 3x + 4y – 5 = 0 से निरूपित सरल रेखीय पथों के संधि बिन्दुओं (junction/crossing) पर खड़ा है और समीकरण 6x – 7y + 8 = 0 से निरूपित पथ पर न्यूनतम समय में पहुँचना चाहता है। उसके द्वारा अनुसरित पथ का समीकरण ज्ञात कीजिए।
हल:
AB और BC दो रेखीय पथ हैं। AB वे BC रेखाओं के समीकरण
2x – 3y + 4 = 0 ………(1)
और 3x +4y – 5 = 0 ……..(2)

We hope the UP Board Solutions for Class 11 Maths Chapter 10 Straight Lines (सरल रेखाएँ) help you. If you have any query regarding UP Board Solutions for Class 11 Maths Chapter 10 Straight Lines (सरल रेखाएँ), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning (गणितीय विवेचन)

These Solutions are part of UP Board Solutions for Class 11 Maths. Here we have given UP Board Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning (गणितीय विवेचन).

प्रश्नावली 14.1

प्रश्न 1.
निम्नलिखित वाक्यों में से कौन से कथन हैं ? अपने उत्तर के लिए कारण भी बतलाइए।
(i) एक महीने में 35 दिन होते हैं।
(ii) गणित एक कठिन विषय है।
(iii) 5 और 7 का योगफल 10 से अधिक होता है।
(iv) किसी संख्या का वर्ग एक सम संख्या होती है।
(v) किसी चतुर्भुज की भुजाएँ बराबर (समान) लंबाई की होती हैं।
(vi) इस प्रश्न का उत्तर दीजिए।
(vii) -1 और 8 का गुणनफल 8 है।
(viii) किसी त्रिभुज के सभी अंत: कोणों का योगफल 180° होता है।
(ix) आज एक तूफानी दिन है।
(x) सभी वास्तविक संख्याएँ सम्मिश्र संख्याएँ होती हैं।
हल:
(i) कथन : यह असत्य है क्योंकि महीने में 35 दिन नहीं होते।
(ii) वाक्य : गणित एक कठिन विषय है। इसकी कोई (UPBoardSolutions.com) परिभाषा नहीं है। किसी एक के लिए सरल और दूसरे के लिए कठिन विषय हो सकता है।
(iii) कथन : यह कथन सत्य है।
(iv) कथन : यह असत्य है क्योंकि वर्ग संख्या विषम भी हो सकती है। जैसे 9, 25,….
(v) कथन : यह कथन असत्य है क्योंकि किसी चतुर्भुज की लंबाई असमान भी होती है।
(vi) वाक्य : यह एक आदेश है, इसलिए यह एक कथन नहीं है।
(vii) कथन : यह कथन असत्य है, -1 x 8 = – 8 ≠ 8.
(viii) कथन : यह कथन सत्य है। त्रिभुज के तीनों अंतः कोणों का योग 180° होता है।
(ix) वाक्य : यह स्पष्ट नहीं है कि कौन-सा दिन तूफानी है?
(x) कथन : यह सत्य कथन है।

प्रश्न 2.
वाक्यों मैं तीन ऐसे उदाहरण दीजिए जो कथन नहीं हैं। उत्तर के लिए कारण भी बताइए।
हल:
तीन उदाह्ररण इस प्रकार हो सकते हैं:
(i) इस कमरे में उपस्थित प्रत्येक व्यक्ति निडर है। यह एक कथन नहीं है, क्योंकि संदर्भ से स्पष्ट नहीं है कि यहाँ पर किस कमरे के बारे में कहा जा रहा है और निडर शब्द भी स्पष्ट रूप से परिभाषित नहीं है।
(ii) वह अभियान्त्रिकी की छात्री है। यह भी एक कथन नहीं है क्योंकि यह स्पष्ट नहीं है कि ‘वह’ वह कौन है।
(iii) “cos² θ का मान सदैव [latex s=2]\frac { 1 }{ 2 }[/latex] ” से अधिक होता है। जब तक हमें यह ज्ञात न हो कि 8 क्या है हम यह नहीं कह सकते कि वाक्य सत्य है या नहीं।

प्रश्नावली 14.2

प्रश्न 1.
निम्नलिखित कथन का निषेधन लिखिए।
(i) चैन्नई, तमिलनाडु की राजधानी है।
(ii) √2 एक सम्मिश्र संख्या नहीं है।
(iii) सभी त्रिभुज समबाहु त्रिभुज नहीं होते हैं।
(iv) संख्या 2 संख्या 7 से अधिक है।
(v) प्रत्येक प्राकृत संख्या एक पूर्णाक होती है।
हल:
(i) चैन्नई, तमिलनाडु की राजधानी नहीं है।
(ii) √2 एक सम्मिश्र संख्या है।
(iii) सभी त्रिभुज समबाहु त्रिभुज हैं।
(iv) संख्या 2 संख्या 7 से (UPBoardSolutions.com) बड़ी नहीं है।
(v) प्रत्येक प्राकृत संख्या एक पूर्णीक नहीं है।

प्रश्न 2.
क्या निम्नलिखित कथन युग्म (कथन के जोड़े) एक दूसरे के निषेधन हैं?
(i) संख्या x एक परिमेय संख्या नहीं है।
संग्ख्या x एक अपरिमेय संख्या नहीं है।
हल:
कथन ” संख्या x एक परिमेय संख्या नहीं है।” का निषेधन संख्या x एक परिमेय संख्या है। यो x एक अपरिमेय संख्या नहीं है। यही दूसरा कथन है। अतः दिए गए कथन एक दूसरे के निषेधन हैं।

(ii) संख्या एक परिमेय संख्या है।
संख्या एक अपरिमेय संख्या है।
हल:
कथन ” संख्या x एक परिमेय संख्या है।” का निषेधन संख्या ४ एक अपरिमेय संख्या है। जो कि दूसरे कथन के समान है।
अतः यह कथन एक दूसरे के निषेधन हैं।

प्रश्न 3.
निम्नलिखित मिश्र कथन के घटक कथन ज्ञात कीजिए और जाँचिए कि वे सत्य हैं या असत्य हैं।
(i) संख्या 3 अभाज्य है या विषम है।
(ii) समस्त (सभी) पूर्णांक धन या ऋण हैं।
(iii) संख्या 100 संख्याओं 3, 11 और 5 से भाज्य हैं।
हल:
(i) p : संख्या 3 अभाज्य है। यह कथन सत्य है।
q : संख्या 3 विषम संख्या है। यह कथन सत्य है।
(ii) p : सभी पूर्णांक धन हैं। यह कथन सत्य है।
q : सभी पूर्णांक ऋण हैं। यह कथन सत्य है।
(iii) p : 100, 3 से भाज्य है। यह कथन असत्य है।
q : 100, 11 से भाज्य है। यह कथन असत्य है।
r : 100, 5 से भाज्य है। यह कथन सत्य है।

प्रश्नावली 14.3

प्रश्न 1.
निम्नलिखित मिश्र कथनों में पहले संयोजक शब्दों को पहचानिए और फिर उनको घटक कथनों में विघटित कीजिए:
(i) सभी परिमेय संख्याएँ वास्तविक संख्याएँ होती हैं और सभी वास्तविक संख्याएँ सम्मिश्र संख्याएँ नहीं होती हैं।
हल:
संयोजक शब्द ‘और’
घटक p : सभी परिमेय संख्याएँ वास्तविक संख्याएँ होती हैं।
q : सभी वास्तविक संख्याएँ सम्मिश्र (UPBoardSolutions.com) संख्याएँ नहीं होती हैं।

(ii) किसी पूर्णांक का वर्ग धन या ऋण होता है।
हल:
संयोजक शब्द ‘या’
घटक p : किसी पूर्णांक का वर्ग धन होता है।
q : किसी पूर्णा का वर्ग ऋण होता है।

(iii) रेत (बालू घूप में शीघ्र गर्म हो जाती है और रात्रि में शीघ्र ठंडी नहीं होती है।
हल:
संयोजक शब्द ‘और’
घटक p : रेत (बालू) धूप में शीघ्र गर्म हो जाती है।
q : रेत (बालू) रात्रि में शीघ्र ठंडी नहीं होती।

(iv) x = 2 और x = 3, समीकरण 3x² – x – 10 = 0 के मूल हैं।
हल:
संयोजक शब्द ‘और’
घटक p : x = 2, समीकरण 3x² – x – 10 = 0 का मूल है।
q : x = 3 समीकरण 3x² – x – 10 = 0 को मूल है।

प्रश्न 2.
निम्नलिखित कथनों में परिमाण वाचक वाक्यांश पहचानिए और कथनों के निषेधन लिखिए:
(i) एक ऐसी संख्या का अस्तित्व है, जो अपने वर्ग के बराबर है।
हल:
परिमाणवाचक वाक्यांश : एक ऐसी संख्या का अस्तित्व है।
कथन का निषेधन : ऐसी संख्या का (UPBoardSolutions.com) अस्तित्व नहीं है जो अपने वर्ग के बराबर हो।

(ii) प्रत्येक वास्तविक संख्या x के लिए x, (x + 1) से कम होता है।
हल:
परिमाणवाचक वाक्यांश : ” प्रत्येक के लिए ”
p : प्रत्येक वास्तविक संख्या x के लिए x, x + 1 से कम होता है।
p का निषेधन = ~p = कम से कम एक वास्तविक संख्या 7 ऐसी है जो x + 1 से कम नहीं है।

(iii) भारत के हर एक राज्य/प्रदेश के लिए एक राजधानी का अस्तित्व है।
हल:
परिमाणवाचक वाक्यांश : एक ऐसे का अस्तित्व है।
कथन p : भारत के हर एक राज्य/प्रदेश के लिए एक राजधानी का अस्तित्व है।
p का निषेधन : ~p = भारत के हर एक राज्य/ प्रदेश के लिए एक राजधानी का अस्तित्व नहीं है।

प्रश्न 3.
जाँचिए कि क्या नीचे लिखे कथनों के जोड़े (युग्म) एक दूसरे के निषेधन हैं। अपने उत्तर के लिए कारण भी बतलाइए।
(i) प्रत्येक वास्तविक संख्याओं x और y के लिए x + y = y + x सत्य है।
(ii) ऐसी वास्तविक संख्याओं x और y का अस्तित्व है जिनके लिए x + y = y + x सत्य है।
हल:
कथन (i) और (ii) एक दूसरे के निषेधन (UPBoardSolutions.com) नहीं है।

प्रश्न 4.
बतलाइए कि निम्नलिखित कथनों में प्रयुक्त ‘या’ ‘अपवर्जित है’ अथवा ‘अंतर्विष्ट’ है। अपने उत्तर के लिए कारण भी बतलाइए।
(i) सूर्य उदय होता है या चन्द्रमा अस्त होता है।
हल:
अपवर्जित : सूर्य उदय होता है और चन्द्रमा अस्त होता है। एक समय पर सूर्य उदय होगा या चन्द्रमा

(ii) ड्राइविंग लाइसेंस के आवेदन हेतु आपके पास राशन कार्ड या पासपोर्ट होना चाहिए।
हल:
अंतर्विष्ट : ड्राइविंग लाइसेंस के आवेदन हेतु राशन कार्ड या पास पोर्ट या दोनों मान्य है।
(iii) सभी पूर्णांक धन या ऋण होते है।
हल:
अपवर्जित : सभी पूर्णांक धन या ऋण होते हैं। परन्तु धन या ऋण दोनों नहीं हो सकते।

प्रश्नावली 14.4

प्रश्न 1.
निम्नलिखित कथन को वाक्यांश “यदि- तो” का प्रयोग करते हुए पाँच विभिन्न रूप में इस प्रकार लिखिए कि उनके अर्थ समान हों।
यदि एक प्राकृत संख्या विषम है तो उसका वर्ग भी विषम है।
हल:
(i) यदि एक प्राकृत संख्या विषम है तो अंर्तभाव है उसको वर्ग भी विषम है।
(ii) कोई प्राकृत संख्या विषम संख्या है केवल यदि उसका वर्ग विषम है।
(iii) यदि प्राकृत संख्या का वर्ग विषम नहीं है तो वह (UPBoardSolutions.com) प्राकृत संख्या भी विषम नहीं होगी।
(iv) एक प्राकृत संख्या विषम है, इसके लिए यह अनिवार्य है कि उनका वर्ग भी विषम होगा।
(v) एक प्राकृत संख्या का वर्ग विषम है, इसके लिए यह पर्याप्त होगा कि वह संख्या विषम है।

प्रश्न 2.
निम्नलिखित कथनों के प्रतिधनात्मक और विलोम कथन लिखिए:
(i) यदि x एक अभाज्य संख्या है, तो x एक विषम है।
हल:
प्रतिधनात्मक कथन : यदि एक संख्या x विषम नहीं है तो x एक अभाज्य संख्या नहीं है।
विलोम कथन : यदि एक संख्या x विषम है तो x एक अभाज्य संख्या है।

(ii) यदि दो रेखाएँ समांतर हैं तो वे एक दूसरे को एक समतल में नहीं काटती हैं।
हल:
प्रतिधनात्मक कथन : यदि दो रेखाएँ एक दूसरे को समतल में काटती हैं तो रेखाएँ समांतर नहीं हैं।
विलोम कथन : अदि दो रेखाएँ एक दूसरे को एक ही (UPBoardSolutions.com) समतल में नही काटती हैं तो रेखाएँ समांतर हैं।

(iii) किसी वस्तु के ठंडे होने का तात्पर्य (अंतर्भाव) है कि उसका तापक्रम कम है।
हल:
प्रतिधनात्मक कथन : यदि किसी वस्तु का तापमान कम नहीं है तो वह वस्तु ठंडी नहीं है।
विलोम कथन : यदि किसी वस्तु का तापमान कम है तो वह वस्तु ठंडी है।

(iv) आप ज्यामिति विषय को आत्मसात नहीं कर सकते यदि आपको यह ज्ञान नहीं है कि निगमनात्मक विवेचन किस प्रकार किया जाता है।
हल:
प्रतिधनात्मक कथन : यदि आपको यह ज्ञात है कि निगमनात्मक विवेचन किस प्रकार किया है तो आप ज्यामिति विषय को आत्मसात कर सकते हैं।
विलोम कथन : यदि आपको यह ज्ञात नहीं है कि निगमनात्मक (UPBoardSolutions.com) विवेचन किस प्रकार किया जाता है तो आप ज्यामिन्नि विषय को आत्मसात नहीं कर सकते हैं।

(v) “x एक सम संख्या है” से तात्पर्य (अंतर्भाव) है कि x संख्या 4 से भाज्य है।
हल:
प्रतिधनात्मक कथन : यदि x संख्या 4 से भाज्य नहीं है तो x एक सम संख्या नहीं है।
विलोम कथन : यदि संख्या x, 4 से भाज्य है तो यह एक सम संख्या है।

प्रश्न 3.
निम्नलिखित कथनों में से प्रत्येक को ‘यदि–तो’ रूप में लिखिए:
(i) आपको नौकरी (काम) मिलने का तात्पर्य (अंतर्भाव) है कि आपकी विश्वसनियता अच्छी है।
हल:
यदि आपको नौकरी मिल गई है तो आपकी विश्वसनियता अच्छी है।

(ii) केले का पेड़ फूलेगा यदि वह एक माह तक गरम बना रहे।
हल:
यदि केले का पेड़ एक माह तक गरम बना रहे तो केले का पेड़ फूलेगा।

(iii) एक चतुर्भुज समांतर चतुर्भुज है यदि उसके विकर्ण एक-दूसरे को समद्विभाजित करे।
हल:
यदि किसी चतुर्भुज के विकर्ण एक दूसरे को (UPBoardSolutions.com) समद्विभाजित करते हैं तो वह एक समांतर चतुर्भुज है।

(iv) कक्षा में ग्रेड A पाने के लिए यह अनिवार्य है कि आप पुस्तक के सभी प्रश्नों को सरल कर लेते है।
हल:
यदि आप कक्षा में A ग्रेड पाते हैं, तो आप पुस्तक के सभी प्रश्न हल कर लेते हैं।

प्रश्न 4.
नीचे (a) और (b) में प्रदत्त कथनों में से प्रत्येक के (i) में दिए कथन का प्रतिधनात्मक और विलोम कथन पहचानिए।
(a) यदि आप दिल्ली में रहते हैं तो आपके पास जाड़े के कपड़े हैं।
(i) यदि आपके पास जाड़े के कपड़े नहीं हैं, तो आप दिल्ली में नहीं रहते हैं।
हल:
प्रतिधनात्मक।

(ii) यदि आपके पास जाड़े के कपड़े हैं, तो आप दिल्ली में रहते हैं।
हल:
विलोम

(b) यदि एक चतुर्भुज समांतर चतुर्भुज है, तो उसके विकर्ण एक दूसरे को समद्विभाजित करते हैं।
(i) यदि किसी चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित नहीं करते हैं तो चतुर्भुज एक समांतर चतुर्भुज नहीं है।
हल:
प्रतिधमात्मक।

(ii) यदि चतुर्भुज के विकर्ण एक दूसरे को समद्विभाजित करते हैं तो वह समांतर चतुर्भुज है।
हल:
विलोम।

प्रश्नावली 14.5

प्रश्न 1.
सिद्ध कीजिए कि कथन यदि x एक ऐसी वास्तविक संख्या है कि x³ + 4x = 0, तो x = 0
(i) प्रत्यक्ष विधि द्वारा
(ii) विरोधोक्ति द्वारा
(iii) प्रतिधनात्मक कथन द्वारा
हल:
(i) प्रत्यक्ष विधि द्वारा
x³ + 4x = 0 या x (x² + 4) = 0
x = 0 या x² + 4 = 0
परन्तु x² + 4 ≠ 0, x ∈ R
अतः x = 0.

(ii) विरोधोक्ति द्वारा : माना x ≠ 0
यदि समीकरण x² + 4x = 0 का एक मूल p हो, तब
p³ + 4p = 0 या p(p² + 4) = 0
p = 0 या p² + 4 = 0
p² + 4 ≠ 0
p= 0 विरोधात्मक है x ≠ p के जो पूर्व निर्धारित है।
अर्थात् p = 0 या x = 0

(iii) प्रतिधनात्मक कथन द्वारा:
माना x = 0 सत्य नहीं है।
x ∈ R, x³ + 4x ≠ 0, और x ≠ 0 (माना गया है)
x (x² + 4) ≠ 0 यह सिद्ध करता (UPBoardSolutions.com) है कि x² + 4x = 0 का x = 0 मूल है।

प्रश्न 2.
प्रत्युदाहरण द्वारा सिद्ध कीजिए कि कथन ” किसी भी ऐसी वास्तविक संख्याओं a और b के लिए, जहाँ a² = b² का तात्पर्य है कि a = b ” सत्य नहीं है।
हल:
माना जब a = 1, b = -1 तो a² = b²
परन्तु a ≠ b. अतः दिया गया कथन सत्य नहीं है।

प्रश्न 3.
प्रतिधनात्मक विधि द्वारा सिद्ध कीजिए कि निम्नलिखित कथन सत्य है।
p : यदि x एक पूर्णांक है और x² सम है तो x सम है।
हल:
माना x एक सम संख्या नहीं हैं।
x = 2n + 1
x² = (2n + 1)² = 4n² + 4n + 1 = 2 (2n² + 2n) + 1
यह एक विषम संख्या है। इस प्रकार यदि q सत्य नहीं है तो p भी सत्य नहीं है। अर्थात दिया हुआ कथन सत्य है।

प्रश्न 4.
प्रत्युदाहरण द्वारा सिद्ध कीजिए कि निम्नलिखित कथन सत्य नहीं हैं।
(i) p : यदि किसी त्रिभुज के कोण समान हैं, तो त्रिभुज एक अधिक कोण त्रिभुज है।
हल:
माना एक कोण = 90 + θ
तीनों कोण समान हों, तब
त्रिभुज के तीनों कोणों का योग = 3 (90 + θ) = 270 + 3θ
यह 180° के बराबर नहीं है।
त्रिभुज को कोई भी कोण अधिक कोण नहीं हो (UPBoardSolutions.com) सकता अर्थात वह त्रिभुज अधिक कोण त्रिभुज नहीं हो सकता है।

(ii) q : समीकरण x² – 1 = 0 के मूल 0 और 2 के बीच स्थित नहीं है।
हल:
0 और 2 के बीच की संख्या 1 लीजिए।
x² – 1 = 0 में x = 1 रखने पर,
1 – 1 = 0,
अत: x = 1, दिए हुए समीकरण को संतुष्ट करता है।
इसलिए x = 1, समीकरण x² – 1 = 0 का मूल है और 0 और 2 के बीच स्थित हैं।
अतः दिया गया कथन सत्य नहीं है।

प्रश्न 5.
निम्नलिखित कथनों में से कौन से सत्य हैं और कौन से असत्य हैं। प्रत्येक दशा में अपने उत्तर के लिए वैध कारण बतलाइए:
(i) p : किसी वृत्त की प्रत्येक त्रिज्या वृत्त की जीवा होती है।
हल:
असत्य : त्रिज्या का एक सिरा केंद्र पर ओर दूसरा सिरा वृत्त पर होता हो तो वह जीवा नहीं होती है। अत: यह वृत्त की जीवा नहीं है।

(ii) q : किसी वृत्त का केंद्र वृत्त की प्रत्येक जीवा को समद्विभाजित करता है।
हल:
असत्य : वृत्त का केंद्र केवल व्यास को समद्विभाजित करता है। प्रत्येक जीवा केंद्र से होकर नहीं जाती है।
अत: वृत्त का केंद्र प्रत्येक जीवा को समद्विभाजित (UPBoardSolutions.com) नहीं करता है।

(iii) r : एक वृत्त किसी दीर्घवृत्त की एक विशेष स्थिति है।
हल:
सत्य : दीर्घवृत्त का समीकरण [latex s=2]\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =\quad 1[/latex]
जब a = b तब [latex s=2]\frac { { x }^{ 2 } }{ { a }^{ 2 } } +\frac { { y }^{ 2 } }{ { b }^{ 2 } } =\quad 1[/latex] या x² + y² = a²
अत: यह वृत्त का समीकरण है।

(iv) s : यदि x औरy ऐसे पूर्णाक हैं कि x > y, तो -x < -y हैं।
हल:
सत्य यदि x और y पूर्णांक हैं और x > y तो -x < -y (असमिकाओं के नियम से)

(v) t : √11 एक परिमेय संख्या है।
हल:
असत्य : √11 एक अपरिमेय संख्या है।

अध्याय 14 पर विविध प्रश्नावली

प्रश्न 1.
निम्नलिखित कथनों के निषेधन लिखिए:
(i) प्रत्येक धन वास्तविक संख्या x के लिए, संख्या x – 1 भी धन संख्या है।
हल:
एक ऐसी धन वास्तविक संख्या x को अस्तित्व है कि x – 1 धन संख्या नहीं है।

(ii) सभी बिल्लियाँ खरोंचती हैं।
हल:
सभी बिल्लियाँ खरोंचती नहीं हैं।

(iii) प्रत्येक वास्तविक संख्या के लिए या तो x > 1 या x < 1.
हल:
एक ऐसी वास्तविक संख्या x का अस्तित्व है कि न तो x > 1 और न ही x < 1.

(iv) एक ऐसी संख्या ४ का अस्तित्व है कि 0 < x < 1.
हल:
किसी ऐसी वास्तविक संख्या x का अस्तित्व नहीं है कि 0 < x < 1.

प्रश्न 2.
निम्नलिखित सप्रतिबंध कथनों (अंतर्भाव) में से प्रत्येक का विलोम तथा प्रतिधनात्मक कथन लिखिए:
(i) एक धन पूर्णाक अभाज्य संख्या है केवल यदि 1 और पूर्णांक स्वयं के अतिरिक्त उसका कोई अन्य भाजक नहीं है।
हल:
विलोम कथन : यदि एक धन पूर्णांक अभाज्य है, तो 1 तथा स्वयं के अतिरिक्त इसका कोई अन्य भाजक नहीं है।
प्रतिधनात्मक कथन : यदि एक धन पूर्णांक के 1 तथा स्वयं के अतिरिक्त अन्य भाजक भी हैं, तो वह धन पूर्णांक अभाज्य संख्या नहीं है।

(ii) मैं समुद्र तट पर जाता हूँ जब कभी धूप वाला दिन होता है।
हल:
विलोम कथन : यदि कभी धूप वाला दिन हो तो मैं समुद्र तट पर जाता हूँ।
प्रतिधनात्मक कथन : जब कभी धूप वाला दिन नहीं होता तो मैं समुद्र तट पर नहीं जाता।

(iii) यदि बाहर गर्म है, तो आपको प्यास लगती है।
हल:
विलोम कथन : यदि आपको प्यास लगी है, तो बाहर गर्म है।
प्रतिधनात्मक कथन : यदि आपको प्यास नहीं लगती है तो बाहर गर्म नहीं है।

प्रश्न 3.
निम्नलिखित कथनों में से प्रत्येक को ” यदि p तो q” के रूप में लिखिए।:
(i) सर्वर पर लॉग आन करने के लिए पासवर्ड का होना आवश्यक है।
(ii) जब कभी वर्षा होती है यातायात में अवरोध उत्पन्न होता है।
(iii) आप वेबसाइट में प्रवेश कर सकते हैं केवल यदि आपने निर्धारित शुल्क का भुगतान किया हो।
हल:
” यदि p तो q” के रूप में कथन
(i) यदि सर्वर पर लॉग आन है, तो पासवर्ड ज्ञात है।
(ii) यदि वर्षा होती है, तो यातायात में अवरोध उत्पन्न होता है।
(iii) यदि आप निर्धारित शुल्क का भुगतान करते हैं, तो आप बेवसाइट में प्रवेश कर सकते हैं।

प्रश्न 4.
निम्नलिखित कथनों में से प्रत्येक को ‘p यदि और केवल यदि q’ के रूप में पुनः लिखिएः
(i) यदि आप दूरदर्शन (टेलीविजन) देखते हैं, तो आपका मन मुक्त होता है तथा यदि आपका मन मुक्त है तो आप दूरदर्शन देखते हैं।
(ii) आपके द्वारा A ग्रेड प्राप्त करने के लिए यह अनिवार्य और पर्याप्त है कि आप गृहकार्य नियमित रूप से । करते हैं।
(iii) यदि एक चतुर्भुज समान कोणिक है, तो वह एक आयत होता है तथा यदि एक चतुर्भुज आयत है, तो वह समान कोणिक होता है।
हल:
‘p यदि और केवल यदि q’ के रूप में कथन
(i) आप टेलीविज़न देखते हैं यदि और केवल यदि आपका मन मुक्त होता है।
(ii) आप A ग्रेड प्राप्त करते हैं यदि और केवल (UPBoardSolutions.com) यदि आप नियमित रूप से समस्त गृहकार्य करते हैं।
(iii) एक चतुर्भुज समान कोणिक है यदि और केवल यदि वह एक आयत है।

प्रश्न 5.
नीचे दो कथन दिए हैं,
p : 25 संख्या 5 का एक गुणज है।
q : 25 संख्या 8 का एक गुणज है।
उपरोक्त कथनों का संयोजक ‘और’ तथा ‘या’ द्वारा संयोजन करके मिश्र कथन लिखिए। दोनों दशाओं में प्राप्त मिश्र कथनों की वैधता जाँचिए।
हल:
(i) ‘और’ संयोजन द्वारा मिश्र कथन: 25 संख्या 5 और 8 का गुणज है। यह असत्य कथन है क्योंकि p और q दोनों सत्य नहीं हैं।
(ii) संयोजक ‘या’ द्वारा मिश्र कथने: 25 संख्या 5 या 8 का गुणज है। यह कथन सत्य है।

प्रश्न 6.
नीचे लिखे कथनों की वैधता की जाँच उनके सामने लिखित विधि द्वारा कीजिए।
(i) p : एक अपरिमेय संख्या और एक परिमेय संख्या का योगफल अपरिमेय होता है। (विरोधोक्ति विधि)
(ii) q : यदि n एक ऐसी वास्तविक संख्या है कि n > 3 तो n² > 9 (विरोधोक्ति विधि)
हल:
(i) मान लीजिए √a अपरिमेय और b परिमेय सेख्याएँ हों, तब
दोनों का योग b + √a = s
माना यह योग अपरिमेय नहीं है।
यदि s अपरिमेय नहीं है तो यह परिमेय संख्या है।
b + √a = [latex s=2]\frac { p }{ q }[/latex] …..(1)
जबकि p और q पूर्णांक हैं, q ≠ 0 तथा उनमें कोई समान गुणनखण्ड नहीं है।
समीकरण (1) से, √a = [latex s=2]\frac { p }{ q }[/latex] – b
बायाँ पक्ष = √a = एक अपरिमेय संख्या
दायाँ पक्ष = [latex s=2]\frac { p }{ q }[/latex] – b = एक परिमेय संख्या
चूँकि यह दोनों विरोधात्मक हैं।
अतः योग s परिमेय संख्या नहीं हो सकती।

(ii) माना n² > 9 नहीं है जबकि n > 3
n = 3 + a रखने पर
n = a + 3
n² = (a + 3)² = a² + 6a + 9 = 9 + (a² + 6a)
n² > 9
पूर्वनिर्धारित कथन और यह कथन (UPBoardSolutions.com) विरोधात्मक है।
अतः जब x > 3 तो x² > 9

प्रश्न 7.
निम्नलिखित कथन को पाँच भिन्न-भिन्न तरीकों से इस प्रकार व्यक्त कीजिए कि उनके अर्थ समान हों।
q : यदि एक त्रिभुज समान कोणिक है तो वह एक अधिक कोण त्रिभुज है।
हल:
पाँच समान अर्थ वाले कथन :
(i) कथन ”एक त्रिभुज समान कोणिक है’ का अंतर्भाव है कि यह अधिक कोण त्रिभुज है।
(ii) एक त्रिभुज के अधिक कोण त्रिभुज होने के लिए यह पर्याप्त है कि यह समान कोणिक है।
(iii) एक त्रिभुज समान कोणिक है यदि और केवल यदि त्रिभुज अधिक कोण त्रिभुज है।
(iv) एक त्रिभुज को समान कोणिक होने के लिए यह अनिवार्य है कि त्रिभुज अधिक कोण त्रिभुज हो।
(v) यदि एक त्रिभुज अधिक कोण त्रिभुज नहीं है तो वह (UPBoardSolutions.com) समान कोणिक त्रिभुज नहीं है।

We hope the UP Board Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning (गणितीय विवेचन) help you. If you have any query regarding UP Board Solutions for Class 11 Maths Chapter 14 Mathematical Reasoning (गणितीय विवेचन), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry (त्रिविमीय ज्यामिति का परिचय)

These Solutions are part of UP Board Solutions for Class 11 Maths. Here we have given UP Board Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry (त्रिविमीय ज्यामिति का परिचय).

प्रश्नावली 12.1

प्रश्न 1.
एक बिन्दु x-अक्ष पर स्थित है। इस के y-निर्देशांक तथा z-निर्देशांक क्या हैं ?
हल:
x-अक्ष पर किसी बिन्दु के निर्देशांक (x, 0, 0) होते हैं जिसमें y = 0, z = 0.

प्रश्न 2.
एक बिन्दु XZ तल में है। इसके y – निर्देशांक के बारे में आप क्या कह सकते हैं?
हल:
XZ तल में y- निर्देशांक 0 होता है। इस तल का बिन्दु (x, 0, z) के रूप में होता है।

प्रश्न 3.
अष्टाशों के नाम बताइए, जिनमें निम्नलिखित बिन्दु स्थित हैं:
(1, 2, 3), (4, -2, 3), ( 4, -2, -5), (4, 2, -5), (-4, 2, -5), (-4, 2, 5), (-3, -1, 6), (2, -4, -7)
हल:
दिए हुए बिन्दुओं के अष्टांश हैं:
(i) (1, 2, 3) – XOYZ – पहला
(ii) (4, -2, 3) – XOYZ. – चौथा
(iii) (4, 2, -5) – XOY’Z’ – आठवाँ
(iv) (4, 2, -5) – XOYZ’ – पाँचवाँ
(v) (-4, 2, -5) – XOYZ’ – छटा
(vi) (-4, 2, 5) – (XOYZ) – दूसरी
(vii) (-3, -1, 6) – (XOY’Z) – तीसरा
(viii) (2, -4, -7) – (XOY’Z’) – आठवाँ

प्रश्न 4.
रिक्त स्थानों की पूर्ति कीजिए:
(i) x-अक्ष और y-अक्ष दोनों एक साथ मिल कर एक तल बनाते हैं, उस तल को …………. कहते हैं।
(ii) XY- तल में एक बिन्दु के निर्देशांक ……… रूप के होते हैं।
(iii) निर्देशांक तल अंतरिक्ष को ………. अष्टांश में विभाजित करते हैं।
हल:
(i) x-अक्ष और y-अक्ष दोनों एक साथ मिलकर एक तल बनाते है उस तल को XY-तल कहते हैं।
(ii) XY- तल में एक बिन्दु के निर्देशांक (x, y, 0) रूप के होते हैं।
(iii) निर्देशांक तल अंतरिक्ष को 8 क्षेत्र में विभाजित करते हैं।

प्रश्नावली 12.2

प्रश्न 1.
निम्नलिखित बिन्दु-युग्मों के बीच की दूरी ज्ञात कीजिए:
(i) (2, 3, 5) और (4, 3, 1)

प्रश्न 2.
दर्शाइए कि बिन्दु (-2, 3, 5), (1, 2, 3) और (7, 0, -1) संरेख हैं।

प्रश्न 3.
निम्नलिखित को सत्यापित कीजिए:
(i) (0, 7, -10), (1, 6, -6), और (4, 9, – 6) एक समद्विबाहु त्रिभुज के शीर्ष हैं।

प्रश्न 4.
ऐसे बिन्दुओं के समुच्चय का समीकरण ज्ञात कीजिए जो बिन्दु (1, 2, 3) और (3, 2, -1) से समदूरस्थ हैं।

प्रश्न 5.
बिन्दुओं P से बने समुच्चय का समीकरण ज्ञात कीजिए जिनकी बिन्दुओं A(4, 0, 0) और B(-4, 0, 0) से दूरियों का योगफल 10 है।
हल:
माना बिन्दु P के निर्देशांक (x, y, z) हैं।

प्रश्नावली 12.3

प्रश्न 1.
बिन्दुओं (-2, 3, 5) और (1, -4, 6) को मिलाने से बने रेखाखण्ड को अनुपात (i) 2 : 3 में अंतः (ii) 2 : 3 में बाह्यतः विभाजित करने वाले बिन्दु के निर्देशांक ज्ञात कीजिए।

प्रश्न 2.
दिया गया है कि बिन्दु P(3, 2, -4), Q(5, 4, -6) और R(9, 8, -10) संरेख हैं। वह अनुपात ज्ञात कीजिए जिसमें Q, PR को विभाजित करता है।

प्रश्न 3.
बिन्दुओ (-2, 4, 7) और (3, -5, 8) को मिलाने वाली रेखाखण्ड, YZ- तले द्वारा जिस अनुपात में विभक्त होता है, उसे ज्ञात कीजिए।
हल:
मान लीजिए बिन्दु P पर तल YZ रेखाखण्ड AB क k : 1 के अनुपात में प्रतिच्छेद करता है, तब YZ – तल पर प्रत्येक बिन्दु (0, y, z) के रूप में होगा।

प्रश्न 4.
विभाजन सूत्र का प्रयोग करके दिखाइए A(2, -3, 4), B(-1, 2, 1) तथा C(0, [latex]\frac { 1 }{ 3 }[/latex], 2) संरेख हैं।

प्रश्न 5.
P(4, 2, -6) और Q(10, -16, 6) के मिलाने वाली रेखाखण्ड PQ को सम-त्रिभाजित करने वाले बिन्दुओं के निर्देशांक ज्ञात कीजिए।
हल:
माना बिन्दु A, B रेखाखण्ड PQ को 3 समान भागों में विभाजित करती है।

अध्याय 12 पर विविध प्रश्नावली

प्रश्न 1.
समातेर चतुर्भुज के तीन शीर्ष A(3, -1, 2), B(1, 2, -4) व C(-1, 1, 2) हैं। चौथे शीर्ष D के निर्देशांक ज्ञात कीजिए।
हल:
शीर्ष A और C क्रमशः (3, -1, 2), (-1, 1, 2) हैं।

प्रश्न 2.
एक त्रिभुज ABC के शीर्षों के निर्देशांक क्रमशः A(0, 0, 6), B(0, 4, 0) तथा C(6, 0, 0) हैं। त्रिभुज की माध्यिकाओं की लंबाई ज्ञात कीजिए।

प्रश्न 3.
यदि त्रिभुज PQR का केन्द्रक मूल बिन्दु है और शीर्ष P(2a, 2, 6), Q(-4, 3b, -10) और R(8, 14, 2c) हैं तो a, b और c का मान ज्ञात कीजिए:

प्रश्न 4.
y-अक्ष पर उस बिन्दु के निर्देशांक ज्ञात कीजिए जिसकी बिन्दु P(3, -2, 5) से दूरी 5√2 है।

प्रश्न 5.
P(2, -3, 4) और (8, 0, 10) को मिलाने वाली रेखाखण्ड पर स्थित एक बिन्दु R का x- निर्देशांक 4 है। बिन्दु R के निर्देशांक ज्ञात कीजिए।

प्रश्न 6.
यदि बिन्दु A और B क्रमशः (3, 4, 5) तथा (-1, 3, -7) हैं। चर बिन्दु P द्वारा निर्मित समुच्चय से संबंधित समीकरण ज्ञात कीजिए जहाँ PA² + PB² = k² जब कि k अचर है।

We hope the UP Board Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry (त्रिविमीय ज्यामिति का परिचय) help you. If you have any query regarding UP Board Solutions for Class 11 Maths Chapter 12 Introduction to Three Dimensional Geometry (त्रिविमीय ज्यामिति का परिचय), drop a comment below and we will get back to you at the earliest.

UP Board Solutions for Class 11 Maths Chapter 13 Limits and Derivatives (सीमा और अवकलज)

These Solutions are part of UP Board Solutions for Class 11 Maths. Here we have given UP Board Solutions for Class 11 Maths Chapter 13 Limits and Derivatives (सीमा और अवकलज).

प्रश्नावली 13.1

प्रश्न 1 से 22 तक निम्नलिखित सीमाओं के मान प्राप्त कीजिए:

प्रश्नावली 13.2

प्रश्न 1.
x = 10 पर x² – 2 का अवकलज ज्ञात कीजिए।

प्रश्न 2.
x = 100 पर 99x का अवकलज ज्ञात कीजिए।

प्रश्न 3.
x = 1 पर x का अवकलज ज्ञात कीजिए।

प्रश्न 4.
प्रथम सिद्धांत से निम्नलिखित फलनों का अवकलज ज्ञात कीजिए:

प्रश्न 7.
किन्हीं अचरों a और b के लिए

प्रश्न 9.
निम्नलिखित के अवकलज ज्ञात कीजिए:

प्रश्न 10.
प्रथम सिद्धांत से cos x का अवकलज ज्ञात कीजिए।

प्रश्न 11.
निम्नलिखित फलनों के अवकलज ज्ञात कीजिए:

अध्याय 13 पर विविध प्रश्नावली

प्रश्न 1.
प्रथम सिद्धांत से निम्नलिखित फलनों का अवकलज ज्ञात कीजिए:

निम्नलिखित फलनों के अवकलज ज्ञात कीजिए (यह समझा जाए कि a, b, c, p, q, r और s निश्चित शून्येत्तर अचर हैं और m तथा n पूर्णाक हैं।)

प्रश्न 2.
(x + a)

प्रश्न 3.
(px + q) ([latex s=2]\frac { r }{ x }[/latex] + s)

प्रश्न 4.
(ax + b) (cx + d)²

प्रश्न 11.
4√x – 2.

प्रश्न 12.
(ax + b)ⁿ

प्रश्न 13.
(ax + b)ⁿ (cx + d)^m

प्रश्न 14.
sin (x + a).

प्रश्न 15.
cosec x cot x.

We hope the UP Board Solutions for Class 11 Maths Chapter 13 Limits and Derivatives (सीमा और अवकलज) help you. If you have any query regarding UP Board Solutions for Class 11 Maths Chapter 13 Limits and Derivatives (सीमा और अवकलज), drop a comment below and we will get back to you at the earliest.