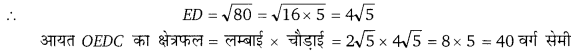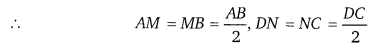Class 9

Balaji Class 9 Maths Solutions Chapter 8 Coordinate Geometry Ex 8.1 निर्देशांक ज्यामिति

Ex 8.1 Coordinate Geometry अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
किसी बिन्दु का भुज किस चतुर्थांश में ऋणात्मक होता है?
हलः
II तथा III चतुर्थांश में।

प्रश्न 2.
दो निर्देशांक अक्षों के प्रतिच्छेद बिन्दु का नाम बताओ। (NCERT Exemplar)
हलः
दो निर्देशांक अक्षों का प्रतिच्छेद बिन्दु मूल बिन्दु कहलाता है।

प्रश्न 3.
बिन्दु (0, -9) किस अक्ष पर स्थित है?
हलः
∵ X-अक्ष निर्देशांक 0 है। इसलिए बिन्दु (0, -9) Y-अक्ष पर स्थित है।

प्रश्न 4.
बिन्दु (0, -6) की मूल बिन्दु से दूरी ज्ञात करो।
हलः
बिन्दु (0, -6) में x-अक्ष निर्देशांक 0 है तथा y-अक्ष निर्देशांक -6 है इसलिए बिन्दु (0, -6) की मूल बिन्दु से दूरी 6 मात्रक है।

प्रश्न 5.
यदि बिन्दु A(2, 0), B(-6, 0) तथा C(3, a – 3) x-अक्ष पर स्थित है तो a का मान ज्ञात करो।
हलः
∵ बिन्दु C, x-अक्ष पर स्थित है।
∴ बिन्दु C का y-अक्ष निर्देशांक = 0
a – 3 = 0 ⇒ a = 3

Ex 8.1 Coordinate Geometry लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 6.
वह चतुर्थांश ज्ञात कीजिए जिसमें निम्न बिन्दु स्थित हैं
(i) (-1,-4)
(ii) (4, 1)
(iii) (3, -2)
(iv) (-3, 1)
(v) (7, 2)
(vi) (-3, -2)
(vii) (-6, 4)
(viii) (2, -2)
हल:
(i) (-1, -4) स्थित होगा – तृतीय चतुर्थांश
(ii) (4, 1) स्थित होगा – प्रथम चतुर्थांश
(iii) (3, -2) स्थित होगा। – चतुर्थ चतुर्थांश
(iv) (-3, 1) स्थित होगा – द्वितीय चतुर्थांश
(v) (7, 2) स्थित होगा। – प्रथम चतुर्थांश
(vi) (-3, -2) स्थित होगा – तृतीय चतुर्थांश
(vii) (-6, 4) स्थित होगा – द्वितीय चतुर्थांश
(viii) (2, -2) स्थित होगा – चतुर्थ चतुर्थांश

Ex 8.1 Coordinate Geometry लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 11.
निम्न अंकित बिन्दुओं के निर्देशांक ज्ञात कीजिए

हलः
बिन्दु P = (4, -6)
बिन्दु G = (3, 2)
बिन्दु N = (-1, -1)
बिन्दु Q = (-1, 3)
बिन्दु H = (-3, 1)
बिन्दु S = (5, 6)
बिन्दु I = (3, -2)

Ex 8.1 Coordinate Geometry बहविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
किसी बिन्दु A(4, 3) की y-अक्ष से लम्बवत् दूरी
(a) 4 इकाई
(b) 3 इकाई
(c) 2 इकाई
(d) इनमें से कोई नहीं
हलः
बिन्दु A (4, 3) की y-अक्ष से लम्बवत् दूरी = 4 इकाई

अतः विकल्प (a) सही है।

प्रश्न 2.
वह बिन्दु जिसके दोनों निर्देशांक ऋणात्मक हों, वह किस चतुर्थांश में स्थित होगा (NCERT Exemplar)
(a) IV
(b) III
(c) II
(d) I
हल:
जिस बिन्दु के दोनों निर्देशांक ऋणात्मक हों, वह बिन्दु तीसरे चतुर्थांश में होगा।.

अतः विकल्प (b) सही है।

प्रश्न 3.
बिन्दु A(7, 5) की y-अक्ष से लम्बवत् दूरी (इकाई में)- .
(a) 35 इकाई
(b) 12 इकाई
(c) 7 इकाई
(d) इनमें से कोई नहीं
हलः
x = 7
अतः विकल्प (c) सही है।

प्रश्न 4.
द्वितीय चतुर्थांश में किसी बिन्दु के भुज एवं कोटि के चिह्न हैं (NCERT Exemplar)
(a) (+, +)
(b) (+, -)
(c) (-, +)
(d) (-, -)
हलः
द्वितीय चतुर्थांश में किसी बिन्दु के भुज एवं कोटि के चिह्न (-, +) होगा।
अतः विकल्प (c) सही है।

प्रश्न 5.
किसी बिन्दु की कोटि धनात्मक किस चतुर्थांश में होती है?
(a) I, II
(b) II, III
(c) III, IV
(d) इनमें से कोई नहीं
हल:
किसी बिन्दु की कोटि धानात्मक प्रथम तथा द्वितीय चतुर्थांश में होगी।
अतः विकल्प (a) सही है।

प्रश्न 6.
x-अक्ष पर सभी बिन्दुओं के भुज का मान (NCERT Exemplar)
(a) 0
(b) धनात्मक वास्तविक संख्या
(c) कोई वास्तविक संख्या
(d) इनमें से कोई नहीं
हलः
कोई वास्तविक संख्या।
अतः विकल्प (c) सही है।

प्रश्न 7.
वह बिन्दु, जिसके दोनों निर्देशांक धनात्मक हो, किस चतुर्थांश में स्थित होगा?
(a) I
(b) II
(c) III
(d) इनमें से कोई नहीं
हलः
प्रथम चतुर्थांश।
अतः विकल्प (a) सही है।

प्रश्न 8.
यदि x ≠ y, तब (x, y) + (y, x), परन्तु यदि x = y तब
(a) (x, y) ≠ (y, x)
(b) (x, y) = (y, x)
(c) (x, y) = (-x, y)
(d) इनमें से कोई नहीं
हलः
(x, y) = (y, x)
अतः विकल्प (b) सही है।

प्रश्न 9.
यदि A = A(-2, 3), B = B(-3, 5 ) तब (A का भुज) – (B का भुज) = (NCERT Exemplar)
(a) 1
(b) 2
(c) 3
(d) -3
हलः
A का भुज – B का भुज = -2 + 3 = 1
अतः विकल्प (a) सही है।

प्रश्न 10.
यदि 0(0, 0), A(4, 0) तथा B (0, 6) तब ∆OAB का क्षेत्रफल (वर्ग इकाई में)
(a) 8
(b) 10
(c) 12
(d) इनमें से कोई नहीं
हल:
∆OAB का क्षेत्रफल = [latex]\frac{1}{2}[/latex] × OA × OB
= [latex]\frac{1}{2}[/latex] × 4 × 6 = 12 वर्ग इकाई

अतः विकल्प (c) सही है।

Ex 8.1 Coordinate Geometry स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
निम्न बिन्दुओं को ग्राफ पेपर पर अंकित करें।
(i) (3, 5)
(ii) (-3, 4)
(iii) (-3, -4)
हलः

प्रश्न 2.
बिन्दु A(2, 0), B(5, 0) तथा C(5, 3) को ग्राफ पर अंकित करें तथा एक बिन्द D के निर्देशांक ज्ञात कीजिए जिसके लिए ABCD एक वर्ग है।
हल:
ABCD एक वर्ग होगा यदि AB = BC = CD = DA
ग्राफ से स्पष्ट है कि AB = BC = CD = DA = 3 इकाई
∴ बिन्दु D के निर्देशांक = (2, 3)

प्रश्न 3.
x-अक्ष पर मूल बिन्दु के दायीं ओर, y-अक्ष से 5 इकाई दूरी पर एक बिन्दु है। यदि यह y-अक्ष पर मूल बिन्दु से नीचे x-अक्ष से 5 इकाई दूरी पर है तो उस बिन्दु के निर्देशांक ज्ञात करो।
हलः
बिन्दु M के निर्देशांक = (5, 0)
बिन्दु N के निर्देशांक = (0, -5)

प्रश्न 4.
वे क्रमित युग्म ज्ञात कीजिए जिसके लिए x + 3y = 6 तथा उनका अभिलम्ब ज्ञात कीजिए। इस तरह के कितने क्रमित युग्म प्राप्त किये जा सकते हैं तथा कितनों का आलेखन किया जा सकता है?
हलः
x + 3y = 6
x = 6 – 3y …………..(1)

x	6	3	0
y	0	1	2

इस प्रकार (6, 0) (3, 1) तथा (0, 2) क्रमित युग्म प्राप्त हो सकते हैं।
इस प्रकार अनन्त क्रमित युग्मों का आलेखन किया जा सकता है।

प्रश्न 5.
संलग्न चित्र में, ABCD एक आयत है जिसकी लम्बाई 6 सेमी तथा चौड़ाई 3 सेमी है। 0, रेखा AB का मध्य बिन्दु है। A, B, C व D के निर्देशांक ज्ञात कीजिए।
हल:
बिन्दु A = (-3, 0)
बिन्दु B = (3, 0)
बिन्दु C = (3, 3)
बिन्दु D = (-3, 3)

प्रश्न 6.
बिन्दु P = (2, -6) को ग्राफ पेपर पर आलेखित कीजिए तथा x व y-अक्ष पर इस बिन्दु से लम्ब क्रमशः PM व PN डालें तो M तथा N के निर्देशांक ज्ञात कीजिए।
हलः
बिन्दु P = (2, -6) से x-अक्ष पर PM तथा y-अक्ष पर PN लम्ब
डालें। बिन्दु M के निर्देशांक = (2, 0)
M बिन्दु N के निर्देशांक = (0, -6)

प्रश्न 7.
तृतीय चतुर्थांश में स्थित उस आयत के शीर्षों के निर्देशांक ज्ञात कीजिए। जिसकी लम्बाई x-अक्ष पर p इकाई तथा y-अक्ष पर चौड़ाई q इकाई है।
हलः
II चतुर्थांश में आयत OPQR स्थित है।
बिन्दु O के निर्देशांक = (0, 0)
बिन्दु P के निर्देशांक = (0, -q)
बिन्दु Q के निर्देशांक = (-p, -4)
बिन्दु R के निर्देशांक = (-p, 0)

प्रश्न 8.
बिन्दुओं B(-5, 3), E(-3, -2), S(4, -2) तथा T(1, 3) को ग्राफ पेपर पर आलेखन करें तथा इनको क्रम से मिलायें, यह भी बताइये कि ये बिन्दु किस चतुर्थांश में स्थित हैं?
हलः
बिन्दु B, II चतुर्थांश में स्थित है।
बिन्दु E, III चतुर्थांश में स्थित है।
बिन्दु S, IV चतुर्थांश में स्थित है।’
बिन्दु T, I चतुर्थांश में स्थित है।

प्रश्न 9.
बिन्दु M के निर्देशांक (-2, 9) है इसको (1 + x, y²) तथा y > 0 से भी निरूपित करते हैं। निम्न बिन्दु किस चतुर्थांश में स्थित है, यह ज्ञात कीजिए। P(y, x), Q(s, x), R(x², y – 1), S(2x, -3y)
हलः
∵ बिन्दु M के निर्देशांक = (-2, 9)
बिन्दु M के निर्देशांक = (1 + x, y²)
x निर्देशांक की तुलना से, 1 + x = -2
x = -2 – 1 = -3
Y निर्देशांक की तुलना से, y² = 9
y = [latex]\sqrt{9}=[/latex] = +3 [∵ y > 0]
∴ बिन्दु P के निर्देशांक = (y, x) = (3, – 3) जो IV चतुर्थांश में है।
बिन्दु Q के निर्देशांक = (z, x) = (2, – 3) जो IV चतुर्थांश में है।
बिन्दु R के निर्देशांक = (x², y – 1) = (9, 2) जो I चतुर्थांश में है।
बिन्दु S के निर्देशांक = (2x, -3y) = (-6, -9) जो III चतुर्थांश में है।

प्रश्न 10.
संलग्न चित्र में, PQR एक समबाहु त्रिभुज है जिसके बिन्दु व R के निर्देशांक क्रमशः (0, 6) व (0, -6) हैं। शीर्ष P के निर्देशांक ज्ञात करो।
हलः
बिन्दु Q = (0, 6), बिन्दु R = (0, -6)
∴ OQ = 6 मात्रक, OR = 6 मात्रक
∴ QR = 6 + 6 = 12 मात्रक
∴ PR = PQ = 12 मात्रक
समबाहु त्रिभुज की ऊँचाई OP = QR × [latex]\frac{\sqrt{3}}{2}[/latex] = 12 × [latex]\frac{\sqrt{3}}{2}[/latex] = [latex]6 \sqrt{3}[/latex]
∴ बिन्दु P = ([latex]6 \sqrt{3}[/latex], 0)

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 7 Linear Equation in Two Variables Ex 7.1 दो चरों के रैखिक समीकरण

प्रश्न 1.
एक समीकरण का ग्राफ खींचिए, यदि
(i) x = 0, y = 4 समीकरण का एक हल है।
(ii) x = 1, y = 5 समीकरण का एक हल है।
(iii) (-4, -4) समीकरण के ग्राफ पर स्थित है।
(iv) रेखा (y – 2x = 4) और अक्षों के निर्देशांक के द्वारा निर्मित त्रिभुज का क्षेत्रफल
हलः

प्रश्न 2.
निम्नलिखित प्रत्येक का ग्राफ खींचिए।
(i) x = 2
(ii) x = -4
(iii) x = -4
हलः

प्रश्न 3.
नीचे दिये गये समीकरणों के ग्राफ खींचिए।
(i) y = 2x (NCERT)
(ii) y = -3x
(iii) 3x + 4y =0
हलः

प्रश्न 4.
निम्नलिखित प्रत्येक समीकरण के लिए चार हल ज्ञात कीजिए।
(i) 12x + 5y = 0
(ii) 5x – 3y = 0
(iii) 2(x – 1) + 3y = 4
(iv) 2x – 3(y – 2) = 1
हलः
(i) 12x + 5y = 0

प्रश्न 5.
समीकरण x + 2y – 4 = 0 का ग्राफ खींचिए तथा उस बिन्दु के निर्देशांक ज्ञात कीजिए। जहाँ ग्राफ y-अक्ष को काटता है।
हलः

प्रश्न 6.
समीकरण y = 3x का ग्राफ खींचिए। ग्राफ से x का मान ज्ञात कीजिए। जब y = -3
हलः

प्रश्न 7.
समीकरण 2x + 3y = 11 का ग्राफ खींचिए। ग्राफ से y का मान ज्ञात कीजिए। जब x = 1
हलः

प्रश्न 8.
एक त्रिभुज खींचिए जिसकी भुजाएं x = 0, y = 0 और x + y = 3.द्वारा निरूपित है।
हल:

Ex 7.1 Linear Equation in Two Variables बहविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
समीकरण 2x – y = 4 का आलेख x – अक्ष को किस बिन्दु पर काटेगा?
(a) (0, 2)
(b) (2, 0)
(c) (-2, 0)
(d) इनमें से कोई नहीं
हल:
x-अक्ष पर बिन्दु के लिए y = 0 रखने पर,
2x – 0 = 4 ⇒ x = 2
अतः बिन्दु (2, 0) है।
अतः विकल्प (b) सही है।

प्रश्न 2.
यदि (2a – 1, a) समीकरण 10x – 9y = 12 का हल है तो a =
(a) 2
(b) 1
(c) 1/2
(d) इनमें से कोई नहीं
हलः
यदि (2a – 1, a) दी गई समीकरण का हल है, तो यह समीकरण को सन्तुष्ट करेगा।
10(2a – 1) – 9a = 12
20a – 10 – 9a = 12
11a = 22 ⇒ a = 2
अतः विकल्प (a) सही है।

प्रश्न 3.
x = 2 तथा y = -4 से सन्तुष्ट होने वाली समीकरणों की संख्या
(a) केवल एक
(b) केवल दो
(c) अनन्त
(d) इनमें से कोई नहीं
हलः
अनन्त
अतः विकल्प (c) सही है।

प्रश्न 4.
y = -1 तथा y = 3 के ग्राफों के बीच की दूरी =
(a) 2
(b) 3
(c) 4
(d) इनमें से कोई नहीं
हलः
y = -1 तथा y = 3 के ग्राफों के बीच की दूरी = 3 + 1 = 4

अतः विकल्प (c) सही है।

प्रश्न 5.
बिन्दु (a, a), a ≠ 0 स्थित है (NCERT Exemplar)
(a) x-अक्ष पर
(b) y-अक्ष पर
(c) रेखा y = x पर
(d) इनमें से कोई नहीं
हलः
दिए गए बिन्दु का भुज तथा कोटि समान है, अतः यह बिन्दु y = x रेखा पर स्थित है।
अतः विकल्प (c) सही है।

प्रश्न 6.
रैखिक समीकरण 3x + 2y = 6 का ग्राफ y-अक्ष को किस बिन्दु पर प्रतिच्छेद करेगा?
(a) (3, 0)
(b) (0, 3)
(c) (2, 0)
(d) (0, 2)
हल:
y-अक्ष पर प्रतिच्छेद बिन्दु के लिए x = 0 रखने पर,
3 × 0 + 2y = 6
⇒ y = 3
अतः y-अक्ष पर प्रतिच्छेद बिन्दु (0, 3) होगा।
अतः विकल्प (b) सही है।

प्रश्न 7.
रेखा x = 3 निम्न में से किस बिन्दु से गुजरेगा?
(a) (3, 2)
(b) (2, 3)
(c) (0, 3)
(d) इनमें से कोई नहीं
हलः
(3, 0) से
अतः विकल्प (d) सही है।

प्रश्न 8.
y-अक्ष पर स्थित बिन्दु का रूप है
(a) (0, y),(y ≠ 0)
(b) (y, 0)
(c) (-y, 0)
(d) (x, x)
हलः
y-अक्ष पर स्थित बिन्दु के लिए x = 0
अतः बिन्दु (0, y) है।
अतः विकल्प (a) सही है।

प्रश्न 9.
2x + 5y = 10 को निरूपित करने वाली रेखा y-अक्ष के किस बिन्दु से मिलेगी?
(a) (2, 0)
(b) (0, 2)
(c) (1/2, 2)
(d) इनमें से कोई नहीं
हल:
y-अक्ष के लिए x = 0 रखने पर,
2 × 0 + 5y = 10 ⇒ y = [latex]\frac{10}{5}[/latex] = 2
रेखा बिन्दु (0, 2) पर मिलेगी।
अतः विकल्प (b) सही है।

प्रश्न 10.
बिन्दुओं (-1,1),(0, 0) तथा (1, -1) से गुजरने वाली सरल रेखा का समीकरण
(a) y = x
(b) x – y = 0
(c) x + y = 0
(d) इनमें से कोई नहीं
हलः
दिए गए विकल्पों में से x + y = 0, को प्रत्येक बिन्दु सन्तुष्ट करता है। अतः इन बिन्दुओं से गुजरने वाली रेखा का
समीकरण x + y = 0 है।
अतः विकल्प (c) सही है।

प्रश्न 11.
यदि (3, 2) समीकरण 3x – ky = 5 का हल है तब k =
(a) 1
(b) 2
(c) 3
(d) 4
हलः
∵ (3, 2) समीकरण 3x – ky = 5 का हल है, तो यह बिन्दु (3, 2), दी गयी समीकरण को सन्तुष्ट करेगा।
– 3 × 3 – k × 2 = 5 ⇒ -2k = -4 ⇒ k = 2
अतः विकल्प (b) सही है।

प्रश्न 12.
x = 2 व y = -1 निम्न में से किसका हल होगा?
(a) x + y = 3
(b) x – y = 3
(c) x + y + 3 = 0
(d) इनमें से कोई नहीं
हलः
दिए गए विकल्पों में x – y = 3 समीकरण x = 2 व y = -1 से सन्तुष्ट हो जाता है।
अतः विकल्प (b) सही है।

प्रश्न 13.
ax + by + c = 0 का ज्यामितीय निरूपण
(a) सरल रेखा
(b) वृत्त
(c) बिन्दु .
(d) इनमें से कोई नहीं
हलः
सरल रेखा।
अतः विकल्प (a) सही है।

प्रश्न 14.
x = 5, y = 2 निम्न में से किसका हल है? (NCERT Exemplar)
(a) x – y = 7
(b) x + y = 7
(c) x + 2y = 7
(d) इनमें से कोई नहीं
हलः
दिए गए विकल्पों में x + y = 7 समीकरण x = 5, y = 2 से सन्तुष्ट हो जाती है।
अतः विकल्प (b) सही है।

प्रश्न 15.
y = 8 का आलेख एक रेखा है जो
(a) x-अक्ष के समान्तर तथा मूलबिन्दु से 8 इकाई दूरी पर
(b) y-अक्ष के समान्तर तथा मूलबिन्दु से 8 इकाई दूरी पर
(c) (a) व (b) दोनों सत्य हैं।
(d) इनमें से कोई नहीं
हल:
x-अक्ष के समान्तर तथा मूल बिन्दु से 8 इकाई दूरी पर।
अतः विकल्प (a) सही है।

Ex 7.1 Linear Equation in Two Variables स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
एक पुस्तक का मूल्य, एक पैन के मूल्य से दोगुना है। इसे व्यक्त करने के लिए दो चरों का रैखिक समीकरण लिखिये।
हलः
माना पुस्तक का मूल्य = ₹ x तथा पैन का मूल्य = ₹ y
प्रश्नानुसार, x = 2y
x – 2y =0

प्रश्न 2.
विवेचना कीजिए, दो चरों के रैखिक समीकरण का आलेख, एक रेखा नहीं होती।
हलः
दो चरों के रैखिक समीकरण का ग्राफ हमेशा एक सरल रेखा होगी जो उस पर स्थित प्रत्येक बिन्दु को संतुष्ट करेगी।

प्रश्न 3.
उस रेखा का समीकरण ज्ञात कीजिए। जिसके निर्देशांकों का योग 10 इकाई है।
हलः
x+ y = 10

प्रश्न 4.
2x + 3y = 12 का आलेख बनाइये। किस बिन्दु पर यह x-अक्ष तथा y-अक्ष को काटती है?
हलः

प्रश्न 5.
3x + 4y = 6 का आलेख बनाइए। किस बिन्दु पर यह :-अक्ष तथा y-अक्ष को काटती है?
हलः

प्रश्न 6.
c के किस मान के लिए समीकरण 2x + cy = 8 में x व y के मान समान होंगे?
हलः
2x + cy = 8
cy = 8 – 2x ……………(1)
c = [latex]\frac{8-2 x}{y}[/latex]
SHERPREE
∵ x तथा y के मान समान है।
∴ c = [latex]\frac{8-2 x}{x}[/latex] जहाँ x ≠ 0

प्रश्न 7.
किस बिन्दु पर रेखा x + y = 5, y-अक्ष के समान्तर तथा मूल बिन्दु से धनात्मक दिशा में 2 इकाई दूरी पर स्थित रेखा से मिलता है?
हल:
y-अक्ष के समान्तर तथा मूल बिन्दु से +2 इकाई दूरी पर स्थित रेखा का समीकरण x = 2 ………..(1)
तथा x + y = 5 ………………. (2) रेखा का समीकरण है।
समीकरण (1) से मान रखने पर 2 + y = 5
y = 5 – 2 = 3
∴ बिन्दु = (2, 3) पर रेखा मिलती है।

प्रश्न 8.
एक शहर में ऑटो रिक्शा पहले किमी के लिए ₹ 10 तथा आगे के अन्य दूरी के प्रति किमी ₹ 4 लेता है। इस तथ्य को रैखिक समीकरण के रूप में व्यक्त करके, उसके आलेख खींचें।
हलः

प्रश्न 9.
एक गाड़ी को खींचने के लिए, उसके द्वारा प्रदत्त बल, त्वरण के समानुपाती है। इस कथन को दो चरों के रैखिक समीकरण के रूप में व्यक्त कीजिए तथा उसका ग्राफ खींचिए। स्थिर द्रव्यमान 6 किग्रा वह बल ज्ञात कीजिए जो निम्न त्वरण के द्वारा लगेगा। (NCERT Exemplar)
(i) 5 मी/से²
(ii) 6 मी/से²
हलः
y = mx जहाँ y = बल, x = चर तथा m अचर है।
(i) m = 6 किग्रा, त्वरण x = 5 मी/सेकण्ड²
बल y = mx = 5 × 6 = 30 न्यूटन
(ii) m = 6 किग्रा, त्वरण x = 6 मी/सेकण्ड²
बल y = mx = 6 × 6 = 36 न्यूटन

प्रश्न 10.
एक पिता एवं उसके पुत्र की वर्तमान आयु क्रमशः x तथा y है। 5 वर्ष पहले पिता की आयु, अपने पुत्र की आयु के 7 गुने से 2 अधिक है। इस कथन को रैखिक समीकरण द्वारा व्यक्त कीजिए।
हलः
x – 5 = 7(y – 5) + 2
x – 5 = 7y – 35 + 2
x – 7y – 5 + 33 = 0
x – 7y + 28 = 0

प्रश्न 11.
यदि x = 2, y =1 समीकरण 2x + 3y = m का हल है तो n का मान ज्ञात कीजिए।
हलः
2x + 3y =m
2 × 2 + 3 × 1 = m
4 + 3 = m ⇒ m = 7

प्रश्न 12.
एक आयताकार बाग का परिमाप 80 मीटर है। यदि लम्बाई 5 मीटर कम कर दी जाए तथा चौड़ाई 5 मीटर बढ़ा दी जाए तब इसका क्षेत्रफल 55 वर्ग मीटर बढ़ जाता है, इस कथन को रैखिक समीकरण द्वारा व्यक्त कीजिए।
हलः
माना आयताकार बाग की लम्बाई = x मीटर
आयताकार बाग की चौड़ाई = y मीटर
आयताकार बाग का परिमाप = 2(लम्बाई + चौड़ाई) = 2(x + y)
2(x + y) = 80 ………………(1)
आयताकार बाग का क्षेत्रफल = लम्बाई x चौड़ाई = xy
तथा (x – 5)(y + 5) = xy + 55

प्रश्न 13.
एक नाव धारा के विपरीत 8 किमी तथा धारा की दिशा में 16 किमी की दूरी 6 घण्टे में पूरी करती है। इस कथन को रैखिक समीकरण में व्यक्त कीजिए।
हलः
माना नाव की चाल = x किमी/घण्टा
धारा की चाल = y किमी/घण्टा
धारा की दिशा में नाव की चाल = (x + y) किमी/घण्टा
धारा की विपरीत दिशा में नाव की चाल = (x – y) किमी/घण्टा

प्रश्न 14.
3x – 2y = 4 तथा x + y – 3 = 0 के आलेख एक ही पेपर पर खींचकर दोनों रेखाओं का प्रतिच्छेद बिन्दु ज्ञात कीजिए।
हल:

प्रश्न 15.
यदि बिन्दु A(3, 5) तथा B(1, 4) रेखा ax + by = 7 के आलेख पर स्थित हो तो a व b के मान ज्ञात कीजिए।
हल:
यदि रेखा ax + by = 7, बिन्दु A व बिन्दु B से जाती है, तो दिए गए बिन्दु, रेखा को सन्तुष्ट करते हैं, अतः
x = 3, y = 5 रखने पर,
3a + 5b = 7 ……………….. (1)
x = 1, y = 4 रखने पर,
a + 4b = 7 ……………… (2)
समीकरण (1) व (2) को हल करने पर,
a = -1, b = 2

प्रश्न 16.
रेखाओं 2x + y = 6 तथा 2x – y + 2 = 0 के आलेख खींचे तथा दोनों रेखाओं से घिरे क्षेत्र को छायांकित कर, छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 17.
एक संख्या, उसके अंकों को पलटकर बनी संख्या से 27 अधिक है। यदि इकाई व दहाई के अंक क्रमशः x व y हैं तो उपरोक्त कथन को प्रदर्शित करने वाली रैखिक समीकरण ज्ञात कीजिए।
हलः
माना इकाई का अंक = x तथा दहाई का अंक = y
अतः संख्या = 10y + x
तथा अंकों को पलटकर बनने वाली संख्या = 10x + y
प्रश्नानुसार, (10y + x) – (10x + y) = 27
-9x + 9y = 27
या x – y = -3
x – y + 3 = 0

प्रश्न 18.
रैखिक समीकरण 4x – 3y + 4 = 0 तथा 4x + 3y – 20 = 0 का आलेख बनाइये तथा इन रेखाओं व x-अक्ष के बीच का क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 19.
यदि बिन्दु (2, -2) रैखिक समीकरण 5x + ky = 4 पर स्थित है तो k का मान ज्ञात कीजिए।
हलः
दी गई रैखिक समीकरण 5x + ky = 4
x = 2, y = -2 रखने पर,
5 × 2 + k(-2) = 4
10 – 2k = 4
-2k = -6 ⇒ k = 3

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 14 Parallelogram and Triangles Ex 14.1 समान्तर चतुर्भुज व त्रिभुज के क्षेत्रफल

Ex 14.1 Parallelogram and Triangles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
एक समान्तर चतुर्भुज के विकर्ण इसे कितने भागों में विभक्त करते हैं?
हलः
समान्तर चतुर्भुज में विकर्ण एक-दूसरे को दो बराबर भागों में काटते हैं।

प्रश्न 2.
समचतुर्भुज का क्षेत्रफल इसके विकर्णों के गुणनफल से कितने गुना होगा?
हलः
समचतुर्भुज का क्षेत्रफल [latex]=\frac{1}{2} \times[/latex] विकर्णों का गुणनफल

प्रश्न 3.
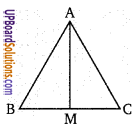
यदि माध्यिका किसी त्रिभुज को दो भागों में बाँटती है तो इनके क्षेत्रफल में सम्बन्ध ज्ञात कीजिए।
हलः
यदि ∆ में माध्यिका ∆ को दो भागों में बाँटती है तो उनके क्षेत्रफल समान होंगे।

प्रश्न 4.
समलम्ब चतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हलः
समलम्ब चतुर्भुज का क्षेत्रफल [latex]=\frac{1}{2} \times[/latex] समान्तर भुजाओं का योगफल × ऊँचाई

प्रश्न 5.
समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए।
हलः
समचतुर्भुज का क्षेत्रफल [latex]=\frac{1}{2} \times[/latex] विकर्णों का गुणनफल

Ex 14.1 Parallelogram and Triangles लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 6.
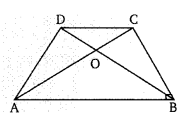
किसी समलम्ब चतुर्भुज ABCD के विकर्ण AC व BD (AB||DC) बिन्दु O पर प्रतिच्छेद करते हैं। सिद्ध कीजिए कि ∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल। [NCERT]
हलः
ज्ञात है: AB||DC जो एक-दूसरे को बिन्दु O पर काटते हैं।
सिद्ध करना है: ar(∆AOD) = ar(∆BOC)
उपपत्तिः एक ही आधार और दो समान्तर रेखाओं के बीच बने त्रिभुजों के क्षेत्रफल समान होते हैं।
∴ ∆ABD का क्षेत्रफल = ∆ABC का क्षेत्रफल …(1)
दोनों पक्षों से ∆AOB का क्षेत्रफल घटाने पर
∆ABD का क्षेत्रफल – ∆AOB का क्षेत्रफल
= ∆ABC का क्षेत्रफल – ∆AOB का क्षेत्रफल
∴ ∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल

प्रश्न 7.
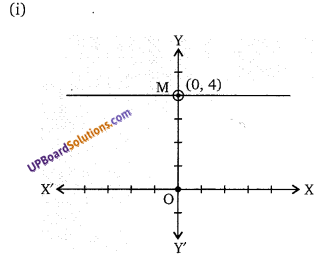
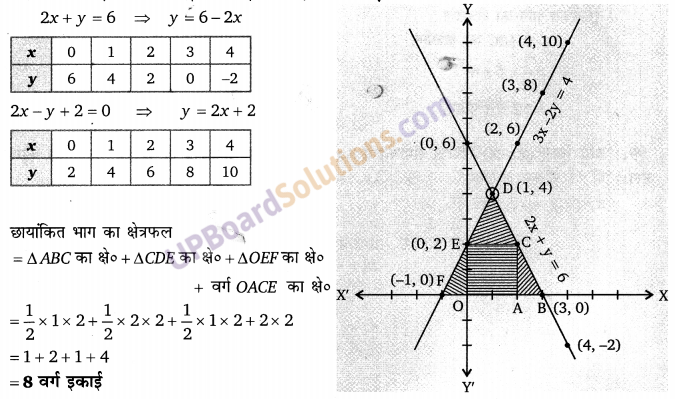
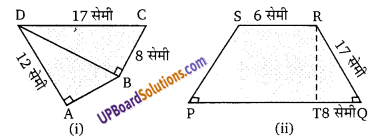
(i) चित्र (i) में दिये गये चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
(ii) चित्र (ii) में दिये गये समलम्ब चतुर्भुज PQRS का क्षेत्रफल ज्ञात कीजिए।

हलः

प्रश्न 8.
चित्र में BD, चतुर्भुज ABCD का विकर्ण है। सिद्ध कीजिए कि 5 सेमी ABCD एक समान्तर चतुर्भुज है तथा समान्तर चतुर्भुज ABCD का क्षेत्रफल भी ज्ञात कीजिए।
हलः

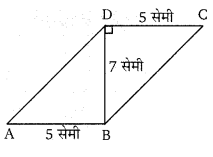
∠CDB = ∠DBA = 900
परन्तु ये एकान्तर कोण हैं।
∴ AB|| DC
∆ABD तथा ∆BCD में, AB = DC = 5 सेमी
BD (उभयनिष्ठ)
∴ ∠ABD = ∠BDC (प्रत्येक समकोण)
∴ ∆ABD ≅ ∆BDC
∠ADB = ∠DBC (परन्तु ये एकान्तर कोण हैं)
∴ AD||BC
तथा AD = BC
∴ ABCD एक समान्तर चतुर्भुज है।
समान्तर चतुर्भुज ABCD का क्षेत्रफल = AB × BD = 5 × 7 = 35 सेमी²

प्रश्न 9.
ABCD एक समान्तर चतुर्भुज है। BC को L तक इस प्रकार बढ़ाते हैं कि BC = CL, रेखा AL, CD से बिन्दु M पर प्रतिच्छेद करती है। सिद्ध कीजिए कि
ar(∆BCM) = ar(∆DML)
हलः

प्रश्न 10.
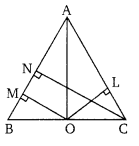
त्रिभुज ABC में AB = AC, BC पर कोई बिन्दु O है। बिन्दु O से OL व OM क्रमश: AC व AB पर लम्ब है। सिद्ध कीजिए कि OL + OM = C से AB पर लम्ब की लम्बाई।
हलः

प्रश्न 11.
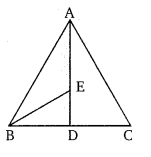
∆ABC में बिन्दु D, BC का तथा E, AD का मध्य बिन्दु है। सिद्ध कीजिए कि ∆BED का क्षेत्रफल = [latex ]\frac{1}{4}[/latex] × ∆ABC का क्षेत्रफल [NCERT]
हल:
D, भुजा BC का मध्य बिन्दु है। अत: AD इसे दो समान त्रिभुजों में बाँटता है। इसी प्रकार AD का मध्य बिन्दु E है, B को E से मिलाया।
∴ ∆ABE का क्षेत्रफल = ∆BED का क्षेत्रफल
∴ ∆ABC का क्षेत्रफल = ∆ADC का क्षेत्रफल + ∆ABD का क्षेत्रफल
∵ ∆ABC का क्षेत्रफल = 2∆BED का क्षेत्रफल + 2∆BED का क्षेत्रफल = 4∆BED का क्षेत्रफल
∴ ∆BED का क्षेत्रफल = [latex ]\frac{1}{4}[/latex] ∆ABC का क्षेत्रफल

प्रश्न 12.
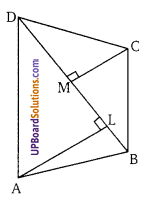
चित्र में, ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण BD = 20 सेमी। यदि AL ⊥ BD व CM ⊥ BD इस प्रकार हैं कि AL = 10 सेमी व CM = 5 सेमी है। चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
हल:


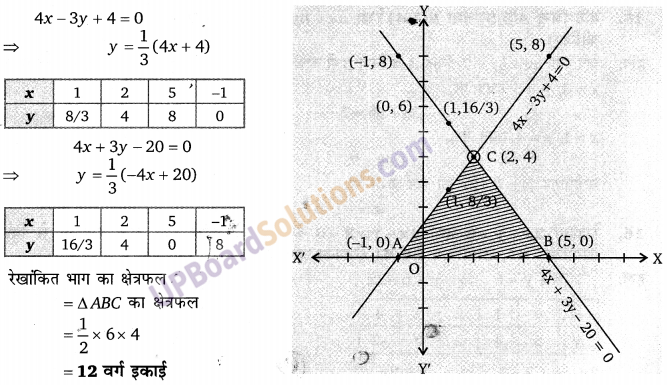
प्रश्न 13.
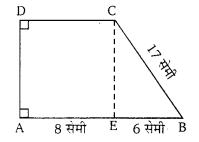
चित्र में, समलम्ब चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
हलः

प्रश्न 14.
चित्र में, समलम्ब चतुर्भुज ABCD में AB = 7 सेमी, AD = BC = 5 सेमी, DC = x सेमी। AB व DC के बीच की दूरी 4 सेमी है। तब x का मान व ABCD का क्षेत्रफल ज्ञात कीजिए।
हल:

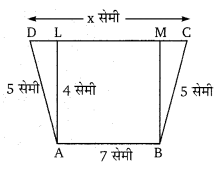
प्रश्न 15.
सिद्ध कीजिए कि किसी त्रिभुज की दो भुजाओं के मध्य बिन्दुओं को मिलाने से बने त्रिभुज का क्षेत्रफल पूरी लम्बाई के त्रिभुज के क्षेत्रफल का [latex]\frac{1}{4}[/latex] होगा।
हलः

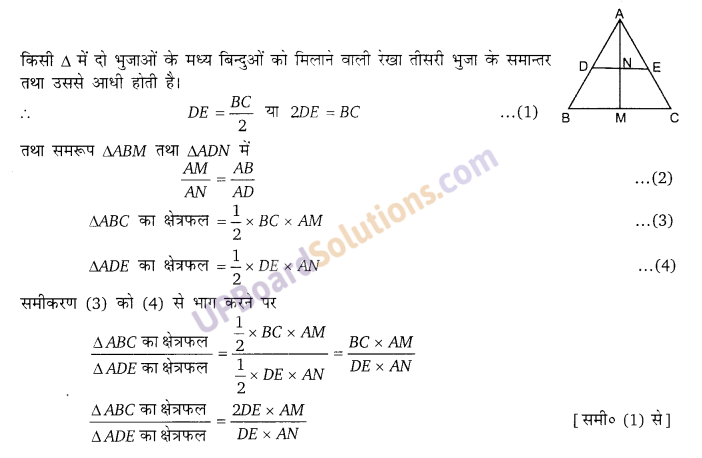
प्रश्न 16.
सिद्ध कीजिए कि a भुजा वाले समबाहु त्रिभुज का क्षेत्रफल [latex]\frac{\sqrt{3}}{4} a^{2}[/latex] होता है।
हलः

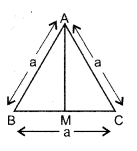
प्रश्न 17.
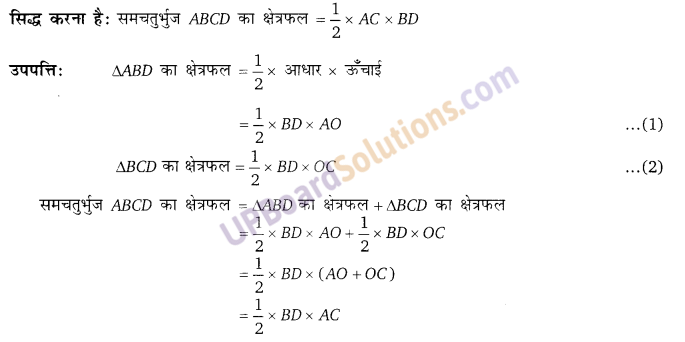
सिद्ध कीजिए कि समचतुर्भुज का क्षेत्रफल उसके विकर्णों के गुणनफल का आधा होता है।
हलः

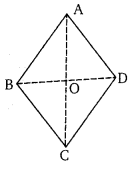
ज्ञात हैः समचतुर्भुज ABCD जिसके विकर्ण AC तथा BD परस्पर बिन्दु O पर प्रतिच्छेद करते हैं तथा ये विकर्ण परस्पर लम्ब हैं।
सिद्ध करना है: समचतुर्भुज ABCD का क्षेत्रफल = [latex]\frac{1}{2}[/latex] × AC × BD

प्रश्न 18.
एक समान्तर चतुर्भुज ABCD की भुजाओं BC व AD पर क्रमशः बिन्दु E व F हैं। सिद्ध कीजिए कि त्रिभुज AED व DFC के क्षेत्रफल बराबर होंगे।
हलः
ज्ञात है: ABCD एक समान्तर चतुर्भुज है जिसमें BC पर बिन्दु E तथा AD पर बिन्दु F हैं।

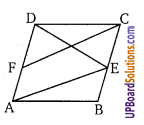
सिद्ध करना है: ∆AED का क्षेत्रफल = ∆DFC का क्षेत्रफल
उपपत्तिः एक ही आधार तथा दो समान्तर रेखाओं के बीच बने दो त्रिभुजों के क्षेत्रफल – समान होते हैं।
∆AED का क्षेत्रफल = ∆DFC का क्षेत्रफल

प्रश्न 19.
चित्र में, चतुर्भुज का प्रत्येक विकर्ण इसे दो समान क्षेत्रफल वाले त्रिभुजों में विभक्त करता है। सिद्ध कीजिए कि यह एक समान्तर चतुर्भुज है।
हलः
विकर्ण BD, समान्तर चतुर्भुज को दो त्रिभुजों में बाँटता है।
∆ABD का क्षेत्रफल = ∆BCD का क्षेत्रफल
∆ABD ≅ ABCD

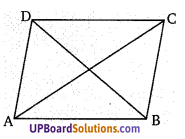
∴ AB = DC तथा AD = BC तथा ∠ABD = ∠BDC परन्तु ये एकान्तर कोण हैं।
∴ AB || DC
∴ विकर्ण AC, समान्तर चतुर्भुज को दो त्रिभुजों में बाँटता है।
∆ADC का क्षेत्रफल = ∆ABC का क्षेत्रफल
∆ADC ≅ ∆ABC
∴ ∠CAB = ∠DCA
परन्तु ये एकान्तर कोण हैं
∴ AD|| BC
∴ ABCD एक समान्तर चतुर्भुज है।

प्रश्न 20.
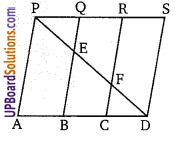
चित्र में, समान्तर चतुर्भुज PSDA में PQ = QR = RS तथा AP||BQ||CR तो सिद्ध कीजिए कि
∆PQE का क्षेत्रफल = ∆CFD का क्षेत्रफल (NCERT Exemplar)

हलः
ज्ञात हैः PSDA एक समान्तर चतुर्भुज है जिसमें PQ = QR = RS तथा AP|| BQ||CR
सिद्ध करना हैः क्षेत्रफल (∆PQE) = क्षेत्रफल (∆CFD)
उपपत्तिः ∆PQE तथा ∆CFD में,
PQ = CD (ज्ञात है)
∠EPQ = ∠FDC (एकान्तर कोण)
∠PQE = ∠FCD
(∵ ∠PQB = ∠PRC (संगत कोण), ∠PRC = ∠QBC, ∠QBC = ∠FCD, ∠PQB = ∠FCD)
अतः
∆PQE ≅ ∆DFB
∆PQE का क्षेत्रफल = ∆FCD का क्षेत्रफल

प्रश्न 21.
चित्र में, ABCD एक समान्तर चतुर्भुज है। तो सिद्ध कीजिए कि ar(∆BCP) = ar(∆DPQ) [NCERT]
हल:

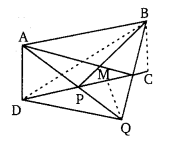
प्रश्न 22.
∆ABC में, P भुजा BC पर कोई बिन्दु है। एक रेखा CQ||AP इस प्रकार खींचे कि यह Q पर BA से मिले। सिद्ध कीजिए कि
ar(∆BQP) = ar(∆ABC)
हल:

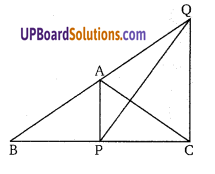
∵ ∆PAC तथा ∆PAQ एक ही आधार तथा दो समान्तर भुजाओं के बीच बने है।
∆PAC का क्षेत्रफल = ∆PAQ का क्षेत्रफल
∆ABP का क्षेत्रफल दोनों पक्षों में जोडने पर
∆ABP का क्षेत्रफल + ∆PAC का क्षेत्रफल = ∆PAQ का क्षेत्रफल + ∆ABP का क्षेत्रफल
∆ABC का क्षेत्रफल = ∆PBQ का क्षेत्रफल

प्रश्न 23.
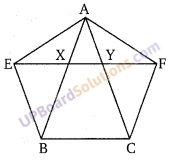
चित्र में, समलम्ब चतुर्भुज ABCD में AB||DC व DC = 40 सेमी, AB = 60 सेमी हैं। यदि X व Y क्रमशः AD व BC के मध्य बिन्दु हैं तो सिद्ध कीजिए कि
(i) XY = 50 सेमी
(ii) DCYX एक समलम्ब चतुर्भुज है।
(iii) समलम्ब चतुर्भुज DCYX का क्षेत्रफल


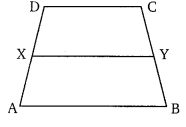
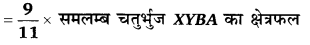
हल:

प्रश्न 24.
एक त्रिभुज ABC की भुजा BC के समान्तर XY एक रेखा है। यहाँ BE|| AC व CF|| AB बढ़ाने पर XY से क्रमशः E व F पर मिलती हैं। सिद्ध कीजिए। कि ar(∆ABE) = ar(∆ACF) [NCERT]
हलः
दिया है: XY एक रेखा है जो ∆ABC में BC के समान्तर है तथा BE|| AC तथा
CF|| AB| AB रेखा XY को E तथा F पर काटती है।
सिद्ध करना है: ∆ABE का क्षेत्रफल = ∆ACE का क्षेत्रफल
उपपत्ति: ∆ABE तथा ∆ACF में,
∠BAC = ∠ACF (एकान्तर कोण)
परन्तु ∠BAC = ∠ABE (एकान्तर कोण)
∠ABE = ∠ACF
BE = CF (समान्तर चतुर्भुज की भुजाएं)
तथा AB = AC
अतः
∆ABE ≅ ∆ACF
∴ ∆ABE का क्षेत्रफल = ∆ACF का क्षेत्रफल

प्रश्न 25.
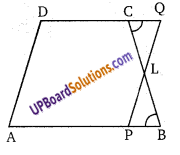
एक समलम्ब चतुर्भुज ABCD में AB||CD तथा L, BC का मध्य बिन्दु है। L से एक रेखा PQ|| AD इस प्रकार खींचे कि यह AB से P तथा DC से Q पर मिलती है। सिद्ध कीजिए कि
ar (समलम्ब ABCD) = ar(समान्तर चतुर्भुज APQD) (NCERT Exemplar)
हलः
ज्ञात है: ABCD एक समलम्ब है जहाँ AB||CD तथा L, BC का मध्य बिन्दु है, PQ|| AD खींची गयी है जो AB को P तथा BC को Q पर काटती है।

सिद्ध करना है: समलम्ब ABCD का क्षेत्रफल = समान्तर चतुर्भुज APQD का क्षेत्रफल
उपपत्ति: ∆CLQ तथा ∆LPB में,
CL = LB (ज्ञात है)
∠BCQ = ∠CBP (एकान्तर कोण)
∠CLQ = ∠PLB (शीर्षाभिमुख कोण)
अतः
∆CLQ = ∆LPB
∴ ∆CLQ का क्षेत्रफल = ∆LPB का क्षेत्रफल
आकृति APLCD + ∆LPB का क्षेत्रफल = आकृति APLCD + ∆CLQ का क्षेत्रफल
समलम्ब ABCD का क्षेत्रफल = समान्तर चतुर्भुज APQD का क्षेत्रफल

प्रश्न 26.
चित्र में, ABCD व AEFD दो समान्तर चतुर्भुज हैं। सिद्ध कीजिए कि ।
(i) PE = FQ
(ii) ar(∆PEA) = ar(∆QFD)
हलः

ज्ञात है: ABCD तथा AEFD दो समान्तर चतुर्भुज हैं।
सिद्ध करना है:
(i) PE = FQ
(ii) ∆PEA का क्षेत्रफल = ∆QFD का क्षेत्रफल
उपपत्तिः ∆PEA तथा ∆FQD में
AE||DF तथा EQ तिर्यक रेखा काटती है।
∠AEP = ∠DFQ (संगत कोण)
AE = DF (समान्तर चतुर्भुज AEFD की भुजाएं)
तथा ∠EAP’= ∠FDQ (∵ AB||DC)
अतः ∆PEA ≅ ∆FQD
∴ PE = FQ तथा ∆PEA का क्षेत्रफल = ∆FQD का क्षेत्रफल

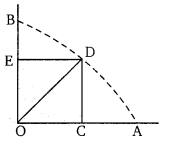
प्रश्न 27.
चित्र में, OCDE एक 10 सेमी त्रिज्या के वृत्त के एक चतुर्थाश में एक आयत है। यदि OE [latex]=2 \sqrt{5}[/latex] है तो आयत का क्षेत्रफल ज्ञात कीजिए।
हलः
समकोण ∆OED में,
OD² = OE² + ED²
(10)² = (275)² + ED²
100 = 20 + ED²
100 – 20 = ED

80 = ED²

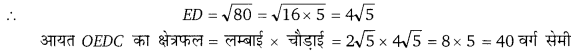
प्रश्न 28.
एक समान्तर चतुर्भुज ABCD के विकर्ण AC व BD बिन्दु O पर मिलते हैं। AD के मध्य बिन्दु से एक
रेखा MH खींचे जो DB से समान्तर है तथा A0 से H पर मिलती है तथा MH || AO, DO से K पर मिलती है। सिद्ध कीजिए कि

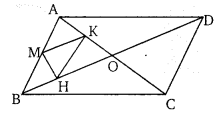
हलः

Ex 14.1 Parallelogram and Triangles बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
एक समलम्ब चतुर्भुज की दो समांतर भुजाएँ क्रमशः 1 मी और 2 मी हैं तथा इनके बीच की लम्बवत् दूरी 6 मी है। समलम्ब चतुर्भुज का क्षेत्रफल है-
(a) 9 मी²
(b) 18 मी²
(c) 12 मी²
(d) इनमें से कोई नहीं
हलः
समलम्ब चतुर्भुज का क्षेत्रफल

अतः विकल्प (a) सही है।

प्रश्न 2.
एक समांतर चतुर्भुज ABCD में, AB = 20 सेमी भुजाओं AB और DC की संगत ऊँचाईयाँ क्रमश: 14 सेमी तथा 10 सेमी हैं। तब AD की लम्बाई =
(a) 26 सेमी
(b) 28 सेमी
(c) 25 सेमी
(d) इनमें से कोई नहीं
हलः
समान्तर चतुर्भुज ABCD का क्षेत्रफल = 20 × 14
= 280 वर्ग सेमी

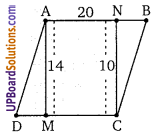
समान्तर चतुर्भुज ABCD का क्षेत्रफल = 10 × AD
10 × AD = 280
AD = 28 सेमी
अतः विकल्प (b) सही है।

प्रश्न 3.
यदि एक वर्ग और एक समचतुर्भुज समान आधार पर है तथा समान समांतरों के बीच स्थित है तब वर्ग और समचतुर्भुज के क्षेत्रफलों का अनुपात है-
(a) 1 : 2
(b) 1 : 3
(c) 1 : 1
(d) इनमें से कोई नहीं
हलः
∵ एक ही आधार पर तथा समान समांतरों के बीच बने समान्तर चतुर्भुजों के क्षेत्रफल बराबर होते हैं।
अतः वर्ग और समचतुर्भुजों के क्षेत्रफलों का अनुपात = 1 : 1
अतः विकल्प (c) सही है।

प्रश्न 4.
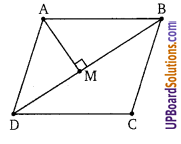
एक समचतुर्भुज की एक भुजा और एक विकर्ण क्रमशः 5 सेमी और 8 सेमी हैं। तब समचतुर्भुज का क्षेत्रफल है
(a) 20 सेमी²
(b) 22 सेमी²
(c) 24 सेमी²
(d) इनमें से कोई नहीं
हल:
AB = BC = CD = DA = 5 सेमी, BD = 8 सेमी समचतुर्भुज में शीर्ष से विकर्ण पर डाला गया लम्ब, विकर्ण को समद्विभाजित करता है। तब

प्रश्न 5.
यदि एक त्रिभुज और एक समांतर चतुर्भुज समान आधार पर हैं तथा समान समांतरों के बीच स्थित हैं तब त्रिभुज और समांतर चतुर्भुज के क्षेत्रफलों का अनुपात है- (NCERT Exemplar)
(a) 1 : 2
(b) 1 : 1
(c) 1 : 3
(d) 1 : 4
हलः

प्रश्न 6.
संलग्न चित्र में एक समांतर चतुर्भुज ABCD है जिसमें DC = 6 सेमी तथा AE ⊥ DC, AE = 4 सेमी तब
∆ DCF का क्षे० =
(a) 10 सेमी²
(b) 24 सेमी²
(c) 12 सेमी²
(d) इनमें से कोई नहीं
हलः

वर्ग सेमी अतः विकल्प (c) सही है।

प्रश्न 7.
संलग्न चित्र में, एक समांतर चतुर्भुज ABCD है। यदि (∆BFC) का क्षेत्रफल = 40 सेमी² तब (∆AEB) का क्षेत्रफल =
(a) 30 सेमी²
(b) 40 सेमी²
(c) 20 सेमी²
(d) इनमें से कोई नहीं
हल:

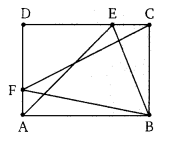
∵ दो समान्तर रेखाओं के बीच बने त्रिभुजों का क्षेत्रफल समान होता है। अतः ∆AEB का क्षेत्रफल = ∆BFC का क्षेत्रफल = 40 वर्ग सेमी
अतः विकल्प (b) सही है।

प्रश्न 8.
यदि एक ∆ABC में,E माध्यिका AD का मध्य बिंदु है तब ∆BED और ∆ABC के क्षेत्रफलों का अनुपात होगा-
(a) 1 : 2
(b) 1 : 4
(c) 2 : 1
(d) 4 : 1
हलः

अतः विकल्प (c) सही है।

प्रश्न 9.
∆ABC में, D, E तथा F क्रमशः BC, CA और AB के मध्य बिंदु हैं यदि (∆ABC) का क्षेत्रफल = 56 सेमी²
तब ∆DEF का क्षेत्रफल =
(a) 28 सेमी²
(b) 26 सेमी²
(c) 21 सेमी²
(d) इनमें से कोई नहीं
हलः

प्रश्न 10.
यदि P, Q,R और S क्रमशः एक समान्तर चतुर्भुज ABCD की भुजाओं के मध्य बिंदु हैं तथा (||^gm PQRS) का क्षे० = 32.5 सेमी² तब (||^gm ABCD) का क्षेत्रफल =
(a) 65 सेमी²
(b) 130 सेमी²
(c) 135 सेमी²
(d) इनमें से कोई नहीं ।
हलः

प्रश्न 11.
एक ∆ABC में, AD एक माध्यिका है, E, माध्यिका का मध्य बिंदु है। यदि (∆BED) का क्षेत्रफल = 20 सेमी² तब (∆ABC) का क्षेत्रफल =
(a) 20 सेमी²
(b) 10 सेमी²
(c) 60 सेमी²
(d) इनमें से कोई नहीं
हलः
प्रश्न संख्या 8 से

अतः विकल्प (a) सही है।

प्रश्न 12.
संलग्न चित्र में, यदि समांतर चतुर्भुज ABCD का क्षेत्रफल 30 सेमी है तब शीर्षलम्ब AQ की लम्बाई है-
(a) 6 सेमी
(b) 5 सेमी
(c) 4 सेमी
(d) इनमें से कोई नहीं
हलः
समान्तर चतुर्भुज ABCD का क्षेत्रफल = BC × AQ
30 = 6 × AQ


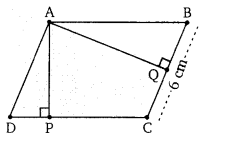
अतः विकल्प (b) सही है।

प्रश्न 13.
संलग्न चित्र में, AD माध्यिका है, तथा AC पर कोई बिन्दुE इस प्रकार है, कि ∆ADE का क्षेत्रफल : ∆ABD का क्षेत्रफल = 2 : 3 तब (∆EDC) का क्षेत्रफल : ∆ABC का क्षेत्रफल =
(a) 1 : 2
(b) 1 : 3
(c) 1 : 4
(d) 1 : 6
हलः


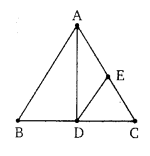
अतः विकल्प (d) सही है।

प्रश्न 14.
संलग्न चित्र में, एक समांतर चतुर्भुज ABCD है तब (∆APB) का क्षेत्रफल =
(a) 12 सेमी²
(b) 10 सेमी²
(c) 16 सेमी²
(d) 18 सेमी²
हल:

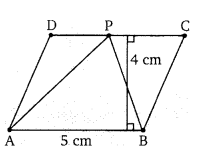
प्रश्न 15.
एक बराबर आधार के दो समांतर चतुर्भुज हैं तथा समान समांतरों के बीच स्थित हैं, उनके क्षेत्रफलों का अनुपात है
(NCERT Exemplar)
(a) 1 : 1
(b) 1 : 2
(c) 2 : 1
(d) 1 : 3
हलः
1 : 1
अतः विकल्प (a) सही है।

प्रश्न 16.
एक त्रिभुज की भुजाओं के मध्य बिन्दु त्रिभुज के किसी शीर्ष को चौथा बिंदु मानकर बने एक समान्तर चतुर्भुज का क्षेत्रफल- (NCERT Exemplar)
(a) [latex]\frac{1}{2}(\Delta A B C)[/latex] का क्षेत्रफल
(b) (∆ABC) का क्षेत्रफल
(c) [latex]\frac{1}{3}(\Delta A B C)[/latex] का क्षेत्रफल
(d) इनमें से कोई नहीं
हलः

अतः विकल्प (a) सही है।

प्रश्न 17.
एक त्रिभुज की माध्यिका इसे दो में विभाजित करती है- (NCERT Exemplar)
(a) सम त्रिभुजों
(b) बराबर क्षेत्रफलों के त्रिभुजों
(c) सर्वांगसम त्रिभुजों
(d) समद्विबाहु त्रिभुज
हलः
बराबर क्षेत्रफलों के त्रिभज।
अतः विकल्प (b) सही है।

प्रश्न 18.
एक समचतुर्भुज जिसके विकर्ण 16 सेमी और 12 सेमी हैं, की आसन्न भुजाओं के मध्य बिंदुओं को मिलाने पर प्राप्त आकृति का क्षेत्रफल है-
(a) 48 सेमी²
(b) 24 सेमी²
(c) 96 सेमी²
(d) इनमें से कोई नहीं
हलः

अतः विकल्प (a) सही है।

प्रश्न 19.
एक समलम्ब चतुर्भुज ABCD है जिसमें AB||DC के विकर्ण AC और BD, परस्पर O पर प्रतिच्छेद करते हैं ∆AOD के क्षेत्रफल के बराबर क्षे० का त्रिभुज है-
(a) BOC
(b) AOB
(c) DOC
(d) इनमें से कोई नहीं
हलः

प्रश्न 20.
एक समचतुर्भुज के विकर्णों की लम्बाईयाँ 12 सेमी तथा 16 सेमी हैं। समचतुर्भुज का क्षेत्रफल है
(a) 196 सेमी²
(b) 96 सेमी²
(c) 98 सेमी²
(d) 144 सेमी²
हलः

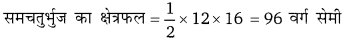
अतः विकल्प (b) सही है।

Ex 14.1 Parallelogram and Triangles स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
एक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु 0 पर इस प्रकार प्रतिच्छेद करते हैं कि AOD का क्षेत्रफल = BOC का क्षेत्रफल तो सिद्ध कीजिए कि ABCD एक समलम्ब चतुर्भुज है।
हलः

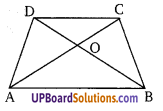
∵ ∆AOD का क्षेत्रफल = ∆BOC का क्षेत्रफल ….. (1)
दोनों पक्षों में ADOC जोड़ने पर
∆AOD का क्षेत्रफल + ∆DOC का क्षेत्रफल = ∆BOC का क्षेत्रफल + ∆DOC का क्षेत्रफल
∴ ∆ADC का क्षेत्रफल = ∴BCD का क्षेत्रफल
एक ही आधार पर बने दो त्रिभुज समान क्षेत्रफल के हैं तो वे समान्तर भुजाओं के बीच बनेगें। अत: AB||DC तथा AD व BC असमान्तर रेखायें हैं।
अतः चतुर्भुज ABCD एक समलम्ब चतुर्भुज होगा।

प्रश्न 2.
∆ABC की भुजा AB का मध्य बिन्दु D है। BC पर कोई बिन्दु P है। CQ, PD के समान्तर है तो सिद्ध कीजिए कि PQ, ∆ABC को समद्विभाजित करती है।
हलः
ज्ञात है: बिन्दु D, भुजा AB का मध्य बिन्दु है। P, BC पर कोई बिन्दु है तथा CQ||PD
सिद्ध करना है: PQ, AABC को समद्विभाजित करता है।

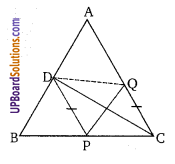
∴ DPCQ एक समान्तर चतुर्भुज है तथा PQ रेखा ∆ABC को समद्विभाजित करती है।

प्रश्न 3.
दर्शाइए कि एक समान्तर चतुर्भुज की विपरीत भुजाओं के एक युग्म D के मध्य बिन्दुओं को मिलाने वाला रेखाखण्ड, इसे दो बराबर समान्तर चतुर्भुजों में बाँटता है।
हल:

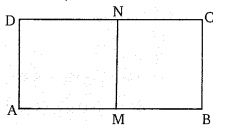
ABCD एक समान्तर चतुर्भुज है यदि M तथा N समान्तर चतुर्भुज की भुजाओं AB तथा DC के मध्य बिन्दु हैं।

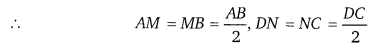
AB||DC
∴ AM || DN तथा MB||NC
अत: AMND तथा MBCN भी समान्तर चतुर्भुज होंगे।
इसी प्रकार,

इस चित्र में भी सिद्ध कर सकते हैं कि ABNM तथा DCNM भी समान्तर चतुर्भुज होंगे। इतिसिद्धम्

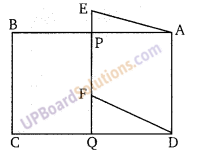
प्रश्न 4.
किसी समलम्ब चतुर्भुज में बडी भुजा का मध्य बिन्दु दूसरी बडी भुजा के बाहरी बिन्दु से मिलकर जो त्रिभुज बनाता है। सिद्ध कीजिए कि उसका क्षेत्रफल, समलम्ब चतुर्भुज का आधा होगा।

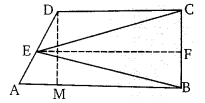
हलः
समलम्ब की भुजा AD का मध्य बिन्दु E से खींची गयी रेखा इसे दो समान क्षेत्रफल वाले समलम्ब में बाँटती है तथा समलम्ब EFCD का क्षेत्रफल = 2. ∆EFC का क्षेत्रफल …(1)
समलम्ब EFBA का क्षेत्रफल = 2. ∆EFB का क्षेत्रफल …(2)
समीकरण (1) व (2) को जोड़ने पर
समलम्ब EFCD का क्षेत्रफल + समलाब EFB का क्षेत्रफल = 2∆EFC का क्षेत्रफल + 2∆EFB का क्षेत्रफल
समलम्ब ABCD का क्षेत्रफल = 2(∆EFB + ∆EFC का क्षेत्रफल)
= 2. ∆BCE का क्षेत्रफल

प्रश्न 5.
दो बिन्दु P व Q, एक समान्तर चतुर्भुज ABCD की क्रमशः भुजाओं DC व AD पर स्थित हैं। दर्शाइए कि (NCERT) (∆APB) का क्षेत्रफल = (∆BQC) का क्षेत्रफल
हल:

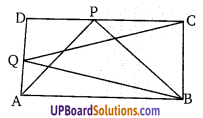
∆APB का क्षेत्रफल = [latex]\frac{1}{2}[/latex] समान्तर चतुर्भुज ABCD का क्षेत्रफल …(1)
तथा ∆BQC का क्षेत्रफल = [latex]\frac{1}{2}[/latex] समान्तर चतुर्भुज ABCD का क्षेत्रफल
समीकरण (1) व (2) की तुलना से
∆APB का क्षेत्रफल = ∆BQC का क्षेत्रफल

प्रश्न 6.
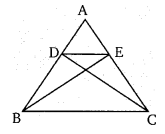
बिन्दु D और E, ∆ABC की क्रमशः भुजाओं AB और AC पर इस प्रकार हैं कि (∆DBC) का क्षेत्रफल = (∆EBC) का क्षेत्रफल, तो सिद्ध कीजिए कि
DE||BC
हल:
∆DBC तथा ∆EBC क्षेत्रफल में समान हैं जिनका आधार BC समान है।
∆DBC के बिन्दु D से डाला गया लम्ब = ∆EBC के बिन्दु E से डाला गया लम्ब
तथा ∆DBC तथा ∆EBC एक ही समान्तर रेखाओं के बीच बने हैं।

प्रश्न 7.
एक समान्तर चतुर्भुज ABCD की दो भुजाओं को किसी बिन्दु P तक बढ़ाया गया है। A से, तथा CP के समान्तर एक रेखा, CB के बढ़े भाग Q पर मिलती है तथा तब पूर्ण समान्तर चतुर्भुज PBQR है तो दर्शाइए कि
(ABCD) का क्षेत्रफल = (PBQR) का क्षेत्रफल
हल:

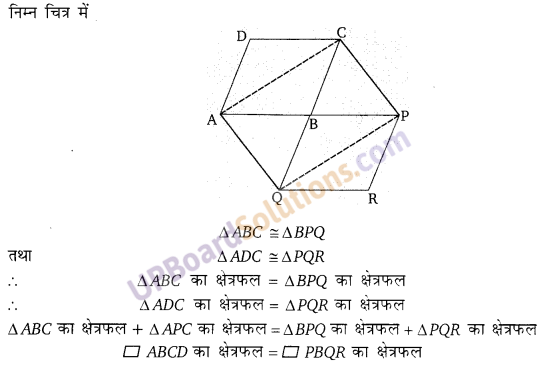
प्रश्न 8.
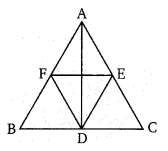
एक ∆ABC की भुजाओं BC, CA और AB के मध्य बिन्दु क्रमश: D, E व F हैं। तो दर्शाइए कि
(i) BDEF एक समान्तर चतुर्भुज है।
(ii) (DEF) का क्षेत्रफल = [latex]\frac{1}{4} \times[/latex] (ABC) का क्षेत्रफल
(iii) (BDEF) का क्षेत्रफल = [latex]\frac{1}{2} \times[/latex] (ABC) का क्षेत्रफल
हलः
∴ D तथा E, भुजा BC तथा AC के मध्य बिन्दु हैं।
∴ DE || BA या DE || BF
इसी प्रकार FE || BD अत: BDEF एक समान्तर चतुर्भुज है इसी प्रकार DCEF तथा AFDE समान्तर चतुर्भुज है। अब DF, समान्तर चतुर्भुज BDEF का विकर्ण है।
ar(∆BDF) = ar(∆DEF) …(1)
DF, समान्तर चतुर्भुज DCEF का विकर्ण है।

∴ ar(∆DCE) = ar(∆DEF)

प्रश्न 9.
आधार के एक ∆ABC में,  कोई बिंदु D लिया गया है तथा AD को तक बढाया है जो AD के बराबर, DE बना रहा है तो दर्शाइए कि, (∆ABC) का क्षेत्रफल का क्षेत्रफल
हल:

प्रश्न 10.
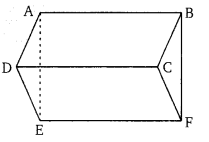
संलग्न चित्र में, समान्तर चतुर्भुज ABCD, ABFE तथा CDEF हैं, तो सिद्ध कीजिए कि
(∆ADE ) का क्षेत्रफल = (∆BCF) का क्षेत्रफल
हल:

प्रश्न 11.
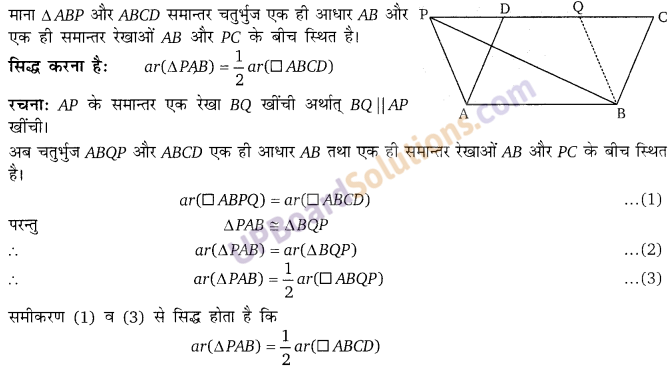
यदि एक त्रिभुज और एक समान्तर चतुर्भुज समान आधार पर है तथा समान समान्तरों के बीच स्थित है
तो सिद्ध कीजिए कि त्रिभुज का क्षेत्रफल, समान्तर चतुर्भुज के क्षेत्रफल के आधे के बराबर है।
हलः

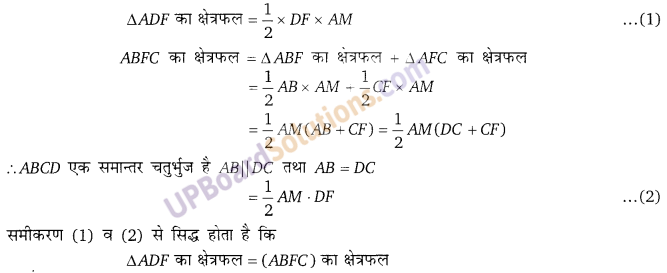
प्रश्न 12.
एक समान्तर चतुर्भुज की भुजा BC पर, एक बिन्दु E लिया गया है। AE और DC को बढ़ाने पर, ये F पर मिलती है तो सिद्ध कीजिए कि (∆ADF) का क्षेत्रफल = (ABFC) का क्षेत्रफल (NCERT Exemplar)

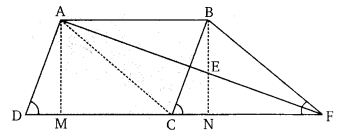
हलः

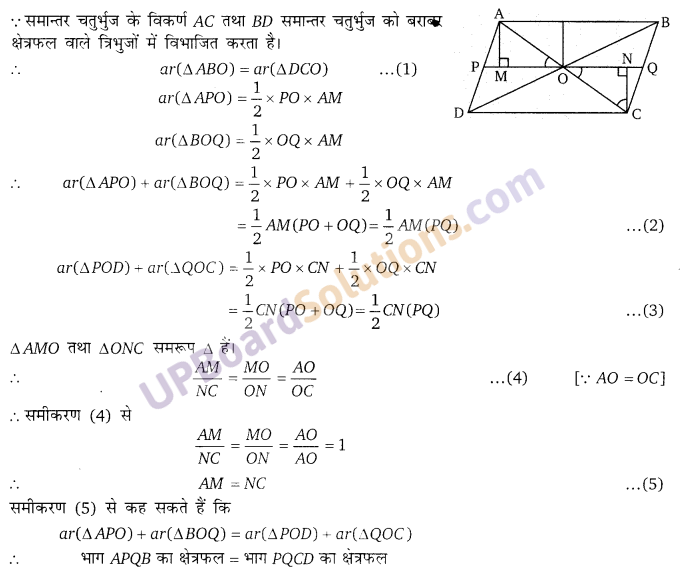
प्रश्न 13.
एक समान्तर चतुर्भुज ABCD के विकर्ण, एक बिन्दु O पर प्रतिच्छेद करते हैं। O से, एक रेखा खींची गई है जो AD को P पर तथा BC को Q पर प्रतिच्छेद करती है तो दर्शाइये कि PQ समान्तर चतुर्भुज को दो बराबर क्षेत्रफलों के भागों में विभाजित करती है। (NCERT Exemplar)
हलः

प्रश्न 14.
एक समलम्ब चतुर्भुज ABCD है जिसमें AB || DC, DC = 30 सेमी तथा AB = 50 सेमी है यदि AD और BC के मध्य बिन्दु क्रमश: X और Y हैं तो सिद्ध कीजिए कि (NCERT Exemplar)

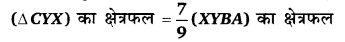
हलः

प्रश्न 15.
यदि एक त्रिभुज की माध्यिकाएं G पर प्रतिच्छेद करती हैं तो दर्शाइए कि
(∆AGB) का क्षेत्रफल = (∆AGC) का क्षेत्रफल = (∆BGC) का क्षेत्रफल = [latex]\frac{1}{3}[/latex](∆ABC) का क्षेत्रफल (NCERT Exemplar)
हलः

अतः ar(∆AGB) = ar(∆AGC) = ar(∆BGC) = [latex]\frac{1}{3}[/latex](∆ABC)

प्रश्न 16.
एक त्रिभुज ABC की माध्यिकाएं BE तथा CF, G पर प्रतिच्छेद करती हैं दर्शाइए कि ∆GBC का क्षेत्रफल = चतुर्भुज AFGE का क्षेत्रफल (NCERT Exemplar)
हलः

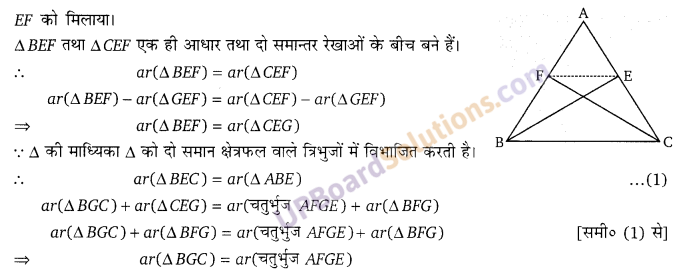
प्रश्न 17.
एक त्रिभुज ABC में, यदि AB और AC पर क्रमशः बिन्दु L और M इस प्रकार है कि LM ||BC तो सिद्ध कीजिए कि (∆LOB) का क्षेत्रफल = (∆MOC) का क्षेत्रफल (NCERT Exemplar)
हलः

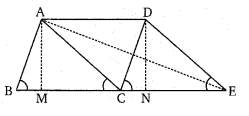
प्रश्न 18.
एक त्रिभुज ABC में, D, AB का मध्य बिन्दु है। BC पर कोई बिन्दु P है। cQ||PD, AB से Q पर मिलती
है। तो सिद्ध कीजिए कि (∆BPQ) का क्षेत्रफल = [latex]\frac{1}{2}[/latex] (∆ABC) का क्षेत्रफल
हलः
रचनाः CD को मिलाया।

प्रश्न 19.
एक समान्तर चतुर्भुज ABCD है तथा AC के समान्तर DE . खींची गई है जो BC के बढे भाग E पर प्रतिच्छेद करती है तो सिद्ध कीजिए कि


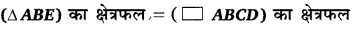
हलः

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 6 Remainder Theorem and Factor Theorem Ex 6.4 शेषफल प्रमेय तथा गुणनखण्ड प्रमेय

प्रश्न 1.
सिद्ध कीजिए कि (3x – 2), बहुपद p(x) = 3x³ + x² – 20x + 12 का एक गुणनखण्ड है।
हलः
(3x – 2), बहुपद p(x) का एक गुणनखण्ड होगा यदि p(2/3) = 0

अतः (3x – 2) बहुपद p(x) = 3x³ + x² – 20x + 12 का एक गुणनखण्ड है।

प्रश्न 2.
सिद्ध कीजिए कि (x – 1), बहुपद x²⁰ – 1 तथा x²¹ – 1 का एक गुणनखण्ड है।
हल:
p(x) = x²⁰ – 1
∵ x – 1 = 0 = x = 1 रखने पर,
p(1) = 1²⁰ – 1 = 1 – 1 = 0
x = 1 रखने पर p(1) = 0
अतः (x – 1) बहुपद x²⁰ – 1 का एक गुणनखण्ड होगा।
इसी प्रकार, p(x) = x²¹ – 1
p(1) = 1²¹ – 1 = 0
अतः (x – 1), बहुपद x²¹ – 1 का भी एक गुणनखण्ड है।

प्रश्न 3.
यदि 4x⁴ – ax³ + 2x² + 4x + 3 का एक गुणनखण्ड (1 – 2x) है तो a का मान ज्ञात कीजिए।
हलः
1 – 2x = 0 ⇒ x = [latex]\frac{1}{2}[/latex] रखने पर,

प्रश्न 4.
यदि R₁ तथा R₂ दो शेषफल हैं। जब क्रमश: x³ + 2x² – 5ax + 7 को (x + 1) तथा x³ + ax² – 12x + 6 को (x – 2) से विभाजित किया जाता है। यदि R₁ – R₂ = 20, तो सिद्ध कीजिए a = 2।
हलः
R₁ = p( – 1) = (-1)³ + 2(- 1)² – 5a (-1) + 7 = – 1 + 2 + 5a + 7 = (5a + 8)
R₂ = P(2) = 2³ + a(2)² – 12 × 2 + 6 = 8 + 4a – 24 + 6 = 4a – 10
तब दिया है, R₁ – R₂ = 20
⇒ (5a + 8) – (4a – 10) = 20
⇒ a + 8 + 10 = 20 ⇒ a = 2

प्रश्न 5.
यदि R₁ तथा R₂ दो शेषफल हैं जब क्रमशः f(x) = x³ + 2ax² – 5x – 7 को (x + 1) तथा g(x) = x³ + x² – 12x + 6a को (x – 2) से विभाजित किया जाता है। यदि 2R₁ + R₂ = 12 तो सिद्ध कीजिए a = 3।
हल:
R₁ = f(-1) = (-1)³ + 2a (-1)² – 5(-1) – 7 = – 1 + 2a + 5 – 7 = 2a – 3
R₂ = g (2) = (2)³ + 2² – 12 × 2 + 6a = 8 + 4 – 24 + 6a = 6a – 12
दिया है,
2R₁ + R₂ = 12 .
2(2a – 3) + 6a – 12 = 12
10a – 18 = 12
10a = 30 ⇒ a = [latex]\frac{30}{10}[/latex] = 3

प्रश्न 6.
यदि बहुपद ax³ + 3x² – 3 तथा 2x³ – 5x + a को (x – 4) से भाग देने पर क्रमशः R₁ तथा R₂ शेषफल प्राप्त होते हैं तब a का मान ज्ञात कीजिए, यदि
(i) R₁ = R₂
(iii) 2R₁ – R₂ =0
हलः
R₁ = P(4) = a (4)³ + 3(4)² – 3 = 64a + 48 – 3 = 64a + 45
R₂ = q(4) = 2(4)³ – 5(4) + a = 128 – 20 + a = a + 108
तब (i)
R₁ = R₂
⇒ 64a + 45 = a + 108
⇒ 63a = 63 ⇒ a = 1

(ii) 2R₁ – R₂ = 0
2(64a + 45) – (a + 108) = 0
128a + 90 – a – 108 = 0
127a – 18 = 0 ⇒ a = [latex]\frac{18}{127}[/latex]

प्रश्न 7.
यदि (x + α), x² + px + q तथा x² + mx + n, का गुणनखण्ड है तब सिद्ध कीजिए कि α = [latex]\frac{n-q}{m-p}[/latex]
हलः
यदि (x + α), x² + px + q का एक गुणनखण्ड है, तब x = – α रखने पर शेषफल शून्य प्राप्त होगा। अतः
(-α)² + p(-α) + q = 0
α² – αp + q = 0 ………………… (1)
इसी प्रकार यदि (x + α), x² + mx + n का एक गुणनखण्ड है, तब x = – α रखने पर शेषफल शून्य प्राप्त होता है, अतः
(α)² + m(α) + n = 0
α² – mα + n = 0 ……………………… (2)
समी० (1) व (2) से,

प्रश्न 8.
यदि (x + 2), व्यंजक ax² + bx + c तथा bx² + ax + c का महत्तम समापवर्तक (HCF) है तो सिद्ध कीजिए a = b तथा a + b + c = 0
हलः
यदि (x + 2) व्यंजक ax² + bx + c तथा bx² + ax + c का म०स० है, तब यह उभयनिष्ठ गुणनखण्ड होगा।
अत: x = – 2 रखने पर,
a( – 2)² + b( – 2) + c = 0
या 4a – 2b + c = 0 …………………….. (1)
4b – 2a + c = 0 ……………….(2)
समी० (1) व (2) को जोड़ने पर,
2a + 2b + 2c = 0
⇒ a + b + c = 0
समी० (1) व (2) को घटाने पर, a = b

प्रश्न 9.
यदि (x – 1), व्यंजक x² – 1 तथा ax² – b(x + 1), का महत्तम समापवर्तक (HCF) है तो सिद्ध कीजिए a = 2b
हलः
यदि (x – 1), व्यंजक (x² – 1) और ax² – b(x + 1) का म०स० है, तो (x – 1) इसका उभयनिष्ठ गुणनखण्ड होगा। अतः
a(1)² – b(1 + 1) = 0
a – 2b = 0
a = 2b

Ex 6.4 Remainder Theorem and Factor Theorem स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
x³ + 3x² + 3x + 1 को 5 + 2x से भाग करने पर शेषफल ज्ञात कीजिए।
हल:
5 + 2x = 0 या 2x = – 5
∴ x = [latex]-\frac{5}{2}[/latex] को बहुपद में रखने पर

प्रश्न 2.
गुणनखण्ड प्रमेय का प्रयोग करके 2y³ + y² – 2y – 1 के गुणनखण्ड कीजिए।
हलः
2y³ + y² – 2y – 1 में y = 1 रखने पर
शेषफल = 2(1)³ + (1)² – 2(1) – 1 = 2 + 1 – 2 – 1 = 0
अतः (y – 1) बहुपद 2y³ + y² – 2y – 1 का एक गुणनखण्ड है।

∴ 2y² + 3y + 1 = 2y² + (2 + 1)y + 1
= 2y² + 2y + y + 1
= 2y(y + 1) + 1(y + 1) = (2y + 1)(y + 1)
∴ गुणनखण्ड = (y – 1)(y + 1)(2y + 1)

प्रश्न 3.
x⁴ + x³ – 2x² + x + 1 को (x – 1) से भाग करने पर शेषफल ज्ञात कीजिए। .
हलः
∵ x – 1 = 0 या x = 1 का मान बहुपद में रखने पर
शेषफल = (1)⁴ + (1)³ – 2(1)² + 1 + 1
= 1 + 1 – 2 + 1 + 1 = 2

प्रश्न 4.
सिद्ध कीजिए कि (x + 2) बहुपद x³ + 3x² + 5x + 6 व 2x + 4 का गुणनखण्ड है।
हलः
∵ x + 2 = 0 ∴x = 0 – 2 = – 2 रखने पर
बहुपद x³ + 3x² + 5x + 6 का शेषफल
=(-2)³ + 3(-2)² + 5(-2) + 6 = – 8 + 12 – 10 + 6 = 0
बहुपद 2x + 4 का शेषफल = 2(-2) + 4 = – 4 + 4 = 0
∴ (x + 2), बहुपद x³ + 3x² + 5x + 6 व 2x + 4 का गुणनखण्ड है।

प्रश्न 5.
गुणनखण्ड प्रमेय से 6x² + 17x + 5 के गुणनखण्ड कीजिए।
हल:

प्रश्न 6.
गुणनखण्ड प्रमेय से y² – 5y + 6 के गुणनखण्ड कीजिए।
हलः
बहुपद y² – 5y + 6 में y = 2 रखने पर
(2)² – 5(2) + 6
4 – 10 + 6 = 0
अतः (y – 2) इसका एक गुणनखण्ड है।

∴ गुणनखण्ड = (y – 2)(y – 3)

प्रश्न 7.
सिद्ध कीजिए कि (x + 2), बहुपद x³ + 3x² + 3x + 2 का एक गुणनखण्ड है।
हलः
∵ x + 2 = 0 इसलिए x = – 2 का मान बहुपद में रखने पर
(-2)³ + 3(-2)² + 38 – 2) + 2
– 8 + 12 – 6 + 2 = 0
अतः (x + 2), बहुपद x³ + 3x² + 3x + 2 का एक गुणनखण्ड है।

प्रश्न 8.
बहुपद 9x³ + 3x² – 13 व 2x³ – 5x + α को (x + 2) से भाग देने पर समान शेषफल प्राप्त होते हैं तब α का मान ज्ञात कीजिए।
हलः
बहुपद 9x³ + 3x² – 13 को (x + 2) से भाग देने पर
x + 2 = 0 या x = – 2 रखने पर
शेषफल = 9(-2)³ + 3(-2)² – 13
= 9(-8) + 3(4) – 13 = – 72 + 12 – 13 = – 73
बहुपद 2x³ – 5x + α को (x + 2) से भाग देने पर शेषफल
= 2(-2)³ – 5( – 2) + α = – 16 + 10 + α = – 6 + α
दोनों शेषफल समान होने की दिशा में
– 6 + α = – 73
α = – 73 + 6 = – 67

प्रश्न 9.
सिद्ध कीजिए कि (x + 1) तथा (2x – 3) बहुपद 2x³ – 9x² + x + 12 के गुणनखण्ड है। (NCERT Exemplar)
हलः
(i) बहुपद 2x³ – 9x² + x + 12 में x + 1 = 0 या x = 0 – 1 = – 1 रखने पर
शेषफल = 2(-1)³ – 9(-1)² + (-1) + 12
= 2(-1) – 9(1) – 1 + 12 = – 2 – 9 – 1 + 12 = 0
अतः (x + 1), बहुपद 2x³ – 9x² + x + 12 का गुणनखण्ड है।

(ii) 2x – 3 = 0 या x = [latex]\frac{3}{2}[/latex] का मान बहुपद 2x³ – 9x² + x + 12 में रखने पर

अतः (2x – 3) बहुपद 2x³ – 9x² + x + 12 का गुणनखण्ड है।

प्रश्न 10.
α के किस मान के लिए बहुपद 2x³ + 9x² + 11x + α + 3, 2x – 1 से पूर्णतया विभाजित है।
हल:
2x – 1 = 0 या x = [latex]\frac{1}{2}[/latex] का मान बहुपद में रखने पर, शेषफल = 0

प्रश्न 11.
4x⁴ – 2x³ – 6x² + x – 5 से क्या घटाया जाए कि वह 2x² + x – 1 से पूर्णतया विभाजित है।
हल:
2x² + x – 1 = 2x² + (2 – 1)x – 1
= 2x + 2x – x – 1
= 2x(x + 1) – 1(x + 1) = (x + 1)(2x – 1)
(x + 1) से पूर्णतया विभाजित होने पर x + 1 = 0 या x = – 1 रखने पर
शेषफल = 4(-1)⁴ – 2(-1)³ – 6(-1)² + (-1) – 5 .
= 4(1) – 2(-1) – 6(1) – 1 – 5 = 4 + 2 – 6 – 1 – 5 = – 6
इसी प्रकार 2x – 1 = 0 या x = [latex]\frac{1}{2}[/latex] रखने पर

∴ 2x² + x – 1 के दोनों गुणनखण्डों से विभाजित करने पर बहुपद 4x⁴ – 2x³ – 6x² + x – 5 के शेषफल = – 6

प्रश्न 12.
यदि x³ + ax² – bx + 10, x² – 3x + 2 से पूर्णतया विभाजित हो तो a तथा b के मान ज्ञात कीजिए।
हल:
x² – 3x + 2 = x² – (2 + 1) x + 2 = x² – 2x – x + 2
= x (x – 2) – 1(x – 2)= (x – 2)(x – 1)
∵ x – 2 = 0 ∴ x = 2 का मान बहुपद x³ + ax² – bx + 10 में रखने पर
शेषफल = (2)³ + a(2)² – b(2) + 10
= 8 + 4a – 2b + 10 = 4a – 2b + 18 ………………….. (1)
∵ x – 1 = 0 ∴ x = 1 का मान बहुपद x³ + ax² – bx + 10 में रखने पर
शेषफल = (1)³ + a(1)² – b(1) + 10
= 1 + a – b + 10
= 11 + a – b ………………… (2)
दोनों शेषफल = 0 रखने पर
4a – 2b + 18 = 0
⇒ 4a – 2b = – 18 ………………(3)
11 + a – b = 0
a – b = – 11 ……………… (4)
समी (4) में 2 से गुणा करने पर, समीकरण (3) घटाने पर

समी (4) में a का मान रखने पर
2 – b = – 11
–b = – 11 – 2 = – 13 ⇒ b = 13

प्रश्न 13.
सिद्ध कीजिए कि (x – 2),(x + 3) तथा (x – 4) बहुपद x³ – 3x² – 10x + 24 के गुणनखण्ड है।
हलः
∵ x – 2 = 0 या x = 2 रखने पर
शेषफल = (2)³ – 3(2)² – 10(2) + 24 = 8 – 12 – 20 + 24 = 0
∵ x + 3 = 0 या x = – 3 रखने पर
शेषफल = (-3)³ – 3(-3)² – 10(-3) + 24 = – 27 – 27 + 30 + 24 = 0
∵ x – 4 = 0 या x = 4 रखने पर
शेषफल = (4)³ – 3(4)² – 10(4) + 24 = 64 – 48 – 40 + 24 = 88 – 88 = 0
∵ शेषफल 0 है
∵ (x – 2), (x + 3), (x – 4) बहुपद x³ – 3x² – 10x + 24 के गुणनखण्ड है।

प्रश्न 14.
x³ – 3x² – 12x + 9 में क्या जोड़ें कि परिणामी x² + x – 6 से पूर्णतया विभाजित हो जाए।
हल:

शेषफल = – (2x + 15)
अर्थात् (2x + 15) जोड़ने पर परिणामी x² + x – 6 से पूर्णतया विभाजित हो जाता है।

प्रश्न 15.
3x³ + x² – 22x + 9 में क्या जोड़ें कि परिणामी 3x² + 7x – 6 से पूर्णतया विभाजित हो जाए।
हलः

शेषफल = – (2x + 3) अर्थात् 2x + 3 जोड़ने पर परिणामी 3x² + 7x – 6 से पूर्णतया विभाजित होगा।

प्रश्न 16.
x³ – 6x² – 15x + 80 में क्या घटायें कि परिणामी x² + x – 12 से पूर्णतया विभाजित हो जाए।
हल:

∴ शेषफल = 4x – 4
अतः (4x – 4) घटाने पर परिणामी पूर्णतया विभाजित होगा।

प्रश्न 17.
सिद्ध कीजिए कि (x – 2), बहुपद f (x) = 2x³ – 3x² – 17x + 30 का एक गुणनखण्ड है।
हलः
∵ x – 2 = 0 ∴ x = 2 रखने पर।
f(2) = 2(2)³ – 3(2)² – 17(2) + 30
= 16 – 12 – 34 + 30 = 0
∴ (x – 2), बहुपद f(x) का एक गुणनखण्ड है।

प्रश्न 18.
गुणनखण्ड प्रमेय से x³ – 6x² + 11x – 6 के गुणनखण्ड कीजिए। (NCERT Exemplar)
हल:
x³ – 6x² + 11x – 6
x = 1 रखने पर, शेषफल = (1)³ – 6(1)² + 11(1) – 6 = 1 – 6 + 11 – 6 = 0
अतः (x – 1) इसका एक गुणनखण्ड है।

x² – 5x + 6 = x 2 – (2 + 3)x + 6
= x² – 2x – 3x + 6 = x(x – 2) – 3(x – 2) = (x – 2)(x – 3)
गुणनखण्ड = (x – 1)(x – 2)(x – 3)

प्रश्न 19.
यदि (2x + 3) बहुपद 4x³ + 20x² + 33x + 18 का एक गुणनखण्ड है तो इसके शेष गुणनखण्ड ज्ञात कीजिए।
हलः
(2x + 3), बहुपद 4x³ + 20x² + 33x + 18 का एक गुणनखण्ड है

2x² + 7x + 6 = 2x² + (3 + 4)x + 6
= 2x² + 3x + 4x + 6 = x(2x + 3) + 2(2x + 3) = (2x + 3)(x + 2)
∴ गुणनखण्ड = (2x + 3)(2x + 3)(x + 2) = (2x + 3)² (x + 2)

प्रश्न 20.
f(x) = x⁴ – 4x³ + 3x² – ax – bको (x – 1) से विभाजित किया जाता है तो शेषफल 6 आता है तब सिद्ध कीजिए कि a + b = – 6
हल:
f(x), (x – 1) से विभाजित होता है।
∴ x – 1 = 0 या x = 1 रखने पर
f(1) = (1)⁴ – 4(1)³ + 3(1)² – a(1) – b
6 = 1 – 4 + 3 – a – b
1 – 4 + 3 – a – b = 6
4 – 4 – a – b = 6 ⇒ – a – b = 6
a + b = – 6

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 4 Algebraic Identities Ex 4.5 बीजगणितीय सर्वसमिकाऐं

प्रश्न 1.
निम्न के मान ज्ञात कीजिए।
(a) (25)³ – (75)³ + (50)³
(b) (0.2)³ – (0.3)³ + (0.1)³ (NCERT Exemplar)
(c) (1.5)³ – (0.9)³ – (0.6)³
(d) (-12)³ + 7³ + 5³
हलः
(a) (25)³ – (75)³ + (50)³
= (25)³ – (25 + 50)³ + (50)³
= (25)³ – (25)³ – (50)³ – 3 × 25 × 50(25 + 50) + (50)³
=-3 × 25 × 50 × 75 = -281250

(b) (0.2)³ – (0.3)³ + (0.1)³
= (0.2)³ – (0.2 + 0.1) + (0.1) ³
= (0.2)3 s – (0.2)³ – (0.1)³ – 3 × 0.2 × 0.1 × (0.2 + 0.1) + (0.1)³
=-3 × 0.2 × 0.1 × (0.3) = -0.018

(c) (1.5)³ – (0.9)³ – (0.6)³
= (0.9 + 0.6)³ – (0.9)³ – (0.6)³
= (0.9)³ + (0.6)³ + 3 × 0.9 × 0.6 × (0.9 + 0.6) – (0.9)³ – (0.6)³
= 3 × 0.9 × 0.6 × 1.5 = 2.430

(d) (-12)³ + 7³ + 5³
⇒ 7³ + (-7 – 5)³ + 5³
⇒ 7³ + (-7)³ + (-5)³ + 3 × (-7)(-5)(-7 – 5) + 5³
= 3 × -7 × -5(-12)= 105 × (-12) = -1260

प्रश्न 2.
यदि x + y + z = 9 और x² + y² + z² = 35, तब x³ + y³ + z³ – 3xyz के मान ज्ञात कीजिए।
हल:
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx) ……..(1)
∵ x + y + z = 9
वर्ग करने पर .
x² + y² + z² + 2(xy + y + zx) = 81
35 + 2(xy + yz + zx) = 81
2(xy + yz + zx) = 81 – 35 = 46
xy + yz + zx = [latex]\frac{46}{2}[/latex] = 23
समी० (1) से
x³ + y³ + z³ – 3xyz = 9(35 – 23) = 9 × 12 = 108

प्रश्न 3.
यदि x + y + z = 8 और xy + yz + z x = 26, तब x³ + y³ + x ³ – 3xyz के मान ज्ञात कीजिए।
हलः
∵ x + y + z = 8
वर्ग करने पर
(x + y + z) = (8)
x² + y² + z² + 2(xy + yz + zx) = 64
x² + y² + z² + 2(26) = 64
x² + y² + z² = 64 – 52 = 12
∵ x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
= (8)(12 – 26)
= (8)(-14) = – 112

प्रश्न 4.
निम्न के मान ज्ञात कीजिए।
(i) (3x – 4y + 5z)(9x² + 16y² + 25z² + 12xy – 15yz + 20yz)
(ii) (3x + 2y + 2z)(9x² + 4y² + 4z² -6xy – 4yz – 6xz)
(iii) (2x – y + 3z)(4x² + y² + 9z² + 2xy + 3yz -6xz) (NCERT Exemplar)
हलः
(i) (3x – 4y + 5z)(9x² + 16y² + 25z² + 12xy – 15xz + 20yz)
= (3x) + (-4y) + (5z)³ – 3[3x × – 4y × 5z]
=27x³ – 64y³ + 125z³ + 180xyz

(ii) (3x + 2y + 2z(9x² + 4y² + 4z² – 6xy -4yz – 6zx)
= (3x)³ + (2y) + (2z)³ – 3[3x × 2y × 2z]
=27x² + 8y² + 8z² – 36xyz

(iii) (2x – y + 3z)(4x² + y² – 9z² + 2xy + 3yz – 6xz)
= (2x)³ + (-y)³ + (3z)³ – 3[2x × -y × 3z]
= 8x³ – y³ + 27z³ + 18xyz

Ex 4.5 Algebraic Identities विविध प्रश्नावली

प्रश्न 1.
सर्वसमिका का प्रयोग करके निम्न के मान ज्ञात कीजिए। [NCERT]
(1) 103 × 107
(ii) 95 × 96
(iii) 104 × 96
हलः
(i) 103 × 107 = (100 + 3) × (100 + 7)
= (100)² + (3 + 7) × 100 + 3 × 7
=10000 + 1000 + 21 = 11021

(ii) 95 × 96 = (100 – 5) × (100 – 4)
= (100)² (5 + 4) × 100 + 5 × 4
= 10000 – 900 + 20 = 9120

(iii) 104 × 96 = (100 + 4) × (100 – 4)
= (100)² – (4)²
= 10000 – 16 = 9984

प्रश्न 2.

हल:

प्रश्न 3.
यदि [latex]x+\frac{1}{x}[/latex] = 11, सिद्ध कीजिए कि [latex]x^{2}+\frac{1}{x^{2}}[/latex] = 119
हल:

प्रश्न 4.
यदि [latex]x^{2}+\frac{1}{x^{2}}[/latex] = 66, सिद्ध कीजिए कि [latex]x-\frac{1}{x}[/latex] = ±8
हलः

प्रश्न 5.
यदि x = 4, y =3, z = 2 तब सिद्ध कीजिए कि 4x² + y² + 25z² + 4xy – 10yz – 20xz =1
हल:
L.H.S. = 4x² + y² + 25z² + 4xy -10yz – 20xz
= (-2x)² + (-y)² + (58)² + 2(-2x)(-y) + 2(-y) (5z) + 2(5z)(-2x)
= (-2x – y + 5z)²
= (-2 × 4 – 3 + 5 × 2)² = (-1)² = 1 = R.H.S.

प्रश्न 6.
यदि x + y = 12 व xy = 27, तब सिद्ध कीजिए कि x³ + y³ = 756
हलः
∵ x + y = 12
घन करने पर x³ + y³ + 3xy (x + y) = 1728
x³ + y³ + 3 × 27 (12) = 1728
x³ + y³ + 972 = 1728
x³ + y³ = 1728 – 972 = 756

प्रश्न 7.
यदि [latex]x^{2}+\frac{1}{x^{2}}[/latex] = 83, तब सिद्ध कीजिए कि [latex]x^{3}-\frac{1}{x^{3}}[/latex] = 756
हलः

प्रश्न 8.
यदि x + y + z =8 व xy + yz + zx=20, तब सिद्ध कीजिए कि x³ + y³ + z³ – 3xyz = 32
हल:
∵ x + y + x = 8 ……….(1)
वर्ग करने पर
x² + y² + z² + 2(xy + ys + ax) = 64
x² + y² + z² = 64-2(xy + yz + zx)
∵ x³ + y³ + z³ – 3xyz = (x + y + 2)(x² + y² + z² – xy – yz – zx)
= (8)[64 – 2(xy + yz + zx)-(xy + yz + zx)]
= 8[64 – 3(xy + yz + zx)]
= 8[64 – 3 × 20] = 8 × 4 = 32

प्रश्न 9.
सिद्ध कीजिए कि 2x² + 2y² + 2z² – 2xy – 2yz – 2zx = [(x – y)² + (y – z)² + (z – x)²]
हलः
L.H.S. = 2x² + 2y² + 2z² – 2xy -2yz – 2zx
= x² + x² + y² + y² + z² + z² – 2xy -2yz – 2zx
= (x² + y² – 2xy) + (y² + x² – 2yz) + (x² + x² – 2zx)
= (x – y)² + (y – z)² + (z – x)² = R.H.S.

प्रश्न 10.
[latex]\left(\frac{1}{4} a-\frac{1}{2} b+1\right)^{2}[/latex] का विस्तार कीजिए। [NCERT]
हलः

प्रश्न 11.
विस्तार कीजिए – (-2x + 5y – 3z)² [NCERT]
हलः
(-2x + 5y – 3z)² = (-2x)² + (5y)² + (-3z)² + 2(-2x)(5y) + 2(5y)(-3z) + 2(-2x)(-3z)
= 4x² + 25y² + 9z² – 20xy – 30yz + 12xz

प्रश्न 12.
[latex]\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{3}\right)^{3}-\left(\frac{5}{6}\right)^{3}[/latex] का मान ज्ञात कीजिए। (NCERT Exemplar)
हलः

Ex 4.5 Algebraic Identities बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.

(a) 320
(b) 322
(c) 321
(d) 222
हलः

अतः विकल्प (b) सही है।

प्रश्न 2.
यदि x – y = 5 व xy = 12, तब x² + y² =
(a) 49
(b) 25
(c) 144
(d) इनमें से कोई नहीं
हलः
x – y = 5
दोनों पक्षों का वर्ग करने पर,
(x – y)² = 5²
⇒ x² + y² – 2xy = 25
⇒ x² + y² – 2(12) = 25
⇒ x² + y² = 49
अतः विकल्प (a) सही है।

प्रश्न 3.

(a) 100
(b) 127
(c) 10
(d) 12
हलः

अतः विकल्प (c) सही है।

प्रश्न 4.

(a) 194
(b) 144
(c) 124
(d) इनमें से कोई नहीं
हलः

अतः विकल्प (a) सही है।

प्रश्न 5.

(a) 15
(b) 105
(c) 25 .
(d) 5
हलः

अतः विकल्प (d) सही है।

प्रश्न 6.

(a) 17
(b) 4
(c) 17/4
(d) 19/4
हलः

अतः विकल्प (c) सही है।

प्रश्न 7.
यदि x + y + z =9, xy + yz + xz = 23, तब x³ + y³ + z³ – 3xyz =
(a) 100
(b) 81
(c) 108
(d) 123
हलः
x + y + z = 9
दोनों पक्षों का वर्ग करने पर,
(x + y + z)² = 81
⇒ x² + y² + z² + 2(xy + yz + zx) = 81
⇒ x² + y² + z² = 81 – 2 × 23 = 35
∵ x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² –xy –yz – zx)
= 9 × (35 – 23)
= 9 × 12 = 108
अतः विकल्प (c) सही है।

प्रश्न 8.
यदि [latex]\frac{x}{y}+\frac{y}{x}[/latex] = 1, तब x³ + y³ =
(a) 1
(b) 2
(c) 3
(d) 0
हलः

अतः विकल्प (d) सही है।

प्रश्न 9.
यदि x – y = -8 व xy = -12, तब x³ – y³ =
(a) 224
(b) -224
(c) 234
(d) -234
हलः
x – y = -8
दोनों पक्षों का घन करने पर,
(x – y)³ = (-8)³
⇒ x³ – y³ – 3xy (x – y) = -512
⇒ x³ – y³ = -512 + 3xy (x – y)
⇒ x³ – y³ = -512 + 3(-12)(-8) = -512 + 288
⇒ x³ – y³ = -224
अतः विकल्प (b) सही है।

प्रश्न 10.
यदि x + y + z = 9 व xy + yz + zx = 23, तब x² + y² + z² =
(a) 25
(b) 35
(c) 45
(d) 305
हलः
x + y + z =9
दोनों पक्षों का वर्ग करने पर,
(x + y + z)² = 9²
⇒ x² + y² + z² + 2(xy + yz + zx) = 81
⇒ x² + y² + z² = 81 – 2(xy + yz + zx)
= 81 – 2 × 23 (∵ xy + yz + zx = 23)
= 81 – 46 = 35
अतः विकल्प (b) सही है।

Ex 4.5 Algebraic Identities स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
(2x – y + z)² का विस्तार कीजिए।
हलः
(2x – y + z)² = (2x)² + (-y)² + (z)² – 2. 2x . y + 2(-y) (z) + 2(2x)(z)
=4x² + y² + z² – 4xy – 2yz + 4xz

प्रश्न 2.
(3a + 4b + 5c)² का विस्तार कीजिए।
हलः
(3a + 4b + 5c)² = 9a² + 16b² + 25c² + 24ab + 40 bc + 30ac

प्रश्न 3.
(4a – 2b – 3c)² का विस्तार कीजिए।
हलः
(4a – 2b – 3c)² = (4a)² + (-2b)² + (-3c)² – 16ab + 12bc – 24ac
= 16a² + 4b² + 9c² – 16ab + 12bc – 24ac

प्रश्न 4.
सर्वसमिका का प्रयोग करके (28)³ + (-15)³ + (-13)³ का मान ज्ञात कीजिए।
हलः
(28)³ + (-15)³ + (-13)³ = (15 + 13)³ + (-15)³ + (-13)³
= (15)³ + (13)³ + 3 × 15 × 13(15 + 13) – (15)³ – (13)³
= 3 × 15 × 13(15 + 13) = 16380

प्रश्न 5.
(104)³ का मान सर्वसमिका का प्रयोग करके ज्ञात कीजिए। .
हलः
(104)³ = (100 + 4)³
(100)³ + (4)³ + 3 × 100 × 4(100 + 4)
= 1000000 + 64 + 124800 = 1124864

प्रश्न 6.
यदि 3x – 7y = 10 व xy = -1, तब सिद्ध कीजिए कि 9x² + 49y² = 58
हलः
3x – 7y = 10
दोनों ओर का वर्ग करने पर
9x² + 49y² – 42xy = 100
9x² + 49y² – 42 × (-1) = 100
9x² + 49y² = 100 – 42 = 58

प्रश्न 7.
सिद्ध कीजिए कि x² + y² + z² – xy – y – zx; x, y व z के सभी मानों के लिए सदैव धनात्मक होगा।
हल:
x² + y² + z² – xy – yz – zx = [latex]\frac{1}{2}[/latex] [(x – y)² + (y – z)² + (z – x)²]
∵ (x – y)²,(y – z)², (z – x)²
पूर्ण वर्ग है जो हमेशा धनात्मक होते हैं।
अतः इसका योग सदैव धनात्मक होगा।

प्रश्न 8.
यदि x² + y² + z² = 20 व x + y + z = 0, तब सिद्ध कीजिए xy + yz + zx = -10
हल:
x + y + z = 0
वर्ग करने पर, (x + y + z)² = 0
x² + y² + z² + 2(xy + yz + zx) = 0
20 + 2(xy + yz + zx) = 0
2(xy + yz + zx) = 0 – 20 = -20
xy + yz + zx = [latex]\frac{-20}{2}[/latex] = -10

प्रश्न 9.
यदि x + y + z = 6 व xy + yz + zx = 11, तब सिद्ध कीजिए x³ + y³ + z³ -3xyz = 18
हलः
∵ x + y + z = 6 ……………. (1)
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx) ……..(2)
समी० (1) का वर्ग करने पर
x² + y² + z² + 2(xy + yz + zx) = 36
x² + y² + z² + 2(11) = 36
x² + y² + z² = 36 – 22 = 14
समी० (2) में x² + y² + z² का मान रखने पर
x³ + y³ + z³ – 3xyz = (6) (14 – 11) = (6) (3) = 18

प्रश्न 10.
x³ + y³ + z³ का मान ज्ञात कीजिए, यदि x + y + z = 11, x² + y² + z² = 45 व xyz = 40
हलः
x + y + z = 11 …………….(1)
समी० (1) का वर्ग करने पर
∵ (x + y + z)² = 121
x² + y² + z² + 2(xy + yz + zx) = 121
2(xy + yz + zx) = 121 – 45 = 76
∴ xy + yz + zx = [latex]\frac{76}{2}[/latex] = 38
x³ + y³+ z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ – 3 × 40 = (11)(45 – 38) = (11)(7) = 77
x³ + y³ + z³ = 77 + 120 = 197

प्रश्न 11.
x³ + y³ + z³ का मान ज्ञात कीजिए, यदि x + y + z = 15, ‘xy + yz + zx = 71 व xys = 10
हलः
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ – 3 × 10 = (15) [x² + y² z² – 71] ………… (1)
x + y + z = 15 …………………. (2)
समी० (2) का वर्ग करने पर
x² + y² + z² + 2(xy + yz + zx) = 225
x² + y² + z² + 2(71) = 225
x² + y² + z² = 225 – 142
x² + y² + z² = 83 का मान समी० (1) में रखने पर
समी० (1) से, x³ + y³ + z³ – 30 = 15[83 – 71]
x³ + y³ + z³ – 30 = 15 × 12 = 180
x³ + y³ + z³ = 180 + 30 = 210

प्रश्न 12.
x³ – 8y³ – 36xy – 216 का मान ज्ञात कीजिए, यदि x = 2y + 6
हल:
x = 2y + 6 का मान रखने पर,
(2y + 6)³ – 8y³ – 36(2y + 6)y – 216
= 8y³ + 216 + 36y (2y + 6) – 8y³ – 72y² – 216y – 216
= 72y² + 216y – 72y² – 216y = 0

प्रश्न 13.
x³ + y³ + z³ – 3xyz का मान ज्ञात कीजिए, यदि x + y + z = 14 व x² + y² + z² = 60
हलः
x + y + z = 14 ………………(1)
वर्ग करने पर,
x² + y² + z² + 2(xy + yz + zx) = 196
60 + 2(xy + yz + zx) = 196
2(xy + yz + zx) = 196 – 60 = 136
xy + yz + zx = [latex]\frac{136}{2}[/latex] = 68
x³ + y³ + z³ – 3xyz = (x + y + z)[x² + y² + z² – xy – yz – zx]
= (14)[60 – 68] = 14 × (-8) = -112

प्रश्न 14.
यदि 4x² + y² = 40 व xy =6, तब सिद्ध कीजिए कि 2x + y = ± 8
हलः
4x² + y² = 40
⇒ (2x)² + (y)² + 2(2x)(y) = 40 + 2(2x)(y)
⇒ (2x + y)² = 40 + 4(6) = 40 + 24
⇒ (2x + y)² = 64 ⇒ (2x + y) = ± 8

प्रश्न 15.

हलः

प्रश्न 16.
यदि 2x + 3y = 8 व xy = 2, तब सिद्ध कीजिए कि 4x² + 9y² = 40
हलः
2x + 3y = 8
वर्ग करने पर, 4x² + 9y² + 2(2x)(3y) = 64
⇒ 4x² + 9y² = 64 – 12(xy) = 64 – 12 × 2 = 40

प्रश्न 17.

हलः

प्रश्न 18.

हलः

प्रश्न 19.
सिद्ध कीजिए कि (x + y + z)² – (x – y – z)² = 4x ( y + z)
हलः
L.H.S. = (x + y + z)² – (x – y – z)²
= x² + y² + z² + 2(xy + yz + zx) – (x² +  y² + z² – 2xy + 2yz – 2zx)
= 4xy + 4xz = 4x(y + z) = R.H.S.

प्रश्न 20.
सिद्ध कीजिए कि (4x + 2y)³ – (4x – 2y)³ = 16y³ + 192x²y
हलः
माना a = 4x + 2y, b = 4x – 2y
a³ – b³ = (a – b) (a² + b² + ab)
अब a² = (4x + 2y)² = 16x² + 4y² + 16xy
b² =(4x – 2y)² =16x² + 4y² – 16xy
ab =16x² – 4y²
तब बायाँ पक्ष =(4x + 2y)³ – (4x – 2y)³
= (4y)[16x² + 4y² + 16xy +16x² + 4y² – 16xy + 16x² – 4y²]
= 4y(48x² + 4y²) = 16y³ + 192x²y = दायाँ पक्ष

प्रश्न 21.
सिद्ध कीजिए कि 7x³ + 8y³ -(4x + 3y)(16x² – 12xy + 9y³) = -57x³ – 19y³
हलः
L.H.S. = 7x³ +8y³ – (4x + 3y)(16x² – 12xy + 9y²)
= 7x³ + 8y³ – [(4x)³ +(3y)³]
= 7x³ + 8y³ – (64x³ + 27y³)
= 7x³ + 8y³ – 64x³ – 27y³
= – 57x³ – 19y³ = R.HS.

Balaji Publications Mathematics Class 9 Solutions