Balaji Class 9 Maths Solutions Chapter 20 Statistics Ex 20.8 सांख्यिकी
Ex 20.8 Statistics अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
आँकड़ों का बहुलक ज्ञात कीजिए : 2, 6, 4, 5, 0, 2, 1, 3, 2, 3
हलः
बहुलक = 2
![]()
प्रश्न 2.
आँकड़ों का बहुलक ज्ञात कीजिए : 14, 25, 14, 28, 17, 18, 14, 23, 22, 14, 18
हलः
बहुलक = 14
प्रश्न 3.
आँकड़ों का बहुलक ज्ञात कीजिए : 15, 14, 19, 20, 14, 15, 16, 14, 15, 18, 14, 19, 15, 17, 15
हलः
बहुलक = 15
प्रश्न 4.
यदि स्कोर 3, 4, 3, 5, 4, 6, 6, x का बहुलक 4 है तो x का मान ज्ञात कीजिए।
हल:
x = 4
प्रश्न 5.
बहुलक है :
(a) कम बारंबारता वाला मान
(b) अधिक बारंबारता वाला मान
(c) सबसे मध्य वाला मान
(d) इनमें से कोई नहीं
हलः
(b) अधिक बारम्बारता वाला मान
![]()
Ex 20.8 Statistics लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 6.
निम्नलिखित आँकड़ों से बहुलक ज्ञात कीजिए :
125, 175, 225, 125, 225, 175, 325, 375, 225, 125
हलः
125
प्रश्न 7.
किसी विशेष दिन पर एक दुकान द्वारा बेची गई कमीजों की निम्नलिखित मापों के बहुलक की गणना कीजिए :
35, 39, 38, 36, 39, 34, 33, 39, 31, 36, 33, 39, 37, 31, 32, 35, 39
हल:
39
प्रश्न 8.
निम्नलिखित आँकड़ों से बहुलक ज्ञात कीजिए। यदि 15 को 24 से बदल दिया जाये तो बहुलक में क्या बदलाव होगा?
7, 4, 10, 9, 15, 11, 7, 9, 9
हलः
बहुलक = 9 यदि 15 को 24 से बदल दिया जाए तो बहुलक 9 ही रहेगा।
![]()
प्रश्न 9.
K का वह मान ज्ञात कीजिए जिसके लिए निम्नलिखित आँकड़ों का बहुलक 7 है :
(i) 3, 5, 5, 7, 3, 6, 7, 9, 6, 7, 3, 5, 7, 3, K
(ii) 3, 5, 6, 7, 5, 4, 7, 5, 6, K, 8, 7
हलः
(i) 3, 5, 5, 7, 3, 6, 7, 9, 6, 7, 3, 5, 7, 3, K
K = 7
(ii) 3, 5, 6, 7, 5, 4, 7, 5, 6, K, 8, 7
K = 7
Ex 20.8 Statistics दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 10.
संख्याएँ 2, 3, 4, 4, (x +3), 5, 5, 6, 7 आरोही क्रम में रखी गयी है। यदि माध्यक 5 है तो x ज्ञात कीजिए तथा उपरोक्त आँकड़ों का बहुलक ज्ञात कीजिए।
हलः
आरोही क्रम = 2, 3, 4, 4, (x + 3), 5, 5, 6, 7
n = 9 (विषम संख्या)।
![]()
5 = x + 3
5-3 = x ⇒ x = 2
अतः संख्याएँ = 2, 3, 4, 4, 5, 5, 5, 6, 7
∴ बहुलक = 5
प्रश्न 11.
12 एकदिवसीय क्रिकेट मैचों में एक बल्लेबाज ने निम्नलिखित रन स्कोर किये :
50, 30, 9, 32, 60, 50, 28, 50, 19, 27, 35
बहुलक स्कोर ज्ञात कीजिए।
हल:
बहुलक = 50
![]()
प्रश्न 12.
निम्नलिखित आँकड़ों के लिए बहुलक ज्ञात कीजिए। यदि 15 की बारंबारता को 3 से बदलकर 9 कर दिया जाये तो नया बहुलक भी ज्ञात कीजिए :

हलः
∵ 12 की बारम्बारता 6 सबसे अधिक है
∵ बहुलक = 12
यदि 15 की बारम्बारता को 3 से बदलकर 9 कर दिया जाए तो नया बहुलक = 15
प्रश्न 13.
संख्याएं 42, 43, 44,44, (2x +3), 45, 45, 46, 47 आरोही क्रम में व्यवस्थित है। यदि माध्यक 45 है तो x ज्ञात कीजिए तथा उपरोक्त आँकड़ों का बहुलक ज्ञात कीजिए।
हल:
आरोही क्रम = 42, 43, 44, 44, (2x + 3), 45, 45, 46, 47
n = 9 (विषम)
![]()
45 = 2x +3
45 – 3 = 2x
42 = 2x
![]()
∴ संख्याएँ = 42, 43, 44, 44, 45, 45, 45, 46, 47
अतः बहुलक = 45
प्रश्न 14.
x के किस मान के लिए निम्नलिखित आँकड़ों का बहुलक 27 है?
25, 26, 27, 23, 27, 26, 24, x, 27, 26, 25, 25
हलः
27
Ex 20.8 Statistics विविध प्रश्नावली
प्रश्न 1.
16 संख्याओं का माध्य 8 है। यदि प्रत्येक संख्या में 2 जोड़ दिया जाये तो नया माध्य क्या होगा?
हलः
16 संख्याओं का माध्य = 8
16 संख्याओं का योग = 16 × 8 = 128
प्रत्येक संख्या में 2 जोडने पर 16 संख्याओं का योग = 128 + 2 × 16 = 128 + 32 = 160
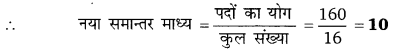
![]()
प्रश्न 2.
यदि M, x1, x1….,x6 का माध्य है तो सिद्ध कीजिए कि,
(x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M) = 0
हलः
⇒ L.H.S. (x1 – M) + (x2 – M) + (x3 – M) + (x4 – M) + (x5 – M) + (x6 – M) = (x1 + x2 + x3 + x4 + x5 + x6) – (M + M + M + M + M + M)
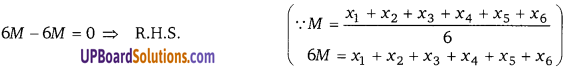
प्रश्न 3.
200 वस्तुओं का माध्य 50 था। बाद में पता चला कि 192 की जगह 92 तथा 88 की जगह 8 पढ़ लिया गया था। सही माध्य ज्ञात कीजिए।
हलः
200 वस्तुओं का माध्य = 50
200 वस्तुओं का योग = 50 × 200 = 10000
192 की जगह 92 तथा 88 की जगह 8 की त्रुटि होने पर 200
वस्तुओं का योग = 10, 000 – 92 + 192 – 8+ 88 = 10,180
![]()
प्रश्न 4.
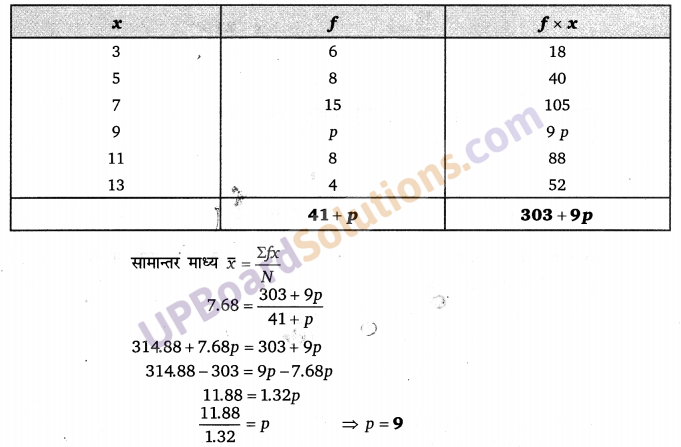
निम्नलिखित बंटन के लिए अज्ञात बारंबारता (p) ज्ञात कीजिए जिसका माध्य 7.68 है।

हलः
प्रश्न 5.
![]()
हल:
n = 5 (विषम संख्या)

प्रश्न 6.
5 संख्याओं का माध्य 28 है। यदि एक संख्या को हटा दिया जाये तो माध्य 2 कम हो जाता है। हटायी गयी संख्या ज्ञात कीजिए।
हलः
5 सँख्याओं का माध्य = 28
5 सँख्याओं का योग = 28 × 5 = 140
हटायी गयी संख्या = x
1 संख्या हटाने पर 4 संख्याओं का योग = 140 – x
4 संख्याओं का माध्य = 28 – 2 = 26
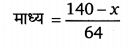
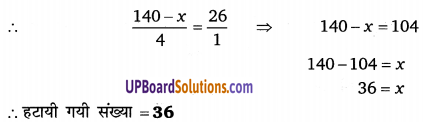
प्रश्न 7.
एक बल्लेबाज अपनी 12वीं पारी में 63 रन बनाता है जिससे उसका कुल औसत 2 बढ़ जाता है। उसका 12वीं पारी के बाद का औसत ज्ञात कीजिए।
हलः
12 वीं पारी में रन = 63
11 पारी तक औसत = x
11 पारी तक कुल रन = 11x
12 पारी तक कुल रन = 11x + 63

11x + 63 = 12x + 24
63 – 24 = x
39 =x
∴ 12 वीं पारी को बढ़ने के बाद औसत = 39+ 2 = 41
प्रश्न 8.
निम्नलिखित सारणी एक कक्षा के 41 विद्यार्थियों के द्वारा प्राप्त अंकों को दर्शाती है। बहुलक ज्ञात कीजिए।

हलः

प्रश्न 9.
यदि 10 प्रेक्षण 10, 13, 15, 18, x + 1, x + 3, 30, 32, 35, 41 एक आरोही क्रम में व्यवस्थित है, जिनका माध्यक 24 है तो x ज्ञात कीजिए।
हलः

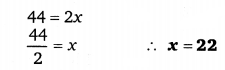
प्रश्न 10.
निम्नलिखित आँकड़ों का बहुलक ज्ञात कीजिए :

हलः
प्राप्तांक 20 प्राप्त करने वाले विद्यार्थियों की संख्या = 36 जो सबसे अधिक है।
अतः बहुलक = 20
Ex 20.8 Statistics बहुविकल्पीय प्रश्न (Multiple Choice Questions)
सही विकल्प का चयन कीजिए।
![]()
प्रश्न 1.
एक बारंबारता बंटन में एक वर्ग का मध्यमान 10 है तथा वर्ग की चौड़ाई 6 है। वर्ग की निम्न सीमा है-
(a) 5
(b) 7
(c) 8
(d) इनमें से कोई नहीं
हलः

प्रश्न 2.
माना एक सतत् बारंबारता बंटन में एक वर्ग का मध्यमान m तथा ऊपरी वर्ग सीमा । है। वर्ग की निम्न सीमा है-
(a) 2m
(b) 2m + l
(c) 2m – l
(d) इनमें से कोई नहीं
हलः
माना वर्ग की निम्न सीमा l1 है तब
![]()
अतः विकल्प (c) सही है।
प्रश्न 3.
वर्ग अन्तराल 10-20 व 20-30 में संख्या 20 किस अन्तराल में स्थित है-
(a) 10 – 20
(b) 20 – 30
(c) दोनों अन्तराल
(d) इनमें से कोई नहीं
हल:
20 – 30
अतः विकल्प (b) सही है।
प्रश्न 4.
![]()
(a) [latex]\overline{x}+\overline{y}[/latex]
(b) [latex]\frac{\overline{x}+\overline{y}}{n}[/latex]
(c) [latex]\frac{\overline{x}+\overline{y}}{2}[/latex]
(d) इनमें से कोई नहीं
हलः

प्रश्न 5.
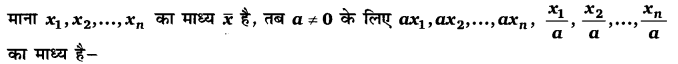
(a) [latex]\left(\boldsymbol{a}+\frac{\mathbf{1}}{\boldsymbol{a}}\right) \frac{\overline{\boldsymbol{x}}}{\mathbf{2}}[/latex]
(b) [latex]\left(\boldsymbol{a}+\frac{\mathbf{1}}{\boldsymbol{a}}\right) \overline{\boldsymbol{x}}[/latex]
(c) [latex]\left(\boldsymbol{a}+\frac{\mathbf{1}}{\boldsymbol{a}}\right) \frac{\overline{\boldsymbol{x}}}{\boldsymbol{x}}[/latex]
(d) इनमें से कोई नहीं
हलः

प्रश्न 6.
माना एक बारंबारता बंटन में, एक वर्ग की निम्न सीमा । है तथा m वर्ग का मध्य बिन्दु है तब वर्ग की ऊपरी सीमा है
(a) m + l
(b) 2m + l
(c) 2m – l
(d) इनमें से कोई नहीं
हलः

प्रश्न 7.
एक समूह में 6 लड़कों का माध्य भार 48 किग्रा है उनमें से 5 लड़कों का भार 51, 45, 49, 46 व 44 किग्रा है। तब 6वें लड़के का भार
(a) 52 किग्रा
(b) 53 किग्रा
(c) 54 किग्रा
(d) इनमें से कोई नहीं
हलः
माना 6वें लड़के का भार x किग्रा है।
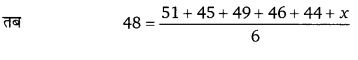
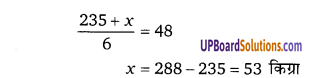
अतः विकल्प (b) सही है।
प्रश्न 8.
100 नगों का माध्य 64 है। बाद में पाया गया कि 36 के स्थान पर 26 तथा 90 के स्थान पर 9 पढ़ लिया गया था। सही माध्य ज्ञात कीजिए-
(a) 64.91
(b) 49.61
(c) 64.49
(d) इनमें से कोई नहीं
हलः
कुल योग = 100 × 64 = 6400
सही योग = 6400 + (36 – 26) + (90 – 9)
= 6400 + 10 + 81 = 6491
![]()
अतः विकल्प (a) सही है।
![]()
प्रश्न 9.
पाँच संख्याओं का माध्य 30 है। यदि एक संख्या हटा दी जाये, तब उनका माध्य 28 है। हटायी गयी संख्या है-
(a) 35
(b) 36
(c) 38
(d) इनमें से कोई नहीं
हलः
पाँच संख्याओं का कुल योग = 5 × 30 = 150
चार संख्याओं का कुल योग = 4 × 28 = 112
हटायी गयी संख्या = 150 -112 = 38
अतः विकल्प (c) सही है।
प्रश्न 10.
25 प्रेक्षणों का माध्य 36 है। इन प्रेक्षणों के प्रथम 13 का माध्य 32 है तथा अन्तिम 13 का माध्य 40 है। 13वां प्रेक्षण है-
(a) 34
(b) 36
(c) 38
(d) इनमें से कोई नहीं
हलः
25 प्रेक्षणों का कुल योग = 25 × 36 = 900
प्रथम 13 प्रेक्षणों का योग = 13 × 32 = 416
अन्तिम 13 प्रेक्षणों का योग = 13 × 40 = 520
13 वाँ प्रेक्षण = -900 + (416 + 520)
= -900 + 936 = 36
अतः विकल्प (b) सही है।
प्रश्न 11.
50 विद्यार्थियों द्वारा प्राप्त अंकों का औसत 39 है। बाद में पता चला कि एक अंक 43 को 23 पढ़ लिया गया था। सही समान्तर माध्य ज्ञात कीजिए।
(a) 39
(b) 39.2
(c) 39.4
(d) इनमें से कोई नहीं
हलः
50 अंकों का कुल योग = 50 × 39 = 1950
सही योग = 1950 + (43 – 23)
= 1950 + 20 = 1970
सही समान्तर माध्य = [latex]\frac{1970}{50}[/latex] = 39.4
अतः विकल्प (c) सही है।
![]()
प्रश्न 12.
आँकड़े 8, 9, 12, 18, (x + 2), (x + 4), 30, 31, 34, 39 आरोही क्रम में व्यवस्थित है इनका माध्यक 24 है। x का मान है-
(a) 19
(b) 20
(c) 21
(d) इनमें से कोई नहीं
हल:
n = 10 (सम)

अतः विकल्प (c) सही है।
Ex 20.8 Statistics स्वमूल्यांकन परीक्षण (Self Assessment Test)
प्रश्न 1.
तीन सिक्के 30 बार उछाले गये। प्रत्येक बार आये चितों की संख्या निम्न प्रकार लिखी गयी :

उपरोक्त आँकड़ों के लिए एक बारंबारता बंटन सारणी तैयार कीजिए।
हलः
बारंबारता बंटन सारणी-
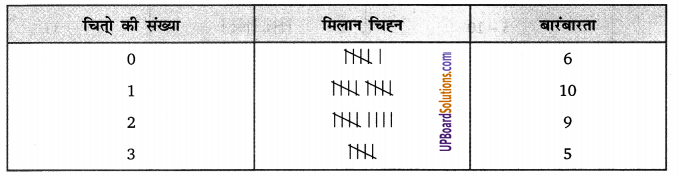
प्रश्न 2.
तीस बच्चों से यह पूछा गया कि पिछले सप्ताह उन्होंने कितने घंटों तक टीवी के प्रोग्राम देखे। प्राप्त परिणाम निम्न हैं:

(i) वर्ग चौड़ाई 5 लेकर और एक वर्ग अंतराल को 5-10 लेकर इन आँकड़ों की एक वगीकृत बंटन सारणी बनाइए।
(ii) कितने बच्चों ने सप्ताह में 15 या अधिक घंटो तक टेलीविजन देखा?
हलः
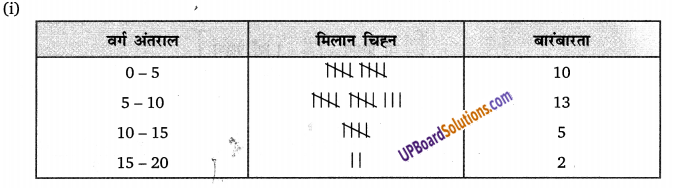
(ii) 2
प्रश्न 3.
40 महिला इंजीनियरों की उनके आवास से उनके कार्यस्थल की दूरी (किमी में) निम्न प्रकार है:

0-5 को (जिसमें 5 सम्मिलित नहीं है) पहला अंतराल लेकर ऊपर दिए गए आँकड़ों से वर्ग-माप 5 वाली एक वर्गीकृत बारंबारता बंटन सारणी बनाइए। इस सारणी बद्ध निरूपण से आपको कौन-से मुख्य लक्षण देखने को मिलते हैं?
हलः
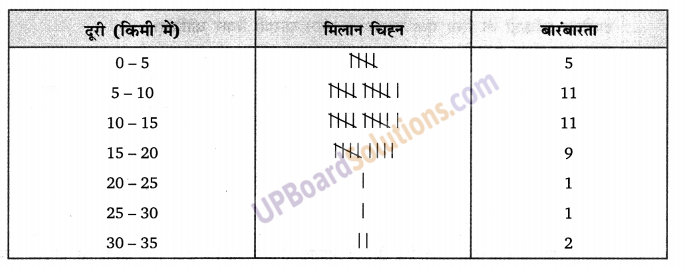
प्रश्न 4.
50 दशमलव स्थान तक शुद्ध 1 का मान नीचे दिया गया है :
3.141592653589793238462643383279502884419716939937510
(i) दशमलव बिंदु के बाद आने वाले 0 से 9 तक के अंकों का एक बारंबारता बंटन बनाइए।
(ii) सबसे अधिक बार और सबसे कम बार आने वाले अंक कौन-कौन से हैं?
हलः
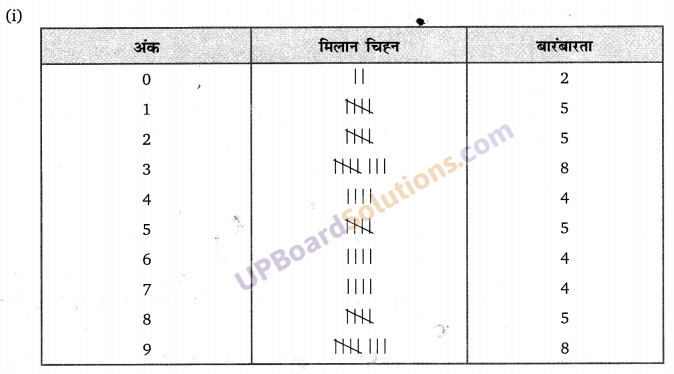
(ii) 3 या 9, 0
प्रश्न 5.
गणित की एक परीक्षा में 10 विद्यार्थियों द्वारा प्राप्त अंकों को नीचे दर्शाया गया है :
55, 36, 95, 73, 60, 42, 25, 78, 75, 62 ज्ञात कीजिए :
(i) अधिकतम और निम्नतम अंक
(ii) आँकड़ों का परास
(iii) आँकड़ों का आरोही क्रम में व्यवस्थितिकरण
हलः
(i) 95, 25
(ii) 70
(iii) 25, 36, 42, 55, 60, 62, 73, 75, 78, 95
![]()
प्रश्न 6.
भारतीय समाज के विभिन्न क्षेत्रों में प्रति हजार लड़कों पर लड़कियों की (निकटतम दस तक की) संख्या के आँकड़े नीचे दिए गए हैं :

(i) ऊपर दी गई सूचनाओं को एक दण्ड आलेख द्वारा निरूपित कीजिए।
(ii) कक्षा में चर्चा करके बताइए कि आप इस आलेख से कौन-कौन से निष्कर्ष निकाल सकते हैं?
हलः
(i) दण्ड आलेख
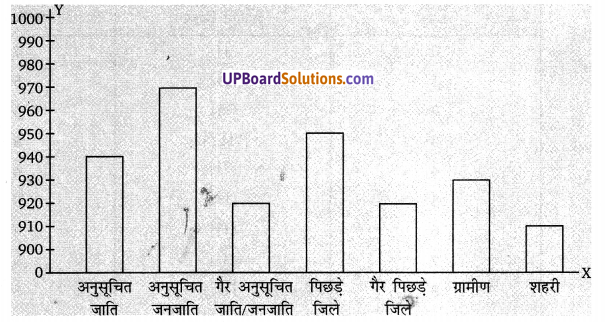
(ii) अनुसूचित जनजाति में प्रति 1000 लड़कों पर लड़कियों की संख्या अधिकतम (अर्थात् 970) है तथा शहरी क्षेत्र में निम्नतम् अर्थात् (910) है।
प्रश्न 7.
एक कक्षा के 80 विद्यार्थियों द्वारा (100 में से) प्राप्त अंक नीचे दिए हैं :

उपरोक्त आँकड़ों के निरूपण के लिए एक आयत चित्र बनाइये।
हलः
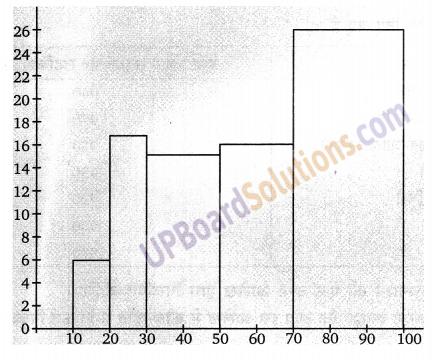
प्रश्न 8.
नीचे की दो सारणियों में प्राप्त किए गए अंकों के अनुसार दो सेक्शनों के विद्यार्थियों का बंटन दिया गया है :
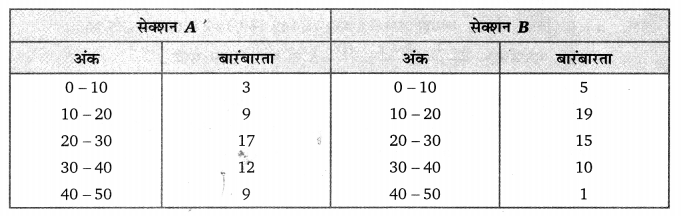
दो बारंबारता बहुभुजों की सहायता से एक ही आलेख पर दोनों सेक्शनों के विद्यार्थियों के प्राप्तांक निरूपित कीजिए। दोनों बहुभुजों अध्ययन करके दोनों सेक्शनों के निष्पादनों की तुलना कीजिए।
हलः
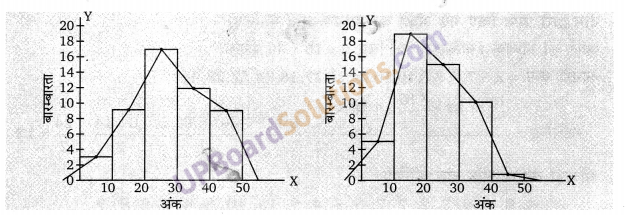
प्रश्न 9.
निम्नलिखित प्रेक्षण आरोही क्रम में व्यवस्थित हैं :
26, 29, 42, 53, x, x + 2, 70, 75, 82, 93 यदि माध्यक 65 है तो x का मान ज्ञात कीजिए।
हलः
n = 10 (सम संख्या)

प्रश्न 10.
एक कक्षा के 9 विद्यार्थियों की लम्बाइयाँ (सेमी में) निम्न है-
155, 160, 145, 140, 150, 147, 152, 144, 149 माध्यक ज्ञात कीजिए।
हल:
n = 9 (विषम संख्या) आरोही क्रम = 140, 144, 145, 147, 149, 150, 152, 155, 160
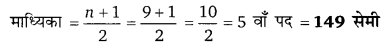
प्रश्न 11.
5 व्यक्तियों से यह पूछा गया कि अपने समुदाय के सामाजिक कार्य करने में वे एक सप्ताह में कितना समय देते हैं। उनका कहना था क्रमशः 10, 7, 13, 20 और 15 घंटे। एक सप्ताह में उनके द्वारा सामाजिक कार्य में लगाए गए समयों का माध्य ज्ञात कीजिए।
हल:
![]()
![]()
प्रश्न 12.
एक टीम द्वारा मैचों की एक श्रृंखला में प्राप्त किए गए अंक हैं :
17, 2, 7, 27, 15, 5, 14, 8, 10, 24, 48, 10, 8, 7, 18, 28
टीम द्वारा प्राप्त किए गए अंकों का माध्यक ज्ञात कीजिए।
हलः
अंको का माध्यक (माध्यिका) के लिए n = 16 (सम संख्या)
आरोही क्रम = 2,5,7,7,8,8,10,10,14,15,17,18, 24, 27, 28,48

प्रश्न 13.
आँकड़ों का बहुलक ज्ञात कीजिए:
4, 6, 5, 9, 3, 2, 7, 7, 6, 5, 4, 9, 10, 10, 3, 4, 7, 6, 9, 9
हलः
१
प्रश्न 14.
बॉस्केट-बॉल की एक टीम द्वारा अनेक मैचों में प्राप्त किए गए अंक निम्न हैं :
17, 2, 7, 27, 25, 5, 14, 18, 10, 24, 48, 10, 8, 7, 10, 28 उपरोक्त आँकड़ों का माध्यक और बहुलक ज्ञात कीजिए। हल:
आरोही क्रम = 2, 5,7,7, 8, 10, 10, 10,14,17,18,24, 25, 27, 28, 48
n = 16 (सम संख्या)

प्रश्न 15.

हलः
(x1 – 2) + (x2 – 2) + (x3 – 2)+…(xn – 2) = 110

प्रश्न 16.
n आँकड़ों x, x2,…,xn का संख्या 50 से विचलन -10 है तथा 46 से विचलन 70 है। n का मान व समान्तर माध्य ज्ञात कीजिए।
हलः

प्रश्न 17.
एक पार्क में खेल रहे विभिन्न आयु वर्गों के बच्चों की संख्या का एक यादृच्छिक सर्वेक्षण करने पर निम्नलिखित आँकड़े प्राप्त हुए :
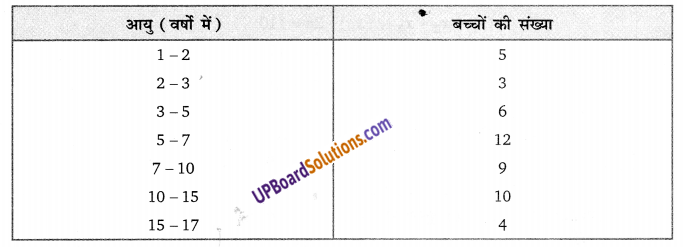
ऊपर दिए गए आँकड़ों को निरूपित करने वाला एक आयत चित्र खींचिए।
हलः
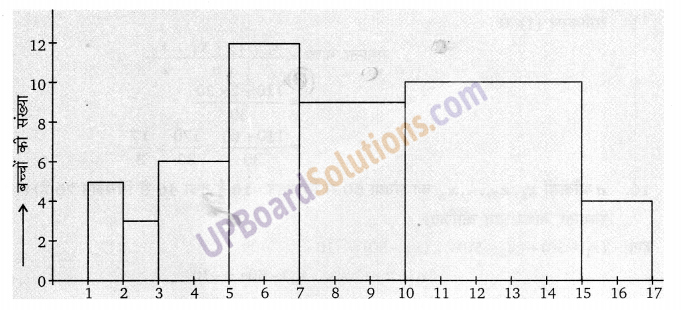
प्रश्न 18.
एक स्थानीय टेलीफोन निर्देशिका से 100 कुलनाम (Surname) यादृच्छया लिए गए और उनसे अंग्रेजी वर्णमाला के अक्षरों की संख्या का निम्न बारंबारता बंटन प्राप्त किया गया।

(i) दी हुई सूचनाओं को निरूपित करने वाला एक आयत चित्र खींचिए।
(ii) वह वर्ग अन्तराल बताइए जिसमें अधिकतम संख्या में कुलनाम है।
हलः
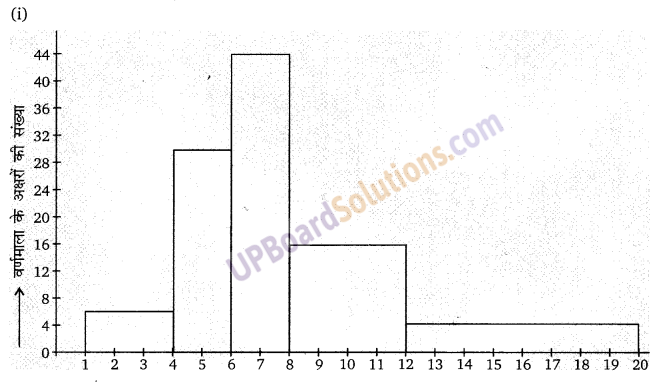
(ii) वर्गअन्तराल (6-8) में अधिकतम संख्या में कुल नाम है।
प्रश्न 19.
गणित की एक परीक्षा में एक कक्षा के 90 विद्यार्थियों द्वारा 100 में से प्राप्त किए गए अंक निम्न सारणी में दिए गए हैं:
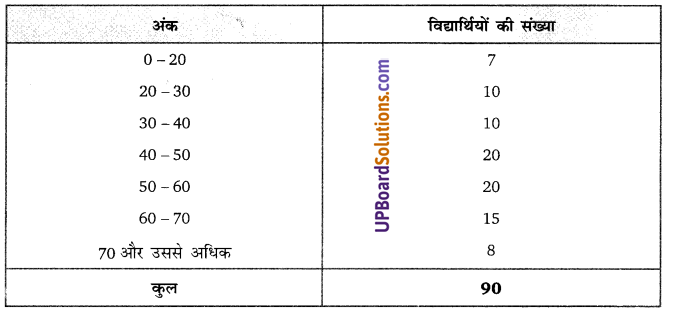
उपरोक्त आँकड़ों को निरूपित करने वाला एक आयत चित्र खींचिए।
हलः
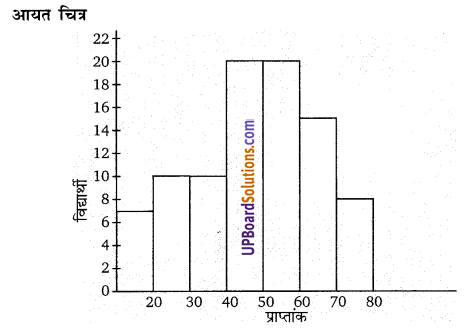
प्रश्न 20.
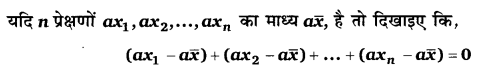
हलः