Safia

These Sample papers are part of CBSE Sample Papers for Class 10 Maths. Here we have given CBSE Sample Papers for Class 10 Maths Paper 3.

CBSE Sample Papers for Class 10 Maths Paper 1

Board	CBSE
Class	X
Subject	Maths
Sample Paper Set	Paper 3
Category	CBSE Sample Papers

Students who are going to appear for CBSE Class 10 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 3 of Solved CBSE Sample Paper for Class 10 Maths is given below with free pdf download solutions.

Time allowed: 3 Hours
Maximum Marks: 80

General Instructions

•  All questions are compulsory.
• The question paper consists of 30 questions divided into four sections A, B, C andD.
• Section A contains 6 questions of 1 mark each. Section B contains 6 questions of 2 marks each. Section C contains 10 questions of 3 marks each. Section D contains 8 questions of 4 marks each,
• There is no overall choice. However, an internal choice has been provided in four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternatives in all such questions.
• Use of calculators is not permitted.

Section-A

Question 1.
Find an irrational between 3 and 5.

Question 2.
Find the distance between the points A(4, 5) and B(0, -3)

Question 3.

Question 4.
Find the common difference ofthe AP [latex s=2]\frac { 1 }{ p } ,\frac { 1-p }{ p } ,\frac { 1-2p }{ p } ,[/latex] …….

Question 5.
Let ∆ABC ~ ∆DEF. Ifar (∆ABC) = 100 cm², ar(∆DEF) = 196 cm² andDE= 7, then find AB.

Question 6.
Solve the equation [latex s=2]\frac { 4 }{ x } [/latex] – 3 = [latex s=2]\frac { 5 }{ 2x+3 } [/latex] ; x ≠ 0, -[latex s=2]\frac { 3 }{ 2 } [/latex], for x.

Section-B

Question 7.
Find how many integers between 200 and 500 are divisible by 8.

Question 8.
Find the ratio in which the line segment joining the points A (3, -3) and B (-2, 7) is divided by x-axis. Also find the coordinates of the point of division.

Question 9.
Which type of equations x + 2y = 4 and 2x + y = 5 will be?

Question 10.
Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.

Question 11.
A bag contains 15 white and some black balls. If the probability of drawing a black ball from the bag is thrice that of drawing a white ball, find the number of black balls in the bag.

Question 12.
Find the probability that in a family of 3 children, there will be at least one boy.

Section-C

Question 13.
If the H.C.F of 210 and 55 is expressible in the form 210 × 5 + 55y, find y.

Question 14.
If the polynomial f{x) = 3x⁴ + 3x³ – 11x² – 5x + 10 is completely divisible by 3x² – 5, find all its zeroes.

Question 15.
If sin 0 + cos 0 = p and sec 0 + cosec 0 = q, show that q (p² -1) = 2p

Question 16.
Following frequency distribution shows the daily expenditure on milk of 30 households in a locality:

Find the mode for the above data.

Question 17.
Solve the system of equations:
a(x + y) + b{x-y) = a² – ab + b²
a(x + y)-b(x-y) = a² + ab + b²

Question 18.
∆ ABC is right-angled at A. DEFG is a square as shown in the figure. Prove that DE² = BD × EC

OR
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, then prove that the other two sides are divided in the same ratio.

Question 19.
Ifthe distances of P(x, y) from A(5, 1) and B (-1,5) are equal, then prove that 3x = 2y.
OR
Prove that the points (3,0), (6,4) and (-1, 3) are the vertices of a right angled isosceles triangle.

Question 20.
PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T (see Fig.). Find the length of TP.

Question 21.
In fig., a circle is inscribed in an equilateral triangle ABC of side 12 cm. Find the radius of inscribed circle and the area of the shaded region.
[Use n = 3.14 and [latex]\sqrt { 3 } [/latex] = 1.73]

Question 22.
A conical vessel, with base radius 5 cm and height 24 cm, is full of water. This water is emptied into a cylindrical vessel ofbase radius 10 cm. Find the height to which the water will rise in the cylindrical vessel. 22
[Use π = [latex s=2]\frac { 22 }{ 7 } [/latex] ]
OR
A sphere of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by 3[latex s=2]\frac { 5 }{ 9 } [/latex] cm. Find the diameter of the cylindrical vessel.

Section-D

Question 23.
The pth term of an A.P. is a and qth term is A Prove that the sum of its (p + q) terms is [latex s=2]\frac { p+q }{ 2 } \left\{ a+d+\frac { a-b }{ p-q } \right\} [/latex]

Question 24.
A man standing on the deck of a ship, which is 10 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base ofhillas30°. Find the distance of the hill from the ship and the height of the hill
OR
The angle of elevation of a bird from a point 50 metres above a lake is 30° and the angle of depression of its reflection in the lake is 60°. Find the height of the bird above the lake.

Question 25.
For the following frequency distribution, find the value of f₁ and f₂, ifmean is given to be 50,

OR
The following distribution gives the daily income of 50 workers of a factory.

Convert the distribution above to a less than type cummulative frequency distribution and draw its ogive.

Question 26.
The sum of the radius of base and height of a solid right circular cylinder is 37 cm. Ifthe total surface area
of the solid cylinder is 1628 sq. cm, find the volume of the cylinder. [Use π = [latex s=2]\frac { 22 }{ 7 } [/latex] ]

Question 27.
Sove for x : [latex]\frac { 1 }{ x+1 } +\frac { 3 }{ 5x+1 } =\frac { 5 }{ x+4 } [/latex] x ≠-1, -[latex s=2]\frac { 1 }{ 5 } [/latex],-4
OR
Two taps running together can fill a tank in 3[latex s=2]\frac { 1 }{ 13 } [/latex] hours. If one tap takes 3 hours more than the other to fill

Question 28.
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then prove that the angle opposite to the first side is a right angle.

Question 29.
Solve [latex]\frac { \cos ^{ 2 }{ \theta } -3\cos { \theta } +2 }{ \sin ^{ 2 }{ \theta } } [/latex] =1; (θ < 90°)

Question 30.
Draw a circle ofradius 2.5 cm. From a point P, 6 cm apart from the centre of the circle, draw two tangents to the circle.

Solutions
Section-A

Solution 1.
[latex]\sqrt { 3\times 5 } =\sqrt { 15 } [/latex] is an irrational between 3 and 5  (1)

Solution 2.
Here x₁ = 4, y₁ = 5, x₂ = 0, y₂ = -3
Using distance formula

Solution 3.

Solution 4.

Solution 5.

Solution 6.

Section-B

Solution 7.
First number divisible by 8 between 200 and 500 is 208.
If form an A.P. = 208,216,224,……..,496.
Here, a_n = 496, a = 208, d = 8
a_n = a + (n – l)d  (1)
496 = 208 + (n-l)8
(n-1)8 = 496-208
(n-1) = [latex s=2]\frac { 288 }{ 8 } [/latex] ⇒ n-1=36 ⇒n=37   (1)

Solution 8.

Solution 9.

Solution 10.
Natural numbers between 101 and 999 divisible by 5 and 2 both, must be divisible by 10.
∴ {110,120,………, 990} are numbers divisible by both 2 and 5.   (1/2)
If forms anA.P., in which a = 110, d = 10 and a_n = 990.   (1/2)
a_n = a + (n-1)d ⇒ 990 = 110 + (n- 1) 10
⇒ 99 =11+ (n-1)=>88 + 1= n ⇒n = 89   (1)

Solution 11.
Since, number of white balls in the bag = 15
Let the number of black balls in the bag = x
As, P (drawing a black ball) = 3 x P (drawing a white ball)   (1)
[latex s=2]\frac { x }{ 15+x } =3\times \frac { 15 }{ 15+x } [/latex] ⇒ x=45 [∵x+15 ≠ 0]   (1)
Hence, the number ofblack balls in the bag is 45.

Solution 12.
S = {BBB, BBQ BGB, BGQ GBB, GBQ GGB, GGG} ; n(S) = 8
E = {BBB, BBQ BGB, BGQ GBB, GBQ GGB}; n(E) = 7  (1)
∴ P(E) = [latex]\frac { n(E) }{ n(S) } =\frac { 7 }{ 8 } [/latex] (1)

Section-C

Solution 13.
Let us first find the H.C.F. of 210and 55.
Applying Euclid’s division lemma on 210 and 55, we get
210=55 x3 + 45 ….(i) (1)
Since, the remainder 45 ^ 0. So, we now apply division lemma on the divisor 55 and the remainder 45 to get
55 = 45 × 1 + 10 ….(ii)     (1/2)
We consider the divisor 45 and the remainder 10 and apply division lemma to get
45 = 4 × 10 + 5 …(iii)   (1/2)
We consider the divisor 10 and the remainder 5 and apply division lemma to get
10=5 × 2 + 0….(iv)
We observe that the remainder at this stage is zero. So, the last divisor i.e., 5 is the H.C.F of210 and 55.
∴ 5 = 210 × 5 + 55y ⇒ y = [latex]\frac { -1045 }{ 55 } [/latex] = (-19)   (1)

Solution 14.
As 3x² – 5 divides f(x) completely
∴ (3x² – 5) is a factor of f(x)
⇒ 3[latex]\left( { x }^{ 2 }-\frac { 5 }{ 3 } \right) [/latex] is a factor of f(x)

Solution 15.

Solution 16.

Solution 17.

Solution 18.


OR

Solution 19.
Since, distance between (x, y) and (5,1) = Distance between (x, y) and (-1,5)
So, [latex]\sqrt { { (x-5) }^{ 2 }+{ (y-1) }^{ 2 } } =\sqrt { { (x-(-1)) }^{ 2 }+{ (y-5) }^{ 2 } } [/latex]  (1)
Squaring on both sides, we get
(x-5)² + (y- 1)² = (x+ 1)²+(y-5)²
(x²– lOx + 25) + (y² -2y + 1) = (x² + 2x + 1)+ (y²-10y + 25)  (1)
So, -12x = -8y ⇒ 12x = 8y ⇒ 3x = 2y (Hence proved).  (1)
OR
Let A (3,0), B(6,4) andC (-1,3) be the vertices of the triangle.
Using distance formula,
AB = [latex]\sqrt { { (4-0) }^{ 2 }+{ (6-3) }^{ 2 } } =\sqrt { 25 } [/latex] = 5 units   (1/2)
BC = [latex]\sqrt { { (3-4) }^{ 2 }+{ (-1-6) }^{ 2 } } =\sqrt { 50 } =5\sqrt { 2 } [/latex]  (1/2)
CA = [latex]\sqrt { { (0-3) }^{ 2 }+{ (3+1) }^{ 2 } } =\sqrt { 25 } [/latex] = 5 units   (1/2)
Now, (5)² + (5)² = [latex]{ \left( 2\sqrt { 5 } \right) }^{ 2 }[/latex]
=> AB² + CA² = BC² [Follow Pythagoras theorem]   (1)
Also, AB = CA = 5 units
So, ∆ABC is a right-angled isosceles triangle.   (1/2)
Hence, the given points are the vertices of a right-angled isosceles triangle.

Solution 20.

Solution 21.
Median and altitude of an equilateral triangle are same and passing through the centre of incircle and centre divides the median in ratio 2:1.
∴ In ∆ABD, ∠D = 90°

By Pythagoras theorem
AD² = AB²-BD² ⇒ AD² = 12² – 6²
⇒ AD² = 144-36
⇒ AD = [latex]\sqrt { 108 } [/latex] = 6[latex]\sqrt { 3 } [/latex] cm
AO:OD = 2: 1   (1)
∴OD = [latex s=2]\frac { 1 }{ 3 } [/latex] AD = [latex s=2]\frac { 1 }{ 3 } [/latex] × 6[latex]\sqrt { 3 } [/latex] = 2[latex]\sqrt { 3 } [/latex]   (1/2)
Now, radius of circle = 2[latex]\sqrt { 3 } [/latex] = 2 × 1.73 = 3.46 cm   (1/2)
Area of shaded region = Area of equilateral ∆ABC – Area of circle   (1)
= [latex]\frac { \sqrt { 3 } }{ 4 } [/latex](12)² -(2[latex]\sqrt { 3 } [/latex])² × π
= 1.73 × 36 – 12 × 3.14 = 62.28 – 37.68 = 24.6 cm².

Solution 22.
Suppose,
r = Radius of the conical vessel = 5 cm
h = Height of the conical vessel = 24 cm
r2 = Radius of the cylindrical vessel = 10 cm
Suppose water rises up to a height h2 cm in the cylindrical vessel.
A.T.Q,
Volume of the water in cylindrical vessel = Volume of water in conical vessel
⇒[latex ]\pi { r }_{ 2 }^{ 2 }{ h }_{ 2 }=\frac { 1 }{ 3 } \pi { r }_{ 1 }^{ 2 }{ h }_{ 1 }[/latex] (1)
⇒[latex ]3{ r }_{ 2 }^{ 2 }{ h }_{ 2 }={ r }_{ 1 }^{ 2 }{ h }_{ 1 }[/latex] ⇒ 3 × 10 × 10 × h₂ = 5 × 5 × 24 (1)
h₂ = [latex s=2]\frac { 5\times 5\times 24 }{ 3\times 10\times 10 } [/latex] ⇒ h2 = 2 cm  (1)
Hence, the rise in the water level in the cylindrical vessel = 2 cm.
OR
Increase in the height of water level in the cylindrical vessel due to sphere (h) = [latex s=2]\frac { 32 }{ 9 } [/latex] cm
Radius of the sphere (R) = 6 cm  (1/2)
Suppose radius of the cylindrical vessel be r.
Volume ofwater in cylinder = Volume of sphere  (1)
πr²h = [latex s=2]\frac { 4 }{ 3 } [/latex]πR³
⇒ r² = [latex s=2]\frac { 4\times { 6 }^{ 3 }\times 9 }{ 3\times 32 } [/latex] ⇒ r = [latex]\sqrt { 27\times 3 } [/latex] = 9cm (1)
Hence, diameter of the cylindrical vessel = 18 cm. (1/2)

Section-D

Solution 23.

Solution 24.

Suppose the man is standing on the deck of the ship at point A.
Suppose CE be the hill with base at C.  (1)
Given that the angle of elevation of point E from A is 60° and the angle of depression of point C from A is 30°.
∠DAE = 60°, ∠CAD = 30°  (1/2)
Now, ∠CAD = ∠ACB = 30° [Alternate angles]
AB = 10 m   (1/2)
Let ED = h m and BC = x m.
In ∆EAD, tan 60° = [latex s=2]\frac { ED }{ AD } [/latex] ⇒ [latex]\sqrt { 3 } [/latex] = [latex s=2]\frac { h }{ x } [/latex] ⇒ h = x[latex]\sqrt { 3 } [/latex] …..(i)   (1/2)

In ∆ABC, tan30° = [latex s=2]\frac { AB }{ BC } [/latex] ⇒ [latex]\frac { 1 }{ \sqrt { 3 } } [/latex] = [latex s=2]\frac { 10 }{ x } [/latex] ⇒ x = 10[latex]\sqrt { 3 } [/latex] …(ii)  (1/2)
So, distance of the hill from the ship = 10[latex]\sqrt { 3 } [/latex]m
From (i) and (ii), h = 10[latex]\sqrt { 3 } [/latex]×[latex]\sqrt { 3 } [/latex] = 30m
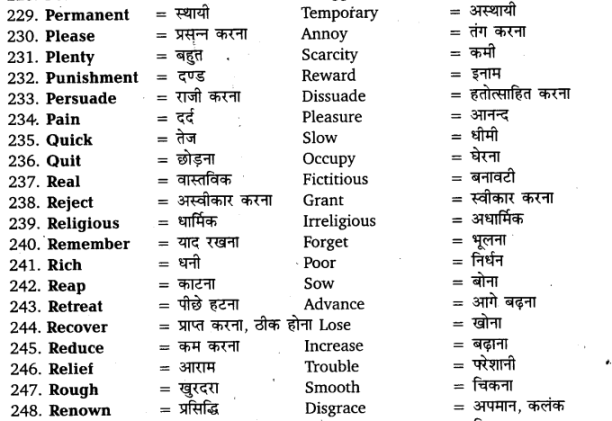
Hence, height of the hill = h+ 10 = 30+ 10 = 40 m. (1)
OR
Let A be the reflection ofthe bird B in the lake, then CB = CA = h metres (say).

∴NB-{h — 50) m and    (1)
AN =(h + 50) m
Let ON be dmetres.
tan 60° = [latex s=2]\frac { h+50 }{ d } [/latex] ⇒ [latex]\sqrt { 3 } [/latex] =[latex s=2]\frac { h+50 }{ d } [/latex] and

tan 30° = [latex s=2]\frac { h-50 }{ d } [/latex] ⇒d = (h-50)[latex]\sqrt { 3 } [/latex]

Thus, 3 = [latex s=2]\frac { h+50 }{ h-50 } [/latex] ⇒ h = 100      (1)

Solution 25.
Let a = 50 and h = 20

OR
Less than type frequency distribution

We first draw the coordinate x-axis with lower limits of the daily income (in ?) along the horizontal axis and the cummulative frequency along the vertical axis. Then, we plot the points (120, 12), (140, 26), (160,34), (180,40), (200,50) and join these points by a free hand smooth curve.

Solution 26.
Let the radius of base and height of the solid right circular cylinder be r cm and h cm, respectively,
Here, r + h = 37 ….(i)  (1/2)
Total surface area = 1628 sq cm
∴ 2πr(r + h)= 1628 …(ii)  (1/2)
From (i) and (ii), we get
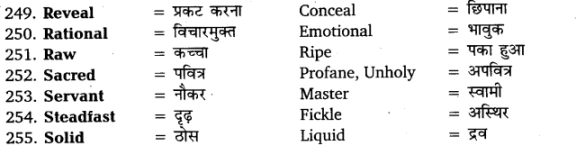
2πr(37) =1628 => 2×[latex s=2]\frac { 22 }{ 7 } [/latex]×r = 44
∴ r =7cm  (1)
After substituting the value of r in (i), we get
7 + h = 37
∴ h = 30cm  (1)
Then, volume of the cylinder = πr²h
= [latex s=2]\frac { 22 }{ 7 } [/latex] ×7×7×30 = 4630 cm²    (1)
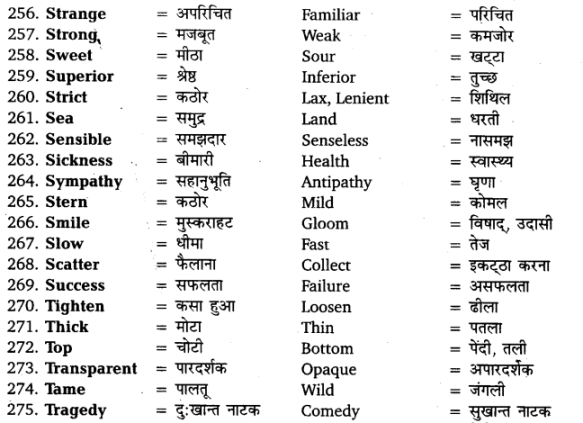
Therefore, the volume of the cylinder is 4,620 cm³.

Solution 27.

OR

Solution 28.

Solution 29.

Solution 30.
Given : Apoint P is at a distance of 6 cm. from the centre of a circle ofradius 2.5 cm.
Required : To draw two tangents to the circle from the given point P. (1)

Step of construction:
1. DrawalinesegmentOPoflength6cm.
2. With centre O and radius equal to 2.5 cm, draw a circle.
3. Draw the right bisector of OP, intersecting OP at M. Let M be mid-point of OP.
4. Taking M as centre and MO as radius draw a circle which intersect the given circle in two points, say AandB.
5. Join PA and PB. These are the required tangents from P to the given circle. (1)