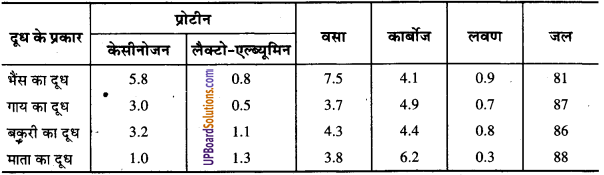
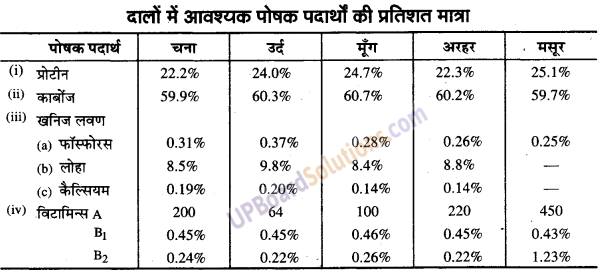
UP Board Solutions for Class 10 Social Science Chapter 6 आर्थिक नियोजन (अनुभाग – चार)
These Solutions are part of UP Board Solutions for Class 10 Social Science. Here we have given UP Board Solutions for Class 10 Social Science Chapter 6 आर्थिक नियोजन (अनुभाग – चार)
विरतृत उत्तरीय प्रश्न
प्रश्न 1.
भारत की पंचवर्षीय योजनाओं का संक्षिप्त विवरण दीजिए।
उत्तर :
भारत की पंचवर्षीय योजनाएँ
स्वतन्त्रता के बाद देश के बहुमुखी विकास के लिए पंचवर्षीय योजनाएँ कार्यान्वित की गयीं। अब तक दस योजनाएँ पूर्ण हो चुकी हैं तथा ग्यारहवीं योजना चालू है। इन परियोजनाओं की प्राथमिकताएँ (उद्देश्य) तथा उपलब्धियाँ निम्नवत् रही हैं –
प्रथम योजना (1951-56 ई०) – इस योजना के तीन उद्देश्य थे—
- देश विभाजन के फलस्वरूप उत्पन्न आर्थिक असन्तुलन की समस्याओं का समाधान करना,
- देश की अर्थव्यवस्था को सन्तुलित बनाना तथा
- उत्पादन में वृद्धि करके जनसाधारण के जीवन स्तर में वृद्धि करना तथा धन के वितरण की असमानता को दूर करना। इसके लिए कृषि के विकास को प्राथमिकता दी गयी। इस दौरान आर्थिक प्रगति सन्तोषजनक रही। राष्ट्रीय आय (UPBoardSolutions.com) में वृद्धि के लक्ष्य से अधिक वृद्धि दर्ज की गयी। भूमि-सुधार कार्यक्रमों के फलस्वरूप कृषि उत्पादन में भी वृद्धि हुई। औद्योगिक उत्पादन 40% बढ़ा। चिकित्सा एवं स्वास्थ्य तथा परिवहन के क्षेत्र में भी विकास हुआ, जिससे औद्योगिक विकास की भूमिका तैयार हो गयी।
द्वितीय योजना (1956-61 ई०) – इस योजना में औद्योगिक विकास पर बल दिया गया। आधारभूत तथा भारी उद्योगों की स्थापना की गयी। रोजगार सुविधाओं का विकास तथा आर्थिक विषमताओं को दूर करना इस योजना के अन्य लक्ष्य थे, किन्तु इस काल में खाद्यान्नों के उत्पादन का लक्ष्य पूरा न हो सका। राष्ट्रीय आय में भी आशा से कम वृद्धि हुई और भारतीय अर्थव्यवस्था आर्थिक संकट में डूब गयी।
तृतीय योजना (1961-66 ई०) – इस योजना के खाद्यान्न उत्पादन में आत्मनिर्भरता प्राप्त करना, उद्योगों की आवश्यकताओं को पूरा करने के लिए कृषि उत्पादन में वृद्धि करना, आधारभूत उद्योगों का विस्तार करना, मशीनरी उद्योगों की स्थापना करना, बेरोजगारी दूर करना (UPBoardSolutions.com) आदि लक्ष्य थे किन्तु इन लक्ष्यों में भी वांछित सफलता न मिल सकी। चीन तथा पाकिस्तान के आक्रमणों के कारण देश का विकास बाधित रहा। इस योजना-काल में केवल आंशिक सफलताएँ ही प्राप्त हुईं।
तीन वार्षिक योजनाएँ – सन् 1966 से 1969 ई० तक तीन वर्षों के लिए पंचवर्षीय योजनाओं को स्थगित कर दिया गया और तीन वार्षिक योजनाएँ बनायी गयीं। इन वार्षिक योजनाओं की अवधि में साधनों का अभाव रहा, जिससे विकास की गति मन्द रही।
चौथी योजना (1969-74 ई०) – इस योजना का लक्ष्य विकास की दर को तेज करना, कृषि उत्पादन में उतार-चढ़ाव को कम करना, विदेशी सहायता पर निर्भरता को कम करना, जन-जीवन के स्तर को ऊँचा उठाना, दुर्बल वर्ग के लोगों की दशा सुधारना, सम्पत्ति, आय तथा आर्थिक शक्ति के केन्द्रीकरण को रोकना आदि थे, किन्तु ये सभी लक्ष्य पूरे न हो सके। निर्यात के क्षेत्र में अवश्य वृद्धि हुई।
![]()
पाँचवीं योजना (1974-79 ई०) – इस योजना के मुख्य लक्ष्य आत्मनिर्भरता प्राप्त करना, निर्धनता रेखा के नीचे रहने वालों का जीवन-स्तर सुधारना, मुद्रास्फीति (महँगाई) पर नियन्त्रण करना, राष्ट्रीय आय में वृद्धि करना आदि थे। योजना को एक वर्ष पूर्व ही अर्थात् 1978 ई० में समाप्त कर दिया गया। इसका कारण देश में राजनीतिक उथल-पुथल के वातावरण का होना था।
दो वार्षिक योजनाएँ – इन दो वार्षिक योजनाओं (सन् 1978-79 एवं 1979-80) के (UPBoardSolutions.com) द्वारा पिछड़े हुए। लक्ष्यों को प्राप्त करने का प्रयास किया गया।
छठी योजना (1980-85 ई०) – इस योजना में कृषि तथा उद्योग के आधारभूत ढाँचे को एक-साथ विकसित करने, रोजगार के अवसर जुटाने, गरीबी दूर करने, परिवार नियोजन का प्रसार करने, क्षेत्रीय विषमताओं को दूर करने आदि का लक्ष्य रखा गया। ग्रामीण क्षेत्रों के विकास पर अधिक बल दिया गया। सन्तुलित आर्थिक विकास के कार्यक्रम चलाये गये, किन्तु जनसंख्या की तीव्र दर से वृद्धि होने के कारण ये सभी कार्यक्रम लक्ष्यों को पूरा न कर सके। इस योजना ने सातवीं पंचवर्षीय योजना के लिए एक स्वस्थ वातावरण अवश्य तैयार किया।
सातवीं योजना (1985-90 ई०) – इस योजना के प्रमुख उद्देश्य थे—सुनियोजित विकास, आम लोगों के जीवन-स्तर में सुधार, उत्पादन में वृद्धि, कमजोर वर्गों को संरक्षण, निर्धनता को दूर करना, रोजगार के अवसरों में वृद्धि, निर्यातों में वृद्धि, पर्यावरण-प्रदूषण दूर करना, ऊर्जा, परिवहन संचार आदि क्षेत्रों का विस्तार करना, आवासों के निर्माण में वृद्धि करना आदि। यह योजना निश्चित ही उपलब्धियों से पूर्ण थी।
दो वार्षिक योजनाएँ – आठवीं पंचवर्षीय योजना को ध्यान में रखकर तैयार की गयी इन वार्षिक योजनाओं (सन् 1990-91 एवं 1991-92)में मुख्य रूप से अधिकतम रोजगार प्रदान करने और सामाजिक स्थानान्तरण पर बल दिया गया।
आठवीं योजना (1992-97 ई०) – इस योजना में मानव संसाधन विकास पर विशेष बल दिया गया। इसके लिए गाँवों में पेयजल उपलब्ध कराना, सिर पर मैला उठाने की कुप्रथा को दूर करना, पर्यावरण स्वच्छ रखना, परिवहन, ऊर्जा, सिंचाई आदि का प्रसार करना तथा ग्रामीण क्षेत्रों में विशेष रूप से शिक्षा, रोजगार तथा समाजकल्याण की योजनाओं का विकास करना मुख्य लक्ष्य निर्धारित किये गये। किन्तु ये उपलब्धियाँ हासिल न हो सकीं। गरीबों और दलितों को अपेक्षित लाभ न मिल सका। क्षेत्रीय विषमताओं में वृद्धि हुई। कृषि विकास के बावजूद कुल सम्भावनाओं का दोहन नहीं किया जा सका। अन्य आधारभूत (UPBoardSolutions.com) क्षेत्रों के लक्ष्य भी अधूरे रहे।
- नवीं योजना (1997-2002 ई०) – विस्तृत उत्तरीय प्रश्न संख्या 6 का उत्तर देखें।
- दसवीं योजना (2002-2007 ई०) – विस्तृत उत्तरीय प्रश्न संख्या 3 का उत्तर देखें।
- ग्यारहवीं पंचवर्षीय योजना (2007-2012) – लघु उत्तरीय प्रश्न संख्या 6 का उत्तर देखें।
- बारहवीं पंचवर्षीय योजना (2012-2017) – विस्तृत उत्तरीय प्रश्न संख्या 8 का उत्तर देखें।
![]()
प्रश्न 2.
भारत में आर्थिक नियोजन के उद्देश्यों पर प्रकाश डालिए।
या
भारतीय अर्थव्यवस्था में ‘आर्थिक नियोजन’ क्यों आवश्यक है ? इसके उद्देश्य भी लिखिए। आर्थिक नियोजन के दो महत्त्व बताइट। [2010]
या
भारत में आर्थिक नियोजन के महत्व पर प्रकाश डालिए। [2018]
या
आर्थिक नियोजन के दो उद्देश्यों का उल्लेख कीजिए। [2009, 10, 11]
या
आर्थिक नियोजन में चार उद्देश्यों को स्पष्ट कीजिए। [2013, 15,16, 18]
या
आर्थिक नियोजन की आवश्यकता क्यों होती है? दो कारण दीजिए। [2016]
उत्तर :
आर्थिक नियोजन की आवश्यकता
भारत एक विकासशील देश है, जो शताब्दियों तक गुलामी की जंजीरों में जकड़े रहने के कारण आर्थिक शोषण का शिकार रहा। भारत में आर्थिक नियोजन की आवश्यकता निम्नलिखित कारणों से है
1. आर्थिक संसाधनों के उचित प्रयोग के लिए – भारत में आर्थिक संसाधन प्रचुर मात्रा में हैं, किन्तु उनका अभी तक सदुपयोग नहीं हुआ है। आर्थिक नियोजन का सबसे बड़ा लाभ यह होगा कि हमारे प्राकृतिक (आर्थिक) संसाधनों का विवेकपूर्ण तथा इष्टतम उपयोग हो सकेगा।
2. राष्ट्रीय आय में वृद्धि के लिए – भारत एक जनसंकुल देश है। प्रति व्यक्ति (UPBoardSolutions.com) आय की दृष्टि से यह विश्व के निर्धन देशों में गिना जाता है। राष्ट्रीय तथा प्रति व्यक्ति आय बढ़ाने के लिए आर्थिक नियोजन की बहुत आवश्यकता है।
![]()
3. धन के समान वितरण के लिए – भारत में राष्ट्रीय आय के वितरण में प्रादेशिक विषमताएँ अधिक हैं। नियोजित विकास से धन का न्यायपूर्ण तथा समान वितरण सम्भव है। समाजवादी नियोजन आर्थिक समानता के सिद्धान्त को आधार मानता है।
4. आत्मनिर्भरता के लिए – यद्यपि विश्व का कोई भी देश पूर्णत: आत्मनिर्भर नहीं है, तथापि भारत आत्मनिर्भर बनने के लिए चेष्टारत है। यह कार्य आर्थिक नियोजन द्वारा ही सम्भव है।
भारत में आर्थिक नियोजन का महत्त्व
भारतीय अर्थव्यवस्था में आर्थिक नियोजन का अत्यधिक महत्त्व है। टी०टी० कृष्णामाचारी के शब्दों में, आर्थिक क्षेत्र में नियोजन का वही महत्त्व है, जो आध्यात्मिक क्षेत्र में ईश्वर का है। आर्थिक नियोजन के महत्त्व को निम्नवत् स्पष्ट किया जा सकता है –
- उपलब्ध सीमित संसाधनों का सर्वोत्तम उपयोग किया जाता है।
- अन्तर्राष्ट्रीय संस्थाओं द्वारा योजनाबद्ध आर्थिक विकास के लिए आर्थिक सहायता उपलब्ध हो जाती है।
- स्वतन्त्रता से पूर्व युद्धकालीन जर्जरित अर्थव्यवस्था का स्वतन्त्रता के पश्चात् पुनरुत्थान सम्भव हुआ।
- आर्थिक नियोजन के द्वारा आर्थिक विकास की गति को तीव्र किया जा सकता है।
- आर्थिक नियोजन के द्वारा पूँजी-निर्माण की दर में वृद्धि होगी, विनियोग (UPBoardSolutions.com) में वृद्धि होगी और अर्थव्यवस्था को गरीबी के दुश्चक्र से बाहर निकाला जा सकेगा।
- भारत में बेरोजगारी एवं अर्द्ध-बेरोजगारी की व्यापक समस्या विद्यमान है। आर्थिक नियोजन के द्वारा ही । इस समस्या का समाधान किया जा सकता है।
- नियोजन, आर्थिक एवं सामाजिक आधारिक संरचना (सड़क, रेल, बिजलीघर, शिक्षा एवं चिकित्सालय संस्थान आदि) का निर्माण जो निजी विनियोगों को प्रोत्साहन प्रदान करता है, में सहायक है।
- नियोजन द्वारा उत्पादन तकनीकी में परिवर्तन की गति को तीव्र किया जा सकता है।
निष्कर्ष रूप में कहा जा सकता है कि आर्थिक नियोजन देश के आर्थिक विकास में सहायक है।
उद्देश्य
भारत में आर्थिक नियोजन के मुख्य उद्देश्य निम्नलिखित हैं –
- राष्ट्रीय आय एवं प्रति व्यक्ति आय में दीर्घकालीन वृद्धि।
- निर्धनता के दुश्चक्र की समाप्ति।
- देश को आत्मनिर्भर बनाना।
- प्राकृतिक एवं मानवीय संसाधनों का उचित दोहन।
- देश की योजनाबद्ध एवं सन्तुलित आर्थिक विकास।
- देश में रोजगार के अवसरों का विस्तार।
- सामाजिक एवं आर्थिक आधारिक संरचना का निर्माण।
- शिक्षा, प्रशिक्षण एवं तकनीक के उच्च स्तर की प्राप्ति।
- संविधान के नीति-निदेशक सिद्धान्तों का क्रियान्वयन।
- समाजवादी ढंग से लोकतान्त्रिक समाज की स्थापना।
![]()
प्रश्न 3.
दसवीं पंचवर्षीय योजना पर एक लेख लिखिए। [2009]
या
भारत की दसवीं पंचवर्षीय योजना के किन्हीं दो उद्देश्यों का उल्लेख कीजिए। [2009]
उत्तर :
दसवीं पंचवर्षीय योजना (सन् 2002-2007 ई०)
1 सितम्बर, 2001 ई० को राष्ट्रीय विकास परिषद् (National Development Council) ने अपनी 49वीं बैठक में दसवीं पंचवर्षीय योजना (2002-2007 ई०) के दृष्टिकोण-पत्र को अपना अनुमोदन प्रदान किया। अनुमोदित दृष्टिकोण-पत्र के विशिष्ट (UPBoardSolutions.com) बिन्दु (उद्देश्य) निम्नलिखित थे
- सकल राष्ट्रीय उत्पाद के 8% वार्षिक दर का लक्ष्य प्राप्त करना।
- उद्योग क्षेत्र की वृद्धि दर 10% वार्षिक करनी।
- निर्धनता अनुपात 2007 ई० तक 20% तथा 2012 ई० तक 10% लाना।
- वर्ष 2007 तक सभी को प्राथमिक शिक्षा उपलब्ध कराना।
- 2001-11 के दशक में जनसंख्या की दशकीय वृद्धि को 16.2% तक सीमित रखना।
- साक्षरता दर को 2007 ई० तक 72% तथा 2012 ई० तक 80% करना।
- सन् 2012 ई० तक सभी गाँवों में स्वच्छ पेयजल की व्यवस्था करना।
- श्रम-शक्ति को लाभपूर्ण रोजगार उपलब्ध कराना।
- शिशु मृत्यु-दर को 45 प्रति हजार जीवित जन्मों तक कम करना।
- वनों और वृक्षों से घिरे क्षेत्र को 25% तक बढ़ाना।
- सभी मुख्य नदियों की सफाई करना।
- सकल बजटीय समर्थन में 18.3% वार्षिक की वृद्धि, जिससे 2007 ई० में इसे GDP के 5% तक लाया जा सके।
- GDP के प्रतिशत रुपये में सकल कर राजस्व (डीजल उपकर सहित) को वर्ष 2001-02 में 9.16% से बढ़ाकर 2006-07 ई० तक 11.7% करना।
- ‘सेवा कर के दायरे का विस्तार।
- विनिवेश में वृद्धि (2002-05) की अवधि में 16-17 (UPBoardSolutions.com) हजार करोड़ रुपये की वार्षिक निवेश प्राप्तियाँ।
- राजकोषीय घाटे को GDP के 5% से घटाकर 2.5% तक ले जाना।
![]()
दसवीं पंचवर्षीय योजना के प्रारम्भ के समय यानि वर्ष 2002-03 में कृषि उत्पादन में गिरावट आ गयी। वर्ष 2003-04 में यह उत्पादन 10% बढ़ा, जब कि 2004-05 और 2005-06 में क्रमश: 0.7% और 2.3% की ही वृद्धि हुई। वर्ष 2002-03 में 7%, 2003-04 में 7.6%, 2004–05 में 8.6% और 2005-06 में 9% की दर से औद्योगिक उत्पादन बढ़ा। भारतीय अर्थव्यवस्था की संवृद्धि दर को आगे बढ़ाने में सबसे महत्त्वपूर्ण भूमिका सेवाओं के क्षेत्र की रही है। सेवाओं में संवृद्धि की दर वर्ष 2002-03, 2003-04, 2004-05 और 2005-06 में क्रमश: 7.3,8.2, 9.9 और 9.8 प्रतिशत रही। आज सेवाओं का सकल घरेलू उत्पाद में हिस्सा 54.1% है। विनिर्माण के क्षेत्र में उत्पादने वर्ष 2004-05 के 7.1% की तुलना में 2005-06 में 9.4% की दर से बढ़ा है। शेयर बाजार का संवेदी सूचकांक भी बढ़ (UPBoardSolutions.com) रहा है। यह 2004 ई० में 11% बढ़ा और 2005 ई० में 36% 6 फरवरी, 2006 ई० को दस हजार के अंक के ऊपर चला गया और बारह हजार के अंक तक चढ़ने के बाद ही गिरा। सकल घरेलू उत्पाद के अनुपात के रूप में निवेश वर्ष 2004-05 में 30.1% तक हो गया था।
दसवीं पंचवर्षीय योजना की समीक्षा के आधार पर यह कहा जा सकता है कि यह योजना अपने लक्ष्यों को प्राप्त करने में एक सीमा तक अवश्य सफल हुई है।
प्रश्न 4.
भारत में पंचवर्षीय योजनाओं के उद्देश्यों पर विस्तार से प्रकाश डालिए।
या
पंचवर्षीय योजनाओं के क्या उद्देश्य हैं?
उत्तर :
भारत में पंचवर्षीय योजनाओं के उद्देश्य स्वतन्त्रता के पश्चात् देश का तेजी से आर्थिक विकास करने के लिए भारत में सरकारी स्तर पर सर्वप्रथम 1950 ई० में योजना आयोग की स्थापना की गयी। भारत के प्रथम प्रधानमन्त्री पण्डित जवाहरलाल नेहरू इसके अध्यक्ष थे। देश की पहली पंचवर्षीय योजना 1 अप्रैल, 1951 ई० से आरम्भ हुई। भारत में पंचवर्षीय योजनाओं के उद्देश्य निम्नलिखित रहे हैं –
1. उपलब्ध साधनों का सर्वोत्तम प्रयोग – भारत के सीमित उपलब्ध साधनों का पूर्ण दोहन नहीं हो पाया है; अत: उपलब्ध साधनों का अधिकतम और श्रेष्ठतम उपयोग योजनाबद्ध दोहन का प्रमुख पहलू
2. राष्ट्रीय आय तथा प्रति व्यक्ति आय में वृद्धि करना – देश की गरीबी को दूर करने के लिए प्रत्येक योजना में राष्ट्रीय आय तथा प्रति व्यक्ति आय में वृद्धि करने के प्रयास किये जा रहे हैं।
3. जनसंख्या-वृद्धि पर नियन्त्रण – देश में तीव्र गति से बढ़ती जनसंख्या देश के विकास में सबसे बड़ी बाधा है। इसलिए प्रत्येक योजना में जनसंख्या वृद्धि को रोकने की प्रयत्न किया गया है।
4. जनता के जीवन-स्तर में सुधार करना – राष्ट्रीय आय और प्रति व्यक्ति आय में वृद्धि करके तथा जन्म-दर में कमी करके जीवन-स्तर को ऊँचा उठाना योजनाओं का उद्देश्य रहा है।
5. समाजवादी समाज की स्थापना – भारत की पंचवर्षीय योजनाओं का उद्देश्य समाजवादी समाज की स्थापना रहा है; अर्थात् इस बात पर विशेष बल दिया गया है कि आर्थिक विकास का लाभ कुछ लोगों को न मिलकर सम्पूर्ण समाज़ के विशेष (UPBoardSolutions.com) रूप से पिछड़े और निर्धन लोगों को अधिक मिल सके।
6. सार्वजनिक क्षेत्र का विस्तार – भारत सरकार की नीति सार्वजनिक क्षेत्र के विस्तार की रही है। सरकारी क्षेत्र में इस्पात, रसायन, उर्वरक, तेल इत्यादि कारखानों की स्थापना, यातायात और संचार सेवाएँ, सिंचाई की सुविधा, सरकारी विपणन, बैंक व बीमा की सरकारी सेवाएँ इसी उद्देश्य को पूरा करने के लिए प्रदान की गयी हैं।
7. रोजगार के अवसरों में वृद्धि करना – नियोजन काल में नये-नये उद्योगों की स्थापना, पुराने उद्योगों और कृषि का सुधार, सरकारी कारखानों की संख्या में वृद्धि, कुटीर उद्योगों का विस्तार आदि का उद्देश्य रोजगार की अधिकाधिक सुविधाएँ प्रदान करना रहा है, जिससे रोजगार के अवसरों में वृद्धि की जा सके तथा बढ़ती हुई बेरोजगारी कम हो सके।
![]()
8. आर्थिक समानता लाना – योजनाओं में इस बात पर विशेष बल दिया गया है कि योजनाओं का लाभ समाज के पिछड़े और गरीब लोगों को अधिक-से-अधिक मिल सके। इससे आर्थिक असमानता दूर होगी; क्योंकि समाज के कमजोर वर्गों का कल्याण सरकार ही कर सकती है।
9. जन-सुविधाओं का विस्तार – आर्थिक समानता लाने के लिए देश के पिछड़े हुए क्षेत्रों में, गाँवों में अनुसूचित जाति एवं जनजाति व पिछड़े वर्गों के लोगों के लिए विभिन्न योजनाओं के द्वारा अच्छा भोजन, वस्त्र, मकान, स्कूल, अस्पताल, बिजली, पक्की सड़कें इत्यादि जन-सुविधाओं को निरन्तर बढ़ाया जा रहा है।
10. कल्याणकारी राज्य की स्थापना – देश की योजनाओं का उद्देश्य कल्याणकारी राज्य की स्थापना करना है। विशेषतः पाँचवीं और छठी योजना में जिस न्यूनतम आवश्यकता कार्यक्रम पर बल दिया गया था उसका उद्देश्य देश की जनता के कल्याण को सरकारी स्तर पर बढ़ाना है। इसमें आवश्यक वस्तुओं की वितरण-व्यवस्था को सुधारना, गरीबों को उचित मूल्य पर वस्तुएँ प्रदान करना, मूल्य तथा मजदूरी आय में सन्तुलन लाना, शिक्षा, स्वास्थ्य व पौष्टिक आहार, पीने के पानी व आवास, वृद्धावस्था व अन्य आपत्तियों के समय सहायता करना इत्यादि से जन-कल्याण में वृद्धि की जा रही है। यही कल्याणकारी राज्य का उद्देश्य होता है।
11. आत्मनिर्भरता की प्राप्ति – यद्यपि योजना के प्रारम्भ से ही देश में आत्मनिर्भरता प्राप्त करने का उद्देश्य रखा गया, लेकिन तीसरी योजना-अवधि में इस पर विशेष बल दिया गया कि बिना विदेशी सहायता के देश अपने पैरों पर खड़ा होकर आर्थिक विकास करे।
प्रश्न 5.
आर्थिक नियोजन की विशेषताएँ स्पष्ट कीजिए।
या
आर्थिक नियोजन की किन्हीं तीन विशेषताओं का वर्णन कीजिए। [2010, 13, 17]
उत्तर :
आर्थिक नियोजन की विशेषताएँ आर्थिक नियोजन की प्रमुख विशेषताएँ निम्नलिखित हैं –
1. निश्चित उद्देश्य के लिए – आर्थिक नियोजन की सबसे महत्त्वपूर्ण विशेषता यह है कि यह सदैव विचारयुक्त होता है तथा इसका एक निश्चित उद्देश्य होता है। ये उद्देश्य भिन्न-भिन्न हो सकते हैं; जैसे-आर्थिक विकास की गति तीव्र करना या पूर्ण रोजगार (UPBoardSolutions.com) की स्थिति प्राप्त करना आदि।
2. केन्द्रीय नियोजन सत्ता – नियोजन के लिए यह आवश्यक है कि देश में एक केन्द्रीय सत्ता हो, जो नियोजन का कार्य करे। भारत में योजना आयोग इस कार्य को करता है।
3. सम्पूर्ण नियोजन – नियोजन सम्पूर्ण अर्थव्यवस्था का होता है। यह केवल कुछ क्षेत्रों तक ही सीमित नहीं होना चाहिए अर्थात् नियोजन आंशिक नहीं होना चाहिए।
![]()
4. साधनों का विवेकपूर्ण विभाजन – आर्थिक नियोजन के अन्तर्गत देश के सीमित साधनों का विवेकपूर्ण बँटवारा इस ढंग से किया जाता है, जिससे सामाजिक कल्याण अधिकतम किया जा सके।
5. नियोजन उत्पादन तक ही सीमित नहीं – एक नियोजित अर्थव्यवस्था में उत्पादन के साथ-साथ वितरण का भी नियोजन किया जाता है। नियोजन जहाँ इस बात को निश्चित करता है कि क्या और कितना उत्पन्न किया जाए, वहाँ वह इस बात को भी निश्चित करता है कि बँटवारा किन लोगों के बीच किया जाए।
6. नियन्त्रण आवश्यक – अपने उद्देश्यों एवं लक्ष्यों को प्राप्त करने के लिए अर्थव्यवस्था के विभिन्न क्षेत्रों में नियन्त्रण लगाये जाते हैं।
7. जनसहयोग आवश्यक – आर्थिक नियोजन की सफलता के लिए जनता का सहयोग आवश्यक होता है। बिना जनता के सहयोग के आर्थिक नियोजन की प्रक्रिया सफल नहीं हो सकती।
8. दीर्घकालीन प्रक्रिया – आर्थिक नियोजन एक दीर्घकालीन प्रक्रिया है। यह तभी सफल होती है, जबकि इसका आयोजन सतत व लम्बे समय के लिए किया जाए।
प्रश्न 6.
नवीं पंचवर्षीय योजना के उद्देश्य, वित्त-व्यवस्था एवं उपलब्धियों का मूल्यांकन कीजिए।
उत्तर :
नवीं पंचवर्षीय योजना (सन् 1997-2002 ई०)
नवीं पंचवर्षीय योजना 1997 ई० से आरम्भ हुई थी और यह 2002 ई० (UPBoardSolutions.com) तक चली। इस योजना के उद्देश्य (प्राथमिकताएँ) तथा लक्ष्य निम्नलिखित थे
उद्देश्य – नवीं पंचवर्षीय योजना के उद्देश्य (प्राथमिकताएँ) निम्नलिखित थे –
- पर्याप्त उत्पादक रोजगार सृजित करना
- कृषि एवं ग्रामीण विकास
- निर्धनता का उन्मूलन
- सभी के लिए स्वच्छ पेयजल
- प्राथमिक स्वास्थ्य सुविधाएँ
- सार्वभौमिक प्राथमिक शिक्षा
- आवास की सुविधाओं सहित न्यूनतम आवश्यकताओं की समयबद्ध आपूर्ति
- जनसंख्या-वृद्धि पर अंकुश
- महिलाओं व दलित वर्ग का उत्थान
- मूल्यों में स्थिरता आदि। नवीं पंचवर्षीय योजना की असफलताएँ एवं उपलब्धियाँ निम्नलिखित हैं
![]()
1. आठवीं पंचवर्षीय योजना में सकल घरेलू उत्पाद की दर लगभग 6.7% थी, जो नवीं योजना में घटकर 5.35% हो गयी।
2. नवीं पंचवर्षीय योजना में कृषि विकास दर आठवीं पंचवर्षीय योजना के 4.7% से घटकर 2.1% रह गयी, जब कि संशोधित लक्ष्य 3.7% का था।
3. नवीं योजना में सार्वजनिक क्षेत्र में परिव्यय का आकार 18% घटा दिया गया।
4. नंवीं योजना में विनिर्माण क्षेत्र में विकास-दर आठवीं योजना के 7.6% से घटकर 4.5% रह गयी, जब कि लक्ष्य 8.2% का था।
5. नवी योजना बचत एवं निवेश के लक्ष्य को भी प्राप्त नहीं कर सकी। सकल (UPBoardSolutions.com) घरेलू उत्पाद में बचत-दर 23.3% रही, जब कि लक्ष्य 26.3% का था। इसी प्रकार सकल घरेलू उत्पाद में निवेश-दर 24.2% रही, जब कि लक्ष्य 28.3% का था।
6. नवीं योजना में बेरोजगारी की दर में भी वृद्धि हुई।
7. नवीं योजना में कर और सकल घरेलू उत्पाद के अनुपात में कमी आयी, परन्तु व्यय और सकल घरेलू उत्पाद के अनुपात में तुलनात्मक रूप से अधिक वृद्धि हुई।
8. नवीं योजना निर्यात-क्षेत्र में भी असफल सिद्ध हुई। 11.8% वृद्धि के लक्ष्य की तुलना में निर्यातों में मात्र 5% की वृद्धि हुई। संक्षेप में, नवी योजना अपने लक्ष्यों को प्राप्त करने में असफल रही।
प्रश्न 7.
भारतीय आर्थिक नियोजन की उपलब्धियों पर निबन्ध लिखिए।
या
आर्थिक नियोजन की किन्हीं तीन उपलब्धियों का वर्णन कीजिए। [2011, 13, 17]
या
योजना-काल में भारत के आर्थिक विकास पर टिप्पणी लिखिए।
उत्तर :
आर्थिक नियोजन की उपलब्धियाँ
भारत की पहली पंचवर्षीय योजना 1951-52 ई० में आरम्भ हुई थी। नियोजित विकास के वर्षों के दौरान देश के आर्थिक विकास के प्रमुख तथ्य निम्नलिखित हैं –
1. विकास दर – कुछ पंचवर्षीय योजनाओं को छोड़कर हम निर्धारित विकास दर को प्राप्त करने में सफल रहे हैं। प्रथम योजना काल में प्राप्त विकास दर 3.6% वार्षिक थी, जब कि लक्ष्य 2.1% वार्षिक का था। इसी प्रकार नवीं योजना में प्राप्त आर्थिक (UPBoardSolutions.com) विकास की दर का लक्ष्य 9 प्रतिशत है।
2. राष्ट्रीय आय – शुद्ध राष्ट्रीय आय में 6.8 गुनी वृद्धि हुई है। वर्ष 2010-11 में राष्ट्रीय आय (चालू मूल्यों पर) ₹ 6466860 करोड़ है। अतः सम्पूर्ण योजना-काल में शुद्ध राष्ट्रीय आय में निरन्तर वृद्धि हुई है।
3. प्रति व्यक्ति आय – इसमें चार गुनी वृद्धि हुई है। जनसंख्या में तीव्र वृद्धि होने के कारण प्रति व्यक्ति आय में वृद्धि-दर आशा से कम ही रही है।
4. सकल घरेलू उत्पाद – सकल घरेलू उत्पाद में 6.9 गुनी वृद्धि हुई है।
![]()
5. खाद्यान्न उत्पादन – यह 550 लाख टन (1950-51) से बढ़कर 2003-04 ई० में 2,135 लाख टन . हो गया है। वाणिज्यिक फसलों में आशातीत वृद्धि हुई है।
6. सिंचाई क्षमता – सन् 1950-51 ई० में बड़ी, मझोली और छोटी योजनाओं की कुल क्षमता 2 करोड़ 26 लाख हेक्टेयर थी, जो दसवीं योजना की मध्यावधि तक 8 करोड़ 93 लाख 10 हजार हेक्टेयर तक पहुँच गयी है।
7. विद्युत उत्पादन-क्षमता – 11वीं योजना में 62,374 मेगावाट के संशोधित क्षमता निर्माण के लक्ष्य के मुकाबले 54,964 मेगावट क्षमता बढ़ायी जा चुकी है, जिसमें केन्द्रीय क्षेत्र में 15,220 मेगावट, राज्य क्षेत्र में 16,732 मेगावाट और निजी क्षेत्र में 23,012 मेगावाट रहा। यह 10वीं योजना के मुकाबले ढाई गुना अधिक है। 2012 में प्रतिस्थिापित विद्युत क्षमता 1400 मेगावाट थी जो 31 मई, 2012 को बढ़कर 20297.03 मेगावाट हो गई, जिसमें 39,060.40 मेगावाट जल विद्युत, 134,635.18 मेगावाट तापीय । (गैस और डीजल सहित) बिजली, 4780.00 मेगावाट परमाणु ऊर्जा और 24,503.45 मेगावाट पवन सहित नवीकरणीय ऊर्जा शामिल है।
8. औद्योगिक विकास – सन् 1948 ई० के औद्योगिक नीति प्रस्ताव के साथ औद्योगिक विकास कार्यक्रम का आरम्भ हुआ। इसमें सार्वजनिक क्षेत्र को प्रोत्साहन दिया गया। सन् 1956 ई० के औद्योगिक नीति प्रस्ताव में भी सार्वजनिक क्षेत्र को प्राथमिकता देते हुए निजी क्षेत्र के विकास की. व्यवस्था की गयी। सन् 1993 ई० की औद्योगिक नीति के बाद से भारतीय उद्योगों को मजबूती प्रदान करने तथा अन्तर्राष्ट्रीय स्तर पर प्रतिस्पर्धी बनाने की प्रक्रिया तेज हुई। फलतः अप्रैल, 2001 ई० से औद्योगिक नीति को अधिक उदार बनाया जा रहा है। अधिकांश उद्योगों में लाइसेन्स व्यवस्था समाप्त कर दी गयी है। रक्षा, पेट्रोलियम, (UPBoardSolutions.com) परमाणु, खनिज तथा रेल क्षेत्र को छोड़कर सभी उद्योगों को लाइसेन्स मुक्त कर दिया गया है। विदेशी पूँजी निवेश को बढ़ावा दिया गया है। परिणामतः सभी उद्योगों में उत्पादन की वृद्धि हुई है।
9. परिवहन एवं संचार – परिवहन एवं संचार के क्षेत्र में योजनी-काल में उल्लेखनीय प्रगति हुई। रेलवे लाइनों की लम्बाई 76,197 किमी, सड़कों की लम्बाई 33 लाख किमी तथा जहाजरानी की क्षमता 6.28 लाख G.R.T. हो गयी। हवाई परिवहन, बन्दरगाहों की स्थिति और आन्तरिक जलमार्गों को भी विकास किया गया है। संचार-व्यवस्था के अंन्तर्गत विकास के क्षेत्रों में डाकखानों, टेलीफोन, टेलीग्राफ, रेडियो स्टेशन एवं प्रसारण केन्द्रों की संख्या में भी पर्याप्त वृद्धि हुई है।
10. शिक्षा एवं स्वास्थ्य सुविधाएँ – योजना-काल में शिक्षा का भी व्यापक प्रसार हुआ है। भारत में साक्षरता की दर 1951 ई० में 16.7% थी, जो 2011 ई० में 74.04% हो गयी। इसी प्रकार योजना-काल में देश में स्वास्थ्य सुविधाओं में उल्लेखनीय वृद्धि हुई है।
11. बैंकिंग संरचना – योजना-काल में बैंकिंग संरचना में उल्लेखनीय वृद्धि हुई है। 30 जून, 1969 ई० को व्यापारिक बैंकों की शाखाओं की संख्या 8,262 थी; जो 30 जून, 2004 ई० को बढ़कर 67,283 हो गयी। राष्ट्रीयकरण के पश्चात् ग्रामीण क्षेत्रों में बैंकिंग शाखाओं का व्यापक विस्तार हुआ है।
![]()
12. आत्मनिर्भरता – हमारा देश योजना-काल में आत्मनिर्भरता की ओर अग्रसर हुआ है। पहले जिन वस्तुओं का आयात किया जाता था, आज वे वस्तुएँ हमारे देश में ही बनने लगी हैं खाद्यान्न उत्पादन में हमारा देश लगभग आत्मनिर्भर हो चुका है तथा विदेशी सहायता में भी कमी आयी है।
13. सामाजिक न्याय – हमारे देश में आर्थिक नियोजन का लक्ष्य ‘सामाजिक न्याय के साथ आर्थिक विकास’ रहा है। योजना-काल में समाज के निर्धन वर्ग के उत्थान के लिए तथा गरीबी व बेरोजगारी जैसी भयावह समस्याओं के समाधान के लिए सरकार द्वारा अनेक योजनाएँ चालू की गयी हैं, जिनके सार्थक परिणाम धीरे-धीरे सामने आने लगे हैं।
प्रश्न 8.
बारहवीं पंचवर्षीय योजना का विस्तारपूर्वक वर्णन कीजिए। [2013]
उत्तर :
बारहवीं पंचवर्षीय योजना (2012-2017)–भारत की 12वीं पंचवर्षीय योजना (2012-17) के निर्माण की दिशा का मार्ग अक्टूबर 2011 में उस समय प्रशस्त हो गया जब इस योजना के दृष्टि पत्र (दृष्टिकोण पत्र/दिशा पत्र/Approach Paper) को राष्ट्रीय विकास परिषद् (NDC) ने स्वीकृति प्रदान कर दी। 1 अप्रैल, 2012 से प्रारम्भ हो चुकी इस पंचवर्षीय योजना के दृष्टि पत्र को योजना आयोग की 20 अगस्त, 2011 की बैठक में स्वीकार कर लिया था तथा केन्द्रीय मन्त्रिपरिषद् ने इसका अनुमोदन 15 सितम्बर, 2011 की अपनी बैठक में किया था। प्रधानमन्त्री डॉ० मनमोहन सिंह की अध्यक्षता में राष्ट्रीय विकास परिषद् की नई दिल्ली में 22 अक्टूबर, 2011 को सम्पन्न हुई इस 56वीं बैठक में दिशा पत्र को कुछेक शर्तों के साथ स्वीकार किया गया। राज्यों द्वारा सुझाए गए कुछ संशोधनों को समायोजन योजना दस्तावेज तैयार करते समय योजना आयोग द्वारा किया जायेगा। 12वीं पंचवर्षीय योजना में वार्षिक विकास दर का लक्ष्य 9 प्रतिशत है। इस लक्ष्य को प्राप्त करने में राज्यों के सहयोग (UPBoardSolutions.com) की अपेक्षा प्रधानमन्त्री मनमोहन सिंह ने की है। इस लक्ष्य को प्राप्त करने के लिए कृषि, उद्योग व सेवाओं के क्षेत्र में क्रमशः 4.0 प्रतिशत, 9.6 प्रतिशत व 10.0 प्रतिशत की वार्षिक वृद्धि प्राप्त करने के लक्ष्य तय किये गये हैं। इनके लिए निवेश दर सकल घरेलू उत्पाद (GDP) की 387 प्रतिशत प्राप्त करनी होगी। बचत की दर जीडीपी के 36.2 प्रतिशत प्राप्त करने का लक्ष्य दृष्टि पत्र में निर्धारित किया गया है। समाप्त हुई 11वीं पंचवर्षीय योजना में निवेश की दर 36.4 प्रतिशत तथा बचत की दर 34.0 प्रतिशत रहने का अनुमान था। 11वीं पंचवर्षीय योजना में वार्षिक विकास दर 8.2 प्रतिशत रहने का अनुमान लगाया गया था। 11वीं पंचवर्षीय योजना में थोक मूल्य सूचकांक (Wholesale Price Index) में औसत वार्षिक वृद्धि लगभग 6.0 प्रतिशत अनुमानित था, जो 12वीं पंचवर्षीय योजना में 4.5 – 5.0 प्रतिशत तक सीमित रखने का लक्ष्य है। योजनावधि में केन्द्र सरकार को औसत वार्षिक राजकोषीय घाटा जीडीपी के 3.25 प्रतिशत तक सीमित रखने का लक्ष्य इस योजना के दृष्टि पत्र में निर्धारित किया गया है।
लघु उत्तरीय प्रश्न
प्रश्न 1.
आर्थिक नियोजन से क्या तात्पर्य है ? स्पष्ट कीजिए। [2009, 13, 14, 17, 18]
उत्तर :
नियोजन का शाब्दिक अर्थ ‘पहले से आयोजन करना है। यह एक ऐसी विवेकपूर्ण व्यवस्था है, जिसका उद्देश्य किसी ‘न्यायपूर्ण आर्थिक विकास एवं अधिकतम सामाजिक कल्याण के लक्ष्य को प्राप्त करना है। आर्थिक नियोजन को निम्नलिखित प्रकार से परिभाषित किया जा सकता है –
आर्थिक नियोजन से आशय पूर्व-निर्धारित और निश्चित सामाजिक और आर्थिक उद्देश्यों की पूर्ति हेतु अर्थव्यवस्था के सभी अंगों को एकीकृत और समन्वित करते हुए राष्ट्र के संसाधनों के सम्बन्ध में सोच-विचारकर रूपरेखा तैयार करने और (UPBoardSolutions.com) केन्द्रीय नियन्त्रण से है।”
प्रश्न 2.
पंचवर्षीय योजनाओं से देश को क्या लाभ हुआ है ? [2014]
या
आर्थिक नियोजन के दो लाभों का उल्लेख कीजिए। [2009, 16, 17]
या
पंचवर्षीय योजनाओं के चार लाभों का उल्लेख कीजिए। [2014]
उत्तर :
पंचवर्षीय योजनाओं से देश को निम्नलिखित लाभ हुए हैं –
- उपलब्ध सीमित संसाधनों का दोहन एवं सर्वोत्तम उपयोग सम्भव हुआ है।
- कृषि जो देश के अर्थतन्त्र की रीढ़ है, उसका विकास हुआ है। कृषि उत्पादकता तथा उत्पादन में वृद्धि होने से देश खाद्यान्नों में आत्मनिर्भर बन सका है। वाणिज्यिक फसलों का उत्पादन बढ़ने से कृषिपरक उद्योगों में भी विस्तार एवं वृद्धि हुई है।
- उद्योगों का विकास हुआ है। इससे देश की आर्थिक समृद्धि में वृद्धि हुई है।
- उद्योगों के नियोजित विकास से विदेशी व्यापार भी विकसित हुआ है।
- देश में परिवहन तथा संचार के साधनों तथा ऊर्जा उत्पादन में भी वृद्धि हुई है।
- आर्थिक विकास के फलस्वरूप रोजगार के अवसरों में वृद्धि हुई है।
- शिक्षा, प्रशिक्षण, शोध, अनुसन्धान तथा तकनीकी क्षेत्रों में प्रगति के कारण देश का सामाजिक विकास सम्भव हुआ है।
- देशवासियों को जीवनस्तर ऊँचा उठा है।
- नियोजन काल में भारत में राष्ट्रीय आय एवं प्रति व्यक्ति आय दोनों में वृद्धि हुई है। इस प्रकार पंचवर्षीय योजनाओं के अन्तर्गत भारत में तीव्र आर्थिक विकास हुआ है।
- देश में निवेश की मात्रा एवं निवेश-दर में निरन्तर वृद्धि (UPBoardSolutions.com) हुई है, जिससे देश का आर्थिक विकास हुआ है।
- नियोजन काल में देश के बड़े-बड़े बैंकों का राष्ट्रीयकरण किया गया। राष्ट्रीयकरण के पश्चात् बैंकिंग व्यवस्था सुदृढ़ हुई एवं उसका व्यापक विस्तार हुआ।
- ग्रामों का विद्युतीकरण, जल-व्यवस्था एवं गरीबी की रेखा से नीचे जीवन-यापन करने वाले लोगों को ऊपर उठाने के प्रयास किये गये, जिनका लाभ समाज के कमजोर लोगों को प्राप्त हुआ है।
![]()
प्रश्न 3.
विभिन्न योजना-काल की प्राथमिकताओं का उल्लेख कीजिए।
उत्तर :
भारत की विभिन्न पंचवर्षीय योजनाओं में यद्यपि विकास का उद्देश्य समान रूप से देखने को मिलता है, लेकिन भिन्न-भिन्न योजनाओं की प्राथमिकताओं में भी परिवर्तन किये गये, जो निम्नलिखित हैं –
- पहली योजना में कृषि विकास को सर्वोच्च प्राथमिकता दी गयी।
- दूसरी योजना में औद्योगिक विकास को प्राथमिकता दी गयी।
- तीसरी योजना में कृषि एवं उद्योग दोनों को प्राथमिकता दी गयी।
- चौथी योजना में कृषि क्षेत्र में आत्मनिर्भरता को सर्वोच्च प्राथमिकता दी गयी।
- पाँचवीं योजना में गरीबी उन्मूलन, औद्योगिक विकास एवं खनन को प्राथमिकता दी गयी।
- छठी योजना में गरीबी उन्मूलन और आत्मनिर्भरता को प्रमुख लक्ष्य रखा गया।
- सातवीं योजना में आधारभूत वस्तुओं के उत्पादन को प्राथमिकता दी गयी।
- आठवीं योजना में रोजगार वृद्धि को प्राथमिकता दी गयी।
- नवी योजना में मानव संसाधनों के विकास पर (UPBoardSolutions.com) विशेष बल दिया गया।
- दसवीं योजना में सभी को प्राथमिक शिक्षा उपलब्ध कराने पर जोर दिया गया।
- ग्यारहवीं योजना का प्रमुख उद्देश्य सभी गाँवों को फोन व ब्रॉड बैंड सुविधा देना था।
- बारहवीं योजना में वार्षिक विकास दर का लक्ष्य 9% रखा गया है।
प्रश्न 4.
आर्थिक नियोजन के मार्ग में आने वाली कठिनाइयों का वर्णन कीजिए।
उत्तर :
यद्यपि ग्यारह पंचवर्षीय योजनाएँ एवं सात एकवर्षीय योजनाएँ पूरी हो चुकी हैं और बारहवीं पंचवर्षीय योजना कार्यरत है, तथापि हम नियोजन के लक्ष्यों को पूर्ण रूप से प्राप्त नहीं कर पाये हैं। देश में आर्थिक नियोजन के मार्ग में प्रमुख निम्नलिखित कठिनाइयाँ हैं –
- जनसंख्या में तीव्र वृद्धि के कारण प्रति व्यक्ति आय में वृद्धि की गति धीमी रही है।
- मूल्यों में तीव्र और निरन्तर वृद्धि ने योजनाओं की लागत को तेजी से बढ़ाया है।
- सार्वजनिक उपक्रमों का निष्पादन घटिया और अकुशल रहा है।
- श्रम-शक्ति में वृद्धि के अनुपात में रोजगार के अवसरों में वृद्धि नहीं हो पायी है।
- आर्थिक विषमताओं की बढ़ती खाई ने ‘सामाजिक न्याय के लक्ष्य को झुठला दिया है।
- सरकार की नियन्त्रण नीति दोषपूर्ण ही नहीं, अपितु एकांगी रही है। निष्कर्ष रूप में कहा जा सकता है कि लगभग सभी योजनाएँ विशाल आकार की रही हैं। इनका निर्माण भी गलत धारणाओं पर आधारित रहा है और योजनाओं की सफलता को आँकड़ों के माध्यम से दिखाने का प्रयास किया गया है।
![]()
प्रश्न 5.
आर्थिक नियोजन को सफल बनाने के लिए आप क्या सुझाव देंगे ?
उत्तर :
भारत में आर्थिक नियोजन को सफल बनाने के लिए कुछ सुझाव दिये जा सकते हैं, जो निम्नलिखित हैं –
- आवश्यक वस्तुओं की आपूर्ति एवं उनके मूल्यों पर प्रभावी नियन्त्रण स्थापित किया जाना चाहिए।
- शिक्षा-प्रणाली को कार्यपरक बनाया जाना चाहिए।
- आर्थिक नीतियों को प्रभावी ढंग से लागू किया जाना चाहिए।
- जनता का पूर्ण सहयोग प्राप्त करने के लिए प्रयास किये जाने चाहिए।
- सार्वजनिक एवं निजी क्षेत्र के उद्योगों में उचित समन्वय स्थापित किया जाना चाहिए।
- गाँवों में गैर-कृषि क्षेत्रों (दुग्ध उद्योग, मुर्गीपालन, कुटीर उद्योग) का विकास किया जाना चाहिए।
- केन्द्र एवं राज्यों के बीच उचित सम्बन्ध स्थापित किये जाने (UPBoardSolutions.com) चाहिए, जिससे सम्पूर्ण राष्ट्र के समन्वित आर्थिक विकास को गति दी जा सके।
- योजनाओं का निर्माण साधनों को ध्यान में रखकर किया जाना चाहिए।
- प्रशासकीय व्यवस्था को चुस्त एवं दुरुस्त किया जाना चाहिए।
- वित्त-प्रधान योजनाओं के साथ-साथ भौतिक योजनाओं की ओर भी ध्यान दिया जाना चाहिए।
प्रश्न 6.
ग्यारहवीं पंचवर्षीय योजना पर संक्षिप्त टिप्पणी लिखिए।
उतर :
ग्यारहवीं योजना (2007-2012)–19 दिसम्बर, 2007 को नई दिल्ली में आयोजित राष्ट्रीय विकास परिषद् की 54वीं बैठक में 11वीं पंचवर्षीय योजना के प्रारूप को सर्वसम्मति से मंजूर कर लिया गया।
प्रमुख लक्ष्य
- 2012 तक सभी गाँवों को टेलीफोन से जोड़ना और ब्रॉडबैंड कनेक्शन उपलब्ध कराना।
- सभी गाँवों व निर्धनता रेखा से नीचे के परिवारों को 2009 तक बिजली व योजना के अंत तक 24 घंटे बिजली उपलब्ध कराना।
- 2012 तक सभी भूमिहीनों को घर और जमीन उपलब्ध कराना।
- 0-3 वर्ष के बच्चों में कुपोषण को घटाकर आधा करना।
- प्रजनन दर को घटाकर 2-1 करना।
- वर्ष 2009 तक सभी को पीने का पानी उपलब्ध कराना।
- मातृ मृत्यु-दर को घटाकर 2 प्रतिशत करना और मातृ मृत्यु-अनुपात को एक हजार पर एक करना।
- विकास दर का लक्ष्य 9 प्रतिशत प्रतिवर्ष
- 5.8 करोड़ नए रोजगार के अवसर पैदा करना।
- 2011-2012 तक प्राथमिक शिक्षा में बीच में स्कूल छोड़ने वालों की संख्या में 52.2 प्रतिशत से घटाकर 20 प्रतिशत की कटौती करना।
- उच्च शिक्षा प्राप्त करने वालों की संख्या 10 से बढ़ाकर (UPBoardSolutions.com) 15 प्रतिशत करना।
- महिलाओं के लिए केन्द्र सरकार की योजनाओं में प्रत्यक्ष तौर पर 33 प्रतिशत आरक्षण करना।
![]()
प्रश्न 7.
भारत में योजना आयोग की स्थापना क्यों की गयी ? दो कारण दीजिए।
उत्तर :
द्वितीय विश्वयुद्ध एवं स्वतन्त्रता-प्राप्ति के बाद भारत की आर्थिक स्थिति अत्यधिक बिगड़ चुकी थी और सरकार के सामने अनेक समस्याएँ एवं कठिनाइयाँ मुँह खोले खड़ी थीं। इन समस्याओं के समाधान हेतु 1950 ई० में भारत में योजना आयोग की स्थापना की गयी। योजना आयोग की स्थापना के दो प्रमुख कारण निम्नलिखित हैं
1. आर्थिक संसाधनों के उचित प्रयोग के लिए – भारत में आर्थिक संसाधन प्रंचुर मात्रा में हैं, किन्तु उनका अभी तक सदुपयोग नहीं हुआ है। आर्थिक नियोजन का सबसे बड़ा लाभ यह होगा कि हमारे प्राकृतिक (आर्थिक) संसाधनों का विवेकपूर्ण तथा इष्टतम उपयोग हो सकेगा।
2. राष्ट्रीय आय में वृद्धि के लिए – भारत एक जनसंकुल देश है। प्रति व्यक्ति आय की दृष्टि से यह विश्व के निर्धन देशों में गिना जाता है। राष्ट्रीय तथा प्रति व्यक्ति आय बढ़ाने के लिए आर्थिक नियोजन की बहुत आवश्यकता है।
प्रश्न 8.
तृतीय पंचवर्षीय योजना की वित्त-व्यवस्था लिखिए।
उत्तर :
तृतीय योजना के लक्ष्यों में खाद्यान्न उत्पादन में आत्मनिर्भरता प्राप्त करना, उद्योगों की आवश्यकताओं को पूरा करने के लिए कृषि उत्पादन में वृद्धि करना, आधारभूत उद्योगों का विस्तार करना, मशीनरी उद्योगों की स्थापना करना, बेरोजगारी दूर करना, आर्थिक विषमताओं को यथासम्भव कम करना, राष्ट्रीय आय में वृद्धि करना आदि थे। किन्तु इन लक्ष्यों में भी वांछित सफलता न मिल सकी। चीन (1962 ई०) तथा पाकिस्तान (1965 ई०) के आक्रमणों के कारण देश का विकास बाधित रहा। इन युद्धों के कारण महँगाई में 25% की वृद्धि हुई, विदेशी मुद्रा का अभाव उत्पन्न हुआ तथा अर्थव्यवस्था पर वित्तीय बोझ बढ़ा। इस अवधि में दो बार सूखा पड़ा, जिससे खाद्यान्न उत्पादन पूर्ववत् रहा तथा विदेशों से अनाज का भारी आयात करना पड़ा। तृतीय योजना का काल भारतीय अर्थव्यवस्था (UPBoardSolutions.com) के लिए कठिनाइयों का काल रहा। अधिक व्यय के बाद भी सामान्य रूप से इस योजना की प्रगति निराशाजनक रही। परिणामस्वरूप इस योजना-काल में केवल आंशिक सफलताएँ ही प्राप्त हुईं।
तीन वार्षिक योजनाएँ–सन् 1966 से 1969 ई० तक तीन वर्षों के लिए योजनाओं को स्थगित कर दिया गया। इसके लिए प्रमुख कारण थे(i) तृतीय योजना-अवधि में हुए दो युद्ध तथा (ii) वर्ष 1966-67 के दौरान पड़े दो सूखे। इन वार्षिक योजनाओं का प्रमुख उद्देश्य स्वयं स्फूर्त विकास, पूर्ण रोजगार तथा आर्थिक विषमताओं की समाप्ति के लिए सुदृढ़ आधार प्रदान करना था। यद्यपि इन वार्षिक योजनाओं की अवधि में साधनों का अभाव रहा, जिससे विकास की गति मन्द रही; तथापि इन योजनाओं ने चौथी पंचवर्षीय योजना को एक ठोस आधार प्रदान किया।
प्रश्न 9.
आठवीं पंचवर्षीय योजना के प्रमुख लक्ष्य क्या थे ?
उत्तर :
आठवीं योजना में मानव संसाधन विकास पर विशेष बल दिया गया। इसके लिए गाँवों में पेयजल उपलब्ध कराना, सिर पर मैला उठाने की कुप्रथा को दूर करना, पर्यावरण स्वच्छ रखना, परिवहन, ऊर्जा, सिंचाई आदि का प्रसार करना तथा ग्रामीण क्षेत्रों में विशेष रूप से शिक्षा, रोजगार तथा समाजकल्याण की योजनाओं का विकास करना, खाद्यान्नों में आत्मनिर्भरता पैदा करना, 15-35 वर्ष के आयु-वर्ग के सभी व्यक्यिों को साक्षर बनाना आदि मुख्य लक्ष्य निर्धारित किये गये। किन्तु ये उपलब्धियाँ पूर्णरूप में प्राप्त न हो सकीं। गरीबों और दलितों को अपेक्षित लाभ न मिल सका, क्षेत्रीय विषमताओं में वृद्धि हुई, कृषि विकास के बावजूद कुल सम्भावनाओं का दोहन नहीं किया जा सका तथा अन्य आधारभूत क्षेत्रों के लक्ष्य भी अधूरे रहे। इस योजना की प्रमुख उपलब्धियाँ इस प्रकार रहीं–साधन-लागत पर जीडीपी (UPBoardSolutions.com) की वृद्धि दर लक्ष्य से अधिक रही। कृषि क्षेत्र में विकास की औसत वृद्धि दर तथा औद्योगिक क्षेत्र में औसत संवृद्धि दर लक्ष्य से अधिक रही। सेवा-क्षेत्र में भी औसत वार्षिक वृद्धि दर लक्ष्य से अधिक रही।
![]()
प्रश्न 10
महिला समृद्धि योजना पर टिप्पणी लिखिए। [2014]
उत्तर :
ग्रामीण महिलाओं को सशक्त बनाने के उद्देश्य से 2 अक्टूबर 1993 ई० को महिला समृद्धि योजना आरम्भ की गई थी। इसका लक्ष्य ग्रामीण महिलाओं में बचत की आदत डालना तथा उन्हें आत्मनिर्भर बनाना था। हालांकि प्रारम्भ के दो वर्षों में इस योजना का प्रदर्शन निराशाजनक था परन्तु वर्तमान में यह योजना सफल भी हो रही है। इस योजना के अन्तर्गत 18 वर्ष से ऊपर उम्र की महिलाएँ अपना बचत खाता खोल सकती हैं। यह खाता निकटतम डाकघर में एक न्यूनतम धनराशि द्वारा 4 वर्ष या उसके गुणक में खोला जा सकता है। इस योजना के अन्तर्गत यदि खाताधारक महिला प्रथम वर्ष में धनराशि नहीं निकालती है तो उसमें जमाधन की 25% राशि सरकार उसे प्रोत्साहन के रूप में प्रदान करती है।
अतिलघु उत्तरीय प्रश्न
प्रश्न 1.
प्रथम पंचवर्षीय योजना की कार्य-अवधि क्या थी ? [2013, 16]
उत्तर :
1 अप्रैल, 1951 ई० से 31 मार्च, 1956 ई० तक।
प्रश्न 2.
भारत की कौन-सी पंचवर्षीय योजना एक वर्ष पूर्व समाप्त हो गयी थी ?
उत्तर :
पाँचवीं पंचवर्षीय योजना को एक वर्ष पूर्व समाप्त कर दिया गया।
प्रश्न 3.
दसवीं पंचवर्षीय योजना की समयावधि क्या थी ?
उत्तर :
1 अप्रैल, 2002 से 31 मार्च, 2007 तक।
प्रश्न 4.
ग्यारहवीं पंचवर्षीय योजना की कार्य-अवधि क्या थी?
उत्तर :
ग्यारहवीं पंचवर्षीय योजना 1 अप्रैल, 2007 से 31 मार्च, 2012 तक चली।
प्रश्न 5.
भारत में योजना आयोग की स्थापना कब और क्यों हुई ? एक उद्देश्य लिखिए।
उत्तर :
भारत में योजना आयोग की स्थापना सन् (UPBoardSolutions.com) 1950 ई० में हुई थी। इसका एक उद्देश्य देश में रोजगार अवसरों का विस्तार करना था।
प्रश्न 6
आर्थिक नियोजन के किन्हीं दो लाभों को लिखिए। [2009, 16, 17]
उत्तर :
- उपलब्ध सीमित संसाधनों का सर्वोत्तम उपयोग किया जाता है।
- आर्थिक नियोजन के द्वारा आर्थिक विकास की गति को तीव्र किया जा सकता है।
प्रश्न 7.
भारतीय आर्थिक आयोजन की किन्हीं तीन असफलताओं की ओर संकेत कीजिए।
उत्तर :
भारतीय आर्थिक आयोजन की तीन असफलताएँ इस प्रकार हैं-
- प्रति व्यक्ति वास्तविक आय में असन्तोषजनक प्रगति
- धन तथा आय की असमानता में वृद्धि तथा
- जनसंख्या पर नियन्त्रण तथा बेरोजगारी की समस्या के समाधान में असफलता।
![]()
प्रश्न 8.
पंचवर्षीय योजना क्या है ?
उत्तर :
आर्थिक योजना का वह प्रारूप जिसकी अवधि 5 (UPBoardSolutions.com) वर्ष होती है; अर्थात् जिसमें लक्ष्य प्राप्ति की अवधि 5 वर्ष रखी जाती है, पंचवर्षीय योजना कहलाती है।
प्रश्न 9.
छठवीं पंचवर्षीय योजना का प्रारम्भ कब हुआ ?
उत्तर :
छठवीं पंचवर्षीय योजना 1 अप्रैल, 1980 ई० को प्रारम्भ हुई थी।
प्रश्न 10.
आठवीं पंचवर्षीय योजना की अवधि लिखिए।
उत्तर :
आठवीं पंचवर्षीय योजना की अवधि थी-1 अप्रैल, 1992 से 31 मार्च, 1997 ई० तक।
प्रश्न 11.
आठवीं योजना के दो मुख्य उद्देश्य लिखिए।
उत्तर :
आठवीं योजना के दो मुख्य उद्देश्य थे—
- जनसंख्या-वृद्धि दर को नियन्त्रित करना तथा
- रोजगार के अधिकाधिक अवसरों का सृजन करना।
प्रश्न 12.
देश की कौन-सी पंचवर्षीय योजना केवल चार वर्ष चली ?
उत्तर :
पाँचवीं पंचवर्षीय योजना केवल चार वर्ष चली थी।
प्रश्न 13.
नवीं योजना का कार्यकाल क्या था ?
उत्तर :
नवीं योजना का कार्यकाल 1 अप्रैल, 1997 से 31 मार्च, 2002 ई० था।
प्रश्न 14.
नवीं पंचवर्षीय योजना में उद्योगों के विकास पर व्यय हेतु कितनी धनराशि प्रस्तावित की गयी है ?
उत्तर :
नवीं पंचवर्षीय योजना (संशोधित) में उद्योग व खनिज पर (UPBoardSolutions.com) ₹ 69,972 करोड़ का व्यय प्रस्तावित किया गया था।
प्रश्न 15.
दसवीं योजना के प्रमुख उद्देश्य क्या थे ?
उत्तर :
दसवीं योजना में यह प्रमुख उद्देश्य रखा गया है कि विकास दर बढ़े और सामाजिक न्याय के उद्देश्य को पाया जा सके। दसवीं योजना में कृषि पर विशेष ध्यान दिया गया है।
![]()
प्रश्न 16.
भारत में योजना आयोग का पदेन अध्यक्ष कौन होता है ?
उत्तर :
भारत में योजना आयोग का पदेन अध्यक्ष भारत का प्रधानमन्त्री होता है।
प्रश्न 17.
आर्थिक नियोजन के दो उद्देश्य लिखिए। [2010, 12, 15, 18]
उत्तर :
आर्थिक नियोजन के दो उद्देश्य हैं –
- देश को आत्मनिर्भर बनाना तथा
- देश में रोजगार के अवसरों का विस्तार।
प्रश्न 18.
बारहवीं पंचवर्षीय योजना की अवधि लिखिए। [2013]
उत्तर :
बारहवीं पंचवर्षीय योजना 2012 से 2017 ई० तक चलेगी।
प्रश्न 19.
भारतीय योजना आयोग के चार कार्य लिखिए। [2013]
या
योजना आयोग के दो प्रमुख कार्यों का उल्लेख कीजिए। [2009, 10, 11, 13]
उत्तर :
भारतीय योजना आयोग के अनेक उद्देश्य तथा कार्य हैं, जिनमें निम्नलिखित प्रमुख हैं
- देश में उपलब्ध समस्त भौतिक, आर्थिक तथा मानवीय संसाधनों का आकलन करना
- सभी संसाधनों के सन्तुलित तथा इष्टतम (UPBoardSolutions.com) उपयोग की योजना बनाना
- योजना को लागू करने के लिए प्रशासन तन्त्र की रूपरेखा बनाना
- योजना के प्रत्येक चरण पर उसके क्रियान्वयन का मूल्यांकन करना।
![]()
बहुविकल्पीय प्रश्न
1. योजना आयोग कब गठित किया गया? [2009, 10, 14, 15, 16, 17]
(क) 1947 ई० में
(ख) 1948 ई० में
(ग) 1949 ई० में
(घ) 1950 ई० में
2. भारत में अब तक कुल कितनी पंचवर्षीय योजनाएँ लागू हो चुकी हैं? [2015, 16]
(क) दस
(ख) ग्यारह
(ग) बारह
(घ) तेरह
3. इस समय कौन-सी पंचवर्षीय योजना चल रही है?
(क) आठवीं
(ख) नवीं
(ग) दसवीं
(घ) बारहवीं
4. किस पंचवर्षीय योजना में प्रथम बार उद्योगों के विकास पर बल दिया गया?
(क) प्रथम
(ख) द्वितीय
(ग) तृतीय
(घ) चतुर्थ
![]()
5. किस पंचवर्षीय योजना में गरीबी उन्मूलन को प्राथमिकता दी गई?
(क) तृतीय
(ख) चतुर्थ
(ग) पाँचवीं
(घ) छठी
6. रोजगार तथा पर्यावरण विकास किस पंचवर्षीय योजना की प्राथमिकता थे?
(क) आठवीं
(ख) सातवीं
(ग) छठी
(घ) नवीं
7. आठवीं पंचवर्षीय योजना का कार्यकाल निम्नलिखित में से कौन-सा है?
(क) 1990-95 ई०
(ख) 1991-96 ई०
(ग) 1992-97 ई०
(घ) 1993-98 ई०
8. योजना आयोग का पदेन अध्यक्ष होता है [2009, 11, 12, 14, 15]
(क) योजना मन्त्री
(ख) राष्ट्रपति
(ग) उपराष्ट्रपति
(घ) प्रधानमन्त्री
![]()
9. नवीं पंचवर्षीय योजना में कितने प्रतिशत की आर्थिक वृद्धि-दर निर्धारित की गई थी?
(क) 6%
(ख) 8%
(ग) 7%
(घ) 5%
10. दसवीं पंचवर्षीय योजना में कितने प्रतिशत की आर्थिक वृद्धि-दर निर्धारित की गई थी?
(क) 6%
(ख) 8%
(ग) 7%
(घ) 9%
11. निम्नलिखित में से कौन-सी पंचवर्षीय योजना निर्धारित समय से पहले समाप्त हो गई? [2015]
(क) तृतीय
(ख) चतुर्थ
(ग) पंचम
(घ) सातवीं
12. भारत की किस पंचवर्षीय योजना में प्रति व्यक्ति आय सर्वाधिक रही?
(क) द्वितीय
(ख) प्रथम
(ग) चतुर्थ
(घ) तृतीय
13. भारत की दसवीं पंचवर्षीय योजना की अवधि क्या थी?
(क) 1995-2000 ई०
(ख) 1999-2004 ई०
(ग) 2001-2006 ई०
(घ) 2002-2007 ई०
![]()
14. प्रधानमन्त्री रोजगार योजना कब आरम्भ की गई?
(क) पाँचवीं पंचवर्षीय योजना में
(ख) सातवीं पंचवर्षीय योजना में
(ग) आठवीं पंचवर्षीय योजना में
(घ) नवीं पंचवर्षीय योजना में
15. आर्थिक नियोजन का अर्थ है [2015, 18]
(क) प्रत्येक व्यक्ति की आय को बराबर करना
(ख) संसाधनों का उचित उपयोग करना।
(ग) आर्थिक प्रतियोगिता को प्रोत्साहित करना
(घ) साम्प्रदायिक सद्भावना उत्पन्न करना
16. भारत में आर्थिक नियोजन का प्रमुख उद्देश्य है
(क) देश की सामाजिक कुरीतियों को दूर करना
(ख) हिन्दू धर्म का प्रसार करना
(ग) समाजवादी समाज की स्थापना करना
(घ) साम्प्रदायिक सद्भावना पैदा करनी
17. ग्यारहवीं पंचवर्षीय योजना की समयावधि क्या थी?
(क) 2008-13
(ख) 2007-12
(ग) 2006-11
(घ) इनमें से कोई नहीं
18. बारहवीं पंचवर्षीय योजना की समयावधि क्या है? [2013]
(क) 2011-16
(ख) 2012-17
(ग) 2013-18
(घ) 2010-15
![]()
19. निम्नलिखित में से कौन-सा आर्थिक नियोजन का प्रमुख उद्देश्य है? [2015, 18]
(क) आर्थिक प्रतियोगिता को प्रोत्साहित करना
(ख) संसाधनों का जनकल्याण में समुचित उपयोग करना
(ग) सामुदायिक सद्भाव उत्पन्न करना
(घ) राजनैतिक लक्ष्य प्राप्त करना।
20. ‘योजना आयोग’ के स्थान पर किस आयोग का गठन वर्ष 2015 में किया गया? [2018]
(क) वाणिज्य आयोग
(ख) नीति आयोग
(ग) वित्त आयोग
(घ) सूचना आयोग
21. राष्ट्रीय भारत परिवर्तन संस्थान (नीति आयोग) का अध्यक्ष कौन होता है? [2018]
(क) भारत का राष्ट्रपति
(ख) प्रधानमंत्री
(ग) वित्तमंत्री
(घ) मानव संसाधन विकास मंत्री
उत्तरमाला

Hope given UP Board Solutions for Class 10 Social Science Chapter 6 are helpful to complete your homework.
If you have any doubts, please comment below. UP Board Solutions try to provide online tutoring for you.