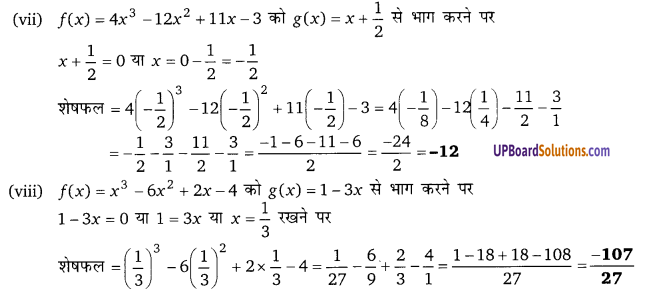Safia

Balaji Class 9 Maths Solutions Chapter 6 Remainder Theorem and Factor Theorem Ex 6.3 शेषफल प्रमेय तथा गुणनखण्ड प्रमेय

गुणनखण्ड प्रमेय का प्रयोग करके निम्न बहुपदों के गुणनफल ज्ञात कीजिए।
प्रश्न 1.
x³ +13x² + 32x + 20; यदि (x + 2) इसका एक गुणनखण्ड है।
हलः
x³ + 13x² + 32x + 20 का (x + 2) एक गुणनखण्ड है।

गुणनखण्ड = (x + 2)[x² +11x + 10]
= (x + 2)[x² + (10 + 1)x + 10]
= (x + 2)[x² + 10x + x + 10]
= (x + 2)[x(x + 10) + 1(x + 10)]
= (x + 2)(x + 10)(x + 1)

प्रश्न 2.
x³ – 6x² + 3x + 10; यदि (x – 2) इसका एक गुणनखण्ड है।
हल:
x³ – 6x² + 3x + 10 का एक गुणनखण्ड (x – 2) है।

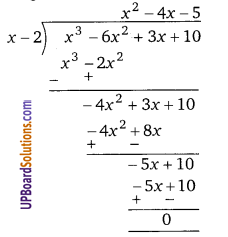
गुणनखण्ड = (x – 2)[x² – 4x – 5]
= (x – 2)[x² – (5 – 1)x – 5]
= (x – 2)[x² – 5x + x – 5]
= (x – 2)[x(x – 5) + 1(x – 5)]
= (x – 2)(x – 5)(x + 1)

प्रश्न 3.
x³ + 13x² + 31x – 45; यदि (x + 9) इसका एक गुणनखण्ड है।
हलः
x³ + 13x² + 31x – 45 का एक गुणनखण्ड (x + 9) है।

गुणनखण्ड = (x + 9)[x² + 4x – 5]
= (x + 9)[x² + (5 – 1)x -5]
= (x + 9)[x² + 5x – x -5]
= (x + 9)[x(x + 5) – 1(x + 5)]
= (x + 9)(x + 5)(x – 1)

प्रश्न 4.
9x³ – 27x² – 100x + 300; यदि (3x + 10) इसका एक गुणनखण्ड है।
हल:
9x³ – 27x² – 100x + 300 का एक गुणनखण्ड (3x + 10) है।

गुणनखण्ड = (3x + 10)[3x² – 19x + 30]
= (3x + 10)[3x² – (10 + 9)x + 30]
= (3x + 10)[3x² – 10x – 9x + 30]
= (3x + 10)[x(3x – 10) – 3(3x – 10)]
= (3x + 10)(3x – 10)(x – 3)

प्रश्न 5.
x⁴ – 7x³ + 9x² + 7x – 10; यदि (x – 1) इसका एक गुणनखण्ड है।
हल:
x⁴ – 7x³ + 9x² – 10 का एक गुणनखण्ड (x – 1) है।

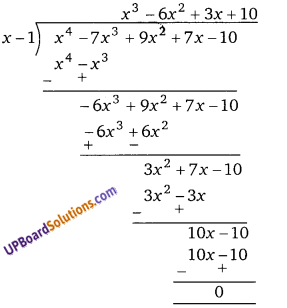
x³ – 6x² + 3x + 10 में x = -1 रखने पर
शेषफल = (-1)³ – 6(-1)² + 3(-1) + 10
= -1 – 6 – 3 + 10 = 0
∴ (x + 1) भी इसका एक गुणनखण्ड होगा।

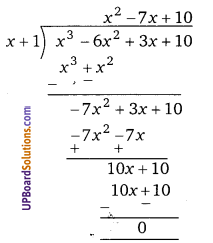
गुणनखण्ड = (x -1)(x + 1)[x² – 7x + 10]
= (x – 1)(x + 1)[x² – (5 + 2)x + 10]
= (x – 1)(x + 1)[x² – 5x – 2x + 10]
= (x – 1)(x + 1)[x(x – 5) – 2(x – 5)]
= (x – 1)(x + 1)(x – 5)(x – 2)

प्रश्न 6.
x³ + 6x² + 11x + 6
हल:
x³ + 6x² + 11x + 6
अतः इनमें से ऋणात्मक मान रखे जायेंगे।
x = -1 रखने पर = (-1)³ + 6(-1)² + 11(-1) + 6 = -1 + 6 – 11 + 6 = 0
अतः (x + 1) इसका एक गुणनखण्ड है।

गुणनखण्ड = (x + 1)[x² + 5x + 6]
= (x + 1)[x² + (2 + 3)x + 6]
= (x + 1)[x² + 2x + 3x + 6]
= (x + 1)[x(x + 2) + 3(x + 2)]
= (x + 1)(x + 2)(x + 3)

प्रश्न 7.
x³ + 7x² + 7x – 15
हल:
x³ + 7x² + 7x – 15                 (∵ 15 = 1 × 3 × 5)
x = 1 रखने पर = (1)³ + 7(1)² + 7(1) – 15 = 1 + 7 + 7 – 15 = 0
अतः (x – 1) इसका एक गुणनखण्ड है।

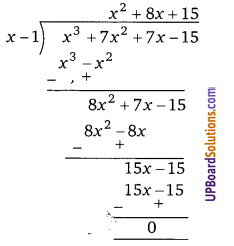
∴ गुणनखण्ड = (x – 1)[x² + 8x +15]
= (x – 1)[x² + (3 + 5)x + 15]
= (x – 1)[x² + 3x + 5x + 15]
= (x – 1)[x(x + 3) + 5(x + 3)]
= (x – 1)(x + 3)(x + 5)

प्रश्न 8.
a³ + b³ + c³ – 3abc
हल:
a³ + b³ + c³ – 3abc में a = -(b + c) रखने पर
=[-(b + c)]³ + b³ + c³ + 3(b + c)bc = -[b³ + c³ + 3bc(b + c)] + b³ + c³ + 3b²c + 3bc³ = 0
अतः (a + b + c) इसका एक गुणनखण्ड है।

∴ a³ + b³ + c³ – 3abc के गुणनखण्ड = (a + b + c)(a² + b² + c² – ab – bc – ca)

प्रश्न 9.
x⁴ + x³ – 7x² – x + 6
हलः
x⁴ + x³ – 7x² – x + 6 (∵ 6 = 1 × 2 × 3)
x = 1 रखने पर = (1)⁴ + (1)³ – 7(1)² – 1 + 6 = 1 + 1 – 7 – 1 + 6 = 0
अतः (x – 1) इसका एक गुणनखण्ड है। .
x = -1 रखने पर = (-1)⁴ + (-1)³ – 7(-1)² – (-1) + 6 = 1 – 1 – 7 + 1 + 6 = 8 – 8 = 0
अतः (x + 1) भी इसका एक गुणनखण्ड है।
∴ (x + 1)(x – 1) = (x² – 1) बहुपद का गुणनखण्ड होगा।

∴ गुणनखण्ड = (x + 1)(x – 1)[x² + x – 6]
= (x + 1)(x – 1)[x² + (3 – 2)x – 6] = (x + 1)(x – 1)[x² + 3x – 2x – 6]
= (x + 1)(x – 1)[x(x + 3) – 2(x + 3)]
= (x + 1)(x – 1)(x + 3)(x – 2)

प्रश्न 10.
2y³ – 5y² – 19y + 42
हलः
2y³ – 5y² – 19y + 42 (∵ 42 = 2 × 3 × 7)
y = 2 रखने पर = 2(2)³ – 5(2)² – 19(2) + 42 = 16 – 20 – 38 + 42 = 58 – 58 = 0
अतः (y – 2) इसका एक गुणनखण्ड है।

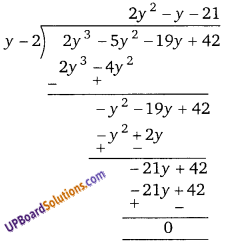
∴ गुणनखण्ड = (y – 2)[2y² – y – 21]
= (y – 2)[2y² – (7 – 6)y – 21] = (y – 2)[2y² – 7y + 6y – 21]
= (y – 2)[y (2y – 7) + 3(2y – 7)]
= (y – 2)(y + 3)(2y – 7)

प्रश्न 11.
x⁴ – 5x³ – 7x² + 41x – 30
हल:
x⁴ – 5x³ – 7x² + 41x – 30 (∵ 30 = 1 × 2 × 3 × 5)
x = 1 रखने पर = (1)⁴ – 5(1)³ – 7(1)² + 41(1) – 30 = 1 – 5 – 7 + 4 1 – 30 = 42 – 42 = 0
अतः (x -1) इसका एक गुणनखण्ड है।
x = 2 रखने पर = (2)⁴ – 5(2)³ – 7(2)² + 41(2) – 30 = 16 – 40 – 28 + 82 – 30 = 98 – 98 = 0
अतः (x – 2) भी इसका एक गुणनखण्ड है।।
(x – 1)(x – 2) = x² – 2x – x + 2 = x² – 3x + 2 इसके गुणनखण्ड है।

∴ गुणनखण्ड = (x – 1)(x – 2)[x² – 2x – 15]
= (x – 1)(x – 2)[x² – (5 – 3)x – 15] = (x -1)(x – 2)[x² – 5x + 3x – 15]
= (x – 1)(x – 2)[x(x – 5) + 3(x – 5)] = (x – 1)(x – 2)(x – 5)(x + 3)

प्रश्न 12.
a⁴ + 2a³ – 2a² + 2a – 3
हलः
a⁴ + 2a³ – 2a² + 2a – 3 (∵ 3 = 1 × 3)
a = 1 रखने पर = (1)⁴ + 2(1)³ – 2(1)² + 2(1) – 3 = 1 + 2 – 2 + 2 – 3 = 5 – 5 = 0
अतः (a – 1) इसका एक गुणनखण्ड है।
a = -3 रखने पर = (-3)⁴ + 2(-3)³ – 2(-3)² + 2(-3) – 3 = 81 – 54 – 18 – 6 – 3 = 81 – 81 = 0
अतः (a + 3) भी इसका एक गुणनखण्ड है।
इसलिए (a – 1)(a + 3) = a² + 3a – a – 3 = a² + 2a – 3 इसका गुणनखण्ड है।

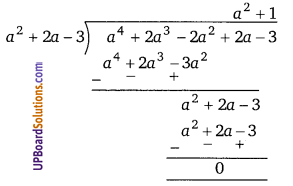
∴ गुणनखण्ड = (a – 1)(a + 3)(a² + 1)

प्रश्न 13.
4x⁴ – 12x³ – x² + 27x – 18
हलः
4x⁴ – 12x³ – x² + 27x – 18 (∵ 18 = 1 × 2 × 3 × 3)
x = 1 रखने पर = 4(1)⁴ – 12(1)³ – (1)² + 27(1) – 18 = 4 – 12 – 1 + 27 – 18 = 31 – 31 = 0
अतः (x – 1) इसका एक गुणनखण्ड है।
इसी प्रकार x = 2 रखने पर = 4(2)⁴ – 12(2)³ – (2)² + 27(2) – 18
= 4 × 16 – 12 × 8 – 4 + 27 × 2 – 18
= 64 – 96 – 4 + 54 – 18 = 118 – 118 = 0
अतः (x – 2) इसका एक गुणनखण्ड है।
(x – 1)(x – 2) = x² – 2x – x + 2 = x² – 3x + 2 इसका गुणनखण्ड है।

∴ गुणनखण्ड = (x – 1)(x – 2)(4x² – 9) = (x – 1)(x – 2)(2x + 3)(2x – 3)

प्रश्न 14.
x⁴ + 10x³ + 35x² + 50x + 24
हल:
x⁴ + 10x³ + 35x² + 50x + 24 (∵ 24 = 1 × 2 × 2 × 2 × 3)
x = -1 रखने पर = (-1)⁴ + 10(-1)³ + 35(-1)² + 50(-1) + 24
= 1 – 10 + 35 – 50 + 24 = 60 – 60 = 0
अतः (x + 1) इसका एक गुणनखण्ड है।
x = -2 रखने पर = (-2)⁴ + 10(-2)³ + 35(-2)² + 50(-2) + 24
= 16 – 80 + 140 – 100 + 24 = 180 – 180 = 0
अतः (x + 2) भी इसका एक गुणनखण्ड है।
∴ (x + 1)(x + 2) = x² + 3x + 2 इसका गुणनखण्ड है।

गुणनखण्ड = (x + 1)(x + 2)[x² + 7x + 12]
= (x + 1)(x + 2)[x² + (3 + 4)x + 12] = (x + 1)(x + 2)[x² + 3x + 4x + 12]
= (x + 1)(x + 2)[x(x + 3)+ 4(x + 3)] = (x + 1)(x + 2)(x + 3)(x + 4)

प्रश्न 15.
3a⁴ + 28a³ + 87a² + 98a + 24
हलः
3a⁴ + 28a³ + 87a² + 98a + 24      (∵ 24 = 1 × 2 × 3 × 4)
a = -2 रखने पर = 3(-2)⁴ + 28(-2)³ + 87(-2)² + 98(-2) + 24
= 48 – 224 + 348 – 196 + 24 = 420 – 420 = 0
अतः (a + 2) इसका एक गुणनखण्ड है।
a = -3 रखने पर = 3(-3)⁴ + 28(-3)³ + 87(-3)² + 98(-3) + 24
= 243 – 756 + 783 – 294 + 24 = 1050 – 1050 = 0
अतः (a + 3) भी इसका एक गुणनखण्ड है।
(a + 2)(a + 3) = a² + 5a + 6 इसका गुणनखण्ड है।

∴ गुणनखण्ड = (a + 2)(a + 3)[3a² + 13a + 4] = (a + 2)(a + 3)[3a² + (12 + 1)a + 4]
= (a + 2)(a + 3)[3a² + 12a + a + 4] = (a + 2)(a + 3)[3a(a + 4) + 1(a + 4)]
= (a + 2)(a + 3)(3a + 1)(a + 4)

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 10 Maths Solutions Chapter 11 Height and Distance Ex 11.2 ऊँचाई एवं दूरी

Ex 11.2 Height and Distance बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.
एक ऊर्ध्वाधर खम्भे की छाया उसकी ऊँचाई के बराबर है तो सूर्य का उन्नयन कोण होगा-
(a) 30°
(b) 45°
(c) 60°
(d) इनमें से कोई नहीं
हलः
माना सूर्य का उन्नयन (UPBoardSolutions.com) कोण = θ
दिया है, खम्भे की ऊँचाई AB = खम्भे की छाया BC


अतः विकल्प (b) सही है।

प्रश्न 2.
50 मीटर ऊँची मीनार का पृथ्वी के किसी बिन्दु पर अवनमन कोण 30° है तब मीनार के आधार से उस बिन्दु की दूरी है-
(a) 25 मीटर
(b) 25[latex] \sqrt{{3}} [/latex] मीटर
(c) 50[latex] \sqrt{{3}} [/latex] मीटर
(d) इनमें से कोई नहीं
हलः
बिन्दु A पर बना अवनमन कोण = 30°
∠ PAC = ∠ACB = 30°


अतः विकल्प (c) सही है।

प्रश्न 3.
एक खम्भे के शीर्ष के उन्नयन कोण A की स्पर्शज्या उसकी छाया की [latex]\frac{3}{4}[/latex] गुणा है। खम्भे की ऊँचाई तथा छाया की लम्बाई का अनुपात है-
(a) 3 : 4
(b) 4 : 3
(c) 2 : 3
(d) इनमें से कोई नहीं
हल:

प्रश्न 4.
एक झण्डा पताका के पाद से  एक बिन्दु A, 50 मीटर की दूरी पर है यदि ∠ PAB = 60°, तो झण्डा पताका की ऊँचाई है-
(a) 25[latex] \sqrt{{3}} [/latex] मीटर
(b) 25[latex] \sqrt{{2}} [/latex] मीटर
(c) 50[latex] \sqrt{{3}} [/latex] मीटर
(d) इनमें से कोई नहीं
हलः

अतः विकल्प (c) सही है।

Ex 11.2 Height and Distance लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 5.
यदि सूर्य का उन्नयन कोण 30° से 60° हो जाता है तो सिद्ध कीजिए कि 15 मीटर ऊँचे खम्भे की छाया का अन्तर 10[latex] \sqrt{{3}} [/latex] मीटर होगा।
हलः
खम्भे की ऊँचाई PQ = 15 मीटर
माना QR = x मीटर
RS = y मीटर

∴ खम्भे की छाया की लम्बाई (UPBoardSolutions.com) में अन्तर y = 10[latex] \sqrt{{3}} [/latex] मीटर इति सिद्धम्

प्रश्न 6.
एक 5 मीटर ऊँचे बिजली के खम्भे के पाद से एक मीनार के शीर्ष का उन्नयन कोण 60° तथा खम्भे के शीर्ष से मीनार के शीर्ष का उन्नयन कोण 30° है। मीनार की ऊँचाई ज्ञात कीजिए। [UP 2003]
हलः
माना BQ = AM = x मीटर तथा PM = y मीटर
AB = MQ = 5 मीटर

प्रश्न 7.
दो बिन्दुओं A व B जो मीनार के आधार से क्रमश: 100 मीटर व 25 मीटर की दूरी पर है। एक ही क्षैतिज रेखा में हैं तथा कोटिपूरक हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हलः
माना ∠ PAQ = 0
कोटिपूरक कोण (UPBoardSolutions.com) ∠PBQ = 90° – θ
माना मीनार की ऊँचाई PQ = h मीटर



∴ मीनार की ऊँचाई h = 50 मीटर

प्रश्न 8.
क्षैतिज तल पर खडे एक ऊर्ध्वाधर मीनार के शीर्ष का उसी तल पर स्थित बिन्दु O से उन्नयन कोण 15° है। मीनार की ओर 80 मीटर चलने पर उन्नयन कोण 30° हो जाता है। मीनार की ऊँचाई ज्ञात कीजिए। [UP 2006, 11]
हलः
माना AB मीनार की ऊँचाई १ मीटर है। (UPBoardSolutions.com) बिन्दु 0 से शीर्ष पर 15° का कोण बनता है।
OP = 80 मीटर
माना PB = x मीटर

प्रश्न 9.
क्षैतिज समतल के किसी बिन्दु से उसी समतल में स्थित एक टीले की चोटि का उन्नयन कोण θ है। उस बिन्दु से ϕ के कोण पर टीले की चोटी की ओर k दूरी तय करने के उपरान्त टीले का उन्नयन कोण α हो जाता है। सिद्ध कीजिए कि टीले की ऊँचाई [latex]\frac{k(\cos \phi-\sin \phi \cot \alpha)}{(\cot \theta-\cot \alpha)}[/latex] है।[UP 2007]
हलः
माना बिन्दु O से टीले की चोटी B का उन्नयन कोण θ है जबकि B के ठीक नीचे बिन्दु A है।
∠AOB = θ
∠AOC = ϕ
OC = k ?
बिन्दु C से AB तथा OA (UPBoardSolutions.com) पर क्रमशः लम्ब CD तथा CE डाले।
∠DCB = α
टीले की ऊँचाई AB = h
समकोण ∆OEC में,

प्रश्न 10.
एक वृक्ष का ऊपरी भाग हवा से टूटकर भूमि से जा लगा है तथा भूमि से 45° माप का कोण बनाता है। वृक्ष की जड़ से उस बिन्दु की दूरी जहाँ वृक्ष का शीर्ष भूमि को छूता है, 6 मीटर हो तो वृक्ष की ऊँचाई ज्ञात कीजिए। [UP 2008]
हलः
माना वृक्ष PAQ का ऊपरी भाग AP, हवा (UPBoardSolutions.com) से बिन्दु A पर टूटकर AO स्थिति ग्रहण कर लेता है, अर्थात् वृक्ष का शिखर P, भूमि को बिन्दु O पर छूता है।
∴ OA = AP
OQ = 6 मीटर
∠QOA = 45°
माना AQ = x मीटर, OA = y मीटर
समकोण ∆OQA में,


∴ वृक्ष की ऊँचाई = PA + AQ = x + y
= 6 + 6[latex] \sqrt{{2}} [/latex] = 6 (1 + [latex] \sqrt{{2}} [/latex])
= 6 (1 + 1.414) = 6 (2.414) = 14.48 मीटर

प्रश्न 11.
दो मीनारों के बीच की दूरी 140 मीटर है। दूसरी मीनार के शीर्ष से देखने पर प्रथम मीनार के शीर्ष का उन्नयन कोण 30° है। यदि दूसरी मीनार की ऊँचाई 60 मीटर है, तो प्रथम मीनार की ऊँचाई ज्ञात कीजिए। NCERT; UP 2010]
हलः
PM = QB = 140 मीटर
माना AM = x मीटर
MB = PQ = 60 मीटर

प्रश्न 12.
सूर्य के प्रकाश में 45 मीटर ऊँची मीनार की छाया 4573 मीटर है तो सूर्य का उन्नयन कोण ज्ञात कीजिए। [UP 2004,01]
हलः
समकोण ∆ ABC में, (UPBoardSolutions.com)

प्रश्न 13.
60 मीटर ऊँचे पहाड़ की चोटि से एक मीनार के शीर्ष तथा आधार के अवनमन कोण 30° व 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए। [UP 2006]
हलः
माना मीनार की (UPBoardSolutions.com) ऊँचाई AB = h मीटर
तथा BQ = AM = x मीटर
समकोणं ∆PAM में,
tan30° = [latex]\frac{P M}{x}[/latex]

प्रश्न 14.
एक अपूर्ण मन्दिर के आधार से 30 मीटर क्षैतिज दूरी पर स्थित किसी बिन्दु से मन्दिर के शिखर का उन्नयन कोण 30° है तो ज्ञात कीजिए कि मन्दिर को कितना ऊँचा और बनाया जाये कि उसी बिन्दु पर मन्दिर के नये शिखर का उन्नयन कोण 60° हो जाये। ([latex] \sqrt{{3}} [/latex] = 1.732) [UP 2009]
हलः
माना मन्दिर को h ऊँचाई (UPBoardSolutions.com) तक ऊपर उठाया जाए।
∴ PR = h मीटर
माना PQ = x मीटर
समकोण ∆PQA में,

प्रश्न 15.
क्षैतिज तल पर स्थित एक बिन्दु से किसी ऊर्ध्वाधर स्तम्भ की चोटी के उन्नयन कोण की माप θ है। स्तम्भ की ओर a दूरी बढ़ने पर उन्नयन कोण 45° तथा पुनः b दूरी बढ़ने पर वह (90° – θ) हो जाता है। स्तम्भ की ऊँचाई ज्ञात कीजिए। [UP 2011]
हलः
माना स्तम्भ की ऊँचाई = h
SR = a, MS = b, QM = x (माना)
समकोण ∆ PQM में,

प्रश्न 16.
सड़क के एक ओर एक मीनार तथा दूसरी ओर एक मकान स्थित है। मीनार के शीर्ष से मकान के शीर्ष तथा आधार के अवनमन कोण क्रमशः 45° व 60° हैं। यदि मकान की ऊँचाई 10 मीटर है तो मीनार की ऊँचाई ज्ञात कीजिए। [UP 2005]
हलः
माना MQ = NR = x मीटर
मकान की ऊँचाई MN (UPBoardSolutions.com) = 10 मीटर
मीनार की ऊँचाई PR = h मीटर
MN = QR = 10 मीटर
∴ PQ = PR – QR
= (h -10) मीटर

प्रश्न 17.
किसी बिन्दु पर एक मीनार के शिखर के उन्नयन कोण की स्पर्शज्या [latex]\frac{5}{3}[/latex] है। मीनार की ओर 32 मीटर चलने पर शिखर के उन्नयन कोण की स्पर्श [latex]\frac{5}{2}[/latex] हो जाती है। मीनार की ऊँचाई ज्ञात कीजिए। [UP 2011]
हलः

Ex 11.2 Height and Distance दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 18.
एक वायुयान, जो 1200 मीटर की ऊँचाई पर उड़ रहा है। दो जलयान, जो एक ही दिशा में है, अपनी ओर आते हुए पाता है। जलयानों के अवनमन कोण क्रमश: 60° व 30° हैं। जलयानों के बीच की दूरी ज्ञात कीजिए।
हलः

प्रश्न 19.
100 मीटर चौडी सड़क के दोनों ओर एक समान ऊँचाई के दो खम्भे हैं। सड़क पर स्थित किसी बिन्दु से खम्भों के शीर्षों के उन्नयन कोण 60° व 30° हैं। उस बिन्दु की स्थिति तथा खम्भों की ऊँचाई ज्ञात कीजिए।
हलः
माना दोनों खम्भों की (UPBoardSolutions.com) ऊँचाई = h मीटर
QT = x मीटर
∴ TS = (100 – x) मीटर

समी० (2) में समी० (1) से h का मान रखने पर
100 – x = 13([latex] \sqrt{{3}} [/latex]x)
100 – x = 3x
100 = 3x + x ⇒ 100 = 4x
x = [latex]\frac{100}{4}[/latex] ⇒ x = 25 मीटर
∴ बिन्दु T, पहले खम्भे से 25 मीटर तथा दूसरे खम्भे से (100 – 25) = 75 मीटर दूर स्थित होगा। समीकरण (1) में x का मान रखने पर
h = [latex] \sqrt{{3}} [/latex]x = 13 x 25 = 2513 मीटर
∴ खम्भों की ऊँचाई = 25[latex] \sqrt{{3}} [/latex] मीटर

प्रश्न 20.
एक 60 मीटर ऊँचे भवन से एक मीनार के शीर्ष एवं आधार के अवनमन कोण क्रमशः 30° व 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हलः
भवन MN की ऊँचाई (UPBoardSolutions.com) = 60 मीटर
माना मीनार PQ की ऊँचाई = h मीटर
∠MPT = 30°, ∠ MQN = 60°
समकोण ∆MTP में,

प्रश्न 21.
क्षैतिज पर एक बिन्दु जो मीनार के पाद से 40 मीटर दूर स्थित है, उस पर मीनार के शीर्ष का उन्नयन कोण 30° है। मीनार के ऊपर रखे टैंक का उन्नयन कोण 45° है। मीनार की ऊँचाई तथा टैंक की गहराई ज्ञात कीजिए। [NCERT]
हलः
माना मीनार की ऊँचाई PQ = h मीटर
तथा टैंक की ऊँचाई TP = x मीटर
समकोण ∆ PQM में,

प्रश्न 22.
15 मीटर ऊँचे भवन के शीर्ष से मीनार के शीर्ष का उन्नयन कोण 30° है तथा भवन के पाद से मीनार के शीर्ष का उन्नयन कोण 60° है। तब मीनार की ऊँचाई तथा भवन से मीनार की दूरी ज्ञात कीजिए।
हलः
भवन की ऊँचाई (UPBoardSolutions.com) AB = 15 मीटर
मीनार की ऊँचाई PQ = h मीटर
माना AM = BQ = x मीटर
∵ AB = MQ = 15 मीटर
PM = PQ – MQ = h – 15 मीटर
समकोण ∆ AMP में,

प्रश्न 23.
एक ऊर्ध्वाधर मीनार के ऊपरी सिरे पर 5 मीटर लम्बा एक झण्डे का डण्डा लगा है। मीनार के पाद के क्षैतिज तल के एक बिन्दु से झण्डे के निचले तथा ऊपरी सिरों के उन्नयन कोण 30° व 60° हैं। मीनार की ऊँचाई ज्ञात कीजिए।
हलः
माना मीनार BP की ऊँचाई (UPBoardSolutions.com) = h मीटर, QP = x मीटर
तथा AB = 5 मीटर

प्रश्न 24.
एक लड़का जमीन पर खडे होकर पतंग उड़ा रहा है। जिसकी डोरी 100 मीटर लम्बी तथा उन्नयन कोण 30° है। दूसरा लड़का 10 मीटर ऊँचे एक मकान की छत पर खड़ा होकर पतंग उड़ा रहा है। जिसका उन्नयन कोण 45° है। दोनों लड़के पतंगों के विपरीत ओर खड़े हैं। पहली पतंग से लड़ाने के लिए दूसरी पतंग की डोरी की लम्बाई ज्ञात कीजिए।
हलः
दोनों लड़के क्रमशः (UPBoardSolutions.com) B व P पर स्थित हैं।
समकोण ∆ ABC में,

प्रश्न 25.
एक प्रकाश गृह के शीर्ष से दो जलयानों के अवनमन कोण 45° व 30° पूर्व की ओर हैं। यदि जलयानों के बीच की दूरी 200 मीटर है तो प्रकाश गृह की ऊँचाई ज्ञात कीजिए।
हलः
माना प्रकाश गृह की (UPBoardSolutions.com) ऊँचाई PQ = h मीटर
QA = x मीटर


∴ प्रकाश गृह की ऊँचाई h = 273.2 मीटर

प्रश्न 26.
एक जलयान की छत पर जो पानी की सतह से 10 मीटर ऊपर है, एक व्यक्ति का किसी पहाड़ी के शीर्ष से उन्नयन कोण 60° तथा पहाड़ी के तल का अवनमन कोण 30° देखता है। पहाड़ी की जलयान से दूरी तथा पहाड़ी की ऊँचाई ज्ञात कीजिए।
हलः
माना पहाड़ी की ऊँचाई = h मीटर व AB = MQ = 10 मीटर
पुनः . माना BQ = AM = x मीटर
समकोण ∆ PAM में, (UPBoardSolutions.com)


समीकरण (1) में x का मान रखने पर
[latex] \sqrt{{3}} [/latex] × 10[latex] \sqrt{{3}} [/latex] = h – 10
30 = h – 10 (UPBoardSolutions.com)
30 + 10 = h
h = 40 मीटर
∴ पहाड़ी की जलयान से दूरी = 10[latex] \sqrt{{3}} [/latex]मीटर
तथा पहाड़ी की ऊँचाई = 40 मीटर

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 20 Statistics Ex 20.1 सांख्यिकी

प्रश्न 1.
शब्द “सांख्यिकी’ द्वारा
(i) एकवचन रूप में,
(ii) बहुवचन रूप में तुम क्या समझते हो?
हलः
सांख्यिकी वह विज्ञान है जिसमें किसी अनुसन्धान क्षेत्र से सम्बन्धित आँकडो का संकलन, वर्गीकरण, सारणीकरण, प्रस्तुतीकरण, विश्लेषण निर्वचन तथा पूर्वानुमान, किसी निश्चित उद्देश्य की पूर्ति हेतू किया जाता है।

प्रश्न 2.
30 विद्यार्थियों ने एक परीक्षा में निम्न अंक प्राप्त किए-
20, 23, 28, 30, 32, 34, 35, 36, 36, 40, 41, 42, 43, 44, 45, 45, 48, 44, 50, 50, 52, 53, 54, 56, 56, 58, 61, 62, 65, 65
वर्ग अन्तराल 20-29, 30-39, 40-49, 50-59 तथा 60-69 लेकर इन्हें बारंबारता बंटनीय रूप में दर्शाइये।
हलः

प्रश्न 3.
एक सोसाइटी में 30 घरों के पानी के बिल (र में ) नीचे दिये गये हैं।
वर्ग-माप 10 लेकर एक वर्गीकृत बारंबारता बंटन सारणी के रूप में निरूपित कीजिए:
30, 32, 45, 54, 74, 78, 108, 112, 66, 76, 88, 40, 14, 20, 15, 35, 44, 66 , 75, 84, 95, 96, 102, 110, 88, 74, 112, 14, 34, 44
हलः

प्रश्न 4.
निम्नलिखित आँकड़ों के प्रयोग से एक बारंबारता सारणी बनाइयेः
315, 320, 324, 317, 324, 319, 320, 317, 323, 325, 316, 318, 321, 322, 325, 319, 324, 321, 316, 319, 320, 320, 322, 323.
हल:

प्रश्न 5.
नीचे 16 विद्यार्थियों की लम्बाइयाँ इंचों में दी गई हैं। 5 के वर्ग-अन्तराल के प्रयोग से एक बारंबारता
बंटन सारणी बनाइये :
62, 70, 72, 64, 65, 71, 70, 60, 64, 72, 60, 61, 69, 70, 64, 71
हलः

प्रश्न 6.
एक बंटन के वर्ग-चिह्न 104, 114, 124, 134, 144, 154 तथा 164 हैं। वर्ग-माप तथा वर्ग-सीमा निकालिये।
हलः
वर्ग माप = 10
वर्ग सीमा = 100-110,110-120, 120-130,130-140,140-150, 150-160,160-170, 170-180 है।

प्रश्न 7.
एक सोसाइटी के 40 घरों के बिजली के बिल (र में) नीचे दिये गये हैं :
116, 127, 107, 100, 80, 82, 91, 101, 65, 95,87,81, 105, 129, 92, 75, 89, 78,87, 81, 59,52, 65, 101, 115, 108,95, 65, 98, 62,84, 76, 63, 128, 121, 61, 118, 108, 116, 130.
वर्गीकृत-बारंबारता सारणी बनाइये।
हलः

प्रश्न 8.
नीचे दिये गये आँकड़ों से एक बारंबारता सारणी तैयार कीजिए।
90, 97, 92, 95, 93, 95, 93, 85, 93, 85, 83, 77, 83, 77, 74, 60, 71, 65, 74, 80, 87, 82, 81, 76, 61, 63, 58, 58, 56, 57
हलः

प्रश्न 9.
30 विद्यार्थियों के गणित में अन्तिम अंक निम्न प्रकार दिये गये हैं:
53, 61, 48, 60, 78, 68, 55, 100, 67, 90, 75, 88, 77, 37, 84, 58, 60, 48, 62, 56, 44, 58, 52, 64, 98, 59, 70, 39, 56, 60.
(i) इन अंकों को आरोही क्रम में व्यवस्थित कीजिए। जैसे – 30-39 एक समूह, 40-49 दूसरा समूह आदि।
(ii) अधिकतम स्कोर क्या है?
(iii) निम्नतम स्कोर क्या है?
(iv) परास क्या है?
(v) यदि उत्तीर्ण अंक 40 है तो कितने अनुत्तीर्ण हैं?
(vi) 75 या अधिक अंक कितने विद्यार्थियों ने प्राप्त किए?
(vii) 50 से 60 के बीच कौन-सा प्रेक्षण वास्तव में नहीं होगा।
(viii) 50 से कम अंक कितनों ने प्राप्त किए?
हलः
(i) सारणी 30-49, 40-49, 50-59, 60-69, 70-79, 80-89, 90-99 तथा 100-109 तक बनाओ।
(ii) 100
(iii) 37
(iv) 63
(v) 2
(vi) 8
(vii) 51, 54,57
(viii) 5

प्रश्न 10.
दी गई समावेशी श्रृंखला को अपवर्जी श्रृंखला में बदलिए :

हलः
अपवर्जी सारणी

प्रश्न 11.
वर्ग अन्तराल 13.5 – 15.5 का मध्य-बिन्दु क्या है?
हल:
14.5

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 10 Maths Solutions Chapter 7 Triangles Ex 7.1 त्रिभुज

प्रश्न 1.
दी गई आकृति में DE ||BC यदि AD = 2.5 सेमी, DB = 3 सेमी तथा AE = 3.75 सेमी है तो AC का मान ज्ञात कीजिए।
हलः
दिया है,

AD = 2.5 cm
DB = 3 cm
AE = 3.75
अब ∆ABC में, DE||BC
तब आधारभूत समानुपातिका (UPBoardSolutions.com) प्रमेय से,

अतः AC = AE + EC
= 3.75 +4.5 = 8.25 सेमी

प्रश्न 2.
दी गई आकृति में DE ||BC यदि AD = 1.7 सेमी, AB = 6.8 सेमी तथा AC = 9 सेमी है तो AE का मान ज्ञात कीजिए।
हल:
दिया है,

AD = 1.7 सेमी
AB = 6.8 सेमी
AC = 9 सेमी (UPBoardSolutions.com)
अतः हम जानते हैं कि

प्रश्न 3.
दो समान त्रिभुजों ABC तथा PQR का परिमाप क्रमशः 32 सेमी तथा 24 सेमी हैं। यदि PQ = 12 सेमी है तो AB का मान ज्ञात कीजिए।
हलः
चूँकि समान त्रिभुजों की संगत भुजाओं का (UPBoardSolutions.com) अनुपात उनके परिमाप के अनुपात के बराबर होता है।

प्रश्न 4.
एक त्रिभुज ABC में, AD, ∠A का अर्द्धक है। जो भुजा BC पर D पर मिलता है।
(i) यदि AB = 5.6 सेमी, AC = 6 सेमी, DC = 3 सेमी है तो BC ज्ञात कीजिए।
(ii) यदि AD = 5.6 सेमी, BC = 6 सेमी, BD = 3.2 सेमी है तो AC ज्ञात कीजिए।
हल:
(i) AB = 5.6 cm
AC = 6 cm
DC = 3cm (UPBoardSolutions.com)
BC = ?

चित्र से, BC = BD + DC
BC = BD + 3 …(1)
हम जानते हैं त्रिभुज के किसी कोण से (UPBoardSolutions.com) भुजा पर डाला गया लम्ब समकोण होता है। अतः ∆ADC से,
AC² = AD² + DC²
6² = AD² +3²
36 = AD² + 9
AD² = 27
AD = [latex] \sqrt{{27}} [/latex] = 3[latex] \sqrt{{3}} [/latex] cm
इसी प्रकार ∆ABD में,
AB² = BD² + AD²
(5.6)² = BD² + 27
BD² = 4.36
BD = 2.08 cm
अतः BC = BD + DC
= 2.08 +3
= 5.08 सेमी

(ii) दिया है,
AD = 5.6 सेमी
BC = 6 सेमी
BD = 3.2 सेमी
AC = ?

∆ABC में,
BC = BD + DC
6 = 3.2 + DC
DC = 6 – 3.2
DC = 2.8 सेमी
∆ADC में,
AC² = AD² + DC²
AC² = (5.6)² + (2.8)²
AC² = 31.36 + 7.84
AC² = 39.2
AC = 6.26 सेमी

प्रश्न 5.
एक समान्तर चतुर्भज ABCD है, भुजा BC पर एक बिन्दु P है तथा DP को बढ़ाने पर AB से बिन्दु L पर मिलती है तो सिद्ध कीजिए कि
(i) [latex]\frac{D P}{P L}=\frac{D C}{B L}[/latex]
(ii) [latex]\frac{D L}{D P}=\frac{A L}{D C}[/latex]
हल:
(i) ∆ALD में, ज्ञात है

प्रश्न 6.
एक चतुर्भुज ABCD है तथा P,Q, R तथा S क्रमशः AB, BC, CD व DA के ट्राईसैक्सन बिन्दु A व C के सम्मुख हैं। तो सिद्ध कीजिए कि PQRS एक समान्तर चतुर्भुज होगा।
हलः
माना चतुर्भुज ABCD इस प्रकार है कि (UPBoardSolutions.com) इनकी भुजाओं के मध्य बिन्दु क्रमशः P, Q, R, S हैं।
अब AC को मिलाया

∆ABC में, P तथा Q, AB तथा BC के मध्य बिन्दु हैं।
तब PQ|| AC …(1)
इसी प्रकार ∆ACD में, R तथा S क्रमशः DC तथा DA के मध्य बिन्दु हैं
तब SR || AC …(2)
समी० (1) तथा (2) से,
PQ || AC तथा SR || AC
इसलिये PQ|| SR
इसी प्रकार, ∆ ABD तथा ABDC हैं।
PS||QR
अतः PQRS एक समान्तर चतुर्भुज है।

प्रश्न 7.
एक ∆ ABC की भुजा BC का अर्द्धक D है। O AD पर कोई बिन्दु है। AC तथा AB में बिन्दु E तथा F मिल जाने पर BO तथा CO बनते हैं। AD को x तक बढ़ाया इसलिए D,OX का मध्य बिन्दु है तो सिद्ध कीजिए कि
(i) AO : AX = AF : AB
(ii) FE||BC
हल:
B और CX को मिलाया।
दिया है, BD = CD और OD = DX
इस प्रकार, BC तथा Ox (UPBoardSolutions.com) एक-दूसरे को काटते हैं।

⇒ OB, XC समान्तर है।
⇒ BX||CO और CX||BO
⇒ BX ||CF और CX||BE
⇒ BX ||OF और CX||OE

इस प्रकार E तथा F, AB तथा AC इस प्रकार है जोकि AB तथा AC को समान अनुपात में बाँटते हैं। अतः थेल्स प्रमेय के व्युत्क्रम से,
FE || BC

प्रश्न 8.
एक ∆ ABC में, बिन्दु D तथा E क्रमशः भुजाओं AB व AC पर हैं। तब प्रत्येक निम्नलिखित के लिए सिद्ध कीजिए कि DE || BC
(i) AD = 5.7 सेमी, BD = 9.5 सेमी, AE = 3.3 सेमी, EC = 5.5 सेमी
(ii) AB = 12 सेमी, AD = 8 सेमी, AE = 12 सेमी तथा AC = 18 सेमी
हलः
(i) दिया है, AD = 5.7 सेमी, (UPBoardSolutions.com) BD = 9.5 सेमी, AE = 3.3 सेमी, EC = 5.5 सेमी
हम जानते हैं कि

[latex]\frac{A D}{B D}=\frac{A E}{E C}[/latex]
⇒ AD × EC = AE × BD
⇒ [latex]\frac{5.7}{9.5}=\frac{3.3}{5.5}[/latex]
⇒ 5.7 × 5.5 = 9.5 × 3.3
⇒ 31.35 = 31.35
यदि एक रेखा त्रिभुज की दो भुजाओं को एक अनुपात में प्रतिच्छेद करती है तब वह तीसरी भुजा के समान्तर होती है आधारभूत समानुपातिका की मूल प्रमेय की व्युत्क्रमानुपाती सिद्धान्त से, DE ||BC यही सिद्ध करना था।

(ii) दिया है, AB = 12 सेमी, AD = 8 सेमी, AE = 12 सेमी तथा AC = 18 सेमी


यदि एक रेखा त्रिभुज की दो भुजाओं को एक अनुपात (UPBoardSolutions.com) में प्रतिच्छेद करती है तब वह तीसरी भुजा के समान्तर होती है, आधारभूत समानुपातिका की मूल प्रमेय की व्युत्क्रमानुपाती सिद्धान्त से, DE ||BC यही सिद्ध करना था।

प्रश्न 9.
एक ∆ABC में, भुजाओं AB तथा AC पर क्रमशः बिन्दु D तथा E है तथा DE||BC है। यदि AD = 2.4 सेमी, AE = 3.2 सेमी, DE = 2 सेमी, BC = 5 सेमी है तो BD तथा CE ज्ञात कीजिए।
हल:
∆ABC में, भुजाओं AB तथा AC पर क्रमशः बिन्दु D व E हैं तथा DE ||BC है।
दिया है, AD = 2.4 सेमी, AE = 3.2 सेमी, (UPBoardSolutions.com) DE = 2 सेमी तथा BC = 5 सेमी BD = ? तथा CE = ?


यदि BD = 3.6 सेमी तथा CE = 4.8 सेमी

प्रश्न 10.
एक ∆ABC की भुजाओं AB तथा AC पर क्रमशः बिन्दु D तथा E हैं तथा DE ||BC और BD = CE है। तो सिद्ध कीजिए कि ∆ABC एक समद्विबाहु त्रिभुज है।
हलः
यहाँ ∆ABC है जिसमें बिन्दु D तथा E भुजाओं AB तथा AC के मध्य बिन्दु हैं तथा DE ||BC अतः हमें सिद्ध करना है कि AB = AC
∆ ABC में ∠B का अर्द्धक BE है, इसलिये
[latex]\frac{A B}{B C}=\frac{A E}{E C}[/latex] …(1)
∆ ABC में, ∠C का अर्द्धक CD है इसलिये
[latex]\frac{A C}{B C}=\frac{A D}{D B}[/latex] …(2)
अब BD||CE तब आधारभूत (UPBoardSolutions.com) समानुपातिक प्रमेय के विलोम द्वारा,
[latex]\frac{A D}{B D}=\frac{A E}{E C}[/latex] …(3)
समी० (1), (2) तथा (3) से,
[latex]\frac{A B}{B C}=\frac{A C}{B C}[/latex]
⇒ AB = AC
अत: ∆ ABC समद्विबाहु है।

प्रश्न 11.
बिन्दुओं L, M, N के तीन रेखाखण्ड OA,OB तथा Oc ऐसे लिए गए हैं कि LM ||AB तथा MN||BC लेकिन न तो L, M, N न ही A,B,C समरेख हैं। तो सिद्ध कीजिए कि LN||AC
हलः
बिन्दुओं L,M, N के तीन रेखाखण्ड OA, OB तथा OC ऐसे लिए गए हैं कि LM ||AB तथा MN ||BC
परन्तु, L, M, N तथा A, B, C समरेख नहीं हैं।

⇒ ∆ONL में C तथा A क्रमश: ON तथा OL (UPBoardSolutions.com) को समान अनुपात में बाँटते हैं। अत: तब थेल्स के आधारभत समानुपातिक प्रमेय के विलोम से, LN || AC यही सिद्ध करना था।

प्रश्न 12.
त्रिभुज ABC का कोई अन्तः बिन्दु ० है। ∠AOB, ∠BOC तथा ∠COA का अर्द्धक भुजाओं AB, BC तथा CA से क्रमशः बिन्दुओं D, E तथा F में मिलता है। तो सिद्ध कीजिए कि
AD × BE × CF = DB × EC × FA
हल:
∆AOD में,
OD, ∠AOB का लम्बर्द्धक है।

प्रश्न 13.
माना ∆ABC का मध्य AD है। ∠ADB तथा ∠ADC के अर्द्धक, AB तथा AC में क्रमशः E तथा F मिलते हैं तो सिद्ध कीजिए कि EF ||BC
हलः
दिया है- ∆ABC में माध्यिका AD और DE और (UPBoardSolutions.com) DF, कोण ADB तथा ∠ADC के लम्बर्द्धक हैं।
सिद्ध करना है- EF||BC

उपपत्ति-∆ADB में, DE, ∠ADB का लम्बर्द्धक है।
[latex]\frac{A D}{D B}=\frac{A E}{E B}[/latex] …(1)
∆ADC में,
DF, ∠ADC का लम्बर्द्धक है,
[latex]\frac{A D}{D C}=\frac{A F}{F C}[/latex] …(2) [∵ AD माध्यिका है, ∴ BD = DC]
समी० (1) तथा (2) से,
[latex]\frac{A E}{E B}=\frac{A F}{F C}[/latex]
इस प्रकार ∆ABC में रेखाखण्ड EF, (UPBoardSolutions.com) भुजाओं AB तथा AC को समान अनुपात में बाँटता है।
अतः EF || BC

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 6 Remainder Theorem and Factor Theorem Ex 6.1 शेषफल प्रमेय तथा गुणनखण्ड प्रमेय

Ex 6.1 Remainder Theorem and Factor Theorem अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
बहुपद 5x³ – 2x² – 7x + 1 को x से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब 5x³ – 2x² – 7x + 1 को x से विभाजित किया जाता है तो x = 0 रखने पर
शेषफल = 0 – 0 – 0 + 1 = 1

प्रश्न 2.
बहुपद p(x) को (x – a) से भाग देने पर शेषफल ज्ञात कीजिए।
हल:
जब P(x) को (x – a) से विभाजित किया जाता है तो x – a = 0
∴ x = a रखने पर
शेषफल = P(a)

प्रश्न 3.
बहुपद p(x) को (ax – b) से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब P(x) को (ax – b) से विभाजित किया जाता है तो ax – b = 0 या x = [latex]\frac{b}{a}[/latex] रखने पर
शेषफल = [latex]\boldsymbol{P}\left(\frac{\boldsymbol{b}}{\boldsymbol{a}}\right)[/latex]

प्रश्न 4.
बहुपद x³ – 2x² + x + 1 को (x – 1) से भाग देने पर शेषफल ज्ञात कीजिए।
हल:
x³ – 2x² + x + 1 को (x – 1) से विभाजित किया जाता है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)³ – 2(1)² + 1 + 1 = 1 – 2 + 1 + 1 = 1

प्रश्न 5.
बहुपद x³¹ + 31 को (x + 1) से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब x³¹ + 31 को (x + 1) से विभाजित किया जाता है तो x + 1 = 0 या x = 0 – 1 = -1
शेषफल = (-1)³¹ + 31 = -1 + 31 = 30

प्रश्न 6.
बहुपद 3x³ – 4x² + 7x – 5 को (x – 3) से भाग देने पर शेषफल ज्ञात कीजिए।
हलः
जब 3x³ – 4x³ + 7x – 5 को (x – 3) से विभाजित किया जाता है तो x – 3 = 0 या x = 3 रखने पर
शेषफल = 3(3)³ – 4(3)² + 7(3) – 5 = 3. 27 – 36 + 21 – 5 = 81 – 36 + 21 – 5 = 102 – 41 = 61

प्रश्न 7.
बहुपद x³ + 5x² – 2 को (x – 1) से भाग देने पर शेषफल ज्ञात कीजिए।
हल:
x³ + 5x² – 2 को (x – 1) से विभाजित किया जाता है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)³ + 5(1)² – 2 = 1 + 5 – 2 = 4

Ex 6.1 Remainder Theorem and Factor Theorem लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 8.
शेषफल ज्ञात कीजिए यदि 3x³ – 4x² + 7x – 5 को (x + 3) से भाग दिया जाता है।
हलः
जब 3x³ – 4x² + 7x – 5 को (x + 3) से विभाजित किया जाता है तो
x + 3 = 0 या X = 0 – 3 = -3 रखने पर
शेषफल = 3(-3)³ – 4(-3)² + 7(-3) – 5 = 3(-27) – 4(9) – 21 – 5
= -81 – 36 – 21 – 5 = -143

प्रश्न 9.
x = 3 पर p(x) का मान ज्ञात कीजिए यदि p(x) = 3x² – 4x + [latex]\sqrt{17}[/latex]
हल:
P(x) = 3x² – 4x + [latex]\sqrt{17}[/latex], यदि x = 3
शेषफल = 3(3)² – 4 × 3 + [latex]\sqrt{17}[/latex] = 27 – 12 + [latex]\sqrt{17}[/latex] = 15 + [latex]\sqrt{17}[/latex]

प्रश्न 10.
शेषफल ज्ञात कीजिए यदि f (x) = 3x⁴ + 29x³ – 5a²x² + 5x को (x – a) से भाग दिया जाता है।
हल:
f(x) = 3x⁴ + 29x³ – 5a²x² + 5x को (x – a) से विभाजित किया जाता है तो
x – a = 0 या x = 0 + a = a
शेषफल = 3a⁴ + 29a³ – 5a². a² + 5a = 3a⁴ + 29a³ – 5a⁴ + 5a = -2a⁴ + 29a³ + 5a

प्रश्न 11.
शेषफल ज्ञात कीजिए यदि P(x) = x³ – 3x² + 4x + 50 को (x – 3) से भाग दिया जाता है।
हल:
P(x) = x³ – 3x² + 4x + 50 को (x -3) से भाग किया जाता है तो x – 3 = 0 या x = 3 रखने पर
शेषफल = (3)³ – 3(3)² + 4 × 3 + 50 = 27 – 27 + 12 + 50 = 62

Ex 6.1 Remainder Theorem and Factor Theorem लघु उत्तरीय प्रश्न – II (Short Answer Type Questions – II)

प्रश्न 12.
शेषफल प्रमेय का प्रयोग करते हुए निम्न में शेषफल ज्ञात कीजिए जब f(x) को g(x) से भाग दिया जाता है।

हल:

प्रश्न 13.
सिद्ध कीजिए कि 2x³ + 13x² + x – 70, (x – 2) से विभाजित है।
हल:
2x³ + 13x³ + x – 70 को (x – 2) से भाग करने पर x – 2 = 0 या x = 2 रखने पर
शेषफल = 2(2)³ + 13(2)² + 2 – 70 = 16 + 52 + 2 – 70 = 0
अत: 2x³ + 13x² + x – 70, (x – 2) से पूर्णतया विभाजित होगा।

प्रश्न 14.
यदि बहुपदों px³ + 4x² + 3x – 4 व x³ – 4x + p को (x – 3) से भाग करने पर समान शेषफल प्राप्त होते हैं तो सिद्ध कीजिए कि p = -1 (NCERT Exemplar)
हलः
जब Px³ + 4x² + 3x – 4 को (x – 3) से भाग करने पर x – 3 = 0 या x = 3 रखने पर
शेषफल = P(3)³ + 4(3)² + 3(3) – 4 = 27P + 36 + 9 – 4 = 27P + 41
जब x³ – 4x + P को (x – 3) से भाग करने पर x – 3 = 0 या x = 3 रखने पर
शेषफल = 3³ – 4(3) + P = 27 – 12 + P = 15 + P
∴ 27P + 41 = 15 + P
27P – P = 15 – 41
26P = -26.
P = [latex]\frac{-26}{26}[/latex] = -1

प्रश्न 15.
यदि px³ + 9x² + 4x – 10 को (x + 3) से भाग देने पर -22 शेषफल प्राप्त होता है तो p का मान ज्ञात कीजिए।
हलः
जब Px³ + 9x³ + 4x – 10 को (x + 3) से भाग किया जाता है तो x + 3 = 0 या x = -3 रखने पर
शेषफल = P(-3)³ + 9(-3)² + 4(-3) – 10 = -22
-27P + 81 – 12 – 10 = -22
-27P = -22 – 81 + 22
– 27P = -81
P = [latex]\frac{-81}{-27}[/latex] = 3

प्रश्न 16.
यदि बहुपद f (x) = x⁴ – 2x³ + 3x² – ax + b को (x – 1) और (x + 1) से भाग देने पर शेषफल क्रमशः 5 व 19 प्राप्त होते हैं, तो a व b के मान ज्ञात कीजिए।
हलः
यदि f(x) = x⁴ – 2x³ + 3x² – ax + b को (x – 1) से भाग किया जाता है तो x – 1 = 0 या x = 1 रखने पर
शेषफल = (1)⁴ – 2(1)³ + 3(1)² – a(1) + b = 1 – 2 + 3 – a + b = 2 – a + b
प्रश्नानुसार, 2 – a + b = 5
-a + b = 5 – 2 = 3 ⇒ – a + b = 3 ………………(1)
प्रश्नानुसार, यदि f(x) को (x + 1) से भाग किया जाता है तो
x + 1 = 0 या x = -1 रखने पर
शेषफल = (-1)⁴ – 2(-1)³ + 3(-1)² – a(-1) + b
= 1 + 2 + 3 + a + b
= 6 + a + b
तथा 6 + a + b = 19
a + b = 19 – 6
a + b = 13 ………………(2)
(1) व (2) जोडने पर,
2b = 16
b = [latex]\frac{16}{2}[/latex] = 8
समी० (2) मे b का मान रखने पर, a + 8 = 13
a = 13 – 8 = 5
अतः a = 5 व b = 8

प्रश्न 17.
बहुपद x³ + px² + qx + 6 को जब (x – 3) से भाग दिया जाता है तो शेषफल 3 तथा जब (x – 2) से भाग दिया जाता है तो शेषफल शून्य प्राप्त होता है। p व 4 के मान ज्ञात कीजिए।
हलः
यदि x³ + px² + qx + 6 को (x – 3) से भाग किया जाता है तो x – 3 = 0 या x = 3 रखने पर
शेषफल = (3)³ + p(3)² + q(3) + 6 = 3
27 + 9p + 3q + 6 = 3
9p + 3q + 33 = 3
9p + 3q = 3 – 33
9p + 3q = -30
3(3p + q) = -30
3p + q =[latex]\frac{-33}{3}[/latex] = -10 ……………(1)
यदि x³ + px² + qx + 6 को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर
शेषफल = (2)³ + p(2)³ + q(2) + 6 = 0
8 + 4p + 2q + 6 = 0
4p + 2q = -14
2(2p + q) = -14
2p + q =[latex]\frac{-14}{2}[/latex] =-7 …………….(2)
समीकरण (1) व (2) को हल करने पर,

समीकरण (1) में p का मान रखने पर,
3 × -3 + q = -10
-9 + q = -10
q = -10 + 9 = -1
अतः p = -3,    q = -1

प्रश्न 18.
बहुपद kr⁴ + 3x³ + 6 को (x – 2) से भाग देने पर प्राप्त शेषफल, दूसरे बहुपद 2x³ + 17x + k को (x – 2) से भाग देने पर प्राप्त शेषफल का दोगुना है। k का मान ज्ञात कीजिए।
हलः
बहुपद kr⁴ + 3x³ + 6 को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर शेषफल
= k(2)⁴ + 3(2)³ + 6
= 16k + 24 + 6 = 16k + 30
और जब 2x³ + 17x + k को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर
शेषफल = 2(2)³ + 17(2) + k = 2 × 8 + 34 + k = 50 + k
प्रश्नानुसार,
16k + 30 = 2(50 + k)
16k + 30 = 100 + 2k
16k – 2k = 100 – 30
14k = 70
k = [latex]\frac{70}{14}[/latex] = 5

प्रश्न 19.
यदि बहुपदों 9x³ + 3x² – 13 तथा 2x³ – 5x + a को (x – 2) से भाग देने पर समान शेषफल प्राप्त होते हैं तो a का मान ज्ञात कीजिए।
हलः
बहुपद 9x³ + 3x² – 13 को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर,
शेषफल = 9(2)³ + 3(2)² – 13 = 72 + 12 – 13 = 71
बहुपद 2x³ – 5x + a को (x – 2) से भाग किया जाता है तो x – 2 = 0 या x = 2 रखने पर,
शेषफल = 2(2)³ – 5(2) + a = 16 – 10 + a या 6 + a
प्रश्नानुसार, 6 + a = 71
a = 71 – 6 = 65

Balaji Publications Mathematics Class 9 Solutions