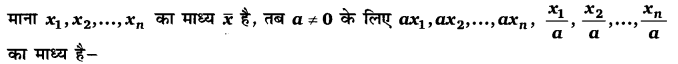Balaji Class 10 Maths Solutions Chapter 7 Triangles Ex 7.2 त्रिभुज
प्रश्न 1.
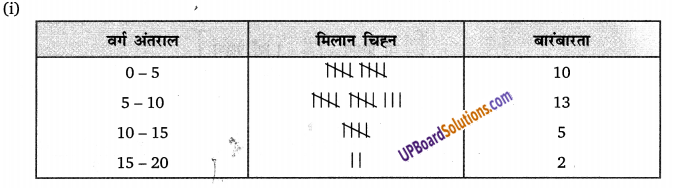
दी गई आकृति में ∆ ACB ~ ∆ APQ है यदि BC = 8 सेमी, PQ = 4 सेमी, BA = 6.5 सेमी, AP = 2.8 सेमी है तो CA तथा AQ ज्ञात कीजिए।
हलः
दिया है,
BC = 8 सेमी PQ = 4 सेमी, (UPBoardSolutions.com) BA = 6.5 सेमी

AP = 2.8 सेमी
दिया है, ∆ACB ~ ∆APQ

⇒ AC = 5.6 cm
तथा AQ = 3.25 cm
![]()
प्रश्न 2.
दी गई आकृति में, QA तथा PB, AB के लम्बवत् है। यदि AQ = 10 सेमी, BO = 6 सेमी तथा PB = 9 सेमी है तो AQ ज्ञात कीजिए।
हलः
दिया है,
AO = 10 सेमी
BO = 6 सेमी
PB = 9 सेमी

∵ AQ तथा PB रेखा AB के (UPBoardSolutions.com) लम्बवत् है अत: ∆OAQ तथा ∆OPB समकोणीय त्रिभुज है।
अतः ∆OPB में,
(OP)2 = (OB)2 + (PB)2
OP2 = (6)2 + (9)2
OP2 = 36 + 81
OP2 = 117
OP2 = [latex]\sqrt{117}=\sqrt{13 \times 9}[/latex]
= 3[latex] \sqrt{{13}} [/latex] सेमी
∆OAQ तथा ∆OPB समरूप हैं।
[latex]\frac{O A}{O B}=\frac{O Q}{O P}[/latex]
⇒ [latex]\frac{10}{6}=\frac{O Q}{3 \sqrt{13}}[/latex]
⇒ OQ = 5[latex] \sqrt{{13}} [/latex] सेमी
अब ∆OAQ में,
![]()
OQ2 = OA2 + AQ2
⇒ (5[latex] \sqrt{{13}} [/latex])2 = 102 + AQ2
⇒ AQ2 = 25 × 13 – 100
⇒ AQ2 = 325 – 100
⇒ AQ2 = 225
⇒ AQ = 15 सेमी
प्रश्न 3.
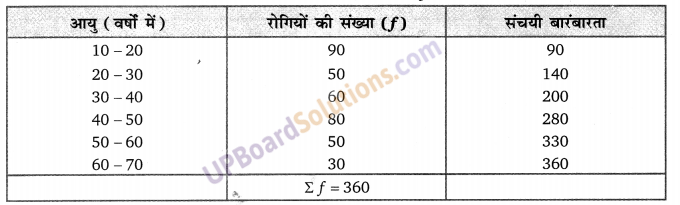
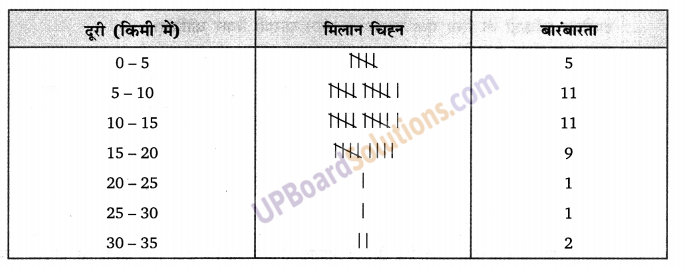
10 सेमी ऊँची एक ऊर्ध्वाधर छड़ी की छाया 8 सेमी लम्बी बनती है। ठीक उसी समय एक मीनार की छाया 30 सेमी है तो मीनार की ऊँचाई ज्ञात कीजिए।
हलः
ऊर्ध्वाधर छड़ी की लम्बाई CE = 10 cm जमीन पर 8 cm की छाया बनाती है।
माना कि मीनार की ऊँचाई h (UPBoardSolutions.com) है।
मीनार की छाया की लम्बाई = 30 सेमी

अब ∆ ABD तथा ∆ DEC
में ∠ABD = ∠ECD
∠D = ∠D
तब समरूपता की AA-कसौटी द्वारा
∆ABD ~ ∆ DEC

![]()
प्रश्न 4.
एक समकोण त्रिभुज की भुजाएँ a तथा b और कर्ण c हैं। कर्ण पर एक ऊँचाई x है तो सिद्ध कीजिए कि ab = cx
हलः
दिया है, AC = b, BC = a
AB = c और CD = x

∆ABC तथा ∆BCD में
∠BCA = ∠CDB [प्रत्येक कोण = 90°]
और ∠B = ∠B
अतः समरूपता की (UPBoardSolutions.com) AA – कसौटी से,
∆ABC ~ BCD
[latex]\frac{A C}{C D}=\frac{B A}{B C}[/latex]
[latex]\frac{b}{x}=\frac{c}{a}[/latex]
⇒ ab = cx
![]()
प्रश्न 5.
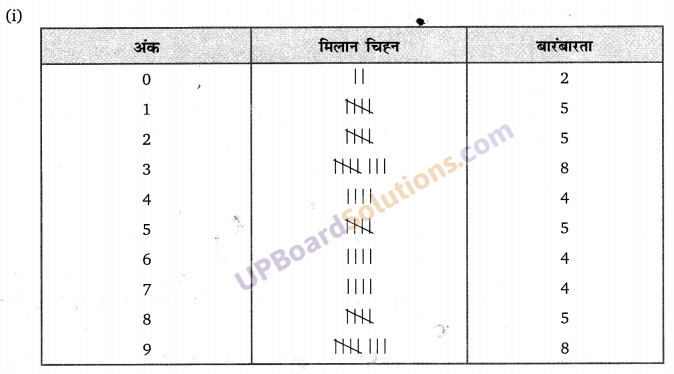
दी गई आकृति में ∠A = ∠CED है तो सिद्ध कीजिए कि ∆CAB ~ ∆CED तथा x का मान भी ज्ञात कीजिए।
हलः

दिया है, ∠A = ∠CED
∆EDC में,
(EC)2 = DC2 + DE 2
(10)2 = 82 + x2
100 = 64 + x2
x2 = 100 – 64
x = [latex] \sqrt{{36}} [/latex]
x = 6 सेमी
∆ABC तथा ∆ADE
∠ABC = ∠EDC में
∠ABC = ∠EDC [प्रत्येक कोण = 90°]
तथा ∠C = ∠C
यह समरूपता की (UPBoardSolutions.com) AA-कसौटी का पालन करती है।
∆CAB ~ ∆CED
![]()
प्रश्न 6.
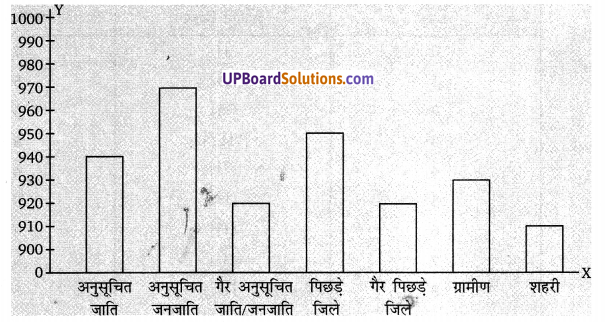
दी गई आकृति में ∠CAB = 90° तथा AD ⊥BC है। यदि AC = 75 सेमी, AB = 1 मी० तथा BD = 1.25 मीटर है तो AD का मान ज्ञात कीजिए।
हलः

दिया है, AB = 1 मीटर = 100 सेमी
AC = 75 सेमी और BD = 125 सेमी
∆ BAC और ∆ BDA में यहाँ,
∠BAC = ∠ BDA (UPBoardSolutions.com) (समकोण)
और ∠B = ∠B
अतः (AA-समरूपता से)

![]()
प्रश्न 7.
दी गई आकृति में, यदि AB ⊥ BC तथा DE ⊥ AC है तो सिद्ध कीजिए कि ∆ ABC ~ ∆ AED
हल:

∆ ABC तथा ∆ AED में
∠ABC = ∠AED = 90°
∠ BAC = ∠EAD (समान कोण)
= ∠A
अतः समरूपता की AA-कसौटी से,
∆ABC ~∆ AED (UPBoardSolutions.com) यही सिद्ध करना था।
प्रश्न 8.
दी गई आकृति में, यदि ∠A = ∠C है तो सिद्ध कीजिए कि ∆AOB ~ ∆COD
हलः

दिया है,
∠A = ∠C = 90°
तथा ∠1 = ∠2 (शीर्षाभिमुख कोण)
∆ AOB तथा ∆CDO में,

अतः SAS समरूपता द्वारा,
∠A = ∠C
तथा ∠B = ∠D
अतः ∆ AOB ~ ∆CDO (UPBoardSolutions.com) यही सिद्ध करना था।
![]()
प्रश्न 9.
दी गई आकृति में, ∠ ABC = 90° तथा BD ⊥ AC है यदि AB = 5.7 सेमी०, BD = 3.8 सेमी० तथा CD = 5.4 सेमी० हो तो BC ज्ञात कीजिए।
हलः

दिया है,
∠ABC = 90°
AB = 5.7 सेमी, BD = 3.8 सेमी
CD = 5.4 सेमी, BC = ?
∵ ∆ABC तथा ∆BDC में यहाँ
∠ABC = ∠CDA (UPBoardSolutions.com) = 90°
और ∠C = ∠C
अतः (AA-समरूपता से)
∆BAC ~ ∆BDA

![]()
प्रश्न 10.
∆ ABC तथा ∆ DEF में, यह दिया गया है कि, AB = 5 सेमी०, BC = 4 सेमी०, CA = 4.2 सेमी०, DE = 10 सेमी०, EF = 8 सेमी० तथा FD = 8.4 सेमी० है। यदि AL I BC तथा DM L EF है तो AL:DM ज्ञात कीजिए।
हलः

प्रश्न 11.
दी गई आकृति में, दो त्रिभुज BEP तथा CPD दिये गये हैं तो सिद्ध कीजिए कि
BP × PD = EP × PC
हल:

∆ EPB तथा ∆DPC में,
∠ PEB = ∠ PDC = 90°
∠ EPB = ∠DPC (शीर्षाभिमुख कोण)
इस प्रकार AA-कसौटी की समरूपता से,
∆ EPB ~ ∆DPC
⇒ [latex]\frac{E P}{D P}=\frac{P B}{P C}[/latex]
⇒ BP × DP = EP × PC यही सिद्ध करना था।
![]()
प्रश्न 12.
∆ ABC की भुजाओं AB तथा AC पर क्रमशः बिन्दु P तथा Q हैं। यदि AP = 3 सेमी०, PB = 6 सेमी०, AQ = 5 सेमी० तथा QC = 10 सेमी० है तो सिद्ध कीजिए कि BC = 3PQ
हलः
दिया है,

AP = 3 सेमी, PB = 6 सेमी,
AQ = 5 सेमी, QC = 10 सेमी
∆ ABC में, PQ ||BC (UPBoardSolutions.com)
⇒ [latex]\frac{A B}{A P}=\frac{A Q}{A E}[/latex]
तथा ∠A = ∠A
तब समरूपता की कसौटी (SAS) द्वारा

प्रश्न 13.
ABCD एक समान्तर चतुर्भुज है तथा APQ एक सरल रेखा है जो बढ़ाने पर BC से बिन्दु P पर तथा DC से बिन्दु Q पर मिलती है। सिद्ध कीजिए कि BP व DQ से बना आयत AB व AD से बने आयत के बराबर होता है।
हलः
स्वयं हल (UPBoardSolutions.com) कीजिए।
![]()
प्रश्न 14.
एक चतुर्भुज ABCD है। जिसमें AD = BC यदि P, Q, R तथा S क्रमशः AB, BC, CD तथा AD के मध्य बिन्दु हैं तो सिद्ध कीजिए कि PQRS एक समचतुर्भुज है।
हलः
माना कि एक चतुर्भुज ABCD इस प्रकार है कि इसकी भुजाओं AB, BC,CD तथा DA के क्रमशः मध्य-बिन्दु P,Q, R, S हैं तब हमें सिद्ध करना है कि PQRS एक समचतुर्भुज है।
अब AC को मिलाया।
∆ABC में, P तथा Q, AB तथा BC के मध्य बिन्दु हैं।
∵ दिया है
AB = BC
अतः AP = PB = BQ = CQ
PQ || AC …(1)
इसी प्रकार ∆ ACD में, R तथा S क्रमशः CD तथा DA के मध्य-बिन्दु हैं।
तब SR || AC …(2)

समीकरण (1) तथा (2) से यहाँ है
PQ || AC तथा SR || AC
इसलिये PQ || SR (UPBoardSolutions.com)
इसी प्रकार ∆ABD, ∆BCD हैं
PS ||QR
अत: PQRS एक समचतुर्भुज है।
प्रश्न 15.
दी गई आकृति में, ABCD एक समलम्ब चतुर्भुज है तथा AB||DC यदि ∆ AED तथा ∆ BEC समरूप है तो सिद्ध कीजिए कि AD = BC

हलः
स्वयं हल कीजिए।
![]()
प्रश्न 16.
एक समलम्ब चतुर्भुज ABCD में, AB||DC तथा DC = 2AB, AB के आगे EF दर्शायी गयी है। AD, F द्वारा तथा BC, E द्वारा काटे गये हैं तथा [latex]\frac{B E}{E C}=\frac{3}{4}[/latex] विकर्ण DB, EF को G पर प्रतिच्छेद करता है तो सिद्ध कीजिए कि 7FE = 10AB
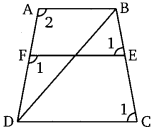
हल:
∆DFG तथा ∆ DAB में ज्ञात हैं।
∠1 = ∠2 [∵ AB ||DC ∴ ∠1 तथा ∠2 संगत कोण है।]
∠ FDG = ∠ADB (सर्वनिष्ठ)
अतः समरूपता (UPBoardSolutions.com) की AA-कसौटी से,
∆DFG ~ ∆DAB


![]()
प्रश्न 17.
दी गई आकृति में, एक त्रिभुज ABC है जो C पर समकोण है तथा DE ⊥ AB है। तो सिद्ध कीजिए कि ∆ ABC ~ ∆ ADE तथा AE और DE की लम्बाई ज्ञात कीजिए।
हलः
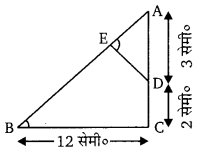
त्रिभुज ABC तथा ∆ ADE में
∠ACB = ∠ AED = 90°
और ∠BAC = ∠ DAE (UPBoardSolutions.com)
अतः समरूपता की AA-कसौटी से,
∆ABC ~ ∆ ADE

![]()
प्रश्न 18.
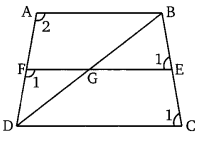
एक समान्तर चतुर्भुज ABCD के शीर्ष D से, एक रेखा खींची गई है जो भुजा BA तथा BC को क्रमशः E तथा F पर प्रतिच्छेद करती है। तो सिद्ध कीजिए कि :
![]()
हलः
त्रिभुज EAD तथा ∆ DCF में,
∠1 = ∠2 [∵ AB ||DC ∴ संगत कोण बराबर है।]
∠3 = ∠4 [∵ AD||BC ∴ संगत कोण बराबर है।]
इसलिये समरूपता की (UPBoardSolutions.com) AA-कसौटी द्वारा,
∆ EAD ~ ∆DCF