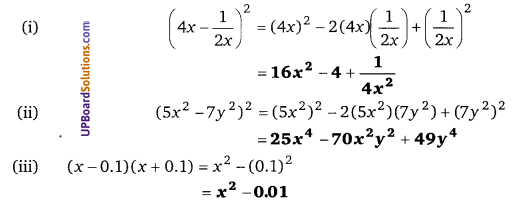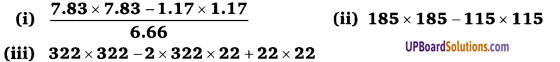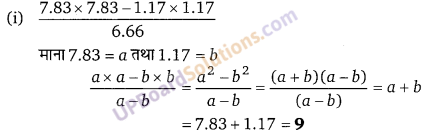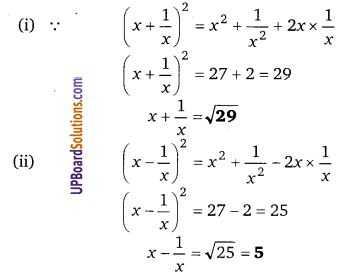Balaji Class 9 Maths Solutions Chapter 4 Algebraic Identities Ex 4.2 बीजगणितीय सर्वसमिकाऐं
Ex 4.2 Algebraic Identities अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
(x + 2y + 4x) का विस्तार ज्ञात कीजिए। [NCERT]
हलः
(x + 2y + 4z)2 = x2 + (2y)2 + (4z)2 + 2x . 2y + 2.2y . 4z + 2. x. 4z
= x2 + 4y2 + 16z2 + 4xy +16yz +8xz
![]()
प्रश्न 2.
(-2x + 3y + 2z)2 का विस्तार ज्ञात कीजिए। [NCERT]
हलः
(-2x + 3y + 2x)2 = (-2x)2 + (3y)2 + (2z)2 + 2(-2x)(3y) + 2(3y) (2z) + 2(-2x)(2z)
= 4x2 + 9y2 + 4z2 – 12xy + 12yz – 8xz
Ex 4.2 Algebraic Identities लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 3.
निम्न के विस्तार ज्ञात कीजिए।
(i) (-3x + y + z2
(ii) (-x + 2y + z)2
(iii) (3x + 2y – z)2
(iv) (2 + x – 2y)2
(v) (m + 2n – 5p)2
(vi) (ab + bc + ca)2
हलः
(i) (-3x + y + x)2 = (–3x)2 + (y)2 +(z)2 + 2(–3x)(y) + 2(y) (z) + 2(-3x)(z)
=9x2 + y2 +z2 – 6xy + 2yz – 6xz
(ii) (-x + 2y + z)2 = (-x)2 + (2y)2 +(z)2 + 2(-x)(2y) + 2(2y)(z) + 2(-x)(z)
= x2 + y2 + z2 – 4xy + 4yz – 2xz
(iii) (3x + 2y – z)2 = (3x)2 + (2y)2 +(+z)2 + 2(3x)(2y) + 2(2y)(-z) + 2(3x)(-z)
= 9x2 + 4y2 + z2 + 12xy – 4yz – 6xz
(iv) (2 + x – 2y)2 = (2)2 + (x)2 + (-2y)2 + 2.2.x + 2. x(-2y) + 2.2(-2y)
=4 + x2 + 4y2 + 4x – 4xy – 8y
(v) (m + 2n – 5p)2 = (m)2 + (2n)2 + (-5p)2 + 2. m. 2n + 2. 2n(-5p) +2. m(-5p)
= m2 + 4n2 +25p2 + 4mn – 20np – 10mp
(vi) (ab + bc + ca)2 = (ab)2 + (bc)2 + (ca)2 + 2ab.bc + 2bc.ca + 2ab.ca
=a2b2 + b2c2 +c2a2 +2ab2c + 2abc2 + 2a2bc
![]()
प्रश्न 4.
सरल कीजिए।
(i) (2x + p – c)2 – (2x – p + c)2
(ii) (x2 + y2 – 2)2 – (x2 – y2 +z2)2
(iii) (a + b + c)2 + (a – b + c)2 + (a + b – c)2
हलः
(i) (2x + y – c)2 – (2x -p + c)2
= (2x + P – c + 2x – P + c)(2x + p – c – 2x + p – c)
= (4x)(2p – 2c)
= (4x)2(p – c) = 8x(p – c)
(ii) (x2 + y2 – z2)2 – (x2 – y2 + z2)2
= (x2 + y2 – 2 + x2 – y2 + z2)(x2 + y2 – z2 – x2 + y2 – z2)
= (2x2)(2y2 – 2z2)
= (2x2)2(y2 – z2)
= 4x2(y2 – z2)
(iii) (a + b + c)2 + (a – b + c)2 + (a + b – c)2
=a2 + b2 + c2 + 2ab + 2bc + 2ac + a2 + b2 + c2 – 2ab – 2bc + 2ac
+ a2 + b2 + c2 + 2ab – 2bc – 2ac
= 3 (a2 + b2 + c2) + 2ab – 2bc + 2ca
Ex 4.2 Algebraic Identities दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 5.
यदि a2 + b2 + c2 = 20 व a + b+ c =0, तब ab+ bc + ca का मान ज्ञात कीजिए।
हलः
a + b + c = 0 )
वर्ग करने पर
a2 + b2 + c2 + 2(ab + bc + ca) = 0
20 + 2(ab + bc + ca) = 0
2(ab + bc + ca) = 0 – 20
ab + bc + ca = [latex]-\frac{20}{2}[/latex] = -10
![]()
प्रश्न 6.
यदि a + b + c = 9 व ab+ bc + ca = 40, तब a2 + b2 + c2 का मान ज्ञात कीजिए।
हलः
यदि a + b + c = 9
वर्ग करने पर
a2 + b2 + c2 + 2(ab + bc + ca) = 81
a2 + b2 + c2 + 2 × 40 = 81
a + b + c = 81 – 80 = 1
प्रश्न 7.
यदि a2 + b2 + c2 = 16 व ab+ bc + ca = 10, तब a + b + c का मान ज्ञात कीजिए।
हलः
(a + b + c)2 = a2 + b2 + c2 + 2(ab + bc + ca)
= 16 + 2 × 10 = 16 + 20 = 36
∴ a + b + c = [latex]\sqrt{36}[/latex] = 6