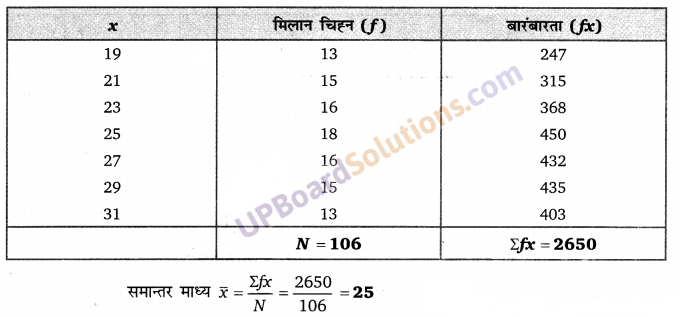
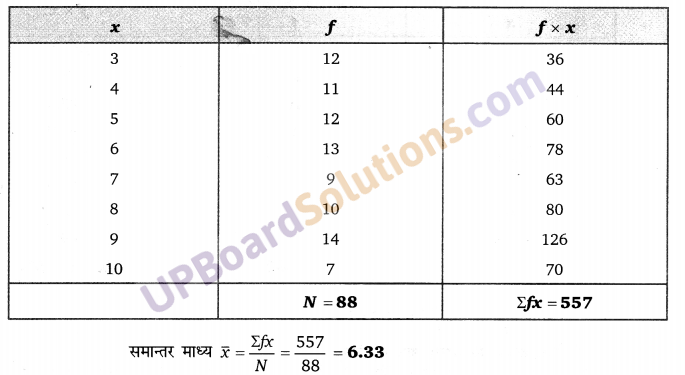
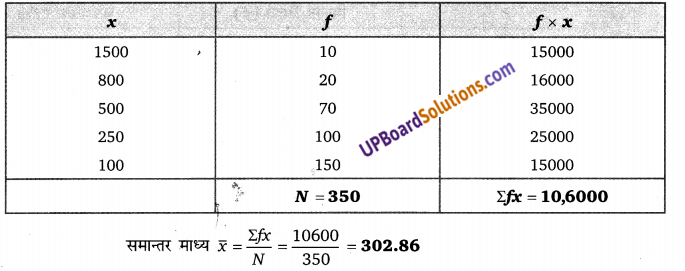
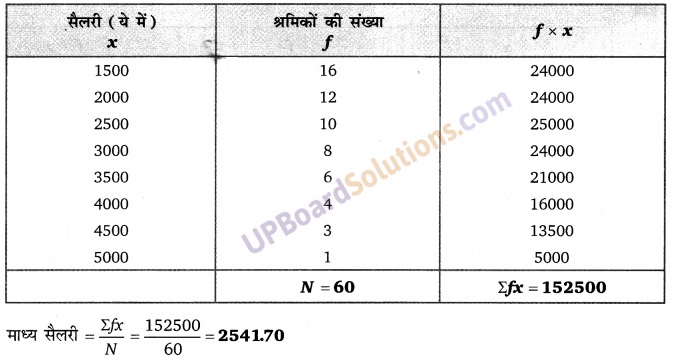
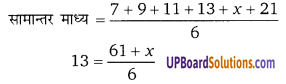Balaji Class 10 Maths Solutions Chapter 7 Triangles Ex 7.4 त्रिभुज
प्रश्न 1.
एक त्रिभुज की निम्न भुजाएँ दी गई हैं। ज्ञात कीजिए कि यह त्रिभुज समकोण है या नहीं? a = 6 सेमी, b = 8 सेमी, c = 10 सेमी
हल:
a = 6 सेमी, b = 8 सेमी, c = 10 सेमी
a2 + b2 = (6)2 + (UPBoardSolutions.com) (8)2 = 36 + 64
= 100 = c2
∴ a2 + b2 = c2
पाइथागोरस प्रमेय द्वारा दिया गया त्रिभुज समकोण है।
![]()
प्रश्न 2.
एक त्रिभुज ABC की भुजाओं की लम्बाई AB = 9 सेमी, BC = 40 सेमी तथा AC = 41 सेमी है तो सिद्ध कीजिए कि त्रिभुज ABC एक समकोण त्रिभुज है।
हल:
∆ ABC में, AB = 9 सेमी
BC = 40 सेमी, AC = 41 सेमी
(AB)2 + (BC)2 = (9)2 + (40)2 = 81 +1600 = 1681
= (AC)2
⇒ (AB)2 + (BC)2 = (AC)2
पाइथागोरस प्रमेय द्वारा ∆ ABC समकोण त्रिभुज है।
प्रश्न 3.
एक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AB = AC = 13 सेमी, BC पर A की ऊँचाई की लम्बाई 5 सेमी है तो BC ज्ञात कीजिए।
हलः
समद्विबाहु त्रिभुज ABC में, AB = 13 सेमी
AC = (UPBoardSolutions.com) 13 सेमी
AD = 5 सेमी
AD ⊥ BC

हमें BC ज्ञात करना है।
∆ ABD में पाइथागोरस प्रमेय द्वारा
AB2 = AD2 + BD2
132 = 52 + BD2
BD2 = 169 – 25 = 144
BD = 12 सेमी
∆ ADC में पाइथागोरस प्रमेय द्वारा
AC2 = AD2 + DC2
132 = 52 + DC2
DC2 = 169 – 25 = 144
DC = 12 सेमी
BC = BD + DC
BC = 12 + 12 = 24 सेमी
![]()
प्रश्न 4.
एक समचतुर्भुज की भुजा 10 सेमी है। इसके एक विकर्ण की लम्बाई 12 सेमी है तो इसके दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हलः
माना ABCD एक समचतुर्भुज है।
AB = BC = CD = DA = 10 सेमी
विकर्ण BD = 12 सेमी
हमें विकर्ण AC की लम्बाई ज्ञात करनी है।
चूँकि समचतुर्भुज के विकर्ण समकोण पर समद्विभाजित करते है तो विकर्ण AC और BD बिन्दु E पर समकोण पर समद्विभाजित करेंगे।

BE = ED = [latex]\frac{B D}{2}=\frac{12}{2}[/latex] = 6 सेमी
∆ AEB में पाइथागोरस प्रमेय द्वारा
AB2 = AE2 + BE2
102 = AE2 + 62 (BE = 6 सेमी)
100 – 36 = AE2
AE2 = 64 (UPBoardSolutions.com)
AE = 8 सेमी
∆ BEC में पाइथागोरस प्रमेय द्वारा
BC2 = BE2 + EC2
102 = 62 + EC2
100 -36 = EC2
EC2 = 64
EC = 8 सेमी
विकर्ण AC = AE + EC
= 8 + 8 = 16 सेमी
![]()
प्रश्न 5.
एक समकोण त्रिभुज का कर्ण, उसकी छोटी भुजा के दोगुने से 6 मीटर अधिक है। यदि तीसरी भुजा कर्ण से 2 मीटर कम है। तो त्रिभुज की भुजाएँ ज्ञात कीजिए।
हलः
माना ∆ ABC, B पर समकोण है
दिया है, AC = (2AB +6) मीटर
BC = (AC – 2) मीटर …(1)
हमें त्रिभुज की भुजा AB, BC और AC ज्ञात करनी है।
दिया है AC = 2AB +6
[latex]\frac{(A C-6)}{2}[/latex] = AB
∆ ABC में पाइथागोरस प्रमेय द्वारा,
AC2 = AB2 + BC2

4AC2 = 5AC2 – 28AC + 52
AC2 – 28AC + 52 = 0
AC2 – (26 +2)AC + 52 = 0
AC2 – 26AC – 2AC + 52 = 0
AC(AC – 26) -2(AC – 26) = 0
(AC – 26)(AC – 2) = 0
AC – 26 = 0
AC = 26 मीटर
AC = 26, समी० (UPBoardSolutions.com) (1) में रखने पर,
BC = AC – 2 = 26 – 2 = 24 मीटर
AC = 26, समी० (2) में रखने पर,
AB = [latex]\frac{A C-6}{2}=\frac{26-6}{2}=\frac{20}{2}[/latex]
AB = 10 मीटर
AB = 10 मीटर, BC = 24 मीटर, AC = 26 मीटर
![]()
प्रश्न 6.
एक 15 मीटर लम्बी सीढ़ी एक गली में सतह से 9 मीटर ऊँची खिड़की पर लगी है। यदि इसके पाद को उसी स्थान पर रखकर, सीढ़ी गली के दूसरी ओर 12 मीटर ऊँची खिड़की पर पहुँचती है। गली की चौड़ाई ज्ञात कीजिए।
हलः
माना खिड़की की ऊँचाई गली के दोनों और क्रमशः AB = 9 मीटर और ED = 12 मीटर हैं।
सीड़ी की लम्बाई AC = EC = 15 मीटर
हमें गली की चौड़ाई BD ज्ञात करनी है।

∆ ABC में पाइथागोरस प्रमेय द्वारा
AC2 = AB2 + BC2
152 = 92 + BC2
BC2 = 225 – 81 = 144
BC = 12 मीटर
अब ∆ EDC में (UPBoardSolutions.com) पाइथागोरस प्रमेय द्वारा
EC2 = ED2 + CD2
152 = 122 + CD2
CD2 = 225 – 144 = 81
CD = 9 मीटर
गली की चौड़ाई BD = BC +CD
= 12 + 9 = 21 मीटर
![]()
प्रश्न 7.
एक खेल के मैदान पर ऊर्ध्वाधर खड़े दो खम्भों की ऊँचाई 9 मीटर तथा 14 मीटर है यदि उनके पादों के बीच की दूरी 12 मीटर है तो उनके शीर्षों के बीच की दूरी ज्ञात कीजिए।
हलः

माना AB और CD दो खम्भे हैं।
दिया है, AB = 9 मीटर
CD = 14 मीटर
BC = 12 मीटर
हमें शीर्षों के बीच की दूरी AD ज्ञात करनी है।
12 मीटर शीर्ष A से CD पर E बिन्दु पर लम्ब AE डाला गया।
AE = BC = 12 मीटर
EC = AB = 9 मीटर
DE = CD – EC
DE = 14 – 9 = 5 मीटर
अब ∆ AED में पाइथागोरस प्रमेय द्वारा,
AD2 = AE2 + ED2
AD2 = 122 + 52
AD2 = 144 + 25 = 169
AD = 13 मीटर
प्रश्न 8.
∆ ABC एक समद्विबाहु त्रिभुज है जिसका ∠C समकोण है। सिद्ध कीजिए कि AB2 = 2 AC2 (NCERT)
हल:
∆ ABC समद्विबाहु त्रिभुज है।

∠C = 90°
AC = BC
∆ ABC में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा
AB2 = AC2 + BC2
AB2 = AC2 + AC2 (∵ BC = AC)
AB2 = 2AC2
![]()
प्रश्न 9.
एक ∆ ABC का ∠B समकोण है तथा भुजाओं AB और AC के मध्य बिन्दु क्रमशः L और M हैं तो सिद्ध कीजिए कि 4LC2 = AB2 + 4 BC2
हल:

∆ LCB में पाइथागोरस प्रमेय द्वारा,
LC2 = LB2 + BC2
दोनों और 4 से गुणा करने पर
4LC2 = 4LB2 + 4BC2
4LC2 = (2LB)2 + 4BC2
4LC2 = (AB)2 + 4BC2 (∵ AB = 2LB)
प्रश्न 10.
एक समबाहु ∆ ABC में, BC के बिन्दु D पर मिलने वाला लम्ब AD डाला गया है। सिद्ध कीजिए कि AD2 = 3BD2
हल:

∆ ABC समबाहु है
AB = BC = AC
∠A = ∠B = ∠C = 60°
∆ ADB तथा (UPBoardSolutions.com) ∆ADC में,
AB = AC (दिया है)
∠B = ∠C (60°)
∠ADB = ∠ADC (90°)
∴ ∆ ADB ≅ ∆ ADC
⇒ इसलिए BD = DC
⇒ BD = DC = [latex]\frac{1}{2}[/latex] BC
∆ ADB में पाइथागोरस प्रमेय द्वारा
AB2 = AD2 + BD2
BC2 = AD2 + BD2
(2BD)2 = AD2 + BD2 (∵ BC = 2BD)
4 BD2 = AD2 + BD2
AD2 = 4 BD2 – BD2
AD2 = 3 BD2
![]()
प्रश्न 11.
2a इकाई का एक समबाहु त्रिभुज है। इसकी प्रत्येक ऊँचाई ज्ञात कीजिए। (NCERT)
हलः

माना, ∆ ABC एक समबाहु त्रिभुज है।
AD ऊँचाई BC पर
BE ऊँचाई AC पर
CF ऊँचाई AB पर
दिया है, AB = BC = CA = 2a
हमें ऊँचाई AD, BE, CF ज्ञात करनी है।
∆ ADB तथा ∆ ADC में,
AB = AC (समबाहु A) (UPBoardSolutions.com)
∠B = LC (प्रत्येक 60°)
∠ ADB = ∠ ADC (प्रत्येक 90°)
∴ ∆ ADB ≅ ∆ ADC
इसलिए BD = DC
इसी प्रकार AE = EC और AF = FB

∆ ADB में पाइथागोरस प्रमेय द्वारा,
AB2 = AD2 + DB2
(2a)2 = AD2 + a2
AD2 = 4a2 – a2 = 3a2
ऊँचाई AD = a[latex] \sqrt{{3}} [/latex] इकाई
इसी प्रकार BE = CF = a[latex] \sqrt{{3}} [/latex] इकाई
![]()
प्रश्न 12.
∆ ABC का ∆C समकोण है तथा भुजाओं CA और CB के मध्य बिन्दु क्रमशः P और Q हैं तो सिद्ध कीजिए कि 4(AQ2 + BP2) = 5AB2 (NCERT)
हलः

दिया है, ∆ ABC में,
∆C = 90°
P और Q क्रमशः CA और CB मध्य बिन्दु हैं
CP = PA
और CQ = QB
हमें सिद्ध करना है 4(AQ2 + BP2) = 5AB2
∆AQC में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा,
AQ2 = AC2 + CQ
⇒ 4AQ2 = 4AC2 + 4CQ
4AQ2 = 4AC2 + (2CQ2
4AQ2 = 4AC2 + CB2 (CB = 2CQ)
⇒ 4AQ2 = 4AC2 + CB2 …(1)
अब ∆ PCB में, पाइथागोरस प्रमेय द्वारा
BP2 = PC2 + CB2
⇒ 4BP2 = 4PC2 + 4CB2
⇒ 4BP2 = (2PC)2 + 4CB2
⇒ 4BP2 = AC2 +4CB2 …(2) (2PC = AC)
समीकरण (1) तथा (2) को जोड़ने पर
4AQ2 + 4BP2 = 4AC2 + CB2 + AC2 + 4CB2
4(AQ2 + BP2) = 5(AC2 + CB)
4(AQ2 + BP2) = 5AB2 (∵ AB2 = AC2 + BC2)
प्रश्न 13.
एक समद्विबाहु ∆ ABC में, AB = AC तथा BD, B से भुजा AC के लम्बवत् है तो सिद्ध कीजिए कि BD2 – CD 2 = 2 CD AD
हलः
दिया है, ∆ ABC में,
AB = AC

BD ⊥ AC
सिद्ध करना है
BD2 – CD22 = 2CD · AD
∆ ABD में पाइथागोरस प्रमेय द्वारा
AB2 = AD2 + BD2
⇒ BD2 = AB2 – AD
⇒ BD2 = AC2 – AD2 (∵ AB = AC)
⇒ BD2 = (CD + AD)2 – (UPBoardSolutions.com) AD2 (∴ AC = CD + AD)
⇒ BD2 = CD2 + AD2 + 2CD × AD – AD2 [(a + b)2 = a2 + b2 +2ab]
⇒ BD2 = CD2 + 2CD – AD
⇒ BD2 – CD2 = 2CD·AD
![]()
प्रश्न 14.
एक ∆ ABC में, कोण B तथा कोण C न्यून कोण हैं। यदि AC तथा AB पर क्रमशः लम्ब BE तथा CF खींचे गये हैं तो सिद्ध कीजिए कि BC2 = AB × BF + AC × CE
हल:
∆ ABC में दिया है
∠B और ∠C न्यून कोण हैं

BE ⊥ AC
CF ⊥ AB
हमें सिद्ध करना है, BC2 = AB × BF + AC × CE
∆ ABC में ऊँचाई BE के साथ
चूँकि ∠C न्यून कोण है ।
इसलिए, AB2 = BC2 + AC2 – 2AC · CE …(1)
अब ∆ ABC में ऊँचाई CF के साथ
चूँकि ∠B न्यून कोण है ।
इसलिए, AC2 = BC2 + AB2 – 2AB · BF …(2)
समीकरण (1) और (2) को जोड़ने पर
AB2 + AC2 = BC2 + BC2 + AC2 + AB2 – 2AC · CE – 2AB · BF
-2BC2 = -2(AB · BF + AC · CE)
⇒ BC2 = AB × BF + AC × CE
प्रश्न 15.
एक समकोण त्रिभुज ABC में, ∠C समकोण है तथा AC = [latex] \sqrt{{3}} [/latex] · BC हो तो सिद्ध कीजिए कि, ∠ABC = 60°
हल:
∆ABC में दिया है, ∠C = 90°
AC = [latex] \sqrt{{3}} [/latex]BC

[latex]\frac{A C}{B C}=\sqrt{3}[/latex]
सिद्ध करना है (UPBoardSolutions.com) ∠ABC = 60°
∆ ABC में, tan B = [latex]\frac{A C}{B C}[/latex]
tan B = 13
tanB = tan60°
∴ B = 60°
अतः ∠ABC = 60°
![]()
प्रश्न 16.
∆ PQR में, QM ⊥ PR तथा PR2 – PQ2 = QR2 है तो सिद्ध कीजिए कि QM2 = PM × MR (NCERT)
हल:

∆ PQR में, दिया है QM 2 PR
PR2 – PQ2 = QR2
हमें सिद्ध करना है-
QM2 = PM × MR
चूँकि दिया है PR2 – PQ2 = QR2
⇒ (PM + MR)2 – (QM2 + PM2) = (QM2 + MR2
(∵ PR = PM + MR, ∆PQM में PQ2 = QM2 + PM2, ∆QMR में, QR2 = QM2 + MR2)
⇒ PM2 + MR2 + 2PM · MR (UPBoardSolutions.com) – QM2 – PM2 = QM2 + MR 2
⇒ 2QM2 = 2PM – MR
⇒ QM2 = PM × MR
प्रश्न 17.
एक सीढ़ी का पाद एक दीवार से 6 मीटर की दूरी पर है तथा यह जमीन से 8 मीटर ऊँची एक खिड़की तक पहुंचती है। यदि सीढ़ी को इस तरह विस्थापित किया जाता है कि इसका पाद, तल से 8 मीटर दूर हो। इसकी टिप (शीर्ष) किस ऊँचाई तक पहुँचेगी।
हलः
हमें EB ज्ञात करना है।
∆ ABC में पाइथागोरस प्रमेय द्वारा,

AC2 = AB2 + BC2
AC2 = 82 +62
AC2 = 64 + 36
AC2 = 100 = (10)2
AC = 10 मीटर
चूँकि सीड़ी की लम्बाई = AC = DE = 10 मीटर
अब ∆ EBD में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा
ED2 = EB2 + BD2
102 = EB2 + 82
100 – 64 = EB2
EB2 = 36 = (6)2
EB = 6 मीटर
![]()
प्रश्न 18.
एक त्रिभुज की भुजाएं 5 सेमी, 12 सेमी तथा 13 सेमी हैं। 13 सेमी वाली भुजा पर उसके सम्मुख शीर्ष से डाले गये लम्ब की लम्बाई (दशमलव के एक अंक तक) ज्ञात कीजिए।
हल:

∆ABC में, AC2 + BC2 = 52 + 122
= 25 + 144 = 169
= (13)2
∴ AC2 + BC2 = AB2
∴ ∆ ABC समकोण त्रिभुज है और ∠C = 90°
∴ ∠A और ∠B न्यून कोण होंगे।
⇒ ∴ CD2 = AD × BD
CD2 = (AB – BD) × BD
CD2 = AB · BD – BD2

प्रश्न 19.
एक समचतुर्भुज की प्रत्येक भुजा 10 सेमी है। यदि इसका एक विकर्ण 16 सेमी है तो दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हलः
समचतुर्भुज ABCD में,
दिया है, AB = BC = CD = DA = 10 सेमी
विकर्ण AC = 16 सेमी
हमें विकर्ण BD ज्ञात करना है

समचतुर्भुज के (UPBoardSolutions.com) विकर्ण समकोण पर समद्विभाजित करते हैं।
∴ AE = EC = [latex]\frac{16}{2}[/latex] = 8 सेमी
और BE = ED
अब ∆ABE में पाइथागोरस प्रमेय द्वारा,
AB2 = AE2 + BE2
102 = 82 + BE2
100 – 64 = BE2
BE2 = 36 = 62
BE = 6 सेमी
∴ ED = BE = 6 सेमी
विकर्ण BD = BE + ED
= 6 + 6 = 12 सेमी
![]()
प्रश्न 20.
18 मीटर ऊँचे एक ऊर्ध्वाधर खम्भे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूटे से जुड़ा हुआ है। खम्भे के आधार से खूटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लम्बाई 24 मीटर है। (NCERT)
हलः

दिया है, AB = 18 मीटर
AC = 24 मीटर
हमें खम्भे से खूटे की दूरी (BC) ज्ञात करनी है
∆ABC में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा
AC2 = AB2 + BC2
242 = 182 + BC2
BC2 = 576 – 324
BC2 = 252
BC = [latex] \sqrt{{125}} [/latex]
BC = 6[latex] \sqrt{{7}} [/latex] मीटर
प्रश्न 21.
एक त्रिभुज की भुजाएँ (a -1) सेमी०, 2[latex] \sqrt{{a}} [/latex] सेमी० तथा (a + 1) सेमी० हैं। तो ज्ञात कीजिए कि क्या त्रिभुज समकोण है ?
हलः
दिया है ∆ ABC में, AB = (a – 1) सेमी
BC = 2[latex] \sqrt{{a}} [/latex], CA = (a +1) सेमी
AB2 + BC2 = (a – 1)2 + (2[latex] \sqrt{{a}} [/latex])2
= a2 + 1 – 2a + 4a
= a2 + 1 + 2a = (a + 1)2
AB2 + BC2 = (AC)
अतः पाइथागोरस प्रमेय द्वारा ∆ ABC (समकोण है)
![]()
प्रश्न 22.
एक समकोण त्रिभुज में, यदि कर्ण के समकोण से एक लम्ब खींचा गया है तो सिद्ध कीजिए कि लम्ब का वर्ग, कर्ण की दो रेखाखण्डों के गुणनफल बराबर है।
हलः
माना ABC समकोण त्रिभुज है

∠B = 90°
B से AC पर लम्ब BD खींचा गया। हमें सिद्ध करना है
BD2 = CD × AD
∆ABC में, ∠B = 90° तब पाइथागोरस प्रमेय द्वारा
AC2 = AB2 + BC2
∆ ADB में, ∠D = 90° तब पाइथागोरस प्रमेय द्वारा
AB2 = AD2 + DB2
∆BDC में ∠D = 90° तब (UPBoardSolutions.com) पाइथागोरस प्रमेय द्वारा
BC2 = BD2 + DC2
समीकरण (2) और (3) को जोड़ने पर,
AB2 + BC2 = AD2 + DB2 + BD2 + CD2
AC2 = AD2 + 2BD2 + CD2 [(1) के प्रयोग से]
(AD + DC)2 = AD2 + 2BD2 + CD2
AD2 + DC2 + 2AD × CD = AD2 + 2BD2 + CD2
2AD × CD = 2BD2
⇒ BD2 = AD × CD
प्रश्न 23.
एक त्रिभुज ABC है। जिसमें AB = AC तथा D, BC पर कोई बिन्दु है तो सिद्ध कीजिए कि AB2 – AD2 = BD·CD
हल:
∆ ABC में, दिया है AB = AC
तथा D,BC पर कोई बिन्दु है।
हमें सिद्ध करना है— AB2 – AD2 = BD·CD
AE ⊥ BC खींचा।

∆AEB तथा ∆AEC में,) AB = AC
AE = AE [उभयनिष्ठ]
∠B = ∠c [∵ AB = AC]
∴ ∆AEB ≅ ∆AEC
⇒ BE = CE
∵ ∆AED और ∆AEB, बिन्दु E (UPBoardSolutions.com) पर समकोण त्रिभुज हैं
इसलिए AD2 = AE2 + DE2
और AB2 = AE2 + BE2
AB2 – AD2 = BE2 – DE2
AB2 – AD2 = (DE + DE) (BE – DE)
AB2 – AD2 = (CE + DE) (BE – DE)
AB2 – AD2 = CD × BD
इस प्रकार AB2 – AD2 = BD × CD