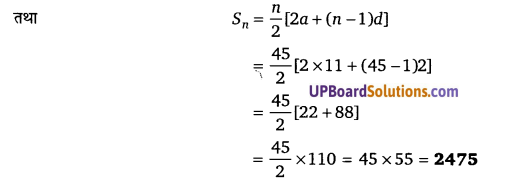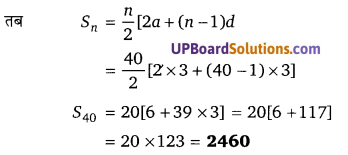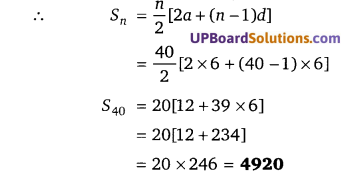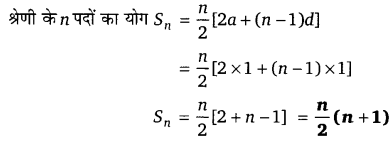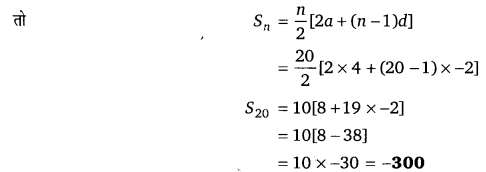Class 10

Balaji Class 10 Maths Solutions Chapter 7 Triangles Ex 7.2 त्रिभुज

प्रश्न 1.
दी गई आकृति में ∆ ACB ~ ∆ APQ है यदि BC = 8 सेमी, PQ = 4 सेमी, BA = 6.5 सेमी, AP = 2.8 सेमी है तो CA तथा AQ ज्ञात कीजिए।
हलः
दिया है,
BC = 8 सेमी PQ = 4 सेमी, (UPBoardSolutions.com) BA = 6.5 सेमी

AP = 2.8 सेमी
दिया है, ∆ACB ~ ∆APQ

⇒ AC = 5.6 cm
तथा AQ = 3.25 cm

प्रश्न 2.
दी गई आकृति में, QA तथा PB, AB के  लम्बवत् है। यदि AQ = 10 सेमी, BO = 6 सेमी तथा PB = 9 सेमी है तो AQ ज्ञात कीजिए।
हलः
दिया है,
AO = 10 सेमी
BO = 6 सेमी
PB = 9 सेमी

∵ AQ तथा PB रेखा AB के (UPBoardSolutions.com) लम्बवत् है अत: ∆OAQ तथा ∆OPB समकोणीय त्रिभुज है।
अतः ∆OPB में,
(OP)² = (OB)² + (PB)²
OP² = (6)² + (9)²
OP² = 36 + 81
OP² = 117
OP² = [latex]\sqrt{117}=\sqrt{13 \times 9}[/latex]
= 3[latex] \sqrt{{13}} [/latex] सेमी
∆OAQ तथा ∆OPB समरूप हैं।
[latex]\frac{O A}{O B}=\frac{O Q}{O P}[/latex]
⇒ [latex]\frac{10}{6}=\frac{O Q}{3 \sqrt{13}}[/latex]
⇒ OQ = 5[latex] \sqrt{{13}} [/latex] सेमी
अब ∆OAQ में,

OQ² = OA² + AQ²
⇒ (5[latex] \sqrt{{13}} [/latex])² = 10² + AQ²
⇒ AQ² = 25 × 13 – 100
⇒ AQ² = 325 – 100
⇒ AQ² = 225
⇒ AQ = 15 सेमी

प्रश्न 3.
10 सेमी ऊँची एक ऊर्ध्वाधर छड़ी की छाया 8 सेमी लम्बी बनती है। ठीक उसी समय एक मीनार की छाया 30 सेमी है तो मीनार की ऊँचाई ज्ञात कीजिए।
हलः
ऊर्ध्वाधर छड़ी की लम्बाई CE = 10 cm जमीन पर 8 cm की छाया बनाती है।
माना कि मीनार की ऊँचाई h (UPBoardSolutions.com) है।
मीनार की छाया की लम्बाई = 30 सेमी

अब ∆ ABD तथा ∆ DEC
में ∠ABD = ∠ECD
∠D = ∠D
तब समरूपता की AA-कसौटी द्वारा
∆ABD ~ ∆ DEC

प्रश्न 4.
एक समकोण त्रिभुज की भुजाएँ a तथा b और कर्ण c हैं। कर्ण पर एक ऊँचाई x है तो सिद्ध कीजिए कि ab = cx
हलः
दिया है, AC = b, BC = a
AB = c और CD = x

∆ABC तथा ∆BCD में
∠BCA = ∠CDB [प्रत्येक कोण = 90°]
और ∠B = ∠B
अतः समरूपता की (UPBoardSolutions.com) AA – कसौटी से,
∆ABC ~ BCD
[latex]\frac{A C}{C D}=\frac{B A}{B C}[/latex]
[latex]\frac{b}{x}=\frac{c}{a}[/latex]
⇒ ab = cx

प्रश्न 5.
दी गई आकृति में ∠A = ∠CED है तो सिद्ध कीजिए कि ∆CAB ~ ∆CED तथा x का मान भी ज्ञात कीजिए।
हलः

दिया है, ∠A = ∠CED
∆EDC में,
(EC)² = DC² + DE ²
(10)² = 8² + x²
100 = 64 + x²
x² = 100 – 64
x = [latex] \sqrt{{36}} [/latex]
x = 6 सेमी
∆ABC तथा ∆ADE
∠ABC = ∠EDC में
∠ABC = ∠EDC [प्रत्येक कोण = 90°]
तथा ∠C = ∠C
यह समरूपता की (UPBoardSolutions.com) AA-कसौटी का पालन करती है।
∆CAB ~ ∆CED

प्रश्न 6.
दी गई आकृति में ∠CAB = 90° तथा AD ⊥BC है। यदि AC = 75 सेमी, AB = 1 मी० तथा BD = 1.25 मीटर है तो AD का मान ज्ञात कीजिए।
हलः

दिया है, AB = 1 मीटर = 100 सेमी
AC = 75 सेमी और BD = 125 सेमी
∆ BAC और ∆ BDA में यहाँ,
∠BAC = ∠ BDA (UPBoardSolutions.com) (समकोण)
और ∠B = ∠B
अतः (AA-समरूपता से)

प्रश्न 7.
दी गई आकृति में, यदि AB ⊥ BC तथा DE ⊥ AC है तो सिद्ध कीजिए कि ∆ ABC ~ ∆ AED
हल:

∆ ABC तथा ∆ AED में
∠ABC = ∠AED = 90°
∠ BAC = ∠EAD (समान कोण)
= ∠A
अतः समरूपता की AA-कसौटी से,
∆ABC ~∆ AED (UPBoardSolutions.com) यही सिद्ध करना था।

प्रश्न 8.
दी गई आकृति में, यदि ∠A = ∠C है तो सिद्ध कीजिए कि ∆AOB ~ ∆COD
हलः

दिया है,
∠A = ∠C = 90°
तथा ∠1 = ∠2 (शीर्षाभिमुख कोण)
∆ AOB तथा ∆CDO में,

अतः SAS समरूपता द्वारा,
∠A = ∠C
तथा ∠B = ∠D
अतः ∆ AOB ~ ∆CDO (UPBoardSolutions.com) यही सिद्ध करना था।

प्रश्न 9.
दी गई आकृति में, ∠ ABC = 90° तथा BD ⊥ AC है यदि AB = 5.7 सेमी०, BD = 3.8 सेमी० तथा CD = 5.4 सेमी० हो तो BC ज्ञात कीजिए।
हलः

दिया है,
∠ABC = 90°
AB = 5.7 सेमी, BD = 3.8 सेमी
CD = 5.4 सेमी, BC = ?
∵ ∆ABC तथा ∆BDC में यहाँ
∠ABC = ∠CDA (UPBoardSolutions.com) = 90°
और ∠C = ∠C
अतः (AA-समरूपता से)
∆BAC ~ ∆BDA

प्रश्न 10.
∆ ABC तथा ∆ DEF में, यह दिया गया है कि, AB = 5 सेमी०, BC = 4 सेमी०, CA = 4.2 सेमी०, DE = 10 सेमी०, EF = 8 सेमी० तथा FD = 8.4 सेमी० है। यदि AL I BC तथा DM L EF है तो AL:DM ज्ञात कीजिए।
हलः

प्रश्न 11.
दी गई आकृति में, दो त्रिभुज BEP तथा CPD दिये गये हैं तो सिद्ध कीजिए कि
BP × PD = EP × PC
हल:

∆ EPB तथा ∆DPC में,
∠ PEB = ∠ PDC = 90°
∠ EPB = ∠DPC (शीर्षाभिमुख कोण)
इस प्रकार AA-कसौटी की समरूपता से,
∆ EPB ~ ∆DPC
⇒ [latex]\frac{E P}{D P}=\frac{P B}{P C}[/latex]
⇒ BP × DP = EP × PC यही सिद्ध करना था।

प्रश्न 12.
∆ ABC की भुजाओं AB तथा AC पर क्रमशः बिन्दु P तथा Q हैं। यदि AP = 3 सेमी०, PB = 6 सेमी०, AQ = 5 सेमी० तथा QC = 10 सेमी० है तो सिद्ध कीजिए कि BC = 3PQ
हलः
दिया है,

AP = 3 सेमी, PB = 6 सेमी,
AQ = 5 सेमी, QC = 10 सेमी
∆ ABC में, PQ ||BC (UPBoardSolutions.com)
⇒ [latex]\frac{A B}{A P}=\frac{A Q}{A E}[/latex]
तथा ∠A = ∠A
तब समरूपता की कसौटी (SAS) द्वारा

प्रश्न 13.
ABCD एक समान्तर चतुर्भुज है तथा APQ एक सरल रेखा है जो बढ़ाने पर BC से बिन्दु P पर तथा DC से बिन्दु Q पर मिलती है। सिद्ध कीजिए कि BP व DQ से बना आयत AB व AD से बने आयत के बराबर होता है।
हलः
स्वयं हल (UPBoardSolutions.com) कीजिए।

प्रश्न 14.
एक चतुर्भुज ABCD है। जिसमें AD = BC यदि P, Q, R तथा S क्रमशः AB, BC, CD तथा AD के मध्य बिन्दु हैं तो सिद्ध कीजिए कि PQRS एक समचतुर्भुज है।
हलः
माना कि एक चतुर्भुज ABCD इस प्रकार है कि इसकी भुजाओं AB, BC,CD तथा DA के क्रमशः मध्य-बिन्दु P,Q, R, S हैं तब हमें सिद्ध करना है कि PQRS एक समचतुर्भुज है।
अब AC को मिलाया।
∆ABC में, P तथा Q, AB तथा BC के मध्य बिन्दु हैं।
∵ दिया है
AB = BC
अतः AP = PB = BQ = CQ
PQ || AC …(1)
इसी प्रकार ∆ ACD में, R तथा S क्रमशः CD तथा DA के मध्य-बिन्दु हैं।
तब SR || AC …(2)

समीकरण (1) तथा (2) से यहाँ है
PQ || AC तथा SR || AC
इसलिये PQ || SR (UPBoardSolutions.com)
इसी प्रकार ∆ABD, ∆BCD हैं
PS ||QR
अत: PQRS एक समचतुर्भुज है।

प्रश्न 15.
दी गई आकृति में, ABCD एक समलम्ब चतुर्भुज है तथा AB||DC यदि ∆ AED तथा ∆ BEC समरूप है तो सिद्ध कीजिए कि AD = BC

हलः
स्वयं हल कीजिए।

प्रश्न 16.
एक समलम्ब चतुर्भुज ABCD में, AB||DC तथा DC = 2AB, AB के आगे EF दर्शायी गयी है। AD, F द्वारा तथा BC, E द्वारा काटे गये हैं तथा [latex]\frac{B E}{E C}=\frac{3}{4}[/latex] विकर्ण DB, EF को G पर प्रतिच्छेद करता है तो सिद्ध कीजिए कि 7FE = 10AB

हल:
∆DFG तथा ∆ DAB में ज्ञात हैं।
∠1 = ∠2 [∵ AB ||DC ∴ ∠1 तथा ∠2 संगत कोण है।]
∠ FDG = ∠ADB (सर्वनिष्ठ)
अतः समरूपता (UPBoardSolutions.com) की AA-कसौटी से,
∆DFG ~ ∆DAB

प्रश्न 17.
दी गई आकृति में, एक त्रिभुज ABC है जो C पर समकोण है तथा DE ⊥ AB है। तो सिद्ध कीजिए कि ∆ ABC ~ ∆ ADE तथा AE और DE की लम्बाई ज्ञात कीजिए।
हलः

त्रिभुज ABC तथा ∆ ADE में
∠ACB = ∠ AED = 90°
और ∠BAC = ∠ DAE (UPBoardSolutions.com)
अतः समरूपता की AA-कसौटी से,
∆ABC ~ ∆ ADE

प्रश्न 18.
एक समान्तर चतुर्भुज ABCD के शीर्ष D से, एक रेखा खींची गई है जो भुजा BA तथा BC को क्रमशः E तथा F पर प्रतिच्छेद करती है। तो सिद्ध कीजिए कि :

हलः
त्रिभुज EAD तथा ∆ DCF में,
∠1 = ∠2 [∵ AB ||DC ∴ संगत कोण बराबर है।]
∠3 = ∠4 [∵ AD||BC ∴ संगत कोण बराबर है।]
इसलिये समरूपता की (UPBoardSolutions.com) AA-कसौटी द्वारा,
∆ EAD ~ ∆DCF

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 8 Circles Ex 8.2 वृत्त

Ex 8.2 Circles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
दिये गये चित्र में 0 केन्द्र वाले एक वृत्त के  बिन्दु A पर PAQ एक स्पर्शी है तथा ∠BAQ = 60° तब ∠ABC का मान ज्ञात कीजिए।
हलः

∠ACB = ∠BAQ = 60° (एकान्तर वृत्त खण्ड के कोण बराबर होते हैं।)
∠BAC = 90° (UPBoardSolutions.com) (अर्द्धवृत्त में बना कोण समकोण होता है।)
∠ACB + ∠BAC + ∠ABC = 180°
∴ ∠ABC = 180° – (∠ACB + ∠BAC)
= 180° – (60° + 90° )
= 180° -150°
= 30°

प्रश्न 2.
दिये गये चित्र में, O केन्द्र वाले वृत्त के किसी बिन्दु P पर TPT’ एक स्पर्शी है। यदि ∠ APT = 65° तथा ∠ POA = x° हो तो x का मान क्या होगा?
हलः
वृत्त की परिधि पर एक बिन्दु M लिया। A को (UPBoardSolutions.com) M से तथा P को M से मिलाया।

∴ ∠ AMP = ∠APT = 65° (एकान्तर वृत्त खण्ड के कोण)
∠POA = x
2 × ∠AMP
= 2 × 65°
= 130°

प्रश्न 3.
दिये गये चित्र में ∠AOB = 108° तथा AT वृत्त के बिन्दु A पर स्पर्शी है तथा AB एक जीवा है। तब ∠ BAT का मान ज्ञात कीजिए।
हलः
∵ ∠AOB = 2 × ∠APB
एक ही वृत्तखण्ड द्वारा वृत्त के केन्द्र पर बना कोण उसी वृत्तखण्ड द्वारा परिधि पर बने कोण का दोगुना होता है।

∠APB = [latex]\frac{\angle A O B}{2}[/latex]
= [latex]\frac{108^{\circ}}{2}[/latex]
= 54°
∠BAT = ∠ APB = 54° (UPBoardSolutions.com) [एकान्तर वृत्तखण्ड के कोण]

प्रश्न 4.
दिये गये चित्र में, O वृत्त का केन्द्र है। वृत्त के बिन्दु P से स्पर्श रेखा PQ पर एक बिन्दु Q इस प्रकार है कि PQ = 4 सेमी तथा ∠PQO = 45°। तब वृत्त की त्रिज्या की माप ज्ञात कीजिए।
हलः
O से बिन्दु P को मिलाया।
∵ वृत्त की त्रिज्या स्पर्श रेखा पर लम्ब होती है।

∠OPQ = 90°
∠PQO + ∠OPQ + ∠ POQ = 180°
∴ ∠POQ = 180° – (90° + 45°)
= 180° -135°
= 45°
∵ ∠PQO = ∠POQ = 45°
∴ PQ = PO = 4 सेमी

प्रश्न 5.
दिये गये चित्र में, PQ बिन्दु K पर स्पर्शी है। यदि ∠N वृत्त का व्यास है तथा ∠ KLN = 30° तब ∠ PKL का मान ज्ञात कीजिए।
हल:

∆KLN में, ∠LKN = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)
∠ LNK = 180° – (∠ LKN + ∠ KLN)
= 180° – (90°+ 30°)
= 180° – 120°
= 60°
∠PKL = ∠ LNK = 60° [एकान्तर वृत्तखण्ड के कोण बराबर होते हैं।]

प्रश्न 6.
दिये गये चित्र में AOB, O केन्द्र वाले वृत्त का व्यास है। तथा ∠ ADC = 125° तब ∠ BAC का मान ज्ञात कीजिए।
हलः
∵ ABCD एक चक्रीय चतुर्भुज है।

∠ABC + ∠ADC = 180°
∠ABC +125° = 180°
∠ABC = 180°-125°
∠ABC = 550
तथा ∠ACB = 90° (अर्द्धवृत्त में बना कोण समकोण होता है।)
∴ ∆ ABC में,
∠ABC + ∠ACB + ∠ BAC = 180°
∠ BAC = 180° – (55° + 90° )
= 180° – 145°
= 35°

प्रश्न 7.
दिये गये चित्र में, 0 वृत्त का केन्द्र है तथा वृत्त के बिन्दु P पर T’PT एक स्पर्शी है। इसके अन्दर एक ∆ ABP खींचा गया है। यदि ∠ BPT = 60° तब ∠ BAP का मान ज्ञात कीजिए।
हलः
∠BAP = ∠ BPT = 60° [एकान्तर वृत्तखण्ड के कोण ]

प्रश्न 8.
दिये गये चित्र में ABCD एक चक्रीय चतुर्भुज है। वृत्त के एक बिन्दु B पर PBQ एक स्पर्शी है। यदि ∠DBP = 65° तब ∠ BCD का मान ज्ञात कीजिए।
हलः
∠BAD = ∠DBP = 65° [एकान्तर (UPBoardSolutions.com) वृत्तखण्ड के कोण बराबर होते हैं ]

∵ ABCD चक्रीय चतुर्भुज में,
∠BCD + ∠BAD = 180°
∠BCD + 65° = 180°
∠BCD = 180°- 65°
= 115°

प्रश्न 9.
दिये गये चित्र में ABCD एक चक्रीय चतुर्भुज है। बिन्दु A व C पर खींची गई स्पर्शी एक-दूसरे से बिन्दु P पर मिलती हैं। यदि । ∠ABC = 100° तब ∠ APC का मान ज्ञात कीजिए।

हलः
O को A तथा C से मिलाया।
∠OCP = ∠OAP = 90° [त्रिज्या का स्पर्श रेखा के साथ बना कोण ]
∵ ∠ABC + ∠ADC = 180°
∠ADC = 180° – 100°
= 80°
लघु ∠AOC = 2 × ∠ADC
= 2 × 80°
= 160° [ केन्द्र पर बना कोण वृत्त की परिधि पर बने कोण का दोगुना होता है।]
∴ चतुर्भुज APCO में,
∠OCP + ∠ APC + ∠OAP + लघु ∠AOC = 360°
90°+ ∠ APC + 90° + 160° = 360°
∠APC + 340° = 360°
∠APC = 360° – 340°
= 20°

प्रश्न 10.
वृत्त के बाहर एक बिन्दु P से वृत्त पर दो स्पर्शियाँ PA व PC खींची गयी हैं। इनके बीच का कोण θ है। बिन्दु C से PA के समान्तर एक जीवा CB खींची जाती है। तब ∠ BAC का मान ज्ञात कीजिए।
हलः

∵ PA||CB तथा PM तिर्यक रेखा काटती है।
∴ ∠ MCB = ∠CPA = θ (UPBoardSolutions.com) (संगत कोण)
∠BAC = ∠ MCB = θ (एकान्तर वृत्तखण्ड के कोण)

प्रश्न 11.
दिये गये चित्र में, O वृत्त का केन्द्र है। वृत्त के बाहर एक बिन्दु T से वृत्त पर दो स्पर्शी TP व TQ खींची गयी हैं। यहाँ स्पर्श जीवा वृत्त के शेष भाग से ∠ PAQ = 70° बनाती है। तब दोनों स्पर्शियों के बीच का कोण ज्ञात कीजिए।
हलः

∠ PAQ = ∠PQT = 70° [ एकान्तर वृत्तखण्ड के कोण ]
∵ TP = TQ
∴ ∠PQT = ∠QPT = 70°
∆ PQT में, ∠ PTQ = 180° – (70° + 70°)
= 180°- 140°
= 40°

Ex 8.2 Circles लघु उत्तरीय प्रश्न-1(Short Answer Type Questions-I)

प्रश्न 12.
दिये गये चित्र में, एक रेखा PAT वृत्त को बिन्दु A पर स्पर्श करती है। यदि ∠PAC = 40° तथा ∠BAT = 55° तब ∠CAB का मान ज्ञात कीजिए।
हलः

∠CAB = 180° – (∠CAP + ∠BAT)
= 180° – (40° + 55°)
= 180°- 95°
= 85°

प्रश्न 13.
दिये गये चित्र में रेखा PAT वृत्त को बिन्दु A पर स्पर्श करती है। बिन्दु A से एक जीवा AB इस प्रकार खींची जाती है जो रेखा PAT से 46° का कोण बनाती है। ∠ ACB, रेखाखण्ड ACB में कोण है। ∠ACB की माप ज्ञात कीजिए।
हलः

वृत्त की परिधि पर एक बिन्दु M लिया। M को A तथा B से मिलाया।
∠AMB = ∠ BAT = 46° (UPBoardSolutions.com) [एकान्तर वृत्तखण्ड के कोण ]
∵ AMBC एक चक्रीय चतुर्भुज है।
∴ ∠AMB + ∠ ACB = 180°
46°+ ∠ACB = 180°
∠ACB = 180° – 46° = 134°

प्रश्न 14.
दिये गये चित्र में, O वृत्त का केन्द्र है। वृत्त के बिन्दु P पर एक स्पर्शी T’PT खींची जाती है। जो कि केन्द्र पर ∠ POQ बनाती है। यदि ∠QPT = α तब ∠ POQ का मान ज्ञात कीजिए।
हलः

∵ ∠OPT = 90° [त्रिज्या का स्पर्श रेखा के साथ कोण ]
∠OPQ = 90° – α
∠OQP = ∠OPQ = 90° – α
∠OQP = ∠OPQ = 90° – α [∆OPQ में, OP = OQ (वृत्त की त्रिज्याएँ)]
∆OPQ में, OP = OQ (वृत्त की त्रिज्याएँ)
∆OPQ में, ∠POQ = 180° – (∠OPQ + ∠OQP)
= 180° – (90° – α + 90° – a)
= 180° – (180° – 2α)
= 180° – 180° + 2α
= 2α

प्रश्न 15.
दिये गये चित्र में, PQRS एक चक्रीय चतुर्भुज है। वृत्त के एक बिन्दु Q पर एक स्पर्शी AQT खींची जाती है। यदि ∠ SQA = 65° तब ∠QRS की माप ज्ञात कीजिए।
हलः

∠ SPQ = ∠ SQA = 65° (एकान्तर वृत्तखण्ड के कोण)
∵ PQRS एक चक्रीय (UPBoardSolutions.com) चतुर्भुज है।
∠ SPQ + ∠ SRQ = 180°
65°+ ∠SRQ = 180°
∠SRQ = 180° – 65°
∠SRQ = 115°

प्रश्न 16.
दिये गये चित्र में, वृत्त के बिन्दु A पर PAT एक स्पर्शी है। BC वृत्त का व्यास P है तथा ∠ ABC = 30° तब ∠ PAB व ∠ TAC के मान ज्ञात कीजिए।
हल:
∆ ABC में,

∠ BAC = 90° [अर्द्धवृत्त में बना कोण समकोण होता है।]
∠ ACB = 180° – (30° + 90°)
= 180° – 120° = 60°
∴ ∠ PAB = ∠ ACB = 60° (एकान्तर वृत्तखण्ड के कोण)
∠ TAC = ∠ABC = 30° (एकान्तर वृत्तखण्ड के कोण)

Ex 8.2 Circles लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 17.
दिये गये चित्र में ∆ ABC एक समद्विबाहु त्रिभुज है तथा AB = AC सिद्ध कीजिए कि ∆ ABC के परिवृत्त के बिन्दु A पर खींची गई स्पर्शी BC के समान्तर होगी।
हलः
ज्ञात हैः

∆ ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC तथा उसका परिवृत्त खींचा गया है। उसके बिन्दु A पर परिवृत्त की स्पर्श रेखा PAQ खींची गयी है।
सिद्ध करना है: PQ || BC
उपपत्तिः समद्विबाहु ∆ ABC में,
AB = AC
∠ ABC = ∠ ACB …(1)
∠ PAB = ∠ ACB …(2) (UPBoardSolutions.com) [एकान्तर वृत्तखण्ड के कोण]
समीकरण (1) व (2) से,
∠ PAB = ∠ABC …(3)
इसी प्रकार ∠QAC = ∠ ACB
परन्तु समीकरण (3) व (4) संगत कोण हैं तथा बराबर हैं। परन्तु यह तभी सम्भव है
जब PQ||BC इति सिद्धम्

प्रश्न 18.
दिये गये चित्र में, AB वृत्त का व्यास तथा AC वृत्त की जीवा है तथा ∠ BAC = 30° है। बिन्दु C पर स्पर्शी AB को बढ़ाने पर मिले बिन्दु D पर प्रतिच्छेद करती है। सिद्ध कीजिए कि BC = BD
हलः
ज्ञात है: AB वृत्त का व्यास तथा AC वृत्त की जीवा है। ∠ BAC = 30° तथा C पर एक स्पर्श रेखा खींची गई है।

सिद्ध करना है: BC = BD
उपपत्तिः ∆BCD में, ∠CBD = 30° + 90° = 120° [∆ का बहिष्कोण अपने सम्मुख अन्तः कोणों के योग के बराबर होता है।]
∠BCD = ∠CAB = 30° [एकान्तर वृत्तखण्ड के कोण ]
अब ∆ BCD में,
∠BDC = 180° – (∠ BCD + ∠CBD)
= 180° – (30° + 120°)
= 180° – 150° = 30°
∴ ∆BCD संमद्विबाहु त्रिभुज होगा जिसमें BC = BD होगी। इति सिद्धम्

प्रश्न 19.
सिद्ध कीजिए कि वृत्त की जीवा के शीर्षों पर खींची गई स्पर्शी, जीवा से समान कोण बनाती है।
हलः
दिया हैः O केन्द्र वाला वृत्त तथा जीवा MN जिसके बिन्दु M व N पर दो स्पर्श रेखायें खींची गई हैं।

सिद्ध करना है: ∠ PMN = ∠ MNR
तथा ∠QMN = ∠ SNM
रचनाः वृत्त की परिधि पर दो बिन्दु T व S लिये तथा M,N को T तथा M,N को S से भी मिलाया।
उपपत्तिः ∠ PMN = ∠ MSN …(1)
तथा ∠RNM = ∠MSN …(2) [ एकान्तर वृत्तखण्ड के कोण ]
समीकरण (1) व (2) की तुलना करने पर
∠PMN = ∠RNM
इसी प्रकार (UPBoardSolutions.com) ∠QMN = ∠MTN …(3) [एकान्तर वृत्तखण्ड के कोण]
∠ SNM = ∠ MTN …(4)
समीकरण (3) व (4) की तुलना करने पर
∠QMN = ∠ SNM
इस प्रकार प्रत्येक जीवा के सिरों पर खींची गई स्पर्श रेखायें जीवा पर समान कोण बनायेंगी। इति सिद्धम्

प्रश्न 20.
चित्र में, O वृत्त का केन्द्र है और TPQ इसकी स्पर्श रेखा है। यदि ∠RPQ = 60° है तो ∠POR का मान ज्ञात कीजिए।
हलः

∵ ∠OPQ = 90° [त्रिज्या का स्पर्श रेखा के साथ कोण ]
∠OPR = 90° – 60°
⇒ ∠OPR = 30°
∠ORP = ∠OPQ = 30° [∆OPQ में, OP = OQ (वृत्त की त्रिज्याएँ)]
∆OPQ में, ∠ POR = 180° – (∠OPR + ∠ORP)
= 180 – (30° + 30°)
= 180°- 600
= 120°

प्रश्न 21.
वृत्त के केन्द्र से 5 सेमी दूरी पर स्थित एक बिन्दु A से स्पर्शी की लम्बाई 4 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
∵ वृत्त की स्पर्शी, वृत्त (UPBoardSolutions.com) के स्पर्श बिन्दु से होकर जाने वाली त्रिज्या के लम्बवत् है।

∴ ∠OTA = 90°
∴ ∆OTA में, OA² = OT² + AT²
(5)² = OT² + (4)²
25 – 16 = OT²
OT² = 9
OT = 3 सेमी
अतः वृत्त की त्रिज्या = 3 सेमी

प्रश्न 22.
संलग्न चित्र में, 3 सेमी त्रिज्या वाले वृत्त के परिगत एक ∆ ABC इस प्रकार है कि रेखाखण्ड BD व DC की लम्बाई क्रमशः 6 व 9 सेमी हैं। यदि त्रिभुज का क्षेत्रफल 54 सेमी² है, तो AB व AC की लम्बाई ज्ञात कीजिए।
हलः

स्वयं हल कीजिए।

प्रश्न 23.
O केन्द्र वाले वृत्त पर एक बाह्य बिन्दु P से दो स्पर्शी PA व PB खींची गयी हैं। यदि ∠ PAB = 50° तब ∠AOB का मान ज्ञात कीजिए।
हलः

दिया है, बाह्य बिन्दु P से दो स्पर्शी PA तथा PB हैं
तथा ∠ PAB = 50°, ∠AOB = ?
∵ PA ⊥ OA ⇒ ∠OAP = 90°
तथा PB ⊥ OB ⇒ ∠OBP = 90°
∵ बाह्य बिन्दु से वृत्त के केन्द्र पर (UPBoardSolutions.com) बने कोण बिन्दु पर बने कोण का दोगुना होता है।
अतः ∠AOB = 2 × ∠APB
= 2 × 50 = 100°

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 8 Circles Ex 8.1 वृत्त

Ex 8.1 Circles अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
6 सेमी त्रिज्या के एक वृत्त के केन्द्र से 8 सेमी दूर स्थित एक बिन्दु से खींची गई स्पर्श रेखा की लम्बाई ज्ञात कीजिए।
हलः
∵ वृत्त की त्रिज्या स्पर्श रेखा पर लम्ब होती है।

∆OPQ में, (PQ)² = (OQ)² + (OP)²
(PQ)² = (6)² + (8)²
= 36 + 64
= 100
PQ = [latex] \sqrt{{100}} [/latex] (UPBoardSolutions.com) = 10 सेमी

प्रश्न 2.
चित्र में, O वृत्त का केन्द्र है। जिसकी दो जीवाएँ AB व CD परस्पर बिन्दु E पर प्रतिच्छेद करती हैं। यदि CE = 4 सेमी तथा ED = 2 सेमी है तब AE EB का मान ज्ञात कीजिए
हलः

AE · EB = CE · ED
= 4 × 2 (UPBoardSolutions.com)
= 8 सेमी²

प्रश्न 3.
चित्र में, O वृत्त का केन्द्र है। जिसकी दो जीवाएँ AB व CD परस्पर बिन्दु E पर प्रतिच्छेद करती हैं। यदि CE = 4 सेमी तथा ED = 6 सेमी है तब AE व EB आसन्न भुजाओं वाले आयत का क्षेत्रफल ज्ञात कीजिए।
हलः

AE · EB = CE · ED
= 4 × 6 (UPBoardSolutions.com)
= 24 सेमी²

प्रश्न 4.
चित्र में PT एक स्पर्शी है। यदि PT = 12 सेमी तथा PB = 8 सेमी तब जीवा AB की लम्बाई ज्ञात कीजिए।
हलः

AP · BP = PT²
AP·8 = (12)²
AP = [latex]\frac{144}{8}[/latex] (UPBoardSolutions.com) = 18 सेमी
जीवा AB = AP – BP
= 18 – 8
= 10 सेमी

प्रश्न 5.
चित्र में, PAB वृत्त की एक छेदक रेखा है तथा PT वृत्त की स्पर्शी है। यदि PA = 5 सेमी, AB = 15 सेमी तब PT की लम्बाई क्या होगी?
हलः

PA · PB = (PT)²
5·20 = (PT)² (UPBoardSolutions.com) (∵ PB = PA + AB)
PT = [latex] \sqrt{{100}} [/latex] = 10 सेमी

Ex 8.1 Circles लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-1)

प्रश्न 6.
एक बिन्दु A, वृत्त के केन्द्र से 26 सेमी दूर है तथा A से वृत्त पर स्पर्शी की लम्बाई 24 सेमी है। वृत्त की त्रिज्या ज्ञात कीजिए।
हल:
∵ वृत्त की त्रिज्या, स्पर्श बिन्दु P पर (UPBoardSolutions.com) स्पर्श रेखा के साथ 90° का कोण बनाती है।
∴ समकोण ∆OPA में,

(OA)² = (OP)² + (PA)²
(26) = (OP)² + (24)²
676 = (OP)² + 576
676 – 576 = (OP)²
(OP)² = 100
OP = [latex] \sqrt{{100}} [/latex] = 10 सेमी
∴ वृत्त की त्रिज्या 10 सेमी है।

प्रश्न 7.
चित्र में PT, O केन्द्र वाले वृत्त की स्पर्शी है। यदि OP = 17 सेमी तथा OT = 8 सेमी तब स्पर्शी PT की लम्बाई ज्ञात कीजिए।
हल:

OP = 17 सेमी तथा OT = 8 सेमी
∵ वृत्त की त्रिज्या OT (UPBoardSolutions.com) स्पर्श रेखा TP के बिन्दु T पर लम्ब है।
∴ समकोण ∆OTP में,
(OP)² = (OT)² + (TP)²
(17)² = (8)² + (TP)²
289 = 64 + (TP)²
289 – 64 = (TP)²
225 = (TP)²
∴ TP = [latex] \sqrt{{1225}} [/latex] = 15 सेमी
∴ स्पर्श रेखा की लम्बाई = 15 सेमी

प्रश्न 8.
चित्र में O वृत्त का केन्द्र है तथा इसकी त्रिज्या 1.5 सेमी है। बिन्दु P, O से 3.9 सेमी दूरी पर है। बिन्दु P से वृत्त पर स्पर्शी PT है। PT की लम्बाई ज्ञात कीजिए।
हलः

∠OTP = 90° 1 (UPBoardSolutions.com) [वृत्त की त्रिज्या तथा स्पर्श रेखा के बीच का कोण ]
समकोण ∆OTP में,
(OP)² = (OT )² + (TP)²
(3.9)² = (1.5)² + (TP)²
15.21 = 2.25 + (TP)²
15.21 – 2.25 = (TP)²
12.96 = (TP)²
∴ TP = [latex] \sqrt{{12.96}} [/latex] = 3.6 सेमी

प्रश्न 9.
चित्र में यदि AP = 8 सेमी, CP = 6 सेमी तथा PD = 4 सेमी है तब AB की लम्बाई ज्ञात कीजिए।
हलः

∵ AP · PB = CP · PD
8 × PB = 6 × 4
PB = [latex]\frac{6 \times 4}{8}[/latex] = 3 सेमी
∴ जीवा AB = AP + (UPBoardSolutions.com) PB = 8 + 3 = 11 सेमी

प्रश्न 10.
निम्न प्रत्येक चित्र में x के मान ज्ञात कीजिए-

हलः
(i) AE·EB = CE · ED (∵ AE = x, EB = 2.5 सेमी, CE = 3 सेमी, ED = 5 सेमी)
x × 2.5 = 3 × 5
x = [latex]\frac{3 \times 5}{2.5}[/latex]= 6 सेमी

(ii) PA · PB = PC · PD
7 × 16 = 6 × (6 + x) (UPBoardSolutions.com) [∵ PB = 9 + 7 = 16 व PD = (6 + x)]
112 = 6(6 + x)
[latex]\frac{112}{6}[/latex] = (6 + x) या 18.67 = 6 + x
या x = 18.67 – 6 = 12.67 सेमी

प्रश्न 11.
चित्र में किसी वृत्त के बिन्दु T पर स्पर्शी PT है तथा PAB वृत्त की एक छेदक रेखा है। यदि PA = 9 सेमी तथा AB = 7 सेमी तब PT की माप ज्ञात कीजिए।
हल:

∵ PA = 9 सेमी
PB = PA + AB
= 9 + 7 = 16 सेमी
PA · PB = (PT)²
9 × 16 = (PT)²
144 = (PT)²
∴ PT = [latex] \sqrt{{144}} [/latex] = 12 सेमी

Ex 8.1 Circles लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

प्रश्न 12.
चित्र में PA व PB स्पर्शी इस प्रकार हैं कि PA = 9 सेमी तथा ∠ APB = 60° है तब जीवा AB की लम्बाई ज्ञात कीजिए।
हलः
∵ किसी बाह्य बिन्दु P से वृत्त पर खींची गई स्पर्श रेखायें

PA = PB = 9 सेमी
∴ ∠ PAB = ∠ PBA
∵ ∠PAB + ∠ PBA + ∠APB = 180°
2∠PBA + LAPB = 180°
2∠PBA + 60° = 180°
2∠PBA = (UPBoardSolutions.com) 120°
⇒ ∠PBA = 60°
∴ ∠PAB = 60°
∴ ∆ PAB एक समबाहु A है।
PA = PB = AB = 9 सेमी

प्रश्न 13.
चित्र में, O वृत्त का केन्द्र है। बिन्दु से वृत्त के बिन्दु P पर स्पर्शी PQ इस प्रकार है कि PQ = 4 सेमी तथा ∠PQO = 45°। वृत्त की त्रिज्या ज्ञात कीजिए।
हल:

∵ वृत्त की त्रिज्या, स्पर्श रेखा के बिन्दु P पर लम्बवत् होगी।
∴ ∠OPQ = 90°
∠PQO = 45°
∆OPQ में, ∠POQ = 180° – (90° +45°)
= 180° -135°
= 45°
∴ समद्विबाहु ∆OPQ में,
PQ = PO = 4 सेमी
∴ वृत्त की त्रिज्या OP = 4 सेमी

प्रश्न 14.
O केन्द्र वाले वृत्त पर दो स्पर्श रेखाखण्ड BC व BD इस प्रकार हैं कि ∠CBD = 120° है। सिद्ध कीजिए कि OB = 2BC
हलः

चतुर्भुज BCOD में,
∠BCO = ∠BDO = 90° (वृत्त की त्रिज्या और स्पर्श रेखा के बीच का कोण)
∠CBD + ∠COD = 180°
120° + ∠COD (UPBoardSolutions.com) = 180°
∠COD = 180° – 120° = 60°

प्रश्न 15.
∆ ABC एक समकोण त्रिभुज है जिसमें BC = 6 सेमी तथा AB = 8 सेमी है। ∆ ABC के अन्तर्गत एक 0 केन्द्र तथा x त्रिज्या का वृत्त है। x का मान ज्ञात कीजिए।
हल:

BMON एक वर्ग होगा, क्योंकि
∠ABC = 90°
∠BNO = ∠BMO = 90° [त्रिज्या तथा स्पर्श रेखाओं के बीच का कोण]
शेष ∠MBN = ∠MON = 90° (UPBoardSolutions.com) [चतुर्भुज के चारों कोणों का योग 360° होता है व ∠ABC = 90° (दिया है)]
∴ BMON एक वर्ग है।
माना MB = BN = a
AN = AT = b
CM – CT = c
समकोण त्रिभुज में,

∴ वर्ग BMON की भुजा a = x = 2 सेमी

प्रश्न 16.
एक चतुर्भुज ABCD के अन्दर एक वृत्त इस प्रकार है कि BC = 38 सेमी, BQ = 27 सेमी, DC = 25 सेमी तथा AD, DC पर लम्ब है। वृत्त की त्रिज्या ज्ञात कीजिए।
हलः

∠PDS = 90°
∠OPD = ∠OSD = 90° [स्पर्श रेखा तथा त्रिज्या के बीच का कोण]
∠ PDS + ∠OPD + ∠OSD + ∠POS = 360°
∠POS = 360° – (UPBoardSolutions.com) (90° +90° + 90°)
= 360°- 270° = 90°
∴ POSD एक वर्ग है।
माना DS = DP = x
SC = CR = y
BQ = BR = 27 [ एक ही बिन्दु से वृत्त की स्पर्श रेखाएँ]
∴ y = BC – BR
= 38 – 27
= 11
DC = x + y = 25
y का मान रखने पर x +11 = 25
x = 25 – 11
= 14 सेमी
अतः DS = DP = OP = OS एक वर्ग की भुजाएँ हैं।
∴ वृत्त की त्रिज्या = 14 सेमी

प्रश्न 17.
एक वृत्त, त्रिभुज ABC की भुजाओं AB, BC व CA को क्रमशः बिन्दु P,Q व R पर अन्तः स्पर्श करता है। सिद्ध कीजिए कि AP + BQ + CR = PB +QC + RA = [latex]\frac{1}{2}[/latex] (∆ ABC का परिमाप)
हलः
दिया है: ∆ ABC में, अन्तः वृत्त का केन्द्र O है। जो त्रिभुज की भुजाओं AB, BC तथा CA को क्रमशः P, Q तथा R पर स्पर्श करता है।
सिद्ध करना है: AP + BQ + CR = PB + QC + RA = [latex]\frac{1}{2}[/latex] (∆ ABC का परिमाप)

उपपत्तिः ∵ किसी (UPBoardSolutions.com) बिन्दु से वृत्त पर खींची दोनों स्पर्शियाँ बराबर होती हैं।
∴ AP = AR …(1)
BQ = BP …(2)
CR = CQ …(3)
समीकरण (1), (2) व (3) को जोड़ने पर
AP + BQ + CR = AR + PB + QC
= [latex]\frac{1}{2}[/latex][AB + BC + CA)

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 7 Triangles Ex 7.4 त्रिभुज

प्रश्न 1.
एक त्रिभुज की निम्न भुजाएँ दी गई हैं। ज्ञात कीजिए कि यह त्रिभुज समकोण है या नहीं? a = 6 सेमी, b = 8 सेमी, c = 10 सेमी
हल:
a = 6 सेमी, b = 8 सेमी, c = 10 सेमी
a² + b² = (6)² + (UPBoardSolutions.com) (8)² = 36 + 64
= 100 = c²
∴ a² + b² = c²
पाइथागोरस प्रमेय द्वारा दिया गया त्रिभुज समकोण है।

प्रश्न 2.
एक त्रिभुज ABC की भुजाओं की लम्बाई AB = 9 सेमी, BC = 40 सेमी तथा AC = 41 सेमी है तो सिद्ध कीजिए कि त्रिभुज ABC एक समकोण त्रिभुज है।
हल:
∆ ABC में, AB = 9 सेमी
BC = 40 सेमी, AC = 41 सेमी
(AB)² + (BC)² = (9)² + (40)² = 81 +1600 = 1681
= (AC)²
⇒ (AB)² + (BC)² = (AC)²
पाइथागोरस प्रमेय द्वारा ∆ ABC समकोण त्रिभुज है।

प्रश्न 3.
एक समद्विबाहु त्रिभुज ABC इस प्रकार है कि AB = AC = 13 सेमी, BC पर A की ऊँचाई की लम्बाई 5 सेमी है तो BC ज्ञात कीजिए।
हलः
समद्विबाहु त्रिभुज ABC में, AB = 13 सेमी
AC = (UPBoardSolutions.com) 13 सेमी
AD = 5 सेमी
AD ⊥ BC

हमें BC ज्ञात करना है।
∆ ABD में पाइथागोरस प्रमेय द्वारा
AB² = AD² + BD²
132 = 5² + BD²
BD² = 169 – 25 = 144
BD = 12 सेमी
∆ ADC में पाइथागोरस प्रमेय द्वारा
AC² = AD² + DC²
132 = 52 + DC²
DC² = 169 – 25 = 144
DC = 12 सेमी
BC = BD + DC
BC = 12 + 12 = 24 सेमी

प्रश्न 4.
एक समचतुर्भुज की भुजा 10 सेमी है। इसके एक विकर्ण की लम्बाई 12 सेमी है तो इसके दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हलः
माना ABCD एक समचतुर्भुज है।
AB = BC = CD = DA = 10 सेमी
विकर्ण BD = 12 सेमी
हमें विकर्ण AC की लम्बाई ज्ञात करनी है।
चूँकि समचतुर्भुज के विकर्ण समकोण पर समद्विभाजित करते  है तो विकर्ण AC और BD बिन्दु E पर समकोण पर समद्विभाजित करेंगे।

BE = ED = [latex]\frac{B D}{2}=\frac{12}{2}[/latex] = 6 सेमी
∆ AEB में पाइथागोरस प्रमेय द्वारा
AB² = AE² + BE²
10² = AE²  + 6² (BE = 6 सेमी)
100 – 36 = AE²
AE² = 64 (UPBoardSolutions.com)
AE = 8 सेमी
∆ BEC में पाइथागोरस प्रमेय द्वारा
BC² = BE² + EC²
10² = 6² + EC²
100 -36 = EC²
EC² = 64
EC = 8 सेमी
विकर्ण AC = AE + EC
= 8 + 8 = 16 सेमी

प्रश्न 5.
एक समकोण त्रिभुज का कर्ण, उसकी छोटी भुजा के दोगुने से 6 मीटर अधिक है। यदि तीसरी भुजा कर्ण से 2 मीटर कम है। तो त्रिभुज की भुजाएँ ज्ञात कीजिए।
हलः
माना ∆ ABC, B पर समकोण है
दिया है, AC = (2AB +6) मीटर
BC = (AC – 2) मीटर …(1)
हमें त्रिभुज की भुजा AB, BC और AC ज्ञात करनी है।
दिया है AC = 2AB +6
[latex]\frac{(A C-6)}{2}[/latex] = AB
∆ ABC में पाइथागोरस प्रमेय द्वारा,
AC² = AB² + BC²

4AC² = 5AC² – 28AC + 52
AC² – 28AC + 52 = 0
AC² – (26 +2)AC + 52 = 0
AC² – 26AC – 2AC + 52 = 0
AC(AC – 26) -2(AC – 26) = 0
(AC – 26)(AC – 2) = 0
AC – 26 = 0
AC = 26 मीटर
AC = 26, समी० (UPBoardSolutions.com) (1) में रखने पर,
BC = AC – 2 = 26 – 2 = 24 मीटर
AC = 26, समी० (2) में रखने पर,
AB = [latex]\frac{A C-6}{2}=\frac{26-6}{2}=\frac{20}{2}[/latex]
AB = 10 मीटर
AB = 10 मीटर, BC = 24 मीटर, AC = 26 मीटर

प्रश्न 6.
एक 15 मीटर लम्बी सीढ़ी एक गली में सतह से 9 मीटर ऊँची खिड़की पर लगी है। यदि इसके पाद को उसी स्थान पर रखकर, सीढ़ी गली के दूसरी ओर 12 मीटर ऊँची खिड़की पर पहुँचती है। गली की चौड़ाई ज्ञात कीजिए।
हलः
माना खिड़की की ऊँचाई गली के दोनों और क्रमशः AB = 9 मीटर और ED = 12 मीटर हैं।
सीड़ी की लम्बाई AC = EC = 15 मीटर
हमें गली की चौड़ाई BD ज्ञात करनी है।

∆ ABC में पाइथागोरस प्रमेय द्वारा
AC² = AB² + BC²
15² = 9² + BC²
BC² = 225 – 81 = 144
BC = 12 मीटर
अब ∆ EDC में (UPBoardSolutions.com) पाइथागोरस प्रमेय द्वारा
EC² = ED² + CD²
15² = 12² + CD²
CD² = 225 – 144 = 81
CD = 9 मीटर
गली की चौड़ाई BD = BC +CD
= 12 + 9 = 21 मीटर

प्रश्न 7.
एक खेल के मैदान पर ऊर्ध्वाधर खड़े दो खम्भों की ऊँचाई 9 मीटर तथा 14 मीटर है यदि उनके पादों के बीच की दूरी 12 मीटर है तो उनके शीर्षों के बीच की दूरी ज्ञात कीजिए।
हलः

माना AB और CD दो खम्भे हैं।
दिया है, AB = 9 मीटर
CD = 14 मीटर
BC = 12 मीटर
हमें शीर्षों के बीच की दूरी AD ज्ञात करनी है।
12 मीटर शीर्ष A से CD पर E बिन्दु पर लम्ब AE डाला गया।
AE = BC = 12 मीटर
EC = AB = 9 मीटर
DE = CD – EC
DE = 14 – 9 = 5 मीटर
अब ∆ AED में पाइथागोरस प्रमेय द्वारा,
AD² = AE² + ED²
AD² = 12² + 5²
AD² = 144 + 25 = 169
AD = 13 मीटर

प्रश्न 8.
∆ ABC एक समद्विबाहु त्रिभुज है जिसका ∠C समकोण है। सिद्ध कीजिए कि AB² = 2 AC² (NCERT)
हल:
∆ ABC समद्विबाहु त्रिभुज है।

∠C = 90°
AC = BC
∆ ABC में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा
AB² = AC² + BC²
AB² = AC² + AC² (∵ BC = AC)
AB² = 2AC²

प्रश्न 9.
एक ∆ ABC का ∠B समकोण है तथा भुजाओं AB और AC के मध्य बिन्दु क्रमशः L और M हैं तो सिद्ध कीजिए कि 4LC² = AB² + 4 BC²
हल:

∆ LCB में पाइथागोरस प्रमेय द्वारा,
LC² = LB² + BC²
दोनों और 4 से गुणा करने पर
4LC² = 4LB² + 4BC²
4LC² = (2LB)² + 4BC²
4LC² = (AB)² + 4BC² (∵ AB = 2LB)

प्रश्न 10.
एक समबाहु ∆ ABC में, BC के बिन्दु D पर मिलने वाला लम्ब AD डाला गया है। सिद्ध कीजिए कि AD² = 3BD²
हल:

∆ ABC समबाहु है
AB = BC = AC
∠A = ∠B = ∠C = 60°
∆ ADB तथा (UPBoardSolutions.com) ∆ADC में,
AB = AC (दिया है)
∠B = ∠C (60°)
∠ADB = ∠ADC (90°)
∴ ∆ ADB ≅ ∆ ADC
⇒ इसलिए BD = DC
⇒ BD = DC = [latex]\frac{1}{2}[/latex] BC
∆ ADB में पाइथागोरस प्रमेय द्वारा
AB² = AD² + BD²
BC² = AD² + BD²
(2BD)² = AD² + BD² (∵ BC = 2BD)
4 BD² = AD² + BD²
AD² = 4 BD² – BD²
AD² = 3 BD²

प्रश्न 11.
2a इकाई का एक समबाहु त्रिभुज है। इसकी प्रत्येक ऊँचाई ज्ञात कीजिए। (NCERT)
हलः

माना, ∆ ABC एक समबाहु त्रिभुज है।
AD ऊँचाई BC पर
BE ऊँचाई AC पर
CF ऊँचाई AB पर
दिया है, AB = BC = CA = 2a
हमें ऊँचाई AD, BE, CF ज्ञात करनी है।
∆ ADB तथा ∆ ADC में,
AB = AC (समबाहु A) (UPBoardSolutions.com)
∠B = LC (प्रत्येक 60°)
∠ ADB = ∠ ADC (प्रत्येक 90°)
∴ ∆ ADB ≅ ∆ ADC
इसलिए BD = DC
इसी प्रकार AE = EC और AF = FB

∆ ADB में पाइथागोरस प्रमेय द्वारा,
AB² = AD² + DB²
(2a)² = AD² + a²
AD² = 4a² – a² = 3a²
ऊँचाई AD = a[latex] \sqrt{{3}} [/latex] इकाई
इसी प्रकार BE = CF = a[latex] \sqrt{{3}} [/latex] इकाई

प्रश्न 12.
∆ ABC का ∆C समकोण है तथा भुजाओं CA और CB के मध्य बिन्दु क्रमशः P और Q हैं तो सिद्ध कीजिए कि 4(AQ² + BP²) = 5AB² (NCERT)
हलः

दिया है, ∆ ABC में,
∆C = 90°
P और Q क्रमशः CA और CB मध्य बिन्दु हैं
CP = PA
और CQ = QB
हमें सिद्ध करना है 4(AQ² + BP²) = 5AB²
∆AQC में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा,
AQ² = AC² + CQ
⇒ 4AQ² = 4AC² + 4CQ
4AQ² = 4AC² + (2CQ²
4AQ² = 4AC² + CB² (CB = 2CQ)
⇒ 4AQ² = 4AC² + CB²  …(1)
अब ∆ PCB में, पाइथागोरस प्रमेय द्वारा
BP² = PC² + CB²
⇒ 4BP² = 4PC² + 4CB²
⇒ 4BP² = (2PC)² + 4CB²
⇒ 4BP² = AC² +4CB² …(2) (2PC = AC)
समीकरण (1) तथा (2) को जोड़ने पर
4AQ² + 4BP² = 4AC² + CB² + AC² + 4CB²
4(AQ² + BP²) = 5(AC² + CB)
4(AQ² + BP²) = 5AB² (∵ AB² = AC² + BC²)

प्रश्न 13.
एक समद्विबाहु ∆ ABC में, AB = AC तथा BD, B से भुजा AC के लम्बवत् है तो सिद्ध कीजिए कि BD² – CD ² = 2 CD AD
हलः
दिया है, ∆ ABC में,
AB = AC

BD ⊥ AC
सिद्ध करना है
BD² – CD²2 = 2CD · AD
∆ ABD में पाइथागोरस प्रमेय द्वारा
AB² = AD² + BD²
⇒ BD² = AB² – AD
⇒ BD² = AC² – AD² (∵ AB = AC)
⇒ BD² = (CD + AD)² – (UPBoardSolutions.com) AD² (∴ AC = CD + AD)
⇒ BD² = CD² + AD² + 2CD × AD – AD² [(a + b)² = a² + b² +2ab]
⇒ BD² = CD² + 2CD – AD
⇒ BD² – CD² = 2CD·AD

प्रश्न 14.
एक ∆ ABC में, कोण B तथा कोण C न्यून कोण हैं। यदि AC तथा AB पर क्रमशः लम्ब BE तथा CF खींचे गये हैं तो सिद्ध कीजिए कि BC² = AB × BF + AC × CE
हल:
∆ ABC में दिया है
∠B और ∠C न्यून कोण हैं

BE ⊥ AC
CF ⊥ AB
हमें सिद्ध करना है, BC² = AB × BF + AC × CE
∆ ABC में ऊँचाई BE के साथ
चूँकि ∠C न्यून कोण है ।
इसलिए, AB² = BC² + AC² – 2AC · CE …(1)
अब ∆ ABC में ऊँचाई CF के साथ
चूँकि ∠B न्यून कोण है ।
इसलिए, AC² = BC² + AB² – 2AB · BF …(2)
समीकरण (1) और (2) को जोड़ने पर
AB² + AC² = BC² + BC² + AC² + AB² – 2AC · CE – 2AB · BF
-2BC² = -2(AB · BF + AC · CE)
⇒ BC² = AB × BF + AC × CE

प्रश्न 15.
एक समकोण त्रिभुज ABC में, ∠C समकोण है तथा AC = [latex] \sqrt{{3}} [/latex] · BC हो तो सिद्ध कीजिए कि, ∠ABC = 60°
हल:
∆ABC में दिया है, ∠C = 90°
AC = [latex] \sqrt{{3}} [/latex]BC

[latex]\frac{A C}{B C}=\sqrt{3}[/latex]
सिद्ध करना है (UPBoardSolutions.com) ∠ABC = 60°
∆ ABC में, tan B = [latex]\frac{A C}{B C}[/latex]
tan B = 13
tanB = tan60°
∴ B = 60°
अतः ∠ABC = 60°

प्रश्न 16.
∆ PQR में, QM ⊥ PR तथा PR² – PQ² = QR² है तो सिद्ध कीजिए कि QM² = PM × MR (NCERT)
हल:

∆ PQR में, दिया है QM ² PR
PR² – PQ² = QR²
हमें सिद्ध करना है-
QM² = PM × MR
चूँकि दिया है PR² – PQ² = QR²
⇒ (PM + MR)² – (QM² + PM²) = (QM² + MR²
(∵ PR = PM + MR, ∆PQM में PQ² = QM² + PM², ∆QMR में, QR² = QM² + MR²)
⇒ PM² + MR² + 2PM · MR (UPBoardSolutions.com) – QM² – PM² = QM² + MR 2
⇒ 2QM² = 2PM – MR
⇒ QM² = PM × MR

प्रश्न 17.
एक सीढ़ी का पाद एक दीवार से 6 मीटर की दूरी पर है तथा यह जमीन से 8 मीटर ऊँची एक खिड़की तक पहुंचती है। यदि सीढ़ी को इस तरह विस्थापित किया जाता है कि इसका पाद, तल से 8 मीटर दूर हो। इसकी टिप (शीर्ष) किस ऊँचाई तक पहुँचेगी।
हलः
हमें EB ज्ञात करना है।
∆ ABC में पाइथागोरस प्रमेय द्वारा,

AC² = AB² + BC²
AC² = 8² +6²
AC² = 64 + 36
AC² = 100 = (10)²
AC = 10 मीटर
चूँकि सीड़ी की लम्बाई = AC = DE = 10 मीटर
अब ∆ EBD में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा
ED² = EB² + BD²
10² = EB² + 82
100 – 64 = EB²
EB² = 36 = (6)²
EB = 6 मीटर

प्रश्न 18.
एक त्रिभुज की भुजाएं 5 सेमी, 12 सेमी तथा 13 सेमी हैं। 13 सेमी वाली भुजा पर उसके सम्मुख शीर्ष से डाले गये लम्ब की लम्बाई (दशमलव के एक अंक तक) ज्ञात कीजिए।
हल:

∆ABC में, AC² + BC² = 52 + 122
= 25 + 144 = 169
= (13)²
∴ AC² + BC² = AB²
∴ ∆ ABC समकोण त्रिभुज है और ∠C = 90°
∴ ∠A और ∠B न्यून कोण होंगे।
⇒ ∴ CD² = AD × BD
CD² = (AB – BD) × BD
CD² = AB · BD – BD²

प्रश्न 19.
एक समचतुर्भुज की प्रत्येक भुजा 10 सेमी है। यदि इसका एक विकर्ण 16 सेमी है तो दूसरे विकर्ण की लम्बाई ज्ञात कीजिए।
हलः
समचतुर्भुज ABCD में,
दिया है, AB = BC = CD = DA = 10 सेमी
विकर्ण AC = 16 सेमी
हमें विकर्ण BD ज्ञात करना है

समचतुर्भुज के (UPBoardSolutions.com) विकर्ण समकोण पर समद्विभाजित करते हैं।
∴ AE = EC = [latex]\frac{16}{2}[/latex] = 8 सेमी
और BE = ED
अब ∆ABE में पाइथागोरस प्रमेय द्वारा,
AB² = AE² + BE²
10² = 8² + BE²
100 – 64 = BE²
BE² = 36 = 6²
BE = 6 सेमी
∴ ED = BE = 6 सेमी
विकर्ण BD = BE + ED
= 6 + 6 = 12 सेमी

प्रश्न 20.
18 मीटर ऊँचे एक ऊर्ध्वाधर खम्भे के ऊपरी सिरे से एक तार का एक सिरा जुड़ा हुआ है तथा तार का दूसरा सिरा एक खूटे से जुड़ा हुआ है। खम्भे के आधार से खूटे को कितनी दूरी पर गाड़ा जाए कि तार तना रहे जबकि तार की लम्बाई 24 मीटर है। (NCERT)
हलः

दिया है, AB = 18 मीटर
AC = 24 मीटर
हमें खम्भे से खूटे की दूरी (BC) ज्ञात करनी है
∆ABC में पाइथागोरस (UPBoardSolutions.com) प्रमेय द्वारा
AC² = AB² + BC²
24² = 18² + BC²
BC² = 576 – 324
BC² = 252
BC = [latex] \sqrt{{125}} [/latex]
BC = 6[latex] \sqrt{{7}} [/latex] मीटर

प्रश्न 21.
एक त्रिभुज की भुजाएँ (a -1) सेमी०, 2[latex] \sqrt{{a}} [/latex] सेमी० तथा (a + 1) सेमी० हैं। तो ज्ञात कीजिए कि क्या त्रिभुज समकोण है ?
हलः
दिया है ∆ ABC में, AB = (a – 1) सेमी
BC = 2[latex] \sqrt{{a}} [/latex], CA = (a +1) सेमी
AB² + BC² = (a – 1)² + (2[latex] \sqrt{{a}} [/latex])²
= a² + 1 – 2a + 4a
= a² + 1 + 2a = (a + 1)²
AB² + BC² = (AC)
अतः पाइथागोरस प्रमेय द्वारा ∆ ABC (समकोण है)

प्रश्न 22.
एक समकोण त्रिभुज में, यदि कर्ण के समकोण से एक लम्ब खींचा गया है तो सिद्ध कीजिए कि लम्ब का वर्ग, कर्ण की दो रेखाखण्डों के गुणनफल बराबर है।
हलः
माना ABC समकोण त्रिभुज है

∠B = 90°
B से AC पर लम्ब BD खींचा गया। हमें सिद्ध करना है
BD² = CD × AD
∆ABC में, ∠B = 90° तब पाइथागोरस प्रमेय द्वारा
AC² = AB² + BC²
∆ ADB में, ∠D = 90° तब पाइथागोरस प्रमेय द्वारा
AB² = AD² + DB²
∆BDC में ∠D = 90° तब (UPBoardSolutions.com) पाइथागोरस प्रमेय द्वारा
BC² = BD² + DC²
समीकरण (2) और (3) को जोड़ने पर,
AB² + BC² = AD² + DB² + BD² + CD²
AC² = AD² + 2BD² + CD² [(1) के प्रयोग से]
(AD + DC)² = AD² + 2BD² + CD²
AD² + DC² + 2AD × CD = AD² + 2BD² + CD²
2AD × CD = 2BD²
⇒ BD² = AD × CD

प्रश्न 23.
एक त्रिभुज ABC है। जिसमें AB = AC तथा D, BC पर कोई बिन्दु है तो सिद्ध कीजिए कि AB² – AD² = BD·CD
हल:
∆ ABC में, दिया है AB = AC
तथा D,BC पर कोई बिन्दु है।
हमें सिद्ध करना है— AB² – AD² = BD·CD
AE ⊥ BC खींचा।

∆AEB तथा ∆AEC में,) AB = AC
AE = AE [उभयनिष्ठ]
∠B = ∠c [∵ AB = AC]
∴ ∆AEB ≅ ∆AEC
⇒ BE = CE
∵ ∆AED और ∆AEB, बिन्दु E (UPBoardSolutions.com) पर समकोण त्रिभुज हैं
इसलिए AD² = AE² + DE²
और AB² = AE² + BE²
AB² – AD² = BE² – DE²
AB² – AD² = (DE + DE) (BE – DE)
AB² – AD² = (CE + DE) (BE – DE)
AB² – AD² = CD × BD
इस प्रकार AB² – AD² = BD × CD

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.2 समान्तर श्रेणी

Ex 5.2 Arithmetic Progressions अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
1 से 100 तक सभी प्राकृतिक संख्याओं (UPBoardSolutions.com) का योग ज्ञात कीजिए।
हल:
1 से 100 तक सभी प्राकृतिक संख्याओं से बनी समान्तर श्रेणी 1, 2, 3, 4…..100
प्रथम पद a = 1, सार्वअन्तर d = 2 – 1 = 1 तथा n = 100
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
S₁₀₀ = [latex]\frac{100}{2}[/latex][2 × 1 + (100 – 1) × 1]
= 50[2 + 99] = 50 × 101
= 5050

प्रश्न 2.
प्रथम 200 प्राकृतिक संख्याओं का योग ज्ञात कीजिए।
हलः
प्रथम 200 प्राकृतिक संख्यायें : 1, 2, 3, 4,…. 200
a = 1, d = 2 – 1 = 1, n = 200
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
S₁₀₀ = [latex]\frac{200}{2}[/latex][2 × 1 + (200 – 1) × 1]
= 100[2 + 199]
= 100 × 201
= 20100

प्रश्न 3.
100 से छोटी सभी सम प्राकृतिक संख्याओं का योग ज्ञात कीजिए।
हलः
100 से छोटी सभी सम प्राकृतिक (UPBoardSolutions.com) संख्यायें निम्न है।
2, 4, 6, 8….98
a = 2,d = 4 – 2 = 2 तथा अन्तिम पद l = 98, n = ?
l = a + (n – 1)d
98 = 2 + (n – 1) × 2
98 = 2 + 2n – 2
98 = 2n या n = [latex]\frac{98}{2}[/latex] = 49

प्रश्न 4.
तीन अंकों की सभी संख्याओं का योग ज्ञात कीजिए जो 11 से विभाज्य है।
हल:
तीन अंकों की सभी संख्यायें जो 11 से विभाज्य है
110, 121, 132,…… 990
a = 110, d = 121 – 110 = 11 तथा अन्तिम पद l = 990
माना श्रेणी में पदों की संख्या = n
तब l = a + (n – 1)d
या 990 = 110 + (n – 1) × 11
990 = 110 + 11n – 11
या 990 = 99 + 11n
990 – 99 = 11n
11n = 891
n = [latex]\frac{891}{11}[/latex] = 81

प्रश्न 5.
सभी दो अंकों वाली विषम धनात्मक संख्याओं का योग ज्ञात कीजिए।
हलः
सभी दो अंकों वाली विषम संख्यायें .
11, 13, 15, 17….99
a = 11, d = 13 – 11 = 2 तथा l = 99
माना श्रेणी में पदों की संख्या n है।
∴ l = a + (n – 1)d या 99 = 11 + (n – 1) × 2
99 = 11 + 2n – 2 या 99 = 9 + 2n
99 – 9= 2n या 2n = 90 या n = [latex]\frac{90}{2}[/latex] = 45

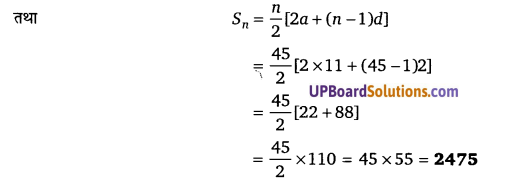
प्रश्न 6.
तीन अंकों वाली सभी संख्याओं (UPBoardSolutions.com) का योग ज्ञात कीजिए जो 7 की गुणज है।
हल:
तीन अंकों की सभी संख्याये जो 7 की गुणज है।
105, 112, 119,….994
तब a = 105, d = 112 – 105 = 7 तथा l = 994
l = a + (n – 1)d या 994 = 105 + (n – 1) × 7
994 = 105 + 7n – 7 या 994 = 98 + 7n

प्रश्न 7.
तीन अंकों की सभी प्राकृतिक संख्याओं का योगफल ज्ञात कीजिए जो 13 से विभाज्य हैं।
हल:
तीन अंकों की सभी संख्याये जो 13 से विभाज्य है : 104, 117, 130,… 988
अब a = 104, d = 117 – 104 = 13, l = 988, n = ?
l = a + (n – 1)d या 988 = 104 + (n – 1) × 13
988 = 104 + 13n – 13 या 988 = 91 – 13n
988 – 91 = 13n या 13n = 897 या n = [latex]\frac{897}{13}[/latex] = 69

प्रश्न 8.
निम्न का योग ज्ञात कीजिए :
(i) 8 के प्रथम 15 गुणजों का (NCERT)
(ii) प्रथम 40 धन पूर्णांकों का जो विभाजित है
(a) 3
(b) 5
(c) 6 से (NCERT)
हलः
(i) 8 के प्रथम 15 गुणज निम्नलिखित है।
8, 16, 24…..120
तब a = 8, d = 16 – 8 = 8 तथा l = 120
और n = 5

(ii) (a) प्रथम 40 धनपूर्णांक जो 3 से विभाजित है—
3, 6, 9…..120
∴ a = 3, d = 6 – 3 = 3 तथा l = 120, n = 40

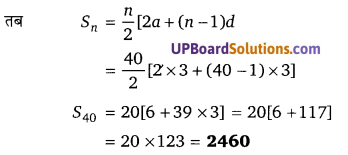
(b) प्रथम 40 धन पूर्णांक जो 5 से विभाजित हैं-
5, 10, 15,…. 200
तब a = 5, d = 10 – 5 = 5 तथा n = 40

(c) प्रथम 40 धन पूर्णांक जो 6 से विभाजित हैं—
6, 12, 18,….240
तब, a = 6,d = 12 – 6 = 6 तथा n = 40

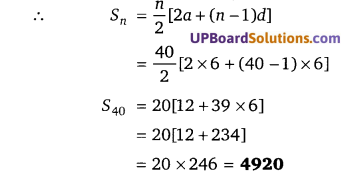
प्रश्न 9.
निम्न में प्रथम n पदों का (UPBoardSolutions.com) योगफल ज्ञात कीजिए :
(i) प्राकृतिक संख्याएँ
(ii) विषम संख्याएँ
(iii) सम संख्याएँ
हल:
(i) प्राकृतिक संख्याएँ 1, 2, 3, 4…. n
a = 1, d = 2 – 1 = 1

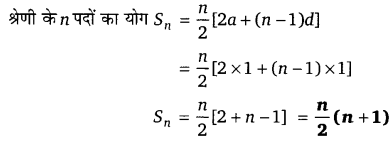
(ii) विषम संख्यायें 1, 3, 5, 7….n
a = 1, d = 3 – 1 = 2

(iii) सम संख्यायें 2, 4, 6,……n
a = 2, d = 4 – 2 = 2

प्रश्न 10.
(i) प्रथम 100 सम प्राकृतिक संख्याओं का योग ज्ञात कीजिए, जो 5 से विभाज्य हैं।
(ii) 1 तथा 100 के बीच की सभी प्राकृतिक संख्याओं का योग ज्ञात कीजिए, जो3 से विभाज्य हैं।
(iii) 100 तथा 1000 के बीच की सभी (UPBoardSolutions.com) प्राकृतिक संख्याओं का योग ज्ञात कीजिए जो 5 से विभाज्य
(iv) 50 तथा 500 के बीच के सभी पूर्णाकों का योग ज्ञात कीजिए, जो 7 से विभाज्य हैं।
(v) 100 तथा 800 के बीच की सभी प्राकृतिक संख्याओं का योग ज्ञात कीजिए, जो 7 से विभाज्य
(vi) 1 तथा 100 की बीच की सभी प्राकृतिक संख्याओं का योग ज्ञात कीजिए, जो 5 से विभाज्य नहीं ैं।
हल:
(i) प्रथम 100 सम प्राकृतिक संख्यायें जो 5 से विभाज्य है।
10, 20, 30…..
a = 10, d = 20 – 10, n = 100
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]= [latex]\frac{100}{2}[/latex] [2 × 10 + (100 – 1) × 10]
S₁₀₀ = 50[20 + 99 × 10] = 50[20 + 990] = 50 × 1010 = 50500

(ii) 1 तथा 100 के बीच सभी प्राकृतिक संख्यायें जो 3 से विभाज्य हैं।
3, 6, 9, 12,…..99
a = 3,d = 6 – 3 = 3 तथा अन्तिम पद l = 99
तब l = a + (n – 1)d या 99 = 3 + (n – 1) × 3
99 = 3 + 3n – 3 या 99 = 3n या n = [latex]\frac{99}{3}[/latex] = 33

(iii) 100 तथा 1000 के बीच सभी प्राकृतिक संख्यायें जो 5 से विभाज्य है।
105, 110, 115, …..995
a = 105, d = 110 – 105 = 5, तथा l = 995
तब, l = a + (n – 1)d या 995 = 105 + (n – 1) × 5
995 = 105 + 5n – 5 या 995 = 100 + 5n
995 – 100 = 5n या 5n = 895 या n = [latex]\frac{895}{5}[/latex] = 179

(iv) 50 तथा 500 के बीच के सभी पूर्णांक, जो 7 से विभाज्य हैं :
56, 63, 70,…..497
a = 56,d = 63 – 56 = 7 तथा l = 497
तब, l = a + (n – 1)d या 497 = 56 + (n – 1) × 7
497 = 56 + 7n – 7 या 497 = 49 + 7n
497 – 49 = 7n या 7n = 448 या n = [latex]\frac{448}{7}[/latex] = 64

= 32[112 + 63 × 7]
= 32[112 + 445] = 32 × 553 = 17696

(v) 100 तथा 800 के बीच सभी प्राकृतिक संख्यायें, जो 7 से विभाज्य हैं :
105, 112, 119,……798
a = 105, d = 112 – 105 = 7 तथा l = 798
तब, l = a + (n – 1)d या 798 = 105 + (n – 1) × 7
798 = 105 + 7n – 7 या 798 = 7n + 98
798 – 98 = 7n या 7n = 700 या (UPBoardSolutions.com) n = [latex]\frac{700}{7}[/latex] = 100
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
= [latex]\frac{100}{2}[/latex][2 × 105 + (100 – 1) × 7]
S₁₀₀ = 50[210 + 99 × 7]
= 50[210 + 693] = 50 × 903 = 45150

(vi) 1 तथा 100 के बीच सभी प्राकृतिक संख्यायें
2, 3, 4, 5, 6,……99
तब a = 2, d = 3 – 2 = 1 तथा l = 99
l = a + (n – 1)d या 99 = 2 + (n – 1) × 1 या 99 = 2 + n – l
99 = n + 1 या n = 99 – 1 = 98
तथा, 1 और 100 के बीच सभी प्राकृतिक संख्याओं का योग
S_n =[latex]\frac{n}{2}[/latex] [2a + (n – 1)d]
= [latex]\frac{98}{2}[/latex][2 × 2 + (98 – 1) × 1]
= 49[4 + 97] = 49 × 101 = 4949
अब वें संख्यायें, जो 5 से विभाज्य है। उनका योग :
5, 10, 15,…..95
a = 5, d = 10 – 5 = 5 तथा l = 95
तब l = a + (n – 1)d
या 95 = 5 + (n – 1) × 5 या 95 = 5 + 5n – 5
95 = 5n या n = [latex]\frac{95}{5}[/latex] = 19
तथा S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
= [latex]\frac{19}{2}[/latex][2 × 5 + (19 – 1) × 5]
= [latex]\frac{19}{2}[/latex] [10+ 18 × 5] = [latex]\frac{19}{2}[/latex][10 + 90]
= [latex]\frac{19}{2}[/latex] × 100 = 19 × 50 = 950
अतः 1 तथा 100 के बीच उन सभी प्राकृतिक संख्याओं का योग जो 5 से विभाज्य नहीं हैं
= 4949 – 950 = 3999

Ex 5.2 Arithmetic Progressions लघु उत्तरीय प्रश्न – I (Short Answer Type Questions – I)

प्रश्न 11.
समान्तर श्रेणी 10, 6, 2… के प्रथम 16 पदों का योग ज्ञात कीजिए।
हलः
समान्तर श्रेणी 10, 6, 2…. के प्रथम (UPBoardSolutions.com) 16 पदों का योग
a = 10, d = 6 – 10 = – 4 तथा n = 16
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
= [latex]\frac{16}{2}[/latex][2 × 10 + (16 – 1) × – 4]
S₁₆ = 8[20 + 15 × – 4]
= 8[20 – 60] = 8 × – 40 = – 320

प्रश्न 12.
एक समान्तर श्रेणी 1, 3, 5, 7, 9… के प्रथम 20 पदों का योग ज्ञात कीजिए।
हलः
समान्तर श्रेणी 1, 3, 5, 7, 9…. के प्रथम 20 पदों का योग
यहाँ, प्रथम पद a = 1,
सार्वअन्तर d = 3 – 1 = 2 तथा n = 20
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
= [latex]\frac{20}{2}[/latex][2 × 1 + (20 – 1) × 2]
S₂₀ = 10[2 + 19 × 2] = 10[2 + 38]
= 10 × 40 = 400

प्रश्न 13.
समान्तर श्रेणी 5, 8, 11, 14… के प्रथम 24 पदों का योग ज्ञात कीजिए।
हलः
समान्तर श्रेणी 5, 8, 11, 14… के प्रथम 24 पदों का योग
यहाँ, a = 5, d = 8 – 5 = 3, n = 24
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
S₂₄ = [2 × 5 + (24 – 1) × 3]
= 12[10 + 23 × 3] = 12[10 + 69]
= 12 × 79 = 948

प्रश्न 14.
5 + 13 + 21 + … + 181 का योग ज्ञात कीजिए।
हलः
5 + 13 + 21 + ….. + 181 का योग
a = 5, d = 13 – 5 = 8 तथा l = 181, n = ?
अब l = a + (n – 1)d या 181 = 5 + (n – 1) × 8
181 = 5 + 8n – 8 या 181 = 8n – 3
181 + 3 =8n या 8n = 184 या (UPBoardSolutions.com) n = [latex]\frac{184}{8}[/latex] = 23
तथा S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
= [latex]\frac{23}{2}[/latex][ 2 × 5 + (23 – 1) × 8]
S₂₃ = [latex]\frac{23}{2}[/latex] [10 + 22 × 8]
= [latex]\frac{23}{2}[/latex][10 + 176]
= [latex]\frac{23}{2}[/latex] × 186 = 23 × 93 = 2139

प्रश्न 15.
5 + 9 + 13 + … + 81 का योग ज्ञात कीजिए।
हलः
5 + 9 + 13 + …. + 81 का योग
a = 5, d = 9 – 5 = 4,1 = 81, n= ? तथा S_n = ?
तब l = a + (n – 1)d या 81 = 5 + (n – 1) × 4
81 = 5 + 4n – 4 या 81 = 1 + 4n
81 – 1 = 4n या 4n = 80 या n = [latex]\frac{80}{4}[/latex] = 20
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
S₂₀ = [latex]\frac{20}{2}[/latex][2 × 5 + (20 – 1)4]
तथा S₂₀ = 10[10 + 19 × 4]
= 10[10 + 76] = 10 × 86 = 860

प्रश्न 16.
18 + 15, + 13 + …. ( – 49[latex]\frac{1}{2}[/latex]) का योग ज्ञात कीजिए।
हलः

प्रश्न 17.
श्रेणी 18,16,14… के कितने (UPBoardSolutions.com) पदों का योग शून्य होगा?
हलः
श्रेणी 18, 16, 14….
माना श्रेणी के n पदों का योग शून्य है।
अर्थात् S_n = 0 तथा a = 18, d = 16 – 18 = – 2
[latex]\frac{n}{2}[/latex][2a + (n – 1)d] = 0
[latex]\frac{n}{2}[/latex][2 × 18 + (n – 1) × – 2] = 0
n[36 – 2n + 2] = 0
36 – 2n + 2 = 0
38 = 2n या n = [latex]\frac{38}{2}[/latex] = 19
अत : n = 19

प्रश्न 18.
निम्नलिखित श्रेणियों का योगफल ज्ञात कीजिए :
(i) 1, 3, 5, 7… 12 पदों तक।
(ii) 0.7 + 0.71 + 0.72 + … 100 पदों तक।
(iii) a + b, a – b, a – 3b…22 पदों तक।
(iv) (a – b)² + (a² + b²) + (a² + b²) + … + [(a + b)² + 6(ab)]
हल:
(i) 1, 3, 5, 7,…. 12 पदों तक योग ।
a = 1, d = 3 – 1 = 2, n = 12
तथा S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
S₁₂ = [latex]\frac{12}{2}[/latex][2 × 1 + (12 – 1) × 2]
= 6[2 + 11 × 2] = 6[2 + 22]
= 6 × 24 = 144

(ii) 0.7 + 0.71 + 0.72 + ….100 पदों तक
a = 0.7, d = 0.71 – 0.7 = 0.01, n = 100
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
= [latex]\frac{100}{2}[/latex] [2 × 0.7 + (100 – 1) × 0.01]
S₁₀₀ = 50[1.4 + 99 × 0.01]
= 50[1.4 + 0.99]
= 50 × 2.39
= 119.5

(iii) a + b, a – b, a – 3b,…. 22 पदों की (UPBoardSolutions.com) संख्या
a = a + b, d = a – b – a – b = – 2b, n = 22
S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d] = [latex]\frac{22}{2}[/latex] [2(a + b) + (22 – 1) × – 2b]
S₂₂ = 11[2a + 2b – 42b]
= 11[2a – 40b]
S₂₂ = (22a – 440b)

(iv) (a – b)² + (a² + b²) + (a + b)² + …. + [(a + b)² + 6(ab)]
a = (a – b)², d = (a² + b²) – (a – b)² = (a² + b²) – (a² + b² – 2ab)
a = a² + b² – 2ab, d = a² + b² – a² – b² + 2ab = 2ab
तथा l = (a + b)² + 6(ab) = a² + b² + 2ab + 6ab = a² + b² + 8ab
माना, श्रेणी में पदों की संख्या = n
तब l = a + (n – 1)d
a² + b² + 8ab = a² + b² – 2ab + (n – 1) × 2ab
a² + b² + 8ab = a² + b² – 2ab + 2abn – 2ab
a² + b² + 8ab – a² – b² + 4ab = 2abn
[latex]\frac{12ab}{2ab}[/latex] = n या n = 6
तथा श्रेणी के n पदों का योग S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
S₆ = [latex]\frac{6}{2}[/latex][2(a² + b² – 2ab) + (6 – 1) × 2ab]
3[2a² + 2b² – 4ab + 10ab]
= 3[2a² + 2b² + 6ab]
=3 × 2[a² + b² + 3ab]
अत : S₆ = 6(a² + b² + 3ab)

प्रश्न 19.
निम्नलिखित समीकरणों (UPBoardSolutions.com) को हल कीजिए :
(i) 1 + 6 + 11 + 16 + … + x = 148
(ii) 2 + 5 + 8 + 11 + … + x = 345
हलः
(i) 1 + 6 + 11 + 16 + ….. + x = 118
a = 1, d = 6 – 1 = 5 तथा l = x
माना, समान्तर श्रेणी में पदों की संख्या = n
तब l = a + (n – 1)d
x = 1 + (n – 1) × 5
x = 1 + 5n – 5
x = 5n – 4

x + x² + 4 + 4x = 1480
x² + 5x + 4 – 1480 = 0
x² + 5x – 1476 = 0
x² + 41x – 36x – 1476 = 0
x (x + 41) – 36(x + 41) = 0
(x + 41)(x – 36) = 0
x + 41 = 0 तथा x – 36 = 0
x = – 41 (अमान्य), x = 36
अतः x = 36

(ii) 2 + 5 + 8 + 11 + …. + x = 345
a= 2,d = 5 – 2 = 3 तथा l = x
माना श्रेणी में पदों की (UPBoardSolutions.com) संख्या = n
तब l = a + (n – 1)d
x = 2 + (n – 1) × 3
x = 2 + 3n – 3
x = 3n – 1 या x + 1 = 3n या n = [latex]\frac{x+1}{3}[/latex]
तथा S_n = 345
[latex]\frac{n}{2}[/latex](a + l) = 345
[latex]\left(\frac{x+1}{6}\right)[/latex](2 + x ) = 345
2x + x² + 2 + x = 345 × 6
x² + 3x + 2 = 2070
x² + 3x + 2 – 2070 = 0
x² + 3x – 2068 = 0
x² + 47x – 44x – 2068 = 0
x(x + 47) – 44(x + 47) = 0
(x + 47)(x – 44) = 0
x + 47 = 0 तथा x – 44 = 0
x = – 47 (अमान्य), x = 44
x = 44

प्रश्न 20.
एक समान्तर श्रेणी के 15 पदों का योग ज्ञात कीजिए (UPBoardSolutions.com) जिसका पहला पद तथा अन्तिम पद क्रमशः 5 तथा 75 हैं।
हलः
पहला पद a = 5, अन्तिम पद l = 75, n = 15

प्रश्न 21.
तीन संख्याएँ, एक समान्तर श्रेणी में हैं जिनका योग 24 है तथा उनके वर्गों का योग 200 है। संख्याएँ ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी की तीन संख्याये (a – d), a , (a + d) हैं।
प्रश्नानुसार, I – शर्त a – d + a + a + d = 24
3a = 24 या a = [latex]\frac{24}{2}[/latex] = 8
तथा II – शर्त (a – d)² + a² + (a + d) = 200
a = 8 रखने पर
(8 – d)²2 + (8)² + (8 + d)² = 200
64 + d² – 16d + 64 + 64 + d² + 16d = 200
192 + 2d² = 200
2d² = 200 – 192
d² = [latex]\frac{8}{2}[/latex] या d = [latex] \sqrt{{4}} [/latex] = 2
अतः तीनों संख्यायें a – d, a, a + d
= 8 – 2, 8, 8 + 2
= 6, 8, 10

प्रश्न 22.
यदि एक समान्तर श्रेणी के प्रथम n पदों (UPBoardSolutions.com) का योग दिया है, S_n = (3n² – n) तो ज्ञात कीजिए।
(i) n वाँ पद
(ii) इसका पहला पद
(iii) सार्वअन्तर
हलः
दिया है, S_n = 3n² – n
n = n – 1 रखने पर
S_n-1 = 3(n – 1)² – (n – 1) = 3(n² + 1 – 2n) – n + 1
= 3n² + 3 – 6n – n + 1 = 3n² – 7n + 4
(i) T_n = S_n – S_n-1 = (3n² – n) – (3n² – 7n + 4)
= 3n² – n – 3n² + 7n – 4 = 6n – 4
अतः समान्तर श्रेणी का n वाँ पद = (6n – 4)

(ii) T_n = 6n – 4
n = 1, 2, 3…. रखने पर
T₁ = 6 × 1 – 4 = 6 – 4 = 2
T₂ = 6 × 2 – 4 = 12 – 4 = 8
T₃ = 6 × 3 – 4 = 18 – 4 = 14
तब, समान्तर श्रेणी 2, 8, 14..
अतः श्रेणी का पहला पद a = 2

(iii) सार्वअन्तर d = 8 – 2 = 6

प्रश्न 23.
एक समान्तर श्रेणी के प्रथम n पदों का योग (UPBoardSolutions.com) [latex]\frac{1}{2}[/latex](3n² + 7n) है, तब इसका n वाँ पद ज्ञात कीजिए तथा इसका 20 वाँ पद भी लिखिए।
हलः
समान्तर श्रेणी के प्रथम n पदों का योग S_n = [latex]\frac{1}{2}[/latex](3n² + 7n)

Ex 5.2 Arithmetic Progressions लघु उत्तरीय प्रश्न – II (Short Answer Type Questions)

प्रश्न 24.
एक समान्तर श्रेणी के प्रथम n पदों का योग 4n² + 2n है तो समान्तर श्रेणी का n वाँ पद ज्ञात कीजिए।
हलः
दिया है S_n = 4n² + 2n
तब n = (n – 1) रखने पर
S_n-1 = 4(n – 1)² + 2(n – 1)
= 4(n² + 1 – 2n) + 2n – 2
= 4n² + 4 – 8n + 2n – 2
= 4n² – 6n + 2
तो समान्तर श्रेणी का n वाँ पद
T_n = S_n – S_n-1 = (4n² + 2n) – (4n² – 6n + 2)
T_n = 4n² + 2n – 4n² + 6n – 2 = (8n – 2)

प्रश्न 25.
एक समान्तर श्रेणी के प्रथम n पदों का (UPBoardSolutions.com) योग 5n² + 3n है यदि इसका n वाँ पद 168 है तो n का मान ज्ञात कीजिए।
हलः
समान्तर श्रेणी के प्रथम n पदों का योग S_n = 5n² + 3n
तब, माना = 5n² + 3n तथा t_n = 168
n = (n – 1) रखने पर
S_n-1 = 5(n – 1)² + 3(n – 1) = 5(n² + 1 – 2n) + 3n – 3
S_n-1 = 5n² + 5 – 10n + 3n – 3 = 5n² – 7n + 2
तब, T_n = S_n – S_n-1
T_n = (5n² + 3n) – (5n² – 7n + 2)
T_n = 5n² + 3n – 5n² + 7n – 2
T_n = 10n – 2
168 = 10n – 2 या 168 + 2 = 10n
10n = 170 या n = [latex]\frac{170}{10}[/latex]
n = 17

प्रश्न 26.
यदि एक समान्तर श्रेणी के n पदों का योग (3n² + 4n) है। इसका n वाँ पद ज्ञात कीजिए तथा समान्तर श्रेणी भी ज्ञात कीजिए।
हलः
माना, S_n = 3n² + 4n
तब, n = (n – 1) रखने पर
S_n-1 = 3(n – 1) + 4(n – 1) = 3(n² + 1 – 2n) + 4n – 4
S_n-1 = 3n² + 3 – 6n + 4n – 4 = 3n² – 2n – 1
समान्तर श्रेणी का n वाँ पद T_n = S_n – S_n-1 से
T_n = (3n² + 4n) – (3n² – 2n – 1)
= 3n² + 4n – 3n² + 2n – 1
T_n = (6n + 1)
अब n = 1, 2, 3….. रखने पर,
T₁ = 6 × 1 + 1 = 6 + 1 = 7
T₂ = 6 × 2 + 1 = 12 + 1 = 13
T₃ = 6 × 3 + 1 = 18 + 1 = 19
अतः श्रेणी का n वाँ पद = (6n + 1)
तथा समान्तर श्रेणी 7,13,19,

प्रश्न 27.
एक समान्तर श्रेणी के प्रथम 25 पदों का (UPBoardSolutions.com) योग ज्ञात कीजिए जिसका n वाँ पद a_n = 7 – 3n है।
हलः
समान्तर श्रेणी का n वाँ पद a_n = 7 – 3n
n = 1, 2, 3…. रखने पर
a₁ = 7 – 3 × 1 = 7 – 3 = 4
a₂ = 7 – 3 × 2 = 7 – 6 = 1
a₃ = 7 – 3 × 3 = 7 – 9 = – 2
समान्तर श्रेणी 4, 1, – 2….
तब a = 4, d = 1 – 4 = – 3 तथा n = 25

प्रश्न 28.
एक समान्तर श्रेणी का n वाँ पद (- 4n + 15) दिया है। इस समान्तर श्रेणी के प्रथम 20 पदों का योग ज्ञात कीजिए।
हलः
समान्तर श्रेणी का n वाँ पद T_n = – 4n + 15 दिया है।
तब, n = 1, 2, 3…. रखने पर
T₁ = – 4 × 1 + 15 = – 4 + 15 = 11
T₂ = – 4 × 2 + 15 = – 8 + 15 = 7
T₃ = – 4 × 3 + 15 = – 12 + 15 = 3
अतः समान्तर श्रेणी, 11,7,3….
तब, a= 11, d = 7 – 11 = – 4 तथा n = 20

प्रश्न 29.
एक समान्तर श्रेणी के n पदों का योग S_n = 3n² + 5n दिया है। इसका कौन – सा पद 164 है?
हलः
माना, समान्तर श्रेणी का n वाँ पद 164 है। अर्थात् T_n = 164 तब, .
S_n = 3n² + 5n
n = n – 1 रखने पर
S_n-1 = 3(n – 1)² + 5(n – 1)
= 3(n² + 1 – 2n) + 5n – 5
S_n-1 = 3n² + 3 – 6n + 5n – 5 = 3n² – n – 2
∴ T_n = S_n – S_n-1 = 2n² + 5n – (3n² – n – 2)
T_n = 3n² + 5n – 3n² + n + 2 = 6n + 2
∵ T_n = 164
164 = 6n + 2
164 – 2 = 6n
या 162 = 6n
या n = [latex]\frac{162}{6}[/latex] ⇒ n = 27
n = 27 वाँ पद

प्रश्न 30.
यदि प्रथम n सम प्राकृतिक संख्याओं का (UPBoardSolutions.com) योग, प्रथम n विषम संख्याओं के योग के k गुने के बराबर है। तब k ज्ञात कीजिए।
हलः
प्रथम n सम – प्राकृतिक संख्याये = 2, 4, 6,….n
तब a = 2, d = 4 – 2 = 2, n = n

प्रश्न 31.
यदि एक समान्तर श्रेणी का पहला पद, दूसरा तथा अन्तिम पद क्रमशः a, b तथा 2a हैं। इसका योग ज्ञात कीजिए।
हलः
समान्तर श्रेणी का पहला पद = a तथा दूसरा पद = b
और अन्तिम पद l = 2a तब d = b – a
∵ l = a + (n – 1)d
2a = a + (n – 1)(b – a)
2a = a + nb – na – b + a
2a = 2a – b + nb – na
2a – 2a + b= n(b – a)
b = n(b – a) या n = [latex]\frac{b}{b-a}[/latex]

प्रश्न 32.
समान्तर श्रेणी के प्रथम 21 पदों का योग ज्ञात कीजिए जिसका दूसरा पद 8 है तथा चौथा पद 14 है।
हलः
माना, समान्तर श्रेणी का प्रथम पद (UPBoardSolutions.com) a तथा सार्वअन्तर d है।
प्रश्नानुसार, दूसरा पद = 8
a + d = 8 …(1)
तथा चौथा पद = 14

प्रश्न 33.
एक समान्तर श्रेणी के प्रथम 20 पदों का योग ज्ञात कीजिए, जिसमें 3 वाँ पद 7 है तथा 7 वाँ पद, तीसरे – पद के 3 गुने से 2 अधिक है।
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब, समान्तर श्रेणी का 3 वाँ पद 7
a + 2d = 7 …(1)
समान्तर श्रेणी का 7 वाँ पद = a + 6d
प्रश्नानुसार, a + 6d = 3(a + 2d) + 2
a + 6d = 3a + 6d + 2
a + 6d – 3a – 6d = 2
– 2a = 2 या – a = [latex]\frac{2}{2}[/latex] या a = – 1
a का मान समीकरण (1) में रखने पर,
– 1 + 2d = 7 या 2d = 7 + 1 या d = [latex]\frac{2}{2}[/latex] = 4
a = – 1, d = 4 तथा n = 20

प्रश्न 34.
यदि एक समान्तर श्रेणी के प्रथम n पदों (UPBoardSolutions.com) का योग S_n दिया गया है, S_n = (3n² – 4n), तब इसका n वाँ पद ज्ञात कीजिए।
हलः
दिया गया है, S_n = (3n² – 4n)
n = n – 1 रखने पर
S_n-1 = 3(n – 1)² – 4(n – 1) = 3(n² + 1 – 2n) – 4n + 4
S_n-1 = 3n² + 3 – 6n – 4n + 4 = 3n² – 10n + 7
अतः श्रेणी का n वाँ पद T_n = S_n – S_n-1
= 3n² – 4n – (3n² – 10n + 7)
= 3n² – 4n – 3n² + 10n – 7
= 6n – 7

प्रश्न 35.
एक समान्तर श्रेणी के प्रथम 8 पदों का योग 100 है तथा इसके प्रथम 19 पदों का योग 551 है तो समान्तर श्रेणी ज्ञात कीजिए।
हल:
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब प्रश्नानुसार, श्रेणी के प्रथम 8 पदों का योग = 100

प्रश्न 36.
समान्तर श्रेणी के 51 पदों का योग ज्ञात कीजिए जिसका दूसरा पद 2 है तथा 4 वाँ पद 8 है।
हलः
माना समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब, प्रश्नानुसार, दूसरा पद = 2
a + d = 2 …(1)
तथा 4 वाँ पद = 8

d का मान समीकरण (1) में रखने पर
a + 3 = 2 या a = 2 – 3 = – 1
a = – 1, d = 3, n = 51

प्रश्न 37.
यदि समान्तर श्रेणी का 5 वाँ पद तथा 12 वाँ पद क्रमशः (UPBoardSolutions.com) – 4 तथा – 18 हैं तो समान्तर श्रेणी के प्रथम 20 पदों का योग ज्ञात कीजिए।
हलः
माना समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब प्रश्नानुसार, 5 वाँ पद = – 4
a + 4d = – 4 …..(1)
तथा 12 वाँ पद = – 18 ….(2)

d का मान समीकरण (1) में रखने पर
a + 4 × – 2 = – 4
a – 8 = – 4
a = – 4 + 8 = 4
a = 4, d = –2, n = 20

प्रश्न 38.
एक समान्तर श्रेणी में पहला पद 22 है,n वाँ पद (UPBoardSolutions.com) – 11 है तथा प्रथम n पदों का योग 66 है। n तथा सार्वअन्तर d ज्ञात कीजिए।
हलः
समान्तर श्रेणी का पहला पद a = 22
प्रश्नानुसार, n वाँ पद = – 11
a + (n – 1)d = – 11
22 + nd – d = – 11
nd – d = – 11 – 22
nd – d= – 33 …(1)
तथा प्रथम n पदों का योग = 66
[latex]\frac{n}{6}[/latex][2a + (n – 1)d] = 66
n[2 × 22 + nd – d] = 132
समीकरण (1) से,
n[44 + ( – 33)] = 132
n[44 – 33] = 132
11n= 132
या n = [latex]\frac{132}{11}[/latex] = 12
n का मान समीकरण (1) में रखने पर, (UPBoardSolutions.com)
12d – d = – 33
या 11d = – 33
d= [latex]\frac{-33}{11}[/latex] = – 3
अतः n = 12, d= – 3

प्रश्न 39.
यदि एक समान्तर श्रेणी का 10 वाँ पद 21 है तथा इसके प्रथम 10 पदों का योग 120 है तो इसका n वाँ पद ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
प्रश्नानुसार, 10 वाँ पद 21
a + 9d = 21 …(1)
तथा प्रथम 10 पदों का योग = 120
[latex]\frac{10}{2}[/latex][2a + (10 – 1)d] = 120
5[2a + 9d] = 120
[2a + 9d] = [latex]\frac{120}{5}[/latex]

a = 3 a का मान समीकरण (1) में रखने पर
3 + 9d = 21
या 9d = 21 – 3 या d = [latex]\frac{19}{2}[/latex] = 2
अतः श्रेणी का n वाँ पद = a + (n – 1)d
= 3 + (n – 1) × 2
= 3 + 2n – 2 = (2n + 1)

प्रश्न 40.
एक समान्तर श्रेणी के प्रथम 7 पदों का योग (UPBoardSolutions.com) 63 है तथा इसके अगले 7 पदों का योग 161 है तो इस समान्तर श्रेणी का 28 वाँ पद ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब, प्रश्नानुसार, प्रथम 7 पदों का योग = 63
a + a + d + a + 2d + a + 3d + a + 4d + a + 5d + a + 6d = 63
7a + 21d = 63
a + 3d = 9 …(1)
तथा इसके अगले 7 पदों का योग = 161
a + 7d + a + 8d + a + 9d + a + 10d + a + 11d + a + 12d + a + 13d = 161
7a + 70d = 161

d का मान समीकरण (1) में रखने पर
a + 3 × 2 = 9
या a + 6 = 9
या a = 9 – 6 = 3
a = 3 तथा d = 2
तो समान्तर श्रेणी का 28 वाँ पद = a + 27d
= 3 + 27 × 2 = 3 + 54 = 57

प्रश्न 41.
एक समान्तर श्रेणी के प्रथम सात पदों का योग (UPBoardSolutions.com) 182 है। यदि इसका 4 वाँ पद तथा 17 वाँ पद 1 : 5 के अनुपात में है तो समान्तर श्रेणी ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब, प्रश्नानुसार, समान्तर श्रेणी के प्रथम 7 पदों का योग = 182
∴ a + a + d + a + 2d + a + 3d + a + 4d + a + 5d + a + 6d = 182
7a + 21d = 182
a + 3d = 26 …(1)

d का मान समीकरण (1) में रखने पर
a + 3 × 8 = 26
या a + 24 = 26
या a = 26 – 24 = 2
a = 2 तथा d = 8
अतः समान्तर श्रेणी a, a + d, a + 2d….
= 2, 2 + 8, 2 + 2 × 8….
= 2, 10, 2 + 16….
= 2, 10, 18, ….

प्रश्न 42.
एक समान्तर श्रेणी के प्रथम १ पदों का योग 63q – 3q² है यदि (UPBoardSolutions.com) इसका p वाँ पद – 60 है। तो p का मान ज्ञात कीजिए तथा इसका 11 वाँ पद भी ज्ञात कीजिए।
हलः
माना समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
प्रश्नानुसार, दिया है S_q = 63q – 3q²
तथा q = q – 1 रखने पर
S_q-1 = 63(q – 1) – 3(q – 1)²
= 63(q – 1) – 3(q² + 1 – 2q)
S_q-1 = 63q – 63 – 3q² – 3 + 6q
= – 3q² + 69q – 66
अतः श्रेणी का q वाँ पद T_q = S_q – S_q-1
T_q = (63q – 3q²) – (- 3q² + 69q – 66)
= 63q – 3q² + 3q² – 69q + 66
T_q = – 6q + 66
q = 1, 2, 3…. रखने पर
T₁ = – 6 × 1 + 66 = – 6 + 66 = 60
T₂ = – 6 × 2 + 66 = – 12 + 66 = 54
T₃ = – 6 × 3 + 66 = – 18 + 66 = 48
तब समान्तर श्रेणी 60, 54, 48….
a = 60,d = 54 – 60 = – 6
अतः श्रेणी का P वाँ पद = – 60
a + (P – 1)d = – 60
60 + (P – 1) × – 6 = – 60
60 – 6p + 6 = – 60
66 – 6p = – 60
या 66 + 60 = 6p
126 = 6p या p = [latex]\frac{126}{6}[/latex] = 21 (UPBoardSolutions.com)
तथा श्रेणी का 11 वाँ पद = a + 10d
= 60 + 10 × – 6 = 60 – 60 = 0
अतः P = 21 तथा श्रेणी का 11 वाँ पद = 0

प्रश्न 43.
एक समान्तर श्रेणी के प्रथम n पदों का योग S_n द्वारा निरूपित किया है तो सिद्ध कीजिए S₁₂ = 3(S₈ – S₄) (NCERT Exemplar)
हलः
समान्तर श्रेणी के n पदों का योग = S_n
या  S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
तब,   S₁₂ = [latex]\frac{12}{2}[/latex][2a + (12 – 1d]
S₁₂ = 6[2a + 11d] …(1)
S₈ = [latex]\frac{8}{2}[/latex][2a + (8 – 1)d]
S₈ = 4[2a + 7d] ..(2)
S₄ = [latex]\frac{4}{2}[/latex][2a + (4 – 1)d]
S₄ = 2[2a + 3d] …(3)
सिद्ध करना है S₁₂ = 3(S₈ – S₄)
R.H.S = 3(S₈ – S₄)
= 3[4(2a + 7d) – 2(2a + 3d)] [समीकरण (2) व समीकरण (3) से]
= 3[8a + 28d – 4a – 6d]
= 3[4a + 22d]
= 3 × 2[2a + 11d]
= 6[2a + 11d]
= S₁₂ = L.H.S

प्रश्न 44.
एक समान्तर श्रेणी का पहला तथा अन्तिम पद (UPBoardSolutions.com) क्रमशः 5 तथा 45 हैं। यदि इसके सभी पदों का योग 400 है तो इसका सार्वअन्तर ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी का सार्वअन्तर d और पदों की संख्या n है।
तब, a = 5 तथा l = 45, S_n = 400

प्रश्न 45.
एक समान्तर श्रेणी के प्रथम 9 पदों का योग 162 है। इसके 6 वें पद तथा 13 वें पद का अनुपात 1 : 2 है। समान्तर श्रेणी का पहला तथा 15 वाँ पद ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब, प्रश्नानुसार, समान्तर श्रेणी के प्रथम 9 पदों का योग = 162
[latex]\frac{9}{2}[/latex][2a + (9 – 1)d] = 162
2a + 8d = [latex]\frac{162 \times 2}{9}[/latex]
2a + 8d = 18 × 2 या 2a + 8d = 36
a + 4d = 18 …(1)

d का मान समीकरण (2) में रखने पर
a – 2 × 3 = 0
या a – 6 = 0 या a = 6
श्रेणी का 15 वाँ पद= a + 14d = 6 + 14 × 3
= 6 + 42
= 48
अतः पहला पद = 6 तथा 15 वाँ पद = 48

प्रश्न 46.
एक समान्तर श्रेणी के प्रथम 14 पदों का योग 1505 है (UPBoardSolutions.com) तथा इसका पहला पद 10 है। इसका 25 वाँ पद ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी का प्रथम पद, a = 10 तथा सार्वअन्तर d है।
तब प्रश्नानुसार, श्रेणी के प्रथम 14 पदों का योग 1505
[latex]\frac{n}{2}[/latex][2a + (n – 1)d] = 1505
[latex]\frac{14}{2}[/latex][2 × 10 + (14 – 1)d] = 1505
7[20 + 13d] = 1505
20 + 13d = [latex]\frac{1505}{7}[/latex]
20 + 13d = 215
13d = 215 – 20 = 195
d = [latex]\frac{195}{13}[/latex] = 15
अतः श्रेणी का 25 वाँ पद = a + 24d = 10 + 24 × 15
= 10 + 360 = 370

प्रश्न 47.
यदि एक समान्तर श्रेणी के 7 पदों का योग 49 है तथा 17 पदों (UPBoardSolutions.com) का योग 289 है तो इसके n पदों का योग ज्ञात कीजिए। (NCERT)
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब प्रश्नानुसार, श्रेणी के 7 पदों का योग = 49
[latex]\frac{7}{2}[/latex][2a + (7 – 1)d] = 49

d का मान समीकरण (1) में रखने पर
2a + 6 × 2 = 14 या 2a + 12 = 14
2a = 14 – 12
या 2a = 2 या a = [latex]\frac{-2}{2}[/latex] = 1
a = 1, d = 2
तो श्रेणी के n के पदों का योग = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
S_n = [latex]\frac{n}{2}[/latex][2 × 1 + (n – 1) × 2]
= [latex]\frac{n}{2}[/latex][2 + 2n – 2]
= [latex]\frac{n}{2}[/latex] × 2n = n²

प्रश्न 48.
एक समान्तर श्रेणी का पहला पद तथा अन्तिम पद क्रमशः 7 तथा 49 है। यदि इसके सभी पदों का योग 420 है तो इसका सार्वअन्तर ज्ञात कीजिए।
हलः
माना, समान्तर श्रेणी का सार्वअन्तर d है।
तथा पहला पद a = 7 तथा अन्तिम पद = 49
तब श्रेणी के सभी पदों का योग = 420
[latex]\frac{n}{2}[/latex](a + l) = 420
n(7 + 49) = 420 × 2
56n = 840
n = [latex]\frac{840}{56}[/latex] = 15
तथा l = a + (n – 1)d
49 = 7 + (15 – 1)d
49 – 7 = 14d
[latex]\frac{42}{14}[/latex] = d या d = 3
अतः सार्वअन्तर d = 3

प्रश्न 49.
समान्तर.श्रेणी – 12, – 9, – 6,…21 के पदों की संख्या ज्ञात (UPBoardSolutions.com) कीजिए, यदि इस श्रेणी के प्रत्येक पद में 1 जोड़ दिया जाये तो इस प्रकार की बनी समान्तर श्रेणी के सभी पदों का योग ज्ञात कीजिए।
हलः
समान्तर श्रेणी – 12, – 9, – 6,…….21
a = – 12, d = (- 9) – (-12) = –9 + 12 = 3, l = 21
माना श्रेणी में पदों की संख्या’ = n
l = a + (n – 1)d
21 = – 12 + (n – 1) × 3
21 = – 12 + 3n – 3
21 = – 15 + 3n
21 + 15 = 3n
या 3n = 36
n = [latex]\frac{36}{3}[/latex] = 12
∴ n = 12
यदि श्रेणी के प्रत्येक पद में 1 जोड़ दिया जाये तो श्रेणी
– 12 + 1, – 9 + 1, – 6 + 1,…….,21 + 1
– 11, – 8, – 5, ……. 22
तब a = – 11, तथा n = 22
समान्तर श्रेणी के सभी पदों का यो = [latex]\frac{n}{2}[/latex](a + l)
= [latex]\frac{12}{2}[/latex] (-11 + 22)
= 6 × 11 = 66
अत: n = 12 तथा सभी पदों का योग = 66

Ex 5.2 Arithmetic Progressions दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 50.
(i) एक समान्तर श्रेणी के n पदों का योग ज्ञात कीजिए, जिसका 7 वाँ पद 30 है तथा 13 वाँ पद 54
(ii) श्रेणी 15 + 11 + 7… के कितने पदों का योग 35 है?
(iii) एक समान्तर श्रेणी 25, 22, 19,… के कुछ (UPBoardSolutions.com) पदों का योग 116 है। इसका अन्तिम पद ज्ञात कीजिए तथा पदों की संख्या ज्ञात कीजिए।
(iv) एक समान्तर श्रेणी में पहला पद तथा अन्तिम पद क्रमशः 7 तथा 57 है। यदि इसके सभी पदों का योग 352 है। तो पदों की संख्या ज्ञात कीजिए।
हलः
(i) माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब प्रश्नानुसार,
7वाँ पद = 30
a + 6d = 30 …(1)
13 वाँ पद = 54

(ii) श्रेणी 15 + 11 + 7 ……
a = 15, d = 11 – 15 = – 4
माना श्रेणी के n पदों का योग = 35
[latex]\frac{n}{2}[/latex][2a + (n – 1)d] = 35
n[2 × 15 + (n – 1) × – 4] = 35 × 2
n[30 – 4n + 4] = 70
n[34 – 4n] = 70
34n – 4n² – 70 = 0
-4n² + 34n – 70 = 0
– 2[2n² – 17n + 35] = 0
2n² – 17n + 35 = 0
2n² – 10n – 7n + 35 = 0
2n(n – 5) – 7(n – 5) = 0
(n – 5)(2n – 7) = 0
n – 5 = 0 तथा 2n – 7 = 0
n = 5, n = [latex]\frac{7}{2}[/latex] (अमान्य)
अतः n – 5

(iii) समान्तर श्रेणी 25, 22, 19….
a = 25, d = 22 – 25 = – 3
माना श्रेणी के n पदों का योग (UPBoardSolutions.com) = 116
तब [latex]\frac{n}{2}[/latex][2a + (n – 1)d] = 116
n[2 × 25 + (n – 1) × – 3] = 232
n[50 – 3n + 3] = 232
n[53 – 3n] = 232
53n – 3n² = 232
-3n² + 53n – 232 = 0
3n² – 53n + 232 = 0
3n² – 29n – 24n + 232 = 0
n(3n – 29) – 8(3n – 29) = 0
(3n – 29)(n – 8) = 0
3n – 29 = 0 तथा n – 8 = 0
n = [latex]\frac{29}{3}[/latex] (अमान्य) n = 8
तथा l = a + (n – 1)d
l = 25 + (8 – 1) × – 3 = 25 – 7 × 3
l = 25 – 21 = 4
अतः अन्तिम पद l = 4 तथा पदों की संख्या = 8

(iv) समान्तर श्रेणी का प्रथम पद a = 7 तथा अन्तिम पद l = 57
माना, श्रेणी के n पदों का योग = 352
तब [latex]\frac{n}{2}[/latex](a + l) = 352
[latex]\frac{n}{2}[/latex](7 + 57) = 352
[latex]\frac{n}{2}[/latex] × 64 = 352
32n = 352
n = [latex]\frac{352}{32}[/latex] = 11
अतः पदों की संख्या = 11

प्रश्न 51.
एक समान्तर श्रेणी के 35 पदों का योग ज्ञात कीजिए जिसका दूसरा पद 2 है तथा 7 वाँ पद 22 है।
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
तब प्रश्नानुसार, श्रेणी का दूसरा पद = 2
a + d = 2 …(1)

प्रश्न 52.
यदि एक समान्तर श्रेणी का पहला पद 2 है तथा इसके (UPBoardSolutions.com) प्रथम पाँच पदों का योग, अगले पाँच पदों के योग का [latex]\frac{1}{4}[/latex] है। तब सिद्ध कीजिए कि समान्तर श्रेणी का 20 वाँ पद – 112 है।
हलः
माना, समान्तर श्रेणी का पहला पद a = 2 तथा सार्वअन्तर d है।
तब, प्रश्नानुसार,
a + a + d + a + 2d + a + 3d + a + 4 = [latex]\frac{1}{4}[/latex](a + 5d + a + 6d + a + 7d + a + 8d + a + 9d)
5a + 10d = [latex]\frac{1}{4}[/latex](5a + 35d)
20a + 40d = 5a + 35d या 20a – 5a + 40d – 35d = 0
15a + 5d = 0
a = 2 रखने पर 15 × 2 + 5d = 0 या 30 + 5d = 0 या 5d = – 30 या d = – 6
अतः a_n = a + (n – 1)d
a₂₀ = 2 + (20 – 1) × – 6
a₂₀ = 2 – 19 × 6 = 2 – 114 = – 112
अतः समान्तर श्रेणी का 20 वाँ पद = – 112

प्रश्न 53.
यदि एक समान्तर श्रेणी में m पदों का योग, n पदों के योग के बराबर है तो सिद्ध कीजिए कि (m + n) वें पद का योग शून्य है।
हलः
माना समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर (UPBoardSolutions.com) d है:
तब, प्रश्नानुसार, m पदों का योग = n पदों का योग
[latex]\frac{m}{2}[/latex][2a + (m – 1)d] = [latex]\frac{n}{2}[/latex][2a + (n – 1)d]
m[2a + (m – 1)d] = n[2a + (n – 1)d]
2am + (m – 1)md = 2an + (n – 1)nd
2am – 2an = (n – 1)nd – (m – 1)md
2a(m – n) = [n² – n – m² + m]d
2a(m – n) = [n² – m² – n + m]d
2a(m – n) = [(n + m)(n – m) – 1(n – m)]d
2a(m – n) = (n – m)(m + n – 1)d

प्रश्न 54.
यदि एक समान्तर श्रेणी के p, q तथा r पदों का योग क्रमशः a, b तथा c है। तो सिद्ध कीजिए कि

(NCERT Exemplar)
हलः
माना समान्तर श्रेणी का प्रथम पद A तथा सार्वअन्तर D है, तब प्रश्नानुसार,

प्रश्न 55.
यदि दो समान्तर श्रेणी के n पदों के योग का अनुपात (UPBoardSolutions.com) 14 – 4n : 3n + 5 है। उनके 8 वें पदों का अनुपात ज्ञात कीजिए।
हलः
माना, दो समान्तर श्रेणी के प्रथम पद क्रमशः a₁ तथा a₂ और सार्वअन्तर क्रमश: d₁ तथा d₂ हैं।

प्रश्न 56.
यदि एक समान्तर श्रेणी के p वाँ पद [latex]\frac{1}{q}[/latex] तथा q वाँ पद [latex]\frac{1}{p}[/latex] है तो सिद्ध कीजिए कि प्रथम pq पदों का योग [latex]\frac{1}{2}[/latex](pq + 1) है।
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d हैं।

प्रश्न 57.
यदि एक समान्तर श्रेणी के प्रथम p पदों का योग q है तथा प्रथम व पदों का योग p है तो निम्न का योग ज्ञात कीजिए :
(i) (p + q) पदों का
(ii) (p – q) पदों का
हल:
(i) माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।

प्रश्न 58.
यदि एक समान्तर श्रेणी के n, 2n तथा 3n पदों (UPBoardSolutions.com) का योग क्रमशः S₁, S₃ तथा S₃ है तो सिद्ध कीजिए कि S₃ = 3(S₂ – S₁) (NCERT)
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।

प्रश्न 59.
यदि समीकरण (b – c)x² + (c – a)x + (a – b) = 0 के मूल बराबर हैं, तो सिद्ध कीजिए कि a, b तथा c एक समान्तर श्रेणी में हैं।
हलः
समीकरण (b – c)x² + (c – a)x + (a – b) = 0
A = (b – c), B = (c – a), C = (a – b)
∵ समीकरण के मूल बराबर हैं।
∴ B² – 4AC = 0
(c – a)² – 4(b – c)(a – b) = 0
c² + a² – 2ca – 4(ab – b² – ca + bc) = 0
c² + a² – 2ca – 4ab + 4b²+ 4ca – 4bc = 0
4b² – 4ab – 4bc = -c² – a² + 2ca – 4ca
4b² – 4b(a + c) = -c² – a² – 2ca
4b² – 4b(a + c) = -(c² + a² + 2ca)
4b² – 4b(a + c) = -(a + c)²
4b² = 4b(a + c) – (a + c)²
4b² = (a + c)[4b – a – c]
∵ a, b, c समान्तर श्रेणी में हैं।
∴ 2b = a + c
4b² = 2b(4b – a – c)
[latex]\frac{4 b^{2}}{2 b}[/latex] = 4b – a – c
2b = 4b – a – c
a + c = 4b – 2b
a + c = 2b
या 2b = a + c
अतः a, b तथा c एक समान्तर श्रेणी में है।

प्रश्न 60.
यदि S_n = n²p तथा S_m = m²p, m ≠ n है (UPBoardSolutions.com) तो सिद्ध कीजिए कि S_p = p³
हलः
माना, समान्तर श्रेणी का प्रथम पद a तथा सार्वअन्तर d है।
यदि S_n = n²p

d का मान समीकरण (1) में रखने पर,
2a + (n – 1)2p = 2np
2a + 2np – 2p = 2np
2a = 2np – 2np + 2p
2a = 2p
सिद्ध करना हैं S_p = p³
L. H. S. S_p = [latex]\frac{p}{2}[/latex][2a + (p – 1)d]
2a व d का मान रखने पर,
S_p = [latex]\frac{p}{2}[/latex][2p + (p – 1)2p]
= [latex]\frac{p}{2}[/latex] × 2p[1 + p – 1]
= p² × p = p³ = R.H.S.

प्रश्न 61.
यदि S₁, S₂, S₃ तीन समान्तर श्रेणी के n पदों का योग है। (UPBoardSolutions.com) जिनका प्रथम पद 1 है तथा सार्वअन्तर क्रमशः 1, 2 तथा 3 है तो सिद्ध कीजिए कि S₁ + S₃ = 2S₂
हलः

Balaji Publications Mathematics Class 10 Solutions