Class 10

Balaji Class 10 Maths Solutions Chapter 3 Pair of Linear Equation in Two Variables Ex 3.1 दो चर वाले रैखिक समीकरण युग्म

प्रश्न 1.
आलेखीय विधि द्वारा सिद्ध (UPBoardSolutions.com) कीजिए कि रैखिक समीकरण युग्म
2x – 3y = 5 और
6y – 4x = 3
असंगत है अर्थात् कोई हल नहीं रखता।
हल:
रैखिक समीकरण युग्म
2x – 3y = 5 ….(1)
और 6y – 4x = 3 …(2)
समी० (1) से,

∵ दोनों रेखायें समान्तर हैं।
∴ रेखायें असंगत हैं अर्थात् कोई हल (UPBoardSolutions.com) नहीं है। इति सिद्धम्।

प्रश्न 2.
निम्नलिखित रेखा युग्म निकाय को आलेखीय विधि द्वारा हल कीजिए।
(i) 2x + 3y = 4; 3x – y = – 5
(ii) 2x + 3y = 2; x – 2y = 8
हल:
(i) रेखायुग्म 2x + 3y = 4 …..(1)
और 3x – y = – 5 ………..(2)
समी० (1) से,

उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखाएँ बिन्दु (UPBoardSolutions.com) A (- 1, 2) पर प्रतिच्छेद करती है।
अतः x = – 1 y = 2

(ii) रेखायुग्म 2x + 3y = 2 ……..(1)
और x – 2y = 8 ………….(2)
समी० (1) से,

चूँकि दोनों रेखायें अंतः बिन्दु (4, – 2) पर प्रतिच्छेद करती है।
अतः निकाय का हल है। अतः
x = 4 y = – 2

प्रश्न 3.
निम्न समीकरण निकाय को आलेखीय विधि द्वारा हल कीजिए।
4x – 5 = 20 = 0; 3x + 5y – 15 = 0
तथा इन दो रेखाओं तथा y – अक्ष से बने (UPBoardSolutions.com) त्रिभुज के शीर्ष के निर्देशांक भी ज्ञात कीजिए।
हलः
समीकरण निकाय 4x – 5y – 20 = 0 या 4x – 5y = 20 …………(1)
3x + 5y – 15 = 0 या 3x + 5y = 15 ………(2)
समी० (1) से, 4x – 20 = 5y


उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखायें बिन्दु B (5, 0) पर प्रतिच्छेद करती है।
अतः x = 5, y = 0
तथा दोनों रेखाओं व y – अक्ष से बने त्रिभुज (UPBoardSolutions.com) के शीर्ष (0, – 4), (5, 0), (0, 3) हैं।

प्रश्न 4.
निम्न रैखिक समीकरण निकाय को आलेखीय विधि द्वारा हल कीजिए।
2x – y = 1; x – y = – 1
तथा इन रेखाओं तथा y – अक्ष से घिरे क्षेत्र को छायांकित कीजिए।
हलः
समीकरण निकाय 2x – y = 1 …..(1)
और x – y = – 1 ……………(2)
समी० (1) से, 2x – 1 = y
या y = 2x – 1


उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखायें बिन्दु C (2, 3) पर काटती है।
अतः x = 2, y = 3

प्रश्न 5.
आलेखीय विधि से जाँचिए कि निम्न रैखिक समीकरण (UPBoardSolutions.com) निकाय 3x + 5y = 15 तथा x – y = 5 संगत निकाय है तथा उस बिन्दु के निर्देशांक भी ज्ञात कीजिए जहाँ इन समीकरणों का ग्राफ, y – अक्ष को काटता है।
हलः
रैखिक समीकरण निकाय 3x + 5y = 15 …(1)
और x – y = 5 …(2)
समी० (1) से,

उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखायें एक – दूसरे को बिन्दु D (5, 0) पर काटती है।
अतः समीकरण संगत निकाय है।
तथा उन बिन्दुओं के निर्देशांक जहाँ इन समीकरणों का ग्राफ, y – अक्ष को काटता है।
A(0, 3) तथा B(0, – 5)

प्रश्न 6.
निम्न रैखिक समीकरण निकाय को आलेखीय विधि द्वारा हल कीजिए।
4x – 5y + 16 = 0; 2x + y – 6 = 0
तथा इन रेखाओं तथा x – अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए।
हलः
समीकरण निकाय 4x – 5y + 16 = 0 ……….(1)
और 2x + y – 6 = 0 ……..(2)
समी० (1) से, 4y – 5y + 16 = 0
⇒ 5y = 4x + 16

चूँकि दोनों रेखायें बिन्दु A(1, 4) पर एक – दूसरे को काटती हैं, अत: x = 1 तथा y = 4 समीकरण के हल हैं।
तथा x – अक्ष से बने त्रिभुज के शीर्षों के निर्देशांक (UPBoardSolutions.com) A(1, 4), B( – 4, 0), C(3, 0) हैं।

प्रश्न 7.
आलेखीय विधि द्वारा हल सिद्ध कीजिए कि निम्न रैखिक समीकरण निकाय का कोई हल नहीं है।
2x + 4y = 10; 3x + 6y = 12
हलः
रेखायुग्म 2x + 4y = 10 ………….(1)
और 3x + 6y = 12 ….(2)
समी० (1) से, 4y = 10 – 2x


चूँकि दोनों रेखायें समान्तर हैं। अतः निकाय का कोई हल नहीं है।

प्रश्न 8.
निम्न रैखिक समीकरण निकाय को (UPBoardSolutions.com) आलेखीय विधि द्वारा हल कीजिए।
(i) 2x – 5y + 4 = 0
2x + 5y – 8 = 0
(ii) x + 2y – 7 = 0
2x – y – 4 = 0
(iii) 3x + y – 5 = 0
2x – y – 5 = 0
(iv) 3x + 2y = 12
5x – 2y = 4
हल:
(i) समीकरण निकाय 2x – 5y + 4 = 0 ………..(1)
और 2x + 5y – 8 = 0 ……(2)
समी० (1) से, 2x + 4 = 5y या [latex]\frac{2 x+4}{5}[/latex] = y

उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखाएँ (UPBoardSolutions.com) एक – दूसरे को बिन्दु (1, [latex]\frac{6}{5}[/latex]) पर काटती हैं।
अतः x=1 तथा y = [latex]\frac{6}{5}[/latex]

(ii) समीकरण निकाय x + 2y – 7 = 0 ……(1)
और 2x – y – 4 = 0 …………..(2)
समी० (1) से,
2y = 7 – x


∵ दोनों रेखाएँ एक – दूसरे को बिन्दु (3, 2) पर काटती हैं।
अतः x = 3 तथा y = 2

(iii) समीकरण निकाय 3x + 5 = 0 …………(1)
और 2x – y – 5 = 0 …….(2)
समी० (1) से, y = 5 – 3x

चूँकि दोनों रेखायें एक – दूसरे को बिन्दु (2, – 1) पर काटती हैं।
अत: x = 2 तथा y = – 1 समीकरण के हल हैं (UPBoardSolutions.com) तथा x – अक्ष तथा रेखाओं द्वारा बने त्रिभुज के निर्देशांक (2, – 1), (3, 0) तथा (2, 0) है।

(iv) समीकरण निकाय 3x + 2y = 12 …(1)
और 5x – 2y = 4 …(2)
समी० (1) से, 2y = 12 – 3x या y = [latex]\frac{12-3 x}{2}[/latex]

∵ दोनों रेखायें एक – दूसरे को बिन्दु (2, 3) पर काटती हैं।
∴ x = 2 तथा y = 3

प्रश्न 9.
निम्न रैखिक समीकरण निकाय को आलेखीय विधि द्वारा हल कीजिए।
3x + y – 11 = 0
x – y – 1 = 0
इन रेखाओं तथा y – अक्ष से घिरे क्षेत्र को छायांकित (UPBoardSolutions.com) कीजिए तथा छायांकित क्षेत्र का क्षेत्रफल भी ज्ञात कीजिए।
हलः
समीकरण 3x + y – 11 = 0
या 3x + y = 11 …(1)
और x – y – 1 = 0
या x – y = 1 ……(2)
समी० (1) से, y = 11 – 3x

उपरोक्त ग्राफ से स्पष्ट है कि दोनों रेखायें बिन्दु B (3, 2) पर प्रतिच्छेद करती हैं।
अतः x = 3, y = 2
तथा छायांकित भाग (त्रिभुज) के शीर्ष के निर्देशांक
0(0, 0), D(0, – 1) तथा E (1, 0)
∆ODE का क्षेत्रफल = [latex]\frac{1}{2}[/latex] [x₁ (y₂ – y₃) + x₂(y₃ – y₁) + x₃ (y₁ – y₂)]
= [latex]\frac{1}{2}[/latex] [0(1 – 0) + 0 (0 – 0) + 1 (0 + 1)]
= [latex]\frac{1}{2}[/latex][0 + 0 + 1] = [latex]\frac{1}{2}[/latex] × 1 = [latex]\frac{1}{2}[/latex] वर्ग इकाई

प्रश्न 10.
निम्न रैखिक समीकरण निकाय को आलेखीय विधि द्वारा हल कीजिए।
4x – 5y – 20 = 0; 3x + 5y – 15 = 0
तथा इन समीकरणों द्वारा निरूपित रेखाओं तथा y – अक्ष से बने त्रिभुज के शीर्ष के निर्देशांक भी ज्ञात कीजिए।
हलः
समीकरण निकाय 4x – 5y – 20 = 0 ……..(1)
और 3x + 5y – 15 = 0 …………..(2)
समी० (1) से, 4x – 20 = 5y


∵ ‘दोनों रेखायें एक – दूसरे को बिन्दु (5, 0) पर काटती हैं।
अतः x= 5 तथा y = 0
तथा इन रेखाओं तथा y – अक्ष से बने ∆ABC के निर्देशांक A = (5, 0), B =(0, – 3) तथा C = (0, – 4) हैं।

प्रश्न 11.
कक्षा – 10 के 10 विद्यार्थीयों ने एक गणित की पहेली (UPBoardSolutions.com) प्रतियोगिता में भाग लिया। यदि लडकियों की संख्या, लड़कों की संख्या से 4 अधिक है, तो प्रतियोगिता में भाग लेने वाले लड़के तथा लड़कियों की संख्या ज्ञात कीजिए। (NCERT)
हलः
माना लड़कों की संख्या = x तथा लड़कियों की संख्या = x + 4
प्रश्नानुसार, कुल विद्यार्थी = 10
x + x + 4 = 10
2x = 10 – 4
2x = 6x = [latex]\frac{6}{2}[/latex]
x = 3
अतः लड़कों की संख्या, x = 3
तथा लड़कियों की संख्या, x + 4 = 3 + 4 = 7

प्रश्न 12.
c के किन मानों के लिए निम्न रैखिक समीकरण निकाय अपरिमित हल रखता है?
(i) 2x + 3y = 2; (c + 2)x + (2c + 1)y = 2(c – 1)
(ii) (c – 1)x + y = 5; (c + 1)x + (1 – c)y = 3x + 1
(iii) cx + 3y – (c – 3) = 0; 12x + cy – c= 0
हलः
(i) 2x + 3y = 2 तथा (c + 2)x + (2c + 1)y = 2(c – 1)

प्रश्न 13.
a के किन मानों के लिए निम्न रैखिक (UPBoardSolutions.com) समीकरण निकाय कोई हल नहीं रखते हैं?
(i) ax + 3y = a – 2; 12x + ay = a
(ii) (3a + 1)x + 3y – 2 = 0; (a + 1)x + (a – 2)y – 5 = 0
(iii) x + 2y = 5; 3x + ay + 15 = 0
हलः
(i) समीकरण निकाय
ar + 3y = a – 2
12x + ay = a
∵ रैखिक समीकरण निकाय का कोई हल नहीं है।

प्रश्न 14.
a व b के वे मान ज्ञात कीजिए जिनके लिए निम्न निकाय अपरिमित हल रखता है।
(i) 2x + 3y = 7; (a + b + 1)x + (a + 2b + 2)y = 4(a + b) + 1
(ii) 2x + 3y = 7; (a + b)x + (2a – b)y = 3(a + b + 1)
(iii) 3x + 4y = 12; (a + b)x + 2(a – b)y = 5a – 1
हलः
(i) समीकरण निकाय 2x + 3y = 7
और (a + b + 1)x + (a + 2b + 2)y = 4(a + b) + 1
∵ समीकरण निकाय अपरिमित हल रखता है।





अतः.a = 5, b = 1

प्रश्न 15.
चाँदनी एक ‘सेल’ में कुछ पेंट और शर्ट खरीदने गई। (UPBoardSolutions.com) जब उसकी सहेलियों ने पूछा कि प्रत्येक के कितने नग खरीदे, तो उसने उत्तर दिया “शर्ट की संख्या खरीदी गयी पेंटों की संख्या की दोगुनी से दो कम है तथा पुनः शर्ट की संख्या खरीदी गयी पेंटों की संख्या के चार गुना से 4 कम है। सहेलियों की यह जानने के लिए सहायता कीजिए कि चाँदनी ने कितनी पेंट व शर्ट खरीदी? [NCERT]
हलः
माना पेंटों की संख्या = x
तथा शर्टों की संख्या = y
प्रश्नानुसार, पहली शर्त : 2x – 2 = y
2x – y = 2 …(1)
तथा दूसरी शर्त : 4x – y = 4

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 6 Coordinate Geometry Ex 6.1 निर्देशांक ज्यामिति

प्रश्न 1.
वह चतुर्थांश ज्ञात (UPBoardSolutions.com) कीजिए जिसमें निम्न बिन्दु स्थित हैं –
(i) (-1, -4)
(ii) (4, 1)
(iii) (3, -2)
(iv) (-3, 1)
(v) (7, 2)
(vi) (-3, -2)
(vii) (-6, 4)
(viii) (2, -2)
हलः
(i) (-1, -4) स्थित होगा – तृतीय चतुर्थांश
(ii) (4, 1) स्थित होगा प्रथम चतुर्थांश
(iii) (3, -2) स्थित होगा – चतुर्थ चतुर्थांश
(iv) (-3,1) स्थित होगा – द्वितीय चतुर्थांश
(v) (7, 2) स्थित होगा प्रथम चतुर्थांश
(vi) (-3, -2) स्थित होगा – तृतीय चतुर्थांश
(vii) (-6, 4) स्थित होगा (UPBoardSolutions.com) – द्वितीय चतुर्थांश
(viii) (2, -2) स्थित होगा – चतुर्थ चतुर्थांश

प्रश्न 2.
निम्न में से कौन-से बिन्दु -अक्ष पर स्थित है?
(i) A(2, 3)
(ii) B(2, 0)
(iii) C(0, 2)
(iv) D(0, 0)
(v) E(-1, 0)
(vi) F(0, -2)
(vii) G(6, 0)
(viii) H(0, -7)
हलः
(ii) B(2, 0), x-अक्ष पर होगा।
(v) E(-1, 0), x-अक्ष पर होगा।
(vii) G(6, 0), x-अक्ष पर होगा।

प्रश्न 3.
निम्न प्रत्येक बिन्दु को अक्षों पर (UPBoardSolutions.com) निरूपित कीजिए तथा वह चतुर्थांश भी ज्ञात कीजिए जिसमें ये स्थित हैं
(i) (-2, 0)
(ii) (0, 5)
(iii) (0, 0)
(iv) (3, -2)
(v) (-5, -1)
(vi) (0, -3/2)
हलः

(i) (-2, 0) स्थित होगा द्वितीय चतुर्थांश में।
(ii) (0, 5) स्थित होगा y-अक्ष पर प्रथम चतुर्थांश में।
(iii) (0, 0),x-अक्ष तथा (UPBoardSolutions.com) y-अक्ष के कटान बिन्दु या मूल बिन्दु पर है।
(iv) (3, -2) चतुर्थ चतुर्थांश में है।
(v) (-5, -1) तृतीय चतुर्थांश में है।
(vi) (0, [latex]\frac{-3}{2}[/latex]) चतुर्थ चतुर्थांश में स्थित होगा।

प्रश्न 4.
(i) (-4, 5) का भुज ज्ञात कीजिए।
(ii) (-6, 6) की कोटि ज्ञात कीजिए।
(iii) मूल बिन्दु के निर्देशांक क्या होते हैं?
(iv) भुज 0 वाला बिन्दु कहाँ स्थित होगा?
(v) कोटि 0 वाला बिन्दु कहाँ स्थित होगा?
हलः
(i) (-4, 5) का भुज = -4
(ii) (-6, 6) की कोटि = 6
(iii) मूल बिन्दु के निर्देशांक = (0, 0)
(iv) यदि भुज 0 है तो सभी बिन्दु y-अक्ष पर होंगे।
(v) यदि कोटि 0 है तो सभी बिन्दु x-अक्ष पर होंगे।

प्रश्न 5.
बिन्दु P(-4, 2) को निरूपित कर बिन्दु के (UPBoardSolutions.com) निर्देशांक ज्ञात कीजिए यदि रेखाखण्ड PQ, x-अक्ष का लम्ब समद्विभाजक है।
हलः

∵ रेखाखण्ड PQ, x-अक्ष का लम्बसमद्विभाजक है।
अतः बिन्दु Q के निर्देशांक = (-4, -2)

प्रश्न 6.
निम्न अंकित बिन्दुओं के निर्देशांक (UPBoardSolutions.com) ज्ञात कीजिए-

हलः
बिन्दु P = (4, -6)
बिन्दु Q = (-1, 3)
बिन्दु S = (5, 6)
बिन्दु N = (-1, -1)
बिन्दु G = (3, 2)
बिन्दु H = (-3, 1)
बिन्दु I = (3, -2)

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 5 Arithmetic Progressions Ex 5.3 समान्तर श्रेणी

Ex 5.3 Arithmetic Progressions अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

प्रश्न 1.
0 व 500 के बीच 7 के गुणांकों का योग ज्ञात कीजिए।
हल:
0 व 500 के बीच 7 के गुणांक
7, 14, 21,……, 497
a = 7, d = 14 – 7 = 7 तथा (UPBoardSolutions.com) l = 497
तब l = a + (n – 1)d
या 497 = 7 + (n – 1) × 7
497 = 7 + 7n – 7

प्रश्न 2.
5 से विभाजित होने वाली सभी दो अंकों की संख्याओं का योग ज्ञात कीजिए।
हल:
5 से विभाजित दो अंकों की सभी (UPBoardSolutions.com) संख्यायें :
10, 15, 20,……..95
a = 10, d = 15 – 10 = 5 तथा l = 95
तब l = a + (n – 1)d या 95 = 10 + (n – 1) × 5
95 = 10 + 5n – 5 या 95 = 5n + 5
95 – 5 = 5n या 5n = 90 या n = [latex]\frac{90}{5}[/latex] = 18
तथा S_n = [latex]\frac{n}{2}[/latex][2a + (n – 1)d] = [latex]\frac{18}{2}[/latex][2 × 10 + (18 – 1) × 5]
S₁₈ = 9[20 + 17 × 5]
= 9[20 + 85]
= 9 × 105 = 945

प्रश्न 3.
यदि S_r, किसी समान्तर श्रेणी के r पदों का योग है तो S_3n:(S_2n – S_n) का अनुपात ज्ञात कीजिए।
हलः
दिया है S_r = [latex]\frac{r}{2}[/latex][2a + (r – 1)d]

प्रश्न 4.
संख्या 5 व 7 का समान्तर माध्य ज्ञात कीजिए।
हलः
संख्या 5 व 7 का स०मा० = [latex]\frac{5+7}{2}=\frac{12}{6}[/latex] = 6

Ex 5.3 Arithmetic Progressions लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 5.
यदि दो संख्याओं का अन्तर 4 तथा उनका (UPBoardSolutions.com) समान्तर माध्य 6 हो तो संख्याएँ ज्ञात कीजिए।
हलः
माना वे दोनों संख्याये a व b हैं।
तब प्रश्नानुसार, a – b = 4 …(1)
तथा समान्तर माध्य = 6
[latex]\frac{a+b}{2}[/latex] = 6
a + b = 12 …(2)

a का मान समीकरण (2) में रखने पर
8 + b = 12
या b = 12 – 8 = 4
अतः दोनों संख्यायें 8,4 हैं।

प्रश्न 6.
यदि संख्याएं a,b व c समान्तर श्रेणी में हैं तथा a व b का समान्तर माध्य (UPBoardSolutions.com) p तथा b व c का समान्तर माध्य q हो तो सिद्ध कीजिए कि p वq का समान्तर माध्य b होगा।
हल:
∵ संख्याये a, b व c समान्तर श्रेणी में है।
∴ 2b = a + c
प्रश्नानुसार, a व b का समान्तर माध्य = p
[latex]\frac{a+b}{2}[/latex] = P
या a + b = 2p …(1)
तथा b व c का समान्तर माध्य = q
[latex]\frac{b+c}{2}[/latex] = q
या c + b = 2q …(2)
समीकरण (1) व (2) को जोड़ने पर
a + 2b + c = 2p + 2q
a + c + 2b = 2(p + q)
∵ a + c = 2b
तो 2b + 2b = 2(p + q)
[latex]\frac{4 b}{2}[/latex] = p + q
2b = p + q
[latex]\frac{p+q}{2}[/latex] = b
अतः इससे स्पष्ट है कि p व १ का समान्तर (UPBoardSolutions.com) माध्य b है।

प्रश्न 7.
यदि a व b का समान्तर माध्य A है तो सिद्ध कीजिए कि

हलः
∵ a व b का समान्तर माध्य A है।

प्रश्न 8.
(i) माना 3 व 17 के बीच n समान्तर माध्य है तथा पहले व (UPBoardSolutions.com) अन्तिम समान्तर माध्य का अनुपात 3 : 1 है तो n का मान ज्ञात कीजिए।
(ii) 7 व 37 के बीच 9 समान्तर माध्य ज्ञात कीजिए।
हल:
(i) माना 3 व 17 के बीच n समान्तर माध्य है।
तब समान्तर श्रेणी में
3, A₁, A₂, A₃……A_n, 17
पदों की संख्या = n + 2 ,a = 3, l = 17
तब l = a + (n – 1)d
17 = 3 + (n + 2 – 1)d
17 = 3 + (n + 1)d
17 – 3 = (n + 1)d

(ii) माना, 7, A₁, A₂, A₃, A₄, A₅, A₆, A₇, A₈, A₉, 37
तब a = 7, l = 37 तथा पदों की संख्या = 11
l = a + (n – 1)d से
37 = 7 + (11 – 1)d
37 – 7 = 10d
या 10d = 30, (UPBoardSolutions.com) d = [latex]\frac{30}{10}[/latex] = 3
A₁ = a + d = 7 + 3 = 10,
A₂ = a + 2d = 7 + 6 = 13
A₃ = a + 3d = 7 + 9 = 16,
इसी प्रकार A₄ = 19, A₅ = 22, A₆ = 25
A₇ = 28, A₈ = 31, A₉ = 34
अतः 10, 13, 16, 19, 22, 25, 28, 31, 34

Ex 5.3 Arithmetic Progressions दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 9.
यदि x, y, z समान्तर श्रेणी में हैं तो सिद्ध कीजिए कि
(x + 2y – z)(2y + z – x) (z + x – y) = 4xyz
हल:
∵ x, y व z समान्तर श्रेणी में है।
∴ 2y = x + z
सिद्ध करना हैं (x + 2y – z)(2y + z – x)(z + x – y) = 4xyz
L. H. S. = (x + 2y – z)(2y + z – x)(z + x – y)
∵ 2y = x + z
∴ (x + x + z – z)(x + z + z – x) (2y – y)
= (2x)(2z)(y)
= 4xyz = R.H.S

प्रश्न 10.
यदि a, b, c समान्तर श्रेणी में हैं तो सिद्ध कीजिए कि
(i) b + c, c + a, a + b भी समान्तर (UPBoardSolutions.com) श्रेणी में होंगे।
(ii) b + c – a, c + a – b, a + b – c भी समान्तर श्रेणी में होंगे।
(iii) [latex]\boldsymbol{a}\left(\frac{\mathbf{1}}{\boldsymbol{b}}+\frac{\mathbf{1}}{\mathbf{c}}\right), \mathbf{b}\left(\frac{\mathbf{1}}{\mathbf{c}}+\frac{\mathbf{1}}{\boldsymbol{a}}\right), \mathbf{c}\left(\frac{\mathbf{1}}{\boldsymbol{a}}+\frac{\mathbf{1}}{\mathbf{b}}\right)[/latex] भी समान्तर श्रेणी में होंगे।
(iv) a²(b + c), b²(c + a), c²(a + b) भी समान्तर श्रेणी में होंगे यदि ab + bc + ca = 0
हलः
यदि a, b, c समान्तर श्रेणी में हैं।
तब 2b = a + c
(i) b + c, c + a, a + b भी समान्तर श्रेणी में हैं।
2(c + a) = b + c + a + b
2c + 2a – c – a = 2b
2b = a + c
अतः इससे स्पष्ट हैं कि b + c, c + a, a + b (UPBoardSolutions.com) भी समान्तर श्रेणी हैं।

(ii) b + c – a, c + a – b, a + b – c समान्तर श्रेणी में हैं।
2(c + a – b) = b + c – a + a + b – c
2c + 2a – 2b = 2b
2c + 2a = 2b + 2b
या 4b = 2(c + a)
[latex]\frac{4 b}{2}[/latex] = (c + a)
या 2b = c + a
अत: b + c – a, c + a – b, a + b – c समान्तर श्रेणी में हैं।

(iv) ∵ a²(b + c), b²(c + a), c²(a + b) समान्तर श्रेणी में हैं।
प्रत्येक पद में abc जोड़ने पर
a²(b + c) + abc, b²(c + a) + abc, c²(a + b) + abc (UPBoardSolutions.com) भी समान्तर श्रेणी में हैं।
a(ab + ac + bc), b(bc + ab + ac), c(ca + bc + ab) समान्तर श्रेणी में हैं।
2 × b(ab + bc + ac) = (a + c)(ab + bc + ca)
(2b – a – c)(ab + bc + ab) = 0
ab + bc + ac = 0

प्रश्न 11.
यदि b² + c², c² + a², a² + b² समान्तर श्रेणी में हैं तो सिद्ध कीजिए कि [latex]\frac{1}{b+c}, \frac{1}{c+a}, \frac{1}{a+b}[/latex] भी समान्तर श्रेणी में होंगे।
हल: ∵ b² + c², c² + ad, a² + b² समान्तर श्रेणी में हैं।
2(c² + a²) = b² + c² + a² + b²
2c² + 2a² – c² – a² = 2b²
c² + a² = 2b²
या 2b² = c² + a²

2ab + 2ac + 2b² + 2bc = ac + c² + 2bc (UPBoardSolutions.com) + a² + ac + 2ab
2b² = c² + a² + 2ab + 2bc + 2ac – 2ab – 2ac – 2bc
2b² = c² + a² …(2)
समीकरण (1) व (2) से स्पष्ट है कि [latex]\frac{1}{b+c}, \frac{1}{c+a}, \frac{1}{a+b}[/latex] समान्तर श्रेणी में हैं।

प्रश्न 12.
यदि a, b, c समान्तर श्रेणी में हैं तो सिद्ध कीजिए कि [latex]\frac{1}{b c}, \frac{1}{c a}, \frac{1}{a b}[/latex] भी समान्तर श्रेणी में होंगे।
हलः
∵ a, b, c समान्तर श्रेणी में हैं।
∴ प्रत्येक पद में abc में भाग देने पर,
[latex]\frac{a}{a b c}, \frac{b}{a b c}, \frac{c}{a b c}[/latex] भी समान्तर श्रेणी में हैं।
[latex]\frac{1}{b c}, \frac{1}{a c}, \frac{1}{a b}[/latex] भी समान्तर श्रेणी में हैं।

प्रश्न 13.
यदि a², b², c² समान्तर श्रेणी में हैं तो सिद्ध कीजिए (UPBoardSolutions.com) कि [latex]\frac{1}{b+c}, \frac{1}{c+a}, \frac{1}{a+b}[/latex] भी समान्तर श्रेणी में होंगे।
हलः
∵ a², b², c² समान्तर श्रेणी में हैं।
∴ प्रत्येक पद में (ab + bc + ca) जोड़ने पर
(a² + ab + bc + ca), (b² + ab + bc + ca), (c² + ab + bc + ca)
(a + b)(c + a), (a + b)(b + c), (c + a)(b + c) समान्तर श्रेणी में हैं।
प्रत्येक पद में (a + b)(b + c)(c + a) से भाग देने पर
[latex]\frac{1}{b+c}, \frac{1}{c+a}, \frac{1}{a+b}[/latex] समान्तर श्रेणी में हैं।

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.3 द्विघात समीकरण

निम्नलिखित समीकरणों को हल कीजिए –
प्रश्न 1.
(i) x(x + 1)(x + 3)(x + 4) = 180
(ii) (2x + 3)(2x + 5)(x – 1)(x – 2) = 30
(iii) (x – 5)(x – 7)(x + 4) (UPBoardSolutions.com) (x + 6) = 504
(iv) x(2x + 1)(x – 2)(2x – 3) = 63
(v) (x² – 3x – 10)(x² – 5x – 6) = 144
(vi) (x + 2)(3x + 4)(3x + 7)(x + 3) = 2400
हलः
(i) दिया गया समीकरण
{x(x + 1)(x + 3)(x + 4)} = 180
{x(x + 4)}{(x + 1)(x + 3)} = 180
(x² + 4x)(x² + x + 3x + 3) = 180
(x² + 4x)(x² + 4x + 3) = 180
माना x² + 4x = y
∴ दिया हुआ समीकरण, y(y + 3) = 180
y² + 3y – 180 = 0

अब y = 12 लेने पर, x² + 4x = 12
x² + 4x – 12 = 0
x² + 6x (UPBoardSolutions.com) – 2x – 12 = 0
x(x + 6) – 2(x + 6) = 0
(x + 6)(x – 2) = 0
x = 2, – 6
y = 15 लेने पर, x² + 4x = – 15
x² + 4x + 15 = 0

(ii) दिया गया समीकरण
(2x + 3) (2x + 5)(x – 1)(x – 2) = 30
{(2x + 3)(x – 1)}{(2x + 5)(x – 2)} = 30
(2x² – 2x + 3x – 3)(2x² – 4x + 5x – 10) = 30
(2x² + x – 3)(2x² + x – 10) = 30
माना 2x² + x = y
∴ दिया गया समीकरण
(y – 3)(y – 10) = 30
y² – 10y – 3y + 30 = 30
y² – 13y = 0
y(y – 13) = 0
y= 0 व y = 13
जब y = 0, 2x² (UPBoardSolutions.com) + x = 0
x(2x + 1) = 0
⇒ x = 0, x = [latex]-\frac{1}{2}[/latex]
y = 13 लेने पर, 2x² + x = 13
2x² + x – 13 = 0

(iii) दिया गया समीकरण
{(x – 5)(x + 4)}{(x – 7)(x + 6)} = 504
(x² – 5x + 4x – 20)(x² – 7x + 6x – 42) = 504
(x² – x – 20)(x² – x – 42) = 504
माना x² – x = y
∴ दिया गया समीकरण
(y – 20)(y – 42) = 504
y² – 20y – 42y + 840 – 504 = 0
y² – 62y + 336 = 0
y² – 6y – 56y + 336 (UPBoardSolutions.com) = 0
y(y – 6) – 56(y – 6) = 0
(y – 6)(y – 56) = 0
जब y – 6 = 0 तब y = 6
जब y – 56 = 0
तब y = 56
y = 6 लेने पर, x² – x = 6
x² – x – 6 = 0
x² + 2x – 3x – 6 = 0
x(x + 2) – 3(x + 2) = 0
(x + 2)(x – 3) = 0
x = – 2, 3
y = 56 लेने पर, x² – x = 56
x² – x – 56 = 0
x² – 8x + 7x – 56 = 0
x(x – 8) + 7(x – 8) = 0
(x + 7)(x – 8) = 0
जब x + 7 = 0 तब x = – 7
जब x – 8 = 0 तब x = 8

(iv) दिया गया समीकरण
x(2x + 1)(x – 2)(2x – 3) = 63
{x(2x – 3)} {(2x + 1)(x – 2)} = 63
(2x² – 3x)(2x² – 4x + x – 2) = 63
(2x² – 3x)(2x² – 3x – 2) = 63
माना 2x² – 3x (UPBoardSolutions.com) = y
y(y – 2) = 63
y² – 2y – 63 = 0
y² – 9y + 7y – 63 = 0
y(y – 9) + 7(y – 9) = 0
(y + 7)(y – 9) = 0
जब y + 7 = 0 तब y = – 7
जब y – 9 = 0 तब y = 9
y = – 7 लेने पर, 2x² – 3x = – 7
2x² – 3x + 7 = 0

y = 9 लेने पर, 2x² – 3x = 9
2x² – 3x – 9 = 0
2x² + 3x – 6x – 9 = 0
x(2x + 3) – 3(2x + 3) = 0
(x – 3)(2x + 3) = 0
जब x – 3 = 0 तब (UPBoardSolutions.com) x = 3
जब 2x + 3 = 0 तब x = [latex]\frac{-3}{2}[/latex]

(v) दिया गया समीकरण
(x² – 3x – 10)(x² – 5x – 6) = 144
(x² – 5x + 2x – 10)(x² – 6x + x – 6) = 144
[x(x – 5) + 2(x – 5)][x(x – 6) + 1(x – 6)] = 144
(x – 5)(x + 2)(x + 1)(x – 6) = 144
{(x – 5)(x + 1)}{(x + 2)(x – 6)} = 144
(x² – 4x – 5) (x² – 4x – 12) = 144
माना x² – 4x = y
∴ दिया गया समीकरण,
(y – 5)(y – 12) = 144
y² – 5y – 12y + 60 – 144 = 0
y² – 17y – 84 = 0
y² + 4y – 21y – 84 = 0
y(y + 4) – 21 (y + 4) = 0
(y + 4)(y – 21) = 0
जब y + 4 = 0, (UPBoardSolutions.com) तब y = -4
जब y – 21 = 0, तब y = 21
y = – 4 लेने पर, x² – 4x + 4 = 0
x² – 2x – 2x + 4 = 0
x(x – 2) – 2(x – 2) = 0
(x – 2)(x – 2) = 0
x = 2, 2
y = 21 लेने पर, x² – 4x = 21
x² – 4x – 21 = 0
x² – 7x + 3x – 21 = 0
x(x – 7) + 3(x – 7) = 0
x = – 3, 7

(vi) दिया गया समीकरण,
{(x + 2)(3x + 7)} {(3x + 4)(x + 3)} = 2400
(3x² + 7x + 6x + 14)(3x² + 9x + 4x + 12) = 2400
(3x² + 13x + 14) (UPBoardSolutions.com) (3x² + 13x + 12) = 2400
माना 3x² + 13x = y
∴ दिया गया समीकरण (y + 14)(y + 12) = 2400
y² + 14y + 12y + 168 = 2400
y² + 26y + 168 – 2400 = 0
y² + 26y – 2232 = 0
y² – 36y + 62y – 2232 = 0
y(y – 36) + 62(y – 36) = 0
(y – 36)(y + 62) = 0
जब y – 36 = 0 तब y = 36
जब y + 62 = 0 तब y = – 62
y = 36 लेने पर, 3x² + 13x = 36
3x² + 13x – 36 = 0

प्रश्न 2.

हल:
(i) दिया गया समीकरण
[latex]\sqrt{3 x+1}-\sqrt{x-1}[/latex] = 2
[latex]\sqrt{3 x+1}[/latex] = 2 + [latex]\sqrt{x-1}[/latex]
3x + 1 = 4 + (x – 1) + 4[latex]\sqrt{x-1}[/latex] (दोनों पक्षों का वर्ग करने पर)
3x – x + 1 – 4 + 1 = 4[latex]\sqrt{x-1}[/latex]
2x – 2 = 4[latex]\sqrt{x-1}[/latex] (UPBoardSolutions.com)
2(x – 1) = 2.2[latex]\sqrt{x-1}[/latex]
(x – 1) = 2[latex]\sqrt{x-1}[/latex]
x² – 2x + 1 = 4(x – 1) (दोनों पक्षों का पुनः वर्ग करने पर)
x² – 2x – 4x + 1 + 4 = 0
x² – 6x + 5 = 0
x² –x – 5x + 5 = 0
x(x – 1) – 5(x – 1)
(x – 1)(x – 5) = 0
जब (x – 1) = 0 तब x = 1
तथा जब (x – 5) = 0 तब x = 5

(ii) दिया गया समीकरण.
[latex]\sqrt{2 x+8}[/latex] + [latex]\sqrt{x+5}[/latex] = 7
[latex]\sqrt{2 x+8}[/latex] = 7 – [latex]\sqrt{x+5}[/latex]
2x + 8 = 49 + (x + 5) (UPBoardSolutions.com) – 14[latex]\sqrt{x+5}[/latex] (दोनों पक्षों का वर्ग करने पर)
2x + 8 – x – 49 – 5 = – 14[latex]\sqrt{x+5}[/latex]
x – 46 = – 14[latex]\sqrt{x+5}[/latex]
(x – 46)² = ( – 14[latex]\sqrt{x+5}[/latex])² (दोनों पक्षों का पुनः वर्ग करने पर)
x² – 92x + (46)² = 196(x + 5)
x² – 92x – 196x + 2116 – 980 = 0
x² – 288x + 1136 = 0
x² – 4x – 284x + 1136 = 0
x(x – 4) – 284(x – 4) = 0
यदि x – 4 = 0 तब x = 4
तथा यदि x – 284 = 0 तब x = 284
परन्तु x = 284 समीकरण को सन्तुष्ट नहीं करता।
अतः x = 4

(iii) दिया गया समीकरण,
[latex]\sqrt{x+4}[/latex] + [latex]\sqrt{x+20}[/latex] = 2[latex]\sqrt{x+11}[/latex]
x + 4 + x + 20 + 2/[latex]\sqrt{(x+4)} \sqrt{x+20}[/latex] = 4(x + 11) (दोनों पक्षों का वर्ग करने पर)
2x + 24 + 21[latex]\sqrt{x^{2}+24 x+80}[/latex] = 4x + 44
2x + 24 – 4x – 44 = [latex]\sqrt{x^{2}+24 x+80}[/latex]
– 2x – 20 = – 2[latex]\sqrt{x^{2}+24 x+80}[/latex]
– 2(x + 10) = -2[latex]\sqrt{x^{2}+24 x+80}[/latex]
(x + 10) = [latex]\sqrt{x^{2}+24 x+80}[/latex]
x² + 20x + 100 = x² + 24x + 80 (दोनों पक्षों का पुन: वर्ग करने पर)
x² + 20x + 100 – x² – 24x – 80 = 0
– 4x + 20 = 0
– 4x = – 20
x = 5

(iv) दिया गया समीकरण,
[latex]\sqrt{x+1}[/latex] – [latex]\sqrt{x-1}[/latex] = [latex]\sqrt{4x-1}[/latex]
x + 1 + x – 1 – 2[latex]\sqrt{x^{2}-1}[/latex] = 4x – 1 (दोनों पक्षों का वर्ग करने पर)
2x – 4x + 1 = 20[latex]\sqrt{x^{2}-1}[/latex] (UPBoardSolutions.com)
– 2x + 1 = 2[latex]\sqrt{x^{2}-1}[/latex]
4x² + 1 – 4x = 4(x² – 1) (दोनों पक्षों का पुनः वर्ग करने पर)
4x² – 4x + 1 – 4x² + 4 = 0
– 4x + 5 = 0
– 4x = – 5
x = [latex]\frac{5}{4}[/latex]

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 3 Pair of Linear Equation in Two Variables Ex 3.4 दो चर वाले रैखिक समीकरण युग्म

(A) सामान खर्चा तथा कीमतों पर आधारित

प्रश्न 1.
4 कुसियों और 3 मेजों का मूल्य ₹ 2100 तथा 5 कुर्सियों और 2 (UPBoardSolutions.com) मेजों का मूल्य ₹1750 है तो एक कुर्सी तथा एक मेज का मूल्य अलग – अलग ज्ञात कीजिए।
हलः
माना एक कुर्सी का मूल्य = ₹ x
तथा एक मेज का मूल्य = ₹y
प्रश्नानुसार,
पहली शर्त, 4x + 3y = 2100 ………(1)
तथा दूसरी शर्त, 5x + 2y = 1750 …..(2)
समी० (1) को 2 से तथा समी० (2) को 3 से गुणा करने पर,

x का मान समी० (1) में रखने पर,
4 × 150 + 3y = 2100
600 + 3y = 2100
3y = 2100 – 600 = 1500
y = [latex]\frac{1500}{3}[/latex] = 500
अतः एक कुर्सी का मूल्य = ₹ 150 और एक मेज (UPBoardSolutions.com) का मूल्य = ₹ 500

प्रश्न 2.
2 मेजों और 3 कुर्सियों का एक – साथ मूल्य ₹ 2000 है तथा 3 मेजों और 2 कुर्सियों का एक – साथ मूल्य ₹ 2500 है, तो एक मेज और 5 कुर्सियों का कुल मूल्य ज्ञात कीजिए।
हलः
माना एक मेज का मूल्य = ₹ x
तथा एक कुर्सी का मूल्य = ₹ y
प्रश्नानुसार, पहली शर्त, 2x + 3y = 2000 …………(1)
तथा दूसरी शर्त, 3x + 2y = 2500 …..(2)
समी० (1) को 3 से तथा समी० (2) को 2 से गुणा करने पर,

y का मान समी० (1) में रखने पर,
2x + 3 × 200 = 2000
2x + 600 = 2000
2x = 2000 – 600 = 1400
1400 700
x= [latex]\frac{1500}{2}[/latex] (UPBoardSolutions.com) = 700
∵ एक मेज का मूल्य = ₹ 700
तथा एक कुर्सी का मूल्य = ₹ 200
अतः एक मेज तथा 5 कुर्सियों का मूल्य = x + 5y = 700 + 5 × 200
= 700 + 1000 = ₹1700

प्रश्न 3.
एक मित्र दूसरे से कहता है कि यदि तुम मुझे एक सौ दे दो, तो मैं (UPBoardSolutions.com) आपसे दोगना धनी बन जाऊँगा। दूसरा उत्तर देता है, यदि आप मुझे दस दे दें, तो मैं आपसे छः गुना धनी बन जाऊँगा। बताइए कि उनकी क्रमशः क्या सम्पत्तियाँ हैं? (NCERT)
हलः
माना पहले मित्र के पास धन = ₹ x
तथा दूसरे मित्र के पास धन = ₹ y
प्रश्नानुसार,
पहली शर्त, x + 100 = 2(y – 100)
x + 100 = 2y – 200
x – 2y = –200 – 100
x – 2y = – 300 ……(1)
तथा दूसरी शर्त, 6 (x – 10) = y + 10
6x – 60 = y + 10
6x – y = 10 + 60
6x – y = 70 ………..(2)
समी० (2) को 2 से गुणा करने पर,

x का मान समी० (1) में रखने पर,
6 × 40 – y = 70
240 – y = 70
– y = 70 – 240 = – 170
y = 170
अतः पहले मित्र के पास धन = ₹ 40 तथा दूसरे मित्र के पास धन = ₹ 170

प्रश्न 4.
एक व्यक्ति के पर्स में 20 पैसे तथा 25 पैसे के सिक्के हैं। उसके (UPBoardSolutions.com) पास कुल ₹ 11.25 हैं। जिनमें सिक्कों की संख्या 50 है। उसके पास दोनों प्रकार के कितने – कितने सिक्के हैं?
हलः
माना 20 पैसे के सिक्कों की संख्या = x
तथा 25 पैसे के सिक्कों की संख्या = y
प्रश्नानुसार, उसके पास कुल रुपये = 11.25
पहली शर्त, [latex]\frac{x}{5}+\frac{y}{4}[/latex] = 11.25 (∵ 1 रुपया = 100 पैसे)
[latex]\frac{4 x+5 y}{20}[/latex] = 11.25
4x + 5y = 11.25 × 20
4x + 5y = 225 ……….(1)
तथा दूसरी शर्त, सिक्कों की संख्या = 50
x + y = 50
समी० (2) को 4 से गुणा करने पर,

y का मान समी० (2) में रखने पर,
x + 25 = 50
x = 50 – 25 या x = 25
अतः 20 पैसे के सिक्कों की संख्या = 25
तथा 25 पैसे के सिक्कों की संख्या = 25

प्रश्न 5.
3 बैग और 4 पेनों का एक साथ मूल्य ₹ 257 है। ऐसे ही 4 बैग (UPBoardSolutions.com) और 3 पेनों का एक साथ मूल्य ₹ 324 है तो एक बैग और 10 पेनों का कुल मूल्य ज्ञात कीजिए।
हलः
माना एक बैग का मूल्य = ₹ x
तथा एक पैन का मूल्य = ₹ y
प्रश्नानुसार,
3x + 4y = 257 ……….(1)
4x + 3y = 324 ………(2)
समी० (1) को 4 से तथा समी० (2) को 3 से गुणा करने पर,

y का मान समी० (1) में रखने पर,
3x + 4 × 8 = 257
3x + 32 = 257
3x = 257 – 32 = 225
x = [latex]\frac{225}{3}[/latex] = 75
अतः एक बैग का मूल्य = ₹ 75
तथा एक पेन का मूल्य = ₹ 8
अतः एक बैग और 10 पेनों का मूल्य = x + 10y
= 75 + 10 × 8 = 75 + 80 = ₹ 155

(A) संख्याओं पर आधारित

प्रश्न 6.
दो अंकों की एक संख्या में दहाई का अंक, इकाई के अंक से (UPBoardSolutions.com) तीन गुना है। यदि इस संख्या में 54 जोड़ा जाये तो उसके अंक पलट जाते हैं। संख्या ज्ञात कीजिए।
हलः
माना दहाई का अंक = x
तथा इकाई का अंक = y
मूल संख्या = 10x + y
प्रश्नानुसार,
पहली शर्त, दहाई का अंक = 3 × इकाई का अंक
x = 3y
x – 3y = 0 ………(1)
दूसरी शर्त, अंकों को पलट देने पर प्राप्त संख्या = 10 y + x
मूल संख्या + 54 = 10 y + x
10x + y + 54 = 10 y + x
10x + y – 10y – x = – 54
9x – 9y = – 54
9(x – y) = – 54
x – y = [latex]\frac{54}{9}[/latex]

y का मान समी० (1) में रखने पर,
x – 3 × 3 = 0
x – 9 = 0 ⇒ x = 9
अतः
मूल संख्या = 10x + y
= 10 × 9 + 3 = 90 + 3 = 93

प्रश्न 7.
एक दो अंकों की संख्या तथा उसके अंकों को उलटने (UPBoardSolutions.com) पर बनी संख्या का योग 121 है। उसके दोनों अंकों का अन्तर 3 है। संख्या ज्ञात कीजिए।
हलः
माना दहाई का अंक = x
तथा इकाई का अंक = y
मूल संख्या = 10x + y
तथा अंकों को उलटने पर बनी संख्या = 10 y + x
प्रश्नानुसार,
पहली शर्त, 10x + y + 10y + x = 121
11x + 11y = 121
11(x + y) = 121

x का मान समी० (1) में रखने पर,
7 + y = 11
या y = 11 – 7 – 4
अतः अभीष्ट संख्या = 10x + y
= 10 × 7 + 4 = 70 + 4 = 74

प्रश्न 8.
एक दो अंकों की संख्या तथा उसके अंकों को उलटने पर (UPBoardSolutions.com) बनी संख्या का योग 165 है तथा इसके दोनों अंकों का अन्तर 3 है। संख्या ज्ञात कीजिए।
हलः
माना दहाई का अंक = x
तथा इकाई का अंक = y
मूल संख्या = 10x + y
तथा अंकों को उलटने पर बनी संख्या = 10 y + x
प्रश्नानुसार,
पहली शर्त, 10x + y + 10 y + x = 165
11x + 11y = 165
11(x + y) = 165
x + y = [latex]\frac{165}{11}[/latex]
x + y = 15 ….(1)
दूसरी शर्त, x – y = 3 ………..(2)
समी० (1) व (2) को जोड़ने पर,

x का मान समी० (1) में रखने पर,
9 + y = 15
या y = 15 – 9 ⇒ y = 6
अभीष्ट संख्या = 10x + y
= 10 × 9 + 6 = 96

प्रश्न 9.
एक दो अंकों की संख्या तथा उसके अंकों को उलटने पर बनी संख्या का (UPBoardSolutions.com) योग 132 है। यदि इस संख्या में 12 जोड़ा जाये तो नई संख्या, अंकों के योग से 5 गुनी होगी। संख्या ज्ञात कीजिए।
हलः
माना दहाई का अंक = x
तथा इकाई का अंक = y
तब मूल संख्या = 10x + y
तथा अंकों को उलटने पर प्राप्त नई संख्या = 10y + x
प्रश्नानुसार,
पहली शर्त, 10x + y + 10 y + x = 165
11x + 11y = 132
11(x + y) = 132
x + y = [latex]\frac{132}{11}[/latex]
x + y = 12 ……..(1)
दूसरी शर्त, 10x + y + 12 = (UPBoardSolutions.com) 5(x + y)
10x + y + 12 = 5x + 5y
10x + y – 5x – 5y = – 12
5x – 4y = – 12 ……(2)
समी० (1) को 4 से गुणा करने पर,

x = [latex]\frac{36}{9}[/latex] या x = 4
x का मान समी० (1) में रखने पर,
4 + y = 12
या y = 12 – 4 = 8
अतः अभीष्ट संख्या = 10x + y
= 10 × 4 + 8 = 40 + 8 = 48

प्रश्न 10.
एक दो अंकों की संख्या, उसके अंकों के योग से 4 गुनी है। (UPBoardSolutions.com) यदि संख्या में 18 जोड़ा जाये तो संख्या के अंक आपस में बदल जाते हैं। संख्या ज्ञात कीजिए।
हलः
माना दहाई का अंक = x
तथा इकाई का अंक = y
तब अभीष्ट संख्या = 10x + y
प्रश्नानुसार,
पहली शर्त, 10x + y = 4(x + y)
10x + y = 4x + 4y
10x + y – 4x – 4y = 0
6x – 3y = 0
3(2x – y) = 0
2x – y = 0 …..(1)
दूसरी शर्त, अंकों को बदलने पर (UPBoardSolutions.com) प्राप्त संख्या = 10 y + x
10x + y + 18 = 10 y + x
10x + y – 10y – x = – 18
9x – 9y = – 18
9(x – y) = – 18
x – y = [latex]-\frac{18}{9}[/latex]
x – y = – 2 ….(2)
समी० (1) में से समी० (2) घटाने पर,

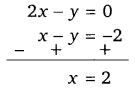
x का मान समी० (1) में रखने पर,
2 × 2 – y = 0 या 4 – y = 0
– y = – 4 या y = 4
अतः अभीष्ट संख्या = 10x + y
= 10 × 2 + 4 = 20 + 4 = 24

प्रश्न 11.
दो अंकों से बनी एक संख्या तथा उसके अंकों को (UPBoardSolutions.com) बदलकर बनी संख्या का योग 66 है। यदि दोनों अंकों का अन्तर 2 है तो संख्या ज्ञात कीजिए। (NCERT)
हलः
माना दहाई का अंक = x
तथा इकाई का अंक = y
मूल संख्या = 10x + y
तथा अंकों को बदलने पर प्राप्त संख्या = 10 y + x
प्रश्नानुसार,
पहली शर्त, 10x + y + 10y + x = 66
11x + 11y = 66
11(x + y) = 66
x + y = [latex]\frac{66}{11}[/latex]
x + y = 6 ……..(1)
दूसरी शर्त, x – y = 2 ……(2)
समी० (1) व (2) को जोड़ने पर,

x का मान समी० (1) में रखने पर,
4 + y = 6
या y = 6 – 4 ⇒ y = 2
अतः अभीष्ट संख्या = 10x + y
= 10 × 4 + 2
= 40 + 2 = 42

प्रश्न 12.
एक दो अंकों से बनी संख्या उसके अंकों के योग से चार (UPBoardSolutions.com) गुनी तथा अंकों की गुणा से दोगुनी है। संख्या ज्ञात कीजिए।
हलः
माना दहाई का अंक = x
तथा इकाई का अंक = y
तब मूल संख्या = 10x + y
प्रश्नानुसार,
पहली शर्त, 10x + y = 4x(x + y)
10x + y = 4x + 4y
10x + y – 4x – 4y = 0
6x – 3y = 0
3(2x – y) = 0
2x – y = 0 ……….(1)
दूसरी शर्त, 10x + y = 2xy ……(2)
समी० (1) व (2) को जोड़ने पर,

y का मान समी० (1) में रखने पर,
2x – 6 = 0 या 2x = 6
x = [latex]\frac{6}{2}[/latex] या x = 3
अतः
मूल संख्या = 10x + y
= 10 × 3 + 6 = 30 + 6 = 36

(C) भिन्नों पर आधारित

प्रश्न 13.
एक भिन्न के अंश को 3 से गुणा करने तथा हर में से 3 घटाने पर वह [latex]\frac{18}{11}[/latex] होती है। लेकिन यदि अंश में 8 जोड़ा जाये तथा हर को 2 गुना किया जाये तो वह [latex]\frac{2}{3}[/latex] हो जाती है। (UPBoardSolutions.com) भिन्न ज्ञात कीजिए।
हलः
माना भिन्न का अंश = x तथा हर = y
तब अभीष्ट भिन्न = [latex]\frac{x}{y}[/latex]
प्रश्नानुसार,
पहली शर्त, [latex]\frac{3 x}{y-3}=\frac{18}{11}[/latex]
3x = 18y – 54
33x = 18y – 54 ………..(1)
33x – 18y = – 54
दूसरी शर्त, [latex]\frac{x+8}{2 y}=\frac{2}{5}[/latex]
5x + 40 = 4y
5x – 4y = – 40
समी० (1) को 2 से तथा समी० (2) को 9 से गुणा करने पर,

x = [latex]\frac{252}{21}[/latex] = 12
x का मान समी० (2) में रखने पर,
5 × 12 – 4y = – 40
60 – 4y = – 40 या – 4y = – 40 – 60
– 4y = – 100 या y = [latex]\frac{100}{2}[/latex] = 25
अतः अभीष्ट भिन्न = [latex]\frac{x}{y}=\frac{12}{25}[/latex]

प्रश्न 14.
एक भिन्न के अंश व हर में यदि 2 जोड़ा जाये (UPBoardSolutions.com) तो वह [latex]\frac{9}{11}[/latex] हो जाती है। लेकिन यदि भिन्न के अंश व हर में 3 जोड़ा जाये तो यह [latex]\frac{5}{6}[/latex] हो जाती है। भिन्न ज्ञात कीजिए। (NCERT)
हलः
माना भिन्न का अंश = x तथा हर = y
तब अभीष्ट भिन्न = [latex]\frac{x}{y}[/latex]
प्रश्नानुसार,
पहली शर्त, [latex]\frac{x+2}{y+2}=\frac{9}{11}[/latex]
11 (x + 2) = 9 (y + 2)
11x + 22 = 9y + 18
11x – 9y + 22 – 18 = 0
11x – 9y + 4 = 0
11x – 9y = – 4 ………(1)
दूसरी शर्त, [latex]\frac{x+3}{y+3}=\frac{5}{6}[/latex]
6 (x + 3) = 5(y + 3)
6x + 18 = 5y + 15
6x – 5y + 18 – 15 = 0
6x – 5y + 3 = 0
6x – 5y = – 3 ………(2)
समी० (1) को 5 से तथा समी० (2) को 9 से गुणा करने पर,

x का मान समी० (2) में रखने पर,
6 × 7 – 5y = – 3
42 – 5y = – 3
– 5y = – 3 – 42
या – 5y = – 45
y = [latex]\frac{45}{5}[/latex] ⇒ y = 9
अतः अभीष्ट भिन्न = [latex]\frac{x}{y}=\frac{7}{9}[/latex]

प्रश्न 15.
एक भिन्न के अंश व हर का योग अंश के दोगुने से 4 अधिक है। (UPBoardSolutions.com) यदि अंश व हर में 3 जोड़ा जाता है तो वे 2 : 3 के अनुपात में होते हैं। भिन्न ज्ञात कीजिए।
हलः
माना अभीष्ट भिन्न =
प्रश्नानुसार, पहली शर्त, x + y = 2x + 4
x + y – 2x = 4
-x + y = 4 …….(1)
दूसरी शर्त, [latex]\frac{x+3}{y+3}=\frac{2}{3}[/latex]
3x + 9 = 2y + 6 या 3x – 2y = 6 – 9
3x – 2y = – 3
समी० (1) को 3 से गुणा करने पर,

y का मान समी० (1) में रखने पर,
– x + 9 = 4 या – x = 4 – 9 = – 5
x = 5
अतः अभीष्ट भिन्न = [latex]\frac{x}{y}=\frac{5}{9}[/latex]

प्रश्न 16.
एक भिन्न के अंश व हर का योग 18 है। यदि हर में  (UPBoardSolutions.com) जोड़ा जाये तो वह [latex]\frac{1}{3}[/latex] हो जाती है। भिन्न ज्ञात कीजिए।
हलः
माना अभीष्ट भिन्न =
प्रश्नानुसार, पहली शर्त, x + y = 18 …………(10
दूसरी शर्त, [latex]\frac{x}{y+2}=\frac{1}{3}[/latex]
3x = y + 2
3x – y = 2 ………..(2)
समी० (1) व समी० (2) को जोड़ने पर,

x का मान समी० (1) में रखने पर,
5 + y = 18
या y = 18 – 5
y = 13
अतः अभीष्ट भिन्न = [latex]\frac{x}{y}=\frac{5}{13}[/latex]

प्रश्न 17.
एक भिन्न के अंश व हर का योग उसके हर के दोगुने से 3 कम है। यदि (UPBoardSolutions.com) अंश व हर में 1 घटा दिया जाये तो उसका अंश हर का आधा हो जाता है। भिन्न ज्ञात कीजिए।
हलः
माना भिन्न का अंश = x तथा हर = y
तब अभीष्ट भिन्न = [latex]\frac{x}{y}[/latex]
प्रश्नानुसार, पहली शर्त, x + y = 2y – 3
x + y – 2y = – 3
या x – y = – 3 …..(1)
दूसरी शर्त, (x – 1) = [latex]\frac{1}{2}[/latex] × (y – 1)
2x – 2 = y – 1
या 2x – y = – 1 + 2

y का मान समी० (1) में रखने पर,
4 – y = – 3
या – y = – 3 – 4 = – 7
y = 7
अतः अभीष्ट भिन्न = x = [latex]\frac{x}{y}=\frac{4}{7}[/latex]

(D) आयु पर आधारित

प्रश्न 18.
पिता की उम्र तथा उसके बेटे की उम्र के दोगुने का योग 70 है। यदि पिता की (UPBoardSolutions.com) उम्र का दोगुना पुत्र की उम्र में जोड़ा जाये तो वह 95 हो जाती है। पिता व पुत्र की उम्र ज्ञात कीजिए।
हलः
माना पिता की उम्र = x वर्ष तथा पुत्र की उम्र = y
प्रश्नानुसार, पहली शर्त, x + 2y = 70 …….(1)
दूसरी शर्त, 2x + y = 95
समी० (1) को 2 से गुणा करने पर,

y का मान समी० (1) में रखने पर,
x + 2 × 15 = 70 या x + 30 = 70
x = 70 – 30 = 40
अतः पिता की उम्र = 40 वर्ष तथा पुत्र की उम्र = 15 वर्ष

प्रश्न 19.
10 वर्ष बाद, A की आयु B से दोगुनी है तथा 5 वर्ष पहले, A की उम्र, B की उम्र से 3 गुनी थी। A व B की वर्तमान आयु ज्ञात कीजिए।
हलः
माना, A की वर्तमान आयु = x वर्ष
तथा B की वर्तमान आयु = y वर्ष
प्रश्नानुसार, प्रथम शर्त, x + 10 = 2 × (y + 10)
x + 10 = 2y + 20
x – 2y = 20 – 10
x – 2y = 10 ….(1)
दूसरी शर्त, x – 5 = 3 × (y – 5)
x – 3y = – 15 + 5

y का मान समी० (1) में रखने पर,
x – 2 × 20 = 10
या x – 40 = 10
x = 10 + 40 या x = 50
अतः A की आयु = 50 वर्ष तथा B की आयु = 20 वर्ष

प्रश्न 20.
पिता की आयु, उसके दो बच्चों की आयु से 3 गुना है। 5 वर्ष बाद उसकी (UPBoardSolutions.com) आयु, उसके बच्चों की आयु के योग की दोगुनी होगी। पिता की आयु ज्ञात कीजिए।
हलः
माना पिता की वर्तमान आयु = x वर्ष
तथा दो बच्चों की आयु = y वर्ष
प्रश्नानुसार, पहली शर्त, x = 3y
x – 3y = 0 ……….(1)
दूसरी शर्त, (x + 5) = 2 × (y + 10)
x + 5 = 2y + 20
या x – 2y = 20 – 5

y का मान समी० (1) में रखने पर,
x – 3 × 15 = 0
या x – 45 = 0 ⇒ x = 45
अतः पिता की उम्र = 45 वर्ष

प्रश्न 21.
दो मित्रों A व B की आयु में 3 वर्ष का अन्तर है। A के पिता D की आयु (UPBoardSolutions.com) A से दोगुनी है तथा B की आयु उसकी बहन C से दोगुनी है। C व D की आयु में अन्तर 30 वर्ष का है। A व B की आयु ज्ञात कीजिए। (NCERT)
हलः
माना A की आयु = x वर्ष तथा C आयु = y वर्ष
तब D की आयु = 2x वर्ष तथा B की आयु = 2y वर्ष
प्रश्नानुसार, पहली शर्त, 2y – x = 3
या – x + 2y = 3 …..(1)
दूसरी शर्त, 2x – y = 30 ……..(2)
समी० (1) को 2 से गुणा करने पर,

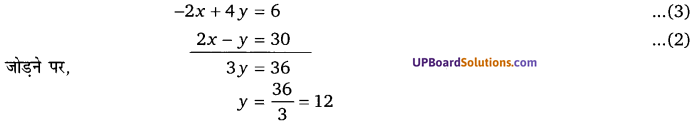
y का मान समी० (1) में रखने पर,
– x + 2 × 12 = 3
या – x + 24 = 3
या – x = 3 – 24 = – 21
x = 21
अतः A की आयु = 21 वर्ष, B की आयु 2y = 2 × 12 = 24 वर्ष

प्रश्न 22.
6 वर्ष बाद, एक व्यक्ति की आयु उसके बेटे की आयु की तीन गुनी (UPBoardSolutions.com) होगी। तीन वर्ष पहले वह अपने पुत्र की आयु से 9 गुनी थी। उनकी वर्तमान आयु ज्ञात कीजिए।
हलः
माना व्यक्ति की वर्तमान आयु = x वर्ष
तथा पुत्र की वर्तमान आयु = y वर्ष
प्रश्नानुसार, पहली शर्त, x + 6 = 3 × (y + 6)
x + 6 = 3y + 18
x – 3y = 18 – 6
x – 3y = 12
दूसरी शर्त, x – 3 = 9 × (y – 3)
x – 3 = 9y – 27
x – 9y = – 27 + 3

y का मान समी० (1) में रखने पर,
x – 3 × 6 = 12
या x – 18 = 12
x = 12 + 18 या x = 30
अतः पिता की आयु = 30 वर्ष तथा पुत्र की आयु = 6 वर्ष

(E) दूरी एवं चाल पर आधारित

प्रश्न 23.
एक हाइवे के दो बिन्दुओं A व B के बीच 90 किमी की दूरी है। एक (UPBoardSolutions.com) कार बिन्दु A से तथा दूसरी बिन्दु B से समान समय पर चलना प्रारम्भ करती है। एक ही दिशा में चलने पर वे 9 घण्टे बाद मिलती हैं तथा विपरीत दिशा में चलने पर वे [latex]\frac{9}{7}[/latex] घण्टे बाद मिलती हैं। उनकी गति ज्ञात कीजिए।
हलः
माना पहली कार की गति = x किमी/घण्टा
तथा दूसरी कार की गति = y किमी/घण्टा
प्रश्नानुसार, दो बिन्दुओं A व B के बीच की दूरी = 90 किमी
पहली शर्त, एक ही दिशा में चलने पर कारों की गति = (x – y) किमी/घण्टा
तथा समय = 9 घण्टे

x का मान समी० (2) में रखने पर,
40 + y = 70
या y = 70 – 40 = 30
अतः पहली कार की गति = 40 किमी/घण्टा
तथा दूसरी कार की गति = 30 किमी/घण्टा

प्रश्न 24.
एक हाइवे पर दो बिन्दु A व B, 70 किमी० की दूरी पर हैं। एक (UPBoardSolutions.com) कार बिन्दु A से तथा दूसरी कार बिन्दु B से एक ही समय पर चलना प्रारम्भ करती है। यदि वे एक ही दिशा में चलती हैं तो वे 7 घण्टे बाद मिलती है और विपरीत दिशा में चलने पर एक घण्टे बाद मिलती हैं। दोनों कार की गति ज्ञात कीजिए।
हलः
माना पहली कार की गति = x किमी/घण्टा
तथा दूसरी कार की गति = y किमी/घण्टा
प्रश्नानुसार, दो बिन्दुओं A व B के बीच की दूरी = 70 किमी
पहली शर्त, एक ही दिशा में चलने पर कारों की गति = (x – y) किमी/घण्टा
तथा समय = 7 घण्टे

या x – y = 10
दूसरी शर्त, विपरीत दिशा में चलने पर कारों की गति = (x + y)
किमी/घण्टा तथा समय = 1 घण्टा

x का मान समी० (2) में रखने पर,
40 + y = 70
y = 70 – 40
या y = 30
अत: पहली कार की गति = 40 किमी/घण्टा
तथा दूसरी कार की गति = 30 किमी/घण्टा

प्रश्न 25.
एक हाइवे पर A व B दो स्थान 80 किमी की दूरी पर हैं। एक कार बिन्दु A से तथा दूसरी कार बिन्दु B से एक ही समय पर चलना शुरू करती हैं। यदि वे एक ही दिशा में चलती हैं तो वे 8 घण्टे पश्चात् तथा विपरीत दिशा में चलने पर एक घण्टा 20 मिनट में मिलती (UPBoardSolutions.com) हैं। कारों की चाल ज्ञात कीजिए।
हलः
माना पहली कार की चाल = x किमी/घण्टा
तथा दूसरी कार की चाल = y किमी/घण्टा
प्रश्नानुसार, स्थान A तथा B के बीच की दूरी = 80 किमी/घण्टा
पहली शर्त, एक ही दिशा में कारों की चाल = (x – y) किमी/घण्टा
तथा समय = 8 घण्टे


x का मान समी० (2) में रखने पर,
35 + y = 60 या y = 60 – 35 = 25
अतः पहली कार की चाल = 35 किमी/घण्टा
तथा दूसरी कार की चाल = 25 किमी/घण्टा

प्रश्न 26.
एक हाइवे पर दो स्थान A व B की दूरी 160 किमी है। एक कार A से (UPBoardSolutions.com) तथा दूसरी B से एक ही समय पर चलना प्रारम्भ करती हैं। एक ही दिशा में चलने पर वे 8 घण्टे बाद तथा विपरीत दिशा में चलने पर 2 घण्टे बाद मिलती हैं। कारों की चाल ज्ञात कीजिए। (NCERT)
हलः
माना पहली कार की चाल = x किमी/घण्टा
तथा दूसरी कार की चाल = y किमी/घण्टा
प्रश्नानुसार, दो स्थान A तथा B के बीच की दूरी = 160 किमी/घण्टा
पहली शर्त, एक ही दिशा में कारों की चाल = (x – y) किमी/घण्टा
तथा समय = 8 घण्टे

x का मान समी० (2) में रखने पर,
50 + y = 80
y = 80 – 50 ⇒ y = 30
अतः पहली कार की चाल = 50 किमी/घण्टा
तथा दूसरी कार की चाल = 30 किमी/घण्टा

प्रश्न 27.
एक नाव 7 घण्टे में धारा के विपरीत 32 किमी तथा धारा की दिशा में (UPBoardSolutions.com) 36 किमी चलती है और यह नाव धारा के प्रतिकूल 40 किमी तथा धारा की दिशा में 60 किमी समान समय में चलती है। शांत जल में नाव की चाल तथा धारा की चाल ज्ञात कीजिए।
हलः
माना नाव की चाल = x किमी/घण्टा
तथा धारा की चाल = y किमी/घण्टा
तब धारा की दिशा में नाव की चाल = (x + y) किमी/घण्टा
तथा धारा की विपरीत दिशा में नाव की चाल = (x – y) किमी/घण्टा
प्रश्नानुसार,

x का मान समी० (5) में रखने पर,
10 + y = 12
या y = 12 – 10 = 2
अतः नाव की चाल = 10 किमी/घण्टा
तथा धारा की चाल = 2 किमी/घण्टा

प्रश्न 28.
एक नाव 6 घण्टे में धारा की दिशा में 24 किमी तथा विपरीत दिशा (UPBoardSolutions.com) में 16 किमी चलती है तथा वह विपरीत दिशा में 12 किमी तथा धारा की दिशा में 36 किमी उसी समय में चलती है। शांत जल में नाव की चाल तथा धारा की चाल ज्ञात कीजिए।
हलः
माना नाव की चाल = x किमी/घण्टा
तथा धारा की चाल = y किमी/घण्टा
तब धारा की दिशा में नाव की चाल = (x + y) किमी/घण्टा
तथा धारा की विपरीत दिशा में नाव की चाल = (x – y) किमी/घण्टा
प्रश्नानुसार,

x का मान समी० (6) में रखने पर,
8 + y = 12
या y = 12 – 8 ⇒ y = 4
अतः नाव की चाल = 8 किमी/घण्टा तथा (UPBoardSolutions.com) धारा की चाल = 4 किमी/घण्टा

Balaji Publications Mathematics Class 10 Solutions