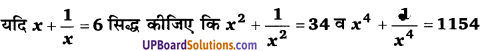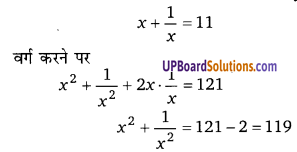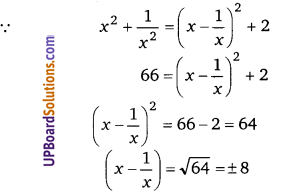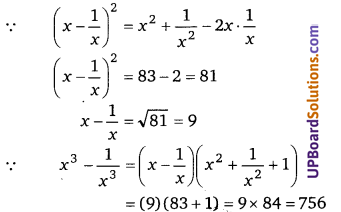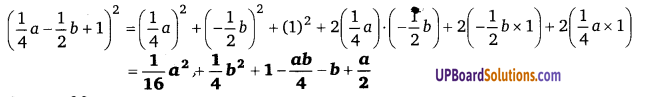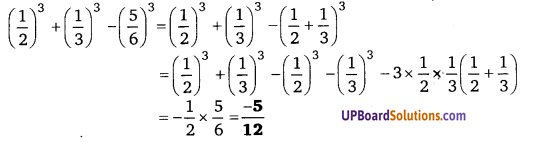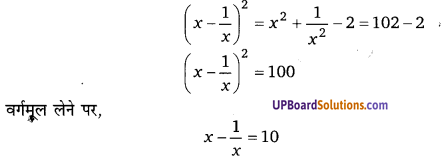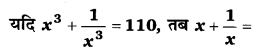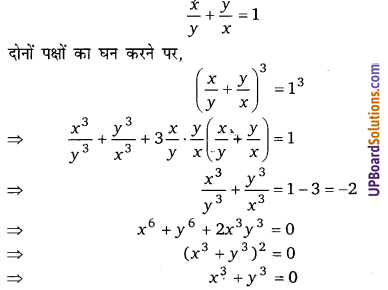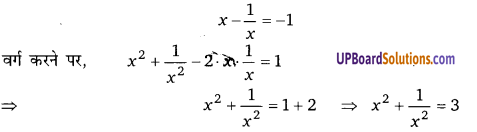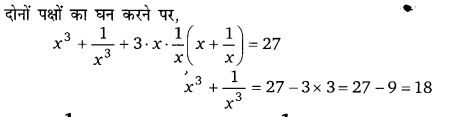Safia

Balaji Class 10 Maths Solutions Chapter 12 Area Related to Circles Ex 12.3 वृत्तों से सम्बन्धित क्षेत्रफल

प्रश्न 1.
एक जीवा PQ की लम्बाई 12 सेमी है जो वृत्त के केन्द्र पर 120° का कोण बनाती है। जीवा PQ द्वारा काटे गये लघु वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए। (NCERT)
हलः
जीवा PQ की लम्बाई 12 सेमी तथा (UPBoardSolutions.com) वृत्त के केन्द्र पर बना कोण θ = 120° है।
माना, वृत्त की त्रिज्या OP = r सेमी
तब समकोण ∆ PRO में

प्रश्न 2.
10 सेमी त्रिज्या वाले वृत्त की एक जीवा AB वृत्त के केन्द्र पर एक समकोण बनाती है। दीर्घ तथा लघु वृत्तखण्डों का क्षेत्रफल ज्ञात कीजिए। (NCERT)
हलः
वृत्त की त्रिज्या r = 10 सेमी तथा (UPBoardSolutions.com) केन्द्र पर बना कोण θ = 90°

वृत्त का क्षेत्रफल = πr² = [latex]\frac{22}{7}[/latex](10)²
= [latex]\frac{22 \times 100}{7}=\frac{2200}{7}[/latex] = 314.3 सेमी²
दीर्घ वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड का क्षेत्रफल
= 314.3 – 28.5 = 285.8 सेमी²
अतः लघु वृत्तखण्ड का क्षेत्रफल 28.5 सेमी² तथा दीर्घ वृत्तखण्ड का क्षेत्रफल 285.8 सेमी²

प्रश्न 3.
वृत्त की एक जीवा केन्द्र पर एक कोण θ बनाती है। यदि जीवा द्वारा काटे गये लघु वृत्तखण्ड का क्षेत्रफल, वृत्त के क्षेत्रफल का [latex]\frac{1}{8}[/latex] है तो सिद्ध कीजिए कि-

हलः
माना, वृत्त की त्रिज्या = r इकाई तथा कोण θ है।
तब, प्रश्नानुसार
[latex]\frac{1}{8}[/latex] × वृत्त का क्षेत्रफल (UPBoardSolutions.com) = जीवा द्वारा काटे गये लघु वृत्तखण्ड का क्षेत्रफल

प्रश्न 4.
दो चाप A व B चित्र में दर्शाये गये हैं। चाप A,0 केन्द्र व OP त्रिज्या वाले वृत्त का भाग है तथा चाप B, M केन्द्र तथा PM त्रिज्या वाले वृत्त का भाग है। यहाँ M, PQ का मध्य बिन्दु है। सिद्ध कीजिए कि दोनों चापों द्वारा सीमाबद्ध क्षेत्र का क्षेत्रफल 25 ([latex] \sqrt{{3}} [/latex] – [latex]\frac{\pi}{6}[/latex]) सेमी² है।

हलः
O केन्द्र वाले वृत्त की त्रिज्या (UPBoardSolutions.com) OP = 10 सेमी, ∵ OP = OQ

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 6 Remainder Theorem and Factor Theorem Ex 6.4 शेषफल प्रमेय तथा गुणनखण्ड प्रमेय

प्रश्न 1.
सिद्ध कीजिए कि (3x – 2), बहुपद p(x) = 3x³ + x² – 20x + 12 का एक गुणनखण्ड है।
हलः
(3x – 2), बहुपद p(x) का एक गुणनखण्ड होगा यदि p(2/3) = 0

अतः (3x – 2) बहुपद p(x) = 3x³ + x² – 20x + 12 का एक गुणनखण्ड है।

प्रश्न 2.
सिद्ध कीजिए कि (x – 1), बहुपद x²⁰ – 1 तथा x²¹ – 1 का एक गुणनखण्ड है।
हल:
p(x) = x²⁰ – 1
∵ x – 1 = 0 = x = 1 रखने पर,
p(1) = 1²⁰ – 1 = 1 – 1 = 0
x = 1 रखने पर p(1) = 0
अतः (x – 1) बहुपद x²⁰ – 1 का एक गुणनखण्ड होगा।
इसी प्रकार, p(x) = x²¹ – 1
p(1) = 1²¹ – 1 = 0
अतः (x – 1), बहुपद x²¹ – 1 का भी एक गुणनखण्ड है।

प्रश्न 3.
यदि 4x⁴ – ax³ + 2x² + 4x + 3 का एक गुणनखण्ड (1 – 2x) है तो a का मान ज्ञात कीजिए।
हलः
1 – 2x = 0 ⇒ x = [latex]\frac{1}{2}[/latex] रखने पर,

प्रश्न 4.
यदि R₁ तथा R₂ दो शेषफल हैं। जब क्रमश: x³ + 2x² – 5ax + 7 को (x + 1) तथा x³ + ax² – 12x + 6 को (x – 2) से विभाजित किया जाता है। यदि R₁ – R₂ = 20, तो सिद्ध कीजिए a = 2।
हलः
R₁ = p( – 1) = (-1)³ + 2(- 1)² – 5a (-1) + 7 = – 1 + 2 + 5a + 7 = (5a + 8)
R₂ = P(2) = 2³ + a(2)² – 12 × 2 + 6 = 8 + 4a – 24 + 6 = 4a – 10
तब दिया है, R₁ – R₂ = 20
⇒ (5a + 8) – (4a – 10) = 20
⇒ a + 8 + 10 = 20 ⇒ a = 2

प्रश्न 5.
यदि R₁ तथा R₂ दो शेषफल हैं जब क्रमशः f(x) = x³ + 2ax² – 5x – 7 को (x + 1) तथा g(x) = x³ + x² – 12x + 6a को (x – 2) से विभाजित किया जाता है। यदि 2R₁ + R₂ = 12 तो सिद्ध कीजिए a = 3।
हल:
R₁ = f(-1) = (-1)³ + 2a (-1)² – 5(-1) – 7 = – 1 + 2a + 5 – 7 = 2a – 3
R₂ = g (2) = (2)³ + 2² – 12 × 2 + 6a = 8 + 4 – 24 + 6a = 6a – 12
दिया है,
2R₁ + R₂ = 12 .
2(2a – 3) + 6a – 12 = 12
10a – 18 = 12
10a = 30 ⇒ a = [latex]\frac{30}{10}[/latex] = 3

प्रश्न 6.
यदि बहुपद ax³ + 3x² – 3 तथा 2x³ – 5x + a को (x – 4) से भाग देने पर क्रमशः R₁ तथा R₂ शेषफल प्राप्त होते हैं तब a का मान ज्ञात कीजिए, यदि
(i) R₁ = R₂
(iii) 2R₁ – R₂ =0
हलः
R₁ = P(4) = a (4)³ + 3(4)² – 3 = 64a + 48 – 3 = 64a + 45
R₂ = q(4) = 2(4)³ – 5(4) + a = 128 – 20 + a = a + 108
तब (i)
R₁ = R₂
⇒ 64a + 45 = a + 108
⇒ 63a = 63 ⇒ a = 1

(ii) 2R₁ – R₂ = 0
2(64a + 45) – (a + 108) = 0
128a + 90 – a – 108 = 0
127a – 18 = 0 ⇒ a = [latex]\frac{18}{127}[/latex]

प्रश्न 7.
यदि (x + α), x² + px + q तथा x² + mx + n, का गुणनखण्ड है तब सिद्ध कीजिए कि α = [latex]\frac{n-q}{m-p}[/latex]
हलः
यदि (x + α), x² + px + q का एक गुणनखण्ड है, तब x = – α रखने पर शेषफल शून्य प्राप्त होगा। अतः
(-α)² + p(-α) + q = 0
α² – αp + q = 0 ………………… (1)
इसी प्रकार यदि (x + α), x² + mx + n का एक गुणनखण्ड है, तब x = – α रखने पर शेषफल शून्य प्राप्त होता है, अतः
(α)² + m(α) + n = 0
α² – mα + n = 0 ……………………… (2)
समी० (1) व (2) से,

प्रश्न 8.
यदि (x + 2), व्यंजक ax² + bx + c तथा bx² + ax + c का महत्तम समापवर्तक (HCF) है तो सिद्ध कीजिए a = b तथा a + b + c = 0
हलः
यदि (x + 2) व्यंजक ax² + bx + c तथा bx² + ax + c का म०स० है, तब यह उभयनिष्ठ गुणनखण्ड होगा।
अत: x = – 2 रखने पर,
a( – 2)² + b( – 2) + c = 0
या 4a – 2b + c = 0 …………………….. (1)
4b – 2a + c = 0 ……………….(2)
समी० (1) व (2) को जोड़ने पर,
2a + 2b + 2c = 0
⇒ a + b + c = 0
समी० (1) व (2) को घटाने पर, a = b

प्रश्न 9.
यदि (x – 1), व्यंजक x² – 1 तथा ax² – b(x + 1), का महत्तम समापवर्तक (HCF) है तो सिद्ध कीजिए a = 2b
हलः
यदि (x – 1), व्यंजक (x² – 1) और ax² – b(x + 1) का म०स० है, तो (x – 1) इसका उभयनिष्ठ गुणनखण्ड होगा। अतः
a(1)² – b(1 + 1) = 0
a – 2b = 0
a = 2b

Ex 6.4 Remainder Theorem and Factor Theorem स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
x³ + 3x² + 3x + 1 को 5 + 2x से भाग करने पर शेषफल ज्ञात कीजिए।
हल:
5 + 2x = 0 या 2x = – 5
∴ x = [latex]-\frac{5}{2}[/latex] को बहुपद में रखने पर

प्रश्न 2.
गुणनखण्ड प्रमेय का प्रयोग करके 2y³ + y² – 2y – 1 के गुणनखण्ड कीजिए।
हलः
2y³ + y² – 2y – 1 में y = 1 रखने पर
शेषफल = 2(1)³ + (1)² – 2(1) – 1 = 2 + 1 – 2 – 1 = 0
अतः (y – 1) बहुपद 2y³ + y² – 2y – 1 का एक गुणनखण्ड है।

∴ 2y² + 3y + 1 = 2y² + (2 + 1)y + 1
= 2y² + 2y + y + 1
= 2y(y + 1) + 1(y + 1) = (2y + 1)(y + 1)
∴ गुणनखण्ड = (y – 1)(y + 1)(2y + 1)

प्रश्न 3.
x⁴ + x³ – 2x² + x + 1 को (x – 1) से भाग करने पर शेषफल ज्ञात कीजिए। .
हलः
∵ x – 1 = 0 या x = 1 का मान बहुपद में रखने पर
शेषफल = (1)⁴ + (1)³ – 2(1)² + 1 + 1
= 1 + 1 – 2 + 1 + 1 = 2

प्रश्न 4.
सिद्ध कीजिए कि (x + 2) बहुपद x³ + 3x² + 5x + 6 व 2x + 4 का गुणनखण्ड है।
हलः
∵ x + 2 = 0 ∴x = 0 – 2 = – 2 रखने पर
बहुपद x³ + 3x² + 5x + 6 का शेषफल
=(-2)³ + 3(-2)² + 5(-2) + 6 = – 8 + 12 – 10 + 6 = 0
बहुपद 2x + 4 का शेषफल = 2(-2) + 4 = – 4 + 4 = 0
∴ (x + 2), बहुपद x³ + 3x² + 5x + 6 व 2x + 4 का गुणनखण्ड है।

प्रश्न 5.
गुणनखण्ड प्रमेय से 6x² + 17x + 5 के गुणनखण्ड कीजिए।
हल:

प्रश्न 6.
गुणनखण्ड प्रमेय से y² – 5y + 6 के गुणनखण्ड कीजिए।
हलः
बहुपद y² – 5y + 6 में y = 2 रखने पर
(2)² – 5(2) + 6
4 – 10 + 6 = 0
अतः (y – 2) इसका एक गुणनखण्ड है।

∴ गुणनखण्ड = (y – 2)(y – 3)

प्रश्न 7.
सिद्ध कीजिए कि (x + 2), बहुपद x³ + 3x² + 3x + 2 का एक गुणनखण्ड है।
हलः
∵ x + 2 = 0 इसलिए x = – 2 का मान बहुपद में रखने पर
(-2)³ + 3(-2)² + 38 – 2) + 2
– 8 + 12 – 6 + 2 = 0
अतः (x + 2), बहुपद x³ + 3x² + 3x + 2 का एक गुणनखण्ड है।

प्रश्न 8.
बहुपद 9x³ + 3x² – 13 व 2x³ – 5x + α को (x + 2) से भाग देने पर समान शेषफल प्राप्त होते हैं तब α का मान ज्ञात कीजिए।
हलः
बहुपद 9x³ + 3x² – 13 को (x + 2) से भाग देने पर
x + 2 = 0 या x = – 2 रखने पर
शेषफल = 9(-2)³ + 3(-2)² – 13
= 9(-8) + 3(4) – 13 = – 72 + 12 – 13 = – 73
बहुपद 2x³ – 5x + α को (x + 2) से भाग देने पर शेषफल
= 2(-2)³ – 5( – 2) + α = – 16 + 10 + α = – 6 + α
दोनों शेषफल समान होने की दिशा में
– 6 + α = – 73
α = – 73 + 6 = – 67

प्रश्न 9.
सिद्ध कीजिए कि (x + 1) तथा (2x – 3) बहुपद 2x³ – 9x² + x + 12 के गुणनखण्ड है। (NCERT Exemplar)
हलः
(i) बहुपद 2x³ – 9x² + x + 12 में x + 1 = 0 या x = 0 – 1 = – 1 रखने पर
शेषफल = 2(-1)³ – 9(-1)² + (-1) + 12
= 2(-1) – 9(1) – 1 + 12 = – 2 – 9 – 1 + 12 = 0
अतः (x + 1), बहुपद 2x³ – 9x² + x + 12 का गुणनखण्ड है।

(ii) 2x – 3 = 0 या x = [latex]\frac{3}{2}[/latex] का मान बहुपद 2x³ – 9x² + x + 12 में रखने पर

अतः (2x – 3) बहुपद 2x³ – 9x² + x + 12 का गुणनखण्ड है।

प्रश्न 10.
α के किस मान के लिए बहुपद 2x³ + 9x² + 11x + α + 3, 2x – 1 से पूर्णतया विभाजित है।
हल:
2x – 1 = 0 या x = [latex]\frac{1}{2}[/latex] का मान बहुपद में रखने पर, शेषफल = 0

प्रश्न 11.
4x⁴ – 2x³ – 6x² + x – 5 से क्या घटाया जाए कि वह 2x² + x – 1 से पूर्णतया विभाजित है।
हल:
2x² + x – 1 = 2x² + (2 – 1)x – 1
= 2x + 2x – x – 1
= 2x(x + 1) – 1(x + 1) = (x + 1)(2x – 1)
(x + 1) से पूर्णतया विभाजित होने पर x + 1 = 0 या x = – 1 रखने पर
शेषफल = 4(-1)⁴ – 2(-1)³ – 6(-1)² + (-1) – 5 .
= 4(1) – 2(-1) – 6(1) – 1 – 5 = 4 + 2 – 6 – 1 – 5 = – 6
इसी प्रकार 2x – 1 = 0 या x = [latex]\frac{1}{2}[/latex] रखने पर

∴ 2x² + x – 1 के दोनों गुणनखण्डों से विभाजित करने पर बहुपद 4x⁴ – 2x³ – 6x² + x – 5 के शेषफल = – 6

प्रश्न 12.
यदि x³ + ax² – bx + 10, x² – 3x + 2 से पूर्णतया विभाजित हो तो a तथा b के मान ज्ञात कीजिए।
हल:
x² – 3x + 2 = x² – (2 + 1) x + 2 = x² – 2x – x + 2
= x (x – 2) – 1(x – 2)= (x – 2)(x – 1)
∵ x – 2 = 0 ∴ x = 2 का मान बहुपद x³ + ax² – bx + 10 में रखने पर
शेषफल = (2)³ + a(2)² – b(2) + 10
= 8 + 4a – 2b + 10 = 4a – 2b + 18 ………………….. (1)
∵ x – 1 = 0 ∴ x = 1 का मान बहुपद x³ + ax² – bx + 10 में रखने पर
शेषफल = (1)³ + a(1)² – b(1) + 10
= 1 + a – b + 10
= 11 + a – b ………………… (2)
दोनों शेषफल = 0 रखने पर
4a – 2b + 18 = 0
⇒ 4a – 2b = – 18 ………………(3)
11 + a – b = 0
a – b = – 11 ……………… (4)
समी (4) में 2 से गुणा करने पर, समीकरण (3) घटाने पर

समी (4) में a का मान रखने पर
2 – b = – 11
–b = – 11 – 2 = – 13 ⇒ b = 13

प्रश्न 13.
सिद्ध कीजिए कि (x – 2),(x + 3) तथा (x – 4) बहुपद x³ – 3x² – 10x + 24 के गुणनखण्ड है।
हलः
∵ x – 2 = 0 या x = 2 रखने पर
शेषफल = (2)³ – 3(2)² – 10(2) + 24 = 8 – 12 – 20 + 24 = 0
∵ x + 3 = 0 या x = – 3 रखने पर
शेषफल = (-3)³ – 3(-3)² – 10(-3) + 24 = – 27 – 27 + 30 + 24 = 0
∵ x – 4 = 0 या x = 4 रखने पर
शेषफल = (4)³ – 3(4)² – 10(4) + 24 = 64 – 48 – 40 + 24 = 88 – 88 = 0
∵ शेषफल 0 है
∵ (x – 2), (x + 3), (x – 4) बहुपद x³ – 3x² – 10x + 24 के गुणनखण्ड है।

प्रश्न 14.
x³ – 3x² – 12x + 9 में क्या जोड़ें कि परिणामी x² + x – 6 से पूर्णतया विभाजित हो जाए।
हल:

शेषफल = – (2x + 15)
अर्थात् (2x + 15) जोड़ने पर परिणामी x² + x – 6 से पूर्णतया विभाजित हो जाता है।

प्रश्न 15.
3x³ + x² – 22x + 9 में क्या जोड़ें कि परिणामी 3x² + 7x – 6 से पूर्णतया विभाजित हो जाए।
हलः

शेषफल = – (2x + 3) अर्थात् 2x + 3 जोड़ने पर परिणामी 3x² + 7x – 6 से पूर्णतया विभाजित होगा।

प्रश्न 16.
x³ – 6x² – 15x + 80 में क्या घटायें कि परिणामी x² + x – 12 से पूर्णतया विभाजित हो जाए।
हल:

∴ शेषफल = 4x – 4
अतः (4x – 4) घटाने पर परिणामी पूर्णतया विभाजित होगा।

प्रश्न 17.
सिद्ध कीजिए कि (x – 2), बहुपद f (x) = 2x³ – 3x² – 17x + 30 का एक गुणनखण्ड है।
हलः
∵ x – 2 = 0 ∴ x = 2 रखने पर।
f(2) = 2(2)³ – 3(2)² – 17(2) + 30
= 16 – 12 – 34 + 30 = 0
∴ (x – 2), बहुपद f(x) का एक गुणनखण्ड है।

प्रश्न 18.
गुणनखण्ड प्रमेय से x³ – 6x² + 11x – 6 के गुणनखण्ड कीजिए। (NCERT Exemplar)
हल:
x³ – 6x² + 11x – 6
x = 1 रखने पर, शेषफल = (1)³ – 6(1)² + 11(1) – 6 = 1 – 6 + 11 – 6 = 0
अतः (x – 1) इसका एक गुणनखण्ड है।

x² – 5x + 6 = x 2 – (2 + 3)x + 6
= x² – 2x – 3x + 6 = x(x – 2) – 3(x – 2) = (x – 2)(x – 3)
गुणनखण्ड = (x – 1)(x – 2)(x – 3)

प्रश्न 19.
यदि (2x + 3) बहुपद 4x³ + 20x² + 33x + 18 का एक गुणनखण्ड है तो इसके शेष गुणनखण्ड ज्ञात कीजिए।
हलः
(2x + 3), बहुपद 4x³ + 20x² + 33x + 18 का एक गुणनखण्ड है

2x² + 7x + 6 = 2x² + (3 + 4)x + 6
= 2x² + 3x + 4x + 6 = x(2x + 3) + 2(2x + 3) = (2x + 3)(x + 2)
∴ गुणनखण्ड = (2x + 3)(2x + 3)(x + 2) = (2x + 3)² (x + 2)

प्रश्न 20.
f(x) = x⁴ – 4x³ + 3x² – ax – bको (x – 1) से विभाजित किया जाता है तो शेषफल 6 आता है तब सिद्ध कीजिए कि a + b = – 6
हल:
f(x), (x – 1) से विभाजित होता है।
∴ x – 1 = 0 या x = 1 रखने पर
f(1) = (1)⁴ – 4(1)³ + 3(1)² – a(1) – b
6 = 1 – 4 + 3 – a – b
1 – 4 + 3 – a – b = 6
4 – 4 – a – b = 6 ⇒ – a – b = 6
a + b = – 6

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 10 Maths Solutions Chapter 12 Area Related to Circles Ex 12.2 वृत्तों से सम्बन्धित क्षेत्रफल

प्रश्न 1.
21 सेमी त्रिज्या वाले एक वृत्त से एक त्रिज्यखण्ड काटा जाता है। त्रिज्यखण्ड का कोण 150° है। चाप की लम्बाई तथा क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 21 सेमी तथा त्रिज्यखण्ड (UPBoardSolutions.com) का कोण θ = 150°, चाप को लम्बाई l सेमी है।

अतः चाप की लम्बाई 55 सेमी तथा क्षेत्रफल = 577.5 सेमी²

प्रश्न 2.
एक वृत्त की त्रिज्या 35 सेमी तथा एक चाप द्वारा केन्द्र पर बनाया गया कोण 72° है। चाप की लम्बाई तथा त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 35 सेमी तथा केन्द्र पर बनाया गया कोण θ = 72°


अतः चाप की लम्बाई l = 44 सेमी, क्षेत्रफल = 770 सेमी²

प्रश्न 3.
21 सेमी त्रिज्या के एक वृत्त से एक त्रिज्यखण्ड काटा गया है। त्रिज्यखण्ड का कोण 120° है। चाप की लम्बाई तथा क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 21 सेमी (UPBoardSolutions.com) तथा त्रिज्यखण्ड का कोण θ = 120°

अतः चाप की लम्बाई 1 = 44 सेमी, क्षेत्रफल A = 462 सेमी²

प्रश्न 4.
वृत्त के एक चाप की लम्बाई 20 π सेमी है तथा जिसका केन्द्र पर कोण 144° है। वृत्त की त्रिज्या ज्ञात कीजिए।
हलः
वृत्त के एक चाप की लम्बाई l = 20 π सेमी तथा केन्द्र पर बना कोण θ = 144°
तथा माना, वृत्त की (UPBoardSolutions.com) त्रिज्या = r सेमी है।।

अतः वृत्त की त्रिज्या 25 सेमी है।

प्रश्न 5.
एक वृत्त से 56° के कोण पर काटे गये त्रिज्यखण्ड का क्षेत्रफल 4.4 सेमी² है। वृत्त की त्रिज्या ज्ञात कीजिए।
हलः
माना, वृत्त की त्रिज्या = r सेमी
तथा त्रिज्यखण्ड का कोण θ = 56°
तब, प्रश्नानुसार, त्रिज्यखण्ड का (UPBoardSolutions.com) क्षेत्रफल = 4.4 सेमी²

प्रश्न 6.
5.2 सेमी की त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड की परिधि 16.4 सेमी है। त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 5.2 सेमी तथा त्रिज्यखण्ड की परिधि = 16.4 सेमी
l + 2r = 16.4
l + 2 × 5.2 = 16.4
l + 10.4 = 16.4
l = 16.4 – 10.4 = 6 सेमी
त्रिज्यखण्ड का क्षेत्रफल = [latex]\frac{1}{2} l r=\frac{1}{2}[/latex] × 6 × 5.2 = 15.6 सेमी²

प्रश्न 7.
एक घड़ी की छोटी तथा बडी सुइयाँ क्रमश: 4 सेमी तथा 6 सेमी लम्बी हैं। दो दिन में इनके द्वारा चली गयी दूरियों का योग ज्ञात कीजिए।
हलः
माना, घड़ी की छोटी सुई की लम्बाई (त्रिज्या) r₁ = 4 सेमी
तथा घड़ी की बड़ी सुई की लम्बाई (त्रिज्या) r₂ = 6 सेमी
∵ घड़ी की छोटी सुई 12 घण्टे में एक चक्कर लगाती है।
∴ 2 दिन (48 घण्टे) में 4 चक्कर लगायेंगी
अतः घड़ी की छोटी सुई (UPBoardSolutions.com) द्वारा 2 दिन में चली गयी दूरी = 2π₁ × 4
= 2 × [latex]\frac{22}{7}[/latex] × 4 × 4 = [latex]\frac{704}{7}[/latex] सेमी
तथा घड़ी की बड़ी सुई 1 घण्टे में एक चक्कर लगाती है तब वह 2 दिन (48 घण्टे) में 48 चक्कर लगायेंगी।
अतः घड़ी की बड़ी सुई द्वारा 2 दिन में चली गई दूरी = 2πr₂ × 48
= 2 × [latex]\frac{22}{7}[/latex] × 6 × 48 = [latex]\frac{12672}{7}[/latex] सेमी
दोनों सुईयों द्वारा 2 दिनों में चली गई दूरियों का योग
[latex]\frac{704}{7}+\frac{12672}{7}=\frac{13376}{7}[/latex] = 1910.85 सेमी

प्रश्न 8.
एक वृत्त मे केन्द्र O तथा त्रिज्या 5 सेमी, एक जीवा AB की लम्बाई 5[latex] \sqrt{{3}} [/latex] सेमी है। त्रिज्यखण्ड AOB का क्षेत्रफल ज्ञात कीजिए।
हल:
वृत्त की त्रिज्या r = 5 सेमी तथा जीवा AB की लम्बाई = 5[latex] \sqrt{{3}} [/latex] सेमी
माना, त्रिज्यखण्ड AOB का कोण = θ

प्रश्न 9.
एक घड़ी की मिनट की सुई की लम्बाई [latex] \sqrt{{21}} [/latex] सेमी है। घड़ी की मिनट की सुई द्वारा 7:00 A.M. तथा 7:05 A.M. के बीच में रचित क्षेत्रफल ज्ञात कीजिए।
हलः
घड़ी की मिनट की सुई की लम्बाई r = [latex] \sqrt{{21}} [/latex] सेमी
घड़ी की मिनट की सुई द्वारा 7:00 A.M. तथा 7:05 A.M. तक का समय = 5 मिनट
∵ 60 मिनट में घड़ी की मिनट की सुई द्वारा बना कोण = 360°
∴ 5 मिनट में घड़ी की मिनट की (UPBoardSolutions.com) सुई द्वारा बना कोण = [latex]\frac{360 \times 5}{60}[/latex]
θ = 30°
घड़ी की मिनट की सुई द्वारा 7:00 A.M. तथा 7:05 A.M. के बीच में रचित क्षेत्रफल

प्रश्न 10.
5 सेमी त्रिज्या की एक पुली के रिम पर प्रत्यास्थ (elastic) बेल्ट रखी है। बेल्ट के एक बिन्दु को केन्द्र 0 से 10 सेमी दूर बिन्दु P तक खींचा जाता है। पुली के रिम के सम्पर्क में आने वाली बेल्ट की लम्बाई ज्ञात कीजिए।
हलः
स्वयं हल (UPBoardSolutions.com) करें।

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 4 Algebraic Identities Ex 4.5 बीजगणितीय सर्वसमिकाऐं

प्रश्न 1.
निम्न के मान ज्ञात कीजिए।
(a) (25)³ – (75)³ + (50)³
(b) (0.2)³ – (0.3)³ + (0.1)³ (NCERT Exemplar)
(c) (1.5)³ – (0.9)³ – (0.6)³
(d) (-12)³ + 7³ + 5³
हलः
(a) (25)³ – (75)³ + (50)³
= (25)³ – (25 + 50)³ + (50)³
= (25)³ – (25)³ – (50)³ – 3 × 25 × 50(25 + 50) + (50)³
=-3 × 25 × 50 × 75 = -281250

(b) (0.2)³ – (0.3)³ + (0.1)³
= (0.2)³ – (0.2 + 0.1) + (0.1) ³
= (0.2)3 s – (0.2)³ – (0.1)³ – 3 × 0.2 × 0.1 × (0.2 + 0.1) + (0.1)³
=-3 × 0.2 × 0.1 × (0.3) = -0.018

(c) (1.5)³ – (0.9)³ – (0.6)³
= (0.9 + 0.6)³ – (0.9)³ – (0.6)³
= (0.9)³ + (0.6)³ + 3 × 0.9 × 0.6 × (0.9 + 0.6) – (0.9)³ – (0.6)³
= 3 × 0.9 × 0.6 × 1.5 = 2.430

(d) (-12)³ + 7³ + 5³
⇒ 7³ + (-7 – 5)³ + 5³
⇒ 7³ + (-7)³ + (-5)³ + 3 × (-7)(-5)(-7 – 5) + 5³
= 3 × -7 × -5(-12)= 105 × (-12) = -1260

प्रश्न 2.
यदि x + y + z = 9 और x² + y² + z² = 35, तब x³ + y³ + z³ – 3xyz के मान ज्ञात कीजिए।
हल:
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx) ……..(1)
∵ x + y + z = 9
वर्ग करने पर .
x² + y² + z² + 2(xy + y + zx) = 81
35 + 2(xy + yz + zx) = 81
2(xy + yz + zx) = 81 – 35 = 46
xy + yz + zx = [latex]\frac{46}{2}[/latex] = 23
समी० (1) से
x³ + y³ + z³ – 3xyz = 9(35 – 23) = 9 × 12 = 108

प्रश्न 3.
यदि x + y + z = 8 और xy + yz + z x = 26, तब x³ + y³ + x ³ – 3xyz के मान ज्ञात कीजिए।
हलः
∵ x + y + z = 8
वर्ग करने पर
(x + y + z) = (8)
x² + y² + z² + 2(xy + yz + zx) = 64
x² + y² + z² + 2(26) = 64
x² + y² + z² = 64 – 52 = 12
∵ x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
= (8)(12 – 26)
= (8)(-14) = – 112

प्रश्न 4.
निम्न के मान ज्ञात कीजिए।
(i) (3x – 4y + 5z)(9x² + 16y² + 25z² + 12xy – 15yz + 20yz)
(ii) (3x + 2y + 2z)(9x² + 4y² + 4z² -6xy – 4yz – 6xz)
(iii) (2x – y + 3z)(4x² + y² + 9z² + 2xy + 3yz -6xz) (NCERT Exemplar)
हलः
(i) (3x – 4y + 5z)(9x² + 16y² + 25z² + 12xy – 15xz + 20yz)
= (3x) + (-4y) + (5z)³ – 3[3x × – 4y × 5z]
=27x³ – 64y³ + 125z³ + 180xyz

(ii) (3x + 2y + 2z(9x² + 4y² + 4z² – 6xy -4yz – 6zx)
= (3x)³ + (2y) + (2z)³ – 3[3x × 2y × 2z]
=27x² + 8y² + 8z² – 36xyz

(iii) (2x – y + 3z)(4x² + y² – 9z² + 2xy + 3yz – 6xz)
= (2x)³ + (-y)³ + (3z)³ – 3[2x × -y × 3z]
= 8x³ – y³ + 27z³ + 18xyz

Ex 4.5 Algebraic Identities विविध प्रश्नावली

प्रश्न 1.
सर्वसमिका का प्रयोग करके निम्न के मान ज्ञात कीजिए। [NCERT]
(1) 103 × 107
(ii) 95 × 96
(iii) 104 × 96
हलः
(i) 103 × 107 = (100 + 3) × (100 + 7)
= (100)² + (3 + 7) × 100 + 3 × 7
=10000 + 1000 + 21 = 11021

(ii) 95 × 96 = (100 – 5) × (100 – 4)
= (100)² (5 + 4) × 100 + 5 × 4
= 10000 – 900 + 20 = 9120

(iii) 104 × 96 = (100 + 4) × (100 – 4)
= (100)² – (4)²
= 10000 – 16 = 9984

प्रश्न 2.

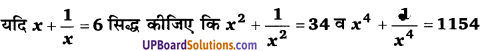
हल:

प्रश्न 3.
यदि [latex]x+\frac{1}{x}[/latex] = 11, सिद्ध कीजिए कि [latex]x^{2}+\frac{1}{x^{2}}[/latex] = 119
हल:

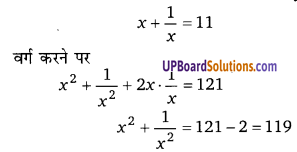
प्रश्न 4.
यदि [latex]x^{2}+\frac{1}{x^{2}}[/latex] = 66, सिद्ध कीजिए कि [latex]x-\frac{1}{x}[/latex] = ±8
हलः

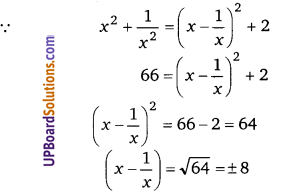
प्रश्न 5.
यदि x = 4, y =3, z = 2 तब सिद्ध कीजिए कि 4x² + y² + 25z² + 4xy – 10yz – 20xz =1
हल:
L.H.S. = 4x² + y² + 25z² + 4xy -10yz – 20xz
= (-2x)² + (-y)² + (58)² + 2(-2x)(-y) + 2(-y) (5z) + 2(5z)(-2x)
= (-2x – y + 5z)²
= (-2 × 4 – 3 + 5 × 2)² = (-1)² = 1 = R.H.S.

प्रश्न 6.
यदि x + y = 12 व xy = 27, तब सिद्ध कीजिए कि x³ + y³ = 756
हलः
∵ x + y = 12
घन करने पर x³ + y³ + 3xy (x + y) = 1728
x³ + y³ + 3 × 27 (12) = 1728
x³ + y³ + 972 = 1728
x³ + y³ = 1728 – 972 = 756

प्रश्न 7.
यदि [latex]x^{2}+\frac{1}{x^{2}}[/latex] = 83, तब सिद्ध कीजिए कि [latex]x^{3}-\frac{1}{x^{3}}[/latex] = 756
हलः

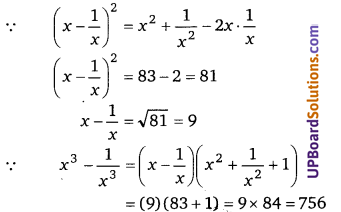
प्रश्न 8.
यदि x + y + z =8 व xy + yz + zx=20, तब सिद्ध कीजिए कि x³ + y³ + z³ – 3xyz = 32
हल:
∵ x + y + x = 8 ……….(1)
वर्ग करने पर
x² + y² + z² + 2(xy + ys + ax) = 64
x² + y² + z² = 64-2(xy + yz + zx)
∵ x³ + y³ + z³ – 3xyz = (x + y + 2)(x² + y² + z² – xy – yz – zx)
= (8)[64 – 2(xy + yz + zx)-(xy + yz + zx)]
= 8[64 – 3(xy + yz + zx)]
= 8[64 – 3 × 20] = 8 × 4 = 32

प्रश्न 9.
सिद्ध कीजिए कि 2x² + 2y² + 2z² – 2xy – 2yz – 2zx = [(x – y)² + (y – z)² + (z – x)²]
हलः
L.H.S. = 2x² + 2y² + 2z² – 2xy -2yz – 2zx
= x² + x² + y² + y² + z² + z² – 2xy -2yz – 2zx
= (x² + y² – 2xy) + (y² + x² – 2yz) + (x² + x² – 2zx)
= (x – y)² + (y – z)² + (z – x)² = R.H.S.

प्रश्न 10.
[latex]\left(\frac{1}{4} a-\frac{1}{2} b+1\right)^{2}[/latex] का विस्तार कीजिए। [NCERT]
हलः

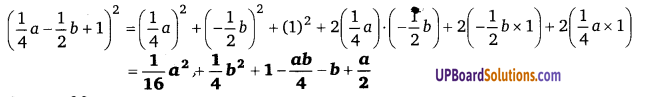
प्रश्न 11.
विस्तार कीजिए – (-2x + 5y – 3z)² [NCERT]
हलः
(-2x + 5y – 3z)² = (-2x)² + (5y)² + (-3z)² + 2(-2x)(5y) + 2(5y)(-3z) + 2(-2x)(-3z)
= 4x² + 25y² + 9z² – 20xy – 30yz + 12xz

प्रश्न 12.
[latex]\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{3}\right)^{3}-\left(\frac{5}{6}\right)^{3}[/latex] का मान ज्ञात कीजिए। (NCERT Exemplar)
हलः

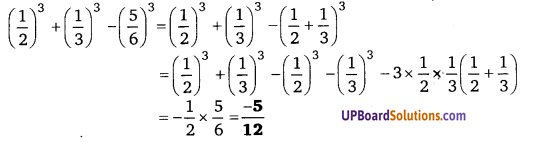
Ex 4.5 Algebraic Identities बहुविकल्पीय प्रश्न (Multiple Choice Questions)

सही विकल्प का चयन कीजिए।
प्रश्न 1.

(a) 320
(b) 322
(c) 321
(d) 222
हलः

अतः विकल्प (b) सही है।

प्रश्न 2.
यदि x – y = 5 व xy = 12, तब x² + y² =
(a) 49
(b) 25
(c) 144
(d) इनमें से कोई नहीं
हलः
x – y = 5
दोनों पक्षों का वर्ग करने पर,
(x – y)² = 5²
⇒ x² + y² – 2xy = 25
⇒ x² + y² – 2(12) = 25
⇒ x² + y² = 49
अतः विकल्प (a) सही है।

प्रश्न 3.

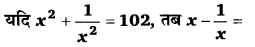
(a) 100
(b) 127
(c) 10
(d) 12
हलः

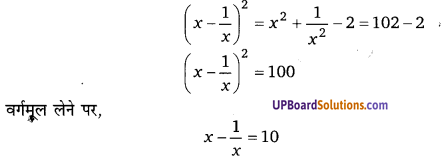
अतः विकल्प (c) सही है।

प्रश्न 4.

(a) 194
(b) 144
(c) 124
(d) इनमें से कोई नहीं
हलः

अतः विकल्प (a) सही है।

प्रश्न 5.

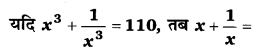
(a) 15
(b) 105
(c) 25 .
(d) 5
हलः

अतः विकल्प (d) सही है।

प्रश्न 6.

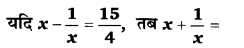
(a) 17
(b) 4
(c) 17/4
(d) 19/4
हलः

अतः विकल्प (c) सही है।

प्रश्न 7.
यदि x + y + z =9, xy + yz + xz = 23, तब x³ + y³ + z³ – 3xyz =
(a) 100
(b) 81
(c) 108
(d) 123
हलः
x + y + z = 9
दोनों पक्षों का वर्ग करने पर,
(x + y + z)² = 81
⇒ x² + y² + z² + 2(xy + yz + zx) = 81
⇒ x² + y² + z² = 81 – 2 × 23 = 35
∵ x³ + y³ + z³ – 3xyz = (x + y + z) (x² + y² + z² –xy –yz – zx)
= 9 × (35 – 23)
= 9 × 12 = 108
अतः विकल्प (c) सही है।

प्रश्न 8.
यदि [latex]\frac{x}{y}+\frac{y}{x}[/latex] = 1, तब x³ + y³ =
(a) 1
(b) 2
(c) 3
(d) 0
हलः

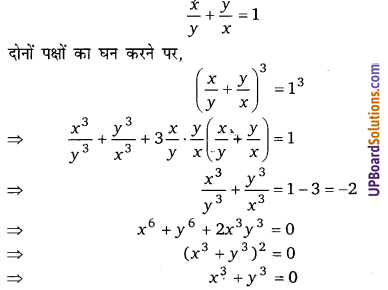
अतः विकल्प (d) सही है।

प्रश्न 9.
यदि x – y = -8 व xy = -12, तब x³ – y³ =
(a) 224
(b) -224
(c) 234
(d) -234
हलः
x – y = -8
दोनों पक्षों का घन करने पर,
(x – y)³ = (-8)³
⇒ x³ – y³ – 3xy (x – y) = -512
⇒ x³ – y³ = -512 + 3xy (x – y)
⇒ x³ – y³ = -512 + 3(-12)(-8) = -512 + 288
⇒ x³ – y³ = -224
अतः विकल्प (b) सही है।

प्रश्न 10.
यदि x + y + z = 9 व xy + yz + zx = 23, तब x² + y² + z² =
(a) 25
(b) 35
(c) 45
(d) 305
हलः
x + y + z =9
दोनों पक्षों का वर्ग करने पर,
(x + y + z)² = 9²
⇒ x² + y² + z² + 2(xy + yz + zx) = 81
⇒ x² + y² + z² = 81 – 2(xy + yz + zx)
= 81 – 2 × 23 (∵ xy + yz + zx = 23)
= 81 – 46 = 35
अतः विकल्प (b) सही है।

Ex 4.5 Algebraic Identities स्वमूल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
(2x – y + z)² का विस्तार कीजिए।
हलः
(2x – y + z)² = (2x)² + (-y)² + (z)² – 2. 2x . y + 2(-y) (z) + 2(2x)(z)
=4x² + y² + z² – 4xy – 2yz + 4xz

प्रश्न 2.
(3a + 4b + 5c)² का विस्तार कीजिए।
हलः
(3a + 4b + 5c)² = 9a² + 16b² + 25c² + 24ab + 40 bc + 30ac

प्रश्न 3.
(4a – 2b – 3c)² का विस्तार कीजिए।
हलः
(4a – 2b – 3c)² = (4a)² + (-2b)² + (-3c)² – 16ab + 12bc – 24ac
= 16a² + 4b² + 9c² – 16ab + 12bc – 24ac

प्रश्न 4.
सर्वसमिका का प्रयोग करके (28)³ + (-15)³ + (-13)³ का मान ज्ञात कीजिए।
हलः
(28)³ + (-15)³ + (-13)³ = (15 + 13)³ + (-15)³ + (-13)³
= (15)³ + (13)³ + 3 × 15 × 13(15 + 13) – (15)³ – (13)³
= 3 × 15 × 13(15 + 13) = 16380

प्रश्न 5.
(104)³ का मान सर्वसमिका का प्रयोग करके ज्ञात कीजिए। .
हलः
(104)³ = (100 + 4)³
(100)³ + (4)³ + 3 × 100 × 4(100 + 4)
= 1000000 + 64 + 124800 = 1124864

प्रश्न 6.
यदि 3x – 7y = 10 व xy = -1, तब सिद्ध कीजिए कि 9x² + 49y² = 58
हलः
3x – 7y = 10
दोनों ओर का वर्ग करने पर
9x² + 49y² – 42xy = 100
9x² + 49y² – 42 × (-1) = 100
9x² + 49y² = 100 – 42 = 58

प्रश्न 7.
सिद्ध कीजिए कि x² + y² + z² – xy – y – zx; x, y व z के सभी मानों के लिए सदैव धनात्मक होगा।
हल:
x² + y² + z² – xy – yz – zx = [latex]\frac{1}{2}[/latex] [(x – y)² + (y – z)² + (z – x)²]
∵ (x – y)²,(y – z)², (z – x)²
पूर्ण वर्ग है जो हमेशा धनात्मक होते हैं।
अतः इसका योग सदैव धनात्मक होगा।

प्रश्न 8.
यदि x² + y² + z² = 20 व x + y + z = 0, तब सिद्ध कीजिए xy + yz + zx = -10
हल:
x + y + z = 0
वर्ग करने पर, (x + y + z)² = 0
x² + y² + z² + 2(xy + yz + zx) = 0
20 + 2(xy + yz + zx) = 0
2(xy + yz + zx) = 0 – 20 = -20
xy + yz + zx = [latex]\frac{-20}{2}[/latex] = -10

प्रश्न 9.
यदि x + y + z = 6 व xy + yz + zx = 11, तब सिद्ध कीजिए x³ + y³ + z³ -3xyz = 18
हलः
∵ x + y + z = 6 ……………. (1)
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx) ……..(2)
समी० (1) का वर्ग करने पर
x² + y² + z² + 2(xy + yz + zx) = 36
x² + y² + z² + 2(11) = 36
x² + y² + z² = 36 – 22 = 14
समी० (2) में x² + y² + z² का मान रखने पर
x³ + y³ + z³ – 3xyz = (6) (14 – 11) = (6) (3) = 18

प्रश्न 10.
x³ + y³ + z³ का मान ज्ञात कीजिए, यदि x + y + z = 11, x² + y² + z² = 45 व xyz = 40
हलः
x + y + z = 11 …………….(1)
समी० (1) का वर्ग करने पर
∵ (x + y + z)² = 121
x² + y² + z² + 2(xy + yz + zx) = 121
2(xy + yz + zx) = 121 – 45 = 76
∴ xy + yz + zx = [latex]\frac{76}{2}[/latex] = 38
x³ + y³+ z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ – 3 × 40 = (11)(45 – 38) = (11)(7) = 77
x³ + y³ + z³ = 77 + 120 = 197

प्रश्न 11.
x³ + y³ + z³ का मान ज्ञात कीजिए, यदि x + y + z = 15, ‘xy + yz + zx = 71 व xys = 10
हलः
x³ + y³ + z³ – 3xyz = (x + y + z)(x² + y² + z² – xy – yz – zx)
x³ + y³ + z³ – 3 × 10 = (15) [x² + y² z² – 71] ………… (1)
x + y + z = 15 …………………. (2)
समी० (2) का वर्ग करने पर
x² + y² + z² + 2(xy + yz + zx) = 225
x² + y² + z² + 2(71) = 225
x² + y² + z² = 225 – 142
x² + y² + z² = 83 का मान समी० (1) में रखने पर
समी० (1) से, x³ + y³ + z³ – 30 = 15[83 – 71]
x³ + y³ + z³ – 30 = 15 × 12 = 180
x³ + y³ + z³ = 180 + 30 = 210

प्रश्न 12.
x³ – 8y³ – 36xy – 216 का मान ज्ञात कीजिए, यदि x = 2y + 6
हल:
x = 2y + 6 का मान रखने पर,
(2y + 6)³ – 8y³ – 36(2y + 6)y – 216
= 8y³ + 216 + 36y (2y + 6) – 8y³ – 72y² – 216y – 216
= 72y² + 216y – 72y² – 216y = 0

प्रश्न 13.
x³ + y³ + z³ – 3xyz का मान ज्ञात कीजिए, यदि x + y + z = 14 व x² + y² + z² = 60
हलः
x + y + z = 14 ………………(1)
वर्ग करने पर,
x² + y² + z² + 2(xy + yz + zx) = 196
60 + 2(xy + yz + zx) = 196
2(xy + yz + zx) = 196 – 60 = 136
xy + yz + zx = [latex]\frac{136}{2}[/latex] = 68
x³ + y³ + z³ – 3xyz = (x + y + z)[x² + y² + z² – xy – yz – zx]
= (14)[60 – 68] = 14 × (-8) = -112

प्रश्न 14.
यदि 4x² + y² = 40 व xy =6, तब सिद्ध कीजिए कि 2x + y = ± 8
हलः
4x² + y² = 40
⇒ (2x)² + (y)² + 2(2x)(y) = 40 + 2(2x)(y)
⇒ (2x + y)² = 40 + 4(6) = 40 + 24
⇒ (2x + y)² = 64 ⇒ (2x + y) = ± 8

प्रश्न 15.

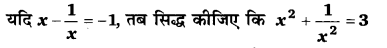
हलः

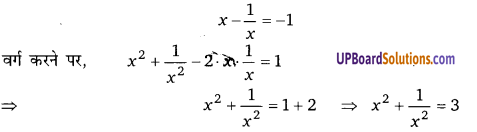
प्रश्न 16.
यदि 2x + 3y = 8 व xy = 2, तब सिद्ध कीजिए कि 4x² + 9y² = 40
हलः
2x + 3y = 8
वर्ग करने पर, 4x² + 9y² + 2(2x)(3y) = 64
⇒ 4x² + 9y² = 64 – 12(xy) = 64 – 12 × 2 = 40

प्रश्न 17.

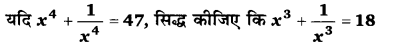
हलः

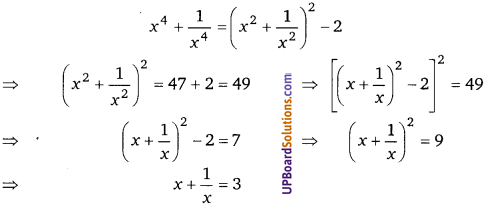
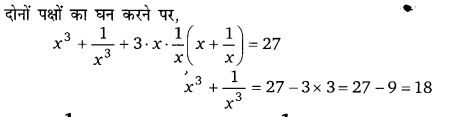
प्रश्न 18.

हलः

प्रश्न 19.
सिद्ध कीजिए कि (x + y + z)² – (x – y – z)² = 4x ( y + z)
हलः
L.H.S. = (x + y + z)² – (x – y – z)²
= x² + y² + z² + 2(xy + yz + zx) – (x² +  y² + z² – 2xy + 2yz – 2zx)
= 4xy + 4xz = 4x(y + z) = R.H.S.

प्रश्न 20.
सिद्ध कीजिए कि (4x + 2y)³ – (4x – 2y)³ = 16y³ + 192x²y
हलः
माना a = 4x + 2y, b = 4x – 2y
a³ – b³ = (a – b) (a² + b² + ab)
अब a² = (4x + 2y)² = 16x² + 4y² + 16xy
b² =(4x – 2y)² =16x² + 4y² – 16xy
ab =16x² – 4y²
तब बायाँ पक्ष =(4x + 2y)³ – (4x – 2y)³
= (4y)[16x² + 4y² + 16xy +16x² + 4y² – 16xy + 16x² – 4y²]
= 4y(48x² + 4y²) = 16y³ + 192x²y = दायाँ पक्ष

प्रश्न 21.
सिद्ध कीजिए कि 7x³ + 8y³ -(4x + 3y)(16x² – 12xy + 9y³) = -57x³ – 19y³
हलः
L.H.S. = 7x³ +8y³ – (4x + 3y)(16x² – 12xy + 9y²)
= 7x³ + 8y³ – [(4x)³ +(3y)³]
= 7x³ + 8y³ – (64x³ + 27y³)
= 7x³ + 8y³ – 64x³ – 27y³
= – 57x³ – 19y³ = R.HS.

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 10 Maths Solutions Chapter 10 Trigonometrical Ratios and Identities Ex 10.3 त्रिकोणमितीय अनुपात एवं असमिकाएँ

Ex 10.3 Trigonometrical Ratios and Identities अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

निम्न के मान ज्ञात कीजिए
प्रश्न 1.
sin(90° – θ)
हल:
sin(90° – θ) = cosθ

प्रश्न 2.
tan(90° + θ)
हल:
tan(90° + θ) = – cotθ

प्रश्न 3.
cos(180° – θ)
हलः
cos(180° – θ) (UPBoardSolutions.com) = – cosθ

प्रश्न 4.
cos37° cosec53°
हल:
cos37° cosec53° = cos 37°.cosec(90° – 37°) = cos 37° sec37° = cos 37°.[latex]\frac{1}{\cos 37^{\circ}}[/latex] = 1

प्रश्न 5.
tan210°
हलः
tan210° = tan(180° + 30°) = tan30° = [latex]\frac{1}{\sqrt{3}}[/latex]

प्रश्न 6.
[latex]\frac{\cos 55^{\circ}}{\sin 35^{\circ}}[/latex]
हलः

प्रश्न 7.
sin 225°
हलः
sin 225° = sin(180° + 45°) (UPBoardSolutions.com) = – sin 45° = [latex]\frac{1}{\sqrt{2}}[/latex]

Ex 10.3 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-I (Short Answer Type Questions-I)

प्रश्न 8.
sin 27° sec63° का मान ज्ञात कीजिए|
हलः
sin 27°.sec 63° = sin 27°.sec(90° – 27°)
= sin 27°.cosec27°
=sin 27°.[latex]\frac{1}{\sin 27^{\circ}}[/latex] = 1

प्रश्न 9.
tan 37° tan 53° का मान ज्ञात कीजिए|
हलः
tan 37°.tan 53°= tan 37°. (UPBoardSolutions.com) tan(90° – 37°)
= tan37°.cot 37°
= tan37°.[latex]\frac{1}{\tan 37^{\circ}}[/latex] = 1

प्रश्न 10.
सिद्ध कीजिए: sin (180° + θ) = cos(90° + θ)
हलः
LHS → sin(180° + θ) = – sinθ
RHS → cos (90° + θ) = – sinθ
RHS = LHS

प्रश्न 11.
सिद्ध कीजिए: tan 45° – cot 45° = 0
हलः
LHS = tan 45° – cot (UPBoardSolutions.com) 45° = 1 – 1 = 0 = RHS

प्रश्न 12.
सिद्ध कीजिए: [latex]\frac{\cos 21^{\circ}}{\sin 69^{\circ}}+\frac{\sin 59^{\circ}}{\cos 31^{\circ}}[/latex] = 2
हलः

Ex 10.3 Trigonometrical Ratios and Identities लघु उत्तरीय प्रश्न-II (Short Answer Type Questions-II)

सिद्ध कीजिए कि
प्रश्न 13.
(i) sin 210°= – 1/2
(ii) tan 225°= 1
(iii) sec 210° = [latex]-\frac{2}{\sqrt{3}}[/latex]
(iv) cosec 225°= [latex]- \sqrt{{2}} [/latex]
हलः
(i) LHS = sin 210°= sin(180° + 30°) = – sin 30° = [latex]-\frac{1}{2}[/latex] = RHS
(ii) LHS = tan 225° = tan(180° + 45°) = tan 45° = 1 = RHS
(iii) LHS = sec 210° = sec(180° + 30°) (UPBoardSolutions.com) = – sec 30°= [latex]-\frac{2}{\sqrt{3}}[/latex] = RHS
(iv) LHS = cosec 225° = cosec(180° + 45° ) = – sec 45° = [latex]- \sqrt{{2}} [/latex] = RHS

प्रश्न 14.
[latex]\frac{\sin 35^{\circ}}{\cos 55^{\circ}}+\frac{\cos 55^{\circ}}{\sin 35^{\circ}}[/latex] – 4cos60° = 0
हलः

प्रश्न 15.

हलः

Ex 10.3 Trigonometrical Ratios and Identities दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

सिद्ध कीजिए कि –
प्रश्न 16.

हलः

प्रश्न 17.

हलः

प्रश्न 18.
tan240° + sin120° = [latex]\frac{3 \sqrt{3}}{2}[/latex]
हलः

Balaji Publications Mathematics Class 10 Solutions