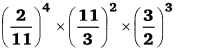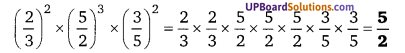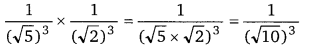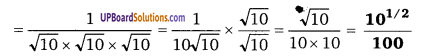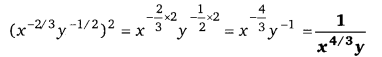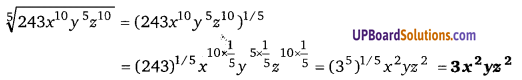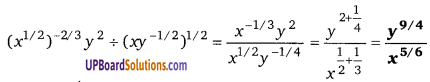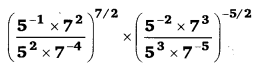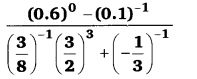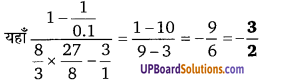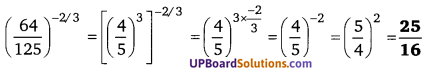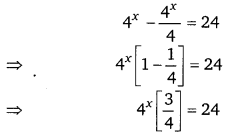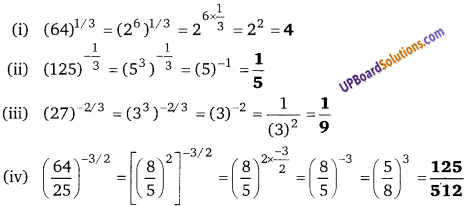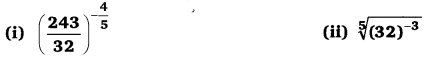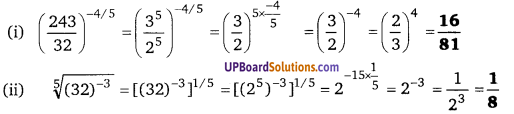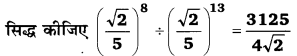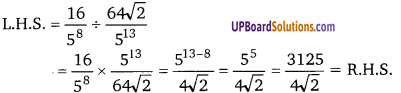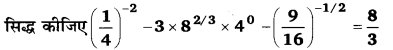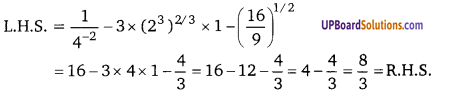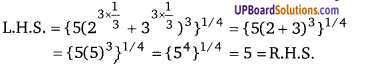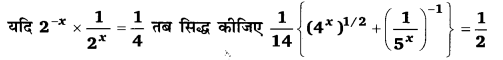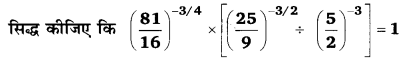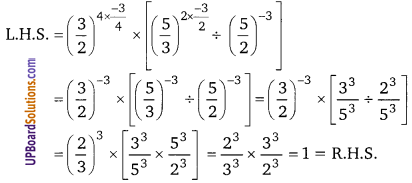Safia

UP Board Solutions for Class 12 Civics Chapter 9 Recent Developments in Indian Politics (भारतीय राजनीति : नए बदलाव)

UP Board Class 12 Civics Chapter 9 Text Book Questions

UP Board Class 12 Civics Chapter 9 पाठ्यपुस्तक से अभ्यास प्रश्न

प्रश्न 1.
उन्नी-मुन्नी ने अखबार की कुछ कतरनों को बिखेर दिया है। आप इन्हें कालक्रम के अनुसार व्यवस्थित करें
(क) मण्डल आयोग की सिफारिशों और आरक्षण विरोधी हंगामा
(ख) जनता दल का गठन
(ग) बाबरी मस्जिद का विध्वंस
(घ) इन्दिरा गांधी की हत्या
(ङ) राजग सरकार का गठन
(च) संप्रग सरकार का गठन
(छ) गोधरा की दुर्घटना और उसके परिणाम।
उत्तर:
(घ) इन्दिरा गांधी की हत्या (1984)
(ख) जनता दल का गठन (1988)
(क) मण्डल आयोग की सिफारिशों और आरक्षण विरोधी हंगामा (1990)
(ग) बाबरी मस्जिद का विध्वंस (1992)
(ङ) राजग सरकार का गठन (1999)
(छ) गोधरा की दुर्घटना और उसके परिणाम (2002)
(च) संप्रग सरकार का गठन (2004)।

प्रश्न 2.
निम्नलिखित में मेल करें-

उत्तर

प्रश्न 3.
1989 के बाद की अवधि में भारतीय राजनीति के मुख्य उद्देश्य क्या रहे हैं? इन मुद्दों से राजनीतिक दलों के आपसी जुड़ाव के क्या रूप सामने आए हैं?
उत्तर:
1989 के बाद भारतीय राजनीति के मुख्य मुद्दे – सन् 1989 के बाद भारतीय राजनीति में कई बदलाव आए जिनमें कांग्रेस का कमजोर होना, मण्डल आयोग की सिफारिशें एवं आन्दोलन, आर्थिक सुधारों को लागू करना, राजीव गांधी की हत्या तथा अयोध्या मामला प्रमुख हैं। इन स्थितियों में भारतीय राजनीति में अग्र मुद्दे प्रमुख रूप से उभरे-

1. कांग्रेस ने स्थिर सरकार का मुद्दा उठाया।
2. भाजपा ने राम मन्दिर बनाने का मुद्दा उठाया।
3. लोकदल व जनता दल ने मण्डल आयोग की सिफारिशों का मुद्दा उठाया।

इन मुद्दों में कांग्रेस ने दूसरे दलों की गैर-कांग्रेस सरकारों की अस्थिरता का मुद्दा उठाकर कहा कि देश में स्थिर सरकार कांग्रेस दल ही दे सकता है। दूसरी तरफ भाजपा ने अयोध्या में राम मन्दिर का मुद्दा उठाकर हिन्दू मतों को अपने पक्ष में कर अपने जनाधार को ग्रामीण क्षेत्रों में व्यापक करने का प्रयास किया।

तीसरी तरफ लोक मोर्चा, जनता पार्टी व लोकदल आदि दलों ने पिछड़ी जातियों को अपने पक्ष में लामबन्द करने के उद्देश्य से मण्डल की 27 प्रतिशत पिछड़ी जातियों के आरक्षण का मुद्दा उठाया।

प्रश्न 4.
“गठबन्धन की राजनीति के इस दौर में राजनीतिक दल विचारधारा को आधार मानकर गठजोड़ नहीं करते हैं।” इस कथन के पक्ष या विपक्ष में आप कौन-कौन से तर्क देंगे?
उत्तर:
वर्तमान युग में गठबन्धन की राजनीति का दौर चल रहा है। इस दौर में राजनीतिक दल विचारधारा को आधार बनाकर गठजोड़ नहीं कर रहे बल्कि अपने निजी स्वार्थी हितों की पूर्ति के लिए गठजोड़ करते हैं। वर्तमान समय में अधिकांश राजनीतिक दलों को राष्ट्रीय हित की चिन्ता नहीं रहती, बल्कि वे सदैव इस प्रयास में रहते हैं कि किस प्रकार अपने राजनीतिक हितों को पूरा किया जाए, इसी कारण अधिकांश राजनीतिक दल विचारधारा और सिद्धान्तों के आधार पर गठजोड़ न करके स्वार्थी हितों की पूर्ति के लिए गठजोड़ करते हैं।

पक्ष में तर्क-गठबन्धन की राजनीति के भारत में चल रहे नए दौर में राजनीतिक दल विचारधारा को आधार मानकर गठजोड़ नहीं करते। इनके समर्थन में निम्नलिखित तर्क दिए जा सकते हैं-

(1) सन् 1977 में जे०पी० नारायण के आह्वान पर जो जनता दल बना था उसमें कांग्रेस के विरोधी प्रायः सी०पी०आई० को छोड़कर अधिकांश विपक्षी दल जिनमें भारतीय जनसंघ, कांग्रेस फॉर डेमोक्रेसी, भारतीय क्रान्ति दल, तेलुगू देशम, समाजवादी पार्टी, अकाली दल आदि शामिल थे। इन सभी दलों को हम एक ही विचारधारा वाले दल नहीं कह सकते।

(2) जनता दल की सरकार गिरने के बाद केन्द्र में राष्ट्रीय मोर्चा बना जिसमें एक ओर जनता पार्टी के वी०पी० सिंह तो दूसरी तरफ उन्हें समर्थन देने वाले सी०पी०एम० वामपन्थी और भाजपा जैसे तथाकथित हिन्दुत्व समर्थक गांधीवादी राष्ट्रवादी दल भी थे। कुछ महीनों बाद वी०पी० सिंह प्रधानमन्त्री नहीं रहे तो केवल सात महीनों के लिए कांग्रेस ने चन्द्रशेखर को समर्थन देकर प्रधानमन्त्री बनाया। चन्द्रशेखर वही नेता थे जिन्होंने इन्दिरा गांधी के आपातकाल के दौरान श्रीमती गांधी का विरोध किया था और श्रीमती गांधी ने चन्द्रशेखर और मोरारजी को कारावास में डाल दिया था।

(3) कांग्रेस की सरकार, सन् 1991 से सन् 1996 तक नरसिंह राव के नेतृत्व में अल्पमत होते हुए भी इसलिए चलती रही क्योंकि उसे अनेक दलों का समर्थन प्राप्त था।

(4) अटल बिहारी वाजपेयी के नेतृत्व में जनतान्त्रिक गठबन्धन (एन०डी०ए०) की सरकार लगभग 6 वर्ष तक चली लेकिन उसे जहाँ एक ओर अकालियों ने तो दूसरी ओर तृणमूल कांग्रेस, बीजू पटनायक कांग्रेस, कुछ समय के लिए समता दल, जनता पार्टी आदि ने भी सहयोग और समर्थन दिया।

संक्षेप में हम कह सकते हैं कि राजनीति में किसी का कोई स्थायी शत्रु नहीं होता। अवसरवादिता हकीकत में सर्वाधिक महत्त्वपूर्ण है।
विपक्ष में तर्क-उपर्युक्त कथन के विपक्ष में निम्नलिखित तर्क दिए जा सकते हैं-

1. गठबन्धन की राजनीति के नए दौर में भी वामपन्थ के चारों दल अर्थात् सी०पी०एम०; सी०पी०आई०, फारवर्ड ब्लॉक, आर०एस० ने भारतीय जनता पार्टी से हाथ नहीं मिलाया, वे उसे अब भी राजनीतिक दृष्टि से अस्पर्शीय पार्टी मानती है।
2. समाजवादी पार्टी, वामपन्थी मोर्चा, डी०पी०के० जैसे क्षेत्रीय दल किसी भी उस प्रत्याशी को खुला समर्थन नहीं देना चाहते जो एन०डी०ए० अथवा भाजपा का प्रत्याशी हो क्योंकि उनकी वोटों की राजनीति को ठेस पहुँचती है।
3. कांग्रेस पार्टी ने अधिकांश मोर्चों पर बीजेपी विरोधी और बीजेपी ने कांग्रेस विरोधी रुख अपनाया है।

प्रश्न 5.
आपातकाल के बाद के दौर में भाजपा एक महत्त्वपूर्ण शक्ति के रूप में उभरी। इस दौर में इस पार्टी के विकास-क्रम का उल्लेख करें।
उत्तर:
भारतीय जनता पार्टी का विकासक्रम आपातकाल के बाद भारतीय जनता पार्टी की शक्ति में निरन्तर वृद्धि हुई और एक सशक्त राजनीतिक दल के रूप में उभरी। भाजपा की इस विकास यात्रा को निम्न प्रकार से समझा जा सकता है-

1. जनता पार्टी सरकार के पतन के बाद जनता पार्टी के भारतीय जनसंघ घटक ने वर्ष 1980 में भारतीय जनता पार्टी का गठन किया। श्री अटल बिहारी वाजपेयी इसके संस्थापक अध्यक्ष बने।
2. सन् 1984 के चुनावों में कांग्रेस के पक्ष में श्रीमती इन्दिरा गांधी की हत्या हो जाने के बाद पैदा हुई सहानुभूति की लहर में भाजपा को लोकसभा में केवल दो सीटें प्राप्त हुईं।
3. सन् 1989 के चुनावों में वी०पी० सिंह के जनमोर्चा के साथ गठजोड़ कर भाजपा ने चुनाव में भाग लिया तथा राम मन्दिर बनवाने के नारे को उछाला। फलत: इस चुनाव में भाजपा को आशा से अधिक सफलता मिली। भाजपा ने वी०पी० सिंह को बाहर से समर्थन देकर संयुक्त मोर्चा सरकार का गठन करने में सहयोग दिया।
4. सन् 1991 के चुनाव में इसने अपनी स्थिति को लगातार मजबूत किया। इस चुनाव में राम मन्दिर निर्माण का नारा विशेष लाभदायक सिद्ध हुआ।
5. सन् 1996 के चुनावों में यह लोकसभा में सबसे बड़ी पार्टी के रूप में उभरी लेकिन लोकसभा में स्पष्ट बहुमत का समर्थन प्राप्त नहीं कर सकी।
6. सन् 1998 के चुनावों में इसने कुछ क्षेत्रीय दलों से गठबन्धन कर सरकार बनाई तथा सन् 1999 के चुनावों में भाजपानीत गठबन्धन ने फिर सत्ता प्राप्त की। राष्ट्रीय जनतान्त्रिक गठबन्धन के काल में अटल बिहारी वाजपेयी प्रधानमन्त्री बने।
7. सन् 2004 तथा सन् 2009 के चुनावों में भाजपा को पुनः अपेक्षित सफलता नहीं मिल पायी। फिर भी कांग्रेस के बाद आज यह दूसरी सबसे बड़ी पार्टी है।

प्रश्न 6.
कांग्रेस के प्रभुत्व का दौर समाप्त हो गया है। इसके बावजूद देश की राजनीति पर कांग्रेस का असर लगातार कायम है। क्या आप इस बात से सहमत हैं? अपने उत्तर के पक्ष में तर्क दीजिए।
उत्तर:
देश की राजनीति से यद्यपि कांग्रेस का प्रभुत्व समाप्त हो गया है परन्तु अभी कांग्रेस का असर कायम है, क्योंकि अब भी भारतीय राजनीति कांग्रेस के इर्द-गिर्द घूम रही है तथा सभी राजनीतिक दल अपनी नीतियाँ एवं योजनाएँ कांग्रेस को ध्यान में रखकर बनाते हैं। सन् 2004 के 14वें लोकसभा के चुनावों में इसने अन्य दलों के सहयोग से केन्द्र में सरकार बनाई। इसके साथ-साथ जुलाई 2007 में हुए राष्ट्रपति के चुनाव में भी इस दल की महत्त्वपूर्ण भूमिका रही। सन् 2009 के आम चुनावों में पहले से काफी अधिक सीटों पर जीत प्राप्त कर गठबन्धन की सरकार बनाई। अत: कहा जा सकता है कि कांग्रेस के कमजोर होने के बावजूद इसका असर भारतीय राजनीति पर कायम है।

प्रश्न 7.
अनेक लोग सोचते हैं कि सफल लोकतन्त्र के लिए दो-दलीय व्यवस्था जरूरी है। पिछले बीस सालों के भारतीय अनुभवों को आधार बनाकर एक लेख लिखिए और इसमें बताइए कि भारत की मौजूदा बहुदलीय व्यवस्था के क्या फायदे हैं।
उत्तर:
कुछ लोगों का मानना है कि सफल लोकतन्त्र के लिए दो-दलीय व्यवस्था जरूरी है। इनका मानना है कि द्वि-दलीय व्यवस्था में साधारण बहुमत के दोष समाप्त हो जाते हैं, सरकार स्थायी होती हैं, भ्रष्टाचार कम फैलता है, निर्णय शीघ्रता से लिए जा सकते हैं।

भारत में बहुदलीय प्रणाली भारत में बहुदलीय प्रणाली है। कई विद्वानों का मत है कि भारत में बहुदलीय प्रणाली उचित ढंग से कार्य नहीं कर पा रही है। यह भारतीय लोकतन्त्र के लिए बाधा उत्पन्न कर रही है अत: भारत को द्वि-दलीय पद्धति अपनानी चाहिए परन्तु पिछले बीस वर्षों के अनुभव के आधार पर यह कहा जा सकता है कि बहुदलीय प्रणाली से भारतीय राजनीतिक व्यवस्था को निम्नलिखित फायदे हुए हैं-

1. विभिन्न मतों का प्रतिनिधित्व-बहुदलीय प्रणाली के कारण भारतीय राजनीति में सभी वर्गों तथा हितों को प्रतिनिधित्व मिल जाता है। इस प्रणाली से सच्चे लोकतन्त्र की स्थापना होती है।
2. मतदाताओं को अधिक स्वतन्त्रता-अधिक दलों के कारण मतदाताओं को अपने वोट का प्रयोग करने के लिए अधिक स्वतन्त्रताएँ होती हैं। मतदाताओं के लिए अपने विचारों से मिलते-जुलते दल को वोट देना आसान हो जाता है।
3. राष्ट्र दो गुटों में नहीं बँटता-बहुदलीय प्रणाली होने के कारण भारत कभी भी दो विरोधी गुटों में . विभाजित नहीं हुआ।
4. मन्त्रिमण्डल की तानाशाही स्थापित नहीं होती-बहुदलीय प्रणाली के कारण भारत में मन्त्रिमण्डल तानाशाह नहीं बन सकता।
5. अनेक विचारधाराओं का प्रतिनिधित्व-बहुदलीय प्रणाली में व्यवस्थापिका में देश की अनेक विचारधाराओं का प्रतिनिधित्व हो सकता है।

प्रश्न 8.
निम्नलिखित अवतरण को पढ़ें और इसके आधार पर पूछे गए प्रश्नों के उत्तर दें-
भारत की दलगत राजनीति ने कई चुनौतियों का सामना किया है। कांग्रेस प्रणाली ने अपना खात्मा ही नहीं किया बल्कि कांग्रेस के जमावड़े के बिखर जाने से आत्म-प्रतिनिधित्व की नयी प्रवृत्ति का भी जोर बढ़ा। इससे दलगत व्यवस्था और विभिन्न हितों की समाई करने की इसकी क्षमता पर भी सवाल उठे। राज-व्यवस्था के सामने एक महत्त्वपूर्ण काम एक ऐसी दलगत व्यवस्था खड़ी करने अथवा राजनीतिक दलों को गढ़ने की है, जो कारगर तरीके से विभिन्न हितों को मुखर और एकजुट करें। -जोया हसन
(क)इस अध्याय को पढ़ने के बाद क्या आपदलगत व्यवस्था की चुनौतियों की सूची बना सकते हैं?
(ख) विभिन्न हितों का समाहार और उनमें एकजुटता का होना क्यों जरूरी है?
(ग) इस अध्याय में आपने अयोध्या विवाद के बारे में पढ़ा। इस विवाद ने भारत के राजनीतिक दलों की समाहार की क्षमता के आगे क्या चुनौती पेश की?
उत्तर:
(क) इस अध्याय में दलगत व्यवस्था की निम्नलिखित चुनौतियाँ उभरकर सामने आती हैं-

1. गठबन्धन की राजनीति को चलाना।
2. कांग्रेस के कमजोर होने से खाली हुए स्थान को भरना।
3. पिछड़े वर्गों की राजनीति का उभरना।
4. अयोध्या विवाद का उभरना।
5. गैर-सैद्धान्तिक राजनीतिक समझौते का होना।
6. गुजरात दंगों से साम्प्रदायिक दंगे होना।

(ख) विभिन्न हितों का समाहार और उनमें एकजुटता का होना जरूरी है, क्योंकि तभी भारत अपनी एकता और अखण्डता को बनाए रखकर विकास कर सकता है।
(ग) अयोध्या विवाद ने भारत में राजनीतिक दलों के सामने साम्प्रदायिकता की चुनौती पेश की तथा भारत में साम्प्रदायिक आधार पर राजनीतिक दलों की राजनीति बढ़ गई।

UP Board Class 12 Civics Chapter 9 InText Questions

UP Board Class 12 Civics Chapter 9 पाठान्तर्गत प्रश्नोत्तर

प्रश्न 1.
अगर हर सरकार एक-सी नीति पर अमल करे, तो मुझे नहीं लगता कि इससे राजनीति में कोई बदलाव आएगा।
उत्तर:
यदि सभी सरकारें या उनसे सम्बद्ध राजनीतिक दल एक ही प्रकार की नीतियाँ अपनाएँ तो इससे राजनीतिक व्यवस्था स्थिर व जड़ हो जाएगी।

लेकिन लोकतान्त्रिक व्यवस्था में इस प्रकार की नीति लागू होना सम्भव नहीं है क्योंकि लोकतान्त्रिक व्यवस्था में जनमत सर्वोपरि होता है और जनसामान्य के हित अलग-अलग होते हैं और यह हित समय और परिस्थितियों के अनुसार निरन्तर परिवर्तित भी होते रहते हैं, इसलिए प्रत्येक सरकार को जन इच्छाओं को ध्यान में रखते हुए कार्य करना पड़ता है। ऐसी स्थिति में सभी सरकारें एक जैसी नीति का अनुसरण नहीं कर सकतीं।

इसके अलावा भारत जैसे बहुदलीय व्यवस्था वाले देश में तो इस प्रकार की नीति लागू करना बिल्कुल भी सम्भव नहीं है क्योंकि भारत में प्रत्येक दल की विचारधारा व कार्यक्रमों में व्यापक अन्तर है और ये राजनीतिक दल सत्ता में आने पर अलग-अलग ढंग से निर्णय लेते हैं।

प्रश्न 2.
चलो मान लिया कि भारत जैसे देश में लोकतान्त्रिक राजनीति का तकाजा ही गठबन्धन बनाना है। लेकिन क्या इसका मतलब यह निकाला जाए कि हमारे देश में हमेशा से गठबन्धन बनते चले आ रहे हैं। अथवा, राष्ट्रीय स्तर के दल एक बार फिर से अपना बुलन्द मुकाम हासिल करके दिखाएँगे।
उत्तर:
भारतीय राजनीतिक व्यवस्था में गठबन्धन का दौर हमेशा से चला आ रहा है। यह बात कुछ हद तक सही है, लेकिन इन गठबन्धनों के स्वरूप में व्यापक अन्तर है। पहले जहाँ एक ही पार्टी के भीतर गठबन्धन (जैसे—कांग्रेस पार्टी में क्रान्तिकारी और शान्तिवादी, कंजरवेटिव और रेडिकल, गरमपन्थी और नरमपन्थी, दक्षिणपन्थी और वामपन्थी आदि) होता था अब पार्टियों के बीच गठबन्धन होता है।

जहाँ तक राष्ट्रीय दलों के प्रभुत्व का सवाल है, वर्तमान दलीय व्यवस्था के बदलते दौर में अपना बुलन्द मुकाम पाना बहुत कठिन है। क्योंकि वर्तमान में भारतीय दलीय व्यवस्था का स्वरूप बहुदलीय हो गया है, जिसमें राष्ट्रीय दलों के साथ-साथ क्षेत्रीय दलों के महत्त्व को भी नकारा नहीं जा सकता। यही कारण है कि आज राष्ट्रीय स्तर पर किसी भी एक दल को स्पष्ट बहुमत नहीं मिल पा रहा और मिली-जुली सरकारों का निर्माण हो रहा है। भारत में नब्बे के दशक में गठबन्ध सरकारों का दौर शुरू हुआ और यह सिलसिला अभी तक जारी है।

प्रश्न 3.
मुझे इसकी चिन्ता नहीं है कि सरकार किसी एक पार्टी की है यां गठबन्धन की। मसला तो यह है कि कोई सरकार काम कौन-से कर रही है। क्या गठबन्धन सरकार में ज्यादा समझौते करने पड़ते हैं? क्या गठबन्धन सरकार साहसी और कल्पनाशील नीतियाँ नहीं अपना सकती?
उत्तर:
सरकारों का स्वरूप चाहे कैसा भी हो। चाहे वह गठबन्धन सरकार हो या एक ही दल की सरकार हो लेकिन सरकार जनता की कसौटियों पर खरी उतरे वही सफल सरकार है।

गठबन्धन सरकारों में विभिन्न दल आपसी समझौतों या शर्तों के आधार पर सरकार का गठन करते हैं। इन दलों के सभी के अपने-अपने हित व स्वार्थ होते हैं जिन्हें पूरा करने हेतु निरन्तर प्रयास करते रहते हैं। जहाँ आपसी हितों में रुकावट या टकराव आता है वहीं दल अलग हो जाते हैं और सरकारें गिर जाती हैं। इस प्रकार गठबन्धन सरकारों में स्थिरता बहुत कम पायी जाती है। इस प्रकार की सरकारों में स्वतन्त्र निर्णय लेना सम्भव नहीं है। इस प्रकार गठबन्धन सरकार साहसी और कल्पनाशील नीतियाँ नहीं अपना सकतीं।

प्रश्न 4.
क्या हम यह सुनिश्चित कर सकते हैं कि जो लोग ऐसे जनसंहार की योजनाए बनाएँ, अमल करें और उसे समर्थन दें, वे कानून के हाथों से बच न पाएँ? ऐसे लोगों को कम-से-कम राजनीतिक रूप से तो सबक सिखाया ही जा सकता है।
उत्तर:
भारत में धर्म, जाति व सम्प्रदाय के नाम पर अनेक बार साम्प्रदायिक दंगे हुए तथा देश की शान्ति और व्यवस्था पर प्रश्न चिह्न भी लगा। इन साम्प्रदायिक दंगों के पीछे प्रत्यक्ष या अप्रत्यक्ष रूप से विभिन्न राजनीतिक दलों का हाथ रहा है। यह दल अपने राजनीतिक स्वार्थों की पूर्ति हेतु दुष्प्रचार करते हैं जिसमें जनसामान्य इनके बहकावे में आकर गलत कदम उठाते हैं। भारत में सन् 1984 के सिक्ख दंगे हों, सन् 1992 की अयोध्या की घटना हो या सन् 2002 में गुजरात का गोधरा काण्ड, इन सभी चटनाओं के पीछे राजनीतिक दलों की स्वार्थपूर्ण नीति रही है।

इस प्रकार ये सभी घटनाएँ हमें आगाह करती हैं कि राजनीतिक उद्देश्यों के लिए धार्मिक भावनाओं को भड़काना खतरनाक है। इससे हमारी लोकतान्त्रिक व्यवस्था को खतरा उत्पन्न हो सकता है, अतः यह जरूरत है कि ऐसी घटनाओं को रोका जाए। इन घटनाओं को रोकने के लिए आवश्यक है कि ऐसे राजनीतिक दल व उनके नेतृत्वकर्ता जिनका आपराधिक रिकॉर्ड रहा है या साम्प्रदायिक दंगों में लिप्त रहे हैं उन पर चुनावी प्रक्रिया में भाग लेने पर आजीवन प्रतिबन्ध लगा दिया जाना चाहिए।

UP Board Class 12 Civics Chapter 9 Other Important Questions

UP Board Class 12 Civics Chapter 9 अन्य महत्वपूर्ण प्रश्नोत्तर

प्रश्न 1.
वर्तमान में भारतीय दलीय व्यवस्था की उभरती प्रवृत्तियों का विवेचन कीजिए।
उत्तर:
भारतीय दलीय व्यवस्था की उभरती प्रवृत्तियाँ वर्तमान में भारतीय दलीय व्यवस्था की उभरती हुई प्रवृत्तियाँ निम्नलिखित हैं-

1. एक दल से साझा सरकारों की ओर-भारतीय राजनीति में सन् 1989 के बाद कांग्रेस की एक दलीय प्रभुत्व की स्थिति भी नहीं रही। 11वीं, 12वीं, 13वीं, 14वीं तथा 15वीं लोकसभा के चुनावों में किसी भी दल को स्पष्ट बहुमत नहीं मिला। परिणामतः साझा सरकारें अस्तित्व में आईं।
2. क्षेत्रीय दलों का बढ़ता वर्चस्व-वर्तमान राजनीतिक दलीय स्थिति में क्षेत्रीय दलों की भूमिका बढ़ी है। किसी भी दल को स्पष्ट बहुमत के अभाव में सत्ता की जोड़-तोड़ में इन दलों की भूमिका बढ़ रही है।
3. निर्दलीय सदस्यों की बढ़ती भूमिका-भारत में प्रत्येक लोकसभा और राज्य विधानसभा के चुनावों में निर्दलीय उम्मीदवार बड़ी संख्या में रहे हैं। किसी भी दल को स्पष्ट बहुमत न मिलने की स्थिति में निर्दलीय उम्मीदवारों की भूमिका बढ़ जाती है।
4. दलीय प्रणाली का सत्ता केन्द्रित स्वरूप-वर्तमान समय में राजनीतिक दलों का उद्देश्य केवल सत्ता प्राप्त करना रह गया है तथा उनके लिए विचारधाराएँ समस्याएँ गौण हो गई हैं।
5. भाषावाद, जातिवाद, सम्प्रदायवाद का प्रभाव-सत्ता प्राप्ति के लिए राजनीतिक दल भाषा, जाति एवं सम्प्रदायों का भी सहारा लेते हैं। चुनावी घोषणा-पत्र में इनका विरोध करते हैं, परन्तु दलीय प्रत्याशी खड़ा करते समय इन आधारों को महत्त्व प्रदान करते हैं।
6. दलों में आन्तरिक गुटबन्दी–भारत की दल प्रणाली का एक प्रमुख लक्षण विभिन्न दलों में आन्तरिक गुटबन्दी का होना है। सभी राजनीतिक दल इस समस्या से पीड़ित हैं। इन दलों में एक गुट तो वह होता है जो संगठन तथा सत्ता में पद प्राप्त किए हुए है और दूसरा गुट इन पदों से अलग रहने वाला असन्तुष्ट गुट होता है।
   भारतीय राजनीतिक दलों में व्याप्त गुटबन्दी की स्थिति भारतीय राजनीति का अभिशाप बनी हुई है।
7. राजनीतिक अपराधीकरण-राजनीतिक व्यवस्था में आपराधिक प्रवृत्ति के लोगों की संख्या निरन्तर बढ़ती जा रही है। प्रायः सभी राजनीतिक दलों द्वारा आपराधिक प्रवृत्ति के लोगों को चुनावों में खड़ा किया जा रहा है जो धन-बल व भुज-बल के आधार पर मत प्राप्त करते हैं।
8. दल की कथनी व करनी में अन्तर—यद्यपि लोकतान्त्रिक देशों में राजनीतिक दलों व उनके नेताओं की कथनी और करनी में अन्तर रहता है लेकिन पिछले कुछ वर्षों में भारत में यह अन्तर अपने भीषणतम रूप में उभरा है।
9. केन्द्र व राज्य में टकराहट केन्द्र व राज्यों में अलग-अलग दलों की सरकारें होती हैं जिससे केन्द्र व राज्यों के मध्य विभिन्न राजनीतिक मुद्दों को लेकर टकराहट की स्थिति बनी रहती है। केन्द्र, राज्य की दूसरे दलों की सरकार को किसी-न-किसी बहाने दबाव व उलझन में रखते हैं।

प्रश्न 2.
भारतीय दलीय व्यवस्था की प्रमुख समस्याओं की व्याख्या कीजिए।
उत्तर:
भारतीय दलीय व्यवस्था की समस्याएँ भारतीय दलीय व्यवस्था की प्रमुख समस्याएँ निम्नलिखित हैं-

1. दलों की संख्या में वृद्धि-भारत में बहुदलीय व्यवस्था है। बहुदलीय व्यवस्था में राजनीतिक अस्थिरता का दौर जारी है। राजनीतिक दलों की भरमार ने अस्थिर राजनीतिक स्थिति के साथ-साथ अन्य समस्याओं को भी जन्म दिया है।
2. वैचारिक प्रतिबद्धता का अभाव-राजनीतिक दल आर्थिक और राजनीतिक विचारधारा पर आधारित होना चाहिए तथा दल एवं उसके सदस्यों में वैचारिक प्रतिबद्धता होनी चाहिए लेकिन भारतीय राजनीतिक दलों में वैचारिक प्रतिबद्धता का अभाव है।
   वैचारिक प्रतिबद्धता से रहित इन दलों का मुख्य उद्देश्य येन-केन प्रकारेण सत्ता प्राप्त करना होता है तथा सत्ता से जुड़े लाभ प्राप्त करने के लिए ये अपने सिद्धान्तों की तिलांजलि देने में तत्पर रहते हैं।
3. दलीय व्यवस्था में अस्थायित्व-भारतीय राजनीतिक दल निरन्तर बिखराव और विभाजन के शिकार हैं। इस कारण इन दलों में तथा भारतीय दलीय व्यवस्था में स्थायित्व का अभाव है। कई बार तो राज्यों में सत्ता हेतु पूरे-के-पूरे राजनीतिक दल ने अपना चरित्र बदल दिया।
4. दलों में आन्तरिक लोकतन्त्र का अभाव-भारत के अधिकांश राजनीतिक दलों में आन्तरिक लोकतन्त्र का अभाव है और वे घोर अनुशासनहीनता से पीड़ित हैं।
5. राजनीतिक दलों में गुटीय राजनीति-लगभग सभी राजनीतिक दल तीव्र आन्तरिक गुटबन्दी की समस्या से पीड़ित हैं। लगभग सभी राजनीतिक दलों में अनेक छोटे-बड़े गुट विद्यमान हैं। इन दलों में गुटीय राजनीति इतनी तीव्र है कि चुनावों में एक गुट के समर्थन प्राप्त उम्मीदवार को उसी दल के दूसरे गुट के सदस्य पराजित करने की भरसक कोशिश करते हैं।
6. सत्ता के लिए संविधानेतर और विघटनकारी प्रवृत्तियों को अपनाना-वैचारिक प्रतिबद्धता के अभाव तथा गहरी सत्ता लिप्सा के कारण राजनीतिक दलों ने पिछले दशक की राजनीति में बहुत अधिक मात्रा में संविधानेतर और विघटनकारी प्रवृत्तियों को अपना लिया है।
7. नेतृत्व का संकट-भारत में वर्तमान में राजनीतिक दलों के समक्ष नेतृत्व का संकट भी बना हुआ है। अधिकांश राजनीतिक दलों के पास ऐसा नेतृत्व नहीं है, जिसका अपना ऊँचा राजनीतिक कद हो। प्रायः बौना नेतृत्व बना हुआ है। नेतृत्व का यह बौना कद न तो दल को एकजुट रख पा रहा है और न ही वह अपने दल या देश की राजनीति को कोई दिशा दे पा रहा है।

लघु उत्तरीय प्रश्नोत्तर

प्रश्न 1.
शाहबानो मामला क्या था? इस मामले पर भारतीय जनता पार्टी ने कांग्रेस विरोधी रुख क्यों अपनाया?
उत्तर:
शाहबानो मामला-शाहबानो मामला एक 62 वर्षीय तलाकशुदा मुस्लिम महिला शाहबानो का है। उसने अपने भूतपूर्व पति से गुजारा भत्ता हासिल करने के लिए अदालत में एक अर्जी दायर की थी। सर्वोच्च न्यायालय ने शाहबानो के पक्ष में निर्णय लिया। पुरातनपन्थी मुसलमानों ने अदालत के इस निर्णय को अपने ‘पर्सनल लॉ’ में हस्तक्षेप माना। कुछ मुस्लिम नेताओं की माँग पर सरकार ने मुस्लिम महिला अधिनियम, 1986 पास किया जिसमें सर्वोच्च फैसले के निर्णय को निरस्त कर दिया गया।

भाजपा ने कांग्रेस सरकार के इस कदम की आलोचना की और इसे अल्पसंख्यक समुदाय को दी गई अनावश्यक रियायत तथा तुष्टीकरण करार दिया।

प्रश्न 2.
जनता दल के प्रमुख कार्यक्रमों एवं नीतियों का उल्लेख कीजिए।
उत्तर:
जनता दल के कार्यक्रम एवं नीतियाँ-जनता दल के प्रमुख कार्यक्रम एवं नीतियाँ निम्नलिखित हैं-

1. जनता दल का लोकतन्त्र में दृढ़ विश्वास है और उत्तरदायी प्रशासनिक व्यवस्था को अपनाने के पक्ष में है।
2. जनता दल ने भ्रष्टाचार को समाप्त करने के लिए सात-सूत्रीय कार्यक्रम को अपनाने की बात कही है।
3. पार्टी राजनीति में बढ़ते हुए भ्रष्टाचार को रोकने के लिए लोकपाल की नियुक्ति के पक्ष में है।
4. पार्टी पंचायती राज संस्थाओं को अधिक स्वायत्तता देने के पक्ष में है।
5. जनता दल महिलाओं को संसद और राज्य विधानमण्डलों में 33 प्रतिशत और सरकारी, सार्वजनिक व निजी क्षेत्र की नौकरियों में 30 प्रतिशत आरक्षण दिलाने के पक्ष में है।

प्रश्न 3.
भारत में गठबन्धन की राजनीति के प्रभाव समझाइए।
उत्तर:
सन् 1989 में भारत में गठबन्धन की राजनीति का श्रीगणेश हुआ। इस गठबन्धन की राजनीति के निम्नलिखित प्रमुख प्रभाव पड़े-

1. एक दलीय प्रभुत्व की समाप्ति-गठबन्धन की राजनीति में कांग्रेस के दबदबे की समाप्ति हुई और बहुदलीय प्रणाली का युग शुरू हुआ।
2. क्षेत्रीय पार्टियों का बढ़ता प्रभाव क्षेत्रीय पार्टियों ने गठबन्धन सरकार बनाने में महत्त्वपूर्ण भूमिका निभायी। प्रान्तीय और राष्ट्रीय दल का भेद अब लगातार कम होता जा रहा है और प्रान्तीय दल केन्द्र सरकार में साझेदार बन रहे हैं।
3. विचारधारा की जगह कार्यसिद्धि पर जोर-गठबन्धन की राजनीति के इस दौर में राजनीतिक दल विचारधारागत अन्तर की जगह सत्ता में भागीदारी की बातों पर जोर दे रहे हैं।
4. जन-आन्दोलन और संगठन विकास के नए रूप-गठबन्धन की राजनीति में प्रतिस्पर्धी राजनीति के बीच राजनीतिक दलों में कुछ मसलों पर सहमति है, वहीं जन-आन्दोलन और संगठन विकास के नए रूप सामने आ रहे हैं। ये रूप गरीबी, विस्थापन, न्यूनतम मजदूरी, भ्रष्टाचार विरोध, आजीविका और सामाजिक सुरक्षा के मुद्दों पर जन-आन्दोलन के जरिए राजनीति में उभर रहे हैं।

प्रश्न 4.
1990 का दशक भारतीय राजनीति में नए बदलाव का दशक माना जाता है? कारण बताइए।
उत्तर:
1990 का दशक भारतीय राजनीति में नए बदलाव का दशक निम्नलिखित कारणों से माना जाता है-

1. सन् 1984 में भारत की प्रथम महिला प्रधानमन्त्री इन्दिरा गांधी की हत्या। लोकसभा के चुनाव व सहानुभूति की लहर में कांग्रेस का विजयी होना। लेकिन सन् 1989 में कांग्रेस की हार तथा सन् 1991 में मध्यावधि चुनाव होना तथा सन् 1991 में राजीव गांधी की हत्या।
2. राष्ट्रीय राजनीति में अन्य पिछड़ा वर्ग से सम्बन्धित मण्डल मुद्दे का उदय होना।
3. अयोध्या में स्थित एक विवादित ढाँचे का विध्वंस, राष्ट्र में साम्प्रदायिक तनाव व दंगे।
4. देश में गठबन्धन की राजनीति का तीव्रता से उदय होना तथा नए राजनीतिक दलों के रूप में भाजपा, उसके सहयोगी एवं संयुक्त प्रगतिशील गठबन्धन के समर्थक दलों का तेजी से उत्थान।
5. विभिन्न सरकारों द्वारा नवीन आर्थिक नीति व सुधारों को अपनाकर उदारीकरण एवं वैश्वीकरण को बढ़ावा देना।
   ये सभी महत्त्वपूर्ण बदलाव हैं और आगामी राजनीति इन्हीं बदलावों के दायरे में आकार लेगी। इस . प्रतिस्पर्धी राजनीति के बीच मुख्य राजनीतिक दलों में कुछ मसलों पर सहमति है। अगर राजनीतिक दल इस सहमति के दायरे में सक्रिय हैं तो जन-आन्दोलन और संगठन विकास के नए रूप, स्वप्न और तरीकों की पहचान कर रहे हैं।

प्रश्न 5.
1990 के दशक में कांग्रेस के पतन के प्रमुख कारणों पर प्रकाश डालिए।
उत्तर:
1990 के दशक में कांग्रेस के पतन के प्रमुख कारण निम्नलिखित हैं-

1. अन्य पिछड़ा वर्ग ओ०बी०सी० के कारण मण्डल एवं कमण्डल की राजनीति कुछ समय तक देश के क्षितिज पर छा गई।
2. देश की बहुदलीय प्रणाली व गठबन्धन राजनीति की बढ़ती लोकप्रियता।
3. बहुजन समाज पार्टी का जन्म, उदय एवं विकास होना।
4. कई प्रान्तों एवं क्षेत्रों में क्षेत्रीय दलों का उदय तथा अनेक वर्ग समूहों का कांग्रेस से हटकर अन्य बड़े राजनीतिक दलों से जुड़ना।
5. कुछ राजनीतिक दलों द्वारा साम्प्रदायिकता की राजनीति करने में सफल होना।
6. सन् 1971 के बाद बहुत बड़ी संख्या में बंगलादेशियों का आगमन तथा वोट की राजनीति के कारण उनकी वापसी के बारे में टालमटोल की राजनीति।
7. सन् 1984 के सिक्ख दंगे तथा उससे पूर्व अमृतसर के स्वर्ण मन्दिर में सैन्य बलों का प्रवेश अथवा ऑपरेशन ब्लू स्टार की घटना।

प्रश्न 6.
‘मण्डल कमीशन’ अथवा ‘मण्डल आयोग’ की नियुक्ति क्यों की गयी? इसकी प्रमुख सिफारिशें बताइए।
उत्तर:
मण्डल आयोग का गठन-केन्द्र सरकार ने सन् 1978 में एक आयोग का गठन किया और इसको पिछड़ा वर्ग की स्थिति को सुधारने के उपाय बताने का कार्य सौंपा गया। आमतौर पर इस आयोग को इसके अध्यक्ष बिन्देश्वरी प्रसाद मण्डल के नाम पर ‘मण्डल कमीशन’ कहा जाता है। मण्डल आयोग का गठन भारतीय समाज के विभिन्न वर्गों के बीच शैक्षिक और सामाजिक पिछड़ेपन की व्यापकता का पता लगाने और इन पिछड़े वर्गों की पहचान के तरीके बताने के लिए किया गया था। आयोग से यह भी अपेक्षा की गयी थी कि वह इन वर्गों के पिछड़ेपन को दूर करने के उपाय सुझाएगा।

मण्डल आयोग की सिफारिशें-आयोग ने सन् 1980 में अपनी सिफारिशें पेश की। इस समय तक जनता पार्टी की सरकार गिर चुकी थी। आयोग का मशविरा था कि पिछड़ा वर्ग को पिछड़ी जाति के अर्थ में स्वीकार किया जाए। आयोग ने एक सर्वेक्षण किया और पाया कि इन पिछड़ी जातियों की शिक्षा संस्थाओं तथा सरकारी नौकरियों में बड़ी कम मौजूदगी है। इस वजह से आयोग ने इन समूहों के लिए शिक्षा संस्थाओं तथा सरकारी नौकरियों में 27 प्रतिशत सीट आरक्षित करने की सिफारिश की। मण्डल आयोग ने अन्य पिछड़ा वर्ग की स्थिति सुधारने के लिए कई और समाधान सुझाए जिनमें भूमि-सुधार भी एक था।

अति उत्तरीय प्रश्नोत्तर

प्रश्न 1.
भारतीय जनता पार्टी की स्थापना कब हुई? इसके प्रथम अध्यक्ष कौन थे?
उत्तर:
भारतीय जनता पार्टी की स्थापना सन् 1980 में हुई। अटल बिहारी वाजपेयी पार्टी के प्रथम अध्यक्ष थे।

प्रश्न 2.
दल-बदल से क्या अभिप्राय है?
उत्तर:
कोई जन-प्रतिनिधि किसी खास दल के चुनाव चिह्न को लेकर चुनाव लड़े और चुनाव जीतने के बाद इस दल को छोड़कर किसी दूसरे दल में शामिल हो जाए, तो इसे ‘दल-बदल’ कहते हैं।

प्रश्न 3.
संयुक्त मोर्चा सरकार कब और किसके नेतृत्व में बनी?
उत्तर:
संयुक्त मोर्चा सरकार 1 जून, 1996 को एच०डी० देवगौड़ा के नेतृत्व में बनी।

प्रश्न 4.
भारतीय दलीय व्यवस्था की दो विशेषताएँ बताइए।
उत्तर:

1. बहुदलीय व्यवस्था, एवं
2. विभिन्न मतों का प्रतिनिधित्व।

प्रश्न 5.
राजनीतिक दल के कोई दो कार्य बताइए।
उत्तर:

1. राजनीतिक चेतना का प्रसार, एवं
2. शासन सत्ता को मर्यादित करना।

प्रश्न 6.
वर्तमान दलीय व्यवस्था की उभरती हुई दो प्रवृत्तियाँ बताइए।
उत्तर:

1. जाति आधारित दलों का गठन, एवं
2. राजनीतिक अपराधीकरण।

प्रश्न 7.
भारतीय दलीय व्यवस्था के कोई दो अवगुण/दोष/कमियाँ बताइए।
उत्तर:

1. साम्प्रदायिकता तथा क्षेत्रवाद की प्रबलता, एवं
2. नैतिकता का अभाव।

प्रश्न 8.
राजनीतिक दलों के दो आवश्यक तत्त्व बताइए।
उत्तर:

1. संगठन, एवं
2. सामान्य सिद्धान्तों की एकता।

प्रश्न 9.
किन्हीं चार क्षेत्रीय दलों के नाम लिखिए।
उत्तर:

1. डी०एम०के०
2. ए०डी०एम०के०
3. अकाली दल, एवं
4. तेलुगू देशम।

प्रश्न 10.
जन मोर्चा का गठन किसने और कब किया?
उत्तर:
जन मोर्चा का गठन वी०पी० सिंह ने 2 अक्टूबर, 1987 को किया।

प्रश्न 11.
बाबरी मस्जिद कब गिराई गई, उस समय केन्द्र में किस पार्टी की सरकार थी?
उत्तर:
बाबरी मस्जिद 6 दिसम्बर, 1992 को गिराई गई, उस समय केन्द्र में कांग्रेस पार्टी की सरकार थी तथा पी०वी० नरसिम्हा राव प्रधानमन्त्री थे।

बहुविकल्पीय प्रश्नोत्तर

प्रश्न 1.
भारतीय दलीय व्यवस्था का स्वरूप है-
(a) एकदलीय
(b) द्विदलीय
(c) बहुदलीय
(d) इनमें से कोई नहीं।
उत्तर:
(c) बहुदलीय।

प्रश्न 2.
निर्बल व अस्थिर जिस शासन-प्रणाली का दोष है, वह है-
(a) एकदल की तानाशाही
(b) द्विदलीय प्रणाली
(c) बहुदलीय प्रणाली
(d) दलविहीन प्रणाली।
उत्तर:
(c) बहुदलीय प्रणाली।

प्रश्न 3.
जनता पार्टी का उदय कब हुआ-
(a) सन् 1980 में
(b) सन् 1998 में
(c) सन् 1999 में
(d) सन् 1977 में।
उत्तर:
(d) सन् 1977 में।

प्रश्न 4.
निम्नलिखित में कौन-सा दल अखिल भारतीय दल है-
(a) तेलुगू देशम
(b) कांग्रेस
(c) समाजवादी पार्टी
(d) राष्ट्रीय जनता दल।
उत्तर:
(b) कांग्रेस।

प्रश्न 5.
केन्द्र में मिली-जुली सरकार कब बनी-
(a) सन् 1977 में
(b) सन् 1978 में
(c) सन् 1979 में
(d) सन् 1980 में।
उत्तर:
(a) सन् 1977 में।

UP Board Solutions for Class 12 Civics

Balaji Class 10 Maths Solutions Chapter 7 Triangles Ex 7.3 त्रिभुज

प्रश्न 1.
यदि ∆ ABC ~ ∆ DEF तथा AB = 1.2 सेमी तथा DE = 1.4 सेमी है तो ∆ ABC और ∆ DEF के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हलः

दिया है
∆ ABC ~ ∆ DEF
AB = 1.2 सेमी
DE = 1.4 सेमी
चूँकि दो समरूप त्रिभुजों के क्षेत्रफलों का (UPBoardSolutions.com) अनुपात उनकी संगत B भुजाओं के वर्गों के अनुपात के बराबर होता है।
इसलिए, (∆ ABC) का क्षेत्रफल = (AB)²
(∆ DEF) का क्षेत्रफल = (DE)²

प्रश्न 2.
यदि ∆ ABC ~ ∆ DEF तथा ∆ ABC का क्षेत्रफल 9 सेमी² है और ∆ DEF का क्षेत्रफल 16 सेमी² है व BC = 2.1 सेमी है तो EF ज्ञात कीजिए।
हलः
दिया है,
∆ABC ~ ∆DEF
∆ ABC का क्षेत्रफल = 9 सेमी²
∆DEF का क्षेत्रफल = 16 सेमी²
BC = 2.1 सेमी
ज्ञात करना है EF का (UPBoardSolutions.com) मान
चूँकि ∆ABC ~ ∆DEF

प्रश्न 3.
यदि ∆ ABC ~ ∆DEF है, यदि (∆ ABC) का क्षेत्रफल = 36 सेमी², (∆ DEF) का क्षेत्रफल = 64 सेमी² तथा DE = 6.2 सेमी है तो AB की लम्बाई ज्ञात कीजिए।
हलः
दिया है, ∆ABC ~ ∆DEF
∆ABC का क्षेत्रफल = 36 सेमी²
∆ DEF का क्षेत्रफल = 64 सेमी²
DE = 6.2 सेमी
हमें AB की लम्बाई ज्ञात (UPBoardSolutions.com) करनी है।
चूँकि ∆ABC ~ ∆ DEF

प्रश्न 4.
यदि ∆ ABC ~ ∆DEF तथा (∆ ABC) का क्षेत्रफल = 16 सेमी², (∆DEF) का क्षेत्रफल = 25 सेमी² तथा BC = 2.3 सेमी है तो EF ज्ञात कीजिए।
हलः
दिया है, ∆ ABC ~ ∆ DEF
∆ ABC का क्षेत्रफल = 16 सेमी²
∆ DEF का क्षेत्रफल (UPBoardSolutions.com) = 25 सेमी²
BC = 2.3 सेमी
हमें EF का मान ज्ञात करना है।
चूँकि, ∆ABC ~ ∆ DEF

प्रश्न 5.
दो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 81 सेमी² तथा 49 सेमी² हैं। उनकी संगत ऊँचाईयों का अनुपात ज्ञात कीजिए तथा उनकी संगत माध्यिकाओं का अनुपात भी ज्ञात कीजिए।
हलः
माना दो समरूप त्रिभुज क्रमशः हैं ∆ ABC और ∆ DEF
दिया है, ∆ ABC ~ ∆ DEF
∆ ABC का क्षेत्रफल = 81 सेमी²
∆DEF का क्षेत्रफल = 49 (UPBoardSolutions.com) सेमी² 

प्रश्न 6.
यदि ∆ ABC ~ ∆DEF तथा BC = 3 सेमी, EF = 4 सेमी और (∆ ABC) का क्षेत्रफल = 54 सेमी² है तो ∆ DEF का क्षेत्रफल ज्ञात कीजिए।
हलः
दिया है, ∆ ABC ~ ∆ DEF
BC = 3 सेमी
EF = 4 सेमी
∆ ABC का क्षेत्रफल = 54 सेमी²
हमें ∆ DEF का क्षेत्रफल (UPBoardSolutions.com) ज्ञात करना है।
चूँकि ∆ ABC ~ ∆ DEF

प्रश्न 7.
दो समद्विबाहु त्रिभुजों के शीर्ष कोण समान हैं तथा उनके क्षेत्रफलों का अनुपात 36 : 25 है। तब उनकी संगत ऊँचाईयों का अनुपात ज्ञात कीजिए।
हलः
माना दो समद्विबाहु त्रिभुज क्रमशः ∆ ABC और ∆ DEF हैं।
∆ ABC में AB = AC
∆DEF में DE = DF
और दिया है, ∠A = ∠D

प्रश्न 8.
∆ ABC में, D तथा E क्रमशः AB तथा AC के मध्य बिन्दु हैं। ∆ ADE और ∆ ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए। (NCERT)
हलः
दिया है, D और E क्रमश: ∆ABC की. भुजा AB तथा AC के मध्य बिन्दु हैं।

अतः AD = DB
AE = EC
∵ AB = AD + DB
∴ AB = AD + AD (AD = DB)
AB = 2AD
[latex]\frac{A B}{A D}[/latex] = 2 …(1)
और AC = AE + EC
AC = AE + AE (AE = EC)
AC = 2AE
[latex]\frac{A C}{A E}[/latex] = 2 …(2)
समीकरण (1) और (2) द्वारा, (UPBoardSolutions.com)

∴ ∆ADE का क्षेत्रफल : ∆ABC का क्षेत्रफल = 1 : 4

प्रश्न 9.
दो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 169 सेमी² तथा 121 सेमी² हैं। यदि बड़े त्रिभुज की बड़ी भुजा 26 सेमी हैं तो छोटे त्रिभुज की बड़ी भुजा ज्ञात कीजिए।
हलः
माना दो त्रिभुज ∆ ABC और ∆ DEF हैं।
दिया है ∆ABC ~ ∆ DEF
∆ABC का क्षेत्रफल = 121 सेमी²
∆ DEF का क्षेत्रफल = 169 सेमी², DF = 26 सेमी
माना ∆ DEF की बड़ी भुजा = DF
और ∆ ABC की बड़ी भुआ = AC
अब चूंकि, ∆ DEF ~ ∆ ABC

प्रश्न 10.
दिये गये चित्र में, PB तथा QA, रेखाखण्ड AB के लम्बवत् है। यदि PO = 5 सेमी,QO = 7 सेमी तथा ∆ POB का क्षेत्रफल = 150 सेमी² है। तो ∆QOA का क्षेत्रफल ज्ञात कीजिए।

हलः
दिया है,
∠OBP = 90°
∠OAQ = 90°
OQ = 7 सेमी
OP = 5 सेमी
∆ POB का क्षेत्रफल = 150 सेमी²

हमें ∆QOA का क्षेत्रफल ज्ञात करना है।
∆ POB और ∆QOA में, (UPBoardSolutions.com)
∆ POB = ∆QOA (शीर्षाभिमुख कोण)
∆OBP = ∆QAO = (90°)
∴ ∆POB ~ ∆QOA (AA-समरूपता)

प्रश्न 11.
दो समरूप त्रिभुजों ABC तथा PQR के क्षेत्रफलों का अनुपात 9 : 16 है यदि BC = 4.5 सेमी है तो QR की लम्बाई ज्ञात कीजिए।
हलः

प्रश्न 12.
दो समरूप त्रिभुजों के क्षेत्रफल क्रमशः 100 सेमी² तथा 49 सेमी² हैं। यदि बड़े त्रिभुज की ऊँचाई 5 सेमी है तो दूसरे त्रिभुज की संगत ऊँचाई ज्ञात कीजिए।
हलः
माना दो त्रिभुज ∆ ABC और ∆ DEF हैं।
दिया है, ∆ DEF का (UPBoardSolutions.com) क्षेत्रफल = 100 सेमी²
∆ABC का क्षेत्रफल = 49 सेमी²
∆ DEF की ऊँचाई = 5 सेमी
और ∆DEF ~ ∆ ABC
हमें ∆ ABC की ऊँचाई ज्ञात करनी है।
चूँकि ∆DEF ~ ∆ ABC

प्रश्न 13.
सिद्ध कीजिए कि एक वर्ग ABCD की एक भुजा BC को आधार लेकर बने एक त्रिभुज BCE का क्षेत्रफल, विकर्ण AC को आधार लेकर बने त्रिभुज के क्षेत्रफल का आधा होता है।
हलः
दिया है, ABCD एक वर्ग है तथा समबाहु त्रिभुज BCE तथा ACF क्रमशः भुजा BC तथा विकर्ण AC पर बने हैं।
हमें सिद्ध करना है कि ∆ BCE का क्षेत्रफल = [latex]\frac{1}{2}[/latex] × ∆ ACF का क्षेत्रफल
चूँकि त्रिभुज BCE तथा ∆ ACF समबाहु हैं इसलिए उनके कोण भी बराबर होंगें। (प्रत्येक = 60°)

प्रश्न 14.
एक समकोण त्रिभुज की एक भुजा पर समबाहु त्रिभुज खींचा गया है। तो सिद्ध कीजिए कि कर्ण पर बने त्रिभुज का क्षेत्रफल, अन्य दो भुजाओं पर बने त्रिभुज के क्षेत्रफलों के योग के बराबर है।
हलः

माना ∆ ABC एक समकोण त्रिभुज है
∆ ADB, ∆ BEC, (UPBoardSolutions.com) ∆ AFC समबाहु त्रिभुज है।
AFC और ∆ BEC में सभी कोण बराबर होंगे।

प्रश्न 15.
एक त्रिभुज ABC है। PQ एक सीधी रेखा है। AB, P में मिल रही है। तथा AC, Q में, यदि AP = 1 सेमी, PB = 3 सेमी, AQ = 1.5 सेमी, QC = 4.5 सेमी है। तो सिद्ध कीजिए कि ∆APQ का क्षेत्रफल, ∆ ABC के क्षेत्रफल का [latex]\frac{1}{16}[/latex] है।
हलः

प्रश्न 16.
दो समरूप त्रिभुजों की संगत ऊँचाईयाँ क्रमश: 6 सेमी तथा 9 सेमी हैं। उनके क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हलः
माना, दो त्रिभुज ∆ ABC और ∆ DEF हैं
∆ ABC की ऊँचाई = AL = 6 सेमी
∆DEF की (UPBoardSolutions.com) ऊँचाई = AM = 9 सेमी
दिया है, ∆ ABC ~ ∆DEF

⇒ ∆ABC का क्षेत्रफल : ∆DEF का क्षेत्रफल = 4 : 9

प्रश्न 17.
∆ ABC में, भुजा AB, P द्वारा विभाजित है तथा AP : PB = 1 : 2, AC पर एक बिन्दु 0 है तथा PQ||BC है। ∆ ABC के क्षेत्रफल तथा समलम्ब चतुर्भुज BPQC के क्षेत्रफल का अनुपात ज्ञात कीजिए।
हलः
दिया है, AP : PB = 1 : 2
PQ || BC
∆ ABC और ∆APQ में,
∠ABC = ∠APQ (संगत कोण)
∠A = ∠A (उभयनिष्ठ)
∴ ∆ABC ~ ∆APQ


⇒ ∆ABC का क्षेत्रफल : समलम्ब चतुर्भुज PBCQ का क्षेत्रफल = 9 : 8

प्रश्न 18.
दो समरूप त्रिभुजों के क्षेत्रफल क्रमश: 100 सेमी² तथा 64 सेमी² हैं। यदि छोटे त्रिभुज की माध्यिका 5.6 सेमी है। तो दूसरे की संगत माध्यिका ज्ञात कीजिए।
हलः
माना दो त्रिभुज हैं ABC तथा DEF
दिया है, ∆ ABC ~ ∆ DEF
∆ ABC का क्षेत्रफल = 64 सेमी²
∆DEF का क्षेत्रफल = 100 सेमी²
∆ ABC की (UPBoardSolutions.com) माध्यिका = 5.6 सेमी
हमें ∆ DEF की माध्यिका ज्ञात करनी है।

प्रश्न 19.
∆ ABC, A पर समकोण है तथा AD ⊥ BC है। यदि BC = 13 सेमी और AC = 5 सेमी है तो ∆ ABC तथा ∆ ADC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
हलः
दिया है (UPBoardSolutions.com) ∠ BAC = 90°
AD ⊥ BC
BC = 13 सेमी, AC = 5 सेमी


⇒ ∆ ABC का क्षेत्रफल : ∆ ADC का क्षेत्रफल = 169 : 25

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 4 Quadratic Equations Ex 4.4 द्विघात समीकरण

प्रश्न 1.
k का वह मान ज्ञात कीजिए, जिसके लिए (UPBoardSolutions.com) समीकरण x² – 4x + k = 0 के मूल वास्तविक और भिन्न
हलः
x² – 4x + k = 0
यहाँ a = 1, b = – 4, c = k
∵ समीकरण के मूल वास्तविक और भिन्न हैं
∴ विविक्तकर, D > 0
या b² – 4ac > 0
( – 4)² – 4 × 1 × k > 0
16 – 4k > 0
16 > 4k   या   [latex]\frac{16}{4}[/latex] > k
k < 4

प्रश्न 2.
यदि P, q और r वास्तविक हैं तथा p ≠ q तब सिद्ध (UPBoardSolutions.com) कीजिए कि समीकरण (p – q)x² + 5(p + q)x – 2(p – q) = 0 के मूल वास्तविक और असमान हैं।
हलः
समीकरण (p – q)x² + 5(p + q)x – 2(p – q) = 0
विविक्तकर, D = b² – 4ac
= {5 (p + q)}² – 4(p – q) × – 2(p – q)
= 25 (p² + q² + 2pq) + 8(p – q)²
= 25p2²+ 25q² + 50 pq + 8(p² + q² – 2pq)
= 25p² + 25q² + 50pq + 8p² + 8q² – 16pq
= 33p² + 33q² + 34pq
∵ D > 0
∴ दी गई समीकरण के मूल वास्तविक और असमान हैं। इति सिद्धम्।

प्रश्न 3.
k का मान ज्ञात कीजिए जिसके लिए समीकरण x² + 5kx + 16 = 0 के मूल वास्तविक नहीं हैं।
हलः
x² + 5kx + 16 = 0
यहाँ a = 1, b = 5k, c = 16
∵ समीकरण के मूल वास्तविक नहीं हैं
∴ b² – 4ac < 0
(5k)² – 4 × 1 × 16 < 0
25k² – 64 < 0
k² < [latex]\frac{64}{25}[/latex] k < [latex]\sqrt{\frac{64}{25}}[/latex]
या k < [latex]\pm \frac{8}{5}[/latex]
या -[latex]\frac{8}{5}[/latex] < k < [latex]\frac{8}{5}[/latex] [∵ x² – a < 0 ⇒ – a < x < a]

प्रश्न 4.
k के किस मान के लिए, (4 – k)x² + (2k + 4)x + (8k + 1) = 0 पूर्ण वर्ग है?
हलः
(4 – k)x² + (2k + 4)x + (8k + 1) = 0
यहाँ a = (4 – k), b = (2k + 4), c = (8k + 1)
∵ मूल पूर्ण वर्ग हैं।
∴ b² – 4ac > 0
(2k + 4)² – 4(4 – k)(8k + 1) > 0
4k² + 16 + 16k – 4(32k + 4 – 8k² – k) > 0 (UPBoardSolutions.com)
4k² + 16 + 16k – 4( – 8k² + 31k + 4) > 0
4[k² + 4 + 4k + 8k² – 31k – 4] > 0
9k² – 27k > 0
9k(k – 3) > 0
जब 9k > 0 तब k > 0
जब k – 3 > 0 तब k > 3

प्रश्न 5.
k का वह मान ज्ञात कीजिए जिसके लिए समीकरण x² + k(2x + k – 1) + 2 = 0 के मूल वास्तविक और बराबर हैं।
हलः
समीकरण x² + k (2x + k – 1) + 2 = 0
x² + 2kx + k² – k + 2 = 0
यहाँ a = 1, b = 2k, c = k² – k + 2
∵ समीकरण के मूल वास्तविक और बराबर हैं।
∴ b² – 4ac = 0
(2k)² – 4 × 1 × (k² – k + 2) = 0
4k² – 4k² + 4k – 8 = 0
4k – 8 = 0
k = [latex]\frac{8}{4}[/latex] ⇒ k = 2

प्रश्न 6.
निम्नलिखित प्रत्येक में k का मान ज्ञात कीजिए (UPBoardSolutions.com) जिसके लिए निम्न समीकरण के मूल वास्तविक और बराबर हैं।
(i) x² – 2(k + 1)x + k² = 0
(ii) k²x² – 2(2k – 1)x + 4 = 0
(iii) (k + 1)x² – 2(k – 1)x + 1 = 0
(iv) kx(x – 2) + 6 = 0 (NCERT)
(v) x² – 4kx + k = 0
हलः
(i) x² – 2(k + 1)x + k² = 0
यहाँ a = 1, b = – 2(k + 1), c = k²
∵ समीकरण के मूल वास्तविक और बराबर हैं।
∴ b² – 4ac = 0
[- 2(k + 1)]² – 4 × 1 × k² = 0
4(k + 1)² – 4k² = 0
4 (k² + 1 + 2k – k²) = 0
1 + 2k = 0 या k= [latex]-\frac{1}{2}[/latex]

(ii) k²x² – 2(2k – 1)x + 4 = 0
यहाँ a = k², b = – 2(2k – 1), c = 4
∵ समीकरण के मूल वास्तविक (UPBoardSolutions.com) और बराबर हैं।
∴ b² – 4ac = 0
[- 2(2k – 1)]² – 4 × k² × 4 = 0
4(2k – 1)² – 16k² = 0
4[(2k – 1)² – 4k²] = 0
4k² + 1 – 4k – 4k² = 0
1 – 4k = 0 या 1 = 4k
k = [latex]\frac{1}{4}[/latex]

(iii) (k + 1)x² – 2(k – 1)x + 1 = 0
यहाँ a = (k + 1), b = – 2(k – 1), c = 1
∵ समीकरण के मूल वास्तविक और बराबर हैं।
∴ b² – 4ac = 0
[- 2(k – 1)]² – 4 × (k + 1) × 1 = 0
4 (k – 1)² – 4(k + 1) = 0
4[(k – 1)² – (k + 1)] = 0
k² + 1 – 2k – k – 1 = 0
k² – 3k = 0 या k(k – 3) = 0
∴ k = 0 तथा k – 3 = 0 या k = 3
अत: k = 0, 3

(iv) kx(x – 2) + 6 = 0
या kx² – 2kx + 6 = 0
यहाँ a = k, b = – 2k, c = 6
∵ समीकरण के मूल वास्तविक और बराबर हैं।
∴ b² – 4ac = 0
(- 2k)² – 4 × k × 6 = 0
4k² – 24k = 0
4k (k – 6) = 0
∴ 4k = 0 तथा k – 6 = 0
k = 0 , k = 6
अत: k = 0, 6

(v) x² – 4kx + k = 0
यहाँ a = 1, b = – 4k, c = k
∵ समीकरण के मूल वास्तविक और बराबर हैं।
∴ b² – 4ac = 0
(- 4k)² – 4 × 1 × k = 0
16k² – 4k = 0
4k (4k – 1) = 0
∴ 4k = 0 तथा 4k – 1 = 0
k = 0, k = [latex]\frac{1}{4}[/latex]
अत:k = 0, [latex]\frac{1}{4}[/latex]

प्रश्न 7.
यदि समीकरण (b – c)x² + (c – a)x + (a – b) = 0 (UPBoardSolutions.com) के मूल बराबर हैं तब सिद्ध कीजिए कि 2b = a + c अर्थात् a, b और c समान्तर श्रेणी में हैं।
हलः
(b – c)x² + (c – a)x + (a – b) = 0
यहाँ a = (b – c), b = (c – a), c = (a – b)
∵ समीकरण के मूल बराबर हैं।
∴ b² – 4ac = 0
(c – a)² – 4(b – c)(a – b) = 0
c² + a² – 2ca – – 4(ab – b² – ca + bc) = 0
c² + a² – 2ca – 4ab + 4b² + 4ca – 4bc = 0
c² + a² + 2ca + 4b² – 4ab – 4bc = 0
c² + a² + (- 2b)² + 2ca + 2a(- 2b) + 2(- 2b)c = 0
(c + a – 2b)² = 0
c + a = 2b
या 2b = a + c
अर्थात् a, b और c समान्तर श्रेणी में हैं। इति सिद्धम्।

प्रश्न 8.
k के किस मान के लिए, द्विघात समीकरण (UPBoardSolutions.com) (3k + 1)x² + 2(k + 1)x + 1 = 0 के मूल बराबर हैं?
हलः
(3k + 1) x² + 2(k + 1)x + 1 = 0
यहाँ a = (3k + 1), b = 2(k + 1), c = 1
∵ समीकरण के मूल बराबर हैं।
∴ b² – 4ac = 0
[2(k + 1)]² – 4(3k + 1) × 1 = 0
4(k + 1)² – 4(3k + 1) = 0
4 [(k + 1)² – (3k + 1)] = 0
k² + 1 + 2k – 3k – 1 = 0
k² – k = 0
k(k – 1) = 0
तब, k = 0 तथा k – 1 = 0 ⇒ k = 1
अत: k = 0, k = 1

प्रश्न 9.
k का मान ज्ञात कीजिए जिसके लिए द्विघात समीकरण (UPBoardSolutions.com) (k + 1)x² – 6(k + 1)x + 3(k + 9) = 0, k ≠ – 1 के मूल बराबर हैं तथा मूलों को भी ज्ञात कीजिए।
हलः
(k + 1)x² – 6(k + 1)x + 3(k + 9) = 0 जहाँ k ≠ – 1
यहाँ a = (k + 1), b = – 6(k + 1), c = 3(k + 9)
∵ समीकरण के मूल बराबर हैं। अतः
∴ b² – 4ac = 0
[- 6(k + 1)]² – 4 × (k + 1) × 3 (k + 9) = 0
36(k + 1)² – 12(k + 1) (k + 9) = 0
12(k + 1)[3 (k + 1) – (k + 9)] = 0
(k + 1)(3k + 3 – k – 9) = 0
(k + 1)(2k – 6) = 0
अतः 2k – 6 = 0 (∵ k≠ – 1)
या 2k = 6
या k = 3
k का मान समीकरण में रखने पर, (3 + 1)x² – 6(3 + 1)x + 3(3 + 9) = 0
4x² – 24x + 3 × 12 = 0
4x² – 24x + 36 = 0
x² – 6x + 9 = 0
(x)² – 2 × 3 × x + (3)² = 0
(x – 3)² = 0
अतः x = 3, 3

प्रश्न 10.
यदि – 5, एक द्विघात समीकरण 2x² + px – 15 = 0 का मूल है और द्विघात समीकरण p(x² + x) + k = 0 के मूल बराबर हैं, तो k का मान ज्ञात कीजिए।
हलः
द्विघात समीकरण 2x² + px – 15 = 0 का एक मूल –5 है।
तो x = – 5 रखने पर,
2(- 5)² + p(- 5) – 15 = 0
या 50 – 5p – 15 = 0
35 – 5p = 0 या 35 = 5p
या [latex]\frac{35}{5}[/latex] = p या p = 7
तथा द्विघात समीकरण p(x² + x) (UPBoardSolutions.com) + k = 0
∵ p = 7
∴ 7(x² + x) + k = 0
या 7x² + 7x + k = 0
यहाँ a = 7, b = 7, c = k
∵ समीकरण के मूल बराबर हैं।
∴ b² – 4ac = 0
(7)² – 4 × 7 × k = 0
49 – 28k = 0 या – 28k = – 49
28k = 49 या k = [latex]\frac{49}{28}=\frac{7}{4}[/latex]

प्रश्न 11.
यदि समीकरण (c² – ab)x² – 2(a² – bc)x + b² – ac = 0 के मूल बराबर हैं तो सिद्ध कीजिए कि a = 0 या a³ + b³ + c³ = 3abc
हलः
समीकरण (c² – ab)x² – 2(a² – bc)x + b² – ac = 0
A = c² – ab, B = -2(a² – bc), C = b² – ac
∵ समीकरण के मूल बराबर हैं।
∴ (B)² – 4AC = 0
[- 2(a² – bc)]² – 4(c² – ab)(b² – ac) = 0
4(a² – bc)² – 4(b²c² – ac³ – ab³ + a²bc) = 0
4(a⁴ + b²c² – 2a²bc – b²c² + ac³ + ab³ – a²bc) = 0
a⁴ + ab³ + ac³ – 3a²bc = 0
a(a³ + b³ + c³ – 3abc) = 0
a = 0 तथा a³ + b³ + c³ – 3abc = 0
a³ + b³ + c³ = 3abc
अतः a = 0 या a³ + b³ + c³ = 3abc इति सिद्धम्।(UPBoardSolutions.com)

प्रश्न 12.
यदि समीकरण (a + b)x² – 2(ac + bd) x + (c² + d²) = 0 के मूल बराबर हैं, तो सिद् कीजिए कि [latex]\frac{a}{b}=\frac{c}{d}[/latex]
हलः
समीकरण (a² + b²)x² – 2(ac + bd)x + (c² + d²) = 0
A = a² + b², B = – 2(ac + bd), C = (c² + d²)
∵ समीकरण के मूल बराबर हैं।
∴ B² – 4AC = 0
[- 2 (ac + bd)]² – 4(a² + b²)(c² + d²) = 0
4(ac + bd)² – 4(a²c² + a²d² + b²c² + b²d²)= 0
4[a²c² + b²d² + 2acbd – a²c² – a²d² – b²c² – b²d²] = 0
-a²d² – b²c² + 2acbd = 0
– [(ad)² + (bc)² – 2acbd] = 0
(ad – bc)² = 0
ad – bc = 0
ad = bc
[latex]\frac{a}{b}=\frac{c}{d}[/latex] इति सिद्धम्।

प्रश्न 13.
यदि द्विघात समीकरण 3x² + px – 8 = 0 का एक मूल 2 है और(UPBoardSolutions.com) द्विघात समीकरण 4x² – 2px + k = 0 के मूल बराबर हैं, तो k का मान ज्ञात कीजिए।
हल:
द्विघात समीकरण 3x² + px – 8 = 0 का एक मूल 2 है।
तो x = 2 रखने पर,
3(2)² + px2 – 8 = 0
या 3 × 4 + p × 2 – 8 = 0
12 + 2p – 8 = 0
या 4 + 2p = 0
या 2p = – 4 या p = [latex]-\frac{4}{2}[/latex]
p = – 2
तथा द्विघात समीकरण 4x² – 2px + k = 0 में p = – 2 रखने पर,
∴ 4x² – 2( – 2)x + k = 0
या 4x² + 4x + k = 0
यहाँ a = 4, b = 4, c = k
∵ समीकरण के मूल बराबर हैं।
∴ b² – 4ac = 0
(4)² – 4 × 4 × k = 0
16 – 16k = 0
या – 16k = – 16
या k = [latex]\frac{16}{16}[/latex] ⇒ k = 1

प्रश्न 14.
यदि समीकरण ax² + 2bx + c = 0 और bx² – 2[latex] \sqrt{{ac}} [/latex] x + b = 0 के मूल साथ – साथ वास्तविक हैं तो सिद्ध कीजिए कि b² = ac अर्थात् a, b, c गुणोत्तर श्रेणी में हैं।
हलः
यदि समीकरण ax² + 2bx + c = 0 और bx² – 2[latex] \sqrt{{ac}} [/latex]x + b = 0 के मूल वास्तविक हैं।
(2b)² – 4ac = (- 2[latex] \sqrt{{ac}} [/latex])² – 4b × b
4b² – 4ac = 4ac – 4b²
4b² + 4b² = 4ac + 4ac
8b² = 8ac
b² = ac
अर्थात् a, b, c गुणोत्तर श्रेणी में हैं। इति सिद्धम्।

प्रश्न 15.
यदि समीकरण lx² + nx + n = 0 के मूलों का (UPBoardSolutions.com) अनुपात p : q है तब सिद्ध कीजिए-
[latex]\sqrt{\frac{p}{q}}+\sqrt{\frac{q}{p}}+\sqrt{\frac{n}{l}}=0[/latex] (UP 2006, 08, 15)
हलः
माना समीकरण lx² + nx + n = 0 के मूल α व β हैं।

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 9 Maths Solutions Chapter 2 Exponents of Real Numbers Ex 2.1 वास्तविक संख्याओं के घातांक

Ex 2.1 Exponents of Real Numbers अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)

निम्न के मान ज्ञात कीजिए। ( प्रश्न 1 – 5)
प्रश्न 1.
5⁸ ÷ 5³
हलः
[latex]\frac{5^{8}}{5^{3}}[/latex] = 5^8-3 = 5⁵ = 5 × 5 × 5 × 5 × 5 = 3125

प्रश्न 2.
5² × 5⁴
हलः
5²⁺⁴ = 5⁶ = 5 × 5 × 5 × 5 × 5 × 5 = 15625

प्रश्न 3
[latex]\left(\frac{3}{4}\right)^{-3}[/latex]
हल:

प्रश्न 4.

हल:

प्रश्न 5.

हल:

निम्न का सरलीकरण कीजिए। (प्रश्न 6 – 16)

प्रश्न 6.
[latex](\sqrt{4})^{-3}[/latex]
हलः

प्रश्न 7.
[latex](\sqrt{5})^{-3} \times(\sqrt{2})^{-3}[/latex]
हलः

प्रश्न 8.
(x^-2/3y^-1/2)²
हलः

प्रश्न 9.
[latex]\sqrt[5]{243 x^{10} y^{5} z^{10}}[/latex]
हलः

प्रश्न 10.

हलः

प्रश्न 11.
(0.001)^1/3
हलः
(0.001)^1/3 = (10^-3 )^1/3 = 10^-3×1/3 = 10^-1 = [latex]\frac{1}{10}[/latex] = 0.1

प्रश्न 12.

हलः

प्रश्न 13.

हलः

प्रश्न 14.

हलः

प्रश्न 15.

हलः

प्रश्न 16.

हलः

प्रश्न 17.
यदि 2^5x ÷ 2^x = [latex]\sqrt[5]{2^{20}}[/latex] तब x का मान ज्ञात कीजिए।
हलः

प्रश्न 18.
यदि (2³)⁴ = (2²)^x तब x का मान ज्ञात कीजिए।
हलः
(2³)⁴ = (2²)^x ⇒ 2¹² = 2^2x
दोनों पक्षों के घातांकों की तुलना से
2x = 12 ⇒ x = [latex]\frac{12}{2}[/latex] = 6

प्रश्न 19.
[latex]\sqrt[3]{125 \times 27}[/latex] का मान ज्ञात कीजिए।
हलः

प्रश्न 20.
यदि 3^x-1 = 9 व 4^y+2 = 64, तब [latex]\frac{x}{y}[/latex] का मान ज्ञात कीजिए।
हलः
3^x-1 = 9
∴ 3^x-1 = 3²
घातांकों की तुलना करने से
x – 1 = 2
इसी प्रकार x = 3
4^y+2 = 64
4^y+2 = 4³
घातांकों की तुलना करने से
y + 2 = 3
∴ y = 3 – 2 = 1
∴ [latex]\frac{x}{y}=\frac{3}{1}[/latex] = 3

प्रश्न 21.
यदि (x – 1)³ = 8, तब (x + 1)² का मान ज्ञात कीजिए।
हलः
(x – 1)³ = 8
⇒ x – 1 = [latex]\sqrt[3]{8}[/latex]= (2³)^1/3 = 2
∴ x = 2 + 1 = 3
अतः (x + 1)² = (3 + 1)² = (4)² =16

Ex 2.1 Exponents of Real Numbers लघु उत्तरीय प्रश्न (Short Answer Type Questions)

प्रश्न 22.
[latex]\frac{2^{0}+8^{0}}{6^{0}}[/latex] का मान ज्ञात कीजिए।
हल:

प्रश्न 23.
[latex]\left(\frac{64}{125}\right)^{-2 / 3}[/latex] का मान ज्ञात कीजिए।
हल:

प्रश्न 24.
यदि 4^x – 4^x-1 = 24 तब (2x)^x का मान ज्ञात कीजिए।
हल:

प्रश्न 25.
यदि 8^x+1 =64 तब 3^2x+1 का मान ज्ञात कीजिए।
हलः
दिया है: 8^x+1 = 64
⇒ (2³)^x+1 = 26
⇒ 2^3x+3 = 26
दोनों पक्षों के घातांकों की तुलना से
∴ 3x + 3 = 6
⇒ 3x = 6 – 3 = 3
⇒ x = [latex]\frac{3}{3}[/latex] =1
∴ 3^2x+1 = 3^2×1×1 = 3²⁺¹= 3³ = 27

प्रश्न 26.
यदि x^-2 = 64 तब x^1/3 + x⁰ का मान ज्ञात कीजिए।
हलः

प्रश्न 27.
यदि (2³)² = 4^x तब x³ का मान ज्ञात कीजिए।
हलः
यहाँ 2⁶ = 4^x
⇒ 2⁶ = (2)^2x
दोनों पक्षों के घातांकों की तुलना से
2x = 6
x = = 3
∴ x³ = (3)³ = 27

प्रश्न 28.
यदि (16)^2x+3 = (64)^x+3, तब 4^2x-2 का मान ज्ञात कीजिए।
हलः
(16)^2x+3 = (64)^x+3
⇒ (2⁴)^2x+3 = (2⁶)^x+3
(2)^8x+12 = (2)^6x+18
दोनों पक्षों में 2 के घातांकों की तुलना से
8x + 12 = 6x + 18
⇒ 8x – 6x = 18 – 12
⇒ 2x = 6
⇒ x = [latex]\frac{6}{2}[/latex] = 3
∴ 4^2x-2 = 4^2×3-2 = 4^6-2 = 4⁴ = 256

प्रश्न 29.

हलः

दोनों पक्षों के. घातांकों की तुलना से
x = 4

प्रश्न 30.

हलः

दोनों पक्षों के समान आधार वाले घातांकों की तुलना करने से x = 3

प्रश्न 31.
यदि x एक धनात्मक वास्तविक संख्या है तथा x² = 2, तब x³ का मान ज्ञात कीजिए।
हलः
यहाँ x² = 2
∴ x = (2)^1/2
∴ x³ = [(2)^1/2]³ = (2)^3/2 = [latex]\sqrt{2 \times 2 \times 2}=2 \sqrt{2}[/latex]

प्रश्न 32.
(256) ^-(4-3/2 का मान ज्ञात कीजिए।   (NCERT Exemplar)
हलः

Ex 2.1 Exponents of Real Numbers दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)

प्रश्न 33.
निम्न में से प्रत्येक का मान ज्ञात कीजिए (NCERT)
(i) (64)^1/3
(ii) (125)^-1/3
(iii) (27)^-2/3
(iv) [latex]\left(\frac{64}{25}\right)^{-3 / 2}[/latex]
हल:

प्रश्न 34.
यदि x,y, धनात्मक वास्तविक संख्याएं हैं तब निम्न का सरलीकरण कीजिए।

हल:

प्रश्न 35.
निम्न को सिद्ध कीजिए

हल:

प्रश्न 36.
(i) यदि 2^x = 3^y = 12^x, तब सिद्ध कीजिए कि [latex]\frac{1}{z}=\frac{1}{y}+\frac{2}{x}[/latex]
(ii) यदि 2^x = 3^y =6^x, तब सिद्ध कीजिए कि [latex]\frac{1}{x}+\frac{1}{y}+\frac{1}{x}=0[/latex]
(iii) यदि 3^x = 5^y = (75)^x, तब सिद्ध कीजिए z = [latex]\frac{x y}{2 x+y}[/latex]
(iv) यदि x = 2^1/3 + 2^2/3, तब सिद्ध कीजिए कि x³ – 6x = 6
हलः

प्रश्न 37.
सिद्ध कीजिए:

हलः

प्रश्न 38.
सिद्ध कीजिए:

हलः

प्रश्न 39.

हलः

Ex 2.1 Exponents of Real Numbers स्वमल्यांकन परीक्षण (Self Assessment Test)

प्रश्न 1.
निम्न का सरलीकरण कीजिए

हलः

प्रश्न 2.
सिद्ध कीजिए [(16)^-1/5]^5/2 = [latex]\frac{1}{4}[/latex]
हल:

प्रश्न 3.

हल:

प्रश्न 4.

हल:

प्रश्न 5.
यदि 27^x = [latex]\frac{9}{3^{x}}[/latex] तो सिद्ध कीजिए कि x = [latex]\frac{1}{2}[/latex]
हलः
L.H.S. = 27^x = [latex]\frac{9}{3^{x}}[/latex]
⇒ 27^x . 3^x = 9
⇒ (3³)^x = 3²
⇒ 3^3x . 3^x = 3²
⇒ 3^3x+x = 3²
⇒ 3^4x = 3^x
दोनों पक्षों के घातों की तुलना से
4x = 2
x = [latex]\frac{2}{4}=\frac{1}{2}[/latex]

प्रश्न 6.
सिद्ध कीजिए {5(8^1/3 + 27^1/3)³}^1/4 = 5
हलः

प्रश्न 7.
वास्तविक संख्या x के लिए सिद्ध कीजिए कि

हलः

प्रश्न 8.

हलः

प्रश्न 9.

हलः

प्रश्न 10.

हलः

प्रश्न 11.
यदि x,y, धनात्मक वास्तविक संख्याएं हैं तो सिद्ध कीजिए कि [latex]\sqrt{x^{-1} y} \sqrt{y^{-1} z} \sqrt{x^{-1} x}[/latex] =1
हलः

प्रश्न 12.

हलः

प्रश्न 13.
निम्न में से प्रत्येक में x का मान ज्ञात कीजिए

हलः
(i) (2³)⁴ = (2²)^x
2¹² = 2^2x

Balaji Publications Mathematics Class 9 Solutions

Balaji Class 9 Maths Solutions Chapter 20 Statistics Ex 20.3 (सांख्यिकी)

प्रश्न 1.
निम्नलिखित आँकड़ों के लिए आयत-चित्र बनाइये:

हलः

प्रश्न 2.
निम्नलिखित आँकड़ों के लिए आयत-चित्र बनाइये:

हलः

निम्नलिखित आँकड़ों के लिए एक आयत-चित्र बनाइये-

प्रश्न 3.
एक प्रवेश परीक्षा में, 100 विद्यार्थियों द्वारा प्राप्त अंकों को निम्नलिखित सारणी में दर्शाया गया है।

आँकड़ों को आयत-चित्र के रूप में निरूपित कीजिए।
हल:

प्रश्न 4.
निम्नलिखित आँकड़ों से एक बारंबारता बहुभुज बनाइये।

हलः
बारंबारता सारणी

प्रश्न 5.
निम्नलिखित आँकड़ों से एक बारंबारता बहुभुज बनाइये।

हलः

प्रश्न 6.
निम्नलिखित आँकड़ों के लिए एक आयत-चित्र बनाइये:

हलः
इसके लिए बारबारता सारणी है।

प्रश्न 7.
एक शहर में श्रमिकों के कुल घर का खर्च ( ₹ में) का बंटन निम्नलिखित है:

हलः

प्रश्न 8.
निम्नलिखित आँकड़ों का बारंबारता बहुभुज बनाइये।

हलः

प्रश्न 9.
नीचे दी गई सारणी में एक चिड़ियाघर के 840 पशु पक्षियों को इस प्रकार दर्शाया गया है:

उपरोक्त आँकड़ों का दण्ड आलेख निरूपित कीजिए।
हलः

प्रश्न 10.
दिल्ली से चार शहरों की हवाई दूरी (किमी में) नीचे दी गई है:

उपरोक्त आँकड़ों का दण्ड आलेख निरूपित कीजिए।
हलः

प्रश्न 11.
दिया है। वर्ष

उपरोक्त आँकड़ों का दण्ड आलेख निरूपित कीजिए
हलः

प्रश्न 12.
दिया है:

उपरोक्त आँकड़ों का दण्ड आलेख निरूपित कीजिए
हलः

प्रश्न 13.
दिया है:

उपरोक्त आँकड़ों का दण्ड आलेख निरूपित कीजिए
हलः

Balaji Publications Mathematics Class 9 Solutions