Class 10

Balaji Class 10 Maths Solutions Chapter 13 Surface Area and Volumes Ex 13.2 पृष्ठीय क्षेत्रफल और आयतन

प्रश्न 1.
एक कमरा बेलन के आकार का है। इस पर एक अर्द्धगोलाकार गुम्बद बना है। जिसमें 17.7 सेमी³ हवा है। भवन का आन्तरिक व्यास, गुम्बद की फर्श से ऊँचाई के बराबर है। ऊँचाई ज्ञात कीजिए।
हलः

माना, बेलनाकार कमरे की त्रिज्या = r सेमी
गुम्बद की फर्श से ऊँचाई (UPBoardSolutions.com) = भवन का व्यास
= 2r सेमी
बेलनाकार कमरे की ऊँचाई h = r सेमी
तथा अर्द्धगोलाकार गुम्बद की त्रिज्या= r सेमी
तब, प्रश्नानुसार,
भवन में हवा का आयतन= 17.7 सेमी³
πr²h + [latex]\frac{2}{3}[/latex] πr³ = 17.7

अतः गुम्बद की फर्श से ऊँचाई = 2r = 2 × 1.5 = 3 सेमी

प्रश्न 2.
3.3 मीटर ऊँचाई का एक टैंट एक लम्ब वृत्तीय बेलन के रूप का है। इसका व्यास 12 मीटर तथा ऊँचाई 2.2 मीटर है। इस पर समान व्यास की एक लम्बवृत्तीय शंकु अध्यारोपित है। टैंट में लगे कैनवास का खर्च ज्ञात करें यदि कैनवास की दर ₹ 500 प्रति वर्ग मीटर है।
हलः

बेलन तथा शंकु का व्यास = 12 मीटर
तब, बेलन तथा शंकु की त्रिज्या r = [latex]\frac{12}{2}[/latex] = 6 मीटर
बेलन की ऊँचाई h₁ = 2.2 (UPBoardSolutions.com) मीटर
तथा शंकु की ऊँचाई h₂ = 3.3 – 2.2 = 1.1 मीटर

प्रश्न 3.
77 डेमी ऊँचाई का एक टैंट लम्बवृत्तीय बेलन के आकार का है। जिसका व्यास 36 मीटर और ऊँचाई 44 डेमी है। इस पर एक लम्बवृत्तीय शंकु अध्यारोपित है। ₹ 3.50 प्रति मीटर की दर से टैन्ट में प्रयुक्त कैनवास का खर्च ज्ञात कीजिए।
हलः

टैंट की ऊँचाई = 77 डेमी = [latex]\frac{77}{10}[/latex] = 7.7 मीटर
बेलन तथा शंकु का व्यास = 36 मीटर
बेलन तथा शंकु की त्रिज्या r = [latex]\frac{36}{2}[/latex] = 18 मीटर
बेलन की ऊँचाई H = 44 डेमी (UPBoardSolutions.com) = [latex]\frac{44}{10}[/latex] = 4.4 मीटर
शंकु की ऊँचाई h = 7.7 – 4.4 = 3.3 मीटर

प्रश्न 4.
एक भवन का आन्तरिक भाग एक बेलन के आकार का है। जिसका व्यास 4.3 मीटर और ऊँचाई 3.8 मीटर है। इस पर एक शंकु अध्यारोपित है। जिसका शीर्षकोण एक समकोण है। भवन का पृष्ठीय क्षेत्रफल एवं आयतन ज्ञात कीजिए।
हलः
बेलन तथा शंकु का व्यास = 4.3 मीटर तथा बेलन की ऊँचाई H = 3.8 मीटर
बेलन तथा शंकु की त्रिज्या r = [latex]\frac{4.3}{2}[/latex] = 2.15 मीटर
माना, शंकु की ऊँचाई h मीटर है।



अतः भवन का पृष्ठीय क्षेत्रफल = 71.83 मी² तथा आयतन = 65.55 मी³

प्रश्न 5.
9 सेमी भुजा के घन को काटकर बने सबसे बड़े लम्ब वृत्तीय शंकु का आयतन ज्ञात कीजिए।
हलः
घन की भुजा = 9 सेमी
शंकु का व्यास = शंकु की ऊँचाई = घन की भुजा = 9 सेमी
∴ r = [latex]\frac{9}{2}[/latex] (UPBoardSolutions.com) = 4.5 सेमी तथा h = 9 सेमी
तब, शंकु का आयतन = [latex]\frac{1}{3}[/latex]πr²h
[latex]\frac{1}{3} \times \frac{22}{7}[/latex] × 4.5 × 9
= 190.93 सेमी³

प्रश्न 6.
21 सेमी भुजा वाले ठोस घन से एक सबसे बडा शंकु बनाया गया है। शेष बचे ठोस का आयतन ज्ञात कीजिए।
हलः
घन की भुजा a = 21 सेमी
तब, शंकु का व्यास = शंकु की ऊँचाई = घन की भुजा = 21 सेमी
∴ r = [latex]\frac{21}{2}[/latex] = 10.5 सेमी, h = 21 सेमी
घन का आयतन = a³ = (21)³ = 9261 सेमी³
शंकु का आयतन = [latex]\frac{3}{3}[/latex]πr²h = [latex]\frac{21}{2}[/latex] × 10.5 × 10.5 × 21
= 22 × 10.5 × 10.5 = 2425.5 सेमी
शेष बचे ठोस का आयतन = घन का आयतन – शंकु का आयतन
= 9261 – 2425.5 = 6835.5 सेमी³

प्रश्न 7.
7 मी भुजा वाले ठोस लकड़ी के घन से महत्तम सम्भव गोला बनाया गया है। शेष बची लकडी का आयतन ज्ञात कीजिए।
हलः
घन की भुजा a = 7 सेमी
तब, घन का आयतन = (a)³ = (7)³ = 343 सेमी³
∵ घन में से एक गोला (UPBoardSolutions.com) बनाया जाता है।
∴ गोले का व्यास = घन की भुजा = 7 सेमी

प्रश्न 8.
एक लौह-स्तम्भ जिसके बेलनाकार भाग की ऊँचाई 110 सेमी और आधार का व्यास 12 सेमी है जिसके ऊपर एक 9 सेमी ऊँचा एक शंकु अध्यारोपित है। यदि 1 सेमी³ लौह का द्रव्यमान 8 ग्राम है, तो लौह स्तम्भ का द्रव्यमान ज्ञात कीजिए।
हलः
आधार का व्यास = 12 सेमी

प्रश्न 9.
कागज के बने एक शंकु की ऊँचाई 3 h तथा ऊर्ध्वाधर कोण 2α है। इसके अन्दर 2h व h ऊँचाई तथा क्रमशः ऊर्ध्वाधर कोण 4α व 6α के दो शंकु रखे हैं। शंकुओं के आयतन का अनुपात ज्ञात कीजिए।
हलः
माना, शंकु की त्रिज्या BO = r इकाई
शंकु ABC के लिए, (UPBoardSolutions.com)
∆AOB में, tanα = [latex]\frac{B O}{A O}[/latex]

प्रश्न 10.
शंकु के आधार का एक ठोस, अर्द्ध गोले पर अध्यारोपित है। इनमें प्रत्येक की त्रिज्या 3.5 सेमी तथा ठोस की कुल ऊँचाई 9.5 सेमी है। ठोस का आयतन ज्ञात कीजिए।
हलः
अर्द्धगोले तथा शंकु की त्रिज्या r = 3.5 सेमी
ठोस की कुल ऊँचाई = 9.5 सेमी
शंकु की ऊँचाई h = 9.5 – 3.5 = 6 सेमी
ठोस का आयतन (UPBoardSolutions.com) = अर्द्धगोले का आयतन + शंकु का आयतन

प्रश्न 11.
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्द्धगोला खोदकर निकालते हुए एक खिलौना बनाया गया है। यदि बेलन की ऊँचाई 10 सेमी तथा आधार की त्रिज्या 3.5 सेमी है तो खिलौने में लगी लकड़ी का आयतन ज्ञात कीजिए।
हलः
आधार की त्रिज्या r = 3.5 सेमी
बेलन की ऊँचाई h = 10 सेमी
खिलौने में लगी लकड़ी का आयतन (UPBoardSolutions.com) = बेलन का आयतन – दोनों अर्द्धगोलों का आयतन

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 13 Surface Area and Volumes Ex 13.1 पृष्ठीय क्षेत्रफल और आयतन

प्रश्न 1.
तीन घनों, जिनकी भुजाएँ क्रमशः 3 सेमी, 4 सेमी, 5 सेमी हैं, से एक घन बनायें तथा नये घन का पृष्ठीय क्षेत्रफल भी ज्ञात करें।
हलः
माना नये घन की भुजा = a सेमी
तथा दिये गये तीन घनों की भुजायें a₁ = 3 सेमी, a₂ = 4 सेमी तथा a₃ = 5 सेमी हैं।
तब, नये घन का (UPBoardSolutions.com) आयतन = तीनों घनों का आयतन
a³ = a₁³ + a₂³ + a₃³
a³ = (3)³ + (4)³ + (5)³
a³ = 27 + 64 +125
a³ = 216
a³ = (6)³
a = 6 सेमी
नये घन का पृष्ठीय क्षेत्रफल = 6a² = 6 × (6)² = 6 × 36 = 216 सेमी²

प्रश्न 2.
53 सेमी × 40 सेमी × 15 सेमी आकार का एक ठोस घनाभ पिघलाया जाता है तथा उससे बेलनाकार पाईप बनाये जाते हैं जिनका बाह्य एवं आन्तरिक व्यास क्रमशः 8 सेमी तथा 7 सेमी हैं। पाईप की लम्बाई ज्ञात कीजिए।
हलः
ठोस घनाभ की मापे, लम्बाई l = 53 सेमी, चौड़ाई b = 40 सेमी तथा ऊँचाई h = 15 सेमी
बेलनाकार पाईप का बाह्य तथा आन्तरिक व्यास क्रमशः 8 सेमी तथा 7 सेमी
तब R = [latex]\frac{8}{2}[/latex] = 4 = सेमी, r = [latex]\frac{7}{2}[/latex] = 3.5 सेमी
माना, पाईप की लम्बाई l सेमी है।
तब, प्रश्नानुसार, बेलनाकार पाईप का (UPBoardSolutions.com) आयतन = ठोस घनाभ का आयतन
π(R² – r²)l = l × b × h
[latex]\frac{22}{7}[/latex] (4)² – (3.5)²] × l = 53 × 40 × 15

प्रश्न 3.
5.5 सेमी × 10 सेमी × 14 सेमी के एक घनाभ को पिघलाकर 1.75 सेमी व्यास तथा 2 मिमी मोटाई के कितने सिक्के बनाये जाते हैं?
हलः
घनाभ का आयतन = 5.5 × 10 × 14 = 770 सेमी³
सिक्के का व्यास = 1.75 सेमी
सिक्के की त्रिज्या r = [latex]\frac{1.75}{2}[/latex] सेमी
सिक्के की मोटाई h = 2 मिमी = [latex]\frac{2}{10}[/latex] = 0.2 सेमी
तब, एक सिक्के का आयतन = πr²h

प्रश्न 4.
11 डेकामी × 1 मी × 5 डेकामी  आकार की एक धातु की शीट से 5 सेमी व्यास की कितनी गोलियाँ बनायी जा सकती हैं?
हलः
धातु का आयतन = 11 डेकामी × 1 मीटर × 5 डेकामी
= 11 × 10 सेमी × 1 × 100 सेमी × 5 × 10 सेमी
= 110 × 100 × 50 = 550000 सेमी³
तथा गोली का व्यास = 5 (UPBoardSolutions.com) सेमी
तब गोली की त्रिज्या r = [latex]\frac{5}{2}[/latex] सेमी

प्रश्न 5.
दो घनों जिनमें प्रत्येक की भुजा 10 सेमी है, के संलग्न फलकों को मिलाकर एक घनाभ बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः

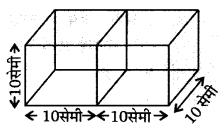
दो घनों जिनमें प्रत्येक भुजा = 10 सेमी है।
तब, घनाभ की लम्बाई l = 10 +10 = 20 सेमी
चौड़ाई b = 10 सेमी तथा (UPBoardSolutions.com) ऊँचाई h = 10 सेमी
घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2(20 × 10 + 10 × 10 + 10 × 20)
= 2(200 + 100 + 200) = 2 × 500 = 1000 सेमी²

प्रश्न 6.
2.2 डेकामी घन धातु से 0.25 सेमी व्यास का एक तार खींचा जाता है। तार की लम्बाई ज्ञात कीजिए।
हलः
तार का व्यास = 0.25 सेमी तब तार की त्रिज्या r = [latex]\frac{0.25}{2}[/latex] सेमी
माना, तार की लम्बाई = h सेमी
तब, प्रश्नानुसार, धातु का आयतन = 2.2 डेकामी घन
= 2.2 × 10 × 10 × 10 घन सेमी = 2200 घन सेमी
∵ धातु में से तार बनाया जाता है।
∴ तार का आयतन = घातु का आयतन

प्रश्न 7.
तीन घनों, जिनमें प्रत्येक की भुजा 5 सेमी है, के संलग्न फलकों को मिलाकर एक घनाभ बनाया जाता है। इससे प्राप्त धनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
हलः
तीन घनों, जिनमें प्रत्येक की (UPBoardSolutions.com) भुजा = 5 सेमी

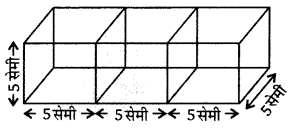
तब, घनाभ की मांपें क्रमशः
लम्बाई l = 5 + 5 + 5 = 15 सेमी, चौड़ाई b = 5 सेमी तथा ऊँचाई h = 5 सेमी
अतः घनाभ का पृष्ठीय क्षेत्रफल = 2(lb + bh + hl)
= 2(15 × 5 + 5 × 5 + 5 × 15)
= 2(75 + 25 + 75)
= 2 × 175 = 350 सेमी²

प्रश्न 8.
2 सेमी व्यास के ठोस बेलन की लम्बाई ज्ञात कीजिए जिससे 16 सेमी लम्बाई, बाह्य व्यास 20 सेमी तथा मोटाई 2.5 मिमी से एक खोखला बेलन बनाया जा सके।
हलः
माना, ठोस बेलन की लम्बाई । सेमी है।
ठोस बेलन का व्यास = 2 सेमी
ठोस बेलन की त्रिज्या r = [latex]\frac{2}{2}[/latex] = 1 सेमी
खोखले बेलन की लम्बाई H = 16 सेमी
खोखले बेलन का बाह्य व्यास (UPBoardSolutions.com) = 20 सेमी
खोखले बेलन की बाह्य त्रिज्या r₁ = [latex]\frac{20}{2}[/latex] = 10 सेमी
तथा मोटाई = 2.5 मिमी = [latex]\frac{2.5}{10}[/latex] सेमी = 0.25 सेमी
खोखले बेलन की भीतरी त्रिज्या r₂ = 10 – 0.25 = 9.75 सेमी
तब, प्रश्नानुसार, ठोस बेलन का आयतन = खोखले बेलन का आयतन
πr²h = π(r₁² – r₂²)H
(1)² × h = [(10)² – (9.75)²] × 16
1 × h = [100 – 95.0625] × 16 = 4.9375 × 16
h = 79 सेमी

प्रश्न 9.
9 सेमी आन्तरिक त्रिज्या वाले एक अर्द्धगोलीय कटोरा एक द्रव से भरा है। इस दव को 3 सेमी व्यास और 4 सेमी ऊँचाई वाले छोटे-छोटे बेलनाकार बोतलों में भरना है। कटोरा खाली करने के लिए कितनी बोतलों की आवश्यकता होगी?
हलः
अर्द्धगोलीय कटोरे की आन्तरिक त्रिज्या R = 9 सेमी

प्रश्न 10.
25 वृत्तीय प्लेटों, जिनमें प्रत्येक की त्रिज्या 10.5 सेमी तथा मोटाई 1.6 सेमी है, को एक के ऊपर एक ठोस वृत्तीय बेलन के रूप में रखा गया है। प्राप्त बेलन के वक्र पृष्ठ का क्षेत्रफल और आयतन ज्ञात कीजिए।
हलः
वृत्तीय प्लेट की त्रिज्या r = 10.5 सेमी तथा मोटाई h = 1.6 सेमी
माना, ठोस बेलन की त्रिज्या (UPBoardSolutions.com) R = 10.5 सेमी तथा ऊँचाई H = 1.6 × 25, H = 40 सेमी
बेलन का वक्रपृष्ठ = 2πRH = 2 × [latex]\frac{22}{7}[/latex] × 10.5 × 40 = 2640 सेमी²
तथा बेलन का आयतन = πr²h = [latex]\frac{22}{7}[/latex] × 10.5 × 40 = 13860 सेमी³

प्रश्न 11.
एक धातुई गोले का व्यास 6 सेमी है। इसे पिघलाकर, एक व्यास 0.2 सेमी अनुप्रस्थ काट का तार बनाया जाता है। तार की लम्बाई ज्ञात कीजिए।
हलः
धातुई गोले का व्यास = 6 सेमी, तथा तार का व्यास = 0.2 सेमी
धातुई गोले की त्रिज्या R = [latex]\frac{6}{2}[/latex] = 3 सेमी, तथा तार की त्रिज्या r = [latex]\frac{0.2}{2}[/latex] = 0.1 सेमी
माना, तार की लम्बाई = h सेमी है।
तब, प्रश्नानुसार, तार का आयतन = धातुई गोले का आयतन

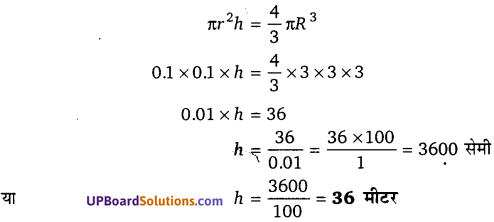
प्रश्न 12.
यदि खोखले गोले का आन्तरिक एवं बाह्य व्यास क्रमशः 6 सेमी तथा 10 सेमी है। यदि इसे पिघलाकर 14 सेमी व्यास के एक ठोस बेलन के रूप में बनाया जाता है। तो बेलन की ऊँचाई ज्ञात कीजिए।
हलः
खोखले गोले की आन्तरिक त्रिज्या r = [latex]\frac{6}{2}[/latex] = 3 सेमी
खोखले गोले की बाह्य त्रिज्या (UPBoardSolutions.com) R = [latex]\frac{10}{2}[/latex] = 5 सेमी
ठोस बेलन की त्रिज्या r₁ = [latex]\frac{14}{2}[/latex] = 7 सेमी
माना, बेलन की ऊँचाई = h सेमी
तब, प्रश्नानुसार, ठोस बेलन का आयतन = खोखले गोले का आयतन

प्रश्न 13.
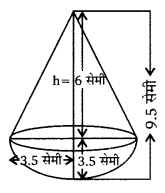
एक लम्बवृत्तीय शंकु की ऊँचाई 8.4 सेमी तथा इसके आधार की त्रिज्या 2.1 सेमी है। इसे पिघलाकर, एक गोला बनाया जाता है। गोले की त्रिज्या ज्ञात कीजिए।
हलः
माना, गोले की त्रिज्या = r सेमी तथा शंकु की त्रिज्या R = 2.1 सेमी
और शंकु की ऊँचाई H = 8.4
सेमी तब, प्रश्नानुसार, गोले का आयतन = शंकु का आयतन

प्रश्न 14.
80 मी लम्बे तथा 50 मीटर चौड़े एक आयताकार टैंक में 500 व्यक्तियों को डुबाया जाता है। यदि प्रत्येक व्यक्ति द्वारा पानी के स्तर में 0.04 मीटर³ की वृद्धि की जाती है तो टैंक के पानी के स्तर में कुल बढ़ोतरी ज्ञात कीजिए।
हलः
आयताकार टैंक की लम्बाई l = 80 मीटर, चौड़ाई b = 50 मीटर
माना, पानी के स्तर में बढ़ोत्तरी = h मीटर
तब, प्रश्नानुसार, आयताकार टैंक (UPBoardSolutions.com) में ऊपर उठे पानी का आयतन = 500 × 0.04 मीटर³
l × b × h = 20 मी³
80 × 50 × h = 20
h = [latex]\frac{20}{80 \times 50}=\frac{1}{4 \times 50}=\frac{1}{200}[/latex] = 0.005 मीटर
h = 0.005 × 100 = 0.500 = 0.5 सेमी

प्रश्न 15.
12 सेमी आधार त्रिज्या तथा 24 सेमी ऊँचाई के धातु के एक शंकु को पिघलाकर 6 सेमी व्यास की कितनी ठोस वृत्तीय गेंद बनायी जा सकती हैं?
हलः
शंकु के आधार की त्रिज्या R = 12 सेमी तथा ऊँचाई H = 24 सेमी
ठोस वृत्तीय गेंद की त्रिज्या r = [latex]\frac{6}{2}[/latex] = 3 सेमी
तब, शंकु का आयतन = [latex]\frac{1}{3}[/latex]πR²H

प्रश्न 16.
21 सेमी व्यास के एक धातु के गोले को पिघलाकर 3.5 सेमी व्यास का तथा 3 सेमी ऊँचाई के छोटे कितने शंकु बनाये जा सकते हैं?
हलः
धातु के गोले का व्यास = 21 सेमी
धातु के गोले की त्रिज्या R = [latex]\frac{21}{2}[/latex] सेमी

प्रश्न 17.
एक गोल कैरम बाल जिसका व्यास 28 सेमी है, को पिघलाकर 35 सेमी आधार के व्यास वाला लम्ब वृत्तीय शंकु बनाया गया है। शंकु की ऊँचाई ज्ञात कीजिए।
हलः
गोल कैरम बाल का व्यास = 28 सेमी
गोल कैरम बाल की त्रिज्या r₁ = [latex]\frac{28}{2}[/latex] = 14 सेमी
तथा लम्बवृत्तीय शंकु का व्यास (UPBoardSolutions.com) = 35 सेमी व ऊँचाई h = ?
लम्बवृत्तीय शंकु की त्रिज्या r₂ = [latex]\frac{35}{2}[/latex] = 17.5 सेमी
तब, प्रश्नानुसार, शंकु का आयतन = गोल कैरम बॉल का आयतन

प्रश्न 18.
1 सेमी आन्तरिक त्रिज्या वाले वत्ताकार पाईप से 80 सेमी/सेकण्ड की दर से एक खाली बेलनाकार टैंक जिसके आधार की त्रिज्या 40 सेमी है, में पानी भर रहा है। आधे घण्टे में टैंक में पानी का स्तर कितना ऊँचा उठेगा?
हल:
वृत्ताकार पाईप की आन्तरिक त्रिज्या r = 1 सेमी
तथा वृत्ताकार पाईप से पानी निकलने की रफ्तार = 80 सेमी/सेकण्ड
अर्थात् 1 सेकण्ड में पानी की ऊँचाई (UPBoardSolutions.com) h = 80 सेमी
तथा बेलनाकार टैंक के आधार की त्रिज्या R = 40 सेमी
माना, बेलनाकार टैंक में पानी के स्तर की ऊँचाई H सेमी है।
तब, प्रश्नानुसार,
बेलनाकार टेंक में ऊपर उठे पानी का आयतन = [latex]\frac{1}{2}[/latex] घण्टे (1800 सेकण्ड) में वृत्ताकार पाईप द्वारा भरे पानी का आयतन
πR²H = πr²h × 1800
π × 40 × 40 × H = π × 1 × 1 × 80 × 1800
H =[latex]\frac{80 \times 1800}{40 \times 40}[/latex]
= 5 × 18 = 90 सेमी

प्रश्न 19.
एक खाली अर्द्धगोलीय बर्तन के आन्तरिक व बाह्य व्यास क्रमशः 21 सेमी तथा 25.2 सेमी हैं। 1 सेमी² सतह को पेंट करने में 10 पैसे लगते हैं। पूरे बर्तन को पेंट करने में कुल लागत ज्ञात कीजिए।
हलः
अर्द्धगोलीय बर्तन के आन्तरिक व बाह्य व्यास क्रमशः 21 सेमी तथा 25.2 सेमी है।
तब, बर्तन की बाह्य त्रिज्या R = [latex]\frac{25.2}{2}[/latex] = 12.6 सेमी
और बर्तन की आन्तरिक त्रिज्या r = [latex]\frac{21}{2}[/latex] = 10.5 सेमी
अर्द्धगोलीय बर्तन का सम्पूर्ण पृष्ठ = 3πR² + πr²
3 × [latex]\frac{22}{7}[/latex] × 12.6 × 12.6 + [latex]\frac{22}{7}[/latex] × 10.5 × 10.5
= 1496.88 + 346.5
= 1843.38 सेमी
∵ 1 सेमी² सतह को पेंट कराने की लागत = 10 पैसे
∴ 1843.38 सेमी² सतह को पेंट कराने की कुल लागत = 1843.38 × 10
= 18433.80 पैसे
= ₹[latex]\frac{18433.80}{100}[/latex] = ₹184.34
= ₹184.34

प्रश्न 20.
एक खोखले 14 सेमी लम्बे लम्ब वृत्तीय बेलन के आन्तरिक एवं बाह्य वक्र पृष्ठों का अन्तर 88 सेमी है। यदि बेलन को बनाने में लगी धातु का आयतन 176 सेमी³ है तो बेलन के आन्तरिक व बाह्य व्यास ज्ञात कीजिए। (π = [latex]\frac{22}{7}[/latex])
हल:
माना, खोखले बेलन की बाह्य त्रिज्या r₁ तथा आन्तरिक त्रिज्या r₂ सेमी है।
तथा खोखले बेलन की लम्बाई (UPBoardSolutions.com) h = 14 सेमी
तब, प्रश्नानुसार, बेलन के आन्तरिक व बाह्य वक्रपृष्ठों का अन्तर = 88 सेमी

प्रश्न 21.
40 सेमी आधार त्रिज्या के बेलनाकार टैंक, एक बेलनाकार पाईप से 2.52 किमी/घण्टा की दर से पानी भर रहा है। आधे घण्टे में टैंक में पानी का स्तर 3.15 मीटर बहता है तो पाईप का आन्तरिक व्यास ज्ञात कीजिए।
हल:
माना, पाईप की आन्तरिक त्रिज्या = r सेमी तथा पाईप से निकले पानी की ऊँचाई h = 2.52 किमी
h = 2.52 × 1000 × 100 सेमी
h = 252000 सेमी
तथा बेलनाकार टैंक के आधार की त्रिज्या (UPBoardSolutions.com) R = 40 सेमी तथा टैंक में पानी के स्तर की ऊँचाई H = 3.15 मीटर
= 3.15 × 100 = 315 सेमी
तब, प्रश्नानुसार, [latex]\frac{1}{2}[/latex] घण्टे में पाईप द्वारा भरे पानी का आयतन = बेलनाकार टैंक में पानी का आयतन

अतः पाईप का आन्तरिक व्यास = 2r = 2 × 2 = 4 सेमी

प्रश्न 22.
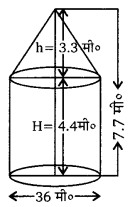
एक 5 मीटर चौड़े कपड़े से 14 मीटर व्यास तथा 24 मीटर ऊँचाई का एक शंक्वाकार तम्बु बनाया गया है। यदि इसमें लगे कपडे का मूल्य ₹ 25 प्रति मीटर है तो कुल लागत ज्ञात कीजिए।
हलः
शंक्वाकार तम्बु का व्यास = 14 मीटर तथा ऊँचाई h = 24 मीटर
तब, शंक्वाकार तम्बु की त्रिज्या r = [latex]\frac{14}{2}[/latex] = 7 मीटर

तम्बु में लगे कपड़े की कुल लागत = 110 × 25 = ₹ 2750

प्रश्न 23.
पानी से भरे एक बेलनाकार टैंक को 225 लीटर प्रति मिनट की दर से खाली किया जाता है। यदि इसके आधार का व्यास 3 मीटर तथा ऊँचाई 3.5 मीटर है तो कितने समय बाद आधा टैंक खाली हो जायेगा?
हलः
बेलनाकार टैंक का व्यास = 3 मीटर तथा ऊँचाई h = 3.5 मीटर
बेलनाकार टैंक की त्रिज्या r = [latex]\frac{3}{2}[/latex] × 100 = 150 सेमी, h = 3.5 × 100 = 350 सेमी
बेलनाकार टैंक में पूरे भरे पानी का आयतन = πr²h
[latex]\frac{22}{7}[/latex] × 150 × 150 × 350 = 24750000 सेमी³
तब आधे बेलनाकार टैंक का आयतन = [latex]\frac{1}{2}[/latex] × 24750000 = 12375000 सेमी³
1 मिनट में खाली टैंक का आयतन = 225 लीटर = 225 × 1000 = 225000 सेमी³
अतः आधे टैंक को खाली करने में लगा समय = [latex]\frac{12375000}{225000}[/latex] = 55 मीटर

प्रश्न 24.
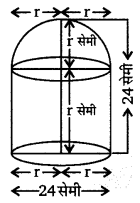
1.4 सेमी व्यास के 150 मारबल के गोले, 7 सेमी व्यास के बेलनाकार बर्तन, जिसमें कुछ पानी है, में डुबोये जाते हैं। बर्तन में पानी का बढ़ा स्तर ज्ञात कीजिए।
हलः
मारबल के गोले का व्यास = 1.4 सेमी
मारबल के गोले की त्रिज्या r = [latex]\frac{1.4}{2}[/latex] = 0.7 सेमी
तथा बेलनाकार बर्तन का (UPBoardSolutions.com) व्यास = 7 सेमी
बेलनाकार बर्तन की त्रिज्या R = [latex]\frac{7}{2}[/latex] = 3.5 सेमी
माना, बेलनाकार बर्तन में पानी का बढ़ा स्तर = h सेमी
तब, प्रश्नानुसार, बेलनाकार बर्तन में बढ़े पानी का आयतन = 150 मारबल के गोलो का आयतन

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 12 Area Related to Circles Ex 12.4 वृत्तों से सम्बन्धित क्षेत्रफल

प्रश्न 1.
वर्गाकार टैंक की भुजा 40 मीटर है। उसके चारों ओर अर्द्धवृत्ताकार चार प्लॉट हैं। ₹ 1.25 प्रति वर्ग मीटर की दर से उन्हें सींचने का कुल मूल्य ज्ञात कीजिए। (π = 3.14)
हलः
वर्गाकार टैंक की भुजा = 40 मीटर।

₹ 1.25 प्रति वर्ग मीटर की दर (UPBoardSolutions.com) से प्लॉटो को सींचने का कुल मूल्य
= 2512 × 1.25 = ₹3140

प्रश्न 2.
सिद्ध कीजिए कि r त्रिज्या के वृत्ताकार क्षेत्र के चारों ओर h मीटर चौड़ाई के एक वृत्ताकार रास्ते का क्षेत्रफल πh(2r + h) वर्ग मीटर है।
हलः
वृत्ताकार क्षेत्र की आन्तरिक त्रिज्या = r मीटर तथा वृत्ताकार रास्ते की चौड़ाई = h मीटर
तब, वृत्ताकार क्षेत्र की बाा त्रिज्या R = (r + h) मीटर

वृत्ताकार रास्ते का क्षेत्रफल = π(R² – r²)
= π[(r + h)² – r²]
= π[r² + h² +2rh – r²]
= π[h² +2rh]
= πh(h + 2r) वर्ग मीटर

प्रश्न 3.
एक 40 सेमी भुजा के वर्ग के रूप में डेन कवर है जिसके अन्दर 441 छेद हैं। जिनमें प्रत्येक का व्यास 1 सेमी है। छेद से अलग वर्गाकार प्लेट का क्षेत्रफल ज्ञात कीजिए।
हलः
वर्ग की भुजा a = 40 सेमी तब
वर्ग का क्षेत्रफल = a² = (40)² = 1600 सेमी²
छेद का व्यास (UPBoardSolutions.com) r = [latex]\frac{1}{2}[/latex] सेमी


अतः छेद से अलग वर्गाकार प्लेट का क्षेत्रफल
= 1600 – 346.5 = 1253.5 सेमी²

प्रश्न 4.
O केन्द्र तथा 21 सेमी व 7 सेमी त्रिज्या के दो संकेन्द्रीय वृत्तों की चाप क्रमशः AB व CD हैं। यदि ∠AOB = 30° तब छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (NCERT)

हलः
केन्द्र O वाले संकेन्द्रीय वृत्तों की त्रिज्यायें क्रमशः 21 सेमी व 7 सेमी हैं।
तथा ∠AOB = 30°
तब छायांकित क्षेत्र का क्षेत्रफल (UPBoardSolutions.com) = त्रिज्यखण्ड AOB का क्षेत्रफल – त्रिज्यखण्ड COD का क्षेत्रफल

प्रश्न 5.
40 मीटर व्यास का एक वृत्ताकार प्लॉट है। जिसके चारों ओर 3.5 मीटर चौड़ा एक रास्ता है। उस रास्ते पर ₹ 4 प्रति वर्ग मीटर के हिसाब से घास लगाने में कितना खर्च आयेगा?
हलः
वृत्ताकार प्लॉट का व्यास = 40 मीटर
वृत्ताकार प्लॉट की त्रिज्या r = [latex]\frac{40}{2}[/latex] = 20 मीटर
रास्ते की चौड़ाई = 3.5 मीटर
रास्ते सहित वृत्ताकार प्लॉट की त्रिज्या R = 20 + 3.5 = 23.5 मीटर
तब रास्ते का क्षेत्रफल = π [R² – r²]
= [latex]\frac{22}{7}[/latex](23.5)² – (20)²]
= [latex]\frac{22}{7}[/latex][552.25 – 400]
= [latex]\frac{22}{7}[/latex] × 152.25 = 22 × 21.75
= 478.5 सेमी²
रास्ते पर ₹ 4 प्रति वर्ग मीटर की दर से घास लगाने का खर्च = 478.5 × 4 = ₹1914

प्रश्न 6.
एक वृत्ताकार तालाब जिसका व्यास 17.5 मीटर है, के चारों ओर 2 मीटर चौड़ा एक रास्ता है। ₹ 25 प्रति वर्ग मीटर की दर से रास्ते बनाने में कुल लागत ज्ञात कीजिए। (π = 3.14)
हलः
वृत्ताकार तालाब का व्यास = 17.5 मीटर
वृत्ताकार तालाब की त्रिज्या r = [latex]\frac{17.5}{2}[/latex] = 8.75 मीटर
रास्ते की चौड़ाई = 2 मीटर
तब, रास्ते सहित वृत्ताकार तालाब की त्रिज्या R = 8.75 + 2
R = 10.75 मीटर
वृत्ताकार रास्ते का क्षेत्रफल = π(R² – r²)
= 3.14[(10.75)² – (8.75)²]
= 3.14[115.5625 – 76.5625]
= 3.14 × 39 = 122.46 मीटर²
₹ 25 प्रति वर्ग मीटर की दर से (UPBoardSolutions.com) रास्ता बनाने में कुल लागत = 122.46 × 25 = ₹ 3061.50

प्रश्न 7.
72 मीटर परिमाप वाले अर्द्धवृत्ताकार क्षेत्र के चारों ओर 3.5 मीटर चौड़ा एक रास्ता है। रास्ते का क्षेत्रफल ज्ञात कीजिए।
हलः
माना, अर्द्धवृत्ताकार क्षेत्र की त्रिज्या r मीटर है।
तब प्रश्नानुसार, अर्द्धवृत्ताकार क्षेत्र का परिमाप = 72 मीटर
2r + πr = 72 या r(2 + π) = 72

अर्द्धवृत्ताकार क्षेत्र के चारों ओर रास्ते की चौड़ाई = 3.5 मीटर
तब, रास्ते सहित अर्द्धवृत्ताकार क्षेत्र की (UPBoardSolutions.com) त्रिज्या R = 14 + 3.5 = 17.5 मीटर

प्रश्न 8.
24 सेमी भुजा वाले एक समबाहु त्रिभुज में उसकी भुजाओं को स्पर्श करते हुए एक वृत्त खींचा गया है। त्रिभुज के शेष भाग का क्षेत्रफल ज्ञात कीजिए। ([latex] \sqrt{{3}} [/latex] = 1.732)
हलः
माना, वृत्त की त्रिज्या ON = r सेमी
तथा समबाहु ∆ ABC की प्रत्येक भुजा a = 24 सेमी
∵ समबाहु A का प्रत्येक कोण 60° का होता है।
∴ ∠OBN = 30°

प्रश्न 9.
संलग्न चित्र में, AB व CD, O केन्द्र वाले एक वृत्त के व्यास हैं जो परस्पर लम्बवत् हैं। OD उसके समरूप वृत्त का व्यास है। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए। (NCERT)

हलः
O केन्द्र वाले वृत्त के व्यास AB = CD = 14 सेमी
तथा समरूप वृत्त का व्यास OD = 7
सेमी माना, O केन्द्र वाले (UPBoardSolutions.com) वृत्त की त्रिज्य R = [latex]\frac{14}{2}[/latex] = 7 सेमी
तथा समरूप वृत्त की त्रिज्या r = [latex]\frac{7}{2}[/latex] सेमी
तब, छायांकित क्षेत्र का क्षेत्रफल = OD व्यास वाले वृत्त का क्षेत्रफल + अर्द्धवृत्त OACB का क्षेत्रफल – ∆ ABC का क्षेत्रफल

प्रश्न 10.
संलग्न चित्र में एक समबाहु त्रिभुज ABC जोकि O केन्द्र तथा 4 सेमी त्रिज्या वाले वृत्त के अन्दर स्थित है। छायांकित क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 4 सेमी

∵ समबाहु A ABC का प्रत्येक कोण 60° है। अर्थात् ∠ABC = 60°
∴ केन्द्र O पर बना कोण (UPBoardSolutions.com) AOC = 120°

प्रश्न 11.
50 मीटर भुजा वाले वर्गाकार क्षेत्र के चारों कोनों पर चार गाय इस प्रकार बांधी गयी हैं कि वे कभी भी एक-दूसरे से नहीं मिल सकती। कितना क्षेत्र बिना चरे रह जायेगा?

हलः
वर्गाकार क्षेत्र की भुजा a = 50 मीटर
∵ वर्गाकार क्षेत्र के चारों कोनों पर चार गाय बाँधी गयी हैं।
∴ गाय की रस्सी की लम्बाई (UPBoardSolutions.com) r = [latex]\frac{50}{2}[/latex] = 25 मीटर
तब बिना चरे क्षेत्र का क्षेत्रफल = वर्गाकार क्षेत्र का क्षेत्रफल – गाय द्वारा चरे भाग का क्षेत्रफल
= a² – 4 × त्रिज्यखण्ड का क्षेत्रफल

प्रश्न 12.
आयताकार मैदान की छोटी भुजाओं को व्यास मानकर दो अर्द्धवृत्त उसकी छोटी भुजाओं में जोड़े गये हैं। यदि आयत की भुजाएँ 36 मीटर व 24.5 मीटर हों तो मैदान का क्षेत्रफल ज्ञात कीजिए। (π = [latex]\frac{22}{7}[/latex])
हलः
आयताकार मैदान की लम्बाई = 36 मीटर
तथा आयताकार मैदान की चौड़ाई = 24.5 मीटर
आयत का क्षेत्रफल = लम्बाई × चौड़ाई
= 36 × 24.5 = 882 मीटर² 
∵ दो अर्द्धवृत्त आयत की छोटी भुजाओं (UPBoardSolutions.com) में जोड़े गये हैं।

अतः पूरे मैदान का क्षेत्रफल = 882 + 471.625
= 1353.625 मीटर²

प्रश्न 13.
एक आयताकार टुकडे की लम्बाई 20 मीटर व चौडाई 15 मीटर है। इसके चारों कोनों से 3.5 मीटर त्रिज्या के चार चतुर्थांश काटे गये हैं। शेष भाग का क्षेत्रफल ज्ञात कीजिए।
हलः
आयताकार टुकडे की लम्बाई l = 20 मीटर
आयताकार टुकडे की चौड़ाई b = 15 मीटर
चतुर्थांश की त्रिज्या r = 3.5 मीटर
तब शेष भाग का क्षेत्रफल = आयताकार (UPBoardSolutions.com) टुकडे का क्षेत्रफल – चारों चतुर्थांशों का क्षेत्रफल

प्रश्न 14.
एक समषटभुज, एक वृत्त के अन्दर स्थित है। यदि समषटभुज का क्षेत्रफल 24[latex] \sqrt{{3}} [/latex] वर्ग सेमी है तो वृत्त का क्षेत्रफल ज्ञात कीजिए। (π = 3.14)
हलः
समषटभुज ABCDEF का क्षेत्रफल = (UPBoardSolutions.com) 24[latex] \sqrt{{3}} [/latex] सेमी²

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 12 Area Related to Circles Ex 12.3 वृत्तों से सम्बन्धित क्षेत्रफल

प्रश्न 1.
एक जीवा PQ की लम्बाई 12 सेमी है जो वृत्त के केन्द्र पर 120° का कोण बनाती है। जीवा PQ द्वारा काटे गये लघु वृत्तखण्ड का क्षेत्रफल ज्ञात कीजिए। (NCERT)
हलः
जीवा PQ की लम्बाई 12 सेमी तथा (UPBoardSolutions.com) वृत्त के केन्द्र पर बना कोण θ = 120° है।
माना, वृत्त की त्रिज्या OP = r सेमी
तब समकोण ∆ PRO में

प्रश्न 2.
10 सेमी त्रिज्या वाले वृत्त की एक जीवा AB वृत्त के केन्द्र पर एक समकोण बनाती है। दीर्घ तथा लघु वृत्तखण्डों का क्षेत्रफल ज्ञात कीजिए। (NCERT)
हलः
वृत्त की त्रिज्या r = 10 सेमी तथा (UPBoardSolutions.com) केन्द्र पर बना कोण θ = 90°

वृत्त का क्षेत्रफल = πr² = [latex]\frac{22}{7}[/latex](10)²
= [latex]\frac{22 \times 100}{7}=\frac{2200}{7}[/latex] = 314.3 सेमी²
दीर्घ वृत्तखण्ड का क्षेत्रफल = वृत्त का क्षेत्रफल – लघु वृत्तखण्ड का क्षेत्रफल
= 314.3 – 28.5 = 285.8 सेमी²
अतः लघु वृत्तखण्ड का क्षेत्रफल 28.5 सेमी² तथा दीर्घ वृत्तखण्ड का क्षेत्रफल 285.8 सेमी²

प्रश्न 3.
वृत्त की एक जीवा केन्द्र पर एक कोण θ बनाती है। यदि जीवा द्वारा काटे गये लघु वृत्तखण्ड का क्षेत्रफल, वृत्त के क्षेत्रफल का [latex]\frac{1}{8}[/latex] है तो सिद्ध कीजिए कि-

हलः
माना, वृत्त की त्रिज्या = r इकाई तथा कोण θ है।
तब, प्रश्नानुसार
[latex]\frac{1}{8}[/latex] × वृत्त का क्षेत्रफल (UPBoardSolutions.com) = जीवा द्वारा काटे गये लघु वृत्तखण्ड का क्षेत्रफल

प्रश्न 4.
दो चाप A व B चित्र में दर्शाये गये हैं। चाप A,0 केन्द्र व OP त्रिज्या वाले वृत्त का भाग है तथा चाप B, M केन्द्र तथा PM त्रिज्या वाले वृत्त का भाग है। यहाँ M, PQ का मध्य बिन्दु है। सिद्ध कीजिए कि दोनों चापों द्वारा सीमाबद्ध क्षेत्र का क्षेत्रफल 25 ([latex] \sqrt{{3}} [/latex] – [latex]\frac{\pi}{6}[/latex]) सेमी² है।

हलः
O केन्द्र वाले वृत्त की त्रिज्या (UPBoardSolutions.com) OP = 10 सेमी, ∵ OP = OQ

Balaji Publications Mathematics Class 10 Solutions

Balaji Class 10 Maths Solutions Chapter 12 Area Related to Circles Ex 12.2 वृत्तों से सम्बन्धित क्षेत्रफल

प्रश्न 1.
21 सेमी त्रिज्या वाले एक वृत्त से एक त्रिज्यखण्ड काटा जाता है। त्रिज्यखण्ड का कोण 150° है। चाप की लम्बाई तथा क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 21 सेमी तथा त्रिज्यखण्ड (UPBoardSolutions.com) का कोण θ = 150°, चाप को लम्बाई l सेमी है।

अतः चाप की लम्बाई 55 सेमी तथा क्षेत्रफल = 577.5 सेमी²

प्रश्न 2.
एक वृत्त की त्रिज्या 35 सेमी तथा एक चाप द्वारा केन्द्र पर बनाया गया कोण 72° है। चाप की लम्बाई तथा त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 35 सेमी तथा केन्द्र पर बनाया गया कोण θ = 72°


अतः चाप की लम्बाई l = 44 सेमी, क्षेत्रफल = 770 सेमी²

प्रश्न 3.
21 सेमी त्रिज्या के एक वृत्त से एक त्रिज्यखण्ड काटा गया है। त्रिज्यखण्ड का कोण 120° है। चाप की लम्बाई तथा क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 21 सेमी (UPBoardSolutions.com) तथा त्रिज्यखण्ड का कोण θ = 120°

अतः चाप की लम्बाई 1 = 44 सेमी, क्षेत्रफल A = 462 सेमी²

प्रश्न 4.
वृत्त के एक चाप की लम्बाई 20 π सेमी है तथा जिसका केन्द्र पर कोण 144° है। वृत्त की त्रिज्या ज्ञात कीजिए।
हलः
वृत्त के एक चाप की लम्बाई l = 20 π सेमी तथा केन्द्र पर बना कोण θ = 144°
तथा माना, वृत्त की (UPBoardSolutions.com) त्रिज्या = r सेमी है।।

अतः वृत्त की त्रिज्या 25 सेमी है।

प्रश्न 5.
एक वृत्त से 56° के कोण पर काटे गये त्रिज्यखण्ड का क्षेत्रफल 4.4 सेमी² है। वृत्त की त्रिज्या ज्ञात कीजिए।
हलः
माना, वृत्त की त्रिज्या = r सेमी
तथा त्रिज्यखण्ड का कोण θ = 56°
तब, प्रश्नानुसार, त्रिज्यखण्ड का (UPBoardSolutions.com) क्षेत्रफल = 4.4 सेमी²

प्रश्न 6.
5.2 सेमी की त्रिज्या वाले एक वृत्त के एक त्रिज्यखण्ड की परिधि 16.4 सेमी है। त्रिज्यखण्ड का क्षेत्रफल ज्ञात कीजिए।
हलः
वृत्त की त्रिज्या r = 5.2 सेमी तथा त्रिज्यखण्ड की परिधि = 16.4 सेमी
l + 2r = 16.4
l + 2 × 5.2 = 16.4
l + 10.4 = 16.4
l = 16.4 – 10.4 = 6 सेमी
त्रिज्यखण्ड का क्षेत्रफल = [latex]\frac{1}{2} l r=\frac{1}{2}[/latex] × 6 × 5.2 = 15.6 सेमी²

प्रश्न 7.
एक घड़ी की छोटी तथा बडी सुइयाँ क्रमश: 4 सेमी तथा 6 सेमी लम्बी हैं। दो दिन में इनके द्वारा चली गयी दूरियों का योग ज्ञात कीजिए।
हलः
माना, घड़ी की छोटी सुई की लम्बाई (त्रिज्या) r₁ = 4 सेमी
तथा घड़ी की बड़ी सुई की लम्बाई (त्रिज्या) r₂ = 6 सेमी
∵ घड़ी की छोटी सुई 12 घण्टे में एक चक्कर लगाती है।
∴ 2 दिन (48 घण्टे) में 4 चक्कर लगायेंगी
अतः घड़ी की छोटी सुई (UPBoardSolutions.com) द्वारा 2 दिन में चली गयी दूरी = 2π₁ × 4
= 2 × [latex]\frac{22}{7}[/latex] × 4 × 4 = [latex]\frac{704}{7}[/latex] सेमी
तथा घड़ी की बड़ी सुई 1 घण्टे में एक चक्कर लगाती है तब वह 2 दिन (48 घण्टे) में 48 चक्कर लगायेंगी।
अतः घड़ी की बड़ी सुई द्वारा 2 दिन में चली गई दूरी = 2πr₂ × 48
= 2 × [latex]\frac{22}{7}[/latex] × 6 × 48 = [latex]\frac{12672}{7}[/latex] सेमी
दोनों सुईयों द्वारा 2 दिनों में चली गई दूरियों का योग
[latex]\frac{704}{7}+\frac{12672}{7}=\frac{13376}{7}[/latex] = 1910.85 सेमी

प्रश्न 8.
एक वृत्त मे केन्द्र O तथा त्रिज्या 5 सेमी, एक जीवा AB की लम्बाई 5[latex] \sqrt{{3}} [/latex] सेमी है। त्रिज्यखण्ड AOB का क्षेत्रफल ज्ञात कीजिए।
हल:
वृत्त की त्रिज्या r = 5 सेमी तथा जीवा AB की लम्बाई = 5[latex] \sqrt{{3}} [/latex] सेमी
माना, त्रिज्यखण्ड AOB का कोण = θ

प्रश्न 9.
एक घड़ी की मिनट की सुई की लम्बाई [latex] \sqrt{{21}} [/latex] सेमी है। घड़ी की मिनट की सुई द्वारा 7:00 A.M. तथा 7:05 A.M. के बीच में रचित क्षेत्रफल ज्ञात कीजिए।
हलः
घड़ी की मिनट की सुई की लम्बाई r = [latex] \sqrt{{21}} [/latex] सेमी
घड़ी की मिनट की सुई द्वारा 7:00 A.M. तथा 7:05 A.M. तक का समय = 5 मिनट
∵ 60 मिनट में घड़ी की मिनट की सुई द्वारा बना कोण = 360°
∴ 5 मिनट में घड़ी की मिनट की (UPBoardSolutions.com) सुई द्वारा बना कोण = [latex]\frac{360 \times 5}{60}[/latex]
θ = 30°
घड़ी की मिनट की सुई द्वारा 7:00 A.M. तथा 7:05 A.M. के बीच में रचित क्षेत्रफल

प्रश्न 10.
5 सेमी त्रिज्या की एक पुली के रिम पर प्रत्यास्थ (elastic) बेल्ट रखी है। बेल्ट के एक बिन्दु को केन्द्र 0 से 10 सेमी दूर बिन्दु P तक खींचा जाता है। पुली के रिम के सम्पर्क में आने वाली बेल्ट की लम्बाई ज्ञात कीजिए।
हलः
स्वयं हल (UPBoardSolutions.com) करें।

Balaji Publications Mathematics Class 10 Solutions