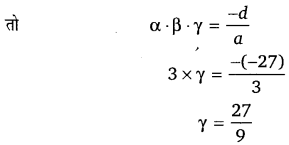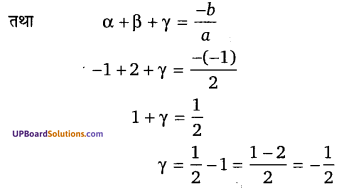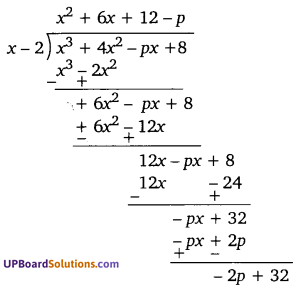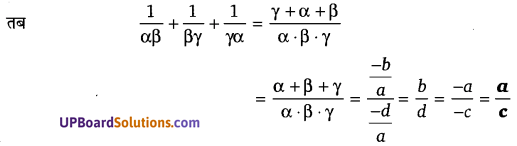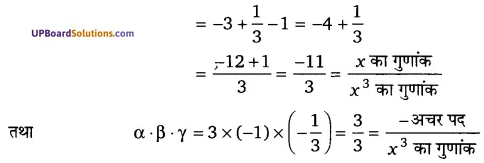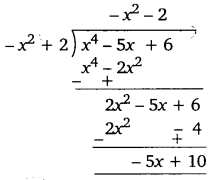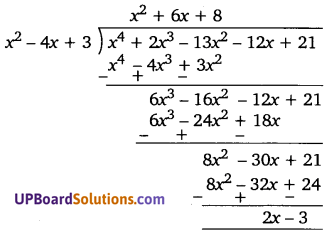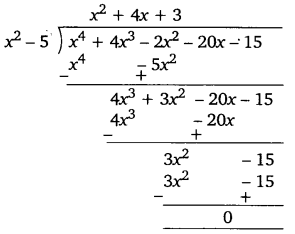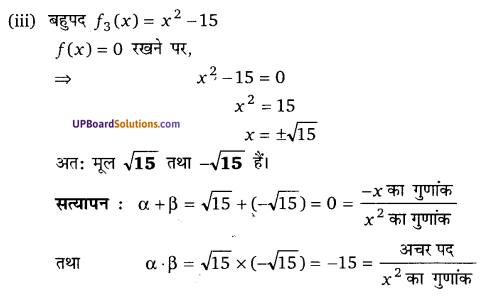Balaji Class 10 Maths Solutions Chapter 2 Polynomials Ex 2.2 बहुपद
Ex 2.2 Polynomials अतिलघु उत्तरीय प्रश्न (Very Short Answer Type Questions)
प्रश्न 1.
यदि α, β, γ बहुपद 2x3 + x2 – 13x + 16 के मूल हैं, तब αβγ का मान ज्ञात कीजिए।
हलः
यदि 2x3 + x2 – 13x + 16 के मूल α,β,γ हैं, तब
मूलों का गुणनफल (α · β · γ) = [latex]\frac{-d}{a}=\frac{-16}{2}[/latex] = – 8
प्रश्न 2.
यदि त्रिघात बहुपद ax3 + bx2 + cx + d के दो मूल 0 हैं तब तीसरा मूल ज्ञात कीजिए।
हलः
यदि त्रिघात बहुपद ax3 + bx2 + cx + d के (UPBoardSolutions.com) दो मूल α व β, शून्य हैं तब तीसरा मूल


प्रश्न 3.
यदि बहुपद 3x3 + 5x2 – 7x – 27 के दो मूलों का गुणनफल 3 है, तब तीसरा मूल ज्ञात कीजिए।
हलः
बहुपद 3x3 + 5x2 – 7x – 27 के दो (UPBoardSolutions.com) मूलों का गुणनफल 3 है।
अतः α · β = 3 तथा तीसरा मूल γ = ?
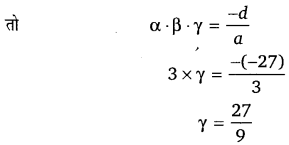
अतः तीसरा मूल γ = 3
प्रश्न 4.
यदि बहुपद 2x3 – x2 – 5x – 2 के दो मूल -1 और 2 हैं तब इसका तीसरा मूल ज्ञात कीजिए। (NCERT)
हलः
बहुपद 2x3 – x2 – 5x – 2
माना बहुपद के दो दिए गए मूल α = -1 तथा β = 2 हैं।
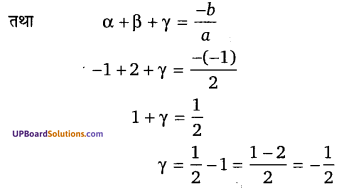
अतः बहुपद का तीसरा मूल γ = [latex]-\frac{1}{2}[/latex]

प्रश्न 5.
यदि बहुपद x3 – 4x2 – 7x + 10 के दो (UPBoardSolutions.com) मूल 1 और -2 हैं, तो इसका तीसरा मूल ज्ञात कीजिए।
हलः
बहुपद x3 – 4x2 – 7x + 10
बहुपद के दो मूल α = 1 तथा β = -2 हैं।
माना बहुपद का तीसरा मूल γ है।

अतः बहुपद का तीसरा मूल γ = 5

प्रश्न 6.
यदि बहुपद x3 – 4x2 + x + 6 का एक मूल -1 है तो अन्य मूल ज्ञात कीजिए।
हलः
मानां f (x) = x3 – 4x2 + x + 6
तथा बहुपद का एक मूल α = -1, β तथा γ हैं।


अतः बहुपद के अन्य मूल 3 व 2 हैं।

प्रश्न 7.
यदि त्रिघात बहुपद x3 + ax2 + bx + c का (UPBoardSolutions.com) एक मूल -1 है तब अन्य दो मूलों का गुणनफल ज्ञात कीजिए।
हलः
त्रिघात बहुपद x3 + ax2 + bx + c में,
α = -1, β = ?, γ = ?
तब मूलों का गुणनफल (α · β · γ) = [latex]\frac{-d}{a}[/latex]
⇒ α · β · γ = [latex]\frac{-c}{1}[/latex]
∵ α = -1 तो -1 × β, γ = -c ⇒ βγ = c
अतः दो मूलों का गुणनफल, βγ = c
प्रश्न 8.
यदि त्रिघात बहुपद ax3 + bx2 + cx + d का एक मूल 0 है तब अन्य दो मूलों का गुणनफल ज्ञात कीजिए।
हलः
त्रिघात बहुपद ax3 + bx2 + cx +d में, α = 0
तब αβ + βγ + γα = [latex]\frac{c}{a}[/latex]
0 × β + βγ × γ × 0 = [latex]\frac{c}{a}[/latex]
0 + βγ + 0 = [latex]\frac{c}{a}[/latex]
अतः दो मूलों का गुणनफल, βγ = [latex]\frac{c}{a}[/latex]

प्रश्न 9.
यदि बहुपद f (x) = x3 – 3px2 + qx – r के (UPBoardSolutions.com) मूल समान्तर श्रेणी में हैं तब p,q और r के बीच में सम्बन्ध ज्ञात कीजिए।
हलः
यदि f (x) = x3 – 3px2 + qx – 7
∵ मूल समान्तर श्रेणी में हैं।
अतः माना α = a – d, β = a, γ = a + d
∴ α + β + γ = [latex]\frac{-b}{a}[/latex]
⇒ a – d + a + a + d = [latex]\frac{3 p}{1}[/latex]
⇒ 3a = 3p
⇒ a = P
तथा α·β + β·γ + γ·α = [latex]\frac{c}{a}[/latex]
(a – d) × a + a × (a + d) + (a + d) (a – d) = [latex]\frac{q}{1}[/latex]
a = p रखने पर,
(p – d) × p + px (p + d) + (p + d) (p – d) = q
p2 – pd + p2 + pd + p2 – d2 = q
3p2 – d2 = q
3p2 – q = d2
या d2 = 3p2 – q
अब α·β·γ = [latex]\frac{-d}{a}[/latex]
(a – d) × a × (a + d) = [latex]\frac{-(-r)}{1}[/latex]
a × (a2 – d2) = r
a = p तथा d2 = 3p2 – q रखने पर,
p × [p2 – (3p2 – q)] = r
p(p2 – 3p + q) = r
p(-2p2 + q) = r
-2p3 + pq = r
Pq – r = 2p3

प्रश्न 10.
p का वह मान ज्ञात कीजिए जिसके लिए बहुपद x3 + 4x2 – px + 8, (x – 2) से पूरी तरह विभाजित है।
हलः
यदि बहुपद x3 + 4x2 – px + 8, (x – 2) से (UPBoardSolutions.com) पूरी तरह विभाजित है तो शेषफल शून्य होगा।
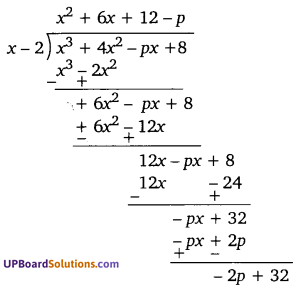
चूँकि शेषफल = 0
-2p + 32 = 0
-2p = -32
2p = 32
p = [latex]\frac{32}{2}[/latex]
p = 16
Ex 2.2 Polynomials लघु उत्तरीय प्रश्न (Short Answer Type Questions)
प्रश्न 11.
एक त्रिघात बहुपद ज्ञात कीजिए जिसके मूल -2, -3 और -1 हैं।
हलः
माना α = –2, β = -3 और γ = -1
तब α + β + γ = (-2) + (-3) + (-1) = -2 – 3 – 1 = -6
αβ + βγ + γα = (-2)(-3) + (-3)(-1) + (-1)(-2) = 6 + 3 + 2 = 11
तथा αβγ = (-2)(-3)(-1) = -6
अतः अभीष्ट बहुपद = x3 – (α + β + γ)x2 + (αβ + βγ + γα)x – α·β·γ
= x3 – (-6)x2 + 11x – (-6)
= x3 + 6x2 + 11x + 6

प्रश्न 12.
एक त्रिघात बहुपद ज्ञात कीजिए जिसके (UPBoardSolutions.com) मूल 3, [latex]\frac{1}{2}[/latex] और -1 हैं।
हलः
माना α = 3, β = 7 और γ = -1

प्रश्न 13.
एक त्रिघात बहुपद ज्ञात कीजिए, जिसके मूलों का (UPBoardSolutions.com) योगफल, दो-दो करके मूलों के गुणनफल का योगफल और इसके मूलों का गुणनफल क्रमशः 3,-1 और -3 है। (NCERT)
हलः
माना त्रिघात बहुपद के मूल क्रमशः α, β तथा γ हैं।
प्रश्नानुसार, मूलों का योगफल (α + β + γ) = 3
तथा αβ + βγ + γα = -1
और α·β·γ = -3
तब. त्रिघात बहुपद = x3 – (α + β + γ)x2 + (αβ + βγ + γα)x -α·β·γ
= x3 – 3x2 + (-1)x – (-3)
= x3 – 3x2 – x + 3

प्रश्न 14.
यदि α, β, γ बहुपद f (x) = ax3 + bx2 + cx + d के मूल हैं तब [latex]\frac{1}{\alpha}+\frac{1}{\beta}+\frac{1}{\gamma}[/latex] का मान ज्ञात कीजिए।
हल:
यदि f(x) = ax3 + bx2 + cx + d

प्रश्न 15.
यदि α, β, γ बहुपद f (x) = x3 – ax2 + bx – c के मूल हैं तब [latex]\frac{1}{\alpha \beta}+\frac{1}{\beta \gamma}+\frac{1}{\gamma \alpha}[/latex] का मान ज्ञातकीजिए।
हलः
यदि f (x) = x3 – ax2 + bx – c
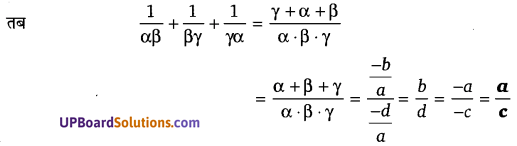

प्रश्न 16.
5x3 – 13x2 + 21x – 14 को 3 – 2x + x2 द्वारा विभाजित (UPBoardSolutions.com) करो और विभाजन एल्गोरिथम का सत्यापन करो।
हलः

भागफल = 5x – 3, शेषफल = -5
सत्यापन : विभाजन एल्गोरिथम से,
भाज्य = भाजक × भागफल + शेषफल
= (x2 – 2x + 3) × (5x – 3) + (-5)
= 5x3 – 10x2 + 15x – 3x2 + 6x – 9 – 5
= 5x3 – 13x2 + 21x – 14
प्रश्न 17.
विभाजन एल्गोरिथम का प्रयोग करके सिद्ध कीजिए कि
3x2 + 5, 6x5 + 15x4 + 16x3 + 4x2 + 10x – 35 का एक गुणनखण्ड है।
हलः
माना f (x) = 6x5 + 15x4 +16x3 + 4x2 + 10x – 35 तथा g(x) = 3x2 + 5

∵ शेषफल शून्य है।
∴ g(x), f (x) का एक गुणनखण्ड है।

प्रश्न 18.
यदि बहुपद f (x) = x3 – 3x2 + x + 1 के मूल a – b, a, a + b हैं तो a और b के मान ज्ञात कीजिए। (NCERT)
हलः
बहुपद x3 – 3x2 + x + 1
∵ बहुपद के मूल a – b, a, a + b हैं।

प्रश्न 19.
यदि x = 1 बहुपद f (x) = x3 – 2x2 + 4x + k का एक मूल है तो k का मान ज्ञात कीजिए।
हलः
बहुपद f(x) = x3 – 2x2 + 4x + k
यदि x = 1 बहुपद का एक मूल है तथा f(x) = 0
0 = (1)3 – 2(1)2 + 4 × 1 + k
0 = 1 – 2 + 4 + k
0 = 3 + k
-3 = k या k = -3

प्रश्न 20.
विभाजन एल्गोरिथम का प्रयोग करके यह जाँच कीजिए (UPBoardSolutions.com) कि क्या प्रथम बहुपद, दूसरे बहुपद का एक गुणनखण्ड है?
(i) g(x) = x2 – 3, f (x) = 2x4 + 3x3 – 2x2 – 9x – 12 (NCERT)
(ii) g(x) = 2x2 – x + 3, f(x) = 6x5 – x4 + 4x3 – 5x2 – x – 15
हल:
(i) g(x) = x2 – 3, f(x) = 2x4 + 3x3 – 2x2 – 9x – 12

∵ शेषफल शून्य है।
∴ g(x), f(x) का एक गुणनखण्ड है।
(ii) g(x) = 2x2 – x + 3, f(x) = 6x5 – x4 + 4x3 – 5x2 – x -15

∵ शेषफल शून्य है।
∴ g(x), f(x) का एक गुणनखण्ड है।

Ex 2.2 Polynomials दीर्घ उत्तरीय प्रश्न (Long Answer Type Questions)
प्रश्न 21.
सत्यापित कीजिए कि 3, -1 और [latex]\frac{-1}{3}[/latex] घात (UPBoardSolutions.com) बहुपद f (x) = 3x3 – 5x2 – 11x – 3 के मूल हैं और तब इसके मूलों एवं गुणांकों के बीच में सम्बन्ध की सत्यता की जाँच कीजिए। (NCERT)
हलः
बहुपद f (x) = 3x3 – 5x2 – 11x – 3
3, बहुपद f(x) का एक मूल है यदि f (3) = 0
अब f(3) = 3 × (33 – 5(3)2 – 11(3) – 3
= 81 – 45 – 33- 3
= 81 – 81 = 0
इसी प्रकार,
f(-1) = 3(-1)3 – 5(-1)2 – 11(-1) – 3
= -3 – 5 + 11 – 3
= -11 + 11 = 0

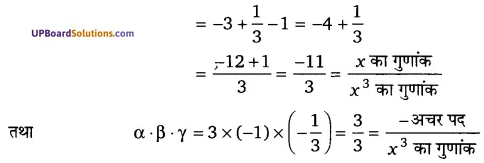
प्रश्न 22.
बहुपद f (x) = x3 + 3px2 + 3qr + r के मूलों के समान्तर श्रेणी में होने के प्रतिबन्ध ज्ञात कीजिए।
हलः
यदि f (x) = x3 + 3px2 + 3qx + r
∵ मूल समान्तर श्रेणी में हैं।
अतः माना α = a – d, β = a, γ = a + d
∴ α + β + γ = [latex]\frac{-b}{a}[/latex]
a – d + a + a + d = [latex]\frac{-3 p}{1}[/latex]
⇒ 3a = -3p
⇒ a = -p
तथा α·β + β·γ + γ·α = [latex]\frac{c}{a}[/latex]
(a – d) × a + a × (a + d) + (a + d)·(a – d) = [latex]\frac{3 q}{1}[/latex]
a2 – ad + a2 + ad + a2 – d2 = 3q
3a2 – d2 = 3q
a = -p रखने पर,
3(-p)2 – d2 = 3q
-3p2 – d2 = 3q
d2 = 3p2 – 3q
अब α·β·γ = [latex]\frac{-d}{a}[/latex]
(a – d) × a × (a + d) = [latex]\frac{-r}{1}[/latex]
a × (a2 – d2) = -r
a = -p तथा d2 = 3p2 – 3q रखने पर,
(-p) x [p2 – (3p2 – 3q)] = -r
-p(p2 – 3p2 + 3q) = -r
p(-2p2 + 3q) = r
-2p3 + 3pq = r
-2p3 + 3pq – r = 0
2p3 – 3pq + r = 0

प्रश्न 23.
यदि बहुपद f (x) = ax3 + 3bx2 + 3cr + d के मूल (UPBoardSolutions.com) समान्तर श्रेणी में है तब सिद्ध कीजिए 2b3 – 3abc + a2d = 0
हलः
यदि f (x) = ax3 + 3bx2 + 3cx + d
∵ मूल समान्तर श्रेणी में हैं।
अतः माना बहुपद के मूल α = A – D, β = A तथा γ = A + D




प्रश्न 24.
निम्न में विभाजन एल्गोरिथम का प्रयोग करके, f(x) को g(x) (UPBoardSolutions.com) द्वारा विभाजित करने पर, भागफल और शेषफल ज्ञात कीजिए।
(i) f(x) = x3 – 3x + 5x – 3; g(x) = x2 – 2 (NCERT)
(ii) f(x) = x4 – 3x + 4x + 5; g(x) = x2 – x + 1 (NCERT)
(iii) f(x) = x4 – 5x + 6; g(x) = 2 – x2 (NCERT)
हल:
(i) f(x) = x3 – 3x2 + 5x – 3; g(x) = x2 – 2

भागफल = (x – 3) तथा शेषफल = (7x – 9)
(ii) f(x) = x4 – 3x2 + 4x + 5; 8(x) = x2 – x + 1
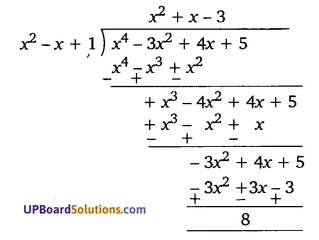
अतः भागफल = x2 + x – 3 तथा शेषफल = 8
(iii) f(x) = x4 – 5x + 6; g(x) = 2 – x2
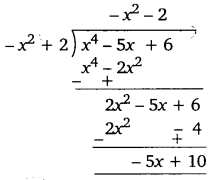
अतः भागफल = -x2 – 2 तथा शेषफल = -5x + 10

प्रश्न 25.
यदि बहुपद x4 – 6x3 – 26x2 + 138x – 35 के दो पद (UPBoardSolutions.com) [latex]2 \pm \sqrt{3}[/latex] हैं, तो अन्य मूल ज्ञात कीजिए। (NCERT)
हलः
बहुपद x4 – 6x3 – 26x2 + 138x – 35
माना बहुपद के मूल α = 2 + [latex] \sqrt{{3}} [/latex], β = 2 – [latex] \sqrt{{3}} [/latex], γ तथा δ हैं।
तब α + β + γ + δ = [latex]\frac{-b}{a}[/latex]
2 + [latex] \sqrt{{3}} [/latex] + 2 – [latex] \sqrt{{3}} [/latex] + y + δ = [latex]\frac{-(-6)}{1}[/latex]
4 + γ + δ = 6
γ + δ = 6 – 4
γ + δ = 2 …(1)
α · β · γ· δ = [latex]\frac{l}{a}[/latex]
(2 + [latex] \sqrt{{3}} [/latex])(2 – [latex] \sqrt{{3}} [/latex]).γδ = [latex]\frac{-35}{1}[/latex]
(4 – 3)γδ = -35
γδ = -35 …(2)
समी० (2) से 8 का मान समी० (1) में रखने पर,

प्रश्न 26.
f(x) = 4x4 + 2x3 – 2x2 + x – 1 में क्या जोड़ें कि प्राप्त बहुपद g(x) = x2 + 2x – 3 से विभाजित हो जाये?
हल:
f(x) = 4x4 + 2x3 – 2x2 + x -1 तथा g(x) = x2 + 2x – 3

अत: बहुपद में, -(-61x + 65) अर्थात् 61x – 65 जोड़ना पड़ेगा।

प्रश्न 27.
बहुपद f (x) = x4 + 2x3 – 13x2 – 12x + 21 में क्या (UPBoardSolutions.com) घटायें कि प्राप्त बहुपद x2 – 4x + 3 से पूरी तरह विभाजित हो जाये।
हलः
बहुपद f(x) = x4 + 2x3 – 13x2 – 12x + 21
g(x) = x2 – 4x + 3
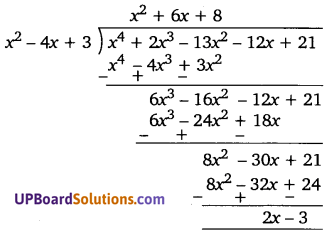
अतः बहुपद में से (2x – 3) घटाना होगा।
प्रश्न 28.
x4 + 4x3 – 2x2 -20x – 15 के अन्य सभी मूल ज्ञात (UPBoardSolutions.com) कीजिए यदि इसके दो मूल [latex] \sqrt{{5}} [/latex] और -[latex] \sqrt{{5}} [/latex]
हलः
माना बहुपद f (x) = x4 + 4x3 – 2x2 – 20x – 15
प्रश्नानुसार, [latex] \sqrt{{5}} [/latex] और -[latex] \sqrt{{5}} [/latex], f(x) के मूल हैं।
= (x – [latex] \sqrt{{5}} [/latex]) और (x + [latex] \sqrt{{5}} [/latex]), f (x) के गुणनखण्ड हैं।
= (x – [latex] \sqrt{{5}} [/latex])· (x + [latex] \sqrt{{5}} [/latex]), f(x) का एक गुणनखण्ड है।
= (x2 – 5), f(x) का एक गुणनखण्ड है।
अत: f (x) को x2 – 5 से विभाजित करने पर,
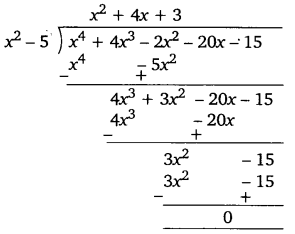
⇒ f(x) = (x2 – 5)(x2 + 4x + 3)
अतः f(x) = 0
तब x2 – 5 = 0 तथा x2 +4x +3 = 0
x2 = 5 तथा x2 + 3x + x + 3 = 0
x = ±[latex] \sqrt{{5}} [/latex] x(x + 3) + 1(x + 3) = 0
(x + 3)(x + 1) = 0
x + 3 = 0 या x + 1 = 0
x = -3 या x = -1
अतः बहुपद f(x) के अन्य मूल -3 और -1 हैं।
प्रश्न 29.
बहुपद f (x) = x4 + 2x3 – 2x2 + x – 1 में क्या जोड़ें कि प्राप्त बहुपद x2 + 2x – 3 से पूरी तरह विभाजित हो जाये।
हलः
f(x) = x4 + 2x3 – 2x2 + x – 1
तथा g(x) = x2 + 2x – 3

अतः बहुपद में, (-x + 2) अर्थात् (x – 2) जोड़ना पड़ेगा।

प्रश्न 30.
बहुपद 3x3 + 10x2 – 14x + 9 में से क्या वास्तविक (UPBoardSolutions.com) संख्या घटायें कि यह (3x – 2) से पूरी तरह विभाजित हो जाये?
हलः
माना f(x) = 3x3 + 10x2 – 14x + 9
तथा g(x) = (3x – 2)

∵ f(x) को g(x) से भाग देने पर 5 शेषफल आता है।
∴ बहुपद f (x) में से वास्तविक संख्या 5 घटाने पर f(x), g(x) से पूरी तरह विभाजित हो जाता है।
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()


![]()
![]()



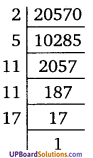
 ⇒ [latex] \sqrt{{5}} [/latex] एक परिमेय संख्या है, चूँकि [latex]\frac{p^{2}+2 q^{2}}{2 p q}[/latex] एक परिमेय संख्या है जोकि एक विरोधाभास है।
⇒ [latex] \sqrt{{5}} [/latex] एक परिमेय संख्या है, चूँकि [latex]\frac{p^{2}+2 q^{2}}{2 p q}[/latex] एक परिमेय संख्या है जोकि एक विरोधाभास है।